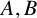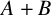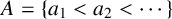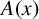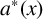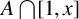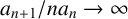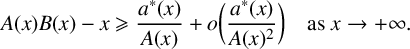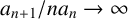1 Introduction
Two sets
![]() $A,B$
of positive integers are called additive complements, if
$A,B$
of positive integers are called additive complements, if
![]() $A+B$
contains all sufficiently large integers. Let
$A+B$
contains all sufficiently large integers. Let
![]() $A=\{a_1<a_2<\cdots \}$
be a set of positive integers. Denote by
$A=\{a_1<a_2<\cdots \}$
be a set of positive integers. Denote by
![]() $A(x)$
the counting function of A and by
$A(x)$
the counting function of A and by
![]() $a^*(x)$
the largest element in
$a^*(x)$
the largest element in
![]() $A\bigcap [1,x]$
. If additive complements
$A\bigcap [1,x]$
. If additive complements
![]() $A,B$
satisfy
$A,B$
satisfy
then we call such
![]() $A,B$
exact additive complements. In 2001, Ruzsa [Reference Ruzsa2] introduced the following notation which is powerful for the proof of additive complements. Let
$A,B$
exact additive complements. In 2001, Ruzsa [Reference Ruzsa2] introduced the following notation which is powerful for the proof of additive complements. Let
![]() ${m>a_1}$
be an integer and let
${m>a_1}$
be an integer and let
![]() $k=A(m)$
. Denote by
$k=A(m)$
. Denote by
![]() $L(m)$
the smallest number l for which there are integers
$L(m)$
the smallest number l for which there are integers
![]() $b_1,\ldots ,b_l$
such that the numbers
$b_1,\ldots ,b_l$
such that the numbers
![]() $a_i+b_j,1\leqslant i\leqslant k, 1\leqslant j\leqslant l$
, contain every residue modulo m. Obviously,
$a_i+b_j,1\leqslant i\leqslant k, 1\leqslant j\leqslant l$
, contain every residue modulo m. Obviously,
![]() $L(m)\geqslant m/k$
.
$L(m)\geqslant m/k$
.
Theorem 1.1 (Ruzsa [Reference Ruzsa2]).
If
then A has an exact complement.
Theorem 1.2 (Ruzsa [Reference Ruzsa2]).
Let A be a set satisfying
![]() ${A(2x)}/{A(x)}\rightarrow 1$
. The following are equivalent.
${A(2x)}/{A(x)}\rightarrow 1$
. The following are equivalent.
-
(a) A has an exact complement.
-
(b)
 $A(m)L(m)/m\rightarrow 1$
.
$A(m)L(m)/m\rightarrow 1$
. -
(c) There is a sequence
 $m_1\kern1.5pt{<}\kern1.5pt m_2\kern1.5pt{<}\kern1.2pt\cdots $
of positive integers such that
$m_1\kern1.5pt{<}\kern1.5pt m_2\kern1.5pt{<}\kern1.2pt\cdots $
of positive integers such that
 ${A(m_{i+1})/ A(m_i)\kern1.2pt{\rightarrow}\kern1.2pt 1}$
and
${A(m_{i+1})/ A(m_i)\kern1.2pt{\rightarrow}\kern1.2pt 1}$
and
 $A(m_i)L(m_i)/m_i\rightarrow 1$
.
$A(m_i)L(m_i)/m_i\rightarrow 1$
.
Theorem 1.3 (Ruzsa [Reference Ruzsa3]).
For exact additive complements
![]() $A,B$
with
$A,B$
with
![]() ${A(2x)}/ {A(x)}\rightarrow 1$
,
${A(2x)}/ {A(x)}\rightarrow 1$
,
In 2019, Chen and Fang [Reference Chen and Fang1] improved Theorem 1.3 by removing the exact condition. Chen and Fang also showed in [Reference Chen and Fang1] that Theorem 1.3 is the best possible.
Theorem 1.4 (Chen and Fang [Reference Chen and Fang1]).
There exist exact additive complements
![]() $A,B$
with
$A,B$
with
![]() ${A(2x)}/{A(x)}\rightarrow 1$
such that
${A(2x)}/{A(x)}\rightarrow 1$
such that
for infinitely many positive integers x.
In this paper, under condition (1.1) from [Reference Ruzsa2], we obtain the following result.
Theorem 1.5. For exact additive complements
![]() $A,B$
with (1.1),
$A,B$
with (1.1),
Moreover, we also show that
![]() ${a^*(x)}/{A(x)^2}$
is the best possible.
${a^*(x)}/{A(x)^2}$
is the best possible.
Theorem 1.6. There exist exact additive complements
![]() $A,B$
with (1.1) such that
$A,B$
with (1.1) such that
 $$ \begin{align} \liminf_{x\to \infty }\frac{A(x)B(x)-x-\frac{a^*(x)}{A(x)}}{\frac{a^*(x)}{A(x)^2}}\leqslant 1. \end{align} $$
$$ \begin{align} \liminf_{x\to \infty }\frac{A(x)B(x)-x-\frac{a^*(x)}{A(x)}}{\frac{a^*(x)}{A(x)^2}}\leqslant 1. \end{align} $$
2 Proofs of the main results
Let
and
The ideas used in the proofs of the main results come from [Reference Chen and Fang1–Reference Ruzsa3]. We use the following lemma of Ruzsa in the proof of Theorem 1.5.
Lemma 2.1 [Reference Ruzsa3, Lemma 2.1].
Let U and V be finite sets of integers and let
and
Then
 $$ \begin{align*}\sum_{\sigma (n)>1} (\sigma (n)-1) \geqslant \frac 1{|U|} \sum_{\delta (n)>1} (\delta (n)-1).\end{align*} $$
$$ \begin{align*}\sum_{\sigma (n)>1} (\sigma (n)-1) \geqslant \frac 1{|U|} \sum_{\delta (n)>1} (\delta (n)-1).\end{align*} $$
Proof of Theorem 1.5.
Assume the contrary. Suppose that (1.2) does not hold. Then there exist a positive number
![]() $\delta _0(<1)$
and a sequence
$\delta _0(<1)$
and a sequence
![]() $x_1<x_2<\cdots <x_k<\cdots $
such that
$x_1<x_2<\cdots <x_k<\cdots $
such that
 $$ \begin{align} A(x_k)B(x_k)-x_k\leqslant \frac{a^*(x_k)}{A(x_k)}-\delta _0\frac{a^*(x_k)}{A(x_k)^2}. \end{align} $$
$$ \begin{align} A(x_k)B(x_k)-x_k\leqslant \frac{a^*(x_k)}{A(x_k)}-\delta _0\frac{a^*(x_k)}{A(x_k)^2}. \end{align} $$
We know that
 $$ \begin{align*} A(x_k)B(x_k)-x_k&=\sum_{\substack{a\leqslant x_k, b\leqslant x_k\\ a\in A, b\in B}} 1 -x_k=\sum_{n=1}^{2x_k} \sigma (x_k, n)-x_k \\ & =\sum_{\substack{n=1\\ \sigma (x_k, n)\geqslant 1}}^{x_k} (\sigma(x_k, n)-1)+ \sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1}}^{2x_k} \sigma (x_k, n) \\ & = \sum_{\substack{n=1\\ \sigma (x_k, n)\geqslant 1}}^{2x_k} (\sigma (x_k, n)-1) + \sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1} }^{2x_k} 1 \\ & =\sum_{\substack{n=1\\ \sigma (x_k,n)>1}}^{2x_k} (\sigma (x_k, n)-1) + \sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1} }^{2x_k} 1. \end{align*} $$
$$ \begin{align*} A(x_k)B(x_k)-x_k&=\sum_{\substack{a\leqslant x_k, b\leqslant x_k\\ a\in A, b\in B}} 1 -x_k=\sum_{n=1}^{2x_k} \sigma (x_k, n)-x_k \\ & =\sum_{\substack{n=1\\ \sigma (x_k, n)\geqslant 1}}^{x_k} (\sigma(x_k, n)-1)+ \sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1}}^{2x_k} \sigma (x_k, n) \\ & = \sum_{\substack{n=1\\ \sigma (x_k, n)\geqslant 1}}^{2x_k} (\sigma (x_k, n)-1) + \sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1} }^{2x_k} 1 \\ & =\sum_{\substack{n=1\\ \sigma (x_k,n)>1}}^{2x_k} (\sigma (x_k, n)-1) + \sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1} }^{2x_k} 1. \end{align*} $$
Since
![]() $a^*(x_k)\in A$
and
$a^*(x_k)\in A$
and
![]() $a^*(x_k)+b>x_k$
for all
$a^*(x_k)+b>x_k$
for all
![]() $b\in B$
with
$b\in B$
with
![]() $x_k-a^*(x_k)<b\leqslant x_k$
,
$x_k-a^*(x_k)<b\leqslant x_k$
,
 $$ \begin{align*}\sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1} }^{2x_k} 1\geqslant B(x_k)-B(x_k-a^*(x_k)).\end{align*} $$
$$ \begin{align*}\sum_{\substack{n=x_k+1\\ \sigma (x_k, n)\geqslant 1} }^{2x_k} 1\geqslant B(x_k)-B(x_k-a^*(x_k)).\end{align*} $$
Thus,
 $$ \begin{align*} A(x_k)B(x_k)-x_k\geqslant \sum_{\substack{n\\ \sigma(x_k, n)>1} } (\sigma (x_k,n)-1)+B(x_k)-B(x_k-a^*(x_k)).\end{align*} $$
$$ \begin{align*} A(x_k)B(x_k)-x_k\geqslant \sum_{\substack{n\\ \sigma(x_k, n)>1} } (\sigma (x_k,n)-1)+B(x_k)-B(x_k-a^*(x_k)).\end{align*} $$
From Ruzsa’s Lemma 2.1,
 $$ \begin{align} A(x_k)B(x_k)-x_k\geqslant \frac{1}{A(x_k)}\sum_{\substack{n\\ \delta(x_k, n)>1} } (\delta (x_k,n)-1)+B(x_k)-B(x_k-a^*(x_k)).\end{align} $$
$$ \begin{align} A(x_k)B(x_k)-x_k\geqslant \frac{1}{A(x_k)}\sum_{\substack{n\\ \delta(x_k, n)>1} } (\delta (x_k,n)-1)+B(x_k)-B(x_k-a^*(x_k)).\end{align} $$
Let
Then
 $$ \begin{align} \sum_{\substack{n\\ \delta(x_k, n)>1} } (\delta (x_k,n)-1)=\sum_{\substack{n\\ \delta(x_k, n)\geqslant 1} } (\delta (x_k,n)-1)\geqslant |D|-(x_k-a^*(x_k)+1). \end{align} $$
$$ \begin{align} \sum_{\substack{n\\ \delta(x_k, n)>1} } (\delta (x_k,n)-1)=\sum_{\substack{n\\ \delta(x_k, n)\geqslant 1} } (\delta (x_k,n)-1)\geqslant |D|-(x_k-a^*(x_k)+1). \end{align} $$
Now we need a lower bound for
![]() $|D|$
. We consider the following two cases.
$|D|$
. We consider the following two cases.
Case 1:
![]() $a^*(x_k)>\frac 12x_k$
for infinitely many k. By (1.1),
$a^*(x_k)>\frac 12x_k$
for infinitely many k. By (1.1),
Thus, in this case, by Theorem 1.3 and
![]() $A(x)B(x)/x\rightarrow 1$
,
$A(x)B(x)/x\rightarrow 1$
,
 $$ \begin{align*} |D|&\geqslant \sum_{\substack{\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\leqslant b\leqslant x_k-a^*(x_k)\\ b\in B}} A(b) \geqslant A\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg(B(x_k-a^*(x_k))-B\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg) \\ &= (A(x_k)-1)B(x_k-a^*(x_k))-A\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &= A(x_k)B(x_k)+A(x_k)(B(x_k-a^*(x_k))-B(x_k))-B(x_k-a^*(x_k)) \\ & \quad -A\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &\geqslant x_k+\bigg(1-\frac{\delta _0}{4}\bigg)\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k))-B(a^*(x_k))-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)} \\ &\geqslant x_k+\bigg(1-\frac{\delta _0}{4}\bigg)\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \\&\quad -\bigg(1+\frac{\delta _0}{4}\bigg)\frac{a^*(x_k)}{A(x_k)}-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)} \\ &= x_k-\frac{3\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \end{align*} $$
$$ \begin{align*} |D|&\geqslant \sum_{\substack{\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\leqslant b\leqslant x_k-a^*(x_k)\\ b\in B}} A(b) \geqslant A\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg(B(x_k-a^*(x_k))-B\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg) \\ &= (A(x_k)-1)B(x_k-a^*(x_k))-A\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &= A(x_k)B(x_k)+A(x_k)(B(x_k-a^*(x_k))-B(x_k))-B(x_k-a^*(x_k)) \\ & \quad -A\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{5}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &\geqslant x_k+\bigg(1-\frac{\delta _0}{4}\bigg)\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k))-B(a^*(x_k))-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)} \\ &\geqslant x_k+\bigg(1-\frac{\delta _0}{4}\bigg)\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \\&\quad -\bigg(1+\frac{\delta _0}{4}\bigg)\frac{a^*(x_k)}{A(x_k)}-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)} \\ &= x_k-\frac{3\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \end{align*} $$
for sufficiently large k. It follows from (2.2) and (2.3) that
 $$ \begin{align*} A(x_k)B(x_k)-x_k &\geqslant \frac{x_k}{A(x_k)}-\frac{3\delta _0}{4}\frac{a^*(x_k)}{A(x_k)^2} +B(x_k-a^*(x_k))-B(x_k)-\frac{x_k-a^*(x_k)+1}{A(x_k)} \\ & \quad +B(x_k)-B(x_k-a^*(x_k) )\\ &>\frac{a^*(x_k)}{A(x_k)}-\delta _0\frac{a^*(x_k)}{A(x_k)^2} \end{align*} $$
$$ \begin{align*} A(x_k)B(x_k)-x_k &\geqslant \frac{x_k}{A(x_k)}-\frac{3\delta _0}{4}\frac{a^*(x_k)}{A(x_k)^2} +B(x_k-a^*(x_k))-B(x_k)-\frac{x_k-a^*(x_k)+1}{A(x_k)} \\ & \quad +B(x_k)-B(x_k-a^*(x_k) )\\ &>\frac{a^*(x_k)}{A(x_k)}-\delta _0\frac{a^*(x_k)}{A(x_k)^2} \end{align*} $$
for sufficiently large k, which is in contradiction with (2.1).
Case 2:
![]() $a^*(x_k)\leqslant \tfrac 12x_k$
for infinitely many k. By (1.1),
$a^*(x_k)\leqslant \tfrac 12x_k$
for infinitely many k. By (1.1),
Thus, in this case, by Theorem 1.3 and
![]() $A(x)B(x)/x\rightarrow 1$
,
$A(x)B(x)/x\rightarrow 1$
,
 $$ \begin{align*} |D| & \geqslant \sum_{\substack{\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}<b\leqslant x_k-a^*(x_k)\\ b\in B}} A\bigg(b-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ & =\sum_{\substack{\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}<b<a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\\ b\in B}} A\bigg(b-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)+ \sum_{\substack{a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\leqslant b\leqslant x_k-a^*(x_k)\\b\in B}} A\bigg(b-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ & =(A(x_k)-1)\bigg(B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)-B\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg) \\ &\quad +A(x_k)\bigg(B( x_k-a^*(x_k))-B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg) \\ & =A\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)-B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &\quad -A\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)+A(x_k)B(x_k)+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \\ &\quad -A\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ & =A(x_k)B(x_k)+A(x_k)(B(x_k-a^*(x_k))-B(x_k))-B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &\quad -A\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg) \\& \geqslant x_k+\bigg(1-\frac{\delta _0}{10}\bigg)\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \\ &\quad -\bigg(1+\frac{\delta _0}{10}\bigg)\frac{a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}}{A(x_k)} -\frac{3\delta _0}{5}\frac{a^*(x_k)}{A(x_k)} \\ &\geqslant x_k-\frac{9\delta _0}{10}\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)), \end{align*} $$
$$ \begin{align*} |D| & \geqslant \sum_{\substack{\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}<b\leqslant x_k-a^*(x_k)\\ b\in B}} A\bigg(b-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ & =\sum_{\substack{\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}<b<a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\\ b\in B}} A\bigg(b-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)+ \sum_{\substack{a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\leqslant b\leqslant x_k-a^*(x_k)\\b\in B}} A\bigg(b-\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ & =(A(x_k)-1)\bigg(B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)-B\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg) \\ &\quad +A(x_k)\bigg(B( x_k-a^*(x_k))-B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)\bigg) \\ & =A\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)-B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &\quad -A\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)+A(x_k)B(x_k)+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \\ &\quad -A\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ & =A(x_k)B(x_k)+A(x_k)(B(x_k-a^*(x_k))-B(x_k))-B\bigg(a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}\bigg) \\ &\quad -A\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg)B\bigg(\frac{\delta _0}{2}\frac{a^*(x_k)}{A(x_k)}\bigg) \\& \geqslant x_k+\bigg(1-\frac{\delta _0}{10}\bigg)\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)) \\ &\quad -\bigg(1+\frac{\delta _0}{10}\bigg)\frac{a^*(x_k)+\frac{\delta _0}{4}\frac{a^*(x_k)}{A(x_k)}}{A(x_k)} -\frac{3\delta _0}{5}\frac{a^*(x_k)}{A(x_k)} \\ &\geqslant x_k-\frac{9\delta _0}{10}\frac{a^*(x_k)}{A(x_k)}+A(x_k)(B(x_k-a^*(x_k))-B(x_k)), \end{align*} $$
for sufficiently large k. It follows from (2.2) and (2.3) that
 $$ \begin{align*} A(x_k)B(x_k)-x_k &\geqslant \frac{x_k}{A(x_k)}-\frac{9\delta _0}{10}\frac{a^*(x_k)}{A(x_k)^2}+B(x_k-a^*(x_k))-B(x_k)-\frac{x_k-a^*(x_k)+1}{A(x_k)} \\ &\quad +B(x_k)-B(x_k-a^*(x_k))\\ &> \frac{a^*(x_k)}{A(x_k)}-\delta_0\frac{a^*(x_k)}{A(x_k)^2} \end{align*} $$
$$ \begin{align*} A(x_k)B(x_k)-x_k &\geqslant \frac{x_k}{A(x_k)}-\frac{9\delta _0}{10}\frac{a^*(x_k)}{A(x_k)^2}+B(x_k-a^*(x_k))-B(x_k)-\frac{x_k-a^*(x_k)+1}{A(x_k)} \\ &\quad +B(x_k)-B(x_k-a^*(x_k))\\ &> \frac{a^*(x_k)}{A(x_k)}-\delta_0\frac{a^*(x_k)}{A(x_k)^2} \end{align*} $$
for sufficiently large k, which is in contradiction with (2.1).
This completes the proof of Theorem 1.5.
Proof of Theorem 1.6.
Let
![]() $a_1=1$
and
$a_1=1$
and
![]() $a_2=4$
. We construct the sequence
$a_2=4$
. We construct the sequence
![]() $a_3,a_4,\dots $
with
$a_3,a_4,\dots $
with
and a sequence
![]() $n_1,n_2,\dots $
such that
$n_1,n_2,\dots $
such that
![]() $a_1,a_2,\dots ,a_{n_k}$
form a complete residue system modulo
$a_1,a_2,\dots ,a_{n_k}$
form a complete residue system modulo
![]() $n_k$
and
$n_k$
and
![]() $n_k\mid a_{n_k}$
. We get such a sequence by a greedy algorithm: let
$n_k\mid a_{n_k}$
. We get such a sequence by a greedy algorithm: let
![]() $n_1=2$
, and if
$n_1=2$
, and if
![]() $n_1,n_2,\dots ,n_k$
are already defined, then let
$n_1,n_2,\dots ,n_k$
are already defined, then let
![]() $n_{k+1}=a_{n_k}$
. Since
$n_{k+1}=a_{n_k}$
. Since
![]() $a_1,\dots ,a_{n_k}$
are distinct residues modulo
$a_1,\dots ,a_{n_k}$
are distinct residues modulo
![]() $a_{n_k}$
, we can choose
$a_{n_k}$
, we can choose
![]() $a_{n_k+1},\dots ,a_{n_{k+1}}$
such that
$a_{n_k+1},\dots ,a_{n_{k+1}}$
such that
![]() $a_{m+1}\gg m^4a_m$
for
$a_{m+1}\gg m^4a_m$
for
![]() ${m=n_k,\ldots , n_{k+1}-1}$
,
${m=n_k,\ldots , n_{k+1}-1}$
,
![]() $a_{n_k}\mid a_{a_{n_k}}$
and
$a_{n_k}\mid a_{a_{n_k}}$
and
![]() $a_1,\dots ,a_{n_{k+1}}$
form a complete residue system modulo
$a_1,\dots ,a_{n_{k+1}}$
form a complete residue system modulo
![]() $n_{k+1}$
.
$n_{k+1}$
.
For every positive integer k, we further take
Then
![]() $a_i+b_j$
for
$a_i+b_j$
for
![]() $1\leqslant i\leqslant p, 1\leqslant j\leqslant {a_{n_k}}/{n_k}$
, form a complete residue system modulo
$1\leqslant i\leqslant p, 1\leqslant j\leqslant {a_{n_k}}/{n_k}$
, form a complete residue system modulo
![]() $a_{n_k}$
. From the definition of
$a_{n_k}$
. From the definition of
![]() $L(a_{n_k})$
,
$L(a_{n_k})$
,
For the set
![]() $A=\{a_k\}_{k=1}^{\infty }$
and every positive integer k, define
$A=\{a_k\}_{k=1}^{\infty }$
and every positive integer k, define
![]() $q_k$
by
$q_k$
by
Define the same sets
![]() $A,B$
as in [Reference Ruzsa2, Theorem 3] (replacing
$A,B$
as in [Reference Ruzsa2, Theorem 3] (replacing
![]() $m_k$
by
$m_k$
by
![]() $a_k$
) and write
$a_k$
) and write
![]() ${A_k=A\bigcap [1,a_k]}$
. Take
${A_k=A\bigcap [1,a_k]}$
. Take
![]() $U_k\subseteq [1,a_k]$
so that
$U_k\subseteq [1,a_k]$
so that
![]() $|U_k|=L(a_k)$
and
$|U_k|=L(a_k)$
and
![]() $A_k+U_k$
contains every residue module
$A_k+U_k$
contains every residue module
![]() $a_k$
. Let
$a_k$
. Let
 $$ \begin{align*} V_k=U_k+\bigg\{(q_k-1)a_k,q_ka_k,(q_k+1)a_k,\ldots, \bigg\lfloor \frac{q_{k+1}a_{k+1}}{a_k}\bigg\rfloor a_k\bigg\} \quad\mbox{and}\quad B=\bigcup_{k=1}^\infty V_k.\end{align*} $$
$$ \begin{align*} V_k=U_k+\bigg\{(q_k-1)a_k,q_ka_k,(q_k+1)a_k,\ldots, \bigg\lfloor \frac{q_{k+1}a_{k+1}}{a_k}\bigg\rfloor a_k\bigg\} \quad\mbox{and}\quad B=\bigcup_{k=1}^\infty V_k.\end{align*} $$
Let
![]() $q_ka_k\leqslant x\leqslant q_{k+1}a_{k+1}$
. The sequence
$q_ka_k\leqslant x\leqslant q_{k+1}a_{k+1}$
. The sequence
![]() $\{q_k\}_{k=1}^{\infty }$
defined in (2.6) is increasing to infinity by (2.4) and
$\{q_k\}_{k=1}^{\infty }$
defined in (2.6) is increasing to infinity by (2.4) and
![]() $A(q_ka_k)\sim A(a_k)$
. (In fact,
$A(q_ka_k)\sim A(a_k)$
. (In fact,
![]() $A(q_ka_k)=k=A(a_k)$
by (2.6).) By the same proof as in [Reference Ruzsa2, Theorem 3],
$A(q_ka_k)=k=A(a_k)$
by (2.6).) By the same proof as in [Reference Ruzsa2, Theorem 3],
![]() $A,B$
are additive complements and
$A,B$
are additive complements and
![]() $A(x)B(x)\sim x$
. Thus, the set A with (2.4) has an exact complement B. Obviously, such an A with (2.4) satisfies (1.1).
$A(x)B(x)\sim x$
. Thus, the set A with (2.4) has an exact complement B. Obviously, such an A with (2.4) satisfies (1.1).
Finally, we prove that (1.3) holds for infinitely many
![]() $x_k$
. For x with
$x_k$
. For x with
![]() $q_ka_k\leqslant x<(q_{k+1}-1)a_{k+1}$
, we have
$q_ka_k\leqslant x<(q_{k+1}-1)a_{k+1}$
, we have
![]() $k\leqslant A(x)\leqslant k+1$
and
$k\leqslant A(x)\leqslant k+1$
and
 $$ \begin{align} B(x)\leqslant \bigg(\bigg\lfloor\frac{x}{a_k}\bigg\rfloor-q_k+2\bigg)L(a_k) +\sum_{i=2}^k\bigg(\bigg\lfloor\frac{q_ia_i}{a_{i-1}}\bigg\rfloor-q_{i-1}+2\bigg)L(a_{i-1}). \end{align} $$
$$ \begin{align} B(x)\leqslant \bigg(\bigg\lfloor\frac{x}{a_k}\bigg\rfloor-q_k+2\bigg)L(a_k) +\sum_{i=2}^k\bigg(\bigg\lfloor\frac{q_ia_i}{a_{i-1}}\bigg\rfloor-q_{i-1}+2\bigg)L(a_{i-1}). \end{align} $$
By Theorem 1.2(b),
![]() $L(a_{k-1})\leqslant {2a_{k-1}}/{(k-1)} \mbox { for large } k$
. From (2.6),
$L(a_{k-1})\leqslant {2a_{k-1}}/{(k-1)} \mbox { for large } k$
. From (2.6),
 $$ \begin{align*} \sum_{i=2}^k\bigg(\bigg\lfloor\frac{q_ia_i}{a_{i-1}}\bigg\rfloor-q_{i-1}+2\bigg)L(a_{i-1}) \leqslant (k-1)\frac{2q_ka_k}{k-1}=O(q_ka_k)=O\bigg(\frac{a_{k+1}}{(k+1)^4}\bigg).\end{align*} $$
$$ \begin{align*} \sum_{i=2}^k\bigg(\bigg\lfloor\frac{q_ia_i}{a_{i-1}}\bigg\rfloor-q_{i-1}+2\bigg)L(a_{i-1}) \leqslant (k-1)\frac{2q_ka_k}{k-1}=O(q_ka_k)=O\bigg(\frac{a_{k+1}}{(k+1)^4}\bigg).\end{align*} $$
It is easy to see that, for large k,
It follows from (2.7) that
Choose
![]() $x_k=a_{n_k+1}$
, where
$x_k=a_{n_k+1}$
, where
![]() $n_k$
is the index satisfying (2.5). Then by (2.8),
$n_k$
is the index satisfying (2.5). Then by (2.8),
 $$ \begin{align*} A(x_k)B(x_k)-x_k-\frac{a^*(x_k)}{A(x_k)} &\leqslant(n_k+1)\frac{x_k}{n_k}-x_k-\frac{x_k}{n_k+1} +O\bigg(\frac{x_k}{(n_k+1)^3}\bigg)\\ &=\frac{x_k}{A(x_k)^2}+O\bigg(\frac{x_k}{A(x_k)^3}\bigg). \end{align*} $$
$$ \begin{align*} A(x_k)B(x_k)-x_k-\frac{a^*(x_k)}{A(x_k)} &\leqslant(n_k+1)\frac{x_k}{n_k}-x_k-\frac{x_k}{n_k+1} +O\bigg(\frac{x_k}{(n_k+1)^3}\bigg)\\ &=\frac{x_k}{A(x_k)^2}+O\bigg(\frac{x_k}{A(x_k)^3}\bigg). \end{align*} $$
This completes the proof of Theorem 1.6.