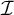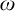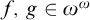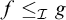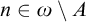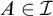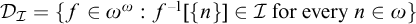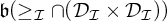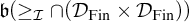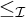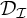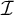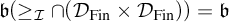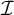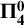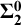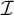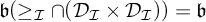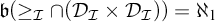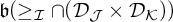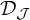1 Introduction
For an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
we denote
$\omega $
we denote
![]() $\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$
(in particular,
$\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$
(in particular,
![]() $\mathcal {D}_{\mathrm {Fin}}$
denotes the family of all finite-to-one functions) and write
$\mathcal {D}_{\mathrm {Fin}}$
denotes the family of all finite-to-one functions) and write
![]() $f\leq _{\mathcal {I}} g$
if
$f\leq _{\mathcal {I}} g$
if
![]() $\{n\in \omega :f(n)>g(n)\}\in \mathcal {I}$
, where
$\{n\in \omega :f(n)>g(n)\}\in \mathcal {I}$
, where
![]() $f,\,g\in \omega ^{\omega }$
. By
$f,\,g\in \omega ^{\omega }$
. By
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}} \times \mathcal {D}_{\mathcal {K}}))$
we denote the smallest sizes of sets in
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}} \times \mathcal {D}_{\mathcal {K}}))$
we denote the smallest sizes of sets in
![]() $\mathcal {D}_{\mathcal {K}}$
not bounded from below with respect to the order
$\mathcal {D}_{\mathcal {K}}$
not bounded from below with respect to the order
![]() $\leq _{\mathcal {I}}$
by any member of
$\leq _{\mathcal {I}}$
by any member of
![]() $\mathcal {D}_{\mathcal {J}}$
. (We restrict ourself to functions from
$\mathcal {D}_{\mathcal {J}}$
. (We restrict ourself to functions from
![]() $\mathcal {D}_{\mathcal {J}}$
instead of all functions from
$\mathcal {D}_{\mathcal {J}}$
instead of all functions from
![]() $\omega ^{\omega }$
, because every subset of
$\omega ^{\omega }$
, because every subset of
![]() $\omega ^{\omega }$
is bounded from below with respect to
$\omega ^{\omega }$
is bounded from below with respect to
![]() $\leq _{\mathcal {I}}$
by the constant zero function.)
$\leq _{\mathcal {I}}$
by the constant zero function.)
In 1980s, Canjar [Reference Canjar11, Reference Canjar12, Reference RecŁaw13] studied the smallest sizes of cofinal and coinitial subsets in ultrapowers
![]() $\omega ^{\omega }/\mathcal {U}$
ordered by
$\omega ^{\omega }/\mathcal {U}$
ordered by
![]() $\leq _{\mathcal {I}}$
for ultrafilters
$\leq _{\mathcal {I}}$
for ultrafilters
![]() $\mathcal {U}=\mathcal {I}^*$
. Among others, Conjar proved that consistently
$\mathcal {U}=\mathcal {I}^*$
. Among others, Conjar proved that consistently
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$
can be equal to any regular cardinal between
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$
can be equal to any regular cardinal between
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\mathfrak {b}$
for some maximal ideal
$\mathfrak {b}$
for some maximal ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
In this paper, we examine cardinals
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
for various triples of ideals
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
for various triples of ideals
![]() $(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
, but we do not require from ideals
$(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
, but we do not require from ideals
![]() $\mathcal {I},\,\mathcal {J}$
and
$\mathcal {I},\,\mathcal {J}$
and
![]() $\mathcal {K}$
to be maximal. We obtained some facts for arbitrary ideals
$\mathcal {K}$
to be maximal. We obtained some facts for arbitrary ideals
![]() $\mathcal {I},\, \mathcal {J}$
and
$\mathcal {I},\, \mathcal {J}$
and
![]() $\mathcal {K}$
, however, the most interesting results we proved for Borel ideals. For instance, we showed that there are Borel ideals
$\mathcal {K}$
, however, the most interesting results we proved for Borel ideals. For instance, we showed that there are Borel ideals
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\aleph _1$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\aleph _1$
and
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}} \times \mathcal {D}_{\mathrm {Fin}}))=\mathfrak {b}$
provable in ZFC.
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}} \times \mathcal {D}_{\mathrm {Fin}}))=\mathfrak {b}$
provable in ZFC.
To make life easier, we restrict our study only to eight cases with at most two different ideals among
![]() $\mathcal {I},\,\mathcal {J},\,\mathcal {K}$
and with at least one of them equal to the ideal
$\mathcal {I},\,\mathcal {J},\,\mathcal {K}$
and with at least one of them equal to the ideal
![]() $\mathrm {Fin}$
. It will follow from results of Section 4 that in fact we can restrict our study only to four cases:
$\mathrm {Fin}$
. It will follow from results of Section 4 that in fact we can restrict our study only to four cases:
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
,
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
,
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathcal {I}}))$
,
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathcal {I}}))$
,
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
![]() $\mathfrak {b}(\geq _{\mathrm {Fin}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
.
$\mathfrak {b}(\geq _{\mathrm {Fin}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
.
The paper is organized in the following way. In Section 3 we show that
![]() $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) = \mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
and
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) = \mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
and
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) = \mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
, where
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) = \mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
, where
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
and
$\mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
and
![]() $\mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
are cardinals considered by Filipów and Stanszewski in [Reference Filipów and Staniszewski18, Reference Šupina35]. This provides us with a very useful combinatorial characterizations of the considered cardinals, which we use almost exclusively in the rest of the paper.
$\mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
are cardinals considered by Filipów and Stanszewski in [Reference Filipów and Staniszewski18, Reference Šupina35]. This provides us with a very useful combinatorial characterizations of the considered cardinals, which we use almost exclusively in the rest of the paper.
Section 4 is devoted to showing the basic properties of considered
![]() $\mathfrak {b}$
-like numbers. Also, we prove that
$\mathfrak {b}$
-like numbers. Also, we prove that
![]() $\mathfrak {b}(\geq _{\mathrm {Fin}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))=\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
and present some diagrams summarizing basic relationships between considered
$\mathfrak {b}(\geq _{\mathrm {Fin}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))=\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
and present some diagrams summarizing basic relationships between considered
![]() $\mathfrak {b}$
-like numbers
$\mathfrak {b}$
-like numbers
In Section 5, we calculate
![]() $\mathfrak {b}$
-like numbers for direct sums and Fubini products of ideals. Moreover, we compute
$\mathfrak {b}$
-like numbers for direct sums and Fubini products of ideals. Moreover, we compute
![]() $\mathfrak {b}$
-like numbers for not tall ideals. The results of that section are used in Section 8 to obtain examples of ideals with distinct values of various
$\mathfrak {b}$
-like numbers for not tall ideals. The results of that section are used in Section 8 to obtain examples of ideals with distinct values of various
![]() $\mathfrak {b}$
-like cardinals.
$\mathfrak {b}$
-like cardinals.
In Section 6, we examine
![]() $\mathfrak {b}$
-like cardinals for nice ideals, where nice means ideals with the Baire property,
$\mathfrak {b}$
-like cardinals for nice ideals, where nice means ideals with the Baire property,
![]() $\omega $
-diagonalizable ideals or definable ideals. We show that
$\omega $
-diagonalizable ideals or definable ideals. We show that
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) =\mathfrak {b}$
for all ideals
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) =\mathfrak {b}$
for all ideals
![]() $\mathcal {I}$
with the Baire property and infer that for P-ideals with the Baire property all considered cardinals equal
$\mathcal {I}$
with the Baire property and infer that for P-ideals with the Baire property all considered cardinals equal
![]() $\mathfrak {b}$
. Moreover, we show that
$\mathfrak {b}$
. Moreover, we show that
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathcal {I}})) =\mathfrak {b}$
for coanalytic weak P-ideals. The latter gives an upper bound for
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathcal {I}})) =\mathfrak {b}$
for coanalytic weak P-ideals. The latter gives an upper bound for
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
in the case of coanalytic weak P-ideals (by a result of Debs and Saint Raymond, this class contains all
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
in the case of coanalytic weak P-ideals (by a result of Debs and Saint Raymond, this class contains all
![]() $\bf {\Pi ^0_4}$
ideals).
$\bf {\Pi ^0_4}$
ideals).
Section 7 is devoted to ideals
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))=\aleph _1$
. In particular, we give examples of such ideals among not tall
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))=\aleph _1$
. In particular, we give examples of such ideals among not tall
![]() $\bf {\Sigma ^0_2}$
ideals and among tall
$\bf {\Sigma ^0_2}$
ideals and among tall
![]() $\bf {\Sigma ^0_2}$
ideals.
$\bf {\Sigma ^0_2}$
ideals.
In Section 8, we show that consistently the values of considered cardinals can be pairwise distinct.
In the literature, there are considered other ideal versions of the bounding number
![]() $\mathfrak {b}$
. For instance, Farkas and Soukup [Reference Farkas and Soukup17] consider
$\mathfrak {b}$
. For instance, Farkas and Soukup [Reference Farkas and Soukup17] consider
![]() $\mathfrak {b}(\leq _{\mathcal {I}}\cap (\omega ^{\omega }\times \omega ^{\omega })$
(Canjar in [Reference Canjar12] proved that consistently there are ideals
$\mathfrak {b}(\leq _{\mathcal {I}}\cap (\omega ^{\omega }\times \omega ^{\omega })$
(Canjar in [Reference Canjar12] proved that consistently there are ideals
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
![]() $\mathfrak {b}(\leq _{\mathcal {I}}\cap (\omega ^{\omega }\times \omega ^{\omega })\neq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
; see also [Reference RecŁaw13]), and Brendle and Mejía [Reference Brendle and Mejía3] consider the number
$\mathfrak {b}(\leq _{\mathcal {I}}\cap (\omega ^{\omega }\times \omega ^{\omega })\neq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
; see also [Reference RecŁaw13]), and Brendle and Mejía [Reference Brendle and Mejía3] consider the number
![]() $\mathfrak {b}(\mathcal {I})$
defined as the smallest
$\mathfrak {b}(\mathcal {I})$
defined as the smallest
![]() $\kappa $
such that there is an
$\kappa $
such that there is an
![]() $\mathcal {I}-(\omega ,\,\kappa )$
-gap in
$\mathcal {I}-(\omega ,\,\kappa )$
-gap in
![]() $(\mathcal {P}(\omega ),\subseteq ^{\mathcal {I}})$
and call it the Rothberger number of
$(\mathcal {P}(\omega ),\subseteq ^{\mathcal {I}})$
and call it the Rothberger number of
![]() $\mathcal {I}$
(in general,
$\mathcal {I}$
(in general,
![]() $\mathfrak {b}(\mathcal {I})\neq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
because the former is not defined for maximal ideals whereas the latter is).
$\mathfrak {b}(\mathcal {I})\neq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
because the former is not defined for maximal ideals whereas the latter is).
2 Preliminaries
By
![]() $\omega $
we denote the set of all natural numbers. We identify a natural number n with the set
$\omega $
we denote the set of all natural numbers. We identify a natural number n with the set
![]() $\{0, 1,\dots , n-1\}$
. (Thus, for instance,
$\{0, 1,\dots , n-1\}$
. (Thus, for instance,
![]() $n\setminus k$
means the set
$n\setminus k$
means the set
![]() $\{i\in \omega : k\leq i<n\}$
). We write
$\{i\in \omega : k\leq i<n\}$
). We write
![]() $A\subseteq ^*B$
or
$A\subseteq ^*B$
or
![]() $B\supseteq ^* A$
if
$B\supseteq ^* A$
if
![]() $A\setminus B$
is finite. For a set A and a finite or infinite cardinal number
$A\setminus B$
is finite. For a set A and a finite or infinite cardinal number
![]() $\kappa $
, we write
$\kappa $
, we write
![]() $[A]^{\kappa } =\{B\subseteq A: |B|=\kappa \}$
.
$[A]^{\kappa } =\{B\subseteq A: |B|=\kappa \}$
.
2.1 Ideals
An ideal on a set X (in short ideal) is a family
![]() $\mathcal {I}\subseteq \mathcal {P}(X)$
that satisfies the following properties:
$\mathcal {I}\subseteq \mathcal {P}(X)$
that satisfies the following properties:
-
(1) if
 $A,B\in \mathcal {I}$
then
$A,B\in \mathcal {I}$
then
 $A\cup B\in \mathcal {I}$
,
$A\cup B\in \mathcal {I}$
, -
(2) if
 $A\subseteq B$
and
$A\subseteq B$
and
 $B\in \mathcal {I}$
then
$B\in \mathcal {I}$
then
 $A\in \mathcal {I}$
,
$A\in \mathcal {I}$
, -
(3)
 $\mathcal {I}$
contains all finite subsets of X, and
$\mathcal {I}$
contains all finite subsets of X, and -
(4)
 $X\notin \mathcal {I}$
.
$X\notin \mathcal {I}$
.
For an ideal
![]() $\mathcal {I}$
, we write
$\mathcal {I}$
, we write
![]() $\mathcal {I}^+=\{A\subseteq X: A\notin \mathcal {I}\}$
and call it the coideal of
$\mathcal {I}^+=\{A\subseteq X: A\notin \mathcal {I}\}$
and call it the coideal of
![]() $\mathcal {I}$
, and we write
$\mathcal {I}$
, and we write
![]() $\mathcal {I}^*=\{A\subseteq X: X\setminus A\in \mathcal {I}\}$
and call it the dual filter of
$\mathcal {I}^*=\{A\subseteq X: X\setminus A\in \mathcal {I}\}$
and call it the dual filter of
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
The ideal of all finite subsets of an infinite set X is denoted by
![]() $\mathrm {Fin}(X)$
(or
$\mathrm {Fin}(X)$
(or
![]() $\mathrm {Fin}$
for short).
$\mathrm {Fin}$
for short).
Let
![]() $\mathcal {A}\subseteq \mathcal {P}(X)$
. If X cannot be covered by finitely many members of
$\mathcal {A}\subseteq \mathcal {P}(X)$
. If X cannot be covered by finitely many members of
![]() $\mathcal {A}$
then the smallest ideal containing
$\mathcal {A}$
then the smallest ideal containing
![]() $\mathcal {A}$
i.e., the ideal
$\mathcal {A}$
i.e., the ideal
![]() $\mathcal {I}=\{B\subset X: \exists A_1,\dots ,A_n \in \mathcal {A}\, (B\subseteq ^* A_1\cup \dots \cup A_n)\}$
is called the ideal generated by
$\mathcal {I}=\{B\subset X: \exists A_1,\dots ,A_n \in \mathcal {A}\, (B\subseteq ^* A_1\cup \dots \cup A_n)\}$
is called the ideal generated by
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
An ideal
![]() $\mathcal {I}$
on X is P-ideal (weak P-ideal, resp.) if for any countable family
$\mathcal {I}$
on X is P-ideal (weak P-ideal, resp.) if for any countable family
![]() $\mathcal {A}\subseteq \mathcal {I}$
there is
$\mathcal {A}\subseteq \mathcal {I}$
there is
![]() $B\in \mathcal {I}^*$
(
$B\in \mathcal {I}^*$
(
![]() $B\in \mathcal {I}^{+}$
, resp.) such that
$B\in \mathcal {I}^{+}$
, resp.) such that
![]() $A\cap B\in \mathrm {Fin}(X)$
for every
$A\cap B\in \mathrm {Fin}(X)$
for every
![]() $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
While P-ideals can be considered as a classical notion, weak P-ideals are gaining in popularity nowadays. Usefulness of weak P-ideals follows from the fact that this property can be characterized in various manners. For instance, an ideal
![]() $\mathcal {I}$
is a weak P-ideal if and only if one of the following conditions hold:
$\mathcal {I}$
is a weak P-ideal if and only if one of the following conditions hold:
-
•
 $\mathcal {I}$
is not above the ideal
$\mathcal {I}$
is not above the ideal
 $\mathrm {Fin}\otimes \mathrm {Fin}$
in the Katětov order (see e.g., [Reference Talagrand36] where also other orders are used for similar characterizations);
$\mathrm {Fin}\otimes \mathrm {Fin}$
in the Katětov order (see e.g., [Reference Talagrand36] where also other orders are used for similar characterizations); -
•
 $\mathcal {I}$
and
$\mathcal {I}$
and
 $\mathcal {I}^*$
can be separated by an
$\mathcal {I}^*$
can be separated by an
 $F_\sigma $
set [Reference Laczkovich and RecŁaw26];
$F_\sigma $
set [Reference Laczkovich and RecŁaw26]; -
• Player I does not have a winning strategy in a game introduce by Laflamme in [Reference Laflamme27] (see Subsection 6.3 of the present paper for a definition of this game);
-
•
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $\omega $
-diagonalizable by
$\omega $
-diagonalizable by
 $\mathcal {I}^*$
-universal sets (see Section 6.2 for a definition of this notion).
$\mathcal {I}^*$
-universal sets (see Section 6.2 for a definition of this notion).
The last characterization is technical, but its combinatorial character turns out to be very useful for working with weak P-ideals: we use it for examining some
![]() $\mathfrak {b}$
-like numbers in Section 6.2 (for other applications of this characterization see e.g., [Reference Filipów and Szuca19, Reference Kwela and RecŁaw23, Reference Kwela and Staniszewski25, Reference Laczkovich and RecŁaw26]).
$\mathfrak {b}$
-like numbers in Section 6.2 (for other applications of this characterization see e.g., [Reference Filipów and Szuca19, Reference Kwela and RecŁaw23, Reference Kwela and Staniszewski25, Reference Laczkovich and RecŁaw26]).
We say that ideals
![]() $\mathcal {I},\mathcal {J}$
on X are orthogonal (in short:
$\mathcal {I},\mathcal {J}$
on X are orthogonal (in short:
![]() $\mathcal {I}\perp \mathcal {J}$
) if there is
$\mathcal {I}\perp \mathcal {J}$
) if there is
![]() $A\in \mathcal {J}$
with
$A\in \mathcal {J}$
with
![]() $X\setminus A\in \mathcal {I}$
.
$X\setminus A\in \mathcal {I}$
.
An ideal
![]() $\mathcal {I}$
on X is tall if for every infinite
$\mathcal {I}$
on X is tall if for every infinite
![]() $A\subseteq X$
there is an infinite
$A\subseteq X$
there is an infinite
![]() $B\in \mathcal {I}$
such that
$B\in \mathcal {I}$
such that
![]() $B\subset A$
.
$B\subset A$
.
For an ideal
![]() $\mathcal {I}$
on X and for
$\mathcal {I}$
on X and for
![]() $A\notin \mathcal {I}$
we define
$A\notin \mathcal {I}$
we define
![]() $\mathcal {I}\restriction A = \{B\subseteq A: B\in \mathcal {I}\}$
. It is easy to see that
$\mathcal {I}\restriction A = \{B\subseteq A: B\in \mathcal {I}\}$
. It is easy to see that
![]() $\mathcal {I}\restriction A$
is an ideal on A.
$\mathcal {I}\restriction A$
is an ideal on A.
The vertical section of a set
![]() $A\subseteq X\times Y$
at a point
$A\subseteq X\times Y$
at a point
![]() $x\in X$
is defined by
$x\in X$
is defined by
![]() $(A)_x = \{y\in Y : (x,y)\in A\}$
.
$(A)_x = \{y\in Y : (x,y)\in A\}$
.
For ideals
![]() $\mathcal {I},\mathcal {J}$
on X and Y respectively we define the following new ideals:
$\mathcal {I},\mathcal {J}$
on X and Y respectively we define the following new ideals:
-
(1)
 $\mathcal {I}\oplus \mathcal {J} = \{A\subseteq X\times \{0\}\cup Y\times \{1\}: \{x:(x,0)\in A\}\in \mathcal {I}\land \{y:(y,1)\in A\}\in \mathcal {J}\}\}$
,
$\mathcal {I}\oplus \mathcal {J} = \{A\subseteq X\times \{0\}\cup Y\times \{1\}: \{x:(x,0)\in A\}\in \mathcal {I}\land \{y:(y,1)\in A\}\in \mathcal {J}\}\}$
, -
(2)
 $\mathcal {I}\oplus \mathcal {P}(\omega ) = \{A\subseteq X\times \{0\}\cup \omega \times \{1\}: \{n:(n,0)\in A\}\in \mathcal {I}\}$
,
$\mathcal {I}\oplus \mathcal {P}(\omega ) = \{A\subseteq X\times \{0\}\cup \omega \times \{1\}: \{n:(n,0)\in A\}\in \mathcal {I}\}$
, -
(3)
 $\mathcal {I}\otimes \mathcal {J} = \{A\subseteq X\times Y: \{x:(A)_x\notin \mathcal {J}\}\in \mathcal {I}\}$
,
$\mathcal {I}\otimes \mathcal {J} = \{A\subseteq X\times Y: \{x:(A)_x\notin \mathcal {J}\}\in \mathcal {I}\}$
, -
(4)
 $\mathcal {I}\otimes \{\emptyset \} = \{A\subseteq X\times \omega : \{x:(A)_x\ne \emptyset \}\in \mathcal {I}\}$
, and
$\mathcal {I}\otimes \{\emptyset \} = \{A\subseteq X\times \omega : \{x:(A)_x\ne \emptyset \}\in \mathcal {I}\}$
, and -
(5)
 $\{\emptyset \} \otimes \mathcal {J}= \{A\subseteq \omega \times Y : (A)_x\in \mathcal {J}\text { for all } x\}$
.
$\{\emptyset \} \otimes \mathcal {J}= \{A\subseteq \omega \times Y : (A)_x\in \mathcal {J}\text { for all } x\}$
.
For any
![]() $n\geq 1$
we define the ideals
$n\geq 1$
we define the ideals
![]() $\mathrm {Fin}^n$
in the following manner:
$\mathrm {Fin}^n$
in the following manner:
![]() $\mathrm {Fin}^1=\mathrm {Fin}$
, and
$\mathrm {Fin}^1=\mathrm {Fin}$
, and
![]() $\mathrm {Fin}^{n+1}=\mathrm {Fin}\otimes \mathrm {Fin}^n$
.
$\mathrm {Fin}^{n+1}=\mathrm {Fin}\otimes \mathrm {Fin}^n$
.
By identifying sets of natural numbers with their characteristic functions, we equip
![]() $\mathcal {P}(\omega )$
with the topology of the Cantor space
$\mathcal {P}(\omega )$
with the topology of the Cantor space
![]() $\{0,1\}^{\omega }$
and therefore we can assign topological complexity to ideals on
$\{0,1\}^{\omega }$
and therefore we can assign topological complexity to ideals on
![]() $\omega $
. In particular, an ideal
$\omega $
. In particular, an ideal
![]() $\mathcal {I}$
is Borel (has the Baire property) if
$\mathcal {I}$
is Borel (has the Baire property) if
![]() $\mathcal {I}$
is Borel (has the Baire property) as a subset of the Cantor space.
$\mathcal {I}$
is Borel (has the Baire property) as a subset of the Cantor space.
In the sequel, we use the convention that
![]() $\min \emptyset = \mathfrak {c}^+$
.
$\min \emptyset = \mathfrak {c}^+$
.
For an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
we define
$\omega $
we define
Note that
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\aleph _0$
for every non P-ideal and
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\aleph _0$
for every non P-ideal and
![]() $\operatorname {\mathrm {add}}(\mathcal {I})\geq \aleph _1$
for every P-ideal. Moreover, it is easy to see that
$\operatorname {\mathrm {add}}(\mathcal {I})\geq \aleph _1$
for every P-ideal. Moreover, it is easy to see that
![]() $\operatorname {\mathrm {add}}^*(\mathcal {I})=\mathfrak {c}^+$
if and only if
$\operatorname {\mathrm {add}}^*(\mathcal {I})=\mathfrak {c}^+$
if and only if
![]() $\,\mathcal {I}=\{C\subseteq \omega : |C\setminus A|<\aleph _0\}$
for some
$\,\mathcal {I}=\{C\subseteq \omega : |C\setminus A|<\aleph _0\}$
for some
![]() $A\subset \omega $
. For instance,
$A\subset \omega $
. For instance,
![]() $\operatorname {\mathrm {add} ^{*}}(\mathrm {Fin})=\mathfrak {c}^+$
.
$\operatorname {\mathrm {add} ^{*}}(\mathrm {Fin})=\mathfrak {c}^+$
.
3 Various bounding numbers
3.1 The ordinary bounding number
For
![]() $f,g\in \omega ^{\omega }$
we write
$f,g\in \omega ^{\omega }$
we write
![]() $f\leq ^*g$
if
$f\leq ^*g$
if
![]() $f(n)\leq g(n)$
for all but finitely many
$f(n)\leq g(n)$
for all but finitely many
![]() $n\in \omega $
. The bounding number
$n\in \omega $
. The bounding number
![]() $\mathfrak {b}$
is the smallest size of
$\mathfrak {b}$
is the smallest size of
![]() $\leq ^*$
-unbounded subset of
$\leq ^*$
-unbounded subset of
![]() $\omega ^{\omega }$
i.e.,
$\omega ^{\omega }$
i.e.,
The dominating number
![]() $\mathfrak {d}$
is the smallest size of
$\mathfrak {d}$
is the smallest size of
![]() $\leq ^*$
-dominating subset of
$\leq ^*$
-dominating subset of
![]() $\omega ^{\omega }$
i.e.,
$\omega ^{\omega }$
i.e.,
3.2 The bounding numbers à la Vojtáš
If R is a binary relation, then by
![]() $\operatorname {\mathrm {dom}}(R)$
and
$\operatorname {\mathrm {dom}}(R)$
and
![]() $\operatorname {\mathrm {ran}}(R)$
we denote the domain and range of R respectively i.e.,
$\operatorname {\mathrm {ran}}(R)$
we denote the domain and range of R respectively i.e.,
![]() $\operatorname {\mathrm {dom}}(R)=\{x:\exists y\, (x,y)\in R\}$
and
$\operatorname {\mathrm {dom}}(R)=\{x:\exists y\, (x,y)\in R\}$
and
![]() $\operatorname {\mathrm {ran}}(R) = \{y: \exists x\, (x,y)\in R\}$
. A set
$\operatorname {\mathrm {ran}}(R) = \{y: \exists x\, (x,y)\in R\}$
. A set
![]() $B\subseteq \operatorname {\mathrm {dom}}(R)$
is called R-unbounded if for every
$B\subseteq \operatorname {\mathrm {dom}}(R)$
is called R-unbounded if for every
![]() $y\in \operatorname {\mathrm {ran}}(R)$
there is
$y\in \operatorname {\mathrm {ran}}(R)$
there is
![]() $x\in B$
with
$x\in B$
with
![]() $(x,y)\notin R$
. A set
$(x,y)\notin R$
. A set
![]() $D\subseteq \operatorname {\mathrm {ran}}(R)$
is called R-dominating if for every
$D\subseteq \operatorname {\mathrm {ran}}(R)$
is called R-dominating if for every
![]() $x\in \operatorname {\mathrm {dom}}(R)$
there is
$x\in \operatorname {\mathrm {dom}}(R)$
there is
![]() $y\in D$
with
$y\in D$
with
![]() $(x,y)\in R$
.
$(x,y)\in R$
.
Definition 3.1 (Vojtáš [Reference Vojtáš39]).
Let R be a binary relation.
 $$ \begin{align*} \begin{aligned} \mathfrak{b}(R) & = \min(\{|B|: B \text{ is } R\text{-unbounded set}\}.\\ \mathfrak{d}(R) & = \min(\{|D|: D \text{ is } R\text{-dominating set}\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathfrak{b}(R) & = \min(\{|B|: B \text{ is } R\text{-unbounded set}\}.\\ \mathfrak{d}(R) & = \min(\{|D|: D \text{ is } R\text{-dominating set}\}. \end{aligned} \end{align*} $$
It is easy to see that the bounding number
![]() $\mathfrak {b}$
is equal to the bounding number of the relation
$\mathfrak {b}$
is equal to the bounding number of the relation
![]() $\leq ^*\cap (\omega ^{\omega }\times \omega ^{\omega })$
i.e.,
$\leq ^*\cap (\omega ^{\omega }\times \omega ^{\omega })$
i.e.,
![]() $\mathfrak {b} = \mathfrak {b}(\leq ^*\cap (\omega ^{\omega }\times \omega ^{\omega }))$
, and similarly
$\mathfrak {b} = \mathfrak {b}(\leq ^*\cap (\omega ^{\omega }\times \omega ^{\omega }))$
, and similarly
![]() $\mathfrak {d} = \mathfrak {d}(\leq ^*\cap (\omega ^{\omega }\times \omega ^{\omega }))$
.
$\mathfrak {d} = \mathfrak {d}(\leq ^*\cap (\omega ^{\omega }\times \omega ^{\omega }))$
.
3.3 The bounding numbers à la Canjar
Definition 3.2. For an ideal
![]() $\mathcal {I}$
we define the relation
$\mathcal {I}$
we define the relation
![]() $\leq _{\mathcal {I}} = \{(f,g)\in \omega ^{\omega }\times \omega ^{\omega }: \{n\in \omega : f(n)>g(n)\}\in \mathcal {I}\}$
. We write
$\leq _{\mathcal {I}} = \{(f,g)\in \omega ^{\omega }\times \omega ^{\omega }: \{n\in \omega : f(n)>g(n)\}\in \mathcal {I}\}$
. We write
![]() $f\leq _{\mathcal {I}} g$
if
$f\leq _{\mathcal {I}} g$
if
![]() $(f,g)\in \leq _{\mathcal {I}}$
. In a similar manner we define
$(f,g)\in \leq _{\mathcal {I}}$
. In a similar manner we define
![]() $<_{\mathcal {I}}$
,
$<_{\mathcal {I}}$
,
![]() $\geq _{\mathcal {I}}$
and
$\geq _{\mathcal {I}}$
and
![]() $>_{\mathcal {I}}$
.
$>_{\mathcal {I}}$
.
Definition 3.3. For an ideal
![]() $\mathcal {I}$
we define
$\mathcal {I}$
we define
In [Reference Canjar11, Reference Canjar12, Reference RecŁaw13], Canjar studied cardinals
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
and
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
for some maximal ideals
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
for some maximal ideals
![]() $\mathcal {I}$
. In this paper we will examine the bounding numbers
$\mathcal {I}$
. In this paper we will examine the bounding numbers
![]() $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
and
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
and
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
for various triples of ideals
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
for various triples of ideals
![]() $(\mathcal {I},\mathcal {J},\mathcal {K})$
.
$(\mathcal {I},\mathcal {J},\mathcal {K})$
.
Proposition 3.4. Let
![]() $\mathcal {I},\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {I},\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1)
 $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
.
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
. -
(2)
 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}})) \leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
.
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}})) \leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
. -
(3)
 $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}})) \leq \operatorname {\mathrm {cf}}(\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
.
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}})) \leq \operatorname {\mathrm {cf}}(\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
. -
(4) If
 $\mathcal {J}\subseteq \mathcal {K}$
, then
$\mathcal {J}\subseteq \mathcal {K}$
, then
 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
and
 $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
are regular cardinals.
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
are regular cardinals.
Proof. (1) Obvious.
(2) Let
![]() $\mathcal {F}\subset \mathcal {D}_{\mathcal {K}}$
be an
$\mathcal {F}\subset \mathcal {D}_{\mathcal {K}}$
be an
![]() $\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})$
-unbounded family of cardinality
$\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})$
-unbounded family of cardinality
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
and
![]() $\mathcal {F} = \bigcup _{\alpha <\operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))}\mathcal {F}_\alpha $
with
$\mathcal {F} = \bigcup _{\alpha <\operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))}\mathcal {F}_\alpha $
with
![]() $|\mathcal {F}_\alpha |<\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
for every
$|\mathcal {F}_\alpha |<\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
for every
![]() $\alpha $
.
$\alpha $
.
For every
![]() $\alpha $
we find
$\alpha $
we find
![]() $g_\alpha \in \mathcal {D}_{\mathcal {J}}$
with
$g_\alpha \in \mathcal {D}_{\mathcal {J}}$
with
![]() $f\geq _{\mathcal {I}} g_\alpha $
for every
$f\geq _{\mathcal {I}} g_\alpha $
for every
![]() $f\in \mathcal {F}_\alpha $
. Let
$f\in \mathcal {F}_\alpha $
. Let
![]() $\mathcal {G}=\{g_\alpha :\alpha <\operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\}$
.
$\mathcal {G}=\{g_\alpha :\alpha <\operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\}$
.
Suppose to the contrary that
![]() $\operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))<\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))$
.
$\operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))<\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))$
.
Since
![]() $\mathcal {G}\subseteq \mathcal {D}_{\mathcal {J}}$
and
$\mathcal {G}\subseteq \mathcal {D}_{\mathcal {J}}$
and
![]() $|\mathcal {G}|\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))<\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}})$
, there is
$|\mathcal {G}|\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))<\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}})$
, there is
![]() $g\in \mathcal {D}_{\mathcal {J}}$
with
$g\in \mathcal {D}_{\mathcal {J}}$
with
![]() $g_\alpha \geq _{\mathcal {I}} g$
for every
$g_\alpha \geq _{\mathcal {I}} g$
for every
![]() $\alpha $
. Consequently,
$\alpha $
. Consequently,
![]() $f\geq _{\mathcal {I}} g$
for every
$f\geq _{\mathcal {I}} g$
for every
![]() $f\in \mathcal {F}$
, a contradiction.
$f\in \mathcal {F}$
, a contradiction.
(3) This can be proved in a similar way as item 2.
(4) If
![]() $\mathcal {J}\subseteq \mathcal {K}$
, then
$\mathcal {J}\subseteq \mathcal {K}$
, then
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))$
and
![]() $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))$
. Now using (2) and (3), we get
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))$
. Now using (2) and (3), we get
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
and
![]() $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
.⊣
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}}\times \mathcal {D}_{\mathcal {J}}))\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})))$
.⊣
3.4 The bounding numbers à la Staniszewski
Definition 3.5. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
. By
$\omega $
. By
![]() $ \widehat {\mathcal {P}}_{\mathcal {I}}$
we will denote the family of all sequences
$ \widehat {\mathcal {P}}_{\mathcal {I}}$
we will denote the family of all sequences
![]() $\langle A_n : n\in \omega \rangle $
such that
$\langle A_n : n\in \omega \rangle $
such that
![]() $A_n\in \mathcal {I}$
for all
$A_n\in \mathcal {I}$
for all
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $A_n\cap A_k=\emptyset $
for
$A_n\cap A_k=\emptyset $
for
![]() $n\neq k$
. By
$n\neq k$
. By
![]() $ \mathcal {P}_{\mathcal {I}}$
we will denote the family of all sequences
$ \mathcal {P}_{\mathcal {I}}$
we will denote the family of all sequences
![]() $\langle A_n : n\in \omega \rangle $
such that
$\langle A_n : n\in \omega \rangle $
such that
![]() $\langle A_n : n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathcal {I}}$
and
$\langle A_n : n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathcal {I}}$
and
![]() $\bigcup \{A_n: n\in \omega \} = \omega $
.
$\bigcup \{A_n: n\in \omega \} = \omega $
.
Definition 3.6. For ideals
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathcal {J}$
and
$\mathcal {J}$
and
![]() $\mathcal {K}$
on
$\mathcal {K}$
on
![]() $\omega $
we define
$\omega $
we define
 $$ \begin{align*} \begin{aligned} \mathfrak{b}(\mathcal{I},\mathcal{J},\mathcal{K}) & = \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\widehat{\mathcal{P}}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}}\, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{n\in\omega}\left(A_n\cap \bigcup_{i\leq n}E_i\right)\notin\mathcal{I}\right\},\\ \mathfrak{b}_s(\mathcal{I},\mathcal{J},\mathcal{K}) & = \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\widehat{\mathcal{P}}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}}\, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{n\in\omega}\left(A_{n+1}\cap \bigcup_{i\leq n}E_i\right)\notin\mathcal{I}\right\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathfrak{b}(\mathcal{I},\mathcal{J},\mathcal{K}) & = \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\widehat{\mathcal{P}}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}}\, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{n\in\omega}\left(A_n\cap \bigcup_{i\leq n}E_i\right)\notin\mathcal{I}\right\},\\ \mathfrak{b}_s(\mathcal{I},\mathcal{J},\mathcal{K}) & = \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\widehat{\mathcal{P}}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}}\, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{n\in\omega}\left(A_{n+1}\cap \bigcup_{i\leq n}E_i\right)\notin\mathcal{I}\right\}. \end{aligned} \end{align*} $$
Remark. A topological space X is a QN-space if it does not distinguish pointwise and quasi-normal convergence of sequences of real-valued continuous functions defined on X. QN-spaces were introduced by Bukovský et al. in [Reference Calbrix9], and were thoroughly examined in papers [Reference Bukovský5, Reference Bukovský, Das and Šupina6, Reference Bukovský, RecŁaw and Repický8, Reference Calbrix9, Reference Repický30, Reference Šottová and Šupina33, Reference Staniszewski34, Reference Vojtáš39]. The research on ideal-QN-spaces was initiated by Das and Chandra in [Reference Das and Chandra14] and has been continued in [Reference Bukovský and Haleš7, Reference Kwela22, Reference Staniszewski34, Reference Talagrand36].
In [Reference Calbrix9], the authors proved that the smallest size of non-QN-space is equal to the bounding number
![]() $\mathfrak {b}$
. The cardinal numbers
$\mathfrak {b}$
. The cardinal numbers
![]() $\mathfrak {b}(\mathcal {I},J,K)$
and
$\mathfrak {b}(\mathcal {I},J,K)$
and
![]() $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
were introduced by Filipów and Staniszewski [Reference Filipów and Staniszewski18, Reference Šupina35] to characterize the smallest size of a space which is not ideal-QN. Recently, Repický [Reference Repický31, Reference Sakai32] thoroughly examined ideal-QN spaces and, among others, characterized the smallest size of non-ideal-QN-spaces in terms of the cardinal
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
were introduced by Filipów and Staniszewski [Reference Filipów and Staniszewski18, Reference Šupina35] to characterize the smallest size of a space which is not ideal-QN. Recently, Repický [Reference Repický31, Reference Sakai32] thoroughly examined ideal-QN spaces and, among others, characterized the smallest size of non-ideal-QN-spaces in terms of the cardinal
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
. Taking into account Theorem 3.10, we see that both Repický and Staniszewski obtained the same conclusion but coming from different directions.
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
. Taking into account Theorem 3.10, we see that both Repický and Staniszewski obtained the same conclusion but coming from different directions.
In [Reference Talagrand36], Šupina introduced the cardinal
![]() $\kappa (\mathcal {I},\mathcal {J})$
which is equal to
$\kappa (\mathcal {I},\mathcal {J})$
which is equal to
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {I})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {I})$
.
Proposition 3.7. Let
![]() $\mathcal {I}, \mathcal {J}$
and
$\mathcal {I}, \mathcal {J}$
and
![]() $\mathcal {K}$
be ideals on
$\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1)
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
. -
(2) If
 $\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
, then
$\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) = \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) = \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
. -
(3)
 $\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}) = \mathfrak {b}_s(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}) =\mathfrak {b}$
.
$\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}) = \mathfrak {b}_s(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}) =\mathfrak {b}$
.
Proof. (1) Obvious.
(2) It is enough to show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
.
Let
![]() $\mathcal {E}\subseteq \widehat {\mathcal {P}}_{\mathcal {K}}$
be such that for every
$\mathcal {E}\subseteq \widehat {\mathcal {P}}_{\mathcal {K}}$
be such that for every
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
For every
![]() $E = \langle E_n\rangle \in \mathcal {E}$
we define
$E = \langle E_n\rangle \in \mathcal {E}$
we define
![]() $F^E_0=E_0\cup E_1$
and
$F^E_0=E_0\cup E_1$
and
![]() $F^E_n=E_{n+1}$
for
$F^E_n=E_{n+1}$
for
![]() $n\geq 1$
. Then
$n\geq 1$
. Then
![]() $\mathcal {F}=\{\langle F^E_n\rangle :E\in \mathcal {E}\}\subseteq \widehat {\mathcal {P}}_{\mathcal {K}}$
and
$\mathcal {F}=\{\langle F^E_n\rangle :E\in \mathcal {E}\}\subseteq \widehat {\mathcal {P}}_{\mathcal {K}}$
and
![]() $|\mathcal {F}|\leq |\mathcal {E}|$
.
$|\mathcal {F}|\leq |\mathcal {E}|$
.
Let
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $B = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$B = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Since
![]() $A_0\cap E_0\in \mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
and
$A_0\cap E_0\in \mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
and
![]() $ \bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}F^E_i) = (\bigcup _{n\in \omega }(A_{n}\cap \bigcup _{i\leq n}E_i))\setminus (A_0\cap E_0) = B\setminus (A_0\cap E_0)$
, we get
$ \bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}F^E_i) = (\bigcup _{n\in \omega }(A_{n}\cap \bigcup _{i\leq n}E_i))\setminus (A_0\cap E_0) = B\setminus (A_0\cap E_0)$
, we get
![]() $\bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}F^E_i) \notin \mathcal {I}$
, and the proof is finished.
$\bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}F^E_i) \notin \mathcal {I}$
, and the proof is finished.
(3) It was proved in [Reference Filipów and Staniszewski18, Reference Šupina35].⊣
Proposition 3.8. Let
![]() $\mathcal {I},\mathcal {I}',\mathcal {J},\mathcal {J}',\mathcal {K},\mathcal {K}'$
be ideals on
$\mathcal {I},\mathcal {I}',\mathcal {J},\mathcal {J}',\mathcal {K},\mathcal {K}'$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\mathcal {I}\subseteq \mathcal {I}'$
, then
$\mathcal {I}\subseteq \mathcal {I}'$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}(\mathcal {I}',\mathcal {J},\mathcal {K})$
and
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}(\mathcal {I}',\mathcal {J},\mathcal {K})$
and
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I}',\mathcal {J},\mathcal {K})$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I}',\mathcal {J},\mathcal {K})$
. -
(2) If
 $\mathcal {J}\subseteq \mathcal {J}'$
, then
$\mathcal {J}\subseteq \mathcal {J}'$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}(\mathcal {I},\mathcal {J}',\mathcal {K})$
and
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}(\mathcal {I},\mathcal {J}',\mathcal {K})$
and
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I},\mathcal {J}',\mathcal {K})$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I},\mathcal {J}',\mathcal {K})$
. -
(3) If
 $\mathcal {K}\subseteq \mathcal {K}'$
, then
$\mathcal {K}\subseteq \mathcal {K}'$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}')$
and
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}')$
and
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K}')$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K}')$
.
Proof. Straightforward.⊣
In the sequel we will often use the following equivalent forms of
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
without any reference.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
without any reference.
Proposition 3.9. Let
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathcal {J}$
and
$\mathcal {J}$
and
![]() $\mathcal {K}$
be ideals on
$\mathcal {K}$
be ideals on
![]() $\omega $
. Then
$\omega $
. Then
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) = \mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_3(\mathcal {I},\mathcal {J},\mathcal {K})$
, where
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) = \mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_3(\mathcal {I},\mathcal {J},\mathcal {K})$
, where
 $$ \begin{align*} \begin{aligned} \mathfrak{b}_1(\mathcal{I},\mathcal{J},\mathcal{K}) =& \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\mathcal{P}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}}\, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{n\in\omega}\left(A_n\cap \bigcup_{i\leq n}E_i\right)\notin\mathcal{I}\right\},\\ \mathfrak{b}_2(\mathcal{I},\mathcal{J},\mathcal{K}) = & \min \left\{|\mathcal{G}|:\mathcal{G}\subseteq\mathcal{K}^{\omega} \land \forall_{\langle A_n\rangle \in\mathcal{P}_{\mathcal{J}}} \, \exists_{\langle G_n\rangle \in\mathcal{G}} \, \bigcup_{n\in\omega}\left(A_n\cap G_n\right)\notin\mathcal{I}\right\}, \\ \mathfrak{b}_3(\mathcal{I},\mathcal{J},\mathcal{K}) = & \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\widehat{\mathcal{P}}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}} \, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{k\in\omega}\left(E_k\setminus \bigcup_{n<k}A_n\right)\notin\mathcal{I}\right\}. \\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathfrak{b}_1(\mathcal{I},\mathcal{J},\mathcal{K}) =& \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\mathcal{P}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}}\, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{n\in\omega}\left(A_n\cap \bigcup_{i\leq n}E_i\right)\notin\mathcal{I}\right\},\\ \mathfrak{b}_2(\mathcal{I},\mathcal{J},\mathcal{K}) = & \min \left\{|\mathcal{G}|:\mathcal{G}\subseteq\mathcal{K}^{\omega} \land \forall_{\langle A_n\rangle \in\mathcal{P}_{\mathcal{J}}} \, \exists_{\langle G_n\rangle \in\mathcal{G}} \, \bigcup_{n\in\omega}\left(A_n\cap G_n\right)\notin\mathcal{I}\right\}, \\ \mathfrak{b}_3(\mathcal{I},\mathcal{J},\mathcal{K}) = & \min \left\{|\mathcal{E}|:\mathcal{E}\subseteq\widehat{\mathcal{P}}_{\mathcal{K}} \land \forall_{\langle A_n\rangle\in\mathcal{P}_{\mathcal{J}}} \, \exists_{\langle E_n\rangle\in\mathcal{E}} \, \bigcup_{k\in\omega}\left(E_k\setminus \bigcup_{n<k}A_n\right)\notin\mathcal{I}\right\}. \\ \end{aligned} \end{align*} $$
Proof. First we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})$
. Since
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})$
. Since
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})$
is obvious, we only show
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})$
is obvious, we only show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
![]() $\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
be such that for every
$\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
be such that for every
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
. For every
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
. For every
![]() $E=\langle E_n\rangle \in \mathcal {E}$
we define
$E=\langle E_n\rangle \in \mathcal {E}$
we define
![]() $F^E_n = E_n\cup \{e_n\}$
, where
$F^E_n = E_n\cup \{e_n\}$
, where
![]() $e_1,e_2,\dots $
is an enumeration of
$e_1,e_2,\dots $
is an enumeration of
![]() $B=\omega \setminus \bigcup _{n\in \omega } E_n$
(if B is finite, we put
$B=\omega \setminus \bigcup _{n\in \omega } E_n$
(if B is finite, we put
![]() $F^E_n = E_n$
for
$F^E_n = E_n$
for
![]() $n>|B|$
). Let
$n>|B|$
). Let
![]() $\mathcal {F}=\{\langle F^E_n\rangle :E\in \mathcal {E}\}$
, and notice that
$\mathcal {F}=\{\langle F^E_n\rangle :E\in \mathcal {E}\}$
, and notice that
![]() $\mathcal {F}\subseteq \mathcal {P}_{\mathcal {K}}$
and
$\mathcal {F}\subseteq \mathcal {P}_{\mathcal {K}}$
and
![]() $|\mathcal {F}|\leq |\mathcal {E}|$
. Let
$|\mathcal {F}|\leq |\mathcal {E}|$
. Let
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. There is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. There is
![]() $E=\langle E_n\rangle \in \mathcal {E}$
with
$E=\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
. Then
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
. Then
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i) \subseteq \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}F^E_i)$
, so
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i) \subseteq \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}F^E_i)$
, so
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}F^E_i)\notin \mathcal {I}$
. Thus
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}F^E_i)\notin \mathcal {I}$
. Thus
![]() $\mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
.
$\mathfrak {b}_1(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
.
Now we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
![]() $\mathcal {G}\subset \mathcal {K}^{\omega }$
such that for every
$\mathcal {G}\subset \mathcal {K}^{\omega }$
such that for every
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\langle G_n\rangle \in \mathcal {G}$
with
$\langle G_n\rangle \in \mathcal {G}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap G_n)\notin \mathcal {I}$
. For every
$\bigcup _{n\in \omega }(A_n\cap G_n)\notin \mathcal {I}$
. For every
![]() $G=\langle G_n\rangle \in \mathcal {G}$
we define
$G=\langle G_n\rangle \in \mathcal {G}$
we define
![]() $E^G_0=G_0$
and
$E^G_0=G_0$
and
![]() $E^G_{n}=G_n\setminus \bigcup _{i<n}G_i$
for
$E^G_{n}=G_n\setminus \bigcup _{i<n}G_i$
for
![]() $n\geq 1$
. Let
$n\geq 1$
. Let
![]() $\mathcal {E} = \{\langle E^G_n\rangle : G\in \mathcal {G}\}$
, and notice that
$\mathcal {E} = \{\langle E^G_n\rangle : G\in \mathcal {G}\}$
, and notice that
![]() $\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
and
$\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
and
![]() $|\mathcal {E}|\leq |\mathcal {G}|$
. Let
$|\mathcal {E}|\leq |\mathcal {G}|$
. Let
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then there is
![]() $G=\langle G_n\rangle \in \mathcal {G}$
with
$G=\langle G_n\rangle \in \mathcal {G}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap G_n)\notin \mathcal {I}$
. But
$\bigcup _{n\in \omega }(A_n\cap G_n)\notin \mathcal {I}$
. But
![]() $\bigcup _{n\in \omega }(A_n\cap G_n)= \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n} E^G_i)$
, so
$\bigcup _{n\in \omega }(A_n\cap G_n)= \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n} E^G_i)$
, so
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq |\mathcal {G}|$
and the proof of this case is finished.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq |\mathcal {G}|$
and the proof of this case is finished.
Now we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\geq \mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
![]() $\mathcal {E}\subset \widehat {\mathcal {P}_{\mathcal {K}}}$
such that for every
$\mathcal {E}\subset \widehat {\mathcal {P}_{\mathcal {K}}}$
such that for every
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
. For every
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
. For every
![]() $E=\langle E_n\rangle \in \mathcal {E}$
we define
$E=\langle E_n\rangle \in \mathcal {E}$
we define
![]() $G^E_{n}=\bigcup _{i\leq n}E_i$
for
$G^E_{n}=\bigcup _{i\leq n}E_i$
for
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\mathcal {G}= \{\langle G^E_n\rangle : E\in \mathcal {E}\}$
, and notice that
$\mathcal {G}= \{\langle G^E_n\rangle : E\in \mathcal {E}\}$
, and notice that
![]() $\mathcal {G}\subseteq \mathcal {K}^{\omega }$
and
$\mathcal {G}\subseteq \mathcal {K}^{\omega }$
and
![]() $|\mathcal {G}|\leq |\mathcal {E}|$
. Let
$|\mathcal {G}|\leq |\mathcal {E}|$
. Let
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then there is
![]() $E=\langle E_n\rangle \in \mathcal {E}$
with
$E=\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n} E_i)\notin \mathcal {I}$
. But
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n} E_i)\notin \mathcal {I}$
. But
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n} E_i) = \bigcup _{n\in \omega }(A_n\cap G_n)$
, so
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n} E_i) = \bigcup _{n\in \omega }(A_n\cap G_n)$
, so
![]() $\mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})\leq |\mathcal {E}|$
and the proof of this case is finished.
$\mathfrak {b}_2(\mathcal {I},\mathcal {J},\mathcal {K})\leq |\mathcal {E}|$
and the proof of this case is finished.
Finally, we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_3(\mathcal {I},\mathcal {J},\mathcal {K})$
. Actually, it suffices to observe (using the fact that
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {b}_3(\mathcal {I},\mathcal {J},\mathcal {K})$
. Actually, it suffices to observe (using the fact that
![]() $\langle A_n\rangle $
is a partition of
$\langle A_n\rangle $
is a partition of
![]() $\omega $
) that
$\omega $
) that
 $$ \begin{align*} \begin{aligned} x\in\bigcup_{n\in\omega}\left(A_n\cap \bigcup_{i\leq n}E_i\right) &\iff (\exists n\in\omega)(\exists k\leq n)(x\in A_n \land x\in E_k)\\[-3pt] & \iff (\exists k\in\omega)(\exists n\geq k)(x\in E_k \land x\in A_n)\\[-3pt] &\iff (\exists k\in\omega)(\forall n<k)(x\in E_k \land x\notin A_n)\\[-3pt] &\iff x\in\bigcup_{k\in\omega}\left(E_k\setminus \bigcup_{n<k}A_n\right).\\[-2pc] \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} x\in\bigcup_{n\in\omega}\left(A_n\cap \bigcup_{i\leq n}E_i\right) &\iff (\exists n\in\omega)(\exists k\leq n)(x\in A_n \land x\in E_k)\\[-3pt] & \iff (\exists k\in\omega)(\exists n\geq k)(x\in E_k \land x\in A_n)\\[-3pt] &\iff (\exists k\in\omega)(\forall n<k)(x\in E_k \land x\notin A_n)\\[-3pt] &\iff x\in\bigcup_{k\in\omega}\left(E_k\setminus \bigcup_{n<k}A_n\right).\\[-2pc] \end{aligned} \end{align*} $$
⊣
3.5 Staniszewski and Canjar bounding numbers are the same
Theorem 3.10. Let
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathcal {J}$
and
$\mathcal {J}$
and
![]() $\mathcal {K}$
be ideals on
$\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1)
 $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))=\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}).$
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))=\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}).$
-
(2)
 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) = \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K}).$
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) = \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K}).$
Proof. (1) First we show
![]() $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\leq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\leq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
![]() $\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
be such that for every
$\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
be such that for every
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
For every
![]() $E=\langle E_n\rangle \in \mathcal {E}$
let
$E=\langle E_n\rangle \in \mathcal {E}$
let
![]() $f_E\in \omega ^{\omega }$
be such that
$f_E\in \omega ^{\omega }$
be such that
![]() $f_E^{-1}[\{n\}] = E_n$
for every
$f_E^{-1}[\{n\}] = E_n$
for every
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\mathcal {F} = \{f_E:E\in \mathcal {E}\}$
. Then
$\mathcal {F} = \{f_E:E\in \mathcal {E}\}$
. Then
![]() $\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
and
$\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
and
![]() $|\mathcal {F}|=|\mathcal {E}|$
.
$|\mathcal {F}|=|\mathcal {E}|$
.
Let
![]() $g\in \mathcal {D}_{\mathcal {J}}$
and
$g\in \mathcal {D}_{\mathcal {J}}$
and
![]() $A_n=g^{-1}[\{n\}]$
for every
$A_n=g^{-1}[\{n\}]$
for every
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
, there is
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
, there is
![]() $E=\langle E_n\rangle \in \mathcal {E}$
with
$E=\langle E_n\rangle \in \mathcal {E}$
with
![]() $B = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$B = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Once we show
![]() $B \subseteq \{k\in \omega : f_E(k)\leq g(k)\}$
, the proof will be finished in this case. Let
$B \subseteq \{k\in \omega : f_E(k)\leq g(k)\}$
, the proof will be finished in this case. Let
![]() $k\in B$
. Then
$k\in B$
. Then
![]() $k\in A_n\cap E_i$
for some
$k\in A_n\cap E_i$
for some
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $i\leq n$
. Hence
$i\leq n$
. Hence
![]() $g(k) = n \geq i = f_E(k)$
.
$g(k) = n \geq i = f_E(k)$
.
Now we show
![]() $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\geq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) $
. Let
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))\geq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) $
. Let
![]() $\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
be such that there is no
$\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
be such that there is no
![]() $g\in \mathcal {D}_{\mathcal {J}}$
such that for all
$g\in \mathcal {D}_{\mathcal {J}}$
such that for all
![]() $f\in \mathcal {F}$
we have
$f\in \mathcal {F}$
we have
![]() $f>_{\mathcal {I}} g$
.
$f>_{\mathcal {I}} g$
.
For every
![]() $f\in \mathcal {F}$
and
$f\in \mathcal {F}$
and
![]() $n\in \omega $
we define
$n\in \omega $
we define
![]() $E^f_n = f^{-1}[\{n\}]$
, and we notice that
$E^f_n = f^{-1}[\{n\}]$
, and we notice that
![]() $\mathcal {E}=\{ \langle E^f_n\rangle : f\in \mathcal {F}\}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
and
$\mathcal {E}=\{ \langle E^f_n\rangle : f\in \mathcal {F}\}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
and
![]() $|\mathcal {E}|=|\mathcal {F}|$
.
$|\mathcal {E}|=|\mathcal {F}|$
.
Let
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
and
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
and
![]() $g\in \omega ^{\omega }$
be such that
$g\in \omega ^{\omega }$
be such that
![]() $g^{-1}[\{n\}] = A_n$
. Since
$g^{-1}[\{n\}] = A_n$
. Since
![]() $g\in \mathcal {D}_{\mathcal {J}}$
, there is
$g\in \mathcal {D}_{\mathcal {J}}$
, there is
![]() $f\in \mathcal {F}$
with
$f\in \mathcal {F}$
with
![]() $\neg (f>_{\mathcal {I}} g)$
. Thus,
$\neg (f>_{\mathcal {I}} g)$
. Thus,
![]() $B = \{k\in \omega : f(k)\leq g(k)\}\notin \mathcal {I}$
.
$B = \{k\in \omega : f(k)\leq g(k)\}\notin \mathcal {I}$
.
Once we show
![]() $B \subseteq \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E^f_i)$
, the proof will be finished in this case.
$B \subseteq \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E^f_i)$
, the proof will be finished in this case.
Let
![]() $k\in B$
. Since
$k\in B$
. Since
![]() $k\in A_{g(k)}\cap E^f_{f(k)}$
and
$k\in A_{g(k)}\cap E^f_{f(k)}$
and
![]() $f(k)\leq g(k)$
,
$f(k)\leq g(k)$
,
![]() $k\in A_{g(k)}\cap \bigcup _{i\leq g(k)}E^f_i$
.
$k\in A_{g(k)}\cap \bigcup _{i\leq g(k)}E^f_i$
.
(2) First we show
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \leq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
![]() $\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
be such that for every
$\mathcal {E}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
be such that for every
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$\bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
For every
![]() $E=\langle E_n\rangle \in \mathcal {E}$
let
$E=\langle E_n\rangle \in \mathcal {E}$
let
![]() $f_E\in \omega ^{\omega }$
be such that
$f_E\in \omega ^{\omega }$
be such that
![]() $f_E^{-1}[\{n\}] = E_n$
for every
$f_E^{-1}[\{n\}] = E_n$
for every
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\mathcal {F} = \{f_E:E\in \mathcal {E}\}$
. Then
$\mathcal {F} = \{f_E:E\in \mathcal {E}\}$
. Then
![]() $\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
and
$\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
and
![]() $|\mathcal {F}|=|\mathcal {E}|$
.
$|\mathcal {F}|=|\mathcal {E}|$
.
Let
![]() $g\in \mathcal {D}_{\mathcal {J}}$
and
$g\in \mathcal {D}_{\mathcal {J}}$
and
![]() $A_n=g^{-1}[\{n\}]$
for every
$A_n=g^{-1}[\{n\}]$
for every
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
, there is
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
, there is
![]() $E=\langle E_n\rangle \in \mathcal {E}$
with
$E=\langle E_n\rangle \in \mathcal {E}$
with
![]() $B = \bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$B = \bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Once we show
![]() $B \subseteq \{k\in \omega : f_E(k)<g(k)\}$
, the proof will be finished in this case. Let
$B \subseteq \{k\in \omega : f_E(k)<g(k)\}$
, the proof will be finished in this case. Let
![]() $k\in B$
. Then
$k\in B$
. Then
![]() $k\in A_{n+1}\cap E_i$
for some
$k\in A_{n+1}\cap E_i$
for some
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $i\leq n$
. Hence
$i\leq n$
. Hence
![]() $g(k) = n+1\geq i+1>i = f_E(k)$
.
$g(k) = n+1\geq i+1>i = f_E(k)$
.
Now we show
![]() $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \geq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}})) \geq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
. Let
![]() $\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
be such that for every
$\mathcal {F}\subseteq \mathcal {D}_{\mathcal {K}}$
be such that for every
![]() $g\in \mathcal {D}_{\mathcal {J}}$
there is
$g\in \mathcal {D}_{\mathcal {J}}$
there is
![]() $f\in \mathcal {F}$
with
$f\in \mathcal {F}$
with
![]() $\neg (f\geq _I g)$
. For every
$\neg (f\geq _I g)$
. For every
![]() $f\in \mathcal {F}$
and
$f\in \mathcal {F}$
and
![]() $n\in \omega $
we define
$n\in \omega $
we define
![]() $E^f_n=f^{-1}[\{n\}]$
, and we notice that
$E^f_n=f^{-1}[\{n\}]$
, and we notice that
![]() $\mathcal {E}=\{\langle E^f_n\rangle :f\in \mathcal {F}\}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
and
$\mathcal {E}=\{\langle E^f_n\rangle :f\in \mathcal {F}\}\subseteq \widehat {\mathcal {P}_{\mathcal {K}}}$
and
![]() $|\mathcal {E}|\leq |\mathcal {F}|$
.
$|\mathcal {E}|\leq |\mathcal {F}|$
.
Take any
![]() $\langle A_k\rangle \in \mathcal {P}_{\mathcal {J}}$
and define
$\langle A_k\rangle \in \mathcal {P}_{\mathcal {J}}$
and define
![]() $g\in \omega ^{\omega }$
by
$g\in \omega ^{\omega }$
by
![]() $g(n)=k$
for every
$g(n)=k$
for every
![]() $n\in A_k$
,
$n\in A_k$
,
![]() $k\in \omega $
. Since
$k\in \omega $
. Since
![]() $g\in \mathcal {D}_{\mathcal {J}}$
, there is
$g\in \mathcal {D}_{\mathcal {J}}$
, there is
![]() $f\in \mathcal {F}$
with
$f\in \mathcal {F}$
with
![]() $B = \{n\in \omega :f(n)<g(n)\}\notin \mathcal {I}$
. Once we show that
$B = \{n\in \omega :f(n)<g(n)\}\notin \mathcal {I}$
. Once we show that
![]() $B\subseteq \bigcup _{k\in \omega }(A_{k+1}\cap \bigcup _{i\leq k}E^f_i)$
, the proof will be finished in this case.
$B\subseteq \bigcup _{k\in \omega }(A_{k+1}\cap \bigcup _{i\leq k}E^f_i)$
, the proof will be finished in this case.
Let
![]() $n\in \omega $
be such that
$n\in \omega $
be such that
![]() $f(n)<g(n)$
and let
$f(n)<g(n)$
and let
![]() $k\in \omega $
be such that
$k\in \omega $
be such that
![]() $n\in A_k$
. Notice that
$n\in A_k$
. Notice that
![]() $k\geq 1$
. (Indeed, if
$k\geq 1$
. (Indeed, if
![]() $k=0$
then
$k=0$
then
![]() $n\in A_0$
, so
$n\in A_0$
, so
![]() $g(n)=0$
, and consequently
$g(n)=0$
, and consequently
![]() $f(n)<0$
, a contradiction.) Since
$f(n)<0$
, a contradiction.) Since
![]() $f(n)<g(n)=k$
,
$f(n)<g(n)=k$
,
![]() $n\in \bigcup _{i<k}E^f_i$
. Let
$n\in \bigcup _{i<k}E^f_i$
. Let
![]() $l=k-1$
. Then
$l=k-1$
. Then
![]() $n\in A_{l+1}\cap \bigcup _{i\leq l}E^f_i$
.⊣
$n\in A_{l+1}\cap \bigcup _{i\leq l}E^f_i$
.⊣
Corollary 3.11. Let
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathcal {J}$
and
$\mathcal {J}$
and
![]() $\mathcal {K}$
be ideals on
$\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
, then
$\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
, then
 $\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))= \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
.
$\mathfrak {b}(>_{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))= \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {K}}\times \mathcal {D}_{\mathcal {J}}))$
. -
(2)
 $\mathfrak {b}(\geq _{\mathrm {Fin}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) = \mathfrak {b}(>_{\mathrm {Fin}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) = \mathfrak {b}$
.
$\mathfrak {b}(\geq _{\mathrm {Fin}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) = \mathfrak {b}(>_{\mathrm {Fin}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) = \mathfrak {b}$
.
Corollary 3.12. Let
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathcal {J}$
and
$\mathcal {J}$
and
![]() $\mathcal {K}$
be ideals on
$\mathcal {K}$
be ideals on
![]() $\omega $
. If
$\omega $
. If
![]() $\mathcal {J}\subseteq \mathcal {K}$
, then
$\mathcal {J}\subseteq \mathcal {K}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
and
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
and
![]() $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
are regular cardinals.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
are regular cardinals.
3.6 Extreme cases
Proposition 3.13. Let
![]() $\mathcal {I},\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {I},\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1)
 $1\leq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {c}^+$
.
$1\leq \mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {c}^+$
. -
(2) If
 $\mathcal {K}\not \subseteq \mathcal {I}$
, then
$\mathcal {K}\not \subseteq \mathcal {I}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=1$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=1$
. -
(3) If
 $\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
and
$\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
and
 $\mathcal {K}\not \subseteq \mathcal {I}$
, then
$\mathcal {K}\not \subseteq \mathcal {I}$
, then
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})=1$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})=1$
. -
(4) If
 $\mathcal {K}\subseteq \mathcal {J}$
, then
$\mathcal {K}\subseteq \mathcal {J}$
, then
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K}) \geq \aleph _0$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K}) \geq \aleph _0$
. -
(5) If
 $\mathcal {J}\subseteq \mathcal {K}$
and
$\mathcal {J}\subseteq \mathcal {K}$
and
 $\mathcal {I}\not \perp \mathcal {J}$
, then
$\mathcal {I}\not \perp \mathcal {J}$
, then
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {c}$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {c}$
. -
(6) If
 $\mathcal {J}\subseteq \mathcal {K}$
, then
$\mathcal {J}\subseteq \mathcal {K}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {c}$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq \mathfrak {c}$
. -
(7) If
 $\mathcal {I}\perp \mathcal {J}$
, then
$\mathcal {I}\perp \mathcal {J}$
, then
 $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {c}^+$
.
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {c}^+$
. -
(8) If
 $\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
and
$\mathcal {J}\cap \mathcal {K}\subseteq \mathcal {I}$
and
 $\mathcal {I}\perp \mathcal {J}$
, then
$\mathcal {I}\perp \mathcal {J}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {c}^+$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {c}^+$
.
Proof. (1) Obvious.
(2) By (1) it is enough to show that
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq 1$
. Let
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq 1$
. Let
![]() $E\in \mathcal {K}\setminus \mathcal {I}$
and
$E\in \mathcal {K}\setminus \mathcal {I}$
and
![]() $\mathcal {E} = \{\langle E,\emptyset ,\emptyset ,\dots \rangle \}$
. Since
$\mathcal {E} = \{\langle E,\emptyset ,\emptyset ,\dots \rangle \}$
. Since
![]() $E\in \mathcal {K}$
,
$E\in \mathcal {K}$
,
![]() $\mathcal {E}\in \widehat {\mathcal {P}_{\mathcal {K}}}$
. Let
$\mathcal {E}\in \widehat {\mathcal {P}_{\mathcal {K}}}$
. Let
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {J}}$
. Then
![]() $ \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i) = \bigcup _{n\in \omega }(A_n\cap E) = (\bigcup _{n\in \omega }A_n)\cap E = \omega \cap E=E\notin \mathcal {I}$
. Consequently,
$ \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i) = \bigcup _{n\in \omega }(A_n\cap E) = (\bigcup _{n\in \omega }A_n)\cap E = \omega \cap E=E\notin \mathcal {I}$
. Consequently,
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq |\mathcal {E}|=1$
.
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})\leq |\mathcal {E}|=1$
.
(3) Follows from (2) and Proposition 3.7(2).
(4) It follows from [Reference Šupina35, Theorem 4.9(5)].
(5) It follows from [Reference Šupina35, Theorem 4.9(2)].
(6) If
![]() $\mathcal {I}\not \perp \mathcal {J}$
, it follows from (5). If
$\mathcal {I}\not \perp \mathcal {J}$
, it follows from (5). If
![]() $\mathcal {I}\perp \mathcal {J}$
, then
$\mathcal {I}\perp \mathcal {J}$
, then
![]() $\mathcal {K}\not \subseteq \mathcal {I}$
in this case, so (2) finishes the proof.
$\mathcal {K}\not \subseteq \mathcal {I}$
in this case, so (2) finishes the proof.
(7) It follows from [Reference Šupina35, Theorem 4.9(1)].
Example 3.14. Let
![]() $\mathcal {I}=\{A\subseteq \omega : A\cap \{2n:n\in \omega \}\in \mathrm {Fin}\}$
and
$\mathcal {I}=\{A\subseteq \omega : A\cap \{2n:n\in \omega \}\in \mathrm {Fin}\}$
and
![]() $\mathcal {J}=\mathcal {K}=\{A\subseteq \omega : A\cap \{2n+1:n\in \omega \}\in \mathrm {Fin}\}$
. Then by Proposition 3.13 we have
$\mathcal {J}=\mathcal {K}=\{A\subseteq \omega : A\cap \{2n+1:n\in \omega \}\in \mathrm {Fin}\}$
. Then by Proposition 3.13 we have
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) =1$
and
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K}) =1$
and
![]() $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {c}^+ .$
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})=\mathfrak {c}^+ .$
4 Basic relationships between the bounding numbers
In the rest of the paper we examine the cardinals
![]() $\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
and
$\mathfrak {b}(\mathcal {I},\mathcal {J},\mathcal {K})$
and
![]() $\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
only in the case when
$\mathfrak {b}_s(\mathcal {I},\mathcal {J},\mathcal {K})$
only in the case when
![]() $|\{\mathcal {I},\mathcal {J},\mathcal {K}\}\setminus \{\mathrm {Fin}\}|\leq 1$
i.e., a priori one could consider cardinals for 8 triples:
$|\{\mathcal {I},\mathcal {J},\mathcal {K}\}\setminus \{\mathrm {Fin}\}|\leq 1$
i.e., a priori one could consider cardinals for 8 triples:
![]() $(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})$
,
$(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})$
,
![]() $(\mathrm {Fin},\mathrm {Fin},\,\mathcal {I})$
,
$(\mathrm {Fin},\mathrm {Fin},\,\mathcal {I})$
,
![]() $(\mathrm {Fin},\,\mathcal {I},\mathrm {Fin})$
,
$(\mathrm {Fin},\,\mathcal {I},\mathrm {Fin})$
,
![]() $(\mathrm {Fin},\,\mathcal {I},\,\mathcal {I})$
,
$(\mathrm {Fin},\,\mathcal {I},\,\mathcal {I})$
,
![]() $(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
,
$(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
,
![]() $(\mathcal {I},\mathrm {Fin},\,\mathcal {I})$
,
$(\mathcal {I},\mathrm {Fin},\,\mathcal {I})$
,
![]() $(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
,
$(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
,
![]() $(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
. However, it will follow from Corollary 4.1 and Theorem 4.2 that in fact we can restrict our study to four nontrivial cases:
$(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
. However, it will follow from Corollary 4.1 and Theorem 4.2 that in fact we can restrict our study to four nontrivial cases:
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
,
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
,
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
,
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
,
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
and
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
and
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\,\mathcal {I})$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\,\mathcal {I})$
.
In the second part of this section we present diagrams which summarize most results proved in the first part.
4.1 Basic properties and relationships
Corollary 4.1.
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})=\mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
for any triple
$\mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})=\mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
for any triple
![]() $(\mathcal {I},\,\mathcal {J},\,\mathcal {K}) \in \{(\mathrm {Fin},\mathrm {Fin}, \mathrm {Fin}),$
$(\mathcal {I},\,\mathcal {J},\,\mathcal {K}) \in \{(\mathrm {Fin},\mathrm {Fin}, \mathrm {Fin}),$
![]() $(\mathrm {Fin},\mathrm {Fin},\mathcal {I}),$
$(\mathrm {Fin},\mathrm {Fin},\mathcal {I}),$
![]() $(\mathrm {Fin},\mathcal {I},\mathrm {Fin}),$
$(\mathrm {Fin},\mathcal {I},\mathrm {Fin}),$
![]() $(\mathcal {I},\mathrm {Fin},\mathrm {Fin}),$
$(\mathcal {I},\mathrm {Fin},\mathrm {Fin}),$
![]() $(\mathcal {I},\mathrm {Fin},\,\mathcal {I}),$
$(\mathcal {I},\mathrm {Fin},\,\mathcal {I}),$
![]() $(\mathcal {I},\,\mathcal {I},\mathrm {Fin}),$
$(\mathcal {I},\,\mathcal {I},\mathrm {Fin}),$
![]() $(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\}$
.
$(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\}$
.
Theorem 4.2. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
such that
$\omega $
such that
![]() $\mathcal {I}\neq \mathrm {Fin}$
.
$\mathcal {I}\neq \mathrm {Fin}$
.
-
(1)
 $\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathcal {I})=\mathfrak {b}(\mathrm {Fin},\mathcal {I},\,\mathcal {I})=1$
.
$\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathcal {I})=\mathfrak {b}(\mathrm {Fin},\mathcal {I},\,\mathcal {I})=1$
. -
(2)
 $\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
.
$\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
. -
(3)
-
(a) If
 $\mathcal {I}$
is not a P-ideal,
$\mathcal {I}$
is not a P-ideal,
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\,\mathcal {I})=1$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\,\mathcal {I})=1$
. -
(b) If
 $\mathcal {I}$
is a P-ideal,
$\mathcal {I}$
is a P-ideal,
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\,\mathcal {I})=\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\,\mathcal {I})=\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
.
-
-
(4)
-
(a) If
 $\mathcal {I}$
is not a weak P-ideal,
$\mathcal {I}$
is not a weak P-ideal,
 $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})=\mathfrak {c}^+$
.
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})=\mathfrak {c}^+$
. -
(b) If
 $\mathcal {I}$
is a weak P-ideal,
$\mathcal {I}$
is a weak P-ideal,
 $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})\leq \mathfrak {d}$
.
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})\leq \mathfrak {d}$
.
-
-
(5)
 $\aleph _1\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I}) \leq \mathfrak {c}$
.
$\aleph _1\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I}) \leq \mathfrak {c}$
. -
(6)
 $\mathfrak {b}\leq \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) \leq \mathfrak {d}$
.
$\mathfrak {b}\leq \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) \leq \mathfrak {d}$
. -
(7)
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
. -
(8)
 $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
and
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
and
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
are regular.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
are regular. -
(9)
 $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I}) \leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathrm {Fin}))\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I}) \leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathrm {Fin}))\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
Proof. (1) It follows from Proposition 3.13(2).
(2) It follows from [Reference Filipów and Staniszewski18, Proposition 4.5].
(3a) It follows from [Reference Filipów and Staniszewski18, Proposition 4.1].
(3b) It follows from [Reference Filipów and Staniszewski18, Corollary 4.4].
(4a) It follows from [Reference Šupina35, Theorem 4.9(1)]
(4b) It follows from [Reference Kwela22, Corollary 2.10].
(5) It follows from [Reference Filipów and Staniszewski18, Proposition 4.1].
(6) By (2) and Proposition 3.8 we have
![]() $\mathfrak {b}=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
. Now we show
$\mathfrak {b}=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
. Now we show
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {d}$
. Let
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {d}$
. Let
![]() $\mathcal {F}\subset \omega ^{\omega }$
be a dominating family in
$\mathcal {F}\subset \omega ^{\omega }$
be a dominating family in
![]() $(\omega ^{\omega },\leq ^*)$
. Without loss of generality we can assume that every
$(\omega ^{\omega },\leq ^*)$
. Without loss of generality we can assume that every
![]() $f\in \mathcal {F}$
is increasing. We define
$f\in \mathcal {F}$
is increasing. We define
![]() $E^f_n = [f(n-1), f(n))\cap \omega $
for every
$E^f_n = [f(n-1), f(n))\cap \omega $
for every
![]() $f\in \mathcal {F}$
,
$f\in \mathcal {F}$
,
![]() $n\in \omega $
(here we put
$n\in \omega $
(here we put
![]() $f(-1) = 0$
).
$f(-1) = 0$
).
Notice that
![]() $\langle E^f_n:n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathrm {Fin}}$
for every
$\langle E^f_n:n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathrm {Fin}}$
for every
![]() $f\in \mathcal {F}$
. Let
$f\in \mathcal {F}$
. Let
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}}$
. Let
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}}$
. Let
![]() $g\in \omega ^{\omega }$
be given by
$g\in \omega ^{\omega }$
be given by
![]() $g(n) = \max (\bigcup _{i\leq n} A_i)$
. Note that if
$g(n) = \max (\bigcup _{i\leq n} A_i)$
. Note that if
![]() $g(n)<f(n)$
, then
$g(n)<f(n)$
, then
![]() $A_n \subseteq \bigcup _{i\leq n} A_i \subseteq [0,f(n)) = \bigcup _{i\leq n}E^f_i$
.
$A_n \subseteq \bigcup _{i\leq n} A_i \subseteq [0,f(n)) = \bigcup _{i\leq n}E^f_i$
.
Since
![]() $\mathcal {F}$
is dominating, there is
$\mathcal {F}$
is dominating, there is
![]() $f\in \mathcal {F}$
with
$f\in \mathcal {F}$
with
![]() $g<^* f$
. Let
$g<^* f$
. Let
![]() $N\in \omega $
be such that
$N\in \omega $
be such that
![]() $g(n)<f(n)$
for all
$g(n)<f(n)$
for all
![]() $n\geq N$
.
$n\geq N$
.
Then
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E^f_i) \supseteq \bigcup _{n\geq N}(A_n\cap \bigcup _{i\leq n}E^f_i) = \bigcup _{n\geq N}(\bigcup _{i\leq n}E^f_i) =\omega \notin \mathcal {I} $
, and the proof is finished.
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E^f_i) \supseteq \bigcup _{n\geq N}(A_n\cap \bigcup _{i\leq n}E^f_i) = \bigcup _{n\geq N}(\bigcup _{i\leq n}E^f_i) =\omega \notin \mathcal {I} $
, and the proof is finished.
(7) It follows from Proposition 3.8.
(8) It follows from Theorem 3.10(1, 2) and Proposition 3.4(4).
(9) The second inequality is obvious and the first inequality follows from Theorem 3.10(1) and Proposition 3.4(2).⊣
Corollary 4.3.
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
and
$\mathfrak {b}(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
and
![]() $\mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
are regular cardinals for any triple
$\mathfrak {b}_s(\mathcal {I},\,\mathcal {J},\,\mathcal {K})$
are regular cardinals for any triple
![]() $(\mathcal {I},\,\mathcal {J},\,\mathcal {K}) \in \{(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}),$
$(\mathcal {I},\,\mathcal {J},\,\mathcal {K}) \in \{(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}),$
![]() $(\mathrm {Fin},\mathrm {Fin},\mathcal {I}),$
$(\mathrm {Fin},\mathrm {Fin},\mathcal {I}),$
![]() $(\mathrm {Fin},\,\mathcal {I},\mathrm {Fin}),$
$(\mathrm {Fin},\,\mathcal {I},\mathrm {Fin}),$
![]() $(\mathrm {Fin},\,\mathcal {I},\,\mathcal {I}),$
$(\mathrm {Fin},\,\mathcal {I},\,\mathcal {I}),$
![]() $(\mathcal {I},\mathrm {Fin},\mathrm {Fin}),$
$(\mathcal {I},\mathrm {Fin},\mathrm {Fin}),$
![]() $(\mathcal {I},\mathrm {Fin},\,\mathcal {I}),$
$(\mathcal {I},\mathrm {Fin},\,\mathcal {I}),$
![]() $(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\}$
.
$(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\}$
.
Proof. By Corollary 4.1 and Theorem 4.2(2),
![]() $\mathfrak {b}(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
, which is a regular cardinal. The remaining cases follow from Corollary 3.12.⊣
$\mathfrak {b}(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
, which is a regular cardinal. The remaining cases follow from Corollary 3.12.⊣
We were not able to show that
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
is regular. However, the next result shows that some values of
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
is regular. However, the next result shows that some values of
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
are prohibited (for instance, this is the case for
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
are prohibited (for instance, this is the case for
![]() $\aleph _\omega $
, as
$\aleph _\omega $
, as
![]() $\operatorname {\mathrm {cf}}(\aleph _\omega )=\omega $
).
$\operatorname {\mathrm {cf}}(\aleph _\omega )=\omega $
).
Corollary 4.4.
![]() $\aleph _1\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))=\operatorname {\mathrm {cf}}(\mathfrak {b}_s(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))$
for any ideal
$\aleph _1\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))=\operatorname {\mathrm {cf}}(\mathfrak {b}_s(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))$
for any ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Proof. By Proposition 3.4(2) and Theorem 3.10 we have
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))$
,
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})\leq \operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))$
,
![]() $\operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))=\operatorname {\mathrm {cf}}(\mathfrak {b}_s(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))$
follows from Corollary 4.1 and
$\operatorname {\mathrm {cf}}(\mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))=\operatorname {\mathrm {cf}}(\mathfrak {b}_s(\mathcal {I},\,\mathcal {I},\mathrm {Fin}))$
follows from Corollary 4.1 and
![]() $\aleph _1\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
follows from Theorem 4.2(5).⊣
$\aleph _1\leq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I})$
follows from Theorem 4.2(5).⊣
As shown in the next result, for P-ideals the situation is much simpler—many considered cardinals coincide.
Theorem 4.5. If
![]() $\mathcal {I}$
is a P-ideal, then
$\mathcal {I}$
is a P-ideal, then
Proof. Taking into account the previous results and the fact that every P-ideal is a weak P-ideal, it is enough to show
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) \geq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
and
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) \geq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
and
![]() $\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I}) \geq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\,\mathcal {I},\,\mathcal {I}) \geq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
First we show
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) \geq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) \geq \mathfrak {b}(\mathcal {I},\,\mathcal {I},\mathrm {Fin})$
.
Let
![]() $\mathcal {E}\in \mathcal {P}_{\mathrm {Fin}}$
be such that for every
$\mathcal {E}\in \mathcal {P}_{\mathrm {Fin}}$
be such that for every
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathrm {Fin}}$
there is
$\langle A_n\rangle \in \mathcal {P}_{\mathrm {Fin}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Let
![]() $\langle B_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. Since
$\langle B_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. Since
![]() $\mathcal {I}$
is a P-ideal, there is
$\mathcal {I}$
is a P-ideal, there is
![]() $B\in \mathcal {I}$
with
$B\in \mathcal {I}$
with
![]() $B_n\setminus B\in \mathrm {Fin}$
for every
$B_n\setminus B\in \mathrm {Fin}$
for every
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $B=\{b_n:n\in \omega \}$
and set
$B=\{b_n:n\in \omega \}$
and set
![]() $A_n = (B_n\setminus B)\cup \{b_n\}$
for every
$A_n = (B_n\setminus B)\cup \{b_n\}$
for every
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathrm {Fin}}$
, so there is
$\langle A_n\rangle \in \mathcal {P}_{\mathrm {Fin}}$
, so there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $C = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$C = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Once we show
![]() $C\setminus B \subseteq \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E_i)$
, the proof of this case will be finished.
$C\setminus B \subseteq \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E_i)$
, the proof of this case will be finished.
Let
![]() $k\in C\setminus B$
. Then there is
$k\in C\setminus B$
. Then there is
![]() $n\in \omega $
with
$n\in \omega $
with
 $k\in [A_n\cap \bigcup _{i\leq n}E_i]\setminus B = [((B_n\setminus B)\cup \{b_n\})\cap \bigcup _{i\leq n}E_i]\setminus B = (B_n\setminus B)\cap \bigcup _{i\leq n}E_i \subseteq B_n\cap \bigcup _{i\leq n}E_i $
.
$k\in [A_n\cap \bigcup _{i\leq n}E_i]\setminus B = [((B_n\setminus B)\cup \{b_n\})\cap \bigcup _{i\leq n}E_i]\setminus B = (B_n\setminus B)\cap \bigcup _{i\leq n}E_i \subseteq B_n\cap \bigcup _{i\leq n}E_i $
.
Now we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}) \geq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}) \geq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
.
Let
![]() $\mathcal {E}\in \mathcal {P}_{\mathcal {I}}$
be such that for every
$\mathcal {E}\in \mathcal {P}_{\mathcal {I}}$
be such that for every
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
there is
![]() $\langle E_n\rangle \in \mathcal {E}$
with
$\langle E_n\rangle \in \mathcal {E}$
with
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Since
![]() $\mathcal {I}$
is a P-ideal, for every
$\mathcal {I}$
is a P-ideal, for every
![]() $E=\langle E_n\rangle \in \mathcal {E}$
there is
$E=\langle E_n\rangle \in \mathcal {E}$
there is
![]() $B_E\in \mathcal {I}$
such that
$B_E\in \mathcal {I}$
such that
![]() $D_n^E = E_n\setminus B_E\in \mathrm {Fin}$
for every
$D_n^E = E_n\setminus B_E\in \mathrm {Fin}$
for every
![]() $n\in \omega $
. Note that
$n\in \omega $
. Note that
![]() $D_n^E\cap D_k^E=\emptyset $
for every
$D_n^E\cap D_k^E=\emptyset $
for every
![]() $E\in \mathcal {E}$
and
$E\in \mathcal {E}$
and
![]() $n\neq k$
.
$n\neq k$
.
Let
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. Then there is
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. Then there is
![]() $E=\langle E_n\rangle \in \mathcal {E}$
with
$E=\langle E_n\rangle \in \mathcal {E}$
with
![]() $C = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
$C = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)\notin \mathcal {I}$
.
Once we show
![]() $C\setminus B_E \subseteq \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}D^E_i)$
, the proof of this case will be finished.
$C\setminus B_E \subseteq \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}D^E_i)$
, the proof of this case will be finished.
Let
![]() $k\in C\setminus B_E$
. Then there is
$k\in C\setminus B_E$
. Then there is
![]() $n\in \omega $
with
$n\in \omega $
with
 $k \in [\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)]\setminus B_E = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}(E_i\setminus B_E)) = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}D_i^E) $
.⊣
$k \in [\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E_i)]\setminus B_E = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}(E_i\setminus B_E)) = \bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}D_i^E) $
.⊣
The rest of this subsection is devoted to
![]() $\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I}, \mathcal {I})$
.
$\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I}, \mathcal {I})$
.
Lemma 4.6. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\mathcal {I}$
is not a P-ideal, then
$\mathcal {I}$
is not a P-ideal, then
 $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
. -
(2) If
 $\mathcal {I}$
is a P-ideal, then
$\mathcal {I}$
is a P-ideal, then
 $\aleph _1\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}$
.
$\aleph _1\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}$
.
Proof. (1) By Theorem 3.13(4),
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\geq \aleph _0$
. The revers inequality follows from [Reference Šupina35, Theorem 4.9(3)].
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\geq \aleph _0$
. The revers inequality follows from [Reference Šupina35, Theorem 4.9(3)].
(2) The first inequality follows from [Reference Šupina35, Theorem 4.9(4)], whereas the second one follows from Theorem 4.2(2) and the observation that
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
.⊣
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
.⊣
Lemma 4.7.
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {I})$
for any ideal
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {I})$
for any ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Proof. If
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\mathfrak {c}^+$
, we are done. Assume that
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\mathfrak {c}^+$
, we are done. Assume that
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\leq \mathfrak {c}$
. Then there is a family
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\leq \mathfrak {c}$
. Then there is a family
![]() $\mathcal {F}=\{F_\alpha :\alpha <\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}\subseteq \mathcal {I}$
such that for every
$\mathcal {F}=\{F_\alpha :\alpha <\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}\subseteq \mathcal {I}$
such that for every
![]() $A\in \mathcal {I}$
there is
$A\in \mathcal {I}$
there is
![]() $\alpha $
with
$\alpha $
with
![]() $|F_\alpha \setminus A|=\aleph _0$
. For every
$|F_\alpha \setminus A|=\aleph _0$
. For every
![]() $\alpha $
, we define
$\alpha $
, we define
![]() $E^{\alpha }_0=F_\alpha $
and
$E^{\alpha }_0=F_\alpha $
and
![]() $E^{\alpha }_n=\emptyset $
for
$E^{\alpha }_n=\emptyset $
for
![]() $n\geq 1$
. Then
$n\geq 1$
. Then
![]() $\langle E^{\alpha }_n:n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathcal {I}}$
.
$\langle E^{\alpha }_n:n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathcal {I}}$
.
Take any
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. If we show that
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. If we show that
![]() $\bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n} E^{\alpha }_i)\notin \mathrm {Fin}$
for some
$\bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n} E^{\alpha }_i)\notin \mathrm {Fin}$
for some
![]() $\alpha $
, the proof will be finished.
$\alpha $
, the proof will be finished.
Since
![]() $A_0\in \mathcal {I}$
, there is
$A_0\in \mathcal {I}$
, there is
![]() $\alpha $
with
$\alpha $
with
![]() $|F_\alpha \setminus A_0|=\aleph _0$
. On the other hand, it is easy to see that
$|F_\alpha \setminus A_0|=\aleph _0$
. On the other hand, it is easy to see that
![]() $F_\alpha \setminus A_0 = E^{\alpha }_0\setminus A_0 \subseteq \bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n} E^{\alpha }_i)$
, so we are done.⊣
$F_\alpha \setminus A_0 = E^{\alpha }_0\setminus A_0 \subseteq \bigcup _{n\in \omega }(A_{n+1}\cap \bigcup _{i\leq n} E^{\alpha }_i)$
, so we are done.⊣
Theorem 4.8.
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
for any ideal
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
for any ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Proof. If
![]() $\mathcal {I}$
is not a P-ideal, then
$\mathcal {I}$
is not a P-ideal, then
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
(by Lemma 4.6(1)) and
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
(by Lemma 4.6(1)) and
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\aleph _0$
. Since
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\aleph _0$
. Since
![]() $\mathfrak {b}>\aleph _0$
, we obtain
$\mathfrak {b}>\aleph _0$
, we obtain
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
.
Assume that
![]() $\mathcal {I}$
is a P-ideal. The inequality “
$\mathcal {I}$
is a P-ideal. The inequality “
![]() $\leq $
” follows from Lemma 4.6(2) and Lemma 4.7. Below we show the inequality “
$\leq $
” follows from Lemma 4.6(2) and Lemma 4.7. Below we show the inequality “
![]() $\geq $
.”
$\geq $
.”
Take
![]() $\kappa <\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
. We will show that
$\kappa <\min \{\mathfrak {b},\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\}$
. We will show that
![]() $\kappa <\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})$
.
$\kappa <\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})$
.
Let
![]() $\langle E^{\alpha }_n:n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathcal {I}}$
for
$\langle E^{\alpha }_n:n\in \omega \rangle \in \widehat {\mathcal {P}}_{\mathcal {I}}$
for
![]() $\alpha <\kappa $
. Since
$\alpha <\kappa $
. Since
![]() $\kappa \cdot \aleph _0 <\operatorname {\mathrm {add} ^{*}}(\mathcal {I})$
, there is
$\kappa \cdot \aleph _0 <\operatorname {\mathrm {add} ^{*}}(\mathcal {I})$
, there is
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $|E^{\alpha }_n\setminus A|<\aleph _0$
for every
$|E^{\alpha }_n\setminus A|<\aleph _0$
for every
![]() $\alpha <\kappa $
and
$\alpha <\kappa $
and
![]() $n\in \omega $
.
$n\in \omega $
.
Let
![]() $B = \omega \setminus A$
. Since
$B = \omega \setminus A$
. Since
![]() $\langle E^{\alpha }_n\cap B\rangle \in \widehat {\mathcal {P}}_{\mathrm {Fin}(B)}$
for every
$\langle E^{\alpha }_n\cap B\rangle \in \widehat {\mathcal {P}}_{\mathrm {Fin}(B)}$
for every
![]() $\alpha <\kappa $
and
$\alpha <\kappa $
and
![]() $\kappa <\mathfrak {b}=\mathfrak {b}(\mathrm {Fin}(B),\mathrm {Fin}(B),\mathrm {Fin}(B))$
, there is
$\kappa <\mathfrak {b}=\mathfrak {b}(\mathrm {Fin}(B),\mathrm {Fin}(B),\mathrm {Fin}(B))$
, there is
![]() $\langle B_n\rangle \in \mathcal {P}_{\mathrm {Fin}(B)}$
such that
$\langle B_n\rangle \in \mathcal {P}_{\mathrm {Fin}(B)}$
such that
 $$ \begin{align*}\bigcup_{n\in \omega}\left(B_{n}\cap \bigcup_{i\leq n} \left(E^{\alpha}_i\cap B\right)\right)\in \mathrm{Fin}(B)\end{align*} $$
$$ \begin{align*}\bigcup_{n\in \omega}\left(B_{n}\cap \bigcup_{i\leq n} \left(E^{\alpha}_i\cap B\right)\right)\in \mathrm{Fin}(B)\end{align*} $$
for every
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Let
![]() $A_0=A$
and
$A_0=A$
and
![]() $A_n=B_{n-1}$
for
$A_n=B_{n-1}$
for
![]() $n\geq 1$
. Then
$n\geq 1$
. Then
![]() $\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
and for every
$\langle A_n\rangle \in \mathcal {P}_{\mathcal {I}}$
and for every
![]() $\alpha <\kappa $
we have
$\alpha <\kappa $
we have
 $$ \begin{align*}\bigcup_{n\in \omega}\left(A_{n+1}\cap \bigcup_{i\leq n} E^{\alpha}_i\right) = \bigcup_{n\in \omega}\left(B_{n}\cap \bigcup_{i\leq n} E^{\alpha}_i\right) = \bigcup_{n\in \omega}\left(B_{n}\cap \bigcup_{i\leq n} (E^{\alpha}_i\cap B)\right)\in \mathrm{Fin}.\end{align*} $$
$$ \begin{align*}\bigcup_{n\in \omega}\left(A_{n+1}\cap \bigcup_{i\leq n} E^{\alpha}_i\right) = \bigcup_{n\in \omega}\left(B_{n}\cap \bigcup_{i\leq n} E^{\alpha}_i\right) = \bigcup_{n\in \omega}\left(B_{n}\cap \bigcup_{i\leq n} (E^{\alpha}_i\cap B)\right)\in \mathrm{Fin}.\end{align*} $$
⊣
4.2 Diagrams
In this subsection we present some diagrams which show inequalities proved above. In all diagrams, “
![]() $A\to B$
” means “
$A\to B$
” means “
![]() $A\leq B$
.” Moreover, to make diagrams fit into the page, we sometimes write “
$A\leq B$
.” Moreover, to make diagrams fit into the page, we sometimes write “
![]() $\mathrm {F}$
” instead of “
$\mathrm {F}$
” instead of “
![]() $\mathrm {Fin}$
.”
$\mathrm {Fin}$
.”

Figure 2 Nontrivial bounding numbers and inequalities valid for arbitrary ideals.

Figure 3 Inequalities valid for weak P-ideals.

Figure 4 Inequalities valid for non weak P-ideals.

Figure 5 Inequalities valid for P-ideals.
5 Sums and products of ideals
In this section we examine the considered cardinals for ideals of the form
![]() $\mathcal {I}\oplus \mathcal {J}$
or
$\mathcal {I}\oplus \mathcal {J}$
or
![]() $\mathcal {I}\otimes \mathcal {J}$
. Additionally, we compute the considered cardinals in the case of not tall ideals.
$\mathcal {I}\otimes \mathcal {J}$
. Additionally, we compute the considered cardinals in the case of not tall ideals.
5.1 Disjoint sums
Theorem 5.1. Let
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
be ideals on
$\mathcal {J}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1)
 $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J}, \mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})=\min \{\mathfrak {b}(\mathcal {I}, \mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
.
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J}, \mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})=\min \{\mathfrak {b}(\mathcal {I}, \mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
. -
(2)
 $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J}, \mathcal {I}\oplus \mathcal {J},\mathrm {Fin})=\min \{\mathfrak {b}(\mathcal {I}, \mathcal {I},\mathrm {Fin}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})\}$
.
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J}, \mathcal {I}\oplus \mathcal {J},\mathrm {Fin})=\min \{\mathfrak {b}(\mathcal {I}, \mathcal {I},\mathrm {Fin}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})\}$
. -
(3)
 $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J}, \mathrm {Fin},\mathrm {Fin})=\min \{\mathfrak {b}(\mathcal {I},\mathrm {Fin}, \mathrm {Fin}),\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})\}$
, and
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J}, \mathrm {Fin},\mathrm {Fin})=\min \{\mathfrak {b}(\mathcal {I},\mathrm {Fin}, \mathrm {Fin}),\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})\}$
, and -
(4)
 $\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})=\min \{\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I},\mathcal {I}),\mathfrak {b}_s(\mathrm {Fin},\mathcal {J},\mathcal {J})\}$
.
$\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})=\min \{\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I},\mathcal {I}),\mathfrak {b}_s(\mathrm {Fin},\mathcal {J},\mathcal {J})\}$
.
Proof. We will only prove the first item. The remaining items can be proved in a similar way.
First we prove that
![]() $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\leq \min \{\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
. We will prove that
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\leq \min \{\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
. We will prove that
![]() $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
(the proof of
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
(the proof of
![]() $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\leq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
goes in a similar way).
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\leq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
goes in a similar way).
There is a family
![]() $\{\langle E^{\alpha }_n:n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}}$
with the property that for every
$\{\langle E^{\alpha }_n:n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}}$
with the property that for every
![]() $\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
there is
$\langle A_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
there is
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
such that
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
such that
![]() $\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\notin \mathcal {I}$
.
$\bigcup _{n\in \omega }(A_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\notin \mathcal {I}$
.
Consider the family
![]() $\{\langle E^{\alpha }_n\times \{0\}: n\in \omega \rangle :\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}\oplus \mathcal {J}}$
. Let
$\{\langle E^{\alpha }_n\times \{0\}: n\in \omega \rangle :\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}\oplus \mathcal {J}}$
. Let
![]() $\langle B_n\oplus C_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}\oplus \mathcal {J}}$
. Since
$\langle B_n\oplus C_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}\oplus \mathcal {J}}$
. Since
![]() $\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
, there is
$\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
, there is
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
such that
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
such that
![]() $C = \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\notin \mathcal {I}$
. Then
$C = \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\notin \mathcal {I}$
. Then
![]() $C\times \{0\}\notin \mathcal {I}\oplus \mathcal {J}$
, and
$C\times \{0\}\notin \mathcal {I}\oplus \mathcal {J}$
, and
![]() $ C \times \{0\}\subseteq \bigcup _{n\in \omega }(B_n\oplus C_n\cap \bigcup _{i\leq n}(E^{\alpha }_i\times \{0\})) $
. That finishes this part of the proof.
$ C \times \{0\}\subseteq \bigcup _{n\in \omega }(B_n\oplus C_n\cap \bigcup _{i\leq n}(E^{\alpha }_i\times \{0\})) $
. That finishes this part of the proof.
Now we prove
![]() $\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\geq \min \{\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
. Let
$\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})\geq \min \{\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
. Let
![]() $\kappa <\min \{\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
and
$\kappa <\min \{\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}),\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})\}$
and
![]() $\{\langle E^{\alpha }_n\oplus F^{\alpha }_n: n\in \omega \rangle : \alpha <\kappa \}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}\oplus \mathcal {J}}$
. Since
$\{\langle E^{\alpha }_n\oplus F^{\alpha }_n: n\in \omega \rangle : \alpha <\kappa \}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}\oplus \mathcal {J}}$
. Since
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
and
$\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
and
![]() $\{\langle E^{\alpha }_n: n\in \omega \rangle :\alpha <\kappa \}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}}$
, there is
$\{\langle E^{\alpha }_n: n\in \omega \rangle :\alpha <\kappa \}\subseteq \widehat {\mathcal {P}}_{\mathcal {I}}$
, there is
![]() $\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
such that
$\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\in \mathcal {I}$
for all
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\in \mathcal {I}$
for all
![]() $\alpha <\kappa $
. Similarly, there is
$\alpha <\kappa $
. Similarly, there is
![]() $\langle C_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
such that
$\langle C_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
such that
![]() $\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}F^{\alpha }_i)\in \mathcal {J}$
for all
$\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}F^{\alpha }_i)\in \mathcal {J}$
for all
![]() $\alpha <\kappa $
. Then
$\alpha <\kappa $
. Then
![]() $\langle B_n\oplus C_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}\oplus \mathcal {J}}$
and
$\langle B_n\oplus C_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}\oplus \mathcal {J}}$
and
![]() $\bigcup _{n\in \omega }((B_n\oplus C_n)\cap \bigcup _{i\leq n}(E^{\alpha }_i\oplus F^{\alpha }_i))\in \mathcal {I}\oplus \mathcal {J}$
for all
$\bigcup _{n\in \omega }((B_n\oplus C_n)\cap \bigcup _{i\leq n}(E^{\alpha }_i\oplus F^{\alpha }_i))\in \mathcal {I}\oplus \mathcal {J}$
for all
![]() $\alpha <\kappa $
. Thus,
$\alpha <\kappa $
. Thus,
![]() $\kappa <\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})$
.⊣
$\kappa <\mathfrak {b}(\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J},\mathcal {I}\oplus \mathcal {J})$
.⊣
5.2 Not tall ideals
Using the results of the previous subsection, we are able to compute the considered cardinals for not tall ideals.
Theorem 5.2. If
![]() $\mathcal {I}$
is not a tall ideal, then
$\mathcal {I}$
is not a tall ideal, then
Proof. By Theorem 4.2,
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
and
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
and
![]() $\mathfrak {b}\leq \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
, so it is enough to show
$\mathfrak {b}\leq \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
, so it is enough to show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}$
.
Let
![]() $A\subseteq \omega $
be infinite such that for every
$A\subseteq \omega $
be infinite such that for every
![]() $B\subseteq A$
,
$B\subseteq A$
,
![]() $B\in \mathcal {I} \iff B\text { is finite}$
. Let
$B\in \mathcal {I} \iff B\text { is finite}$
. Let
![]() $\mathrm {Fin}(A)$
denote the family of all finite subsets of A. Then
$\mathrm {Fin}(A)$
denote the family of all finite subsets of A. Then
![]() $\mathcal {I}=\mathrm {Fin}(A)\oplus (\mathcal {I}\restriction (\omega \setminus A))$
and, by Theorem 5.1(2), we have
$\mathcal {I}=\mathrm {Fin}(A)\oplus (\mathcal {I}\restriction (\omega \setminus A))$
and, by Theorem 5.1(2), we have
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}(\mathrm {Fin}(A),\mathrm {Fin}(A),\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.⊣
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}(\mathrm {Fin}(A),\mathrm {Fin}(A),\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.⊣
Corollary 5.3. If
![]() $\mathcal {I}$
is a not tall P-ideal, then
$\mathcal {I}$
is a not tall P-ideal, then
Example 5.4. If
![]() $\mathcal {I} = \{\emptyset \}\otimes \mathrm {Fin}$
, then
$\mathcal {I} = \{\emptyset \}\otimes \mathrm {Fin}$
, then
Indeed, it is known that
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\mathfrak {b}$
(see e.g., [Reference Hrušák21, p. 43]), so
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\mathfrak {b}$
(see e.g., [Reference Hrušák21, p. 43]), so
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\mathfrak {b}$
. The remaining equalities follows from Corollary 5.3, because
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\mathfrak {b}$
. The remaining equalities follows from Corollary 5.3, because
![]() $\mathcal {I}$
is a P-ideal (see [Reference Farah16, Example 1.2.3(b)]) and it is not tall (indeed, if
$\mathcal {I}$
is a P-ideal (see [Reference Farah16, Example 1.2.3(b)]) and it is not tall (indeed, if
![]() $A=\{0\}\times \omega $
, then for every
$A=\{0\}\times \omega $
, then for every
![]() $B\subseteq A$
,
$B\subseteq A$
,
![]() $B\in \{\emptyset \}\otimes \mathrm {Fin} \iff B \text { is finite}$
).
$B\in \{\emptyset \}\otimes \mathrm {Fin} \iff B \text { is finite}$
).
5.3 Fubini products
In this subsection we compute the considered cardinals for Fubini products of ideals. We state the lemmas in a more general form than needed in this section, because we will apply some of them also in other sections.
5.3.1 The cardinal
 $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})$
.
Theorem 5.5. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
or
$\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
or
 $\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
$\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
 $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
. -
(2) If
 $\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
$\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
 $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
.
Proof.
-
(1) It suffices to observe that
 $\mathcal {J}\otimes \mathcal {K}$
and
$\mathcal {J}\otimes \mathcal {K}$
and
 $\mathcal {J}\otimes \{\emptyset \}$
are not P-ideals.
$\mathcal {J}\otimes \{\emptyset \}$
are not P-ideals. -
(2) First we will show
 $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
.
If
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {K})=\mathfrak {c}^+$
, then
$\operatorname {\mathrm {add} ^{*}}(\mathcal {K})=\mathfrak {c}^+$
, then
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}=\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
by Theorem 4.8. So assume that
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\leq \mathfrak {b}=\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
by Theorem 4.8. So assume that
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {K})\leq \mathfrak {c}$
and let
$\operatorname {\mathrm {add} ^{*}}(\mathcal {K})\leq \mathfrak {c}$
and let
![]() $\mathcal {F}\subseteq \mathcal {K}$
be such that
$\mathcal {F}\subseteq \mathcal {K}$
be such that
![]() $|\mathcal {F}|=\operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
and for any
$|\mathcal {F}|=\operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
and for any
![]() $A\in \mathcal {K}$
there is
$A\in \mathcal {K}$
there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $F\setminus A\notin \mathrm {Fin}$
.
$F\setminus A\notin \mathrm {Fin}$
.
Consider the family
![]() $\left \{\{0\}\times F: F\in \mathcal {F}\right \}\subseteq \mathcal {I}$
. We claim that it witnesses
$\left \{\{0\}\times F: F\in \mathcal {F}\right \}\subseteq \mathcal {I}$
. We claim that it witnesses
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
.
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
.
Fix
![]() $A\in \mathcal {I}$
. Then
$A\in \mathcal {I}$
. Then
![]() $(A)_0\in \mathcal {K}$
, so there is
$(A)_0\in \mathcal {K}$
, so there is
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $|F\setminus (A)_0|=\aleph _0$
. We get
$|F\setminus (A)_0|=\aleph _0$
. We get
![]() $|\{0\}\times F\setminus A|=|F\setminus (A)_0|=\aleph _0$
. Thus
$|\{0\}\times F\setminus A|=|F\setminus (A)_0|=\aleph _0$
. Thus
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
which implies
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
which implies
![]() $\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I},\mathcal {I})\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
by Theorem 4.8.
$\mathfrak {b}_s(\mathrm {Fin}, \mathcal {I},\mathcal {I})\leq \mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
by Theorem 4.8.
Now we show
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\geq \mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})\geq \mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
.
If
![]() $\mathcal {K}$
is not a P-ideal, then
$\mathcal {K}$
is not a P-ideal, then
![]() $\mathcal {I}$
is not a P-ideal as well and we have
$\mathcal {I}$
is not a P-ideal as well and we have
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})=\aleph _0$
. So we can assume that
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})=\aleph _0$
. So we can assume that
![]() $\mathcal {K}$
is a P-ideal.
$\mathcal {K}$
is a P-ideal.
Let
![]() $\kappa <\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
. We will show that
$\kappa <\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})$
. We will show that
![]() $\kappa <\operatorname {\mathrm {add} ^{*}}(\mathcal {I})$
. By Theorem 4.8, it will finish the proof.
$\kappa <\operatorname {\mathrm {add} ^{*}}(\mathcal {I})$
. By Theorem 4.8, it will finish the proof.
Fix
![]() $\left \{A^{\alpha }: \alpha <\kappa \right \}\subseteq \mathcal {I}$
. Then
$\left \{A^{\alpha }: \alpha <\kappa \right \}\subseteq \mathcal {I}$
. Then
![]() $\left \{(A^{\alpha })_n: n\in \omega ,\alpha <\kappa \right \}\subseteq \mathcal {K}$
has cardinality
$\left \{(A^{\alpha })_n: n\in \omega ,\alpha <\kappa \right \}\subseteq \mathcal {K}$
has cardinality
![]() $|\omega \cdot \kappa |<\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
, so there is
$|\omega \cdot \kappa |<\mathfrak {b}_s(\mathrm {Fin},\mathcal {K},\mathcal {K})\leq \operatorname {\mathrm {add} ^{*}}(\mathcal {K})$
, so there is
![]() $A\in \mathcal {K}$
such that
$A\in \mathcal {K}$
such that
![]() $(A^{\alpha })_n\setminus A\in \mathrm {Fin}$
for all
$(A^{\alpha })_n\setminus A\in \mathrm {Fin}$
for all
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Define
![]() $f_\alpha (n)=\max ((A^{\alpha })_n\setminus A)$
for all
$f_\alpha (n)=\max ((A^{\alpha })_n\setminus A)$
for all
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\kappa $
. Since
$\alpha <\kappa $
. Since
![]() $\kappa <\mathfrak {b}_s (\mathrm {Fin},\mathcal {K},\mathcal {K})\leq \mathfrak {b}$
, there is
$\kappa <\mathfrak {b}_s (\mathrm {Fin},\mathcal {K},\mathcal {K})\leq \mathfrak {b}$
, there is
![]() $g\in \omega ^{\omega }$
such that
$g\in \omega ^{\omega }$
such that
![]() $f_\alpha \leq ^* g$
for all
$f_\alpha \leq ^* g$
for all
![]() $\alpha <\kappa $
. Define
$\alpha <\kappa $
. Define
![]() $B\subseteq \omega \times \omega $
by
$B\subseteq \omega \times \omega $
by
![]() $(B)_n=A\cup \{0,1,\ldots ,g(n)\}$
. Observe that
$(B)_n=A\cup \{0,1,\ldots ,g(n)\}$
. Observe that
![]() $B\in \mathcal {I}$
. If we will show that
$B\in \mathcal {I}$
. If we will show that
![]() $A^{\alpha }\setminus B$
is finite for all
$A^{\alpha }\setminus B$
is finite for all
![]() $\alpha <\kappa $
, the proof will be finished.
$\alpha <\kappa $
, the proof will be finished.
Fix
![]() $\alpha <\kappa $
. There is
$\alpha <\kappa $
. There is
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $f_\alpha (n)\leq g(n)$
for all
$f_\alpha (n)\leq g(n)$
for all
![]() $n\geq k$
. Then
$n\geq k$
. Then
![]() $(A^{\alpha }\setminus B)_{n}\subseteq (A^{\alpha })_{n}\setminus A$
is finite for all
$(A^{\alpha }\setminus B)_{n}\subseteq (A^{\alpha })_{n}\setminus A$
is finite for all
![]() $n<k$
and
$n<k$
and
![]() $(A^{\alpha }\setminus B)_{n}=(A^{\alpha })_{n}\setminus (B)_{n}=(A^{\alpha })_{n}\setminus (A\cup \{0,1,\ldots ,g(n)\})=\emptyset $
for all
$(A^{\alpha }\setminus B)_{n}=(A^{\alpha })_{n}\setminus (B)_{n}=(A^{\alpha })_{n}\setminus (A\cup \{0,1,\ldots ,g(n)\})=\emptyset $
for all
![]() $n\geq k$
. Hence
$n\geq k$
. Hence
![]() $A^{\alpha }\setminus B$
is finite.⊣
$A^{\alpha }\setminus B$
is finite.⊣
5.3.2 The cardinal
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
.
The following three lemmas will be useful in our considerations.
Lemma 5.6. Let
![]() $\langle B_n\rangle $
and
$\langle B_n\rangle $
and
![]() $\langle C_n\rangle $
be partitions of
$\langle C_n\rangle $
be partitions of
![]() $\omega $
. If
$\omega $
. If
![]() $C_n\subseteq \bigcup _{m\geq n}B_m$
(i.e.,
$C_n\subseteq \bigcup _{m\geq n}B_m$
(i.e.,
![]() $C_n\cap \bigcup _{m<n}B_m=\emptyset $
) for all
$C_n\cap \bigcup _{m<n}B_m=\emptyset $
) for all
![]() $n\in \omega $
, then
$n\in \omega $
, then
![]() $\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}A_i)\subseteq \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A_i)$
for any
$\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}A_i)\subseteq \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A_i)$
for any
![]() $\langle A_n\rangle $
.
$\langle A_n\rangle $
.
Proof. If
![]() $x\in C_n\cap \bigcup _{i\leq n}A_i$
for some
$x\in C_n\cap \bigcup _{i\leq n}A_i$
for some
![]() $n\in \omega $
, then there is
$n\in \omega $
, then there is
![]() $m\geq n$
with
$m\geq n$
with
![]() $x\in B_m$
and we have
$x\in B_m$
and we have
![]() $x\in B_m\cap \bigcup _{i\leq n}A_i\subseteq B_m\cap \bigcup _{i\leq m}A_i$
.⊣
$x\in B_m\cap \bigcup _{i\leq n}A_i\subseteq B_m\cap \bigcup _{i\leq m}A_i$
.⊣
Lemma 5.7. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
(here we also allow
$\omega $
(here we also allow
![]() $\mathcal {J}=\{\emptyset \}$
) and
$\mathcal {J}=\{\emptyset \}$
) and
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega ^2$
. If
$\omega ^2$
. If
![]() $\mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
, then
$\mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))\leq \mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))\leq \mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
.
Proof. Let
![]() $\{\langle E^{\alpha }_n:n\in \omega \rangle : \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega )}$
witness
$\{\langle E^{\alpha }_n:n\in \omega \rangle : \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega )}$
witness
![]() $\kappa =\mathfrak {b}(\mathcal {K},\mathrm {Fin},\mathrm {Fin})$
.
$\kappa =\mathfrak {b}(\mathcal {K},\mathrm {Fin},\mathrm {Fin})$
.
For each
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\kappa $
define
$\alpha <\kappa $
define
![]() $A^{\alpha }_n=(\{0,\ldots ,n-1\}\times E^{\alpha }_n)\cup (\{n\}\times \bigcup _{i\leq n}E^{\alpha }_i)$
. Then
$A^{\alpha }_n=(\{0,\ldots ,n-1\}\times E^{\alpha }_n)\cup (\{n\}\times \bigcup _{i\leq n}E^{\alpha }_i)$
. Then
![]() $\mathcal {A}=\{\langle A^{\alpha }_n:n\in \omega \rangle : \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
.
$\mathcal {A}=\{\langle A^{\alpha }_n:n\in \omega \rangle : \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
.
We will show that
![]() $\mathcal {A}$
witnesses
$\mathcal {A}$
witnesses
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))\leq \kappa $
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))\leq \kappa $
.
Let
![]() $\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
. Then
$\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
. Then
![]() $\langle (B_n)_i:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}(\omega )}$
for each
$\langle (B_n)_i:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}(\omega )}$
for each
![]() $i\in \omega $
.
$i\in \omega $
.
Now we inductively define
 $$ \begin{align*}C_n=\left(\bigcup_{i\leq n}((B_n)_i\cup (B_i)_n)\right)\setminus\left(\bigcup_{i<n}C_i\right),\end{align*} $$
$$ \begin{align*}C_n=\left(\bigcup_{i\leq n}((B_n)_i\cup (B_i)_n)\right)\setminus\left(\bigcup_{i<n}C_i\right),\end{align*} $$
and observe that
![]() $\langle C_n:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}(\omega )}$
. Therefore, there is
$\langle C_n:n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}(\omega )}$
. Therefore, there is
![]() $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
![]() $\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\notin \mathcal {K}$
.
$\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\notin \mathcal {K}$
.
If we show that
![]() $(\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i))_j\notin \mathcal {K}$
for every
$(\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i))_j\notin \mathcal {K}$
for every
![]() $j\in \omega $
, then
$j\in \omega $
, then
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\notin \mathcal {I}$
, and the proof will be finished.
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\notin \mathcal {I}$
, and the proof will be finished.
Fix
![]() $j\in \omega $
and note that if
$j\in \omega $
and note that if
![]() $n>j$
then
$n>j$
then
![]() $(\bigcup _{i\leq n}A^{\alpha }_i)_j =(\bigcup _{i\leq n}E^{\alpha }_i)_j$
, and
$(\bigcup _{i\leq n}A^{\alpha }_i)_j =(\bigcup _{i\leq n}E^{\alpha }_i)_j$
, and
![]() $(B_n)_j\cap \bigcup _{i\leq n}(E^{\alpha }_i)_j \supseteq C_n\cap \bigcup _{i\leq n}(E^{\alpha }_i)_j$
(the inclusion follows from Lemma 5.6 because
$(B_n)_j\cap \bigcup _{i\leq n}(E^{\alpha }_i)_j \supseteq C_n\cap \bigcup _{i\leq n}(E^{\alpha }_i)_j$
(the inclusion follows from Lemma 5.6 because
![]() $C_n\cap \bigcup _{m<n}(B_m)_j=\emptyset $
). Thus, we have
$C_n\cap \bigcup _{m<n}(B_m)_j=\emptyset $
). Thus, we have
 $$ \begin{align*} &\left(\bigcup_{n\in\omega}\left(B_{n}\cap \bigcup_{i\leq n}A^{\alpha}_{i}\right)\right)_{j} \supseteq\left( \bigcup_{n>j}\left(B_{n}\cap \bigcup_{i\leq n}A^{\alpha}_{i}\right)\right)_{j} = \bigcup_{n>j}\left((B_{n})_{j}\cap \left(\bigcup_{i\leq n}A^{\alpha}_{i}\right)_{j}\right) \\ & \quad = \bigcup_{n>j}\left((B_{n})_{j}\cap \left(\bigcup_{i\leq n}E^{\alpha}_{i}\right)_{j}\right) \supseteq \bigcup_{n>j}\left(C_{n} \cap \left(\bigcup_{i\leq n}E^{\alpha}_{i}\right)_{j} \right)\notin {\mathcal{K}}. \end{align*} $$
$$ \begin{align*} &\left(\bigcup_{n\in\omega}\left(B_{n}\cap \bigcup_{i\leq n}A^{\alpha}_{i}\right)\right)_{j} \supseteq\left( \bigcup_{n>j}\left(B_{n}\cap \bigcup_{i\leq n}A^{\alpha}_{i}\right)\right)_{j} = \bigcup_{n>j}\left((B_{n})_{j}\cap \left(\bigcup_{i\leq n}A^{\alpha}_{i}\right)_{j}\right) \\ & \quad = \bigcup_{n>j}\left((B_{n})_{j}\cap \left(\bigcup_{i\leq n}E^{\alpha}_{i}\right)_{j}\right) \supseteq \bigcup_{n>j}\left(C_{n} \cap \left(\bigcup_{i\leq n}E^{\alpha}_{i}\right)_{j} \right)\notin {\mathcal{K}}. \end{align*} $$
⊣
Lemma 5.8. Let
![]() $\mathcal {K}$
be an ideal on
$\mathcal {K}$
be an ideal on
![]() $\omega $
and
$\omega $
and
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega ^2$
. If
$\omega ^2$
. If
![]() $\{\emptyset \}\otimes \mathcal {K}\subseteq \mathcal {I}$
, then
$\{\emptyset \}\otimes \mathcal {K}\subseteq \mathcal {I}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))\geq \mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))\geq \mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
.
Proof. We will show that
![]() $\kappa <\mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
implies
$\kappa <\mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
implies
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2), \mathrm {Fin}(\omega ^2))$
. Let
$\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin}(\omega ^2), \mathrm {Fin}(\omega ^2))$
. Let
![]() $\kappa <\mathfrak {b}(\mathcal {K},\mathrm {Fin},\mathrm {Fin})$
and
$\kappa <\mathfrak {b}(\mathcal {K},\mathrm {Fin},\mathrm {Fin})$
and
![]() $\{\langle E^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
.
$\{\langle E^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
.
For each
![]() $n,j\in \omega $
and
$n,j\in \omega $
and
![]() $\alpha <\kappa $
define
$\alpha <\kappa $
define
![]() $A^{\alpha ,j}_n= (E^{\alpha }_n)_j$
. Then
$A^{\alpha ,j}_n= (E^{\alpha }_n)_j$
. Then
![]() $\{\langle A^{\alpha ,j}_n:n\in \omega \rangle :j\in \omega , \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega )}$
.
$\{\langle A^{\alpha ,j}_n:n\in \omega \rangle :j\in \omega , \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}(\omega )}$
.
Since
![]() $|\omega \times \kappa |=\kappa <\mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
, there is
$|\omega \times \kappa |=\kappa <\mathfrak {b}(\mathcal {K},\mathrm {Fin}(\omega ),\mathrm {Fin}(\omega ))$
, there is
![]() $\langle B_n\rangle \in \mathcal {P}_{\mathrm {Fin}(\omega )}$
with
$\langle B_n\rangle \in \mathcal {P}_{\mathrm {Fin}(\omega )}$
with
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha ,j}_i)\in \mathcal {K}$
for all
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha ,j}_i)\in \mathcal {K}$
for all
![]() $j\in \omega $
and
$j\in \omega $
and
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Define
![]() $\langle C_n\rangle \in \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
by
$\langle C_n\rangle \in \mathcal {P}_{\mathrm {Fin}(\omega ^2)}$
by
![]() $C_n=(\bigcup _{i<n}\{i\}\times B_n)\cup (\{n\}\times \bigcup _{i\leq n}B_i)$
for all
$C_n=(\bigcup _{i<n}\{i\}\times B_n)\cup (\{n\}\times \bigcup _{i\leq n}B_i)$
for all
![]() $n\in \omega $
.
$n\in \omega $
.
Fix
![]() $\alpha <\kappa $
and denote
$\alpha <\kappa $
and denote
![]() $X=\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}E^{\alpha }_i)$
. If we show that
$X=\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}E^{\alpha }_i)$
. If we show that
![]() $X\in \mathcal {I}$
, the proof will be finished. Since
$X\in \mathcal {I}$
, the proof will be finished. Since
![]() $\{\emptyset \}\otimes \mathcal {K}\subseteq \mathcal {I}$
, it is enough to show that
$\{\emptyset \}\otimes \mathcal {K}\subseteq \mathcal {I}$
, it is enough to show that
![]() $(X)_j\in \mathcal {K}$
for every
$(X)_j\in \mathcal {K}$
for every
![]() $j\in \omega $
.
$j\in \omega $
.
Take
![]() $j\in \omega $
. If
$j\in \omega $
. If
![]() $n>j$
, then
$n>j$
, then
![]() $(C_n)_j=B_n$
, so
$(C_n)_j=B_n$
, so
 $$ \begin{align*}(X)_j= \bigcup_{n\in\omega}\left((C_n)_j\cap \bigcup_{i\leq n}(E^{\alpha}_i)_j\right) \subseteq \left(\bigcup_{n\leq j}B_n\right) \cup \bigcup_{n>j}\left(B_n\cap\bigcup_{i\leq n}A^{\alpha,j}_i\right)\in\mathcal{K}.\end{align*} $$
$$ \begin{align*}(X)_j= \bigcup_{n\in\omega}\left((C_n)_j\cap \bigcup_{i\leq n}(E^{\alpha}_i)_j\right) \subseteq \left(\bigcup_{n\leq j}B_n\right) \cup \bigcup_{n>j}\left(B_n\cap\bigcup_{i\leq n}A^{\alpha,j}_i\right)\in\mathcal{K}.\end{align*} $$
⊣
Theorem 5.9. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\,\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
or
$\,\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
or
 $\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
$\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathcal {K},\mathrm {Fin},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathcal {K},\mathrm {Fin},\mathrm {Fin})$
. -
(2) If
 $\,\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
$\,\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.
Proof. (1) The inequality “
![]() $\leq $
” follows from Lemma 5.7, and “
$\leq $
” follows from Lemma 5.7, and “
![]() $\geq $
” follows from Lemma 5.8. (2) Since
$\geq $
” follows from Lemma 5.8. (2) Since
![]() $\mathcal {I}\subseteq \mathcal {J}\otimes \mathrm {Fin}$
, by Lemma 5.7 we get
$\mathcal {I}\subseteq \mathcal {J}\otimes \mathrm {Fin}$
, by Lemma 5.7 we get
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})$
. By 4.2(2), we have
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})$
. By 4.2(2), we have
![]() $\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
and the inequality “
$\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
and the inequality “
![]() $\geq $
” follows from Theorem 4.2(6).⊣
$\geq $
” follows from Theorem 4.2(6).⊣
The last item of Theorem 5.9 may be surprising:
![]() $\mathfrak {b}(\mathcal {J}\otimes \{\emptyset \},\mathrm {Fin},\mathrm {Fin})$
does not depend on
$\mathfrak {b}(\mathcal {J}\otimes \{\emptyset \},\mathrm {Fin},\mathrm {Fin})$
does not depend on
![]() $\mathcal {J}$
.
$\mathcal {J}$
.
5.3.3 The cardinal
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
We will need three lemmas.
Lemma 5.10. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
(here we allow
$\omega $
(here we allow
![]() $\mathcal {K}=\{\emptyset \}$
) and
$\mathcal {K}=\{\emptyset \}$
) and
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega ^2$
. If
$\omega ^2$
. If
![]() $\mathcal {J}\otimes \{\emptyset \}\subseteq \mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
, then
$\mathcal {J}\otimes \{\emptyset \}\subseteq \mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
.
Proof. We will show that
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
implies
$\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
implies
![]() $\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
. Let
$\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
. Let
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
and
$\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
and
![]() $\{\langle A^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {P}_{\mathcal {J}}$
.
$\{\langle A^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {P}_{\mathcal {J}}$
.
For each
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\kappa $
define
$\alpha <\kappa $
define
![]() $E^{\alpha }_n=A^{\alpha }_n\times \omega $
. Then
$E^{\alpha }_n=A^{\alpha }_n\times \omega $
. Then
![]() $\{\langle E^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {P}_{\mathcal {I}}$
(as
$\{\langle E^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {P}_{\mathcal {I}}$
(as
![]() $\mathcal {J}\otimes \{\emptyset \}\subseteq \mathcal {I}$
).
$\mathcal {J}\otimes \{\emptyset \}\subseteq \mathcal {I}$
).
Since
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
, there is
$\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
, there is
![]() $\langle B_n\rangle \in \mathcal {P}_{\mathcal {I}}$
such that
$\langle B_n\rangle \in \mathcal {P}_{\mathcal {I}}$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\in \mathcal {I}$
for all
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\in \mathcal {I}$
for all
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Define
We will show that
![]() $V\in \mathcal {J}$
. Fix
$V\in \mathcal {J}$
. Fix
![]() $k\in V$
. There is
$k\in V$
. There is
![]() $m\in \omega $
such that
$m\in \omega $
such that
![]() $k\in A^0_m$
. Then
$k\in A^0_m$
. Then
 $$ \begin{align*}\left(\bigcup_{n\in\omega}\left(B_n\cap \bigcup_{i\leq n}E^0_i\right)\right)_k = \left(\bigcup_{n\geq m} B_n\right)_k = \omega\setminus \left(\bigcup_{n<m} B_n\right)_k\notin\mathcal{K}.\end{align*} $$
$$ \begin{align*}\left(\bigcup_{n\in\omega}\left(B_n\cap \bigcup_{i\leq n}E^0_i\right)\right)_k = \left(\bigcup_{n\geq m} B_n\right)_k = \omega\setminus \left(\bigcup_{n<m} B_n\right)_k\notin\mathcal{K}.\end{align*} $$
Since
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^0_i)\in \mathcal {I}$
and
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^0_i)\in \mathcal {I}$
and
![]() $\mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
, we get
$\mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
, we get
 $$ \begin{align*}V\subseteq \left\{k\in\omega: \left(\bigcup_{n\in\omega}\left(B_n\cap \bigcup_{i\leq n}E^0_i\right)\right)_k\notin\mathcal{K}\right\}\in\mathcal{J}.\end{align*} $$
$$ \begin{align*}V\subseteq \left\{k\in\omega: \left(\bigcup_{n\in\omega}\left(B_n\cap \bigcup_{i\leq n}E^0_i\right)\right)_k\notin\mathcal{K}\right\}\in\mathcal{J}.\end{align*} $$
Define
![]() $\langle C_n\rangle \in \mathcal {P}_{\mathcal {J}}$
by
$\langle C_n\rangle \in \mathcal {P}_{\mathcal {J}}$
by
![]() $V\subseteq C_0$
and
$V\subseteq C_0$
and
for
![]() $k\notin V$
(each
$k\notin V$
(each
![]() $C_n$
belongs to
$C_n$
belongs to
![]() $\mathcal {J}$
as
$\mathcal {J}$
as
![]() $\langle B_i\rangle \subseteq \mathcal {I}$
and
$\langle B_i\rangle \subseteq \mathcal {I}$
and
![]() $\mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
).
$\mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
).
Fix
![]() $\alpha <\kappa $
and denote
$\alpha <\kappa $
and denote
![]() $X=\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}A^{\alpha }_i)$
. If we show that
$X=\bigcup _{n\in \omega }(C_n\cap \bigcup _{i\leq n}A^{\alpha }_i)$
. If we show that
![]() $X\in \mathcal {J}$
, the proof will be finished. Suppose to the contrary that
$X\in \mathcal {J}$
, the proof will be finished. Suppose to the contrary that
![]() $X\notin \mathcal {J}$
. Then
$X\notin \mathcal {J}$
. Then
 $$ \begin{align*} \begin{aligned} \mathcal{J}\not\ni X\setminus V & = \left\{k\in\omega:\exists n\in\omega\ k\in C_n \land k\in\bigcup_{i\leq n}A^{\alpha}_i \land (B_n)_k\notin \mathcal{K}\right\}\\ & = \left\{k\in\omega: \exists n\in\omega\ k\in C_n \land \left(\bigcup_{i\leq n}E^{\alpha}_i\right)_k=\omega \land (B_n)_k\notin\mathcal{K}\right\}\\ & \subseteq \left\{k\in\omega:\left(\bigcup_{n\in\omega}\left(B_n\cap \bigcup_{i\leq n}E^{\alpha}_i\right)\right)_k\notin\mathcal{K}\right\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{J}\not\ni X\setminus V & = \left\{k\in\omega:\exists n\in\omega\ k\in C_n \land k\in\bigcup_{i\leq n}A^{\alpha}_i \land (B_n)_k\notin \mathcal{K}\right\}\\ & = \left\{k\in\omega: \exists n\in\omega\ k\in C_n \land \left(\bigcup_{i\leq n}E^{\alpha}_i\right)_k=\omega \land (B_n)_k\notin\mathcal{K}\right\}\\ & \subseteq \left\{k\in\omega:\left(\bigcup_{n\in\omega}\left(B_n\cap \bigcup_{i\leq n}E^{\alpha}_i\right)\right)_k\notin\mathcal{K}\right\}, \end{aligned} \end{align*} $$
which contradicts
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\in \mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
.⊣
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}E^{\alpha }_i)\in \mathcal {I}\subseteq \mathcal {J}\otimes \mathcal {K}$
.⊣
Lemma 5.11. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
(here we allow
$\omega $
(here we allow
![]() $\mathcal {K}=\{\emptyset \}$
). If
$\mathcal {K}=\{\emptyset \}$
). If
![]() $\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
, then
$\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\geq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\geq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
.
Proof. We will show that
![]() $\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
implies
$\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
implies
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
$\kappa <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
Let
![]() $\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
and
$\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
and
![]() $\{\langle E^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {I}^{\omega }$
.
$\{\langle E^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {I}^{\omega }$
.
For each
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\kappa $
define
$\alpha <\kappa $
define
![]() $A^{\alpha }_n=\{i\in \omega :(E^{\alpha }_n)_i\notin \mathcal {K}\}$
. Then
$A^{\alpha }_n=\{i\in \omega :(E^{\alpha }_n)_i\notin \mathcal {K}\}$
. Then
![]() $\{\langle A^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {J}^{\omega }$
.
$\{\langle A^{\alpha }_n:n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathcal {J}^{\omega }$
.
Since
![]() $\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
, there is
$\kappa <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
, there is
![]() $\langle B_n\rangle \in \mathcal {P}_{\mathcal {J}}$
such that
$\langle B_n\rangle \in \mathcal {P}_{\mathcal {J}}$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\in \mathcal {J}$
for all
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\in \mathcal {J}$
for all
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Define
![]() $\langle C_n\rangle \in \mathcal {P}_{\mathcal {I}}$
by
$\langle C_n\rangle \in \mathcal {P}_{\mathcal {I}}$
by
![]() $C_n=B_n\times \omega $
for all
$C_n=B_n\times \omega $
for all
![]() $n\in \omega $
.
$n\in \omega $
.
Fix
![]() $\alpha <\kappa $
and denote
$\alpha <\kappa $
and denote
![]() $X=\bigcup _{n\in \omega }(C_n\cap E^{\alpha }_n)$
. If we show that
$X=\bigcup _{n\in \omega }(C_n\cap E^{\alpha }_n)$
. If we show that
![]() $X\in \mathcal {I}$
, the proof will be finished. Since
$X\in \mathcal {I}$
, the proof will be finished. Since
![]() $\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
, it is enough to show that
$\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
, it is enough to show that
![]() $\{i\in \omega : (X)_i\notin \mathcal {K}\} \subseteq \bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)$
.
$\{i\in \omega : (X)_i\notin \mathcal {K}\} \subseteq \bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)$
.
Take
![]() $i\notin \bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)$
. Since
$i\notin \bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)$
. Since
![]() $\langle B_n\rangle $
is a partition, there is
$\langle B_n\rangle $
is a partition, there is
![]() $n\in \omega $
with
$n\in \omega $
with
![]() $i\in B_n$
. Then
$i\in B_n$
. Then
![]() $i\notin A_n^{\alpha }$
, so
$i\notin A_n^{\alpha }$
, so
![]() $(E_n^{\alpha })_i\in \mathcal {K}$
. Moreover,
$(E_n^{\alpha })_i\in \mathcal {K}$
. Moreover,
![]() $i\in B_n$
implies
$i\in B_n$
implies
![]() $(C_n)_i=\omega $
, so
$(C_n)_i=\omega $
, so
![]() $(X)_i = (B_n\cap E^{\alpha }_n)_i = \omega \cap (E_n^{\alpha })_i\in \mathcal {K}$
.⊣
$(X)_i = (B_n\cap E^{\alpha }_n)_i = \omega \cap (E_n^{\alpha })_i\in \mathcal {K}$
.⊣
Lemma 5.12. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
,
$\omega $
,
![]() $\mathcal {J}'$
be an ideal on
$\mathcal {J}'$
be an ideal on
![]() $\omega ^2$
and denote
$\omega ^2$
and denote
![]() $\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
.
$\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
.
-
(1) If
 $\{\{0\}\times A: A\in \mathcal {J}\}\subseteq \mathcal {J}'$
, then
$\{\{0\}\times A: A\in \mathcal {J}\}\subseteq \mathcal {J}'$
, then
 $\mathfrak {b}(\mathcal {I}, \mathcal {I},\mathcal {J}') \leq \mathfrak {b}(\mathcal {K}, \mathcal {K},\mathcal {J})$
.
$\mathfrak {b}(\mathcal {I}, \mathcal {I},\mathcal {J}') \leq \mathfrak {b}(\mathcal {K}, \mathcal {K},\mathcal {J})$
. -
(2) If
 $\mathcal {J}'\subseteq \{\emptyset \}\otimes \mathcal {J}$
, then
$\mathcal {J}'\subseteq \{\emptyset \}\otimes \mathcal {J}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')\geq \mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')\geq \mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})$
.
Proof. (1) Let
![]() $\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})\}\subseteq \mathcal {J}^{\omega }$
be such that for any
$\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})\}\subseteq \mathcal {J}^{\omega }$
be such that for any
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {K}}$
there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {K}}$
there is
![]() $\alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})$
such that
$\alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {K}$
. Consider the family
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {K}$
. Consider the family
![]() $\{\langle \{0\}\times A^{\alpha }_n : n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})\}\subseteq (\mathcal {J}')^{\omega }$
. Fix any
$\{\langle \{0\}\times A^{\alpha }_n : n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})\}\subseteq (\mathcal {J}')^{\omega }$
. Fix any
![]() $\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
and define
$\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
and define
![]() $B_n=\{i\in \omega : (0,i)\in C_n\}$
for all
$B_n=\{i\in \omega : (0,i)\in C_n\}$
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {K}}$
, so there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {K}}$
, so there is
![]() $\alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})$
such that
$\alpha <\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {J})$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {K}$
. We have
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {K}$
. We have
 $$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap (\{0\}\times A^{\alpha}_n))\supseteq \{0\}\times \left(\,\bigcup_{n\in\omega}(B_n\cap A^{\alpha}_n)\right)\notin\mathcal{I}.\end{align*} $$
$$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap (\{0\}\times A^{\alpha}_n))\supseteq \{0\}\times \left(\,\bigcup_{n\in\omega}(B_n\cap A^{\alpha}_n)\right)\notin\mathcal{I}.\end{align*} $$
(2) Let
![]() $\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')\}\subseteq (\mathcal {J}')^{\omega }$
be such that for any
$\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')\}\subseteq (\mathcal {J}')^{\omega }$
be such that for any
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
there is
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')$
such that
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. For each
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. For each
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')$
and
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')$
and
![]() $n,k\in \omega $
define
$n,k\in \omega $
define
![]() $E^{\alpha ,k}_n=(A^{\alpha }_n)_{k}$
. Consider the family
$E^{\alpha ,k}_n=(A^{\alpha }_n)_{k}$
. Consider the family
![]() $\{\langle E^{\alpha ,k}_n: n\in \omega \rangle : k\in \omega ,\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')\}\subseteq \mathcal {J}^{\omega }$
. Fix any
$\{\langle E^{\alpha ,k}_n: n\in \omega \rangle : k\in \omega ,\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')\}\subseteq \mathcal {J}^{\omega }$
. Fix any
![]() $\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {K}}$
and define
$\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {K}}$
and define
![]() $B_n=\omega \times C_n$
for all
$B_n=\omega \times C_n$
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
, so there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
, so there is
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')$
such that
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {J}')$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. Thus, there is
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. Thus, there is
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $(\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n))_{k}\notin \mathcal {K}$
. We have
$(\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n))_{k}\notin \mathcal {K}$
. We have
 $$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap E^{\alpha,k}_n)\supseteq \left(\,\bigcup_{n\in\omega}(B_n\cap A^{\alpha}_n)\right)_{k}\notin\mathcal{K}.\\[-3.5pc] \end{align*} $$
$$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap E^{\alpha,k}_n)\supseteq \left(\,\bigcup_{n\in\omega}(B_n\cap A^{\alpha}_n)\right)_{k}\notin\mathcal{K}.\\[-3.5pc] \end{align*} $$
⊣
Theorem 5.13. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
or
$\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
or
 $\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
$\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
. -
(2) If
 $\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
$\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {K})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathcal {K},\mathcal {K},\mathcal {K})$
.
5.3.4 The cardinal
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
.
Theorem 5.14. Let
![]() $\mathcal {J},\mathcal {K}$
be ideals on
$\mathcal {J},\mathcal {K}$
be ideals on
![]() $\omega $
.
$\omega $
.
-
(1) If
 $\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
, then
$\mathcal {I}=\mathcal {J}\otimes \mathcal {K}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {c}^+$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {c}^+$
. -
(2) If
 $\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
$\mathcal {I}=\mathcal {J}\otimes \{\emptyset \}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
. -
(3) If
 $\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
$\mathcal {I}=\{\emptyset \}\otimes \mathcal {K}$
, then
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {b}(\mathcal {K},\mathcal {K},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {b}(\mathcal {K},\mathcal {K},\mathrm {Fin})$
.
Proof. (1) Follows from Theorem 4.2(4) since
![]() $\mathcal {J}\otimes \mathcal {K}$
is not a weak P-ideal.
$\mathcal {J}\otimes \mathcal {K}$
is not a weak P-ideal.
(2) First we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
.
Let
![]() $\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})\}\subseteq \mathrm {Fin}^{\omega }$
be such that for any
$\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})\}\subseteq \mathrm {Fin}^{\omega }$
be such that for any
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
there is
![]() $\alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
such that
$\alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {J}$
. Consider the family
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {J}$
. Consider the family
![]() $\{\langle A^{\alpha }_n\times \{0\}: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})\}\subseteq \mathrm {Fin}(\omega ^2)^{\omega }$
. Fix any
$\{\langle A^{\alpha }_n\times \{0\}: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})\}\subseteq \mathrm {Fin}(\omega ^2)^{\omega }$
. Fix any
![]() $\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
and define
$\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
and define
![]() $B_n=\{i\in \omega : (i,0)\in C_n\}$
for all
$B_n=\{i\in \omega : (i,0)\in C_n\}$
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
, so there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
, so there is
![]() $\alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
such that
$\alpha <\mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {J}$
. We have
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {J}$
. We have
 $$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap (A^{\alpha}_n\times \{0\}))\supseteq \left(\bigcup_{n\in\omega}(B_n\cap A^{\alpha}_n)\right)\times\{0\}\notin\mathcal{I}.\end{align*} $$
$$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap (A^{\alpha}_n\times \{0\}))\supseteq \left(\bigcup_{n\in\omega}(B_n\cap A^{\alpha}_n)\right)\times\{0\}\notin\mathcal{I}.\end{align*} $$
Now we show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\geq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\geq \mathfrak {b}(\mathcal {J},\mathcal {J},\mathrm {Fin})$
.
Let
![]() $\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\}\subseteq \mathrm {Fin}(\omega ^2)^{\omega }$
be such that for any
$\{\langle A^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\}\subseteq \mathrm {Fin}(\omega ^2)^{\omega }$
be such that for any
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
there is
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
such that
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. For each
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. For each
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
and
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
and
![]() $n\in \omega $
define
$n\in \omega $
define
![]() $E^{\alpha }_n=\{i\in \omega : (\exists j\in \omega )((i,j)\in A^{\alpha }_n)\}$
. Consider the family
$E^{\alpha }_n=\{i\in \omega : (\exists j\in \omega )((i,j)\in A^{\alpha }_n)\}$
. Consider the family
![]() $\{\langle E^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\}\subseteq \mathrm {Fin}^{\omega }$
. Fix any
$\{\langle E^{\alpha }_n: n\in \omega \rangle : \alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\}\subseteq \mathrm {Fin}^{\omega }$
. Fix any
![]() $\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
and define
$\langle C_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {J}}$
and define
![]() $B_n=C_n\times \omega $
for all
$B_n=C_n\times \omega $
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
, so there is
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
, so there is
![]() $\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
such that
$\alpha <\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. Thus,
$\bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n)\notin \mathcal {I}$
. Thus,
![]() $\{i\in \omega : (\exists j\in \omega )((i,j)\in \bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n))\}\notin \mathcal {J}$
. We have
$\{i\in \omega : (\exists j\in \omega )((i,j)\in \bigcup _{n\in \omega }(B_n\cap A^{\alpha }_n))\}\notin \mathcal {J}$
. We have
 $$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap E^{\alpha}_n)\supseteq \left\{i\in\omega: (\exists j\in\omega)\left((i,j)\in \bigcup_{n\in\omega}\left(B_n\cap A^{\alpha}_n\right)\right)\right\}\notin\mathcal{J}.\end{align*} $$
$$ \begin{align*}\bigcup_{n\in\omega}(C_n\cap E^{\alpha}_n)\supseteq \left\{i\in\omega: (\exists j\in\omega)\left((i,j)\in \bigcup_{n\in\omega}\left(B_n\cap A^{\alpha}_n\right)\right)\right\}\notin\mathcal{J}.\end{align*} $$
Example 5.15. If
![]() $\mathcal {I}=\mathrm {Fin}\otimes \{\emptyset \}$
, then
$\mathcal {I}=\mathrm {Fin}\otimes \{\emptyset \}$
, then
Indeed,
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
by Theorem 5.5(1). Moreover,
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
by Theorem 5.5(1). Moreover,
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
by Theorem 5.9(2), and
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
by Theorem 5.9(2), and
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
by Theorems 5.14(2) and 4.2(2). Hence, it is enough to show
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})=\mathfrak {b}$
by Theorems 5.14(2) and 4.2(2). Hence, it is enough to show
![]() $\mathfrak {b}\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
. But this inequality follows from Theorem 5.13(1).
$\mathfrak {b}\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
. But this inequality follows from Theorem 5.13(1).
6 Nice ideals
In this section we will compute
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
for ideals
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
for ideals
![]() $\mathcal {I}$
with the Baire property and
$\mathcal {I}$
with the Baire property and
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
for coanalytic weak P-ideals. The latter gives an upper bound for
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
for coanalytic weak P-ideals. The latter gives an upper bound for
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
in the case of coanalytic weak P-ideals (by a result of Debs and Saint Raymond, this class contains all
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
in the case of coanalytic weak P-ideals (by a result of Debs and Saint Raymond, this class contains all
![]() $\bf {\Pi ^0_4}$
ideals).
$\bf {\Pi ^0_4}$
ideals).
6.1 Ideals with the Baire property
In this subsection an interval
![]() $[a,b)$
will mean
$[a,b)$
will mean
![]() $[a,b)\cap \omega $
i.e., the set
$[a,b)\cap \omega $
i.e., the set
![]() $\{n\in \omega : a\leq n<b\}$
.
$\{n\in \omega : a\leq n<b\}$
.
Theorem 6.1 (Talagrand [Reference Tsaban and Zdomskyy37, Théorème 21] (see also [Reference Bartoszyński and Judah1, Theorem 4.1.2])).
An ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
has the Baire property if and only if there is an increasing sequence
$\omega $
has the Baire property if and only if there is an increasing sequence
![]() $n_1<n_2<\cdots $
such that if there are infinitely many k with
$n_1<n_2<\cdots $
such that if there are infinitely many k with
![]() $[n_k,n_{k+1})\subseteq A$
, then
$[n_k,n_{k+1})\subseteq A$
, then
![]() $A\notin \mathcal {I}$
.
$A\notin \mathcal {I}$
.
Corollary 6.2. Let
![]() $\mathcal {I}$
be an ideal with the Baire property. For every
$\mathcal {I}$
be an ideal with the Baire property. For every
![]() $g\in \omega ^{\omega }$
there is
$g\in \omega ^{\omega }$
there is
![]() $h\in \omega ^{\omega }$
such that
$h\in \omega ^{\omega }$
such that
-
(1) h is strictly increasing,
-
(2)
 $g\leq h$
,
$g\leq h$
, -
(3) if
 $A\in \mathcal {I}$
, then the set
$A\in \mathcal {I}$
, then the set
 $\{n : [h(n),h(n+1))\subseteq A\}$
is finite.
$\{n : [h(n),h(n+1))\subseteq A\}$
is finite.
Proof. By Theorem 6.1 there is a sequence
![]() $n_0<n_1<\cdots $
such that
$n_0<n_1<\cdots $
such that
![]() $\{k: [n_k,n_{k+1})\subseteq A\}$
is finite for every
$\{k: [n_k,n_{k+1})\subseteq A\}$
is finite for every
![]() $A\in \mathcal {I}$
.
$A\in \mathcal {I}$
.
It is enough to define h such that h is increasing,
![]() $g\leq h$
and
$g\leq h$
and
![]() $[h(n),h(n+1))$
contains at least one interval
$[h(n),h(n+1))$
contains at least one interval
![]() $[n_k,n_{k+1})$
for every
$[n_k,n_{k+1})$
for every
![]() $n\in \omega $
. We can define h inductively in the following manner. Let
$n\in \omega $
. We can define h inductively in the following manner. Let
![]() $h(0)=g(0)$
. Suppose that
$h(0)=g(0)$
. Suppose that
![]() $h(i)$
has been defined for
$h(i)$
has been defined for
![]() $i\leq n$
. Let
$i\leq n$
. Let
![]() $k_0=\min \{k: h(n)\leq n_k\}$
. We put
$k_0=\min \{k: h(n)\leq n_k\}$
. We put
![]() $h(n+1)=\max \{n_{k_0+1},h(n)+1,g(n+1)\}$
.⊣
$h(n+1)=\max \{n_{k_0+1},h(n)+1,g(n+1)\}$
.⊣
Theorem 6.3. If an ideal
![]() $\mathcal {I}$
has the Baire property, then
$\mathcal {I}$
has the Baire property, then
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.
Proof. By Theorem 4.2(6) we only have to show that
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}$
. We will show that
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})\leq \mathfrak {b}$
. We will show that
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
implies
$\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
implies
![]() $\kappa <\mathfrak {b}$
.
$\kappa <\mathfrak {b}$
.
Let
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
and
$\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
and
![]() $g_\alpha \in \omega ^{\omega }$
for
$g_\alpha \in \omega ^{\omega }$
for
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
By Corollary 6.2 we can assume that
![]() $g_\alpha $
are strictly increasing and
$g_\alpha $
are strictly increasing and
for every infinite
![]() $A\subseteq \omega $
and
$A\subseteq \omega $
and
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
For
![]() $\alpha <\kappa $
we define
$\alpha <\kappa $
we define
![]() $A^{\alpha }_0 = [0,g_\alpha (1))$
and
$A^{\alpha }_0 = [0,g_\alpha (1))$
and
![]() $A^{\alpha }_n = [g_\alpha (n),g_\alpha (n+1))$
for
$A^{\alpha }_n = [g_\alpha (n),g_\alpha (n+1))$
for
![]() $n\geq 1$
.
$n\geq 1$
.
Since
![]() $\{\langle A^{\alpha }_n:n\in \omega \rangle : \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}}$
and
$\{\langle A^{\alpha }_n:n\in \omega \rangle : \alpha <\kappa \}\subseteq \mathcal {P}_{\mathrm {Fin}}$
and
![]() $\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
, there is a partition
$\kappa <\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
, there is a partition
![]() $\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}}$
such that
$\langle B_n: n\in \omega \rangle \in \mathcal {P}_{\mathrm {Fin}}$
such that
![]() $\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\in \mathcal {I}$
for every
$\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\in \mathcal {I}$
for every
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
We define
![]() $g\in \omega ^{\omega }$
by
$g\in \omega ^{\omega }$
by
![]() $g(n) = \max (\bigcup _{i\leq n} B_i)$
. If we show that
$g(n) = \max (\bigcup _{i\leq n} B_i)$
. If we show that
![]() $g_\alpha \leq ^* g$
for every
$g_\alpha \leq ^* g$
for every
![]() $\alpha <\kappa $
, the proof will be finished.
$\alpha <\kappa $
, the proof will be finished.
Let
![]() $\alpha <\kappa $
. Since
$\alpha <\kappa $
. Since
![]() $B = \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\in \mathcal {I}$
, the set
$B = \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\in \mathcal {I}$
, the set
![]() $A = \{n: [g_\alpha (n), g_\alpha (n+1))\subseteq B\}$
is finite.
$A = \{n: [g_\alpha (n), g_\alpha (n+1))\subseteq B\}$
is finite.
Now we show that
![]() $g_\alpha (n)\leq g(n)$
for every
$g_\alpha (n)\leq g(n)$
for every
![]() $n\in \omega \setminus A$
(i.e.
$n\in \omega \setminus A$
(i.e.
![]() $g_\alpha \leq ^* g$
). Let
$g_\alpha \leq ^* g$
). Let
![]() $n\in \omega \setminus A$
. Since
$n\in \omega \setminus A$
. Since
![]() $[g_\alpha (n),g_\alpha (n+1))\cap (\omega \setminus B)\neq \emptyset $
, there is
$[g_\alpha (n),g_\alpha (n+1))\cap (\omega \setminus B)\neq \emptyset $
, there is
![]() $m\in [g_\alpha (n),g_\alpha (n+1))\cap (\omega \setminus B)$
. Then
$m\in [g_\alpha (n),g_\alpha (n+1))\cap (\omega \setminus B)$
. Then
![]() $g_\alpha (n)\leq m$
. On the other hand,
$g_\alpha (n)\leq m$
. On the other hand,
![]() $m\notin B = \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)$
and
$m\notin B = \bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)$
and
![]() $m\in [g_\alpha (n), g_\alpha (n+1)) = A^{\alpha }_n$
. Thus
$m\in [g_\alpha (n), g_\alpha (n+1)) = A^{\alpha }_n$
. Thus
![]() $m\notin B_i$
for every
$m\notin B_i$
for every
![]() $i\geq n$
, so
$i\geq n$
, so
![]() $m\in B_i$
for some
$m\in B_i$
for some
![]() $i<n$
. Hence
$i<n$
. Hence
![]() $g(n) = \max (\bigcup _{i\leq n} B_i) \geq m \geq g_\alpha (n)$
.⊣
$g(n) = \max (\bigcup _{i\leq n} B_i) \geq m \geq g_\alpha (n)$
.⊣
Corollary 6.4. If
![]() $\mathcal {I}$
is a P-ideal with the Baire property, then
$\mathcal {I}$
is a P-ideal with the Baire property, then
For
![]() $f:\omega \to [0,\infty )$
satisfying
$f:\omega \to [0,\infty )$
satisfying
![]() $\sum _{n\in \omega }f(n)=\infty $
we define the summable ideal by
$\sum _{n\in \omega }f(n)=\infty $
we define the summable ideal by
 $$ \begin{align*}\mathcal{I}_f=\left\{A\subset\omega:\sum_{n\in A}f(n)<\infty\right\}\end{align*} $$
$$ \begin{align*}\mathcal{I}_f=\left\{A\subset\omega:\sum_{n\in A}f(n)<\infty\right\}\end{align*} $$
(for instance,
![]() $\mathcal {I}_{1/n} = \{A\subseteq \omega : \sum _{n\in A}1/(n+1)<\infty \}$
is the summable ideal), and for
$\mathcal {I}_{1/n} = \{A\subseteq \omega : \sum _{n\in A}1/(n+1)<\infty \}$
is the summable ideal), and for
![]() $f:\omega \to [0,\infty )$
satisfying
$f:\omega \to [0,\infty )$
satisfying
![]() $\sum _{n\in \omega }f(n)=\infty $
and
$\sum _{n\in \omega }f(n)=\infty $
and
![]() $\lim _{n\to \infty }f(n)/(\sum _{i\leq n}f(i))=0$
, we define the Erdoős–Ulam ideals by
$\lim _{n\to \infty }f(n)/(\sum _{i\leq n}f(i))=0$
, we define the Erdoős–Ulam ideals by
 $$ \begin{align*}EU_f=\left\{A\subset\omega: \limsup_{n\to\infty}\frac{\sum_{i\in A\cap n}f(i)}{\sum_{i\in n}f(i)}=0\right\}\end{align*} $$
$$ \begin{align*}EU_f=\left\{A\subset\omega: \limsup_{n\to\infty}\frac{\sum_{i\in A\cap n}f(i)}{\sum_{i\in n}f(i)}=0\right\}\end{align*} $$
(for instance, the ideal
![]() $\mathcal {I}_d = \{A:\lim _n|A\cap n|/n=0\}$
of all sets of asymptotic density zero is an Erdoős-Ulam ideal).
$\mathcal {I}_d = \{A:\lim _n|A\cap n|/n=0\}$
of all sets of asymptotic density zero is an Erdoős-Ulam ideal).
Corollary 6.5. If
![]() $\mathcal {I}$
is a tall summable ideal or a tall Erdoős–Ulam ideal, then
$\mathcal {I}$
is a tall summable ideal or a tall Erdoős–Ulam ideal, then
where
![]() $\operatorname {\mathrm {add}}(\mathcal {N})$
is the smallest size of a family of Lebesgue null sets with non-null union.
$\operatorname {\mathrm {add}}(\mathcal {N})$
is the smallest size of a family of Lebesgue null sets with non-null union.
Proof. It was proved by Hernández and Hrušák [Reference Hernández-Hernández and Hrušák20, Theorem 2.2] that
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\operatorname {\mathrm {add}}(\mathcal {N})$
in these cases. Since
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\operatorname {\mathrm {add}}(\mathcal {N})$
in these cases. Since
![]() $\operatorname {\mathrm {add}}(\mathcal {N})\leq \mathfrak {b}$
(see e.g., [Reference Bartoszyński and Judah1, p. 35]), we get
$\operatorname {\mathrm {add}}(\mathcal {N})\leq \mathfrak {b}$
(see e.g., [Reference Bartoszyński and Judah1, p. 35]), we get
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \operatorname {\mathrm {add}}(\mathcal {N})$
. Moreover, since
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \operatorname {\mathrm {add}}(\mathcal {N})$
. Moreover, since
![]() $\mathcal {I}$
is a P-ideal with the Baire property (see e.g., [Reference Farah16, Examples 1.2.3(c,d)]), Corollary 6.4 finishes the proof.⊣
$\mathcal {I}$
is a P-ideal with the Baire property (see e.g., [Reference Farah16, Examples 1.2.3(c,d)]), Corollary 6.4 finishes the proof.⊣
Corollary 6.6. Let
![]() $n\in \omega \setminus \{0,1\}$
. If
$n\in \omega \setminus \{0,1\}$
. If
![]() $\mathcal {I}=\mathrm {Fin}^n$
, then
$\mathcal {I}=\mathrm {Fin}^n$
, then
Proof. Since
![]() $\mathcal {I}$
in not a P-ideal, we get
$\mathcal {I}$
in not a P-ideal, we get
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \aleph _0$
. Since
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \aleph _0$
. Since
![]() $\mathcal {I}$
has the Baire property (see e.g., [Reference Hrušák21]), we can apply Theorem 6.3 to obtain
$\mathcal {I}$
has the Baire property (see e.g., [Reference Hrušák21]), we can apply Theorem 6.3 to obtain
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) = \mathfrak {b}$
. Since
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin}) = \mathfrak {b}$
. Since
![]() $\mathcal {I} = \mathrm {Fin}^n = \mathrm {Fin}\otimes \mathrm {Fin}^{n-1}$
, we can apply Theorem 5.13(1) to obtain
$\mathcal {I} = \mathrm {Fin}^n = \mathrm {Fin}\otimes \mathrm {Fin}^{n-1}$
, we can apply Theorem 5.13(1) to obtain
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}) = \mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}) = \mathfrak {b}$
. Since
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I}) = \mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin}) = \mathfrak {b}$
. Since
![]() $\mathcal {I}$
is not a weak P-ideal, we can apply Proposition 4.2(4a) to obtain
$\mathcal {I}$
is not a weak P-ideal, we can apply Proposition 4.2(4a) to obtain
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin}) = \mathfrak {c}^+$
.⊣
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin}) = \mathfrak {c}^+$
.⊣
6.2
 $\omega $
-diagonalizable ideals
$\omega $
-diagonalizable ideals
We need to recall the following technical notion. We will apply it in the next subsection to the cases of coanalytic weak P-ideals and
![]() $\bf {\Pi ^0_4}$
ideals.
$\bf {\Pi ^0_4}$
ideals.
Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
. A family
$\omega $
. A family
![]() $\mathcal {Z}\subseteq [\omega ]^{<\omega }\setminus \{\emptyset \}$
is
$\mathcal {Z}\subseteq [\omega ]^{<\omega }\setminus \{\emptyset \}$
is
![]() $\mathcal {I}^*$
-universal if for each
$\mathcal {I}^*$
-universal if for each
![]() $F\in \mathcal {I}^*$
there is
$F\in \mathcal {I}^*$
there is
![]() $Z\in \mathcal {Z}$
with
$Z\in \mathcal {Z}$
with
![]() $Z\subseteq F$
. We say that
$Z\subseteq F$
. We say that
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\omega $
-diagonalizable by
$\omega $
-diagonalizable by
![]() $\mathcal {I}^*$
-universal sets if there exists a family
$\mathcal {I}^*$
-universal sets if there exists a family
![]() $\{\mathcal {Z}_k:k\in \omega \}$
of
$\{\mathcal {Z}_k:k\in \omega \}$
of
![]() $\mathcal {I}^*$
-universal families such that for each
$\mathcal {I}^*$
-universal families such that for each
![]() $F\in \mathcal {I}^*$
there is
$F\in \mathcal {I}^*$
there is
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $Z\cap F\neq \emptyset $
for every
$Z\cap F\neq \emptyset $
for every
![]() $Z\in \mathcal {Z}_k$
.
$Z\in \mathcal {Z}_k$
.
Theorem 6.7. If an ideal
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\omega $
-diagonalizable by
$\omega $
-diagonalizable by
![]() $\mathcal {I}^*$
-universal sets, then
$\mathcal {I}^*$
-universal sets, then
Proof. By Theorem 4.2, we only need to show
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}$
.
Let
![]() $\{f_\alpha :\alpha <\mathfrak {b}\}$
be an unbounded family on
$\{f_\alpha :\alpha <\mathfrak {b}\}$
be an unbounded family on
![]() $\omega ^{\omega }$
. Without loss of generality we can assume that each
$\omega ^{\omega }$
. Without loss of generality we can assume that each
![]() $f_\alpha $
is strictly increasing.
$f_\alpha $
is strictly increasing.
For each
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\mathfrak {b}$
define
$\alpha <\mathfrak {b}$
define
![]() $F^{\alpha }_n=\{i\in \omega :i\leq f_\alpha (n)\}$
. We will show that
$F^{\alpha }_n=\{i\in \omega :i\leq f_\alpha (n)\}$
. We will show that
![]() $\{\langle F^{\alpha }_n:n\in \omega \rangle : \alpha <\mathfrak {b}\}\subseteq \mathrm {Fin}^{\omega }$
witnesses
$\{\langle F^{\alpha }_n:n\in \omega \rangle : \alpha <\mathfrak {b}\}\subseteq \mathrm {Fin}^{\omega }$
witnesses
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \mathfrak {b}$
.
Fix
![]() $\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
. Let
$\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
. Let
![]() $\{\mathcal {Z}_k:k\in \omega \}$
be a family of
$\{\mathcal {Z}_k:k\in \omega \}$
be a family of
![]() $\mathcal {I}^*$
-universal sets
$\mathcal {I}^*$
-universal sets
![]() $\omega $
-diagonalizing
$\omega $
-diagonalizing
![]() $\mathcal {I}$
. For each k, let
$\mathcal {I}$
. For each k, let
![]() $\mathcal {Z}_k=\{Z_k^n:n\in \omega \}$
.
$\mathcal {Z}_k=\{Z_k^n:n\in \omega \}$
.
For each
![]() $k,n\in \omega $
find
$k,n\in \omega $
find
![]() $i(k,n)\in \omega $
such that
$i(k,n)\in \omega $
such that
![]() $Z_k^{i(k,n)}\cap (B_0\cup \cdots \cup B_n)=\emptyset $
and define
$Z_k^{i(k,n)}\cap (B_0\cup \cdots \cup B_n)=\emptyset $
and define
![]() $g_k\in \omega ^{\omega }$
by
$g_k\in \omega ^{\omega }$
by
![]() $g_k(n)=\max Z_k^{i(k,n)}$
. Let
$g_k(n)=\max Z_k^{i(k,n)}$
. Let
![]() $g\in \omega ^{\omega }$
be given by
$g\in \omega ^{\omega }$
be given by
![]() $g(i)=\max \{g_1(i),\ldots ,g_i(i)\}$
.
$g(i)=\max \{g_1(i),\ldots ,g_i(i)\}$
.
There is
![]() $\alpha <\mathfrak {b}$
such that
$\alpha <\mathfrak {b}$
such that
![]() $f_\alpha (i)>g(i)$
for infinitely many i. If we show that for each
$f_\alpha (i)>g(i)$
for infinitely many i. If we show that for each
![]() $k\in \omega $
there is
$k\in \omega $
there is
![]() $i\in \omega $
with
$i\in \omega $
with
![]() $Z_k^i\subseteq \bigcup _{j\in \omega }(B_j\cap F^{\alpha }_j)$
, then, by
$Z_k^i\subseteq \bigcup _{j\in \omega }(B_j\cap F^{\alpha }_j)$
, then, by
![]() $\omega $
-diagonalizability of
$\omega $
-diagonalizability of
![]() $\mathcal {I}$
, it will follow that
$\mathcal {I}$
, it will follow that
![]() $\bigcup _{j\in \omega }(B_j\cap F^{\alpha }_j)\notin \mathcal {I}$
, and the proof will be finished.
$\bigcup _{j\in \omega }(B_j\cap F^{\alpha }_j)\notin \mathcal {I}$
, and the proof will be finished.
Fix
![]() $k\in \omega $
. There is
$k\in \omega $
. There is
![]() $n>k$
such that
$n>k$
such that
![]() $f_\alpha (n)>g(n)\geq g_k(n)=\max Z_k^{i(k,n)}$
. Thus,
$f_\alpha (n)>g(n)\geq g_k(n)=\max Z_k^{i(k,n)}$
. Thus,
![]() $Z_k^{i(k,n)}\subseteq F^{\alpha }_n\subseteq F^{\alpha }_{n+1}\subseteq \cdots $
and
$Z_k^{i(k,n)}\subseteq F^{\alpha }_n\subseteq F^{\alpha }_{n+1}\subseteq \cdots $
and
![]() $Z_k^{i(k,n)}\subseteq B_{n+1}\cup B_{n+2}\cup \cdots $
. Hence,
$Z_k^{i(k,n)}\subseteq B_{n+1}\cup B_{n+2}\cup \cdots $
. Hence,
![]() $Z_k^{i(k,n)}\subseteq \bigcup _{j>n}(B_j\cap F^{\alpha }_j)\subseteq \bigcup _{j\in \omega }(B_j\cap F^{\alpha }_j)$
and we are done.⊣
$Z_k^{i(k,n)}\subseteq \bigcup _{j>n}(B_j\cap F^{\alpha }_j)\subseteq \bigcup _{j\in \omega }(B_j\cap F^{\alpha }_j)$
and we are done.⊣
6.3 Coanalytic weak P-ideals and
 $\bf {\Pi ^0_4}$
ideals
$\bf {\Pi ^0_4}$
ideals
Theorem 6.8. If
![]() $\mathcal {I}$
is a coanalytic weak P-ideal, then
$\mathcal {I}$
is a coanalytic weak P-ideal, then
Proof. Consider the game
![]() $G\left (\mathcal {I}\right )$
, defined by Laflamme (see [Reference Laflamme27]) as follows: Player I in his n’th move plays an element
$G\left (\mathcal {I}\right )$
, defined by Laflamme (see [Reference Laflamme27]) as follows: Player I in his n’th move plays an element
![]() $C_{n}\in \mathcal {I}$
, and then Player II responses with any
$C_{n}\in \mathcal {I}$
, and then Player II responses with any
![]() $F_{n}\in \left [\omega \right ]^{<\omega }$
such that
$F_{n}\in \left [\omega \right ]^{<\omega }$
such that
![]() $F_{n}\cap C_{n}=\emptyset $
. Player I wins if
$F_{n}\cap C_{n}=\emptyset $
. Player I wins if
![]() $\bigcup _{n\in \omega } F_{n}\in \mathcal {I}$
. Otherwise, Player II wins.
$\bigcup _{n\in \omega } F_{n}\in \mathcal {I}$
. Otherwise, Player II wins.
By [Reference Kwela and Staniszewski25, Theorem 5.1],
![]() $G\left (\mathcal {I}\right )$
is determined for coanalytic ideals (see also [Reference Kwela and Sabok24, Theorem 1.6]). Moreover, by [Reference Laflamme27, Theorem 2.16], Player I has a winning strategy in
$G\left (\mathcal {I}\right )$
is determined for coanalytic ideals (see also [Reference Kwela and Sabok24, Theorem 1.6]). Moreover, by [Reference Laflamme27, Theorem 2.16], Player I has a winning strategy in
![]() $G\left (\mathcal {I}\right )$
if and only if
$G\left (\mathcal {I}\right )$
if and only if
![]() $\mathcal {I}$
is not a weak P-ideal. Thus, in our case Player II has a winning strategy. Again by [Reference Laflamme27, Theorem 2.16], this is in turn equivalent to
$\mathcal {I}$
is not a weak P-ideal. Thus, in our case Player II has a winning strategy. Again by [Reference Laflamme27, Theorem 2.16], this is in turn equivalent to
![]() $\mathcal {I}$
being
$\mathcal {I}$
being
![]() $\omega $
-diagonalizable by
$\omega $
-diagonalizable by
![]() $\mathcal {I}^*$
-universal sets. Using Theorem 6.7 we get
$\mathcal {I}^*$
-universal sets. Using Theorem 6.7 we get
![]() $\aleph _1\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b} = \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
and we are done.⊣
$\aleph _1\leq \mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b} = \mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
and we are done.⊣
Corollary 6.9. If
![]() $\mathcal {I}$
is a
$\mathcal {I}$
is a
![]() $\bf {\Pi ^0_4}$
ideal, then
$\bf {\Pi ^0_4}$
ideal, then
Proof. By [Reference Debs and Raymond15, Theorems 7.5 and 9.1], each
![]() $\bf {\Pi ^0_4}$
ideal is a weak P-ideal. Thus, the corollary follows from Theorem 6.8.⊣
$\bf {\Pi ^0_4}$
ideal is a weak P-ideal. Thus, the corollary follows from Theorem 6.8.⊣
Example 6.10. The eventually different ideal is defined by
If
![]() $\mathcal {I} =\mathcal {ED}$
, then
$\mathcal {I} =\mathcal {ED}$
, then
Indeed, since
![]() $\mathcal {I}$
is not a P-ideal,
$\mathcal {I}$
is not a P-ideal,
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
(see Lemma 4.6(1)). Since
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})=\aleph _0$
(see Lemma 4.6(1)). Since
![]() $\mathcal {I}$
is a
$\mathcal {I}$
is a
![]() $\bf {\Sigma ^0_2}$
ideal, we can use Theorem 6.9 to obtain the remaining (in)equality. (Note that since
$\bf {\Sigma ^0_2}$
ideal, we can use Theorem 6.9 to obtain the remaining (in)equality. (Note that since
![]() $\mathrm {Fin}\otimes \{\emptyset \}\subseteq \mathcal {ED} \subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
, we could also use Lemma 5.10 to obtain the inequality
$\mathrm {Fin}\otimes \{\emptyset \}\subseteq \mathcal {ED} \subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
, we could also use Lemma 5.10 to obtain the inequality
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}$
.)
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}$
.)
7 Ideals with
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
In this section we will show that
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
for some ideals (even
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
for some ideals (even
![]() $\bf {\Sigma ^0_2}$
ideals). All results of this section follow from the next lemma.
$\bf {\Sigma ^0_2}$
ideals). All results of this section follow from the next lemma.
Lemma 7.1. Let
![]() $\mathcal {A}\subseteq [\omega ]^{\omega }$
be an uncountable family with the property that
$\mathcal {A}\subseteq [\omega ]^{\omega }$
be an uncountable family with the property that
![]() $A\setminus (A_0\cup \cdots \cup A_n)\notin \mathrm {Fin}$
for all
$A\setminus (A_0\cup \cdots \cup A_n)\notin \mathrm {Fin}$
for all
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $A,A_0,\ldots A_n\in \mathcal {A}$
with
$A,A_0,\ldots A_n\in \mathcal {A}$
with
![]() $A\neq A_i$
for all
$A\neq A_i$
for all
![]() $i\leq n$
. If
$i\leq n$
. If
![]() $\mathcal {I}$
is an ideal generated by
$\mathcal {I}$
is an ideal generated by
![]() $\mathcal {A}$
, then
$\mathcal {A}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
.
Proof. Let
![]() $\left \{A^{\alpha }_n\in \mathcal {A}: n\in \omega ,\alpha <\aleph _1\right \}$
be such that
$\left \{A^{\alpha }_n\in \mathcal {A}: n\in \omega ,\alpha <\aleph _1\right \}$
be such that
![]() $A^{\alpha }_n\neq A^{\beta }_m$
whenever
$A^{\alpha }_n\neq A^{\beta }_m$
whenever
![]() $(\alpha ,n)\neq (\beta ,m)$
. We will show that
$(\alpha ,n)\neq (\beta ,m)$
. We will show that
![]() $\{\langle \bigcup _{i\leq n} A^{\alpha }_i: n\in \omega \rangle : \alpha <\aleph _1\}\subseteq \mathcal {I}^{\omega }$
witnesses
$\{\langle \bigcup _{i\leq n} A^{\alpha }_i: n\in \omega \rangle : \alpha <\aleph _1\}\subseteq \mathcal {I}^{\omega }$
witnesses
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
.
Let
![]() $\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
. Then there is
$\langle B_n:n\in \omega \rangle \in \mathcal {P}_{\mathcal {I}}$
. Then there is
![]() $\alpha <\aleph _1$
such that
$\alpha <\aleph _1$
such that
![]() $A^{\alpha }_n\setminus \bigcup _{i<m}B_i\notin \mathrm {Fin}$
for all
$A^{\alpha }_n\setminus \bigcup _{i<m}B_i\notin \mathrm {Fin}$
for all
![]() $n,m\in \omega $
. Indeed, for each m there are
$n,m\in \omega $
. Indeed, for each m there are
![]() $C^m_0,\ldots ,C^m_{l_m}\in \mathcal {A}$
such that
$C^m_0,\ldots ,C^m_{l_m}\in \mathcal {A}$
such that
![]() $\bigcup _{i<m}B_i\subseteq ^* C^m_0\cup \cdots \cup C^m_{l_m}$
. Since
$\bigcup _{i<m}B_i\subseteq ^* C^m_0\cup \cdots \cup C^m_{l_m}$
. Since
![]() $\mathcal {C}=\{C^m_{i}: m\in \omega , i\leq l_m\}$
is countable, there is
$\mathcal {C}=\{C^m_{i}: m\in \omega , i\leq l_m\}$
is countable, there is
![]() $\alpha <\aleph _1$
with
$\alpha <\aleph _1$
with
![]() $\{A^{\alpha }_n:n\in \omega \}\cap \mathcal {C}=\emptyset $
. Then
$\{A^{\alpha }_n:n\in \omega \}\cap \mathcal {C}=\emptyset $
. Then
for each
![]() $n,m\in \omega $
.
$n,m\in \omega $
.
Let
![]() $B=\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)$
. If we show that
$B=\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)$
. If we show that
![]() $B\notin \mathcal {I}$
, the proof will be finished. Suppose to the contrary that
$B\notin \mathcal {I}$
, the proof will be finished. Suppose to the contrary that
![]() $B=\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\in \mathcal {I}$
. Then there are
$B=\bigcup _{n\in \omega }(B_n\cap \bigcup _{i\leq n}A^{\alpha }_i)\in \mathcal {I}$
. Then there are
![]() $D_0,\ldots ,D_k\in \mathcal {A}$
with
$D_0,\ldots ,D_k\in \mathcal {A}$
with
![]() $B\subseteq ^* D_0\cup \cdots \cup D_k$
. Find
$B\subseteq ^* D_0\cup \cdots \cup D_k$
. Find
![]() $j\in \omega $
such that
$j\in \omega $
such that
![]() $A^{\alpha }_j\neq D_i$
for all
$A^{\alpha }_j\neq D_i$
for all
![]() $i=0,\ldots ,k$
.
$i=0,\ldots ,k$
.
We have
![]() $A^{\alpha }_j\setminus \bigcup _{n<j}B_n\notin \mathrm {Fin}$
and
$A^{\alpha }_j\setminus \bigcup _{n<j}B_n\notin \mathrm {Fin}$
and
 $$ \begin{align*}A^{\alpha}_j\setminus\bigcup_{n<j}B_n=A^{\alpha}_j\cap\bigcup_{n\geq j}B_n\subseteq \bigcup_{n\geq j}\left(B_n\cap\bigcup_{i\leq n}A^{\alpha}_i\right)\subseteq\bigcup_{n\in\omega}\left(B_n\cap\bigcup_{i\leq n}A^{\alpha}_i\right)=B.\end{align*} $$
$$ \begin{align*}A^{\alpha}_j\setminus\bigcup_{n<j}B_n=A^{\alpha}_j\cap\bigcup_{n\geq j}B_n\subseteq \bigcup_{n\geq j}\left(B_n\cap\bigcup_{i\leq n}A^{\alpha}_i\right)\subseteq\bigcup_{n\in\omega}\left(B_n\cap\bigcup_{i\leq n}A^{\alpha}_i\right)=B.\end{align*} $$
On the other hand,
 $(A^{\alpha }_j\setminus \bigcup _{n<j}B_n)\setminus \bigcup _{n\leq k}D_n=A^{\alpha }_j\setminus (\bigcup _{n<j}B_n\cup \bigcup _{n\leq k}D_n)\supseteq ^* A^{\alpha }_j\setminus (\bigcup _{n\leq l_j}C^j_{n}\cup \bigcup _{n\leq k}D_n)\notin \mathrm {Fin}$
. This contradicts
$(A^{\alpha }_j\setminus \bigcup _{n<j}B_n)\setminus \bigcup _{n\leq k}D_n=A^{\alpha }_j\setminus (\bigcup _{n<j}B_n\cup \bigcup _{n\leq k}D_n)\supseteq ^* A^{\alpha }_j\setminus (\bigcup _{n\leq l_j}C^j_{n}\cup \bigcup _{n\leq k}D_n)\notin \mathrm {Fin}$
. This contradicts
![]() $B\subseteq ^* D_0\cup \cdots \cup D_k$
and finishes the proof.⊣
$B\subseteq ^* D_0\cup \cdots \cup D_k$
and finishes the proof.⊣
Theorem 7.2. Let
![]() $\mathcal {A}\subseteq [\omega ]^{\omega }$
be an uncountable almost disjoint family. If
$\mathcal {A}\subseteq [\omega ]^{\omega }$
be an uncountable almost disjoint family. If
![]() $\mathcal {I}$
is an ideal generated by
$\mathcal {I}$
is an ideal generated by
![]() $\mathcal {A}$
, then
$\mathcal {A}$
, then
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
.
Proof. This follows directly from Lemma 7.1 – it suffices to observe that for any almost disjoint family
![]() $\mathcal {A}$
, if
$\mathcal {A}$
, if
![]() $A,A_0,\ldots A_n\in \mathcal {A}$
are such that
$A,A_0,\ldots A_n\in \mathcal {A}$
are such that
![]() $A\neq A_i$
for all
$A\neq A_i$
for all
![]() $i\leq n$
, then
$i\leq n$
, then
![]() $A\cap (A_0\cup \cdots \cup A_n)$
is finite, so
$A\cap (A_0\cup \cdots \cup A_n)$
is finite, so
![]() $A\setminus (A_0\cup \cdots \cup A_n)$
is infinite.⊣
$A\setminus (A_0\cup \cdots \cup A_n)$
is infinite.⊣
Let
![]() $2^{<\omega }$
be the set of all finite sequences of zeros and ones. Let
$2^{<\omega }$
be the set of all finite sequences of zeros and ones. Let
![]() $\mathcal {I}_b$
denote the ideal on
$\mathcal {I}_b$
denote the ideal on
![]() $2^{<\omega }$
generated by all branches i.e., sets of the form
$2^{<\omega }$
generated by all branches i.e., sets of the form
![]() $B_x=\{s\in 2^{<\omega }:s\subseteq x\}$
for
$B_x=\{s\in 2^{<\omega }:s\subseteq x\}$
for
![]() $x\in 2^{\omega }$
. It is easy to see that the ideal
$x\in 2^{\omega }$
. It is easy to see that the ideal
![]() $\mathcal {I}_b$
is
$\mathcal {I}_b$
is
![]() $\bf {\Sigma ^0_2}$
and not tall.
$\bf {\Sigma ^0_2}$
and not tall.
Corollary 7.3.
![]() $\mathfrak {b}(\mathcal {I}_b,\mathcal {I}_b,\mathcal {I}_b)=\aleph _1$
.
$\mathfrak {b}(\mathcal {I}_b,\mathcal {I}_b,\mathcal {I}_b)=\aleph _1$
.
Proof. It follows from Theorem 7.2, as the family
![]() $\{B_x:x\in 2^{\omega }\}$
is almost disjoint of size
$\{B_x:x\in 2^{\omega }\}$
is almost disjoint of size
![]() $\mathfrak {c}$
.⊣
$\mathfrak {c}$
.⊣
Let
![]() $\Omega $
be the set of all clopen subsets of the Cantor space
$\Omega $
be the set of all clopen subsets of the Cantor space
![]() $2^{\omega }$
having Lebesgue measure
$2^{\omega }$
having Lebesgue measure
![]() $1/2$
(note that
$1/2$
(note that
![]() $\Omega $
is countable). Let
$\Omega $
is countable). Let
![]() $\mathcal {S}$
denote the Solecki’s ideal on
$\mathcal {S}$
denote the Solecki’s ideal on
![]() $\Omega $
i.e., the ideal generated by sets of the form
$\Omega $
i.e., the ideal generated by sets of the form
![]() $G_x=\{A\in \Omega :x\in A\}$
for all
$G_x=\{A\in \Omega :x\in A\}$
for all
![]() $x\in 2^{\omega }$
.
$x\in 2^{\omega }$
.
![]() $\mathcal {S}$
is a tall
$\mathcal {S}$
is a tall
![]() $\bf {\Sigma ^0_{2}}$
ideal (see e.g., [Reference Hrušák21]).
$\bf {\Sigma ^0_{2}}$
ideal (see e.g., [Reference Hrušák21]).
Theorem 7.4.
![]() $\mathfrak {b}(\mathcal {S},\mathcal {S},\mathcal {S})=\aleph _1$
.
$\mathfrak {b}(\mathcal {S},\mathcal {S},\mathcal {S})=\aleph _1$
.
Proof. It follows from Lemma 7.1, as the family
![]() $\{G_x:x\in 2^{\omega }\}$
has cardinality
$\{G_x:x\in 2^{\omega }\}$
has cardinality
![]() $\mathfrak {c}$
and for any
$\mathfrak {c}$
and for any
![]() $x,x_0,\ldots ,x_n\in 2^{\omega }$
with
$x,x_0,\ldots ,x_n\in 2^{\omega }$
with
![]() $x\neq x_i$
for all
$x\neq x_i$
for all
![]() $i\leq n$
, we have
$i\leq n$
, we have
![]() $G_x\setminus (G_{x_0}\cup \ldots \cup G_{x_n})=\{A\in \Omega : x\in A \land \forall i\leq n \, (x_i\notin A)\}$
is infinite.⊣
$G_x\setminus (G_{x_0}\cup \ldots \cup G_{x_n})=\{A\in \Omega : x\in A \land \forall i\leq n \, (x_i\notin A)\}$
is infinite.⊣
8 Consistency results
In this section we apply some known consistency results to the case of the considered cardinals. The main aim of this section is to show that consistently the values of considered cardinals can be pairwise distinct. We start with two results about
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})$
.
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I})$
.
Proposition 8.1. It is consistent that there is a P-ideal
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
Proof. It follows from Corollary 6.5 and the fact that it is consistent that
![]() $\operatorname {\mathrm {add}}(\mathcal {N})<\mathfrak {b}$
(see e.g., [Reference Blass2]).⊣
$\operatorname {\mathrm {add}}(\mathcal {N})<\mathfrak {b}$
(see e.g., [Reference Blass2]).⊣
Theorem 8.2 (Essentially Louveau).
Under Martin’s axiom, there is a maximal ideal
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \kappa $
for all regular
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \kappa $
for all regular
![]() $\aleph _1\leq \kappa \leq \mathfrak {c}$
.
$\aleph _1\leq \kappa \leq \mathfrak {c}$
.
Proof. Louveau [Reference Louveau28, Théorèmes 3.9 and 3.12] proved that there is a maximal ideal
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
![]() $\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\kappa $
(see also [Reference Brendle and Shelah4, p. 2647]). On the other hand, it is well known that
$\operatorname {\mathrm {add} ^{*}}(\mathcal {I})=\kappa $
(see also [Reference Brendle and Shelah4, p. 2647]). On the other hand, it is well known that
![]() $\mathfrak {b}=\mathfrak {c}$
under Martin’s axiom. Thus,
$\mathfrak {b}=\mathfrak {c}$
under Martin’s axiom. Thus,
![]() $\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \kappa $
.⊣
$\mathfrak {b}_s(\mathrm {Fin},\mathcal {I},\mathcal {I}) = \kappa $
.⊣
Now we want to reformulate Canjar’s results from [Reference Canjar11, Reference Canjar12, Reference RecŁaw13]. He studied
![]() $\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
$\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
![]() $\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
in the case of maximal ideals
$\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
in the case of maximal ideals
![]() $\mathcal {I}$
. It is not difficult to see that for a maximal ideal
$\mathcal {I}$
. It is not difficult to see that for a maximal ideal
![]() $\mathcal {I}$
we have
$\mathcal {I}$
we have
![]() $\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) = \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
$\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}})) = \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
![]() $\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}})) = \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
. On the other hand, by Theorem 3.10(2),
$\mathfrak {d}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}})) = \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
. On the other hand, by Theorem 3.10(2),
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
and
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
. Thus, we have the following two results.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}}\times \mathcal {D}_{\mathcal {I}}))$
. Thus, we have the following two results.
Theorem 8.3 (Canjar [Reference Canjar11, Reference Canjar12]).
The following is true in the model obtained by adding
![]() $\lambda $
Cohen reals to a model of GCH.
$\lambda $
Cohen reals to a model of GCH.
-
(1) There exists an ideal
 $\mathcal {I}$
with
$\mathcal {I}$
with
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\kappa $
for all regular cardinals
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\kappa $
for all regular cardinals
 $\aleph _1\leq \kappa < \lambda $
.
$\aleph _1\leq \kappa < \lambda $
. -
(2) There exist
 $2^{\kappa }$
ideals
$2^{\kappa }$
ideals
 $\mathcal {I}$
with
$\mathcal {I}$
with
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\kappa $
for all regular cardinals
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\kappa $
for all regular cardinals
 $\aleph _1\leq \kappa < \lambda $
.
$\aleph _1\leq \kappa < \lambda $
.
Theorem 8.4 (Essentially Canjar [Reference RecŁaw13]).
-
(1) There is an ideal
 $\mathcal {I}$
such that
$\mathcal {I}$
such that
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\text {cf}(\mathfrak {d})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\text {cf}(\mathfrak {d})$
. -
(2) If
 $\mathfrak {d}=\mathfrak {c}$
, then there is a P-ideal
$\mathfrak {d}=\mathfrak {c}$
, then there is a P-ideal
 $\mathcal {I}$
such that
$\mathcal {I}$
such that
 $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\operatorname {\mathrm {cf}}(\mathfrak {d})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\operatorname {\mathrm {cf}}(\mathfrak {d})$
.
Recall that consistency of
![]() $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
and
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
and
![]() $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})\leq \mathfrak {d}=\mathfrak {c}$
follows for instance from [Reference Blass2, Theorem 2.5].
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})\leq \mathfrak {d}=\mathfrak {c}$
follows for instance from [Reference Blass2, Theorem 2.5].
Corollary 8.5.
-
(1) If
 $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
, then there is an ideal
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
, then there is an ideal
 $\mathcal {I}$
such that
$\mathcal {I}$
such that
 $\mathfrak {b}<\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\text {cf}(\mathfrak {d})$
.
$\mathfrak {b}<\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\text {cf}(\mathfrak {d})$
. -
(2) If
 $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})\leq \mathfrak {d}=\mathfrak {c}$
, then there is a P-ideal
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})\leq \mathfrak {d}=\mathfrak {c}$
, then there is a P-ideal
 $\mathcal {I}$
such that
$\mathcal {I}$
such that  $$ \begin{align*}\mathfrak{b}<\mathfrak{b}(\mathcal{I},\mathrm{Fin},\mathrm{Fin})=\mathfrak{b}(\mathcal{I}, \mathcal{I},\mathcal{I})=\mathfrak{b}(\mathcal{I},\mathcal{I},\mathrm{Fin})=\text{cf}(\mathfrak{d}).\end{align*} $$
$$ \begin{align*}\mathfrak{b}<\mathfrak{b}(\mathcal{I},\mathrm{Fin},\mathrm{Fin})=\mathfrak{b}(\mathcal{I}, \mathcal{I},\mathcal{I})=\mathfrak{b}(\mathcal{I},\mathcal{I},\mathrm{Fin})=\text{cf}(\mathfrak{d}).\end{align*} $$
Next three results will establish that consistently the values of
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
,
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
,
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
and
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
and
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
can be pairwise distinct
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
can be pairwise distinct
Theorem 8.6. If
![]() $\mathfrak {b}<\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
for some ideal
$\mathfrak {b}<\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
for some ideal
![]() $\mathcal {J}$
(e.g. if
$\mathcal {J}$
(e.g. if
![]() $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
), then there is an ideal
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
), then there is an ideal
![]() $\mathcal {I}$
, which is not a weak P-ideal, such that
$\mathcal {I}$
, which is not a weak P-ideal, such that
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}<\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}<\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})$
.
Proof. Consider the ideal
![]() $\mathcal {I}=\mathrm {Fin}\otimes \mathcal {J}$
. Obviously,
$\mathcal {I}=\mathrm {Fin}\otimes \mathcal {J}$
. Obviously,
![]() $\mathcal {I}$
is not a weak P-ideal as
$\mathcal {I}$
is not a weak P-ideal as
![]() $\mathrm {Fin}\otimes \mathrm {Fin}\subseteq \mathcal {I}$
. By Theorems 5.13(1), 5.9(1) and 4.2(2) we have
$\mathrm {Fin}\otimes \mathrm {Fin}\subseteq \mathcal {I}$
. By Theorems 5.13(1), 5.9(1) and 4.2(2) we have
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
and
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
and
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})>\mathfrak {b}$
.⊣
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})>\mathfrak {b}$
.⊣
Theorem 8.7. If
![]() $\mathfrak {b}<\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
for some ideal
$\mathfrak {b}<\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
for some ideal
![]() $\mathcal {J}$
(e.g. if
$\mathcal {J}$
(e.g. if
![]() $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})\leq \mathfrak {d}=\mathfrak {c}$
), then there is an ideal
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})\leq \mathfrak {d}=\mathfrak {c}$
), then there is an ideal
![]() $\mathcal {I}$
, which is not a weak P-ideal, such that
$\mathcal {I}$
, which is not a weak P-ideal, such that
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
Proof. Consider the ideal
![]() $\mathcal {I}=\mathcal {J}\otimes \mathrm {Fin}$
. Obviously,
$\mathcal {I}=\mathcal {J}\otimes \mathrm {Fin}$
. Obviously,
![]() $\mathcal {I}$
is not a weak P-ideal as
$\mathcal {I}$
is not a weak P-ideal as
![]() $\mathrm {Fin}\otimes \mathrm {Fin}\subseteq \mathcal {I}$
. By Theorems 5.13(1), 5.9(1) and 4.2(2) we have
$\mathrm {Fin}\otimes \mathrm {Fin}\subseteq \mathcal {I}$
. By Theorems 5.13(1), 5.9(1) and 4.2(2) we have
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})>\mathfrak {b}$
and
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})>\mathfrak {b}$
and
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.⊣
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
.⊣
Theorem 8.8. If
![]() $\mathfrak {b}<\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
for some ideal
$\mathfrak {b}<\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
for some ideal
![]() $\mathcal {J}$
(e.g. if
$\mathcal {J}$
(e.g. if
![]() $\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
), then there is a weak P-ideal
$\mathfrak {b}<\operatorname {\mathrm {cf}}(\mathfrak {d})$
), then there is a weak P-ideal
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
Proof. Consider the ideal
![]() $\mathcal {I}=(\mathrm {Fin}\otimes \mathrm {Fin})\cap (\mathcal {J}\otimes \{\emptyset \})$
.
$\mathcal {I}=(\mathrm {Fin}\otimes \mathrm {Fin})\cap (\mathcal {J}\otimes \{\emptyset \})$
.
First we show that
![]() $\mathcal {I}$
is a weak P-ideal (this fact is also shown in [Reference Kwela22, Lemma 2.3], however we prove it here for the sake of completeness). Fix a partition
$\mathcal {I}$
is a weak P-ideal (this fact is also shown in [Reference Kwela22, Lemma 2.3], however we prove it here for the sake of completeness). Fix a partition
![]() $\langle X_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. Define by induction two sequences
$\langle X_n\rangle \in \mathcal {P}_{\mathcal {I}}$
. Define by induction two sequences
![]() $\langle m_n\rangle ,\langle k_n\rangle \in \omega ^{\omega }$
such that for each
$\langle m_n\rangle ,\langle k_n\rangle \in \omega ^{\omega }$
such that for each
![]() $n\in \omega $
we have
$n\in \omega $
we have
![]() $(n,m_n)\in X_{k_n}$
and
$(n,m_n)\in X_{k_n}$
and
 $$ \begin{align*}m_n= \begin{cases} \min\{m\in\omega:m\notin(\bigcup\{X_{k_i}:i<n\})_n\} & \text{if } \omega\not\subseteq(\bigcup_{i<n}X_{k_i})_n,\\ \min\{m\in\omega:m\in(\bigcup\{X_{k}:|(X_k)_n|=\omega\})_n\} & \text{otherwise.}\\ \end{cases}\end{align*} $$
$$ \begin{align*}m_n= \begin{cases} \min\{m\in\omega:m\notin(\bigcup\{X_{k_i}:i<n\})_n\} & \text{if } \omega\not\subseteq(\bigcup_{i<n}X_{k_i})_n,\\ \min\{m\in\omega:m\in(\bigcup\{X_{k}:|(X_k)_n|=\omega\})_n\} & \text{otherwise.}\\ \end{cases}\end{align*} $$
Then
![]() $Y=\{(n,m_n):n\in \omega \}\notin \mathcal {I}$
as
$Y=\{(n,m_n):n\in \omega \}\notin \mathcal {I}$
as
![]() $\{n\in \omega : (Y)_n\neq \emptyset \}=\omega \notin \mathcal {J}$
. Moreover,
$\{n\in \omega : (Y)_n\neq \emptyset \}=\omega \notin \mathcal {J}$
. Moreover,
![]() $Y\cap X_n$
is finite for all n (otherwise we would have
$Y\cap X_n$
is finite for all n (otherwise we would have
![]() $|(X_n)_k|=\omega $
for infinitely many
$|(X_n)_k|=\omega $
for infinitely many
![]() $k\in \omega $
). Thus
$k\in \omega $
). Thus
![]() $\mathcal {I}$
is a weak P-ideal.
$\mathcal {I}$
is a weak P-ideal.
As
![]() $\mathcal {I}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
and
$\mathcal {I}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
and
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
is meager,
$\mathrm {Fin}\otimes \mathrm {Fin}$
is meager,
![]() $\mathcal {I}$
is meager as well. Thus,
$\mathcal {I}$
is meager as well. Thus,
![]() $\mathcal {I}$
has the Baire property and
$\mathcal {I}$
has the Baire property and
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
by Theorem 6.3.
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
by Theorem 6.3.
By Lemma 5.10 we have
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
, as
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {b}(\mathrm {Fin},\mathrm {Fin},\mathrm {Fin})=\mathfrak {b}$
, as
![]() $\mathrm {Fin}\otimes \{\emptyset \}\subseteq \mathcal {I}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
.
$\mathrm {Fin}\otimes \{\emptyset \}\subseteq \mathcal {I}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
.
To finish the proof we need to show that
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\geq \mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
. Let
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\geq \mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
. Let
![]() $\kappa <\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
and
$\kappa <\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
and
![]() $\{\langle E^{\alpha }_n: n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathrm {Fin}(\omega ^2)^{\omega }$
. We will show that this family does not witness
$\{\langle E^{\alpha }_n: n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathrm {Fin}(\omega ^2)^{\omega }$
. We will show that this family does not witness
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \kappa $
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})\leq \kappa $
.
For each
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha <\kappa $
define
$\alpha <\kappa $
define
Since
![]() $\{\langle A^{\alpha }_n: n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathrm {Fin}^{\omega }$
and
$\{\langle A^{\alpha }_n: n\in \omega \rangle :\alpha <\kappa \}\subseteq \mathrm {Fin}^{\omega }$
and
![]() $\kappa <\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
, there is
$\kappa <\mathfrak {b}(\mathcal {J},\mathrm {Fin},\mathrm {Fin})$
, there is
![]() $\langle B_n\rangle \in \mathcal {P}_{\mathrm {Fin}}$
such that
$\langle B_n\rangle \in \mathcal {P}_{\mathrm {Fin}}$
such that
![]() $\bigcup _{n\in \omega }\left (B_n\cap A^{\alpha }_n\right )\in \mathcal {J}$
for all
$\bigcup _{n\in \omega }\left (B_n\cap A^{\alpha }_n\right )\in \mathcal {J}$
for all
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Define
![]() $C_n=B_n\times \omega $
for all
$C_n=B_n\times \omega $
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\langle C_n\rangle \in \mathcal {P}_{\mathcal {I}}$
.
$\langle C_n\rangle \in \mathcal {P}_{\mathcal {I}}$
.
Fix
![]() $\alpha <\kappa $
and denote
$\alpha <\kappa $
and denote
![]() $X=\bigcup _{n\in \omega }\left (C_n\cap E^{\alpha }_n\right )$
. If we show that
$X=\bigcup _{n\in \omega }\left (C_n\cap E^{\alpha }_n\right )$
. If we show that
![]() $X\in \mathcal {I}$
, the proof will be finished.
$X\in \mathcal {I}$
, the proof will be finished.
Observe that for each
![]() $k\in \omega $
there is
$k\in \omega $
there is
![]() $j\in \omega $
with
$j\in \omega $
with
![]() $k\in B_j$
. Then
$k\in B_j$
. Then
![]() $(X)_k=(E^{\alpha }_j)_k$
, so
$(X)_k=(E^{\alpha }_j)_k$
, so
![]() $(X)_k$
is finite. Thus,
$(X)_k$
is finite. Thus,
![]() $X\in \{\emptyset \}\otimes \mathrm {Fin}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
.
$X\in \{\emptyset \}\otimes \mathrm {Fin}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
.
Moreover,
 $$ \begin{align*} \begin{aligned} \left\{k\in\omega: (X)_k\neq\emptyset\right\}& = \left\{k\in\omega: \exists n\in\omega\,\exists i\in\omega\, (k,i)\in C_n\cap E^{\alpha}_n\right\}\\ & = \bigcup_{n\in\omega} \left\{k\in\omega: \exists i\in\omega\, \left(i \in \left(C_n\cap E^{\alpha}_n\right)_k\right)\right\}\\ &\subseteq \bigcup_{n\in\omega} \left(\left\{k\in\omega: \exists i\in\omega\left(i\in \left(C_n\right)_k\right)\right\}\right.\\ & \left.\cap \left\{k\in\omega: \exists i\in\omega \left(i \in \left(E^{\alpha}_n\right)_k\right)\right\}\right)\\ &= \bigcup_{n\in\omega}\left(B_n\cap A^{\alpha}_n\right)\in\mathcal{J}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\{k\in\omega: (X)_k\neq\emptyset\right\}& = \left\{k\in\omega: \exists n\in\omega\,\exists i\in\omega\, (k,i)\in C_n\cap E^{\alpha}_n\right\}\\ & = \bigcup_{n\in\omega} \left\{k\in\omega: \exists i\in\omega\, \left(i \in \left(C_n\cap E^{\alpha}_n\right)_k\right)\right\}\\ &\subseteq \bigcup_{n\in\omega} \left(\left\{k\in\omega: \exists i\in\omega\left(i\in \left(C_n\right)_k\right)\right\}\right.\\ & \left.\cap \left\{k\in\omega: \exists i\in\omega \left(i \in \left(E^{\alpha}_n\right)_k\right)\right\}\right)\\ &= \bigcup_{n\in\omega}\left(B_n\cap A^{\alpha}_n\right)\in\mathcal{J}. \end{aligned} \end{align*} $$
Thus,
![]() $X\in \mathcal {J}\otimes \{\emptyset \}$
and we can conclude that
$X\in \mathcal {J}\otimes \{\emptyset \}$
and we can conclude that
![]() $X\in \mathcal {I}$
.⊣
$X\in \mathcal {I}$
.⊣
We were not able to compute the exact value of
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
in Theorem 8.8. Thus, we have the following open question.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
in Theorem 8.8. Thus, we have the following open question.
Question 1. Is it consistent that there is a weak P-ideal
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})<\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
?
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})<\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
?
There is another closely related open question.
Question 2. Is it consistent that there is a weak P-ideal
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
![]() $\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
?
$\mathfrak {b}(\mathcal {I},\mathrm {Fin},\mathrm {Fin})<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathrm {Fin})$
?
9 Questions and remarks about
 $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
In this section we collect some remarks indicating difficulties in obtaining any general results concerning
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
for Borel ideals.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
for Borel ideals.
Remark. Observe that
![]() $\mathcal {I}\subseteq \mathcal {J}$
does not give us any information about the relation between
$\mathcal {I}\subseteq \mathcal {J}$
does not give us any information about the relation between
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
and
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
and
![]() $\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
. Indeed, let
$\mathfrak {b}(\mathcal {J},\mathcal {J},\mathcal {J})$
. Indeed, let
![]() $\mathcal {I}$
be an ideal generated by an uncountable family
$\mathcal {I}$
be an ideal generated by an uncountable family
![]() $\mathcal {F}\subseteq \omega ^{\omega }$
of pairwise almost disjoint graphs (i.e.,
$\mathcal {F}\subseteq \omega ^{\omega }$
of pairwise almost disjoint graphs (i.e.,
![]() $\{n\in \omega :f(n)=g(n)\}\in \mathrm {Fin}$
for any
$\{n\in \omega :f(n)=g(n)\}\in \mathrm {Fin}$
for any
![]() $f,g\in \mathcal {F}$
,
$f,g\in \mathcal {F}$
,
![]() $f\neq g$
). Then
$f\neq g$
). Then
![]() $\mathrm {Fin}(\omega ^2)\subseteq \mathcal {I}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
, however
$\mathrm {Fin}(\omega ^2)\subseteq \mathcal {I}\subseteq \mathrm {Fin}\otimes \mathrm {Fin}$
, however
![]() $\mathfrak {b}(\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))=\mathfrak {b}(\mathrm {Fin}\otimes \mathrm {Fin},\mathrm {Fin}\otimes \mathrm {Fin},\mathrm {Fin}\otimes \mathrm {Fin})=\mathfrak {b}$
(by Corollary 6.6) and
$\mathfrak {b}(\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2),\mathrm {Fin}(\omega ^2))=\mathfrak {b}(\mathrm {Fin}\otimes \mathrm {Fin},\mathrm {Fin}\otimes \mathrm {Fin},\mathrm {Fin}\otimes \mathrm {Fin})=\mathfrak {b}$
(by Corollary 6.6) and
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
(by Theorem 7.2).
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
(by Theorem 7.2).
Remark. We have non-tall ideals with
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
(e.g. the branching ideal
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
(e.g. the branching ideal
![]() $\mathcal {I}_b$
) as well as non-tall ideals with
$\mathcal {I}_b$
) as well as non-tall ideals with
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}$
(this is the case for instance for
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}$
(this is the case for instance for
![]() $\mathrm {Fin}$
,
$\mathrm {Fin}$
,
![]() $\mathrm {Fin}\otimes \{\emptyset \}$
or
$\mathrm {Fin}\otimes \{\emptyset \}$
or
![]() $\{\emptyset \}\otimes \mathrm {Fin}$
). The same holds for tall ideals –
$\{\emptyset \}\otimes \mathrm {Fin}$
). The same holds for tall ideals –
![]() $\mathcal {S}$
is a tall ideal with
$\mathcal {S}$
is a tall ideal with
![]() $\mathfrak {b}(\mathcal {S},\mathcal {S},\mathcal {S})=\aleph _1$
whereas the ideal
$\mathfrak {b}(\mathcal {S},\mathcal {S},\mathcal {S})=\aleph _1$
whereas the ideal
![]() $\mathcal {I}_d$
is a tall ideal with
$\mathcal {I}_d$
is a tall ideal with
![]() $\mathfrak {b}(\mathcal {I}_d,\mathcal {I}_d,\mathcal {I}_d)=\mathfrak {b}$
.
$\mathfrak {b}(\mathcal {I}_d,\mathcal {I}_d,\mathcal {I}_d)=\mathfrak {b}$
.
Remark.
![]() $\bf {\Sigma ^0_{2}}$
ideals may have different values of
$\bf {\Sigma ^0_{2}}$
ideals may have different values of
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
. Indeed, there are
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
. Indeed, there are
![]() $\bf {\Sigma ^0_{2}}$
ideals with
$\bf {\Sigma ^0_{2}}$
ideals with
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
(e.g. the branching ideal
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\aleph _1$
(e.g. the branching ideal
![]() $\mathcal {I}_b$
or the Solecki’s ideal
$\mathcal {I}_b$
or the Solecki’s ideal
![]() $\mathcal {S}$
) as well as
$\mathcal {S}$
) as well as
![]() $\bf {\Sigma ^0_{2}}$
ideals with
$\bf {\Sigma ^0_{2}}$
ideals with
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}$
(e.g., ideals
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})=\mathfrak {b}$
(e.g., ideals
![]() $\mathrm {Fin}$
,
$\mathrm {Fin}$
,
![]() $\mathrm {Fin}\otimes \{\emptyset \}$
or
$\mathrm {Fin}\otimes \{\emptyset \}$
or
![]() $\{\emptyset \}\otimes \mathrm {Fin}$
).
$\{\emptyset \}\otimes \mathrm {Fin}$
).
Remark. Note that actually we cannot compute
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
basing on the descriptive complexity of
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
basing on the descriptive complexity of
![]() $\mathcal {I}$
. Indeed, for each
$\mathcal {I}$
. Indeed, for each
![]() $n\geq 1$
the ideal
$n\geq 1$
the ideal
![]() $\mathrm {Fin}^n$
is an
$\mathrm {Fin}^n$
is an
![]() $\bf {\Sigma ^0_{2n}}$
-complete ideal such that
$\bf {\Sigma ^0_{2n}}$
-complete ideal such that
![]() $\mathfrak {b}(\mathrm {Fin}^n,\mathrm {Fin}^n,\mathrm {Fin}^n)=\mathfrak {b}$
(see Corollary 6.6). On the other hand, Calbrix in [Reference Canjar10] proved that given a
$\mathfrak {b}(\mathrm {Fin}^n,\mathrm {Fin}^n,\mathrm {Fin}^n)=\mathfrak {b}$
(see Corollary 6.6). On the other hand, Calbrix in [Reference Canjar10] proved that given a
![]() $\bf {\Sigma ^0_\alpha }$
-complete,
$\bf {\Sigma ^0_\alpha }$
-complete,
![]() $\alpha>1$
, (respectively:
$\alpha>1$
, (respectively:
![]() $\bf {\Pi ^0_\alpha }$
-complete,
$\bf {\Pi ^0_\alpha }$
-complete,
![]() $\alpha>2$
) subset A of
$\alpha>2$
) subset A of
![]() $2^{\omega }$
, the ideal
$2^{\omega }$
, the ideal
![]() $\mathcal {I}_{A}$
on
$\mathcal {I}_{A}$
on
![]() $2^{<\omega }$
generated by the family
$2^{<\omega }$
generated by the family
![]() $\{B_x: x\in A\}$
is
$\{B_x: x\in A\}$
is
![]() $\bf {\Sigma ^0_\alpha }$
-complete (respectively:
$\bf {\Sigma ^0_\alpha }$
-complete (respectively:
![]() $\bf {\Pi ^0_\alpha }$
-complete). Moreover, since the family
$\bf {\Pi ^0_\alpha }$
-complete). Moreover, since the family
![]() $\{B_x: x\in A\}$
is almost disjoint, by Theorem 7.2 we get
$\{B_x: x\in A\}$
is almost disjoint, by Theorem 7.2 we get
![]() $\mathfrak {b}(\mathcal {I}_A,\mathcal {I}_A,\mathcal {I}_A)=\aleph _1$
.
$\mathfrak {b}(\mathcal {I}_A,\mathcal {I}_A,\mathcal {I}_A)=\aleph _1$
.
We end with two natural open questions about
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})$
.
Question 3. Is
![]() $\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {d}$
for every ideal
$\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})\leq \mathfrak {d}$
for every ideal
![]() $\mathcal {I}$
?
$\mathcal {I}$
?
Question 4. Is it consistent that
![]() $\aleph _1<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})<\mathfrak {b}$
for some ideal
$\aleph _1<\mathfrak {b}(\mathcal {I},\mathcal {I},\mathcal {I})<\mathfrak {b}$
for some ideal
![]() $\mathcal {I}$
?
$\mathcal {I}$
?