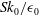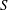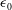1. Introduction
The motion of small passive and inertial particles in turbulence has been extensively studied in recent years, from both the experimental and the theoretical viewpoints. This has been motivated by a broad range of applications such as the spread of pollutants in the atmosphere and oceans, the process of rain and ice formation in cloud, and the transport of sediments in rivers and estuaries, see e.g. the reviews of Shaw (Reference Shaw2003) and Toschi & Bodenschatz (Reference Toschi and Bodenschatz2009). Progress in the understanding has on the one hand been made possible by recent improvements in Lagrangian measurements through particle tracking methodologies, resulting in part from rapid advances in high-speed imaging (Virant & Dracos Reference Virant and Dracos1997; Ott & Mann Reference Ott and Mann2000; Voth et al. Reference Voth, Porta, Crawford, Alexander and Bodenschatz2002; Xu, Ouelette & Bodenschatz Reference Xu, Ouelette and Bodenschatz2008), and on the other hand by increased computational capabilities of numerical simulations (Yeung & Pope Reference Yeung and Pope1998; Celani Reference Celani2007).
The objective of this work is to investigate the effects of flow straining on the Lagrangian dynamics of small, sub-Kolmogorov scale, passive and inertial particles. Our motivation stems from the fact that many practical turbulent flows are subject to straining motions, such as the external flows over bluff or streamlined bodies and internal flows in variable cross-sections (Batchelor Reference Batchelor1953; Hunt Reference Hunt1973; Warhaft Reference Warhaft1980; Hunt & Carruthers Reference Hunt and Carruthers1990; Ayyalasomayajula & Warhaft Reference Ayyalasomayajula and Warhaft2006; Chen, Meneveau & Katz Reference Chen, Meneveau and Katz2006; Gualtieri & Meneveau Reference Gualtieri and Meneveau2010). A mean straining flow naturally appears in the proximity of stagnation points. Flow straining is furthermore of fundamental interest since it induces a scale-dependent anisotropy; the smallest scales of the flow may be nearly isotropic, whereas the largest scales are highly anisotropic (Biferale & Procaccia Reference Biferale and Procaccia2005).
Furthermore, many flows naturally combine straining geometries and inertial particles. The flow geometry presented here, namely particle-laden turbulent flow undergoing an axisymmetric expansion, has similarities with combustor diffusers in jet engines (Klein Reference Klein1995), where liquid fuel is injected in an expanding flow, and with the flow in the combustion chamber in an internal combustion engine during the compression stroke of the fuel–air mixture (Han & Reitz Reference Han and Reitz1995).
While significant attention has been given to the study of Lagrangian acceleration statistics in isotropic turbulence, less attention has been paid to the implications of anisotropic large-scale flow geometry on the Lagrangian dynamics. Recent experimental and numerical work on the Lagrangian behaviour of inertial particles in shear flows and turbulent boundary layers has shown pronounced effects on the inertial particle statistics (Shotorban & Balachandar Reference Shotorban and Balachandar2006; Gerashchenco et al. Reference Gerashchenco, Sharp, Neuscamman and Warhaft2008; Gualtieri, Picano & Casciola Reference Gualtieri, Picano and Casciola2009; Lavezzo et al. Reference Lavezzo, Soldati, Gerashchenko, Warhaft and Collins2010; Gualtieri et al. Reference Gualtieri, Picano, Sardina and Casciola2012; Alipchenkov & Beketov Reference Alipchenkov and Beketov2013). The persistent small-scale anisotropy has been found to influence the geometry and alignment of particle clusters and relative particle pair velocities. In addition, the combined effects of gravity and shear on particle acceleration variance result in an increase in magnitude with the Stokes number. As a consequence, the acceleration probability distribution functions (p.d.f.s) became increasingly narrow and skewed with inertia. Here, we address a related topic, namely the complexity introduced in the Lagrangian dynamics of tracer and inertial particles due to flow straining.
In an effort to realize the effects of anisotropy in the particle dynamics, we numerically simulate axisymmetric expansion of initially isotropic turbulence. The flow is seeded with infinitesimal tracer and inertial particles of varied Stokes numbers. We measure the particle velocity and acceleration statistics, including variances and p.d.f.s for different strain rates and Stokes numbers. Comparisons are made with predictions of rapid-distortion theory on tracer accelerations, and the solutions of Newton’s equations for the motion of inertial particles in the straining flow.
The paper is organized as follows. In § 2 we briefly introduce the numerical methods for simulating an axisymmetric turbulence and particle movements. The parameters of the simulations are listed. Section 3 presents the underlying flow field. We discuss our main findings on particle acceleration variances and p.d.f.s in simulation data with the support of theoretical estimations in § 4. We also discuss our results in the context of previous work in shear flows. In § 5 we present our conclusions.
2. Methodology
2.1. Flow equations and flow simulation
The equations describing the motion of an incompressible Newtonian fluid are the continuity equation and the Navier–Stokes equations respectively:
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \tilde{\boldsymbol{u}}}{\partial t}+\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\tilde{\boldsymbol{u}}+\boldsymbol{{\rm\nabla}}\tilde{p}={\it\nu}{\rm\nabla}^{2}\tilde{\boldsymbol{u}}. & \displaystyle\end{eqnarray}$$
$\tilde{\boldsymbol{u}}$
is the instantaneous flow velocity,
$\tilde{p}=p/{\it\rho}$
is the pressure field rescaled by the density of the fluid, and
${\it\nu}$
is the kinematic viscosity of the fluid.
In this paper we are concerned with a turbulent fluid undergoing an axisymmetric expansion, where the mean flow field is described by
$$\begin{eqnarray}\boldsymbol{U}=(-2Sx,Sy,Sz).\end{eqnarray}$$
Here,
$S$
is the constant mean strain rate
$S=(\bar{\unicode[STIX]{x1D61A}}_{ij}\bar{\unicode[STIX]{x1D61A}}_{ij})^{1/2}/\sqrt{6}$
, and
$\bar{\unicode[STIX]{x1D61A}}_{ij}=(\partial U_{i}/\partial x_{j}+\partial U_{j}/\partial x_{i})/2$
is the mean rate of strain tensor. The mean flow corresponds to an ideal flow onto a flat plate, and is realized in the flow between contracting pistons or in the expanding flow through a diffuser. Figure 1(a) shows a sketch of the mean flow field, namely streamlines of the mean field, and the coordinate system employed.
Figure 1. A sketch of the deformation of the simulation domain under straining. The mean flow
$\boldsymbol{U}=(-2Sx,Sy,Sz)$
corresponds to an ideal flow onto a flat plate. The deforming domain is initially elongated in the
$x$
direction but becomes wider in the
$y$
and
$z$
directions with time. Arrows indicate the directions of the streamlines of the induced mean flow.
By applying the Reynolds decomposition and expressing (2.2) in terms of the vector potential
$\boldsymbol{b}$
, with
$\boldsymbol{u}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{b}$
, one obtains
$$\begin{eqnarray}-\partial _{t}{\rm\nabla}^{2}\boldsymbol{b}-\boldsymbol{{\rm\nabla}}\times (\boldsymbol{u}\times {\bf\omega})+2Sx\partial _{x}{\rm\nabla}^{2}\boldsymbol{b}-Sy\partial _{y}{\rm\nabla}^{2}\boldsymbol{b}-Sz\partial _{z}{\rm\nabla}^{2}\boldsymbol{b}+S{\rm\nabla}^{2}\boldsymbol{b}-3S{\rm\nabla}^{2}b_{1}\hat{e}_{1}=-{\it\nu}{\rm\nabla}^{4}\boldsymbol{b},\end{eqnarray}$$
where
$\boldsymbol{u}=\tilde{\boldsymbol{u}}-\boldsymbol{U}$
is the velocity fluctuation,
${\bf\omega}$
is the vorticity, defined as
${\bf\omega}\equiv \boldsymbol{{\rm\nabla}}\times \boldsymbol{u}=-{\rm\nabla}^{2}\boldsymbol{b}$
,
$b_{1}$
is the first component of
$\boldsymbol{b}$
and
$\hat{e}_{1}$
is the unit vector in the
$x$
direction. In the following we briefly outline the numerical algorithm.
As in Gylfason et al. (Reference Gylfason, Lee, Perlekar and Toschi2011), in order to solve (2.4) we apply a pseudo-spectral method with Rogallo’s algorithm (Rogallo Reference Rogallo1981), where the following variable transformations are performed:
$$\begin{eqnarray}\displaystyle x^{\prime }=\text{e}^{2St}x,\quad y^{\prime }=\text{e}^{-St}y,\quad z^{\prime }=\text{e}^{-St}z,\quad t^{\prime }=t, & & \displaystyle\end{eqnarray}$$
and hence the vector potential of the velocity fluctuation satisfies
$$\begin{eqnarray}\partial _{t^{\prime }}{\rm\nabla}^{^{\prime }2}\boldsymbol{b}-\boldsymbol{{\rm\nabla}}^{\prime }\times (\boldsymbol{u}\times {\bf\omega})+S{\rm\nabla}^{^{\prime }2}\boldsymbol{b}-3S{\rm\nabla}^{^{\prime }2}b_{1}\hat{e}_{1}=-{\it\nu}{\rm\nabla}^{^{\prime }4}\boldsymbol{b},\end{eqnarray}$$
where
$\boldsymbol{{\rm\nabla}}^{\prime }=(\text{e}^{2St}\partial _{x^{\prime }},\text{e}^{-St}\partial _{y^{\prime }},\text{e}^{-St}\partial _{z^{\prime }})$
. By adopting this new coordinate system, the physical domain deforms with time while the computational lattice grid is time-independent, and the flow equations become periodic. Figure 1 depicts the deformation of the physical domain. We then apply the pseudo-spectral method to the equations in (2.6). More details about the numerical method can be found in Gylfason et al. (Reference Gylfason, Lee, Perlekar and Toschi2011).
Numerical simulations of this axisymmetric expansion flow were carried out on a Cartesian grid with 1024
$\times$
256
$\times$
256 and 2048
$\times$
512
$\times$
512 grid points in the
$x$
,
$y$
and
$z$
directions respectively. The initial configurations were derived from statistically independent homogeneous and isotropic flow simulations which had reached a stationary state after more than five large-eddy turnover times. The Reynolds numbers, based on the Taylor microscale
${\it\lambda}_{0}$
, were
$Re_{{\it\lambda}0}=117$
and
$Re_{{\it\lambda}0}=193$
before the straining was applied and the integral scales
$\ell _{0}$
were 2.68 and 2.66 for the lower and higher grid resolutions respectively. Relevant flow parameters at the beginning of the straining are listed in table 1. Initially, the physical domain size was
$[0,8{\rm\pi}]\times [0,2{\rm\pi}]\times [0,2{\rm\pi}]$
in the
$x$
,
$y$
and
$z$
directions respectively, and the simulation was terminated when the domain had reached
$[0,1.1{\rm\pi}]\times [0,5.4{\rm\pi}]\times [0,5.4{\rm\pi}]$
to prevent the physical domain from becoming too flattened.
Figure 2(a–c) shows snapshots of the fluctuating velocity magnitude at three time instants during the straining. From (a) to (c), the non-dimensional times are
$S\times t=0.08$
(shortly after the mean strain is applied),
$S\times t=0.64$
and
$S\times t=0.96$
(just before the strain simulation is terminated due the large deformation of the physical domain). Additionally, the figure shows the coordinate system adopted in the text, and the geometry of the simulation domain selected and its deformation. Production of turbulence overwhelms dissipation during the straining, reflected in an increase in the turbulent kinetic energy, most notably in the compressed component (
$x$
). This can be seen in the warmer colours in figure 2(c). Figure 2(d–f) shows isosurfaces of non-dimensional vorticity,
${\it\omega}/({\it\varepsilon}_{0}/{\it\nu})^{1/2}=3.17$
, with
${\it\varepsilon}_{0}=({\it\nu}/2)\langle (\partial u_{i0}/\partial x_{j})(\partial u_{i0}/\partial x_{j})\rangle$
being the initial energy dissipation rate, at the same time instants as above, which is respectively 4.36, 2.86 and 2.43 standard deviations above the mean vorticity magnitude at the three time instants. From the increased number and size of the filaments, we observe that the vorticity is intensified during straining, and the filaments are found to gradually align with the
$y,z$
-plane due to the mean flow extension in the plane.
Figure 2. Snapshots of the magnitude of the fluctuating flow velocity (a–c) and isosurface of the magnitude of vorticity
${\it\omega}=\Vert \boldsymbol{{\rm\nabla}}\times \boldsymbol{u}\Vert$
(d–f) in the deforming domain in a realization of the axisymmetrically expanding flow, from the onset of the straining simulation to the end of the straining simulation at time instants
$S\times t=0.08$
, (a,d),
$0.64$
(b,e) and
$0.96$
(c,f). The size of the simulation domain is denoted in the figure, and its deformation is displayed. The coordinate system adopted in the text is also shown. We simulated the axisymmetric turbulence with two resolutions using
$2048\times 512\times 512$
and
$1024\times 256\times 256$
computational nodes. The illustration shows one of the realizations of the
$1024\times 256\times 256$
, simulations with
$S^{\ast }=21$
(
$S=10$
). The isosurfaces plotted have non-dimensional vorticity
${\it\omega}/({\it\varepsilon}_{0}/{\it\nu})^{1/2}=3.17$
, which is respectively 4.36, 2.86 and 2.43 standard deviations above the mean vorticity magnitude at the three time instants and is chosen to illustrate the flow structure. It should be noted that
${\it\varepsilon}_{0}\equiv ({\it\nu}/2)\langle (\partial u_{i0}/\partial x_{j})(\partial u_{i0}/\partial x_{j})\rangle$
is the initial energy dissipation rate.
Table 1. Flow parameters in the direct numerical simulations, based on the homogeneous isotropic simulation prior to the application of the straining. Here,
$k_{0}\equiv (\langle u_{10}^{2}\rangle +\langle u_{20}^{2}\rangle +\langle u_{30}^{2}\rangle )/2$
is the turbulent kinetic energy,
${\it\epsilon}_{0}\equiv ({\it\nu}/2)\langle (\partial u_{i0}/\partial x_{j})(\partial u_{i0}/\partial x_{j})\rangle$
is the energy dissipation rate,
$\ell _{0}\equiv (u_{0}^{rms})^{3}/{\it\epsilon}_{0}$
is the integral length scale, and the Kolmogorov length scale
${\it\eta}_{0}\equiv ({\it\nu}^{3}/{\it\epsilon}_{0})^{1/4}$
. The subscript
$0$
indicates that the parameter values are taken prior to the straining. (Units are arbitrary.)
2.2. Equations for particle movements
To study Lagrangian aspects of this flow we seed the flow with tracers and inertial particles. Here, we are concerned with particles that are small compared with the smallest length scales present in the flow, and their densities are considerably higher than the fluid density. The particle number densities are furthermore assumed to be sufficiently low so that particle–particle interactions can be ignored. Under the above approximations, the coupling of the particles with the carrier fluid can be ignored.
The Lagrangian equation of inertial particle motion is derived from Newton’s second law, and represents the balance between the forces acting on the particles (inertia and Stokes drag). The equations describing the motion of a particle of diameter
$d_{p}$
and density
${\it\rho}_{p}$
, located at
$\boldsymbol{x}_{p}$
and with instantaneous velocity
$\tilde{\boldsymbol{v}}_{p}$
are (Maxey & Riley Reference Maxey and Riley1983; Bec et al.
Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\boldsymbol{x}_{p}}{\text{d}t}=\tilde{\boldsymbol{v}}_{p}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\tilde{\boldsymbol{v}}_{p}}{\text{d}t}=\frac{1}{{\it\tau}_{p}}(\tilde{\boldsymbol{u}}(\boldsymbol{x}_{p})-\tilde{\boldsymbol{v}}_{p}), & \displaystyle\end{eqnarray}$$
${\it\tau}_{p}={\it\beta}d_{p}^{2}/18{\it\nu}$
is the Stokes relaxation time for the particle and
${\it\beta}=({\it\rho}_{p}-{\it\rho}_{f})/{\it\rho}_{f}$
is the relative density ratio between the particle and the fluid. The Stokes number
$St={\it\tau}_{p}/{\it\tau}_{{\it\eta}}$
characterizes the inertia of a particle in the flow, where
${\it\tau}_{{\it\eta}}$
is the Kolmogorov time scale of the flow.
For the tracer particles (zero inertia), the particle velocity is the same as the fluid velocity at the particle location, which yields the kinematic relation
$$\begin{eqnarray}\frac{\text{d}\boldsymbol{x}_{p}}{\text{d}t}=\tilde{\boldsymbol{u}}(\boldsymbol{x}_{p}).\end{eqnarray}$$
The ordinary differential equations (2.7)–(2.9) are solved numerically by the second-order Adams–Bashforth method. In (2.8) and (2.9), the instantaneous flow velocity at the particle location
$\boldsymbol{x}_{p}$
is evaluated as
$$\begin{eqnarray}\displaystyle \tilde{\boldsymbol{u}}(\boldsymbol{x}_{p})=\boldsymbol{U}(\boldsymbol{x}_{p})+\boldsymbol{u}(\boldsymbol{x}_{p}); & & \displaystyle\end{eqnarray}$$
that is, the mean flow velocity is evaluated at the location of the particle through the formula
$\boldsymbol{U}(\boldsymbol{x}_{p})=(-2Sx_{p},Sy_{p},Sz_{p})$
, and the flow velocity fluctuation is interpolated to the particle position.
We initialize the particles and the fluid velocity with steady-state homogeneous isotropic simulations. The particles are uniformly distributed over the domain prior to the forced homogeneous isotropic simulation being carried out. At the beginning of the straining, at
$t=0$
, we add the mean flow velocity and the acceleration component due to the strain geometry to the existing particle velocity. We conduct simulations with
$1024\times 256^{2}$
and
$2048\times 512^{2}$
collocation points. For the lower-resolution simulation we use 16 independent flow realizations with
$5\times 10^{5}$
particles of each type (six different Stokes numbers) and for the higher-resolution simulations we perform 10 independent flow realizations with
$4\times 10^{5}$
particles of each type. On average, there are 20 particles in a box in Taylor scale and 0.002 in a box in Kolmogorov scale in each realization in the lower-Reynolds-number simulations. In the higher-Reynolds-number simulations, the averages are 4.3 and 0.0002 for a box in the Taylor scale and the Kolmogorov scale respectively. Therefore, for each time instant we have at least
$4\times 10^{6}$
measurements for each type of particle. The numbers of particles were chosen according to previous simulation works in homogeneous isotropic turbulence (Bec et al.
Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006). The error bars in our figures are an estimate of the stability of the measurements by subdividing the full statistics into several smaller subsets.
Table 1 shows the various flow parameters for the simulations performed. The range of strain rates selected is such that its effect on the smallest scales of the flow ranges from being negligible to substantial. The higher strain rates are felt intensely by the large-scale flow, whereas the lower strain rates have mild effects on the large scales. The values of the strain parameters,
$S{\it\tau}_{{\it\eta}0}$
and
$Sk_{0}/{\it\epsilon}_{0}$
, which compare the strain time with the local and global time scales of the flow, indicate the importance of the various terms in the evolution equation of the velocity field.
3. Underlying flow field
We first report the evolution of the turbulent kinetic energy
$k=\langle u_{i}u_{i}\rangle /2$
and vorticity
${\it\omega}=\Vert \boldsymbol{{\rm\nabla}}\times \boldsymbol{u}\Vert$
of the flow in figure 3. The kinetic energy increases exponentially with time for all of the strain rates, although the lower rates display an initial drop in energy and then a subsequent long-term increase. The vorticity grows monotonically with the strain time, but the growth rate displays more sensitivity to the rate of strain applied than in the case of the kinetic energy, as expected.
The short-term rapid-distortion theory (RDT) prediction plotted in figure 3 is derived from the Reynolds stress equation (Pope Reference Pope2000),
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\langle u_{i}u_{j}\rangle =\unicode[STIX]{x1D617}_{ij}+\unicode[STIX]{x1D619}_{ij}^{(r)},\end{eqnarray}$$
where
$\unicode[STIX]{x1D617}_{ij}\equiv -\langle u_{i}u_{k}\rangle (\partial U_{j}/\partial x_{k})-\langle u_{j}u_{k}\rangle (\partial U_{i}/\partial x_{k})$
is the production rate of Reynolds stress,
$\unicode[STIX]{x1D619}_{ij}^{(r)}\equiv \langle (p^{(r)}/{\it\rho})(\partial u_{i}/\partial x_{j}+\partial u_{j}/\partial x_{i})\rangle$
is the rapid pressure rate of strain tensor and
$p^{(r)}$
is the rapid pressure which satisfies
$(1/{\it\rho}){\rm\nabla}^{2}p^{(r)}=-2(\partial U_{i}/\partial x_{j})(\partial u_{j}/\partial x_{i})$
. Right before the straining starts, the initial configuration of the flow is isotropic, and
$\unicode[STIX]{x1D619}_{ij}^{(r)}=-(3/5)\unicode[STIX]{x1D617}_{ij}$
(Pope Reference Pope2000). In an axisymmetric expansion flow, the production rates are
$\unicode[STIX]{x1D617}_{11}=4S\langle (u_{1})^{2}\rangle ,\unicode[STIX]{x1D617}_{22}=-2S\langle (u_{2})^{2}\rangle$
and
$\unicode[STIX]{x1D617}_{33}=-2S\langle (u_{3})^{2}\rangle$
. Therefore, at early times RDT predicts
$$\begin{eqnarray}\langle (u_{1})^{2}\rangle =\langle (u_{10})^{2}\rangle \text{e}^{(8/5)St},\quad \langle (u_{2})^{2}\rangle =\langle (u_{20})^{2}\rangle \text{e}^{-(4/5)St},\quad \langle (u_{3})^{2}\rangle =\langle (u_{30})^{2}\rangle \text{e}^{-(4/5)St},\end{eqnarray}$$
where
$\langle (u_{i0})^{2}\rangle$
represents the initial value of the Reynolds stress (
$\langle (u_{i})^{2}\rangle ,i=1,2,3$
). The turbulent kinetic energy would then have the approximation
$$\begin{eqnarray}\frac{k}{k_{0}}=\frac{1}{3}(\text{e}^{(8/5)st}+2\text{e}^{-(4/5)st}),\end{eqnarray}$$
if we assume
$\langle (u_{10})^{2}\rangle =\langle (u_{20})^{2}\rangle =\langle (u_{30})^{2}\rangle$
in the homogeneous isotropic turbulence right before the application of straining. However, in order for RDT to apply, the parameters must satisfy
$S{\it\tau}_{{\it\eta}}\gg 1$
and
$Sk/{\it\epsilon}\gg 1$
(Batchelor Reference Batchelor1953). Only at the highest rate of strain is the latter constraint weakly satisfied, and therefore one does not observe close matches between the predictions of RDT and the turbulent kinetic energy in simulation data.
Figure 3. (a) Normalized turbulent kinetic energy
$k/k_{0}=(\langle u_{i}u_{i}\rangle /2)/(\langle u_{i0}u_{i_{0}}\rangle /2)$
versus strain time
$S\times t$
. (b) Normalized vorticity
${\it\omega}/{\it\omega}_{0}$
versus strain time. Lines with circle (○), square (▫) and triangle (▵) symbols represent data from
$S^{\ast }=2.1,8.4,21$
in the
$Re_{{\it\lambda}0}=117$
flow respectively. Lines with crosses (
$\times$
), asterisks (*) and pluses (
$+$
) indicate the data from
$S^{\ast }=2.3,9.3,23$
in the
$Re_{{\it\lambda}0}=193$
flow. The solid line with no symbols represents short-term RDT predictions (3.3). Estimates of statistical error bars are shown and are computed according to (3.4), with
$X_{j}$
being
$k/k_{0}$
and
${\it\omega}/{\it\omega}_{0}$
in the
$j$
th realization.
Figure 4(a) shows the evolution of the Reynolds stresses (
$\langle u_{i}^{2}\rangle$
) normalized by the initial turbulent kinetic energy (
$k_{0}$
). The component along the compressed direction (
$x_{1}$
) grows rapidly in most cases, whereas the components along the expanding directions are suppressed or remain roughly constant. At the lowest strain rate all component are suppressed during the simulation time. For large times, RDT predicts an exponential growth of the Reynolds stresses, in the proportions
$\langle u_{1}^{2}\rangle =2\langle u_{2}^{2}\rangle =2\langle u_{3}^{2}\rangle$
. Figure 4(b) shows the evolution of the anisotropy tensor
$\unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /\langle u_{i}u_{i}\rangle -{\it\delta}_{ij}/3$
with time. The curves corresponding to the lowest strain rates markedly deviate from the others as the turbulent kinetic energy decreases during the straining, and the straining motions are fairly mild, even for the largest scales of motions.
Figure 4. (a) The normalized Reynolds stress
$\langle u_{i}^{2}\rangle /k_{0}$
versus the strain time
$S\times t$
. (b) The flow anisotropy tensor
$\displaystyle \unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /\langle u_{i}u_{i}\rangle -{\it\delta}_{ij}/3$
versus the strain time. Solid symbols represent the
$i=1$
component and open symbols represent the
$i=2$
component;
$k_{0}$
is the initial kinetic energy of the fluid prior to the straining. The diamond (♢), pentagram (✩), circle (○), square (▫) and triangle (▵) symbols represent data from
$S^{\ast }=0.21,1.05,2.1,8.4,21$
in the
$Re_{{\it\lambda}0}=117$
flow respectively. The blue, green and red lines indicate the data from
$S^{\ast }=2.3,9.3,23$
in the
$Re_{{\it\lambda}0}=193$
flow; solid and dashed lines represent the
$i=1$
and
$i=2$
components. The black solid and dashed lines represent the short-term RDT predictions (3.2). Estimates of statistical error bars on data from
$S^{\ast }=0.21,2.1,21$
in the
$Re_{{\it\lambda}0}=117$
set are shown and are computed according to (3.4), with
$X_{j}$
being
$\langle u_{i}^{2}\rangle /k_{0}$
and
$\unicode[STIX]{x1D623}_{ii}$
in the
$j$
th realization.
Again, only at the highest rate of strain does the situation weakly satisfy the
$Sk/{\it\epsilon}\gg 1$
constraint for RDT. Therefore, the predictions from RDT in (3.2) and the Reynolds stresses in the simulation data are not matched. The global anisotropy is much less sensitive, and short-term RDT predicts the anisotropy well.
The error bars in figures 3 and 4 indicate the statistical error of the quantities estimated from the finite number of realizations of the flow. That is, in
$N$
realizations of the turbulent flow with a particular strain rate
$S$
, one obtains samples
$\{X_{1},X_{2},\ldots ,X_{N}\}$
of a quantity
$X$
. The estimated standard error is the sample standard deviation of
$\{X_{1},X_{2},\ldots ,X_{N}\}$
divided by
$\sqrt{N}$
. That is,
$$\begin{eqnarray}\frac{\displaystyle \sqrt{\mathop{\sum }_{j=1}^{N}(X_{j}-\overline{X})^{2}}}{\sqrt{N-1}\sqrt{N}}\end{eqnarray}$$
for data from
$N$
realizations; here,
$\overline{X}$
is the mean of
$\{X_{j}\}_{j=1}^{N}$
. In this work, the length of the symmetric error bars in figures 4–9 is twice the estimated statistical error.
Since tracer and inertial particle accelerations occur primarily at the smallest scales of motion, it is useful to look at the effects of the straining on small scales. Figure 5 shows a measure of the small-scale anisotropy, the ratio of the variances of the longitudinal derivatives of the transverse and longitudinal velocity components
$\langle (\partial _{x}u_{2})^{2}\rangle /\langle (\partial _{x}u_{1})^{2}\rangle$
with respect to time. At the highest strain rates, the anisotropy due to the straining is present at the smallest scales of motion, whereas for the lower strain rates, the flow appears to be nearly isotropic at small scales. It should be noted that the isotropic prediction for the ratio is
$\langle (\partial _{x}u_{2})^{2}\rangle /\langle (\partial _{x}u_{1})^{2}\rangle =2$
. The small-scale anisotropy appears to become close to a constant after an initial transition period for the lower strain rates, but a stationary state is not reached at the highest rate of strain for this quantity.
Figure 5. Ratios of the variances of velocity derivatives
$\langle (\partial _{x}u_{2})^{2}\rangle /\langle (\partial _{x}u_{1})^{2}\rangle$
versus the strain time
$S\times t$
. The circle (○), square (▫) and triangle (▵) symbols represent strain rates
$S^{\ast }=Sk_{0}/{\it\epsilon}_{0}=2.1,8.4,21$
from the
$Re_{{\it\lambda}0}=117$
set, and the crosses (
$\times$
), asterisks (*) and pluses (
$+$
) represent strain rates
$S^{\ast }=Sk_{0}/{\it\epsilon}_{0}=2.3,9.3,23$
from the
$Re_{{\it\lambda}0}=193$
set. An estimate of the statistical error bar is shown (within the symbols) and is computed according to (3.4), with
$X_{j}$
being
$\langle (\partial _{x}u_{2})^{2}\rangle /\langle (\partial _{x}u_{1})^{2}\rangle$
in the
$j$
th realization. The solid line shows the theoretical prediction for this ratio in the isotropic turbulence.
Figure 6(a) shows the time evolution of the longitudinal derivative skewness, along the directions of compression and expansion in the flow. Before the straining is applied, the skewness has a value between
$-0.5$
and
$-0.4$
, as expected, but the straining causes a marked change in its value and becomes positive in the expanding direction. The effect in the compressed direction is more subtle, but an increase in magnitude (larger negative values) appears to occur for all strain rates given that the simulation is run for a sufficiently long time. The sign change indicates a change in the small-scale structure of turbulence, namely that vortex structures dominate sheet-like structures, resulting in an inhibition of the energy cascade (Townsend Reference Townsend1951; Betchov Reference Betchov1956; Davidson Reference Davidson2004; Ayyalasomayajula & Warhaft Reference Ayyalasomayajula and Warhaft2006). In figure 2(d–f) the isosurfaces of fixed value of non-dimensional vorticity increase in quantity during the straining, and this increase of vortex structures qualitatively agrees with what we expect from the trend of the skewness.
Figure 6(b) shows the longitudinal kurtosis, a measure of the flow intermittency. Here, the effects are milder in both directions, although a small increase in the kurtosis is noted in the expanding directions (from the expected value of approximately 5–6, Gylfason, Ayyalasomayajula & Warhaft (Reference Gylfason, Ayyalasomayajula and Warhaft2004)).
Figure 6. (a) The skewness in the compression and expansion directions. Solid lines (——):
$\langle (\partial _{x}u_{1})^{3}\rangle /\langle (\partial _{x}u_{1})^{2}\rangle ^{3/2}$
. Dashed lines (– – –):
$\langle (\partial _{y}u_{2})^{3}\rangle /\langle (\partial _{y}u_{2})^{2}\rangle ^{3/2}$
. (b) The kurtosis in the compression and expansion directions. Solid lines (——):
$\langle (\partial _{x}u_{1})^{4}\rangle /\langle (\partial _{x}u_{1})^{2}\rangle ^{2}$
. Dashed lines (– – –):
$\langle (\partial _{y}u_{2})^{4}\rangle /\langle (\partial _{y}u_{2})^{2}\rangle ^{2}$
. In both plots the circles (○), squares (▫) and triangles (▵) represent strain rates
$S^{\ast }=Sk_{0}/{\it\epsilon}_{0}=2.1,8.4,21$
from the
$Re_{{\it\lambda}0}=117$
set, and the crosses (
$\times$
), asterisks (*) and pluses (
$+$
) represent strain rates
$S^{\ast }=Sk_{0}/{\it\epsilon}_{0}=2.3,9.3,23$
from the
$Re_{{\it\lambda}0}=193$
set. An estimate of the statistical error bar is shown and is computed according to (3.4), with
$X_{j}$
being the skewness and kurtosis in the
$j$
th realization.
4. Particle acceleration statistics and discussion
The non-uniform mean velocity field has a significant effect on the dynamics of tracers and inertial particles, both directly via the mean flow velocity and indirectly through the strained turbulent field.
4.1. Tracer accelerations in straining flow
The full acceleration of tracer particles in our flow is given by the equation
$$\begin{eqnarray}\widetilde{a}_{p_{i}}=\frac{\text{D}\tilde{u} _{p_{i}}}{\text{D}t}=\frac{\text{D}u_{p_{i}}}{\text{D}t}+u_{p_{j}}\frac{\partial U_{p_{i}}}{\partial x_{j}}+U_{p_{j}}\frac{\partial U_{p_{i}}}{\partial x_{j}},\quad i=1,2,3,\end{eqnarray}$$
where the material derivative
$\text{D}/\text{D}t=\partial /\partial t+\tilde{u} _{p_{i}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}$
. The subscript
$p$
indicates that the full instantaneous flow velocity
$\tilde{u} _{p_{i}}$
, the fluctuating flow velocity
$u_{p_{j}}$
and the mean flow velocity
$U_{p_{i}}$
are taken at the location of the tracer. Here, we have assumed that the mean flow is time-independent. The mean of the tracer acceleration is
$U_{p_{j}}(\partial U_{p_{i}}/\partial x_{j})$
, equal to the acceleration in a laminar flow of the same strain geometry. We are interested in the statistics of the tracer acceleration fluctuation, that is, when the pure mean flow contribution to the acceleration has been subtracted:
$$\begin{eqnarray}a_{p_{i}}=\frac{\text{D}u_{p_{i}}}{\text{D}t}+u_{p_{j}}\frac{\partial U_{p_{i}}}{\partial x_{j}},\quad i=1,2,3.\end{eqnarray}$$
The first term on the right-hand side refers to the material derivative of the fluctuating velocity field and represents the acceleration experienced by the fluid particle advected by the fluctuating flow field, and the second term refers to the tracer acceleration induced by turbulent transport in the mean velocity field.
In the variance of acceleration, the cross-terms give rise to
$\langle (\text{D}u_{p_{i}}/\text{D}t)u_{p_{i}}\rangle$
(no sum over
$i$
), representing the time derivative of the kinetic energy in the
$i$
th component of velocity. In addition, the latter term describes contributions of velocity variances, notably
$(2S)^{2}\langle (u_{p_{1}})^{2}\rangle$
and
$S^{2}\langle (u_{p_{2}})^{2}\rangle$
for the first and second component respectively. These terms are easily evaluated if the statistics of flow velocity fluctuations are available.
4.1.1. Approximate tracer acceleration variances using RDT
When the straining is sufficiently rapid, the nonlinear and viscous forces can be neglected in the Navier–Stokes equations, for (adequately) short times (e.g. see Pope Reference Pope2000), and therefore their solution is particularly convenient in comparison to solving the full Navier–Stokes equations. Below, we rederive the RDT predictions for the evolution of the fluctuating velocity variances, as well as deriving the prediction of RDT on the evolution of the tracer acceleration variance.
In RDT, each Fourier mode evolves independently. Let us consider a single mode of the fluctuating velocity,
$$\begin{eqnarray}\displaystyle \boldsymbol{u}(\boldsymbol{x},t)=\hat{\boldsymbol{u}}_{{\bf\kappa}}(t)\text{e}^{\text{i}{\bf\kappa}(t)\boldsymbol{\cdot }\boldsymbol{x}}. & & \displaystyle\end{eqnarray}$$
The wavenumber and the Fourier coefficients evolve according to the following set of equations (Pope Reference Pope2000):
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}{\it\kappa}_{\ell }}{\text{d}t}=-{\it\kappa}_{j}\frac{\partial U_{j}}{\partial x_{\ell }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\hat{u} _{j}}{\text{d}t}=-\hat{u} _{k}\frac{\partial U_{\ell }}{\partial x_{k}}\left({\it\delta}_{j\ell }-2\frac{{\it\kappa}_{j}{\it\kappa}_{\ell }}{|{\bf\kappa}|^{2}}\right). & \displaystyle\end{eqnarray}$$
$\boldsymbol{U}=(-2Sx,Sy,Sz)$
, has been applied, equation (4.4) results in 
$$\begin{eqnarray}{\it\kappa}_{\ell }(t)={\it\kappa}_{\ell }^{0}\text{e}^{-\unicode[STIX]{x1D61A}_{\ell }t},\quad \ell =1,2,3,\end{eqnarray}$$
where
$\unicode[STIX]{x1D61A}_{1}=-2S,\unicode[STIX]{x1D61A}_{2}=\unicode[STIX]{x1D61A}_{3}=S$
and
$|{\bf\kappa}|^{2}=({\it\kappa}_{1}^{0})^{2}\text{e}^{4St}+({\it\kappa}_{2}^{0})^{2}\text{e}^{-2St}+({\it\kappa}_{3}^{0})^{2}\text{e}^{-2St}$
. Similarly, for
$\hat{u} _{j}$
, equation (4.5) gives
$$\begin{eqnarray}\displaystyle \frac{\text{d}\hat{u} _{j}}{\text{d}t}=2S\hat{u} _{1}\left({\it\delta}_{1j}-2\frac{{\it\kappa}_{j}{\it\kappa}_{1}}{|{\bf\kappa}|^{2}}\right)-S\hat{u} _{2}\left({\it\delta}_{2j}-2\frac{{\it\kappa}_{j}{\it\kappa}_{2}}{|{\bf\kappa}|^{2}}\right)-S\hat{u} _{3}\left({\it\delta}_{3j}-2\frac{{\it\kappa}_{j}{\it\kappa}_{3}}{|{\bf\kappa}|^{2}}\right). & & \displaystyle\end{eqnarray}$$
In particular, when
$S$
is large and
$t$
is small, we have
$$\begin{eqnarray}\displaystyle \frac{\text{d}\hat{u} _{1}}{\text{d}t}\approx -2S,\quad \frac{\text{d}\hat{u} _{2}}{\text{d}t}\approx -S,\quad \frac{\text{d}\hat{u} _{3}}{\text{d}t}\approx -S. & & \displaystyle\end{eqnarray}$$
Taking the material derivative of the single-mode-flow fluctuating velocity, we have
$$\begin{eqnarray}\frac{\text{D}u_{1}}{\text{D}t}\approx -2Su_{1},\quad \frac{\text{D}u_{2}}{\text{D}t}\approx -Su_{2},\quad \frac{\text{D}u_{3}}{\text{D}t}\approx -Su_{3}.\end{eqnarray}$$
Figure 7. Normalized acceleration variances of passive tracers in the compressed and expanding directions versus the strain time at various strain rates. The solid and empty symbols represent the compressed and expanding directions respectively. The solid (——) and dashed (– – –) lines indicate RDT long-term predictions of the tracer acceleration variances from the straining together with normalized flow acceleration variances in homogeneous isotropic turbulence (HIT) shown in (4.10). The dash-dot line (– ⋅ – ⋅ –) indicates the term
$a_{0}/(\langle {\it\epsilon}\rangle ^{3}/{\it\nu})^{1/2}$
for the
$S^{\ast }=Sk_{0}/{\it\epsilon}_{0}=0.21$
case. The diamonds (♢), circles (○), squares (▫) and triangles (▵) mark the normalized tracer acceleration variances in dimensionless strain rates
$S^{\ast }=Sk_{0}/{\it\epsilon}_{0}=0.21,2.1,8.4$
and
$21$
. (a) Tracer acceleration variances in different strain rates in
$Re_{{\it\lambda}0}=117$
. (b) Tracer acceleration variances in
$S^{\ast }=8.4$
in
$Re_{{\it\lambda}0}=117$
(squares (▪, ▫), compressed and expanding directions respectively) and
$S^{\ast }=9.3$
in
$Re_{{\it\lambda}0}=193$
(asterisks (*) and pluses (
$+$
), compressed and expanding directions respectively). An estimate of the statistical error bar is shown and is computed according to (3.4), with
$X_{j}$
being
$\langle a_{p_{i}}^{2}\rangle /\sqrt{{\it\epsilon}_{0}^{3}/{\it\nu}}$
in the
$j$
th realization.
Therefore, the anisotropic contribution to
$\langle (\text{D}u_{i}/\text{D}t)^{2}\rangle$
can be estimated as
$\unicode[STIX]{x1D61A}_{(i)}^{2}\langle (u_{i})^{2}\rangle$
, where
$\unicode[STIX]{x1D61A}_{1}=-2S,\unicode[STIX]{x1D61A}_{2}=\unicode[STIX]{x1D61A}_{3}=S$
represent the strain rates in different directions. Together with the normalized acceleration variances
$a_{0}\equiv (1/3)\langle a_{i}a_{i}\rangle /(\langle {\it\epsilon}_{0}\rangle ^{3}/{\it\nu})^{1/2}$
at the beginning of the straining (Voth et al.
Reference Voth, Porta, Crawford, Alexander and Bodenschatz2002), the magnitude of tracer fluctuating acceleration variance can be approximated as
$$\begin{eqnarray}\langle (a_{p_{i}})^{2}\rangle \approx a_{0}\left(\frac{\langle {\it\epsilon}\rangle ^{3}}{{\it\nu}}\right)^{1/2}+2\unicode[STIX]{x1D61A}_{(i)}^{2}\langle (u_{i})^{2}\rangle +\unicode[STIX]{x1D61A}_{(i)}\frac{\text{d}\langle (u_{i})^{2}\rangle }{\text{d}t},\quad i=1,2,3,\end{eqnarray}$$
where the first term represents the isotropic contribution to acceleration variances with dependence on the turbulence intensity, and all of the terms on the right-hand side are Eulerian quantities of the straining flow. Here,
$\langle {\it\epsilon}_{0}\rangle$
is the mean energy dissipation rate in homogeneous isotropic turbulence across all realizations, and
$\langle {\it\epsilon}\rangle$
is the time-dependent mean energy dissipation rate in the straining turbulence across all realizations.
Figure 7 shows the acceleration variances of passive tracers in the straining flow. The variance is higher in the compression direction than in the expanding directions due to the mean straining geometry, and the effects are seen immediately after the strain has been imposed. The approximations derived above, applying RDT, fit nicely to the simulation data, as shown. The change in the isotropic dissipation rate due to straining is accounted for in the first term of (4.10), and the rest of the terms involve the mean strain and the velocity fluctuations. The mean strain causes a rapid increase in the acceleration variance as the strain is applied, particularly at the higher rate of strain. The subsequent increase and the differences between the individual components are partially due to the evolution of the velocity variances for each component; namely that the compressed velocity components are emphasized (increasing energy content) whereas the expanding velocity components are either suppressed or maintained.
4.2. Inertial particle accelerations in straining flow
The differential equations for the particle position as a function of time, obtained by combining the mean flow components in (2.3) with (2.7) and (2.8), are second-order linear ordinary differential equations with constant coefficients:
$$\begin{eqnarray}\displaystyle \frac{\text{d}^{2}x_{p_{i}}}{\text{d}t^{2}}+\frac{1}{{\it\tau}_{p}}\frac{\text{d}x_{p_{i}}}{\text{d}t}-\frac{\unicode[STIX]{x1D61A}_{i}}{{\it\tau}_{p}}x_{p_{i}}=\frac{1}{{\it\tau}_{p}}u_{i},\quad i=1,2,3. & & \displaystyle\end{eqnarray}$$
The roots
$\displaystyle {\it\lambda}_{1,2}=(-1\pm \sqrt{1+4\unicode[STIX]{x1D61A}_{i}{\it\tau}_{p}})/(2{\it\tau}_{p})$
of the characteristic equations of these equations prescribe the behaviour of particle movements in the absence of turbulence. In the compression direction, the combination of strain rates
$S$
and the Stokes relaxation time
${\it\tau}_{p}$
in our simulations gives rise to the discriminant
$D_{1}=1-8S{\it\tau}_{p}$
, which separates two possible movements: an overdamped decay motion towards the stagnation plane
$x=0$
or an underdamped oscillation about the stagnation plane. In the expanding direction the discriminant
$D_{2,3}=1+4S{\it\tau}_{p}$
is always positive, and particles move away from the axis
$y=z=0$
exponentially in time when only mean flow is considered. The accelerations of particles follow a similar patten.
When turbulent fluctuations are present in the strained flow, the statistical description of the dynamics of the inertial particles becomes much more complicated. Treating the fluctuating flow velocity as a source term, one can solve the equations formally using the Laplace transform. Specifically, the formal expressions of the particle accelerations are as follows.
In the compression direction,
$$\begin{eqnarray}\displaystyle D_{1}>0, & & \displaystyle \nonumber\\ \displaystyle \widetilde{a}_{p_{1}}(t) & = & \displaystyle \frac{1}{{\it\lambda}_{1}-{\it\lambda}_{2}}\left[({\it\lambda}_{2}^{2}({\it\lambda}_{1}+2S)\text{e}^{{\it\lambda}_{2}t}-{\it\lambda}_{1}^{2}({\it\lambda}_{2}+2S)\text{e}^{{\it\lambda}_{1}t})x_{p0}+({\it\lambda}_{1}^{2}\text{e}^{{\it\lambda}_{1}t}-{\it\lambda}_{2}^{2}\text{e}^{{\it\lambda}_{2}t})v_{p_{1}0}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{1}{{\it\tau}_{p}}\int _{0}^{t}u_{1}(\boldsymbol{x}_{p}({\it\tau}),{\it\tau})({\it\lambda}_{1}^{2}\text{e}^{{\it\lambda}_{1}(t-{\it\tau})}-{\it\lambda}_{2}^{2}\text{e}^{{\it\lambda}_{2}(t-{\it\tau})})\,\text{d}{\it\tau}\right]+\frac{1}{{\it\tau}_{p}}u_{1}(\boldsymbol{x}_{p}(t),t);\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{1}<0, & & \displaystyle \nonumber\\ \displaystyle \widetilde{a}_{p_{1}}(t) & = & \displaystyle \text{e}^{-t/(2{\it\tau}_{p})}\left[-\frac{1}{{\it\tau}_{p}}v_{p_{1}0}\cos ({\it\omega}t)+\frac{1}{2{\it\tau}_{p}^{2}{\it\omega}}((1-4S{\it\tau}_{p})v_{p_{1}0}+8S^{2}{\it\tau}_{p}x_{p0})\sin ({\it\omega}t)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{1}{{\it\tau}_{p}^{2}}\int _{0}^{t}u_{1}(\boldsymbol{x}_{p}({\it\tau}),{\it\tau})\text{e}^{{\it\tau}/(2{\it\tau}_{p})}\left(\cos ({\it\omega}(t-{\it\tau}))+\frac{4S{\it\tau}_{p}-1}{2{\it\tau}_{p}{\it\omega}}\sin ({\it\omega}(t-{\it\tau}))\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{{\it\tau}_{p}}u_{1}(\boldsymbol{x}_{p}(t),t).\end{eqnarray}$$
In these expressions,
$$\begin{eqnarray}{\it\lambda}_{1,2}=-\frac{1}{2{\it\tau}_{p}}(1\pm \sqrt{1-8S{\it\tau}_{p}}),\quad {\it\omega}=\frac{1}{2{\it\tau}_{p}}\sqrt{8S{\it\tau}_{p}-1}\end{eqnarray}$$
as well as the Stokes relaxation time
${\it\tau}_{p}$
determine the time scales for various contributions to inertial particle accelerations.
$x_{p0}$
and
$v_{p_{1}0}$
are the position and velocity of the particle right before the straining starts (at
$t=0^{-}$
). In the expanding direction
$y$
(the expression in the
$z$
direction is similar),
$$\begin{eqnarray}\displaystyle \widetilde{a}_{p_{2}}(t) & = & \displaystyle \frac{1}{{\it\lambda}_{1}-{\it\lambda}_{2}}\left[({\it\lambda}_{2}^{2}({\it\lambda}_{1}-S)\text{e}^{{\it\lambda}_{2}t}-{\it\lambda}_{1}^{2}({\it\lambda}_{2}-S)\text{e}^{{\it\lambda}_{1}t})y_{p0}+({\it\lambda}_{1}^{2}\text{e}^{{\it\lambda}_{1}t}-{\it\lambda}_{2}^{2}\text{e}^{{\it\lambda}_{2}t})v_{p_{2}0}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{1}{{\it\tau}_{p}}\int _{0}^{t}u_{2}(\boldsymbol{x}_{p}({\it\tau}),{\it\tau})({\it\lambda}_{1}^{2}\text{e}^{{\it\lambda}_{1}(t-{\it\tau})}-{\it\lambda}_{2}^{2}\text{e}^{{\it\lambda}_{2}(t-{\it\tau})})\,\text{d}{\it\tau}\right]+\frac{1}{{\it\tau}_{p}}u_{2}(\boldsymbol{x}_{p}(t),t).\end{eqnarray}$$
Similarly,
$y_{p0}$
and
$v_{p_{2}0}$
are the position and velocity of the particle at
$t=0^{-}$
, and
$$\begin{eqnarray}{\it\lambda}_{1,2}=-\frac{1}{2{\it\tau}_{p}}(1\pm \sqrt{1+4S{\it\tau}_{p}}).\end{eqnarray}$$
The mean flow influences the variances when the full acceleration is considered, and this is also the case for other statistics involving the full particle velocity or acceleration. Since the magnitude of the mean flow velocity depends on the location in the domain, the magnitudes of the variances of acceleration components are characterized by the domain size in the respective directions (through the initial positions
$x_{p0}$
,
$y_{p0}$
in the acceleration expressions (4.12), (4.13) and (4.15)) in addition to the rate of strain.
In an attempt to minimize the influence of the mean flow, in addition to ensuring that our statistics are deduced from sufficiently many independent samples, we condition our inertial particle analysis on particles that started in a thin layer parallel to and next to the
$x=0$
plane for the
$x$
component statistics and a thin layer parallel to and next to the
$y=0$
plane for the
$y$
component statistics. For the dimensionless strain rates
$S^{\ast }=2.1$
and
$S^{\ast }=21$
we use layers with thicknesses of eight lattice units in the
$Re_{{\it\lambda}0}=117$
simulations. For
$S^{\ast }=8.4$
and
$S^{\ast }=21$
flows, we use layers with thicknesses of four and two lattice units. With the selected thicknesses, we ensure that the difference of the mean flow velocities within the layers does not exceed 55 % of
$u_{1}^{rms}$
in the compression direction and does not exceed 77 % of
$u_{2}^{rms}$
in the expanding direction. The numbers of particles available in the layers decreases with the thickness of the layers from approximately 61 500 in
$S^{\ast }=2.1$
flows to 15 500 in
$S=21$
flows in the compression direction. In the expanding direction, the number of particles used for the analysis decreases from 240 000 in
$S^{\ast }=2.1$
to 60 700 in
$S^{\ast }=21$
. We also apply the symmetry with respect to the planes
$x=0$
and
$y=0$
.
Figure 8 shows the acceleration variance of inertial particles in the straining flow for two particle types,
${\it\tau}_{p}=0.015$
and
${\it\tau}_{p}=0.05$
, which correspond to
$St_{0}={\it\tau}_{p}/{\it\tau}_{{\it\eta}0}=0.3$
and
$1$
at the beginning of the straining. These two types of particles have positive discriminants in
$S^{\ast }=2.1$
, correspond to
$D_{1}>0$
and
$D_{1}<0$
in
$S^{\ast }=8.4$
, and have negative discriminants in
$S^{\ast }=21$
.
Figure 8. Acceleration variances of inertial particles in the compressed (solid symbols) and expanding (empty symbols) directions versus the strain time for two types of particles, (a)
$St_{0}=0.3$
and (b)
$St_{0}=1$
. The symbols refer to different strain rates: diamond (♢),
$S^{\ast }=0.21$
; circle (○),
$S^{\ast }=2.1$
; square (▫),
$S^{\ast }=8.4$
; triangle (▵),
$S^{\ast }=21$
. The data are from the data set
$Re_{{\it\lambda}0}=117$
. An estimate of the statistical error bar is shown and is computed according to (3.4), with
$X_{j}$
being particle acceleration variances in the
$j$
th realization.
4.2.1. Initial transition period of acceleration variances
The acceleration variances of the inertial particles show a transition period at the beginning of the straining that is not seen in the tracer accelerations. Equations (4.12) and (4.13) indicate that the initial position
$x_{p0}$
and velocity
$v_{p_{1}0}$
of an inertial particle affect its acceleration. The time scale of this influence depends on the exponents of the exponential terms in the acceleration expressions. In the compression direction, if
$D_{1}<0$
the decaying rate is
$2{\it\tau}_{p}$
. If
$D_{1}>0$
, both
${\it\lambda}_{1}$
and
${\it\lambda}_{2}$
are negative, so the decaying rate is
$\min (1/|{\it\lambda}_{1}|,1/|{\it\lambda}_{2}|)=1/|{\it\lambda}_{2}|$
. This explains the different lengths of the initial transition period for particles with different Stokes numbers in flows with a fixed strain rate. In figure 9(a) we show acceleration variances of particles with
${\it\tau}_{p}=0.01$
and
$0.1$
, which correspond to
$St_{0}=0.2$
and
$2$
, in
$S^{\ast }=8.4$
to elucidate the time scale for initial transition. The ratio between the decaying rates of these two types of particles is approximately 1.75.
Figure 9. Acceleration variances for tracers and inertial particles with
$St_{0}=0.2,2$
. Lines with circles (○),
$St_{0}=2$
; lines with triangles (▵),
$St_{0}=0.2$
; solid lines with solid symbols,
$\langle (\widetilde{a}_{p_{1}})^{2}\rangle$
; dashed lines with empty symbols,
$\langle (\widetilde{a}_{p_{2}})^{2}\rangle$
; solid lines (——), tracers
$\langle (a_{p_{1}})^{2}\rangle$
; dashed lines (– – –), tracers
$\langle (a_{p_{2}})^{2}\rangle$
; (a)
$S^{\ast }=8.4$
, (b)
$S^{\ast }=21$
. The data are from the data set
$Re_{{\it\lambda}0}=117$
. An estimate of the statistical error bar is shown and is computed according to (3.4), with
$X_{j}$
being particle acceleration variances in the
$j$
th realization.
Although
$\langle (u_{2})^{2}\rangle$
decreases with straining,
$\langle \widetilde{a}_{p2}^{2}\rangle$
increases at the beginning and a maximum occurs. This is because
${\it\lambda}_{2}$
is positive in the expanding direction. Similarly to the case discussed in the
$x$
direction, the exponents determine the time scale of the behaviour of acceleration variances. From (4.15) one can estimate the time when the maximum takes place by ignoring the flow fluctuation, and obtain the ratio between the times of maximum acceleration variances of the two particles presented in the figure to be 1.52. It appears that our simulation data confirm such an estimation. For
$S^{\ast }=21$
, our simulations were too short to display the post-transition period.
4.2.2. Magnitude of the acceleration variance
Figure 8 shows that the acceleration variance of inertial particles increases with the strain rate. This is mainly due to the mean flow contributing to the acceleration in terms of the factors
$2S$
and
$S$
in the expressions (4.12), (4.13) and (4.15), and, in a smaller part, through the exponents that regulate the influence of the initial conditions.
At the onset of straining, the acceleration variance in the expanding direction is higher than that in the compression direction. This could be explained through the exponents of the kernels. In the compression direction, the coefficients
${\it\lambda}_{1},{\it\lambda}_{2}$
and
$-1/(2{\it\tau}_{p})$
in the exponents of the kernels in (4.12) and (4.13) are all negative and indicate decay with time. However, for the expanding direction,
${\it\lambda}_{2}=(-1+\sqrt{1+4S{\it\tau}_{p}})/$
$(2{\it\tau}_{p})$
is positive, which leads to the increase of magnitude. For sufficiently long time, the influence of the initial condition is diminished. The magnitude of the flow velocity fluctuation (in the last two terms of the acceleration expressions) in the expanding direction remains roughly constant, while in the compression direction the flow velocity fluctuation grows exponentially. As a result, the acceleration variance in the compression direction overtakes that in the expanding direction.
In contrast to isotropic homogeneous turbulence (Ayyalasomayajula et al.
Reference Ayyalasomayajula, Gylfason, Collins, Bodenschatz and Warhaft2006; Bec et al.
Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006), the acceleration variances of inertial particles do not necessary have lower magnitudes compared with those of tracers in strained flow. The inertial particle with
${\it\tau}_{p}=0.01$
in figure 9(b) depicts such a situation. We recall that (4.10) provides an approximation of tracer acceleration variances, and in higher strain rates the terms
$2\unicode[STIX]{x1D61A}_{i}^{2}\langle (u_{i})^{2}\rangle +\unicode[STIX]{x1D61A}_{i}\text{d}\langle (u_{i})^{2}\rangle /\text{d}t$
are the main contributors to the variances. From figure 4 we know that the variance of the flow fluctuating velocity grows exponentially in time, so its time derivative can be estimated as a constant multiple
$c_{1}S$
(
$c_{1}$
is a constant) of the variance itself. Hence, the main terms in the tracer acceleration variance increase in the order of
$\unicode[STIX]{x1D61A}_{i}^{2}\langle (u_{i})^{2}\rangle$
with the strain rate. For the inertial particles, however, their long-term variance depends on the term
$\langle (u_{i})^{2}\rangle /{\it\tau}_{p}^{2}$
. When
${\it\tau}_{p}$
is small enough, the factor
$1/{\it\tau}_{p}^{2}$
is larger than the magnitude of
$\unicode[STIX]{x1D61A}_{i}^{2}$
, and the inertial particle acceleration variances surpass the tracer acceleration variances.
4.3. Probability density functions of particle accelerations
Figures 10–12 show the particle acceleration p.d.f.s at various rates of strain and at two Reynolds numbers (
$S^{\ast }=2.1,8.4,21$
in
$Re_{{\it\lambda}0}=117$
and
$S^{\ast }=2.3,9.3,23$
in
$Re_{{\it\lambda}0}=193$
) for tracers and inertial particles (
$St_{0}=0.3$
and
$St_{0}=1$
) respectively. The effect of increasing the rate of strain is most notably seen by the narrowed p.d.f. tails for the tracer and inertial particle accelerations.
Figure 10. Normalized p.d.f.s of tracer acceleration and tracer acceleration flatness. (a) The p.d.f. (
$a_{p_{1}}$
) in HIT (circle, ●), straining flow
$S^{\ast }=8.4$
(square, ▪), and
$S^{\ast }=21$
(triangle, ▴). (b) The p.d.f. (
$a_{p_{1}}$
) in HIT (circle, ●,
$Re_{{\it\lambda}0}=117$
; ○:
$Re_{{\it\lambda}0}=193$
) and in straining flow
$S^{\ast }=21$
(▴,
$Re_{{\it\lambda}0}=117$
);
$S^{\ast }=23$
(▵,
$Re_{{\it\lambda}0}=193$
). (c) The p.d.f. (
$a_{p_{1}}$
) and the p.d.f. (
$a_{p_{2}}$
) in
$Re_{{\it\lambda}0}=117$
flow. Circles (●, ○), HIT; squares (▪, ▫),
$S^{\ast }=8.4$
; triangles (▴, ▵),
$S^{\ast }=21$
. Solid symbols,
$i=1$
component; empty symbols,
$i=2$
component. (d) Tracer acceleration flatness,
$\langle (a_{p_{i}}-\overline{a_{p_{i}}})^{4}\rangle /\langle (a_{p_{i}}-\overline{a_{p_{i}}})^{2}\rangle ^{2}$
, at
$Re_{{\it\lambda}0}=117$
. Solid line (——), HIT; squares (▪, ▫),
$S^{\ast }=8.4$
; triangles (▴, ▵),
$S^{\ast }=21$
. Solid symbols,
$i=1$
component; empty symbols,
$i=2$
component. The p.d.f.s in the straining flow are plotted at a strain time of
$S\times t=0.5$
.
Figure 10(a) demonstrates the narrowing of the tracer acceleration p.d.f.s in straining flow. Figure 10(b) shows that the narrowing effect is milder at the higher Reynolds number due to the faster time response of smaller scales at the higher Reynolds number. The increase in the magnitude of acceleration variances due to the mean straining appears to be the primary reason for the tail narrowing. Figure 10(c) indicates the response of acceleration in the compressed and expanding directions. Although the flow field is very different component-wise, the acceleration p.d.f.s, resulting from tracers following trajectories of small-scale structures in the fluid, are more or less identical. Additionally, the evolution of the acceleration flatness
$\langle (a_{p_{i}}-\overline{a_{p_{i}}})^{4}\rangle /\langle (a_{p_{i}}-\overline{a_{p_{i}}})^{2}\rangle ^{2}$
(a measure of the intermittency of the acceleration) is shown in figure 10(d) for the lower Reynolds number
$Re_{{\it\lambda}0}=117$
, emphasizing the narrowing effect of straining and the difference between components.
Figure 11. Normalized p.d.f.s of particle acceleration components
$\widetilde{a}_{p_{i}}$
for different strain rates, for particles originating in thin slices parallel to the
$x=0$
plane for the
$i=1$
component and to the
$y=0$
plane for the
$i=2$
component. (a,c) Particles with
$St_{0}=0.3$
in
$Re_{{\it\lambda}0}=117$
. (b,d) particles with
$St_{0}=1$
in
$Re_{{\it\lambda}0}=117$
. (a,b) The
$i=1$
component. (c,d) The
$i=2$
component. Circles (●), HIT; squares (▪),
$S^{\ast }=8.4$
; triangles (▴),
$S^{\ast }=21$
. The p.d.f.s in the straining flow are plotted at a strain time of
$S\times t=0.5$
.
In terms of inertial particles, as for isotropic homogeneous turbulence, narrowing of the p.d.f. tails follows an increase in the Stokes number. Figure 11 illustrates the narrowing effects. Such behaviour has been demonstrated in a number of previous studies (Ayyalasomayajula et al.
Reference Ayyalasomayajula, Gylfason, Collins, Bodenschatz and Warhaft2006; Bec et al.
Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006), due to the heavier particles passing through, or selectively filtering, the most rapid motions in the flow field. However, here the situation is more complex, since the acceleration variance is not necessarily smaller for inertial particles, due to the strong effect of the mean flow, as discussed above. Figure 12 shows that the higher Reynolds number has an expanding effect on lighter inertial particle acceleration p.d.f. tails. However, for the heavier particles (
$St_{0}=1$
) in higher strain,
$S^{\ast }=21$
in
$Re_{{\it\lambda}0}=117$
and
$S^{\ast }=23$
in
$Re_{{\it\lambda}0}=193$
, the effect is not as evident in the expanding direction. We note that the Stokes number of a particle increases during the straining due to a decrease in the Kolmogorov time scale. In the lower-Reynolds-number simulations, particle Stokes numbers increase by 24 %, 38 % and 53 % during the straining when the dimensionless strain rate is
$S^{\ast }=2.1,8.4,21$
. In the higher-Reynolds-number simulations, particle Stokes numbers increase by 6 %, 14 % and 21 % during the straining when the dimensionless strain rates are
$S^{\ast }=2.3,9.3,23$
. For example, the Stokes numbers of particles with
$St_{0}=0.3,1$
in the
$Re_{{\it\lambda}0}=117$
flow become
$St=0.36,1.19$
when
$S^{\ast }=8.4$
and
$St=0.39,1.26$
when
$S^{\ast }=21$
at the time instant
$S\times t=0.5$
. The Stokes numbers of particles with
$St_{0}=0.34,1.12$
in the
$Re_{{\it\lambda}0}=193$
flow become
$St=0.41,1.37$
when
$S^{\ast }=23$
at the time instant
$S\times t=0.5$
. The increase of Stokes numbers contributes to the narrowing of the acceleration p.d.f. tails, but to a lesser effect than the increased variances.
Figure 12. Normalized p.d.f.s of particle acceleration components
$\widetilde{a}_{p_{i}}$
for two Reynolds numbers, for particles originating in thin slices parallel to the
$x=0$
plane for the
$i=1$
component and to the
$y=0$
plane for the
$i=2$
component. (a,c) Particles with
$St_{0}=0.3$
in
$Re_{{\it\lambda}0}=117$
and
$St_{0}=0.34$
in
$Re_{{\it\lambda}0}=193$
. (b,d) Particles with
$St_{0}=1$
in
$Re_{{\it\lambda}0}=117$
and
$St_{0}=1.12$
in
$Re_{{\it\lambda}0}=193$
. (a,b) The
$i=1$
component. (c,d) The
$i=2$
component. Circles (●, ○), HIT; triangles (▴, ▵),
$S=10$
. Solid symbols,
$S^{\ast }=21$
,
$Re_{{\it\lambda}0}=117$
; empty symbols,
$S^{\ast }=23$
,
$Re_{{\it\lambda}0}=193$
. The p.d.f.s in the straining flow are plotted at a strain time of
$S\times t=0.5$
.
It is interesting to consider our results in a wider context of flows with non-zero mean components, for example by comparing with the dynamics in shear flow. Gerashchenco et al. (Reference Gerashchenco, Sharp, Neuscamman and Warhaft2008) and Lavezzo et al. (Reference Lavezzo, Soldati, Gerashchenko, Warhaft and Collins2010) considered tracers and inertial particles in a non-uniform shear, namely a turbulent boundary layer. An increased rate of shear, closer to the wall, resulted in an increased acceleration variance in the lateral component but a milder effect in the transverse component, which appears to be consistent with the predictions of (4.2) for their geometry. As a result of the increased acceleration variances, attenuation was found in the tails of the inertial particle acceleration p.d.f.s, as observed in this work.
5. Conclusions
Our results show a strong effect of the mean flow straining on the Lagrangian acceleration statistics, for both passive tracers and inertial particles. The effect of straining is primarily felt in the acceleration variances and p.d.f.s when the rate of strain is sufficiently high such that the strain time scale is of a comparable magnitude to the Kolmogorov time scale. For high rates of strain the magnitude of the acceleration variances is increased significantly and the tails of the normalized acceleration p.d.f.s for tracers and inertial particles narrow. The former effect is well explained by observing the predicted behaviour of the acceleration variance by RDT. Rapid-distortion theory provides us with a relation between the flow velocity variance and the acceleration variance, and illustrates the dependence of the acceleration variance on the rate of strain.
However, the effect is complex, partly due to the connection, or lack thereof, between the particle acceleration component in one direction and the fluid flow in the same direction; a particle trajectory around a strong vortex will result in large acceleration values in the directions normal to the axis of the vortex. However, there is also a direct contribution from the mean straining and fluctuating velocity in the acceleration, resulting, for example, in an increased variance value of the acceleration in both the compressing and expanding directions.
For tracers, the narrowing of the normalized acceleration p.d.f.s stems, therefore, in a complex manner from both of these effects. The same effect is also felt by the lighter inertial particles, given that their inertia is sufficiently small to sample the small-scale motions. Because of their small inertia, the interplay with the mean flow enables their acceleration variance to rise beyond that of the tracers.
When the inertia is further increased, the ballistic particle motion in the rapidly accelerating mean flow becomes increasingly important, leading to Gaussian p.d.f. tails. Here, the particles are swept through the fluid, and the slower large scales of motions are more likely to influence the particles. This could also be seen by the lower magnitude of acceleration variances of the heavier particles compared with the lighter inertial particles. We derived the formal expressions for inertial particle acceleration, and these expressions reveal the complex interplay between flow straining and particle inertia.
Our findings emphasize the importance of the presence of strong mean motions and imposed small-scale anisotropy in particle-laden flows. It is our opinion that the results have relevance to the understanding and modelling of a range of practical deforming or straining flows where inertial particles are important aspects of the process. In particular, we believe that our findings may help in the development of subgrid Lagrangian models for particles in the proximity of straining regimes near stagnation points.
Acknowledgements
We thank Z. Warhaft, P. Gualtieri and M. van Hinsberg for their comments and suggestions. C.-M.L. acknowledges the hospitality of the School of Science and Engineering at Reykjavík University and the Department of Mathematics and Computer Science and the Department of Applied Physics at Eindhoven University of Technology. C.-M.L. and F.T. acknowledge the hospitality from the National Center for Theoretical Sciences (NCTS) in Taipei, Taiwan and from National Taiwan University. This work was partially supported by the Icelandic Research Fund and was partially supported by a research programme of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). Support from COST Actions MP0806 and MP1305 is also kindly acknowledged.
