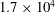1. Introduction
1.1. Background
One of the classical problems in fluid mechanics is predicting the forces imparted to an airfoil in a flow. While solutions for steady lift and drag on an airfoil are well-known, adding airfoil motion to the problem vastly increases its difficulty in every aspect. Because unsteady airfoil motion mandates resolving time-dependent forces, solutions becomes more elaborate theoretically and significantly more expensive computationally. Experimentally, measuring unsteady fluid forces is also much more difficult than measuring steady ones; techniques that work well for steady forces, such as measuring momentum deficit in the wake, can break down in the case of highly unsteady flow. Further, even with direct force measurement one encounters a problem of scale. The experimental apparatus must be robust enough to measure extremely large oscillating forces, yet sensitive enough to accurately report relatively tiny mean forces.
There is more than a just a pedagogic reason for studying the forces on an unsteady airfoil. Just as steady models for airfoil lift and drag find use in designing airplanes, there is recent interest in using oscillating bodies for propulsion and manoeuvering in micro-air vehicles and autonomous underwater vehicles (see, for instance, Platzer & Jones Reference Platzer and Jones2000; Read, Hover & Triantafyllou Reference Read, Hover and Triantafyllou2003; Jones et al. Reference Jones, Bradshaw, Papadopoulos and Platzer2005). Oscillating airfoils have also gained attention as a means of energy extraction from a fluid, such as McKinney & DeLaurier (Reference McKinney and DeLaurier1981), Jones & Platzer (Reference Jones and Platzer1997) and Bryant & Garcia (Reference Bryant and Garcia2009). Finally, understanding the mechanics of flight and propulsion of animals was recognized as a motivation for early theoretical efforts regarding unsteady airfoils, as specifically noted in Garrick (Reference Garrick1936). Researchers have used unsteady fluid mechanics as a tool to understand aspects of biology, such as the theoretical model of fish swimming by Lighthill (Reference Lighthill1970) and calculation of optimal propulsion parameters for aquatic animals (see Triantafyllou, Triantafyllou & Grosenbaugh Reference Triantafyllou, Triantafyllou and Grosenbaugh1993; Triantafyllou, Triantafyllou & Yue Reference Triantafyllou, Triantafyllou and Yue2000; Eloy Reference Eloy2012).
The theoretical groundwork for analysing unsteady airfoils was laid in the first part of the 20th century. The mean propulsive force produced by an airfoil undergoing pitching and/or heaving motions was investigated by Garrick in 1936, building off results by Theodorsen (Reference Theodorsen1935) for unsteady lift forces and von Kármán & Burgers (Reference von Kármán, Burgers and Durand1935) for streamwise forces. This analysis assumes inviscid flow, small amplitudes in the airfoil’s motion, and a non-deforming vortex wake behind the airfoil. Given these conditions, Garrick was doubtful of the theory’s ability to make experimental predictions, noting that ‘quantitative agreement with experimental values …can hardly be expected’. While this concern bears true with the mean thrust (where viscous drag and wake deformation are important), we will show that linear theory is surprisingly accurate in predicting the thrust’s unsteady amplitude and phase.
More recently, there has been a wealth of experimental and computational research on flapping airfoils and plates and their suitability for propulsion. Apart from a variety of outstanding papers dealing with more biomimetic systems, noteworthy reviews of elementary flat-plate and airfoil studies include McCroskey (Reference McCroskey1982), Rozhdestvensky & Ryzhov (Reference Rozhdestvensky and Ryzhov2003) and Platzer et al. (Reference Platzer, Jones, Young and Lai2008). In the present study, we are interested in the 2D fluid mechanics of an oscillating NACA 0012 airfoil at low Reynolds number. A direct numerical simulation of heaving motion by Tuncer & Platzer (Reference Tuncer and Platzer1996) at a Reynolds number of
$3\times 10^{6}$
reported propulsive efficiencies reaching 70 % for this type of airfoil section. For the case of combined pitching and heaving of a NACA 0012 airfoil, experiments by Anderson et al. (Reference Anderson, Streitlien, Barrett and Triantafyllou1998) showed that certain parameter choices could produce a propulsive efficiency reaching 87 % at a Reynolds number of 40 000. An experimental study by Heathcote & Gursul (Reference Heathcote and Gursul2007) for pure heaving at Reynolds numbers of 10 000, 20 000 and 30 000 showed propulsive efficiencies under 28 %. These figures agree with computations by Ashraf, Young & Lai (Reference Ashraf, Young and Lai2012) for the same heaving airfoil at a Reynolds number of 20 000 that show propulsive efficiencies under 30 %. Experimental studies of finite-span pitching plates by Buchholz & Smits (Reference Buchholz and Smits2008) show much lower propulsive efficiencies in the range of 10–20 %. Interestingly, the researchers find that the panel aspect ratio does not strongly affect measurements of propulsive efficiency. This conclusion is echoed in an earlier computational study by Dong, Mittal & Najjar (Reference Dong, Mittal and Najjar2006) at a much lower Reynolds number of 200.
1.2. Previous results for pure pitching
The analysis by Garrick treats a flat-plate airfoil with specified heaving amplitude, pitching amplitude, pitching axis, phase between heaving and pitching, as well as motion of an attached aileron. Because there are too many independent kinematic parameters to allow for a complete experimental confirmation, it is useful to examine a simpler case where the airfoil only performs pitching motion. This leaves us with three kinematic parameters: the pitching amplitude, frequency and location of the rotational axis. It is also instructive to study pitching-only motion because thrust is produced through purely unsteady means. For a heaving airfoil at low values of reduced frequency, a component of thrust can be attributed as the result of steady effects due to the non-zero apparent angle of attack. In comparison, a pitching foil never has a steady mechanism in its thrust. Further, in the case where both pitching and heaving motion are present and in phase, we can approximate the system as one with pure pitching about a different axis.
One of the principal experimental investigations of thrust from a pitching airfoil comes from Koochesfahani (Reference Koochesfahani1989). In addition to producing flow visualization of the oscillating NACA 0012 airfoil, Koochesfahani estimated its thrust by calculating momentum deficit in the mean wake profile. However, this technique of measuring thrust falls apart as the flow becomes more unsteady, and tends to greatly over-predict the net force (Jones, Dohring & Platzer Reference Jones, Dohring and Platzer1998; Streitlien & Triantafyllou Reference Streitlien and Triantafyllou1998; Ramamurti & Sandberg Reference Ramamurti and Sandberg2001). The presence of strong vortices in the airfoil’s wake invalidates several assumptions used in the mean momentum analysis. Bohl & Koochesfahani (Reference Bohl and Koochesfahani2009) improve on the earlier experiment by presenting a revised set of thrust measurements for a pitching foil after measuring the full unsteady flowfield in the wake. By including a careful accounting of unsteady terms in their thrust calculations, the authors were able to produce thrust estimates that agree much better with existing models and simulations. The present study, by employing direct force measurement, may be compared directly with this type of thrust calculation.
1.3. Research objectives
Our overarching goal is to produce a set of direct, accurate measurements of the forces on a pitching airfoil, parametrized by oscillation amplitude, frequency and Reynolds number. These results are necessary to gauge the accuracy of previous theoretical, computational and experimental approaches to this classical problem. In addition to the mean thrust produced by the airfoil, we are interested in exploring the unsteady forces acting on the airfoil: these have typically attracted less attention in the literature. For the case of unsteady thrust, we are not aware of any previous experimental treatment.
By understanding the true forces on a pitching airfoil, we can make conclusions as to when certain models are appropriate to the problem. When does linear theory or a fast panel code sufficiently capture the fluid dynamics? As another angle towards this question, we examine the flow structure behind the pitching airfoil to look for any connection between its vortex wake and the forces we measure.
1.4. Terms and definitions
One of the difficulties in characterizing the behaviour of an oscillating foil is the large number of parameters that characterize the foil kinematics and fluid mechanics. We can deal with fewer parameters by restricting ourselves to the scenario of pure pitching about a fixed point. We define the kinematics of the airfoil as a sinusoidal oscillation given about its quarter-chord point with frequency
$f$
and amplitude
${\it\theta}_{0}$
, so that
${\it\theta}(t)={\it\theta}_{0}\sin (2{\rm\pi}ft)$
. In terms of fluid mechanics, the flapping frequency of the foil is non-dimensionalized with the freestream velocity
$U_{\infty }$
and airfoil chord length
$c$
to produce the Garrick reduced frequency
$k$
, defined as
$$\begin{eqnarray}k=\frac{2{\rm\pi}fc}{2U_{\infty }}.\end{eqnarray}$$
The reduced frequency is proportional to the number of flapping wavelengths per airfoil chord length. A related definition is the Strouhal number based on the wake width
$A$
:
$\mathit{St}_{A}=fA/U_{\infty }$
. Because the wake width is difficult to determine in practice, we replace it with the vertical peak-to-peak excursion of the airfoil’s trailing edge:
$$\begin{eqnarray}\mathit{St}_{A}=\frac{fA}{U_{\infty }}=\frac{f2cr_{p}\sin {\it\theta}_{0}}{U_{\infty }}.\end{eqnarray}$$
Here,
$r_{p}$
is the non-dimensional distance from the pivot point to the trailing edge (for pitching at the quarter-chord,
$r_{p}=0.75$
). For small values of
${\it\theta}_{0}$
, the Strouhal number is proportional to the reduced frequency times the oscillation amplitude.
The quantities we are most interested in for the pitching airfoil are its thrust, power and propulsive efficiency. We report these quantities non-dimensionally as
$C_{T}=\overline{F_{x}}/(({\it\rho}U_{\infty }^{2}ch/2))$
,
$C_{P}=\overline{P}/(({\it\rho}U_{\infty }^{3}ch/2))$
and
${\it\eta}=C_{T}/C_{P}$
, respectively, where
$h$
is the submerged length of the foil section. The propulsive efficiency represents the ratio of useful thrust power to the total power imparted to produce the airfoil’s oscillatory motion.
Figure 1. Illustration of the experimental set-up on the Cornell-AFOSR hybrid water channel facility. The flow direction is from left to right.
2. Experimental set-up
2.1. Physical description
Our experiment is conducted in the Cornell-AFOSR hybrid water channel facility, shown in figure 1. The water channel has a test section width of 38 cm and maximum depth of 46 cm. To facilitate comparison to existing unsteady airfoil studies, we choose a NACA 0012 profile for our airfoil section. The airfoil has a chord length of 10 cm and an aspect ratio of 2.4. We command the channel velocity to produce a desired chord-based Reynolds number for our experiments. In this paper, we examine some cases at
$\mathit{Re}=12\,000$
for the purpose of comparison with previous work, otherwise we use a slightly higher Reynolds number of 16 000 to achieve higher force resolution. To limit airfoil end-effects, we use an endplate attached to the bottom of the channel, positioned with a gap of
$3~\text{mm}$
between itself and the airfoil tip.
Figure 2. Characterization of two-dimensional flow: here we show PIV measurements of the airfoil pitching vigorously at a Reynolds number of 16 600, amplitude
${\it\theta}_{0}=16^{\circ }$
, and reduced frequency
$k=2.35$
. Measurement (a) represents a slice of spanwise vorticity at the airfoil mid-span. Measurement (b) shows vorticity at a plane located
$1/8$
-span from the endplate (airfoil end-effects will be most pronounced on this side). Measurement (c) was performed at the same location, but with the endplate removed.
Although the aspect ratio of the airfoil section is relatively low, it should be noted that the free surface allows the vortex lines to extend upwards and increase their effective aspect ratio. One can also make the case that the aspect ratio of the vortices themselves (rather than the airfoil) is a more relevant parameter for the current arrangement, especially at high oscillating frequencies. Nevertheless, we show an example from a particle image velocimetry (PIV) study to confirm that our end conditions are adequate in creating a nominally two-dimensional flowfield. The PIV measurement in figure 2(b) shows spanwise vorticity produced by a pitching airfoil at a plane located
$1/8$
-span from the endplate. If the flow was highly three-dimensional, vortex lines near the tip would bend back towards the airfoil along the chordwise direction. This bending, in turn, would cause most of the vorticity to leave the plane of the PIV measurement. With the endplate removed, figure 2(c) demonstrates this effect.
Figure 2(b) almost completely matches the vorticity distribution found at the airfoil mid-span (shown in figure 2 a). This tells us that the endplate serves its purpose of keeping shed vortices aligned in the spanwise direction along the vast majority of the airfoil length. While the endplate is able to keep the flow primarily two-dimensional in the vicinity of the airfoil, the shed vorticity will inevitably form three-dimensional structures as it advects downstream. However, by this point the structures are far enough from the airfoil surface that the forces they exert on it are minimal.
The airfoil is attached to a rotational stage driven by a stepper motor, with position feedback provided by a high-resolution rotary encoder. The rotational stage is mounted on a transverse (
$Y$
) stage powered by a brushless linear motor (producing up to 60 pounds force, with an integral
$1~{\rm\mu}\text{m}$
linear encoder). The transverse stage is mounted atop a second stage that provides motion in the streamwise (
$X$
) direction (this one producing up to 120 pounds force, also with a
$1~{\rm\mu}\text{m}$
linear encoder). A computer control system running at 1000 Hz controls the
$X$
and
$Y$
linear motors, both of which achieve less than
$5^{\circ }$
of phase lag while oscillating at 10 Hz. A separate control loop commands the rotational stage, which is capable of oscillating at 8 Hz with
$7^{\circ }$
of phase lag.
2.2. Force measurement
To measure fluid forces and moments, we employ a three-axis force/torque sensor (calibrated to 20 N and 1 N m). To compensate for forces caused by the airfoil section’s inertia, we mount an identical airfoil and sensor out of the flow to directly measure inertial forces. After we rotate and orient force measurements from both sensors back to the lab reference frame, we simply subtract the inertial forces from measurements by the in-fluid airfoil, leaving us with only the fluid forces.
Fluid forces on the pitching airfoil can be very small; for instance, the drag force on our airfoil while stationary is about the equivalent weight of
$0.7~\text{g}$
. On the other hand, unsteady lift forces can reach the equivalent weight of
$0.27~\text{kg}$
. The latter forces and moments dictate the requirements for the force/torque sensor’s measurement range (with an additional safety margin on top). Unfortunately, this means that measurements of the comparatively tiny thrust or drag forces are susceptible to drift and random fluctuations. To achieve precise readings it is therefore necessary to take ensemble averages of repeated experiments; every data point shown in the following figures is the average of 120 identical experiments, each up to 2 min long and rounded to an integer number of oscillation cycles. The process of performing and interpreting these experiments is entirely automated, including stopping the water channel and zeroing the force/torque sensors before and after each run.
At the free surface, we choose our experimental parameters so that significant sloshing or waves do not occur. As an added precaution, each experiment takes place at a randomized position within 3 cm of the channel centreline and inside a 14 cm region in the streamwise direction. Randomizing the initial position controls for some of the electromagnetic interference from the linear stages on the force/torque sensor, as well as helping to reduce resonant wave action within the test section. We use laser Doppler velocimetry (LDV) measurements to confirm flow speed in the airfoil vicinity. While it is difficult to predict blockage for an unsteady flow, models from Garner et al. (Reference Garner, Rogers, Acum and Maskell1966) indicate that steady blockage effects are small for our airfoil section and off-centre effects are negligible for the
$\pm 3~\text{cm}$
experimental region in the transverse direction. Computations by Lian (Reference Lian2010) indicate that blockage effects for a pitching airfoil decrease with increasing reduced frequency and increase with pitching amplitude, an the effects are minimal for a domain width greater than about two chord lengths.
2.3. Pitching about an arbitrary axis
The airfoil section is mounted in such a way that its centre of mass (located 42.04 % of the chord length from the leading edge) is aligned with the axis of the rotational stage, which is coaxial with the force/torque sensors. However, our desired axis of rotation is the quarter-chord point, as illustrated in figure 3. To produce rotation about the desired axis, we combine rotation with translation in the
$X$
and
$Y$
directions such that there is zero velocity at the pivot point (i.e.
${\dot{x}}_{p}={\dot{y}}_{p}=0$
).
Figure 3. Schematic showing coordinates for the airfoil section. The physical attachment point is at the foil’s centroid, while the pivot point is at the quarter-chord.
We specify the foil’s rotation as
$\dot{{\it\theta}}(t)=2{\rm\pi}f{\it\theta}_{0}\cos (2{\rm\pi}ft)$
, where
${\it\theta}_{0}$
is the pitching amplitude. To move the axis of rotation to the quarter-chord point, we introduce the additional kinematics
${\dot{x}}(t)=r\sin ({\it\theta})\dot{{\it\theta}}$
and
${\dot{y}}(t)=-r\cos ({\it\theta})\dot{{\it\theta}}$
. Here,
$r$
represents the distance from the physical attachment point to the desired pitching point. Because the axis of pitching is now different from the axis of the force/torque sensor, we must include these translational velocities when calculating the power input to the airfoil, giving
$P_{in}=-(M_{z}\dot{{\it\theta}}+F_{x}{\dot{x}}+F_{y}{\dot{y}})$
.
2.4. PIV measurements
We take selected PIV measurements of the flow’s velocity field with a
$1600\times 1200$
resolution camera and a light sheet (produced by dual, pulsed Nd:YAG lasers) positioned halfway down the airfoil’s span. The computer control system that commands airfoil motion can additionally output trigger pulses to the PIV camera and laser firing inputs. We use this functionality to produce phase-averaged PIV measurements. By linking the PIV timing directly to the foil movement, we can precisely specify the phase of every PIV image taken, obviating the need for oversampling and grouping PIV measurements. We use a customized MATLAB program based upon the open-source PIVlab software (Thielicke & Stamhuis Reference Thielicke and Stamhuis2012) to analyse and process PIV image pairs.
3. Measurements of mean thrust and efficiency
We show measurements of the airfoil’s mean thrust in figure 4, along with comparisons with existing experimental data. As a point of reference, we have included static drag measurements for the same airfoil at zero angle of attack from Laitone (Reference Laitone1997) and Sheldahl & Klimas (Reference Sheldahl and Klimas1981). These reported values for the static value of thrust coincide well with the corresponding datum in Koochesfahani (Reference Koochesfahani1989) and that of the present study.
Figure 4. Experimentally determined values of thrust coefficient for a NACA 0012 airfoil pitching about its quarter-chord point,
${\it\theta}_{0}=2^{\circ }$
. Present measurements have a 95 % confidence interval of approximately
$\pm 0.0034$
.
The results in figure 4 illustrate the amount by which a simple, steady momentum deficit calculation is liable to overestimate the thrust force on a flapping airfoil, as encountered in Koochesfahani (Reference Koochesfahani1989). Data from Bohl & Koochesfahani (Reference Bohl and Koochesfahani2009), computed from an updated momentum analysis and unsteady wake velocity measurements, agree reasonably well with the present direct force measurements. The agreement fares best at moderate to high values of reduced frequency. However, at lower values of reduced frequency, results from the aforementioned study indicate abnormally high levels of drag on the airfoil, up to twice the static amount. While accounting for unsteady terms in a momentum-deficit thrust calculation produces significant improvement over the steady model, the present results indicate that there is opportunity for further improvement in the unsteady momentum-deficit approach at low flapping frequencies.
Figure 5. Theoretical and computational values for the thrust coefficient of a NACA 0012 airfoil pitching about its quarter-chord point,
${\it\theta}_{0}=2^{\circ }$
: (a) inviscid methods (linear theory and panel codes) with static profile drag added in to facilitate comparison; (b) viscous simulations.
It is also instructive to compare our direct force measurements of thrust with results from theory and simulation. Figure 5 includes a comparison with the inviscid linear theory in Garrick (Reference Garrick1936) and panel codes from Jones & Platzer (Reference Jones and Platzer1997) and Ramamurti & Sandberg (Reference Ramamurti and Sandberg2001). A constant offset representing the viscous, static drag of the airfoil section has been added to these results to present a more meaningful comparison with measured data. The difference in thrust between linear theory and the panel codes is chiefly due to the ability of the vortex wake to leave the plane of the
$x$
-axis and deform under its own influence. The fact that linear theory overestimates thrust much more than the panel codes indicates that the presence of a non-planar wake plays an important role in the propulsion process.
As expected, results from direct numerical simulation of the Navier–Stokes equations (see the lower part of figure 5) match much better with experimental results than the inviscid methods (shown in the upper part of the figure). Our direct force measurement data shows very good agreement with the viscous simulation by Ramamurti & Sandberg (Reference Ramamurti and Sandberg2001). The numerical study by Young & Lai (Reference Young and Lai2004) does not fare as well, though still matches the trend of thrust coefficient versus pitching frequency.
Figure 6. Experimentally determined values of propulsive efficiency for a NACA 0012 airfoil pitching about its quarter-chord point, shown for different values of maximum pitch angle
${\it\theta}_{0}$
. Data are shown for a Reynolds number of 16 600.
In terms of propulsive efficiency, the pitching airfoil performed far below the limit from linear theory (
${\it\eta}=50\,\%$
) and well below peak measured efficiencies for heaving airfoils. Figure 6 shows measured values of propulsive efficiency for different pitching amplitudes as a function of the Strouhal number. Moderate values of
${\it\theta}_{0}$
give similar results for efficiency, reaching a maximum of 12 % for the case of an
$8^{\circ }$
pitching amplitude. As predicted by linear theory, higher pitching amplitudes attain their best efficiency at slightly larger values of Strouhal number.
While the system geometry here is different than that employed in the pitching study by Buchholz & Smits (Reference Buchholz and Smits2008) (which investigates a finite-span section), the results for propulsive efficiency are reasonably similar. This affirms the notion that pure pitching is an inefficient method of producing thrust, even in approximately two-dimensional flow conditions. It is also worth noting that the aforementioned study, along with others such as Triantafyllou et al. (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993), have found that efficiency is maximized at a Strouhal number of around 0.25. However, the presence of surface waves and sloshing at high amplitudes and frequencies prevented us from exploring higher Strouhal numbers with our current experimental arrangement.
Figure 7. The value of reduced frequency
$k$
at which an airfoil pitching at
${\it\theta}_{0}=2^{\circ }$
transitions from net drag to net thrust. At higher Reynolds numbers, the airfoil produces more thrust at a given non-dimensional flapping frequency.
3.1. Effect of Reynolds number on thrust production
Our experimental technique allows us to examine how the thrust properties of the pitching airfoil change with Reynolds number. Figure 7 shows the value of the reduced frequency
$k$
at which the airfoil transitions from producing net drag to net thrust. This crossover point decreases monotonically, indicating that the airfoil becomes more capable of producing thrust at higher Reynolds numbers (recall that
$k$
is already non-dimensionalized by the flow speed).
As the Reynolds number changes we also experience a change in the airfoil’s static drag coefficient
$C_{D0}$
. However, while the decrease of
$C_{D0}$
with Reynolds number does contribute to a decrease in the drag–thrust crossover point, the magnitude of this effect is not enough to produce the data shown in figure 7. The trend of this plot is to be expected given that at higher Reynolds numbers, the inviscid assumption behind Garrick’s analysis becomes more valid. As the thrust predictions from Garrick (Reference Garrick1936) rise quickly with reduced frequency, we in turn see a crossover from drag to thrust at a low value of
$k$
.
Physically speaking, the trend in drag–thrust crossover point versus Reynolds number results from the effect of viscosity on the process of vortex roll-up and shedding. At low Reynolds numbers, it is likely that a thick boundary layer along the airfoil inhibits a sharply localized buildup of vorticity at the airfoil’s trailing edge. With weaker, globular vortices shed behind the airfoil it becomes harder to produce a jet profile in the wake, resulting in decreased thrust production.
Figure 8. Amplitude of the time-varying component of the airfoil’s thrust coefficient, shown for various values of maximum pitch angle
${\it\theta}_{0}$
and compared with predictions from linear theory. Experiments performed at a Reynolds number of 16 600.
4. Measurements of unsteady forces
4.1. Thrust
We can approximate the unsteady part of the thrust force on the airfoil as a sinusoidal force with a frequency double that of the oscillation frequency, i.e.
$F_{T}=A_{T}\sin (2\cdot [2{\rm\pi}f_{{\it\theta}}t-{\it\phi}_{T}])$
. Here,
${\it\phi}_{T}$
represents the phase of the unsteady thrust force behind the pitch oscillation. From before, we concluded that while the linear theory compiled by Garrick (Reference Garrick1936) captured the trend of the mean thrust with frequency, it was not capable of making quantitative predictions. However, figure 8 shows that linear theory is capable of making quantitatively accurate predictions for the oscillation amplitude of the thrust coefficient, even at surprisingly high pitching angles.
Figure 9. Collapse of the data sets shown in figure 8 by scaling with
${\it\theta}_{0}^{2}$
, following the relationship from linear theory.
Figure 9 shows the unsteady thrust amplitude normalized by the square of the pitching angle, as suggested by the linear theory. This scaling works remarkably well across the entire range of pitching angles. Figure 10 presents measurements of the phase
${\it\phi}_{T}$
of the thrust force compared with the prediction from linear theory. Overall, it is remarkable that linear theory, which assumes inviscid flow, a non-deforming wake, and small pitching amplitudes, is able to match experimental measurements to this extent. This result suggests that the unsteady part of the thrust force on a pitching airfoil is (i) largely an inviscid phenomenon and (ii) not strongly dependent on wake features.
At high pitching amplitudes, we would ordinarily expect massively stalled, separated flow to ruin the applicability of inviscid theory. However, it is possible that for medium to high oscillation frequencies we encounter an effect analogous to dynamic stall. The intense vorticity concentrations produced by flapping likely help keep flow attached to the airfoil surface, at least to the extent that inviscid theory produces a passable approximation of the overall fluid dynamics.
Figure 10. Phase of the oscillating component of the airfoil’s thrust coefficient compared with the prediction from linear theory. Phase values represent a delay behind
${\it\theta}(t)$
.
In figures 9 and 10 one can discern a slight jump in thrust amplitude and phase between reduced frequencies of three and four. The point
$k={\rm\pi}$
corresponds to the scenario where the freestream fluid advances one chord length during each oscillation cycle. In other words, this point represents the transition where the oscillation wavelength becomes shorter than a chord length. Physically speaking, the point
$k={\rm\pi}$
occurs during a transition where vorticity shed from the airfoil’s trailing edge begins to roll up and coalesce closer to the airfoil itself, in the near-wake region. This vorticity, which was previously convected downstream, is now concentrated in discrete vortices which exert more thrust on the airfoil.
Figure 11. Amplitude of the lift force acting on the airfoil for different values of pitching angle,
$\mathit{Re}=16\,600$
.
4.2. Lift
For completeness, in addition to the thrust force we measured the unsteady amplitude and phase of the lift force produced by the airfoil. Figure 11 shows the lift force amplitude as a function of reduced frequency for a range of pitching angles. As with the thrust amplitude, the oscillating lift force agrees very well with linear theory from Theodorsen (Reference Theodorsen1935), even at low values of reduced frequency where added-mass effects are less important. While the thrust amplitudes scale with
${\it\theta}_{0}^{2}$
, the theory indicates that the unsteady lift amplitudes scale with
${\it\theta}_{0}$
. As figure 12 demonstrates, this scaling produces a remarkably good collapse of the measured data.
Figure 12. Collapse of the data sets shown in figure 11, produced by scaling with the pitching angle
${\it\theta}_{0}$
.
The good agreement here between unsteady lift forces and linear theory was noted in a combined experimental/computational study by Kang et al. (Reference Kang, Baik, Bernal, Ol and Shyy2009). The authors found that Theodorsen’s model did an excellent job capturing time-varying lift forces when the flow on the airfoil was attached. When there was significant flow separation, the linear theory fared worse, however, the overall force characteristics (i.e. amplitude and phase) were still a reasonably good match.
Figure 13 shows the measured phase of the lift force behind the pitching oscillation. The match with linear theory is reasonable for all pitching amplitudes. As with the thrust force, we see a slight jump in the lift force’s amplitude and phase between reduced frequencies of three and four.
Figure 13. Phase of the lift force behind pitching oscillations, compared with linear theory.
4.3. High-amplitude pitching
Figure 14 shows measurements of mean thrust on the airfoil as a function of Strouhal number for the full series of pitching angles. Thrust measurements for small angle cases (two, four and to a certain extent
$8^{\circ }$
) collapse reasonably well with Strouhal number. However, for larger amplitudes of oscillation a different trend emerges. At a low Strouhal number, the mean thrust force is consistent with its quasi-static value (the asymptote of force as flapping frequency approaches zero). We compute the quasi-static thrust force by integrating the airfoil’s static drag force through a cycle of oscillation, then dividing by the oscillation period. It is interesting that with increasing oscillation frequency, the thrust coefficient for these large-amplitude cases actually decreases. The magnitude of the drag force for the oscillating foil represents a sizeable portion of the static drag force at
${\it\theta}_{0}$
, as illustrated by the bottom portion of the shaded regions in figure 14. One could use this effect in a flapping-foil vehicle to produce a braking force for manoeuvering.
Figure 14. Mean thrust coefficient as a function of Strouhal number, measured for all pitching amplitudes at a Reynolds number of 16 600. Lines shown represent a curve fit through the data. The shaded bands for pitching amplitudes of 8, 16 and
$32^{\circ }$
show a reference interval. The lower bound of the interval represents the airfoil’s maximum static drag force at this angle of attack. The upper part of the interval represents the thrust force as the flapping frequency asymptotically approaches zero, computed from static force data.
5. Vortex dynamics of thrust production
5.1. Motivation for PIV study
In this section we examine PIV vorticity measurements behind the pitching airfoil to elucidate the physical flow processes behind our force measurements. It has long been known that the crossover from net drag to net thrust approximately corresponds to a change in wake from a von Kármán street (vK) to an inverse-vK arrangement (von Kármán & Burgers Reference von Kármán, Burgers and Durand1935). The latter phenomenon is illustrated in figure 2(c) for our airfoil pitching at a Reynolds number of 16 600. Because of profile drag, the inverse-vK arrangement appears slightly before the airfoil produces positive thrust. At somewhat lower values of reduced frequency, previous studies (for example Koochesfahani Reference Koochesfahani1989) have observed the 2P-type vortex arrangement shown in figure 2(b). Here, we borrow the nomenclature of Williamson & Roshko (Reference Williamson and Roshko1988), where
$nS+mP$
indicates
$n$
single vortices and
$m$
vortex pairs per cycle.
Figure 15. Phase-averaged PIV measurements of spanwise vorticity for an airfoil pitching with amplitude
${\it\theta}_{0}=2^{\circ }$
. The vorticity contour levels are identical across all images. (a) At
$k=2$
, we observe synchronization between the flapping motion and small vortices shed from boundary layer rollup. (b) At
$k=5$
there is a distinct 2P vortex mode in the wake. (c) At
$k=9$
, where the airfoil is close to producing net thrust, we observe an inverse-vK wake structure.
We seek to understand how much further the connection extends between vortex shedding modes and forces imparted on the airfoil. Comparison between linear theory and panel codes demonstrates that the presence of discrete vortex formation affects thrust production, however, the role of particular vortex arrangements remains to be determined. Researchers have approached the problem of airfoil flapping through classifying and mapping the observed wake structure. Godoy-Diana, Aider & Wesfreid (Reference Godoy-Diana, Aider and Wesfreid2008) investigated the wake structure behind a pitching airfoil at a Reynolds number on the order of
$10^{4}$
, producing a map of vortex shedding modes and comparing it with a map of net thrust coefficient. Using a soap-film experiment, Schnipper, Andersen & Bohr (Reference Schnipper, Andersen and Bohr2009) produced an even more detailed map of wake vortex structure (including complex modes such as
$6\text{P}+2\text{S}$
). As with the aforementioned studies, we find a vast array of vortex arrangements as we vary the pitching amplitude and frequency. However, aside from the eventual transition to an inverse-vK vortex arrangement, we see no evidence of particular vortex patterns having a distinct effect on force characteristics. The plot of thrust versus frequency shown in figure 4 has a smooth trend, even though the vortex wake transitions through multiple arrangements (some of which are shown in figure 15).
5.2. Why do we see no effects of vortex patterns in force data?
The apparent insensitivity of airfoil force to vortex arrangements hints that the underlying process of thrust production is dominated by the inviscid mechanisms captured in Garrick’s analysis. Although the presence of viscosity and vortex roll-up works to diminish the magnitude of thrust produced, both our measurements and linear theory exhibit a smooth trend in thrust, unaffected by the presence of vortex patterns in the wake. The unexpected agreement of unsteady forces with linear theory echoes this conclusion. (It is important to note, however, that for other types of oscillation (e.g. heaving) the airfoil’s leading edge may play a larger role in shedding vortices that produce a noticeable effect on the thrust force.)
When we consider the flow physics, there are a couple features that may contribute to the disconnect between vortex patterns and thrust forces. For one, vortices downstream of the airfoil exert most of their influence in a direction normal to the airfoil chord line. Even as we move a wake vortex away from the centreline, the incremental change in its
$x$
-direction influence is small. Further, by the time the wake vortex arrangement has stabilized, its effect on the airfoil surface may be small enough that the particular arrangement of vortices is insignificant.
5.3. Effect of vorticity at large pitching amplitudes
One scenario where we do see a clear connection between vortex arrangements and force measurements is when the airfoil pitches at large amplitudes. In figure 14, we observe pronounced dips in the thrust coefficient for 8, 16 and
$32^{\circ }$
oscillations. The Strouhal number where this phenomenon occurs tends to be higher for higher pitching amplitudes (roughly at a value of
$k/{\it\theta}_{0}$
of 0.4). We can explain this drop in thrust force by looking at the wake structure behind the pitching airfoil. Figure 16 shows two PIV measurements at the same pitching phase for a
$32^{\circ }$
oscillation. At a reduced frequency of 0.025 (
$\mathit{St}_{A}=0.0063$
), the flow is entirely separated. The airfoil here experiences forces that are essentially quasi-static. However, at a higher reduced frequency of 0.25 (
$\mathit{St}_{A}=0.063$
), we see a strong vortex retained behind the airfoil’s leading edge. The higher frequency of oscillation allows for a process analogous to dynamic stall, amalgamating leading-edge vorticity into a coherent structure that resists being convected downstream. The low-pressure region created by this leading-edge vortex causes the dramatic increase in drag (decrease in
$C_{T}$
) shown in figure 14.
Figure 16. Phase-averaged PIV measurements of vorticity for pitching with
${\it\theta}_{0}=32^{\circ }$
, both taken at a phase of
$108^{\circ }$
: (a) corresponds to pitching at a reduced frequency
$k=0.025$
, while (b) depicts
$k=0.25$
.
6. Conclusions
We have experimentally investigated the forces acting upon a NACA 0012 airfoil pitching about its quarter-chord point at low Reynolds number. This problem serves as an elementary test case for the study of oscillating foils, and by extension various methods of aquatic and aerial propulsion. By measuring fluid forces directly, we are able to bypass issues related to deriving force measurements from the local flowfield. Our results generally confirm the experimental method employed by Bohl & Koochesfahani (Reference Bohl and Koochesfahani2009), although measurements from the present study are more reasonable at low values of reduced frequency.
By itself, a pure pitching motion is a relatively inefficient mechanism of propulsion, reaching a peak efficiency of only 12 % in our tests. We note that this low efficiency seems to be typical of pitching-only mechanisms. Our measurements of thrust on the airfoil lie slightly below inviscid predictions from panel codes, and significantly below predictions from linear theory. This suggests that the presence of a deforming, non-planar wake influences the mean propulsive force on a pitching airfoil. However, the same cannot be said for the unsteady component of the propulsive force. Linear theory reasonably predicts the unsteady amplitude and phase of both the thrust and lift forces acting on the airfoil, even at high amplitudes of oscillation where one might expect flow separation. We postulate that an effect similar to dynamic stall helps to diminish flow separation effects at moderate to high oscillation frequencies, explaining why linear theory produces a reasonable approximation.
The fact that linear theory produced any utility for our low-Reynolds-number experiments leads us to believe that thrust production of a pitching airfoil is dominated by the inviscid effects captured in Garrick’s analysis. Viscous effects are observed to limit the total magnitude of thrust produced, but do not seem to significantly affect the unsteady dynamics.
Regarding the unsteady lift force on the airfoil, our results confirm the conclusion of Hall & Hall (Reference Hall, Hall and Mueller2001), who compare flapping-wing numerical studies with and without the effects of wake rollup. They find that there is no significant difference in the airfoil’s unsteady lift coefficient between a prescribed wake model and one that is free to deform. Remarkably, our experimental results show an even more drastic relation: unsteady lift forces from small-amplitude, inviscid linear theory agree well with measured forces in an actual viscous flow, even at surprisingly high amplitudes of pitch oscillation (
${\it\theta}_{0}=32^{\circ }$
).
We also use PIV to investigate the vortex wake behind the airfoil at different pitching conditions. Even though we conclude that the presence of a non-planar wake is important in predicting the mean thrust force on the airfoil, at the same time we find little correspondence between the measured mean thrust coefficient and the particular arrangement of vortices in the airfoil’s wake. The mean thrust coefficient tends to increase smoothly and monotonically with flapping frequency (with the exception of the high-amplitude, low-frequency cases discussed in § 3.1), even as the flow passes through several regimes of vortex patterns. This result starkly contrasts with bluff bodies undergoing vortex-induced vibration, where the mode of vortex shedding in the wake is closely related to fluid forces on the immersed body.
The aforementioned observations lead us to believe that the effect of vorticity on the airfoil’s thrust production is highly localized. This would explain why the myriad vortex arrangements that eventually form downstream leave no distinguishing trace on force measurements. Unlike a bluff body, the mode of the vortex wake behind a pitching airfoil seems to be a remnant of force generation, rather than a driver.
Acknowledgements
This work was supported by the Air Force Office of Scientific Research under AFOSR award No. FA9550-11-1-0155, monitored by Dr D. Smith.
