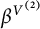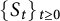1 Introduction
Broadly speaking, the subject of irreversible non-commutative dynamics is concerned with the study of dynamical systems where instead of a group action on a non-commutative space (Hilbert spaces,
![]() $C^{*}$
-algebras, von Neumann algebras), we have a semigroup action. The operator algebraic aspects of such irreversible dynamical systems have received the attention of many authors over the years. Some of the topics that were investigated in detail and continue to be a source for much research are semigroup
$C^{*}$
-algebras, von Neumann algebras), we have a semigroup action. The operator algebraic aspects of such irreversible dynamical systems have received the attention of many authors over the years. Some of the topics that were investigated in detail and continue to be a source for much research are semigroup
![]() $C^{*}$
-algebras [Reference Cuntz, Echterhoff, Li and Yu11], semi-crossed products of non self-adjoint algebras [Reference Davidson, Fuller and Kakariadis13], dilation theory of semigroups of contractions and CP-semigroups [Reference Shalit, Bastos, Castro and Karlovich28],
$C^{*}$
-algebras [Reference Cuntz, Echterhoff, Li and Yu11], semi-crossed products of non self-adjoint algebras [Reference Davidson, Fuller and Kakariadis13], dilation theory of semigroups of contractions and CP-semigroups [Reference Shalit, Bastos, Castro and Karlovich28],
![]() $E_0$
-semigroups and product systems [Reference Arveson8]. This paper comes under the topic of
$E_0$
-semigroups and product systems [Reference Arveson8]. This paper comes under the topic of
![]() $E_0$
-semigroups and product systems.
$E_0$
-semigroups and product systems.
An
![]() $E_0$
-semigroup (CP-semigroup) over a semigroup P on
$E_0$
-semigroup (CP-semigroup) over a semigroup P on
![]() $B(\mathcal {H})$
is a semigroup
$B(\mathcal {H})$
is a semigroup
![]() $\alpha :=\{\alpha _x\}_{x \in P}$
of unital, normal
$\alpha :=\{\alpha _x\}_{x \in P}$
of unital, normal
![]() $^*$
-endomorphisms (CP-maps) of
$^*$
-endomorphisms (CP-maps) of
![]() $B(\mathcal {H})$
. If P has a topology, we require the semigroup
$B(\mathcal {H})$
. If P has a topology, we require the semigroup
![]() $\alpha $
to satisfy an appropriate continuity hypothesis. The study of such semigroups, when
$\alpha $
to satisfy an appropriate continuity hypothesis. The study of such semigroups, when
![]() $P=[0,\infty )$
, has a long history which dates back to Powers’ works [Reference Powers19, Reference Powers20]. Arveson wrote several influential papers on the subject [Reference Arveson4–Reference Arveson7] and also authored [Reference Arveson8] which is the standard reference for the subject. More on Arveson’s contribution and by others to the subject of
$P=[0,\infty )$
, has a long history which dates back to Powers’ works [Reference Powers19, Reference Powers20]. Arveson wrote several influential papers on the subject [Reference Arveson4–Reference Arveson7] and also authored [Reference Arveson8] which is the standard reference for the subject. More on Arveson’s contribution and by others to the subject of
![]() $E_0$
-semigroups can be found in a survey article [Reference Izumi15] by Izumi.
$E_0$
-semigroups can be found in a survey article [Reference Izumi15] by Izumi.
In the last 15 years, several papers [Reference Arjunan1–Reference Arjunan and Sundar3, Reference Murugan and Sundar17, Reference Shalit and Skeide25–Reference Shalit27, Reference Shalit and Solel30, Reference Solel32, Reference Sundar36] appeared where semigroups of endomorphisms/CP-maps and product systems, over more general monoids, were considered. Moreover, it was demonstrated that significant differences show up in the multiparameter case. A few features that are in stark contrast to the
![]() $1$
-parameter case are listed below.
$1$
-parameter case are listed below.
-
(1) A CP-semigroup over
 $\mathbb {N}^{3}$
need not have a dilation to an
$\mathbb {N}^{3}$
need not have a dilation to an
 $E_0$
-semigroup [Reference Shalit and Skeide29].
$E_0$
-semigroup [Reference Shalit and Skeide29]. -
(2) CCR and CAR flows need not be cocycle conjugate in the multiparameter case [Reference Srinivasan33].
-
(3) In the multiparameter case, decomposable product systems need not be spatial [Reference Namitha and Sundar18, Reference Sundar36].
These contrasting phenomena make the multiparameter theory interesting, and the authors believe that multiparameter
![]() $E_0$
-semigroups are objects worthy of investigation. Here, we study a class of
$E_0$
-semigroups are objects worthy of investigation. Here, we study a class of
![]() $E_0$
-semigroups called CAR flows and classify a subclass of them.
$E_0$
-semigroups called CAR flows and classify a subclass of them.
In view of the bijective correspondence between the class of product systems and the class of
![]() $E_0$
-semigroups [Reference Arveson9, Reference Murugan and Sundar17, Reference Skeide31], we explain the problem studied and the results obtained in the language of product systems. A product system is a measurable field of separable Hilbert spaces
$E_0$
-semigroups [Reference Arveson9, Reference Murugan and Sundar17, Reference Skeide31], we explain the problem studied and the results obtained in the language of product systems. A product system is a measurable field of separable Hilbert spaces
![]() $E:=\{E(x)\}_{x \in P}$
endowed with a multiplication that is compatible with the measurable structure.
$E:=\{E(x)\}_{x \in P}$
endowed with a multiplication that is compatible with the measurable structure.
The two simplest product systems, whose definitions we recall, are the ones associated with CCR and CAR flows. Let
![]() $\mathcal {H}$
be a separable Hilbert space. (All Hilbert spaces considered in this paper are tacitly assumed to be separable.) We denote the symmetric Fock space of
$\mathcal {H}$
be a separable Hilbert space. (All Hilbert spaces considered in this paper are tacitly assumed to be separable.) We denote the symmetric Fock space of
![]() $\mathcal {H}$
by
$\mathcal {H}$
by
![]() $\Gamma _s(\mathcal {H})$
and the antisymmetric Fock space of
$\Gamma _s(\mathcal {H})$
and the antisymmetric Fock space of
![]() $\mathcal {H}$
by
$\mathcal {H}$
by
![]() $\Gamma _a(\mathcal {H})$
. Throughout this paper, the letter P stands for a closed, convex cone in
$\Gamma _a(\mathcal {H})$
. Throughout this paper, the letter P stands for a closed, convex cone in
![]() $\mathbb {R}^d$
that is pointed, i.e.,
$\mathbb {R}^d$
that is pointed, i.e.,
![]() $P \cap -P=\{0\}$
and spanning, i.e.,
$P \cap -P=\{0\}$
and spanning, i.e.,
![]() $P-P=\mathbb {R}^d$
. Let
$P-P=\mathbb {R}^d$
. Let
![]() $V:=\{V_x\}_{x \in P}$
be a strongly continuous semigroup of isometries on
$V:=\{V_x\}_{x \in P}$
be a strongly continuous semigroup of isometries on
![]() $\mathcal {H}$
. We call such a semigroup of isometries an isometric representation of P on
$\mathcal {H}$
. We call such a semigroup of isometries an isometric representation of P on
![]() $\mathcal {H}$
. We assume V is pure, i.e.,
$\mathcal {H}$
. We assume V is pure, i.e.,
![]() $\displaystyle \bigcap _{x \in P}V_x\mathcal {H}=\{0\}$
.
$\displaystyle \bigcap _{x \in P}V_x\mathcal {H}=\{0\}$
.
Consider the field of Hilbert spaces
![]() $F^V:=\{F^V(x)\}_{x \in P}$
,
$F^V:=\{F^V(x)\}_{x \in P}$
,
![]() $F^V(x):=\Gamma _s(Ker(V_x^*))$
for
$F^V(x):=\Gamma _s(Ker(V_x^*))$
for
![]() $x \in P$
. We impose a measurable structure on
$x \in P$
. We impose a measurable structure on
![]() $F^V$
as follows. For every
$F^V$
as follows. For every
![]() $x \in P$
, we can view
$x \in P$
, we can view
![]() $F^V(x)$
as a subspace of
$F^V(x)$
as a subspace of
![]() $\Gamma _s(\mathcal {H})$
, as the embedding
$\Gamma _s(\mathcal {H})$
, as the embedding
![]() $Ker(V_x^*) \subset \mathcal {H}$
induces an embedding of
$Ker(V_x^*) \subset \mathcal {H}$
induces an embedding of
![]() $\Gamma _s(Ker(V_x^*))$
in
$\Gamma _s(Ker(V_x^*))$
in
![]() $\Gamma _s(\mathcal {H})$
. Let
$\Gamma _s(\mathcal {H})$
. Let
![]() $\Gamma $
be the set of all maps
$\Gamma $
be the set of all maps
![]() $t:P \to \Gamma _s(\mathcal {H})$
such that
$t:P \to \Gamma _s(\mathcal {H})$
such that
-
(a) the map t is weakly measurable, and
-
(b) for
 $x \in P$
,
$x \in P$
,
 $t(x) \in F^V(x)$
.
$t(x) \in F^V(x)$
.
Then,
![]() $F^V$
is a measurable field of Hilbert spaces with
$F^V$
is a measurable field of Hilbert spaces with
![]() $\Gamma $
being the space of measurable sections. Define a product rule on
$\Gamma $
being the space of measurable sections. Define a product rule on
![]() $F^V$
by
$F^V$
by
for
![]() $\xi \in Ker(V_x^*)$
and
$\xi \in Ker(V_x^*)$
and
![]() $\eta \in Ker(V_y^*)$
. Here,
$\eta \in Ker(V_y^*)$
. Here,
![]() $\{e(\xi ):\xi \in Ker(V_x^*)\}$
denotes the collection of exponential vectors in the symmetric Fock space
$\{e(\xi ):\xi \in Ker(V_x^*)\}$
denotes the collection of exponential vectors in the symmetric Fock space
![]() $\Gamma _s(Ker(V_x^*)) $
. Then, the multiplication is compatible with the measurable structure making
$\Gamma _s(Ker(V_x^*)) $
. Then, the multiplication is compatible with the measurable structure making
![]() $F^V$
a product system. The product system
$F^V$
a product system. The product system
![]() $F^V$
is called the product system of the CCR flow associated with V. The corresponding
$F^V$
is called the product system of the CCR flow associated with V. The corresponding
![]() $E_0$
-semigroup
$E_0$
-semigroup
![]() $\alpha ^V$
is called the CCR flow associated with V. Concrete examples of multiparameter CCR flows and their intrinsic properties like index, gauge group, type were analyzed in [Reference Arjunan, Srinivasan and Sundar2, Reference Arjunan and Sundar3] and in [Reference Sarkar and Sundar23].
$\alpha ^V$
is called the CCR flow associated with V. Concrete examples of multiparameter CCR flows and their intrinsic properties like index, gauge group, type were analyzed in [Reference Arjunan, Srinivasan and Sundar2, Reference Arjunan and Sundar3] and in [Reference Sarkar and Sundar23].
For
![]() $x \in P$
, let
$x \in P$
, let
![]() $\Omega _x$
be the vacuum vector of
$\Omega _x$
be the vacuum vector of
![]() $\Gamma _a(Ker(V_x^{*}))$
. Consider the field of Hilbert spaces
$\Gamma _a(Ker(V_x^{*}))$
. Consider the field of Hilbert spaces
![]() $E^{V}:=\{E^{V}(x)\}_{x\in P}$
, where
$E^{V}:=\{E^{V}(x)\}_{x\in P}$
, where
![]() $E^{V}(x):=\Gamma _{a}(Ker(V_{x}^{*}))$
for
$E^{V}(x):=\Gamma _{a}(Ker(V_{x}^{*}))$
for
![]() $x\in P$
. The measurable structure on
$x\in P$
. The measurable structure on
![]() $E^V$
is defined as in the CCR case. Define a multiplication on
$E^V$
is defined as in the CCR case. Define a multiplication on
![]() $E^{V}$
as follows:
$E^{V}$
as follows:
for
![]() $\xi =\xi _1 \wedge \xi _2 \cdots \wedge \xi _m\in \Gamma _a(Ker(V_{x}^{*})$
,
$\xi =\xi _1 \wedge \xi _2 \cdots \wedge \xi _m\in \Gamma _a(Ker(V_{x}^{*})$
,
![]() $\eta =\eta _1 \wedge \eta _2 \wedge \ldots \wedge \eta _n \in \Gamma _a(Ker(V_{y}^{*}))$
and
$\eta =\eta _1 \wedge \eta _2 \wedge \ldots \wedge \eta _n \in \Gamma _a(Ker(V_{y}^{*}))$
and
![]() $x,y\in P$
. For
$x,y\in P$
. For
![]() $m=0$
or
$m=0$
or
![]() $n=0$
, (1.2) is interpreted as follows:
$n=0$
, (1.2) is interpreted as follows:
 $$ \begin{align*} \Omega_x \cdot \Omega_y&=\Omega_{x+y},\\ \Omega_x \cdot \eta&=V_{x}\eta_1 \wedge V_x \eta_2 \wedge \ldots \wedge V_x \eta_n, \\ \xi \cdot \Omega_y&=\xi_1 \wedge \xi_2 \wedge \ldots \wedge \xi_m. \end{align*} $$
$$ \begin{align*} \Omega_x \cdot \Omega_y&=\Omega_{x+y},\\ \Omega_x \cdot \eta&=V_{x}\eta_1 \wedge V_x \eta_2 \wedge \ldots \wedge V_x \eta_n, \\ \xi \cdot \Omega_y&=\xi_1 \wedge \xi_2 \wedge \ldots \wedge \xi_m. \end{align*} $$
Then,
![]() $E^V$
is a product system and is called the product system of the CAR flow associated with V. The corresponding
$E^V$
is a product system and is called the product system of the CAR flow associated with V. The corresponding
![]() $E_0$
-semigroup
$E_0$
-semigroup
![]() $\beta ^V$
is called the CAR flow associated with V.
$\beta ^V$
is called the CAR flow associated with V.
It is known that in the
![]() $1$
-parameter case, i.e., when
$1$
-parameter case, i.e., when
![]() $P=[0,\infty )$
,
$P=[0,\infty )$
,
![]() $E^V$
and
$E^V$
and
![]() $F^V$
are isomorphic [Reference Powers and Robinson21]. Then, it follows from the work of Arveson [Reference Arveson4] that
$F^V$
are isomorphic [Reference Powers and Robinson21]. Then, it follows from the work of Arveson [Reference Arveson4] that
![]() $1$
-parameter CAR flows are classified by a single numerical invariant called index that takes values in
$1$
-parameter CAR flows are classified by a single numerical invariant called index that takes values in
![]() $\{0, 1,2,\ldots \} \cup \{\infty \}$
. In particular, the map
$\{0, 1,2,\ldots \} \cup \{\infty \}$
. In particular, the map
is injective. Also,
![]() $1$
-parameter CAR flows are type I. Here, we take up the multiparameter case, and we completely classify type I CAR flows associated with isometric representations with commuting range projections.
$1$
-parameter CAR flows are type I. Here, we take up the multiparameter case, and we completely classify type I CAR flows associated with isometric representations with commuting range projections.
Before we state our results, we mention here that, in the multiparameter case, the study of CCR flows and CAR flows are not the same thing. For, it was demonstrated in [Reference Srinivasan33] that
![]() $E^V$
and
$E^V$
and
![]() $F^V$
need not be isomorphic. In [Reference Arjunan1], Arjunan studied the decomposability of the product system
$F^V$
need not be isomorphic. In [Reference Arjunan1], Arjunan studied the decomposability of the product system
![]() $E^V$
when V is the shift semigroup associated with a free and transitive action of P. He showed that for a large class of isometric representations V,
$E^V$
when V is the shift semigroup associated with a free and transitive action of P. He showed that for a large class of isometric representations V,
![]() $E^V$
fails to be decomposable, and hence not isomorphic to the product system of a CCR flow.
$E^V$
fails to be decomposable, and hence not isomorphic to the product system of a CCR flow.
Our first result concerning CAR flows is given below.
Theorem 1.1 Let
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
be pure isometric representations of P on Hilbert spaces
$V^{(2)}$
be pure isometric representations of P on Hilbert spaces
![]() $\mathcal {H}_1$
and
$\mathcal {H}_1$
and
![]() $\mathcal {H}_2$
respectively. The product systems
$\mathcal {H}_2$
respectively. The product systems
![]() $E^{V^{(1)}}$
and
$E^{V^{(1)}}$
and
![]() $E^{V^{(2)}}$
are isomorphic if and only if
$E^{V^{(2)}}$
are isomorphic if and only if
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
are unitarily equivalent, i.e., there exists a unitary
$V^{(2)}$
are unitarily equivalent, i.e., there exists a unitary
![]() $U:\mathcal {H}_1 \to \mathcal {H}_2 $
such that for every
$U:\mathcal {H}_1 \to \mathcal {H}_2 $
such that for every
![]() $a \in P$
,
$a \in P$
,
The above theorem was statedin [Reference Srinivasan33, Proposition 4.7]. However, the proof given there is incorrect. The author argues that in view of [Reference Srinivasan33, Proposition 4.1], it suffices to prove that the gauge group of a CAR flow acts transitively on the set of normalized units, and he gives an incorrect proof of this assertion. In fact, the last assertion is false. We show by counterexamples that the gauge group of a CAR flow need not act transitively on the set of normalized units.
Theorem 1.1 says that the task of parametrizing/listing CAR flows is equivalent to the problem of parametrizing isometric representations of P. However, the process of inducing isometric representations [Reference Dahya12, Reference Sarkar and Sundar23] of
![]() $\mathbb {N}^2$
to that of
$\mathbb {N}^2$
to that of
![]() $\mathbb {R}_+^2$
allows us to conclude that the classification problem of isometric representations of
$\mathbb {R}_+^2$
allows us to conclude that the classification problem of isometric representations of
![]() $\mathbb {R}_{+}^{2}$
is at least as hard as describing the dual of
$\mathbb {R}_{+}^{2}$
is at least as hard as describing the dual of
![]() $C^{*}(\mathbb {Z}_2*\mathbb {Z})$
which is known to be pathological, i.e., it is not a standard Borel space. Thus, describing a good parameterization of all CAR flows is beyond the scope of this paper and the authors. Neverthless, we show that a suitable subclass, i.e., the class of type I CAR flows associated with isometric representations with commuting range projections can be completely classified and described in concrete terms.
$C^{*}(\mathbb {Z}_2*\mathbb {Z})$
which is known to be pathological, i.e., it is not a standard Borel space. Thus, describing a good parameterization of all CAR flows is beyond the scope of this paper and the authors. Neverthless, we show that a suitable subclass, i.e., the class of type I CAR flows associated with isometric representations with commuting range projections can be completely classified and described in concrete terms.
Recall that an isometric representation
![]() $V=\{V_a\}_{a \in P}$
is said to have commuting range projections if
$V=\{V_a\}_{a \in P}$
is said to have commuting range projections if
![]() $\{V_aV_{a}^{*}:a \in P\}$
is a commuting family of projections, and recall that a product system E is said to be type I if the only subsystem of E that contains all the units of E is E. A unit of E is a non-zero multiplicative section of E.
$\{V_aV_{a}^{*}:a \in P\}$
is a commuting family of projections, and recall that a product system E is said to be type I if the only subsystem of E that contains all the units of E is E. A unit of E is a non-zero multiplicative section of E.
We fix notation to describe our results. Let
![]() $\mathbb {N}_\infty :=\{1,2,\ldots \} \cup \{\infty \}$
. Let
$\mathbb {N}_\infty :=\{1,2,\ldots \} \cup \{\infty \}$
. Let
![]() $P^{*}$
be the dual cone of P, i.e.,
$P^{*}$
be the dual cone of P, i.e.,
We denote by
![]() $S(P^*)$
the unit sphere of
$S(P^*)$
the unit sphere of
![]() $P^*$
, i.e.,
$P^*$
, i.e.,
Let
![]() $\lambda \in S(P^*)$
, let
$\lambda \in S(P^*)$
, let
![]() $k \in \mathbb {N}_\infty $
, and let
$k \in \mathbb {N}_\infty $
, and let
![]() $\mathcal {K}$
be a Hilbert space of dimension k. Denote the one parameter shift semigroup on
$\mathcal {K}$
be a Hilbert space of dimension k. Denote the one parameter shift semigroup on
![]() $\mathcal {H}:=L^{2}([0,\infty ),\mathcal {K})$
by
$\mathcal {H}:=L^{2}([0,\infty ),\mathcal {K})$
by
![]() $S^{(k)}:=\{S_t^{(k)}\}_{t \geq 0}$
. Recall that for
$S^{(k)}:=\{S_t^{(k)}\}_{t \geq 0}$
. Recall that for
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $S_t^{(k)}$
is the isometry on
$S_t^{(k)}$
is the isometry on
![]() $\mathcal {H}$
defined by
$\mathcal {H}$
defined by
 $$ \begin{align*} S_t^{(k)}f(x):=\begin{cases} f(x-t) & \text{if } x-t \geq 0,\\ &\\ 0 & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} S_t^{(k)}f(x):=\begin{cases} f(x-t) & \text{if } x-t \geq 0,\\ &\\ 0 & \text{ otherwise}. \end{cases} \end{align*} $$
For
![]() $a \in P$
, let
$a \in P$
, let
![]() $S_a^{(\lambda ,k)}:=S_{\langle \lambda |a \rangle }^{(k)}$
. Then,
$S_a^{(\lambda ,k)}:=S_{\langle \lambda |a \rangle }^{(k)}$
. Then,
![]() $S^{(\lambda ,k)}:=\{S_{a}^{(\lambda ,k)}\}_{a \in P}$
is an isometric representation of P on
$S^{(\lambda ,k)}:=\{S_{a}^{(\lambda ,k)}\}_{a \in P}$
is an isometric representation of P on
![]() $\mathcal {H}$
. If
$\mathcal {H}$
. If
![]() $k=1$
, we denote
$k=1$
, we denote
![]() $S^{(\lambda ,k)}$
by
$S^{(\lambda ,k)}$
by
![]() $S^\lambda $
.
$S^\lambda $
.
For a non-empty countable subset I, an injective map
![]() $\lambda :I \to S(P^*)$
and a map
$\lambda :I \to S(P^*)$
and a map
![]() $k:I \to \mathbb {N}_\infty $
, set
$k:I \to \mathbb {N}_\infty $
, set
Let
![]() $E^{(\lambda ,k)}$
be the product system of the CAR flow associated with
$E^{(\lambda ,k)}$
be the product system of the CAR flow associated with
![]() $S^{(\lambda ,k)}$
.
$S^{(\lambda ,k)}$
.
With the above notation, we have the following classification result which is the main result of this paper.
Theorem 1.2 For every non-empty countable set I, an injective map
![]() $\lambda :I \to S(P^*)$
and a map
$\lambda :I \to S(P^*)$
and a map
![]() $k:I \to \mathbb {N}_\infty $
, the product system
$k:I \to \mathbb {N}_\infty $
, the product system
![]() $E^{(\lambda ,k)}$
is type I. Conversely, suppose V is an isometric representation of P with commuting range projections such that
$E^{(\lambda ,k)}$
is type I. Conversely, suppose V is an isometric representation of P with commuting range projections such that
![]() $E^V$
is type I. Then,
$E^V$
is type I. Then,
![]() $E^V$
is isomorphic to
$E^V$
is isomorphic to
![]() $E^{(\lambda ,k)}$
(equivalently, V is unitarily equivalent to
$E^{(\lambda ,k)}$
(equivalently, V is unitarily equivalent to
![]() $S^{(\lambda ,k)}$
) for a non-empty countable set I, an injective map
$S^{(\lambda ,k)}$
) for a non-empty countable set I, an injective map
![]() $\lambda :I \to S(P^*)$
and a map
$\lambda :I \to S(P^*)$
and a map
![]() $k:I \to \mathbb {N}_\infty $
. Moroever, the maps
$k:I \to \mathbb {N}_\infty $
. Moroever, the maps
![]() $\lambda $
and k are unique up to conjugacy.
$\lambda $
and k are unique up to conjugacy.
We explain briefly the ideas involved in the the proof of the converse part. A certain “universal irreversible” dynamical system that encodes all pure semigroups of isometries with commuting range projections was constructed in [Reference Sundar35] (see also [Reference Sundar37]). The irreversible system is given by the pair
![]() $(X_u,P)$
where
$(X_u,P)$
where
The topology that we impose on
![]() $X_u$
is the Fell topology. The semigroup P acts on
$X_u$
is the Fell topology. The semigroup P acts on
![]() $X_u$
by translations.
$X_u$
by translations.
The results of [Reference Sundar34] allow us to conclude that if we focus on one unit
![]() $u:=\{u_a\}_{a \in P}$
at a time, then we can assume that V is the shift semigroup
$u:=\{u_a\}_{a \in P}$
at a time, then we can assume that V is the shift semigroup
![]() $V ^\mu $
on
$V ^\mu $
on
![]() $X_u$
associated with a translation invariant Radon measure
$X_u$
associated with a translation invariant Radon measure
![]() $\mu $
on
$\mu $
on
![]() $X_u$
. Making use of the equality
$X_u$
. Making use of the equality
and by few computations, we show that the support of
![]() $\mu $
can be identified with
$\mu $
can be identified with
![]() $[0,\infty )$
. Under this identification, the action of P on
$[0,\infty )$
. Under this identification, the action of P on
![]() $[0,\infty )$
is then given by
$[0,\infty )$
is then given by
for a unique
![]() $\lambda \in S(P^*)$
. Then, it is clear that
$\lambda \in S(P^*)$
. Then, it is clear that
![]() $V^{\mu }$
is unitarily equivalent to
$V^{\mu }$
is unitarily equivalent to
![]() $S^\lambda $
. The proof of the converse part of Theorem 1.2 is completed by a Zorn’s lemma argument.
$S^\lambda $
. The proof of the converse part of Theorem 1.2 is completed by a Zorn’s lemma argument.
We also compute the index and the gauge group, i.e., the group of automorphisms, of the product system
![]() $E^{(\lambda ,k)}$
. For
$E^{(\lambda ,k)}$
. For
![]() $\ell \in \mathbb {N}_\infty $
, the unitary group of a Hilbert space of dimension
$\ell \in \mathbb {N}_\infty $
, the unitary group of a Hilbert space of dimension
![]() $\ell $
will be denoted by
$\ell $
will be denoted by
![]() $U(\ell )$
. We denote the gauge group of
$U(\ell )$
. We denote the gauge group of
![]() $E^{(\lambda ,k)}$
by G.
$E^{(\lambda ,k)}$
by G.
Theorem 1.3 Let I be a non-empty countable set, let
![]() $\lambda :I \to S(P^*)$
be an injective map, and let
$\lambda :I \to S(P^*)$
be an injective map, and let
![]() $k:I \to \mathbb {N}_\infty $
be a map. Then,
$k:I \to \mathbb {N}_\infty $
be a map. Then,
-
(1) If
 $I=\{i\}$
is singleton, then
$I=\{i\}$
is singleton, then
 $E^{(\lambda ,k)}$
is isomorphic to the product system of the CCR flow associated with
$E^{(\lambda ,k)}$
is isomorphic to the product system of the CCR flow associated with
 $S^{(\lambda _i,k_{i})}$
. In this case, the gauge group G acts transitively on the set of normalized units, and G is isomorphic to the gauge group of the CCR flow associated with
$S^{(\lambda _i,k_{i})}$
. In this case, the gauge group G acts transitively on the set of normalized units, and G is isomorphic to the gauge group of the CCR flow associated with
 $S^{(\lambda _i,k_{i})}$
.
$S^{(\lambda _i,k_{i})}$
. -
(2) If the cardinality of I is at least two, then the gauge group G does not act transitively on the set of normalized units. In this case, G is isomorphic to
 $\displaystyle \mathbb {R}^d \times \prod _{i \in I}U(k_i)$
.
$\displaystyle \mathbb {R}^d \times \prod _{i \in I}U(k_i)$
.
The organization of this paper is as follows.
After this introductory section, in Section 2, we collect a few definitions concerning product systems, additive decomposable vectors and units. To keep the paper self contained, we give an overview of the results derived in [Reference Margetts and Srinivasan16] and in [Reference Arjunan1] concerning the exponential map that plays a crucial role in our analysis. Theorem 1.1 is proved in Section 3. In Section 4, we prove Theorem 1.2. In Section 5, we prove Theorem 1.3. We also prove that the gauge group of a CAR flow need not act transitively on the set of normalized units.
2 Additive decomposable vectors and the exponential map
We will make extensive use of the exponential map defined initially for “addits” in [Reference Margetts and Srinivasan16] and later extended to “coherent sections of additive decomposable vectors” in [Reference Arjunan1]. To keep the paper fairly self contained, we give a quick overview of the results of [Reference Margetts and Srinivasan16] and [Reference Arjunan1]. We start by first recalling the definition of product systems, units, and what it means for a product system to be type I.
Let P be a closed, convex cone in
![]() $\mathbb {R}^d$
, where
$\mathbb {R}^d$
, where
![]() $d \geq 1$
, which is spanning, i.e.,
$d \geq 1$
, which is spanning, i.e.,
![]() $P-P=\mathbb {R}^d$
and pointed, i.e.,
$P-P=\mathbb {R}^d$
and pointed, i.e.,
![]() $P \cap -P=\{0\}$
. The letter P is reserved to denote such a cone for the rest of this paper. Let
$P \cap -P=\{0\}$
. The letter P is reserved to denote such a cone for the rest of this paper. Let
![]() $P_\infty :=P \cup \{\infty \}$
. For
$P_\infty :=P \cup \{\infty \}$
. For
![]() $x,y \in \mathbb {R}^d$
, we say
$x,y \in \mathbb {R}^d$
, we say
![]() $x \leq y$
if
$x \leq y$
if
![]() $y-x \in P$
. For
$y-x \in P$
. For
![]() $x \in P$
, set
$x \in P$
, set
For
![]() $x=\infty $
, we let
$x=\infty $
, we let
![]() $[0,x]=P$
.
$[0,x]=P$
.
Let
![]() $E:=\{E(x)\}_{x \in P}$
be a measurable field of non-zero separable Hilbert spaces together with an associative multiplication defined on the disjoint union
$E:=\{E(x)\}_{x \in P}$
be a measurable field of non-zero separable Hilbert spaces together with an associative multiplication defined on the disjoint union
![]() $\displaystyle \coprod _{x \in P}E(x)$
. Then, E together with the multiplication is called a product system if the following properties are satisfied.
$\displaystyle \coprod _{x \in P}E(x)$
. Then, E together with the multiplication is called a product system if the following properties are satisfied.
-
(1) If
 $u \in E(x)$
and
$u \in E(x)$
and
 $v \in E(y)$
, then
$v \in E(y)$
, then
 $uv \in E(x+y)$
.
$uv \in E(x+y)$
. -
(2) For
 $x,y \in P$
, the map
$x,y \in P$
, the map  $$\begin{align*}E(x) \otimes E(y) \ni u \otimes v \to uv \in E(x+y) \end{align*}$$
$$\begin{align*}E(x) \otimes E(y) \ni u \otimes v \to uv \in E(x+y) \end{align*}$$
is a unitary operator.
-
(3) For measurable sections
 $r,s,t$
, the map is measurable.
$r,s,t$
, the map is measurable. $$\begin{align*}P \times P \ni (x,y) \to \langle r(x)s(y)|t(x+y) \rangle \in \mathbb{C}\end{align*}$$
$$\begin{align*}P \times P \ni (x,y) \to \langle r(x)s(y)|t(x+y) \rangle \in \mathbb{C}\end{align*}$$
Let
![]() $E:=\{E(x)\}_{x \in P}$
be a product system. A measurable section
$E:=\{E(x)\}_{x \in P}$
be a product system. A measurable section
![]() $\displaystyle u:P \to \coprod _{x \in P}E(x)$
is called a unit if
$\displaystyle u:P \to \coprod _{x \in P}E(x)$
is called a unit if
-
(1) for
 $x \in P$
,
$x \in P$
,
 $u_x \neq 0 $
, and
$u_x \neq 0 $
, and -
(2) for
 $x,y \in P$
,
$x,y \in P$
,
 $u_xu_y=u_{x+y}$
.
$u_xu_y=u_{x+y}$
.
We denote the set of units of E by
![]() $\mathcal {U}_E$
. We say that E is spatial if
$\mathcal {U}_E$
. We say that E is spatial if
![]() $\mathcal {U}_E$
is non-empty.
$\mathcal {U}_E$
is non-empty.
Let
![]() $F:=\{F(x)\}_{x \in P}$
be a field of non-zero Hilbert spaces such that, for
$F:=\{F(x)\}_{x \in P}$
be a field of non-zero Hilbert spaces such that, for
![]() $x \in P$
,
$x \in P$
,
![]() $F(x) \subset E(x)$
. We say F is a subsystem of E if for every
$F(x) \subset E(x)$
. We say F is a subsystem of E if for every
![]() $x,y \in P$
,
$x,y \in P$
,
Let
![]() $u \in \mathcal {U}_E$
. We say a subsystem F contains u if
$u \in \mathcal {U}_E$
. We say a subsystem F contains u if
![]() $u_x \in F(x)$
for every
$u_x \in F(x)$
for every
![]() $x \in P$
. We say F contains
$x \in P$
. We say F contains
![]() $\mathcal {U}_E$
if F contains u for every
$\mathcal {U}_E$
if F contains u for every
![]() $u \in \mathcal {U}_E$
. The product system E is said to be type I if E is spatial and the only subsystem of E that contains
$u \in \mathcal {U}_E$
. The product system E is said to be type I if E is spatial and the only subsystem of E that contains
![]() $\mathcal {U}_E$
is E.
$\mathcal {U}_E$
is E.
We denote the gauge group of E, i.e., the group of automorphisms of E, by
![]() $G_E$
. For
$G_E$
. For
![]() $u\in \mathcal {U}_{E}$
and
$u\in \mathcal {U}_{E}$
and
![]() $\Psi \in G_{E}$
, let
$\Psi \in G_{E}$
, let
![]() $\Psi .u\in \mathcal {U}_{E}$
be given by
$\Psi .u\in \mathcal {U}_{E}$
be given by
for
![]() $x\in P$
. A unit
$x\in P$
. A unit
![]() $u=\{u_{x}\}_{x\in P}$
of E is said to be normalized if
$u=\{u_{x}\}_{x\in P}$
of E is said to be normalized if
![]() $||u_{x}||=1$
for each
$||u_{x}||=1$
for each
![]() $x\in P$
. The set of normalized units of E is denoted by
$x\in P$
. The set of normalized units of E is denoted by
![]() $\mathcal {U}^{n}_{E}$
. We say that the gauge group acts transitively on the set of normalized units if the action of
$\mathcal {U}^{n}_{E}$
. We say that the gauge group acts transitively on the set of normalized units if the action of
![]() $G_E$
on
$G_E$
on
![]() $\mathcal {U}^{n}_E$
given by
$\mathcal {U}^{n}_E$
given by
is transitive.
In [Reference Margetts and Srinivasan16], Margetts and Srinivasan introduced the notion of addits of a
![]() $1$
-parameter product system and constructed an exponential map that, after suitable normalization, sets up a bijective correspondence between addits and units. The notion of addits was also considered independentely by Bhat, Lindsay, and Mukherjee in [Reference Rajarama Bhat, Martin Lindsay and Mukherjee22]. In [Reference Srinivasan33], Srinivasan introduced the concept of additive decomposable vectors. Imitating the techniques of [Reference Margetts and Srinivasan16], Arjunan in [Reference Arjunan1] showed that there is a bijective correspondence between the set of additive decomposable vectors and the set of decomposable vectors. Since this bijection and the exponential map play a key role in what follows, we summarize the main resuls of [Reference Srinivasan33] and [Reference Arjunan1].
$1$
-parameter product system and constructed an exponential map that, after suitable normalization, sets up a bijective correspondence between addits and units. The notion of addits was also considered independentely by Bhat, Lindsay, and Mukherjee in [Reference Rajarama Bhat, Martin Lindsay and Mukherjee22]. In [Reference Srinivasan33], Srinivasan introduced the concept of additive decomposable vectors. Imitating the techniques of [Reference Margetts and Srinivasan16], Arjunan in [Reference Arjunan1] showed that there is a bijective correspondence between the set of additive decomposable vectors and the set of decomposable vectors. Since this bijection and the exponential map play a key role in what follows, we summarize the main resuls of [Reference Srinivasan33] and [Reference Arjunan1].
Let
![]() $E=\{E(x)\}_{x \in P}$
be a spatial product system over P with a reference unit
$E=\{E(x)\}_{x \in P}$
be a spatial product system over P with a reference unit
![]() $e:=\{e_x\}_{x \in P}$
that is normalized, i.e.,
$e:=\{e_x\}_{x \in P}$
that is normalized, i.e.,
![]() $||e_x||=1$
for
$||e_x||=1$
for
![]() $x \in P$
. Such a pair
$x \in P$
. Such a pair
![]() $(E,e)$
was called a pointed product system in [Reference Rajarama Bhat, Martin Lindsay and Mukherjee22]. The reference unit e is fixed until further mention.
$(E,e)$
was called a pointed product system in [Reference Rajarama Bhat, Martin Lindsay and Mukherjee22]. The reference unit e is fixed until further mention.
Definition 2.1 [Reference Srinivasan33]
Let
![]() $x \in P$
, and let
$x \in P$
, and let
![]() $b \in E(x)$
. We say that b is an additive decomposable vector if
$b \in E(x)$
. We say that b is an additive decomposable vector if
![]() $b \perp e_x$
and for
$b \perp e_x$
and for
![]() $y \leq x$
, there exists
$y \leq x$
, there exists
![]() $b_y \in E(y)$
and
$b_y \in E(y)$
and
![]() $b(y,x) \in E(y-x)$
(that are necessarily unique) such that
$b(y,x) \in E(y-x)$
(that are necessarily unique) such that
-
(1)
 $b_y \perp e_y$
,
$b_y \perp e_y$
,
 $b(y,x) \perp e_{x-y}$
, and
$b(y,x) \perp e_{x-y}$
, and -
(2)
 $b=b_y e_{x-y}+e_y b(y,x)$
.
$b=b_y e_{x-y}+e_y b(y,x)$
.
For
![]() $x \in P$
, let
$x \in P$
, let
Let
![]() $x \in P_\infty $
, and let
$x \in P_\infty $
, and let
![]() $\{b_y\}_{y \in [0,x]}$
be a family of additive decomposable vectors such that
$\{b_y\}_{y \in [0,x]}$
be a family of additive decomposable vectors such that
![]() $b_y \in \mathcal {A}_e(y)$
for every
$b_y \in \mathcal {A}_e(y)$
for every
![]() $y \in [0,x]$
. We call such a family a coherent section of additive decomposable vectors if for every
$y \in [0,x]$
. We call such a family a coherent section of additive decomposable vectors if for every
![]() $y,z \in [0,x]$
with
$y,z \in [0,x]$
with
![]() $y\leq z$
, there exists, a necessarily unique,
$y\leq z$
, there exists, a necessarily unique,
![]() $b(y,z) \in E(z-y)$
such that
$b(y,z) \in E(z-y)$
such that
A coherent section of additive decomposable vectors
![]() $\{b_y\}_{y \in P}$
is called an addit if
$\{b_y\}_{y \in P}$
is called an addit if
![]() $b(y,z)=b_{z-y}$
whenever
$b(y,z)=b_{z-y}$
whenever
![]() $y \leq z$
.
$y \leq z$
.
Suppose
![]() $\{b_y\}_{y \in [0,x]}$
is a coherent section of additive decomposable vectors. It is clear that the collection
$\{b_y\}_{y \in [0,x]}$
is a coherent section of additive decomposable vectors. It is clear that the collection
![]() $\{b(y,z): y,z \in [0,x], y \leq z\}$
satisfies the following propagator equation: for
$\{b(y,z): y,z \in [0,x], y \leq z\}$
satisfies the following propagator equation: for
![]() $y_1 \leq y_2 \leq y_3$
,
$y_1 \leq y_2 \leq y_3$
,
Let
![]() $x \in P$
. Given
$x \in P$
. Given
![]() $b \in A_{e}(x)$
, it follows from [Reference Srinivasan33, Lemma 3.2] that there exists a unique coherent section of additive decomposable vectors
$b \in A_{e}(x)$
, it follows from [Reference Srinivasan33, Lemma 3.2] that there exists a unique coherent section of additive decomposable vectors
![]() $\{b_y\}_{y \in [0,x]}$
such that
$\{b_y\}_{y \in [0,x]}$
such that
![]() $b_x=b$
.
$b_x=b$
.
Next, we recall the definition of decomposable vectors. Let
![]() $x \in P$
, and let
$x \in P$
, and let
![]() $u \in E(x)$
be a non-zero vector. We say that u is decomposable if whenever
$u \in E(x)$
be a non-zero vector. We say that u is decomposable if whenever
![]() $y \leq x$
, there exists
$y \leq x$
, there exists
![]() $v \in E(y)$
and
$v \in E(y)$
and
![]() $w \in E(x-y)$
such that
$w \in E(x-y)$
such that
![]() $u=vw$
. For
$u=vw$
. For
![]() $x \in P$
, let
$x \in P$
, let
Let
![]() $x \in P_\infty $
, and let
$x \in P_\infty $
, and let
![]() $\{u_y\}_{y \in [0,x]}$
be a family of decomposable vectors such that
$\{u_y\}_{y \in [0,x]}$
be a family of decomposable vectors such that
![]() $u_y \in D_{e}(y)$
for every
$u_y \in D_{e}(y)$
for every
![]() $y \in [0,x]$
. We say that
$y \in [0,x]$
. We say that
![]() $\{u_y\}_{y \in [0,x]}$
is a left coherent section of decomposable vectors if for
$\{u_y\}_{y \in [0,x]}$
is a left coherent section of decomposable vectors if for
![]() $y,z \in [0,x]$
with
$y,z \in [0,x]$
with
![]() $y \leq z$
, there exists a unique
$y \leq z$
, there exists a unique
![]() $u(y,z) \in D_{e}(z-y)$
such that
$u(y,z) \in D_{e}(z-y)$
such that
![]() $u_z=u_yu(y,z)$
.
$u_z=u_yu(y,z)$
.
Next, we recall the definition of the exponential map, in the
![]() $1$
-parameter setting, that sets up a bijective correspondence between
$1$
-parameter setting, that sets up a bijective correspondence between
![]() $\mathcal {A}_{e}(\cdot )$
and
$\mathcal {A}_{e}(\cdot )$
and
![]() $D_{e}(\cdot )$
. Let
$D_{e}(\cdot )$
. Let
![]() $E:=\{E(t)\}_{t \geq 0}$
be a
$E:=\{E(t)\}_{t \geq 0}$
be a
![]() $1$
-parameter product system with a reference unit
$1$
-parameter product system with a reference unit
![]() $\{e_t\}_{t \geq 0}$
that is normalized. Suppose
$\{e_t\}_{t \geq 0}$
that is normalized. Suppose
![]() $t \geq 0$
. Let
$t \geq 0$
. Let
![]() $b \in \mathcal {A}_{e}(t)$
be given. Let
$b \in \mathcal {A}_{e}(t)$
be given. Let
![]() $\{b_s\}_{s \in [0,t]}$
be the coherent section of additive decomposable vectors such that
$\{b_s\}_{s \in [0,t]}$
be the coherent section of additive decomposable vectors such that
![]() $b_t=b$
.
$b_t=b$
.
For every
![]() $n \in \{0,1,2,\ldots \}$
, define a section
$n \in \{0,1,2,\ldots \}$
, define a section
![]() $x^{(n)}:[0,t] \to \displaystyle \coprod _{s \in [0,t]}E(s)$
inductively as follows: for
$x^{(n)}:[0,t] \to \displaystyle \coprod _{s \in [0,t]}E(s)$
inductively as follows: for
![]() $s \in [0,t]$
, set
$s \in [0,t]$
, set
![]() $x^{(0)}_s:=e_s$
and
$x^{(0)}_s:=e_s$
and
![]() $x^{(1)}_s:=b_s$
, and for
$x^{(1)}_s:=b_s$
, and for
![]() $n \geq 2$
, let
$n \geq 2$
, let
Then, we set
It was proved in [Reference Arjunan1, Proposition 3] that the series
![]() $\sum _{n=1}^{\infty }x_t^{(n)}$
is norm convergent in
$\sum _{n=1}^{\infty }x_t^{(n)}$
is norm convergent in
![]() $E(t)$
. The integral
$E(t)$
. The integral
![]() $\int _{0}^{s}x_{r}^{(n-1)}db_r$
is called Itô integral whose definition is recalled below for the reader’s benefit.
$\int _{0}^{s}x_{r}^{(n-1)}db_r$
is called Itô integral whose definition is recalled below for the reader’s benefit.
Let
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $s \in [0,t]$
be given. For every
$s \in [0,t]$
be given. For every
![]() $k \geq 1$
, partition
$k \geq 1$
, partition
![]() $[0,s]$
into k intervals of length
$[0,s]$
into k intervals of length
![]() $\frac {s}{k}$
. For
$\frac {s}{k}$
. For
![]() $i=0,1,2,\ldots ,k-1$
, set
$i=0,1,2,\ldots ,k-1$
, set
![]() $r_i^{(k)}:=\frac {is}{k}$
. Define
$r_i^{(k)}:=\frac {is}{k}$
. Define
 $$ \begin{align} S_k:=\sum_{i=0}^{k-1}x_{r_i^{(k)}}^{(n-1)}b(r_{i}^{(k)},r_{i+1}^{(k)})e_{s-r_{i+1}^{(k)}} \end{align} $$
$$ \begin{align} S_k:=\sum_{i=0}^{k-1}x_{r_i^{(k)}}^{(n-1)}b(r_{i}^{(k)},r_{i+1}^{(k)})e_{s-r_{i+1}^{(k)}} \end{align} $$
Note that
![]() $S_k \in E(s)$
for every
$S_k \in E(s)$
for every
![]() $k \geq 1$
. Moreover, the sequence
$k \geq 1$
. Moreover, the sequence
![]() $(S_k)_k$
converges in norm whose limit we denote by
$(S_k)_k$
converges in norm whose limit we denote by
![]() $\int _{0}^{s}x_r^{(n-1)}db_r$
. The norm convergence of
$\int _{0}^{s}x_r^{(n-1)}db_r$
. The norm convergence of
![]() $(S_k)_k$
was shown in [Reference Margetts and Srinivasan16] when
$(S_k)_k$
was shown in [Reference Margetts and Srinivasan16] when
![]() $\{b_s\}_{s \geq 0}$
is an addit (see [Reference Margetts and Srinivasan16, Proposition 5.4]). It was observed in [Reference Arjunan1] that the same proof works if we replace an addit by a coherent section of additive decomposable vectors (see [Reference Arjunan1, Proposition 2]).
$\{b_s\}_{s \geq 0}$
is an addit (see [Reference Margetts and Srinivasan16, Proposition 5.4]). It was observed in [Reference Arjunan1] that the same proof works if we replace an addit by a coherent section of additive decomposable vectors (see [Reference Arjunan1, Proposition 2]).
Proposition 2.1 [Reference Margetts and Srinivasan16], [Reference Arjunan1]
The exponential map satisfies the following key properties.
-
(1) Let
 $t\geq 0$
. For
$t\geq 0$
. For
 $b \in \mathcal {A}_e(t)$
,
$b \in \mathcal {A}_e(t)$
,
 $Exp(b) \in \mathcal {D}_e(t)$
. Moreover, the map is a bijection. For
$Exp(b) \in \mathcal {D}_e(t)$
. Moreover, the map is a bijection. For $$\begin{align*}\mathcal{A}_e(t) \ni b \to Exp(b) \in D_e(t) \end{align*}$$
$$\begin{align*}\mathcal{A}_e(t) \ni b \to Exp(b) \in D_e(t) \end{align*}$$
 $b_1,b_2 \in \mathcal {A}_e(t)$
,
$b_1,b_2 \in \mathcal {A}_e(t)$
,  $$\begin{align*}\langle Exp(b_1)|Exp(b_2) \rangle=exp(\langle b_1|b_2 \rangle). \end{align*}$$
$$\begin{align*}\langle Exp(b_1)|Exp(b_2) \rangle=exp(\langle b_1|b_2 \rangle). \end{align*}$$
For
 $b \in A_{e}(t)$
, let
$b \in A_{e}(t)$
, let
 $\{b_s\}_{s \in [0,t]}$
be the unique coherent section of additive decomposable vectors such that
$\{b_s\}_{s \in [0,t]}$
be the unique coherent section of additive decomposable vectors such that
 $b_t=b$
. Then, (2.2)for
$b_t=b$
. Then, (2.2)for $$ \begin{align} Exp(b_r)Exp(b(r,s))=Exp(b_s). \end{align} $$
$$ \begin{align} Exp(b_r)Exp(b(r,s))=Exp(b_s). \end{align} $$
 $0 \leq r \leq s \leq t$
.
$0 \leq r \leq s \leq t$
.
-
(2) If
 $\{b_t\}_{t \in [0,\infty )}$
is an addit, then
$\{b_t\}_{t \in [0,\infty )}$
is an addit, then
 $\{Exp(b_t)\}_{t \in [0,\infty )}$
is a unit. Conversely, if
$\{Exp(b_t)\}_{t \in [0,\infty )}$
is a unit. Conversely, if
 $\{u_t\}_{t \in [0,\infty )}$
is a unit and
$\{u_t\}_{t \in [0,\infty )}$
is a unit and
 $u_t \in D_e(t)$
for every t, then there exists an addit
$u_t \in D_e(t)$
for every t, then there exists an addit
 $\{b_t\}_{t \in [0,\infty )}$
such that
$\{b_t\}_{t \in [0,\infty )}$
such that
 $u_t=Exp(b_t)$
for every
$u_t=Exp(b_t)$
for every
 $t \geq 0$
.
$t \geq 0$
.
For a proof of the above proposition, we refer the reader to [Reference Margetts and Srinivasan16] and [Reference Arjunan1].
Definition 2.2 Let
![]() $E:=\{E(x)\}_{x \in P}$
be a spatial product system over P with a normalized reference unit
$E:=\{E(x)\}_{x \in P}$
be a spatial product system over P with a normalized reference unit
![]() $\{e_x\}_{x \in P}$
. For
$\{e_x\}_{x \in P}$
. For
![]() $x \in P$
, let
$x \in P$
, let
![]() $\widetilde {E}:=\{\widetilde {E}(tx)\}_{t \geq 0}$
be the spatial
$\widetilde {E}:=\{\widetilde {E}(tx)\}_{t \geq 0}$
be the spatial
![]() $1$
-product system with reference unit
$1$
-product system with reference unit
![]() $\{\widetilde {e}_{tx}\}_{t \geq 0}$
. We denote the exponential map of
$\{\widetilde {e}_{tx}\}_{t \geq 0}$
. We denote the exponential map of
![]() $\widetilde {E}$
by
$\widetilde {E}$
by
![]() $Exp_x$
. In particular, if
$Exp_x$
. In particular, if
![]() $b \in \mathcal {A}_e(x)$
, then
$b \in \mathcal {A}_e(x)$
, then
![]() $Exp_x(b)$
is a well defined vector in
$Exp_x(b)$
is a well defined vector in
![]() $E(x)$
. If
$E(x)$
. If
![]() $P=[0,\infty )$
, then for
$P=[0,\infty )$
, then for
![]() $s \geq 0$
, we omit the subscript “s” from
$s \geq 0$
, we omit the subscript “s” from
![]() $Exp_s$
and simply denote it by
$Exp_s$
and simply denote it by
![]() $Exp$
.
$Exp$
.
Suppose V is a pure isometric representation of P on a separable Hilbert space
![]() $\mathcal {H}$
, and let
$\mathcal {H}$
, and let
![]() $E^V:=\{E^V(x)\}_{x \in P}$
be the product system of the CAR flow
$E^V:=\{E^V(x)\}_{x \in P}$
be the product system of the CAR flow
![]() $\beta ^V$
. Recall that, for
$\beta ^V$
. Recall that, for
![]() $x \in P$
,
$x \in P$
,
![]() $E^V(x)=\Gamma _a(Ker (V_x^*))$
and the multiplication rule is given by (1.2). For
$E^V(x)=\Gamma _a(Ker (V_x^*))$
and the multiplication rule is given by (1.2). For
![]() $x \in P$
, let
$x \in P$
, let
![]() $\Omega _x$
be the vacuum vector of
$\Omega _x$
be the vacuum vector of
![]() $\Gamma _a(Ker(V_x^*))$
. Then,
$\Gamma _a(Ker(V_x^*))$
. Then,
![]() $\Omega :=\{\Omega _x\}_{x \in P}$
is a unit which we call the vacuum unit. We always consider the vacuum unit as the reference unit of
$\Omega :=\{\Omega _x\}_{x \in P}$
is a unit which we call the vacuum unit. We always consider the vacuum unit as the reference unit of
![]() $E^V$
while considering the exponential map. The set of additive decomposable vectors was determined by Srinivasan in [Reference Srinivasan33], and we summarize the results in the next remark. A couple of definitions are in order before we make the remark.
$E^V$
while considering the exponential map. The set of additive decomposable vectors was determined by Srinivasan in [Reference Srinivasan33], and we summarize the results in the next remark. A couple of definitions are in order before we make the remark.
For
![]() $x \in P$
, we denote the range projection of
$x \in P$
, we denote the range projection of
![]() $V_x$
by
$V_x$
by
![]() $E_x$
.
$E_x$
.
Definition 2.3 A map
![]() $\xi :P \to \mathcal {H}$
is called an additive cocycle if for
$\xi :P \to \mathcal {H}$
is called an additive cocycle if for
![]() $x \in P$
,
$x \in P$
,
![]() $E_x\xi _x=0$
, and for
$E_x\xi _x=0$
, and for
![]() $x,y \in P$
,
$x,y \in P$
,
The set of additive cocycles is denoted by
![]() $\mathcal {A}(V)$
.
$\mathcal {A}(V)$
.
Let
![]() $u:=\{u_x\}_{x \in P}$
be a unit of
$u:=\{u_x\}_{x \in P}$
be a unit of
![]() $E^V$
. We say that u is an exponential unit if
$E^V$
. We say that u is an exponential unit if
![]() $u_x \in \mathcal {D}_{\Omega }(x)$
for every
$u_x \in \mathcal {D}_{\Omega }(x)$
for every
![]() $x \in P$
, i.e.,
$x \in P$
, i.e.,
![]() $\langle u_x|\Omega _x\rangle =1$
for
$\langle u_x|\Omega _x\rangle =1$
for
![]() $x \in P$
.
$x \in P$
.
Remark 2.2 With the foregoing notation, we have the following.
-
(1) Let
 $x \in P$
. Then, it follows from [Reference Srinivasan33, Proposition 4.1] that
$x \in P$
. Then, it follows from [Reference Srinivasan33, Proposition 4.1] that
 $\mathcal {A}_{\Omega }(x)=Ker(V_x^*)$
. It is easy to see that
$\mathcal {A}_{\Omega }(x)=Ker(V_x^*)$
. It is easy to see that
 $Ker(V_x^*) \subset \mathcal {A}_{\Omega }(x)$
. To see this suppose
$Ker(V_x^*) \subset \mathcal {A}_{\Omega }(x)$
. To see this suppose
 $x \in P$
and
$x \in P$
and
 $\xi \in Ker(V_x^{*})$
. Let
$\xi \in Ker(V_x^{*})$
. Let
 $y \in P$
be such that
$y \in P$
be such that
 $y \leq x$
. Set
$y \leq x$
. Set
 $\xi _y:=E_y^{\perp }\xi $
and
$\xi _y:=E_y^{\perp }\xi $
and
 $\xi (y,x):=V_y^*\xi $
. Then, it is clear from the definition of the multiplication rule that (2.3)
$\xi (y,x):=V_y^*\xi $
. Then, it is clear from the definition of the multiplication rule that (2.3) $$ \begin{align} \xi_y \cdot \Omega_{x-y}+\Omega_y \cdot \xi(y,x)=\xi. \end{align} $$
$$ \begin{align} \xi_y \cdot \Omega_{x-y}+\Omega_y \cdot \xi(y,x)=\xi. \end{align} $$
Suppose
 $P=[0,\infty )$
,
$P=[0,\infty )$
,
 $t \geq 0$
and
$t \geq 0$
and
 $\xi \in Ker(V_t^*)$
. It follows from (2.2) that for
$\xi \in Ker(V_t^*)$
. It follows from (2.2) that for $$\begin{align*}Exp(E_s^\perp \xi)Exp(V_s^*\xi)=Exp(\xi) \end{align*}$$
$$\begin{align*}Exp(E_s^\perp \xi)Exp(V_s^*\xi)=Exp(\xi) \end{align*}$$
 $s \leq t$
. Equivalently, if
$s \leq t$
. Equivalently, if
 $P=[0,\infty )$
, then for
$P=[0,\infty )$
, then for
 $s,t \geq 0$
,
$s,t \geq 0$
,
 $\xi \in Ker(V_s^*)$
and
$\xi \in Ker(V_s^*)$
and
 $\eta \in Ker(V_t^*)$
, (2.4)
$\eta \in Ker(V_t^*)$
, (2.4) $$ \begin{align} Exp(\xi)Exp(\eta)=Exp(\xi+V_s\eta). \end{align} $$
$$ \begin{align} Exp(\xi)Exp(\eta)=Exp(\xi+V_s\eta). \end{align} $$
-
(2) Let
 $\xi :P \to \mathcal {H}$
be a map such that
$\xi :P \to \mathcal {H}$
be a map such that
 $\xi _x \in Ker(V_x^{*})$
for every
$\xi _x \in Ker(V_x^{*})$
for every
 $x \in P$
. It is clear from the definition of an addit, (2.3) and (1.2) that
$x \in P$
. It is clear from the definition of an addit, (2.3) and (1.2) that
 $\{\xi _x\}_{x \in P}$
is an addit if and only if
$\{\xi _x\}_{x \in P}$
is an addit if and only if
 $\xi $
is an additive cocycle for V.
$\xi $
is an additive cocycle for V. -
(3) Let u be an exponential unit of
 $E^V$
. Let
$E^V$
. Let
 $x \in P$
. Note that
$x \in P$
. Note that
 $\{u_{tx}\}_{t \geq 0}$
is a unit for the one parameter product system
$\{u_{tx}\}_{t \geq 0}$
is a unit for the one parameter product system
 $\{E(tx)\}_{t \geq 0}$
. It follows from Proposition 2.1 that there exists a unique
$\{E(tx)\}_{t \geq 0}$
. It follows from Proposition 2.1 that there exists a unique
 $\xi _x \in Ker(V_x^*)$
such that
$\xi _x \in Ker(V_x^*)$
such that
 $u_x=Exp_x(\xi _x)$
. It follows from the definition of
$u_x=Exp_x(\xi _x)$
. It follows from the definition of
 $Exp_x$
that the
$Exp_x$
that the
 $1$
-particle vector of
$1$
-particle vector of
 $u_x$
is
$u_x$
is
 $\xi _x$
. Comparing the
$\xi _x$
. Comparing the
 $1$
-particle vectors of the equation we see that for
$1$
-particle vectors of the equation we see that for $$\begin{align*}Exp_{x+y}(\xi_{x+y})=u_{x+y}=u_x \cdot u_y=Exp_x(\xi_x) \cdot Exp_y(\xi_y)\end{align*}$$
$$\begin{align*}Exp_{x+y}(\xi_{x+y})=u_{x+y}=u_x \cdot u_y=Exp_x(\xi_x) \cdot Exp_y(\xi_y)\end{align*}$$
 $x,y \in P$
,
$x,y \in P$
,
 $\xi _{x+y}=\xi _x+V_x\xi _y$
, i.e.,
$\xi _{x+y}=\xi _x+V_x\xi _y$
, i.e.,
 $\xi :=\{\xi _x\}_{x \in P}$
is an additive cocycle for V.
$\xi :=\{\xi _x\}_{x \in P}$
is an additive cocycle for V.
Thus, if u is an exponential unit, then u is of the form
 $\{Exp_x(\xi _x)\}_{x \in P}$
for a unique
$\{Exp_x(\xi _x)\}_{x \in P}$
for a unique
 $\xi \in \mathcal {A}(V)$
. However, it is not necessary that
$\xi \in \mathcal {A}(V)$
. However, it is not necessary that
 $Exp(\xi ):=\{Exp_x(\xi _x)\}_{x \in P}$
is a unit if
$Exp(\xi ):=\{Exp_x(\xi _x)\}_{x \in P}$
is a unit if
 $\xi \in \mathcal {A}(V)$
(see Proposition 4.16).
$\xi \in \mathcal {A}(V)$
(see Proposition 4.16).
3 Injectivity of the CAR functor
In this section, we prove Theorem 1.1. Suppose V is a pure isometric representation of
![]() $[0,\infty )$
. Let
$[0,\infty )$
. Let
![]() $F:=\{F(t)\}_{t \geq 0}$
be the product system of the associated CCR flow
$F:=\{F(t)\}_{t \geq 0}$
be the product system of the associated CCR flow
![]() $\alpha ^V$
. Recall that for
$\alpha ^V$
. Recall that for
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $F(t):=\Gamma _s(Ker(V_t^*))$
and the multiplication rule is given by
$F(t):=\Gamma _s(Ker(V_t^*))$
and the multiplication rule is given by
for
![]() $\xi \in Ker(V_s^*)$
and
$\xi \in Ker(V_s^*)$
and
![]() $\eta \in Ker(V_t^*)$
. Here,
$\eta \in Ker(V_t^*)$
. Here,
![]() $\{e(\xi ):\xi \in Ker(V_s^*)\}$
denotes the set of exponential vectors. The vacuum unit of F is denoted by
$\{e(\xi ):\xi \in Ker(V_s^*)\}$
denotes the set of exponential vectors. The vacuum unit of F is denoted by
![]() $\Omega :=\{\Omega _t\}_{t \geq 0}$
. We use the same letter
$\Omega :=\{\Omega _t\}_{t \geq 0}$
. We use the same letter
![]() $\Omega $
to denote the vacuum unit of both CCR and CAR flows. Let E denote the product system of the CAR flow
$\Omega $
to denote the vacuum unit of both CCR and CAR flows. Let E denote the product system of the CAR flow
![]() $\beta ^V$
with the reference unit
$\beta ^V$
with the reference unit
![]() $\Omega $
. For
$\Omega $
. For
![]() $t\geq 0$
, let
$t\geq 0$
, let
![]() $D^{E}(t)$
and
$D^{E}(t)$
and
![]() $D^{F}(t)$
denote the decomposable vectors in
$D^{F}(t)$
denote the decomposable vectors in
![]() $E(t)$
and
$E(t)$
and
![]() $F(t)$
, respectively.
$F(t)$
, respectively.
For
![]() $t\geq 0$
, let
$t\geq 0$
, let
and
![]() $D_{\Omega }^{F}(t)$
is defined similarly. From Remark 2.2 and Proposition 2.1, we have
$D_{\Omega }^{F}(t)$
is defined similarly. From Remark 2.2 and Proposition 2.1, we have
and from [Reference Sundar36, Proposition 2.2], we have
It is known that E and F are isomorphic, a fact first proved by Robinson and Powers in [Reference Powers and Robinson21]. For our purposes, we need the following coordinate free isomorphism.
Lemma 3.1 For each
![]() $t\geq 0$
, the map
$t\geq 0$
, the map
![]() $\Psi _{t}:D_{\Omega }^{E}(t)\to D_{\Omega }^{F}(t)$
defined by
$\Psi _{t}:D_{\Omega }^{E}(t)\to D_{\Omega }^{F}(t)$
defined by
is a bijection. Moreover,
for
![]() $s,t \geq 0$
,
$s,t \geq 0$
,
![]() $\xi \in Ker(V^{*}_{s})$
and
$\xi \in Ker(V^{*}_{s})$
and
![]() $\eta \in Ker(V^{*}_{t})$
. The map
$\eta \in Ker(V^{*}_{t})$
. The map
![]() $\Psi _{t}$
extends uniquely to a unitary (again denoted by
$\Psi _{t}$
extends uniquely to a unitary (again denoted by
![]() $\Psi _{t}$
)
$\Psi _{t}$
)
![]() $\Psi _t: E(t)\to F(t)$
for
$\Psi _t: E(t)\to F(t)$
for
![]() $t\geq 0$
. The field of maps
$t\geq 0$
. The field of maps
![]() $\Psi :=\{\Psi _{t}\}_{t\geq 0}$
is an isomorphism from E onto F.
$\Psi :=\{\Psi _{t}\}_{t\geq 0}$
is an isomorphism from E onto F.
Proof From [Reference Arveson8, Corollary 6.8.3],
![]() $D_{\Omega }^{E}(t)$
is total in
$D_{\Omega }^{E}(t)$
is total in
![]() $E(t)$
, and
$E(t)$
, and
![]() $D_{\Omega }^{F}(t)$
is total in
$D_{\Omega }^{F}(t)$
is total in
![]() $F(t)$
for
$F(t)$
for
![]() $t\geq 0$
. Also, by Proposition 2.1,
$t\geq 0$
. Also, by Proposition 2.1,
for
![]() $\eta ,\xi \in Ker(V_{t}^{*})$
for
$\eta ,\xi \in Ker(V_{t}^{*})$
for
![]() $t\geq 0$
. Hence,
$t\geq 0$
. Hence,
![]() $\Psi _{t}$
can be extended to a unitary operator, again denoted
$\Psi _{t}$
can be extended to a unitary operator, again denoted
![]() $\Psi _t$
,
$\Psi _t$
,
![]() $\Psi _{t}:E(t)\to F(t)$
, for
$\Psi _{t}:E(t)\to F(t)$
, for
![]() $t\geq 0$
. It follows from (2.4) and (3.1) that
$t\geq 0$
. It follows from (2.4) and (3.1) that
![]() $\Psi :=\{\Psi _t\}_{t \geq 0}:E \to F$
is an isomorphism. Hence the proof.
$\Psi :=\{\Psi _t\}_{t \geq 0}:E \to F$
is an isomorphism. Hence the proof.
Suppose
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
are pure isometric representations of
$V^{(2)}$
are pure isometric representations of
![]() $[0,\infty )$
on
$[0,\infty )$
on
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {K}$
, respectively. Denote the product systems of the respective CAR flows by
$\mathcal {K}$
, respectively. Denote the product systems of the respective CAR flows by
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. Let
$E_{2}$
. Let
 $$\begin{align*}&\mathscr{U}(V^{(1)}, V^{(2)})\\ &\quad :=\{U:\mathcal{H}\to\mathcal{K}:U \text{ is a unitary}, UV^{(1)}_{t}=V^{(2)}_{t}U, UV^{(1)*}_{t}=V^{(2)*}_{t}U \text{for} t\geq 0\}.\end{align*}$$
$$\begin{align*}&\mathscr{U}(V^{(1)}, V^{(2)})\\ &\quad :=\{U:\mathcal{H}\to\mathcal{K}:U \text{ is a unitary}, UV^{(1)}_{t}=V^{(2)}_{t}U, UV^{(1)*}_{t}=V^{(2)*}_{t}U \text{for} t\geq 0\}.\end{align*}$$
The proof of the next lemma is essentially an application of Lemma 3.1 and the gauge group computation of CCR flows due to Arveson.
Lemma 3.2 Suppose
![]() $\Psi : E_{1}\to E_{2}$
is an isomorphism of product systems. Then, there exists
$\Psi : E_{1}\to E_{2}$
is an isomorphism of product systems. Then, there exists
![]() $U\in \mathscr {U}(V^{(1)}, V^{(2)})$
,
$U\in \mathscr {U}(V^{(1)}, V^{(2)})$
,
![]() $\xi =\{\xi _{t}\}_{t\geq 0}\in \mathcal {A}(V^{(2)})$
, and
$\xi =\{\xi _{t}\}_{t\geq 0}\in \mathcal {A}(V^{(2)})$
, and
![]() $\lambda \in \mathbb {R}$
such that
$\lambda \in \mathbb {R}$
such that
for
![]() $\eta \in Ker(V^{(1)*}_{t})$
,
$\eta \in Ker(V^{(1)*}_{t})$
,
![]() $t\geq 0$
.
$t\geq 0$
.
Proof We denote by
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
the product systems of the CCR flows associated with
$F_{2}$
the product systems of the CCR flows associated with
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
respectively. For
$V^{(2)}$
respectively. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\Theta _{i}=\{\Theta _{i}(t)\}_{t \geq 0}$
be the isomorphism from
$\Theta _{i}=\{\Theta _{i}(t)\}_{t \geq 0}$
be the isomorphism from
![]() $E_{i}$
onto
$E_{i}$
onto
![]() $F_{i}$
given by
$F_{i}$
given by
for
![]() $\eta \in Ker(V^{(i)*}_{t})$
and
$\eta \in Ker(V^{(i)*}_{t})$
and
![]() $t\geq 0$
. The isomorphism
$t\geq 0$
. The isomorphism
![]() $\Theta _i$
for
$\Theta _i$
for
![]() $i=1,2$
is guaranteed by Lemma 3.1. Then,
$i=1,2$
is guaranteed by Lemma 3.1. Then,
![]() $\Delta =\Theta _{2}\circ \Psi \circ \Theta _{1}^{-1}$
is an isomorphism from
$\Delta =\Theta _{2}\circ \Psi \circ \Theta _{1}^{-1}$
is an isomorphism from
![]() $F_{1}$
onto
$F_{1}$
onto
![]() $F_{2}$
.
$F_{2}$
.
It follows from [Reference Arveson8, Corollary 2.6.10] that
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
are unitarily equivalent. Suppose
$V^{(2)}$
are unitarily equivalent. Suppose
![]() $W:\mathcal {H}\to \mathcal {K}$
is a unitary such that
$W:\mathcal {H}\to \mathcal {K}$
is a unitary such that
![]() $WV^{(1)}_{t}=V^{(2)}_{t}W$
for
$WV^{(1)}_{t}=V^{(2)}_{t}W$
for
![]() $t\geq 0$
. For
$t\geq 0$
. For
![]() $t\geq 0$
, let
$t\geq 0$
, let
![]() $\Lambda _t:F_1(t) \to F_2(t)$
be the unitary operator such that
$\Lambda _t:F_1(t) \to F_2(t)$
be the unitary operator such that
for
![]() $\xi \in Ker(V^{(1)*}_t)$
. Clearly,
$\xi \in Ker(V^{(1)*}_t)$
. Clearly,
![]() $\Lambda :=\{\Lambda _{t}\}_{t\geq 0}:F_{1}\to F_{2}$
is an isomorphism.
$\Lambda :=\{\Lambda _{t}\}_{t\geq 0}:F_{1}\to F_{2}$
is an isomorphism.
Now consider the map
![]() $T:=\Lambda ^{-1}\circ \Delta $
. The map T is an automorphism of
$T:=\Lambda ^{-1}\circ \Delta $
. The map T is an automorphism of
![]() $F_{1}$
. By [Reference Arveson8, Theorem 3.8.4], there exists
$F_{1}$
. By [Reference Arveson8, Theorem 3.8.4], there exists
![]() $U \in \mathscr {U}(V^{(1)},V^{(1)})$
, an additive cocycle
$U \in \mathscr {U}(V^{(1)},V^{(1)})$
, an additive cocycle
![]() $\xi =\{\xi _{t}\}_{t\geq 0}$
for
$\xi =\{\xi _{t}\}_{t\geq 0}$
for
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $\lambda \in \mathbb {R}$
such that
$\lambda \in \mathbb {R}$
such that
for
![]() $\eta \in Ker(V_t^{(1)*})$
. For
$\eta \in Ker(V_t^{(1)*})$
. For
![]() $t \geq 0$
, set
$t \geq 0$
, set
![]() $\widetilde {\xi }_t:=W\xi _t$
and
$\widetilde {\xi }_t:=W\xi _t$
and
![]() $\widetilde {U}:=WU$
. Then,
$\widetilde {U}:=WU$
. Then,
![]() $\widetilde {U} \in \mathscr {U}(V^{(1)},V^{(2)})$
and
$\widetilde {U} \in \mathscr {U}(V^{(1)},V^{(2)})$
and
![]() $\widetilde {\xi }:=\{\widetilde {\xi }_t\}_{t\geq 0}$
is an additive cocycle for
$\widetilde {\xi }:=\{\widetilde {\xi }_t\}_{t\geq 0}$
is an additive cocycle for
![]() $V^{(2)}$
.
$V^{(2)}$
.
Since
![]() $\Delta :=\Lambda \circ T$
, it follows that for for
$\Delta :=\Lambda \circ T$
, it follows that for for
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $\eta \in Ker(V^{(1)*}_{t})$
,
$\eta \in Ker(V^{(1)*}_{t})$
,
 $$ \begin{align*} \Delta_{t}e(\eta)&=e^{i\lambda t}e^{-\frac{||\xi_{t}||^{2}}{2}-\langle U\eta|\xi_{t}\rangle}e(WU\eta+W\xi_{t})\\ &=e^{i\lambda t}e^{-\frac{||W\xi_{t}||^{2}}{2}-\langle WU\eta|W\xi_{t}\rangle}e(WU\eta+\widetilde{\xi}_{t})\\ &=e^{i \lambda t}e^{-\frac{||\widetilde{\xi}_t||^{2}}{2}-\langle \widetilde{U}\eta|\widetilde{\xi}_t\rangle}e(\widetilde{U}\eta+\widetilde{\xi}_t). \end{align*} $$
$$ \begin{align*} \Delta_{t}e(\eta)&=e^{i\lambda t}e^{-\frac{||\xi_{t}||^{2}}{2}-\langle U\eta|\xi_{t}\rangle}e(WU\eta+W\xi_{t})\\ &=e^{i\lambda t}e^{-\frac{||W\xi_{t}||^{2}}{2}-\langle WU\eta|W\xi_{t}\rangle}e(WU\eta+\widetilde{\xi}_{t})\\ &=e^{i \lambda t}e^{-\frac{||\widetilde{\xi}_t||^{2}}{2}-\langle \widetilde{U}\eta|\widetilde{\xi}_t\rangle}e(\widetilde{U}\eta+\widetilde{\xi}_t). \end{align*} $$
Since
![]() $\Psi =\Theta _2^{-1} \circ \Delta \circ \Theta _1$
, it is immediate that
$\Psi =\Theta _2^{-1} \circ \Delta \circ \Theta _1$
, it is immediate that
for
![]() $\eta \in Ker(V^{(1)*}_{t})$
and
$\eta \in Ker(V^{(1)*}_{t})$
and
![]() $t\geq 0$
. Hence the proof.
$t\geq 0$
. Hence the proof.
Let P be a closed convex cone in
![]() $\mathbb {R}^d$
which is spanning and pointed. Let
$\mathbb {R}^d$
which is spanning and pointed. Let
![]() $V^{(1)}$
,
$V^{(1)}$
,
![]() $V^{(2)}$
be two pure isometric representations of P on Hilbert spaces
$V^{(2)}$
be two pure isometric representations of P on Hilbert spaces
![]() $\mathcal {H}_1$
and
$\mathcal {H}_1$
and
![]() $\mathcal {H}_2$
, respectively. We denote the product systems of the corresponding CAR flows by
$\mathcal {H}_2$
, respectively. We denote the product systems of the corresponding CAR flows by
![]() $E^{(1)}$
and
$E^{(1)}$
and
![]() $E^{(2)}$
, respectively.
$E^{(2)}$
, respectively.
Theorem 3.3 The product systems
![]() $E^{(1)}$
and
$E^{(1)}$
and
![]() $E^{(2)}$
are isomorphic if and only if
$E^{(2)}$
are isomorphic if and only if
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
are unitarily equivalent.
$V^{(2)}$
are unitarily equivalent.
Proof Suppose
![]() $E^{(1)}$
and
$E^{(1)}$
and
![]() $E^{(2)}$
are isomorphic. Let
$E^{(2)}$
are isomorphic. Let
![]() $\Psi =\{\Psi _{a}\}_{a\in P}:E^{(1)}\to E^{(2)}$
be an isomorphism. Let
$\Psi =\{\Psi _{a}\}_{a\in P}:E^{(1)}\to E^{(2)}$
be an isomorphism. Let
![]() $a\in Int(P)$
. Consider the one parameter product system
$a\in Int(P)$
. Consider the one parameter product system
![]() $E_{a}^{(1)}:= \{E_{a}^{(1)} (t)\}_{t \geq 0}$
, where for
$E_{a}^{(1)}:= \{E_{a}^{(1)} (t)\}_{t \geq 0}$
, where for
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $E_{a}^{(1)}(t):=E^{(1)}(ta)$
. Similarly, consider the one parameter product system
$E_{a}^{(1)}(t):=E^{(1)}(ta)$
. Similarly, consider the one parameter product system
![]() $E_{a}^{(2)}:= \{E_{a}^{(2)}(t)\}_{t \geq 0}$
, where
$E_{a}^{(2)}:= \{E_{a}^{(2)}(t)\}_{t \geq 0}$
, where
![]() $E_{a}^{(2)}(t):=E^{(2)}(ta)$
for
$E_{a}^{(2)}(t):=E^{(2)}(ta)$
for
![]() $t\geq 0$
. Then,
$t\geq 0$
. Then,
![]() $\{\Psi _{ta}\}_{t \geq 0}:E_a^{(1)} \to E_a^{(2)}$
is an isomorphism.
$\{\Psi _{ta}\}_{t \geq 0}:E_a^{(1)} \to E_a^{(2)}$
is an isomorphism.
By Lemma 3.2, there exists a unitary
![]() $U_{a}:\mathcal {H}_1\to \mathcal {H}_2$
intertwining
$U_{a}:\mathcal {H}_1\to \mathcal {H}_2$
intertwining
![]() $\{V^{(1)}_{ta}\}_{t\geq 0}$
and
$\{V^{(1)}_{ta}\}_{t\geq 0}$
and
![]() $\{V^{(2)}_{ta}\}_{t\geq 0}$
, an additive cocycle
$\{V^{(2)}_{ta}\}_{t\geq 0}$
, an additive cocycle
![]() $ \{\xi ^{a}_{t}\}_{t\geq 0}$
of
$ \{\xi ^{a}_{t}\}_{t\geq 0}$
of
![]() $\{V^{(2)}_{ta}\}_{t\geq 0}$
and
$\{V^{(2)}_{ta}\}_{t\geq 0}$
and
![]() $\lambda _{a}\in \mathbb {R}$
such that
$\lambda _{a}\in \mathbb {R}$
such that
![]() $\Psi _{ta}$
is of the form
$\Psi _{ta}$
is of the form
for
![]() $\xi \in Ker(V^{(1)*}_{ta}) $
and
$\xi \in Ker(V^{(1)*}_{ta}) $
and
![]() $t>0$
. We will denote
$t>0$
. We will denote
![]() $\xi ^{a}_{1}$
by
$\xi ^{a}_{1}$
by
![]() $\xi _{a}$
. Hence,
$\xi _{a}$
. Hence,
for
![]() $a \in Int(P)$
and
$a \in Int(P)$
and
![]() $\xi \in Ker(V^{(1)*}_a)$
.
$\xi \in Ker(V^{(1)*}_a)$
.
Let
![]() $a, b\in Int(P)$
. Since
$a, b\in Int(P)$
. Since
![]() $\Psi $
is an isomorphism, we have
$\Psi $
is an isomorphism, we have
for
![]() $\xi \in Ker(V^{(1)*}_{a}) $
and
$\xi \in Ker(V^{(1)*}_{a}) $
and
![]() $\eta \in Ker(V^{(1)*}_{b}) $
.
$\eta \in Ker(V^{(1)*}_{b}) $
.
In particular,
i.e.,
Comparing the
![]() $0$
-particle vectors in LHS and RHS of (3.4), we have
$0$
-particle vectors in LHS and RHS of (3.4), we have
Now, comparing the
![]() $1$
-particle vectors of LHS and RHS in (3.4), we have
$1$
-particle vectors of LHS and RHS in (3.4), we have
Let
![]() $\xi \in Ker(V^{(1)*}_{a})$
. Consider the equation
$\xi \in Ker(V^{(1)*}_{a})$
. Consider the equation
Considering the exponential map in the one parameter product system
![]() $E^{(1)}_a$
, we have
$E^{(1)}_a$
, we have
where for
![]() $r \in (0,1]$
,
$r \in (0,1]$
,
![]() $x_r^{(0)}=\Omega _{ra}$
,
$x_r^{(0)}=\Omega _{ra}$
,
![]() $x_r^{(1)}= (1-V_{ra}^{(1)}V_{ra}^{(1)*})\xi $
and
$x_r^{(1)}= (1-V_{ra}^{(1)}V_{ra}^{(1)*})\xi $
and
![]() $x_r^{(n)}=\int _{0}^{r}x_t^{(n-1)}d\xi _{t}$
. Here, for
$x_r^{(n)}=\int _{0}^{r}x_t^{(n-1)}d\xi _{t}$
. Here, for
![]() $t \in (0,1]$
,
$t \in (0,1]$
,
![]() $\xi _{t}=(1-V^{(1)}_{ta}V^{(1)*}_{ta})\xi $
.
$\xi _{t}=(1-V^{(1)}_{ta}V^{(1)*}_{ta})\xi $
.
Let
![]() $s \in \mathbb {R}$
. Suppose
$s \in \mathbb {R}$
. Suppose
where the summands are obtained via Itô integration. A moment’s reflection on the definition of the Itô integral reveals that
for
![]() $n=0,1,2,\cdots $
.
$n=0,1,2,\cdots $
.
Note that
for
![]() $t \in \mathbb {R}$
. Since the power series in (3.8) is norm convergent for every
$t \in \mathbb {R}$
. Since the power series in (3.8) is norm convergent for every
![]() $t \in \mathbb {R}$
, it may be differentiated term by term, and the derivative is given by
$t \in \mathbb {R}$
, it may be differentiated term by term, and the derivative is given by
Hence,
From (3.3) we have,
 $$ \begin{align*} & \frac{d}{dt}\Psi_{a}Exp_{a}(t\xi) \\ &\quad =\frac{d}{dt} e^{i\lambda_{a}}e^{-\frac{||\xi_{a}||^{2}}{2}}e^{-t\langle U_{a}\xi|\xi_{a}\rangle}Exp_{a}(tU_{a}\xi+\xi_{a})\\ &\quad =e^{i\lambda_{a}}e^{-\frac{||\xi_{a}||^{2}}{2}}\Big(Exp_{a}(tU_{a}\xi+\xi_{a})\frac{d}{dt}e^{-t\langle U_{a}\xi|\xi_{a}\rangle}+ e^{-t\langle U_{a}\xi|\xi_{a}\rangle}\frac{d}{dt}Exp_{a}(tU_{a}\xi+\xi_{a})\Big)\\ &\quad =e^{i\lambda_{a}-\frac{||\xi_{a}||^{2}}{2}}e^{-t\langle U_{a}\xi|\xi_{a}\rangle}\Big(-\langle U_{a}\xi|\xi_{a}\rangle Exp_{a}(tU_{a}\xi+\xi_{a})+U_{a}\xi+q_{a}(t,\xi)\Big) \end{align*} $$
$$ \begin{align*} & \frac{d}{dt}\Psi_{a}Exp_{a}(t\xi) \\ &\quad =\frac{d}{dt} e^{i\lambda_{a}}e^{-\frac{||\xi_{a}||^{2}}{2}}e^{-t\langle U_{a}\xi|\xi_{a}\rangle}Exp_{a}(tU_{a}\xi+\xi_{a})\\ &\quad =e^{i\lambda_{a}}e^{-\frac{||\xi_{a}||^{2}}{2}}\Big(Exp_{a}(tU_{a}\xi+\xi_{a})\frac{d}{dt}e^{-t\langle U_{a}\xi|\xi_{a}\rangle}+ e^{-t\langle U_{a}\xi|\xi_{a}\rangle}\frac{d}{dt}Exp_{a}(tU_{a}\xi+\xi_{a})\Big)\\ &\quad =e^{i\lambda_{a}-\frac{||\xi_{a}||^{2}}{2}}e^{-t\langle U_{a}\xi|\xi_{a}\rangle}\Big(-\langle U_{a}\xi|\xi_{a}\rangle Exp_{a}(tU_{a}\xi+\xi_{a})+U_{a}\xi+q_{a}(t,\xi)\Big) \end{align*} $$
where the projection of
![]() $q_{a}(t,\xi )$
onto
$q_{a}(t,\xi )$
onto
![]() $0$
-particle and
$0$
-particle and
![]() $1$
-particle space is zero. By (3.9),
$1$
-particle space is zero. By (3.9),
Similarly,
where the projection of
![]() $q_{a+b}(0,\xi )$
onto
$q_{a+b}(0,\xi )$
onto
![]() $0$
-particle and
$0$
-particle and
![]() $1$
-particle space is zero.
$1$
-particle space is zero.
Therefore, (3.7) implies,
 $$ \begin{align*} &e^{i(\lambda_{a}+\lambda_{b})-\frac{(||\xi_{a}||^{2}+||\xi_{b}||^{2})}{2}}\Big(\!\!-\langle U_{a}\xi|\xi_{a}\rangle Exp_{a}(\xi_{a})+U_{a}\xi+q_{a}(0,\xi)\Big).Exp_{b}(\xi_{b})\\ & \quad =e^{i\lambda_{a+b}-\frac{||\xi_{a+b}||^{2}}{2}}\Big(\!\!-\langle U_{a+b}\xi|\xi_{a+b}\rangle Exp_{a+b}(\xi_{a+b})+U_{a+b}\xi+q_{a+b}(0,\xi)\Big). \end{align*} $$
$$ \begin{align*} &e^{i(\lambda_{a}+\lambda_{b})-\frac{(||\xi_{a}||^{2}+||\xi_{b}||^{2})}{2}}\Big(\!\!-\langle U_{a}\xi|\xi_{a}\rangle Exp_{a}(\xi_{a})+U_{a}\xi+q_{a}(0,\xi)\Big).Exp_{b}(\xi_{b})\\ & \quad =e^{i\lambda_{a+b}-\frac{||\xi_{a+b}||^{2}}{2}}\Big(\!\!-\langle U_{a+b}\xi|\xi_{a+b}\rangle Exp_{a+b}(\xi_{a+b})+U_{a+b}\xi+q_{a+b}(0,\xi)\Big). \end{align*} $$
Using (3.5), the above equation reduces to
 $$ \begin{align} &\big(\!\!-\langle U_{a}\xi|\xi_{a}\rangle Exp_{a}(\xi_{a})+U_{a}\xi+q_{a}(0,\xi)\Big).Exp_{b}(\xi_{b}) \nonumber \\ &\quad =-\langle U_{a+b}\xi|\xi_{a+b}\rangle Exp_{a+b}(\xi_{a+b})+U_{a+b}\xi+q_{a+b}(0,\xi). \end{align} $$
$$ \begin{align} &\big(\!\!-\langle U_{a}\xi|\xi_{a}\rangle Exp_{a}(\xi_{a})+U_{a}\xi+q_{a}(0,\xi)\Big).Exp_{b}(\xi_{b}) \nonumber \\ &\quad =-\langle U_{a+b}\xi|\xi_{a+b}\rangle Exp_{a+b}(\xi_{a+b})+U_{a+b}\xi+q_{a+b}(0,\xi). \end{align} $$
By equating the
![]() $0$
-particle vectors in the above equation, we see that
$0$
-particle vectors in the above equation, we see that
Equating the
![]() $1$
-particle vectors in (3.10), we have
$1$
-particle vectors in (3.10), we have
Thus, if
![]() $\xi \in Ker( V^{(1)*}_{a})$
and
$\xi \in Ker( V^{(1)*}_{a})$
and
![]() $\xi \in Ker( V^{(1)*}_{b})$
for
$\xi \in Ker( V^{(1)*}_{b})$
for
![]() $a,b\in Int(P)$
,
$a,b\in Int(P)$
,
![]() $U_{a}\xi =U_{a+b}\xi =U_{b}\xi $
. Since
$U_{a}\xi =U_{a+b}\xi =U_{b}\xi $
. Since
![]() $ \bigcup _{a \in Int(P)}Ker(V_a^{(1)*})$
is dense in
$ \bigcup _{a \in Int(P)}Ker(V_a^{(1)*})$
is dense in
![]() $\mathcal {H}_1$
, it follows that there exists a unitary operator
$\mathcal {H}_1$
, it follows that there exists a unitary operator
![]() $U: \mathcal {H}_1\to \mathcal {H}_2$
such that
$U: \mathcal {H}_1\to \mathcal {H}_2$
such that
if
![]() $\xi \in Ker(V^{(1)*}_{a})$
.
$\xi \in Ker(V^{(1)*}_{a})$
.
Similarly, considering the equation
for
![]() $\eta \in Ker(V^{(1)*}_{b})$
and comparing
$\eta \in Ker(V^{(1)*}_{b})$
and comparing
![]() $0$
and
$0$
and
![]() $1$
-particle vectors as before, it is not difficult to see that for
$1$
-particle vectors as before, it is not difficult to see that for
![]() $a,b \in Int(P)$
and
$a,b \in Int(P)$
and
![]() $\eta \in Ker(V_b^{(1)*})$
$\eta \in Ker(V_b^{(1)*})$
Since
![]() $\displaystyle \bigcup _{b \in Int(P)}Ker(V_b^{(1)*})$
is dense in
$\displaystyle \bigcup _{b \in Int(P)}Ker(V_b^{(1)*})$
is dense in
![]() $\mathcal {H}_1$
, it follows that
$\mathcal {H}_1$
, it follows that
![]() $UV^{(1)}_a=V^{(2)}_aU$
for every
$UV^{(1)}_a=V^{(2)}_aU$
for every
![]() $a \in Int(P)$
. As
$a \in Int(P)$
. As
![]() $Int(P)$
is dense in P, U intertwines
$Int(P)$
is dense in P, U intertwines
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
. This completes the proof.
$V^{(2)}$
. This completes the proof.
4 Type I CAR flows associated with isometric representations with commuting range projections
In this section, we characterize pure isometric representations of P with commuting range projections that give rise to type I CAR flows. Recall that a pure isometric representation V of P is said to have commuting range projections if
![]() $\{V_{a}V_{a}^{*}: a \in P\}$
is a commuting family of projections. First, we recall the dynamical system that encodes all pure isometric representations with commuting range projections. Let
$\{V_{a}V_{a}^{*}: a \in P\}$
is a commuting family of projections. First, we recall the dynamical system that encodes all pure isometric representations with commuting range projections. Let
![]() $\mathcal {C}(\mathbb {R}^{d})$
denote the set of closed subsets of
$\mathcal {C}(\mathbb {R}^{d})$
denote the set of closed subsets of
![]() $\mathbb {R}^{d}$
which we equip with the Fell topology.
$\mathbb {R}^{d}$
which we equip with the Fell topology.
Let
![]() $(A_n)$
be a sequence in
$(A_n)$
be a sequence in
![]() $\mathcal {C}(\mathbb {R}^d)$
, and let
$\mathcal {C}(\mathbb {R}^d)$
, and let
![]() $A \in \mathcal {C}(\mathbb {R}^d)$
. Then,
$A \in \mathcal {C}(\mathbb {R}^d)$
. Then,
![]() $(A_n) \to A$
if and only if
$(A_n) \to A$
if and only if
![]() $\limsup A_n=\liminf A_n=A$
, where
$\limsup A_n=\liminf A_n=A$
, where
 $$ \begin{align*} \liminf A_n & :=\{x \in \mathbb{R}^d: \text{for every} n, \text{there exists } x_n \in A_n \text{ such that } (x_n) \to x\}\\ \limsup A_n & := \{x \in \mathbb{R}^d: \text{there exists a subsequence } (n_k) \text{ and } x_{n_k} \in A_{n_k}\\ &\qquad \text{ such that } (x_{n_k})_k \to x\}. \end{align*} $$
$$ \begin{align*} \liminf A_n & :=\{x \in \mathbb{R}^d: \text{for every} n, \text{there exists } x_n \in A_n \text{ such that } (x_n) \to x\}\\ \limsup A_n & := \{x \in \mathbb{R}^d: \text{there exists a subsequence } (n_k) \text{ and } x_{n_k} \in A_{n_k}\\ &\qquad \text{ such that } (x_{n_k})_k \to x\}. \end{align*} $$
Let
 $$ \begin{align*}Y_{u}:&=\{A\in\mathcal{C}(\mathbb{R}^{d}): { -P+A\subset A, A\neq \emptyset, A\neq \mathbb{R}^d}\},\\ X_{u}:&=\{A\in Y_{u}:{ 0\in A}\}. \end{align*} $$
$$ \begin{align*}Y_{u}:&=\{A\in\mathcal{C}(\mathbb{R}^{d}): { -P+A\subset A, A\neq \emptyset, A\neq \mathbb{R}^d}\},\\ X_{u}:&=\{A\in Y_{u}:{ 0\in A}\}. \end{align*} $$
The space
![]() $Y_{u}$
is locally compact, Hausdorff and second countable on which the group
$Y_{u}$
is locally compact, Hausdorff and second countable on which the group
![]() $\mathbb {R}^d$
acts. The action is given by the map
$\mathbb {R}^d$
acts. The action is given by the map
Note that
![]() $X_u+P \subset X_u$
and
$X_u+P \subset X_u$
and
![]() $Y_u=\displaystyle \bigcup _{a \in P}(X_u-a)$
.
$Y_u=\displaystyle \bigcup _{a \in P}(X_u-a)$
.
Remark 4.1 In the
![]() $1$
-dimensional case, the space
$1$
-dimensional case, the space
![]() $Y_u$
has a very simple description. Let
$Y_u$
has a very simple description. Let
![]() $P=[0,\infty )$
. Suppose
$P=[0,\infty )$
. Suppose
![]() $A \in Y_u$
. The fact that
$A \in Y_u$
. The fact that
![]() $A-[0,\infty ) \subset A$
implies that A is an interval that is not bounded below. Since
$A-[0,\infty ) \subset A$
implies that A is an interval that is not bounded below. Since
![]() $A \neq \mathbb {R}$
, and since A is closed, it follows that
$A \neq \mathbb {R}$
, and since A is closed, it follows that
![]() $A=(-\infty ,a]$
for a unique
$A=(-\infty ,a]$
for a unique
![]() $a \in \mathbb {R}$
. It is not difficult to show that the map
$a \in \mathbb {R}$
. It is not difficult to show that the map
is an
![]() $\mathbb {R}$
-equivariant homeomorphism. Here, the action of
$\mathbb {R}$
-equivariant homeomorphism. Here, the action of
![]() $\mathbb {R}$
on
$\mathbb {R}$
on
![]() $\mathbb {R}$
is by translations. With this identification of
$\mathbb {R}$
is by translations. With this identification of
![]() $Y_u$
with
$Y_u$
with
![]() $\mathbb {R}$
, we have
$\mathbb {R}$
, we have
![]() $X_u=[0,\infty )$
.
$X_u=[0,\infty )$
.
It was proved in [Reference Sundar37] that there is a bijective correspondence between the class of pure isometric representations of P with commuting range projections and the class of covariant representations of the dynamical system
![]() $(Y_u,\mathbb {R}^d)$
. For us, the most important examples of isometric representations are the “shift semigroups on
$(Y_u,\mathbb {R}^d)$
. For us, the most important examples of isometric representations are the “shift semigroups on
![]() $X_u$
” that arise from invariant measures on
$X_u$
” that arise from invariant measures on
![]() $Y_u$
.
$Y_u$
.
Let
![]() $\mu $
be a non-zero Radon measure on
$\mu $
be a non-zero Radon measure on
![]() $Y_{u}$
which is also invariant under the above mentioned action of
$Y_{u}$
which is also invariant under the above mentioned action of
![]() $\mathbb {R}^{d}$
. Define an isometric representation
$\mathbb {R}^{d}$
. Define an isometric representation
![]() $V^{\mu }$
of P on
$V^{\mu }$
of P on
![]() $L^{2}(X_{u},\mu )$
by
$L^{2}(X_{u},\mu )$
by
 $$\begin{align*}V^{\mu}_{a}f(A):=\begin{cases}f(A-a) & \text{~if~}A-a\in X_{u},\\ 0 & \text{~if~}A-a \notin X_u. \end{cases}\end{align*}$$
$$\begin{align*}V^{\mu}_{a}f(A):=\begin{cases}f(A-a) & \text{~if~}A-a\in X_{u},\\ 0 & \text{~if~}A-a \notin X_u. \end{cases}\end{align*}$$
for
![]() $a\in P$
. Clearly,
$a\in P$
. Clearly,
![]() $V^{\mu }$
has commuting range projections.
$V^{\mu }$
has commuting range projections.
It follows from [Reference Sundar34, Lemmas 3.8 and 3.9] that the set
![]() $X_{u}\setminus (X_{u}+a)$
has compact closure for
$X_{u}\setminus (X_{u}+a)$
has compact closure for
![]() $a \in P$
and has positive measure if
$a \in P$
and has positive measure if
![]() $a \in Int(P)$
. It is now clear that
$a \in Int(P)$
. It is now clear that
![]() $\{1_{X_{u}\setminus (X_{u}+a)}\}_{a\in P}$
is a non-zero additive cocycle for
$\{1_{X_{u}\setminus (X_{u}+a)}\}_{a\in P}$
is a non-zero additive cocycle for
![]() $V^{\mu }$
.
$V^{\mu }$
.
Recall that
![]() $P^*$
stands for the dual cone of P, and
$P^*$
stands for the dual cone of P, and
![]() $S(P^*):=\{\lambda \in P^*: ||\lambda ||=1\}$
. Suppose
$S(P^*):=\{\lambda \in P^*: ||\lambda ||=1\}$
. Suppose
![]() $\lambda \in S(P^{*})$
. Define
$\lambda \in S(P^{*})$
. Define
Define
and
Note that
![]() $X_{u}^{\lambda }$
,
$X_{u}^{\lambda }$
,
![]() $Y_{u}^{\lambda }\subset Y_{u}$
are closed. Also, observe that
$Y_{u}^{\lambda }\subset Y_{u}$
are closed. Also, observe that
![]() $Y_u^{\lambda }$
is
$Y_u^{\lambda }$
is
![]() $\mathbb {R}^d$
-invariant and
$\mathbb {R}^d$
-invariant and
![]() $X_u^{\lambda }+ P \subset P$
.
$X_u^{\lambda }+ P \subset P$
.
Let
![]() $S:=\{S_{t}\}_{t\geq 0}$
be the one parameter shift semigroup on
$S:=\{S_{t}\}_{t\geq 0}$
be the one parameter shift semigroup on
![]() $L^{2}[0,\infty )$
defined by
$L^{2}[0,\infty )$
defined by
For
![]() $\lambda \in S(P^{*})$
, define the isometric representation
$\lambda \in S(P^{*})$
, define the isometric representation
![]() $S^{\lambda }$
of P on
$S^{\lambda }$
of P on
![]() $L^{2}[0,\infty )$
by
$L^{2}[0,\infty )$
by
for
![]() $a\in P$
.
$a\in P$
.
Let
![]() $\mu $
be a non-zero
$\mu $
be a non-zero
![]() $\mathbb {R}^d$
-invariant Radon measure on
$\mathbb {R}^d$
-invariant Radon measure on
![]() $Y_u$
. Denote the product system of the CAR flow associated with
$Y_u$
. Denote the product system of the CAR flow associated with
![]() $V^{\mu }$
by
$V^{\mu }$
by
![]() $E^{\mu }$
. For
$E^{\mu }$
. For
![]() $a\in P$
, let
$a\in P$
, let
![]() $\eta _{a}:=1_{X_{u}\setminus X_{u}+a}$
, let
$\eta _{a}:=1_{X_{u}\setminus X_{u}+a}$
, let
![]() $\eta :=\{\eta _{a}\}_{a\in P}$
, and let
$\eta :=\{\eta _{a}\}_{a\in P}$
, and let
![]() $Exp(\eta ):=\{Exp_a(\eta _a)\}_{a \in P}$
.
$Exp(\eta ):=\{Exp_a(\eta _a)\}_{a \in P}$
.
Lemma 4.2 Suppose
![]() $supp(\mu )=Y^{\lambda }_{u}$
for some
$supp(\mu )=Y^{\lambda }_{u}$
for some
![]() $\lambda \in S(P^*)$
. Then,
$\lambda \in S(P^*)$
. Then,
-
(i)
 $V^{\mu }$
is unitarily equivalent to
$V^{\mu }$
is unitarily equivalent to
 $S^{\lambda }$
, and
$S^{\lambda }$
, and -
(ii)
 $Exp(\eta )$
is a unit for
$Exp(\eta )$
is a unit for
 $E^{\mu }$
.
$E^{\mu }$
.
Proof We first show that
![]() $V^{\mu }$
is unitarily equivalent to
$V^{\mu }$
is unitarily equivalent to
![]() $S^{\lambda }$
. The reader may verify that the map
$S^{\lambda }$
. The reader may verify that the map
![]() $\mathcal {F}: Y^{\lambda }_{u}\to \mathbb {R}$
defined by
$\mathcal {F}: Y^{\lambda }_{u}\to \mathbb {R}$
defined by
is a homeomorphism, and
![]() $\mathcal {F}(X_u^{\lambda })=[0,\infty )$
. Also,
$\mathcal {F}(X_u^{\lambda })=[0,\infty )$
. Also,
for
![]() $t \in \mathbb {R}$
and
$t \in \mathbb {R}$
and
![]() $a \in \mathbb {R}^d$
. Since
$a \in \mathbb {R}^d$
. Since
![]() $\mu $
is an invariant measure, the push forward measure
$\mu $
is an invariant measure, the push forward measure
![]() $\mathcal {F}_{*}\mu $
is the Lebesgue measure, denoted by m. Define a unitary operator
$\mathcal {F}_{*}\mu $
is the Lebesgue measure, denoted by m. Define a unitary operator
![]() $U: L^{2}([0,\infty ),m)\to L^{2}(X_{u}^{\lambda },\mu )$
by
$U: L^{2}([0,\infty ),m)\to L^{2}(X_{u}^{\lambda },\mu )$
by
It is routine to verify that U intertwines
![]() $S^{\lambda }$
and
$S^{\lambda }$
and
![]() $V^{\mu }$
. Note that
$V^{\mu }$
. Note that
![]() $U^{-1}(1_{X_{u}\setminus X_{u}+a})=1_{(0,\langle \lambda |a\rangle )}$
for
$U^{-1}(1_{X_{u}\setminus X_{u}+a})=1_{(0,\langle \lambda |a\rangle )}$
for
![]() $a\in P$
. By abusing notation, we may assume that
$a\in P$
. By abusing notation, we may assume that
![]() $V^{\mu }=S^{\lambda }$
and
$V^{\mu }=S^{\lambda }$
and
![]() $\eta _{a}=1_{(0,\langle \lambda |a\rangle )}$
for
$\eta _{a}=1_{(0,\langle \lambda |a\rangle )}$
for
![]() $a\in P$
.
$a\in P$
.
Let
![]() $Exp$
denote the exponential map of the one parameter product system
$Exp$
denote the exponential map of the one parameter product system
![]() $\widetilde {E} $
of the CAR flow associated with
$\widetilde {E} $
of the CAR flow associated with
![]() $\{S_{t}\}_{t\geq 0}$
. Let
$\{S_{t}\}_{t\geq 0}$
. Let
![]() $u_{t}=Exp(1_{(0,t)})$
for
$u_{t}=Exp(1_{(0,t)})$
for
![]() $t\geq 0$
. It follows from Remark 2.2 and Propostion 2.1 that
$t\geq 0$
. It follows from Remark 2.2 and Propostion 2.1 that
![]() $u=\{u_t\}_{t \geq 0}$
is a unit for
$u=\{u_t\}_{t \geq 0}$
is a unit for
![]() $\widetilde {E}$
. Note that
$\widetilde {E}$
. Note that
![]() $Exp_{a}(\eta _{a})=u_{\langle \lambda |a\rangle }$
for
$Exp_{a}(\eta _{a})=u_{\langle \lambda |a\rangle }$
for
![]() $a\in P$
. Observe that
$a\in P$
. Observe that
for
![]() $a, b\in P$
, i.e.,
$a, b\in P$
, i.e.,
![]() $Exp(\eta )$
is a unit.
$Exp(\eta )$
is a unit.
Remark 4.3 In the
![]() $1$
-dimensional case, it is clear from Remark 4.1 that, up to a scalar multiple, there is a unique invariant Radon measure on
$1$
-dimensional case, it is clear from Remark 4.1 that, up to a scalar multiple, there is a unique invariant Radon measure on
![]() $Y_u$
. This is not true in the higher dimensional case. Nor is it true that such a measure is supported on
$Y_u$
. This is not true in the higher dimensional case. Nor is it true that such a measure is supported on
![]() $Y^{\lambda }_u$
for some
$Y^{\lambda }_u$
for some
![]() $\lambda \in S(P^*)$
.
$\lambda \in S(P^*)$
.
Consider
![]() $P=\mathbb {R}_{+}^{2}$
as an example. Let
$P=\mathbb {R}_{+}^{2}$
as an example. Let
![]() $A \in Y_u$
, and let
$A \in Y_u$
, and let
![]() $G_A:=\{z \in \mathbb {R}^2: A+z=A\}$
. Denote the map
$G_A:=\{z \in \mathbb {R}^2: A+z=A\}$
. Denote the map
by T. As T is equivariant, the push-forward measure
![]() $T_*\lambda $
is an invariant measure on
$T_*\lambda $
is an invariant measure on
![]() $Y_u$
and is supported on the orbit of A. Here,
$Y_u$
and is supported on the orbit of A. Here,
![]() $\lambda $
is the Haar measure on
$\lambda $
is the Haar measure on
![]() $\mathbb {R}^2/G_A$
. However,
$\mathbb {R}^2/G_A$
. However,
![]() $T_*\lambda $
need not be a Radon measure. For example, let
$T_*\lambda $
need not be a Radon measure. For example, let
![]() $A=-\mathbb {R}_{+}^{2}$
. In this case,
$A=-\mathbb {R}_{+}^{2}$
. In this case,
![]() $G_A=\{0\}$
and
$G_A=\{0\}$
and
which has infinite measure if
![]() $a \geq 0$
and
$a \geq 0$
and
![]() $b \geq 0$
.
$b \geq 0$
.
Let
![]() $\displaystyle \phi =\sum _{n \in \mathbb {Z}}-n1_{[n,n+1)}$
. Note that the graph of
$\displaystyle \phi =\sum _{n \in \mathbb {Z}}-n1_{[n,n+1)}$
. Note that the graph of
![]() $\phi $
is an infinite staircase. Let
$\phi $
is an infinite staircase. Let
In this case,
![]() $G_A=\mathbb {Z}(1,-1)$
. Let
$G_A=\mathbb {Z}(1,-1)$
. Let
![]() $\pi :\mathbb {R}^2 \to \mathbb {R}^2/G_A$
be the quotient map. By drawing a “few pictures”, it is immediate to see that
$\pi :\mathbb {R}^2 \to \mathbb {R}^2/G_A$
be the quotient map. By drawing a “few pictures”, it is immediate to see that
![]() $T^{-1}(X_u\setminus (X_u+(a,b)))=\pi (A \setminus (A+(a,b)))$
has compact closure. For example, mod
$T^{-1}(X_u\setminus (X_u+(a,b)))=\pi (A \setminus (A+(a,b)))$
has compact closure. For example, mod
![]() $G_A$
,
$G_A$
,
![]() $A \setminus (A+(1,1))$
is just a bounded square. In this case,
$A \setminus (A+(1,1))$
is just a bounded square. In this case,
![]() $T_*\lambda $
is a Radon measure. In fact, given
$T_*\lambda $
is a Radon measure. In fact, given
![]() $A \in Y_u$
, if
$A \in Y_u$
, if
![]() $G_A \neq 0$
, then it can proved, by appealing to a few results from [Reference Sarkar and Sundar24], that
$G_A \neq 0$
, then it can proved, by appealing to a few results from [Reference Sarkar and Sundar24], that
![]() $T_*\lambda $
is a Radon measure. Since this fact is not needed and since we don’t make use of the fact that there are enough invariant measures on
$T_*\lambda $
is a Radon measure. Since this fact is not needed and since we don’t make use of the fact that there are enough invariant measures on
![]() $Y_u$
in this paper, we omit details and proofs.
$Y_u$
in this paper, we omit details and proofs.
Next, we next explain that a typical element of
![]() $Y_u$
can be described by a continuous function. We exploit this description to make computations. This is akin to introducing coordinates to compute. Let us first consider the case of the quadrant, i.e., let
$Y_u$
can be described by a continuous function. We exploit this description to make computations. This is akin to introducing coordinates to compute. Let us first consider the case of the quadrant, i.e., let
![]() $P=\mathbb {R}_{+}^{2}=[0,\infty )\times [0,\infty )$
. Let
$P=\mathbb {R}_{+}^{2}=[0,\infty )\times [0,\infty )$
. Let
![]() $A \in Y_u$
be given. For each
$A \in Y_u$
be given. For each
![]() $x \in \mathbb {R}$
, consider the x-section, i.e.,
$x \in \mathbb {R}$
, consider the x-section, i.e.,
It is possible that
![]() $A_x$
is empty. Since
$A_x$
is empty. Since
![]() $A-(0,t) \subset A$
for
$A-(0,t) \subset A$
for
![]() $t>0$
, it follows that
$t>0$
, it follows that
![]() $A_x$
is an interval and is not bounded below if
$A_x$
is an interval and is not bounded below if
![]() $A_x \neq \emptyset $
. Since A is closed,
$A_x \neq \emptyset $
. Since A is closed,
![]() $A_x$
is closed. Hence, there exists a unique
$A_x$
is closed. Hence, there exists a unique
![]() $\phi (x) \in [-\infty ,\infty ]$
such that
$\phi (x) \in [-\infty ,\infty ]$
such that
![]() $A_x=[-\infty ,\phi (x)] \cap \mathbb {R}$
. Since
$A_x=[-\infty ,\phi (x)] \cap \mathbb {R}$
. Since
![]() $A=\displaystyle \bigcup _{x \in \mathbb {R}}(\{x\} \times A_x)$
, it follows that A is the closed region below the graph of
$A=\displaystyle \bigcup _{x \in \mathbb {R}}(\{x\} \times A_x)$
, it follows that A is the closed region below the graph of
![]() $\phi $
, i.e.,
$\phi $
, i.e.,
The fact that
![]() $A-(s,0) \subset A$
implies that
$A-(s,0) \subset A$
implies that
![]() $\phi $
is decreasing. If
$\phi $
is decreasing. If
![]() $A=-\mathbb {R}_{+}^2$
, then
$A=-\mathbb {R}_{+}^2$
, then
![]() $\phi $
is given by
$\phi $
is given by
 $$\begin{align*}\phi(x):=\begin{cases}0 & \text{~if~}x \leq 0,\\ -\infty & \text{~if~}x>0. \end{cases}\end{align*}$$
$$\begin{align*}\phi(x):=\begin{cases}0 & \text{~if~}x \leq 0,\\ -\infty & \text{~if~}x>0. \end{cases}\end{align*}$$
In this case,
![]() $\phi $
is not continuous, and
$\phi $
is not continuous, and
![]() $\phi $
takes values in the extended real line. However, we can ensure that
$\phi $
takes values in the extended real line. However, we can ensure that
![]() $\phi $
is continuous and
$\phi $
is continuous and
![]() $\phi $
takes only finite values by changing the coordinate system. This is the content of the next lemma which is [Reference Arjunan1, Lemma 4.3].
$\phi $
takes only finite values by changing the coordinate system. This is the content of the next lemma which is [Reference Arjunan1, Lemma 4.3].
We return to the general case now, and let
![]() $P \subset \mathbb {R}^d$
be a closed convex cone which is spanning and pointed. Let us first fix a few notation that we will use for the rest of this section. Let
$P \subset \mathbb {R}^d$
be a closed convex cone which is spanning and pointed. Let us first fix a few notation that we will use for the rest of this section. Let
![]() $\{v_{1},v_{2},\ldots , v_{d}\}$
be a basis for
$\{v_{1},v_{2},\ldots , v_{d}\}$
be a basis for
![]() $\mathbb {R}^{d}$
such that
$\mathbb {R}^{d}$
such that
![]() $v_{i}\in Int(P)$
for
$v_{i}\in Int(P)$
for
![]() $i\in \{1,2,\ldots , d\}$
. Fix
$i\in \{1,2,\ldots , d\}$
. Fix
![]() $i\in \{1,2,\ldots , d\}$
. Let
$i\in \{1,2,\ldots , d\}$
. Let
Let
![]() $f:Q_{i}\to \mathbb {R}$
be a map. Define
$f:Q_{i}\to \mathbb {R}$
be a map. Define
 $$\begin{align*}A_{f}:=\left\{\sum_{j=1}^{d}x_{j}v_{j}: { x_{i}\leq f \left(\sum_{j\neq i}x_{j}v_{j}\right)}\right\}.\end{align*}$$
$$\begin{align*}A_{f}:=\left\{\sum_{j=1}^{d}x_{j}v_{j}: { x_{i}\leq f \left(\sum_{j\neq i}x_{j}v_{j}\right)}\right\}.\end{align*}$$
The following assertion is [Reference Arjunan1, Lemma 4.3]. For completeness, we include a proof.
Lemma 4.4 Let
![]() $i \in \{1,2,\ldots ,d\}$
, and let
$i \in \{1,2,\ldots ,d\}$
, and let
![]() $A \in Y_u$
. Then, there exists a unique continuous function
$A \in Y_u$
. Then, there exists a unique continuous function
![]() $f:Q_i \to \mathbb {R}$
such that
$f:Q_i \to \mathbb {R}$
such that
![]() $A=A_f$
.
$A=A_f$
.
Proof Uniqueness is clear. Without loss of generality, we assume
![]() $i=d$
and write
$i=d$
and write
![]() $Q_{d}= Q$
. For
$Q_{d}= Q$
. For
![]() $x \in Q$
, let
$x \in Q$
, let
Since
![]() $\mathbb {R}^d \cong Q \times \mathbb {R}$
,
$\mathbb {R}^d \cong Q \times \mathbb {R}$
,
![]() $A=\{x+tv_d: x \in Q, t \in A_x\}$
. Since A is closed,
$A=\{x+tv_d: x \in Q, t \in A_x\}$
. Since A is closed,
![]() $A_x$
is closed for each
$A_x$
is closed for each
![]() $x \in Q$
.
$x \in Q$
.
Claim: For each
![]() $x \in Q$
,
$x \in Q$
,
![]() $A_x \neq \emptyset $
and
$A_x \neq \emptyset $
and
![]() $A_x \neq \mathbb {R}$
.
$A_x \neq \mathbb {R}$
.
Note that since
![]() $-P+A \subset A$
,
$-P+A \subset A$
,
![]() $-Int(P)+A \subset Int(A)$
and
$-Int(P)+A \subset Int(A)$
and
![]() $-P+Int(A) \subset Int(A)$
. Let
$-P+Int(A) \subset Int(A)$
. Let
![]() $B= \mathbb {R}^{d}\setminus Int(A)$
. Then, B is a proper closed subset of
$B= \mathbb {R}^{d}\setminus Int(A)$
. Then, B is a proper closed subset of
![]() $\mathbb {R}^{d}$
such that
$\mathbb {R}^{d}$
such that
![]() $P+B\subset B$
. Also,
$P+B\subset B$
. Also,
![]() $Int(B)=\mathbb {R}^{d}\setminus A$
. It is clear that
$Int(B)=\mathbb {R}^{d}\setminus A$
. It is clear that
![]() $\mathbb {R}^d \setminus A \subset Int(B)$
as A is closed. If
$\mathbb {R}^d \setminus A \subset Int(B)$
as A is closed. If
![]() $z \in \partial A$
, then every neighbourhood of z intersects
$z \in \partial A$
, then every neighbourhood of z intersects
![]() $Int(A)$
. This is because
$Int(A)$
. This is because
![]() $-Int(P)+A \subset Int(A)$
which in turn implies that
$-Int(P)+A \subset Int(A)$
which in turn implies that
![]() $-tv_d+z \in Int(A)$
as
$-tv_d+z \in Int(A)$
as
![]() $t \to 0+$
. Thus,
$t \to 0+$
. Thus,
![]() $Int(B)=\mathbb {R}^d\backslash A$
.
$Int(B)=\mathbb {R}^d\backslash A$
.
Let
![]() $x \in Q$
be given. For
$x \in Q$
be given. For
![]() $y\in \mathbb {R}^{d}$
, there exists
$y\in \mathbb {R}^{d}$
, there exists
![]() $n_{0} \in \mathbb {N}$
such that
$n_{0} \in \mathbb {N}$
such that
![]() $y-n_{0}v_{d}\in -Int(P)$
. For,
$y-n_{0}v_{d}\in -Int(P)$
. For,
![]() $-Int(P)$
is an open cone,
$-Int(P)$
is an open cone,
![]() $v_d \in Int(P)$
and
$v_d \in Int(P)$
and
![]() $\frac {y}{n}-v_{d}\in -Int(P)$
for large
$\frac {y}{n}-v_{d}\in -Int(P)$
for large
![]() $n\in \mathbb {N}$
. Fix
$n\in \mathbb {N}$
. Fix
![]() $z_0\in A$
. Since
$z_0\in A$
. Since
![]() $-Int(P) +z_0 \subset Int(A)$
, given
$-Int(P) +z_0 \subset Int(A)$
, given
![]() $y\in \mathbb {R}^{d}$
, there exists a natural number
$y\in \mathbb {R}^{d}$
, there exists a natural number
![]() $n_{0}\in \mathbb {N}$
such that
$n_{0}\in \mathbb {N}$
such that
![]() $y-n_{0}v_{d}\in -Int(P) \subset Int(A)-z_0$
. Setting
$y-n_{0}v_{d}\in -Int(P) \subset Int(A)-z_0$
. Setting
![]() $y=x-z_0$
, we see that there exists
$y=x-z_0$
, we see that there exists
![]() $n_{0}\in \mathbb {N}$
such that
$n_{0}\in \mathbb {N}$
such that
![]() $x-n_{0}v_{d}\in Int(A)$
. Replacing A by B, P by
$x-n_{0}v_{d}\in Int(A)$
. Replacing A by B, P by
![]() $-P$
and
$-P$
and
![]() $v_{d}$
by
$v_{d}$
by
![]() $-v_{d}$
and arguing similarly, we see that there exists
$-v_{d}$
and arguing similarly, we see that there exists
![]() $n_{1}\in \mathbb {N}$
such that
$n_{1}\in \mathbb {N}$
such that
![]() $x+n_{1}v_{d}\in Int(B)= \mathbb {R}^{d}\setminus A$
. In particular, there exists
$x+n_{1}v_{d}\in Int(B)= \mathbb {R}^{d}\setminus A$
. In particular, there exists
![]() $m,n\in \mathbb {Z}$
such that
$m,n\in \mathbb {Z}$
such that
![]() $m\in A_{x}$
and
$m\in A_{x}$
and
![]() $n\in \mathbb {R}\setminus A_{x}$
. This proves the claim.
$n\in \mathbb {R}\setminus A_{x}$
. This proves the claim.
As
![]() $-P+A \subset A$
, note that if
$-P+A \subset A$
, note that if
![]() $x+tv_{d}\in A$
for
$x+tv_{d}\in A$
for
![]() $t\in \mathbb {R}$
, then
$t\in \mathbb {R}$
, then
![]() $x+sv_{d}\in A$
for every
$x+sv_{d}\in A$
for every
![]() $s<t$
. Thus, for each
$s<t$
. Thus, for each
![]() $x \in Q$
,
$x \in Q$
,
![]() $A_x$
is a closed interval which is not bounded below. Since
$A_x$
is a closed interval which is not bounded below. Since
![]() $A_x \neq \mathbb {R}$
,
$A_x \neq \mathbb {R}$
,
![]() $A_x=(-\infty ,f(x)]$
, where
$A_x=(-\infty ,f(x)]$
, where
Hence,
![]() $A=A_f$
.
$A=A_f$
.
Next, we prove that f is continuous. Let
![]() $x\in Q$
and let
$x\in Q$
and let
![]() $\epsilon>0$
be given. Let
$\epsilon>0$
be given. Let
![]() $s_{0},s_{1}\in \mathbb {R}$
be such that
$s_{0},s_{1}\in \mathbb {R}$
be such that
![]() $f(x)>s_{0}>f(x)-\epsilon $
and
$f(x)>s_{0}>f(x)-\epsilon $
and
![]() $f(x)+\epsilon>s_{1}>f(x)$
. Since
$f(x)+\epsilon>s_{1}>f(x)$
. Since
![]() $x+f(x)v_d \in A$
and
$x+f(x)v_d \in A$
and
![]() $-Int(P)+A \subset Int(A)$
,
$-Int(P)+A \subset Int(A)$
,
![]() $x+s_0v_d \in Int(A)$
. Also,
$x+s_0v_d \in Int(A)$
. Also,
![]() $x+s_{1}v_{d}\in \mathbb {R}^d \setminus A$
. Let
$x+s_{1}v_{d}\in \mathbb {R}^d \setminus A$
. Let
![]() $\delta>0$
be such that the open ball
$\delta>0$
be such that the open ball
![]() $B(x+s_{0}v_{d},\delta )\subset Int(A)$
and
$B(x+s_{0}v_{d},\delta )\subset Int(A)$
and
![]() $B(x+s_{1}v_{d},\delta )\subset \mathbb {R}^d \setminus A$
, respectively. Let
$B(x+s_{1}v_{d},\delta )\subset \mathbb {R}^d \setminus A$
, respectively. Let
![]() $y\in Q$
be such that
$y\in Q$
be such that
![]() $|x-y|<\delta $
. Since
$|x-y|<\delta $
. Since
![]() $|(x+s_{0}v_{d})-(y+s_{0}v_{d})|=|x-y|<\delta $
,
$|(x+s_{0}v_{d})-(y+s_{0}v_{d})|=|x-y|<\delta $
,
![]() $y+s_{0}v_{d}\in A$
. Hence,
$y+s_{0}v_{d}\in A$
. Hence,
Similarly, since
![]() $|(x+s_{1}v_{d})-(y+s_{1}v_{d})|=|x-y|<\delta $
,
$|(x+s_{1}v_{d})-(y+s_{1}v_{d})|=|x-y|<\delta $
,
![]() $y+s_{1}v_{d}\in \mathbb {R}^d\setminus A $
, i.e.,
$y+s_{1}v_{d}\in \mathbb {R}^d\setminus A $
, i.e.,
This implies
![]() $|f(x)-f(y)|<\epsilon $
. Hence, f is continuous. This completes the proof.
$|f(x)-f(y)|<\epsilon $
. Hence, f is continuous. This completes the proof.
Let
![]() $i\in \{1,2,\ldots , d\}$
. Let
$i\in \{1,2,\ldots , d\}$
. Let
![]() $f:Q_{i}\to \mathbb {R}$
be a function. Define
$f:Q_{i}\to \mathbb {R}$
be a function. Define
 $$\begin{align*}\left(\Psi_{i}(a) f\right)\left(\sum_{ j\neq i}x_{j}v_{j}\right)=f \left(\sum_{j\neq i}(x_{j}-a_{j})v_{j}\right)+a_{i}\end{align*}$$
$$\begin{align*}\left(\Psi_{i}(a) f\right)\left(\sum_{ j\neq i}x_{j}v_{j}\right)=f \left(\sum_{j\neq i}(x_{j}-a_{j})v_{j}\right)+a_{i}\end{align*}$$
for
![]() $a=\sum _{i=1}^{d}a_{i}v_{i}\in \mathbb {R}^d$
. Let
$a=\sum _{i=1}^{d}a_{i}v_{i}\in \mathbb {R}^d$
. Let
Remark 4.5 Let
![]() $P=[0,\infty )\times [0,\infty )$
. Let
$P=[0,\infty )\times [0,\infty )$
. Let
![]() $v_{1}=(1,1)$
and
$v_{1}=(1,1)$
and
![]() $v_{2}=(2,1)$
. In this case, we identify
$v_{2}=(2,1)$
. In this case, we identify
![]() $Q_1$
with
$Q_1$
with
![]() $\mathbb {R}$
. Let
$\mathbb {R}$
. Let
![]() $e_1=(1,0)=v_2-v_1$
and
$e_1=(1,0)=v_2-v_1$
and
![]() $e_2=(0,1)=2v_1-v_2$
be the standard basis. Note that for
$e_2=(0,1)=2v_1-v_2$
be the standard basis. Note that for
![]() $A \subset \mathbb {R}^2$
,
$A \subset \mathbb {R}^2$
,
![]() $-P+A \subset A$
if and only if
$-P+A \subset A$
if and only if
![]() $A-se_1 \subset A$
and
$A-se_1 \subset A$
and
![]() $A-se_2 \subset A$
for
$A-se_2 \subset A$
for
![]() $s>0$
. Thus, for a continuous function
$s>0$
. Thus, for a continuous function
![]() $f:\mathbb {R}=Q_1 \to \mathbb {R}$
,
$f:\mathbb {R}=Q_1 \to \mathbb {R}$
,
![]() $f \in \mathcal {F}_1$
if and only if
$f \in \mathcal {F}_1$
if and only if
![]() $A_f \in Y_u$
if and only if
$A_f \in Y_u$
if and only if
![]() $\Psi _1(-se_1)f \leq f$
and
$\Psi _1(-se_1)f \leq f$
and
![]() $\Psi _1(-se_2)f \leq f$
for
$\Psi _1(-se_2)f \leq f$
for
![]() $s>0$
. Hence,
$s>0$
. Hence,
![]() $\mathcal {F}_1$
is given by
$\mathcal {F}_1$
is given by
 $$\begin{align*}\mathcal{F}_{1} &=\{f: \mathbb{R}\to \mathbb{R}: f \text{ is continuous},\\ &\quad f(x+s)+s\leq f(x)\leq f(x+s)+2s \text{ for } x\in\mathbb{R}, s\geq 0\}.\end{align*}$$
$$\begin{align*}\mathcal{F}_{1} &=\{f: \mathbb{R}\to \mathbb{R}: f \text{ is continuous},\\ &\quad f(x+s)+s\leq f(x)\leq f(x+s)+2s \text{ for } x\in\mathbb{R}, s\geq 0\}.\end{align*}$$
Similarly,
![]() $\mathcal {F}_2$
is given by
$\mathcal {F}_2$
is given by
 $$\begin{align*}\mathcal{F}_{2} &=\{f: \mathbb{R}\to \mathbb{R}: f \text{ is continuous},\\ &\quad f(x+2s)+s\leq f(x)\leq f(x+s)+s \text{ for } x\in\mathbb{R}, s\geq 0\}.\end{align*}$$
$$\begin{align*}\mathcal{F}_{2} &=\{f: \mathbb{R}\to \mathbb{R}: f \text{ is continuous},\\ &\quad f(x+2s)+s\leq f(x)\leq f(x+s)+s \text{ for } x\in\mathbb{R}, s\geq 0\}.\end{align*}$$
Note that if
![]() $f \in \mathcal {F}_1$
, f is decreasing and is also Lipschitz.
$f \in \mathcal {F}_1$
, f is decreasing and is also Lipschitz.
Hereafter, the letter P stands for a closed, convex cone in
![]() $\mathbb {R}^d$
that is pointed and spanning. The notation introduced in this section will be used for the rest of this paper. Fix
$\mathbb {R}^d$
that is pointed and spanning. The notation introduced in this section will be used for the rest of this paper. Fix
![]() $i\in \{1,2,\ldots ,d\}$
. Let
$i\in \{1,2,\ldots ,d\}$
. Let
![]() $f:Q_i \to \mathbb {R}$
be continuous. Note that
$f:Q_i \to \mathbb {R}$
be continuous. Note that
![]() $a+A_{f}= A_{\Psi _{i}(a)f}$
for
$a+A_{f}= A_{\Psi _{i}(a)f}$
for
![]() $a\in \mathbb {R}^d$
. Hence
$a\in \mathbb {R}^d$
. Hence
![]() $-P+A_f \subset A_f$
if and only if
$-P+A_f \subset A_f$
if and only if
![]() $\Psi _i(a)f \leq f$
for every
$\Psi _i(a)f \leq f$
for every
![]() $a \in -P$
. In other words,
$a \in -P$
. In other words,
![]() $A_f \in Y_u$
if and only if
$A_f \in Y_u$
if and only if
![]() $f \in \mathcal {F}_i$
.
$f \in \mathcal {F}_i$
.
Conversely, suppose
![]() $A\in Y_{u}$
. By Lemma 4.4, there exists a unique continuous function
$A\in Y_{u}$
. By Lemma 4.4, there exists a unique continuous function
![]() $f^{A}_{i}:Q_i \to \mathbb {R}$
such that
$f^{A}_{i}:Q_i \to \mathbb {R}$
such that
 $$\begin{align*}A=A_{f^A_i}= \left\{\sum_{j=1}^{d}x_{j}v_{j}\in \mathbb{R}^{d}:{ x_{i}\leq f^{A}_{i}\left( \sum_{k\neq i}x_{k}v_{k}\right)}\right\}.\end{align*}$$
$$\begin{align*}A=A_{f^A_i}= \left\{\sum_{j=1}^{d}x_{j}v_{j}\in \mathbb{R}^{d}:{ x_{i}\leq f^{A}_{i}\left( \sum_{k\neq i}x_{k}v_{k}\right)}\right\}.\end{align*}$$
Since
![]() $-P+A \subset A$
,
$-P+A \subset A$
,
![]() $f_i^A \in \mathcal {F}_i$
. Hence, the map
$f_i^A \in \mathcal {F}_i$
. Hence, the map
is a bijection. Clearly,
Proposition 4.6 Suppose
![]() $(A_{n})_{n\in \mathbb {N}}$
is a sequence in
$(A_{n})_{n\in \mathbb {N}}$
is a sequence in
![]() $Y_{u}$
such that
$Y_{u}$
such that
![]() $A_{n}\to A$
in
$A_{n}\to A$
in
![]() $Y_{u}$
. Then, the sequence
$Y_{u}$
. Then, the sequence
![]() $\{f^{A_{n}}_{i}\}_{n\in \mathbb {N}}$
converges pointwise to
$\{f^{A_{n}}_{i}\}_{n\in \mathbb {N}}$
converges pointwise to
![]() $f^{A}_{i}$
for each
$f^{A}_{i}$
for each
![]() $i\in \{1,2,\ldots , d\}$
.
$i\in \{1,2,\ldots , d\}$
.
Proof Fix
![]() $i\in \{1,2,\ldots ,d\}$
. Suppose
$i\in \{1,2,\ldots ,d\}$
. Suppose
![]() $(A_{n})$
is a sequence in
$(A_{n})$
is a sequence in
![]() $Y_{u}$
converging to
$Y_{u}$
converging to
![]() $A\in Y_{u}$
. For simplicity, we denote
$A\in Y_{u}$
. For simplicity, we denote
![]() $f_i^{A_{n}}$
and
$f_i^{A_{n}}$
and
![]() $f_i^{{A}}$
by
$f_i^{{A}}$
by
![]() $f_{n}$
and f respectively. From the proof of [Reference Hilgert and Neeb14, Proposition II.13],
$f_{n}$
and f respectively. From the proof of [Reference Hilgert and Neeb14, Proposition II.13],
![]() $1_{A_{n}}(a)\to 1_{A}(a)$
pointwise for every
$1_{A_{n}}(a)\to 1_{A}(a)$
pointwise for every
![]() $a \in \mathbb {R}^{d}\setminus \partial A$
, where
$a \in \mathbb {R}^{d}\setminus \partial A$
, where
![]() $\partial A$
is the boundary of A. Recall that
$\partial A$
is the boundary of A. Recall that
 $$\begin{align*}A=\left\{\sum_{i=1}^{d}x_{j}v_{j}\in \mathbb{R}^{d}: { x_{i}\leq f\left(\sum_{k\neq i}x_{k}v_{k}\right)}\right\}.\end{align*}$$
$$\begin{align*}A=\left\{\sum_{i=1}^{d}x_{j}v_{j}\in \mathbb{R}^{d}: { x_{i}\leq f\left(\sum_{k\neq i}x_{k}v_{k}\right)}\right\}.\end{align*}$$
Let
![]() $x\in Q_{i}$
and
$x\in Q_{i}$
and
![]() $t>0$
. Let
$t>0$
. Let
![]() $y=x+(f(x)-t)v_{i}$
. Since
$y=x+(f(x)-t)v_{i}$
. Since
![]() $y\in Int(A)$
,
$y\in Int(A)$
,
![]() $y\in A_{n}$
eventually, i.e., for
$y\in A_{n}$
eventually, i.e., for
![]() $n\in \mathbb {N}$
sufficiently large, there exists
$n\in \mathbb {N}$
sufficiently large, there exists
![]() $s_{n} \geq 0$
and
$s_{n} \geq 0$
and
![]() $x_n \in Q_i$
such that
$x_n \in Q_i$
such that
![]() $y=x_{n}+(f_{n}(x)-s_{n})v_{i}$
. Now,
$y=x_{n}+(f_{n}(x)-s_{n})v_{i}$
. Now,
for sufficiently large
![]() $n\in \mathbb {N}$
. In particular,
$n\in \mathbb {N}$
. In particular,
for large
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Let
![]() $z= x+(f(x)+t)v_{i}$
. Then,
$z= x+(f(x)+t)v_{i}$
. Then,
![]() $z\in \mathbb {R}^{d}\setminus A$
. Therefore,
$z\in \mathbb {R}^{d}\setminus A$
. Therefore,
![]() $z\in \mathbb {R}^{d}\setminus A_{n}$
eventually, i.e., for sufficiently large
$z\in \mathbb {R}^{d}\setminus A_{n}$
eventually, i.e., for sufficiently large
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $t_{n}>0$
and
$t_{n}>0$
and
![]() $z_n \in Q_i$
such that
$z_n \in Q_i$
such that
![]() $z=z_n+(f_{n}(x)+t_{n})v_{i}$
. Now,
$z=z_n+(f_{n}(x)+t_{n})v_{i}$
. Now,
for large
![]() $n\in \mathbb {N}$
. Therefore, for large n,
$n\in \mathbb {N}$
. Therefore, for large n,
Since
![]() $t>0$
is arbitrary, we conclude that
$t>0$
is arbitrary, we conclude that
![]() $f_{n}(x)\to f(x)$
. This completes the proof.
$f_{n}(x)\to f(x)$
. This completes the proof.
For
![]() $i\in \{1,2,\ldots , d\}$
, let
$i\in \{1,2,\ldots , d\}$
, let
![]() $Y^{i}_{u}:=\{A\in Y_{u}: { f^{A}_{i}(0)=0}\}$
. Then,
$Y^{i}_{u}:=\{A\in Y_{u}: { f^{A}_{i}(0)=0}\}$
. Then,
![]() $Y^{i}_{u}$
is a closed subset of
$Y^{i}_{u}$
is a closed subset of
![]() $Y_{u}$
by Proposition 4.6. Define
$Y_{u}$
by Proposition 4.6. Define
![]() $\Psi _{i}:Y^{i}_{u}\times \mathbb {R} \to Y_u$
by
$\Psi _{i}:Y^{i}_{u}\times \mathbb {R} \to Y_u$
by
The map
![]() $\Psi _i$
is a homeomorphism with the inverse given by
$\Psi _i$
is a homeomorphism with the inverse given by
![]() $\Psi _{i}^{-1}(A)=(A-f^{A}_{i}(0)v_{i}, f_i^{A}(0))$
. Observe that
$\Psi _{i}^{-1}(A)=(A-f^{A}_{i}(0)v_{i}, f_i^{A}(0))$
. Observe that
for
![]() $A\in Y_{u}$
,
$A\in Y_{u}$
,
![]() $s,t\in \mathbb {R}$
.
$s,t\in \mathbb {R}$
.
Remark 4.7 Let
![]() $i \in \{1,2,\ldots ,d\}$
, and let
$i \in \{1,2,\ldots ,d\}$
, and let
![]() $X^{(i)}_{u+}:=\{A \in X_u: f_i^A(0)>0\}$
. Then,
$X^{(i)}_{u+}:=\{A \in X_u: f_i^A(0)>0\}$
. Then,
![]() $X^{(i)}_{u+}$
is open in
$X^{(i)}_{u+}$
is open in
![]() $Y_u$
whose closure is
$Y_u$
whose closure is
![]() $X_u$
. This is because
$X_u$
. This is because
![]() $\Psi _i$
is a homeomorphism,
$\Psi _i$
is a homeomorphism,
![]() $X_u=\Psi _i(Y_u^{(i)} \times [0,\infty ))$
and
$X_u=\Psi _i(Y_u^{(i)} \times [0,\infty ))$
and
![]() $X^{(i)}_{u+}=\Psi _i(Y_u^{(i)}\times (0,\infty ))$
.
$X^{(i)}_{u+}=\Psi _i(Y_u^{(i)}\times (0,\infty ))$
.
Let
![]() $\mu $
be an invariant, non-zero Radon measure on
$\mu $
be an invariant, non-zero Radon measure on
![]() $Y_u$
which is fixed until further mention. The measure that we consider on
$Y_u$
which is fixed until further mention. The measure that we consider on
![]() $Y_u \times Y_u$
is the product measure
$Y_u \times Y_u$
is the product measure
![]() $\mu \times \mu $
.
$\mu \times \mu $
.
Lemma 4.8 With the forgoing notation,
-
(i) for each
 $i\in \{1,2,\ldots ,d\}$
,
$i\in \{1,2,\ldots ,d\}$
,
 $Y^{i}_{u}\subset Y_{u}$
has measure zero, and
$Y^{i}_{u}\subset Y_{u}$
has measure zero, and -
(ii) the set
 $\mathcal {N}=\{(A,B): {f^{A}_{i}(0)=f^{B}_{i}(0)}\}\subset Y_{u}\times Y_{u}$
has measure zero.
$\mathcal {N}=\{(A,B): {f^{A}_{i}(0)=f^{B}_{i}(0)}\}\subset Y_{u}\times Y_{u}$
has measure zero.
Proof Fix
![]() $i\in \{1,2,\ldots , d\}$
. Let
$i\in \{1,2,\ldots , d\}$
. Let
![]() $\nu =(\Psi _{i}^{-1})_{*}\mu $
. Since
$\nu =(\Psi _{i}^{-1})_{*}\mu $
. Since
![]() $\mu $
is invariant, it follows from (4.2) that
$\mu $
is invariant, it follows from (4.2) that
![]() $\nu $
is invariant under the action of
$\nu $
is invariant under the action of
![]() $\mathbb {R}$
on
$\mathbb {R}$
on
![]() $Y^{i}_{u} \times \mathbb {R}$
given by
$Y^{i}_{u} \times \mathbb {R}$
given by
![]() $s.(A,t)=(A,s+t)$
. Hence,
$s.(A,t)=(A,s+t)$
. Hence,
![]() $\nu $
is a product measure of the form
$\nu $
is a product measure of the form
![]() $\nu _0 \times m$
where m is the Lebesgue measure on
$\nu _0 \times m$
where m is the Lebesgue measure on
![]() $\mathbb {R}$
. Now,
$\mathbb {R}$
. Now,
![]() $\mu (Y^{i}_{u})=\nu (Y^{i}_{u}\times \{0\})=0$
. This proves
$\mu (Y^{i}_{u})=\nu (Y^{i}_{u}\times \{0\})=0$
. This proves
![]() $(i)$
.
$(i)$
.
Fix
![]() $B\in Y_{u}$
, and let
$B\in Y_{u}$
, and let
![]() $t:=f^{B}_{i}(0)$
. Then,
$t:=f^{B}_{i}(0)$
. Then,
![]() $1_{\mathcal {N}}(A,B)=1$
if and only if
$1_{\mathcal {N}}(A,B)=1$
if and only if
![]() $f^{A}_{i}(0)=f^{B}_{i}(0)=t$
. But
$f^{A}_{i}(0)=f^{B}_{i}(0)=t$
. But
![]() $\{A \in Y_u: {f_i^{A}(0)=t}\}=Y^{i}_{u}+tv_{i}$
is a null set. Now
$\{A \in Y_u: {f_i^{A}(0)=t}\}=Y^{i}_{u}+tv_{i}$
is a null set. Now
![]() $(ii)$
follows from Fubini’s theorem.
$(ii)$
follows from Fubini’s theorem.
For
![]() $n\in \mathbb {N}\cup \{0\}$
, we denote the projection from
$n\in \mathbb {N}\cup \{0\}$
, we denote the projection from
![]() $ \Gamma _{a}(L^{2}(X_{u}))$
onto its n-particle space by
$ \Gamma _{a}(L^{2}(X_{u}))$
onto its n-particle space by
![]() $P_{n}$
. For
$P_{n}$
. For
![]() $A,B\in Y_{u}$
, define
$A,B\in Y_{u}$
, define
 $$\begin{align*}\epsilon_{i}(A,B):= \begin{cases} 1 & \text{if } f^{A}_{i}(0)>f^{B}_{i}(0) ,\\ -1 & \text{if } f^{A}_{i}(0)<f^{B}_{i}(0),\\ 0 &\text{ if } f^{A}_{i}(0)=f^{B}_{i}(0). \end{cases}\end{align*}$$
$$\begin{align*}\epsilon_{i}(A,B):= \begin{cases} 1 & \text{if } f^{A}_{i}(0)>f^{B}_{i}(0) ,\\ -1 & \text{if } f^{A}_{i}(0)<f^{B}_{i}(0),\\ 0 &\text{ if } f^{A}_{i}(0)=f^{B}_{i}(0). \end{cases}\end{align*}$$
Consider the additive cocycle
![]() $\eta =\{\eta _{a}\}_{a\in P}$
for
$\eta =\{\eta _{a}\}_{a\in P}$
for
![]() $ V^{\mu }$
, where
$ V^{\mu }$
, where
![]() $\eta _{a}=1_{X_{u}\setminus X_{u}+a}$
for
$\eta _{a}=1_{X_{u}\setminus X_{u}+a}$
for
![]() $a\in P$
. Let
$a\in P$
. Let
![]() $Exp_{i}$
denote the exponential map of the one parameter product system
$Exp_{i}$
denote the exponential map of the one parameter product system
![]() $\{E^{\mu }(tv_{i})\}_{t\geq 0}$
.
$\{E^{\mu }(tv_{i})\}_{t\geq 0}$
.
Lemma 4.9 For
![]() $i\in \{1,2,\ldots ,d\}$
and
$i\in \{1,2,\ldots ,d\}$
and
![]() $t>0$
,
$t>0$
,
for almost every
![]() $(A,B)\in X_{u}\times X_{u}$
.
$(A,B)\in X_{u}\times X_{u}$
.
Proof The computation is similar to the computation done in [Reference Arjunan1, Proposition 5]. Fix
![]() $t>0$
and
$t>0$
and
![]() $i\in \{1,2,\ldots , d\}$
. For simplicity, write
$i\in \{1,2,\ldots , d\}$
. For simplicity, write
![]() $\eta _{sv_{i}}=\eta _{s}$
for
$\eta _{sv_{i}}=\eta _{s}$
for
![]() $s\geq 0$
. Let
$s\geq 0$
. Let
![]() $x_{s}^{(1)}=\eta _{s}$
.
$x_{s}^{(1)}=\eta _{s}$
.
By definition,
 $$ \begin{align} &=\lim_{n\to\infty} \sum_{j=0}^{n-1}\eta_{\frac{jt}{n}}.\eta_{\frac{t}{n}}\nonumber\\ &=\lim_{n\to\infty} \sum_{j=0}^{n-1}V_{\frac{jtv_{i}}{n}}\eta_{\frac{t}{n}}\wedge \eta_{\frac{jt}{n}}\nonumber\\ &=\lim_{n\to\infty} \sum_{j=0}^{n-1}(\eta_{\frac{(j+1)t}{n}}-\eta_{\frac{jt}{n}})\wedge \eta_{\frac{jt}{n}}\nonumber\\ &=\lim_{n\to\infty} \sum_{j=0}^{n-1}\eta_{\frac{(j+1)t}{n}}\wedge \eta_{\frac{jt}{n}}.\end{align} $$
$$ \begin{align} &=\lim_{n\to\infty} \sum_{j=0}^{n-1}\eta_{\frac{jt}{n}}.\eta_{\frac{t}{n}}\nonumber\\ &=\lim_{n\to\infty} \sum_{j=0}^{n-1}V_{\frac{jtv_{i}}{n}}\eta_{\frac{t}{n}}\wedge \eta_{\frac{jt}{n}}\nonumber\\ &=\lim_{n\to\infty} \sum_{j=0}^{n-1}(\eta_{\frac{(j+1)t}{n}}-\eta_{\frac{jt}{n}})\wedge \eta_{\frac{jt}{n}}\nonumber\\ &=\lim_{n\to\infty} \sum_{j=0}^{n-1}\eta_{\frac{(j+1)t}{n}}\wedge \eta_{\frac{jt}{n}}.\end{align} $$
Let
 $s_{n}= \displaystyle \sum _{j=0}^{n-1}\eta _{\frac {(j+1)t}{n}}\wedge \eta _{\frac {jt}{n}}$
for
$s_{n}= \displaystyle \sum _{j=0}^{n-1}\eta _{\frac {(j+1)t}{n}}\wedge \eta _{\frac {jt}{n}}$
for
![]() $n\in \mathbb {N}$
. The proof will be over if we show that
$n\in \mathbb {N}$
. The proof will be over if we show that
for almost every
![]() $(A,B)\in X_{u}\setminus (X_u+tv_i) \times X_u\setminus (X_u+tv_i)$
.
$(A,B)\in X_{u}\setminus (X_u+tv_i) \times X_u\setminus (X_u+tv_i)$
.
For
![]() $n\in \mathbb {N}$
, suppose
$n\in \mathbb {N}$
, suppose
![]() $A,B\in X_{u}$
are such that
$A,B\in X_{u}$
are such that
![]() $f^{A}_{i}(0)<\frac {jt}{n}$
,
$f^{A}_{i}(0)<\frac {jt}{n}$
,
![]() $\frac {jt}{n} \leq f^{B}_{i}(0)< \frac {(j+1)t}{m}$
for some
$\frac {jt}{n} \leq f^{B}_{i}(0)< \frac {(j+1)t}{m}$
for some
![]() $j\in \{1,2,\ldots ,n-1\}$
. Then,
$j\in \{1,2,\ldots ,n-1\}$
. Then,
Since
![]() $A \in X_u\setminus (X_u+\frac {jtv_i}{n})$
and
$A \in X_u\setminus (X_u+\frac {jtv_i}{n})$
and
![]() $B \in (X_u+\frac {jtv_i}{n})\setminus (X_u+\frac {(j+1)tv_i}{n})$
,
$B \in (X_u+\frac {jtv_i}{n})\setminus (X_u+\frac {(j+1)tv_i}{n})$
,
Let
![]() $A,B\in X_{u}\setminus X_{u}+tv_{i}$
. Suppose
$A,B\in X_{u}\setminus X_{u}+tv_{i}$
. Suppose
![]() $f^{A}_{i}(0)<f^{B}_{i}(0)$
. For sufficiently large
$f^{A}_{i}(0)<f^{B}_{i}(0)$
. For sufficiently large
![]() $n\in \mathbb {N}$
, there exists a unique
$n\in \mathbb {N}$
, there exists a unique
![]() $j_{n}\in \{1,2,\ldots , n-1\}$
such that
$j_{n}\in \{1,2,\ldots , n-1\}$
such that
![]() $f^{A}_{i}(0)< \frac {j_{n}t}{n}$
,
$f^{A}_{i}(0)< \frac {j_{n}t}{n}$
,
![]() $\frac {j_{n}t}{n}\leq f^{B}_{i}(0)< \frac {(j_{n}+1)t}{n}$
. By (4.5), for sufficiently large n,
$\frac {j_{n}t}{n}\leq f^{B}_{i}(0)< \frac {(j_{n}+1)t}{n}$
. By (4.5), for sufficiently large n,
 $$ \begin{align*} s_n(A,B)&=-\frac{1}{\sqrt{2}} \\ &=\frac{1}{\sqrt{2}}\Big(\epsilon_{i}(A,B)\eta_{tv_{i}}(A) \eta_{tv_{i}}(B)\Big). \end{align*} $$
$$ \begin{align*} s_n(A,B)&=-\frac{1}{\sqrt{2}} \\ &=\frac{1}{\sqrt{2}}\Big(\epsilon_{i}(A,B)\eta_{tv_{i}}(A) \eta_{tv_{i}}(B)\Big). \end{align*} $$
Similarly, it may be proved that, when
![]() $f^A_i(0)>f_i^B(0)$
, for n sufficiently large,
$f^A_i(0)>f_i^B(0)$
, for n sufficiently large,
The result follows from Lemma 4.8. The proof is complete.
Lemma 4.10 Suppose
![]() $\{Exp_{a}(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
$\{Exp_{a}(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
![]() $E^{\mu }$
. Then, for every
$E^{\mu }$
. Then, for every
![]() $i,j\in \{1,2,\ldots , d\}$
,
$i,j\in \{1,2,\ldots , d\}$
,
![]() $\epsilon _{i}(A,B)=\epsilon _{j}(A,B)$
for almost every
$\epsilon _{i}(A,B)=\epsilon _{j}(A,B)$
for almost every
![]() $(A,B)\in X_{u}\times X_{u}$
.
$(A,B)\in X_{u}\times X_{u}$
.
Proof Write
![]() $V^{\mu }=V$
, and let
$V^{\mu }=V$
, and let
![]() $\eta _{a}=1_{X_{u}\setminus (X_{u}+a)}$
for
$\eta _{a}=1_{X_{u}\setminus (X_{u}+a)}$
for
![]() $a\in P$
. Let
$a\in P$
. Let
![]() $i,j \in \{1,2,\ldots ,d\}$
be given. Since
$i,j \in \{1,2,\ldots ,d\}$
be given. Since
![]() $Exp(\eta )$
is a unit,
$Exp(\eta )$
is a unit,
for
![]() $i,j\in \{1,2,\ldots , d\}$
and
$i,j\in \{1,2,\ldots , d\}$
and
![]() $s,t> 0$
.
$s,t> 0$
.
Hence,
for
![]() $i,j\in \{1,2,\ldots , d\}$
and
$i,j\in \{1,2,\ldots , d\}$
and
![]() $s,t> 0$
.
$s,t> 0$
.
Thanks to Lemma 4.9,
 $$ \begin{align*}P_{2}\Big(Exp_{i}(\eta_{sv_{i}}).Exp_{j}(\eta_{tv_{j}})\Big)(A,B)&=\epsilon_i(A,B) \eta_{sv_{i}}(A) \eta_{sv_{i}}(B)+V_{sv_{i}}\eta_{tv_{j}}\wedge \eta_{sv_{i}}(A,B)\\ &\quad +\epsilon_{j}(A-sv_i,B-sv_i)V_{sv_{i}}\eta_{tv_{j}}(A) V_{sv_{i}}\eta_{tv_{j}}(B)\end{align*} $$
$$ \begin{align*}P_{2}\Big(Exp_{i}(\eta_{sv_{i}}).Exp_{j}(\eta_{tv_{j}})\Big)(A,B)&=\epsilon_i(A,B) \eta_{sv_{i}}(A) \eta_{sv_{i}}(B)+V_{sv_{i}}\eta_{tv_{j}}\wedge \eta_{sv_{i}}(A,B)\\ &\quad +\epsilon_{j}(A-sv_i,B-sv_i)V_{sv_{i}}\eta_{tv_{j}}(A) V_{sv_{i}}\eta_{tv_{j}}(B)\end{align*} $$
for almost every
![]() $(A,B)\in X_{u}\times X_{u}$
. Similarly,
$(A,B)\in X_{u}\times X_{u}$
. Similarly,
 $$ \begin{align*}P_{2}\Big(Exp_{j}(\eta_{tv_{j}}).Exp_{i}(\eta_{sv_{i}})\Big)(A,B)&=\epsilon_j(A,B) \eta_{tv_{j}}(A) \eta_{tv_{j}}(B)+V_{tv_{j}}\eta_{sv_{i}}\wedge \eta_{tv_{j}}(A,B)\\ & \quad +\epsilon_{i}(A-tv_j,B-tv_j)V_{tv_{j}}\eta_{sv_{i}}(A) V_{tv_{j}}\eta_{sv_{i}}(B)\end{align*} $$
$$ \begin{align*}P_{2}\Big(Exp_{j}(\eta_{tv_{j}}).Exp_{i}(\eta_{sv_{i}})\Big)(A,B)&=\epsilon_j(A,B) \eta_{tv_{j}}(A) \eta_{tv_{j}}(B)+V_{tv_{j}}\eta_{sv_{i}}\wedge \eta_{tv_{j}}(A,B)\\ & \quad +\epsilon_{i}(A-tv_j,B-tv_j)V_{tv_{j}}\eta_{sv_{i}}(A) V_{tv_{j}}\eta_{sv_{i}}(B)\end{align*} $$
for almost every
![]() $(A,B)\in X_{u}\times X_{u}$
.
$(A,B)\in X_{u}\times X_{u}$
.
For
![]() $s>0$
and
$s>0$
and
![]() $i\in \{1,2,\ldots , d\}$
, let
$i\in \{1,2,\ldots , d\}$
, let
![]() $L_{i,s}:=(1_{X_{u}}\setminus X_{u}+sv_{i})\times (1_{X_{u}}\setminus X_{u}+sv_{i})$
. Let
$L_{i,s}:=(1_{X_{u}}\setminus X_{u}+sv_{i})\times (1_{X_{u}}\setminus X_{u}+sv_{i})$
. Let
![]() $s,t>0$
. For almost all
$s,t>0$
. For almost all
![]() $(A,B)\in L_{i,s}\cap L_{j,t}$
,
$(A,B)\in L_{i,s}\cap L_{j,t}$
,
and
Therefore, (4.7) implies,
for almost every
![]() $(A,B)\in L_{i,s}\cap L_{j,t}$
. Now observe that
$(A,B)\in L_{i,s}\cap L_{j,t}$
. Now observe that
![]() $X_{u}\times X_{u}=\displaystyle {\bigcup _{m,n\in \mathbb {N}}}L_{i,m}\cap L_{j,n}$
. Hence the proof follows.
$X_{u}\times X_{u}=\displaystyle {\bigcup _{m,n\in \mathbb {N}}}L_{i,m}\cap L_{j,n}$
. Hence the proof follows.
Notation: Let
![]() $X:=supp(\mu ) \cap X_u$
. Recall that
$X:=supp(\mu ) \cap X_u$
. Recall that
![]() $Y_u\setminus supp(\mu )$
is the largest open set that has
$Y_u\setminus supp(\mu )$
is the largest open set that has
![]() $\mu $
measure zero. Since
$\mu $
measure zero. Since
![]() $\mu $
is invariant,
$\mu $
is invariant,
![]() $supp(\mu )$
is
$supp(\mu )$
is
![]() $\mathbb {R}^d$
-invariant. It follows from Remark 4.7 that
$\mathbb {R}^d$
-invariant. It follows from Remark 4.7 that
![]() $\mu |_{X}$
has full support.
$\mu |_{X}$
has full support.
Proposition 4.11 Suppose
![]() $\{Exp_{a}(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
$\{Exp_{a}(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
![]() $E^{\mu }$
. Then, for
$E^{\mu }$
. Then, for
![]() $A,B\in supp(\mu )$
,
$A,B\in supp(\mu )$
,
![]() $A\subset B$
or
$A\subset B$
or
![]() $B\subset A$
.
$B\subset A$
.
Proof Write
![]() $\eta _{a}=1_{X_{u}\setminus X_{u}+a}$
for
$\eta _{a}=1_{X_{u}\setminus X_{u}+a}$
for
![]() $a\in P$
. Assume that
$a\in P$
. Assume that
![]() $Exp(\eta )$
is a unit for
$Exp(\eta )$
is a unit for
![]() $E^{\mu }$
. For
$E^{\mu }$
. For
![]() $A,B\in Y_{u}$
and
$A,B\in Y_{u}$
and
![]() $i\in \{1,2,\ldots ,d\}$
, note that
$i\in \{1,2,\ldots ,d\}$
, note that
![]() $A\subset B$
if and only if
$A\subset B$
if and only if
![]() $f_{i}^{A}(x)\leq f^{B}_{i}(x)$
for each
$f_{i}^{A}(x)\leq f^{B}_{i}(x)$
for each
![]() $x\in Q_{i}$
.
$x\in Q_{i}$
.
Let
![]() $A,B\in X$
, and
$A,B\in X$
, and
![]() $i\in \{1,2,\ldots ,d\}$
. Suppose
$i\in \{1,2,\ldots ,d\}$
. Suppose
![]() $f^{A}_{i}(0)\leq f^{B}_{i}(0)$
. Then, we claim the following.
$f^{A}_{i}(0)\leq f^{B}_{i}(0)$
. Then, we claim the following.
-
(i)
 $f^{A}_{j}(0)\leq f^{B}_{j}(0)$
for each
$f^{A}_{j}(0)\leq f^{B}_{j}(0)$
for each
 $j\in \{1,2,\ldots ,d\}$
, and
$j\in \{1,2,\ldots ,d\}$
, and -
(ii) if
 $t_{j}>0$
for
$t_{j}>0$
for
 $j\in \{1,2,\ldots ,d-1\}$
, then
$j\in \{1,2,\ldots ,d-1\}$
, then  $$\begin{align*}f^{A}_{d} \left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right)\leq f^{B}_{d} \left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right).\end{align*}$$
$$\begin{align*}f^{A}_{d} \left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right)\leq f^{B}_{d} \left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right).\end{align*}$$
Observe that X is a measurable subset of
![]() $X_{u}$
such that
$X_{u}$
such that
![]() $X+P \subset X$
. Consider the set
$X+P \subset X$
. Consider the set
for
![]() $i,j\in \{1,2,\ldots , d\}$
. By Proposition 4.6,
$i,j\in \{1,2,\ldots , d\}$
. By Proposition 4.6,
![]() $N_{i,j}$
is an open set, and by Lemma 4.10,
$N_{i,j}$
is an open set, and by Lemma 4.10,
![]() $N_{i,j}$
is a null set. Therefore,
$N_{i,j}$
is a null set. Therefore,
![]() $N_{i,j}$
is empty. Similarly, consider the set
$N_{i,j}$
is empty. Similarly, consider the set
for
![]() $i,j\in \{1,2,\ldots ,d\}$
. Fix
$i,j\in \{1,2,\ldots ,d\}$
. Fix
![]() $i,j\in \{1,2,\ldots ,d\}$
with
$i,j\in \{1,2,\ldots ,d\}$
with
![]() $i \neq j$
. Suppose
$i \neq j$
. Suppose
![]() $(A^{'},B^{'})\in M_{i,j}$
. Let
$(A^{'},B^{'})\in M_{i,j}$
. Let
![]() $s,t>0$
be sufficiently small such that
$s,t>0$
be sufficiently small such that
![]() $s<t$
and
$s<t$
and
![]() $f^{A^{'}}_{j}(0)>f^{B^{'}}_{j}(-tv_{i})$
. Then,
$f^{A^{'}}_{j}(0)>f^{B^{'}}_{j}(-tv_{i})$
. Then,
Since
![]() $f^{A^{'}}_{j} \in \mathcal {F}_j$
,
$f^{A^{'}}_{j} \in \mathcal {F}_j$
,
This implies
![]() $(A^{'}+sv_{i},B^{'}+tv_{i})\in N_{i,j}$
, which is a contradiction. Hence,
$(A^{'}+sv_{i},B^{'}+tv_{i})\in N_{i,j}$
, which is a contradiction. Hence,
![]() $M_{i,j}=\emptyset $
. Therefore, for
$M_{i,j}=\emptyset $
. Therefore, for
![]() $A^{'},B^{'}\in X$
and
$A^{'},B^{'}\in X$
and
![]() $i,j\in \{1,2,\ldots d\}$
,
$i,j\in \{1,2,\ldots d\}$
,
![]() $f^{A^{'}}_{i}(0)\leq f^{B^{'}}_{i}(0)$
if and only if
$f^{A^{'}}_{i}(0)\leq f^{B^{'}}_{i}(0)$
if and only if
![]() $f^{A^{'}}_{j}(0)\leq f^{B^{'}}_{j}(0)$
, which proves
$f^{A^{'}}_{j}(0)\leq f^{B^{'}}_{j}(0)$
, which proves
![]() $(i)$
.
$(i)$
.
For each
![]() $j \in \{1,2,\ldots ,d-1\}$
, let
$j \in \{1,2,\ldots ,d-1\}$
, let
![]() $t_{j}>0$
. Let
$t_{j}>0$
. Let
![]() $A,B \in X$
be such that
$A,B \in X$
be such that
![]() $f_i^A(0) \leq f_i^B(0)$
for some i. Since
$f_i^A(0) \leq f_i^B(0)$
for some i. Since
![]() $f_{i}^{A}(0)\leq f_{i}^{B}(0)$
, by
$f_{i}^{A}(0)\leq f_{i}^{B}(0)$
, by
![]() $(i)$
,
$(i)$
,
![]() $f_{1}^{A}(0)\leq f_{1}^{B}(0)$
. Since
$f_{1}^{A}(0)\leq f_{1}^{B}(0)$
. Since
![]() $f^{A+t_{1}v_{1}}_{1}(0)\leq f^{B+t_{1}v_{1}}_{1}(0)$
, by
$f^{A+t_{1}v_{1}}_{1}(0)\leq f^{B+t_{1}v_{1}}_{1}(0)$
, by
![]() $(i)$
,
$(i)$
,
![]() $f^{A+t_{1}v_{1}}_{2}(0)\leq f^{B+t_{1}v_{1}}_{2}(0)$
, i.e.,
$f^{A+t_{1}v_{1}}_{2}(0)\leq f^{B+t_{1}v_{1}}_{2}(0)$
, i.e.,
Since
![]() $f_{2}^{A+t_{1}v_{1}}(0)+t_{2}\leq f^{B+t_{1}v_{1}}_{2}(0)+t_{2}$
,
$f_{2}^{A+t_{1}v_{1}}(0)+t_{2}\leq f^{B+t_{1}v_{1}}_{2}(0)+t_{2}$
,
Once again by
![]() $(i)$
,
$(i)$
,
Inductively,
 $$ \begin{align}f^{A}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right)\leq f^{B}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right).\end{align} $$
$$ \begin{align}f^{A}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right)\leq f^{B}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right).\end{align} $$
We have proved
![]() $(ii)$
.
$(ii)$
.
It follows from
![]() $(i)$
that for
$(i)$
that for
![]() $i \in \{1,2,\ldots ,d\}$
and
$i \in \{1,2,\ldots ,d\}$
and
![]() $A,B \in X$
,
$A,B \in X$
,
![]() $f_i^A(0)>f_i^B(0)$
if and only if
$f_i^A(0)>f_i^B(0)$
if and only if
![]() $f_j^A(0)>f_j^B(0)$
for every
$f_j^A(0)>f_j^B(0)$
for every
![]() $j \in \{1,2,\ldots ,d\}$
. Suppose
$j \in \{1,2,\ldots ,d\}$
. Suppose
![]() $f_i^A(0)>f_i^B(0)$
for
$f_i^A(0)>f_i^B(0)$
for
![]() $A,B \in X$
and
$A,B \in X$
and
![]() $i \in \{1,2,\ldots ,d\}$
. Arguing as before, we see that
$i \in \{1,2,\ldots ,d\}$
. Arguing as before, we see that
 $$ \begin{align} f^{A}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right)>f^{B}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right) \end{align} $$
$$ \begin{align} f^{A}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right)>f^{B}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right) \end{align} $$
whenever
![]() $t_{j}>0$
for
$t_{j}>0$
for
![]() $j\in \{1,2,\ldots ,d-1\}$
.
$j\in \{1,2,\ldots ,d-1\}$
.
Let
![]() $A,B\in X$
. Without loss of generality, we can assume that
$A,B\in X$
. Without loss of generality, we can assume that
![]() $f^{A}_{d}(0)\leq f^{B}_{d}(0)$
. Then,
$f^{A}_{d}(0)\leq f^{B}_{d}(0)$
. Then,
 $$ \begin{align} f^{A}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right) \leq f^{B}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right) \end{align} $$
$$ \begin{align} f^{A}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right) \leq f^{B}_{d}\left(-\sum_{j=1}^{d-1}t_{j}v_{j}\right) \end{align} $$
whenever
![]() $t_{j}>0$
for
$t_{j}>0$
for
![]() $j\in \{1,2,\ldots ,d-1\}$
.
$j\in \{1,2,\ldots ,d-1\}$
.
Let
![]() $x \in Q_d$
. Choose
$x \in Q_d$
. Choose
![]() $t>0$
such that
$t>0$
such that
![]() $A-x+tv_{d}\in X$
and
$A-x+tv_{d}\in X$
and
![]() $B-x+tv_{d}\in X$
, i.e.,
$B-x+tv_{d}\in X$
, i.e.,
and
Let
![]() $\widetilde {A}=A-x+tv_{d}$
and
$\widetilde {A}=A-x+tv_{d}$
and
![]() $\widetilde {B}=B-x+tv_{d}$
. Suppose
$\widetilde {B}=B-x+tv_{d}$
. Suppose
![]() $f^{A}_{d}(x)>f^{B}_{d}(x)$
. Then,
$f^{A}_{d}(x)>f^{B}_{d}(x)$
. Then,
By (4.9),
 $$\begin{align*}f^{\widetilde{A}}_{d}\left(-\sum_{j=1}^{d-1}r_{j}v_{j}\right)>f^{\widetilde{B}}_{d}\left(-\sum_{j=1}^{d-1}r_{j}v_{j}\right)\end{align*}$$
$$\begin{align*}f^{\widetilde{A}}_{d}\left(-\sum_{j=1}^{d-1}r_{j}v_{j}\right)>f^{\widetilde{B}}_{d}\left(-\sum_{j=1}^{d-1}r_{j}v_{j}\right)\end{align*}$$
whenever
![]() $r_{j}>0$
for
$r_{j}>0$
for
![]() $j=1,2,\ldots , d-1$
. This implies
$j=1,2,\ldots , d-1$
. This implies
 $$\begin{align*}f^{A}_{d}\left(\sum_{j=1}^{d-1}(x_{j}-r_{j})v_{j}\right)>f^{B}_{d} \left(\sum_{j=1}^{d-1}(x_{j}-r_{j})v_{j}\right)\end{align*}$$
$$\begin{align*}f^{A}_{d}\left(\sum_{j=1}^{d-1}(x_{j}-r_{j})v_{j}\right)>f^{B}_{d} \left(\sum_{j=1}^{d-1}(x_{j}-r_{j})v_{j}\right)\end{align*}$$
whenever
![]() $r_{j}>0$
for
$r_{j}>0$
for
![]() $j=1,2,\ldots , d-1$
. This contradicts (4.10). Hence,
$j=1,2,\ldots , d-1$
. This contradicts (4.10). Hence,
![]() $f^{A}_{d}(x)\leq f^{B}_{d}(x)$
for every
$f^{A}_{d}(x)\leq f^{B}_{d}(x)$
for every
![]() $x\in Q_{d}$
, i.e.,
$x\in Q_{d}$
, i.e.,
![]() $A\subset B$
.
$A\subset B$
.
Now suppose
![]() $A,B\in supp(\mu )$
. Then, there exists
$A,B\in supp(\mu )$
. Then, there exists
![]() $t>0$
such that
$t>0$
such that
![]() $A+tv_{1}, B+tv_{1}\in X$
. Without loss of generality, assume that
$A+tv_{1}, B+tv_{1}\in X$
. Without loss of generality, assume that
![]() $A+tv_{1}\subset B+tv_{1}$
. Then,
$A+tv_{1}\subset B+tv_{1}$
. Then,
![]() $A\subset B$
. Therefore, if
$A\subset B$
. Therefore, if
![]() $A,B\in supp(\mu )$
,
$A,B\in supp(\mu )$
,
![]() $A\subset B$
or
$A\subset B$
or
![]() $B\subset A$
. The proof is complete.
$B\subset A$
. The proof is complete.
Theorem 4.12 The following statements are equivalent.
-
(i)
 $\{Exp(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
$\{Exp(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
 $E^{\mu }$
.
$E^{\mu }$
. -
(ii) There exists
 $\lambda \in S(P^{*})$
such that
$\lambda \in S(P^{*})$
such that
 $supp(\mu )=Y^{\lambda }_{u}$
.
$supp(\mu )=Y^{\lambda }_{u}$
.
Proof By Lemma 4.2, if
![]() $supp(\mu )=Y^{\lambda }_{u}$
for some
$supp(\mu )=Y^{\lambda }_{u}$
for some
![]() $\lambda \in S(P^{*})$
, then
$\lambda \in S(P^{*})$
, then
![]() $\{Exp(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
$\{Exp(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
![]() $E^{\mu }$
.
$E^{\mu }$
.
To prove the converse, let
![]() $A\in supp(\mu )$
. Since
$A\in supp(\mu )$
. Since
![]() $\mu $
is invariant,
$\mu $
is invariant,
![]() $supp(\mu )$
is
$supp(\mu )$
is
![]() $\mathbb {R}^d$
-invariant. By Lemma 4.11, for
$\mathbb {R}^d$
-invariant. By Lemma 4.11, for
![]() $x\in \mathbb {R}^{d}$
, either
$x\in \mathbb {R}^{d}$
, either
![]() $A+x\subset A$
or
$A+x\subset A$
or
![]() $A\subset A+x$
. Define
$A\subset A+x$
. Define
![]() $Q_{A}:=\{x\in \mathbb {R}^{d}: {A+x\subset A}\}$
. Then,
$Q_{A}:=\{x\in \mathbb {R}^{d}: {A+x\subset A}\}$
. Then,
![]() $Q_{A}\cup -Q_{A}=\mathbb {R}^{d}$
. Note that
$Q_{A}\cup -Q_{A}=\mathbb {R}^{d}$
. Note that
![]() $-P\subset Q_{A}$
and
$-P\subset Q_{A}$
and
![]() $-P+Q_A \subset Q_A$
. Let
$-P+Q_A \subset Q_A$
. Let
![]() $Q:=Q_{A}\cap -Q_{A}$
. We claim the following:
$Q:=Q_{A}\cap -Q_{A}$
. We claim the following:
-
(i)
 $\partial Q_{A}=Q$
, where
$\partial Q_{A}=Q$
, where
 $\partial Q_A$
is the boundary of
$\partial Q_A$
is the boundary of
 $Q_{A}$
, and
$Q_{A}$
, and -
(ii) Q is a vector subspace of
 $\mathbb {R}^{d}$
.
$\mathbb {R}^{d}$
.
We identify
![]() $span\{v_{1},v_{2},\ldots v_{d-1}\}$
with
$span\{v_{1},v_{2},\ldots v_{d-1}\}$
with
![]() $\mathbb {R}^{d-1}$
. Let
$\mathbb {R}^{d-1}$
. Let
![]() $f:\mathbb {R}^{d-1}\to \mathbb {R}$
be a continuous function such that
$f:\mathbb {R}^{d-1}\to \mathbb {R}$
be a continuous function such that
![]() $A=\{(x,t): {t\leq f(x)}\}$
. Note that
$A=\{(x,t): {t\leq f(x)}\}$
. Note that
and
It is not difficult to deduce using the fact that
![]() $Q_A \cup -Q_A=\mathbb {R}^d$
that
$Q_A \cup -Q_A=\mathbb {R}^d$
that
Suppose
![]() $(y,t) \in Q$
. Set
$(y,t) \in Q$
. Set
![]() $t_n:=t-\frac {1}{n}$
and
$t_n:=t-\frac {1}{n}$
and
![]() $s_n:=t+\frac {1}{n}$
. Then,
$s_n:=t+\frac {1}{n}$
. Then,
![]() $(y,t_n) \in Q_A$
and
$(y,t_n) \in Q_A$
and
![]() $(y,t_n) \to (y,t)$
. Also,
$(y,t_n) \to (y,t)$
. Also,
![]() $(y,s_n) \notin Q_A$
and
$(y,s_n) \notin Q_A$
and
![]() $(y,s_n) \to (y,t)$
. Therefore,
$(y,s_n) \to (y,t)$
. Therefore,
![]() $(y,t) \in \partial Q_A$
. Hence,
$(y,t) \in \partial Q_A$
. Hence,
![]() $\partial Q_A=Q$
.
$\partial Q_A=Q$
.
Let
![]() $g:\mathbb {R}^{d-1}\to \mathbb {R}$
be a continuous function such that
$g:\mathbb {R}^{d-1}\to \mathbb {R}$
be a continuous function such that
![]() $Q_{A}=\{(x,t): {t\leq g(x)}\}$
. Clearly,
$Q_{A}=\{(x,t): {t\leq g(x)}\}$
. Clearly,
![]() $Q=\{x \in \mathbb {R}^d:A +x=A\}$
is a closed subgroup of
$Q=\{x \in \mathbb {R}^d:A +x=A\}$
is a closed subgroup of
![]() $\mathbb {R}^{d}$
. Since
$\mathbb {R}^{d}$
. Since
![]() $Q=\partial Q_A$
is the graph of the continuous function g, it is connected. Therefore, Q is a vector space and consequently, g is linear. Hence, there exists
$Q=\partial Q_A$
is the graph of the continuous function g, it is connected. Therefore, Q is a vector space and consequently, g is linear. Hence, there exists
![]() $\lambda \in \mathbb {R}^d$
,
$\lambda \in \mathbb {R}^d$
,
![]() $||\lambda ||=1$
such that
$||\lambda ||=1$
such that
Since
![]() $-P\subset Q_{A}$
,
$-P\subset Q_{A}$
,
![]() $\lambda \in S(P^{*})$
.
$\lambda \in S(P^{*})$
.
Since
![]() $Q_{A}+A\subset A$
, there exists
$Q_{A}+A\subset A$
, there exists
![]() $y\in \mathbb {R}^{d}$
such that
$y\in \mathbb {R}^{d}$
such that
![]() $A=y+Q_{A}$
, i.e.,
$A=y+Q_{A}$
, i.e.,
![]() $A \in Y_u^{\lambda }$
. Since
$A \in Y_u^{\lambda }$
. Since
![]() $supp(\mu ) \subset Y_{u}$
is invariant,
$supp(\mu ) \subset Y_{u}$
is invariant,
![]() $x+A=x+y+Q_A\in supp(\mu )$
for each
$x+A=x+y+Q_A\in supp(\mu )$
for each
![]() $x\in \mathbb {R}^{d}$
, i.e.,
$x\in \mathbb {R}^{d}$
, i.e.,
![]() $Y^{\lambda }_{u}\subset supp(\mu )$
. To stress the dependence of
$Y^{\lambda }_{u}\subset supp(\mu )$
. To stress the dependence of
![]() $\lambda $
on A, we write
$\lambda $
on A, we write
![]() $\lambda =\lambda _{A}$
. We have proved that
$\lambda =\lambda _{A}$
. We have proved that
Suppose
![]() $A, B\in supp(\mu )$
. Note that
$A, B\in supp(\mu )$
. Note that
![]() $Q_{A}\in Y^{\lambda _{A}}_{u}\subset supp(\mu )$
and
$Q_{A}\in Y^{\lambda _{A}}_{u}\subset supp(\mu )$
and
![]() $Q_{B}\in Y^{\lambda _{B}}_{u}\subset supp(\mu )$
. Then, by Proposition 4.11, either
$Q_{B}\in Y^{\lambda _{B}}_{u}\subset supp(\mu )$
. Then, by Proposition 4.11, either
![]() $Q_{A}\subset Q_{B}$
or
$Q_{A}\subset Q_{B}$
or
![]() $Q_{B}\subset Q_{A}$
. But this can happen only if
$Q_{B}\subset Q_{A}$
. But this can happen only if
![]() $\lambda _{A}=\lambda _{B}$
. In that case,
$\lambda _{A}=\lambda _{B}$
. In that case,
![]() $Y^{\lambda _{A}}_{u}=Y^{\lambda _{B}}_{u}$
. Therefore, there exists
$Y^{\lambda _{A}}_{u}=Y^{\lambda _{B}}_{u}$
. Therefore, there exists
![]() $\lambda \in S(P^{*})$
such that
$\lambda \in S(P^{*})$
such that
![]() $supp(\mu )=Y^{\lambda }_{u}$
. Now the proof is complete.
$supp(\mu )=Y^{\lambda }_{u}$
. Now the proof is complete.
Notation and Convention: Let V be an isometric representation of P on a Hilbert space
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
. We define
$\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
. We define
![]() $\mathcal {H}^{\xi }$
to be the smallest, closed, reducing subspace of
$\mathcal {H}^{\xi }$
to be the smallest, closed, reducing subspace of
![]() $\mathcal {H}$
containing
$\mathcal {H}$
containing
![]() $\{\xi _{a}:{ a\in P}\}$
. (Hereafter, all reducing subspaces will be assumed to be closed.) If W is a direct summand of V, we view the product system
$\{\xi _{a}:{ a\in P}\}$
. (Hereafter, all reducing subspaces will be assumed to be closed.) If W is a direct summand of V, we view the product system
![]() $E^W$
as a subsystem of
$E^W$
as a subsystem of
![]() $E^V$
. Similarly, we view
$E^V$
. Similarly, we view
![]() $\mathcal {A}(W)$
as a subspace of
$\mathcal {A}(W)$
as a subspace of
![]() $\mathcal {A}(V)$
.
$\mathcal {A}(V)$
.
Proposition 4.13 Let V be a pure isometric representation of P on a Hilbert space
![]() $\mathcal {H}$
with commuting range projections. Let
$\mathcal {H}$
with commuting range projections. Let
![]() $\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
be non-zero. Then,
$\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
be non-zero. Then,
-
(1) there exists an
 $\mathbb {R}^d$
-invariant, non-zero Radon measure
$\mathbb {R}^d$
-invariant, non-zero Radon measure
 $\mu $
on
$\mu $
on
 $Y_u$
such that
$Y_u$
such that
 $V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
$V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
 $V^{\mu }$
, and
$V^{\mu }$
, and -
(2) if
 $Exp(\xi )$
is a unit for
$Exp(\xi )$
is a unit for
 $E^{V}$
, then there exists
$E^{V}$
, then there exists
 $\lambda \in S(P^{*})$
such that
$\lambda \in S(P^{*})$
such that
 $V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
$V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
 $S^{\lambda }$
.
$S^{\lambda }$
.
Proof For the proof of
![]() $(1)$
, we refer the reader to [Reference Sundar34, Theorem 3.16 and Remark 3.17]. From
$(1)$
, we refer the reader to [Reference Sundar34, Theorem 3.16 and Remark 3.17]. From
![]() $(1)$
,
$(1)$
,
![]() $V^{\xi }:=V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
$V^{\xi }:=V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
![]() $V^{\mu }$
. We can see from the proof of [Reference Sundar34, Theorem 3.16] that the unitary U intertwining
$V^{\mu }$
. We can see from the proof of [Reference Sundar34, Theorem 3.16] that the unitary U intertwining
![]() $V^{\xi }$
and
$V^{\xi }$
and
![]() $V^{\mu }$
can be chosen such that
$V^{\mu }$
can be chosen such that
![]() $U\xi _{a}=1_{X_{u}\setminus X_{u}+a}$
for
$U\xi _{a}=1_{X_{u}\setminus X_{u}+a}$
for
![]() $a\in P$
. Suppose
$a\in P$
. Suppose
![]() $Exp(\xi )$
is a unit for
$Exp(\xi )$
is a unit for
![]() $E^{V}$
. Note that the subsystem
$E^{V}$
. Note that the subsystem
![]() $E^{V^\xi }$
contains
$E^{V^\xi }$
contains
![]() $Exp(\xi )$
. Hence,
$Exp(\xi )$
. Hence,
![]() $\{Exp(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
$\{Exp(1_{X_{u}\setminus X_{u}+a})\}_{a\in P}$
is a unit for
![]() $E^{V^\mu }$
. It follows from Theorem 4.12 and Lemma 4.2 that
$E^{V^\mu }$
. It follows from Theorem 4.12 and Lemma 4.2 that
![]() $V^{\mu }$
is unitarily equivalent to
$V^{\mu }$
is unitarily equivalent to
![]() $S^{\lambda }$
for some
$S^{\lambda }$
for some
![]() $\lambda \in S(P^{*})$
. This proves
$\lambda \in S(P^{*})$
. This proves
![]() $(2)$
.
$(2)$
.
Before proceeding further, let us recall the notation introduced in the introduction. For
![]() $\lambda \in S(P^{*})$
and
$\lambda \in S(P^{*})$
and
![]() $k\in \mathbb {N}_\infty $
, let
$k\in \mathbb {N}_\infty $
, let
![]() $S^{(\lambda , k)}$
denote the isometric representation
$S^{(\lambda , k)}$
denote the isometric representation
![]() $\{S_{\langle \lambda |a\rangle }\otimes 1\}_{a\in P}$
of P acting on the Hilbert space
$\{S_{\langle \lambda |a\rangle }\otimes 1\}_{a\in P}$
of P acting on the Hilbert space
![]() $L^{2}[0,\infty )\otimes \mathcal {K}$
where
$L^{2}[0,\infty )\otimes \mathcal {K}$
where
![]() $\mathcal {K}$
is a Hilbert space of dimension k. For
$\mathcal {K}$
is a Hilbert space of dimension k. For
![]() $k=1$
, we denote
$k=1$
, we denote
![]() $S^{(\lambda ,1)}$
by
$S^{(\lambda ,1)}$
by
![]() $S^\lambda $
. For a non-empty countable set I, an injective map
$S^\lambda $
. For a non-empty countable set I, an injective map
![]() $\lambda :I \to S(P^*)$
and a function
$\lambda :I \to S(P^*)$
and a function
![]() $k:I \to \mathbb {N}_\infty $
, set
$k:I \to \mathbb {N}_\infty $
, set
Let
![]() $E^{(\lambda ,k)}$
be the product system of the CAR flow associated with
$E^{(\lambda ,k)}$
be the product system of the CAR flow associated with
![]() $S^{(\lambda ,k)}$
.
$S^{(\lambda ,k)}$
.
Remark 4.14 A few properties concerning the representation
![]() $S^{(\lambda ,k)}$
are summarized below.
$S^{(\lambda ,k)}$
are summarized below.
-
(1) For
 $\lambda _{1},\lambda _{2}\in S(P^*)$
and for
$\lambda _{1},\lambda _{2}\in S(P^*)$
and for
 $k_1,k_2 \in \mathbb {N}_\infty $
,
$k_1,k_2 \in \mathbb {N}_\infty $
,
 $S^{(\lambda _{1}, k_{1})}$
is unitarily equivalent to
$S^{(\lambda _{1}, k_{1})}$
is unitarily equivalent to
 $S^{(\lambda _{2}, k_{2})}$
if and only if
$S^{(\lambda _{2}, k_{2})}$
if and only if
 $\lambda _{1}=\lambda _{2}$
and
$\lambda _{1}=\lambda _{2}$
and
 $k_{1}=k_{2}$
. Also,
$k_{1}=k_{2}$
. Also,
 $S^{\lambda }$
is irreducible for every
$S^{\lambda }$
is irreducible for every
 $\lambda \in S(P^{*})$
, i.e., it has no non-zero non-trivial reducing subspace. Thus, if
$\lambda \in S(P^{*})$
, i.e., it has no non-zero non-trivial reducing subspace. Thus, if
 $\lambda _1 \neq \lambda _2$
, the representations
$\lambda _1 \neq \lambda _2$
, the representations
 $S^{(\lambda _1,k_1)}$
and
$S^{(\lambda _1,k_1)}$
and
 $S^{(\lambda _2,k_2)}$
are disjoint. Recall that two isometric representations V and W, acting on
$S^{(\lambda _2,k_2)}$
are disjoint. Recall that two isometric representations V and W, acting on
 $\mathcal {H}$
and
$\mathcal {H}$
and
 $\mathcal {K}$
, respectively, are said to be disjoint if
$\mathcal {K}$
, respectively, are said to be disjoint if  $$\begin{align*}\{T \in B(\mathcal{H},\mathcal{K}): TV_a=W_aT, TV_a^*=W_a^*T \text{~~for all } a \in P\}=0. \end{align*}$$
$$\begin{align*}\{T \in B(\mathcal{H},\mathcal{K}): TV_a=W_aT, TV_a^*=W_a^*T \text{~~for all } a \in P\}=0. \end{align*}$$
-
(2) Consider a countable (non-empty) indexing set I. Let
 $\lambda : I\to S(P^{*})$
be injective, and let
$\lambda : I\to S(P^{*})$
be injective, and let
 $k:I\to \mathbb {N}_{\infty }$
be a map. Consider
$k:I\to \mathbb {N}_{\infty }$
be a map. Consider
 $V=S^{(\lambda ,k)}=\bigoplus _{i \in I}S^{(\lambda _i,k_{i})}$
acting on the Hilbert space
$V=S^{(\lambda ,k)}=\bigoplus _{i \in I}S^{(\lambda _i,k_{i})}$
acting on the Hilbert space
 $\mathcal {H}=\displaystyle {\bigoplus _{i\in I}}L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
, where
$\mathcal {H}=\displaystyle {\bigoplus _{i\in I}}L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
, where
 $\mathcal {K}_{i}$
is of dimension
$\mathcal {K}_{i}$
is of dimension
 $k_{i}$
. Write
$k_{i}$
. Write
 $V^{(i)}= S^{(\lambda _{i}, k_{i})}$
. Then,
$V^{(i)}= S^{(\lambda _{i}, k_{i})}$
. Then,
 $V^{(i)}$
acts on
$V^{(i)}$
acts on
 $\mathcal {H}_i:=L^{2}[0,\infty )\otimes \mathcal {K}_i$
. Since
$\mathcal {H}_i:=L^{2}[0,\infty )\otimes \mathcal {K}_i$
. Since
 $\lambda _{i}\neq \lambda _{j}$
whenever
$\lambda _{i}\neq \lambda _{j}$
whenever
 $i\neq j$
, the isometric representations
$i\neq j$
, the isometric representations
 $V^{(i)}$
and
$V^{(i)}$
and
 $V^{(j)}$
are disjoint wh enever
$V^{(j)}$
are disjoint wh enever
 $i \neq j$
. Thus, a bounded operator
$i \neq j$
. Thus, a bounded operator
 $T \in \{V_{a}, V^{*}_{a}: { a\in P}\}^{'}$
if and only if there exists
$T \in \{V_{a}, V^{*}_{a}: { a\in P}\}^{'}$
if and only if there exists
 $T_{i}\in \{V^{(i)}_{a}, V^{(i)*}_{a}: { a\in P}\}^{'}$
such that
$T_{i}\in \{V^{(i)}_{a}, V^{(i)*}_{a}: { a\in P}\}^{'}$
such that
 $T|_{\mathcal {H}_{i}}=T_{i}$
for each
$T|_{\mathcal {H}_{i}}=T_{i}$
for each
 $i\in I$
. Moreover,
$i\in I$
. Moreover,
 $\{V^{(i)}_a, V^{(i)*}_a:a \in P\}^{'}=\{1 \otimes R: R \in B(\mathcal {K}_i)\}$
. Hence,
$\{V^{(i)}_a, V^{(i)*}_a:a \in P\}^{'}=\{1 \otimes R: R \in B(\mathcal {K}_i)\}$
. Hence,  $$\begin{align*}\{V_a,V_a^*:a \in P\}^{'}=\bigoplus_{i \in I}B(\mathcal{K}_i). \end{align*}$$
$$\begin{align*}\{V_a,V_a^*:a \in P\}^{'}=\bigoplus_{i \in I}B(\mathcal{K}_i). \end{align*}$$
-
(3) It follows from
 $(2)$
that the reducing subspaces of V are of the form
$(2)$
that the reducing subspaces of V are of the form
 $\displaystyle \bigoplus _{j\in J}L^{2}[0,\infty )\otimes \mathcal {W}_{j}$
for some non-empty subset J of I, and where, for j,
$\displaystyle \bigoplus _{j\in J}L^{2}[0,\infty )\otimes \mathcal {W}_{j}$
for some non-empty subset J of I, and where, for j,
 $\mathcal {W}_j$
is a subspace of
$\mathcal {W}_j$
is a subspace of
 $\mathcal {K}_j$
. Suppose
$\mathcal {K}_j$
. Suppose
 $\mathcal {W}$
is a non-zero reducing subspace for V such that
$\mathcal {W}$
is a non-zero reducing subspace for V such that
 $V|_{\mathcal {W}}$
is irreducible. Then, there exists
$V|_{\mathcal {W}}$
is irreducible. Then, there exists
 $i \in I$
and a one dimensional subspace
$i \in I$
and a one dimensional subspace
 $\mathcal {W}_i$
of
$\mathcal {W}_i$
of
 $\mathcal {K}_i$
such that
$\mathcal {K}_i$
such that
 $\mathcal {W} \subset \mathcal {H}_i=L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
and
$\mathcal {W} \subset \mathcal {H}_i=L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
and
 $\mathcal {W}=L^2[0,\infty ) \otimes \mathcal {W}_i$
. Moreover,
$\mathcal {W}=L^2[0,\infty ) \otimes \mathcal {W}_i$
. Moreover,
 $V|_{\mathcal {W}}$
is unitarily equivalent to
$V|_{\mathcal {W}}$
is unitarily equivalent to
 $S^{\lambda _{i}}$
.
$S^{\lambda _{i}}$
.
The next proposition is the “only if part” of Theorem 1.2. The “uniqueness” part of Theorem 1.2 follows from the fact that if an isometric representation admits a direct sum decomposition of irreducible representations, then the decomposition is “unique”.
Proposition 4.15 Let V be a pure isometric representation of P with commuting range projections on a Hilbert space
![]() $\mathcal {H}$
. Suppose the product system
$\mathcal {H}$
. Suppose the product system
![]() $E^{V}$
of the CAR flow associated with V is type I. Then, there exists a non-empty, countable set I, a map
$E^{V}$
of the CAR flow associated with V is type I. Then, there exists a non-empty, countable set I, a map
![]() $\lambda :I\to S(P^{*})$
which is injective, and a map
$\lambda :I\to S(P^{*})$
which is injective, and a map
![]() $k:I\to \mathbb {N}_{\infty }$
such that V is unitarily equivalent to
$k:I\to \mathbb {N}_{\infty }$
such that V is unitarily equivalent to
![]() $S^{(\lambda ,k)}$
. Equivalently,
$S^{(\lambda ,k)}$
. Equivalently,
![]() $E^V$
is isomorphic to
$E^V$
is isomorphic to
![]() $E^{(\lambda ,k)}$
.
$E^{(\lambda ,k)}$
.
Proof A family
![]() $\mathscr {S}$
of closed subspaces of
$\mathscr {S}$
of closed subspaces of
![]() $\mathcal {H}$
is said to be “shift reducing” if
$\mathcal {H}$
is said to be “shift reducing” if
-
(1) each
 $\mathcal {K}\in \mathscr {S}$
is a non-zero reducing subspace for V,
$\mathcal {K}\in \mathscr {S}$
is a non-zero reducing subspace for V, -
(2) for each
 $\mathcal {K}\in \mathscr {S}$
, there exists
$\mathcal {K}\in \mathscr {S}$
, there exists
 $\lambda \in S(P^*)$
such that
$\lambda \in S(P^*)$
such that
 $V|_{\mathcal {K}}$
is unitarily equivalent to
$V|_{\mathcal {K}}$
is unitarily equivalent to
 $S^{\lambda }$
, and
$S^{\lambda }$
, and -
(3) if
 $\mathcal {K},\mathcal {L}\in \mathscr {S}$
and
$\mathcal {K},\mathcal {L}\in \mathscr {S}$
and
 $\mathcal {K}\neq \mathcal {L}$
, then
$\mathcal {K}\neq \mathcal {L}$
, then
 $\mathcal {K}\perp \mathcal {L}$
.
$\mathcal {K}\perp \mathcal {L}$
.
Let
![]() $\mathcal {W}:=\{\mathscr {S}: {\mathscr {S}} \text { is shift reducing}\}$
. Note that
$\mathcal {W}:=\{\mathscr {S}: {\mathscr {S}} \text { is shift reducing}\}$
. Note that
![]() $\mathcal {W}$
is partially ordered where the partial order on
$\mathcal {W}$
is partially ordered where the partial order on
![]() $\mathcal {W}$
is given by inclusion.
$\mathcal {W}$
is given by inclusion.
Since
![]() $E^{V}$
is type I, there exists a non-zero additive cocycle
$E^{V}$
is type I, there exists a non-zero additive cocycle
![]() $\xi =\{\xi _{a}\}_{a\in P}$
such that
$\xi =\{\xi _{a}\}_{a\in P}$
such that
![]() $Exp(\xi )$
is a unit for
$Exp(\xi )$
is a unit for
![]() $E^{V}$
. Hence,
$E^{V}$
. Hence,
![]() $\{\mathcal {H}^{\xi }\}$
is in
$\{\mathcal {H}^{\xi }\}$
is in
![]() $\mathcal {W}$
by Proposition 4.13. Therefore,
$\mathcal {W}$
by Proposition 4.13. Therefore,
![]() $\mathcal {W}$
is non-empty. A routine application of Zorn’s lemma allows us to get a maximal shift reducing family
$\mathcal {W}$
is non-empty. A routine application of Zorn’s lemma allows us to get a maximal shift reducing family
![]() $\mathscr {K}$
of closed subspaces.
$\mathscr {K}$
of closed subspaces.
Define
Note that for each
![]() $W\in \mathcal {K}$
, there exists
$W\in \mathcal {K}$
, there exists
![]() $\lambda _{W}\in S(P^{*})$
such that
$\lambda _{W}\in S(P^{*})$
such that
![]() $V|_{W}$
is unitarily equivalent to
$V|_{W}$
is unitarily equivalent to
![]() $S^{\lambda _{W}}$
. Hence,
$S^{\lambda _{W}}$
. Hence,
![]() $V|_{\mathcal {K}}=\displaystyle {\bigoplus _{W\in \mathcal {K}}}S^{\lambda _{W}}$
. Let
$V|_{\mathcal {K}}=\displaystyle {\bigoplus _{W\in \mathcal {K}}}S^{\lambda _{W}}$
. Let
![]() $\mathcal {L}:=\mathcal {K}^{\perp }$
. Note that
$\mathcal {L}:=\mathcal {K}^{\perp }$
. Note that
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {L}$
are reducing subspaces for V. Denote the restriction of V to
$\mathcal {L}$
are reducing subspaces for V. Denote the restriction of V to
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {L}$
by
$\mathcal {L}$
by
![]() $V^{(1)}$
and
$V^{(1)}$
and
![]() $V^{(2)}$
, respectively. Also, denote the projection of
$V^{(2)}$
, respectively. Also, denote the projection of
![]() $\mathcal {H}$
onto
$\mathcal {H}$
onto
![]() $\mathcal {L}$
by Q.
$\mathcal {L}$
by Q.
It suffices to prove that
![]() $V=V^{(1)}$
. Denote by
$V=V^{(1)}$
. Denote by
![]() $E^{V^{(1)}}$
the product system of the CAR flow associated with
$E^{V^{(1)}}$
the product system of the CAR flow associated with
![]() $V^{(1)}$
. We consider
$V^{(1)}$
. We consider
![]() $E^{V^{(1)}}$
as a subsystem of
$E^{V^{(1)}}$
as a subsystem of
![]() $E^{V}$
. We claim that
$E^{V}$
. We claim that
![]() $E^{V^{(1)}}=E^{V}$
. Suppose
$E^{V^{(1)}}=E^{V}$
. Suppose
![]() $u=\{u_{a}\}_{a\in P}$
is a unit for
$u=\{u_{a}\}_{a\in P}$
is a unit for
![]() $E^{V}$
. We claim that
$E^{V}$
. We claim that
![]() $E^{V^{(1 )}}$
contains u. Without loss of generality, we can assume u is exponential. Then, there exists
$E^{V^{(1 )}}$
contains u. Without loss of generality, we can assume u is exponential. Then, there exists
![]() $\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
such that
$\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
such that
![]() $u_{a}=Exp_{a}(\xi _{a})$
for
$u_{a}=Exp_{a}(\xi _{a})$
for
![]() $a\in P$
. For
$a\in P$
. For
![]() $a\in P$
, let
$a\in P$
, let
![]() $\xi ^{(1)}_{a}=(1-Q)\xi _{a}$
and
$\xi ^{(1)}_{a}=(1-Q)\xi _{a}$
and
![]() $\xi ^{(2)}_{a}=Q\xi _{a}$
. Then,
$\xi ^{(2)}_{a}=Q\xi _{a}$
. Then,
![]() $\xi ^{(i)}=\{\xi ^{(i)}_{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
for
$\xi ^{(i)}=\{\xi ^{(i)}_{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
for
![]() $i=1,2$
.
$i=1,2$
.
Note that
![]() $\mathcal {Q}=\{\mathcal {Q}_{a}\}_{a\in P}:E^{V}\to E^{V}$
given by
$\mathcal {Q}=\{\mathcal {Q}_{a}\}_{a\in P}:E^{V}\to E^{V}$
given by
is multiplicative, where
![]() $\Gamma (Q)$
is the second quantisation of Q. Also,
$\Gamma (Q)$
is the second quantisation of Q. Also,
![]() $\Gamma (Q)u_a=Exp_a(\xi ^{(2)}_a)$
. Therefore,
$\Gamma (Q)u_a=Exp_a(\xi ^{(2)}_a)$
. Therefore,
![]() $\{Exp_{a}(\xi ^{(2)}_{a})\}_{a\in P}$
is a unit for
$\{Exp_{a}(\xi ^{(2)}_{a})\}_{a\in P}$
is a unit for
![]() $E^{V}$
.
$E^{V}$
.
Assume that
![]() $\xi ^{(2)}$
is non-zero. Consider the reducing subspace
$\xi ^{(2)}$
is non-zero. Consider the reducing subspace
![]() $\mathcal {H}^{\xi ^{(2)}}$
of V. Then, by Proposition 4.13 there exists
$\mathcal {H}^{\xi ^{(2)}}$
of V. Then, by Proposition 4.13 there exists
![]() $\lambda \in S(P^{*})$
such that
$\lambda \in S(P^{*})$
such that
![]() $V|_{\mathcal {H}^{\xi ^{(2)}}}$
is unitarily equivalent to
$V|_{\mathcal {H}^{\xi ^{(2)}}}$
is unitarily equivalent to
![]() $S^{\lambda }$
. Now,
$S^{\lambda }$
. Now,
![]() $\mathscr {K}\cup \{\mathcal {H}^{\xi ^{(2)}}\}\in \mathcal {W}$
and contains
$\mathscr {K}\cup \{\mathcal {H}^{\xi ^{(2)}}\}\in \mathcal {W}$
and contains
![]() $\mathscr {K}$
as a proper subset. This contradicts the maximality of
$\mathscr {K}$
as a proper subset. This contradicts the maximality of
![]() $\mathscr {K}$
. Therefore,
$\mathscr {K}$
. Therefore,
![]() $\xi ^{(2)}=0$
. Thus,
$\xi ^{(2)}=0$
. Thus,
![]() $E^{V^{(1)}}$
contains u. Hence, every unit of
$E^{V^{(1)}}$
contains u. Hence, every unit of
![]() $E^{V}$
is contained in
$E^{V}$
is contained in
![]() $E^{V^{(1)}}$
. Since
$E^{V^{(1)}}$
. Since
![]() $E^{V}$
is type I,
$E^{V}$
is type I,
![]() $E^{V}=E^{V^{(1)}}$
.
$E^{V}=E^{V^{(1)}}$
.
Since
for
![]() $a\in P$
,
$a\in P$
,
![]() $Ker(V^{(1)*}_{a})=Ker(V_{a}^{*})$
for
$Ker(V^{(1)*}_{a})=Ker(V_{a}^{*})$
for
![]() $a\in P$
. Since
$a\in P$
. Since
![]() $\displaystyle {\bigcup _{a\in P}}Ker(V_{a}^{*})$
is dense in
$\displaystyle {\bigcup _{a\in P}}Ker(V_{a}^{*})$
is dense in
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $\mathcal {H}=\mathcal {K}$
. Therefore,
$\mathcal {H}=\mathcal {K}$
. Therefore,
![]() $V=V^{(1)}$
. The proof is complete.
$V=V^{(1)}$
. The proof is complete.
Fix a countable (non-empty) indexing set I. Let
![]() $\lambda : I\to S(P^{*})$
be injective, and let
$\lambda : I\to S(P^{*})$
be injective, and let
![]() $k:I\to \mathbb {N}_{\infty }$
be a map. Let
$k:I\to \mathbb {N}_{\infty }$
be a map. Let
![]() $V=S^{(\lambda ,k)}$
. Denote the space
$V=S^{(\lambda ,k)}$
. Denote the space
![]() $\displaystyle {\bigoplus _{i\in I}}L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
(on which V acts) by
$\displaystyle {\bigoplus _{i\in I}}L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
(on which V acts) by
![]() $\mathcal {H}$
, where
$\mathcal {H}$
, where
![]() $\mathcal {K}_{i}$
is a Hilbert space of dimension
$\mathcal {K}_{i}$
is a Hilbert space of dimension
![]() $k_{i}\in \mathbb {N}_{\infty }$
. For each
$k_{i}\in \mathbb {N}_{\infty }$
. For each
![]() $i\in I$
, let
$i\in I$
, let
![]() $V^{(i)}=S^{(\lambda _{i}, k_{i})}$
, and write
$V^{(i)}=S^{(\lambda _{i}, k_{i})}$
, and write
![]() $\mathcal {H}_{i}:=L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
(the Hilbert space on which
$\mathcal {H}_{i}:=L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
(the Hilbert space on which
![]() $V^{(i)}$
acts). Note that for
$V^{(i)}$
acts). Note that for
![]() $i\in I$
, we may view
$i\in I$
, we may view
![]() $\mathcal {A}(S^{(\lambda _i,k_{i})})$
as a subspace of
$\mathcal {A}(S^{(\lambda _i,k_{i})})$
as a subspace of
![]() $\mathcal {A}(V)$
under the natural inclusion.
$\mathcal {A}(V)$
under the natural inclusion.
Proposition 4.16 Let
![]() $\xi \in \mathcal {A}(V)$
. Then,
$\xi \in \mathcal {A}(V)$
. Then,
![]() $\{Exp_{a}(\xi _{a})\}_{a\in P}$
is a unit of
$\{Exp_{a}(\xi _{a})\}_{a\in P}$
is a unit of
![]() $E^V$
if and only if there exists
$E^V$
if and only if there exists
![]() $i\in I$
such that
$i\in I$
such that
![]() $\xi \in \mathcal {A}(S^{(\lambda _i,k_{i})})$
.
$\xi \in \mathcal {A}(S^{(\lambda _i,k_{i})})$
.
Proof Suppose
![]() $\xi =\{\xi _{a}\}_{a\in P} \in \mathcal {A}(V)$
is non-zero and is such that
$\xi =\{\xi _{a}\}_{a\in P} \in \mathcal {A}(V)$
is non-zero and is such that
![]() $Exp(\xi )$
is a unit of
$Exp(\xi )$
is a unit of
![]() $E^{V}$
. Consider the reducing subspace
$E^{V}$
. Consider the reducing subspace
![]() $\mathcal {H}^{\xi }$
of V. By Proposition 4.13,
$\mathcal {H}^{\xi }$
of V. By Proposition 4.13,
![]() $V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
$V|_{\mathcal {H}^{\xi }}$
is unitarily equivalent to
![]() $S^{\lambda }$
for some
$S^{\lambda }$
for some
![]() $\lambda \in S(P^{*})$
. Since
$\lambda \in S(P^{*})$
. Since
![]() $S^{\lambda }$
is irreducible, by Remark 4.14,
$S^{\lambda }$
is irreducible, by Remark 4.14,
![]() $\mathcal {H}^{\xi }$
is a subspace of
$\mathcal {H}^{\xi }$
is a subspace of
![]() $\mathcal {H}_{i}$
and
$\mathcal {H}_{i}$
and
![]() $\lambda =\lambda _{i}$
for some
$\lambda =\lambda _{i}$
for some
![]() $i\in I$
. In particular,
$i\in I$
. In particular,
![]() $\xi \in \mathcal {A}(S^{\lambda _{i}, k_{i})})$
.
$\xi \in \mathcal {A}(S^{\lambda _{i}, k_{i})})$
.
Conversely, suppose
![]() $\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(S^{(\lambda _{i},k_{i})})$
for some
$\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(S^{(\lambda _{i},k_{i})})$
for some
![]() $i\in I$
. Then, there exists an additive cocycle
$i\in I$
. Then, there exists an additive cocycle
![]() $\eta =\{\eta _{a}\}\in \mathcal {A}(S^{\lambda _{i}})$
and
$\eta =\{\eta _{a}\}\in \mathcal {A}(S^{\lambda _{i}})$
and
![]() $\gamma \in \mathcal {K}_{i}$
such that
$\gamma \in \mathcal {K}_{i}$
such that
![]() $\xi _{a}=\eta _{a}\otimes \gamma $
for
$\xi _{a}=\eta _{a}\otimes \gamma $
for
![]() $a\in P$
. In turn, there is an additive cocycle
$a\in P$
. In turn, there is an additive cocycle
![]() $\widetilde {\eta }=\{\widetilde {\eta }_{t}\}_{t\geq 0}$
of
$\widetilde {\eta }=\{\widetilde {\eta }_{t}\}_{t\geq 0}$
of
![]() $\{S_{t}\}_{t\geq 0}$
such that
$\{S_{t}\}_{t\geq 0}$
such that
![]() $\eta _{a}=\widetilde {\eta }_{\langle \lambda _{i}|a\rangle }$
for
$\eta _{a}=\widetilde {\eta }_{\langle \lambda _{i}|a\rangle }$
for
![]() $a\in P$
. Denote the exponential map of the product system of the
$a\in P$
. Denote the exponential map of the product system of the
![]() $1$
-parameter CAR flow associated with
$1$
-parameter CAR flow associated with
![]() $\{S_{t}\otimes 1\}_{t\geq 0}$
acting on
$\{S_{t}\otimes 1\}_{t\geq 0}$
acting on
![]() $\mathcal {H}_{i}$
by
$\mathcal {H}_{i}$
by
![]() $Exp$
. By Remark 2.2,
$Exp$
. By Remark 2.2,
for
![]() $s,t\geq 0$
. Then, for
$s,t\geq 0$
. Then, for
![]() $a,b \in P$
,
$a,b \in P$
,
 $$ \begin{align*}Exp_{a}(\xi_{a}).Exp_{b}(\xi_{b})&=Exp_{a}(\eta_{a}\otimes\gamma).Exp_{b}(\eta_{b}\otimes \gamma)\\ &= Exp(\widetilde{\eta}_{\langle\lambda_{i}|a\rangle}\otimes\gamma).Exp(\widetilde{\eta}_{\langle\lambda_{i}|b\rangle}\otimes\gamma)\\ &=Exp(\widetilde{\eta}_{\langle\lambda_{i}|a+b\rangle}\otimes\gamma)\\ &= Exp_{a+b}(\xi_{a+b}) \end{align*} $$
$$ \begin{align*}Exp_{a}(\xi_{a}).Exp_{b}(\xi_{b})&=Exp_{a}(\eta_{a}\otimes\gamma).Exp_{b}(\eta_{b}\otimes \gamma)\\ &= Exp(\widetilde{\eta}_{\langle\lambda_{i}|a\rangle}\otimes\gamma).Exp(\widetilde{\eta}_{\langle\lambda_{i}|b\rangle}\otimes\gamma)\\ &=Exp(\widetilde{\eta}_{\langle\lambda_{i}|a+b\rangle}\otimes\gamma)\\ &= Exp_{a+b}(\xi_{a+b}) \end{align*} $$
for
![]() $a,b\in P$
, i.e.,
$a,b\in P$
, i.e.,
![]() $Exp(\xi )$
is a unit. This completes the proof.
$Exp(\xi )$
is a unit. This completes the proof.
The following is the “if part” of Theorem 1.2.
Proposition 4.17 Keeping the forgoing notation, the CAR flow associated with V is type I.
Proof Let F be a subsystem of
![]() $E^{V}$
containing all the units of
$E^{V}$
containing all the units of
![]() $E^{V}$
. For
$E^{V}$
. For
![]() $a\in P$
, let
$a\in P$
, let
![]() $\Psi _{a}$
be the projection of
$\Psi _{a}$
be the projection of
![]() $E^{V}(a)$
onto
$E^{V}(a)$
onto
![]() $F(a)$
. Then,
$F(a)$
. Then,
![]() $\Psi =\{\Psi _{a}\}_{a\in P}$
is multiplicative, i.e.,
$\Psi =\{\Psi _{a}\}_{a\in P}$
is multiplicative, i.e.,
for
![]() $a,b\in P$
. Let
$a,b\in P$
. Let
![]() $a\in P$
. Consider the one parameter product system
$a\in P$
. Consider the one parameter product system
![]() $E_{a}=\{E(ta)\}_{t\geq 0}$
and the multiplicative section of maps
$E_{a}=\{E(ta)\}_{t\geq 0}$
and the multiplicative section of maps
![]() $\{\Psi _{ta}\}_{t\geq 0}$
. Let
$\{\Psi _{ta}\}_{t\geq 0}$
. Let
![]() $\widetilde {E}_{a}$
be the product system of the
$\widetilde {E}_{a}$
be the product system of the
![]() $1$
-parameter CCR flow associated with
$1$
-parameter CCR flow associated with
![]() $\{V_{ta}\}_{t\geq 0}$
. Suppose
$\{V_{ta}\}_{t\geq 0}$
. Suppose
![]() $\widetilde {\Psi }=\{\mathcal {Q}_{t}\}_{t\geq 0}:\widetilde {E}_{a}\to \widetilde {E}_{a}$
is such that
$\widetilde {\Psi }=\{\mathcal {Q}_{t}\}_{t\geq 0}:\widetilde {E}_{a}\to \widetilde {E}_{a}$
is such that
-
(i)
 $\mathcal {Q}_{t}$
is a projection for
$\mathcal {Q}_{t}$
is a projection for
 $t\geq 0$
, and
$t\geq 0$
, and -
(ii)
 $\mathcal {Q}_{s}.\mathcal {Q}_{t}=\mathcal {Q}_{s+t}$
for
$\mathcal {Q}_{s}.\mathcal {Q}_{t}=\mathcal {Q}_{s+t}$
for
 $s,t\geq 0$
.
$s,t\geq 0$
.
Then, by [Reference Rajarama Bhat10, Theorem 7.6] (see also [Reference Sundar36, Proposition 6.12]), there exists an additive cocycle
![]() $\{\xi _{t}^{a}\}_{t\geq 0}$
of
$\{\xi _{t}^{a}\}_{t\geq 0}$
of
![]() $\{V_{ta}\}_{t\geq 0}$
, a projection
$\{V_{ta}\}_{t\geq 0}$
, a projection
![]() $Q^{a} \in \{V_{ta},V_{ta}^{*}: { t\geq 0}\}^{'}$
such that
$Q^{a} \in \{V_{ta},V_{ta}^{*}: { t\geq 0}\}^{'}$
such that
![]() $(1-Q^{a})\xi ^{a}_{t}=\xi ^{a}_{t}$
for
$(1-Q^{a})\xi ^{a}_{t}=\xi ^{a}_{t}$
for
![]() $t\geq 0$
, and
$t\geq 0$
, and
![]() $\mu _{a}\in \mathbb {R}$
such that
$\mu _{a}\in \mathbb {R}$
such that
for
![]() $\eta \in Ker(V_{ta}^{*})$
and
$\eta \in Ker(V_{ta}^{*})$
and
![]() $t\geq 0$
.
$t\geq 0$
.
By Lemma 3.1, the map
![]() $\widetilde {E}_{a}(t)\ni exp(\xi )\to Exp_{a}(\xi )\in E_{a}(t)$
extends to an isomorphism from
$\widetilde {E}_{a}(t)\ni exp(\xi )\to Exp_{a}(\xi )\in E_{a}(t)$
extends to an isomorphism from
![]() $\widetilde {E}_{a}$
onto
$\widetilde {E}_{a}$
onto
![]() $E_{a}$
. Therefore, there exists an additive cocycle
$E_{a}$
. Therefore, there exists an additive cocycle
![]() $\{\xi _{t}^{a}\}_{t\geq 0}$
of
$\{\xi _{t}^{a}\}_{t\geq 0}$
of
![]() $\{V_{ta}\}_{t\geq 0}$
, a projection
$\{V_{ta}\}_{t\geq 0}$
, a projection
![]() $Q^{a}\in \{V_{ta}, V_{ta}^{*}: { {t\geq 0}}\}^{'}$
with
$Q^{a}\in \{V_{ta}, V_{ta}^{*}: { {t\geq 0}}\}^{'}$
with
![]() $(1-Q^{a})\xi ^{a}_{t}=\xi ^{a}_{t}$
for
$(1-Q^{a})\xi ^{a}_{t}=\xi ^{a}_{t}$
for
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $\mu _a \in \mathbb {R}$
, such that
$\mu _a \in \mathbb {R}$
, such that
for
![]() $\eta \in Ker(V_{ta}^{*})$
.
$\eta \in Ker(V_{ta}^{*})$
.
For
![]() $a\in P$
, let
$a\in P$
, let
![]() $\xi _{a}:=\xi ^{a}_{1}$
. Proceeding as in the proof of Theorem 3.3, we can prove that
$\xi _{a}:=\xi ^{a}_{1}$
. Proceeding as in the proof of Theorem 3.3, we can prove that
-
(i)
 $\{\xi _{a}\}_{a\in P}$
is an additive cocycle for V,
$\{\xi _{a}\}_{a\in P}$
is an additive cocycle for V, -
(ii) there exists a projection
 $Q \in \{V_{a}, V_{a}^{*}: {a\in P}\}^{'}$
such that
$Q \in \{V_{a}, V_{a}^{*}: {a\in P}\}^{'}$
such that
 $Q|_{Ker(V_{a}^{*})}=Q_{a}$
$Q|_{Ker(V_{a}^{*})}=Q_{a}$
-
(iii) the map
 $P\ni a\mapsto \mu _{a}$
is a continuous homomorphism. Hence, there exists
$P\ni a\mapsto \mu _{a}$
is a continuous homomorphism. Hence, there exists
 $\mu \in \mathbb {R}^{d}$
such that
$\mu \in \mathbb {R}^{d}$
such that
 $\mu _{a}=\langle \mu |a\rangle $
for
$\mu _{a}=\langle \mu |a\rangle $
for
 $a\in P$
.
$a\in P$
.
Therefore, there exists an additive cocycle
![]() $\xi =\{\xi _{a}\}_{a\in P}$
, a projection
$\xi =\{\xi _{a}\}_{a\in P}$
, a projection
![]() $Q\in \{V_{a}, V_{a}^{*}: { a\in P}\}^{'}$
and a vector
$Q\in \{V_{a}, V_{a}^{*}: { a\in P}\}^{'}$
and a vector
![]() $\mu \in \mathbb {R}^{d}$
such that
$\mu \in \mathbb {R}^{d}$
such that
for
![]() $a\in P$
,
$a\in P$
,
![]() $\eta \in Ker(V_{a}^{*})$
.
$\eta \in Ker(V_{a}^{*})$
.
Suppose
![]() $u=\{u_{a}\}_{a\in P}$
is an exponential unit for
$u=\{u_{a}\}_{a\in P}$
is an exponential unit for
![]() $E^{V}$
. Let
$E^{V}$
. Let
![]() $\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V)$
be such that
$\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V)$
be such that
![]() $u_{a}=Exp_{a}(\eta _{a})$
for
$u_{a}=Exp_{a}(\eta _{a})$
for
![]() $a\in P$
. Since F contains all the units, it follows that
$a\in P$
. Since F contains all the units, it follows that
![]() $\Psi _{a}Exp_{a}(\eta _{a})=Exp_{a}(\eta _{a})$
for
$\Psi _{a}Exp_{a}(\eta _{a})=Exp_{a}(\eta _{a})$
for
![]() $a \in P$
. In particular,
$a \in P$
. In particular,
for
![]() $a\in P$
. By (4.11),
$a\in P$
. By (4.11),
for
![]() $a\in P$
. This implies,
$a\in P$
. This implies,
![]() $\xi _{a}=0$
for
$\xi _{a}=0$
for
![]() $a\in P$
and
$a\in P$
and
![]() $\mu =0$
.
$\mu =0$
.
Note that since
![]() $Q\in \{V_{a}, V_{a}^{*}: { a\in P}\}^{'}$
, by Remark 4.14, Q is a diagonal operator, i.e., for
$Q\in \{V_{a}, V_{a}^{*}: { a\in P}\}^{'}$
, by Remark 4.14, Q is a diagonal operator, i.e., for
![]() $i\in I$
, there exists a projection
$i\in I$
, there exists a projection
![]() $Q^{(i)}\in \{V^{(i)}_{a}, V^{(i)*}_{a}: { a\in P}\}^{'}$
such that
$Q^{(i)}\in \{V^{(i)}_{a}, V^{(i)*}_{a}: { a\in P}\}^{'}$
such that
![]() $Q|_{\mathcal {H}_{i}}=Q^{(i)}$
. Fix
$Q|_{\mathcal {H}_{i}}=Q^{(i)}$
. Fix
![]() $i\in I$
. By Proposition 4.16, for any
$i\in I$
. By Proposition 4.16, for any
![]() $\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
,
$\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
,
![]() $Exp(\eta )$
is a unit for
$Exp(\eta )$
is a unit for
![]() $E^{V}$
. Hence
$E^{V}$
. Hence
for
![]() $\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
. This implies that
$\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
. This implies that
for
![]() $a\in P$
and
$a\in P$
and
![]() $\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
. Note that for
$\eta =\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
. Note that for
![]() $\gamma \in \mathcal {K}_i$
,
$\gamma \in \mathcal {K}_i$
,
![]() $\{1_{(0,\langle \lambda _{i}|a\rangle )}\otimes \gamma \}_{a\in P}$
is an additive cocycle for
$\{1_{(0,\langle \lambda _{i}|a\rangle )}\otimes \gamma \}_{a\in P}$
is an additive cocycle for
![]() $V^{(i)}$
. Therefore, the set
$V^{(i)}$
. Therefore, the set
![]() $\{\eta _{a}: { \{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)}), a\in P}\}$
is total in
$\{\eta _{a}: { \{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)}), a\in P}\}$
is total in
![]() $\mathcal {H}_{i}$
. Now, (4.12) implies that
$\mathcal {H}_{i}$
. Now, (4.12) implies that
for
![]() $\eta \in \mathcal {H}_{i}$
for
$\eta \in \mathcal {H}_{i}$
for
![]() $i\in I$
, i.e., Q is the identity operator. Hence,
$i\in I$
, i.e., Q is the identity operator. Hence,
for
![]() $\xi \in Ker(V_{a}^{*})$
and
$\xi \in Ker(V_{a}^{*})$
and
![]() $a\in P$
. Since
$a\in P$
. Since
![]() $\{Exp_{a}(\xi ): {\xi \in Ker(V_{a}^{*})}\}$
is total in
$\{Exp_{a}(\xi ): {\xi \in Ker(V_{a}^{*})}\}$
is total in
![]() $E^{V}(a)$
, it follows that
$E^{V}(a)$
, it follows that
![]() $\Psi _{a}$
is the identity operator for each
$\Psi _{a}$
is the identity operator for each
![]() $a\in P$
. Therefore,
$a\in P$
. Therefore,
![]() $F=E^{V}$
. Hence the proof.
$F=E^{V}$
. Hence the proof.
5 Computation of index and gauge Group
In this section, we compute the index and the gauge group of the product system
![]() $E^{(\lambda ,k)}$
. Arveson’s definition of index for a
$E^{(\lambda ,k)}$
. Arveson’s definition of index for a
![]() $1$
-parameter product system was extended to the multiparameter case in [Reference Sarkar and Sundar24] which we first recall. Let E be a product system over P. Denote the set of units of E by
$1$
-parameter product system was extended to the multiparameter case in [Reference Sarkar and Sundar24] which we first recall. Let E be a product system over P. Denote the set of units of E by
![]() $\mathcal {U}_{E}$
. Assume that
$\mathcal {U}_{E}$
. Assume that
![]() $\mathcal {U}_{E}\neq \emptyset $
. Fix
$\mathcal {U}_{E}\neq \emptyset $
. Fix
![]() $a\in Int(P)$
. For
$a\in Int(P)$
. For
![]() $u,v\in \mathcal {U}_{E}$
, let
$u,v\in \mathcal {U}_{E}$
, let
![]() $c_{a}(u,v)\in \mathbb {C}$
be such that
$c_{a}(u,v)\in \mathbb {C}$
be such that
for
![]() $t\geq 0$
. The function
$t\geq 0$
. The function
![]() $\mathcal {U}_{E}\times \mathcal {U}_{E} \ni (u,v)\to c_{a}(u,v)\in \mathbb {C}$
is conditionally positive definite and is called the covariance function of E with respect to a.
$\mathcal {U}_{E}\times \mathcal {U}_{E} \ni (u,v)\to c_{a}(u,v)\in \mathbb {C}$
is conditionally positive definite and is called the covariance function of E with respect to a.
Let
![]() $\mathcal {H}(\mathcal {U}_{E})$
be the Hilbert space obtained from the covariance function using the GNS construction. For the sake of completeness and also to fix notation, we brief the construction of
$\mathcal {H}(\mathcal {U}_{E})$
be the Hilbert space obtained from the covariance function using the GNS construction. For the sake of completeness and also to fix notation, we brief the construction of
![]() $\mathcal {H}(\mathcal {U}_{E})$
. Let
$\mathcal {H}(\mathcal {U}_{E})$
. Let
![]() $\mathbb {C}_{c}(\mathcal {U}_{E})$
denote the vector space of finitely supported complex valued functions on
$\mathbb {C}_{c}(\mathcal {U}_{E})$
denote the vector space of finitely supported complex valued functions on
![]() $\mathcal {U}_{E}$
. Set
$\mathcal {U}_{E}$
. Set
Define a semi-definite inner product on
![]() $\mathbb {C}_{0}(\mathcal {U}_{E})$
by
$\mathbb {C}_{0}(\mathcal {U}_{E})$
by
Let
![]() $\mathcal {H}(\mathcal {U}_{E})$
be the Hilbert space obtained by completing the semi-definite inner product space
$\mathcal {H}(\mathcal {U}_{E})$
be the Hilbert space obtained by completing the semi-definite inner product space
![]() $\mathbb {C}_0(\mathcal {U}_E)$
.
$\mathbb {C}_0(\mathcal {U}_E)$
.
For
![]() $u\in \mathcal {U}_{E}$
, let
$u\in \mathcal {U}_{E}$
, let
![]() $\delta _{u}:\mathcal {U}_E \to \mathbb {C}$
be the indicator function
$\delta _{u}:\mathcal {U}_E \to \mathbb {C}$
be the indicator function
![]() $1_{\{u\}}$
. Clearly,
$1_{\{u\}}$
. Clearly,
![]() $\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}_{E}}\}$
is total in
$\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}_{E}}\}$
is total in
![]() $\mathcal {H}(\mathcal {U}_{E})$
. The dimension of the space
$\mathcal {H}(\mathcal {U}_{E})$
. The dimension of the space
![]() $\mathcal {H}(\mathcal {U}_{E})$
is independent of the choice of
$\mathcal {H}(\mathcal {U}_{E})$
is independent of the choice of
![]() $a\in Int(P)$
and is called the index of E denoted
$a\in Int(P)$
and is called the index of E denoted
![]() $Ind(E)$
. The reader is referred to [Reference Sarkar and Sundar24, Proposition 2.4] for a proof of this statement.
$Ind(E)$
. The reader is referred to [Reference Sarkar and Sundar24, Proposition 2.4] for a proof of this statement.
Consider the isometric representation
![]() $V=S^{(\lambda ,k)}$
for a non-empty countable indexing set I, an injective map
$V=S^{(\lambda ,k)}$
for a non-empty countable indexing set I, an injective map
![]() $\lambda :I\to S(P^{*})$
and a map
$\lambda :I\to S(P^{*})$
and a map
![]() $k: I\to \mathbb {N}_{\infty }$
. The isometric representation V shall remain fixed for the rest of this section. Let
$k: I\to \mathbb {N}_{\infty }$
. The isometric representation V shall remain fixed for the rest of this section. Let
![]() $\mathcal {H}:=\displaystyle {\bigoplus _{i\in I}}L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
be the Hilbert space on which V acts, where
$\mathcal {H}:=\displaystyle {\bigoplus _{i\in I}}L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
be the Hilbert space on which V acts, where
![]() $\mathcal {K}_{i}$
is a Hilbert space of dimension
$\mathcal {K}_{i}$
is a Hilbert space of dimension
![]() $k_{i}\in \mathbb {N}_{\infty }$
for
$k_{i}\in \mathbb {N}_{\infty }$
for
![]() $i\in I$
. For
$i\in I$
. For
![]() $i\in I$
, let
$i\in I$
, let
![]() $V^{(i)}=S^{(\lambda _{i}, k_{i})}$
, which acts on
$V^{(i)}=S^{(\lambda _{i}, k_{i})}$
, which acts on
![]() $\mathcal {H}_{i}=L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
. Denote the set of units of
$\mathcal {H}_{i}=L^{2}[0,\infty )\otimes \mathcal {K}_{i}$
. Denote the set of units of
![]() $E^{V}$
by
$E^{V}$
by
![]() $\mathcal {U}$
. Similarly, denote the set of units of
$\mathcal {U}$
. Similarly, denote the set of units of
![]() $E^{V^{(i)}}$
by
$E^{V^{(i)}}$
by
![]() $\mathcal {U}_{i}$
for each
$\mathcal {U}_{i}$
for each
![]() $i\in I$
. Then,
$i\in I$
. Then,
![]() $\mathcal {U}_{i}\subset \mathcal {U}$
for
$\mathcal {U}_{i}\subset \mathcal {U}$
for
![]() $i\in I$
. Let
$i\in I$
. Let
![]() $c(.,.)$
be the covariance function of
$c(.,.)$
be the covariance function of
![]() $E^{V}$
with respect to a fixed
$E^{V}$
with respect to a fixed
![]() $a\in Int(P)$
. Let
$a\in Int(P)$
. Let
![]() $\mathcal {U}^{\Omega }$
,
$\mathcal {U}^{\Omega }$
,
![]() $\mathcal {U}^{\Omega }_{i}$
respectively denote the set of exponential units of
$\mathcal {U}^{\Omega }_{i}$
respectively denote the set of exponential units of
![]() $E^{V}$
and
$E^{V}$
and
![]() $E^{V^{(i)}}$
. By Proposition 4.16,
$E^{V^{(i)}}$
. By Proposition 4.16,
![]() $\mathcal {U}^{\Omega }=\displaystyle {\bigcup _{i\in I}}~\mathcal {U}^{\Omega }_{i}$
.
$\mathcal {U}^{\Omega }=\displaystyle {\bigcup _{i\in I}}~\mathcal {U}^{\Omega }_{i}$
.
Remark 5.1 Let
![]() $u\in \mathcal {U}$
. Let
$u\in \mathcal {U}$
. Let
![]() $\widetilde {u}\in \mathcal {U}^{\Omega }$
be given by
$\widetilde {u}\in \mathcal {U}^{\Omega }$
be given by
![]() $\widetilde {u}_{b}=\frac {u_b}{\langle u_{b}|\Omega _{b}\rangle }$
for
$\widetilde {u}_{b}=\frac {u_b}{\langle u_{b}|\Omega _{b}\rangle }$
for
![]() $b\in P$
, where
$b\in P$
, where
![]() $\Omega _{b}$
is the vacuum vector in
$\Omega _{b}$
is the vacuum vector in
![]() $E^{V}(b)$
. Fix
$E^{V}(b)$
. Fix
![]() $a\in Int(P)$
. Now, for
$a\in Int(P)$
. Now, for
![]() $v\in \mathcal {U}$
,
$v\in \mathcal {U}$
,
Since the map
![]() $[0,\infty )\ni t\to \langle u_{ta}|\Omega _{ta}\rangle \in \mathbb {C}^{*}$
is multiplicative, there exists
$[0,\infty )\ni t\to \langle u_{ta}|\Omega _{ta}\rangle \in \mathbb {C}^{*}$
is multiplicative, there exists
![]() $z_{u}\in \mathbb {C}$
such that
$z_{u}\in \mathbb {C}$
such that
![]() $\langle u_{ta}|\Omega _{ta}\rangle =e^{tz_{u}}$
for
$\langle u_{ta}|\Omega _{ta}\rangle =e^{tz_{u}}$
for
![]() $t\geq 0$
. Hence,
$t\geq 0$
. Hence,
It is now routine to verify that if
![]() $w,z\in \mathcal {U}$
, then
$w,z\in \mathcal {U}$
, then
for every
![]() $u,v\in \mathcal {U}$
. Thus, for
$u,v\in \mathcal {U}$
. Thus, for
![]() $u,v \in \mathcal {U}$
,
$u,v \in \mathcal {U}$
,
in
![]() $\mathcal {H}(\mathcal {U})$
. Hence, the set
$\mathcal {H}(\mathcal {U})$
. Hence, the set
![]() $\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}^{\Omega }}\}$
is total in
$\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}^{\Omega }}\}$
is total in
![]() $\mathcal {H}(\mathcal {U})$
. Similarly,
$\mathcal {H}(\mathcal {U})$
. Similarly,
![]() $\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}^{\Omega }_{i}}\}$
is total in
$\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}^{\Omega }_{i}}\}$
is total in
![]() $\mathcal {H}(\mathcal {U}_{i})$
for
$\mathcal {H}(\mathcal {U}_{i})$
for
![]() $i\in I$
.
$i\in I$
.
Lemma 5.2 If
![]() $u\in \mathcal {U}^{\Omega }_{i}$
and
$u\in \mathcal {U}^{\Omega }_{i}$
and
![]() $v\in \mathcal {U}^{\Omega }_{j}$
for
$v\in \mathcal {U}^{\Omega }_{j}$
for
![]() $i\neq j$
, then
$i\neq j$
, then
![]() $c(u,v)=0$
.
$c(u,v)=0$
.
Proof Let
![]() $\xi =\{\xi _{b}\}_{b\in P}\in \mathcal {A}(V^{(i)})$
and
$\xi =\{\xi _{b}\}_{b\in P}\in \mathcal {A}(V^{(i)})$
and
![]() $\eta =\{\eta _{b}\}_{b\in P}\in \mathcal {A}(V^{(j)})$
be such that
$\eta =\{\eta _{b}\}_{b\in P}\in \mathcal {A}(V^{(j)})$
be such that
![]() $u_{b}=Exp_{b}(\xi _{b})$
and
$u_{b}=Exp_{b}(\xi _{b})$
and
![]() $v_{b}=Exp_{b}(\eta _{b})$
for
$v_{b}=Exp_{b}(\eta _{b})$
for
![]() $b \in P$
. Then, for
$b \in P$
. Then, for
![]() $t\geq 0$
,
$t\geq 0$
,
 $$ \begin{align*}\langle u_{ta}|v_{ta}\rangle=&e^{\langle\xi_{ta}|\eta_{ta}\rangle} \text{ (by Proposition 2.1)}\\ =&1 \text{ (since} \langle\xi_{ta}|\eta_{ta}\rangle=0).\end{align*} $$
$$ \begin{align*}\langle u_{ta}|v_{ta}\rangle=&e^{\langle\xi_{ta}|\eta_{ta}\rangle} \text{ (by Proposition 2.1)}\\ =&1 \text{ (since} \langle\xi_{ta}|\eta_{ta}\rangle=0).\end{align*} $$
Therefore,
![]() $c(u,v)=0$
. Hence the proof.
$c(u,v)=0$
. Hence the proof.
Let
![]() $a\in Int(P)$
and
$a\in Int(P)$
and
![]() $i\in I$
. Denote the covariance function of
$i\in I$
. Denote the covariance function of
![]() $E^{V}$
,
$E^{V}$
,
![]() $E^{V^{(i)}}$
(with respect to a) by c,
$E^{V^{(i)}}$
(with respect to a) by c,
![]() $c_{i}$
, respectively. Note that if
$c_{i}$
, respectively. Note that if
![]() $u,v\in \mathcal {U}_{i}$
,
$u,v\in \mathcal {U}_{i}$
,
![]() $c_{i}(u,v)=c(u,v)$
. For each
$c_{i}(u,v)=c(u,v)$
. For each
![]() $i\in I$
, the map
$i\in I$
, the map
![]() $\mathcal {H}(\mathcal {U}_{i})\ni \delta _{u}-\delta _{v}\to \delta _{u}-\delta _{v}\in \mathcal {H}(\mathcal {U})$
extends to an isometry from
$\mathcal {H}(\mathcal {U}_{i})\ni \delta _{u}-\delta _{v}\to \delta _{u}-\delta _{v}\in \mathcal {H}(\mathcal {U})$
extends to an isometry from
![]() $\mathcal {H}(\mathcal {U}_{i})$
into
$\mathcal {H}(\mathcal {U}_{i})$
into
![]() $\mathcal {H}(\mathcal {U})$
. Hence, we may consider
$\mathcal {H}(\mathcal {U})$
. Hence, we may consider
![]() $\mathcal {H}(\mathcal {U}_{i})$
as a subspace of
$\mathcal {H}(\mathcal {U}_{i})$
as a subspace of
![]() $\mathcal {H}(\mathcal {U})$
.
$\mathcal {H}(\mathcal {U})$
.
Proposition 5.3 With the foregoing notation, we have the following.
-
(i)
 $\mathcal {H}(\mathcal {U}_{i})\perp \mathcal {H}(\mathcal {U}_{j})$
if
$\mathcal {H}(\mathcal {U}_{i})\perp \mathcal {H}(\mathcal {U}_{j})$
if
 $i\neq j$
,
$i\neq j$
, -
(ii)
 $\mathcal {H}(\mathcal {U})=\displaystyle {\bigoplus _{i\in I}}\mathcal {H}(\mathcal {U}_{i})$
, and
$\mathcal {H}(\mathcal {U})=\displaystyle {\bigoplus _{i\in I}}\mathcal {H}(\mathcal {U}_{i})$
, and -
(iii)
 $Ind(E^{V})=\displaystyle {\sum _{i\in I}}Ind(E^{V^{(i)}})$
.
$Ind(E^{V})=\displaystyle {\sum _{i\in I}}Ind(E^{V^{(i)}})$
.
Proof Clearly, it suffices to prove
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
. For
$(ii)$
. For
![]() $i\in I$
, let
$i\in I$
, let
![]() $\mathcal {W}_{i}:=\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}^{\Omega }_{i}}\}$
. As observed in Remark 5.1,
$\mathcal {W}_{i}:=\{\delta _{u}-\delta _{v}: {u,v\in \mathcal {U}^{\Omega }_{i}}\}$
. As observed in Remark 5.1,
![]() $\mathcal {W}_{i}$
is total in
$\mathcal {W}_{i}$
is total in
![]() $\mathcal {H}(\mathcal {U}_{i})$
for
$\mathcal {H}(\mathcal {U}_{i})$
for
![]() $i\in I$
. Using Lemma 5.2, it is routine to verify that
$i\in I$
. Using Lemma 5.2, it is routine to verify that
whenever
![]() $u_{1},v_{1}\in \mathcal {U}_{i}^{\Omega } $
and
$u_{1},v_{1}\in \mathcal {U}_{i}^{\Omega } $
and
![]() $u_{2},v_{2}\in \mathcal {U}_{j}^{\Omega }$
and
$u_{2},v_{2}\in \mathcal {U}_{j}^{\Omega }$
and
![]() $i\neq j$
. Now
$i\neq j$
. Now
![]() $(i)$
follows.
$(i)$
follows.
Consider
![]() $\mathcal {W}=\displaystyle {\bigcup _{i\in I}}~\mathcal {W}_{i}\subset \bigoplus _{i\in I}\mathcal {H}(\mathcal {U}_{i})$
. Note that if
$\mathcal {W}=\displaystyle {\bigcup _{i\in I}}~\mathcal {W}_{i}\subset \bigoplus _{i\in I}\mathcal {H}(\mathcal {U}_{i})$
. Note that if
![]() $u\in \mathcal {U}_{i}^{\Omega }$
, then
$u\in \mathcal {U}_{i}^{\Omega }$
, then
![]() $\delta _{u}-\delta _{\Omega }\in \mathcal {W}$
, where
$\delta _{u}-\delta _{\Omega }\in \mathcal {W}$
, where
![]() $\Omega $
is the vacuum unit. Let
$\Omega $
is the vacuum unit. Let
![]() $u,v \in \mathcal {U}^{\Omega }$
. Then, there exist
$u,v \in \mathcal {U}^{\Omega }$
. Then, there exist
![]() $i,j \in I$
such that
$i,j \in I$
such that
![]() $u\in \mathcal {U}_{i}^{\Omega }$
and
$u\in \mathcal {U}_{i}^{\Omega }$
and
![]() $v\in \mathcal {U}_{j}^{\Omega }$
. Then,
$v\in \mathcal {U}_{j}^{\Omega }$
. Then,
![]() $\delta _{u}-\delta _{v}=(\delta _{u}-\delta _{\Omega })+(\delta _{\Omega }-\delta _{v})$
. Consequently,
$\delta _{u}-\delta _{v}=(\delta _{u}-\delta _{\Omega })+(\delta _{\Omega }-\delta _{v})$
. Consequently,
![]() $\delta _{u}-\delta _{v}\in span (\mathcal {W})$
. Therefore,
$\delta _{u}-\delta _{v}\in span (\mathcal {W})$
. Therefore,
![]() $\mathcal {W}$
is total in
$\mathcal {W}$
is total in
![]() $\mathcal {H}(\mathcal {U})$
, and hence
$\mathcal {H}(\mathcal {U})$
, and hence
![]() $\displaystyle \mathcal {H}(\mathcal {U})=\bigoplus _{i\in I}\mathcal {H}(\mathcal {U}_{i})$
. This proves
$\displaystyle \mathcal {H}(\mathcal {U})=\bigoplus _{i\in I}\mathcal {H}(\mathcal {U}_{i})$
. This proves
![]() $(ii)$
.
$(ii)$
.
Let G denote the group of automorphisms of
![]() $E^V$
, also called the gauge group of
$E^V$
, also called the gauge group of
![]() $E^V$
. Denote the set of normalized units of
$E^V$
. Denote the set of normalized units of
![]() $E^{V}$
by
$E^{V}$
by
![]() $\mathcal {U}^{n}$
. It follows from Proposition 4.16 that the normalized units of
$\mathcal {U}^{n}$
. It follows from Proposition 4.16 that the normalized units of
![]() $E^{V}$
are of the form
$E^{V}$
are of the form
![]() $\Big \{e^{i\langle \lambda |a\rangle }e^{\frac {-||\xi _{a}||^{2}}{2}}Exp_{a}(\xi _{a})\Big \}_{a \in P}$
for some
$\Big \{e^{i\langle \lambda |a\rangle }e^{\frac {-||\xi _{a}||^{2}}{2}}Exp_{a}(\xi _{a})\Big \}_{a \in P}$
for some
![]() $\xi =\{\xi _{a}\}\in \mathcal {A}(V^{(i)})$
and
$\xi =\{\xi _{a}\}\in \mathcal {A}(V^{(i)})$
and
![]() $\lambda \in \mathbb {R}^{d}$
. For each
$\lambda \in \mathbb {R}^{d}$
. For each
![]() $i\in I$
, we denote the unitary group of
$i\in I$
, we denote the unitary group of
![]() $\mathcal {K}_{i}$
by
$\mathcal {K}_{i}$
by
![]() $U(k_{i})$
.
$U(k_{i})$
.
Proof of Theorem 1.3:
-
(1) Suppose that
 $I=\{i\}$
is singleton. Denote
$I=\{i\}$
is singleton. Denote
 $\mathcal {K}_i$
by
$\mathcal {K}_i$
by
 $\mathcal {K}$
,
$\mathcal {K}$
,
 $\lambda _i$
by
$\lambda _i$
by
 $\lambda $
and
$\lambda $
and
 $k_i$
by k. Let
$k_i$
by k. Let
 $E^{(\lambda ,k)}$
be the product system of the CAR flow associated with
$E^{(\lambda ,k)}$
be the product system of the CAR flow associated with
 $V=S^{(\lambda ,k)}$
. Since V is a pull back of the one parameter shift semigroup
$V=S^{(\lambda ,k)}$
. Since V is a pull back of the one parameter shift semigroup
 $\{S_t \otimes 1\}$
on
$\{S_t \otimes 1\}$
on
 $L^2[0,\infty ) \otimes \mathcal {K}$
by the homomorphism
$L^2[0,\infty ) \otimes \mathcal {K}$
by the homomorphism
 $P \ni a \to \langle \lambda |a \rangle \in \mathbb {C}$
, and since the product systems of CAR and CCR flows associated with the one-parameter shift semigroup
$P \ni a \to \langle \lambda |a \rangle \in \mathbb {C}$
, and since the product systems of CAR and CCR flows associated with the one-parameter shift semigroup
 $\{S_t \otimes 1\}_{t \geq 0}$
are isomorphic,
$\{S_t \otimes 1\}_{t \geq 0}$
are isomorphic,
 $E^{(\lambda ,k)}$
is isomorphic to the product system
$E^{(\lambda ,k)}$
is isomorphic to the product system
 $F^{(\lambda ,k)}$
of the CCR flow associated with V. In fact, the map
$F^{(\lambda ,k)}$
of the CCR flow associated with V. In fact, the map
 $T=\{T_{a}\}_{a\in P}:E^{(\lambda , k)}\to F^{(\lambda , k)}$
defined by for
$T=\{T_{a}\}_{a\in P}:E^{(\lambda , k)}\to F^{(\lambda , k)}$
defined by for $$\begin{align*}T_{a}( Exp_{a}(\xi))= e(\xi), \end{align*}$$
$$\begin{align*}T_{a}( Exp_{a}(\xi))= e(\xi), \end{align*}$$
 $\xi \in Ker(V_{a}^{*})$
and
$\xi \in Ker(V_{a}^{*})$
and
 $a\in P$
is an isomorphism. Hence, G is isomorphic to the automorphism group of
$a\in P$
is an isomorphism. Hence, G is isomorphic to the automorphism group of
 $F^{(\lambda ,k)}$
. Since the automorphism group of a CCR flow acts transitively on the set of normalized units, the conclusion follows. The fact that the gauge group of a CCR flow acts transitively on the set of normalized units can been seen from the explicit description of units and the gauge group obtained in [Reference Arjunan, Srinivasan and Sundar2, Theorems 5.1 and 7.3].
$F^{(\lambda ,k)}$
. Since the automorphism group of a CCR flow acts transitively on the set of normalized units, the conclusion follows. The fact that the gauge group of a CCR flow acts transitively on the set of normalized units can been seen from the explicit description of units and the gauge group obtained in [Reference Arjunan, Srinivasan and Sundar2, Theorems 5.1 and 7.3].
Since
 $E^{(\lambda ,k)}$
and
$E^{(\lambda ,k)}$
and
 $F^{(\lambda ,k)}$
are isomorphic, they have the same index. But, by [Reference Sarkar and Sundar24, Proposition 2.7],
$F^{(\lambda ,k)}$
are isomorphic, they have the same index. But, by [Reference Sarkar and Sundar24, Proposition 2.7],  $$\begin{align*}Ind(F^{(\lambda,k)})=\dim \mathcal{A}(S^{(\lambda,k)}).\end{align*}$$
$$\begin{align*}Ind(F^{(\lambda,k)})=\dim \mathcal{A}(S^{(\lambda,k)}).\end{align*}$$
Note that for every
 $\eta \in \mathcal {K}$
,
$\eta \in \mathcal {K}$
,
 $\{1_{(0,\langle \lambda |a \rangle )} \otimes \eta \}_{a \in P}$
is an additive cocycle for
$\{1_{(0,\langle \lambda |a \rangle )} \otimes \eta \}_{a \in P}$
is an additive cocycle for
 $S^{(\lambda ,k)}$
, and it is not difficult to see that every additive cocycle is of this form. Thus,
$S^{(\lambda ,k)}$
, and it is not difficult to see that every additive cocycle is of this form. Thus,  $$\begin{align*}Ind(E^{(\lambda,k)})=Ind(F^{(\lambda,k)})=\dim \mathcal{K}=k.\end{align*}$$
$$\begin{align*}Ind(E^{(\lambda,k)})=Ind(F^{(\lambda,k)})=\dim \mathcal{K}=k.\end{align*}$$
-
(2) Next assume that I has at least two elements. It is clear from Proposition 5.3 and
 $(1)$
that
$(1)$
that  $$\begin{align*}Ind(E^V)=\sum_{i \in I}k_i.\end{align*}$$
$$\begin{align*}Ind(E^V)=\sum_{i \in I}k_i.\end{align*}$$
Let
 $\Psi =\{\Psi _a\}_{a \in P} \in G$
be given. For
$\Psi =\{\Psi _a\}_{a \in P} \in G$
be given. For
 $a\in P$
, consider the one-parameter product system
$a\in P$
, consider the one-parameter product system
 $E_{a}=\{E(ta)\}_{t\geq 0}$
. By Lemma 3.2, there exists a unitary
$E_{a}=\{E(ta)\}_{t\geq 0}$
. By Lemma 3.2, there exists a unitary
 $U_{a} \in \{V_{ta}, V_{ta}^{*}: { t\geq 0}\}^{'}$
, an additive cocycle
$U_{a} \in \{V_{ta}, V_{ta}^{*}: { t\geq 0}\}^{'}$
, an additive cocycle
 $\xi ^{a}=\{\xi ^{a}_{t}\}_{t\geq 0}$
and
$\xi ^{a}=\{\xi ^{a}_{t}\}_{t\geq 0}$
and
 $\mu _{a}\in \mathbb {R}^{d}$
such that for
$\mu _{a}\in \mathbb {R}^{d}$
such that for $$\begin{align*}\Psi_{ta}Exp_{a}(\eta)=e^{i\mu_{a}t}e^{-\frac{||\xi^{a}_{t}||^{2}}{2}-\langle U_{a}\eta|\xi^{a}_{t}\rangle}Exp_{a}(U_{a}\eta+\xi^{a}_{t})\end{align*}$$
$$\begin{align*}\Psi_{ta}Exp_{a}(\eta)=e^{i\mu_{a}t}e^{-\frac{||\xi^{a}_{t}||^{2}}{2}-\langle U_{a}\eta|\xi^{a}_{t}\rangle}Exp_{a}(U_{a}\eta+\xi^{a}_{t})\end{align*}$$
 $\eta \in Ker(V_{ta}^{*})$
. Proceeding as in the proof of Theorem 3.3, we see that there exists
$\eta \in Ker(V_{ta}^{*})$
. Proceeding as in the proof of Theorem 3.3, we see that there exists
 $\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
, a unitary
$\xi =\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V)$
, a unitary
 $U\in \{V_{a}, V_{a}^{*}: { a\in P}\}^{'}$
and
$U\in \{V_{a}, V_{a}^{*}: { a\in P}\}^{'}$
and
 $\mu \in \mathbb {R}^{d}$
such that (5.1)for
$\mu \in \mathbb {R}^{d}$
such that (5.1)for $$ \begin{align}\Psi_{a}Exp_{a}(\eta)=e^{i\langle\mu|a\rangle}e^{-\frac{||\xi_{a}||^{2}}{2}-\langle U\eta|\xi_{a}\rangle}Exp_{a}(U\eta+\xi_{a})\end{align} $$
$$ \begin{align}\Psi_{a}Exp_{a}(\eta)=e^{i\langle\mu|a\rangle}e^{-\frac{||\xi_{a}||^{2}}{2}-\langle U\eta|\xi_{a}\rangle}Exp_{a}(U\eta+\xi_{a})\end{align} $$
 $\eta \in Ker(V_{a}^{*})$
and
$\eta \in Ker(V_{a}^{*})$
and
 $a\in P$
.
$a\in P$
.
Assume that the additive cocycle
 $\{\xi _{a}\}_{a\in P}$
is non-zero. Note that
$\{\xi _{a}\}_{a\in P}$
is non-zero. Note that
 $\{\Psi _{a}Exp_{a}(0)\}_{a\in P}$
is a unit of
$\{\Psi _{a}Exp_{a}(0)\}_{a\in P}$
is a unit of
 $E^{V}$
. Hence,
$E^{V}$
. Hence,
 $\{Exp_{a}(\xi _{a})\}_{a\in P}$
is a unit for
$\{Exp_{a}(\xi _{a})\}_{a\in P}$
is a unit for
 $E^{V}$
(the map
$E^{V}$
(the map
 $P \ni a \to \langle \xi _a|\eta _a \rangle \in \mathbb {C}$
is additive if
$P \ni a \to \langle \xi _a|\eta _a \rangle \in \mathbb {C}$
is additive if
 $\xi ,\eta \in \mathcal {A}(V)$
). By Proposition 4.16, there exists
$\xi ,\eta \in \mathcal {A}(V)$
). By Proposition 4.16, there exists
 $i\in I$
such that
$i\in I$
such that
 $\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
. Let
$\{\xi _{a}\}_{a\in P}\in \mathcal {A}(V^{(i)})$
. Let
 $j\in I$
,
$j\in I$
,
 $j\neq i$
. Let
$j\neq i$
. Let
 $\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(j)})$
be non-zero. By Proposition 4.16,
$\{\eta _{a}\}_{a\in P}\in \mathcal {A}(V^{(j)})$
be non-zero. By Proposition 4.16,
 $\{Exp_{a}(\eta _{a})\}_{a\in P}$
is a unit for
$\{Exp_{a}(\eta _{a})\}_{a\in P}$
is a unit for
 $E^{V}$
. Therefore,
$E^{V}$
. Therefore,
 $\{\Psi _{a}Exp_{a}(\eta _{a})\}_{a\in P}$
is a unit for
$\{\Psi _{a}Exp_{a}(\eta _{a})\}_{a\in P}$
is a unit for
 $E^{V}$
. (5.1) implies that
$E^{V}$
. (5.1) implies that
 $\{Exp_{a}(U\eta _{a}+\xi _{a})\}_{a\in P}$
is a unit for
$\{Exp_{a}(U\eta _{a}+\xi _{a})\}_{a\in P}$
is a unit for
 $E^{V}$
. Note that since
$E^{V}$
. Note that since
 $U\in \{V_{a},V_{a}^{*}: { a\in P}\}^{'}$
, U is a diagonal operator, i.e., there exists a unitary operator
$U\in \{V_{a},V_{a}^{*}: { a\in P}\}^{'}$
, U is a diagonal operator, i.e., there exists a unitary operator
 $U_{i}\in \{V^{(i)}_{ta},V^{(i)*}_{ta}: {t\geq 0}\}^{'}$
such that
$U_{i}\in \{V^{(i)}_{ta},V^{(i)*}_{ta}: {t\geq 0}\}^{'}$
such that
 $U|_{\mathcal {H}_{i}}=U_{i}$
for
$U|_{\mathcal {H}_{i}}=U_{i}$
for
 $i\in I$
. Therefore,
$i\in I$
. Therefore,
 $U\eta _{a}\in Ker(V^{(j)*}_{a})$
for
$U\eta _{a}\in Ker(V^{(j)*}_{a})$
for
 $a\in P$
. Hence,
$a\in P$
. Hence,
 $\{U\eta _{a}+\xi _{a}\}_{a\in P}\not \in \mathcal {A}(V^{(\ell )})$
for any
$\{U\eta _{a}+\xi _{a}\}_{a\in P}\not \in \mathcal {A}(V^{(\ell )})$
for any
 $\ell \in I$
, contradicting Proposition4.16. As a consequence,
$\ell \in I$
, contradicting Proposition4.16. As a consequence,
 $\xi _{a}=0$
for
$\xi _{a}=0$
for
 $a\in P$
. Therefore, for
$a\in P$
. Therefore, for $$\begin{align*}\Psi_{a}Exp_{a}(\xi)=e^{i\langle\mu |a\rangle}Exp_{a}(U\xi)\end{align*}$$
$$\begin{align*}\Psi_{a}Exp_{a}(\xi)=e^{i\langle\mu |a\rangle}Exp_{a}(U\xi)\end{align*}$$
 $\xi \in Ker(V_{a}^{*})$
and
$\xi \in Ker(V_{a}^{*})$
and
 $a\in P$
.
$a\in P$
.
Suppose
 $\mu \in \mathbb {R}^{d}$
and
$\mu \in \mathbb {R}^{d}$
and
 $U\in \{V_{a},V_{a}^{*}: {a\in P}\}^{'}$
. Then, there exists
$U\in \{V_{a},V_{a}^{*}: {a\in P}\}^{'}$
. Then, there exists
 $\Psi ^{(\mu ,U)} \in G$
such that for
$\Psi ^{(\mu ,U)} \in G$
such that for $$\begin{align*}\Psi^{(\mu ,U)}_{a}Exp_{a}(\xi)=e^{i\langle\mu |a\rangle}Exp_{a}(U\xi)\end{align*}$$
$$\begin{align*}\Psi^{(\mu ,U)}_{a}Exp_{a}(\xi)=e^{i\langle\mu |a\rangle}Exp_{a}(U\xi)\end{align*}$$
 $\xi \in Ker(V_{a}^{*})$
and
$\xi \in Ker(V_{a}^{*})$
and
 $a\in P$
. Note that
$a\in P$
. Note that
 $\Psi \in G$
because
$\Psi \in G$
because
 $\Psi _a=e^{i \langle \mu |a \rangle }\Gamma (U)$
for
$\Psi _a=e^{i \langle \mu |a \rangle }\Gamma (U)$
for
 $a \in P$
, where
$a \in P$
, where
 $\Gamma (U)$
is the second quantisation map.
$\Gamma (U)$
is the second quantisation map.
Let
 $M:=\{V_a,V_a^*:a \in P\}^{'}$
and denote the unitary group of M by
$M:=\{V_a,V_a^*:a \in P\}^{'}$
and denote the unitary group of M by
 $\mathcal {U}(M)$
. By Remark 4.14, we have
$\mathcal {U}(M)$
. By Remark 4.14, we have
 $\mathcal {U}(M)=\displaystyle \prod _{i \in I}U(k_i)$
. We have shown that the map is an isomorphism of groups. Hence, if
$\mathcal {U}(M)=\displaystyle \prod _{i \in I}U(k_i)$
. We have shown that the map is an isomorphism of groups. Hence, if $$\begin{align*}\mathbb{R}^d \times \mathcal{U}(M) \ni (\mu ,U) \to \Psi^{(\mu ,U)} \in G \end{align*}$$
$$\begin{align*}\mathbb{R}^d \times \mathcal{U}(M) \ni (\mu ,U) \to \Psi^{(\mu ,U)} \in G \end{align*}$$
 $\Psi $
is an automorphism of
$\Psi $
is an automorphism of
 $E^{V}$
, then for
$E^{V}$
, then for
 $a \in P$
, (5.2)for some
$a \in P$
, (5.2)for some $$ \begin{align} \Psi_a \Omega_a=\Psi_{a}Exp_{a}(0)=e^{i\langle \mu |a\rangle}Exp_{a}(0)=e^{i\langle \mu |a \rangle}\Omega_a \end{align} $$
$$ \begin{align} \Psi_a \Omega_a=\Psi_{a}Exp_{a}(0)=e^{i\langle \mu |a\rangle}Exp_{a}(0)=e^{i\langle \mu |a \rangle}\Omega_a \end{align} $$
 $\mu \in \mathbb {R}^{d}$
. Let
$\mu \in \mathbb {R}^{d}$
. Let
 $\eta =\{\eta _{a}\}_{a\in P}$
be a non-zero additive cocycle such that
$\eta =\{\eta _{a}\}_{a\in P}$
be a non-zero additive cocycle such that
 $Exp(\eta )$
is a unit. Then,
$Exp(\eta )$
is a unit. Then,
 $u=\{u_{a}\}_{a\in P}$
given by
$u=\{u_{a}\}_{a\in P}$
given by
 $u_{a}= e^{-\frac {||\eta _{a}||^{2}}{2}}Exp(\eta _{a})$
is a normalized unit, but, by (5.2),
$u_{a}= e^{-\frac {||\eta _{a}||^{2}}{2}}Exp(\eta _{a})$
is a normalized unit, but, by (5.2),
 $\Psi .\Omega \neq u$
for every
$\Psi .\Omega \neq u$
for every
 $\Psi \in G$
. Hence, the action of G on
$\Psi \in G$
. Hence, the action of G on
 $\mathcal {U}^{n}$
is not transitive.
$\mathcal {U}^{n}$
is not transitive.
Remark 5.4 Suppose
![]() $d \geq 2$
. Then,
$d \geq 2$
. Then,
![]() $S(P^*)$
is uncountable. This is because, as P is pointed,
$S(P^*)$
is uncountable. This is because, as P is pointed,
![]() $P^*$
spans
$P^*$
spans
![]() $\mathbb {R}^d$
. It follows from Theorems 1.3 and 1.2 that there are uncountably many CAR flows that are type I and for which the action of the gauge group on the set of normalized units is not transitive.
$\mathbb {R}^d$
. It follows from Theorems 1.3 and 1.2 that there are uncountably many CAR flows that are type I and for which the action of the gauge group on the set of normalized units is not transitive.
Remark 5.5 It is immediate from Theorems 1.2 and 1.3 that if V is an isometric representation with commuting range projections such that
![]() $E^V$
is type I and has index one, then V is unitarily equivalent to
$E^V$
is type I and has index one, then V is unitarily equivalent to
![]() $S^\lambda $
for some
$S^\lambda $
for some
![]() $\lambda \in S(P^*)$
, i.e.,
$\lambda \in S(P^*)$
, i.e.,
![]() $E^V$
is “a pullback” of a one parameter CAR flow. The analogous statement for
$E^V$
is “a pullback” of a one parameter CAR flow. The analogous statement for
![]() $F^V$
, the product system of the CCR flow associated with V, is not true (see [Reference Sarkar and Sundar24]).
$F^V$
, the product system of the CCR flow associated with V, is not true (see [Reference Sarkar and Sundar24]).
Question Is it possible to construct an isometric representation V of P such that
![]() $E^V$
is type I, has index one, but V is not unitarily equivalent to
$E^V$
is type I, has index one, but V is not unitarily equivalent to
![]() $S^\lambda $
for any
$S^\lambda $
for any
![]() $\lambda \in S(P^*)$
?
$\lambda \in S(P^*)$
?