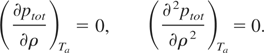2. BRIEF REVIEW OF EARLIER WORK

Starting with Van der Waal's theory (Novikov, 1965) of inpenetrable hard spheres (HS), with a weak long ranged attractive tail, various models have been used up to now to estimate the critical constants of liquid metals. Though the liquid-vapor co-existence curves for metals are nearly quadratic like that of the Van der Waals gas, the theoretical critical compressibility ratio (0.375) differs from experimental values found between 0.2–0.4. As a first step toward improving the Van der Waal's model, Young and Alder (1971) replaced its repulsive component of pressure by a more accurate formula for HS pressure (Carnahan & Starling, 1969). The HS pressure is derived by using the Percus–Yevic theory of dense fluids. The improved model provides critical temperature of alkali metals in agreement with other experiments, but is unable to predict accurate values for the critical volume and pressure.

It was realized that the impenetrable HS theory can not be used for liquid metals, which are known to be compressible. Moreover, the large number of free electrons present in a metal, and the configuration of ions have to be taken into account in the EOS. Young (1977) then replaced the HS model by the so called soft sphere (SS) model introduced by Hoover et al. (1975). This model is based on computer calculations for the “effective” free energy of particles in the fluid. The modified SS pressure and energy, in standard notation is given by Young (1977):

and

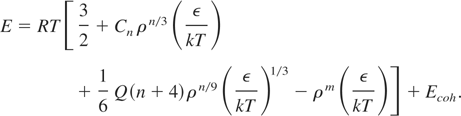
In the above, C_n ρ^n/3 represents the static lattice energy term with C_n as the face-centered-cubic (FCC) Medulung constant, and

. The first term of Eq. (1) refers to the thermal pressure of the ions in the ideal gas approximation. Pressure generated due to thermal excitation of electrons is described by the third term. The second and fourth terms jointly describe the “cold pressure,” with ρ^n/3 and ρ^m dependence arising from repulsion and attraction between neighboring ions. Eq. (2) for energy also has similar interpretation. By adjusting five parameters (ε, σ, n, m, and Q), Young (1977) then obtained the total energy and pressure of a liquid metal at any density and temperature. The critical constants of this model show significant improvements over the HS model. However, there are still discrepancies between SS estimates and the experimental values (Young, 1977). The reason for this discrepancy has not been explained, one possible reason could be that the thermal pressure due to the large number of free electrons needs some further refinements. Also, at this temperature the ions do not really behave like an ideal gas.

3. GLOBAL EOS MODEL

In order to construct a more general and thermodynamically complete multi-phase wide range EOS model, like QEOS, one defines the thermodynamic free energy as:

which consists of elastic contribution at zero temperature (F_cold), and the thermal contributions by ions (F_i) and electrons (F_e). The global QEOS uses this additivity property of free energy. The electronic contributions in this model has been adopted from Thomas–Fermi (TF) statistical model of Feynman et al. (1949). However, for density (ρ) greater than solid density (ρ_s), TF contribution to F_cold is supplemented by a semi-empirical bonding correction, originally proposed by Barnes (1967). The ion EOS of this global model combines Debye, Gruneisen, and liquid scaling laws based on the work of Cowan (More et al., 1988). For density lower than solid density, F_cold is taken as the zero temperature TF energy. As discussed by More et al. (1988), this model leads to over-estimation of the critical pressure and temperature. Also, for some of the materials, the QEOS estimates for the cohesive energy are negative, leading to disappearance of the liquid-vapor region itself, which is totally unphysical.

The problem of over estimation of critical temperature and pressure in the original QEOS model has been addressed by Young and Corey (1995). They replaced the TF cold curve for low density region, ρ < ρ_s, with Lennard–Jones type of soft sphere function. According to this model, the cold energy for ρ < ρ_s is given by:

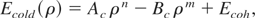
where E_coh is the experimental cohesive energy. The coefficients A_c and B_c are estimated by setting the energy and pressure values at standard condition. The exponents m and n are adjustable parameters. The results of this model for critical temperature and pressure are not in very good agreement with experimentally known values for metals (Young & Corey, 1995). Morever, difficulties arise when one tries to reproduce the critical isotherm for any metal using the reported values of m and n. It is also reported (Young & Corey, 1995) that this model is not able to verify the liquid-gas co-existence region with the experimental isobaric expansion data (Gathers, 1986) for most of the metals.

One of the main aims of the present work is to show that, for obtaining the correct set of critical constants and liquid-gas phase boundary, it is necessary to model the electron and the ion thermal pressure more appropriately.

4. PROPOSED SCHEME

Following the QEOS approach, we have constructed a global theoretical EOS model assuming the additivity of electron, and ion free energies for all temperature and density. Accordingly, we express the total energy for ρ < ρ_s as:

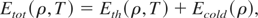
where

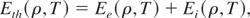
is the thermal energy of the electrons and ions, and E_cold is the cold energy. The total pressure defined as:

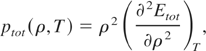
assumes the form:

where p_cold refers to the cold pressure. p_th is the thermal pressure arising due to electrons and ions, that is,

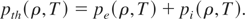
In this paper, we are proposing a scheme for determining the EOS of metals in the liquid-vapor region, that compares the experimental results. The new scheme is based on the use of more experimental data for physical and thermodynamic parameters, like melting temperature, electron specific heat, etc. We also propose a simple approach for finding the parameters of SS function defining the cold part. In the following subsections, we discuss the improvements in electron and ion contribution to EOS, and cold part separately.

4.1. Ion EOS

The ion thermal pressure in the QEOS model has been estimated by the structural and phenomenological models of Cowan. We also treat the ion contribution to EOS by Cowan's model, however, with some modifications. Depending on the temperature of interest, Cowan's model treats ions in three distinct phases, namely, the low-temperature solid phase, followed by high temperature solid, and finally fluid phase. The fluid phase is reached when temperature is greater than the melting temperature of the solid. Since we are interested in the liquid-vapor phase transition region, we will consider the fluid region only, that is T > T_m. Following More et al. (1988), we express the energy and the pressure of the ions in this region as:

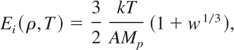
where, w = T_m(ρ)/T and γ_F are the fluid phase. Gruneisen (1912) parameter, which depends on density through the relation

From Eqs. (10) and (11), it can be easily seen that for very high temperature, T >> T_m, or w << 1, ion internal energy and pressure reduce to the ideal gas expressions, that is,

As the temperature at which the liquid-gas phase transition takes place is much higher than the melting temperature of metals, the ideal gas treatment of Young (1977) in the SS model was not in serious error. But this is not true in general.

We modify the ion model with the observation by More et al. (1988) that there are important differences between Cowan model melting temperatures with the corresponding experimental values for transition metals, even at normal density ρ_s. This resulted in over-estimation of the critical pressure in QEOS. To that end, we normalized Cowan's melting temperature at ρ_s with the corresponding experimental value, and express it as:

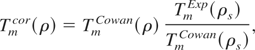
where T_m^cor refers to the corrected melting temperature. It can be easily shown from Eq. (12) that the fluid phase Gruneisen (1912) parameter, remains unaltered with this correction. We find that this correction improves the critical pressure for transition metals significantly.

4.2. Electron EOS

In all the global models, including QEOS, the electron contribution has been treated by the TF theory. However, we know that the TF theory gives an accurate representation of the free electron pressure for temperatures above ∼10 eV. The largest inaccuracy in the TF electron pressure occurs near the solid density and T = 0. Since the critical temperature for most of the elements are less than 2 eV, the TF theory is not a very good candidate for treating the liquid-gas region. Therefore, electron thermal pressure, in the region ρ < ρ_s, needs adjustment with some experimental data .

In our model, we use McCloskey's (1964) semi-empirical formula for estimating the contribution to pressure from thermal excitation of electrons. Therefore, the thermal energy and pressure at any temperature are given by

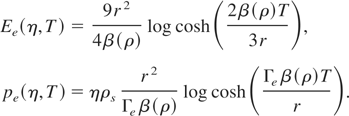
In these equations, T is in eV, Z is the atomic number of the element, η = ρ/ρ_s and β(ρ) is the coefficient of electronic specific heat. The following fitting formulas are used for other parameters in Eq. (15):

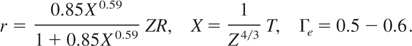
Note that for very high temperature, the energy and the pressure relations given in (15) reduce to that of ideal electron gas, that is,

On the other hand, for very low temperature, the electron EOS given in (15) reduces to that of a degenerate electron gas

Thus, McCloskey's (1964) formula interpolates the electron EOS at any temperature appropriately. The coefficient of electronic specific heat β(ρ) depends on the density by the relation

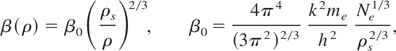
where, N_e is the number of free electrons per unit mass, and β₀ is the theoretical estimate for β(ρ_s). It is known that the experimental values of β₀ differ from this estimate for most metals (Kittel, 1971).

On expanding the TF expression for electron energy at very low temperature and keeping the terms up to T² one obtains Eq. (18), with the theoretical β₀. Even if one replaces this theoretical estimate of β₀ with its experimental value, the question whether the temperature is sufficiently low for such expansion remains debatable. Both the facts cause TF theory to estimate the electron pressure incorrectly. In this regard, McCloskey (1964) formula seems to be a better choice, as it finds the energy and pressure for any temperature by using proper fitting constants. We therefore used McCloskey's formula together with the measured value of β₀. This approach provides the correct electron pressure and energy upto about two to three times the critical temperature. Above this temperature, the TF theory is appropriate.

4.3. Cold Curve

Following Al'tshuler et al. (1980), we express the cold energy as:

where E_coh is the experimental cohesive energy and ρ_r = ρ/ρ_s. Hence, the cold pressure is

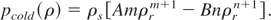
The parameters A and B are obtained by the requirements that the total energy and pressure vanishes at ρ = ρ_s and T = 0. Thus we get

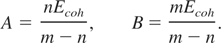
With the help of Eq. (22), we can now rewrite the expression for the cold energy and pressure as:

and

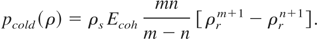
Thus, the total pressure of Eq. (8) reduces to

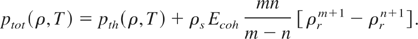
Using the expressions for thermal pressure of ions (Eq. (11)) and electrons (Eq. (15)), we obtain

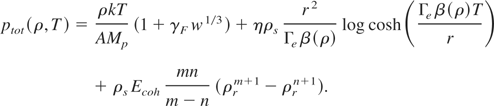
In next section, we present our approach for finding the exponents m and n.

5. FINDING CRITICAL CONSTANTS

Our formulation for total pressure can now be used to determine the critical constants for metals. Instead of adjusting the parameters m and n arbitrarily, we find them explicitly using a set of experimental values for certain thermodynamic variables. First, we match the bulk modulus calculated by using Eq. (26) with it's experimental value, B₀, at solid density ρ_s, that is,

Since the thermal contribution to pressure p_th is zero at T = 0 and ρ = ρ_s, Eqs. (26) and (27) give

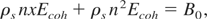
where we have introduced a new variable x defined as:

Eq. (28) is rewritten as:

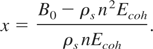
From the definition of cold pressure, it is evident that m and n are both positive and m > n. Hence, x is also positive. The positivity of x demands that n is bounded above by:

Next we follow the steps outlined below:

1. Choose the experimental value of B₀ at ρ = ρ_s.
2. Estimate critical temperature T_c either by the Partington (1949) formula or Jing's modification (1984), wherein it is shown that the critical temperature is related to the sum of melting and boiling temperatures. Now, choose a temperature T_a close to this estimate.
3. Choose a value of n much smaller than y₀.
4. Find x and hence, m using Eqs. (30) and (29), and use Eq. (26) to get total pressure at the chosen temperature T_a.
5. As we know that the first and second derivatives of total pressure vanish at T_c, determine densities ρ₁ and ρ₂ using the relations:
   

1. If ρ₁ and ρ₂ are equal to the required accuracy, then accept this density as the critical density, that is, ρ_c = ρ₁ = ρ₂. Thus the chosen temperature is nothing but the critical temperature, T_c = T_a. Finally the critical pressure is p_c = p_tot(ρ_c,T_c).
2. If ρ₁ and ρ₂ are not the same, increase the value of n by a small amount and repeat from step 3.
3. If necessary, repeat the procedure from step 2 by increasing T_a until the correct set of exponents (m and n) are obtained for which ρ₁ and ρ₂ are the same.
4. If the above steps are not successful then change the value of B₀ and follow the steps 2–8. We find that the value of B₀ that staisfies the condition given in step 5 happens for less than its experimental value at ρ_s. This is due to the fact that slopes of the pressure-density curve at two sides of the solid density are slightly different. The value of B₀ is further tuned so as to match other experimental results described in the next section.

We have applied the above described approach to predict the critical constants for all metals. Table 1 presents the values of the Lennard–Jones exponent m and n, and the parameters of critical points for 10 metals obtained by our method, along with other theoretical estimates and experimental results, if available. For most of the metals, our estimates of critical temperature are lower than the hard-sphere model of Young and Alder (1971) and higher than the soft-sphere model (Young, 1977).

Estimations of Lennard–Jones and critical parameters for metals

For Mercury, our estimate of all the four parameters including the critical compressibility ratio, Z_c = p_c /Rρ_cT_c, are very close to experimental values. However, our predicted value of p_c for Lead is higher than other evaluation, leading to larger Z_c.

6. VALIDATION OF THE PROPOSED MODEL

For validating our model, we first compared the predicted and experimental data for the critical isotherm of Mercury (Young & Alder, 1971). Figure 1 shows the density dependence of pressure (both normalized to their respective critical values) for temperatures T = 1.01 T_c and T = 1.13 T_c, with solid lines corresponding to our results and points refering to experimental values. The agreement is quite satisfactory.

Comparison of experimental isotherm with our model for Mercury.

6.1. Isobaric Expansion

The thermodynamic properties of a metallic liquid are studied either by density measurements at normal pressure (Lang, 1995), or by isobaric expansion techniques (Gathers, 1986). In the second technique, the metal is rapidly heated by a powerful pulse of current and then allowed to expand in an atmosphere of an inert gas maintaining a prescribed constant pressure P_IEX. The density, enthalpy at melting and the sound velocity are then measured at different temperatures. On extrapolation, these data embraces the critical density ρ_c. In order to compare these liquid metal expansion data, we determine the densities ρ_i and the corresponding temperatures T_i for which the total pressure given in (26) is equal to P_IEX, by an interpolation method.

In Figure 2 we show comparisons for Aluminum, Tantalum, and Lead, with solid lines and points refering to our calculation and measured data, respectively.

The comparison of isobaric expansion data. Density versus temperature for (a) Aluminum, (b) Tantalum, and (c) Lead. The experimental values are shown by points whereas lines refer to our model result.

Next, we find the total energy for the above values of density and temperature, that is, E_i = E_tot(ρ_i,T_i) and then calculate the enthalpy as H_i = E_tot(ρ_i,T_i) + P_IEX /ρ_i. We show the experimental and calculated values of enthalpy for Aluminum, Tantalum, and Lead in Figure 3. It is clear from these figures that the enthalpy data agrees quite well for all the elements. The experimental data used are taken from Gathers (1983a, 1983b) and Shaner et al. (1977).

Comparison of isobaric expansion data. Enthalpy versus temperature for (a) Aluminum, (b) Tantalum, and (c) Lead. The experimental values are shown by points whereas lines refer to our model result.

6.2. Release Isentrope

The study of release isentrope of strongly compressed materials provide another way to characterize the liquid-vapor phase region. Release isentrope experiments to cover the complete liquid-vapor region uses porous materials (Al'tshuler et al., 1980), which has not been incorporated in the present model. However, for the normal metals, the release isentrope usually corresponds to the solid and partially melted regions, which has been tested by our model.

The experimental data on release isentropes of shocked solids, in the form of unloading pressure versus free-surface velocity, give indirect information about the phases of the material it passes through while shock unloading. A released isentrope corresponds to specific values of initial shock pressure P = P_ri and particle velocity U_p = U_ri. As the shock unloads at a free-surface, pressure decreases to zero and free-surface velocity increases to two times U_ri. This increase is due to the isentropic conversion of internal energy to kinetic energy.

Starting with given P = P_ri and U_p = U_ri, we used the following Hugoniot relations

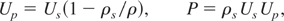
to obtain the initial shock speed U_s, and the compressed solid density, ρ_ri as:

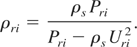
From our model, we also find the entropy S_ri of the compressed state corresponding to ρ_ri and P_ri. This entropy identifies the unloading isentrope.

We then use the Riemann invariant condition to estimate the isentropic flow, that is,

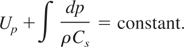
where

refers to the isentropic sound speed. The free-surface velocity, U₂ corresponding to any lower pressure P₂ is then obtained as:

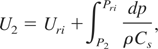
which can also be expressed as:

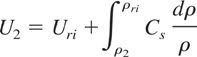
For ρ₂ very close to ρ_ri, this can be approximated as:

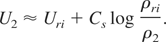
where we have approximated C_s inside the integral with C_s(ρ_ri).

Using an interpolation method, we first generate the isentrope corresponding to S_ri. Then eq. (38) is applied successively, by replacing U_ri and ρ_ri with U₂ and ρ₂ respectively. Thus we generate the free-surface velocity vs pressure curve along the isentrope. In Figure 4 we show the experimental (points) and calculated (lines) results for Copper and Molybdenum. The experimental results are taken from (Zhernokletov et al., 1984; Zhernokletov et al., 1995). The good agreement observed in these figure validates our model further.

Comparison of isentropic expansion data. The pressure versus free-surface velocity for (a) Copper and (b) Molybdenum. The lines correspond to our model and points refer to experimental data.