2.1 Limit of strong magnetic field

All of the applications of Braginskii MHD cited in the introduction are in the strong-field regime $(x_{i}\gg 1)$ . By considering (2.8)–(2.9), it is clear that in the strong-field limit, the parallel viscosity dominates and the viscous stress tensor can be simplified to

In the solar corona, it is also the case that $x_{i}\gg 1$ . For example, consider a relatively weak coronal field of 10 G. Then it can be shown that $x_{i}\sim 10^{5}$ (Hollweg Reference Hollweg1986). Hence, equation (2.12) would apply throughout most of the corona.

Hollweg (Reference Hollweg1985) gives a physical interpretation of (2.12) as being due to small pressure anisotropies that develop as the flows evolve. He shows that (2.12) can be derived from assuming a diagonal pressure tensor and equations analogous to the double adiabatic equations (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956). Hollweg (Reference Hollweg1986) extends the analysis of (2.12) to include the effects of resistivity. In doing this, he notes that the use of (2.12) would not be suitable for reconnection-type flows, like those described in Sonnerup & Priest (Reference Sonnerup and Priest1975). Such flows involve the compression of the magnetic field to null points.

Compared to coronal models that use only isotropic viscosity, those with Braginskii viscosity are in the minority. Many of the earlier studies of Braginskii MHD in the corona are in the strong-field limit (e.g. van der Linden, Goossens & Hood Reference van der Linden, Goossens and Hood1988; Hood, van der Linden & Goossens Reference Hood, van der Linden and Goossens1989; Ofman, Davila & Steinolfson Reference Ofman, Davila and Steinolfson1994; Ruderman et al. Reference Ruderman, Verwichte, Erdélyi and Goossens1996). Several recent works study two-dimensional null point reconnection in the incompressible regime (Craig Reference Craig2010; Craig & Litvinenko Reference Craig and Litvinenko2010; Armstrong, Craig & Litvinenko Reference Armstrong, Craig and Litvinenko2011; Armstrong & Craig Reference Armstrong and Craig2013, Reference Armstrong and Craig2014). To deal with the concerns mentioned above, they interpolate between (2.12) when the field is strong and the standard expression for isotropic viscosity at null points. We shall now consider Braginskii viscosity in the limit $|\boldsymbol{B}|\rightarrow 0$ .

2.2 Limit of weak magnetic field

The Braginskii tensors, as written in (2.2)–(2.4), are not in a suitable form for studying how the viscosity behaves in the limit $|\boldsymbol{B}|\rightarrow 0$ . For example, let us momentarily consider only the parallel viscosity given by (2.12). Since the unit vector $\boldsymbol{b}$ is not defined when $|\boldsymbol{B}|=0$ , we would require that $\unicode[STIX]{x1D702}_{0}/|\boldsymbol{B}|^{4}\rightarrow l\in \mathbb{R}$ as $|\boldsymbol{B}|\rightarrow 0$ . However, since the parallel viscosity coefficient $\unicode[STIX]{x1D702}_{0}$ is constant, $\unicode[STIX]{x1D702}_{0}/|\boldsymbol{B}|^{4}$ is singular at null points. This means that, as we shall demonstrate shortly, we require combinations of $\{\unicode[STIX]{x1D652}^{(0)},\unicode[STIX]{x1D652}^{(1)},\unicode[STIX]{x1D652}^{(2)}\}$ in order to correctly describe Braginskii’s model in the limit $|\boldsymbol{B}|\rightarrow 0$ . Before doing this, and in order to make the analysis clearer, we relabel the numerical values in the viscosity coefficients (2.8) and write

We also write $x_{i}=\unicode[STIX]{x1D6FC}|\boldsymbol{B}|$ , with $\unicode[STIX]{x1D6FC}=|e|\unicode[STIX]{x1D70F}_{i}/m_{i}$ . Therefore, the viscosity coefficients (2.13) can be written as

From expressions (2.14), we deduce that as $|\boldsymbol{B}|\rightarrow 0$ ,

Simplifying and rearranging (2.1)–(2.4) gives

For (2.17) to be well defined at null points, we require

as $|\boldsymbol{B}|\rightarrow 0$ . By virtue of expressions (2.15) and (2.16), it is clear that the asymptotic requirements (2.18)–(2.19) are satisfied. Hence, the Braginskii tensor (2.17) is well defined as $|\boldsymbol{B}|\rightarrow 0$ .

For the implementation of Braginskii viscosity in simulations, the form given in (2.17) is recommended in order to make sure that there is no singular behaviour in the limit $|\boldsymbol{B}|\rightarrow 0$ . As highlighted above, considering the Braginskii tensor written in the form of (2.1) could lead to singular behaviour in numerical implementations. A similar analysis for the drift terms is given in Appendix A.

3.1 General form

We start by considering the Cauchy stress tensor as the sum of three contributions:

The isotropic tensor

with $p_{s}$ being the hydrostatic pressure, is the hydrostatic stress tensor. The second contribution is due to the Lorentz force, which can be viewed as the elastic response of the magnetic field on the plasma. This force can be expressed as the divergence of the Maxwell stress tensor,

The combination of $\unicode[STIX]{x1D748}_{H}$ and $\unicode[STIX]{x1D748}_{M}$ represents the stress tensor for an inviscid plasma. To model the viscous stress tensor $\unicode[STIX]{x1D748}_{V}$ , we assume that it depends on both the rate of strain and the distribution of the orientations of momentum transport relative to the magnetic field lines. We then assume that $\unicode[STIX]{x1D748}_{V}$ is given by a constitutive relation of the form

where, as before, $\unicode[STIX]{x1D63F}$ is the strain rate tensor and $\unicode[STIX]{x1D643}$ is a structure tensor describing the distribution of the orientations of momentum transport throughout the plasma. If $\unicode[STIX]{x1D643}=\unicode[STIX]{x1D64A}$ , as would be required if $\boldsymbol{B}=\mathbf{0}$ , $\hat{\unicode[STIX]{x1D748}}_{V}(\unicode[STIX]{x1D63F},\unicode[STIX]{x1D64A},0)$ gives the (isotropic) viscous stress tensor for non-magnetic plasmas.

3.2 Structure tensor

To derive a suitable form for the structure tensor $\unicode[STIX]{x1D643}$ , we shall borrow ideas that are more common in nonlinear elasticity and the theory of liquid crystals. We start by assuming that the magnetic field $\boldsymbol{B}$ is non-zero throughout the plasma. Hence, the unit vector field $\boldsymbol{b}=\boldsymbol{B}/|\boldsymbol{B}|$ gives the direction of the magnetic field at any point. Since, at kinetic length scales, particles are constrained to follow magnetic field lines when the field is strong, the direction of the magnetic field represents the preferred orientation of momentum transport in the plasma.

Next, we introduce an orientation density function $f_{\boldsymbol{x}}:\mathbb{S}^{2}\rightarrow \mathbb{R}^{+}$ , $\mathbb{S}^{2}$ being the unit sphere, such that $f_{\boldsymbol{x}}(\boldsymbol{t})\,\text{d}\unicode[STIX]{x1D714}$ gives the probability that, at $\boldsymbol{x}\in \mathbb{R}^{3}$ , the direction of momentum transport through $\boldsymbol{x}$ orients along $\boldsymbol{t}$ within the solid angle $\text{d}\unicode[STIX]{x1D714}$ . The orientation density function $f_{\boldsymbol{x}}$ must then satisfy the normalization condition

We now assume that the viscosity of the plasma depends only on the orientation of the magnetic field lines and not on the directions they point in. In other words, we assume, based on considerations described earlier, that the viscosity is invariant under inversion of the magnetic field direction $\boldsymbol{b}\rightarrow -\boldsymbol{b}$ . Consequently, as far as the probability density function is concerned, $\boldsymbol{t}$ is ‘headless’ and $f_{\boldsymbol{x}}(\boldsymbol{t})=f_{\boldsymbol{x}}(-\boldsymbol{t})$ . Because of this property, the first moment of the distribution $f_{\boldsymbol{x}}$ is zero.

The second moment of the distribution is the variance tensor

Introducing an orthonormal basis ${\mathcal{B}}=\{\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}\}$ , the variance tensor can be written in the compact form

where

$(t_{1},t_{2},t_{3})$ being the components of $\boldsymbol{t}$ with respect to ${\mathcal{B}}$ .

To make progress with the form of the structure tensor, we choose, without loss of generality, $\boldsymbol{e}_{3}=\boldsymbol{b}$ , and characterize $\boldsymbol{t}$ in terms of the two Euler angles $\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}]$ and $\unicode[STIX]{x1D719}\in [0,2\unicode[STIX]{x03C0})$ :

Because of the arbitrariness of the basis vectors $\boldsymbol{e}_{1}$ and $\boldsymbol{e}_{2}$ , we assume that the orientation density function is independent of $\unicode[STIX]{x1D719}$ , i.e.

Consequently, the normalization condition (3.5) becomes

the off-diagonal terms of $\unicode[STIX]{x1D648}$ vanish and the diagonal terms remaining are, on use of the normalization condition, given by

Thus, the variance tensor can be written in the compact form

The parameter $\unicode[STIX]{x1D705}$ , defined through equation (3.12c ), is called the dispersion parameter and represents the degree of anisotropy. Furthermore, since $\unicode[STIX]{x1D648}$ is positive semi-definite, the dispersion parameter must satisfy the inequalities

The perfect alignment of momentum transport through $\boldsymbol{x}$ along the magnetic field is attained for $\unicode[STIX]{x1D705}=0$ , whereas for $\unicode[STIX]{x1D705}=1/3$ there is no preferred alignment and all orientations are equiprobable. For $\unicode[STIX]{x1D705}=1/2$ , instead, the momentum transport through $\boldsymbol{x}$ orients perpendicularly to the magnetic field and all the directions orthogonal to $\boldsymbol{b}$ are equiprobable. However, since the magnetic field direction is the preferred direction, we require that the probability that the momentum transport through $\boldsymbol{x}$ orients along $\boldsymbol{b}$ be greater than or equal to the probability that it orients along a direction perpendicular to the magnetic field. Therefore $1-2\unicode[STIX]{x1D705}\geqslant \unicode[STIX]{x1D705}$ and, in the light of (3.14), we shall limit our analysis to the interval

In order to discuss the dispersion parameter $\unicode[STIX]{x1D705}$ we consider a transversely isotropic and $\unicode[STIX]{x03C0}$ -periodic von Mises distribution. More precisely, we modify the standard $\unicode[STIX]{x03C0}$ -periodic von Mises distribution to satisfy the normalization condition (3.11), giving

where $\text{erfi}(x)=-\text{i}\,\text{erf}(\text{i}\,x)$ is the imaginary error function and $a$ is a positive quantity called the concentration parameter. The orientation density function (3.16), used also by Gasser, Ogden & Holzapfel (Reference Gasser, Ogden and Holzapfel2006) to model collagen fibre distributions in arteries, can be interpreted as the normal distribution projected onto the unit sphere. The modified von Mises distribution (3.16) tends uniformly to the uniform distribution $f_{\boldsymbol{x}}\equiv 1$ as $a\rightarrow 0$ , while it tends to the Dirac delta $\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D703})$ centred at $\unicode[STIX]{x1D703}=0$ as $a\rightarrow +\infty$ (figure 1). Therefore, this distribution gives the required directional behaviour for momentum transport when $|\boldsymbol{B}|$ is weak or strong.

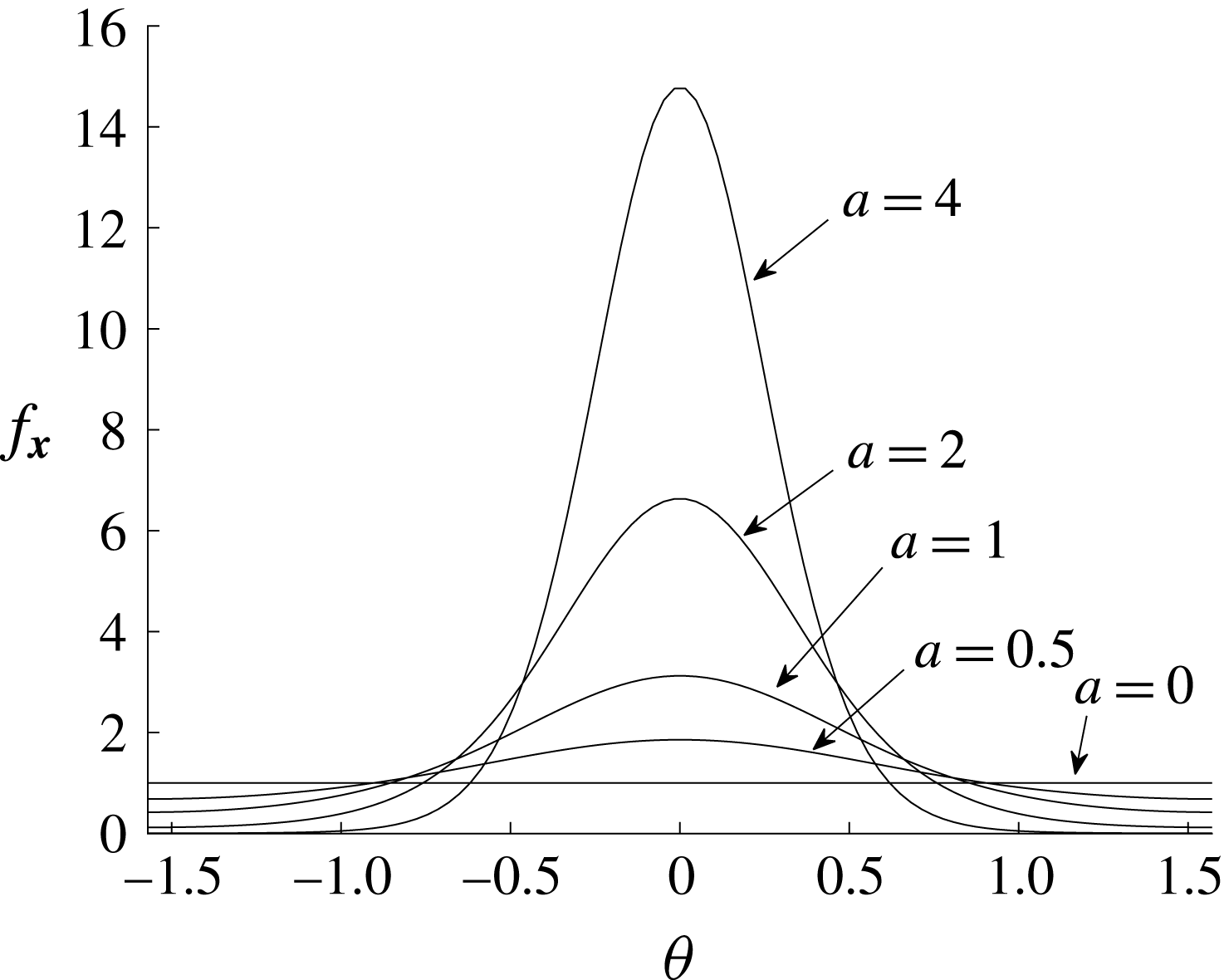
Figure 1. Modified von Mises distribution for various values of the concentration parameter.

Inserting (3.16) into (3.12c ) results, after integration, in an analytical expression for the dispersion parameter,

from which we deduce that the dispersion parameter decreases as $a$ increases, tends to 0 as $a\rightarrow +\infty$ , and tends to $1/3$ as $a\rightarrow 0$ (figure 2 a). As a consequence, the momentum transport through $\boldsymbol{x}$ can orient along any direction with the same probability as $a\rightarrow 0$ , whereas it tends to align perfectly along the magnetic field for a very large concentration parameter.

Later it will be convenient to work with the traceless part of the variance tensor $\unicode[STIX]{x1D648}$ ,

Readers familiar with liquid crystal theory will recognize $\unicode[STIX]{x1D643}$ as similar to the order tensor for nematics (e.g. Napoli & Vergori Reference Napoli and Vergori2012). Here, instead, in line with the nomenclature adopted in the theory of nonlinear anisotropic elasticity, we call $\unicode[STIX]{x1D643}$ the structure tensor. In view of (3.15), the order parameter $s$ lies in the interval $[0,1]$ . Thus, the orientation of momentum transport through $\boldsymbol{x}$ aligns perfectly along the magnetic field direction for $s=1$ , while it has no preferred direction for $s=0$ . Asymptotically, we have

and $s\rightarrow 1$ as $a\rightarrow +\infty$ (figure 2 b).

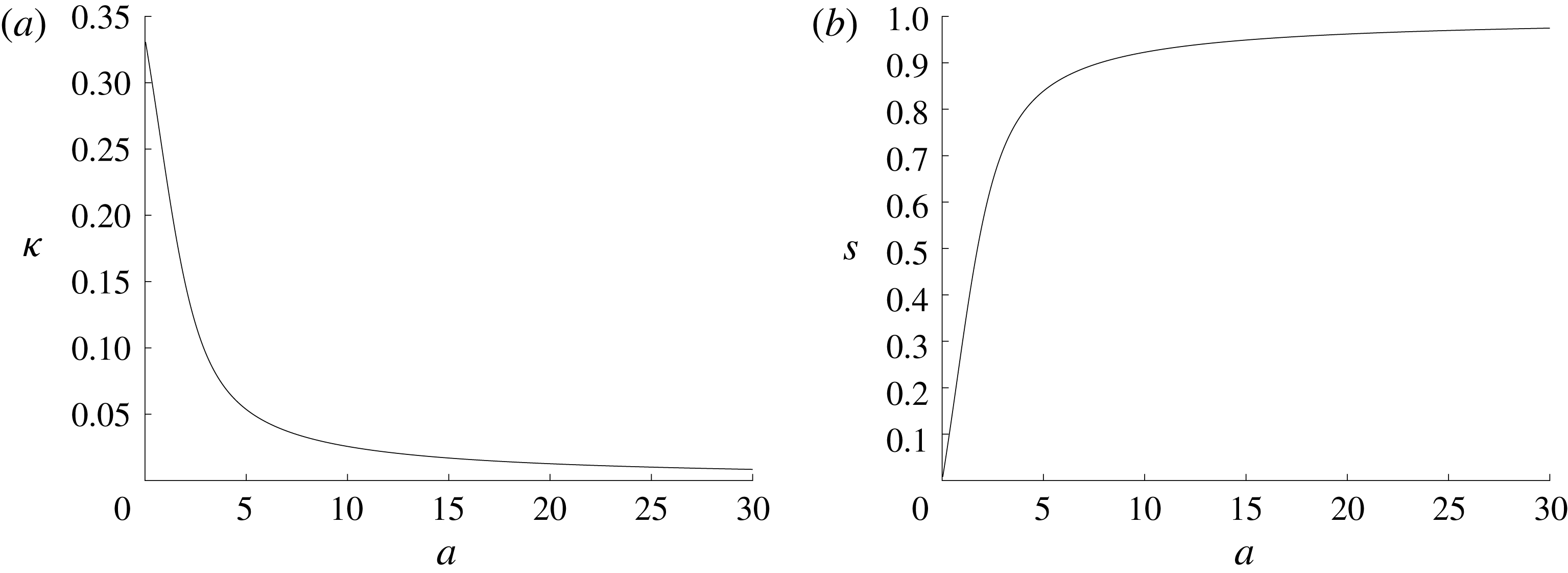
Figure 2. (a) Dispersion parameter and (b) order parameter versus concentration parameter.

If the viscous stress tensor $\unicode[STIX]{x1D748}_{V}$ is to be applicable to magnetic fields of arbitrary topology, the order parameter $s$ must represent some measure of the magnetic field strength. If a magnetic field contains a null point, where $\boldsymbol{B}=\mathbf{0}$ , any anisotropic effect must ‘switch off’, with viscosity reverting to an isotropic form. In order to determine a constitutive function for $s$ relating the order parameter to the magnetic field strength, we assume that the (non-dimensional) concentration parameter $a$ depends on $|\boldsymbol{B}|$ ,

Since

1. (1) the probability that momentum transport orients along the magnetic field lines increases as the magnetic field strength increases,

2. (2) the momentum transport tends to orient perfectly along the magnetic field lines if the magnetic field is strong enough,

3. (3) the momentum transport tends to have no preferred direction for weak (or zero) magnetic fields,

we require the constitutive function $\hat{a}$ to satisfy the following properties:

1. (i) $\hat{a}$ is a non-negative increasing function of $|\boldsymbol{B}|$ ;

2. (ii) $\hat{a}(|\boldsymbol{B}|)\rightarrow +\infty$ as $|\boldsymbol{B}|\rightarrow +\infty$ ;

3. (iii) $\lim _{\boldsymbol{B}\rightarrow \mathbf{0}}(\hat{a}(|\boldsymbol{B}|)/|\boldsymbol{B}|^{2})\in \mathbb{R}$ .

Property (iii) requires that the constitutive function for the concentration parameter be an infinitesimal in the magnetic field strength of order greater than or equal to 2. The reason for this requirement will be clear in a few lines.

From (3.18) and the definition of $\boldsymbol{b}$ , the structure tensor $\unicode[STIX]{x1D643}$ can be rewritten as

where, in view of (3.17) and (3.20),

Finally, thanks to (3.19) and property (iii), we can define the structure tensor also at points where the magnetic field vanishes, i.e. equation (3.21) applies to arbitrary magnetic topologies. The simplest (non-trivial) form for the concentration parameter that satisfies conditions (i)–(iii) is $a=a_{0}|\boldsymbol{B}|^{2}$ , for some constant $a_{0}>0$ .

3.3 Viscosity tensor

Now that a suitable form for the structure tensor $\unicode[STIX]{x1D643}$ has been developed, we can focus on what kind of expression the viscous stress tensor of (3.4) can take. The constitutive equation for $\unicode[STIX]{x1D748}_{V}$ (3.4) must be objective (that is, invariant with respect to a change of observer) and hence satisfy the identity

for all proper orthogonal tensors $\unicode[STIX]{x1D64C}$ . Following Ericksen (Reference Ericksen1960), Spencer (Reference Spencer and Eringen1971) and Dorfmann, Ogden & Wineman (Reference Dorfmann, Ogden and Wineman2007), and noting that

we can write down the most general constitutive relation for $\unicode[STIX]{x1D748}_{V}$ satisfying (3.23):

which, as required by the balance of angular momentum, is symmetric. The six viscosity coefficients $\unicode[STIX]{x1D6FC}_{i}$ ( $i=0,\ldots ,5$ ) are functions of $|\boldsymbol{B}|$ and the integrity basis of the two tensors $\unicode[STIX]{x1D63F}$ and $\unicode[STIX]{x1D643}$ . In view of (3.24), the integrity basis for the current problem consists of the following five invariants:

This is a minimal set of invariants since the trace of the product of two second-order Cartesian tensors is equal to the trace of the tensor product with the factors written in reverse (Spencer Reference Spencer and Eringen1971). The first three invariants in (3.26) account for the dependence on the strain rate tensor $\unicode[STIX]{x1D63F}$ ; the remaining two invariants account for the interaction of the deformation rate and the structure tensor and are sometimes referred to as pseudo-invariants (Holzapfel Reference Holzapfel2000).

Taking into account (2.7), the viscous stress tensor $\unicode[STIX]{x1D748}_{V}$ can be written as

where

is the hydrodynamic pressure and

Obviously, $\overset{\circ }{\unicode[STIX]{x1D748}}_{V}$ is traceless. Then, from (3.1) and (3.27), the full stress tensor becomes

where $p=p_{s}+p_{d}$ is the plasma pressure; $\overset{\circ }{\unicode[STIX]{x1D748}}_{V}$ represents the most general form of the viscous stress tensor in our model. There are many possible specializations and we shall now consider two.

3.4 Model 1: single-fluid Braginskii

As mentioned previously, the single-fluid Braginskii tensor (2.17) is a special case of $\overset{\circ }{\unicode[STIX]{x1D748}}_{V}$ . This is easily shown by setting

with $\unicode[STIX]{x1D702}_{0}$ constant and with $\unicode[STIX]{x1D702}_{1}$ and $\unicode[STIX]{x1D702}_{2}$ as in (2.14), and the remaining values of $\unicode[STIX]{x1D6FD}$ to zero. A family of Braginskii-like viscosity coefficients can be found by first specifying the correct asymptotic behaviour of $\unicode[STIX]{x1D6FD}_{1}$ , $\unicode[STIX]{x1D6FD}_{3}$ and $\unicode[STIX]{x1D6FD}_{4}$ , i.e. the viscosity tensor produces parallel viscosity in the strong-field limit and isotropic viscosity in the weak-field limit. We shall not pursue this approach here but, instead, consider a simplified model that could be useful in large-scale coronal simulations.

3.5 Model 2: parallel–isotropic switch

Most of the work concerning Braginskii MHD that we have cited in this paper has focused on the strong-field limit. We have also highlighted that this regime applies almost everywhere in the solar corona. For simulations of large-scale coronal phenomena, where null points exist at isolated locations throughout the domain (and are perhaps spread over only a few grid points), the effects of the full Braginskii tensor may not be adequately resolved. Instead, a simpler model where the direct switch between parallel and isotropic viscosity can be controlled may prove more useful. At null points, the parallel viscosity cannot be separated from the perpendicular viscosity in the limit as $|\boldsymbol{B}|\rightarrow 0$ in the Braginskii tensor (2.17). In (3.27), however, we can choose the coefficients depending on our requirements. Setting

where $\unicode[STIX]{x1D702}_{0}$ is the viscosity in an unmagnetized plasma, gives the parallel viscosity (2.12) in the strong-field limit regime and isotropic viscosity when the field goes to zero. The viscous stress tensor can be written as

Equation (3.35) represents an improvement on current coronal models that only consider isotropic viscosity. It also represents a simple extension of the many models that have only parallel viscosity. Later, we shall demonstrate that the ‘region of switching’ from parallel to isotropic viscosity can be controlled using the concentration parameter $\hat{a}$ .

4.1 Concentration parameter

For the parallel–isotropic model, we are required to choose a form for the non-dimensional concentration parameter $\hat{a}$ . As mentioned earlier we assume that $\hat{a}=a_{0}|\boldsymbol{B}|^{2}$ . In order to make a simple comparison between the different models, we shall choose $a_{0}=\unicode[STIX]{x1D6FC}^{2}$ so that $\hat{a}=x_{i}^{2}$ . For this particular numerical experiment, we set $\unicode[STIX]{x1D6FC}|\boldsymbol{B}_{r}|=6$ . This choice allows for a simple comparison between the models and for the different heating contributions to be easily visualized. In the discussion at the end of the paper, we shall return to the consequences of choosing different expressions for $\hat{a}$ and $x_{i}$ .

4.2 Heating profiles

We shall now examine how the different viscosity models heat the plasma. The viscous heating in the fully isotropic model is

In the Braginskii model, the heating terms from the isotropic and anisotropic parts are

In the parallel–isotropic model, the heating terms from the isotropic and anisotropic parts are

From (2.14) and (4.11)–(4.14) we deduce that, at null points, the total viscous heating in both models $(i=1,2)$ equals the viscous heating in the fully isotropic model, specifically

while in the limit of a strong magnetic field we have

That is, the parallel–isotropic model reproduces the asymptotic limits of the full Braginskii model.

Figure 4 displays slices of $Q^{iso}$ in the $y=0$ plane at two different times.

Figure 4. $Q^{iso}$ slices in the $y=0$ plane.

As the motions on the upper and lower boundaries continue to be driven, torsional waves are transmitted towards the null point. Initially, the waves follow the path of the spine, a vertical line through the null point. As the field lines then splay out into the fan, a plane through the null orthogonal to the spine, the plasma follows the magnetic field. In the fully isotropic model, viscous heating occurs on the fan plane and in vertical locations near the spine. As time increases, more of the domain becomes heated by viscosity. By comparison, the viscous heating due to the isotropic parts ( $Q_{1}^{iso}$ and $Q_{2}^{iso}$ ) of the other models exhibits different behaviour. Their profiles are displayed in figure 5.

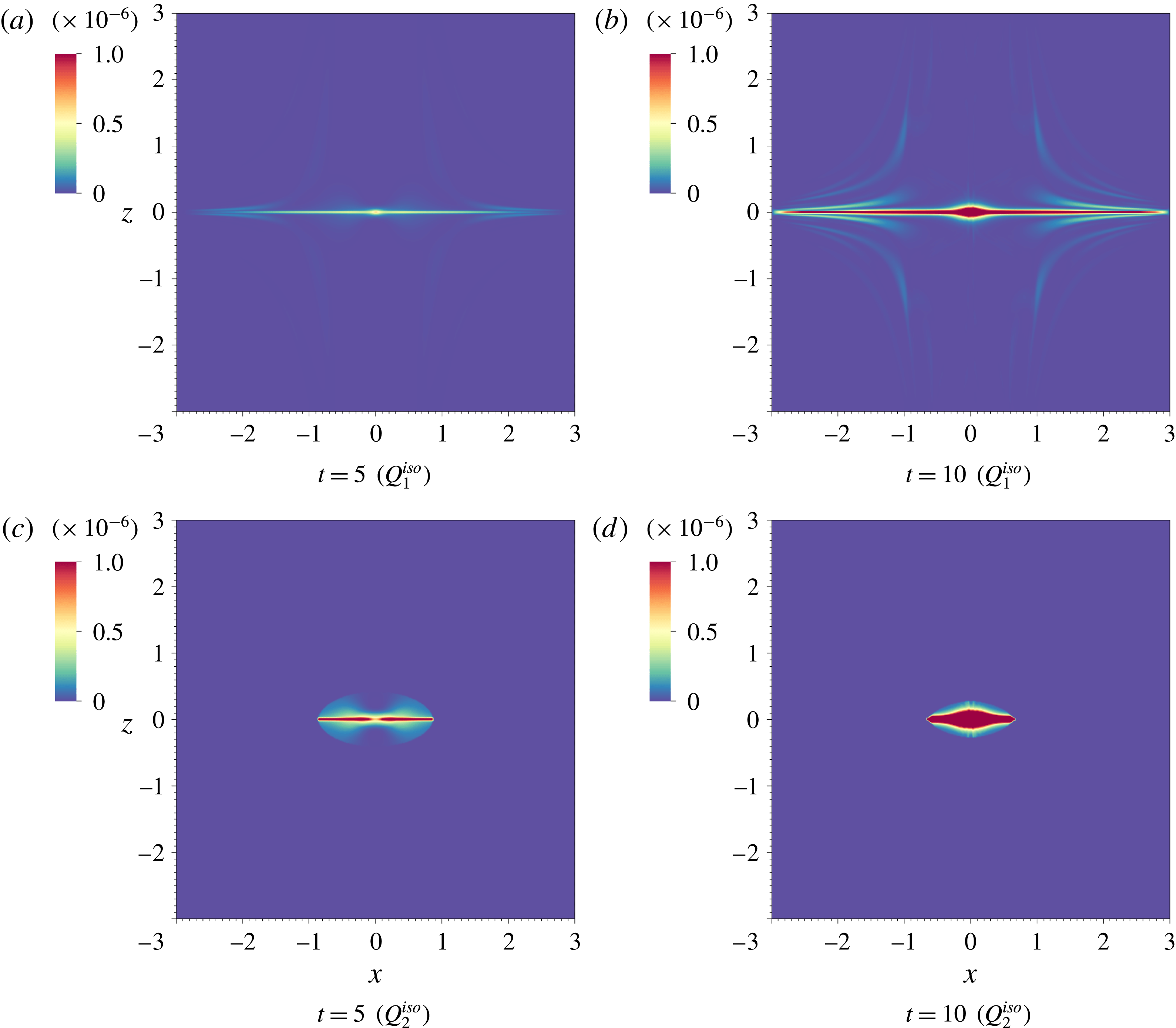
Figure 5. $Q_{1}^{iso}$ and $Q_{2}^{iso}$ slices in the $y=0$ plane.

Note that the magnitude of heating shown on the colour bar in figure 5 is an order of magnitude less than that of figure 4 in order to reveal structure. Considering the Braginskii model first (figure 5 a,b), viscous heating is almost entirely confined to the fan plane. This behaviour is to be expected as the imposed twisting motions generate a shear layer in the fan plane. Unlike in the fully isotropic model, however, the heating does not spread significantly beyond the fan plane. The viscous heating of the parallel–isotropic model (figure 5 c,d) is also concentrated on the fan plane but is truncated compared to the Braginskii model.

Figure 6 displays slices of viscous heating due to the anisotropic parts ( $Q_{1}^{ani}$ and $Q_{2}^{ani}$ ) of the models at $t=5,10$ .

Figure 6. $Q_{1}^{ani}$ and $Q_{2}^{ani}$ slices in the $y=0$ plane.

Comparing figures 6(a) and 6(b) of the Braginskii model with figures 6(c) and 6(d) of the parallel–isotropic model, the viscous heating profiles have many similarities. The main differences occur close to the null point. At $t=5$ , the heating due to the Braginskii model contains small-scale structures very close to the null point; see figure 6(a). The parallel–isotropic model does not include these small-scale structures; see figure 6(c). Away from the null point, the two heating profiles are very similar. This is to be expected from (4.16).

Later, at $t=10$ , the anisotropic heating from the Braginskii model has spread to the null point itself; see figure 6(b). The parallel–isotropic model produces a very similar heating profile but now there is no anisotropic heating at the null point; see figure 6(d).

Comparing the heating profiles of the anisotropic models, figures 5 and 6, with that of the fully isotropic model, figure 4, reveals significant differences in the magnitude of the heating and its spatial distribution. Throughout large parts of the magnetic field, including both the spine and the fan, isotropic viscous heating is an order of magnitude greater than the heating from both the anisotropic models.