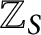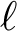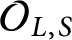1 Introduction
A leading problem in arithmetic geometry is to determine whether an equation with coefficients in a number field F has any solutions. Since there can be no algorithm determining whether a given Diophantine equation is soluble in the integers
![]() $\mathbb {Z}$
, one usually tries to understand the problem under strong constraints of the geometry of the variety defined by such equation or by assuming the existence of many local solutions. In the case of curves, for example, Skorobogatov [Reference Skorobogatov38] asked whether the Brauer-Manin obstruction is the only obstruction to the existence of rational points. The question, or variations thereof, attracted the attention of Bruin, Harari, Helm, Poonen, Stoll, and Voloch among others. In particular, Helm and Voloch [Reference Helm and Voloch26] studied a form of the finite Galois descent obstruction for the integral points of modular curves. The goal of our paper is to present a class of arbitrarily large dimensional varieties that can be treated similarly to curves. More precisely, we give sufficient conditions for the existence of
$\mathbb {Z}$
, one usually tries to understand the problem under strong constraints of the geometry of the variety defined by such equation or by assuming the existence of many local solutions. In the case of curves, for example, Skorobogatov [Reference Skorobogatov38] asked whether the Brauer-Manin obstruction is the only obstruction to the existence of rational points. The question, or variations thereof, attracted the attention of Bruin, Harari, Helm, Poonen, Stoll, and Voloch among others. In particular, Helm and Voloch [Reference Helm and Voloch26] studied a form of the finite Galois descent obstruction for the integral points of modular curves. The goal of our paper is to present a class of arbitrarily large dimensional varieties that can be treated similarly to curves. More precisely, we give sufficient conditions for the existence of
![]() $\mathcal {O}_{L,S}$
-integral points on (twists of) Hilbert modular varieties associated with K, where both L and K are totally real fields.
$\mathcal {O}_{L,S}$
-integral points on (twists of) Hilbert modular varieties associated with K, where both L and K are totally real fields.
1.1 What is a Point of a Shimura Variety?
A point of a Shimura variety attached to a Shimura datum
![]() $(G,X)$
corresponds to a Hodge structure (once a faithful linear representation of the group G is fixed). Of course, not every Hodge structure can arise in this way. Even when the Shimura variety parametrises motives, there is no description of the Hodge structures coming from geometry, nor a conjecture predicting this. However, Shimura varieties have canonical models over number fields. Hence, we can associate with an algebraic point a Galois representation, and, conjecturally at least, we can predict which
$(G,X)$
corresponds to a Hodge structure (once a faithful linear representation of the group G is fixed). Of course, not every Hodge structure can arise in this way. Even when the Shimura variety parametrises motives, there is no description of the Hodge structures coming from geometry, nor a conjecture predicting this. However, Shimura varieties have canonical models over number fields. Hence, we can associate with an algebraic point a Galois representation, and, conjecturally at least, we can predict which
![]() $\ell $
-adic Galois representations come from geometry. This is the content of the Fontaine–Mazur conjecture [Reference Fontaine and Mazur19]. Our study of rational and integral points of Hilbert modular varieties begins with an attempt to understand when a suitable system of Galois representations comes from an abelian variety with
$\ell $
-adic Galois representations come from geometry. This is the content of the Fontaine–Mazur conjecture [Reference Fontaine and Mazur19]. Our study of rational and integral points of Hilbert modular varieties begins with an attempt to understand when a suitable system of Galois representations comes from an abelian variety with
![]() $\mathcal {O}_{K}$
-multiplication; see Section 2.1 for a more precise formulation of the question.
$\mathcal {O}_{K}$
-multiplication; see Section 2.1 for a more precise formulation of the question.
Our strategy arises from predictions of the Langlands’ programme, which link the worlds of
We refer the reader to [Reference Clozel12] for an introduction to this circle of ideas. More precisely, from a system of Galois representations that “looks like” the one coming from an abelian variety with
![]() $\mathcal {O}_{K}$
-multiplication, we want to produce, via Serre’s modularity conjecture, a Hilbert modular form over L with Fourier coefficients in K. Eichler–Shimura theory attaches to this modular form an abelian variety over L with
$\mathcal {O}_{K}$
-multiplication, we want to produce, via Serre’s modularity conjecture, a Hilbert modular form over L with Fourier coefficients in K. Eichler–Shimura theory attaches to this modular form an abelian variety over L with
![]() $\mathcal {O}_{K}$
-multiplication, which will correspond to an L-point on the Hilbert modular variety for K. If
$\mathcal {O}_{K}$
-multiplication, which will correspond to an L-point on the Hilbert modular variety for K. If
![]() $L=\mathbb {Q}$
, Serre’s conjecture is known to hold true by the work of Khare and Wintenberger [Reference Khare and Wintenberger27], and the Eichler–Shimura theory has been worked out by Shimura [Reference Shimura37]. If
$L=\mathbb {Q}$
, Serre’s conjecture is known to hold true by the work of Khare and Wintenberger [Reference Khare and Wintenberger27], and the Eichler–Shimura theory has been worked out by Shimura [Reference Shimura37]. If
![]() $L\neq \mathbb {Q}$
, to make such a strategy work, we need to assume Serre’s conjecture for the totally real field L and also (a special case of) the absolute Hodge conjecture, where the latter is required by Blasius in [Reference Blasius6] in order to attach abelian varieties to Hilbert modular forms. In the next section, we present in more detail the main results of the paper.
$L\neq \mathbb {Q}$
, to make such a strategy work, we need to assume Serre’s conjecture for the totally real field L and also (a special case of) the absolute Hodge conjecture, where the latter is required by Blasius in [Reference Blasius6] in order to attach abelian varieties to Hilbert modular forms. In the next section, we present in more detail the main results of the paper.
1.2 Main Results
Let
![]() $L,K$
be totally real extensions of
$L,K$
be totally real extensions of
![]() $\mathbb {Q}$
and set
$\mathbb {Q}$
and set
We denote by w a place of L and by v a place of K. In what follows, one should think of L as the field of definition and of K as the Hecke field. We denote by
![]() $\mathcal {O}_{L}$
and
$\mathcal {O}_{L}$
and
![]() $\mathcal {O}_{K}$
the rings of integers of L and K, by
$\mathcal {O}_{K}$
the rings of integers of L and K, by
![]() $L_{w}$
(resp.
$L_{w}$
(resp.
![]() $K_{v}$
) the completion of L at w (resp. of K at v) and by
$K_{v}$
) the completion of L at w (resp. of K at v) and by
![]() $\mathcal {O}_{L_{w}}$
(resp.
$\mathcal {O}_{L_{w}}$
(resp.
![]() $\mathcal {O}_{K_{v}}$
) the ring of integers of
$\mathcal {O}_{K_{v}}$
) the ring of integers of
![]() $L_{w}$
(resp.
$L_{w}$
(resp.
![]() $K_{v}$
). Finally,
$K_{v}$
). Finally,
![]() $G_{L}$
denotes the absolute Galois group of L.
$G_{L}$
denotes the absolute Galois group of L.
Let S be a finite set of places of L (including all archimedean places), and consider a system of Galois representations
for every finite place v of K, such that:
-
𝒮.1
 $\{\rho _{v}\}_{v}$
is a weakly compatible system of Galois representations (see Definition 3.1);
$\{\rho _{v}\}_{v}$
is a weakly compatible system of Galois representations (see Definition 3.1); -
𝒮.2
 $\det (\rho _{v})=\chi _{\ell }$
, where
$\det (\rho _{v})=\chi _{\ell }$
, where
 $\chi _{\ell }$
is the
$\chi _{\ell }$
is the
 $\ell $
-adic cyclotomic character and
$\ell $
-adic cyclotomic character and
 $v\mid \ell $
;
$v\mid \ell $
; -
𝒮.3 the residual representation
 $\bar {\rho }_{v}$
is finite flat at
$\bar {\rho }_{v}$
is finite flat at
 $w\mid \ell $
, for all
$w\mid \ell $
, for all
 $v\mid \ell $
such that
$v\mid \ell $
such that
 $\bar {\rho }_{v}$
is irreducible and
$\bar {\rho }_{v}$
is irreducible and
 $\ell $
is not divisible by any prime in S;
$\ell $
is not divisible by any prime in S; -
𝒮.4
 $\bar {\rho }_{v}$
is absolutely irreducible for all but finitely many v;
$\bar {\rho }_{v}$
is absolutely irreducible for all but finitely many v; -
𝒮.5 the field generated by the trace of
 $\rho _{v}(\text {Frob}_{w})$
for every w is K.
$\rho _{v}(\text {Frob}_{w})$
for every w is K.
To make it clear which case is conjectural and which is not, we separate the statement of our first theorem into two cases depending on whether
![]() $n_{L}=1$
or
$n_{L}=1$
or
![]() $n_{L}>1$
.
$n_{L}>1$
.
Theorem 1.A If
![]() $L=\mathbb {Q}$
, there exists an
$L=\mathbb {Q}$
, there exists an
![]() $n_{K}$
-dimensional abelian variety
$n_{K}$
-dimensional abelian variety
![]() $A/\mathbb {Q}$
with
$A/\mathbb {Q}$
with
![]() $\mathcal {O}_{K}$
-multiplication, such that, for every v, the v-adic Tate module of A, denoted by
$\mathcal {O}_{K}$
-multiplication, such that, for every v, the v-adic Tate module of A, denoted by
![]() $T_{v} A$
, is isomorphic to
$T_{v} A$
, is isomorphic to
![]() $\rho _{v}$
as representation of
$\rho _{v}$
as representation of
![]() $G_{\mathbb {Q}}$
.
$G_{\mathbb {Q}}$
.
Theorem 1.B Assume
![]() $n_{L}>1$
. Under the validity of the absolute Hodge–conjecture (more precisely Conjecture 1.1) and a suitable generalisation of Serre’s conjecture (Conjecture 1.2), there exists an
$n_{L}>1$
. Under the validity of the absolute Hodge–conjecture (more precisely Conjecture 1.1) and a suitable generalisation of Serre’s conjecture (Conjecture 1.2), there exists an
![]() $n_{K}$
-dimensional abelian variety
$n_{K}$
-dimensional abelian variety
![]() $A/L$
with
$A/L$
with
![]() $\mathcal {O}_{K}$
-multiplication, such that, for every v,
$\mathcal {O}_{K}$
-multiplication, such that, for every v,
![]() $T_{v} A$
is isomorphic to
$T_{v} A$
is isomorphic to
![]() $\rho _{v}$
as representation of
$\rho _{v}$
as representation of
![]() $G_{L}$
.
$G_{L}$
.
We apply the above to study the finite descent obstruction, as explored in [Reference Skorobogatov38, Reference Stoll39, Reference Harari and Voloch25], of Hilbert modular varieties. A recap is given in Section 4.1. More precisely, denote by
![]() $Y_{K}$
the Hilbert modular variety associated with K. Let
$Y_{K}$
the Hilbert modular variety associated with K. Let
![]() $\mathfrak {N}$
be an ideal in
$\mathfrak {N}$
be an ideal in
![]() $\mathcal {O}_{K}$
and denote by
$\mathcal {O}_{K}$
and denote by
![]() $Y_{K}(\mathfrak {N})$
the moduli space of
$Y_{K}(\mathfrak {N})$
the moduli space of
![]() $n_{K}$
-dimensional abelian varieties, principally
$n_{K}$
-dimensional abelian varieties, principally
![]() $\mathcal {O}_{K}$
-polarized and with
$\mathcal {O}_{K}$
-polarized and with
![]() $\mathfrak {N}$
-level structure (see Section 2.2.1 for a precise definition). As a corollary of the above theorems, we prove that the finite Galois descent obstruction (as defined in Section 4) is the only obstruction to the existence of S-integral points on integral models of twists of Hilbert modular varieties, denoted by
$\mathfrak {N}$
-level structure (see Section 2.2.1 for a precise definition). As a corollary of the above theorems, we prove that the finite Galois descent obstruction (as defined in Section 4) is the only obstruction to the existence of S-integral points on integral models of twists of Hilbert modular varieties, denoted by
![]() $\mathcal {Y}_{K}(\mathfrak {N})$
, over the ring of S-integers of a totally real field L, generalising [Reference Helm and Voloch26, Theorem 3]. Assume that S contains the places of bad reduction of
$\mathcal {Y}_{K}(\mathfrak {N})$
, over the ring of S-integers of a totally real field L, generalising [Reference Helm and Voloch26, Theorem 3]. Assume that S contains the places of bad reduction of
![]() $Y_{K}(\mathfrak {N})$
. The set
$Y_{K}(\mathfrak {N})$
. The set
 $\mathcal {Y}_\rho ^{f-cov} (\mathcal {O}_{L,S})$
is defined in Section 4.1. We prove the following theorem.
$\mathcal {Y}_\rho ^{f-cov} (\mathcal {O}_{L,S})$
is defined in Section 4.1. We prove the following theorem.
Theorem 2 If
![]() $n_{L}>1$
, assume that the conjectures of Theorem 1.B hold. Let
$n_{L}>1$
, assume that the conjectures of Theorem 1.B hold. Let
![]() $\mathcal {Y}_\rho $
be the S-integral model of a twist of
$\mathcal {Y}_\rho $
be the S-integral model of a twist of
![]() $\mathcal {Y}_{K}(\mathfrak {N})$
, corresponding to a representation
$\mathcal {Y}_{K}(\mathfrak {N})$
, corresponding to a representation
![]() $\rho : G_{L} \to \mathrm {GL}_{2}(\mathcal {O}_{K}/\mathfrak {N})$
. If
$\rho : G_{L} \to \mathrm {GL}_{2}(\mathcal {O}_{K}/\mathfrak {N})$
. If
 $\mathcal {Y}_\rho ^{f-cov} (\mathcal {O}_{L,S})$
is non-empty, then
$\mathcal {Y}_\rho ^{f-cov} (\mathcal {O}_{L,S})$
is non-empty, then
![]() $\mathcal {Y}_\rho (\mathcal {O}_{L,S})$
is non-empty.
$\mathcal {Y}_\rho (\mathcal {O}_{L,S})$
is non-empty.
In the work of Helm–Voloch,
![]() $\mathcal {Y}$
is the integral model of an affine curve. In the case of curves, there are also other tools to establish (variants of) such results, without invoking Serre’s conjecture. Indeed, as noticed after the proof of [Reference Helm and Voloch26, Theorem 3], Stoll [Reference Stoll39, Corollary 8.8] proved a similar result, under some extra assumptions, knowing that a factor of the Jacobian of such modular curves has finite Mordell–Weil and Tate–Shafarevich groups. The goal of this paper is to push Helm–Voloch’s strategy to a particular class of varieties of arbitrarily large dimension and whose associated Albanese variety is trivial (see Theorem 2.2), thereby showing that the method could also be applied to study L-points.
$\mathcal {Y}$
is the integral model of an affine curve. In the case of curves, there are also other tools to establish (variants of) such results, without invoking Serre’s conjecture. Indeed, as noticed after the proof of [Reference Helm and Voloch26, Theorem 3], Stoll [Reference Stoll39, Corollary 8.8] proved a similar result, under some extra assumptions, knowing that a factor of the Jacobian of such modular curves has finite Mordell–Weil and Tate–Shafarevich groups. The goal of this paper is to push Helm–Voloch’s strategy to a particular class of varieties of arbitrarily large dimension and whose associated Albanese variety is trivial (see Theorem 2.2), thereby showing that the method could also be applied to study L-points.
Another reason for studying rational points of Hilbert modular varieties is the following. By [Reference Cohen, Itzykson and Wolfart13, Theorem 1], every smooth projective geometrically connected curve
![]() $C/\overline {\mathbb {Q}}$
of genus at least two admits a non-constant
$C/\overline {\mathbb {Q}}$
of genus at least two admits a non-constant
![]() $\overline {\mathbb {Q}}$
-morphism to either a Hilbert or a Quaternionic modular variety for K, where K is a totally real number field depending on C and the choice of a Belyi function
$\overline {\mathbb {Q}}$
-morphism to either a Hilbert or a Quaternionic modular variety for K, where K is a totally real number field depending on C and the choice of a Belyi function
![]() $\beta : C\to \mathbb {P}^{1}$
. See [Reference Cohen, Itzykson and Wolfart13, Remark 2] for a detailed description of the ambiguities of such a construction. Inspired by [Reference Patrikis, Voloch and Zarhin32, Theorem 5.2], where the role of the Belyi embedding is played by the Kodaira–Parshin construction [Reference Martin-Deschamps30], we have the following corollary of Theorem 2. For simplicity, we consider rational points of projective curves, even if our main theorems are about integral points.
$\beta : C\to \mathbb {P}^{1}$
. See [Reference Cohen, Itzykson and Wolfart13, Remark 2] for a detailed description of the ambiguities of such a construction. Inspired by [Reference Patrikis, Voloch and Zarhin32, Theorem 5.2], where the role of the Belyi embedding is played by the Kodaira–Parshin construction [Reference Martin-Deschamps30], we have the following corollary of Theorem 2. For simplicity, we consider rational points of projective curves, even if our main theorems are about integral points.
Corollary Let
![]() $C/\mathbb {Q}$
be a smooth projective curve of genus
$C/\mathbb {Q}$
be a smooth projective curve of genus
![]() $g \geq 2$
. Assume the following:
$g \geq 2$
. Assume the following:
-
(i)
 $C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}}\neq \emptyset $
;
$C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}}\neq \emptyset $
; -
(ii) there exist two totally real number fields
 $L,K$
and a non-constant L-morphism where
$L,K$
and a non-constant L-morphism where $$ \begin{align*} f: C_{L}:=C\times_{\mathbb{Q}} L \longrightarrow Y_{K}(\mathfrak{N}), \end{align*} $$
$$ \begin{align*} f: C_{L}:=C\times_{\mathbb{Q}} L \longrightarrow Y_{K}(\mathfrak{N}), \end{align*} $$
 $Y_{K}(\mathfrak {N})$
denotes, as above, the Hilbert modular variety for K of some level
$Y_{K}(\mathfrak {N})$
denotes, as above, the Hilbert modular variety for K of some level
 $\mathfrak {N}$
;
$\mathfrak {N}$
;
-
(iii) if
 $L\neq \mathbb {Q}$
, the conjectures of Theorem 1.B hold true.
$L\neq \mathbb {Q}$
, the conjectures of Theorem 1.B hold true.
Then
![]() $C(\mathbb {Q})\neq \emptyset $
.
$C(\mathbb {Q})\neq \emptyset $
.
Stoll [Reference Stoll39, Conjecture 9.1] conjectured that every smooth projective curve is very good. That is, the closure of
![]() $C({\mathbb {Q}})$
in the adelic points of C is equal to
$C({\mathbb {Q}})$
in the adelic points of C is equal to
![]() $C(\mathbb {A}_{\mathbb {Q}})^{\text {f-ab}}$
. For the definition of
$C(\mathbb {A}_{\mathbb {Q}})^{\text {f-ab}}$
. For the definition of
![]() $C(\mathbb {A}_{\mathbb {Q}})^{\text {f-ab}}$
, we refer the reader to [Reference Stoll39, Definition 6.1]. For the moment, we just need to know that
$C(\mathbb {A}_{\mathbb {Q}})^{\text {f-ab}}$
, we refer the reader to [Reference Stoll39, Definition 6.1]. For the moment, we just need to know that
 $$ \begin{align*} C({\mathbb{Q}})\subset C(\mathbb{A}_{\mathbb{Q}})^{\text{f-cov}} \subset C(\mathbb{A}_{\mathbb{Q}})^{\text{f-ab}} \subset C(\mathbb{A}_{\mathbb{Q}}). \end{align*} $$
$$ \begin{align*} C({\mathbb{Q}})\subset C(\mathbb{A}_{\mathbb{Q}})^{\text{f-cov}} \subset C(\mathbb{A}_{\mathbb{Q}})^{\text{f-ab}} \subset C(\mathbb{A}_{\mathbb{Q}}). \end{align*} $$
Hence, Stoll’s conjecture predicts the following implication:
 $$ \begin{align*} C(\mathbb{A}_{\mathbb{Q}})^{\text{f-cov}}\neq \emptyset \Longrightarrow C({\mathbb{Q}})\neq \emptyset, \end{align*} $$
$$ \begin{align*} C(\mathbb{A}_{\mathbb{Q}})^{\text{f-cov}}\neq \emptyset \Longrightarrow C({\mathbb{Q}})\neq \emptyset, \end{align*} $$
which we are able to prove, as a consequence of Theorem 2, for curves satisfying (i), (ii), and (iii) from the above corollary.
Proof Fix a point
![]() $(P_{w})\in C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}}$
, which is not empty by (i). Let
$(P_{w})\in C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}}$
, which is not empty by (i). Let
![]() $X/L$
be the image of C in
$X/L$
be the image of C in
![]() $Y:=Y_{K}(\mathfrak {N})$
under the map f of assumption (ii). Notice that, since
$Y:=Y_{K}(\mathfrak {N})$
under the map f of assumption (ii). Notice that, since
![]() $C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}}\neq \emptyset $
,
$C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}}\neq \emptyset $
,
![]() $C(\mathbb {A}_{L})^{\text {f-cov}}\neq \emptyset $
, and therefore, by [Reference Stoll39, Proposition 5.9.],
$C(\mathbb {A}_{L})^{\text {f-cov}}\neq \emptyset $
, and therefore, by [Reference Stoll39, Proposition 5.9.],
![]() $X(\mathbb {A}_{L})^{\text {f-cov}}$
and
$X(\mathbb {A}_{L})^{\text {f-cov}}$
and
![]() $Y(\mathbb {A}_{L})^{\text {f-cov}}$
are not empty. The untwisted version of Theorem 2, for a suitable choice of a finite set S of places of L, implies that
$Y(\mathbb {A}_{L})^{\text {f-cov}}$
are not empty. The untwisted version of Theorem 2, for a suitable choice of a finite set S of places of L, implies that
![]() $Y(L)\neq \emptyset $
(this is the only step where (iii) is needed). The proof of Theorem 2 (cf. Section 4.3) actually guarantees the existence of a point in
$Y(L)\neq \emptyset $
(this is the only step where (iii) is needed). The proof of Theorem 2 (cf. Section 4.3) actually guarantees the existence of a point in
![]() $Y(L)$
inducing the fixed
$Y(L)$
inducing the fixed
![]() $f(P_{w})\in Y (\mathbb {A}_{L,S})^{\text {f-cov}}$
. Since
$f(P_{w})\in Y (\mathbb {A}_{L,S})^{\text {f-cov}}$
. Since
![]() $Y(L)$
injects into
$Y(L)$
injects into
![]() $Y(\mathbb {A}_{L,S})^{\text {f-cov}}$
, there exists a unique
$Y(\mathbb {A}_{L,S})^{\text {f-cov}}$
, there exists a unique
![]() $Q \in Y(L)$
inducing
$Q \in Y(L)$
inducing
![]() $f(P_{w})\in Y(\mathbb {A}_{L})^{\text {f-cov}}$
. Moreover, by construction,
$f(P_{w})\in Y(\mathbb {A}_{L})^{\text {f-cov}}$
. Moreover, by construction,
![]() $f(P_{w})$
lies in
$f(P_{w})$
lies in
![]() $X(\mathbb {A}_{L})^{\text {f-cov}}$
, and
$X(\mathbb {A}_{L})^{\text {f-cov}}$
, and
![]() $X(L)=Y(L)\cap X(\mathbb {A}_{L})^{\text {f-cov}}$
. Eventually, we conclude that Q lies in
$X(L)=Y(L)\cap X(\mathbb {A}_{L})^{\text {f-cov}}$
. Eventually, we conclude that Q lies in
![]() $X(L)$
.
$X(L)$
.
Let Z be the finite
![]() ${\mathbb {Q}}$
-subscheme of C given by the
${\mathbb {Q}}$
-subscheme of C given by the
![]() $G_{{\mathbb {Q}}}$
-orbit of the pull-back of Q along the surjective map
$G_{{\mathbb {Q}}}$
-orbit of the pull-back of Q along the surjective map
By construction,
![]() $(P_{w})\in C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}} \subset C(\mathbb {A}_{\mathbb {Q}})^{\text {f-ab}} $
lies in
$(P_{w})\in C(\mathbb {A}_{\mathbb {Q}})^{\text {f-cov}} \subset C(\mathbb {A}_{\mathbb {Q}})^{\text {f-ab}} $
lies in
![]() $Z(\mathbb {A}_{\mathbb {Q}})$
. In particular, [Reference Stoll39, Theorem 8.2] implies that
$Z(\mathbb {A}_{\mathbb {Q}})$
. In particular, [Reference Stoll39, Theorem 8.2] implies that
![]() $Z({\mathbb {Q}})\neq \emptyset $
. That is, C has at least one
$Z({\mathbb {Q}})\neq \emptyset $
. That is, C has at least one
![]() ${\mathbb {Q}}$
-rational point, concluding the proof of the corollary. ▪
${\mathbb {Q}}$
-rational point, concluding the proof of the corollary. ▪
1.3 Conjectures
We briefly state the conjectures appearing in Theorem 1.B.
1.3.1 Absolute Hodge Conjecture
We only give a brief overview for the purpose of understanding the conjecture. For more details, we refer the reader to Deligne–Milne’s paper [Reference Deligne, Milne, Ogus and Shih16, Section 6], where Deligne’s category of absolute motives is described. Let
![]() $X,Y /\mathbb {C}$
be smooth projective varieties. A morphism of Hodge structures between their Betti cohomology groups corresponds to a Hodge class in the cohomology of
$X,Y /\mathbb {C}$
be smooth projective varieties. A morphism of Hodge structures between their Betti cohomology groups corresponds to a Hodge class in the cohomology of
![]() $X\times Y$
:
$X\times Y$
:
 $$ \begin{align*} \mathrm{Hom} \big(H^*_\text {\rm Betti}(X,{\mathbb{Q}}), H^*_\text {\rm Betti}(Y,{\mathbb{Q}}) \big) \cong H^{2*}_\text {\rm Betti}(X\times Y, {\mathbb{Q}}). \end{align*} $$
$$ \begin{align*} \mathrm{Hom} \big(H^*_\text {\rm Betti}(X,{\mathbb{Q}}), H^*_\text {\rm Betti}(Y,{\mathbb{Q}}) \big) \cong H^{2*}_\text {\rm Betti}(X\times Y, {\mathbb{Q}}). \end{align*} $$
We say that a Hodge class
![]() $\alpha \in H^{2i}_{\text {\rm Betti} }(X\times Y, {\mathbb {Q}})$
, or a morphism of Hodge structures between their
$\alpha \in H^{2i}_{\text {\rm Betti} }(X\times Y, {\mathbb {Q}})$
, or a morphism of Hodge structures between their
![]() $H^{i}$
’s, is absolute Hodge if, for every automorphism
$H^{i}$
’s, is absolute Hodge if, for every automorphism
![]() $\sigma $
of
$\sigma $
of
![]() $\mathbb {C}$
, the class
$\mathbb {C}$
, the class
![]() $\alpha ^\sigma \in H^{2i}(X^\sigma \times Y^\sigma , \mathbb {C})$
is again a Hodge class. With this definition, we can split the classical Hodge conjecture into two parts:
$\alpha ^\sigma \in H^{2i}(X^\sigma \times Y^\sigma , \mathbb {C})$
is again a Hodge class. With this definition, we can split the classical Hodge conjecture into two parts:
For the purpose of this paper, the following conjecture is enough.
Conjecture 1.1 If
![]() $X,Y /\mathbb {C}$
are smooth projective complex varieties such that, for some i, we have an isomorphism of Hodge structures
$X,Y /\mathbb {C}$
are smooth projective complex varieties such that, for some i, we have an isomorphism of Hodge structures
then there exists an absolute Hodge class inducing this isomorphism.
More precisely, Conjecture 1.1 will be applied when X is a Picard modular variety and Y is an abelian variety.
1.3.2 Serre’s Weak Conjecture Over Totally Real Fields
We now explain the version of Serre’s conjecture we need to assume to obtain the main theorems when
![]() $L\neq {\mathbb {Q}}$
(see, for example, [Reference Buzzard, Diamond and Jarvis10, Conjecture 1.1], where it is referred to as a folklore generalisation of Serre’s conjecture). For more details, we refer the reader to the introduction of [Reference Buzzard, Diamond and Jarvis10] and references therein. Given a prime
$L\neq {\mathbb {Q}}$
(see, for example, [Reference Buzzard, Diamond and Jarvis10, Conjecture 1.1], where it is referred to as a folklore generalisation of Serre’s conjecture). For more details, we refer the reader to the introduction of [Reference Buzzard, Diamond and Jarvis10] and references therein. Given a prime
![]() $\ell ,$
we denote by
$\ell ,$
we denote by
![]() $\mathbb {F}_\ell $
a finite field with
$\mathbb {F}_\ell $
a finite field with
![]() $\ell $
elements and by
$\ell $
elements and by
![]() $\overline {\mathbb {F}}_\ell $
a fixed algebraic closure of
$\overline {\mathbb {F}}_\ell $
a fixed algebraic closure of
![]() $\mathbb {F}_\ell $
.
$\mathbb {F}_\ell $
.
Conjecture 1.2 Let
![]() $\ell $
be any odd prime and
$\ell $
be any odd prime and
![]() $\overline {\rho }: G_{L} \to \mathrm {GL}_{2}( \overline {\mathbb {F}}_\ell )$
be an irreducible and totally oddFootnote
1
Galois representation. Then there exists some Hilbert modular eigenform f for L such that
$\overline {\rho }: G_{L} \to \mathrm {GL}_{2}( \overline {\mathbb {F}}_\ell )$
be an irreducible and totally oddFootnote
1
Galois representation. Then there exists some Hilbert modular eigenform f for L such that
![]() $\overline {\rho }$
is isomorphic to the reduction mod
$\overline {\rho }$
is isomorphic to the reduction mod
![]() $\lambda $
of
$\lambda $
of
![]() $\rho _{f,\lambda }$
, where
$\rho _{f,\lambda }$
, where
![]() $\rho _{f,\lambda }$
is the
$\rho _{f,\lambda }$
is the
![]() $\lambda $
-adic Galois representation attached to f and
$\lambda $
-adic Galois representation attached to f and
![]() $\lambda $
is a prime of the Hecke field of f dividing
$\lambda $
is a prime of the Hecke field of f dividing
![]() $\ell $
.
$\ell $
.
Remark 1.1 This is usually referred to as weak Serre’s conjecture, because there is no explicit recipe to compute the weight
![]() $k(\overline {\rho })$
and the level
$k(\overline {\rho })$
and the level
![]() $N(\overline {\rho })$
. It has been proven [Reference Gee, Liu and Savitt23, Reference Fujiwara22] that the refined version follows from the weak version under some assumptions. We state the results we need in Theorem 3.4.
$N(\overline {\rho })$
. It has been proven [Reference Gee, Liu and Savitt23, Reference Fujiwara22] that the refined version follows from the weak version under some assumptions. We state the results we need in Theorem 3.4.
When
![]() $L={\mathbb {Q}}$
, this was proved by Khare and Wintenberger [Reference Khare and Wintenberger27]. When
$L={\mathbb {Q}}$
, this was proved by Khare and Wintenberger [Reference Khare and Wintenberger27]. When
![]() $L\neq {\mathbb {Q}}$
, Conjecture 1.2 is known when the coefficient field is
$L\neq {\mathbb {Q}}$
, Conjecture 1.2 is known when the coefficient field is
![]() $\mathbb {F}_{3}$
(Langlands–Tunnell [Reference Langlands29, Reference Tunnell42]), but we really need to assume that the conjecture holds for all (but finitely many)
$\mathbb {F}_{3}$
(Langlands–Tunnell [Reference Langlands29, Reference Tunnell42]), but we really need to assume that the conjecture holds for all (but finitely many)
![]() $\ell $
’s. Indeed, our strategy follows the lines of the proof of modularity theorems assuming Serre’s conjecture: starting from a system of Galois representations, we produce a Hilbert modular form whose Fourier coefficients are equal to the traces of Frobenii modulo infinitely many primes, and hence are equal as elements of
$\ell $
’s. Indeed, our strategy follows the lines of the proof of modularity theorems assuming Serre’s conjecture: starting from a system of Galois representations, we produce a Hilbert modular form whose Fourier coefficients are equal to the traces of Frobenii modulo infinitely many primes, and hence are equal as elements of
![]() $\mathcal {O}_{K}$
.
$\mathcal {O}_{K}$
.
Finally, a potential version of the above conjecture was proved in [Reference Taylor41, Theorem 1.6]. There, Taylor proves a potential modularity result: if
![]() $\bar {\rho }: G_{L}\to \mathrm {GL}_{2}(\overline {\mathbb {F}}_{\ell })$
is a totally odd irreducible representation with determinant equal to the cyclotomic character, then there exists
$\bar {\rho }: G_{L}\to \mathrm {GL}_{2}(\overline {\mathbb {F}}_{\ell })$
is a totally odd irreducible representation with determinant equal to the cyclotomic character, then there exists
![]() $L'/L$
a finite totally real Galois extension such that all the primes of L above
$L'/L$
a finite totally real Galois extension such that all the primes of L above
![]() $\ell $
split in
$\ell $
split in
![]() $L',$
and there exists f a Hilbert modular form for
$L',$
and there exists f a Hilbert modular form for
![]() $L'$
such that
$L'$
such that
![]() $\bar {\rho }_{f,\lambda '}$
is isomorphic to
$\bar {\rho }_{f,\lambda '}$
is isomorphic to
![]() $\bar {\rho }$
restricted to
$\bar {\rho }$
restricted to
![]() $G_{L'}$
.
$G_{L'}$
.
1.4 Related Work
We compare our results with [Reference Patrikis, Voloch and Zarhin32, Theorems 3.1 and 3.7] (later also extended to the moduli space of K3 surfaces by the first author [Reference Baldi3, Theorem 1.3] and Klevdal [Reference Klevdal28, Theorem 1.1], where a finite extension of the base field is, however, required). In the approach of Patrikis, Voloch, and Zarhin, there are no restrictions on the base field, whereas here it is crucial for L to be a totally real field. We believe that it is easier to make the results of this paper unconditional. We notice here that the absolute Hodge conjecture is not enough for such papers. In [Reference Patrikis, Voloch and Zarhin32, Reference Baldi3, Reference Klevdal28], the Hodge conjecture is not only needed to descend complex abelian varieties over number fields. Finally, the version of Serre’s conjecture we are assuming here is always about
![]() $\mathrm {GL}_{2}$
-coefficients, and so is certainly easier than the full Fontaine–Mazur conjecture [Reference Fontaine and Mazur19].
$\mathrm {GL}_{2}$
-coefficients, and so is certainly easier than the full Fontaine–Mazur conjecture [Reference Fontaine and Mazur19].
Thanks to the recent breakthroughs on potential modularity over CM fields [Reference Allen, Calegari, Caraiani, Gee, Helm, Le Hung, Newton, Scholze, Taylor and Thorne1], it should be possible to extract from the main result of [Reference Allen, Calegari, Caraiani, Gee, Helm, Le Hung, Newton, Scholze, Taylor and Thorne1, Section 7.1] the following. Let
![]() $\{\rho _{v}\}_{v}$
be a compatible system as in Section 1.2, and let
$\{\rho _{v}\}_{v}$
be a compatible system as in Section 1.2, and let
![]() $n_{L}>1$
. Under the validity of Conjecture 1.1, there exist a totally real extension
$n_{L}>1$
. Under the validity of Conjecture 1.1, there exist a totally real extension
![]() $L'/L$
and
$L'/L$
and
![]() $n_{K}$
-dimensional abelian variety
$n_{K}$
-dimensional abelian variety
![]() $A/L'$
with
$A/L'$
with
![]() $\mathcal {O}_{K}$
-multiplication, such that, for every v,
$\mathcal {O}_{K}$
-multiplication, such that, for every v,
![]() $T_{v} A$
is isomorphic to
$T_{v} A$
is isomorphic to
![]() $\rho _{v}$
as representations of
$\rho _{v}$
as representations of
![]() $G_{L'}$
.
$G_{L'}$
.
Since Conjecture 1.1 can be avoided in many interesting cases, as recalled in Remark 2.7, a potential but unconditional version of Theorem 2 can therefore be obtained. Unfortunately, the extension
![]() $L'/L$
depends on the system of Galois representations
$L'/L$
depends on the system of Galois representations
![]() $\{\rho _{v}\}_{v}$
, and it is not easy to control a priori its degree over L.
$\{\rho _{v}\}_{v}$
, and it is not easy to control a priori its degree over L.
1.5 Outline of the Paper
In Section 2, we collect all the results we need about Hilbert modular forms (especially how Eichler–Shimura works in this setting). In Section 3, which is the heart of the paper, we prove Theorems 1.A and 1.B. We then explain how these results are related to the finite descent obstruction for Hilbert modular varieties in Section 4, eventually proving Theorem 2.
2 Recap on Hilbert Modular Varieties and Modular Forms
We recall some general facts about Shimura varieties. The reader interested only in Hilbert modular varieties can skip Section 2.1, which is not fundamental for the main results. We then focus on Hilbert modular varieties and Hilbert modular forms, explaining how they give rise to certain principally polarised abelian varieties.
2.1 A Question on Rational Points on Shimura Varieties
Let
![]() $\mathbb{S} $
denote the real torus
$\mathbb{S} $
denote the real torus
![]() $\mathrm {Res}_{\mathbb {C} / \mathbb {R}} (\mathbb {G}_m)$
, and let
$\mathrm {Res}_{\mathbb {C} / \mathbb {R}} (\mathbb {G}_m)$
, and let
 $\mathbb {A}_{\mathbb {Q}}^{f} $
be the finite adeles of
$\mathbb {A}_{\mathbb {Q}}^{f} $
be the finite adeles of
![]() ${\mathbb {Q}}$
. A Shimura datum is a pair
${\mathbb {Q}}$
. A Shimura datum is a pair
![]() $(G,X)$
where G is a reductive
$(G,X)$
where G is a reductive
![]() ${\mathbb {Q}}$
-algebraic group and X a
${\mathbb {Q}}$
-algebraic group and X a
![]() $G(\mathbb {R})$
-orbit in the set of morphisms of
$G(\mathbb {R})$
-orbit in the set of morphisms of
![]() $\mathbb {R}$
-algebraic groups
$\mathbb {R}$
-algebraic groups
![]() $\mathrm {Hom}(\mathbb{S} , G_{\mathbb {R}})$
, satisfying the Shimura–Deligne axioms ([Reference Deligne15, Conditions 2.1.1(1-3)]); furthermore, in what follows, we also assume that G is the generic Mumford–Tate group on X. The Shimura–Deligne axioms imply that the connected components of X are hermitian symmetric domains and that faithful representations of G induce variations of polarisable
$\mathrm {Hom}(\mathbb{S} , G_{\mathbb {R}})$
, satisfying the Shimura–Deligne axioms ([Reference Deligne15, Conditions 2.1.1(1-3)]); furthermore, in what follows, we also assume that G is the generic Mumford–Tate group on X. The Shimura–Deligne axioms imply that the connected components of X are hermitian symmetric domains and that faithful representations of G induce variations of polarisable
![]() ${\mathbb {Q}}$
-Hodge structures on X. Let
${\mathbb {Q}}$
-Hodge structures on X. Let
![]() $\widetilde {K}$
be a compact open subgroup of
$\widetilde {K}$
be a compact open subgroup of
 $G(\mathbb {A}_{\mathbb {Q}}^{f})$
and set
$G(\mathbb {A}_{\mathbb {Q}}^{f})$
and set
 $$ \begin{align*} \mathrm{Sh}_{\widetilde{K}}(G,X) := G({\mathbb{Q}}) \backslash \big ( X \times G(\mathbb{A}_{\mathbb{Q}}^{f}) / \widetilde{K} \big). \end{align*} $$
$$ \begin{align*} \mathrm{Sh}_{\widetilde{K}}(G,X) := G({\mathbb{Q}}) \backslash \big ( X \times G(\mathbb{A}_{\mathbb{Q}}^{f}) / \widetilde{K} \big). \end{align*} $$
Let
![]() $X^+$
be a connected component of X and let
$X^+$
be a connected component of X and let
![]() $G({\mathbb {Q}})^+$
be the stabiliser of
$G({\mathbb {Q}})^+$
be the stabiliser of
![]() $X^+$
in
$X^+$
in
![]() $G({\mathbb {Q}})$
. The above double coset set is a disjoint union of quotients of
$G({\mathbb {Q}})$
. The above double coset set is a disjoint union of quotients of
![]() $X^+$
by the arithmetic groups
$X^+$
by the arithmetic groups
![]() $\Gamma _{g}:=G({\mathbb {Q}})^+ \cap gKg^{-1}$
, where g runs through a set of representatives for the finite double coset set
$\Gamma _{g}:=G({\mathbb {Q}})^+ \cap gKg^{-1}$
, where g runs through a set of representatives for the finite double coset set
 $G({\mathbb {Q}})^+ \backslash G(\mathbb {A}_{\mathbb {Q}}^{f} )/K$
. Baily and Borel [Reference Baily and Borel2] proved that
$G({\mathbb {Q}})^+ \backslash G(\mathbb {A}_{\mathbb {Q}}^{f} )/K$
. Baily and Borel [Reference Baily and Borel2] proved that
![]() $\mathrm {Sh}_{\widetilde {K}}(G,X)$
has a unique structure of a quasi-projective complex algebraic variety. Thanks to the work of Borovoi, Deligne, Milne, and Milne–Shih, among others, the
$\mathrm {Sh}_{\widetilde {K}}(G,X)$
has a unique structure of a quasi-projective complex algebraic variety. Thanks to the work of Borovoi, Deligne, Milne, and Milne–Shih, among others, the
![]() $\mathbb {C}$
-scheme
$\mathbb {C}$
-scheme
 $$ \begin{align*} \mathrm{Sh} (G,X)= G({\mathbb{Q}}) \backslash \Big ( X \times G\big(\mathbb{A}_{\mathbb{Q}}^{f}\big) \Big), \end{align*} $$
$$ \begin{align*} \mathrm{Sh} (G,X)= G({\mathbb{Q}}) \backslash \Big ( X \times G\big(\mathbb{A}_{\mathbb{Q}}^{f}\big) \Big), \end{align*} $$
together with its
 $G(\mathbb {A}_{\mathbb {Q}}^{f})$
-action, can be naturally defined over a number field
$G(\mathbb {A}_{\mathbb {Q}}^{f})$
-action, can be naturally defined over a number field
![]() $E:= E(G,X) \subset \mathbb {C}$
called the reflex field of
$E:= E(G,X) \subset \mathbb {C}$
called the reflex field of
![]() $(G,X)$
. That is, there exists an E-scheme
$(G,X)$
. That is, there exists an E-scheme
![]() $\mathrm {Sh} (G,X)_{E}$
with an action of
$\mathrm {Sh} (G,X)_{E}$
with an action of
 $G(\mathbb {A}_{\mathbb {Q}}^{f})$
whose base change to
$G(\mathbb {A}_{\mathbb {Q}}^{f})$
whose base change to
![]() $\mathbb {C}$
gives
$\mathbb {C}$
gives
![]() $\mathrm {Sh} (G,X)$
with its
$\mathrm {Sh} (G,X)$
with its
 $G(\mathbb {A}_{\mathbb {Q}}^{f})$
-action.
$G(\mathbb {A}_{\mathbb {Q}}^{f})$
-action.
Let F be a finite extension of E such that there exists a point
![]() $x \in \mathrm {Sh}_{\widetilde {K}}(G,X)_{E}(F)$
. With such a point, we can naturally associate a continuous group homomorphism
$x \in \mathrm {Sh}_{\widetilde {K}}(G,X)_{E}(F)$
. With such a point, we can naturally associate a continuous group homomorphism
 $$ \begin{align*} \rho_{x} : G_{F}:=\mathrm{Gal}(\overline{F}/F) \longrightarrow \widetilde{K} \subset G(\mathbb{A}_{\mathbb{Q}}^{f}). \end{align*} $$
$$ \begin{align*} \rho_{x} : G_{F}:=\mathrm{Gal}(\overline{F}/F) \longrightarrow \widetilde{K} \subset G(\mathbb{A}_{\mathbb{Q}}^{f}). \end{align*} $$
This paper is motivated by the following question.
Question 2.1 Let F be a field as above and let
 $\rho : G_{F} \to \widetilde {K} \subset G(\mathbb {A}_{\mathbb {Q}}^{f})$
be a Galois representation. What are necessary and sufficient conditions such that there exists
$\rho : G_{F} \to \widetilde {K} \subset G(\mathbb {A}_{\mathbb {Q}}^{f})$
be a Galois representation. What are necessary and sufficient conditions such that there exists
![]() $x \in \mathrm {Sh}_{\widetilde {K}}(G,X)_{E}(F)$
and
$x \in \mathrm {Sh}_{\widetilde {K}}(G,X)_{E}(F)$
and
![]() $\rho = \rho _{x}$
?
$\rho = \rho _{x}$
?
When the Shimura variety has a natural interpretation as a moduli space of motives, the above question is naturally related to the Fontaine–Mazur conjecture [Reference Fontaine and Mazur19]. Indeed, both aim to predict when a Galois representation comes from the
![]() $\ell $
-adic (or adelic in our case) realisation of a motive. Even when they are not motivical (see [Reference Baldi4, Remark 1.6] for a discussion about this), representations arising in this way enjoy nice properties. For an example of geometric flavour, we refer the reader to [Reference Baldi4, Theorem 1.3].
$\ell $
-adic (or adelic in our case) realisation of a motive. Even when they are not motivical (see [Reference Baldi4, Remark 1.6] for a discussion about this), representations arising in this way enjoy nice properties. For an example of geometric flavour, we refer the reader to [Reference Baldi4, Theorem 1.3].
2.2 Hilbert Modular Varieties
Let
![]() $F/{\mathbb {Q}}$
be a totally real extension of degree
$F/{\mathbb {Q}}$
be a totally real extension of degree
![]() $n_{F}$
and fix
$n_{F}$
and fix
![]() $\{\sigma _{i}\}_{i=1}^{n_{F}}$
the set of real embeddings of F into
$\{\sigma _{i}\}_{i=1}^{n_{F}}$
the set of real embeddings of F into
![]() $\mathbb {C}$
. We let G be the
$\mathbb {C}$
. We let G be the
![]() ${\mathbb {Q}}$
-algebraic group obtained as the Weil restriction of
${\mathbb {Q}}$
-algebraic group obtained as the Weil restriction of
![]() $\mathrm {GL}_{2}$
from F to
$\mathrm {GL}_{2}$
from F to
![]() ${\mathbb {Q}}$
and let X be
${\mathbb {Q}}$
and let X be
![]() $n_{F}$
copies of
$n_{F}$
copies of
![]() $\mathcal {H}^{\pm }=\{\tau \in \mathbb {C}: \mathrm {Im}(\tau )\neq 0\}$
, on which
$\mathcal {H}^{\pm }=\{\tau \in \mathbb {C}: \mathrm {Im}(\tau )\neq 0\}$
, on which
![]() $G({\mathbb {Q}})=\mathrm {GL}_{2}(F)$
acts on the i-th component via
$G({\mathbb {Q}})=\mathrm {GL}_{2}(F)$
acts on the i-th component via
![]() $\sigma _{i}$
. That is,
$\sigma _{i}$
. That is,
 $$ \begin{align*} \bigg( \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot (\tau_{1},\ldots,\tau_{n_{F}})\bigg)_{i} = \frac{\sigma_{i}(a) \tau_{i}+\sigma_{i}(b)}{\sigma_{i}(c)\tau_{i}+\sigma_{i}(d)}. \end{align*} $$
$$ \begin{align*} \bigg( \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot (\tau_{1},\ldots,\tau_{n_{F}})\bigg)_{i} = \frac{\sigma_{i}(a) \tau_{i}+\sigma_{i}(b)}{\sigma_{i}(c)\tau_{i}+\sigma_{i}(d)}. \end{align*} $$
In this case, the reflex field of
![]() $(G,X)$
is
$(G,X)$
is
![]() ${\mathbb {Q}}$
, and the set of geometrically connected components of the Shimura variety
${\mathbb {Q}}$
, and the set of geometrically connected components of the Shimura variety
 $S:=\mathrm {Sh}_{G(\widehat {\mathbb {Z}})}(G,X)$
is
$S:=\mathrm {Sh}_{G(\widehat {\mathbb {Z}})}(G,X)$
is
![]() $\mathrm {Pic}(\mathcal {O}_{F})^+$
, where
$\mathrm {Pic}(\mathcal {O}_{F})^+$
, where
![]() $\widehat {\mathbb {Z}}$
denotes the profinite completion of
$\widehat {\mathbb {Z}}$
denotes the profinite completion of
![]() $\mathbb {Z}$
(different choices of level structure will appear later).
$\mathbb {Z}$
(different choices of level structure will appear later).
Remark 2.1 To obtain a Shimura variety from the above construction, it is fundamental that F is totally real. Indeed, if F is a number field, and G is an algebraic F-group, then the real points of
![]() $\mathrm {Res}_{F/{\mathbb {Q}}}G$
have a structure of Hermitian symmetric space if and only if F is a totally real field and the symmetric space associated with each real embedding of F is Hermitian.
$\mathrm {Res}_{F/{\mathbb {Q}}}G$
have a structure of Hermitian symmetric space if and only if F is a totally real field and the symmetric space associated with each real embedding of F is Hermitian.
It is interesting to notice here a first difference between modular curves (i.e., when
![]() $F={\mathbb {Q}}$
) and higher dimensional Hilbert modular varieties. We recall the following folklore result (see [Reference Blasius6, Section 2.3.2.]) to see how it follows from Matsushima’s formula [Reference Borel and Wallach8, Theorem VII.5.2].
$F={\mathbb {Q}}$
) and higher dimensional Hilbert modular varieties. We recall the following folklore result (see [Reference Blasius6, Section 2.3.2.]) to see how it follows from Matsushima’s formula [Reference Borel and Wallach8, Theorem VII.5.2].
Theorem 2.2 Let
![]() $(G,X)$
be a Shimura datum as above and let
$(G,X)$
be a Shimura datum as above and let
![]() $\widetilde {K}$
be a neatFootnote
2
subgroup of
$\widetilde {K}$
be a neatFootnote
2
subgroup of
 $G(\mathbb {A}_{{\mathbb {Q}}}^{f})$
. Consider
$G(\mathbb {A}_{{\mathbb {Q}}}^{f})$
. Consider
![]() $S_{\widetilde {K}}$
, the Shimura variety associated with
$S_{\widetilde {K}}$
, the Shimura variety associated with
![]() $(G,X)$
and
$(G,X)$
and
![]() $\widetilde {K}$
. Unless
$\widetilde {K}$
. Unless
![]() $n_{F}=1$
, the first group of Betti cohomology of
$n_{F}=1$
, the first group of Betti cohomology of
![]() $S_{\widetilde {K}}$
with rational coefficients is trivial. In particular, there are no non-constant maps from
$S_{\widetilde {K}}$
with rational coefficients is trivial. In particular, there are no non-constant maps from
![]() $S_{\widetilde {K}}$
to an abelian variety.
$S_{\widetilde {K}}$
to an abelian variety.
To have a better interpretation as moduli space, we actually consider the subgroup
![]() $G^*$
of G given by its elements whose determinant is in
$G^*$
of G given by its elements whose determinant is in
![]() ${\mathbb {Q}}$
. More precisely, we let
${\mathbb {Q}}$
. More precisely, we let
![]() $G^*$
be the pull-back of
$G^*$
be the pull-back of
to
![]() $\mathbb {G}_m/{\mathbb {Q}}$
. The Shimura variety
$\mathbb {G}_m/{\mathbb {Q}}$
. The Shimura variety
 $Y_{F}:=\mathrm {Sh}_{G^*(\widehat {\mathbb {Z}})}(G^*,X^*)(\mathbb {C})$
is connected and comes with a finite map to
$Y_{F}:=\mathrm {Sh}_{G^*(\widehat {\mathbb {Z}})}(G^*,X^*)(\mathbb {C})$
is connected and comes with a finite map to
![]() $S/\mathbb {C}$
. It is a quasi projective
$S/\mathbb {C}$
. It is a quasi projective
![]() $n_{F}$
-dimensional
$n_{F}$
-dimensional
![]() ${\mathbb {Q}}$
-scheme.
${\mathbb {Q}}$
-scheme.
In the next section, we present the moduli problem solved by
![]() $Y_{F}$
. It will be also clear from such moduli interpretation that the reflex field of
$Y_{F}$
. It will be also clear from such moduli interpretation that the reflex field of
![]() $Y_{F}$
is the field of rational numbers.
$Y_{F}$
is the field of rational numbers.
2.2.1 Hilbert Modular Varieties as Moduli Spaces
As explained, for example, in [Reference Edixhoven17, Section 3], the Shimura variety
![]() $Y_{F}$
represents the (coarse) moduli space for triplets
$Y_{F}$
represents the (coarse) moduli space for triplets
![]() $(A, \alpha , \lambda )$
where:
$(A, \alpha , \lambda )$
where:
-
• A is a complex abelian variety of dimension
 $n_{F}$
;
$n_{F}$
; -
•
 $\alpha : \mathcal {O}_{F} \hookrightarrow \mathrm {End} (A)$
is a morphism of rings;
$\alpha : \mathcal {O}_{F} \hookrightarrow \mathrm {End} (A)$
is a morphism of rings; -
•
 $\lambda : A \to A^*$
is a principal
$\lambda : A \to A^*$
is a principal
 $\mathcal {O}_{F}$
-polarisation.
$\mathcal {O}_{F}$
-polarisation.
By
![]() $A^*,$
we denoted the
$A^*,$
we denoted the
![]() $\mathcal {O}_{F}$
-dual abelian variety of A, i.e,. it is defined as
$\mathcal {O}_{F}$
-dual abelian variety of A, i.e,. it is defined as
![]() $\mathrm {Ext}^{1}(A,\mathcal {O}_{F}\otimes \mathbb {G}_m)$
. Otherwise, one can obtain such abelian variety considering
$\mathrm {Ext}^{1}(A,\mathcal {O}_{F}\otimes \mathbb {G}_m)$
. Otherwise, one can obtain such abelian variety considering
![]() $A^\vee $
(the dual of A, in the standard sense) and tensoring it over
$A^\vee $
(the dual of A, in the standard sense) and tensoring it over
![]() $\mathcal {O}_{F}$
with the different ideal of the extension
$\mathcal {O}_{F}$
with the different ideal of the extension
![]() $F/{\mathbb {Q}}$
. By principal
$F/{\mathbb {Q}}$
. By principal
![]() $\mathcal {O}_{F}$
-polarisation we mean an isomorphism
$\mathcal {O}_{F}$
-polarisation we mean an isomorphism
![]() $\lambda : A \to A^*$
, such that the induced map
$\lambda : A \to A^*$
, such that the induced map
![]() $A\to A^\vee $
is a polarisation.
$A\to A^\vee $
is a polarisation.
Furthermore, the Shimura variety of level
 $$ \begin{align*} U_{0}(\mathfrak{N}):= \big\lbrace \gamma\in G(\widehat{\mathbb{Z}}): \gamma \equiv \bigg(\begin{matrix}* &*\\0& 1\end{matrix}\bigg) \text{ mod } \mathfrak{N}\big\rbrace, \end{align*} $$
$$ \begin{align*} U_{0}(\mathfrak{N}):= \big\lbrace \gamma\in G(\widehat{\mathbb{Z}}): \gamma \equiv \bigg(\begin{matrix}* &*\\0& 1\end{matrix}\bigg) \text{ mod } \mathfrak{N}\big\rbrace, \end{align*} $$
where
![]() $\mathfrak {N}$
is an integral ideal of
$\mathfrak {N}$
is an integral ideal of
![]() $\mathcal {O}_{F}$
, parametrises triplets as above, equipped with a
$\mathcal {O}_{F}$
, parametrises triplets as above, equipped with a
![]() $\mathfrak {N}$
-level structure as follows. We fix an isomorphism of
$\mathfrak {N}$
-level structure as follows. We fix an isomorphism of
![]() $\mathcal {O}_{F}$
-modules
$\mathcal {O}_{F}$
-modules
 $$ \begin{align*} \big(\mathcal{O}_{F}/\mathfrak{N} \mathcal{O}_{F} \big)^{2} \to A[\mathfrak{N}] \end{align*} $$
$$ \begin{align*} \big(\mathcal{O}_{F}/\mathfrak{N} \mathcal{O}_{F} \big)^{2} \to A[\mathfrak{N}] \end{align*} $$
making the following diagram commutative:

where
![]() $(N)=\mathbb {Z}\cap \mathfrak {N}$
,
$(N)=\mathbb {Z}\cap \mathfrak {N}$
,
![]() $\psi _{\mathfrak {N}}$
is the pairing given by
$\psi _{\mathfrak {N}}$
is the pairing given by
 $\bigg(\begin{matrix}0 &1\\-1&0\end{matrix}\bigg)$
,
$\bigg(\begin{matrix}0 &1\\-1&0\end{matrix}\bigg)$
,
![]() $e_{\lambda ,\mathfrak {N}}$
is the perfect Weil pairing on
$e_{\lambda ,\mathfrak {N}}$
is the perfect Weil pairing on
![]() $A[\mathfrak {N}]$
induced by the
$A[\mathfrak {N}]$
induced by the
![]() $\mathcal {O}_{F}$
-polarisation
$\mathcal {O}_{F}$
-polarisation
![]() $\lambda ,$
and
$\lambda ,$
and
![]() $\mathcal {O}_{F}\otimes \mathbb {Z}/N\mathbb {Z}\to \mathcal {O}_{F} \otimes \mu _{N}$
is an arbitrarily chosen isomorphism. When a level structure is needed, we always assume that
$\mathcal {O}_{F}\otimes \mathbb {Z}/N\mathbb {Z}\to \mathcal {O}_{F} \otimes \mu _{N}$
is an arbitrarily chosen isomorphism. When a level structure is needed, we always assume that
![]() $N>3$
in order to have a fine moduli space. A rational point of
$N>3$
in order to have a fine moduli space. A rational point of
![]() $Y_{F}(\mathfrak {N}):=\mathrm {Sh}_{U_{0}(\mathfrak {N})\cap G^*}(G^*,X)$
then represents a triple, as above, together with such level structure. In Section 4.2, we will see a similar description for
$Y_{F}(\mathfrak {N}):=\mathrm {Sh}_{U_{0}(\mathfrak {N})\cap G^*}(G^*,X)$
then represents a triple, as above, together with such level structure. In Section 4.2, we will see a similar description for
![]() $\mathcal {O}_{L,S}$
-points of an integral model of
$\mathcal {O}_{L,S}$
-points of an integral model of
![]() $Y_{F}(\mathfrak {N})$
.
$Y_{F}(\mathfrak {N})$
.
2.3 Eichler–Shimura Theory
We discuss Eichler–Shimura theory for classical and Hilbert modular forms, reviewing results that attach opportune abelian varieties to modular forms.
2.3.1 Classical Modular Eigenform
The following is [Reference Shimura37, Theorem 7.14, p. 183 and Theorem 7.24, p. 194].
Theorem 2.3 (Shimura)
Let f be a holomorphic newform of weight
![]() $2$
with rational Fourier coefficients
$2$
with rational Fourier coefficients
![]() $(a_{n}(f))_{n}$
. There exists an elliptic curve
$(a_{n}(f))_{n}$
. There exists an elliptic curve
![]() $E/{\mathbb {Q}}$
such that, for all primes p at which E has good reduction, one has
$E/{\mathbb {Q}}$
such that, for all primes p at which E has good reduction, one has
where
![]() $N_{p}(E)$
denotes the number of points of the reduction mod p of E, over the field with p-elements. In other words, up to a finite number of Euler factors,
$N_{p}(E)$
denotes the number of points of the reduction mod p of E, over the field with p-elements. In other words, up to a finite number of Euler factors,
![]() $L(s,E/{\mathbb {Q}})$
and
$L(s,E/{\mathbb {Q}})$
and
![]() $L(s,f)$
coincide.
$L(s,f)$
coincide.
More generally, let
![]() $K(f)$
be the subfield of
$K(f)$
be the subfield of
![]() $\mathbb {C}$
generated over
$\mathbb {C}$
generated over
![]() ${\mathbb {Q}}$
by
${\mathbb {Q}}$
by
![]() $(a_{n}(f))_{n}$
for all n. Then there exists an abelian variety
$(a_{n}(f))_{n}$
for all n. Then there exists an abelian variety
![]() $A/{\mathbb {Q}}$
and an isomorphism
$A/{\mathbb {Q}}$
and an isomorphism
 $K(f) \cong \mathrm {End}^{0}(A)$
with the following properties:
$K(f) \cong \mathrm {End}^{0}(A)$
with the following properties:
-
•
 $\dim (A)=[K(f):{\mathbb {Q}}]$
;
$\dim (A)=[K(f):{\mathbb {Q}}]$
; -
• up to a finite number of Euler factors at primes at which A has good reduction,
 $L(s,A/{\mathbb {Q}},K(f))$
coincides with
$L(s,A/{\mathbb {Q}},K(f))$
coincides with
 $L(s,f)$
;
$L(s,f)$
;
where the L-function
![]() $L(s,A/{\mathbb {Q}},K(f))$
is defined by the product of the following local factors where v is a prime of
$L(s,A/{\mathbb {Q}},K(f))$
is defined by the product of the following local factors where v is a prime of
![]() $K(f)$
not dividing
$K(f)$
not dividing
![]() $\ell $
$\ell $
 $$ \begin{align*} \det\big(1-\ell^{-s}\operatorname{Frob}_{\ell}|T_{v}(A)\big). \end{align*} $$
$$ \begin{align*} \det\big(1-\ell^{-s}\operatorname{Frob}_{\ell}|T_{v}(A)\big). \end{align*} $$
Shimura considers the Jacobian of the modular curve of level N and takes the quotient by the kernel of the homomorphism giving the Hecke action on f. What happens if we want to produce an abelian variety with such properties, defined over our totally real field F, when
![]() ${\mathbb {Q}}\subsetneq F$
? Here is where Hilbert modular forms come into play. In the next section, we recall what we need from such theory, and explain Blasius’ generalisation of Theorem 2.3 and why the absolute Hodge conjecture is needed.
${\mathbb {Q}}\subsetneq F$
? Here is where Hilbert modular forms come into play. In the next section, we recall what we need from such theory, and explain Blasius’ generalisation of Theorem 2.3 and why the absolute Hodge conjecture is needed.
2.3.2 Hilbert Modular Forms for F
Let
![]() $\mathcal {H}_{F}$
denote
$\mathcal {H}_{F}$
denote
![]() $n_{F}$
copies of the upper half plane
$n_{F}$
copies of the upper half plane
![]() $\mathcal {H}^+$
. We consider subgroups
$\mathcal {H}^+$
. We consider subgroups
![]() $\Gamma \subset \mathrm {GL}_{2}(\mathcal {O}_{F})$
of the form
$\Gamma \subset \mathrm {GL}_{2}(\mathcal {O}_{F})$
of the form
![]() $U_{0}(\mathfrak {N}) \cap G({\mathbb {Q}})^+$
. Moreover, for
$U_{0}(\mathfrak {N}) \cap G({\mathbb {Q}})^+$
. Moreover, for
![]() $\lambda \in F$
and
$\lambda \in F$
and
![]() $\underline {r}=(r_{1},\ldots , r_{n_{F}})\in \mathbb {Z}^{n_{F}}$
, we write
$\underline {r}=(r_{1},\ldots , r_{n_{F}})\in \mathbb {Z}^{n_{F}}$
, we write
 $\lambda ^{\underline {r}}=\lambda _{1}^{r_{1}}\cdots \lambda _{n_{F}}^{r_{n_{F}}}$
, where
$\lambda ^{\underline {r}}=\lambda _{1}^{r_{1}}\cdots \lambda _{n_{F}}^{r_{n_{F}}}$
, where
![]() $\lambda _{i}=\sigma _{i}(\lambda )$
. Similarly, if
$\lambda _{i}=\sigma _{i}(\lambda )$
. Similarly, if
![]() $\underline {\tau }=(\tau _{1},\ldots ,\tau _{n_{F}})\in \mathcal {H}_{F}$
, we write
$\underline {\tau }=(\tau _{1},\ldots ,\tau _{n_{F}})\in \mathcal {H}_{F}$
, we write
 $\underline {\tau }^{\lambda }=\tau _{1}^{r_{1}}\cdots \tau _{n_{F}}^{r_{n_{F}}}$
.
$\underline {\tau }^{\lambda }=\tau _{1}^{r_{1}}\cdots \tau _{n_{F}}^{r_{n_{F}}}$
.
Definition 2.1 A Hilbert modular form of level
![]() $\mathfrak {N}$
and weight
$\mathfrak {N}$
and weight
![]() $(\underline {r},w)\in \mathbb {Z}^{n_{F}}\times \mathbb {Z}$
, with
$(\underline {r},w)\in \mathbb {Z}^{n_{F}}\times \mathbb {Z}$
, with
![]() $r_{i}\equiv w \mod 2$
(and trivial nebentype character) is a holomorphic function
$r_{i}\equiv w \mod 2$
(and trivial nebentype character) is a holomorphic function
![]() $f: \mathcal {H}_{F} \rightarrow \mathbb {C}$
such that
$f: \mathcal {H}_{F} \rightarrow \mathbb {C}$
such that
 $$ \begin{align*} f(\gamma \cdot \underline{\tau})= (\det\gamma)^{-\underline{r}/2}(c\underline{\tau}+d)^{\underline{r}}f(\underline{\tau}), \end{align*} $$
$$ \begin{align*} f(\gamma \cdot \underline{\tau})= (\det\gamma)^{-\underline{r}/2}(c\underline{\tau}+d)^{\underline{r}}f(\underline{\tau}), \end{align*} $$
for every
 $\gamma =\bigg(\begin{matrix}a & b \\ c & d\end{matrix}\bigg) \in U_{0}(\mathfrak {N}) \cap G({\mathbb {Q}})^+$
and for every
$\gamma =\bigg(\begin{matrix}a & b \\ c & d\end{matrix}\bigg) \in U_{0}(\mathfrak {N}) \cap G({\mathbb {Q}})^+$
and for every
![]() $\underline {\tau }=(\tau _{1},\ldots ,\tau _{n_{F}})\in \mathcal {H}_{F}$
.
$\underline {\tau }=(\tau _{1},\ldots ,\tau _{n_{F}})\in \mathcal {H}_{F}$
.
Since Hilbert modular forms are holomorphic functions on
![]() $\mathcal {H}_{F}$
invariant under the lattice
$\mathcal {H}_{F}$
invariant under the lattice
![]() $\mathcal {O}_{F}$
, they admit a q-expansion over
$\mathcal {O}_{F}$
, they admit a q-expansion over
![]() $\mathcal {O}_{F}^{\vee }=\mathfrak {d}^{-1}$
, where
$\mathcal {O}_{F}^{\vee }=\mathfrak {d}^{-1}$
, where
![]() $q=e^{2\pi i \sum \tau _{i}}$
; see [Reference Goren24, Definition 3.1] for more details.
$q=e^{2\pi i \sum \tau _{i}}$
; see [Reference Goren24, Definition 3.1] for more details.
2.3.3 Hecke Operators and Hilbert Eigenforms
On the space of Hilbert modular forms of level
one has Hecke operators
![]() $T(\mathfrak {n})$
for every integral ideal of
$T(\mathfrak {n})$
for every integral ideal of
![]() $\mathcal {O}_{F}$
coprime with
$\mathcal {O}_{F}$
coprime with
![]() $\mathfrak {N}$
. The definition is analogous to the one for classical modular forms. For example, if
$\mathfrak {N}$
. The definition is analogous to the one for classical modular forms. For example, if
![]() $\mathfrak {p}$
does not divide
$\mathfrak {p}$
does not divide
![]() $\mathfrak {N}$
and x is a totally positive generator of
$\mathfrak {N}$
and x is a totally positive generator of
![]() $\mathfrak {p}$
, one defines
$\mathfrak {p}$
, one defines
 $$ \begin{align*} (T(\mathfrak{p})f)(\underline{\tau}):=\text{Nm}(\mathfrak{p}) f(x\cdot\underline{\tau})+ \frac{1}{\text{Nm}(\mathfrak{p})}\sum\limits_{a\in\mathcal{O}_{F}/\mathfrak{p}}f(\gamma_{a} \cdot \underline{\tau}), \end{align*} $$
$$ \begin{align*} (T(\mathfrak{p})f)(\underline{\tau}):=\text{Nm}(\mathfrak{p}) f(x\cdot\underline{\tau})+ \frac{1}{\text{Nm}(\mathfrak{p})}\sum\limits_{a\in\mathcal{O}_{F}/\mathfrak{p}}f(\gamma_{a} \cdot \underline{\tau}), \end{align*} $$
where
 $\gamma _{a}:= \bigg(\begin{matrix}1 & a \\ 0 & x\end{matrix}\bigg)$
. We recall the following definition.
$\gamma _{a}:= \bigg(\begin{matrix}1 & a \\ 0 & x\end{matrix}\bigg)$
. We recall the following definition.
Definition 2.2 A cuspidal Hilbert modular form (i.e., such that the
![]() $0$
-th Fourier coefficient
$0$
-th Fourier coefficient
![]() $a_{0}(f)$
vanishes) is an eigenform if it is an eigenvector for every Hecke operator
$a_{0}(f)$
vanishes) is an eigenform if it is an eigenvector for every Hecke operator
![]() $T(\mathfrak {n})$
.
$T(\mathfrak {n})$
.
As in the case of classical modular forms, if f is an eigenform, normalised so that
![]() $a_{1}(f) = 1$
, then the eigenvalues of the Hecke operators are the Fourier coefficients, i.e.,
$a_{1}(f) = 1$
, then the eigenvalues of the Hecke operators are the Fourier coefficients, i.e.,
![]() $T(\mathfrak {n})f = a_{\mathfrak {n}}(f)\cdot f$
; moreover, they are algebraic integers lying in the number field
$T(\mathfrak {n})f = a_{\mathfrak {n}}(f)\cdot f$
; moreover, they are algebraic integers lying in the number field
![]() $K(f):={\mathbb {Q}}((a_{\mathfrak {n}}(f))_{\mathfrak {n}})$
, as shown in [Reference Shimura36,
$K(f):={\mathbb {Q}}((a_{\mathfrak {n}}(f))_{\mathfrak {n}})$
, as shown in [Reference Shimura36,
![]() $\S $
2].
$\S $
2].
2.3.4 Eichler–Shimura for Hilbert Modular Forms
Blasius and Rogawski [Reference Blasius and Rogawski7], Carayol [Reference Carayol11], and Taylor [Reference Taylor40] proved that to any Hilbert eigenform, one can attach representations of
![]() $G_{F}$
, similarly to the classical case. More precisely, one has the following result.
$G_{F}$
, similarly to the classical case. More precisely, one has the following result.
Theorem 2.4 If f is a Hilbert eigenform for F of weight
![]() $(\underline {r},t)$
, level
$(\underline {r},t)$
, level
![]() $\mathfrak {N,}$
and trivial nebentype character and
$\mathfrak {N,}$
and trivial nebentype character and
![]() $K(f)$
is the number field generated by its eigenvalues, then for every finite place
$K(f)$
is the number field generated by its eigenvalues, then for every finite place
![]() $\lambda $
of
$\lambda $
of
![]() $K(f),$
there is an irreducible
$K(f),$
there is an irreducible
![]() $2$
-dimensional Galois representation
$2$
-dimensional Galois representation
such that for every prime
![]() $w\nmid \mathfrak {N}\operatorname {Nm}_{K(f)/{\mathbb {Q}}}(\lambda )$
in F,
$w\nmid \mathfrak {N}\operatorname {Nm}_{K(f)/{\mathbb {Q}}}(\lambda )$
in F,
![]() $\rho _{f,\lambda }$
is unramified at w and
$\rho _{f,\lambda }$
is unramified at w and
 $$ \begin{align*} \det(1-X\rho_{f,\lambda}(\operatorname{Frob}_{w}))=X^{2}-a_{w}(f)X+\operatorname{Nm}_{F/{\mathbb{Q}}}^{t-1}(w). \end{align*} $$
$$ \begin{align*} \det(1-X\rho_{f,\lambda}(\operatorname{Frob}_{w}))=X^{2}-a_{w}(f)X+\operatorname{Nm}_{F/{\mathbb{Q}}}^{t-1}(w). \end{align*} $$
Assume that f is of weight
![]() $(2,\ldots ,2 )$
. As in the classical case, we would like to have such Galois representations to be attached to opportune abelian varieties. The existence of abelian varieties associated with f was first considered by Oda in [Reference Oda31], and Blasius gave a conjectural solution to such a problem.
$(2,\ldots ,2 )$
. As in the classical case, we would like to have such Galois representations to be attached to opportune abelian varieties. The existence of abelian varieties associated with f was first considered by Oda in [Reference Oda31], and Blasius gave a conjectural solution to such a problem.
Theorem 2.5 (Blasius)
Let f be a Hilbert eigenform for F of parallel weight
![]() $2$
. Denote by
$2$
. Denote by
![]() $K(f)$
the number field generated by the
$K(f)$
the number field generated by the
![]() $a_{w}(f)$
for all w. Assume Conjecture 1.1. There exists a
$a_{w}(f)$
for all w. Assume Conjecture 1.1. There exists a
![]() $[K(f):{\mathbb {Q}}]$
-dimensional abelian variety
$[K(f):{\mathbb {Q}}]$
-dimensional abelian variety
![]() $A_{f}/F$
with
$A_{f}/F$
with
![]() $\mathcal {O}_{K(f)}$
-multiplication such that for all but finitely many of the finite places w of F at which
$\mathcal {O}_{K(f)}$
-multiplication such that for all but finitely many of the finite places w of F at which
![]() $A_{f}$
has good reduction, we have
$A_{f}$
has good reduction, we have
 $$ \begin{align*} L\big(s,A_{f},K(f)\big)=L(f,s), \end{align*} $$
$$ \begin{align*} L\big(s,A_{f},K(f)\big)=L(f,s), \end{align*} $$
where the L-function
![]() $L(s,A_{f},K(f))$
is defined by the product of local factors
$L(s,A_{f},K(f))$
is defined by the product of local factors
 $$ \begin{align*} \det\big(1-\operatorname{Nm}(w)^{-s}\operatorname{Frob}_{w}|T_{v}(A)^{I_{w}}\big), \end{align*} $$
$$ \begin{align*} \det\big(1-\operatorname{Nm}(w)^{-s}\operatorname{Frob}_{w}|T_{v}(A)^{I_{w}}\big), \end{align*} $$
where v is a prime of K, w is a prime of
![]() $F,$
and w and v lay above distinct rational primes.
$F,$
and w and v lay above distinct rational primes.
Proof If
![]() $K(f)={\mathbb {Q}}$
, this is precisely [Reference Blasius6, Theorem 1, p. 3]. As noticed by Blasius [Reference Blasius6, 1.10], the proof easily adapts to the general case (where the necessary changes are hinted at in the remarks in [Reference Blasius6, Sections 5.4., 5.7., and 7.6.]). ▪
$K(f)={\mathbb {Q}}$
, this is precisely [Reference Blasius6, Theorem 1, p. 3]. As noticed by Blasius [Reference Blasius6, 1.10], the proof easily adapts to the general case (where the necessary changes are hinted at in the remarks in [Reference Blasius6, Sections 5.4., 5.7., and 7.6.]). ▪
Remark 2.6 The proof is completely different from the one of Shimura, since, as noticed in Theorem 2.2, we cannot obtain a non-trivial abelian variety as quotient of the Albanese variety of a Hilbert modular variety. Blasius instead considers the symmetric square of the automorphic representation of
![]() $\mathrm {GL}_{2,F}$
associated with the Hilbert eigenform; it is an automorphic representation of
$\mathrm {GL}_{2,F}$
associated with the Hilbert eigenform; it is an automorphic representation of
![]() $\mathrm {GL}_{3,F,}$
and its base change to a quadratic imaginary field appears in the middle degree cohomology of a Picard modular variety. He then considers the associated motive and shows that its Betti realisation is the symmetric square of a polarised Hodge structure of type
$\mathrm {GL}_{3,F,}$
and its base change to a quadratic imaginary field appears in the middle degree cohomology of a Picard modular variety. He then considers the associated motive and shows that its Betti realisation is the symmetric square of a polarised Hodge structure of type
![]() $(1,0), (0,1)$
. This gives a complex abelian variety A and Conjecture 1.1 (applied to the product of the Picard modular variety and A) allows us to conclude that A is defined over a number field containing F. He then finds the desired abelian variety inside the restriction of scalars of A over F.
$(1,0), (0,1)$
. This gives a complex abelian variety A and Conjecture 1.1 (applied to the product of the Picard modular variety and A) allows us to conclude that A is defined over a number field containing F. He then finds the desired abelian variety inside the restriction of scalars of A over F.
Remark 2.7 Theorem 2.5 is known to hold unconditionally in many interesting cases (for example, when
![]() $n_{F}$
is odd, by the work of Hida). For more details, we refer the reader to [Reference Blasius6, Theorem 3] and references therein. The proof of such unconditional cases actually follows Shimura’s proof of Theorem 2.3, rather than the strategy described in the previous remark.
$n_{F}$
is odd, by the work of Hida). For more details, we refer the reader to [Reference Blasius6, Theorem 3] and references therein. The proof of such unconditional cases actually follows Shimura’s proof of Theorem 2.3, rather than the strategy described in the previous remark.
2.4 A Remark on Polarisations
To use Theorems 2.3 and 2.5 to produce F-points of a Hilbert modular variety, we need, of course, the abelian varieties produced to be principally polarised (up to isogeny would actually be enough for our applications, if the isogeny is defined over the base field F). An abelian variety over an algebraically closed base field always admits an isogeny to a principally polarised abelian variety. But since the same does not hold over number fields, some considerations are needed. The first observation is that every weight one Hodge structure of dimension
![]() $2$
with an action by
$2$
with an action by
![]() $\mathcal {O}_{K(f)}$
is automatically
$\mathcal {O}_{K(f)}$
is automatically
![]() $\mathcal {O}_{K(f)}$
-polarised, as explained for example in [Reference Edixhoven17, Appendix B].
$\mathcal {O}_{K(f)}$
-polarised, as explained for example in [Reference Edixhoven17, Appendix B].
As noticed in [Reference Blasius6, Remark 5.7.], Blasius first finds a principally polarised abelian variety A over a finite extension
![]() $L'/F$
. Actually, we can assume that A has a principal
$L'/F$
. Actually, we can assume that A has a principal
![]() $\mathcal {O}_{K(f)}$
-polarisation
$\mathcal {O}_{K(f)}$
-polarisation
![]() $\lambda $
. As explained above, the proof then considers the Weil restriction of A to F, which is again principally
$\lambda $
. As explained above, the proof then considers the Weil restriction of A to F, which is again principally
![]() $\mathcal {O}_{K(f)}$
-polarised. It is not hard to see that the construction of [Reference Blasius6, section 7] behaves well with respect to the
$\mathcal {O}_{K(f)}$
-polarised. It is not hard to see that the construction of [Reference Blasius6, section 7] behaves well with respect to the
![]() $\mathcal {O}_{K(f)}$
-polarisation, and, therefore, the proof actually produces an
$\mathcal {O}_{K(f)}$
-polarisation, and, therefore, the proof actually produces an
![]() $\mathcal {O}_{K(f)}$
-polarised abelian variety over F.
$\mathcal {O}_{K(f)}$
-polarised abelian variety over F.
3 Producing Abelian Varieties via Serre’s Conjecture
In this section, we prove Theorems 1.A and 1.B. As in Section 1.2, consider two totally real fields L and K. We work with a compatible system of Galois representations of
![]() $G_{L}$
with values in
$G_{L}$
with values in
 $\mathrm {Res}_{K/{\mathbb {Q}}}(\mathrm {GL}_{2}) (\mathbb {A}^{f}_{\mathbb {Q}})=\mathrm {GL}_{2}(\mathbb {A}_{K}^{f})$
, where
$\mathrm {Res}_{K/{\mathbb {Q}}}(\mathrm {GL}_{2}) (\mathbb {A}^{f}_{\mathbb {Q}})=\mathrm {GL}_{2}(\mathbb {A}_{K}^{f})$
, where
 $\mathbb {A}_{K}^{f}$
denotes the finite adeles of K that “looks like” an algebraic point of the Hilbert modular variety for K. We then produce a Hilbert modular form for L of weight
$\mathbb {A}_{K}^{f}$
denotes the finite adeles of K that “looks like” an algebraic point of the Hilbert modular variety for K. We then produce a Hilbert modular form for L of weight
![]() $(2,\ldots ,2)$
, and of opportune explicit conductor. Eventually, we obtain an abelian variety over L that allows us to produce an L-rational point on the Hilbert modular variety for K.
$(2,\ldots ,2)$
, and of opportune explicit conductor. Eventually, we obtain an abelian variety over L that allows us to produce an L-rational point on the Hilbert modular variety for K.
3.1 Weakly Compatible Systems
The definition of weakly compatible families presented is due to Serre, who called them strictly compatible in [Reference Serre35, p. I-11]. It follows from the Weil conjectures that the
![]() $\ell $
-adic Tate modules of abelian varieties form a weakly compatible system of Galois representations.
$\ell $
-adic Tate modules of abelian varieties form a weakly compatible system of Galois representations.
Definition 3.1 (Weakly compatible system)
A system
![]() $\{\rho _{v}:G_{L}\to \mathrm {GL}_{2}(K_{v})\}_{v}$
is weakly compatible if there exists a finite set of places S of L such that the following hold.
$\{\rho _{v}:G_{L}\to \mathrm {GL}_{2}(K_{v})\}_{v}$
is weakly compatible if there exists a finite set of places S of L such that the following hold.
-
(i) For all places w of L,
 $\rho _{v}$
is unramified outside the set
$\rho _{v}$
is unramified outside the set
 $S_{v}$
. Here, we denote by
$S_{v}$
. Here, we denote by
 $S_{v}$
the union of S and all the primes of L dividing
$S_{v}$
the union of S and all the primes of L dividing
 $\ell $
where
$\ell $
where
 $\ell $
is the residue characteristic of
$\ell $
is the residue characteristic of
 $K_{v}$
.
$K_{v}$
. -
(ii) For all
 $w \notin S_{v}$
, denoting by
$w \notin S_{v}$
, denoting by
 $\text {Frob}_w$
a Frobenius element at w, the characteristic polynomial of
$\text {Frob}_w$
a Frobenius element at w, the characteristic polynomial of
 $\rho _{v}(\text {Frob}_w)$
has K-rational coefficients, and it is independent of v.
$\rho _{v}(\text {Frob}_w)$
has K-rational coefficients, and it is independent of v.
Recall that
![]() $\rho _{v}$
is said to be unramified at a place w of L if the image of the inertia at w is trivial. If
$\rho _{v}$
is said to be unramified at a place w of L if the image of the inertia at w is trivial. If
![]() $\rho _{v}$
is attached to the v-adic cohomology of a smooth proper variety defined over a number field, the smooth and proper base change theorems (see, for example, [Reference Deligne14, I, Theorems 5.3.2 and 4.1.1]) imply that
$\rho _{v}$
is attached to the v-adic cohomology of a smooth proper variety defined over a number field, the smooth and proper base change theorems (see, for example, [Reference Deligne14, I, Theorems 5.3.2 and 4.1.1]) imply that
![]() $\rho _{v}$
is unramified at every place
$\rho _{v}$
is unramified at every place
![]() $w\notin S_{v}$
such that X has good reduction at w.
$w\notin S_{v}$
such that X has good reduction at w.
3.2 Key Proposition
Fix a finite set of places S of L, containing all the archimedean places. To prove Theorem 1.A and Theorem 1.B, we need the following proposition.
Proposition 3.1 Assume Conjecture 1.2 and let
![]() $\{\rho _{v}\}_{v}$
be a system of representations satisfying conditions
$\{\rho _{v}\}_{v}$
be a system of representations satisfying conditions
![]() $(\mathcal {S}.1)$
–
$(\mathcal {S}.1)$
–
![]() $(\mathcal {S}.4)$
. For every
$(\mathcal {S}.4)$
. For every
![]() $w\not \in S$
, let
$w\not \in S$
, let
![]() $a_{w}\in \mathcal {O}_{K}$
be the trace of
$a_{w}\in \mathcal {O}_{K}$
be the trace of
![]() $\rho _{v}(\operatorname {Frob}_{w})$
. Then there exists f a normalised Hilbert eigenform for L with Fourier coefficients in
$\rho _{v}(\operatorname {Frob}_{w})$
. Then there exists f a normalised Hilbert eigenform for L with Fourier coefficients in
![]() $\mathcal {O}_{K}$
, such that for every
$\mathcal {O}_{K}$
, such that for every
![]() $w\not \in S$
,
$w\not \in S$
,
![]() $a_{w}(f)=a_{w}$
. Moreover, f is of weight
$a_{w}(f)=a_{w}$
. Moreover, f is of weight
![]() $(2,\ldots ,2)$
and conductor divisible only by primes in S.
$(2,\ldots ,2)$
and conductor divisible only by primes in S.
Remark 3.2 If we start with an abelian variety
![]() $A/L$
with
$A/L$
with
![]() $\mathcal {O}_{K}$
-multiplication, we can produce a system
$\mathcal {O}_{K}$
-multiplication, we can produce a system
which satisfies the four conditions of (𝒮) for S the union of infinite places and the set of places of bad reduction; see [Reference Ribet33,
![]() $\S $
3]. Proposition 3.1 hence implies that A is modular; i.e., there exists a Hilbert modular form for the totally real field L such that
$\S $
3]. Proposition 3.1 hence implies that A is modular; i.e., there exists a Hilbert modular form for the totally real field L such that
up to a finite number of Euler factors. Unconditionally, it has been proven that elliptic curves over real quadratic fields are modular (see [Reference Freitas, Le Hung and Siksek21]), and, more generally, the work of Taylor and Kisin implies that elliptic curves over L become modular (in this sense) after a totally real extension
![]() $L'/L$
. See [Reference Buzzard9, Theorem 1.16] and reference therein.
$L'/L$
. See [Reference Buzzard9, Theorem 1.16] and reference therein.
In the proof of Proposition 3.1, we use Conjecture 1.2 and the following result due to Serre (for the proof, see [Reference Serre34, 4.9.4]).
Proposition 3.3 (Serre)
Let q be a power of
![]() $\ell $
. Let
$\ell $
. Let
![]() $r: G_{E} \to \mathrm {GL}_{2}(\mathbb {F}_{q})$
be a continuous homomorphism, where
$r: G_{E} \to \mathrm {GL}_{2}(\mathbb {F}_{q})$
be a continuous homomorphism, where
![]() $q=\ell ^{t}$
and E is a local field of residue characteristic
$q=\ell ^{t}$
and E is a local field of residue characteristic
![]() $p\neq \ell $
and discrete valuation
$p\neq \ell $
and discrete valuation
![]() $v_{E}$
. Let
$v_{E}$
. Let
![]() $e_{E}:=v_{E}(p)$
and
$e_{E}:=v_{E}(p)$
and
![]() $c\geq 0$
be an integer such that the image via r of the wild inertia of E has cardinality
$c\geq 0$
be an integer such that the image via r of the wild inertia of E has cardinality
![]() $p^{c}$
. We denote by
$p^{c}$
. We denote by
![]() $n(r,E)$
the exponent of the conductor of r. We have
$n(r,E)$
the exponent of the conductor of r. We have
 $$ \begin{align*} n(r,E)\leq 2\big(1+e_{E}\cdot c + \tfrac{e_{E}}{p-1}\big). \end{align*} $$
$$ \begin{align*} n(r,E)\leq 2\big(1+e_{E}\cdot c + \tfrac{e_{E}}{p-1}\big). \end{align*} $$
We also need to compute the weight and the conductor of the modular forms produced by Conjecture 1.2. As anticipated in Remark 1.1, this is a known result under some assumptions. The weight part stated in the following theorem is a special case of the work [Reference Gee, Liu and Savitt23]; the conductor part follows from automorphy lifting methods or can be seen as a consequence of the main theorem of [Reference Fujiwara22].
Theorem 3.4 [Reference Gee, Liu and Savitt23, Reference Fujiwara22]
Let
![]() $\ell>5$
and
$\ell>5$
and
![]() $\bar {\rho }: G_{L}\to \mathrm {GL}_{2}(\overline {\mathbb {F}}_{\ell })$
be an irreducible totally odd representation such that its determinant is the cyclotomic character and it is finite flat at all places
$\bar {\rho }: G_{L}\to \mathrm {GL}_{2}(\overline {\mathbb {F}}_{\ell })$
be an irreducible totally odd representation such that its determinant is the cyclotomic character and it is finite flat at all places
![]() $w\mid \ell $
. Assume, furthermore, that
$w\mid \ell $
. Assume, furthermore, that
![]() $\bar {\rho }$
satisfies the Taylor–Wiles assumption; namely,
$\bar {\rho }$
satisfies the Taylor–Wiles assumption; namely,
 $$ \begin{align} \bar{\rho}_{\mid G_{L(\zeta_{\ell})}} \text{ is irreducible}, \end{align} $$
$$ \begin{align} \bar{\rho}_{\mid G_{L(\zeta_{\ell})}} \text{ is irreducible}, \end{align} $$
where
![]() $\zeta _{\ell }$
is a primitive
$\zeta _{\ell }$
is a primitive
![]() $\ell $
-th root of unity. Then if
$\ell $
-th root of unity. Then if
![]() $\bar {\rho }$
is modular, there exists a Hilbert modular form of parallel weight
$\bar {\rho }$
is modular, there exists a Hilbert modular form of parallel weight
![]() $2$
and conductor equal to the Artin conductor of
$2$
and conductor equal to the Artin conductor of
![]() $\bar {\rho }$
giving rise to
$\bar {\rho }$
giving rise to
![]() $\bar {\rho }$
.
$\bar {\rho }$
.
We are now ready to prove Proposition 3.1.
Proof Our goal is to apply Serre’s conjecture to
![]() $\bar {\rho }_{v}$
, the reduction modulo v of the representation
$\bar {\rho }_{v}$
, the reduction modulo v of the representation
![]() $\rho _{v}$
, for infinitely many
$\rho _{v}$
, for infinitely many
![]() $v\notin S_{K}$
, where
$v\notin S_{K}$
, where
![]() $S_{K}$
is the following finite set of primes of
$S_{K}$
is the following finite set of primes of
![]() $K:$
$K:$
Let v be such a prime, and let
![]() $\ell $
be its residue characteristic.
$\ell $
be its residue characteristic.
We first compute the conductor
![]() $N(\bar {\rho }_{v})$
. Since
$N(\bar {\rho }_{v})$
. Since
![]() $\bar {\rho }_{v}$
is unramified outside
$\bar {\rho }_{v}$
is unramified outside
![]() $S_{v}$
, the conductor is divisible only by primes in S. We then apply Proposition 3.3 to
$S_{v}$
, the conductor is divisible only by primes in S. We then apply Proposition 3.3 to
![]() $E=L_{w}$
and
$E=L_{w}$
and
![]() $r=\bar {\rho }_{v}$
. The image of
$r=\bar {\rho }_{v}$
. The image of
![]() $\bar {\rho }_{v}$
s contained in
$\bar {\rho }_{v}$
s contained in
![]() $\mathrm {GL}_{2}(\mathbb {F}_{\ell ^{t}})$
, where
$\mathrm {GL}_{2}(\mathbb {F}_{\ell ^{t}})$
, where
![]() $t\leq [K:{\mathbb {Q}}]=n_{K}$
. The cardinality of this group is
$t\leq [K:{\mathbb {Q}}]=n_{K}$
. The cardinality of this group is
![]() $\ell ^{t}(\ell ^{2t}-1)(\ell ^{t}-1)$
. Let
$\ell ^{t}(\ell ^{2t}-1)(\ell ^{t}-1)$
. Let
![]() $W_{w}$
denote the wild inertia subgroup of
$W_{w}$
denote the wild inertia subgroup of
![]() $G_{L_{w}}$
. If
$G_{L_{w}}$
. If
![]() $\ell $
satisfies the following congruences:
$\ell $
satisfies the following congruences:
 $$ \begin{align} \ell^{n_{K}} \not\equiv \begin{cases} \pm 1 \mod p &\text{ if } p\neq 2,3\\ \pm 1 \mod 8 &\text{ if } p=2,\\ \pm 1, 4,7 \mod 9 &\text{ if } p=3, \end{cases} \end{align} $$
$$ \begin{align} \ell^{n_{K}} \not\equiv \begin{cases} \pm 1 \mod p &\text{ if } p\neq 2,3\\ \pm 1 \mod 8 &\text{ if } p=2,\\ \pm 1, 4,7 \mod 9 &\text{ if } p=3, \end{cases} \end{align} $$
then the same congruences hold for
![]() $\ell ^{t},$
and hence
$\ell ^{t},$
and hence
![]() $\bar {\rho }_{v}(W_{w})$
is trivial if
$\bar {\rho }_{v}(W_{w})$
is trivial if
![]() $p\neq 2,3$
and is at most
$p\neq 2,3$
and is at most
![]() $p^{5}$
if
$p^{5}$
if
![]() $p=2$
and at most p if
$p=2$
and at most p if
![]() $p=3$
. Hence for
$p=3$
. Hence for
![]() $v\notin S$
laying above
$v\notin S$
laying above
![]() $\ell $
satisfying the above conditions, using that
$\ell $
satisfying the above conditions, using that
![]() $e_{E}\leq [L:{\mathbb {Q}}]=n_{L}$
, the inequality of Proposition 3.3 implies that
$e_{E}\leq [L:{\mathbb {Q}}]=n_{L}$
, the inequality of Proposition 3.3 implies that
 $$ \begin{align*} n_{K}(\bar{\rho}_{v},L_{w})\leq \begin{cases} 2(1+n_{L}) &\text{ if } p\neq 2,3,\\ 2(1+6n_{L}) &\text{ if } p=2,\\ 2(1+2n_{L}) &\text{ if } p=3. \end{cases} \end{align*} $$
$$ \begin{align*} n_{K}(\bar{\rho}_{v},L_{w})\leq \begin{cases} 2(1+n_{L}) &\text{ if } p\neq 2,3,\\ 2(1+6n_{L}) &\text{ if } p=2,\\ 2(1+2n_{L}) &\text{ if } p=3. \end{cases} \end{align*} $$
Writing
![]() $\mathfrak {p}_{w}$
for the prime ideal of L corresponding to w, we hence find that the conductor of
$\mathfrak {p}_{w}$
for the prime ideal of L corresponding to w, we hence find that the conductor of
![]() $\bar {\rho }_{v}$
divides
$\bar {\rho }_{v}$
divides
 $$ \begin{align*} \mathfrak{C}:= \prod\limits_{\substack{w\in S,\\ w\nmid 2,3}} \mathfrak{p}_{w}^{2+2n_{L}}\cdot \prod\limits_{\substack{w\in S,\\ w\mid 2}}\mathfrak{p}_{w}^{2+12n_{L}}\cdot \prod\limits_{\substack{w\in S,\\ w\mid 3}}\mathfrak{p}_{w}^{2+4n_{L}}. \end{align*} $$
$$ \begin{align*} \mathfrak{C}:= \prod\limits_{\substack{w\in S,\\ w\nmid 2,3}} \mathfrak{p}_{w}^{2+2n_{L}}\cdot \prod\limits_{\substack{w\in S,\\ w\mid 2}}\mathfrak{p}_{w}^{2+12n_{L}}\cdot \prod\limits_{\substack{w\in S,\\ w\mid 3}}\mathfrak{p}_{w}^{2+4n_{L}}. \end{align*} $$
Finally, notice that
![]() $\rho _{v}$
is odd thanks to the condition on the determinant, and, moreover, [Reference Barnet-Lamb, Gee, Geraghty and Taylor5, Proposition 5.3.2] implies that there exists a density one set of primes such that
$\rho _{v}$
is odd thanks to the condition on the determinant, and, moreover, [Reference Barnet-Lamb, Gee, Geraghty and Taylor5, Proposition 5.3.2] implies that there exists a density one set of primes such that
 $(\bar {\rho }_{v})_{\mid G_{L(\zeta _{\ell })}}$
is irreducible, i.e., (TW) is satisfied.
$(\bar {\rho }_{v})_{\mid G_{L(\zeta _{\ell })}}$
is irreducible, i.e., (TW) is satisfied.
We can apply Conjecture 1.2 to
![]() $\bar {\rho }_{v}$
for
$\bar {\rho }_{v}$
for
![]() $v\in \Sigma $
, where
$v\in \Sigma $
, where
![]() $\Sigma $
is the infinite set of primes
$\Sigma $
is the infinite set of primes
![]() $v\mid \ell $
such that
$v\mid \ell $
such that
![]() $v\not \in S_{K}$
,
$v\not \in S_{K}$
,
![]() $\ell $
satisfies (⋆);
$\ell $
satisfies (⋆);
![]() $\bar {\rho }_{v}$
is absolutely irreducible and satisfies (TW). We have produced infinitely many
$\bar {\rho }_{v}$
is absolutely irreducible and satisfies (TW). We have produced infinitely many
![]() $f_{v}$
Hilbert modular eigenform, which by Theorem 3.4 are of parallel weight 2 and level dividing
$f_{v}$
Hilbert modular eigenform, which by Theorem 3.4 are of parallel weight 2 and level dividing
![]() $\mathfrak {C}$
. Their Fourier coefficients are defined over a ring
$\mathfrak {C}$
. Their Fourier coefficients are defined over a ring
![]() $\mathcal {O}(v)\subset \mathcal {O}_{K},$
and at a prime
$\mathcal {O}(v)\subset \mathcal {O}_{K},$
and at a prime
![]() $\lambda \mid v,$
the associated Galois representation
$\lambda \mid v,$
the associated Galois representation
![]() $\rho _{f_{v},\lambda }$
is isomorphic to
$\rho _{f_{v},\lambda }$
is isomorphic to
![]() $\bar {\rho }_{v}$
modulo
$\bar {\rho }_{v}$
modulo
![]() $\lambda $
. Since the space of Hilbert modular form of fixed weight and with conductor dividing
$\lambda $
. Since the space of Hilbert modular form of fixed weight and with conductor dividing
![]() $\mathfrak {C}$
is finite dimensional (see [Reference Freitag20, Theorem 6.1]), we can find at least one Hilbert modular eigenform f of parallel weight 2 and level dividing
$\mathfrak {C}$
is finite dimensional (see [Reference Freitag20, Theorem 6.1]), we can find at least one Hilbert modular eigenform f of parallel weight 2 and level dividing
![]() $\mathfrak {C}$
defined over some
$\mathfrak {C}$
defined over some
![]() $\mathcal {O}\subset \mathcal {O}_{K}$
such that for infinitely many of the v above, the same property holds for
$\mathcal {O}\subset \mathcal {O}_{K}$
such that for infinitely many of the v above, the same property holds for
![]() $\rho _{f,\lambda }$
for
$\rho _{f,\lambda }$
for
![]() $\lambda \mid v$
. This implies that for all
$\lambda \mid v$
. This implies that for all
![]() $w\not \in S,$
the congruence
$w\not \in S,$
the congruence
holds for infinitely many primes
![]() $\lambda ,$
and hence,
$\lambda ,$
and hence,
![]() $a_{w}(f)= a_{w}$
, as required. ▪
$a_{w}(f)= a_{w}$
, as required. ▪
3.3 Proof of Theorem 1
Recall that, as in Section 1.2, the system
![]() $(\rho _{v})_{v}$
is required to satisfy the following additional property:
$(\rho _{v})_{v}$
is required to satisfy the following additional property:
In other words, we have
![]() $K(f)=K$
, where f is the Hilbert modular form for L produced in Proposition 3.1.
$K(f)=K$
, where f is the Hilbert modular form for L produced in Proposition 3.1.
Proof Starting with our initial datum of Galois representations, we have produced a Hilbert modular form f for L. We can then apply Theorem 2.5, which gives an abelian variety
![]() $A_{f}$
over L of dimension
$A_{f}$
over L of dimension
![]() $[K:{\mathbb {Q}}]$
and an embedding of
$[K:{\mathbb {Q}}]$
and an embedding of
![]() $\mathcal {O}_{K}$
into
$\mathcal {O}_{K}$
into
![]() $\mathrm {End}(A)$
. For all but finitely many
$\mathrm {End}(A)$
. For all but finitely many
![]() $w\mid p$
at which
$w\mid p$
at which
![]() $A_{f}$
has good reduction
$A_{f}$
has good reduction
 $$ \begin{align*} \det(1-X\rho_{A_{f},v}(\text{Frob}_{w}))=1-a_{w}(f)X+N_wX^{2}, \end{align*} $$
$$ \begin{align*} \det(1-X\rho_{A_{f},v}(\text{Frob}_{w}))=1-a_{w}(f)X+N_wX^{2}, \end{align*} $$
where v is a finite prime of K not dividing p and
![]() $\rho _{A_{f},v}$
is the
$\rho _{A_{f},v}$
is the
![]() $G_{L}$
-representation on
$G_{L}$
-representation on
![]() $T_{v}(A_{f})$
, the v-adic Tate module of
$T_{v}(A_{f})$
, the v-adic Tate module of
![]() $A_{f}$
. We have therefore produced an abelian variety
$A_{f}$
. We have therefore produced an abelian variety
![]() $A_{f}$
as stated in Theorems 1.A and 1.B.
$A_{f}$
as stated in Theorems 1.A and 1.B.
We just need to stress that we do not require any conjectural statement in the case
![]() $n_{L}=1$
. Indeed, we can use Theorem 2.3 in place of Blasius’ conjectural version, and Serre’s conjecture is fully known thanks to the work of Khare–Wintenberger [Reference Khare and Wintenberger27, Theorem 1.2]. ▪
$n_{L}=1$
. Indeed, we can use Theorem 2.3 in place of Blasius’ conjectural version, and Serre’s conjecture is fully known thanks to the work of Khare–Wintenberger [Reference Khare and Wintenberger27, Theorem 1.2]. ▪
3.4 A Corollary
We rephrase the main results of the section as needed to prove Theorem 2.
Corollary 3.5 Assume that, in the setting of Theorems 1.A and 1.B, we also have a representation
for some integral ideal
![]() $\mathfrak {N}\subset \mathcal {O}_{K}$
, such that for all pairs
$\mathfrak {N}\subset \mathcal {O}_{K}$
, such that for all pairs
![]() $(v, a)$
, where v is a place of K and
$(v, a)$
, where v is a place of K and
![]() $a\in \mathfrak {N}-\{0\}$
, such that
$a\in \mathfrak {N}-\{0\}$
, such that
![]() $v^{a}$
divides
$v^{a}$
divides
![]() $\mathfrak {N}$
, the reductions of
$\mathfrak {N}$
, the reductions of
![]() $\rho $
and
$\rho $
and
![]() $\rho _{v}$
modulo
$\rho _{v}$
modulo
![]() $v^{a}$
agree. Then there exists an
$v^{a}$
agree. Then there exists an
![]() $n_{K}$
-dimensional abelian variety
$n_{K}$
-dimensional abelian variety
![]() $A/L$
with good reduction at all w outside
$A/L$
with good reduction at all w outside
![]() $S,$
and the action of
$S,$
and the action of
![]() $G_{L}$
on
$G_{L}$
on
![]() $A[\mathfrak {N}]$
is given by
$A[\mathfrak {N}]$
is given by
![]() $\rho $
.
$\rho $
.
Proof Theorems 1.A and 1.B give an
![]() $n_{K}$
-dimensional abelian variety
$n_{K}$
-dimensional abelian variety
![]() $A/L$
and, using the Néron–Ogg–Shafarevich criterion, we can see that it has good reduction at all w outside S. Finally,
$A/L$
and, using the Néron–Ogg–Shafarevich criterion, we can see that it has good reduction at all w outside S. Finally,
![]() $G_{L}$
acts on
$G_{L}$
acts on
![]() $A[\mathfrak {N}]$
via
$A[\mathfrak {N}]$
via
![]() $\rho $
, since the reduction modulo
$\rho $
, since the reduction modulo
![]() $v^{a}$
of
$v^{a}$
of
![]() $\rho $
and
$\rho $
and
![]() $\rho _{v}$
agree. ▪
$\rho _{v}$
agree. ▪
4 Finite Descent Obstruction and Proof of Theorem 2
In this final section, we recall the finite descent obstruction for integral points, explaining how it relates to the system of Galois representations considered in the previous section. Using Theorem 1, we indeed produce an
![]() $\mathcal {O}_{L,S}$
-point of integral models of twists of Hilbert modular varieties, which is what we require to prove Theorem 2.
$\mathcal {O}_{L,S}$
-point of integral models of twists of Hilbert modular varieties, which is what we require to prove Theorem 2.
4.1 Recap on the Integral Finite Descent Obstruction
Let
![]() $Y/F$
be a smooth, geometrically connected variety (not necessarily proper) over a number field F. Let S be a finite set of places of
$Y/F$
be a smooth, geometrically connected variety (not necessarily proper) over a number field F. Let S be a finite set of places of
![]() $F,$
and, as before, assume that S contains the archimedean places and all places of bad reduction of Y. Choose and fix a smooth model
$F,$
and, as before, assume that S contains the archimedean places and all places of bad reduction of Y. Choose and fix a smooth model
![]() $\mathcal {Y}$
of Y over
$\mathcal {Y}$
of Y over
![]() $\mathcal {O}_{F,S}$
. In this section, we recall the definition of the set
$\mathcal {O}_{F,S}$
. In this section, we recall the definition of the set
![]() $\mathcal {Y}^{f-cov}$
, which will correspond to the adelic points of
$\mathcal {Y}^{f-cov}$
, which will correspond to the adelic points of
![]() $\mathcal {Y}$
that are unobstructed by all Galois covers. To make the paper self contained, we recall the discussion from [Reference Helm and Voloch26, Section 2] (where the authors work with affine curves). We then recall that, for Hilbert modular varieties, a point unobstructed by finite covers admits an infinite tower of twists of covers with a compatible system of lifts of adelic points along the tower (following [Reference Helm and Voloch26, Proposition 1]).
$\mathcal {Y}$
that are unobstructed by all Galois covers. To make the paper self contained, we recall the discussion from [Reference Helm and Voloch26, Section 2] (where the authors work with affine curves). We then recall that, for Hilbert modular varieties, a point unobstructed by finite covers admits an infinite tower of twists of covers with a compatible system of lifts of adelic points along the tower (following [Reference Helm and Voloch26, Proposition 1]).
Let
![]() $\pi : \mathcal {X} \to \mathcal {Y}$
be a map of
$\pi : \mathcal {X} \to \mathcal {Y}$
be a map of
![]() $\mathcal {O}_{F,S}$
-schemes, such that it becomes a Galois covering over
$\mathcal {O}_{F,S}$
-schemes, such that it becomes a Galois covering over
![]() $\overline {F}$
. Such a map is called a geometrical Galois cover of
$\overline {F}$
. Such a map is called a geometrical Galois cover of
![]() $\mathcal {Y}$
. Denote by
$\mathcal {Y}$
. Denote by
![]() $\operatorname {Tw}(\pi )$
the set of isomorphism classes of twists of
$\operatorname {Tw}(\pi )$
the set of isomorphism classes of twists of
![]() $\pi $
, i.e., of maps
$\pi $
, i.e., of maps
![]() $\pi ':\mathcal {X}'\to \mathcal {Y}$
that become isomorphic to
$\pi ':\mathcal {X}'\to \mathcal {Y}$
that become isomorphic to
![]() $\pi $
over
$\pi $
over
![]() $\overline {F}$
. We have
$\overline {F}$
. We have
 $$ \begin{align*} \mathcal{Y}(\mathcal{O}_{F,S})= \bigcup\limits_{\pi ' \in \operatorname{Tw}_{0}(\pi)} \pi' \big(\mathcal{X}'(\mathcal{O}_{F,S})\big), \end{align*} $$
$$ \begin{align*} \mathcal{Y}(\mathcal{O}_{F,S})= \bigcup\limits_{\pi ' \in \operatorname{Tw}_{0}(\pi)} \pi' \big(\mathcal{X}'(\mathcal{O}_{F,S})\big), \end{align*} $$
where
![]() $\operatorname {Tw}_{0}(\pi )$
is a suitable finite subset of
$\operatorname {Tw}_{0}(\pi )$
is a suitable finite subset of
![]() $\operatorname {Tw}(\pi )$
(for a more detailed discussion, we refer the reader to [Reference Skorobogatov38, pp. 105, 106]), and
$\operatorname {Tw}(\pi )$
(for a more detailed discussion, we refer the reader to [Reference Skorobogatov38, pp. 105, 106]), and
![]() $\pi ':\mathcal {X}'\to \mathcal {Y}$
is a twist of
$\pi ':\mathcal {X}'\to \mathcal {Y}$
is a twist of
![]() $\pi $
. In what follows, w denotes a place of F.
$\pi $
. In what follows, w denotes a place of F.
Definition 4.1 We define
 $\mathcal {Y}^{f-cov}(\mathcal {O}_{F,S})=\mathcal {Y}^{f-cov}$
as the set of
$\mathcal {Y}^{f-cov}(\mathcal {O}_{F,S})=\mathcal {Y}^{f-cov}$
as the set of
![]() $ (P_{w})_{w} \in \prod _{w \notin S} \mathcal {Y}(\mathcal {O}_{F_{w}})$
such that, for each geometrical Galois cover
$ (P_{w})_{w} \in \prod _{w \notin S} \mathcal {Y}(\mathcal {O}_{F_{w}})$
such that, for each geometrical Galois cover
![]() $\pi $
, we can write
$\pi $
, we can write
for some
![]() $\pi ' \in \operatorname {Tw}_{0}(\pi )$
and
$\pi ' \in \operatorname {Tw}_{0}(\pi )$
and
![]() $(Q_{w})_{w}\in \prod _{w \notin S} \mathcal {X}'(\mathcal {O}_{F_{w}})$
.
$(Q_{w})_{w}\in \prod _{w \notin S} \mathcal {X}'(\mathcal {O}_{F_{w}})$
.
Proposition 4.1 A point
![]() $(P_{w})_{w} $
lies in
$(P_{w})_{w} $
lies in
![]() $\mathcal {Y}^{f-cov}$
if and only if, for each geometrical Galois cover
$\mathcal {Y}^{f-cov}$
if and only if, for each geometrical Galois cover
![]() $\pi : \mathcal {X} \to \mathcal {Y} $
, we can choose a twist
$\pi : \mathcal {X} \to \mathcal {Y} $
, we can choose a twist
![]() $\pi ': \mathcal {X}'\to \mathcal {Y}$
and a point
$\pi ': \mathcal {X}'\to \mathcal {Y}$
and a point
![]() $(P_{w})_\pi \in \prod _{w\notin S}\mathcal {X}'(\mathcal {O}_{F_{w}})$
lifting
$(P_{w})_\pi \in \prod _{w\notin S}\mathcal {X}'(\mathcal {O}_{F_{w}})$
lifting
![]() $(P_{w})_{w}$
in a compatible way (i.e., if
$(P_{w})_{w}$
in a compatible way (i.e., if
![]() $\pi _{1} , \pi _{2}$
are Galois covers and
$\pi _{1} , \pi _{2}$
are Galois covers and
![]() $\pi _{2}$
dominates
$\pi _{2}$
dominates
![]() $\pi _{1}$
, then
$\pi _{1}$
, then
![]() $\pi _{2}'$
dominates
$\pi _{2}'$
dominates
![]() $\pi _{1}'$
and
$\pi _{1}'$
and
![]() $(P_{w})_{\pi _{2}'}$
maps to
$(P_{w})_{\pi _{2}'}$
maps to
![]() $(P_{w})_{\pi _{1}'}$
).
$(P_{w})_{\pi _{1}'}$
).
A few words to justify the equivalence between the two definitions are needed. This is explained in [Reference Helm and Voloch26, Proposition 1] for curves, and it relies on results from [Reference Stoll39] (notably [Reference Stoll39, Lemma 5.7]Footnote 3). In [Reference Stoll39], Stoll works with projective varieties and their rational points, but what he says still holds true for the integral points of non-projective varieties. Once such differences are taken into account, the proof works in the same way in our setting.
Clearly, we have
 $\mathcal {Y}(\mathcal {O}_{F,S})\subset \mathcal {Y}^{f-cov},$
and so if
$\mathcal {Y}(\mathcal {O}_{F,S})\subset \mathcal {Y}^{f-cov},$
and so if
![]() $ \mathcal {Y}^{f-cov}$
is empty, then
$ \mathcal {Y}^{f-cov}$
is empty, then
![]() $\mathcal {Y}(\mathcal {O}_{F,S})$
has to be empty as well. What can be said when
$\mathcal {Y}(\mathcal {O}_{F,S})$
has to be empty as well. What can be said when
![]() $ \mathcal {Y}^{f-cov}$
contains a point?
$ \mathcal {Y}^{f-cov}$
contains a point?
Definition 4.2 If
 $\mathcal {Y}^{f-cov}(\mathcal {O}_{F,S})\neq \emptyset$
implies that
$\mathcal {Y}^{f-cov}(\mathcal {O}_{F,S})\neq \emptyset$
implies that
![]() $\mathcal {Y}(\mathcal {O}_{F,S})$
is non-empty, we say that the S-integral finite descent obstruction is the only obstruction for the existence of S-integral points.
$\mathcal {Y}(\mathcal {O}_{F,S})$
is non-empty, we say that the S-integral finite descent obstruction is the only obstruction for the existence of S-integral points.
From now on, we specialise to the case of Hilbert modular varieties (and their twists).
4.2 Integral Points on Hilbert Modular Varieties
Recall the notation from Section 2.2.1. Let
![]() $Y_{K}(\mathfrak {N})$
be the
$Y_{K}(\mathfrak {N})$
be the
![]() $n_{K}$
-dimensional
$n_{K}$
-dimensional
![]() ${\mathbb {Q}}$
-scheme described in Section 2.2.1 and let N be the integer such that
${\mathbb {Q}}$
-scheme described in Section 2.2.1 and let N be the integer such that
![]() $\mathfrak {N}\cap \mathbb {Z}=(N)$
. The set of twists of
$\mathfrak {N}\cap \mathbb {Z}=(N)$
. The set of twists of
![]() $\pi : Y_{K}(\mathfrak {N}) \to Y_{K}(1)$
over a number field F corresponds to the set of Galois representations
$\pi : Y_{K}(\mathfrak {N}) \to Y_{K}(1)$
over a number field F corresponds to the set of Galois representations
![]() $\rho : G_{F} \to \mathrm {GL}_{2}( {\mathcal {O}_{K}}/\mathfrak {N})$
whose determinant is the cyclotomic character
$\rho : G_{F} \to \mathrm {GL}_{2}( {\mathcal {O}_{K}}/\mathfrak {N})$
whose determinant is the cyclotomic character
![]() $\chi : G_{F} \to (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Moreover, a point
$\chi : G_{F} \to (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Moreover, a point
![]() $x \in Y_{K}(1)(F)$
lifts to a F-rational point of the twist of
$x \in Y_{K}(1)(F)$
lifts to a F-rational point of the twist of
![]() $Y_{K}(\mathfrak {N})$
corresponding to a representation
$Y_{K}(\mathfrak {N})$
corresponding to a representation
![]() $\rho $
, if and only if
$\rho $
, if and only if
![]() $\rho $
describes the action of
$\rho $
describes the action of
![]() $G_{F}$
on the
$G_{F}$
on the
![]() $\mathfrak {N}$
-torsion of the underlying abelian variety
$\mathfrak {N}$
-torsion of the underlying abelian variety
![]() $A_{x}$
(as an
$A_{x}$
(as an
![]() $\mathcal {O}_{K}$
-module).
$\mathcal {O}_{K}$
-module).
Using the moduli interpretation of Section 2.2.1, we can construct a model of
![]() $Y_{K}(\mathfrak {N})$
over
$Y_{K}(\mathfrak {N})$
over
![]() $\mathbb {Z}$
, which is smooth over
$\mathbb {Z}$
, which is smooth over
![]() $\mathbb {Z}[1/b]$
, for some natural number b, divisible by N. To be more precise ,b depends on the level structure and the discriminant of K. Fixing such a model, which we denote by
$\mathbb {Z}[1/b]$
, for some natural number b, divisible by N. To be more precise ,b depends on the level structure and the discriminant of K. Fixing such a model, which we denote by
![]() $\mathcal {Y}_{K}(\mathfrak {N})$
, we can talk about
$\mathcal {Y}_{K}(\mathfrak {N})$
, we can talk about
![]() $\mathcal {O}_{F,S}$
-points of
$\mathcal {O}_{F,S}$
-points of
![]() $Y_{K}(\mathfrak {N})$
, for any number field F and set of places S containing the archimedean places and the ones dividing b. Such
$Y_{K}(\mathfrak {N})$
, for any number field F and set of places S containing the archimedean places and the ones dividing b. Such
![]() $\mathcal {O}_{F,S}$
-points then correspond to abelian varieties (with some extra structure), having good reduction outside S. Recall that N is assumed to be bigger than
$\mathcal {O}_{F,S}$
-points then correspond to abelian varieties (with some extra structure), having good reduction outside S. Recall that N is assumed to be bigger than
![]() $3$
, since it is important to have a fine moduli space. For example, the affine line is the moduli space of elliptic curves and has plenty of
$3$
, since it is important to have a fine moduli space. For example, the affine line is the moduli space of elliptic curves and has plenty of
![]() $\mathbb {Z}$
-points, even though there are no elliptic curves defined over
$\mathbb {Z}$
-points, even though there are no elliptic curves defined over
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
We are ready to study the finite descent obstruction for the
![]() $\mathcal {O}_{L,S}$
-points of
$\mathcal {O}_{L,S}$
-points of
![]() $\mathcal {Y}_{K}(\mathfrak {N})$
and its twists, where L is a totally real field (the fact that L is totally real will be used only in the next section). Let
$\mathcal {Y}_{K}(\mathfrak {N})$
and its twists, where L is a totally real field (the fact that L is totally real will be used only in the next section). Let
be a representation whose determinant is the cyclotomic character. Assume that S contains the places w of ramification of
![]() $\rho $
. Under this assumption, arguing as above, we can consider
$\rho $
. Under this assumption, arguing as above, we can consider
![]() $\mathcal {Y}_\rho $
to be the S-integral model of the twist of
$\mathcal {Y}_\rho $
to be the S-integral model of the twist of
![]() $\mathcal {Y}_{K}(\mathfrak {N})$
corresponding to
$\mathcal {Y}_{K}(\mathfrak {N})$
corresponding to
![]() $\rho $
. From now on, we assume that
$\rho $
. From now on, we assume that
![]() $\mathcal {Y}_\rho (\mathcal {O}_{L,S})$
is non-empty. The next lemma relates a point
$\mathcal {Y}_\rho (\mathcal {O}_{L,S})$
is non-empty. The next lemma relates a point
 $(P_{w})_{w} \in \mathcal {Y}_\rho ^{f-cov}$
to a system of Galois representations as considered in the previous section.
$(P_{w})_{w} \in \mathcal {Y}_\rho ^{f-cov}$
to a system of Galois representations as considered in the previous section.
Lemma 4.2 A point
 $(P_{w})_{w} \in \mathcal {Y}_\rho ^{f-cov}(\mathcal {O}_{L,S})$
corresponds to the following data:
$(P_{w})_{w} \in \mathcal {Y}_\rho ^{f-cov}(\mathcal {O}_{L,S})$
corresponds to the following data:
-
• for each finite place v of K a representation
 $\rho _{v} : G_{L} \to \mathrm {GL}_{2}(K_{v})$
;
$\rho _{v} : G_{L} \to \mathrm {GL}_{2}(K_{v})$
; -
• for each finite place w of L such that
 $w\notin S$
an abelian variety
$w\notin S$
an abelian variety
 $A_{w}/ L_{w}$
of dimension
$A_{w}/ L_{w}$
of dimension
 $n_{K}$
, with good reduction and
$n_{K}$
, with good reduction and
 $\mathcal {O}_{K}$
-multiplication;
$\mathcal {O}_{K}$
-multiplication;
satisfying:
-
• for every place v in K the action of
 $G_{L_{w}}$
on
$G_{L_{w}}$
on
 $T_{v}(A_{w})$
is given by the restriction of
$T_{v}(A_{w})$
is given by the restriction of
 $\rho _{v}$
to the decomposition group at w;
$\rho _{v}$
to the decomposition group at w; -
• for all pairs
 $(v, a)$
such that
$(v, a)$
such that
 $v^{a}$
divides
$v^{a}$
divides
 $\mathfrak {N}$
, the reductions of
$\mathfrak {N}$
, the reductions of
 $\rho $
and
$\rho $
and
 $\rho _{v}$
modulo
$\rho _{v}$
modulo
 $v^{a}$
agree.
$v^{a}$
agree.
Moreover, every such system satisfies the first four conditions of (𝒮).
Proof We first check, using Lemma 4.1, that an unobstructed point corresponds to a system of Galois representations as described above, and then we show that every such system enjoys the desired properties.
Thanks to Proposition 4.1, we can fix a compatible system of lifts of
![]() $(P_{w})_{w}$
on
$(P_{w})_{w}$
on
 $\mathcal {Y}_\rho ^{f-cov}(\mathcal {O}_{L,S})$
. In particular, for each
$\mathcal {Y}_\rho ^{f-cov}(\mathcal {O}_{L,S})$
. In particular, for each
![]() $\mathfrak {M}$
divisible by
$\mathfrak {M}$
divisible by
![]() $\mathfrak {N}$
, we obtain a twist
$\mathfrak {N}$
, we obtain a twist
![]() $\mathcal {Y}_{K}(\mathfrak {M})'$
of
$\mathcal {Y}_{K}(\mathfrak {M})'$
of
![]() $\mathcal {Y}_{K}(\mathfrak {M})$
and a compatible family of points
$\mathcal {Y}_{K}(\mathfrak {M})$
and a compatible family of points
![]() $(P_{w})_{\mathfrak {M}}$
of
$(P_{w})_{\mathfrak {M}}$
of
![]() $\mathcal {Y}_{K}(\mathfrak {M})'$
lifting
$\mathcal {Y}_{K}(\mathfrak {M})'$
lifting
![]() $(P_{w})_{w}$
. We remark here that the latter compatible family of points depends on
$(P_{w})_{w}$
. We remark here that the latter compatible family of points depends on
![]() $(P_{w})_{w}$
. Indeed, a priori, we cannot simply lift
$(P_{w})_{w}$
. Indeed, a priori, we cannot simply lift
![]() $\rho $
to mod
$\rho $
to mod
![]() $\mathfrak {M}$
coefficients.
$\mathfrak {M}$
coefficients.
By the interpretation of
![]() $\mathcal {Y}_{K} (\mathfrak {M})'$
as moduli space of abelian varieties discussed above, the point
$\mathcal {Y}_{K} (\mathfrak {M})'$
as moduli space of abelian varieties discussed above, the point
![]() $(P_{w})_{\mathfrak {M}}$
corresponds to an abelian variety
$(P_{w})_{\mathfrak {M}}$
corresponds to an abelian variety
![]() $A_{w}/ L_{w}$
of dimension
$A_{w}/ L_{w}$
of dimension
![]() $n_{K}$
, with good reduction and
$n_{K}$
, with good reduction and
![]() $\mathcal {O}_{K}$
-multiplication and prescribed
$\mathcal {O}_{K}$
-multiplication and prescribed
![]() $\mathfrak {M}$
-torsion. The other conditions are easily checked as at the end of proof of [Reference Helm and Voloch26, Theorem 2].
$\mathfrak {M}$
-torsion. The other conditions are easily checked as at the end of proof of [Reference Helm and Voloch26, Theorem 2].
The fact that the action of
![]() $G_{L_{w}}$
on
$G_{L_{w}}$
on
![]() $T_{v}(A_{w})$
is given by the restriction of
$T_{v}(A_{w})$
is given by the restriction of
![]() $\rho _{v}$
to the decomposition group at w ensures that (
$\rho _{v}$
to the decomposition group at w ensures that (
![]() $\mathcal {S}.1$
) and (
$\mathcal {S}.1$
) and (
![]() $\mathcal {S}.2$
) are satisfied. Moreover, since
$\mathcal {S}.2$
) are satisfied. Moreover, since
![]() $A_{w}$
has good reduction,
$A_{w}$
has good reduction,
![]() $A_{w}[v]\simeq \bar {\rho }_{v}$
is a finite flat group scheme over
$A_{w}[v]\simeq \bar {\rho }_{v}$
is a finite flat group scheme over
![]() $O_{K_{w}}$
for all
$O_{K_{w}}$
for all
![]() $w\mid \ell $
if
$w\mid \ell $
if
![]() $v\mid \ell $
; this implies that (
$v\mid \ell $
; this implies that (
![]() $\mathcal {S}.3$
) also holds.
$\mathcal {S}.3$
) also holds.
Finally, we need to show that (
![]() $\mathcal {S}.4$
) is satisfied. With the three conditions above, one can show, as in the proof of Proposition 3.1, that the conductor of
$\mathcal {S}.4$
) is satisfied. With the three conditions above, one can show, as in the proof of Proposition 3.1, that the conductor of
![]() $\bar {\rho }_{v}$
divides a fixed ideal
$\bar {\rho }_{v}$
divides a fixed ideal
![]() $\mathfrak {C}$
of L. If w is such that
$\mathfrak {C}$
of L. If w is such that
![]() $A_{w}/L_{w}$
is supersingular at v, then
$A_{w}/L_{w}$
is supersingular at v, then
![]() $A_{w}[v]\simeq \bar {\rho }_{v}$
is absolutely irreducible. If there existed infinitely many v such that
$A_{w}[v]\simeq \bar {\rho }_{v}$
is absolutely irreducible. If there existed infinitely many v such that
![]() $\bar {\rho }_{v}$
is absolutely reducible, we could then write the semisemplification of
$\bar {\rho }_{v}$
is absolutely reducible, we could then write the semisemplification of
![]() $\bar {\rho }_{v}$
as direct sum of
$\bar {\rho }_{v}$
as direct sum of
![]() $\phi $
and
$\phi $
and
![]() $\chi _{\ell }\phi ^{-1}$
, for some character
$\chi _{\ell }\phi ^{-1}$
, for some character
![]() $\phi $
. Since
$\phi $
. Since
![]() $\bar {\rho }_{v}\simeq A_{w}[v]$
for
$\bar {\rho }_{v}\simeq A_{w}[v]$
for
![]() $w\mid p$
, we then have that
$w\mid p$
, we then have that
![]() $A_{w}$
is ordinary, and hence
$A_{w}$
is ordinary, and hence
![]() $\phi $
is unramified at w. We also know that the conductor of
$\phi $
is unramified at w. We also know that the conductor of
![]() $\phi $
divides
$\phi $
divides
![]() $\mathfrak {C}$
; hence, if
$\mathfrak {C}$
; hence, if
![]() $w\equiv 1 \mod \mathfrak {C,}$
we have
$w\equiv 1 \mod \mathfrak {C,}$
we have
 $$ \begin{align*} a_{w}(A_{w}):=\mathrm{Tr}\big(\operatorname{Frob}_{w}, T_{v}(A_{w})\big) \equiv \chi_{\ell}(\operatorname{Frob}_{w})+1 \mod v. \end{align*} $$
$$ \begin{align*} a_{w}(A_{w}):=\mathrm{Tr}\big(\operatorname{Frob}_{w}, T_{v}(A_{w})\big) \equiv \chi_{\ell}(\operatorname{Frob}_{w})+1 \mod v. \end{align*} $$
Since
 $\chi _{\ell }(\operatorname {Frob}_{w})=p^{[L_{w}:{\mathbb {Q}}_{p}]}$
, we showed that if we had infinitely many v such that
$\chi _{\ell }(\operatorname {Frob}_{w})=p^{[L_{w}:{\mathbb {Q}}_{p}]}$
, we showed that if we had infinitely many v such that
![]() $\bar {\rho }_{v}$
is absolutely reducible, we would find
$\bar {\rho }_{v}$
is absolutely reducible, we would find
 $a_{w}(A_{w})=p^{[L_{w}:{\mathbb {Q}}_{p}]}+1$
. Since the Weil bound says that
$a_{w}(A_{w})=p^{[L_{w}:{\mathbb {Q}}_{p}]}+1$
. Since the Weil bound says that
 $|a_{w}|\leq 2\sqrt {p^{[L_{w}:{\mathbb {Q}}_{p}]}}$
, we reached a contradiction. ▪
$|a_{w}|\leq 2\sqrt {p^{[L_{w}:{\mathbb {Q}}_{p}]}}$
, we reached a contradiction. ▪
Remark 4.3 As discussed above, for any number field F, we have a map from
![]() $Y_{K}(F)$
to systems of Galois representations satisfying (
$Y_{K}(F)$
to systems of Galois representations satisfying (
![]() $\mathcal {S}.1$
)–(
$\mathcal {S}.1$
)–(
![]() $\mathcal {S}.4$
). Thanks to Faltings [Reference Faltings18, Satz 6], this map has finite fibres. Indeed, if two points give rise to the same system, the two corresponding abelian varieties have the same locus of bad reduction, which we denote by S. It follows from the Shafarevich conjecture that Shimura varieties of abelian type have only finitely many
$\mathcal {S}.4$
). Thanks to Faltings [Reference Faltings18, Satz 6], this map has finite fibres. Indeed, if two points give rise to the same system, the two corresponding abelian varieties have the same locus of bad reduction, which we denote by S. It follows from the Shafarevich conjecture that Shimura varieties of abelian type have only finitely many
![]() $\mathcal {O}_{F,S}$
-points. For more details, we refer the reader to [Reference Ullmo43, Theorem 3.2(A)].
$\mathcal {O}_{F,S}$
-points. For more details, we refer the reader to [Reference Ullmo43, Theorem 3.2(A)].
We are now ready to prove the main theorem about descent obstruction for Hilbert modular varieties
4.3 Proof of Theorem 2
We do not treat the cases
![]() $n_{L}=1$
and
$n_{L}=1$
and
![]() $n_{L}>1$
separately, but, as in the proof of Theorem 1, we emphasize that we do not need any conjectural statement in the case
$n_{L}>1$
separately, but, as in the proof of Theorem 1, we emphasize that we do not need any conjectural statement in the case
![]() $n_{L}=1$
, since we have Shimura’s unconditional result, Theorem 2.3.
$n_{L}=1$
, since we have Shimura’s unconditional result, Theorem 2.3.
Proof Thanks to Lemma 4.2, a point in
 $\mathcal {Y}_\rho ^{f-cov} (\mathcal {O}_{L,S})$
, which is assumed to be non-empty, gives rise to a compatible system of representations of
$\mathcal {Y}_\rho ^{f-cov} (\mathcal {O}_{L,S})$
, which is assumed to be non-empty, gives rise to a compatible system of representations of
![]() $G_{L}$
, denoted by
$G_{L}$
, denoted by
![]() $\{\rho _{v}\}_{v}$
. Let E be the the subfield of K generated by
$\{\rho _{v}\}_{v}$
. Let E be the the subfield of K generated by
![]() $\mathrm {tr} (\rho _{v}(\operatorname {Frob}_{w}))$
for all w. If
$\mathrm {tr} (\rho _{v}(\operatorname {Frob}_{w}))$
for all w. If
![]() $E=K$
, Corollary 3.5 produces an
$E=K$
, Corollary 3.5 produces an
![]() $\mathcal {O}_{L,S}$
-abelian variety A with
$\mathcal {O}_{L,S}$
-abelian variety A with
![]() $\mathcal {O}_{K}$
-multiplication, such that
$\mathcal {O}_{K}$
-multiplication, such that
![]() $G_{L}$
acts on
$G_{L}$
acts on
![]() $A[\mathfrak {N}]$
via
$A[\mathfrak {N}]$
via
![]() $\rho $
. To conclude the proof, we just need to see how A corresponds to a point
$\rho $
. To conclude the proof, we just need to see how A corresponds to a point
![]() $P\in \mathcal {Y}_{\rho }(\mathcal {O}_{L,S})$
. The only issue that is not clear from the quoted corollary is whether A is principally
$P\in \mathcal {Y}_{\rho }(\mathcal {O}_{L,S})$
. The only issue that is not clear from the quoted corollary is whether A is principally
![]() $\mathcal {O}_{K}$
-polarised, but this follows from the discussion in Section 2.4.
$\mathcal {O}_{K}$
-polarised, but this follows from the discussion in Section 2.4.
If E is strictly contained in K, i.e., condition (𝒮.5) is not satisfied, we consider
![]() $S_{E}$
, the Hilbert modular variety associated with E and of level
$S_{E}$
, the Hilbert modular variety associated with E and of level
![]() $\mathfrak {N} \cap \mathcal {O}_{E}$
. For the same reason as above, the system
$\mathfrak {N} \cap \mathcal {O}_{E}$
. For the same reason as above, the system
![]() $\{\rho _{v}\}$
corresponds to a
$\{\rho _{v}\}$
corresponds to a
![]() $\mathcal {O}_{L,S}$
-point P of the twist by
$\mathcal {O}_{L,S}$
-point P of the twist by
![]() $\rho $
of
$\rho $
of
![]() $S_{E}$
. The embedding
$S_{E}$
. The embedding
![]() $\mathrm {Res}_{E/{\mathbb {Q}}}\mathrm {GL}_{2}\hookrightarrow \mathrm {Res}_{K/{\mathbb {Q}}}\mathrm {GL}_{2}$
induces a map of Shimura varieties
$\mathrm {Res}_{E/{\mathbb {Q}}}\mathrm {GL}_{2}\hookrightarrow \mathrm {Res}_{K/{\mathbb {Q}}}\mathrm {GL}_{2}$
induces a map of Shimura varieties
and therefore on their twists by
![]() $\rho $
. Via r, we can regard P as an
$\rho $
. Via r, we can regard P as an
![]() $\mathcal {O}_{L,S}$
-point of
$\mathcal {O}_{L,S}$
-point of
![]() $\mathcal {Y}_\rho $
, which completes the proof of the theorem. The only difference is that the abelian variety constructed in this case is not primitive. This concludes the proof of Theorem 2. ▪
$\mathcal {Y}_\rho $
, which completes the proof of the theorem. The only difference is that the abelian variety constructed in this case is not primitive. This concludes the proof of Theorem 2. ▪
Acknowledgement
It is a pleasure to thank Toby Gee for helpful discussions about the weight part of Serre’s conjecture and the Taylor–Wiles assumption. We thank Matteo Tamiozzo for his comments on an earlier draft of this paper. We would also like to express our gratitude to the anonymous referees whose comments improved the paper.