Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T08:12:40.876Z Has data issue: false hasContentIssue false
  • English
  • Français

A general buoyancy–drag model for the evolution of the Rayleigh–Taylor and Richtmyer–Meshkov instabilities

Published online by Cambridge University Press:  03 March 2004

YAIR SREBRO ,
YONI ELBAZ ,
OREN SADOT ,
LIOR ARAZI  and
DOV SHVARTS
YAIR SREBRO
Affiliation:
Department of Physics, Ben-Gurion University, Beer-Sheva, Israel Department of Physics, Nuclear Research Center–Negev, Israel
YONI ELBAZ
Affiliation:
Department of Physics, Ben-Gurion University, Beer-Sheva, Israel Department of Physics, Nuclear Research Center–Negev, Israel
OREN SADOT
Affiliation:
Department of Physics, Nuclear Research Center–Negev, Israel Department of Mechanical Engineering, Ben-Gurion University, Beer-Sheva, Israel
LIOR ARAZI
Affiliation:
School of Physics and Astronomy, Tel-Aviv University, Tel-Aviv, Israel
DOV SHVARTS
Affiliation:
Department of Physics, Ben-Gurion University, Beer-Sheva, Israel Department of Physics, Nuclear Research Center–Negev, Israel Department of Mechanical Engineering, Ben-Gurion University, Beer-Sheva, Israel
Rights & Permissions [Opens in a new window]

Abstract

The growth of a single-mode perturbation is described by a buoyancy–drag equation, which describes all instability stages (linear, nonlinear and asymptotic) at time-dependent Atwood number and acceleration profile. The evolution of a multimode spectrum of perturbations from a short wavelength random noise is described using a single characteristic wavelength. The temporal evolution of this wavelength allows the description of both the linear stage and the late time self-similar behavior. Model results are compared to full two-dimensional numerical simulations and shock-tube experiments of random perturbations, studying the various stages of the evolution. Extensions to the model for more complicated flows are suggested.

Keywords

Buoyancy–drag modelDirect numerical simulationHydrodynamic instabilityShock tube experiment
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 3 , July 2003 , pp. 347 - 353
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

The Rayleigh–Taylor (RT) instability occurs on the interface between two fluids when an acceleration is directed from the heavy to the light, or, in general, when the pressure gradient is in the opposite direction to the density gradient. The Richtmyer–Meshkov (RM) instability occurs when a shock wave passes through the interface between the two fluids. Small perturbations on unstable interfaces grow with time into a turbulent mixing zone. The evolution of a mixing zone starts from a random perturbation present due to noise and nonuniformities in the system. The multimode spectrum of short-wavelength perturbations evolves into larger structures through an inverse cascade process. Competition and coalescence of large coherent structures drive this process, because of the reduced drag per unit volume of large structures.

It is customary to investigate the instability between two semi-infinite fluids of densities ρ1 and ρ2 in a uniform acceleration field perpendicular to the interface. The Atwood number is then defined as A = (ρ2 − ρ1)/(ρ2 + ρ1). Layzer (1955) solved the problem of a single bubble rising in a heavy fluid by means of a potential flow model, valid for all instability stages from the linear stage through the early nonlinear to the asymptotic, but limited to A = 1. This model has been extended into a class of buoyancy–drag models valid for every A, but limited to the nonlinear stages of the instability (Alon et al., 1995; Arazi, 2001; Oron et al., 2001). These models will be described in more detail in Section 4. Goncharov (2002) has recently presented an extension of the single-mode model to all density ratios. Alon et al. (1993) used a statistical bubble merger model to investigate the self-similar evolution of the mixing zone. Youngs (1984), Freed et al. (1991) and Alon and Shvarts (1995) applied a two-phase flow model for describing the interpenetration of the two fluids. The evolution of a turbulent mixing zone from a random initial perturbation has been studied experimentally by Dimonte and Schneider (2000). Shock-tube experiments were conducted and compared to diffusion-like turbulence models (Andronov et al., 1976; Brouillette & Sturtevant, 1989; Gauthier & Bonnet, 1990).

An effective mix model should describe the mixing based on the one-dimensional (1D) flow. This description includes the mix region boundaries, as well as its internal structure. Turbulent mixing is coupled to the 1D flow and affects it. Hence a good model should include a feedback to the simulation of the 1D flow. The description of the internal structure of the mixing zone includes spatial profiles of density, temperature, and pressure of every material, as well as the degree of mixing. The feedback to the simulation of the 1D flow is done by transferring mass, momentum, and energy due to the mixing between the materials. The model should describe all instability stages. General hydrodynamic instabilities include many complicated effects, such as general acceleration profiles, various geometries (planar, cylindrical, and spherical), compressibility, ablative flow, density gradients, and heat conduction. Moreover the dimensionality of the perturbations may be two-dimensional (2D) or three-dimensional (3D). This paper describes a model that integrates most of these effects, and suggests means of treating some of the further effects.

Section 2 describes new shock-tube experiments, conducted to measure the evolution of a mix region from a random perturbation. Section 3 describes numerical simulations, which attempt to reproduce the experimental results. In Section 4, the buoyancy–drag model is described, its validity is confirmed by comparison to the simulations, and its results are compared to the shock-tube experimental results. Section 5 summarizes the results and presents suggestions for the modification of the model for more general problems.

2. SHOCK-TUBE EXPERIMENTS

The mixing front growth was investigated experimentally in shock-tube experiments, following those published by Erez et al. (2000). A 5.5-m-long horizontal double-diaphragm shock tube with an 8 cm × 8 cm cross section was used to generate a 1.2 Mach number shock wave passing from air to SF6 (A = 0.7). A thin membrane was placed to separate the two gases initially. Upon the incidence of the shock wave, the interface becomes RM unstable. An end wall placed at a distance of 18 cm from the interface reflects the shock to hit the interface again and to induce a second RM instability. Later on, the interface becomes RT unstable when the rarefaction wave, returning from the end wall, starts accelerating the interface.

The evolution of the shock-wave-induced mixing zone was measured by recording a series of Schlieren photographs using a Nd:YAG frequency doubled laser pulsed at intervals of about 40 μs and a shutterless rotating-prism camera. The Schlieren system measures gradients in the index of refraction in the gas. Therefore, material interfaces as well as density discontinuities along shock waves appear as dark lines. The 3D turbulent mixing zone is comprised of complex structures of different sizes; hence the whole mixing region appears as a dark region in the photographs as well. The extent of the turbulent mixing zone was deduced from the photographs using a computerized image analysis, described by Erez et al. (2000). Several experiments with the same experimental setup have been repeated in order to check the reproducibility of the mixing zone measurement. These measurements are compared to the buoyancy–drag model in Section 4 (see Fig. 4).

Figure 1 displays typical frames from the experiment. The contact surface together with the mixing zone being developed around it can clearly be seen as the dark region. The various shock waves can also be seen as the thin black lines. Behind the planar shock waves, a set of shock waves reflected from the tube walls can be seen.

Frames from the experiment at various times. The initial shock wave travels from the air on the left into the SF6 on the right. The end wall is to the right of the right edge of the frames. The dark region around the contact surface is the turbulent mixing zone.

3. NUMERICAL SIMULATIONS

We have performed 2D numerical simulations of multimode perturbations with LEEOR2D to describe the turbulent mixing in the experiments. Hydrodynamic simulations without further mixing models are only capable of reproducing phenomena on a length scale larger than their mesh size. It is impractical to describe all the turbulent length scales in such a simulation. However, since large structures determine the evolution of the mixing zone envelope, it is sufficient to resolve them in the numerical simulation. The initial perturbation in the simulations includes mode numbers 40–60 along the 8-cm width of the shock tube, leaving mode numbers lower than 40 vacant for creation from smaller structures through bubble coalescence. This initial perturbation spectrum has an average wavelength of 〈λ〉 = 0.32 cm and a root-mean-square total amplitude of h = 0.064 cm, which corresponds to h/〈λ〉 = 0.2. The results were found to be insensitive to the numerical resolution by comparing a simulation with 320 cells in the lateral direction to one with 160. These simulations describe the shortest wavelength using roughly 10 and 5 cells, respectively.

The simulation results are displayed in Figure 2, where features similar to those found experimentally may be observed. Another feature observed in the simulations is the coalescence of small bubbles into larger structures, which will enable us to use the assumption of self-similarity for the asymptotic stage. Moreover, the periodicity of bubbles and spikes is similar, which will enable us to use the same typical wavelength, 〈λ〉, for both bubbles and spikes.

Density maps from the 2D multimode simulation of the experiment.

We analyze the simulations by averaging the volume fraction of every one of the gases along the mixing region. The bubble and spike locations are defined where the volume fraction of the air reaches 1% and 99%, respectively. Their heights are defined as the distance between these locations and the instantaneous location of the unperturbed interface. The resulting bubble and spike heights were not very sensitive to cutting off the volume fraction distribution at different percentages. A 3% reduction for the bubbles and a 7% reduction for the spikes were attained when defining with 5% and 95% of the volume fraction. A 9% reduction for the bubbles and a 19% reduction for the spikes were attained when defining with 10% and 90% of the volume fraction. Therefore, we may use the simulations' results up to an accuracy of a few percent.

It is difficult to compare quantitatively between the simulations and the experimental results; therefore we compare the experimental results only to the buoyancy–drag model that will be described in the following section. The experiments are 3D, and the different behavior of the RM instability in 2D versus 3D requires 3D simulations. Because the spikes are narrower, high resolutions are required to describe their behavior. Moreover, the RM instability evolution depends on the initial conditions, and these should be changed to achieve agreement with the experimental results. This will require performing many multimode simulations. The multimode simulations do not include structures smaller than the computational mesh; hence they have a quite ordered perturbation that will exhibit a phase reversal upon the reshocking of the interface. In reality, the mixing zone includes complex structures of all sizes, down to the molecular level, and demixing and phase reversal is not expected to occur.

4. A BUOYANCY–DRAG MODEL

4.1. Existing models

In the case of a single-mode perturbation, we assume that a periodic perturbation of wavelength λ is imposed on the interface. The wave-vector is defined as k = 2π/λ. The amplitude of the lighter fluid bubbles penetrating the heavier fluid is defined as hB, and its derivative as uB = dhB /dt. The amplitude of the heavier fluid spikes penetrating the lighter fluid is defined as hS, and its derivative as uS = dhS /dt.

For an infinite density ratio (A = 1) the perturbation evolution may be described by a potential flow model. Following Layzer (1955) and Hecht et al. (1994) we assume a single-mode perturbation and expand the flow equations to second order around the bubble tips, hence obtaining an ordinary differential equation for the bubble velocity:

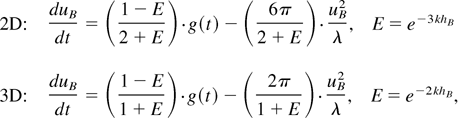
where g(t) is the time-dependent interface acceleration.

The resulting model describes all instability stages—it is correct for small amplitudes up to third order and in the asymptotic stage. It is valid for a general acceleration profile. However, it is limited to A = 1 and to single-mode perturbations.

At late times, when khB increases, E approaches zero and the Layzer model equation may be written as

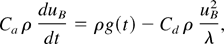
where Ca = 2 (2D), 1 (3D), and Cd = 6π (2D), 2π (3D). The left-hand side of the equation describes the inertia of the added mass—the mass of the heavy fluid, pushed by the rising bubbles. The right-hand side of the equation includes the buoyancy force and the drag force acting on the bubble. This buoyancy–drag equation may now be generalized for every density ratio. Following Alon et al. (1995), Dimonte (2000), Cheng et al. (2000), Arazi (2001), and Oron et al. (2001), we add the bubble's inertia to the added mass's inertia and change the buoyancy term to include the density difference:

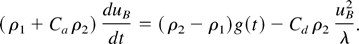
An equation for the spikes is obtained by substituting ρ1 and ρ2 in the inertia term and in the drag term:

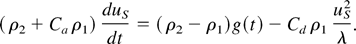
These equations, with Ca and Cd taken from Layzer's model for A = 1, describe correctly the asymptotic stage for a general acceleration profile and for a general density ratio.

4.2. Model description

For single-mode perturbations, we may use the Layzer model for A = 1 and all instability stages, and the buoyancy–drag model for the asymptotic stage at every A. We would now want to expand the validity of the buoyancy–drag model to all instability stages so that it will coincide with the Layzer model as A approaches one. We add the amplitude dependence through the parameter E(t) = e−Ce·k·hB, where Ce = 3 (2D), 2 (3D). And we write the buoyancy–drag equations as

It is evident that as A approaches one, this model coincides with the Layzer model (Eq. (1)) for all instability stages, and that for the asymptotic stage, when khB is large and E approaches zero, it coincides with the buoyancy–drag model (Eqs. (3) and (4)) for all Atwood numbers. In the linear stage, when expanding Eq. (5) to first order in khB, we attain the general acceleration linear stage solution for all Atwood numbers, which is symmetric for bubbles and spikes:

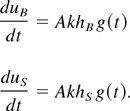
To describe the evolution of a multimode perturbation we limit ourselves to perturbations that have smooth nonpeaked spectra. This is usually the case, because random noise initial perturbations do not have singular lines, and during the self-similar stage an asymptotic spectrum is achieved. We identify the full spectrum of perturbations with an equivalent single-mode perturbation, which grows according to the single-mode model described above (Eq. (5)). The multimode spectrum of perturbations is described by its characteristic wavelength, 〈λ〉. Initially 〈λ〉 is set to be the wavelength of the most dominant mode in the spectrum. During the linear stage, 〈λ〉 is not changed with time. In the asymptotic stage, the mixing fronts behave self-similarly. As the amplitude grows, the wavelength characterizing the perturbation grows, and the ratio between the average amplitude and the average wavelength remains constant: hB /〈λ〉 = b(A). The dependence b(A) has been investigated experimentally by Dimonte and Schneider (2000) and theoretically by Arazi (2001) and Oron et al. (2001). To reproduce the hB = αB Agt2 behavior with αB = 0.05 for constant acceleration RT instability we choose b = 0.5/(1 + A) for 2D and b = 1.6/(1 + A) for 3D, similar to the Atwood-dependent functions given by Hansom et al. (1990). Note that in order to reproduce the RM hB ∼ tθ behavior with θ = 0.4 in 2D and θ = 0.25 in 3D, different functions should be used for b(A). We change 〈λ〉 as

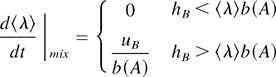
There is a sharp transition at hB = 〈λ〉·b(A) from the linear stage, where 〈λ〉 is not changed, to the asymptotic stage, where self-similarity is assumed. This differential equation for 〈λ〉 is coupled to Eq. (5), which describes the evolution of hB and hS. As pointed out by Alon et al. (1995), and as observed in the simulations presented in the previous section, the spikes and bubbles have the same periodicity because the dominant bubbles generate the dominant spikes. We assume the same periodicity for the bubbles and the spikes, and hence may use a single wavelength for both of the equations in Eq. (5).

The model we have built describes the growth of the mixing fronts for a multimode perturbation and for a general acceleration profile. In the linear stage, it reproduces the theoretical behavior, because the equations are equivalent to

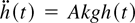
. During the early nonlinear stage, it coincides with the Layzer model as A approaches one; hence it is correct to third order. In the asymptotic stage, it coincides with the buoyancy–drag equations for every A. However, the model is limited to planar geometry and to incompressible flow.

The RT instability occurs only for gA > 0, whereas for gA < 0 the interface is stable. Theoretically, stable interfaces exhibit oscillations in perturbation amplitudes. This is probably the case only for ordered perturbations comprised of a small number of mode numbers. For turbulent mixing where an infinite number of modes is present, demixing is not expected to occur (Hansom et al., 1990); hence we increase the bubble's and spike's amplitudes according to Eq. (5) only when gA > 0 and do not decrease them when gA < 0. The RM instability, on the other hand, occurs also for gA < 0. When a shock wave passes from a heavy fluid to a lighter one, the amplitude of an ordered perturbation will decrease, but will then grow in an unstable manner after reversing its phase. Since we assume there is no demixing for the turbulent flows under consideration in this article, we do not include this phase reversal phenomenon in the model. For the model to describe all RM instability cases, we take the absolute value of gA. This is done only for problems that have a RM-dominated acceleration temporal history.

In compressible flow, the density may depend on location and on time. This is taken into account by defining the Atwood number by using the average densities of every one of the materials in the mixing zone. If there is a 1D flow in the proximity of the bubbles or spikes, the 1D flow velocity should be added to the velocity at which the mixing zone grows. Following Hansom et al. (1990), we change uB to uB + u1D(hB) and uS to uS + u1D(hS), where u1D(hB) and u1D(hS) are the 1D velocities at the locations of the bubbles and at the location of the spikes, respectively.

4.3. Comparison between model and simulations

The 2D version of the model (with Cd = 6π, Ca = 2, Ce = 3, and b = 0.5/(1 + A)) was compared to the 2D multimode simulation with the same initial hB, hS, and 〈λ〉. A good agreement for the bubbles' location and a reasonable agreement for the spikes' location can be seen in Figure 3 after the first shock, after the reshock, and for the acceleration at later times. The difference between simulation and model for the spikes' location is probably due to limited ability of the numerical simulation to describe the thin spikes. When the simulation's resolution was increased, the spikes' envelope approached the model result.

x–t diagram of the interface from a 1D simulation (dotted line) and of the bubble and spike envelope from the 2D multimode simulation (solid lines) and from the 2D mix model (dashed lines).

Size of the mixing zone versus time from two experiments (triangles and circles) compared to the result of the 2D and 3D mix models for different initial values of 〈λ〉.

4.4. Comparison between model and experiments

Due to the 3D nature of the experiments, they are compared to the 3D version of the model (with Cd = 2π, Ca = 1, Ce = 2, and b = 1.6/(1 + A)). Due to the difficulty in defining the unperturbed interface and due to the increased error in subtracting two measured numbers, we compare the total width of the mixing zone, hB + hS, which is easier and more accurate to measure. We do not have information about the initial perturbation; therefore we varied both 〈λ〉 and h, assuming hB = hS. For every value of 〈λ〉, various initial amplitudes were checked until the model result agreed with the RM evolution after the first shock. The result of this fitting is displayed in Figure 4 for two initial wavelengths. An initial value of 〈λ〉 = 0.05 cm and h = 0.06 cm best matches the experimental results. For shorter wavelengths, the amplitude required to fit the experimental results is very large—much larger than the wavelength, which does not seem reasonable to exist on the membrane. For longer wavelengths, small initial amplitudes are required and the growth is dominated by the linear regime, resulting in a larger scaling exponent, as can be observed in Figure 4.

The two separate experiments seem to behave similarly, implying their initial conditions were similar. The model reproduces the growth after the first shock as well as the growth after the reshock; however, the details of the growth after the reshock are different. This may be attributed to the phase reversal of the perturbation when the reflected shock hits the perturbed interface. The effect occurs in the experiment and is included in the simulations, but is not taken into account in the model.

The agreement with the experimental results is quantified by the parameter θ in the h ∼ tθ asymptotic RM behavior. Experimentally, θ = 0.24 for the growth after the first shock, and the model with λ = 0.05 cm results in θ = 0.29, while when starting with λ = 0.5 cm, θ = 0.77. After the reshock, the mixing zone evolves from an existing mixing zone and not from a negligible perturbation like in the case of the first shock; therefore its growth is fitted to (t − t0)θ. After the reshock, the experimental mixing zone grows with θ = 0.93, while the model predicts θ = 0.77 for all initial wavelengths. This growth is faster than the initial growth, both for the experiment and the model. Even though a self-similar mixing zone has already been established during the RM instability after the first shock, the post reshock growth begins with an existing velocity and not only with a perturbation amplitude. Shortly after the reshock, the instability grows faster than the self-similar scaling law. The experiment probably does not allow enough time for the mixing zone to return to its self-similar behavior.

The difference between the 3D model and the 2D model may be seen in Figure 4. In 2D for λ = 0.05 cm, θ = 0.32 after the first shock and θ = 0.8 after the reshock. Due to the lack of information about the initial conditions in the experiment and due to the degree of agreement with the experimental results, it is difficult to distinguish between 3D behavior and 2D behavior. We suggest using the 3D model because of the 3D nature of the experimental setup and not because of a better agreement with the experimental results.

4.5. Extensions to the model

The model is valid for general acceleration profiles, for compressible flows, and for both 2D and 3D perturbations. The model may simply be extended to more complicated flows. Nonplanar geometry introduces two effects, which have been pointed out by Bell (1951) and by Plesset (1954). When the radius of the system changes, all length scales change as well. When the radius is reduced, the radial length scales increase and the azimuthal length scales decrease. The change of length scales in the radial direction (amplitudes) is included in the 1D coupling to the Lagrangian flow. The change of length scales in the azimuthal direction (wavelength) may be described by modifying the equation governing 〈λ〉 (Eq. (7)). A geometric term is then added to this equation:

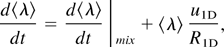
where R1D is the radius of the interface between the two materials.

An automatic discrimination between RT and RM for gA < 0 may be added to the model, according to the criterion of Shvarts et al. (1995): Accelerations changing faster than g ∼ t−2 are RM-like and accelerations changing slower are RT-like. This is important for problems with combined RT and RM, such as a gA < 0 shock wave during a gA < 0 continuous acceleration.

The influence of further effects, such as ablation, density gradients, and heat conduction on the linear growth rates is known. Oron et al. (1998) found that the influence on the asymptotic single-mode evolution is similar and can be approximately derived from it. Knowing this, it is simple to incorporate these effects into the buoyancy–drag model in a phenomenological manner.

5. CONCLUSIONS

A model based on considerations of buoyancy and drag, valid only for the asymptotic stage, has been extended to all instability stages. The evolution of a multimode spectrum of perturbations from a short wavelength random noise is described using a single characteristic wavelength. The temporal evolution of this wavelength allows the description of both the linear stage and the late time self-similar behavior. The model is coupled to the 1D Lagrangian flow in the proximity of the bubbles and the spikes. Good agreement was found in comparing the 2D model to 2D multimode numerical simulations. When comparing the 3D model to shock-tube experiments of random perturbations, the initial perturbation had to be selected for the result to fit the experimental result. Similar scaling laws were found after the first shock; however the experimental mixing zone grew faster than the theoretical prediction.

The model is valid for general acceleration profiles, for compressible flows, and for both 2D and 3D perturbations. Extensions of the model for more complicated flows, including spherical or cylindrical geometries, ablation, density gradients, and heat conduction have been suggested.

ACKNOWLEDGMENT

The authors would like to thank D. Oron for his helpful remarks during the preparation of this article.

References

REFERENCES

Alon, U., Shvarts, D., & Mukamel, D. (1993). Scale invariant regime in Rayleigh–Taylor bubble-front dynamics. Phys. Rev. E 48, 1008–1014.Google Scholar
Alon, U., & Shvarts, D. (1995). Two phase flow model for RT and RM mixing. Proc. Fifth Int. Workshop on Compressible Turbulent Mixing (Young, D., Climm, J. & Boston, B., Eds.), pp. 14–22.
Alon, U., Hecht, J., Ofer, D., & Shvarts, D. (1995). Power Laws and Similarity of Rayleigh-Taylor and Richtmyer-Meshkov Mixing Fronts at All Density Ratios Phys. Rev. Lett. 74, 534–537.Google Scholar
Andronov, V.A., Bakhrakh, S.M., Meshkov, E.E., Mokhov, V.N., Nikiforov, V.V., Pevnitskii, A.V., & Tolshmyakov, A.I. (1976). Turbulent mixing at contact surface accelerated by shockwaves. Sov. Phys. JETP 44, 424–427.Google Scholar
Arazi, L. (2001). A drag-buoyancy based study of the late time RT and RM scaling laws. M.Sc. Thesis, Tel Aviv, Israel: Tel Aviv University.
Bell, G.I. (1951). Taylor instability on cylinders and spheres in the small amplitude approximation. Report LA-1321, Los Alamos, NM: Los Alamos National Laboratory.
Bodner, S.E. (1974). Rayleigh–Taylor instability and laser-pellet fusion. Phys. Rev. Lett. 33, 761–764.Google Scholar
Brouillette, M., & Sturtevant, B. (1989). Growth induced by multiple shock waves normally incident on plane gaseous interfaces. Physica D 37, 248–263.Google Scholar
Cheng, B., Glimm, J., & Sharp, D.H. (2000). Density dependence of Rayleigh–Taylor and Richtmyer–Meshkov mixing fronts. Phys. Lett. A 268, 366–374.Google Scholar
Dimonte, G. (2000). Spanwise homogeneous buoyancy-drag model for Rayleigh–Taylor mixing and experimental evaluation. Phys. Plasmas 7, 2255–2269.Google Scholar
Dimonte, G., & Schneider, M. (2000). Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12, 304–321.Google Scholar
Erez, L., Sadot, O., Oron, D., Erez, G., Levin, L.A., Shvarts, D., & Ben-Dor, G. (2000). Study of the membrane effect on turbulent mixing measurements in shock tubes. Shock Waves 10, 241–251.Google Scholar
Freed, N., Ofer, D., Shvarts, D., & Orszag, S.O. (1991). Two-phase flow analysis of self-similar turbulent mixing by Rayleigh–Taylor in stability. Phys. Fluids A 3, 912–918.Google Scholar
Gauthier, S., & Bonnet, M. (1990). A k-epsilon model for turbulent mixing in shock-tube flows induced by Rayleigh–Taylor instability. Phys. Fluids A 2, 1685–1694.Google Scholar
Goncharov, V.N. (2002). Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502-1-4.Google Scholar
Hansom, J.C.V., Rosen, P.A., Goldack, T.J., Oades, K., Fieldhouse, P., Cowperthwaite, N., Youngs, D.L., Nawhinney, N., & Baxter, A.J. (1990). Radiation driven planer foil instability and mix experiments at the AWE HELEN laser. Laser Part. Beams 8, 51–71.Google Scholar
Hecht, J., Alon, U., & Shvarts, D. (1994). Potential flow models of Rayleigh–Taylor and Richtmyer–Meshkov bubble fronts. Phys. Fluids 6, 4019–4030.Google Scholar
Layzer, D. (1955). On the instability of superposed fluids in a gravitational field. Astrophys. J. 122, 1–12.Google Scholar
Oron, D., Arazi, L., Kartoon, D., Rikanati, A., Alon, U., & Shvarts, D. (2001). Dimensionality dependence of the Rayleigh–Taylor and Richtmyer–Meshkov instability late-time scaling laws. Phys. Plasmas 8, 2883–2889.Google Scholar
Oron, D., Alon, U., & Shvarts, D. (1998). Scaling laws of the Rayleigh–Taylor ablation front mixing zone evolution in inertial confinement fusion. Phys. Plasmas 5, 1467–1476.Google Scholar
Plesset, M.S. (1954). On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.Google Scholar
Shvarts, D., Alon, U., Ofer, D., McCrory, R.L., & Verdon, C.P. (1995). Nonlinear evolution of multimode Rayleigh–Taylor instability in two and three dimensions. Phys. Plasmas 2, 2465–2472.Google Scholar
Youngs, D.L. (1984). Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
Figure 0

Frames from the experiment at various times. The initial shock wave travels from the air on the left into the SF6 on the right. The end wall is to the right of the right edge of the frames. The dark region around the contact surface is the turbulent mixing zone.

Figure 1

Density maps from the 2D multimode simulation of the experiment.

Figure 2

x–t diagram of the interface from a 1D simulation (dotted line) and of the bubble and spike envelope from the 2D multimode simulation (solid lines) and from the 2D mix model (dashed lines).

Figure 3

Size of the mixing zone versus time from two experiments (triangles and circles) compared to the result of the 2D and 3D mix models for different initial values of 〈λ〉.