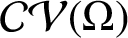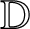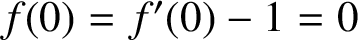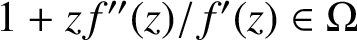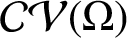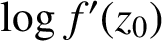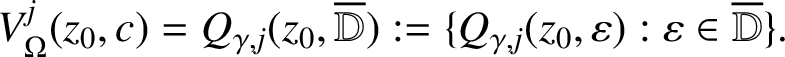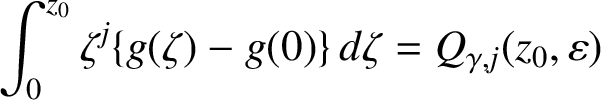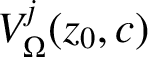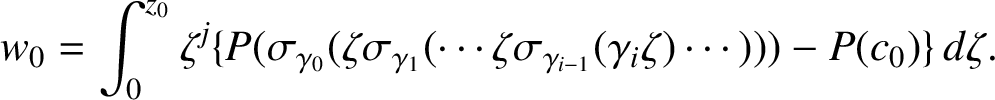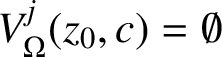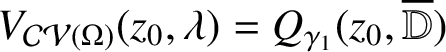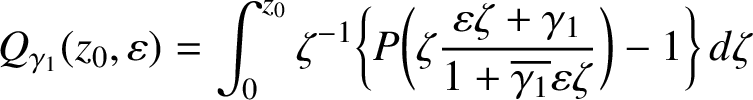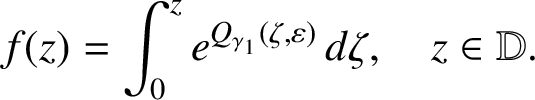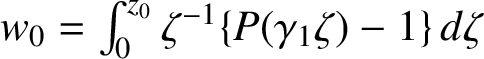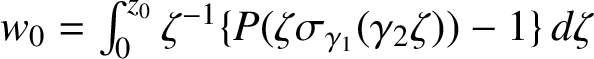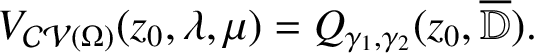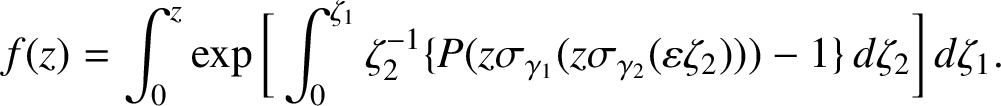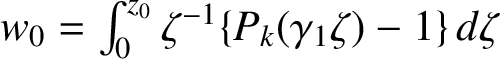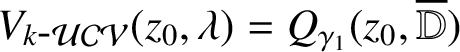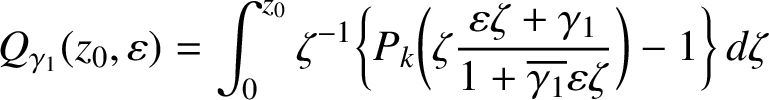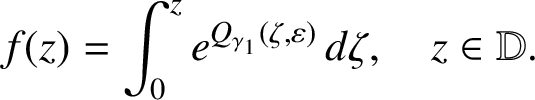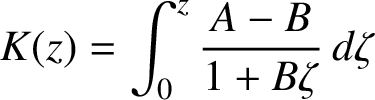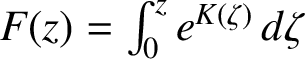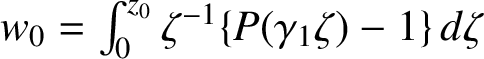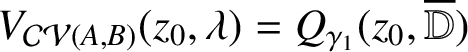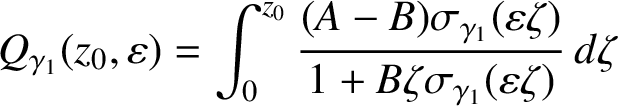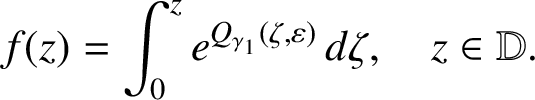1 Introduction
Let
${\mathbb C}$
be the complex plane. For
$c \in {\mathbb C}$
and
$r> 0$
, let
${\mathbb D}(c,r) := \{ z \in {\mathbb C} : |z-c| < r \}$
and
$\overline {\mathbb D}(c,r) := \{ z \in {\mathbb C} : |z-c| \leq r \}$
. In particular, we denote the unit disk by
${\mathbb D} := {\mathbb D}(0,1)$
. Let
${\mathcal A}({\mathbb D})$
be the class of analytic functions in the unit disk
${\mathbb D}$
endowed with the topology of uniform convergence on every compact subset of
${\mathbb D}$
. Denote by
$\mathcal {A}_0$
functions f in
${\mathcal A}({\mathbb D})$
normalised by
$f(0) = f'(0)-1 = 0$
. Further, let
$\mathcal {S}$
denote the standard subclass of
$\mathcal {A}_0$
of normalised univalent functions in
${\mathbb D}$
. A function f in
$\mathcal {A}_0$
is called starlike (respectively convex) if f is univalent and
$f(\mathbb {D})$
is starlike with respect to
$0$
(respectively convex). Let
$\mathcal {S}^*$
and
$\mathcal {CV}$
denote the classes of starlike and convex functions, respectively. It is well known that a function
$f\in \mathcal {A}_0$
is in
$\mathcal {S}^*$
if and only if
$\mathrm {Re}\,(zf'(z)/f(z))>0$
and in
$\mathcal {CV}$
if and only if
$\mathrm {Re} \, \{ zf''(z)/f'(z) \} +1> 0$
for
$z\in \mathbb {D}$
.
Let
${\mathcal F}$
be a subclass of
${\mathcal A}({\mathbb D})$
and
$z_0 \in {\mathbb D}$
. The upper and lower estimates,
$$ \begin{align*} M_1 \leq |f'(z_0)| \leq M_2 \quad\mbox{and}\quad m_1 \leq \text{Arg } f'(z_0) \leq m_2 \quad \mbox{for all } f \in {\mathcal F}, \end{align*} $$
where the
$M_j$
and
$m_j$
are nonnegative constants, are respectively called distortion and rotation theorems at
$z_0$
for
${\mathcal F}$
. These estimates deal only with the absolute value or argument of
$f'(z_0)$
. If one wants to study the complex value
$f'(z_0)$
itself, it is necessary to consider the variability region of
$f'(z_0)$
when f ranges over
${\mathcal F}$
, that is, to consider the set
$\{ f'(z_0) : f \in {\mathcal F } \}$
. For example [Reference Duren4, Ch. 2, Exercises 10, 11 and 13],
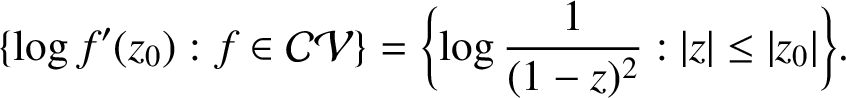$$ \begin{align*} \{ \log f'(z_0) : f \in \mathcal{CV} \} = \bigg\{\!\log \frac{1}{(1-z)^2 } : |z| \leq |z_0| \bigg\}. \end{align*} $$
For
$f \in \mathcal {CV}$
, an easy consequence of Schwarz’s lemma is that
$|f''(0)| \leq 2$
. For fixed
$z_0 \in {\mathbb D}$
and
$\lambda \in \overline {\mathbb D}$
, Gronwall [Reference Gronwall7] obtained the sharp lower and upper estimates for
$|f'(z_0)|$
when
$f \in \mathcal {CV}$
satisfies the additional condition
$f''(0) = 2 \lambda $
(see also [Reference Finkelstein5]). Let
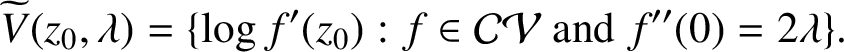$$ \begin{align*} \widetilde{V} (z_0, \lambda) = \{ \log f'(z_0) : f \in \mathcal{CV} \mbox{ and } f''(0) = 2 \lambda \}. \end{align*} $$
If
$| \lambda | =1 $
, then, by Schwarz’s lemma, for
$f \in \mathcal {CV}$
the condition
$f''(0) = 2 \lambda $
forces
$f(z) \equiv z/(1-\lambda z)$
and hence
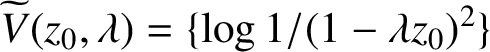$\widetilde {V} (z_0, \lambda ) = \{ \log 1/(1-\lambda z_0)^2 \}$
. Since
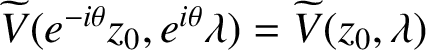$\widetilde {V}(e^{-i \theta }z_0, e^{i \theta }\lambda ) = \widetilde {V}(z_0, \lambda )$
for all
$\theta \in {\mathbb R}$
, without loss of generality we may assume that
$0 \leq \lambda < 1$
. In 2006, Yanagihara [Reference Yanagihara20] obtained the following extension of Gronwall’s result.
Theorem 1.1. For any
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
and
$0 \leq \lambda < 1$
, the set
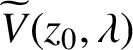$\widetilde {V} (z_0, \lambda ) $
is a convex closed Jordan domain surrounded by the curve
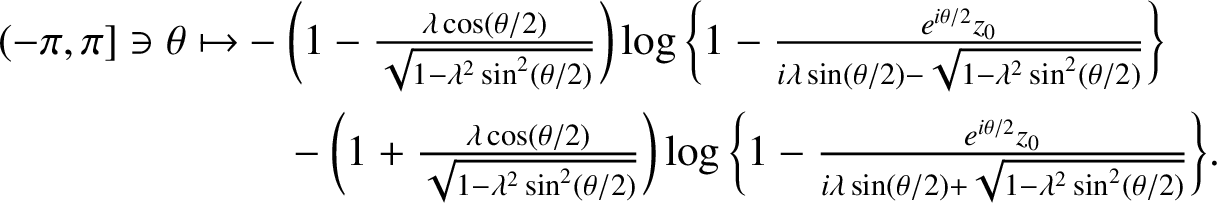$$ \begin{align*} ( - \pi , \pi ] \ni \theta \mapsto & - \bigg( 1 - \tfrac{\lambda \cos ( \theta /2)}{\sqrt{1 - \lambda^2 \sin^2 ( \theta /2) }} \bigg) \log \bigg\{ 1 - \tfrac{e^{i \theta /2} z_0} {i \lambda \sin ( \theta /2) - \sqrt{1 - \lambda^2 \sin^2 ( \theta /2) } } \bigg\}\\ & \quad - \bigg( 1 + \tfrac{\lambda \cos ( \theta /2)}{\sqrt{1 - \lambda^2 \sin^2 ( \theta /2) }} \bigg) \log \bigg\{ 1 - \tfrac{e^{i \theta /2} z_0} {i \lambda \sin ( \theta /2) + \sqrt{1 - \lambda^2 \sin^2 ( \theta /2) } } \bigg\}. \end{align*} $$
Theorem 1.1 can be equivalently written as follows.
Theorem 1.2. Let
${\mathbb H} = \{ w \in {\mathbb C} : \text {Re} \, w> 0 \}$
. For any
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
and
$0 \leq \lambda < 1$
, the variability region
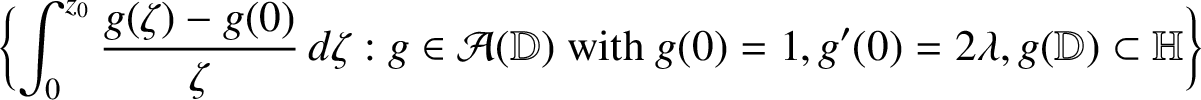$$ \begin{align*} \bigg\{\!\int_0^{z_0} \frac{g(\zeta )-g(0)}{\zeta} \, d \zeta : g \in {\mathcal A}({\mathbb D}) \mbox{ with } g(0)=1, g'(0)= 2 \lambda, g({\mathbb D}) \subset {\mathbb H} \bigg\} \end{align*} $$
coincides with the convex closed Jordan domain defined in Theorem 1.1.
Theorem 1.1 is a direct consequence of Theorem 1.2 with
$g(z) = 1 + zf''(z)/f'(z)$
. For similar results, we refer to [Reference Ali and Vasudevarao1
Reference Ali and Vasudevarao1, Reference Ponnusamy, Vasudevarao and Yanagihara13, Reference Ul-Haq18, Reference Yanagihara19, Reference Yanagihara21] and the references therein.
Recently, the present authors [Reference Ali, Allu and Yanagihara2] extended Theorem 1.2 to the most general setting.
Let
$\Omega $
be a simply connected domain in
${\mathbb C}$
with
$\Omega \not = {\mathbb C}$
and let P be a conformal map of
${\mathbb D}$
onto
$\Omega $
. Let
${\mathcal F}_\Omega $
be the class of analytic functions g in
${\mathbb D}$
with
$g( {\mathbb D}) \subset \Omega $
. Then the map
$P^{-1} \circ g$
maps
${\mathbb D}$
into
${\mathbb D}$
. For
$c = (c_0,c_1, \ldots , c_n ) \in {\mathbb C}^{n+1}$
, let
$$ \begin{align*} {\mathcal F}_\Omega (c ) = \{ g \in {\mathcal F}_\Omega: (P^{-1} \circ g) (z) = c_0 + c_1z+\cdots +c_nz^n + \cdots \ \in {\mathbb D} \}. \end{align*} $$
Let
$H^\infty ({\mathbb D})$
be the Banach space of analytic functions f in
${\mathbb D}$
with the norm defined by
$\| f \|_\infty = \sup _{z \in {\mathbb D}} |f(z)|$
, and
$H_1^\infty ({\mathbb D}) = \{ \omega \in H^\infty ({\mathbb D}) : \| \omega \|_\infty \leq 1 \}$
be the closed unit ball of
$H^\infty ({\mathbb D})$
. The coefficient body
${\mathcal C}(n)$
defined by
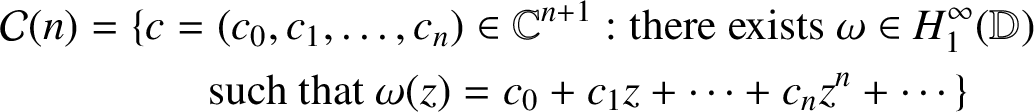$$ \begin{align*} {\mathcal C}(n)= \{ c &= (c_0,c_1, \ldots , c_n ) \in {\mathbb C}^{n+1}: \mbox{there exists } \omega \in H_1^\infty ({\mathbb D})\\ &\quad \mbox{such that } \omega (z) = c_0+c_1 z + \cdots + c_n z^n + \cdots \} \end{align*} $$
is a compact and convex subset of
${\mathbb C}^{n+1}$
. The coefficient body
${\mathcal C}(n)$
has been completely characterised by Schur [Reference Schur15, Reference Schur and Gohberg16]. For a detailed treatment, we refer to [Reference Foias and Frazho6, Ch. I] and [Reference Bakonyi and Constantinescu3, Ch. 1].
We call
$c = (c_0, \ldots , c_n )$
the Carathéodory data of length
$n+1$
. For given Carathéodory data
$c =(c_0,\ldots ,c_n) \in {\mathbb C}^{n+1}$
, the Schur parameter
$\gamma = (\gamma _0 , \ldots , \gamma _k)$
,
$k=0,1, \ldots , n$
, is defined as follows.
For
$j=0,1,\ldots $
, define recursively
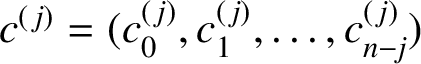$c^{({\kern1.5pt}j)} = (c_0^{({\kern1.5pt}j)},c_1^{({\kern1.5pt}j)}, \ldots , c_{n-j}^{({\kern1.5pt}j)})$
and
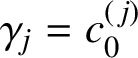$\gamma _j = c_0^{({\kern1.5pt}j)}$
by
$$ \begin{align*} c_0^{({\kern1.5pt}j)} = \frac{c_1^{({\kern1.5pt}j-1)}}{1-|\gamma_{j-1}|^2}, \quad c_p^{({\kern1.5pt}j)} = \frac{c_{p+1}^{({\kern1.5pt}j-1)} + \overline{\gamma_{j-1}} \sum_{\ell =1}^p c_{p-\ell}^{({\kern1.5pt}j)} c_\ell^{({\kern1.5pt}j-1)}}{1-|\gamma_{j-1}|^2} \quad (1 \leq p \leq n- j) \end{align*} $$
with
$c ^{(0)} =c = (c_0,\ldots ,c_n)$
. In the jth step (
$j=0,1,\ldots $
), if
$|\gamma _j|> 1$
, then we put
$k=j$
and
$\gamma = ( \gamma _0, \ldots , \gamma _j )$
; if
$|\gamma _j | =1$
, then we put
$k=n$
and, for
$p=j+1, \ldots , n$
, we take
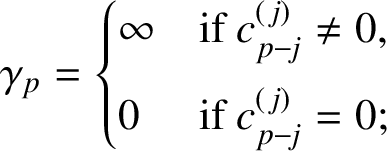$$ \begin{align*}\gamma_p = \begin{cases} \infty & \mbox{if}\ c_{p-j}^{({\kern1.5pt}j)} \not= 0, \\[6pt] 0 & \mbox{if}\ c_{p-j}^{({\kern1.5pt}j)} =0; \end{cases} \end{align*} $$
if
$|\gamma _j | < 1$
, then we proceed to the
$({\kern1.5pt}j+1)$
th step. Applying this procedure recursively, we obtain the Schur parameter
$\gamma = ( \gamma _0 , \ldots , \gamma _k )$
,
$k=0, \ldots , n$
, of
$c =(c_0, \ldots , c_n)$
.
When
$|\gamma _0|<1, \ldots , |\gamma _n| < 1$
, each of
$c=(c_0, \ldots , c_n )= c^{(0)}$
and
$\gamma = (\gamma _0, \ldots , \gamma _n )$
is uniquely determined by the other. For an explicit representation of
$\gamma $
in terms of c, we refer to [Reference Schur15, Reference Schur and Gohberg16]. For given
$c=(c_0, \ldots , c_n) \in {\mathbb C}^{n+1}$
, Schur [Reference Schur15, Reference Schur and Gohberg16] proved that
$c \in \text {Int} \, {\mathcal C}(n)$
,
$c \in \partial {\mathcal C}(n)$
and
$c \not \in {\mathcal C}(n)$
are respectively equivalent to the conditions:
-
(C1)
$k=n$
and
$|\gamma _i|<1$
for
$i=1,2,\ldots ,n$
; -
(C2)
$k=n$
and
$|\gamma _0|<1, \ldots , |\gamma _{i-1}|<1$
,
$|\gamma _i|=1$
,
$\gamma _{i+1}= \cdots = \gamma _n=0$
for some i with
$i=0, \ldots , n$
; and -
(C3) neither
$\mathrm {\mathbf {(C1)}}$
nor
$\mathrm {\mathbf {(C2)}}$
holds.
For
$c \in \text {Int} \, {\mathcal C}(n)$
, the Schur parameter can be computed as follows. Let
$\omega \in H_1^\infty ({\mathbb D})$
be such that
$\omega (z) = c_0+ c_1 z + \cdots + c_n z^n + \cdots $
. Define
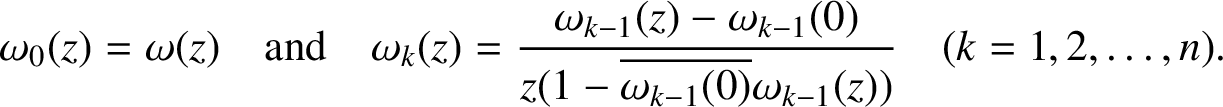$$ \begin{align*} \omega_0(z) = \omega(z) \quad\mbox{and}\quad \omega_k (z) = \displaystyle \frac{\omega_{k-1} (z)-\omega_{k-1}(0)}{z(1-\overline{\omega_{k-1}(0) }\omega_{k-1}(z))} \quad (k=1,2,\ldots,n). \end{align*} $$
Then
$\gamma _p = \omega _p(0)$
and
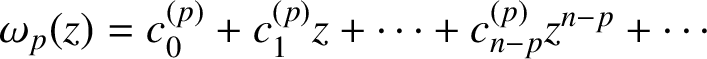$\omega _p(z) = c_0^{(p)}+c_1^{(p)}z+ \cdots + c_{n-p}^{(p)}z^{n-p} + \cdots $
for
$p=0,1, \ldots , n$
. For a detailed proof, we refer to [Reference Foias and Frazho6, Ch. 1].
For
$a \in {\mathbb D}$
, define
$\sigma _a \in \mbox {Aut} ( {\mathbb D})$
by
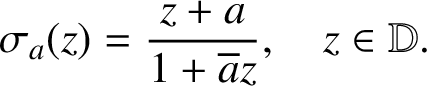$$ \begin{align*}\sigma_a (z) = \frac{z+a}{1+ \overline{a}z}, \quad z \in {\mathbb D}. \end{align*} $$
For
$\varepsilon \in \overline {\mathbb D}$
and the Schur parameter
$\gamma =( \gamma _0,\ldots , \gamma _n)$
of
$c \in \text {Int} \, {\mathcal C}(n)$
, let
$$ \begin{align} \begin{aligned} \omega_{\gamma , \varepsilon }(z) &= \sigma_{\gamma_0} ( z \sigma_{\gamma_1} ( \cdots z \sigma_{\gamma_{n}} ( \varepsilon z) \cdots )), \quad z \in {\mathbb D}, \\ Q_{\gamma , j} (z, \varepsilon ) &= \int_0^z \zeta^j \{ P(\omega_{\gamma,\varepsilon} (\zeta )) - P(c_0) \}\, d \zeta , \quad z \in {\mathbb D} \text{ and } \varepsilon \in \overline{\mathbb D}.\end{aligned} \end{align} $$
Then
$\omega _{\gamma , \varepsilon } \in H_1^\infty ({\mathbb D})$
with Carathéodory data c, that is,
$\omega _{\gamma , \varepsilon }(z) = c_0+c_1z+\cdots + c_nz^n + \cdots $
. By using the Schur algorithm, the present authors [Reference Ali, Allu and Yanagihara2] obtained the following general result for the region of variability.
Theorem 1.3 [Reference Ali, Allu and Yanagihara2]
Let
$n \in {\mathbb N} \cup \{ 0 \}$
,
$j \in \{-1,0, 1,2 , \ldots \}$
and
$c =(c_0, \ldots , c_n) \in {\mathbb C}^{n+1}$
be Carathéodory data. Let
$\Omega $
be a convex domain in
${\mathbb C}$
with
$\Omega \not = {\mathbb C}$
and P be a conformal map of
${\mathbb D}$
onto
$\Omega $
. For each fixed
$z_0 \in {\mathbb D} \backslash \{0 \}$
, let
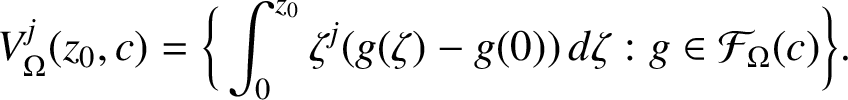$$ \begin{align*} V_\Omega^j (z_0, c ) = \bigg\{ \int_0^{z_0} \zeta^j ( g( \zeta ) - g(0) ) \, d \zeta : g \in {\mathcal F}_\Omega (c ) \bigg\}. \end{align*} $$
-
(i) If
$c = (c_0, \ldots , c_n ) \in \text {Int} \,{\mathcal C}(n)$
and
$\gamma =(\gamma _0, \ldots , \gamma _n )$
is the Schur parameter of c, then
$Q_{\gamma , j}(z_0, \varepsilon )$
defined by (1.1) is a convex univalent function of
$\varepsilon \in \overline {\mathbb D}$
and Furthermore,
$$ \begin{align*}V_\Omega^j (z_0,c) = Q_{\gamma , j}(z_0, \overline{\mathbb D} ) := \{ Q_{\gamma , j}(z_0, \varepsilon ) : \varepsilon \in \overline{\mathbb D} \}. \end{align*} $$
for some
$$ \begin{align*}\int_0^{z_0} \zeta^j \{ g(\zeta ) - g(0) \} \, d \zeta = Q_{\gamma , j}(z_0, \varepsilon ) \end{align*} $$
$g \in {\mathcal F}_\Omega (c )$
and
$\varepsilon \in \partial {\mathbb D}$
if and only if
$g (z) \equiv P( \omega _{\gamma , \varepsilon } (z ))$
.
-
(ii) If
$c \in \partial {\mathcal C}(n)$
and
$\gamma =( \gamma _0, \ldots , \gamma _i, 0, \ldots , 0 )$
is the Schur parameter of c, then
$V_\Omega ^j (z_0,c )$
reduces to a set consisting of a single point
$w_0$
, where
$$ \begin{align*}w_0 = \int_0^{z_0} \zeta^j \{ P( \sigma_{\gamma_0} ( \zeta \sigma_{\gamma_1}(\cdots \zeta \sigma_{\gamma_{i-1}} (\gamma_i \zeta ) \cdots )))- P(c_0) \} \, d \zeta. \end{align*} $$
-
(iii) If
$c \not \in {\mathcal C}(n)$
, then
$V_\Omega ^j (z_0,c ) = \emptyset $
.
In the present article, we first show that in the case
$n=0$
,
$j=-1$
and
$c=0$
, the conclusion of Theorem 1.3 holds when one weakens the assumption that
$\Omega $
is convex to
$\Omega $
is starlike with respect to
$P(0)$
(Theorem 2.1). We then present several applications of Theorems 1.3 and 2.1 to obtain the precise variability region for several well-known subclasses of analytic and univalent functions. We also obtain certain subordination results.
2 Main results
Before we state our first result, let us recall the definition of subordination. For two analytic functions f and g in
$\mathbb {D}$
, we say that f is subordinate to g, written as
$f \prec g$
or
$f(z) \prec g(z)$
, if there exists an analytic function
$\omega : \mathbb {D} \rightarrow \mathbb {D}$
with
$\omega (0)=0$
such that
$f(z)= g(\omega (z))$
for
$z\in \mathbb {D}$
. If g is univalent in
$\mathbb {D}$
, the subordination
$f \prec g$
is equivalent to
$f(0)= g(0)$
and
$f(\mathbb {D})\subseteq g(\mathbb {D})$
.
Theorem 2.1. Let
$b \in {\mathbb C}$
,
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
and
$\Omega $
be a starlike domain with respect to b satisfying
$\Omega \not = {\mathbb C}$
. Let P be a conformal map of
${\mathbb D}$
onto
$\Omega $
with
$P(0) =b$
. Then the region of variability
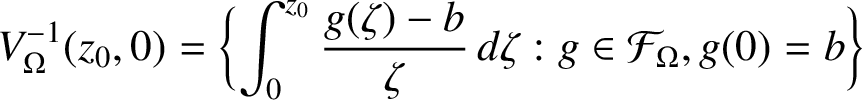$$ \begin{align*} V_\Omega^{-1} (z_0,0) = \bigg\{\!\int_0^{z_0} \frac{g(\zeta ) - b}{\zeta } \, d \zeta : g \in {\mathcal F}_\Omega , g(0) = b \bigg\} \end{align*} $$
is a convex closed Jordan domain that coincides with the set
$K ( \overline {\mathbb D}(0, |z_0| ) )$
, where
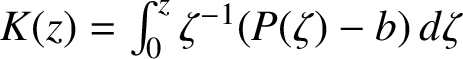$K(z) = \int _0^z \zeta ^{-1} (P(\zeta ) -b) \, d \zeta $
. Furthermore, for
$| \varepsilon | =1$
and
$g \in {\mathcal F}_\Omega $
with
$g(0) = b$
, the relation
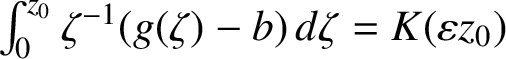$\int _0^{z_0} \zeta ^{-1}(g(\zeta ) - b) \, d \zeta = K(\varepsilon z_0)$
holds if and only if
$g(z) \equiv P ( \varepsilon z )$
.
Proof. Let
$g \in {\mathcal A} ({\mathbb D})$
be such that
$g(0)=b$
and
$g({\mathbb D}) \subset \Omega $
. Then g is subordinate to P. By using a result of Suffridge [Reference Suffridge17], we may conclude that
$$ \begin{align*} \int_0^z \frac{ g(\zeta) -b }{\zeta} \, d \zeta \prec K(z) := \int_0^z \frac{ P(\zeta) -b }{\zeta} \, d \zeta. \end{align*} $$
Thus, there exists
$\omega \in H_1^\infty ({\mathbb D})$
with
$\omega (0)=0$
and
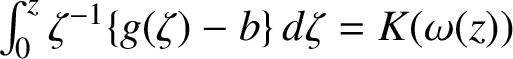$\int _0^z \zeta ^{-1} \{g(\zeta ) -b \}\, d \zeta = K(\omega (z))$
and so
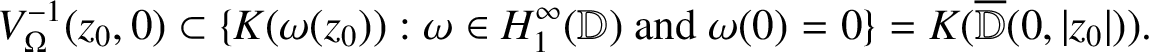$$ \begin{align*}V_\Omega^{-1} (z_0,0) \subset \{ K(\omega (z_0) ) : \omega \in H_1^\infty ({\mathbb D}) \mbox{ and } \omega(0) = 0 \} = K( \overline{\mathbb D}(0,|z_0| )). \end{align*} $$
For
$\varepsilon \in \overline {\mathbb D}$
, let
$g_\varepsilon (z) = P(\varepsilon z)$
. Then
$g_\varepsilon (0) = P(0) = b$
and
$g_\varepsilon ({\mathbb D}) = P({\mathbb D})=\Omega $
. Therefore,
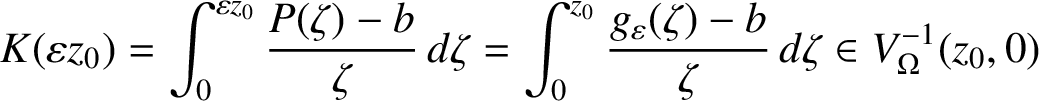$$ \begin{align*}K(\varepsilon z_0)=\int_0^{\varepsilon z_0} \frac{ P(\zeta) -b }{\zeta} \, d \zeta = \int_0^{z_0} \frac{ g_\varepsilon(\zeta) -b }{\zeta} \, d \zeta \in V_\Omega^{-1} (z_0, 0) \end{align*} $$
and hence
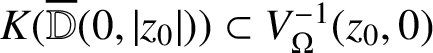$K(\overline {\mathbb D}(0,|z_0|)) \subset V_\Omega ^{-1} (z_0,0)$
.
We now deal with the uniqueness. Suppose that
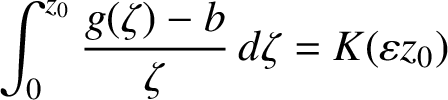$$ \begin{align} \int_0^{z_0} \frac{g( \zeta ) - b}{\zeta} \, d \zeta = K(\varepsilon z_0) \end{align} $$
for some g with
$g(0)=b$
and
$g({\mathbb D}) \subset \Omega $
and
$| \varepsilon | =1$
. Then there exists
$\omega \in H_1^\infty ({\mathbb D})$
with
$\omega (0)=0$
such that
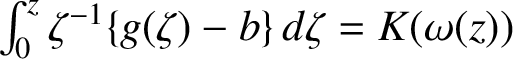$\int _0^z \zeta ^{-1} \{g(\zeta ) -b \} \, d \zeta = K(\omega (z))$
. From (2.1),
$K( \omega (z_0)) = K ( \varepsilon z_0 )$
. Since K is a convex univalent function,
$\omega (z_0) = \varepsilon z_0$
. It follows from Schwarz’s lemma that
$\omega (z) \equiv \varepsilon z$
. Consequently,
$g(z) \equiv P(\varepsilon z)$
.
2.1 The class
$\mathcal {CV} (\Omega )$
Suppose that
$\Omega $
is a simply connected domain with
$1 \in \Omega $
. Define
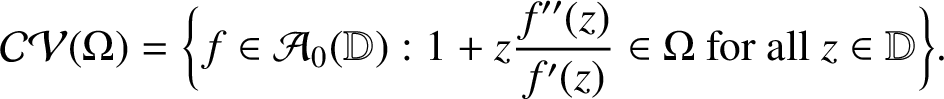$$ \begin{align*} \mathcal{CV} (\Omega ) = \bigg\{ f \in {\mathcal A}_0({\mathbb D}) : 1 + z \frac{f''(z)}{f'(z)} \in \Omega \text{ for all } z\in{\mathbb D} \bigg\}. \end{align*} $$
Let P be the conformal map of
$\mathbb {D}$
onto
$\Omega $
with
$P(0)=1$
. Then
$1+zf''(z)/f'(z)\prec P$
for each
$f\in \mathcal {CV}(\Omega )$
. For
$\alpha \in \mathbb {R}$
, let
$\mathbb {H}_{\alpha }:=\{z\in \mathbb {C}: \mathrm {Re}\, z>\alpha \}$
and
$\mathbb {H}_{0}=\mathbb {H}$
. If
$\Omega = {\mathbb H}$
and
$P(z)=(1+z)/(1-z)$
, then
$\mathcal {CV}({\mathbb H}) = \mathcal {CV}$
is the well-known class of normalised convex functions in
${\mathbb D}$
. If
$\Omega \subset {\mathbb H}$
, then
$\mathcal {CV}(\Omega )$
is a subclass of
$\mathcal {CV}$
. For
$0 \leq \alpha < 1$
,
$\mathcal {CV}(\alpha ):=\mathcal {CV}(\mathbb {H}_{\alpha })$
is the class of convex functions of order
$\alpha $
. In this case, we have
$P(z) \kern-0.6pt =\kern-0.6pt \{1 \kern-0.5pt +\kern-0.5pt (1\kern-0.5pt -2 \alpha )z\}/(1\kern-0.5pt -z)$
. If
$0 \kern-0.5pt<\kern-0.5pt \beta \kern-0.5pt\leq\kern-0.5pt 1$
, then
$\mathcal {CV}_{\beta }\kern-0.5pt:=\mathcal {CV}( \{ w \in {\mathbb C}\kern-0.5pt : |\kern-1.5pt\arg \, w| \kern-0.5pt<\kern-0.5pt \pi \beta /2\})$
is the class of strongly convex functions of order
$\beta $
and
$P(z) = \{(1+z)/(1-z)\}^\beta $
.
As an application of Theorem 2.1, we determine the variability region of
$\log f'(z_0)$
when f ranges over
$\mathcal {CV}(\Omega )$
.
Theorem 2.2. Let
$\Omega $
be a starlike domain with respect to
$1$
and P be a conformal map of
${\mathbb D}$
onto
$\Omega $
with
$P(0)=1$
. Then, for each fixed
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
, the region of variability
$$ \begin{align*} V_{\mathcal{CV}(\Omega)}(z_0):= \{ \log f'(z_0 ) : f \in \mathcal{CV}( \Omega ) \} \end{align*} $$
is a convex closed Jordan domain that coincides with the set
$K( \overline {\mathbb D}(0,|z_0|))$
, where
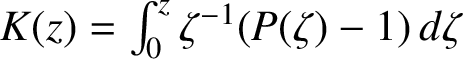$K(z) = \int _0^z \zeta ^{-1} (P( \zeta )- 1) \, d \zeta $
is a convex univalent function in
${\mathbb D}$
. Furthermore,
$\log f'(z_0) = K( \varepsilon z_0)$
for some
$\varepsilon $
with
$|\varepsilon | =1$
and
$f \in \mathcal {CV}( \Omega )$
if and only if
$f(z) = \varepsilon ^{-1}F(\varepsilon z)$
, where
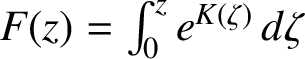$F(z)= \int _0^z e^{K(\zeta )} \, d \zeta $
.
Proof. Let
$c = 0 \in {\mathbb C}^1$
be given Carathéodory data of length one. In that case,
${\mathcal F}_\Omega (0)= \{ g \in {\mathcal A}({\mathbb D}): g({\mathbb D}) \subset \Omega \text { and } (P^{-1} \circ g) (0) = 0 \}$
. It is easy to see that the map
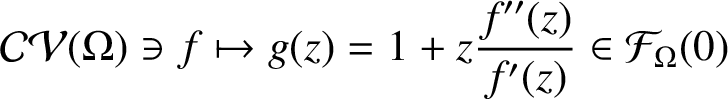$$ \begin{align*}\mathcal{CV}( \Omega ) \ni f \mapsto g(z) = 1 + z \frac{f''(z)}{f'(z)} \in {\mathcal F}_\Omega (0) \end{align*} $$
is bijective. Indeed, since
$g(z) = 1+ zf''(z)/f'(z)$
is analytic in
${\mathbb D}$
,
$f'(z)$
does not have zeros in
${\mathbb D}$
and so
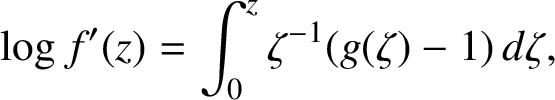$$ \begin{align} \log f'(z)= \int_0^z \zeta^{-1} (g( \zeta )-1)\, d \zeta, \end{align} $$
where
$\log f'$
is a single-valued branch of the logarithm of
$f'$
with
$\log f'(0) = 0$
. The conclusions now follow from Theorem 2.1 and (2.2).
As an application of Theorem 1.3, we determine the variability region of
$\log f'(z_0)$
when f ranges over
$\mathcal {CV}(\Omega )$
with the conditions
$f''(0) = 2 \lambda $
and
$f'''(0) = 6 \mu $
. Here
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
;
$\lambda , \mu \in {\mathbb C}$
are arbitrarily preassigned values. By letting
$\Omega $
be one of the particular domains mentioned above, we can determine variability regions of
$\log f'(z_0)$
for various subclasses of
$\mathcal {CV}$
.
Let
$\Omega $
be a simply connected domain with
$\Omega \not = {\mathbb C}$
and P be a conformal map of
${\mathbb D}$
onto
$\Omega $
with
$P(z)= \alpha _0 + \alpha _1 z + \alpha _2z^2 + \cdots $
. Let g be an analytic function in
${\mathbb D}$
with
$g(z)= b_0+b_1 z + b_2 z^2 +\cdots $
satisfying
$g({\mathbb D}) \subset \Omega $
. For simplicity, we assume that
$P(0)=g(0)$
, that is,
$\alpha _0 =b_0$
. Let
$$ \begin{align*} \omega (z) = (P^{-1}\circ g)(z) = c_0 + c_1 z + c_2 z^2 + \cdots ,\quad z \in {\mathbb D}. \end{align*} $$
Then
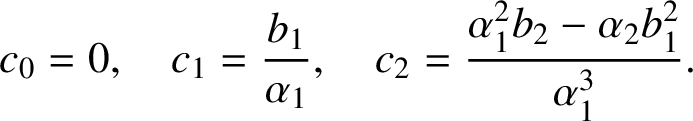$$ \begin{align} c_0 = 0, \quad c_1 = \frac{b_1}{\alpha_1}, \quad c_2 = \frac{\alpha_1^2 b_2 - \alpha_2 b_1^2}{\alpha_1^3}. \end{align} $$
By Schwarz’s lemma,
$|b_1| \leq |\alpha _1|$
with equality if and only if
$g(z) = P(\varepsilon z)$
for some
${\varepsilon \in \partial {\mathbb D}}$
. Let
$\gamma = (\gamma _0,\gamma _1,\gamma _2)$
be the Schur parameter of the Carathéodory data
$c = (0,c_1,c_2)$
. Then
$\gamma _0 = \omega (0) = c_0 = 0$
and
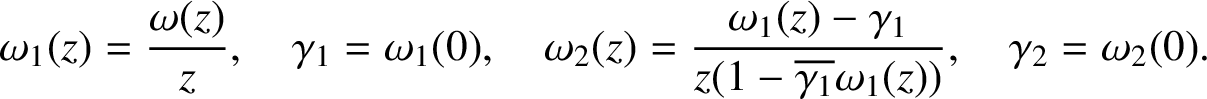$$ \begin{align*} \omega_1(z) = \frac{\omega(z)}{z}, \quad \gamma_1 = \omega_1 (0), \quad \omega_2(z) = \frac{\omega_1 (z)-\gamma_1}{z(1-\overline{\gamma_1}\omega_1(z))}, \quad \gamma_2 = \omega_2 (0). \end{align*} $$
A simple computation shows that
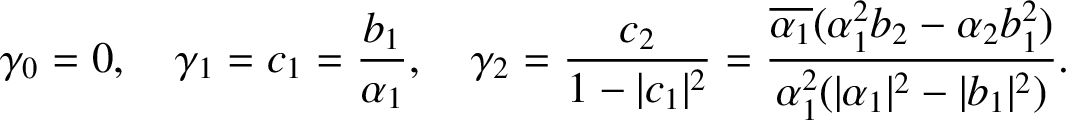$$ \begin{align} \gamma_0 = 0, \quad \gamma_1 = c_1 = \frac{b_1}{\alpha_1}, \quad \gamma_2 = \frac{c_2}{1-|c_1|^2} = \frac{ \overline{\alpha_1} ( \alpha_1^2 b_2 - \alpha_2 b_1^2 )} {\alpha_1^2(|\alpha_1|^2 -|b_1|^2)}. \end{align} $$
For
$f \in \mathcal {CV}( \Omega )$
and
$k \in {\mathbb N}$
, let
$a_k(f) = f^{(k)}(0)/k!$
. Also let
$g(z) = 1 + zf''(z)/f'(z) = 1+b_1z +b_2z^2 +\cdots $
. Then
$$ \begin{align} b_1 = 2 a_2(f) \quad\mbox{and}\quad b_2 = 6 a_3(f) -4 a_2(f)^2. \end{align} $$
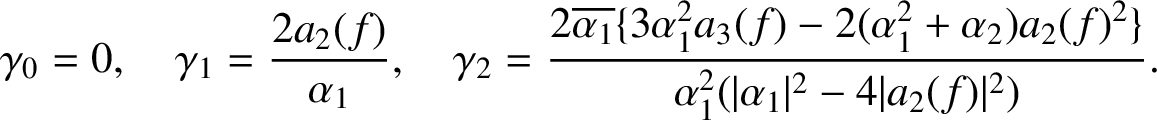$$ \begin{align*} \gamma_0 = 0, \quad \gamma_1 = \frac{2 a_2(f) }{\alpha_1}, \quad \gamma_2 = \frac{ 2\overline{\alpha_1} \{ 3\alpha_1^2 a_3(f) - 2(\alpha_1^2+\alpha_2) a_2(f)^2 \}} {\alpha_1^2(|\alpha_1|^2-4|a_2(f)|^2)}. \end{align*} $$
Let
$ {\mathcal A} (2 , \Omega ) = \{ a_2(f) : f \in \mathcal {CV} ( \Omega )\}.$
By Schwarz’s lemma,
${\mathcal A} (2 , \Omega ) = \overline {\mathbb D}(0, |\alpha _1|/2)$
. For
$f \in \mathcal {CV}(\Omega )$
and
$\lambda \in \partial {\mathcal A} (2 , \Omega )$
, we have
$a_2 (f) = \lambda $
if and only if
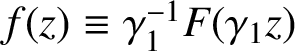$f(z) \equiv \gamma _1^{-1}F(\gamma _1 z)$
, where
$\gamma _1 = 2 \lambda / \alpha _1$
. By applying Theorem 1.3 with
$n=1$
and
$j=-1$
, we obtain the following generalisation of Theorem 1.1.
Theorem 2.3. Let
$\Omega $
be a convex domain with
$1 \in \Omega $
and P be a conformal map of
${\mathbb D}$
onto
$\Omega $
with
$P(z)=1+ \alpha _1 z + \cdots $
. For
$\lambda \in {\mathbb C}$
with
$|\lambda | \leq |\alpha _1|/2 $
and
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
, consider the variability region
$$ \begin{align*}V_{\mathcal{CV}(\Omega)}(z_0,\lambda):= \{ \log f'(z_0) : f \in \mathcal{CV}( \Omega ) \mbox{ with } a_2(f) = \lambda \}. \end{align*} $$
-
(i) If
$|\lambda |= |\alpha _1|/2 $
, then
$V_{\mathcal {CV}(\Omega )}(z_0,\lambda )$
reduces to a set consisting of a single point
$w_0$
, where
$w_0 = \int _0^{z_0} \zeta ^{-1} \{ P(\gamma _1 \zeta )- 1 \} \, d \zeta $
with
$\gamma _1 = 2 \lambda /\alpha _1$
. -
(ii) If
$|\lambda | < |\alpha _1|/2 $
, then
$V_{\mathcal {CV}(\Omega )}(z_0,\lambda ) = Q_{\gamma _1}(z_0, \overline {\mathbb D} )$
, where
$\gamma _1 = 2 \lambda /\alpha _1$
and is a convex, univalent and analytic function of
$$ \begin{align*}Q_{\gamma_1}(z_0, \varepsilon ) = \int_0^{z_0} \zeta^{-1} \bigg\{ P \bigg( \zeta \frac{\varepsilon \zeta + \gamma_1} {1+ \overline{\gamma_1} \varepsilon \zeta} \bigg) -1 \bigg\} \, d \zeta \end{align*} $$
$\varepsilon \in \overline {\mathbb D}$
. Furthermore,
$ \log f'(z_0) = Q_{\gamma _1}(z_0, \varepsilon ) $
for some
$\varepsilon \in \partial {\mathbb D}$
and
$f \in \mathcal {CV}( \Omega )$
with
$a_2(f) = \lambda $
if and only if
$$ \begin{align*}f(z) = \int_0^z e^{Q_{\gamma_1}(\zeta , \varepsilon )} \, d \zeta , \quad z \in {\mathbb D}. \end{align*} $$
Next let
$ {\mathcal A} (3 , \Omega ) = \{ (a_2(f), a_3(f) ) \in {\mathbb C}^2 : f \in \mathcal {CV}( \Omega ) \}$
and, for
$\lambda , \mu \in {\mathbb C}$
, let
$\gamma _1 := \gamma _1 (\lambda ,\mu )$
and
$\gamma _2 := \gamma _2 (\lambda , \mu )$
be given by
$$ \begin{align} \gamma_1 = \frac{2 \lambda }{\alpha_1} \end{align} $$
and
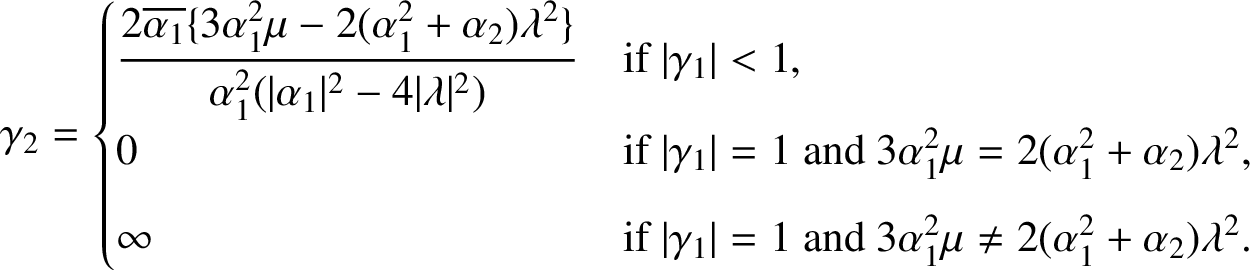$$ \begin{align} \gamma_2 = \begin{cases} \displaystyle \frac{ 2\overline{\alpha_1} \{ 3\alpha_1^2 \mu - 2(\alpha_1^2+\alpha_2)\lambda^2 \}} {\alpha_1^2(|\alpha_1|^2-4|\lambda|^2)} & \text{if } |\gamma_1| < 1, \\[6pt] 0 & \text{if } |\gamma_1| =1 \text{ and } 3\alpha_1^2 \mu = 2(\alpha_1^2+\alpha_2)\lambda^2, \\[6pt] \infty & \text{if } |\gamma_1| = 1 \text{ and } 3\alpha_1^2 \mu \not= 2(\alpha_1^2+\alpha_2)\lambda^2. \end{cases} \end{align} $$
Then
$(\lambda , \mu ) \in {\mathcal A} (3 , \Omega )$
if and only if one of the following conditions holds:
-
(a)
$|\gamma _1 (\lambda , \mu ) | = 1 $
and
$\gamma _2 ( \lambda , \mu )=0$
; -
(b)
$|\gamma _1 (\lambda , \mu ) | < 1 $
and
$ | \gamma _2 ( \lambda , \mu ) |=1$
; -
(c)
$|\gamma _1 (\lambda , \mu ) | < 1 $
and
$| \gamma _2 ( \lambda , \mu )| < 1$
.
In case (a), for
$f \in \mathcal {CV}( \Omega )$
,
$(a_2(f), a_3(f)) = (\lambda , \mu )$
if and only if
$g(z) = P(\gamma _1 z )$
, that is,
$f(z) = \gamma _1 F(\gamma _1 z)$
, where
$\gamma _1 = \gamma _1(\lambda , \mu )$
. Similarly, in case (b), for
$f \in \mathcal {CV}( \Omega )$
,
$(a_2(f), a_3(f)) = (\lambda , \mu ) $
if and only if
$g(z) = P(z \sigma _{\gamma _1}( \gamma _2 z) )$
, that is,
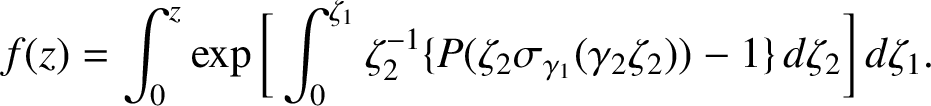$$ \begin{align*}f(z) = \int_0^z \exp\bigg[ \int_0^{\zeta_1} \zeta_2^{-1} \{ P(\zeta_2 \sigma_{\gamma_1}( \gamma_2 \zeta_2) )-1\} \, d \zeta_2 \bigg]\, d \zeta_1. \end{align*} $$
We note that
$(\lambda , \mu ) \in \partial {\mathcal A} (3 , \Omega )$
if and only if either (a) or (b) holds.
Suppose that (c) holds, that is,
$(\lambda , \mu ) \in \text {Int} \, {\mathcal A} (3 , \Omega )$
. Then, for
$f \in \mathcal {CV}( \Omega )$
,
$(a_2(f), a_3(f)) = (\lambda , \mu )$
if and only if there exists
$\omega ^* \in H_1^\infty ({\mathbb D})$
such that
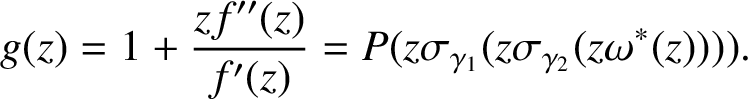$$ \begin{align*}g(z) = 1 + \frac{zf''(z)}{f'(z)} = P(z \sigma_{\gamma_1}(z \sigma_{\gamma_2}(z \omega^*(z))) ). \end{align*} $$
Let
$$ \begin{align} Q_{\gamma_1, \gamma_2}(z, \varepsilon ) = \int_0^z \zeta^{-1} \{ P( \zeta \sigma_{\gamma_1}(\zeta \sigma_{\gamma_2} ( \varepsilon \zeta )) ) -1 \} \, d \zeta , \quad z \in {\mathbb D} \text{ and } \varepsilon \in \overline{\mathbb D}. \end{align} $$
Then, for any fixed
$\varepsilon \in \overline {\mathbb D}$
,
$Q_{\gamma _1, \gamma _2}(z, \varepsilon )$
is an analytic function of
$z \in {\mathbb D}$
and, for each fixed
$z \in {\mathbb D}$
,
$Q_{\gamma _1, \gamma _2}(z, \varepsilon )$
is an analytic function of
$\varepsilon \in \overline {\mathbb D}$
. Theorem 1.3 leads to the following result.
Theorem 2.4. Let
$\Omega $
be a convex domain with
$1 \in \Omega $
and P be a conformal map of
${\mathbb D}$
onto
$\Omega $
with
$P(z)=1+ \alpha _1 z + \cdots $
. Let
$(\lambda , \mu ) \in {\mathbb C}^2$
and
$\gamma _1 = \gamma _1(\lambda , \mu )$
and
$\gamma _2 = \gamma _2(\lambda , \mu )$
be defined by (2.6) and (2.7), respectively. For
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
, consider the variability region
$$ \begin{align*}V_{\mathcal{CV}(\Omega)}(z_0,\lambda,\mu):= \{ \log f'(z_0) : f \in \mathcal{CV}( \Omega ) \text{ with } (a_2(f),a_3(f)) = (\lambda , \mu) \}. \end{align*} $$
-
(i) If
$|\gamma _1(\lambda , \mu )|=1$
and
$|\gamma _2(\lambda , \mu )| =0$
, then
$V_{\mathcal {CV}(\Omega )}(z_0,\lambda ,\mu )$
reduces to a set consisting of a single point
$w_0$
, where
$w_0 = \int _0^{z_0} \zeta ^{-1} \{ P(\gamma _1 \zeta )- 1 \} \, d \zeta $
. -
(ii) If
$|\gamma _1(\lambda , \mu )| <1$
and
$|\gamma _2(\lambda , \mu )| =1$
, then
$V_{\mathcal {CV}(\Omega )}(z_0,\lambda ,\mu )$
reduces to a set consisting of a single point
$w_0$
, where
$w_0 = \int _0^{z_0} \zeta ^{-1} \{ P(\zeta \sigma _{\gamma _1}( \gamma _2 \zeta ))- 1 \} \, d \zeta $
. -
(iii) If
$|\gamma _1(\lambda , \mu )| <1$
and
$|\gamma _2(\lambda , \mu )| <1$
, that is,
$(\lambda , \mu ) \in \text {Int} \, {\mathcal A}(3, \Omega )$
, then
$Q_{\gamma _1, \gamma _2}(z_0, \varepsilon )$
defined by (2.8) is a convex, univalent and analytic function of
$\varepsilon \in \overline {\mathbb D}$
and Furthermore,
$$ \begin{align*}V_{\mathcal{CV}(\Omega)}(z_0,\lambda,\mu) = Q_{\gamma_1, \gamma_2}(z_0, \overline{\mathbb D}). \end{align*} $$
$\log f'(z_0) = Q_{\gamma _1, \gamma _2}(z_0, \varepsilon )$
for some
$\varepsilon $
with
$| \varepsilon | =1$
and
$f \in \mathcal {CV}( \Omega ) $
with
$(a_2(f),a_3(f)) = (\lambda , \mu )$
if and only if
$$ \begin{align*}f(z) = \int_0^z \exp \bigg[ \int_0^{\zeta_1} \zeta_2^{-1} \{ P ( z \sigma_{\gamma_1}(z \sigma_{\gamma_2}(\varepsilon \zeta_2 ))) - 1 \} \, d \zeta_2 \bigg] \, d \zeta_1. \end{align*} $$
Remark 2.5. For a simply connected domain
$\Omega $
with
$1 \in \Omega $
, define
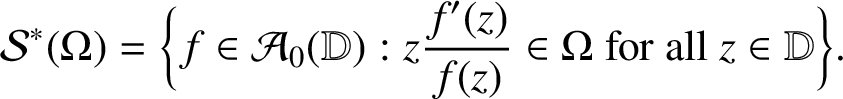$$ \begin{align*}\mathcal{S}^*( \Omega ) = \bigg\{ f \in {\mathcal A}_0({\mathbb D} ) : z \frac{f'(z)}{f(z)} \in \Omega \text{ for all } z\in{\mathbb D} \bigg\}. \end{align*} $$
Then
$f \in \mathcal {CV} (\Omega )$
if and only if
$zf'(z) \in \mathcal {S}^*( \Omega )$
. Thus, we can easily translate the theorems of this section to results about variability regions of
$\log \{ f(z_0)/z_0 \}$
when f ranges over
$\mathcal {S}^* ( \Omega )$
with or without the conditions
$f''(0) = \lambda $
and
$f'''(0) = \mu $
.
2.2 Uniformly convex functions
For
$0\le k < \infty $
, the class
$k\mbox {-}\mathcal {UCV}$
of k-uniformly convex functions is
$\mathcal {CV}(\Omega _k)$
, where
$\Omega _k:=\{ w \in {\mathbb C} : \text {Re} \, w> k |w-1| \}$
. Here
$\Omega _k$
is a convex domain containing
$1$
, bounded by a conic section. The conformal map
$P_k$
that maps the unit disk
$\mathbb {D}$
conformally onto
$\Omega _k$
is given by
$$ \begin{align*}P_k= \begin{cases} \displaystyle \frac{1}{1-k^2}\cosh\bigg(A\log\frac{1+\sqrt{z}}{1-\sqrt{z}}\bigg)-\frac{k^2}{1-k^2} & \mbox{for } 0\le k<1,\\[10pt] \displaystyle 1+\frac{2}{\pi^2}\bigg(\log\frac{1+\sqrt{z}}{1-\sqrt{z}}\bigg)^2 & \mbox{for } k=1,\\[10pt] \displaystyle \frac{1}{k^2-1} \sin \bigg(\frac{\pi}{2K(x)} \int_0^{u(z)/\sqrt{x}} \frac{dt}{\sqrt{(1-t^2)(1-x^2 t^2)}}\bigg) + \frac{k^2}{k^2-1} & \mbox{for } 1<k<\infty, \end{cases} \end{align*} $$
where
$A=(2/\pi )\operatorname {\mathrm {\operatorname {arc}}}\cos k$
,
$u(z)=(z-\sqrt {x})/(1-\sqrt {x}z)$
and
$K(x)$
is the elliptic integral defined by
$$ \begin{align*}K(x)=\int_0^1 \frac{dt}{\sqrt{(1-t^2)(1-x^2 t^2)}},\quad x\in(0,1). \end{align*} $$
For more details concerning uniformly convex functions, we refer to [Reference Kanas and Wiśniowska10, Reference Ronning14]. When
$k=0$
, the class
$0\mbox {-}\mathcal {UCV}$
is essentially the same as
$\mathcal {CV}$
. Let
$P_k(z)= 1+\alpha _{k1}z+\alpha _{k2}z^2+\cdots $
. Then it is a simple exercise to see that
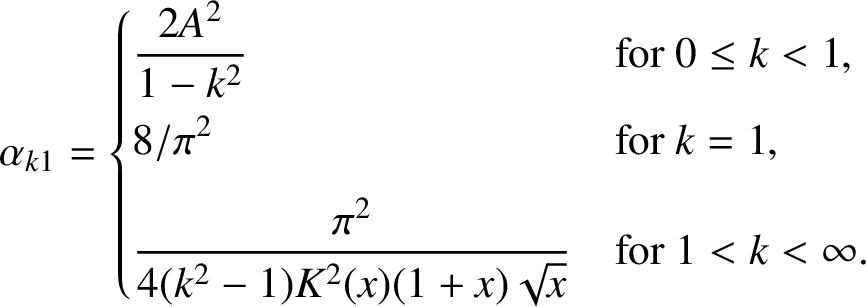$$ \begin{align*}\alpha_{k1}= \begin{cases} \displaystyle \frac{2A^2}{1-k^2} & \mbox{for}\ 0\le k<1,\\[6pt] \displaystyle 8/\pi^2 & \mbox{for}\ k=1,\\[6pt] \displaystyle \frac{\pi^2}{4(k^2-1)K^2(x)(1+x)\sqrt{x}} & \mbox{for}\ 1<k<\infty. \end{cases} \end{align*} $$
Let
$f\in k\mbox {-}\mathcal {UCV}$
be of the form
$f(z)=z+a_2z+a_3z^2+\cdots $
and
$g(z)=1+zf''(z)/f'(z)$
. Then, from (2.3) and (2.5), we obtain
$|a_2|\le \alpha _{k1}/2$
. For
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
and
$|\lambda |\le \alpha _{k1}/2$
, consider the region of variability
$$ \begin{align*}V_{k\mbox{-}\mathcal{UCV}}(z_0,\lambda)= \{ \log f'(z_0) : f \in k\mbox{-}\mathcal{UCV} \mbox{ with } a_2(f) = \lambda \}. \end{align*} $$
The following corollary is a simple consequence of Theorem 2.3.
Corollary 2.6. Let
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
and
$\lambda \in {\mathbb C}$
with
$|\lambda | \leq \alpha _{1k}/2$
. Let
$\gamma _1 = 2 \lambda /\alpha _{1k}$
.
-
(i) If
$|\gamma _1 |= 1 $
, then
$V_{k\mbox {-}\mathcal {UCV}}(z_0,\lambda )=\{w_0\}$
, where
$w_0 = \int _0^{z_0} \zeta ^{-1} \{ P_k(\gamma _1 \zeta )- 1 \} \, d \zeta $
. -
(ii) If
$|\gamma _1 |<1 $
, then
$V_{k\mbox {-}\mathcal {UCV}}(z_0,\lambda ) = Q_{\gamma _1}(z_0, \overline {\mathbb D} )$
, where is a convex, univalent and analytic function of
$$ \begin{align*}Q_{\gamma_1}(z_0, \varepsilon ) = \int_0^{z_0} \zeta^{-1} \bigg\{ P_k \bigg( \zeta \frac{\varepsilon \zeta + \gamma_1} {1+ \overline{\gamma_1} \varepsilon \zeta} \bigg) -1 \bigg\} \, d \zeta \end{align*} $$
$\varepsilon \in \overline {\mathbb D}$
. Furthermore, for some
$$ \begin{align*}\log f'(z_0) = Q_{\gamma_1}(z_0, \varepsilon ) \end{align*} $$
$\varepsilon \in \partial {\mathbb D}$
and
$f \in k\mbox {-}\mathcal {UCV}$
with
$a_2(f) = \lambda $
if and only if
$$ \begin{align*}f(z) = \int_0^z e^{Q_{\gamma_1}(\zeta , \varepsilon )} \, d \zeta , \quad z \in {\mathbb D}. \end{align*} $$
2.3 Janowski starlike and convex functions
For
$A,B\in \mathbb {C}$
with
$|B|\le 1$
and
$A\ne B$
, let
$P_{A,B}(z):=(1+Az)/(1+Bz)$
. Then
$P_{A,B}$
is a conformal map of
$\mathbb {D}$
onto a convex domain
$\Omega _{A,B}$
. In this case, the classes
$\mathcal {S}^* ( \Omega _{A,B} )$
and
$\mathcal {CV} (\Omega _{A,B})$
reduce to
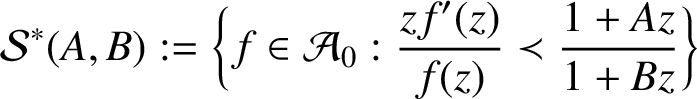$$ \begin{align*}\mathcal{S}^*(A,B):=\bigg\{f \in {\mathcal A}_0: \frac{z f'(z)}{f(z)} \prec \frac{1+A z}{1+B z} \bigg\} \end{align*} $$
and
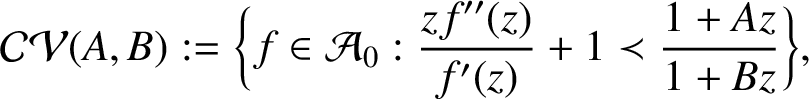$$ \begin{align*}\mathcal{CV}(A,B):=\bigg\{f \in {\mathcal A}_0: \frac{z f''(z)}{f'(z)}+1 \prec \frac{1+A z}{1+B z} \bigg\}, \end{align*} $$
respectively. Since
$P_{A,B}(\mathbb {D})=P_{-A,-B}(\mathbb {D})$
, without loss of generality we may assume that
$A\in \mathbb {C}$
with
$-1\le B\le 0$
and
$A\ne B$
. It is important to note that functions in
$\mathcal {S}^*(A,B)$
with
$A\in \mathbb {C}$
,
$-1\le B\le 0$
and
$A\ne B$
are not in general univalent. For
${-1\le B<A\le 1}$
, it is easy to see that
$\Omega _{A,B}\subset \mathbb {H}$
and so
$\mathcal {S}^*(A,B)\subset \mathcal {S}^*$
. A similar result holds for
$\mathcal {CV}(A,B)$
. For
$-1\le B<A\le 1$
, the class
$\mathcal {S}^*(A,B)$
was first introduced and investigated by Janowski [Reference Janowski9].
Note that
$P_{A,B}(z):=(1+Az)/(1+Bz)=1+(A-B)z+\cdots $
. For
$f\in \mathcal {CV}(A,B)$
, from (2.3) and (2.5) we immediately obtain
$|a_2(f)|\le |A-B|/2$
. For
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
and
$|\lambda |\le |A-B|/2$
, consider
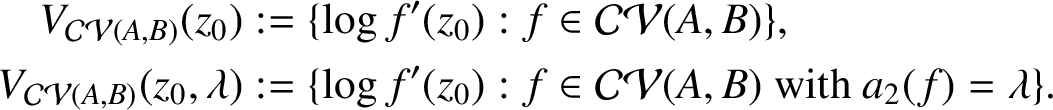$$ \begin{align*} V_{\mathcal{CV}(A,B)}(z_0) &:= \{ \log f'(z_0 ) : f \in \mathcal{CV}(A,B) \},\\ V_{\mathcal{CV}(A,B)}(z_0,\lambda) &:= \{ \log f'(z_0) : f \in \mathcal{CV}(A,B) \mbox{ with } a_2(f) = \lambda \}. \end{align*} $$
The following corollary is a simple consequence of Theorems 2.2 and 2.3.
Corollary 2.7. Let
$z_0 \in {\mathbb D} \backslash \{ 0 \}$
be fixed and
$\lambda \in \mathbb {C}$
be such that
$|\lambda |\le |A-B|/2$
. Also, let
$\gamma _1 = 2 \lambda /(A-B)$
.
-
(i) The region of variability
$V_{\mathcal {CV}(A,B)}(z_0)$
is a convex, closed Jordan domain and coincides with the set
$K( \overline {\mathbb D}(0,|z_0|))$
, where is a convex univalent function in
$$ \begin{align*}K(z) = \int_0^z \frac{A-B}{1+B\zeta} \, d \zeta \end{align*} $$
${\mathbb D}$
. Furthermore,
$\log f'(z_0) = K( \varepsilon z_0)$
for some
$\varepsilon $
with
$|\varepsilon | =1$
and
$f \in \mathcal {CV}(A,B)$
if and only if
$f(z) = \varepsilon ^{-1}F(\varepsilon z)$
, where
$F(z)= \int _0^z e^{K(\zeta )} \, d \zeta $
.
-
(ii) If
$|\gamma _1 |= 1 $
, then
$V_{\mathcal {CV}(A,B)}(z_0,\lambda )=\{w_0\}$
, where
$w_0 = \int _0^{z_0} \zeta ^{-1} \{ P(\gamma _1 \zeta )- 1 \} \, d \zeta $
. -
(iii) If
$|\gamma _1 |< 1 $
, then
$V_{\mathcal {CV}(A,B)}(z_0,\lambda ) = Q_{\gamma _1}(z_0, \overline {\mathbb D} )$
, where is a convex, univalent and analytic function of
$$ \begin{align*} Q_{\gamma_1}(z_0, \varepsilon ) = \int_0^{z_0} \frac{(A-B)\sigma_{\gamma_1}(\varepsilon \zeta)}{1+ B\zeta \sigma_{\gamma_1}(\varepsilon \zeta)} \, d \zeta \end{align*} $$
$\varepsilon \in \overline {\mathbb D}$
. Furthermore, for some
$$ \begin{align*} \log f'(z_0) = Q_{\gamma_1}(z_0, \varepsilon ) \end{align*} $$
$\varepsilon $
with
$\varepsilon \in \partial {\mathbb D}$
and
$f \in \mathcal {CV}( \Omega )$
with
$a_2(f) = \lambda $
if and only if
$$ \begin{align*}f(z) = \int_0^z e^{Q_{\gamma_1}(\zeta , \varepsilon )} \, d \zeta , \quad z \in {\mathbb D}. \end{align*} $$
Remark 2.8. The region of variability
$V_{\mathcal {CV}(A,B)}(z_0,\lambda )$
for the class
$\mathcal {CV}(A,B)$
was first obtained by Ul-Haq [Reference Ul-Haq18] for
$-1\le B<0$
and
$A>B$
. Although Ul-Haq considered the problem for
$A\in \mathbb {C}$
,
$0<B\le 1$
and
$A\ne B$
, the computation is valid only for
$-1\le B<0$
and
$A>B$
. We also note that the Herglotz representation [Reference Ul-Haq18, formula (2)] for functions in
$\mathcal {CV}(A,B)$
is not valid when
$-1< B<0$
.
In particular, for
$A= e^{-2i\alpha }$
with
$\alpha \in (-\pi /2,\pi /2)$
and
$B= -1$
, the class
$\mathcal {CV}(A,B)$
reduces to the class of functions that satisfy
$\mathrm {Re}\, \{e^{i\alpha }(1+zf''(z)/f'(z))\}>0$
for
$z\in \mathbb {D}$
. The functions in this class, denoted by
$\mathcal {S}_{\alpha }$
, are known as Robertson functions. If we choose
$A= e^{-2i\alpha }$
with
$\alpha \in (-\pi /2,\pi /2)$
and
${B= -1}$
in Corollary 2.7, then we obtain the result obtained in [Reference Ponnusamy, Vasudevarao and Yanagihara13].
For
$A= 1-2\alpha $
with
$-1/2\le \alpha <1$
and
$B= -1$
, the class
$\mathcal {CV}(A,B)$
reduces to the class of functions f satisfying
$\mathrm {Re}\, (1+zf''(z)/f'(z))>\alpha $
for
$z\in \mathbb {D}$
. This is the class
$\mathcal {CV}(\alpha )$
of convex functions of order
$\alpha $
. For
$0\le \alpha <1$
,
$\mathcal {CV}(\alpha )\subset \mathcal {CV}$
. On the other hand, for
$-1/2\le \alpha <0$
, functions in
$\mathcal {CV}(\alpha )$
are convex functions in some direction (see [Reference Ali and Vasudevarao1
Reference Ali, Allu and Yanagihara2]). If we choose
$A= 1-2\alpha $
with
$-1/2\le \alpha <1$
and
${B= -1}$
in Corollary 2.7, then we obtain the precise region of variability
$V_{\mathcal {CV}(\alpha )}(z_0):= \{ \log f'(z_0 ) : f \in \mathcal {CV}(\alpha ) \}$
and
$V_{\mathcal {CV}(\alpha )}(z_0,\lambda ):=\{ \log f'(z_0) : f \in \mathcal {CV}(\alpha ) \mbox { and } a_2(f) = \lambda \}$
, which gives a generalisation of Theorem 1.1. In particular, if we choose
$A= 2$
and
$B= -1$
in Corollary 2.7, then we obtain the result obtained by Ponnusamy and Vasudevarao [Reference Ponnusamy and Vasudevarao11, Theorem 2.6]. Similarly, for
$A= -2$
and
$B= -1$
, the class
$\mathcal {CV}(A,B)$
reduces to the class of functions f that satisfy
$\mathrm {Re}\, (1+zf''(z)/f'(z))<3/2$
for
$z\in \mathbb {D}$
. Functions in the class
$\mathcal {CV}(-2,-1)$
are starlike, but not necessarily convex [Reference Ali and Vasudevarao1]. If we choose
$A= -2$
and
$B= -1$
in Corollary 2.7, then we obtain the result in [Reference Ponnusamy and Vasudevarao11, Theorem 2.8].
Since
$f \in \mathcal {CV}(A,B)$
if and only if
$zf'(z) \in \mathcal {S}^*(A,B)$
, we can easily translate the above results about variability regions of
$\log \{ f(z_0)/z_0 \}$
when f ranges over
$\mathcal {S}^*(A,B)$
with or without the condition
$f''(0) = 2\lambda $
.
3 Concluding remark
Theorem 2.1 demonstrates that our results are closely related to the concept of subordination. Our assumption that
$g \in {\mathcal F}_\Omega (c)$
in Theorem 1.3 can be rewritten as
$g \prec P$
when
$c_0=0$
. In this case,
$P^{-1} (g (z)) = c_1z+\cdots +c_n z^n + \cdots $
. However, apart from a few exceptional cases, we cannot express our conclusions in terms of subordination relations. Let
$c = (c_0, \ldots , c_{n-1}) = (0,\ldots , 0)\in {\mathbb C}^n$
. Then the Schur parameter for c is given by
$\gamma = (\gamma _0, \ldots , \gamma _{n-1}) = (0, \ldots , 0)$
. For this particular choice of c, the function
$Q_{\gamma , j}$
defined by (1.1) becomes
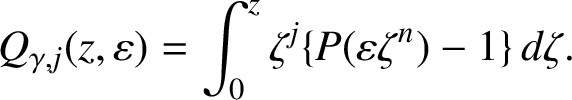$$ \begin{align*} Q_{\gamma , j}(z, \varepsilon) = \int_0^z \zeta^j \{ P( \varepsilon \zeta^n ) -1 \}\, d \zeta. \end{align*} $$
Let
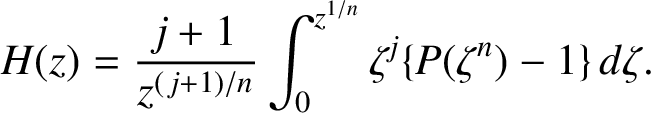$$ \begin{align*} H(z) = \frac{j+1}{z^{({\kern1.5pt}j+1)/n}} \int_0^{z^{1/n}} \zeta^j \{ P( \zeta^n ) -1 \}\, d \zeta. \end{align*} $$
Then
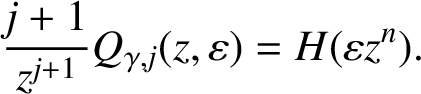$$ \begin{align*}\frac{j+1}{z^{j+1}} Q_{\gamma , j}(z, \varepsilon ) = H( \varepsilon z^n ). \end{align*} $$
By Theorem 1.3, for each fixed
$z \in {\mathbb D} \backslash \{ 0 \}$
,
$Q_{\gamma , j}(z, \varepsilon )$
is a convex univalent function of
$\varepsilon \in \overline {\mathbb D}$
and
$H( \varepsilon z^n )$
is also a convex univalent function of
$\varepsilon \in \overline {\mathbb D}$
. Letting
$z \rightarrow 1$
in
${\mathbb D}$
shows that
$H (\varepsilon )$
is also convex univalent in
${\mathbb D}$
. Let
$g \in {\mathcal F}_\Omega $
with
$g'(0)= \cdots = g^{(n-1)}(0) = 0$
. It follows from Theorem 1.3 that for any
$z \in {\mathbb D} \backslash \{ 0 \}$
, there exists
$\varepsilon \in \overline {\mathbb D}$
satisfying
$$ \begin{align*}\int_0^z \zeta^j \{g(\zeta) -1 \} \, d \zeta = Q_{\gamma , j}(z, \varepsilon ). \end{align*} $$
Thus, for all
$z \in {\mathbb D}$
,
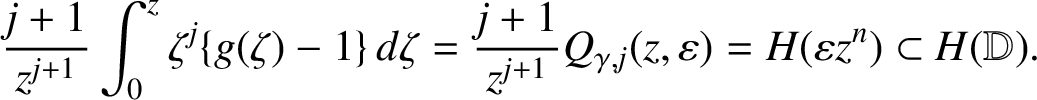$$ \begin{align*}\frac{j+1}{z^{j+1}} \int_0^z \zeta^j \{g(\zeta) -1 \} \, d \zeta = \frac{j+1}{z^{j+1}} Q_{\gamma , j}(z, \varepsilon ) = H( \varepsilon z^n ) \subset H( {\mathbb D }). \end{align*} $$
Consequently, in view of the univalence of H, we obtain the subordination relation
$$ \begin{align*}\frac{j+1}{z^{j+1}} \int_0^z \zeta^j \{g(\zeta) -1 \} \, d \zeta \prec H(z). \end{align*} $$
This was previously proved by Hallenbeck and Ruscheweyh [Reference Hallenbeck and Ruscheweyh8] when
$\text {Re} \, j \geq -1$
with
$j \not = -1$
.
