1. Introduction
It is certainly of great interest to understand how individual preferences are (at least partly) influenced by interpersonal comparison and what implications this has on economic welfare. Although specific results always depend on how exactly social mediation is specified, the assumption by itself has a tremendous impact on the consequences of traditional approaches to economic welfare. This argument holds for different conceptions of economic welfare such as utilitarianism, Rawlsian ethics, Sen's capability approach, or the focus on subjective happiness and well being. Schubert and Cordes (Reference Schubert and Cordes2013) try to explore these consequences by focusing on escalating consumption commitments. They argue that the social mediation of preferences may lead to ever-increasing levels of (aspired) consumption, which eventually decrease economic welfare. While we think that their argument is plausible on a general level, in this comment we develop a mathematical proof running counter to the results presented in Schubert and Cordes (Reference Schubert and Cordes2013, Section 3). Specifically, we claim to have found that the dynamical system specified by Schubert and Cordes (Reference Schubert and Cordes2013) will always stabilize at an equilibrium point.
After first drafting this comment, we directly approached Professors Schubert and Cordes. Professor Cordes sent us a series of replies, in which he explained their approach, which allowed us to identify more clearly where our approaches differ. While our exchange was quite fruitful and instructive for both authors of this comment, the participants as a whole failed to reach a conclusion on the issue, which is why it is now posed to the readers of this journal.
This comment proceeds as follows: first, we describe the model's assumption and illustrate the main point of contention in our controversy with Schubert and Cordes. In doing so, we present a simple argument, which already captures the reasons why the model cannot create self-reinforcing growth. Second, we analyze the long-term behavior of the model and show that it always reaches an equilibrium state. Finally, we describe some interesting properties of the model as implied by Schubert and Cordes’ assumptions: for some special initial data we find that an initially relatively homogeneous society may split into two classes (the ‘rich’ and the ‘poor’). There is only minimal interaction between these two classes over extremely long periods of time until they finally merge into a totally homogeneous society.
1.1 The model's assumptions
The model assumes a society comprised of a finite number of n individuals, which we label with i = 1, . . ., n. Each individual starts with an initial consumption level x i, 0 (a real number) and a preferred level of consumption p i, 0 (another real number). Schubert and Cordes assume in addition that p i, 0 > x i, 0 (something that will be of no importance to our approach but can be assumed if the reader chooses to). Moreover, each individual carries a weightFootnote 1 αi > 0 corresponding to its status in society, which can be taken to be normalized as
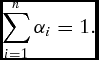\begin{equation*}
\sum \limits_{i = 1}^n \alpha _i = 1.\end{equation*}With regard to cultural transmission, Schubert and Cordes assume a direct bias affecting current consumption as well as an indirect bias affecting preferred consumption levels. To model the former they take a weight function β( ·, ·) of the form
\begin{equation*}
\beta (x,p) = {\rm exp}\left\{ { - a(x - p)^2 } \right\},\end{equation*}where a ≥ 0 is a given parameter. Cultural transmission in form of the direct bias proceeds according to the following equation (equation (1) in Schubert and Cordes, Reference Schubert and Cordes2013):
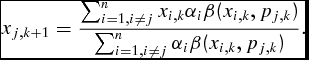\begin{equation*}
x_{j,k + 1} = \frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n x_{i,k} \alpha _i \beta (x_{i,k} ,p_{j,k} )}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \beta (x_{i,k} ,p_{j,k} )}}.\end{equation*}Heuristically speaking, in the next generation an individual's spending is given by an average of the consumption level of those individuals, which are close to the level of consumption considered desirable by the individual. The same mechanism applies to the levels of desired consumption (that is, the indirect bias); a second weight function θ( ·, ·) is given by
\begin{equation*}
\theta (x,p) = {\rm exp}\left\{ { - b(x - p)^2 } \right\},\end{equation*}where b ≥ 0 is a second given parameter. The iteration rule for the desired level of consumption (as specified by equation (2) in Schubert and Cordes, Reference Schubert and Cordes2013) is
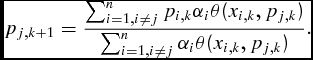\begin{equation*}
p_{j,k + 1} = \frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n p_{i,k} \alpha _i \theta (x_{i,k} ,p_{j,k} )}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \theta (x_{i,k} ,p_{j,k} )}}.\end{equation*}Written as text, the desired level of consumption in the next step is given by an average over the desired level of consumption of certain other people – those people, whose actual spending level is close to my desired spending level.
1.2 Competing statements
Through our exchange with Schubert and Cordes we identified the central tenets fostering our mutual disagreement. They study the difference in means between time period k and k + 1: for the level of spending they consider the change in the average spending level 
$\bar x$, which can be written as
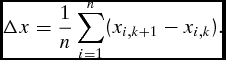\begin{equation*}
\Delta x = \frac{1}{n}\mathop \sum \limits_{i = 1}^n (x_{i,k + 1} - x_{i,k} ).\end{equation*}They then rewrite this expression and use a first-order Taylor series approximation to handle the arising terms (see their Appendix B). Based on this information, they use a stability analysis of the arising quantities. Based on this stability analysis, they conclude that
[. . .] a situation with 
$\bar p > \bar x$ [
$\bar \cdot $ denotes the average of · , JK & SS] (inducing a rise in 
$\bar x$) combined with the role model bias function, β( · ), that continuously updates the preference levels upward, makes social learners adopt ever more accentuated preferences relative to an ‘appropriate’ level of consumption. This results in a self-augmenting ‘treadmill’ of consumption choices. (Schubert and Cordes, Reference Schubert and Cordes2013: 147)
The main mathematical problem lies in the validity of the Taylor series approximation, which they never justify and whose error terms remain unstudied. Indeed, the growth is not self-reinforcingFootnote 2 and does not continue for all time: there is no self-augmenting ‘treadmill’.Footnote 3
2. A basic observation
The purpose of this section is to give a short and simple argument why the claimed ‘self-augmenting “treadmill”’ can never occur in this setup. We start by looking at those individual(s) with the highest amount of desired consumption within the whole population. The largest amount of spending desired by any individual at time k is
\begin{equation*}
\mathop {{\rm max}}\limits_{1 \le i \le n} p_{i,k} .\end{equation*}In this section, we show that the (desired) consumption of these individuals can never grow and that no one else can grow beyond this value. This, however, implies that any individual j at any point in time k satisfies
\begin{equation*}
p_{j,k} \le \mathop {{\rm max}}\limits_{1 \le i \le n} p_{i,0} ,\end{equation*}which says that the desired consumption levels are bounded from above – they have an unsurpassable upper limit.
The formal argument is relatively simple. We define the largest desired spending level in form of a function 
$f:\mathbb{N} \to \mathbb{R}$ via
\begin{equation*}
f(k) : = \mathop {{\rm max}}\limits_{1 \le i \le n} p_{i,k} .\end{equation*}In the model, aspiration levels in the next round are given by a weighted average of the aspiration levels of the current round. Let us assign a name h to the individual with the highest level of aspiration at time k: assume that f(k) = p h, k for some 1 ≤ h ≤ n. Now we study the development of individual consumption aspirations. First, we replace all values p i, k by the maximum p h, k for all 1 ≤ j ≤ n, which certainly increases the quantity
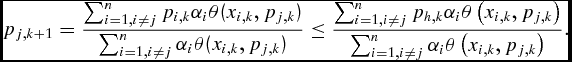\begin{equation*}
p_{j,k + 1} = \frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n p_{i,k} \alpha _i \theta (x_{i,k} ,p_{j,k} )}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \theta (x_{i,k} ,p_{j,k} )}} \le \frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n p_{h,k} \alpha _i \theta \left( {x_{i,k} ,p_{j,k} } \right)}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \theta \left( {x_{i,k} ,p_{j,k} } \right)}}.\end{equation*}Now we observe that there is a common factor p h, k in all the summands: we isolate this common factor and notice that the remaining fraction cancels
\begin{equation*}
\frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n p_{h,k} \alpha _i \theta \left( {x_{i,k} ,p_{j,k} } \right)}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \theta \left( {x_{i,k} ,p_{j,k} } \right)}} = p_{h,k} \left( {\frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \theta \left( {x_{i,k} ,p_{j,k} } \right)}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \theta \left( {x_{i,k} ,p_{j,k} } \right)}}} \right) = p_{h,k} .\end{equation*}Since j was completely arbitrary, this inequality holds for all individuals (including the individual with the highest desired consumption level in period k + 1). This implies that we have also shown that
\begin{equation*}
f(k + 1) \le f(k).\end{equation*}It immediately follows that the desired consumption level of any individual j will never surpass f(0). Therefore, the highest desired level of consumption in the entire evolution of the model can never exceed the highest desired level of consumption found in the initial data.
The same argument holds true for the largest actual spending level max1 ≤ i ≤ nx i, k and, additionally, the inverse results hold true for the minimal spending level as well as the minimal desired spending level (both of which cannot decrease). In particular, this means that all variables are trapped within the smallest and the largest values of the initial data for all time. As such, blow-up cannot occur.
3. Controversy
We encountered this basic property of the model when studying Schubert and Cordes’ original contribution and found it to be at odds with their results. It follows logically that either our or their result must be incorrect and, trivially, that at least one of the two arguments must be erroneous. Their presentation is far from rigorous: the mistake lies in assuming that a first-order Taylor expansion is sufficiently accurate and this mistake goes unnoticed because no analysis of the remainder term is being performed.
We can now pin down the essence of our controversy to the following three statements (the acronyms point to the originators of the statement, numbers refer to the equations in Schubert-Cordes).
• CS1: Equations (5) and (6) lead to result A.
• CS2: Equations (5) and (6) are derived from equations (1) and (2) (they describe the same dynamical system).
• KS1: Equations (1) and (2) lead to result non-A.
In this context, we choose a strategy of proof by contradiction: in this comment, we offer our proof of KS1 for anyone to find an error in. Alternatively, one could also construct an explicit numerical example exhibiting runaway dynamics to show that KS1 is false. If no error is to be found in KS1, an error must reside in CS1, CS2, or both of these statements (as already explained we presume CS1 is wrong).
4. Actual behavior of the model: a concise analysis
We have already discussed that all quantities produced by the model will be bounded. In this section, we give a complete description of the behavior of the model as time goes to infinity. We would like to point out that there is quite a bit of time until infinity and that despite very simple limiting dynamics, the model can exhibit quite interesting behavior until it stabilizes – we discuss one particular phenomenon in the next section.
Note first that for n = 2, it is very easy to see that both citizens will cyclically exchange roles: A imitates B completely while B imitates A. Every two rounds, they assume their previous demeanor. This cyclic exchange will go on forever and nothing will stabilize. Now suppose that the number of citizens is at least three. Then the model will eventually stabilize.
Theorem. Suppose n ≥ 3. Assume β, θ to be continuous weight functions satisfying
\begin{equation*}
\beta (x,y) > 0\quad {\rm and}\quad \theta (x,y) > 0\end{equation*}
or all 
$x,y \in \mathbb{R}$. Let (x i, 0, p i, 0)1 ≤ i ≤ n be any set of real-valued initial data. Then there exist two constants 
$c_1 ,c_2 \in \mathbb{R}$ such that the dynamical system converges in the sense that for all 1 ≤ i ≤ n
\begin{eqnarray*}
\mathop {{\rm lim}}\limits_{k \to \infty } x_{i,k} = c_1 \quad {\rm and}\quad \mathop {{\rm lim}}\limits_{k \to \infty } p_{i,k} = c_2 .\\\end{eqnarray*}In particular, if n ≥ 3, then the Schubert-Cordes model will always evolve into a stable equilibrium state, regardless of the parameters a, b and the initial data (x i, 0, p i, 0).
4.1 Proof of the theorem
In this section, we give a detailed proof of the theorem, which is based on relatively simple ideas and extends our approach for analyzing this model as presented in the preceding section. We prove the convergence statement only for the desired level of consumption p i, k (the proof for x i, k is completely identical). We assume without loss of generality that the weight functions are bounded from above by 1 (as we will show below, their value is only important on a compact interval: we can normalize without changing the dynamics).
Let us study the individuals with the highest level of aspiration at time 
$k \in \mathbb{N}$ and define a function 
$f:\mathbb{N} \to \mathbb{R}$ via
\begin{equation*}
f(k): = \mathop {{\rm max}}\limits_{1 \le i \le n} p_{i,k} .\end{equation*}As was described in the previous section, we have that
\begin{equation*}
f(k + 1) \le f(k).\end{equation*}The very same argument, however, holds for the persons with the lowest level of aspiration. If we define
\begin{equation*}
g(k): = \mathop {{\rm min}}\limits_{1 \le i \le n} p_{i,k} ,\end{equation*}then the inequality
\begin{equation*}
g(k + 1) \ge g(k)\end{equation*}is proven analogously. This already implies that for all k ≥ 0 and all 1 ≤ i ≤ N,
\begin{equation*}
g(0) \le p_{i,k} \le f(0).\end{equation*}Of course, the very same result can be proven for the x i, k. In particular, the p i, k are uniformly bounded in i and k by some numbers: they are trapped in the finite interval
\begin{equation*}
g(0) \le p_{i,k} \le f(0)\end{equation*}from which they can never escape. By simply replacing the variables in the above argument, the very same argument holds for x i, k. Indeed, we claim more: we claim that they are trapped in smaller and smaller intervals that end up shrinking to a point. However, in order to rigorously prove this statement, we do require the fact that they cannot escape from a bounded interval as a stepping stone.
While showing that the model stabilizes within a given interval is sufficient to indicate the invalidity of Schubert and Cordes’ conclusion, it does not suffice to prove our original theorem claiming that minimal and maximal values will eventually coincide in the limit. In doing so, we start with the sequence f(k), which is monotonically decreasing and bounded from below by g(0); therefore
\begin{equation*}
\mathop {{\rm lim}}\limits_{k \to \infty } f(k)\end{equation*}exists. At the same time, the sequence g(k) is monotonically increasing and bounded from above by f(0) and therefore
\begin{equation*}
\mathop {{\rm lim}}\limits_{k \to \infty } g(k)\end{equation*}exists. We need to show that the limits coincide.
To this end, we need to replay the previous argument and refine it a bit. We claim that there exists a number η > 0 such that uniformly for all k ≥ 0
\begin{equation*}
\mathop {{\rm min}}\limits_{i \in \left\{ {1,2, \ldots ,n} \right\}} \alpha _i \theta (x_{i,k} ,p_{j,k} ) \ge \eta > 0.\end{equation*}We have already seen that both p i, k and x i, k are uniformly bounded for all 1 ≤ i ≤ n as well as all k ≥ 0 and that the weight θ is positive and continuous. From this it follows that the term on the left-hand side cannot be arbitrarily close to 0, which in turn implies the existence of η. The number η can be thought of as a measure of the most unimportant person.
Suppose now g(k) < f(k). There exists j 1, j 2 such that p j 1, k + 1 = f(k + 1) and p j 2, k + 1 = g(k + 1). We can assume j 1 ≠ j 2 (we could prove that this is always doable but there is another argument: if they were equal, then minimum and maximum would coincide and we would be done). Since n ≥ 3, there exists a j 3 different from both j 1 and j 2. Here is the dilemma: in our computation of p j 1, k + 1 as well as in our computation of p j 2, k + 1, we take weighted averages over all other individuals: in particular, the individual j 3 appears in both computations. We consider two cases. In the first case, p j 3, k is smaller than or equal to the mean of f(k) and g(k):
\begin{equation*}
p_{j_3 ,k} \le \frac{{g(k) + f(k)}}{2}.\end{equation*}We get that in the worst case (in which j 3 is the most unimportant individual, whose opinion is only given weight η)
\begin{equation*}
f(k + 1) \le (1 - \eta )f(k) + \eta \left( {\frac{{g(k) + f(k)}}{2}} \right)\end{equation*}implying that the maximum level of desired consumption will decrease as long as it is greater than g(k). In the other case, where p j 3, k is higher than or equal to the mean of f(k) and g(k),
\begin{equation*}
p_{j_3 ,k} \ge \frac{{g(k) + f(k)}}{2};\end{equation*}we get by the same reasoning that
\begin{equation*}
g(k + 1) \ge (1 - \eta )g(k) + \eta \left( {\frac{{g(k) + f(k)}}{2}} \right).\end{equation*} Both sequences 
$(f(k))_{k \in \mathbb{N}} $ and 
$(g(k))_{k \in \mathbb{N}} $ are monotone and bounded, in particular
\begin{equation*}
\bar f: = \mathop {{\rm lim}}\limits_{k \to \infty } f(k)\quad {\rm and}\quad \bar g: = \mathop {{\rm lim}}\limits_{k \to \infty } g(k)\end{equation*}
exist. Furthermore, by definition, 
$\bar g \le \bar f$. From the inequalities, we have that
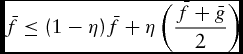\begin{equation*}
\bar f \le (1 - \eta )\bar f + \eta \left( {\frac{{\bar f + \bar g}}{2}} \right)\end{equation*}
and since η > 0, this implies 
$\bar f = \bar g$. The proof for the other inequality as well as for x i, k is completely identical.
4.2 Remarks
First, one could extend the models to societies, where some individuals have weight αi = 0. These individuals have no influence over other individuals and are only themselves influenced. It is easily seen that our theorem still holds true as long as the number of individuals satisfying αi > 0 is at least 3.
Second, this principle proof is an adaptation of the classical maximum principle for parabolic partial differential equations to the particular setting. We refer to Gilbarg and Trudinger (Reference Gilbarg and Trudinger2001) for the classical exposition and Chung (Reference Chung1997) for the discrete case.
5. A non-linear segregation effect
Here we aim to report on a new interesting phenomenon within the Schubert-Cordes model. As we have seen above, the long-time dynamics of the model are very simple: every citizen spends the same amount of money c 1 and desires to spend the same amount of money c 2 and nothing changes. As such, no interesting dynamical behavior can go on forever. However, while doing computer experiments, we have discovered a phenomenon that gives rise to dynamical behavior that persists for very long time.
Let a = 5, b = 10 and let the population size be n = 20. The individual i has societal importance αi = i/210 (individual 5 is five times as important as individual 1). Let the initial data be given by
\begin{equation*}
(x_0 )_j = j\quad {\rm and}\quad (p_0 )_j = \frac{{j^2 }}{{10}}.\end{equation*}This initial distribution is certainly uneven but certainly approximates a continuum: individual 7 spends much more than individual 1, but there is no segregation into ‘rich’ and ‘poor’, because there is also individual 4 spending less than 7, but more than 1. However, after merely three iterations, the system has a curious shape: we have
\begin{equation*}
(x_3 )_j \sim \left\{ {\begin{array}{l@{\hspace*{8pt}}l}
{1.012} & {{\rm if}\;j \le 9} \\
{20} & {{\rm if}\;10 \le j \le 20}
\end{array}} \right.\end{equation*}and
\begin{equation*}
(p_3 )_j \sim \left\{ {\begin{array}{l@{\hspace*{8pt}}l}
{0.1} & {{\rm if}\;j \le 9} \\
{40} & {{\rm if}\;10 \le j \le 20.}
\end{array}} \right.\end{equation*}The society has split into two parts: the first nine individuals 1 ≤ j ≤ 9 have low actual spending (x 3)j ~ 1.012 and desire to spend very little money (p 3)j ~ 0.1. All other individuals 10 ≤ j ≤ 20 spend much money (x 3)j ~ 20 and desire to spend even more (p 3)j ~ 40.
This particular societal configuration now seems stable: running thousands or even millions of additional iterations does not seem to change anything at all. The explanation is relatively simple: both parameters a, b in the weight functions β and θ are very large. This means that weighted averages in the recursion formulae only consider a rather small sample of individuals. In this example, those people, who spend small amounts of money, desire to spend even smaller amounts of money, meaning all weighted averages reduce essentially to taking the data of the individual with the lowest spending level. At the same time, those people, who actually spend lots of money, desire to spend even more, meaning their averages will be dominated by the value of the richest person. This explains why within both parts of society there is roughly the same numerical value.
This example resembles a form of class-society, where the intensity of economic inequality or other social cleavages leads to a kind of social disentanglement – the ‘rich’ and the ‘poor’ are so intensely segregated that they share no common social identity (Hogg and Terry, Reference Hogg and Terry2000) and, thus, do not employ each other as reference persons (Kahnemann, Reference Kahnemann2003) when making consumption decisions. A similar constellation was already addressed by Veblen, when emphasizing that great social or economic cleavages may significantly dampen the effect of emulation:
[. . .] each class envies and emulates the class next above it in the social scale, while it rarely compares itself with those below or with those who are considerably in advance. (Veblen, Reference Veblen1970[1899]: 81, Italics by the authors of this paper)
It follows from our proof that even a configuration like this has to eventually converge. However, it might take a long while. Let us consider a rich individual j considering their spending level in the next round
\begin{equation*}
x_{j,k + 1} = \frac{{\mathop \sum \nolimits_{i = 1,i \ne j}^n x_{i,k} \alpha _i \beta (x_{i,k} ,p_{j,k} )}}{{\mathop \sum \nolimits_{i = 1,i \ne j}^n \alpha _i \beta (x_{i,k} ,p_{j,k} )}},\end{equation*}where
\begin{equation*}
\beta (x,p) = {\rm exp}\left\{ { - 20(x - p)^2 } \right\}.\end{equation*}Then another rich individual h has a very small weight (which means little: through normalization we are interested in its size compared to that of other weights)
\begin{equation*}
\beta (x_{h,k} ,p_{j,k} ) \sim \beta (20,40) = e^{ - 8000} .\end{equation*}However, this weight is many, many times larger than the weight a poor individual l is given as
\begin{equation*}
\beta (x_{l,k} ,p_{j,k} ) \sim \beta (1.012,40) \sim e^{ - 30420} .\end{equation*}This means that, ignoring the weights of societal importance α (which do not contribute much in this regime anyway), a rich individual assigns many magnitudes more importance to another rich person than to a poor person. The same reasoning holds true in the other direction as well, therefore a separation of society occurs: rich people orient themselves according to what other rich people think and the other way around; hence interaction among these groups is minimal and segregation occurs.
This effect is truly non-linear and highly interesting: it shows that despite fairly simple limiting dynamics (convergence to a constant) a model like this can have quite fascinating long-time dynamical behavior with structures that are difficult to predict.
