Introduction
The idea of this paper is originated from the concept of structural instability, when the qualitative behaviour of a mathematical model is sharply changed by small perturbations of its parameters. We start with the model of Newtonian physics.
In Newtonian physics, the concept of probability ρ for a moving particle is introduced via the Liouville equation
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + \nabla \cdot ({\rm \rho} {\bf F}) = 0,\quad \int_{ - \infty} ^\infty {{\rm \rho d}{\bf v} = 1} $$generated by the three-dimensional (3D) vector ODE (ordinary differential equation)
$$\displaystyle{{{\rm d}{\bf v}} \over {{\rm dt}}} = {\bf F}({\bf v}),$$where v is velocity vector, and F is a Newtonian force per unit mass.
It describes the conservation of the probability density flow originated by the error distribution at t = 0
$${\rm \rho} _0 = {\rm \rho} _0 (V),\quad {\rm where}\;{\rm \rho} \ge 0,\;{\rm and}\;\int_{ - \infty} ^\infty {{\rm \rho} _0 {\rm d}V = 1}. $$Remark 1. Here and below we make distinction between the random variable v(t) and its values V in probability space.
Remark 2. In general, the force F can depend upon velocity v and position r of the particle. Then one has to replace equation (2) by the 6D system
$$\displaystyle{{{\rm d}{\bf v}} \over {{\rm d}t}} = {\bf F}({\bf v}),\quad \displaystyle{{{\rm d}{\bf r}} \over {{\rm d}t}} = {\bf v}.$$ The criterion (1) is formally the same if one introduces an extended ‘force’ 
${\bf F}_{\rm e} = {\bf F},{\bf v}$ and consider the operation div in the corresponding 6D space.
Rehabilitation of the Maxwell demon
All the previous attempts to develop models for so-called active systems have been based upon the principles of Newtonian and statistical mechanics (Mikhailov Reference Mikhailov1990). These models appear to be so general that they predict not only physical, but also some biological and economical, as well as social patterns of behaviour exploiting such fundamental properties of non-linear dynamics as attractors. Notwithstanding indisputable successes of that approach (neural networks, distributed active systems, etc.) there is still a fundamental limitation that characterizes these models on a dynamical level of description: they propose no difference between a Solar System, a swarm of insects and a stock market. Such a phenomenological reductionism is incompatible with the first principle of progressive biological evolution associated with Darwin (Prigogine Reference Prigogine1980; Haken Reference Haken1988). According to this principle, the evolution of living systems is directed towards the highest levels of complexity if the complexity is measured by an irreducible number of different parts which interact in a well-regulated manner. At the same time, the solutions to the models based upon dissipative Newtonian dynamics eventually approach attractors where the evolution stops while these attractors dwell on the subspaces of lower dimensionality, and therefore, of the lower complexity (until a ‘master’ reprogrammes the model). Therefore, such models fail to provide an autonomous progressive evolution of living systems (i.e. evolution leading to increase of complexity). In addition to this limitation, there are some problems, and even paradoxes with the second law of thermodynamics when it is applied to intelligent systems. One of the paradoxes of the second law of thermodynamics that is still under discussion is the following: We live in a world that should not be possible. Indeed, the world around us is in a high order, although given the age of the Universe, there is not ‘enough time’ to create a non-vanishingly small probability for such complex world. Ludwig Boltzmann reasoned that brains and other complex, orderly objects on Earth were the result of random fluctuations. But why, then, do we see billions of other complex, orderly objects all around us? Just a short strand of DNA is so intricately constructed that the probability of it arising as a result of ‘random fluctuations’ in physical material is unthinkably small. So how is it that there are billions of base pairs in a single cell, trillions of cells in a complex organism and millions of species on Earth? So, we have another question. If the only requirement of consciousness is a brain like the one in your head, why are you not a Boltzmann brain? If you were assigned to experience a random consciousness, you should almost certainly find yourself alone in the depths of space rather than surrounded by similar consciousness. The easy answers seem to all require a touch of magic. But we will turn to mathematics instead, and replace the Newtonian force 
${\bf F(V)}$ in equations (2) and (3) with an information force, (Zak Reference Zak2017)
$$\displaystyle{{{\rm d}{\bf v}} \over {{\rm d}t}} = {\bf F}[{\rm \rho} ({\bf v})],\quad \int_{ - \infty} ^\infty {{\rm \rho d}{\bf v} = 1}, $$
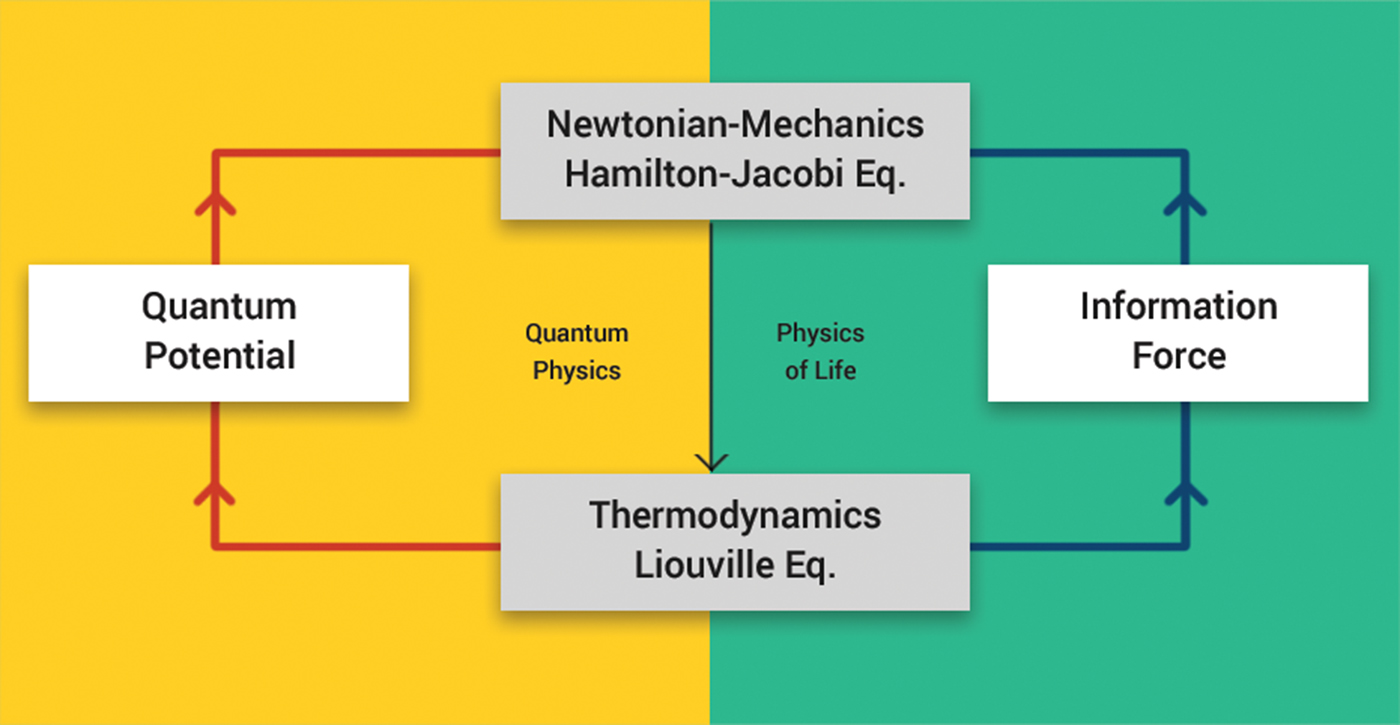
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + \nabla \cdot \{ {\rm \rho} {\bf F}[{\rm \rho} ({\bf V})]\} = 0.$$This is a fundamental step in our approach: in Newtonian dynamics, the probability never explicitly enters the equation of motion. In addition to that, the Liouville equation (6), in contrast to equation (4), is non-linear with respect to the probability density ρ, and therefore, the system (5), (6) departs from Newtonian dynamics. However, although it has the same topology as quantum mechanics (since now the equation of motion is coupled with the equation of continuity of probability density), Zak (Reference Zak2016a), it does not belong to it either. Indeed equation (5) is more general than the Hamilton–Jacoby equation (2): it is not necessarily conservative, and the feedback F is not necessarily the quantum or classical potential although further we will impose some restriction upon it that links F to the concept of information. The relation of the system (5), (6) to Newtonian and quantum physics is illustrated in Fig. 1.
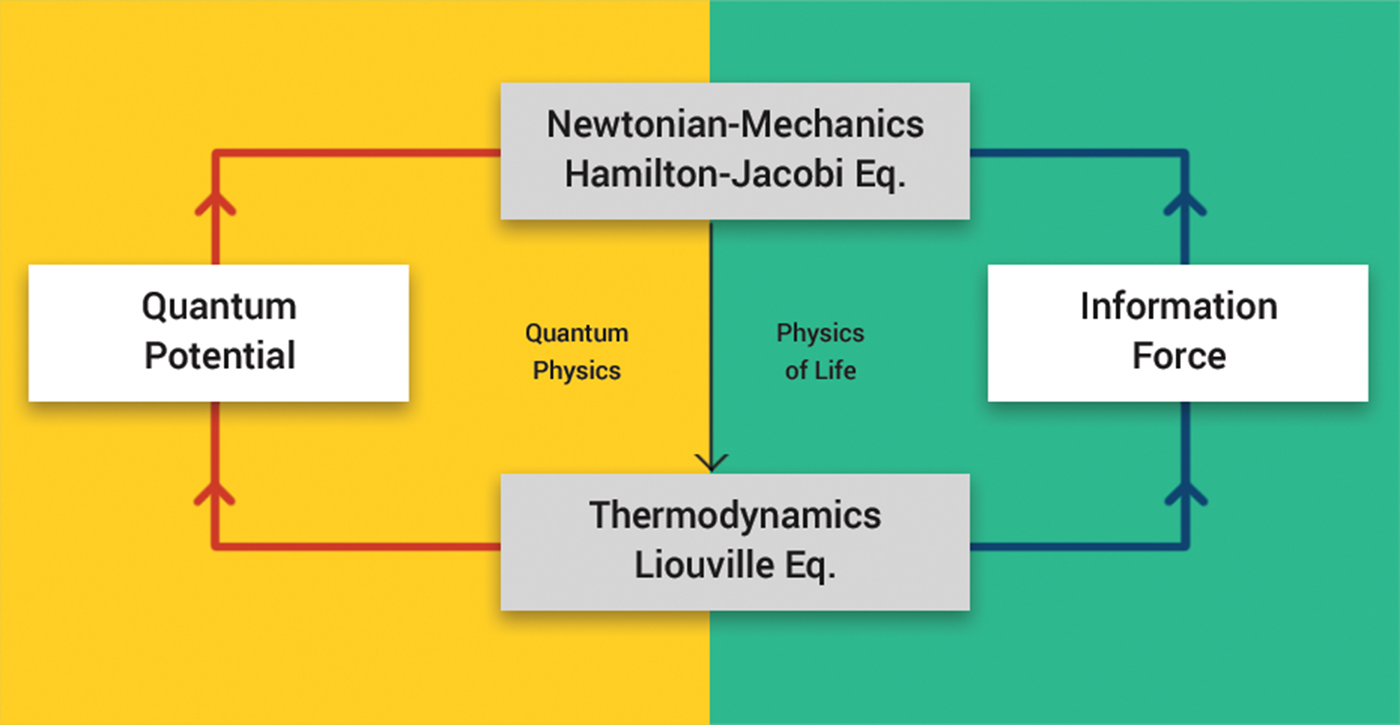
Fig. 1. Classic physics, quantum physics and physics of life.
Following Zak (Reference Zak2016a, Reference Zak2017), we consider the force F that plays the role of a feedback from the Liouville equation (6) to the equation of motion (5). Turning to 1D case, let us specify this feedback as
$$F = c_0 + \displaystyle{1 \over 2}c_1 {\rm \rho} - \displaystyle{{c_2} \over {\rm \rho}} \displaystyle{{\partial {\rm \rho}} \over {\partial v}} + \displaystyle{{c_3} \over {\rm \rho}} \displaystyle{{\partial ^2 {\rm \rho}} \over {\partial v^2}}, $$
$$c_0 \gt 0,\;c_1 \gt 0,\;c_3 \gt 0.$$Then equation (9) can be reduced to the following:
$$\dot v = c_0 + \displaystyle{1 \over 2}c_1 {\rm \rho} - \displaystyle{{c_2} \over {\rm \rho}} \displaystyle{{\partial {\rm \rho}} \over {\partial v}} + \displaystyle{{c_3} \over {\rm \rho}} \displaystyle{{\partial ^2 {\rm \rho}} \over {\partial v^2}}, $$and the corresponding Liouville equation will turn into the non-linear partial differential equations (PDE)
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + (c_0 + c_1 {\rm \rho} )\displaystyle{{\partial {\rm \rho}} \over {\partial V}} - c_2 \displaystyle{{\partial ^2 {\rm \rho}} \over {\partial V^2}} + c_3 \displaystyle{{\partial ^3 {\rm \rho}} \over {\partial V^3}} = 0$$(see the remark above).
This equation is known as KdV-Burgers (Korteweg-de Vries-Burgers) PDE. The mathematical theory behind the KdV equation became rich and interesting, and, in the broad sense, it is a topic of active mathematical research. A homogeneous version of this equation that illustrates its distinguished properties is a non-linear PDE of parabolic type. But a fundamental difference between the standard KdV-Bergers equation and equation (12) is that equation (12) dwells in the probability space, and therefore, it must satisfy the normalization constraint
$$\int_{ - \infty} ^\infty {{\rm \rho d}V = 1}. $$However, as noticed in (Zak Reference Zak2016a), this constraint is satisfied: in physical space, it expresses conservation of mass, and it can be easily scale-down to the constraint (13) in probability space. That allows one to apply all the known results directly to equation (12). However, it should be noticed that all the conservation invariants have different physical meaning: they are not related to conservation of momentum and energy, but rather impose constraints upon the Shannon information.
In physical space, equation (12) has many applications from shallow waves to shock waves and solitons. However, application of solutions of the same equations in probability space is fundamentally different. Analysis of equations (11)–(13) performed in (Zak Reference Zak2016a) discovered non-Newtonian properties of their solutions such as randomness, entanglement and probability interference typical for quantum systems. But the most surprising property of these equations that may have fundamental philosophical implications was a capability of their solutions to violate the second law of thermodynamics, and we will demonstrate it below. For that purpose consider the simplest case of the system (11)–(13) assuming that
$$c_0 = 0,\quad c_2 = 0,\quad c_3 = 0,\quad c_1 \gt 0.$$The closed form analytical solution can be presented in the following implicit form (Whitham Reference Whitham1974)
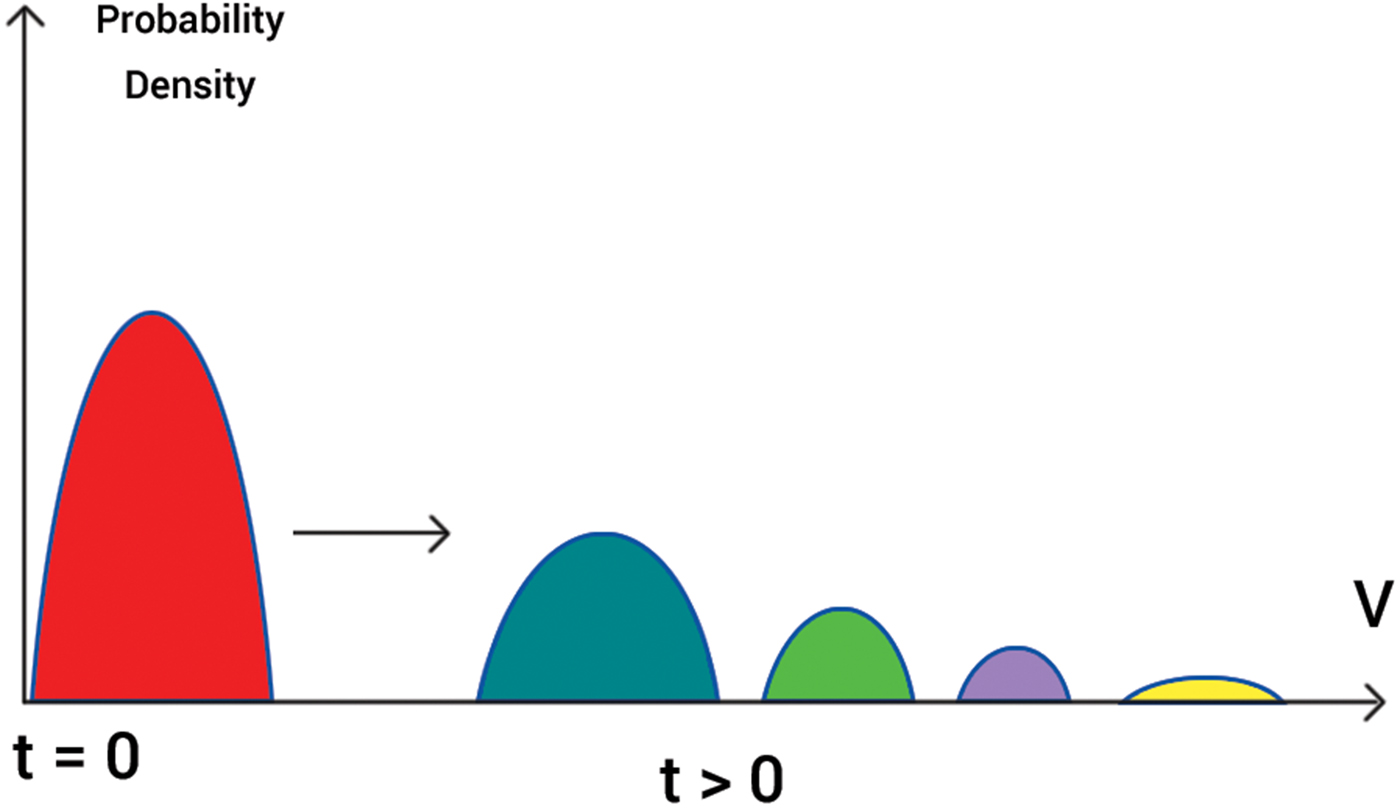
$${\rm \rho} (V,t) = {\rm \rho} _0 (V - {\rm \xi \rho} t),\quad {\rm \rho} _0 = {\rm \rho} _{t = 0}. $$The process of violation of the second law of thermodynamics is illustrated in Fig. 2: the higher values of ρ propagate faster than lower ones. As a result, the moving front becomes steeper and steeper, and that leads to formation of solitons (c 3 > 0), or shock waves (c 3 = 0) in probability space. This process is accompanied by decrease of entropy.
Fig. 2. Formation of shock waves in probability space.
At the same time, the original system (11), (12) is isolated: it has no external interactions. Indeed, the information force equation (9) is generated by the Liouville equation that, in turn, is generated by the equation of motion (11). In addition to that, the particle described by ODE (11) is in equilibrium 
$\dot v = 0$ prior to activation of the feedback (9). Therefore, the solution of equations (11) and (12) can violate the second law of thermodynamics, and that means that this class of dynamical systems does not belong to physics as we know it.
It should be emphasized that despite the mathematical similarity between equation (12) and the KdV-Bergers equation, the physical interpretation of equation (12) is fundamentally different: it is a part of the dynamical system (11), (12) in which equation (12) plays the role of the Liouville equation generated by equation (11). As follows from equation (15), this system, being isolated and being in equilibrium, has the capability to decrease entropy, i.e. to move from disorder to order without external resources. In addition to that, as shown in Zak (Reference Zak2016a), the system displays transition from deterministic state to randomness.
This property represents departure from classical and quantum physics, and, as shown in (Zak Reference Zak2012), provides a link to behaviour of livings. That suggests that this kind of dynamics requires extension of modern physics to include physics of life.
A biological interpretation of the model presented by equations (11) and (12) (that can be associated with motor and mental dynamics, respectively) has been described in (Zak Reference Zak2012; Reference Zak2017). In addition to that, we will notice that the motor dynamics equation (11) is non-conservative and irreversible, while the mental dynamics equation (12), (if c 2 = 0), is conservative and reversible as KdV equation is, (Whitham Reference Whitham1974). Since the mental dynamics (12) can be considered independently from the motor dynamics (11), this means that there is no arrow of time in mental dynamics, i.e. mentally the activity of the livings can be directed from present to future as well as from present to past (memories), and this is another evidence of similarity between the proposed model and behaviour of livings.
So far, the model equations (11) and (12) have been written for a 1D case. It can be easily generalized to 3D case
$${\dot {\rm v}}+ = c_{\rm 0} + \displaystyle{1 \over 2}c_1 {\rm \rho} - \displaystyle{{c_2} \over {\rm \rho}} \nabla {\rm \rho} + \displaystyle{{c_3} \over {\rm \rho}} \Delta {\rm \rho,} $$
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + \nabla \cdot \left[ {{\rm \rho} \left( {c_{\rm 0} + \displaystyle{1 \over 2}c_{\rm 1} {\rm \rho} - \displaystyle{{c_2} \over {\rm \rho}} \nabla {\rm \rho} + \displaystyle{{c_3} \over {\rm \rho}} \Delta {\rm \rho}} \right)} \right] = 0.$$Finally, we will emphasize the rehabilitation of the conceit of the Maxwell demon when it is applied to physics of livings. Actually, the mental dynamics plays the role of the Maxwell sorting demon: it rearranges the probability distribution by creating the information force and converting it into a force that is applied to the particle. One should notice that mental dynamics describes evolution of the whole class of state variables (differed from each other only by initial conditions), and that can be associated with the ability to generalize that is a privilege of living systems.
Remark 1. Maxwell's demon is an imaginary creature that the mathematician James Clerk Maxwell created to contradict the second law of thermodynamics. The demon is trying to create more useful energy from the system than there was originally. Equivalently he was decreasing the randomness of the system (by ordering the molecules according to a certain rule), which is decreasing the entropy. No such violation of the second law of thermodynamics has ever been found in physics.
Structural instability of Newtonian physics
In this section, we demonstrate that the Second Newton Law is structurally unstable with respect to perturbations coming from the Liouville feedback. For this purpose, we discuss transition from determinism to randomness in ODE that coupled with their Liouville PDE. Let us turn to equations (11) and (12).
Without the Liouville feedback, i.e. when
$$c_0 = 0,\quad c_1 = 0,\quad c_2 = 0,\quad c_3 = 0$$they represent the Second Newton's Law and the conservation of probability, respectively.
Let us assume now that
$$c_3 \gt 0.$$In order to complete the solution of the system (11), (12), one has to substitute the solution of equation (12):
$${\rm \rho} = {\rm \rho (}V,t)\quad {\rm at}\;V = v$$into equation (11). Since the transition from determinism to randomness occurs at t → 0, let us turn to equation (12) with sharp initial condition
$${\rm \rho} _0 (V) = {\rm \delta} (V)\quad {\rm at}\;t = 0,$$Then applying one of the standard analytical approximations of the δ-function, one obtains the asymptotic solution
$${\rm \rho} = \displaystyle{1 \over {t\sqrt {\rm \pi}}} {\rm e}^{ - (V^2 /t^2 )} \quad {\rm at}\;t \to 0.$$Substitution of this solution into equation (11) shows that
$$\dot v = \displaystyle{{4c_3 v^2} \over {t^4}} \quad {\rm at}\;t \to 0,\;v \ne 0.$$Equation (23) has the following solution (see Fig. 2)
$$v = \displaystyle{{t^3} \over {4c_3 + Ct^3}} \quad {\rm at}\;t \to 0,\;v \ne 0,$$where C is an arbitrary constant.
This solution has the following property: the Lipchitz condition at t → 0 fails
$${\displaystyle{{\partial \dot v} \over {\partial v}} = \displaystyle{{8c_3 v} \over {t^4}} = \displaystyle{{8c_3 t^3} \over {t^4 (4c_3 + Ct^3 )}} \to \infty \quad {\rm at}\;t \to 0,\;v \ne 0,} $$and as a result of that, the uniqueness of the solution is lost. Indeed, as follows from equation (24), for any value of the arbitrary constant C, the solutions are different, but they satisfy the same initial condition
$$v \to 0\;{\rm at}\;t \to 0.$$Due to violation of the Lipchitz condition (25), the solution becomes unstable. That kind of instability when infinitesimal errors lead to finite deviations from basic motion (the Lipchitz instability) has been discussed in (Zak Reference Zak1992). This instability leads to unpredictable shift of solution from one value of C to another. It means that appearance of any specified solution out of the whole family is random, and that randomness is controlled by the feedback (9) from the Liouville equation (12). Indeed, if the solution (21) runs independently many times with the same initial conditions, and the statistics is collected, the probability density will satisfy the Liouville equation (12) (Fig. 3).
Fig. 3. Family of random solutions describing transition.
But here we will be interested in another property of this solution – its structural instability. Indeed, when
$$C_3 = 0,$$we have an inertial motion of a particle, and with initial condition (26), the particle is in the state of rest. However, any small, even infinitesimal, but positive perturbation of the parameter
$$c_3 \gt 0$$shifts the solution to random non-inertial motion. It can be shown (Zak Reference Zak2016a) that similar qualitative shift occurs when instead of c 3 we consider other parameters in equation (11). Therefore, the solution to equation (11) is structurally unstable since its qualitative behaviour is sharply changed by small perturbations of its parameters.
This suggests the following mathematical scenario of origin and emerging of life: if we postulate the model of Newtonian physics, then due to its structural instability with respect to a certain kind of perturbations of parameters of possible Liouville feedback, the model of the Newtonian physics shifts to the model of life. The appearance of these perturbations could be random, and from physics viewpoint, special conditions of such appearance have to be satisfied. Obviously, these conditions are beyond the mathematical scenario that is under consideration.
In order to make our argumentation more transparent, we will deviate from the main target that is physics of life, and turn to quantum mechanics described by the Madelung equation (Madelung Reference Madelung1926) representing the hydrodynamic version of the Schrödinger equation
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + \nabla \left( {\displaystyle{{\rm \rho} \over m}\nabla S} \right) = 0,$$
$$\displaystyle{{\partial S} \over {\partial t}} + (\nabla S)^2 + F - \displaystyle{{\hbar\!^2 \nabla ^2 \sqrt {\rm \rho}} \over {2m\sqrt {\rm \rho}}} = 0.$$ Here ρ and S are the components of the wave function 
${\rm \psi} = \sqrt {\rm \rho} {\rm e}^{iS/\hbar} $, and 
$\hbar $ is the Planck constant divided by 2π. The last term in equation (30) is known as quantum potential and F represents a classical potential. From the viewpoint of Newtonian mechanics, equation (29) expresses continuity of the flow of probability density, and it can be associated with the Liouville equation, while equation (30) is the Hamilton–Jacobi equation for the action S of the particle of mass m, and it can be associated with the Second Newton's Law. Actually, the quantum potential in equation (30), as a feedback from equation (29) to (30), represents the difference between the Newtonian and quantum mechanics, and therefore, it is solely responsible for fundamental quantum properties. Choosing the Planck constant as a parameter, one finds the similarity between 
$\hbar $ and c 3 in equation (23): the Newtonian model is structurally unstable with respect to perturbations of the quantum potential since we have the model of Newtonian physics as long as 
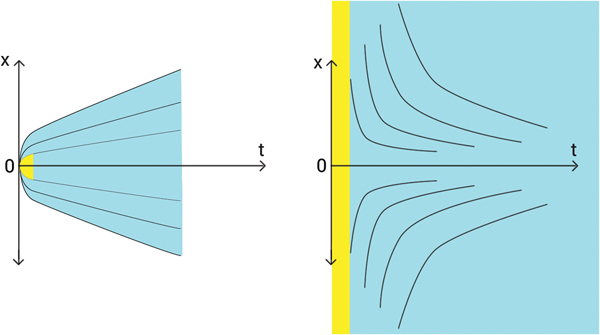
$\hbar $ = 0, and this model shifts to quantum model at 
$\hbar $ > 0. The scenario of this transition has been described in (Zak Reference Zak2016b), see Fig. 4
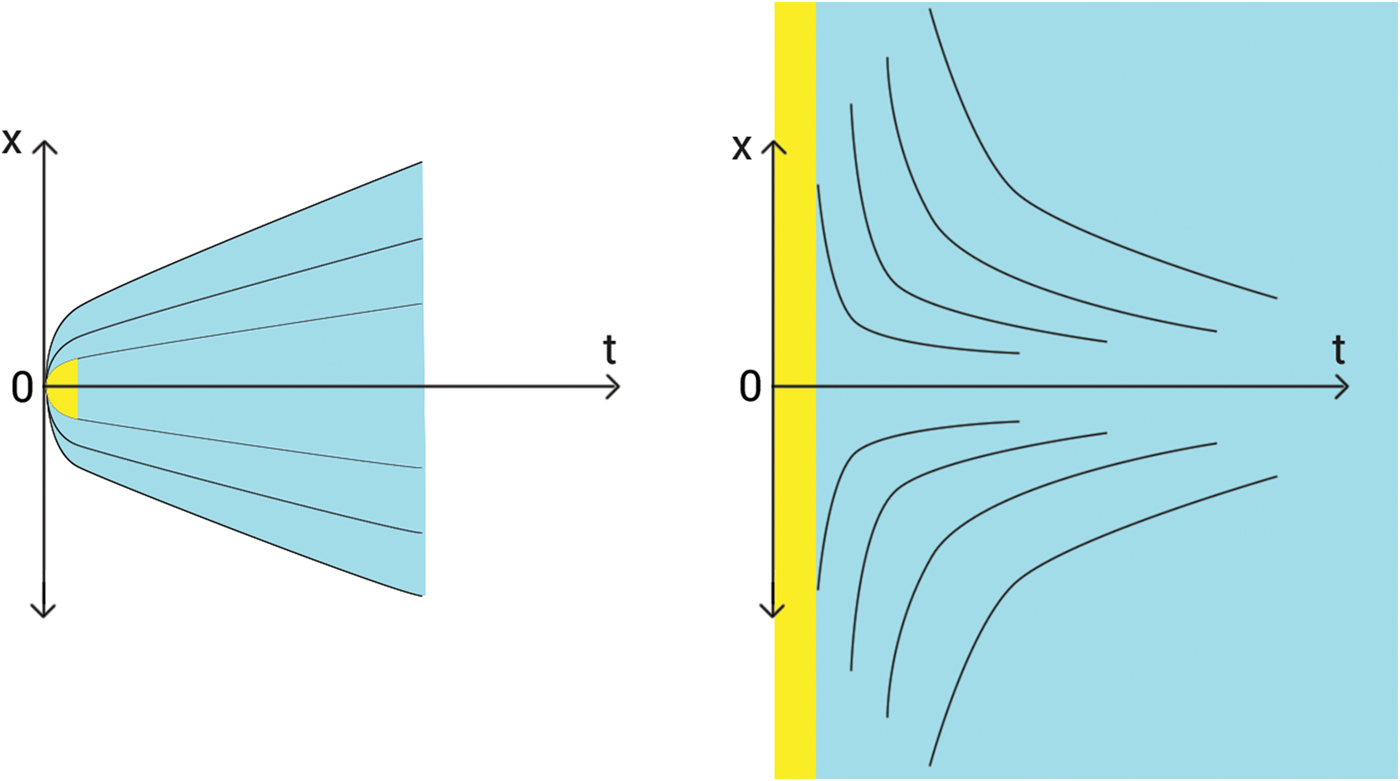
Fig. 4. Family of random trajectories and particle velocities after transition from the deterministic state.
This scenario is qualitatively similar to that of transition to the model of life in Fig. 3.
Structural instability of physics of life
In this section, we investigate the structural instability of physics of life model described by equations (11) and (12). We will start with the linear version of this model by setting
$$c_1 = 0,\quad c_2 = 0,$$
$$\dot v = c_0 + \displaystyle{{c_3} \over {\rm \rho}} \displaystyle{{\partial ^2 {\rm \rho}} \over {\partial v^2}}, $$
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + c_0 \displaystyle{{\partial {\rm \rho}} \over {\partial V}} + c_3 \displaystyle{{\partial ^3 {\rm \rho}} \over {\partial V^3}} = 0.$$The first applications of linear (parabolic) version of KdV equation (1.2) appear in models of shallow water waves. The equation is conservative, and its solution is represented by a train of traveling waves
$${\rm \rho} (v,t) = A{\rm e}^{ikv - {\rm \omega} t}, $$where ω is the frequency, and k is the wave number. For KdV equation, these two constants are connected by the following dispersion relation
$$c_3 \gt 0,\;c_0 \gt 0,\;c_1 \gt 0.$$If the initial profile ρ = u(v, 0) is represented as a sum of the Fourier harmonics, then each of this harmonic will propagate with the phase speed
$$C = {\rm \omega} /k.$$Comparing equations (35) and (36), one can see that each Fourier harmonics will propagate with different phase speed that depends upon its wave number k. Therefore, any initial profile eventually is dispersed over the whole positive subspace (Fig. 5).
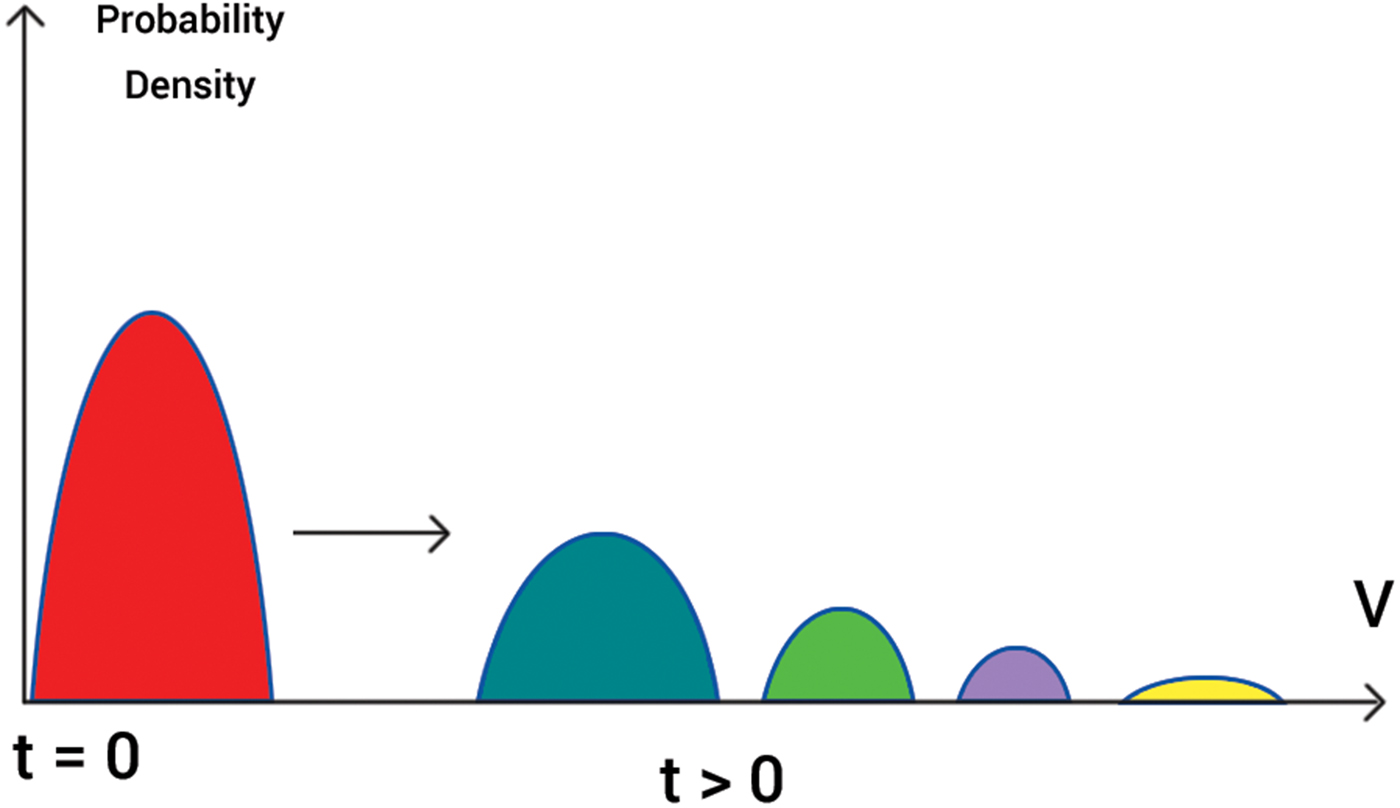
Fig. 5. Linear dispersion of initial profile.
Two important properties of the linear version of the KdV equation should be emphasized. Firstly, its solutions depend on the initial conditions for all times, and secondly, they do not violate the second law of thermodynamics. The latter property provides a reason to attribute the linear model equations (32) and (33) to physics of non-intelligent life.
Let us turn to the feedback (9) at
$$c_2 = 0$$and modify equation (11) as
$$\dot v = c_0 + \displaystyle{1 \over 2}c_1 {\rm \rho} + \displaystyle{{c_3} \over {\rm \rho}} \displaystyle{{\partial ^2 {\rm \rho}} \over {\partial v^2}}, $$
$$c_3 \gt 0,\;c_0 \gt 0,\;c_1 \gt 0.$$Then the corresponding Liouville equation will turn into the following non-linear PDE
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + (c_0 + c_1 {\rm \rho} )\displaystyle{{\partial {\rm \rho}} \over {\partial V}} + c_3 \displaystyle{{\partial ^3 {\rm \rho}} \over {\partial V^3}} = 0$$that is a celebrated KdV equation.
However, a fundamental difference between the standard KdV equation and equation (39) is that equation (39) dwells in the probability space, as well as the KdV-Burgers equation (12), and therefore, it must satisfy the normalization constraint
$$\int_{ - \infty} ^\infty {{\rm \rho d}V = 1}. $$But since the KdV equation has the conservation invariants, (Whitham Reference Whitham1974)
$$\int_{ - \infty} ^\infty {{\rm \rho d}V = {\rm Const}{\rm.,}} $$
$$\int_{ - \infty} ^\infty {{\rm \rho} ^2 {\rm d}V = {\rm Const}{\rm.,}} \;{\rm etc}{\rm.} \; $$the constraint (40) becomes a particular case of the invariant (41); consequently, if the normalization constraint is satisfied at t = 0, it is satisfied all the time. That allows one to apply all the known result directly to equation (39). However, it should be noticed that the conservation invariants (41) and (42) have different physical meaning: they are not related to conservation of momentum and energy, but rather impose constraints upon the Shannon information.
Since closed form solution of equation (39) is not available, we will continue with the solution for large time. The rationale for that is the assumption that eventually the solution tends to a stationary shape as a result of a balance between dispersion and shock wave formation. Therefore, we will seek the solution in the form of a stationary motion
$${\rm \rho} (v,t) = f\,(v - Ut) = u({\rm \zeta} )\quad {\rm at}\;t \to \infty. $$Substituting (43) into (39) one obtains
$$- U\displaystyle{{\partial {\rm \rho}} \over {\partial {\rm \zeta}}} + (c_0 + c_1 {\rm \rho} )\displaystyle{{\partial {\rm \rho}} \over {\partial {\rm \zeta}}} + c_3 \displaystyle{{\partial ^3 {\rm \rho}} \over {\partial {\rm \zeta} ^3}} = 0.$$Integrating this equation with respect to ζand setting the arbitrary constant to zero, one arrives at the ODE in its final form
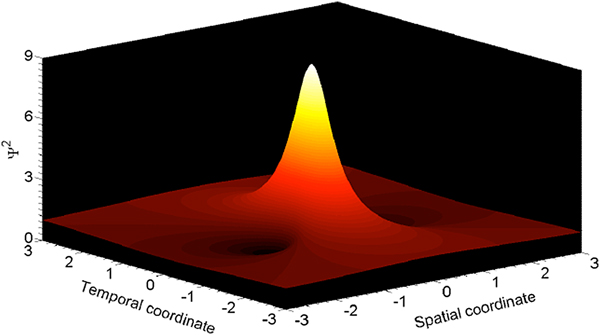
$$c_3 \displaystyle{{\partial ^2 {\rm \rho}} \over {\partial {\rm \zeta} ^2}} + (c_0 - U){\rm \rho} + \displaystyle{{c_1} \over 2}{\rm \rho} ^2 = 0.$$The solution of this equation is a soliton moving with the speed U
$${\rm \rho} = a\;{\rm Sec}h^2 \left[ {\displaystyle{{\sqrt {c_1 a}} \over {\sqrt {12c_3}}} (v - Ut)} \right],$$where
$$U = c_0 + \displaystyle{1 \over 3}c_1 a,$$see Fig. 6. It should be emphasized that the soliton (46) does not depend upon initial conditions, and consequently it can be considered as a static attractor in probability space. This means that in physical space, a solution of equation (38) eventually approach a stochastic attractor.
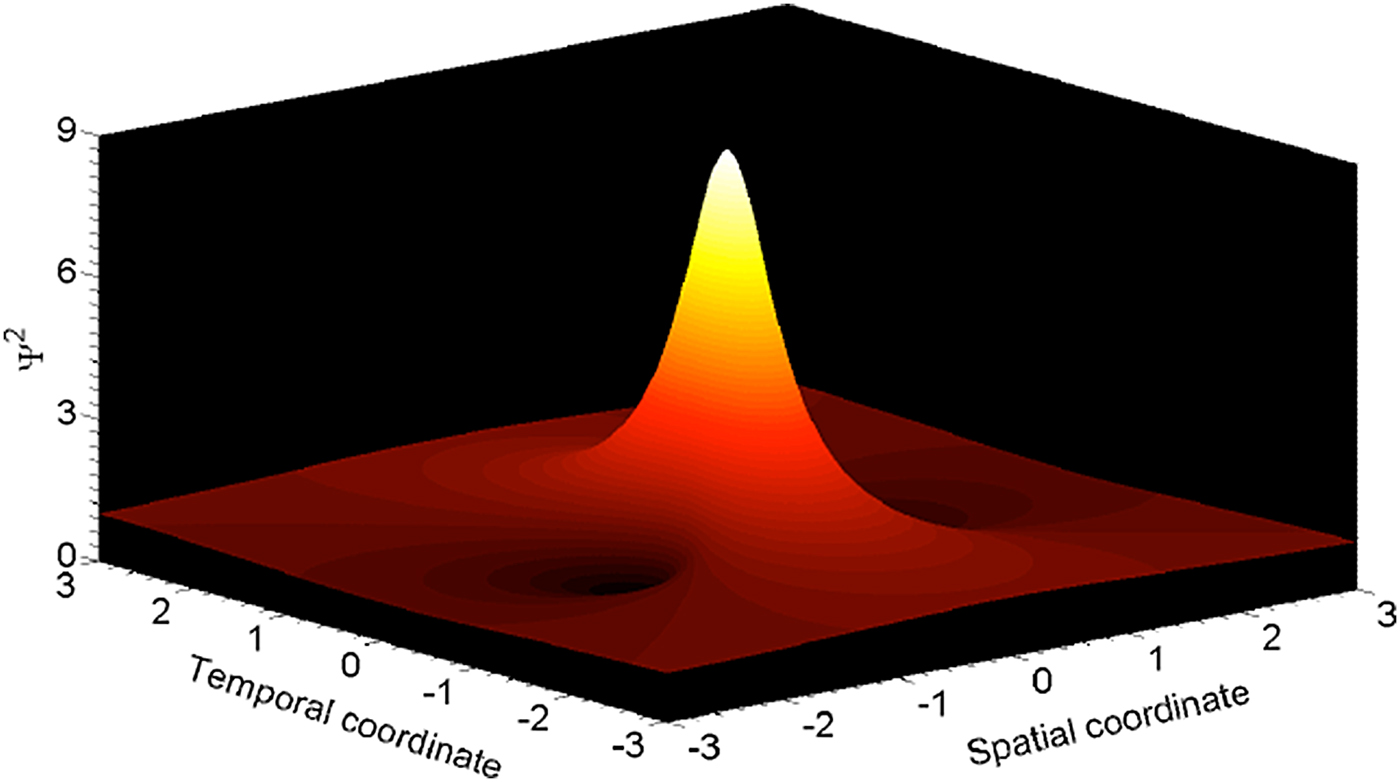
Fig. 6. Soliton as an attractor of KdV solution.
Comparing the solutions (45) and (34) one notice that any small, even infinitesimal, but positive perturbation of the parameter c 1 > 0 shifts the solution (34) from dispersive waves that depend upon initial conditions, to a dynamical attractor soliton in the probability space, while this attractor does not depend upon initial conditions. Therefore, the solution to equation (34) is structurally unstable since its qualitative behaviour is sharply changed by small perturbations of its parameters.
It should be noticed that the solution equation (46) illustrates the failure of the second law of thermodynamics. Indeed, since it does not depend upon initial condition, one can choose the high entropy initial conditions, for instance, the Brownian motion, and regardless of that, this solution, eventually, will be attracted to the lower entropy soliton equation (46) (Fig. 6).
Now we can complete the mathematical scenario of origin and emerging of intelligent life: if we postulate the model of Newtonian physics, then due to its structural instability with respect to a certain kind of perturbations of parameters of possible Liouville feedback, the model of the Newtonian physics shifts to the model of non-intelligent life, i.e. to the model described by equations (32) and (33). Then due to structural instability of the latter with respect to different kind of perturbation of the Liuoville feedback, the model of non-intelligent life equations (32) and (33) shifts to the model of intelligent life described by equations (38) and (39). As was noticed above, the appearance of these perturbations could be random, and special conditions for their appearance should be satisfied while these conditions are beyond the mathematical scenario considered above.
Remark 2. The concept of structural stability/instability is a subject of the mathematical theory of catastrophe that is a branch of bifurcation theory in the study of dynamical systems. It has been originated by Rene Thom and advanced by Arnold (Reference Arnold1992). Small changes in certain parameters of a non-linear system can cause equilibria to appear or disappear, or to change from attracting to repelling and vice versa, leading to large and sudden changes of the behaviour of the system. That what actually happens in the scenario of transition from Newtonian dynamics to intelligent life introduced above.
Formation of collective brains
The model of intelligent life introduced above (see equations (38) and (39)) allows one to advance into a model of collective brain that amplifies intellectual capabilities of individual brains. For illustration, let us introduce the following two brains coupled by the joint probability density <grdel>
$$\dot v_1 = c_1 ^{(1)} {\rm \rho,} $$
$$\dot v_2 = c_1 ^{(2)} {\rm \rho} {\rm.} $$Each of these equations is a simplified version of equation (38) when c 0 = 0, c 2 = 0, c 3 = 0.
The corresponding analogue of the Liouville equation (39) is
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + c_1 ^{(1)} {\rm \rho} \displaystyle{{\partial {\rm \rho}} \over {\partial V_1}} + c_2 ^{(2)} {\rm \rho} \displaystyle{{\partial {\rm \rho}} \over {\partial V_2}} = 0.$$As follows from this equation, the capability to decrease entropy of the joint probability ρ is amplified, and that is the first step in the formation of collective brain. Projecting this result from the model to real life, one can explain the concentration of talents in Gottingen (Einstein, Gauss, Hilbert) or Princeton, (Godel, Hadamard) therefore removing the entropy paradox.
Comments to AI-human competition
Recent publications on artificial intelligence (AI) are abundant with pessimistic predictions about potential superiority of robots over humans. Based upon the proposed model, we express an alternative view on that subject. In the previous sections, we presented a mathematical answer to the ancient philosophical question ‘How mind is related to matter’. We proposed that in mathematical world, the bridge from matter to mind requires extension and modification of quantum physics. In this context, we will comment on the recent statement made by Stephen Hawking on 2 December 2014, in which he warns that AI could end mankind. Based upon our work, part of which is presented in the previous sections, it can be stated that machines composed only out of physical components and without any digital devices being included, cannot, in principle, overperform a human in creativity, regardless of the level of technology. But what happens if a machine does include digital devices? The answer to this question is the subject of Section 8 in reference Zak (Reference Zak2016a). In these sections, we propose a quantum version of recurrent neural nets (QRN) that, along with classical performance, possess the capability to move from disorder to order without external recourses, and that makes their intelligence comparable with that of a human. The QRN incorporate classical feedback loops into conventional quantum networks. It is shown that the dynamical evolution of such networks, which interleave quantum evolution with measurement and reset operations, exhibits novel dynamical properties. Moreover, decoherence in quantum recurrent networks is less problematic than in conventional quantum network architectures due to the modest phase coherence times needed for network operation. It is proven that a hypothetical quantum computer can implement an exponentially larger number of the degrees of freedom within the same size.
Discussion and conclusion
This work is about studying reality via mathematical models. Although models are not identical to reality (the picture of a cat cannot harm the picture of a rat), nevertheless models are supposed to extract the most fundamental features of reality. Therefore, importance of models should not be underestimated. Indeed, theoreticians studying reality via models make great discoveries illuminating the way to proper experiments. The theoretical leadership is especially crucial in astrobiology and cosmology where experiment becomes more and more expensive if it is possible at all.
The most instructive is a story of discovery of quantum entanglement: although the surprising correlation between quantum particles was in apparent disagreement with ‘common sense’, it follows from the Schrödinger equation, and despite the critique by many scientists, including Einstein, those theoreticians, which stood with mathematics, were appeared to be right. That is why the results introduced in this work could be successfully projected from models to reality.
The paper proposes a scenario of origin and emerging of intelligent life in Universe based upon the mathematical discovery of a new class of dynamical systems described by ODE coupled with their Liouville equation. These systems called self-controlled since the role of actuators is played by the probability produced by the Liouville equation. Following the Madelung equation that belongs to this class, non-Newtonian and quantum-like properties such as randomness, entanglement and probability interference typical for quantum systems have been described. At the same time, these systems expose properties of livings: decomposition into motor and mental dynamics, the capability of self-identification and self-awareness, as well as self-supervision. But the most surprising discovery is the existence of a special sub-class, in which the dynamical systems can violate the second law of thermodynamics, and that makes them different from both Newtonian and quantum physics. This sub-class should be associated with intelligent livings due to the capability to move from disorder to order without external help. Based upon the mathematical discovery described above, on can assume that there are good chances that similar dynamical systems representing intelligent livings exist in real physical world. This provides a reason for a ‘rehabilitation’ of the Maxwell demon and put it into physics of intelligent systems. Indeed, the Maxwell demon is implemented by the feedback from the Liouville equation to the original ODE while this feedback is capable to rearrange the probability distribution against the second law of thermodynamics. In addition to that, the same feedback removes the entropy paradox by explaining high order in our surrounding by ‘intelligent life support’. Two-steps transition: from the Newtonian physics to the linear model of life, and from the latter to the model of intelligent life are analysed. The first transition is triggered by the Hadamard instability of the Newtonian physics with respect to small random disturbances in linear terms of the Liouville feedback. The second transition is triggered by instability of linear model of life with respect to small random disturbances of non-linear terms of Liouville feedback. This transition could be implemented by such physical phenomena as shock waves or negative diffusion in probability space. Both transitions can be associated with catastrophe theory, in which sudden shifts in behaviour arises from small changes in parameters of the model.
