1 Introduction
Pension systems around the world have come under severe pressure from the two-sided demographic development: declining fertility rates and increasing life expectancy. The latter aspect is of particular interest, since it represents an ongoing process with considerable and far-reaching budgetary consequences. For the European Union (EU)-countries, e.g., life expectancy at birth is projected to increase over the next 50 years by about 7.5 years. This increase is one of the main factors behind the projected rise in the old-age dependency ratio from 27.8% in 2013 to 50.1% in 2060 (European Commission, 2015). This development is a particular challenge for pay-as-you-go (PAYG) pension systems. In their traditional organization PAYG systems are based on the implicit assumption of a stationary age structure while ideally they should be designed in such a way as to automatically react to the steady increases in longevity. This has been emphasized recently by the Organization for Economic Co-operation and Development (OECD), which states that these life-expectancy adjustments have ‘a strong claim to be the most important innovation of pension policy in recent years’ (OECD, 2011, p. 82).
Despite this claim there does not exist much empirical and – even less though – theoretical work on the basic functioning, the appropriate design and the main properties of these automatic life-expectancy-adjustments. In this paper, I study the effects of increasing life expectancy for notional defined contribution (NDC) systems (cf. Holzmann and Palmer, Reference Holzmann, Palmer, Holzmann, Palmer and Robalino2012). NDC systems are a natural starting point to analyze the linkage between life expectancy and retirement age since they are explicitly designed in a way such as to react to demographic changes and since they are the most popular variant of automatically adjusting PAYG systems. NDC systems take increases in life expectancy into consideration when the notional capital – i.e., the accumulated contributions – are annuitized. Longer life expectancy will, ceteris paribus, decrease pension benefits, while later retirement will increase them.
In order to study the issue in a systematic way, I use a stylized economic and demographic model that is presented in Section 2. In Section 3, I describe the basic structure of NDC systems. I emphasize that it is important to determine the details of the NDC system in an appropriate manner in order to guarantee a self-stabilizing system. In particular, there are three important parameters that determine the financial stability of a NDC system: (i) the ‘notional interest rate’ (or the ‘rate of return’) that specifies how past contributions to the pension system are revalued over time; (ii) the adjustment rate that determines how ongoing pensions are indexed over the years of retirement; (iii) the ‘annuity conversion factor’ that is used to calculate the first pension benefit at the time of retirement. The prevailing opinion on this topic is that one should use the growth rate of the wage bill (or, to be precise, the sum of total contributions) for indexation (i.e., as notional interest and adjustment rates)Footnote 1 and the cohort (i.e., forecasted) life expectancy in order to determine the size of the pension annuity.Footnote 2
In Section 4 of this paper, I show that the conventional wisdom is accurate in a situation with a constant mortality structure and with constant or constantly changing cohort sizes. For decreasing mortality rates and increasing longevity, however, the conventional wisdom fails. This is demonstrated in Section 5, where I use a model with rectangular survivorship, i.e., a situation where every member of a cohort reaches the cohort-specific maximum age that is increasing over time in a linear fashion (cf. Oeppen and Vaupel, Reference Oeppen and Vaupel2002). I show that no combination of the standard choices for the three crucial parameters is able to implement a stable NDC system if the retirement age is either constant or proportional to life expectancy.
In Section 6, I present two alternative specifications of the two indexation rates that can be used to establish a stable system. The first alternative takes the budget constraint of the pension system as a starting point and is thus based on a period perspective. This is first reflected in the fact that the annuity is calculated by using period (remaining) life expectancy. Furthermore, I argue that the use of the growth rate of the wage bill is not appropriate in the case of increasing life expectancy. The reason for this is straightforward. When average longevity increases then the retirement age has to rise as well just in order to keep the dependency ratio constant. This ‘neutralizing’ postponement of retirement, however, increases by itself the total size of the labor force even if the size of cohorts is constant. Using the growth rate of the wage bill would thus grant an ‘excessive’ rate of return. The appropriate notional interest and adjustment rates have to be corrected for this effect. I show that a combination of these corrected indexation rates and period life expectancy (PLE) as the annuity conversion factor establishes a self-stabilizing social security system.
A second alternative specification is based on the cohort perspective. In particular, it can be shown (Knell, Reference Knell2016) that increasing longevity gives rise to a positive internal rate of return. A NDC system that uses cohort life expectancy (CLE) as the annuity conversion factor can use this internal rate of return for indexation without violating the budget constraint. I show that this approach is also related to the ‘turnover duration’ (i.e., the difference between the average ages for active and retired individuals) – a concept that is used in the Swedish NDC system.
The paper mainly uses rather stylized assumptions in order to be able to derive analytical results that are useful in discussing the consequences of increasing longevity and to understand the intuition behind the findings. In particular, I mostly use the assumptions of rectangular survivorship and I look at two polar cases for the development of retirement age (a constant retirement age or a retirement age that moves in proportion to increasing longevity). In Section 7, I study a number of extensions of the basic model. Most importantly, I analyze the case of non-rectangular survivorship. Using numerical simulations it can be shown that the conventional wisdom also fails under these demographic assumptions while the two alternative approaches (based on the period and the cohort view, respectively) will again manage to implement a stable (or at least approximately stable) system. Section 8 concludes.
The related literature includes empirical analyses, simulation studies and also a small number of theoretical papers. Whitehouse (Reference Whitehouse2007), OECD (2011) and OECD (2012) contain information about the links between life expectancy and various parameters in existing pension systems of OECD countries. Alho et al. (Reference Alho, Hougaard Jensen, Lassila and Valkonen2005) and Auerbach and Lee (Reference Auerbach and Lee2009) use stochastic simulation models in order to evaluate and compare the risk-sharing characteristics of alternative public pension schemes. Since these models allow for a stochastic development of mortality rates they also – implicitly – show how different systems react to changing life expectancy. On the other hand, these papers do not include a systematic discussion on the working and the different design features of automatic life expectancy adjustments. Shoven and Goda (Reference Shoven and Goda2008) and Heeringa and Bovenberg (Reference Heeringa and Bovenberg2009) are related papers that study how ‘life expectancy indexation’ could be used to stabilize the budget of the public pension systems in specific countries (the USA and the Netherlands, respectively). The latter work also contains a stylized model of the use of changes in the retirement age in order to balance increases in longevity. The paper, however, does not compare different formulations of such an indexation. Andersen (Reference Andersen2008), on the other hand, uses a two-period model to derive that a ‘social security system cannot be maintained by simply indexing pension ages to longevity’. This contrast to the results of the present paper has to do with a different modelling of the life cycle. Ludwig and Reiter (Reference Ludwig and Reiter2010) study the optimal policy response of a social planner in the presence of demographic shocks. Valdés-Prieto (Reference Valdés-Prieto2000) discusses the ability of NDC system to run on ‘auto-pilot’ but he mainly focuses on the role of changing fertility patterns. Settergren and Mikula (Reference Settergren and Mikula2005) and Palmer (Reference Palmer, Holzmann, Palmer and Robalino2012) present results that are related to the ones of the present paper but they also lack an explicit treatment of the case with constantly increasing life expectancy.
2 The model
2.1 General set-up
I work with a model in continuous time. In every instant of time t a new cohort is born. The maximum age that a member of cohort t can reach is denoted by ω
c
(t). The superscript ‘c’ is used to distinguish the cohort-specific maximum age of cohort t from the maximum age observed in period t, which is denoted by ω
p
(t). S(a,t) gives the probability that a member of cohort t survives to age a. It holds that S(0, t) = 1, S(ω
c
(t), t) = 0 and that survivorship declines with age, i.e., dS(a, t)/da ≤ 0 for a ∈ [0, ω
c
(t)]. The mortality hazard rate of cohort t at age a is given by
![]() $\mu (a,t) \equiv - \displaystyle{{dS(a,t)} \over {da}}\displaystyle{1 \over {S(a,t)}}$
. In line with the empirical evidence, I allow for changing mortality rates, which is the reason why S(a, t) and μ(a, t) are not only age-specific but also include a cohort-specific time index. It holds that:
$\mu (a,t) \equiv - \displaystyle{{dS(a,t)} \over {da}}\displaystyle{1 \over {S(a,t)}}$
. In line with the empirical evidence, I allow for changing mortality rates, which is the reason why S(a, t) and μ(a, t) are not only age-specific but also include a cohort-specific time index. It holds that:
As far as remaining life expectancy is concerned one has to distinguish between CLE and PLE. The first concept uses the cohort-specific mortality rates (which have to be forecasted in real-world estimations) in order to calculate life expectancy, while the latter concept is based on current (cross-section) mortality rates that can actually be observed in period t. The formulas for remaining life expectancy at age z are given byFootnote 3 :
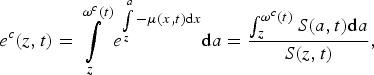 $$e^c (z,t) = \int\limits_z^{\omega ^c (t)} {e^{\int\limits_z^a { - \mu (x,t) {\rm d}x}} {\rm d}a} = \displaystyle{{\int_z^{\omega ^c (t)} {S(a,t) {\rm d}a}} \over {S(z,t)}},$$
$$e^c (z,t) = \int\limits_z^{\omega ^c (t)} {e^{\int\limits_z^a { - \mu (x,t) {\rm d}x}} {\rm d}a} = \displaystyle{{\int_z^{\omega ^c (t)} {S(a,t) {\rm d}a}} \over {S(z,t)}},$$
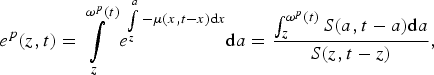 $$e^p (z,t) = \int\limits_z^{\omega ^p (t)} {e^{\int\limits_z^a { - \mu (x,t - x) {\rm d}x}} {\rm d}a} = \displaystyle{{\int_z^{\omega ^p (t)} {S(a,t - a) {\rm d}a}} \over {S(z,t - z)}},$$
$$e^p (z,t) = \int\limits_z^{\omega ^p (t)} {e^{\int\limits_z^a { - \mu (x,t - x) {\rm d}x}} {\rm d}a} = \displaystyle{{\int_z^{\omega ^p (t)} {S(a,t - a) {\rm d}a}} \over {S(z,t - z)}},$$
where CLE e c (z, t) refers to the cohort born in time t (and thus to period t + z) while PLE e p (z, t) refers to period t (and thus to the cohort born in time t − z).
The size of cohort t at age a is given by N(a, t) = N(0, t)S(a, t), where N(0, t) stands for the initial size of the cohort. The total population size in period t can then be written as:
 $$N(t) = \int\limits_0^{\omega ^p (t)} {N(a,t - a) {\rm d}a} = \int\limits_0^{\omega ^p (t)} {N(0,t - a)S(a,t - a) {\rm d}a.} $$
$$N(t) = \int\limits_0^{\omega ^p (t)} {N(a,t - a) {\rm d}a} = \int\limits_0^{\omega ^p (t)} {N(0,t - a)S(a,t - a) {\rm d}a.} $$
All members of generation t start to work as soon as they are born and the surviving members remain in the labor market for R
c
(t) periods, earning a wage W(t + a) during each of these working periods a ∈ [0, R
c
(t)].Footnote
4
The growth rate of wages is denoted by g(t), i.e.,
![]() $W(t) = W(0)e^{\int_0^t g(s) {\rm d}s} $
. I abstract here from the existence of an age-earnings profile and all workers are assumed to earn the same wage at each point in time. Furthermore, I also abstract from intragenerational differences in wages and in the retirement age. The only dimension in which members of the same cohort might differ is their length of life. While working, individuals pay contributions to the PAYG pension system at a fixed rate τ. After retirement, they receive a pension benefit P(a,t) in each period of retirement a ∈ [R
c
(t), ω
c
(t)] (given that they survive that long).
$W(t) = W(0)e^{\int_0^t g(s) {\rm d}s} $
. I abstract here from the existence of an age-earnings profile and all workers are assumed to earn the same wage at each point in time. Furthermore, I also abstract from intragenerational differences in wages and in the retirement age. The only dimension in which members of the same cohort might differ is their length of life. While working, individuals pay contributions to the PAYG pension system at a fixed rate τ. After retirement, they receive a pension benefit P(a,t) in each period of retirement a ∈ [R
c
(t), ω
c
(t)] (given that they survive that long).
The retirement age is assumed to be non-decreasing over time, i.e., R c (t + dt) ≥ R c (t). This makes it possible to express all aggregate values in a compact form without the use of ‘indicator variables’. While R c (t) stands for the retirement age of cohort t the variable R p (t) denotes the number of working years of the generation that retires in period t. In general it will be the case that ω p (t) ≠ ω c (t) and R p (t) ≠ R c (t).
Using these assumptions the total size of the active population L(t) and the retired population M(t) in period t can be written as:
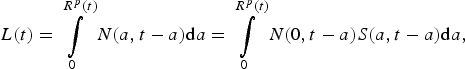 $$L(t) = \int\limits_0^{R^p (t)} {N(a,t - a) {\rm d}a} = \int\limits_0^{R^p (t)} {N(0,t - a)S(a,t - a) {\rm d}a}, $$
$$L(t) = \int\limits_0^{R^p (t)} {N(a,t - a) {\rm d}a} = \int\limits_0^{R^p (t)} {N(0,t - a)S(a,t - a) {\rm d}a}, $$
 $$M(t) = \int\limits_{R^p (t)}^{\omega ^p (t)} {N(a,t - a) {\rm d}a} = \int\limits_{R^p (t)}^{\omega ^p (t)} {N(0,t - a)S(a,t - a) {\rm d}a}. $$
$$M(t) = \int\limits_{R^p (t)}^{\omega ^p (t)} {N(a,t - a) {\rm d}a} = \int\limits_{R^p (t)}^{\omega ^p (t)} {N(0,t - a)S(a,t - a) {\rm d}a}. $$
Note that from (3) to (5) it follows that N(t) = L(t) + M(t).
For later reference it is also useful to look at the average age
![]() $A_W^c (t)$
at which a member of cohort t pays the pension contributions and at the average age
$A_W^c (t)$
at which a member of cohort t pays the pension contributions and at the average age
![]() $A_P^c (t)$
at which he receives the pension benefit:
$A_P^c (t)$
at which he receives the pension benefit:
 $$A_W^c (t) = \displaystyle{{\int_0^{R^c (t)} {aN(a,t) {\rm d}a}} \over {\int_0^{R^c (t)} {N(a,t) {\rm d}a}}}, A_P^c (t) = \displaystyle{{\int_{R^c (t)}^{\omega ^c (t)} {aN(a,t) {\rm d}a}} \over {\int_{R^c (t)}^{\omega ^c (t)} {N(a,t) {\rm d}a}}}. $$
$$A_W^c (t) = \displaystyle{{\int_0^{R^c (t)} {aN(a,t) {\rm d}a}} \over {\int_0^{R^c (t)} {N(a,t) {\rm d}a}}}, A_P^c (t) = \displaystyle{{\int_{R^c (t)}^{\omega ^c (t)} {aN(a,t) {\rm d}a}} \over {\int_{R^c (t)}^{\omega ^c (t)} {N(a,t) {\rm d}a}}}. $$
In contrast, the variables
![]() $A_W^p (t)$
and
$A_W^p (t)$
and
![]() $A_P^p (t)$
measure the average age of contributors and pensioners in period t. They are defined as:
$A_P^p (t)$
measure the average age of contributors and pensioners in period t. They are defined as:
 $$A_W^p (t) = \displaystyle{{\int_0^{R^p (t)} {aN(a,t - a) {\rm d}a}} \over {\int_0^{R^p (t)} {N(a,t - a) {\rm d}a}}}, A_P^p (t) = \displaystyle{{\int_{R^p (t)}^{\omega ^p (t)} {aN(a,t - a) {\rm d}a}} \over {\int_{R^p (t)}^{\omega ^p (t)} {N(a,t - a) {\rm d}a}}}. $$
$$A_W^p (t) = \displaystyle{{\int_0^{R^p (t)} {aN(a,t - a) {\rm d}a}} \over {\int_0^{R^p (t)} {N(a,t - a) {\rm d}a}}}, A_P^p (t) = \displaystyle{{\int_{R^p (t)}^{\omega ^p (t)} {aN(a,t - a) {\rm d}a}} \over {\int_{R^p (t)}^{\omega ^p (t)} {N(a,t - a) {\rm d}a}}}. $$
2.2 Specific demographic assumptions
In the following analysis, I will often make use of specific assumptions concerning the development of the crucial demographic processes.
2.2.1 Cohort sizes
Concerning the development of the size of initial cohorts a popular assumption is that they evolve in an exponential manner:
2.2.2 Mortality rates
As far as survivorship is concerned, I make a number of simplifying assumptions that allow for analytical solutions while at the same time being broadly in line with observable demographic trends. First, I assume that the development of mortality follows a deterministic process that is perfectly known by all agents. Important issues that arise in the case of aggregate and idiosyncratic longevity risk are discussed in Alho et al. (Reference Alho, Bravo and Palmer2012).
Second, in order to model mortality developments, I use a simple survivorship curve that resembles a ‘modified de Moivre function’ (Bruce and Turnovsky, Reference Bruce and Turnovsky2013):
 $$S(a,t) = \left\{ {\matrix{ {\left( {1 - \displaystyle{a \over {\omega ^c (t)}}} \right)^\lambda} & {{\rm for}\;a \in [0,\omega ^c (t)],} \cr 0 & {{\rm for}\;a \ge \omega ^c (t),} \cr}} \right.$$
$$S(a,t) = \left\{ {\matrix{ {\left( {1 - \displaystyle{a \over {\omega ^c (t)}}} \right)^\lambda} & {{\rm for}\;a \in [0,\omega ^c (t)],} \cr 0 & {{\rm for}\;a \ge \omega ^c (t),} \cr}} \right.$$
where λ ≥ 0. This is a quite flexible specification that contains a number of interesting nested cases. For λ = 0, e.g., one gets a ‘rectangular’ survivorship function where S(a,t) = 1 for a ∈ [0, ω c (t)]. For this case there are no premature deaths and all cohort members reach their cohort-specific maximum age ω c (t). In the following I will use this (unrealistic but convenient) extreme case quite frequently in order to establish benchmark results. For λ = 1, on the other hand, one has the original linear de Moivre survivorship curve.Footnote 5 Note that for (9) the mortality rates are given by μ(a, t) = λ/(ω c (t) − a). One can use this expression in (2a) to derive that (see Appendix A):
This means that life expectancy depends linearly on the development of the maximum age ω c (t). Note that life expectancy at birth is given by e c (0, t) = ω c (t)/(1 + λ) while the length of life conditional on having reached age z is larger and given by e c (z, t) + z = (ω c (t) + λz)/(1 + λ).
A straightforward way to capture increasing life expectancy is to assume that the maximum age increases in a linear fashion.Footnote 6 As a third mortality assumption I therefore assume that:
where 0 ≤ γ < 1. This assumption is in line with the empirical literature. Oeppen and Vaupel (Reference Oeppen and Vaupel2002), e.g., analyze ‘record female life expectancy’ (i.e., the highest value for female life expectancy reported in any country for which data are available) from 1840 to 2000 and they show that it follows an almost perfect linear development.Footnote 7
From assumption (11) one can calculate the period maximum life-span ω p (t) from the relation: ω c (t − ω p (t)) = ω p (t). This implies that ω c (t) − γω p (t) = ω p (t) which leads to:
For assumption (9) this can be used in (2b) to derive an expression for remaining PLE:
The increase in PLE is thus given by de p (z, t)/dt = γ/(1 + γ + λ).Footnote 8 Empirical studies (Oeppen and Vaupel, Reference Oeppen and Vaupel2002, Lee, Reference Lee2003) suggest a linear increase in PLE between 1.5 months and 3 months per calendar year, i.e., a slope between 0.15 and 0.25. Using the midpoint 0.2 of this interval suggests a value of γ = 0.25 (for λ = 0) and γ = 0.375 (for λ = 1/2).Footnote 9
2.2.3 Retirement age
For later discussions, I will often use specific assumptions concerning the development of the cohort-specific retirement age R c (t): either a retirement age that is proportional to cohort-specific longevity or a constant retirement age, i.e.:
or
These processes for retirement behavior are interesting since they allow for closed form solutions. Using equation (11) one can calculate R
p
(t), i.e., the retirement age in period t. It holds that R
c
(t − R
p
(t)) = R
p
(t) and thus for (13a) one can derive that R
p
(t) = (ψ/(1 + γψ)) ω
c
(t) while for (13b) one has trivially that
![]() $R^p (t) = \overline R $
.
$R^p (t) = \overline R $
.
2.3 Budget of the pension system
The total revenues I(t) and the total expenditures E(t) of the pension system in a certain period t are:
where
![]() $\overline P (t)$
is the average pension in time t given by:
$\overline P (t)$
is the average pension in time t given by:
 $$\overline P (t) = \displaystyle{1 \over {M(t)}}\int\limits_{R^p (t)}^{\omega ^p (t)} {P(a,t - a)N(a,t - a) {\rm d}a}. $$
$$\overline P (t) = \displaystyle{1 \over {M(t)}}\int\limits_{R^p (t)}^{\omega ^p (t)} {P(a,t - a)N(a,t - a) {\rm d}a}. $$
The total deficit (or surplus) is denoted by D(t) = E(t) − I(t) while the deficit ratio d(t) is written as:
A balanced budget thus requires that the following condition is fulfilled:
or – equivalently – that D(t) = 0 or d(t) = 1,
![]() $\forall t$
.
$\forall t$
.
3 A NDC pension system
Thus far I have left open how the pension levels P(a, t − a) of the various retired cohorts at a certain period t are determined. In the real-world one can observe a wide variety of alternative approaches including flat demogrants, defined benefit and defined contribution systems. In this paper, I focus on the NDC system that has been implemented first in Sweden and has later been also adapted by a number of additional countries like Italy, Poland, Latvia, Mongolia, Turkmenistan etc. It is now also often used as a benchmark PAYG model by international institutions like the World Bank (Holzmann and Hinz, Reference Holzmann and Hinz2005), the OECD (2011) or the European Commission (2015).Footnote 10
3.1 Formal expression of a NDC system
The contributions in a NDC system are credited to a notional account and in period t they are revalued with a ‘notional interest rate’ ρ(a, t) (that is allowed to change over time t and across age groups a). The total value of this account is called the ‘notional capital’ that accumulates over the working periods of an insured person. When the surviving members of cohort t retire at age R c (t) the final notional capital is given by:
 $$K(R^c (t),t) = \int\limits_0^{R^c (t)} {\tau W(t + x)e^{\int\limits_x^{R^c (t)} {\rho (s,t + s) {\rm d}s}} {\rm d}x}, $$
$$K(R^c (t),t) = \int\limits_0^{R^c (t)} {\tau W(t + x)e^{\int\limits_x^{R^c (t)} {\rho (s,t + s) {\rm d}s}} {\rm d}x}, $$
where the cumulative factor
![]() $e^{\int_x^{R^c (t)} \rho (s,t + s) {\rm d}s} $
indicates how the contribution τW(t + x) that is paid into the pension system in period (t + x) is revalued when calculating the final amount of the notional capital in period (t + Rc
(t)), i.e., the period of retirement. The notional interest rate is a crucial magnitude in a NDC system and I will discuss alternative specifications below.
$e^{\int_x^{R^c (t)} \rho (s,t + s) {\rm d}s} $
indicates how the contribution τW(t + x) that is paid into the pension system in period (t + x) is revalued when calculating the final amount of the notional capital in period (t + Rc
(t)), i.e., the period of retirement. The notional interest rate is a crucial magnitude in a NDC system and I will discuss alternative specifications below.
The first pension PF (t) that is received by a (surviving) member of cohort t is given by:
The first pension is calculated by taking the final notional capital K(R c (t), t) and turning it into an annual pension payment by using the annuity conversion factor Γ(R c (t), t), which is based on remaining life expectancy. One can use either CLE or PLE to calculate this annuity conversion factor, which is again an important parameter choice in NDC systems to which I will return later.Footnote 11
Existing pensions are adjusted according to:
 $$P(a,t) = P^F (t)e^{\int\limits_{R^c (t)}^a {\vartheta (s,t + s) {\rm d}s}}, $$
$$P(a,t) = P^F (t)e^{\int\limits_{R^c (t)}^a {\vartheta (s,t + s) {\rm d}s}}, $$
for a ∈ [R
c
(t), ω
c
(t)], where
![]() $\vartheta (x,t)$
stands for the adjustment rate in period t for the cohort that is x years old and the cumulative adjustment factor
$\vartheta (x,t)$
stands for the adjustment rate in period t for the cohort that is x years old and the cumulative adjustment factor
![]() $\exp \,({\int_{{R^{c}} (t)}^{a}} \vartheta (s,t + s) {\rm d}s)$
indicates how the first pension P
F
(t) is adjusted to give the pension payment in period t + a.
$\exp \,({\int_{{R^{c}} (t)}^{a}} \vartheta (s,t + s) {\rm d}s)$
indicates how the first pension P
F
(t) is adjusted to give the pension payment in period t + a.
Inserting equations (18), (19) and (20) into (15) and using N(a, t) = N(0, t)S(a, t) and (1) leads to the following expression of total pension expenditures
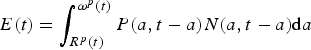 $E(t) = \int_{R^p (t)}^{\omega ^p (t)} P(a,t - a)N(a,t - a){\rm d}a$
(see Appendix B):
$E(t) = \int_{R^p (t)}^{\omega ^p (t)} P(a,t - a)N(a,t - a){\rm d}a$
(see Appendix B):
 $$\eqalign{E(t) = & \tau W(t)\int\limits_{R^p (t)}^{\omega ^p (t)} {\left[ {\displaystyle{{\int\limits_0^{R^c (t - a)} {e^{\int\limits_x^{R^c (t - a)} {(\rho (s,t - a + s) - g(t - a + s)) {\rm d}s}} {\rm d}x}} \over {\Gamma (R^c (t - a),t - a)}} \times} \right.} \cr & \quad \left. {e^{\int\limits_{R^c (t - a)}^a {(\vartheta (s,t - a + s) - g(t - a + s)) {\rm d}s}} N(0,t - a)e^{\int\limits_0^a {( - \mu (s,t - a)) {\rm d}s}}} \right]{\rm d}a.} $$
$$\eqalign{E(t) = & \tau W(t)\int\limits_{R^p (t)}^{\omega ^p (t)} {\left[ {\displaystyle{{\int\limits_0^{R^c (t - a)} {e^{\int\limits_x^{R^c (t - a)} {(\rho (s,t - a + s) - g(t - a + s)) {\rm d}s}} {\rm d}x}} \over {\Gamma (R^c (t - a),t - a)}} \times} \right.} \cr & \quad \left. {e^{\int\limits_{R^c (t - a)}^a {(\vartheta (s,t - a + s) - g(t - a + s)) {\rm d}s}} N(0,t - a)e^{\int\limits_0^a {( - \mu (s,t - a)) {\rm d}s}}} \right]{\rm d}a.} $$
3.2 Crucial choices in NDC systems
Expression (21) for E(t) indicates that a NDC system requires the setting of three parameters: the notional interest rate ρ(a, t), the adjustment rate
![]() $\vartheta (a,t)$
and the annuity conversion factor Γ(a, t). The question is, whether these parameters can be defined in a simple and transparent way such that (21) is equal to the revenues of the pension system given by (14), i.e., I(t) = τW(t)L(t). I focus first on the choices that are discussed in the related literature and that are used in real-world systems.
$\vartheta (a,t)$
and the annuity conversion factor Γ(a, t). The question is, whether these parameters can be defined in a simple and transparent way such that (21) is equal to the revenues of the pension system given by (14), i.e., I(t) = τW(t)L(t). I focus first on the choices that are discussed in the related literature and that are used in real-world systems.
As far as the annuity conversion factor is concerned, there exist two possibilities. It can be based on cohort (forecasted) or on period (cross-section) life expectancy:
or
where Γ(a, t) stands for the annuity conversion factor for cohort t when it retires at age a.
As far as the notional interest rate is concerned the proposed definitions are typically related to three elements: First, to the growth rate of productivity (or of average wages), second to the growth rate of the labor force and third to the ‘inheritance gains’ (i.e., to the distribution of the account values of deceased cohort members). I will focus on two benchmark definitions: an indexation with the growth rate of average wages and one with the growth rate of the wage bill. Both notional interest rates also correct for the inheritance gains μ(a, t − a):
or
where
![]() $g^W (t) \equiv \dot W(t)/W(t)$
,
$g^W (t) \equiv \dot W(t)/W(t)$
,
![]() $g^L (t) \equiv \dot L(t)/L(t)$
,
$g^L (t) \equiv \dot L(t)/L(t)$
,
![]() $\dot W(t) \equiv dW(t)/dt$
and
$\dot W(t) \equiv dW(t)/dt$
and
![]() $\dot L(t) \equiv dL(t)/dt$
. From the definition of
$\dot L(t) \equiv dL(t)/dt$
. From the definition of
![]() $W(t) = W(0)e^{\int_0^t g(s) {\rm d}s} $
it follows that g
W
(t) = g(t).
$W(t) = W(0)e^{\int_0^t g(s) {\rm d}s} $
it follows that g
W
(t) = g(t).
For the adjustment of ongoing pensions
![]() $\vartheta (a,t)$
, I will look at two variants that are parallel to the notional interest rate formulas in equation (23). The only difference is that in these cases there are no inheritance gains and thus the formulas reduce to:
$\vartheta (a,t)$
, I will look at two variants that are parallel to the notional interest rate formulas in equation (23). The only difference is that in these cases there are no inheritance gains and thus the formulas reduce to:
or
It will often be insightful to focus on cases where the adjustment rate is equal to the notional interest rate (except the inheritance gains), i.e.,
![]() $\vartheta (a,t) = \rho (a,t) - \mu (a,t - a)$
. In Section 5, I show that there exists no combination of equation (22), (23) and (24) that leads to a generally stable system for increasing life expectancy. In Section 6, I therefore go beyond the standard specifications and I present two additional specifications of the notional interest rate ((23c) and (23d)) and the adjustment rate ((24c) and (24d)) that can be used to implement a stable NDC system.
$\vartheta (a,t) = \rho (a,t) - \mu (a,t - a)$
. In Section 5, I show that there exists no combination of equation (22), (23) and (24) that leads to a generally stable system for increasing life expectancy. In Section 6, I therefore go beyond the standard specifications and I present two additional specifications of the notional interest rate ((23c) and (23d)) and the adjustment rate ((24c) and (24d)) that can be used to implement a stable NDC system.
Obviously, the development of the retirement age R c (t) is also a crucial determinant of the stability of NDC systems. It is, however, the result of individual decisions that can only be influenced but not entirely selected by the policy-makers. I therefore do not treat the retirement age as a policy variable but rather analyze the evolution of the budget under the two polar assumptions of a constant retirement age (13b) and a retirement age that increases in proportion to the increases in life expectancy (13a). An appropriate NDC system should be able to cope with both retirement patterns.
4 Constant longevity
A natural starting point for discussing the financial stability of NDC systems is a stationary demographic situation with constant (or constantly changing) cohort sizes, a constant retirement age, constant longevity and stable survivorship and mortality rates. The latter assumptions imply that it does not matter whether remaining life expectancy is based on cohort or on period values and that the two annuity conversion factors (22a) and (22b) coincide. The following proposition summarizes under which conditions a NDC system will remain stable in a stationary demographic constellation.
Proposition 1
Assume that the maximum age is constant (ω
c
(t) = ω
p
(t) = ω), the mortality rates are time-independent (μ(a, t) = μ(a)), the cohort size is constant or constantly changing (N(0, t) = Ne
nt
) and the retirement age is constant R
c
(t) = R. In this case a NDC system will be in continuous balance
![]() $(d(t) = 1,\forall t)$
if the notional interest rate and the adjustment factor are set according to (23b) and (24b), i.e., ρ(a, t) = g
W
(t) + g
L
(t) + μ(a) and
$(d(t) = 1,\forall t)$
if the notional interest rate and the adjustment factor are set according to (23b) and (24b), i.e., ρ(a, t) = g
W
(t) + g
L
(t) + μ(a) and
![]() $\vartheta (a,t) = g^W (t) + g^L (t)$
.
$\vartheta (a,t) = g^W (t) + g^L (t)$
.
Proof. For a complete proof see Appendix C.
Here, I want to sketch the proof for rectangular survivorship (assumption (9) with λ = 0) since it is also instructive for understanding the challenges NDC systems face in the presence of increasing life expectancy. For λ = 0 assumption (8) implies that g L (t) = n and one can write equation (21) as:
 $$\displaylines{E(t) = \int\limits_R^\omega {\underbrace {\tau W(t)\left( {\displaystyle{{\int_0^R {e^{\int_x^R {n {\rm d}s}} {\rm d}x}} \over {\omega - R}}} \right)}_{{\scriptstyle {\rm First} \atop \scriptstyle {\rm Pension}}} \underbrace {e^{\int\limits_R^a {n {\rm d}s}}} _{{\scriptstyle {\rm Adjustment} \atop \scriptstyle {\rm Factor}}} \underbrace {e^{ - na} N(0,t)}_{{\scriptstyle {\rm Size}\,{\rm of} \atop \scriptstyle {\rm cohort}\,t - a}} {\rm d}a} \cr = \tau W(t)N(0,t)\int\limits_R^\omega {\displaystyle{{\int_0^R {e^{n(R - x)} {\rm d}x}} \over {\omega - R}}e^{n(a - R)} e^{ - na} {\rm d}a} \cr = \tau W(t)N(0,t)\int\limits_R^\omega {\displaystyle{{\int_0^R {e^{ - nx} {\rm d}x}} \over {\omega - R}} {\rm d}a} \cr = \tau W(t)N(0,t)\int\limits_0^R {e^{ - nx} {\rm d}x = \tau W(t)L(t) = I(t)},} $$
$$\displaylines{E(t) = \int\limits_R^\omega {\underbrace {\tau W(t)\left( {\displaystyle{{\int_0^R {e^{\int_x^R {n {\rm d}s}} {\rm d}x}} \over {\omega - R}}} \right)}_{{\scriptstyle {\rm First} \atop \scriptstyle {\rm Pension}}} \underbrace {e^{\int\limits_R^a {n {\rm d}s}}} _{{\scriptstyle {\rm Adjustment} \atop \scriptstyle {\rm Factor}}} \underbrace {e^{ - na} N(0,t)}_{{\scriptstyle {\rm Size}\,{\rm of} \atop \scriptstyle {\rm cohort}\,t - a}} {\rm d}a} \cr = \tau W(t)N(0,t)\int\limits_R^\omega {\displaystyle{{\int_0^R {e^{n(R - x)} {\rm d}x}} \over {\omega - R}}e^{n(a - R)} e^{ - na} {\rm d}a} \cr = \tau W(t)N(0,t)\int\limits_R^\omega {\displaystyle{{\int_0^R {e^{ - nx} {\rm d}x}} \over {\omega - R}} {\rm d}a} \cr = \tau W(t)N(0,t)\int\limits_0^R {e^{ - nx} {\rm d}x = \tau W(t)L(t) = I(t)},} $$
where the last equality follows from the definition of
![]() $L(t) = N(0,t)\int_0^R e^{ - na} {\rm d}a$
. ■
$L(t) = N(0,t)\int_0^R e^{ - na} {\rm d}a$
. ■
The constantly balanced budget is due to the fact that under the assumptions of a stationary demographic structure various terms in the formulas for expenditures E(t) and revenues I(t) cancel. First, the total pension volume is the same for each retired cohort. This follows from the fact that each cohort starts with a first per-capita pension P
F
(t) that is in later retirement period adjusted to yield P
F
(t)e
n(a−R). But since older cohorts are smaller (for n > 0) the total volume of pension payments P
F
(t)e
n(a−R)
e
−na
N(0, t) = P
F
(t)e
−nR
N(0, t) is the same for each of the (ω − R) retired cohorts. The notional capital, on the other hand, depends (via the notional interest rate) on the growth rate of the labor force during the R working periods. It is given by:
![]() $\tau W(t)\int_0^R e^{ - nx} {\rm d}x$
and this just happens to be proportional to the size of the current labor force (which is due to the assumption of a constant population growth rate n). Finally, remaining life expectancy (that is used to calculate the first pension P
F
(t)) is (ω − R) and this is just equal to the number of retired cohorts (which is due to the assumptions of constant retirement age and constant life expectancy). In the Appendix, I show that the same logic also holds true for a constant mortality pattern μ(a) while, on the other hand, it does not hold if the notional interest rate is based on the growth rate of average wages.
$\tau W(t)\int_0^R e^{ - nx} {\rm d}x$
and this just happens to be proportional to the size of the current labor force (which is due to the assumption of a constant population growth rate n). Finally, remaining life expectancy (that is used to calculate the first pension P
F
(t)) is (ω − R) and this is just equal to the number of retired cohorts (which is due to the assumptions of constant retirement age and constant life expectancy). In the Appendix, I show that the same logic also holds true for a constant mortality pattern μ(a) while, on the other hand, it does not hold if the notional interest rate is based on the growth rate of average wages.
The financial sustainability of a benchmark NDC system, however, is only true for the specific assumptions of proposition 1, i.e., only for the stationary demographic environment (possibly with n ≠ 0) and it no longer holds if, e.g., cohort sizes or retirement ages are determined in an irregular manner.Footnote 12 Finally, and most importantly, financial stability of a standard NDC system is no longer guaranteed if life expectancy increases, which will be discussed in the next section.
5 Increasing longevity
In this section, I am going to analyze whether the conventional choice, i.e., the use of the growth rate of the wage bill for indexation, also guarantees financial sustainability in the scenario with increasing longevity. In order to focus clearly on the issue of increasing life expectancy, I will assume in the following that the size of birth cohorts is constant, i.e., n = 0 or N(0, t) = N (see assumption (8)). Furthermore, I will start with the most simple case of mortality and assume a rectangular survivorship function, (i.e., assumption (9) with λ = 0). In this case all members of cohort t reach the cohort-specific maximum age ω
c
(t). This assumption leads to simple expressions for the central demographic variables: the size of the employed and retired population L(t) = R
p
(t)N and M(t) = (ω
p
(t) − R
p
(t))N, life expectancies e
c
(z, t) = ω
c
(t) − z and e
p
(z, t) = (ω
c
(t) − (1 + γ)z)/(1 + γ) = ω
p
(t) − z and the indexation rates
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t)$
(for the average wage concept) and
$\rho (a,t) = \vartheta (a,t) = g^W (t)$
(for the average wage concept) and
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) + g^L (t)$
(for the wage bill concept). In Section 7.1, I deal with the case where survivorship is non-rectangular (λ > 0).
$\rho (a,t) = \vartheta (a,t) = g^W (t) + g^L (t)$
(for the wage bill concept). In Section 7.1, I deal with the case where survivorship is non-rectangular (λ > 0).
In the next subsection it is shown that the use of the growth rate of the wage bill will not safeguard financial stability and that in fact no combination of the standard parameter choices will lead to a balanced budget for different patterns of retirement. In Section 5.2, I will provide intuition for this result from two angles: one based on the period view (of the system) and one based on the cohort view (of the insured individual). These considerations will then be used in Section 6 to derive rules for the determination of the notional interest rate, the adjustment factor and the annuity conversion factor such as to implement a stable NDC system
5.1 Failure of standard NDC systems
Proposition 2
Survial curves are assumed to be rectangular (assumption (9) with λ = 0). If the maximum age and life expectancy increase (assumption (11) with γ > 0) then there exists no combination of the two notional interest rates ((23a) or (23b)), the two adjustment factors ((24a) or (23b)) and the two annuity conversion factors ((22a) or (22b)) that leads to a constantly balanced budget when retirement ages can develop either according to process (13a) or to process (13b).
Proof: See online Appendix D.
The failure of conventional NDC systems can be gauged by looking at Tables 1 and 2 where I report the implied deficit ratio d(t) for each of the eight possible combinations of the crucial parameters.Footnote 13 In Table 1, I use the assumption that the retirement age is proportional to cohort-specific longevity, as expressed in assumption (13a), i.e., R c (t) = ψω c (t). This seems to be a ‘natural’ and intergenerational equitable reaction to the continuous increase in life expectancy where for every generation the proportion of retirement years to working years stays constant at (ω c (t) − R c (t))/(R c (t)) = (1 − ψ)/ψ.
Table 1. The deficit-ratio for an increasing retirement age (λ = 0)

Note: The table shows the deficit ratio d(t) = E(t)/I(t) for various assumption about the notional interest rate, the adjustment rate and the annuity conversion factor. The annuity conversion factor based on cohort (period) life expectancy is defined as in (22a) [(22b)]. The notional interest rate is given by (23a) or (23b) and the adjustment rate by (24a) or (24b). Furthermore, it is assumed that retirement age increases in a linear fashion according to R c (t) = ψω c (t).
Table 2. The deficit-ratio for a constant retirement age (λ = 0)

Note: The table shows the deficit ratio d(t) = E(t)/I(t) for a annuity conversion factor that is based on either CLE or PLE as defined in (22a) and (22b). The notional interest rates and the adjustment rates are the same for the average-wage and the wage-bill concept since g
L
(t) = 0. This is due to the assumption that the retirement age is constant, i.e.,
![]() $R^c (t) = \overline {R} $
.
$R^c (t) = \overline {R} $
.
Only one of the eight combinations is associated with a balanced budget and a stationary deficit ratio of d(t) = 1. This is the constellation where the notional interest rate and the adjustment rate follow the growth rate of average wages and the annuity conversion factor is based on PLE. This is an interesting contrast to the recommendations in the literature that suggest that the most appropriate NDC design involves a combination of CLE (cf. (22a)) and the growth rate of the wage bill (cf. (23b) and (24b)). The use of this combination, however, would lead to a deficit ratio that is approximately equal to d(t) ≈ 1 − (γ/2). This is a non-trivial magnitude. For a realistic value of γ = 0.25 it would amount to a deficit ratio of about 0.875 or – in other words – to a permanent surplus of 12.5%. A similar (somewhat larger) surplus of d(t) ≈ (1/(1 + γ)) arises if one uses CLE together with average wage growth. The use of CLE (as frequently recommended for NDC systems) is thus ‘overambitious’ as it will lead to excessively small annuities that cause a permanent surplus in the budget. The intuition for this result is the following. CLE is a forward-looking measure while the budget of the social security system is a period, non-forward-looking measure. Put differently, the budget is related to current and not to future pension payments and it is thus sufficient to use PLE for the calculation of the annuity if this is combined with an appropriate notional interest rate. I will elaborate on this issue in Section 5.2, where I will also explain why for this example the appropriate notional interest rate corresponds to the growth rate of average wages.
It is certainly an optimistic scenario to assume that retirement age always adjusts in lockstep with the increases in life expectancy. As the opposite (very ‘pessimistic’) extreme one could also assume that the retirement remains constant despite the advances in longevity as expressed in assumption (13b), i.e.,
![]() $R^c (t) = \overline R $
. Note that in this case the labor force is constant (g
L
(t) = 0) and thus the two notional interest rates and adjustment factors coincide and are given by
$R^c (t) = \overline R $
. Note that in this case the labor force is constant (g
L
(t) = 0) and thus the two notional interest rates and adjustment factors coincide and are given by
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t)$
. Therefore Table 2 just contains two cases, one for an annuity conversion factor based on PLE and one based on CLE. Neither of these two cases is associated with a balanced budget. Using PLE one can calculate that d(t) ≈ 1 + (γ/2). This seems to confirm the belief that the use of PLE is not enough to keep a NDC system in balance. The use of CLE (22a), however, as is often suggested as the better alternative is also not appropriate as it leads to a permanent surplus with d(t) ≈ 1 − (γ/2). The punchline of this consideration is that in the case of constant retirement ages and a notional interest rate
$\rho (a,t) = \vartheta (a,t) = g^W (t)$
. Therefore Table 2 just contains two cases, one for an annuity conversion factor based on PLE and one based on CLE. Neither of these two cases is associated with a balanced budget. Using PLE one can calculate that d(t) ≈ 1 + (γ/2). This seems to confirm the belief that the use of PLE is not enough to keep a NDC system in balance. The use of CLE (22a), however, as is often suggested as the better alternative is also not appropriate as it leads to a permanent surplus with d(t) ≈ 1 − (γ/2). The punchline of this consideration is that in the case of constant retirement ages and a notional interest rate
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t)$
both methods of calculating the remaining life expectancy for annuitization at the time of retirement lead to an unbalanced budget. The first method is too ‘generous’ causing persistent deficits while the second method is too ‘harsh’ leading to ongoing surpluses.
$\rho (a,t) = \vartheta (a,t) = g^W (t)$
both methods of calculating the remaining life expectancy for annuitization at the time of retirement lead to an unbalanced budget. The first method is too ‘generous’ causing persistent deficits while the second method is too ‘harsh’ leading to ongoing surpluses.
Taking together, the results of Tables 1 and 2 thus complete the proof of proposition 2. None of the analyzed combination of the three crucial parameters is compatible with a constantly balanced budget if the retirement age can evolve either according to R
c
(t) = ψω
c
(t) or according to
![]() $R^c (t) = \overline R $
. In fact, it can be shown that the same result holds if retirement age is a linear combination of (13a) and (13b), i.e.,
$R^c (t) = \overline R $
. In fact, it can be shown that the same result holds if retirement age is a linear combination of (13a) and (13b), i.e.,
![]() $R^c (t) = \varsigma \psi \omega ^c (t) + (1 - \varsigma )\overline R $
, for
$R^c (t) = \varsigma \psi \omega ^c (t) + (1 - \varsigma )\overline R $
, for
![]() $0 \le \varsigma \le 1$
.
$0 \le \varsigma \le 1$
.
5.2 Intuition
There are two ways to provide intuition for the failure of the conventional wisdom in the presence of increasing longevity. One is based on the viewpoint of the system – the period perspective – while the other is based on the viewpoint of the insured individual – the cohort perspective. I am going to discuss both approaches in the following.
5.2.1 Period perspective
Why is it the case that for assumption (13a) with R
c
(t) = ψω
c
(t) the use of average wage growth as indexation and PLE for annuity conversion leads to a balanced budget with d(t) = 1? In order to see this, one can use the balanced budget condition (17), i.e.,
![]() $\tau W(t)L(t) = \overline P (t)M(t)$
. This condition can be transformed to deliver a pension payment that will (almost trivially) implement a constantly balanced budget for a PAYG system. This ‘generic’ (i.e., non-NDC) pension simply assigns each retiree in period t an identical benefit level
$\tau W(t)L(t) = \overline P (t)M(t)$
. This condition can be transformed to deliver a pension payment that will (almost trivially) implement a constantly balanced budget for a PAYG system. This ‘generic’ (i.e., non-NDC) pension simply assigns each retiree in period t an identical benefit level
![]() $P(a,t - a) = \tilde P(t)$
given by:
$P(a,t - a) = \tilde P(t)$
given by:
For the case with R
c
(t) = ψω
c
(t) (see Table 1) the NDC system where the notional interest and the adjustment rate are equal to average wage growth just implements this flat ‘generic’ pension
![]() $\tilde P(t)$
. This can be seen by noting that for ρ(a, t) = g(t) the first pension of the cohort born in (t − a) is given by
$\tilde P(t)$
. This can be seen by noting that for ρ(a, t) = g(t) the first pension of the cohort born in (t − a) is given by
![]() $P^F (t - a) = \tau W(t - a)\displaystyle{{R^c (t - a)} \over {\Gamma (R^c (t - a),t - a)}}$
. This reduces to
$P^F (t - a) = \tau W(t - a)\displaystyle{{R^c (t - a)} \over {\Gamma (R^c (t - a),t - a)}}$
. This reduces to
![]() $P^F (t - a) = \tau W(t - a) \displaystyle{\psi \over {1 - \psi}} $
(when the conversion factor is based on CLE) or
$P^F (t - a) = \tau W(t - a) \displaystyle{\psi \over {1 - \psi}} $
(when the conversion factor is based on CLE) or
![]() $P^F (t - a) = \tau W(t - a)\displaystyle{{\psi (1 + \gamma )} \over {1 - \psi}} $
(for PLE). On the other hand, the use of the adjustment rate
$P^F (t - a) = \tau W(t - a)\displaystyle{{\psi (1 + \gamma )} \over {1 - \psi}} $
(for PLE). On the other hand, the use of the adjustment rate
![]() $\vartheta (a,t) = g(t)$
implies that these initial pensions are indexed in such a manner that in period t every pensioner has an equal pension given by
$\vartheta (a,t) = g(t)$
implies that these initial pensions are indexed in such a manner that in period t every pensioner has an equal pension given by
![]() $P(a,t - a) = \tau W(t)\displaystyle{{\psi (1 + \chi \gamma )} \over {1 - \psi}} $
where χ = 0 (for CLE) and χ = 1 (for PLE). Comparing these NDC pensions with the flat generic pension
$P(a,t - a) = \tau W(t)\displaystyle{{\psi (1 + \chi \gamma )} \over {1 - \psi}} $
where χ = 0 (for CLE) and χ = 1 (for PLE). Comparing these NDC pensions with the flat generic pension
![]() $\tilde P(t) = \tau W(t)\displaystyle{{L(t)} \over {M(t)}} = \tau W(t)\displaystyle{{\psi (1 + \gamma )} \over {1 - \psi}} $
one can conclude that for χ = 1 the two magnitudes are identical and thus that the use of PLE for annuity conversion will lead to a constantly balanced budget.
$\tilde P(t) = \tau W(t)\displaystyle{{L(t)} \over {M(t)}} = \tau W(t)\displaystyle{{\psi (1 + \gamma )} \over {1 - \psi}} $
one can conclude that for χ = 1 the two magnitudes are identical and thus that the use of PLE for annuity conversion will lead to a constantly balanced budget.
Put differently, the use of the growth rate of the wage bill g
W
(t) + g
L
(t) for indexation would be inappropriate since the increase in the labor force g
L
(t) is not due to growing cohort sizes but rather a necessary reaction to increasing longevity in order to hold the dependency ratio constant. On the other hand, however, the use of CLE for annuity conversion is ‘overambitious’ to achieve budgetary balance in a NDC system. By using CLE the NDC implicitly assumes that there are as many retired cohorts as there are years of remaining life expectancy. In a stationary demographic constellation this assumption is correct. For example, if ω = 60 and R = 40 then remaining life expectancy is 20 and at the same time there are always 20 retired cohorts. For increasing longevity, however, this equivalence is no longer true and when the cohort with 20 remaining years retires there will be less (e.g., only 18) retired cohorts. By slicing the notional capital in 20 pieces the NDC would do more than is necessary to achieve a stable budget. The use of PLE works as if the conventional annuity calculation is augmented by a factor of 1 + γ to compensate for the gap between period and cohort measures. Similar arguments also hold for the case when
![]() $R^c (t) = \overline R $
and I come back to this discussion in Section 6.1.
$R^c (t) = \overline R $
and I come back to this discussion in Section 6.1.
5.2.2 Cohort perspective
A different way to look at this issue is by focusing on the individual perspective. For the case with R
c
(t) = ψω
c
(t) and assuming (for the sake of simplicity) that wages are constant (W(t) = W) the total contributions paid by a member of cohort t are given by TC(t) = τWR
c
(t) = τWψω
c
(t). For the ‘generic pension system’ that pays a flat benefit of
![]() $\tilde P(t) = \tau W\displaystyle{{L(t)} \over {M(t)}} = \tau W\displaystyle{{\psi (1 + \gamma )} \over {1 - \psi}} $
the total benefits received by a member of cohort t come out as
$\tilde P(t) = \tau W\displaystyle{{L(t)} \over {M(t)}} = \tau W\displaystyle{{\psi (1 + \gamma )} \over {1 - \psi}} $
the total benefits received by a member of cohort t come out as
![]() $TB(t) = \tilde P(t)(\omega ^c (t) - R^c (t)) = \tau W\psi (1 + \gamma )\omega ^c (t)$
. The ratio of total benefits to total contributions is thus given by 1 + γ. For increasing longevity (γ > 0) the total benefits received by insured individuals outstrip the total contributions they have paid. This can be viewed as a special ‘biological interest rate’ as I have discussed in Knell (Reference Knell2016).
$TB(t) = \tilde P(t)(\omega ^c (t) - R^c (t)) = \tau W\psi (1 + \gamma )\omega ^c (t)$
. The ratio of total benefits to total contributions is thus given by 1 + γ. For increasing longevity (γ > 0) the total benefits received by insured individuals outstrip the total contributions they have paid. This can be viewed as a special ‘biological interest rate’ as I have discussed in Knell (Reference Knell2016).
One can also derive an approximation for the implied internal rate of return. For this purpose assume that an individual born in t pays all contributions at the average age of working life
![]() $A_W^c (t)$
and receives all pension benefits at the average age of retirement
$A_W^c (t)$
and receives all pension benefits at the average age of retirement
![]() $A_R^c (t)$
(see equation (6)). The cohort-based internal rate of return σ
c
(t) can then be calculated from
$A_R^c (t)$
(see equation (6)). The cohort-based internal rate of return σ
c
(t) can then be calculated from
![]() $TC(t)e^{\sigma ^c (t)(A_R^c (t) - A_W^c (t))} = TB(t)$
or:
$TC(t)e^{\sigma ^c (t)(A_R^c (t) - A_W^c (t))} = TB(t)$
or:
 $$\sigma ^c (t) = \displaystyle{{\ln \left( {\displaystyle{{TB(t)} \over {TC(t)}}} \right)} \over {A_R^c (t) - A_W^c (t)}}.$$
$$\sigma ^c (t) = \displaystyle{{\ln \left( {\displaystyle{{TB(t)} \over {TC(t)}}} \right)} \over {A_R^c (t) - A_W^c (t)}}.$$
For rectangular survivorship (λ = 0) the average working age is R
c
(t)/2, the average retirement age (ω
c
(t) + R
c
(t))/2 and
![]() $A_R^c (t) - A_W^c (t) = \omega ^c (t)/2$
. For the case with R
c
(t) = ψω
c
(t) where TB(t)/TC(t) = 1 + γ one can thus derive that σ
c
(t) = 2ln(1 + γ)/ω
c
(t) ≈ 2γ/ω
c
(t). For the case with
$A_R^c (t) - A_W^c (t) = \omega ^c (t)/2$
. For the case with R
c
(t) = ψω
c
(t) where TB(t)/TC(t) = 1 + γ one can thus derive that σ
c
(t) = 2ln(1 + γ)/ω
c
(t) ≈ 2γ/ω
c
(t). For the case with
![]() $R^c (t) = \overline R $
, on the other hand, the generic pension in period t amounts to
$R^c (t) = \overline R $
, on the other hand, the generic pension in period t amounts to
![]() $\tilde P(t) = \tau W\displaystyle{{L(t)} \over {M(t)}} = \tau W\displaystyle{{\overline R} \over {\omega ^p (t) - \overline R}} $
. For an individual born in time t the ratio of total benefits to total contributions is given by
$\tilde P(t) = \tau W\displaystyle{{L(t)} \over {M(t)}} = \tau W\displaystyle{{\overline R} \over {\omega ^p (t) - \overline R}} $
. For an individual born in time t the ratio of total benefits to total contributions is given by
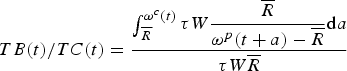 $TB(t)/TC(t) = \displaystyle{{\int_{\overline R} ^{\omega ^c (t)} \tau W\displaystyle{{\overline R} \over {\omega ^p (t + a) - \overline R}} {\rm d}a} \over {\tau W\overline R}} $
which reduces to TB(t)/TC(t) = (1 + γ)ln(1 + γ)/γ. The internal rate of return can then be calculated as σ
c
(t) = 2ln((1 + γ)ln(1 + γ)/γ)/ω
c
(t) ≈ γ/ω
c
(t). It is thus only half as large than for the case with an increasing retirement age but still positive.
$TB(t)/TC(t) = \displaystyle{{\int_{\overline R} ^{\omega ^c (t)} \tau W\displaystyle{{\overline R} \over {\omega ^p (t + a) - \overline R}} {\rm d}a} \over {\tau W\overline R}} $
which reduces to TB(t)/TC(t) = (1 + γ)ln(1 + γ)/γ. The internal rate of return can then be calculated as σ
c
(t) = 2ln((1 + γ)ln(1 + γ)/γ)/ω
c
(t) ≈ γ/ω
c
(t). It is thus only half as large than for the case with an increasing retirement age but still positive.
The reason for the positive internal rate of return even in the case of a constant retirement age has again to do with the difference between PLE and CLE. Each pension benefit can be somewhat more generous than in a stationary situation since the number of retired cohorts at the start of retirement is smaller than the remaining life expectancy of the retiring cohort. For the case with R c (t) = ψω c (t) there is the additional advantage that the continuous postponement of retirement enlarges the size of the PAYG system and thus produces ‘windfall gains’ that double the internal rate of return of all cohorts. This is analyzed and explained in more depth in Knell (Reference Knell2016).
The above derivation for the internal rate of return has been based on the generic pension system with
![]() $\tilde P(t)$
. One would, however, conjecture that each NDC system that manages to implement the same internal rate of return (σ
c
(t) = 2γ/ω
c
(t) for R
c
(t) = ψω
c
(t) and σ
c
(t) = γ/ω
c
(t) for
$\tilde P(t)$
. One would, however, conjecture that each NDC system that manages to implement the same internal rate of return (σ
c
(t) = 2γ/ω
c
(t) for R
c
(t) = ψω
c
(t) and σ
c
(t) = γ/ω
c
(t) for
![]() $R^c (t) = \overline R $
) might also be a candidate for a system with a balanced budget. This is the topic of Section 6.2.
$R^c (t) = \overline R $
) might also be a candidate for a system with a balanced budget. This is the topic of Section 6.2.
6 Stable NDC systems
One can use the considerations from above to derive rules for stable NDC systems. I will again distinguish between approaches that are based on the period and the cohort perspective. The aim is to find general rules that subsume the solutions for the two specific retirement assumptions as special cases.
6.1 A rule based on the period perspective
The starting point is the observation that with increasing longevity an increase in the retirement age is a necessary requirement to keep the dependency ratio M(t)/L(t) constant. In general, this increase in the retirement age will also lead to an increase in the labor force and it appears unjustified that this ‘necessary’ and ‘appropriate’ increase in the labor force should lead to a higher notional interest rate as would be the case if one uses the growth rate of the wage bill (cf. (23b)) as the relevant concept. It seems more reasonable to propose a new concept that defines the notional interest rate as the growth rate of the wage bill corrected for the necessary increase in retirement age due to increasing life expectancy. This leads to an additional concept for the determination of the notional interest rate and the adjustment rate:
where
![]() $g^{R^{*\,p}}$
(t) is the growth rate of the period retirement age R*
p
(t) that is necessary to hold the dependency ratio M(t)/L(t) constant.
$g^{R^{*\,p}}$
(t) is the growth rate of the period retirement age R*
p
(t) that is necessary to hold the dependency ratio M(t)/L(t) constant.
For the case with λ = 0 the dependency ratio is given by M(t)/L(t) = (ω
p
(t) − R
p
(t))/R
p
(t). A constant dependency ratio thus requires that the retirement age increases at the same speed as life expectancy, i.e.,
![]() $g^{R^{*\,p}}$
(t) = g
ω
p
(t) = γ/((1 + γ)ω
p
(t)) = γ/ω
c
(t). In this case the two indexation rates are thus given by
$g^{R^{*\,p}}$
(t) = g
ω
p
(t) = γ/((1 + γ)ω
p
(t)) = γ/ω
c
(t). In this case the two indexation rates are thus given by
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) + g^L (t) - (\gamma /\omega ^c (t))$
(the inheritance gains μ(a, t − a) drop out of (23c) due to the fact that λ = 0).
$\rho (a,t) = \vartheta (a,t) = g^W (t) + g^L (t) - (\gamma /\omega ^c (t))$
(the inheritance gains μ(a, t − a) drop out of (23c) due to the fact that λ = 0).
One can derive the deficit ratios for these indexation rates together with an annuity conversion factor based on PLE. For R
c
(t) = ψω
c
(t) we already know the result since in this case the individuals make the necessary adjustments in their retirement age such as to keep the dependency ratio constant. This means that in this case g
L
(t) = (γ/ω
c
(t)) and the rules (23c) and (24c) reduce to
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t)$
. As reported in Table 1 the use of average wage growth indexation together with an annuity conversion based on PLE leads to a balanced budget with d(t) = 1. It is interesting to note that this parameter constellation corresponds to the actual Swedish NDC system. It has been argued that the Swedish system is unstable by design since it deviates from the conventional wisdom and uses the growth rate of average wages (instead of the wage bill) for indexation and remaining PLE (instead of CLE) as annuity conversion factor. The result of this section, however, suggests that this constellation is in fact the appropriate choice if the retirement increases in line with life expectancy.
$\rho (a,t) = \vartheta (a,t) = g^W (t)$
. As reported in Table 1 the use of average wage growth indexation together with an annuity conversion based on PLE leads to a balanced budget with d(t) = 1. It is interesting to note that this parameter constellation corresponds to the actual Swedish NDC system. It has been argued that the Swedish system is unstable by design since it deviates from the conventional wisdom and uses the growth rate of average wages (instead of the wage bill) for indexation and remaining PLE (instead of CLE) as annuity conversion factor. The result of this section, however, suggests that this constellation is in fact the appropriate choice if the retirement increases in line with life expectancy.
For a constant retirement age
![]() $(R^c (t) = \overline R )$
the labor force stays constant (g
L
(t) = 0) and thus the corrected growth rate of the wage bill (23c) is given by
$(R^c (t) = \overline R )$
the labor force stays constant (g
L
(t) = 0) and thus the corrected growth rate of the wage bill (23c) is given by
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) - \gamma /(\omega ^c (t))$
. When this indexation is combined with an annuity conversion factor based on PLE the deficit ratio is given by (see online Appendix D.2):
$\rho (a,t) = \vartheta (a,t) = g^W (t) - \gamma /(\omega ^c (t))$
. When this indexation is combined with an annuity conversion factor based on PLE the deficit ratio is given by (see online Appendix D.2):
 $$d(t) = \displaystyle{{\overline R} \over {\omega ^p (t)}}\left( {\displaystyle{{(2 + \gamma )\ln (1 + \gamma )} \over {2\gamma}} - 1} \right) + 1 \approx 1,$$
$$d(t) = \displaystyle{{\overline R} \over {\omega ^p (t)}}\left( {\displaystyle{{(2 + \gamma )\ln (1 + \gamma )} \over {2\gamma}} - 1} \right) + 1 \approx 1,$$
where the approximation is around γ = 0. As for the case of increasing retirement the combination of (23c) and (22b) leads to a budget that is (approximately) balanced in every period. The error of approximation in this equation is rather small. Using γ = 0.25,
![]() $\overline R = 45$
and ω
c
(0) = 60 one gets an exact value of d(0) = 1.0039, i.e., expenditures exceed revenues by 0.39%. This is the amount that has to be channelled to the pension system from the general budget in order to keep it stable. This is a rather modest amount, in particular when compared with the alternative methods. The use of PLE and the (uncorrected) growth rate of the wage bill leads to a permanent deficit ratio of 11.6 % while the use of CLE gives rise to a permanent surplus of 10.7%.
$\overline R = 45$
and ω
c
(0) = 60 one gets an exact value of d(0) = 1.0039, i.e., expenditures exceed revenues by 0.39%. This is the amount that has to be channelled to the pension system from the general budget in order to keep it stable. This is a rather modest amount, in particular when compared with the alternative methods. The use of PLE and the (uncorrected) growth rate of the wage bill leads to a permanent deficit ratio of 11.6 % while the use of CLE gives rise to a permanent surplus of 10.7%.
A constant retirement age in the presence of a continuously increasing life expectancy is certainly an unrealistic assumptions that is mainly studied because it is the extreme case of sluggish retirement behavior. As life expectancy increases the annual pension benefit gets smaller and smaller and in the end the pension system stops to fullfill its main purpose to provide sufficient resources for old age. This long-term development implies that the case of constant retirement should be viewed as a thought-experiment that is empirically relevant only in a short-run perspective. Sooner or later the retirement age (or the contribution rate) has to increase in order to counteract the increase in longevity.
6.2 A rule based on the cohort perspective
A second possibility to implement a stable NDC system involves the combination of an annuity conversion factor based on CLE and the cohort-based internal rate of return as derived in Section 5.2.2. For the retirement pattern R
c
(t) = ψω
c
(t) and λ = 0 this means that the indexation rates are given by
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) + \displaystyle{{2\gamma} / {\omega ^c (t)}}$
while for
$\rho (a,t) = \vartheta (a,t) = g^W (t) + \displaystyle{{2\gamma} / {\omega ^c (t)}}$
while for
![]() $R^c (t) = \overline R $
they are given by
$R^c (t) = \overline R $
they are given by
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) + \displaystyle{\gamma / {\omega^c (t)}}$
. In the online Appendices D.1 and D.2 it is shown that this indexation leads to a deficit ratio of d(t) = 1 for the increasing retirement age and approximately d(t) = 1 for the constant retirement age. The intuition behind this result is that by using the internal rate of return as the indexation rates the system exactly distributes the available amount of resources such as to maintain financial stability.
$\rho (a,t) = \vartheta (a,t) = g^W (t) + \displaystyle{\gamma / {\omega^c (t)}}$
. In the online Appendices D.1 and D.2 it is shown that this indexation leads to a deficit ratio of d(t) = 1 for the increasing retirement age and approximately d(t) = 1 for the constant retirement age. The intuition behind this result is that by using the internal rate of return as the indexation rates the system exactly distributes the available amount of resources such as to maintain financial stability.
One can also use a different line of thought to arrive at the same conclusion. This approach is based on the concept of ‘turnover duration’ that is also employed in the Swedish model. This approach is discussed in Settergren and Mikula (Reference Settergren and Mikula2005) who start their analysis of NDC systems with the notion of the ‘pension liabilty’ defined as ‘the present value of future pension benefits to all persons to whom the system has a liability at the time of evaluation, minus the present value of future contributions by the same individuals’ (p.119). They show that in a stationary situation it holds that PL(t) = I(t)TD(t), i.e., total pension liabilities PL(t) of the system are equal to the product of total revenues I(t) = τW(t)L(t) and the ‘turnover duration’ TD(t). The latter magnitude is defined as the difference between the average age of retirees and the average age of contributors (see equation (7)), i.e.,
![]() $TD(t) = A_P^p (t) - A_W^p (t)$
. ‘The turnover duration indicates the size of the pension liability that the present contribution flow can finance, given the present income and mortality patterns’ (p.122). It corresponds to the length of time it takes on average from the payment of pension contributions to the receipt of pension benefits. In the online Appendix E, I derive the expression PL(t) = I(t)TD(t) for rectangular survivorship and increasing retirement and maximum ages.
$TD(t) = A_P^p (t) - A_W^p (t)$
. ‘The turnover duration indicates the size of the pension liability that the present contribution flow can finance, given the present income and mortality patterns’ (p.122). It corresponds to the length of time it takes on average from the payment of pension contributions to the receipt of pension benefits. In the online Appendix E, I derive the expression PL(t) = I(t)TD(t) for rectangular survivorship and increasing retirement and maximum ages.
The growth rate of total pension liabilities is given by g PL (t) = g I (t) + g TD (t). Since the revenues of the system grow at rate g I (t) = g W (t) + g L (t) this can be written as g PL (t) = g W (t) + g L (t) + g TD (t). One could thus conjecture (even for λ > 0) that a stable NDC system can be implemented when both the notional interest rate and the adjustment rate follow the development of total pension liabilities. This is captured in the following expressions:
For the case of rectangular survivorship (λ = 0) it holds that TD(t) = ω
p
(t)/2 and g
TD
(t) = (γ/ω
c
(t)). For R
c
(t) = ψω
c
(t) one has that g
L
(t) = (γ/ω
c
(t)) and thus
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) + (2\gamma /\omega ^c (t))$
. For
$\rho (a,t) = \vartheta (a,t) = g^W (t) + (2\gamma /\omega ^c (t))$
. For
![]() $R^c (t) = \overline R $
, on the other hand, it holds that g
L
(t) = 0 and thus
$R^c (t) = \overline R $
, on the other hand, it holds that g
L
(t) = 0 and thus
![]() $\rho (a,t) = \vartheta (a,t) = g^W (t) + (\gamma /\omega ^c (t))$
. These are exactly the expressions stated above that lead to a balanced (or approximately balanced) NDC system.
$\rho (a,t) = \vartheta (a,t) = g^W (t) + (\gamma /\omega ^c (t))$
. These are exactly the expressions stated above that lead to a balanced (or approximately balanced) NDC system.
6.3 Additional rules
The stable NDC systems of Sections 6.1 and 6.2 are characterized by the fact that the adjustment rates are equal to the notional interest rates, i.e.,
![]() $\vartheta (a,t) = \rho (a,t)$
. It is interesting to see whether there exist additional parameter constellations where this equality does not hold and that are also associated with a balanced budget. In particular, I continue to focus on the case of rectangular survivorship and assume that ρ(a, t) =g
W
(t). I now look at a specification of the adjustment rate
$\vartheta (a,t) = \rho (a,t)$
. It is interesting to see whether there exist additional parameter constellations where this equality does not hold and that are also associated with a balanced budget. In particular, I continue to focus on the case of rectangular survivorship and assume that ρ(a, t) =g
W
(t). I now look at a specification of the adjustment rate
![]() $\vartheta (a,t)$
that is compatible with a balanced system.
$\vartheta (a,t)$
that is compatible with a balanced system.
For R
c
(t) = ψω
c
(t), rectangular survivorship and an annuity conversion factor based on PLE the answer is already known and contained in Table 1. In this case an adjustment rate given by
![]() $\vartheta (a,t) = \rho (a,t) = g^W (t)$
leads to a stable deficit ratio of d(t) = 1. Using an annuity conversion factor based on CLE it can be shown (see the online Appendix D.1) that a choice of
$\vartheta (a,t) = \rho (a,t) = g^W (t)$
leads to a stable deficit ratio of d(t) = 1. Using an annuity conversion factor based on CLE it can be shown (see the online Appendix D.1) that a choice of
![]() $\vartheta (a,t) = g^W (t) + 2\gamma /(\omega ^c (t) - R^c (t)) = g^W (t) +2\gamma /((1 - \psi )\omega ^c (t))$
leads to an approximately balanced budget. For
$\vartheta (a,t) = g^W (t) + 2\gamma /(\omega ^c (t) - R^c (t)) = g^W (t) +2\gamma /((1 - \psi )\omega ^c (t))$
leads to an approximately balanced budget. For
![]() $R^c (t) = \overline R $
, on the other hand, one can show (see the online Appendix D.2) that the same is true if one chooses
$R^c (t) = \overline R $
, on the other hand, one can show (see the online Appendix D.2) that the same is true if one chooses
![]() $\vartheta (a,t) = g^W (t) + \gamma /(\omega ^c (t) - \overline R )$
(for CLE) and
$\vartheta (a,t) = g^W (t) + \gamma /(\omega ^c (t) - \overline R )$
(for CLE) and
![]() $\vartheta (a,t) = g^W (t) - \gamma /(\omega ^c (t) - \overline R )$
(for PLE).
$\vartheta (a,t) = g^W (t) - \gamma /(\omega ^c (t) - \overline R )$
(for PLE).
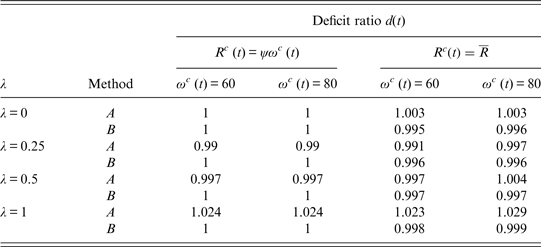
In Tables 3 and 4, I summarize all methods discussed so far that lead to a stable or an approximately stable system for rectangular survivorship (λ = 0). The results indicate that stable NDC systems are compatible with different paths for individual pension benefits. Either the first pension payment P
F
(t) is high and the adjustment rate
![]() $\vartheta (a,t)$
low or the other way round. The first pension payment is influenced both by the notional interest rate and by the annuity conversion factor. It will be larger if the latter is based on PLE. This implies that the first pension will be largest for method A, second largest for method B and smallest for method C that uses CLE and a notional interest rate of ρ(a, t) = g
W
(t). The choice between these different methods will be influenced by the level of individual and social time preferences and by considerations about horizontal and vertical equity.
$\vartheta (a,t)$
low or the other way round. The first pension payment is influenced both by the notional interest rate and by the annuity conversion factor. It will be larger if the latter is based on PLE. This implies that the first pension will be largest for method A, second largest for method B and smallest for method C that uses CLE and a notional interest rate of ρ(a, t) = g
W
(t). The choice between these different methods will be influenced by the level of individual and social time preferences and by considerations about horizontal and vertical equity.
Table 3. Stable NDC systems for an increasing retirement age (λ = 0)

Note: The table shows stable NDC systems, i.e., combinations of the notional interest rate, the adjustment rate and the annuity conversion factor such that the deficit ratio d(t) is exactly or approximately equal to one. PLE (CLE) stand for period (cohort) life expectancy. Retirement follows R c (t) = ω c (t) and survivorship is rectangular (λ = 0). Method A corresponds to the use of (23c) and (24c) and method B to the use of (23d) and (24d).
Table 4. Stable NDC systems for a constant retirement age (λ = 0)

Note: The table shows stable NDC systems, i.e., combinations of the notional interest rate, the adjustment rate and the annuity conversion factor such that the deficit ratio d(t) is approximately equal to one. PLE (CLE) stand for period (cohort) life expectancy. Retirement follows
![]() $R^c (t) = \overline R $
and survivorship is rectangular (λ = 0). Method A corresponds to the use of (23c) and (24c) and method B to the use of (23d) and (24d).
$R^c (t) = \overline R $
and survivorship is rectangular (λ = 0). Method A corresponds to the use of (23c) and (24c) and method B to the use of (23d) and (24d).
7 Extensions
In Sections 5 and 6, I have worked with a number of stylized assumptions in order to be able to derive clear-cut and analytical results. It is, however, interesting to study how the main results concerning the stability of NDC systems are changed by modifications of these assumptions. In this section, I briefly discuss the effects of changing the assumptions concerning the mortality rates, the maximum age and the pattern of retirement behavior.
7.1 Non-rectangular survivorship
The case with rectangular survivorship (λ = 0) has been convenient to illustrate why increasing life expectancy challenges the functioning of a traditional NDC system and how the three crucial parameters could be determined in order to guarantee its financial stability in the long-run. For the general case (λ > 0) the discussion gets more involved. Unfortunately, analytical results are no longer possible (or only for specific assumptions) and one has to resort to numerical examples and simulations. It would be highly informative to set up a numerical model with stochastic demography as in Auerbach and Lee (Reference Auerbach and Lee2009, Reference Auerbach and Lee2011) and study the budgetary implications of various assumptions concerning ρ(a, t),
![]() $\vartheta (a,t)$
and Γ(a, t). This would be particularly interesting since the aforementioned papers looked at the case of mortality rates that do not decrease over time and an analysis with increasing longevity would complement their findings. As shown in Section 5 a constantly increasing longevity has a positive effect on the internal rate of return and one would expect that this will also show up in a stochastic simulation environment. This, however, would require an entirely different set-up and I leave it as an exercise for future research.
$\vartheta (a,t)$
and Γ(a, t). This would be particularly interesting since the aforementioned papers looked at the case of mortality rates that do not decrease over time and an analysis with increasing longevity would complement their findings. As shown in Section 5 a constantly increasing longevity has a positive effect on the internal rate of return and one would expect that this will also show up in a stochastic simulation environment. This, however, would require an entirely different set-up and I leave it as an exercise for future research.
In this section, I stick to the assumption of a deterministic development of mortality rates but I now study the case of non-rectangular survivorship, i.e., λ > 0 in the ‘modified de Moivre function’ (9). To this end, I use numerical examples to calculate the deficit ratio d(t) for two combinations of pension parameters that have shown to guarantee a stable (or approximately stable) NDC system for the rectangular case. The first combination (method A in Tables 3 and 4) uses PLE for the annuity conversion and the indexations (23c) and (24c) that are based on the corrected growth rate of the wage bill. The second combination uses CLE together with the indexations (23d) and (24d) that are based on the turnover duration (method B in Tables 3 and 4).
In order to calculate the indexation rates for the two methods one has to know the growth rates of the labor force L(t), the turnover duration TD(t) and the dependency-ratio-stabilizing retirement age R*
p
(t) for the case with λ > 0. As far as the first two are involved one can show that they again grow (approximately) in lockstep with life expectancy, i.e., g
L
(t) ≈ (γ/ω
c
(t)) and g
TD
(t) ≈ (γ/ω
c
(t)). This means that for method B the indexation rates are given by ρ(a, t) = g(t) + μ(a, t − a) + (2γ/ω
c
(t)) and
![]() $\vartheta (a,t) = g(t) + (2\gamma /\omega ^c (t))$
for increasing retirement (R
c
(t) = ψω
c
(t)) and ρ(a, t) = g(t) + μ(a, t − a) + (γ/ω
c
(t)) and
$\vartheta (a,t) = g(t) + (2\gamma /\omega ^c (t))$
for increasing retirement (R
c
(t) = ψω
c
(t)) and ρ(a, t) = g(t) + μ(a, t − a) + (γ/ω
c
(t)) and
![]() $\vartheta (a,t) = g(t) + (\gamma /\omega ^c (t))$
for constant retirement
$\vartheta (a,t) = g(t) + (\gamma /\omega ^c (t))$
for constant retirement
![]() $(R^c (t) = \overline R )$
.
$(R^c (t) = \overline R )$
.
As far as the required retirement age R*
p
(t) is concerned, however, it is no longer true that it is also proportional to life expectancy. The reason for this is that due to the mortality after retirement the pension expenditures are reduced in every period and thus the increase in the retirement age of the newly retiring cohorts can be less than proportional in order to stabilize the aggregate dependency ratio. This is discussed in the online Appendix F, where I show that the required retirement age can be expressed as R*
p
(t) = ϕ(ω
c
(t))1−λ
. The growth rate of the required retirement age is thus given by: g
R*
p
(t) = (1 − λ) (γ/ω
c
(t)). For the case with λ = 0 this implies that
![]() $g^{R^{*\,p}}$
(t) = (γ/ω
c
(t)), which was the expression used in Section 6.1. For general λ > 0 the indexation rates for method A are given by ρ(a, t) = g(t) + μ(a, t − a) + (λγ/ω
c
(t)) and
$g^{R^{*\,p}}$
(t) = (γ/ω
c
(t)), which was the expression used in Section 6.1. For general λ > 0 the indexation rates for method A are given by ρ(a, t) = g(t) + μ(a, t − a) + (λγ/ω
c
(t)) and
![]() $\vartheta (a,t) = g(t) + (\lambda \gamma /\omega ^c (t))$
for increasing retirement (R
c
(t) = ψω
c
(t)) and ρ(a, t) = g(t) + μ(a, t − a) − ((1 − λ)γ/ω
c
(t)) and
$\vartheta (a,t) = g(t) + (\lambda \gamma /\omega ^c (t))$
for increasing retirement (R
c
(t) = ψω
c
(t)) and ρ(a, t) = g(t) + μ(a, t − a) − ((1 − λ)γ/ω
c
(t)) and
![]() $\vartheta (a,t) = g(t) - ((1 - \lambda )\gamma /\omega ^c (t))$
for constant retirement
$\vartheta (a,t) = g(t) - ((1 - \lambda )\gamma /\omega ^c (t))$
for constant retirement
![]() $(R^c (t) = \overline R )$
.
$(R^c (t) = \overline R )$
.
In Table 5, I use a numerical example to calculate the deficit ratios for methods A and B and various values of λ. Furthermore, in order to illustrate the development over time, I show the deficit ratios for two values of the maximum age (i.e., for ω c (t) = 60 and ω c (t) = 80). The use of method B leads to a stable NDC system. In particular, for an increasing retirement age the deficit ratio is exactly one. In the online Appendix D.3, I prove this for the case of linear survivorship with λ = 1. For the fixed retirement age method B leads to a deficit ratio that is very close to balance (between 0.995 and 0.999) for all cases. Method A, on the other hand, is also in line with an approximately balanced NDC systems for almost all cases considered. Only for the case of linear survivorship (λ = 1) the deficit ratio is above 1%.
Table 5. Stable NDC systems for non-rectangular survivorship
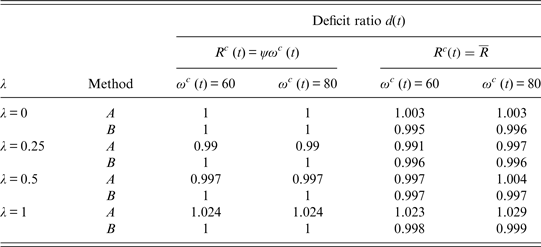
Note: The table shows the deficit ratio for various assumptions concerning the retirement age R
c
(t), the maximum age ω
c
(t) and the shape of the survivorship curve λ. For increasing retirement age the parameter ψ is set for each case of λ such that retirement is a fixed proportion
![]() $\tilde \psi $
of life expectancy at birth, i.e.,
$\tilde \psi $
of life expectancy at birth, i.e.,
![]() $R^c (t) = \tilde \psi e^c (0,t) = \tilde \psi (\omega ^c (t)/1 + \lambda )$
which implies that
$R^c (t) = \tilde \psi e^c (0,t) = \tilde \psi (\omega ^c (t)/1 + \lambda )$
which implies that
![]() $\psi = \tilde \psi /(1 + \lambda )$
. The parameters are given by γ = 0.25, ω
c
(0) = 60,
$\psi = \tilde \psi /(1 + \lambda )$
. The parameters are given by γ = 0.25, ω
c
(0) = 60,
![]() $\tilde \psi = 3/4$
and
$\tilde \psi = 3/4$
and
![]() $\bar R = \psi \omega ^c (0)/(1 + \gamma \psi )$
. Method A (B) uses remaining period (cohort) life expectancy as the annuity conversion factor. The indexation rates for method A are given by ρ(a, t) = g(t) + μ(a, t − a) + g
L
(t) − (1 − λ) γ/ω
c
(t) and
$\bar R = \psi \omega ^c (0)/(1 + \gamma \psi )$
. Method A (B) uses remaining period (cohort) life expectancy as the annuity conversion factor. The indexation rates for method A are given by ρ(a, t) = g(t) + μ(a, t − a) + g
L
(t) − (1 − λ) γ/ω
c
(t) and
![]() $\vartheta (a,t) = g(t) + g^L (t) - (1 - \lambda )\gamma /\omega ^c (t)$
. For method B the indexation rates are ρ(a, t) = g(t) + μ(a, t − a) + g
L
(t) + g
TD
(t) and
$\vartheta (a,t) = g(t) + g^L (t) - (1 - \lambda )\gamma /\omega ^c (t)$
. For method B the indexation rates are ρ(a, t) = g(t) + μ(a, t − a) + g
L
(t) + g
TD
(t) and
![]() $\vartheta (a,t) = g(t) + g^L (t) + g^{TD} (t)$
.
$\vartheta (a,t) = g(t) + g^L (t) + g^{TD} (t)$
.
7.2 An upper limit to longevity
So far, I have assumed that the maximum age ω
c
(t) and thus life expectancy increase in a linear fashion (see (11)). This assumption is in line with the historic development over the last century, but there exists a controversy whether or how long this process might continue into the future. In particular, a group of demographers is arguing that there exists a maximum human life span that cannot be extended. In order to study the effects of this alternative viewpoint, I have also looked at a set-up where the maximum age hits an upper limit ω
max
. In particular, it is assumed that ω
c
(t) = ω
c
(0) + γ · t for
![]() $t \lt \hat {\hskip-2pt t}$
and
$t \lt \hat {\hskip-2pt t}$
and
![]() $\omega ^c (t) = \omega ^c (\,\hat {\hskip-2pt t}\,) = \omega ^{max} $
for
$\omega ^c (t) = \omega ^c (\,\hat {\hskip-2pt t}\,) = \omega ^{max} $
for
![]() $t \ge \hat {\hskip-2pt t}$
.
$t \ge \hat {\hskip-2pt t}$
.
In order to study the budgetary developments of the pension system in this demographic scenario, I had to use numerical simulations. These simulations (not shown) indicate that the parameter combinations that have been shown to lead to a stable NDC system in Section 6 can again be employed to implement a budget that stabilizes over time. Whether and how this automatic stabilization takes place depends, however, crucially on the retirement behavior before and after the transition. In particular, it is important to consider whether the demographic change is an expected event or whether it comes as a surprise.
The above example where ageing stops abruptly after a long path of linear increases is of course unrealistic. One would rather expect a continuous (or step-wise) slow-down (cf. Vallin and Meslé, Reference Vallin and Meslé2009) that approaches the upper limit asymptotically. In the language of the model this could be captured by a time-varying γ(t) where γ(T) = 0 for some time T. I leave a thorough treatment of this case for future research.
7.3 Retirement behavior
A second modification concerns the assumption of the retirement behavior. So far, I have assumed that retirement is either proportional to the maximum age or constant while real-world retirement patterns are less regular. In a previous version of the paper, I used simulations to study the budgetary consequences when retirement follows a stochastic pattern and when the NDC system is based on either method A or method B. The results show that in this case the pension system is unbalanced in almost every year and the deficit ratios fluctuate widely. Over time, however, the surpluses and the deficits counteract each other and the average deficit ratio over a longer time span is approximately equal to one.
8 Conclusion
In this paper, I have studied how to design a NDC pension system that is able to stabilize its budget in the presence of increasing life expectancy. I have shown that the financial sustainability depends on the appropriate determination of three parameters: the notional interest rate, the adjustment rate and the annuity conversion factor, which is based on remaining life expectancy. The analysis has shown that there exist various combinations of the three parameters that are associated with a balanced budget. Two approaches turned out to be particularly interesting since they work under a large variety of assumptions concerning the mortality structure and the retirement patterns and since they can be formulated in general terms. The first approach (method A) uses period (remaining) life expectancy for annuity conversion and a corrected growth rate of the wage bill for indexation (i.e., for the notional interest and the adjustment rate) where the correction takes into consideration that the retirement age and thus the labor force have to increase just to counterbalance the continuous increase in life expectancy. The second approach (method B) uses CLE for the annuity conversion and again a corrected growth rate of the wage bill for indexation where the correction now adds the growth rate of the turnover duration. This correction accounts for the fact that increasing life expectancy leads to a higher internal rate of return, which can be distributed among the insured population without challenging the stability of the system. These findings are a challenge to the conventional wisdom on the appropriate design of NDC systems and none of the countries that are currently organized in such a way uses the combination of parameters that suggests itself in the modelling framework of this paper. These findings might thus be useful for the refinement of existing or the construction of future NDC systems.
The focus of this paper has been to analyze the impact of increasing life expectancy on the stability of PAYG pension systems. Therefore, I have abstracted from all other economic and demographic factors that might also be potential sources of instability for the system. First and foremost this concerns changes along the second demographic dimension: the size of the birth or working cohorts N(0, t). Different fertility scenarios have already been studied in the related literature (cf. in particular Valdés-Prieto, Reference Valdés-Prieto2000). The main finding is that non-monotonic shifts in the development of cohort size can lead to short-run and/or long-run financial instability of the pension system. Besides irregular developments of fertility there exist a number of other factors that might change in an erratic fashion, e.g., sudden changes in the average fertility age, in the average age of labor market entry or in the age-earnings profiles. It is an interesting area for future research to study and systematize the effects of these changes and to analyze their interaction with increasing life expectancy.
Given that there are many sources for unpredictable shocks it seems inevitable that a NDC system includes some additional mechanism that adjusts for unforeseen imbalances like the Swedish ‘automatic balance mechanism’ (Auerbach and Lee, Reference Auerbach and Lee2009; Settergren, Reference Settergren, Holzmann, Palmer and Robalino2012). Independent of the design of such an additional balance mechanism it is important to note, however, that the appropriate definition of the notional interest rate and remaining life expectancy will in any case lead to a more stable system and will make the activation of the automatic balance mechanism a less frequent event.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S1474747216000226.
Appendices
A. Cohort and PLE (Section 2.1)
CLE is given by equation (2a). The second equality follows from the fact that:
 $$e^{\int\limits_z^a { - \mu (x,t) {\rm d}x}} = e^{\int\limits_0^a { - \mu (x,t) {\rm d}x}} e^{\int\limits_0^z {\mu (x,t) {\rm d}x}} = \displaystyle{{S(a,t)} \over {S(z,t)}},$$
$$e^{\int\limits_z^a { - \mu (x,t) {\rm d}x}} = e^{\int\limits_0^a { - \mu (x,t) {\rm d}x}} e^{\int\limits_0^z {\mu (x,t) {\rm d}x}} = \displaystyle{{S(a,t)} \over {S(z,t)}},$$
where I use equation (1), i.e.,
![]() $S(a,t) = e^{\int_0^a - \mu (x,t) {\rm d}x} $
.
$S(a,t) = e^{\int_0^a - \mu (x,t) {\rm d}x} $
.
Inserting the ‘modified de Moivre function’ (9) one can solve:
 $$\int_z^{\omega ^c (t)} S(a,t) {\rm d}a = \displaystyle{{\left( {\displaystyle{1 \over {\omega ^c (t)}}} \right)^\lambda \left( {\omega ^c (t) - z} \right)^{1 + \lambda}} \over {1 + \lambda}} = \displaystyle{{\left( {1 - \displaystyle{z \over {\omega ^c (t)}}} \right)^\lambda \left( {\omega ^c (t) - z} \right)} \over {1 + \lambda}}. $$
$$\int_z^{\omega ^c (t)} S(a,t) {\rm d}a = \displaystyle{{\left( {\displaystyle{1 \over {\omega ^c (t)}}} \right)^\lambda \left( {\omega ^c (t) - z} \right)^{1 + \lambda}} \over {1 + \lambda}} = \displaystyle{{\left( {1 - \displaystyle{z \over {\omega ^c (t)}}} \right)^\lambda \left( {\omega ^c (t) - z} \right)} \over {1 + \lambda}}. $$
Dividing this expression by
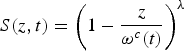 $S(z,t) = \left( {1 - \displaystyle{z \over {\omega ^c (t)}}} \right)^\lambda $
leads to e
c
(z, t) = (ω
c
(t) − z)/(1 + λ) as stated in equation (10a).
$S(z,t) = \left( {1 - \displaystyle{z \over {\omega ^c (t)}}} \right)^\lambda $
leads to e
c
(z, t) = (ω
c
(t) − z)/(1 + λ) as stated in equation (10a).
PLE, on the other hand, is given by equation (2b), i.e.,
![]() $e^p (z,t) = \int_z^{\omega ^p (t)} e^{\int_z^a - \mu (x,t - x) {\rm d}x} {\rm d}a$
. This can also be written as
$e^p (z,t) = \int_z^{\omega ^p (t)} e^{\int_z^a - \mu (x,t - x) {\rm d}x} {\rm d}a$
. This can also be written as
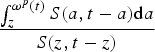 $\displaystyle{{\int_z^{\omega ^p (t)} S(a,t - a) {\rm d}a} \over {S(z,t - z)}}$
as can be shown following similar steps as above for e
c
(z, t). For the ‘modified de Moivre function’ (9) the mortality hazard rate is given by μ(a, t) = λ/(ω
c
(t) − a) and one can write:
$\displaystyle{{\int_z^{\omega ^p (t)} S(a,t - a) {\rm d}a} \over {S(z,t - z)}}$
as can be shown following similar steps as above for e
c
(z, t). For the ‘modified de Moivre function’ (9) the mortality hazard rate is given by μ(a, t) = λ/(ω
c
(t) − a) and one can write:
 $$e^{\int\limits_z^a { - \mu (x,t - x) {\rm d}x}} = e^{\int\limits_z^a {\displaystyle{{ - \lambda} \over {\omega ^c (t - x) - x}} {\rm d}x}} = e^{\int\limits_z^a {\displaystyle{{ - \lambda} \over {\omega ^c (t) - (1 + \gamma )x}} {\rm d}x}} = \left( {\displaystyle{{\omega ^c (t) - (1 + \gamma )a} \over {\omega ^c (t) - (1 + \gamma )z}}} \right)^{\displaystyle{\lambda \over {1 + \gamma}}}. $$
$$e^{\int\limits_z^a { - \mu (x,t - x) {\rm d}x}} = e^{\int\limits_z^a {\displaystyle{{ - \lambda} \over {\omega ^c (t - x) - x}} {\rm d}x}} = e^{\int\limits_z^a {\displaystyle{{ - \lambda} \over {\omega ^c (t) - (1 + \gamma )x}} {\rm d}x}} = \left( {\displaystyle{{\omega ^c (t) - (1 + \gamma )a} \over {\omega ^c (t) - (1 + \gamma )z}}} \right)^{\displaystyle{\lambda \over {1 + \gamma}}}. $$
From this one can derive:
 $$e^p (z,t) = \int_z^{\omega ^p (t)} \left( {\displaystyle{{\omega ^c (t) - (1 + \gamma )a} \over {\omega ^c (t) - (1 + \gamma )z}}} \right)^{\displaystyle{\lambda \over {1 + \gamma}}} {\rm d}a = \displaystyle{{\omega ^c (t) - (1 + \gamma )z} \over {1 + \gamma + \lambda}} $$
$$e^p (z,t) = \int_z^{\omega ^p (t)} \left( {\displaystyle{{\omega ^c (t) - (1 + \gamma )a} \over {\omega ^c (t) - (1 + \gamma )z}}} \right)^{\displaystyle{\lambda \over {1 + \gamma}}} {\rm d}a = \displaystyle{{\omega ^c (t) - (1 + \gamma )z} \over {1 + \gamma + \lambda}} $$
which is stated as equation (10b). Note that:
B. Expenditures E(t) (Section 3)
Inserting equations (18), (19) and (20) into (15) and using (1) leads to the following expression:
 $$\eqalign{& E(t) = \tau \int_{R^p (t)}^{\omega ^p (t)} \left[ {\displaystyle{{\int_0^{R^c (t - a)} W(t - a + x)e^{\int_x^{R^c (t - a)} \rho (s,t - a + s) {\rm d}s} {\rm d}x} \over {\Gamma (R^c (t - a),t - a)}} \times} \right. \cr & \quad \left. {e^{\int\limits_{R^c (t - a)}^a {\vartheta (s,t - a + s) {\rm d}s}} N(0,t - a)e^{\int\limits_0^a {( - \mu (s,t - a)) {\rm d}s}}} \right]{\rm d}a.} $$
$$\eqalign{& E(t) = \tau \int_{R^p (t)}^{\omega ^p (t)} \left[ {\displaystyle{{\int_0^{R^c (t - a)} W(t - a + x)e^{\int_x^{R^c (t - a)} \rho (s,t - a + s) {\rm d}s} {\rm d}x} \over {\Gamma (R^c (t - a),t - a)}} \times} \right. \cr & \quad \left. {e^{\int\limits_{R^c (t - a)}^a {\vartheta (s,t - a + s) {\rm d}s}} N(0,t - a)e^{\int\limits_0^a {( - \mu (s,t - a)) {\rm d}s}}} \right]{\rm d}a.} $$
Note that
![]() $W(t - a + x) = W(t - a)e^{\int_0^x {g(t - a + s) {\rm d}s}} $
and
$W(t - a + x) = W(t - a)e^{\int_0^x {g(t - a + s) {\rm d}s}} $
and
![]() $W(t - a + R^c (t - a)) = W(t - a)e^{\int_0^{R^c (t - a)} {g(t - a + s) {\rm d}s}} $
. Since in the formula above x ≤ R
c
(t − a) one can write that:
$W(t - a + R^c (t - a)) = W(t - a)e^{\int_0^{R^c (t - a)} {g(t - a + s) {\rm d}s}} $
. Since in the formula above x ≤ R
c
(t − a) one can write that:
 $$W(t - a + x) = W(t - a + R^c (t - a))e^{\int\limits_x^{R^c (t - a)} {( - g(t - a + s)) {\rm d}s}} $$
$$W(t - a + x) = W(t - a + R^c (t - a))e^{\int\limits_x^{R^c (t - a)} {( - g(t - a + s)) {\rm d}s}} $$
from which it follows that:
Similarly (since R c (t − a) ≤ a):
which leads to the final expression for E(t) that is stated as equation (21) in the text.
C. Proposition 1 (Section 4)
For the assumptions of proposition 1 the income of the system (14) is given by:
 $$\displaylines{I(t) = \tau W(t)L(t) = \tau W(t)N(0,t)\int_0^R e^{ - na} S(a) {\rm d}a \cr = \tau W(t)N(0,t)\int_0^R e^{ - na} e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a.} $$
$$\displaylines{I(t) = \tau W(t)L(t) = \tau W(t)N(0,t)\int_0^R e^{ - na} S(a) {\rm d}a \cr = \tau W(t)N(0,t)\int_0^R e^{ - na} e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a.} $$
The expenditure level (21), on the other hand, can be simplified to:
 $$\displaylines{E(t) = \int\limits_R^\omega {\underbrace {\tau W(t)\left( {\displaystyle{{\int_0^R e^{\int_x^R (\mu (s) + n) {\rm d}s} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}} \right)}_{{\scriptstyle {\rm First} \atop \scriptstyle {\rm Pension}}} \underbrace {e^{\int_R^a n {\rm d}s}} _{{\scriptstyle {\rm Adjustment} \atop \scriptstyle {\rm Factor}}} \underbrace {e^{\int_0^a ( - \mu (s)) {\rm d}s}} _{{\scriptstyle {\rm Cohort}\,{\rm size} \atop \scriptstyle {\rm at \;age}\; a}} \underbrace {e^{ - na} N(0,t)}_{{\scriptstyle {\rm Initial \;size} \atop \scriptstyle {\rm of}\,{\rm cohort}\,t - a}} {\rm d}a} \cr = \tau W(t)N(0,t)\int_R^\omega \displaystyle{{\int_0^R e^{\int_x^R \mu (s) {\rm d}s} e^{n(R - x)} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}e^{n(a - R)} e^{\int_0^a ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a \cr = \tau W(t)N(0,t)\int_R^\omega \displaystyle{{\int_0^R e^{\int_x^R \mu (s) {\rm d}s} e^{ - nx} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a.} $$
$$\displaylines{E(t) = \int\limits_R^\omega {\underbrace {\tau W(t)\left( {\displaystyle{{\int_0^R e^{\int_x^R (\mu (s) + n) {\rm d}s} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}} \right)}_{{\scriptstyle {\rm First} \atop \scriptstyle {\rm Pension}}} \underbrace {e^{\int_R^a n {\rm d}s}} _{{\scriptstyle {\rm Adjustment} \atop \scriptstyle {\rm Factor}}} \underbrace {e^{\int_0^a ( - \mu (s)) {\rm d}s}} _{{\scriptstyle {\rm Cohort}\,{\rm size} \atop \scriptstyle {\rm at \;age}\; a}} \underbrace {e^{ - na} N(0,t)}_{{\scriptstyle {\rm Initial \;size} \atop \scriptstyle {\rm of}\,{\rm cohort}\,t - a}} {\rm d}a} \cr = \tau W(t)N(0,t)\int_R^\omega \displaystyle{{\int_0^R e^{\int_x^R \mu (s) {\rm d}s} e^{n(R - x)} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}e^{n(a - R)} e^{\int_0^a ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a \cr = \tau W(t)N(0,t)\int_R^\omega \displaystyle{{\int_0^R e^{\int_x^R \mu (s) {\rm d}s} e^{ - nx} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a.} $$
One can use these two expressions for I(t) and E(t) to derive that:
 $$\displaylines{d(t) = \displaystyle{{E(t)} \over {I(t)}} = \int\limits_R^\omega {\displaystyle{{\int_0^R e^{\int_x^R \mu (s) {\rm d}s} e^{ - nx} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}\displaystyle{{e^{\int_0^a ( - \mu (s)) {\rm d}s}} \over {\int_0^R e^{\int_0^x ( - \mu (s)) {\rm d}s} e^{ - nx} {\rm d}x}} {\rm d}a} \cr = \displaystyle{{\int_0^R e^{\int_a^R \mu (s) {\rm d}s} e^{ - na} {\rm d}a} \over {\int_0^R e^{\int_0^a ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a}}\displaystyle{{\int_R^\omega e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a} \over {\int_R^\omega e^{\int_R^a ( - \mu (s)) {\rm d}s} {\rm d}a}},} $$
$$\displaylines{d(t) = \displaystyle{{E(t)} \over {I(t)}} = \int\limits_R^\omega {\displaystyle{{\int_0^R e^{\int_x^R \mu (s) {\rm d}s} e^{ - nx} {\rm d}x} \over {\int_R^\omega e^{\int_R^x ( - \mu (s)) {\rm d}s} {\rm d}x}}\displaystyle{{e^{\int_0^a ( - \mu (s)) {\rm d}s}} \over {\int_0^R e^{\int_0^x ( - \mu (s)) {\rm d}s} e^{ - nx} {\rm d}x}} {\rm d}a} \cr = \displaystyle{{\int_0^R e^{\int_a^R \mu (s) {\rm d}s} e^{ - na} {\rm d}a} \over {\int_0^R e^{\int_0^a ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a}}\displaystyle{{\int_R^\omega e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a} \over {\int_R^\omega e^{\int_R^a ( - \mu (s)) {\rm d}s} {\rm d}a}},} $$
where I have changed two times the name of the integration variable from ‘x’ to ‘a’. Noting that (since a ≥ R):
 $$e^{\int\limits_0^a {( - \mu (s)) {\rm d}s}} = \displaystyle{{e^{\int_R^a ( - \mu (s)) {\rm d}s}} \over {e^{\int_0^R \mu (s) {\rm d}s}}} $$
$$e^{\int\limits_0^a {( - \mu (s)) {\rm d}s}} = \displaystyle{{e^{\int_R^a ( - \mu (s)) {\rm d}s}} \over {e^{\int_0^R \mu (s) {\rm d}s}}} $$
and
 $$\int\limits_R^\omega {e^{\int\limits_R^a {( - \mu (s)) {\rm d}s}} {\rm d}a} = e^{\int\limits_0^R {\mu (s) {\rm d}s}} \int\limits_R^\omega {e^{\int\limits_0^a {( - \mu (s)) {\rm d}s}} {\rm d}a} $$
$$\int\limits_R^\omega {e^{\int\limits_R^a {( - \mu (s)) {\rm d}s}} {\rm d}a} = e^{\int\limits_0^R {\mu (s) {\rm d}s}} \int\limits_R^\omega {e^{\int\limits_0^a {( - \mu (s)) {\rm d}s}} {\rm d}a} $$
this can be simplified to:
 $$d(t) = \displaystyle{{\int_0^R e^{\int_a^R \mu (s) {\rm d}s} e^{ - na} {\rm d}a} \over {\displaystyle{1 \over {e^{\int_0^R \mu (s) {\rm d}s}}} \int_0^R e^{\int_a^R \mu (s) {\rm d}s} e^{ - na} {\rm d}a}}\displaystyle{{\int_R^\omega e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a} \over {e^{\int_0^R \mu (s) {\rm d}s} \int_R^\omega e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a}} = 1.$$
$$d(t) = \displaystyle{{\int_0^R e^{\int_a^R \mu (s) {\rm d}s} e^{ - na} {\rm d}a} \over {\displaystyle{1 \over {e^{\int_0^R \mu (s) {\rm d}s}}} \int_0^R e^{\int_a^R \mu (s) {\rm d}s} e^{ - na} {\rm d}a}}\displaystyle{{\int_R^\omega e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a} \over {e^{\int_0^R \mu (s) {\rm d}s} \int_R^\omega e^{\int_0^a ( - \mu (s)) {\rm d}s} {\rm d}a}} = 1.$$
Overall, proposition 1 shows that for the benchmark case of a stationary (or at least continuously developing) demographic structure a constantly balanced NDC system can be established by simply choosing a notional interest rate that is equal to the growth rate of the wage bill plus a correction for inheritance gains, i.e., ρ(a, t) = g W (t) + g L (t) + μ(a).
The choice of any other notional interest rate, on the other hand, will lead to a permanent budgetary imbalance. This can be seen immediately by noting that the total revenues of the system are always given by I(t) = τW(t)L(t), while the expenditures change with the choice of the notional interest rate. Using the growth rate of average wages ρ(a, t) = g
W
(t) + μ(a) leads to:
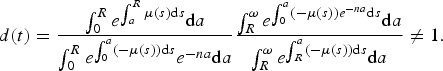 $d(t) = \displaystyle{{\int_0^R e^{\int_a^R \mu (s) {\rm d}s} {\rm d}a} \over {\int_0^R e^{\int_0^a ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a}}\displaystyle{{\int_R^\omega e^{\int_0^a ( - \mu (s))e^{ - na} {\rm d}s} {\rm d}a} \over {\int_R^\omega e^{\int_R^a ( - \mu (s)) {\rm d}s} {\rm d}a}} \ne 1.$
A neglect of the inheritance gains, on the other hand, with ρ(a, t) = g
W
(t) + g
L
(t) leads to
$d(t) = \displaystyle{{\int_0^R e^{\int_a^R \mu (s) {\rm d}s} {\rm d}a} \over {\int_0^R e^{\int_0^a ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a}}\displaystyle{{\int_R^\omega e^{\int_0^a ( - \mu (s))e^{ - na} {\rm d}s} {\rm d}a} \over {\int_R^\omega e^{\int_R^a ( - \mu (s)) {\rm d}s} {\rm d}a}} \ne 1.$
A neglect of the inheritance gains, on the other hand, with ρ(a, t) = g
W
(t) + g
L
(t) leads to
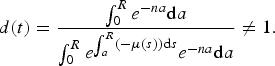 $d(t) = \displaystyle{{\int_0^R e^{ - na} {\rm d}a} \over {\int_0^R e^{\int_a^R ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a}} \ne 1.$
$d(t) = \displaystyle{{\int_0^R e^{ - na} {\rm d}a} \over {\int_0^R e^{\int_a^R ( - \mu (s)) {\rm d}s} e^{ - na} {\rm d}a}} \ne 1.$