2. FULL 3D NUMERICAL SIMULATIONS

2.1. Simulation description

The numerical simulations presented in this work were performed using the 3D arbitrary Lagrangian–Eulerian hydrodynamics code LEEOR3D with interface tracking (Ofer et al., 1996). The program was used in the Eulerian mode with a typical simulation mesh of 80 × 80 × 80 computation cells. Initial conditions for the velocity field were derived from the flow potential φ(x, y, z) = [sum ]_{kx, ky} a₀ cos(k_x x)·cos(k_y y)·e^−kz, were k =

and 20 < k_x /2π, k_y /2π < 40. Final results were found to be insensitive to the choice of the random phases a₀. The velocities were calculated as the gradients of the potential. These initial conditions resulted in the creation of about 450 bubbles in the linear stage. Calculations with different spectra and resolutions did not show significantly different results. A simple P = (ρ − ρ₀)c² equation of state was used for both the heavy and the light fluids, where the sound speed c was taken to the incompressible limit c >> v. Simulations were performed at density ratios ranging from 1.5 to 99, corresponding to Atwood numbers in the range 0.2–0.98. The interface between the light and the heavy fluid in a typical A = 0.5 simulation is plotted in Figure 1 at several stages of the instability evolution.

The interface between the heavy and the light fluid in four typical consecutive frames from the A = 0.5 3D RT simulation. a: t = 0.5, b: t = 1.0, c: t = 1.5, d: t = 2.0.

2.2. Simulation results

The simulations were analyzed using both the one-dimensional (1D) volume fraction and the 3D surface separating the heavy and the light fluids.

The 1D volume fraction of the light fluid obtained from the simulations was used to measure the TMZ width in the same manner used to analyze the experimental results (Dimonte & Schneider, 1996). The threshold values of the percentage for the bubble and the spike fronts were usually taken to be 5% and 95%, respectively, in accordance with the values used by Dimonte.

The 3D surface was analyzed to give the total number of bubbles N_total and their spatial positions. An acceleration criterion was used to define the rising bubbles in the RT case: An accelerating (decelerating) bubble was assumed to be rising (sinking). Following Gardner et al. (1988), a velocity criterion was used to define the rising bubbles N_up in the RM case: A bubble with a positive (negative) velocity was assumed to be rising (sinking). N_up and N_down are the number of rising and sinking bubbles, respectively, where N_total = N_up + N_down (see Fig. 2a). The portion of the rising bubbles out of the whole ensemble was close to 50% for all density ratios (see insert in Fig. 2a). Using this scheme, the bubble-front height was obtained by averaging over the tips of the rising bubbles. This 3D definition showed good agreement with the 1D definition of the bubble-front height. Fitting the bubble-front height to a α_B Agt² law in the RT case and a a_B t^θB law in the RM case gave the 3D α_B and θ_B, respectively, in various density ratios.

Quantitative results taken from the A = 0.5 3D RT simulation. a: The temporal evolution of the total number of bubbles (dashed) and the number of rising bubbles (full line). The insert shows the ratio between the rising and the total number of bubbles. b: The temporal evolution of the mean wavelength of the rising bubbles calculated using two methods: dividing the overall area to the number of rising bubbles (full line), and averaging over the different wavelengths (dashed).

The values of α_B and θ_B calculated from the simulations were found to be in good agreement with the experimental results obtained by Dimonte and Schneider (2000) in the LEM experiments, as shown in Figure 3a and 3b. The two growth parameters show nearly Atwood independent behavior. α_B is similar to its 2D value, as obtained in previous numerical and analytical works (Youngs, 1984; Alon et al., 1995), whereas θ_B appears to have a 3D value of about half its 2D one.

Bubble parameter values as a function of A as obtained from the 3D RT simulations (down triangles), the 3D RM simulations (up triangles), the 3D drag–buoyancy equation assuming αB = 0.05, the 3D statistical model (x) and the Dimonte et al. (2000) experiments (dots). a: αB, b: θB, c: b = hB /〈λ〉.

The average wavelength of the system was calculated using two separate methods: The first one was simply dividing the cross section of the vessel S by the number of the rising bubbles:

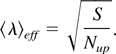
The second method of calculating the average wavelength used the Delaunay triangulation scheme to calculate the average distance l_i of each rising bubble from its closest neighbors:

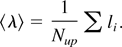
An example of the evolution of the average wavelength in time using the two methods is given in Figure 2b.

The Delaunay triangulation scheme was also used to obtain the wavelength distribution from the simulations and to construct a Voronoi diagram to visualize the distribution of the bubbles, as shown in Figure 4. The wavelength distribution is a key feature of the statistical model that will be discussed in Section 3.

The rising bubble Voronoi cell diagrams in four typical consecutive frames from the A = 0.5 3D RT simulation. a: t = 0.5, b: t = 1.0, c: t = 1.5, d: t = 2.0.

The mean wavelength of the bubbles 〈λ〉 from Eq. 1 was used to calculate the self-similarity parameter b = h_B /〈λ〉, which indicates the mean aspect ratio of the rising bubbles. The values of b (Fig. 3c), which were obtained from both the RT and the RM simulations, are in very good agreement with the experiments. These results also confirm the assumption used in the statistical model, that b^RT ≅ b^RM.

Note that from consistency considerations we compared the mean aspect ratio b of the rising bubbles, rather than the mean aspect ratio of all the bubbles, as done by Dimonte and Schneider (2000). Therefore, the experimental values of b were calculated taking λ to be twice the reported bubble size width d₂ rather than λ = d₂. This estimation of λ is based on the observation mentioned before that at any given time only about half of the bubbles, both in RT and in RM, are rising (see Fig. 2a). Using N_total for the definition of b would have given the same good agreement with the experimental results as reported (λ = d₂).

The simulations' results are supported by the predictions of a simple drag–buoyancy model, also shown in Figure 3, which was taken from Arazi (2001) and Oron et al. (2001). This model is based on the model suggested by Layzer (1955) and Hecht et al. (1994), with an extension to Atwood numbers lower than 1:

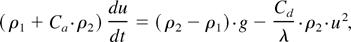
where ρ₁ and ρ₂ are the fluid densities, u is the velocity of the bubble front, g is the acceleration, and λ is the mean wavelength of the bubbles. The added mass coefficient C_a and the drag coefficient C_d are both geometrical constants, independent of A.

Solving this equation for two acceleration profiles—constant for RT and impulsive for RM—gives two equations of motion for the bubble fronts, with three independent parameters: α_B, θ_B, and b = h_B /〈λ〉, the self-similarity parameter that is the same in both the RT and the RM cases (Arazi, 2001), as shown in Figure 3c:

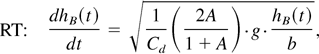
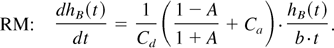
Using the known scaling laws for RT (h_B = α_B Agt²) and RM (h_B = a_B t^θ_B), we obtain the relating equations between the three parameters:

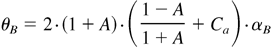
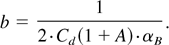
The model's single degree of freedom is degenerated by setting α_B = 0.05, as seen in the simulations, the experiments, and the statistical model that will be presented in Section 3. The model results appearing in Figure 3, which agree well with the experimental results and the simulations, are obtained using the 3D geometrical constants (Layzer, 1955; Hecht et al., 1994; Oron et al., 2001):

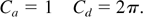
Substituting the 2D values of these constants (C_a = 2, C_d = 6π) into Eqs. (6) and (7) gives the 2D results that agree well with the 2D numerical simulations and statistical model (Alon et al., 1995). These results differ from the experimental results, especially in the values of θ_B (by about a factor of 2) and b (by about a factor of 3).

3. A STATISTICAL BUBBLE-MERGER MODEL

The statistical-mechanics approach to the RT and RM instabilities discussed below is an extension to the 2D model presented by Alon et al. (1993) for the A = 1 case, which was based on the approach suggested by Sharp (1984) and Glimm and Sharp (1990). Adaptations were made to fit the 3D geometry. In this model, we consider an ensemble of bubbles arranged on a surface, characterized only by their diameters d_i. The evolution of the bubbles is divided into two stages:

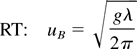
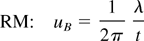
b. Interacting: The interactions between the bubbles occur through merging—two adjacent bubbles merge at a rate ω(λ, λ′) to form a bigger (less drag-detained) bubble with a wavelength

.

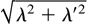
Although in a 3D arrangement of bubbles the average number of neighbors of each bubble is approximately 6, as can be seen in Figure 4, the interactions were assumed to be binary like in the 2D case, only with conservation of area rather than length. This scheme is supported by the simulations, where it was found that at all density ratios, the percentage of rising bubbles out of the whole ensemble was equal to 50% throughout the evolution of the bubble front (see, e.g., Fig. 2a), similar to the 2D simulations.

The evolution equation of the 3D statistical model in the mean-field approximation is

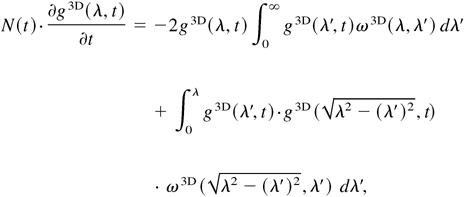
where g^3D(λ, t) is the number of bubbles with a wavelength within dλ of λ at time t, and N(t) is the total number of bubbles at time t. This model results in a self-similar (asymptotic) wavelength distribution

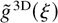
, where ξ = λ/〈λ〉.

In the absence of a bubble-competition potential model in the 3D case, the merger rate between two bubbles ω^3D(λ, λ′) was taken from the 2D model for RT and RM in A = 1 (Alon et al., 1994; Hecht et al., 1994). The 2D merger rate for RM in A = 0 was taken from a vortex competition model (Rikanati et al., 1998). A suitable time-scale adjustment was used due to different time scales in the 2D and the 3D flows: ω^3D = C·ω^2D. The time scale parameter C is the ratio between the 3D and the 2D single-mode velocities (Hecht et al., 1994):

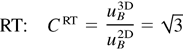
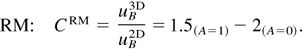
Repeating the model's process numerically with different initial distributions of a large ensemble of bubbles for both the RT and the RM cases gives the asymptotic wavelength distribution

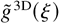
. The distributions are given in Figure 5, with good agreement with the distributions obtained from the 3D simulations using the Delaunay triangulations. The 2D distributions (Alon et al., 1995) are also given in Figure 5 for comparison. Note that the 3D distributions are narrower than the 2D ones, indicating that the 3D bubbles are closer in size. Changing the merger rules between 2 and 6 neighbors had little effect (less than 10%) on the asymptotic distributions, as was demonstrated by Kartoon (2000) and Oron et al. (2001).

The RT (a) and RM (b) scale-invariant wavelength distributions from the 3D simulations in A = 0.5 (full line), the 3D bubble-merger model (dashed, dotted), and the 2D model (dashed-dotted). c: The RT scale-invariant wavelength distribution from the 3D simulations at A = 0.2 (dashed), A = 0.5 (dotted), and A = 0.9 (full line).

The mean bubble-front velocity 〈u〉 and merger rate 〈ω〉 in the self-similar flow regime are calculated by averaging over the asymptotic distributions. These quantities are used to find the scaling parameters (see Kartoon, 2000; Oron et al., 2001):

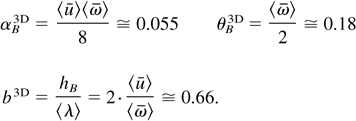
Note that the additional factor of 2 appearing in the denominator of α_B and θ_B and the numerator of b, in comparison to the 2D case (Alon et al., 1994), is due to the area conservation of the merging process.

The growth parameters α_B, θ_B, and b agree well with the experiments, the 3D numerical simulations, and the simple drag–buoyancy model, as seen in Figure 3.

An additional result of the numerical simulations, shown in Figure 5c, is that the asymptotic wavelength distribution is nearly independent of the Atwood number. This, together with the agreement of the results of the model for RM in A = 0 and A = 1, may indicate the validity of the statistical model results over a wide range of Atwood numbers other than A = 1, for which it was originally formulated.

4. THE SPIKE-FRONT EVOLUTION

In contrast to the bubble front, few, if any, analytical models exist for the description of the spike-front evolution. It is commonly accepted that the scaling laws for the spikes are similar to those of the bubbles, only with different scaling parameters α and θ: In the RT case the spike-front height grows as h_S = α_S Agt², and in the RM case it grows as h_S = a_S t^θ_S.

The dependence of α_S and θ_S on the Atwood number, as calculated from the 1D volume fraction in the simulations, is given in Figure 6 and compared to the experimental results of Dimonte et al. In both panels the simulation results are given using three cutoff percentage criteria: 90%, 95%, and 100%. The moderate increase with the Atwood number of α_S taken from the numeric simulations is in good agreement with the experiments, as seen in Figure 6a. Note the same qualitative dependence on A of the three different percentage criteria appearing in the figure. This behavior is also apparent in α_B and θ_B, where three different percentage criteria (0%, 5%, and 10%) are all nearly independent of A, with values within 10%.

Spike parameter values as a function of A as obtained from the 3D simulations using three percentage criteria: 90% (rectangle), 95% (triangles), and 100% (circles), the simple (dashed) and the full 3D drag–buoyancy equation assuming αB = 0.05 (full line) and the Dimonte et al. (1999) experiments (dots). a: αS, b: θS.

The calculated θ_S is consistent with the experimental results up to A ≅ 0.8, whereas it fails to follow the steep increase at Atwood numbers greater than 0.8. This inconsistency is due to the sensitivity of θ_S to different definitions of the cutoff percentage used to determine the height of the spike tips, as can be seen in Figure 6b. A wide spread of the results is also apparent in the experimental results at Atwood numbers greater than 0.8.

A further extension of the drag–buoyancy model, first presented by Alon et al. (1995), gives a prediction of α_S and θ_S as a function of A. The key assumption of the model is that the spike periodicity is equal to that of the dominant bubble, which operates as the driving force for the spikes: 〈λ_S〉(t) = 〈λ_B〉(t). This assumption is supported by the numerical simulations, where at both earlier and later times each pair of bubbles are seen to be separated by a spike, which indicates that the periodicity of the two structures must be the same.

Taking a naïve approach, in which both the bubble and the spike fronts reach their asymptotic velocities together, the ratio between the momentary velocities of the spikes and the bubbles is obtained by simply taking the ratio between their asymptotic velocities. The asymptotic velocities of the spikes are calculated by simply interchanging the two densities ρ₁ and ρ₂ in Eq. (3). This approach gives the approximate expressions

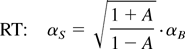
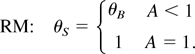
These simple expressions are already in qualitative agreement with the experimental results.

Note that at time t_b, at which the bubble-front height reaches its self-similar value (h_B(t_b) = bλ), the spikes have not yet reached their asymptotic velocity (at Atwood numbers greater than 0). Therefore, more accurate expressions are obtained by taking the ratio between the momentary velocities of the spikes and the bubbles to be the ratio between their velocities at time t_b. Under this assumption, the dependence of the two parameters on the Atwood number is obtained (Arazi, 2001):

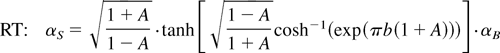
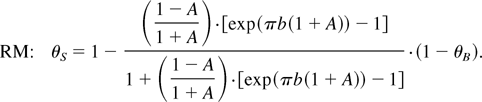
The high sensitivity of θ_B of Eq. (18) to b, in the range 0.9 < A < 1, sheds further light on the spread of the experimental and numerical results presented above. The model results are presented in Figure 6, and are in reasonable agreement with the experiments and the simulations.