1 Introduction
Multi-Agent Systems (MAS) are the systems where autonomous, goal-oriented artificial entities—the agents—participate in. This paper focuses on open MAS, which are systems where the number of agents is unpredictable, as well as their local and interaction behaviours (Piunti, Reference Piunti2009). For these reasons, it is necessary to regulate the agents’ behaviour to conciliate their autonomy with the overall systems’ expectations (Moses & Tennenholtz, Reference Moses and Tennenholtz1995; Castelfranchi, Reference Castelfranchi, Omicini, Tolksdorf and Zambonelli2000; Fasli, Reference Fasli2004). This paper refers to the element that provides such regulation in MAS as artificial institution, or simply institution. Such regulation is usually expressed through regulative norms (henceforth referred just as norms) based on deontic concepts such as obligations, prohibitions, and permissions. Institutions are often viewed as systems where the norms perform their regulative tasks based on an interpretation (also referred in the literature as constitution or classification) of the concrete world (or the environment) where the agents are immersed (Searle, Reference Searle1995; Balke et al., Reference Balke, Pereira, Dignum, Lorini, Rotolo, Vasconcelos, Villata, Andrighetto, Governatori, Noriega and van der Torre2013). Thus, for example, in an auction scenario, norms regulate payments and bids rather than exchanges of paper bills or raising hands. Constitution is usually specified through constitutive rules that specify, for example, that the raising of hands counts as a bid in the context of an auction.
Institutions have thus (i) a constitutive state, which is the institutional interpretation of the current state of the world, according to what is specified by the constitutive rules, and (ii) a normative state, which is the institutional state regarding the expected behaviour of the agents, according to what is specified by the norms. Basing the management of the normative state (i.e. defining norm activations, violations, fulfilments, etc.) on the constitutive state is a key issue in MAS institutions (Boella & van der Torre, Reference Boella, van der Torre, Dubois, Welty and Williams2004; Broersen et al., Reference Broersen, Cranefield, Elrakaiby, Gabbay, Grossi, Lorini, Parent, van der Torre, Tummolini and Turrini2013). Norms and constitutive rules may be combined in a single conceptual model, as proposed, for instance, by Boella and van der Torre (Reference Toni and Torroni2006b), being then jointly managed. In a different direction, some approaches consider that norms and constitutive rules have particular, independent models and management. This is the case of the Situated Artificial Institution (SAI) approach that defines representations and dynamics for the constitutive state (de Brito et al., Reference de Brito, Hübner, Boissier, Bulling, Torre, Villata, Jamroga and Vasconcelos2014, Reference de Brito, Hübner, Boissier, Pereira, Machado, Costa and Cardoso2015a, Reference de Brito, Hübner and Boissier2018), but is not limited to a particular normative model. On the contrary, it assumes that norms, independent of the model they follow, provide the regulation based on a unified representation of constitutive state. This constitutive state is composed of a rich and integrated set of constituted status functions, which are status (or classifications), with corresponding functions, assigned by the institution to the environmental elements (Searle, Reference Searle1995, Reference Searle2009), covering the whole set of abstractions participating in the functioning of the environment: agents acting, events occurring, and states holding. For example, in an auction scenario, (i) an agent may carry the status and perform the function of auctioneer, (ii) the occurrence of an utterance may be an event that carries the status and performs the function of bid, and (iii) a number of agents dwelling in the system may be a state that carries the status and performs the function of minimum quorum.
Basing norms on status functions makes the regulation (i) consistent with the environment under regulation even abstracting from it and (ii) flexible since norms following different models share the same interpretation of the environmental state (de Brito et al., Reference de Brito, Hübner and Boissier2018). However, coupling the management of the normative regulation with a constitutive state composed of constituted status functions, with their particular semantics and dynamics, requires to conceive how the environmental elements of different natures, abstracted under the notion of constituted status functions, are taken into account in the normative management. For example, considering the norm ‘a bidder is obliged to bid’, it is necessary to define (i) how to monitor the norm taking into account every agent considered as bidder, (ii) how to proceed when these agents are no longer considered as bidders (are the obligations kept or revoked?), and (iii) how to verify its compliance when many actions are considered as a bid (is the norm compliance conditioned to the performance of all of these actions or of at least one of them?). This paper addresses such coupling, extending and deepening the initial discussion presented in de Brito et al. (Reference de Brito, Hübner, Boissier, Rovatsos and Vouros2015b). As the main contribution, we define an approach and a formal apparatus to monitor and reason about the norms coupled with a constitutive state composed of constituted status functions. Since it is not possible to investigate the coupling with each existing normative formalism, this paper addresses the coupling with the normative model proposed by Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013), which formalizes the deontic aspects of norms and defines the operational semantics for their monitoring.
This paper is organized as follows: Sections 2 and 3 describe, respectively, the considered normative and constitutive models. While Section 4 describes how normative and constitutive representations are coupled, Section 5 presents our approach to couple the normative and constitutive dynamics. This approach is illustrated in Section 6, discussed in Section 7, and compared with some related works in Section 8, which includes some conclusions and perspectives.
2 Normative model
This section briefly describes the model of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013), firstly defining norms that compose a normative specification and then defining norm instances (i.e. norms enacted in the real world) and their dynamics. The focus is on the essential elements to our proposed coupling. More details about this normative model can be found in Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013).
2.1 Normative specification
Definition 1 (Norm). A norm n is a tuple ![]() $n=\langle \alpha,c_a,c_m, c_d,c_r,c_t\rangle$, where (i)
$n=\langle \alpha,c_a,c_m, c_d,c_r,c_t\rangle$, where (i) ![]() $\alpha$ is the agent obliged to comply with the norm, (ii)
$\alpha$ is the agent obliged to comply with the norm, (ii) ![]() $c_a$ is the activation condition of the norm, (iii)
$c_a$ is the activation condition of the norm, (iii) ![]() $c_m$ is the maintenance condition, (iv)
$c_m$ is the maintenance condition, (iv) ![]() $c_d$ is the deactivation condition, (v)
$c_d$ is the deactivation condition, (v) ![]() $c_r$ is the repair condition, and (vi)
$c_r$ is the repair condition, and (vi) ![]() $c_t$ is the timeout condition. The set of all norms of an institution, noted by
$c_t$ is the timeout condition. The set of all norms of an institution, noted by ![]() $\mathcal{N}$, is called a normative specification.
$\mathcal{N}$, is called a normative specification.
Elements of norms are expressed in first-order predicate language. The element ![]() $\alpha$ is either a constant referring to an agent identifier or a variable that, when grounded, refers to an agent identifier. The remainder c elements are expressed through formulae that may include the connectives
$\alpha$ is either a constant referring to an agent identifier or a variable that, when grounded, refers to an agent identifier. The remainder c elements are expressed through formulae that may include the connectives ![]() $\{\neg,\wedge,\vee\}$. Informally, a norm expresses that if, at some point,
$\{\neg,\wedge,\vee\}$. Informally, a norm expresses that if, at some point, ![]() $c_a$ holds, then the agent
$c_a$ holds, then the agent ![]() $\alpha$ is obliged to see to it that
$\alpha$ is obliged to see to it that ![]() $c_m$ is maintained at least until
$c_m$ is maintained at least until ![]() $c_d$ holds; otherwise,
$c_d$ holds; otherwise, ![]() $\alpha$ is obliged to see to it that
$\alpha$ is obliged to see to it that ![]() $c_r$ holds before the timeout
$c_r$ holds before the timeout ![]() $c_t$. For example, the norm
$c_t$. For example, the norm
expresses that when an agent Ag is driving, he is obliged to not cross the red traffic light LightID until he is not driving; otherwise it has to pay Value before the time 500. Terms starting with uppercase letters are variables that are implicitly universally quantified.
2.2 Normative dynamics
The agents follow norm instances (López y López & Luck, Reference López y López and Luck2003) that are a copy of the specified norms (possibly grounding existing variables). Many instances of the same norm can exist. For example, the norm ‘Buyers are obliged to Pay’ could produce the instances ‘bob is obliged to transfer($100)’ and ‘tom is obliged to deposit($50)’. This section defines how the instances of norms proposed by Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) are represented, and how these instances compose the normative state of an institution.
Definition 2 (Norm instance). Given a norm n and a substitution of variables ![]() $\theta$,Footnote 1 a norm instance is represented by
$\theta$,Footnote 1 a norm instance is represented by ![]() $n^\prime=\langle \alpha^\prime,c_a^\prime,c_m^\prime, c_d^\prime,c_r^\prime,c_t^\prime\rangle$ s.t
$n^\prime=\langle \alpha^\prime,c_a^\prime,c_m^\prime, c_d^\prime,c_r^\prime,c_t^\prime\rangle$ s.t ![]() $\alpha^\prime=\alpha\theta$ is an agent identifier,
$\alpha^\prime=\alpha\theta$ is an agent identifier, ![]() $c_a^\prime=c_a\theta$,
$c_a^\prime=c_a\theta$, ![]() $c_m^\prime=c_m\theta$,
$c_m^\prime=c_m\theta$, ![]() $c_d^\prime=c_d\theta$,
$c_d^\prime=c_d\theta$, ![]() $c_r^\prime=c_r\theta$, and
$c_r^\prime=c_r\theta$, and ![]() $c_t^\prime=c_t\theta$ s.t.
$c_t^\prime=c_t\theta$ s.t. ![]() $\alpha$,
$\alpha$, ![]() $c_a^\prime$ and
$c_a^\prime$ and ![]() $c_t^\prime$ are fully grounded while
$c_t^\prime$ are fully grounded while ![]() $c_m^\prime$,
$c_m^\prime$, ![]() $c_r^\prime$, and
$c_r^\prime$, and ![]() $c_d^\prime$ may be fully or partially grounded.
$c_d^\prime$ may be fully or partially grounded.
Definition 3 (Normative state). The normative state of the institution is a set of norm instances ![]() $N=AS\cup VS\cup DS\cup FS$ s.t. (i) AS is the set of active instances, (ii) VS is the set of violated instances, (iii) DS is the set of deactivated instances, and (iv) FS is the set of failed instances.Footnote 2
$N=AS\cup VS\cup DS\cup FS$ s.t. (i) AS is the set of active instances, (ii) VS is the set of violated instances, (iii) DS is the set of deactivated instances, and (iv) FS is the set of failed instances.Footnote 2
As shown in Figure 1, a norm instance ![]() $n^\prime$ is activated as soon as its activation condition
$n^\prime$ is activated as soon as its activation condition ![]() $c_a^\prime$ is satisfied, getting then into AS, creating an obligation for the agent
$c_a^\prime$ is satisfied, getting then into AS, creating an obligation for the agent ![]() $a^\prime$. The obligation is fulfilled when the deactivation condition
$a^\prime$. The obligation is fulfilled when the deactivation condition ![]() $c_d^\prime$ is satisfied, becoming then deactivated (DS). Active norm instances become violated (VS) when the maintenance condition
$c_d^\prime$ is satisfied, becoming then deactivated (DS). Active norm instances become violated (VS) when the maintenance condition ![]() $c_m^\prime$ is no longer satisfied. Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) consider that violations can be repaired before the timeout
$c_m^\prime$ is no longer satisfied. Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) consider that violations can be repaired before the timeout ![]() $c_t^\prime$. If a norm instance is violated, either (i) satisfying its reparation condition
$c_t^\prime$. If a norm instance is violated, either (i) satisfying its reparation condition ![]() $c_r^\prime$ leads it to deactivated state (DS) or (ii) the occurrence of the timeout condition
$c_r^\prime$ leads it to deactivated state (DS) or (ii) the occurrence of the timeout condition ![]() $c_t^\prime$ leads it to the failure state (FS), when misbehaviours can no longer be repaired.
$c_t^\prime$ leads it to the failure state (FS), when misbehaviours can no longer be repaired.

Figure 1 Life cycle of norm instances, s.t. g(p) is the event of some condition p becoming true (based on Panagiotidi et al., Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013)
The predicates active, viol, deactivated, and failed are defined to check a norm instance with respect to the normative state N as follows:
A normative monitor is the element responsible for checking the current normative state with respect to the current world under regulation. In Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013), a normative monitor is defined as a tuple ![]() $M_N=\langle\mathcal{N},AS,VS,DS,FS,s\rangle$ where (i)
$M_N=\langle\mathcal{N},AS,VS,DS,FS,s\rangle$ where (i) ![]() $\mathcal{N}$ is the set of considered norms, (ii) AS, VS, DS, and FS are the sets of active, violated, deactivated, and failed norm instances, and (iii) s indexes the current state of the normative monitor.The transition system for a normative monitor
$\mathcal{N}$ is the set of considered norms, (ii) AS, VS, DS, and FS are the sets of active, violated, deactivated, and failed norm instances, and (iii) s indexes the current state of the normative monitor.The transition system for a normative monitor ![]() $M_N$ is
$M_N$ is ![]() $TS_{M_N}=\langle\Gamma_{M_N},\triangleright\rangle$, where
$TS_{M_N}=\langle\Gamma_{M_N},\triangleright\rangle$, where ![]() $\Gamma_{M_N}$ is the set of all possible configurations of the normative monitor and
$\Gamma_{M_N}$ is the set of all possible configurations of the normative monitor and ![]() $\triangleright \subseteq {\Gamma _{{M_N}}} \times {\Gamma _{{M_N}}}$ is a transition relation between configurations.The operational semantics of the normative monitor follows the transition rules (5)–(9).
$\triangleright \subseteq {\Gamma _{{M_N}}} \times {\Gamma _{{M_N}}}$ is a transition relation between configurations.The operational semantics of the normative monitor follows the transition rules (5)–(9).
The sets ![]() $\mathcal{N}$, AS, VS, DS, and FS are those of the
$\mathcal{N}$, AS, VS, DS, and FS are those of the ![]() $M_N$. Under a closed world assumption, the conditions
$M_N$. Under a closed world assumption, the conditions ![]() $c_a$,
$c_a$, ![]() $c_d$,
$c_d$, ![]() $c^\prime_m$,
$c^\prime_m$, ![]() $c^\prime_d$,
$c^\prime_d$, ![]() $c^\prime_r$, and
$c^\prime_r$, and ![]() $c^\prime_t$ are evaluated against the state of the world to manage the normative state N as illustrated in Figure 1. For example, by the transition rule (5), if the state of the world satisfies the activation condition but does not satisfy the deactivation condition of a norm—both under a substitution
$c^\prime_t$ are evaluated against the state of the world to manage the normative state N as illustrated in Figure 1. For example, by the transition rule (5), if the state of the world satisfies the activation condition but does not satisfy the deactivation condition of a norm—both under a substitution ![]() $\theta$—then the monitor adds a norm instance
$\theta$—then the monitor adds a norm instance ![]() $n^\prime=\langle \alpha^\prime,c_a\theta,c_m\theta, c_d\theta,c_r\theta,c_t\theta\rangle$ into the set AS. Variables in partially grounded conditions are implicitly universally quantified (Brachman & Levesque, Reference Brachman and Levesque2004).
$n^\prime=\langle \alpha^\prime,c_a\theta,c_m\theta, c_d\theta,c_r\theta,c_t\theta\rangle$ into the set AS. Variables in partially grounded conditions are implicitly universally quantified (Brachman & Levesque, Reference Brachman and Levesque2004).
3 Constitutive model
The SAI model (de Brito et al., Reference de Brito, Hübner and Boissier2018), inspired by the theory of John Searle (Reference Searle1995, Reference Searle2009), considers that, in artificial institutions, the regulation is specified using abstract concepts that do not refer directly to the environment under regulation. For example, the norm ‘the winner of an auction is obliged to pay its offer’ makes sense in the institutional specification of an auction. The norm, however, does not specify (i) what an agent should do to become the winner of the auction or (ii) what an agent must do to perform the payment. In this scenario, winner and payment are status functions: they are status, assigned by the institution to the environmental elements, which impose functions to these elements.Footnote 3 SAI considers that status functions are assigned to agents acting, events occurring, and states holding in the environment. For example, in an auction, an agent may have the agent-status function of winner, the utterance ‘I offer $100’ may have the event-status function of bid, and ‘more than 20 people placed in a room at Friday 10am’ may have the state-status function of minimum quorum for its realization.
The constitution of status functions, that is, their assignment to the environmental elements, produces the constitutive state, which is the institutional interpretation about the environmental state. In SAI, the dynamics of the normative state (i.e. the activation, fulfilment, violation, etc. of the norms) is based on the constitutive state. For example, the norm ‘the winner of the auction is obliged to pay its offer’ is activated when an agent acting in the environment is considered by the institution as carrying the winner status function. The same norm is fulfilled when that agent produces in the environment an event considered by the institution as carrying a payment status function (Figure 2). This section presents the essential background on SAI to base the contribution of this paper. Further details and examples on SAI can be found in de Brito et al. (Reference de Brito, Hübner and Boissier2018) among others. In the following, Section 3.1 describes how the constitution of status functions is specified in SAI, and Section 3.2 describes the dynamics of such constitution.
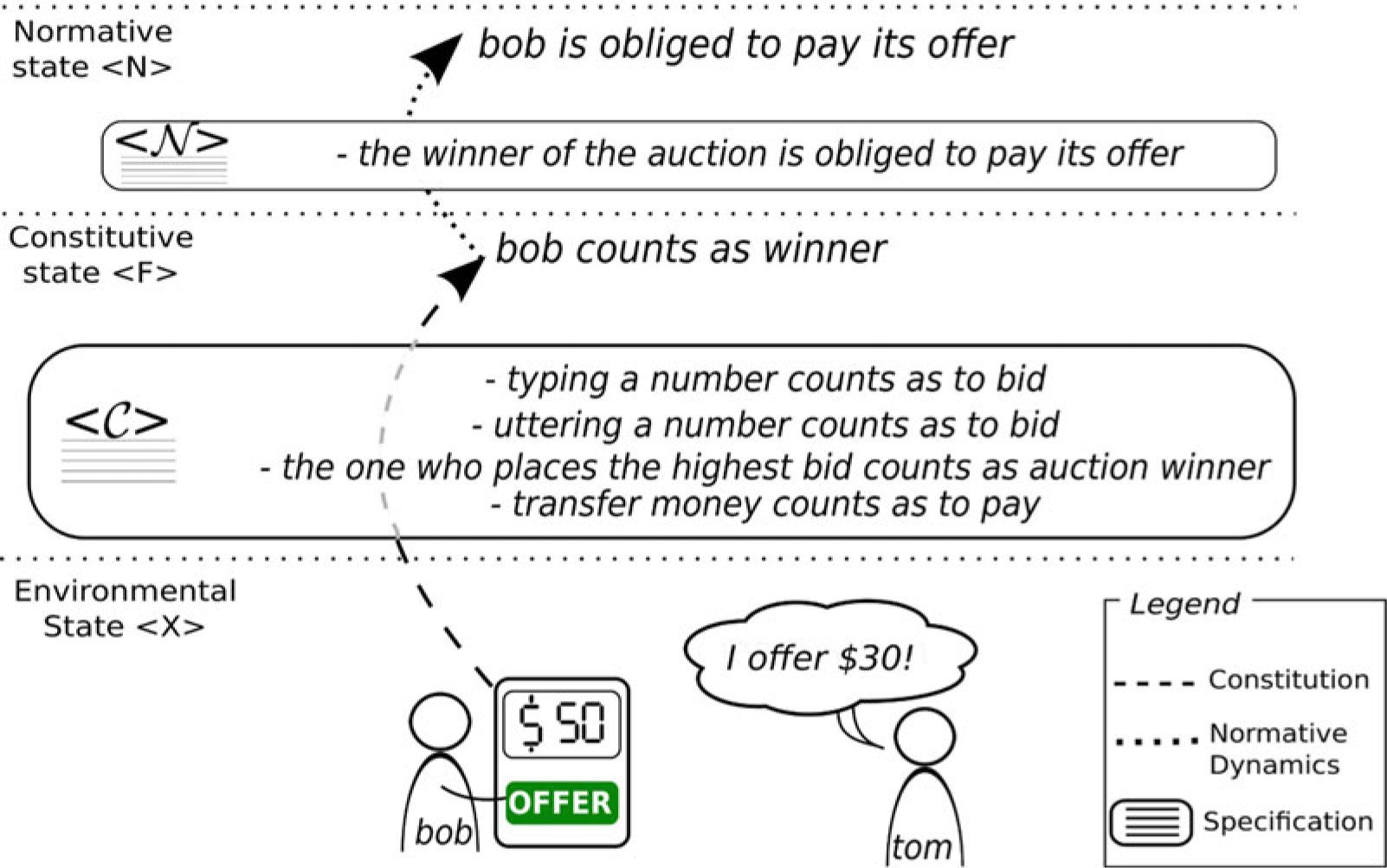
Figure 2 Example of constitution process. In the current environmental state, agents are uttering numbers and are also typing numbers in electronic devices. In the constitutive state, these actions count as bids, and the agent that places the highest bid counts as the winner of the auction, that, according to the normative state, becomes obliged to pay the offer. This obligation can be fulfilled through a money transfer, which, according to a constitutive rule, counts as a payment
3.1 Constitutive specification
The constitutive specification defines, through constitutive rules, how the elements that may be part of the environment, defined below, are considered from the institutional perspective. This section defines constitutive rules according to the SAI model, starting by the elements which they refer to (the environmental elements) and then presenting the elements that are constituted from the environment (the status functions).Footnote 4
Definition 4 (Environmental elements). The environmental elements of interest in SAI are represented by ![]() $\mathcal{X}=\mathcal{A}_{\mathcal{X}}\cup\mathcal{E}_{\mathcal{X}}\cup\mathcal{S}_{\mathcal{X}}$, where
$\mathcal{X}=\mathcal{A}_{\mathcal{X}}\cup\mathcal{E}_{\mathcal{X}}\cup\mathcal{S}_{\mathcal{X}}$, where ![]() $\mathcal{A}_{\mathcal{X}}$ is the set of agents possibly acting in the system,
$\mathcal{A}_{\mathcal{X}}$ is the set of agents possibly acting in the system, ![]() $\mathcal{E}_\mathcal{X}$ is the set of events that may happen in the environment, and
$\mathcal{E}_\mathcal{X}$ is the set of events that may happen in the environment, and ![]() $\mathcal{S}_\mathcal{X}$ is the set of properties used to describe the possible states of the environment.
$\mathcal{S}_\mathcal{X}$ is the set of properties used to describe the possible states of the environment.
Agents ![]() $a_\mathcal{X}\in\mathcal{A}_\mathcal{X}$ are represented by constants (e.g. bob). Events
$a_\mathcal{X}\in\mathcal{A}_\mathcal{X}$ are represented by constants (e.g. bob). Events ![]() $e_\mathcal{X}\in\mathcal{E}_\mathcal{X}$ are pairs (e, a) s.t. e is a first-order logic predicate identifying the event with its arguments and a is (i) either a constant identifying the agent that has triggered the event or (ii)
$e_\mathcal{X}\in\mathcal{E}_\mathcal{X}$ are pairs (e, a) s.t. e is a first-order logic predicate identifying the event with its arguments and a is (i) either a constant identifying the agent that has triggered the event or (ii) ![]() $\varepsilon$ if the event is produced by the environment itself (e.g. a clock tick). Properties
$\varepsilon$ if the event is produced by the environment itself (e.g. a clock tick). Properties ![]() $s_\mathcal{X}\in\mathcal{S_X}$ are represented by first-order logic predicates. It is important to remark that the set
$s_\mathcal{X}\in\mathcal{S_X}$ are represented by first-order logic predicates. It is important to remark that the set ![]() $\mathcal{X}$ is just a representation of the elements that potentially take part in the environment.Footnote 5 For example, when a SAI specification contains an event
$\mathcal{X}$ is just a representation of the elements that potentially take part in the environment.Footnote 5 For example, when a SAI specification contains an event ![]() $e_\mathcal{X}\in\mathcal{E_X}$, it does not mean that
$e_\mathcal{X}\in\mathcal{E_X}$, it does not mean that ![]() $e_\mathcal{X}$ has happened in the environment. Rather, it means that the designer of the institution assumes that
$e_\mathcal{X}$ has happened in the environment. Rather, it means that the designer of the institution assumes that ![]() $e_\mathcal{X}$ may happen.
$e_\mathcal{X}$ may happen.
Definition 5 (Status function). Status functions are functions that the institution assigns to the environmental elements. The status functions of a SAI are represented by ![]() $\mathcal{F}=\mathcal{A_F}\cup\mathcal{E_F}\cup\mathcal{S_F}$, where
$\mathcal{F}=\mathcal{A_F}\cup\mathcal{E_F}\cup\mathcal{S_F}$, where ![]() $\mathcal{A_F}$ is the set of agent-status functions (i.e. status functions assignable to agents
$\mathcal{A_F}$ is the set of agent-status functions (i.e. status functions assignable to agents ![]() $a_\mathcal{X}\in A_\mathcal{X}$),
$a_\mathcal{X}\in A_\mathcal{X}$), ![]() $\mathcal{E_F}$ is the set of event-status functions (i.e. status functions assignable to events
$\mathcal{E_F}$ is the set of event-status functions (i.e. status functions assignable to events ![]() $e_\mathcal{X}\in E_\mathcal{X}$), and
$e_\mathcal{X}\in E_\mathcal{X}$), and ![]() $\mathcal{S_F}$ is the set of state-status functions (i.e. status functions assignable to states
$\mathcal{S_F}$ is the set of state-status functions (i.e. status functions assignable to states ![]() $s_\mathcal{X}\in S_\mathcal{X}$).
$s_\mathcal{X}\in S_\mathcal{X}$).
Agent-status functions are represented by constants. Event- and state-status functions are represented by first-order logic predicates. The assignment of status functions of ![]() $\mathcal{F}$ to the environment elements of
$\mathcal{F}$ to the environment elements of ![]() $\mathcal{X}$ is specified through constitutive rules.
$\mathcal{X}$ is specified through constitutive rules.
Definition 6 (Constitutive rule). The set of all constitutive rules of a SAI is represented by ![]() $\mathcal{C}$. A constitutive rule
$\mathcal{C}$. A constitutive rule ![]() $c\in\mathcal{C}$ is a tuple
$c\in\mathcal{C}$ is a tuple ![]() $\langle x,y,t,m\rangle$ meaning that
$\langle x,y,t,m\rangle$ meaning that ![]() $x\in\mathcal{F}\cup\mathcal{X}\cup Var\cup\lbrace\varepsilon\rbrace$ counts as (i.e. x has the status function)
$x\in\mathcal{F}\cup\mathcal{X}\cup Var\cup\lbrace\varepsilon\rbrace$ counts as (i.e. x has the status function) ![]() $y\in \mathcal{F}$ when the event
$y\in \mathcal{F}$ when the event ![]() $t\in\mathcal{E_F}\cup\mathcal{E_X}\cup\lbrace\varepsilon\rbrace$ has happened and while the condition represented by m holds.Footnote 6
$t\in\mathcal{E_F}\cup\mathcal{E_X}\cup\lbrace\varepsilon\rbrace$ has happened and while the condition represented by m holds.Footnote 6
A constitutive rule where ![]() $x=\varepsilon$ specifies a freestanding assignment of the status function y, that is, an assignment where there is no concrete environmental element carrying y (Searle, Reference Searle2009; de Brito et al., Reference de Brito, Hübner and Boissier2018). In the case of
$x=\varepsilon$ specifies a freestanding assignment of the status function y, that is, an assignment where there is no concrete environmental element carrying y (Searle, Reference Searle2009; de Brito et al., Reference de Brito, Hübner and Boissier2018). In the case of ![]() $t=\varepsilon \wedge m=\top$, the constitutive rule is simply read as x
$t=\varepsilon \wedge m=\top$, the constitutive rule is simply read as x
![]() $\texttt{count-as}$
y since y is assigned to x in any circumstance. The element x may be a variable
$\texttt{count-as}$
y since y is assigned to x in any circumstance. The element x may be a variable ![]() $var\in Var$ that is substituted by an element belonging either to
$var\in Var$ that is substituted by an element belonging either to ![]() $\mathcal{F}$ or to
$\mathcal{F}$ or to ![]() $\mathcal{X}$ when the constitutive rule is interpreted. When x actually counts as y (i.e. when the conditions t and m declared in the constitutive rule are true), we say that there is a status function assignment (SFA) of the status function y to the element x. The establishment of a SFA of y to some x is the constitution of y.
$\mathcal{X}$ when the constitutive rule is interpreted. When x actually counts as y (i.e. when the conditions t and m declared in the constitutive rule are true), we say that there is a status function assignment (SFA) of the status function y to the element x. The establishment of a SFA of y to some x is the constitution of y.
According to Definition 6, the constitution of status functions is conditioned by m. The following BNF grammar defines all the well-formed formulae for m (hereafter m-formulae)Footnote 7
 \begin{align}
m ::=\ & s_\mathcal{X}\ |\ e_\mathcal{X}\ |\ s_\mathcal{F}\ |\ e_\mathcal{F} \ | \neg m \ |\ m \vee m |\ m \wedge m\ | \ \bot\ |\ \top \ | \nonumber\\ & (a_\mathcal{X}|Var)\ \texttt{"is"}(\ a_\mathcal{F}|Var)\ |\ (e_\mathcal{X}|Var)\ \texttt{"is"}\ (e_\mathcal{F}|Var)\ |\ (s_\mathcal{X}|Var)\ \texttt{"is"}\ (s_\mathcal{F}|Var) \nonumber\end{align}
\begin{align}
m ::=\ & s_\mathcal{X}\ |\ e_\mathcal{X}\ |\ s_\mathcal{F}\ |\ e_\mathcal{F} \ | \neg m \ |\ m \vee m |\ m \wedge m\ | \ \bot\ |\ \top \ | \nonumber\\ & (a_\mathcal{X}|Var)\ \texttt{"is"}(\ a_\mathcal{F}|Var)\ |\ (e_\mathcal{X}|Var)\ \texttt{"is"}\ (e_\mathcal{F}|Var)\ |\ (s_\mathcal{X}|Var)\ \texttt{"is"}\ (s_\mathcal{F}|Var) \nonumber\end{align}The semantics of the m-formulae is given in Section 3.2 as it depends on the environmental and constitutive states that are also defined in that section.
3.2 Constitutive dynamics
Status functions are dynamically assigned to the actual environmental elements by the interpretation of constitutive rules. This section introduces the elements that are relevant to coupling this dynamics with the normative one.
Definition 7 (Environmental state). The actual environmental state is represented by ![]() $X=A_X\cup E_X \cup S_X$, where (i)
$X=A_X\cup E_X \cup S_X$, where (i) ![]() $A_X$ is the set of agents participating in the system, (ii)
$A_X$ is the set of agents participating in the system, (ii) ![]() $E_X$ is the set of events occurring in the environment, and (iii)
$E_X$ is the set of events occurring in the environment, and (iii) ![]() $S_X$ is the set of environmental properties describing the environmental state.
$S_X$ is the set of environmental properties describing the environmental state.
Agents ![]() $a_X\in A_X$ are represented by constants referring to their identifiers. States
$a_X\in A_X$ are represented by constants referring to their identifiers. States ![]() $s_X\in S_X$ are represented by atomic formulae. Events
$s_X\in S_X$ are represented by atomic formulae. Events ![]() $e_X\in E_X$ are represented by pairs (e, a) where e is the event, represented by an atomic formulae, triggered by the agent a. Events can be triggered by actions of the agents (e.g. the utterance of a bid in an auction) but can also be produced by the environment itself (e.g. a clock tick). In this case, events are represented by pairs
$e_X\in E_X$ are represented by pairs (e, a) where e is the event, represented by an atomic formulae, triggered by the agent a. Events can be triggered by actions of the agents (e.g. the utterance of a bid in an auction) but can also be produced by the environment itself (e.g. a clock tick). In this case, events are represented by pairs ![]() ${(e,\varepsilon)}$.
${(e,\varepsilon)}$.
Definition 8 (Constitutive state). The constitutive state of a SAI is the set of the existing SFAs. It is represented by ![]() $F= A_F\cup E_F \cup S_F$, where (i)
$F= A_F\cup E_F \cup S_F$, where (i) ![]() $A_F\subseteq A_X\times\mathcal{A_F}$ is the set of agent-SFAs, (ii)
$A_F\subseteq A_X\times\mathcal{A_F}$ is the set of agent-SFAs, (ii) ![]() $E_F\subseteq E_X\times\mathcal{E_F}\times A_X\cup \{\varepsilon\}$ is the set of event-SFAs, and (iii)
$E_F\subseteq E_X\times\mathcal{E_F}\times A_X\cup \{\varepsilon\}$ is the set of event-SFAs, and (iii) ![]() $S_F\subseteq S_X\cup \{\varepsilon\}\times\mathcal{S_F}$ is the set of state-SFAs.
$S_F\subseteq S_X\cup \{\varepsilon\}\times\mathcal{S_F}$ is the set of state-SFAs.
Elements of F are SFAs, that is, relations between environmental elements and status functions. Elements of ![]() $A_F$ are pairs
$A_F$ are pairs ![]() $\langle a_X,a_\mathcal{F}\rangle$ meaning that the agent
$\langle a_X,a_\mathcal{F}\rangle$ meaning that the agent ![]() $a_X$ has the status function
$a_X$ has the status function ![]() $a_\mathcal{F}$. Elements of
$a_\mathcal{F}$. Elements of ![]() $E_F$ are triples
$E_F$ are triples ![]() $\langle e_X, e_\mathcal{F},a_X\rangle$ meaning that the event-status function
$\langle e_X, e_\mathcal{F},a_X\rangle$ meaning that the event-status function ![]() $e_\mathcal{F}$ is assigned to the event
$e_\mathcal{F}$ is assigned to the event ![]() $e_X$ produced by the agent
$e_X$ produced by the agent ![]() $a_X$.Footnote 8 Elements of
$a_X$.Footnote 8 Elements of ![]() $S_F$ are pairs
$S_F$ are pairs ![]() $\langle s_X,s_\mathcal{F}\rangle$ meaning that the state
$\langle s_X,s_\mathcal{F}\rangle$ meaning that the state ![]() $s_X$ carries the status function
$s_X$ carries the status function ![]() $s_\mathcal{F}$.The process of interpretation of constitutive rules that builds the constitutive state is detailed in de Brito et al. (Reference de Brito, Hübner and Boissier2018). Briefly, if the actual environment holds the elements t and m of a constitutive rule
$s_\mathcal{F}$.The process of interpretation of constitutive rules that builds the constitutive state is detailed in de Brito et al. (Reference de Brito, Hübner and Boissier2018). Briefly, if the actual environment holds the elements t and m of a constitutive rule ![]() $\langle x,y,t,m\rangle$, then the environmental element x constitutes the status function y, producing an SFA. If the environment is no longer holding the condition m that maintains an existing SFA, then such SFA is dropped from the constitutive state (as illustrated in Figure 3).
$\langle x,y,t,m\rangle$, then the environmental element x constitutes the status function y, producing an SFA. If the environment is no longer holding the condition m that maintains an existing SFA, then such SFA is dropped from the constitutive state (as illustrated in Figure 3).

Figure 3 Example of constitutive state changes along time. At some moment, while a state m holds, an event t happens (cf. the first arrow in the bottom of the picture). By the constitutive rule ![]() $\texttt{x count-as y when t while m}$ (
$\texttt{x count-as y when t while m}$ (![]() $\langle x,y,t,m\rangle \in \mathcal{C}$), such conditions lead the environmental element x to count as y in the constitutive state (cf. the dashed line). Then, the event
$\langle x,y,t,m\rangle \in \mathcal{C}$), such conditions lead the environmental element x to count as y in the constitutive state (cf. the dashed line). Then, the event ![]() $t^\prime$ occurs while the state
$t^\prime$ occurs while the state ![]() $m^\prime$ holds. By the constitutive rule
$m^\prime$ holds. By the constitutive rule ![]() $\texttt{y count-as y'}$
$\texttt{y count-as y'}$
![]() $\texttt{when t' while m'}$, the element that counts as y (i.e. x) counts also as
$\texttt{when t' while m'}$, the element that counts as y (i.e. x) counts also as ![]() $y^\prime$ (cf. the dotted horizontal line). When the state m ceases to hold, the conditions to x count as y also cease to hold, and as x is no longer counting as y, it also ceases to count
$y^\prime$ (cf. the dotted horizontal line). When the state m ceases to hold, the conditions to x count as y also cease to hold, and as x is no longer counting as y, it also ceases to count ![]() $y^\prime$. For example, if
$y^\prime$. For example, if ![]() $x=bob,y=bidder,\text{ and }y^\prime=auction_\kern0.7ptparticipant$, s.t.
$x=bob,y=bidder,\text{ and }y^\prime=auction_\kern0.7ptparticipant$, s.t. ![]() $bob\in\mathcal{A_X}$ and
$bob\in\mathcal{A_X}$ and ![]() $\{bidder,auction_\kern0.7ptparticipant\}\subseteq\mathcal{A_F}$, then bob counts as (i) bidder from t and (ii)
$\{bidder,auction_\kern0.7ptparticipant\}\subseteq\mathcal{A_F}$, then bob counts as (i) bidder from t and (ii) ![]() $auction_\kern0.7ptparticipant$ from
$auction_\kern0.7ptparticipant$ from ![]() $t^\prime$
$t^\prime$
Both the environmental and constitutive states are used to evaluate the m-formulae defined in Section 3.1. For a model ![]() $M=\langle F,X,\mathcal{F}\rangle$, the semantics of m-formulae is defined as follows:
$M=\langle F,X,\mathcal{F}\rangle$, the semantics of m-formulae is defined as follows:
 \begin{align} M \models m \text{ iff } \exists\theta:& (m\theta\in E_X\vee m\theta\in S_X)\vee\\[3pt]
& (\exists (e,a)\in E_X: \langle e,m\theta,a\rangle\in E_F)\ \vee\nonumber\\[3pt]
& (\exists s_X\in S_X: \langle s_X,m\theta\rangle\in S_F)\nonumber\end{align}
\begin{align} M \models m \text{ iff } \exists\theta:& (m\theta\in E_X\vee m\theta\in S_X)\vee\\[3pt]
& (\exists (e,a)\in E_X: \langle e,m\theta,a\rangle\in E_F)\ \vee\nonumber\\[3pt]
& (\exists s_X\in S_X: \langle s_X,m\theta\rangle\in S_F)\nonumber\end{align} \begin{align}
M \models x\ {\bf is }\ y \text{ iff }\exists\theta: & (x\theta\in A_X\wedge y\theta\in\mathcal{A_F}\wedge\langle x\theta,y\theta\rangle\in A_F)\vee \\[3pt]
& (x\theta\in E_X\wedge x=(e,a)\wedge y\theta\in\mathcal{E_F}\wedge\langle e\theta,y\theta,a\theta \rangle\in E_F)\vee\nonumber\\[3pt]
& (x\theta\in S_X\wedge y\theta\in\mathcal{S_F}\wedge\langle x\theta,y\theta\rangle\in S_F)\nonumber\end{align}
\begin{align}
M \models x\ {\bf is }\ y \text{ iff }\exists\theta: & (x\theta\in A_X\wedge y\theta\in\mathcal{A_F}\wedge\langle x\theta,y\theta\rangle\in A_F)\vee \\[3pt]
& (x\theta\in E_X\wedge x=(e,a)\wedge y\theta\in\mathcal{E_F}\wedge\langle e\theta,y\theta,a\theta \rangle\in E_F)\vee\nonumber\\[3pt]
& (x\theta\in S_X\wedge y\theta\in\mathcal{S_F}\wedge\langle x\theta,y\theta\rangle\in S_F)\nonumber\end{align}From the expression (10), an m-formula m is satisfied by M (i) if it represents either an event actually occurring or a state actually holding in the environment; (ii) if it represents an event-status function assigned to some environmental elements; or (iii) if it represents a state-status function assigned to some environmental state. From the expression (11), an m-formula is satisfied by M if it has the form ![]() $x {\ \text{is}\ } y$ and if, under a substitution
$x {\ \text{is}\ } y$ and if, under a substitution ![]() $\theta$, either (i)
$\theta$, either (i) ![]() $x\theta$ is the identifier of an agent that carries the agent-status function
$x\theta$ is the identifier of an agent that carries the agent-status function ![]() $y\theta$ or (ii)
$y\theta$ or (ii) ![]() $x\theta$ identifies an event that actually carries the event-status function
$x\theta$ identifies an event that actually carries the event-status function ![]() $y\theta$ or (iii)
$y\theta$ or (iii) ![]() $x\theta$ identifies a state that actually carries the state-status function
$x\theta$ identifies a state that actually carries the state-status function ![]() $y\theta$. As usual,
$y\theta$. As usual, ![]() $M\models \top$ and
$M\models \top$ and ![]() $M\not\models\bot$.
$M\not\models\bot$.

Figure 4 Example of constitutive specification
3.3 Example of SAI constitutive specification
Based on the described constitutive model, a language to specify the constitution of status functions is proposed in de Brito et al. (Reference de Brito, Hübner and Boissier2018). In that language, the symbols ![]() $\texttt{"not"}$,
$\texttt{"not"}$, ![]() $\texttt{"|"}$,
$\texttt{"|"}$, ![]() $\rm{"\&"}$,
$\rm{"\&"}$, ![]() $\texttt{"false"}$, and
$\texttt{"false"}$, and ![]() $\texttt{"true"}$ correspond respectively to
$\texttt{"true"}$ correspond respectively to ![]() $\neg$,
$\neg$, ![]() $\vee$,
$\vee$, ![]() $\wedge$,
$\wedge$, ![]() $\bot$, and
$\bot$, and ![]() $\top$ in the m-formulae. Figure 4 shows the constitutive specification for a use case where agents collaborate to manage crisis such as flooding and car crashes in zones that may be either insecure (only professional people intervene) or secure (admits unprofessional intervention) (de Brito et al., Reference de Brito, Thévin, Garbay, Boissier, Hübner, Demazeau, Decker, Pérez and de la Prieta2015c). Norms regulate the collaboration (e.g. firefighters are obliged to evacuate insecure zones). The environment is composed of geographic information systems (GIS) and of tangible tables (Kubicki et al., Reference Kubicki, Lepreux and Kolski2012), where the agents put objects equipped with RFID tags on to signal their intended actions. The relevant information provided by the GIS are
$\top$ in the m-formulae. Figure 4 shows the constitutive specification for a use case where agents collaborate to manage crisis such as flooding and car crashes in zones that may be either insecure (only professional people intervene) or secure (admits unprofessional intervention) (de Brito et al., Reference de Brito, Thévin, Garbay, Boissier, Hübner, Demazeau, Decker, Pérez and de la Prieta2015c). Norms regulate the collaboration (e.g. firefighters are obliged to evacuate insecure zones). The environment is composed of geographic information systems (GIS) and of tangible tables (Kubicki et al., Reference Kubicki, Lepreux and Kolski2012), where the agents put objects equipped with RFID tags on to signal their intended actions. The relevant information provided by the GIS are ![]() $\texttt{security-phase(Zone,Phase)}$, when a
$\texttt{security-phase(Zone,Phase)}$, when a ![]() $\texttt{Zone}$ is in a specific
$\texttt{Zone}$ is in a specific ![]() $\texttt{Phase}$ of the crisis management, and
$\texttt{Phase}$ of the crisis management, and ![]() $\texttt{nb_inhabit(Zone,X)}$ when a
$\texttt{nb_inhabit(Zone,X)}$ when a ![]() $\texttt{Zone}$ has
$\texttt{Zone}$ has ![]() $\texttt{X}$ inhabitants. The event
$\texttt{X}$ inhabitants. The event ![]() $\texttt{put_tangible(Object,X,Y,Agent)}$ is triggered when an
$\texttt{put_tangible(Object,X,Y,Agent)}$ is triggered when an ![]() $\texttt{Agent}$ puts an
$\texttt{Agent}$ puts an ![]() $\texttt{Object}$ on the coordinates (
$\texttt{Object}$ on the coordinates (![]() $\texttt{X}$,
$\texttt{X}$, ![]() $\texttt{Y}$) of a tangible table. The event
$\texttt{Y}$) of a tangible table. The event ![]() $\texttt{send_message(Content,Zone,Agent)}$ is triggered when an
$\texttt{send_message(Content,Zone,Agent)}$ is triggered when an ![]() $\texttt{Agent}$ sends a message with some
$\texttt{Agent}$ sends a message with some ![]() $\texttt{Content}$ with respect to a
$\texttt{Content}$ with respect to a ![]() $\texttt{Zone}$.The actions of the agents upon the tables, as well as the information from the GIS,do not have per se any meaning in the crisis scenario and, thus, they cannot ground, by themselves, the checking of the norm compliance. For instance, an agent putting an object on a specific point of the table does not mean, by itself, a command for the evacuation of a zone. Such action becomes meaningful in the crisis scenario through the interpretation of constitutive rules. For example, agents are recognized as mayor and firefighter according to the table where they are acting in (constitutive rules 1 and 2) and putting a launch_object on the coordinates (2,2) of a table signals the evacuation of the downtown (constitutive rule 3).
$\texttt{Zone}$.The actions of the agents upon the tables, as well as the information from the GIS,do not have per se any meaning in the crisis scenario and, thus, they cannot ground, by themselves, the checking of the norm compliance. For instance, an agent putting an object on a specific point of the table does not mean, by itself, a command for the evacuation of a zone. Such action becomes meaningful in the crisis scenario through the interpretation of constitutive rules. For example, agents are recognized as mayor and firefighter according to the table where they are acting in (constitutive rules 1 and 2) and putting a launch_object on the coordinates (2,2) of a table signals the evacuation of the downtown (constitutive rule 3).
4 Linking normative and constitutive representations
Normative models look to the ‘state of the world’ to check the agents’ expected behaviour. When norms are part of SAI, this ‘state of the world’ is the constitutive state. Basing the normative regulation on the constitutive state requires to define (i) how the ‘world’ represented by the constitutive elements is captured by the representations of norms and norm instances and (ii) how the different components of the norms are evaluated considering the different nature of the constituted elements in the different states of the life cycle of the norm instances. The first point is addressed in this section. The second point is addressed in Section 5.
4.1 Representing norms through status functions
Evaluating norms with respect to the constitutive and to the normative state itself requires to define expressions that can be used to evaluate those states. Conditions over the whole constitutive state are expressed through sf-formulae
![]() $m_\mathcal{F}\in M_\mathcal{F}$. The sf-formulae are particular cases of the m-formulae whose atomic formulae are either event/state-status functions or expressions of the type
$m_\mathcal{F}\in M_\mathcal{F}$. The sf-formulae are particular cases of the m-formulae whose atomic formulae are either event/state-status functions or expressions of the type ![]() $x\ \mathbf{ is }\ y$. The syntax of sf-formulae is given by the grammar (12) and their semantics follows the expressions (10) and (11).
$x\ \mathbf{ is }\ y$. The syntax of sf-formulae is given by the grammar (12) and their semantics follows the expressions (10) and (11).
The sf-formulae can be combined with the predicates active, viol, deactivated, and failed, evaluated according to the expressions (1)–(4) in the n-formulae ********![]() $m_N\in M_N$, that follow the grammar (13).
$m_N\in M_N$, that follow the grammar (13).
To link the representation of norms presented in Section 2 to the constitutive state presented in Section 3, we need to introduce status functions in the norms. For a norm ![]() $n\in\mathcal{N}$, where
$n\in\mathcal{N}$, where ![]() $n=\langle \alpha,c_a,c_m, c_d,c_r,c_t\rangle$, we define that
$n=\langle \alpha,c_a,c_m, c_d,c_r,c_t\rangle$, we define that ![]() $\alpha\in\mathcal{A_F}$,
$\alpha\in\mathcal{A_F}$, ![]() $c_a\in M_N$,
$c_a\in M_N$, ![]() $c_m\in M_N$,
$c_m\in M_N$, ![]() $c_d\in\mathcal{E_F}\cup\mathcal{S_F}$,
$c_d\in\mathcal{E_F}\cup\mathcal{S_F}$, ![]() $c_r\in\mathcal{E_F}\cup\mathcal{S_F}$, and
$c_r\in\mathcal{E_F}\cup\mathcal{S_F}$, and ![]() $c_t\in M_N$. The reasons for linking the elements of the norm with these particular types are:
$c_t\in M_N$. The reasons for linking the elements of the norm with these particular types are:
• A norm is directed to agents carrying an agent-status function (
 $\alpha \in\mathcal{A_F}$) and not to concrete agents.
$\alpha \in\mathcal{A_F}$) and not to concrete agents.• Deactivation and repairing conditions are expressed with event- and state-status functions. From the institutional perspective, agents must behave as prescribed by the norms and then produce, in the environment, events and states that can be interpreted as the corresponding event- and state-status functions.
• Activation, maintenance, and timeout refer to the whole constitutive and normative states and, thus, are referred in norms through particular types of formulae.
Figure 5 shows the norms as conceived in Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) using the status functions defined in the constitutive specification shown in Figure 4 to specify that (i) the mayor is obliged to evacuate secure zones and (ii) firefighters are obliged to evacuate insecure zones.

Figure 5 Norms using status functions
4.2 Linking representations of norm instances to the constitutive state
While norms refer to agent-status functions (i.e. ![]() $\alpha\in\mathcal{A_F}$), their instances prescribe the behaviour of the concrete agents acting in the environment. The obligation of an agent
$\alpha\in\mathcal{A_F}$), their instances prescribe the behaviour of the concrete agents acting in the environment. The obligation of an agent ![]() $a_X$ to follow a norm instance
$a_X$ to follow a norm instance ![]() $n^\prime$ is conditioned by its carrying of the status function
$n^\prime$ is conditioned by its carrying of the status function ![]() $\alpha$ as prescribed in the norm n. As detailed later in the expressions (15)–(18), to check this condition norm instances must record both the agent to whom the norm is directed and the status function carried by that agent when the instance was created. Thus, the representation of norm instance of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) is extended to
$\alpha$ as prescribed in the norm n. As detailed later in the expressions (15)–(18), to check this condition norm instances must record both the agent to whom the norm is directed and the status function carried by that agent when the instance was created. Thus, the representation of norm instance of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) is extended to ![]() $n^\prime=\langle (a_X,\alpha),c_a^\prime,c_m^\prime, c_d^\prime,c_r^\prime,c_t^\prime\rangle$, where
$n^\prime=\langle (a_X,\alpha),c_a^\prime,c_m^\prime, c_d^\prime,c_r^\prime,c_t^\prime\rangle$, where ![]() $a_X\in A_X$ points to the concrete agent targeted by the norm instance and
$a_X\in A_X$ points to the concrete agent targeted by the norm instance and ![]() $\alpha\in\mathcal{A_F}$ is the status function carried by that agent when the instance was created. The remainder elements are those from Definition 2. The elements
$\alpha\in\mathcal{A_F}$ is the status function carried by that agent when the instance was created. The remainder elements are those from Definition 2. The elements ![]() $c_m^\prime, c_d^\prime,c_r^\prime$ may be partially grounded while the remainder ones are fully grounded.
$c_m^\prime, c_d^\prime,c_r^\prime$ may be partially grounded while the remainder ones are fully grounded.
5 Coupling normative and constitutive dynamics
Having defined how normative and constitutive representations are linked, this section explains how the dynamics of the normative and constitutive states are coupled. Section 5.1 explains when, given the constitutive and normative states, norm instances are considered activated, deactivated, violated, and failed. These definitions can be used by the normative monitors that implement the operational semantics of the normative model, as shown in Section 5.2.
5.1 Norm activation, deactivation, violation, and failure
5.1.1 Activation
Given a normative specification ![]() $\mathcal{N}$, a constitutive state F, and a normative state N, the set of norm instances to be created is given by the function activated defined below:
$\mathcal{N}$, a constitutive state F, and a normative state N, the set of norm instances to be created is given by the function activated defined below:
The creation of norm instances is conditioned by the constitutive and normative states satisfying the activation condition ![]() $c_a$ for some substitution
$c_a$ for some substitution ![]() $\theta$ (i.e.
$\theta$ (i.e. ![]() $F\cup N\models c_a\theta$). The evaluation of
$F\cup N\models c_a\theta$). The evaluation of ![]() $c_a$ with respect to N follows the expressions (1)–(4). Its evaluation with respect to F follows the expressions (10) and (11). By the function activated, a norm directed to an agent-status function
$c_a$ with respect to N follows the expressions (1)–(4). Its evaluation with respect to F follows the expressions (10) and (11). By the function activated, a norm directed to an agent-status function ![]() $\alpha$ produces an instance for every concrete agent
$\alpha$ produces an instance for every concrete agent ![]() $a_X$ carrying
$a_X$ carrying ![]() $\alpha$. For example, considering the constitutive specification in Figure 4, if both agents bob and tom carry the status function of firefighter (i.e.
$\alpha$. For example, considering the constitutive specification in Figure 4, if both agents bob and tom carry the status function of firefighter (i.e. ![]() $\{\langle bob,firefighter\rangle,\langle tom, firefighter\rangle\}\subseteq A_F$) and the downtown is in emergency phase of crisis, being thus insecure (i.e.
$\{\langle bob,firefighter\rangle,\langle tom, firefighter\rangle\}\subseteq A_F$) and the downtown is in emergency phase of crisis, being thus insecure (i.e. ![]() $\langle security_\kern0.7ptphase(downtown, emergency), insecure(downtown) \rangle\in S_F $), then (i)
$\langle security_\kern0.7ptphase(downtown, emergency), insecure(downtown) \rangle\in S_F $), then (i) ![]() $F\models insecure(downtown)$, (ii)
$F\models insecure(downtown)$, (ii) ![]() $F\models bob {\bf{is}} firefighter$, and (iii)
$F\models bob {\bf{is}} firefighter$, and (iii) ![]() $F\models tom {\bf{is}} firefighter$. Thus, as illustrated in Figure 6, the following instances of the norm 2 of Figure 5 are created:
$F\models tom {\bf{is}} firefighter$. Thus, as illustrated in Figure 6, the following instances of the norm 2 of Figure 5 are created:

Figure 6 Example of norm activation. The normative specification contains a norm stating that when the downtown is insecure, firefighters are obliged to evacuate it (cf. Figure 5). The environment is in a state that counts as the downtown being insecure in the constitutive state. The holding of such condition in the constitutive state produces an instance of that norm for each agent counting as firefighter
 \begin{align*} \langle (bob,firefighter),insecure(downtown),insecure(downtown),evacuate(downtown),\bot,\neg insecure(downtown)\rangle\\[2pt] \langle (tom,firefighter),insecure(downtown),insecure(downtown),evacuate(downtown),\bot,\neg insecure(downtown)\rangle\end{align*}
\begin{align*} \langle (bob,firefighter),insecure(downtown),insecure(downtown),evacuate(downtown),\bot,\neg insecure(downtown)\rangle\\[2pt] \langle (tom,firefighter),insecure(downtown),insecure(downtown),evacuate(downtown),\bot,\neg insecure(downtown)\rangle\end{align*}5.1.2 Deactivation
In the considered normative model, obligations are fulfilled when norm instances are deactivated. Deactivations are considered separately according to the nature of the deactivation condition (event or state). The functions ![]() $ f\text{-}deactivated^e$ and
$ f\text{-}deactivated^e$ and ![]() $f\text{-}deactivated^s$ deal respectively with deactivations of active instances conditioned by events and by states.
$f\text{-}deactivated^s$ deal respectively with deactivations of active instances conditioned by events and by states.
 \begin{align} f\hbox{-}deactivated^e(F,N) = \{\langle n^\prime\arrowvert &\exists (e_X,a_X)\in E_X: n^\prime \in AS \wedge c_d^\prime\in \mathcal{E}_\mathcal{F} \wedge \nonumber \\[4pt]
& F\models ((e_X,a_X) {\bf{is}} c_d^\prime \vee \neg (a_X\,{\bf{is}}\,\alpha))\wedge F\cup N\models c_m^\prime\} \end{align}
\begin{align} f\hbox{-}deactivated^e(F,N) = \{\langle n^\prime\arrowvert &\exists (e_X,a_X)\in E_X: n^\prime \in AS \wedge c_d^\prime\in \mathcal{E}_\mathcal{F} \wedge \nonumber \\[4pt]
& F\models ((e_X,a_X) {\bf{is}} c_d^\prime \vee \neg (a_X\,{\bf{is}}\,\alpha))\wedge F\cup N\models c_m^\prime\} \end{align} \begin{align} f\hbox{-}deactivated^s(F,N) = \{\langle n^\prime\arrowvert & n^\prime \in AS \wedge \nonumber c_d^\prime\in \mathcal{S_F} \wedge\\[4pt]
& F\models (c_d^\prime \vee \neg (a_X\,{\bf{is}}\,\alpha)) \wedge F\cup N\models c_m^\prime\} \end{align}
\begin{align} f\hbox{-}deactivated^s(F,N) = \{\langle n^\prime\arrowvert & n^\prime \in AS \wedge \nonumber c_d^\prime\in \mathcal{S_F} \wedge\\[4pt]
& F\models (c_d^\prime \vee \neg (a_X\,{\bf{is}}\,\alpha)) \wedge F\cup N\models c_m^\prime\} \end{align}The function ![]() $f\hbox{-}deactivated^e$ captures the notion of events as being considered at the individual agent level. The obligation of an agent
$f\hbox{-}deactivated^e$ captures the notion of events as being considered at the individual agent level. The obligation of an agent ![]() $a_X$ with respect to the occurrence in the environment of an event that counts as the event-status function
$a_X$ with respect to the occurrence in the environment of an event that counts as the event-status function ![]() $c_d^\prime$ is only fulfilled when
$c_d^\prime$ is only fulfilled when ![]() $c_d^\prime$ is assigned to an event
$c_d^\prime$ is assigned to an event ![]() $e_X$ really produced by the agent
$e_X$ really produced by the agent ![]() $a_X$. This is expressed by the element
$a_X$. This is expressed by the element ![]() $ F\models ((e_X,a_X){\bf{is}} c_d^\prime)$, evaluated according to the Expression (11). For instance, if two agents are obliged to produce an event that counts as the event-status function evacuate(downtown), then every obliged agent must produce such an event (Figure 7).
$ F\models ((e_X,a_X){\bf{is}} c_d^\prime)$, evaluated according to the Expression (11). For instance, if two agents are obliged to produce an event that counts as the event-status function evacuate(downtown), then every obliged agent must produce such an event (Figure 7).
By the function ![]() $ f\hbox{-}deactivated^s$, an agent fulfils an obligation to achieve a state when it sees to it that such state holds, no matter by whom it has been produced. This achievement is detected when there is an assignment to the state-status function
$ f\hbox{-}deactivated^s$, an agent fulfils an obligation to achieve a state when it sees to it that such state holds, no matter by whom it has been produced. This achievement is detected when there is an assignment to the state-status function ![]() $c_d^\prime$, evaluated according to the Expression (10). For example, if two agents are obliged to see to them that the environment is in a state that counts as the downtown being evacuated, then the obligations of all the agents are fulfilled when such a state is produced, no matter by whom (Figure 8).
$c_d^\prime$, evaluated according to the Expression (10). For example, if two agents are obliged to see to them that the environment is in a state that counts as the downtown being evacuated, then the obligations of all the agents are fulfilled when such a state is produced, no matter by whom (Figure 8).

Figure 7 Example of norm deactivation—event-status function obligation. Both the agents bob and tom are obliged to produce, in the environment, an event that counts as the evacuation of the downtown. The agent bob produces such an event, fulfilling, thus, his obligation. The obligation of the agent tom remains active until he does the same

Figure 8 Example of norm deactivation—state-status function obligation. Both the agents bob and tom are obliged to see to them that the environment is in a state that counts as the downtown being evacuated. The agent bob produces such state. Then, both bob and tom have their obligation fulfilled
The functions ![]() $f\hbox{-}deactivated^e$ and
$f\hbox{-}deactivated^e$ and ![]() $f\hbox{-}deactivated^s$ capture the idea of norm instances directed to the concrete agents but conditioned by the agent-SFAs. If an instance is assigned to the agent
$f\hbox{-}deactivated^s$ capture the idea of norm instances directed to the concrete agents but conditioned by the agent-SFAs. If an instance is assigned to the agent ![]() $a_X$ because it carries the agent-status function
$a_X$ because it carries the agent-status function ![]() $\alpha$, then it is deactivated if
$\alpha$, then it is deactivated if ![]() $a_X$ ceases to carry
$a_X$ ceases to carry ![]() $\alpha$ (Figure 9).
$\alpha$ (Figure 9).

Figure 9 Example of norm deactivation—loss of agent-status function. The agent bob loses the status function of firefighter and, then, their standing obligations related to that status function are deactivated
The element ![]() $F\cup N\models c_m^\prime$ in expressions (15) and (16) captures the assumption of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) that an active norm instance is deactivated if the deactivation condition starts to hold while the maintenance condition is still holding. While active norm instances are deactivated when the deactivation condition
$F\cup N\models c_m^\prime$ in expressions (15) and (16) captures the assumption of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) that an active norm instance is deactivated if the deactivation condition starts to hold while the maintenance condition is still holding. While active norm instances are deactivated when the deactivation condition ![]() $c_d^\prime$ is satisfied, violated instances are deactivated by the satisfaction of the repair condition
$c_d^\prime$ is satisfied, violated instances are deactivated by the satisfaction of the repair condition ![]() $c_r^\prime$. Deactivations by reparation of violated instances are also considered at the individual agent level when they are conditioned by events (function
$c_r^\prime$. Deactivations by reparation of violated instances are also considered at the individual agent level when they are conditioned by events (function ![]() $r\hbox{-}deactivated^e$). Reparations conditioned by states are achieved when the agents see to them that such state holds (function
$r\hbox{-}deactivated^e$). Reparations conditioned by states are achieved when the agents see to them that such state holds (function ![]() $r\hbox{-}deactivated^s$). Different of deactivations of active instances, the maintenance condition is not considered in the reparations of violated ones. An instance, to be repaired, must be in the violated state, reached when the maintenance condition
$r\hbox{-}deactivated^s$). Different of deactivations of active instances, the maintenance condition is not considered in the reparations of violated ones. An instance, to be repaired, must be in the violated state, reached when the maintenance condition ![]() $c_m^\prime$ ceased to hold in the past. If it is the case that
$c_m^\prime$ ceased to hold in the past. If it is the case that ![]() $c_m^\prime$ holds while the reparation condition of a violated instance is reached, such condition has started to hold again while the instance was violated, having thus no influence on such instance.
$c_m^\prime$ holds while the reparation condition of a violated instance is reached, such condition has started to hold again while the instance was violated, having thus no influence on such instance.
 \begin{align} r\hbox{-}deactivated^e(F,N) = \{ n^\prime\arrowvert &\exists (e_X,a_X)\in E_X: n^\prime\in VS \wedge c_r^\prime\in \mathcal{E}_\mathcal{F} \wedge \nonumber \\[4pt]
& F\models ((e_X,a_X){\bf{is}} c_r^\prime \vee \neg (a_X\,{\bf is }\,\alpha))\} \end{align}
\begin{align} r\hbox{-}deactivated^e(F,N) = \{ n^\prime\arrowvert &\exists (e_X,a_X)\in E_X: n^\prime\in VS \wedge c_r^\prime\in \mathcal{E}_\mathcal{F} \wedge \nonumber \\[4pt]
& F\models ((e_X,a_X){\bf{is}} c_r^\prime \vee \neg (a_X\,{\bf is }\,\alpha))\} \end{align} \begin{align} r\hbox{-}deactivated^s(F,N) = \{n^\prime\arrowvert & n^\prime \in VS \wedge \nonumber c_r^\prime\in \mathcal{S_F} \wedge\\[4pt]
& F\models (c_r^\prime \vee \neg (a_X\,{\bf is }\,\alpha)) \}\end{align}
\begin{align} r\hbox{-}deactivated^s(F,N) = \{n^\prime\arrowvert & n^\prime \in VS \wedge \nonumber c_r^\prime\in \mathcal{S_F} \wedge\\[4pt]
& F\models (c_r^\prime \vee \neg (a_X\,{\bf is }\,\alpha)) \}\end{align}5.1.3 Violation
Active norm instances are considered violated when the constitutive and normative states do not satisfy the maintenance condition (function violated below).
Following the considered normative model, the Expression (19) captures the assumption that a norm instance becomes violated as soon as the maintenance condition ceases to hold, even if the deactivation or any other condition starts to hold at the same time.
5.1.4 Failure
An instance is failed if (i) it is violated and (ii) the current constitutive and normative states satisfy the timeout condition (function failed below).
5.2 Monitoring norms based on the constitutive state
The original operational semantics for norm monitoring proposed by Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) considers that the life cycle of the norm instances evolves based on the satisfaction of the conditions ![]() $c_a$,
$c_a$, ![]() $c_d$,
$c_d$, ![]() $c_m$,
$c_m$, ![]() $c_r$, and
$c_r$, and ![]() $c_t$. Basing the regulation on the constitutive state requires also to consider other conditions captured by the functions (14)–(20). For this reason, to base the operational semantics of the normative monitor proposed by Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) on the SAI constitutive state, we redefine below the transition rules presented in Section 2.
$c_t$. Basing the regulation on the constitutive state requires also to consider other conditions captured by the functions (14)–(20). For this reason, to base the operational semantics of the normative monitor proposed by Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) on the SAI constitutive state, we redefine below the transition rules presented in Section 2.
 \begin{align}\frac{n^\prime\in activated(\mathcal{N},F,N)\ \ \ \ \ n^\prime \notin f\hbox{-}deactivated^e(F,activated(\mathcal{N},F,N))\cup f\hbox{-}deactivated^s(F,activated(\mathcal{N},F,N))}{M_N\triangleright \langle \mathcal{N},AS\cup n^\prime,VS,DS,FS,s_{i+1}\rangle}\end{align}
\begin{align}\frac{n^\prime\in activated(\mathcal{N},F,N)\ \ \ \ \ n^\prime \notin f\hbox{-}deactivated^e(F,activated(\mathcal{N},F,N))\cup f\hbox{-}deactivated^s(F,activated(\mathcal{N},F,N))}{M_N\triangleright \langle \mathcal{N},AS\cup n^\prime,VS,DS,FS,s_{i+1}\rangle}\end{align}6 Example
Considering the proposed coupling and the scenario introduced in Section 3.3, we illustrate the evolving of the normative regulation based on the constitutive state. It is possible thus to observe the dynamics of the norms that abstract from the concrete environment but are still grounded in the concrete environment under regulation. The constitutive specification is shown in Figure 4. The norms are shown in Figure 5. We consider five steps of the environmental dynamics. In each step, the environmental state changes causing changes in the constitutive state and, as consequence, changing the normative state, as described below and summarized in Tables 1 and 2:
Step 1. GIS indicate that the properties security_phase(downtown,preventive) and nb_inhabit(downtown,200) hold in the environment, meaning that (i) the downtown is on preventive phase of the crisis management and (ii) the downtown has 200 inhabitants. By the constitutive rule 5, the downtown counts as a secure zone. At this moment, the actor bob checks in the table_mayor and the actors tom, jim, and ana check in the table_fire_brigade. By the constitutive rules 1 and 2, bob counts as the mayor while tom, jim, and ana count as firefighter. As the downtown is considered secure, bob is obliged to evacuate it.
Step 2. Bob puts the launch_object on the coordinates (2,2). By the constitutive rule 3, this event counts as the evacuation of the downtown, deactivating the previously created obligation.
Step 3. After the evacuation performed by bob, for some reason, the downtown has 50 inhabitants. The security phase of the crisis changes from preventive to emergency, and, from the institutional perspective, the downtown is insecure (constitutive rule 6). Thus, new norm instances are created to be followed by the firefighters.
Step 4. Tom puts the launch_object on the coordinates (2,2) of the table, while jim sends a message. Both the actions count as the evacuation of the downtown (constitutive rules 3 and 4). Thus, tom and jim fulfil their obligations.
Step 5. The security phase of the crisis becomes again preventive, and, from the institutional perspective, the downtown is again secure (constitutive rule 5). The agent ana violates its obligation as it has not evacuated the downtown while it was insecure.
Table 1 Evolution of environmental and constitutive states

Table 2 Evolution of the normative state

7 Discussion
In institutions as conceived by SAI, norms are based on the interpretation of the environment provided by the constitutive state, but they regulate the elements under such interpretation. It is necessary, thus, to define how the elements abstracted under the constitution are considered in the management of the normative state. Since the elements referred by the norms, that is, the status functions, may abstract more than one environmental element, it is necessary to define how such possible one-to-many relation is handled in the normative management. Our proposed coupling explicitly defines that (i) regarding to the addressee ![]() $\alpha$, norms govern all the agents under the same constitution of agent-status function and (ii) the activation, maintenance, deactivation, repair, and timeout conditions
$\alpha$, norms govern all the agents under the same constitution of agent-status function and (ii) the activation, maintenance, deactivation, repair, and timeout conditions ![]() $c_a$,
$c_a$, ![]() $c_m$,
$c_m$, ![]() $c_d$,
$c_d$, ![]() $c_r$, and
$c_r$, and ![]() $c_t$, differently, point to (at least) a single constitution of event- and state-status function. For example, if many agents count as firefighter and two events count as an evacuation (Figure 4—constitutive rules 3 and 4) and if firefighters are obliged to evacuate an insecure zone (Figure 5—norm 2), then the obligation stands to every agent counting as firefighter (cf. step 3 of the example in Section 6). The fulfilment of the obligation requires that every firefighter produces at least one event interpreted as evacuation. By the constitutive rules 3 and 4, they can either put a tangible in the table or send a message (as it is done in step 4 of the example in Section 6).
$c_t$, differently, point to (at least) a single constitution of event- and state-status function. For example, if many agents count as firefighter and two events count as an evacuation (Figure 4—constitutive rules 3 and 4) and if firefighters are obliged to evacuate an insecure zone (Figure 5—norm 2), then the obligation stands to every agent counting as firefighter (cf. step 3 of the example in Section 6). The fulfilment of the obligation requires that every firefighter produces at least one event interpreted as evacuation. By the constitutive rules 3 and 4, they can either put a tangible in the table or send a message (as it is done in step 4 of the example in Section 6).
When the normative regulation is based on the constitutive state, the expected agents’ behaviour is attached to the status functions instead of attaching to the agents themselves. That is why norm instances are deactivated when the responsible agents are no longer carrying the target status function (expressions (15)–(18)). But other coupling approaches can be conceived where, for example, obligations and prohibitions remain active even if the agent-SFAs are revoked. These decisions concern the management of the social meanings of the agents in a society, which is a complex question that can be addressed in different ways (Tessop, Reference Tessop2011).
Keeping in mind that norms following different models may take part in an institution (Criado et al., Reference Criado, Argente and Botti2011), the institutional reality in SAI–that is, the constitutive state–provides a common, shared vocabulary, composed of the status functions, in terms of which all the norms of an institution can be expressed. But more than providing the set of words to be used to write norms, the institutional reality as conceived by SAI provides semantics to the institutional vocabulary through the typing of the status functions. Such semantics is also shared among all the norms in an institution. It is possible, thus, to establish clear relations between the components of the norms and the components of the institutional reality (cf. Section 4.1). For example, it is possible to convention that the addressee of the norms is specified in terms of agent-status functions, and, thus, the ‘![]() $\alpha$’ of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) refers to the same kind of element (i.e. agent-status functions) as the addressee in any other normative representation.
$\alpha$’ of Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013) refers to the same kind of element (i.e. agent-status functions) as the addressee in any other normative representation.
When norms are specified in terms of status functions, they are consistent with the institutional reality and also with the environment under regulation. For instance, if firefighter is an agent-status function and evacuate is an event-status function, evacuate cannot be the bearer and firefighter cannot be the goal of a norm. Such consistency depends neither on the normative model nor on the normative specification. Rather, it is provided by the proper link between the components of the norms and the different kinds of status functions.
Basing the normative regulation on the constitutive state is not just about to specify norms through status functions. It is necessary to define how to manage norms based on an interpretation of the environment to regulate the elements under such interpretation. We addressed this point in two steps: (i) aligning constitutive and normative representations (cf. Section 4) and (ii) defining how the life cycle of the norm instances evolves according to the constitutive state (cf. Section 5). These two steps can be seen as a replicable strategy (a kind of ‘method’) to couple different normative models with the constitutive state.
8 Related work, conclusions, and perspectives
Some works, such as those by Dastani et al. (Reference Dastani, Grossi, Meyer, Tinnemeier, Boella, Noriega, Pigozzi and Verhagen2009) and Aldewereld et al. (Reference Aldewereld, Álvarez Napagao, Dignum, Vázquez-Salceda, Richland, van der Hoek, Kaminka, Lespérance, Luck and Sen2010), consider that deontic notions can be reduced to classification statements based on counts as (Grossi et al., Reference Grossi, Meyer and Dignum2005). In this case, certain circumstances count as norm violations and fulfilments. In our proposal, however, counts-as statements are not used to express regulation. Rather, they have the exclusive function of constituting the conditions evaluated by the norms.
More similar to our direction, some works consider that the normative regulation is based on some kind of interpretation of the environment, usually specified through constitutive rules. Sun and van der Torre (Reference Sun, van der Torre, Cariani, Grossi, Meheus and Parent2014) and Boella and van der Torre (Reference Boella, van der Torre, Dubois, Welty and Williams2004, Reference Boella, van der Torre, Goble and Meyer2006a) discuss logic and semantics aspects of combining norms and constitutive rules without committing with particular constitutive and normative models. While our proposal embodies some of these aspects, such as the simple-minded semantics proposed by Sun and van der Torre (Reference Sun, van der Torre, Cariani, Grossi, Meheus and Parent2014), as well as the notions of conjunction of output (if two status functions ![]() $y_1$
and
$y_1$
and
![]() $y_2$ are simultaneously assigned to some x, then it is possible to say that x counts both as
$y_2$ are simultaneously assigned to some x, then it is possible to say that x counts both as ![]() $y_1$
and
$y_1$
and
![]() $y_2$), disjunction of input (if the status function y is simultaneously assigned to
$y_2$), disjunction of input (if the status function y is simultaneously assigned to ![]() $x_1$
and
$x_1$
and
![]() $x_2$, then it is possible to say that
$x_2$, then it is possible to say that ![]() $x_1$
or
$x_1$
or
![]() $x_2$ count as y), and transitivity (if x counts
$x_2$ count as y), and transitivity (if x counts ![]() $y_1$ and
$y_1$ and ![]() $y_1$ counts
$y_1$ counts ![]() $y_2$, then x counts as
$y_2$, then x counts as ![]() $y_2$) discussed by (Boella and van der Torre Reference Boella, van der Torre, Dubois, Welty and Williams2004, Reference Boella, van der Torre, Dubois, Welty and Williams2006a), it also takes into account the different dynamics of norms directed to event- and state-status functions. Furthermore, we consider that constituted elements base the whole normative life cycle–activation, deactivation,violation, etc.–while the referred works consider that constitution bases exclusively the deactivations of obligations.
$y_2$) discussed by (Boella and van der Torre Reference Boella, van der Torre, Dubois, Welty and Williams2004, Reference Boella, van der Torre, Dubois, Welty and Williams2006a), it also takes into account the different dynamics of norms directed to event- and state-status functions. Furthermore, we consider that constituted elements base the whole normative life cycle–activation, deactivation,violation, etc.–while the referred works consider that constitution bases exclusively the deactivations of obligations.
The semantics of the constituted elements is an important point to be considered when norms are coupled with constitutive rules. In Aldewereld et al. (Reference Aldewereld, Álvarez Napagao, Dignum, Vázquez-Salceda, Richland, van der Hoek, Kaminka, Lespérance, Luck and Sen2010), the constitution, which affects the whole normative life cycle, results in predicates added to the knowledge base accessed by the normative reasoner. Such predicates, however, do not have any associated semantics from the normative perspective. In our approach, differently, norms are coupled in meaningful institutional elements constituted from environmental ones. Other approaches, closer to our one, consider that norms refer to constituted elements with a defined semantics. In Cliffe et al. (Reference Cliffe, De Vos, Padgetm, Inoue, Satoh and Toni2007), norms are fulfilled and violated from the occurrence of either physical or institutional events, which are the institutional interpretation of the facts occurring in the environment, analogous to the event-status functions in SAI. In Cardoso and Oliveira (Reference Cardoso and Oliveira2007), the fulfilment conditions of norms are based exclusively on institutional events, admitting also that norms may prescribe the behaviour to institutional roles, which are analogous to the agent-status functions of SAI. A similar approach is proposed by Fornara et al. (Reference Fornara, Viganò, Verdicchio and Colombetti2008). Viganó and Colombetti (Reference Viganò, Colombetti, Noriega, VÃzquez-Salceda, Boella, Boissier, Dignum, Fornara and Matson2007, Reference Viganò, Colombetti, Sichman, Padget, Ossowski and Noriega2008) also consider institutional events and introduce the notion of status function as an abstraction of the agents acting in the environment. As the referred works do not propose a clear dynamics for the constitution, the coupling of norms with the constituted elements is limited to refer to the constituted elements in the normative specification. Our work, in turn, couples norms on a constitutive state that has a well-defined dynamics that is taken into account in the normative management.
Pieters et al. (Reference Pieters, Padget, Dechesne, Dignum and Aldewereld2015) and García-Camino et al. (Reference Garcá-Camino, Noriega, Rodrǵuez-Aguilar, O’Hare, Ricci, O’Grady and Dikenelli2006) consider that norms can prescribe behaviours composed of sets of sub-activities. The abstraction provided by the status functions makes possible to prescribe such a composition in the case of state-status functions constituted by a set of properties. However, composition of events, which is considered by the referred work, is not envisioned by the SAI model. Analyzing composition of events and states in SAI is a future work.
Coupling the normative regulation with the SAI constitutive state requires to consider the semantics of the different kinds of status functions in both the normative representation and dynamics. This work addresses these issues in Sections 4 and 5. We focused on the reasoning about the normative and constitutive states to define when instances should be activated, deactivated, violated, and failed. We have shown how such reasoning can be used by a normative monitor that manages the regulation on top of the constitutive state. But it can be useful for the agents to plan their actions in the environment as they can reason about the normative impact of the environmental facts in the constitutive state and, then, in the normative one.
The literature on norms presents several normative models that express the expected agents’ behaviour in different ways.Footnote 9 While norms following the NPL normative model (Hübner et al., Reference Hübner, Boissier and Bordini2011) are used in de Brito et al. (Reference de Brito, Hübner and Boissier2018) to illustrate regulation based on constitutive rules in SAI, this paper focuses on the coupling between constitutive rules and regulative norms in general using the normative model proposed by Panagiotidi et al. (Reference Panagiotidi, Álvarez-Napagao, Vázquez-Salceda, Balke, Dignum, van Riemsdijk and Chopra2013).Footnote 10 It discusses in greater depth the main issues of such coupling, describing how the semantics of the different kinds of constituted elements is taken into account both in the normative specifications and in its dynamics. Applying a similar coupling to other normative models is a future work. We also plan to work (i) on agents using the proposed coupling to reason about the normative consequence of their actions in the environment, (ii) on a deeper analysis of implicit changes in the normative state due to revocations of agent-status functions, and (iii) on the analysis of the proposed coupling considering group norms.
Acknowledgements
The authors thank the anonymous reviewers of KER for their valuable remarks that have been taken into account in this paper.













