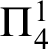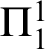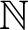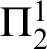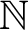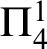1 Introduction
A classical result of Girard [Reference Girard14] and Hirst [Reference Hirst18] shows that the following are equivalent over the usual base theory
![]() $\mathbf {RCA}_0$
of reverse mathematics (see [Reference Simpson29] for an introduction to the latter):
$\mathbf {RCA}_0$
of reverse mathematics (see [Reference Simpson29] for an introduction to the latter):
-
(i) arithmetical comprehension (i.e., the principal axiom of
 $\mathbf {ACA}_0$
) and
$\mathbf {ACA}_0$
) and -
(ii) when
 $(X,\leq _X)$
is a (countable) well order, then so is with the lexicographic order.
$(X,\leq _X)$
is a (countable) well order, then so is with the lexicographic order. $$ \begin{align*} \omega^X:=\{\langle x_0,\dots,x_{n-1}\rangle\,|\,x_0,\dots,x_{n-1}\in X\text{ and }x_{n-1}\leq_X\dots\leq_X x_0\} \end{align*} $$
$$ \begin{align*} \omega^X:=\{\langle x_0,\dots,x_{n-1}\rangle\,|\,x_0,\dots,x_{n-1}\in X\text{ and }x_{n-1}\leq_X\dots\leq_X x_0\} \end{align*} $$
If we think of
![]() $\langle x_0,\dots ,x_{n-1}\rangle \in \omega ^X$
as the Cantor normal form
$\langle x_0,\dots ,x_{n-1}\rangle \in \omega ^X$
as the Cantor normal form
![]() $\omega ^{x_0}+\dots +\omega ^{x_{n-1}}$
, we see that
$\omega ^{x_0}+\dots +\omega ^{x_{n-1}}$
, we see that
![]() $X\mapsto \omega ^X$
represents the familiar operation from ordinal arithmetic. Note that the base theory
$X\mapsto \omega ^X$
represents the familiar operation from ordinal arithmetic. Note that the base theory
![]() $\mathbf {RCA}_0$
proves that
$\mathbf {RCA}_0$
proves that
![]() $\omega ^X$
exists and is a linear order (whenever the same holds for X). A statement such as (ii), which asserts that some computable transformation preserves well foundedness, is called a well ordering principle.
$\omega ^X$
exists and is a linear order (whenever the same holds for X). A statement such as (ii), which asserts that some computable transformation preserves well foundedness, is called a well ordering principle.
Many important principles of reverse mathematics (about iterated arithmetical comprehension [Reference Marcone and Montalbán21, Reference Rathjen, Weiermann, Cooper and Sorbi27] and the existence of
![]() $\omega $
-models [24–26, Reference Thomson30]) have been characterized in terms of well ordering principles. At least in principle, there is no limitation on the consistency strength of statements that can be characterized in this way. There is, however, a limitation in terms of logical complexity: For any computable transformation of orders, the statement that this transformation preserves well foundedness has complexity
$\omega $
-models [24–26, Reference Thomson30]) have been characterized in terms of well ordering principles. At least in principle, there is no limitation on the consistency strength of statements that can be characterized in this way. There is, however, a limitation in terms of logical complexity: For any computable transformation of orders, the statement that this transformation preserves well foundedness has complexity
![]() $\Pi ^1_2$
. Hence a genuine
$\Pi ^1_2$
. Hence a genuine
![]() $\Pi ^1_3$
-statement—such as the principle of
$\Pi ^1_3$
-statement—such as the principle of
![]() $\Pi ^1_1$
-comprehension—cannot be equivalent to a well ordering principle of this form.
$\Pi ^1_1$
-comprehension—cannot be equivalent to a well ordering principle of this form.
In order to characterize statements of higher logical complexity, one needs to consider transformations of higher type. Recall that the usual notion of computability on the natural numbers extends to higher types if one restricts to functionals that are continuous in a suitable sense. In the present context, the continuous transformations between well orders are the dilators of Girard [Reference Girard13] (see below for details). Girard has sketched a proof that
![]() $\Pi ^1_1$
-comprehension is equivalent to the statement that his functor
$\Pi ^1_1$
-comprehension is equivalent to the statement that his functor
![]() $\Lambda $
preserves dilators [Reference Girard15]. As far as the present author is aware, the details of this proof have not been worked out. However, the present author [4–6] has shown that
$\Lambda $
preserves dilators [Reference Girard15]. As far as the present author is aware, the details of this proof have not been worked out. However, the present author [4–6] has shown that
![]() $\Pi ^1_1$
-comprehension is equivalent to the following different well ordering principle: For every dilator D there is a well order X and a collapse
$\Pi ^1_1$
-comprehension is equivalent to the following different well ordering principle: For every dilator D there is a well order X and a collapse
![]() $\vartheta :D(X)\to X$
that is almost order preserving in a suitable sense. Here the order X and the function
$\vartheta :D(X)\to X$
that is almost order preserving in a suitable sense. Here the order X and the function
![]() $\vartheta $
can be computed from a representation of D. Only the fact that X is well founded cannot be proved in
$\vartheta $
can be computed from a representation of D. Only the fact that X is well founded cannot be proved in
![]() $\mathbf {RCA}_0$
.
$\mathbf {RCA}_0$
.
Well ordering principles are relevant because they allow to apply methods from ordinal analysis to questions of reverse mathematics. Together with Rathjen and Weiermann, the present author has used his result on a collapse
![]() $\vartheta :D(X)\to X$
to show that
$\vartheta :D(X)\to X$
to show that
![]() $\Pi ^1_1$
-comprehension is equivalent to a uniform version of Kruskal’s tree theorem [Reference Freund, Rathjen and Weiermann12]. This implies that the uniform Kruskal theorem exhausts the full strength of Nash-Williams’s famous “minimal bad sequence argument” [Reference Nash-Williams22], in contrast to the usual Kruskal theorem. The present author has also shown that iterated applications of the uniform Kruskal theorem yield a systematic reconstruction of H. Friedman’s gap condition [Reference Freund8].
$\Pi ^1_1$
-comprehension is equivalent to a uniform version of Kruskal’s tree theorem [Reference Freund, Rathjen and Weiermann12]. This implies that the uniform Kruskal theorem exhausts the full strength of Nash-Williams’s famous “minimal bad sequence argument” [Reference Nash-Williams22], in contrast to the usual Kruskal theorem. The present author has also shown that iterated applications of the uniform Kruskal theorem yield a systematic reconstruction of H. Friedman’s gap condition [Reference Freund8].
Much of reverse mathematics concerns statements of complexity
![]() $\Pi ^1_2$
and
$\Pi ^1_2$
and
![]() $\Pi ^1_3$
. In some applications, however,
$\Pi ^1_3$
. In some applications, however,
![]() $\Pi ^1_4$
-statements play a central role. An example is the principle of
$\Pi ^1_4$
-statements play a central role. An example is the principle of
![]() $\Pi ^1_2$
-bar induction, which is used in the proof of the graph minor theorem [Reference Krombholz, Rathjen, Schuster, Seisenberger and Weiermann19]. The strongest ordinal analysis due to Rathjen [Reference Rathjen23] is also concerned with a
$\Pi ^1_2$
-bar induction, which is used in the proof of the graph minor theorem [Reference Krombholz, Rathjen, Schuster, Seisenberger and Weiermann19]. The strongest ordinal analysis due to Rathjen [Reference Rathjen23] is also concerned with a
![]() $\Pi ^1_4$
-statement, namely with the principle of
$\Pi ^1_4$
-statement, namely with the principle of
![]() $\Pi ^1_2$
-comprehension. For these reasons it seems particularly relevant to extend well ordering principles to the level of
$\Pi ^1_2$
-comprehension. For these reasons it seems particularly relevant to extend well ordering principles to the level of
![]() $\Pi ^1_4$
-statements, which requires another step in the type structure. As far as the author is aware, the present paper is the first to make this step. Since the paper is intended as a pilot study, we will consider a particularly simple
$\Pi ^1_4$
-statements, which requires another step in the type structure. As far as the author is aware, the present paper is the first to make this step. Since the paper is intended as a pilot study, we will consider a particularly simple
![]() $\Pi ^1_4$
-statement, namely the principle of
$\Pi ^1_4$
-statement, namely the principle of
![]() $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
![]() $\mathbb N$
. Even though the latter was chosen for its simplicity, it is of independent foundational interest: over
$\mathbb N$
. Even though the latter was chosen for its simplicity, it is of independent foundational interest: over
![]() $\mathbf {\Pi ^1_1}\mathbf {-CA}_0$
, the principle of
$\mathbf {\Pi ^1_1}\mathbf {-CA}_0$
, the principle of
![]() $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
![]() $\mathbb N$
is needed to show that the finite trees with Friedman’s gap condition form a well quasi order [Reference Simpson, Harrington, Morley, Sčědrov and Simpson28].
$\mathbb N$
is needed to show that the finite trees with Friedman’s gap condition form a well quasi order [Reference Simpson, Harrington, Morley, Sčědrov and Simpson28].
To state our result, we need some terminology; full details of the following can be found in §2–§4. A predilator is an endofunctor of linear orders that preserves direct limits, pullbacks and the order on morphisms (pointwise domination). If it preserves well foundedness, then it is called a dilator. By a morphism between (pre-)dilators D and E we mean a natural transformation
![]() $\mu :D\Rightarrow E$
of functors. Such a transformation consists of an order embedding
$\mu :D\Rightarrow E$
of functors. Such a transformation consists of an order embedding
![]() $\mu _X:D(X)\to E(X)$
for each linear order X. If the image of each embedding
$\mu _X:D(X)\to E(X)$
for each linear order X. If the image of each embedding
![]() $\mu _X$
is an initial segment of the order
$\mu _X$
is an initial segment of the order
![]() $E(X)$
, then we call
$E(X)$
, then we call
![]() $\mu $
a segment. A 2-preptyx is an endofunctor of predilators that preserves direct limits and pullbacks. If it preserves dilators, then it is called a 2-ptyx (plural: ptykes). The number
$\mu $
a segment. A 2-preptyx is an endofunctor of predilators that preserves direct limits and pullbacks. If it preserves dilators, then it is called a 2-ptyx (plural: ptykes). The number
![]() $2$
indicates the type level, where we think of well orders and dilators as objects of type zero and one, respectively; it will be omitted where the context allows it. We say that a 2-(pre-)ptyx P is normal if
$2$
indicates the type level, where we think of well orders and dilators as objects of type zero and one, respectively; it will be omitted where the context allows it. We say that a 2-(pre-)ptyx P is normal if
![]() $P(\mu ):P(D)\Rightarrow P(E)$
is a segment for any segment
$P(\mu ):P(D)\Rightarrow P(E)$
is a segment for any segment
![]() $\mu :D\Rightarrow E$
. Preservation of direct limits is a continuity property, which allows us to represent predilators and preptykes in second order arithmetic. Based on such a representation, we will show that the following are equivalent over
$\mu :D\Rightarrow E$
. Preservation of direct limits is a continuity property, which allows us to represent predilators and preptykes in second order arithmetic. Based on such a representation, we will show that the following are equivalent over
![]() $\mathbf {ACA}_0$
(cf. Theorem 6.7 below):
$\mathbf {ACA}_0$
(cf. Theorem 6.7 below):
-
(i) the principle of
 $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
 $\mathbb N$
and
$\mathbb N$
and -
(ii) for any normal 2-ptyx P there is a dilator
 $D\cong P(D)$
.
$D\cong P(D)$
.
Since P preserves direct limits, a predilator
![]() $D_P\cong P(D_P)$
can be constructed as the direct limit of the diagram
$D_P\cong P(D_P)$
can be constructed as the direct limit of the diagram

where
![]() $D^0_P$
is the constant dilator with value
$D^0_P$
is the constant dilator with value
![]() $0$
(the empty order). In §6 we will see that this construction can be implemented in
$0$
(the empty order). In §6 we will see that this construction can be implemented in
![]() $\mathbf {ACA}_0$
(and presumably also in
$\mathbf {ACA}_0$
(and presumably also in
![]() $\mathbf {RCA}_0$
). Hence the strength of (ii) does not lie in the existence of
$\mathbf {RCA}_0$
). Hence the strength of (ii) does not lie in the existence of
![]() $D\cong P(D)$
, but rather in the assertion that D is a dilator (i.e., preserves well foundedness). In order to prove that (i) implies (ii), one uses
$D\cong P(D)$
, but rather in the assertion that D is a dilator (i.e., preserves well foundedness). In order to prove that (i) implies (ii), one uses
![]() $\Pi ^1_2$
-induction to show that each predilator
$\Pi ^1_2$
-induction to show that each predilator
![]() $D^n_P$
in the above diagram is a dilator. The assumption that P is normal is needed to conclude that the same holds for the direct limit (by Example 4.4, which shows that
$D^n_P$
in the above diagram is a dilator. The assumption that P is normal is needed to conclude that the same holds for the direct limit (by Example 4.4, which shows that
![]() $P(D)(X):=(D+1)(X):=D(X)+1$
defines a 2-ptyx that is not normal and cannot have a dilator as a fixed point).
$P(D)(X):=(D+1)(X):=D(X)+1$
defines a 2-ptyx that is not normal and cannot have a dilator as a fixed point).
In order to explain the proof that (ii) implies (i), we recall another result on the level of
![]() $\Pi ^1_3$
-statements. A function f on the ordinals is called normal if it is strictly increasing and continuous at limits (i.e., we demand
$\Pi ^1_3$
-statements. A function f on the ordinals is called normal if it is strictly increasing and continuous at limits (i.e., we demand
![]() $f(\lambda )= {\mathrm {sup}} _{\alpha <\lambda }f(\alpha )$
for any limit ordinal
$f(\lambda )= {\mathrm {sup}} _{\alpha <\lambda }f(\alpha )$
for any limit ordinal
![]() $\lambda $
). It is well known that any normal function f has a proper class of fixed points. These are enumerated by another normal function
$\lambda $
). It is well known that any normal function f has a proper class of fixed points. These are enumerated by another normal function
![]() $f'$
, which is called the derivative of f. Together with Rathjen, the present author has shown that
$f'$
, which is called the derivative of f. Together with Rathjen, the present author has shown that
![]() $\Pi ^1_1$
-bar induction is equivalent to a suitable formalization of the statement that every normal function has a derivative [Reference Freund7, Reference Freund and Rathjen11]. Furthermore,
$\Pi ^1_1$
-bar induction is equivalent to a suitable formalization of the statement that every normal function has a derivative [Reference Freund7, Reference Freund and Rathjen11]. Furthermore,
![]() $\Pi ^1_1$
-induction along
$\Pi ^1_1$
-induction along
![]() $\mathbb N$
is equivalent to the statement that each normal function has at least one fixed point [Reference Freund9]. In the following, we recall the intuition behind this result.
$\mathbb N$
is equivalent to the statement that each normal function has at least one fixed point [Reference Freund9]. In the following, we recall the intuition behind this result.
Given a linear order X and an ordinal
![]() $\alpha $
, we write
$\alpha $
, we write
![]() $X\preceq \alpha $
to express that X is well founded with order type at most
$X\preceq \alpha $
to express that X is well founded with order type at most
![]() $\alpha $
. On an intuitive level, the fact that well foundedness is
$\alpha $
. On an intuitive level, the fact that well foundedness is
![]() $\Pi ^1_1$
-complete allows us to write any instance of
$\Pi ^1_1$
-complete allows us to write any instance of
![]() $\Pi ^1_1$
-induction as
$\Pi ^1_1$
-induction as
for some family of linear orders
![]() $X_n$
. Assume that the second conjunct of the premise is witnessed by a function
$X_n$
. Assume that the second conjunct of the premise is witnessed by a function
![]() $h_0$
such that
$h_0$
such that
![]() $X_n\preceq \alpha $
implies
$X_n\preceq \alpha $
implies
![]() $X_{n+1}\preceq h_0(n,\alpha )$
. If we set
$X_{n+1}\preceq h_0(n,\alpha )$
. If we set
![]() $h(\alpha ):={\mathrm {sup}}_{n\in \mathbb N}h_0(n,\alpha )$
, then we obtain
$h(\alpha ):={\mathrm {sup}}_{n\in \mathbb N}h_0(n,\alpha )$
, then we obtain
As h may not be normal, we consider the normal function g with
 $$ \begin{align*} g(\alpha)=\sum_{\gamma<\alpha}h(\gamma)+1. \end{align*} $$
$$ \begin{align*} g(\alpha)=\sum_{\gamma<\alpha}h(\gamma)+1. \end{align*} $$
More formally, this function can be defined by the recursive clauses
![]() $g(0)=0$
,
$g(0)=0$
,
![]() $g(\alpha +1)=g(\alpha )+h(\alpha )+1$
and
$g(\alpha +1)=g(\alpha )+h(\alpha )+1$
and
 $g(\lambda )= {\mathrm {sup}}_{\gamma <\lambda }g(\gamma )$
for
$g(\lambda )= {\mathrm {sup}}_{\gamma <\lambda }g(\gamma )$
for
![]() $\lambda $
limit. We observe
$\lambda $
limit. We observe
To incorporate the premise
![]() $X_0\preceq \alpha _0$
of our induction statement, we transform g into another normal function f with
$X_0\preceq \alpha _0$
of our induction statement, we transform g into another normal function f with
![]() $f(\alpha ):=\alpha _0+1+g(\alpha )$
. If
$f(\alpha ):=\alpha _0+1+g(\alpha )$
. If
![]() $\alpha =f(\alpha )$
is a fixed point, then a straightforward induction over
$\alpha =f(\alpha )$
is a fixed point, then a straightforward induction over
![]() $n\in \mathbb N$
yields
$n\in \mathbb N$
yields
In particular we have
![]() $\forall _{n\in \mathbb N}X_n\preceq \alpha $
, which entails the conclusion of the induction statement above. As shown in [Reference Freund9], the given argument can be formalized in terms of dilators. In that setting, the induction at the end of the argument is not needed: it can be replaced by a construction that builds embeddings
$\forall _{n\in \mathbb N}X_n\preceq \alpha $
, which entails the conclusion of the induction statement above. As shown in [Reference Freund9], the given argument can be formalized in terms of dilators. In that setting, the induction at the end of the argument is not needed: it can be replaced by a construction that builds embeddings
![]() $X_n+1\hookrightarrow \alpha $
by primitive recursion over elements of
$X_n+1\hookrightarrow \alpha $
by primitive recursion over elements of
![]() $X_n$
, simultaneously for all
$X_n$
, simultaneously for all
![]() $n\in \mathbb N$
. The formalized argument deduces
$n\in \mathbb N$
. The formalized argument deduces
![]() $\Pi ^1_1$
-induction along
$\Pi ^1_1$
-induction along
![]() $\mathbb N$
from the assumption that every normal function (represented by a dilator) has a fixed point.
$\mathbb N$
from the assumption that every normal function (represented by a dilator) has a fixed point.
In order to deduce
![]() $\Pi ^1_2$
-induction, we will lift the previous argument to the next type level. This relies, first of all, on Girard’s result [Reference Girard15] that the notion of dilator is
$\Pi ^1_2$
-induction, we will lift the previous argument to the next type level. This relies, first of all, on Girard’s result [Reference Girard15] that the notion of dilator is
![]() $\Pi ^1_2$
-complete. Given an arbitrary
$\Pi ^1_2$
-complete. Given an arbitrary
![]() $\Pi ^1_2$
-formula
$\Pi ^1_2$
-formula
![]() $\psi $
, one can thus construct a family of predilators
$\psi $
, one can thus construct a family of predilators
![]() $D^n_\psi $
such that induction for
$D^n_\psi $
such that induction for
![]() $\psi $
is equivalent to the following statement: If
$\psi $
is equivalent to the following statement: If
 $D^0_\psi $
is a dilator and
$D^0_\psi $
is a dilator and
 $D^{n+1}_\psi $
is a dilator whenever the same holds for
$D^{n+1}_\psi $
is a dilator whenever the same holds for
![]() $D^n_\psi $
, then
$D^n_\psi $
, then
![]() $D^n_\psi $
is a dilator for every
$D^n_\psi $
is a dilator for every
![]() $n\in \mathbb N$
. Assuming the premise of this implication, we will be able to construct a 2-ptyx P that admits a morphism
$n\in \mathbb N$
. Assuming the premise of this implication, we will be able to construct a 2-ptyx P that admits a morphism
 $$ \begin{align*} D^{n+1}_\psi\Rightarrow P(D^n_\psi) \end{align*} $$
$$ \begin{align*} D^{n+1}_\psi\Rightarrow P(D^n_\psi) \end{align*} $$
for each
![]() $n\in \mathbb N$
. Note that P corresponds to the function h from the argument above. Next, we need to transform P into a normal 2-ptyx
$n\in \mathbb N$
. Note that P corresponds to the function h from the argument above. Next, we need to transform P into a normal 2-ptyx
![]() $P^*$
that corresponds to the normal function g. In the author’s opinion, it is somewhat surprising that this is possible: The construction of g relies on the fact that each
$P^*$
that corresponds to the normal function g. In the author’s opinion, it is somewhat surprising that this is possible: The construction of g relies on the fact that each
![]() $\alpha $
has a well ordered set of predecessors. A priori, this fact seems specific to the ordinals. However, Girard has discovered an analogous result on the next type level: Let us temporarily write
$\alpha $
has a well ordered set of predecessors. A priori, this fact seems specific to the ordinals. However, Girard has discovered an analogous result on the next type level: Let us temporarily write
![]() $D\ll E$
to indicate that there is a segment
$D\ll E$
to indicate that there is a segment
![]() $\mu :D\Rightarrow E$
that is not an isomorphism. If E is a predilator, then the isomorphism classes of predilators
$\mu :D\Rightarrow E$
that is not an isomorphism. If E is a predilator, then the isomorphism classes of predilators
![]() $D\ll E$
form a set on which
$D\ll E$
form a set on which
![]() $\ll $
is linear (see [Reference Girard and Normann16, Lemma 2.11]). It is straightforward to define a pointwise sum of predilators. On an informal level, this allows us to set
$\ll $
is linear (see [Reference Girard and Normann16, Lemma 2.11]). It is straightforward to define a pointwise sum of predilators. On an informal level, this allows us to set
 $$ \begin{align*} P^*(E):=\sum_{D\ll E}P(D)+1, \end{align*} $$
$$ \begin{align*} P^*(E):=\sum_{D\ll E}P(D)+1, \end{align*} $$
where
![]() $1$
refers to the constant dilator with that value. In view of
$1$
refers to the constant dilator with that value. In view of
![]() $D\ll D+1$
, we obtain a morphism
$D\ll D+1$
, we obtain a morphism
for each predilator D. This completes the reconstruction of g on the next type level. To define a normal 2-ptyx
![]() $P^+$
that corresponds to the normal function f, it suffices to set
$P^+$
that corresponds to the normal function f, it suffices to set
 $P^+(E):=D^0_{\psi}+1+P^*(E)$
. Given a dilator
$P^+(E):=D^0_{\psi}+1+P^*(E)$
. Given a dilator
![]() $E\cong P^+(E)$
, one can construct morphisms
$E\cong P^+(E)$
, one can construct morphisms
![]() $D^n_{\psi}+1\Rightarrow E$
by (effective) recursion on
$D^n_{\psi}+1\Rightarrow E$
by (effective) recursion on
![]() $n\in \mathbb N$
, as on the previous type level. These ensure that the predilators
$n\in \mathbb N$
, as on the previous type level. These ensure that the predilators
![]() $D^n_{\psi}$
are dilators, which is the conclusion of
$D^n_{\psi}$
are dilators, which is the conclusion of
![]() $\Pi ^1_2$
-induction. The given argument is made precise in §4 and §5.
$\Pi ^1_2$
-induction. The given argument is made precise in §4 and §5.
2 The category of dilators
In this section we recall the definition and basic theory of dilators, both of which are due to Girard [Reference Girard13]. As the latter has observed, the continuity properties of dilators allow to represent them in second order arithmetic. Details of such a representation have been worked out in [Reference Freund6, Section 2] and will also be recalled. Even though the material is known, this section plays a crucial role in the context of our paper: it fixes an efficient formalism upon which we can base our investigation of ptykes. The section also ensures that our paper is reasonably self contained.
Let
![]() $\mathbf {LO}$
be the category of linear orders, with the order embeddings (strictly increasing functions) as morphisms. For morphisms
$\mathbf {LO}$
be the category of linear orders, with the order embeddings (strictly increasing functions) as morphisms. For morphisms
![]() $f,g:X\to Y$
we abbreviate
$f,g:X\to Y$
we abbreviate
We say that a functor
![]() $D:\mathbf {LO}\to \mathbf {LO}$
is monotone if
$D:\mathbf {LO}\to \mathbf {LO}$
is monotone if
![]() $f\leq g$
implies
$f\leq g$
implies
![]() $D(f)\leq D(g)$
. The forgetful functor to the underlying set of an order will be omitted; conversely, subsets of the underlying set will often be considered as suborders. Given a set X, we write
$D(f)\leq D(g)$
. The forgetful functor to the underlying set of an order will be omitted; conversely, subsets of the underlying set will often be considered as suborders. Given a set X, we write
![]() $[X]^{<\omega }$
for the set of its finite subsets. In order to obtain a functor, we define
$[X]^{<\omega }$
for the set of its finite subsets. In order to obtain a functor, we define
![]() $[f]^{<\omega }(a):=\{f(x)\,|\,x\in a\}\in [Y]^{<\omega }$
for
$[f]^{<\omega }(a):=\{f(x)\,|\,x\in a\}\in [Y]^{<\omega }$
for
![]() $f:X\to Y$
and
$f:X\to Y$
and
![]() $a\in [X]^{<\omega }$
. Let us also write
$a\in [X]^{<\omega }$
. Let us also write
![]() $\operatorname {rng}(f):=\{f(x)\,|\,x\in X\}\subseteq Y$
for the range of a function
$\operatorname {rng}(f):=\{f(x)\,|\,x\in X\}\subseteq Y$
for the range of a function
![]() $f:X\to Y$
.
$f:X\to Y$
.
Definition 2.1. A predilator consists of
-
(i) a monotone functor
 $D:\mathbf {LO}\to \mathbf {LO}$
and
$D:\mathbf {LO}\to \mathbf {LO}$
and -
(ii) a natural transformation
 ${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
such that we have for any morphism
${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
such that we have for any morphism $$ \begin{align*} \{\sigma\in D(Y)\,|\,{\operatorname{supp}}_Y(\sigma)\subseteq\operatorname{rng}(f)\}\subseteq\operatorname{rng}(D(f)) \end{align*} $$
$$ \begin{align*} \{\sigma\in D(Y)\,|\,{\operatorname{supp}}_Y(\sigma)\subseteq\operatorname{rng}(f)\}\subseteq\operatorname{rng}(D(f)) \end{align*} $$
 $f:X\to Y$
.
$f:X\to Y$
.
If
![]() $D(X)$
is well founded for every well order X, then
$D(X)$
is well founded for every well order X, then
![]() $D=(D,{\operatorname {supp}})$
is a dilator.
$D=(D,{\operatorname {supp}})$
is a dilator.
The inclusion in part (ii) of Definition 2.1 will be called the support condition. Its converse is automatic by naturality. If we take f to be an inclusion
![]() $\iota _b^Y:X=b\hookrightarrow Y$
with
$\iota _b^Y:X=b\hookrightarrow Y$
with
![]() $\operatorname {rng}(\iota _b^Y)=b\subseteq Y$
, then we see that
$\operatorname {rng}(\iota _b^Y)=b\subseteq Y$
, then we see that
![]() ${\operatorname {supp}}_Y(\sigma )$
is determined as the smallest set
${\operatorname {supp}}_Y(\sigma )$
is determined as the smallest set
![]() $b\in [Y]^{<\omega }$
with
$b\in [Y]^{<\omega }$
with
![]() $\sigma \in \operatorname {rng}(D(\iota _b^Y))$
. The fact that there is always a smallest finite set with this property implies that D preserves direct limits and pullbacks; conversely, if
$\sigma \in \operatorname {rng}(D(\iota _b^Y))$
. The fact that there is always a smallest finite set with this property implies that D preserves direct limits and pullbacks; conversely, if
![]() $D:\mathbf {LO}\to \mathbf {LO}$
preserves direct limits and pullbacks, there is a unique natural transformation
$D:\mathbf {LO}\to \mathbf {LO}$
preserves direct limits and pullbacks, there is a unique natural transformation
![]() ${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
that satisfies the support condition (essentially by Girard’s normal form theorem [Reference Girard13]; see also [Reference Freund3, Remark 2.2.2]). This shows that the given definition of dilator is equivalent to the original one by Girard. The condition that D must be monotone is automatic when
${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
that satisfies the support condition (essentially by Girard’s normal form theorem [Reference Girard13]; see also [Reference Freund3, Remark 2.2.2]). This shows that the given definition of dilator is equivalent to the original one by Girard. The condition that D must be monotone is automatic when
![]() $X\mapsto D(X)$
preserves well foundedness (by [Reference Girard13, Proposition 2.3.10]; see [Reference Freund, Rathjen and Weiermann12, Lemma 5.3] for a proof that uses our terminology). It has been omitted in previous work by the present author but will be important in this paper (see the proof of Lemma 4.9).
$X\mapsto D(X)$
preserves well foundedness (by [Reference Girard13, Proposition 2.3.10]; see [Reference Freund, Rathjen and Weiermann12, Lemma 5.3] for a proof that uses our terminology). It has been omitted in previous work by the present author but will be important in this paper (see the proof of Lemma 4.9).
The present paper considers dilators in second order arithmetic. When we speak of predilators in the sense of Definition 2.1, we will always assume that they are given by
![]() $\Delta ^0_1$
-definitions of the relations
$\Delta ^0_1$
-definitions of the relations
Here
![]() $\sigma ,\tau $
and a (which codes a finite set) range over natural numbers, while X and
$\sigma ,\tau $
and a (which codes a finite set) range over natural numbers, while X and
![]() $f:X\to Y$
are represented by subsets of
$f:X\to Y$
are represented by subsets of
![]() $\mathbb N$
. In particular, this means that we interpret
$\mathbb N$
. In particular, this means that we interpret
![]() $\mathbf {LO}$
as the category of countable linear orders (with underlying sets contained in
$\mathbf {LO}$
as the category of countable linear orders (with underlying sets contained in
![]() $\mathbb N$
). We can use number and set parameters to quantify over families of predilators. In fact, we will see that there is a single
$\mathbb N$
). We can use number and set parameters to quantify over families of predilators. In fact, we will see that there is a single
![]() $\Delta ^0_1$
-definable family that is universal in the sense that any predilator is isomorphic to one in this family. Our universal family will be parameterized by subsets of
$\Delta ^0_1$
-definable family that is universal in the sense that any predilator is isomorphic to one in this family. Our universal family will be parameterized by subsets of
![]() $\mathbb N$
, which are called coded predilators. The existence of such a universal family will be essential for our approach to ptykes, which are supposed to take arbitrary predilators as arguments. As explained after Proposition 2.8 below, the restriction to
$\mathbb N$
, which are called coded predilators. The existence of such a universal family will be essential for our approach to ptykes, which are supposed to take arbitrary predilators as arguments. As explained after Proposition 2.8 below, the restriction to
![]() $\Delta ^0_1$
-definable predilators is inessential in a certain sense.
$\Delta ^0_1$
-definable predilators is inessential in a certain sense.
In order to construct a universal family of predilators, one exploits the fact that these are essentially determined by their restrictions to a small category
![]() $\mathbf {LO}_0$
. The objects of
$\mathbf {LO}_0$
. The objects of
![]() $\mathbf {LO}_0$
are the finite sets
$\mathbf {LO}_0$
are the finite sets
![]() $\{0,\dots ,n-1\}=:n$
with the usual linear order; the morphisms are the strictly increasing functions between them.
$\{0,\dots ,n-1\}=:n$
with the usual linear order; the morphisms are the strictly increasing functions between them.
Definition 2.2. A coded predilator is a pair that consists of a monotone functor
![]() $D:\mathbf {LO}_0\Rightarrow \mathbf {LO}$
and a natural transformation
$D:\mathbf {LO}_0\Rightarrow \mathbf {LO}$
and a natural transformation
![]() ${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
, such that the support condition from part (ii) of Definition 2.1 is satisfied for all morphisms in
${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
, such that the support condition from part (ii) of Definition 2.1 is satisfied for all morphisms in
![]() $\mathbf {LO}_0$
.
$\mathbf {LO}_0$
.
Let us recall that we work with countable linear orders only. In this situation it is straightforward to represent coded predilators by subsets of
![]() $\mathbb N$
. From now on we speak of class-sized predilators when we want to refer to predilators in the sense of Definition 2.1. Recall that any class-sized dilator D is given by a
$\mathbb N$
. From now on we speak of class-sized predilators when we want to refer to predilators in the sense of Definition 2.1. Recall that any class-sized dilator D is given by a
![]() $\Delta ^0_1$
-formula. Working over
$\Delta ^0_1$
-formula. Working over
![]() $\mathbf {RCA}_0$
, this ensures that the restriction
$\mathbf {RCA}_0$
, this ensures that the restriction
![]() $D\!\restriction \!\mathbf {LO}_0$
exists as a set.
$D\!\restriction \!\mathbf {LO}_0$
exists as a set.
Lemma 2.3. If D is a class-sized predilator, then
![]() $D\!\restriction \!\mathbf {LO}_0$
is a coded predilator.
$D\!\restriction \!\mathbf {LO}_0$
is a coded predilator.
Conversely, we will now extend coded predilators into class-sized ones.
Definition 2.4. The trace of a coded predilator D is given by
A class-sized predilator D has trace
![]() $\operatorname {Tr}(D):=\operatorname {Tr}(D\!\restriction \!\mathbf {LO}_0)$
.
$\operatorname {Tr}(D):=\operatorname {Tr}(D\!\restriction \!\mathbf {LO}_0)$
.
The equation
![]() ${\operatorname {supp}}_n(\sigma )=n$
in the definition of the trace is called the minimality condition: it states that the set
${\operatorname {supp}}_n(\sigma )=n$
in the definition of the trace is called the minimality condition: it states that the set
![]() $n=\{0,\dots ,n-1\}$
is minimal in the sense that
$n=\{0,\dots ,n-1\}$
is minimal in the sense that
![]() $\sigma $
depends on all its elements. This can also be understood as a uniqueness property (see, e.g., the proof of [Reference Freund6, Proposition 2.1]). Given a finite order a, we write
$\sigma $
depends on all its elements. This can also be understood as a uniqueness property (see, e.g., the proof of [Reference Freund6, Proposition 2.1]). Given a finite order a, we write
![]() $|a|$
for its cardinality and
$|a|$
for its cardinality and
![]() $\operatorname {en}_a:|a|=\{0,\dots ,|a|-1\}\to a$
for the increasing enumeration. If
$\operatorname {en}_a:|a|=\{0,\dots ,|a|-1\}\to a$
for the increasing enumeration. If
![]() $f:a\to b$
is an embedding between finite orders, then
$f:a\to b$
is an embedding between finite orders, then
![]() $|f|:|a|\to |b|$
is defined as the unique morphism in
$|f|:|a|\to |b|$
is defined as the unique morphism in
![]() $\mathbf {LO}_0$
that satisfies
$\mathbf {LO}_0$
that satisfies
![]() $\operatorname {en}_b\circ |f|=f\circ \operatorname {en}_a$
. Given sets
$\operatorname {en}_b\circ |f|=f\circ \operatorname {en}_a$
. Given sets
![]() $X\subseteq Y$
, we write
$X\subseteq Y$
, we write
![]() $\iota _X^Y:X\hookrightarrow Y$
for the inclusion.
$\iota _X^Y:X\hookrightarrow Y$
for the inclusion.
Definition 2.5. Consider a coded predilator D. For each linear order X we set
 $$ \begin{align*} &\qquad\overline D(X):=\{(a,\sigma)\,|\,a\in[X]^{<\omega}\text{ and }(|a|,\sigma)\in\operatorname{Tr}(D)\},\\ &(a,\sigma)<_{\overline D(X)}(b,\tau)\quad:\Leftrightarrow\quad D(|\iota_a^{a\cup b}|)(\sigma)<_{D(|a\cup b|)}D(|\iota_b^{a\cup b}|)(\tau), \end{align*} $$
$$ \begin{align*} &\qquad\overline D(X):=\{(a,\sigma)\,|\,a\in[X]^{<\omega}\text{ and }(|a|,\sigma)\in\operatorname{Tr}(D)\},\\ &(a,\sigma)<_{\overline D(X)}(b,\tau)\quad:\Leftrightarrow\quad D(|\iota_a^{a\cup b}|)(\sigma)<_{D(|a\cup b|)}D(|\iota_b^{a\cup b}|)(\tau), \end{align*} $$
where
![]() $a\cup b$
is ordered as a subset of X. Given an embedding
$a\cup b$
is ordered as a subset of X. Given an embedding
![]() $f:X\to Y$
, we define
$f:X\to Y$
, we define
![]() $\overline D(f):\overline D(X)\to \overline D(Y)$
by
$\overline D(f):\overline D(X)\to \overline D(Y)$
by
![]() $\overline D(f)(a,\sigma ):=([f]^{<\omega }(a),\sigma )$
, relying on
$\overline D(f)(a,\sigma ):=([f]^{<\omega }(a),\sigma )$
, relying on
![]() $|[f]^{<\omega }(a)|=|a|$
. To define a family of functions
$|[f]^{<\omega }(a)|=|a|$
. To define a family of functions
![]() $\overline {{\operatorname {supp}}}_{X}:\overline D(X)\to [X]^{<\omega }$
, we set
$\overline {{\operatorname {supp}}}_{X}:\overline D(X)\to [X]^{<\omega }$
, we set
![]() $\overline {{\operatorname {supp}}}_{X}(a,\sigma ):=a$
.
$\overline {{\operatorname {supp}}}_{X}(a,\sigma ):=a$
.
Note that the relations
 $(a,\sigma )<_{\overline D(X)}(b,\tau )$
,
$(a,\sigma )<_{\overline D(X)}(b,\tau )$
,
![]() $(a,\sigma )\in \overline D(X)$
,
$(a,\sigma )\in \overline D(X)$
,
![]() $\overline D(f)(a,\sigma )=(b,\tau )$
and
$\overline D(f)(a,\sigma )=(b,\tau )$
and
![]() $\overline {\operatorname {supp}}_X(a,\sigma )=b$
are
$\overline {\operatorname {supp}}_X(a,\sigma )=b$
are
![]() $\Delta ^0_1$
-definable with parameter
$\Delta ^0_1$
-definable with parameter
![]() $D\subseteq \mathbb N$
. By [Reference Freund6, Lemma 2.2] and [Reference Freund, Rathjen and Weiermann12, Lemma 5.2] we have the following:
$D\subseteq \mathbb N$
. By [Reference Freund6, Lemma 2.2] and [Reference Freund, Rathjen and Weiermann12, Lemma 5.2] we have the following:
Proposition 2.6. If D is a coded predilator, then
![]() $\overline D$
is a class-sized predilator.
$\overline D$
is a class-sized predilator.
Starting with a class-sized predilator D, we can first form the restriction
![]() $D\!\restriction \!\mathbf {LO}_0$
and then the extension according to Definition 2.5. In the following, we show that we essentially recover D in this way.
$D\!\restriction \!\mathbf {LO}_0$
and then the extension according to Definition 2.5. In the following, we show that we essentially recover D in this way.
Definition 2.7. Consider a class-sized predilator D. For each order X, we define a function
 $\eta ^D_X:\overline {D\!\restriction \!\mathbf {LO}_0}(X)\to D(X)$
by setting
$\eta ^D_X:\overline {D\!\restriction \!\mathbf {LO}_0}(X)\to D(X)$
by setting
![]() $\eta ^D_X(a,\sigma ):=D(\iota _a^X\circ \operatorname {en}_a)(\sigma )$
.
$\eta ^D_X(a,\sigma ):=D(\iota _a^X\circ \operatorname {en}_a)(\sigma )$
.
By our standing assumption on class-sized predilators, the relation
![]() $D(f)(\sigma )=\tau $
has a
$D(f)(\sigma )=\tau $
has a
![]() $\Delta ^0_1$
-definition, in which f occurs as a set variable. To obtain a
$\Delta ^0_1$
-definition, in which f occurs as a set variable. To obtain a
![]() $\Delta ^0_1$
-definition of
$\Delta ^0_1$
-definition of
![]() $\eta ^D$
, one replaces each occurrence of
$\eta ^D$
, one replaces each occurrence of
![]() $(k,x)\in f$
by the
$(k,x)\in f$
by the
![]() $\Delta ^0_1$
-formula
$\Delta ^0_1$
-formula
![]() $\operatorname {en}_a(k)=x$
(note that the finite enumeration
$\operatorname {en}_a(k)=x$
(note that the finite enumeration
![]() $\operatorname {en}_a:|a|\to a\subseteq X$
can be computed with X as an oracle, and that we have
$\operatorname {en}_a:|a|\to a\subseteq X$
can be computed with X as an oracle, and that we have
![]() $\iota _a^X(x)=x$
). Let us recall [Reference Freund6, Proposition 2.1]:
$\iota _a^X(x)=x$
). Let us recall [Reference Freund6, Proposition 2.1]:
Proposition 2.8. If D is a class-sized predilator, then
![]() $\eta ^D:\overline {D\!\restriction \!\mathbf {LO}_0}\Rightarrow D$
is a natural isomorphism of functors.
$\eta ^D:\overline {D\!\restriction \!\mathbf {LO}_0}\Rightarrow D$
is a natural isomorphism of functors.
We point out that
![]() $\eta ^D$
respects the supports that come with D and
$\eta ^D$
respects the supports that come with D and
![]() $\overline {D\!\restriction \!\mathbf {LO}_0}$
, by a straightforward computation or by the general result of Lemma 2.12. Let us write
$\overline {D\!\restriction \!\mathbf {LO}_0}$
, by a straightforward computation or by the general result of Lemma 2.12. Let us write
and call the right side a normal form of
![]() $\sigma \in D(X)$
if the equation holds and we have
$\sigma \in D(X)$
if the equation holds and we have
![]() $(|a|,\sigma _0)\in \operatorname {Tr}(D)$
, where
$(|a|,\sigma _0)\in \operatorname {Tr}(D)$
, where
![]() $a\in [X]^{<\omega }$
. These conditions amount to
$a\in [X]^{<\omega }$
. These conditions amount to
![]() $\eta ^D_X(a,\sigma _0)=\sigma $
. Hence the proposition shows existence and uniqueness of the given normal forms.
$\eta ^D_X(a,\sigma _0)=\sigma $
. Hence the proposition shows existence and uniqueness of the given normal forms.
Proposition 2.8 is important since it reveals that Definition 2.5 yields a universal
![]() $\Delta ^0_1$
-definable family of class-sized predilators, in which coded predilators serve as set parameters. As promised, the previous considerations also show that the restriction to
$\Delta ^0_1$
-definable family of class-sized predilators, in which coded predilators serve as set parameters. As promised, the previous considerations also show that the restriction to
![]() $\Delta ^0_1$
-definitions is inessential to a certain extent: It was only needed to ensure that the set
$\Delta ^0_1$
-definitions is inessential to a certain extent: It was only needed to ensure that the set
![]() $D\!\restriction \!\mathbf {LO}_0$
and the components
$D\!\restriction \!\mathbf {LO}_0$
and the components
 $\eta ^D_X:\overline {D\!\restriction \!\mathbf {LO}_0}(X)\to D(X)$
can be formed in
$\eta ^D_X:\overline {D\!\restriction \!\mathbf {LO}_0}(X)\to D(X)$
can be formed in
![]() $\mathbf {RCA}_0$
. In a sufficiently strong base theory, the same argument shows that a class-sized predilator D of arbitrary complexity is equivalent to the
$\mathbf {RCA}_0$
. In a sufficiently strong base theory, the same argument shows that a class-sized predilator D of arbitrary complexity is equivalent to the
![]() $\Delta ^0_1$
-definable predilator
$\Delta ^0_1$
-definable predilator
![]() $\overline {D\!\restriction \!\mathbf {LO}_0}$
. Let us now come back to questions of well foundedness.
$\overline {D\!\restriction \!\mathbf {LO}_0}$
. Let us now come back to questions of well foundedness.
Definition 2.9. Consider a coded predilator D. If
![]() $\overline D(X)$
is well founded for every well order X, then we say that D is a coded dilator.
$\overline D(X)$
is well founded for every well order X, then we say that D is a coded dilator.
The following holds since Proposition 2.8 ensures
![]() $\overline {D\!\restriction \!\mathbf {LO}_0}(X)\cong D(X)$
.
$\overline {D\!\restriction \!\mathbf {LO}_0}(X)\cong D(X)$
.
Corollary 2.10. If D is a class-sized dilator, then
![]() $D\!\restriction \!\mathbf {LO}_0$
is a coded dilator. If D is a coded dilator, then
$D\!\restriction \!\mathbf {LO}_0$
is a coded dilator. If D is a coded dilator, then
![]() $\overline D$
is a class-sized dilator.
$\overline D$
is a class-sized dilator.
In view of the close connection that we have established, we will omit the specifications “class-sized” and “coded” when the context allows it. Many constructions and results apply—mutatis mutandis—to both class-sized and coded predilators.
To turn the collection of predilators into a category, we declare that the morphisms between two predilators
![]() $D=(D,\ {\operatorname {supp}}^D)$
and
$D=(D,\ {\operatorname {supp}}^D)$
and
![]() $E=(E,\ {\operatorname {supp}}^E)$
are the natural transformations
$E=(E,\ {\operatorname {supp}}^E)$
are the natural transformations
![]() $\mu :D\Rightarrow E$
of functors. Note that the components of such a transformation are morphisms in
$\mu :D\Rightarrow E$
of functors. Note that the components of such a transformation are morphisms in
![]() $\mathbf {LO}$
, i.e., order embeddings. In the coded case, we assume that
$\mathbf {LO}$
, i.e., order embeddings. In the coded case, we assume that
![]() $\mu $
is given as the set
$\mu $
is given as the set
![]() $\{(n,\sigma ,\tau )\,|\,\mu _n(\sigma )=\tau \}\subseteq \mathbb N$
; in the class-sized case, we require that the relation
$\{(n,\sigma ,\tau )\,|\,\mu _n(\sigma )=\tau \}\subseteq \mathbb N$
; in the class-sized case, we require that the relation
![]() $\mu _X(\sigma )=\tau $
is
$\mu _X(\sigma )=\tau $
is
![]() $\Delta ^0_1$
-definable. The obvious restriction
$\Delta ^0_1$
-definable. The obvious restriction
![]() $\mu \!\restriction \!\mathbf {LO}_0$
will then exist as a set, and we have the following.
$\mu \!\restriction \!\mathbf {LO}_0$
will then exist as a set, and we have the following.
Lemma 2.11. Assume that
![]() $\mu :D\Rightarrow E$
is a morphism of class-sized dilators. Then the restriction
$\mu :D\Rightarrow E$
is a morphism of class-sized dilators. Then the restriction
![]() $\mu \!\restriction \!\mathbf {LO}_0:D\!\restriction \!\mathbf {LO}_0\Rightarrow E\!\restriction \!\mathbf {LO}_0$
is a morphism of coded dilators.
$\mu \!\restriction \!\mathbf {LO}_0:D\!\restriction \!\mathbf {LO}_0\Rightarrow E\!\restriction \!\mathbf {LO}_0$
is a morphism of coded dilators.
In order to prove a converse, we will need the following fact, which applies in the coded as well as in the class-sized case. The result is due to Girard [Reference Girard13, Proposition 2.3.15]; a proof that uses our terminology can be found in [Reference Freund and Rathjen11, Lemma 2.19].
Lemma 2.12. We have
![]() ${\operatorname {supp}}^E\circ \mu ={\operatorname {supp}}^D$
for any morphism
${\operatorname {supp}}^E\circ \mu ={\operatorname {supp}}^D$
for any morphism
![]() $\mu :D\Rightarrow E$
between predilators
$\mu :D\Rightarrow E$
between predilators
![]() $D=(D,\ {\operatorname {supp}}^D)$
and
$D=(D,\ {\operatorname {supp}}^D)$
and
![]() $E=(E,\ {\operatorname {supp}}^E)$
.
$E=(E,\ {\operatorname {supp}}^E)$
.
The lemma ensures that
![]() $(n,\sigma )\in \operatorname {Tr}(D)$
implies
$(n,\sigma )\in \operatorname {Tr}(D)$
implies
![]() $(n,\mu _n(\sigma ))\in \operatorname {Tr}(E)$
, which is needed in order to justify the following construction.
$(n,\mu _n(\sigma ))\in \operatorname {Tr}(E)$
, which is needed in order to justify the following construction.
Definition 2.13. Consider a morphism
![]() $\mu :D\Rightarrow E$
of coded predilators. For each order X we define
$\mu :D\Rightarrow E$
of coded predilators. For each order X we define
![]() $\overline \mu _X:\overline D(X)\to \overline E(X)$
by setting
$\overline \mu _X:\overline D(X)\to \overline E(X)$
by setting
 $\overline \mu _X(a,\sigma )=(a,\mu _{|a|}(\sigma ))$
.
$\overline \mu _X(a,\sigma )=(a,\mu _{|a|}(\sigma ))$
.
The following has been verified in [Reference Freund and Rathjen11, Lemma 2.21].
Lemma 2.14. If
![]() $\mu :D\Rightarrow E$
is a morphism of coded predilators, then
$\mu :D\Rightarrow E$
is a morphism of coded predilators, then
![]() $\overline \mu :\overline D\Rightarrow \overline E$
is a morphism of class-sized predilators.
$\overline \mu :\overline D\Rightarrow \overline E$
is a morphism of class-sized predilators.
It is straightforward to see that
![]() $(\cdot )\!\restriction \!\mathbf {LO}_0$
is a functor from the category of class-sized predilators to the category of coded predilators, and that
$(\cdot )\!\restriction \!\mathbf {LO}_0$
is a functor from the category of class-sized predilators to the category of coded predilators, and that
![]() $\overline {(\cdot )}$
is a functor in the converse direction. Proposition 2.8 and the following result (which can be verified by a straightforward computation) show that
$\overline {(\cdot )}$
is a functor in the converse direction. Proposition 2.8 and the following result (which can be verified by a straightforward computation) show that
![]() $\eta $
is a natural isomorphism between the composition
$\eta $
is a natural isomorphism between the composition
 $\overline {(\cdot )\!\restriction \!\mathbf {LO}_0}$
and the identity on the category of class-sized predilators.
$\overline {(\cdot )\!\restriction \!\mathbf {LO}_0}$
and the identity on the category of class-sized predilators.
Proposition 2.15. We have
![]() $\eta ^E\circ \overline {\mu \!\restriction \!\mathbf {LO}_0}=\mu \circ \eta ^D$
whenever
$\eta ^E\circ \overline {\mu \!\restriction \!\mathbf {LO}_0}=\mu \circ \eta ^D$
whenever
![]() $\mu :D\Rightarrow E$
is a morphism of class-sized predilators.
$\mu :D\Rightarrow E$
is a morphism of class-sized predilators.
One can also start with a coded predilator D, form the class-sized extension
![]() $\overline D$
, and then revert to the coded restriction
$\overline D$
, and then revert to the coded restriction
![]() $\overline D\!\restriction \!\mathbf {LO}_0$
. By mapping
$\overline D\!\restriction \!\mathbf {LO}_0$
. By mapping
![]() $(a,\sigma )\in \overline D(n)$
to the element
$(a,\sigma )\in \overline D(n)$
to the element
![]() $D(\iota _a^X\circ \operatorname {en}_a)(\sigma )\in D(n)$
, we get a natural isomorphism
$D(\iota _a^X\circ \operatorname {en}_a)(\sigma )\in D(n)$
, we get a natural isomorphism
![]() $\overline D\!\restriction \!\mathbf {LO}_0\cong D$
, as verified in [Reference Freund and Rathjen11, Lemma 2.6]. Analogous to the proof of Proposition 2.15, one can show that the construction is natural in D. Together, these considerations show that the category of class-sized predilators is equivalent to the category of coded predilators (in the sense of [Reference Mac Lane20, Section IV.4]).
$\overline D\!\restriction \!\mathbf {LO}_0\cong D$
, as verified in [Reference Freund and Rathjen11, Lemma 2.6]. Analogous to the proof of Proposition 2.15, one can show that the construction is natural in D. Together, these considerations show that the category of class-sized predilators is equivalent to the category of coded predilators (in the sense of [Reference Mac Lane20, Section IV.4]).
In the following, we show that the trace of a predilator plays an analogous role to the underlying set of a linear order. The following is justified by Lemma 2.12.
Definition 2.16. Given a morphism
![]() $\mu :D\Rightarrow E$
of predilators, we define an injective function
$\mu :D\Rightarrow E$
of predilators, we define an injective function
![]() $\operatorname {Tr}(\mu ):\operatorname {Tr}(D)\to \operatorname {Tr}(E)$
by setting
$\operatorname {Tr}(\mu ):\operatorname {Tr}(D)\to \operatorname {Tr}(E)$
by setting
The range of
![]() $\mu $
is defined as the set
$\mu $
is defined as the set
![]() $\operatorname {rng}(\mu ):=\operatorname {rng}(\operatorname {Tr}(\mu ))\subseteq \operatorname {Tr}(E)$
.
$\operatorname {rng}(\mu ):=\operatorname {rng}(\operatorname {Tr}(\mu ))\subseteq \operatorname {Tr}(E)$
.
Girard [Reference Girard13, Theorem 4.2.5] has shown that any subset
![]() $A\subseteq \operatorname {Tr}(D)$
gives rise to a predilator
$A\subseteq \operatorname {Tr}(D)$
gives rise to a predilator
![]() $D[A]$
and a morphism
$D[A]$
and a morphism
![]() $\iota [A]:D[A]\Rightarrow D$
with
$\iota [A]:D[A]\Rightarrow D$
with
![]() $\operatorname {rng}(\iota [A])=A$
. In the following we recover this result in our terminology. As preparation, we consider an order embedding
$\operatorname {rng}(\iota [A])=A$
. In the following we recover this result in our terminology. As preparation, we consider an order embedding
![]() $f:X\to Y$
and an element
$f:X\to Y$
and an element
![]() $\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)\in D(X)$
, using the normal form notation discussed after Proposition 2.8. For
$\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)\in D(X)$
, using the normal form notation discussed after Proposition 2.8. For
![]() $b:=[f]^{<\omega }(a)\in [Y]^{<\omega }$
we have
$b:=[f]^{<\omega }(a)\in [Y]^{<\omega }$
we have
![]() $|b|=|a|$
and
$|b|=|a|$
and
![]() $f\circ\iota _a^X\circ \operatorname {en}_a=\iota _b^Y\circ \operatorname {en}_b$
, as both functions enumerate the finite order b. Hence
$f\circ\iota _a^X\circ \operatorname {en}_a=\iota _b^Y\circ \operatorname {en}_b$
, as both functions enumerate the finite order b. Hence
![]() $D(f)(\sigma )=_{\operatorname {NF}} D(\iota _b^Y\circ \operatorname {en}_b)(\sigma _0)\in D(Y)$
depends on the same trace element
$D(f)(\sigma )=_{\operatorname {NF}} D(\iota _b^Y\circ \operatorname {en}_b)(\sigma _0)\in D(Y)$
depends on the same trace element
![]() $(|b|,\sigma _0)=(|a|,\sigma _0)\in \operatorname {Tr}(D)$
. In the context of the following construction, this justifies the definition of
$(|b|,\sigma _0)=(|a|,\sigma _0)\in \operatorname {Tr}(D)$
. In the context of the following construction, this justifies the definition of
![]() $D[A](f)$
.
$D[A](f)$
.
Definition 2.17. Consider a predilator
![]() $D=(D,{\operatorname {supp}}^D)$
and a set
$D=(D,{\operatorname {supp}}^D)$
and a set
![]() $A\subseteq \operatorname {Tr}(D)$
. For each order X (with
$A\subseteq \operatorname {Tr}(D)$
. For each order X (with
![]() $X\in \mathbf {LO}$
in the class-sized and
$X\in \mathbf {LO}$
in the class-sized and
![]() $X\in \mathbf {LO}_0$
in the coded case) we define a suborder
$X\in \mathbf {LO}_0$
in the coded case) we define a suborder
![]() $D[A](X)\subseteq D(X)$
by stipulating
$D[A](X)\subseteq D(X)$
by stipulating
For a morphism
![]() $f:X\to Y$
, let
$f:X\to Y$
, let
![]() $D[A](f):D[A](X)\to D[A](Y)$
be the restriction of the embedding
$D[A](f):D[A](X)\to D[A](Y)$
be the restriction of the embedding
![]() $D(f):D(X)\to D(Y)$
. We also define
$D(f):D(X)\to D(Y)$
. We also define
 ${\operatorname {supp}}^{D[A]}_X:D[A](X)\to [X]^{<\omega }$
as the restriction of the support function
${\operatorname {supp}}^{D[A]}_X:D[A](X)\to [X]^{<\omega }$
as the restriction of the support function
![]() ${\operatorname {supp}}^D_X:D(X)\to [X]^{<\omega }$
.
${\operatorname {supp}}^D_X:D(X)\to [X]^{<\omega }$
.
Note that the relation
![]() $\sigma \in D[A](X)$
is
$\sigma \in D[A](X)$
is
![]() $\Delta ^0_1$
-definable with set parameter A, by the discussion that precedes Proposition 2.8.
$\Delta ^0_1$
-definable with set parameter A, by the discussion that precedes Proposition 2.8.
Lemma 2.18. If D is a (pre-)dilator, then so is
![]() $D[A]$
, for any
$D[A]$
, for any
![]() $A\subseteq \operatorname {Tr}(D)$
.
$A\subseteq \operatorname {Tr}(D)$
.
Proof We only verify the support condition from part (ii) of Definition 2.1, since all other properties are immediate. Consider an embedding
![]() $f:X\to Y$
and an element
$f:X\to Y$
and an element
![]() $\tau \in D[A](Y)$
with
$\tau \in D[A](Y)$
with
 $\operatorname {rng}(f)\supseteq {\operatorname {supp}}^{D[A]}_Y(\tau )={\operatorname {supp}}^D_Y(\tau )$
. The support condition for D yields
$\operatorname {rng}(f)\supseteq {\operatorname {supp}}^{D[A]}_Y(\tau )={\operatorname {supp}}^D_Y(\tau )$
. The support condition for D yields
![]() $\tau =D(f)(\sigma )$
for some
$\tau =D(f)(\sigma )$
for some
![]() $\sigma \in D(X)$
. Write
$\sigma \in D(X)$
. Write
![]() $\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
, and argue as above to get
$\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
, and argue as above to get
![]() $\tau =_{\operatorname {NF}} D(\iota _b^Y\circ \operatorname {en}_b)(\sigma _0)$
with
$\tau =_{\operatorname {NF}} D(\iota _b^Y\circ \operatorname {en}_b)(\sigma _0)$
with
![]() $b=[f]^{<\omega }(a)$
. In view of
$b=[f]^{<\omega }(a)$
. In view of
![]() $\tau \in D[A](Y)$
we can conclude
$\tau \in D[A](Y)$
we can conclude
![]() $(|a|,\sigma _0)=(|b|,\sigma _0)\in A$
and then
$(|a|,\sigma _0)=(|b|,\sigma _0)\in A$
and then
![]() $\sigma \in D[A](X)$
. It follows that we have
$\sigma \in D[A](X)$
. It follows that we have
![]() $\tau =D(f)(\sigma )=D[A](f)(\sigma )\in \operatorname {rng}(D[A](f))$
, as needed. ⊣
$\tau =D(f)(\sigma )=D[A](f)(\sigma )\in \operatorname {rng}(D[A](f))$
, as needed. ⊣
One readily checks that the following yields a morphism of predilators.
Definition 2.19. Consider a predilator D and a set
![]() $A\subseteq \operatorname {Tr}(D)$
. To define a morphism
$A\subseteq \operatorname {Tr}(D)$
. To define a morphism
![]() $\iota [A]:D[A]\Rightarrow D$
, declare that each component
$\iota [A]:D[A]\Rightarrow D$
, declare that each component
![]() $\iota [A]_X:D[A](X)\hookrightarrow D(X)$
is the inclusion map.
$\iota [A]_X:D[A](X)\hookrightarrow D(X)$
is the inclusion map.
Let us verify the promised property:
Lemma 2.20. We have
![]() $\operatorname {rng}(\iota [A])=A$
for each predilator D and each
$\operatorname {rng}(\iota [A])=A$
for each predilator D and each
![]() $A\subseteq \operatorname {Tr}(D)$
.
$A\subseteq \operatorname {Tr}(D)$
.
Proof To establish the first inclusion, we consider
![]() $(n,\sigma )\in \operatorname {rng}(\iota [A])\subseteq \operatorname {Tr}(D)$
. Since
$(n,\sigma )\in \operatorname {rng}(\iota [A])\subseteq \operatorname {Tr}(D)$
. Since
![]() $\iota [A]_n:D[A](n)\hookrightarrow D(n)$
is the inclusion, we must have
$\iota [A]_n:D[A](n)\hookrightarrow D(n)$
is the inclusion, we must have
![]() $(n,\sigma )\in \operatorname {Tr}(D[A])$
, which entails
$(n,\sigma )\in \operatorname {Tr}(D[A])$
, which entails
![]() $\sigma \in D[A](n)$
. Due to
$\sigma \in D[A](n)$
. Due to
![]() $(n,\sigma )\in \operatorname {Tr}(D)$
we have
$(n,\sigma )\in \operatorname {Tr}(D)$
we have
![]() $\sigma =_{\operatorname {NF}} D(\iota _n^n\circ \operatorname {en}_n)(\sigma )$
, where both
$\sigma =_{\operatorname {NF}} D(\iota _n^n\circ \operatorname {en}_n)(\sigma )$
, where both
![]() $\iota _n^n$
and
$\iota _n^n$
and
![]() $\operatorname {en}_n$
is the identity on
$\operatorname {en}_n$
is the identity on
![]() $n=\{0,\dots ,n-1\}$
. Now
$n=\{0,\dots ,n-1\}$
. Now
![]() $(n,\sigma )\in A$
follows by the equivalence that defines
$(n,\sigma )\in A$
follows by the equivalence that defines
![]() $D[A](n)$
. For the converse inclusion, we consider an arbitrary element
$D[A](n)$
. For the converse inclusion, we consider an arbitrary element
![]() $(n,\sigma )\in A\subseteq \operatorname {Tr}(D)$
. Once again we have
$(n,\sigma )\in A\subseteq \operatorname {Tr}(D)$
. Once again we have
![]() $\sigma =_{\operatorname {NF}} D(\iota _n^n\circ \operatorname {en}_n)(\sigma )$
, so that we get
$\sigma =_{\operatorname {NF}} D(\iota _n^n\circ \operatorname {en}_n)(\sigma )$
, so that we get
![]() $\sigma \in D[A](n)$
. Together with
$\sigma \in D[A](n)$
. Together with
 ${\operatorname {supp}}^{D[A]}_n(\sigma )={\operatorname {supp}}^D_n(\sigma )=n$
we obtain
${\operatorname {supp}}^{D[A]}_n(\sigma )={\operatorname {supp}}^D_n(\sigma )=n$
we obtain
![]() $(n,\sigma )\in \operatorname {Tr}(D[A])$
and then
$(n,\sigma )\in \operatorname {Tr}(D[A])$
and then
![]() $(n,\sigma )=(n,\iota [A]_n(\sigma ))=\operatorname {Tr}(\iota [A])(n,\sigma )\in \operatorname {rng}(\iota [A])$
. ⊣
$(n,\sigma )=(n,\iota [A]_n(\sigma ))=\operatorname {Tr}(\iota [A])(n,\sigma )\in \operatorname {rng}(\iota [A])$
. ⊣
One can characterize
![]() $D[A]$
and
$D[A]$
and
![]() $\iota [A]$
by a universal property:
$\iota [A]$
by a universal property:
Proposition 2.21. For all morphisms
![]() $\mu :D\Rightarrow E$
and
$\mu :D\Rightarrow E$
and
![]() $\mu ':D'\Rightarrow E$
of predilators, the following are equivalent:
$\mu ':D'\Rightarrow E$
of predilators, the following are equivalent:
-
(i) we have
 $\operatorname {rng}(\mu )\subseteq \operatorname {rng}(\mu ')$
and
$\operatorname {rng}(\mu )\subseteq \operatorname {rng}(\mu ')$
and -
(ii) there is a (necessarily unique) morphism
 $\nu :D\Rightarrow D'$
with
$\nu :D\Rightarrow D'$
with
 $\mu '\circ \nu =\mu $
.
$\mu '\circ \nu =\mu $
.
Proof To establish the crucial direction from (i) to (ii), we consider an element
![]() $\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)\in D(X)$
and note
$\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)\in D(X)$
and note
 $(|a|,\mu _{|a|}(\sigma _0))=\operatorname {Tr}(\mu )(|a|,\sigma _0)\in \operatorname {rng}(\mu )$
. Assuming
$(|a|,\mu _{|a|}(\sigma _0))=\operatorname {Tr}(\mu )(|a|,\sigma _0)\in \operatorname {rng}(\mu )$
. Assuming
![]() $\operatorname {rng}(\mu )\subseteq \operatorname {rng}(\mu ')$
, there is a unique
$\operatorname {rng}(\mu )\subseteq \operatorname {rng}(\mu ')$
, there is a unique
![]() $\tau _0\in D'(|a|)$
with
$\tau _0\in D'(|a|)$
with
 $\mu _{|a|}(\sigma _0)=\mu ^{\prime }_{|a|}(\tau _0)$
. For the latter we set
$\mu _{|a|}(\sigma _0)=\mu ^{\prime }_{|a|}(\tau _0)$
. For the latter we set
![]() $\nu _X(\sigma )=D'(\iota _a^X\circ \operatorname {en}_a)(\tau _0)$
. The required properties are readily verified. Essentially, this is the uniqueness part of [Reference Girard13, Theorem 4.2.5]. ⊣
$\nu _X(\sigma )=D'(\iota _a^X\circ \operatorname {en}_a)(\tau _0)$
. The required properties are readily verified. Essentially, this is the uniqueness part of [Reference Girard13, Theorem 4.2.5]. ⊣
Using this characterization of
![]() $D[A]$
and
$D[A]$
and
![]() $\iota [A]$
, it is straightforward to establish the following result, which is due to Girard [Reference Girard13, Theorem 4.2.7].
$\iota [A]$
, it is straightforward to establish the following result, which is due to Girard [Reference Girard13, Theorem 4.2.7].
Proposition 2.22. In the category of predilators, any two morphisms
![]() $\mu ^i:E_i\Rightarrow E$
with
$\mu ^i:E_i\Rightarrow E$
with
![]() $i=0,1$
have a pullback. Two morphisms
$i=0,1$
have a pullback. Two morphisms
![]() $\nu ^i:D\Rightarrow E_i$
with
$\nu ^i:D\Rightarrow E_i$
with
![]() $\mu ^0\circ \nu ^0=\mu ^1\circ \nu ^1$
form a pullback of
$\mu ^0\circ \nu ^0=\mu ^1\circ \nu ^1$
form a pullback of
![]() $\mu ^0$
and
$\mu ^0$
and
![]() $\mu ^1$
if, and only if, we have
$\mu ^1$
if, and only if, we have
![]() $\operatorname {rng}(\mu ^0)\cap \operatorname {rng}(\mu ^1)\subseteq \operatorname {rng}(\mu ^0\circ \nu ^0)$
.
$\operatorname {rng}(\mu ^0)\cap \operatorname {rng}(\mu ^1)\subseteq \operatorname {rng}(\mu ^0\circ \nu ^0)$
.
Proof For existence we set
![]() $A:=\operatorname {rng}(\mu ^0)\cap \operatorname {rng}(\mu ^1)$
and consider
$A:=\operatorname {rng}(\mu ^0)\cap \operatorname {rng}(\mu ^1)$
and consider
![]() $\iota [A]:E[A]\Rightarrow E$
. In view of
$\iota [A]:E[A]\Rightarrow E$
. In view of
![]() $\operatorname {rng}(\iota [A])=A\subseteq \operatorname {rng}(\mu ^i)$
, we get morphisms
$\operatorname {rng}(\iota [A])=A\subseteq \operatorname {rng}(\mu ^i)$
, we get morphisms
![]() $\xi ^i:E[A]\Rightarrow E_i$
with
$\xi ^i:E[A]\Rightarrow E_i$
with
One readily checks that these form a pullback. For missing details and the remaining claim we refer to the cited paper by Girard. ⊣
Girard [Reference Girard13, Theorem 4.4.4] has shown that any direct system in the category of predilators has a limit. However, the limit of a system of dilators does not need to be a dilator itself (i.e., it may not preserve well foundedness). In the next section we will define ptykes in terms of a support condition (analogous to Definition 2.1), which is motivated by the following result (see [Reference Girard13, Proposition 4.2.6]).
Proposition 2.23. In the category of predilators, consider a direct system of objects
![]() $D_i$
and morphisms
$D_i$
and morphisms
![]() $\mu ^{ij}:D_i\Rightarrow D_j$
, indexed by a directed set I. For a collection of morphisms
$\mu ^{ij}:D_i\Rightarrow D_j$
, indexed by a directed set I. For a collection of morphisms
![]() $\nu ^i:D_i\Rightarrow D$
with
$\nu ^i:D_i\Rightarrow D$
with
![]() $\nu ^j\circ \mu ^{ij}=\nu ^i$
, the following are equivalent:
$\nu ^j\circ \mu ^{ij}=\nu ^i$
, the following are equivalent:
-
(i) the morphisms
 $\nu ^i:D_i\Rightarrow D$
form a direct limit of the given system and
$\nu ^i:D_i\Rightarrow D$
form a direct limit of the given system and -
(ii) we have
 $\operatorname {Tr}(D)=\bigcup \{\operatorname {rng}(\nu ^i)\,|\,i\in I\}$
.
$\operatorname {Tr}(D)=\bigcup \{\operatorname {rng}(\nu ^i)\,|\,i\in I\}$
.
3 Ptykes in second order arithmetic
If we consider (well founded) linear orders as objects of ground type, then (pre-) dilators form the first level in a hierarchy of countinuous functionals of finite type. The functionals in this hierarchy are called (pre-)ptykes (singular ptyx; see [Reference Girard and Normann17]). On the second level of this hierarchy, we have transformations that take predilators as input. The output can be a linear order, a predilator, or even another functional from the second level—at least intuitively, these possibilities are equivalent modulo Currying. We will only consider transformations of predilators into predilators, and the term 2-ptyx will be reserved for these. The number
![]() $2$
indicates the type level and will often be omitted. In the present section, we define 2-ptykes in terms of a support condition, which is analogous to part (ii) of Definition 2.1; we show that the given definition is equivalent to the original definition by Girard, which invokes direct limits and pullbacks; and we discuss an example.
$2$
indicates the type level and will often be omitted. In the present section, we define 2-ptykes in terms of a support condition, which is analogous to part (ii) of Definition 2.1; we show that the given definition is equivalent to the original definition by Girard, which invokes direct limits and pullbacks; and we discuss an example.
In the previous section we have discussed the category of predilators. We have seen that the trace
![]() $\operatorname {Tr}(D)$
of a predilator D plays an analogous role to the underlying set of a linear order. Given a morphism
$\operatorname {Tr}(D)$
of a predilator D plays an analogous role to the underlying set of a linear order. Given a morphism
![]() $\nu :D\Rightarrow E$
of predilators, we have constructed a function
$\nu :D\Rightarrow E$
of predilators, we have constructed a function
![]() $\operatorname {Tr}(\nu ):\operatorname {Tr}(D)\to \operatorname {Tr}(E)$
with range
$\operatorname {Tr}(\nu ):\operatorname {Tr}(D)\to \operatorname {Tr}(E)$
with range
![]() $\operatorname {rng}(\nu ):=\operatorname {rng}(\operatorname {Tr}(\nu ))\subseteq \operatorname {Tr}(E)$
. One readily checks that this yields a functor
$\operatorname {rng}(\nu ):=\operatorname {rng}(\operatorname {Tr}(\nu ))\subseteq \operatorname {Tr}(E)$
. One readily checks that this yields a functor
![]() $\operatorname {Tr}(\cdot )$
from the category of predilators to the category of sets, as presupposed in part (ii) of the following definition. The formalization of the definition in second order arithmetic will be discussed below.
$\operatorname {Tr}(\cdot )$
from the category of predilators to the category of sets, as presupposed in part (ii) of the following definition. The formalization of the definition in second order arithmetic will be discussed below.
Definition 3.1. A 2-preptyx consists of
-
(i) a functor P from predilators to predilators and
-
(ii) a natural transformation
 ${\operatorname {Supp}}:\operatorname {Tr}(P(\cdot ))\to [\operatorname {Tr}(\cdot )]^{<\omega }$
such that we have for any morphism
${\operatorname {Supp}}:\operatorname {Tr}(P(\cdot ))\to [\operatorname {Tr}(\cdot )]^{<\omega }$
such that we have for any morphism $$ \begin{align*} \{\sigma\in\operatorname{Tr}(P(E))\,|\,{\operatorname{Supp}}_E(\sigma)\subseteq\operatorname{rng}(\mu)\}\subseteq\operatorname{rng}(P(\mu)) \end{align*} $$
$$ \begin{align*} \{\sigma\in\operatorname{Tr}(P(E))\,|\,{\operatorname{Supp}}_E(\sigma)\subseteq\operatorname{rng}(\mu)\}\subseteq\operatorname{rng}(P(\mu)) \end{align*} $$
 $\mu :D\Rightarrow E$
of predilators.
$\mu :D\Rightarrow E$
of predilators.
If
![]() $P(D)$
is a dilator for every dilator D, then
$P(D)$
is a dilator for every dilator D, then
![]() $P=(P,{\operatorname {Supp}})$
is called a 2-ptyx.
$P=(P,{\operatorname {Supp}})$
is called a 2-ptyx.
As in the case of dilators, we will refer to the inclusion in part (ii) as the support condition. The converse inclusion is, once again, automatic: given an arbitrary element
![]() $\sigma =\operatorname {Tr}(P(\mu ))(\sigma _0)\in \operatorname {rng}(P(\mu ))$
, we can invoke naturality to get
$\sigma =\operatorname {Tr}(P(\mu ))(\sigma _0)\in \operatorname {rng}(P(\mu ))$
, we can invoke naturality to get
Clause (i) of Definition 3.1 is not completely precise, because we have distinguished between coded and class-sized predilators—even though the two notions give rise to equivalent categories (cf. the discussion after Proposition 2.15). We can and will consider preptykes as classes-sized functions. However, the arguments of these functions should certainly be set-sized. This means that the arguments of a preptyx must be coded predilators in the sense of Definition 2.2. We agree that the values of our preptykes are coded predilators as well, even though this is less essential. To define
![]() $P(D)$
as a coded predilator, it suffices to specify its values on finite orders
$P(D)$
as a coded predilator, it suffices to specify its values on finite orders
![]() $n=\{0,\dots ,n-1\}\in \mathbf {LO}_0$
and morphisms between them. In practice, we often define the action of
$n=\{0,\dots ,n-1\}\in \mathbf {LO}_0$
and morphisms between them. In practice, we often define the action of
![]() $P(D)$
on (morphisms of) infinite linear orders as well; this means that we describe a class-sized predilator of which
$P(D)$
on (morphisms of) infinite linear orders as well; this means that we describe a class-sized predilator of which
![]() $P(D)$
is the coded restriction.
$P(D)$
is the coded restriction.
Whenever we speak of a preptyx, we assume that it is given by
![]() $\Delta ^0_1$
-definitions of the following relations, possibly with additional number and set parameters: First, we have the relations
$\Delta ^0_1$
-definitions of the following relations, possibly with additional number and set parameters: First, we have the relations
 $$ \begin{align*} \sigma\in P(D)(X),\quad\sigma<_{P(D)(X)}\tau,\quad P(D)(f)(\sigma)=\tau,\quad {\operatorname{supp}}^{P(D)}_X(\sigma)=a \end{align*} $$
$$ \begin{align*} \sigma\in P(D)(X),\quad\sigma<_{P(D)(X)}\tau,\quad P(D)(f)(\sigma)=\tau,\quad {\operatorname{supp}}^{P(D)}_X(\sigma)=a \end{align*} $$
that define the predilator
![]() $P(D)=(P(D),{\operatorname {supp}}^{P(D)})$
relative to the coded predilator
$P(D)=(P(D),{\operatorname {supp}}^{P(D)})$
relative to the coded predilator
![]() $D\subseteq \mathbb N$
. As before, these
$D\subseteq \mathbb N$
. As before, these
![]() $\Delta ^0_1$
-definitions ensure that the coded predilator
$\Delta ^0_1$
-definitions ensure that the coded predilator
![]() $P(D)$
exists as a set, over
$P(D)$
exists as a set, over
![]() $\mathbf {RCA}_0$
. Secondly, we require a
$\mathbf {RCA}_0$
. Secondly, we require a
![]() $\Delta ^0_1$
-formula
$\Delta ^0_1$
-formula
![]() $P(\mu )_X(\sigma )=\tau $
that defines the morphism
$P(\mu )_X(\sigma )=\tau $
that defines the morphism
![]() $P(\mu )$
relative to the morphism
$P(\mu )$
relative to the morphism
![]() $\mu \subseteq \mathbb N$
(cf. the discussion before Definition 2.11). Finally, we demand a
$\mu \subseteq \mathbb N$
(cf. the discussion before Definition 2.11). Finally, we demand a
![]() $\Delta ^0_1$
-definition of the relation
$\Delta ^0_1$
-definition of the relation
![]() ${\operatorname {Supp}}_D(\sigma )=a$
, where a refers to the numerical code of a finite subset of
${\operatorname {Supp}}_D(\sigma )=a$
, where a refers to the numerical code of a finite subset of
![]() $\operatorname {Tr}(D)$
.
$\operatorname {Tr}(D)$
.
By using parameters, one can quantify over
![]() $\Delta ^0_1$
-definable families of preptykes. In the following, all general definitions and results should be read as schemas, with one instance for each
$\Delta ^0_1$
-definable families of preptykes. In the following, all general definitions and results should be read as schemas, with one instance for each
![]() $\Delta ^0_1$
-definable family. We will not construct a universal family of 2-preptykes in detail, as this is quite technical and not strictly necessary for the present paper. Let us, nevertheless, sketch the construction: Given a predilator D and a finite set
$\Delta ^0_1$
-definable family. We will not construct a universal family of 2-preptykes in detail, as this is quite technical and not strictly necessary for the present paper. Let us, nevertheless, sketch the construction: Given a predilator D and a finite set
![]() $a\in [\operatorname {Tr}(D)]^{<\omega }$
, the constructions from the previous section yield a predilator
$a\in [\operatorname {Tr}(D)]^{<\omega }$
, the constructions from the previous section yield a predilator
![]() $D[a]$
and a morphism
$D[a]$
and a morphism
![]() $\iota [a]:D[a]\Rightarrow D$
with
$\iota [a]:D[a]\Rightarrow D$
with
![]() $\operatorname {rng}(\iota [a])=a$
. For
$\operatorname {rng}(\iota [a])=a$
. For
![]() $a\subseteq b$
, Proposition 2.21 ensures that there is a unique morphism
$a\subseteq b$
, Proposition 2.21 ensures that there is a unique morphism
![]() $\nu ^{ab}:D[a]\Rightarrow D[b]$
with
$\nu ^{ab}:D[a]\Rightarrow D[b]$
with
![]() $\iota [b]\circ \nu ^{ab}=\iota [a]$
. This turns the collection of predilators
$\iota [b]\circ \nu ^{ab}=\iota [a]$
. This turns the collection of predilators
![]() $D[a]$
into a directed system indexed by
$D[a]$
into a directed system indexed by
![]() $a\in [\operatorname {Tr}(D)]^{<\omega }$
. Invoking Proposition 2.23, we learn that the morphisms
$a\in [\operatorname {Tr}(D)]^{<\omega }$
. Invoking Proposition 2.23, we learn that the morphisms
![]() $\iota [a]:D[a]\Rightarrow D$
form a direct limit. Given a preptyx P, Proposition 3.2 below entails that
$\iota [a]:D[a]\Rightarrow D$
form a direct limit. Given a preptyx P, Proposition 3.2 below entails that
![]() $P(D)$
is the (essentially unique) limit of the system of predilators
$P(D)$
is the (essentially unique) limit of the system of predilators
![]() $P(D[a])$
and morphisms
$P(D[a])$
and morphisms
![]() $P(\nu ^{ab}):P(D[a])\Rightarrow P(D[b])$
. In other words, P is essentially determined by its action on (morphisms between) predilators with finite trace. The latter are determined by a finite amount of information (by [Reference Girard13, Proposition 4.3.7] or, implicitly, Definition 2.5 above). By restricting to arguments with finite trace, one can thus define a notion of coded preptyx, analogous to Definition 2.2. The following result is the main ingredient of the construction that we have sketched. It also shows that our definition of 2-ptykes coincides with Girard’s original one.
$P(\nu ^{ab}):P(D[a])\Rightarrow P(D[b])$
. In other words, P is essentially determined by its action on (morphisms between) predilators with finite trace. The latter are determined by a finite amount of information (by [Reference Girard13, Proposition 4.3.7] or, implicitly, Definition 2.5 above). By restricting to arguments with finite trace, one can thus define a notion of coded preptyx, analogous to Definition 2.2. The following result is the main ingredient of the construction that we have sketched. It also shows that our definition of 2-ptykes coincides with Girard’s original one.
Proposition 3.2. The following are equivalent for an endofunctor P of predilators:
-
(i) The functor P preserves direct limits and pullbacks.
-
(ii) There is a natural transformation
 ${\operatorname {Supp}}:\operatorname {Tr}(P(\cdot ))\to [\operatorname {Tr}(\cdot )]^{<\omega }$
that satisfies the support condition from part (ii) of Definition 3.1.
${\operatorname {Supp}}:\operatorname {Tr}(P(\cdot ))\to [\operatorname {Tr}(\cdot )]^{<\omega }$
that satisfies the support condition from part (ii) of Definition 3.1.
If a natural transformation as in (ii) exists, then it is unique.
Proof The argument is very similar to the corresponding proof for dilators (see [Reference Girard13, Propositions 4.2.6 and 4.2.7] or also [Reference Freund3, Remark 2.2.2]), so we only sketch it. In order to show that (ii) implies (i), consider a direct system of predilators
![]() $D_i$
and morphisms
$D_i$
and morphisms
![]() $\mu ^{ij}:D_i\Rightarrow D_j$
. Assume that the morphisms
$\mu ^{ij}:D_i\Rightarrow D_j$
. Assume that the morphisms
![]() $\nu ^i:D_i\Rightarrow D$
form a direct limit. By Proposition 2.23 we have
$\nu ^i:D_i\Rightarrow D$
form a direct limit. By Proposition 2.23 we have
![]() $\operatorname {Tr}(D)=\bigcup \{\operatorname {rng}(\nu ^i)\,|\,i\in I\}$
. To confirm that P preserves direct limits, we need to establish
$\operatorname {Tr}(D)=\bigcup \{\operatorname {rng}(\nu ^i)\,|\,i\in I\}$
. To confirm that P preserves direct limits, we need to establish
![]() $\operatorname {Tr}(P(D))=\bigcup \{\operatorname {rng}(P(\nu ^i))\,|\,i\in I\}$
. This is straightforward, given that the supports from (ii) are finite. Preservation of pullbacks is shown similarly, based on the characterization from Proposition 2.22. For the other direction and the uniqueness result, we point out that the support of
$\operatorname {Tr}(P(D))=\bigcup \{\operatorname {rng}(P(\nu ^i))\,|\,i\in I\}$
. This is straightforward, given that the supports from (ii) are finite. Preservation of pullbacks is shown similarly, based on the characterization from Proposition 2.22. For the other direction and the uniqueness result, we point out that the support of
![]() $\rho \in \operatorname {Tr}(P(D))$
is determined as the smallest set
$\rho \in \operatorname {Tr}(P(D))$
is determined as the smallest set
![]() $a\in [\operatorname {Tr}(D)]^{<\omega }$
such that we have
$a\in [\operatorname {Tr}(D)]^{<\omega }$
such that we have
![]() $\rho \in \operatorname {rng}(P(\iota [a]))$
, where
$\rho \in \operatorname {rng}(P(\iota [a]))$
, where
![]() $\iota [a]:D[a]\Rightarrow D$
is the morphism from Lemma 2.20. Preservation of direct limits (applied to D as a limit of the
$\iota [a]:D[a]\Rightarrow D$
is the morphism from Lemma 2.20. Preservation of direct limits (applied to D as a limit of the
![]() $D[a]$
) ensures that there is a finite set with this property. The fact that there is a smallest one follows from preservation of pullbacks. A detailed verification can be found in a first version of this paper, which is available as arXiv:2006.12111v1. ⊣
$D[a]$
) ensures that there is a finite set with this property. The fact that there is a smallest one follows from preservation of pullbacks. A detailed verification can be found in a first version of this paper, which is available as arXiv:2006.12111v1. ⊣
The following variant of the support functions is convenient, because it does not force us to consider the trace of
![]() $P(D)$
, which can be hard to describe. We recall that every element
$P(D)$
, which can be hard to describe. We recall that every element
![]() $\sigma \in P(D)(X)$
has a unique normal form
$\sigma \in P(D)(X)$
has a unique normal form
![]() $\sigma =_{\operatorname {NF}} P(D)(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
with
$\sigma =_{\operatorname {NF}} P(D)(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
with
![]() $(|a|,\sigma _0)\in \operatorname {Tr}(P(D))$
, as explained after Proposition 2.8 above.
$(|a|,\sigma _0)\in \operatorname {Tr}(P(D))$
, as explained after Proposition 2.8 above.
Definition 3.3. Consider a 2-preptyx
![]() $P=(P,\ {\operatorname {Supp}})$
. For each predilator D and each linear order X, we define a function
$P=(P,\ {\operatorname {Supp}})$
. For each predilator D and each linear order X, we define a function
by setting
![]() ${\operatorname {Supp}}_{D,X}(\sigma ):={\operatorname {Supp}}_D(|a|,\sigma _0)$
for
${\operatorname {Supp}}_{D,X}(\sigma ):={\operatorname {Supp}}_D(|a|,\sigma _0)$
for
![]() $\sigma =_{\operatorname {NF}} P(D)(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
.
$\sigma =_{\operatorname {NF}} P(D)(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
.
One readily checks that our modified support functions inherit the following properties. Details can, once again, be found in arXiv:2006.12111v1.
Lemma 3.4. For any preptyx P, the functions
![]() ${\operatorname {Supp}}_{D,X}$
are natural in D and X, in the sense that we have
${\operatorname {Supp}}_{D,X}$
are natural in D and X, in the sense that we have
for any morphism
![]() $\mu :D\Rightarrow E$
of predilators and any order embedding
$\mu :D\Rightarrow E$
of predilators and any order embedding
![]() $f:X\to Y$
. Furthermore, the support condition
$f:X\to Y$
. Furthermore, the support condition
is satisfied for any morphism
![]() $\mu :D\Rightarrow E$
and any linear order X.
$\mu :D\Rightarrow E$
and any linear order X.
For the following converse, we recall that elements of
![]() $\operatorname {Tr}(P(D))$
have the form
$\operatorname {Tr}(P(D))$
have the form
![]() $(n,\sigma )$
with
$(n,\sigma )$
with
![]() $\sigma \in P(D)(n)$
, where
$\sigma \in P(D)(n)$
, where
![]() $n=\{0,\dots ,n-1\}$
is ordered as usual.
$n=\{0,\dots ,n-1\}$
is ordered as usual.
Lemma 3.5. Consider an endofunctor P of predilators and a family of functions
![]() ${\operatorname {Supp}}_{D,X}$
with the properties from Lemma 3.4. We obtain a preptyx
${\operatorname {Supp}}_{D,X}$
with the properties from Lemma 3.4. We obtain a preptyx
![]() $(P,{\operatorname {Supp}})$
if we define
$(P,{\operatorname {Supp}})$
if we define
![]() ${\operatorname {Supp}}_D:\operatorname {Tr}(P(D))\to [\operatorname {Tr}(D)]^{<\omega }$
by
${\operatorname {Supp}}_D:\operatorname {Tr}(P(D))\to [\operatorname {Tr}(D)]^{<\omega }$
by
![]() ${\operatorname {Supp}}_D(n,\sigma ):={\operatorname {Supp}}_{D,n}(\sigma )$
.
${\operatorname {Supp}}_D(n,\sigma ):={\operatorname {Supp}}_{D,n}(\sigma )$
.
The functions
![]() ${\operatorname {Supp}}_D:\operatorname {Tr}(P(D))\to [\operatorname {Tr}(D)]^{<\omega }$
are unique by Proposition 3.2. As in the proof of the latter, the value
${\operatorname {Supp}}_D:\operatorname {Tr}(P(D))\to [\operatorname {Tr}(D)]^{<\omega }$
are unique by Proposition 3.2. As in the proof of the latter, the value
![]() ${\operatorname {Supp}}_{D,X}(\sigma )$
is uniquely determined as the smallest
${\operatorname {Supp}}_{D,X}(\sigma )$
is uniquely determined as the smallest
![]() $a\subseteq \operatorname {Tr}(D)$
with
$a\subseteq \operatorname {Tr}(D)$
with
![]() $\sigma \in \operatorname {rng}(P(\iota [a])_X)$
. Due to uniqueness, the constructions from the previous two lemmas must be inverse to each other. The proof of Lemma 3.5 does not use the assumption that the functions
$\sigma \in \operatorname {rng}(P(\iota [a])_X)$
. Due to uniqueness, the constructions from the previous two lemmas must be inverse to each other. The proof of Lemma 3.5 does not use the assumption that the functions
![]() ${\operatorname {Supp}}_{D,X}$
are natural in X. Hence the latter is automatic when the other properties from Lemma 3.4 are satisfied.
${\operatorname {Supp}}_{D,X}$
are natural in X. Hence the latter is automatic when the other properties from Lemma 3.4 are satisfied.
The following example reveals a connection with a more familiar topic: it shows that the transformation of a normal function into its derivative is related to the notion of ptyx. A much simpler ptyx will be described in Example 4.4 below.
Example 3.6. A normal predilator consists of a predilator
![]() $D=(D,\ {\operatorname {supp}}^D)$
and a natural family of functions
$D=(D,\ {\operatorname {supp}}^D)$
and a natural family of functions
![]() $\mu ^D_X:X\to D(X)$
such that we have
$\mu ^D_X:X\to D(X)$
such that we have
 $$ \begin{align*} \sigma<_{D(X)}\mu^D_X(x)\quad\Leftrightarrow\quad{\operatorname{supp}}^D_X(\sigma)\subseteq\{x'\in X\,|\,x'<_X x\}, \end{align*} $$
$$ \begin{align*} \sigma<_{D(X)}\mu^D_X(x)\quad\Leftrightarrow\quad{\operatorname{supp}}^D_X(\sigma)\subseteq\{x'\in X\,|\,x'<_X x\}, \end{align*} $$
for any linear order X and arbitrary elements
![]() $x\in X$
and
$x\in X$
and
![]() $\sigma \in D(X)$
. If
$\sigma \in D(X)$
. If
![]() $D=(D,\mu ^D)$
is a normal dilator, then the induced function on the ordinals (which maps
$D=(D,\mu ^D)$
is a normal dilator, then the induced function on the ordinals (which maps
![]() $\alpha $
to the order type of
$\alpha $
to the order type of
![]() $D(\alpha )$
) is normal in the usual sense, due to Aczel [Reference Aczel1, Reference Aczel2]. The latter has also shown that one can transform D into a normal (pre-)dilator
$D(\alpha )$
) is normal in the usual sense, due to Aczel [Reference Aczel1, Reference Aczel2]. The latter has also shown that one can transform D into a normal (pre-)dilator
![]() $\partial D$
that induces the derivative of the normal function induced by D. Together with Rathjen, the present author has established that the construction of
$\partial D$
that induces the derivative of the normal function induced by D. Together with Rathjen, the present author has established that the construction of
![]() $\partial D$
can be implemented in
$\partial D$
can be implemented in
![]() $\mathbf {RCA}_0$
. Over the latter, the statement that
$\mathbf {RCA}_0$
. Over the latter, the statement that
![]() $\partial D$
is a dilator (i.e., preserves well foundedness) when the same holds for D is equivalent to
$\partial D$
is a dilator (i.e., preserves well foundedness) when the same holds for D is equivalent to
![]() $\Pi ^1_1$
-bar induction [Reference Freund7, Reference Freund and Rathjen11]. The transformation of D into
$\Pi ^1_1$
-bar induction [Reference Freund7, Reference Freund and Rathjen11]. The transformation of D into
![]() $P(D):=\partial D$
is no 2-ptyx in the strict sense, since it only acts on normal predilators. Nevertheless, it is instructive to observe that all other conditions from Definition 3.1 are satisfied. For this purpose, we recall that
$P(D):=\partial D$
is no 2-ptyx in the strict sense, since it only acts on normal predilators. Nevertheless, it is instructive to observe that all other conditions from Definition 3.1 are satisfied. For this purpose, we recall that
![]() $\partial D(X)$
is recursively generated by the following clauses (cf. [Reference Freund and Rathjen11, Definition 4.1]):
$\partial D(X)$
is recursively generated by the following clauses (cf. [Reference Freund and Rathjen11, Definition 4.1]):
-
• For each element
 $x\in X$
, there is a term
$x\in X$
, there is a term
 $\mu ^{\partial D}_x\in \partial D(X)$
.
$\mu ^{\partial D}_x\in \partial D(X)$
. -
• Given a finite set
 $a\subseteq \partial D(X)$
, we get a term
$a\subseteq \partial D(X)$
, we get a term
 $\xi \langle a,\sigma \rangle \in \partial D(X)$
for each
$\xi \langle a,\sigma \rangle \in \partial D(X)$
for each
 $\sigma \in D(|a|)$
with
$\sigma \in D(|a|)$
with
 $(|a|,\sigma )\in \operatorname {Tr}(D)$
, except when
$(|a|,\sigma )\in \operatorname {Tr}(D)$
, except when
 $\langle a,\sigma \rangle =\langle \{\mu ^{\partial D}_x\},\mu ^D_1(0)\rangle $
for some
$\langle a,\sigma \rangle =\langle \{\mu ^{\partial D}_x\},\mu ^D_1(0)\rangle $
for some
 $x\in X$
(where
$x\in X$
(where
 $\mu ^D_1:1=\{0\}\to D(1)$
witnesses the normality of D).
$\mu ^D_1:1=\{0\}\to D(1)$
witnesses the normality of D).
The map
![]() $X\mapsto \partial D(X)$
can be turned into a normal (pre-)dilator, as shown in [Reference Freund and Rathjen11]. To turn
$X\mapsto \partial D(X)$
can be turned into a normal (pre-)dilator, as shown in [Reference Freund and Rathjen11]. To turn
![]() $D\mapsto \partial D=P(D)$
into a functor, we consider a morphism
$D\mapsto \partial D=P(D)$
into a functor, we consider a morphism
![]() $\nu :D\Rightarrow E$
of normal predilators (which requires
$\nu :D\Rightarrow E$
of normal predilators (which requires
![]() $\nu _1(\mu ^D_1(0))=\mu ^E_1(0)$
, by [Reference Freund and Rathjen11, Definition 2.20]). In order to obtain a morphism
$\nu _1(\mu ^D_1(0))=\mu ^E_1(0)$
, by [Reference Freund and Rathjen11, Definition 2.20]). In order to obtain a morphism
![]() $P(\nu ):P(D)\Rightarrow P(E)$
, we define the components
$P(\nu ):P(D)\Rightarrow P(E)$
, we define the components
![]() $P(\nu )_X:\partial D(X)\to \partial E(X)$
by the recursive clauses
$P(\nu )_X:\partial D(X)\to \partial E(X)$
by the recursive clauses
![]() $P(\nu )_X(\mu ^{\partial D}_x)=\mu ^{\partial E}_x$
and
$P(\nu )_X(\mu ^{\partial D}_x)=\mu ^{\partial E}_x$
and
To show that we have something like a 2-ptyx (except for the restriction to normal predilators), we need to construct support functions
as in Lemma 3.4. We recursively define
 ${\operatorname {Supp}}_{D,X}(\mu ^{\partial D}_x)=\emptyset $
and
${\operatorname {Supp}}_{D,X}(\mu ^{\partial D}_x)=\emptyset $
and
 $$ \begin{align*} {\operatorname{Supp}}_{D,X}(\xi\langle a,\sigma\rangle)=\{(|a|,\sigma)\}\cup\bigcup\{{\operatorname{Supp}}_{D,X}(\rho)\,|\,\rho\in a\}. \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}_{D,X}(\xi\langle a,\sigma\rangle)=\{(|a|,\sigma)\}\cup\bigcup\{{\operatorname{Supp}}_{D,X}(\rho)\,|\,\rho\in a\}. \end{align*} $$
The required properties are readily verified (see again arXiv:2006.12111v1).
4 Normal 2-ptykes
The present section introduces a normality condition for 2-ptykes, which is related to the notion of normal function on the ordinals. We then show that any 2-ptyx is bounded by a normal one; this amounts to the construction of the ptyx
![]() $P^*$
from the argument that was sketched in the introduction.
$P^*$
from the argument that was sketched in the introduction.
In Example 3.6, we have recalled the notion of normal predilator. The crucial point is that any normal predilator D preserves initial segments, which are determined by the values
![]() $\mu ^D_X(x)\in D(X)$
(cf. Girard’s notion of flower [Reference Girard13]). We now introduce a corresponding notion on the next type level.
$\mu ^D_X(x)\in D(X)$
(cf. Girard’s notion of flower [Reference Girard13]). We now introduce a corresponding notion on the next type level.
Definition 4.1. A morphism
![]() $\nu :D\Rightarrow E$
is called a segment if the range of each component
$\nu :D\Rightarrow E$
is called a segment if the range of each component
![]() $\nu _X:D(X)\to E(X)$
is an initial segment of the linear order
$\nu _X:D(X)\to E(X)$
is an initial segment of the linear order
![]() $E(X)$
.
$E(X)$
.
We point out that the definition applies to both coded and class-sized predilators. In the coded case one only considers orders of the form
![]() $X=n=\{0,\dots ,n-1\}$
. As the following lemma shows, the two variants of the definition are compatible with the equivalence between coded and class-sized predilators (cf. Lemma 2.14). For a detailed verification we refer to arXiv:2006.12111v1.
$X=n=\{0,\dots ,n-1\}$
. As the following lemma shows, the two variants of the definition are compatible with the equivalence between coded and class-sized predilators (cf. Lemma 2.14). For a detailed verification we refer to arXiv:2006.12111v1.
Lemma 4.2. Consider a morphism
![]() $\nu :D\Rightarrow E$
of coded predilators. If
$\nu :D\Rightarrow E$
of coded predilators. If
![]() $\nu $
is a segment, then so is
$\nu $
is a segment, then so is
![]() $\overline \nu :\overline D\Rightarrow \overline E$
.
$\overline \nu :\overline D\Rightarrow \overline E$
.
The following is similar to the corresponding notion for dilators, which is itself related to the usual notion of normal function on the ordinals (cf. Example 3.6).
Definition 4.3. A 2-preptyx P is called normal if
![]() $P(\nu ):P(D)\Rightarrow P(E)$
is a segment whenever the same holds for
$P(\nu ):P(D)\Rightarrow P(E)$
is a segment whenever the same holds for
![]() $\nu :D\Rightarrow E$
.
$\nu :D\Rightarrow E$
.
In §6 we will construct a minimal fixed point
![]() $D\cong P(D)$
of a given 2-preptyx P. We will see that D is a dilator (rather than just a predilator) when P is a normal 2-ptyx. The following example shows that normality is essential. We provide full details, because the construction will be needed later.
$D\cong P(D)$
of a given 2-preptyx P. We will see that D is a dilator (rather than just a predilator) when P is a normal 2-ptyx. The following example shows that normality is essential. We provide full details, because the construction will be needed later.
Example 4.4. Given a linear order X, we define
![]() $X+1=X\cup \{\top \}$
as the order with a new biggest element
$X+1=X\cup \{\top \}$
as the order with a new biggest element
![]() $\top $
. If D is a (pre-)dilator, we get a (pre-)dilator
$\top $
. If D is a (pre-)dilator, we get a (pre-)dilator
![]() $D+1$
by setting
$D+1$
by setting
![]() $(D+1)(X):=D(X)+1$
and
$(D+1)(X):=D(X)+1$
and
 $$ \begin{align*} (D+1)(f)(\sigma)&:=\begin{cases} D(f)(\sigma) & \text{if}\ \sigma\in D(X)\subseteq (D+1)(X),\\ \top & \text{if}\ \sigma=\top, \end{cases}\\ {\operatorname{supp}}^{D+1}_X(\sigma)&:=\begin{cases} {\operatorname{supp}}^D_X(\sigma) & \text{if}\ \sigma\in D(X)\subseteq (D+1)(X),\\ \emptyset & \text{if}\ \sigma=\top, \end{cases} \end{align*} $$
$$ \begin{align*} (D+1)(f)(\sigma)&:=\begin{cases} D(f)(\sigma) & \text{if}\ \sigma\in D(X)\subseteq (D+1)(X),\\ \top & \text{if}\ \sigma=\top, \end{cases}\\ {\operatorname{supp}}^{D+1}_X(\sigma)&:=\begin{cases} {\operatorname{supp}}^D_X(\sigma) & \text{if}\ \sigma\in D(X)\subseteq (D+1)(X),\\ \emptyset & \text{if}\ \sigma=\top, \end{cases} \end{align*} $$
where
![]() $f:X\to Y$
is an embedding. To turn
$f:X\to Y$
is an embedding. To turn
![]() $D\mapsto D+1$
into a functor, we transform each morphism
$D\mapsto D+1$
into a functor, we transform each morphism
![]() $\nu :D\Rightarrow E$
into the morphism
$\nu :D\Rightarrow E$
into the morphism
![]() $\nu +1:D+1\Rightarrow E+1$
with
$\nu +1:D+1\Rightarrow E+1$
with
 $$ \begin{align*} (\nu+1)_X(\sigma):=\begin{cases} \nu_X(\sigma) & \text{if}\ \sigma\in D(X)\subseteq (D+1)(X),\\ \top & \text{if}\ \sigma=\top. \end{cases} \end{align*} $$
$$ \begin{align*} (\nu+1)_X(\sigma):=\begin{cases} \nu_X(\sigma) & \text{if}\ \sigma\in D(X)\subseteq (D+1)(X),\\ \top & \text{if}\ \sigma=\top. \end{cases} \end{align*} $$
By Lemma 3.5, we obtain a ptyx if we define
![]() ${\operatorname {Supp}}_{D,X}:D(X)+1\to [\operatorname {Tr}(D)]^{<\omega }$
by
${\operatorname {Supp}}_{D,X}:D(X)+1\to [\operatorname {Tr}(D)]^{<\omega }$
by
 $$ \begin{align*} {\operatorname{Supp}}_{D,X}(\sigma):=\begin{cases} \{(|a|,\sigma_0)\} & \text{if}\ \sigma=_{\operatorname{NF}} D(\iota_a^X\circ\operatorname{en}_a)(\sigma_0)\in D(X),\\ \emptyset & \text{if}\ \sigma=\top. \end{cases} \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}_{D,X}(\sigma):=\begin{cases} \{(|a|,\sigma_0)\} & \text{if}\ \sigma=_{\operatorname{NF}} D(\iota_a^X\circ\operatorname{en}_a)(\sigma_0)\in D(X),\\ \emptyset & \text{if}\ \sigma=\top. \end{cases} \end{align*} $$
If
![]() $D\cong D+1$
is a fixed point, then
$D\cong D+1$
is a fixed point, then
![]() $D(0)\cong D(0)+1$
cannot be a well order, so that D is no dilator. To see that
$D(0)\cong D(0)+1$
cannot be a well order, so that D is no dilator. To see that
![]() $D\mapsto D+1$
is not normal, we consider the constant dilators with values
$D\mapsto D+1$
is not normal, we consider the constant dilators with values
![]() $D(X)=0$
and
$D(X)=0$
and
![]() $E(X)=1=\{0\}$
. The unique morphism
$E(X)=1=\{0\}$
. The unique morphism
![]() $\nu :D\Rightarrow E$
(with the empty function as components) is a segment. We have
$\nu :D\Rightarrow E$
(with the empty function as components) is a segment. We have
but
![]() $0\notin \operatorname {rng}((\nu +1)_0)$
, which shows that
$0\notin \operatorname {rng}((\nu +1)_0)$
, which shows that
![]() $\nu +1$
is no segment.
$\nu +1$
is no segment.
In the rest of this section, we show that each preptyx P can be majorized by a normal preptyx
![]() $P^*$
, in the sense that there is a morphism
$P^*$
, in the sense that there is a morphism
![]() $P(D)+1\Rightarrow P^*(D+1)$
for each predilator D. Informally, the discussion in the introduction suggests
$P(D)+1\Rightarrow P^*(D+1)$
for each predilator D. Informally, the discussion in the introduction suggests
 $$ \begin{align*} P^*(D):=\sum\{P(D_0)+1\,|\,\text{there is a ``proper" segment~}D_0\Rightarrow D\}. \end{align*} $$
$$ \begin{align*} P^*(D):=\sum\{P(D_0)+1\,|\,\text{there is a ``proper" segment~}D_0\Rightarrow D\}. \end{align*} $$
By a result of Girard (see e.g., [Reference Girard and Normann16, Lemma 2.11]), we can hope to find a linear order on the summands. In order to make precise sense of our informal definition, we analyse the collection of segments
![]() $D_0\Rightarrow D$
in terms of the trace
$D_0\Rightarrow D$
in terms of the trace
![]() $\operatorname {Tr}(D)$
.
$\operatorname {Tr}(D)$
.
Definition 4.5. Given a predilator D, we define a relation
![]() $\ll $
on the trace
$\ll $
on the trace
![]() $\operatorname {Tr}(D)$
by stipulating that
$\operatorname {Tr}(D)$
by stipulating that
![]() $(m,\sigma )\ll (n,\tau )$
holds if, and only if, we have
$(m,\sigma )\ll (n,\tau )$
holds if, and only if, we have
for all embeddings
![]() $f:m\to X$
and
$f:m\to X$
and
![]() $g:n\to X$
into a linear order X.
$g:n\to X$
into a linear order X.
The following shows that the relation
![]() $\ll $
is
$\ll $
is
![]() $\Delta ^0_1$
-definable. It also shows that it makes no difference whether we consider D as a class-sized or as a coded dilator.
$\Delta ^0_1$
-definable. It also shows that it makes no difference whether we consider D as a class-sized or as a coded dilator.
Lemma 4.6. We already have
![]() $(m,\sigma )\ll (n,\tau )$
if the condition from Definition 4.5 is satisfied for all embeddings into
$(m,\sigma )\ll (n,\tau )$
if the condition from Definition 4.5 is satisfied for all embeddings into
![]() $X=m+n=\{0,\dots ,m+n-1\}$
.
$X=m+n=\{0,\dots ,m+n-1\}$
.
Proof Consider embeddings
![]() $f:m\to X$
and
$f:m\to X$
and
![]() $g:n\to X$
into an arbitrary order X. The idea is to factor through the inclusion
$g:n\to X$
into an arbitrary order X. The idea is to factor through the inclusion
![]() $\operatorname {rng}(f)\cup \operatorname {rng}(g)\hookrightarrow X$
, and to consider an embedding
$\operatorname {rng}(f)\cup \operatorname {rng}(g)\hookrightarrow X$
, and to consider an embedding
![]() $\operatorname {rng}(f)\cup \operatorname {rng}(g)\to m+n$
. ⊣
$\operatorname {rng}(f)\cup \operatorname {rng}(g)\to m+n$
. ⊣
Let us verify a basic property:
Lemma 4.7. The relation
![]() $\ll $
on
$\ll $
on
![]() $\operatorname {Tr}(D)$
is irreflexive and transitive.
$\operatorname {Tr}(D)$
is irreflexive and transitive.
Proof Given that the order on
![]() $D(m)$
is irreflexive for all
$D(m)$
is irreflexive for all
![]() $m\in \mathbb N$
, it is straightforward to show that the same holds for
$m\in \mathbb N$
, it is straightforward to show that the same holds for
![]() $\ll $
. To establish transitivity we consider inequalities
$\ll $
. To establish transitivity we consider inequalities
![]() $(m,\sigma )\ll (n,\tau )$
and
$(m,\sigma )\ll (n,\tau )$
and
![]() $(n,\tau )\ll (k,\rho )$
. Given embeddings
$(n,\tau )\ll (k,\rho )$
. Given embeddings
![]() $f:m\to X$
and
$f:m\to X$
and
![]() $g:k\to X$
, pick an order Y that is large enough to admit embeddings
$g:k\to X$
, pick an order Y that is large enough to admit embeddings
![]() $h:X\to Y$
and
$h:X\to Y$
and
![]() $h':n\to Y$
. We get
$h':n\to Y$
. We get
 $$ \begin{align*} D(h\circ f)(\sigma)<_{D(Y)} D(h')(\tau)<_{D(Y)} D(h\circ g)(\rho), \end{align*} $$
$$ \begin{align*} D(h\circ f)(\sigma)<_{D(Y)} D(h')(\tau)<_{D(Y)} D(h\circ g)(\rho), \end{align*} $$
which implies
![]() $D(f)(\sigma )<_{D(X)} D(g)(\rho )$
, as needed for
$D(f)(\sigma )<_{D(X)} D(g)(\rho )$
, as needed for
![]() $(m,\sigma )\ll (k,\rho )$
. ⊣
$(m,\sigma )\ll (k,\rho )$
. ⊣
As promised, the relation
![]() $\ll $
on the trace can be used to characterize segments:
$\ll $
on the trace can be used to characterize segments:
Proposition 4.8. For any morphism
![]() $\nu :D\Rightarrow E$
between predilators D and E, the following are equivalent:
$\nu :D\Rightarrow E$
between predilators D and E, the following are equivalent:
-
(i) the morphism
 $\nu :D\Rightarrow E$
is a segment and
$\nu :D\Rightarrow E$
is a segment and -
(ii) given
 $(m,\sigma )\in \operatorname {rng}(\nu )$
and
$(m,\sigma )\in \operatorname {rng}(\nu )$
and
 $(m,\sigma )\not \ll (n,\tau )\in \operatorname {Tr}(E)$
, we get
$(m,\sigma )\not \ll (n,\tau )\in \operatorname {Tr}(E)$
, we get
 $(n,\tau )\in \operatorname {rng}(\nu )$
.
$(n,\tau )\in \operatorname {rng}(\nu )$
.
Proof To show that (i) implies (ii), assume
![]() $(m,\sigma )\in \operatorname {rng}(\nu )$
and
$(m,\sigma )\in \operatorname {rng}(\nu )$
and
![]() $(m,\sigma )\not \ll (n,\tau )$
. The former is witnessed by an element
$(m,\sigma )\not \ll (n,\tau )$
. The former is witnessed by an element
![]() $\sigma _0\in D(m)$
with
$\sigma _0\in D(m)$
with
![]() $\sigma =\nu _m(\sigma _0)$
, while the latter yields embeddings
$\sigma =\nu _m(\sigma _0)$
, while the latter yields embeddings
![]() $f:m\to X$
and
$f:m\to X$
and
![]() $g:n\to X$
with
$g:n\to X$
with
Given that
![]() $\nu $
is a segment, we obtain
$\nu $
is a segment, we obtain
![]() $E(g)(\tau )=\nu _X(\rho )$
for some element
$E(g)(\tau )=\nu _X(\rho )$
for some element
![]() $\rho \in D(X)$
. Write
$\rho \in D(X)$
. Write
![]() $\rho =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\rho _0)$
and observe
$\rho =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\rho _0)$
and observe
 $$ \begin{align*} E(g)(\tau)=\nu_X\circ D(\iota_a^X\circ\operatorname{en}_a)(\rho_0)=E(\iota_a^X\circ\operatorname{en}_a)\circ\nu_{|a|}(\rho_0). \end{align*} $$
$$ \begin{align*} E(g)(\tau)=\nu_X\circ D(\iota_a^X\circ\operatorname{en}_a)(\rho_0)=E(\iota_a^X\circ\operatorname{en}_a)\circ\nu_{|a|}(\rho_0). \end{align*} $$
Recall that
![]() $(n,\tau )\in \operatorname {Tr}(E)$
entails
$(n,\tau )\in \operatorname {Tr}(E)$
entails
![]() ${\operatorname {supp}}^E_n(\tau )=n$
. Together with Lemma 2.12, this means that
${\operatorname {supp}}^E_n(\tau )=n$
. Together with Lemma 2.12, this means that
![]() $(|a|,\rho _0)\in \operatorname {Tr}(D)$
yields
$(|a|,\rho _0)\in \operatorname {Tr}(D)$
yields
 ${\operatorname {supp}}^E_{|a|}\circ \nu _{|a|}(\rho _0)={\operatorname {supp}}^D_{|a|}(\rho _0)=|a|$
. We obtain
${\operatorname {supp}}^E_{|a|}\circ \nu _{|a|}(\rho _0)={\operatorname {supp}}^D_{|a|}(\rho _0)=|a|$
. We obtain
 $$ \begin{align*} [g]^{<\omega}(n)&={\operatorname{supp}}^E_X(E(g)(\tau))={\operatorname{supp}}^E_X(\nu_X\circ D(\iota_a^X\circ\operatorname{en}_a)(\rho_0))\\ &={\operatorname{supp}}^E_X(E(\iota_a^X\circ\operatorname{en}_a)\circ\nu_{|a|}(\rho_0))=[\iota_a^X\circ\operatorname{en}_a]^{<\omega}({\operatorname{supp}}^E_{|a|}\circ\nu_{|a|}(\rho_0))=a, \end{align*} $$
$$ \begin{align*} [g]^{<\omega}(n)&={\operatorname{supp}}^E_X(E(g)(\tau))={\operatorname{supp}}^E_X(\nu_X\circ D(\iota_a^X\circ\operatorname{en}_a)(\rho_0))\\ &={\operatorname{supp}}^E_X(E(\iota_a^X\circ\operatorname{en}_a)\circ\nu_{|a|}(\rho_0))=[\iota_a^X\circ\operatorname{en}_a]^{<\omega}({\operatorname{supp}}^E_{|a|}\circ\nu_{|a|}(\rho_0))=a, \end{align*} $$
so that
![]() $n=|a|$
and
$n=|a|$
and
![]() $g=\iota _a^X\circ \operatorname {en}_a$
. By the above we get
$g=\iota _a^X\circ \operatorname {en}_a$
. By the above we get
 $\tau =\nu _{|a|}(\rho _0)$
and hence
$\tau =\nu _{|a|}(\rho _0)$
and hence
To show that (ii) implies (i), we consider
![]() $E(X)\ni \tau <_{E(X)}\nu _X(\sigma )$
with
$E(X)\ni \tau <_{E(X)}\nu _X(\sigma )$
with
![]() $\sigma \in D(X)$
. Let us write
$\sigma \in D(X)$
. Let us write
![]() $\tau =_{\operatorname {NF}} E(\iota _b^X\circ \operatorname {en}_b)(\tau _0)$
and
$\tau =_{\operatorname {NF}} E(\iota _b^X\circ \operatorname {en}_b)(\tau _0)$
and
![]() $\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
. Then
$\sigma =_{\operatorname {NF}} D(\iota _a^X\circ \operatorname {en}_a)(\sigma _0)$
. Then
 $$ \begin{align*} E(\iota_a^X\circ\operatorname{en}_a)\circ\nu_{|a|}(\sigma_0)=\nu_X(\sigma)\not<_{E(X)}\tau=E(\iota_b^X\circ\operatorname{en}_b)(\tau_0) \end{align*} $$
$$ \begin{align*} E(\iota_a^X\circ\operatorname{en}_a)\circ\nu_{|a|}(\sigma_0)=\nu_X(\sigma)\not<_{E(X)}\tau=E(\iota_b^X\circ\operatorname{en}_b)(\tau_0) \end{align*} $$
witnesses that we have
By (ii) we get
![]() $(|b|,\tau _0)\in \operatorname {rng}(\nu )$
, say
$(|b|,\tau _0)\in \operatorname {rng}(\nu )$
, say
 $\tau _0=\nu _{|b|}(\tau _1)$
with
$\tau _0=\nu _{|b|}(\tau _1)$
with
![]() $\tau _1\in D(|b|)$
. This yields
$\tau _1\in D(|b|)$
. This yields
 $$ \begin{align*} \tau=E(\iota_b^X\circ\operatorname{en}_b)\circ\nu_{|b|}(\tau_1)=\nu_X\circ D(\iota_b^X\circ\operatorname{en}_b)(\tau_1)\in\operatorname{rng}(\nu_X), \end{align*} $$
$$ \begin{align*} \tau=E(\iota_b^X\circ\operatorname{en}_b)\circ\nu_{|b|}(\tau_1)=\nu_X\circ D(\iota_b^X\circ\operatorname{en}_b)(\tau_1)\in\operatorname{rng}(\nu_X), \end{align*} $$
as needed to show that
![]() $\nu $
is a segment. ⊣
$\nu $
is a segment. ⊣
The following result implies that incomparability under
![]() $\ll $
is an equivalence relation that is compatible with
$\ll $
is an equivalence relation that is compatible with
![]() $\ll $
. Hence one can linearize
$\ll $
. Hence one can linearize
![]() $\ll $
by identifying incomparable elements.
$\ll $
by identifying incomparable elements.
Lemma 4.9. Assume that we have
![]() $(m,\sigma )\ll (n,\tau )$
in
$(m,\sigma )\ll (n,\tau )$
in
![]() $\operatorname {Tr}(D)$
.
$\operatorname {Tr}(D)$
.
-
(a) If we have
 $(m,\sigma )\not \ll (m',\sigma ')$
, then we have
$(m,\sigma )\not \ll (m',\sigma ')$
, then we have
 $(m',\sigma ')\ll (n,\tau )$
.
$(m',\sigma ')\ll (n,\tau )$
. -
(b) If we have
 $(n',\tau ')\not \ll (n,\tau )$
, then we have
$(n',\tau ')\not \ll (n,\tau )$
, then we have
 $(m,\sigma )\ll (n',\tau ')$
.
$(m,\sigma )\ll (n',\tau ')$
.
Proof First note that the contrapositive of (b) is an instance of (a). In order to establish the latter, we deduce
![]() $(m,\sigma )\not \ll (n,\tau )$
from the assumption that we have
$(m,\sigma )\not \ll (n,\tau )$
from the assumption that we have
![]() $(m,\sigma )\not \ll (m',\sigma ')$
and
$(m,\sigma )\not \ll (m',\sigma ')$
and
![]() $(m',\sigma ')\not \ll (n,\tau )$
. The latter yields embeddings
$(m',\sigma ')\not \ll (n,\tau )$
. The latter yields embeddings
![]() $f:m\to X$
,
$f:m\to X$
,
![]() $g:m'\to X$
,
$g:m'\to X$
,
![]() $f':m'\to Y$
and
$f':m'\to Y$
and
![]() $g':n\to Y$
with
$g':n\to Y$
with
 $$ \begin{align*} D(g)(\sigma')\leq_{D(X)} D(f)(\sigma)\quad\text{and}\quad D(g')(\tau)\leq_{D(Y)} D(f')(\sigma'). \end{align*} $$
$$ \begin{align*} D(g)(\sigma')\leq_{D(X)} D(f)(\sigma)\quad\text{and}\quad D(g')(\tau)\leq_{D(Y)} D(f')(\sigma'). \end{align*} $$
Consider a linear order Z that is large enough to admit embeddings
![]() $h:X\to Z$
and
$h:X\to Z$
and
![]() $h':Y\to Z$
with
$h':Y\to Z$
with
![]() $h'(y)\leq _Z h(x)$
for all
$h'(y)\leq _Z h(x)$
for all
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
. This yields
$y\in Y$
. This yields
![]() $h'\circ f'\leq h\circ g$
, in the notation from the beginning of §2. Since the predilator D is monotone (cf. Definition 2.1), we obtain
$h'\circ f'\leq h\circ g$
, in the notation from the beginning of §2. Since the predilator D is monotone (cf. Definition 2.1), we obtain
 $$ \begin{align*} D(h'\circ g')(\tau)\leq_{D(Z)} D(h'\circ f')(\sigma')\leq_{D(Z)} D(h\circ g)(\sigma')\leq_{D(Z)} D(h\circ f)(\sigma), \end{align*} $$
$$ \begin{align*} D(h'\circ g')(\tau)\leq_{D(Z)} D(h'\circ f')(\sigma')\leq_{D(Z)} D(h\circ g)(\sigma')\leq_{D(Z)} D(h\circ f)(\sigma), \end{align*} $$
as needed to witness
![]() $(m,\sigma )\not \ll (n,\tau )$
. ⊣
$(m,\sigma )\not \ll (n,\tau )$
. ⊣
For technical reasons, we will not identify incomparable elements. Instead, we linearize
![]() $\ll $
as follows (cf. [Reference Girard and Normann16, Lemma 2.11]): Each order
$\ll $
as follows (cf. [Reference Girard and Normann16, Lemma 2.11]): Each order
![]() $n=|n|=\{0,\dots ,n-1\}$
can be identified with a suborder of
$n=|n|=\{0,\dots ,n-1\}$
can be identified with a suborder of
![]() $\omega $
. In view of Definition 2.5, this identification yields
$\omega $
. In view of Definition 2.5, this identification yields
![]() $\operatorname {Tr}(D)\subseteq \overline D(\omega )$
, with
$\operatorname {Tr}(D)\subseteq \overline D(\omega )$
, with
![]() $D\!\restriction \!\mathbf {LO}_0$
at the place of D when the latter is class-sized. For elements
$D\!\restriction \!\mathbf {LO}_0$
at the place of D when the latter is class-sized. For elements
![]() $(m,\sigma )$
and
$(m,\sigma )$
and
![]() $(n,\tau )$
of
$(n,\tau )$
of
![]() $\operatorname {Tr}(D)$
we set
$\operatorname {Tr}(D)$
we set
 $$ \begin{align*} (m,\sigma)<_{\operatorname{Tr}(D)}(n,\tau)\quad:\Leftrightarrow\quad (m,\sigma)<_{\overline D(\omega)} (n,\tau). \end{align*} $$
$$ \begin{align*} (m,\sigma)<_{\operatorname{Tr}(D)}(n,\tau)\quad:\Leftrightarrow\quad (m,\sigma)<_{\overline D(\omega)} (n,\tau). \end{align*} $$
Let us observe the following:
Lemma 4.10. The relation
![]() $<_{\operatorname {Tr}(D)}$
is a linear order. It is well founded if the same holds for
$<_{\operatorname {Tr}(D)}$
is a linear order. It is well founded if the same holds for
![]() $<_{\overline D(\omega )}$
. Furthermore, we have
$<_{\overline D(\omega )}$
. Furthermore, we have
for any elements
![]() $(m,\sigma )$
and
$(m,\sigma )$
and
![]() $(n,\tau )$
of
$(n,\tau )$
of
![]() $\operatorname {Tr}(D)$
.
$\operatorname {Tr}(D)$
.
Proof Proposition 2.6 entails that
![]() $\overline D(\omega )$
is a linear order, which yields the first part of the claim. The definition of
$\overline D(\omega )$
is a linear order, which yields the first part of the claim. The definition of
![]() $\ll $
reveals that
$\ll $
reveals that
![]() $(m,\sigma )\ll (n,\tau )$
implies
$(m,\sigma )\ll (n,\tau )$
implies
 $$ \begin{align*} D(|\iota_m^{m\cup n}|)(\sigma)<_{D(|m\cup n|)} D(|\iota_n^{m\cup n}|)(\tau). \end{align*} $$
$$ \begin{align*} D(|\iota_m^{m\cup n}|)(\sigma)<_{D(|m\cup n|)} D(|\iota_n^{m\cup n}|)(\tau). \end{align*} $$
By Definition 2.5 this amounts to
 $(m,\sigma )<_{\overline D(\omega )} (n,\tau )$
, as required for the last part of the lemma. To avoid confusion, we point out that our general notation is unnecessarily complex for the present situation: the function
$(m,\sigma )<_{\overline D(\omega )} (n,\tau )$
, as required for the last part of the lemma. To avoid confusion, we point out that our general notation is unnecessarily complex for the present situation: the function
![]() $|\iota _m^{m\cup n}|=\iota _m^{m\cup n}$
is simply the inclusion of
$|\iota _m^{m\cup n}|=\iota _m^{m\cup n}$
is simply the inclusion of
![]() $m=\{0,\dots ,m-1\}$
into
$m=\{0,\dots ,m-1\}$
into
![]() $m\cup n=\max (m,n)=\{0,\dots ,\max (m,n)-1\}$
. ⊣
$m\cup n=\max (m,n)=\{0,\dots ,\max (m,n)-1\}$
. ⊣
As the following shows, each “proper” segment
![]() $\nu :D\Rightarrow E$
is determined (cf. Proposition 2.21) by an element
$\nu :D\Rightarrow E$
is determined (cf. Proposition 2.21) by an element
![]() $\rho =(k,\rho _0)\in \operatorname {Tr}(E)$
. Usually,
$\rho =(k,\rho _0)\in \operatorname {Tr}(E)$
. Usually,
![]() $\rho $
is not unique: if
$\rho $
is not unique: if
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
are incomparable, then they determine the same subset of
$\rho '$
are incomparable, then they determine the same subset of
![]() $\operatorname {Tr}(E)$
, by Lemma 4.9.
$\operatorname {Tr}(E)$
, by Lemma 4.9.
Corollary 4.11. Consider a morphism
![]() $\nu :D\Rightarrow E$
of predilators and assume that
$\nu :D\Rightarrow E$
of predilators and assume that
![]() $\overline E(\omega )$
is well founded. If we have
$\overline E(\omega )$
is well founded. If we have
![]() $\operatorname {rng}(\nu )\neq \operatorname {Tr}(E)$
, then the following are equivalent:
$\operatorname {rng}(\nu )\neq \operatorname {Tr}(E)$
, then the following are equivalent:
-
(i) the morphism
 $\nu $
is a segment and
$\nu $
is a segment and -
(ii) we have
 $\operatorname {rng}(\nu )=\{\sigma \in \operatorname {Tr}(E)\,|\,\sigma \ll \rho \}$
for some
$\operatorname {rng}(\nu )=\{\sigma \in \operatorname {Tr}(E)\,|\,\sigma \ll \rho \}$
for some
 $\rho \in \operatorname {Tr}(E)$
.
$\rho \in \operatorname {Tr}(E)$
.
Proof Due to
![]() $\operatorname {rng}(\nu )\neq \operatorname {Tr}(E)$
and the previous lemma, we may pick a
$\operatorname {rng}(\nu )\neq \operatorname {Tr}(E)$
and the previous lemma, we may pick a
![]() $\rho \notin \operatorname {rng}(\nu )$
that is
$\rho \notin \operatorname {rng}(\nu )$
that is
![]() $\ll $
-minimal. Assuming (i), we show that any such
$\ll $
-minimal. Assuming (i), we show that any such
![]() $\rho $
witnesses (ii). To see that
$\rho $
witnesses (ii). To see that
![]() $\sigma \ll \rho $
implies
$\sigma \ll \rho $
implies
![]() $\sigma \in \operatorname {rng}(\nu )$
, it suffices to invoke the minimality of
$\sigma \in \operatorname {rng}(\nu )$
, it suffices to invoke the minimality of
![]() $\rho $
. Now assume
$\rho $
. Now assume
![]() $\sigma \in \operatorname {rng}(\nu )$
. If we had
$\sigma \in \operatorname {rng}(\nu )$
. If we had
![]() $\sigma \not \ll \rho $
, then Proposition 4.8 would yield
$\sigma \not \ll \rho $
, then Proposition 4.8 would yield
![]() $\rho \in \operatorname {rng}(\nu )$
, against the choice of
$\rho \in \operatorname {rng}(\nu )$
, against the choice of
![]() $\rho $
. Hence we must have
$\rho $
. Hence we must have
![]() $\sigma \ll \rho $
. Let us now assume that (ii) holds for some given
$\sigma \ll \rho $
. Let us now assume that (ii) holds for some given
![]() $\rho \in \operatorname {Tr}(E)$
. By Lemma 4.9, it follows that
$\rho \in \operatorname {Tr}(E)$
. By Lemma 4.9, it follows that
![]() $\sigma \in \operatorname {rng}(\nu )$
and
$\sigma \in \operatorname {rng}(\nu )$
and
![]() $\sigma \not \ll \tau $
imply
$\sigma \not \ll \tau $
imply
![]() $\tau \in \operatorname {rng}(\nu )$
. Then Proposition 4.8 yields (i). ⊣
$\tau \in \operatorname {rng}(\nu )$
. Then Proposition 4.8 yields (i). ⊣
According to Definition 2.16, each morphism
![]() $\nu :D\Rightarrow E$
of predilators yields a function
$\nu :D\Rightarrow E$
of predilators yields a function
![]() $\operatorname {Tr}(\nu ):\operatorname {Tr}(D)\to \operatorname {Tr}(E)$
. We will need the following:
$\operatorname {Tr}(\nu ):\operatorname {Tr}(D)\to \operatorname {Tr}(E)$
. We will need the following:
Lemma 4.12. Consider a morphism
![]() $\nu :D\Rightarrow E$
. If we have
$\nu :D\Rightarrow E$
. If we have
![]() $\sigma <_{\operatorname {Tr}(D)}\tau $
, then we have
$\sigma <_{\operatorname {Tr}(D)}\tau $
, then we have
![]() $\operatorname {Tr}(\nu )(\sigma )<_{\operatorname {Tr}(E)}\operatorname {Tr}(\nu )(\tau )$
.
$\operatorname {Tr}(\nu )(\sigma )<_{\operatorname {Tr}(E)}\operatorname {Tr}(\nu )(\tau )$
.
Proof In defining
![]() $<_{\operatorname {Tr}(D)}$
, we have identified
$<_{\operatorname {Tr}(D)}$
, we have identified
![]() $\operatorname {Tr}(D)$
with a subset of
$\operatorname {Tr}(D)$
with a subset of
![]() $\overline D(\omega )$
. Under this identification, the value
$\overline D(\omega )$
. Under this identification, the value
![]() $\operatorname {Tr}(\nu )(n,\sigma _0)=(n,\nu _n(\sigma _0))$
from Definition 2.16 coincides with the value
$\operatorname {Tr}(\nu )(n,\sigma _0)=(n,\nu _n(\sigma _0))$
from Definition 2.16 coincides with the value
![]() $\overline \nu _\omega (n,\sigma _0)=(n,\nu _n(\sigma _0))$
from Definition 2.13. From Lemma 2.14 we know that the function
$\overline \nu _\omega (n,\sigma _0)=(n,\nu _n(\sigma _0))$
from Definition 2.13. From Lemma 2.14 we know that the function
![]() $\overline \nu _\omega :\overline D(\omega )\to \overline E(\omega )$
is order preserving. Hence the same holds for the function
$\overline \nu _\omega :\overline D(\omega )\to \overline E(\omega )$
is order preserving. Hence the same holds for the function
![]() $\operatorname {Tr}(\nu )$
. ⊣
$\operatorname {Tr}(\nu )$
. ⊣
We now have all ingredients to make the definition of
![]() $P^*$
official (cf. the discussion before Definition 4.5). For
$P^*$
official (cf. the discussion before Definition 4.5). For
![]() $\rho \in \operatorname {Tr}(D)$
we abbreviate
$\rho \in \operatorname {Tr}(D)$
we abbreviate
where the right side is explained by Definition 2.17. Together with the notation from Example 4.4, this allows us to describe the action of
![]() $P^*$
on predilators:
$P^*$
on predilators:
Definition 4.13. Consider a 2-preptyx P. For each predilator D and each order X, we consider the set
 $$ \begin{align*} P^*(D)(X):=\sum_{\rho\in\operatorname{Tr}(D)}(P(D[\rho])+1)(X), \end{align*} $$
$$ \begin{align*} P^*(D)(X):=\sum_{\rho\in\operatorname{Tr}(D)}(P(D[\rho])+1)(X), \end{align*} $$
which has elements
![]() $(\rho ,\sigma )$
with
$(\rho ,\sigma )$
with
![]() $\rho \in \operatorname {Tr}(D)$
and
$\rho \in \operatorname {Tr}(D)$
and
![]() $\sigma \in P(D[\rho ])(X)\cup \{\top \}$
. We set
$\sigma \in P(D[\rho ])(X)\cup \{\top \}$
. We set
 $$ \begin{align*} (\rho,\sigma)<_{P^*(D)(X)}(\rho',\sigma')\quad:\Leftrightarrow\quad \rho<_{\operatorname{Tr}(D)}\rho'\text{ or }(\rho=\rho'\text{ and }\sigma<_{P(D[\rho])(X)+1}\sigma'). \end{align*} $$
$$ \begin{align*} (\rho,\sigma)<_{P^*(D)(X)}(\rho',\sigma')\quad:\Leftrightarrow\quad \rho<_{\operatorname{Tr}(D)}\rho'\text{ or }(\rho=\rho'\text{ and }\sigma<_{P(D[\rho])(X)+1}\sigma'). \end{align*} $$
Given an embedding
![]() $f:X\to Y$
, we define
$f:X\to Y$
, we define
![]() $P^*(D)(f):P^*(D)(X)\to P^*(D)(Y)$
by
$P^*(D)(f):P^*(D)(X)\to P^*(D)(Y)$
by
Finally, we set
 $$ \begin{align*} {\operatorname{supp}}^{P^*(D)}_X(\rho,\sigma):={\operatorname{supp}}^{P(D[\rho])+1}_X(\sigma) \end{align*} $$
$$ \begin{align*} {\operatorname{supp}}^{P^*(D)}_X(\rho,\sigma):={\operatorname{supp}}^{P(D[\rho])+1}_X(\sigma) \end{align*} $$
to define a family of functions
 ${\operatorname {supp}}^{P^*(D)}_X:P^*(D)(X)\to [X]^{<\omega }$
.
${\operatorname {supp}}^{P^*(D)}_X:P^*(D)(X)\to [X]^{<\omega }$
.
By the discussion after Definition 3.1, the preptyx P comes with
![]() $\Delta ^0_1$
-definitions of
$\Delta ^0_1$
-definitions of
![]() $\sigma \in P(D)(X)$
and other relevant relations. These definitions refer to the coded predilator
$\sigma \in P(D)(X)$
and other relevant relations. These definitions refer to the coded predilator
![]() $D\subseteq \mathbb N$
as a parameter, i.e., they may contain subformulas like
$D\subseteq \mathbb N$
as a parameter, i.e., they may contain subformulas like
![]() $\tau \in D(n)$
. As observed after Definition 2.17, the relation
$\tau \in D(n)$
. As observed after Definition 2.17, the relation
![]() $\tau \in D[A](X)$
is
$\tau \in D[A](X)$
is
![]() $\Delta ^0_1$
-definable relative to
$\Delta ^0_1$
-definable relative to
![]() $D\subseteq \mathbb N$
and
$D\subseteq \mathbb N$
and
![]() $A\subseteq \operatorname {Tr}(D)$
. In order to turn the given definition of
$A\subseteq \operatorname {Tr}(D)$
. In order to turn the given definition of
![]() $\sigma \in P(D)$
into a
$\sigma \in P(D)$
into a
![]() $\Delta ^0_1$
-definition of
$\Delta ^0_1$
-definition of
![]() $\sigma \in P(D[\rho ])$
, it suffices to replace subformulas like
$\sigma \in P(D[\rho ])$
, it suffices to replace subformulas like
![]() $\tau \in D(n)$
by corresponding
$\tau \in D(n)$
by corresponding
![]() $\Delta ^0_1$
-formulas like
$\Delta ^0_1$
-formulas like
![]() $\tau \in D[\rho ](n)$
. Once we have definitions for
$\tau \in D[\rho ](n)$
. Once we have definitions for
![]() $P(D[\rho ])$
, it is straightforward to construct
$P(D[\rho ])$
, it is straightforward to construct
![]() $\Delta ^0_1$
-definitions of
$\Delta ^0_1$
-definitions of
![]() $(\rho ,\sigma )\in P^*(D)(X)$
and the other relations that constitute
$(\rho ,\sigma )\in P^*(D)(X)$
and the other relations that constitute
![]() $P^*(D)$
. The following results will allow us to define the action of
$P^*(D)$
. The following results will allow us to define the action of
![]() $P^*$
on morphisms of predilators.
$P^*$
on morphisms of predilators.
Lemma 4.14. Consider a morphism
![]() $\nu :D\Rightarrow E$
. We have
$\nu :D\Rightarrow E$
. We have
![]() $\sigma \ll \rho $
in
$\sigma \ll \rho $
in
![]() $\operatorname {Tr}(D)$
if, and only if, we have
$\operatorname {Tr}(D)$
if, and only if, we have
![]() $\operatorname {Tr}(\nu )(\sigma )\ll \operatorname {Tr}(\nu )(\rho )$
in
$\operatorname {Tr}(\nu )(\sigma )\ll \operatorname {Tr}(\nu )(\rho )$
in
![]() $\operatorname {Tr}(E)$
.
$\operatorname {Tr}(E)$
.
Proof Write
![]() $\sigma =(m,\sigma _0)$
and
$\sigma =(m,\sigma _0)$
and
![]() $\rho =(n,\rho _0)$
, which yields
$\rho =(n,\rho _0)$
, which yields
![]() $\operatorname {Tr}(\nu )(\sigma )=(m,\nu _m(\sigma _0))$
and
$\operatorname {Tr}(\nu )(\sigma )=(m,\nu _m(\sigma _0))$
and
![]() $\operatorname {Tr}(\nu )(\rho )=(n,\nu _n(\rho _0))$
. In view of Definition 4.5, it suffices to observe that the inequality
$\operatorname {Tr}(\nu )(\rho )=(n,\nu _n(\rho _0))$
. In view of Definition 4.5, it suffices to observe that the inequality
![]() $D(f)(\sigma _0)<_{D(X)} D(g)(\rho _0)$
is equivalent to
$D(f)(\sigma _0)<_{D(X)} D(g)(\rho _0)$
is equivalent to
for arbitrary embeddings
![]() $f:m\to X$
and
$f:m\to X$
and
![]() $g:n\to X$
. ⊣
$g:n\to X$
. ⊣
For each element
![]() $\rho \in \operatorname {Tr}(D)$
, Lemma 2.20 yields a morphism
$\rho \in \operatorname {Tr}(D)$
, Lemma 2.20 yields a morphism
with
![]() $\operatorname {rng}(\iota [\rho ])=\{\sigma \in \operatorname {Tr}(D)\,|\,\sigma \ll \rho \}$
.
$\operatorname {rng}(\iota [\rho ])=\{\sigma \in \operatorname {Tr}(D)\,|\,\sigma \ll \rho \}$
.
Corollary 4.15. For each morphism
![]() $\nu :D\Rightarrow E$
and each
$\nu :D\Rightarrow E$
and each
![]() $\rho \in \operatorname {Tr}(D)$
we have
$\rho \in \operatorname {Tr}(D)$
we have
If
![]() $\nu $
is a segment, then the converse inclusion holds as well.
$\nu $
is a segment, then the converse inclusion holds as well.
Proof Any element of
![]() $\operatorname {rng}(\nu \circ \iota [\rho ])$
has the form
$\operatorname {rng}(\nu \circ \iota [\rho ])$
has the form
![]() $\operatorname {Tr}(\nu )(\sigma )$
with
$\operatorname {Tr}(\nu )(\sigma )$
with
![]() $\sigma \in \operatorname {rng}(\iota [\rho ])$
and hence
$\sigma \in \operatorname {rng}(\iota [\rho ])$
and hence
![]() $\sigma \ll \rho $
. By the previous lemma we get
$\sigma \ll \rho $
. By the previous lemma we get
![]() $\operatorname {Tr}(\nu )(\sigma )\ll \operatorname {Tr}(\nu )(\rho )$
, as needed for
$\operatorname {Tr}(\nu )(\sigma )\ll \operatorname {Tr}(\nu )(\rho )$
, as needed for
![]() $\operatorname {Tr}(\nu )(\sigma )\in \operatorname {rng}(\iota [\operatorname {Tr}(\nu )(\rho )])$
. Now assume that
$\operatorname {Tr}(\nu )(\sigma )\in \operatorname {rng}(\iota [\operatorname {Tr}(\nu )(\rho )])$
. Now assume that
![]() $\nu $
is a segment. For an arbitrary element
$\nu $
is a segment. For an arbitrary element
![]() $\tau \in \operatorname {rng}(\iota [\operatorname {Tr}(\nu )(\rho )])$
we have
$\tau \in \operatorname {rng}(\iota [\operatorname {Tr}(\nu )(\rho )])$
we have
![]() $\tau \ll \operatorname {Tr}(\nu )(\rho )$
and hence
$\tau \ll \operatorname {Tr}(\nu )(\rho )$
and hence
By Proposition 4.8 we get
![]() $\tau \in \operatorname {rng}(\nu )$
, say
$\tau \in \operatorname {rng}(\nu )$
, say
![]() $\tau =\operatorname {Tr}(\nu )(\sigma )$
. The previous lemma yields
$\tau =\operatorname {Tr}(\nu )(\sigma )$
. The previous lemma yields
![]() $\sigma \ll \rho $
and hence
$\sigma \ll \rho $
and hence
![]() $\sigma \in \operatorname {rng}(\iota [\rho ])$
, so that we get
$\sigma \in \operatorname {rng}(\iota [\rho ])$
, so that we get
![]() $\tau =\operatorname {Tr}(\nu )(\sigma )\in \operatorname {rng}(\nu \circ \iota [\rho ])$
. ⊣
$\tau =\operatorname {Tr}(\nu )(\sigma )\in \operatorname {rng}(\nu \circ \iota [\rho ])$
. ⊣
Together with Proposition 2.21, the corollary justifies the following:
Definition 4.16. For a morphism
![]() $\nu :D\Rightarrow E$
and an element
$\nu :D\Rightarrow E$
and an element
![]() $\rho \in \operatorname {Tr}(D)$
, we define
$\rho \in \operatorname {Tr}(D)$
, we define
as the unique morphism with
![]() $\iota [E,\operatorname {Tr}(\nu )(\rho )]\circ \nu ^\rho =\nu \circ \iota [D,\rho ]$
.
$\iota [E,\operatorname {Tr}(\nu )(\rho )]\circ \nu ^\rho =\nu \circ \iota [D,\rho ]$
.
Let us observe that
![]() $\nu ^\rho $
is
$\nu ^\rho $
is
![]() $\Delta ^0_1$
-definable, given that the same holds for
$\Delta ^0_1$
-definable, given that the same holds for
![]() $\nu $
: According to Definition 2.19, the components of
$\nu $
: According to Definition 2.19, the components of
![]() $\iota [\rho ]$
are inclusion maps. For
$\iota [\rho ]$
are inclusion maps. For
![]() $\sigma \in D[\rho ](X)$
, this means that
$\sigma \in D[\rho ](X)$
, this means that
![]() $\nu ^\rho _X(\sigma )=\tau $
is equivalent to
$\nu ^\rho _X(\sigma )=\tau $
is equivalent to
![]() $\nu _X(\sigma )=\tau $
. The following result will be needed to verify the support condition for
$\nu _X(\sigma )=\tau $
. The following result will be needed to verify the support condition for
![]() $P^*$
. In view of Proposition 2.22, it tells us that we are concerned with a pullback.
$P^*$
. In view of Proposition 2.22, it tells us that we are concerned with a pullback.
Corollary 4.17. We have
![]() $\operatorname {rng}(\nu )\cap \operatorname {rng}(\iota [E,\operatorname {Tr}(\nu )(\rho )])\subseteq \operatorname {rng}(\nu \circ \iota [D,\rho ])$
for each morphism
$\operatorname {rng}(\nu )\cap \operatorname {rng}(\iota [E,\operatorname {Tr}(\nu )(\rho )])\subseteq \operatorname {rng}(\nu \circ \iota [D,\rho ])$
for each morphism
![]() $\nu :D\Rightarrow E$
and each element
$\nu :D\Rightarrow E$
and each element
![]() $\rho \in \operatorname {Tr}(D)$
.
$\rho \in \operatorname {Tr}(D)$
.
Proof An arbitrary element of
![]() $\operatorname {rng}(\nu )\cap \operatorname {rng}(\iota [\operatorname {Tr}(\nu )(\rho )])$
has the form
$\operatorname {rng}(\nu )\cap \operatorname {rng}(\iota [\operatorname {Tr}(\nu )(\rho )])$
has the form
![]() $\operatorname {Tr}(\nu )(\sigma )$
and satisfies
$\operatorname {Tr}(\nu )(\sigma )$
and satisfies
![]() $\operatorname {Tr}(\nu )(\sigma )\ll \operatorname {Tr}(\nu )(\rho )$
. By Lemma 4.14 we can conclude
$\operatorname {Tr}(\nu )(\sigma )\ll \operatorname {Tr}(\nu )(\rho )$
. By Lemma 4.14 we can conclude
![]() $\sigma \ll \rho $
. The latter amounts to
$\sigma \ll \rho $
. The latter amounts to
![]() $\sigma \in \operatorname {rng}(\iota [\rho ])$
, which implies
$\sigma \in \operatorname {rng}(\iota [\rho ])$
, which implies
![]() $\operatorname {Tr}(\nu )(\sigma )\in \operatorname {rng}(\nu \circ \iota [\rho ])$
. ⊣
$\operatorname {Tr}(\nu )(\sigma )\in \operatorname {rng}(\nu \circ \iota [\rho ])$
. ⊣
Let us also record the following fact, which will be used to show that the preptyx
![]() $P^*$
is normal (cf. Definition 4.3).
$P^*$
is normal (cf. Definition 4.3).
Corollary 4.18. If
![]() $\nu :D\Rightarrow E$
is a segment, then
$\nu :D\Rightarrow E$
is a segment, then
![]() $\nu ^\rho :D[\rho ]\Rightarrow E[\operatorname {Tr}(\nu )(\rho )]$
is an isomorphism, for each element
$\nu ^\rho :D[\rho ]\Rightarrow E[\operatorname {Tr}(\nu )(\rho )]$
is an isomorphism, for each element
![]() $\rho \in \operatorname {Tr}(D)$
.
$\rho \in \operatorname {Tr}(D)$
.
Proof Due to the second part of Corollary 4.15, we can invoke Proposition 2.21 to get a morphism
![]() $\mu ^\rho :E[\operatorname {Tr}(\nu )(\rho )]\Rightarrow D[\rho ]$
with
$\mu ^\rho :E[\operatorname {Tr}(\nu )(\rho )]\Rightarrow D[\rho ]$
with
![]() $\nu \circ \iota [\rho ]\circ \mu ^\rho =\iota [\operatorname {Tr}(\nu )(\rho )]$
. In view of
$\nu \circ \iota [\rho ]\circ \mu ^\rho =\iota [\operatorname {Tr}(\nu )(\rho )]$
. In view of
the uniqueness part of Proposition 2.21 implies that
![]() $\mu ^\rho \circ \nu ^\rho $
is the identity on
$\mu ^\rho \circ \nu ^\rho $
is the identity on
![]() $D[\rho ]$
. An analogous argument shows that
$D[\rho ]$
. An analogous argument shows that
![]() $\nu ^\rho \circ \mu ^\rho $
is the identity on
$\nu ^\rho \circ \mu ^\rho $
is the identity on
![]() $E[\operatorname {Tr}(\nu )(\rho )]$
. ⊣
$E[\operatorname {Tr}(\nu )(\rho )]$
. ⊣
In order to turn
![]() $P^*$
into a preptyx, we will define support functions
$P^*$
into a preptyx, we will define support functions
![]() ${\operatorname {Supp}}^*_{D,X}$
as in Lemma 3.5. By Lemma 3.4, we may assume that the preptyx P comes with functions
${\operatorname {Supp}}^*_{D,X}$
as in Lemma 3.5. By Lemma 3.4, we may assume that the preptyx P comes with functions
![]() ${\operatorname {Supp}}_{D,X}:P(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
.
${\operatorname {Supp}}_{D,X}:P(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
.
Definition 4.19. Consider a preptyx P. For each morphism
![]() $\nu :D\Rightarrow E$
and each linear order X, we define
$\nu :D\Rightarrow E$
and each linear order X, we define
![]() $P^*(\nu )_X:P^*(D)(X)\Rightarrow P^*(E)(X)$
by
$P^*(\nu )_X:P^*(D)(X)\Rightarrow P^*(E)(X)$
by
 $$ \begin{align*} P^*(\nu)_X(\rho,\sigma):=\begin{cases} (\operatorname{Tr}(\nu)(\rho),P(\nu^\rho)_X(\sigma)) & \text{if}\ \sigma\in P(D[\rho])(X),\\ (\operatorname{Tr}(\nu)(\rho),\top) & \text{if}\ \sigma=\top. \end{cases} \end{align*} $$
$$ \begin{align*} P^*(\nu)_X(\rho,\sigma):=\begin{cases} (\operatorname{Tr}(\nu)(\rho),P(\nu^\rho)_X(\sigma)) & \text{if}\ \sigma\in P(D[\rho])(X),\\ (\operatorname{Tr}(\nu)(\rho),\top) & \text{if}\ \sigma=\top. \end{cases} \end{align*} $$
In order to define functions
![]() ${\operatorname {Supp}}^*_{D,X}:P^*(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
, we set
${\operatorname {Supp}}^*_{D,X}:P^*(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
, we set
 $$ \begin{align*} {\operatorname{Supp}}^*_{D,X}(\rho,\sigma):=\begin{cases} \{\rho\}\cup{\operatorname{Supp}}_{D,X}(P(\iota[\rho])_X(\sigma)) & \text{if}\ \sigma\in P(D[\rho])(X),\\ \{\rho\} & \text{if}\ \sigma=\top, \end{cases} \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}^*_{D,X}(\rho,\sigma):=\begin{cases} \{\rho\}\cup{\operatorname{Supp}}_{D,X}(P(\iota[\rho])_X(\sigma)) & \text{if}\ \sigma\in P(D[\rho])(X),\\ \{\rho\} & \text{if}\ \sigma=\top, \end{cases} \end{align*} $$
for each predilator D and each linear order X.
The relations
![]() $P^*(\nu )_X(\sigma )=\tau $
and
$P^*(\nu )_X(\sigma )=\tau $
and
![]() ${\operatorname {Supp}}^*_{D,X}(\sigma )=a$
are
${\operatorname {Supp}}^*_{D,X}(\sigma )=a$
are
![]() $\Delta ^0_1$
-definable, by the discussion after Definition 4.13. Our constructions culminate in the following result:
$\Delta ^0_1$
-definable, by the discussion after Definition 4.13. Our constructions culminate in the following result:
Theorem 4.20. For any 2-preptyx P we have the following:
-
(a)
 $P^*$
is a normal 2-preptyx,
$P^*$
is a normal 2-preptyx, -
(b) if P is a 2-ptyx (i.e., preserves dilators), then so is
 $P^*$
, and
$P^*$
, and -
(c) there is a family of morphisms
 $\xi ^D:P(D)+1\Rightarrow P^*(D+1)$
that is natural in the predilator D, in the sense that we have
$\xi ^D:P(D)+1\Rightarrow P^*(D+1)$
that is natural in the predilator D, in the sense that we have
 $\xi ^E\circ (P(\nu )+1)=P^*(\nu +1)\circ \xi ^D$
for any morphism
$\xi ^E\circ (P(\nu )+1)=P^*(\nu +1)\circ \xi ^D$
for any morphism
 $\nu :D\Rightarrow E$
.
$\nu :D\Rightarrow E$
.
Proof (a) Given a predilator D, we can invoke Lemma 2.18 to learn that
![]() $D[\rho ]$
is a predilator for each
$D[\rho ]$
is a predilator for each
![]() $\rho \in \operatorname {Tr}(D)$
. Since P is a preptyx, it follows that
$\rho \in \operatorname {Tr}(D)$
. Since P is a preptyx, it follows that
![]() $P(D[\rho ])$
and
$P(D[\rho ])$
and
![]() $P(D[\rho ])+1$
are predilators. It is straightforward to deduce that
$P(D[\rho ])+1$
are predilators. It is straightforward to deduce that
![]() $P^*(D)$
is a predilator as well. Similarly,
$P^*(D)$
is a predilator as well. Similarly,
![]() $P^*(\nu ):P^*(D)\Rightarrow P^*(E)$
is a morphism of predilators when the same holds for
$P^*(\nu ):P^*(D)\Rightarrow P^*(E)$
is a morphism of predilators when the same holds for
![]() $\nu :D\Rightarrow E$
. The claim that
$\nu :D\Rightarrow E$
. The claim that
![]() $P^*$
is functorial can be reduced to the following facts: First, if
$P^*$
is functorial can be reduced to the following facts: First, if
![]() $\nu :D\Rightarrow D$
is the identity, then
$\nu :D\Rightarrow D$
is the identity, then
![]() $\nu ^\rho :D[\rho ]\Rightarrow D[\rho ]$
is the identity for each
$\nu ^\rho :D[\rho ]\Rightarrow D[\rho ]$
is the identity for each
![]() $\rho \in \operatorname {Tr}(D)$
. Secondly, we have
$\rho \in \operatorname {Tr}(D)$
. Secondly, we have
 $$ \begin{align*} (\mu\circ\nu)^\rho=\mu^{\operatorname{Tr}(\nu)(\rho)}\circ\nu^\rho \end{align*} $$
$$ \begin{align*} (\mu\circ\nu)^\rho=\mu^{\operatorname{Tr}(\nu)(\rho)}\circ\nu^\rho \end{align*} $$
for arbitrary morphisms
![]() $\nu :D_0\Rightarrow D_1$
and
$\nu :D_0\Rightarrow D_1$
and
![]() $\mu :D_1\Rightarrow D_2$
and any
$\mu :D_1\Rightarrow D_2$
and any
![]() $\rho \in \operatorname {Tr}(D_0)$
. Both facts follow from the uniqueness part of Proposition 2.21. To show that the functions
$\rho \in \operatorname {Tr}(D_0)$
. Both facts follow from the uniqueness part of Proposition 2.21. To show that the functions
![]() ${\operatorname {Supp}}^*_{D,X}:P^*(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
are natural in D, consider a morphism
${\operatorname {Supp}}^*_{D,X}:P^*(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
are natural in D, consider a morphism
![]() $\nu :D\Rightarrow E$
and an element
$\nu :D\Rightarrow E$
and an element
![]() $(\rho ,\sigma )\in P^*(D)(X)$
. Since P is a preptyx, the support functions
$(\rho ,\sigma )\in P^*(D)(X)$
. Since P is a preptyx, the support functions
![]() ${\operatorname {Supp}}_{D,X}:P(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
are natural (cf. Lemma 3.4). In the more difficult case of
${\operatorname {Supp}}_{D,X}:P(D)(X)\to [\operatorname {Tr}(D)]^{<\omega }$
are natural (cf. Lemma 3.4). In the more difficult case of
![]() $\sigma \neq \top $
, we can deduce
$\sigma \neq \top $
, we can deduce
 $$ \begin{align*} {\operatorname{Supp}}^*_{E,X}(P^*(\nu)_X(\rho,\sigma))&={\operatorname{Supp}}^*_{E,X}(\operatorname{Tr}(\nu)(\rho),P(\nu^\rho)_X(\sigma))\\ {}&=\{\operatorname{Tr}(\nu)(\rho)\}\cup{\operatorname{Supp}}_{E,X}(P(\iota[\operatorname{Tr}(\nu)(\rho)]\circ\nu^\rho)_X(\sigma))\\ {}&=\{\operatorname{Tr}(\nu)(\rho)\}\cup{\operatorname{Supp}}_{E,X}(P(\nu\circ\iota[\rho])_X(\sigma))\\ {}&=\{\operatorname{Tr}(\nu)(\rho)\}\cup[\operatorname{Tr}(\nu)]^{<\omega}({\operatorname{Supp}}_{D,X}(P(\iota[\rho])_X(\sigma)))\\ {}&=[\operatorname{Tr}(\nu)]^{<\omega}({\operatorname{Supp}}^*_{D,X}(\rho,\sigma)). \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}^*_{E,X}(P^*(\nu)_X(\rho,\sigma))&={\operatorname{Supp}}^*_{E,X}(\operatorname{Tr}(\nu)(\rho),P(\nu^\rho)_X(\sigma))\\ {}&=\{\operatorname{Tr}(\nu)(\rho)\}\cup{\operatorname{Supp}}_{E,X}(P(\iota[\operatorname{Tr}(\nu)(\rho)]\circ\nu^\rho)_X(\sigma))\\ {}&=\{\operatorname{Tr}(\nu)(\rho)\}\cup{\operatorname{Supp}}_{E,X}(P(\nu\circ\iota[\rho])_X(\sigma))\\ {}&=\{\operatorname{Tr}(\nu)(\rho)\}\cup[\operatorname{Tr}(\nu)]^{<\omega}({\operatorname{Supp}}_{D,X}(P(\iota[\rho])_X(\sigma)))\\ {}&=[\operatorname{Tr}(\nu)]^{<\omega}({\operatorname{Supp}}^*_{D,X}(\rho,\sigma)). \end{align*} $$
In order to conclude that
![]() $P^*$
is a preptyx, we verify the support condition from Lemma 3.4 (which implies the one from Definition 3.1, by Lemma 3.5). For this purpose, we consider a morphism
$P^*$
is a preptyx, we verify the support condition from Lemma 3.4 (which implies the one from Definition 3.1, by Lemma 3.5). For this purpose, we consider a morphism
![]() $\nu :D\Rightarrow E$
and an element
$\nu :D\Rightarrow E$
and an element
![]() $(\rho ,\sigma )\in P^*(E)(X)$
with
$(\rho ,\sigma )\in P^*(E)(X)$
with
![]() ${\operatorname {Supp}}^*_{E,X}(\rho ,\sigma )\subseteq \operatorname {rng}(\nu )$
. The latter yields
${\operatorname {Supp}}^*_{E,X}(\rho ,\sigma )\subseteq \operatorname {rng}(\nu )$
. The latter yields
![]() $\rho \in \operatorname {rng}(\nu )$
, say
$\rho \in \operatorname {rng}(\nu )$
, say
![]() $\rho =\operatorname {Tr}(\nu )(\rho _0)$
. In case of
$\rho =\operatorname {Tr}(\nu )(\rho _0)$
. In case of
![]() $\sigma \neq \top $
, it also yields
$\sigma \neq \top $
, it also yields
 $$ \begin{align*} &{\operatorname{Supp}}_{E,X}(P(\iota[\rho])_X(\sigma))=[\operatorname{Tr}(\iota[\rho])]^{<\omega}({\operatorname{Supp}}_{D,X}(\sigma))\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{}\subseteq\operatorname{rng}(\nu)\cap\operatorname{rng}(\iota[\rho])\subseteq\operatorname{rng}(\nu\circ\iota[\rho_0]), \end{align*} $$
$$ \begin{align*} &{\operatorname{Supp}}_{E,X}(P(\iota[\rho])_X(\sigma))=[\operatorname{Tr}(\iota[\rho])]^{<\omega}({\operatorname{Supp}}_{D,X}(\sigma))\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{}\subseteq\operatorname{rng}(\nu)\cap\operatorname{rng}(\iota[\rho])\subseteq\operatorname{rng}(\nu\circ\iota[\rho_0]), \end{align*} $$
where the last inclusion relies on Corollary 4.17. By the support condition for the preptyx P, we get an element
![]() $\sigma _0\in P(D[\rho _0])(X)$
with
$\sigma _0\in P(D[\rho _0])(X)$
with
Since
![]() $P(\iota [\rho ])$
is a morphism of predilators, the component
$P(\iota [\rho ])$
is a morphism of predilators, the component
![]() $P(\iota [\rho ])_X$
is an order embedding and in particular injective. We obtain
$P(\iota [\rho ])_X$
is an order embedding and in particular injective. We obtain
![]() $\sigma =P(\nu ^{\rho _0})_X(\sigma _0)$
and then
$\sigma =P(\nu ^{\rho _0})_X(\sigma _0)$
and then
as required by the support condition for
![]() $P^*$
. Finally, we show that the 2-preptyx
$P^*$
. Finally, we show that the 2-preptyx
![]() $P^*$
is normal (cf. Definition 4.3). Consider a segment
$P^*$
is normal (cf. Definition 4.3). Consider a segment
![]() $\nu :D\Rightarrow E$
and an inequality
$\nu :D\Rightarrow E$
and an inequality
 $$ \begin{align*} (\rho,\sigma)<_{P^*(E)(X)} P^*(\nu)_X(\rho',\sigma')\in\operatorname{rng}(P^*(\nu)_X). \end{align*} $$
$$ \begin{align*} (\rho,\sigma)<_{P^*(E)(X)} P^*(\nu)_X(\rho',\sigma')\in\operatorname{rng}(P^*(\nu)_X). \end{align*} $$
The latter entails
![]() $\rho \leq _{\operatorname {Tr}(E)}\operatorname {Tr}(\nu )(\rho ')$
, so that Lemma 4.9 yields
$\rho \leq _{\operatorname {Tr}(E)}\operatorname {Tr}(\nu )(\rho ')$
, so that Lemma 4.9 yields
By Proposition 4.8 we get
![]() $\rho \in \operatorname {rng}(\nu )$
, say
$\rho \in \operatorname {rng}(\nu )$
, say
![]() $\rho =\operatorname {Tr}(\nu )(\rho _0)$
. Now Corollary 4.18 tells us that
$\rho =\operatorname {Tr}(\nu )(\rho _0)$
. Now Corollary 4.18 tells us that
![]() $\nu ^{\rho _0}:D[\rho _0]\Rightarrow E[\rho ]$
is an isomorphism. Since P is a functor, it follows that the natural transformation
$\nu ^{\rho _0}:D[\rho _0]\Rightarrow E[\rho ]$
is an isomorphism. Since P is a functor, it follows that the natural transformation
![]() $P(\nu ^{\rho _0})$
and its component
$P(\nu ^{\rho _0})$
and its component
![]() $P(\nu ^{\rho _0})_X$
are isomorphisms as well. For
$P(\nu ^{\rho _0})_X$
are isomorphisms as well. For
![]() $\sigma \neq \top $
we get
$\sigma \neq \top $
we get
![]() $\sigma =P(\nu ^{\rho _0})_X(\sigma _0)$
for some
$\sigma =P(\nu ^{\rho _0})_X(\sigma _0)$
for some
![]() $\sigma _0\in P(D[\rho _0])_X$
. This yields
$\sigma _0\in P(D[\rho _0])_X$
. This yields
For
![]() $\sigma =\top $
we have
$\sigma =\top $
we have
![]() $(\rho ,\sigma )=(\operatorname {Tr}(\nu )(\rho _0),\top )=P^*(\nu )_X(\rho _0,\top )\in \operatorname {rng}(P^*(\nu )_X)$
.
$(\rho ,\sigma )=(\operatorname {Tr}(\nu )(\rho _0),\top )=P^*(\nu )_X(\rho _0,\top )\in \operatorname {rng}(P^*(\nu )_X)$
.
(b) Consider a dilator D and a well order X. We need to show that
![]() $P^*(D)(X)$
is well founded. The morphisms
$P^*(D)(X)$
is well founded. The morphisms
![]() $\iota [\rho ]:D[\rho ]\Rightarrow D$
ensure that
$\iota [\rho ]:D[\rho ]\Rightarrow D$
ensure that
![]() $D[\rho ]$
is a dilator for each
$D[\rho ]$
is a dilator for each
![]() $\rho \in \operatorname {Tr}(D)$
. Given that P is a ptyx, it follows that each order
$\rho \in \operatorname {Tr}(D)$
. Given that P is a ptyx, it follows that each order
![]() $P(D[\rho ])(X)+1$
is well founded. Now consider a (not necessarily strictly) descending sequence
$P(D[\rho ])(X)+1$
is well founded. Now consider a (not necessarily strictly) descending sequence
The first components form a descending sequence with respect to the order
![]() $<_{\operatorname {Tr}(D)}$
on the trace of D. Given that D is a dilator, we can invoke Lemma 4.9 to find an
$<_{\operatorname {Tr}(D)}$
on the trace of D. Given that D is a dilator, we can invoke Lemma 4.9 to find an
![]() $N\in \mathbb N$
with
$N\in \mathbb N$
with
![]() $\rho _n=\rho _N$
for all
$\rho _n=\rho _N$
for all
![]() $n\geq N$
. Then
$n\geq N$
. Then
![]() $\sigma _N,\sigma _{N+1},\ldots $
is a sequence in the well order
$\sigma _N,\sigma _{N+1},\ldots $
is a sequence in the well order
![]() $P(D[\rho _N])(X)+1$
, and it is easy to conclude.
$P(D[\rho _N])(X)+1$
, and it is easy to conclude.
(c) The element
![]() $\top \in (D+1)(0)$
yields an element
$\top \in (D+1)(0)$
yields an element
![]() $(0,\top )\in \operatorname {Tr}(D+1)$
, which gives rise to a morphism
$(0,\top )\in \operatorname {Tr}(D+1)$
, which gives rise to a morphism
![]() $\iota [D+1,(0,\top )]:(D+1)[(0,\top )]\Rightarrow D+1$
(cf. the discussion before Corollary 4.15). We also have a morphism
$\iota [D+1,(0,\top )]:(D+1)[(0,\top )]\Rightarrow D+1$
(cf. the discussion before Corollary 4.15). We also have a morphism
![]() $\pi ^D:D\Rightarrow D+1$
, where each component
$\pi ^D:D\Rightarrow D+1$
, where each component
![]() $\pi ^D_X:D(X)\hookrightarrow D(X)\cup \{\top \}=(D+1)(X)$
is the obvious inclusion map. Let us show that we have
$\pi ^D_X:D(X)\hookrightarrow D(X)\cup \{\top \}=(D+1)(X)$
is the obvious inclusion map. Let us show that we have
An arbitrary element of
![]() $\operatorname {rng}(\pi ^D)$
can be written as
$\operatorname {rng}(\pi ^D)$
can be written as
![]() $\operatorname {Tr}(\pi ^D)(m,\sigma _0)=(m,\pi ^D_m(\sigma _0))$
for some
$\operatorname {Tr}(\pi ^D)(m,\sigma _0)=(m,\pi ^D_m(\sigma _0))$
for some
![]() $(m,\sigma _0)\in \operatorname {Tr}(D)$
. To show that we have
$(m,\sigma _0)\in \operatorname {Tr}(D)$
. To show that we have
![]() $(m,\pi ^D_m(\sigma _0))\ll (0,\top )$
in
$(m,\pi ^D_m(\sigma _0))\ll (0,\top )$
in
![]() $\operatorname {Tr}(D+1)$
, we consider arbitrary embeddings
$\operatorname {Tr}(D+1)$
, we consider arbitrary embeddings
![]() $f:m\to X$
and
$f:m\to X$
and
![]() $g:0\to X$
into some order X (in fact, g can only be the empty function). In view of
$g:0\to X$
into some order X (in fact, g can only be the empty function). In view of
![]() $\pi ^D_m(\sigma _0)\in D(m)\subseteq D(m)\cup \{\top \}$
, we have
$\pi ^D_m(\sigma _0)\in D(m)\subseteq D(m)\cup \{\top \}$
, we have
![]() $(D+1)(f)(\pi ^D_m(\sigma _0))=D(f)(\pi ^D_m(\sigma _0))\in D(X)\subseteq D(X)\cup \{\top \}$
. This yields
$(D+1)(f)(\pi ^D_m(\sigma _0))=D(f)(\pi ^D_m(\sigma _0))\in D(X)\subseteq D(X)\cup \{\top \}$
. This yields
 $$ \begin{align*} (D+1)(f)(\pi^D_m(\sigma_0))<_{(D+1)(X)}\top=(D+1)(g)(\top), \end{align*} $$
$$ \begin{align*} (D+1)(f)(\pi^D_m(\sigma_0))<_{(D+1)(X)}\top=(D+1)(g)(\top), \end{align*} $$
as needed for
![]() $(m,\pi ^D_m(\sigma _0))\ll (0,\top )$
. Now Proposition 2.21 yields a morphism
$(m,\pi ^D_m(\sigma _0))\ll (0,\top )$
. Now Proposition 2.21 yields a morphism
Since
![]() $\iota [D+1,(0,\top )]$
and
$\iota [D+1,(0,\top )]$
and
![]() $\pi ^D$
are
$\pi ^D$
are
![]() $\Delta ^0_1$
-definable relative to D, the same holds for
$\Delta ^0_1$
-definable relative to D, the same holds for
![]() $\iota ^D$
. As explained after Definition 4.13, we obtain a
$\iota ^D$
. As explained after Definition 4.13, we obtain a
![]() $\Delta ^0_1$
-definition of the morphism
$\Delta ^0_1$
-definition of the morphism
The components of
![]() $\xi ^D:P(D)+1\Rightarrow P^*(D+1)$
can now be defined by
$\xi ^D:P(D)+1\Rightarrow P^*(D+1)$
can now be defined by
 $$ \begin{align*} \xi^D_X(\sigma):=\begin{cases} ((0,\top),P(\iota^D)_X(\sigma)) & \text{if}\ \sigma\in P(D)(X)\subseteq (P(D)+1)(X),\\ ((0,\top),\sigma) & \text{if}\ \sigma=\top\in (P(D)+1)(X). \end{cases} \end{align*} $$
$$ \begin{align*} \xi^D_X(\sigma):=\begin{cases} ((0,\top),P(\iota^D)_X(\sigma)) & \text{if}\ \sigma\in P(D)(X)\subseteq (P(D)+1)(X),\\ ((0,\top),\sigma) & \text{if}\ \sigma=\top\in (P(D)+1)(X). \end{cases} \end{align*} $$
It is straightforward to verify that
![]() $\xi ^D_X$
is an embedding and natural in X, so that
$\xi ^D_X$
is an embedding and natural in X, so that
![]() $\xi ^D$
is a morphism of predilators. To establish naturality in D, we consider
$\xi ^D$
is a morphism of predilators. To establish naturality in D, we consider
![]() $\nu :D\Rightarrow E$
. Note
$\nu :D\Rightarrow E$
. Note
![]() $\operatorname {Tr}(\nu +1)(0,\top )=(0,(\nu +1)_0(\top ))=(0,\top )$
and invoke Definition 4.16 to get
$\operatorname {Tr}(\nu +1)(0,\top )=(0,(\nu +1)_0(\top ))=(0,\top )$
and invoke Definition 4.16 to get
 $$ \begin{align*}\iota[E+1,(0,\top)]\circ(\nu+1)^{(0,\top)}\circ\iota^D&=(\nu+1)\circ\iota[D+1,(0,\top)]\circ\iota^D\\&=(\nu+1)\circ\pi^D=\pi^E\circ\nu=\iota[E+1,(0,\top)]\circ\iota^E\circ\nu. \end{align*} $$
$$ \begin{align*}\iota[E+1,(0,\top)]\circ(\nu+1)^{(0,\top)}\circ\iota^D&=(\nu+1)\circ\iota[D+1,(0,\top)]\circ\iota^D\\&=(\nu+1)\circ\pi^D=\pi^E\circ\nu=\iota[E+1,(0,\top)]\circ\iota^E\circ\nu. \end{align*} $$
This entails
![]() $(\nu +1)^{(0,\top )}\circ \iota ^D=\iota ^E\circ \nu $
, since the components of our morphisms are embeddings. For an element
$(\nu +1)^{(0,\top )}\circ \iota ^D=\iota ^E\circ \nu $
, since the components of our morphisms are embeddings. For an element
![]() $\sigma \in P(D)(X)\subseteq (P(D)+1)(X)$
we can deduce
$\sigma \in P(D)(X)\subseteq (P(D)+1)(X)$
we can deduce
 $$ \begin{align*} \xi^E_X\circ(P(\nu)+1)_X(\sigma)&=\xi^E_X(P(\nu)_X(\sigma))=((0,\top),P(\iota^E)_X\circ P(\nu)_X(\sigma))\\ {}&=(\operatorname{Tr}(\nu+1)(0,\top),P((\nu+1)^{(0,\top)})_X\circ P(\iota^D)_X(\sigma))\\ {}&=P^*(\nu+1)_X((0,\top),P(\iota^D)_X(\sigma))=P^*(\nu+1)_X\circ\xi^D_X(\sigma). \end{align*} $$
$$ \begin{align*} \xi^E_X\circ(P(\nu)+1)_X(\sigma)&=\xi^E_X(P(\nu)_X(\sigma))=((0,\top),P(\iota^E)_X\circ P(\nu)_X(\sigma))\\ {}&=(\operatorname{Tr}(\nu+1)(0,\top),P((\nu+1)^{(0,\top)})_X\circ P(\iota^D)_X(\sigma))\\ {}&=P^*(\nu+1)_X((0,\top),P(\iota^D)_X(\sigma))=P^*(\nu+1)_X\circ\xi^D_X(\sigma). \end{align*} $$
The case of
![]() $\sigma =\top \in (P(D)+1)(X)$
is similar and easier. ⊣
$\sigma =\top \in (P(D)+1)(X)$
is similar and easier. ⊣
5 From fixed points of 2-ptykes to
 $\Pi ^1_2$
-induction
$\Pi ^1_2$
-induction
In this section, we deduce
![]() $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
![]() $\mathbb N$
from the assumption that every normal 2-ptyx has a fixed point that is a dilator. For this purpose, we work out the details of the argument that we have sketched in the introduction.
$\mathbb N$
from the assumption that every normal 2-ptyx has a fixed point that is a dilator. For this purpose, we work out the details of the argument that we have sketched in the introduction.
Consider a
![]() $\Pi ^1_2$
-formula
$\Pi ^1_2$
-formula
![]() $\psi (n)$
with a distinguished number variable, possibly with further number or set parameters. The Kleene normal form theorem (see e.g., [Reference Simpson29, Lemma V.1.4]) yields a
$\psi (n)$
with a distinguished number variable, possibly with further number or set parameters. The Kleene normal form theorem (see e.g., [Reference Simpson29, Lemma V.1.4]) yields a
![]() $\Delta ^0_0$
-formula
$\Delta ^0_0$
-formula
![]() $\theta $
such that
$\theta $
such that
![]() $\mathbf {ACA}_0$
proves
$\mathbf {ACA}_0$
proves
Here
![]() $f[m]=\langle f(0),\dots ,f(m-1)\rangle $
denotes the sequence of the first m values of f, coded by a natural number; in writing
$f[m]=\langle f(0),\dots ,f(m-1)\rangle $
denotes the sequence of the first m values of f, coded by a natural number; in writing
![]() $Z[m]$
, we identify the set
$Z[m]$
, we identify the set
![]() $Z\subseteq \mathbb N$
with its characteristic function. The formulas
$Z\subseteq \mathbb N$
with its characteristic function. The formulas
![]() $\psi $
and
$\psi $
and
![]() $\theta $
will be fixed throughout the following. We also fix
$\theta $
will be fixed throughout the following. We also fix
![]() $\mathbf {ACA}_0$
as base theory.
$\mathbf {ACA}_0$
as base theory.
Let us introduce some notation: We write
![]() $Y^{<\omega }$
for the set of finite sequences with entries from the set Y. In order to refer to the entries of a sequence
$Y^{<\omega }$
for the set of finite sequences with entries from the set Y. In order to refer to the entries of a sequence
![]() $s\in Y^{<\omega }$
of length
$s\in Y^{<\omega }$
of length
![]() $m=\operatorname {len}(s)$
, we will often write it as
$m=\operatorname {len}(s)$
, we will often write it as
![]() $s=\langle s(0),\dots ,s(m-1)\rangle $
. For
$s=\langle s(0),\dots ,s(m-1)\rangle $
. For
![]() $k\leq m$
we put
$k\leq m$
we put
![]() $s[k]:=\langle s(0),\dots ,s(k-1)\rangle $
. If Y is linearly ordered, the Kleene–Brouwer order (also called Lusin–Sierpiński order) on
$s[k]:=\langle s(0),\dots ,s(k-1)\rangle $
. If Y is linearly ordered, the Kleene–Brouwer order (also called Lusin–Sierpiński order) on
![]() $Y^{<\omega }$
is the linear order defined by
$Y^{<\omega }$
is the linear order defined by
 $$ \begin{align*} s<_{\operatorname{KB}(Y)}t\,:\Leftrightarrow\,\begin{cases} \text{either }\operatorname{len}(s)>\operatorname{len}(t)\text{ and }s[\operatorname{len}(t)]=t,\\ \text{or}\ s[k]=t[k]\ \text{and}\ s(k)<_Y t(k)\ \text{for some}\ k<\min\{\operatorname{len}(s),\operatorname{len}(t)\}. \end{cases} \end{align*} $$
$$ \begin{align*} s<_{\operatorname{KB}(Y)}t\,:\Leftrightarrow\,\begin{cases} \text{either }\operatorname{len}(s)>\operatorname{len}(t)\text{ and }s[\operatorname{len}(t)]=t,\\ \text{or}\ s[k]=t[k]\ \text{and}\ s(k)<_Y t(k)\ \text{for some}\ k<\min\{\operatorname{len}(s),\operatorname{len}(t)\}. \end{cases} \end{align*} $$
We say that a subset
![]() $\mathcal T\subseteq Y^{<\omega }$
is a tree if
$\mathcal T\subseteq Y^{<\omega }$
is a tree if
![]() $s\in \mathcal T$
and
$s\in \mathcal T$
and
![]() $k\leq \operatorname {len}(s)$
imply
$k\leq \operatorname {len}(s)$
imply
![]() $s[k]\in \mathcal T$
. Unless indicated otherwise, we assume that any tree
$s[k]\in \mathcal T$
. Unless indicated otherwise, we assume that any tree
![]() $\mathcal T\subseteq Y^{<\omega }$
carries the Kleene–Brouwer order
$\mathcal T\subseteq Y^{<\omega }$
carries the Kleene–Brouwer order
![]() $<_{\operatorname {KB}(Y)}$
. Recall that a branch of
$<_{\operatorname {KB}(Y)}$
. Recall that a branch of
![]() $\mathcal T$
is given by a function
$\mathcal T$
is given by a function
![]() $f:\mathbb N\to Y$
such that
$f:\mathbb N\to Y$
such that
![]() $f[m]\in \mathcal T$
holds for all
$f[m]\in \mathcal T$
holds for all
![]() $m\in \mathcal T$
. If Y is a well order, then
$m\in \mathcal T$
. If Y is a well order, then
![]() $\mathcal T\subseteq Y^{<\omega }$
(with order relation
$\mathcal T\subseteq Y^{<\omega }$
(with order relation
![]() $<_{\operatorname {KB}(Y)}$
) is well founded if, and only if, it has no branch (by the proof of [Reference Simpson29, Lemma V.1.3], which is formulated for
$<_{\operatorname {KB}(Y)}$
) is well founded if, and only if, it has no branch (by the proof of [Reference Simpson29, Lemma V.1.3], which is formulated for
![]() $Y=\mathbb N$
). One can conclude that our
$Y=\mathbb N$
). One can conclude that our
![]() $\Pi ^1_2$
-formula
$\Pi ^1_2$
-formula
![]() $\psi (n)$
fails for
$\psi (n)$
fails for
![]() $n\in \mathbb N$
if, and only if, there is a
$n\in \mathbb N$
if, and only if, there is a
![]() $Z\subseteq \mathbb N$
such that the Kleene–Brouwer order
$Z\subseteq \mathbb N$
such that the Kleene–Brouwer order
![]() $<_{\operatorname {KB}(\mathbb N)}$
is well founded on the tree
$<_{\operatorname {KB}(\mathbb N)}$
is well founded on the tree
In the following we construct predilators
![]() $D_\psi ^n$
such that
$D_\psi ^n$
such that
![]() $D_\psi ^n$
is a dilator if, and only if, the instance
$D_\psi ^n$
is a dilator if, and only if, the instance
![]() $\psi (n)$
holds. This is a version of Girard’s result that the notion of dilator is
$\psi (n)$
holds. This is a version of Girard’s result that the notion of dilator is
![]() $\Pi ^1_2$
-complete. The construction that we present is due to Normann (see [Reference Girard15, Theorem 8.E.1]). We recall it in full detail, because the rest of this section depends on the construction itself, not just on the result. Given a linear order X, the idea is to define
$\Pi ^1_2$
-complete. The construction that we present is due to Normann (see [Reference Girard15, Theorem 8.E.1]). We recall it in full detail, because the rest of this section depends on the construction itself, not just on the result. Given a linear order X, the idea is to define
 $D^n_\psi (X)$
as a subtree of
$D^n_\psi (X)$
as a subtree of
![]() $(2\times X)^{<\omega }$
(recall
$(2\times X)^{<\omega }$
(recall
![]() $m=\{0,\dots ,m-1\}$
with the usual linear order). Along each potential branch of
$m=\{0,\dots ,m-1\}$
with the usual linear order). Along each potential branch of
 $D^n_\psi (X)$
, we aim to construct a set
$D^n_\psi (X)$
, we aim to construct a set
![]() $Z\subseteq \mathbb N$
(determined by the characteristic function
$Z\subseteq \mathbb N$
(determined by the characteristic function
![]() $\mathbb N\to 2$
from the first component of the branch) and, simultaneously, an embedding of
$\mathbb N\to 2$
from the first component of the branch) and, simultaneously, an embedding of
![]() $\mathcal T^n_Z$
into X. If
$\mathcal T^n_Z$
into X. If
![]() $D^n_\psi $
fails to be a dilator, then
$D^n_\psi $
fails to be a dilator, then
 $D^n_\psi (X)$
has a branch for some well order X. The resulting embedding
$D^n_\psi (X)$
has a branch for some well order X. The resulting embedding
![]() $\mathcal T^n_Z\to X$
ensures that
$\mathcal T^n_Z\to X$
ensures that
![]() $\mathcal T^n_Z$
is a well order, so that
$\mathcal T^n_Z$
is a well order, so that
![]() $\psi (n)$
fails. Since Z is not given in advance, we need to approximate
$\psi (n)$
fails. Since Z is not given in advance, we need to approximate
![]() $\mathcal T^n_Z$
by the trees
$\mathcal T^n_Z$
by the trees
for
![]() $s\in 2^{<\omega }$
. The relation
$s\in 2^{<\omega }$
. The relation
![]() $t\in \mathcal T_s^n$
is
$t\in \mathcal T_s^n$
is
![]() $\Delta ^0_1$
-definable, as
$\Delta ^0_1$
-definable, as
![]() $\theta $
is a
$\theta $
is a
![]() $\Delta ^0_0$
-formula. We observe
$\Delta ^0_0$
-formula. We observe
 $\mathcal T_{s[m]}^n=\{t\in \mathcal T_s^n\,|\,\operatorname {len}(t)\leq m\}$
for
$\mathcal T_{s[m]}^n=\{t\in \mathcal T_s^n\,|\,\operatorname {len}(t)\leq m\}$
for
![]() $m\leq \operatorname {len}(s)$
, as well as
$m\leq \operatorname {len}(s)$
, as well as
 $\mathcal T_Z^n=\bigcup \{\mathcal T_{Z[m]}^n\,|\,m\in \mathbb N\}$
.
$\mathcal T_Z^n=\bigcup \{\mathcal T_{Z[m]}^n\,|\,m\in \mathbb N\}$
.
In order to describe the following constructions in an efficient way, we introduce some notation in connection with products. First recall that the product of sets
![]() $Y_0,\dots ,Y_{k-1}$
is given by
$Y_0,\dots ,Y_{k-1}$
is given by
If
![]() $Y_i=(Y_i,<_i)$
is a linear order for each
$Y_i=(Y_i,<_i)$
is a linear order for each
![]() $i<k$
, then we assume that the product carries the lexicographic order, in which
$i<k$
, then we assume that the product carries the lexicographic order, in which
![]() $(y_0,\dots ,y_{k-1})$
precedes
$(y_0,\dots ,y_{k-1})$
precedes
![]() $(y_0',\dots ,y_{k-1}')$
if, and only if, there is an index
$(y_0',\dots ,y_{k-1}')$
if, and only if, there is an index
![]() $j<k$
with
$j<k$
with
 $y_j<_jy_j'$
and
$y_j<_jy_j'$
and
![]() $y_i=y_i'$
for all
$y_i=y_i'$
for all
![]() $i<j$
. Given sequences
$i<j$
. Given sequences
![]() $s_i=\langle s_i(0),\dots ,s_i(m-1)\rangle \in Y_i^{<\omega }$
of the same length, we can construct a sequence
$s_i=\langle s_i(0),\dots ,s_i(m-1)\rangle \in Y_i^{<\omega }$
of the same length, we can construct a sequence
![]() $s_0\times \dots \times s_{k-1}\in (Y_0\times \dots \times Y_{k-1})^{<\omega }$
by setting
$s_0\times \dots \times s_{k-1}\in (Y_0\times \dots \times Y_{k-1})^{<\omega }$
by setting
Note that any sequence in
![]() $(Y_0\times \dots \times Y_{k-1})^{<\omega }$
can be uniquely written in this form. Analogously, we will combine functions
$(Y_0\times \dots \times Y_{k-1})^{<\omega }$
can be uniquely written in this form. Analogously, we will combine functions
![]() $g_i:\mathbb N\to Y_i$
into a function
$g_i:\mathbb N\to Y_i$
into a function
with
![]() $(g_0\times \dots \times g_{k-1})(l):=(g_0(l),\dots ,g_{k-1}(l))$
. For arbitrary
$(g_0\times \dots \times g_{k-1})(l):=(g_0(l),\dots ,g_{k-1}(l))$
. For arbitrary
![]() $m\in \mathbb N$
, we can observe
$m\in \mathbb N$
, we can observe
We use our product notation in a somewhat flexible way, for example by combining
![]() $s_0\in Y_0^{<\omega }$
and
$s_0\in Y_0^{<\omega }$
and
![]() $t=s_1\times s_2\in (Y_1\times Y_2)^{<\omega }$
into
$t=s_1\times s_2\in (Y_1\times Y_2)^{<\omega }$
into
![]() $s_0\times t:=s_0\times s_1\times s_2\in (Y_0\times Y_1\times Y_2)^{<\omega }$
. We can now officially define the predilators
$s_0\times t:=s_0\times s_1\times s_2\in (Y_0\times Y_1\times Y_2)^{<\omega }$
. We can now officially define the predilators
![]() $D^n_\psi $
that were mentioned above.
$D^n_\psi $
that were mentioned above.
Definition 5.1. For each linear order X, we define
 $D^n_\psi (X)$
as the tree of all sequences
$D^n_\psi (X)$
as the tree of all sequences
![]() $s\times t\in (2\times X)^{<\omega }$
with the following property: For all indices
$s\times t\in (2\times X)^{<\omega }$
with the following property: For all indices
![]() $i,j<\operatorname {len}(t)$
that are (numerical codes for) elements of
$i,j<\operatorname {len}(t)$
that are (numerical codes for) elements of
![]() $\mathcal T_s^n\subseteq \mathbb N^{<\omega }$
, we have
$\mathcal T_s^n\subseteq \mathbb N^{<\omega }$
, we have
Given an embedding
![]() $f:X\to Y$
, we define
$f:X\to Y$
, we define
 $D^n_\psi (f):D^n_\psi (X)\to D^n_\psi (Y)$
by
$D^n_\psi (f):D^n_\psi (X)\to D^n_\psi (Y)$
by
 $$ \begin{align*} D^n_\psi(f)(s\times\langle t(0),\dots,t(m-1)\rangle):=s\times\langle f(t(0)),\dots,f(t(m-1))\rangle. \end{align*} $$
$$ \begin{align*} D^n_\psi(f)(s\times\langle t(0),\dots,t(m-1)\rangle):=s\times\langle f(t(0)),\dots,f(t(m-1))\rangle. \end{align*} $$
Finally, we define functions
 ${\operatorname {supp}}^n_X:D^n_\psi (X)\to [X]^{<\omega }$
by setting
${\operatorname {supp}}^n_X:D^n_\psi (X)\to [X]^{<\omega }$
by setting
for each linear order X.
As mentioned before, the following comes from Normann’s proof of Girard’s result that the notion of dilator is
![]() $\Pi ^1_2$
-complete (see [Reference Girard15, Theorem 8.E.1]).
$\Pi ^1_2$
-complete (see [Reference Girard15, Theorem 8.E.1]).
Proposition 5.2. For each
![]() $n\in \mathbb N$
, we have the following:
$n\in \mathbb N$
, we have the following:
-
(a) the constructions from Definition 5.1 yield a predilator
 $D^n_\psi $
and
$D^n_\psi $
and -
(b) the predilator
 $D^n_\psi $
is a dilator if, and only if, the
$D^n_\psi $
is a dilator if, and only if, the
 $\Pi ^1_2$
-formula
$\Pi ^1_2$
-formula
 $\psi (n)$
holds.
$\psi (n)$
holds.
Proof Part (a) can be established by a straightforward verification. In (b), both directions are established by contraposition. First assume that
![]() $\psi (n)$
fails. We can then consider a set
$\psi (n)$
fails. We can then consider a set
![]() $Z\subseteq \mathbb N$
such that
$Z\subseteq \mathbb N$
such that
![]() $\mathcal T_Z^n$
is well founded. Write
$\mathcal T_Z^n$
is well founded. Write
![]() $g:\mathbb N\to 2$
for the characteristic function of Z, and put
$g:\mathbb N\to 2$
for the characteristic function of Z, and put
![]() $X:=\mathcal T_Z^n\cup \{\top \}$
with a new maximal element denoted by
$X:=\mathcal T_Z^n\cup \{\top \}$
with a new maximal element denoted by
![]() $\top $
. Using the latter as a default value, we define
$\top $
. Using the latter as a default value, we define
![]() $h:\mathbb N\to X$
by
$h:\mathbb N\to X$
by
 $$ \begin{align*} h(i):=\begin{cases} i & \text{if}\ i\ \text{codes an element of}~\mathcal T_Z^n\subseteq X,\\ \top & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} h(i):=\begin{cases} i & \text{if}\ i\ \text{codes an element of}~\mathcal T_Z^n\subseteq X,\\ \top & \text{otherwise}. \end{cases} \end{align*} $$
For
![]() $i,j\in \mathcal T_Z^n$
it is then trivial that
$i,j\in \mathcal T_Z^n$
it is then trivial that
![]() $i<_{\operatorname {KB}(\mathbb N)}j$
implies
$i<_{\operatorname {KB}(\mathbb N)}j$
implies
![]() $h(i)<_X h(j)$
. One can conclude that
$h(i)<_X h(j)$
. One can conclude that
![]() $g\times h:\mathbb N\to 2\times X$
is a branch of
$g\times h:\mathbb N\to 2\times X$
is a branch of
 $D_\psi ^n(X)$
. Since X is well founded while
$D_\psi ^n(X)$
. Since X is well founded while
 $D_\psi ^n(X)$
is not, the predilator
$D_\psi ^n(X)$
is not, the predilator
![]() $D_\psi ^n$
fails to be a dilator. To establish the converse, consider some well order X such that
$D_\psi ^n$
fails to be a dilator. To establish the converse, consider some well order X such that
 $D_\psi ^n(X)$
is ill founded. We can then consider a branch
$D_\psi ^n(X)$
is ill founded. We can then consider a branch
![]() $g\times h$
in
$g\times h$
in
 $D_\psi ^n(X)$
. Let
$D_\psi ^n(X)$
. Let
![]() $Z\subseteq \mathbb N$
be the set with characteristic function g. To conclude that
$Z\subseteq \mathbb N$
be the set with characteristic function g. To conclude that
![]() $\psi (n)$
fails, we argue that
$\psi (n)$
fails, we argue that
![]() $\mathcal T_Z^n$
is well founded because h restricts to an embedding of
$\mathcal T_Z^n$
is well founded because h restricts to an embedding of
![]() $\mathcal T_Z^n$
into the well order X: Given sequences
$\mathcal T_Z^n$
into the well order X: Given sequences
![]() $i,j\in \mathcal T_Z^n$
, we observe that
$i,j\in \mathcal T_Z^n$
, we observe that
 $i,j\in \mathcal T_{g[m]}^n$
holds for sufficiently large
$i,j\in \mathcal T_{g[m]}^n$
holds for sufficiently large
![]() $m\in \mathbb N$
(above the length of i and j). Then
$m\in \mathbb N$
(above the length of i and j). Then
 $g[m]\times h[m]\in D_\psi ^n(X)$
ensures that
$g[m]\times h[m]\in D_\psi ^n(X)$
ensures that
![]() $i<_{\operatorname {KB}(\mathbb N)}j$
implies
$i<_{\operatorname {KB}(\mathbb N)}j$
implies
![]() $h(i)<_Xh(j)$
, as desired. ⊣
$h(i)<_Xh(j)$
, as desired. ⊣
Next, we construct a family of 2-preptykes
![]() $P_\psi ^n$
such that
$P_\psi ^n$
such that
![]() $P_\psi ^n$
is a 2-ptyx (i.e., preserves dilators) precisely when the implication
$P_\psi ^n$
is a 2-ptyx (i.e., preserves dilators) precisely when the implication
![]() $\psi (n)\to \psi (n+1)$
holds. The construction is inspired by the one from Definition 5.1 (which is due to Normann). It will be somewhat more technical, because we work at a higher type level; on the other hand, the fact that we are concerned with an implication between
$\psi (n)\to \psi (n+1)$
holds. The construction is inspired by the one from Definition 5.1 (which is due to Normann). It will be somewhat more technical, because we work at a higher type level; on the other hand, the fact that we are concerned with an implication between
![]() $\Pi ^1_2$
-statements (and not with a general
$\Pi ^1_2$
-statements (and not with a general
![]() $\Pi ^1_3$
-statement) allows for some simplifications.
$\Pi ^1_3$
-statement) allows for some simplifications.
Let us recall that the component
![]() $t\in X^{<\omega }$
of an element
$t\in X^{<\omega }$
of an element
 $s\times t\in D_\psi ^n(X)$
encodes a partial embedding of
$s\times t\in D_\psi ^n(X)$
encodes a partial embedding of
![]() $\mathcal T_Z^n$
(or rather of
$\mathcal T_Z^n$
(or rather of
![]() $\mathcal T_s^n$
) into X. To discuss partial embeddings on the next type level, we need some notation: For a predilator D we write
$\mathcal T_s^n$
) into X. To discuss partial embeddings on the next type level, we need some notation: For a predilator D we write
for
![]() $m=\{0,\dots ,m-1\}$
with the usual linear order. To get an order on
$m=\{0,\dots ,m-1\}$
with the usual linear order. To get an order on
![]() $\Sigma D$
, we put
$\Sigma D$
, we put
As before, we write
![]() $\Sigma D+1$
for the extension of
$\Sigma D+1$
for the extension of
![]() $\Sigma D$
by a new maximal element
$\Sigma D$
by a new maximal element
![]() $\top $
(which will, once again, serve as a default value).
$\top $
(which will, once again, serve as a default value).
Definition 5.3. Consider predilators D and E. By a partial morphism
![]() we mean a sequence
we mean a sequence
![]() $r=\langle r(0),\dots ,r(\operatorname {len}(r)-1)\rangle \in (\Sigma E+1)^{<\omega }$
for which the following properties are satisfied:
$r=\langle r(0),\dots ,r(\operatorname {len}(r)-1)\rangle \in (\Sigma E+1)^{<\omega }$
for which the following properties are satisfied:
-
(i) Whenever
 $i<\operatorname {len}(r)$
is (the numerical code of) an element
$i<\operatorname {len}(r)$
is (the numerical code of) an element
 $(m,\sigma )\in \Sigma D$
, we have
$(m,\sigma )\in \Sigma D$
, we have
 $r(i)=(m,\rho )$
for some
$r(i)=(m,\rho )$
for some
 $\rho \in E(m)$
, with the same first component m.
$\rho \in E(m)$
, with the same first component m.To formulate the other conditions, we assume that (i) holds. For
 $(m,\sigma )\in \Sigma D$
with code
$(m,\sigma )\in \Sigma D$
with code
 $i<\operatorname {len}(r)$
, we then define
$i<\operatorname {len}(r)$
, we then define
 $\nu ^r_m(\sigma )\in E(m)$
by stipulating
$\nu ^r_m(\sigma )\in E(m)$
by stipulating
 $r(i)=(m,\nu ^r_m(\sigma ))$
. We say that
$r(i)=(m,\nu ^r_m(\sigma ))$
. We say that
 $\nu ^r_m(\sigma )$
is undefined when
$\nu ^r_m(\sigma )$
is undefined when
 $(m,\sigma )$
does not lie in
$(m,\sigma )$
does not lie in
 $\Sigma D$
or has code
$\Sigma D$
or has code
 $i\geq \operatorname {len}(r)$
.
$i\geq \operatorname {len}(r)$
. -
(ii) When the values
 $\nu ^r_m(\sigma )$
and
$\nu ^r_m(\sigma )$
and
 $\nu ^r_m(\tau )$
are defined, we demand
$\nu ^r_m(\tau )$
are defined, we demand  $$ \begin{align*} \sigma<_{D(m)}\tau\quad\Rightarrow\quad\nu^r_m(\sigma)<_{E(m)}\nu^r_m(\tau). \end{align*} $$
$$ \begin{align*} \sigma<_{D(m)}\tau\quad\Rightarrow\quad\nu^r_m(\sigma)<_{E(m)}\nu^r_m(\tau). \end{align*} $$
-
(iii) If
 $f:m=\{0,\dots ,m-1\}\to \{0,\dots ,k-1\}=k$
is an embedding, we require whenever the values
$f:m=\{0,\dots ,m-1\}\to \{0,\dots ,k-1\}=k$
is an embedding, we require whenever the values $$ \begin{align*} E(f)(\nu^r_m(\sigma))=\nu^r_k(D(f)(\sigma)) \end{align*} $$
$$ \begin{align*} E(f)(\nu^r_m(\sigma))=\nu^r_k(D(f)(\sigma)) \end{align*} $$
 $\nu ^r_m(\sigma )$
and
$\nu ^r_m(\sigma )$
and
 $\nu ^r_k(D(f)(\sigma ))$
are defined.
$\nu ^r_k(D(f)(\sigma ))$
are defined.
To avoid confusion, we explicitly state that both
![]() $r(i)\in \Sigma E$
and
$r(i)\in \Sigma E$
and
![]() $r(i)=\top $
is permitted when
$r(i)=\top $
is permitted when
![]() $i<\operatorname {len}(r)$
does not code an element of
$i<\operatorname {len}(r)$
does not code an element of
![]() $\Sigma D$
. Let us observe that condition (iii) is void for all but finitely many functions f, since there are only finitely many numbers
$\Sigma D$
. Let us observe that condition (iii) is void for all but finitely many functions f, since there are only finitely many numbers
![]() $m\in \mathbb N$
such that
$m\in \mathbb N$
such that
![]() $\nu ^r_m(\sigma )$
is defined for some
$\nu ^r_m(\sigma )$
is defined for some
![]() $\sigma \in D(m)$
. As a consequence, the notion of partial morphism is
$\sigma \in D(m)$
. As a consequence, the notion of partial morphism is
![]() $\Delta ^0_1$
-definable. The following is straightforward but important:
$\Delta ^0_1$
-definable. The following is straightforward but important:
Lemma 5.4. Consider a partial morphism
![]() . For
. For
![]() $k\leq \operatorname {len}(r)$
, the initial segment
$k\leq \operatorname {len}(r)$
, the initial segment
![]() is also a partial morphism, and we have
is also a partial morphism, and we have
 $\nu ^{r[k]}_m(\sigma )=\nu ^r_m(\sigma )$
whenever
$\nu ^{r[k]}_m(\sigma )=\nu ^r_m(\sigma )$
whenever
 $\nu ^{r[k]}_m(\sigma )$
is defined (note that
$\nu ^{r[k]}_m(\sigma )$
is defined (note that
![]() $\nu ^{r}_m(\sigma )$
is also defined in this case).
$\nu ^{r}_m(\sigma )$
is also defined in this case).
In order to define the preptyx
![]() $P_\psi ^n$
, we must specify an endofunctor of predilators and a natural family of support functions. The following definition explains the action of the endofunctor
$P_\psi ^n$
, we must specify an endofunctor of predilators and a natural family of support functions. The following definition explains the action of the endofunctor
![]() $P_\psi ^n$
on objects, i.e., on predilators.
$P_\psi ^n$
on objects, i.e., on predilators.
Definition 5.5. Consider a predilator E. For each order X, we define
 $P_\psi ^n(E)(X)$
as the tree of all sequences
$P_\psi ^n(E)(X)$
as the tree of all sequences
![]() $r\times s\times t\in ((\Sigma E+1)\times 2\times X)^{<\omega }$
such that
$r\times s\times t\in ((\Sigma E+1)\times 2\times X)^{<\omega }$
such that
 is a partial morphism and we have
is a partial morphism and we have
 $s\times t\in D_\psi ^{n+1}(X)$
. Given an embedding
$s\times t\in D_\psi ^{n+1}(X)$
. Given an embedding
![]() $f:X\to Y$
, we define
$f:X\to Y$
, we define
 $P_\psi ^n(E)(f):P_\psi ^n(E)(X)\to P_\psi ^n(E)(Y)$
by
$P_\psi ^n(E)(f):P_\psi ^n(E)(X)\to P_\psi ^n(E)(Y)$
by
 $$ \begin{align*} P_\psi^n(E)(f)(r\times s\times t):=r\times D_\psi^{n+1}(f)(s\times t). \end{align*} $$
$$ \begin{align*} P_\psi^n(E)(f)(r\times s\times t):=r\times D_\psi^{n+1}(f)(s\times t). \end{align*} $$
To define functions
 ${\operatorname {supp}}^{n,E}_X:P_\psi ^n(E)(X)\to [X]^{<\omega }$
, we set
${\operatorname {supp}}^{n,E}_X:P_\psi ^n(E)(X)\to [X]^{<\omega }$
, we set
 $$ \begin{align*} {\operatorname{supp}}^{n,E}_X(r\times s\times t):={\operatorname{supp}}^{n+1}_X(s\times t), \end{align*} $$
$$ \begin{align*} {\operatorname{supp}}^{n,E}_X(r\times s\times t):={\operatorname{supp}}^{n+1}_X(s\times t), \end{align*} $$
where
 ${\operatorname {supp}}^{n+1}_X:D_\psi ^{n+1}(X)\to [X]^{<\omega }$
is the support function from Definition 5.1.
${\operatorname {supp}}^{n+1}_X:D_\psi ^{n+1}(X)\to [X]^{<\omega }$
is the support function from Definition 5.1.
We recall that the arguments and values of our preptykes are coded predilators in the sense of Definition 2.2, rather than class-sized predilators in the sense of Definition 2.1. This is important for foundational reasons but has few practical implications, as the two variants of predilators form equivalent categories (see the first part of §2). In Definition 5.1 we have specified
 $D_\psi ^n(X)$
for an arbitrary order X, which means that we have defined
$D_\psi ^n(X)$
for an arbitrary order X, which means that we have defined
![]() $D_\psi ^n$
as a class-sized predilator. We will also write
$D_\psi ^n$
as a class-sized predilator. We will also write
![]() $D_\psi ^n$
(rather than
$D_\psi ^n$
(rather than
![]() $D_\psi ^n\!\restriction \!\mathbf {LO}_0$
) for the coded restriction given by Lemma 2.3.
$D_\psi ^n\!\restriction \!\mathbf {LO}_0$
) for the coded restriction given by Lemma 2.3.
Assuming that
![]() $P_\psi ^n$
preserves dilators, part (b) of the following proposition entails that
$P_\psi ^n$
preserves dilators, part (b) of the following proposition entails that
 $D_\psi ^{n+1}$
is a dilator if the same holds for
$D_\psi ^{n+1}$
is a dilator if the same holds for
![]() $D_\psi ^n$
. In view of Proposition 5.2, this amounts to the implication
$D_\psi ^n$
. In view of Proposition 5.2, this amounts to the implication
![]() $\psi (n)\to \psi (n+1)$
.
$\psi (n)\to \psi (n+1)$
.
Proposition 5.6. The following holds for any
![]() $n\in \mathbb N$
:
$n\in \mathbb N$
:
-
(a) if E is a predilator, then so is
 $P_\psi ^n(E),$
and
$P_\psi ^n(E),$
and -
(b) there is a morphism
 $\zeta ^n:D_\psi ^{n+1}\Rightarrow P_\psi ^n(D_\psi ^n)$
of predilators.
$\zeta ^n:D_\psi ^{n+1}\Rightarrow P_\psi ^n(D_\psi ^n)$
of predilators.
Proof It is straightforward to check part (a), based on the corresponding result from Proposition 5.2. To establish part (b), we define
![]() $g:\mathbb N\to \Sigma D_\psi ^n+1$
by
$g:\mathbb N\to \Sigma D_\psi ^n+1$
by
 $$ \begin{align*} g(i):=\begin{cases} (m,\sigma) & \text{if}\ i\ \text{is the numerical code of}~(m,\sigma)\in\Sigma D_\psi^n,\\ \top & \text{if}\ i\ \text{does not code an element of}\ \Sigma D_\psi^n. \end{cases} \end{align*} $$
$$ \begin{align*} g(i):=\begin{cases} (m,\sigma) & \text{if}\ i\ \text{is the numerical code of}~(m,\sigma)\in\Sigma D_\psi^n,\\ \top & \text{if}\ i\ \text{does not code an element of}\ \Sigma D_\psi^n. \end{cases} \end{align*} $$
Then
 is a partial morphism for each
is a partial morphism for each
![]() $k\in \mathbb N$
(with
$k\in \mathbb N$
(with
 $\nu ^{g[k]}_m(\sigma )=\sigma $
whenever the value is defined). For each linear order X, we can thus define a function
$\nu ^{g[k]}_m(\sigma )=\sigma $
whenever the value is defined). For each linear order X, we can thus define a function
 $\zeta ^n_X:D_\psi ^{n+1}(X)\to P_\psi ^n(D_\psi ^n)(X)$
by setting
$\zeta ^n_X:D_\psi ^{n+1}(X)\to P_\psi ^n(D_\psi ^n)(X)$
by setting
It is straightforward to verify that this yields a natural family of order embeddings, i.e., a morphism of predilators. ⊣
In order to extend
![]() $P^n_\psi $
into a functor, we need to define its action on a (total) morphism
$P^n_\psi $
into a functor, we need to define its action on a (total) morphism
![]() $\mu :E_0\Rightarrow E_1$
. For
$\mu :E_0\Rightarrow E_1$
. For
 $r\times s\times t\in P^n_\psi (E_0)(X)$
with
$r\times s\times t\in P^n_\psi (E_0)(X)$
with
 , the first component of
, the first component of
 $P_\psi ^n(\mu )_X(r\times s\times t)\in P_\psi ^n(E_1)(X)$
should be a partial morphism from
$P_\psi ^n(\mu )_X(r\times s\times t)\in P_\psi ^n(E_1)(X)$
should be a partial morphism from
![]() $D_\psi ^n$
to
$D_\psi ^n$
to
![]() $E_1$
. To obtain such a morphism, we compose r and
$E_1$
. To obtain such a morphism, we compose r and
![]() $\mu $
in the following way.
$\mu $
in the following way.
Definition 5.7. Consider a (total) morphism
![]() $\mu :E_0\Rightarrow E_1$
of predilators and a sequence
$\mu :E_0\Rightarrow E_1$
of predilators and a sequence
![]() $r=\langle r(0),\dots ,r(k-1)\rangle \in (\Sigma E_0+1)^{<\omega }$
. For
$r=\langle r(0),\dots ,r(k-1)\rangle \in (\Sigma E_0+1)^{<\omega }$
. For
![]() $i<k$
we define
$i<k$
we define
 $$ \begin{align*} \mu\circ r(i):=\begin{cases} (m,\mu_m(\tau)) & \text{if}\ r(i)=(m,\tau)\in\Sigma E_0,\\ \top & \text{if}\ r(i)=\top. \end{cases} \end{align*} $$
$$ \begin{align*} \mu\circ r(i):=\begin{cases} (m,\mu_m(\tau)) & \text{if}\ r(i)=(m,\tau)\in\Sigma E_0,\\ \top & \text{if}\ r(i)=\top. \end{cases} \end{align*} $$
We then set
![]() $\mu \circ r:=\langle \mu \circ r(0),\dots ,\mu \circ r(k-1)\rangle \in (\Sigma E_1+1)^{<\omega }$
.
$\mu \circ r:=\langle \mu \circ r(0),\dots ,\mu \circ r(k-1)\rangle \in (\Sigma E_1+1)^{<\omega }$
.
Let us verify basic properties of our construction:
Lemma 5.8. Consider a predilator D, a (total) morphism
![]() $\mu :E_0\Rightarrow E_1$
of predilators, and a sequence
$\mu :E_0\Rightarrow E_1$
of predilators, and a sequence
![]() $r\in (\Sigma E_0+1)^{<\omega }$
. Then
$r\in (\Sigma E_0+1)^{<\omega }$
. Then
![]() is a partial morphism if, and only if, the same holds for
is a partial morphism if, and only if, the same holds for
 . Assuming that these equivalent statements hold, we have
. Assuming that these equivalent statements hold, we have
whenever the values
![]() $\nu _m^r(\sigma )$
and
$\nu _m^r(\sigma )$
and
![]() $\nu _m^{\mu \circ r}(\sigma )$
are defined.
$\nu _m^{\mu \circ r}(\sigma )$
are defined.
Proof Invoking the definition of
![]() $\mu \circ r$
, it is straightforward to see that condition (i) of Definition 5.3 holds for r if, and only if, it holds for
$\mu \circ r$
, it is straightforward to see that condition (i) of Definition 5.3 holds for r if, and only if, it holds for
![]() $\mu \circ r$
. In the following we assume that r and
$\mu \circ r$
. In the following we assume that r and
![]() $\mu \circ r$
do indeed satisfy condition (i). We can then consider the values
$\mu \circ r$
do indeed satisfy condition (i). We can then consider the values
![]() $\nu _m^r(\sigma )$
and
$\nu _m^r(\sigma )$
and
![]() $\nu _m^{\mu \circ r}(\sigma )$
; note that they are defined for the same arguments, namely for
$\nu _m^{\mu \circ r}(\sigma )$
; note that they are defined for the same arguments, namely for
![]() $(m,\sigma )\in \Sigma D$
with code below
$(m,\sigma )\in \Sigma D$
with code below
![]() $\operatorname {len}(r)=\operatorname {len}(\mu \circ r)$
. The definition of
$\operatorname {len}(r)=\operatorname {len}(\mu \circ r)$
. The definition of
![]() $\mu \circ r$
does also reveal that
$\mu \circ r$
does also reveal that
![]() $\nu _m^{\mu \circ r}(\sigma )=\mu _m(\nu _m^r(\sigma ))$
holds whenever the relevant values are defined. Since the components
$\nu _m^{\mu \circ r}(\sigma )=\mu _m(\nu _m^r(\sigma ))$
holds whenever the relevant values are defined. Since the components
![]() $\mu _m:E_0(m)\to E_1(m)$
are order embeddings, it is straightforward to conclude that condition (ii) of Definition 5.3 holds for r if, and only if, it holds for
$\mu _m:E_0(m)\to E_1(m)$
are order embeddings, it is straightforward to conclude that condition (ii) of Definition 5.3 holds for r if, and only if, it holds for
![]() $\mu \circ r$
. In order to establish the same for condition (iii), we consider an embedding
$\mu \circ r$
. In order to establish the same for condition (iii), we consider an embedding
![]() $f:m\to k$
and assume that the values
$f:m\to k$
and assume that the values
![]() $\nu ^{r}_m(\sigma )$
and
$\nu ^{r}_m(\sigma )$
and
![]() $\nu ^{r}_k(D(f)(\sigma ))$
are defined. If condition (iii) holds for r, we can use the naturality of
$\nu ^{r}_k(D(f)(\sigma ))$
are defined. If condition (iii) holds for r, we can use the naturality of
![]() $\mu $
to get
$\mu $
to get
 $$ \begin{align*} \nu^{\mu\circ r}_k(D(f)(\sigma))=\mu_k(\nu^r_k(D(f)(\sigma)))&=\mu_k(E_0(f)(\nu^r_m(\sigma)))\\ &=E_1(f)(\mu_m(\nu^r_m(\sigma)))=E_1(f)(\nu^{\mu\circ r}_m(\sigma)), \end{align*} $$
$$ \begin{align*} \nu^{\mu\circ r}_k(D(f)(\sigma))=\mu_k(\nu^r_k(D(f)(\sigma)))&=\mu_k(E_0(f)(\nu^r_m(\sigma)))\\ &=E_1(f)(\mu_m(\nu^r_m(\sigma)))=E_1(f)(\nu^{\mu\circ r}_m(\sigma)), \end{align*} $$
as needed to show that condition (iii) holds for
![]() $\mu \circ r$
. Assuming the latter, the same equalities show
$\mu \circ r$
. Assuming the latter, the same equalities show
![]() $\mu _k(\nu ^r_k(D(f)(\sigma )))=\mu _k(E_0(f)(\nu ^r_m(\sigma )))$
. Since
$\mu _k(\nu ^r_k(D(f)(\sigma )))=\mu _k(E_0(f)(\nu ^r_m(\sigma )))$
. Since
![]() $\mu _k$
is injective, we can conclude
$\mu _k$
is injective, we can conclude
![]() $\nu ^r_k(D(f)(\sigma ))=E_0(f)(\nu ^r_m(\sigma ))$
, as required by condition (iii) for r. ⊣
$\nu ^r_k(D(f)(\sigma ))=E_0(f)(\nu ^r_m(\sigma ))$
, as required by condition (iii) for r. ⊣
To turn
![]() $P_\psi ^n$
into a preptyx, we also need to define support functions
$P_\psi ^n$
into a preptyx, we also need to define support functions
 $$ \begin{align*} {\operatorname{Supp}}^n_{E,X}:P_\psi^n(E)(X)\to[\operatorname{Tr}(E)]^{<\omega} \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}^n_{E,X}:P_\psi^n(E)(X)\to[\operatorname{Tr}(E)]^{<\omega} \end{align*} $$
as in Lemmas 3.4 and 3.5. The support of an element
 $r\times s\times t\in P_\psi ^n(E)(X)$
will depend on the entries
$r\times s\times t\in P_\psi ^n(E)(X)$
will depend on the entries
![]() $r(i)\in \Sigma E+1$
with
$r(i)\in \Sigma E+1$
with
![]() $r(i)\neq \top $
and hence
$r(i)\neq \top $
and hence
![]() $r(i)=(m,\tau )\in \Sigma E$
with
$r(i)=(m,\tau )\in \Sigma E$
with
![]() $m\in \mathbb N$
and
$m\in \mathbb N$
and
![]() $\tau \in E(m)$
. As explained after Proposition 2.8, we have a normal form
$\tau \in E(m)$
. As explained after Proposition 2.8, we have a normal form
![]() $\tau =_{\operatorname {NF}} E(\iota _a^m\circ \operatorname {en}_a)(\tau _0)$
with
$\tau =_{\operatorname {NF}} E(\iota _a^m\circ \operatorname {en}_a)(\tau _0)$
with
![]() $a\subseteq m=\{0,\dots ,m-1\}$
and
$a\subseteq m=\{0,\dots ,m-1\}$
and
![]() $(|a|,\tau _0)\in \operatorname {Tr}(E)$
.
$(|a|,\tau _0)\in \operatorname {Tr}(E)$
.
Definition 5.9. Consider a (total) morphism
![]() $\mu :E_0\Rightarrow E_1$
of predilators. For each linear order X, we define a function
$\mu :E_0\Rightarrow E_1$
of predilators. For each linear order X, we define a function
 $P_\psi ^n(\mu )_X:P_\psi ^n(E_0)(X)\to P_\psi ^n(E_1)(X)$
by
$P_\psi ^n(\mu )_X:P_\psi ^n(E_0)(X)\to P_\psi ^n(E_1)(X)$
by
 $$ \begin{align*} P_\psi^n(\mu)_X(r\times s\times t):=(\mu\circ r)\times s\times t. \end{align*} $$
$$ \begin{align*} P_\psi^n(\mu)_X(r\times s\times t):=(\mu\circ r)\times s\times t. \end{align*} $$
To define a family of support functions, we set
 $$ \begin{align*} &{\operatorname{Supp}}^n_{E,X}(r\times s\times t)=\{(|a|,\tau_0)\,|\,\text{there is an}\ i<\operatorname{len}(r)\ \text{with}\\ &\qquad\qquad\qquad\qquad\qquad\qquad r(i)=(m,\tau)\in\Sigma E\ \text{and}\ \tau=_{\operatorname{NF}} E(\iota_a^m\circ\operatorname{en}_a)(\tau_0)\} \end{align*} $$
$$ \begin{align*} &{\operatorname{Supp}}^n_{E,X}(r\times s\times t)=\{(|a|,\tau_0)\,|\,\text{there is an}\ i<\operatorname{len}(r)\ \text{with}\\ &\qquad\qquad\qquad\qquad\qquad\qquad r(i)=(m,\tau)\in\Sigma E\ \text{and}\ \tau=_{\operatorname{NF}} E(\iota_a^m\circ\operatorname{en}_a)(\tau_0)\} \end{align*} $$
for each order X and each element
 $r\times s\times t\in P_\psi ^n(E)(X)$
.
$r\times s\times t\in P_\psi ^n(E)(X)$
.
To complete our construction of
![]() $P_\psi ^n$
, we establish the following properties, which have been promised above.
$P_\psi ^n$
, we establish the following properties, which have been promised above.
Theorem 5.10. For each
![]() $n\in \mathbb N$
, we have the following:
$n\in \mathbb N$
, we have the following:
Proof (a) From Proposition 5.6 we know that
![]() $P_\psi ^n$
maps predilators to predilators. Let us now consider its action on a morphism
$P_\psi ^n$
maps predilators to predilators. Let us now consider its action on a morphism
![]() $\mu :E_0\Rightarrow E_1$
. Since each component
$\mu :E_0\Rightarrow E_1$
. Since each component
![]() $\mu _m:E_0(m)\to E_1(m)$
is an order embedding, the same holds for the map
$\mu _m:E_0(m)\to E_1(m)$
is an order embedding, the same holds for the map
In view of Definition 5.7, one readily infers that the components
 $P_\psi ^n(\mu )_X$
are order embeddings as well (recall that
$P_\psi ^n(\mu )_X$
are order embeddings as well (recall that
 $P_\psi ^n(E_i)(X)\subseteq ((\Sigma E_i+1)\times 2\times X)^{<\omega }$
carries the Kleene–Brouwer order with respect to the lexicographic order on the product). To conclude that
$P_\psi ^n(E_i)(X)\subseteq ((\Sigma E_i+1)\times 2\times X)^{<\omega }$
carries the Kleene–Brouwer order with respect to the lexicographic order on the product). To conclude that
 $P_\psi ^n(\mu )$
is a morphism of predilators, we consider an order embedding
$P_\psi ^n(\mu )$
is a morphism of predilators, we consider an order embedding
![]() $f:X\to Y$
and verify the naturality property
$f:X\to Y$
and verify the naturality property
 $$ \begin{align*} P_\psi^n(\mu)_Y\circ P_\psi^n(E_0)(f)(r\times s\times t)&=P_\psi^n(\mu)_Y(r\times D_\psi^{n+1}(f)(s\times t))\\ &=(\mu\circ r)\times D_\psi^{n+1}(f)(s\times t)\\&=P_\psi^n(E_1)(f)((\mu\circ r)\times s\times t)\\ &=P_\psi^n(E_1)(f)\circ P_\psi^n(\mu)_X(r\times s\times t). \end{align*} $$
$$ \begin{align*} P_\psi^n(\mu)_Y\circ P_\psi^n(E_0)(f)(r\times s\times t)&=P_\psi^n(\mu)_Y(r\times D_\psi^{n+1}(f)(s\times t))\\ &=(\mu\circ r)\times D_\psi^{n+1}(f)(s\times t)\\&=P_\psi^n(E_1)(f)((\mu\circ r)\times s\times t)\\ &=P_\psi^n(E_1)(f)\circ P_\psi^n(\mu)_X(r\times s\times t). \end{align*} $$
The claim that
![]() $P_\psi ^n$
is a functor reduces to
$P_\psi ^n$
is a functor reduces to
![]() $\mu ^1\circ (\mu ^0\circ r)=(\mu ^1\circ \mu ^0)\circ r$
(for partial and total morphisms of suitable (co-)domain), which is readily verified. To show that
$\mu ^1\circ (\mu ^0\circ r)=(\mu ^1\circ \mu ^0)\circ r$
(for partial and total morphisms of suitable (co-)domain), which is readily verified. To show that
![]() $P_\psi ^n$
is a preptyx, we use the criterion from Lemma 3.5. Let us first verify the naturality condition
$P_\psi ^n$
is a preptyx, we use the criterion from Lemma 3.5. Let us first verify the naturality condition
 $$ \begin{align*} {\operatorname{Supp}}^n_{E_1,X}\circ P_\psi^n(\mu)_X(r\times s\times t)=[\operatorname{Tr}(\mu)]^{<\omega}\circ{\operatorname{Supp}}^n_{E_0,X}(r\times s\times t) \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}^n_{E_1,X}\circ P_\psi^n(\mu)_X(r\times s\times t)=[\operatorname{Tr}(\mu)]^{<\omega}\circ{\operatorname{Supp}}^n_{E_0,X}(r\times s\times t) \end{align*} $$
with respect to a morphism
![]() $\mu :E_0\Rightarrow E_1$
. For an arbitrary element
$\mu :E_0\Rightarrow E_1$
. For an arbitrary element
![]() $\operatorname {Tr}(\mu )(|a|,\tau _0)$
of the right side, there is an index
$\operatorname {Tr}(\mu )(|a|,\tau _0)$
of the right side, there is an index
![]() $i<\operatorname {len}(r)$
such that
$i<\operatorname {len}(r)$
such that
![]() $r(i)$
has the form
$r(i)$
has the form
![]() $(m,\tau )\in \Sigma E_0$
with
$(m,\tau )\in \Sigma E_0$
with
![]() $\tau =_{\operatorname {NF}} E_0(\iota _a^m\circ \operatorname {en}_a)(\tau _0)$
. We observe
$\tau =_{\operatorname {NF}} E_0(\iota _a^m\circ \operatorname {en}_a)(\tau _0)$
. We observe
In view of
 $(|a|,\mu _{|a|}(\tau _0))=\operatorname {Tr}(\mu )(|a|,\tau _0)\in \operatorname {Tr}(E_1)$
(cf. Definition 2.16, which relies on Lemma 2.12), this equation yields the normal form of
$(|a|,\mu _{|a|}(\tau _0))=\operatorname {Tr}(\mu )(|a|,\tau _0)\in \operatorname {Tr}(E_1)$
(cf. Definition 2.16, which relies on Lemma 2.12), this equation yields the normal form of
![]() $\mu _m(\tau )\in E_1(m)$
. Together with
$\mu _m(\tau )\in E_1(m)$
. Together with
![]() $\mu \circ r(i)=(m,\mu _m(\tau ))$
, it follows that
$\mu \circ r(i)=(m,\mu _m(\tau ))$
, it follows that
![]() $\operatorname {Tr}(\mu )(|a|,\tau _0)$
lies in the set
$\operatorname {Tr}(\mu )(|a|,\tau _0)$
lies in the set
 $$ \begin{align*} {\operatorname{Supp}}^n_{E_1,X}((\mu\circ r)\times s\times t)={\operatorname{Supp}}^n_{E_1,X}\circ P_\psi^n(\mu)_X(r\times s\times t). \end{align*} $$
$$ \begin{align*} {\operatorname{Supp}}^n_{E_1,X}((\mu\circ r)\times s\times t)={\operatorname{Supp}}^n_{E_1,X}\circ P_\psi^n(\mu)_X(r\times s\times t). \end{align*} $$
Now consider any element
![]() $(|b|,\rho _0)$
of the latter. For some
$(|b|,\rho _0)$
of the latter. For some
![]() $i<\operatorname {len}(\mu \circ r)=\operatorname {len}(r)$
, we have
$i<\operatorname {len}(\mu \circ r)=\operatorname {len}(r)$
, we have
![]() $\mu \circ r(i)=(m,\rho )\in \Sigma E_1$
with
$\mu \circ r(i)=(m,\rho )\in \Sigma E_1$
with
![]() $\rho =_{\operatorname {NF}} E_1(\iota _b^m\circ \operatorname {en}_b)(\rho _0)$
. This yields
$\rho =_{\operatorname {NF}} E_1(\iota _b^m\circ \operatorname {en}_b)(\rho _0)$
. This yields
![]() $r(i)=(m,\tau )$
with
$r(i)=(m,\tau )$
with
![]() $\mu _m(\tau )=\rho $
. Writing
$\mu _m(\tau )=\rho $
. Writing
![]() $\tau =_{\operatorname {NF}} E_0(\iota _a^m\circ \operatorname {en}_a)(\tau _0)$
, we get
$\tau =_{\operatorname {NF}} E_0(\iota _a^m\circ \operatorname {en}_a)(\tau _0)$
, we get
as above. The uniqueness of normal forms (see the paragraph after Proposition 2.8) entails that we have
 $(b,\rho _0)=(a,\mu _{|a|}(\tau _0))$
. We can conclude
$(b,\rho _0)=(a,\mu _{|a|}(\tau _0))$
. We can conclude
 $$ \begin{align*} (|b|,\rho_0)=(|a|,\mu_{|a|}(\tau_0))=\operatorname{Tr}(\mu)(|a|,\tau_0)\in [\operatorname{Tr}(\mu)]^{<\omega}\circ{\operatorname{Supp}}^n_{E_0,X}(r\times s\times t). \end{align*} $$
$$ \begin{align*} (|b|,\rho_0)=(|a|,\mu_{|a|}(\tau_0))=\operatorname{Tr}(\mu)(|a|,\tau_0)\in [\operatorname{Tr}(\mu)]^{<\omega}\circ{\operatorname{Supp}}^n_{E_0,X}(r\times s\times t). \end{align*} $$
The naturality property
 ${\operatorname {Supp}}^n_{E,Y}\circ P_\psi ^n(E)(f)={\operatorname {Supp}}^n_{E,X}$
with respect to an order embedding
${\operatorname {Supp}}^n_{E,Y}\circ P_\psi ^n(E)(f)={\operatorname {Supp}}^n_{E,X}$
with respect to an order embedding
![]() $f:X\to Y$
is straightforward (and in fact automatic, cf. the discussion after Lemma 3.5). It remains to verify the support condition
$f:X\to Y$
is straightforward (and in fact automatic, cf. the discussion after Lemma 3.5). It remains to verify the support condition
 $$ \begin{align*} \{r\times s\times t\in P_\psi^n(E_1)(X)\,|\,{\operatorname{Supp}}_{E_1,X}^n(r\times s\times t)\subseteq\operatorname{rng}(\mu)\}\subseteq\operatorname{rng}(P_\psi^n(\mu)_X) \end{align*} $$
$$ \begin{align*} \{r\times s\times t\in P_\psi^n(E_1)(X)\,|\,{\operatorname{Supp}}_{E_1,X}^n(r\times s\times t)\subseteq\operatorname{rng}(\mu)\}\subseteq\operatorname{rng}(P_\psi^n(\mu)_X) \end{align*} $$
for a morphism
![]() $\mu :E_0\Rightarrow E_1$
. Given an arbitrary element
$\mu :E_0\Rightarrow E_1$
. Given an arbitrary element
![]() $r\times s\times t$
of the left side, we construct
$r\times s\times t$
of the left side, we construct
![]() $r'\in (\Sigma E_0+1)^{<\omega }$
with
$r'\in (\Sigma E_0+1)^{<\omega }$
with
![]() $\operatorname {len}(r')=\operatorname {len}(r)$
as follows: For each
$\operatorname {len}(r')=\operatorname {len}(r)$
as follows: For each
![]() $i<\operatorname {len}(r)$
with
$i<\operatorname {len}(r)$
with
![]() $r(i)=\top $
, we set
$r(i)=\top $
, we set
![]() $r'(i):=\top $
. In the case of
$r'(i):=\top $
. In the case of
![]() $r(i)=(m,\rho )\in \Sigma E_1$
, we consider the unique normal form
$r(i)=(m,\rho )\in \Sigma E_1$
, we consider the unique normal form
![]() $\rho =_{\operatorname {NF}} E_1(\iota _a^m\circ \operatorname {en}_a)(\rho _0)$
and observe
$\rho =_{\operatorname {NF}} E_1(\iota _a^m\circ \operatorname {en}_a)(\rho _0)$
and observe
 $$ \begin{align*} (|a|,\rho_0)\in{\operatorname{Supp}}_{E_1,X}^n(r\times s\times t)\subseteq\operatorname{rng}(\mu). \end{align*} $$
$$ \begin{align*} (|a|,\rho_0)\in{\operatorname{Supp}}_{E_1,X}^n(r\times s\times t)\subseteq\operatorname{rng}(\mu). \end{align*} $$
This allows us to write
 $\rho _0=\mu _{|a|}(\tau _0)$
, where
$\rho _0=\mu _{|a|}(\tau _0)$
, where
![]() $\tau _0\in E_0(|a|)$
is unique since
$\tau _0\in E_0(|a|)$
is unique since
![]() $\mu _{|a|}$
is an embedding. We now set
$\mu _{|a|}$
is an embedding. We now set
![]() $\tau :=E_0(\iota _a^m\circ \operatorname {en}_a)(\tau _0)\in E_0(m)$
and
$\tau :=E_0(\iota _a^m\circ \operatorname {en}_a)(\tau _0)\in E_0(m)$
and
![]() $r'(i):=(m,\tau )\in \Sigma E_0$
. Observe that we have
$r'(i):=(m,\tau )\in \Sigma E_0$
. Observe that we have
![]() $\mu _m(\tau )=\rho $
and hence
$\mu _m(\tau )=\rho $
and hence
![]() $\mu \circ r'=r$
. Crucially, the equivalence from Lemma 5.8 ensures that
$\mu \circ r'=r$
. Crucially, the equivalence from Lemma 5.8 ensures that
 is a partial morphism. This entails that we have
is a partial morphism. This entails that we have
 $r'\times s\times t\in P_\psi ^n(E_0)(X)$
, so that we indeed get
$r'\times s\times t\in P_\psi ^n(E_0)(X)$
, so that we indeed get
 $$ \begin{align*} r\times s\times t=(\mu\circ r')\times s\times t=P_\psi^n(\mu)_X(r'\times s\times t)\in\operatorname{rng}(P_\psi^n(\mu)_X). \end{align*} $$
$$ \begin{align*} r\times s\times t=(\mu\circ r')\times s\times t=P_\psi^n(\mu)_X(r'\times s\times t)\in\operatorname{rng}(P_\psi^n(\mu)_X). \end{align*} $$
(b) For the first direction, we assume that
![]() $P_\psi ^n$
is a ptyx and that
$P_\psi ^n$
is a ptyx and that
![]() $\psi (n)$
holds. By Proposition 5.2, the latter entails that
$\psi (n)$
holds. By Proposition 5.2, the latter entails that
![]() $D_\psi ^n$
is a dilator. Since
$D_\psi ^n$
is a dilator. Since
![]() $P_\psi ^n$
is a ptyx, it follows that
$P_\psi ^n$
is a ptyx, it follows that
 $P_\psi ^n(D_\psi ^n)$
is a dilator as well. Invoking the morphism from Proposition 5.6, we can conclude that
$P_\psi ^n(D_\psi ^n)$
is a dilator as well. Invoking the morphism from Proposition 5.6, we can conclude that
 $D_\psi ^{n+1}$
is a dilator: For each well order X, the component
$D_\psi ^{n+1}$
is a dilator: For each well order X, the component
 $$ \begin{align*} \zeta^n_X:D_\psi^{n+1}(X)\to P_\psi^n(D_\psi^n)(X) \end{align*} $$
$$ \begin{align*} \zeta^n_X:D_\psi^{n+1}(X)\to P_\psi^n(D_\psi^n)(X) \end{align*} $$
is an order embedding, which ensures that
 $D_\psi ^{n+1}(X)$
is well founded. By the other direction of Proposition 5.2, it follows that
$D_\psi ^{n+1}(X)$
is well founded. By the other direction of Proposition 5.2, it follows that
![]() $\psi (n+1)$
holds, as required. To be precise, one needs to switch back and forth between class-sized and coded dilators; this is straightforward with the help of Proposition 2.8, Corollary 2.10 and Lemma 2.14. In order to establish the other direction, we assume that
$\psi (n+1)$
holds, as required. To be precise, one needs to switch back and forth between class-sized and coded dilators; this is straightforward with the help of Proposition 2.8, Corollary 2.10 and Lemma 2.14. In order to establish the other direction, we assume that
![]() $\psi (n)$
holds while
$\psi (n)$
holds while
![]() $\psi (n+1)$
fails. Then
$\psi (n+1)$
fails. Then
![]() $D_\psi ^n$
is a dilator while
$D_\psi ^n$
is a dilator while
 $D_\psi ^{n+1}(X)$
is ill founded for some well order X. To conclude that
$D_\psi ^{n+1}(X)$
is ill founded for some well order X. To conclude that
![]() $P_\psi ^n$
fails to be a ptyx, it suffices to show that
$P_\psi ^n$
fails to be a ptyx, it suffices to show that
 $P_\psi ^n(D_\psi ^n)(X)$
is ill founded. The proof of Proposition 5.2 provides a function
$P_\psi ^n(D_\psi ^n)(X)$
is ill founded. The proof of Proposition 5.2 provides a function
![]() $g:\mathbb N\to \Sigma D_\psi ^n+1$
such that
$g:\mathbb N\to \Sigma D_\psi ^n+1$
such that
 is a partial morphism for each
is a partial morphism for each
![]() $k\in \mathbb N$
. We can also pick a branch
$k\in \mathbb N$
. We can also pick a branch
![]() $h_0\times h_1:\mathbb N\to 2\times X$
of the ill founded tree
$h_0\times h_1:\mathbb N\to 2\times X$
of the ill founded tree
 $D_\psi ^{n+1}(X)\subseteq (2\times X)^{<\omega }$
. It follows that
$D_\psi ^{n+1}(X)\subseteq (2\times X)^{<\omega }$
. It follows that
![]() $g\times h_0\times h_1$
is a branch of the tree
$g\times h_0\times h_1$
is a branch of the tree
 $P_\psi ^n(D_\psi ^n)(X)\subseteq ((\Sigma D_\psi ^n+1)\times 2\times X)^{<\omega }$
, which is thus ill founded. ⊣
$P_\psi ^n(D_\psi ^n)(X)\subseteq ((\Sigma D_\psi ^n+1)\times 2\times X)^{<\omega }$
, which is thus ill founded. ⊣
As a final ingredient for the analysis of
![]() $\Pi ^1_2$
-induction, we discuss the pointwise sum of ptykes. Consider a family of preptykes
$\Pi ^1_2$
-induction, we discuss the pointwise sum of ptykes. Consider a family of preptykes
![]() $P_z$
, indexed by the elements of a linear order Z. We define a preptyx
$P_z$
, indexed by the elements of a linear order Z. We define a preptyx
![]() $P:=\sum _{z\in Z}P_z$
as follows: Given a predilator E and a linear order X, we set
$P:=\sum _{z\in Z}P_z$
as follows: Given a predilator E and a linear order X, we set
 $$ \begin{gather*} P(E)(X):=\{(z,\sigma)\,|\,z\in Z\text{ and }\sigma\in P_z(E)(X)\},\\ (z,\sigma)<_{P(E)(X)}(z',\sigma')\quad:\Leftrightarrow\quad z<_Zz'\text{ or }(z=z'\text{ and }\sigma<_{P_z(E)(X)}\sigma'). \end{gather*} $$
$$ \begin{gather*} P(E)(X):=\{(z,\sigma)\,|\,z\in Z\text{ and }\sigma\in P_z(E)(X)\},\\ (z,\sigma)<_{P(E)(X)}(z',\sigma')\quad:\Leftrightarrow\quad z<_Zz'\text{ or }(z=z'\text{ and }\sigma<_{P_z(E)(X)}\sigma'). \end{gather*} $$
For an embedding
![]() $f:X\to Y$
, we define
$f:X\to Y$
, we define
![]() $P(E)(f):P(E)(X)\to P(E)(Y)$
by
$P(E)(f):P(E)(X)\to P(E)(Y)$
by
The support functions
![]() ${\operatorname {supp}}^z_X:P_z(E)(X)\to [X]^{<\omega }$
of the predilators
${\operatorname {supp}}^z_X:P_z(E)(X)\to [X]^{<\omega }$
of the predilators
![]() $P_z(E)$
can be combined into
$P_z(E)$
can be combined into
![]() ${\operatorname {supp}}_X:P(E)(X)\to [X]^{<\omega }$
with
${\operatorname {supp}}_X:P(E)(X)\to [X]^{<\omega }$
with
![]() ${\operatorname {supp}}_X(z,\sigma ):={\operatorname {supp}}^z_X(\sigma )$
. It is straightforward to check that this defines
${\operatorname {supp}}_X(z,\sigma ):={\operatorname {supp}}^z_X(\sigma )$
. It is straightforward to check that this defines
![]() $P(E)$
as a predilator. To turn P into a functor, consider a morphism
$P(E)$
as a predilator. To turn P into a functor, consider a morphism
![]() $\mu :E_0\Rightarrow E_1$
and define
$\mu :E_0\Rightarrow E_1$
and define
![]() $P(\mu ):P(E_0)\Rightarrow P(E_1)$
by
$P(\mu ):P(E_0)\Rightarrow P(E_1)$
by
Definition 3.3 provides functions
![]() ${\operatorname {Supp}}^z_{E,X}:P_z(E)(X)\to [\operatorname {Tr}(E)]^{<\omega }$
, which we can combine into
${\operatorname {Supp}}^z_{E,X}:P_z(E)(X)\to [\operatorname {Tr}(E)]^{<\omega }$
, which we can combine into
![]() ${\operatorname {Supp}}_{E,X}:P(E)(X)\to [\operatorname {Tr}(E)]^{<\omega }$
with
${\operatorname {Supp}}_{E,X}:P(E)(X)\to [\operatorname {Tr}(E)]^{<\omega }$
with
![]() ${\operatorname {Supp}}_{E,X}(z,\sigma ):={\operatorname {Supp}}^z_{E,X}(\sigma )$
. Invoking Lemma 3.5, one can verify that this turns
${\operatorname {Supp}}_{E,X}(z,\sigma ):={\operatorname {Supp}}^z_{E,X}(\sigma )$
. Invoking Lemma 3.5, one can verify that this turns
![]() $P=\sum _{z\in Z}P_z$
into a preptyx. If
$P=\sum _{z\in Z}P_z$
into a preptyx. If
![]() $P_z$
is a ptyx for all
$P_z$
is a ptyx for all
![]() $z\in Z$
, then so is P. Let us also point out that we have a morphism
$z\in Z$
, then so is P. Let us also point out that we have a morphism
![]() $P_z(E)\Rightarrow P(E)$
for each
$P_z(E)\Rightarrow P(E)$
for each
![]() $z\in Z$
and each predilator E: its components are given by
$z\in Z$
and each predilator E: its components are given by
![]() $P_z(E)(X)\ni \sigma \mapsto (z,\sigma )\in P(E)(X)$
. Finally, we can prove the central result of this paper. Note that the theorem demands less than a dilator
$P_z(E)(X)\ni \sigma \mapsto (z,\sigma )\in P(E)(X)$
. Finally, we can prove the central result of this paper. Note that the theorem demands less than a dilator
![]() $D\cong P(D)$
.
$D\cong P(D)$
.
Theorem 5.11
 $(\mathbf {ACA}_0)$
$(\mathbf {ACA}_0)$
Assume that every normal 2-ptyx P admits a morphism
![]() $P(D)\Rightarrow D$
for some dilator D. Then the principle of
$P(D)\Rightarrow D$
for some dilator D. Then the principle of
![]() $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
![]() $\mathbb N$
holds.
$\mathbb N$
holds.
Let us recall that we can quantify over (coded) dilators, since the latter are represented by subsets of
![]() $\mathbb N$
(cf. the discussion after Definition 2.2). The situation for ptykes is somewhat different: In the paragraph before Proposition 3.2, we have sketched how to construct a universal family of preptykes. However, we have not carried out the details of this construction. For this reason, one should read the previous theorem as a schema: Given a
$\mathbb N$
(cf. the discussion after Definition 2.2). The situation for ptykes is somewhat different: In the paragraph before Proposition 3.2, we have sketched how to construct a universal family of preptykes. However, we have not carried out the details of this construction. For this reason, one should read the previous theorem as a schema: Given a
![]() $\Pi ^1_2$
-formula
$\Pi ^1_2$
-formula
![]() $\psi $
, possibly with parameters, we will specify a
$\psi $
, possibly with parameters, we will specify a
![]() $\Delta ^0_1$
-definable family of preptykes. Assuming that every normal ptyx P from this family admits a morphism
$\Delta ^0_1$
-definable family of preptykes. Assuming that every normal ptyx P from this family admits a morphism
![]() $P(D)\Rightarrow D$
, we will establish the induction principle for
$P(D)\Rightarrow D$
, we will establish the induction principle for
![]() $\psi $
and arbitrary values of the parameters.
$\psi $
and arbitrary values of the parameters.
Proof Let
![]() $\psi (n)$
be an arbitrary
$\psi (n)$
be an arbitrary
![]() $\Pi ^1_2$
-formula with a distinguished number variable, possibly with further parameters. We will use the previous constructions and results for this formula
$\Pi ^1_2$
-formula with a distinguished number variable, possibly with further parameters. We will use the previous constructions and results for this formula
![]() $\psi $
(with respect to some fixed normal form, cf. the second paragraph of this section). Theorem 5.10 provides 2-preptykes
$\psi $
(with respect to some fixed normal form, cf. the second paragraph of this section). Theorem 5.10 provides 2-preptykes
![]() $P^n_\psi $
for all
$P^n_\psi $
for all
![]() $n\in \mathbb N$
. Let us form their pointwise sum
$n\in \mathbb N$
. Let us form their pointwise sum
![]() $P_\psi :=\textstyle \sum _{n\in \mathbb N}P^n_\psi $
. As we have seen above, we have a morphism
$P_\psi :=\textstyle \sum _{n\in \mathbb N}P^n_\psi $
. As we have seen above, we have a morphism
 $P^n_\psi (E)\Rightarrow P_\psi (E)$
for each predilator E and each
$P^n_\psi (E)\Rightarrow P_\psi (E)$
for each predilator E and each
![]() $n\in \mathbb N$
. For the predilators
$n\in \mathbb N$
. For the predilators
![]() $D^n_\psi $
from Proposition 5.2, we will denote these morphisms by
$D^n_\psi $
from Proposition 5.2, we will denote these morphisms by
 $$ \begin{align*} \iota^n:P_\psi^n(D^n_\psi)\Rightarrow P_\psi(D^n_\psi). \end{align*} $$
$$ \begin{align*} \iota^n:P_\psi^n(D^n_\psi)\Rightarrow P_\psi(D^n_\psi). \end{align*} $$
Invoking Theorem 4.20 (and the constructions that precede it), we consider the normal 2-preptyx
 $P^*_\psi :=(P_\psi )^*$
and the morphisms
$P^*_\psi :=(P_\psi )^*$
and the morphisms
 $$ \begin{align*} \xi^n:P_\psi(D^n_\psi)+1\Rightarrow P^*_\psi(D^n_\psi+1). \end{align*} $$
$$ \begin{align*} \xi^n:P_\psi(D^n_\psi)+1\Rightarrow P^*_\psi(D^n_\psi+1). \end{align*} $$
Theorem 5.10 tells us that
![]() $P^n_\psi $
corresponds to the induction step
$P^n_\psi $
corresponds to the induction step
![]() $\psi (n)\to \psi (n+1)$
. To incorporate the base of the induction, we form the 2-preptyx
$\psi (n)\to \psi (n+1)$
. To incorporate the base of the induction, we form the 2-preptyx
![]() $P^+_\psi $
with
$P^+_\psi $
with
 $$ \begin{align*} P^+_\psi(E):=D^0_\psi+1+P^*_\psi(E). \end{align*} $$
$$ \begin{align*} P^+_\psi(E):=D^0_\psi+1+P^*_\psi(E). \end{align*} $$
More formally, this can be explained as the pointwise sum
![]() $P^+_\psi =\sum _{i\in 2}P_i$
, where
$P^+_\psi =\sum _{i\in 2}P_i$
, where
![]() $P_1$
is
$P_1$
is
![]() $P^*_\psi $
and
$P^*_\psi $
and
![]() $P_0$
is the constant preptyx with value
$P_0$
is the constant preptyx with value
 $D^0_\psi +1$
(note that the latter assigns support
$D^0_\psi +1$
(note that the latter assigns support
![]() ${\operatorname {Supp}}_{E,X}(\sigma ):=\emptyset \in [\operatorname {Tr}(E)]^{<\omega }$
to any
${\operatorname {Supp}}_{E,X}(\sigma ):=\emptyset \in [\operatorname {Tr}(E)]^{<\omega }$
to any
 $\sigma \in P_0(E)(X)=D^0_\psi (X)+1$
). It is easy to see that
$\sigma \in P_0(E)(X)=D^0_\psi (X)+1$
). It is easy to see that
![]() $P^+_\psi $
is still normal. The family of preptykes
$P^+_\psi $
is still normal. The family of preptykes
![]() $P^+_\psi $
is
$P^+_\psi $
is
![]() $\Delta ^0_1$
-definable in the parameters of
$\Delta ^0_1$
-definable in the parameters of
![]() $\psi $
, just as all relevant objects that we have constructed in the previous sections. Only ptykes from this family will be used to derive the induction principle for
$\psi $
, just as all relevant objects that we have constructed in the previous sections. Only ptykes from this family will be used to derive the induction principle for
![]() $\psi $
. Fix values of the parameters and assume
$\psi $
. Fix values of the parameters and assume
By Theorem 5.10 we can conclude that
![]() $P^n_\psi $
is a ptyx for every
$P^n_\psi $
is a ptyx for every
![]() $n\in \mathbb N$
. As we have seen, it follows that
$n\in \mathbb N$
. As we have seen, it follows that
![]() $P_\psi =\sum _{n\in \mathbb N}P^n_\psi $
is a ptyx as well. Then
$P_\psi =\sum _{n\in \mathbb N}P^n_\psi $
is a ptyx as well. Then
![]() $P^*_\psi $
is a normal ptyx, by Theorem 4.20. Given that
$P^*_\psi $
is a normal ptyx, by Theorem 4.20. Given that
![]() $\psi (0)$
holds, Proposition 5.2 tells us that
$\psi (0)$
holds, Proposition 5.2 tells us that
 $D^0_\psi $
is a dilator. It is straightforward to conclude that
$D^0_\psi $
is a dilator. It is straightforward to conclude that
![]() $P^+_\psi $
is a normal 2-ptyx. By the assumption of the theorem, we now get a dilator E that admits a morphism
$P^+_\psi $
is a normal 2-ptyx. By the assumption of the theorem, we now get a dilator E that admits a morphism
 $$ \begin{align*} \chi:P^+_\psi(E)\Rightarrow E. \end{align*} $$
$$ \begin{align*} \chi:P^+_\psi(E)\Rightarrow E. \end{align*} $$
In the following, we will construct morphisms
![]() $\kappa ^n:D^n_\psi +1\Rightarrow E$
. Given that E is a dilator, these morphisms will ensure that
$\kappa ^n:D^n_\psi +1\Rightarrow E$
. Given that E is a dilator, these morphisms will ensure that
![]() $D^n_\psi $
is a dilator for each number
$D^n_\psi $
is a dilator for each number
![]() $n\in \mathbb N$
(as in the proof of part (b) of Theorem 5.10). By Proposition 5.2 this yields
$n\in \mathbb N$
(as in the proof of part (b) of Theorem 5.10). By Proposition 5.2 this yields
![]() $\forall _{n\in \mathbb N}\,\psi (n)$
, which is the desired conclusion of induction. To construct
$\forall _{n\in \mathbb N}\,\psi (n)$
, which is the desired conclusion of induction. To construct
![]() $\kappa ^n$
, we first note that the pointwise sum
$\kappa ^n$
, we first note that the pointwise sum
![]() $P^+_\psi $
comes with morphisms
$P^+_\psi $
comes with morphisms
 $$ \begin{align*} \pi^0:D^0_\psi+1\Rightarrow P^+_\psi(E)\quad\text{and}\quad\pi^1:P^*_\psi(E)\Rightarrow P^+_\psi(E). \end{align*} $$
$$ \begin{align*} \pi^0:D^0_\psi+1\Rightarrow P^+_\psi(E)\quad\text{and}\quad\pi^1:P^*_\psi(E)\Rightarrow P^+_\psi(E). \end{align*} $$
Using the morphisms
 $\zeta ^n:D_\psi ^{n+1}\Rightarrow P_\psi ^n(D_\psi ^n)$
from Proposition 5.6 (and the construction from Example 4.4), we can recursively define
$\zeta ^n:D_\psi ^{n+1}\Rightarrow P_\psi ^n(D_\psi ^n)$
from Proposition 5.6 (and the construction from Example 4.4), we can recursively define
![]() $\kappa ^0:=\chi \circ \pi ^0$
and
$\kappa ^0:=\chi \circ \pi ^0$
and
 $$ \begin{align*} \kappa^{n+1}:=\chi\circ\pi^1\circ P^*_\psi(\kappa^n)\circ\xi^n\circ(\iota^n+1)\circ(\zeta^n+1). \end{align*} $$
$$ \begin{align*} \kappa^{n+1}:=\chi\circ\pi^1\circ P^*_\psi(\kappa^n)\circ\xi^n\circ(\iota^n+1)\circ(\zeta^n+1). \end{align*} $$
Working in
![]() $\mathbf {ACA}_0$
, this construction can be implemented as an effective recursion along
$\mathbf {ACA}_0$
, this construction can be implemented as an effective recursion along
![]() $\mathbb N$
(see [Reference Freund10] for a detailed exposition of this principle). To justify this claim, we need to verify that
$\mathbb N$
(see [Reference Freund10] for a detailed exposition of this principle). To justify this claim, we need to verify that
![]() $\kappa ^{n+1}$
is
$\kappa ^{n+1}$
is
![]() $\Delta ^0_1$
-definable relative to
$\Delta ^0_1$
-definable relative to
![]() $\kappa ^n\subseteq \mathbb N$
(cf. the discussion before Lemma 2.11). This brings up a somewhat subtle point: In the discussion before Theorem 4.20, we have noted that the relation
$\kappa ^n\subseteq \mathbb N$
(cf. the discussion before Lemma 2.11). This brings up a somewhat subtle point: In the discussion before Theorem 4.20, we have noted that the relation
 $P^*_\psi (\mu )_X(\sigma )=\tau $
is
$P^*_\psi (\mu )_X(\sigma )=\tau $
is
![]() $\Delta ^0_1$
-definable. More precisely, the relation is defined by a
$\Delta ^0_1$
-definable. More precisely, the relation is defined by a
![]() $\Sigma ^0_1$
- and a
$\Sigma ^0_1$
- and a
![]() $\Pi ^0_1$
-formula that are equivalent when
$\Pi ^0_1$
-formula that are equivalent when
![]() $\mu \subseteq \mathbb N$
represents a morphism of predilators. However, we may not be able to assume that the two formulas are equivalent for any parameter
$\mu \subseteq \mathbb N$
represents a morphism of predilators. However, we may not be able to assume that the two formulas are equivalent for any parameter
![]() $\mu \subseteq \mathbb N$
. To point out one potential issue, we note that it is problematic to compose functions when we do not know whether they are total. A way around this obstacle has been presented in [Reference Freund10]: In defining
$\mu \subseteq \mathbb N$
. To point out one potential issue, we note that it is problematic to compose functions when we do not know whether they are total. A way around this obstacle has been presented in [Reference Freund10]: In defining
![]() $\kappa ^{n+1}$
, we may anticipate the result of the construction and assume that
$\kappa ^{n+1}$
, we may anticipate the result of the construction and assume that
![]() $\kappa ^n$
is a morphism of predilators. This ensures that we can use the aforementioned
$\kappa ^n$
is a morphism of predilators. This ensures that we can use the aforementioned
![]() $\Delta ^0_1$
-definition of the components
$\Delta ^0_1$
-definition of the components
 $$ \begin{align*} P^*_\psi(\kappa^n)_X:P^*_\psi(D^n_\psi+1)(X)\to P^*_\psi(E)(X). \end{align*} $$
$$ \begin{align*} P^*_\psi(\kappa^n)_X:P^*_\psi(D^n_\psi+1)(X)\to P^*_\psi(E)(X). \end{align*} $$
It also ensures that the latter are total functions. Due to this fact, the composition above provides the required
![]() $\Delta ^0_1$
-definition of
$\Delta ^0_1$
-definition of
![]() $\kappa ^{n+1}$
. ⊣
$\kappa ^{n+1}$
. ⊣
6 Constructing fixed points of 2-ptykes
In the present section we show how to construct a predilator
![]() $D_P\cong P(D_P)$
for any given 2-preptyx P. Using
$D_P\cong P(D_P)$
for any given 2-preptyx P. Using
![]() $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
![]() $\mathbb N$
, we then prove that
$\mathbb N$
, we then prove that
![]() $D_P$
is a dilator when P is a normal 2-ptyx.
$D_P$
is a dilator when P is a normal 2-ptyx.
We begin with some foundational considerations. Recall that the arguments and values of our preptykes are coded predilators in the sense of Definition 2.2. If D is a coded predilator, then
![]() $D(X)$
is only defined when X is a finite order of the form
$D(X)$
is only defined when X is a finite order of the form
![]() $m=\{0,\dots ,m-1\}$
; for better readability, we will nevertheless write
$m=\{0,\dots ,m-1\}$
; for better readability, we will nevertheless write
![]() $D(X)$
rather than
$D(X)$
rather than
![]() $D(m)$
. Coded predilators are represented by subsets of
$D(m)$
. Coded predilators are represented by subsets of
![]() $\mathbb N$
, as explained after Definition 2.2. In view of [Reference Freund9, Section 4] it seems plausible that the desired fixed point
$\mathbb N$
, as explained after Definition 2.2. In view of [Reference Freund9, Section 4] it seems plausible that the desired fixed point
![]() $D_P\cong P(D_P)$
can be constructed in
$D_P\cong P(D_P)$
can be constructed in
![]() $\mathbf {RCA}_0$
. We will work in
$\mathbf {RCA}_0$
. We will work in
![]() $\mathbf {ACA}_0$
, as this allows for a less technical approach and ties in with the base theory of Theorem 5.11. Note that the class-sized extension
$\mathbf {ACA}_0$
, as this allows for a less technical approach and ties in with the base theory of Theorem 5.11. Note that the class-sized extension
![]() $\overline {D_P}$
will still be computable (relative to
$\overline {D_P}$
will still be computable (relative to
![]() $D_P\subseteq \mathbb N$
; cf. the discussion after Proposition 2.8).
$D_P\subseteq \mathbb N$
; cf. the discussion after Proposition 2.8).
The idea is to define
![]() $D_P$
as the direct limit over iterated applications of P. To provide a base for the iteration, we point out that any linear order Z gives rise to a constant predilator with values
$D_P$
as the direct limit over iterated applications of P. To provide a base for the iteration, we point out that any linear order Z gives rise to a constant predilator with values
![]() $D(X):=Z$
. For each embedding
$D(X):=Z$
. For each embedding
![]() $f:X\to Y$
, the embedding
$f:X\to Y$
, the embedding
![]() $D(f):D(X)\to D(Y)$
is defined as the identity on Z. To obtain a natural transformation
$D(f):D(X)\to D(Y)$
is defined as the identity on Z. To obtain a natural transformation
![]() ${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
, we need to set
${\operatorname {supp}}:D\Rightarrow [\cdot ]^{<\omega }$
, we need to set
![]() ${\operatorname {supp}}_X(\sigma ):=\emptyset \in [X]^{<\omega }$
for every
${\operatorname {supp}}_X(\sigma ):=\emptyset \in [X]^{<\omega }$
for every
![]() $\sigma \in D(X)$
. It is straightforward to see that this satisfies the support condition from Definition 2.1. Working in
$\sigma \in D(X)$
. It is straightforward to see that this satisfies the support condition from Definition 2.1. Working in
![]() $\mathbf {ACA}_0$
, the following definition can be implemented as an effective recursion along
$\mathbf {ACA}_0$
, the following definition can be implemented as an effective recursion along
![]() $\mathbb N$
(see [Reference Freund10] and the proof of Theorem 5.11 above). This relies on the standing assumption that all our preptykes are given by
$\mathbb N$
(see [Reference Freund10] and the proof of Theorem 5.11 above). This relies on the standing assumption that all our preptykes are given by
![]() $\Delta ^0_1$
-relations (cf. the discussion after Definition 3.1). For the inductive proof that
$\Delta ^0_1$
-relations (cf. the discussion after Definition 3.1). For the inductive proof that
![]() $D^n_P$
is a predilator, we rely on the fact that the notion of (coded) predilator is arithmetical (in contrast to the notion of dilator, which is
$D^n_P$
is a predilator, we rely on the fact that the notion of (coded) predilator is arithmetical (in contrast to the notion of dilator, which is
![]() $\Pi ^1_2$
-complete).
$\Pi ^1_2$
-complete).
Definition 6.1. Given a 2-preptyx P, we define predilators
![]() $D^n_P$
and morphisms
$D^n_P$
and morphisms
 $\nu ^n:D^n_P\Rightarrow D^{n+1}_P$
by recursion over
$\nu ^n:D^n_P\Rightarrow D^{n+1}_P$
by recursion over
![]() $n\in \mathbb N$
: For
$n\in \mathbb N$
: For
![]() $n=0$
we declare that
$n=0$
we declare that
![]() $D^0_P$
is the constant dilator with value
$D^0_P$
is the constant dilator with value
![]() $0$
(the empty order). Assuming that
$0$
(the empty order). Assuming that
![]() $D^n_P$
is already defined, we set
$D^n_P$
is already defined, we set
 $D^{n+1}_P:=P(D^n_P)$
. Each component of the morphism
$D^{n+1}_P:=P(D^n_P)$
. Each component of the morphism
![]() $\nu ^0$
is the empty function. Recursively, we put
$\nu ^0$
is the empty function. Recursively, we put
![]() $\nu ^{n+1}:=P(\nu ^n)$
.
$\nu ^{n+1}:=P(\nu ^n)$
.
To describe the direct limit over the predilators
![]() $D^n_P$
, we will use the following observation with
$D^n_P$
, we will use the following observation with
 $\nu ^n:D^n_P\Rightarrow D^{n+1}_P$
at the place of
$\nu ^n:D^n_P\Rightarrow D^{n+1}_P$
at the place of
![]() $\mu :D\Rightarrow E$
. The proof is straightforward and given in arXiv:2006.12111v1, a first version of this paper.
$\mu :D\Rightarrow E$
. The proof is straightforward and given in arXiv:2006.12111v1, a first version of this paper.
Lemma 6.2. For a morphism
![]() $\mu :D\Rightarrow E$
and an embedding
$\mu :D\Rightarrow E$
and an embedding
![]() $f:X\to Y$
, we have
$f:X\to Y$
, we have
for any element
![]() $\sigma \in E(X)$
.
$\sigma \in E(X)$
.
For
![]() $n\leq k$
we define
$n\leq k$
we define
![]() $\nu ^{nk}:D^n_P\Rightarrow D^k_P$
as
$\nu ^{nk}:D^n_P\Rightarrow D^k_P$
as
![]() $\nu ^{nk}:=\nu ^{k-1}\circ \dots \circ \nu ^n$
. In particular, the morphism
$\nu ^{nk}:=\nu ^{k-1}\circ \dots \circ \nu ^n$
. In particular, the morphism
![]() $\nu ^{nn}$
is the identity on
$\nu ^{nn}$
is the identity on
![]() $D^n_P$
. We can now define the desired limit as follows. Note that the definition of
$D^n_P$
. We can now define the desired limit as follows. Note that the definition of
![]() $D_P(f)$
is justified by the previous lemma.
$D_P(f)$
is justified by the previous lemma.
Definition 6.3. For each (finite) linear order X we put
 $$ \begin{align*} &\qquad D_P(X):=\{(m,\sigma)\,|\,m\in\mathbb N\backslash\{0\}\text{ and }\sigma\in D^m_P(X)\backslash\operatorname{rng}(\nu^{m-1}_X)\},\\ &(m,\sigma)<_{D_P(X)}(n,\tau)\quad:\Leftrightarrow\quad\nu^{mk}_X(\sigma)<_{D^k_P(X)}\nu^{nk}_X(\tau)\text{ for }k=\max\{m,n\}. \end{align*} $$
$$ \begin{align*} &\qquad D_P(X):=\{(m,\sigma)\,|\,m\in\mathbb N\backslash\{0\}\text{ and }\sigma\in D^m_P(X)\backslash\operatorname{rng}(\nu^{m-1}_X)\},\\ &(m,\sigma)<_{D_P(X)}(n,\tau)\quad:\Leftrightarrow\quad\nu^{mk}_X(\sigma)<_{D^k_P(X)}\nu^{nk}_X(\tau)\text{ for }k=\max\{m,n\}. \end{align*} $$
Given an embedding
![]() $f:X\to Y$
, we define
$f:X\to Y$
, we define
![]() $D_P(f):D_P(X)\to D_P(Y)$
by
$D_P(f):D_P(X)\to D_P(Y)$
by
Finally, we define functions
![]() ${\operatorname {supp}}_X:D_P(X)\to [X]^{<\omega }$
by
${\operatorname {supp}}_X:D_P(X)\to [X]^{<\omega }$
by
![]() ${\operatorname {supp}}_X(m,\sigma ):={\operatorname {supp}}^m_X(\sigma )$
, where
${\operatorname {supp}}_X(m,\sigma ):={\operatorname {supp}}^m_X(\sigma )$
, where
![]() ${\operatorname {supp}}^m_X:D^m_P(X)\to [X]^{<\omega }$
is the support function of the predilator
${\operatorname {supp}}^m_X:D^m_P(X)\to [X]^{<\omega }$
is the support function of the predilator
![]() $D^m_P$
.
$D^m_P$
.
Let us verify that we have constructed an object of the intended type:
Lemma 6.4. The constructions from Definition 6.3 yield a predilator
![]() $D_P$
.
$D_P$
.
Proof To show that each value
![]() $D_P(X)$
is a linear order, we first observe that the truth of an equality
$D_P(X)$
is a linear order, we first observe that the truth of an equality
 $\nu ^{mk}_X(\sigma )<_{D^k_P(X)}\nu ^{nk}_X(\tau )$
is independent of
$\nu ^{mk}_X(\sigma )<_{D^k_P(X)}\nu ^{nk}_X(\tau )$
is independent of
![]() $k\geq \max \{m,n\}$
, since all functions
$k\geq \max \{m,n\}$
, since all functions
![]() $\nu ^l_X$
are embeddings. Based on this fact, it is straightforward to show transitivity. Linearity reduces to the claim that
$\nu ^l_X$
are embeddings. Based on this fact, it is straightforward to show transitivity. Linearity reduces to the claim that
![]() $\nu ^{mk}_X(\sigma )=\nu ^{nk}_X(\tau )$
implies
$\nu ^{mk}_X(\sigma )=\nu ^{nk}_X(\tau )$
implies
![]() $m=n$
(and then
$m=n$
(and then
![]() $\sigma =\tau $
, since
$\sigma =\tau $
, since
![]() $\nu ^{mk}_X$
is an embedding). Aiming at a contradiction, we assume
$\nu ^{mk}_X$
is an embedding). Aiming at a contradiction, we assume
![]() $m<n$
. From
$m<n$
. From
 $$ \begin{align*} \nu^{nk}_X(\tau)=\nu^{mk}_X(\sigma)=\nu^{nk}_X\circ\nu^{n-1}_X\circ\nu^{m(n-1)}_X(\sigma)\end{align*} $$
$$ \begin{align*} \nu^{nk}_X(\tau)=\nu^{mk}_X(\sigma)=\nu^{nk}_X\circ\nu^{n-1}_X\circ\nu^{m(n-1)}_X(\sigma)\end{align*} $$
we then get
 $\tau =\nu ^{n-1}_X\circ \nu ^{m(n-1)}_X(\sigma )\in \operatorname {rng}(\nu ^{n-1}_X)$
, which contradicts
$\tau =\nu ^{n-1}_X\circ \nu ^{m(n-1)}_X(\sigma )\in \operatorname {rng}(\nu ^{n-1}_X)$
, which contradicts
![]() $(n,\tau )\in D_P(X)$
. To see that
$(n,\tau )\in D_P(X)$
. To see that
![]() $D_P(f)$
is an order embedding whenever the same holds for
$D_P(f)$
is an order embedding whenever the same holds for
![]() $f:X\to Y$
, we note that
$f:X\to Y$
, we note that
 $\nu ^{mk}_X(\sigma )<_{D^k_P(X)}\nu ^{nk}_X(\tau )$
implies
$\nu ^{mk}_X(\sigma )<_{D^k_P(X)}\nu ^{nk}_X(\tau )$
implies
 $$ \begin{align*} \nu^{mk}_Y\circ D^m_P(f)(\sigma)=D^k_P(f)\circ\nu^{mk}_X(\sigma)<_{D^k_P(Y)} D^k_P(f)\circ\nu^{nk}_X(\tau)=\nu^{nk}_Y\circ D^n_P(\tau). \end{align*} $$
$$ \begin{align*} \nu^{mk}_Y\circ D^m_P(f)(\sigma)=D^k_P(f)\circ\nu^{mk}_X(\sigma)<_{D^k_P(Y)} D^k_P(f)\circ\nu^{nk}_X(\tau)=\nu^{nk}_Y\circ D^n_P(\tau). \end{align*} $$
The fact that
![]() $D_P$
is a monotone endofunctor of linear orders is readily deduced from the corresponding property of the predilators
$D_P$
is a monotone endofunctor of linear orders is readily deduced from the corresponding property of the predilators
![]() $D^m_P$
. The same applies to the naturality of supports. To verify the support condition, we consider an order embedding
$D^m_P$
. The same applies to the naturality of supports. To verify the support condition, we consider an order embedding
![]() $f:X\to Y$
and an element
$f:X\to Y$
and an element
![]() $(m,\tau )\in D_P(Y)$
with
$(m,\tau )\in D_P(Y)$
with
By the support condition for
![]() $D^m_P$
, we get
$D^m_P$
, we get
![]() $\tau =D^m_P(f)(\sigma )$
for some
$\tau =D^m_P(f)(\sigma )$
for some
![]() $\sigma \in D^m_P(X)$
. Due to
$\sigma \in D^m_P(X)$
. Due to
![]() $(m,\tau )\in D_P(Y)$
we have
$(m,\tau )\in D_P(Y)$
we have
![]() $D^m_P(f)(\sigma )\notin \operatorname {rng}(\nu ^{m-1}_Y)$
, which implies
$D^m_P(f)(\sigma )\notin \operatorname {rng}(\nu ^{m-1}_Y)$
, which implies
![]() $\sigma \notin \operatorname {rng}(\nu ^{m-1}_X)$
by Lemma 6.2. This yields
$\sigma \notin \operatorname {rng}(\nu ^{m-1}_X)$
by Lemma 6.2. This yields
![]() $(m,\sigma )\in D_P(X)$
and then
$(m,\sigma )\in D_P(X)$
and then
as required by the support condition for
![]() $D_P$
. ⊣
$D_P$
. ⊣
As promised above, we have the following:
Proposition 6.5. For each 2-preptyx P, the predilator
![]() $D_P$
is a direct limit of the system of predilators
$D_P$
is a direct limit of the system of predilators
![]() $D^m_P$
and morphisms
$D^m_P$
and morphisms
![]() $\nu ^{mn}:D^m_P\Rightarrow D^n_P$
.
$\nu ^{mn}:D^m_P\Rightarrow D^n_P$
.
Proof The promised limit should come with morphisms
![]() $\mu ^k:D^k_P\Rightarrow D_P$
. In order to define these, we observe that any element
$\mu ^k:D^k_P\Rightarrow D_P$
. In order to define these, we observe that any element
![]() $\sigma \in D^k_P(X)$
lies in the range of
$\sigma \in D^k_P(X)$
lies in the range of
![]() $\nu ^{kk}_X$
, since the latter is the identity. Hence there is a minimal
$\nu ^{kk}_X$
, since the latter is the identity. Hence there is a minimal
![]() $m\leq k$
with
$m\leq k$
with
![]() $\sigma \in \operatorname {rng}(\nu ^{mk}_X)$
. In view of
$\sigma \in \operatorname {rng}(\nu ^{mk}_X)$
. In view of
![]() $D^0_P(X)=0$
we must have
$D^0_P(X)=0$
we must have
![]() $m>0$
. We get
$m>0$
. We get
![]() $\sigma \notin \operatorname {rng}(\nu ^{m-1}_X)$
by the minimality of m. Since
$\sigma \notin \operatorname {rng}(\nu ^{m-1}_X)$
by the minimality of m. Since
![]() $\nu ^{mk}_X$
is an embedding (and hence injective), we can define a function
$\nu ^{mk}_X$
is an embedding (and hence injective), we can define a function
![]() $\mu ^k_X:D^k_P(X)\to D_P(X)$
by stipulating
$\mu ^k_X:D^k_P(X)\to D_P(X)$
by stipulating
It is immediate that
![]() $\mu ^k_X$
is an order embedding and that we have
$\mu ^k_X$
is an order embedding and that we have
![]() $\mu ^n_X\circ \nu ^{mn}_X=\mu ^m_X$
for
$\mu ^n_X\circ \nu ^{mn}_X=\mu ^m_X$
for
![]() $m\leq n$
. To show that the functions
$m\leq n$
. To show that the functions
![]() $\mu ^k_X$
are natural in X, we consider an order embedding
$\mu ^k_X$
are natural in X, we consider an order embedding
![]() $f:X\to Y$
. Consider
$f:X\to Y$
. Consider
![]() $\sigma \in D^k_P(X)$
and write
$\sigma \in D^k_P(X)$
and write
![]() $\mu ^k_X(\sigma )=(m,\sigma _0)$
. We get
$\mu ^k_X(\sigma )=(m,\sigma _0)$
. We get
Furthermore,
![]() $\sigma \notin \operatorname {rng}(\nu ^{m-1}_X)$
entails
$\sigma \notin \operatorname {rng}(\nu ^{m-1}_X)$
entails
![]() $D^m_P(f)(\sigma )\notin \operatorname {rng}(\nu ^{m-1}_Y)$
, by Lemma 6.2. This minimality property of m allows us to conclude
$D^m_P(f)(\sigma )\notin \operatorname {rng}(\nu ^{m-1}_Y)$
, by Lemma 6.2. This minimality property of m allows us to conclude
By Proposition 2.23, the claim that we have a direct limit reduces to the inclusion
 $$ \begin{align*} \operatorname{Tr}(D_P)\subseteq\bigcup\{\operatorname{rng}(\mu^n)\,|\,n\in\mathbb N\}. \end{align*} $$
$$ \begin{align*} \operatorname{Tr}(D_P)\subseteq\bigcup\{\operatorname{rng}(\mu^n)\,|\,n\in\mathbb N\}. \end{align*} $$
An arbitrary element of the left side has the form
![]() $(m,(n,\sigma ))$
with
$(m,(n,\sigma ))$
with
![]() $(n,\sigma )\in D_P(m)$
and
$(n,\sigma )\in D_P(m)$
and
![]() ${\operatorname {supp}}_m(n,\sigma )=m$
, where m denotes the finite order
${\operatorname {supp}}_m(n,\sigma )=m$
, where m denotes the finite order
![]() $m=\{0,\dots ,m-1\}$
. By the definition of
$m=\{0,\dots ,m-1\}$
. By the definition of
![]() $D_P$
we have
$D_P$
we have
![]() $\sigma \in D^n_P(m)\backslash \operatorname {rng}(\nu ^{n-1}_m)$
. In view of
$\sigma \in D^n_P(m)\backslash \operatorname {rng}(\nu ^{n-1}_m)$
. In view of
![]() $\sigma =\nu ^{nn}_m(\sigma )$
this yields
$\sigma =\nu ^{nn}_m(\sigma )$
this yields
![]() $\mu ^n_m(\sigma )=(n,\sigma )$
. As
$\mu ^n_m(\sigma )=(n,\sigma )$
. As
![]() ${\operatorname {supp}}^n_m(\sigma )={\operatorname {supp}}_m(n,\sigma )=m$
entails
${\operatorname {supp}}^n_m(\sigma )={\operatorname {supp}}_m(n,\sigma )=m$
entails
![]() $(m,\sigma )\in \operatorname {Tr}(D^n_P)$
, we can invoke Definition 2.16 to conclude
$(m,\sigma )\in \operatorname {Tr}(D^n_P)$
, we can invoke Definition 2.16 to conclude
as required to establish the inclusion above. ⊣
It is now straightforward to draw the desired conclusion:
Corollary 6.6. We have
![]() $D_P\cong P(D_P)$
for any 2-preptyx P.
$D_P\cong P(D_P)$
for any 2-preptyx P.
Proof According to Proposition 3.2, the preptyx P preserves direct limits. In view of Definition 6.1, we can infer that
![]() $P(D_P)$
is a direct limit of the system of predilators
$P(D_P)$
is a direct limit of the system of predilators
![]() $D^m_P$
and morphisms
$D^m_P$
and morphisms
![]() $\nu ^{mn}:D^m\Rightarrow D^n$
for
$\nu ^{mn}:D^m\Rightarrow D^n$
for
![]() $1\leq m\leq n$
. The predilator
$1\leq m\leq n$
. The predilator
![]() $D_P$
is a direct limit of the same system, up to an irrelevant index shift. Now the result follows since direct limits are unique up to isomorphism. ⊣
$D_P$
is a direct limit of the same system, up to an irrelevant index shift. Now the result follows since direct limits are unique up to isomorphism. ⊣
As Example 4.4 shows, it can happen that P is a ptyx (i.e., preserves dilators) but
![]() $D_P$
is no dilator (i.e., does not preserve well orders). In the following we show that
$D_P$
is no dilator (i.e., does not preserve well orders). In the following we show that
![]() $D_P$
is a dilator if we also demand that P is normal in the sense of Definition 4.3. Combined with Theorem 5.11, this yields our main result:
$D_P$
is a dilator if we also demand that P is normal in the sense of Definition 4.3. Combined with Theorem 5.11, this yields our main result:
Theorem 6.7. The following are equivalent over
![]() $\mathbf {ACA}_0$
:
$\mathbf {ACA}_0$
:
-
(i) the principle of
 $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along
 $\mathbb N$
holds,
$\mathbb N$
holds, -
(ii) if P is a normal 2-ptyx, then
 $D_P$
is a dilator,
$D_P$
is a dilator, -
(ii) any normal 2-ptyx P admits a morphism
 $P(D)\Rightarrow D$
for some dilator D.
$P(D)\Rightarrow D$
for some dilator D.
We point out that the theorem asserts an equivalence between schemas (cf. the detailed explanation after the statement of Theorem 5.11).
Proof To see that (ii) implies (iii), it suffices to recall that we have
![]() $P(D_P)\cong D_P$
, by Corollary 6.6. The claim that (iii) implies (i) is the result of Theorem 5.11. To establish the remaining implication from (i) to (ii), we consider a normal 2-ptyx P. In view of Definition 2.9, being a (coded) dilator is a
$P(D_P)\cong D_P$
, by Corollary 6.6. The claim that (iii) implies (i) is the result of Theorem 5.11. To establish the remaining implication from (i) to (ii), we consider a normal 2-ptyx P. In view of Definition 2.9, being a (coded) dilator is a
![]() $\Pi ^1_2$
-property. Given that P is a ptyx, we can use the induction principle from (i) to show that
$\Pi ^1_2$
-property. Given that P is a ptyx, we can use the induction principle from (i) to show that
![]() $D^n_P$
is a dilator for every
$D^n_P$
is a dilator for every
![]() $n\in \mathbb N$
(cf. Definition 6.1). The morphism
$n\in \mathbb N$
(cf. Definition 6.1). The morphism
![]() $\nu ^0:D^0_P\Rightarrow D^1_P$
is a segment in the sense of Definition 4.1, since each of its components is the empty function. Given that P is normal, another (arithmetical) induction over
$\nu ^0:D^0_P\Rightarrow D^1_P$
is a segment in the sense of Definition 4.1, since each of its components is the empty function. Given that P is normal, another (arithmetical) induction over
![]() $\mathbb N$
shows that all morphisms
$\mathbb N$
shows that all morphisms
 $\nu ^n:D^n_P\Rightarrow D^{n+1}_P$
are segments. From Proposition 6.5 we know that
$\nu ^n:D^n_P\Rightarrow D^{n+1}_P$
are segments. From Proposition 6.5 we know that
![]() $D_P$
is a direct limit of the predilators
$D_P$
is a direct limit of the predilators
![]() $D^n_P$
. Let us show that the morphisms
$D^n_P$
. Let us show that the morphisms
![]() $\mu ^n:D^n_P\Rightarrow D_P$
that witness this fact are segments as well. For this purpose, we consider a (finite) order X and an inequality
$\mu ^n:D^n_P\Rightarrow D_P$
that witness this fact are segments as well. For this purpose, we consider a (finite) order X and an inequality
 $\sigma <_{D_P(X)}\mu ^n_X(\tau )$
with
$\sigma <_{D_P(X)}\mu ^n_X(\tau )$
with
![]() $\sigma \in D_P(X)$
and
$\sigma \in D_P(X)$
and
![]() $\tau \in D^n_P(X)$
. We need to show that
$\tau \in D^n_P(X)$
. We need to show that
![]() $\sigma $
lies in the range of
$\sigma $
lies in the range of
![]() $\mu ^n_X$
. Since
$\mu ^n_X$
. Since
![]() $D_P$
is a direct limit, we can write
$D_P$
is a direct limit, we can write
![]() $\sigma =\mu ^k_X(\rho )$
for some
$\sigma =\mu ^k_X(\rho )$
for some
![]() $k\geq n$
. We then get
$k\geq n$
. We then get
 $\mu ^k_X(\rho )=\sigma <_{D_P(X)}\mu ^n_X(\tau )=\mu ^k_X\circ \nu ^{nk}_X(\tau )$
. Since each component of
$\mu ^k_X(\rho )=\sigma <_{D_P(X)}\mu ^n_X(\tau )=\mu ^k_X\circ \nu ^{nk}_X(\tau )$
. Since each component of
![]() $\mu ^k$
is an embedding, this yields
$\mu ^k$
is an embedding, this yields
 $\rho <_{D^k_P(X)}\nu ^{nk}_X(\tau )$
. As a composition of segments, the morphism
$\rho <_{D^k_P(X)}\nu ^{nk}_X(\tau )$
. As a composition of segments, the morphism
![]() $\nu ^{nk}=\nu ^{k-1}\circ \dots \circ \nu ^n$
is a segment itself. We may thus write
$\nu ^{nk}=\nu ^{k-1}\circ \dots \circ \nu ^n$
is a segment itself. We may thus write
![]() $\rho =\nu ^{nk}_X(\rho _0)$
with
$\rho =\nu ^{nk}_X(\rho _0)$
with
![]() $\rho _0\in D^n_P(X)$
. This yields
$\rho _0\in D^n_P(X)$
. This yields
as needed to show that
![]() $\mu ^n$
is a segment. To prove that
$\mu ^n$
is a segment. To prove that
![]() $D_P$
is a (coded) dilator, we need to consider the class-sized extension
$D_P$
is a (coded) dilator, we need to consider the class-sized extension
![]() $\overline {D_P}$
(cf. Definition 2.9). Aiming at a contradiction, we assume that X is a well order with a descending sequence
$\overline {D_P}$
(cf. Definition 2.9). Aiming at a contradiction, we assume that X is a well order with a descending sequence
 $$ \begin{align*} (a_0,\sigma_0)>_{\overline{D_P}(X)}(a_1,\sigma_1)>_{\overline{D_P}(X)}\ldots \end{align*} $$
$$ \begin{align*} (a_0,\sigma_0)>_{\overline{D_P}(X)}(a_1,\sigma_1)>_{\overline{D_P}(X)}\ldots \end{align*} $$
in
![]() $\overline {D_P}(X)$
. Since
$\overline {D_P}(X)$
. Since
![]() $D_P$
is a direct limit, we get
$D_P$
is a direct limit, we get
![]() $(a_0,\sigma _0)\in \operatorname {rng}((\overline {\mu ^n})_X)$
for some
$(a_0,\sigma _0)\in \operatorname {rng}((\overline {\mu ^n})_X)$
for some
![]() $n\in \mathbb N$
, where
$n\in \mathbb N$
, where
 $\overline {\mu ^n}:\overline {D^n_P}\Rightarrow \overline {D_P}$
is the class-sized extension from Lemma 2.14. To see this, recall that Definition 2.5 requires
$\overline {\mu ^n}:\overline {D^n_P}\Rightarrow \overline {D_P}$
is the class-sized extension from Lemma 2.14. To see this, recall that Definition 2.5 requires
![]() $(|a_0|,\sigma _0)\in \operatorname {Tr}(D_P)$
. By Proposition 6.5 we get
$(|a_0|,\sigma _0)\in \operatorname {Tr}(D_P)$
. By Proposition 6.5 we get
 $$ \begin{align*} (|a_0|,\sigma_0)=\operatorname{Tr}(\mu^n)(|a_0|,\tau_0)=(a,\mu^n_{|a_0|}(\tau_0)) \end{align*} $$
$$ \begin{align*} (|a_0|,\sigma_0)=\operatorname{Tr}(\mu^n)(|a_0|,\tau_0)=(a,\mu^n_{|a_0|}(\tau_0)) \end{align*} $$
for some
![]() $n\in \mathbb N$
and some
$n\in \mathbb N$
and some
![]() $(|a_0|,\tau _0)\in \operatorname {Tr}(D^n_P)$
. The latter ensures
$(|a_0|,\tau _0)\in \operatorname {Tr}(D^n_P)$
. The latter ensures
 $(a_0,\tau _0)\in \overline {D^n_P}(X)$
, so that we indeed obtain
$(a_0,\tau _0)\in \overline {D^n_P}(X)$
, so that we indeed obtain
 $$ \begin{align*} (a_0,\sigma_0)=(a,\mu^n_{|a_0|}(\tau_0))=(\overline{\mu^n})_X(a_0,\tau_0)\in\operatorname{rng}((\overline{\mu^n})_X). \end{align*} $$
$$ \begin{align*} (a_0,\sigma_0)=(a,\mu^n_{|a_0|}(\tau_0))=(\overline{\mu^n})_X(a_0,\tau_0)\in\operatorname{rng}((\overline{\mu^n})_X). \end{align*} $$
According to Lemma 4.2, the class-sized extension
![]() $\overline {\mu ^n}$
is also a segment. For the fixed n and any
$\overline {\mu ^n}$
is also a segment. For the fixed n and any
![]() $i>0$
, we can thus rely on
$i>0$
, we can thus rely on
 $(a_i,\sigma _i)<_{\overline {D_P}(X)}(a_0,\sigma _0)\in \operatorname {rng}((\overline {\mu ^n})_X)$
to infer
$(a_i,\sigma _i)<_{\overline {D_P}(X)}(a_0,\sigma _0)\in \operatorname {rng}((\overline {\mu ^n})_X)$
to infer
![]() $(a_i,\sigma _i)\in \operatorname {rng}((\overline {\mu ^n})_X)$
, say
$(a_i,\sigma _i)\in \operatorname {rng}((\overline {\mu ^n})_X)$
, say
![]() $(a_i,\sigma _i)=(\overline {\mu ^n})_X(a_i,\tau _i)$
. Since the components of
$(a_i,\sigma _i)=(\overline {\mu ^n})_X(a_i,\tau _i)$
. Since the components of
![]() $\overline {\mu ^n}$
are embeddings, we have a descending sequence
$\overline {\mu ^n}$
are embeddings, we have a descending sequence
 $(a_0,\tau _0)>_{\overline {D^n_P}(X)}(a_1,\tau _1)>_{\overline {D^n_P}(X)}\ldots $
in
$(a_0,\tau _0)>_{\overline {D^n_P}(X)}(a_1,\tau _1)>_{\overline {D^n_P}(X)}\ldots $
in
 $\overline {D^n_P}(X)$
. This is the desired contradiction: since
$\overline {D^n_P}(X)$
. This is the desired contradiction: since
![]() $D^n_P$
is a dilator (as we have shown by
$D^n_P$
is a dilator (as we have shown by
![]() $\Pi ^1_2$
-induction) and X is a well order, we know that
$\Pi ^1_2$
-induction) and X is a well order, we know that
 $\overline {D^n_P}(X)$
is well founded. ⊣
$\overline {D^n_P}(X)$
is well founded. ⊣