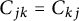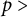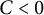1 Introduction and formulation of the problem
The Newtonian planar N-body problem of the Celestial Mechanics with point masses
![]() $m_k>0$
and positions
$m_k>0$
and positions
![]() $\boldsymbol{r}_k \in \mathbb {R}^2$
,
$\boldsymbol{r}_k \in \mathbb {R}^2$
,
![]() $ k=1,\ldots ,N $
is governed by the second-order ordinary differential equations [Reference Wintner12]
$ k=1,\ldots ,N $
is governed by the second-order ordinary differential equations [Reference Wintner12]
 $$ \begin{align} m_k\ddot{\boldsymbol{r}}_k= \sum_{j=1, j\neq k}^{N} \frac{m_k m_j (\boldsymbol{r}_j - \boldsymbol{r}_k)}{\|\boldsymbol{r}_k - \boldsymbol{r}_j \|^3}=\frac{\partial U}{\partial \boldsymbol{r}_k}, \end{align} $$
$$ \begin{align} m_k\ddot{\boldsymbol{r}}_k= \sum_{j=1, j\neq k}^{N} \frac{m_k m_j (\boldsymbol{r}_j - \boldsymbol{r}_k)}{\|\boldsymbol{r}_k - \boldsymbol{r}_j \|^3}=\frac{\partial U}{\partial \boldsymbol{r}_k}, \end{align} $$
for each
![]() $ k=1,\ldots ,N $
with
$ k=1,\ldots ,N $
with
 $$ \begin{align} U=\sum_{1\leq k<j\leq N}\frac{m_k m_j}{\|\boldsymbol{r}_k - \boldsymbol{r}_j\|}, \end{align} $$
$$ \begin{align} U=\sum_{1\leq k<j\leq N}\frac{m_k m_j}{\|\boldsymbol{r}_k - \boldsymbol{r}_j\|}, \end{align} $$
the Newtonian potential. Note that the system defined in (1) is analytic in
![]() $ \mathbb {R}^{2N}\setminus \Delta $
where
$ \mathbb {R}^{2N}\setminus \Delta $
where
![]() $ \displaystyle \Delta _{kj}=\left \lbrace \boldsymbol{r} = (\boldsymbol{r}_1,\ldots ,\boldsymbol{r}_N) \in \mathbb {R}^{2 N}: \boldsymbol{r}_k = \boldsymbol{r}_j \right \rbrace $
.
$ \displaystyle \Delta _{kj}=\left \lbrace \boldsymbol{r} = (\boldsymbol{r}_1,\ldots ,\boldsymbol{r}_N) \in \mathbb {R}^{2 N}: \boldsymbol{r}_k = \boldsymbol{r}_j \right \rbrace $
.
![]() $ \Delta $
represents the set of singularities of the ODE of second order in (1), and
$ \Delta $
represents the set of singularities of the ODE of second order in (1), and
![]() $ \Delta _{kj} $
corresponds to the binary collisions between the particles
$ \Delta _{kj} $
corresponds to the binary collisions between the particles
![]() $ \boldsymbol{r}_k $
and
$ \boldsymbol{r}_k $
and
![]() $ \boldsymbol{r}_j$
. For further details, please refer to [Reference Wintner12].
$ \boldsymbol{r}_j$
. For further details, please refer to [Reference Wintner12].
The present study is motivated by a variation of the significant N-body problem, which we refer to as the
![]() $ N $
-body problem with Manev potential. In 1930, the Bulgarian physicist Georgi Manev [Reference Manev5] considered a model analogous to the Newtonian case, obeying potentials of the form
$ N $
-body problem with Manev potential. In 1930, the Bulgarian physicist Georgi Manev [Reference Manev5] considered a model analogous to the Newtonian case, obeying potentials of the form
 $$ \begin{align} W =\sum_{1\leq k<j\leq N} m_k m_j \left[ \frac{A}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|} + \frac{B}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^2}\right], \end{align} $$
$$ \begin{align} W =\sum_{1\leq k<j\leq N} m_k m_j \left[ \frac{A}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|} + \frac{B}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^2}\right], \end{align} $$
where, as described in [Reference Arribas, Elipe, Kalvouridis and Palacios1],
![]() $ A $
and
$ A $
and
![]() $ B $
are constants, while W represents the sum of two homogeneous potentials of degree
$ B $
are constants, while W represents the sum of two homogeneous potentials of degree
![]() $ -1 $
and
$ -1 $
and
![]() $ -2 $
, respectively. Manev proposes this model as an alternative to the theory of relativity. The significance of this model lies in its ability to address the theoretical requirements of Celestial Mechanics, preserving the fundamental properties and advantages of the Newtonian Mechanics. Some authors have investigated the Manev-type problem under the assumption
$ -2 $
, respectively. Manev proposes this model as an alternative to the theory of relativity. The significance of this model lies in its ability to address the theoretical requirements of Celestial Mechanics, preserving the fundamental properties and advantages of the Newtonian Mechanics. Some authors have investigated the Manev-type problem under the assumption
![]() $ A= B =1 $
, for example, in [Reference Diacu3].
$ A= B =1 $
, for example, in [Reference Diacu3].
In the early of 1990s, Florin Diacu [Reference Diacu3] proposed the study of Manev’s gravitational law, which is a small perturbation of Newton’s universal law of gravitation. In the general context, he referred to it as quasi-homogeneous potentials. In several papers, written independently or in collaboration, he demonstrated that Manev’s law provides a classical explanation for the advance of Mercury, taking
![]() $A=1$
and
$A=1$
and
![]() $B=1/c^2$
, where c is the speed of light. This phenomenon represents a borderline case between Newton’s law of gravity and Manev’s law, as evidenced by [Reference Ureche11].
$B=1/c^2$
, where c is the speed of light. This phenomenon represents a borderline case between Newton’s law of gravity and Manev’s law, as evidenced by [Reference Ureche11].
The equations of motion that model the planar problem of
![]() $ N $
-bodies of the Manev type (4) are as follows:
$ N $
-bodies of the Manev type (4) are as follows:
 $$ \begin{align} m_k\ddot{\boldsymbol{r}_k} = \sum_{j=1, j\neq k}^{N} m_k m_j \left[\frac{A (\boldsymbol{r}_j-\boldsymbol{r}_k) }{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^3}+\frac{B (\boldsymbol{r}_j-\boldsymbol{r}_k)}{\boldsymbol{r}_k-\boldsymbol{r}_j\|^4} \right]= \frac{\partial W}{\partial\boldsymbol{r}_k}, \end{align} $$
$$ \begin{align} m_k\ddot{\boldsymbol{r}_k} = \sum_{j=1, j\neq k}^{N} m_k m_j \left[\frac{A (\boldsymbol{r}_j-\boldsymbol{r}_k) }{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^3}+\frac{B (\boldsymbol{r}_j-\boldsymbol{r}_k)}{\boldsymbol{r}_k-\boldsymbol{r}_j\|^4} \right]= \frac{\partial W}{\partial\boldsymbol{r}_k}, \end{align} $$
and they are analytic in
![]() $ \mathbb {R}^{2 N}\setminus \Delta $
.
$ \mathbb {R}^{2 N}\setminus \Delta $
.
The problem of
![]() $ N $
-bodies with Manev potential has been generalized for a quasi-homogeneous potential of the following form:
$ N $
-bodies with Manev potential has been generalized for a quasi-homogeneous potential of the following form:
 $$ \begin{align} W =\sum_{1\leq k<j\leq N} m_k m_j \left[ \frac{A_{kj}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^a} + \frac{B_{kj}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^b}\right], \end{align} $$
$$ \begin{align} W =\sum_{1\leq k<j\leq N} m_k m_j \left[ \frac{A_{kj}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^a} + \frac{B_{kj}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^b}\right], \end{align} $$
where
![]() $ 0<a<b $
,
$ 0<a<b $
,
![]() $ A_{kj} $
and
$ A_{kj} $
and
![]() $ B_{kj} $
are real constants. In this case, the equations of motion are as follows:
$ B_{kj} $
are real constants. In this case, the equations of motion are as follows:
 $$ \begin{align} m_k\ddot{\boldsymbol{r}}_k = \sum_{j=1, j\neq k}^{N} m_k m_j \left[a \frac{A_{kj} (\boldsymbol{r}_j-\boldsymbol{r}_k) }{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^{a+1}}+\frac{b B_{kj} (\boldsymbol{r}_j-\boldsymbol{r}_k)}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^{b+2}} \right]= \frac{\partial W}{\partial\boldsymbol{r}_k}, \end{align} $$
$$ \begin{align} m_k\ddot{\boldsymbol{r}}_k = \sum_{j=1, j\neq k}^{N} m_k m_j \left[a \frac{A_{kj} (\boldsymbol{r}_j-\boldsymbol{r}_k) }{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^{a+1}}+\frac{b B_{kj} (\boldsymbol{r}_j-\boldsymbol{r}_k)}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^{b+2}} \right]= \frac{\partial W}{\partial\boldsymbol{r}_k}, \end{align} $$
for each
![]() $k=1,\ldots ,N$
. This problem has been the subject of study by several authors, including [Reference Diacu2], [Reference Mioc and Blaga7], [Reference Diacu, Mioc and Stoica4] as well as [Reference Arribas, Elipe, Kalvouridis and Palacios1]. More precisely, Diacu in [Reference Diacu2] examines the collision and ejection orbits of
$k=1,\ldots ,N$
. This problem has been the subject of study by several authors, including [Reference Diacu2], [Reference Mioc and Blaga7], [Reference Diacu, Mioc and Stoica4] as well as [Reference Arribas, Elipe, Kalvouridis and Palacios1]. More precisely, Diacu in [Reference Diacu2] examines the collision and ejection orbits of
![]() $3$
-particle systems with a quasi-homogeneous potential
$3$
-particle systems with a quasi-homogeneous potential
![]() $W=U+V$
, where U and V are homogeneous functions of degree
$W=U+V$
, where U and V are homogeneous functions of degree
![]() $-a$
and
$-a$
and
![]() $-b$
, respectively, with
$-b$
, respectively, with
![]() $1 \leq a< b$
. They show that for values of
$1 \leq a< b$
. They show that for values of
![]() $b \neq 2$
the collision and ejection orbits tend to form asymptotically a central configuration. In the case
$b \neq 2$
the collision and ejection orbits tend to form asymptotically a central configuration. In the case
![]() $b=2$
, which corresponds to Maneff’s gravitational law, they found a set of collision and ejection orbits reaching the triple collision manifold without asymptotic phase. This set contains an uncountable union of manifolds and has positive measure within the set of all rectilinear solutions. In [Reference Arribas, Elipe, Kalvouridis and Palacios1], it is proved that for generalized forces that are a function of the mutual distance, the ring of
$b=2$
, which corresponds to Maneff’s gravitational law, they found a set of collision and ejection orbits reaching the triple collision manifold without asymptotic phase. This set contains an uncountable union of manifolds and has positive measure within the set of all rectilinear solutions. In [Reference Arribas, Elipe, Kalvouridis and Palacios1], it is proved that for generalized forces that are a function of the mutual distance, the ring of
![]() $n + 1$
configuration (with one central mass) is a central configuration. Besides, it is demonstrated that this solution is homographic. The results are applied to quasi-homogeneous potentials of the form
$n + 1$
configuration (with one central mass) is a central configuration. Besides, it is demonstrated that this solution is homographic. The results are applied to quasi-homogeneous potentials of the form
![]() $W= U+ V$
, where
$W= U+ V$
, where
![]() $U=\sum _{0\leq k<j\leq n} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|}$
and
$U=\sum _{0\leq k<j\leq n} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|}$
and
![]() $V=\sum _{0\leq k<j\leq n} \frac {A m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^b}$
with
$V=\sum _{0\leq k<j\leq n} \frac {A m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^b}$
with
![]() $b>0$
. The paper [Reference Mioc and Blaga7] deals with the study of a special five-body configuration (four masses placed at the vertices of a rhombus centered in the fifth mass) in the so-called post-Newtonian gravitational field of Manev of the form
$b>0$
. The paper [Reference Mioc and Blaga7] deals with the study of a special five-body configuration (four masses placed at the vertices of a rhombus centered in the fifth mass) in the so-called post-Newtonian gravitational field of Manev of the form
![]() $W= U+ V$
with
$W= U+ V$
with
![]() $U=\sum _{0\leq k<j\leq 4} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^a}$
and
$U=\sum _{0\leq k<j\leq 4} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^a}$
and
![]() $V=\sum _{0\leq k<j\leq 4} \frac {3 m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^3}$
. It has been shown that the problem with masses
$V=\sum _{0\leq k<j\leq 4} \frac {3 m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^3}$
. It has been shown that the problem with masses
![]() $1$
and m placed at the symmetrical vertices exhibits a monoparametric family of relative equilibria. In their study, Diacu et al. in [Reference Diacu, Mioc and Stoica4] explored the two-body problems with potentials of the type
$1$
and m placed at the symmetrical vertices exhibits a monoparametric family of relative equilibria. In their study, Diacu et al. in [Reference Diacu, Mioc and Stoica4] explored the two-body problems with potentials of the type
![]() $A/r + B/r^2$
, where r represents the distance between the particles, A and B are real constants. By employing McGehee-type transformations and exploiting the rotational symmetry inherent to this class of vector fields, they reduced the equations of motion to a reduced phase space and studied all possible choices of the constants A and B. Santoprete in [Reference Santoprete10] studied the linear stability of the relative equilibria for homogeneous and quasi-homogeneous potentials. First, in the case where the potential is a homogeneous function of degree
$A/r + B/r^2$
, where r represents the distance between the particles, A and B are real constants. By employing McGehee-type transformations and exploiting the rotational symmetry inherent to this class of vector fields, they reduced the equations of motion to a reduced phase space and studied all possible choices of the constants A and B. Santoprete in [Reference Santoprete10] studied the linear stability of the relative equilibria for homogeneous and quasi-homogeneous potentials. First, in the case where the potential is a homogeneous function of degree
![]() $-a$
, they found that every relative equilibrium of the n-body problem with
$-a$
, they found that every relative equilibrium of the n-body problem with
![]() $a> 2$
is spectrally unstable. Moreover, he finds a similar condition in the quasi-homogeneous case. Subsequently, he investigated the stability of the equilateral triangle relative equilibria in the case of three bodies. In the case of homogeneous potentials, he was able to recover the classical result obtained by Routh in a simpler way. In the case of quasi-homogeneous potentials, he found a generalization of the Routh inequality and showed that, for specific values of the masses, the stability of the relative equilibria depends on the size of the configuration. It should be noted that in his study, the quasi-homogeneous potential is of the form
$a> 2$
is spectrally unstable. Moreover, he finds a similar condition in the quasi-homogeneous case. Subsequently, he investigated the stability of the equilateral triangle relative equilibria in the case of three bodies. In the case of homogeneous potentials, he was able to recover the classical result obtained by Routh in a simpler way. In the case of quasi-homogeneous potentials, he found a generalization of the Routh inequality and showed that, for specific values of the masses, the stability of the relative equilibria depends on the size of the configuration. It should be noted that in his study, the quasi-homogeneous potential is of the form
![]() $W= U+ V$
with
$W= U+ V$
with
![]() $U=\sum _{1\leq k<j\leq n} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^a}$
and
$U=\sum _{1\leq k<j\leq n} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^a}$
and
![]() $V=\sum _{1\leq k<j\leq n} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^b}$
with
$V=\sum _{1\leq k<j\leq n} \frac {m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^b}$
with
![]() $0< a < b$
.
$0< a < b$
.
In our study, we will consider the planar problem of
![]() $ N $
-bodies with a quasi-homogeneous potential of the form
$ N $
-bodies with a quasi-homogeneous potential of the form
![]() $ W= U + V $
, where
$ W= U + V $
, where
 $$ \begin{align} U=\sum_{1\leq k<j\leq N} \frac{m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|}, \quad V=\sum_{1\leq k<j\leq N} \frac{C_{kj} m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p}, \end{align} $$
$$ \begin{align} U=\sum_{1\leq k<j\leq N} \frac{m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|}, \quad V=\sum_{1\leq k<j\leq N} \frac{C_{kj} m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p}, \end{align} $$
in other words, U represents the Newtonian potential, whereas V denotes a homogeneous potential of degree
![]() $ -p$
with
$ -p$
with
![]() $p>1$
.
$p>1$
.
![]() $ C_{kj}= C_{jk}= C $
for each
$ C_{kj}= C_{jk}= C $
for each
![]() $ k,j=1,\dots ,N $
are nonzero real constants and
$ k,j=1,\dots ,N $
are nonzero real constants and
![]() $ m_k>0 $
for each
$ m_k>0 $
for each
![]() $k=1,\dots ,N$
.
$k=1,\dots ,N$
.
The main objective of this work is to characterize, identify, and quantify the existence of periodic solutions that, at each instant, form a regular polygon (on a circle with radius
![]() $\rho $
), where the masses are all equal and rotate with constant angular velocity
$\rho $
), where the masses are all equal and rotate with constant angular velocity
![]() $\omega $
. This type of solution is sometimes called a ring solution or a Maxwell-type solution. This designation is attributed to Maxwell (1890) [Reference Maxwell and Niven6], in his attempt to give a simple model of a planet ring. He first studied the relative equilibria N of equal masses situated at the vertices of a regular polygon and rotating rigidly about a point mass at its center.
$\omega $
. This type of solution is sometimes called a ring solution or a Maxwell-type solution. This designation is attributed to Maxwell (1890) [Reference Maxwell and Niven6], in his attempt to give a simple model of a planet ring. He first studied the relative equilibria N of equal masses situated at the vertices of a regular polygon and rotating rigidly about a point mass at its center.
The periodic solutions forming an N-gon are parameterized by
where
In a manner analogous to the N-body problem, we define spectral and linear stability in accordance with the tenets espoused by Moeckel (see reference [Reference Moeckel8] for details).
Definition 1 Suppose that x is a relative equilibrium of the planar N-body problem with quasi-homogeneous potential and that has eigenvalues 0 with some multiplicity. We say that x is nondegenerate if the remaining eigenvalues are nonzero. A nondegenerate equilibrium point x is spectrally stable if the remaining eigenvalues are purely imaginary and it is linearly stable if, in addition, the linear part restricted to the reduced space is diagonalizable.
Our study focuses on the existence of Maxwell-type solutions and the study of their (spectral) stability or instability, depending on the constant
![]() $C= C_{kj} $
, the radius of the circle containing the particles and the masses. The stability is studied in detail for
$C= C_{kj} $
, the radius of the circle containing the particles and the masses. The stability is studied in detail for
![]() $ N=3 $
.
$ N=3 $
.
The study of the regular N-gon solutions in the Newtonian case was developed by Perko and Walter [Reference Perko and Walter9]. They showed that for
![]() $ N\geq 4 $
the given functions (9) are solutions of the N-body problem, if and only if, all the masses are equal. Furthermore, they established that there exists a unique admissible radius set to the value
$ N\geq 4 $
the given functions (9) are solutions of the N-body problem, if and only if, all the masses are equal. Furthermore, they established that there exists a unique admissible radius set to the value
![]() $m= m_k$
,
$m= m_k$
,
![]() $k=1,\ldots , N$
. On the other hand, the study of stability must be understood in the spectral sense, that is, apart from the null eigenvalues, the rest of the eigenvalues must all be purely imaginary for the matrix of the linearized system. It is known from Moeckel [Reference Moeckel8] that the regular polygon solution for problems with gravitational potential (and no central mass) is always unstable for
$k=1,\ldots , N$
. On the other hand, the study of stability must be understood in the spectral sense, that is, apart from the null eigenvalues, the rest of the eigenvalues must all be purely imaginary for the matrix of the linearized system. It is known from Moeckel [Reference Moeckel8] that the regular polygon solution for problems with gravitational potential (and no central mass) is always unstable for
![]() $ N\geq 4$
. Furthermore, for
$ N\geq 4$
. Furthermore, for
![]() $N=3$
the Lagrange equilateral triangle solution with equal mass is also unstable.
$N=3$
the Lagrange equilateral triangle solution with equal mass is also unstable.
In his study of stability for the case
![]() $N=3$
, Santoprete [Reference Santoprete10] considers general exponents
$N=3$
, Santoprete [Reference Santoprete10] considers general exponents
![]() $ a $
and
$ a $
and
![]() $ b $
for the quasi-homogeneous potentials, coefficients of the form
$ b $
for the quasi-homogeneous potentials, coefficients of the form
![]() $ A_{kj}=B_{kj }=1 $
with arbitrary masses
$ A_{kj}=B_{kj }=1 $
with arbitrary masses
![]() $ m_1, m_2, m_3 $
. His analysis shows that when
$ m_1, m_2, m_3 $
. His analysis shows that when
![]() $ 0 < b < 2 < a $
the equilateral triangle solution is unstable if,
$ 0 < b < 2 < a $
the equilateral triangle solution is unstable if,
![]() $ (m_1 m_2 + m_1 m_3 + m_2 m_3) /(m_1 + m_2 + m_3)^2> (1/3) [(b-2)/(b+2)]^2 $
. In comparison with our analysis, we take exponents of the form
$ (m_1 m_2 + m_1 m_3 + m_2 m_3) /(m_1 + m_2 + m_3)^2> (1/3) [(b-2)/(b+2)]^2 $
. In comparison with our analysis, we take exponents of the form
![]() $ a=p $
and
$ a=p $
and
![]() $ b=1 $
,
$ b=1 $
,
![]() $ C_{kj}=C= 1 $
(positive) with masses
$ C_{kj}=C= 1 $
(positive) with masses
![]() $ m_1 = m_2 = m_3 = m $
. It can be seen that our study corresponds in an equivalent way to Santoprete’s Theorem
$ m_1 = m_2 = m_3 = m $
. It can be seen that our study corresponds in an equivalent way to Santoprete’s Theorem
![]() $3$
item (b) case (i). With these notations, we obtain the following result: if
$3$
item (b) case (i). With these notations, we obtain the following result: if
![]() $ 0<1<2<p $
and
$ 0<1<2<p $
and
![]() $ (m_1 m_2 + m_1 m_3 + m_2 m_3) /(m_1 + m_2 + m_3)^2=1/3 $
, then it follows that
$ (m_1 m_2 + m_1 m_3 + m_2 m_3) /(m_1 + m_2 + m_3)^2=1/3 $
, then it follows that
![]() $ 1/3> (1/3) [(b-2)/(b+2)]^2= 1/27$
. Therefore, the equilateral triangle solution is unstable, in agreement with our analysis. It should be noted that in Santoprete’s analysis the case
$ 1/3> (1/3) [(b-2)/(b+2)]^2= 1/27$
. Therefore, the equilateral triangle solution is unstable, in agreement with our analysis. It should be noted that in Santoprete’s analysis the case
![]() $p=2$
and
$p=2$
and
![]() $C \neq 1$
is not considered.
$C \neq 1$
is not considered.
2 Existence of the N-gon periodic solutions with quasi-homogeneous potential
In accordance with (8), the equations of motion for the planar
![]() $ N $
-body problem with quasi-homogeneous potential assuming equal masses
$ N $
-body problem with quasi-homogeneous potential assuming equal masses
![]() $ m_k = m $
for each
$ m_k = m $
for each
![]() $ k=1,\ldots , N $
are as follows:
$ k=1,\ldots , N $
are as follows:
 $$ \begin{align} \ddot{\boldsymbol{r}}_k=m \sum_{j=1, k\neq j}^{N} \left[\frac{\boldsymbol{r}_j-\boldsymbol{r}_k}{r_{jk}^3}+\frac{pC_{kj}(\boldsymbol{r}_j-\boldsymbol{r}_k)}{r_{jk}^{p+2}} \right], \quad k=1,\ldots, N. \end{align} $$
$$ \begin{align} \ddot{\boldsymbol{r}}_k=m \sum_{j=1, k\neq j}^{N} \left[\frac{\boldsymbol{r}_j-\boldsymbol{r}_k}{r_{jk}^3}+\frac{pC_{kj}(\boldsymbol{r}_j-\boldsymbol{r}_k)}{r_{jk}^{p+2}} \right], \quad k=1,\ldots, N. \end{align} $$
Next, our aim will be to characterize the existence of periodic solutions where all the particles have the same mass m, are situated on a circle of radius
![]() $\rho $
, and rotate with a constant angular velocity
$\rho $
, and rotate with a constant angular velocity
![]() $\omega $
, thereby forming a regular polygon (see Figure 1). We propose that such circular solutions are parametrized by
$\omega $
, thereby forming a regular polygon (see Figure 1). We propose that such circular solutions are parametrized by
where

Figure 1: Representation of the periodic solution of the quasi-homogeneous problem (10) forming a regular N-gon.
For the sake of simplicity, we will assume that
![]() $ \theta _0=0 $
, then
$ \theta _0=0 $
, then
From (11), we obtain the first and second derivative of
![]() $ \boldsymbol{r}_{k} $
$ \boldsymbol{r}_{k} $
Next, we calculate the mutual distances
 $$ \begin{align} \boldsymbol{r}_j-\boldsymbol{r}_k &= \rho e^{i(\omega t+\theta_{j})}-\rho e^{i(\omega t+\theta_{k})} \nonumber\\ &= \rho e^{i\omega t}\left(e^{i\theta_{j}}-e^{i\theta_{k}}\right) \nonumber\\ &= \rho e^{i\omega t}e^{i\theta_k}\left( e^{i(\theta_j-\theta_k)}-1\right). \end{align} $$
$$ \begin{align} \boldsymbol{r}_j-\boldsymbol{r}_k &= \rho e^{i(\omega t+\theta_{j})}-\rho e^{i(\omega t+\theta_{k})} \nonumber\\ &= \rho e^{i\omega t}\left(e^{i\theta_{j}}-e^{i\theta_{k}}\right) \nonumber\\ &= \rho e^{i\omega t}e^{i\theta_k}\left( e^{i(\theta_j-\theta_k)}-1\right). \end{align} $$
So,
 $$ \begin{align} r_{jk}=\lVert\boldsymbol{r}_j-\boldsymbol{r}_k\rVert=\rho\underbrace{\lVert e^{i(\theta_j-\theta_k)}-1\rVert}_{d_{jk}}= \rho d_{jk}, \end{align} $$
$$ \begin{align} r_{jk}=\lVert\boldsymbol{r}_j-\boldsymbol{r}_k\rVert=\rho\underbrace{\lVert e^{i(\theta_j-\theta_k)}-1\rVert}_{d_{jk}}= \rho d_{jk}, \end{align} $$
where
Substituting in (10), we have that
 $$ \begin{align*} -\frac{\omega^2}{m} e^{i\theta_k} &=\sum_{j=1, j\neq k}^{N} \left( \frac{(e^{i\theta_j}-e^{i\theta_k})}{\rho^{3}d_{jk}^{3}} +\frac{pC_{kj}(e^{i\theta_j}-e^{i\theta_k})}{\rho^{p+2}d_{jk}^{p+2}}\right)\\ &=\sum_{j=1, j\neq k}^{N}\frac{(e^{i\theta_j}-e^{i\theta_k})}{\rho^3}\left( \frac{1}{d_{jk}^{3}} + \frac{pC_{kj}}{\rho^{p-1}d_{jk}^{p+2}}\right)\\ &=e^{i\theta_k}\sum_{j=1, j\neq k}^{N}\frac{(e^{i(\theta_j-\theta_k)}-1)}{\rho^3}\left( \frac{1}{d_{jk}^{3}} + \frac{pC_{kj}}{\rho^{p-1}d_{jk}^{p+2}}\right). \end{align*} $$
$$ \begin{align*} -\frac{\omega^2}{m} e^{i\theta_k} &=\sum_{j=1, j\neq k}^{N} \left( \frac{(e^{i\theta_j}-e^{i\theta_k})}{\rho^{3}d_{jk}^{3}} +\frac{pC_{kj}(e^{i\theta_j}-e^{i\theta_k})}{\rho^{p+2}d_{jk}^{p+2}}\right)\\ &=\sum_{j=1, j\neq k}^{N}\frac{(e^{i\theta_j}-e^{i\theta_k})}{\rho^3}\left( \frac{1}{d_{jk}^{3}} + \frac{pC_{kj}}{\rho^{p-1}d_{jk}^{p+2}}\right)\\ &=e^{i\theta_k}\sum_{j=1, j\neq k}^{N}\frac{(e^{i(\theta_j-\theta_k)}-1)}{\rho^3}\left( \frac{1}{d_{jk}^{3}} + \frac{pC_{kj}}{\rho^{p-1}d_{jk}^{p+2}}\right). \end{align*} $$
Therefore,
 $$ \begin{align} -\frac{\omega^2}{m} = \sum_{j=1, j\neq k}^{N}\frac{(e^{i(\theta_j-\theta_k)}-1)}{\rho^3}\left( \frac{1}{d_{jk}^{3}} + \frac{pC_{kj}}{\rho^{p-1}d_{jk}^{p+2}}\right). \end{align} $$
$$ \begin{align} -\frac{\omega^2}{m} = \sum_{j=1, j\neq k}^{N}\frac{(e^{i(\theta_j-\theta_k)}-1)}{\rho^3}\left( \frac{1}{d_{jk}^{3}} + \frac{pC_{kj}}{\rho^{p-1}d_{jk}^{p+2}}\right). \end{align} $$
From (12), it follows that
 $$ \begin{align} \theta_j-\theta_k = 2\left(\frac{\pi(j-k)}{N}\right), \end{align} $$
$$ \begin{align} \theta_j-\theta_k = 2\left(\frac{\pi(j-k)}{N}\right), \end{align} $$
and
 $$ \begin{align} 1-\cos(\theta_j-\theta_k)=2\sin^2\left( \frac{(\theta_j-\theta_k)}{2}\right)= 2\sin^2\left( \frac{\pi(j-k)}{N}\right). \end{align} $$
$$ \begin{align} 1-\cos(\theta_j-\theta_k)=2\sin^2\left( \frac{(\theta_j-\theta_k)}{2}\right)= 2\sin^2\left( \frac{\pi(j-k)}{N}\right). \end{align} $$
Thus,
 $$ \begin{align} d_{jk}= 2\left| \sin\left( \frac{\pi(j-k)}{N}\right) \right|. \end{align} $$
$$ \begin{align} d_{jk}= 2\left| \sin\left( \frac{\pi(j-k)}{N}\right) \right|. \end{align} $$
Therefore, taking the real and imaginary parts in the system (17), it is equivalent to
 $$ \begin{align} \frac{\omega^2}{m}\rho^3 = \displaystyle\sum_{j=1, j\neq k}^{N}\left(\frac{1}{4}\left|\csc\left( \frac{\pi(j-k)}{N}\right) \right| + \frac{p C_{kj}}{2^{p+1}} \frac{1}{\rho^{p-1}}\left|\csc\left( \frac{\pi(j-k)}{N}\right)\right|{}^{p} \right), \end{align} $$
$$ \begin{align} \frac{\omega^2}{m}\rho^3 = \displaystyle\sum_{j=1, j\neq k}^{N}\left(\frac{1}{4}\left|\csc\left( \frac{\pi(j-k)}{N}\right) \right| + \frac{p C_{kj}}{2^{p+1}} \frac{1}{\rho^{p-1}}\left|\csc\left( \frac{\pi(j-k)}{N}\right)\right|{}^{p} \right), \end{align} $$
and
 $$ \begin{align} \displaystyle\sum_{j=1, j\neq k}^{N} \left(\frac{1}{8} \frac{\sin\left(\frac{2\pi(j-k)}{N}\right)}{\left|\sin^3\left( \frac{\pi(j-k)}{N}\right) \right|} + \frac{p C_{kj}}{2^{p+2}}\frac{1}{\rho^{p-1}}\frac{\sin\left(\frac{2\pi(j-k)}{N}\right)}{\left|\sin\left( \frac{\pi(j-k)}{N}\right) \right|{}^{p+2}}\right) =0, \end{align} $$
$$ \begin{align} \displaystyle\sum_{j=1, j\neq k}^{N} \left(\frac{1}{8} \frac{\sin\left(\frac{2\pi(j-k)}{N}\right)}{\left|\sin^3\left( \frac{\pi(j-k)}{N}\right) \right|} + \frac{p C_{kj}}{2^{p+2}}\frac{1}{\rho^{p-1}}\frac{\sin\left(\frac{2\pi(j-k)}{N}\right)}{\left|\sin\left( \frac{\pi(j-k)}{N}\right) \right|{}^{p+2}}\right) =0, \end{align} $$
for every
![]() $k=1,\ldots ,N$
.
$k=1,\ldots ,N$
.
In order to study system (21) and (22), from now on, we will assume that
for all
![]() $k,j=1, \ldots , N$
.
$k,j=1, \ldots , N$
.
Next, define
 $$ \begin{align*}f_k= \displaystyle\sum_{j=1, j\neq k}^{N} \frac{\sin^2\left( \frac{(\theta_j-\theta_k)}{2}\right) }{4\left|\sin\left( \frac{\pi(j-k)}{N}\right) \right|{}^3} + \frac{p}{\rho^{p-1}}\frac{C \sin^2\left( \frac{(\theta_j-\theta_k)}{2}\right) }{\left|\sin\left( \frac{\pi(j-k)}{N}\right) \right|{}^3}, \end{align*} $$
$$ \begin{align*}f_k= \displaystyle\sum_{j=1, j\neq k}^{N} \frac{\sin^2\left( \frac{(\theta_j-\theta_k)}{2}\right) }{4\left|\sin\left( \frac{\pi(j-k)}{N}\right) \right|{}^3} + \frac{p}{\rho^{p-1}}\frac{C \sin^2\left( \frac{(\theta_j-\theta_k)}{2}\right) }{\left|\sin\left( \frac{\pi(j-k)}{N}\right) \right|{}^3}, \end{align*} $$
for
![]() $k=1, 2, \ldots , N$
.
$k=1, 2, \ldots , N$
.
Now, we point out that rearranging the sum in
![]() $f_k$
, we observe that the relations
$f_k$
, we observe that the relations
![]() $f_1= f_2= \cdots = f_N$
are valid. On the other hand, since
$f_1= f_2= \cdots = f_N$
are valid. On the other hand, since
 $$ \begin{align*}\displaystyle\sum_{j=2}^{N} \frac{\sin\left(\frac{2\pi(j-1)}{N}\right)}{\left|\sin\left( \frac{\pi(j-1)}{N}\right) \right|{}^{\alpha}}=0, \end{align*} $$
$$ \begin{align*}\displaystyle\sum_{j=2}^{N} \frac{\sin\left(\frac{2\pi(j-1)}{N}\right)}{\left|\sin\left( \frac{\pi(j-1)}{N}\right) \right|{}^{\alpha}}=0, \end{align*} $$
for all
![]() $\alpha>0$
. So
$\alpha>0$
. So
![]() $f_1=0$
and then (22) is always satisfied for
$f_1=0$
and then (22) is always satisfied for
![]() $k=1, \cdots , N$
.
$k=1, \cdots , N$
.
Subsequently, upon rearranging the system of equations in (21), for
![]() $k=1, 2, 3, \ldots , N$
, it becomes evident that all of the equations in the system are equal. So, we can conclude that the following result has been proven.
$k=1, 2, 3, \ldots , N$
, it becomes evident that all of the equations in the system are equal. So, we can conclude that the following result has been proven.
Lemma 1 Assume
![]() $C_{kj}= C$
and maintain the previous notations. Then,
$C_{kj}= C$
and maintain the previous notations. Then,
![]() $\boldsymbol{r}_k(t)= \rho e^{i(\omega t + \theta _k)}, \quad t\in \mathbb {R}$
, where
$\boldsymbol{r}_k(t)= \rho e^{i(\omega t + \theta _k)}, \quad t\in \mathbb {R}$
, where
![]() $\theta _k= 2\pi \left ( \frac {k-1}{N}\right )$
with equal masses
$\theta _k= 2\pi \left ( \frac {k-1}{N}\right )$
with equal masses
![]() $m_k = m$
,
$m_k = m$
,
![]() $k=1,\ldots , N$
is a N-gon solution of the system (10), if and only if, the following condition is satisfied:
$k=1,\ldots , N$
is a N-gon solution of the system (10), if and only if, the following condition is satisfied:
 $$ \begin{align} \begin{array}{rl} \frac{\omega^2}{m} \rho^3 =& \displaystyle\sum_{j= 2}^{N}\left(\frac{1}{4}\left|\csc\left( \frac{\pi(j-1)}{N}\right) \right| + \frac{p C}{2^{p+1}} \frac{1}{\rho^{p-1}}\left|\csc\left( \frac{\pi(j-1)}{N}\right)\right|{}^{p} \right). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \frac{\omega^2}{m} \rho^3 =& \displaystyle\sum_{j= 2}^{N}\left(\frac{1}{4}\left|\csc\left( \frac{\pi(j-1)}{N}\right) \right| + \frac{p C}{2^{p+1}} \frac{1}{\rho^{p-1}}\left|\csc\left( \frac{\pi(j-1)}{N}\right)\right|{}^{p} \right). \end{array} \end{align} $$
Now, we see that the equation (23) can be rewritten as
 $$ \begin{align} \frac{\omega^2}{m} \rho^3 = \frac{1}{4} A + \frac{p B C}{2^{p+1}} \frac{1}{\rho^{p-1}}, \end{align} $$
$$ \begin{align} \frac{\omega^2}{m} \rho^3 = \frac{1}{4} A + \frac{p B C}{2^{p+1}} \frac{1}{\rho^{p-1}}, \end{align} $$
with
 $$ \begin{align} A= \displaystyle\sum_{j= 2}^{N}\left|\csc\left( \frac{\pi(j-1)}{N}\right) \right|,\quad B= \sum_{j=2}^{N} \left|\csc\left( \frac{\pi(j-1)}{N}\right)\right|{}^{p}. \end{align} $$
$$ \begin{align} A= \displaystyle\sum_{j= 2}^{N}\left|\csc\left( \frac{\pi(j-1)}{N}\right) \right|,\quad B= \sum_{j=2}^{N} \left|\csc\left( \frac{\pi(j-1)}{N}\right)\right|{}^{p}. \end{align} $$
From all this, we have proved the following theorem.
Theorem 2.1 Let
![]() $ N\geq 2 $
,
$ N\geq 2 $
,
![]() $ C_{kj}=C\neq 0 $
for each
$ C_{kj}=C\neq 0 $
for each
![]() $k,j=1,\ldots ,N$
,
$k,j=1,\ldots ,N$
,
![]() $m_l=m$
,
$m_l=m$
,
![]() $ \omega>0 $
for
$ \omega>0 $
for
![]() $l= 1,\ldots ,N$
, then the functions
$l= 1,\ldots ,N$
, then the functions
![]() $ \boldsymbol{r}_{k}(t) $
given in (11) define a
$ \boldsymbol{r}_{k}(t) $
given in (11) define a
![]() $ 2\pi /\omega $
-periodic solution of the N-body problem with quasi-homogeneous potential (10), which forms a regular polygon on a circle of radius
$ 2\pi /\omega $
-periodic solution of the N-body problem with quasi-homogeneous potential (10), which forms a regular polygon on a circle of radius
![]() $\rho $
, provided that the following equation is satisfied:
$\rho $
, provided that the following equation is satisfied:
Next, we will study the admissible values of
![]() $ \rho $
that satisfy (26). The subsequent analysis will be divided into two distinct cases: one where
$ \rho $
that satisfy (26). The subsequent analysis will be divided into two distinct cases: one where
![]() $ C>0 $
and another where
$ C>0 $
and another where
![]() $ C <0 $
. It should be noted that, by employing (26) we can determine the mass m as a function of
$ C <0 $
. It should be noted that, by employing (26) we can determine the mass m as a function of
![]() $ \rho $
, assuming that
$ \rho $
, assuming that
![]() $ C, \omega>0 $
and
$ C, \omega>0 $
and
![]() $ p>1 $
are fixed. In fact, we have
$ p>1 $
are fixed. In fact, we have
 $$ \begin{align} m=f(\rho):=\omega^2 \rho^{p+2} \left(\frac{A}{4} \rho^{p-1} + \frac{p C B}{2^{p+1}} \right)^{-1}, \end{align} $$
$$ \begin{align} m=f(\rho):=\omega^2 \rho^{p+2} \left(\frac{A}{4} \rho^{p-1} + \frac{p C B}{2^{p+1}} \right)^{-1}, \end{align} $$
where
![]() $A>0$
,
$A>0$
,
![]() $B>0$
are as in (25).
$B>0$
are as in (25).
For the case
![]() $ C>0$
, the following result is obtained.
$ C>0$
, the following result is obtained.
Theorem 2.2 Assume
![]() $C>0$
,
$C>0$
,
![]() $p>1$
,
$p>1$
,
![]() $N>2$
and
$N>2$
and
![]() $\omega>0$
are arbitrary. For any positive value
$\omega>0$
are arbitrary. For any positive value
![]() $ m$
, then there exists a unique radius
$ m$
, then there exists a unique radius
![]() $ \rho (m) $
which gives rise to a regular N-gon solution to the N-body problem with quasi-homogeneous potential. Furthermore,
$ \rho (m) $
which gives rise to a regular N-gon solution to the N-body problem with quasi-homogeneous potential. Furthermore,
![]() $\rho (m)$
is an increasing function, such that
$\rho (m)$
is an increasing function, such that
![]() $\displaystyle \lim _{m \rightarrow 0} \rho (m)= 0$
and
$\displaystyle \lim _{m \rightarrow 0} \rho (m)= 0$
and
![]() $\displaystyle \lim _{m \rightarrow +\infty } \rho (m)= +\infty $
.
$\displaystyle \lim _{m \rightarrow +\infty } \rho (m)= +\infty $
.
Proof We will show that the function
![]() $ f(\rho ) $
is a monotone increasing. Indeed, differentiating the function
$ f(\rho ) $
is a monotone increasing. Indeed, differentiating the function
![]() $ f $
with respect to
$ f $
with respect to
![]() $ \rho $
yields
$ \rho $
yields
 $$ \begin{align} f'(\rho)= \frac{\omega^2 \rho^{p+1}}{\left(\frac{A}{4} \rho^{p-1} + \frac{p B C}{2^{p+1}} \right)^2} \left(\frac{3 A}{4} \rho^{p-1} + \frac{p(p+2)}{2^{p+1}} B C \right). \end{align} $$
$$ \begin{align} f'(\rho)= \frac{\omega^2 \rho^{p+1}}{\left(\frac{A}{4} \rho^{p-1} + \frac{p B C}{2^{p+1}} \right)^2} \left(\frac{3 A}{4} \rho^{p-1} + \frac{p(p+2)}{2^{p+1}} B C \right). \end{align} $$
Since
![]() $ C>0 $
clearly
$ C>0 $
clearly
![]() $ f'(\rho )>0 $
, then
$ f'(\rho )>0 $
, then
![]() $ f $
is a monotonic increasing function, thus
$ f $
is a monotonic increasing function, thus
![]() $ f(\rho )>f(0)=0 $
. Also,
$ f(\rho )>f(0)=0 $
. Also,
![]() $ \lim _{\rho \rightarrow +\infty } f(\rho )= +\infty $
. Consequently, for any value of
$ \lim _{\rho \rightarrow +\infty } f(\rho )= +\infty $
. Consequently, for any value of
![]() $ m>0 $
, there exists a unique
$ m>0 $
, there exists a unique
![]() $ \rho>0 $
such that
$ \rho>0 $
such that
![]() $ f(\rho )=m $
as in (27) (see Figure (2)). Therefore, we have that
$ f(\rho )=m $
as in (27) (see Figure (2)). Therefore, we have that
![]() $f(\rho (0))=0$
and that
$f(\rho (0))=0$
and that
![]() $f(\rho (m)) \rightarrow +\infty $
as
$f(\rho (m)) \rightarrow +\infty $
as
![]() $m \rightarrow +\infty $
. This concludes the proof of the theorem.
$m \rightarrow +\infty $
. This concludes the proof of the theorem.
Remark 1 Figure 3 illustrates the existence of a unique regular N-gon solution
![]() $ \rho (m) $
for the case
$ \rho (m) $
for the case
![]() $C>0$
. This solution represents the only possible configuration of the
$C>0$
. This solution represents the only possible configuration of the
![]() $ N $
bodies that can be arranged in a regular polygon at any given instant. These results agree with those obtained for the Newtonian case in [Reference Perko and Walter9].
$ N $
bodies that can be arranged in a regular polygon at any given instant. These results agree with those obtained for the Newtonian case in [Reference Perko and Walter9].

Figure 2: Study of the function
![]() $ f $
given in (27) for the case
$ f $
given in (27) for the case
![]() $ C>0 $
and
$ C>0 $
and
![]() $ p>1$
.
$ p>1$
.

Figure 3: Existence of a regular polygon solution given
![]() $ C>0 $
and
$ C>0 $
and
![]() $ p>1 $
.
$ p>1 $
.
The following theorem presents the analysis of the case
![]() $C<0$
.
$C<0$
.
Theorem 2.3 Assume case
![]() $ C<0 $
,
$ C<0 $
,
![]() $ p>1 $
,
$ p>1 $
,
![]() $ N>2 $
and
$ N>2 $
and
![]() $ \omega>0 $
. Then there exists a bifurcation value of the mass, denoted by
$ \omega>0 $
. Then there exists a bifurcation value of the mass, denoted by
 $$ \begin{align} m_{\sharp}= \frac{\omega^2 (p+2) \left(-B C p (p+2) A^{-1} \right)^{3/(p-1)}}{2 A (p-1)}, \end{align} $$
$$ \begin{align} m_{\sharp}= \frac{\omega^2 (p+2) \left(-B C p (p+2) A^{-1} \right)^{3/(p-1)}}{2 A (p-1)}, \end{align} $$
such that the following conditions are satisfied:
-
(1) If
 $ m= m_{\sharp }$
, then there exists a unique of
$ m= m_{\sharp }$
, then there exists a unique of
 $\rho $
, which is given by the formula
$\rho $
, which is given by the formula
 $ \rho _{\sharp }= \frac {1}{2}\left (-\frac {B C}{3 A}p(p+2) \right )^{1/(p-1)}$
which gives rise to a N-gon solution of the N-body problem with quasi-homogeneous potential.
$ \rho _{\sharp }= \frac {1}{2}\left (-\frac {B C}{3 A}p(p+2) \right )^{1/(p-1)}$
which gives rise to a N-gon solution of the N-body problem with quasi-homogeneous potential. -
(2) If
 $ m> m_{\sharp }$
, then there exist two admissible radii,
$ m> m_{\sharp }$
, then there exist two admissible radii,
 $ \rho _1 , \rho _2 $
such that
$ \rho _1 , \rho _2 $
such that
 $ \rho _*= \left (-\frac {p B C}{2^{p-1} A} \right )^{1/(p-1)} < \rho _1 < \rho _{\sharp } < \rho _2 $
which give rise to two N-gon solutions of the N-body problem with quasi-homogeneous potential.
$ \rho _*= \left (-\frac {p B C}{2^{p-1} A} \right )^{1/(p-1)} < \rho _1 < \rho _{\sharp } < \rho _2 $
which give rise to two N-gon solutions of the N-body problem with quasi-homogeneous potential. -
(3) If
 $ 0<m< m_{\sharp }$
, then there are no admissible radii.
$ 0<m< m_{\sharp }$
, then there are no admissible radii.
Proof In accordance with the definition of
![]() $ f(\rho ) $
in (27), it can be established that, in the case
$ f(\rho ) $
in (27), it can be established that, in the case
![]() $ C<0 $
, in order to have
$ C<0 $
, in order to have
![]() $ m>0 $
, it is necessary to impose the following condition:
$ m>0 $
, it is necessary to impose the following condition:
where
 $$ \begin{align} \rho_* = \left(-\frac{p B C}{2^{p-1} A} \right)^{1/(p-1)}= \frac{1}{2}\left(- \frac{p B C}{A} \right)^{1/p-1}. \end{align} $$
$$ \begin{align} \rho_* = \left(-\frac{p B C}{2^{p-1} A} \right)^{1/(p-1)}= \frac{1}{2}\left(- \frac{p B C}{A} \right)^{1/p-1}. \end{align} $$
On the other hand, according to (28), the sign of
![]() $ f'(\rho ) $
is determined by the sign of the expression
$ f'(\rho ) $
is determined by the sign of the expression
It should be noted that
![]() $ f'(\rho )=0 \Leftrightarrow \rho = \rho _\sharp $
where
$ f'(\rho )=0 \Leftrightarrow \rho = \rho _\sharp $
where
 $$ \begin{align} \rho_\sharp = \left( -\frac{p (p+2)}{2^{p-1}} \frac{B C}{3 A} \right)^{1/(p-1)}= \frac{1}{2}\left(-\frac{B C}{3 A}p(p+2) \right)^{1/(p-1)}. \end{align} $$
$$ \begin{align} \rho_\sharp = \left( -\frac{p (p+2)}{2^{p-1}} \frac{B C}{3 A} \right)^{1/(p-1)}= \frac{1}{2}\left(-\frac{B C}{3 A}p(p+2) \right)^{1/(p-1)}. \end{align} $$
Let us determine which domain,
![]() $ f(\rho ) $
and
$ f(\rho ) $
and
![]() $ f'(\rho ) $
, are positive. It can be verified that
$ f'(\rho ) $
, are positive. It can be verified that
 $$ \begin{align*}f(\rho)>0 \,\ \wedge \,\ f'(\rho)>0 \Leftrightarrow \rho> \frac{1}{2}\left(-\frac{ B C}{3 A}p(p+2) \right)^{1/(p-1)}\Leftrightarrow \rho > \rho_\sharp. \end{align*} $$
$$ \begin{align*}f(\rho)>0 \,\ \wedge \,\ f'(\rho)>0 \Leftrightarrow \rho> \frac{1}{2}\left(-\frac{ B C}{3 A}p(p+2) \right)^{1/(p-1)}\Leftrightarrow \rho > \rho_\sharp. \end{align*} $$
Let us now examine which domain
![]() $f(\rho )>0 $
and
$f(\rho )>0 $
and
![]() $f'(\rho )<0 $
. In this case,
$f'(\rho )<0 $
. In this case,
Besides,
![]() $ \lim _{\rho \rightarrow \rho _{*}^{+}} f(\rho )= +\infty $
and
$ \lim _{\rho \rightarrow \rho _{*}^{+}} f(\rho )= +\infty $
and
![]() $\lim _{\rho \rightarrow +\infty } f(\rho ) = +\infty $
.
$\lim _{\rho \rightarrow +\infty } f(\rho ) = +\infty $
.
In this context, we will denote the number obtained by substituting
![]() $ \rho _\sharp $
in (27) by
$ \rho _\sharp $
in (27) by
![]() $ m_\sharp $
, which is,
$ m_\sharp $
, which is,
![]() $ m_\sharp = f(\rho _\sharp ) $
(see Figure 4). In consequence, we can state that:
$ m_\sharp = f(\rho _\sharp ) $
(see Figure 4). In consequence, we can state that:
-
(1) If
 $ m = m_\sharp $
, then there is a unique admissible radius
$ m = m_\sharp $
, then there is a unique admissible radius
 $ \rho>0 $
, denoted by
$ \rho>0 $
, denoted by
 $ \rho _\sharp $
, which yields a N-gon solution.
$ \rho _\sharp $
, which yields a N-gon solution. -
(2) If
 $ m> m_\sharp $
, then there exist two distinct admissible radii, namely
$ m> m_\sharp $
, then there exist two distinct admissible radii, namely
 $ \rho _1 $
and
$ \rho _1 $
and
 $ \rho _2 $
such that
$ \rho _2 $
such that
 $ \rho _1< \rho _\sharp < \rho _2 $
and each gives rise to a N-gon solution.
$ \rho _1< \rho _\sharp < \rho _2 $
and each gives rise to a N-gon solution. -
(3) If
 $ 0<m< m_\sharp $
, there are no admissible radii.
$ 0<m< m_\sharp $
, there are no admissible radii.

Figure 4: Graphic of the function
![]() $ f $
given in (27) for the case
$ f $
given in (27) for the case
![]() $ C<0 $
and
$ C<0 $
and
![]() $ p>1$
.
$ p>1$
.
Thus, we have concluded the proof of the theorem.
Figure 5 illustrates the existence of two N-gon solutions
![]() $ \rho _1 (m) $
and
$ \rho _1 (m) $
and
![]() $ \rho _2 (m) $
, that is, there are at least two possible of arrangements of the
$ \rho _2 (m) $
, that is, there are at least two possible of arrangements of the
![]() $ N $
bodies such that they form a regular polygon at each instant.
$ N $
bodies such that they form a regular polygon at each instant.
Remark 2 The preceding results demonstrate the significant distinction between the case of
![]() $C < 0$
and the situation of
$C < 0$
and the situation of
![]() $C> 0$
.
$C> 0$
.

Figure 5: Existence of two regular polygon solutions given
![]() $ C<0 $
and
$ C<0 $
and
![]() $ p>1$
.
$ p>1$
.
3 Relative equilibrium for the quasi-homogeneous N-body problem
The equations of motion of the particles are given by (10), where the quasi-homogeneous potential is given by
 $$ \begin{align} W(\boldsymbol{r})=\sum_{1\leq k<j\leq N }\left[\frac{m^2}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|}+\frac{m^2 C}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p}\right]. \end{align} $$
$$ \begin{align} W(\boldsymbol{r})=\sum_{1\leq k<j\leq N }\left[\frac{m^2}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|}+\frac{m^2 C}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p}\right]. \end{align} $$
The linear momentum of the
![]() $ k $
th particle is given by the equation
$ k $
th particle is given by the equation
![]() $ \boldsymbol{p}_k= m \dot {\boldsymbol{r}_k} $
with
$ \boldsymbol{p}_k= m \dot {\boldsymbol{r}_k} $
with
![]() $ k=1,\dots ,N $
. Then, the equations of motion are written in their Hamiltonian form
$ k=1,\dots ,N $
. Then, the equations of motion are written in their Hamiltonian form
 $$ \begin{align} \dot{\boldsymbol{r}}&=\boldsymbol{M}^{-1}\boldsymbol{p}=H_{\boldsymbol{p}} \nonumber\\ \dot{\boldsymbol{p}}&=\nabla W(\boldsymbol{r})=-H_{\boldsymbol{r}}, \end{align} $$
$$ \begin{align} \dot{\boldsymbol{r}}&=\boldsymbol{M}^{-1}\boldsymbol{p}=H_{\boldsymbol{p}} \nonumber\\ \dot{\boldsymbol{p}}&=\nabla W(\boldsymbol{r})=-H_{\boldsymbol{r}}, \end{align} $$
whose Hamiltonian function is
where
![]() $ \boldsymbol{r} =(\boldsymbol{r}_1, \boldsymbol{r}_2,\dots ,\boldsymbol{r}_N),\,\ \boldsymbol{p}=(\boldsymbol{p}_1,\boldsymbol{p}_2,\cdots ,\boldsymbol{p}_N) $
and
$ \boldsymbol{r} =(\boldsymbol{r}_1, \boldsymbol{r}_2,\dots ,\boldsymbol{r}_N),\,\ \boldsymbol{p}=(\boldsymbol{p}_1,\boldsymbol{p}_2,\cdots ,\boldsymbol{p}_N) $
and
![]() $ \boldsymbol{M} = diag(M_1,M_2,\dots ,M_N) $
with
$ \boldsymbol{M} = diag(M_1,M_2,\dots ,M_N) $
with
 $$ \begin{align*} M_k=\left( \begin{array}{ccccc} m_k & 0 & 0 & \cdots & 0 \\ 0 & m_k & 0 & \cdots & 0 \\ 0 & 0 & m_k & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & m_k \end{array} \right)_{3N\times 3N}, \end{align*} $$
$$ \begin{align*} M_k=\left( \begin{array}{ccccc} m_k & 0 & 0 & \cdots & 0 \\ 0 & m_k & 0 & \cdots & 0 \\ 0 & 0 & m_k & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & m_k \end{array} \right)_{3N\times 3N}, \end{align*} $$
for each
![]() $ k=1,\dots ,N $
, where
$ k=1,\dots ,N $
, where
![]() $ \boldsymbol{M}=mI $
.
$ \boldsymbol{M}=mI $
.
The system described in (33) can be expressed as follows:
 $$ \begin{align} \dot{\boldsymbol{r}}_k&=m^{-1}\boldsymbol{p}_k=H_{\boldsymbol{p}_k}, \nonumber\\ \dot{\boldsymbol{p}}_k&=\nabla W(\boldsymbol{r}_k)=-H_{\boldsymbol{r}_k}, \, k=1, \ldots, N. \end{align} $$
$$ \begin{align} \dot{\boldsymbol{r}}_k&=m^{-1}\boldsymbol{p}_k=H_{\boldsymbol{p}_k}, \nonumber\\ \dot{\boldsymbol{p}}_k&=\nabla W(\boldsymbol{r}_k)=-H_{\boldsymbol{r}_k}, \, k=1, \ldots, N. \end{align} $$
Let us consider a systems in which the center of mass is fixed at the origin of the coordinates. We assume the existence of equilibrium solutions as described in (11) and then we introduce a time-dependent symplectic change of coordinates (rotating coordinates) by
whose system rotates with constant angular velocity
![]() $ \omega $
and where
$ \omega $
and where
 $ \displaystyle \boldsymbol{L}_k=\left (\begin {matrix} 0 & -1 \\ 1 & 0 \end {matrix}\right ) $
.
$ \displaystyle \boldsymbol{L}_k=\left (\begin {matrix} 0 & -1 \\ 1 & 0 \end {matrix}\right ) $
.
Differentiating the equations in (35), we get
 $$ \begin{align} \dot{\boldsymbol{r}}_k&= \omega \boldsymbol{L}_k e^{\omega \boldsymbol{L}_k t} \boldsymbol{x}_k + e^{\omega \boldsymbol{L}_k t} \dot{\boldsymbol{x}}_k, \nonumber\\ \dot{\boldsymbol{p}}_k&= \omega \boldsymbol{L}_k e^{\omega \boldsymbol{L}_k t} \boldsymbol{y}_k + e^{\omega \boldsymbol{L}_k t} \dot{\boldsymbol{y}}_k, \, k=1, \ldots, N. \end{align} $$
$$ \begin{align} \dot{\boldsymbol{r}}_k&= \omega \boldsymbol{L}_k e^{\omega \boldsymbol{L}_k t} \boldsymbol{x}_k + e^{\omega \boldsymbol{L}_k t} \dot{\boldsymbol{x}}_k, \nonumber\\ \dot{\boldsymbol{p}}_k&= \omega \boldsymbol{L}_k e^{\omega \boldsymbol{L}_k t} \boldsymbol{y}_k + e^{\omega \boldsymbol{L}_k t} \dot{\boldsymbol{y}}_k, \, k=1, \ldots, N. \end{align} $$
Then, substituting the equations of the system (34) in (36), we obtain the new equations of motion
 $$ \begin{align} \dot{\boldsymbol{x}}_k & = m^{-1}\boldsymbol{y}_k-\omega \boldsymbol{L}_k\boldsymbol{x}_k, \nonumber\\ \displaystyle\dot{\boldsymbol{y}}_k &= \sum_{j=1, j\neq k}^{N} \left[ \frac{m^2(\boldsymbol{x}_j-\boldsymbol{x}_k)}{\lVert\boldsymbol{x}_j-\boldsymbol{x}_k\rVert^3} + \frac{pm^2 C (\boldsymbol{x}_j-\boldsymbol{x}_k)}{\lVert\boldsymbol{x}_j-\boldsymbol{x}_k\rVert^{p+2}} - \omega \boldsymbol{L}_k\boldsymbol{y}_k\right], \, k=1, \ldots, N. \end{align} $$
$$ \begin{align} \dot{\boldsymbol{x}}_k & = m^{-1}\boldsymbol{y}_k-\omega \boldsymbol{L}_k\boldsymbol{x}_k, \nonumber\\ \displaystyle\dot{\boldsymbol{y}}_k &= \sum_{j=1, j\neq k}^{N} \left[ \frac{m^2(\boldsymbol{x}_j-\boldsymbol{x}_k)}{\lVert\boldsymbol{x}_j-\boldsymbol{x}_k\rVert^3} + \frac{pm^2 C (\boldsymbol{x}_j-\boldsymbol{x}_k)}{\lVert\boldsymbol{x}_j-\boldsymbol{x}_k\rVert^{p+2}} - \omega \boldsymbol{L}_k\boldsymbol{y}_k\right], \, k=1, \ldots, N. \end{align} $$
These equations have as their Hamiltonian function
with
![]() $ \boldsymbol{L}=diag(\boldsymbol{L}_1,\boldsymbol{L}_2,\dots , \boldsymbol{L}_N) $
and
$ \boldsymbol{L}=diag(\boldsymbol{L}_1,\boldsymbol{L}_2,\dots , \boldsymbol{L}_N) $
and
![]() $ W(x) $
is the quasi-homogeneous potential (32) at the new coordinates.
$ W(x) $
is the quasi-homogeneous potential (32) at the new coordinates.
An equilibrium point of (33) now corresponds to a relative equilibrium of the solutions (37), that is,
hence
By construction, it is clear that
![]() $x= \boldsymbol{x}^*=(\boldsymbol{x}_{1}^{*}, \boldsymbol{x}_{2}^{*},\dots , \boldsymbol{x}_{N}^{*})=\rho \boldsymbol{r}^*$
with
$x= \boldsymbol{x}^*=(\boldsymbol{x}_{1}^{*}, \boldsymbol{x}_{2}^{*},\dots , \boldsymbol{x}_{N}^{*})=\rho \boldsymbol{r}^*$
with
![]() $\boldsymbol{x}_{k}^{*}=\rho \boldsymbol{r}_{k}^{*}$
and
$\boldsymbol{x}_{k}^{*}=\rho \boldsymbol{r}_{k}^{*}$
and
![]() $ \boldsymbol{r}_{k}^{*}= e^{i\theta _k} $
is an equilibrium point of the previous system (or, a relative equilibrium point, since the system is rotating uniformly).
$ \boldsymbol{r}_{k}^{*}= e^{i\theta _k} $
is an equilibrium point of the previous system (or, a relative equilibrium point, since the system is rotating uniformly).
A significant outcome of this section is to demonstrate that the relative equilibrium point, represented by the vector
![]() $ \boldsymbol{x}^* $
, is a simultaneous relative equilibrium for the functions U and V. This implies that both U and V evaluated at the relative equilibrium are multiples of the equilibrium position.
$ \boldsymbol{x}^* $
, is a simultaneous relative equilibrium for the functions U and V. This implies that both U and V evaluated at the relative equilibrium are multiples of the equilibrium position.
Proposition 1 The relative equilibrium solution
![]() $(\boldsymbol{x}^*, \boldsymbol{y}^*)$
of (39), which is associated with the N-gon solution for the quasi-homogeneous N-body problem i.e.,
$(\boldsymbol{x}^*, \boldsymbol{y}^*)$
of (39), which is associated with the N-gon solution for the quasi-homogeneous N-body problem i.e.,
![]() $\boldsymbol{x}^* $
, satisfies (40), more precisely,
$\boldsymbol{x}^* $
, satisfies (40), more precisely,
where
![]() $\boldsymbol{x}_{k}^{*}=\rho \boldsymbol{r}_{k}^{*}$
, and such that
$\boldsymbol{x}_{k}^{*}=\rho \boldsymbol{r}_{k}^{*}$
, and such that
![]() $ \boldsymbol{r}_{k}^{*}= e^{i \frac {2 \pi (k-1)}{N}}$
, is a simultaneous relative equilibrium for
$ \boldsymbol{r}_{k}^{*}= e^{i \frac {2 \pi (k-1)}{N}}$
, is a simultaneous relative equilibrium for
![]() $ U $
and
$ U $
and
![]() $ V $
, that is, there exist
$ V $
, that is, there exist
![]() $\mu , \nu \in \mathbb {R}$
such that
$\mu , \nu \in \mathbb {R}$
such that
Proof By calculating the gradient of
![]() $ U(\boldsymbol{x}^*) $
and given that the imaginary part of the equation (21) is null, we conclude that
$ U(\boldsymbol{x}^*) $
and given that the imaginary part of the equation (21) is null, we conclude that
 $$ \begin{align} \frac{\partial U (\boldsymbol{x}^*)}{\partial \boldsymbol{r}_{k}}&=\sum_{j=1, j\neq k}^{N}\frac{m^2(\boldsymbol{r}_j-\boldsymbol{r}_k)}{\lVert\boldsymbol{r}_j-\boldsymbol{r}_k\rVert^3} \nonumber\\ &= e^{i\theta_k} m^2 \frac{\rho}{\rho^3}\sum_{j=1, j\neq k}^{N} \frac{1}{d_{jk}^{3}}[(\cos(\theta_j-\theta_k)-1),-\sin(\theta_j-\theta_k)] \nonumber\\ &= e^{i\theta_k} m^2 \frac{\rho}{\rho^3}\sum_{j=1, j\neq k}^{N} \frac{[(\cos(\theta_j-\theta_k)-1)]}{d_{jk}^{3}}\\ &= -\left( \frac{Am^2}{4 \rho^3}\right) \rho e^{i\theta_k}= -\left( \frac{Am^2}{4 \rho^3}\right) \rho \boldsymbol{r}_{k}^{*} = -\left( \frac{Am^2}{4 \rho^3}\right) \boldsymbol{x}_{k}^{*}.\nonumber \end{align} $$
$$ \begin{align} \frac{\partial U (\boldsymbol{x}^*)}{\partial \boldsymbol{r}_{k}}&=\sum_{j=1, j\neq k}^{N}\frac{m^2(\boldsymbol{r}_j-\boldsymbol{r}_k)}{\lVert\boldsymbol{r}_j-\boldsymbol{r}_k\rVert^3} \nonumber\\ &= e^{i\theta_k} m^2 \frac{\rho}{\rho^3}\sum_{j=1, j\neq k}^{N} \frac{1}{d_{jk}^{3}}[(\cos(\theta_j-\theta_k)-1),-\sin(\theta_j-\theta_k)] \nonumber\\ &= e^{i\theta_k} m^2 \frac{\rho}{\rho^3}\sum_{j=1, j\neq k}^{N} \frac{[(\cos(\theta_j-\theta_k)-1)]}{d_{jk}^{3}}\\ &= -\left( \frac{Am^2}{4 \rho^3}\right) \rho e^{i\theta_k}= -\left( \frac{Am^2}{4 \rho^3}\right) \rho \boldsymbol{r}_{k}^{*} = -\left( \frac{Am^2}{4 \rho^3}\right) \boldsymbol{x}_{k}^{*}.\nonumber \end{align} $$
In particular, we have that
![]() $ \nabla U(\boldsymbol{x}^*)=-\mu m\boldsymbol{x}^{*} $
, with
$ \nabla U(\boldsymbol{x}^*)=-\mu m\boldsymbol{x}^{*} $
, with
Similarly, by computing
![]() $ \nabla V(\boldsymbol{x}^*) $
and noting that the imaginary part of the equation (21) is zero, we obtain
$ \nabla V(\boldsymbol{x}^*) $
and noting that the imaginary part of the equation (21) is zero, we obtain
 $$ \begin{align} \frac{\partial V (\boldsymbol{x}^*)}{\partial \boldsymbol{r}_{k}}&=\sum_{j=1, j\neq k}^{N}\frac{m^2 pC (\boldsymbol{r}_j-\boldsymbol{r}_k)}{\lVert\boldsymbol{r}_j-\boldsymbol{r}_k\rVert^{p+2}} \nonumber\\ &= e^{i\theta_k} m^2 p C \frac{\rho}{\rho^{p+2}}\sum_{j=1, j\neq k}^{N} \frac{1}{d_{jk}^{p+2}}[(\cos(\theta_j-\theta_k)-1),-\sin(\theta_j-\theta_k)] \nonumber\\ &= e^{i\theta_k} m^2 \frac{pBC}{2^{p+1}} \frac{\rho}{\rho^{p+2}}\sum_{j=1, j\neq k}^{N} \frac{[(\cos(\theta_j-\theta_k)-1)]}{d_{jk}^{p+2}}\\ &= -\left( \frac{m^2 pBC}{2^{p+1} \rho^{p+2}}\right) \rho e^{i\theta_k}= - \left( \frac{m^2 p BC}{2^{p+1} \rho^{p+2}}\right) \boldsymbol{x}_{k}^{*}.\nonumber \end{align} $$
$$ \begin{align} \frac{\partial V (\boldsymbol{x}^*)}{\partial \boldsymbol{r}_{k}}&=\sum_{j=1, j\neq k}^{N}\frac{m^2 pC (\boldsymbol{r}_j-\boldsymbol{r}_k)}{\lVert\boldsymbol{r}_j-\boldsymbol{r}_k\rVert^{p+2}} \nonumber\\ &= e^{i\theta_k} m^2 p C \frac{\rho}{\rho^{p+2}}\sum_{j=1, j\neq k}^{N} \frac{1}{d_{jk}^{p+2}}[(\cos(\theta_j-\theta_k)-1),-\sin(\theta_j-\theta_k)] \nonumber\\ &= e^{i\theta_k} m^2 \frac{pBC}{2^{p+1}} \frac{\rho}{\rho^{p+2}}\sum_{j=1, j\neq k}^{N} \frac{[(\cos(\theta_j-\theta_k)-1)]}{d_{jk}^{p+2}}\\ &= -\left( \frac{m^2 pBC}{2^{p+1} \rho^{p+2}}\right) \rho e^{i\theta_k}= - \left( \frac{m^2 p BC}{2^{p+1} \rho^{p+2}}\right) \boldsymbol{x}_{k}^{*}.\nonumber \end{align} $$
Thus,
![]() $ \nabla V(\boldsymbol{x}^*)=-\nu m\boldsymbol{x}^{*} $
, with
$ \nabla V(\boldsymbol{x}^*)=-\nu m\boldsymbol{x}^{*} $
, with
In particular, we have proved that the gradients of U and V evaluated at the relative equilibrium are multiples of the equilibrium position. It can be concluded that the point
![]() $x^*$
represents a simultaneous relative equilibrium for both potentials.
$x^*$
represents a simultaneous relative equilibrium for both potentials.
Remark 3 In the equations (44) and (46), we note that
![]() $ \mu $
depends on
$ \mu $
depends on
![]() $ (m, \rho ) $
and
$ (m, \rho ) $
and
![]() $ \nu $
depends on
$ \nu $
depends on
![]() $ (m, p, \rho ) $
.
$ (m, p, \rho ) $
.
Remark 4 The relative equilibrium
![]() $ \boldsymbol{x}^* $
satisfies
$ \boldsymbol{x}^* $
satisfies
![]() $\omega ^2 = m \left (\frac {A}{4 \rho ^3} + \frac {p B C}{2^{p+1} \rho ^{p+2}} \right )= m (\mu + \nu )$
.
$\omega ^2 = m \left (\frac {A}{4 \rho ^3} + \frac {p B C}{2^{p+1} \rho ^{p+2}} \right )= m (\mu + \nu )$
.
4 Stability of the relative equilibrium associated with the N-gon for the planar N-body problem with quasi-homogeneous potential
In this section, we will study the linear stability of the relative equilibrium associated with the N-gon periodic solution. We begin rewriting the system (37) by setting
![]() $ \boldsymbol{z}=(\boldsymbol{x},\boldsymbol{y})$
, which allows us to express the equations in the following form:
$ \boldsymbol{z}=(\boldsymbol{x},\boldsymbol{y})$
, which allows us to express the equations in the following form:
where
 $$ \begin{align*} \boldsymbol{J}=\left( \begin{matrix} \boldsymbol{0} & \boldsymbol{I} \\ -\boldsymbol{I} & \boldsymbol{0} \end{matrix}\right), \end{align*} $$
$$ \begin{align*} \boldsymbol{J}=\left( \begin{matrix} \boldsymbol{0} & \boldsymbol{I} \\ -\boldsymbol{I} & \boldsymbol{0} \end{matrix}\right), \end{align*} $$
where
![]() $ \boldsymbol {I} $
is the identity matrix of order
$ \boldsymbol {I} $
is the identity matrix of order
![]() $2n$
.
$2n$
.
Let
![]() $\boldsymbol{z}^*$
be an equilibrium point of (47), then
$\boldsymbol{z}^*$
be an equilibrium point of (47), then
![]() $ \nabla H(\boldsymbol{z}^*)=0 $
and by developing in Taylor series the function
$ \nabla H(\boldsymbol{z}^*)=0 $
and by developing in Taylor series the function
![]() $ H $
around
$ H $
around
![]() $ \boldsymbol{z}^* $
, we arrive to
$ \boldsymbol{z}^* $
, we arrive to
Using this expression, the linearized system of the equations (47) at the equilibrium
![]() $ \boldsymbol{z}^* $
can be expressed as follows:
$ \boldsymbol{z}^* $
can be expressed as follows:
where
![]() $ \boldsymbol {S} $
is the symmetric matrix
$ \boldsymbol {S} $
is the symmetric matrix
![]() $ \boldsymbol {S}=D\nabla H(\boldsymbol{z}^*)= Hess H(\boldsymbol{z}^*)$
,
$ \boldsymbol {S}=D\nabla H(\boldsymbol{z}^*)= Hess H(\boldsymbol{z}^*)$
,
![]() $\boldsymbol {A}=\boldsymbol {J}\boldsymbol {S}$
. In this equation, we have used the same notation
$\boldsymbol {A}=\boldsymbol {J}\boldsymbol {S}$
. In this equation, we have used the same notation
![]() $ \boldsymbol{z} $
for
$ \boldsymbol{z} $
for
![]() $ \boldsymbol{z}-\boldsymbol{z}^* $
. We point out that
$ \boldsymbol{z}-\boldsymbol{z}^* $
. We point out that
 $$ \begin{align} \boldsymbol{A}=\left[\begin{matrix} -\omega \boldsymbol{L} & m^{-1}I \\ D\nabla W(\boldsymbol{x}^*) & -\omega \boldsymbol{L} \end{matrix} \right]. \end{align} $$
$$ \begin{align} \boldsymbol{A}=\left[\begin{matrix} -\omega \boldsymbol{L} & m^{-1}I \\ D\nabla W(\boldsymbol{x}^*) & -\omega \boldsymbol{L} \end{matrix} \right]. \end{align} $$
Lemma 2 The characteristic polynomial
![]() $p(\lambda )$
associated with the matrix
$p(\lambda )$
associated with the matrix
![]() $\boldsymbol {A} $
at the equilibrium
$\boldsymbol {A} $
at the equilibrium
![]() $ \boldsymbol{x}^* $
possesses the factors
$ \boldsymbol{x}^* $
possesses the factors
![]() $\lambda ^2$
and
$\lambda ^2$
and
![]() $ (\lambda ^2-\alpha +3\omega ^2 ) $
where
$ (\lambda ^2-\alpha +3\omega ^2 ) $
where
![]() $ \alpha = 2\mu +(p+1)\nu $
. In particular, the eigenvalue
$ \alpha = 2\mu +(p+1)\nu $
. In particular, the eigenvalue
![]() $ 0 $
has multiplicity
$ 0 $
has multiplicity
![]() $ 2 $
and
$ 2 $
and
![]() $ \pm \sqrt {\alpha -3 \omega ^2} $
are two other eigenvalues.
$ \pm \sqrt {\alpha -3 \omega ^2} $
are two other eigenvalues.
Proof As in Moeckel’s work [Reference Moeckel8], the proof focus on the subspace
![]() $ Q_1(\boldsymbol{x}^*) $
spanned by the vectors of
$ Q_1(\boldsymbol{x}^*) $
spanned by the vectors of
![]() $ \mathbb {R}^{4n} $
$ \mathbb {R}^{4n} $
where
![]() $ \boldsymbol{x}^* $
is the relative equilibrium associated with the N-gon solution defined in (41) for the problem of
$ \boldsymbol{x}^* $
is the relative equilibrium associated with the N-gon solution defined in (41) for the problem of
![]() $ N $
-bodies with quasi-homogeneous potential. Since
$ N $
-bodies with quasi-homogeneous potential. Since
![]() $ \boldsymbol{x}^* $
and
$ \boldsymbol{x}^* $
and
![]() $ \boldsymbol{L}\boldsymbol{x}^* $
are orthogonal, it follows that the dimension of
$ \boldsymbol{L}\boldsymbol{x}^* $
are orthogonal, it follows that the dimension of
![]() $ Q_1(\boldsymbol{x}^*) $
is 4.
$ Q_1(\boldsymbol{x}^*) $
is 4.
Given that the potential functions
![]() $ U $
and
$ U $
and
![]() $ V $
are homogeneous of degrees
$ V $
are homogeneous of degrees
![]() $ -1 $
and
$ -1 $
and
![]() $ -p $
, respectively, we have that their gradients are homogeneous of degrees
$ -p $
, respectively, we have that their gradients are homogeneous of degrees
![]() $ -2 $
and
$ -2 $
and
![]() $ -(p+1) $
. Consequently, by Euler’s theorem for homogeneous functions and since
$ -(p+1) $
. Consequently, by Euler’s theorem for homogeneous functions and since
![]() $ \boldsymbol{x}^* $
is a simultaneous relative equilibrium, we have that
$ \boldsymbol{x}^* $
is a simultaneous relative equilibrium, we have that
 $$ \begin{align} D\nabla W(\boldsymbol{x}^{*}) \boldsymbol{x}&= -2\nabla U(\boldsymbol{x}^{*})-(p+1)\nabla V(\boldsymbol{x}^{*}) \nonumber\\ &= -2(-\mu mI\boldsymbol{x}^*)-(p+1)(-\nu mI\boldsymbol{x}^*) \nonumber\\ & = 2 \mu m\boldsymbol{x}^* + (p+1) \nu m\boldsymbol{x}^*. \end{align} $$
$$ \begin{align} D\nabla W(\boldsymbol{x}^{*}) \boldsymbol{x}&= -2\nabla U(\boldsymbol{x}^{*})-(p+1)\nabla V(\boldsymbol{x}^{*}) \nonumber\\ &= -2(-\mu mI\boldsymbol{x}^*)-(p+1)(-\nu mI\boldsymbol{x}^*) \nonumber\\ & = 2 \mu m\boldsymbol{x}^* + (p+1) \nu m\boldsymbol{x}^*. \end{align} $$
As a consequence of the fact that
![]() $ W $
is invariant under rotations, it follows that
$ W $
is invariant under rotations, it follows that
![]() $ \nabla W $
is also invariant under rotations, in particular,
$ \nabla W $
is also invariant under rotations, in particular,
for all
![]() $ t $
, with
$ t $
, with
![]() $ e^{\boldsymbol{L}t}=diag(e^{\boldsymbol{L}_1t},e^{\boldsymbol{L}_2t}, \ldots , e^{\boldsymbol{L}_nt}) $
. Therefore, it follows that
$ e^{\boldsymbol{L}t}=diag(e^{\boldsymbol{L}_1t},e^{\boldsymbol{L}_2t}, \ldots , e^{\boldsymbol{L}_nt}) $
. Therefore, it follows that
Now, since
![]() $ \boldsymbol{x}^* $
is a relative equilibrium, then from (40) we have
$ \boldsymbol{x}^* $
is a relative equilibrium, then from (40) we have
This equality will be employed to prove that
![]() $ Q_1(\boldsymbol{x}^*) $
is invariant by
$ Q_1(\boldsymbol{x}^*) $
is invariant by
![]() $ \boldsymbol {A} $
. In fact, note that
$ \boldsymbol {A} $
. In fact, note that
-
(1)
 $ \boldsymbol {A} (\boldsymbol{x}^*, \boldsymbol {0})= -\omega (\boldsymbol{L}\boldsymbol{x}^*,0)+(0, D\nabla W(\boldsymbol{x}^*) \boldsymbol{x}^*)= -\omega (\boldsymbol{L}\boldsymbol{x}^*,0)+ m ( 2\mu + (p+1)\nu ) (0,\boldsymbol{x}^*)$
, because
$ \boldsymbol {A} (\boldsymbol{x}^*, \boldsymbol {0})= -\omega (\boldsymbol{L}\boldsymbol{x}^*,0)+(0, D\nabla W(\boldsymbol{x}^*) \boldsymbol{x}^*)= -\omega (\boldsymbol{L}\boldsymbol{x}^*,0)+ m ( 2\mu + (p+1)\nu ) (0,\boldsymbol{x}^*)$
, because
 $ D\nabla W(\boldsymbol{x}^*) \boldsymbol{x}^*= m (2 \mu m+(p+1) \nu ) \boldsymbol{x}^*$
.
$ D\nabla W(\boldsymbol{x}^*) \boldsymbol{x}^*= m (2 \mu m+(p+1) \nu ) \boldsymbol{x}^*$
. -
(2)
 $ \boldsymbol {A} (\boldsymbol {0}, \boldsymbol{x}^*)= m^{-1}(\boldsymbol{x}^*,0)-\omega (0,\boldsymbol{L}\boldsymbol{x}^*) $
.
$ \boldsymbol {A} (\boldsymbol {0}, \boldsymbol{x}^*)= m^{-1}(\boldsymbol{x}^*,0)-\omega (0,\boldsymbol{L}\boldsymbol{x}^*) $
. -
(3)
 $ \boldsymbol {A} (\boldsymbol{L}\boldsymbol{x}^*, \boldsymbol {0})= -\omega (\boldsymbol{L}^2\boldsymbol{x}^*,0)+(0,D\nabla W(\boldsymbol{x}^*) \boldsymbol{L}\boldsymbol{x}^*) = \omega (\boldsymbol{x}^*,0)-\omega ^2 m(0,\boldsymbol{L}\boldsymbol{x}^*)$
, because by (52)
$ \boldsymbol {A} (\boldsymbol{L}\boldsymbol{x}^*, \boldsymbol {0})= -\omega (\boldsymbol{L}^2\boldsymbol{x}^*,0)+(0,D\nabla W(\boldsymbol{x}^*) \boldsymbol{L}\boldsymbol{x}^*) = \omega (\boldsymbol{x}^*,0)-\omega ^2 m(0,\boldsymbol{L}\boldsymbol{x}^*)$
, because by (52)
 $ D\nabla W(\boldsymbol{x}^*) \boldsymbol{L}\boldsymbol{x}^*=-\omega ^2\boldsymbol{L}m\boldsymbol{x}^* $
and as
$ D\nabla W(\boldsymbol{x}^*) \boldsymbol{L}\boldsymbol{x}^*=-\omega ^2\boldsymbol{L}m\boldsymbol{x}^* $
and as
 $ \boldsymbol{L}^2=-I $
.
$ \boldsymbol{L}^2=-I $
. -
(4)
 $ \boldsymbol {A} (\boldsymbol {0}, \boldsymbol{L}\boldsymbol{x}^*) = m^{-1} (\boldsymbol{L}\boldsymbol{x}^*,0)+ \omega (0, \boldsymbol{x}^*) $
.
$ \boldsymbol {A} (\boldsymbol {0}, \boldsymbol{L}\boldsymbol{x}^*) = m^{-1} (\boldsymbol{L}\boldsymbol{x}^*,0)+ \omega (0, \boldsymbol{x}^*) $
.
Thus, we have proved that
![]() $ Q_1(\boldsymbol{x}^*) $
is invariant by
$ Q_1(\boldsymbol{x}^*) $
is invariant by
![]() $ \boldsymbol {A} $
. Moreover,
$ \boldsymbol {A} $
. Moreover,
is a basis for
![]() $ Q_1(\boldsymbol{x}^*) $
, and the matrix of
$ Q_1(\boldsymbol{x}^*) $
, and the matrix of
![]() $ \boldsymbol {A} $
restricted to this invariant subspace has the form
$ \boldsymbol {A} $
restricted to this invariant subspace has the form
 $$ \begin{align} [\boldsymbol{A}]_{\beta}=\left[ \begin{array}{cccc} 0 & m^{-1} & \omega & 0 \\ \left( 2\mu +(p+1)\nu \right) m & 0 & 0 & \omega \\ -\omega & 0 & 0 & m^{-1} \\ 0 & -\omega & -\omega^2 m & 0 \end{array}\right], \end{align} $$
$$ \begin{align} [\boldsymbol{A}]_{\beta}=\left[ \begin{array}{cccc} 0 & m^{-1} & \omega & 0 \\ \left( 2\mu +(p+1)\nu \right) m & 0 & 0 & \omega \\ -\omega & 0 & 0 & m^{-1} \\ 0 & -\omega & -\omega^2 m & 0 \end{array}\right], \end{align} $$
whose factor of the characteristic polynomial is
with
![]() $ \alpha =2\mu +(p+1)\nu $
. Therefore, it follows that the characteristic polynomial is written as the product of two polynomials: one of which is the factor
$ \alpha =2\mu +(p+1)\nu $
. Therefore, it follows that the characteristic polynomial is written as the product of two polynomials: one of which is the factor
![]() $ \lambda ^2 (\lambda ^2-\alpha +3\omega ^2)$
, which is associated with the last block to be found, and the other is a polynomial, which we shall refer to as
$ \lambda ^2 (\lambda ^2-\alpha +3\omega ^2)$
, which is associated with the last block to be found, and the other is a polynomial, which we shall refer to as
![]() $ \hat {p}(\lambda ) $
, the form of which is unknown.
$ \hat {p}(\lambda ) $
, the form of which is unknown.
The following proposition will serve to analyze the eigenvalues
![]() $\lambda = \pm \sqrt {\alpha -3 \omega ^2}$
.
$\lambda = \pm \sqrt {\alpha -3 \omega ^2}$
.
Lemma 3 Let
![]() $ \gamma =\alpha - 3 \omega ^2 $
. If
$ \gamma =\alpha - 3 \omega ^2 $
. If
![]() $ p\geq 2$
with
$ p\geq 2$
with
![]() $C<0$
, then the number
$C<0$
, then the number
![]() $\gamma <0$
. Furthermore, the eigenvalues
$\gamma <0$
. Furthermore, the eigenvalues
![]() $\lambda = \pm \sqrt {\alpha -3 \omega ^2} $
are purely imaginary.
$\lambda = \pm \sqrt {\alpha -3 \omega ^2} $
are purely imaginary.
Proof In fact,
Using the equality in (44) and (46), we arrive at
Then, if
![]() $ p\geq 2 $
with
$ p\geq 2 $
with
![]() $ C<0 $
, it is verified that
$ C<0 $
, it is verified that
![]() $ \gamma <0 $
, which consequently establishes that
$ \gamma <0 $
, which consequently establishes that
![]() $ \lambda $
is a pure imaginary number.
$ \lambda $
is a pure imaginary number.
Remark 5 In the case where
![]() $ C>0 $
, the sign of the number
$ C>0 $
, the sign of the number
![]() $ \gamma $
can be either positive or negative. Consequently, it is not possible to ascertain with certainty whether the eigenvalue
$ \gamma $
can be either positive or negative. Consequently, it is not possible to ascertain with certainty whether the eigenvalue
![]() $ \lambda $
is pure imaginary or not.
$ \lambda $
is pure imaginary or not.
We proceed to define another subspace, denoted
![]() $ Q_2(\boldsymbol{x}^*) $
, of dimension
$ Q_2(\boldsymbol{x}^*) $
, of dimension
![]() $ 4 $
. This subspace is spanned by the vectors of
$ 4 $
. This subspace is spanned by the vectors of
![]() $ \mathbb {R}^{4n} $
$ \mathbb {R}^{4n} $
where
![]() $ \xi =(1,0,1,0,\dots ) $
and
$ \xi =(1,0,1,0,\dots ) $
and
![]() $\eta =(0,1,0,1,\dots )$
are points of
$\eta =(0,1,0,1,\dots )$
are points of
![]() $ \mathbb {R}^{2n} $
. In this case, we have the following result.
$ \mathbb {R}^{2n} $
. In this case, we have the following result.
Lemma 4 The characteristic polynomial of the matrix
![]() $ \boldsymbol {A} $
, restricted to
$ \boldsymbol {A} $
, restricted to
![]() $ Q_2(\boldsymbol{x}^*) $
, can be expressed as a factor of the form
$ Q_2(\boldsymbol{x}^*) $
, can be expressed as a factor of the form
The eigenvalues of this polynomial are
![]() $ \pm i \omega $
, with multiplicity
$ \pm i \omega $
, with multiplicity
![]() $ 2 $
.
$ 2 $
.
Proof It is evident that these vectors are linearly independent in
![]() $ \mathbb {R}^{4n} $
. On the other hand, it is known that the function
$ \mathbb {R}^{4n} $
. On the other hand, it is known that the function
![]() $ W $
is invariant under translations, so
$ W $
is invariant under translations, so
![]() $ \nabla W $
is also invariant under translations. Then,
$ \nabla W $
is also invariant under translations. Then,
By differentiating this equality with respect to
![]() $ t $
and employing the chain rule, we obtain
$ t $
and employing the chain rule, we obtain
and analogously,
Considering (56) and (57), it follows that:
-
(1)
 $ \boldsymbol {A}(\xi , \boldsymbol {0})= (-\omega \boldsymbol{L} \xi , D\nabla W(\boldsymbol{x}) \xi )= -\omega (\eta , 0)$
, because
$ \boldsymbol {A}(\xi , \boldsymbol {0})= (-\omega \boldsymbol{L} \xi , D\nabla W(\boldsymbol{x}) \xi )= -\omega (\eta , 0)$
, because
 $\boldsymbol{L} \xi = \eta $
.
$\boldsymbol{L} \xi = \eta $
. -
(2)
 $ \boldsymbol {A} (\boldsymbol {0}, \xi ) = m^{-1}(\xi , -\omega \boldsymbol{L} \xi )= m^{-1}(\xi ,\boldsymbol {0})-\omega (\boldsymbol {0},\boldsymbol{L} \xi ) = m^{-1}(\xi ,\boldsymbol {0})-\omega (\boldsymbol {0},\eta )$
.
$ \boldsymbol {A} (\boldsymbol {0}, \xi ) = m^{-1}(\xi , -\omega \boldsymbol{L} \xi )= m^{-1}(\xi ,\boldsymbol {0})-\omega (\boldsymbol {0},\boldsymbol{L} \xi ) = m^{-1}(\xi ,\boldsymbol {0})-\omega (\boldsymbol {0},\eta )$
. -
(3)
 $ \boldsymbol {A}(\eta , \boldsymbol {0}) = (-\omega \boldsymbol{L} \eta , D\nabla W(\boldsymbol{x}) \eta )= \omega (\xi ,\boldsymbol {0}) $
, because
$ \boldsymbol {A}(\eta , \boldsymbol {0}) = (-\omega \boldsymbol{L} \eta , D\nabla W(\boldsymbol{x}) \eta )= \omega (\xi ,\boldsymbol {0}) $
, because
 $\boldsymbol{L} \eta = -\xi $
.
$\boldsymbol{L} \eta = -\xi $
. -
(4)
 $ \boldsymbol {A}(\eta , \boldsymbol {0}) = m^{-1}(\eta , -\omega \boldsymbol{L} \eta )=m^{-1}(\eta ,\boldsymbol {0})-\omega (\boldsymbol {0},\boldsymbol{L} \eta )=m^{-1}(\eta ,\boldsymbol {0})+\omega (\boldsymbol {0},\xi ) $
.
$ \boldsymbol {A}(\eta , \boldsymbol {0}) = m^{-1}(\eta , -\omega \boldsymbol{L} \eta )=m^{-1}(\eta ,\boldsymbol {0})-\omega (\boldsymbol {0},\boldsymbol{L} \eta )=m^{-1}(\eta ,\boldsymbol {0})+\omega (\boldsymbol {0},\xi ) $
.
Thus, we have proved that
![]() $ Q_2(\boldsymbol{x}^*) $
is invariant by
$ Q_2(\boldsymbol{x}^*) $
is invariant by
![]() $ \boldsymbol {A} $
. Furthermore,
$ \boldsymbol {A} $
. Furthermore,
is a basis for
![]() $ Q_2(\boldsymbol{x}^*)$
, and the matrix of A associated with this basis has the form
$ Q_2(\boldsymbol{x}^*)$
, and the matrix of A associated with this basis has the form
 $$ \begin{align*} [A]_{\beta'}=\left[ \begin{array}{cccc} 0 & m^{-1} & \omega & 0 \\ 0 & 0 & 0 & \omega \\ -\omega & 0 & 0 & m^{-1} \\ 0 & -\omega & 0 & 0 \end{array}\right]. \end{align*} $$
$$ \begin{align*} [A]_{\beta'}=\left[ \begin{array}{cccc} 0 & m^{-1} & \omega & 0 \\ 0 & 0 & 0 & \omega \\ -\omega & 0 & 0 & m^{-1} \\ 0 & -\omega & 0 & 0 \end{array}\right]. \end{align*} $$
Therefore, it follows that the polynomial
![]() $ (\lambda ^2+\omega ^2)^2 $
is a factor of the characteristic polynomial of A. This finishes the proof.
$ (\lambda ^2+\omega ^2)^2 $
is a factor of the characteristic polynomial of A. This finishes the proof.
Remark 6 The outcome of the aforementioned lemma is independent of the number of bodies, the value of p, and the value of the constant C.
5 Study of the stability of the
 $3$
-gon solution for the planar
$3$
-gon solution for the planar
 $3$
-body problem with quasi-homogeneous potential and
$3$
-body problem with quasi-homogeneous potential and
 $p>1$
arbitrary
$p>1$
arbitrary
In this section, we will study the stability of the N-gon solutions previously obtained, focusing on the case where
![]() $ N=3 $
and
$ N=3 $
and
![]() $ p>1 $
is arbitrary. First, it is observed that for
$ p>1 $
is arbitrary. First, it is observed that for
![]() $N=3$
the relative equilibrium solution is parametrized by
$N=3$
the relative equilibrium solution is parametrized by
 $$ \begin{align} x_1&=\rho, y_1=0, x_2=-\frac{1}{2} \rho, y_2=\frac{\sqrt{3}}{2} \rho, x_3=-\frac{1}{2} \rho, y_3=-\frac{\sqrt{3}}{2} \rho. \nonumber\\ X_1&=0, Y_1=m \rho \omega, X_2=-\frac{\sqrt{3}}{2} m \rho \omega, Y_2=-\frac{1}{2} m \rho \omega,\nonumber\\ X_3&=\frac{\sqrt{3}}{2} m \rho \omega, Y_3=-\frac{1}{2} m \rho \omega, \end{align} $$
$$ \begin{align} x_1&=\rho, y_1=0, x_2=-\frac{1}{2} \rho, y_2=\frac{\sqrt{3}}{2} \rho, x_3=-\frac{1}{2} \rho, y_3=-\frac{\sqrt{3}}{2} \rho. \nonumber\\ X_1&=0, Y_1=m \rho \omega, X_2=-\frac{\sqrt{3}}{2} m \rho \omega, Y_2=-\frac{1}{2} m \rho \omega,\nonumber\\ X_3&=\frac{\sqrt{3}}{2} m \rho \omega, Y_3=-\frac{1}{2} m \rho \omega, \end{align} $$
where
![]() $\rho $
is an admissible radius satisfying the equation (27). In particular, the parameterization of the particles forming the equilateral triangle is given by
$\rho $
is an admissible radius satisfying the equation (27). In particular, the parameterization of the particles forming the equilateral triangle is given by
 $$ \begin{align*} q_1=\rho(1,0),\,\ q_2=\rho\left( -\frac{1}{2},\frac{\sqrt{3}}{2}\right),\,\ q_3=\rho\left( -\frac{1}{2},-\frac{\sqrt{3}}{2}\right). \end{align*} $$
$$ \begin{align*} q_1=\rho(1,0),\,\ q_2=\rho\left( -\frac{1}{2},\frac{\sqrt{3}}{2}\right),\,\ q_3=\rho\left( -\frac{1}{2},-\frac{\sqrt{3}}{2}\right). \end{align*} $$
The velocities of the particles are
 $$ \begin{align*} p_1= m \rho \omega (1,0),\,\ p_2= m \rho \omega \left( \frac{\sqrt{3}}{2},-\frac{1}{2}\right),\,\ p_3= m \rho \omega \left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right). \end{align*} $$
$$ \begin{align*} p_1= m \rho \omega (1,0),\,\ p_2= m \rho \omega \left( \frac{\sqrt{3}}{2},-\frac{1}{2}\right),\,\ p_3= m \rho \omega \left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right). \end{align*} $$
We check that for the case
![]() $ N=3 $
, we must have
$ N=3 $
, we must have
![]() $ \displaystyle \theta _1=0 $
,
$ \displaystyle \theta _1=0 $
,
![]() $ \theta _2= \displaystyle \frac {2\pi }{3} $
,
$ \theta _2= \displaystyle \frac {2\pi }{3} $
,
![]() $ \displaystyle \theta _3=\frac {4\pi }{3} $
. Moreover, it follows by equations in (25) that the values of A and B are as follows:
$ \displaystyle \theta _3=\frac {4\pi }{3} $
. Moreover, it follows by equations in (25) that the values of A and B are as follows:
 $$ \begin{align} A = 2 \csc\left( \frac{\pi}{3}\right) = \frac{4}{\sqrt{3}}, \quad B = 2\csc\left( \frac{\pi}{3}\right)^{p} = \frac{2^{p+1}}{3^{p/2}}. \end{align} $$
$$ \begin{align} A = 2 \csc\left( \frac{\pi}{3}\right) = \frac{4}{\sqrt{3}}, \quad B = 2\csc\left( \frac{\pi}{3}\right)^{p} = \frac{2^{p+1}}{3^{p/2}}. \end{align} $$
Then, substituting the values of A and B into (60), we get that
![]() $ \rho , C, m $
, and
$ \rho , C, m $
, and
![]() $ \omega $
must satisfy
$ \omega $
must satisfy
 $$ \begin{align} \frac{\omega^2}{m}\rho^{p+2} - \frac{\rho^{p-1}}{\sqrt{3}}- 3^{-p/2}Cp=0. \end{align} $$
$$ \begin{align} \frac{\omega^2}{m}\rho^{p+2} - \frac{\rho^{p-1}}{\sqrt{3}}- 3^{-p/2}Cp=0. \end{align} $$
In general, it is not straightforward to ascertain the admissible values of
![]() $\rho $
from the above equation. Nevertheless, the explicit relationship between m and the remaining parameters, or between C and the remaining parameters, can be determined for a given solution
$\rho $
from the above equation. Nevertheless, the explicit relationship between m and the remaining parameters, or between C and the remaining parameters, can be determined for a given solution
![]() $\rho $
, namely:
$\rho $
, namely:
 $$ \begin{align} m =\frac{3^{1+p/2} \rho^{p+3} \omega^2}{3 C p + 3^{(p+1)/2} \rho^p}, \quad C =\frac{3^{p/2-1}}{mp} \rho^{p-1}\left( -\sqrt{3}m + 3\rho^3 \omega^2\right). \end{align} $$
$$ \begin{align} m =\frac{3^{1+p/2} \rho^{p+3} \omega^2}{3 C p + 3^{(p+1)/2} \rho^p}, \quad C =\frac{3^{p/2-1}}{mp} \rho^{p-1}\left( -\sqrt{3}m + 3\rho^3 \omega^2\right). \end{align} $$
For
![]() $N=3$
, the matrix
$N=3$
, the matrix
![]() $ \boldsymbol {A} $
is of dimension
$ \boldsymbol {A} $
is of dimension
![]() $ 12\times 12 $
and in this situation, we have
$ 12\times 12 $
and in this situation, we have
 $$ \begin{align*} Hess\ W(\boldsymbol{x}^*) =\left[ \begin{array}{cccccc} a_{11} & a_{12} & a_{13} & 0 & a_{15} & a_{16} \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{25} & 0 \\ a_{31} & a_{32} & a_{33} & a_{34} & 0 & a_{36} \\ 0 & a_{42} & a_{43} & a_{44} & a_{45} & a_{46} \\ a_{51} & a_{52} & 0 & a_{54} & a_{55} & a_{56} \\ a_{61} & 0 & a_{63} & a_{64} & a_{65} & a_{66} \end{array} \right], \end{align*} $$
$$ \begin{align*} Hess\ W(\boldsymbol{x}^*) =\left[ \begin{array}{cccccc} a_{11} & a_{12} & a_{13} & 0 & a_{15} & a_{16} \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{25} & 0 \\ a_{31} & a_{32} & a_{33} & a_{34} & 0 & a_{36} \\ 0 & a_{42} & a_{43} & a_{44} & a_{45} & a_{46} \\ a_{51} & a_{52} & 0 & a_{54} & a_{55} & a_{56} \\ a_{61} & 0 & a_{63} & a_{64} & a_{65} & a_{66} \end{array} \right], \end{align*} $$
where the entries of this matrix are
 $$ \begin{align*} a_{11}&= \frac{m \left(-\sqrt{3} m (p-1) + (3p+2) \rho^3 \omega^2 \right) }{6 \rho^3}= -2 a_{12}= -2 a_{13}= -2 a_{21}=-2 a_{31},\\ a_{15}&= \frac{m \left(m- mp +\sqrt{3} (p+2) \rho^3 \omega^2 \right) }{12 \rho^3}= a_{24}= a_{36}= a_{42}= a_{51}= a_{63},\\ a_{16}&= \frac{m \left(m (p-1) -\sqrt{3} (p+2) \rho^3 \omega^2 \right) }{12 \rho^3}= a_{25}= a_{34}= a_{43}= a_{52}= a_{61},\\ a_{22}&= -\frac{m \left(\sqrt{3} m (p-1) + (2-3p) \rho^3 \omega^2 \right) }{12 \rho^3}= a_{33},\\ a_{23}&= \frac{m \omega^2}{3}= a_{32},\\ a_{44}&= \frac{m \left(-\sqrt{3} m (p-1) + 3(p-2) \rho^3 \omega^2 \right) }{18 \rho^3}=-2 a_{45}= -2 a_{46}=-2 a_{54}=-2 a_{64},\\ a_{55}&= \frac{m \left(-5 \sqrt{3} m (p-1) + 3 (5p+2) \rho^3 \omega^2 \right) }{36 \rho^3}= a_{66},\\ a_{56}&= \frac{m \left(\sqrt{3} m (p-1) - 3 (p+1) \rho^3 \omega^2 \right) }{9 \rho^3}= a_{65}. \end{align*} $$
$$ \begin{align*} a_{11}&= \frac{m \left(-\sqrt{3} m (p-1) + (3p+2) \rho^3 \omega^2 \right) }{6 \rho^3}= -2 a_{12}= -2 a_{13}= -2 a_{21}=-2 a_{31},\\ a_{15}&= \frac{m \left(m- mp +\sqrt{3} (p+2) \rho^3 \omega^2 \right) }{12 \rho^3}= a_{24}= a_{36}= a_{42}= a_{51}= a_{63},\\ a_{16}&= \frac{m \left(m (p-1) -\sqrt{3} (p+2) \rho^3 \omega^2 \right) }{12 \rho^3}= a_{25}= a_{34}= a_{43}= a_{52}= a_{61},\\ a_{22}&= -\frac{m \left(\sqrt{3} m (p-1) + (2-3p) \rho^3 \omega^2 \right) }{12 \rho^3}= a_{33},\\ a_{23}&= \frac{m \omega^2}{3}= a_{32},\\ a_{44}&= \frac{m \left(-\sqrt{3} m (p-1) + 3(p-2) \rho^3 \omega^2 \right) }{18 \rho^3}=-2 a_{45}= -2 a_{46}=-2 a_{54}=-2 a_{64},\\ a_{55}&= \frac{m \left(-5 \sqrt{3} m (p-1) + 3 (5p+2) \rho^3 \omega^2 \right) }{36 \rho^3}= a_{66},\\ a_{56}&= \frac{m \left(\sqrt{3} m (p-1) - 3 (p+1) \rho^3 \omega^2 \right) }{9 \rho^3}= a_{65}. \end{align*} $$
We verify that the characteristic polynomial associated with the matrix
![]() $ \boldsymbol {A} $
has the form
$ \boldsymbol {A} $
has the form
with
![]() $ \bar {p}(\lambda )$
a polynomial of degree four, given by
$ \bar {p}(\lambda )$
a polynomial of degree four, given by
where,
and
 $$ \begin{align} a_0 &= \frac{1}{12 \rho^6} \left(m^2 (5 p^2 + 6 p + 5) + 4\,\ 3^{1-p} p^2 (p+1)^2 m^2 C^2 \rho^{2(1-p)} \right) \nonumber\\ &\quad + \frac{1}{12 \rho^6} \left( 8\,\ 3^{(1-p)/2} p (p+1)^2 m^2 C \rho^{1-p} - 4 \sqrt{3} m \rho^3 \omega^2\right) \\ & \quad+ \frac{1}{12 \rho^6} \left(- 18 \sqrt{3} p m \rho^3 \omega^2 - 10 \sqrt{3} p^2 m \rho^3 \omega^2 \right) \nonumber\\ & \quad- \frac{1}{12 \rho^6} \left( 8 \,\ 3^{(2-p)/2} p (p+1)^2 m C \rho^{4-p} \omega^2 + 3 (5 p^2 + 12 p + 8) \rho^6 \omega^4 \right)\hspace{-1pt}.\nonumber \end{align} $$
$$ \begin{align} a_0 &= \frac{1}{12 \rho^6} \left(m^2 (5 p^2 + 6 p + 5) + 4\,\ 3^{1-p} p^2 (p+1)^2 m^2 C^2 \rho^{2(1-p)} \right) \nonumber\\ &\quad + \frac{1}{12 \rho^6} \left( 8\,\ 3^{(1-p)/2} p (p+1)^2 m^2 C \rho^{1-p} - 4 \sqrt{3} m \rho^3 \omega^2\right) \\ & \quad+ \frac{1}{12 \rho^6} \left(- 18 \sqrt{3} p m \rho^3 \omega^2 - 10 \sqrt{3} p^2 m \rho^3 \omega^2 \right) \nonumber\\ & \quad- \frac{1}{12 \rho^6} \left( 8 \,\ 3^{(2-p)/2} p (p+1)^2 m C \rho^{4-p} \omega^2 + 3 (5 p^2 + 12 p + 8) \rho^6 \omega^4 \right)\hspace{-1pt}.\nonumber \end{align} $$
At this stage, it is important to highlight that the values of
![]() $ \mu $
and
$ \mu $
and
![]() $ \nu $
, as presented in (44) and (46), respectively, for
$ \nu $
, as presented in (44) and (46), respectively, for
![]() $ N=3 $
and in accordance with (62), assume the following form:
$ N=3 $
and in accordance with (62), assume the following form:
as a function of m, or equivalently,
 $$ \begin{align*}\mu = \frac{p \omega^2}{C p + 3^{(p-1)/2} \rho^{p-1}} \quad\text{and}\quad \nu = \frac{C p \omega^2}{C p + 3^{(p-1)/2} \rho^{p-1}}, \end{align*} $$
$$ \begin{align*}\mu = \frac{p \omega^2}{C p + 3^{(p-1)/2} \rho^{p-1}} \quad\text{and}\quad \nu = \frac{C p \omega^2}{C p + 3^{(p-1)/2} \rho^{p-1}}, \end{align*} $$
as function of C.
On the other hand, as previously established in Lemmas 2 and 4 the characteristic polynomial exhibits eight known eigenvalues: two null eigenvalues, four pure imaginary represented by
![]() $ \pm i\omega $
, and the remaining two eigenvalues are given by
$ \pm i\omega $
, and the remaining two eigenvalues are given by
![]() $ \pm \sqrt {\alpha - 3 \omega ^2}= \pm \sqrt {-\frac {m (p-1) }{\sqrt {3} \rho ^3} + (p-2) \omega ^2} $
. We must therefore characterize the two roots of the polynomial
$ \pm \sqrt {\alpha - 3 \omega ^2}= \pm \sqrt {-\frac {m (p-1) }{\sqrt {3} \rho ^3} + (p-2) \omega ^2} $
. We must therefore characterize the two roots of the polynomial
![]() $\hat {p}(x)$
.
$\hat {p}(x)$
.
At the outset, we note that the discriminant of
![]() $ \hat {p}(x) $
in (64) is given by
$ \hat {p}(x) $
in (64) is given by
 $$ \begin{align} D &= -9 p^2 (p+1)^2 m^2 C^2 \rho^2\nonumber\\ &\quad - 2\,\ 3^{p/2} p (p+1) m C \rho^{p+1} \left(2 \sqrt{3} m (p+2) - 3 (2p+5) \rho^3 \omega^2 \right) \nonumber \\ &- 3^p \rho^{2p} (m^2 (p+1) (p+5) - 2 \sqrt{3} m (p (p+11) + 2) \rho^3 \omega^2\nonumber\\ &+ 3(p (p + 16) + 7) \rho^6 \omega^4 ). \end{align} $$
$$ \begin{align} D &= -9 p^2 (p+1)^2 m^2 C^2 \rho^2\nonumber\\ &\quad - 2\,\ 3^{p/2} p (p+1) m C \rho^{p+1} \left(2 \sqrt{3} m (p+2) - 3 (2p+5) \rho^3 \omega^2 \right) \nonumber \\ &- 3^p \rho^{2p} (m^2 (p+1) (p+5) - 2 \sqrt{3} m (p (p+11) + 2) \rho^3 \omega^2\nonumber\\ &+ 3(p (p + 16) + 7) \rho^6 \omega^4 ). \end{align} $$
To carry out the stability study, we evaluate
![]() $a_1$
and the discriminant D with respect to the mass specified in (62). Then (65) and (67) are equivalent to
$a_1$
and the discriminant D with respect to the mass specified in (62). Then (65) and (67) are equivalent to
 $$ \begin{align} a_1= \frac{\omega^2 \left(-3 p (p-2) C + v \right) }{3 p C + v}, \end{align} $$
$$ \begin{align} a_1= \frac{\omega^2 \left(-3 p (p-2) C + v \right) }{3 p C + v}, \end{align} $$
and
 $$ \begin{align} D= -\frac{8\,\ \omega^4}{(3 p C + v)^2}\left(9 p^3 C^2 + 3 p (p+1) C v + v^2 \right), \end{align} $$
$$ \begin{align} D= -\frac{8\,\ \omega^4}{(3 p C + v)^2}\left(9 p^3 C^2 + 3 p (p+1) C v + v^2 \right), \end{align} $$
where
![]() $ v= \kappa u$
,
$ v= \kappa u$
,
![]() $\kappa = 3^{(p+1)/2} $
and
$\kappa = 3^{(p+1)/2} $
and
![]() $ u= \rho ^{p-1} $
.
$ u= \rho ^{p-1} $
.
The roots of the quadratic polynomial in
![]() $ x $
are given by
$ x $
are given by
and
As demonstrated in Theorem 2.2, for a given
![]() $ C>0 $
and
$ C>0 $
and
![]() $ p>1 $
, there exists a unique admissible radius
$ p>1 $
, there exists a unique admissible radius
![]() $ \rho>0 $
, for the fixed mass
$ \rho>0 $
, for the fixed mass
![]() $ m $
. The following theorem will be employed for the purpose of verifying the type of stability of the associated solution.
$ m $
. The following theorem will be employed for the purpose of verifying the type of stability of the associated solution.
Theorem 5.1 If
![]() $ C>0 $
,
$ C>0 $
,
![]() $ p>1 $
, and
$ p>1 $
, and
![]() $ m>0 $
, then the
$ m>0 $
, then the
![]() $3$
-gon solution of the problem of
$3$
-gon solution of the problem of
![]() $3$
-bodies with quasi-homogeneous potential and
$3$
-bodies with quasi-homogeneous potential and
![]() $ \rho = \rho (m) $
given in Theorem 2.2 is unstable in the Lyapunov sense.
$ \rho = \rho (m) $
given in Theorem 2.2 is unstable in the Lyapunov sense.
Proof Since
![]() $ C>0 $
it follows immediately from (69) that
$ C>0 $
it follows immediately from (69) that
![]() $D <0 $
and hence the roots
$D <0 $
and hence the roots
![]() $ x_- $
and
$ x_- $
and
![]() $ x_+ $
given in (70) and (71), respectively, are complex. In consequence, the
$ x_+ $
given in (70) and (71), respectively, are complex. In consequence, the
![]() $3$
-gon solution is unstable in the sense of Lyapunov.
$3$
-gon solution is unstable in the sense of Lyapunov.
Next we will analyze the case
![]() $C<0$
. We note that the
$C<0$
. We note that the
![]() $ sgn(D)=-sgn(v^2 + 3 p (p+1) C v + 9 p^3 C^2) $
. Therefore, the objective is now to examine the behavior of the quadratic polynomial
$ sgn(D)=-sgn(v^2 + 3 p (p+1) C v + 9 p^3 C^2) $
. Therefore, the objective is now to examine the behavior of the quadratic polynomial
Lemma 5 Let
![]() $C<0$
and
$C<0$
and
![]() $p>1$
. So we have that:
$p>1$
. So we have that:
-
(1)
 $D=0 \Leftrightarrow v=v_+= -3 p^2 C $
or
$D=0 \Leftrightarrow v=v_+= -3 p^2 C $
or
 $ v= v_-= -3 p C $
.
$ v= v_-= -3 p C $
. -
(2)
 $ D>0 \Leftrightarrow v_- < v <v_+ $
.
$ D>0 \Leftrightarrow v_- < v <v_+ $
. -
(3)
 $D <0 \Leftrightarrow v>v_+$
or
$D <0 \Leftrightarrow v>v_+$
or
 $0 < v < v_-$
.
$0 < v < v_-$
.
The graph of D is shown in Figure 6.

Figure 6: Graphic of D with
![]() $ C<0 $
and
$ C<0 $
and
![]() $ p>1 $
.
$ p>1 $
.
Proof In fact,
 $$ \begin{align*} h(v)=0 & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm \sqrt{9 p^2 (p+1)^2 C^2 - 36 p^3 C^2} \right) \\ & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm \sqrt{9 p^2 C^2 ((p+1)^2 - 4p)} \right)\\ & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm 3 p |C| \sqrt{p^2 -2p + 1} \right)\\ & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm 3 p (p-1) C \right)\hspace{-1pt}, \end{align*} $$
$$ \begin{align*} h(v)=0 & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm \sqrt{9 p^2 (p+1)^2 C^2 - 36 p^3 C^2} \right) \\ & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm \sqrt{9 p^2 C^2 ((p+1)^2 - 4p)} \right)\\ & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm 3 p |C| \sqrt{p^2 -2p + 1} \right)\\ & \Leftrightarrow v= \frac{1}{2} \left(-3 p(p+1) C \pm 3 p (p-1) C \right)\hspace{-1pt}, \end{align*} $$
because
![]() $|C|= -C$
. Thus,
$|C|= -C$
. Thus,
clearly
![]() $ v_- < v_+ $
. This proves part 1 of the lemma.
$ v_- < v_+ $
. This proves part 1 of the lemma.
The proofs of items 2 and 3 of the lemma are immediate, as it can be observed that
![]() $ h(v)<0 $
if
$ h(v)<0 $
if
![]() $ v_- < v < v_+ $
and
$ v_- < v < v_+ $
and
![]() $ h(v)>0 $
if
$ h(v)>0 $
if
![]() $ v>v_+ $
. As
$ v>v_+ $
. As
![]() $ sgn(D)=-sgn(h) $
, the proof of the lemma follows.
$ sgn(D)=-sgn(h) $
, the proof of the lemma follows.
Remark 7 According the definition of
![]() $\rho _{\sharp }$
in Theorem 2.3, it can be observed that
$\rho _{\sharp }$
in Theorem 2.3, it can be observed that
![]() $\rho _{\sharp }^{p-1}= -\frac {C}{3^{(p+1)/2}} p (p+2)$
, so
$\rho _{\sharp }^{p-1}= -\frac {C}{3^{(p+1)/2}} p (p+2)$
, so
![]() $v_{\sharp }=- C p(p+2)$
.
$v_{\sharp }=- C p(p+2)$
.
Again, using the definition of
![]() $\rho _*$
in Theorem 2.3, we check that
$\rho _*$
in Theorem 2.3, we check that
![]() $v_*= v_-$
.
$v_*= v_-$
.
By definition of
![]() $v_+$
, the corresponding
$v_+$
, the corresponding
![]() $\rho _+$
satisfies
$\rho _+$
satisfies
![]() $\rho _+^{p-1}= -\frac {3 C p^2}{3^{(p+1)/2}}$
. Analogously, for
$\rho _+^{p-1}= -\frac {3 C p^2}{3^{(p+1)/2}}$
. Analogously, for
![]() $v_-$
we have
$v_-$
we have
![]() $\rho _-^{p-1}= -\frac {3 C p}{3^{(p+1)/2}}$
.
$\rho _-^{p-1}= -\frac {3 C p}{3^{(p+1)/2}}$
.
Moreover, if
![]() $p>1$
then
$p>1$
then
![]() $\rho _{\sharp } < \rho _+$
.
$\rho _{\sharp } < \rho _+$
.
Theorem 5.2 If
![]() $C< 0$
,
$C< 0$
,
![]() $ m_\sharp = \frac {\omega ^2 (p+2) \left (-B C p (p+2) A^{-1} \right )^{3 /(p-1)}}{2 A (p-1)}$
,
$ m_\sharp = \frac {\omega ^2 (p+2) \left (-B C p (p+2) A^{-1} \right )^{3 /(p-1)}}{2 A (p-1)}$
,
![]() $ p>1 $
and
$ p>1 $
and
![]() $ m> m_\sharp $
, then the
$ m> m_\sharp $
, then the
![]() $3$
-gon solution of the planar
$3$
-gon solution of the planar
![]() $3$
-body problem for the quasi-homogeneous potential with radius
$3$
-body problem for the quasi-homogeneous potential with radius
![]() $\rho _2(m)> \rho _+ $
(given in Theorem 2.3) is unstable in the Lyapunov sense.
$\rho _2(m)> \rho _+ $
(given in Theorem 2.3) is unstable in the Lyapunov sense.
Proof Indeed, as established in item
![]() $3$
of Lemma 5, we know that
$3$
of Lemma 5, we know that
![]() $D <0 $
if
$D <0 $
if
![]() $ v> v_+ $
which implies that both
$ v> v_+ $
which implies that both
![]() $ x_- $
and
$ x_- $
and
![]() $ x_+ $
are complex. Thus, the N-gon solution for
$ x_+ $
are complex. Thus, the N-gon solution for
![]() $\rho _2> \rho _+$
which exists if
$\rho _2> \rho _+$
which exists if
![]() $m> m_{\sharp }$
, satisfies
$m> m_{\sharp }$
, satisfies
![]() $v_2> v_+$
. Therefore, this solution is unstable in the Lyapunov sense, which proves the theorem.
$v_2> v_+$
. Therefore, this solution is unstable in the Lyapunov sense, which proves the theorem.
Lemma 6 For
![]() $C<0$
,
$C<0$
,
![]() $p>1$
and
$p>1$
and
![]() $ v> v_- $
, then
$ v> v_- $
, then
![]() $a_1 $
is always positive.
$a_1 $
is always positive.
Proof First, let’s check the sign of the denominator of
![]() $a_1 $
in (68). By hypothesis
$a_1 $
in (68). By hypothesis
![]() $ v> v_- $
, that is,
$ v> v_- $
, that is,
![]() $ v> -3 p C $
, or equivalently,
$ v> -3 p C $
, or equivalently,
![]() $ v + 3 p C> 0 $
.
$ v + 3 p C> 0 $
.
On the other hand, again from the inequality
![]() $v> v_- $
, we have
$v> v_- $
, we have
![]() $ -3 p (p-2) C + v> -3 p (p-1) C >0 $
. So the numerator of
$ -3 p (p-2) C + v> -3 p (p-1) C >0 $
. So the numerator of
![]() $a_1 $
in (68) is positive. This concludes the proof.
$a_1 $
in (68) is positive. This concludes the proof.
Lemma 7 For
![]() $ C<0 $
and
$ C<0 $
and
![]() $ p>1 $
,
$ p>1 $
,
![]() $ v_- \leq v \leq v_+ $
, then
$ v_- \leq v \leq v_+ $
, then
![]() $ x_- $
is always negative.
$ x_- $
is always negative.
Proof The proof is immediate, since by definition in (70)
![]() $x_- = -\frac {a_1 + \sqrt {D}}{2}$
, so by Lemmas 5 and 6, we get
$x_- = -\frac {a_1 + \sqrt {D}}{2}$
, so by Lemmas 5 and 6, we get
![]() $x_- < 0$
. This proves the lemma.
$x_- < 0$
. This proves the lemma.
Next, we will analyze the root
![]() $ x_+ $
of the quadratic polynomial
$ x_+ $
of the quadratic polynomial
![]() $ \hat {p}(x) $
given in (71). Substituting the values of
$ \hat {p}(x) $
given in (71). Substituting the values of
![]() $a_1$
given in (68) and D given in (69), we obtain that
$a_1$
given in (68) and D given in (69), we obtain that
 $$ \begin{align*}x_+ = \frac{\omega^2}{3 p C + v}\left[(3 p (p-2) C - v) + 2 \sqrt{6}\,\ \sqrt{-3 p^3 C^2 + p (p+1) C v + \frac{v^2}{3}} \right]. \end{align*} $$
$$ \begin{align*}x_+ = \frac{\omega^2}{3 p C + v}\left[(3 p (p-2) C - v) + 2 \sqrt{6}\,\ \sqrt{-3 p^3 C^2 + p (p+1) C v + \frac{v^2}{3}} \right]. \end{align*} $$
Now, we know by Lemma 6 that
![]() $ 3 p C + v>0 $
. Let us then define the auxiliary function
$ 3 p C + v>0 $
. Let us then define the auxiliary function
 $$ \begin{align} g(v)= 3 p (p-2) C - v + 2 \sqrt{6}\,\ \sqrt{-3 p^3 C^2 + p (p+1) C v + \frac{v^2}{3}}. \end{align} $$
$$ \begin{align} g(v)= 3 p (p-2) C - v + 2 \sqrt{6}\,\ \sqrt{-3 p^3 C^2 + p (p+1) C v + \frac{v^2}{3}}. \end{align} $$
Of course, it is clear that
![]() $sgn(x_+)= sgn(g(v))$
for
$sgn(x_+)= sgn(g(v))$
for
![]() $v \in (v_-, v_+)$
.
$v \in (v_-, v_+)$
.
Lemma 8 If
![]() $C<0$
and
$C<0$
and
![]() $p>1$
, then the auxiliary function
$p>1$
, then the auxiliary function
![]() $ g(v)<0 $
in
$ g(v)<0 $
in
![]() $ v_- < v < v_+ $
.
$ v_- < v < v_+ $
.
Proof Let
![]() $v \in (v_-, v_+)$
. Differentiating the auxiliary function
$v \in (v_-, v_+)$
. Differentiating the auxiliary function
![]() $ g $
given in (75) with respect to v, we have that
$ g $
given in (75) with respect to v, we have that
 $$ \begin{align} g'(v)=-1-\frac{\sqrt{2}\,\ (3 p (p+1) C + 2v)}{\sqrt{-9 p^3 C^2 - 3 p (p+1) C v - v^2}}, \end{align} $$
$$ \begin{align} g'(v)=-1-\frac{\sqrt{2}\,\ (3 p (p+1) C + 2v)}{\sqrt{-9 p^3 C^2 - 3 p (p+1) C v - v^2}}, \end{align} $$
and differentiating again, we get
 $$ \begin{align} g"(v)= -\frac{9 p^2 (p-1)^2 C^2}{\sqrt{2}\,\ \left[-9 p^3 C^2 - 3 p (p+1) C v - v^2 \right]^{3/2}}. \end{align} $$
$$ \begin{align} g"(v)= -\frac{9 p^2 (p-1)^2 C^2}{\sqrt{2}\,\ \left[-9 p^3 C^2 - 3 p (p+1) C v - v^2 \right]^{3/2}}. \end{align} $$
Note that the second derivative is always negative, so
![]() $ g' $
is decreasing for all
$ g' $
is decreasing for all
![]() $ v $
. In particular, for
$ v $
. In particular, for
![]() $v \in (v_-, v_\sharp )$
it is verified that
$v \in (v_-, v_\sharp )$
it is verified that
We assert that
![]() $ g'(v_\sharp )=0 $
. In fact,
$ g'(v_\sharp )=0 $
. In fact,
 $$ \begin{align*} g'(v_\sharp) &= -1-\frac{\sqrt{2}\,\ [3 p (p+1) C - 2 p (p+2) C]}{\left[-9 p^3 C^2 + 3 p^2 (p+1)(p+2) C^2 - p^2 (p+2)^2 C^2 - p^2 (p+2)^2 C^2\right]^{1/2}}\\ & =-1+\frac{\sqrt{2}\,\ p C (p-1)}{p C \left[-9 p + 3 p (p+1)(p+2) - (p+2)^2\right]^{1/2}}= -1 + \frac{\sqrt{2}\,\ (p-1)}{\sqrt{2 (p-1)^2}}= 0. \end{align*} $$
$$ \begin{align*} g'(v_\sharp) &= -1-\frac{\sqrt{2}\,\ [3 p (p+1) C - 2 p (p+2) C]}{\left[-9 p^3 C^2 + 3 p^2 (p+1)(p+2) C^2 - p^2 (p+2)^2 C^2 - p^2 (p+2)^2 C^2\right]^{1/2}}\\ & =-1+\frac{\sqrt{2}\,\ p C (p-1)}{p C \left[-9 p + 3 p (p+1)(p+2) - (p+2)^2\right]^{1/2}}= -1 + \frac{\sqrt{2}\,\ (p-1)}{\sqrt{2 (p-1)^2}}= 0. \end{align*} $$
Thus,
![]() $ 0 = g'(v_\sharp )< g'(v) < g'(v_-) $
, therefore
$ 0 = g'(v_\sharp )< g'(v) < g'(v_-) $
, therefore
![]() $ g $
is increasing by
$ g $
is increasing by
![]() $v \in (v_*, v_\sharp ) $
. Then,
$v \in (v_*, v_\sharp ) $
. Then,
In an analogous way, we affirm that
![]() $g(v_\sharp )=0$
. In fact,
$g(v_\sharp )=0$
. In fact,
 $$ \begin{align*} g(v_\sharp)&= 3 p (p-2) C + p (p+2) C + 2 \sqrt{6}\,\\ &\quad\sqrt{\left(-3 p^3 C^2 - p^2 (p+1)(p+2) C^2 + \frac{1}{3} (p+2)^2 p^2 C^2\right)}\\ &= 3 p (p-2) C + p (p+2) C + 2 \sqrt{6}\,\\ &\quad\sqrt{p^2 C^2 \left(-3 p - (p+1)(p+2) + \frac{1}{3} (p+2)^2\right)}\\ &= p C \left(4 (p-1) - 2\sqrt{2}\,\ \sqrt{-2 p^2 - 4p + 2} \right)\\ &= p C (4 (p-1) - 4\,\ \sqrt{p^2 - 2p +1})= p C (4 (p-1)-4 (p-1))=0. \end{align*} $$
$$ \begin{align*} g(v_\sharp)&= 3 p (p-2) C + p (p+2) C + 2 \sqrt{6}\,\\ &\quad\sqrt{\left(-3 p^3 C^2 - p^2 (p+1)(p+2) C^2 + \frac{1}{3} (p+2)^2 p^2 C^2\right)}\\ &= 3 p (p-2) C + p (p+2) C + 2 \sqrt{6}\,\\ &\quad\sqrt{p^2 C^2 \left(-3 p - (p+1)(p+2) + \frac{1}{3} (p+2)^2\right)}\\ &= p C \left(4 (p-1) - 2\sqrt{2}\,\ \sqrt{-2 p^2 - 4p + 2} \right)\\ &= p C (4 (p-1) - 4\,\ \sqrt{p^2 - 2p +1})= p C (4 (p-1)-4 (p-1))=0. \end{align*} $$
Then,
![]() $g(v) <0 $
for
$g(v) <0 $
for
![]() $v \in (v_-, v_\sharp ) $
.
$v \in (v_-, v_\sharp ) $
.
Similarly, since
![]() $ g" $
is negative, then
$ g" $
is negative, then
![]() $ g' $
is decreasing in
$ g' $
is decreasing in
![]() $ (v_\sharp , v_+) $
, so
$ (v_\sharp , v_+) $
, so
![]() $ g'(v_+) < g'(v) < g'(v_\sharp ) $
and as
$ g'(v_+) < g'(v) < g'(v_\sharp ) $
and as
![]() $ g'(v_\sharp )=0 $
, we have that
$ g'(v_\sharp )=0 $
, we have that
![]() $ g $
is decreasing in
$ g $
is decreasing in
![]() $ (v_\sharp , v_+) $
. Then
$ (v_\sharp , v_+) $
. Then
![]() $ g(v_+) < g(v) < g(v_\sharp ) $
and again since
$ g(v_+) < g(v) < g(v_\sharp ) $
and again since
![]() $ g(v_\sharp )=0 $
, we conclude that
$ g(v_\sharp )=0 $
, we conclude that
![]() $ g < 0 $
in
$ g < 0 $
in
![]() $ (v_\sharp , v_+ ) $
. This finishes the proof of the lemma.
$ (v_\sharp , v_+ ) $
. This finishes the proof of the lemma.
Now, we know from Theorem 2.3 of Section 2, that for
![]() $ C<0 $
,
$ C<0 $
,
![]() $ p>1 $
, and
$ p>1 $
, and
![]() $ m> m_\sharp $
defined in (29) there exist two radii
$ m> m_\sharp $
defined in (29) there exist two radii
![]() $ \rho _1, \rho _2>0 $
admissible for fixed mass
$ \rho _1, \rho _2>0 $
admissible for fixed mass
![]() $ m $
. Next, we will check the type of stability of these solutions.
$ m $
. Next, we will check the type of stability of these solutions.
Theorem 5.3 If
![]() $ C<0 $
,
$ C<0 $
,
![]() $ p>1 $
and
$ p>1 $
and
![]() $ m> m_\sharp $
fixed, then the
$ m> m_\sharp $
fixed, then the
![]() $3$
-gon solution of the planar
$3$
-gon solution of the planar
![]() $ 3$
-body problem with quasi-homogeneous potential and radius
$ 3$
-body problem with quasi-homogeneous potential and radius
![]() $\rho = \rho _2 (m) $
with
$\rho = \rho _2 (m) $
with
![]() $ \rho _\sharp < \rho _2(m) \leq \rho _+ $
given in Theorem 2.3 is spectrally stable.
$ \rho _\sharp < \rho _2(m) \leq \rho _+ $
given in Theorem 2.3 is spectrally stable.
Proof As a consequence of Lemma 8, it can be deduced that
![]() $ g(v)<0 $
in the interval
$ g(v)<0 $
in the interval
![]() $(v_\sharp , v_+) $
, and therefore
$(v_\sharp , v_+) $
, and therefore
![]() $ x_+ <0 $
in the same interval. On the other hand, Corollary 7 indicates that
$ x_+ <0 $
in the same interval. On the other hand, Corollary 7 indicates that
![]() $ x_- <0 $
in the interval
$ x_- <0 $
in the interval
![]() $(v_\sharp , v_+)$
. This shows that the
$(v_\sharp , v_+)$
. This shows that the
![]() $3$
-gon solution with radius
$3$
-gon solution with radius
![]() $\rho _2$
, where
$\rho _2$
, where
![]() $\rho _\sharp < \rho _2 < \rho _+ $
, is spectrally stable.
$\rho _\sharp < \rho _2 < \rho _+ $
, is spectrally stable.
Now, for the case
![]() $v= v_+$
, it can be demonstrated by means of Lemma 5 that the discriminant
$v= v_+$
, it can be demonstrated by means of Lemma 5 that the discriminant
![]() $D=0$
. Consequently, according to the findings of Lemma 6,
$D=0$
. Consequently, according to the findings of Lemma 6,
![]() $ x_+ = x_- = -a_1 <0$
. This shows that the
$ x_+ = x_- = -a_1 <0$
. This shows that the
![]() $3$
-gon solution with
$3$
-gon solution with
![]() $\rho _2 = \rho _+ $
is also spectrally stable. This concludes the proof of the theorem.
$\rho _2 = \rho _+ $
is also spectrally stable. This concludes the proof of the theorem.
Theorem 5.4 If
![]() $ C<0 $
,
$ C<0 $
,
![]() $ p>1 $
,
$ p>1 $
,
![]() $ m\geq m_\sharp $
, then the
$ m\geq m_\sharp $
, then the
![]() $3$
-gon solution of the planar
$3$
-gon solution of the planar
![]() $ N $
-body problem with quasi-homogeneous potential and
$ N $
-body problem with quasi-homogeneous potential and
![]() $ \rho = \rho _1 (m) $
with
$ \rho = \rho _1 (m) $
with
![]() $ \rho _*=\rho _- < \rho _1 (m) \leq \rho _\sharp $
given in Theorem 2.3 is spectrally stable.
$ \rho _*=\rho _- < \rho _1 (m) \leq \rho _\sharp $
given in Theorem 2.3 is spectrally stable.
Proof Indeed, from Lemma 8, it can be deduced that
![]() $ g(v) < 0$
in the interval
$ g(v) < 0$
in the interval
![]() $(v_-, v_\sharp ) $
which implies that
$(v_-, v_\sharp ) $
which implies that
![]() $ x_+ <0 $
in
$ x_+ <0 $
in
![]() $ (v_-, v_\sharp )$
. Additionally, Corollary 7 indicates that
$ (v_-, v_\sharp )$
. Additionally, Corollary 7 indicates that
![]() $ x_- <0 $
in the interval
$ x_- <0 $
in the interval
![]() $(v_-, v_\sharp )$
. This demonstrates that the
$(v_-, v_\sharp )$
. This demonstrates that the
![]() $3$
-gon solution with
$3$
-gon solution with
![]() $\rho _1 \in (\rho _*, \rho _\sharp ) $
is spectrally stable.
$\rho _1 \in (\rho _*, \rho _\sharp ) $
is spectrally stable.
On the other hand, from Lemma 8, we have that
![]() $ g(v_\sharp )=0 $
, which implies that
$ g(v_\sharp )=0 $
, which implies that
![]() $ x_+=0 $
in
$ x_+=0 $
in
![]() $ (v_-, v_\sharp ) $
, and also by Corollary 7, we have
$ (v_-, v_\sharp ) $
, and also by Corollary 7, we have
![]() $x_- <0 $
in
$x_- <0 $
in
![]() $ v=v_-$
. This shows that the N-gon solution with
$ v=v_-$
. This shows that the N-gon solution with
![]() $ \rho _1=\rho _\sharp $
is spectrally stable. This finishes the proof of the theorem.
$ \rho _1=\rho _\sharp $
is spectrally stable. This finishes the proof of the theorem.
6 Concluding remarks
In this work, we consider the planar N-body problem with quasi-homogeneous potential given by
 $$ \begin{align*}W = \sum_{1\leq k<j\leq N} \left[ \frac{ m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|} +\frac{m_k m_j C_{jk}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p} \right], \end{align*} $$
$$ \begin{align*}W = \sum_{1\leq k<j\leq N} \left[ \frac{ m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|} +\frac{m_k m_j C_{jk}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p} \right], \end{align*} $$
where
![]() $ m_k>0 $
are the masses and
$ m_k>0 $
are the masses and
![]() $C_{jk}= C_{kj}$
is a nonzero real constant, with the exponent
$C_{jk}= C_{kj}$
is a nonzero real constant, with the exponent
![]() $ p> $
1. We characterize the periodic solutions that form a regular polygon with equal masses (
$ p> $
1. We characterize the periodic solutions that form a regular polygon with equal masses (
![]() $m_k= m$
,
$m_k= m$
,
![]() $k=1, \cdots , N$
) and equal constants
$k=1, \cdots , N$
) and equal constants
![]() $C_{jk}$
(
$C_{jk}$
(
![]() $C_{jk}= C$
(
$C_{jk}= C$
(
![]() $j, k=1, \cdots , N$
) (for short, N-gon solutions).
$j, k=1, \cdots , N$
) (for short, N-gon solutions).
Initially, we study the existence of periodic solutions with angular velocity
![]() $ \omega $
and equal masses that form a regular polygon on a circle of radius
$ \omega $
and equal masses that form a regular polygon on a circle of radius
![]() $ \rho $
(as we said before), assuming that
$ \rho $
(as we said before), assuming that
![]() $ C_{kj}=C $
for all
$ C_{kj}=C $
for all
![]() $ k,j=1,\ldots , N $
. We characterize the possible radii as a function of
$ k,j=1,\ldots , N $
. We characterize the possible radii as a function of
![]() $C, m$
, and p. We verify that the existence of an N-gon solution with quasi-homogeneous potential is given by the fulfillment of the following condition:
$C, m$
, and p. We verify that the existence of an N-gon solution with quasi-homogeneous potential is given by the fulfillment of the following condition:
with
 $$ \begin{align*} A= \displaystyle\sum_{j= 2}^{N}\left|\csc\left( \frac{\pi(j-1)}{N}\right) \right|,\quad B= \sum_{j=2}^{N} \left|\csc\left( \frac{\pi(j-1)}{N}\right)\right|{}^{p}, \end{align*} $$
$$ \begin{align*} A= \displaystyle\sum_{j= 2}^{N}\left|\csc\left( \frac{\pi(j-1)}{N}\right) \right|,\quad B= \sum_{j=2}^{N} \left|\csc\left( \frac{\pi(j-1)}{N}\right)\right|{}^{p}, \end{align*} $$
positive constants. We have shown that for
![]() $ C_{kj}=C>0 $
there is a unique admissible radius which leads to a N-gon solution for the planar
$ C_{kj}=C>0 $
there is a unique admissible radius which leads to a N-gon solution for the planar
![]() $N $
-body problem with quasi-homogeneous potential. On the other hand, for
$N $
-body problem with quasi-homogeneous potential. On the other hand, for
![]() $ C_{kj}=C< 0 $
there are 2, 1, or no admissible radii. In fact, there is a critical value of
$ C_{kj}=C< 0 $
there are 2, 1, or no admissible radii. In fact, there is a critical value of
![]() $ m $
denoted by
$ m $
denoted by
![]() $ m_\sharp = \frac {\omega ^2 (p+2) \left (-B C p (p+2) A^{-1} \right )^{3 /(p-1)}}{2 A (p-1) }$
such that if
$ m_\sharp = \frac {\omega ^2 (p+2) \left (-B C p (p+2) A^{-1} \right )^{3 /(p-1)}}{2 A (p-1) }$
such that if
![]() $ m< m_\sharp $
there are no admissible radii. If
$ m< m_\sharp $
there are no admissible radii. If
![]() $ m = m_\sharp $
there is a unique admissible radius which gives rise to a unique N-gon solution. If
$ m = m_\sharp $
there is a unique admissible radius which gives rise to a unique N-gon solution. If
![]() $ m> m_\sharp $
, then there exist two admissible radii denoted by
$ m> m_\sharp $
, then there exist two admissible radii denoted by
![]() $ \rho _1 $
and
$ \rho _1 $
and
![]() $ \rho _2 $
such that
$ \rho _2 $
such that
![]() $ \rho _* = 1/2 \left (- p B C / A \right )^{1/ p-1} < \rho _1 < \rho _\sharp = 1/2 \left (-(B C /3 A) p(p+2) \right )^{1/p-1} $
and
$ \rho _* = 1/2 \left (- p B C / A \right )^{1/ p-1} < \rho _1 < \rho _\sharp = 1/2 \left (-(B C /3 A) p(p+2) \right )^{1/p-1} $
and
![]() $ \rho _2> \rho _\sharp $
each of them gives rise to a N-gon solution.
$ \rho _2> \rho _\sharp $
each of them gives rise to a N-gon solution.
Furthermore, we guarantee that one of the factors of the characteristic polynomial of the Hamiltonian matrix associated with a relative equilibrium is given by the expression
![]() $ \lambda ^2(\lambda ^2-\alpha +3\omega ^2)$
, where
$ \lambda ^2(\lambda ^2-\alpha +3\omega ^2)$
, where
![]() $ \displaystyle \alpha = 2 \mu +(p+1)\nu $
and the values of the parameters are as follows:
$ \displaystyle \alpha = 2 \mu +(p+1)\nu $
and the values of the parameters are as follows:
![]() $ \mu = A m /4 \rho ^3 $
and
$ \mu = A m /4 \rho ^3 $
and
![]() $ \nu = m p B C / 2^{p+1} \rho ^{p+2}$
. The remaining factor of the characteristic polynomial is of the form
$ \nu = m p B C / 2^{p+1} \rho ^{p+2}$
. The remaining factor of the characteristic polynomial is of the form
![]() $ (\lambda ^2+\omega ^2)^2 $
.
$ (\lambda ^2+\omega ^2)^2 $
.
We conclude this work by studying the stability for the case
![]() $ N=3 $
. We find that for
$ N=3 $
. We find that for
![]() $ C>0 $
the
$ C>0 $
the
![]() $3$
-gon solution is always unstable in the Lyapunov sense. For
$3$
-gon solution is always unstable in the Lyapunov sense. For
![]() $ C<0 $
, defining the auxiliary values of
$ C<0 $
, defining the auxiliary values of
![]() $\rho $
, namely,
$\rho $
, namely,
![]() $\rho _*=\left (-3 p C/3^{(p+1)/2}\right )^{1/(p-1)}$
,
$\rho _*=\left (-3 p C/3^{(p+1)/2}\right )^{1/(p-1)}$
,
![]() $\rho _\sharp = \left (-p(p+1)C/3^{(p+1)/2}\right )^{1/(p-1)}$
and
$\rho _\sharp = \left (-p(p+1)C/3^{(p+1)/2}\right )^{1/(p-1)}$
and
![]() $\rho _+ = \left (-3 p^2 C/3^{(p+1)/2}\right )^{1/(p-1)}$
, we have that the
$\rho _+ = \left (-3 p^2 C/3^{(p+1)/2}\right )^{1/(p-1)}$
, we have that the
![]() $3$
-gon solution with
$3$
-gon solution with
![]() $\rho = \rho _1 $
is spectrally stable throughout its entire interval of definition
$\rho = \rho _1 $
is spectrally stable throughout its entire interval of definition
![]() $\left (\rho _*, \rho _\sharp \right ]$
. The solution for
$\left (\rho _*, \rho _\sharp \right ]$
. The solution for
![]() $\rho =\rho _2$
is spectrally stable in the interval
$\rho =\rho _2$
is spectrally stable in the interval
![]() $(\rho _\sharp , \rho _+]$
. It is unstable in the Lyapunov sense in the interval
$(\rho _\sharp , \rho _+]$
. It is unstable in the Lyapunov sense in the interval
![]() $ \rho _2> \rho _+ $
.
$ \rho _2> \rho _+ $
.
Acknowledgments
We deeply appreciate suggestions and comments of the referee which contributed significantly to the improvement and clarity of this paper.