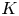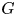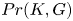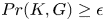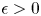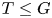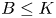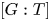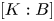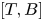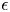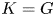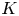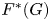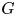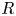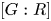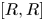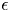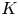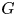1. Introduction
The probability that two randomly chosen elements of a finite group ![]() $G$ commute is given by
$G$ commute is given by
The above number is called the commuting probability (or the commutativity degree) of ![]() $G$. This is a well-studied concept. In the literature one can find publications dealing with problems on the set of possible values of
$G$. This is a well-studied concept. In the literature one can find publications dealing with problems on the set of possible values of ![]() $Pr(G)$ and the influence of
$Pr(G)$ and the influence of ![]() $Pr(G)$ over the structure of
$Pr(G)$ over the structure of ![]() $G$ (see [Reference Eberhard9, Reference Guralnick and Robinson15, Reference Gustafson17, Reference Lescot22, Reference Lescot23] and references therein). The reader can consult [Reference Mann25, Reference Shalev32] and references therein for related developments concerning probabilistic identities in groups.
$G$ (see [Reference Eberhard9, Reference Guralnick and Robinson15, Reference Gustafson17, Reference Lescot22, Reference Lescot23] and references therein). The reader can consult [Reference Mann25, Reference Shalev32] and references therein for related developments concerning probabilistic identities in groups.
P. M. Neumann [Reference Neumann29] proved the following theorem (see also [Reference Eberhard9]).
Theorem 1.1 Let ![]() $G$ be a finite group and let
$G$ be a finite group and let ![]() $\epsilon$ be a positive number such that
$\epsilon$ be a positive number such that ![]() $Pr(G)\geq \epsilon$. Then
$Pr(G)\geq \epsilon$. Then ![]() $G$ has a nilpotent normal subgroup
$G$ has a nilpotent normal subgroup ![]() $R$ of nilpotency class at most
$R$ of nilpotency class at most ![]() $2$ such that both the index
$2$ such that both the index ![]() $[G:R]$ and the order of the commutator subgroup
$[G:R]$ and the order of the commutator subgroup ![]() $[R,R]$ are
$[R,R]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
Throughout the article we use the expression ‘![]() $(a,b,\dots )$-bounded’ to mean that a quantity is bounded from above by a number depending only on the parameters
$(a,b,\dots )$-bounded’ to mean that a quantity is bounded from above by a number depending only on the parameters ![]() $a,b,\dots$.
$a,b,\dots$.
If ![]() $K$ is a subgroup of
$K$ is a subgroup of ![]() $G$, write
$G$, write
This is the probability that an element of ![]() $G$ commutes with an element of
$G$ commutes with an element of ![]() $K$ (the relative commutativity degree of
$K$ (the relative commutativity degree of ![]() $K$ in
$K$ in ![]() $G$).
$G$).
This notion has been studied in several recent papers (see in particular [Reference Erfanian, Rezaei and Lescot10, Reference Nath and Yadav26]). Here we will prove the following proposition.
Proposition 1.2 Let ![]() $K$ be a subgroup of a finite group
$K$ be a subgroup of a finite group ![]() $G$ and let
$G$ and let ![]() $\epsilon$ be a positive number such that
$\epsilon$ be a positive number such that ![]() $Pr(K,G)\geq \epsilon$. Then there is a normal subgroup
$Pr(K,G)\geq \epsilon$. Then there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq K$ such that the indices
$B\leq K$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[K:B]$, and the order of the commutator subgroup
$[K:B]$, and the order of the commutator subgroup ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
Theorem 1.1 can be easily obtained from the above result taking ![]() $K=G$.
$K=G$.
Proposition 1.2 has some interesting consequences. In particular, we will establish the following results.
Recall that the generalized Fitting subgroup ![]() $F^{*}(G)$ of a finite group
$F^{*}(G)$ of a finite group ![]() $G$ is the product of the Fitting subgroup
$G$ is the product of the Fitting subgroup ![]() $F(G)$ and all subnormal quasisimple subgroups; here a group is quasisimple if it is perfect and its quotient by the centre is a non-abelian simple group. Throughout, by a class-
$F(G)$ and all subnormal quasisimple subgroups; here a group is quasisimple if it is perfect and its quotient by the centre is a non-abelian simple group. Throughout, by a class-![]() $c$-nilpotent group we mean a nilpotent group whose nilpotency class is at most
$c$-nilpotent group we mean a nilpotent group whose nilpotency class is at most ![]() $c$.
$c$.
Theorem 1.3 Let ![]() $G$ be a finite group such that
$G$ be a finite group such that ![]() $Pr(F^{*}(G),G)\geq \epsilon$, where
$Pr(F^{*}(G),G)\geq \epsilon$, where ![]() $\epsilon$ is a positive number. Then
$\epsilon$ is a positive number. Then ![]() $G$ has a class-
$G$ has a class-![]() $2$-nilpotent normal subgroup
$2$-nilpotent normal subgroup ![]() $R$ such that both the index
$R$ such that both the index ![]() $[G:R]$ and the order of the commutator subgroup
$[G:R]$ and the order of the commutator subgroup ![]() $[R,R]$ are
$[R,R]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
A somewhat surprising aspect of the above theorem is that information on the commuting probability of a subgroup (in this case ![]() $F^{*}(G)$) enables one to draw a conclusion about
$F^{*}(G)$) enables one to draw a conclusion about ![]() $G$ as strong as in P. M. Neumann's theorem. Yet, several other results with the same conclusion will be established in this paper.
$G$ as strong as in P. M. Neumann's theorem. Yet, several other results with the same conclusion will be established in this paper.
Our next theorem deals with the case where ![]() $K$ is a subgroup containing
$K$ is a subgroup containing ![]() $\gamma _i(G)$ for some
$\gamma _i(G)$ for some ![]() $i\geq 1$. Here and throughout the paper
$i\geq 1$. Here and throughout the paper ![]() $\gamma _i(G)$ denotes the
$\gamma _i(G)$ denotes the ![]() $i$th term of the lower central series of
$i$th term of the lower central series of ![]() $G$.
$G$.
Theorem 1.4 Let ![]() $K$ be a subgroup of a finite group
$K$ be a subgroup of a finite group ![]() $G$ containing
$G$ containing ![]() $\gamma _i(G)$ for some
$\gamma _i(G)$ for some ![]() $i\geq 1$. Suppose that
$i\geq 1$. Suppose that ![]() $Pr(K,G)\geq \epsilon$, where
$Pr(K,G)\geq \epsilon$, where ![]() $\epsilon$ is a positive number. Then
$\epsilon$ is a positive number. Then ![]() $G$ has a nilpotent normal subgroup
$G$ has a nilpotent normal subgroup ![]() $R$ of nilpotency class at most
$R$ of nilpotency class at most ![]() $i+1$ such that both the index
$i+1$ such that both the index ![]() $[G:R]$ and the order of
$[G:R]$ and the order of ![]() $\gamma _{i+1}(R)$ are
$\gamma _{i+1}(R)$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
P. M. Neumann's theorem is a particular case of the above result (take ![]() $i=1$).
$i=1$).
In the same spirit, we conclude that ![]() $G$ has a nilpotent subgroup of
$G$ has a nilpotent subgroup of ![]() $\epsilon$-bounded index if
$\epsilon$-bounded index if ![]() $K$ is a verbal subgroup corresponding to a word implying virtual nilpotency such that
$K$ is a verbal subgroup corresponding to a word implying virtual nilpotency such that ![]() $Pr(K,G)\geq \epsilon$. Given a group-word
$Pr(K,G)\geq \epsilon$. Given a group-word ![]() $w$, we write
$w$, we write ![]() $w(G)$ for the corresponding verbal subgroup of a group
$w(G)$ for the corresponding verbal subgroup of a group ![]() $G$, that is the subgroup generated by the values of
$G$, that is the subgroup generated by the values of ![]() $w$ in
$w$ in ![]() $G$. Recall that a group-word
$G$. Recall that a group-word ![]() $w$ is said to imply virtual nilpotency if every finitely generated metabelian group
$w$ is said to imply virtual nilpotency if every finitely generated metabelian group ![]() $G$ where
$G$ where ![]() $w$ is a law, that is
$w$ is a law, that is ![]() $w(G)=1$, has a nilpotent subgroup of finite index. Such words admit several important characterizations (see [Reference Black2, Reference Burns and Medvedev4, Reference Groves12]). In particular, by a result of Gruenberg [Reference Gruenberg13], the
$w(G)=1$, has a nilpotent subgroup of finite index. Such words admit several important characterizations (see [Reference Black2, Reference Burns and Medvedev4, Reference Groves12]). In particular, by a result of Gruenberg [Reference Gruenberg13], the ![]() $j$-Engel word
$j$-Engel word ![]() $[x,y,\dots,y]$, where
$[x,y,\dots,y]$, where ![]() $y$ appears
$y$ appears ![]() $j \ge 1$ times, implies virtual nilpotency. Burns and Medvedev proved that for any word
$j \ge 1$ times, implies virtual nilpotency. Burns and Medvedev proved that for any word ![]() $w$ implying virtual nilpotency there exist integers
$w$ implying virtual nilpotency there exist integers ![]() $e$ and
$e$ and ![]() $c$ depending only on
$c$ depending only on ![]() $w$ such that every finite group
$w$ such that every finite group ![]() $G$, in which
$G$, in which ![]() $w$ is a law, has a class-
$w$ is a law, has a class-![]() $c$-nilpotent normal subgroup
$c$-nilpotent normal subgroup ![]() $N$ such that
$N$ such that ![]() $G^{e}\leq N$ [Reference Burns and Medvedev4]. Here
$G^{e}\leq N$ [Reference Burns and Medvedev4]. Here ![]() $G^{e}$ denotes the subgroup generated by all
$G^{e}$ denotes the subgroup generated by all ![]() $e$th powers of elements of
$e$th powers of elements of ![]() $G$. Our next theorem provides a probabilistic variation of this result.
$G$. Our next theorem provides a probabilistic variation of this result.
Theorem 1.5 Let ![]() $w$ be a group-word implying virtual nilpotency. Suppose that
$w$ be a group-word implying virtual nilpotency. Suppose that ![]() $K$ is a subgroup of a finite group
$K$ is a subgroup of a finite group ![]() $G$ such that
$G$ such that ![]() $w(G)\leq K$ and
$w(G)\leq K$ and ![]() $Pr(K,G)\geq \epsilon$, where
$Pr(K,G)\geq \epsilon$, where ![]() $\epsilon$ is a positive number. There is an
$\epsilon$ is a positive number. There is an ![]() $(\epsilon,w)$-bounded integer
$(\epsilon,w)$-bounded integer ![]() $e$ and a
$e$ and a ![]() $w$-bounded integer
$w$-bounded integer ![]() $c$ such that
$c$ such that ![]() $G^{e}$ is nilpotent of class at most
$G^{e}$ is nilpotent of class at most ![]() $c$.
$c$.
We also consider finite groups with a given value of ![]() $Pr(P,G)$, where
$Pr(P,G)$, where ![]() $P$ is a Sylow
$P$ is a Sylow ![]() $p$-subgroup of
$p$-subgroup of ![]() $G$.
$G$.
Theorem 1.6 Let ![]() $P$ be a Sylow
$P$ be a Sylow ![]() $p$-subgroup of a finite group
$p$-subgroup of a finite group ![]() $G$ such that
$G$ such that ![]() $Pr(P,G) \ge \epsilon$, where
$Pr(P,G) \ge \epsilon$, where ![]() $\epsilon$ is a positive number. Then
$\epsilon$ is a positive number. Then ![]() $G$ has a class-
$G$ has a class-![]() $2$-nilpotent normal
$2$-nilpotent normal ![]() $p$-subgroup
$p$-subgroup ![]() $L$ such that both the index
$L$ such that both the index ![]() $[P:L]$ and the order of
$[P:L]$ and the order of ![]() $[L,L]$ are
$[L,L]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
Once we have information on the commuting probability of all Sylow subgroups of ![]() $G$, the result is as strong as in P. M. Neumann's theorem.
$G$, the result is as strong as in P. M. Neumann's theorem.
Theorem 1.7 Let ![]() $\epsilon >0$, and let
$\epsilon >0$, and let ![]() $G$ be a finite group such that
$G$ be a finite group such that ![]() $Pr(P,G) \ge \epsilon$ whenever
$Pr(P,G) \ge \epsilon$ whenever ![]() $P$ is a Sylow subgroup. Then
$P$ is a Sylow subgroup. Then ![]() $G$ has a nilpotent normal subgroup
$G$ has a nilpotent normal subgroup ![]() $R$ of nilpotency class at most
$R$ of nilpotency class at most ![]() $2$ such that both the index
$2$ such that both the index ![]() $[G:R]$ and the order of the commutator subgroup
$[G:R]$ and the order of the commutator subgroup ![]() $[R,R]$ are
$[R,R]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
If ![]() $\phi$ is an automorphism of a group
$\phi$ is an automorphism of a group ![]() $G$, the centralizer
$G$, the centralizer ![]() $C_G(\phi )$ is the subgroup formed by the elements
$C_G(\phi )$ is the subgroup formed by the elements ![]() $x\in G$ such that
$x\in G$ such that ![]() $x^{\phi }=x$. In the case where
$x^{\phi }=x$. In the case where ![]() $C_G(\phi )=1$ the automorphism
$C_G(\phi )=1$ the automorphism ![]() $\phi$ is called fixed-point-free. A famous result of Thompson [Reference Thompson33] says that a finite group admitting a fixed-point-free automorphism of prime order is nilpotent. Higman proved that for each prime
$\phi$ is called fixed-point-free. A famous result of Thompson [Reference Thompson33] says that a finite group admitting a fixed-point-free automorphism of prime order is nilpotent. Higman proved that for each prime ![]() $p$ there exists a number
$p$ there exists a number ![]() $h=h(p)$ depending only on
$h=h(p)$ depending only on ![]() $p$ such that whenever a nilpotent group
$p$ such that whenever a nilpotent group ![]() $G$ admits a fixed-point-free automorphism of order
$G$ admits a fixed-point-free automorphism of order ![]() $p$, it follows that
$p$, it follows that ![]() $G$ has nilpotency class at most
$G$ has nilpotency class at most ![]() $h$ [Reference Higman19]. Therefore a finite group admitting a fixed-point-free automorphism of order
$h$ [Reference Higman19]. Therefore a finite group admitting a fixed-point-free automorphism of order ![]() $p$ is nilpotent of class at most
$p$ is nilpotent of class at most ![]() $h$. Khukhro obtained the following ‘almost fixed-point-free’ generalization of this fact [Reference Khukhro21]: if a finite group
$h$. Khukhro obtained the following ‘almost fixed-point-free’ generalization of this fact [Reference Khukhro21]: if a finite group ![]() $G$ admits an automorphism
$G$ admits an automorphism ![]() $\phi$ of prime order
$\phi$ of prime order ![]() $p$ such that
$p$ such that ![]() $C_G(\phi )$ has order
$C_G(\phi )$ has order ![]() $m$, then
$m$, then ![]() $G$ has a nilpotent subgroup of
$G$ has a nilpotent subgroup of ![]() $p$-bounded nilpotency class and
$p$-bounded nilpotency class and ![]() $(m,p)$-bounded index. We will establish a probabilistic variation of the above results. Recall that an automorphism
$(m,p)$-bounded index. We will establish a probabilistic variation of the above results. Recall that an automorphism ![]() $\phi$ of a finite group
$\phi$ of a finite group ![]() $G$ is called coprime if
$G$ is called coprime if ![]() $(|G|,|\phi |)=1$.
$(|G|,|\phi |)=1$.
Theorem 1.8 Let ![]() $G$ be a finite group admitting a coprime automorphism
$G$ be a finite group admitting a coprime automorphism ![]() $\phi$ of prime order
$\phi$ of prime order ![]() $p$ such that
$p$ such that ![]() $Pr(C_G(\phi ),G)\geq \epsilon$ where
$Pr(C_G(\phi ),G)\geq \epsilon$ where ![]() $\epsilon$ is a positive number. Then
$\epsilon$ is a positive number. Then ![]() $G$ has a nilpotent subgroup of
$G$ has a nilpotent subgroup of ![]() $p$-bounded nilpotency class and
$p$-bounded nilpotency class and ![]() $(\epsilon,p)$-bounded index.
$(\epsilon,p)$-bounded index.
An even stronger conclusion will be derived about groups admitting an elementary abelian group of automorphisms of rank at least 2.
Theorem 1.9 Let ![]() $\epsilon >0$, and let
$\epsilon >0$, and let ![]() $G$ be a finite group admitting an elementary abelian coprime group of automorphisms
$G$ be a finite group admitting an elementary abelian coprime group of automorphisms ![]() $A$ of order
$A$ of order ![]() $p^{2}$ such that
$p^{2}$ such that ![]() $Pr(C_G(\phi ),G)\geq \epsilon$ for each nontrivial
$Pr(C_G(\phi ),G)\geq \epsilon$ for each nontrivial ![]() $\phi \in A$. Then
$\phi \in A$. Then ![]() $G$ has a class-
$G$ has a class-![]() $2$-nilpotent normal subgroup
$2$-nilpotent normal subgroup ![]() $R$ such that both the index
$R$ such that both the index ![]() $[G:R]$ and the order of
$[G:R]$ and the order of ![]() $[R,R]$ are
$[R,R]$ are ![]() $(\epsilon,p)$-bounded.
$(\epsilon,p)$-bounded.
Proposition 1.2, which is a key result of this paper, will be proved in the next section. The other results will be established in § 3–5.
2. The key result
A group is said to be a BFC-group if its conjugacy classes are finite and of bounded size. A famous theorem of B. H. Neumann says that in a BFC-group the commutator subgroup ![]() $G'$ is finite [Reference Neumann27]. It follows that if
$G'$ is finite [Reference Neumann27]. It follows that if ![]() $|x^{G}|\leq m$ for each
$|x^{G}|\leq m$ for each ![]() $x\in G$, then the order of
$x\in G$, then the order of ![]() $G'$ is bounded by a number depending only on
$G'$ is bounded by a number depending only on ![]() $m$. A first explicit bound for the order of
$m$. A first explicit bound for the order of ![]() $G'$ was found by J. Wiegold [Reference Wiegold34], and the best known was obtained in [Reference Guralnick and Maroti16] (see also [Reference Neumann and Vaughan-Lee28] and [Reference Segal and Shalev31]). The main technical tools employed in this paper are provided by the recent results [Reference Acciarri and Shumyatsky1, Reference Detomi, Morigi and Shumyatsky6–Reference Dierings and Shumyatsky8] strengthening B. H. Neumann's theorem.
$G'$ was found by J. Wiegold [Reference Wiegold34], and the best known was obtained in [Reference Guralnick and Maroti16] (see also [Reference Neumann and Vaughan-Lee28] and [Reference Segal and Shalev31]). The main technical tools employed in this paper are provided by the recent results [Reference Acciarri and Shumyatsky1, Reference Detomi, Morigi and Shumyatsky6–Reference Dierings and Shumyatsky8] strengthening B. H. Neumann's theorem.
A well-known lemma due to Baer says that if ![]() $A,B$ are normal subgroups of a group
$A,B$ are normal subgroups of a group ![]() $G$ such that
$G$ such that ![]() $[A:C_A(B)]\leq m$ and
$[A:C_A(B)]\leq m$ and ![]() $[B:C_B(A)]\leq m$ for some integer
$[B:C_B(A)]\leq m$ for some integer ![]() $m\geq 1$, then
$m\geq 1$, then ![]() $[A,B]$ has finite
$[A,B]$ has finite ![]() $m$-bounded order (see [Reference Robinson30, 14.5.2]).
$m$-bounded order (see [Reference Robinson30, 14.5.2]).
We will require a stronger result. Here and in the rest of the paper, given an element ![]() $x\in G$ and a subgroup
$x\in G$ and a subgroup ![]() $H\leq G$, we write
$H\leq G$, we write ![]() $x^{H}$ for the set of conjugates of
$x^{H}$ for the set of conjugates of ![]() $x$ by elements from
$x$ by elements from ![]() $H$.
$H$.
Lemma 2.1 Let ![]() $m\geq 1$, and let
$m\geq 1$, and let ![]() $G$ be a group containing normal subgroups
$G$ be a group containing normal subgroups ![]() $A,B$ such that
$A,B$ such that ![]() $[A:C_A(y)]\leq m$ and
$[A:C_A(y)]\leq m$ and ![]() $[B:C_B(x)]\leq m$ for all
$[B:C_B(x)]\leq m$ for all ![]() $x\in A$,
$x\in A$, ![]() $y\in B$. Then
$y\in B$. Then ![]() $[A,B]$ has finite
$[A,B]$ has finite ![]() $m$-bounded order.
$m$-bounded order.
Proof. We first prove that, given ![]() $x\in A$ and
$x\in A$ and ![]() $y\in B$, the order of
$y\in B$, the order of ![]() $[x,y]$ is
$[x,y]$ is ![]() $m$-bounded. Let
$m$-bounded. Let ![]() $H=\langle x,y\rangle$. By assumptions,
$H=\langle x,y\rangle$. By assumptions, ![]() $[A:C_A(y)]\leq m$ and
$[A:C_A(y)]\leq m$ and ![]() $[B:C_B(x)]\leq m$. Hence there exists an
$[B:C_B(x)]\leq m$. Hence there exists an ![]() $m$-bounded number
$m$-bounded number ![]() $l$ such that
$l$ such that ![]() $x^{l}$ and
$x^{l}$ and ![]() $y^{l}$ are contained in
$y^{l}$ are contained in ![]() $Z(H)$ (e.g. we can take
$Z(H)$ (e.g. we can take ![]() $l=m!$). Let
$l=m!$). Let ![]() $D=A\cap B \cap H$ and
$D=A\cap B \cap H$ and ![]() $N=\langle D,x^{l},y^{l}\rangle$. Then
$N=\langle D,x^{l},y^{l}\rangle$. Then ![]() $H/N$ is abelian of order at most
$H/N$ is abelian of order at most ![]() $l^{2}$. Both
$l^{2}$. Both ![]() $x$ and
$x$ and ![]() $y$ have centralizers of index at most
$y$ have centralizers of index at most ![]() $m$ in
$m$ in ![]() $N$. Moreover every element of
$N$. Moreover every element of ![]() $N$ has centralizer of index at most
$N$ has centralizer of index at most ![]() $m$ in
$m$ in ![]() $N$. Indeed
$N$. Indeed ![]() $|d^{N}| \le |d^{A}|\le m$ for every
$|d^{N}| \le |d^{A}|\le m$ for every ![]() $d \in D \le A\cap B$. So, every element of
$d \in D \le A\cap B$. So, every element of ![]() $H$ is a product of at most
$H$ is a product of at most ![]() $l^{2}+1$ elements each of which has centralizer of index at most
$l^{2}+1$ elements each of which has centralizer of index at most ![]() $m$ in
$m$ in ![]() $N$. Therefore each element of
$N$. Therefore each element of ![]() $H$ has centralizer of
$H$ has centralizer of ![]() $m$-bounded index in
$m$-bounded index in ![]() $H$. We conclude that
$H$. We conclude that ![]() $H$ is a BFC-group in which the sizes of conjugacy classes are
$H$ is a BFC-group in which the sizes of conjugacy classes are ![]() $m$-bounded. Hence
$m$-bounded. Hence ![]() $|H'|$ is
$|H'|$ is ![]() $m$-bounded and so the order of
$m$-bounded and so the order of ![]() $[x,y]$ is
$[x,y]$ is ![]() $m$-bounded, too.
$m$-bounded, too.
Now we claim that for every ![]() $x \in A$, the subgroup
$x \in A$, the subgroup ![]() $[x,B]$ has finite
$[x,B]$ has finite ![]() $m$-bounded order. Indeed,
$m$-bounded order. Indeed, ![]() $x$ has at most
$x$ has at most ![]() $m$ conjugates
$m$ conjugates ![]() $\{x^{b_1}, \dots, x^{b_m} \}$ in
$\{x^{b_1}, \dots, x^{b_m} \}$ in ![]() $B$, where
$B$, where ![]() $b_1, \dots, b_m \in B$, so
$b_1, \dots, b_m \in B$, so ![]() $[x,B]$ is generated by at most
$[x,B]$ is generated by at most ![]() $m$ elements. Let
$m$ elements. Let ![]() $C$ be a maximal normal subgroup of
$C$ be a maximal normal subgroup of ![]() $B$ contained in
$B$ contained in ![]() $C_B(x)$. Clearly
$C_B(x)$. Clearly ![]() $C$ has
$C$ has ![]() $m$-bounded index in
$m$-bounded index in ![]() $B$ and centralizes
$B$ and centralizes ![]() $[x,B]$. Thus, the centre of
$[x,B]$. Thus, the centre of ![]() $[x,B]$ has
$[x,B]$ has ![]() $m$-bounded index in
$m$-bounded index in ![]() $[x,B]$. It follows from Schur's theorem [Reference Robinson30, 10.1.4] that the derived subgroup of
$[x,B]$. It follows from Schur's theorem [Reference Robinson30, 10.1.4] that the derived subgroup of ![]() $[x,B]$ has finite
$[x,B]$ has finite ![]() $m$-bounded order. Since
$m$-bounded order. Since ![]() $[x,B]$ is generated by at most
$[x,B]$ is generated by at most ![]() $m$ elements of
$m$ elements of ![]() $m$-bounded order, we deduce that the order of
$m$-bounded order, we deduce that the order of ![]() $[x,B]$ is finite and
$[x,B]$ is finite and ![]() $m$-bounded.
$m$-bounded.
Choose ![]() $a\in A$ such that
$a\in A$ such that ![]() $[B:C_B(a)]=\max _{x \in A} [B:C_B(x)]$ and set
$[B:C_B(a)]=\max _{x \in A} [B:C_B(x)]$ and set ![]() $n=[B:C_B(a)]$, where
$n=[B:C_B(a)]$, where ![]() $n \le m$. Let
$n \le m$. Let ![]() $b_1,\dots, b_n$ be elements of
$b_1,\dots, b_n$ be elements of ![]() $B$ such that
$B$ such that ![]() $a^{B}=\{a^{b_1},\dots, a^{b_n}\}$ is the set of (distinct) conjugates of
$a^{B}=\{a^{b_1},\dots, a^{b_n}\}$ is the set of (distinct) conjugates of ![]() $a$ by elements of
$a$ by elements of ![]() $B$. Set
$B$. Set ![]() $U=C_A(b_1,\dots,b_n)$ and note that
$U=C_A(b_1,\dots,b_n)$ and note that ![]() $U$ has
$U$ has ![]() $m$-bounded index in
$m$-bounded index in ![]() $A$. Given
$A$. Given ![]() $u\in U$, the elements
$u\in U$, the elements ![]() $(ua)^{b_1},\dots, (ua)^{b_n}$ form the conjugacy class
$(ua)^{b_1},\dots, (ua)^{b_n}$ form the conjugacy class ![]() $(ua)^{B}$ because they are all different and their number is the allowed maximum. So, for an arbitrary element
$(ua)^{B}$ because they are all different and their number is the allowed maximum. So, for an arbitrary element ![]() $y\in B$ there exists
$y\in B$ there exists ![]() $i$ such that
$i$ such that ![]() $(ua)^{y}=(ua)^{b_i}=u a^{b_i}$. It follows that
$(ua)^{y}=(ua)^{b_i}=u a^{b_i}$. It follows that ![]() $u^{-1}u^{y}=a^{b_i}a^{-y}$, hence
$u^{-1}u^{y}=a^{b_i}a^{-y}$, hence
Therefore ![]() $[U,B]\leq [a,B]$. Let
$[U,B]\leq [a,B]$. Let ![]() $a_1,\dots,a_s$ be coset representatives of
$a_1,\dots,a_s$ be coset representatives of ![]() $U$ in
$U$ in ![]() $A$ and note that
$A$ and note that ![]() $s$ is
$s$ is ![]() $m$-bounded. As each
$m$-bounded. As each ![]() $[x,B]$ is normal in
$[x,B]$ is normal in ![]() $B$ and
$B$ and ![]() $[U,B]\leq [a,B]$, we deduce that
$[U,B]\leq [a,B]$, we deduce that ![]() $[A,B]=[a,B]\prod [a_i,B]$. So
$[A,B]=[a,B]\prod [a_i,B]$. So ![]() $[A,B]$ is a product of
$[A,B]$ is a product of ![]() $m$-boundedly many subgroups of
$m$-boundedly many subgroups of ![]() $m$-bounded order. These subgroups are normal in
$m$-bounded order. These subgroups are normal in ![]() $B$ and therefore their product has finite
$B$ and therefore their product has finite ![]() $m$-bounded order.
$m$-bounded order.
In the next lemma the subgroup ![]() $B$ is not necessarily normal. Instead, we require that
$B$ is not necessarily normal. Instead, we require that ![]() $B$ is contained in an abelian normal subgroup. Throughout,
$B$ is contained in an abelian normal subgroup. Throughout, ![]() $\langle H^{G}\rangle$ denotes the normal closure of a subgroup
$\langle H^{G}\rangle$ denotes the normal closure of a subgroup ![]() $H$ in
$H$ in ![]() $G$.
$G$.
Lemma 2.2 Let ![]() $m\geq 1$, and let
$m\geq 1$, and let ![]() $G$ be a group containing a normal subgroup
$G$ be a group containing a normal subgroup ![]() $A$ and a subgroup
$A$ and a subgroup ![]() $B$ such that
$B$ such that ![]() $[A:C_A(y)]\leq m$ and
$[A:C_A(y)]\leq m$ and ![]() $[B:C_B(x)]\leq m$ for all
$[B:C_B(x)]\leq m$ for all ![]() $x\in A$,
$x\in A$, ![]() $y\in B$. Assume further that
$y\in B$. Assume further that ![]() $\langle B^{G}\rangle$ is abelian. Then
$\langle B^{G}\rangle$ is abelian. Then ![]() $[A, B]$ has finite
$[A, B]$ has finite ![]() $m$-bounded order.
$m$-bounded order.
Proof. Without loss of generality we can assume that ![]() $G=AB$. Set
$G=AB$. Set ![]() $L=\langle B^{G}\rangle =\langle B^{A}\rangle$.
$L=\langle B^{G}\rangle =\langle B^{A}\rangle$.
Let ![]() $x\in A$. There is an
$x\in A$. There is an ![]() $m$-bounded number
$m$-bounded number ![]() $l$ such that
$l$ such that ![]() $x$ centralizes
$x$ centralizes ![]() $y^{l}$ for every
$y^{l}$ for every ![]() $y\in B$. Since
$y\in B$. Since ![]() $L$ is abelian,
$L$ is abelian, ![]() $[x,y]^{i}=[x,y^{i}]$ for each
$[x,y]^{i}=[x,y^{i}]$ for each ![]() $i$ and therefore the order of
$i$ and therefore the order of ![]() $[x,y]$ is at most
$[x,y]$ is at most ![]() $l$. Thus
$l$. Thus ![]() $[x,B]$ is an abelian subgroup generated by at most
$[x,B]$ is an abelian subgroup generated by at most ![]() $m$ elements of
$m$ elements of ![]() $m$-bounded order, whence
$m$-bounded order, whence ![]() $[x,B]$ has finite
$[x,B]$ has finite ![]() $m$-bounded order.
$m$-bounded order.
Now we choose ![]() $a\in A$ such that
$a\in A$ such that ![]() $[B:C_B(a)]$ is as big as possible. Let
$[B:C_B(a)]$ is as big as possible. Let ![]() $b_1,\dots,b_{m}$ be elements of
$b_1,\dots,b_{m}$ be elements of ![]() $B$ such that
$B$ such that ![]() $a^{B}=\{a^{b_1},\dots,a^{b_{m}}\}$. Set
$a^{B}=\{a^{b_1},\dots,a^{b_{m}}\}$. Set ![]() $U=C_A(b_1,\dots,b_m)$ and note that
$U=C_A(b_1,\dots,b_m)$ and note that ![]() $U$ has
$U$ has ![]() $m$-bounded index in
$m$-bounded index in ![]() $A$. Arguing as in the previous lemma, we see that for arbitrary
$A$. Arguing as in the previous lemma, we see that for arbitrary ![]() $u\in U$ and
$u\in U$ and ![]() $y\in B$, the conjugate
$y\in B$, the conjugate ![]() $(ua)^{y}$ belongs to the set
$(ua)^{y}$ belongs to the set ![]() $\{(ua)^{b_1},\dots, (ua)^{b_m}\}$. Let
$\{(ua)^{b_1},\dots, (ua)^{b_m}\}$. Let ![]() $(ua)^{y}=(ua)^{b_i}$. Then
$(ua)^{y}=(ua)^{b_i}$. Then ![]() $u^{-1}u^{y}=a^{b_i}a^{-y}$ and hence
$u^{-1}u^{y}=a^{b_i}a^{-y}$ and hence ![]() $[u,y]=a^{b_i}a^{-y}\in [a, B]$. Therefore
$[u,y]=a^{b_i}a^{-y}\in [a, B]$. Therefore ![]() $[U,B]\leq [a,B]$.
$[U,B]\leq [a,B]$.
Let ![]() $V=\cap _{x\in A}U^{x}$ be the maximal normal subgroup of
$V=\cap _{x\in A}U^{x}$ be the maximal normal subgroup of ![]() $A$ contained in
$A$ contained in ![]() $U$. We know that
$U$. We know that ![]() $[V,B]$ has
$[V,B]$ has ![]() $m$-bounded order, since
$m$-bounded order, since ![]() $[V,B]\le [a,B]$. Denote the index
$[V,B]\le [a,B]$. Denote the index ![]() $[A:V]$ by
$[A:V]$ by ![]() $s$. Evidently,
$s$. Evidently, ![]() $s$ is
$s$ is ![]() $m$-bounded. Let
$m$-bounded. Let ![]() $a_1,\dots,a_s$ be a transversal of
$a_1,\dots,a_s$ be a transversal of ![]() $V$ in
$V$ in ![]() $A$. As
$A$. As ![]() $[V,B] \le L=\langle B^{A}\rangle$ is abelian, we have
$[V,B] \le L=\langle B^{A}\rangle$ is abelian, we have
 \[ \langle[V,B]^{G}\rangle=\langle[V,B]^{A}\rangle=\prod_{i=1}^{s}[V,B]^{a_i}. \]
\[ \langle[V,B]^{G}\rangle=\langle[V,B]^{A}\rangle=\prod_{i=1}^{s}[V,B]^{a_i}. \]
Thus ![]() $[V,L]=[V, B^{A}] = \langle [V,B]^{A}\rangle$ is a product of
$[V,L]=[V, B^{A}] = \langle [V,B]^{A}\rangle$ is a product of ![]() $m$-boundedly many subgroups of
$m$-boundedly many subgroups of ![]() $m$-bounded order, and hence it has
$m$-bounded order, and hence it has ![]() $m$-bounded order. Write
$m$-bounded order. Write
 \[ L=\langle B^{A}\rangle \leq \langle B^{V a_i} \mid i=1, \dots s \rangle \leq [V,L]\prod_{i=1}^{s}B^{a_i}. \]
\[ L=\langle B^{A}\rangle \leq \langle B^{V a_i} \mid i=1, \dots s \rangle \leq [V,L]\prod_{i=1}^{s}B^{a_i}. \]
Thus, it becomes clear that ![]() $L$ is a product of
$L$ is a product of ![]() $m$-boundedly many conjugates of
$m$-boundedly many conjugates of ![]() $B$. Say
$B$. Say ![]() $L$ is a product of
$L$ is a product of ![]() $t$ conjugates of
$t$ conjugates of ![]() $B$. Then, every
$B$. Then, every ![]() $y \in L$ can be written as a product of at most
$y \in L$ can be written as a product of at most ![]() $t$ conjugates of elements of
$t$ conjugates of elements of ![]() $B$ and consequently
$B$ and consequently ![]() $[A: C_A(y)] \le m^{t}.$ Moreover, as
$[A: C_A(y)] \le m^{t}.$ Moreover, as ![]() $A$ is normal in
$A$ is normal in ![]() $G$ and
$G$ and ![]() $|a^{B}| \le m$ for every
$|a^{B}| \le m$ for every ![]() $a\in A$, the conjugacy class
$a\in A$, the conjugacy class ![]() $x^{L}$ of an element
$x^{L}$ of an element ![]() $x \in A$ has size at most
$x \in A$ has size at most ![]() $m^{t}$. Now lemma 2.1 shows that
$m^{t}$. Now lemma 2.1 shows that ![]() $[A,B] \le [A,L]$ has finite
$[A,B] \le [A,L]$ has finite ![]() $m$-bounded order.
$m$-bounded order.
We will now show that if ![]() $K$ is a subgroup of a finite group
$K$ is a subgroup of a finite group ![]() $G$ and
$G$ and ![]() $N$ is a normal subgroup of
$N$ is a normal subgroup of ![]() $G$, then
$G$, then ![]() $Pr(KN/N,G/N)\geq Pr(K,G)$. More precisely, we will establish the following lemma.
$Pr(KN/N,G/N)\geq Pr(K,G)$. More precisely, we will establish the following lemma.
Lemma 2.3 Let ![]() $N$ be a normal subgroup of a finite group
$N$ be a normal subgroup of a finite group ![]() $G$, and let
$G$, and let ![]() $K\leq G$. Then
$K\leq G$. Then ![]() $Pr(K,G)\leq Pr(KN/N,G/N)Pr(N\cap K,N)$.
$Pr(K,G)\leq Pr(KN/N,G/N)Pr(N\cap K,N)$.
This is an improvement over [Reference Erfanian, Rezaei and Lescot10, theorem 3.9] where the result was obtained under the additional hypothesis that ![]() $N\leq K$.
$N\leq K$.
Proof. In what follows ![]() $\bar {G}=G/N$ and
$\bar {G}=G/N$ and ![]() $\bar {K}=KN/N$. Write
$\bar {K}=KN/N$. Write ![]() $\bar {K_0}$ for the set of cosets
$\bar {K_0}$ for the set of cosets ![]() $(N\cap K)h$ with
$(N\cap K)h$ with ![]() $h\in K$. If
$h\in K$. If ![]() $S_0=(N\cap K)h\in \bar {K_0}$, write
$S_0=(N\cap K)h\in \bar {K_0}$, write ![]() $S$ for the coset
$S$ for the coset ![]() $Nh\in \bar {K}$. Of course, we have a natural one-to-one correspondence between
$Nh\in \bar {K}$. Of course, we have a natural one-to-one correspondence between ![]() $\bar {K_0}$ and
$\bar {K_0}$ and ![]() $\bar {K}$.
$\bar {K}$.
Write
 \begin{align*} |K||G|Pr(K,G)&=\sum_{x\in K}|C_G(x)|=\sum_{S_0\in\bar{K_0}}\sum_{x\in S_0}\frac{|C_G(x)N|}{|N|}|C_N(x)|\\ &\leq\sum_{S_0\in\bar{K_0}}\sum_{x\in S_0}|C_{\bar{G}}(xN)||C_N(x)|=\sum_{S\in\bar{K}}|C_{\bar{G}}(S)|\sum_{x\in S_0}|C_N(x)|\\ &=\sum_{S\in\bar{K}}|C_{\bar{G}}(S)|\sum_{y\in N}|C_{S_0}(y)|.\\ \end{align*}
\begin{align*} |K||G|Pr(K,G)&=\sum_{x\in K}|C_G(x)|=\sum_{S_0\in\bar{K_0}}\sum_{x\in S_0}\frac{|C_G(x)N|}{|N|}|C_N(x)|\\ &\leq\sum_{S_0\in\bar{K_0}}\sum_{x\in S_0}|C_{\bar{G}}(xN)||C_N(x)|=\sum_{S\in\bar{K}}|C_{\bar{G}}(S)|\sum_{x\in S_0}|C_N(x)|\\ &=\sum_{S\in\bar{K}}|C_{\bar{G}}(S)|\sum_{y\in N}|C_{S_0}(y)|.\\ \end{align*}
If ![]() $C_{S_0}(y)\neq \emptyset$, then there is
$C_{S_0}(y)\neq \emptyset$, then there is ![]() $y_0\in C_{S_0}(y)$ and so
$y_0\in C_{S_0}(y)$ and so ![]() $S_0=(N\cap K)y_0$. Therefore
$S_0=(N\cap K)y_0$. Therefore
Conclude that
Observe that
 \[ \sum_{S\in\bar{K}}|C_{\bar{G}}(S)|=\frac{|K|}{|N\cap K|}\frac{|G|}{|N|}Pr(\bar{K},\bar{G}) \]
\[ \sum_{S\in\bar{K}}|C_{\bar{G}}(S)|=\frac{|K|}{|N\cap K|}\frac{|G|}{|N|}Pr(\bar{K},\bar{G}) \]and
It follows that ![]() $Pr(K,G)\leq Pr(\bar {K},\bar {G})Pr(N\cap K,N)$, as required.
$Pr(K,G)\leq Pr(\bar {K},\bar {G})Pr(N\cap K,N)$, as required.
The following theorem is taken from [Reference Acciarri and Shumyatsky1]. It plays a crucial role in the proof of proposition 1.2.
Theorem 2.4 Let ![]() $m$ be a positive integer,
$m$ be a positive integer, ![]() $G$ a group having a subgroup
$G$ a group having a subgroup ![]() $K$ such that
$K$ such that ![]() $|x^{G}| \le m$ for each
$|x^{G}| \le m$ for each ![]() $x\in K$, and let
$x\in K$, and let ![]() $H=\langle K^{G}\rangle$. Then the order of the commutator subgroup
$H=\langle K^{G}\rangle$. Then the order of the commutator subgroup ![]() $[H,H]$ is finite and
$[H,H]$ is finite and ![]() $m$-bounded.
$m$-bounded.
A proof of the next lemma can be found in Eberhard [Reference Eberhard9, lemma 2.1].
Lemma 2.5 Let ![]() $G$ be a finite group and
$G$ be a finite group and ![]() $X$ a symmetric subset of
$X$ a symmetric subset of ![]() $G$ containing the identity. Then
$G$ containing the identity. Then ![]() $\langle X \rangle = X^{3r}$ provided
$\langle X \rangle = X^{3r}$ provided ![]() $(r+1)|X| > |G|$.
$(r+1)|X| > |G|$.
We are now ready to prove proposition 1.2 which we restate here for the reader's convenience:
Let ![]() $\epsilon >0$, and let
$\epsilon >0$, and let ![]() $G$ be a finite group having a subgroup
$G$ be a finite group having a subgroup ![]() $K$ such that
$K$ such that ![]() $Pr(K,G)\geq \epsilon$. Then there is a normal subgroup
$Pr(K,G)\geq \epsilon$. Then there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq K$ such that the indices
$B\leq K$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[K:B]$ and the order of
$[K:B]$ and the order of ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
Proof of proposition 1.2. Set
Note that ![]() $K \setminus X=\{ x\in K \mid |C_G(x)|\leq (\epsilon /2) |G| \}$, whence
$K \setminus X=\{ x\in K \mid |C_G(x)|\leq (\epsilon /2) |G| \}$, whence
 \begin{align*} \epsilon |K||G| &\le | \{ (x,y) \in K\times G \mid xy=yx \} |=\sum_{x\in K}|C_G(x)|\\ &\le \sum_{x \in X} |G| + \sum_{x \in K \setminus X} \frac{\epsilon}{2} |G|\\ &\le |X| |G| +(|K| - |X|)\frac{\epsilon}{2}|G|. \end{align*}
\begin{align*} \epsilon |K||G| &\le | \{ (x,y) \in K\times G \mid xy=yx \} |=\sum_{x\in K}|C_G(x)|\\ &\le \sum_{x \in X} |G| + \sum_{x \in K \setminus X} \frac{\epsilon}{2} |G|\\ &\le |X| |G| +(|K| - |X|)\frac{\epsilon}{2}|G|. \end{align*}
Therefore ![]() $\epsilon |K| \le |X|+ ({\epsilon }/{2}) (|K| - |X|)$, whence
$\epsilon |K| \le |X|+ ({\epsilon }/{2}) (|K| - |X|)$, whence ![]() $({\epsilon }/{2}) |K| < |X|$. Clearly,
$({\epsilon }/{2}) |K| < |X|$. Clearly, ![]() $|B| \ge |X| > ({\epsilon }/{2}) |K|$ and so the index of
$|B| \ge |X| > ({\epsilon }/{2}) |K|$ and so the index of ![]() $B$ in
$B$ in ![]() $K$ is at most
$K$ is at most ![]() $2/\epsilon$. As
$2/\epsilon$. As ![]() $X$ is symmetric and
$X$ is symmetric and ![]() $(2/\epsilon ) |X| > |K|$, it follows from lemma 2.5 that every element of
$(2/\epsilon ) |X| > |K|$, it follows from lemma 2.5 that every element of ![]() $B$ is a product of at most
$B$ is a product of at most ![]() $6/\epsilon$ elements of
$6/\epsilon$ elements of ![]() $X$. Therefore
$X$. Therefore ![]() $|b^{G}| \le (2/\epsilon )^{6/\epsilon }$ for every
$|b^{G}| \le (2/\epsilon )^{6/\epsilon }$ for every ![]() $b \in B$.
$b \in B$.
Let ![]() $L=\langle B^{G}\rangle$. Theorem 2.4 tells us that the commutator subgroup
$L=\langle B^{G}\rangle$. Theorem 2.4 tells us that the commutator subgroup ![]() $[L,L]$ has
$[L,L]$ has ![]() $\epsilon$-bounded order. Let us use the bar notation for the images of the subgroups of
$\epsilon$-bounded order. Let us use the bar notation for the images of the subgroups of ![]() $G$ in
$G$ in ![]() $G/[L,L]$. By lemma 2.3,
$G/[L,L]$. By lemma 2.3,
Moreover, ![]() $[\bar K: \bar B] \le [K:B] \le {\epsilon }/{2}$ and
$[\bar K: \bar B] \le [K:B] \le {\epsilon }/{2}$ and ![]() $|\bar b^{ \bar G}| \le |b^{G}| \le (2/\epsilon )^{6/\epsilon }$. Thus we can pass to the quotient over
$|\bar b^{ \bar G}| \le |b^{G}| \le (2/\epsilon )^{6/\epsilon }$. Thus we can pass to the quotient over ![]() $[L,L]$ and assume that
$[L,L]$ and assume that ![]() $L$ is abelian.
$L$ is abelian.
Now we set
Note that
 \begin{align*} \epsilon |K||G| & \le | \{ (x,y) \in K \times G \mid xy=yx \} |\\ &\le \sum_{y \in Y} |K| + \sum_{y \in G \setminus Y} \frac{\epsilon}{2} |K|\\ &\le |Y| |K| +(|G| - |Y|)\frac{\epsilon}{2}|K| \le |Y| |K|+\frac{\epsilon}{2}|G| |K|. \end{align*}
\begin{align*} \epsilon |K||G| & \le | \{ (x,y) \in K \times G \mid xy=yx \} |\\ &\le \sum_{y \in Y} |K| + \sum_{y \in G \setminus Y} \frac{\epsilon}{2} |K|\\ &\le |Y| |K| +(|G| - |Y|)\frac{\epsilon}{2}|K| \le |Y| |K|+\frac{\epsilon}{2}|G| |K|. \end{align*}
Therefore ![]() $({\epsilon }/{2}) |G| < |Y|.$
$({\epsilon }/{2}) |G| < |Y|.$
Set ![]() $E= \langle Y \rangle$. Thus
$E= \langle Y \rangle$. Thus ![]() $|E| \ge |Y| > ({\epsilon }/{2}) |G|$, and so the index of
$|E| \ge |Y| > ({\epsilon }/{2}) |G|$, and so the index of ![]() $E$ in
$E$ in ![]() $G$ is at most
$G$ is at most ![]() $2/\epsilon$. As
$2/\epsilon$. As ![]() $Y$ is symmetric and
$Y$ is symmetric and ![]() $(2/\epsilon ) |Y| > |G|$, it follows from lemma 2.5 that every element of
$(2/\epsilon ) |Y| > |G|$, it follows from lemma 2.5 that every element of ![]() $E$ is a product of at most
$E$ is a product of at most ![]() $6/\epsilon$ elements of
$6/\epsilon$ elements of ![]() $Y$. Since
$Y$. Since ![]() $|y^{K}|\le 2/\epsilon$ for every
$|y^{K}|\le 2/\epsilon$ for every ![]() $y\in Y$, we conclude that
$y\in Y$, we conclude that ![]() $|e^{K}|\le (2/\epsilon )^{6/\epsilon }$ for every
$|e^{K}|\le (2/\epsilon )^{6/\epsilon }$ for every ![]() $e\in E$. Let
$e\in E$. Let ![]() $T$ be the maximal normal subgroup of
$T$ be the maximal normal subgroup of ![]() $G$ contained in
$G$ contained in ![]() $E$. Clearly, the index
$E$. Clearly, the index ![]() $[G:T]$ is
$[G:T]$ is ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
So, now ![]() $|b^{G}| \le (2/\epsilon )^{6/\epsilon }$ for every
$|b^{G}| \le (2/\epsilon )^{6/\epsilon }$ for every ![]() $b \in B$ and
$b \in B$ and ![]() $|e^{B}| \le (2/\epsilon )^{6/\epsilon }$ for every
$|e^{B}| \le (2/\epsilon )^{6/\epsilon }$ for every ![]() $e\in T$. As
$e\in T$. As ![]() $L$ is abelian, we can apply lemma 2.2 to conclude that
$L$ is abelian, we can apply lemma 2.2 to conclude that ![]() $[T,B]$ has
$[T,B]$ has ![]() $\epsilon$-bounded order and the result follows.
$\epsilon$-bounded order and the result follows.
Remark 2.6 Under the hypotheses of proposition 1.2 the subgroup ![]() $N=\langle [T,B]^{G}\rangle$ has
$N=\langle [T,B]^{G}\rangle$ has ![]() $\epsilon$-bounded order.
$\epsilon$-bounded order.
Proof. Since ![]() $[T,B]$ is normal in
$[T,B]$ is normal in ![]() $T$, it follows that there are only boundedly many conjugates of
$T$, it follows that there are only boundedly many conjugates of ![]() $[T,B]$ in
$[T,B]$ in ![]() $G$ and they normalize each other. Since
$G$ and they normalize each other. Since ![]() $N$ is the product of those conjugates,
$N$ is the product of those conjugates, ![]() $N$ has
$N$ has ![]() $\epsilon$-bounded order.
$\epsilon$-bounded order.
As usual, ![]() $Z_i(G)$ stands for the
$Z_i(G)$ stands for the ![]() $i$th term of the upper central series of a group
$i$th term of the upper central series of a group ![]() $G$.
$G$.
Remark 2.7 Assume the hypotheses of proposition 1.2. If ![]() $K$ is normal, then the subgroup
$K$ is normal, then the subgroup ![]() $T$ can be chosen in such a way that
$T$ can be chosen in such a way that ![]() $K\cap T\leq Z_3(T)$.
$K\cap T\leq Z_3(T)$.
Proof. According to remark 2.6, ![]() $N=\langle [T,B]^{G}\rangle$ has
$N=\langle [T,B]^{G}\rangle$ has ![]() $\epsilon$-bounded order. Let
$\epsilon$-bounded order. Let ![]() $B_0=\langle B^{G}\rangle$ and note that
$B_0=\langle B^{G}\rangle$ and note that ![]() $B_0 \le K$ and
$B_0 \le K$ and ![]() $[T,B_0]\leq N$. Since the index
$[T,B_0]\leq N$. Since the index ![]() $[K:B_0]$ and the order of
$[K:B_0]$ and the order of ![]() $N$ are
$N$ are ![]() $\epsilon$-bounded, the stabilizer in
$\epsilon$-bounded, the stabilizer in ![]() $T$ of the series
$T$ of the series
that is, the subgroup
has ![]() $\epsilon$-bounded index in
$\epsilon$-bounded index in ![]() $G$. Note that
$G$. Note that ![]() $K\cap H\leq Z_3(H)$, whence the result.
$K\cap H\leq Z_3(H)$, whence the result.
3. Probabilistic almost nilpotency of finite groups
Our first goal in this section is to furnish a proof of theorem 1.3. We restate it here.
Let ![]() $G$ be a finite group such that
$G$ be a finite group such that ![]() $Pr(F^{*}(G),G)\geq \epsilon$. Then
$Pr(F^{*}(G),G)\geq \epsilon$. Then ![]() $G$ has a class-
$G$ has a class- ![]() $2$-nilpotent normal subgroup
$2$-nilpotent normal subgroup ![]() $R$ such that both the index
$R$ such that both the index ![]() $[G:R]$ and the order of the commutator subgroup
$[G:R]$ and the order of the commutator subgroup ![]() $[R,R]$ are
$[R,R]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
As mentioned in the introduction, the above result yields a conclusion about ![]() $G$ which is as strong as in P. M. Neumann's theorem.
$G$ which is as strong as in P. M. Neumann's theorem.
Proof of Theorem 1.3. Set ![]() $K=F^{*}(G)$. In view of proposition 1.2 there is a normal subgroup
$K=F^{*}(G)$. In view of proposition 1.2 there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq K$ such that the indices
$B\leq K$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[K:B]$, and the order of the commutator subgroup
$[K:B]$, and the order of the commutator subgroup ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded. As
$\epsilon$-bounded. As ![]() $K$ is normal in
$K$ is normal in ![]() $G$, according to remark 2.7 the subgroup
$G$, according to remark 2.7 the subgroup ![]() $T$ can be chosen in such a way that
$T$ can be chosen in such a way that ![]() $K\cap T\leq Z_3(T)$. By [Reference Huppert and Blackburn20, corollary X.13.11(c)] we have
$K\cap T\leq Z_3(T)$. By [Reference Huppert and Blackburn20, corollary X.13.11(c)] we have ![]() $K\cap T=F^{*}(T)$. Therefore
$K\cap T=F^{*}(T)$. Therefore ![]() $F^{*}(T)\leq Z_3(T)$ and in view of [Reference Huppert and Blackburn20, theorem X.13.6] we conclude that
$F^{*}(T)\leq Z_3(T)$ and in view of [Reference Huppert and Blackburn20, theorem X.13.6] we conclude that ![]() $T=F^{*}(T)$ and so
$T=F^{*}(T)$ and so ![]() $T\leq K$. It follows that the index of
$T\leq K$. It follows that the index of ![]() $K$ in
$K$ in ![]() $G$ is
$G$ is ![]() $\epsilon$-bounded. By remark 2.6 the subgroup
$\epsilon$-bounded. By remark 2.6 the subgroup ![]() $N=\langle [T,B]^{G}\rangle$ has
$N=\langle [T,B]^{G}\rangle$ has ![]() $\epsilon$-bounded order. Conclude that
$\epsilon$-bounded order. Conclude that ![]() $R=\langle B^{G}\rangle \cap C_G(N)$ has
$R=\langle B^{G}\rangle \cap C_G(N)$ has ![]() $\epsilon$-bounded index in
$\epsilon$-bounded index in ![]() $G$. Moreover
$G$. Moreover ![]() $R$ is nilpotent of class at most 2 and
$R$ is nilpotent of class at most 2 and ![]() $[R,R]$ has
$[R,R]$ has ![]() $\epsilon$-bounded order. This completes the proof.
$\epsilon$-bounded order. This completes the proof.
Now focus on theorem 1.4, which deals with the case where ![]() $\gamma _i(G)\leq K$. Start with a couple of remarks on the result. Let
$\gamma _i(G)\leq K$. Start with a couple of remarks on the result. Let ![]() $G$ and
$G$ and ![]() $R$ be as in theorem 1.4. The fact that both the index
$R$ be as in theorem 1.4. The fact that both the index ![]() $[G:R]$ and the order of
$[G:R]$ and the order of ![]() $\gamma _{i+1}(R)$ are
$\gamma _{i+1}(R)$ are ![]() $\epsilon$-bounded implies that for any
$\epsilon$-bounded implies that for any ![]() $x_1,\dots,x_i\in R$ the centralizer of the long commutator
$x_1,\dots,x_i\in R$ the centralizer of the long commutator ![]() $[x_1,\dots,x_i]$ has
$[x_1,\dots,x_i]$ has ![]() $\epsilon$-bounded index in
$\epsilon$-bounded index in ![]() $G$. Therefore there is an
$G$. Therefore there is an ![]() $\epsilon$-bounded number
$\epsilon$-bounded number ![]() $e$ such that
$e$ such that ![]() $G^{e}$ centralizes all commutators
$G^{e}$ centralizes all commutators ![]() $[x_1,\dots,x_i]$ where
$[x_1,\dots,x_i]$ where ![]() $x_1,\dots,x_i\in R$. Then
$x_1,\dots,x_i\in R$. Then ![]() $G_0=G^{e}\cap R$ is a nilpotent normal subgroup of nilpotency class at most
$G_0=G^{e}\cap R$ is a nilpotent normal subgroup of nilpotency class at most ![]() $i$ with
$i$ with ![]() $G/G_0$ of
$G/G_0$ of ![]() $\epsilon$-bounded exponent (recall that a positive integer
$\epsilon$-bounded exponent (recall that a positive integer ![]() $e$ is the exponent of a finite group
$e$ is the exponent of a finite group ![]() $G$ if
$G$ if ![]() $e$ is the minimal number for which
$e$ is the minimal number for which ![]() $G^{e}=1$).
$G^{e}=1$).
If ![]() $G$ is additionally assumed to be
$G$ is additionally assumed to be ![]() $m$-generated for some
$m$-generated for some ![]() $m\geq 1$, then
$m\geq 1$, then ![]() $G$ has a nilpotent normal subgroup of nilpotency class at most
$G$ has a nilpotent normal subgroup of nilpotency class at most ![]() $i$ and
$i$ and ![]() $(\epsilon,m)$-bounded index. Indeed, we know that for any
$(\epsilon,m)$-bounded index. Indeed, we know that for any ![]() $x_1,\dots,x_i\in R$ the centralizer of the long commutator
$x_1,\dots,x_i\in R$ the centralizer of the long commutator ![]() $[x_1,\dots,x_i]$ has
$[x_1,\dots,x_i]$ has ![]() $\epsilon$-bounded index in
$\epsilon$-bounded index in ![]() $G$. An
$G$. An ![]() $m$-generated group has only
$m$-generated group has only ![]() $(j,m)$-boundedly many subgroups of any given index
$(j,m)$-boundedly many subgroups of any given index ![]() $j$ [Reference Hall18, theorem 7.2.9]. Therefore
$j$ [Reference Hall18, theorem 7.2.9]. Therefore ![]() $G$ has a subgroup
$G$ has a subgroup ![]() $J$ of
$J$ of ![]() $(\epsilon,m)$-bounded index that centralizes all commutators
$(\epsilon,m)$-bounded index that centralizes all commutators ![]() $[x_1,\dots,x_i]$ with
$[x_1,\dots,x_i]$ with ![]() $x_1,\dots,x_i\in R$. Then
$x_1,\dots,x_i\in R$. Then ![]() $J\cap R$ is a nilpotent normal subgroup of nilpotency class at most
$J\cap R$ is a nilpotent normal subgroup of nilpotency class at most ![]() $i$ and
$i$ and ![]() $(\epsilon,m)$-bounded index in
$(\epsilon,m)$-bounded index in ![]() $G$.
$G$.
These observations are in parallel with Shalev's results on probabilistically nilpotent groups [Reference Shalev32].
Our proof of theorem 1.4 requires the following result from [Reference Detomi, Donadze, Morigi and Shumyatsky7].
Theorem 3.1 Let ![]() $G$ be a group such that
$G$ be a group such that ![]() $|x^{\gamma _k(G)}|\leq n$ for any
$|x^{\gamma _k(G)}|\leq n$ for any ![]() $x\in G$. Then
$x\in G$. Then ![]() $\gamma _{k+1}(G)$ has finite
$\gamma _{k+1}(G)$ has finite ![]() $(k,n)$-bounded order.
$(k,n)$-bounded order.
We can now prove theorem 1.4.
Proof of theorem 1.4. Recall that ![]() $K$ is a subgroup of the finite group
$K$ is a subgroup of the finite group ![]() $G$ such that
$G$ such that ![]() $\gamma _k(G)\leq K$ and
$\gamma _k(G)\leq K$ and ![]() $Pr(K,G)\geq \epsilon$. In view of [Reference Erfanian, Rezaei and Lescot10, theorem 3.7] observe that
$Pr(K,G)\geq \epsilon$. In view of [Reference Erfanian, Rezaei and Lescot10, theorem 3.7] observe that ![]() $Pr(\gamma _k(G),G)\geq \epsilon$. Therefore without loss of generality we can assume that
$Pr(\gamma _k(G),G)\geq \epsilon$. Therefore without loss of generality we can assume that ![]() $K=\gamma _k(G)$.
$K=\gamma _k(G)$.
Proposition 1.2 tells us that there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq K$ such that the indices
$B\leq K$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[K:B]$ and the order of
$[K:B]$ and the order of ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded. In particular,
$\epsilon$-bounded. In particular, ![]() $|x^{B}|$ is
$|x^{B}|$ is ![]() $\epsilon$-bounded for every
$\epsilon$-bounded for every ![]() $x\in T$. Since
$x\in T$. Since ![]() $B$ has
$B$ has ![]() $\epsilon$-bounded index in
$\epsilon$-bounded index in ![]() $K$, we deduce that
$K$, we deduce that ![]() $|x^{\gamma _k(G)}|$ is
$|x^{\gamma _k(G)}|$ is ![]() $\epsilon$-bounded for every
$\epsilon$-bounded for every ![]() $x\in T$. Now theorem 3.1 implies that
$x\in T$. Now theorem 3.1 implies that ![]() $\gamma _{k+1}(T)$ has
$\gamma _{k+1}(T)$ has ![]() $\epsilon$-bounded order. Set
$\epsilon$-bounded order. Set ![]() $R=C_T(\gamma _{k+1}(T))$. It follows that
$R=C_T(\gamma _{k+1}(T))$. It follows that ![]() $R$ is as required.
$R$ is as required.
Our next goal is a proof of theorem 1.5. As mentioned in the introduction, a group-word ![]() $w$ implies virtual nilpotency if every finitely generated metabelian group
$w$ implies virtual nilpotency if every finitely generated metabelian group ![]() $G$ where
$G$ where ![]() $w$ is a law, that is
$w$ is a law, that is ![]() $w(G)=1$, has a nilpotent subgroup of finite index. A theorem, due to Burns and Medvedev, states that for any word
$w(G)=1$, has a nilpotent subgroup of finite index. A theorem, due to Burns and Medvedev, states that for any word ![]() $w$ implying virtual nilpotency there exist integers
$w$ implying virtual nilpotency there exist integers ![]() $e$ and
$e$ and ![]() $c$ depending only on
$c$ depending only on ![]() $w$ such that every finite group
$w$ such that every finite group ![]() $G$, in which
$G$, in which ![]() $w$ is a law, has a nilpotent of class at most
$w$ is a law, has a nilpotent of class at most ![]() $c$ normal subgroup
$c$ normal subgroup ![]() $N$ with
$N$ with ![]() $G^{e}\leq N$ [Reference Burns and Medvedev4].
$G^{e}\leq N$ [Reference Burns and Medvedev4].
Proof of theorem 1.5. Recall that ![]() $w$ is a group-word implying virtual nilpotency while
$w$ is a group-word implying virtual nilpotency while ![]() $K$ is a subgroup of a finite group
$K$ is a subgroup of a finite group ![]() $G$ such that
$G$ such that ![]() $w(G)\leq K$ and
$w(G)\leq K$ and ![]() $Pr(K,G)\geq \epsilon$. We need to show that there is an
$Pr(K,G)\geq \epsilon$. We need to show that there is an ![]() $(\epsilon,w)$-bounded integer
$(\epsilon,w)$-bounded integer ![]() $e$ and a
$e$ and a ![]() $w$-bounded integer
$w$-bounded integer ![]() $c$ such that
$c$ such that ![]() $G^{e}$ is nilpotent of class at most
$G^{e}$ is nilpotent of class at most ![]() $c$.
$c$.
As in the proof of theorem 1.4 without loss of generality we can assume that ![]() $K=w(G)$. Proposition 1.2 tells us that there is a normal subgroup
$K=w(G)$. Proposition 1.2 tells us that there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq K$ such that the indices
$B\leq K$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[K:B]$ and the order of the commutator subgroup
$[K:B]$ and the order of the commutator subgroup ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded. According to remark 2.7 the subgroup
$\epsilon$-bounded. According to remark 2.7 the subgroup ![]() $T$ can be chosen in such a way that
$T$ can be chosen in such a way that ![]() $K\cap T\leq Z_3(T)$. In particular
$K\cap T\leq Z_3(T)$. In particular ![]() $w(T)\leq Z_3(T)$. Taking into account that the word
$w(T)\leq Z_3(T)$. Taking into account that the word ![]() $w$ implies virtual nilpotency, we deduce from the Burns–Medvedev theorem that there are
$w$ implies virtual nilpotency, we deduce from the Burns–Medvedev theorem that there are ![]() $w$-bounded numbers
$w$-bounded numbers ![]() $i$ and
$i$ and ![]() $c$ such that the subgroup generated by the
$c$ such that the subgroup generated by the ![]() $i$th powers of elements of
$i$th powers of elements of ![]() $T$ is nilpotent of class at most
$T$ is nilpotent of class at most ![]() $c$. Recall that the index of
$c$. Recall that the index of ![]() $T$ in
$T$ in ![]() $G$ is
$G$ is ![]() $\epsilon$-bounded. Hence there is an
$\epsilon$-bounded. Hence there is an ![]() $\epsilon$-bounded integer
$\epsilon$-bounded integer ![]() $e$ such that every
$e$ such that every ![]() $e$th power in
$e$th power in ![]() $G$ is an
$G$ is an ![]() $i$th power of an element of
$i$th power of an element of ![]() $T$. The result follows.
$T$. The result follows.
If ![]() $[x^{i},y_1,\dots,y_j]$ is a law in a finite group
$[x^{i},y_1,\dots,y_j]$ is a law in a finite group ![]() $G$, then
$G$, then ![]() $\gamma _{j+1}(G)$ has
$\gamma _{j+1}(G)$ has ![]() $\{i,j\}$-bounded exponent (the case
$\{i,j\}$-bounded exponent (the case ![]() $j=1$ is a well-known result, due to Mann [Reference Mann24]; see [Reference Caldeira and Shumyatsky5, lemma 2.2] for the case
$j=1$ is a well-known result, due to Mann [Reference Mann24]; see [Reference Caldeira and Shumyatsky5, lemma 2.2] for the case ![]() $j\geq 2$). If the
$j\geq 2$). If the ![]() $j$-Engel word
$j$-Engel word ![]() $[x,y,\dots,y]$, where
$[x,y,\dots,y]$, where ![]() $y$ is repeated
$y$ is repeated ![]() $j$ times, is a law in a finite group
$j$ times, is a law in a finite group ![]() $G$, then
$G$, then ![]() $G$ has a normal subgroup
$G$ has a normal subgroup ![]() $N$ such that the exponent of
$N$ such that the exponent of ![]() $N$ is
$N$ is ![]() $j$-bounded while
$j$-bounded while ![]() $G/N$ is nilpotent with
$G/N$ is nilpotent with ![]() $j$-bounded class [Reference Burns and Medvedev3]. Note that both words
$j$-bounded class [Reference Burns and Medvedev3]. Note that both words ![]() $[x^{i},y_1,\dots,y_j]$ and
$[x^{i},y_1,\dots,y_j]$ and ![]() $[x,y,\dots,y]$ imply virtual nilpotency.
$[x,y,\dots,y]$ imply virtual nilpotency.
Therefore, in addition to theorem 1.5, we deduce
Theorem 3.2 Assume the hypotheses of theorem 1.5.
• If
 $w=[x^{n},y_1,\dots,y_k]$, then
$w=[x^{n},y_1,\dots,y_k]$, then  $G$ has a normal subgroup
$G$ has a normal subgroup  $T$ such that the index
$T$ such that the index  $[G:T]$ is
$[G:T]$ is  $\epsilon$-bounded and the exponent of
$\epsilon$-bounded and the exponent of  $\gamma _{k+4}(T)$ is
$\gamma _{k+4}(T)$ is  $w$-bounded.
$w$-bounded.• There are
 $k$-bounded numbers
$k$-bounded numbers  $e_1$ and
$e_1$ and  $c_1$ with the property that if
$c_1$ with the property that if  $w$ is the
$w$ is the  $k$-Engel word, then
$k$-Engel word, then  $G$ has a normal subgroup
$G$ has a normal subgroup  $T$ such that the index
$T$ such that the index  $[G:T]$ is
$[G:T]$ is  $\epsilon$-bounded and the exponent of
$\epsilon$-bounded and the exponent of  $\gamma _{c_1}(T)$ divides
$\gamma _{c_1}(T)$ divides  $e_1$.
$e_1$.
Proof. By [Reference Erfanian, Rezaei and Lescot10, theorem 3.7], without loss of generality we can assume that ![]() $K=w(G)$. Proposition 1.2 tells us that there is a normal subgroup
$K=w(G)$. Proposition 1.2 tells us that there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq w(G)$ such that the indices
$B\leq w(G)$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[w(G):B]$ and the order of
$[w(G):B]$ and the order of ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded. Since
$\epsilon$-bounded. Since ![]() $K$ is normal in
$K$ is normal in ![]() $G$, according to remark 2.7 the subgroup
$G$, according to remark 2.7 the subgroup ![]() $T$ can be chosen in such a way that
$T$ can be chosen in such a way that ![]() $w(G)\cap T\leq Z_3(T)$. If
$w(G)\cap T\leq Z_3(T)$. If ![]() $w=[x^{n},y_1,\dots,y_k]$, then
$w=[x^{n},y_1,\dots,y_k]$, then ![]() $[x^{n},y_1,\dots,y_{k+3}]$ is a law in
$[x^{n},y_1,\dots,y_{k+3}]$ is a law in ![]() $T$, whence the exponent of
$T$, whence the exponent of ![]() $\gamma _{k+4}(T)$ is
$\gamma _{k+4}(T)$ is ![]() $w$-bounded. If
$w$-bounded. If ![]() $w$ is the
$w$ is the ![]() $k$-Engel word, then the
$k$-Engel word, then the ![]() $(k+3)$-Engel word is a law in
$(k+3)$-Engel word is a law in ![]() $T$ and the theorem follows from the Burns–Medvedev theorem [Reference Burns and Medvedev3].
$T$ and the theorem follows from the Burns–Medvedev theorem [Reference Burns and Medvedev3].
4. Sylow subgroups
As usual, ![]() $O_p(G)$ denotes the maximal normal
$O_p(G)$ denotes the maximal normal ![]() $p$-subgroup of a finite group
$p$-subgroup of a finite group ![]() $G$. For the reader's convenience we restate theorem 1.6:
$G$. For the reader's convenience we restate theorem 1.6:
Let ![]() $P$ be a Sylow
$P$ be a Sylow ![]() $p$-subgroup of a finite group
$p$-subgroup of a finite group ![]() $G$ such that
$G$ such that ![]() $Pr(P,G) \ge \epsilon$. Then
$Pr(P,G) \ge \epsilon$. Then ![]() $G$ has a class-
$G$ has a class- ![]() $2$-nilpotent normal
$2$-nilpotent normal ![]() $p$-subgroup
$p$-subgroup ![]() $L$ such that both the index
$L$ such that both the index ![]() $[P:L]$ and the order of the commutator subgroup
$[P:L]$ and the order of the commutator subgroup ![]() $[L,L]$ are
$[L,L]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
Proof of Theorem 1.6. Proposition 1.2 tells us that there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq P$ such that the indices
$B\leq P$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[P:B]$ and the order of the commutator subgroup
$[P:B]$ and the order of the commutator subgroup ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded. In view of remark 2.6 the subgroup
$\epsilon$-bounded. In view of remark 2.6 the subgroup ![]() $N=\langle [T,B]^{G}\rangle$ has
$N=\langle [T,B]^{G}\rangle$ has ![]() $\epsilon$-bounded order. Therefore
$\epsilon$-bounded order. Therefore ![]() $C=C_T(N)$ has
$C=C_T(N)$ has ![]() $\epsilon$-bounded index in
$\epsilon$-bounded index in ![]() $G$. Set
$G$. Set ![]() $B_0=B\cap C$ and note that
$B_0=B\cap C$ and note that ![]() $[C,B_0]\leq Z(C)$. It follows that
$[C,B_0]\leq Z(C)$. It follows that ![]() $B_0\leq Z_2(C)$ and we conclude that
$B_0\leq Z_2(C)$ and we conclude that ![]() $B_0\leq O_p(G)$. Let
$B_0\leq O_p(G)$. Let ![]() $L=\langle {B_0}^{G}\rangle$. As
$L=\langle {B_0}^{G}\rangle$. As ![]() $B_0 \le L \le O_p(G)$, it is clear that
$B_0 \le L \le O_p(G)$, it is clear that ![]() $L$ is contained in
$L$ is contained in ![]() $P$ as a subgroup of
$P$ as a subgroup of ![]() $\epsilon$-bounded index. Moreover
$\epsilon$-bounded index. Moreover ![]() $[L,L]\leq N$ and so the order of
$[L,L]\leq N$ and so the order of ![]() $[L,L]$ is
$[L,L]$ is ![]() $\epsilon$-bounded. Hence the result.
$\epsilon$-bounded. Hence the result.
We will now prove theorem 1.7.
Proof of theorem 1.7. Recall that ![]() $G$ is a finite group such that
$G$ is a finite group such that ![]() $Pr(P,G) \ge \epsilon$ whenever
$Pr(P,G) \ge \epsilon$ whenever ![]() $P$ is a Sylow subgroup. We wish to show that
$P$ is a Sylow subgroup. We wish to show that ![]() $G$ has a nilpotent normal subgroup
$G$ has a nilpotent normal subgroup ![]() $R$ of nilpotency class at most
$R$ of nilpotency class at most ![]() $2$ such that both the index
$2$ such that both the index ![]() $[G:R]$ and the order of the commutator subgroup
$[G:R]$ and the order of the commutator subgroup ![]() $[R,R]$ are
$[R,R]$ are ![]() $\epsilon$-bounded.
$\epsilon$-bounded.
For each prime ![]() $p\in \pi (G)$ choose a Sylow
$p\in \pi (G)$ choose a Sylow ![]() $p$-subgroup
$p$-subgroup ![]() $S_p$ in
$S_p$ in ![]() $G$. Theorem 1.6 shows that
$G$. Theorem 1.6 shows that ![]() $G$ has a normal
$G$ has a normal ![]() $p$-subgroup
$p$-subgroup ![]() $L_p$ of class at most
$L_p$ of class at most ![]() $2$ such that both
$2$ such that both ![]() $[S_p:L_p]$ and
$[S_p:L_p]$ and ![]() $|[L_p,L_p]|$ are
$|[L_p,L_p]|$ are ![]() $\epsilon$-bounded. Since the bounds on
$\epsilon$-bounded. Since the bounds on ![]() $[S_p:L_p]$ and
$[S_p:L_p]$ and ![]() $|[L_p,L_p]|$ do not depend on
$|[L_p,L_p]|$ do not depend on ![]() $p$, it follows that there is an
$p$, it follows that there is an ![]() $\epsilon$-bounded constant
$\epsilon$-bounded constant ![]() $C$ such that
$C$ such that ![]() $S_p=L_p$ and
$S_p=L_p$ and ![]() $[L_p,L_p]=1$ whenever
$[L_p,L_p]=1$ whenever ![]() $p\geq C$. Set
$p\geq C$. Set ![]() $R=\prod _{p\in \pi (G)}L_p$. Then all Sylow subgroups of
$R=\prod _{p\in \pi (G)}L_p$. Then all Sylow subgroups of ![]() $G/R$ have
$G/R$ have ![]() $\epsilon$-bounded order and therefore the index of
$\epsilon$-bounded order and therefore the index of ![]() $R$ in
$R$ in ![]() $G$ is
$G$ is ![]() $\epsilon$-bounded. Moreover,
$\epsilon$-bounded. Moreover, ![]() $R$ is of class at most
$R$ is of class at most ![]() $2$ and
$2$ and ![]() $|[R,R]|$ is
$|[R,R]|$ is ![]() $\epsilon$-bounded, as required.
$\epsilon$-bounded, as required.
5. Coprime automorphisms and their fixed points
If ![]() $A$ is a group of automorphisms of a group
$A$ is a group of automorphisms of a group ![]() $G$, we write
$G$, we write ![]() $C_G(A)$ for the centralizer of
$C_G(A)$ for the centralizer of ![]() $A$ in
$A$ in ![]() $G$. The symbol
$G$. The symbol ![]() $A^{\#}$ stands for the set of nontrivial elements of the group
$A^{\#}$ stands for the set of nontrivial elements of the group ![]() $A$.
$A$.
The next lemma is well-known (see e.g. [Reference Gorenstein11, theorem 6.2.2 (iv)]). In the sequel we use it without explicit references.
Lemma 5.1 Let ![]() $A$ be a group of automorphisms of a finite group
$A$ be a group of automorphisms of a finite group ![]() $G$ such that
$G$ such that ![]() $(|G|,|A|)=1$. Then
$(|G|,|A|)=1$. Then ![]() $C_{G/N}(A)=NC_G(A)/N$ for any
$C_{G/N}(A)=NC_G(A)/N$ for any ![]() $A$-invariant normal subgroup
$A$-invariant normal subgroup ![]() $N$ of
$N$ of ![]() $G$.
$G$.
Proof of theorem 1.8. Recall that ![]() $G$ is a finite group admitting a coprime automorphism
$G$ is a finite group admitting a coprime automorphism ![]() $\phi$ of prime order
$\phi$ of prime order ![]() $p$ such that
$p$ such that ![]() $Pr(K,G)\geq \epsilon$, where
$Pr(K,G)\geq \epsilon$, where ![]() $K=C_G(\phi )$. We need to show that
$K=C_G(\phi )$. We need to show that ![]() $G$ has a nilpotent subgroup of
$G$ has a nilpotent subgroup of ![]() $p$-bounded nilpotency class and
$p$-bounded nilpotency class and ![]() $(\epsilon,p)$-bounded index.
$(\epsilon,p)$-bounded index.
By proposition 1.2 there is a normal subgroup ![]() $T\leq G$ and a subgroup
$T\leq G$ and a subgroup ![]() $B\leq K$ such that the indices
$B\leq K$ such that the indices ![]() $[G:T]$ and
$[G:T]$ and ![]() $[K:B]$ and the order of the commutator subgroup
$[K:B]$ and the order of the commutator subgroup ![]() $[T,B]$ are
$[T,B]$ are ![]() $\epsilon$-bounded. Let
$\epsilon$-bounded. Let ![]() $T_0$ be the maximal
$T_0$ be the maximal ![]() $\phi$-invariant subgroup of
$\phi$-invariant subgroup of ![]() $T$. Evidently,
$T$. Evidently, ![]() $T_0$ is normal and the index
$T_0$ is normal and the index ![]() $[G:T_0]$ is
$[G:T_0]$ is ![]() $(\epsilon,p)$-bounded. Since
$(\epsilon,p)$-bounded. Since ![]() $\langle [T_0,B]^{G}\rangle \leq \langle [T,B]^{G}\rangle$, remark 2.6 implies that
$\langle [T_0,B]^{G}\rangle \leq \langle [T,B]^{G}\rangle$, remark 2.6 implies that ![]() $M=\langle [T_0,B]^{G}\rangle$ has
$M=\langle [T_0,B]^{G}\rangle$ has ![]() $\epsilon$-bounded order. Moreover,
$\epsilon$-bounded order. Moreover, ![]() $M$ is
$M$ is ![]() $\phi$-invariant. Set
$\phi$-invariant. Set ![]() $D=C_G(M)\cap T_0$ and
$D=C_G(M)\cap T_0$ and ![]() $\bar {D}=D/Z_2(D)$, and note that
$\bar {D}=D/Z_2(D)$, and note that ![]() $D$ is
$D$ is ![]() $\phi$-invariant.
$\phi$-invariant.
In a natural way ![]() $\phi$ induces an automorphism of
$\phi$ induces an automorphism of ![]() $\bar {D}$ which we will denote by the same symbol
$\bar {D}$ which we will denote by the same symbol ![]() $\phi$. We note that
$\phi$. We note that ![]() $C_{\bar {D}}(\phi )=C_D(\phi ) Z_2(D)/Z_2(D)$, so its order is
$C_{\bar {D}}(\phi )=C_D(\phi ) Z_2(D)/Z_2(D)$, so its order is ![]() $\epsilon$-bounded because
$\epsilon$-bounded because ![]() $B\cap D\leq Z_2(D)$. The Khukhro theorem [Reference Khukhro21] now implies that
$B\cap D\leq Z_2(D)$. The Khukhro theorem [Reference Khukhro21] now implies that ![]() $\bar {D}$ has a nilpotent subgroup of
$\bar {D}$ has a nilpotent subgroup of ![]() $p$-bounded class and
$p$-bounded class and ![]() $(\epsilon,p)$-bounded index. Since
$(\epsilon,p)$-bounded index. Since ![]() $\bar {D}=D/Z_2(D)$ and since the index of
$\bar {D}=D/Z_2(D)$ and since the index of ![]() $D$ in
$D$ in ![]() $G$ is
$G$ is ![]() $(\epsilon,p)$-bounded, we deduce that
$(\epsilon,p)$-bounded, we deduce that ![]() $G$ has a nilpotent subgroup of
$G$ has a nilpotent subgroup of ![]() $p$-bounded class and
$p$-bounded class and ![]() $(\epsilon,p)$-bounded index. The proof is complete.
$(\epsilon,p)$-bounded index. The proof is complete.
A proof of the next lemma can be found in [Reference Guralnick and Shumyatsky14].
Lemma 5.2 If ![]() $A$ is a noncyclic elementary abelian
$A$ is a noncyclic elementary abelian ![]() $p$-group acting on a finite
$p$-group acting on a finite ![]() $p'$-group
$p'$-group ![]() $G$ in such a way that
$G$ in such a way that ![]() $|C_G(a)|\leq m$ for each
$|C_G(a)|\leq m$ for each ![]() $a\in A^{\#}$, then the order of
$a\in A^{\#}$, then the order of ![]() $G$ is at most
$G$ is at most ![]() $m^{p+1}$.
$m^{p+1}$.
We will now prove theorem 1.9.
Proof of theorem 1.9. By hypotheses, ![]() $G$ is a finite group admitting an elementary abelian coprime group of automorphisms
$G$ is a finite group admitting an elementary abelian coprime group of automorphisms ![]() $A$ of order
$A$ of order ![]() $p^{2}$ such that
$p^{2}$ such that ![]() $Pr(C_G(\phi ),G)\geq \epsilon$ for each
$Pr(C_G(\phi ),G)\geq \epsilon$ for each ![]() $\phi \in A^{\#}$. We need to show that
$\phi \in A^{\#}$. We need to show that ![]() $G$ has a nilpotent normal subgroup
$G$ has a nilpotent normal subgroup ![]() $R$ of nilpotency class at most
$R$ of nilpotency class at most ![]() $2$ such that both the index
$2$ such that both the index ![]() $[G:R]$ and the order of the commutator subgroup
$[G:R]$ and the order of the commutator subgroup ![]() $[R,R]$ are
$[R,R]$ are ![]() $(\epsilon,p)$-bounded.
$(\epsilon,p)$-bounded.
Let ![]() $A_1,\dots,A_{p+1}$ be the subgroups of order
$A_1,\dots,A_{p+1}$ be the subgroups of order ![]() $p$ of
$p$ of ![]() $A$ and set
$A$ and set ![]() $G_i=C_G(A_i)$ for
$G_i=C_G(A_i)$ for ![]() $i=1,\dots,p+1$. According to proposition 1.2 for each
$i=1,\dots,p+1$. According to proposition 1.2 for each ![]() $i=1,\dots,p+1$ there is a normal subgroup
$i=1,\dots,p+1$ there is a normal subgroup ![]() $T_i\leq G$ and a subgroup
$T_i\leq G$ and a subgroup ![]() $B_i\leq G_i$ such that the indices
$B_i\leq G_i$ such that the indices ![]() $[G:T_i]$ and
$[G:T_i]$ and ![]() $[G_i:B_i]$ and the order of the commutator subgroup
$[G_i:B_i]$ and the order of the commutator subgroup ![]() $[T_i,B_i]$ are
$[T_i,B_i]$ are ![]() $\epsilon$-bounded. We let
$\epsilon$-bounded. We let ![]() $U_i$ denote the maximal
$U_i$ denote the maximal ![]() $A$-invariant subgroup of
$A$-invariant subgroup of ![]() $T_i$ so that each
$T_i$ so that each ![]() $U_i$ is a normal subgroup of
$U_i$ is a normal subgroup of ![]() $(\epsilon,p)$-bounded index. The intersection of all
$(\epsilon,p)$-bounded index. The intersection of all ![]() $U_i$ will be denoted by
$U_i$ will be denoted by ![]() $U$. Further, we let
$U$. Further, we let ![]() $D_i$ denote the maximal
$D_i$ denote the maximal ![]() $A$-invariant subgroup of
$A$-invariant subgroup of ![]() $B_i$ so that each
$B_i$ so that each ![]() $D_i$ has
$D_i$ has ![]() $(\epsilon,p)$-bounded index in
$(\epsilon,p)$-bounded index in ![]() $G_i$. Note that a modification of remark 2.6 implies that
$G_i$. Note that a modification of remark 2.6 implies that ![]() $N_i=\langle [U_i,D_i]^{G}\rangle$ is
$N_i=\langle [U_i,D_i]^{G}\rangle$ is ![]() $A$-invariant and has
$A$-invariant and has ![]() $\epsilon$-bounded order. It follows that the order of
$\epsilon$-bounded order. It follows that the order of ![]() $N=\prod _iN_i$ is
$N=\prod _iN_i$ is ![]() $(\epsilon,p)$-bounded. Let
$(\epsilon,p)$-bounded. Let ![]() $V$ denote the minimal (
$V$ denote the minimal (![]() $A$-invariant) normal subgroup of
$A$-invariant) normal subgroup of ![]() $G$ containing all
$G$ containing all ![]() $D_i$ for
$D_i$ for ![]() $i=1,\dots,p+1$. It is easy to see that
$i=1,\dots,p+1$. It is easy to see that ![]() $[U,V]\leq N$.
$[U,V]\leq N$.
Obviously, ![]() $U$ has
$U$ has ![]() $(\epsilon,p)$-bounded index in
$(\epsilon,p)$-bounded index in ![]() $G$. Let us check that this also holds with respect to
$G$. Let us check that this also holds with respect to ![]() $V$. Let
$V$. Let ![]() $\bar {G}=G/V$. Since
$\bar {G}=G/V$. Since ![]() $V$ contains
$V$ contains ![]() $D_i$ for each
$D_i$ for each ![]() $i=1,\dots,p+1$ and since
$i=1,\dots,p+1$ and since ![]() $D_i$ has
$D_i$ has ![]() $(\epsilon,p)$-bounded index in
$(\epsilon,p)$-bounded index in ![]() $G_i$, we conclude that the image of
$G_i$, we conclude that the image of ![]() $G_i$ in
$G_i$ in ![]() $\bar {G}$ has
$\bar {G}$ has ![]() $(\epsilon,p)$-bounded order. Now lemma 5.2 tells us that the order of
$(\epsilon,p)$-bounded order. Now lemma 5.2 tells us that the order of ![]() $\bar {G}$ is
$\bar {G}$ is ![]() $(\epsilon,p)$-bounded and we conclude that indeed
$(\epsilon,p)$-bounded and we conclude that indeed ![]() $V$ has
$V$ has ![]() $(\epsilon,p)$-bounded index in
$(\epsilon,p)$-bounded index in ![]() $G$. Also note that since
$G$. Also note that since ![]() $N$ has
$N$ has ![]() $(\epsilon,p)$-bounded order,
$(\epsilon,p)$-bounded order, ![]() $C_G(N)$ has
$C_G(N)$ has ![]() $(\epsilon,p)$-bounded index in
$(\epsilon,p)$-bounded index in ![]() $G$. Let
$G$. Let
Then ![]() $R$ is as required since the subgroups
$R$ is as required since the subgroups ![]() $U,V,C_G(N)$ have
$U,V,C_G(N)$ have ![]() $(\epsilon,p)$-bounded index in
$(\epsilon,p)$-bounded index in ![]() $G$ while
$G$ while ![]() $[R,R]\leq N\leq C_G(R)$. The proof is complete.
$[R,R]\leq N\leq C_G(R)$. The proof is complete.
Acknowledgments
The first author is a member of GNSAGA (Indam). The second author was supported by FAPDF and CNPq.