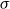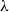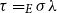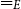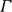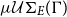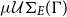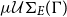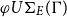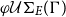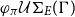1. Introduction
Ordering is a well-established concept in mathematics and it plays an important role in many areas of theoretical computer science too. Quasi-orderings (qo) and most notably well-founded quasi-orderings (wfqo) and well-quasi-orderings (wqo) in particular are of great general interest, see Kruskal (Reference Kruskal1972). Probably the most popular application within our own field is the use of quasi-orders and well-quasi-orders on first-order terms to prove the termination of rewriting rules, see Dershowitz (1982,Reference Dershowitz1987) and logic programs see Leuschel (1998,Reference Leuschel2002).
In the theory of E-unification of terms based on an alphabet
![]() $\Sigma=F\cup X$
, with signature F and variables X and an equational theory E, the set
$\Sigma=F\cup X$
, with signature F and variables X and an equational theory E, the set
![]() $\mathcal{U}\Sigma_{E}(\Gamma)$
denotes the set of all E-unifiers of a unification problem
$\mathcal{U}\Sigma_{E}(\Gamma)$
denotes the set of all E-unifiers of a unification problem
![]() $\Gamma$
. Of great interest is now to find a complete and minimal subset of
$\Gamma$
. Of great interest is now to find a complete and minimal subset of
![]() $\mathcal{U}\Sigma_{E}(\Gamma)$
, denoted as
$\mathcal{U}\Sigma_{E}(\Gamma)$
, denoted as
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
, from which all other E-unifiers can be obtained.
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
, from which all other E-unifiers can be obtained.
Equality on terms induced by the equational theory E will be denoted as =
![]() $_{E}$
and the subsumption order on terms is denoted as
$_{E}$
and the subsumption order on terms is denoted as
![]() $\leq_{E}$
. So, if there are two unifiers
$\leq_{E}$
. So, if there are two unifiers
![]() $\tau$
and
$\tau$
and
![]() $\sigma$
for terms s and t, such that
$\sigma$
for terms s and t, such that
![]() $s\tau=_{E}t\tau$
and
$s\tau=_{E}t\tau$
and
![]() $s\sigma=_{E}t\sigma$
and there is a substitution
$s\sigma=_{E}t\sigma$
and there is a substitution
![]() $\lambda$
, such that
$\lambda$
, such that
![]() $\tau=_{E}\sigma\lambda$
, then
$\tau=_{E}\sigma\lambda$
, then
![]() $\tau$
is an instance of
$\tau$
is an instance of
![]() $\sigma$
, or
$\sigma$
, or
![]() $\sigma$
subsumes
$\sigma$
subsumes
![]() $\tau$
, denoted as
$\tau$
, denoted as
![]() $\sigma\leq_{E}\tau$
. This led to the notion of a most general E-unifier (mgu), that is an E-unifier, which is not an instance of any other E-unifier. The set of most general unifiers is denoted as
$\sigma\leq_{E}\tau$
. This led to the notion of a most general E-unifier (mgu), that is an E-unifier, which is not an instance of any other E-unifier. The set of most general unifiers is denoted as
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
and every E-unifier is subsumed by some element of
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
and every E-unifier is subsumed by some element of
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
, that is, it can be obtained by instantiation in an automated reasoning process, such as resolution (Robinson, Reference Robinson1965). Often we shall drop the E from E-unifiers if it is understood from the context.
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
, that is, it can be obtained by instantiation in an automated reasoning process, such as resolution (Robinson, Reference Robinson1965). Often we shall drop the E from E-unifiers if it is understood from the context.
To illustrate the role of orderings in E-unification, consider the equational theory A for free semigroups with the axiom of associativity for terms built over a binary function symbol f with
![]() $A=\{f(x,f(y,z))=f(f(x,y),z)\}$
. This is also known as the word (or string) algebra and the notation is that of words (strings), where we just drop the function symbol f and have concatenation of symbols.
$A=\{f(x,f(y,z))=f(f(x,y),z)\}$
. This is also known as the word (or string) algebra and the notation is that of words (strings), where we just drop the function symbol f and have concatenation of symbols.
For example, the string unification problem
![]() $\Gamma_{1}=\{ax=^{?}xa\}$
has most general unifiers of the form
$\Gamma_{1}=\{ax=^{?}xa\}$
has most general unifiers of the form
![]() $\sigma_{n}=\{x\mapsto a^{n}:n\geqq1\}$
. Because the
$\sigma_{n}=\{x\mapsto a^{n}:n\geqq1\}$
. Because the
![]() $\sigma_{n}$
are ground substitutions, they are incomparable with respect to the subsumption order, so
$\sigma_{n}$
are ground substitutions, they are incomparable with respect to the subsumption order, so
![]() $\mu\mathcal{U}\Sigma_{A}(\Gamma_{1})=\{\sigma_{n}:n\geqq1\}$
is an infinite set and therefore
$\mu\mathcal{U}\Sigma_{A}(\Gamma_{1})=\{\sigma_{n}:n\geqq1\}$
is an infinite set and therefore
![]() $\Gamma_{1}$
is of unification type infinitary. Furthermore, since the subsumption order is not a well-quasi-order, there are equational theories such that the set of mgus does not exist, see Baader (Reference Baader1988) and Hoche (2016).
$\Gamma_{1}$
is of unification type infinitary. Furthermore, since the subsumption order is not a well-quasi-order, there are equational theories such that the set of mgus does not exist, see Baader (Reference Baader1988) and Hoche (2016).
In order to address these problems, we proposed a generalization of the encompassment of terms to equational encompassment of substitutions, whereby a term s is encompassed by a term t, denoted as
![]() $s\sqsubseteq t$
, iff an instance of s, say
$s\sqsubseteq t$
, iff an instance of s, say
![]() $s\sigma$
, is a subterm of t. This allows a decomposition of t in the following sense: if we denote with t’ the replacement of the subterm
$s\sigma$
, is a subterm of t. This allows a decomposition of t in the following sense: if we denote with t’ the replacement of the subterm
![]() $s\sigma$
of t by a new variable z’, then the term t can be written as
$s\sigma$
of t by a new variable z’, then the term t can be written as
![]() $t=t'\{z'\rightarrow s\}\sigma$
. Equational encompassment of terms, denoted as
$t=t'\{z'\rightarrow s\}\sigma$
. Equational encompassment of terms, denoted as
![]() $\sqsubseteq_{E}$
, is then lifted component-wise to substitutions and applied to the set of E-unifiers. We then introduced the notion of an essential E-unifier by saying that
$\sqsubseteq_{E}$
, is then lifted component-wise to substitutions and applied to the set of E-unifiers. We then introduced the notion of an essential E-unifier by saying that
![]() $\sigma$
is E-encompassed by
$\sigma$
is E-encompassed by
![]() $\tau$
,
$\tau$
,
![]() $\sigma\sqsubseteq_{E}\tau$
, iff each domain variable x of
$\sigma\sqsubseteq_{E}\tau$
, iff each domain variable x of
![]() $\tau$
is also a domain variable of
$\tau$
is also a domain variable of
![]() $\sigma$
and
$\sigma$
and
![]() $x\tau$
has an instance of
$x\tau$
has an instance of
![]() $x\sigma$
as a subterm (modulo E). E-unifiers, which are not encompassed by any other unifier, are then called essential E-unifiers and the complete set of essential E-unifiers is denoted as
$x\sigma$
as a subterm (modulo E). E-unifiers, which are not encompassed by any other unifier, are then called essential E-unifiers and the complete set of essential E-unifiers is denoted as
![]() $e\mathcal{U}\Sigma_{E}(\Gamma)$
for a unification problem
$e\mathcal{U}\Sigma_{E}(\Gamma)$
for a unification problem
![]() $\Gamma$
. If
$\Gamma$
. If
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
exists, we have
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
exists, we have
![]() $e\mathcal{U}\Sigma_{E}(\Gamma)\subseteq\mu\mathcal{U}\Sigma_{E}(\Gamma)$
, that is, the encompassment order generalizes the subsumption order and there are cases where an E-unification problem with an infinite set of mgus reduces to a finite set of essential unifiers (Hoche and Szabo, Reference Hoche and Szabo2006; Szabo et al., Reference Szabo, Siekmann and Hoche2016). Moreover it can happen that an equational theory E, for which
$e\mathcal{U}\Sigma_{E}(\Gamma)\subseteq\mu\mathcal{U}\Sigma_{E}(\Gamma)$
, that is, the encompassment order generalizes the subsumption order and there are cases where an E-unification problem with an infinite set of mgus reduces to a finite set of essential unifiers (Hoche and Szabo, Reference Hoche and Szabo2006; Szabo et al., Reference Szabo, Siekmann and Hoche2016). Moreover it can happen that an equational theory E, for which
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
does not exist, may have a minimal and complete set of essential unifiers
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
does not exist, may have a minimal and complete set of essential unifiers
![]() $e\mathcal{U}\Sigma_{E}(\Gamma)$
.
$e\mathcal{U}\Sigma_{E}(\Gamma)$
.
For example, the unification type of
![]() $\Gamma_{1}$
from above changes drastically using the encompassment order: the essential unifier
$\Gamma_{1}$
from above changes drastically using the encompassment order: the essential unifier
![]() $\sigma_{1}=\{x\mapsto a\}$
encompasses all the other most general unifiers
$\sigma_{1}=\{x\mapsto a\}$
encompasses all the other most general unifiers
![]() $\sigma_{n}=\{x\mapsto a^{n}\},\:n>1$
, because
$\sigma_{n}=\{x\mapsto a^{n}\},\:n>1$
, because
![]() $\sigma_{1}\sqsubseteq_{A}\sigma_{n},\:n>1$
. More precisely, the decomposition of a term, which encompasses another term, as shown above, is also valid for substitutions. In this case, encompassment allows the decomposition
$\sigma_{1}\sqsubseteq_{A}\sigma_{n},\:n>1$
. More precisely, the decomposition of a term, which encompasses another term, as shown above, is also valid for substitutions. In this case, encompassment allows the decomposition
![]() $\sigma_{n}=\lambda_{n}\sigma_{1}$
, where
$\sigma_{n}=\lambda_{n}\sigma_{1}$
, where
![]() $\lambda_{n}=\{x\mapsto a^{n}x\},\:n\geqq0$
. So the minimal and complete set of essential unifiers for
$\lambda_{n}=\{x\mapsto a^{n}x\},\:n\geqq0$
. So the minimal and complete set of essential unifiers for
![]() $\Gamma_{1}$
is
$\Gamma_{1}$
is
![]() $e\mathcal{U}\Sigma_{E}(\Gamma_{1})=\{\sigma_{1}\}$
, that is, it is unitary instead of infinitary as it is under the subsumption ordering.
$e\mathcal{U}\Sigma_{E}(\Gamma_{1})=\{\sigma_{1}\}$
, that is, it is unitary instead of infinitary as it is under the subsumption ordering.
Nevertheless there are still essentially infinitary string unification problems, as the following example shows. Let
![]() $\Gamma_{2}=\{xby=^{?}ayayb\}$
be the string unification problem, which has
$\Gamma_{2}=\{xby=^{?}ayayb\}$
be the string unification problem, which has
![]() $eU\Sigma_{A}(\varGamma_{2})=\{\{x\mapsto ab^{n}a,y\mapsto b^{n}\}:n>0\}$
as its minimal and complete set of essential unifiers. The unifiers are incomparable with respect to encompassment, because
$eU\Sigma_{A}(\varGamma_{2})=\{\{x\mapsto ab^{n}a,y\mapsto b^{n}\}:n>0\}$
as its minimal and complete set of essential unifiers. The unifiers are incomparable with respect to encompassment, because
![]() $ab^{n}a$
cannot be a substring of
$ab^{n}a$
cannot be a substring of
![]() $ab^{m}a$
for
$ab^{m}a$
for
![]() $m\neq~n$
. Furthermore, as the encompassment order on unifying substitutions is not a wqo, unfortunately again, there are theories with a solvable unification problem
$m\neq~n$
. Furthermore, as the encompassment order on unifying substitutions is not a wqo, unfortunately again, there are theories with a solvable unification problem
![]() $\Gamma$
, for which
$\Gamma$
, for which
![]() $e\mathcal{U}\Sigma_{E}(\Gamma)$
does not exist, see Baader (Reference Baader1988), Hoche (2008), and Szabo et al. (Reference Szabo, Siekmann and Hoche2016).
$e\mathcal{U}\Sigma_{E}(\Gamma)$
does not exist, see Baader (Reference Baader1988), Hoche (2008), and Szabo et al. (Reference Szabo, Siekmann and Hoche2016).
This paper deals with a further generalization, namely the extension of the well-known homeomorphic embedding of terms to a homeomorphic embedding modulo E of terms and of substitutions, called E-embedding of terms or substitutions, respectively.Footnote 1 Informally, the homeomorphic embedding of terms is understood as follows:
Let
![]() $s=f(s_{1},...,s_{n})$
and
$s=f(s_{1},...,s_{n})$
and
![]() $t=f(t_{1},....,t_{n})$
be terms, then s is syntactically embedded into t, denoted as
$t=f(t_{1},....,t_{n})$
be terms, then s is syntactically embedded into t, denoted as
![]() $s\trianglelefteq t$
iff
$s\trianglelefteq t$
iff
![]() $s=t$
or
$s=t$
or
![]() $s\trianglelefteq t_{i}$
for some i or
$s\trianglelefteq t_{i}$
for some i or
![]() $s_{i}\trianglelefteq t_{i}$
for all i. For example,
$s_{i}\trianglelefteq t_{i}$
for all i. For example,
![]() $\ f(x,\,b)\trianglelefteq\mathbf{f}(g(a,\,\mathbf{x}),\,f(x,\,\textbf{b}))$
and also
$\ f(x,\,b)\trianglelefteq\mathbf{f}(g(a,\,\mathbf{x}),\,f(x,\,\textbf{b}))$
and also
![]() $f(x,b)\trianglelefteq\textbf{f}(f(a,h(\textbf{x})),f(\textbf{b},a))$
and
$f(x,b)\trianglelefteq\textbf{f}(f(a,h(\textbf{x})),f(\textbf{b},a))$
and
![]() $f(a,x)\trianglelefteq\textbf{f}(g(\textbf{a},b),\textbf{x})$
, but
$f(a,x)\trianglelefteq\textbf{f}(g(\textbf{a},b),\textbf{x})$
, but
![]() $f(a,b)\ntrianglelefteq f(g(a,b),x)$
.
$f(a,b)\ntrianglelefteq f(g(a,b),x)$
.
The E-embedding order for terms, denoted as
![]() $\trianglelefteq_{E}$
, will then be extended to an E-embedding order for substitutions similar to the encompassment order in Szabo et al. (Reference Szabo, Siekmann and Hoche2016). We define
$\trianglelefteq_{E}$
, will then be extended to an E-embedding order for substitutions similar to the encompassment order in Szabo et al. (Reference Szabo, Siekmann and Hoche2016). We define
![]() $\sigma\trianglelefteq_{E}\tau$
iff each domain variable x of
$\sigma\trianglelefteq_{E}\tau$
iff each domain variable x of
![]() $\tau$
is also a domain variable of
$\tau$
is also a domain variable of
![]() $\sigma$
and
$\sigma$
and
![]() $x\tau$
homeomorphically E-embeds
$x\tau$
homeomorphically E-embeds
![]() $x\sigma$
, that is if
$x\sigma$
, that is if
![]() $\tau=\{x_{i}\mapsto t_{i}\}\:\:\textrm{and}\:\;\sigma=\{x_{i}\mapsto s_{i}\},\:1\leqq i\leqq n$
, then
$\tau=\{x_{i}\mapsto t_{i}\}\:\:\textrm{and}\:\;\sigma=\{x_{i}\mapsto s_{i}\},\:1\leqq i\leqq n$
, then
![]() $\sigma\trianglelefteq_{E}\tau\:\textrm{iff}\:s_{i}\trianglelefteq_{E}t_{i}$
. To illustrate the effect of this E-embedding order, take
$\sigma\trianglelefteq_{E}\tau\:\textrm{iff}\:s_{i}\trianglelefteq_{E}t_{i}$
. To illustrate the effect of this E-embedding order, take
![]() $\varGamma_{2}$
from above as an example, where E is the equational theory A for strings. In this case,
$\varGamma_{2}$
from above as an example, where E is the equational theory A for strings. In this case,
![]() $aba\trianglelefteq_{A}ab......ba$
and
$aba\trianglelefteq_{A}ab......ba$
and
![]() $b\trianglelefteq_{A}b.....b$
, hence with
$b\trianglelefteq_{A}b.....b$
, hence with
![]() $\sigma_{1}=\{x\mapsto aba,y\mapsto b\}$
we have
$\sigma_{1}=\{x\mapsto aba,y\mapsto b\}$
we have
![]() $\sigma_{1}\trianglelefteq_{A}\sigma_{n}$
for all
$\sigma_{1}\trianglelefteq_{A}\sigma_{n}$
for all
![]() $n>1$
. Consequently,
$n>1$
. Consequently,
![]() $\sigma_{1}$
is the only minimal unifier and the set of embedment free unifiers for
$\sigma_{1}$
is the only minimal unifier and the set of embedment free unifiers for
![]() $\Gamma_{2}$
is
$\Gamma_{2}$
is
![]() $\lambda\mathcal{U}\Sigma_{A}(\Gamma_{2})=\{\sigma_{1}\}$
and it is finite. In fact, it can be shown that in general the theory is unitary instead of infinitary as before.
$\lambda\mathcal{U}\Sigma_{A}(\Gamma_{2})=\{\sigma_{1}\}$
and it is finite. In fact, it can be shown that in general the theory is unitary instead of infinitary as before.
But in order to generalize the encompassment order for terms to the embedment order for unification problems, we need a more general notion of embedment. This is achieved by defining that a term s is instance E-embedded into a term t iff an instance of s, say
![]() $s\lambda$
, is E-embedded into t, which we call
$s\lambda$
, is E-embedded into t, which we call
![]() $\lambda_{E}$
-embedding. This is denoted as
$\lambda_{E}$
-embedding. This is denoted as
![]()
and E-unifiers, which have no
![]() $\lambda_{E}$
-embedded unifier, are called free
$\lambda_{E}$
-embedded unifier, are called free
![]() $\lambda_{E}$
-unifiers. If the set of free
$\lambda_{E}$
-unifiers. If the set of free
![]() $\lambda_{E}$
-unifiers is complete, then it is denoted as
$\lambda_{E}$
-unifiers is complete, then it is denoted as
![]() $\varphi U\Sigma_{E}(\Gamma)$
for a unification problem
$\varphi U\Sigma_{E}(\Gamma)$
for a unification problem
![]() $\Gamma$
.
$\Gamma$
.
This paper is organized as follows: The next chapter presents the notions and notation in unification theory, term rewriting, and automated theorem proving giving it an algebraic flair. This is then extended to a chapter on quasi-ordering, the basic algebraic notion of this paper. The third chapter presents the main results on E-unification based on equational homeomorphic embedding.
2. Notions and Notation
Notation and basic definitions in unification theory are well known (see, e.g., Baader and Nipkow (1988)) and have found their way into many and diverse academic fields. Most monographs and textbooks on automated reasoning have sections on unification.
In the following, we unify the various presentations of the necessary concepts for unification toward a concise notation which serves our purpose and we show how the additional concepts for ordering E-unifiers based on homeomorphic embedding can be built upon these definitions. The notion of an algebra given below embraces algebraic structures and the original notions in computational logic, recursive function theory, theory of automata, and automated theorem proving are compatible and natural applications.
2.1 Signatures, terms, and term algebras
A signature is a finite set F of function symbols that come with a nonnegative integer n, called arity, which is assigned to each member f of F. f is an n-ary function symbol. The subset of n-ary function symbols in F is denoted by
![]() $F_{n}$
. An algebra of type F is an ordered pair
$F_{n}$
. An algebra of type F is an ordered pair
![]() $\mathfrak{A}$
=
$\mathfrak{A}$
=
![]() $\langle A,F\rangle$
, where A is a nonempty set and F is a family of finitary operations on A indexed by the signature F such that corresponding to each n-ary function symbol f in
$\langle A,F\rangle$
, where A is a nonempty set and F is a family of finitary operations on A indexed by the signature F such that corresponding to each n-ary function symbol f in
![]() $F_{n}$
there is an n-ary operation
$F_{n}$
there is an n-ary operation
![]() $f^{A}$
on A. The set A is called the carrier of the algebra.
$f^{A}$
on A. The set A is called the carrier of the algebra.
Let X be a set of (distinct) variables. Let F be a signature. The set T(F,X) of (syntactic) terms of F over X is the smallest set
-
(i) comprising X and
 $F_{0}$
and
$F_{0}$
and -
(ii) if
 $t_{1},\ldots,t_{n}$
in T(F,X) and f in
$t_{1},\ldots,t_{n}$
in T(F,X) and f in
 $F_{n}$
, then
$F_{n}$
, then
 $f(t_{1},\ldots,t_{n})$
in T(F,X)
$f(t_{1},\ldots,t_{n})$
in T(F,X)
The set of variable-free terms are called ground terms. The set of variables occurring in a term t is denoted by
![]() $\mathbf{Var}(t)$
. The set of subterms of a term
$\mathbf{Var}(t)$
. The set of subterms of a term
![]() $f(t_{1},\ldots,t_{n})$
contains the term itself and is closed recursively by containing
$f(t_{1},\ldots,t_{n})$
contains the term itself and is closed recursively by containing
![]() $t_{1},\ldots,t_{n}$
. It is denoted by
$t_{1},\ldots,t_{n}$
. It is denoted by
![]() $\mathbf{Sub}(t)$
.
$\mathbf{Sub}(t)$
.
The set of terms can be given an algebraic structure called term algebra as usual.
2.2 Substitutions
A substitution is a (unique) homomorphism in the term algebra generated by a mapping
![]() $\sigma:X\longrightarrow T(F,X)$
from a finite set of variables to terms. Substitutions are generally denoted by small Greek letters
$\sigma:X\longrightarrow T(F,X)$
from a finite set of variables to terms. Substitutions are generally denoted by small Greek letters
![]() $\alpha,\beta,\gamma,\sigma$
, etc. and they are represented explicitly as a function by a set of variable bindings
$\alpha,\beta,\gamma,\sigma$
, etc. and they are represented explicitly as a function by a set of variable bindings
![]() $\sigma=\{x_{1}\mapsto s_{1},\ldots,x_{m}\mapsto s_{m}\}$
.
$\sigma=\{x_{1}\mapsto s_{1},\ldots,x_{m}\mapsto s_{m}\}$
.
![]() $\mathcal{S}_{F,X}$
denotes the set of all substitutions. The application of the substitution
$\mathcal{S}_{F,X}$
denotes the set of all substitutions. The application of the substitution
![]() $\sigma$
to a term t, denoted
$\sigma$
to a term t, denoted
![]() $t\sigma$
, is defined by induction on the structure of terms
$t\sigma$
, is defined by induction on the structure of terms
 \[t\sigma=\left\{ \begin{array}{ll}s_{i} & \textrm{if} \, t=x_{i}\\f(t_{1}\sigma,\ldots,t_{n}\sigma) & \textrm{if} \, t=f(t_{1},\ldots,t_{n})\\t & otherwise\end{array}\right.\]
\[t\sigma=\left\{ \begin{array}{ll}s_{i} & \textrm{if} \, t=x_{i}\\f(t_{1}\sigma,\ldots,t_{n}\sigma) & \textrm{if} \, t=f(t_{1},\ldots,t_{n})\\t & otherwise\end{array}\right.\]
The substitution
![]() $\varepsilon=\{\}$
with
$\varepsilon=\{\}$
with
![]() $t\varepsilon=t$
for all terms t in T(F,X) is called the identity. A substitution
$t\varepsilon=t$
for all terms t in T(F,X) is called the identity. A substitution
![]() $\sigma=\{x_{1}\mapsto s_{1},\ldots,x_{m}\mapsto s_{m}\}$
has the finite domain:
$\sigma=\{x_{1}\mapsto s_{1},\ldots,x_{m}\mapsto s_{m}\}$
has the finite domain:
The range of the substitution
![]() $\sigma$
is the set of terms
$\sigma$
is the set of terms
The set of variables occurring in the range is
![]() $\textbf{VRan}(\sigma)\;:=\;\textbf{Var}(\textbf{Ran}(\sigma))$
and
$\textbf{VRan}(\sigma)\;:=\;\textbf{Var}(\textbf{Ran}(\sigma))$
and
![]() $\textbf{Var}(\sigma)=\textbf{Dom}(\sigma)\cup\textbf{VRan}(\sigma)$
. The restriction of a substitution
$\textbf{Var}(\sigma)=\textbf{Dom}(\sigma)\cup\textbf{VRan}(\sigma)$
. The restriction of a substitution
![]() $\sigma$
to a set of variables
$\sigma$
to a set of variables
![]() $Y\subseteq X$
, denoted by
$Y\subseteq X$
, denoted by
![]() $\sigma_{|Y}$
, is the substitution which is equal to the identity everywhere except over
$\sigma_{|Y}$
, is the substitution which is equal to the identity everywhere except over
![]() $Y\cap\textbf{Dom}(\sigma)$
, where it is equal to
$Y\cap\textbf{Dom}(\sigma)$
, where it is equal to
![]() $\sigma$
. The composition of two substitutions
$\sigma$
. The composition of two substitutions
![]() $\sigma$
and
$\sigma$
and
![]() $\theta$
is written
$\theta$
is written
![]() $\sigma\circ\theta$
(to emphasize the composition) or just as
$\sigma\circ\theta$
(to emphasize the composition) or just as
![]() $\sigma\theta$
. The application is defined by
$\sigma\theta$
. The application is defined by
![]() $t\sigma\theta=(t\sigma)\theta$
. This is fine if
$t\sigma\theta=(t\sigma)\theta$
. This is fine if
![]() $\sigma\theta$
has no contradictory variable bindings, otherwise there are several solutions proposed in the literature which solve this problem and preserve functional composition, see, for example, Baader and Nipkow (1988) and Baader and Snyder (Reference Baader and Snyder2001).
$\sigma\theta$
has no contradictory variable bindings, otherwise there are several solutions proposed in the literature which solve this problem and preserve functional composition, see, for example, Baader and Nipkow (1988) and Baader and Snyder (Reference Baader and Snyder2001).
Relations such as
![]() $=,\geq,\ldots$
between substitutions sometimes hold only if they are restricted to a certain set of variables V. A relation R which is restricted to V is denoted as
$=,\geq,\ldots$
between substitutions sometimes hold only if they are restricted to a certain set of variables V. A relation R which is restricted to V is denoted as
![]() $R^{V}$
, and defined as
$R^{V}$
, and defined as
![]() $\sigma R^{V}\tau\Longleftrightarrow x\sigma Rx\tau$
for all x in V. Two substitutions
$\sigma R^{V}\tau\Longleftrightarrow x\sigma Rx\tau$
for all x in V. Two substitutions
![]() $\sigma$
and
$\sigma$
and
![]() $\theta$
are equal, denoted
$\theta$
are equal, denoted
![]() $\sigma=\theta$
iff
$\sigma=\theta$
iff
![]() $x\sigma=x\theta$
for every variable x; they are equal restricted to V, x
$x\sigma=x\theta$
for every variable x; they are equal restricted to V, x
![]() $\sigma$
$\sigma$
![]() $=^{V}\textit{x}\theta$
, iff
$=^{V}\textit{x}\theta$
, iff
![]() $x\sigma=x\theta$
for all variables x in V.
$x\sigma=x\theta$
for all variables x in V.
2.3 Congruences and equations
An equivalence relation
![]() $\Theta$
on the underlying set (the carrier) of an algebra of type F is a congruence, if for each n-ary function symbol f in F and elements
$\Theta$
on the underlying set (the carrier) of an algebra of type F is a congruence, if for each n-ary function symbol f in F and elements
![]() $a_{i},b_{i}$
of A, for all i in
$a_{i},b_{i}$
of A, for all i in
![]() $1\leq i\leq n$
we have
$1\leq i\leq n$
we have
The quotient algebra is the algebra whose carrier are the equivalence classes
![]() $A/\Theta$
and whose operations satisfy
$A/\Theta$
and whose operations satisfy
We are interested in quotient algebras, where the congruence is defined by a set of equations E, which is denoted as
![]() $=_{E}$
. For a term t in T(F,X) and the congruence E the equivalence class of t is denoted as
$=_{E}$
. For a term t in T(F,X) and the congruence E the equivalence class of t is denoted as
![]() $[t]_{E}$
.
$[t]_{E}$
.
2.4 Ordering
Our main interest in this paper is to investigate if the set of most general, minimal, and complete unifiers
![]() $\varphi U\Sigma_{E}(\Gamma)$
exists under certain conditions and the main technique for showing this result is based on orderings, in particular on well-quasi-orderings.
$\varphi U\Sigma_{E}(\Gamma)$
exists under certain conditions and the main technique for showing this result is based on orderings, in particular on well-quasi-orderings.
Definition 1. A quasi-order (also called a pre-order) is a binary relation that is reflexive and transitive.
A term t is (syntactically) an instance of a term s, if
![]() $s\sigma=t$
for some substitution
$s\sigma=t$
for some substitution
![]() $\sigma$
. We also say s subsumes t and this relation is a quasi-order. It is called the subsumption order on terms.
$\sigma$
. We also say s subsumes t and this relation is a quasi-order. It is called the subsumption order on terms.
A term t (syntactically) encompasses a term s, if an instance of s is a subterm of t. Encompassment conveys the notion that s appears in t with some context “above” (in tree notation) and a substitution instance “below.” We say t encompasses s or s is encompassed by t. In particular, encompassment is called strict encompassment, if
![]() $s\sigma$
is a proper subterm of t.
$s\sigma$
is a proper subterm of t.
A term s is homeomorphically embedded into t iff s can be obtained from t by erasing some “parts” in t. We usually abbreviate homeomorphical embedding just to embedding. Embedment conveys the notion that the structure of s and some corresponding symbols appear within t. A term s is instance-embedded into t, we also say it is
![]() $\lambda$
-embedded into t, iff an instance of s, that is
$\lambda$
-embedded into t, iff an instance of s, that is
![]() $s\lambda$
, is embedded into t. This is the main notion of this paper, which we will generalize to embedment of substitutions later on.
$s\lambda$
, is embedded into t. This is the main notion of this paper, which we will generalize to embedment of substitutions later on.
More formally, we have the following orders on terms. Footnote 2
Definition 2 (syntactic)
-
(1) A term s is a subterm of t if
 $s\in\textbf{Sub}(t)$
and we denote this by
$s\in\textbf{Sub}(t)$
and we denote this by
 $s\preceq t$
. If s is a proper subterm of t, we write
$s\preceq t$
. If s is a proper subterm of t, we write
 $s\prec t$
.
$s\prec t$
. -
(2) A term s subsumes t, denoted
 $s\leq t$
, iff there exists a substitution
$s\leq t$
, iff there exists a substitution
 $\sigma$
with
$\sigma$
with
 $s\sigma=t$
$s\sigma=t$
-
(3) A term s is encompassed by t, denoted
 $s\sqsubseteq t$
, iff there exists a substitution
$s\sqsubseteq t$
, iff there exists a substitution
 $\sigma$
such that
$\sigma$
such that
 $s\sigma\in\textbf{Sub}(t)$
.
$s\sigma\in\textbf{Sub}(t)$
. -
(4) A term s is embedded into a term t, denoted
 $s\trianglelefteq t$
, if
$s\trianglelefteq t$
, if
 $s=t$
or s is embedded into an argument of t or the argument terms of s and t embed, respectively:
We denote strictly embedding by
$s=t$
or s is embedded into an argument of t or the argument terms of s and t embed, respectively:
We denote strictly embedding by \[s\trianglelefteq t\,\iff\left\{ \begin{array}{ll}s=t,\:\textrm{or}\\t=f(t_{1},\ldots,t_{n})\;\textrm{and}\;\textrm{for}\;\textrm{some}\;i,\;1\leq i\leq n:\:s\trianglelefteq t_{i},\:\textrm{or}\\t=f(t_{1},\,.\,.\,.,t_{n}),\:s=f(s_{1},.\,.\,.,s_{n})\\\:\;\:\;\:\;\:\;\:\textrm{and}\:\;\forall i:\:s_{i}\trianglelefteq t_{i},\:1\leq i\leq n.\end{array}\right.\]
\[s\trianglelefteq t\,\iff\left\{ \begin{array}{ll}s=t,\:\textrm{or}\\t=f(t_{1},\ldots,t_{n})\;\textrm{and}\;\textrm{for}\;\textrm{some}\;i,\;1\leq i\leq n:\:s\trianglelefteq t_{i},\:\textrm{or}\\t=f(t_{1},\,.\,.\,.,t_{n}),\:s=f(s_{1},.\,.\,.,s_{n})\\\:\;\:\;\:\;\:\;\:\textrm{and}\:\;\forall i:\:s_{i}\trianglelefteq t_{i},\:1\leq i\leq n.\end{array}\right.\]
 $s\vartriangleleft t$
if s and t are not equal.
$s\vartriangleleft t$
if s and t are not equal.
We also say that t embeds s,
![]() $t\trianglerighteq s$
, and use it either way depending on the context. Embedding is of practical interest, notably in term rewriting systems and logic programming languages, where it is used in termination proofs. Sometimes an equivalent definition is used in these fields based on a reduction system:
$t\trianglerighteq s$
, and use it either way depending on the context. Embedding is of practical interest, notably in term rewriting systems and logic programming languages, where it is used in termination proofs. Sometimes an equivalent definition is used in these fields based on a reduction system:
Definition 3. For a set of terms T(F,X), the Embedding Reduction System,
![]() $\mathcal{R_{\textrm{F}}}$
, associated with the signature F is defined as
$\mathcal{R_{\textrm{F}}}$
, associated with the signature F is defined as
![]() $\mathcal{R_{\textrm{F}}}\;:=\;\{f(x_{1},....x_{n})\longrightarrow x_{i}:\;n\geq1,\;f\in F_{n}\subseteq\Sigma,\;for\;i,\;1\leq i\leq n\}$
.
$\mathcal{R_{\textrm{F}}}\;:=\;\{f(x_{1},....x_{n})\longrightarrow x_{i}:\;n\geq1,\;f\in F_{n}\subseteq\Sigma,\;for\;i,\;1\leq i\leq n\}$
.
The following Proposition states a well-known fact, see, for example, Dershowitz and Jouannaud (Reference Dershowitz and Jouannaud1991) and Baader and Nipkow (1988).
Proposition 4. For terms s,t:
![]() $\;$
t embeds s,
$\;$
t embeds s,
![]() $t\trianglerighteq s$
, iff
$t\trianglerighteq s$
, iff
![]() $t\xrightarrow[\mathcal{\mathcal{R_{\textrm{F}}}}]{*}s$
.
$t\xrightarrow[\mathcal{\mathcal{R_{\textrm{F}}}}]{*}s$
.
The next definition for embedding involves instances of terms.
Definition 5. A term s is instance-embedded into a term t, denoted
![]() ,
,
if there is an instantiating substitution
![]() $\lambda$
for s, such that
$\lambda$
for s, such that
![]() $s\lambda$
is embedded into t:
$s\lambda$
is embedded into t:
![]() $s\lambda\trianglelefteq t$
. We also say that s is
$s\lambda\trianglelefteq t$
. We also say that s is
![]() $\lambda$
-embedded into t.
$\lambda$
-embedded into t.
Some remarks: embedding implies
![]() $\lambda$
-embedding, but
$\lambda$
-embedding, but
![]() $\lambda$
-embedding does not necessarily imply embedding.
$\lambda$
-embedding does not necessarily imply embedding.
Remark 6. For terms s and t and a substitution
![]() $\lambda$
:
$\lambda$
:
if
![]() $s\trianglelefteq t$
, then s is
$s\trianglelefteq t$
, then s is
![]() $\lambda$
-embedded into t,
$\lambda$
-embedded into t,
![]() $s\varepsilon\trianglelefteq t$
, with the empty substitution
$s\varepsilon\trianglelefteq t$
, with the empty substitution
![]() $\varepsilon$
.
$\varepsilon$
.
Otherwise:
![]()
does not imply
![]() $s\trianglelefteq t$
, for example,
$s\trianglelefteq t$
, for example,
![]() $s=f(a,x)$
and
$s=f(a,x)$
and
![]() $t=f(g(a,b),\,f(b,h(a)))$
and
$t=f(g(a,b),\,f(b,h(a)))$
and
![]() $\lambda=\{x\mapsto a\}$
. We have
$\lambda=\{x\mapsto a\}$
. We have
![]() ,
,
because
![]() $s\lambda\trianglelefteq t$
,
$s\lambda\trianglelefteq t$
,
but
![]() $s\ntrianglelefteq t$
since
$s\ntrianglelefteq t$
since
![]() $s=f(a,x)\ntrianglelefteq f(g(a,b),\,f(b,h(a)))=t$
.
$s=f(a,x)\ntrianglelefteq f(g(a,b),\,f(b,h(a)))=t$
.
These standard order relations are now extended to equality modulo E for the congruences induced by the equations in E.
Definition 7. Let E be an equational theory:
-
(1) A term s is a subterm of t modulo E, denoted
 $s\preceq_{E}t$
, iff there exists an
$s\preceq_{E}t$
, iff there exists an
 $s'=_{E}s$
and a term
$s'=_{E}s$
and a term
 $t'=_{E}t$
such that
$t'=_{E}t$
such that
 $s'\preceq t'$
. We say s is an E-subterm of t.
$s'\preceq t'$
. We say s is an E-subterm of t. -
(2) A term s subsumes t modulo E,
 $s\leqslant_{E}t$
, iff there exists a substitution
$s\leqslant_{E}t$
, iff there exists a substitution
 $\sigma$
with
$\sigma$
with
 $s\sigma=_{E}t$
. We say s E-subsumes t.
$s\sigma=_{E}t$
. We say s E-subsumes t. -
(3) A term s is encompassed by t modulo E,
 $s\sqsubseteq_{E}t$
iff there is a substitution
$s\sqsubseteq_{E}t$
iff there is a substitution
 $\sigma$
such that
$\sigma$
such that
 $s\sigma\preceq_{E}t$
. We say s is E-encompassed by t.
$s\sigma\preceq_{E}t$
. We say s is E-encompassed by t.
The subterm and the encompassment order are quasi-orders (reflexive and transitive). Fortunately, the extension to E-subterm and E-encompassment order preserves transitivity, so they are quasi-orders too:
Proposition 8. The E-subterm order,
![]() $\preceq_{E}$
, is a quasi-order, that is, it is reflexive and transitive
$\preceq_{E}$
, is a quasi-order, that is, it is reflexive and transitive
Proof.
Reflexivity: for a term t it is obvious, that
![]() $t\preceq_{E}t$
.
$t\preceq_{E}t$
.
Transitivity: for terms r,s,t if
![]() $r\preceq_{E}s,\:s\preceq_{E}t\Longrightarrow r\preceq_{E}t$
.
$r\preceq_{E}s,\:s\preceq_{E}t\Longrightarrow r\preceq_{E}t$
.
![]() $r\preceq_{E}s\Longrightarrow\exists r'\in[r]_{E},s'\in[s]_{E}:r'\preceq s'$
and
$r\preceq_{E}s\Longrightarrow\exists r'\in[r]_{E},s'\in[s]_{E}:r'\preceq s'$
and
![]() $s\preceq_{E}t\Longrightarrow\exists s''\in[s]_{E},t''\in[t]_{E}:s''\preceq t''$
. Now because
$s\preceq_{E}t\Longrightarrow\exists s''\in[s]_{E},t''\in[t]_{E}:s''\preceq t''$
. Now because
![]() $s''=_{E}s'$
we get a new term t’ from t” by replacing s” by s’.
$s''=_{E}s'$
we get a new term t’ from t” by replacing s” by s’.
And then we have
![]() $s'\preceq t'$
.
$s'\preceq t'$
.
That is:
![]() $r'\preceq s'\preceq t'$
and transitivity of
$r'\preceq s'\preceq t'$
and transitivity of
![]() $\preceq$
yields
$\preceq$
yields
![]() $r'\preceq t'$
.
$r'\preceq t'$
.
Hence,
![]() $r=_{E}r'\preceq t'=_{E}t\Longrightarrow r\preceq_{E}t$
.
$r=_{E}r'\preceq t'=_{E}t\Longrightarrow r\preceq_{E}t$
.
The important observation for the following is that the term r’ in the above proof is not necessarily a subterm of t’. It is a subterm of t’ only when t” is transformed under
![]() $=_{E}$
into t’. This property is not valid for E-embedding and hence transitivity does not hold for this and other reasons. Thus, we cannot prove its quasi-order property. The reason is that if a term t embeds a term p, then there is not necessarily a
$=_{E}$
into t’. This property is not valid for E-embedding and hence transitivity does not hold for this and other reasons. Thus, we cannot prove its quasi-order property. The reason is that if a term t embeds a term p, then there is not necessarily a
![]() $t'\in[t]_{E}$
, such that for a given E-variant of p,
$t'\in[t]_{E}$
, such that for a given E-variant of p,
![]() $p'\in[p]_{E}$
, t’
$p'\in[p]_{E}$
, t’
![]() $\trianglerighteq_{E}$
p’. To see this and in order to motivate our Definition 10 below, consider the usual method to extend a quasi-order (relation) R to “R modulo E,” which is to take the transitive closure
$\trianglerighteq_{E}$
p’. To see this and in order to motivate our Definition 10 below, consider the usual method to extend a quasi-order (relation) R to “R modulo E,” which is to take the transitive closure
![]() $=_{E}\circ R\circ=_{E}$
. Originally, we used this idea, where E-embedding is defined as:
$=_{E}\circ R\circ=_{E}$
. Originally, we used this idea, where E-embedding is defined as:
![]() $t\trianglerighteq_{E}s$
iff
$t\trianglerighteq_{E}s$
iff
![]() $t=_{E}s,\:or\:\:\:\exists t'\in[t]_{E},s'\in[s]_{E}:\:t'\trianglerighteq s'$
. The problem is, however, that transitivity, namely:
$t=_{E}s,\:or\:\:\:\exists t'\in[t]_{E},s'\in[s]_{E}:\:t'\trianglerighteq s'$
. The problem is, however, that transitivity, namely:
![]() $t\trianglerighteq_{E}s\trianglerighteq_{E}r\Rightarrow t\trianglerighteq_{E}r$
does not hold in this case. Consider the following example:
$t\trianglerighteq_{E}s\trianglerighteq_{E}r\Rightarrow t\trianglerighteq_{E}r$
does not hold in this case. Consider the following example:
Let
![]() $F=\{f,g,h,a,b,c\}$
be a signature and
$F=\{f,g,h,a,b,c\}$
be a signature and
![]() $E=\{f(b,b)=g(c,h(a))\}$
$E=\{f(b,b)=g(c,h(a))\}$
be an equational theory.
Now consider
![]() $t=f(g(b,a),f(b,a))$
and
$t=f(g(b,a),f(b,a))$
and
![]() $s=f(b,b)$
and
$s=f(b,b)$
and
![]() $r=h(a)$
, where
$r=h(a)$
, where
transitivity of
![]() $\trianglerighteq_{E}$
:
$\trianglerighteq_{E}$
:
![]() $t\trianglerighteq_{E}s\trianglerighteq_{E}r\Rightarrow t\trianglerighteq_{E}r$
does not hold:
$t\trianglerighteq_{E}s\trianglerighteq_{E}r\Rightarrow t\trianglerighteq_{E}r$
does not hold:
![]() $t\trianglerighteq_{E}s$
because
$t\trianglerighteq_{E}s$
because
![]() $t\trianglerighteq s$
and
$t\trianglerighteq s$
and
![]() $s\trianglerighteq_{E}r$
because
$s\trianglerighteq_{E}r$
because
![]() $s=_{E}s'=g(c,h(a))\trianglerighteq h(a)=r$
.
$s=_{E}s'=g(c,h(a))\trianglerighteq h(a)=r$
.
But there is no
![]() $t'\in[t]_{E}$
and no
$t'\in[t]_{E}$
and no
![]() $r'\in[r]_{E}$
, such that
$r'\in[r]_{E}$
, such that
![]() $t'\trianglerighteq r'$
.
$t'\trianglerighteq r'$
.
Therefore, we propose an enhanced definition for equational embedding by requiring that if an embedded term p of a term t E-embeds a term s, then t also E-embeds s. For our contribution, it is important that this E-embedding, respectively
![]() $\lambda_{E}-$
embedding, enhances the comparison of objects (i.e. unifying substitutions) and allows us to use the famous tree-embedding theorem Kruskal (Reference Kruskal1960). This theorem is valid for first-order terms and can be lifted to substitutions and we show later on that it holds for E-embeddings as well. E-embedment, respectively
$\lambda_{E}-$
embedding, enhances the comparison of objects (i.e. unifying substitutions) and allows us to use the famous tree-embedding theorem Kruskal (Reference Kruskal1960). This theorem is valid for first-order terms and can be lifted to substitutions and we show later on that it holds for E-embeddings as well. E-embedment, respectively
![]() $\lambda_{E}-$
embedment, is then our fundamental tool in the rest of this paper. In the following definition and for the rest of this paper note: if two terms are equal under E, then they are embedment equivalent
$\lambda_{E}-$
embedment, is then our fundamental tool in the rest of this paper. In the following definition and for the rest of this paper note: if two terms are equal under E, then they are embedment equivalent
![]() $\equiv_{E}$
too, because
$\equiv_{E}$
too, because
![]() $s=_{E}t$
implies
$s=_{E}t$
implies
![]() $\exists s'\in[s]_{E}$
and
$\exists s'\in[s]_{E}$
and
![]() $\exists t'\in[t]$
with
$\exists t'\in[t]$
with
![]() $s'=t'$
which implies
$s'=t'$
which implies
![]() $s'\trianglelefteq t'$
and
$s'\trianglelefteq t'$
and
![]() $s'\trianglerighteq t'$
, hence
$s'\trianglerighteq t'$
, hence
![]() $s\equiv_{E}t$
. So we just use
$s\equiv_{E}t$
. So we just use
![]() $=_{E}$
in the following.
$=_{E}$
in the following.
Definition 9. For a term t and an equational theory E:
Let
![]() $\mathbf{Emb_{E}}$
(t) :=
$\mathbf{Emb_{E}}$
(t) :=
![]() $\left\{ p:\;p=_{E}p'\;and\;p'\trianglelefteq t\right\} $
be the set of the closure under E of all embedded terms in t.
$\left\{ p:\;p=_{E}p'\;and\;p'\trianglelefteq t\right\} $
be the set of the closure under E of all embedded terms in t.
The following is the crucial definition in this paper:
Definition 10. (E-embedding) A term t E-embeds a term s, denoted
![]() $t\trianglerighteq_{E}s$
, if
$t\trianglerighteq_{E}s$
, if
![]() $s=_{E}t$
, or there are terms
$s=_{E}t$
, or there are terms
![]() $t'=_{E}t$
and
$t'=_{E}t$
and
![]() $s'=_{E}s$
and there is an embedded term
$s'=_{E}s$
and there is an embedded term
![]() $p\in\mathbf{Emb_{E}}(t')$
such that
$p\in\mathbf{Emb_{E}}(t')$
such that
![]() $p\vartriangleright s'$
:
$p\vartriangleright s'$
:
 \[t\trianglerighteq_{E}s\,\iff\begin{cases}s=_{E}t\;\;or\\\exists t'\in[t]_{E},s'\in\left[s\right]_{E}\;and\:\exists p\in\mathbf{Emb_{E}}(t'):p\vartriangleright s'\end{cases}\]
\[t\trianglerighteq_{E}s\,\iff\begin{cases}s=_{E}t\;\;or\\\exists t'\in[t]_{E},s'\in\left[s\right]_{E}\;and\:\exists p\in\mathbf{Emb_{E}}(t'):p\vartriangleright s'\end{cases}\]
Note that if
![]() $p=t'$
and
$p=t'$
and
![]() $t\trianglerighteq_{E}s$
then
$t\trianglerighteq_{E}s$
then
![]() $\exists t'\in[t]_{E},s'\in[s]_{E}:\:t'\vartriangleright s'$
is just a special case of the above definition for
$\exists t'\in[t]_{E},s'\in[s]_{E}:\:t'\vartriangleright s'$
is just a special case of the above definition for
![]() $t\trianglerighteq_{E}s$
.
$t\trianglerighteq_{E}s$
.
In order to show that
![]() $t\trianglerighteq_{E}s$
, we can use an E-embedding-chain of the following form:
$t\trianglerighteq_{E}s$
, we can use an E-embedding-chain of the following form:
![]() $t=_{E}t'_{1}\vartriangleright t_{2}=_{E}t'_{2}\vartriangleright t_{3}=_{E}t'_{3}\vartriangleright.....\vartriangleright t_{n}=_{E}s$
$t=_{E}t'_{1}\vartriangleright t_{2}=_{E}t'_{2}\vartriangleright t_{3}=_{E}t'_{3}\vartriangleright.....\vartriangleright t_{n}=_{E}s$
where
![]() $\vartriangleright$
denotes strict embedding as in Definition 2. We abbreviate this chain as
$\vartriangleright$
denotes strict embedding as in Definition 2. We abbreviate this chain as
![]() $t\blacktriangleright_{E}^{n}s$
,
$t\blacktriangleright_{E}^{n}s$
,
![]() $n\geq1$
.
$n\geq1$
.
Note that this embedding chain has the typical regular structure where =
![]() $_{E}$
and
$_{E}$
and
![]() $\vartriangleright$
alternate. The
$\vartriangleright$
alternate. The
![]() $t_{i}$
may be an embedded term as denoted by p in the second line of Definition 10.
$t_{i}$
may be an embedded term as denoted by p in the second line of Definition 10.
Lemma 11. Let s,t be terms, t E-embeds s,
![]() $t\trianglerighteq_{E}s$
, iff
$t\trianglerighteq_{E}s$
, iff
![]() $t=_{E}s$
, or there exists a strictly descending chain of the form:
$t=_{E}s$
, or there exists a strictly descending chain of the form:
![]() $t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}t_{3}'\vartriangleright.....\vartriangleright t'_{n}=_{E}s$
, abbreviated as
$t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}t_{3}'\vartriangleright.....\vartriangleright t'_{n}=_{E}s$
, abbreviated as
![]() $t\blacktriangleright_{E}^{n}s$
.
$t\blacktriangleright_{E}^{n}s$
.
Proof. The first case in Definition 10 is obvious and we show the existence of the E-embedding chain by induction:
![]() $t\blacktriangleright_{E}^{1}s:$
by Definition 10
$t\blacktriangleright_{E}^{1}s:$
by Definition 10
![]() $\exists t_{1}'\in[t]_{E},\exists s'\in[s]_{E}\;and\;\exists p\in\mathbf{Emb_{E}}(t'):p\vartriangleright s'$
.
$\exists t_{1}'\in[t]_{E},\exists s'\in[s]_{E}\;and\;\exists p\in\mathbf{Emb_{E}}(t'):p\vartriangleright s'$
.
Hence,
![]() $t=_{E}t_{1}'\vartriangleright s'=_{E}s$
.
$t=_{E}t_{1}'\vartriangleright s'=_{E}s$
.
![]() $t\blacktriangleright_{E}^{n+1}s$
: that is
$t\blacktriangleright_{E}^{n+1}s$
: that is
![]() $t\blacktriangleright_{E}^{n}t_{n}$
and
$t\blacktriangleright_{E}^{n}t_{n}$
and
![]() $t_{n}\blacktriangleright_{E}^{1}s$
. By induction hypothesis, we have the chain
$t_{n}\blacktriangleright_{E}^{1}s$
. By induction hypothesis, we have the chain
![]() $t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright......\vartriangleright t_{n}$
and
$t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright......\vartriangleright t_{n}$
and
![]() $t_{n}\blacktriangleright_{E}^{1}s$
with
$t_{n}\blacktriangleright_{E}^{1}s$
with
![]() $t_{n}=_{E}t_{n}'\vartriangleright t_{n+1}$
, where
$t_{n}=_{E}t_{n}'\vartriangleright t_{n+1}$
, where
![]() $t_{n+1}=s'$
.
$t_{n+1}=s'$
.
So the whole E-embedding-chain is the following:
![]() $t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}........\vartriangleright t_{n}=_{E}t_{n}'\vartriangleright t_{n+1}=_{E}s$
.
$t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}........\vartriangleright t_{n}=_{E}t_{n}'\vartriangleright t_{n+1}=_{E}s$
.
The next definition extends instance-embedding to instance embedding modulo an equational theory E.
Definition 12. (instance E-embedding) A term s is instance-embedded modulo E into t, denoted
![]() ,
,
if an instance of s is E-embedded into t, that is
![]() $s\lambda\trianglelefteq_{E}t$
for a substitution
$s\lambda\trianglelefteq_{E}t$
for a substitution
![]() $\lambda$
. We say s is
$\lambda$
. We say s is
![]() $\lambda_{E}$
-embedded into t.
$\lambda_{E}$
-embedded into t.
The relation E-embedding is recursively defined in Definition 10 and it can be computed using Proposition 4 as follows:
Proposition 13. For a set of terms T(F,X) and an equational theory E the
E-embedding Rewrite System,
![]() $\mathcal{E_{\textrm{F}}}$
, is defined as
$\mathcal{E_{\textrm{F}}}$
, is defined as
![]() $\mathcal{E_{\textrm{F}}}$
:=
$\mathcal{E_{\textrm{F}}}$
:=
![]() $(\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}.\stackrel{*}{\longrightarrow}_{E})$
.
$(\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}.\stackrel{*}{\longrightarrow}_{E})$
.
Then for terms s,t:
![]() $t\trianglerighteq_{E}s$
iff
$t\trianglerighteq_{E}s$
iff
![]() $\exists t'\in[t]_{E},\exists s'\in[s]_{E}:\:$
$\exists t'\in[t]_{E},\exists s'\in[s]_{E}:\:$
![]() $t'\overset{*}{\longrightarrow_{\mathcal{E_{\textrm{F}}}}}s'$
.
$t'\overset{*}{\longrightarrow_{\mathcal{E_{\textrm{F}}}}}s'$
.
That is: there is a finite chain of the form:
![]() $\;\;\;\;+t\stackrel{*}{\longrightarrow_{E}}t'\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}t_{1}\stackrel{*}{\longrightarrow_{E}}t'_{1}\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}t_{2}....\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}t_{n}\stackrel{*}{\longrightarrow_{E}}s$
.
$\;\;\;\;+t\stackrel{*}{\longrightarrow_{E}}t'\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}t_{1}\stackrel{*}{\longrightarrow_{E}}t'_{1}\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}t_{2}....\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}t_{n}\stackrel{*}{\longrightarrow_{E}}s$
.
Proof. Follows from Lemma 11 by replacing
![]() $=_{E}$
by its equivalent rewrite system
$=_{E}$
by its equivalent rewrite system
![]() $\stackrel{*}{\longrightarrow_{E}}$
and
$\stackrel{*}{\longrightarrow_{E}}$
and
![]() $\trianglerighteq_{E}$
by its reduction system
$\trianglerighteq_{E}$
by its reduction system
![]() $\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}$
.
$\stackrel{*}{\longrightarrow_{\mathcal{R_{\textrm{F}}}}}$
.
With Definition 10 and Lemma 11, we obtain our first main result:
Theorem 14. The E-embedment order
![]() $\trianglerighteq_{E}$
is a quasi-order on terms.
$\trianglerighteq_{E}$
is a quasi-order on terms.
Proof. Let r,s,t be terms and let E be an equational theory.
reflexivity: Because terms embed themselves.
transitivity:
![]() $t\trianglerighteq_{E}s\trianglerighteq_{E}r\Longrightarrow t\trianglerighteq_{E}r$
.
$t\trianglerighteq_{E}s\trianglerighteq_{E}r\Longrightarrow t\trianglerighteq_{E}r$
.
By Definition 10 and Lemma 11, we have
![]() $t\blacktriangleright_{E}^{m}s$
and
$t\blacktriangleright_{E}^{m}s$
and
![]() $s\blacktriangleright_{E}^{n}r$
$s\blacktriangleright_{E}^{n}r$
that is
![]() $t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}t'_{3}........\vartriangleright t_{m}=_{E}s$
and
$t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}t'_{3}........\vartriangleright t_{m}=_{E}s$
and
![]() $s=_{E}s_{1}'\vartriangleright s_{2}=_{E}s_{2}'\vartriangleright s_{3}=_{E}s'_{3}........\vartriangleright s_{n}=_{E}r$
.
$s=_{E}s_{1}'\vartriangleright s_{2}=_{E}s_{2}'\vartriangleright s_{3}=_{E}s'_{3}........\vartriangleright s_{n}=_{E}r$
.
But since
![]() $t_{m}=_{E}s_{1}'$
we have the correct chain
$t_{m}=_{E}s_{1}'$
we have the correct chain
![]() $t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}t_{3}........\vartriangleright t_{m}=_{E}s_{1}'\vartriangleright s_{2}=_{E}s_{2}'\vartriangleright s_{3}=_{E}s'_{3}........\vartriangleright s_{n}=_{E}r$
$t=_{E}t_{1}'\vartriangleright t_{2}=_{E}t_{2}'\vartriangleright t_{3}=_{E}t_{3}........\vartriangleright t_{m}=_{E}s_{1}'\vartriangleright s_{2}=_{E}s_{2}'\vartriangleright s_{3}=_{E}s'_{3}........\vartriangleright s_{n}=_{E}r$
Hence,
![]() $t\blacktriangleright_{E}^{n+m}r$
, which means
$t\blacktriangleright_{E}^{n+m}r$
, which means
![]() $t\trianglerighteq_{E}r$
.
$t\trianglerighteq_{E}r$
.
The negation of E-subsumption and E-encompassment is obvious:
![]() $s\nleq_{E}t$
iff there exists no substitution
$s\nleq_{E}t$
iff there exists no substitution
![]() $\sigma$
with
$\sigma$
with
![]() $s\sigma=_{E}t$
and
$s\sigma=_{E}t$
and
![]()
iff there is no substitution
![]() $\sigma$
such that
$\sigma$
such that
![]() $s\sigma\preceq_{E}t$
. But the notions “not embedded” and “incomparable” with respect to
$s\sigma\preceq_{E}t$
. But the notions “not embedded” and “incomparable” with respect to
![]() $\trianglelefteq_{E}$
should be made more explicit.
$\trianglelefteq_{E}$
should be made more explicit.
Definition 15. (not embedded modulo E)
-
(1) A term s is not embedded modulo E into a term t,
 $s\ntrianglelefteq_{E}t$
, iff for every element s’ of the class
$s\ntrianglelefteq_{E}t$
, iff for every element s’ of the class
 $[s]_{E}$
there exists no element t’ of the class
$[s]_{E}$
there exists no element t’ of the class
 $[t]_{E}$
such that
$[t]_{E}$
such that
 $s'\trianglelefteq_{E}t'$
.
$s'\trianglelefteq_{E}t'$
. -
(2) Terms s and t are incomparable with respect to
 $\trianglelefteq_{E}$
iff
$\trianglelefteq_{E}$
iff
 $s\ntrianglelefteq_{E}t$
and
$s\ntrianglelefteq_{E}t$
and
 $t\ntrianglelefteq_{E}s$
.
$t\ntrianglelefteq_{E}s$
. -
(3) Terms s and t are incomparable with respect to

iff there exist no substitutions
 $\lambda_{1}$
and
$\lambda_{1}$
and
 $\lambda_{2}$
with
$\lambda_{2}$
with
 $s\lambda_{1}\trianglelefteq_{E}t$
and
$s\lambda_{1}\trianglelefteq_{E}t$
and
 $t\lambda_{2}\trianglelefteq_{E}s$
.
$t\lambda_{2}\trianglelefteq_{E}s$
.
We shall lift these orderings modulo E on terms now component-wise to orderings on substitutions in the sense that for all variables in the domain of the substitution we require that the corresponding images fulfill the order relation modulo E.
Definition 16. (ordering modulo E for substitutions restricted to a set of variables)
In the following, let
![]() $\sigma,\tau$
be substitutions with
$\sigma,\tau$
be substitutions with
![]() $\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau)\supseteq$
V, where V is some set of variables.
$\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau)\supseteq$
V, where V is some set of variables.
-
(1) A substitution
 $\sigma$
is a sub-substitution modulo E of
$\sigma$
is a sub-substitution modulo E of
 $\tau$
restricted to V, denoted as
$\tau$
restricted to V, denoted as
 $\sigma\preceq_{E}^{V}\tau$
, if for all x in V,
$\sigma\preceq_{E}^{V}\tau$
, if for all x in V,
 $x\sigma$
is a subterm of
$x\sigma$
is a subterm of
 $x\tau$
modulo E, that is
$x\tau$
modulo E, that is
 $x\sigma\preceq_{E}x\tau$
.
$x\sigma\preceq_{E}x\tau$
. -
(2) A substitution
 $\sigma$
E-subsumes a substitution
$\sigma$
E-subsumes a substitution
 $\tau$
restricted to V, denoted as
$\tau$
restricted to V, denoted as
 $\sigma\leq_{E}^{V}\tau$
, if there exists a substitution
$\sigma\leq_{E}^{V}\tau$
, if there exists a substitution
 $\lambda$
such that
$\lambda$
such that
 $\sigma\lambda=_{E}^{V}\tau$
. The relation
$\sigma\lambda=_{E}^{V}\tau$
. The relation
 $\leq_{E}^{V}$
is called the E-subsumption order for substitutions restricted to V.
$\leq_{E}^{V}$
is called the E-subsumption order for substitutions restricted to V.
We denote E-subsumption equivalence as
![]() $\sigma\thicksim_{E}^{V}\tau$
, if
$\sigma\thicksim_{E}^{V}\tau$
, if
![]() $\sigma\leq_{E}^{V}\tau\;and\;\tau\leq_{E}^{V}\sigma$
.
$\sigma\leq_{E}^{V}\tau\;and\;\tau\leq_{E}^{V}\sigma$
.
-
(3) A substitution
 $\sigma$
is E-encompassed by
$\sigma$
is E-encompassed by
 $\tau$
restricted to V, denoted
$\tau$
restricted to V, denoted
 $\sigma\sqsubseteq_{E}^{V}\tau$
, if there exists
$\sigma\sqsubseteq_{E}^{V}\tau$
, if there exists
 $\lambda$
, such that
$\lambda$
, such that
 $(\sigma\lambda)$
restricted to V is a sub-substitution of
$(\sigma\lambda)$
restricted to V is a sub-substitution of
 $\tau$
modulo E,
$\tau$
modulo E,
 $\sigma\lambda\preceq_{E}^{V}\tau$
.
$\sigma\lambda\preceq_{E}^{V}\tau$
.
We denote E-encompassment equivalence as
![]() $\sigma\thickapprox_{E}^{V}\tau$
if
$\sigma\thickapprox_{E}^{V}\tau$
if
![]() $\sigma\sqsubseteq_{E}^{V}\tau\;and\;\tau\sqsubseteq_{E}^{V}\sigma$
.
$\sigma\sqsubseteq_{E}^{V}\tau\;and\;\tau\sqsubseteq_{E}^{V}\sigma$
.
-
(4) A substitution
 $\sigma$
is E-embedded into a substitution
$\sigma$
is E-embedded into a substitution
 $\tau$
restricted to V, denoted as
$\tau$
restricted to V, denoted as
 $\sigma\trianglelefteq_{E}^{V}\tau$
, iff for all x in V we have
$\sigma\trianglelefteq_{E}^{V}\tau$
, iff for all x in V we have
 $x\sigma\trianglelefteq_{E}^{V}x\tau$
.
$x\sigma\trianglelefteq_{E}^{V}x\tau$
. -
(5) A substitution
 $\sigma$
is
$\sigma$
is
 $\lambda_{E}$
-embedded into a substitution
$\lambda_{E}$
-embedded into a substitution
 $\tau$
restricted to V, denoted as
$\tau$
restricted to V, denoted as ,
,iff there is a substitution
 $\lambda$
, such that
$\lambda$
, such that
 $\forall x\in V:\:x(\sigma\lambda)$
is E-embedded into
$\forall x\in V:\:x(\sigma\lambda)$
is E-embedded into
 $x\tau$
.
$x\tau$
.
The encompassment and embedment order on terms are well known as quasi-orderings, but the modulo E extension to substitutions requires verification.
Theorem 17 The E-encompassment order is a quasi-order on substitutions.
Proof. This is an improved version of the proof published before in Szabo et al. (Reference Szabo, Siekmann and Hoche2016) and even earlier in Hoche and Szabo (Reference Hoche and Szabo2006).
reflexivity:
![]() $\sigma\sqsubseteq_{E}\sigma$
by Definition 16 .3 means
$\sigma\sqsubseteq_{E}\sigma$
by Definition 16 .3 means
![]() $\sigma\lambda\preceq_{E}^{V}\sigma$
, setting
$\sigma\lambda\preceq_{E}^{V}\sigma$
, setting
![]() $\lambda$
to the
$\lambda$
to the
substitution identity
![]() $\varepsilon$
we have
$\varepsilon$
we have
![]() $\sigma=_{E}\varepsilon\sigma=\sigma$
.
$\sigma=_{E}\varepsilon\sigma=\sigma$
.
transitivity:
![]() $\sigma\sqsubseteq_{E}^{V}\tau$
and
$\sigma\sqsubseteq_{E}^{V}\tau$
and
![]() $\tau\sqsubseteq_{E}^{V}\psi$
implies
$\tau\sqsubseteq_{E}^{V}\psi$
implies
![]() $\sigma\sqsubseteq_{E}^{V}\psi$
, where by definition we have
$\sigma\sqsubseteq_{E}^{V}\psi$
, where by definition we have
![]() $\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau)=\mathbf{Dom}(\psi)$
, so by Definition 16. 3.:
$\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau)=\mathbf{Dom}(\psi)$
, so by Definition 16. 3.:
and by composition with
![]() $\lambda_{2}$
from the right
$\lambda_{2}$
from the right
Theorem 18 The E-embedment order is a quasi-order on substitutions.
Proof. Let
![]() $\sigma,\tau,\psi$
be substitutions and
$\sigma,\tau,\psi$
be substitutions and
![]() $V\;:=\;\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau)=\mathbf{Dom}(\psi)$
.
$V\;:=\;\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau)=\mathbf{Dom}(\psi)$
.
reflexivity:
![]() $\sigma\trianglelefteq_{E}^{V}\sigma$
since
$\sigma\trianglelefteq_{E}^{V}\sigma$
since
![]() $x\sigma$
embeds itself for all x in V.
$x\sigma$
embeds itself for all x in V.
transitivity: we show:
![]() $\sigma\trianglelefteq_{E}^{V}\tau\trianglelefteq_{E}^{V}\psi$
implies
$\sigma\trianglelefteq_{E}^{V}\tau\trianglelefteq_{E}^{V}\psi$
implies
![]() $\sigma\trianglelefteq_{E}^{V}\psi$
$\sigma\trianglelefteq_{E}^{V}\psi$
By Definition 16.(4) : For
![]() $\sigma\trianglelefteq_{E}^{V}\tau$
we have
$\sigma\trianglelefteq_{E}^{V}\tau$
we have
![]() $\forall x\in V:\:x\sigma\trianglelefteq_{E}x\tau$
$\forall x\in V:\:x\sigma\trianglelefteq_{E}x\tau$
and for
![]() $\tau\trianglelefteq_{E}^{V}\psi$
we have
$\tau\trianglelefteq_{E}^{V}\psi$
we have
![]() $\forall x\in V:\:x\tau\trianglelefteq_{E}x\psi$
.
$\forall x\in V:\:x\tau\trianglelefteq_{E}x\psi$
.
Now
![]() $\forall x\in V:\:x\sigma\trianglelefteq_{E}x\tau\;and\;x\tau\trianglelefteq_{E}x\psi$
are assertions on terms,
$\forall x\in V:\:x\sigma\trianglelefteq_{E}x\tau\;and\;x\tau\trianglelefteq_{E}x\psi$
are assertions on terms,
so using Theorem 14 we have
![]() $\forall x\in V:\:x\sigma\trianglelefteq_{E}x\psi$
$\forall x\in V:\:x\sigma\trianglelefteq_{E}x\psi$
and then by Definition 16.(4) we have
![]() $\sigma\trianglelefteq_{E}^{V}\psi$
.
$\sigma\trianglelefteq_{E}^{V}\psi$
.
The following lemma asserts that if a term s (a substitution
![]() $\sigma$
) is embedded into a term t (a substitution
$\sigma$
) is embedded into a term t (a substitution
![]() $\tau$
) then their instances are embedded too, that is, the relation
$\tau$
) then their instances are embedded too, that is, the relation
![]() $\trianglelefteq$
is right composable with substitutions.
$\trianglelefteq$
is right composable with substitutions.
Lemma 19 Let
![]() $s,\:t$
be terms and let
$s,\:t$
be terms and let
![]() $\sigma$
,
$\sigma$
,
![]() $\tau$
, and
$\tau$
, and
![]() $\lambda$
be a substitution. Then
$\lambda$
be a substitution. Then
-
(1) For all
 $\lambda$
, if
$\lambda$
, if
 $s\trianglelefteq t$
, then
$s\trianglelefteq t$
, then
 $s\lambda\trianglelefteq t\lambda$
$s\lambda\trianglelefteq t\lambda$
-
(2) For all
 $\lambda$
, if
$\lambda$
, if
 $s\trianglelefteq_{E}t$
, then
$s\trianglelefteq_{E}t$
, then
 $s\lambda\trianglelefteq_{E}t\lambda$
$s\lambda\trianglelefteq_{E}t\lambda$
-
(3) For all
 $\lambda$
, if
$\lambda$
, if
 $\sigma\trianglelefteq_{E}\tau$
, then
$\sigma\trianglelefteq_{E}\tau$
, then
 $\sigma\lambda\trianglelefteq_{E}\tau\lambda$
$\sigma\lambda\trianglelefteq_{E}\tau\lambda$
Proof.
-
(1)
 $s\trianglelefteq t$
implies
$s\trianglelefteq t$
implies
 $s\lambda\trianglelefteq t\lambda$
:
$s\lambda\trianglelefteq t\lambda$
:
By Definition 2.(4), we have three cases:
-
(i)
 $s=t$
is trivial.
$s=t$
is trivial. -
(ii) Let
 $t=f(t_{1},\ldots,t_{n})$
and
$t=f(t_{1},\ldots,t_{n})$
and
 $s\trianglelefteq t_{j}$
for some
$s\trianglelefteq t_{j}$
for some
 $j\leq n$
. Now
$j\leq n$
. Now
 $t\lambda=f(t_{1},\ldots,t_{n})\lambda=f(t_{1}\lambda,\ldots,\,t_{n}\lambda)$
. Since
$t\lambda=f(t_{1},\ldots,t_{n})\lambda=f(t_{1}\lambda,\ldots,\,t_{n}\lambda)$
. Since
 $t_{j}$
is smaller than t we obtain by an inductive argument that
$t_{j}$
is smaller than t we obtain by an inductive argument that
 $s\lambda\trianglelefteq t_{j}\lambda$
. Hence,
$s\lambda\trianglelefteq t_{j}\lambda$
. Hence,
 $s\lambda\trianglelefteq t\lambda$
.
$s\lambda\trianglelefteq t\lambda$
. -
(iii) Let
 $s=f(s_{1},\ldots,s_{n})$
and
$s=f(s_{1},\ldots,s_{n})$
and
 $t=f(t_{1},\ldots,t_{n})$
with
$t=f(t_{1},\ldots,t_{n})$
with
 $s_{1}\trianglelefteq t_{1},...,\,s_{n}\trianglelefteq t_{n}$
. We have
$s_{1}\trianglelefteq t_{1},...,\,s_{n}\trianglelefteq t_{n}$
. We have
 $s\lambda=f(s_{1}\lambda,\ldots,\,s_{n}\lambda)$
and
$s\lambda=f(s_{1}\lambda,\ldots,\,s_{n}\lambda)$
and
 $f(t_{1}\lambda,\ldots t_{n}\lambda)=t\lambda$
and again by an inductive argument, we obtain
$f(t_{1}\lambda,\ldots t_{n}\lambda)=t\lambda$
and again by an inductive argument, we obtain
 $s_{i}\lambda\trianglelefteq t_{i}\lambda$
for
$s_{i}\lambda\trianglelefteq t_{i}\lambda$
for
 $1\leq i\leq n$
. Hence,
$1\leq i\leq n$
. Hence,
 $s\lambda\trianglelefteq t\lambda$
.
$s\lambda\trianglelefteq t\lambda$
. -
(2) This is shown using the
 $\trianglerighteq_{E}$
-chain of Lemma 11
$\trianglerighteq_{E}$
-chain of Lemma 11
 $t\overset{n}{\blacktriangleright_{E}}s$
, that is, there is a
$t\overset{n}{\blacktriangleright_{E}}s$
, that is, there is a
 $\vartriangleright_{E}$
-chain
$\vartriangleright_{E}$
-chain
 $t=_{E}t_{1}\vartriangleright t'_{1}=_{E}t_{2}\vartriangleright........\vartriangleright t'_{n}=_{E}s$
. Applying assertion (1) of this lemma to every element of the chain yields:
$t=_{E}t_{1}\vartriangleright t'_{1}=_{E}t_{2}\vartriangleright........\vartriangleright t'_{n}=_{E}s$
. Applying assertion (1) of this lemma to every element of the chain yields:
 $t=_{E}t_{1}\Longrightarrow t\lambda=_{E}t_{1}\lambda$
,
$t=_{E}t_{1}\Longrightarrow t\lambda=_{E}t_{1}\lambda$
,
 $t_{1}\vartriangleright t'_{1}\Longrightarrow t_{1}\lambda\vartriangleright t'_{1}\lambda$
, …….,
$t_{1}\vartriangleright t'_{1}\Longrightarrow t_{1}\lambda\vartriangleright t'_{1}\lambda$
, …….,
 $t'_{n}=_{E}s\Longrightarrow t'_{n}\lambda=_{E}s\lambda$
. Combining these into one chain yields:
$t'_{n}=_{E}s\Longrightarrow t'_{n}\lambda=_{E}s\lambda$
. Combining these into one chain yields:
 $t\lambda=_{E}t_{1}\lambda\vartriangleright{t_{1}}\lambda=_{E}t_{2}\lambda\vartriangleright......{t_{n}}\lambda=_{E}s\lambda$
. Hence,
$t\lambda=_{E}t_{1}\lambda\vartriangleright{t_{1}}\lambda=_{E}t_{2}\lambda\vartriangleright......{t_{n}}\lambda=_{E}s\lambda$
. Hence,
 $t\lambda\trianglerighteq_{E}s\lambda$
, resp.
$t\lambda\trianglerighteq_{E}s\lambda$
, resp.
 $s\lambda\trianglelefteq_{E}t\lambda$
.
$s\lambda\trianglelefteq_{E}t\lambda$
. -
(3) By Definition 16.(4)
 $\sigma\trianglelefteq_{E}\tau$
:
$\sigma\trianglelefteq_{E}\tau$
:
 $\forall x\in\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau):x\sigma\trianglelefteq_{E}x\tau$
and since these are terms, we have with 19(2) that
$\forall x\in\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau):x\sigma\trianglelefteq_{E}x\tau$
and since these are terms, we have with 19(2) that
 $\forall x\in\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau):x\sigma\lambda\trianglelefteq_{E}x\tau\lambda$
and thus
$\forall x\in\mathbf{Dom}(\sigma)=\mathbf{Dom}(\tau):x\sigma\lambda\trianglelefteq_{E}x\tau\lambda$
and thus
 $\sigma\lambda\trianglelefteq_{E}\tau\lambda$
.
$\sigma\lambda\trianglelefteq_{E}\tau\lambda$
.
The next theorem shows that instance E-embedding is also a quasi-order on first-order terms.
Theorem 20 The
![]() $\lambda_{E}$
-embedment order
$\lambda_{E}$
-embedment order
![]()
is a quasi-order on terms.
Proof. Let r,s,t be terms:
reflexivity: is obvious because every term
![]() $\lambda$
-embeds itself.
$\lambda$
-embeds itself.
transitivity: we show
![]()
implies
![]() .
.
By Definition 12, we have:
![]()
implies
![]() $\exists\sigma:s\trianglerighteq_{E}r\sigma$
and
$\exists\sigma:s\trianglerighteq_{E}r\sigma$
and
![]()
implies
![]() $\exists\tau:t\trianglerighteq_{E}s\tau$
.
$\exists\tau:t\trianglerighteq_{E}s\tau$
.
Furthermore with Lemma 20 and Theorem 14:
![]() $s\trianglerighteq_{E}r\sigma\Longrightarrow$
$s\trianglerighteq_{E}r\sigma\Longrightarrow$
![]() $\exists m:s\overset{m}{\blacktriangleright_{E}}r\sigma$
and
$\exists m:s\overset{m}{\blacktriangleright_{E}}r\sigma$
and
![]() $t\trianglerighteq_{E}s\tau\Longrightarrow\exists n:t\overset{n}{\blacktriangleright_{E}}s\tau$
.
$t\trianglerighteq_{E}s\tau\Longrightarrow\exists n:t\overset{n}{\blacktriangleright_{E}}s\tau$
.
By Lemma 19
![]() $\blacktriangleright$
is substitution-composable from the right, hence we have
$\blacktriangleright$
is substitution-composable from the right, hence we have
![]() $s\tau\overset{m}{\blacktriangleright_{E}}r\sigma\tau$
, which implies
$s\tau\overset{m}{\blacktriangleright_{E}}r\sigma\tau$
, which implies
![]() $t\overset{n}{\blacktriangleright_{E}}s\tau\overset{m}{\blacktriangleright_{E}}r\sigma\tau$
.
$t\overset{n}{\blacktriangleright_{E}}s\tau\overset{m}{\blacktriangleright_{E}}r\sigma\tau$
.
Using the transitivity of
![]() $\trianglerighteq_{E}$
we get:
$\trianglerighteq_{E}$
we get:
![]() $t\overset{n+m}{\blacktriangleright_{E}}r\sigma\tau$
and hence
$t\overset{n+m}{\blacktriangleright_{E}}r\sigma\tau$
and hence
![]() $t\trianglerighteq_{E}r(\sigma\tau)$
,
$t\trianglerighteq_{E}r(\sigma\tau)$
,
that is
![]() .
.
Using Theorem 20, we can now show that instance E-embedding of terms lifted to substitutions is also a quasi-order:
Theorem 21 The
![]() $\lambda_{E}$
-embedment order
$\lambda_{E}$
-embedment order
![]()
is a quasi-order on substitutions.
Proof.
reflexivity: is a trivial consequence with the identity substitution
![]() $\varepsilon$
:
$\varepsilon$
:
![]()
transitivity:
![]()
implies
![]()
By Definition 16.(5), we have:
![]()
implies
![]() $\exists\lambda:\sigma\trianglerighteq_{E}\varrho\lambda$
and
$\exists\lambda:\sigma\trianglerighteq_{E}\varrho\lambda$
and
![]()
implies
![]() $\exists\delta:\tau\trianglelefteq_{E}\sigma\delta$
. Hence, by Lemma 19.(3) on the components of
$\exists\delta:\tau\trianglelefteq_{E}\sigma\delta$
. Hence, by Lemma 19.(3) on the components of
![]() $\sigma$
and
$\sigma$
and
![]() $\varrho$
$\varrho$
we have
![]() $\sigma\delta\trianglerighteq_{E}\varrho(\lambda\delta)$
, which implies by definition
$\sigma\delta\trianglerighteq_{E}\varrho(\lambda\delta)$
, which implies by definition
![]() .
.
The following definition lists some well-known notions (see Kruskal (Reference Kruskal1960) and Nash-Williams (Reference Nash-Williams1963)) on quasi-orderings, which we shall use later on.
Definition 22 Let
![]() $\leq$
be a quasi-ordering on a set S, then:
$\leq$
be a quasi-ordering on a set S, then:
-
(1) An infinite sequence of elements of S,
 $a_{1},a_{2},a_{3},...$
is called a
$a_{1},a_{2},a_{3},...$
is called a
 $\mathbf{\leq}-$
chain if
$\mathbf{\leq}-$
chain if
 $a_{i}\leq a_{i+1}$
for all
$a_{i}\leq a_{i+1}$
for all
 $i\geq1$
. The sequence
$i\geq1$
. The sequence
 $a_{1},a_{2},a_{3},...$
is said to contain a chain if it has a subsequence that is a chain.
$a_{1},a_{2},a_{3},...$
is said to contain a chain if it has a subsequence that is a chain. -
(2) The infinite sequence
 $a_{1},a_{2},a_{3},...$
is called an anti-chain if neither
$a_{1},a_{2},a_{3},...$
is called an anti-chain if neither
 $a_{i}\leq a_{j}$
nor
$a_{i}\leq a_{j}$
nor
 $a_{j}\leq a_{i}$
, for all
$a_{j}\leq a_{i}$
, for all
 $1\leq i<j$
.
$1\leq i<j$
. -
(3) The quasi-ordering
 $\leq$
is well-founded (wfo) if it contains no infinite strictly descending
$\leq$
is well-founded (wfo) if it contains no infinite strictly descending
 $<$
-chain; that is, there is no infinite sequence
$<$
-chain; that is, there is no infinite sequence
 $a_{1},a_{2},a_{3},...$
of elements of S such that
$a_{1},a_{2},a_{3},...$
of elements of S such that
 $a_{i}>a_{i+1}$
for every
$a_{i}>a_{i+1}$
for every
 $i\;in\;\mathbb{N}$
.
$i\;in\;\mathbb{N}$
. -
(4) A well-quasi-ordering on S (wqo),
 $\leq$
, is a quasi-ordering which is well-founded and it has no infinite anti-chains in S with respect to
$\leq$
, is a quasi-ordering which is well-founded and it has no infinite anti-chains in S with respect to
 $\leq$
.
$\leq$
.
Lemma 23 Let E be an equational theory and let
![]()
be an infinitely descending
![]()
-chain of terms
![]() $t_{i},1\leqq i$
. Then there exists an infinitely descending
$t_{i},1\leqq i$
. Then there exists an infinitely descending
![]() $\trianglerighteq_{E}$
-chain of instances of
$\trianglerighteq_{E}$
-chain of instances of
![]() $t_{i}$
with corresponding instantiating substitutions
$t_{i}$
with corresponding instantiating substitutions
![]() $\sigma_{i}$
:
$\sigma_{i}$
:
![]() $t_{1}\trianglerighteq_{E}t{}_{2}\sigma_{2}\trianglerighteq_{E}t_{3}\sigma_{3}\trianglerighteq_{E}t_{4}\sigma_{4}\trianglerighteq_{E}....$
, where the
$t_{1}\trianglerighteq_{E}t{}_{2}\sigma_{2}\trianglerighteq_{E}t_{3}\sigma_{3}\trianglerighteq_{E}t_{4}\sigma_{4}\trianglerighteq_{E}....$
, where the
![]() $\sigma_{i}$
are composed from the
$\sigma_{i}$
are composed from the
![]() $\sigma_{k}$
for
$\sigma_{k}$
for
![]() $1\leq k\leq i$
.
$1\leq k\leq i$
.
Proof. By Definition 12, we have
![]()
and
![]() .
.
With Lemma 19.(2), we get
![]() $t_{2}\lambda_{2}\trianglerighteq_{E}t_{3}\lambda_{3}\lambda_{2}$
. Hence,
$t_{2}\lambda_{2}\trianglerighteq_{E}t_{3}\lambda_{3}\lambda_{2}$
. Hence,
![]() $t_{1}\trianglerighteq_{E}t_{2}\lambda_{2}\trianglerighteq_{E}t_{3}\lambda_{3}\lambda_{2}$
.
$t_{1}\trianglerighteq_{E}t_{2}\lambda_{2}\trianglerighteq_{E}t_{3}\lambda_{3}\lambda_{2}$
.
Now we have the following induction hypotheses: with
![]() $\sigma_{2}\;:=\;\lambda_{2}$
and for
$\sigma_{2}\;:=\;\lambda_{2}$
and for
![]() $n>2$
$n>2$
![]()
![]() $t_{1}\trianglerighteq_{E}t_{2}\lambda_{2}\trianglerighteq_{E}t_{3}\lambda_{3}\lambda_{2}\trianglerighteq_{E}....\trianglerighteq_{E}t_{n}\lambda_{n}\lambda_{n-1}\lambda_{n\text{-2}}...\lambda_{2}$
$t_{1}\trianglerighteq_{E}t_{2}\lambda_{2}\trianglerighteq_{E}t_{3}\lambda_{3}\lambda_{2}\trianglerighteq_{E}....\trianglerighteq_{E}t_{n}\lambda_{n}\lambda_{n-1}\lambda_{n\text{-2}}...\lambda_{2}$
For more readability, let us use the following notation:
(*1)
![]() $\sigma_{1}\;:=\;\varepsilon,\sigma_{2}\;:=\;\lambda_{2},\sigma_{3}\;:=\;\lambda_{3}\lambda_{2}$
, that is:
$\sigma_{1}\;:=\;\varepsilon,\sigma_{2}\;:=\;\lambda_{2},\sigma_{3}\;:=\;\lambda_{3}\lambda_{2}$
, that is:
![]() $\sigma_{i}\;:=\;\lambda_{i}\sigma_{i-1}$
,
$\sigma_{i}\;:=\;\lambda_{i}\sigma_{i-1}$
,
![]() $i\geq2$
.
$i\geq2$
.
Now by induction.
![]() $n=2:$
$n=2:$
![]()
and using (*1) we have:
![]() $t_{1}\trianglerighteq_{E}t_{2}\sigma_{2}$
$t_{1}\trianglerighteq_{E}t_{2}\sigma_{2}$
![]() $n\rightarrow n+1:$
by induction hypotheses there exist substitutions
$n\rightarrow n+1:$
by induction hypotheses there exist substitutions
![]() $\lambda_{2},\lambda_{3},...,\lambda_{n}$
$\lambda_{2},\lambda_{3},...,\lambda_{n}$
such that
![]() $t_{1}\trianglerighteq_{E}t_{2}\sigma_{2}\trianglerighteq_{E}t_{3}\sigma_{3}\trianglerighteq_{E}....\trianglerighteq_{E}t_{n}\sigma_{n}$
, where
$t_{1}\trianglerighteq_{E}t_{2}\sigma_{2}\trianglerighteq_{E}t_{3}\sigma_{3}\trianglerighteq_{E}....\trianglerighteq_{E}t_{n}\sigma_{n}$
, where
![]() $\sigma_{i}\;:=\;\lambda_{i}\sigma_{i-1}$
,
$\sigma_{i}\;:=\;\lambda_{i}\sigma_{i-1}$
,
![]() $i\geq2$
,
$i\geq2$
,
as notated in (*1).
Now at the tail of the chain, we have
![]()
and by Definition 12 there is a
substitution
![]() $\lambda_{n+1}$
, such that
$\lambda_{n+1}$
, such that
![]() $t_{n}\trianglerighteq_{E}t_{n+1}\lambda_{n+1}$
. Moreover with Lemma 19.(2) :
$t_{n}\trianglerighteq_{E}t_{n+1}\lambda_{n+1}$
. Moreover with Lemma 19.(2) :
![]() $t_{n}\sigma_{n}\trianglerighteq_{E}t_{n+1}\lambda_{n+1}\sigma_{n}$
, and using notation (*1):
$t_{n}\sigma_{n}\trianglerighteq_{E}t_{n+1}\lambda_{n+1}\sigma_{n}$
, and using notation (*1):
![]() $t_{n}\sigma_{n}\trianglerighteq_{E}t_{n+1}\sigma_{n+1}$
.
$t_{n}\sigma_{n}\trianglerighteq_{E}t_{n+1}\sigma_{n+1}$
.
Hence in the limit we obtain
![]() $t_{1}\trianglerighteq_{E}t_{2}\sigma_{2}\trianglerighteq_{E}t_{3}\sigma_{3}\trianglerighteq_{E}....$
.
$t_{1}\trianglerighteq_{E}t_{2}\sigma_{2}\trianglerighteq_{E}t_{3}\sigma_{3}\trianglerighteq_{E}....$
.
The following Tree Theorem was first proposed as a hypothesis by A. Vonyi and proved by Kruskal (Reference Kruskal1960); Kruskal (Reference Kruskal1972), and later with a more elegant proof by Nash-Williams (Reference Nash-Williams1963). It states that the set of finite trees over a well-quasi-ordered set of labels is itself well-quasi-ordered under homeomorphic embedding. Kruskal uses a notation, where T(Y) denotes the collection of all (structured) trees over an alphabet Y.
Theorem 24 The Tree Theorem If Y is well-quasi-ordered, then T(Y) is well-quasi-ordered too.
The following theorem is a consequence of the tree theorem for the set of first-order terms T(F,X), built over a finite signature F and a finite set of variable symbols X. Hereby, we refer to the work of Gallier (Reference Gallier1991), whose terminology we like to use. He proves that “Given a finite alphabet
![]() $\Sigma$
=
$\Sigma$
=
![]() $F\cup X$
which is well quasi ordered then
$F\cup X$
which is well quasi ordered then
![]() $\trianglerighteq$
is also a well quasi order on
$\trianglerighteq$
is also a well quasi order on
![]() $T(F,\,X)$
” and the next theorem is a generalization to “modulo E.” In the following, we assume that
$T(F,\,X)$
” and the next theorem is a generalization to “modulo E.” In the following, we assume that
![]() $\Sigma$
is well-quasi-ordered.
$\Sigma$
is well-quasi-ordered.
Theorem 25 Let E be an equational theory. The E-embedding quasi-order
![]() $\trianglerighteq_{E}$
is a well-quasi-order on the set of terms built over a finite alphabet
$\trianglerighteq_{E}$
is a well-quasi-order on the set of terms built over a finite alphabet
![]() $\Sigma$
=
$\Sigma$
=
![]() $F\cup X$
.
$F\cup X$
.
Proof.
-
(i)
 $\trianglerighteq_{E}$
is well founded.
$\trianglerighteq_{E}$
is well founded.
If not, then there exists an infinite strictly descending
![]() $\vartriangleright_{E}-$
chain over a finite alphabet:
$\vartriangleright_{E}-$
chain over a finite alphabet:
![]() $t_{1}\vartriangleright_{E}t_{2}\vartriangleright_{E}t_{3}\vartriangleright_{E}...$
.
$t_{1}\vartriangleright_{E}t_{2}\vartriangleright_{E}t_{3}\vartriangleright_{E}...$
.
From this chain, we obtain the (sub-) sequence
![]() $s_{1},s{}_{2},s{}_{3},....$
where each
$s_{1},s{}_{2},s{}_{3},....$
where each
![]() $s_{i}$
corresponds to some
$s_{i}$
corresponds to some
![]() $t_{j}$
with
$t_{j}$
with
![]() $s_{i}=_{E}t_{j}$
.
$s_{i}=_{E}t_{j}$
.
Then by the tree embedding theorem, there are indices
![]() $i<j$
such that
$i<j$
such that
![]() $t_{i}\trianglelefteq t{}_{j}$
.
$t_{i}\trianglelefteq t{}_{j}$
.
(see Gallier (Reference Gallier1991) for this formulation).
But
![]() $t_{i}\trianglelefteq t{}_{j}$
implies in particular
$t_{i}\trianglelefteq t{}_{j}$
implies in particular
![]() $t_{i}\trianglelefteq_{E}t{}_{j}$
and hence contradicts that there is a
$t_{i}\trianglelefteq_{E}t{}_{j}$
and hence contradicts that there is a
strictly descending
![]() $\vartriangleright_{E}-$
chain.
$\vartriangleright_{E}-$
chain.
-
(ii) There are no infinite anti-chains with respect to
 $\trianglerighteq_{E}$
.
$\trianglerighteq_{E}$
.
The argument is in the same spirit by contradiction, reducing
![]() $\trianglerighteq_{E}$
to
$\trianglerighteq_{E}$
to
![]() $\trianglerighteq$
.
$\trianglerighteq$
.
Theorem 26 Let E be an equational theory. The
![]() $\lambda_{E-}$
embedding quasi-order
$\lambda_{E-}$
embedding quasi-order
![]()
is a well-quasi-order on the set of terms built over a finite alphabet
![]() $\Sigma=F\cup X$
.
$\Sigma=F\cup X$
.
Proof. Similar to Theorem 25 Footnote 3 .
E-unification of first-order terms is based on an infinite set of variable symbols and it is well known that the embedding order of terms with an infinite set of variable symbols is not a well-quasi-order, since we have the anti-chain
![]() $x_{1},x_{2},x_{3},....$
. Of course the same is the case then for embedment modulo E.
$x_{1},x_{2},x_{3},....$
. Of course the same is the case then for embedment modulo E.
But well foundedness of the syntactic embedding ordering is valid, since the number of symbols decreases in a strictly descending syntactic
![]() $\vartriangleright-$
chain. This well-known fact is stated in the next proposition.
$\vartriangleright-$
chain. This well-known fact is stated in the next proposition.
Proposition 27 In a strictly descending
![]() $\vartriangleright-$
chain the number of occurrences of symbols decreases.
$\vartriangleright-$
chain the number of occurrences of symbols decreases.
Our interest in this paper is the extension to equational theories. But with an infinite set of variables Proposition 27 is not applicable, since in an infinite strictly decreasing
![]() $\trianglerighteq_{E}$
-chain the number of occurrences of symbols could increase. So one would conjecture that the E-embedding order is not a well-founded order (WFO). Unfortunately, we have yet no proof either way.
$\trianglerighteq_{E}$
-chain the number of occurrences of symbols could increase. So one would conjecture that the E-embedding order is not a well-founded order (WFO). Unfortunately, we have yet no proof either way.
For an infinite set of variable symbols, we have to look for appropriate constraints on the equational theory E and a possible candidate is that for a term t the total number of variable symbols in
![]() $[t]_{E}$
is finite. This is achieved by requiring that every axiom
$[t]_{E}$
is finite. This is achieved by requiring that every axiom
![]() $l=r$
in E has the property, that
$l=r$
in E has the property, that
![]() $\mathbf{Var}(l)=\mathbf{Var}(r)$
, a class of theories called regular theories.
$\mathbf{Var}(l)=\mathbf{Var}(r)$
, a class of theories called regular theories.
Lemma 28 Let E=
![]() $\{l_{1}=r_{1},l_{2}=r_{2},...,l_{k}=r_{k}\}$
be a regular equational theory, that is for each
$\{l_{1}=r_{1},l_{2}=r_{2},...,l_{k}=r_{k}\}$
be a regular equational theory, that is for each
![]() $i\in\{1,...,n\}:\mathbf{Var}(l_{i})=\mathbf{Var}(r_{i})$
. For any term
$i\in\{1,...,n\}:\mathbf{Var}(l_{i})=\mathbf{Var}(r_{i})$
. For any term
![]() $t\in T(F,X)$
, the total number of variable symbols in the equational class
$t\in T(F,X)$
, the total number of variable symbols in the equational class
![]() $[t]_{E}$
is finite.
$[t]_{E}$
is finite.
Proof. Consider
![]() $t'\in[t]_{E}$
and a number
$t'\in[t]_{E}$
and a number
![]() $n\geqq1$
of rewrite steps
$n\geqq1$
of rewrite steps
![]() $t\stackrel{n}{\longrightarrow_{E}}t'$
.
$t\stackrel{n}{\longrightarrow_{E}}t'$
.
Then for every rewrite step:
![]() $t_{i}\longrightarrow_{l_{i}\rightarrow r_{i}}t_{i+1}$
or
$t_{i}\longrightarrow_{l_{i}\rightarrow r_{i}}t_{i+1}$
or
![]() $t_{i}\longrightarrow_{r_{i}\rightarrow l_{i}}t_{i+1}$
$t_{i}\longrightarrow_{r_{i}\rightarrow l_{i}}t_{i+1}$
there is a substitution
![]() $\lambda_{i}$
such that
$\lambda_{i}$
such that
![]() $l_{i}\lambda_{i}$
(or
$l_{i}\lambda_{i}$
(or
![]() $r_{i}\lambda_{i}$
) is a subterm of
$r_{i}\lambda_{i}$
) is a subterm of
![]() $t_{i}$
,
$t_{i}$
,
![]() $l_{i}\lambda\preceq t$
(or
$l_{i}\lambda\preceq t$
(or
![]() $l_{i}\lambda\preceq t$
) and
$l_{i}\lambda\preceq t$
) and
![]() $t_{i+1}$
is the result of replacing
$t_{i+1}$
is the result of replacing
![]() $l_{i}\lambda$
by
$l_{i}\lambda$
by
![]() $r_{i}\lambda$
(or
$r_{i}\lambda$
(or
![]() $r_{i}\lambda$
by
$r_{i}\lambda$
by
![]() $l_{i}\lambda$
).
$l_{i}\lambda$
).
But since
![]() $\mathbf{Var}(l_{i})=\mathbf{Var}(r_{i})$
this cannot introduce new variables in
$\mathbf{Var}(l_{i})=\mathbf{Var}(r_{i})$
this cannot introduce new variables in
![]() $t_{i+1}$
and
$t_{i+1}$
and
hence
![]() $\mathbf{Var}(t')\subseteq\mathbf{Var}(t)$
.
$\mathbf{Var}(t')\subseteq\mathbf{Var}(t)$
.
Well foundedness of E-embedding is now an easy consequence.
Theorem 29 Let E be a regular equational theory. E-embedding
![]() $\trianglerighteq_{E}$
is a well-founded quasi-order on the set of terms.
$\trianglerighteq_{E}$
is a well-founded quasi-order on the set of terms.
Proof. If not, then there exists an infinite strictly descending
![]() $\vartriangleright_{E}$
-chain
$\vartriangleright_{E}$
-chain
![]() $t_{1}\vartriangleright_{E}t_{2}\vartriangleright_{E}t_{3}...\vartriangleright_{E}t_{i}\vartriangleright_{E}.....$
$t_{1}\vartriangleright_{E}t_{2}\vartriangleright_{E}t_{3}...\vartriangleright_{E}t_{i}\vartriangleright_{E}.....$
With Definition 10 and Lemma 11, this chain has the form:
![]() $t_{1}=_{E}t_{1}'\overset{n_{1}}{\blacktriangleright_{E}}t{}_{2}=_{E}t_{2}'\overset{n_{2}}{\blacktriangleright_{E}}t{}_{3}=_{E}t_{3}'\overset{n_{3}}{\blacktriangleright_{E}}t{}_{4}.....$
which consists of E-variants of embedded
$t_{1}=_{E}t_{1}'\overset{n_{1}}{\blacktriangleright_{E}}t{}_{2}=_{E}t_{2}'\overset{n_{2}}{\blacktriangleright_{E}}t{}_{3}=_{E}t_{3}'\overset{n_{3}}{\blacktriangleright_{E}}t{}_{4}.....$
which consists of E-variants of embedded
terms. Now with Lemma 28 and
![]() $W\;:=\;\mathbf{Var}(t_{1})\bigcup V_{E}$
we have,
$W\;:=\;\mathbf{Var}(t_{1})\bigcup V_{E}$
we have,
that for all terms ˆ, which appear in the chain: Var(ˆ
![]() $)\subseteq W$
.
$)\subseteq W$
.
But then all elements of the chain and its E-equivalents are built over a finite
alphabet. Hence by Theorem 25, the
![]() $\trianglerighteq_{E}$
ordering is well founded.
$\trianglerighteq_{E}$
ordering is well founded.
The next theorem is similar and shows that
![]() $\lambda_{E}$
-embedding preserves well foundedness.
$\lambda_{E}$
-embedding preserves well foundedness.
Theorem 30 Let E be a regular equational theory.
![]() $\lambda_{E}-$
embedding
$\lambda_{E}-$
embedding
![]()
is a well-founded quasi-order on the set of terms.
Proof. If not, then there is an infinite strictly descending
![]() $\gtrdot_{E}$
-chain
$\gtrdot_{E}$
-chain
![]() $t_{1}\gtrdot_{E}t_{2}\gtrdot_{E}t_{3}...\gtrdot_{E}t_{i}\gtrdot_{E}.....$
$t_{1}\gtrdot_{E}t_{2}\gtrdot_{E}t_{3}...\gtrdot_{E}t_{i}\gtrdot_{E}.....$
By Lemma 23, there exists a corresponding infinite strictly descending
![]() $\vartriangleright_{E}$
-chain
$\vartriangleright_{E}$
-chain
![]() $t_{1}\vartriangleright_{E}t{}_{2}\sigma_{2}\vartriangleright_{E}t_{3}\sigma_{3}\vartriangleright_{E}t_{4}\sigma_{4}\vartriangleright_{E}....$
contradicting Theorem 29.
$t_{1}\vartriangleright_{E}t{}_{2}\sigma_{2}\vartriangleright_{E}t_{3}\sigma_{3}\vartriangleright_{E}t_{4}\sigma_{4}\vartriangleright_{E}....$
contradicting Theorem 29.
3. Ordering E-unifiers under homeomorphic embedding
We shall now look at unification under
![]() $\lambda_{E}$
-embedding, which is our main interest in this paper, and we start with a recapitulation of the standard notions of E-unification.
$\lambda_{E}$
-embedding, which is our main interest in this paper, and we start with a recapitulation of the standard notions of E-unification.
3.1
 $\mathbf{E}$
-Unification
$\mathbf{E}$
-Unification
Let E be an equational theory and let F be the signature of the term algebra. An E-unification problem is a finite set of equations
Let V denote the set of variables in
![]() $\varGamma$
,
$\varGamma$
,
![]() $V=\mathbf{Var}(\varGamma)$
. An
E-unifier for
$V=\mathbf{Var}(\varGamma)$
. An
E-unifier for
![]() $\Gamma$
is a substitution
$\Gamma$
is a substitution
![]() $\sigma$
such that
$\sigma$
such that
The set of all E-unifiers of
![]() $\Gamma$
is denoted
$\Gamma$
is denoted
![]() $\mathcal{U}\Sigma_{E}(\Gamma)$
. A complete set of E-unifiers
$\mathcal{U}\Sigma_{E}(\Gamma)$
. A complete set of E-unifiers
![]() $c\mathcal{U}\Sigma_{E}(\Gamma)$
for
$c\mathcal{U}\Sigma_{E}(\Gamma)$
for
![]() $\Gamma$
is a set of E-unifiers, such that for every E-unifier
$\Gamma$
is a set of E-unifiers, such that for every E-unifier
![]() $\tau$
there exists
$\tau$
there exists
![]() $\sigma\in c\mathcal{U}\Sigma_{E}(\Gamma)$
with
$\sigma\in c\mathcal{U}\Sigma_{E}(\Gamma)$
with
![]() $\sigma\leq_{E}^{V}\tau$
. The set
$\sigma\leq_{E}^{V}\tau$
. The set
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
is called a minimal complete set of E-unifiers for
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
is called a minimal complete set of E-unifiers for
![]() $\Gamma$
, if it is complete and for all distinct elements
$\Gamma$
, if it is complete and for all distinct elements
![]() $\sigma$
and
$\sigma$
and
![]() $\sigma'$
in
$\sigma'$
in
![]() $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
if
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
if
![]() $\sigma\leq_{E}^{V}\sigma'$
then
$\sigma\leq_{E}^{V}\sigma'$
then
![]() $\sigma=_{E}^{V}\sigma'$
.
$\sigma=_{E}^{V}\sigma'$
.
When a minimal complete set of E-unifiers of a unification problem
![]() $\Gamma$
exists, it is unique up to E-subsumption equivalence
$\Gamma$
exists, it is unique up to E-subsumption equivalence
![]() $\thicksim_{E}^{V}$
. Minimal complete sets of E-unifiers need not always exist, and if they do, they might be singular, finite, or infinite. Since minimal complete sets of E-unifiers are isomorphic whenever they exist, they can be used to classify theories with respect to their corresponding unification problem. This leads naturally to the concept of a unification hierarchy, see Siekmann (Reference Siekmann1989), Knight (Reference Knight1989), Gallier (Reference Gallier1991), Baader and Siekmann (Reference Baader and Siekmann1994), and Baader and Snyder (Reference Baader and Snyder2001) for the standard surveys on this aspect.
$\thicksim_{E}^{V}$
. Minimal complete sets of E-unifiers need not always exist, and if they do, they might be singular, finite, or infinite. Since minimal complete sets of E-unifiers are isomorphic whenever they exist, they can be used to classify theories with respect to their corresponding unification problem. This leads naturally to the concept of a unification hierarchy, see Siekmann (Reference Siekmann1989), Knight (Reference Knight1989), Gallier (Reference Gallier1991), Baader and Siekmann (Reference Baader and Siekmann1994), and Baader and Snyder (Reference Baader and Snyder2001) for the standard surveys on this aspect.
A unification problem
![]() $\Gamma$
is
$\Gamma$
is
-
nullary, if
 $\Gamma$
is unifiable, but the minimal complete set of E-unifiers does not exist.
$\Gamma$
is unifiable, but the minimal complete set of E-unifiers does not exist. -
unitary, if it is not nullary and the minimal complete set of E-unifiers for
 $\Gamma$
is of cardinality less than or equal to 1.
$\Gamma$
is of cardinality less than or equal to 1. -
finitary, if it is not nullary and the minimal complete set of E-unifiers is always finite.
-
infinitary, if it is not nullary and the minimal complete set of E-unifiers is infinite.
An equational theory E is
-
unitary, if all unification problems for E are unitary
-
finitary, if all unification problems are finitary.
-
infinitary, if there is at least one infinitary unification problem and all unification problems have minimal complete sets of E-unifiers.
-
If there exists a solvable unification problem
 $\Gamma$
not having a minimal complete set of E-unifiers, then the equational theory E is nullary or of type zero.
$\Gamma$
not having a minimal complete set of E-unifiers, then the equational theory E is nullary or of type zero.
3.2 E-Unifiers ordered by homeomorphic embedding
The essential problem in unification theory is to determine the relationship between the solutions of term equations. In other words: what is the structure of the solution space?
In the case of syntactic unification, the structural relationship between the unifiers is based on the fact that terms form a lattice under the subsumption order, that is, there is a least upper bound and a max lower bound. Hence, if a unification problem is solvable, then there is a single most general unifier. But for unification under an equational theory the answer is not as easy, because:
-
the complete set of most general unifiers is mostly infinite
-
the complete set of most general unifiers may not even exist for a solvable E-unification problem.
So the search for an order relation better than subsumption comes naturally. Our first idea was based on the observation that certain solutions contain the instances of other solutions as a sub-structure. We captured this idea technically with the encompassment order on terms and substitutions, which led to the notion of an E-essential unifier Footnote 4 . Sub-structure means, in this case, that a unifying substitution encompasses other unifiers and hence they need not necessarily be part of the new set that represents all solutions. Unfortunately, the encompassment order is not a wqo either and hence there are equational theories for which there are solvable E-unification problems, but the minimal and complete set of essential E-unifiers does not exist, so they are E-nullary w.r.t. encompassment (Baader, Reference Baader1988; Hoche, 2016; Szabo et al., Reference Szabo, Siekmann and Hoche2016).
This paper is based on the observation that certain solutions embed the instances of other solutions in the sense of the homeomorphic tree embedding theorem or Kruskal’s theorem. That is, the components of a unifying substitution embed the components of another unifying substitution. This then leads to the notion of free (instance embedment-) E-unifiers, free
![]() $\lambda_{E}$
-unifiers, where these free
$\lambda_{E}$
-unifiers, where these free
![]() $\lambda_{E}$
-unifiers are the candidates of our new minimal and complete set of unifiers, which we name
$\lambda_{E}$
-unifiers are the candidates of our new minimal and complete set of unifiers, which we name
![]() $\varphi U\varSigma_{E}(\varGamma)$
.
$\varphi U\varSigma_{E}(\varGamma)$
.
Definition 31. Let E be an equational theory,
![]() $\varGamma$
be a solvable E-unification problem, and
$\varGamma$
be a solvable E-unification problem, and
![]() $\mathcal{U}\Sigma_{E}(\Gamma)$
be the set of all E-unifiers for
$\mathcal{U}\Sigma_{E}(\Gamma)$
be the set of all E-unifiers for
![]() $\varGamma$
. If an E-unifier
$\varGamma$
. If an E-unifier
![]() $\sigma$
in
$\sigma$
in
![]() $\mathcal{U}\Sigma_{E}(\Gamma)$
does not have any
$\mathcal{U}\Sigma_{E}(\Gamma)$
does not have any
![]() $\lambda_{E}$
-embedded unifier, then
$\lambda_{E}$
-embedded unifier, then
![]() $\sigma$
is called a free
$\sigma$
is called a free
![]() $\lambda_{E}$
-unifier. If the set of free
$\lambda_{E}$
-unifier. If the set of free
![]() $\lambda_{E}$
-unifiers is complete, it will be denoted as
$\lambda_{E}$
-unifiers is complete, it will be denoted as
![]() $\varphi\mathcal{U}\varSigma_{E}(\varGamma)$
.
$\varphi\mathcal{U}\varSigma_{E}(\varGamma)$
.
Since homeomorphic embedding is not a well-quasi-order on the set of terms with infinitely many variable symbols, we cannot use Theorem 25. But for all practical purposes it may be possible for an automated deduction system to set a limit to the number of new variables and the theorem may still be useful in that case.
Nevertheless, the infinite sequence of variables
![]() $x_{1},x_{2},x_{3},....$
is normally used as a case in point that we have an anti-chain and hence Kruskal’s theorem cannot be applied. But for the instance embedding order
$x_{1},x_{2},x_{3},....$
is normally used as a case in point that we have an anti-chain and hence Kruskal’s theorem cannot be applied. But for the instance embedding order
![]()
this is not the case: For example,
![]() $x_{1}$
instance embeds
$x_{1}$
instance embeds
![]() $x_{2}$
with the instantiating substitution
$x_{2}$
with the instantiating substitution
![]() $\lambda=\{x_{2}\rightarrow x_{1}\}.$
So there is the open problem whether or not the
$\lambda=\{x_{2}\rightarrow x_{1}\}.$
So there is the open problem whether or not the
![]() $\lambda_{E}$
-embedding is a well-quasi-order. Unfortunately, currently we have neither a counter example nor a proof – so we state it here as an:
$\lambda_{E}$
-embedding is a well-quasi-order. Unfortunately, currently we have neither a counter example nor a proof – so we state it here as an:
Open problem: Is the
![]()
-order a WQO even for an infinite number of variables?
For the rest of the paper, we shall also employ a standard technique used in the quest for termination proofs in logic programming Leuschel (Reference Leuschel1998); Leuschel (Reference Leuschel2002) as well as termination of term rewriting systems Dershowitz and Jouannaud (Reference Dershowitz and Jouannaud1990), namely to disregard the name of a variable and simply treat all variables as the same. In other words, the unification procedure processes them as if they were embedment equivalent. This observation leads to the notion of pure embedding, which we abbreviate to
![]() $\pi$
-embedding in the following and denote it as
$\pi$
-embedding in the following and denote it as
![]() $t\trianglerighteq^{\pi}s$
. As before, we generalize embedding to pure instance embedding or
$t\trianglerighteq^{\pi}s$
. As before, we generalize embedding to pure instance embedding or
![]() $\lambda^{\pi}$
-embedding by saying a term s is
$\lambda^{\pi}$
-embedding by saying a term s is
![]() $\lambda^{\pi}$
-embedded into a term t, if it is
$\lambda^{\pi}$
-embedded into a term t, if it is
![]() $\lambda$
-embedded and in addition all variables are embedding equivalent. It is defined (almost identical to Definition 2.(4), Definition 5 and 10) as follows:
$\lambda$
-embedded and in addition all variables are embedding equivalent. It is defined (almost identical to Definition 2.(4), Definition 5 and 10) as follows:
Definition 32. (Pure embedding,
![]() $\pi-$
embedding)
$\pi-$
embedding)
-
(1) A term t
 $\pi$
-embeds a term s if:
$\pi$
-embeds a term s if:
 \begin{align*}t\trianglerighteq^{\pi}s\,\iff\left\{ \begin{array}{ll}s=t\;or\;s,t\in X\:or\\t=f(t_{1},\ldots,\:t_{n})\;and\:for\:some\;i,\:1\leq i\leq n,\:t_{i}\trianglerighteq^{\pi}s,or\\t=f(t_{1},\,.\,.\,.t_{n}),\:\;s=f(s_{1},.\,.\,.s_{n})\;and\:\;\forall i:\:t_{i}\trianglerighteq^{\pi}s_{i},\:1\leq i\leq n.\end{array}\right.\end{align*}
\begin{align*}t\trianglerighteq^{\pi}s\,\iff\left\{ \begin{array}{ll}s=t\;or\;s,t\in X\:or\\t=f(t_{1},\ldots,\:t_{n})\;and\:for\:some\;i,\:1\leq i\leq n,\:t_{i}\trianglerighteq^{\pi}s,or\\t=f(t_{1},\,.\,.\,.t_{n}),\:\;s=f(s_{1},.\,.\,.s_{n})\;and\:\;\forall i:\:t_{i}\trianglerighteq^{\pi}s_{i},\:1\leq i\leq n.\end{array}\right.\end{align*}
-
(2) A term s is instance
 $\pi$
-embedded (
$\pi$
-embedded (
 $\lambda^{\pi}$
-embedded) into a term t, denoted
$\lambda^{\pi}$
-embedded) into a term t, denoted ,
,if there is an instantiating substitution
 $\lambda$
such that
$\lambda$
such that
 $s\lambda$
is
$s\lambda$
is
 $\pi$
-embedded into t:
$\pi$
-embedded into t:
 $s\lambda\trianglelefteq^{\pi}t$
. We also say that s is
$s\lambda\trianglelefteq^{\pi}t$
. We also say that s is
 $\lambda^{\pi}$
-embedded into t.
$\lambda^{\pi}$
-embedded into t. -
(3) A term t
 $\pi_{E}$
-embeds a term s modulo E, denoted
$\pi_{E}$
-embeds a term s modulo E, denoted
 $t\trianglerighteq_{E}^{\pi}s$
, if s and t are variables, or
$t\trianglerighteq_{E}^{\pi}s$
, if s and t are variables, or
 $s=_{E}t$
, or there is a term
$s=_{E}t$
, or there is a term
 $s'=_{E}s$
and a term
$s'=_{E}s$
and a term
 $t'=_{E}t$
and there is an embedded term p in
$t'=_{E}t$
and there is an embedded term p in
 $\mathbf{Emb_{E}}(t')$
such that
$\mathbf{Emb_{E}}(t')$
such that
 $p\vartriangleright^{\pi}s'$
. More precisely:
$p\vartriangleright^{\pi}s'$
. More precisely:
 \[t\trianglerighteq_{E}^{\pi}s\,\iff\begin{cases}s=_{E}t,\:or\:s,t\in X\;or\\\exists t'\in[t]_{E},s'\in\left[s\right]_{E}\;and\:\:\exists p\in\mathbf{Emb_{E}}(t'):p\vartriangleright^{\pi}s'\end{cases}\]
\[t\trianglerighteq_{E}^{\pi}s\,\iff\begin{cases}s=_{E}t,\:or\:s,t\in X\;or\\\exists t'\in[t]_{E},s'\in\left[s\right]_{E}\;and\:\:\exists p\in\mathbf{Emb_{E}}(t'):p\vartriangleright^{\pi}s'\end{cases}\]
-
(4) Similar to Definition 10 and Definition 12, we define that a term s is instance
 $\pi$
-embedded modulo E (
$\pi$
-embedded modulo E (
 $\lambda_{E}^{\pi}$
-embedded) into a term t,
$\lambda_{E}^{\pi}$
-embedded) into a term t, .
. -
(5) A substitution
 $\sigma$
is
$\sigma$
is
 $\pi$
-embedded into a substitution
$\pi$
-embedded into a substitution
 $\tau$
for a set of variables V, denoted as
$\tau$
for a set of variables V, denoted as ,
,iff V
 $\subseteq$
$\subseteq$
 $\mathbf{Dom}(\sigma)$
and
$\mathbf{Dom}(\sigma)$
and
 $\forall x\in V:x\sigma$
is
$\forall x\in V:x\sigma$
is
 $\pi-$
embedded into
$\pi-$
embedded into
 $x\tau$
.
$x\tau$
. -
(6) A substitution
 $\sigma$
is instance
$\sigma$
is instance
 $\pi-$
embedded modulo E (
$\pi-$
embedded modulo E (
 $\lambda_{E}^{\pi}$
-embedded) into a substitution
$\lambda_{E}^{\pi}$
-embedded) into a substitution
 $\tau$
for a set of variables V, denoted as
$\tau$
for a set of variables V, denoted as ,
,iff V
 $\subseteq+\mathbf{Dom}(\sigma)$
and there is a substitution
$\subseteq+\mathbf{Dom}(\sigma)$
and there is a substitution
 $\lambda$
, such that
$\lambda$
, such that
 $\forall x\in V:x(\sigma\lambda)$
is
$\forall x\in V:x(\sigma\lambda)$
is
 $\pi$
-embedded into
$\pi$
-embedded into
 $x\tau$
.
$x\tau$
.
![]() $\pi_{E}$
-embedding and
$\pi_{E}$
-embedding and
![]() $\lambda_{E}^{\pi}$
-embedding are special cases of E-embedding and
$\lambda_{E}^{\pi}$
-embedding are special cases of E-embedding and
![]() $\lambda_{E}$
-embedding, so we can use Theorem 25 using the fact that we now have only one variable (see also Leuschel (Reference Leuschel1998)):
$\lambda_{E}$
-embedding, so we can use Theorem 25 using the fact that we now have only one variable (see also Leuschel (Reference Leuschel1998)):
Corollary 33.
![]() $\pi_{E}$
-embedding and
$\pi_{E}$
-embedding and
![]() $\lambda_{E}^{\pi}$
-embedding are well-quasi-orders on the set of terms.
$\lambda_{E}^{\pi}$
-embedding are well-quasi-orders on the set of terms.
In order to show the results below, we recall some well-known notions originally found in Higman (Reference Higman1952) and Nash-Williams (Reference Nash-Williams1963) and others, but now restricted to first-order terms (Gallier, Reference Gallier1991). Moreover, we define that a list of terms
![]() $l_{1}=(s_{1},s_{2},s_{3},...,s_{n})$
is
$l_{1}=(s_{1},s_{2},s_{3},...,s_{n})$
is
![]() $\lambda_{E}$
-embedded (is
$\lambda_{E}$
-embedded (is
![]() $\lambda_{E}^{\pi}$
-embedded) into a list of terms
$\lambda_{E}^{\pi}$
-embedded) into a list of terms
![]() $l_{2}=(t_{1},t_{2},t_{3},...,t_{n})$
,
$l_{2}=(t_{1},t_{2},t_{3},...,t_{n})$
,
![]() $n\geq1$
, if there is an instantiating substitution
$n\geq1$
, if there is an instantiating substitution
![]() $\sigma$
, such that
$\sigma$
, such that
![]() $l_{1}\sigma$
is E-embedded into
$l_{1}\sigma$
is E-embedded into
![]() $l_{2}$
. That is every component
$l_{2}$
. That is every component
![]() $s_{i}\sigma$
of the list
$s_{i}\sigma$
of the list
![]() $l_{1}$
is E-embedded into the component
$l_{1}$
is E-embedded into the component
![]() $t_{i}$
of the list
$t_{i}$
of the list
![]() $l_{2}\;for\:1\leqslant i\leqslant n$
.
$l_{2}\;for\:1\leqslant i\leqslant n$
.
In the following proofs, we use two standard notions:
Definition 34. (good and bad sequences)
-
(1) A sequence of terms
 $t_{1},t_{2},t_{3},.....$
is called
good
, if there are indices i,j, and
$t_{1},t_{2},t_{3},.....$
is called
good
, if there are indices i,j, and
 $i<j:t_{i}\trianglelefteq t_{j}$
otherwise it is called
bad
. A well-quasi-ordering (wqo) is a quasi-ordering over which every infinite sequence is good.
$i<j:t_{i}\trianglelefteq t_{j}$
otherwise it is called
bad
. A well-quasi-ordering (wqo) is a quasi-ordering over which every infinite sequence is good. -
(2) Let
 $l_{1}\;:=\;(s_{1},s_{2},s_{3},....s_{n}),l_{2}\;:=\;(t_{1},t_{2},t_{3},....t_{n})$
be lists of terms (of equal length). Then
$l_{1}\;:=\;(s_{1},s_{2},s_{3},....s_{n}),l_{2}\;:=\;(t_{1},t_{2},t_{3},....t_{n})$
be lists of terms (of equal length). Then
 $l_{1}$
is embedded into
$l_{1}$
is embedded into
 $l_{2}$
,
$l_{2}$
,
 $l_{1}\trianglelefteq l_{2}$
, iff
$l_{1}\trianglelefteq l_{2}$
, iff
 $s_{i}\trianglelefteq t_{i},1\leqq i\leqq n$
.
$s_{i}\trianglelefteq t_{i},1\leqq i\leqq n$
.
Since a substitution is in fact a list of terms labeled with a variable, we have:
Lemma 35. Let T(F,X) be a well-quasi-ordered set of terms with respect to term-embedding
![]() $\trianglelefteq$
. Then every infinite sequence of terms
$\trianglelefteq$
. Then every infinite sequence of terms
![]() $t_{1},t_{2},t_{3},....$
has an infinite ascending sub-sequence, (
$t_{1},t_{2},t_{3},....$
has an infinite ascending sub-sequence, (
![]() $\trianglelefteq$
-chain),
$\trianglelefteq$
-chain),
![]() $t'_{1}\trianglelefteq t'_{2}\trianglelefteq t'_{3},.....$
$t'_{1}\trianglelefteq t'_{2}\trianglelefteq t'_{3},.....$
Proof. See the proof in, for example, Nash-Williams (Reference Nash-Williams1963) and Gallier (Reference Gallier1991)
This lemma can now be extended to equational embedding:
Corollary 36. Let T(F,X) be a well-quasi-ordered set of terms and E an equational theory. Then every infinite sequence of terms
![]() $t_{1},t_{2},t_{3},....$
has an infinite ascending sub-sequence, (
$t_{1},t_{2},t_{3},....$
has an infinite ascending sub-sequence, (
![]() $\trianglelefteq_{E}$
-chain),
$\trianglelefteq_{E}$
-chain),
![]() $t'_{1}\trianglelefteq_{E}t'_{2}\trianglelefteq_{E}t'_{3}\trianglelefteq_{E}.....$
$t'_{1}\trianglelefteq_{E}t'_{2}\trianglelefteq_{E}t'_{3}\trianglelefteq_{E}.....$
Proof. See Gallier (Reference Gallier1991) where this is proved in a more general setting.
Lemma 37. Let T(F,X) be a well founded, resp. a well-quasi-ordered set of terms with respect to embedding. Then the set of finite lists of terms
![]() $T(F,X)^{\omega}$
is also well founded, resp. well-quasi-ordered.
$T(F,X)^{\omega}$
is also well founded, resp. well-quasi-ordered.
Proof. See the proof in Nash-Williams (Reference Nash-Williams1963), Gallier (Reference Gallier1991), and Singh et al. (Reference Singh, Shuaibu and Ndayawo2013).
The following lemma lifts the previous results from terms to substitutions and note we have only a finite set of variables, since the terms are wqo:
Lemma 38. Let T(F,X), where X is finite, be a well-quasi-ordered set of terms with respect to E-embedding, then the set of substitutions
![]() $\mathcal{S}_{F,X}$
is also well-quasi-ordered.
$\mathcal{S}_{F,X}$
is also well-quasi-ordered.
Proof. A substitution can be seen as a list of terms, so by induction on the size of the associated lists.
![]() $\mathbf{n=1}$
: If T(F,X) is wqo, then for every infinite sequence of substitutions
$\mathbf{n=1}$
: If T(F,X) is wqo, then for every infinite sequence of substitutions
with a single component
![]() $\sigma_{1}=\{x\rightarrow s_{1}\},\sigma_{2}=\{x\rightarrow s_{2}\},\sigma_{3}=\{x\rightarrow s_{3}\},...$
$\sigma_{1}=\{x\rightarrow s_{1}\},\sigma_{2}=\{x\rightarrow s_{2}\},\sigma_{3}=\{x\rightarrow s_{3}\},...$
the associated sequence of lists is
![]() $l_{1},l_{2},...,l_{i}$
,… where
$l_{1},l_{2},...,l_{i}$
,… where
![]() $l_{i}=(s_{i})$
,
$l_{i}=(s_{i})$
,
![]() $i\geq1$
$i\geq1$
and the corresponding infinite sequence is
![]() $s_{1},s_{2},s_{3},....$
$s_{1},s_{2},s_{3},....$
Now because
![]() $s_{1},s_{2},s_{3},...$
is good, that is there exists an
$s_{1},s_{2},s_{3},...$
is good, that is there exists an
![]() $i,\,j$
,
$i,\,j$
,
![]() $i<j$
:
$i<j$
:
![]() $s_{i}\trianglelefteq_{E}s_{j}$
$s_{i}\trianglelefteq_{E}s_{j}$
the sequence
![]() $l_{1},l_{2},l_{3},...$
is also good. Consequently,
$l_{1},l_{2},l_{3},...$
is also good. Consequently,
![]() $\sigma_{1},\sigma_{2},\sigma_{3},....$
is good.
$\sigma_{1},\sigma_{2},\sigma_{3},....$
is good.
![]() $\mathbf{n\rightarrow n+1}:$
By induction hypothesis
$\mathbf{n\rightarrow n+1}:$
By induction hypothesis
![]() $\sigma_{1},\sigma_{2},\sigma_{3},....$
$\sigma_{1},\sigma_{2},\sigma_{3},....$
with
![]() $\sigma_{i}=\{x_{1}\rightarrow s_{i1},x_{2}\rightarrow s_{i2},...,x_{n}\rightarrow s_{in}\}$
has the associated sequences of lists
$\sigma_{i}=\{x_{1}\rightarrow s_{i1},x_{2}\rightarrow s_{i2},...,x_{n}\rightarrow s_{in}\}$
has the associated sequences of lists
![]() $l_{1},l_{2},...,l_{i}$
,… with
$l_{1},l_{2},...,l_{i}$
,… with
![]() $l_{i}=(s_{i1},s_{i2},...,s_{in})$
which is good and therefore
$l_{i}=(s_{i1},s_{i2},...,s_{in})$
which is good and therefore
![]() $\sigma_{1},\sigma_{2},\sigma_{3},....$
is also good.
$\sigma_{1},\sigma_{2},\sigma_{3},....$
is also good.
Now Lemma 35 can be used, which says that there exists an infinite ascending
E-embedding sub-chain
![]() $l'_{1}\trianglelefteq_{E}l'_{2}\trianglelefteq_{E}l'_{3}\trianglelefteq_{E}...+\trianglelefteq_{E}l'_{i}\trianglelefteq_{E}...$
where
$l'_{1}\trianglelefteq_{E}l'_{2}\trianglelefteq_{E}l'_{3}\trianglelefteq_{E}...+\trianglelefteq_{E}l'_{i}\trianglelefteq_{E}...$
where
![]() $l'_{i}=(s'_{i1},s'_{i2},...,s'_{in})$
.
$l'_{i}=(s'_{i1},s'_{i2},...,s'_{in})$
.
Looking now for lists with size
![]() $n+1$
we have a similar list but with
$n+1$
we have a similar list but with
![]() $l'_{i}=(s'_{i1},s'_{i2},...,s'_{in},s'_{in+1})$
,
$l'_{i}=(s'_{i1},s'_{i2},...,s'_{in},s'_{in+1})$
,
![]() $i\geq1$
and its ascending
$i\geq1$
and its ascending
![]() $\trianglelefteq_{E}$
-subchain
$\trianglelefteq_{E}$
-subchain
![]() $l'_{1}\trianglelefteq_{E}l'_{2}\trianglelefteq_{E}l'_{3}\trianglelefteq_{E}...$
.
$l'_{1}\trianglelefteq_{E}l'_{2}\trianglelefteq_{E}l'_{3}\trianglelefteq_{E}...$
.
Now because T(F,X) is a wqo set w.r.t. E-embedding, the corresponding infinite sequence consisting of the
![]() $n+1$
’th members,
$n+1$
’th members,
![]() $s'_{1n+1,}s'_{2n+1},...,s'_{in+1},...$
must be good; therefore, there are indices i’,j’ such that
$s'_{1n+1,}s'_{2n+1},...,s'_{in+1},...$
must be good; therefore, there are indices i’,j’ such that
![]() $s'_{i'n+1}\leq s'_{j'n+1}$
which implies
$s'_{i'n+1}\leq s'_{j'n+1}$
which implies
![]() $l'_{i'}=(s'_{i'1},s'_{i'2},...,s'_{i'n+1})\trianglelefteq_{E}l'_{j'}=(s'_{j'1},s'_{j'2},...,s'_{j'n+1})$
, hence
$l'_{i'}=(s'_{i'1},s'_{i'2},...,s'_{i'n+1})\trianglelefteq_{E}l'_{j'}=(s'_{j'1},s'_{j'2},...,s'_{j'n+1})$
, hence
![]() $l'_{1},l'_{2},l'_{3},...$
is good. So if we assume that l
$l'_{1},l'_{2},l'_{3},...$
is good. So if we assume that l
![]() $_{1},l{}_{2},l{}_{3},...$
is bad then
$_{1},l{}_{2},l{}_{3},...$
is bad then
![]() $\sigma_{1},\sigma_{2},\sigma_{3},....$
is also bad, but the infinite subsequence
$\sigma_{1},\sigma_{2},\sigma_{3},....$
is also bad, but the infinite subsequence
![]() $l'_{1},l'{}_{2},l'{}_{3},...$
is good; therefore, l
$l'_{1},l'{}_{2},l'{}_{3},...$
is good; therefore, l
![]() $_{1},l{}_{2},l{}_{3},...$
must also be good from which follows that
$_{1},l{}_{2},l{}_{3},...$
must also be good from which follows that
![]() $\sigma_{1},\sigma_{2},\sigma_{3},....$
. is also good. Hence,
$\sigma_{1},\sigma_{2},\sigma_{3},....$
. is also good. Hence,
![]() $\mathcal{S}_{F,X}$
is a well-quasi-ordered set.
$\mathcal{S}_{F,X}$
is a well-quasi-ordered set.
The proofs for our various E-embeddings on substitutions are almost identical to those in Lemma 38; hence, we collect them in one lemma:
Lemma 39. Let T(F,X), where X is finite, be a well-quasi-ordered set of terms with respect to
![]() $\lambda_{E}$
-embedding,
$\lambda_{E}$
-embedding,
![]() $\pi_{E}$
-embedding and
$\pi_{E}$
-embedding and
![]() $\lambda_{E}^{\pi}$
-embedding then the set of substitutions
$\lambda_{E}^{\pi}$
-embedding then the set of substitutions
![]() $\mathcal{S}_{F,X}$
is also a well-quasi-ordered set with respect to these embeddings.
$\mathcal{S}_{F,X}$
is also a well-quasi-ordered set with respect to these embeddings.
The results so far, namely the (homeomorphic) embedding of first-order terms and substitutions extended to various equational embeddings, namely E-embedding (
![]() $\trianglelefteq_{E})$
, instance E-embedding (
$\trianglelefteq_{E})$
, instance E-embedding (
![]()
), pure E-embedding (
![]() $\trianglelefteq_{E}^{\pi}$
), and pure instance E-embedding (
$\trianglelefteq_{E}^{\pi}$
), and pure instance E-embedding (
![]()
) can now be used to show the following properties for the set of E-unifiers, more importantly for the set of minimal E-unifiers, which is of course our main interest.
Theorem 40. Let T(F,X) be the set of first-order terms and E a regular equational theory. Then for a solvable E-unification problem
![]() $\varGamma$
, the set of free
$\varGamma$
, the set of free
![]() $\lambda_{E}$
-unifiers,
$\lambda_{E}$
-unifiers,
![]() $\varphi U\varSigma_{E}(\varGamma)$
always exists and it is minimal and complete (but not necessarily finite).
$\varphi U\varSigma_{E}(\varGamma)$
always exists and it is minimal and complete (but not necessarily finite).
Proof. T(F,X) is a well-founded quasi-order with respect to instance E-embedding as a consequence of Theorem 30 and Lemma 37.
Definition 41. An E-unification problem
![]() $\Gamma_{E}$
is bounded if there is a number N such that
$\Gamma_{E}$
is bounded if there is a number N such that
![]() $U\varSigma_{E}(\varGamma)$
uses at most N variables. A theory E is bounded if every E-unification problem
$U\varSigma_{E}(\varGamma)$
uses at most N variables. A theory E is bounded if every E-unification problem
![]() $\Gamma_{E}$
is bounded.
$\Gamma_{E}$
is bounded.
If the alphabet is finite and
![]() $\Gamma_{E}$
is bounded, we have the following stronger result :Footnote
5
$\Gamma_{E}$
is bounded, we have the following stronger result :Footnote
5
Theorem 42. Let T(F, X) be the set of first-order terms built over a finite alphabet
![]() $\Sigma=F\cup X$
and let E be an equational theory. Then for a solvable bounded E-unification problem
$\Sigma=F\cup X$
and let E be an equational theory. Then for a solvable bounded E-unification problem
![]() $\varGamma$
, the set of free
$\varGamma$
, the set of free
![]() $\lambda_{E}$
-unifiers,
$\lambda_{E}$
-unifiers,
![]() $\varphi U\varSigma_{E}(\varGamma)$
, always exists, it is minimal, complete, and finite.
$\varphi U\varSigma_{E}(\varGamma)$
, always exists, it is minimal, complete, and finite.
Proof. A consequence of the tree embedding theorem extended to equational instance embedding.
For our final result, let us say a purified E-unification problem is a problem where we define all variables as embedment equivalent. Let
![]() $\varphi_{\pi}U\varSigma_{E}(\varGamma)$
be the corresponding complete set of pure and free
$\varphi_{\pi}U\varSigma_{E}(\varGamma)$
be the corresponding complete set of pure and free
![]() $\lambda_{E}$
-unifiers, then:
$\lambda_{E}$
-unifiers, then:
Theorem 43. Let T(F, X) be the set of first-order terms and let E be an equational theory, then for a solvable E-unification problem
![]() $\varGamma$
the set of pure and free
$\varGamma$
the set of pure and free
![]() $\lambda_{E}$
-unifiers,
$\lambda_{E}$
-unifiers,
![]() $\varphi_{\pi}U\varSigma_{E}(\varGamma)$
exists, it is minimal, complete, and finite.
$\varphi_{\pi}U\varSigma_{E}(\varGamma)$
exists, it is minimal, complete, and finite.
4. Conclusion and Future Work
This paper sets forth an abstract setting for equational unification problems, where we redefine the notion of the set of most general unifiers. We now have:
“Unification based on E-subsumption”
“Unification based on E-encompassment”
“Unification based on E-embedding”
where each approach is a generalization of the previous one. For terms s,t, and an instantiating substitution
![]() $\lambda$
, this can be illustrated for the syntactic case as:
$\lambda$
, this can be illustrated for the syntactic case as:
![]() $\blacktriangleright$
$\blacktriangleright$
![]() ,
,
that is t instance embeds s, is defined using
homeomorphic embedding
![]() $\trianglerighteq$
:
$\trianglerighteq$
:

![]() $\blacktriangleright$
$\blacktriangleright$
![]() $t\sqsupseteq s$
, that is
t encompasses s, is defined by deleting the third line of the previous definition:
$t\sqsupseteq s$
, that is
t encompasses s, is defined by deleting the third line of the previous definition:
 $t\sqsupseteq s\,\iff\exists\lambda:\begin{cases}s\lambda=t,\:or\\t=f(t_{1},\ldots,t_{n}),\;i\in\{1,....,n\}:\:t_{i}\sqsupseteq s\lambda\end{cases}$
$t\sqsupseteq s\,\iff\exists\lambda:\begin{cases}s\lambda=t,\:or\\t=f(t_{1},\ldots,t_{n}),\;i\in\{1,....,n\}:\:t_{i}\sqsupseteq s\lambda\end{cases}$
![]() $\blacktriangleright$
$\blacktriangleright$
![]() $t\geq s\,$
, that is
t subsumes s, is defined by deleting the second line of
$t\geq s\,$
, that is
t subsumes s, is defined by deleting the second line of
the previous definition:
![]() $t\geq s\,\iff\exists\lambda:s=t\lambda$
$t\geq s\,\iff\exists\lambda:s=t\lambda$
Extending this to E-unification, we have the three notions:
![]() $\mu U\varSigma_{E}(\varGamma)$
, the standard notion today, essential unification
$\mu U\varSigma_{E}(\varGamma)$
, the standard notion today, essential unification
![]() $eU\varSigma_{E}(\varGamma)$
, and finally
$eU\varSigma_{E}(\varGamma)$
, and finally
![]() $\varphi U\varSigma_{E}(\varGamma)$
under homeomorphic embedding as presented in this paper. In a sequel to this paper, we will show how to compute the set
$\varphi U\varSigma_{E}(\varGamma)$
under homeomorphic embedding as presented in this paper. In a sequel to this paper, we will show how to compute the set
![]() $\varphi U\varSigma_{E}(\varGamma)$
and its closure and whether it can be used in an inference system like resolution.
$\varphi U\varSigma_{E}(\varGamma)$
and its closure and whether it can be used in an inference system like resolution.
Using this general framework, the next tasks are then to look again at the standard unification problems like associativity, commutativity, or idempotency and their combination as well as on the wealth of results about other algebras, in order to see what the potential practical (and theoretical) gains are. A first investigation into these practical problems has been made within the logic programming paradigmFootnote
6
(Alpuente et al., Reference Alpuente, Cuenca-Ortega, Escobar and Meseguer2018). As in the 1970s, when we started unification theory with a table listing the now standard unification problems in one column and in the adjacent column the type within the unification hierarchy, we could now have a similar table, but with an additional column for the type of
![]() $eU\varSigma_{E}(\varGamma)$
and
$eU\varSigma_{E}(\varGamma)$
and
![]() $\varphi U\varSigma_{E}(\varGamma)$
.
$\varphi U\varSigma_{E}(\varGamma)$
.
Secondly, there is far more theoretical work needed to better understand the actual structure of and relationship between these unification settings and also how this work relates to similar results obtained within different theoretical settings, like those of Cabrer and Metcalfe (Reference Cabrer and Metcalfe2014); Cabrer and Metcalfe (Reference Cabrer and Metcalfe2015). Moreover how to relate all this to the wealth of theoretical results obtained by Ghilardi (Reference Ghilardi1997) and his students (see, e.g., Ghilardi (Reference Ghilardi2018)) and by Franz Baader (see, e.g., Baader and Ghilardi (Reference Baader and Ghilardi2011)).
Acknowledgements
This paper has taken a very long time to take its present form. Starting from the basic observation that a subset of infinitely many most general unifiers more often than not share a basic structure until we came to the more theoretical characterization as presented here. We very much like to thank Michael Hoche who worked with us on earlier drafts of these ideas and we hope that he will soon recover and come back to us, in order to continue our joint work on the problems this paper left open. We also like to thank the referees of UNIF18 for their work and critical ideas. In particular, we like to thank the reviewers of this journal, who contributed substantially to the final formulation and shape of this paper. Not least, they found an embarrassing flaw in the previous version and pointed us to related work in the literature.