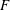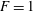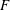1. Introduction
1.1. Statement of the main results
We consider the motion of a two-dimensional fluid which is bounded above by a free surface under constant (atmospheric) pressure and below by a horizontal bed. Gravity acts as an external force, and there is no surface tension on the free surface. Inside the fluid, the velocity
![]() $(u,v)$
and pressure
$(u,v)$
and pressure
![]() $P$
satisfy the incompressible Euler equations. We denote the horizontal bed by
$P$
satisfy the incompressible Euler equations. We denote the horizontal bed by
![]() $y=-d$
and the free surface by
$y=-d$
and the free surface by
![]() $y={\it\eta}(x,t)$
. Fixing the constant wave speed
$y={\it\eta}(x,t)$
. Fixing the constant wave speed
![]() $c>0$
, we assume that the motion is steady in that
$c>0$
, we assume that the motion is steady in that
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() $u$
,
$u$
,
![]() $v$
, and
$v$
, and
![]() $P$
depend on
$P$
depend on
![]() $x$
and
$x$
and
![]() $t$
only through the combination
$t$
only through the combination
![]() $x-ct$
, which we henceforth abbreviate to
$x-ct$
, which we henceforth abbreviate to
![]() $x$
. We also assume that the wave is solitary in that
$x$
. We also assume that the wave is solitary in that
uniformly in
![]() $y$
. We assume that the horizontal velocity
$y$
. We assume that the horizontal velocity
![]() $u$
in the fluid is everywhere strictly less than the wave speed
$u$
in the fluid is everywhere strictly less than the wave speed
![]() $c$
, and similarly for the horizontal velocity
$c$
, and similarly for the horizontal velocity
![]() $U$
of the shear flow at
$U$
of the shear flow at
![]() $x=\pm \infty$
. Otherwise
$x=\pm \infty$
. Otherwise
![]() $U$
is an arbitrary function of
$U$
is an arbitrary function of
![]() $-d\leqslant y\leqslant 0$
. We call a solitary wave trivial if
$-d\leqslant y\leqslant 0$
. We call a solitary wave trivial if
![]() ${\it\eta}\equiv 0$
,
${\it\eta}\equiv 0$
,
![]() $v\equiv 0$
, and
$v\equiv 0$
, and
![]() $u\equiv U$
. In the context of this paper, we will also call a solitary wave a wave of elevation if
$u\equiv U$
. In the context of this paper, we will also call a solitary wave a wave of elevation if
![]() ${\it\eta}(x)\geqslant 0$
for all
${\it\eta}(x)\geqslant 0$
for all
![]() $x$
but
$x$
but
![]() ${\it\eta}\not\equiv 0$
. Similarly we call a solitary wave a wave of depression if
${\it\eta}\not\equiv 0$
. Similarly we call a solitary wave a wave of depression if
![]() ${\it\eta}(x)\leqslant 0$
for all
${\it\eta}(x)\leqslant 0$
for all
![]() $x$
but
$x$
but
![]() ${\it\eta}\not\equiv 0$
.
${\it\eta}\not\equiv 0$
.
The classical Froude number is the dimensionless ratio
![]() $c/\sqrt{gd}$
, where
$c/\sqrt{gd}$
, where
![]() $g$
is the acceleration due to gravity. When working with solitary waves on shear flows, however, we find it more convenient to define the Froude number
$g$
is the acceleration due to gravity. When working with solitary waves on shear flows, however, we find it more convenient to define the Froude number
![]() $F$
by
$F$
by
where the denominator in the integrand is uniformly bounded away from zero thanks to our assumption
![]() $U<c$
. This definition reduces to the classical one when
$U<c$
. This definition reduces to the classical one when
![]() $U$
vanishes identically, and it has the advantage that the critical Froude number is
$U$
vanishes identically, and it has the advantage that the critical Froude number is
![]() $F=1$
regardless of the shear flow
$F=1$
regardless of the shear flow
![]() $U$
. In particular, with this convention the small-amplitude solitary waves with vorticity constructed in Ter-Krikorov (Reference Ter-Krikorov1961), Groves & Wahlén (Reference Groves and Wahlén2008) and Hur (Reference Hur2008a
) have Froude numbers
$U$
. In particular, with this convention the small-amplitude solitary waves with vorticity constructed in Ter-Krikorov (Reference Ter-Krikorov1961), Groves & Wahlén (Reference Groves and Wahlén2008) and Hur (Reference Hur2008a
) have Froude numbers
![]() $F$
slightly bigger than 1.
$F$
slightly bigger than 1.
The reader may assume that
![]() $u,v,P,{\it\eta},U$
are all
$u,v,P,{\it\eta},U$
are all
![]() $C^{2}$
or even smooth. On the other hand, our arguments go through unchanged for solutions with the more limited regularity
$C^{2}$
or even smooth. On the other hand, our arguments go through unchanged for solutions with the more limited regularity
where here
![]() $0<{\it\alpha}<1$
,
$0<{\it\alpha}<1$
,
![]() $r=2/(1-{\it\alpha})$
, and
$r=2/(1-{\it\alpha})$
, and
![]() $D_{{\it\eta}}=\{(x,y):-d<y<{\it\eta}(x)\}$
denotes the fluid domain. By
$D_{{\it\eta}}=\{(x,y):-d<y<{\it\eta}(x)\}$
denotes the fluid domain. By
![]() $w\in W_{\mathit{loc}}^{1,r}(\overline{D_{{\it\eta}}})$
we mean that
$w\in W_{\mathit{loc}}^{1,r}(\overline{D_{{\it\eta}}})$
we mean that
![]() $w\in W^{1,r}(D^{\prime })$
whenever
$w\in W^{1,r}(D^{\prime })$
whenever
![]() $\overline{D^{\prime }}\subset \overline{D_{{\it\eta}}}$
is compact, and similarly for
$\overline{D^{\prime }}\subset \overline{D_{{\it\eta}}}$
is compact, and similarly for
![]() $C_{\mathit{loc}}^{{\it\alpha}}(\overline{D_{{\it\eta}}})$
. The regularity (1.3) is an analogue for solitary waves of the regularity assumed in Theorem 2 of Constantin & Strauss (Reference Constantin and Strauss2011) for periodic waves.
$C_{\mathit{loc}}^{{\it\alpha}}(\overline{D_{{\it\eta}}})$
. The regularity (1.3) is an analogue for solitary waves of the regularity assumed in Theorem 2 of Constantin & Strauss (Reference Constantin and Strauss2011) for periodic waves.
Theorem 1.1. Consider a solitary wave with
![]() $\sup u<c$
and the regularity (1.3). Then
$\sup u<c$
and the regularity (1.3). Then
![]() $F\neq 1$
. Moreover,
$F\neq 1$
. Moreover,
![]() $F>1$
if it is a wave of elevation, and
$F>1$
if it is a wave of elevation, and
![]() $F<1$
if it is a wave of depression.
$F<1$
if it is a wave of depression.
In the irrotational case where the vorticity
![]() ${\it\omega}=v_{x}-u_{y}$
vanishes identically and
${\it\omega}=v_{x}-u_{y}$
vanishes identically and
![]() $U$
is constant, the assumption
$U$
is constant, the assumption
![]() $\sup u<c$
is automatically satisfied (Toland Reference Toland1996) and the bound
$\sup u<c$
is automatically satisfied (Toland Reference Toland1996) and the bound
![]() $F>1$
for waves of elevation is well-known (Starr Reference Starr1947; Amick & Toland Reference Amick and Toland1981; McLeod Reference McLeod1984). While the assumption
$F>1$
for waves of elevation is well-known (Starr Reference Starr1947; Amick & Toland Reference Amick and Toland1981; McLeod Reference McLeod1984). While the assumption
![]() $\sup u<c$
is still reasonable for waves with vorticity (Constantin & Strauss Reference Constantin and Strauss2004; Constantin Reference Constantin2011), it rules out the existence of critical layers or stagnation points in flow.
$\sup u<c$
is still reasonable for waves with vorticity (Constantin & Strauss Reference Constantin and Strauss2004; Constantin Reference Constantin2011), it rules out the existence of critical layers or stagnation points in flow.
We emphasize that, to our knowledge, there is no evidence of any kind for the existence of solitary waves of depression, or indeed for any solitary waves other than symmetric waves of elevation. In the irrotational case, it is known that there do not exist waves of depression which are in addition symmetric and monotone in that, after a translation,
![]() ${\it\eta}$
is an even function of
${\it\eta}$
is an even function of
![]() $x$
with
$x$
with
![]() ${\it\eta}^{\prime }(x)>0$
for
${\it\eta}^{\prime }(x)>0$
for
![]() $x>0$
(Keady & Pritchard Reference Keady and Pritchard1974).
$x>0$
(Keady & Pritchard Reference Keady and Pritchard1974).
In some cases, the argument leading to Theorem 1.1 can be extended to give an upper bound on the Froude number for waves of elevation. Before giving this result, we define a dimensionless quantity
![]() ${\it\Lambda}\geqslant 1$
by
${\it\Lambda}\geqslant 1$
by
We note that
![]() ${\it\Lambda}$
, like
${\it\Lambda}$
, like
![]() $F$
, only depends on the shear flow
$F$
, only depends on the shear flow
![]() $U$
at infinity and the wave speed
$U$
at infinity and the wave speed
![]() $c$
.
$c$
.
Theorem 1.2. For any solitary wave of elevation with the regularity (1.3),
![]() $\sup u<c$
, and
$\sup u<c$
, and
![]() ${\it\Lambda}<2/\sqrt{3}$
, the Froude number
${\it\Lambda}<2/\sqrt{3}$
, the Froude number
![]() $F$
satisfies the upper bound
$F$
satisfies the upper bound
For irrotational waves,
![]() $U$
is constant, so clearly
$U$
is constant, so clearly
![]() ${\it\Lambda}=1<2/\sqrt{3}$
and hence Theorem 1.2 gives the well-known bound
${\it\Lambda}=1<2/\sqrt{3}$
and hence Theorem 1.2 gives the well-known bound
![]() $F<2$
(Starr Reference Starr1947; Amick & Toland Reference Amick and Toland1981; McLeod Reference McLeod1984). More generally, if the vorticity
$F<2$
(Starr Reference Starr1947; Amick & Toland Reference Amick and Toland1981; McLeod Reference McLeod1984). More generally, if the vorticity
![]() ${\it\omega}\leqslant 0$
, then
${\it\omega}\leqslant 0$
, then
![]() $U(y)\leqslant U(0)$
for
$U(y)\leqslant U(0)$
for
![]() $-d\leqslant y\leqslant 0$
so that again
$-d\leqslant y\leqslant 0$
so that again
![]() ${\it\Lambda}=1$
, and Theorem 1.2 gives the same bound
${\it\Lambda}=1$
, and Theorem 1.2 gives the same bound
![]() $F<2$
. In terms of the antiderivative
$F<2$
. In terms of the antiderivative
![]() ${\it\Gamma}(p)$
of the vorticity function and Bernoulli constant
${\it\Gamma}(p)$
of the vorticity function and Bernoulli constant
![]() ${\it\lambda}$
defined in § 2, the condition
${\it\lambda}$
defined in § 2, the condition
![]() ${\it\Lambda}<2/\sqrt{3}$
can be rephrased as
${\it\Lambda}<2/\sqrt{3}$
can be rephrased as
![]() ${\it\lambda}>-8\min _{p}{\it\Gamma}(p)$
.
${\it\lambda}>-8\min _{p}{\it\Gamma}(p)$
.
In addition to their own independent interest, Theorems 1.1 and 1.2 have implications for the existence theory for large-amplitude solitary waves; see §§ 1.3 and 6.
1.2. Historical discussion
1.2.1. Irrotational waves
For irrotational waves, the asymptotic shear flow
![]() $U$
is constant, and can be taken to be zero by switching to an appropriate reference frame. Our formula (1.2) for
$U$
is constant, and can be taken to be zero by switching to an appropriate reference frame. Our formula (1.2) for
![]() $F$
then reduces to the classical ratio
$F$
then reduces to the classical ratio
which is named in honor of William Froude, who in the 1870s argued that in order to compare the resistances felt by scaled models of a ship, the ratio of the speed of the ship to the square root of its length must be kept constant (Froude Reference Froude1874).
The importance of the critical speed
![]() $c=\sqrt{gd}$
corresponding to
$c=\sqrt{gd}$
corresponding to
![]() $F=1$
was known long before Froude. In 1781, Lagrange showed that long irrotational waves in shallow water travel with nearly this speed (Darrigol Reference Darrigol2003), and in 1828 Bélanger showed that a hydraulic jump can occur only if the upstream flow has
$F=1$
was known long before Froude. In 1781, Lagrange showed that long irrotational waves in shallow water travel with nearly this speed (Darrigol Reference Darrigol2003), and in 1828 Bélanger showed that a hydraulic jump can occur only if the upstream flow has
![]() $F>1$
(Bélanger Reference Bélanger1828; Chanson Reference Chanson2009). More pertinent to this article is John Scott Russell’s famous 1844 report (Darrigol Reference Darrigol2003), which gives the empirical formula
$F>1$
(Bélanger Reference Bélanger1828; Chanson Reference Chanson2009). More pertinent to this article is John Scott Russell’s famous 1844 report (Darrigol Reference Darrigol2003), which gives the empirical formula
for the speed of small-amplitude irrotational solitary waves. Theoretical justifications of (1.7) came decades later with the work of Boussinesq in 1871 and Rayleigh in 1876 (Darrigol Reference Darrigol2003).
In 1947, Starr gave a formal proof of the strikingly simple exact formula
for irrotational solitary waves (Starr Reference Starr1947); see Longuet-Higgins (Reference Longuet-Higgins1974) for an alternative derivation. Given this identity, the upper and lower bounds
![]() $1<F<2$
for waves of elevation are straightforward. Indeed, since
$1<F<2$
for waves of elevation are straightforward. Indeed, since
![]() ${\it\eta}\geqslant 0$
does not vanish identically, (1.8) immediately implies
${\it\eta}\geqslant 0$
does not vanish identically, (1.8) immediately implies
![]() $F>1$
. On the other hand, (1.8) also implies the upper bound
$F>1$
. On the other hand, (1.8) also implies the upper bound
Since
![]() $\max {\it\eta}\leqslant F^{2}d/2$
by Bernoulli’s law, (1.9) in turn implies
$\max {\it\eta}\leqslant F^{2}d/2$
by Bernoulli’s law, (1.9) in turn implies
![]() $F^{2}<1+3F^{2}/4$
and hence
$F^{2}<1+3F^{2}/4$
and hence
![]() $F<2$
. Substituting
$F<2$
. Substituting
![]() $F<2$
back into Bernoulli’s law we also obtain the bound
$F<2$
back into Bernoulli’s law we also obtain the bound
![]() $\max {\it\eta}<2d$
on the amplitude.
$\max {\it\eta}<2d$
on the amplitude.
In fact, Starr showed the improved upper bound
in which the coefficient
![]() $3/2$
in (1.9) has been reduced to the 1 appearing in the asymptotic formula (1.7). See Keady & Pritchard (Reference Keady and Pritchard1974) for an alternative derivation. Arguing as in the previous paragraph, (1.10) leads to the bounds
$3/2$
in (1.9) has been reduced to the 1 appearing in the asymptotic formula (1.7). See Keady & Pritchard (Reference Keady and Pritchard1974) for an alternative derivation. Arguing as in the previous paragraph, (1.10) leads to the bounds
![]() $F<\sqrt{2}$
and
$F<\sqrt{2}$
and
![]() $\max {\it\eta}<d$
on the Froude number and amplitude. We note that the proofs of (1.10) in Starr (Reference Starr1947) and Keady & Pritchard (Reference Keady and Pritchard1974) do not depend on the identity (1.8).
$\max {\it\eta}<d$
on the Froude number and amplitude. We note that the proofs of (1.10) in Starr (Reference Starr1947) and Keady & Pritchard (Reference Keady and Pritchard1974) do not depend on the identity (1.8).
Amick & Toland (Reference Amick and Toland1981) gave rigorous proofs of the bounds
![]() $1<F<2$
in their construction of large-amplitude irrotational solitary waves, which involves reformulating the water wave problem as a Nekrasov-type integral equation on the free surface. They objected to the assumption that the ‘mass’
$1<F<2$
in their construction of large-amplitude irrotational solitary waves, which involves reformulating the water wave problem as a Nekrasov-type integral equation on the free surface. They objected to the assumption that the ‘mass’
![]() $\int {\it\eta}\text{d}x$
was finite in the earlier proofs, and instead, as McLeod (Reference McLeod1984) puts it, ‘take sixteen pages and much complicated estimating of integrals to prove
$\int {\it\eta}\text{d}x$
was finite in the earlier proofs, and instead, as McLeod (Reference McLeod1984) puts it, ‘take sixteen pages and much complicated estimating of integrals to prove
![]() $F>1$
without the assumption of finite mass’. In response, McLeod (Reference McLeod1984) showed that the earlier proofs could be easily modified to avoid the assumption of finite mass. Both Amick & Toland (Reference Amick and Toland1981) and McLeod (Reference McLeod1984) showed as a consequence of
$F>1$
without the assumption of finite mass’. In response, McLeod (Reference McLeod1984) showed that the earlier proofs could be easily modified to avoid the assumption of finite mass. Both Amick & Toland (Reference Amick and Toland1981) and McLeod (Reference McLeod1984) showed as a consequence of
![]() $F>1$
that the mass is necessarily finite.
$F>1$
that the mass is necessarily finite.
Craig & Sternberg (Reference Craig and Sternberg1988) proved that all solitary waves with
![]() $F\geqslant 1$
are waves of elevation and furthermore that waves with
$F\geqslant 1$
are waves of elevation and furthermore that waves with
![]() $F>1$
are symmetric and monotone in that, after a translation,
$F>1$
are symmetric and monotone in that, after a translation,
![]() ${\it\eta}$
is an even function of
${\it\eta}$
is an even function of
![]() $x$
with
$x$
with
![]() ${\it\eta}^{\prime }(x)<0$
for
${\it\eta}^{\prime }(x)<0$
for
![]() $x>0$
. Thus a solitary wave has
$x>0$
. Thus a solitary wave has
![]() $F>1$
if and only if it is a wave of elevation, and such waves are also symmetric and monotone. Waves with
$F>1$
if and only if it is a wave of elevation, and such waves are also symmetric and monotone. Waves with
![]() $F<1$
, if they exist, cannot be of elevation, nor can they be symmetric and monotone waves of depression (Keady & Pritchard Reference Keady and Pritchard1974). In the infinite depth setting, on the other hand, there do not exist any solitary waves whose free surfaces
$F<1$
, if they exist, cannot be of elevation, nor can they be symmetric and monotone waves of depression (Keady & Pritchard Reference Keady and Pritchard1974). In the infinite depth setting, on the other hand, there do not exist any solitary waves whose free surfaces
![]() ${\it\eta}(x)$
decay faster than
${\it\eta}(x)$
decay faster than
![]() $|x|^{-1-{\it\varepsilon}}$
for some
$|x|^{-1-{\it\varepsilon}}$
for some
![]() ${\it\varepsilon}>0$
(Hur Reference Hur2012b
); also see Sun (Reference Sun1999).
${\it\varepsilon}>0$
(Hur Reference Hur2012b
); also see Sun (Reference Sun1999).
For later reference we also mention a third upper bound
which was obtained by Keady & Pritchard (Reference Keady and Pritchard1974) using maximum principle arguments. It is easy to check that (1.11) is strictly weaker than (1.9) and (1.10). In particular, it cannot be combined with Bernoulli’s law to obtain a bound on the Froude number which is independent of the amplitude
![]() $\max {\it\eta}$
.
$\max {\it\eta}$
.
Numerics suggest that there is a one-parameter family of irrotational solitary waves connecting small-amplitude waves with
![]() $F$
slightly bigger than 1 and the so-called wave of greatest height, which has a stagnation point at its crest where there is a corner with a
$F$
slightly bigger than 1 and the so-called wave of greatest height, which has a stagnation point at its crest where there is a corner with a
![]() $120^{\circ }$
interior angle. The maximum value of the Froude number (as well as the maxima of mass, momentum, and energy) for this family is achieved before the wave of greatest height is reached, and there are values of the Froude number for which there exist two distinct solitary waves (Longuet-Higgins & Fenton Reference Longuet-Higgins and Fenton1974; Miles Reference Miles1980). The wave with maximum Froude number has
$120^{\circ }$
interior angle. The maximum value of the Froude number (as well as the maxima of mass, momentum, and energy) for this family is achieved before the wave of greatest height is reached, and there are values of the Froude number for which there exist two distinct solitary waves (Longuet-Higgins & Fenton Reference Longuet-Higgins and Fenton1974; Miles Reference Miles1980). The wave with maximum Froude number has
![]() $F=1.294$
and
$F=1.294$
and
![]() $\max {\it\eta}/d=0.790$
. The maximum amplitude is
$\max {\it\eta}/d=0.790$
. The maximum amplitude is
![]() $\max {\it\eta}/d=0.83322$
(Longuet-Higgins & Tanaka Reference Longuet-Higgins and Tanaka1997) and hence the corresponding Froude number is
$\max {\it\eta}/d=0.83322$
(Longuet-Higgins & Tanaka Reference Longuet-Higgins and Tanaka1997) and hence the corresponding Froude number is
![]() $F=1.29091$
. We note that the existence of a wave of extreme form was proved rigorously in Amick & Toland (Reference Amick and Toland1981) and Amick, Fraenkel & Toland (Reference Amick, Fraenkel and Toland1982), while the existence of bifurcation or turning points in the connected set of solutions containing small-amplitude solitary waves was proved in Plotnikov (Reference Plotnikov1991).
$F=1.29091$
. We note that the existence of a wave of extreme form was proved rigorously in Amick & Toland (Reference Amick and Toland1981) and Amick, Fraenkel & Toland (Reference Amick, Fraenkel and Toland1982), while the existence of bifurcation or turning points in the connected set of solutions containing small-amplitude solitary waves was proved in Plotnikov (Reference Plotnikov1991).
1.2.2. Waves with vorticity
With vorticity, the importance of the critical value
![]() $F=1$
for long waves in shallow water was recognized by Burns (Reference Burns1953);
$F=1$
for long waves in shallow water was recognized by Burns (Reference Burns1953);
![]() $F=1$
is sometimes called the ‘Burns condition’. Periodic solutions of the linearized equations exist if and only if
$F=1$
is sometimes called the ‘Burns condition’. Periodic solutions of the linearized equations exist if and only if
![]() $F<1$
, and
$F<1$
, and
![]() $F\rightarrow 1$
as the period tends to infinity; see for instance Groves & Wahlén (Reference Groves and Wahlén2008), Hur & Lin (Reference Hur and Lin2008), and Kozlov, Kuznetsov & Lokharu (Reference Kozlov, Kuznetsov and Lokharu2014). On the other hand the small-amplitude solitary waves constructed by Ter-Krikorov (Reference Ter-Krikorov1961) and later by Hur (Reference Hur2008a
) and then Groves & Wahlén (Reference Groves and Wahlén2008) all have
$F\rightarrow 1$
as the period tends to infinity; see for instance Groves & Wahlén (Reference Groves and Wahlén2008), Hur & Lin (Reference Hur and Lin2008), and Kozlov, Kuznetsov & Lokharu (Reference Kozlov, Kuznetsov and Lokharu2014). On the other hand the small-amplitude solitary waves constructed by Ter-Krikorov (Reference Ter-Krikorov1961) and later by Hur (Reference Hur2008a
) and then Groves & Wahlén (Reference Groves and Wahlén2008) all have
![]() $F$
slightly bigger than 1.
$F$
slightly bigger than 1.
Besides the existence results mentioned above, there are to our knowledge no lower bounds in the literature on the Froude number for solitary waves with vorticity. We note that the lower bound in Ter-Krikorov (Reference Ter-Krikorov1961) applies only to the small-amplitude waves constructed in that paper. The only upper bounds on the Froude number which we know of (Kozlov & Kuznetsov Reference Kozlov and Kuznetsov2012; Wheeler Reference Wheeler2013; also see Keady & Norbury Reference Keady and Norbury1982) are proved by maximum principle arguments and reduce to (1.11) for irrotational waves. In particular, these bounds seem not to lead to bounds on the Froude number which are independent of the amplitude
![]() $\max {\it\eta}$
.
$\max {\it\eta}$
.
There are, however, many results on solitary waves with vorticity which require the assumption that
![]() $F>1$
. Hur proved exponential asymptotics (Hur Reference Hur2008b
) and analyticity of streamlines (Hur Reference Hur2012a
) for waves with
$F>1$
. Hur proved exponential asymptotics (Hur Reference Hur2008b
) and analyticity of streamlines (Hur Reference Hur2012a
) for waves with
![]() $F>1$
, and symmetry for waves with
$F>1$
, and symmetry for waves with
![]() $F>1$
which are also waves of elevation (Hur Reference Hur2008b
) (see Matioc & Matioc Reference Matioc and Matioc2012 for some related results without the assumption
$F>1$
which are also waves of elevation (Hur Reference Hur2008b
) (see Matioc & Matioc Reference Matioc and Matioc2012 for some related results without the assumption
![]() $F>1$
). Upper and lower bounds (or the lack thereof) on the Froude number also feature prominently in the construction by the author of large-amplitude solitary waves in Wheeler (Reference Wheeler2013), where it was also shown that waves with
$F>1$
). Upper and lower bounds (or the lack thereof) on the Froude number also feature prominently in the construction by the author of large-amplitude solitary waves in Wheeler (Reference Wheeler2013), where it was also shown that waves with
![]() $F\geqslant 1$
are necessarily waves of elevation. See § 5 for more on the consequences of our main results for the amplitude, elevation, symmetry, monotonicity, and decay of solitary waves, and § 6 for more on the existence of large-amplitude waves.
$F\geqslant 1$
are necessarily waves of elevation. See § 5 for more on the consequences of our main results for the amplitude, elevation, symmetry, monotonicity, and decay of solitary waves, and § 6 for more on the existence of large-amplitude waves.
With large positive constant vorticity, numerics seem to suggest the existence of overhanging waves with arbitrarily large Froude number (Vanden-Broeck Reference Vanden-Broeck1994), a phenomenon which cannot occur for irrotational waves. See § 7 for versions of Theorems 1.1 and 1.2 in the special case of constant vorticity. Note that overhanging waves must have
![]() $u=c$
somewhere along their free surfaces, and hence do not satisfy our assumption
$u=c$
somewhere along their free surfaces, and hence do not satisfy our assumption
![]() $\sup u<c$
.
$\sup u<c$
.
It is worth noting that Burns (Reference Burns1953), as well as for instance Thompson (Reference Thompson1949) and Freeman & Johnson (Reference Freeman and Johnson1970), are not restricted to waves with
![]() $\sup u<c$
, nor are the bounds in Kozlov & Kuznetsov (Reference Kozlov and Kuznetsov2012). The assumption
$\sup u<c$
, nor are the bounds in Kozlov & Kuznetsov (Reference Kozlov and Kuznetsov2012). The assumption
![]() $\sup u<c$
is made, however, in all of the existence results for solitary waves mentioned earlier (Ter-Krikorov Reference Ter-Krikorov1961; Groves & Wahlén Reference Groves and Wahlén2008; Hur Reference Hur2008a
; Wheeler Reference Wheeler2013). See Wahlén (Reference Wahlén2009) and Ehrnström, Escher & Wahlén (Reference Ehrnström, Escher and Wahlén2011) for the construction of periodic waves where
$\sup u<c$
is made, however, in all of the existence results for solitary waves mentioned earlier (Ter-Krikorov Reference Ter-Krikorov1961; Groves & Wahlén Reference Groves and Wahlén2008; Hur Reference Hur2008a
; Wheeler Reference Wheeler2013). See Wahlén (Reference Wahlén2009) and Ehrnström, Escher & Wahlén (Reference Ehrnström, Escher and Wahlén2011) for the construction of periodic waves where
![]() $u-c$
changes sign, and Kozlov & Kuznetsov (Reference Kozlov and Kuznetsov2014) for a quite general discussion of the dispersion relation.
$u-c$
changes sign, and Kozlov & Kuznetsov (Reference Kozlov and Kuznetsov2014) for a quite general discussion of the dispersion relation.
Lastly, we emphasize that our definition (1.2) of the Froude number
![]() $F$
is made only for convenience and that there are many other conventions in the literature. Fenton (Reference Fenton1973), for instance, uses
$F$
is made only for convenience and that there are many other conventions in the literature. Fenton (Reference Fenton1973), for instance, uses
![]() $(c-U(0))/\sqrt{gd}$
, while Benjamin (Reference Benjamin1962) uses the ratio between the mean of
$(c-U(0))/\sqrt{gd}$
, while Benjamin (Reference Benjamin1962) uses the ratio between the mean of
![]() $c-U$
and
$c-U$
and
![]() $\sqrt{gd}$
. Our definition is essentially that of Ter-Krikorov (Reference Ter-Krikorov1961), who calls our
$\sqrt{gd}$
. Our definition is essentially that of Ter-Krikorov (Reference Ter-Krikorov1961), who calls our
![]() $F\sqrt{gd}$
the ‘speed of propagation’.
$F\sqrt{gd}$
the ‘speed of propagation’.
1.3. Method of proof and further consequences
1.3.1. Integral identities with vorticity
The main ingredient in the proof of Theorem 1.1 is an integral identity, Lemma 3.1, which seems to be completely new. In particular, we emphasize that this lemma is not a straightforward generalization of the identity (1.8) used in the irrotational case. Indeed, following the proof of (1.8) but retaining the extra terms coming from vorticity, one obtains a different identity, Lemma 4.2 (which we use in the proof of Theorem 1.2). Under the relatively strong assumption that vorticity is non-negative, Lemma 4.2 implies a lower bound on the relative speed
![]() $c-U(0)$
of asymptotic shear flow at the free surface. Except in the irrotational case where
$c-U(0)$
of asymptotic shear flow at the free surface. Except in the irrotational case where
![]() $U(y)$
is constant, however, this bound is not sufficient to show that the Froude number
$U(y)$
is constant, however, this bound is not sufficient to show that the Froude number
![]() $F$
is greater than the critical value 1. Indeed, the definition (1.2) of
$F$
is greater than the critical value 1. Indeed, the definition (1.2) of
![]() $F$
involves the values
$F$
involves the values
![]() $U(y)$
for all
$U(y)$
for all
![]() $-d\leqslant y\leqslant 0$
, not just
$-d\leqslant y\leqslant 0$
, not just
![]() $y=0$
, and the lower bound
$y=0$
, and the lower bound
![]() $F>1$
is sharp for small-amplitude waves.
$F>1$
is sharp for small-amplitude waves.
After reading a preprint of this paper, Evgeniy Lokharu pointed out to the author that the proof of Lemma 3.1 can be extended to prove an analogue of
![]() $F\neq 1$
for periodic waves, or even for waves which are neither periodic nor solitary. Here the relevant quantity is not what we call the Froude number, but instead an appropriately defined Bernoulli constant. This result has since appeared in Kozlov, Kuznetsov & Lokharu (Reference Kozlov, Kuznetsov and Lokharu2015).
$F\neq 1$
for periodic waves, or even for waves which are neither periodic nor solitary. Here the relevant quantity is not what we call the Froude number, but instead an appropriately defined Bernoulli constant. This result has since appeared in Kozlov, Kuznetsov & Lokharu (Reference Kozlov, Kuznetsov and Lokharu2015).
1.3.2. Existence of large-amplitude waves
In Wheeler (Reference Wheeler2013), the author constructed a connected set
![]() $\mathscr{C}$
of solitary waves of elevation whose asymptotic shear flows are given by
$\mathscr{C}$
of solitary waves of elevation whose asymptotic shear flows are given by
for some arbitrary but fixed positive function
![]() $U^{\ast }$
satisfying a normalization condition. It is easy to see from (1.12) that the dimensionless parameter
$U^{\ast }$
satisfying a normalization condition. It is easy to see from (1.12) that the dimensionless parameter
![]() ${\it\Lambda}$
is constant along
${\it\Lambda}$
is constant along
![]() $\mathscr{C}$
; when
$\mathscr{C}$
; when
![]() ${\it\Lambda}<2/\sqrt{3}$
, we can combine Theorems 1.1 and 1.2 with the results in Wheeler (Reference Wheeler2013) to show that there exists a sequence of waves in
${\it\Lambda}<2/\sqrt{3}$
, we can combine Theorems 1.1 and 1.2 with the results in Wheeler (Reference Wheeler2013) to show that there exists a sequence of waves in
![]() $\mathscr{C}$
which approach stagnation in that
$\mathscr{C}$
which approach stagnation in that
![]() $\sup u_{n}\rightarrow c$
. This significant improvement is presented in detail in § 6 (Corollary 6.2), along with a related result for
$\sup u_{n}\rightarrow c$
. This significant improvement is presented in detail in § 6 (Corollary 6.2), along with a related result for
![]() ${\it\Lambda}\geqslant 2/\sqrt{3}$
(Corollary 6.1).
${\it\Lambda}\geqslant 2/\sqrt{3}$
(Corollary 6.1).
1.3.3. Waves with surface tension
For irrotational waves with surface tension, Amick & Kirchgässner (Reference Amick and Kirchgässner1989) prove the analogue
of (1.8), where
![]() ${\it\sigma}>0$
is the constant coefficient of surface tension. This identity implies that solitary waves of elevation have
${\it\sigma}>0$
is the constant coefficient of surface tension. This identity implies that solitary waves of elevation have
![]() $F>1$
while solitary waves of depression have
$F>1$
while solitary waves of depression have
![]() $F<1$
. In § 8, we will show that the same is true for waves with vorticity; indeed, with slightly stronger regularity assumptions, Lemma 3.1 and Theorem 1.1 continue to hold in the presence of surface tension and with nearly identical proofs.
$F<1$
. In § 8, we will show that the same is true for waves with vorticity; indeed, with slightly stronger regularity assumptions, Lemma 3.1 and Theorem 1.1 continue to hold in the presence of surface tension and with nearly identical proofs.
While the existence of solitary waves of depression with Bond number
![]() ${\it\sigma}/gd^{2}>1/3$
is well-established (Amick & Kirchgässner Reference Amick and Kirchgässner1989; Groves & Wahlén Reference Groves and Wahlén2007), there is both numerical and analytical evidence that solitary waves of elevation do not exist for any values of
${\it\sigma}/gd^{2}>1/3$
is well-established (Amick & Kirchgässner Reference Amick and Kirchgässner1989; Groves & Wahlén Reference Groves and Wahlén2007), there is both numerical and analytical evidence that solitary waves of elevation do not exist for any values of
![]() ${\it\sigma}$
(Sun Reference Sun1999; Champneys, Vanden-Broeck & Lord Reference Champneys, Vanden-Broeck and Lord2002). In their place are so-called generalized solitary waves with small trains of periodic waves at infinity (Beale Reference Beale1991), as well as families of oscillatory waves whose free surfaces vanish at infinity (Iooss & Kirchgässner Reference Iooss and Kirchgässner1990; Buffoni, Groves & Toland Reference Buffoni, Groves and Toland1996; Groves & Wahlén Reference Groves and Wahlén2007).
${\it\sigma}$
(Sun Reference Sun1999; Champneys, Vanden-Broeck & Lord Reference Champneys, Vanden-Broeck and Lord2002). In their place are so-called generalized solitary waves with small trains of periodic waves at infinity (Beale Reference Beale1991), as well as families of oscillatory waves whose free surfaces vanish at infinity (Iooss & Kirchgässner Reference Iooss and Kirchgässner1990; Buffoni, Groves & Toland Reference Buffoni, Groves and Toland1996; Groves & Wahlén Reference Groves and Wahlén2007).
1.4. Outline
In § 2, we perform a standard change of variables and collect some formulae which will be used later. The main benefit of this change of variables is that it transforms the fluid domain into a fixed infinite strip, enabling us to multiply the Euler equations by functions defined in terms of the asymptotic shear flow
![]() $U(y)$
appearing in the definition (1.2) of the Froude number
$U(y)$
appearing in the definition (1.2) of the Froude number
![]() $F$
.
$F$
.
In § 3, we give a short and elementary proof of Theorem 1.1, based on an integral identity, Lemma 3.1, in the transformed variables. The argument is perhaps even simpler than the argument in McLeod (Reference McLeod1984), provided the change of variables in § 2 is taken for granted.
In § 4, we prove the upper bound Theorem 1.2 using two additional integral identities. The first, Lemma 4.2, is essentially (1.8) with an extra term coming from the vorticity, and is proved mostly in the original physical variables. The second, Lemma 4.3 is proved similarly to Lemma 3.1, but with a different test function.
In § 5, we collect some implications of Theorems 1.1 and 1.2 for the amplitude, mass, symmetry, monotonicity, and exponential decay of solitary waves of elevation.
In § 6, we show how Theorems 1.1 and 1.2 can be used to improve the existence theory for large-amplitude solitary waves with vorticity developed by the author in Wheeler (Reference Wheeler2013).
In § 7, we specialize Theorems 1.1 and 1.2 to the case where the vorticity is constant and more explicit formulae can be given.
Finally, in § 8 we prove that, with slightly modified regularity assumptions, Lemma 3.1 and Theorem 1.1 still hold for waves with surface tension.
2. Preliminaries
With the conventions from § 1.1, we assume that
![]() $u,v,P\in W_{\mathit{loc}}^{1,r}(\overline{D_{{\it\eta}}})$
satisfy the stationary incompressible Euler equations
$u,v,P\in W_{\mathit{loc}}^{1,r}(\overline{D_{{\it\eta}}})$
satisfy the stationary incompressible Euler equations
in
![]() $L_{\mathit{loc}}^{r}(\overline{D_{{\it\eta}}})$
, together with the boundary conditions
$L_{\mathit{loc}}^{r}(\overline{D_{{\it\eta}}})$
, together with the boundary conditions
pointwise, and the asymptotic conditions
uniformly in
![]() $y$
. The free surface elevation
$y$
. The free surface elevation
![]() ${\it\eta}$
has the regularity
${\it\eta}$
has the regularity
![]() ${\it\eta}\in C^{1+{\it\alpha}}(\mathbb{R})$
, and
${\it\eta}\in C^{1+{\it\alpha}}(\mathbb{R})$
, and
![]() $U\in W^{1,r}(-d,0)$
. Here for convenience we have normalized
$U\in W^{1,r}(-d,0)$
. Here for convenience we have normalized
![]() $P$
to vanish on the free surface;
$P$
to vanish on the free surface;
![]() $P$
therefore represents the difference between the pressure in the fluid and the atmospheric pressure.
$P$
therefore represents the difference between the pressure in the fluid and the atmospheric pressure.
Because of incompressibility (2.1c
), there exists a stream function
![]() ${\it\psi}\in W_{\mathit{loc}}^{2,r}(\overline{D_{{\it\eta}}})\subset C_{\mathit{loc}}^{1+{\it\alpha}}(\overline{D_{{\it\eta}}})$
which satisfies
${\it\psi}\in W_{\mathit{loc}}^{2,r}(\overline{D_{{\it\eta}}})\subset C_{\mathit{loc}}^{1+{\it\alpha}}(\overline{D_{{\it\eta}}})$
which satisfies
![]() ${\it\psi}_{y}=u-c$
and
${\it\psi}_{y}=u-c$
and
![]() ${\it\psi}_{x}=v$
. From now on we will always assume
${\it\psi}_{x}=v$
. From now on we will always assume
![]() $\sup u<c$
, or equivalently
$\sup u<c$
, or equivalently
![]() $\sup {\it\psi}_{y}<0$
. By the kinematic boundary conditions (2.1d
)–(2.1e
),
$\sup {\it\psi}_{y}<0$
. By the kinematic boundary conditions (2.1d
)–(2.1e
),
![]() ${\it\psi}$
is constant on
${\it\psi}$
is constant on
![]() $y=-d$
and
$y=-d$
and
![]() $y={\it\eta}(x)$
. Thus the flux
$y={\it\eta}(x)$
. Thus the flux
is independent of
![]() $x$
. We normalize
$x$
. We normalize
![]() ${\it\psi}$
so that
${\it\psi}$
so that
![]() ${\it\psi}=0$
on
${\it\psi}=0$
on
![]() $y={\it\eta}(x)$
and
$y={\it\eta}(x)$
and
![]() ${\it\psi}=-m$
on
${\it\psi}=-m$
on
![]() $y=-d$
. The vorticity
$y=-d$
. The vorticity
![]() ${\it\omega}$
is given in terms of
${\it\omega}$
is given in terms of
![]() ${\it\psi}$
by
${\it\psi}$
by
for some function
![]() ${\it\gamma}\in L^{r}[-m,0]$
called the vorticity function (Constantin & Strauss Reference Constantin and Strauss2011). Because of the asymptotic condition (2.1g
),
${\it\gamma}\in L^{r}[-m,0]$
called the vorticity function (Constantin & Strauss Reference Constantin and Strauss2011). Because of the asymptotic condition (2.1g
),
so that
![]() ${\it\gamma}$
is completely determined by
${\it\gamma}$
is completely determined by
![]() $U$
and
$U$
and
![]() $c$
.
$c$
.
Using
as independent variables, we can rewrite (2.1) in terms of the so-called height function
![]() $h(q,p)$
defined by
$h(q,p)$
defined by
The advantage of this formulation is that
![]() $h$
is defined on the fixed domain
$h$
is defined on the fixed domain
Defining the asymptotic height function
![]() $H(p)$
in a similar way,
$H(p)$
in a similar way,
where
![]() ${\it\Psi}(y)$
is as in (2.4), we have
${\it\Psi}(y)$
is as in (2.4), we have
![]() $H(0)=d$
and
$H(0)=d$
and
![]() $H(-m)=0$
. Since (2.6) implies
$H(-m)=0$
. Since (2.6) implies
![]() $h_{p}^{-1}=-{\it\psi}_{y}$
, we necessarily have
$h_{p}^{-1}=-{\it\psi}_{y}$
, we necessarily have
![]() $\inf h_{p}>0$
and
$\inf h_{p}>0$
and
![]() $\min H_{p}>0$
.
$\min H_{p}>0$
.
The arguments in Constantin & Strauss (Reference Constantin and Strauss2011) show that, under the crucial assumption
![]() $\sup u<c$
, the solitary water wave problem (2.1) is equivalent to the system
$\sup u<c$
, the solitary water wave problem (2.1) is equivalent to the system
for
![]() $h\in W_{\mathit{loc}}^{2,r}(\overline{{\it\Omega}})\subset C_{\mathit{loc}}^{1+{\it\alpha}}(\overline{{\it\Omega}})$
and
$h\in W_{\mathit{loc}}^{2,r}(\overline{{\it\Omega}})\subset C_{\mathit{loc}}^{1+{\it\alpha}}(\overline{{\it\Omega}})$
and
![]() $H\in W^{2,r}[-m,0]$
together with the asymptotic conditions
$H\in W^{2,r}[-m,0]$
together with the asymptotic conditions
The velocity field
![]() $(u,v)$
and free surface
$(u,v)$
and free surface
![]() ${\it\eta}$
can be recovered from
${\it\eta}$
can be recovered from
![]() $h$
via
$h$
via
We note that the divergence-form equation (2.9a
) expresses the balance of the
![]() $y$
-component of momentum and that (2.9b
) is Bernoulli’s law evaluated on the free surface.
$y$
-component of momentum and that (2.9b
) is Bernoulli’s law evaluated on the free surface.
Defining the antiderivative
![]() ${\it\Gamma}\in W^{1,r}[-m,0]\subset C^{{\it\alpha}}[-m,0]$
of the vorticity function
${\it\Gamma}\in W^{1,r}[-m,0]\subset C^{{\it\alpha}}[-m,0]$
of the vorticity function
![]() ${\it\gamma}$
and the Bernoulli constant
${\it\gamma}$
and the Bernoulli constant
![]() ${\it\lambda}$
by
${\it\lambda}$
by
we have the following useful relation between
![]() ${\it\gamma}$
,
${\it\gamma}$
,
![]() $H$
, and
$H$
, and
![]() $U$
:
$U$
:
In particular, the Froude number
![]() $F$
is given in terms of
$F$
is given in terms of
![]() $H$
by
$H$
by
In addition, Bernoulli’s law can be written as
Indeed, one can see that the left-hand side is constant by differentiating and using (2.1a
) and (2.1b
). The fact that this constant is zero follows by sending
![]() $x\rightarrow \pm \infty$
in the dynamic boundary condition (2.1f
).
$x\rightarrow \pm \infty$
in the dynamic boundary condition (2.1f
).
3. Lower bound
Lemma 3.1. Any solitary wave with
![]() $\sup u<c$
and the regularity (1.3) satisfies
$\sup u<c$
and the regularity (1.3) satisfies
Proof. Defining the function
(which solves the linearization of (2.9a
) and (2.9c
) around
![]() $h=H$
), we note that (2.13) implies
$h=H$
), we note that (2.13) implies
![]() $g{\it\Phi}(0)=1/F^{2}$
. Multiplying (2.9a
) by
$g{\it\Phi}(0)=1/F^{2}$
. Multiplying (2.9a
) by
![]() ${\it\Phi}$
and integrating by parts, we then have, for any
${\it\Phi}$
and integrating by parts, we then have, for any
![]() $M>0$
,
$M>0$
,
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left[\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)_{p}{\it\Phi}+\left(\frac{h_{q}}{h_{p}}\right)_{q}{\it\Phi}\right]\!\text{d}p\text{d}q\nonumber\\ \displaystyle & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right)H_{p}^{3}\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{gF^{2}}\int _{-M}^{M}\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)(q,0)\text{d}q+\left.\int _{-m}^{0}\frac{h_{q}}{h_{p}}{\it\Phi}\text{d}p\right|_{q=-M}^{q=M}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left[\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)_{p}{\it\Phi}+\left(\frac{h_{q}}{h_{p}}\right)_{q}{\it\Phi}\right]\!\text{d}p\text{d}q\nonumber\\ \displaystyle & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right)H_{p}^{3}\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{gF^{2}}\int _{-M}^{M}\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)(q,0)\text{d}q+\left.\int _{-m}^{0}\frac{h_{q}}{h_{p}}{\it\Phi}\text{d}p\right|_{q=-M}^{q=M}.\end{eqnarray}$$
Since
![]() $h_{q}\rightarrow 0$
as
$h_{q}\rightarrow 0$
as
![]() $q\rightarrow \pm \infty$
by (2.9d
), the third term in (3.3) vanishes as
$q\rightarrow \pm \infty$
by (2.9d
), the third term in (3.3) vanishes as
![]() $M\rightarrow \infty$
. Using the boundary condition (2.9b
) to simplify the second term, we obtain
$M\rightarrow \infty$
. Using the boundary condition (2.9b
) to simplify the second term, we obtain
as
![]() $M\rightarrow \infty$
. Rewriting the first integrand in (3.4) as
$M\rightarrow \infty$
. Rewriting the first integrand in (3.4) as
we see that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right)H_{p}^{3}\text{d}p\text{d}q=-\int _{-M}^{M}(h(q,0)-H(0))\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{108.0pt}\quad +\,\int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}}\text{d}p\text{d}q.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right)H_{p}^{3}\text{d}p\text{d}q=-\int _{-M}^{M}(h(q,0)-H(0))\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{108.0pt}\quad +\,\int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}}\text{d}p\text{d}q.\end{eqnarray}$$
Plugging (3.6) into (3.4), rearranging terms, and using the identity
![]() $h(q,0)-H(0)={\it\eta}(q)$
from (2.10), we obtain (3.1) as desired.
$h(q,0)-H(0)={\it\eta}(q)$
from (2.10), we obtain (3.1) as desired.
Proof of Theorem 1.1. Consider a non-trivial solitary wave. Then
![]() $H_{p}$
and
$H_{p}$
and
![]() $h_{p}$
are strictly positive, and
$h_{p}$
are strictly positive, and
![]() $h_{q}(q,0)={\it\eta}_{x}(q)$
does not vanish identically. Thus the second integral in (3.1) is a non-decreasing function of
$h_{q}(q,0)={\it\eta}_{x}(q)$
does not vanish identically. Thus the second integral in (3.1) is a non-decreasing function of
![]() $M$
and is strictly positive for
$M$
and is strictly positive for
![]() $M$
sufficiently large, and therefore the limit in (3.1) implies
$M$
sufficiently large, and therefore the limit in (3.1) implies
Since the left-hand side of (3.7) vanishes if
![]() $F=1$
, we must have
$F=1$
, we must have
![]() $F\neq 1$
. For a wave of elevation,
$F\neq 1$
. For a wave of elevation,
![]() ${\it\eta}(x)\geqslant 0$
for all
${\it\eta}(x)\geqslant 0$
for all
![]() $x$
but
$x$
but
![]() ${\it\eta}\not\equiv 0$
, so (3.7) implies that the coefficient
${\it\eta}\not\equiv 0$
, so (3.7) implies that the coefficient
![]() $1/F^{2}-1$
is strictly negative, i.e. that
$1/F^{2}-1$
is strictly negative, i.e. that
![]() $F>1$
. Similarly, for a wave of depression,
$F>1$
. Similarly, for a wave of depression,
![]() ${\it\eta}(x)\leqslant 0$
for all
${\it\eta}(x)\leqslant 0$
for all
![]() $x$
but
$x$
but
![]() ${\it\eta}\not\equiv 0$
, so (3.7) implies that
${\it\eta}\not\equiv 0$
, so (3.7) implies that
![]() $1/F^{2}-1$
is strictly positive, i.e. that
$1/F^{2}-1$
is strictly positive, i.e. that
![]() $F<1$
.
$F<1$
.
4. Upper bound
In this section we will make use of the vorticity function
![]() ${\it\gamma}(-p)$
, Bernoulli constant
${\it\gamma}(-p)$
, Bernoulli constant
![]() ${\it\lambda}=(c-U(0))^{2}$
, and antiderivative
${\it\lambda}=(c-U(0))^{2}$
, and antiderivative
![]() ${\it\Gamma}(p)$
of
${\it\Gamma}(p)$
of
![]() ${\it\gamma}$
defined in § 2. We begin by giving a formula in our notation for an invariant called the flow force.
${\it\gamma}$
defined in § 2. We begin by giving a formula in our notation for an invariant called the flow force.
Lemma 4.1. For any solitary wave with
![]() $\sup u<c$
and the regularity (1.3) and for any
$\sup u<c$
and the regularity (1.3) and for any
![]() $x$
, the flow force
$x$
, the flow force
Proof. That
![]() $S$
is independent of
$S$
is independent of
![]() $x$
is well-known, and can be proved, for instance, by integrating the identity
$x$
is well-known, and can be proved, for instance, by integrating the identity
![]() $(P+(u-c)^{2})_{x}+((u-c)v)_{y}=0$
over a region of the form
$(P+(u-c)^{2})_{x}+((u-c)v)_{y}=0$
over a region of the form
![]() $\{(x,y):a<x<b,-d<y<{\it\eta}(x)\}$
using the divergence theorem and then applying the boundary conditions. To obtain the formula (4.1), we use Bernoulli’s law (2.14) to rewrite
$\{(x,y):a<x<b,-d<y<{\it\eta}(x)\}$
using the divergence theorem and then applying the boundary conditions. To obtain the formula (4.1), we use Bernoulli’s law (2.14) to rewrite
The asymptotic condition (2.9d ) gives
uniformly in
![]() $p$
, and hence, since
$p$
, and hence, since
![]() $S$
is independent of
$S$
is independent of
![]() $x$
,
$x$
,
 $$\begin{eqnarray}\displaystyle S & = & \displaystyle \lim _{q\rightarrow \pm \infty }\int _{-m}^{0}\left(\frac{1-h_{q}^{2}}{2h_{p}^{2}}-g(h-d)+\frac{{\it\lambda}}{2}+{\it\Gamma}\right)h_{p}\text{d}p\nonumber\\ \displaystyle & = & \displaystyle \int _{-m}^{0}\left({\it\lambda}+2{\it\Gamma}-g(H-d)\right)H_{p}\text{d}p\nonumber\\ \displaystyle & = & \displaystyle -2\int _{-m}^{0}{\it\gamma}H\text{d}p+{\it\lambda}d+\frac{gd^{2}}{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S & = & \displaystyle \lim _{q\rightarrow \pm \infty }\int _{-m}^{0}\left(\frac{1-h_{q}^{2}}{2h_{p}^{2}}-g(h-d)+\frac{{\it\lambda}}{2}+{\it\Gamma}\right)h_{p}\text{d}p\nonumber\\ \displaystyle & = & \displaystyle \int _{-m}^{0}\left({\it\lambda}+2{\it\Gamma}-g(H-d)\right)H_{p}\text{d}p\nonumber\\ \displaystyle & = & \displaystyle -2\int _{-m}^{0}{\it\gamma}H\text{d}p+{\it\lambda}d+\frac{gd^{2}}{2},\end{eqnarray}$$
where in the last step we integrated by parts using
![]() $H(-m)={\it\Gamma}(0)=0$
and
$H(-m)={\it\Gamma}(0)=0$
and
![]() ${\it\Gamma}_{p}={\it\gamma}$
.
${\it\Gamma}_{p}={\it\gamma}$
.
The following integral identity is (1.8) but with an extra term coming from the vorticity. Unlike Lemmas 3.1 and 4.3, it is proved mostly in the original physical variables.
Lemma 4.2. Any solitary wave with
![]() $\sup u<c$
and the regularity (1.3) satisfies
$\sup u<c$
and the regularity (1.3) satisfies
Proof. Consider the fluid region
and the two
![]() $W^{1,r}(D)$
vector fields
$W^{1,r}(D)$
vector fields
 $$\begin{eqnarray}\displaystyle \text{div}(x\boldsymbol{A}+(y+d)\boldsymbol{B}) & = & \displaystyle \boldsymbol{A}^{1}+\boldsymbol{B}^{2}\nonumber\\ \displaystyle & = & \displaystyle 2P+(u-c)^{2}+v^{2}+gy\nonumber\\ \displaystyle & = & \displaystyle {\it\lambda}+2{\it\Gamma}(-{\it\psi})-gy\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{div}(x\boldsymbol{A}+(y+d)\boldsymbol{B}) & = & \displaystyle \boldsymbol{A}^{1}+\boldsymbol{B}^{2}\nonumber\\ \displaystyle & = & \displaystyle 2P+(u-c)^{2}+v^{2}+gy\nonumber\\ \displaystyle & = & \displaystyle {\it\lambda}+2{\it\Gamma}(-{\it\psi})-gy\end{eqnarray}$$
in
![]() $L^{r}(D)$
, where in the last step we have used Bernoulli’s law (2.14). Integrating (4.9) over
$L^{r}(D)$
, where in the last step we have used Bernoulli’s law (2.14). Integrating (4.9) over
![]() $D$
, the divergence theorem gives
$D$
, the divergence theorem gives
where
![]() $\boldsymbol{n}$
is an outward pointing normal. We will obtain (4.5) by simplifying both sides of (4.10) and using Lemma 4.1.
$\boldsymbol{n}$
is an outward pointing normal. We will obtain (4.5) by simplifying both sides of (4.10) and using Lemma 4.1.
First consider the left-hand side of (4.10). On the free surface, the two boundary conditions
![]() $v={\it\eta}_{x}(u-c)$
and
$v={\it\eta}_{x}(u-c)$
and
![]() $P=0$
give
$P=0$
give
while on the bottom
![]() $y=-d$
the boundary condition
$y=-d$
the boundary condition
![]() $v=0$
implies
$v=0$
implies
![]() $\boldsymbol{A}^{2}=(y+d)\boldsymbol{B}^{2}=0$
. Thus we see
$\boldsymbol{A}^{2}=(y+d)\boldsymbol{B}^{2}=0$
. Thus we see
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\partial D}(x\boldsymbol{A}+(y+d)\boldsymbol{B})\boldsymbol{\cdot }\boldsymbol{n}\text{d}s=\left.x\int _{-d}^{{\it\eta}(x)}(P+(u-c)^{2})\text{d}y\right|_{x=-M}^{x=M}\nonumber\\ \displaystyle & & \displaystyle \hspace{72.0pt}\quad +\,\left.\int _{-d}^{{\it\eta}(x)}(y+d)(u-c)v\text{d}y\right|_{x=-M}^{x=M}+\int _{-M}^{M}g({\it\eta}+d){\it\eta}\text{d}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\partial D}(x\boldsymbol{A}+(y+d)\boldsymbol{B})\boldsymbol{\cdot }\boldsymbol{n}\text{d}s=\left.x\int _{-d}^{{\it\eta}(x)}(P+(u-c)^{2})\text{d}y\right|_{x=-M}^{x=M}\nonumber\\ \displaystyle & & \displaystyle \hspace{72.0pt}\quad +\,\left.\int _{-d}^{{\it\eta}(x)}(y+d)(u-c)v\text{d}y\right|_{x=-M}^{x=M}+\int _{-M}^{M}g({\it\eta}+d){\it\eta}\text{d}x.\end{eqnarray}$$
By Lemma 4.1, we have
for all
![]() $x$
, and since
$x$
, and since
![]() $v\rightarrow 0$
uniformly in
$v\rightarrow 0$
uniformly in
![]() $y$
as
$y$
as
![]() $x\rightarrow \pm \infty$
, the second term on the right-hand side of (4.12) vanishes as
$x\rightarrow \pm \infty$
, the second term on the right-hand side of (4.12) vanishes as
![]() $M\rightarrow \infty$
. Thus (4.12) implies
$M\rightarrow \infty$
. Thus (4.12) implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\partial D}(x\boldsymbol{A}+(y+d)\boldsymbol{B})\boldsymbol{\cdot }\boldsymbol{n}\text{d}s-g\int _{-M}^{M}{\it\eta}^{2}\text{d}x\nonumber\\ \displaystyle & & \displaystyle \hspace{60.0pt}\qquad -\,gd\int _{-M}^{M}{\it\eta}\text{d}x-2M\left({\it\lambda}d+\frac{gd^{2}}{2}-2\int _{-m}^{0}{\it\gamma}H\text{d}p\right)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\partial D}(x\boldsymbol{A}+(y+d)\boldsymbol{B})\boldsymbol{\cdot }\boldsymbol{n}\text{d}s-g\int _{-M}^{M}{\it\eta}^{2}\text{d}x\nonumber\\ \displaystyle & & \displaystyle \hspace{60.0pt}\qquad -\,gd\int _{-M}^{M}{\it\eta}\text{d}x-2M\left({\it\lambda}d+\frac{gd^{2}}{2}-2\int _{-m}^{0}{\it\gamma}H\text{d}p\right)\rightarrow 0\end{eqnarray}$$
as
![]() $M\rightarrow \infty$
.
$M\rightarrow \infty$
.
Now we turn to the right-hand side of (4.10). Changing variables and integrating by parts,
where we have used that
![]() ${\it\Gamma}$
vanishes on
${\it\Gamma}$
vanishes on
![]() $p=0$
while
$p=0$
while
![]() $h$
vanishes on
$h$
vanishes on
![]() $p=-m$
. Thus
$p=-m$
. Thus
 $$\begin{eqnarray}\displaystyle \iint _{D}({\it\lambda}-gy+2{\it\Gamma}(-{\it\psi}))\text{d}y\text{d}x & = & \displaystyle {\it\lambda}\int _{-M}^{M}{\it\eta}\text{d}x-\frac{g}{2}\int _{-M}^{M}{\it\eta}^{2}\text{d}x\nonumber\\ \displaystyle & & \displaystyle -\,2\int _{-M}^{M}\int _{-m}^{0}{\it\gamma}h\text{d}p\text{d}q+2M\left({\it\lambda}d+\frac{gd^{2}}{2}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \iint _{D}({\it\lambda}-gy+2{\it\Gamma}(-{\it\psi}))\text{d}y\text{d}x & = & \displaystyle {\it\lambda}\int _{-M}^{M}{\it\eta}\text{d}x-\frac{g}{2}\int _{-M}^{M}{\it\eta}^{2}\text{d}x\nonumber\\ \displaystyle & & \displaystyle -\,2\int _{-M}^{M}\int _{-m}^{0}{\it\gamma}h\text{d}p\text{d}q+2M\left({\it\lambda}d+\frac{gd^{2}}{2}\right)\!.\end{eqnarray}$$
Substituting (4.14) and (4.16) into (4.10), most of the terms drop out and we are left with (4.5) as desired.
Lemma 4.3. Any solitary wave with
![]() $u<c$
and the regularity (1.3) satisfies
$u<c$
and the regularity (1.3) satisfies
Proof. We argue as in the proof of Lemma 3.1, but with the function
![]() ${\it\Phi}$
replaced by
${\it\Phi}$
replaced by
![]() $H$
, and then appeal to Lemma 4.2. Multiplying (2.9a
) by
$H$
, and then appeal to Lemma 4.2. Multiplying (2.9a
) by
![]() $H$
and integrating by parts, we have, for any
$H$
and integrating by parts, we have, for any
![]() $M>0$
,
$M>0$
,
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left[\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)_{p}H+\left(\frac{h_{q}}{h_{p}}\right)_{q}H\right]\text{d}p\text{d}q\nonumber\\ \displaystyle & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right)H_{p}\text{d}p\text{d}q+gd\int _{-M}^{M}{\it\eta}\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\left.\int _{-m}^{0}\frac{h_{q}}{h_{p}}H\text{d}p\right|_{q=-M}^{q=M},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left[\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)_{p}H+\left(\frac{h_{q}}{h_{p}}\right)_{q}H\right]\text{d}p\text{d}q\nonumber\\ \displaystyle & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right)H_{p}\text{d}p\text{d}q+gd\int _{-M}^{M}{\it\eta}\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\left.\int _{-m}^{0}\frac{h_{q}}{h_{p}}H\text{d}p\right|_{q=-M}^{q=M},\end{eqnarray}$$
where we have used the boundary condition (2.9b
) as well as
![]() $h(q,0)-H(0)={\it\eta}(q)$
and
$h(q,0)-H(0)={\it\eta}(q)$
and
![]() $H(0)=d$
. As in the proof of Lemma 3.1, the asymptotic conditions (2.9d
) imply that the last term in (4.18) vanishes as
$H(0)=d$
. As in the proof of Lemma 3.1, the asymptotic conditions (2.9d
) imply that the last term in (4.18) vanishes as
![]() $M\rightarrow \infty$
. The integrand in the first term of (4.18) can be rewritten as
$M\rightarrow \infty$
. The integrand in the first term of (4.18) can be rewritten as
as can be seen by dividing (3.5) by
![]() $H_{p}^{2}$
. Since
$H_{p}^{2}$
. Since
we can integrate the first term of (4.19) by parts to get
 $$\begin{eqnarray}\displaystyle -\int _{-m}^{0}\frac{h_{p}-H_{p}}{H_{p}^{2}}(q,p)\text{d}p & = & \displaystyle 2\int _{-m}^{0}\left(\frac{1}{H_{p}^{2}}\right)_{p}(h(q,p)-H(p))\text{d}p-{\it\lambda}(h(q,0)-H(0))\nonumber\\ \displaystyle & = & \displaystyle 2\int _{-m}^{0}{\it\gamma}(h(q,p)-H(p))\text{d}p-{\it\lambda}{\it\eta}(q).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\int _{-m}^{0}\frac{h_{p}-H_{p}}{H_{p}^{2}}(q,p)\text{d}p & = & \displaystyle 2\int _{-m}^{0}\left(\frac{1}{H_{p}^{2}}\right)_{p}(h(q,p)-H(p))\text{d}p-{\it\lambda}(h(q,0)-H(0))\nonumber\\ \displaystyle & = & \displaystyle 2\int _{-m}^{0}{\it\gamma}(h(q,p)-H(p))\text{d}p-{\it\lambda}{\it\eta}(q).\end{eqnarray}$$
Putting everything together, we see that (4.18) implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}H_{p}^{2}}\text{d}p\text{d}q+2\int _{-M}^{M}\int _{-m}^{0}{\it\gamma}(h-H)\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle \quad +\,(gd-{\it\lambda})\int _{-M}^{M}{\it\eta}\text{d}q\longrightarrow 0\quad \text{as }M\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}H_{p}^{2}}\text{d}p\text{d}q+2\int _{-M}^{M}\int _{-m}^{0}{\it\gamma}(h-H)\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle \quad +\,(gd-{\it\lambda})\int _{-M}^{M}{\it\eta}\text{d}q\longrightarrow 0\quad \text{as }M\rightarrow \infty .\end{eqnarray}$$
Adding (4.22) with the conclusion (4.5) of Lemma 4.2, most of the terms cancel and we are left with (4.17) as desired.
Using Lemmas 3.1 and 4.3, we can now prove Theorem 1.2.
Proof of Theorem 1.2. The key observation is that the integrands of the double integrals in (3.1) and (4.17) differ only by a factor of
![]() $H_{p}^{2}$
. Plugging the crude estimate
$H_{p}^{2}$
. Plugging the crude estimate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}}\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{60.0pt}\quad \leqslant \max H_{p}^{2}\int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}H_{p}^{2}}\text{d}p\text{d}q\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}}\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{60.0pt}\quad \leqslant \max H_{p}^{2}\int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}H_{p}^{2}}\text{d}p\text{d}q\end{eqnarray}$$
into the result (3.1) of Lemma 3.1, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \limsup _{M\rightarrow \infty }\left\{\!\left(1-\frac{1}{F^{2}}\right)\int _{-M}^{M}{\it\eta}\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{36.0pt}\left.\quad -\,\max H_{p}^{2}\int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}H_{p}^{2}}\text{d}p\text{d}q\right\}\leqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \limsup _{M\rightarrow \infty }\left\{\!\left(1-\frac{1}{F^{2}}\right)\int _{-M}^{M}{\it\eta}\text{d}x\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{36.0pt}\left.\quad -\,\max H_{p}^{2}\int _{-M}^{M}\int _{-m}^{0}\frac{H_{p}^{3}h_{q}^{2}+(2h_{p}+H_{p})(h_{p}-H_{p})^{2}}{2h_{p}^{2}H_{p}^{2}}\text{d}p\text{d}q\right\}\leqslant 0.\end{eqnarray}$$
Subtracting the conclusion (4.17) of Lemma 4.3 multiplied by
![]() $\max H_{p}^{2}$
, we then get
$\max H_{p}^{2}$
, we then get
But from Bernoulli’s law (2.14) evaluated at the crest we have
![]() $g\max {\it\eta}<{\it\lambda}/2$
, so that (4.25) implies
$g\max {\it\eta}<{\it\lambda}/2$
, so that (4.25) implies
and hence
By (2.11) and (2.12),
![]() ${\it\lambda}=(U-c)^{2}(0)$
and
${\it\lambda}=(U-c)^{2}(0)$
and
![]() $H_{p}^{2}=(U-c)^{-2}$
, so
$H_{p}^{2}=(U-c)^{-2}$
, so
and (4.27) becomes
which, assuming
![]() ${\it\Lambda}<2/\sqrt{3}$
, is equivalent to the desired upper bound on
${\it\Lambda}<2/\sqrt{3}$
, is equivalent to the desired upper bound on
![]() $F$
in (1.5).
$F$
in (1.5).
5. Amplitude, elevation, symmetry, monotonicity, and decay
In this section we will give several corollaries of Theorems 1.1 and 1.2 and their proofs. Some of these will require stronger regularity and decay assumptions than (1.3) and (2.1g ), namely
where
![]() ${\it\beta}\in (0,1)$
is arbitrary and the limit in (5.2) is uniform in
${\it\beta}\in (0,1)$
is arbitrary and the limit in (5.2) is uniform in
![]() $p$
.
$p$
.
Corollary 5.1 (Bound on the amplitude).
In the setting of Theorem 1.2, the maximum amplitude
![]() $\max _{x}{\it\eta}(x)$
satisfies the following upper bound:
$\max _{x}{\it\eta}(x)$
satisfies the following upper bound:
Proof. The first inequality in (5.3) is just Bernoulli’s law (2.14) evaluated at the crest. Next, we note that the definitions (1.2), (1.4), and (2.11) of
![]() $F$
and
$F$
and
![]() ${\it\Lambda}$
immediately imply the simple inequality
${\it\Lambda}$
immediately imply the simple inequality
![]() $(c-U(0))^{2}\leqslant gd{\it\Lambda}^{2}F^{2}$
. The second inequality in (5.3) then follows from the upper bound on
$(c-U(0))^{2}\leqslant gd{\it\Lambda}^{2}F^{2}$
. The second inequality in (5.3) then follows from the upper bound on
![]() $F$
in Theorem 1.2.
$F$
in Theorem 1.2.
When
![]() $U(y)\leqslant U(0)$
for
$U(y)\leqslant U(0)$
for
![]() $-d\leqslant y\leqslant 0$
, such as for instance when
$-d\leqslant y\leqslant 0$
, such as for instance when
![]() ${\it\omega}\leqslant 0$
so that
${\it\omega}\leqslant 0$
so that
![]() $U_{y}\geqslant 0$
, we have
$U_{y}\geqslant 0$
, we have
![]() ${\it\Lambda}=1$
and hence that the second inequality in (5.3) is the simple bound
${\it\Lambda}=1$
and hence that the second inequality in (5.3) is the simple bound
![]() $\max {\it\eta}\leqslant 2d$
. See § 7 for the case of constant vorticity.
$\max {\it\eta}\leqslant 2d$
. See § 7 for the case of constant vorticity.
The following is a partial converse of Theorem 1.1.
Proposition 5.2. A solitary wave with
![]() $\sup u<c$
,
$\sup u<c$
,
![]() $F\geqslant 1$
, and the regularity (5.1) and decay (5.2) is a strict wave of elevation in that
$F\geqslant 1$
, and the regularity (5.1) and decay (5.2) is a strict wave of elevation in that
![]() ${\it\eta}(x)>0$
for all
${\it\eta}(x)>0$
for all
![]() $x\in \mathbb{R}$
.
$x\in \mathbb{R}$
.
Proof. This is a slightly simplified version of Proposition 2.1 in Wheeler (Reference Wheeler2013).
Corollary 5.3 (Elevation).
A solitary wave with
![]() $\sup u<c$
and the regularity (5.1) and decay (5.2) is a wave of elevation if and only if
$\sup u<c$
and the regularity (5.1) and decay (5.2) is a wave of elevation if and only if
![]() $F\geqslant 1$
, and in this case it is a strict wave of elevation in that
$F\geqslant 1$
, and in this case it is a strict wave of elevation in that
![]() ${\it\eta}(x)>0$
for all
${\it\eta}(x)>0$
for all
![]() $x\in \mathbb{R}$
and moreover
$x\in \mathbb{R}$
and moreover
![]() $F>1$
.
$F>1$
.
While there are no symmetric and monotone irrotational solitary waves of depression (Keady & Pritchard Reference Keady and Pritchard1974), it is an open question if the same is true with vorticity. More generally, it is unknown if there are any solitary waves with subcritical Froude number
![]() $F<1$
. By Theorem 1.1, no such wave could be a wave of elevation, and in fact (3.1) implies something stronger.
$F<1$
. By Theorem 1.1, no such wave could be a wave of elevation, and in fact (3.1) implies something stronger.
Corollary 5.4 (Negative mass for subcritical waves).
Any non-trivial solitary wave with
![]() $\sup u<c$
, the regularity (1.3), and subcritical Froude number
$\sup u<c$
, the regularity (1.3), and subcritical Froude number
![]() $F<1$
must have
$F<1$
must have
Proof. This follows immediately from (3.7).
The following corollary is interesting only in the method of proof; the conclusion of Corollary 5.6, which follows from Hur (Reference Hur2008b ), is much stronger.
Corollary 5.5 (Finite mass).
For any solitary wave of elevation with
![]() $\sup u<c$
and the regularity (1.3), all of the definite integrals appearing in Lemmas 3.1 , 4.2 and 4.3 , have a (finite) limit as
$\sup u<c$
and the regularity (1.3), all of the definite integrals appearing in Lemmas 3.1 , 4.2 and 4.3 , have a (finite) limit as
![]() $M\rightarrow \infty$
. In particular, the limits in (3.1), (4.5), and (4.17) become equalities when
$M\rightarrow \infty$
. In particular, the limits in (3.1), (4.5), and (4.17) become equalities when
![]() $M$
is replaced by
$M$
is replaced by
![]() $+\infty$
.
$+\infty$
.
Proof. We argue as in Section 3 of McLeod (Reference McLeod1984). Assume for contradiction that
Since
![]() ${\it\eta}\rightarrow 0$
as
${\it\eta}\rightarrow 0$
as
![]() $x\rightarrow \pm \infty$
, we have
$x\rightarrow \pm \infty$
, we have
 $$\begin{eqnarray}\frac{\displaystyle \int _{-M}^{M}{\it\eta}^{2}\text{d}x}{\displaystyle \int _{-M}^{M}{\it\eta}\text{d}x}\rightarrow 0\quad \text{as }M\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\frac{\displaystyle \int _{-M}^{M}{\it\eta}^{2}\text{d}x}{\displaystyle \int _{-M}^{M}{\it\eta}\text{d}x}\rightarrow 0\quad \text{as }M\rightarrow \infty .\end{eqnarray}$$
But then, since
![]() $F>1$
by Theorem 1.1, the left-hand side of (4.25) tends to
$F>1$
by Theorem 1.1, the left-hand side of (4.25) tends to
![]() $+\infty$
as
$+\infty$
as
![]() $M\rightarrow \infty$
, a contradiction. Thus
$M\rightarrow \infty$
, a contradiction. Thus
![]() $\int _{-\infty }^{\infty }{\it\eta}\text{d}x$
and hence
$\int _{-\infty }^{\infty }{\it\eta}\text{d}x$
and hence
![]() $\int _{-\infty }^{\infty }{\it\eta}^{2}\text{d}x$
are both finite. The statement then follows by combining this result with the limits in (3.1), (4.5), and (4.17).
$\int _{-\infty }^{\infty }{\it\eta}^{2}\text{d}x$
are both finite. The statement then follows by combining this result with the limits in (3.1), (4.5), and (4.17).
In order to state the final corollary in this section, we introduce the Sturm–Liouville problem
Corollary 5.6 (Symmetry, monotonicity, and decay).
Any solitary wave of elevation with
![]() $\sup u<c$
and the regularity (5.1) and decay (5.2) has the following properties.
$\sup u<c$
and the regularity (5.1) and decay (5.2) has the following properties.
-
(a) (Symmetry and monotonicity). The wave is symmetric and monotone in that, after shifting the definition of the horizontal variable
 $q$
, the height function
$q$
, the height function
 $h$
is even in
$h$
is even in
 $q$
and has
$q$
and has
 $h_{q}<0$
for
$h_{q}<0$
for
 $q>0$
and
$q>0$
and
 $-m<p\leqslant 0$
. In particular, after this shift
$-m<p\leqslant 0$
. In particular, after this shift
 ${\it\eta}$
is an even function of
${\it\eta}$
is an even function of
 $x$
with
$x$
with
 ${\it\eta}_{x}<0$
for
${\it\eta}_{x}<0$
for
 $x>0$
.
$x>0$
. -
(b) (Decay and asymptotics). The difference
 $w:=h-H$
decays exponentially as
$w:=h-H$
decays exponentially as
 $q\rightarrow \pm \infty$
, and satisfies the asymptotic estimate (5.9)for some constants
$q\rightarrow \pm \infty$
, and satisfies the asymptotic estimate (5.9)for some constants $$\begin{eqnarray}|D^{k}(w(q,p)-r{\it\varphi}_{1}(p)\text{e}^{-\sqrt{{\it\mu}_{1}}|q|})|\leqslant C\text{e}^{-s_{1}|q|}\quad \text{for }k\leqslant 1,|q|>1,\end{eqnarray}$$
$$\begin{eqnarray}|D^{k}(w(q,p)-r{\it\varphi}_{1}(p)\text{e}^{-\sqrt{{\it\mu}_{1}}|q|})|\leqslant C\text{e}^{-s_{1}|q|}\quad \text{for }k\leqslant 1,|q|>1,\end{eqnarray}$$
 $C,r>0$
depending on
$C,r>0$
depending on
 $w$
, where
$w$
, where
 ${\it\mu}_{1}>0$
and
${\it\mu}_{1}>0$
and
 ${\it\varphi}_{1}$
are defined above in terms of the Sturm–Liouville problem (5.7), and the exponent
${\it\varphi}_{1}$
are defined above in terms of the Sturm–Liouville problem (5.7), and the exponent
 $s_{1}$
appearing on the right-hand side satisfies
$s_{1}$
appearing on the right-hand side satisfies
 $\sqrt{{\it\mu}_{1}}<s_{1}<\min (2\sqrt{{\it\mu}_{1}},\sqrt{{\it\mu}_{2}})$
.
$\sqrt{{\it\mu}_{1}}<s_{1}<\min (2\sqrt{{\it\mu}_{1}},\sqrt{{\it\mu}_{2}})$
.
Proof. Since the waves considered in this corollary have
![]() $F>1$
by Theorem 1.1, part (a) follows immediately from Theorem 3.1 in Hur (Reference Hur2008b
), while part (b) follows from Proposition 4.6 in the same paper.
$F>1$
by Theorem 1.1, part (a) follows immediately from Theorem 3.1 in Hur (Reference Hur2008b
), while part (b) follows from Proposition 4.6 in the same paper.
6. Existence of large-amplitude waves
In this section we observe the implications of Theorems 1.1 and 1.2 for the existence theory of large-amplitude solitary waves with vorticity developed in Wheeler (Reference Wheeler2013). This theory involves a one-parameter family of shear flows
where
![]() $U^{\ast }$
is an arbitrary but fixed strictly positive function satisfying the normalization condition
$U^{\ast }$
is an arbitrary but fixed strictly positive function satisfying the normalization condition
The normalization (6.2) ensures that the parameter
![]() $F$
in (6.1) is indeed the Froude number
$F$
in (6.1) is indeed the Froude number
![]() $F$
defined in (1.2). In the corollary below we call a solitary wave symmetric if
$F$
defined in (1.2). In the corollary below we call a solitary wave symmetric if
![]() $u$
and
$u$
and
![]() ${\it\eta}$
are even in
${\it\eta}$
are even in
![]() $x$
, and
$x$
, and
![]() $v$
is odd in
$v$
is odd in
![]() $x$
, and monotone if in addition
$x$
, and monotone if in addition
![]() ${\it\eta}(x)$
is strictly decreasing for
${\it\eta}(x)$
is strictly decreasing for
![]() $x>0$
.
$x>0$
.
Corollary 6.1 (Existence of large-amplitude waves).
Fix
![]() $g,c,d>0$
, a Hölder parameter
$g,c,d>0$
, a Hölder parameter
![]() $0<{\it\beta}\leqslant 1/2$
, and a strictly positive function
$0<{\it\beta}\leqslant 1/2$
, and a strictly positive function
![]() $U^{\ast }\in C^{2+{\it\beta}}[-d,0]$
satisfying the normalization condition (6.2). Then there exists a connected set
$U^{\ast }\in C^{2+{\it\beta}}[-d,0]$
satisfying the normalization condition (6.2). Then there exists a connected set
![]() $\mathscr{C}$
of solitary waves
$\mathscr{C}$
of solitary waves
where
![]() $F$
determines the asymptotic shear flow
$F$
determines the asymptotic shear flow
![]() $U$
via (6.1), with the following properties. Each wave in
$U$
via (6.1), with the following properties. Each wave in
![]() $\mathscr{C}$
is a symmetric and monotone wave of elevation with
$\mathscr{C}$
is a symmetric and monotone wave of elevation with
![]() $\sup u<c$
and
$\sup u<c$
and
![]() $F>1$
. Moreover, at least one of the following two conditions holds:
$F>1$
. Moreover, at least one of the following two conditions holds:
-
(i) (Stagnation). There is a sequence of flows
 $(u_{n},v_{n},{\it\eta}_{n},F_{n})\in \mathscr{C}$
and sequence of points
$(u_{n},v_{n},{\it\eta}_{n},F_{n})\in \mathscr{C}$
and sequence of points
 $(x_{n},y_{n})$
such that
$(x_{n},y_{n})$
such that
 $u_{n}(x_{n},y_{n}){\nearrow}c$
; or
$u_{n}(x_{n},y_{n}){\nearrow}c$
; or -
(ii) (Large Froude number). There exists a sequence of flows
 $(u_{n},v_{n},{\it\eta}_{n},F_{n})\in \mathscr{C}$
with
$(u_{n},v_{n},{\it\eta}_{n},F_{n})\in \mathscr{C}$
with
 $F_{n}{\nearrow}\infty$
.
$F_{n}{\nearrow}\infty$
.
Proof. The statement of the corollary is a simplified version of Theorem 1.1 in Wheeler (Reference Wheeler2013), except that in that theorem there is the additional possibility (iii) that there exists a solitary wave
![]() $(u,v,{\it\eta},F)$
in the closure of
$(u,v,{\it\eta},F)$
in the closure of
![]() $\mathscr{C}$
with critical Froude number
$\mathscr{C}$
with critical Froude number
![]() $F=1$
. So let
$F=1$
. So let
![]() $(u,v,{\it\eta},F)$
be a wave in the closure of
$(u,v,{\it\eta},F)$
be a wave in the closure of
![]() $\mathscr{C}$
, and assume that condition (i) does not hold. Then
$\mathscr{C}$
, and assume that condition (i) does not hold. Then
![]() $\sup u<c$
, so by Theorem 1.1 we have
$\sup u<c$
, so by Theorem 1.1 we have
![]() $F\neq 1$
. Thus (iii) cannot hold and hence (ii) must hold.
$F\neq 1$
. Thus (iii) cannot hold and hence (ii) must hold.
We note that, even when (i) occurs in Corollary 6.1, the shear flow
![]() $U$
is bounded away from
$U$
is bounded away from
![]() $c$
uniformly along the continuum
$c$
uniformly along the continuum
![]() $\mathscr{C}$
. Indeed, every wave in
$\mathscr{C}$
. Indeed, every wave in
![]() $\mathscr{C}$
has
$\mathscr{C}$
has
![]() $F>1$
and hence
$F>1$
and hence
In many cases, we can apply Theorem 1.2 to further simplify Corollary 6.1.
Corollary 6.2. In the setting of Corollary 6.1 , suppose that the fixed profile
![]() $U^{\ast }$
satisfies
$U^{\ast }$
satisfies
Then condition
![]() $\text{(ii)}$
cannot occur, so that
$\text{(ii)}$
cannot occur, so that
![]() $\text{(i)}$
must hold.
$\text{(i)}$
must hold.
Proof. Thanks to (6.1), any wave in
![]() $\mathscr{C}$
satisfies
$\mathscr{C}$
satisfies
Thus by Theorem 1.2 all waves in
![]() $\mathscr{C}$
have
$\mathscr{C}$
have
![]() $F<(1-3({\it\Lambda}^{\ast })^{2}/4)^{-1/2}<\infty$
.
$F<(1-3({\it\Lambda}^{\ast })^{2}/4)^{-1/2}<\infty$
.
The conclusion of Corollary 6.2, that there exists a sequence of solutions along the continuum with
![]() $\sup u_{n}$
approaching
$\sup u_{n}$
approaching
![]() $c$
, is the same conclusion that was proved for periodic waves in Constantin & Strauss (Reference Constantin and Strauss2004). It remains an open question if the same is true for solitary waves with
$c$
, is the same conclusion that was proved for periodic waves in Constantin & Strauss (Reference Constantin and Strauss2004). It remains an open question if the same is true for solitary waves with
![]() ${\it\Lambda}^{\ast }\geqslant 2/\sqrt{3}$
, though it seems doubtful that the restriction
${\it\Lambda}^{\ast }\geqslant 2/\sqrt{3}$
, though it seems doubtful that the restriction
![]() ${\it\Lambda}^{\ast }<2/\sqrt{3}$
is sharp.
${\it\Lambda}^{\ast }<2/\sqrt{3}$
is sharp.
7. The case of constant vorticity
In this section we specialize the above results to asymptotic shear flows
![]() $U$
which are linear in
$U$
which are linear in
![]() $y$
, or equivalently to waves whose vorticity
$y$
, or equivalently to waves whose vorticity
is constant. In this case more explicit formulae are available; to make these formulae appear simpler, we define the dimensionless constants
In terms of
![]() ${\it\lambda}^{\ast }$
and
${\it\lambda}^{\ast }$
and
![]() ${\it\gamma}^{\ast }$
, the asymptotic shear flow
${\it\gamma}^{\ast }$
, the asymptotic shear flow
![]() $U$
is given by
$U$
is given by
Plugging
![]() $y=-d$
into (7.3), we see that
$y=-d$
into (7.3), we see that
![]() $\sup U<c$
implies
$\sup U<c$
implies
![]() ${\it\gamma}^{\ast }<1$
. Substituting (7.3) into the definitions (1.2) of
${\it\gamma}^{\ast }<1$
. Substituting (7.3) into the definitions (1.2) of
![]() $F$
and (1.4) of
$F$
and (1.4) of
![]() ${\it\Lambda}$
, we find
${\it\Lambda}$
, we find
Using (7.4) in Theorems 1.1 and 1.2, we can then easily prove the following.
Corollary 7.1 (Constant vorticity).
Consider a solitary wave of elevation with constant vorticity
![]() ${\it\gamma}$
, regularity (1.3), and
${\it\gamma}$
, regularity (1.3), and
![]() $\sup u<c$
so that in particular
$\sup u<c$
so that in particular
![]() ${\it\gamma}^{\ast }<1$
. Then we have the following bounds on
${\it\gamma}^{\ast }<1$
. Then we have the following bounds on
![]() ${\it\lambda}^{\ast }$
and
${\it\lambda}^{\ast }$
and
![]() ${\it\gamma}^{\ast }$
:
${\it\gamma}^{\ast }$
:
Proof. The first inequality (7.5) is
![]() $F>1$
from Theorem 1.1, while (7.6) and (7.7) are (1.5) from Theorem 1.2. Since Bernoulli’s law (2.14) implies
$F>1$
from Theorem 1.1, while (7.6) and (7.7) are (1.5) from Theorem 1.2. Since Bernoulli’s law (2.14) implies
![]() $\max {\it\eta}<d{\it\lambda}^{\ast }/2$
, the bounds (7.8) and (7.9) on the amplitude follow immediately from (7.6) and (7.7).
$\max {\it\eta}<d{\it\lambda}^{\ast }/2$
, the bounds (7.8) and (7.9) on the amplitude follow immediately from (7.6) and (7.7).
From (7.6) and (7.7) we see that, for any fixed
![]() ${\it\gamma}^{\ast }<1-\sqrt{3}/2\approx 0.134$
, waves of elevation with
${\it\gamma}^{\ast }<1-\sqrt{3}/2\approx 0.134$
, waves of elevation with
![]() $\sup u<c$
have
$\sup u<c$
have
![]() ${\it\lambda}^{\ast }$
bounded above by a constant depending only on
${\it\lambda}^{\ast }$
bounded above by a constant depending only on
![]() ${\it\gamma}^{\ast }$
. It is interesting to compare this to the numerical results in Vanden-Broeck (Reference Vanden-Broeck1994), which suggest that for any fixed
${\it\gamma}^{\ast }$
. It is interesting to compare this to the numerical results in Vanden-Broeck (Reference Vanden-Broeck1994), which suggest that for any fixed
![]() ${\it\gamma}^{\ast }>{\it\gamma}_{cr}^{\ast }\approx 0.33$
there exist overhanging waves with
${\it\gamma}^{\ast }>{\it\gamma}_{cr}^{\ast }\approx 0.33$
there exist overhanging waves with
![]() ${\it\lambda}^{\ast }$
arbitrarily large. Note however that overhanging waves necessarily violate our assumption
${\it\lambda}^{\ast }$
arbitrarily large. Note however that overhanging waves necessarily violate our assumption
![]() $\sup u<c$
.
$\sup u<c$
.
8. Surface tension
In this section we prove that Theorem 1.1 continues to hold in the presence of surface tension. For waves with surface tension, the dynamic boundary condition (2.1f ) is replaced by
where the constant
![]() ${\it\sigma}>0$
is the coefficient of surface tension. The corresponding boundary condition (2.9b
) in the height equation becomes
${\it\sigma}>0$
is the coefficient of surface tension. The corresponding boundary condition (2.9b
) in the height equation becomes
For irrotational solitary waves with surface tension, Amick & Kirchgässner (Reference Amick and Kirchgässner1989) prove the analogue
of the integral identity (1.8). For irrotational waves of depression, such as those constructed in Amick & Kirchgässner (Reference Amick and Kirchgässner1989) with Bond number
![]() ${\it\sigma}/gd^{2}>1/3$
, (8.3) immediately implies that the Froude number
${\it\sigma}/gd^{2}>1/3$
, (8.3) immediately implies that the Froude number
![]() $F<1$
. As a consequence of Theorem 8.1 below, the same bound
$F<1$
. As a consequence of Theorem 8.1 below, the same bound
![]() $F<1$
holds for waves with vorticity.
$F<1$
holds for waves with vorticity.
We will work with solutions which have the regularity
where, as in § 1.1,
![]() $0<{\it\alpha}<1$
and
$0<{\it\alpha}<1$
and
![]() $r=2/(1-{\it\alpha})$
; see Martin & Matioc (Reference Martin and Matioc2014) for the equivalence of various formulations for periodic waves with surface tension.
$r=2/(1-{\it\alpha})$
; see Martin & Matioc (Reference Martin and Matioc2014) for the equivalence of various formulations for periodic waves with surface tension.
Theorem 8.1. Theorem 1.1 holds for waves with surface tension, provided we replace the regularity (1.3) with (8.4).
Lemma 8.2. Lemma 3.1 holds for waves with surface tension, provided we replace the regularity (1.3) with (8.4).
Proof. We will follow the proof of Lemma 3.1 and notice that the term involving surface tension drops out of the calculation entirely. Multiplying (2.9a
) by
![]() ${\it\Phi}(p)=\int _{-m}^{p}H_{p}^{3}(s)\text{d}s$
and integrating by parts, we obtain (3.3) as before,
${\it\Phi}(p)=\int _{-m}^{p}H_{p}^{3}(s)\text{d}s$
and integrating by parts, we obtain (3.3) as before,
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right){\it\Phi}_{p}\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{gF^{2}}\int _{-M}^{M}\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)(q,0)\text{d}q+\left.\int _{-m}^{0}\frac{h_{q}}{h_{p}}{\it\Phi}\text{d}p\right|_{q=-M}^{q=M}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{-M}^{M}\int _{-m}^{0}\left(\frac{1+h_{q}^{2}}{2h_{p}^{2}}-\frac{1}{2H_{p}^{2}}\right){\it\Phi}_{p}\text{d}p\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{gF^{2}}\int _{-M}^{M}\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)(q,0)\text{d}q+\left.\int _{-m}^{0}\frac{h_{q}}{h_{p}}{\it\Phi}\text{d}p\right|_{q=-M}^{q=M}.\end{eqnarray}$$
We claim that (8.5) implies (3.4). Indeed, the first and last terms in (8.5) can be treated as in the proof of Lemma 3.1, so (3.4) follows from the following computation involving the middle term:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{gF^{2}}\int _{-M}^{M}\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)(q,0)\text{d}q-\frac{1}{F^{2}}\int _{-M}^{M}(h(q,0)-H(0))\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{108.0pt}\quad =-\frac{{\it\sigma}}{gF^{2}}\int _{-M}^{M}\left(\frac{h_{q}}{(1+h_{q}^{2})^{1/2}}\right)_{q}(q,0)\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{108.0pt}\quad =\left.-\frac{{\it\sigma}}{gF^{2}}\frac{h_{q}}{(1+h_{q}^{2})^{1/2}}\right|_{(-M,0)}^{(M,0)}\rightarrow 0\quad \text{as }M\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{gF^{2}}\int _{-M}^{M}\left(-\frac{1+h_{q}^{2}}{2h_{p}^{2}}+\frac{1}{2H_{p}^{2}}\right)(q,0)\text{d}q-\frac{1}{F^{2}}\int _{-M}^{M}(h(q,0)-H(0))\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{108.0pt}\quad =-\frac{{\it\sigma}}{gF^{2}}\int _{-M}^{M}\left(\frac{h_{q}}{(1+h_{q}^{2})^{1/2}}\right)_{q}(q,0)\text{d}q\nonumber\\ \displaystyle & & \displaystyle \hspace{108.0pt}\quad =\left.-\frac{{\it\sigma}}{gF^{2}}\frac{h_{q}}{(1+h_{q}^{2})^{1/2}}\right|_{(-M,0)}^{(M,0)}\rightarrow 0\quad \text{as }M\rightarrow \infty ,\end{eqnarray}$$
where we have used the boundary condition (8.2) and the asymptotic conditions (2.9d ). With (3.4) established, we can then complete the argument exactly as in the proof of Lemma 3.1.
Acknowledgements
This work was partially supported by the National Science Foundation under award no. DMS-1400926. The author would also like to thank the anonymous referees for helpful comments.