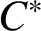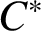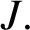1. Introduction
If E is a graph and
![]() $L_K(E)$
is its Leavitt path algebra, it is known that every graded ideal I of
$L_K(E)$
is its Leavitt path algebra, it is known that every graded ideal I of
![]() $L_K(E)$
is uniquely determined by a pair
$L_K(E)$
is uniquely determined by a pair
![]() $(H,S)$
of certain subsets of vertices, known as an admissible pair (we review the definition in Section 2.2). For every such admissible pair, one can define a graph, referred to as the generalised hedgehog graph in [Reference Abrams, Ara and Siles Molina1], such that I is isomorphic to the Leavitt path algebra of this graph. The name ‘hedgehog’ comes from the construction in which one attaches new edges (the ‘spines’) to
$(H,S)$
of certain subsets of vertices, known as an admissible pair (we review the definition in Section 2.2). For every such admissible pair, one can define a graph, referred to as the generalised hedgehog graph in [Reference Abrams, Ara and Siles Molina1], such that I is isomorphic to the Leavitt path algebra of this graph. The name ‘hedgehog’ comes from the construction in which one attaches new edges (the ‘spines’) to
![]() $H\cup S$
(the ‘body’). We modify this construction by replacing the added edges with possibly fewer paths which are then necessarily of length larger than one. Because of the longer spines, we call the resulting graph the porcupine graph of
$H\cup S$
(the ‘body’). We modify this construction by replacing the added edges with possibly fewer paths which are then necessarily of length larger than one. Because of the longer spines, we call the resulting graph the porcupine graph of
![]() $(H,S).$
In the main result of the paper, Theorem 3.3, we construct a graded
$(H,S).$
In the main result of the paper, Theorem 3.3, we construct a graded
![]() $*$
-isomorphism of I and the Leavitt path algebra of the porcupine graph of the admissible pair corresponding to
$*$
-isomorphism of I and the Leavitt path algebra of the porcupine graph of the admissible pair corresponding to
![]() $I.$
$I.$
We adapt our result to graph
![]() $C^*$
-algebras also. In Corollary 3.4, we show that, for every closed gauge-invariant ideal J of a graph
$C^*$
-algebras also. In Corollary 3.4, we show that, for every closed gauge-invariant ideal J of a graph
![]() $C^*$
-algebra, there is a gauge-invariant (and graded in the
$C^*$
-algebra, there is a gauge-invariant (and graded in the
![]() $C^*$
-algebra sense)
$C^*$
-algebra sense)
![]() $*$
-isomorphism which maps the graph
$*$
-isomorphism which maps the graph
![]() $C^*$
-algebra of the porcupine graph of J onto
$C^*$
-algebra of the porcupine graph of J onto
![]() $J.$
Just as in the algebraic case, it is known that such an ideal J is
$J.$
Just as in the algebraic case, it is known that such an ideal J is
![]() $*$
-isomorphic to a graph
$*$
-isomorphic to a graph
![]() $C^*$
-algebra, but it was not clear whether there is a gauge-invariant
$C^*$
-algebra, but it was not clear whether there is a gauge-invariant
![]() $*$
-isomorphism between J and a graph
$*$
-isomorphism between J and a graph
![]() $C^*$
-algebra. We show that such an isomorphism indeed exists.
$C^*$
-algebra. We show that such an isomorphism indeed exists.
2. Prerequisites
2.1. Graded rings and
 $\ast $
-rings
$\ast $
-rings
A ring R (not necessarily unital) is graded by a group
![]() $\Gamma $
if
$\Gamma $
if
 $R=\bigoplus _{\gamma \in \Gamma } R_\gamma $
for additive subgroups
$R=\bigoplus _{\gamma \in \Gamma } R_\gamma $
for additive subgroups
![]() $R_\gamma $
and
$R_\gamma $
and
![]() $R_\gamma R_\delta \subseteq R_{\gamma \delta }$
for all
$R_\gamma R_\delta \subseteq R_{\gamma \delta }$
for all
![]() $\gamma ,\delta \in \Gamma .$
The elements of the set
$\gamma ,\delta \in \Gamma .$
The elements of the set
![]() $\bigcup _{\gamma \in \Gamma } R_\gamma $
are said to be homogeneous and
$\bigcup _{\gamma \in \Gamma } R_\gamma $
are said to be homogeneous and
![]() $\gamma $
is the degree of any nonzero element of
$\gamma $
is the degree of any nonzero element of
![]() $R_\gamma .$
The grading is trivial if
$R_\gamma .$
The grading is trivial if
![]() $R_\gamma =0$
for every
$R_\gamma =0$
for every
![]() $\gamma \in \Gamma $
which is not the group identity. We adopt the standard definitions of graded ring homomorphisms, graded algebras and graded ideals as defined in [Reference Hazrat4].
$\gamma \in \Gamma $
which is not the group identity. We adopt the standard definitions of graded ring homomorphisms, graded algebras and graded ideals as defined in [Reference Hazrat4].
A ring R is an involutive ring, or a
![]() $*$
-ring, if there is an antiautomorphism
$*$
-ring, if there is an antiautomorphism
![]() $*:R\to R$
of order two. If R is also a K-algebra for some commutative, involutive ring K, then R is a
$*:R\to R$
of order two. If R is also a K-algebra for some commutative, involutive ring K, then R is a
![]() $*$
-algebra if
$*$
-algebra if
![]() $(kx)^*=k^*x^*$
for all
$(kx)^*=k^*x^*$
for all
![]() $k\in K$
and
$k\in K$
and
![]() $x\in R.$
If R and S are
$x\in R.$
If R and S are
![]() $*$
-rings, a ring homomorphism
$*$
-rings, a ring homomorphism
![]() $\phi : R\to S$
is a
$\phi : R\to S$
is a
![]() $*$
-homomorphism if
$*$
-homomorphism if
![]() $\phi (x^*)=\phi (x)^*$
for every
$\phi (x^*)=\phi (x)^*$
for every
![]() $x\in R.$
$x\in R.$
2.2. Leavitt path algebras
Let E be a directed graph. Let
![]() $E^0$
denote the set of vertices, let
$E^0$
denote the set of vertices, let
![]() $E^1$
denote the set of edges and let
$E^1$
denote the set of edges and let
![]() $\mathbf {s}$
and
$\mathbf {s}$
and
![]() $\mathbf {r}$
be the source and range maps of E, respectively. A sink of E is a vertex which emits no edges, and an infinite emitter is a vertex which emits infinitely many edges. A vertex of E is regular if it is neither a sink nor an infinite emitter. A path is a single vertex or a sequence of edges
$\mathbf {r}$
be the source and range maps of E, respectively. A sink of E is a vertex which emits no edges, and an infinite emitter is a vertex which emits infinitely many edges. A vertex of E is regular if it is neither a sink nor an infinite emitter. A path is a single vertex or a sequence of edges
![]() $e_1e_2\ldots e_n$
for some positive integer n such that
$e_1e_2\ldots e_n$
for some positive integer n such that
![]() $\mathbf {r}(e_i)=\mathbf {s}(e_{i+1})$
for
$\mathbf {r}(e_i)=\mathbf {s}(e_{i+1})$
for
![]() $i=1,\ldots , n-1.$
$i=1,\ldots , n-1.$
Extend a graph E to the graph which has the same vertices and whose edges are
![]() $E^1\cup \{e^*\mid e\in E^1\}$
, where the range and source functions are the same as in E for
$E^1\cup \{e^*\mid e\in E^1\}$
, where the range and source functions are the same as in E for
![]() $e\in E^1$
and
$e\in E^1$
and
![]() $\mathbf {s}(e^*)=\mathbf {r}(e)$
and
$\mathbf {s}(e^*)=\mathbf {r}(e)$
and
![]() $\mathbf {r}(e^*)=\mathbf {s}(e)$
for the added edges. If K is any field, the Leavitt path algebra
$\mathbf {r}(e^*)=\mathbf {s}(e)$
for the added edges. If K is any field, the Leavitt path algebra
![]() $L_K(E)$
of E over K is a free K-algebra generated by the set
$L_K(E)$
of E over K is a free K-algebra generated by the set
![]() ${E^0\cup E^1\cup \{e^\ast \mid e\in E^1\}}$
such that, for all vertices
${E^0\cup E^1\cup \{e^\ast \mid e\in E^1\}}$
such that, for all vertices
![]() $v,w$
and edges
$v,w$
and edges
![]() $e,f$
:
$e,f$
:
-
(V)
 $vw =0$
if
$vw =0$
if
 $v\neq w$
and
$v\neq w$
and
 $vv=v$
;
$vv=v$
; -
(E1)
 $\mathbf {s}(e)e=e\mathbf {r}(e)=e$
;
$\mathbf {s}(e)e=e\mathbf {r}(e)=e$
; -
(E2)
 $\mathbf {r}(e)e^\ast =e^\ast \mathbf {s}(e)=e^\ast $
;
$\mathbf {r}(e)e^\ast =e^\ast \mathbf {s}(e)=e^\ast $
; -
(CK1)
 $e^\ast f=0$
if
$e^\ast f=0$
if
 $e\neq f$
and
$e\neq f$
and
 $e^\ast e=\mathbf {r}(e)$
; and
$e^\ast e=\mathbf {r}(e)$
; and -
(CK2)
 $v=\sum _{e\in \mathbf {s}^{-1}(v)} ee^\ast $
for each regular vertex v.
$v=\sum _{e\in \mathbf {s}^{-1}(v)} ee^\ast $
for each regular vertex v.
By the first four axioms, every element of
![]() $L_K(E)$
can be represented as a sum of the form
$L_K(E)$
can be represented as a sum of the form
![]() $\sum _{i=1}^n k_ip_iq_i^\ast $
for some n, paths
$\sum _{i=1}^n k_ip_iq_i^\ast $
for some n, paths
![]() $p_i$
and
$p_i$
and
![]() $q_i$
and elements
$q_i$
and elements
![]() $k_i\in K,$
for
$k_i\in K,$
for
![]() $i=1,\ldots ,n$
, where
$i=1,\ldots ,n$
, where
![]() $v^*=v$
for
$v^*=v$
for
![]() $v\in E^0$
and
$v\in E^0$
and
![]() $p^*=e_n^*\ldots e_1^*$
for a path
$p^*=e_n^*\ldots e_1^*$
for a path
![]() $p=e_1\ldots e_n.$
Using this representation, one can make
$p=e_1\ldots e_n.$
Using this representation, one can make
![]() $L_K(E)$
into an involutive ring by defining
$L_K(E)$
into an involutive ring by defining
![]() $(\sum _{i=1}^n k_ip_iq_i^\ast )^*=\sum _{i=1}^n k_i^*q_ip_i^\ast $
, where
$(\sum _{i=1}^n k_ip_iq_i^\ast )^*=\sum _{i=1}^n k_i^*q_ip_i^\ast $
, where
![]() $k_i\mapsto k_i^*$
is any involution on K. For more details on these basic properties, see [Reference Abrams, Ara and Siles Molina1].
$k_i\mapsto k_i^*$
is any involution on K. For more details on these basic properties, see [Reference Abrams, Ara and Siles Molina1].
If we consider K to be trivially graded by
![]() $\mathbb Z, L_K(E)$
is naturally graded by
$\mathbb Z, L_K(E)$
is naturally graded by
![]() $\mathbb Z$
so that the n-component
$\mathbb Z$
so that the n-component
![]() $L_K(E)_n$
is the K-linear span of the elements
$L_K(E)_n$
is the K-linear span of the elements
![]() $pq^\ast $
for paths
$pq^\ast $
for paths
![]() $p, q$
with
$p, q$
with
![]() $|p|-|q|=n$
, where
$|p|-|q|=n$
, where
![]() $|p|$
denotes the length of a path
$|p|$
denotes the length of a path
![]() $p.$
Although one can grade a Leavitt path algebra by any group (see [Reference Hazrat4, Section 1.6.1]), we consider only the natural grading by
$p.$
Although one can grade a Leavitt path algebra by any group (see [Reference Hazrat4, Section 1.6.1]), we consider only the natural grading by
![]() $\mathbb Z.$
$\mathbb Z.$
If a K-algebra R contains elements
![]() $a_v, b_e$
and
$a_v, b_e$
and
![]() $c_{e^*}$
which satisfy the axioms (V), (E1), (E2), (CK1) and (CK2), where
$c_{e^*}$
which satisfy the axioms (V), (E1), (E2), (CK1) and (CK2), where
![]() $v\in E^0$
and
$v\in E^0$
and
![]() $e\in E^1$
for some graph E, the Universal Property of
$e\in E^1$
for some graph E, the Universal Property of
![]() $L_K(E)$
ensures that the map
$L_K(E)$
ensures that the map
![]() $\phi : v\mapsto a_v, e\mapsto b_e, e^*\mapsto c_{e^*}$
has a unique K-algebra homomorphism extension
$\phi : v\mapsto a_v, e\mapsto b_e, e^*\mapsto c_{e^*}$
has a unique K-algebra homomorphism extension
![]() $\phi : L_K(E)\to R$
(see [Reference Abrams, Ara and Siles Molina1, Remark 1.2.5]). If R is
$\phi : L_K(E)\to R$
(see [Reference Abrams, Ara and Siles Molina1, Remark 1.2.5]). If R is
![]() $\mathbb Z$
-graded and the elements
$\mathbb Z$
-graded and the elements
![]() $\phi (v), \phi (e)$
and
$\phi (v), \phi (e)$
and
![]() $\phi (e^*)$
have degrees 0, 1 and
$\phi (e^*)$
have degrees 0, 1 and
![]() $-1$
, respectively, then such an extension is graded and the Graded Uniqueness Theorem [Reference Abrams, Ara and Siles Molina1, Theorem 2.2.15] states that
$-1$
, respectively, then such an extension is graded and the Graded Uniqueness Theorem [Reference Abrams, Ara and Siles Molina1, Theorem 2.2.15] states that
![]() $\phi $
is injective if and only if
$\phi $
is injective if and only if
![]() $\phi (v)\neq 0$
for every
$\phi (v)\neq 0$
for every
![]() $v\in E^0.$
If R is involutive and if
$v\in E^0.$
If R is involutive and if
![]() $a_v^*=a_v$
for every
$a_v^*=a_v$
for every
![]() $v\in E^0$
and
$v\in E^0$
and
![]() $(b_e)^*=c_{e^*}$
for every
$(b_e)^*=c_{e^*}$
for every
![]() $e\in E^1,$
then
$e\in E^1,$
then
![]() $\phi $
is a
$\phi $
is a
![]() $*$
-homomorphism (see [Reference Vaš7, Lemma 4.7]).
$*$
-homomorphism (see [Reference Vaš7, Lemma 4.7]).
2.3. Graded ideals of a Leavitt path algebra
A subset H of
![]() $E^0$
is said to be hereditary if
$E^0$
is said to be hereditary if
![]() $\mathbf {r}(p)\in H$
for any path p such that
$\mathbf {r}(p)\in H$
for any path p such that
![]() $\mathbf {s}(p)\in H.$
The set H is saturated if
$\mathbf {s}(p)\in H.$
The set H is saturated if
![]() $v\in H$
for any regular vertex v such that
$v\in H$
for any regular vertex v such that
![]() $\mathbf {r}(\mathbf {s}^{-1}(v))\subseteq H.$
We recall a construction from [Reference Tomforde6]. If H is hereditary and saturated, let
$\mathbf {r}(\mathbf {s}^{-1}(v))\subseteq H.$
We recall a construction from [Reference Tomforde6]. If H is hereditary and saturated, let
 $$ \begin{align*}B_H&=\{v\in E^0-H\,|\, v\mbox{ an infinite emitter and } \\ &\qquad\qquad\qquad \ \ \mathbf{s}^{-1}(v)\cap \mathbf{r}^{-1}(E^0-H)\mbox{ is nonempty and finite}\}, \end{align*} $$
$$ \begin{align*}B_H&=\{v\in E^0-H\,|\, v\mbox{ an infinite emitter and } \\ &\qquad\qquad\qquad \ \ \mathbf{s}^{-1}(v)\cap \mathbf{r}^{-1}(E^0-H)\mbox{ is nonempty and finite}\}, \end{align*} $$
 $$ \begin{align*}v^H=v-\sum_{e\in \mathbf{s}^{-1}(v)\cap \mathbf{r}^{-1}(E^0-H)}ee^*\quad\mbox{for all }v\in B_H.\end{align*} $$
$$ \begin{align*}v^H=v-\sum_{e\in \mathbf{s}^{-1}(v)\cap \mathbf{r}^{-1}(E^0-H)}ee^*\quad\mbox{for all }v\in B_H.\end{align*} $$
An admissible pair is an ordered pair
![]() $(H, S)$
, where
$(H, S)$
, where
![]() $H\subseteq E^0$
is hereditary and saturated and
$H\subseteq E^0$
is hereditary and saturated and
![]() $S\subseteq B_H.$
For such a pair, let
$S\subseteq B_H.$
For such a pair, let
![]() $I(H,S)$
denote the graded ideal generated by homogeneous elements
$I(H,S)$
denote the graded ideal generated by homogeneous elements
![]() $H\cup \{v^H \,|\, v\in S \}.$
The ideal
$H\cup \{v^H \,|\, v\in S \}.$
The ideal
![]() $I(H,S)$
is the K-linear span of the elements
$I(H,S)$
is the K-linear span of the elements
![]() $pq^*$
for paths
$pq^*$
for paths
![]() $p,q$
with
$p,q$
with
![]() $\mathbf {r}(p)=\mathbf {r}(q)\in H$
and the elements
$\mathbf {r}(p)=\mathbf {r}(q)\in H$
and the elements
![]() $pv^Hq^*$
for paths
$pv^Hq^*$
for paths
![]() $p,q$
with
$p,q$
with
![]() $\mathbf {r}(p)=\mathbf {r}(q)=v\in S$
(see [Reference Tomforde6, Lemma 5.6]). The converse holds as well: for every graded ideal I, the vertices in I form a hereditary and saturated set H and the set of infinite emitters such that
$\mathbf {r}(p)=\mathbf {r}(q)=v\in S$
(see [Reference Tomforde6, Lemma 5.6]). The converse holds as well: for every graded ideal I, the vertices in I form a hereditary and saturated set H and the set of infinite emitters such that
![]() $v^H\in I$
is a subset of
$v^H\in I$
is a subset of
![]() $B_H$
(see [Reference Tomforde6, Theorem 5.7] and also [Reference Abrams, Ara and Siles Molina1, Theorem 2.5.8]). For an admissible pair
$B_H$
(see [Reference Tomforde6, Theorem 5.7] and also [Reference Abrams, Ara and Siles Molina1, Theorem 2.5.8]). For an admissible pair
![]() $(H, S),$
let
$(H, S),$
let
![]() $E_{(H,S)}$
be the graph defined by
$E_{(H,S)}$
be the graph defined by
 $$ \begin{align*} F_1(H,S) &=\{e_1\ldots e_n\mbox{ is a path of }E\mid \mathbf{r}(e_n)\in H, \mathbf{s}(e_n)\notin H\cup S\}, \\ F_2(H,S) &=\{p\mbox{ is a path of }E\mid \mathbf{r}(p)\in S,\; |p|>0\}, \\ \overline{F_i}(H,S) & \mbox{ is a copy of }F_i(H,S) \mbox{ for } i=1,2,\\ E_{(H,S)}^0 &= H\cup S\cup F_1(H,S)\cup F_2(H,S), \\ E_{(H,S)}^1 &=\{e\in E^1\,|\, \mathbf{s}(e)\in H\}\cup \{e\in E^1\,|\, \mathbf{s}(e)\in S, \mathbf{r}(e)\in H\}\cup \overline{F_1}(H,S)\cup \overline{F_2}(H,S), \end{align*} $$
$$ \begin{align*} F_1(H,S) &=\{e_1\ldots e_n\mbox{ is a path of }E\mid \mathbf{r}(e_n)\in H, \mathbf{s}(e_n)\notin H\cup S\}, \\ F_2(H,S) &=\{p\mbox{ is a path of }E\mid \mathbf{r}(p)\in S,\; |p|>0\}, \\ \overline{F_i}(H,S) & \mbox{ is a copy of }F_i(H,S) \mbox{ for } i=1,2,\\ E_{(H,S)}^0 &= H\cup S\cup F_1(H,S)\cup F_2(H,S), \\ E_{(H,S)}^1 &=\{e\in E^1\,|\, \mathbf{s}(e)\in H\}\cup \{e\in E^1\,|\, \mathbf{s}(e)\in S, \mathbf{r}(e)\in H\}\cup \overline{F_1}(H,S)\cup \overline{F_2}(H,S), \end{align*} $$
with
![]() $\mathbf {s}$
and
$\mathbf {s}$
and
![]() $\mathbf {r}$
the same as on
$\mathbf {r}$
the same as on
![]() $E^1$
for
$E^1$
for
 $e\in E^1\cap E^1_{(H,S)}$
and
$e\in E^1\cap E^1_{(H,S)}$
and
![]() $\mathbf {s}(\overline p)=p, \mathbf {r}(\overline p)=\mathbf {r}(p)$
for
$\mathbf {s}(\overline p)=p, \mathbf {r}(\overline p)=\mathbf {r}(p)$
for
![]() $\overline p\in \overline {F_1}(H,S)\cup \overline {F_2}(H,S)$
. By [Reference Ruiz and Tomforde5, Theorem 6.1] (also [Reference Abrams, Ara and Siles Molina1, Theorem 2.5.22]), the ideal
$\overline p\in \overline {F_1}(H,S)\cup \overline {F_2}(H,S)$
. By [Reference Ruiz and Tomforde5, Theorem 6.1] (also [Reference Abrams, Ara and Siles Molina1, Theorem 2.5.22]), the ideal
![]() $I(H,S)$
is isomorphic to
$I(H,S)$
is isomorphic to
![]() $L_K (E_{(H,S)}).$
$L_K (E_{(H,S)}).$
In [Reference Abrams, Ara and Siles Molina1], the graph
![]() $E_{(H,\emptyset )}$
is referred to as the hedgehog graph and the graph
$E_{(H,\emptyset )}$
is referred to as the hedgehog graph and the graph
![]() $E_{(H,S)}$
is referred to as the generalised hedgehog graph. The term ‘hedgehog’ is chosen since the added edges ending at
$E_{(H,S)}$
is referred to as the generalised hedgehog graph. The term ‘hedgehog’ is chosen since the added edges ending at
![]() $H\cup S$
resemble spines of the hedgehog body
$H\cup S$
resemble spines of the hedgehog body
![]() $H\cup S.$
The isomorphism
$H\cup S.$
The isomorphism
![]() $L_K(E_{(H,S)})\to I(H,S)$
is defined so that the edges of
$L_K(E_{(H,S)})\to I(H,S)$
is defined so that the edges of
![]() $E_{(H,S)}$
are mapped to certain homogeneous elements of
$E_{(H,S)}$
are mapped to certain homogeneous elements of
![]() $I(H,S)$
of positive degree, not necessarily degree one. Thus, the degrees are not necessarily preserved under this map and so this isomorphism may not be graded.
$I(H,S)$
of positive degree, not necessarily degree one. Thus, the degrees are not necessarily preserved under this map and so this isomorphism may not be graded.
In [Reference Aranda Pino, Rangaswamy and Siles Molina2], the authors consider a version of
![]() $E_{(H,S)}$
, which they denote
$E_{(H,S)}$
, which they denote
![]() $_HE_S$
(see [Reference Ruiz and Tomforde5] for details on differences in definitions); [Reference Aranda Pino, Rangaswamy and Siles Molina2, Proposition 3.7] states that
$_HE_S$
(see [Reference Ruiz and Tomforde5] for details on differences in definitions); [Reference Aranda Pino, Rangaswamy and Siles Molina2, Proposition 3.7] states that
![]() $I(H,S)$
and
$I(H,S)$
and
![]() $L_K(_HE_S)$
are graded isomorphic. However, the map
$L_K(_HE_S)$
are graded isomorphic. However, the map
![]() $L_K(_HE_S)\to I(H,S)$
in the proof is defined analogously to the map
$L_K(_HE_S)\to I(H,S)$
in the proof is defined analogously to the map
![]() $L_K(E_{(H,S)})\to I(H,S)$
and, as we noted above, this map is not necessarily a graded map. The last section of [Reference Ruiz and Tomforde5] contains some further details on a problem with the definition of
$L_K(E_{(H,S)})\to I(H,S)$
and, as we noted above, this map is not necessarily a graded map. The last section of [Reference Ruiz and Tomforde5] contains some further details on a problem with the definition of
![]() $_HE_S$
and [Reference Aranda Pino, Rangaswamy and Siles Molina2, Proposition 3.7].
$_HE_S$
and [Reference Aranda Pino, Rangaswamy and Siles Molina2, Proposition 3.7].
3. The main result
We modify the construction of the generalised hedgehog graph of an admissible pair
![]() $(H,S)$
by making the spines added to the body
$(H,S)$
by making the spines added to the body
![]() $H\cup S$
possibly fewer in number but then necessarily longer in length. Because of the longer spines, we call the resulting graph the porcupine graph and denote it by
$H\cup S$
possibly fewer in number but then necessarily longer in length. Because of the longer spines, we call the resulting graph the porcupine graph and denote it by
![]() $P_{(H,S)}.$
The modified construction enables us to create a degree-preserving isomorphism
$P_{(H,S)}.$
The modified construction enables us to create a degree-preserving isomorphism
![]() $L_K(P_{(H,S)})\to I(H,S).$
$L_K(P_{(H,S)})\to I(H,S).$
Definition 3.1. For an admissible pair
![]() $(H,S),$
we keep the definitions of
$(H,S),$
we keep the definitions of
![]() $F_1(H,S)$
and
$F_1(H,S)$
and
![]() $F_2(H,S).$
For each
$F_2(H,S).$
For each
![]() $e\in (F_1(H,S)\cup F_2(H,S))\cap E^1,$
let
$e\in (F_1(H,S)\cup F_2(H,S))\cap E^1,$
let
![]() $w^e$
be a new vertex and let
$w^e$
be a new vertex and let
![]() $f^e$
be a new edge such that
$f^e$
be a new edge such that
![]() $\mathbf {s}(f^e)=w^e$
and
$\mathbf {s}(f^e)=w^e$
and
![]() $\mathbf {r}(f^e)=\mathbf {r}(e).$
Continue this process inductively as follows. For each path
$\mathbf {r}(f^e)=\mathbf {r}(e).$
Continue this process inductively as follows. For each path
![]() $p=eq$
, where
$p=eq$
, where
![]() $q\in F_1(H,S)\cup F_2(H,S)$
and
$q\in F_1(H,S)\cup F_2(H,S)$
and
![]() $|q|\geq 1,$
add a new vertex
$|q|\geq 1,$
add a new vertex
![]() $w^p$
and a new edge
$w^p$
and a new edge
![]() $f^p$
such that
$f^p$
such that
![]() $\mathbf {s}(f^p)=w^p$
and
$\mathbf {s}(f^p)=w^p$
and
![]() $\mathbf {r}(f^p)=w^q.$
$\mathbf {r}(f^p)=w^q.$
We define the porcupine graph
![]() $P_{(H,S)}$
as follows. The set of vertices of
$P_{(H,S)}$
as follows. The set of vertices of
![]() $P_{(H,S)}$
is
$P_{(H,S)}$
is
The set of edges of
![]() $P_{(H,S)}$
is
$P_{(H,S)}$
is
The
![]() $\mathbf {s}$
and
$\mathbf {s}$
and
![]() $\mathbf {r}$
maps of
$\mathbf {r}$
maps of
![]() $P_{(H,S)}$
are the same as in E for the common edges and they are defined as above for the new edges.
$P_{(H,S)}$
are the same as in E for the common edges and they are defined as above for the new edges.
Before formulating and proving the main result, we present some examples that compare and contrast the generalised hedgehog and the porcupine graphs of an admissible pair.
Example 3.2. Let E be the Toeplitz graph

and let
![]() $H=\{v\}.$
The hedgehog graph of
$H=\{v\}.$
The hedgehog graph of
![]() $(H, \emptyset )$
is shown first and the porcupine graph is second.
$(H, \emptyset )$
is shown first and the porcupine graph is second.

The graded isomorphism of Theorem 3.3 is such that the path
![]() $e^{n-1}g$
of length n corresponds to the path
$e^{n-1}g$
of length n corresponds to the path
 $f^{e^{n-1}g}f^{e^{n-2}g}\ldots f^g$
, which is also of length n.
$f^{e^{n-1}g}f^{e^{n-2}g}\ldots f^g$
, which is also of length n.
We consider another example with an infinite emitter. Let E be the graph

and consider
![]() $H=\{v\}, S=\{w\}$
. In this case,
$H=\{v\}, S=\{w\}$
. In this case,
![]() $F_1(H,S)=\{e_3, e_2e_3, e_1e_2e_3\} $
and
$F_1(H,S)=\{e_3, e_2e_3, e_1e_2e_3\} $
and
![]() $F_2(H,S)=\{e_1\}.$
The generalised hedgehog graph of
$F_2(H,S)=\{e_1\}.$
The generalised hedgehog graph of
![]() $(H,S)$
is shown first and the porcupine graph is second.
$(H,S)$
is shown first and the porcupine graph is second.


Theorem 3.3. For an admissible pair
![]() $(H,S)$
of a graph
$(H,S)$
of a graph
![]() $E, I(H,S)$
and
$E, I(H,S)$
and
![]() $L_K (P_{(H,S)})$
are graded
$L_K (P_{(H,S)})$
are graded
![]() $*$
-isomorphic. Thus, every graded ideal of a Leavitt path algebra is graded
$*$
-isomorphic. Thus, every graded ideal of a Leavitt path algebra is graded
![]() $*$
-isomorphic to a Leavitt path algebra.
$*$
-isomorphic to a Leavitt path algebra.
Proof. We define a function
![]() $\phi $
which maps the vertices and edges of
$\phi $
which maps the vertices and edges of
![]() $P_{(H,S)}$
to elements of
$P_{(H,S)}$
to elements of
![]() $ I(H,S)$
, as follows. For a vertex v of
$ I(H,S)$
, as follows. For a vertex v of
![]() $P_{(H,S)},$
we let
$P_{(H,S)},$
we let
 $$ \begin{align*} \phi(v)=\left\{\begin{array}{@{}ll} v & \text{if } v\in H,\\ v^H & \text{if } v\in S,\\ pp^* & \text{if } v=w^p\mbox{ and }p\in F_1(H,S), \\ p\mathbf{r}(p)^Hp^* & \text{if } v=w^p\mbox{ and }p\in F_2(H,S). \end{array}\right.\end{align*} $$
$$ \begin{align*} \phi(v)=\left\{\begin{array}{@{}ll} v & \text{if } v\in H,\\ v^H & \text{if } v\in S,\\ pp^* & \text{if } v=w^p\mbox{ and }p\in F_1(H,S), \\ p\mathbf{r}(p)^Hp^* & \text{if } v=w^p\mbox{ and }p\in F_2(H,S). \end{array}\right.\end{align*} $$
For an edge g of
![]() $P_{(H,S)},$
we let
$P_{(H,S)},$
we let
 $$ \begin{align*} \phi(g)=\left\{\begin{array}{@{}ll} e & \text{if } g=e\in E^1\mbox{ or if }g=f^e\mbox{ for some }e\in F_1(H,S)\cap E^1,\\ e\mathbf{r}(e)^H & \text{if } g=f^e\;\; \mbox{ for some }e\in F_2(H,S)\cap E^1,\\ epp^* & \text{if } g=f^{ep} \;\mbox{ for some }e\in E^1\mbox{ and }p\in F_1(H,S),\\ ep\mathbf{r}(p)^Hp^* & \text{if } g=f^{ep} \;\mbox{ for some }e\in E^1\mbox{ and }p\in F_2(H,S). \end{array}\right.\end{align*} $$
$$ \begin{align*} \phi(g)=\left\{\begin{array}{@{}ll} e & \text{if } g=e\in E^1\mbox{ or if }g=f^e\mbox{ for some }e\in F_1(H,S)\cap E^1,\\ e\mathbf{r}(e)^H & \text{if } g=f^e\;\; \mbox{ for some }e\in F_2(H,S)\cap E^1,\\ epp^* & \text{if } g=f^{ep} \;\mbox{ for some }e\in E^1\mbox{ and }p\in F_1(H,S),\\ ep\mathbf{r}(p)^Hp^* & \text{if } g=f^{ep} \;\mbox{ for some }e\in E^1\mbox{ and }p\in F_2(H,S). \end{array}\right.\end{align*} $$
Extend
![]() $\phi $
to
$\phi $
to
![]() $g^*$
for
$g^*$
for
 $g\in P_{(H,S)}^1$
by
$g\in P_{(H,S)}^1$
by
![]() $\phi (g^*)=\phi (g)^*$
and use the definitions to check that (V), (E1), (E2) and (CK1) hold for
$\phi (g^*)=\phi (g)^*$
and use the definitions to check that (V), (E1), (E2) and (CK1) hold for
 $\phi (v), \phi (g), \phi (g^*), v\in P_{(H,S)}^0, g\in P_{(H,S)}^1.$
We present more details for checking that (CK2) holds. If v is a regular vertex of
$\phi (v), \phi (g), \phi (g^*), v\in P_{(H,S)}^0, g\in P_{(H,S)}^1.$
We present more details for checking that (CK2) holds. If v is a regular vertex of
![]() $P_{(H,S)},$
then v cannot be in
$P_{(H,S)},$
then v cannot be in
![]() $S,$
so
$S,$
so
![]() $v\in H$
or
$v\in H$
or
![]() $v=w^p$
for some
$v=w^p$
for some
![]() $p\in F_1(H,S)\cup F_2(H,S).$
In the first case, the edges v emits are in E since H is hereditary and the relation
$p\in F_1(H,S)\cup F_2(H,S).$
In the first case, the edges v emits are in E since H is hereditary and the relation
![]() $v=\sum _{e\in \mathbf {s}^{-1}(v)} ee^*$
holds in
$v=\sum _{e\in \mathbf {s}^{-1}(v)} ee^*$
holds in
![]() $L_K(P_{(H,S)})$
since it holds in
$L_K(P_{(H,S)})$
since it holds in
![]() $L_K(E).$
In the second case, consider the four possible cases:
$L_K(E).$
In the second case, consider the four possible cases:
![]() $p=e\in F_1(H,S)\cap E^1, p=e\in F_2(H,S)\cap E^1, p=eq$
for
$p=e\in F_1(H,S)\cap E^1, p=e\in F_2(H,S)\cap E^1, p=eq$
for
![]() $e\in E^1, q\in F_1(H,S),$
and
$e\in E^1, q\in F_1(H,S),$
and
![]() $p=eq$
for
$p=eq$
for
![]() $e\in E^1, q\in F_2(H,S).$
Note that, in each case, v emits only one edge
$e\in E^1, q\in F_2(H,S).$
Note that, in each case, v emits only one edge
![]() $f^p$
so it is sufficient to check that
$f^p$
so it is sufficient to check that
![]() $\phi (f^p)\phi ((f^p)^*)=\phi (v)$
in each case.
$\phi (f^p)\phi ((f^p)^*)=\phi (v)$
in each case.
-
(i) If
 $p=e\in F_1(H,S)\cap E^1,$
then
$p=e\in F_1(H,S)\cap E^1,$
then
 $\phi (f^e)\phi ((f^e)^*)=ee^*=\phi (v).$
$\phi (f^e)\phi ((f^e)^*)=ee^*=\phi (v).$
-
(ii) If
 $p=e\in F_2(H,S)\cap E^1,$
then
$p=e\in F_2(H,S)\cap E^1,$
then
 $\phi (f^e)\phi ((f^e)^*)=e\mathbf {r}(e)^H \mathbf {r}(e)^H e^*=e\mathbf {r}(e)^H e^*=\phi (v).$
$\phi (f^e)\phi ((f^e)^*)=e\mathbf {r}(e)^H \mathbf {r}(e)^H e^*=e\mathbf {r}(e)^H e^*=\phi (v).$
-
(iii) If
 $p=eq$
for
$p=eq$
for
 $e\in E^1, q\in F_1(H,S),$
then
$e\in E^1, q\in F_1(H,S),$
then  $$ \begin{align*}\phi(f^p)\phi((f^p)^*)=eqq^*qq^*e^*=eqq^*e^*=pp^*=\phi(v).\end{align*} $$
$$ \begin{align*}\phi(f^p)\phi((f^p)^*)=eqq^*qq^*e^*=eqq^*e^*=pp^*=\phi(v).\end{align*} $$
-
(iv) If
 $p=eq$
for
$p=eq$
for
 $e\in E^1, q\in F_2(H,S),$
then
$e\in E^1, q\in F_2(H,S),$
then  $$ \begin{align*}\phi(f^p)\phi((f^p)^*)=eq\mathbf{r}(p)^Hq^*q\mathbf{r}(p)^Hq^*e^*=eq\mathbf{r}(p)^Hq^*e^*=p\mathbf{r}(p)^Hp^*=\phi(v).\end{align*} $$
$$ \begin{align*}\phi(f^p)\phi((f^p)^*)=eq\mathbf{r}(p)^Hq^*q\mathbf{r}(p)^Hq^*e^*=eq\mathbf{r}(p)^Hq^*e^*=p\mathbf{r}(p)^Hp^*=\phi(v).\end{align*} $$
This shows that (CK2) holds.
By the Universal Property,
![]() $\phi $
has a unique extension to a K-algebra homomorphism
$\phi $
has a unique extension to a K-algebra homomorphism
![]() $L_K(P_{(H,S)})\to I(H,S).$
Since
$L_K(P_{(H,S)})\to I(H,S).$
Since
![]() $\phi $
preserves degrees of
$\phi $
preserves degrees of
 $v\in P_{(H,S)}^0$
and of g and
$v\in P_{(H,S)}^0$
and of g and
![]() $g^*$
for
$g^*$
for
 $g\in P_{(H,S)}^1,$
this extension, which we denote also by
$g\in P_{(H,S)}^1,$
this extension, which we denote also by
![]() $\phi ,$
is a graded homomorphism. As
$\phi ,$
is a graded homomorphism. As
![]() $\phi (v)^*=\phi (v)$
for
$\phi (v)^*=\phi (v)$
for
 $v\in P_{(H,S)}^0$
and
$v\in P_{(H,S)}^0$
and
![]() $\phi (g^*)=\phi (g)^*$
for
$\phi (g^*)=\phi (g)^*$
for
 $g\in P_{(H,S)}^1, \phi $
is a
$g\in P_{(H,S)}^1, \phi $
is a
![]() $*$
-homomorphism. The map
$*$
-homomorphism. The map
![]() $\phi $
is nonzero on every vertex of
$\phi $
is nonzero on every vertex of
![]() $P_{(H,S)},$
so
$P_{(H,S)},$
so
![]() $\phi $
is injective by the Graded Uniqueness Theorem.
$\phi $
is injective by the Graded Uniqueness Theorem.
Since
![]() $\phi $
is a
$\phi $
is a
![]() $*$
-homomorphism, to show surjectivity of
$*$
-homomorphism, to show surjectivity of
![]() $\phi ,$
it is sufficient to show (1) and (2), where (1) denotes the condition that p is in the image of
$\phi ,$
it is sufficient to show (1) and (2), where (1) denotes the condition that p is in the image of
![]() $\phi $
for every path such that
$\phi $
for every path such that
![]() $\mathbf {r}(p)\in H,$
and (2) denotes the condition that
$\mathbf {r}(p)\in H,$
and (2) denotes the condition that
![]() $p\mathbf {r}(p)^H$
is in the image of
$p\mathbf {r}(p)^H$
is in the image of
![]() $\phi $
for every path p such that
$\phi $
for every path p such that
![]() $\mathbf {r}(p)\in S.$
Both claims hold for paths of zero length since
$\mathbf {r}(p)\in S.$
Both claims hold for paths of zero length since
![]() $\phi (v)=v$
if
$\phi (v)=v$
if
![]() $v\in H$
and
$v\in H$
and
![]() $\phi (v)=v^H$
if
$\phi (v)=v^H$
if
![]() $v\in S.$
Thus, consider a path
$v\in S.$
Thus, consider a path
![]() $p=e_1\ldots e_n$
for a positive integer
$p=e_1\ldots e_n$
for a positive integer
![]() $n.$
$n.$
To show (1), assume that
![]() $\mathbf {r}(p)\in H.$
If
$\mathbf {r}(p)\in H.$
If
![]() $\mathbf {s}(p)\in H,$
then
$\mathbf {s}(p)\in H,$
then
![]() $\phi (p)=p$
so the claim holds. If
$\phi (p)=p$
so the claim holds. If
![]() $\mathbf {s}(p)\notin H,$
let
$\mathbf {s}(p)\notin H,$
let
![]() $i\in \{1,2,\ldots , n\}$
be the largest such that
$i\in \{1,2,\ldots , n\}$
be the largest such that
![]() $\mathbf {s}(e_i)\notin H.$
We consider three cases: (i)
$\mathbf {s}(e_i)\notin H.$
We consider three cases: (i)
![]() $\mathbf {s}(e_i)\notin S,$
(ii)
$\mathbf {s}(e_i)\notin S,$
(ii)
![]() $\mathbf {s}(e_i)\in S$
and
$\mathbf {s}(e_i)\in S$
and
![]() $i=1$
and (iii)
$i=1$
and (iii)
![]() $\mathbf {s}(e_i)\in S$
and
$\mathbf {s}(e_i)\in S$
and
![]() $i>1.$
$i>1.$
In case (i),
![]() $e_j\ldots e_i\in F_1(H,S)$
for all
$e_j\ldots e_i\in F_1(H,S)$
for all
![]() $j=1,\ldots i$
and
$j=1,\ldots i$
and
 $$ \begin{align*} &\phi(f^{e_1\ldots e_i}f^{e_2\ldots e_i}\ldots f^{e_i} e_{i+1}\ldots e_n) \\[-3pt] &\quad =e_1\ldots e_i(e_2\ldots e_i)^*(e_2\ldots e_i)(e_3\ldots e_i)^*\;\ldots\; e_{i-1}e_ie_i^*e_i \;\;e_{i+1}\ldots e_n \\[-3pt] &\quad =e_1\ldots e_i\;e_{i+1}\ldots e_n=e_1\ldots e_n=p \end{align*} $$
$$ \begin{align*} &\phi(f^{e_1\ldots e_i}f^{e_2\ldots e_i}\ldots f^{e_i} e_{i+1}\ldots e_n) \\[-3pt] &\quad =e_1\ldots e_i(e_2\ldots e_i)^*(e_2\ldots e_i)(e_3\ldots e_i)^*\;\ldots\; e_{i-1}e_ie_i^*e_i \;\;e_{i+1}\ldots e_n \\[-3pt] &\quad =e_1\ldots e_i\;e_{i+1}\ldots e_n=e_1\ldots e_n=p \end{align*} $$
if
![]() $i<n$
, and the analogous argument applies to the case
$i<n$
, and the analogous argument applies to the case
![]() $i=n.$
$i=n.$
In case (ii),
![]() $\phi (e_j)=e_j$
for every
$\phi (e_j)=e_j$
for every
![]() $j=1,\ldots , n$
and
$j=1,\ldots , n$
and
![]() $\phi (p)=p.$
$\phi (p)=p.$
In case (iii),
![]() $e_j\ldots e_{i-1}\in F_2(H,S)$
for every
$e_j\ldots e_{i-1}\in F_2(H,S)$
for every
![]() $j=1,\ldots i-1$
and
$j=1,\ldots i-1$
and
![]() $\mathbf {r}(e_{i-1})^He_i=e_i$
, so
$\mathbf {r}(e_{i-1})^He_i=e_i$
, so
 $$ \begin{align*} &\phi(f^{e_1\ldots e_{i-1}}f^{e_2\ldots e_{i-1}} \ldots f^{e_{i-1}}e_i\ldots e_n) \\[-3pt] &\quad =e_1\ldots e_{i-1}\mathbf{r}(e_{i-1})^H(e_2\ldots e_{i-1})^* e_2\ldots e_{i-1}\mathbf{r}(e_{i-1})^H\ldots e_{i-1}^*e_{i-1}\mathbf{r}(e_{i-1})^He_ie_{i+1}\ldots e_n \\[-3pt] &\quad =e_1\ldots e_{i-1}\mathbf{r}(e_{i-1})^He_ie_{i+1}\ldots e_n= e_1\ldots e_{i-1}e_ie_{i+1}\ldots e_n=p. \end{align*} $$
$$ \begin{align*} &\phi(f^{e_1\ldots e_{i-1}}f^{e_2\ldots e_{i-1}} \ldots f^{e_{i-1}}e_i\ldots e_n) \\[-3pt] &\quad =e_1\ldots e_{i-1}\mathbf{r}(e_{i-1})^H(e_2\ldots e_{i-1})^* e_2\ldots e_{i-1}\mathbf{r}(e_{i-1})^H\ldots e_{i-1}^*e_{i-1}\mathbf{r}(e_{i-1})^He_ie_{i+1}\ldots e_n \\[-3pt] &\quad =e_1\ldots e_{i-1}\mathbf{r}(e_{i-1})^He_ie_{i+1}\ldots e_n= e_1\ldots e_{i-1}e_ie_{i+1}\ldots e_n=p. \end{align*} $$
This shows that (1) holds.
To show (2), assume that
![]() $\mathbf {r}(p)\in S.$
Then
$\mathbf {r}(p)\in S.$
Then
![]() $e_i\ldots e_n$
is in
$e_i\ldots e_n$
is in
![]() $F_2(H,S)$
for every
$F_2(H,S)$
for every
![]() $i=1,\ldots , n$
and
$i=1,\ldots , n$
and
 $$ \begin{align*} \phi(f^{e_1\ldots e_n}f^{e_2\ldots e_n}\ldots f^{e_n}) & =e_1\ldots e_n\mathbf{r}(p)^H(e_2\ldots e_n)^*(e_2\ldots e_n)\mathbf{r}(p)^H(e_3\ldots e_n)^*\;\ldots \\ &\quad \ldots e_{n-1}e_n\mathbf{r}(p)^He_n^*e_n\mathbf{r}(p)^H=e_1\ldots e_n\mathbf{r}(p)^H=p\mathbf{r}(p)^H. \end{align*} $$
$$ \begin{align*} \phi(f^{e_1\ldots e_n}f^{e_2\ldots e_n}\ldots f^{e_n}) & =e_1\ldots e_n\mathbf{r}(p)^H(e_2\ldots e_n)^*(e_2\ldots e_n)\mathbf{r}(p)^H(e_3\ldots e_n)^*\;\ldots \\ &\quad \ldots e_{n-1}e_n\mathbf{r}(p)^He_n^*e_n\mathbf{r}(p)^H=e_1\ldots e_n\mathbf{r}(p)^H=p\mathbf{r}(p)^H. \end{align*} $$
This shows that
![]() $\phi $
is surjective.
$\phi $
is surjective.
The second sentence of the theorem is a direct corollary of the first sentence and [Reference Tomforde6, Theorem 5.7] (also [Reference Abrams, Ara and Siles Molina1, Theorem 2.5.8]).
3.1. Graph
 ${\textit{C}}^{\boldsymbol{*}}$
-algebras
${\textit{C}}^{\boldsymbol{*}}$
-algebras
Theorem 3.3 has its graph
![]() $C^*$
-algebra version. If E is a graph, then the graph
$C^*$
-algebra version. If E is a graph, then the graph
![]() $C^*$
-algebra of E is the universal
$C^*$
-algebra of E is the universal
![]() $C^*$
-algebra generated by mutually orthogonal projections
$C^*$
-algebra generated by mutually orthogonal projections
![]() $\{p_v\mid v\in E^0\}$
and partial isometries with mutually orthogonal ranges
$\{p_v\mid v\in E^0\}$
and partial isometries with mutually orthogonal ranges
![]() $\{s_e\mid e\in E^1\}$
satisfying the analogues of the (CK1) and (CK2) axioms and the axiom (CK3) stating that
$\{s_e\mid e\in E^1\}$
satisfying the analogues of the (CK1) and (CK2) axioms and the axiom (CK3) stating that
![]() $s_es_e^*\leq p_{\mathbf {s}(e)}$
for every
$s_es_e^*\leq p_{\mathbf {s}(e)}$
for every
![]() $e\in E^1.$
The term ‘universal’ in the definition means that the
$e\in E^1.$
The term ‘universal’ in the definition means that the
![]() $C^*$
-algebra version of the algebraic Universal Property, mentioned before, holds (see [Reference Abrams, Ara and Siles Molina1, Definition 5.2.5]). By letting
$C^*$
-algebra version of the algebraic Universal Property, mentioned before, holds (see [Reference Abrams, Ara and Siles Molina1, Definition 5.2.5]). By letting
![]() $s_{e_1\ldots e_n}$
be
$s_{e_1\ldots e_n}$
be
![]() $s_{e_1}\ldots s_{e_n}$
and
$s_{e_1}\ldots s_{e_n}$
and
![]() $s_v=p_v$
for
$s_v=p_v$
for
![]() $e_1,\ldots ,e_n\in E^1$
and
$e_1,\ldots ,e_n\in E^1$
and
 $v\in E^0, s_p$
is defined for every path
$v\in E^0, s_p$
is defined for every path
![]() $p.$
$p.$
The set
![]() $\{p_v, s_e\mid v\in E^0, e\in E^1\}$
is referred to as a Cuntz–Krieger E-family. For such an E-family and an element z of the unit sphere
$\{p_v, s_e\mid v\in E^0, e\in E^1\}$
is referred to as a Cuntz–Krieger E-family. For such an E-family and an element z of the unit sphere
![]() $\mathbb T$
, one defines a map
$\mathbb T$
, one defines a map
![]() $\gamma ^E_z$
by
$\gamma ^E_z$
by
 $\gamma ^E_z(p_v)=p_v$
and
$\gamma ^E_z(p_v)=p_v$
and
 $\gamma ^E_z(s_e)=zs_e$
and then uniquely extends this map to a
$\gamma ^E_z(s_e)=zs_e$
and then uniquely extends this map to a
![]() $*$
-automorphism of
$*$
-automorphism of
![]() $C^*(E)$
(we assume a homomorphism of a
$C^*(E)$
(we assume a homomorphism of a
![]() $C^*$
-algebra to be bounded). The gauge action
$C^*$
-algebra to be bounded). The gauge action
![]() $\gamma ^E$
on
$\gamma ^E$
on
![]() $\mathbb T$
is given by
$\mathbb T$
is given by
 $\gamma ^E(z)=\gamma ^E_z.$
Note that
$\gamma ^E(z)=\gamma ^E_z.$
Note that
 $\gamma ^E_z(s_ps_q^*)=z^{|p|-|q|}s_ps_q^*$
for
$\gamma ^E_z(s_ps_q^*)=z^{|p|-|q|}s_ps_q^*$
for
![]() $z\in \mathbb T$
and paths p and
$z\in \mathbb T$
and paths p and
![]() $q.$
The presence of the degree
$q.$
The presence of the degree
![]() $|p|-|q|$
of
$|p|-|q|$
of
![]() $pq^*$
in the previous formula explains the connection between this action and the
$pq^*$
in the previous formula explains the connection between this action and the
![]() $\mathbb Z$
-grading of
$\mathbb Z$
-grading of
![]() $L_{\mathbb C}(E)$
. If the integral of a continuous function
$L_{\mathbb C}(E)$
. If the integral of a continuous function
![]() $f:\mathbb T\to \mathbb C$
over
$f:\mathbb T\to \mathbb C$
over
![]() $\mathbb T$
is defined by
$\mathbb T$
is defined by
 $\int _{\mathbb T}f(z)\,dz=\int _0^1 f(e^{2\pi i t})\,dt,$
then the gauge action on
$\int _{\mathbb T}f(z)\,dz=\int _0^1 f(e^{2\pi i t})\,dt,$
then the gauge action on
![]() $C^*(E)$
determines a
$C^*(E)$
determines a
![]() $\mathbb Z$
-grading of
$\mathbb Z$
-grading of
![]() $C^*(E)$
(see [Reference Abrams, Ara and Siles Molina1, Proposition 5.2.11]) so that
$C^*(E)$
(see [Reference Abrams, Ara and Siles Molina1, Proposition 5.2.11]) so that
 $$ \begin{align}C^*(E)_n=\bigg\{x\in C^*(E)\,\bigg|\, \int_{\mathbb T}z^{-n}\gamma^E_z(x)\,dz=x\bigg\} \end{align} $$
$$ \begin{align}C^*(E)_n=\bigg\{x\in C^*(E)\,\bigg|\, \int_{\mathbb T}z^{-n}\gamma^E_z(x)\,dz=x\bigg\} \end{align} $$
is the completion of
![]() $L_{\mathbb C}(E)_n$
and
$L_{\mathbb C}(E)_n$
and
![]() $C^*(E)$
is the completion of
$C^*(E)$
is the completion of
 $\bigoplus _{n\,\in\,\mathbb Z} C^*(E)_n.$
We note that this grading is not a grading in the algebraic sense, but in the
$\bigoplus _{n\,\in\,\mathbb Z} C^*(E)_n.$
We note that this grading is not a grading in the algebraic sense, but in the
![]() $C^*$
-algebra sense (see the paragraph following [Reference Abrams, Ara and Siles Molina1, Theorem 5.2.9.]).
$C^*$
-algebra sense (see the paragraph following [Reference Abrams, Ara and Siles Molina1, Theorem 5.2.9.]).
A closed ideal J of a graph
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(E)$
is gauge-invariant if
$C^*(E)$
is gauge-invariant if
 $\gamma ^E_z(J)=J$
for every
$\gamma ^E_z(J)=J$
for every
![]() $z\in \mathbb T.$
By [Reference Bates, Hong, Raeburn and Szymański3, Theorem 3.6], every such ideal J is the completion of the linear span of the elements
$z\in \mathbb T.$
By [Reference Bates, Hong, Raeburn and Szymański3, Theorem 3.6], every such ideal J is the completion of the linear span of the elements
![]() $s_ps_q^*$
for paths
$s_ps_q^*$
for paths
![]() $p,q$
with
$p,q$
with
![]() $\mathbf {r}(p)=\mathbf {r}(q)\in H$
and the elements
$\mathbf {r}(p)=\mathbf {r}(q)\in H$
and the elements
 $s_pp_v^Hs_q^*$
for paths
$s_pp_v^Hs_q^*$
for paths
![]() $p,q$
with
$p,q$
with
![]() $\mathbf {r}(p)=\mathbf {r}(q)=v\in S$
, where
$\mathbf {r}(p)=\mathbf {r}(q)=v\in S$
, where
 $p_v^H=p_v-\sum _{e\in \mathbf {s}^{-1}(v)\cap \mathbf {r}^{-1}(E^0-H)}s_es_e^*$
for
$p_v^H=p_v-\sum _{e\in \mathbf {s}^{-1}(v)\cap \mathbf {r}^{-1}(E^0-H)}s_es_e^*$
for
![]() $v\in B_H$
, and where
$v\in B_H$
, and where
![]() $(H, S)$
is the admissible pair uniquely determined by J and defined analogously as for an ideal of
$(H, S)$
is the admissible pair uniquely determined by J and defined analogously as for an ideal of
![]() $L_K(E)$
. Also as before, an admissible pair
$L_K(E)$
. Also as before, an admissible pair
![]() $(H,S)$
uniquely determines a closed gauge-invariant ideal
$(H,S)$
uniquely determines a closed gauge-invariant ideal
![]() $J(H,S)$
which is graded in the
$J(H,S)$
which is graded in the
![]() $C^*$
-algebra sense.
$C^*$
-algebra sense.
If R is a
![]() $C^*$
-algebra with an action
$C^*$
-algebra with an action
![]() $\beta : \mathbb T\to $
Aut
$\beta : \mathbb T\to $
Aut
![]() $(R),$
then we say that a
$(R),$
then we say that a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : C^*(E)\to R$
is gauge-invariant if
$\phi : C^*(E)\to R$
is gauge-invariant if
 $\beta _z\circ \phi =\phi \circ \gamma ^E_z$
for every
$\beta _z\circ \phi =\phi \circ \gamma ^E_z$
for every
![]() $z\in \mathbb T.$
Thus, if J is a closed gauge-invariant ideal of
$z\in \mathbb T.$
Thus, if J is a closed gauge-invariant ideal of
![]() $C^*(E), F$
is a graph and
$C^*(E), F$
is a graph and
![]() $\phi : C^*(F)\to J$
is a
$\phi : C^*(F)\to J$
is a
![]() $*$
-homomorphism, then
$*$
-homomorphism, then
![]() $\phi $
is gauge-invariant if
$\phi $
is gauge-invariant if
 $\gamma _z^E|_J\circ \phi =\phi \circ \gamma ^F_z$
for every
$\gamma _z^E|_J\circ \phi =\phi \circ \gamma ^F_z$
for every
![]() $z\in \mathbb T.$
It is direct to see that every such gauge-invariant map
$z\in \mathbb T.$
It is direct to see that every such gauge-invariant map
![]() $\phi $
is graded. Indeed, using the formula (*) and the fact that
$\phi $
is graded. Indeed, using the formula (*) and the fact that
![]() $\phi $
is bounded, one directly checks that
$\phi $
is bounded, one directly checks that
![]() $\phi (C^*(F)_n)\subseteq J_n.$
$\phi (C^*(F)_n)\subseteq J_n.$
Corollary 3.4. For an admissible pair
![]() $(H,S)$
of a graph
$(H,S)$
of a graph
![]() $E,$
there is a gauge-invariant (thus graded)
$E,$
there is a gauge-invariant (thus graded)
![]() $*$
-isomorphism
$*$
-isomorphism
Thus, for every closed gauge-invariant ideal J of a graph
![]() $C^*$
-algebra, there is a gauge-invariant (and thus graded)
$C^*$
-algebra, there is a gauge-invariant (and thus graded)
![]() $*$
-isomorphism mapping the graph
$*$
-isomorphism mapping the graph
![]() $C^*$
-algebra of the porcupine graph corresponding to J onto
$C^*$
-algebra of the porcupine graph corresponding to J onto
![]() $J.$
$J.$
Proof. One defines a map
![]() $\phi $
on
$\phi $
on
 $\{p_v, s_g\mid v\in P_{(H,S)}^0, g\in P_{(H,S)}^1\}$
analogously as in Theorem 3.3. We claim that the image of this map constitutes a Cuntz–Krieger
$\{p_v, s_g\mid v\in P_{(H,S)}^0, g\in P_{(H,S)}^1\}$
analogously as in Theorem 3.3. We claim that the image of this map constitutes a Cuntz–Krieger
![]() $P_{(H,S)}$
-family. Indeed,
$P_{(H,S)}$
-family. Indeed,
 $\{\phi (p_v)\mid v\in P_{(H,S)}^0\}$
is a set of orthogonal projections in
$\{\phi (p_v)\mid v\in P_{(H,S)}^0\}$
is a set of orthogonal projections in
![]() $J(H,S)$
and
$J(H,S)$
and
 $\{\phi (s_g)\mid g\in P_{(H,S)}^1\}$
is a set of partial isometries in
$\{\phi (s_g)\mid g\in P_{(H,S)}^1\}$
is a set of partial isometries in
![]() $I(H,S)$
with mutually orthogonal ranges. One checks that (CK1) and (CK2) hold in the same way as in the proof of Theorem 3.3. If
$I(H,S)$
with mutually orthogonal ranges. One checks that (CK1) and (CK2) hold in the same way as in the proof of Theorem 3.3. If
 $g\in P_{(H,S)}^1$
and
$g\in P_{(H,S)}^1$
and
![]() $\mathbf {s}(g)$
is regular, then the requirement
$\mathbf {s}(g)$
is regular, then the requirement
![]() $\phi (s_g)\phi (s_g)^*\leq \phi (p_{\mathbf {s}(g)})$
follows from (CK2). If
$\phi (s_g)\phi (s_g)^*\leq \phi (p_{\mathbf {s}(g)})$
follows from (CK2). If
 $g\in P_{(H,S)}^1$
and
$g\in P_{(H,S)}^1$
and
![]() $\mathbf {s}(g)$
is an infinite emitter, then the
$\mathbf {s}(g)$
is an infinite emitter, then the
![]() $\mathbf {s}(g)\in H\cup S$
and g is an edge in
$\mathbf {s}(g)\in H\cup S$
and g is an edge in
![]() $E^1.$
Thus, (CK3) holds for
$E^1.$
Thus, (CK3) holds for
![]() $s_g$
in
$s_g$
in
![]() $C^*(P_{(H,S)})$
since it holds for
$C^*(P_{(H,S)})$
since it holds for
![]() $s_g$
in
$s_g$
in
![]() $C^*(E).$
$C^*(E).$
The map
![]() $\phi $
has a unique extension to a
$\phi $
has a unique extension to a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi :C^*(P_{(H,S)})\to J(H,S)$
by the Universal Property. To show that
$\phi :C^*(P_{(H,S)})\to J(H,S)$
by the Universal Property. To show that
![]() $\phi $
is gauge-invariant, it is sufficient to check that the condition
$\phi $
is gauge-invariant, it is sufficient to check that the condition
 $\gamma _z^E|_I\circ \phi =\phi \circ \gamma ^{P_{(H,S)}}_z$
holds on
$\gamma _z^E|_I\circ \phi =\phi \circ \gamma ^{P_{(H,S)}}_z$
holds on
 $\{p_v, s_g\mid v\in P_{(H,S)}^0, g\in P_{(H,S)}^1\}$
, which is done directly using the definitions.
$\{p_v, s_g\mid v\in P_{(H,S)}^0, g\in P_{(H,S)}^1\}$
, which is done directly using the definitions.
The map
![]() $\phi $
is nonzero on every element
$\phi $
is nonzero on every element
![]() $p_v$
for
$p_v$
for
 $v\in P_{(H,S)}^0,$
so
$v\in P_{(H,S)}^0,$
so
![]() $\phi $
is injective by the Gauge-Invariant Uniqueness Theorem (see [Reference Abrams, Ara and Siles Molina1, Theorem 5.2.12]). The surjectivity of
$\phi $
is injective by the Gauge-Invariant Uniqueness Theorem (see [Reference Abrams, Ara and Siles Molina1, Theorem 5.2.12]). The surjectivity of
![]() $\phi $
holds by arguments analogous to those in the proof of Theorem 3.3.
$\phi $
holds by arguments analogous to those in the proof of Theorem 3.3.
Acknowledgement
The author is very grateful to the referee for the suggestion to consider formulating and proving the
![]() $C^*$
-algebra version of the main result (now Corollary 3.4).
$C^*$
-algebra version of the main result (now Corollary 3.4).