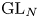1. Introduction
1.1 Reminder on geometric Satake
Let ![]() ${\mathbf {F}}={\mathbb {C}}(\!(t)\!)\supset {\mathbb {C}}[\![t]\!]={\mathbf {O}}$. Throughout the paper, we fix an integer
${\mathbf {F}}={\mathbb {C}}(\!(t)\!)\supset {\mathbb {C}}[\![t]\!]={\mathbf {O}}$. Throughout the paper, we fix an integer ![]() $N\geq 1$, set
$N\geq 1$, set ![]() ${\mathbf {G}}_{\mathbf {F}}=\operatorname{GL}(N,{\mathbf {F}})$ and
${\mathbf {G}}_{\mathbf {F}}=\operatorname{GL}(N,{\mathbf {F}})$ and ![]() ${\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N,{\mathbf {O}})$, and let
${\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N,{\mathbf {O}})$, and let ![]() ${\mathbf {Gr}}={\mathbf {G}}_{\mathbf {F}}/{\mathbf {G}}_{\mathbf {O}}$ be the affine Grassmannian of
${\mathbf {Gr}}={\mathbf {G}}_{\mathbf {F}}/{\mathbf {G}}_{\mathbf {O}}$ be the affine Grassmannian of ![]() $\operatorname{GL}_N$. This is an ind-scheme equipped with a natural action of the group
$\operatorname{GL}_N$. This is an ind-scheme equipped with a natural action of the group ![]() ${\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times$, where
${\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times$, where ![]() ${\mathbb {C}}^\times$ acts by loop rotation. Let
${\mathbb {C}}^\times$ acts by loop rotation. Let ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ (respectively,
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ (respectively, ![]() $D_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$) be the
$D_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$) be the ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant (respectively,
${\mathbf {G}}_{\mathbf {O}}$-equivariant (respectively, ![]() ${\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times$-equivariant) constructible derived category of
${\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times$-equivariant) constructible derived category of ![]() ${\mathbf {Gr}}$.Footnote 1 This is a monoidal category with respect to convolution (which coincides with fusion); cf. [Reference Mirković and VilonenMV07].
${\mathbf {Gr}}$.Footnote 1 This is a monoidal category with respect to convolution (which coincides with fusion); cf. [Reference Mirković and VilonenMV07].
Let ![]() ${\mathfrak {gl}}_N$ be the complex vector space of
${\mathfrak {gl}}_N$ be the complex vector space of ![]() $N\times N$ matrices and let
$N\times N$ matrices and let ![]() $\operatorname{GL}_N$ act on
$\operatorname{GL}_N$ act on ![]() ${\mathfrak {gl}}_N$ by conjugation. Write
${\mathfrak {gl}}_N$ by conjugation. Write ![]() ${\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2])$ for the symmetric algebra of
${\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2])$ for the symmetric algebra of ![]() ${\mathfrak {gl}}_N$ viewed as a dg-algebra such that the space
${\mathfrak {gl}}_N$ viewed as a dg-algebra such that the space ![]() ${\mathfrak {gl}}_N$, of generators, is placed in degree
${\mathfrak {gl}}_N$, of generators, is placed in degree ![]() $2$ and the differential is equal to zero. Let
$2$ and the differential is equal to zero. Let ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N}({\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2]))$ be the triangulated category of perfect
$D_{\operatorname{perf}}^{\operatorname{GL}_N}({\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2]))$ be the triangulated category of perfect ![]() $\operatorname{GL}_N$-equivariant dg-modules over
$\operatorname{GL}_N$-equivariant dg-modules over ![]() ${\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2])$, localized with respect to quasi-isomorphisms. The tensor product of dg-modules gives this category a monoidal structure. One of the versions of derived Satake equivalence proved in [Reference Bezrukavnikov and FinkelbergBF08] states that there is an equivalence
${\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2])$, localized with respect to quasi-isomorphisms. The tensor product of dg-modules gives this category a monoidal structure. One of the versions of derived Satake equivalence proved in [Reference Bezrukavnikov and FinkelbergBF08] states that there is an equivalence ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N}({\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2])){\buildrel \sim \over \longrightarrow} D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ of triangulated monoidal categories.
$D_{\operatorname{perf}}^{\operatorname{GL}_N}({\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2])){\buildrel \sim \over \longrightarrow} D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ of triangulated monoidal categories.
It will be convenient for us to reformulate the above result as follows. Let ![]() $T^*\operatorname{GL}_N[2]$ be the shifted cotangent bundle on
$T^*\operatorname{GL}_N[2]$ be the shifted cotangent bundle on ![]() $\operatorname{GL}_N$, viewed as a dg-scheme equipped with zero differential. The action of
$\operatorname{GL}_N$, viewed as a dg-scheme equipped with zero differential. The action of ![]() $\operatorname{GL}_N$ on itself by left and right translations induces a
$\operatorname{GL}_N$ on itself by left and right translations induces a ![]() $\operatorname{GL}_N\times \operatorname{GL}_N$-action on
$\operatorname{GL}_N\times \operatorname{GL}_N$-action on ![]() $T^*\operatorname{GL}_N[2]$. Let
$T^*\operatorname{GL}_N[2]$. Let ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2])$ be the triangulated category of
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2])$ be the triangulated category of ![]() $\operatorname{GL}_N\times \operatorname{GL}_N$-equivariant perfect complexes of
$\operatorname{GL}_N\times \operatorname{GL}_N$-equivariant perfect complexes of ![]() ${\mathcal {O}}_{T^*\operatorname{GL}_N[2]}$-modules on
${\mathcal {O}}_{T^*\operatorname{GL}_N[2]}$-modules on ![]() $T^*\operatorname{GL}_N[2]$. The fiber of
$T^*\operatorname{GL}_N[2]$. The fiber of ![]() $T^*\operatorname{GL}_N[2]$ over
$T^*\operatorname{GL}_N[2]$ over ![]() $1\in \operatorname{GL}_N$ may (and will) be identified with
$1\in \operatorname{GL}_N$ may (and will) be identified with ![]() $({\mathfrak {gl}}_N[-2])^*={\mathfrak {gl}}_N^*[2]$. Restriction to this fiber induces a monoidal equivalence
$({\mathfrak {gl}}_N[-2])^*={\mathfrak {gl}}_N^*[2]$. Restriction to this fiber induces a monoidal equivalence ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2]){\buildrel \sim \over \longrightarrow} D_{\operatorname{perf}}^{\operatorname{GL}_N}({\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2]))$, where the category on the right is identified with the triangulated category of
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2]){\buildrel \sim \over \longrightarrow} D_{\operatorname{perf}}^{\operatorname{GL}_N}({\operatorname{Sym}}^\bullet ({\mathfrak {gl}}_N[-2]))$, where the category on the right is identified with the triangulated category of ![]() $\operatorname{GL}_N$-equivariant perfect complexes on
$\operatorname{GL}_N$-equivariant perfect complexes on ![]() $({\mathfrak {gl}}_N[-2])^*$. Thus, the derived Satake equivalence stated above may be interpreted as an equivalence
$({\mathfrak {gl}}_N[-2])^*$. Thus, the derived Satake equivalence stated above may be interpreted as an equivalence ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2]){\buildrel \sim \over \longrightarrow} D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2]){\buildrel \sim \over \longrightarrow} D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
There is also a natural ‘quantum’ counterpart of the latter equivalence, where the category ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2])$ is replaced by an appropriately defined category of asymptotic shifted weakly equivariant
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}(T^*\operatorname{GL}_N[2])$ is replaced by an appropriately defined category of asymptotic shifted weakly equivariant ![]() $D$-modules on
$D$-modules on ![]() $\operatorname{GL}_N$, and the category
$\operatorname{GL}_N$, and the category ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is replaced by
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is replaced by ![]() $D_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$; see [Reference Bezrukavnikov and FinkelbergBF08].
$D_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$; see [Reference Bezrukavnikov and FinkelbergBF08].
1.2 Mirabolic Satake category
In the present paper we will be interested in a mirabolic analogue of the above setting. To explain this, fix an ![]() $N$-dimensional vector space
$N$-dimensional vector space ![]() $V$ and put
$V$ and put ![]() ${\mathbf {V}}=V\,{\otimes}\, {\mathbf {F}}$,
${\mathbf {V}}=V\,{\otimes}\, {\mathbf {F}}$, ![]() ${\mathbf {V}}_0= V\,{\otimes}\ {\mathbf {O}}$ and
${\mathbf {V}}_0= V\,{\otimes}\ {\mathbf {O}}$ and ![]() ${\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}= {\mathbf {V}}\,{\smallsetminus}\,\{0\}$. We identify
${\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}= {\mathbf {V}}\,{\smallsetminus}\,\{0\}$. We identify ![]() ${\mathbf {G}}=\operatorname{GL}_N$ with
${\mathbf {G}}=\operatorname{GL}_N$ with ![]() $\operatorname{GL}(V)$, so that
$\operatorname{GL}(V)$, so that ![]() ${\mathbf {G}}_{\mathbf {F}}$ acts on
${\mathbf {G}}_{\mathbf {F}}$ acts on ![]() ${\mathbf {V}}$ and
${\mathbf {V}}$ and ![]() ${\mathbf {G}}_{\mathbf {O}}$ is the stabilizer of
${\mathbf {G}}_{\mathbf {O}}$ is the stabilizer of ![]() ${\mathbf {V}}_0$. Following [Reference Finkelberg, Ginzburg and TravkinFGT09], the mirabolic affine Grassmannian is defined as
${\mathbf {V}}_0$. Following [Reference Finkelberg, Ginzburg and TravkinFGT09], the mirabolic affine Grassmannian is defined as ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$. We let
${\mathbf {Gr}}\times {\mathbf {V}}$. We let ![]() ${\mathbf {G}}_{\mathbf {O}}$ act on
${\mathbf {G}}_{\mathbf {O}}$ act on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$ diagonally. The orbits of
${\mathbf {Gr}}\times {\mathbf {V}}$ diagonally. The orbits of ![]() ${\mathbf {G}}_{\mathbf {O}}$ in
${\mathbf {G}}_{\mathbf {O}}$ in ![]() ${\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$ are, unlike the case of
${\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$ are, unlike the case of ![]() ${\mathbf {G}}_{\mathbf {O}}$-orbits in
${\mathbf {G}}_{\mathbf {O}}$-orbits in ![]() ${\mathbf {Gr}}$, not finite-dimensional. Heuristically, these orbits are of semi-infinite type in the sense that the ‘closure’ of an orbit projects onto a (finite dimensional) Schubert variety in
${\mathbf {Gr}}$, not finite-dimensional. Heuristically, these orbits are of semi-infinite type in the sense that the ‘closure’ of an orbit projects onto a (finite dimensional) Schubert variety in ![]() ${\mathbf {Gr}}$ and onto a lattice in
${\mathbf {Gr}}$ and onto a lattice in ![]() ${\mathbf {V}}$.
${\mathbf {V}}$.
In view of the above, defining the correct mirabolic analogue of the equivariant derived Satake category requires some care. According to our definition, an object of this category is supported on the product of a finite-dimensional Schubert variety in ![]() ${\mathbf {Gr}}$ and a lattice inside the Tate vector space
${\mathbf {Gr}}$ and a lattice inside the Tate vector space ![]() ${\mathbf {V}}$; moreover, this object is pulled back from a finite-dimensional quotient of this lattice. According to three possible choices (
${\mathbf {V}}$; moreover, this object is pulled back from a finite-dimensional quotient of this lattice. According to three possible choices (![]() $!$-,
$!$-, ![]() $*$-, and
$*$-, and ![]() $!*$-) of pullback, one gets the three versions
$!*$-) of pullback, one gets the three versions ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$,
$D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant constructible derived categories on
${\mathbf {G}}_{\mathbf {O}}$-equivariant constructible derived categories on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$. These categories are related to each other by certain renormalization equivalences.
${\mathbf {Gr}}\times {\mathbf {V}}$. These categories are related to each other by certain renormalization equivalences.
We equip the above categories with monoidal structures given by various types of convolution operation. The convolution along the Grassmannian, the first factor in ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$, is defined similarly to the case of the usual Satake category. The convolution along the second factor depends on the choice of category. Specifically, the convolution operation
${\mathbf {Gr}}\times {\mathbf {V}}$, is defined similarly to the case of the usual Satake category. The convolution along the second factor depends on the choice of category. Specifically, the convolution operation ![]() ${\stackrel{!}\circledast}$ in
${\stackrel{!}\circledast}$ in ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ involves the
$D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ involves the ![]() $!$-tensor product of constructible sheaves on
$!$-tensor product of constructible sheaves on ![]() ${\mathbf {V}}$. The convolution operation
${\mathbf {V}}$. The convolution operation ![]() ${\stackrel {*}*}$ on
${\stackrel {*}*}$ on ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ involves a
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ involves a ![]() $*$-pushforward along
$*$-pushforward along ![]() $+\colon {\mathbf {V}}\times {\mathbf {V}}\to {\mathbf {V}}$, the map given by addition. These two types of convolution are related to each other via Fourier transform (along
$+\colon {\mathbf {V}}\times {\mathbf {V}}\to {\mathbf {V}}$, the map given by addition. These two types of convolution are related to each other via Fourier transform (along ![]() ${\mathbf {V}}$). Finally, we define a monoidal structure
${\mathbf {V}}$). Finally, we define a monoidal structure ![]() $\star$ on
$\star$ on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ via the fusion operation on a mirabolic analogue of the Beilinson–Drinfeld Grassmannian.
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ via the fusion operation on a mirabolic analogue of the Beilinson–Drinfeld Grassmannian.
The categories above have natural counterparts involving the action of ![]() ${\mathbb {C}}^\times$ on
${\mathbb {C}}^\times$ on ![]() ${\mathbf {Gr}}$ by loop rotation. These are
${\mathbf {Gr}}$ by loop rotation. These are ![]() ${\mathbb {C}}[\hbar ]$-linear categories where
${\mathbb {C}}[\hbar ]$-linear categories where ![]() ${\mathbb {C}}[\hbar ]=H^\bullet _{{\mathbb {C}}^\times }({\operatorname {pt}})$. Thus, there is a category
${\mathbb {C}}[\hbar ]=H^\bullet _{{\mathbb {C}}^\times }({\operatorname {pt}})$. Thus, there is a category ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})$ (respectively,
$D_{!{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})$ (respectively, ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})$) equipped with a similarly defined monoidal structure
$D_{*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})$) equipped with a similarly defined monoidal structure ![]() ${\stackrel{!}\circledast}$ (respectively,
${\stackrel{!}\circledast}$ (respectively, ![]() ${\stackrel {*}*}$). The fusion operation
${\stackrel {*}*}$). The fusion operation ![]() $\star$ on
$\star$ on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ has no
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ has no ![]() ${\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times$-equivariant counterpart, however.
${\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times$-equivariant counterpart, however.
1.3 Mirabolic Satake equivalence
The category on the ‘other side’ of mirabolic Satake equivalence is an appropriately defined triangulated category of ‘equivariant asymptotic shifted ![]() $D$-modules’ on the vector space
$D$-modules’ on the vector space ![]() ${\mathfrak {gl}}_N$ of
${\mathfrak {gl}}_N$ of ![]() $N\times N$ matrices. More formally, we introduce a
$N\times N$ matrices. More formally, we introduce a ![]() ${\mathbb {C}}[\hbar ]$-algebra
${\mathbb {C}}[\hbar ]$-algebra ![]() ${\mathfrak {D}}^\bullet$, a graded version of the algebra of differential operators on
${\mathfrak {D}}^\bullet$, a graded version of the algebra of differential operators on ![]() ${\mathfrak {gl}}_N$ (where
${\mathfrak {gl}}_N$ (where ![]() $\deg \hbar =2$). The action of
$\deg \hbar =2$). The action of ![]() $\operatorname{GL}_N$ on
$\operatorname{GL}_N$ on ![]() ${\mathfrak {gl}}_N$ by left and right multiplication induces a
${\mathfrak {gl}}_N$ by left and right multiplication induces a ![]() $\operatorname{GL}_N\times \operatorname{GL}_N$-action on
$\operatorname{GL}_N\times \operatorname{GL}_N$-action on ![]() ${\mathfrak {D}}^\bullet$. The relevant category is then defined to be the derived category of weakly
${\mathfrak {D}}^\bullet$. The relevant category is then defined to be the derived category of weakly ![]() $\operatorname{GL}_N\times \operatorname{GL}_N$-equivariant perfect dg-modules over
$\operatorname{GL}_N\times \operatorname{GL}_N$-equivariant perfect dg-modules over ![]() ${\mathfrak {D}}^\bullet$, where
${\mathfrak {D}}^\bullet$, where ![]() ${\mathfrak {D}}^\bullet$ is viewed as a dg-algebra with zero differential. Similarly to the constructible story, we actually define three versions,
${\mathfrak {D}}^\bullet$ is viewed as a dg-algebra with zero differential. Similarly to the constructible story, we actually define three versions, ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{1,1})$,
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{1,1})$, ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{0,2})$ and
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{0,2})$ and ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{2,0})$, of such a category that correspond to three different choices of grading on our algebra. The algebra of asymptotic differential operators specializes at
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{2,0})$, of such a category that correspond to three different choices of grading on our algebra. The algebra of asymptotic differential operators specializes at ![]() $\hbar =0$ to the algebra
$\hbar =0$ to the algebra ![]() ${\mathbb {C}}[T^*{\mathfrak {gl}}_N]$. We denote the specialization of
${\mathbb {C}}[T^*{\mathfrak {gl}}_N]$. We denote the specialization of ![]() ${\mathfrak {D}}^\bullet _{i,2-i}$ at
${\mathfrak {D}}^\bullet _{i,2-i}$ at ![]() $\hbar =0$ by
$\hbar =0$ by ![]() ${\mathfrak {S}}^\bullet _{i,2-i}$. Accordingly, the above-defined
${\mathfrak {S}}^\bullet _{i,2-i}$. Accordingly, the above-defined ![]() ${\mathbb {C}}[\hbar ]$-linear categories specialize at
${\mathbb {C}}[\hbar ]$-linear categories specialize at ![]() $\hbar =0$ to various versions of the derived category of
$\hbar =0$ to various versions of the derived category of ![]() $\operatorname{GL}_N\times \operatorname{GL}_N$-equivariant coherent sheaves on the shifted cotangent bundle
$\operatorname{GL}_N\times \operatorname{GL}_N$-equivariant coherent sheaves on the shifted cotangent bundle ![]() $T^*{\mathfrak {gl}}_N$.
$T^*{\mathfrak {gl}}_N$.
Next, we equip the above-defined categories with monoidal structures. The monoidal structure ![]() $\stackrel {A}*$ on
$\stackrel {A}*$ on ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{2,0})$ is defined as a convolution operation on
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{2,0})$ is defined as a convolution operation on ![]() $D$-modules associated with the map
$D$-modules associated with the map ![]() ${\mathfrak {gl}}_N\times {\mathfrak {gl}}_N\to {\mathfrak {gl}}_N$, given by matrix multiplication. The monoidal structure
${\mathfrak {gl}}_N\times {\mathfrak {gl}}_N\to {\mathfrak {gl}}_N$, given by matrix multiplication. The monoidal structure ![]() $\stackrel {B}*$ on
$\stackrel {B}*$ on ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{0,2})$ is defined as
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {D}}^\bullet _{0,2})$ is defined as ![]() ${\mathsf {F}}^{-1}\circ (\stackrel {A}*)\circ (\mathsf {F}\times \mathsf {F})$, where
${\mathsf {F}}^{-1}\circ (\stackrel {A}*)\circ (\mathsf {F}\times \mathsf {F})$, where ![]() $\mathsf {F}$ is the functor of Fourier transform on
$\mathsf {F}$ is the functor of Fourier transform on ![]() $D$-modules. Each of these monoidal structures has a quasiclassical limit at
$D$-modules. Each of these monoidal structures has a quasiclassical limit at ![]() $\hbar =0$, defined as a convolution of coherent sheaves arising from a certain Lagrangian correspondence. Finally, the tensor product of coherent sheaves, that is, the functor
$\hbar =0$, defined as a convolution of coherent sheaves arising from a certain Lagrangian correspondence. Finally, the tensor product of coherent sheaves, that is, the functor ![]() ${\mathcal {M}},{\mathcal {M}}'\mapsto {\mathcal {M}}\,{\otimes}_{{{\mathfrak {S}}_{1,1}^\bullet }}\ {\mathcal {M}}'$, gives a monoidal structure on
${\mathcal {M}},{\mathcal {M}}'\mapsto {\mathcal {M}}\,{\otimes}_{{{\mathfrak {S}}_{1,1}^\bullet }}\ {\mathcal {M}}'$, gives a monoidal structure on ![]() $D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1})$. This monoidal structure has no counterpart for
$D_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1})$. This monoidal structure has no counterpart for ![]() $D$-modules (i.e. for
$D$-modules (i.e. for ![]() $\hbar \ne 0$)z.
$\hbar \ne 0$)z.
One of the main results of the present paper (see Theorems 3.6.1 and 5.1.1) states that one has the following equivalences of triangulated monoidal categories, called mirabolic Satake equivalences:
 \begin{align*} \big(D_{{\operatorname{perf}}}^{{{\operatorname{GL}}}_N\times{{\operatorname{GL}}}_N}({\mathfrak{D}}^\bullet_{2,0}),\ \stackrel{A}*\big)\ \ &\xrightarrow[{}^{{\cong}}]{\Phi^{2,0}_\hbar} \ \ \big(D_{!{\mathbf{G}}_{\mathbf{O}}\rtimes{\mathbb{C}}^\times}({\mathbf{Gr}}\times{\mathbf{V}}),\ {\stackrel{!}\circledast}\big),\\ \big(D_{{\operatorname{perf}}}^{{{\operatorname{GL}}}_N\times{{\operatorname{GL}}}_N}({\mathfrak{D}}^\bullet_{0,2}),\ \stackrel{B}*\big)\ \ &\xrightarrow[{}^{{\cong}}]{\Phi^{0,2}_\hbar}\ \ \ \ \big(D_{*{\mathbf{G}}_{\mathbf{O}}\rtimes{\mathbb{C}}^\times}({\mathbf{Gr}}\times{\mathbf{V}}),\ \stackrel{*}*\big),\\ \big(D_{{\operatorname{perf}}}^{{{\operatorname{GL}}}_N\times{{\operatorname{GL}}}_N}({{\mathfrak{S}}^\bullet_{1,1}}),\ \,{\otimes}_{_{{{\mathfrak{S}}_{1,1}^\bullet}}}\big)\ \ &\xrightarrow[{}^{{\cong}}]{\Phi^{1,1}}\ \ \ \ \big(D_{!*{\mathbf{G}}_{\mathbf{O}}}({\mathbf{Gr}}\times{\mathbf{V}}),\ \star\big). \end{align*}
\begin{align*} \big(D_{{\operatorname{perf}}}^{{{\operatorname{GL}}}_N\times{{\operatorname{GL}}}_N}({\mathfrak{D}}^\bullet_{2,0}),\ \stackrel{A}*\big)\ \ &\xrightarrow[{}^{{\cong}}]{\Phi^{2,0}_\hbar} \ \ \big(D_{!{\mathbf{G}}_{\mathbf{O}}\rtimes{\mathbb{C}}^\times}({\mathbf{Gr}}\times{\mathbf{V}}),\ {\stackrel{!}\circledast}\big),\\ \big(D_{{\operatorname{perf}}}^{{{\operatorname{GL}}}_N\times{{\operatorname{GL}}}_N}({\mathfrak{D}}^\bullet_{0,2}),\ \stackrel{B}*\big)\ \ &\xrightarrow[{}^{{\cong}}]{\Phi^{0,2}_\hbar}\ \ \ \ \big(D_{*{\mathbf{G}}_{\mathbf{O}}\rtimes{\mathbb{C}}^\times}({\mathbf{Gr}}\times{\mathbf{V}}),\ \stackrel{*}*\big),\\ \big(D_{{\operatorname{perf}}}^{{{\operatorname{GL}}}_N\times{{\operatorname{GL}}}_N}({{\mathfrak{S}}^\bullet_{1,1}}),\ \,{\otimes}_{_{{{\mathfrak{S}}_{1,1}^\bullet}}}\big)\ \ &\xrightarrow[{}^{{\cong}}]{\Phi^{1,1}}\ \ \ \ \big(D_{!*{\mathbf{G}}_{\mathbf{O}}}({\mathbf{Gr}}\times{\mathbf{V}}),\ \star\big). \end{align*}
Furthermore, it turns out that the triangulated category ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is equivalent to the bounded derived category of the abelian category
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is equivalent to the bounded derived category of the abelian category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant perverse sheaves on
${\mathbf {G}}_{\mathbf {O}}$-equivariant perverse sheaves on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$, the heart of the perverse
${\mathbf {Gr}}\times {\mathbf {V}}$, the heart of the perverse ![]() $t$-structure on
$t$-structure on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
Remark 1.3.1 The counterpart of the last statement in the case of the usual Satake category is false: the triangulated category ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is not equivalent to the derived category of the category
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is not equivalent to the derived category of the category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$, which is well known to be a semisimple abelian category.
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$, which is well known to be a semisimple abelian category.
Remark 1.3.2 One can view the group ![]() $\operatorname{GL}_N$ as a Zariski open subset of the vector space
$\operatorname{GL}_N$ as a Zariski open subset of the vector space ![]() ${\mathfrak {gl}}_N$ of all
${\mathfrak {gl}}_N$ of all ![]() $N\times N$ matrices. Associated with the open embedding
$N\times N$ matrices. Associated with the open embedding ![]() $\operatorname{GL}_N{\hookrightarrow} {\mathfrak {gl}}_N$, one has a restriction functor on
$\operatorname{GL}_N{\hookrightarrow} {\mathfrak {gl}}_N$, one has a restriction functor on ![]() $D$-modules. It turns out that the counterpart of this functor for constructible derived categories is a suitably defined version of restriction with respect to the ‘zero section’
$D$-modules. It turns out that the counterpart of this functor for constructible derived categories is a suitably defined version of restriction with respect to the ‘zero section’ ![]() ${\mathbf {Gr}}\times \{0\}{\hookrightarrow} {\mathbf {Gr}}\times {\mathbf {V}}$. That is, one has a natural functor
${\mathbf {Gr}}\times \{0\}{\hookrightarrow} {\mathbf {Gr}}\times {\mathbf {V}}$. That is, one has a natural functor ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ ![]() $\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$. We will show that the latter functor makes the derived Satake category
$\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$. We will show that the latter functor makes the derived Satake category ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ a localization of the mirabolic derived Satake category
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ a localization of the mirabolic derived Satake category ![]() ${D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}$. Moreover, the mirabolic Satake equivalence is compatible with the standard Satake equivalence in the sense that there is a commutative diagram of functors
${D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}$. Moreover, the mirabolic Satake equivalence is compatible with the standard Satake equivalence in the sense that there is a commutative diagram of functors

1.4 Conjectural Iwahori-equivariant version
Let ![]() ${\mathbf {I}}\subset {\mathbf {G}}_{\mathbf {O}}$ be an Iwahori subgroup and
${\mathbf {I}}\subset {\mathbf {G}}_{\mathbf {O}}$ be an Iwahori subgroup and ![]() ${\mathbf {Fl}}:={\mathbf {G}}_{\mathbf {F}}/{\mathbf {I}}$ the affine flag variety. In [Reference BezrukavnikovBez16], Bezrukavnikov established an equivalence of
${\mathbf {Fl}}:={\mathbf {G}}_{\mathbf {F}}/{\mathbf {I}}$ the affine flag variety. In [Reference BezrukavnikovBez16], Bezrukavnikov established an equivalence of ![]() $D_{\mathbf {I}}({\mathbf {Fl}})$, the
$D_{\mathbf {I}}({\mathbf {Fl}})$, the ![]() ${\mathbf {I}}$-equivariant constructible derived category of
${\mathbf {I}}$-equivariant constructible derived category of ![]() ${\mathbf {Fl}}$, and the derived category of
${\mathbf {Fl}}$, and the derived category of ![]() $\operatorname{GL}_N$-equivariant coherent sheaves on an appropriate dg-version of the Steinberg variety. Motivated by this result, we expect that there is a mirabolic counterpart of this equivalence.
$\operatorname{GL}_N$-equivariant coherent sheaves on an appropriate dg-version of the Steinberg variety. Motivated by this result, we expect that there is a mirabolic counterpart of this equivalence.
To explain this, fix a pair ![]() $V_1,V_2$, of
$V_1,V_2$, of ![]() $N$-dimensional vector spaces and let
$N$-dimensional vector spaces and let ![]() ${\mathcal {F}\ell }_i,\ i=1,2$, denote the variety of complete flags in
${\mathcal {F}\ell }_i,\ i=1,2$, denote the variety of complete flags in ![]() $V_i$. Further, consider a dg-scheme with zero differential
$V_i$. Further, consider a dg-scheme with zero differential
Footnote 2
Write ![]() $A$ (respectively,
$A$ (respectively, ![]() $B$) for an element of
$B$) for an element of ![]() ${\operatorname{Hom}}(V_1,V_2)[1]$ (respectively,
${\operatorname{Hom}}(V_1,V_2)[1]$ (respectively, ![]() ${\operatorname{Hom}}(V_2,V_1)[1]$), and
${\operatorname{Hom}}(V_2,V_1)[1]$), and ![]() $F_i=(F^{(1)}_i\subset F^{(2)}_i\subset \cdots \subset F^{(N)}_i=V_i)$ for an element of
$F_i=(F^{(1)}_i\subset F^{(2)}_i\subset \cdots \subset F^{(N)}_i=V_i)$ for an element of ![]() ${\mathcal {F}\ell }_i$.
${\mathcal {F}\ell }_i$.
We define the mirabolic Steinberg scheme to be a dg-subscheme ![]() $\operatorname {St}_{\operatorname {mir}}$ of
$\operatorname {St}_{\operatorname {mir}}$ of ![]() $\operatorname {H}_{\operatorname {mir}}$ cut out by the equations saying that the flag
$\operatorname {H}_{\operatorname {mir}}$ cut out by the equations saying that the flag ![]() $F_2$ is stable under the composition
$F_2$ is stable under the composition ![]() $AB$ and the flag
$AB$ and the flag ![]() $F_1$ is stable under the composition
$F_1$ is stable under the composition ![]() $BA$. Thus the mirabolic Steinberg scheme is a shifted variety of quadruples:
$BA$. Thus the mirabolic Steinberg scheme is a shifted variety of quadruples:
Let ![]() $D_{\mathbf {I}}({\mathbf {Fl}}\times {\mathbf {V}})$ be the
$D_{\mathbf {I}}({\mathbf {Fl}}\times {\mathbf {V}})$ be the ![]() ${\mathbf {I}}$-equivariant constructible derived category of
${\mathbf {I}}$-equivariant constructible derived category of ![]() ${\mathbf {Fl}}\times {\mathbf {V}}$. We propose the following conjecture.
${\mathbf {Fl}}\times {\mathbf {V}}$. We propose the following conjecture.
Conjecture 1.4.1 There exists an equivalence of triangulated categories
This conjecture would explain, in particular, the appearance of the same polynomials, called the Kostka–Shoji polynomials, in two different problems. On the one hand, it was proved in [Reference Finkelberg, Ginzburg and TravkinFGT09] that these polynomials are equal to the Poincaré polynomials of the stalks of ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant intersection cohomology (IC) sheaves on the mirabolic affine Grassmannian. On the other hand, it was proved in [Reference Finkelberg and IonovFI18] that the Kostka–Shoji polynomials are equal to the Poincaré polynomials of graded multiplicities of the natural
${\mathbf {G}}_{\mathbf {O}}$-equivariant intersection cohomology (IC) sheaves on the mirabolic affine Grassmannian. On the other hand, it was proved in [Reference Finkelberg and IonovFI18] that the Kostka–Shoji polynomials are equal to the Poincaré polynomials of graded multiplicities of the natural ![]() $\operatorname{GL}_N\times \operatorname{GL}_N$-action on the space of global sections of line bundles on a convolution diagram of the cyclic
$\operatorname{GL}_N\times \operatorname{GL}_N$-action on the space of global sections of line bundles on a convolution diagram of the cyclic ![]() $\tilde {A}_1$-quiver.
$\tilde {A}_1$-quiver.
1.5 Satake equivalence for some Lie supergroups
We consider the Lie superalgebra ![]() ${\mathfrak {gl}}(M|N)$ of endomorphisms of a super vector space
${\mathfrak {gl}}(M|N)$ of endomorphisms of a super vector space ![]() ${\mathbb {C}}^{M|N}$, and the corresponding Lie supergroup
${\mathbb {C}}^{M|N}$, and the corresponding Lie supergroup ![]() $\operatorname{GL}(M|N)=\operatorname {Aut}({\mathbb {C}}^{M|N})$. We also consider a degenerate version
$\operatorname{GL}(M|N)=\operatorname {Aut}({\mathbb {C}}^{M|N})$. We also consider a degenerate version ![]() $\underline {\mathfrak {gl}}(M|N)$ where the supercommutator of the even elements (with even or odd elements) is the same as in
$\underline {\mathfrak {gl}}(M|N)$ where the supercommutator of the even elements (with even or odd elements) is the same as in ![]() ${\mathfrak {gl}}(M|N)$, while the supercommutator of any two odd elements is set to zero. In other words, the even part
${\mathfrak {gl}}(M|N)$, while the supercommutator of any two odd elements is set to zero. In other words, the even part ![]() $\underline {\mathfrak {gl}}(M|N){}_{\bar 0}={\mathfrak {gl}}_M\oplus {\mathfrak {gl}}_N$ acts naturally on the odd part
$\underline {\mathfrak {gl}}(M|N){}_{\bar 0}={\mathfrak {gl}}_M\oplus {\mathfrak {gl}}_N$ acts naturally on the odd part ![]() $\underline {\mathfrak {gl}}(M|N){}_{\bar 1}={\operatorname{Hom}}({\mathbb {C}}^M,{\mathbb {C}}^N)\oplus {\operatorname{Hom}}({\mathbb {C}}^N,{\mathbb {C}}^M)$, but the supercommutator
$\underline {\mathfrak {gl}}(M|N){}_{\bar 1}={\operatorname{Hom}}({\mathbb {C}}^M,{\mathbb {C}}^N)\oplus {\operatorname{Hom}}({\mathbb {C}}^N,{\mathbb {C}}^M)$, but the supercommutator ![]() $\underline {\mathfrak {gl}}(M|N){}_{\bar 1}\times \underline {\mathfrak {gl}}(M|N){}_{\bar 1}\to \underline {\mathfrak {gl}}(M|N){}_{\bar 0}$ equals zero.
$\underline {\mathfrak {gl}}(M|N){}_{\bar 1}\times \underline {\mathfrak {gl}}(M|N){}_{\bar 1}\to \underline {\mathfrak {gl}}(M|N){}_{\bar 0}$ equals zero.
The category of finite-dimensional representations of the corresponding supergroup ![]() $\underline{\operatorname{GL}}(M|N)$ (in vector superspaces) is denoted by
$\underline{\operatorname{GL}}(M|N)$ (in vector superspaces) is denoted by ![]() ${\operatorname {Rep}}(\underline{\operatorname{GL}}(M|N))$, and its bounded derived category is denoted by
${\operatorname {Rep}}(\underline{\operatorname{GL}}(M|N))$, and its bounded derived category is denoted by ![]() $SD(\underline{\operatorname{GL}}(M|N))$.
$SD(\underline{\operatorname{GL}}(M|N))$.
There is a Koszul equivalence ![]() $\varkappa \colon SD(\underline{\operatorname{GL}}(N|N)){\buildrel \sim \over \longrightarrow} SD_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1})$ (equivariant perfect dg-supermodules over dg-superalgebra
$\varkappa \colon SD(\underline{\operatorname{GL}}(N|N)){\buildrel \sim \over \longrightarrow} SD_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1})$ (equivariant perfect dg-supermodules over dg-superalgebra ![]() ${\mathfrak {S}}^\bullet _{1,1}$); see, for example, [Reference Mirković and RicheMR10]. It intertwines the usual tensor product of
${\mathfrak {S}}^\bullet _{1,1}$); see, for example, [Reference Mirković and RicheMR10]. It intertwines the usual tensor product of ![]() $\underline{\operatorname{GL}}(N|N)$-modules with the tensor product
$\underline{\operatorname{GL}}(N|N)$-modules with the tensor product ![]() ${\otimes}_{{\mathfrak {S}}^\bullet _{1,1}}$ on
${\otimes}_{{\mathfrak {S}}^\bullet _{1,1}}$ on ![]() $SD_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1})$. Composing the Koszul equivalence
$SD_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1})$. Composing the Koszul equivalence ![]() $\varkappa$ with the mirabolic Satake equivalence
$\varkappa$ with the mirabolic Satake equivalence ![]() $\Phi ^{1,1}\colon SD_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1}){\buildrel \sim \over \longrightarrow} SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (constructible sheaves of supervector spaces) we obtain a super Satake equivalence
$\Phi ^{1,1}\colon SD_{\operatorname{perf}}^{\operatorname{GL}_N{\!\times\!} \operatorname{GL}_N}({\mathfrak {S}}^\bullet _{1,1}){\buildrel \sim \over \longrightarrow} SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (constructible sheaves of supervector spaces) we obtain a super Satake equivalence ![]() $SD(\underline{\operatorname{GL}}(N|N)){\buildrel \sim \over \longrightarrow} SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ that intertwines the usual tensor product of
$SD(\underline{\operatorname{GL}}(N|N)){\buildrel \sim \over \longrightarrow} SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ that intertwines the usual tensor product of ![]() $\underline{\operatorname{GL}}(N|N)$-modules with the fusion product on
$\underline{\operatorname{GL}}(N|N)$-modules with the fusion product on ![]() $SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Moreover, this derived equivalence is exact with respect to the tautological
$SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Moreover, this derived equivalence is exact with respect to the tautological ![]() $t$-structure on
$t$-structure on ![]() $SD(\underline{\operatorname{GL}}(N|N))$ with the heart
$SD(\underline{\operatorname{GL}}(N|N))$ with the heart ![]() ${\operatorname {Rep}}(\underline{\operatorname{GL}}(N|N))$ (respectively, the perverse
${\operatorname {Rep}}(\underline{\operatorname{GL}}(N|N))$ (respectively, the perverse ![]() $t$-structure on
$t$-structure on ![]() $SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ with the heart
$SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ with the heart ![]() $S{\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$).
$S{\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$).
Similarly, we construct equivalences
where ![]() $\bar {\mathfrak {S}}{}^\bullet _{1,1}={\operatorname{Sym}}\!{}^\bullet \big ({\operatorname{Hom}}({\mathbb {C}}^{N-1},{\mathbb {C}}^N)[-1]\oplus {\operatorname{Hom}}({\mathbb {C}}^N,{\mathbb {C}}^{N-1})[-1]\big )$.Footnote 3 The composition is again
$\bar {\mathfrak {S}}{}^\bullet _{1,1}={\operatorname{Sym}}\!{}^\bullet \big ({\operatorname{Hom}}({\mathbb {C}}^{N-1},{\mathbb {C}}^N)[-1]\oplus {\operatorname{Hom}}({\mathbb {C}}^N,{\mathbb {C}}^{N-1})[-1]\big )$.Footnote 3 The composition is again ![]() $t$-exact with respect to the tautological
$t$-exact with respect to the tautological ![]() $t$-structure on
$t$-structure on ![]() $SD(\underline{\operatorname{GL}}(N-1|N))$ with the heart
$SD(\underline{\operatorname{GL}}(N-1|N))$ with the heart ![]() ${\operatorname {Rep}}(\underline{\operatorname{GL}}(N-1|N))$ (respectively, the perverse
${\operatorname {Rep}}(\underline{\operatorname{GL}}(N-1|N))$ (respectively, the perverse ![]() $t$-structure on
$t$-structure on ![]() $SD_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$ with the heart
$SD_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$ with the heart ![]() $S{\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$). Moreover, the composition intertwines the usual tensor product of
$S{\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$). Moreover, the composition intertwines the usual tensor product of ![]() $\underline{\operatorname{GL}}(N-1|N)$-modules with the fusion product on
$\underline{\operatorname{GL}}(N-1|N)$-modules with the fusion product on ![]() $S{\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$. Similarly to § 1.3, the functor
$S{\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$. Similarly to § 1.3, the functor ![]() $\bar \Phi$ can be extended to an equivalence
$\bar \Phi$ can be extended to an equivalence ![]() $\bar \Phi {}_\hbar \colon SD_{\operatorname{perf}}^{\operatorname{GL}_{N-1}{\!\times\!} \operatorname{GL}_N}(\bar {\mathfrak {D}}{}^\bullet ){\buildrel \sim \over \longrightarrow} SD_{\operatorname{GL}(N-1,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}_{\operatorname{GL}_{N}})$, where
$\bar \Phi {}_\hbar \colon SD_{\operatorname{perf}}^{\operatorname{GL}_{N-1}{\!\times\!} \operatorname{GL}_N}(\bar {\mathfrak {D}}{}^\bullet ){\buildrel \sim \over \longrightarrow} SD_{\operatorname{GL}(N-1,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}_{\operatorname{GL}_{N}})$, where ![]() $\bar {\mathfrak {D}}{}^\bullet$ is the graded Weyl algebra of shifted differential operators on
$\bar {\mathfrak {D}}{}^\bullet$ is the graded Weyl algebra of shifted differential operators on ![]() ${\operatorname{Hom}}({\mathbb {C}}^{N-1},{\mathbb {C}}^N)$ (with
${\operatorname{Hom}}({\mathbb {C}}^{N-1},{\mathbb {C}}^N)$ (with ![]() $\deg \hbar =2$ and all the other generators in degree 1).
$\deg \hbar =2$ and all the other generators in degree 1).
1.6 Gaiotto conjectures
One may wonder if there is a geometric realization of categories of representations of non-degenerate supergroups ![]() $\operatorname{GL}(N|N),\ \operatorname{GL}(N-1|N)$. It turns out that such a realization exists (conjecturally) for the categories of integrable representations of quantized algebras
$\operatorname{GL}(N|N),\ \operatorname{GL}(N-1|N)$. It turns out that such a realization exists (conjecturally) for the categories of integrable representations of quantized algebras ![]() $U_q({\mathfrak {gl}}(N|N)),\ U_q({\mathfrak {gl}}(N-1|N))$. First of all, similarly to the classical Kazhdan–Lusztig equivalence, it is expected that
$U_q({\mathfrak {gl}}(N|N)),\ U_q({\mathfrak {gl}}(N-1|N))$. First of all, similarly to the classical Kazhdan–Lusztig equivalence, it is expected that ![]() $U_q({\mathfrak {gl}}(M|N))\operatorname {-mod}\cong \operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$, where
$U_q({\mathfrak {gl}}(M|N))\operatorname {-mod}\cong \operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$, where ![]() $q=\exp (\pi \sqrt {-1}/c)$, and
$q=\exp (\pi \sqrt {-1}/c)$, and ![]() $\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ stands for the derived category of
$\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ stands for the derived category of ![]() $\operatorname{GL}(M,{\mathbf {O}})\times \operatorname{GL}(N,{\mathbf {O}})$-equivariant
$\operatorname{GL}(M,{\mathbf {O}})\times \operatorname{GL}(N,{\mathbf {O}})$-equivariant ![]() $\widehat {\mathfrak {gl}}(M|N)$-modules at the level corresponding to the invariant bilinear form
$\widehat {\mathfrak {gl}}(M|N)$-modules at the level corresponding to the invariant bilinear form ![]() $(X,Y)=c\cdot \operatorname {sTr}(XY)-\frac 12\operatorname {Killing}_{{\mathfrak {gl}}(M|N)}(X,Y)$ on
$(X,Y)=c\cdot \operatorname {sTr}(XY)-\frac 12\operatorname {Killing}_{{\mathfrak {gl}}(M|N)}(X,Y)$ on ![]() ${\mathfrak {gl}}(M|N)$. Second, it is expected that the category
${\mathfrak {gl}}(M|N)$. Second, it is expected that the category ![]() $\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N-1|N))$ is equivalent to the
$\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N-1|N))$ is equivalent to the ![]() $q$-monodromic
$q$-monodromic ![]() $\operatorname{GL}(N-1,{\mathbf {O}})$-equivariant derived constructible category of the complement
$\operatorname{GL}(N-1,{\mathbf {O}})$-equivariant derived constructible category of the complement ![]() ${\mathcal {L}}^\bullet$ of the zero section of the determinant line bundle on
${\mathcal {L}}^\bullet$ of the zero section of the determinant line bundle on ![]() ${\mathbf {Gr}}_{\operatorname{GL}_N}$, and this equivalence takes the standard
${\mathbf {Gr}}_{\operatorname{GL}_N}$, and this equivalence takes the standard ![]() $t$-structure of
$t$-structure of ![]() $\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N-1|N))$ to the perverse
$\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N-1|N))$ to the perverse ![]() $t$-structure.
$t$-structure.
Further, it is expected that ![]() $\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N|N))$ is equivalent to the
$\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N|N))$ is equivalent to the ![]() $q$-monodromic
$q$-monodromic ![]() $\operatorname{GL}(N,{\mathbf {O}})$-equivariant derived constructible category of
$\operatorname{GL}(N,{\mathbf {O}})$-equivariant derived constructible category of ![]() ${\mathcal {L}}^\bullet \times {\mathbf {V}}$, and this equivalence takes the standard
${\mathcal {L}}^\bullet \times {\mathbf {V}}$, and this equivalence takes the standard ![]() $t$-structure of
$t$-structure of ![]() $\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N|N))$ to the perverse
$\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(N|N))$ to the perverse ![]() $t$-structure. For
$t$-structure. For ![]() $M< N-1$ it is expected that
$M< N-1$ it is expected that ![]() $\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(M|N))$ is equivalent to the
$\operatorname {KL}_c(\widehat {{\mathfrak {gl}}}(M|N))$ is equivalent to the ![]() $q$-monodromic
$q$-monodromic ![]() $\operatorname{GL}(M,{\mathbf {O}})$-equivariant derived constructible category of
$\operatorname{GL}(M,{\mathbf {O}})$-equivariant derived constructible category of ![]() ${\mathcal {L}}^\bullet$ with certain Whittaker conditions; cf. § 2.6 for more details. In particular, the special case
${\mathcal {L}}^\bullet$ with certain Whittaker conditions; cf. § 2.6 for more details. In particular, the special case ![]() $M=0$ of this conjecture follows from the fundamental local equivalence [Reference GaitsgoryGai08, Reference GaitsgoryGai16, Reference GaitsgoryGai20] of the geometric Langlands program.
$M=0$ of this conjecture follows from the fundamental local equivalence [Reference GaitsgoryGai08, Reference GaitsgoryGai16, Reference GaitsgoryGai20] of the geometric Langlands program.
There are similar expectations for other classical (i.e. orthosymplectic) Lie superalgebras; the interested reader may try to find them in [Reference Gaiotto and WittenGW09].
1.7 Conjectures of Ben-Zvi, Sakellaridis and Venkatesh
In an ongoing project of D. Ben-Zvi, Y. Sakellaridis and A. Venkatesh, the authors propose the Periods–![]() $L$-functions duality conjectures. Their conjectures predict, among other things, that, given a reductive group
$L$-functions duality conjectures. Their conjectures predict, among other things, that, given a reductive group ![]() $\operatorname {G}$ and its spherical homogeneous variety
$\operatorname {G}$ and its spherical homogeneous variety ![]() $X=\operatorname {G}/\operatorname {H}$, there is a subgroup
$X=\operatorname {G}/\operatorname {H}$, there is a subgroup ![]() $\operatorname {G}^\vee _X\subset \operatorname {G}^\vee$, its graded representation
$\operatorname {G}^\vee _X\subset \operatorname {G}^\vee$, its graded representation ![]() $V^\vee _X=\bigoplus _{i\in {\mathbb {Z}}}V^\vee _{X,i}[i]$, and an equivalence
$V^\vee _X=\bigoplus _{i\in {\mathbb {Z}}}V^\vee _{X,i}[i]$, and an equivalence ![]() $D{\mathsf {Coh}}(V^\vee _X/\operatorname {G}^\vee _X)=D{\mathsf {Coh}}\big ((\bigoplus _{i\in {\mathbb {Z}}}V^\vee _{X,i}[i])/\operatorname {G}^\vee _X\big ) \simeq D_{\operatorname {G}({\mathbf {O}})}(X({\mathbf {F}}))$. For a partial list of examples, see the table at the end of [Reference SakellaridisSak13]. The relevant representations
$D{\mathsf {Coh}}(V^\vee _X/\operatorname {G}^\vee _X)=D{\mathsf {Coh}}\big ((\bigoplus _{i\in {\mathbb {Z}}}V^\vee _{X,i}[i])/\operatorname {G}^\vee _X\big ) \simeq D_{\operatorname {G}({\mathbf {O}})}(X({\mathbf {F}}))$. For a partial list of examples, see the table at the end of [Reference SakellaridisSak13]. The relevant representations ![]() $V^\vee _X$ (constructed in terms of the Luna diagram of
$V^\vee _X$ (constructed in terms of the Luna diagram of ![]() $X$) can be read off from the fourth column of the table.
$X$) can be read off from the fourth column of the table.
It turns out that the equivalences discussed in § 1.5 fit into the general setting outlined in the previous paragraph. Thus the case of [Reference SakellaridisSak13, Example 13] corresponds to the equivalence ![]() $\bar {\Phi }\colon D_{\operatorname{perf}}^{\operatorname{GL}_{N-1}{\!\times\!} \operatorname{GL}_N}(\bar {\mathfrak {S}}{}^\bullet _{1,1}){\buildrel \sim \over \longrightarrow} D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$ of § 1.5. To explain this, let
$\bar {\Phi }\colon D_{\operatorname{perf}}^{\operatorname{GL}_{N-1}{\!\times\!} \operatorname{GL}_N}(\bar {\mathfrak {S}}{}^\bullet _{1,1}){\buildrel \sim \over \longrightarrow} D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$ of § 1.5. To explain this, let ![]() $\operatorname {G}:=\operatorname{GL}_{N-1}\times \operatorname{GL}_N$ and
$\operatorname {G}:=\operatorname{GL}_{N-1}\times \operatorname{GL}_N$ and ![]() $\operatorname {H}:=\operatorname{GL}_{N-1}$. We view
$\operatorname {H}:=\operatorname{GL}_{N-1}$. We view ![]() $\operatorname {H}$ as a block-diagonal subgroup of
$\operatorname {H}$ as a block-diagonal subgroup of ![]() $\operatorname {G}$ and put
$\operatorname {G}$ and put ![]() $X=\operatorname {G}/\operatorname {H}$. Then, loosely speaking, we have
$X=\operatorname {G}/\operatorname {H}$. Then, loosely speaking, we have ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_{N}})$ ![]() $\simeq D\big (\operatorname{GL}(N-1,{\mathbf {O}})\backslash \operatorname{GL}(N,{\mathbf {F}})/\operatorname{GL}(N,{\mathbf {O}})\big )$
$\simeq D\big (\operatorname{GL}(N-1,{\mathbf {O}})\backslash \operatorname{GL}(N,{\mathbf {F}})/\operatorname{GL}(N,{\mathbf {O}})\big )$ ![]() $\simeq D\big (\operatorname {G}({\mathbf {O}})\backslash \operatorname {G}({\mathbf {F}})/\operatorname {H}({\mathbf {F}})\big )\simeq D\big (\operatorname {G}({\mathbf {O}})\backslash X({\mathbf {F}})\big )\simeq D_{\operatorname {G}({\mathbf {O}})}(X({\mathbf {F}}))$. On the other hand, we consider a graded
$\simeq D\big (\operatorname {G}({\mathbf {O}})\backslash \operatorname {G}({\mathbf {F}})/\operatorname {H}({\mathbf {F}})\big )\simeq D\big (\operatorname {G}({\mathbf {O}})\backslash X({\mathbf {F}})\big )\simeq D_{\operatorname {G}({\mathbf {O}})}(X({\mathbf {F}}))$. On the other hand, we consider a graded ![]() $\operatorname {G}^\vee$-module
$\operatorname {G}^\vee$-module ![]() $V^\vee _X:={\operatorname{Hom}}({\mathbb {C}}^{N-1},{\mathbb {C}}^N)[1]\oplus {\operatorname{Hom}}({\mathbb {C}}^N,{\mathbb {C}}^{N-1})[1]$ (similarly to the footnote in § 1.5, we view
$V^\vee _X:={\operatorname{Hom}}({\mathbb {C}}^{N-1},{\mathbb {C}}^N)[1]\oplus {\operatorname{Hom}}({\mathbb {C}}^N,{\mathbb {C}}^{N-1})[1]$ (similarly to the footnote in § 1.5, we view ![]() $V^\vee _X$ as an odd vector space placed in cohomological degree
$V^\vee _X$ as an odd vector space placed in cohomological degree ![]() $-1$; note also that
$-1$; note also that ![]() $\operatorname {G}^\vee \simeq \operatorname {G}=\operatorname{GL}_{N-1}\times \operatorname{GL}_N$). Hence, the equivalence
$\operatorname {G}^\vee \simeq \operatorname {G}=\operatorname{GL}_{N-1}\times \operatorname{GL}_N$). Hence, the equivalence ![]() $\bar {\Phi }$ of § 1.5 takes the form
$\bar {\Phi }$ of § 1.5 takes the form ![]() $D{\mathsf {Coh}}(V^\vee _X/\operatorname {G}^\vee )\simeq D_{\operatorname {G}({\mathbf {O}})}(X({\mathbf {F}}))$.
$D{\mathsf {Coh}}(V^\vee _X/\operatorname {G}^\vee )\simeq D_{\operatorname {G}({\mathbf {O}})}(X({\mathbf {F}}))$.
Similarly, [Reference SakellaridisSak13, Example 14] matches the Gaiotto conjecture of § 1.6 for an orthosymplectic Lie superalgebra.
1.8 Organization of the paper
In § 2 (which is not necessary for understanding subsequent sections) we formulate the Gaiotto conjectures and explain their relation to the geometric Langlands program and, in particular, with the fundamental local equivalence. Section 3 is the technical core of the paper. In this section we establish a coherent description of the spherical mirabolic affine Hecke category ![]() $D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}})$ with its three monoidal structures. Also, as preparation for § 4 we give a coherent description of the restriction functor
$D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}})$ with its three monoidal structures. Also, as preparation for § 4 we give a coherent description of the restriction functor ![]() $D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}}_0)$.Footnote 4 In § 4 we establish a coherent description of the category
$D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}}_0)$.Footnote 4 In § 4 we establish a coherent description of the category ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ along with its fusion monoidal structure. In § 5 we prove the quantum analogues, that is, counterparts for categories equivariant with respect to the loop rotations, of the results above.
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ along with its fusion monoidal structure. In § 5 we prove the quantum analogues, that is, counterparts for categories equivariant with respect to the loop rotations, of the results above.
2. Gaiotto conjectures
The purpose of the present section is to put the main results of this paper into a wider framework which has to do with the local geometric Langlands correspondence. This section will be used for motivation purposes only. It can be safely skipped by readers who are not interested in the geometric Langlands correspondence. The ideas of this section are due to D. Gaiotto (private communication). Gaiotto informed us that his ideas were motivated, to a large extent, by his discussions with P. Yoo as well as by [Reference Mikhaylov and WittenMW15].
2.1 Reminder on strong actions on categories
Let ![]() $G$ be a connected reductive group over
$G$ be a connected reductive group over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\kappa$ denote an invariant symmetric bilinear form on the Lie algebra
$\kappa$ denote an invariant symmetric bilinear form on the Lie algebra ![]() $\mathfrak {g}$ of
$\mathfrak {g}$ of ![]() $G$ (when
$G$ (when ![]() $G$ is simple, the vector space of such bilinear forms is one-dimensional, so we can think of
$G$ is simple, the vector space of such bilinear forms is one-dimensional, so we can think of ![]() $\kappa$ as an element of
$\kappa$ as an element of ![]() $\mathbb {C}$). Then there is a notion of strong action of the group
$\mathbb {C}$). Then there is a notion of strong action of the group ![]() $G_{\mathbf {F}}$ on a category
$G_{\mathbf {F}}$ on a category ![]() $\mathcal {C}$ of level
$\mathcal {C}$ of level ![]() $\kappa$. We refer the reader to [Reference GaitsgoryGai16] for details of the definition. It will be important for us later that this definition is, in some sense, invariant under integral shifts. Specifically, any category
$\kappa$. We refer the reader to [Reference GaitsgoryGai16] for details of the definition. It will be important for us later that this definition is, in some sense, invariant under integral shifts. Specifically, any category ![]() $\mathcal {C}$ endowed with a
$\mathcal {C}$ endowed with a ![]() $G_{\mathbf {F}}$-action of level
$G_{\mathbf {F}}$-action of level ![]() $\kappa$ has a natural
$\kappa$ has a natural ![]() $G_{\mathbf {F}}$-action of level
$G_{\mathbf {F}}$-action of level ![]() $\kappa +\kappa '$, where
$\kappa +\kappa '$, where ![]() $\kappa '$ is another form as above which is, moreover, integral in the sense that the corresponding quadratic form is integral and even on elements of the coweight lattice of
$\kappa '$ is another form as above which is, moreover, integral in the sense that the corresponding quadratic form is integral and even on elements of the coweight lattice of ![]() $G$. Here are two important examples.
$G$. Here are two important examples.
(1) Let ![]() $\hat {\mathfrak {g}}_{\kappa }$ denote the central extension of
$\hat {\mathfrak {g}}_{\kappa }$ denote the central extension of ![]() $\mathfrak {g}_{\mathbf {F}}$ associated with the form
$\mathfrak {g}_{\mathbf {F}}$ associated with the form ![]() $\kappa$. Let
$\kappa$. Let ![]() $\hat {\mathfrak {g}}_{\kappa }$-mod be the category of continuous (with respect to
$\hat {\mathfrak {g}}_{\kappa }$-mod be the category of continuous (with respect to ![]() $t$-adic topology) modules over
$t$-adic topology) modules over ![]() $\hat {\mathfrak {g}}_{\kappa }$ such that the element 1 of the center acts on the module as the identity. Then the adjoint action of
$\hat {\mathfrak {g}}_{\kappa }$ such that the element 1 of the center acts on the module as the identity. Then the adjoint action of ![]() $G_{\mathbf {F}}$ on
$G_{\mathbf {F}}$ on ![]() $\hat {\mathfrak {g}}_{\kappa }$ has a natural lift to a strong action of
$\hat {\mathfrak {g}}_{\kappa }$ has a natural lift to a strong action of ![]() $G_{\mathbf {F}}$ on
$G_{\mathbf {F}}$ on ![]() $\hat {\mathfrak {g}}_{\kappa }$-mod of level
$\hat {\mathfrak {g}}_{\kappa }$-mod of level ![]() $\kappa$. More generally, let
$\kappa$. More generally, let ![]() $\mathfrak a=\mathfrak a_{\bar 0}\oplus \mathfrak a_{\bar 1}$ be a Lie superalgebra. Make the following assumptions.
$\mathfrak a=\mathfrak a_{\bar 0}\oplus \mathfrak a_{\bar 1}$ be a Lie superalgebra. Make the following assumptions.
(i)
 $G$ acts on
$G$ acts on  $\mathfrak a$.
$\mathfrak a$.(ii) We are given a map
 $\iota \colon \mathfrak {g}\to \mathfrak a_{\bar 0}$ such that the corresponding adjoint action of
$\iota \colon \mathfrak {g}\to \mathfrak a_{\bar 0}$ such that the corresponding adjoint action of  $\mathfrak {g}$ on
$\mathfrak {g}$ on  $\mathfrak a$ is equal to the derivative of the
$\mathfrak a$ is equal to the derivative of the  $G$-action from (i).
$G$-action from (i).(iii) The algebra
 $\mathfrak a$ is equipped with an invariant symmetric (in the super sense) bilinear form
$\mathfrak a$ is equipped with an invariant symmetric (in the super sense) bilinear form  $\kappa _{\mathfrak a}$. Let
$\kappa _{\mathfrak a}$. Let  $\kappa _{\mathfrak {g}}$ be its pullback to
$\kappa _{\mathfrak {g}}$ be its pullback to  $\mathfrak {g}$.
$\mathfrak {g}$.
Associated with the form ![]() $\kappa _{\mathfrak a}$, there is a canonical Kac–Moody extension
$\kappa _{\mathfrak a}$, there is a canonical Kac–Moody extension ![]() $\hat {\mathfrak a}$ of
$\hat {\mathfrak a}$ of ![]() $\mathfrak a_{\mathbf {F}}$. As before, we denote by
$\mathfrak a_{\mathbf {F}}$. As before, we denote by ![]() $\hat {\mathfrak a}$-mod the category of continuous modules
$\hat {\mathfrak a}$-mod the category of continuous modules ![]() $M$ over
$M$ over ![]() $\hat {\mathfrak a}$ such that the element 1 of the center acts on
$\hat {\mathfrak a}$ such that the element 1 of the center acts on ![]() $M$ by the identity. This category comes equipped with a
$M$ by the identity. This category comes equipped with a ![]() $G_{\mathbf {F}}$-action of level
$G_{\mathbf {F}}$-action of level ![]() $\kappa _{\mathfrak {g}}$.
$\kappa _{\mathfrak {g}}$.
We will mostly be interested in the following special case of the above construction. Fix a pair ![]() $M,N$, of non-negative integers. Let
$M,N$, of non-negative integers. Let ![]() $\mathfrak a=\mathfrak {gl}(M|N)$,
$\mathfrak a=\mathfrak {gl}(M|N)$, ![]() $G=\operatorname{GL}_M\times \operatorname{GL}_N$. Let
$G=\operatorname{GL}_M\times \operatorname{GL}_N$. Let ![]() $\kappa _{\mathfrak a}(x,y)=c\cdot \operatorname {sTr}(xy)$, where
$\kappa _{\mathfrak a}(x,y)=c\cdot \operatorname {sTr}(xy)$, where ![]() $\operatorname {sTr}$ stands for ‘super-trace’ and
$\operatorname {sTr}$ stands for ‘super-trace’ and ![]() $c\in \mathbb {C}$.
$c\in \mathbb {C}$.
(2) Assume that the form ![]() $\kappa$ is integral and even. Then this form gives rise to a central extension
$\kappa$ is integral and even. Then this form gives rise to a central extension ![]() $\hat {G}$ of
$\hat {G}$ of ![]() $G_{\mathbf {F}}$. Let
$G_{\mathbf {F}}$. Let ![]() $X$ be an ind-scheme equipped with a
$X$ be an ind-scheme equipped with a ![]() $\hat {G}$-equivariant line bundle
$\hat {G}$-equivariant line bundle ![]() $\mathcal {L}$. Then, for any
$\mathcal {L}$. Then, for any ![]() $c\in \mathbb {C}$, one has the category
$c\in \mathbb {C}$, one has the category ![]() $D_c(X)$-mod of
$D_c(X)$-mod of ![]() $c$-twisted
$c$-twisted ![]() $D$-modules on
$D$-modules on ![]() $X$. This category has a natural strong
$X$. This category has a natural strong ![]() $G_{\mathbf {F}}$-action of level
$G_{\mathbf {F}}$-action of level ![]() $c\cdot \kappa$.
$c\cdot \kappa$.
2.2 Digression on the local (quantum) geometric Langlands correspondence
Let ![]() $G$ and
$G$ and ![]() $\kappa$ be as above and assume in addition that the form
$\kappa$ be as above and assume in addition that the form ![]() $\kappa$ is non-degenerate. Let
$\kappa$ is non-degenerate. Let ![]() $G^{\vee }$ denote the Langlands dual group. Since
$G^{\vee }$ denote the Langlands dual group. Since ![]() $\kappa$ is non-degenerate it gives a similar form
$\kappa$ is non-degenerate it gives a similar form ![]() $\kappa ^{\vee }$ for
$\kappa ^{\vee }$ for ![]() $G^{\vee }$. Further, put
$G^{\vee }$. Further, put ![]() $\kappa _{\operatorname {crit}}=-\frac 12{\operatorname {Killing}}_{\mathfrak {g}}$, where
$\kappa _{\operatorname {crit}}=-\frac 12{\operatorname {Killing}}_{\mathfrak {g}}$, where ![]() ${\operatorname {Killing}}_{\mathfrak {g}}$ stands for the Killing form on the Lie algebra
${\operatorname {Killing}}_{\mathfrak {g}}$ stands for the Killing form on the Lie algebra ![]() ${\mathfrak {g}}$ of
${\mathfrak {g}}$ of ![]() $G$.
$G$.
The local quantum geometric Langlands conjecture is, roughly speaking, an equivalence of 2-categories
and
The form ![]() $\kappa _{\operatorname {crit}}$ being integral, the shift by
$\kappa _{\operatorname {crit}}$ being integral, the shift by ![]() $\kappa _{\operatorname {crit}}$ in the above formulation is not essential. However, it is convenient for many applications to make this shift.
$\kappa _{\operatorname {crit}}$ in the above formulation is not essential. However, it is convenient for many applications to make this shift.
To give a rigorous meaning to the above conjecture one needs, first of all, to replace all ‘categories’ by suitable ‘dg-categories’. This upgrades each side of the equivalence to an ![]() $(\infty ,2)$-category. Then, for generic (i.e. non-rational)
$(\infty ,2)$-category. Then, for generic (i.e. non-rational) ![]() $\kappa$, the above equivalence is expected to hold as stated. For general
$\kappa$, the above equivalence is expected to hold as stated. For general ![]() $\kappa$, more corrections are necessary but we will not discuss this here since the local geometric Langlands correspondence will only serve as a guiding principle.
$\kappa$, more corrections are necessary but we will not discuss this here since the local geometric Langlands correspondence will only serve as a guiding principle.
There is a ‘limiting version’ of the above conjecture for ![]() $\kappa =0$. To explain this, we use the notion of a ‘category over a stack
$\kappa =0$. To explain this, we use the notion of a ‘category over a stack ![]() $\mathcal {S}$’; cf. [Reference GaitsgoryGai16, § 6] and references therein. Write
$\mathcal {S}$’; cf. [Reference GaitsgoryGai16, § 6] and references therein. Write ![]() $\mathcal {D}^\circ ={\operatorname{Spec}}({\mathbf {F}})$ and let
$\mathcal {D}^\circ ={\operatorname{Spec}}({\mathbf {F}})$ and let ![]() $\operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ )$ be the classifying stack of principal
$\operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ )$ be the classifying stack of principal ![]() $G^{\vee }$-bundles on
$G^{\vee }$-bundles on ![]() $\mathcal {D}^\circ$ equipped with a connection. The ‘classical’ local geometric Langlands conjecture predicts a close relationship between
$\mathcal {D}^\circ$ equipped with a connection. The ‘classical’ local geometric Langlands conjecture predicts a close relationship between
and
Here, ![]() $\kappa _{\operatorname {crit}}$ can be replaced by
$\kappa _{\operatorname {crit}}$ can be replaced by ![]() $0$, since
$0$, since ![]() $\kappa _{\operatorname {crit}}$ is integral. Again, it is possible to make the informal relation above a rigorous mathematical conjecture; cf. again [Reference GaitsgoryGai16, § 6] for a more detailed discussion.
$\kappa _{\operatorname {crit}}$ is integral. Again, it is possible to make the informal relation above a rigorous mathematical conjecture; cf. again [Reference GaitsgoryGai16, § 6] for a more detailed discussion.
In the remainder of this section we will pretend that both quantum and classical geometric Langlands conjectures hold as stated. We will write ![]() $\mathcal {C}\mapsto \mathcal {C}^{\vee }$ for the resulting correspondence.
$\mathcal {C}\mapsto \mathcal {C}^{\vee }$ for the resulting correspondence.
An important example of such a correspondence is as follows. Fix a non-degenerate form ![]() $\kappa$ and let
$\kappa$ and let ![]() $\mathcal {C}=D_{\kappa +\kappa _{\operatorname {crit}}}({\mathbf {Gr}}_G)$-mod be the category of
$\mathcal {C}=D_{\kappa +\kappa _{\operatorname {crit}}}({\mathbf {Gr}}_G)$-mod be the category of ![]() $(\kappa -\kappa _{\operatorname {crit}})$-twisted
$(\kappa -\kappa _{\operatorname {crit}})$-twisted ![]() $D$-modules on the affine Grassmannian
$D$-modules on the affine Grassmannian ![]() ${\mathbf {Gr}}_G$ of
${\mathbf {Gr}}_G$ of ![]() $G$. It is expected that in this case the category
$G$. It is expected that in this case the category ![]() $\mathcal {C}^{\vee }$ is the category
$\mathcal {C}^{\vee }$ is the category ![]() $D_{-\kappa ^{\vee }-\kappa ^{\vee }_{\operatorname {crit}}}({\mathbf {Gr}}_{G^{\vee }})$-mod. In the limiting case
$D_{-\kappa ^{\vee }-\kappa ^{\vee }_{\operatorname {crit}}}({\mathbf {Gr}}_{G^{\vee }})$-mod. In the limiting case ![]() $\kappa =0$ category
$\kappa =0$ category ![]() $\mathcal {C}^{\vee }$ is expected to be a pushforward of category
$\mathcal {C}^{\vee }$ is expected to be a pushforward of category ![]() $\operatorname {QCoh}({\operatorname {pt}}/G^{\vee })$ under the natural map
$\operatorname {QCoh}({\operatorname {pt}}/G^{\vee })$ under the natural map ![]() ${\operatorname {pt}}/G^{\vee }\to \operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ )$ induced by the embedding of the trivial local system. These expectations would have the following implication.
${\operatorname {pt}}/G^{\vee }\to \operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ )$ induced by the embedding of the trivial local system. These expectations would have the following implication.
(i) If
 $\kappa$ is non-degenerate, then
$\kappa$ is non-degenerate, then  $\mathcal {C}^{G_{\mathbf {O}}}\simeq (\mathcal {C}^{\vee })^{G^{\vee }_{\mathbf {O}}}$ (here
$\mathcal {C}^{G_{\mathbf {O}}}\simeq (\mathcal {C}^{\vee })^{G^{\vee }_{\mathbf {O}}}$ (here  $\mathcal {C}^{G_{\mathbf {O}}}$ denotes the category of
$\mathcal {C}^{G_{\mathbf {O}}}$ denotes the category of  $G_{\mathbf {O}}$-equivariant objects in
$G_{\mathbf {O}}$-equivariant objects in  $\mathcal {C}$).
$\mathcal {C}$).(ii) If
 $\kappa =0$ then
$\kappa =0$ then  $\mathcal {C}^{G_{\mathbf {O}}}$ is equivalent to the pullback of the category
$\mathcal {C}^{G_{\mathbf {O}}}$ is equivalent to the pullback of the category  $\mathcal {C}^{\vee }$ under the map
$\mathcal {C}^{\vee }$ under the map  ${\operatorname {pt}}/G^{\vee }\to \operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ )$ corresponding to the trivial local system.
${\operatorname {pt}}/G^{\vee }\to \operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ )$ corresponding to the trivial local system.
2.3 Whittaker category and the fundamental local equivalence
In this subsection we discuss another important example of Langlands dual categories. We refer to [Reference GaitsgoryGai16, Reference GaitsgoryGai20] for details.
Let ![]() $U$ be a maximal unipotent subgroup of
$U$ be a maximal unipotent subgroup of ![]() $G$ and let
$G$ and let ![]() $\chi _0\colon U\to \mathbb {G}_a$ be a non-degenerate character. We define a character
$\chi _0\colon U\to \mathbb {G}_a$ be a non-degenerate character. We define a character ![]() $\chi \colon U_{\mathbf {F}}\to \mathbb {G}_a$ by
$\chi \colon U_{\mathbf {F}}\to \mathbb {G}_a$ by
Given a (cocomplete, dg) category ![]() $\mathcal {C}$ with a strong
$\mathcal {C}$ with a strong ![]() $G_{\mathbf {F}}$-action of a fixed level, one can define a category
$G_{\mathbf {F}}$-action of a fixed level, one can define a category ![]() $\operatorname {Whit}(\mathcal {C})$ of
$\operatorname {Whit}(\mathcal {C})$ of ![]() $(U_{\mathbf {F}},\chi )$-equivariant objects in
$(U_{\mathbf {F}},\chi )$-equivariant objects in ![]() $\mathcal {C}$.
$\mathcal {C}$.
We consider the category ![]() $D_{\kappa }(G_{\mathbf {F}})$-mod of
$D_{\kappa }(G_{\mathbf {F}})$-mod of ![]() $\kappa$-twisted
$\kappa$-twisted ![]() $D$-modules on
$D$-modules on ![]() $G_{\mathbf {F}}$. According to [Reference Arkhipov and GaitsgoryAG02], this category has a natural action of
$G_{\mathbf {F}}$. According to [Reference Arkhipov and GaitsgoryAG02], this category has a natural action of ![]() $G_{\mathbf {F}}$ of level
$G_{\mathbf {F}}$ of level ![]() $\kappa$ that comes from left translations, and also another action of
$\kappa$ that comes from left translations, and also another action of ![]() $G_{\mathbf {F}}$ of level
$G_{\mathbf {F}}$ of level ![]() $-\kappa +2\kappa _{\operatorname {crit}}$ that comes from right translations.
$-\kappa +2\kappa _{\operatorname {crit}}$ that comes from right translations.
Let ![]() $\operatorname {Whit}^r_{\kappa }(G_{\mathbf {F}})$ denote its Whittaker category with respect to the right action. This category inherits the left action of level
$\operatorname {Whit}^r_{\kappa }(G_{\mathbf {F}})$ denote its Whittaker category with respect to the right action. This category inherits the left action of level ![]() $\kappa$. One could ask what is its Langlands dual category.
$\kappa$. One could ask what is its Langlands dual category.
For simplicity, below we will only consider either the case where ![]() $\kappa$ is not rational (i.e. the value of the corresponding quadratic form on any coroot is not a rational number) or the case
$\kappa$ is not rational (i.e. the value of the corresponding quadratic form on any coroot is not a rational number) or the case ![]() $\kappa =0$.
$\kappa =0$.
Assume first that ![]() $\kappa$ is non-degenerate and not rational. Then it is expected (cf. [Reference GaitsgoryGai16]) that
$\kappa$ is non-degenerate and not rational. Then it is expected (cf. [Reference GaitsgoryGai16]) that
In the case ![]() $\kappa =0$ the expected answer is the category
$\kappa =0$ the expected answer is the category ![]() $\operatorname {QCoh}(\operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ ))$.
$\operatorname {QCoh}(\operatorname {LocSys}_{G^{\vee }}(\mathcal {D}^\circ ))$.
Let ![]() $\operatorname {Whit}_{\kappa }({\mathbf {Gr}}_G)$ denote the category of
$\operatorname {Whit}_{\kappa }({\mathbf {Gr}}_G)$ denote the category of ![]() $\kappa$-twisted
$\kappa$-twisted ![]() $D$-modules on
$D$-modules on ![]() ${\mathbf {Gr}}_G$ and let
${\mathbf {Gr}}_G$ and let ![]() $\operatorname {KL}_{\kappa }(\mathfrak {g})=(\hat {\mathfrak {g}}_{\kappa }\text {-mod})^{G_{\mathbf {O}}}$. Then, statements (i) and (ii) of § 2.2 imply the following result, which has been proved rigorously in [Reference GaitsgoryGai20, Reference GaitsgoryGai08] (it goes under the name ‘fundamental local equivalence’).
$\operatorname {KL}_{\kappa }(\mathfrak {g})=(\hat {\mathfrak {g}}_{\kappa }\text {-mod})^{G_{\mathbf {O}}}$. Then, statements (i) and (ii) of § 2.2 imply the following result, which has been proved rigorously in [Reference GaitsgoryGai20, Reference GaitsgoryGai08] (it goes under the name ‘fundamental local equivalence’).
Theorem 2.3.1 Assume that ![]() $\kappa$ is non-degenerate and not rational. Then
$\kappa$ is non-degenerate and not rational. Then
Moreover, these equivalences hold at the level of abelian categories.
Remarks 2.3.2 (1) The critical shifts in (2.3.2) are not important for irrational ![]() $\kappa$ if one only cares about both sides as abstract categories. However, we still prefer to keep them, since in this way one can also extend the statement to rational
$\kappa$ if one only cares about both sides as abstract categories. However, we still prefer to keep them, since in this way one can also extend the statement to rational ![]() $\kappa$; in addition, the shifts are important if we keep track of some natural structures on these categories (cf. (4)) below.
$\kappa$; in addition, the shifts are important if we keep track of some natural structures on these categories (cf. (4)) below.
(2) Note the absence of a negative sign before ![]() $\kappa ^{\vee }+\kappa ^{\vee }_{\operatorname {crit}}$ on the right-hand side of (2.3.2). This has to do with the fact that
$\kappa ^{\vee }+\kappa ^{\vee }_{\operatorname {crit}}$ on the right-hand side of (2.3.2). This has to do with the fact that ![]() $\operatorname {Whit}_{\kappa +\kappa _{\operatorname {crit}}}({\mathbf {Gr}}_G)$ is actually the category of
$\operatorname {Whit}_{\kappa +\kappa _{\operatorname {crit}}}({\mathbf {Gr}}_G)$ is actually the category of ![]() $G_{\mathbf {O}}$-equivariant objects with respect to the left action of
$G_{\mathbf {O}}$-equivariant objects with respect to the left action of ![]() $G_{\mathbf {O}}$ on the category of
$G_{\mathbf {O}}$ on the category of ![]() $D$-modules on
$D$-modules on ![]() $G_{\mathbf {F}}$ which are Whittaker on the right. This change from right to left is what is responsible for the change of sign.
$G_{\mathbf {F}}$ which are Whittaker on the right. This change from right to left is what is responsible for the change of sign.
(3) The fact that the above equivalences respect the natural ![]() $t$-structures does not follow (to the best of our knowledge) from any geometric Langlands considerations. In fact, at the level of (unbounded) derived categories the statement holds for all
$t$-structures does not follow (to the best of our knowledge) from any geometric Langlands considerations. In fact, at the level of (unbounded) derived categories the statement holds for all ![]() $\kappa$, but when
$\kappa$, but when ![]() $\kappa$ is positive rational it is very far from an abelian equivalence.
$\kappa$ is positive rational it is very far from an abelian equivalence.
(4) The above equivalences are in fact not only equivalences of abstract categories, but also equivalences of categories with factorization structure, a notion closely related to the notion of a braided monoidal category (it is also worthwhile to note that as an abstract category, ![]() $\operatorname {KL}_{\kappa }(\hat {\mathfrak {g}})$ is independent of
$\operatorname {KL}_{\kappa }(\hat {\mathfrak {g}})$ is independent of ![]() $\kappa$ if
$\kappa$ if ![]() $\kappa$ is irrational; but it is not so if we take into account the factorization structure).
$\kappa$ is irrational; but it is not so if we take into account the factorization structure).
2.4 Gaiotto conjectures: geometric Langlands form in the case  $N>M$
$N>M$
There is one more series of examples which are relevant to the subject of this paper. Fix two non-negative integers ![]() $N$ and
$N$ and ![]() $M$ such that
$M$ such that ![]() $N\geq M$ and set
$N\geq M$ and set ![]() $G_{M,N}=\operatorname{GL}_M\times \operatorname{GL}_N$. Note that
$G_{M,N}=\operatorname{GL}_M\times \operatorname{GL}_N$. Note that ![]() $G_{M,N}$ is isomorphic to
$G_{M,N}$ is isomorphic to ![]() $G_{M,N}^{\vee }$.
$G_{M,N}^{\vee }$.
We are going to produce an example of Langlands dual categories for ![]() $G_{M,N}$; for
$G_{M,N}$; for ![]() $M=0$ we will recover (2.3.1). First, we describe the analogue of the right-hand side. Let
$M=0$ we will recover (2.3.1). First, we describe the analogue of the right-hand side. Let ![]() $c\in \mathbb {C}$. Then the category in question will be the category
$c\in \mathbb {C}$. Then the category in question will be the category ![]() $\widehat {\mathfrak {gl}}(M|N)_c$-mod of modules over the affine Lie superalgebra
$\widehat {\mathfrak {gl}}(M|N)_c$-mod of modules over the affine Lie superalgebra ![]() $\widehat {\mathfrak {gl}}(M|N)$ of level
$\widehat {\mathfrak {gl}}(M|N)$ of level ![]() $c\cdot \kappa _{M,N}+\frac 12{\operatorname {Killing}}_{M,N}$, where
$c\cdot \kappa _{M,N}+\frac 12{\operatorname {Killing}}_{M,N}$, where
(1)
 $\kappa _{M,N}(x,y)=\operatorname {sTr}(x y)$,
$\kappa _{M,N}(x,y)=\operatorname {sTr}(x y)$,(2)
 ${\operatorname {Killing}}_{M,N}$ is the restriction of the Killing form of
${\operatorname {Killing}}_{M,N}$ is the restriction of the Killing form of  $\mathfrak {gl}(M|N)$ to the even part (note that it is degenerate if
$\mathfrak {gl}(M|N)$ to the even part (note that it is degenerate if  $M=N$).
$M=N$).
This category has a natural action of the group ![]() $G_{M,N}({\mathbf {F}})$ of a certain level which is an integral shift of
$G_{M,N}({\mathbf {F}})$ of a certain level which is an integral shift of ![]() $(c\cdot \kappa _M,-c\cdot \kappa _N)$ (here
$(c\cdot \kappa _M,-c\cdot \kappa _N)$ (here ![]() $\kappa _N$ denotes the standard invariant bilinear form on the Lie algebra
$\kappa _N$ denotes the standard invariant bilinear form on the Lie algebra ![]() $\mathfrak {gl}_N$ equal to
$\mathfrak {gl}_N$ equal to ![]() $\operatorname {Tr}(X\cdot Y)$). As has been explained above, one can twist the action of
$\operatorname {Tr}(X\cdot Y)$). As has been explained above, one can twist the action of ![]() $G_{M,N}({\mathbf {F}})$ on this category so that the twist becomes equal to
$G_{M,N}({\mathbf {F}})$ on this category so that the twist becomes equal to ![]() $(c\cdot \kappa _M,-c\cdot \kappa _N)-\kappa _{\operatorname {crit}}$ (here by
$(c\cdot \kappa _M,-c\cdot \kappa _N)-\kappa _{\operatorname {crit}}$ (here by ![]() $\kappa _{\operatorname {crit}}$ we mean the critical bilinear form for the Lie algebra
$\kappa _{\operatorname {crit}}$ we mean the critical bilinear form for the Lie algebra ![]() $\mathfrak {g}_{M,N}$). Hence it makes sense to consider its Langlands dual. This should be a category with a strong action of
$\mathfrak {g}_{M,N}$). Hence it makes sense to consider its Langlands dual. This should be a category with a strong action of ![]() $G_{M,N}({\mathbf {F}})$ of level
$G_{M,N}({\mathbf {F}})$ of level ![]() $c^{-1}\cdot (\kappa _M,-\kappa _N)-\kappa _{\operatorname {crit}}$. However, we can again twist the action and think of it as a category with an action of
$c^{-1}\cdot (\kappa _M,-\kappa _N)-\kappa _{\operatorname {crit}}$. However, we can again twist the action and think of it as a category with an action of ![]() $G_{M,N}({\mathbf {F}})$ of level
$G_{M,N}({\mathbf {F}})$ of level ![]() $c^{-1}\cdot (\kappa _M,-\kappa _N)$. Let us give a conjectural description of the Langlands dual category according to a prediction of D. Gaiotto.
$c^{-1}\cdot (\kappa _M,-\kappa _N)$. Let us give a conjectural description of the Langlands dual category according to a prediction of D. Gaiotto.
Next, let ![]() $M< N$. We define a unipotent subgroup
$M< N$. We define a unipotent subgroup ![]() $U_{M,N}$ of
$U_{M,N}$ of ![]() $\operatorname{GL}_N$ as follows. If
$\operatorname{GL}_N$ as follows. If ![]() $M=N-1$ this subgroup is trivial, and if
$M=N-1$ this subgroup is trivial, and if ![]() $M=0$ it is the group
$M=0$ it is the group ![]() $U_N$ of unipotent upper-triangular matrices. In the general case,
$U_N$ of unipotent upper-triangular matrices. In the general case, ![]() $U_{M,N}$ is a subgroup of
$U_{M,N}$ is a subgroup of ![]() $U_N$ defined as follows.
$U_N$ defined as follows.
Let ![]() $e_{M,N}\in \mathfrak {gl}_N$ be the standard upper-triangular Jordan block of size
$e_{M,N}\in \mathfrak {gl}_N$ be the standard upper-triangular Jordan block of size ![]() $N-M$, that is,
$N-M$, that is,
 \[ e_{M,N}=\sum_{i=1}^{N-M-1} E_{i,i+1}, \]
\[ e_{M,N}=\sum_{i=1}^{N-M-1} E_{i,i+1}, \]
where ![]() $E_{ij}$ stands for the matrix whose
$E_{ij}$ stands for the matrix whose ![]() $(i,j)$th entry is equal to 1 and all other entries are equal to 0. The element
$(i,j)$th entry is equal to 1 and all other entries are equal to 0. The element ![]() $e_{M,N}$ is part of an
$e_{M,N}$ is part of an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $(e_{M,N},h_{M,N},f_{M,N})$. Here
$(e_{M,N},h_{M,N},f_{M,N})$. Here ![]() $f_{M,N}=\sum _{i=1}^{N-M-1} i(N-M-i) E_{i+1,i}$ and
$f_{M,N}=\sum _{i=1}^{N-M-1} i(N-M-i) E_{i+1,i}$ and ![]() $h_{M,N}$ is the diagonal matrix which has diagonal entries
$h_{M,N}$ is the diagonal matrix which has diagonal entries ![]() $(N-M-1,N-M-3,\ldots ,-N+M+1,0,\ldots ,0)$. For any integer
$(N-M-1,N-M-3,\ldots ,-N+M+1,0,\ldots ,0)$. For any integer ![]() $l$ we let
$l$ we let ![]() $\mathfrak {g}_l$ denote the
$\mathfrak {g}_l$ denote the ![]() $l$-eigenspace of the adjoint action of
$l$-eigenspace of the adjoint action of ![]() $h_{M,N}$ on
$h_{M,N}$ on ![]() $\mathfrak {gl}_N$. We set
$\mathfrak {gl}_N$. We set
where ![]() $\mathfrak {g}_1^+$ is the intersection of
$\mathfrak {g}_1^+$ is the intersection of ![]() $\mathfrak {g}_1$ with the Lie algebra of upper-triangular matrices. We define a Lie algebra homomorphism
$\mathfrak {g}_1$ with the Lie algebra of upper-triangular matrices. We define a Lie algebra homomorphism ![]() $\chi ^0_{M,N}\colon \mathfrak {u}_{M,N}\to \mathbb {C}$ by sending a matrix
$\chi ^0_{M,N}\colon \mathfrak {u}_{M,N}\to \mathbb {C}$ by sending a matrix ![]() $(u_{ij})$ to
$(u_{ij})$ to ![]() $\sum _{i=1}^{N-M-1} u_{i,i+1}$. Let
$\sum _{i=1}^{N-M-1} u_{i,i+1}$. Let ![]() $U_{M,N}$ be a unipotent subgroup of
$U_{M,N}$ be a unipotent subgroup of ![]() $\operatorname{GL}_N$ with Lie algebra
$\operatorname{GL}_N$ with Lie algebra ![]() $\mathfrak {u}_{M,N}$ and let
$\mathfrak {u}_{M,N}$ and let ![]() $U_{M,N}\to \mathbb {G}_a$ be the homomorphism induced by
$U_{M,N}\to \mathbb {G}_a$ be the homomorphism induced by ![]() $\chi _{M,N}^0$ (which we denote by the same symbol
$\chi _{M,N}^0$ (which we denote by the same symbol ![]() $\chi _{M,N}^0$).
$\chi _{M,N}^0$).
We embed the group ![]() $\operatorname{GL}_M$ into the centralizer of the element
$\operatorname{GL}_M$ into the centralizer of the element ![]() $h_{M,N}$ in
$h_{M,N}$ in ![]() $\operatorname{GL}_N$ (this is the block-diagonal embedding corresponding to rows
$\operatorname{GL}_N$ (this is the block-diagonal embedding corresponding to rows ![]() ${N-M+1},\ldots ,N$). It is easy to see that the group
${N-M+1},\ldots ,N$). It is easy to see that the group ![]() $\operatorname{GL}_M$ normalizes the subgroup
$\operatorname{GL}_M$ normalizes the subgroup ![]() $U_{M,N}$, and the homomorphism
$U_{M,N}$, and the homomorphism ![]() $\chi ^0_{M,N}$ is fixed by the
$\chi ^0_{M,N}$ is fixed by the ![]() $\operatorname{GL}_M$-action on
$\operatorname{GL}_M$-action on ![]() $U_{M,N}$ by conjugation.
$U_{M,N}$ by conjugation.
Remark 2.4.1 ![]() $U_{M,N}$ is conjugate to the subgroup
$U_{M,N}$ is conjugate to the subgroup ![]() $U'_{M,N}$ formed by the block-upper-triangular matrices
$U'_{M,N}$ formed by the block-upper-triangular matrices
 \[ \begin{pmatrix}U_r & {*} & {*}\\0 & 1_{M+1} & {*}\\0 & 0 & U_s\end{pmatrix},\quad \text{where } r=\lceil(N-M-1)/2\rceil,\ s=\lfloor(N-M-1)/2\rfloor; \]
\[ \begin{pmatrix}U_r & {*} & {*}\\0 & 1_{M+1} & {*}\\0 & 0 & U_s\end{pmatrix},\quad \text{where } r=\lceil(N-M-1)/2\rceil,\ s=\lfloor(N-M-1)/2\rfloor; \]
in particular, ![]() $r+s=N-M-1$. Here
$r+s=N-M-1$. Here ![]() $U_p$ stands for an arbitrary unipotent upper-triangular matrix in
$U_p$ stands for an arbitrary unipotent upper-triangular matrix in ![]() $\operatorname{GL}_p$, and the notation ‘
$\operatorname{GL}_p$, and the notation ‘![]() $*$’ is used for arbitrary matrices of an appropriate size. Moreover, the conjugation can be chosen so that the character
$*$’ is used for arbitrary matrices of an appropriate size. Moreover, the conjugation can be chosen so that the character ![]() $\chi _{M,N}^0$ corresponds to the character
$\chi _{M,N}^0$ corresponds to the character ![]() $\chi _{M,N}^{(r,s)}$ on
$\chi _{M,N}^{(r,s)}$ on ![]() $\mathfrak u_{M,N}^{(r,s)}:=\operatorname {Lie} U_{M,N}^{(r,s)}$ given by
$\mathfrak u_{M,N}^{(r,s)}:=\operatorname {Lie} U_{M,N}^{(r,s)}$ given by ![]() $(u_{ij})\mapsto \sum _{i=1}^{r-1} u_{i,i+1} + u_{rk} + u_{k,N-s+1} + \sum _{i=N-s+1}^{N-1} u_{i,i+1}$ for any choice of
$(u_{ij})\mapsto \sum _{i=1}^{r-1} u_{i,i+1} + u_{rk} + u_{k,N-s+1} + \sum _{i=N-s+1}^{N-1} u_{i,i+1}$ for any choice of ![]() $k\in \{r+1,\ldots ,N-s\}$. The subgroup
$k\in \{r+1,\ldots ,N-s\}$. The subgroup ![]() $U_{M,N}^{(r,s)}\subset \operatorname{GL}_N$ and the character
$U_{M,N}^{(r,s)}\subset \operatorname{GL}_N$ and the character ![]() $\chi _{M,N}^{(r,s)}$ are defined for an arbitrary pair
$\chi _{M,N}^{(r,s)}$ are defined for an arbitrary pair ![]() $(r,s)\in {\mathbb {N}}^2:={\mathbb {Z}}_{\geq 0}^2$ with
$(r,s)\in {\mathbb {N}}^2:={\mathbb {Z}}_{\geq 0}^2$ with ![]() $r+s=N-M-1$. (In the two extreme cases
$r+s=N-M-1$. (In the two extreme cases ![]() $\{r,s\}=\{0,N-M-1\}$, one of the middle terms in the formula for
$\{r,s\}=\{0,N-M-1\}$, one of the middle terms in the formula for ![]() $\chi _{M,N}^{(r,s)}$ is undefined and should be omitted.) Moreover,
$\chi _{M,N}^{(r,s)}$ is undefined and should be omitted.) Moreover, ![]() $\chi _{M,N}^{(r,s)}$ can be replaced by an arbitrary representative of the open
$\chi _{M,N}^{(r,s)}$ can be replaced by an arbitrary representative of the open ![]() $N_{\operatorname{GL}_N}(U_{M,N}^{(r,s)})$-orbit in
$N_{\operatorname{GL}_N}(U_{M,N}^{(r,s)})$-orbit in ![]() $\mathfrak u_{M,N}^{(r,s)*}$.
$\mathfrak u_{M,N}^{(r,s)*}$.
Remark 2.4.2 ![]() $U_{M,N}^{(0,N-M-1)}$ is also conjugate to the unipotent radical
$U_{M,N}^{(0,N-M-1)}$ is also conjugate to the unipotent radical ![]() $U_{(M+1,1,\ldots ,1)}$ of the standard parabolic subgroup
$U_{(M+1,1,\ldots ,1)}$ of the standard parabolic subgroup ![]() $P_{(M+1,1,\ldots ,1)}$ of
$P_{(M+1,1,\ldots ,1)}$ of ![]() $\operatorname{GL}_N$ corresponding to the partition
$\operatorname{GL}_N$ corresponding to the partition ![]() $(M+1,1,\ldots ,1)$ of
$(M+1,1,\ldots ,1)$ of ![]() $N$. The character
$N$. The character ![]() $\chi ^0_{M,N}$ is conjugate to the restriction of the regular character
$\chi ^0_{M,N}$ is conjugate to the restriction of the regular character ![]() $u\mapsto \sum _{i=1}^{N-1}u_{i,i+1}$ of the upper-triangular subgroup to
$u\mapsto \sum _{i=1}^{N-1}u_{i,i+1}$ of the upper-triangular subgroup to ![]() $U_{(M+1,1,\ldots ,1)}$; cf. [Reference Jacquet, Piatetski-Shapiro and ShalikaJPS83, §(2.11)] and [Reference CogdellCog04, beginning of § 2 of Lecture 5].
$U_{(M+1,1,\ldots ,1)}$; cf. [Reference Jacquet, Piatetski-Shapiro and ShalikaJPS83, §(2.11)] and [Reference CogdellCog04, beginning of § 2 of Lecture 5].
As before, we define a homomorphism ![]() $\chi _{M,N}\colon U_{M,N}({\mathbf {F}})\to \mathbb {G}_a$ to be
$\chi _{M,N}\colon U_{M,N}({\mathbf {F}})\to \mathbb {G}_a$ to be ![]() $\operatorname {Res}_{t=0}\chi ^0_{M,N}$.
$\operatorname {Res}_{t=0}\chi ^0_{M,N}$.
For any ![]() $c'\in \mathbb {C}$, we now consider the category
$c'\in \mathbb {C}$, we now consider the category ![]() $D_{c'}(\operatorname{GL}(N,{\mathbf {F}}))^{U_{M,N}({\mathbf {F}}),\chi _{M,N}}$. By definition this is the derived category of
$D_{c'}(\operatorname{GL}(N,{\mathbf {F}}))^{U_{M,N}({\mathbf {F}}),\chi _{M,N}}$. By definition this is the derived category of ![]() $D$-modules on
$D$-modules on ![]() $\operatorname{GL}(N,{\mathbf {F}})$ twisted by
$\operatorname{GL}(N,{\mathbf {F}})$ twisted by ![]() $c'\cdot \kappa _N$ that are equivariant on the left with respect to
$c'\cdot \kappa _N$ that are equivariant on the left with respect to ![]() $(U_{M,N}({\mathbf {F}}),\chi _{M,N})$. This category has a natural action of
$(U_{M,N}({\mathbf {F}}),\chi _{M,N})$. This category has a natural action of ![]() $\operatorname{GL}(M,{\mathbf {F}})$ of level
$\operatorname{GL}(M,{\mathbf {F}})$ of level ![]() $c'\cdot \kappa _M$ coming from left multiplication and an action of
$c'\cdot \kappa _M$ coming from left multiplication and an action of ![]() $\operatorname{GL}(N,{\mathbf {F}})$ of level
$\operatorname{GL}(N,{\mathbf {F}})$ of level ![]() $-c'\cdot \kappa _M-\operatorname {Killing}_{{\mathfrak {gl}}_N}$ coming from right multiplication (recall that
$-c'\cdot \kappa _M-\operatorname {Killing}_{{\mathfrak {gl}}_N}$ coming from right multiplication (recall that ![]() $\operatorname {Killing}_{{\mathfrak {gl}}_N}$ denotes the Killing form on
$\operatorname {Killing}_{{\mathfrak {gl}}_N}$ denotes the Killing form on ![]() $\mathfrak {gl}_N$). As before, we can twist the second action to make it an action of level
$\mathfrak {gl}_N$). As before, we can twist the second action to make it an action of level ![]() $-c'\cdot \kappa _M$.
$-c'\cdot \kappa _M$.
Remark 2.4.3 In fact, using the Fourier transform for ![]() $D$-modules, one can show that replacing
$D$-modules, one can show that replacing ![]() $(r,s)$ in Remark 2.4.1 with any pair of non-negative integers whose sum equals
$(r,s)$ in Remark 2.4.1 with any pair of non-negative integers whose sum equals ![]() $N-M-1$ produces a category equivalent to
$N-M-1$ produces a category equivalent to ![]() $D_{c'}(\operatorname{GL}(N,{\mathbf {F}}))^{U_{M,N}({\mathbf {F}}),\chi _{M,N}}$.
$D_{c'}(\operatorname{GL}(N,{\mathbf {F}}))^{U_{M,N}({\mathbf {F}}),\chi _{M,N}}$.
We now take ![]() $c'=1/c$. Then, according to a conjecture of D. Gaiotto, the category
$c'=1/c$. Then, according to a conjecture of D. Gaiotto, the category ![]() $D_{1/c}(\operatorname{GL}(N,{\mathbf {F}}))^{U_{M,N}({\mathbf {F}}),\chi _{M,N}}$ is Langlands dual to
$D_{1/c}(\operatorname{GL}(N,{\mathbf {F}}))^{U_{M,N}({\mathbf {F}}),\chi _{M,N}}$ is Langlands dual to ![]() $\widehat {\mathfrak {gl}}(M|N)_c$-mod.
$\widehat {\mathfrak {gl}}(M|N)_c$-mod.
We can also consider the limit ![]() $c\to \infty$. To simplify the discussion we will not do it now, but we will discuss it later when we turn to
$c\to \infty$. To simplify the discussion we will not do it now, but we will discuss it later when we turn to ![]() $G_{\mathbf {O}}$-equivariant objects.
$G_{\mathbf {O}}$-equivariant objects.
2.5 Gaiotto conjectures: geometric Langlands form for  $N=M$
$N=M$
Let us also discuss the case ![]() $N=M$. In this case on the left we again take the same category
$N=M$. In this case on the left we again take the same category ![]() $\widehat {\mathfrak {gl}}(N|N)_c$-mod of modules over the affine Lie superalgebra
$\widehat {\mathfrak {gl}}(N|N)_c$-mod of modules over the affine Lie superalgebra ![]() $\widehat {\mathfrak {gl}}(N|N)$ of level
$\widehat {\mathfrak {gl}}(N|N)$ of level ![]() $c\cdot \kappa _{N,N}-\frac 12{\operatorname {Killing}}_{N,N}$ (note that the Killing form is zero for
$c\cdot \kappa _{N,N}-\frac 12{\operatorname {Killing}}_{N,N}$ (note that the Killing form is zero for ![]() ${N=M}$). The Langlands dual category (according to Gaiotto) is the derived category
${N=M}$). The Langlands dual category (according to Gaiotto) is the derived category ![]() $D_{1/c}(\operatorname{GL}(N,{\mathbf {F}})\times {\mathbf {V}})$ of
$D_{1/c}(\operatorname{GL}(N,{\mathbf {F}})\times {\mathbf {V}})$ of ![]() $1/c$-twisted
$1/c$-twisted ![]() $D$-modules on
$D$-modules on ![]() $\operatorname{GL}(N,{\mathbf {F}})\times {\mathbf {V}}$ where
$\operatorname{GL}(N,{\mathbf {F}})\times {\mathbf {V}}$ where
(1) the twisting is with respect to the first factor,
(2) the two actions of
 $\operatorname{GL}(N,{\mathbf {F}})$ come from the diagonal action coming from the left action of
$\operatorname{GL}(N,{\mathbf {F}})$ come from the diagonal action coming from the left action of  $\operatorname{GL}(N,{\mathbf {F}})$ on the first factor and the natural action of
$\operatorname{GL}(N,{\mathbf {F}})$ on the first factor and the natural action of  $\operatorname{GL}(N,{\mathbf {F}})$ on the second factor, and the right multiplication action
$\operatorname{GL}(N,{\mathbf {F}})$ on the second factor, and the right multiplication action  $\operatorname{GL}(N,{\mathbf {F}})$ on the first factor.
$\operatorname{GL}(N,{\mathbf {F}})$ on the first factor.
2.6 Gaiotto conjectures: ‘simple-minded’ form
The above statements are not really well-formulated mathematical conjectures, since the local geometric Langlands duality is not known at present. However, we can turn them into precise conjectures by using (i) at the end of § 2.2, that is, we are going to take ![]() $G_{M,N}({\mathbf {O}})$-invariants on both sides. We get the following conjectures.
$G_{M,N}({\mathbf {O}})$-invariants on both sides. We get the following conjectures.
Conjecture 2.6.1 Assume that ![]() $N>M$ and assume that
$N>M$ and assume that ![]() $c\neq 0$ is not a rational number. The categories
$c\neq 0$ is not a rational number. The categories ![]() $D_{1/c}^{(\operatorname{GL}(M,{\mathbf {O}})\ltimes U_{M,N}({\mathbf {F}}),\chi _{M,N})}({\mathbf {Gr}}_{\operatorname{GL}_N})$ and
$D_{1/c}^{(\operatorname{GL}(M,{\mathbf {O}})\ltimes U_{M,N}({\mathbf {F}}),\chi _{M,N})}({\mathbf {Gr}}_{\operatorname{GL}_N})$ and ![]() $\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ are equivalent as factorization categories. Here
$\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ are equivalent as factorization categories. Here ![]() $\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ is the category of
$\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ is the category of ![]() $G_{M,N}({\mathbf {O}})$-equivariant objects in the category
$G_{M,N}({\mathbf {O}})$-equivariant objects in the category ![]() $\widehat {\mathfrak {gl}}(M|N)_c$-mod.
$\widehat {\mathfrak {gl}}(M|N)_c$-mod.
Similarly, the category ![]() $D_{1/c}^{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_N}\times {\mathbf {V}})$ is equivalent to
$D_{1/c}^{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_N}\times {\mathbf {V}})$ is equivalent to ![]() $\operatorname {KL}_c(\widehat {\mathfrak {gl}}(N|N))$.
$\operatorname {KL}_c(\widehat {\mathfrak {gl}}(N|N))$.
We now want to take the limit ![]() $c\to \infty$. In this case
$c\to \infty$. In this case ![]() $1/c$ goes to
$1/c$ goes to ![]() $0$ and the category of
$0$ and the category of ![]() $1/c$-twisted
$1/c$-twisted ![]() $D$-modules in Conjecture 2.6.1 just becomes the category of usual
$D$-modules in Conjecture 2.6.1 just becomes the category of usual ![]() $D$-modules. The
$D$-modules. The ![]() $c\to \infty$ limit of the category
$c\to \infty$ limit of the category ![]() $\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ is not canonically defined: one has to choose some nice extension of the corresponding family of categories from
$\operatorname {KL}_c(\widehat {\mathfrak {gl}}(M|N))$ is not canonically defined: one has to choose some nice extension of the corresponding family of categories from ![]() ${\mathbb{A}}^1$ to
${\mathbb{A}}^1$ to ![]() $\mathbb {P}^1$; cf. [Reference ZhaoZha17, § 6]. Naively, one might think that the correct extension is just the category of representations of the supergroup
$\mathbb {P}^1$; cf. [Reference ZhaoZha17, § 6]. Naively, one might think that the correct extension is just the category of representations of the supergroup ![]() $\operatorname{GL}(M|N)$. However, it turns out that this is not the right choice. Instead, one needs to consider the category of representations of the group
$\operatorname{GL}(M|N)$. However, it turns out that this is not the right choice. Instead, one needs to consider the category of representations of the group ![]() $\underline{\operatorname{GL}}(M|N))$ defined in § 1.5. With these conventions one gets the following conjecture.
$\underline{\operatorname{GL}}(M|N))$ defined in § 1.5. With these conventions one gets the following conjecture.
Conjecture 2.6.2 Assume that ![]() $N>M$. Then the category
$N>M$. Then the category ![]() $D^{(\operatorname{GL}(M,{\mathbf {O}})\ltimes U_{M,N}({\mathbf {F}}),\chi _{M,N})}({\mathbf {Gr}}_{\operatorname{GL}_N})$ is equivalent to the category of modules over the group
$D^{(\operatorname{GL}(M,{\mathbf {O}})\ltimes U_{M,N}({\mathbf {F}}),\chi _{M,N})}({\mathbf {Gr}}_{\operatorname{GL}_N})$ is equivalent to the category of modules over the group ![]() $\underline{\operatorname{GL}}(M|N))$.
$\underline{\operatorname{GL}}(M|N))$.
Similarly, for ![]() $N=M$, the category
$N=M$, the category ![]() $D^{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_N}\times {\mathbf {V}})$ is equivalent to the category of modules over the group
$D^{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_{\operatorname{GL}_N}\times {\mathbf {V}})$ is equivalent to the category of modules over the group ![]() $\underline{\operatorname{GL}}(N|N))$.
$\underline{\operatorname{GL}}(N|N))$.
These equivalences should hold for both derived and abelian categories.
In the present work we prove Conjecture 2.6.2 for ![]() $M=N$ and
$M=N$ and ![]() $M=N-1$.
$M=N-1$.
3. A coherent realization of  $D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}})$
$D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}\times {\mathbf {V}})$
3.1 Setup and notation
We follow the notation of [Reference Finkelberg, Ginzburg and TravkinFGT09]. Recall that ![]() ${\mathbf {Gr}}={\mathbf {Gr}}_{\operatorname{GL}_N}={\mathbf {G}}_{\mathbf {F}}/{\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N,{\mathbf {F}})/\operatorname{GL}(N,{\mathbf {O}})$, where
${\mathbf {Gr}}={\mathbf {Gr}}_{\operatorname{GL}_N}={\mathbf {G}}_{\mathbf {F}}/{\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N,{\mathbf {F}})/\operatorname{GL}(N,{\mathbf {O}})$, where ![]() ${\mathbf {F}}={\mathbb {C}}(\!(t)\!)\supset {\mathbb {C}}[\![t]\!]={\mathbf {O}}$. We consider a complex vector space
${\mathbf {F}}={\mathbb {C}}(\!(t)\!)\supset {\mathbb {C}}[\![t]\!]={\mathbf {O}}$. We consider a complex vector space ![]() $V$ with a basis
$V$ with a basis ![]() $e_1,\ldots ,e_N$. We set
$e_1,\ldots ,e_N$. We set ![]() ${\mathbf {V}}=V\,{\otimes}\, {\mathbf {F}}\supset V\,{\otimes}\, {\mathbf {O}}={\mathbf {V}}_0$.
${\mathbf {V}}=V\,{\otimes}\, {\mathbf {F}}\supset V\,{\otimes}\, {\mathbf {O}}={\mathbf {V}}_0$.
Recall that the ![]() ${\mathbf {G}}_{\mathbf {F}}$-orbits in
${\mathbf {G}}_{\mathbf {F}}$-orbits in ![]() ${\mathbf {Gr}}\times {\mathbf {Gr}}$ (respectively, in
${\mathbf {Gr}}\times {\mathbf {Gr}}$ (respectively, in ![]() ${\mathbf {Gr}}\times {\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$) are numbered in [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3.1] by signaturesFootnote 5 (respectively, by bisignatures, i.e. pairs of signatures) in such a way that the
${\mathbf {Gr}}\times {\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$) are numbered in [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3.1] by signaturesFootnote 5 (respectively, by bisignatures, i.e. pairs of signatures) in such a way that the ![]() ${\mathbf {G}}_{\mathbf {F}}$-orbits on
${\mathbf {G}}_{\mathbf {F}}$-orbits on ![]() ${\mathbf {Gr}}\times {\mathbf {Gr}}$ numbered by partitions
${\mathbf {Gr}}\times {\mathbf {Gr}}$ numbered by partitions ![]() ${\boldsymbol {\nu }}=(\nu _1\geq \cdots \geq \nu _N\geq 0)$ correspond to the pairs of lattices
${\boldsymbol {\nu }}=(\nu _1\geq \cdots \geq \nu _N\geq 0)$ correspond to the pairs of lattices ![]() $L^1\subset L^2$. More precisely, the orbit corresponding to a bisignature
$L^1\subset L^2$. More precisely, the orbit corresponding to a bisignature ![]() $({\boldsymbol {\lambda }},{\boldsymbol {\mu }})$ contains a point
$({\boldsymbol {\lambda }},{\boldsymbol {\mu }})$ contains a point
 \[ \bigg(L^1={\mathbf{O}}\langle e_1,e_2,\ldots,e_N\rangle,\ L^2={\mathbf{O}}\langle t^{-\lambda_1-\mu_1}e_1, t^{-\lambda_2-\mu_2}e_2,\ldots,t^{-\lambda_N-\mu_N}e_N\rangle,\ v=\sum_{i=1}^Nt^{-\lambda_i}e_i\bigg). \]
\[ \bigg(L^1={\mathbf{O}}\langle e_1,e_2,\ldots,e_N\rangle,\ L^2={\mathbf{O}}\langle t^{-\lambda_1-\mu_1}e_1, t^{-\lambda_2-\mu_2}e_2,\ldots,t^{-\lambda_N-\mu_N}e_N\rangle,\ v=\sum_{i=1}^Nt^{-\lambda_i}e_i\bigg). \] Irreducible representations of ![]() $\operatorname{GL}_N=\operatorname{GL}(V)$ are also numbered by the signatures, so that, for example, the determinant character
$\operatorname{GL}_N=\operatorname{GL}(V)$ are also numbered by the signatures, so that, for example, the determinant character ![]() $\det V$ corresponds to
$\det V$ corresponds to ![]() $(1^N)$. To a signature
$(1^N)$. To a signature ![]() ${\boldsymbol {\nu }}=(\nu _1\geq \cdots \geq \nu _N)$ we associate an irreducible representation
${\boldsymbol {\nu }}=(\nu _1\geq \cdots \geq \nu _N)$ we associate an irreducible representation ![]() $V_{\boldsymbol {\nu }}$ with the highest weight
$V_{\boldsymbol {\nu }}$ with the highest weight ![]() ${\boldsymbol {\nu }}$. The geometric Satake equivalence takes the irreducible perverse sheaf
${\boldsymbol {\nu }}$. The geometric Satake equivalence takes the irreducible perverse sheaf ![]() ${\operatorname {IC}}_{\boldsymbol {\nu }}$ to the irreducible representation
${\operatorname {IC}}_{\boldsymbol {\nu }}$ to the irreducible representation ![]() $V^*_{\boldsymbol {\nu }}$. Thus if
$V^*_{\boldsymbol {\nu }}$. Thus if ![]() ${\boldsymbol {\nu }}$ is a partition (respectively, a negative partition
${\boldsymbol {\nu }}$ is a partition (respectively, a negative partition ![]() $(0\geq \nu _1\geq \cdots \geq \nu _N)$), then
$(0\geq \nu _1\geq \cdots \geq \nu _N)$), then ![]() $V^*_{\boldsymbol {\nu }}$ is an antipolynomial (respectively, polynomial) representation of
$V^*_{\boldsymbol {\nu }}$ is an antipolynomial (respectively, polynomial) representation of ![]() $\operatorname{GL}_N$ (a polynomial functor in
$\operatorname{GL}_N$ (a polynomial functor in ![]() $V^*$,
$V^*$, ![]() $V$, respectively).
$V$, respectively).
A word of apology for our weird convention is in order. The numbering of ![]() ${\mathbf {G}}_{\mathbf {O}}$-orbits in
${\mathbf {G}}_{\mathbf {O}}$-orbits in ![]() ${\mathbf {Gr}}$ such that the orbits of sublattices
${\mathbf {Gr}}$ such that the orbits of sublattices ![]() $L\subset {\mathbf {V}}_0$ are numbered by partitions goes back at least to [Reference LusztigLus81]. We choose the numbering such that the orbits of sublattices are numbered by negative partitions since under this numbering the adjacency order of
$L\subset {\mathbf {V}}_0$ are numbered by partitions goes back at least to [Reference LusztigLus81]. We choose the numbering such that the orbits of sublattices are numbered by negative partitions since under this numbering the adjacency order of ![]() ${\mathbf {G}}_{\mathbf {O}}$-orbits in
${\mathbf {G}}_{\mathbf {O}}$-orbits in ![]() ${\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$ goes to Shoji's order ([Reference ShojiSho04], [Reference Finkelberg, Ginzburg and TravkinFGT09, Proposition 12]) on the set of bisignatures. Furthermore, we choose the Satake equivalence
${\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$ goes to Shoji's order ([Reference ShojiSho04], [Reference Finkelberg, Ginzburg and TravkinFGT09, Proposition 12]) on the set of bisignatures. Furthermore, we choose the Satake equivalence ![]() ${\operatorname {IC}}_{\boldsymbol {\nu }}\mapsto V^*_{\boldsymbol {\nu }}$ (as opposed to
${\operatorname {IC}}_{\boldsymbol {\nu }}\mapsto V^*_{\boldsymbol {\nu }}$ (as opposed to ![]() ${\operatorname {IC}}_{\boldsymbol {\nu }}\mapsto V_{\boldsymbol {\nu }}$) since it makes the statement of our main result Theorem 3.6.1 neater.
${\operatorname {IC}}_{\boldsymbol {\nu }}\mapsto V_{\boldsymbol {\nu }}$) since it makes the statement of our main result Theorem 3.6.1 neater.
3.2 Constructible mirabolic category and convolutions
The triangulated category ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}})$ is defined as in [Reference Finkelberg, Ginzburg and TravkinFGT09, § 2.6]. We will denote it by
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}})$ is defined as in [Reference Finkelberg, Ginzburg and TravkinFGT09, § 2.6]. We will denote it by ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Recall that an object
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Recall that an object ![]() ${\mathcal {F}}$ of
${\mathcal {F}}$ of ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is supported on
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is supported on ![]() ${\mathbf {Gr}}\times t^m{\mathbf {V}}_0$ for certain
${\mathbf {Gr}}\times t^m{\mathbf {V}}_0$ for certain ![]() $m\in {\mathbb {Z}}$, and there exist
$m\in {\mathbb {Z}}$, and there exist ![]() $n>m$ and a
$n>m$ and a ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant sheaf
${\mathbf {G}}_{\mathbf {O}}$-equivariant sheaf ![]() ${\mathcal {F}}_n$ on
${\mathcal {F}}_n$ on ![]() ${\mathbf {Gr}}\times (t^m{\mathbf {V}}_0/t^n{\mathbf {V}}_0)$ such that
${\mathbf {Gr}}\times (t^m{\mathbf {V}}_0/t^n{\mathbf {V}}_0)$ such that ![]() ${\mathcal {F}}=p_n^*{\mathcal {F}}_n$, where
${\mathcal {F}}=p_n^*{\mathcal {F}}_n$, where
is the natural projection. In other words, ![]() ${\mathcal {F}}$ is a collection of
${\mathcal {F}}$ is a collection of ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant sheaves
${\mathbf {G}}_{\mathbf {O}}$-equivariant sheaves ![]() ${\mathcal {F}}_{n'}$ on
${\mathcal {F}}_{n'}$ on ![]() ${\mathbf {Gr}}\times (t^m{\mathbf {V}}_0/t^{n'}{\mathbf {V}}_0)$ for
${\mathbf {Gr}}\times (t^m{\mathbf {V}}_0/t^{n'}{\mathbf {V}}_0)$ for ![]() $n'\geq n$ along with a compatible system of isomorphisms
$n'\geq n$ along with a compatible system of isomorphisms ![]() $p_{n''/n'}^*{\mathcal {F}}_{n'}{\buildrel \sim \over \longrightarrow} {\mathcal {F}}_{n''}$ for
$p_{n''/n'}^*{\mathcal {F}}_{n'}{\buildrel \sim \over \longrightarrow} {\mathcal {F}}_{n''}$ for ![]() $n''\geq n'$, where
$n''\geq n'$, where
are the natural projections.
If in the above definition we replace ![]() $p_n^*$ by
$p_n^*$ by ![]() $p_n^!$ and
$p_n^!$ and ![]() $p_{n''/n'}^*$ by
$p_{n''/n'}^*$ by ![]() $p_{n''/n'}^!$, then we obtain a triangulated category
$p_{n''/n'}^!$, then we obtain a triangulated category ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Note that
$D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Note that ![]() $p_{n''/n'}$ is a smooth morphism of relative dimension
$p_{n''/n'}$ is a smooth morphism of relative dimension ![]() $N(n''-n')$, so we have a canonical isomorphism
$N(n''-n')$, so we have a canonical isomorphism ![]() $p_{n''/n'}^!\cong p_{n''/n'}^*[2N(n''-n')]$. We also consider the intermediate version
$p_{n''/n'}^!\cong p_{n''/n'}^*[2N(n''-n')]$. We also consider the intermediate version
exact for the perverse ![]() $t$-structure. The corresponding triangulated category will be denoted
$t$-structure. The corresponding triangulated category will be denoted ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
We will make use of an identification ![]() ${\mathbf {Gr}}\times {\mathbf {V}}={\mathbf {G}}_{\mathbf {F}}\stackrel {{\mathbf {G}}_{\mathbf {O}}}{\times }{\mathbf {V}}=({\mathbf {G}}_{\mathbf {F}}\times {\mathbf {V}})/{\mathbf {G}}_{\mathbf {O}}$ (quotient with respect to the diagonal right-left action). We will denote the orbit of
${\mathbf {Gr}}\times {\mathbf {V}}={\mathbf {G}}_{\mathbf {F}}\stackrel {{\mathbf {G}}_{\mathbf {O}}}{\times }{\mathbf {V}}=({\mathbf {G}}_{\mathbf {F}}\times {\mathbf {V}})/{\mathbf {G}}_{\mathbf {O}}$ (quotient with respect to the diagonal right-left action). We will denote the orbit of ![]() $(g,v)\in {\mathbf {G}}_{\mathbf {F}}\times {\mathbf {V}}$ by
$(g,v)\in {\mathbf {G}}_{\mathbf {F}}\times {\mathbf {V}}$ by ![]() $[g,v]$. Note that the left diagonal action of
$[g,v]$. Note that the left diagonal action of ![]() ${\mathbf {G}}_{\mathbf {O}}$ on
${\mathbf {G}}_{\mathbf {O}}$ on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$ in terms of the above identification is
${\mathbf {Gr}}\times {\mathbf {V}}$ in terms of the above identification is ![]() $h\cdot [g,v]=[hg,v]$. We consider the following convolution diagram:
$h\cdot [g,v]=[hg,v]$. We consider the following convolution diagram:

Given ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define ![]() ${\mathcal {F}}_1{\stackrel {!}\circledast} {\mathcal {F}}_2:={\mathbf {m}}_*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2)$, where
${\mathcal {F}}_1{\stackrel {!}\circledast} {\mathcal {F}}_2:={\mathbf {m}}_*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2)$, where ![]() ${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}\times ({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of
${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}\times ({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of ![]() ${\mathbf {p}}^!({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along
${\mathbf {p}}^!({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along ![]() ${\mathbf {q}}$. Similarly, given
${\mathbf {q}}$. Similarly, given ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define ![]() ${\mathcal {F}}_1{\stackrel {*}\circledast} {\mathcal {F}}_2:={\mathbf {m}}_*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2)$, where
${\mathcal {F}}_1{\stackrel {*}\circledast} {\mathcal {F}}_2:={\mathbf {m}}_*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2)$, where ![]() ${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of
${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of ![]() ${\mathbf {p}}^*({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along
${\mathbf {p}}^*({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along ![]() ${\mathbf {q}}$, a unique sheaf such that
${\mathbf {q}}$, a unique sheaf such that ![]() ${\mathbf {p}}^*({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)={\mathbf {q}}^*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2)$.
${\mathbf {p}}^*({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)={\mathbf {q}}^*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2)$.
We also consider another convolution diagram:

Given ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define ![]() ${\mathcal {F}}_1{\stackrel {!}*}{\mathcal {F}}_2:={\mathfrak {m}}_!({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2)$, where
${\mathcal {F}}_1{\stackrel {!}*}{\mathcal {F}}_2:={\mathfrak {m}}_!({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2)$, where ![]() ${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}}\times {\mathbf {V}})\big )$ is the canonical descent of
${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^!{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}}\times {\mathbf {V}})\big )$ is the canonical descent of ![]() ${\mathfrak {p}}^!({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along
${\mathfrak {p}}^!({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along ![]() ${\mathfrak {q}}$. Similarly, given
${\mathfrak {q}}$. Similarly, given ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define ![]() ${\mathcal {F}}_1{\stackrel {*}*}{\mathcal {F}}_2:={\mathfrak {m}}_*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2)$, where
${\mathcal {F}}_1{\stackrel {*}*}{\mathcal {F}}_2:={\mathfrak {m}}_*({\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2)$, where ![]() ${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}}\times {\mathbf {V}})\big )$ is the canonical descent of
${\mathcal {F}}_1{\mathop \boxtimes \limits^{\sim}}^*{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}\big ({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}}\times {\mathbf {V}})\big )$ is the canonical descent of ![]() ${\mathfrak {p}}^*({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along
${\mathfrak {p}}^*({\mathcal {F}}_1\boxtimes {\mathcal {F}}_2)$ along ![]() ${\mathfrak {q}}$.
${\mathfrak {q}}$.
If we formally put ![]() $v_1=0$ in (3.2.2), we obtain the convolution diagram
$v_1=0$ in (3.2.2), we obtain the convolution diagram

and if we put ![]() $v_2=0$, we obtain
$v_2=0$, we obtain

Given ![]() ${\mathcal {P}}\in D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ and
${\mathcal {P}}\in D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ and ![]() ${\mathcal {F}}\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (where
${\mathcal {F}}\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (where ![]() $?=!,*,!*$), we define
$?=!,*,!*$), we define ![]() ${\mathcal {P}}*{\mathcal {F}}:={\mathfrak {m}}_*({\mathcal {P}}{\stackrel {\sim}\boxtimes} {\mathcal {F}})$, where
${\mathcal {P}}*{\mathcal {F}}:={\mathfrak {m}}_*({\mathcal {P}}{\stackrel {\sim}\boxtimes} {\mathcal {F}})$, where ![]() ${\mathcal {P}}{\stackrel {\sim}\boxtimes} {\mathcal {F}}\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of
${\mathcal {P}}{\stackrel {\sim}\boxtimes} {\mathcal {F}}\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of ![]() ${\mathfrak {p}}_{\operatorname {left}}^*({\mathcal {P}}\boxtimes {\mathcal {F}})$ along
${\mathfrak {p}}_{\operatorname {left}}^*({\mathcal {P}}\boxtimes {\mathcal {F}})$ along ![]() ${\mathfrak {q}}$. We also define
${\mathfrak {q}}$. We also define ![]() ${\mathcal {F}}*{\mathcal {P}}:={\mathfrak {m}}_*({\mathcal {F}}{\stackrel {\sim}\boxtimes} {\mathcal {P}})$, where
${\mathcal {F}}*{\mathcal {P}}:={\mathfrak {m}}_*({\mathcal {F}}{\stackrel {\sim}\boxtimes} {\mathcal {P}})$, where ![]() ${\mathcal {F}}{\stackrel {\sim}\boxtimes} {\mathcal {P}}\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of
${\mathcal {F}}{\stackrel {\sim}\boxtimes} {\mathcal {P}}\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {G}}_{\mathbf {F}}\overset {{\mathbf {G}}_{\mathbf {O}}}{\times }({\mathbf {Gr}}\times {\mathbf {V}})\big )$ is the canonical descent of ![]() ${\mathfrak {p}}_{\operatorname {right}}^*({\mathcal {F}}\boxtimes {\mathcal {P}})$ along
${\mathfrak {p}}_{\operatorname {right}}^*({\mathcal {F}}\boxtimes {\mathcal {P}})$ along ![]() ${\mathfrak {q}}$. Both the left and right convolutions are biexact for the perverse
${\mathfrak {q}}$. Both the left and right convolutions are biexact for the perverse ![]() $t$-structures on
$t$-structures on ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ and
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ and ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$; see [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3.9].
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$; see [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3.9].
3.3 Fusion
Let ![]() $X$ be a smooth curve. For any integer
$X$ be a smooth curve. For any integer ![]() $k>0$, and a collection
$k>0$, and a collection ![]() $x=(x_i)_{i=1}^k$ of
$x=(x_i)_{i=1}^k$ of ![]() $S$-points of
$S$-points of ![]() $X$, we denote by
$X$, we denote by ![]() ${\mathcal {D}}_x$ the formal neighborhood of the union of graphs
${\mathcal {D}}_x$ the formal neighborhood of the union of graphs ![]() $|x| := {\bigcup} _{i=1}^k \Gamma _{x_i}\subset S\times X$, and we denote by
$|x| := {\bigcup} _{i=1}^k \Gamma _{x_i}\subset S\times X$, and we denote by ![]() ${\mathcal {D}} _x^\circ :={\mathcal {D}}_x \,{\smallsetminus}\, |x|$ the punctured formal neighborhood. The mirabolic version of the Beilinson–Drinfeld Grassmannian is the ind-scheme
${\mathcal {D}} _x^\circ :={\mathcal {D}}_x \,{\smallsetminus}\, |x|$ the punctured formal neighborhood. The mirabolic version of the Beilinson–Drinfeld Grassmannian is the ind-scheme ![]() ${\mathbf {Gr}}^{\operatorname {mir}}_{BD,k}$ over
${\mathbf {Gr}}^{\operatorname {mir}}_{BD,k}$ over ![]() $X^k$ parametrizing the following collections of data:
$X^k$ parametrizing the following collections of data:
where ![]() ${\mathcal {E}}$ is a rank-
${\mathcal {E}}$ is a rank-![]() $N$ vector bundle on
$N$ vector bundle on ![]() ${\mathcal {D}}_x$. If
${\mathcal {D}}_x$. If ![]() $X={\mathbb {A}}^1$, we have over the complement to the diagonals a canonical isomorphism
$X={\mathbb {A}}^1$, we have over the complement to the diagonals a canonical isomorphism
We denote the projection ![]() $({\mathbb {A}}^k\,{\smallsetminus}\, \Delta )\times ({\mathbf {Gr}}\times {\mathbf {V}})^k\to ({\mathbf {Gr}}\times {\mathbf {V}})^k$ by
$({\mathbb {A}}^k\,{\smallsetminus}\, \Delta )\times ({\mathbf {Gr}}\times {\mathbf {V}})^k\to ({\mathbf {Gr}}\times {\mathbf {V}})^k$ by ![]() $\operatorname {pr}_2$. Given
$\operatorname {pr}_2$. Given ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (where
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (where ![]() $?={}!,*,!*$) we take
$?={}!,*,!*$) we take ![]() $k=2$ and define the fusion
$k=2$ and define the fusion
where ![]() $x,y$ are coordinates on
$x,y$ are coordinates on ![]() ${\mathbb {A}}^2$ (so that
${\mathbb {A}}^2$ (so that ![]() $x-y=0$ is the equation of the diagonal
$x-y=0$ is the equation of the diagonal ![]() $\Delta \subset {\mathbb {A}}^2$), and
$\Delta \subset {\mathbb {A}}^2$), and ![]() $\psi _{x-y}$ is the nearby cycles functor for the pullback of the function
$\psi _{x-y}$ is the nearby cycles functor for the pullback of the function ![]() $x-y$ to
$x-y$ to ![]() ${\mathbf {Gr}}^{\operatorname {mir}}_{BD,2}$, normalized so as to preserve the perverse
${\mathbf {Gr}}^{\operatorname {mir}}_{BD,2}$, normalized so as to preserve the perverse ![]() $t$-structure. Note that the leftmost occurrence of
$t$-structure. Note that the leftmost occurrence of ![]() ${\operatorname {pr}}_2$ in the above definition projects
${\operatorname {pr}}_2$ in the above definition projects ![]() ${\mathbb {A}}^1\times {\mathbf {Gr}}\times {\mathbf {V}}$ to
${\mathbb {A}}^1\times {\mathbf {Gr}}\times {\mathbf {V}}$ to ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$, while the rightmost occurrence of
${\mathbf {Gr}}\times {\mathbf {V}}$, while the rightmost occurrence of ![]() ${\operatorname {pr}}_2$ projects
${\operatorname {pr}}_2$ projects ![]() $({\mathbb {A}}^2\,{\smallsetminus}\, \Delta )\times ({\mathbf {Gr}}\times {\mathbf {V}})^2$ to
$({\mathbb {A}}^2\,{\smallsetminus}\, \Delta )\times ({\mathbf {Gr}}\times {\mathbf {V}})^2$ to ![]() $({\mathbf {Gr}}\times {\mathbf {V}})^2$.
$({\mathbf {Gr}}\times {\mathbf {V}})^2$.
3.4 Coherent mirabolic category and convolutions
We write ![]() $\Pi E$ for an odd vector space obtained from a vector space
$\Pi E$ for an odd vector space obtained from a vector space ![]() $E$ by reversing the parity.
$E$ by reversing the parity.
We fix a pair of ![]() $N$-dimensional vector spaces
$N$-dimensional vector spaces ![]() $V_1\simeq {\mathbb {C}}^N\simeq V_2$. We consider the Lie superalgebra
$V_1\simeq {\mathbb {C}}^N\simeq V_2$. We consider the Lie superalgebra ![]() ${\mathfrak {g}}{\mathfrak {l}}(N|N)={\mathfrak {g}}{\mathfrak {l}}(V_1\oplus \Pi V_2)$. We have
${\mathfrak {g}}{\mathfrak {l}}(N|N)={\mathfrak {g}}{\mathfrak {l}}(V_1\oplus \Pi V_2)$. We have ![]() ${\mathfrak {g}}{\mathfrak {l}}(N|N)={\mathfrak {g}}_{\bar 0}\oplus {\mathfrak {g}}_{\bar 1}$, where
${\mathfrak {g}}{\mathfrak {l}}(N|N)={\mathfrak {g}}_{\bar 0}\oplus {\mathfrak {g}}_{\bar 1}$, where ![]() ${\mathfrak {g}}_{\bar 1}=\Pi {\operatorname{Hom}}(V_1,V_2)\oplus \Pi {\operatorname{Hom}}(V_2,V_1)$, and
${\mathfrak {g}}_{\bar 1}=\Pi {\operatorname{Hom}}(V_1,V_2)\oplus \Pi {\operatorname{Hom}}(V_2,V_1)$, and ![]() ${\mathfrak {g}}_{\bar 0}=\operatorname{End}(V_1)\oplus \operatorname{End}(V_2)$. We set
${\mathfrak {g}}_{\bar 0}=\operatorname{End}(V_1)\oplus \operatorname{End}(V_2)$. We set ![]() $G_{\bar 0}=\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)$. We consider the dg-algebraFootnote 6
$G_{\bar 0}=\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)$. We consider the dg-algebraFootnote 6 ![]() ${\mathfrak {G}}_{1,1}^\bullet ={\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$ with zero differential, and the triangulated category
${\mathfrak {G}}_{1,1}^\bullet ={\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$ with zero differential, and the triangulated category ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ obtained by localization (with respect to quasi-isomorphisms) of the category of perfect
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ obtained by localization (with respect to quasi-isomorphisms) of the category of perfect ![]() $G_{\bar 0}$-equivariant dg-
$G_{\bar 0}$-equivariant dg-![]() ${\mathfrak {G}}_{1,1}^\bullet$-modules. The category
${\mathfrak {G}}_{1,1}^\bullet$-modules. The category ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is monoidal with respect to
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is monoidal with respect to ![]() ${\mathcal {M}},{\mathcal {M}}'\mapsto {\mathcal {M}}\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }\ {\mathcal {M}}'$; see § 3.7 below.
${\mathcal {M}},{\mathcal {M}}'\mapsto {\mathcal {M}}\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }\ {\mathcal {M}}'$; see § 3.7 below.
We will also need two more versions of ![]() ${\mathfrak {G}}_{1,1}^\bullet$, namely
${\mathfrak {G}}_{1,1}^\bullet$, namely
 \begin{gather*} {\mathfrak{G}}_{0,2}^\bullet{=}{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}2]),\\ {\mathfrak{G}}_{2,0}^\bullet{=}{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)), \end{gather*}
\begin{gather*} {\mathfrak{G}}_{0,2}^\bullet{=}{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}2]),\\ {\mathfrak{G}}_{2,0}^\bullet{=}{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)), \end{gather*}
and the corresponding triangulated categories ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet )$ and
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet )$ and ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$. We will now define the monoidal structures on
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$. We will now define the monoidal structures on ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet )$ and
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet )$ and ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$.
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$.
We consider the variety ![]() ${\mathcal {Q}}^A$ (respectively,
${\mathcal {Q}}^A$ (respectively, ![]() ${\mathcal {Q}}^B$) of sextuples
${\mathcal {Q}}^B$) of sextuples
such that
(here ![]() $V'_1$ is a copy of
$V'_1$ is a copy of ![]() $V_1$). Clearly,
$V_1$). Clearly, ![]() ${\mathcal {Q}}^A\simeq {\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)$, and
${\mathcal {Q}}^A\simeq {\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)$, and ![]() ${\mathcal {Q}}^B\simeq {\operatorname{Hom}}(V'_1,V_1)\times {\operatorname{Hom}}(V_2,V'_1)\times {\operatorname{Hom}}(V_1,V_2)$. We have
${\mathcal {Q}}^B\simeq {\operatorname{Hom}}(V'_1,V_1)\times {\operatorname{Hom}}(V_2,V'_1)\times {\operatorname{Hom}}(V_1,V_2)$. We have

We denote ![]() ${\operatorname{Hom}}(V_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Hom}}(V'_1,V_2)$
${\operatorname{Hom}}(V_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Hom}}(V'_1,V_2)$ ![]() $\times {\operatorname{Hom}}(V_2,V'_1)\times {\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_1)$ by
$\times {\operatorname{Hom}}(V_2,V'_1)\times {\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_1)$ by ![]() ${\mathcal {H}}$. We have the natural projections
${\mathcal {H}}$. We have the natural projections
The group ![]() $G_{\mathcal {Q}}:=\operatorname{GL}(V_1)\times \operatorname{GL}(V'_1)\times \operatorname{GL}(V_2)$ naturally acts on
$G_{\mathcal {Q}}:=\operatorname{GL}(V_1)\times \operatorname{GL}(V'_1)\times \operatorname{GL}(V_2)$ naturally acts on ![]() ${\mathcal {H}}$:
${\mathcal {H}}$:
The projections ![]() ${\operatorname {pr}}_{12},{\operatorname {pr}}_{1'2},{\operatorname {pr}}_{11'}$ are equivariant with respect to the same-named projections from
${\operatorname {pr}}_{12},{\operatorname {pr}}_{1'2},{\operatorname {pr}}_{11'}$ are equivariant with respect to the same-named projections from ![]() $G_{\mathcal {Q}}$ to
$G_{\mathcal {Q}}$ to ![]() $\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)$,
$\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)$, ![]() $\operatorname{GL}(V'_1)\times \operatorname{GL}(V_2)$,
$\operatorname{GL}(V'_1)\times \operatorname{GL}(V_2)$, ![]() $\operatorname{GL}(V_1)\times \operatorname{GL}(V'_1)$.
$\operatorname{GL}(V_1)\times \operatorname{GL}(V'_1)$.
Given ![]() ${\mathcal {M}}_{1'2}\in {\mathsf {Coh}}^{\operatorname{GL}(V'_1)\times \operatorname{GL}(V_2)}\big ({\operatorname{Hom}}(V'_1,V_2)\times {\operatorname{Hom}}(V_2,V'_1)\big )$ and
${\mathcal {M}}_{1'2}\in {\mathsf {Coh}}^{\operatorname{GL}(V'_1)\times \operatorname{GL}(V_2)}\big ({\operatorname{Hom}}(V'_1,V_2)\times {\operatorname{Hom}}(V_2,V'_1)\big )$ and ![]() ${\mathcal {M}}_{11'}\in {\mathsf {Coh}}^{\operatorname{GL}(V_1)\times \operatorname{GL}(V'_1)}$
${\mathcal {M}}_{11'}\in {\mathsf {Coh}}^{\operatorname{GL}(V_1)\times \operatorname{GL}(V'_1)}$ ![]() $\big ({\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_1)\big )$, we set
$\big ({\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_1)\big )$, we set
 \begin{align*} {\mathcal{M}}_{11'}{\stackrel {A}*}{\mathcal{M}}_{1'2}&:= {\operatorname{pr}}_{12*}({\operatorname{pr}}_{11'}^*{\mathcal{M}}_{11'}\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\mathbb{C}}[{\mathcal{Q}}^A]\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\operatorname{pr}}_{1'2}^*{\mathcal{M}}_{1'2})^{{{\operatorname{GL}}}(V'_1)}\\ &\quad \in {\mathsf{Coh}}^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\big({{\operatorname{Hom}}}(V_1,V_2)\times{{\operatorname{Hom}}}(V_2,V_1)\big),\end{align*}
\begin{align*} {\mathcal{M}}_{11'}{\stackrel {A}*}{\mathcal{M}}_{1'2}&:= {\operatorname{pr}}_{12*}({\operatorname{pr}}_{11'}^*{\mathcal{M}}_{11'}\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\mathbb{C}}[{\mathcal{Q}}^A]\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\operatorname{pr}}_{1'2}^*{\mathcal{M}}_{1'2})^{{{\operatorname{GL}}}(V'_1)}\\ &\quad \in {\mathsf{Coh}}^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\big({{\operatorname{Hom}}}(V_1,V_2)\times{{\operatorname{Hom}}}(V_2,V_1)\big),\end{align*} \begin{align*} {\mathcal{M}}_{11'}{\stackrel {B}*}{\mathcal{M}}_{1'2}&:= {\operatorname{pr}}_{12*}({\operatorname{pr}}_{11'}^*{\mathcal{M}}_{11'}\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\mathbb{C}}[{\mathcal{Q}}^B]\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\operatorname{pr}}_{1'2}^*{\mathcal{M}}_{1'2})^{{{\operatorname{GL}}}(V'_1)}\\ &\quad\in {\mathsf{Coh}}^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\big({{\operatorname{Hom}}}(V_1,V_2) \times{{\operatorname{Hom}}}(V_2,V_1)\big).\end{align*}
\begin{align*} {\mathcal{M}}_{11'}{\stackrel {B}*}{\mathcal{M}}_{1'2}&:= {\operatorname{pr}}_{12*}({\operatorname{pr}}_{11'}^*{\mathcal{M}}_{11'}\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\mathbb{C}}[{\mathcal{Q}}^B]\,{\otimes}_{{\mathbb{C}}[{\mathcal{H}}]}\ {\operatorname{pr}}_{1'2}^*{\mathcal{M}}_{1'2})^{{{\operatorname{GL}}}(V'_1)}\\ &\quad\in {\mathsf{Coh}}^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\big({{\operatorname{Hom}}}(V_1,V_2) \times{{\operatorname{Hom}}}(V_2,V_1)\big).\end{align*}We will actually need the following modifications of these functors:
obtained using the dg-algebras with trivial differentials ![]() ${\mathbb {C}}[{\mathcal {H}}]_{0,2}^\bullet$ and
${\mathbb {C}}[{\mathcal {H}}]_{0,2}^\bullet$ and ![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$ respectively, where
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$ respectively, where
 \begin{align*} {\mathbb{C}}[{\mathcal{H}}]_{0,2}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}2]) \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_2))\\ &\quad \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V'_1)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V'_1))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_1)[{-}2]), \end{align*}
\begin{align*} {\mathbb{C}}[{\mathcal{H}}]_{0,2}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}2]) \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_2))\\ &\quad \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V'_1)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V'_1))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_1)[{-}2]), \end{align*} \begin{align*} {\mathbb{C}}[{\mathcal{H}}]_{2,0}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)) \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_2)[{-}2])\\ &\quad \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V'_1))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V'_1)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_1)). \end{align*}
\begin{align*} {\mathbb{C}}[{\mathcal{H}}]_{2,0}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)) \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_2)[{-}2])\\ &\quad \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V'_1))\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V'_1)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_1)). \end{align*}
(we identify ![]() ${\mathbb {C}}[{\operatorname{Hom}}(U,W)]$ with
${\mathbb {C}}[{\operatorname{Hom}}(U,W)]$ with ![]() ${\operatorname{Sym}}{\operatorname{Hom}}(W,U)$).
${\operatorname{Sym}}{\operatorname{Hom}}(W,U)$).
3.5 Localization, coherent
We identify
so that
We have an open subvariety ![]() ${\operatorname{Isom}}(V_2,V_1)\subset {\operatorname{Hom}}(V_2,V_1)$, so that
${\operatorname{Isom}}(V_2,V_1)\subset {\operatorname{Hom}}(V_2,V_1)$, so that ![]() ${\mathbb {C}}[{\operatorname{Hom}}(V_2,V_1)]\subset {\mathbb {C}}[{\operatorname{Isom}}(V_2,V_1)]$. We set
${\mathbb {C}}[{\operatorname{Hom}}(V_2,V_1)]\subset {\mathbb {C}}[{\operatorname{Isom}}(V_2,V_1)]$. We set
(a dg-algebra with trivial differential). Similarly, we define
An equivalent formulation of [Reference Bezrukavnikov and FinkelbergBF08, Theorem 5] is an existence of a monoidal equivalence ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {A}}^\bullet )\cong D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ (and, changing the roles of
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {A}}^\bullet )\cong D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ (and, changing the roles of ![]() $V_1,V_2$, a monoidal equivalence
$V_1,V_2$, a monoidal equivalence ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {B}}^\bullet )\cong D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$).
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {B}}^\bullet )\cong D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$).
Since ![]() ${\mathfrak {A}}^\bullet$ (respectively,
${\mathfrak {A}}^\bullet$ (respectively, ![]() ${\mathfrak {B}}^\bullet$) is a localization of
${\mathfrak {B}}^\bullet$) is a localization of ![]() ${\mathfrak {G}}_{2,0}^\bullet$ (respectively, of
${\mathfrak {G}}_{2,0}^\bullet$ (respectively, of ![]() ${\mathfrak {G}}_{0,2}^\bullet$), we have the restriction of scalars functors
${\mathfrak {G}}_{0,2}^\bullet$), we have the restriction of scalars functors
where ![]() $\hat {D}{}^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{?,?}^\bullet )$ stands for the Ind-completion of
$\hat {D}{}^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{?,?}^\bullet )$ stands for the Ind-completion of ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{?,?}^\bullet )$.
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{?,?}^\bullet )$.
However, one can check that, for ![]() ${\mathcal {N}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {A}}^\bullet )$ and
${\mathcal {N}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {A}}^\bullet )$ and ![]() ${\mathcal {M}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$, both convolutions
${\mathcal {M}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$, both convolutions ![]() $\operatorname {Res}_A({\mathcal {N}}){\stackrel {A}*}{\mathcal {M}}$ and
$\operatorname {Res}_A({\mathcal {N}}){\stackrel {A}*}{\mathcal {M}}$ and ![]() ${\mathcal {M}}{\stackrel {A}*}\operatorname {Res}_A({\mathcal {N}})$ lie in
${\mathcal {M}}{\stackrel {A}*}\operatorname {Res}_A({\mathcal {N}})$ lie in ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\subset \hat {D}{}^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$. Thus we have the left and right convolution actions
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\subset \hat {D}{}^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$. Thus we have the left and right convolution actions
and similarly,
3.6 Renormalizations
The action of the center ![]() $Z(\operatorname{GL}(V_1))\cong {\mathbb {G}}_m$ on an object
$Z(\operatorname{GL}(V_1))\cong {\mathbb {G}}_m$ on an object ![]() ${\mathcal {M}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ defines a grading, and the corresponding degrees will be denoted by
${\mathcal {M}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ defines a grading, and the corresponding degrees will be denoted by ![]() $\deg _1$. Similarly, the action of
$\deg _1$. Similarly, the action of ![]() $Z(\operatorname{GL}(V_2))\cong {\mathbb {G}}_m$ gives rise to another grading with degrees denoted by
$Z(\operatorname{GL}(V_2))\cong {\mathbb {G}}_m$ gives rise to another grading with degrees denoted by ![]() $\deg _2$. The cohomological degrees will be denoted simply by
$\deg _2$. The cohomological degrees will be denoted simply by ![]() $\deg$. Clearly, the degrees of the generators are as follows:
$\deg$. Clearly, the degrees of the generators are as follows:
Hence changing cohomological degrees by the formula ![]() $\deg \leadsto \deg +\deg _1$ (respectively,
$\deg \leadsto \deg +\deg _1$ (respectively, ![]() $\deg \leadsto \deg -\deg _2$) yields equivalences
$\deg \leadsto \deg -\deg _2$) yields equivalences
 \begin{gather*} D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{2,0}^\bullet)\xrightarrow{\varrho_{\operatorname{right}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{1,1}^\bullet) \xrightarrow{\varrho_{\operatorname{right}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{0,2}^\bullet),\\ D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{2,0}^\bullet)\xrightarrow{\varrho_{\operatorname{left}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{1,1}^\bullet) \xrightarrow{\varrho_{\operatorname{left}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{0,2}^\bullet), \end{gather*}
\begin{gather*} D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{2,0}^\bullet)\xrightarrow{\varrho_{\operatorname{right}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{1,1}^\bullet) \xrightarrow{\varrho_{\operatorname{right}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{0,2}^\bullet),\\ D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{2,0}^\bullet)\xrightarrow{\varrho_{\operatorname{left}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{1,1}^\bullet) \xrightarrow{\varrho_{\operatorname{left}}}D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{G}}_{0,2}^\bullet), \end{gather*}
respectively. The notation is due to the fact that ![]() $\varrho _{\operatorname {left}}$ commutes with the left action of
$\varrho _{\operatorname {left}}$ commutes with the left action of ![]() ${\operatorname {Rep}}(\operatorname{GL}(V_1))$ on our categories, while
${\operatorname {Rep}}(\operatorname{GL}(V_1))$ on our categories, while ![]() $\varrho _{\operatorname {right}}$ commutes with the right action of
$\varrho _{\operatorname {right}}$ commutes with the right action of ![]() ${\operatorname {Rep}}(\operatorname{GL}(V_2))$ on our categories.
${\operatorname {Rep}}(\operatorname{GL}(V_2))$ on our categories.
Now recall the notation in the definition of categories ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (where
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (where ![]() $?={!},\ *,\ !*$) of § 3.1. Given
$?={!},\ *,\ !*$) of § 3.1. Given ![]() ${\mathcal {F}}=({\mathcal {F}}_n)_{n>m}\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define
${\mathcal {F}}=({\mathcal {F}}_n)_{n>m}\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we define ![]() $\varrho _{\operatorname {right}}{\mathcal {F}}:=({\mathcal {F}}_n[-Nn])_{n>m}\in D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Similarly, given
$\varrho _{\operatorname {right}}{\mathcal {F}}:=({\mathcal {F}}_n[-Nn])_{n>m}\in D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Similarly, given ![]() ${\mathcal {F}}=({\mathcal {F}}_n)_{n>m}\in D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ we define
${\mathcal {F}}=({\mathcal {F}}_n)_{n>m}\in D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ we define ![]() $\varrho _{\operatorname {right}}{\mathcal {F}}:=({\mathcal {F}}_n[-Nn])_{n>m}\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. The functors
$\varrho _{\operatorname {right}}{\mathcal {F}}:=({\mathcal {F}}_n[-Nn])_{n>m}\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. The functors ![]() $\varrho _{\operatorname {right}}$ commute with the action of the monoidal category
$\varrho _{\operatorname {right}}$ commute with the action of the monoidal category ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ by right convolutions. Recall also that the affine Grassmannian is a union of connected components
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ by right convolutions. Recall also that the affine Grassmannian is a union of connected components ![]() ${\mathbf {Gr}}={\bigsqcup} _{k\in {\mathbb {Z}}}{\mathbf {Gr}}^{(k)}$, where
${\mathbf {Gr}}={\bigsqcup} _{k\in {\mathbb {Z}}}{\mathbf {Gr}}^{(k)}$, where ![]() ${\mathbf {Gr}}^{(k)}$ parametrizes the lattices of virtual dimension
${\mathbf {Gr}}^{(k)}$ parametrizes the lattices of virtual dimension ![]() $k$ (e.g.
$k$ (e.g. ![]() $\dim (t{\mathbf {V}}_0)=-N$). For
$\dim (t{\mathbf {V}}_0)=-N$). For ![]() ${\mathcal {F}}$ supported on
${\mathcal {F}}$ supported on ![]() ${\mathbf {Gr}}^{(k)}\times {\mathbf {V}}$ we set
${\mathbf {Gr}}^{(k)}\times {\mathbf {V}}$ we set ![]() $\varrho _{\operatorname {left}}({\mathcal {F}}):=\varrho _{\operatorname {right}}({\mathcal {F}})[-k]$. Then the functors
$\varrho _{\operatorname {left}}({\mathcal {F}}):=\varrho _{\operatorname {right}}({\mathcal {F}})[-k]$. Then the functors
commute with the action of the monoidal category ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ by the left convolutions.
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ by the left convolutions.
Our goal is the following theorem.
Theorem 3.6.1 There exist monoidalFootnote 7 equivalences of triangulated categories

(the vertical equivalences are not monoidal). The squares are commutative. The horizontal equivalences commute with the actions of the monoidal spherical Hecke category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ by the left and right convolutions.
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ by the left and right convolutions.
The proof will be given in § 3.16 after some necessary preparation.
3.7 Super
Strictly speaking, in accordance with the footnote at the beginning of § 3.4, we should consider the category ![]() $SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ of super dg-modules over the superalgebra
$SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ of super dg-modules over the superalgebra ![]() ${\mathfrak {G}}_{1,1}^\bullet ={\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$. The latter superalgebra is supercommutative, hence we have a symmetric monoidal structure
${\mathfrak {G}}_{1,1}^\bullet ={\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$. The latter superalgebra is supercommutative, hence we have a symmetric monoidal structure ![]() $\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$ on the category
$\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$ on the category ![]() $SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$. The equivalence
$SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$. The equivalence ![]() $\Phi ^{1,1}$ of Theorem 3.6.1 can be upgraded to a monoidal equivalence
$\Phi ^{1,1}$ of Theorem 3.6.1 can be upgraded to a monoidal equivalence ![]() $S\Phi ^{1,1}\colon \big (SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet ),\ \,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }\big ){\buildrel \sim \over \longrightarrow} \big (SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}}),\ \star \big )$ to the derived category of sheaves with coefficients in super vector spaces.
$S\Phi ^{1,1}\colon \big (SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet ),\ \,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }\big ){\buildrel \sim \over \longrightarrow} \big (SD_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}}),\ \star \big )$ to the derived category of sheaves with coefficients in super vector spaces.
However, the action of the central element ![]() $({\operatorname{Id}}_{V_1},-{\operatorname{Id}}_{V_2})\in G_{\bar 0}$ on an object of
$({\operatorname{Id}}_{V_1},-{\operatorname{Id}}_{V_2})\in G_{\bar 0}$ on an object of ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ equips this object with an extra
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ equips this object with an extra ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-grading, and thus defines a fully faithful functor
${\mathbb {Z}}/2{\mathbb {Z}}$-grading, and thus defines a fully faithful functor ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )\to SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ of a ‘superization’, such that its essential image is closed under the monoidal structure
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )\to SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ of a ‘superization’, such that its essential image is closed under the monoidal structure ![]() $\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$. This defines the desired monoidal structure
$\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$. This defines the desired monoidal structure ![]() $\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$ on the category
$\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$ on the category ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$.
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$.
3.8 Koszul equivalence
We consider the following complex ![]() $H^\bullet$ of odd vector spaces living in degrees
$H^\bullet$ of odd vector spaces living in degrees ![]() $0,1\colon {\mathfrak {g}}_{\bar 1}\stackrel {{\operatorname{Id}}}{\longrightarrow }{\mathfrak {g}}_{\bar 1}$. We define the Koszul complex
$0,1\colon {\mathfrak {g}}_{\bar 1}\stackrel {{\operatorname{Id}}}{\longrightarrow }{\mathfrak {g}}_{\bar 1}$. We define the Koszul complex ![]() $K^\bullet$ as the symmetric algebra
$K^\bullet$ as the symmetric algebra ![]() ${\operatorname{Sym}}(H^\bullet )$. The degree-
${\operatorname{Sym}}(H^\bullet )$. The degree-![]() $0$ part
$0$ part
(as a vector space, with a superstructure disregarded). We turn ![]() $K^\bullet$ into a dg-
$K^\bullet$ into a dg-![]() ${\mathfrak {G}}^\bullet _{1,1}-\Lambda$-bimodule by letting
${\mathfrak {G}}^\bullet _{1,1}-\Lambda$-bimodule by letting ![]() ${\mathfrak {G}}^\bullet _{1,1}$ act by multiplication, and
${\mathfrak {G}}^\bullet _{1,1}$ act by multiplication, and ![]() $\Lambda$ by differentiation. Note that
$\Lambda$ by differentiation. Note that ![]() $K^{\bullet}$ is quasi-isomorphic to
$K^{\bullet}$ is quasi-isomorphic to ![]() ${\mathbb {C}}$ in degree 0 as a complex of vector spaces, but not as a dg-
${\mathbb {C}}$ in degree 0 as a complex of vector spaces, but not as a dg-![]() ${\mathfrak {G}}^\bullet _{1,1}-\Lambda$-bimodule. We consider the derived category
${\mathfrak {G}}^\bullet _{1,1}-\Lambda$-bimodule. We consider the derived category ![]() $D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ of finite-dimensional complexes of
$D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ of finite-dimensional complexes of ![]() $G_{\bar 0}\ltimes \Lambda$-modules. If we remember the superstructure of
$G_{\bar 0}\ltimes \Lambda$-modules. If we remember the superstructure of ![]() $\Lambda$, we obtain the corresponding category of super dg-modules
$\Lambda$, we obtain the corresponding category of super dg-modules ![]() $SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$. We have the Koszul equivalence functors
$SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$. We have the Koszul equivalence functors
Here is an equivalent definition of the category ![]() $SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$. We consider the following degeneration
$SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$. We consider the following degeneration ![]() $\underline {\mathfrak {gl}}(N|N)$ of the Lie superalgebra
$\underline {\mathfrak {gl}}(N|N)$ of the Lie superalgebra ![]() ${\mathfrak {gl}}({N|N})$: the supercommutator of the even elements (with even or odd elements) remains intact, but the supercommutator of any two odd elements is set to zero. Let
${\mathfrak {gl}}({N|N})$: the supercommutator of the even elements (with even or odd elements) remains intact, but the supercommutator of any two odd elements is set to zero. Let ![]() $SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N))$ denote the derived category of bounded complexes of integrable
$SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N))$ denote the derived category of bounded complexes of integrable ![]() $\underline {\mathfrak {gl}}(N|N)$-modules (note that the even part of
$\underline {\mathfrak {gl}}(N|N)$-modules (note that the even part of ![]() $\underline {\mathfrak {gl}}(N|N)$ is just
$\underline {\mathfrak {gl}}(N|N)$ is just ![]() ${\mathfrak {g}}_{\bar 0}$, and the integrability is nothing but
${\mathfrak {g}}_{\bar 0}$, and the integrability is nothing but ![]() ${\mathfrak {g}}_{\bar 0}$-integrability, i.e.
${\mathfrak {g}}_{\bar 0}$-integrability, i.e. ![]() $G_{\bar 0}$-equivariance). Then
$G_{\bar 0}$-equivariance). Then ![]() $SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N))\cong SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ tautologically. The resulting Koszul equivalence
$SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N))\cong SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ tautologically. The resulting Koszul equivalence ![]() $\varkappa \colon SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N)){\buildrel \sim \over \longrightarrow} SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is monoidal with respect to the usual tensor structure on the left-hand side and
$\varkappa \colon SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N)){\buildrel \sim \over \longrightarrow} SD^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is monoidal with respect to the usual tensor structure on the left-hand side and ![]() $\,{\otimes} _{{\mathfrak {G}}^\bullet _{1,1}}$ on the right-hand side.
$\,{\otimes} _{{\mathfrak {G}}^\bullet _{1,1}}$ on the right-hand side.
As in § 3.7, the action of ![]() $({\operatorname{Id}}_{V_1},-{\operatorname{Id}}_{V_2})\in G_{\bar 0}$ gives rise to a ‘superization’ fully faithful functor
$({\operatorname{Id}}_{V_1},-{\operatorname{Id}}_{V_2})\in G_{\bar 0}$ gives rise to a ‘superization’ fully faithful functor ![]() $D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )\to SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )\cong SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N))$ with the essential image closed under the tensor structure. This defines the tensor structure on
$D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )\to SD_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )\cong SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N|N))$ with the essential image closed under the tensor structure. This defines the tensor structure on ![]() $D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ such that the Koszul equivalence
$D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ such that the Koszul equivalence ![]() $\varkappa \colon D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda ){\buildrel \sim \over \longrightarrow} D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is monoidal.
$\varkappa \colon D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda ){\buildrel \sim \over \longrightarrow} D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is monoidal.
Corollary 3.8.1 (of Theorem 3.6.1)
(a) The composed equivalence
is exact with respect to the tautological ![]() $t$-structure on
$t$-structure on ![]() $D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ and the perverse
$D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ and the perverse ![]() $t$-structure on
$t$-structure on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
(b) This equivalence is monoidal with respect to the tensor structure on ![]() $D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ and the fusion
$D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ and the fusion ![]() $\star$ on
$\star$ on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
(c) The equivariant derived category ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is equivalent to the bounded derived category of the abelian category
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is equivalent to the bounded derived category of the abelian category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
Proof. We consider an irreducible ![]() $G_{\bar 0}$-module
$G_{\bar 0}$-module ![]() $V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$ as a
$V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$ as a ![]() $G_{\bar 0}\ltimes \Lambda$-module with the trivial action of
$G_{\bar 0}\ltimes \Lambda$-module with the trivial action of ![]() $\Lambda$. Then
$\Lambda$. Then ![]() $\varkappa (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, V_{2,{\boldsymbol {\mu }}})=V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$, and
$\varkappa (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, V_{2,{\boldsymbol {\mu }}})=V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$, and ![]() $\Phi ^{1,1}(V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})={\operatorname {IC}}_{({\boldsymbol {\lambda }}^*,{\boldsymbol {\mu }}^*)}$ by construction of
$\Phi ^{1,1}(V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})={\operatorname {IC}}_{({\boldsymbol {\lambda }}^*,{\boldsymbol {\mu }}^*)}$ by construction of ![]() $\Phi ^{1,1}$. Here, for a signature
$\Phi ^{1,1}$. Here, for a signature ![]() ${\boldsymbol {\nu }}=(\nu _1\geq \cdots \geq \nu _N)$, we set
${\boldsymbol {\nu }}=(\nu _1\geq \cdots \geq \nu _N)$, we set ![]() ${\boldsymbol {\nu }}^*:=(-\nu _N\geq \cdots \geq -\nu _1)$.
${\boldsymbol {\nu }}^*:=(-\nu _N\geq \cdots \geq -\nu _1)$.
Finally, since ![]() $D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ is equivalent to the bounded derived category of its heart
$D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ is equivalent to the bounded derived category of its heart ![]() ${\operatorname {Rep}}(G_{\bar 0}\ltimes \Lambda )$, (c) follows from (a).
${\operatorname {Rep}}(G_{\bar 0}\ltimes \Lambda )$, (c) follows from (a).
3.9 De-equivariantized Ext algebra
Recall from [Reference Finkelberg, Ginzburg and TravkinFGT09, Proposition 8] that the ![]() ${\mathbf {G}}_{\mathbf {O}}$-orbits in
${\mathbf {G}}_{\mathbf {O}}$-orbits in ![]() ${\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$ are numbered by bisignatures
${\mathbf {Gr}}\times {\vphantom {j^{X^2}}\smash {\overset {\circ }{\vphantom {\rule {0pt}{0.55em}}\smash {\mathbf {V}}}}}$ are numbered by bisignatures ![]() $({\boldsymbol {\lambda }},{\boldsymbol {\mu }})$ where both
$({\boldsymbol {\lambda }},{\boldsymbol {\mu }})$ where both ![]() ${\boldsymbol {\lambda }}$ and
${\boldsymbol {\lambda }}$ and ![]() ${\boldsymbol {\mu }}$ have length
${\boldsymbol {\mu }}$ have length ![]() $N$. The IC extension of the constant one-dimensional local system on such an orbit is denoted by
$N$. The IC extension of the constant one-dimensional local system on such an orbit is denoted by ![]() ${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$. In particular,
${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$. In particular, ![]() ${\operatorname {IC}}_{(0^N,0^N)}$ is the constant sheaf on
${\operatorname {IC}}_{(0^N,0^N)}$ is the constant sheaf on ![]() ${\mathbf {Gr}}^0\times {\mathbf {V}}_0$, to be denoted by
${\mathbf {Gr}}^0\times {\mathbf {V}}_0$, to be denoted by ![]() $E_0$ for short. Also recall from [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3] that the left and right actions of the monoidal Satake category
$E_0$ for short. Also recall from [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3] that the left and right actions of the monoidal Satake category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ on
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ by convolutions respect the perverse
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ by convolutions respect the perverse ![]() $t$-structure with the heart
$t$-structure with the heart ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\subset D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. As has been mentioned in § 3.6, the right actions of
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\subset D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. As has been mentioned in § 3.6, the right actions of ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ on
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ on ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ commute with the equivalences
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ commute with the equivalences ![]() $\varrho _{\operatorname {right}}$, but the left actions only commute with
$\varrho _{\operatorname {right}}$, but the left actions only commute with ![]() $\varrho _{\operatorname {right}}$ up to cohomological shifts depending on the connected components of
$\varrho _{\operatorname {right}}$ up to cohomological shifts depending on the connected components of ![]() ${\mathbf {Gr}}$.
${\mathbf {Gr}}$.
We restrict the left and right actions of ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ on
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ on ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ to the left and right actions of
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ to the left and right actions of ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$. Thus we obtain the action of
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$. Thus we obtain the action of ![]() ${\operatorname {Rep}}({\mathsf {G}})$ for
${\operatorname {Rep}}({\mathsf {G}})$ for ![]() ${\mathsf {G}}=\operatorname{GL}_N\times \operatorname{GL}_N$. Let
${\mathsf {G}}=\operatorname{GL}_N\times \operatorname{GL}_N$. Let ![]() $D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ denote the corresponding de-equivariantized category (see [Reference Arkhipov and GaitsgoryAG03] in the setting of abelian categories and [Reference GaitsgoryGai15] in the setting of dg-categories). Recall that to construct
$D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ denote the corresponding de-equivariantized category (see [Reference Arkhipov and GaitsgoryAG03] in the setting of abelian categories and [Reference GaitsgoryGai15] in the setting of dg-categories). Recall that to construct ![]() $D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we first consider objects of the ind-completion of
$D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we first consider objects of the ind-completion of ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ endowed with an action of
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ endowed with an action of ![]() $R_{\mathsf {G}}$ where
$R_{\mathsf {G}}$ where ![]() $R_{\mathsf {G}}$ is the regular representation of
$R_{\mathsf {G}}$ is the regular representation of ![]() ${\mathsf {G}}$ considered as a ring object in
${\mathsf {G}}$ considered as a ring object in ![]() ${\operatorname {Rep}}({\mathsf {G}})$. Then we take compact objects of the resulting category. More explicitly, an object of
${\operatorname {Rep}}({\mathsf {G}})$. Then we take compact objects of the resulting category. More explicitly, an object of ![]() $D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is an object
$D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is an object ![]() ${\mathcal {F}}$ of
${\mathcal {F}}$ of ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ together with a system of isomorphisms
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ together with a system of isomorphisms ![]() ${\operatorname {IC}}_{\boldsymbol {\lambda }}*{\mathcal {F}}*{\operatorname {IC}}_{\boldsymbol {\mu }}{\buildrel \sim \over \longrightarrow} V^*_{\boldsymbol {\lambda }}\,{\otimes}\, V^*_{\boldsymbol {\mu }}\,{\otimes}\, {\mathcal {F}}$ (recall that the geometric Satake equivalence takes
${\operatorname {IC}}_{\boldsymbol {\lambda }}*{\mathcal {F}}*{\operatorname {IC}}_{\boldsymbol {\mu }}{\buildrel \sim \over \longrightarrow} V^*_{\boldsymbol {\lambda }}\,{\otimes}\, V^*_{\boldsymbol {\mu }}\,{\otimes}\, {\mathcal {F}}$ (recall that the geometric Satake equivalence takes ![]() ${\operatorname {IC}}_{\boldsymbol {\lambda }}$ to
${\operatorname {IC}}_{\boldsymbol {\lambda }}$ to ![]() $V^*_{\boldsymbol {\lambda }}$) for any signatures
$V^*_{\boldsymbol {\lambda }}$) for any signatures ![]() ${\boldsymbol {\lambda }},{\boldsymbol {\mu }}$, satisfying some natural compatibilities with respect to direct sums and tensor products. By definition we have a natural forgetful functor
${\boldsymbol {\lambda }},{\boldsymbol {\mu }}$, satisfying some natural compatibilities with respect to direct sums and tensor products. By definition we have a natural forgetful functor ![]() $D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. This functor admits a left adjoint that sends an object
$D^{{\operatorname{deeq}}}_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. This functor admits a left adjoint that sends an object ![]() ${\mathcal {F}}$ to
${\mathcal {F}}$ to ![]() $R_{\mathsf {G}}*{\mathcal {F}}=\bigoplus _{{\boldsymbol {\lambda }},{\boldsymbol {\mu }}}V_{\boldsymbol {\lambda }}\,{\otimes}\, V_{\boldsymbol {\mu }}\,{\otimes}\, {\operatorname {IC}}_{\boldsymbol {\lambda }}*{\mathcal {F}}*{\operatorname {IC}}_{\boldsymbol {\mu }}$.
$R_{\mathsf {G}}*{\mathcal {F}}=\bigoplus _{{\boldsymbol {\lambda }},{\boldsymbol {\mu }}}V_{\boldsymbol {\lambda }}\,{\otimes}\, V_{\boldsymbol {\mu }}\,{\otimes}\, {\operatorname {IC}}_{\boldsymbol {\lambda }}*{\mathcal {F}}*{\operatorname {IC}}_{\boldsymbol {\mu }}$.
Thus, given ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we denote the corresponding objects of the de-equivariantized category by the same symbols, and we have
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we denote the corresponding objects of the de-equivariantized category by the same symbols, and we have
Lemma 3.9.1 The dg-algebra ![]() $\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ is formal, that is, it is quasi-isomorphic to the graded algebra
$\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ is formal, that is, it is quasi-isomorphic to the graded algebra ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ with trivial differential.
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ with trivial differential.
Proof. We change the setting to the base field ![]() ${\mathbb {F}}_q$. Then a
${\mathbb {F}}_q$. Then a ![]() ${\mathbf {G}}_{\mathbf {O}}$-equivariant irreducible perverse sheaf
${\mathbf {G}}_{\mathbf {O}}$-equivariant irreducible perverse sheaf ![]() ${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ on
${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$ carries a natural Weil structure (see [Reference Finkelberg, Ginzburg and TravkinFGT09, § 2.6]) and
${\mathbf {Gr}}\times {\mathbf {V}}$ carries a natural Weil structure (see [Reference Finkelberg, Ginzburg and TravkinFGT09, § 2.6]) and ![]() ${\operatorname{Ext}}^\bullet _{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$ is pure. Indeed, if
${\operatorname{Ext}}^\bullet _{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$ is pure. Indeed, if ![]() $\bar \imath _0$ denotes the closed embedding
$\bar \imath _0$ denotes the closed embedding ![]() ${\mathbf {V}}_0\cong {\mathbf {Gr}}^0\times {\mathbf {V}}_0\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$, then
${\mathbf {V}}_0\cong {\mathbf {Gr}}^0\times {\mathbf {V}}_0\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$, then ![]() ${\operatorname{Ext}}^\bullet _{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})= H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {V}}_0,\bar \imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$. Let us consider the loop rotation action
${\operatorname{Ext}}^\bullet _{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})= H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {V}}_0,\bar \imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$. Let us consider the loop rotation action ![]() ${\mathbb {G}}_m\curvearrowright ({\mathbf {Gr}}\times {\mathbf {V}})$. We have an embedding
${\mathbb {G}}_m\curvearrowright ({\mathbf {Gr}}\times {\mathbf {V}})$. We have an embedding ![]() ${\mathbb {A}}^1\hookrightarrow {\mathbf {V}}$ (constant Laurent series), and
${\mathbb {A}}^1\hookrightarrow {\mathbf {V}}$ (constant Laurent series), and ![]() ${\mathbf {Gr}}^0\times {\mathbb {A}}^1$ is a fixed point component of the
${\mathbf {Gr}}^0\times {\mathbb {A}}^1$ is a fixed point component of the ![]() ${\mathbb {G}}_m$-action, so that
${\mathbb {G}}_m$-action, so that ![]() $H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {V}}_0,\bar \imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$ is the hyperbolic restriction to this component (more precisely, the hyperbolic restriction is a geometrically constant complex on
$H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {V}}_0,\bar \imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$ is the hyperbolic restriction to this component (more precisely, the hyperbolic restriction is a geometrically constant complex on ![]() ${\mathbb {A}}^1$ with the above stalks) [Reference BradenBra03, Reference Drinfeld and GaitsgoryDG14]. But the hyperbolic restriction preserves purity.
${\mathbb {A}}^1$ with the above stalks) [Reference BradenBra03, Reference Drinfeld and GaitsgoryDG14]. But the hyperbolic restriction preserves purity.
Now, given the purity of ![]() ${\operatorname{Ext}}^\bullet _{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$, the desired result follows by an application of [Reference Bezrukavnikov and FinkelbergBF08, Lemma 15] (and then of [Reference Bezrukavnikov and FinkelbergBF08, Proposition 5]).
${\operatorname{Ext}}^\bullet _{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$, the desired result follows by an application of [Reference Bezrukavnikov and FinkelbergBF08, Lemma 15] (and then of [Reference Bezrukavnikov and FinkelbergBF08, Proposition 5]).
We denote the dg-algebra ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ (with trivial differential) by
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ (with trivial differential) by ![]() ${\mathfrak {E}}^\bullet$. Since it is an Ext-algebra in the de-equivariantized category between objects induced from the original category, it is automatically equipped with an action of
${\mathfrak {E}}^\bullet$. Since it is an Ext-algebra in the de-equivariantized category between objects induced from the original category, it is automatically equipped with an action of ![]() $\operatorname{GL}_N\times \operatorname{GL}_N=\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)=G_{\bar 0}$, and we can consider the corresponding triangulated category
$\operatorname{GL}_N\times \operatorname{GL}_N=\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)=G_{\bar 0}$, and we can consider the corresponding triangulated category ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}^\bullet )$.
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}^\bullet )$.
Lemma 3.9.2 There is a canonical equivalence ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
Proof. The desired functor is constructed as in [Reference Bezrukavnikov and FinkelbergBF08, § 6.5, Propositions 5,6]. Since ![]() $E_0$ generates the triangulated category
$E_0$ generates the triangulated category ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (with respect to the left and right actions of the Satake category), the claim follows from Lemma 3.9.1.
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (with respect to the left and right actions of the Satake category), the claim follows from Lemma 3.9.1.
We also consider the left and right actions of the monoidal Satake category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ on
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ on ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ by convolutions. Let
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ by convolutions. Let ![]() $D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ denote the corresponding de-equivariantized category. Then the dg-algebra
$D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ denote the corresponding de-equivariantized category. Then the dg-algebra ![]() $\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0,{\operatorname {IC}}_0)$ is formal, that is, it is quasi-isomorphic to the graded algebra
$\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0,{\operatorname {IC}}_0)$ is formal, that is, it is quasi-isomorphic to the graded algebra ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0,{\operatorname {IC}}_0)$ with trivial differential. Furthermore, it follows from [Reference Bezrukavnikov and FinkelbergBF08, Theorem 5] that there is a natural isomorphism
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0,{\operatorname {IC}}_0)$ with trivial differential. Furthermore, it follows from [Reference Bezrukavnikov and FinkelbergBF08, Theorem 5] that there is a natural isomorphism ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0,{\operatorname {IC}}_0)\cong {\mathfrak {A}}^\bullet$ (in the notation of § 3.5).
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0,{\operatorname {IC}}_0)\cong {\mathfrak {A}}^\bullet$ (in the notation of § 3.5).
3.10 Localization, constructible
We have an automorphism ![]() $\alpha \colon {\mathbf {Gr}}\times {\mathbf {V}}{\buildrel \sim \over \longrightarrow} {\mathbf {Gr}}\times {\mathbf {V}}$,
$\alpha \colon {\mathbf {Gr}}\times {\mathbf {V}}{\buildrel \sim \over \longrightarrow} {\mathbf {Gr}}\times {\mathbf {V}}$, ![]() $(L,v)\mapsto (L,tv)$. We have a morphism of endofunctors
$(L,v)\mapsto (L,tv)$. We have a morphism of endofunctors ![]() $\alpha ^*\to {\operatorname{Id}}\colon D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ constructed as follows. We consider a family of automorphisms
$\alpha ^*\to {\operatorname{Id}}\colon D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ constructed as follows. We consider a family of automorphisms ![]() $\boldsymbol {\alpha }\colon {\mathbb {A}}^1\times {\mathbf {Gr}}\times {\mathbf {V}}\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$,
$\boldsymbol {\alpha }\colon {\mathbb {A}}^1\times {\mathbf {Gr}}\times {\mathbf {V}}\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$, ![]() $(c,L,v)\mapsto (L,(c+t)v)$, so that
$(c,L,v)\mapsto (L,(c+t)v)$, so that ![]() $\boldsymbol {\alpha }_0=\alpha$. Note that
$\boldsymbol {\alpha }_0=\alpha$. Note that ![]() $\boldsymbol {\alpha }_c^*\cong {\operatorname{Id}}$ on
$\boldsymbol {\alpha }_c^*\cong {\operatorname{Id}}$ on ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ for
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ for ![]() $c\ne 0$. Now the desired morphism
$c\ne 0$. Now the desired morphism ![]() $\alpha ^*\to {\operatorname{Id}}$ is just the cospecializationFootnote 8 morphism from the stalk at
$\alpha ^*\to {\operatorname{Id}}$ is just the cospecializationFootnote 8 morphism from the stalk at ![]() $0\in {\mathbb {A}}^1$ to the nearby stalk. For
$0\in {\mathbb {A}}^1$ to the nearby stalk. For ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we have an inductive system
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we have an inductive system
Note that it stabilizes since, by definition of ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, the restriction of
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, the restriction of ![]() $(\alpha ^n)^*{\mathcal {F}}_1$ to the support of
$(\alpha ^n)^*{\mathcal {F}}_1$ to the support of ![]() ${\mathcal {F}}_2$ becomes the pullback of an appropriate sheaf in
${\mathcal {F}}_2$ becomes the pullback of an appropriate sheaf in ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ for
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ for ![]() $n\gg 0$.
$n\gg 0$.
We define the localized category ![]() $D^{\operatorname {loc}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ as the category with the same objects as
$D^{\operatorname {loc}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ as the category with the same objects as ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, and with morphisms
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, and with morphisms
The tautological functor ![]() $D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D^{\operatorname {loc}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is denoted by
$D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D^{\operatorname {loc}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is denoted by ![]() $u_0^*$ (‘restriction to
$u_0^*$ (‘restriction to ![]() $v\thickapprox 0$’).
$v\thickapprox 0$’).
We also have the Verdier dual (to the above ![]() $\alpha ^*\to {\operatorname{Id}}$) morphism of endofunctors
$\alpha ^*\to {\operatorname{Id}}$) morphism of endofunctors ![]() ${\operatorname{Id}}\to \alpha ^! \colon D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. This gives rise to an inductive system for
${\operatorname{Id}}\to \alpha ^! \colon D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. This gives rise to an inductive system for ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$,
${\mathcal {F}}_1,{\mathcal {F}}_2\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$,
stabilizing for reasons similar to those above. We define the localized category ![]() $D^{{\operatorname {loc}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ as the category with the same objects as
$D^{{\operatorname {loc}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ as the category with the same objects as ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, and with morphisms
$D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, and with morphisms
The tautological functor ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D^{{\operatorname {loc}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is denoted by
$D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D^{{\operatorname {loc}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is denoted by ![]() $u_0^!$ (‘corestriction to
$u_0^!$ (‘corestriction to ![]() $v\thickapprox 0$’).
$v\thickapprox 0$’).
We also have the projection ![]() ${\operatorname {pr}}\colon {\mathbf {Gr}}\times {\mathbf {V}}_0\to {\mathbf {Gr}}$, and the corresponding pullbacks
${\operatorname {pr}}\colon {\mathbf {Gr}}\times {\mathbf {V}}_0\to {\mathbf {Gr}}$, and the corresponding pullbacks ![]() ${\operatorname {pr}}^*\colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and
${\operatorname {pr}}^*\colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and ![]() ${\operatorname {pr}}^!\colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (with the essential images supported on
${\operatorname {pr}}^!\colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ (with the essential images supported on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}_0\subset {\mathbf {Gr}}\times {\mathbf {V}}$).
${\mathbf {Gr}}\times {\mathbf {V}}_0\subset {\mathbf {Gr}}\times {\mathbf {V}}$).
Lemma 3.10.1 The compositions
are equivalences of categories sending ![]() ${\operatorname {IC}}_0$ to
${\operatorname {IC}}_0$ to ![]() $\varrho _{\operatorname {right}} E_0$,
$\varrho _{\operatorname {right}} E_0$, ![]() $\varrho _{\operatorname {right}}^{-1}E_0$, respectively.
$\varrho _{\operatorname {right}}^{-1}E_0$, respectively.
Proof. Clear.
The localizations of the de-equivariantized categories ![]() $D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and
$D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and ![]() $D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ will be denoted by
$D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ will be denoted by ![]() $D^{{\operatorname {loc}},{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and
$D^{{\operatorname {loc}},{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and ![]() $D^{{\operatorname {loc}},{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, respectively.
$D^{{\operatorname {loc}},{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, respectively.
Recall the dg-algebras ![]() ${\mathfrak {A}}^\bullet ,{\mathfrak {B}}^\bullet$ introduced in § 3.5.
${\mathfrak {A}}^\bullet ,{\mathfrak {B}}^\bullet$ introduced in § 3.5.
Corollary 3.10.2 There are canonical isomorphisms
(a)
 ${\operatorname{Ext}}^\bullet _{D^{{\operatorname {loc}},{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}}^{-1}E_0, \varrho _{{\operatorname {right}}}^{-1}E_0)\cong {\mathfrak {A}}^\bullet ,$
${\operatorname{Ext}}^\bullet _{D^{{\operatorname {loc}},{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}}^{-1}E_0, \varrho _{{\operatorname {right}}}^{-1}E_0)\cong {\mathfrak {A}}^\bullet ,$(b)
 ${\operatorname{Ext}}^\bullet _{D^{{\operatorname {loc}},{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0, \varrho _{\operatorname {right}} E_0)\cong {\mathfrak {B}}^\bullet$.
${\operatorname{Ext}}^\bullet _{D^{{\operatorname {loc}},{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0, \varrho _{\operatorname {right}} E_0)\cong {\mathfrak {B}}^\bullet$.
Note that the dg-algebra ![]() $\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\!\times\! {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0,\varrho _{\operatorname {right}} E_0)$ (respectively,
$\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\!\times\! {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0,\varrho _{\operatorname {right}} E_0)$ (respectively, ![]() $\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\!\times\! {\mathbf {V}})}$
$\operatorname {RHom}_{D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\!\times\! {\mathbf {V}})}$ ![]() $(\varrho _{\operatorname {right}}^{-1}E_0,\varrho _{\operatorname {right}}^{-1}E_0)$) is also formal, that is, it is quasi-isomorphic to
$(\varrho _{\operatorname {right}}^{-1}E_0,\varrho _{\operatorname {right}}^{-1}E_0)$) is also formal, that is, it is quasi-isomorphic to ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0,$
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0,$ ![]() $\varrho _{\operatorname {right}} E_0)$ (respectively,
$\varrho _{\operatorname {right}} E_0)$ (respectively, ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}}^{-1}E_0,\varrho _{\operatorname {right}}^{-1}E_0)$) with trivial differential. If we disregard their gradings, they are both isomorphic to
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}}^{-1}E_0,\varrho _{\operatorname {right}}^{-1}E_0)$) with trivial differential. If we disregard their gradings, they are both isomorphic to ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$. We will denote the algebra
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$. We will denote the algebra ![]() ${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ with grading forgotten by
${\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ with grading forgotten by ![]() ${\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$; the same applies to
${\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$; the same applies to ![]() ${\mathfrak {A}}^\bullet ,{\mathfrak {B}}^\bullet ,{\mathfrak {E}}^\bullet ,{\mathfrak {G}}^\bullet$. Thus we have equalities
${\mathfrak {A}}^\bullet ,{\mathfrak {B}}^\bullet ,{\mathfrak {E}}^\bullet ,{\mathfrak {G}}^\bullet$. Thus we have equalities ![]() ${\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0,\varrho _{\operatorname {right}} E_0)= {\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)= {\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}}^{-1}E_0,\varrho _{\operatorname {right}}^{-1}E_0)$.
${\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}} E_0,\varrho _{\operatorname {right}} E_0)= {\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)= {\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(\varrho _{\operatorname {right}}^{-1}E_0,\varrho _{\operatorname {right}}^{-1}E_0)$.
Lemma 3.10.3 The natural morphism
is injective.
Proof. We have ![]() $\alpha ^!\varrho _{\operatorname {right}}^{-1}{\operatorname {IC}}_{(-1^N,1^N)}[N]\simeq \varrho _{\operatorname {right}}^{-1}E_0$, and we need to check that, for any
$\alpha ^!\varrho _{\operatorname {right}}^{-1}{\operatorname {IC}}_{(-1^N,1^N)}[N]\simeq \varrho _{\operatorname {right}}^{-1}E_0$, and we need to check that, for any ![]() ${\boldsymbol {\lambda }},{\boldsymbol {\mu }}$, the natural morphism
${\boldsymbol {\lambda }},{\boldsymbol {\mu }}$, the natural morphism
 \begin{align} & \vartheta\colon\operatorname{RHom}_{D_{!{\mathbf{G}}_{\mathbf{O}}}({\mathbf{Gr}}\times{\mathbf{V}})}(\varrho_{\operatorname{right}}^{{-}1}E_0, \varrho_{\operatorname{right}}^{{-}1}{\operatorname{IC}}_{({\boldsymbol{\lambda}},{\boldsymbol{\mu}})})\nonumber\\ &\quad \to\operatorname{RHom}_{D_{!{\mathbf{G}}_{\mathbf{O}}}({\mathbf{Gr}}\times{\mathbf{V}})}(\varrho_{\operatorname{right}}^{{-}1}{\operatorname{IC}}_{({-}1^N,1^N)}[{-}N], \varrho_{\operatorname{right}}^{{-}1}{\operatorname{IC}}_{({\boldsymbol{\lambda}},{\boldsymbol{\mu}})}) \end{align}
\begin{align} & \vartheta\colon\operatorname{RHom}_{D_{!{\mathbf{G}}_{\mathbf{O}}}({\mathbf{Gr}}\times{\mathbf{V}})}(\varrho_{\operatorname{right}}^{{-}1}E_0, \varrho_{\operatorname{right}}^{{-}1}{\operatorname{IC}}_{({\boldsymbol{\lambda}},{\boldsymbol{\mu}})})\nonumber\\ &\quad \to\operatorname{RHom}_{D_{!{\mathbf{G}}_{\mathbf{O}}}({\mathbf{Gr}}\times{\mathbf{V}})}(\varrho_{\operatorname{right}}^{{-}1}{\operatorname{IC}}_{({-}1^N,1^N)}[{-}N], \varrho_{\operatorname{right}}^{{-}1}{\operatorname{IC}}_{({\boldsymbol{\lambda}},{\boldsymbol{\mu}})}) \end{align}
is injective. Indeed, since ![]() $\alpha ^!$ is a Hecke transformation endofunctor (namely, it is given by convolution
$\alpha ^!$ is a Hecke transformation endofunctor (namely, it is given by convolution ![]() ${\operatorname {IC}}_{(1^N)}*?*{\operatorname {IC}}_{(-1)^N}$ with invertible objects of the Satake category), the morphism
${\operatorname {IC}}_{(1^N)}*?*{\operatorname {IC}}_{(-1)^N}$ with invertible objects of the Satake category), the morphism ![]() $\vartheta$ is an endomorphism of the identity endofunctor of the de-equivariantized category
$\vartheta$ is an endomorphism of the identity endofunctor of the de-equivariantized category ![]() $D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. In other words,
$D^{{\operatorname{deeq}}}_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. In other words, ![]() $\vartheta$ is an element of the center of this category. But the natural morphism from the center to its localization is injective if and only if the multiplication by
$\vartheta$ is an element of the center of this category. But the natural morphism from the center to its localization is injective if and only if the multiplication by ![]() $\vartheta$ is injective.
$\vartheta$ is injective.
We change the setting to the base field ![]() ${\mathbb {F}}_q$ as in the proof of Lemma 3.9.1. Then all the IC sheaves in question carry a natural Weil structure, and it was proved in the proof of Lemma 3.9.1 that both the left- and right-hand side of (3.10.1) are pure; it is immediate to see that they are pure of the same weight
${\mathbb {F}}_q$ as in the proof of Lemma 3.9.1. Then all the IC sheaves in question carry a natural Weil structure, and it was proved in the proof of Lemma 3.9.1 that both the left- and right-hand side of (3.10.1) are pure; it is immediate to see that they are pure of the same weight ![]() $w$. The cone of
$w$. The cone of ![]() $\vartheta$ is
$\vartheta$ is ![]() $H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}(\Omega _{(0^N,0^N)},\imath _0^!\varrho _{\operatorname {right}}^{-1}{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$, where
$H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}(\Omega _{(0^N,0^N)},\imath _0^!\varrho _{\operatorname {right}}^{-1}{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$, where ![]() $\imath _0$ stands for the locally closed embedding of the
$\imath _0$ stands for the locally closed embedding of the ![]() ${\mathbf {G}}_{\mathbf {O}}$-orbit
${\mathbf {G}}_{\mathbf {O}}$-orbit ![]() $\Omega _{(0^N,0^N)}={\mathbf {Gr}}^0\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0)\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$. Due to the pointwise purity of
$\Omega _{(0^N,0^N)}={\mathbf {Gr}}^0\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0)\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$. Due to the pointwise purity of ![]() ${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3],
${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ [Reference Finkelberg, Ginzburg and TravkinFGT09, § 3], ![]() $\imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ is a pure local system on
$\imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ is a pure local system on ![]() $\Omega _{(0^N,0^N)}$; hence
$\Omega _{(0^N,0^N)}$; hence ![]() $H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}(\Omega _{(0^N,0^N)},\imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$ is also pure of weight
$H^\bullet _{{\mathbf {G}}_{\mathbf {O}}}(\Omega _{(0^N,0^N)},\imath _0^!{\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})})$ is also pure of weight ![]() $w$. It follows that the kernel of
$w$. It follows that the kernel of ![]() $\vartheta$ vanishes, and
$\vartheta$ vanishes, and ![]() $\vartheta$ is injective.
$\vartheta$ is injective.
Corollary 3.10.4 The algebra ![]() ${\mathfrak {E}}={\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ is a commutative integrally closed domain.
${\mathfrak {E}}={\operatorname{Ext}}_{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ is a commutative integrally closed domain.
3.11 Calculation of the Ext algebra
Recall that the first fundamental coweight of ![]() $\operatorname{GL}_N$ is
$\operatorname{GL}_N$ is ![]() $\omega _1=(1,0,\ldots ,0)$, and
$\omega _1=(1,0,\ldots ,0)$, and ![]() $\omega _1^*=(0,\ldots ,0,-1)$. We have
$\omega _1^*=(0,\ldots ,0,-1)$. We have ![]() $\operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}({\operatorname {IC}}_{\omega _1}*E_0,E_0*{\operatorname {IC}}_{\omega _1})$
$\operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}({\operatorname {IC}}_{\omega _1}*E_0,E_0*{\operatorname {IC}}_{\omega _1})$ ![]() $= \operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{\omega _1^*}*E_0*{\operatorname {IC}}_{\omega _1})$,
$= \operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{\omega _1^*}*E_0*{\operatorname {IC}}_{\omega _1})$, ![]() $\operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0*{\operatorname {IC}}_{\omega _1},{\operatorname {IC}}_{\omega _1}*E_0)$
$\operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0*{\operatorname {IC}}_{\omega _1},{\operatorname {IC}}_{\omega _1}*E_0)$ ![]() $= \operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{\omega _1}*E_0*{\operatorname {IC}}_{\omega _1^*})$. Now
$= \operatorname {RHom}_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,{\operatorname {IC}}_{\omega _1}*E_0*{\operatorname {IC}}_{\omega _1^*})$. Now ![]() ${\operatorname {IC}}_{\omega _1}*E_0$ is the constant IC sheaf of the stratum closure formed by all the pairs
${\operatorname {IC}}_{\omega _1}*E_0$ is the constant IC sheaf of the stratum closure formed by all the pairs ![]() $(L,v)$ such that the lattice
$(L,v)$ such that the lattice ![]() $L$ contains
$L$ contains ![]() ${\mathbf {V}}_0$ as a hyperplane, and
${\mathbf {V}}_0$ as a hyperplane, and ![]() $v\in L$. Furthermore,
$v\in L$. Furthermore, ![]() $E_0*{\operatorname {IC}}_{\omega _1}$ is the constant IC sheaf of the stratum closure formed by all the pairs
$E_0*{\operatorname {IC}}_{\omega _1}$ is the constant IC sheaf of the stratum closure formed by all the pairs ![]() $(L,v)$ such that the lattice
$(L,v)$ such that the lattice ![]() $L$ contains
$L$ contains ![]() ${\mathbf {V}}_0$ as a hyperplane, and
${\mathbf {V}}_0$ as a hyperplane, and ![]() $v\in {\mathbf {V}}_0$. In particular, the latter stratum closure is a smooth divisor in the former stratum closure, so we have canonical elements
$v\in {\mathbf {V}}_0$. In particular, the latter stratum closure is a smooth divisor in the former stratum closure, so we have canonical elements ![]() $h\in {\operatorname{Ext}}^1_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}({\operatorname {IC}}_{\omega _1}*E_0,E_0*{\operatorname {IC}}_{\omega _1})$ and
$h\in {\operatorname{Ext}}^1_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}({\operatorname {IC}}_{\omega _1}*E_0,E_0*{\operatorname {IC}}_{\omega _1})$ and ![]() $h^*\in {\operatorname{Ext}}^1_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0*{\operatorname {IC}}_{\omega _1},{\operatorname {IC}}_{\omega _1}*E_0)$. Hence we obtain the subspaces
$h^*\in {\operatorname{Ext}}^1_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0*{\operatorname {IC}}_{\omega _1},{\operatorname {IC}}_{\omega _1}*E_0)$. Hence we obtain the subspaces ![]() $h\,{\otimes}\, V_{\omega _1^*}\,{\otimes}\, V_{\omega _1}\subset {\mathfrak {E}}^1$ and
$h\,{\otimes}\, V_{\omega _1^*}\,{\otimes}\, V_{\omega _1}\subset {\mathfrak {E}}^1$ and ![]() $h^*\,{\otimes}\, V_{\omega _1}\,{\otimes}\, V_{\omega _1^*}\subset {\mathfrak {E}}^1$ (see § 3.9 for the definition of
$h^*\,{\otimes}\, V_{\omega _1}\,{\otimes}\, V_{\omega _1^*}\subset {\mathfrak {E}}^1$ (see § 3.9 for the definition of ![]() ${\mathfrak {E}}^\bullet$ and (3.9.1)). We identify the former subspace with
${\mathfrak {E}}^\bullet$ and (3.9.1)). We identify the former subspace with ![]() ${\operatorname{Hom}}(V_1,V_2)$ and the latter one with
${\operatorname{Hom}}(V_1,V_2)$ and the latter one with ![]() ${\operatorname{Hom}}(V_2,V_1)$. Thus we obtain a homomorphism
${\operatorname{Hom}}(V_2,V_1)$. Thus we obtain a homomorphism ![]() $\phi ^\bullet \colon {\operatorname{Sym}}\big (\Pi {\operatorname{Hom}}(V_1,V_2)[-1]\oplus \Pi {\operatorname{Hom}}(V_2,V_1)[-1]\big )$
$\phi ^\bullet \colon {\operatorname{Sym}}\big (\Pi {\operatorname{Hom}}(V_1,V_2)[-1]\oplus \Pi {\operatorname{Hom}}(V_2,V_1)[-1]\big )$ ![]() $= {\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])={\mathfrak {G}}_{1,1}^\bullet \to {\mathfrak {E}}^\bullet$ (due to commutativity of
$= {\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])={\mathfrak {G}}_{1,1}^\bullet \to {\mathfrak {E}}^\bullet$ (due to commutativity of ![]() ${\mathfrak {E}}$).
${\mathfrak {E}}$).
Lemma 3.11.1 ![]() $\phi ^\bullet$ is an isomorphism.
$\phi ^\bullet$ is an isomorphism.
Proof. We can and will disregard the grading. The morphism ![]() $\phi$ induces the morphism
$\phi$ induces the morphism ![]() $\phi ^*\colon {\operatorname{Spec}}{\mathfrak {E}}\to {\mathfrak {g}}^*_{\bar 1}$ that is an isomorphism over the open subset
$\phi ^*\colon {\operatorname{Spec}}{\mathfrak {E}}\to {\mathfrak {g}}^*_{\bar 1}$ that is an isomorphism over the open subset ![]() ${\operatorname{Isom}}(V_2,V_1)\times {\operatorname{Hom}}(V_1,V_2)\subset {\mathfrak {g}}^*_{\bar 1}$ due to Corollary 3.10.2(a). Similarly,
${\operatorname{Isom}}(V_2,V_1)\times {\operatorname{Hom}}(V_1,V_2)\subset {\mathfrak {g}}^*_{\bar 1}$ due to Corollary 3.10.2(a). Similarly, ![]() $\phi ^*$ is an isomorphism over the open subset
$\phi ^*$ is an isomorphism over the open subset ![]() ${\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Isom}}(V_1,V_2)$ due to Corollary 3.10.2(b).
${\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Isom}}(V_1,V_2)$ due to Corollary 3.10.2(b).
Since the complement to the union of these two open subsets has codimension 2 in ![]() ${\mathfrak {g}}_{\bar 1}^*$, we can apply Lemma 3.11.2 below. Note that the irreducibility of
${\mathfrak {g}}_{\bar 1}^*$, we can apply Lemma 3.11.2 below. Note that the irreducibility of ![]() ${\operatorname{Spec}}{\mathfrak {E}}$ is guaranteed by Corollary 3.10.4. It remains only to check that the ratio of the above isomorphisms is the identity birational isomorphism between the varieties
${\operatorname{Spec}}{\mathfrak {E}}$ is guaranteed by Corollary 3.10.4. It remains only to check that the ratio of the above isomorphisms is the identity birational isomorphism between the varieties ![]() ${\operatorname{Isom}}(V_2,V_1)\times {\operatorname{Hom}}(V_1,V_2)$ and
${\operatorname{Isom}}(V_2,V_1)\times {\operatorname{Hom}}(V_1,V_2)$ and ![]() ${\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Isom}}(V_1,V_2)$.
${\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Isom}}(V_1,V_2)$.
The composition ![]() $h\circ h^*\in {\operatorname{Ext}}^2_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0*{\operatorname {IC}}_{\omega _1},E_0*{\operatorname {IC}}_{\omega _1})$ is multiplication by the first Chern class of the normal line bundle
$h\circ h^*\in {\operatorname{Ext}}^2_{D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0*{\operatorname {IC}}_{\omega _1},E_0*{\operatorname {IC}}_{\omega _1})$ is multiplication by the first Chern class of the normal line bundle ![]() ${\mathcal {N}}$ to the divisor
${\mathcal {N}}$ to the divisor ![]() $\operatorname {supp}(E_0*{\operatorname {IC}}_{\omega _1})$ in
$\operatorname {supp}(E_0*{\operatorname {IC}}_{\omega _1})$ in ![]() $\operatorname {supp}({\operatorname {IC}}_{\omega _1}*E_0)$. Recall that
$\operatorname {supp}({\operatorname {IC}}_{\omega _1}*E_0)$. Recall that ![]() ${\mathbf {Gr}}^{\omega _1}\simeq {\mathbb {P}}^{N-1}$. The line bundle
${\mathbf {Gr}}^{\omega _1}\simeq {\mathbb {P}}^{N-1}$. The line bundle ![]() ${\mathcal {N}}$ is pulled back from the line bundle
${\mathcal {N}}$ is pulled back from the line bundle ![]() ${\mathcal {O}}(1)$ on
${\mathcal {O}}(1)$ on ![]() ${\mathbb {P}}^{N-1}\simeq {\mathbf {Gr}}^{\omega _1}$. Recall also that the restriction of the determinant line bundle
${\mathbb {P}}^{N-1}\simeq {\mathbf {Gr}}^{\omega _1}$. Recall also that the restriction of the determinant line bundle ![]() ${\mathcal {L}}$ from
${\mathcal {L}}$ from ![]() ${\mathbf {Gr}}$ to
${\mathbf {Gr}}$ to ![]() ${\mathbf {Gr}}^{\omega _1}$ is also isomorphic to
${\mathbf {Gr}}^{\omega _1}$ is also isomorphic to ![]() ${\mathcal {O}}(1)$. We conclude that
${\mathcal {O}}(1)$. We conclude that ![]() $h\circ h^*=c_1({\mathcal {L}})$.
$h\circ h^*=c_1({\mathcal {L}})$.
On the other hand, in the equivariant Satake category
the first Chern class ![]() $c_1({\mathcal {L}})\in {\operatorname{Ext}}^2_{D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0*{\operatorname {IC}}_{\omega _1},{\operatorname {IC}}_0*{\operatorname {IC}}_{\omega _1})\subset {\mathfrak {A}}^2$ corresponds to the identity element (shifted by 2)
$c_1({\mathcal {L}})\in {\operatorname{Ext}}^2_{D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})}({\operatorname {IC}}_0*{\operatorname {IC}}_{\omega _1},{\operatorname {IC}}_0*{\operatorname {IC}}_{\omega _1})\subset {\mathfrak {A}}^2$ corresponds to the identity element (shifted by 2) ![]() ${\operatorname{Id}}\in {\operatorname{Hom}}(V_2,V_1)^*\,{\otimes}\, {\operatorname{Hom}}(V_2,V_1)$.
${\operatorname{Id}}\in {\operatorname{Hom}}(V_2,V_1)^*\,{\otimes}\, {\operatorname{Hom}}(V_2,V_1)$.
The lemma is proved.
Lemma 3.11.2 Let ![]() $\pi \colon X\to {\mathbb {A}}^n$ be a morphism from an irreducible affine algebraic variety to an affine space. Let
$\pi \colon X\to {\mathbb {A}}^n$ be a morphism from an irreducible affine algebraic variety to an affine space. Let ![]() $f,g\in {\mathbb {C}}[{\mathbb {A}}^n]$ be such that the codimension of the closed subvariety
$f,g\in {\mathbb {C}}[{\mathbb {A}}^n]$ be such that the codimension of the closed subvariety ![]() ${\mathbb {A}}^n\,{\smallsetminus}\, (U_f\cup U_g)$ in
${\mathbb {A}}^n\,{\smallsetminus}\, (U_f\cup U_g)$ in ![]() ${\mathbb {A}}^n$ is at least
${\mathbb {A}}^n$ is at least ![]() $2$, where
$2$, where ![]() $U_f=\{ u\in {\mathbb {A}}^n\mid f(u)\neq 0\}$. Assume, moreover, that each of the morphisms
$U_f=\{ u\in {\mathbb {A}}^n\mid f(u)\neq 0\}$. Assume, moreover, that each of the morphisms ![]() $\pi ^{-1}(U_f)\to U_f$ and
$\pi ^{-1}(U_f)\to U_f$ and ![]() $\pi ^{-1}(U_g)\to U_g$, induced by
$\pi ^{-1}(U_g)\to U_g$, induced by ![]() $\pi$, is an isomorphism. Then
$\pi$, is an isomorphism. Then ![]() $\pi$ is an isomorphism.
$\pi$ is an isomorphism.
Proof. Let ![]() $X_f=\pi ^{-1}(U_f)$ (respectively,
$X_f=\pi ^{-1}(U_f)$ (respectively, ![]() $X_g=\pi ^{-1}(U_g)$), and write
$X_g=\pi ^{-1}(U_g)$), and write ![]() $j\colon U_f\cup U_g\hookrightarrow {\mathbb {A}}^n$ (respectively,
$j\colon U_f\cup U_g\hookrightarrow {\mathbb {A}}^n$ (respectively, ![]() $j_X\colon X_f\cup X_g\hookrightarrow X$) for the open embedding. We have the commutative diagram
$j_X\colon X_f\cup X_g\hookrightarrow X$) for the open embedding. We have the commutative diagram

The map ![]() $j^*$ in this diagram is an isomorphism by the assumption of codimension at least
$j^*$ in this diagram is an isomorphism by the assumption of codimension at least ![]() $2$. The map
$2$. The map ![]() $j_X^*$ is injective since
$j_X^*$ is injective since ![]() $X$ is irreducible. The assumptions imply also that the vertical map
$X$ is irreducible. The assumptions imply also that the vertical map ![]() $(\pi |_{X_f})^*\oplus (\pi |_{X_g})^*$ on the right is an isomorphism. It follows that the vertical map
$(\pi |_{X_f})^*\oplus (\pi |_{X_g})^*$ on the right is an isomorphism. It follows that the vertical map ![]() $\pi ^*$ on the left must be an isomorphism, as required.
$\pi ^*$ on the left must be an isomorphism, as required.
3.12 Restriction to  ${\mathbf {Gr}}\times {\mathbf {V}}_0$
${\mathbf {Gr}}\times {\mathbf {V}}_0$
The existence of the desired equivalence ![]() $\Phi ^{1,1}$ of Theorem 3.6.1 follows from Lemmas 3.9.2 and 3.11.1. The equivalences
$\Phi ^{1,1}$ of Theorem 3.6.1 follows from Lemmas 3.9.2 and 3.11.1. The equivalences ![]() $\Phi ^{0,2}$ and
$\Phi ^{0,2}$ and ![]() $\Phi ^{2,0}$ are obtained by conjugating with
$\Phi ^{2,0}$ are obtained by conjugating with ![]() $\varrho _{\operatorname {right}}^{\pm 1}$. It remains to check their compatibility with monoidal structures.
$\varrho _{\operatorname {right}}^{\pm 1}$. It remains to check their compatibility with monoidal structures.
We denote by ![]() $\bar \jmath _0$ (respectively,
$\bar \jmath _0$ (respectively, ![]() $\bar \jmath _{-1}$) the closed embedding
$\bar \jmath _{-1}$) the closed embedding ![]() ${\mathbf {Gr}}\times {\mathbf {V}}_0\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$ (respectively,
${\mathbf {Gr}}\times {\mathbf {V}}_0\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$ (respectively, ![]() ${\mathbf {Gr}}\times t{\mathbf {V}}_0\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$). We also denote by
${\mathbf {Gr}}\times t{\mathbf {V}}_0\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$). We also denote by ![]() $\jmath _0$ the locally closed embedding
$\jmath _0$ the locally closed embedding ![]() ${\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0)\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$. Our goal in this section is a description in terms of
${\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0)\hookrightarrow {\mathbf {Gr}}\times {\mathbf {V}}$. Our goal in this section is a description in terms of ![]() $\Phi ^{1,1}$ of the endofunctors
$\Phi ^{1,1}$ of the endofunctors ![]() $\bar \jmath _{0*}\bar \jmath {}_0^!$,
$\bar \jmath _{0*}\bar \jmath {}_0^!$, ![]() $\jmath _{0*}\jmath _0^!\colon D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$\jmath _{0*}\jmath _0^!\colon D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
Recall the setup and notation of § 3.4. We have the natural morphisms
 \begin{gather*} p\colon{\mathcal{Q}}^A\to{{\operatorname{Hom}}}(V_1,V_2)\times{{\operatorname{Hom}}}(V_2,V_1)=\Pi{\mathfrak{g}}^*_{\bar1},\\ q\colon{\mathcal{Q}}^A\to{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)=\Pi{\mathfrak{g}}^*_{\bar1};\\ p(A,A',A'',B,B',B'')=(A,B),\quad q(A,A',A'',B,B',B'')=(A',B'). \end{gather*}
\begin{gather*} p\colon{\mathcal{Q}}^A\to{{\operatorname{Hom}}}(V_1,V_2)\times{{\operatorname{Hom}}}(V_2,V_1)=\Pi{\mathfrak{g}}^*_{\bar1},\\ q\colon{\mathcal{Q}}^A\to{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)=\Pi{\mathfrak{g}}^*_{\bar1};\\ p(A,A',A'',B,B',B'')=(A,B),\quad q(A,A',A'',B,B',B'')=(A',B'). \end{gather*}We also have the natural morphisms
Clearly, ![]() $p,q\colon {\mathcal {Q}}^A\to \Pi {\mathfrak {g}}^*_{\bar 1}$ are equivariant with respect to
$p,q\colon {\mathcal {Q}}^A\to \Pi {\mathfrak {g}}^*_{\bar 1}$ are equivariant with respect to ![]() $p,q\colon G_{\mathcal {Q}}\to G_{\bar 0}$. Hence we have the convolution functor
$p,q\colon G_{\mathcal {Q}}\to G_{\bar 0}$. Hence we have the convolution functor
(in particular, ![]() $p_*$ involves taking
$p_*$ involves taking ![]() $\operatorname{GL}(V'_1)$-invariants). We will actually need the same-named functor
$\operatorname{GL}(V'_1)$-invariants). We will actually need the same-named functor ![]() $p_*q^*\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ defined similarly using the dg-algebra with trivial differential
$p_*q^*\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ defined similarly using the dg-algebra with trivial differential ![]() ${\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}(V_1,V'_1)]$ (the grading on
${\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}(V_1,V'_1)]$ (the grading on ![]() ${\mathbb {C}}[{\operatorname{Hom}}(V_1,V'_1)]$ is trivial, and if we disregard the grading, then
${\mathbb {C}}[{\operatorname{Hom}}(V_1,V'_1)]$ is trivial, and if we disregard the grading, then ![]() ${\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}(V_1,V'_1)]\simeq {\mathbb {C}}[{\mathcal {Q}}^A]$).
${\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}(V_1,V'_1)]\simeq {\mathbb {C}}[{\mathcal {Q}}^A]$).
We also have a ![]() $G_{\mathcal {Q}}$-invariant subvariety
$G_{\mathcal {Q}}$-invariant subvariety ![]() ${\mathcal {Q}}^A_0\subset {\mathcal {Q}}^A$ given by the equation that
${\mathcal {Q}}^A_0\subset {\mathcal {Q}}^A$ given by the equation that ![]() $A''$ is non-invertible. The restriction of
$A''$ is non-invertible. The restriction of ![]() $p,q$ to
$p,q$ to ![]() ${\mathcal {Q}}^A_0$ will be denoted by
${\mathcal {Q}}^A_0$ will be denoted by ![]() $p_0,q_0$. As above, we obtain the functor
$p_0,q_0$. As above, we obtain the functor ![]() $p_{0*}q_0^*\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$.
$p_{0*}q_0^*\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$.
Proposition 3.12.1 (a) There is an isomorphism of functors
(b) The isomorphism in (a) can be extended to the following commutative diagram of morphisms:

(c) There is an isomorphism of functors
Proof. (a) The support of ![]() ${\operatorname {IC}}_{({\boldsymbol {\nu }},{\boldsymbol {\mu }})}$ lies in
${\operatorname {IC}}_{({\boldsymbol {\nu }},{\boldsymbol {\mu }})}$ lies in ![]() ${\mathbf {Gr}}\times {\mathbf {V}}_0$ if and only if
${\mathbf {Gr}}\times {\mathbf {V}}_0$ if and only if ![]() ${\boldsymbol {\nu }}$ is a negative partition (
${\boldsymbol {\nu }}$ is a negative partition (![]() $0\geq \nu _1\geq \cdots \geq \nu _N$) (see [Reference Finkelberg, Ginzburg and TravkinFGT09, Proof of Proposition 8]). So
$0\geq \nu _1\geq \cdots \geq \nu _N$) (see [Reference Finkelberg, Ginzburg and TravkinFGT09, Proof of Proposition 8]). So ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}}_0)$ is generated by the collection of objects
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}}_0)$ is generated by the collection of objects ![]() ${\operatorname {IC}}_{({\boldsymbol {\nu }},{\boldsymbol {\mu }})}$ where
${\operatorname {IC}}_{({\boldsymbol {\nu }},{\boldsymbol {\mu }})}$ where ![]() ${\boldsymbol {\nu }}$ is a negative partition. Thus we see that
${\boldsymbol {\nu }}$ is a negative partition. Thus we see that ![]() $\bar \jmath _{0*}$ is a fully faithful functor whose image is generated by
$\bar \jmath _{0*}$ is a fully faithful functor whose image is generated by ![]() $\{{\operatorname {IC}}_{({\boldsymbol {\nu }},{\boldsymbol {\mu }})}\mid {\boldsymbol {\nu }}\le 0\}$ and
$\{{\operatorname {IC}}_{({\boldsymbol {\nu }},{\boldsymbol {\mu }})}\mid {\boldsymbol {\nu }}\le 0\}$ and ![]() $\bar \jmath _0^!$ is the right adjoint of
$\bar \jmath _0^!$ is the right adjoint of ![]() $\bar \jmath _{0*}$. Recall that
$\bar \jmath _{0*}$. Recall that ![]() $V^*_{\boldsymbol {\nu }}$ denotes an irreducible representation of
$V^*_{\boldsymbol {\nu }}$ denotes an irreducible representation of ![]() $\operatorname{GL}(V)$ obtained by applying the corresponding Schur functor to
$\operatorname{GL}(V)$ obtained by applying the corresponding Schur functor to ![]() $V^*$. The result of application of the same Schur functor to
$V^*$. The result of application of the same Schur functor to ![]() $V^*_1$ (respectively,
$V^*_1$ (respectively, ![]() $V^{\prime *}_1,V^*_2$) will be denoted by
$V^{\prime *}_1,V^*_2$) will be denoted by ![]() $V^*_{1,{\boldsymbol {\nu }}}$ (respectively,
$V^*_{1,{\boldsymbol {\nu }}}$ (respectively, ![]() $V^{\prime *}_{1,{\boldsymbol {\nu }}},V^*_{2,{\boldsymbol {\nu }}}$). Since
$V^{\prime *}_{1,{\boldsymbol {\nu }}},V^*_{2,{\boldsymbol {\nu }}}$). Since
(where ![]() ${\boldsymbol {\nu }}^*=(-\nu _N,-\nu _{N-1},\ldots ,-\nu _2,-\nu _1)$ for
${\boldsymbol {\nu }}^*=(-\nu _N,-\nu _{N-1},\ldots ,-\nu _2,-\nu _1)$ for ![]() ${\boldsymbol {\nu }}=(\nu _1,\ldots ,\nu _N)$), we have to show that
${\boldsymbol {\nu }}=(\nu _1,\ldots ,\nu _N)$), we have to show that ![]() $p_*q^*$ lands in the subcategory
$p_*q^*$ lands in the subcategory ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ generated by objects
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ generated by objects ![]() $\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$ and to construct the adjunction isomorphism
$\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$ and to construct the adjunction isomorphism
 \begin{align*} & {{\operatorname{Hom}}}_{D_{{\operatorname{perf}}}^{G_{\bar0}}({\mathfrak{G}}_{1,1}^\bullet)}(V_{1,{\boldsymbol{\lambda}}}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}}, V_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}'})\\ &\quad {\buildrel \sim \over \longrightarrow} {{\operatorname{Hom}}}_{D_{{\operatorname{perf}}}^{G_{\bar0}}({\mathfrak{G}}_{1,1}^\bullet)}(V_{1,{\boldsymbol{\lambda}}}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}}, p_*q^*(V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}'})) \end{align*}
\begin{align*} & {{\operatorname{Hom}}}_{D_{{\operatorname{perf}}}^{G_{\bar0}}({\mathfrak{G}}_{1,1}^\bullet)}(V_{1,{\boldsymbol{\lambda}}}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}}, V_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}'})\\ &\quad {\buildrel \sim \over \longrightarrow} {{\operatorname{Hom}}}_{D_{{\operatorname{perf}}}^{G_{\bar0}}({\mathfrak{G}}_{1,1}^\bullet)}(V_{1,{\boldsymbol{\lambda}}}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}}, p_*q^*(V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathfrak{G}}_{1,1}^\bullet{\,{\otimes}\,} V_{2,{\boldsymbol{\mu}}'})) \end{align*}
for a partition ![]() ${\boldsymbol {\lambda }}$. Equivalently, we have to construct an isomorphism
${\boldsymbol {\lambda }}$. Equivalently, we have to construct an isomorphism
 \begin{align*} & \big((V_{1,{\boldsymbol{\lambda}}}^{\prime*}\,{\otimes}\, V'_{1,{\boldsymbol{\lambda}}'})\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)] \,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}\\ &\quad {\buildrel \sim \over \longrightarrow} \big(V_{1,{\boldsymbol{\lambda}}}^*\,{\otimes}\, p_*q^*(V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)]\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'}) \,{\otimes}\, V_{2,{\boldsymbol{\mu}}}^*\big)^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\\ &\quad :=\big(V^*_{1,{\boldsymbol{\lambda}}}\,{\otimes}\, V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{\mathcal{Q}}^A]\,{\otimes}\,(V^*_{2,{\boldsymbol{\mu}}}\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{G_{\mathcal{Q}}}. \end{align*}
\begin{align*} & \big((V_{1,{\boldsymbol{\lambda}}}^{\prime*}\,{\otimes}\, V'_{1,{\boldsymbol{\lambda}}'})\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)] \,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}\\ &\quad {\buildrel \sim \over \longrightarrow} \big(V_{1,{\boldsymbol{\lambda}}}^*\,{\otimes}\, p_*q^*(V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)]\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'}) \,{\otimes}\, V_{2,{\boldsymbol{\mu}}}^*\big)^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\\ &\quad :=\big(V^*_{1,{\boldsymbol{\lambda}}}\,{\otimes}\, V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{\mathcal{Q}}^A]\,{\otimes}\,(V^*_{2,{\boldsymbol{\mu}}}\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{G_{\mathcal{Q}}}. \end{align*}
Recall that ![]() ${\mathcal {Q}}^A={\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)$. We apply Lemma 3.13.1(c) below to
${\mathcal {Q}}^A={\operatorname{Hom}}(V_1,V'_1)\times {\operatorname{Hom}}(V'_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)$. We apply Lemma 3.13.1(c) below to ![]() $U_1=V_2$,
$U_1=V_2$, ![]() $U_2=V_1$,
$U_2=V_1$, ![]() $U_3=V'_1$,
$U_3=V'_1$, ![]() ${\boldsymbol {\nu }}={\boldsymbol {\lambda }}$ (in the notation of § 3.13) to obtain an isomorphism
${\boldsymbol {\nu }}={\boldsymbol {\lambda }}$ (in the notation of § 3.13) to obtain an isomorphism
whose inverse induces the desired adjunction isomorphism.
We still have to check that the essential image of ![]() $p_*q^*$ lies in the subcategory
$p_*q^*$ lies in the subcategory ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ generated by
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ generated by ![]() $\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$. We consider the homomorphism
$\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$. We consider the homomorphism ![]() ${\mathfrak {G}}_{1,1}^\bullet \to {\mathbb {C}}$ killing all the generators, and for
${\mathfrak {G}}_{1,1}^\bullet \to {\mathbb {C}}$ killing all the generators, and for ![]() ${\mathcal {M}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ we set
${\mathcal {M}}\in D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ we set ![]() $z_0^*{\mathcal {M}}:={\mathbb {C}}\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }^L {\mathcal {M}}\in D^{G_{\bar 0}}({\mathbb {C}})$ (‘the fiber at
$z_0^*{\mathcal {M}}:={\mathbb {C}}\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }^L {\mathcal {M}}\in D^{G_{\bar 0}}({\mathbb {C}})$ (‘the fiber at ![]() $0\in {\operatorname{Hom}}(V_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)$’). Note that
$0\in {\operatorname{Hom}}(V_1,V_2)\times {\operatorname{Hom}}(V_2,V_1)$’). Note that ![]() $z_0^*p_*q^*$ lands in the category generated by
$z_0^*p_*q^*$ lands in the category generated by ![]() $\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$, that is, the category of modules with polynomial action of
$\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$, that is, the category of modules with polynomial action of ![]() $\operatorname{GL}(V_1)$. Indeed, recall that
$\operatorname{GL}(V_1)$. Indeed, recall that ![]() $G_{\mathcal {Q}}$ acts on
$G_{\mathcal {Q}}$ acts on ![]() ${\mathcal {Q}}^A$ via
${\mathcal {Q}}^A$ via
Since we impose the conditions ![]() $B=0=A:=A'A''$, the action of
$B=0=A:=A'A''$, the action of ![]() $\operatorname{GL}(V_1)$ on
$\operatorname{GL}(V_1)$ on ![]() $z_0^*p_*q^*{\mathcal {N}}$ (for a free dg-
$z_0^*p_*q^*{\mathcal {N}}$ (for a free dg-![]() ${\mathfrak {G}}_{1,1}^\bullet$-module
${\mathfrak {G}}_{1,1}^\bullet$-module ![]() ${\mathcal {N}}$) comes from its action on functions of
${\mathcal {N}}$) comes from its action on functions of ![]() $A''$, and the latter action is polynomial.
$A''$, and the latter action is polynomial.
Finally, we claim that if the action of ![]() $\operatorname{GL}(V_1)$ on
$\operatorname{GL}(V_1)$ on ![]() $z_0^*{\mathcal {M}}$ is polynomial, then
$z_0^*{\mathcal {M}}$ is polynomial, then ![]() ${\mathcal {M}}$ lies in the subcategory generated by
${\mathcal {M}}$ lies in the subcategory generated by ![]() $\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$. To this end we apply the Koszul equivalence
$\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$. To this end we apply the Koszul equivalence ![]() $\varkappa \colon D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda ){\buildrel \sim \over \longrightarrow} D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ of § 3.8. It is easy to see that if the action of
$\varkappa \colon D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda ){\buildrel \sim \over \longrightarrow} D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ of § 3.8. It is easy to see that if the action of ![]() $\operatorname{GL}(V_1)$ on the total cohomology of
$\operatorname{GL}(V_1)$ on the total cohomology of ![]() ${\mathcal {K}}\in D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ is polynomial, then
${\mathcal {K}}\in D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ is polynomial, then ![]() ${\mathcal {K}}$ lies in the subcategory
${\mathcal {K}}$ lies in the subcategory ![]() $\operatorname {Pol}\subset D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ generated by the
$\operatorname {Pol}\subset D_{\operatorname {fd}}^{G_{\bar 0}}(\Lambda )$ generated by the ![]() $G_{\bar 0}\ltimes \Lambda$-modules with polynomial action of
$G_{\bar 0}\ltimes \Lambda$-modules with polynomial action of ![]() $\operatorname{GL}(V_1)$ and trivial action of
$\operatorname{GL}(V_1)$ and trivial action of ![]() $\Lambda$. Now
$\Lambda$. Now ![]() $\varkappa (\operatorname {Pol})$ is the subcategory
$\varkappa (\operatorname {Pol})$ is the subcategory ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$. And if the action of
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$. And if the action of ![]() $\operatorname{GL}(V_1)$ on
$\operatorname{GL}(V_1)$ on ![]() $z_0^*{\mathcal {M}}$ is polynomial, then
$z_0^*{\mathcal {M}}$ is polynomial, then ![]() ${\mathcal {M}}\simeq \varkappa ({\mathcal {K}})$, where the action of
${\mathcal {M}}\simeq \varkappa ({\mathcal {K}})$, where the action of ![]() $\operatorname{GL}(V_1)$ on the total cohomology of
$\operatorname{GL}(V_1)$ on the total cohomology of ![]() ${\mathcal {K}}$ is polynomial. This completes the proof of (a).
${\mathcal {K}}$ is polynomial. This completes the proof of (a).
(b) As ![]() $\alpha ^*\bar \jmath _{-1*}\bar \jmath {}_{-1}^!\simeq \bar \jmath _{0*}\bar \jmath {}_0^!\alpha ^*$ (in the notation of § 3.10), we deduce an isomorphism of functors
$\alpha ^*\bar \jmath _{-1*}\bar \jmath {}_{-1}^!\simeq \bar \jmath _{0*}\bar \jmath {}_0^!\alpha ^*$ (in the notation of § 3.10), we deduce an isomorphism of functors
Thus the upper and lower rectangles of the diagram in (b) are commutative by construction. We have to prove the commutativity of the big curved quadrangle. The endofunctors ![]() $\bar \jmath _{0*}\bar \jmath {}_0^!$,
$\bar \jmath _{0*}\bar \jmath {}_0^!$, ![]() $\bar \jmath _{-1*}\bar \jmath {}_{-1}^!$ of
$\bar \jmath _{-1*}\bar \jmath {}_{-1}^!$ of ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ are equipped with the structure of idempotent comonads. The desired commutativity follows from the fact that, given two idempotent comonads
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ are equipped with the structure of idempotent comonads. The desired commutativity follows from the fact that, given two idempotent comonads ![]() $T_0,T_1\colon {\mathcal {C}}\to {\mathcal {C}}$, there is at most one morphism of functors
$T_0,T_1\colon {\mathcal {C}}\to {\mathcal {C}}$, there is at most one morphism of functors ![]() $\chi \colon T_1\to T_0$ such that
$\chi \colon T_1\to T_0$ such that ![]() $\varepsilon _1=\varepsilon _0\circ \chi$ for the counits
$\varepsilon _1=\varepsilon _0\circ \chi$ for the counits ![]() $\varepsilon _i\colon T_i\to {\operatorname{Id}}_{\mathcal {C}}$. Indeed,
$\varepsilon _i\colon T_i\to {\operatorname{Id}}_{\mathcal {C}}$. Indeed, ![]() $\chi =T_0(\varepsilon _1)\circ \chi _1$, where
$\chi =T_0(\varepsilon _1)\circ \chi _1$, where ![]() $\chi _1$ is defined as the composition
$\chi _1$ is defined as the composition
We claim that ![]() $\chi _1$ is an isomorphism uniquely defined as the inverse to the morphism
$\chi _1$ is an isomorphism uniquely defined as the inverse to the morphism ![]() $\varepsilon _0\circ T_1\colon T_0\circ T_1{\buildrel \sim \over \longrightarrow} T_1$. In effect, the composition
$\varepsilon _0\circ T_1\colon T_0\circ T_1{\buildrel \sim \over \longrightarrow} T_1$. In effect, the composition
equals the composition
which in turn equals ![]() ${\operatorname{Id}}_{T_1}$. Conversely, the composition
${\operatorname{Id}}_{T_1}$. Conversely, the composition
equals the composition
which in turn equals ![]() ${\operatorname{Id}}_{T_0\circ T_1}$.
${\operatorname{Id}}_{T_0\circ T_1}$.
This completes the proof of (b), but we would like to give one more independent argument that will prove useful later on.
Recall that we have to prove the commutativity of the big curved quadrangle. To this end we change the setting to the base field ![]() ${\mathbb {F}}_q$ as in the proof of Lemma 3.9.1. That is, we replace
${\mathbb {F}}_q$ as in the proof of Lemma 3.9.1. That is, we replace ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ by the equivalent equivariant derived category of sheaves on
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ by the equivalent equivariant derived category of sheaves on ![]() $({\mathbf {Gr}}\times {\mathbf {V}})_{\bar {\mathbb {F}}_q}$ as in [Reference Bezrukavnikov and FinkelbergBF08, Proposition 5] (in particular, choosing an isomorphism
$({\mathbf {Gr}}\times {\mathbf {V}})_{\bar {\mathbb {F}}_q}$ as in [Reference Bezrukavnikov and FinkelbergBF08, Proposition 5] (in particular, choosing an isomorphism ![]() ${\mathbb {C}}\simeq \bar {\mathbb {Q}}_\ell$). However, we preserve the notation
${\mathbb {C}}\simeq \bar {\mathbb {Q}}_\ell$). However, we preserve the notation ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ for this category in order not to overload our notation (anyway, it will only be used during the current proof). All the irreducible perverse sheaves
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ for this category in order not to overload our notation (anyway, it will only be used during the current proof). All the irreducible perverse sheaves ![]() ${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ carry a natural Tate Weil structure by [Reference Finkelberg, Ginzburg and TravkinFGT09, Proposition 11]. They (along with their Tate twists) generate a subcategoryFootnote 9
${\operatorname {IC}}_{({\boldsymbol {\lambda }},{\boldsymbol {\mu }})}$ carry a natural Tate Weil structure by [Reference Finkelberg, Ginzburg and TravkinFGT09, Proposition 11]. They (along with their Tate twists) generate a subcategoryFootnote 9 ![]() $\hat {D}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of the mixed version
$\hat {D}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of the mixed version ![]() $D^{\operatorname {mix}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of
$D^{\operatorname {mix}}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ of ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. We will use a particular dg-model of
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. We will use a particular dg-model of ![]() $\hat {D}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ viewed as a category enriched over complexes equipped with an action of the Frobenius automorphism
$\hat {D}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ viewed as a category enriched over complexes equipped with an action of the Frobenius automorphism ![]() $\operatorname {Fr}$. Note that the absolute values of the eigenvalues of
$\operatorname {Fr}$. Note that the absolute values of the eigenvalues of ![]() $\operatorname {Fr}$ lie in
$\operatorname {Fr}$ lie in ![]() $\sqrt {q}^{\mathbb {Z}}$, and hence our complexes carry an additional grading according to the absolute values of the eigenvalues of
$\sqrt {q}^{\mathbb {Z}}$, and hence our complexes carry an additional grading according to the absolute values of the eigenvalues of ![]() $\operatorname {Fr}$. If we forget the mixed structure and remember only this additional grading, we obtain a category
$\operatorname {Fr}$. If we forget the mixed structure and remember only this additional grading, we obtain a category ![]() $\tilde {\underline D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ enriched over complexes equipped with an additional grading. Its localization with respect to quasi-isomorphisms will be denoted
$\tilde {\underline D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ enriched over complexes equipped with an additional grading. Its localization with respect to quasi-isomorphisms will be denoted ![]() $\tilde {D}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$\tilde {D}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
On the other hand, we consider the category ![]() $\underline {D}{}_{\operatorname{perf}}^{G_{\bar 0}\times {\mathbb {C}}^\times }({\mathfrak {G}}^\bullet _{1,1})$ of perfect
$\underline {D}{}_{\operatorname{perf}}^{G_{\bar 0}\times {\mathbb {C}}^\times }({\mathfrak {G}}^\bullet _{1,1})$ of perfect ![]() $G_{\bar 0}\times {\mathbb {C}}^\times$-equivariant dg-
$G_{\bar 0}\times {\mathbb {C}}^\times$-equivariant dg-![]() ${\mathfrak {G}}^\bullet _{1,1}$-modules and its localization (with respect to quasi-isomorphisms)
${\mathfrak {G}}^\bullet _{1,1}$-modules and its localization (with respect to quasi-isomorphisms) ![]() $D_{\operatorname{perf}}^{G_{\bar 0}\times {\mathbb {C}}^\times }({\mathfrak {G}}^\bullet _{1,1})$. Here all the generators of
$D_{\operatorname{perf}}^{G_{\bar 0}\times {\mathbb {C}}^\times }({\mathfrak {G}}^\bullet _{1,1})$. Here all the generators of ![]() ${\mathfrak {G}}^\bullet _{1,1}$ have weight 1 with respect to the action of
${\mathfrak {G}}^\bullet _{1,1}$ have weight 1 with respect to the action of ![]() ${\mathbb {C}}^\times$. Then the standard modification of our construction of the equivalence
${\mathbb {C}}^\times$. Then the standard modification of our construction of the equivalence ![]() $\Phi ^{1,1}\colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ produces a functor
$\Phi ^{1,1}\colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ produces a functor ![]() $\tilde {\underline \Phi }{}^{1,1}\colon \underline {D}{}^{G_{\bar 0}\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )\to \tilde {\underline D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and its localization
$\tilde {\underline \Phi }{}^{1,1}\colon \underline {D}{}^{G_{\bar 0}\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )\to \tilde {\underline D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and its localization ![]() $\tilde {\Phi }{}^{1,1}\colon D^{G_{\bar 0}\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} \tilde {D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
$\tilde {\Phi }{}^{1,1}\colon D^{G_{\bar 0}\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} \tilde {D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$.
We have the similar diagram of morphisms of functors ![]() $D^{G_{\bar 0}\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )\to \tilde {D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ with commutative upper and lower rectangles
$D^{G_{\bar 0}\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )\to \tilde {D}{}_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ with commutative upper and lower rectangles

and we have to prove the commutativity of the big curved quadrangle. The endofunctors ![]() $\det V_1\,{\otimes}\, (p_*q^*)\circ (\det \!{}^{-1}V'_1\,{\otimes}\, {-})$,
$\det V_1\,{\otimes}\, (p_*q^*)\circ (\det \!{}^{-1}V'_1\,{\otimes}\, {-})$, ![]() ${\operatorname{Id}}$,
${\operatorname{Id}}$, ![]() $p_*q^*$ of
$p_*q^*$ of ![]() $D^{G_{\bar 0}\times {\mathbb {C}}^{\times}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ are given by their respective kernels
$D^{G_{\bar 0}\times {\mathbb {C}}^{\times}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ are given by their respective kernels ![]() $K_1,K_2,K_3$ in
$K_1,K_2,K_3$ in ![]() $\underline {D}{}^{G_{\bar 0}^2{\times} {\mathbb {C}}^{\times} }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet )$. Note that the equivariance with respect to
$\underline {D}{}^{G_{\bar 0}^2{\times} {\mathbb {C}}^{\times} }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet )$. Note that the equivariance with respect to ![]() ${\mathbb {C}}^{\times}$ (as opposed to
${\mathbb {C}}^{\times}$ (as opposed to ![]() $({\mathbb {C}}^{\times} )^2$) suffices since all the three functors under consideration commute with the shifts of the additional grading. Similarly, all the three functors on the constructible side commute with the Tate twists. All three kernels are pure of weight 0, that is, their additional gradings coincide with their cohomological gradings. The category of pure weight 0 objects in
$({\mathbb {C}}^{\times} )^2$) suffices since all the three functors under consideration commute with the shifts of the additional grading. Similarly, all the three functors on the constructible side commute with the Tate twists. All three kernels are pure of weight 0, that is, their additional gradings coincide with their cohomological gradings. The category of pure weight 0 objects in ![]() $D^{G_{\bar 0}^2\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet )$ is equivalent to the abelian category of
$D^{G_{\bar 0}^2\times {\mathbb {C}}^\times }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet )$ is equivalent to the abelian category of ![]() $G_{\bar 0}^2\times {\mathbb {C}}^\times$-equivariant
$G_{\bar 0}^2\times {\mathbb {C}}^\times$-equivariant ![]() ${\mathfrak {G}}_{1,1}\,{\otimes}\, {\mathfrak {G}}_{1,1}$-modules (the equivalence being obtained by taking cohomology). Therefore, the morphisms of functors
${\mathfrak {G}}_{1,1}\,{\otimes}\, {\mathfrak {G}}_{1,1}$-modules (the equivalence being obtained by taking cohomology). Therefore, the morphisms of functors ![]() $(\det V_1\,{\otimes}\, {-})\circ (p_*q^*)\circ (\det \!{}^{-1}V'_1\,{\otimes}\, {-})\to {\operatorname{Id}}$ and
$(\det V_1\,{\otimes}\, {-})\circ (p_*q^*)\circ (\det \!{}^{-1}V'_1\,{\otimes}\, {-})\to {\operatorname{Id}}$ and ![]() $p_*q^*\to {\operatorname{Id}}$ arise from the morphisms between the respective kernels that are injective as morphisms of
$p_*q^*\to {\operatorname{Id}}$ arise from the morphisms between the respective kernels that are injective as morphisms of ![]() ${\mathfrak {G}}_{1,1}\,{\otimes}\, {\mathfrak {G}}_{1,1}$-modules. We have to compare certain morphisms to
${\mathfrak {G}}_{1,1}\,{\otimes}\, {\mathfrak {G}}_{1,1}$-modules. We have to compare certain morphisms to ![]() $\tilde {\underline \Phi }{}^{1,1}K_3$, and we know that their compositions with the monomorphism
$\tilde {\underline \Phi }{}^{1,1}K_3$, and we know that their compositions with the monomorphism ![]() $\tilde {\underline \Phi }{}^{1,1}K_3\to \tilde {\underline \Phi }{}^{1,1}K_2$ coincide, hence the desired equality of morphisms. This completes our second proof of (b).
$\tilde {\underline \Phi }{}^{1,1}K_3\to \tilde {\underline \Phi }{}^{1,1}K_2$ coincide, hence the desired equality of morphisms. This completes our second proof of (b).
(c) This follows from the comparison of the distinguished triangles
and
The proposition is proved.
3.13 Some invariant theory
Let ![]() $U_1,U_2,U_3$ be vector spaces of dimensions
$U_1,U_2,U_3$ be vector spaces of dimensions ![]() $n_1,n_2,n_3$. The irreducible polynomial (respectively, antipolynomial) representations of
$n_1,n_2,n_3$. The irreducible polynomial (respectively, antipolynomial) representations of ![]() $\operatorname{GL}(U_i)$ are realized in the Schur spaces
$\operatorname{GL}(U_i)$ are realized in the Schur spaces ![]() ${\mathbb {S}}_{\boldsymbol {\lambda }} U_i$ (respectively,
${\mathbb {S}}_{\boldsymbol {\lambda }} U_i$ (respectively, ![]() ${\mathbb {S}}_{\boldsymbol {\lambda }} U_i^*$), where
${\mathbb {S}}_{\boldsymbol {\lambda }} U_i^*$), where ![]() ${\boldsymbol {\lambda }}$ is a partition with
${\boldsymbol {\lambda }}$ is a partition with ![]() $\ell ({\boldsymbol {\lambda }})\leq n_i$. We will also write
$\ell ({\boldsymbol {\lambda }})\leq n_i$. We will also write ![]() ${\mathbb {S}}_{{\boldsymbol {\lambda }}^*}U_i$ for
${\mathbb {S}}_{{\boldsymbol {\lambda }}^*}U_i$ for ![]() ${\mathbb {S}}_{\boldsymbol {\lambda }} U_i^*$, where
${\mathbb {S}}_{\boldsymbol {\lambda }} U_i^*$, where
for ![]() ${\boldsymbol {\lambda }}=(\lambda _1,\ldots ,\lambda _{n_i})$. We set
${\boldsymbol {\lambda }}=(\lambda _1,\ldots ,\lambda _{n_i})$. We set ![]() ${\mathbb {S}}_{\boldsymbol {\lambda }} U_i=0={\mathbb {S}}_{{\boldsymbol {\lambda }}^*}U_i$ for
${\mathbb {S}}_{\boldsymbol {\lambda }} U_i=0={\mathbb {S}}_{{\boldsymbol {\lambda }}^*}U_i$ for ![]() $\ell ({\boldsymbol {\lambda }})>n_i$. We denote by
$\ell ({\boldsymbol {\lambda }})>n_i$. We denote by ![]() ${\operatorname{Hom}}_{\leq n_2}(U_1,U_3)\subset {\operatorname{Hom}}(U_1,U_3)$ the subvariety formed by all the homomorphisms of rank at most
${\operatorname{Hom}}_{\leq n_2}(U_1,U_3)\subset {\operatorname{Hom}}(U_1,U_3)$ the subvariety formed by all the homomorphisms of rank at most ![]() $n_2$.
$n_2$.
Lemma 3.13.1 The composition of homomorphisms induces the following isomorphisms of ![]() $\operatorname{GL}(U_1)\times \operatorname{GL}(U_3)$-modules.
$\operatorname{GL}(U_1)\times \operatorname{GL}(U_3)$-modules.
(a)
 ${\mathbb {C}}[{\operatorname{Hom}}_{\leq n_2}(U_1,U_3)]{\buildrel \sim \over \longrightarrow} \big ({\mathbb {C}}[{\operatorname{Hom}}(U_1,U_2)]\,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}(U_2,U_3)]\big )^{\operatorname{GL}(U_2)}$.
${\mathbb {C}}[{\operatorname{Hom}}_{\leq n_2}(U_1,U_3)]{\buildrel \sim \over \longrightarrow} \big ({\mathbb {C}}[{\operatorname{Hom}}(U_1,U_2)]\,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}(U_2,U_3)]\big )^{\operatorname{GL}(U_2)}$.(b) If
 $n_1\leq n_2$, for a partition
$n_1\leq n_2$, for a partition  ${\boldsymbol {\nu }}$,
${\boldsymbol {\nu }}$,
 \[ {\mathbb{S}}_{\boldsymbol{\nu}} U_1\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_3)]{\buildrel \sim \over \longrightarrow} \big({\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2)]\,{\otimes}\,{\mathbb{S}}_{\boldsymbol{\nu}} U_2\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_3)]\big)^{{{\operatorname{GL}}}(U_2)}. \]
\[ {\mathbb{S}}_{\boldsymbol{\nu}} U_1\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_3)]{\buildrel \sim \over \longrightarrow} \big({\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2)]\,{\otimes}\,{\mathbb{S}}_{\boldsymbol{\nu}} U_2\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_3)]\big)^{{{\operatorname{GL}}}(U_2)}. \](c) If
 $n_3\leq n_2$, for a partition
$n_3\leq n_2$, for a partition  ${\boldsymbol {\nu }}$,
${\boldsymbol {\nu }}$,
 \[ {\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_3)]\,{\otimes}\,{\mathbb{S}}_{\boldsymbol{\nu}} U^*_3{\buildrel \sim \over \longrightarrow} \big({\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2)]\,{\otimes}\,{\mathbb{S}}_{\boldsymbol{\nu}} U^*_2\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_3)]\big)^{{{\operatorname{GL}}}(U_2)}. \]
\[ {\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_3)]\,{\otimes}\,{\mathbb{S}}_{\boldsymbol{\nu}} U^*_3{\buildrel \sim \over \longrightarrow} \big({\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2)]\,{\otimes}\,{\mathbb{S}}_{\boldsymbol{\nu}} U^*_2\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_3)]\big)^{{{\operatorname{GL}}}(U_2)}. \]
Proof. (a) We have ![]() ${\mathbb {C}}[{\operatorname{Hom}}(U_i,U_j)]=\bigoplus _{m\geq 0}{\operatorname{Sym}}^m(U_j^*\,{\otimes}\, U_i)= \bigoplus _{\boldsymbol {\lambda }}{\mathbb {S}}_{\boldsymbol {\lambda }} U_i\,{\otimes}\, {\mathbb {S}}_{{\boldsymbol {\lambda }}^*} U_j$ as a
${\mathbb {C}}[{\operatorname{Hom}}(U_i,U_j)]=\bigoplus _{m\geq 0}{\operatorname{Sym}}^m(U_j^*\,{\otimes}\, U_i)= \bigoplus _{\boldsymbol {\lambda }}{\mathbb {S}}_{\boldsymbol {\lambda }} U_i\,{\otimes}\, {\mathbb {S}}_{{\boldsymbol {\lambda }}^*} U_j$ as a ![]() $\operatorname{GL}(U_i)\times \operatorname{GL}(U_j)$-module. Also,
$\operatorname{GL}(U_i)\times \operatorname{GL}(U_j)$-module. Also, ![]() ${\mathbb {C}}[{\operatorname{Hom}}_{\leq r}(U_i,U_j)]= \bigoplus _{\ell ({\boldsymbol {\lambda }})\leq r}{\mathbb {S}}_{\boldsymbol {\lambda }} U_i\,{\otimes}\, {\mathbb {S}}_{{\boldsymbol {\lambda }}^*} U_j$ as a
${\mathbb {C}}[{\operatorname{Hom}}_{\leq r}(U_i,U_j)]= \bigoplus _{\ell ({\boldsymbol {\lambda }})\leq r}{\mathbb {S}}_{\boldsymbol {\lambda }} U_i\,{\otimes}\, {\mathbb {S}}_{{\boldsymbol {\lambda }}^*} U_j$ as a ![]() $\operatorname{GL}(U_i)\times \operatorname{GL}(U_j)$-module. Clearly,
$\operatorname{GL}(U_i)\times \operatorname{GL}(U_j)$-module. Clearly, ![]() $({\mathbb {S}}_{{\boldsymbol {\lambda }}^*}U_2\,{\otimes}\, {\mathbb {S}}_{\boldsymbol {\mu }} U_2)^{\operatorname{GL}(U_2)}={\mathbb {C}}^{\delta _{{\boldsymbol {\lambda }}{\boldsymbol {\mu }}}}$. So the two sides of (a) are isomorphic as
$({\mathbb {S}}_{{\boldsymbol {\lambda }}^*}U_2\,{\otimes}\, {\mathbb {S}}_{\boldsymbol {\mu }} U_2)^{\operatorname{GL}(U_2)}={\mathbb {C}}^{\delta _{{\boldsymbol {\lambda }}{\boldsymbol {\mu }}}}$. So the two sides of (a) are isomorphic as ![]() $\operatorname{GL}(U_1)\times \operatorname{GL}(U_3)$-modules. On the other hand, the morphism in question is injective since the composition morphism
$\operatorname{GL}(U_1)\times \operatorname{GL}(U_3)$-modules. On the other hand, the morphism in question is injective since the composition morphism ![]() ${\operatorname{Hom}}(U_1,U_2)\times {\operatorname{Hom}}(U_2,U_3)\to {\operatorname{Hom}}_{\leq n_2}(U_1,U_3)$ is dominant. Hence the morphism in question is an isomorphism.
${\operatorname{Hom}}(U_1,U_2)\times {\operatorname{Hom}}(U_2,U_3)\to {\operatorname{Hom}}_{\leq n_2}(U_1,U_3)$ is dominant. Hence the morphism in question is an isomorphism.
(b) We consider a copy ![]() $U'_2$ of
$U'_2$ of ![]() $U_2$, we tensor both sides of (b) with
$U_2$, we tensor both sides of (b) with ![]() ${\mathbb {S}}_{{\boldsymbol {\nu }}^*}U'_2$, and take the direct sum over all partitions
${\mathbb {S}}_{{\boldsymbol {\nu }}^*}U'_2$, and take the direct sum over all partitions ![]() ${\boldsymbol {\nu }}$ with
${\boldsymbol {\nu }}$ with ![]() $\ell ({\boldsymbol {\nu }})\leq n_2$. Then we have to prove that the morphism
$\ell ({\boldsymbol {\nu }})\leq n_2$. Then we have to prove that the morphism
 \begin{align*} &\gamma\colon {\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2')]\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_3)]\\ &\quad\to \big({\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2)]\,{\otimes}\, {\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_2')]\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_3)]\big)^{{{\operatorname{GL}}}(U_2)}, \end{align*}
\begin{align*} &\gamma\colon {\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2')]\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_3)]\\ &\quad\to \big({\mathbb{C}}[{{\operatorname{Hom}}}(U_1,U_2)]\,{\otimes}\, {\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_2')]\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(U_2,U_3)]\big)^{{{\operatorname{GL}}}(U_2)}, \end{align*}
induced by the composition of arrows of the ![]() $D_4$-quiver in
$D_4$-quiver in

is an isomorphism. Now the statement can be reduced to (a) using the substitution ![]() $U_3 \rightsquigarrow U_3\oplus U'_2$. Alternatively, the condition
$U_3 \rightsquigarrow U_3\oplus U'_2$. Alternatively, the condition ![]() $n_1\leq n_2$ guarantees that the morphism from the representation space of the
$n_1\leq n_2$ guarantees that the morphism from the representation space of the ![]() $D_4$-quiver to the representation space of the dashed
$D_4$-quiver to the representation space of the dashed ![]() $A_3$-quiver is dominant. Hence
$A_3$-quiver is dominant. Hence ![]() $\gamma$ is injective. The surjectivity of
$\gamma$ is injective. The surjectivity of ![]() $\gamma$ follows, for example, from [Reference Le Bruyn and ProcesiLP90, Theorem 1].
$\gamma$ follows, for example, from [Reference Le Bruyn and ProcesiLP90, Theorem 1].
(c) This is dual to (b).
3.14 The monoidal property of  $\Phi ^{2,0}$
$\Phi ^{2,0}$
Recall the notation of § 3.4. The monoidal structure ![]() ${\stackrel {A}*}$ on
${\stackrel {A}*}$ on ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$ is defined via the kernel
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$ is defined via the kernel ![]() ${\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet$: a
${\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet$: a ![]() $G_{\mathcal {Q}}$-equivariant dg-
$G_{\mathcal {Q}}$-equivariant dg-![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$-module. The monoidal structure
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$-module. The monoidal structure ![]() ${\stackrel{*}*}$ on
${\stackrel{*}*}$ on ![]() $D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ transferred to
$D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ transferred to ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$ via the equivalence
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )$ via the equivalence ![]() $\Phi ^{2,0}$ is also defined via a kernel
$\Phi ^{2,0}$ is also defined via a kernel ![]() ${\mathcal {K}}^\bullet$ (a
${\mathcal {K}}^\bullet$ (a ![]() $G_{\mathcal {Q}}$-equivariant dg-
$G_{\mathcal {Q}}$-equivariant dg-![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$-module). We have to construct an isomorphism of
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$-module). We have to construct an isomorphism of ![]() $G_{\mathcal {Q}}$-equivariant dg-
$G_{\mathcal {Q}}$-equivariant dg-![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$-modules
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$-modules ![]() ${\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}^\bullet$.
${\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}^\bullet$.
We denote by ![]() ${\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet$ the localization of
${\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet$ the localization of ![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$ defined as
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$ defined as ![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet [\det ^{-1}\!\!A,\det ^{-1}\!\!A',$
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet [\det ^{-1}\!\!A,\det ^{-1}\!\!A',$ ![]() $\det ^{-1}\!\!A'']$. We define
$\det ^{-1}\!\!A'']$. We define ![]() ${\mathcal {K}}_{\operatorname {loc}}^\bullet :={\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet \,{\otimes} _{{\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet }\ {\mathcal {K}}^\bullet$ and
${\mathcal {K}}_{\operatorname {loc}}^\bullet :={\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet \,{\otimes} _{{\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet }\ {\mathcal {K}}^\bullet$ and ![]() ${\mathbb {C}}[{\mathcal {Q}}^A_{\operatorname {loc}}]_{2,0}^\bullet := {\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet \,{\otimes} _{{\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet }\ {\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet$.
${\mathbb {C}}[{\mathcal {Q}}^A_{\operatorname {loc}}]_{2,0}^\bullet := {\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet \,{\otimes} _{{\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet }\ {\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet$.
We have ![]() $\Phi ^{2,0}{\mathfrak {G}}_{2,0}^\bullet \simeq \varrho _{\operatorname {right}}^{-1}E_0$. Also, for
$\Phi ^{2,0}{\mathfrak {G}}_{2,0}^\bullet \simeq \varrho _{\operatorname {right}}^{-1}E_0$. Also, for ![]() ${\mathcal {F}}\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we have
${\mathcal {F}}\in D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, we have ![]() $\varrho _{\operatorname {right}}^{-1}E_0{\stackrel{*}*} {\mathcal {F}}=\bar \jmath _{0*}\bar \jmath _0^!{\mathcal {F}}$. Thus Proposition 3.12.1(a) yields an isomorphism of functors
$\varrho _{\operatorname {right}}^{-1}E_0{\stackrel{*}*} {\mathcal {F}}=\bar \jmath _{0*}\bar \jmath _0^!{\mathcal {F}}$. Thus Proposition 3.12.1(a) yields an isomorphism of functors ![]() $\Phi ^{2,0}({\mathfrak {G}}_{2,0}^\bullet {\stackrel {A}*}-){\buildrel \sim \over \longrightarrow} (\Phi ^{2,0}{\mathfrak {G}}_{2,0}^\bullet ){\stackrel{*}*} \Phi ^{2,0}-$. This isomorphism yields in turn an isomorphism of kernels
$\Phi ^{2,0}({\mathfrak {G}}_{2,0}^\bullet {\stackrel {A}*}-){\buildrel \sim \over \longrightarrow} (\Phi ^{2,0}{\mathfrak {G}}_{2,0}^\bullet ){\stackrel{*}*} \Phi ^{2,0}-$. This isomorphism yields in turn an isomorphism of kernels ![]() ${\mathbb {C}}[{\mathcal {Q}}_{\operatorname {forg}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}_{\operatorname {forg}}^\bullet$, where the subscript
${\mathbb {C}}[{\mathcal {Q}}_{\operatorname {forg}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}_{\operatorname {forg}}^\bullet$, where the subscript ![]() $_{\operatorname {forg}}$ denotes the restriction of the dg-module structure from
$_{\operatorname {forg}}$ denotes the restriction of the dg-module structure from ![]() ${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$ to
${\mathbb {C}}[{\mathcal {H}}]_{2,0}^\bullet$ to ![]() ${\mathbb {C}}[{\mathcal {H}}_{\operatorname {forg}}]_{2,0}^\bullet :={\operatorname{Sym}}({\operatorname{Hom}}(V_1,V_2)[-2])\,{\otimes}\, {\operatorname{Sym}}({\operatorname{Hom}}(V_2,V_1)) \,{\otimes}\, {\operatorname{Sym}}({\operatorname{Hom}}(V'_1,V_2)[-2])\,{\otimes}\, {\operatorname{Sym}}({\operatorname{Hom}}(V_2,V'_1))$.
${\mathbb {C}}[{\mathcal {H}}_{\operatorname {forg}}]_{2,0}^\bullet :={\operatorname{Sym}}({\operatorname{Hom}}(V_1,V_2)[-2])\,{\otimes}\, {\operatorname{Sym}}({\operatorname{Hom}}(V_2,V_1)) \,{\otimes}\, {\operatorname{Sym}}({\operatorname{Hom}}(V'_1,V_2)[-2])\,{\otimes}\, {\operatorname{Sym}}({\operatorname{Hom}}(V_2,V'_1))$.
According to Proposition 3.12.1(b), the following diagram of functors ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\to D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ commutes:
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\to D_{!{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ commutes:

Hence the diagram

commutes as well, and in particular the multiplication by ![]() $\det A''$ is injective on
$\det A''$ is injective on ![]() ${\mathcal {K}}^\bullet$, and hence
${\mathcal {K}}^\bullet$, and hence ![]() ${\mathcal {K}}^\bullet \hookrightarrow {\mathcal {K}}_{\operatorname {loc}}^\bullet$.
${\mathcal {K}}^\bullet \hookrightarrow {\mathcal {K}}_{\operatorname {loc}}^\bullet$.
Now since ![]() $\Phi ^{2,0}_{\operatorname {loc}}\colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {A}}^\bullet ){\buildrel \sim \over \longrightarrow} D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong D_{!{\mathbf {G}}_{\mathbf {O}}}^{\operatorname {loc}}({\mathbf {Gr}}\times {\mathbf {V}})$ (see Lemma 3.10.1 and Corollary 3.10.2) coincides with the equivariant Satake equivalence, and the latter is monoidal, we obtain an isomorphism of localized kernels
$\Phi ^{2,0}_{\operatorname {loc}}\colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {A}}^\bullet ){\buildrel \sim \over \longrightarrow} D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\cong D_{!{\mathbf {G}}_{\mathbf {O}}}^{\operatorname {loc}}({\mathbf {Gr}}\times {\mathbf {V}})$ (see Lemma 3.10.1 and Corollary 3.10.2) coincides with the equivariant Satake equivalence, and the latter is monoidal, we obtain an isomorphism of localized kernels ![]() ${\mathbb {C}}[{\mathcal {Q}}_{\operatorname {loc}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}_{\operatorname {loc}}^\bullet$ as
${\mathbb {C}}[{\mathcal {Q}}_{\operatorname {loc}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}_{\operatorname {loc}}^\bullet$ as ![]() $G_{\mathcal {Q}}$-equivariant
$G_{\mathcal {Q}}$-equivariant ![]() ${\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet$-modules. By the argument in the second proof of Proposition 3.12.1(b) (using the additional grading and purity of
${\mathbb {C}}[{\mathcal {H}}_{\operatorname {loc}}]_{2,0}^\bullet$-modules. By the argument in the second proof of Proposition 3.12.1(b) (using the additional grading and purity of ![]() ${\mathcal {K}}^\bullet$), it remains to verify that this isomorphism restricts to the desired isomorphism from
${\mathcal {K}}^\bullet$), it remains to verify that this isomorphism restricts to the desired isomorphism from ![]() ${\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet \subset {\mathbb {C}}[{\mathcal {Q}}_{\operatorname {loc}}^A]_{2,0}^\bullet$ to
${\mathbb {C}}[{\mathcal {Q}}^A]_{2,0}^\bullet \subset {\mathbb {C}}[{\mathcal {Q}}_{\operatorname {loc}}^A]_{2,0}^\bullet$ to ![]() ${\mathcal {K}}^\bullet \subset {\mathcal {K}}_{\operatorname {loc}}^\bullet$. For this verification it suffices to restrict the scalars to
${\mathcal {K}}^\bullet \subset {\mathcal {K}}_{\operatorname {loc}}^\bullet$. For this verification it suffices to restrict the scalars to ![]() ${\mathbb {C}}[{\mathcal {H}}_{\operatorname {forg}}]_{2,0}^\bullet$. But we have already seen that over
${\mathbb {C}}[{\mathcal {H}}_{\operatorname {forg}}]_{2,0}^\bullet$. But we have already seen that over ![]() ${\mathbb {C}}[{\mathcal {H}}_{\operatorname {forg}}]_{2,0}^\bullet$ we obtain an isomorphism
${\mathbb {C}}[{\mathcal {H}}_{\operatorname {forg}}]_{2,0}^\bullet$ we obtain an isomorphism ![]() ${\mathbb {C}}[{\mathcal {Q}}_{\operatorname {forg}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}_{\operatorname {forg}}^\bullet$.
${\mathbb {C}}[{\mathcal {Q}}_{\operatorname {forg}}^A]_{2,0}^\bullet {\buildrel \sim \over \longrightarrow} {\mathcal {K}}_{\operatorname {forg}}^\bullet$.
This completes the proof of the monoidal property of ![]() $\Phi ^{2,0}$.
$\Phi ^{2,0}$.
3.15 Fourier transform
We have the Fourier transform functors (along ![]() ${\mathbf {V}}$)
${\mathbf {V}}$)
Strictly speaking, the Fourier transform goes not to ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, but to
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$, but to ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times (V^*\,{\otimes}\, {\mathbf {F}}))$. However, we identify
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times (V^*\,{\otimes}\, {\mathbf {F}}))$. However, we identify ![]() $V^*$ with
$V^*$ with ![]() $V$ using our choice of (self-dual) basis
$V$ using our choice of (self-dual) basis ![]() $e_1,\ldots ,e_N$, and accordingly change the action of
$e_1,\ldots ,e_N$, and accordingly change the action of ![]() ${\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N,{\mathbf {O}})$ by composing it with the automorphism
${\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N,{\mathbf {O}})$ by composing it with the automorphism ![]() $g\mapsto {}^t\!g^{-1}$. Note that the resulting Fourier transform to
$g\mapsto {}^t\!g^{-1}$. Note that the resulting Fourier transform to ![]() $D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is independent of the choice of basis in
$D_{?{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ is independent of the choice of basis in ![]() $V$.
$V$.
To describe the effect of ![]() ${\operatorname {FT}}$ on the coherent side, we identify
${\operatorname {FT}}$ on the coherent side, we identify ![]() $V_1\cong V_1^*$ and
$V_1\cong V_1^*$ and ![]() $V_2\cong V_2^*$ using our bases. Furthermore, we identify
$V_2\cong V_2^*$ using our bases. Furthermore, we identify
 \begin{align*} {{\operatorname{Hom}}}(V_1,V_2)&\cong{{\operatorname{Hom}}}(V_2^*,V_1^*)\cong{{\operatorname{Hom}}}(V_2,V_1),\quad A\mapsto B:={-}{}^t\!\!A,\\ {{\operatorname{Hom}}}(V_2,V_1)&\cong{{\operatorname{Hom}}}(V_1^*,V_2^*)\cong{{\operatorname{Hom}}}(V_1,V_2),\quad B\mapsto A:={}^t\!B. \end{align*}
\begin{align*} {{\operatorname{Hom}}}(V_1,V_2)&\cong{{\operatorname{Hom}}}(V_2^*,V_1^*)\cong{{\operatorname{Hom}}}(V_2,V_1),\quad A\mapsto B:={-}{}^t\!\!A,\\ {{\operatorname{Hom}}}(V_2,V_1)&\cong{{\operatorname{Hom}}}(V_1^*,V_2^*)\cong{{\operatorname{Hom}}}(V_1,V_2),\quad B\mapsto A:={}^t\!B. \end{align*}
Thus we obtain an ![]() $\iota$-equivariant transposition isomorphism
$\iota$-equivariant transposition isomorphism
 \begin{align*} \tau\colon{\mathfrak{G}}_{2,0}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2))\,{\otimes}\, {\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}2])\nonumber\\ &\to{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1))={\mathfrak{G}}_{0,2}^\bullet, \end{align*}
\begin{align*} \tau\colon{\mathfrak{G}}_{2,0}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2))\,{\otimes}\, {\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}2])\nonumber\\ &\to{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}2])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1))={\mathfrak{G}}_{0,2}^\bullet, \end{align*}
where ![]() $\iota \colon G_{\bar 0}\to G_{\bar 0}$ is an automorphism
$\iota \colon G_{\bar 0}\to G_{\bar 0}$ is an automorphism ![]() $(g_1,g_2)\mapsto ({}^t\!g_1^{-1},{}^t\!g_2^{-1})$. We denote the extension of scalars via
$(g_1,g_2)\mapsto ({}^t\!g_1^{-1},{}^t\!g_2^{-1})$. We denote the extension of scalars via ![]() $\tau$ by
$\tau$ by ![]() $\phi \tau \colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\to D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet ).$ Clearly, the functor
$\phi \tau \colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\to D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet ).$ Clearly, the functor ![]() $\phi \tau \colon \big (D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet ),\, {\stackrel {A}*}\big )\to \big (D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet ),\, {\stackrel {B}*}\big )$ is monoidal. Also, by the standard properties of the Fourier transform, the functor
$\phi \tau \colon \big (D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet ),\, {\stackrel {A}*}\big )\to \big (D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{0,2}^\bullet ),\, {\stackrel {B}*}\big )$ is monoidal. Also, by the standard properties of the Fourier transform, the functor
is monoidal. Thus the monoidal property of ![]() $\Phi ^{0,2}$ is a corollary of the following proposition.
$\Phi ^{0,2}$ is a corollary of the following proposition.
Proposition 3.15.1 The functors ![]() ${\operatorname {FT}}\circ \Phi ^{2,0}\colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\to D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and
${\operatorname {FT}}\circ \Phi ^{2,0}\colon D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{2,0}^\bullet )\to D_{*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ and ![]() $\Phi ^{0,2}\circ \phi \tau$ are isomorphic.
$\Phi ^{0,2}\circ \phi \tau$ are isomorphic.
Proof. Going over the construction of equivalences of ![]() $\Phi ^{0,2},\Phi ^{2,0}$, we see that it suffices to construct the isomorphisms
$\Phi ^{0,2},\Phi ^{2,0}$, we see that it suffices to construct the isomorphisms ![]() ${\operatorname {FT}}(E_0){\buildrel \sim \over \longrightarrow} E_0$ (evident), and
${\operatorname {FT}}(E_0){\buildrel \sim \over \longrightarrow} E_0$ (evident), and
(left and right convolution functors ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\times D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times V)\times D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times V)$). Here
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\times D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times V)\times D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times V)$). Here ![]() $\iota \colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is a monoidal autoequivalence induced by the automorphism
$\iota \colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is a monoidal autoequivalence induced by the automorphism ![]() $\iota \colon g\mapsto {}^t\!g^{-1}$ of
$\iota \colon g\mapsto {}^t\!g^{-1}$ of ![]() ${\mathbf {G}}_{\mathbf {F}}$. Note that the Satake equivalence intertwines
${\mathbf {G}}_{\mathbf {F}}$. Note that the Satake equivalence intertwines ![]() $\iota \colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ with the same-named autoequivalence of
$\iota \colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ with the same-named autoequivalence of ![]() ${\operatorname {Rep}}(\operatorname{GL}_N)$. Also note that
${\operatorname {Rep}}(\operatorname{GL}_N)$. Also note that ![]() $\iota \colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is induced by the automorphism
$\iota \colon D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is induced by the automorphism ![]() $L\mapsto L^\perp$ of
$L\mapsto L^\perp$ of ![]() ${\mathbf {Gr}}$. Here
${\mathbf {Gr}}$. Here ![]() $L^\perp :=\{v\in {\mathbf {V}} : (v,L)\in {\mathbf {O}}\}$, and
$L^\perp :=\{v\in {\mathbf {V}} : (v,L)\in {\mathbf {O}}\}$, and ![]() $(\cdot ,\cdot )$ stands for the
$(\cdot ,\cdot )$ stands for the ![]() ${\mathbf {F}}$-bilinear pairing on
${\mathbf {F}}$-bilinear pairing on ![]() ${\mathbf {V}}$ such that
${\mathbf {V}}$ such that ![]() $(e_i,e_j)=\delta _{ij}$. Now the existence of the desired isomorphism (3.15.1) follows from the definitions of
$(e_i,e_j)=\delta _{ij}$. Now the existence of the desired isomorphism (3.15.1) follows from the definitions of ![]() ${\operatorname {FT}}$ and convolutions (3.2.3) and (3.2.4).
${\operatorname {FT}}$ and convolutions (3.2.3) and (3.2.4).
3.16 The monoidal property of  $\Phi ^{1,1}$
$\Phi ^{1,1}$
The argument is very similar to that of § 3.14. We introduce
 \begin{align*} {\mathbb{C}}[{\mathcal{H}}]_{1,1}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}1])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}1]) \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_2)[{-}1])\\ &\quad \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V'_1)[{-}1])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V'_1)[{-}1])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_1)[{-}1]). \end{align*}
\begin{align*} {\mathbb{C}}[{\mathcal{H}}]_{1,1}^\bullet&={\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V_2)[{-}1])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V_1)[{-}1]) \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_2)[{-}1])\\ &\quad \,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_2,V'_1)[{-}1])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V_1,V'_1)[{-}1])\,{\otimes}\,{\operatorname{Sym}}({{\operatorname{Hom}}}(V'_1,V_1)[{-}1]). \end{align*}
Then the monoidal structure ![]() $\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$ on
$\,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }$ on ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is defined via the kernel
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ is defined via the kernel ![]() ${\mathbb {C}}[\Delta ]_{1,1}^\bullet$: the diagonal
${\mathbb {C}}[\Delta ]_{1,1}^\bullet$: the diagonal ![]() $G_{\bar 0}$-equivariant dg-
$G_{\bar 0}$-equivariant dg-![]() ${\mathfrak {G}}_{1,1}^\bullet$-trimodule. The fusion monoidal structure
${\mathfrak {G}}_{1,1}^\bullet$-trimodule. The fusion monoidal structure ![]() $\star$ on
$\star$ on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ transferred to
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ transferred to ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ via the equivalence
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ via the equivalence ![]() $\Phi ^{1,1}$ is also defined via a kernel
$\Phi ^{1,1}$ is also defined via a kernel ![]() ${\mathsf {K}}^\bullet$ (a
${\mathsf {K}}^\bullet$ (a ![]() $G_{\bar 0}$-equivariant dg-
$G_{\bar 0}$-equivariant dg-![]() ${\mathfrak {G}}_{1,1}^\bullet$-trimodule). Note that we have a different equivariant structure than for
${\mathfrak {G}}_{1,1}^\bullet$-trimodule). Note that we have a different equivariant structure than for ![]() ${\mathcal {K}}^\bullet$ (in the notation of § 3.14) because of the different compatibility with the Hecke action. We have to construct an isomorphism of
${\mathcal {K}}^\bullet$ (in the notation of § 3.14) because of the different compatibility with the Hecke action. We have to construct an isomorphism of ![]() $G_{\bar 0}$-equivariant dg-
$G_{\bar 0}$-equivariant dg-![]() ${\mathfrak {G}}_{1,1}^\bullet$-trimodules
${\mathfrak {G}}_{1,1}^\bullet$-trimodules ![]() ${\mathbb {C}}[\Delta ]_{1,1}^\bullet {\buildrel \sim \over \longrightarrow} {\mathsf {K}}^\bullet$.
${\mathbb {C}}[\Delta ]_{1,1}^\bullet {\buildrel \sim \over \longrightarrow} {\mathsf {K}}^\bullet$.
We have ![]() $\Phi ^{1,1}{\mathfrak {G}}_{1,1}^\bullet \simeq E_0$. Also, we have an isomorphism of endofunctors
$\Phi ^{1,1}{\mathfrak {G}}_{1,1}^\bullet \simeq E_0$. Also, we have an isomorphism of endofunctors ![]() $E_0\star -\cong {\operatorname{Id}}\colon D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Thus we obtain an isomorphism of functors
$E_0\star -\cong {\operatorname{Id}}\colon D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. Thus we obtain an isomorphism of functors ![]() $\Phi ^{1,1}({\mathfrak {G}}_{1,1}^\bullet \,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }-){\buildrel \sim \over \longrightarrow} (\Phi ^{1,1}{\mathfrak {G}}_{1,1}^\bullet )\star \Phi ^{1,1}-$. This isomorphism yields an isomorphism of kernels
$\Phi ^{1,1}({\mathfrak {G}}_{1,1}^\bullet \,{\otimes} _{{\mathfrak {G}}_{1,1}^\bullet }-){\buildrel \sim \over \longrightarrow} (\Phi ^{1,1}{\mathfrak {G}}_{1,1}^\bullet )\star \Phi ^{1,1}-$. This isomorphism yields an isomorphism of kernels ![]() ${\mathbb {C}}[\Delta _{\operatorname {forg}}]_{1,1}^\bullet {\buildrel \sim \over \longrightarrow} {\mathsf {K}}_{\operatorname {forg}}^\bullet$ (the notation is explained in § 3.14).
${\mathbb {C}}[\Delta _{\operatorname {forg}}]_{1,1}^\bullet {\buildrel \sim \over \longrightarrow} {\mathsf {K}}_{\operatorname {forg}}^\bullet$ (the notation is explained in § 3.14).
The following diagram commutes:

Hence the diagram

commutes as well, and the rest of the argument proceeds just as in § 3.14.
This completes the proof of the monoidal property of ![]() $\Phi ^{1,1}$ along with Theorem 3.6.1.
$\Phi ^{1,1}$ along with Theorem 3.6.1.
4. A coherent realization of  $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$
4.1 Notation
We consider a complex vector space ![]() $\bar {V}\!_1$ with a basis
$\bar {V}\!_1$ with a basis ![]() $e_2,e_3,\ldots ,e_N$. We consider the Lie superalgebra
$e_2,e_3,\ldots ,e_N$. We consider the Lie superalgebra ![]() ${\mathfrak {g}}{\mathfrak {l}}(N-1|N)={\mathfrak {g}}{\mathfrak {l}}(\bar {V}\!_1\oplus \Pi V_2)$. We have a decomposition
${\mathfrak {g}}{\mathfrak {l}}(N-1|N)={\mathfrak {g}}{\mathfrak {l}}(\bar {V}\!_1\oplus \Pi V_2)$. We have a decomposition ![]() ${\mathfrak {g}}{\mathfrak {l}}(N-1|N)=\bar {\mathfrak {g}}_{\bar 0}\oplus \bar {\mathfrak {g}}_{\bar 1}$, where
${\mathfrak {g}}{\mathfrak {l}}(N-1|N)=\bar {\mathfrak {g}}_{\bar 0}\oplus \bar {\mathfrak {g}}_{\bar 1}$, where ![]() $\bar {\mathfrak {g}}_{\bar 1}=\Pi {\operatorname{Hom}}(\bar {V}\!_1,V_2)\oplus \Pi {\operatorname{Hom}}(V_2,\bar {V}\!_1)$, and
$\bar {\mathfrak {g}}_{\bar 1}=\Pi {\operatorname{Hom}}(\bar {V}\!_1,V_2)\oplus \Pi {\operatorname{Hom}}(V_2,\bar {V}\!_1)$, and ![]() $\bar {\mathfrak {g}}_{\bar 0}=\operatorname{End}(\bar {V}\!_1)\oplus \operatorname{End}(V_2)$. We set
$\bar {\mathfrak {g}}_{\bar 0}=\operatorname{End}(\bar {V}\!_1)\oplus \operatorname{End}(V_2)$. We set ![]() $\bar {G}_{\bar 0}=\operatorname{GL}(\bar {V}\!_1)\times \operatorname{GL}(V_2)$. We consider the dg-algebra
$\bar {G}_{\bar 0}=\operatorname{GL}(\bar {V}\!_1)\times \operatorname{GL}(V_2)$. We consider the dg-algebra ![]() $\bar {\mathfrak {G}}{}^\bullet ={\operatorname{Sym}}(\bar {\mathfrak {g}}_{\bar 1}[-1])$ with trivial differential, and the triangulated category
$\bar {\mathfrak {G}}{}^\bullet ={\operatorname{Sym}}(\bar {\mathfrak {g}}_{\bar 1}[-1])$ with trivial differential, and the triangulated category ![]() $D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ obtained by localization (with respect to quasi-isomorphisms) of the category of perfect
$D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ obtained by localization (with respect to quasi-isomorphisms) of the category of perfect ![]() $\bar {G}_{\bar 0}$-equivariant dg-
$\bar {G}_{\bar 0}$-equivariant dg-![]() $\bar {\mathfrak {G}}{}^\bullet$-modules. Finally, we set
$\bar {\mathfrak {G}}{}^\bullet$-modules. Finally, we set ![]() $\bar {\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N-1,{\mathbf {O}})$.
$\bar {\mathbf {G}}_{\mathbf {O}}=\operatorname{GL}(N-1,{\mathbf {O}})$.
Theorem 4.1.1 There exists an equivalence of triangulated categories ![]() $\bar \Phi \colon D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ commuting with the left convolution action of the monoidal spherical Hecke category
$\bar \Phi \colon D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ commuting with the left convolution action of the monoidal spherical Hecke category ![]() ${\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1})\cong {\operatorname {Rep}}(\operatorname{GL}_{N-1})$ and with the right convolution action of the monoidal spherical Hecke category
${\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1})\cong {\operatorname {Rep}}(\operatorname{GL}_{N-1})$ and with the right convolution action of the monoidal spherical Hecke category ![]() ${\operatorname {Perv}}_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N)\cong {\operatorname {Rep}}(\operatorname{GL}_N)$.
${\operatorname {Perv}}_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N)\cong {\operatorname {Rep}}(\operatorname{GL}_N)$.
The proof will be given in § 4.4 after some preparations in §§ 4.2 and 4.3.
Similarly to § 3.8, we define ![]() $\bar {\Lambda }:=\Lambda \big ({\operatorname{Hom}}(\bar {V}\!_1,V_2)\oplus {\operatorname{Hom}}(V_2,\bar {V}\!_1)\big )$. We consider the derived category
$\bar {\Lambda }:=\Lambda \big ({\operatorname{Hom}}(\bar {V}\!_1,V_2)\oplus {\operatorname{Hom}}(V_2,\bar {V}\!_1)\big )$. We consider the derived category ![]() $D_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$ of finite-dimensional complexes of
$D_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$ of finite-dimensional complexes of ![]() $\bar {G}_{\bar 0}\ltimes \bar \Lambda$-modules. We have the Koszul equivalence functors
$\bar {G}_{\bar 0}\ltimes \bar \Lambda$-modules. We have the Koszul equivalence functors
We also consider the degeneration ![]() $\underline {\mathfrak {gl}}(N-1|N)$ of the Lie superalgebra
$\underline {\mathfrak {gl}}(N-1|N)$ of the Lie superalgebra ![]() ${\mathfrak {gl}}(N-1|N)$ (defined as in § 1.5), and the derived category of bounded complexes of integrable
${\mathfrak {gl}}(N-1|N)$ (defined as in § 1.5), and the derived category of bounded complexes of integrable ![]() $\underline {\mathfrak {gl}}(N-1|N)$-modules
$\underline {\mathfrak {gl}}(N-1|N)$-modules ![]() $SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N-1|N))\cong SD_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$. The following corollary of Theorem 4.1.1 is proved just like Corollary 3.8.1.
$SD_{\operatorname {int}}(\underline {\mathfrak {gl}}(N-1|N))\cong SD_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$. The following corollary of Theorem 4.1.1 is proved just like Corollary 3.8.1.
Corollary 4.1.2 (a) The composed equivalence
is exact with respect to the tautological ![]() $t$-structure on
$t$-structure on ![]() $D_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$ and the perverse
$D_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$ and the perverse ![]() $t$-structure on
$t$-structure on ![]() $D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
$D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
(b) This equivalence is monoidal with respect to the tensor structure on ![]() $D_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$ and the fusion
$D_{\operatorname {fd}}^{\bar {G}_{\bar 0}}(\bar {\Lambda })$ and the fusion ![]() $\star$ on
$\star$ on ![]() $D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
$D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
(c) The equivariant derived category ![]() $D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is equivalent to the bounded derived category of the abelian category
$D_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ is equivalent to the bounded derived category of the abelian category ![]() ${\operatorname {Perv}}_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
${\operatorname {Perv}}_{\bar {\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$.
In case ![]() $N=2$, both Theorem 4.1.1 and Corollary 4.1.2(a) were proved in [Reference Braverman and FinkelbergBF18] by a rather different argument.
$N=2$, both Theorem 4.1.1 and Corollary 4.1.2(a) were proved in [Reference Braverman and FinkelbergBF18] by a rather different argument.
4.2 Constructible mirabolic restriction
Clearly, ![]() ${\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0$ is a single
${\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0$ is a single ![]() ${\mathbf {G}}_{\mathbf {O}}$-orbit, and the stabilizer of the vector
${\mathbf {G}}_{\mathbf {O}}$-orbit, and the stabilizer of the vector ![]() $e_1\in {\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0$ is the mirabolic subgroup
$e_1\in {\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0$ is the mirabolic subgroup ![]() ${\mathbf {M}}_{\mathbf {O}}\subset {\mathbf {G}}_{\mathbf {O}}$. Hence
${\mathbf {M}}_{\mathbf {O}}\subset {\mathbf {G}}_{\mathbf {O}}$. Hence ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))\cong D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$. We will denote
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))\cong D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$. We will denote ![]() ${\mathbf {Gr}}={\mathbf {Gr}}_{\operatorname{GL}_N}$ by
${\mathbf {Gr}}={\mathbf {Gr}}_{\operatorname{GL}_N}$ by ![]() ${\mathbf {Gr}}_N$ to distinguish it from
${\mathbf {Gr}}_N$ to distinguish it from ![]() ${\mathbf {Gr}}_{N-1}:={\mathbf {Gr}}_{\operatorname{GL}_{N-1}}$. We will also denote by
${\mathbf {Gr}}_{N-1}:={\mathbf {Gr}}_{\operatorname{GL}_{N-1}}$. We will also denote by ![]() ${\mathbf {Gr}}_N^\subset \subset {\mathbf {Gr}}_N$ (respectively,
${\mathbf {Gr}}_N^\subset \subset {\mathbf {Gr}}_N$ (respectively, ![]() ${\mathbf {Gr}}_{N-1}^\subset \subset {\mathbf {Gr}}_{N-1}$) the closed subvariety classifying the sublattices in the standard one
${\mathbf {Gr}}_{N-1}^\subset \subset {\mathbf {Gr}}_{N-1}$) the closed subvariety classifying the sublattices in the standard one ![]() ${\mathbf {V}}_0$ (respectively, in
${\mathbf {V}}_0$ (respectively, in ![]() $\bar {\mathbf {V}}\!_0:={\mathbf {O}} e_2\oplus {\mathbf {O}} e_3\oplus \cdots \oplus {\mathbf {O}} e_N$). It is a union of the Schubert varieties numbered by the negative partitions of length
$\bar {\mathbf {V}}\!_0:={\mathbf {O}} e_2\oplus {\mathbf {O}} e_3\oplus \cdots \oplus {\mathbf {O}} e_N$). It is a union of the Schubert varieties numbered by the negative partitions of length ![]() $\leq N$ (respectively,
$\leq N$ (respectively, ![]() $\leq N-1$). The category
$\leq N-1$). The category ![]() ${\operatorname {Perv}}_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N^\subset )$ (respectively,
${\operatorname {Perv}}_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N^\subset )$ (respectively, ![]() ${\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1}^\subset )$) is monoidal and the Satake equivalence takes it to the monoidal category of polynomial representations of
${\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1}^\subset )$) is monoidal and the Satake equivalence takes it to the monoidal category of polynomial representations of ![]() $\operatorname{GL}_N$ (respectively,
$\operatorname{GL}_N$ (respectively, ![]() $\operatorname{GL}_{N-1}$).
$\operatorname{GL}_{N-1}$).
We have a closed embedding ![]() $\varsigma \colon {\mathbf {Gr}}_{N-1}^\subset \hookrightarrow {\mathbf {Gr}}_N^\subset$,
$\varsigma \colon {\mathbf {Gr}}_{N-1}^\subset \hookrightarrow {\mathbf {Gr}}_N^\subset$, ![]() $(\bar {L}\subset \bar {\mathbf {V}}\!_0)\mapsto ({\mathbf {O}} e_1\oplus \bar {L}\subset {\mathbf {V}}_0)$.
$(\bar {L}\subset \bar {\mathbf {V}}\!_0)\mapsto ({\mathbf {O}} e_1\oplus \bar {L}\subset {\mathbf {V}}_0)$.
Lemma 4.2.1 (a) The functor ![]() $\varsigma ^!\colon D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N^\subset )\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1}^\subset )$ is monoidal.
$\varsigma ^!\colon D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N^\subset )\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1}^\subset )$ is monoidal.
(b) For a negative partition ![]() ${\boldsymbol {\lambda }}$ we have
${\boldsymbol {\lambda }}$ we have ![]() $\varsigma ^!{\operatorname {IC}}_{\boldsymbol {\lambda }}={\operatorname {IC}}_{\boldsymbol {\lambda }}[|{\boldsymbol {\lambda }}|]$ in the notation of § 3.13 (i.e. if
$\varsigma ^!{\operatorname {IC}}_{\boldsymbol {\lambda }}={\operatorname {IC}}_{\boldsymbol {\lambda }}[|{\boldsymbol {\lambda }}|]$ in the notation of § 3.13 (i.e. if ![]() $\lambda _1<0$, then
$\lambda _1<0$, then ![]() $\varsigma ^!{\operatorname {IC}}_{\boldsymbol {\lambda }}=0$, and if
$\varsigma ^!{\operatorname {IC}}_{\boldsymbol {\lambda }}=0$, and if ![]() $\lambda _1=0$, then
$\lambda _1=0$, then ![]() $\varsigma ^!{\operatorname {IC}}_{\boldsymbol {\lambda }}={\operatorname {IC}}_{(\lambda _2\geq \cdots \geq \lambda _N)}[\lambda _2+\cdots +\lambda _N]$).
$\varsigma ^!{\operatorname {IC}}_{\boldsymbol {\lambda }}={\operatorname {IC}}_{(\lambda _2\geq \cdots \geq \lambda _N)}[\lambda _2+\cdots +\lambda _N]$).
Proof. (a) The Grassmannian of sublattices ![]() ${\mathbf {Gr}}_N^\subset$ (respectively,
${\mathbf {Gr}}_N^\subset$ (respectively, ![]() ${\mathbf {Gr}}_{N-1}^\subset$) is the union of connected components
${\mathbf {Gr}}_{N-1}^\subset$) is the union of connected components ![]() ${\bigsqcup} _{n\in {\mathbb {N}}}{\mathbf {Gr}}_N^{\subset ,(-n)}$ (respectively,
${\bigsqcup} _{n\in {\mathbb {N}}}{\mathbf {Gr}}_N^{\subset ,(-n)}$ (respectively, ![]() ${\bigsqcup} _{n\in {\mathbb {N}}}{\mathbf {Gr}}_{N-1}^{\subset ,(-n)}$) parametrizing sublattices of codimension
${\bigsqcup} _{n\in {\mathbb {N}}}{\mathbf {Gr}}_{N-1}^{\subset ,(-n)}$) parametrizing sublattices of codimension ![]() $n$. Clearly,
$n$. Clearly, ![]() $\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})\subset {\mathbf {Gr}}_N^{\subset ,(-n)}$. Moreover,
$\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})\subset {\mathbf {Gr}}_N^{\subset ,(-n)}$. Moreover, ![]() $\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})$ is a connected component of the intersection of the Levi Grassmannian
$\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})$ is a connected component of the intersection of the Levi Grassmannian ![]() ${\mathbf {Gr}}_{\operatorname{GL}_1{\!\times\!} \operatorname{GL}_{N-1}}\subset {\mathbf {Gr}}_N$ with
${\mathbf {Gr}}_{\operatorname{GL}_1{\!\times\!} \operatorname{GL}_{N-1}}\subset {\mathbf {Gr}}_N$ with ![]() ${\mathbf {Gr}}_N^{\subset ,(-n)}$. We have the monoidal functor of hyperbolic restriction to the Levi Grassmannian; see for example, [Reference Beilinson and DrinfeldBD, 5.3.28 at p. 213]. Since
${\mathbf {Gr}}_N^{\subset ,(-n)}$. We have the monoidal functor of hyperbolic restriction to the Levi Grassmannian; see for example, [Reference Beilinson and DrinfeldBD, 5.3.28 at p. 213]. Since ![]() $({\mathbf {M}}_{\mathbf {F}}\cdot \varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)}))\cap {\mathbf {Gr}}_N^{\subset ,(-n)}=\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})$, the hyperbolic restriction to the component
$({\mathbf {M}}_{\mathbf {F}}\cdot \varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)}))\cap {\mathbf {Gr}}_N^{\subset ,(-n)}=\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})$, the hyperbolic restriction to the component ![]() $\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})$ coincides with the corestriction
$\varsigma ({\mathbf {Gr}}_{N-1}^{\subset ,(-n)})$ coincides with the corestriction ![]() $\varsigma ^!$.
$\varsigma ^!$.
(b) We have ![]() $({\mathbb {S}}_{\boldsymbol {\lambda }} V_1^*)^{\operatorname{GL}_1}={\mathbb {S}}_{\boldsymbol {\lambda }}\bar {V}{}^*\!\!\!\!_1$. Now the desired claim follows from [Reference Beilinson and DrinfeldBD, Proposition 5.3.29].
$({\mathbb {S}}_{\boldsymbol {\lambda }} V_1^*)^{\operatorname{GL}_1}={\mathbb {S}}_{\boldsymbol {\lambda }}\bar {V}{}^*\!\!\!\!_1$. Now the desired claim follows from [Reference Beilinson and DrinfeldBD, Proposition 5.3.29].
Recall that the monoidal Hecke category ![]() $D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N)=D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ acts by left convolution on
$D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N)=D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}})$ acts by left convolution on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. In particular, the monoidal subcategory
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. In particular, the monoidal subcategory ![]() $D_{\mathbf{G}_\mathbf{O}} ({\mathbf {Gr}}_N^\subset )\subset D_{\mathbf{G}_\mathbf{O}} ({\mathbf {Gr}})$ acts on
$D_{\mathbf{G}_\mathbf{O}} ({\mathbf {Gr}}_N^\subset )\subset D_{\mathbf{G}_\mathbf{O}} ({\mathbf {Gr}})$ acts on ![]() $D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. We define the action of
$D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$. We define the action of ![]() $D_{\mathbf{G}_\mathbf{O}} ({\mathbf {Gr}}_N^\subset )$ by the left convolution on
$D_{\mathbf{G}_\mathbf{O}} ({\mathbf {Gr}}_N^\subset )$ by the left convolution on ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))$ as follows:
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))$ as follows: ![]() ${\mathcal {A}}*{\mathcal {F}}:=\jmath _0^!({\mathcal {A}}*\jmath _{0*}{\mathcal {F}})$ (in the notation of § 3.12). Also, the monoidal Hecke category
${\mathcal {A}}*{\mathcal {F}}:=\jmath _0^!({\mathcal {A}}*\jmath _{0*}{\mathcal {F}})$ (in the notation of § 3.12). Also, the monoidal Hecke category ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1})$ acts by left convolution on
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_{N-1})$ acts by left convolution on ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_N)$. Finally, we denote by
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_N)$. Finally, we denote by ![]() $\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}}_N)\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_N)$ the functor of restriction of equivariance under
$\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}}_N)\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}}_N)$ the functor of restriction of equivariance under ![]() $\operatorname{GL}(N-1,{\mathbf {O}})\hookrightarrow {\mathbf {M}}_{\mathbf {O}}$.
$\operatorname{GL}(N-1,{\mathbf {O}})\hookrightarrow {\mathbf {M}}_{\mathbf {O}}$.
Lemma 4.2.2 We have a compatible system of isomorphisms for all ![]() ${\mathcal {A}}\in D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N^\subset )$ and
${\mathcal {A}}\in D_{\operatorname{GL}(N,{\mathbf {O}})}({\mathbf {Gr}}_N^\subset )$ and ![]() ${\mathcal {F}}\in D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))\cong D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$:
${\mathcal {F}}\in D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))\cong D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$:
Proof. Comparison of definitions.
4.3 Coherent mirabolic restriction
Recall the subcategory ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ generated by
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$ generated by ![]() $\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$ introduced in the proof of Proposition 3.12.1(a). The equivalence
$\{V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}\mid {\boldsymbol \lambda} \geq 0\}$ introduced in the proof of Proposition 3.12.1(a). The equivalence ![]() $\Phi ^{1,1}\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ restricts to the same-named equivalence
$\Phi ^{1,1}\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}})$ restricts to the same-named equivalence ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}}_0)$, and the functor
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times {\mathbf {V}}_0)$, and the functor ![]() $p_*q^*\colon D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$ (in the notation of § 3.12) is isomorphic to
$p_*q^*\colon D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$ (in the notation of § 3.12) is isomorphic to ![]() ${\operatorname{Id}}$. Thus we have a natural morphism
${\operatorname{Id}}$. Thus we have a natural morphism ![]() ${\operatorname{Id}}\cong p_*q^*\to p_{0*}q_0^*$ (again in the notation of § 3.12) of endofunctors of
${\operatorname{Id}}\cong p_*q^*\to p_{0*}q_0^*$ (again in the notation of § 3.12) of endofunctors of ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$. Composing with another copy of
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$. Composing with another copy of ![]() $p_{0*}q_0^*$, we obtain a morphism
$p_{0*}q_0^*$, we obtain a morphism ![]() $p_{0*}q_0^*\to p_{0*}q_0^*\circ p_{0*}q_0^*$ of endofunctors of
$p_{0*}q_0^*\to p_{0*}q_0^*\circ p_{0*}q_0^*$ of endofunctors of ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$ that is easily seen to be an isomorphism. Indeed, according to Proposition 3.12.1(c),
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$ that is easily seen to be an isomorphism. Indeed, according to Proposition 3.12.1(c), ![]() $\Phi ^{1,1}$ takes
$\Phi ^{1,1}$ takes ![]() $p_{0*}q_0^*$ to
$p_{0*}q_0^*$ to ![]() $\jmath _{0*}\jmath _0^!$, and
$\jmath _{0*}\jmath _0^!$, and ![]() $\jmath _{0*}\jmath _0^!{\buildrel \sim \over \longrightarrow} \jmath _{0*}\jmath _0^!\circ \jmath _{0*}\jmath _0^!$. Inverting the isomorphism
$\jmath _{0*}\jmath _0^!{\buildrel \sim \over \longrightarrow} \jmath _{0*}\jmath _0^!\circ \jmath _{0*}\jmath _0^!$. Inverting the isomorphism ![]() $p_{0*}q_0^*{\buildrel \sim \over \longrightarrow} p_{0*}q_0^*\circ p_{0*}q_0^*$, we obtain an isomorphism
$p_{0*}q_0^*{\buildrel \sim \over \longrightarrow} p_{0*}q_0^*\circ p_{0*}q_0^*$, we obtain an isomorphism ![]() $p_{0*}q_0^*\circ p_{0*}q_0^*{\buildrel \sim \over \longrightarrow} p_{0*}q_0^*$ that, together with the morphism
$p_{0*}q_0^*\circ p_{0*}q_0^*{\buildrel \sim \over \longrightarrow} p_{0*}q_0^*$ that, together with the morphism ![]() ${\operatorname{Id}}\to p_{0*}q_0^*$, equips
${\operatorname{Id}}\to p_{0*}q_0^*$, equips ![]() $p_{0*}q_0^*$ with a structure of (idempotent) monad in
$p_{0*}q_0^*$ with a structure of (idempotent) monad in ![]() $D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$.
$D_{\operatorname{perf}}^{G_{\bar 0},\geq }({\mathfrak {G}}_{1,1}^\bullet )$.
We denote the dg-algebra with trivial differential ![]() ${\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}_{\leq N-1}(V_1,V'_1)]$ (the grading on
${\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, {\mathbb {C}}[{\operatorname{Hom}}_{\leq N-1}(V_1,V'_1)]$ (the grading on ![]() ${\mathbb {C}}[{\operatorname{Hom}}_{\leq N-1}(V_1,V'_1)]$ is trivial) by
${\mathbb {C}}[{\operatorname{Hom}}_{\leq N-1}(V_1,V'_1)]$ is trivial) by ![]() ${\mathfrak {F}}^\bullet$ (here
${\mathfrak {F}}^\bullet$ (here ![]() ${\operatorname{Hom}}_{\leq N-1}(V_1,V'_1)\subset {\operatorname{Hom}}(V_1,V'_1)$ stands for the subvariety formed by the non-invertible homomorphisms). It is acted upon by
${\operatorname{Hom}}_{\leq N-1}(V_1,V'_1)\subset {\operatorname{Hom}}(V_1,V'_1)$ stands for the subvariety formed by the non-invertible homomorphisms). It is acted upon by ![]() $G_{\mathcal {Q}}$. By Theorem 3.6.1 and Proposition 3.12.1, we have an equivalence of categories
$G_{\mathcal {Q}}$. By Theorem 3.6.1 and Proposition 3.12.1, we have an equivalence of categories ![]() $\Phi '$ from the Kleisli category (see [Reference Mac LaneMac98, VI.5])
$\Phi '$ from the Kleisli category (see [Reference Mac LaneMac98, VI.5]) ![]() $D(p_{0*}q_0^*)$ of the monad
$D(p_{0*}q_0^*)$ of the monad ![]() $p_{0*}q_0^*$ in
$p_{0*}q_0^*$ in ![]() $D^{G_{\bar 0},\geq }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ to
$D^{G_{\bar 0},\geq }_{\operatorname{perf}}({\mathfrak {G}}_{1,1}^\bullet )$ to ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))$. For the modules
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))$. For the modules ![]() $V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$,
$V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$, ![]() $V_{1,{\boldsymbol {\lambda }}'}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}'}$ over the monad
$V_{1,{\boldsymbol {\lambda }}'}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}'}$ over the monad ![]() $p_{0*}q_0^*$ (here both
$p_{0*}q_0^*$ (here both ![]() ${\boldsymbol {\lambda }},{\boldsymbol {\lambda }}'$ are partitions), we have
${\boldsymbol {\lambda }},{\boldsymbol {\lambda }}'$ are partitions), we have
Recall the equivalence ![]() $D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))\cong D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$. By an abuse of notation, we will denote the composed equivalence
$D_{{\mathbf {G}}_{\mathbf {O}}}({\mathbf {Gr}}\times ({\mathbf {V}}_0\,{\smallsetminus}\, t{\mathbf {V}}_0))\cong D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$. By an abuse of notation, we will denote the composed equivalence ![]() $D(p_{0*}q_0^*){\buildrel \sim \over \longrightarrow} D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ also by
$D(p_{0*}q_0^*){\buildrel \sim \over \longrightarrow} D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ also by ![]() $\Phi '$.
$\Phi '$.
On the other hand, we consider a full subcategory ![]() $D^{\bar {G}_{\bar 0},\geq 0}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )\subset D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ generated by the free modules
$D^{\bar {G}_{\bar 0},\geq 0}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )\subset D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ generated by the free modules ![]() $\bar {V}\!_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, \bar {\mathfrak {G}}{}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$ for partitions
$\bar {V}\!_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, \bar {\mathfrak {G}}{}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$ for partitions ![]() ${\boldsymbol {\lambda }}$ (of length
${\boldsymbol {\lambda }}$ (of length ![]() $\leq ~N-1$). We construct an equivalence
$\leq ~N-1$). We construct an equivalence ![]() $\Phi \colon D(p_{0*}q_0^*){\buildrel \sim \over \longrightarrow} D^{\bar {G}_{\bar 0},\geq 0}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ as follows. We consider the variety
$\Phi \colon D(p_{0*}q_0^*){\buildrel \sim \over \longrightarrow} D^{\bar {G}_{\bar 0},\geq 0}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ as follows. We consider the variety ![]() ${\mathcal {P}}$ of sextuples
${\mathcal {P}}$ of sextuples
such that ![]() $A=\bar {A}b$,
$A=\bar {A}b$, ![]() $\bar {B}=bB$,
$\bar {B}=bB$, ![]() $a=B\bar {A}$. Clearly,
$a=B\bar {A}$. Clearly,

We have the natural morphisms
The variety ![]() ${\mathcal {P}}$ is acted upon by
${\mathcal {P}}$ is acted upon by ![]() $G_{\mathcal {P}}:=\operatorname{GL}(V_1)\times \operatorname{GL}(\bar {V}\!_1)\times \operatorname{GL}(V_2)$:
$G_{\mathcal {P}}:=\operatorname{GL}(V_1)\times \operatorname{GL}(\bar {V}\!_1)\times \operatorname{GL}(V_2)$:
We have the natural morphisms
Clearly, the morphisms ![]() ${\mathsf {p}}\colon {\mathcal {P}}\to \Pi {\mathfrak {g}}^*_{\bar 1}$,
${\mathsf {p}}\colon {\mathcal {P}}\to \Pi {\mathfrak {g}}^*_{\bar 1}$, ![]() ${\mathsf {q}}\colon {\mathcal {P}}\to \Pi \bar {\mathfrak {g}}{}^*_{\bar 1}$ are equivariant with respect to
${\mathsf {q}}\colon {\mathcal {P}}\to \Pi \bar {\mathfrak {g}}{}^*_{\bar 1}$ are equivariant with respect to ![]() ${\mathsf {p}}\colon G_{\mathcal {P}}\to G_{\bar 0}$,
${\mathsf {p}}\colon G_{\mathcal {P}}\to G_{\bar 0}$, ![]() ${\mathsf {q}}\colon G_{\mathcal {P}}\to \bar {G}_{\bar 0}$. Hence we have the convolution functor
${\mathsf {q}}\colon G_{\mathcal {P}}\to \bar {G}_{\bar 0}$. Hence we have the convolution functor
(in particular, ![]() ${\mathsf {q}}_*$ involves taking
${\mathsf {q}}_*$ involves taking ![]() $\operatorname{GL}(V_1)$-invariants). We will actually need the same-named functor
$\operatorname{GL}(V_1)$-invariants). We will actually need the same-named functor ![]() ${\mathsf {q}}_*{\mathsf {p}}^*\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )$ defined similarly using the dg-algebra with trivial differential
${\mathsf {q}}_*{\mathsf {p}}^*\colon D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )\to D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )$ defined similarly using the dg-algebra with trivial differential
(the grading on ![]() ${\operatorname{Sym}}{\operatorname{Hom}}(\bar {V}\!_1,V_1)$ is trivial, and if we disregard the grading, then
${\operatorname{Sym}}{\operatorname{Hom}}(\bar {V}\!_1,V_1)$ is trivial, and if we disregard the grading, then ![]() ${\operatorname{Sym}}\big ({\operatorname{Hom}}(V_1,V_2)[-1]\oplus {\operatorname{Hom}}(\bar {V}\!_1,V_1)[-1]\big )\,{\otimes}\, {\operatorname{Sym}}{\operatorname{Hom}}(\bar {V}\!_1,V_1) \simeq {\mathbb {C}}[{\mathcal {P}}]$).
${\operatorname{Sym}}\big ({\operatorname{Hom}}(V_1,V_2)[-1]\oplus {\operatorname{Hom}}(\bar {V}\!_1,V_1)[-1]\big )\,{\otimes}\, {\operatorname{Sym}}{\operatorname{Hom}}(\bar {V}\!_1,V_1) \simeq {\mathbb {C}}[{\mathcal {P}}]$).
Now recall that ![]() $D(p_{0*}q_0^*)$ is a full subcategory of
$D(p_{0*}q_0^*)$ is a full subcategory of ![]() $D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$. The desired functor
$D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$. The desired functor ![]() $\Phi \colon D(p_{0*}q_0^*)\to D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ is nothing but the restriction of
$\Phi \colon D(p_{0*}q_0^*)\to D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$ is nothing but the restriction of ![]() ${\mathsf {q}}_*{\mathsf {p}}^*$ to the full subcategory
${\mathsf {q}}_*{\mathsf {p}}^*$ to the full subcategory ![]() $D(p_{0*}q_0^*)\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$. The full subcategory
$D(p_{0*}q_0^*)\subset D_{\operatorname{perf}}^{G_{\bar 0}}({\mathfrak {G}}_{1,1}^\bullet )$. The full subcategory ![]() $D(p_{0*}q_0^*)$ is generated by the objects
$D(p_{0*}q_0^*)$ is generated by the objects ![]() $p_{0*}q_0^*(V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}) \cong _{D(p_{0*}q_0^*)} V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$ (the left- and right-hand sides are isomorphic in the Kleisli category
$p_{0*}q_0^*(V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}) \cong _{D(p_{0*}q_0^*)} V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}}$ (the left- and right-hand sides are isomorphic in the Kleisli category ![]() $D(p_{0*}q_0^*)$) with
$D(p_{0*}q_0^*)$) with ![]() ${\boldsymbol {\lambda }}$ running through the set of partitions. For a partition
${\boldsymbol {\lambda }}$ running through the set of partitions. For a partition ![]() ${\boldsymbol {\lambda }}$ we have
${\boldsymbol {\lambda }}$ we have
in the notation of § 3.13 (i.e. if ![]() ${\boldsymbol {\lambda }}=(\lambda _1\geq \lambda _2\geq \cdots \geq \lambda _N\geq 0)$ and
${\boldsymbol {\lambda }}=(\lambda _1\geq \lambda _2\geq \cdots \geq \lambda _N\geq 0)$ and ![]() $\lambda _N>0$, then
$\lambda _N>0$, then ![]() ${\Phi} (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})=0$, and if
${\Phi} (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})=0$, and if ![]() $\lambda _N=0$, then
$\lambda _N=0$, then ![]() $\Phi (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})= \bar {V}\!_{1,(\lambda _1\geq \cdots \geq \lambda _{N-1})}\,{\otimes}\, \bar {\mathfrak {G}}{}^\bullet \,{\otimes}$
$\Phi (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})= \bar {V}\!_{1,(\lambda _1\geq \cdots \geq \lambda _{N-1})}\,{\otimes}\, \bar {\mathfrak {G}}{}^\bullet \,{\otimes}$ ![]() $V_{2,{\boldsymbol {\mu }}}$). Hence
$V_{2,{\boldsymbol {\mu }}}$). Hence ![]() $\Phi (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})$ actually lies in
$\Phi (V_{1,{\boldsymbol {\lambda }}}\,{\otimes}\, {\mathfrak {G}}_{1,1}^\bullet \,{\otimes}\, V_{2,{\boldsymbol {\mu }}})$ actually lies in ![]() $D^{\bar {G}_{\bar 0},\geq 0}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )\subset D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$. It remains to check that
$D^{\bar {G}_{\bar 0},\geq 0}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )\subset D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {G}}{}^\bullet )$. It remains to check that ![]() $\Phi$ is fully faithful.
$\Phi$ is fully faithful.
For partitions ![]() ${\boldsymbol {\lambda }},{\boldsymbol {\lambda }}'$, we have to check that the following morphism is an isomorphism:
${\boldsymbol {\lambda }},{\boldsymbol {\lambda }}'$, we have to check that the following morphism is an isomorphism:
 \begin{align*} & \big(V_{1,{\boldsymbol{\lambda}}}^*\,{\otimes}\, p_{0*}q_0^*(V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)] \,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\,{\otimes}\, V_{2,{\boldsymbol{\mu}}}^*\big)^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\\ &\quad:=\big(V_{1,{\boldsymbol{\lambda}}}^*\,{\otimes}\, V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{\mathcal{Q}}_0]\,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{G_{\mathcal{Q}}} =\big({\mathbb{S}}_{\boldsymbol{\lambda}} V_1^*\,{\otimes}\,{\mathbb{S}}_{{\boldsymbol{\lambda}}'}V_1'\,{\otimes}\,{\mathbb{C}}[{\mathcal{Q}}_0] \,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{G_{\mathcal{Q}}}\\ &\quad{\buildrel \sim \over \longrightarrow}\big({\mathbb{S}}_{\boldsymbol{\lambda}}\bar{V}{}_{\!\!1}^*\,{\otimes}\,{\mathbb{S}}_{{\boldsymbol{\lambda}}'}\bar{V}{}_{\!\!1}\,{\otimes}\, {\mathbb{C}}[{{\operatorname{Hom}}}(\bar{V}\!_1,V_2)\times{{\operatorname{Hom}}}(V_2,\bar{V}\!_1)] \,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{{{\operatorname{GL}}}(\bar{V}\!_1)\times{{\operatorname{GL}}}(V_2)}. \end{align*}
\begin{align*} & \big(V_{1,{\boldsymbol{\lambda}}}^*\,{\otimes}\, p_{0*}q_0^*(V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_2,V'_1)] \,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\,{\otimes}\, V_{2,{\boldsymbol{\mu}}}^*\big)^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}\\ &\quad:=\big(V_{1,{\boldsymbol{\lambda}}}^*\,{\otimes}\, V'_{1,{\boldsymbol{\lambda}}'}\,{\otimes}\,{\mathbb{C}}[{\mathcal{Q}}_0]\,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{G_{\mathcal{Q}}} =\big({\mathbb{S}}_{\boldsymbol{\lambda}} V_1^*\,{\otimes}\,{\mathbb{S}}_{{\boldsymbol{\lambda}}'}V_1'\,{\otimes}\,{\mathbb{C}}[{\mathcal{Q}}_0] \,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{G_{\mathcal{Q}}}\\ &\quad{\buildrel \sim \over \longrightarrow}\big({\mathbb{S}}_{\boldsymbol{\lambda}}\bar{V}{}_{\!\!1}^*\,{\otimes}\,{\mathbb{S}}_{{\boldsymbol{\lambda}}'}\bar{V}{}_{\!\!1}\,{\otimes}\, {\mathbb{C}}[{{\operatorname{Hom}}}(\bar{V}\!_1,V_2)\times{{\operatorname{Hom}}}(V_2,\bar{V}\!_1)] \,{\otimes}\,(V_{2,{\boldsymbol{\mu}}}^*\,{\otimes}\, V_{2,{\boldsymbol{\mu}}'})\big)^{{{\operatorname{GL}}}(\bar{V}\!_1)\times{{\operatorname{GL}}}(V_2)}. \end{align*}
The desired isomorphism is equal to the composition of the following three. The first is induced by
see Lemma 3.13.1(a). The second is induced by the inverse of
see Lemma 3.13.1(b). The third is induced by the inverse of
see Lemma 3.13.1(c).
4.4 Proof of Theorem 4.1.1
We consider an ![]() ${\mathbf {F}}$-linear automorphism
${\mathbf {F}}$-linear automorphism ![]() $\xi$ of
$\xi$ of ![]() ${\mathbf {V}}\colon \xi (e_1)=e_1$,
${\mathbf {V}}\colon \xi (e_1)=e_1$, ![]() $\xi (e_i)=te_i$ for
$\xi (e_i)=te_i$ for ![]() $i=2,\ldots ,N$, and the same-named induced automorphism of
$i=2,\ldots ,N$, and the same-named induced automorphism of ![]() ${\mathbf {Gr}}$. It is given by the action of an element
${\mathbf {Gr}}$. It is given by the action of an element ![]() $\operatorname {diag}(1,t,\ldots ,t)$ of the diagonal Cartan torus
$\operatorname {diag}(1,t,\ldots ,t)$ of the diagonal Cartan torus ![]() ${\mathbf {T}}_{\mathbf {F}}$. Note that
${\mathbf {T}}_{\mathbf {F}}$. Note that ![]() $\operatorname {diag}(1,t,\ldots ,t){\mathbf {M}}_{\mathbf {O}}\operatorname {diag}(1,t^{-1},\ldots ,t^{-1})\supset {\mathbf {M}}_{\mathbf {O}}$. Hence
$\operatorname {diag}(1,t,\ldots ,t){\mathbf {M}}_{\mathbf {O}}\operatorname {diag}(1,t^{-1},\ldots ,t^{-1})\supset {\mathbf {M}}_{\mathbf {O}}$. Hence ![]() $\xi _*$ acts on the equivariant category
$\xi _*$ acts on the equivariant category ![]() $D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ (by restricting equivariance from
$D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ (by restricting equivariance from ![]() $\operatorname {diag}(1,t,\ldots ,t){\mathbf {M}}_{\mathbf {O}}\operatorname {diag}(1,t^{-1},\ldots ,t^{-1})$ to
$\operatorname {diag}(1,t,\ldots ,t){\mathbf {M}}_{\mathbf {O}}\operatorname {diag}(1,t^{-1},\ldots ,t^{-1})$ to ![]() ${\mathbf {M}}_{\mathbf {O}}$). Clearly,
${\mathbf {M}}_{\mathbf {O}}$). Clearly, ![]() $\xi _*$ acts on the equivariant category
$\xi _*$ acts on the equivariant category ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ as well. Recall that
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ as well. Recall that ![]() $\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ denotes the functor of restriction of equivariance under
$\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ denotes the functor of restriction of equivariance under ![]() $\operatorname{GL}(N-1,{\mathbf {O}})\hookrightarrow {\mathbf {M}}_{\mathbf {O}}$. We denote by
$\operatorname{GL}(N-1,{\mathbf {O}})\hookrightarrow {\mathbf {M}}_{\mathbf {O}}$. We denote by ![]() $\operatorname {Av}^{{\mathbf {M}}_{\mathbf {O}}}_{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})\to D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ the corresponding right adjoint
$\operatorname {Av}^{{\mathbf {M}}_{\mathbf {O}}}_{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})\to D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ the corresponding right adjoint ![]() $*$-averaging functor.
$*$-averaging functor.
Lemma 4.4.1 (a) Given ![]() ${\mathcal {F}}\in D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$, for
${\mathcal {F}}\in D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$, for ![]() $n\gg 0$ the canonical morphism
$n\gg 0$ the canonical morphism ![]() $\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}$
$\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}$ ![]() $\operatorname {Av}^{{\mathbf {M}}_{\mathbf {O}}}_{\operatorname{GL}(N-1,{\mathbf {O}})}\xi ^n_*{\mathcal {F}}\to \xi ^n_*{\mathcal {F}}$ is an isomorphism.
$\operatorname {Av}^{{\mathbf {M}}_{\mathbf {O}}}_{\operatorname{GL}(N-1,{\mathbf {O}})}\xi ^n_*{\mathcal {F}}\to \xi ^n_*{\mathcal {F}}$ is an isomorphism.
(b) ![]() $\xi _*$ is an auto-equivalence of
$\xi _*$ is an auto-equivalence of ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$, and hence the natural functor from
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$, and hence the natural functor from ![]() $D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ to
$D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ to ![]() $\operatorname {colim}_{\xi _*}D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ is an equivalence.
$\operatorname {colim}_{\xi _*}D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ is an equivalence.
(c) The restriction of equivariance functor ![]() $\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ induces the same-named equivalence of the colimits
$\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})\to D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ induces the same-named equivalence of the colimits ![]() $\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon \operatorname {colim}_{\xi _*}D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})\to \operatorname {colim}_{\xi _*}D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})\cong D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$.
$\operatorname {Res}_{{\mathbf {M}}_{\mathbf {O}}}^{\operatorname{GL}(N-1,{\mathbf {O}})}\colon \operatorname {colim}_{\xi _*}D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})\to \operatorname {colim}_{\xi _*}D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})\cong D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$.
Proof. It suffices to prove (a) for an irreducible perverse ![]() ${\mathcal {F}}\in D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$. This in turn follows from the fact that, for any
${\mathcal {F}}\in D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$. This in turn follows from the fact that, for any ![]() $\operatorname{GL}(N-1,{\mathbf {O}})$-orbit
$\operatorname{GL}(N-1,{\mathbf {O}})$-orbit ![]() ${\mathbb {O}}\subset {\mathbf {Gr}}$ and
${\mathbb {O}}\subset {\mathbf {Gr}}$ and ![]() $n\gg 0$, the shift
$n\gg 0$, the shift ![]() $\xi ^{-n}{\mathbb {O}}$ becomes
$\xi ^{-n}{\mathbb {O}}$ becomes ![]() ${\mathbf {M}}_{\mathbf {O}}$-invariant. Indeed,
${\mathbf {M}}_{\mathbf {O}}$-invariant. Indeed, ![]() ${\mathbf {M}}_{\mathbf {O}}$ is generated by its radical
${\mathbf {M}}_{\mathbf {O}}$ is generated by its radical ![]() ${\mathbf {U}}_{\mathbf {O}}$ and
${\mathbf {U}}_{\mathbf {O}}$ and ![]() $\operatorname{GL}(N-1,{\mathbf {O}})$. As
$\operatorname{GL}(N-1,{\mathbf {O}})$. As ![]() $n$ grows,
$n$ grows, ![]() ${\mathbf {U}}_{\mathbf {O}}^{(n)}:=\operatorname {diag}(1,t^{-n},\ldots ,t^{-n}){\mathbf {U}}_{\mathbf {O}}\operatorname {diag}(1,t^n,\ldots ,t^n)$ forms a system of shrinking subgroups of
${\mathbf {U}}_{\mathbf {O}}^{(n)}:=\operatorname {diag}(1,t^{-n},\ldots ,t^{-n}){\mathbf {U}}_{\mathbf {O}}\operatorname {diag}(1,t^n,\ldots ,t^n)$ forms a system of shrinking subgroups of ![]() ${\mathbf {U}}_{\mathbf {O}}$, and we take
${\mathbf {U}}_{\mathbf {O}}$, and we take ![]() $n$ big enough so that the action of
$n$ big enough so that the action of ![]() ${\mathbf {U}}_{\mathbf {O}}^{(n)}$ on
${\mathbf {U}}_{\mathbf {O}}^{(n)}$ on ![]() ${\mathbb {O}}$ is trivial (recall that the action of
${\mathbb {O}}$ is trivial (recall that the action of ![]() ${\mathbf {U}}_{\mathbf {O}}$ on any Schubert subvariety of
${\mathbf {U}}_{\mathbf {O}}$ on any Schubert subvariety of ![]() ${\mathbf {Gr}}$ factors through a finite-dimensional quotient group).
${\mathbf {Gr}}$ factors through a finite-dimensional quotient group).
(b) is evident, and (c) follows from (a) and (b).
On the coherent side we consider an endofunctor ![]() $\eta$ of
$\eta$ of ![]() $D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet )$ obtained by tensoring with the polynomial representation
$D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet )$ obtained by tensoring with the polynomial representation ![]() $\det (\bar {V}\!_1)$ of
$\det (\bar {V}\!_1)$ of ![]() $\operatorname{GL}(\bar {V}\!_1)$. The full embedding
$\operatorname{GL}(\bar {V}\!_1)$. The full embedding ![]() $D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet )\hookrightarrow D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )$ gives rise to an equivalence of colimits
$D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet )\hookrightarrow D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )$ gives rise to an equivalence of colimits ![]() $\operatorname {colim}_\eta D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} \operatorname {colim}_\eta D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )\cong D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )$.
$\operatorname {colim}_\eta D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} \operatorname {colim}_\eta D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )\cong D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet )$.
Composing the inverse of ![]() $\Phi$ with
$\Phi$ with ![]() $\Phi '$ (in the notation of § 4.3), we obtain an equivalence
$\Phi '$ (in the notation of § 4.3), we obtain an equivalence ![]() $\bar {\Phi }{}'\colon D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$. According to Lemma 4.2.2, the equivalence
$\bar {\Phi }{}'\colon D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$. According to Lemma 4.2.2, the equivalence ![]() $\bar {\Phi }{}'\colon D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ intertwines the endofunctors
$\bar {\Phi }{}'\colon D_{\operatorname{perf}}^{\bar {G}_{\bar 0},\geq 0}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{{\mathbf {M}}_{\mathbf {O}}}({\mathbf {Gr}})$ intertwines the endofunctors ![]() $\eta$ and
$\eta$ and ![]() $\xi _*$, and hence induces the desired equivalence
$\xi _*$, and hence induces the desired equivalence ![]() $\bar {\Phi }\colon D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ between the colimits. Theorem 4.1.1 is proved.
$\bar {\Phi }\colon D_{\operatorname{perf}}^{\bar {G}_{\bar 0}}(\bar {\mathfrak {G}}{}^\bullet ){\buildrel \sim \over \longrightarrow} D_{\operatorname{GL}(N-1,{\mathbf {O}})}({\mathbf {Gr}})$ between the colimits. Theorem 4.1.1 is proved.
5. Loop rotation and quantization
5.1 Graded differential operators and convolutions
We have ![]() $H^\bullet _{{\mathbb {G}}_m}({\operatorname {pt}})={\mathbb {C}}[\hbar ]$. We consider the algebra
$H^\bullet _{{\mathbb {G}}_m}({\operatorname {pt}})={\mathbb {C}}[\hbar ]$. We consider the algebra ![]() ${\mathfrak {D}}$ of ‘graded differential operators’ on
${\mathfrak {D}}$ of ‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_2,V_1)$: a
${\operatorname{Hom}}(V_2,V_1)$: a ![]() ${\mathbb {C}}[\hbar ]$-algebra generated by
${\mathbb {C}}[\hbar ]$-algebra generated by ![]() ${\operatorname{Hom}}(V_2,V_1)$ and
${\operatorname{Hom}}(V_2,V_1)$ and ![]() ${\operatorname{Hom}}(V_1,V_2)$ with relations
${\operatorname{Hom}}(V_1,V_2)$ with relations ![]() $[h,h']=[f,f']=0$,
$[h,h']=[f,f']=0$, ![]() $[h,f]=\langle h,f\rangle \hbar$ for
$[h,f]=\langle h,f\rangle \hbar$ for ![]() $h,h'\in {\operatorname{Hom}}(V_2,V_1)$,
$h,h'\in {\operatorname{Hom}}(V_2,V_1)$, ![]() $f,f'\in {\operatorname{Hom}}(V_1,V_2)$. It is equipped with the grading
$f,f'\in {\operatorname{Hom}}(V_1,V_2)$. It is equipped with the grading ![]() $\deg f=\deg h=1$,
$\deg f=\deg h=1$, ![]() $\deg \hbar =2$. We denote by
$\deg \hbar =2$. We denote by ![]() ${\mathfrak {D}}_{1,1}^\bullet$ this graded algebra viewed as a dg-algebra with trivial differential. We will also need two more versions of
${\mathfrak {D}}_{1,1}^\bullet$ this graded algebra viewed as a dg-algebra with trivial differential. We will also need two more versions of ![]() ${\mathfrak {D}}_{1,1}^\bullet$ differing by the gradings of generators: in
${\mathfrak {D}}_{1,1}^\bullet$ differing by the gradings of generators: in ![]() ${\mathfrak {D}}_{0,2}^\bullet$ we set
${\mathfrak {D}}_{0,2}^\bullet$ we set ![]() $\deg f=0$ and
$\deg f=0$ and ![]() $\deg h=2$, while in
$\deg h=2$, while in ![]() ${\mathfrak {D}}_{2,0}^\bullet$ we set
${\mathfrak {D}}_{2,0}^\bullet$ we set ![]() $\deg f=2$ and
$\deg f=2$ and ![]() $\deg h=0$.
$\deg h=0$.
Recall the setup and notation of § 3.4. So we have another copy ![]() $V'_1$ of
$V'_1$ of ![]() $V_1$, we rebaptize the algebra
$V_1$, we rebaptize the algebra ![]() ${\mathfrak {D}}$ of ‘graded differential operators’ on
${\mathfrak {D}}$ of ‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_2,V_1)$ as
${\operatorname{Hom}}(V_2,V_1)$ as ![]() ${\mathfrak {D}}_{21}$, and along with it we consider
${\mathfrak {D}}_{21}$, and along with it we consider ![]() ${\mathfrak {D}}_{21'}$ (‘graded differential operators’ on
${\mathfrak {D}}_{21'}$ (‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_2,V'_1)$) and
${\operatorname{Hom}}(V_2,V'_1)$) and ![]() ${\mathfrak {D}}_{1'1}$ (‘graded differential operators’ on
${\mathfrak {D}}_{1'1}$ (‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V'_1,V_1)$). Note that
${\operatorname{Hom}}(V'_1,V_1)$). Note that ![]() ${\mathfrak {D}}_{21}\cong {\mathfrak {D}}_{12}$ (‘graded differential operators’ on
${\mathfrak {D}}_{21}\cong {\mathfrak {D}}_{12}$ (‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_1,V_2)$), and similarly
${\operatorname{Hom}}(V_1,V_2)$), and similarly ![]() ${\mathfrak {D}}_{21'}\cong {\mathfrak {D}}_{1'2}$, and
${\mathfrak {D}}_{21'}\cong {\mathfrak {D}}_{1'2}$, and ![]() ${\mathfrak {D}}_{1'1}\cong {\mathfrak {D}}_{11'}$.
${\mathfrak {D}}_{1'1}\cong {\mathfrak {D}}_{11'}$.
We have morphisms
 \begin{gather*} {\mathsf{m}}^A\colon{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_1,V'_1)\to{{\operatorname{Hom}}}(V_1,V_2),\quad (A',A'')\mapsto A'A'',\\ {\mathsf{m}}^B\colon{{\operatorname{Hom}}}(V'_1,V_1)\times{{\operatorname{Hom}}}(V_2,V'_1)\to{{\operatorname{Hom}}}(V_2,V_1),\quad (B'',B')\mapsto B''B'. \end{gather*}
\begin{gather*} {\mathsf{m}}^A\colon{{\operatorname{Hom}}}(V'_1,V_2)\times{{\operatorname{Hom}}}(V_1,V'_1)\to{{\operatorname{Hom}}}(V_1,V_2),\quad (A',A'')\mapsto A'A'',\\ {\mathsf{m}}^B\colon{{\operatorname{Hom}}}(V'_1,V_1)\times{{\operatorname{Hom}}}(V_2,V'_1)\to{{\operatorname{Hom}}}(V_2,V_1),\quad (B'',B')\mapsto B''B'. \end{gather*}They give rise to the functors
 \begin{gather*} D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}_{1'2})\times D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V'_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{11'})\to D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}_{12}),\\ ({\mathcal{M}}_{1'2},{\mathcal{M}}_{11'})\mapsto\big({\mathsf{m}}^A_*({\mathcal{M}}_{1'2}\boxtimes{\mathcal{M}}_{11'})\big)^{{{\operatorname{GL}}}(V'_1)}, \end{gather*}
\begin{gather*} D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}_{1'2})\times D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V'_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{11'})\to D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}_{12}),\\ ({\mathcal{M}}_{1'2},{\mathcal{M}}_{11'})\mapsto\big({\mathsf{m}}^A_*({\mathcal{M}}_{1'2}\boxtimes{\mathcal{M}}_{11'})\big)^{{{\operatorname{GL}}}(V'_1)}, \end{gather*} \begin{gather*} D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{1'1})\times D^{{{\operatorname{GL}}}(V_2)\times{{\operatorname{GL}}}(V'_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{21'})\to D^{{{\operatorname{GL}}}(V_2)\times{{\operatorname{GL}}}(V_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{21}),\\ ({\mathcal{M}}_{1'1},{\mathcal{M}}_{21'})\mapsto\big({\mathsf{m}}^B_*({\mathcal{M}}_{1'1}\boxtimes{\mathcal{M}}_{21'})\big)^{{{\operatorname{GL}}}(V'_1)} \end{gather*}
\begin{gather*} D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{1'1})\times D^{{{\operatorname{GL}}}(V_2)\times{{\operatorname{GL}}}(V'_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{21'})\to D^{{{\operatorname{GL}}}(V_2)\times{{\operatorname{GL}}}(V_1)}_{{\operatorname{perf}}}({\mathfrak{D}}_{21}),\\ ({\mathcal{M}}_{1'1},{\mathcal{M}}_{21'})\mapsto\big({\mathsf{m}}^B_*({\mathcal{M}}_{1'1}\boxtimes{\mathcal{M}}_{21'})\big)^{{{\operatorname{GL}}}(V'_1)} \end{gather*}
(here ![]() ${\mathsf {m}}^A_*$ and
${\mathsf {m}}^A_*$ and ![]() ${\mathsf {m}}^B_*$ stand for the direct images in the category of
${\mathsf {m}}^B_*$ stand for the direct images in the category of ![]() ${\mathfrak {D}}$-modules).
${\mathfrak {D}}$-modules).
We will actually need the corresponding functors on the categories of dg-modules
The multiplicative group ![]() ${\mathbb {G}}_m$ acts on
${\mathbb {G}}_m$ acts on ![]() ${\mathbf {Gr}}\times {\mathbf {V}}$ as loop rotations. The goal of this section is the following theorem.
${\mathbf {Gr}}\times {\mathbf {V}}$ as loop rotations. The goal of this section is the following theorem.
Theorem 5.1.1 There exist monoidal equivalences of triangulated categories

(the vertical and middle row equivalences are not monoidal). The horizontal equivalences commute with the actions of the monoidal spherical Hecke category ![]() ${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ by left and right convolutions.
${\operatorname {Perv}}_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})\cong {\operatorname {Rep}}(\operatorname{GL}_N)$ by left and right convolutions.
The proof will be given in § 5.3.
5.2 Construction of equivalences
We set ![]() ${\mathfrak {E}}_\hbar ^\bullet :={\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {G}}_m}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ (a dg-algebra with trivial differential). Since it is an Ext-algebra in the de-equivariantized category, it is automatically equipped with an action of
${\mathfrak {E}}_\hbar ^\bullet :={\operatorname{Ext}}^\bullet _{D^{{\operatorname{deeq}}}_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {G}}_m}({\mathbf {Gr}}\times {\mathbf {V}})}(E_0,E_0)$ (a dg-algebra with trivial differential). Since it is an Ext-algebra in the de-equivariantized category, it is automatically equipped with an action of ![]() $\operatorname{GL}_N\times \operatorname{GL}_N=\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)=G_{\bar 0}$, and we can consider the corresponding triangulated category
$\operatorname{GL}_N\times \operatorname{GL}_N=\operatorname{GL}(V_1)\times \operatorname{GL}(V_2)=G_{\bar 0}$, and we can consider the corresponding triangulated category ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}_\hbar ^\bullet )$. Similarly to Lemma 3.9.2, there is a canonical equivalence
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}_\hbar ^\bullet )$. Similarly to Lemma 3.9.2, there is a canonical equivalence ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}_\hbar ^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {G}}_m}({\mathbf {Gr}}\times {\mathbf {V}})$. It remains to construct an isomorphism
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {E}}_\hbar ^\bullet ){\buildrel \sim \over \longrightarrow} D_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {G}}_m}({\mathbf {Gr}}\times {\mathbf {V}})$. It remains to construct an isomorphism ![]() $\phi _\hbar ^\bullet \colon {\mathfrak {D}}_{1,1}^\bullet {\buildrel \sim \over \longrightarrow} {\mathfrak {E}}_\hbar ^\bullet$.
$\phi _\hbar ^\bullet \colon {\mathfrak {D}}_{1,1}^\bullet {\buildrel \sim \over \longrightarrow} {\mathfrak {E}}_\hbar ^\bullet$.
Note that ![]() ${\mathfrak {E}}_\hbar ^\bullet$ is a
${\mathfrak {E}}_\hbar ^\bullet$ is a ![]() ${\mathbb {C}}[\hbar ]$-algebra, and
${\mathbb {C}}[\hbar ]$-algebra, and ![]() ${\mathfrak {E}}_\hbar ^\bullet /(\hbar =0)= {\mathfrak {E}}^\bullet ={\mathfrak {G}}_{1,1}^\bullet ={\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$, so that
${\mathfrak {E}}_\hbar ^\bullet /(\hbar =0)= {\mathfrak {E}}^\bullet ={\mathfrak {G}}_{1,1}^\bullet ={\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$, so that ![]() ${\mathfrak {E}}^\bullet$ acquires a Poisson bracket from this deformation. We claim that this Poisson bracket arises from the canonical symplectic form on
${\mathfrak {E}}^\bullet$ acquires a Poisson bracket from this deformation. We claim that this Poisson bracket arises from the canonical symplectic form on ![]() ${\mathfrak {g}}_{\bar 1}^*$. Indeed, the isomorphism
${\mathfrak {g}}_{\bar 1}^*$. Indeed, the isomorphism ![]() $\phi ^*$ (see the proof of Lemma 3.11.1) over
$\phi ^*$ (see the proof of Lemma 3.11.1) over ![]() ${\operatorname{Isom}}(V_2,V_1)\times {\operatorname{Hom}}(V_1,V_2)$ and
${\operatorname{Isom}}(V_2,V_1)\times {\operatorname{Hom}}(V_1,V_2)$ and ![]() ${\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Isom}}(V_1,V_2)$ is Poisson. Here the Poisson structure on these open subsets arises from the deformations
${\operatorname{Hom}}(V_2,V_1)\times {\operatorname{Isom}}(V_1,V_2)$ is Poisson. Here the Poisson structure on these open subsets arises from the deformations ![]() ${\mathfrak {A}}_\hbar ^\bullet ,{\mathfrak {B}}_\hbar ^\bullet$ which in turn arise from the loop-rotation-equivariant Satake category
${\mathfrak {A}}_\hbar ^\bullet ,{\mathfrak {B}}_\hbar ^\bullet$ which in turn arise from the loop-rotation-equivariant Satake category ![]() $D_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {G}}_m}({\mathbf {Gr}})$. The corresponding Poisson brackets are the standard ones on the cotangent bundles
$D_{{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {G}}_m}({\mathbf {Gr}})$. The corresponding Poisson brackets are the standard ones on the cotangent bundles ![]() $T^*{\operatorname{Isom}}(V_2,V_1),T^*{\operatorname{Isom}}(V_1,V_2)$, as follows from [Reference Bezrukavnikov and FinkelbergBF08, Theorem 5].
$T^*{\operatorname{Isom}}(V_2,V_1),T^*{\operatorname{Isom}}(V_1,V_2)$, as follows from [Reference Bezrukavnikov and FinkelbergBF08, Theorem 5].
Now ![]() ${\mathfrak {D}}_{1,1}^\bullet$ is a unique graded
${\mathfrak {D}}_{1,1}^\bullet$ is a unique graded ![]() ${\mathbb {C}}[\hbar ]$-algebra with
${\mathbb {C}}[\hbar ]$-algebra with ![]() ${\mathfrak {D}}_{1,1}^\bullet /(\hbar =0)= {\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$ such that the corresponding Poisson bracket on
${\mathfrak {D}}_{1,1}^\bullet /(\hbar =0)= {\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$ such that the corresponding Poisson bracket on ![]() ${\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$ is the standard one. Thus
${\operatorname{Sym}}({\mathfrak {g}}_{\bar 1}[-1])$ is the standard one. Thus ![]() $\phi _\hbar ^\bullet$ and
$\phi _\hbar ^\bullet$ and ![]() $\Phi ^{1,1}_\hbar$ are constructed.
$\Phi ^{1,1}_\hbar$ are constructed.
5.3 Restriction to  ${\mathbf {Gr}}\times {\mathbf {V}}_0$ with loop rotation
${\mathbf {Gr}}\times {\mathbf {V}}_0$ with loop rotation
Similarly to § 3.12, our goal in this section is a description in terms of equivalence of Theorem 5.1.1 of the endofunctors ![]() $\bar \jmath _{0*}\bar \jmath {}_0^!$,
$\bar \jmath _{0*}\bar \jmath {}_0^!$, ![]() $\jmath _{0*}\jmath _0^!\colon D_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})$. To this end we will need the algebra
$\jmath _{0*}\jmath _0^!\colon D_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})\to D_{!*{\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}\times {\mathbf {V}})$. To this end we will need the algebra ![]() ${\mathfrak {H}}$ of ‘graded differential operators’ on
${\mathfrak {H}}$ of ‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_1,V_2)\oplus {\operatorname{Hom}}(V_1,V'_1)\oplus {\operatorname{Hom}}(V'_1,V_2)$ defined similarly to
${\operatorname{Hom}}(V_1,V_2)\oplus {\operatorname{Hom}}(V_1,V'_1)\oplus {\operatorname{Hom}}(V'_1,V_2)$ defined similarly to ![]() ${\mathfrak {D}}$ of § 5.1. It is equipped with the grading where the generators from
${\mathfrak {D}}$ of § 5.1. It is equipped with the grading where the generators from ![]() ${\operatorname{Hom}}(V_2,V_1)$,
${\operatorname{Hom}}(V_2,V_1)$, ![]() ${\operatorname{Hom}}(V_1,V_2)$,
${\operatorname{Hom}}(V_1,V_2)$, ![]() ${\operatorname{Hom}}(V'_1,V_2)$ and
${\operatorname{Hom}}(V'_1,V_2)$ and ![]() ${\operatorname{Hom}}(V_2,V'_1)$ have degree 1, while the generators from
${\operatorname{Hom}}(V_2,V'_1)$ have degree 1, while the generators from ![]() ${\operatorname{Hom}}(V_1,V'_1)$ and
${\operatorname{Hom}}(V_1,V'_1)$ and ![]() ${\operatorname{Hom}}(V'_1,V_1)$ have degrees 2 and 0 respectively, and
${\operatorname{Hom}}(V'_1,V_1)$ have degrees 2 and 0 respectively, and ![]() $\deg \hbar =2$. We denote by
$\deg \hbar =2$. We denote by ![]() ${\mathfrak {H}}^\bullet$ this graded algebra viewed as a dg-algebra with trivial differential. If we denote the similar dg-algebras of ‘graded differential operators’ on
${\mathfrak {H}}^\bullet$ this graded algebra viewed as a dg-algebra with trivial differential. If we denote the similar dg-algebras of ‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_1,V_2)$,
${\operatorname{Hom}}(V_1,V_2)$, ![]() ${\operatorname{Hom}}(V_1,V'_1)$ and
${\operatorname{Hom}}(V_1,V'_1)$ and ![]() ${\operatorname{Hom}}(V'_1,V_2)$ by
${\operatorname{Hom}}(V'_1,V_2)$ by ![]() ${\mathfrak {D}}^\bullet _{12}$,
${\mathfrak {D}}^\bullet _{12}$, ![]() ${\mathfrak {D}}^\bullet _{11'}$ and
${\mathfrak {D}}^\bullet _{11'}$ and ![]() ${\mathfrak {D}}^\bullet _{1'2}$, then
${\mathfrak {D}}^\bullet _{1'2}$, then ![]() ${\mathfrak {H}}^\bullet ={\mathfrak {D}}^\bullet _{12}\,{\otimes}\, {\mathfrak {D}}^\bullet _{11'}\,{\otimes}\, {\mathfrak {D}}^\bullet _{1'2}$. Since the canonical line bundle on an affine space carries a canonical flat connection, the algebras
${\mathfrak {H}}^\bullet ={\mathfrak {D}}^\bullet _{12}\,{\otimes}\, {\mathfrak {D}}^\bullet _{11'}\,{\otimes}\, {\mathfrak {D}}^\bullet _{1'2}$. Since the canonical line bundle on an affine space carries a canonical flat connection, the algebras ![]() ${\mathfrak {D}}^{\bullet} _{ij}$ admit
${\mathfrak {D}}^{\bullet} _{ij}$ admit ![]() $(\operatorname{GL}(V_i)\times \operatorname{GL}(V_j))$-equivariant anti-involutions. Thus we can identify
$(\operatorname{GL}(V_i)\times \operatorname{GL}(V_j))$-equivariant anti-involutions. Thus we can identify ![]() ${\mathfrak {H}}^\bullet {\buildrel \sim \over \longrightarrow} {\mathfrak {D}}^\bullet _{12}\,{\otimes}\, ({\mathfrak {D}}^\bullet _{11'}\,{\otimes}\, {\mathfrak {D}}^\bullet _{1'2})^{{\rm op}}$.
${\mathfrak {H}}^\bullet {\buildrel \sim \over \longrightarrow} {\mathfrak {D}}^\bullet _{12}\,{\otimes}\, ({\mathfrak {D}}^\bullet _{11'}\,{\otimes}\, {\mathfrak {D}}^\bullet _{1'2})^{{\rm op}}$.
The algebra ![]() ${\mathfrak {H}}^\bullet$ has a cyclic holonomic left dg-module
${\mathfrak {H}}^\bullet$ has a cyclic holonomic left dg-module ![]() ${\mathfrak {Q}}^\bullet$ of ‘delta-functions along the subvariety cut out by the equation
${\mathfrak {Q}}^\bullet$ of ‘delta-functions along the subvariety cut out by the equation ![]() $A=A'A''$’; see (3.4.1). We also consider the
$A=A'A''$’; see (3.4.1). We also consider the ![]() $\operatorname{GL}(V_1)\times \operatorname{GL}(V_1')$-equivariant cyclic
$\operatorname{GL}(V_1)\times \operatorname{GL}(V_1')$-equivariant cyclic ![]() ${\mathfrak {D}}^{\bullet} _{11'}$-module
${\mathfrak {D}}^{\bullet} _{11'}$-module ![]() ${\mathfrak {D}}^{\bullet} _{11'0}$ corresponding to the
${\mathfrak {D}}^{\bullet} _{11'0}$ corresponding to the ![]() ${\mathfrak {D}} _{11'}:={\mathfrak {D}} _{{\operatorname{Hom}}(V_1,V_1')}$-module given by
${\mathfrak {D}} _{11'}:={\mathfrak {D}} _{{\operatorname{Hom}}(V_1,V_1')}$-module given by
We define the following endofunctors of ![]() $D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {D}}_{1,1}^\bullet )$:
$D^{G_{\bar 0}}_{\operatorname{perf}}({\mathfrak {D}}_{1,1}^\bullet )$:
 \begin{align*} D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet)&=D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{1'2})\ni M \mapsto p_*q^*M\\ &:= \big({\mathfrak{Q}}^\bullet\,{\otimes}_{{\mathfrak{D}}^\bullet_{11'}{\otimes}{\mathfrak{D}}^\bullet_{1'2}}({\mathfrak{D}}^\bullet_{11'}\,{\otimes}\, M)\big)^{{{\operatorname{GL}}}(V'_1)}\in D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{12})=D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet), \end{align*}
\begin{align*} D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet)&=D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{1'2})\ni M \mapsto p_*q^*M\\ &:= \big({\mathfrak{Q}}^\bullet\,{\otimes}_{{\mathfrak{D}}^\bullet_{11'}{\otimes}{\mathfrak{D}}^\bullet_{1'2}}({\mathfrak{D}}^\bullet_{11'}\,{\otimes}\, M)\big)^{{{\operatorname{GL}}}(V'_1)}\in D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{12})=D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet), \end{align*} \begin{align*} D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet)&=D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{1'2})\ni M \mapsto p_{0*}q_0^*M\\ &:= \big({\mathfrak{Q}}^\bullet\,{\otimes}_{{\mathfrak{D}}^\bullet_{11'}{\otimes}{\mathfrak{D}}^\bullet_{1'2}}({\mathfrak{D}}^\bullet_{11'0}\,{\otimes}\, M)\big)^{{{\operatorname{GL}}}(V'_1)}\in D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{12})=D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet). \end{align*}
\begin{align*} D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet)&=D^{{{\operatorname{GL}}}(V'_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{1'2})\ni M \mapsto p_{0*}q_0^*M\\ &:= \big({\mathfrak{Q}}^\bullet\,{\otimes}_{{\mathfrak{D}}^\bullet_{11'}{\otimes}{\mathfrak{D}}^\bullet_{1'2}}({\mathfrak{D}}^\bullet_{11'0}\,{\otimes}\, M)\big)^{{{\operatorname{GL}}}(V'_1)}\in D^{{{\operatorname{GL}}}(V_1)\times{{\operatorname{GL}}}(V_2)}_{{\operatorname{perf}}}({\mathfrak{D}}^\bullet_{12})=D^{G_{\bar0}}_{{\operatorname{perf}}}({\mathfrak{D}}_{1,1}^\bullet). \end{align*}Then, similarly to Proposition 3.12.1, one proves the following proposition.
Proposition 5.3.1 (a) There is an isomorphism of functors
(b) There is an isomorphism of functors
Now, using Proposition 5.3.1 in place of Proposition 3.12.1, one checks the monoidal properties of ![]() $\Phi ^{2,0}_\hbar$ and
$\Phi ^{2,0}_\hbar$ and ![]() $\Phi ^{0,2}_\hbar$ similarly to the monoidal properties of
$\Phi ^{0,2}_\hbar$ similarly to the monoidal properties of ![]() $\Phi ^{2,0}$ and
$\Phi ^{2,0}$ and ![]() $\Phi ^{0,2}$ checked in §§ 3.14 and 3.15, respectively. This completes the proof of Theorem 5.1.1.
$\Phi ^{0,2}$ checked in §§ 3.14 and 3.15, respectively. This completes the proof of Theorem 5.1.1.
5.4  ${\mathfrak {D}}$-modules and
${\mathfrak {D}}$-modules and  $D_{\operatorname{GL}(N-1,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$
$D_{\operatorname{GL}(N-1,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$
Similarly to § 5.1, we consider the dg-algebra (with trivial differential) ![]() $\bar {\mathfrak {D}}{}^\bullet$ of ‘graded differential operators’ on
$\bar {\mathfrak {D}}{}^\bullet$ of ‘graded differential operators’ on ![]() ${\operatorname{Hom}}(V_2,\bar {V}\!_1$). Then, similarly to Theorem 4.1.1, one proves the following theorem.
${\operatorname{Hom}}(V_2,\bar {V}\!_1$). Then, similarly to Theorem 4.1.1, one proves the following theorem.
Theorem 5.4.1 There exists an equivalence of triangulated categories ![]() $\bar \Phi {}_\hbar \colon D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {D}}{}^\bullet ){\buildrel \sim \over \longrightarrow}s D_{\bar {\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$ commuting with the left convolution action of the monoidal spherical Hecke category
$\bar \Phi {}_\hbar \colon D^{\bar {G}_{\bar 0}}_{\operatorname{perf}}(\bar {\mathfrak {D}}{}^\bullet ){\buildrel \sim \over \longrightarrow}s D_{\bar {\mathbf {G}}_{\mathbf {O}}\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}})$ commuting with the left convolution action of the monoidal spherical Hecke category ![]() ${\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}_{N-1})\cong {\operatorname {Rep}}(\operatorname{GL}_{N-1})$ and with the right convolution action of the monoidal spherical Hecke category
${\operatorname {Perv}}_{\operatorname{GL}(N-1,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}_{N-1})\cong {\operatorname {Rep}}(\operatorname{GL}_{N-1})$ and with the right convolution action of the monoidal spherical Hecke category ![]() ${\operatorname {Perv}}_{\operatorname{GL}(N,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}_N)\cong {\operatorname {Rep}}(\operatorname{GL}_N)$.
${\operatorname {Perv}}_{\operatorname{GL}(N,{\mathbf {O}})\rtimes {\mathbb {C}}^\times }({\mathbf {Gr}}_N)\cong {\operatorname {Rep}}(\operatorname{GL}_N)$.
Acknowledgements
We are grateful to R. Bezrukavnikov, D. Ben-Zvi, I. Entova-Aizenbud, P. Etingof, B. Feigin, D. Gaiotto, D. Gaitsgory, J. Hilburn, D. Leites, C. Mautner, Y. Sakellaridis, V. Serganova, A. Venkatesh and P. Yoo for very useful discussions. A.B. was partially supported by NSERC. M.F. was partially funded within the framework of the HSE University Basic Research Program and the Russian Academic Excellence Project ‘5-100’. The work of V.G. was supported in part by an NSF award DMS-1602111.