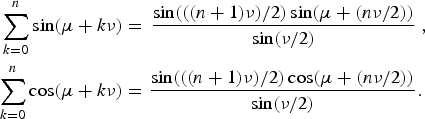I. INTRODUCTION
A piezoelectric actuator has ideal properties for RF-MEMS switches and variable capacitors that require large displacement with low voltage and low power. So far, several groups are pursuing this approach [Reference Lee, Park and Park1–Reference Ikehashi, Ogawa, Yamazaki and Ohguro5]. The use of a piezoelectric actuator, however, requires special care in controlling actuator bending, since the multilayered beam can easily bend owing to its residual stress. The bending can be controlled, in principle, by optimizing the thickness and/or stress of layers that constitute the beam. It is, however, not easy to carry out this process, because the layer thickness must be optimized to maximize piezoelectric displacement. Tuning the stress values is also not easy because they are affected by the process temperatures of succeeding process steps.
In view of this, we have proposed the lithographical bending control (LBC) method [Reference Ikehashi, Ogawa, Yamazaki and Ohguro5], which uses a lithographical pattern formed on top of the actuator to control the bending. The use of lithographical degrees of freedom enables one to control the bending without fine process tuning. This paper aims to supplement our previous paper by presenting a detailed theoretical framework of LBC. The theoretical model is then compared with measurements using a test structure designed for this purpose.
This paper is organized as follows: In section II, a practical model describing the bending of a multilayered beam and piezoelectric displacement is reported. The theoretical model of LBC is explained in section III. A unique actuator structure is introduced in section IV to verify the theoretical model. The measurement and discussion are also presented in section IV.
II. BENDING AND DISPLACEMENT OF A PIEZOELECTRIC ACTUATOR
A) Bending of a multilayered beam
Understanding the behavior of a multilayered beam is indispensable in designing piezoelectric actuators. In this section, we briefly summarize the key features.
The theoretical model of a piezoelectric actuator is presented by several authors [Reference Klaasse, Puers and Tilmans3], [Reference Smits and Choi6–Reference Weinberg9]. Smits have derived the static and dynamic behavior of bimorphs [Reference Smits and Choi6]. DeVoe has extended the approach to n-layer multimorphs [Reference DeVoe and Pisano7]. DeVoe's formulation, however, requires inversion of an n × n matrix. More practical models are presented by Klaasse et al. [Reference Klaasse, Puers and Tilmans3], Tilmans [Reference Tilmans8] and Weinberg [Reference Weinberg9], which are essentially identical. The formulation presented below is based on Weinberg's approach, but is further extended to a case in which the residual stresses of all layers are taken into account.
To start with, let us consider a multilayer cantilever beam of length L, width W and thickness T. The beam consists of n layers and is fixed at the left edge as shown in Fig. 1. The thickness, Young's modulus and residual stress of the ith layer are denoted as T i, E i and σi (i = 1, …n), respectively. For an isotropic beam of W ≫ T, Young’s modulus E i should be replaced by plate modulus E i/(1 − νi2), with νi being a Poisson's ratio of the ith layer [Reference DeVoe and Pisano7, Reference Weinberg9]. The t i's of Fig. 1 are related to T i via T i = t i − t i−1 and the total thickness is T = ∑i=1nT i. The stress at position z of the ith layer is given by:
where ρ is the radius of curvature and 
is the neutral axis. The second term represents the stress caused by bending. Note that ρ ≫ L holds for our beam. The internal axial force F and internal bending moment M can be written as
Fig. 1. Multilayered beam.
For a free cantilever, we have F = 0 and M = 0. By solving these equations, the unknown parameters ρ and 
can be determined. The resulting radius is:
where 
and 
(k = 0, 1, 2) are k-th moments defined by:
The beam deflection Z thus becomes:
The analytic expression (7) suggests that the bending can be controlled by tuning the residual stress of a specific layer. However, the stress value is often affected by a high-temperature annealing process. This implies that a number of process iterations are needed to optimize the bending.
B) Piezoelectric displacement
Next we will derive piezoelectric displacement. Suppose the jth layer is a piezoelectric material with the transverse piezoelectric coupling constant d 31. By applying a voltage difference V piezo to the piezoelectric layer, the stress σj changes as:
where
is a stress change caused by the piezoelectric effect. The change 
is positive for upward electric field and positive d 31. It should be noticed that in actual piezoelectric material, 
is non-linear with respect to the electric field. Especially, in the case of ferroelectric material, d 31 has non-trivial electric field dependence owing to the hysteresis effect. Note also that d 31 should be replaced by d 31(1 + νj) for an isotropic beam of W ≫ T.
The piezoelectric displacement is given by:
From equation (7), (9), (10), the explicit form of piezoelectric displacement can be written as:
As we can see, piezoelectric displacement is unaffected by the residual stresses of layers i ≠ j, since Z is a linear function of stresses. This expression thus coincides with those derived by Klaasse et al. [Reference Klaasse, Puers and Tilmans3] and Weinberg [Reference Weinberg9].
The above formulation can be extended to a case with external loads. The deformation of the beam in this case can be derived by solving the differential equation that represents the matching of the external loads to the internal bending moment [Reference Senturia10]. For example, if a vertical point load F ext is applied to the beam tip, the beam deflection changes as:
where
is the effective beam spring constant. Equation (12) can be used to calculate the contact force of the piezoelectric actuator, if we recall Newton's third law on action–reaction forces. Namely, the actuator force pushing the substrate at a certain V piezo is identical to the F ext that gives the same deflection at the same voltage.
III. LITHOGRAPHICAL BENDING CONTROL
This section reports a theoretical formulation of LBC that is not shown in our previous paper [Reference Ikehashi, Ogawa, Yamazaki and Ohguro5]. Before going into the details, we shall explain the concept of LBC. As shown in Fig. 2, a thin film is deposited and patterned on top of the beam, so that after the sacrificial layer etching, the portions with and without the top film become convex and concave shape, respectively. The beam of length L is divided into n concaves and convexes. If the ratio of the concave and convex portion is set to α: 1 – α, the bending Z can be controlled by the parameter α. In the following, we will derive beam deflection as a function of α and n. In doing this, we make two assumptions:
Fig. 2. Concept of LBC.
1) The concave and convex portions are represented by arcs with radii of ρ1 and ρ2, respectively, as in Fig. 3.
2) Each portion is jointed smoothly, i.e., the first derivatives are continuous at the arc joints.
From now on, we try to find the tip coordinate Ξn = (X n, Z n)T in the xz Cartesian coordinate system. As we shall see, the analytical expression of Ξn can be derived, thanks to the assumptions. As in Fig. 3, we denote the central angles of the concave and convex as θ1/n and θ2/n, respectively. Since the cantilever length is L, there exists a constraint:
Fig. 3. Model of the cantilever.
The angles θ1 and θ2 are related to the ratio α via θ1ρ1 = Lα and θ2ρ2 = L(1 − α). We also introduce angles Θi and Φi (i = 1, … , n) as in Fig. 4. The vectors Ai and Bi are the centers of arcs that constitute the beam. Because of the assumptions, the vector Bi − Ai is perpendicular to the beam tangent. We thus obtain:
Fig. 4. Definition of angles Θi and Φi (i = 1, … , n).
The coordinate of the cantilever tip can be written in terms of An+1 as
By solving the recurrence equations (15) and (16), the vector An+1 can be expressed as
where
Now, from Fig. 4, we can write down relationships between Θi and Φi as;
These recurrence equations can be solved to yield:
The analytic expression of the tip coordinate can be derived by inserting the above result in equation (18). Using the sum rules of trigonometric functions,Footnote 1 the result can be written as
where φ is defined by:
and
This is the analytic result. For practical purposes, it is useful to derive some approximate formulas.
Firstly, in the n → ∞ limit, the tip coordinate converges to a non-trivial value. Recalling the constraint of equation (14), the limit becomes:
At φ → 0, this converges to (L 0)T, as it should.
Secondly, we derive an expression when the radii ρ1 and ρ2 are much longer than the actuator length L. This is the case that holds for most MEMS actuators. The expression for this case is obtained by retaining the first order terms of θi's in equation (24). For later purposes, it is useful to recast the result in terms of the ratio α. The resulting bending Z n becomes:
where
is a term that survives at n → ∞. The expression of Z ∞ can also be derived by setting θi ≪ 1 in equation (26). In Fig. 5, we, show the α-dependence of Z n for some n's. As can be see Z n becomes linear for large n, and the bending can be changed from −L Reference Kawakubo, Nagano, Nishigaki and Itaya2/(2ρ2) to +L Reference Kawakubo, Nagano, Nishigaki and Itaya2/(2ρ1) by the parameter.
Fig. 5. Theoretical plot of Z n.
IV. FABRICATION AND MEASUREMENT OF AN LBC-APPLIED ACTUATOR
A) Actuator structure
To see the applicability of the above approach, we have fabricated a piezoelectric actuator to which LBC is applied. As a piezoelectric material, lead zirconate titanate (PZT) is used. The composition of the actuator is depicted in Fig. 6. The two Pt layers are used as actuation electrodes. The residual stresses of the top SiO2 film and Al are compressive and tensile, respectively. Thus, the portions with and without the top layer become convex and concave, respectively, after sacrificial layer removal. The actuator is fabricated in a surface micromachining process with a polysilicon sacrificial layer. Details of the process flow are reported in [Reference Ikehashi, Ohguro, Ogawa, Yamazaki, Kojima, Matsuo, Ishimaru and Ishiuchi4].
Fig. 6. Composition of the piezoelectric actuator.
The cantilever-type actuator presented in our previous paper [Reference Ikehashi, Ogawa, Yamazaki and Ohguro5] is not suited for verification of LBC, since the cantilever tip touches the substrate when the beam shape is in convex form. We have thus introduced a weakly-fixed-bridge (WFB) structure. The top view and corresponding xz-axis of the WFB structure are shown in Fig. 7. The actuator portion is fixed at both ends, but thanks to the flexures, the actuator can bend freely according to its internal stress. The flexures also serve as bias lines to the top/bottom actuation electrodes. Thus, the actuator curvature changes when a voltage is applied. The PZT layer shrinks in the lateral direction when the downward electric field is applied. Because of the thick Al layer, the displacement Z decreases by electric field application. We confirmed that the curvature change is identical to the cantilever case, which implies that the flexure spring constant is weak enough.
Fig. 7. Top view of the weakly-fixed-bridge (WFB) structure and definition of Z in the cross section.
B) Measurement and analysis of initial deflection
The dimension L shown in Fig. 7 is set to 150 µm and n = 19 for the L section. The interference microscope images for some values of α are shown in Figs. 8(a) and (b). The measured α-dependence of the initial displacement is plotted in Fig. 9. The radii are found to be ρ1 = 5.4 mm and ρ2 = 2.3 mm. As expected, the deflection Z increases monotonically with α. However, the naive theoretical model (the dotted line) does not fit well with the measurements. The discrepancy can be explained by assuming an offset in the stress distribution. This model is illustrated in Fig. 10. As shown in the figure, the non-zero stress exists only in the central portion of the top layer, and the stress is zero in the offset region of length Δ. The offset is caused by a stress relaxation at the edge. Over-etching of the top layer can also induce the offset. If the stress distribution is abrupt as in Fig. 10, the displacement becomes:
for 0 < α ≤ 1 − nΔ/L and
for 1 − nΔ/L ≤ α≤ 1. This model succeeds in explaining the tendency of the measured plot as shown in Fig. 9. The fitted offset value is Δ = 1.8 µm. The offset model may be improved by incorporating smooth stress distribution instead of the abrupt one. Note also that if the offset value is independent of n, which is plausible, the discrepancy between the measurement and the naive model of equation (27) becomes smaller for small n, since the offset is negligible for this case.
Fig. 8. Images of fabricated WFB structure taken by an interference microscope.
Fig. 9. Measured and theoretical initial deflection.
Fig. 10. Offset model.
C) Piezoelectric displacement
The measured piezoelectric displacement is shown in Fig. 11. As expected from the theoretical analysis, the displacement is nearly independent of α. The piezoelectric actuator of L = 150 µm enables 2.7 µm displacement at V piezo = 3 V. This actuator is used to realize the 3 V-operation RF-MEMS variable capacitor [Reference Ikehashi, Ogawa, Yamazaki and Ohguro5].
Fig. 11. Measured piezoelctric displacement.
D) Cancellation of temperature dependence
The essence of the present approach is in the use of the additional degrees of freedom α, brought about by the lithography. This implies that in case the bending can be controlled simply by stress tuning, the additional parameter α can be used for other purposes. For example, the parameter can be used to eliminate the dependence of Z with respect to temperature τ. This can be accomplished as in the band-gap reference circuit, which is a circuit generating temperature-independent reference voltage [Reference Kuijk11]. Namely, in our case, the τ-dependence can be eliminated to the first order in τ by tuning α so that ∂Z/∂τ becomes zero at a certain τ.
V. SUMMARY
In this paper, we have presented a theoretical model of LBC in which a lithographical pattern is used to control the bending. The model succeeds in explaining the measured data obtained from the WFB structure. The additional degrees of freedom introduced by the lithographical method enable simple and practical curvature tuning. In this sense, the method can be applied to various kinds of microstructures.
ACKNOWLEDGEMENTS
The authors thank K. Yamakawa and Dr. H. Kanaya for support and advice on fabrication of the PZT actuator. They also thank M. Matsuo, H. Ishiuchi, K. Ishimaru and Y. Toyoshima for support and encouragement.
Tamio Ikehashi received his Ph.D. degree in theoretical physics from the University of Tokyo in 1995. In 1995, he joined Semiconductor Device Laboratory, Toshiba Corporation, Yokohama, Japan, where he has been engaged in the development of semiconductor memories. Since 2004, he has been engaged in the research and development of MEMS devices.
Etsuji Ogawa received his B.S. degree in metallurgical engineering in 1987. He joined Toshiba Corporation in 1987. He is currently engaged in the research and development of RF MEMS devices.
Hiroaki Yamazaki received his B.S. and M.S. degrees in electronic engineering from Tohoku University, Sendai, Japan, in 2003 and 2005, respectively. He joined Toshiba Corporation Semiconductor Company, Yokohama, Japan, in 2005. He is currently engaged in the research and development of RF MEMS devices.
Tatsuya Ohguro received his B.S. and M.S. degrees in physics from Hokkaido University, Sapporo, Japan, in 1987 and 1989, respectively. He joined Toshiba Corporation in 1989, where he has been engaged in the research and development of advanced logic CMOS devices, mixed signal and RF CMOS, passive elements and advance device processes such as Ni salicide technology, epitaxial channel structure, elevated source and drain, and so on. He is a member of Semiconductor Technology Academic Research Center (STARC) and supports the development of the HiSIM model for RF circuits design. He won the Nikkei BP Grand Prize in (1994). He is a member of IEEE and the Japan Society of Applied Physics.
