Introduction
Landscape genetics that combine high resolution genetic markers with spatial data analysis have been particularly relevant when assessing the influence of landscape characteristics on the genetic variability and the identification of barriers to gene flow (Storfer et al., Reference Storfer, Murphy, Evans, Goldberg, Robinson, Spear, Dezzani, Delmelle, Vierling and Waits2007). Geographic barriers can interrupt gene flow between neighbouring populations independently from geographical distances and, thus, must be tested properly (Bossart & Prowell, Reference Bossart and Prowell1998; Storfer et al., Reference Storfer, Murphy, Evans, Goldberg, Robinson, Spear, Dezzani, Delmelle, Vierling and Waits2007).
Several studies on landscape genetics of insect species, as endangered organisms or biodiversity indicators in forest and agricultural landscapes, have been performed during the last decade (Darvill et al., Reference Darvill, Ellis, Lye and Goulson2006; Sander et al., Reference Sander, Purtauf, Holzhauer and Wolters2006a,Reference Sander, Purtauf, Wolters and Dauberb; Herrmann et al., Reference Herrmann, Westphal, Moritz and Steffan-Dewenter2007; Vandergast et al., Reference Vandergast, Bohonak, Weissman and Fisher2007). However, much less attention has been devoted to forest and agricultural pests, although molecular markers are available for many species (Behura, Reference Behura2006), and area-wide pest management programs provide valuable information about landscape attributes (Calkins & Faust, Reference Calkins and Faust2003; Carrière et al., Reference Carrière, Dutilleul, Ellers-Kirk, Pedersen, Haller, Antilla, Dennehy and Tabashnik2004; Beckler et al., Reference Beckler, French and Chandler2005; Park et al., Reference Park, Perring, Farrar and Gispert2006). Linking current practices of area-wide pest management information on pest population genetics and geographical barriers would increase the efficiency of these programs.
The woolly apple aphid, Eriosoma lanigerum (Hausmann) (Hemiptera: Aphididae), is an important pest of apple orchards worldwide (Blommers, Reference Blommers1994). In North America, this aphid seems to be holocyclic (i.e. cyclic parthenogenesis alternating sexual reproduction with parthenogenesis), with sexual forms on elm trees (Ulmus americana L.) and asexual forms on apple (Malus domestica Borkh) (Blackman & Eastop, Reference Blackman and Eastop1994). In other regions of the world, this aphid is anholocyclic (i.e. with loss of the sexual phase), with year round asexual forms occurring on apple trees (Blackman & Eastop, Reference Blackman and Eastop1994). Production of sexual forms in areas with mild winters and the absence of the primary host has been reported; however, the genetic contribution of sexual genotypes to populations infesting apple trees has not been clarified (Sandanayaka & Bus, Reference Sandanayaka and Bus2005; Timm et al., Reference Timm, Pringle and Warnich2005).
E. lanigerum can disperse through infested plant material and wind (Asante et al., Reference Asante, Danthanarayana and Cairns1993). In regions where holocyclic genotypes are present, the production of sexual alates allows long distance aerial dispersal (Sandanayaka & Bus, Reference Sandanayaka and Bus2005). There geographic barriers, such as mountains and rivers, could limit wind flow, therefore acting as barriers to dispersal and potentially modulating the population genetic structure (Westbrook & Isard, Reference Westbrook and Isard1999). Genetic diversity of E. lanigerum has been studied only in South Africa, where a low genetic variation within and between locations was found, probably associated with predominantly asexual reproduction and dispersal through infested plant material (Timm et al., Reference Timm, Pringle and Warnich2005).
Since genetic variability and structure of insect pest populations, associated with life cycle characteristics, can provide some insights into the dispersal mechanisms of these, in the present study, we tested whether geographical parameters affected genetic diversity and gene flow of E. lanigerum in central Chile (33° to 37° latitude south). Geographical variables as possible barriers to gene flow were then individually tested in order to explain the genetic structure found.
Materials and methods
Samples from ten orchards in different locations were collected in central Chile during spring and summer of 2005/06. Sampling locations were: Ancoa (S 35.91943 W 71.33041, 404 m), Colín (S 35.46507 W 71.73353, 47.5 m), El Colorado (S 35.62074 W 71.27864, 405 m), Villa Alemana (S 33.19079 W 71.37163, 106 m), Los Niches (S 35.04175 W 71.18500, 235 m), Panguilemo (S 35.37091 W 71.59524, 121 m), Pencahue (S 35.38667 W 71.81009, 65.3 m), San Fernando (S 34.57442 W 70.98117, 314 m), Colbún (S 35.68596 W 71.47453, 234 m) and Chillán (S 36.59805 W 72.08192, 133 m). From each location 30–40 wingless adult females of E. lanigerum were collected in 95% alcohol to avoid DNA degradation (Sunnucks & Hales, Reference Sunnucks and Hales1996). To avoid collecting specimens from the same asexual lineage (clones), all individuals were collected from different trees. Individuals were examined under the microscope, and parasitized aphids were discarded to avoid amplification of parasitoid DNA.
DNA extraction and PCR amplification
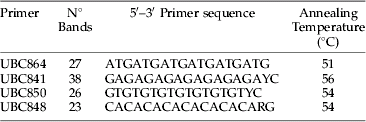
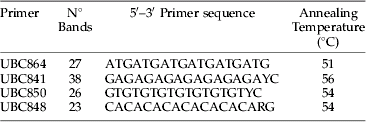
The genomic DNA was obtained following the ‘salting out’ procedure from Sunnucks & Hales (Reference Sunnucks and Hales1996). DNA template was suspended in 40 μl of distilled sterile water. A total of 18 ISSR primers (Biotechnology Laboratory from University of British Columbia, Vancouver) were tested. The inter-simple sequence repeats (ISSR) are a very useful tool for studies of genetic diversity (Wolfe et al., Reference Wolfe, Xiang and Kephart1998), which are based on the use of the microsatellites sequences as primers to generate multiple band patterns. This is a dominant genetic marker, which does not allow differentiating between homozygote and heterozygote genotypes, which are necessary to calculate allele frequencies. However, its main advantage is that no previous knowledge of the genome is necessary, which makes this technique a quick and economic alternative with higher reliability than random amplification of polymorphic DNA (RAPDs) when more informative co-dominant markers are not available (Zietkiewicz et al., Reference Zietkiewicz, Rafalski and Labuda1994; Abbot, Reference Abbot2001).
PCR reactions were carried out in a Mastercycler® gradient Eppendorf thermocycler with a 0.5 ng μl−1 DNA template, 2.5 mM MgCl, 0.2 mM dNTP, one U Taq DNA polymerase Invitrogen, 0.75 μM primers in a final volume of 20 μl. PCR consisted of a program of 5 min initial denaturation at 94°C and then 35 cycles of a 1 min denaturation at 94°C, 1.5 min annealing (see table 1 for annealing temperatures), 7 min extension at 74°C and a final extension at 74°C for 4 min. PCR products were separated in a 2% agarose gel with a GeneRulerTM 100 bp DNA ladder plus (Fermentas). Band weight, presence and absence were determined for all samples.
Table 1. Primer sequence, number of bands, polymorphic bands and annealing temperatures for E. lanigerum.
Mixed based positions Y: (C, T) R: (A, G).
Statistical analysis
A total of 114 loci generated from the best four ISSR primers, based on the consistency of the resulting PCR products, were considered for analysis (table 1). Analysis of molecular variance (AMOVA), pairwise genetic difference between loci and a Mantel test to check for isolation by distance (IBD) was done using Arlequin 3.1 software (Excoffier et al., Reference Excoffier, Laval and Schneider2005). Nei's (Reference Nei1973) gene diversity for each location was calculated with software Popgene version 1.31 (Nei & Li, Reference Nei and Li1979). Using GenAlEx version 6 (Peakall & Smouse, Reference Peakall and Smouse2006), ΦPT, which is the proportion of the variance among populations relative to the total variance and pairwise ΦPT between locations, was calculated in order to assess total variance between all populations and the proportion of variance between the different collecting locations (orchards). ΦPT is analogous to F st when the data are haploid or binary (Maguire et al., Reference Maguire, Peakall and Saenger2002).
Population structure
The use of different methods to study the spatial genetic structure of organisms in a sampled region has been strongly recommended in the literature (Pearse & Crandall, Reference Pearse and Crandall2005; Frantz et al., Reference Frantz, Pourtois, Heuertz, Schley, Flamand, Krier, Bertouille, Chaumont and Burke2006; Storfer et al., Reference Storfer, Murphy, Evans, Goldberg, Robinson, Spear, Dezzani, Delmelle, Vierling and Waits2007). Analyses methods such as AMOVA have the disadvantage that populations must be defined a priori; therefore, the significance of values may change depending on a priori grouping. In contrast, Bayesian methods have the advantage of inferring populations based on the frequencies of the alleles, thus clustering individuals based on there genetic values (Bolstad, Reference Bolstad2004). Therefore, we selected two Bayesian methods for determining the genetic structure of E. lanigerum. In the first method, population structure within E. lanigerum samples was inferred using a Bayesian model clustering algorithm implemented in the computer programme structure version 2.1 (Pritchard et al., Reference Pritchard, Stephens and Donnelly2000; Pritchard & Wen, Reference Pritchard and Wen2003). To run the programme, a number K of genetic clusters, characterized by the matrices of allele frequencies at each locus, is first assumed. Then, for each individual, the proportion of its genome derived from each genetic cluster (proportion of ancestry) is estimated. Five independent runs of the algorithm, assuming values of K from 1 to 11 with 600,000 Markov chain Monte Carlo (MCMC) repetitions and a burning period of 60,000, were performed, assuming population admixture. The posterior probability (probability of K given the data) was then calculated for each mean value of K using the mean estimated log-likelihood of K in order to choose the optimal K. The proportion of ancestry in a given cluster was calculated as an assignment rate (q), in general a level of 0.8 determines a correct assignment to a single cluster (Vialatte et al., Reference Vialatte, Dedryver, Simon, Galman and Plantegenest2005). The algorithm used by structure may be poorly suited for inferring the number of genetic clusters in a data set that has an IBD relationship (Pritchard & Wen, Reference Pritchard and Wen2003; Evanno et al., Reference Evanno, Regnaut and Goudet2005). Considering the latter, the second method was a Bayesian clustering method described in Corander et al., (Reference Corander, Waldmann and Sillanpaa2003) and implemented in software Baps version 4.14 (Corander et al., Reference Corander, Marttinen, Sirén and Tang2006). In contrast with structure, it uses stochastic optimization to infer the genetic structure; and it can use a spatial model that takes into account individual geo-referenced multilocus genotypes to assign the biologically relevant structure, thereby increasing the power to detect correctly the underlying population structure (Corander et al., Reference Corander, Marttinen, Sirén and Tang2006). Ten independent repetitions for each K from 1 to 11 were carried out.
Barriers to gene flow
Models have shown that wind plays a significant role in the distribution of aphids (Loxdale & Lushai, Reference Loxdale and Lushai1999; Zhu et al., Reference Zhu, Radcliffe, Ragsdale, MacRae and Seeley2006) and, thus, their persistence in habitat patches (Parry et al., Reference Parry, Evans and Morgan2006). In particular, rivers and mountains could alter normal wind conditions (through vertical flow or canyon-like transversal winds) (DGA, 1998) affecting aphid movement. By performing multiple stepwise regressions of gene flow and standardized genetic differentiation (ΦPT×(1−ΦPT)−1) (response variables) between locations and the pairwise landscape parameters, we selected possible landscape features (for example, rivers and mountains) that were influencing the population structure from official geographic charts of Chile at a 1:250,000 scale.
The pairwise landscape parameters were defined in two steps. First, for each location, the following variables were measured: distance among populations in meters (d); distance to main rivers (dr) (the minimum distance in meters (m) from each population to a main river); distance to main mountain chains in meters (dm) (the minimum distance (m) from each population to main mountain chains); distance to main populated areas (dp) (the minimum distance in meters from each location to a main populated area); road density (rd) (kilometers of road per 25 km2 of terrain).
Second, using this information for each location, pairwise values were calculated as the Euclidean distance among them using the following expression:
Where LB are the landscape variables: d, dr, dm, dp or rd; i,j are two different locations; and ΔLBi,j is the Euclidean distance between population i and j for the landscape variable (D, DR, DM, DP and RD).
In the study site, the general landscape corresponds to an agricultural flat surrounded by mountains of a generally abrupt topography and elevations reaching up to 500 m.a.s.l. In central Chile, main inhabited areas are located in the north-south direction and rivers cut the landscape in the east-west direction. Thus, landscape parameters were extracted from an image mosaic, using a geographical information system in ArcView. The image mosaic was geographically projected using the coordinates systems UTM -WGS84 and all landscape parameter were measured in meters. All coding and analyses were performed with SPLUS version 6.0 (Insightful, Reference Insightful2001), and ArcView version 3.2.
Pairwise gene flow (Nm) between locations was calculated using GenAlEx version 6. A second matrix was generated from the location coordinates containing the pairwise geographic distances between the individuals.
From the variables that entered the stepwise models (DR and DM), we selected the features that could influence gene flow (rivers and mountains). In order to test whether particular rivers and mountains were impeding gene flow between locations independent from the geographical distance effect, a third matrix was built. To build the third matrix, combinations of individuals from locations on one side of the selected barrier were recorded as 1 and pairs from different sides as 0. Putative barriers from the map were chosen based on the spatial analyses preformed by Baps version 4.14, which were effective interruptions in the landscape (rivers and mountains) between the generated genetic clusters. Using zt version 1.0 (Bonnet & Van de Peer, Reference Bonnet and Van de Peer2002), a partial Mantel test was carried out estimating the correlation and significance for each putative barrier, with 10,000 permutations (Frantz et al., Reference Frantz, Pourtois, Heuertz, Schley, Flamand, Krier, Bertouille, Chaumont and Burke2006). Thus, a significant correlation would be indicative of a barrier to gene flow between clusters other than distance.
Results
Genetic diversity and population differentiation
A total of 215 individual from the ten localities were considered for analyses. The four ISSR primers amplified a total of 114 loci. There were no repeated haplotypes (for numbers of bands, common and private bands per population see table 2). Mean location polymorphism was 60.53%, ranging from 47.37% to 68.42% (table 2). Nei's gene diversity per site ranged from 0.14 to 0.18 (table 2). Total ΦPT was 0.18, with 0.825 of the variation corresponding to within population variation. ΦPT values between pairs of locations varied from 0.04 to 0.32 (table3).
Table 2. Sample size, totals for binary band patterns, percent polymorphisms and Nei's (Reference Nei1973) gene diversity per location.

Table 3. Pairwise genetic differentiation between populations ΦPT values (below diagonal) and corresponding significance after 10,000 permutations (above diagonal) are reported.

** , highly significant, P<0.01.
Population structure
When assigning individuals to clusters using structure, log-likelihood values increased, with posterior probability reaching its highest value (~1) at K=10. Clustering did not respond to sampling origin or geographical regions, and individuals were not clearly assigned to a given genetic population. More than 40% of the individuals were assigned to more than one cluster, thus the resultant clustering was non reliable. The Mantel test was significant with ΦPT×(1−ΦPT)−1 correlating positively with the pairwise geographical distance (r=0.554, P=0.004) (fig. 1).

Fig. 1. Correlation between standardized genetic differentiation (ΦPT×(1−ΦPT)−1) and the logarithm of the geographical distance (km) between locations (R2=0.55; Mantel test: r=0.554. P=0.004).
The number of clusters in optimal partition assignment with Baps determined K=4, with a log -marginal likelihood of optimal partition of −8074.93 and the posterior probability reaching its highest value (~1). Aphids from locations Villa Alemana, Colín and Ancoa formed one cluster, whereas aphids from Panguilemo alone formed a second cluster. Aphids from Colbún, Colorado and Chillán formed a third cluster, and aphids from San Fernando, Los Niches and Pencahue formed a fourth cluster (figs 2 and 3).

Fig. 2. Voronoi tessellations of the spatial clustering of individuals from ten locations. A cell of the tessellation corresponds to the physical neighbourhood of an observed data point and is shaded according to cluster membership. (1) Chillán, (2) Ancoa, (3) Colbún, (4) Colorado, (5) Pencahue, (6) Colín, (7) Panguilemo, (8) Los Niches, (9) San Fernando and (10) Villa Alemana (![]() , Cluster 1;
, Cluster 1; ![]() , Cluster 2; □, Cluster 3; ■, Cluster 4).
, Cluster 2; □, Cluster 3; ■, Cluster 4).

Fig. 3. Schematic diagram of putative barriers and relative position of locations to these barriers. (B1) Villa Alemana Mountains, (B2) Claro River, (B3) Lircay River, (B4) Maule River, and (B5) Ancoa Mountains. ![]() , Cluster one;
, Cluster one; ![]() , Cluster two;
, Cluster two; ![]() , Cluster three and
, Cluster three and ![]() , Cluster four.
, Cluster four.
Barriers to gene flow
When regressing the logarithm of gene flow against the landscape pairwise parameters, D and DR entered the model (D: α=−0.00107, SS=0.40048, P=0.0021; DR: α=−0.00515, SS=0.10716, P=0.0974). When regressing the standardized genetic differentiation (ΦPT×(1−ΦPT)−1) values with the landscape parameters D and DM entered the model (D: α=0.00051761, SS=0.08499, P=0.0015; DM: α=0.00262, SS=0.01694, P=0.1357). The only significant variable that entered in the regressions was geographical distance.
Some main rivers and mountains separated clusters on the map, while others did not. For instance, mountains around Villa Alemana, the Claro River, the Lircay River, the Maule River and the mountains around Ancoa separated clusters (see fig. 3). A partial Mantel test confirmed that Villa Alemana mountains were barriers to gene flow other than distance (r=−0.44, P=0.01). The Claro River also was confirmed as a significant barrier to gene flow other than distance between clusters (r=−0.45, P=0.01). A partial Mantel test also confirmed the Lircay River as a significant barrier to gene flow other than distance (r=−0.44, P=0.01) and the same for the Maule River and the Ancoa mountains (r=−0.42, P=0.02 and r=−0.45, P=0.005, respectively).
Discussion
Genetic diversity and population differentiation
Polymorphism percentage and Nei's gene diversity in our study were higher than those from the only other study on the genetic variation of E. lanigerum published to date (Timm et al., Reference Timm, Pringle and Warnich2005). Gene diversity in South African populations was extremely low, with the highest values reaching 0.024, as compared to our study where gene diversity was highest at Panguilemo with 0.18. In fact, the Villiersdorp population in South Africa was invariant (Timm et al., Reference Timm, Pringle and Warnich2005). In contrast, in our data, the lowest gene diversity was 0.14 (Chillán and Villa Alemana). Such values are similar to those reported in studies from other aphid species (Hales et al., Reference Hales, Tomiuk, Wohrmann and Sunnucks1997) but do not provide a clear insight in terms of sexuality and life cycle predominance in aphid populations (Halkett et al., Reference Halkett, Simon and Balloux2005). Significant absence of linkage disequilibrium using codominant markers would suggest the possibility of sexual reproduction in E. lanigerum populations from Chile. Production of sexual males and females able to successfully oviposit on apple trees were reported from New Zealand (Sandanayaka & Bus, Reference Sandanayaka and Bus2005), and a similar situation might be occurring in central Chile.
Proper testing of the presence of sexual populations of E. lanigerum in Chile will require more informative co-dominant molecular markers (Halkett et al., Reference Halkett, Simon and Balloux2005), as well as biological studies to identify functionality of putative sexual morphs (Sandanayaka & Bus, Reference Sandanayaka and Bus2005). Isolation of microsatellites from E. lanigerum is underway in order to readily assess the contribution of sexual reproduction to the population genetics of this aphid species in Chile.
Genetic differentiation in our data was modest, with ΦPT values reaching 0.18. This estimate is based on genetic distance data and could be comparable with the population divergence estimates obtained for the South African populations (Timm et al., Reference Timm, Pringle and Warnich2005). This latter study also reported a low genetic differentiation probably related with asexual reproduction and spread to other regions through infested plant material from the Elgin area nurseries. The relative isolation of apple producing areas in the Western Cape and the absence of wild host for E. lanigerum are further factors of the South African landscape that could explain the variability found. In our study, a higher differentiation between populations could be expected if holocyclic genotypes are present and abandoned apple orchards could act as reservoirs and corridors between areas.
Population structure
Structure software failed to cluster individuals properly and, as noted before, did not perform well under IBD (Frantz et al., Reference Frantz, Pourtois, Heuertz, Schley, Flamand, Krier, Bertouille, Chaumont and Burke2006). The resulting grouping of individuals in ten clusters did not have any biological meaning, nor correlate with geography, and a great number of individuals were not assigned to a single cluster. The resulting clustering did not agree with AMOVA results. In contrast, Baps assigned individuals to four distinct groups. These same grouping were observed when considering the location of individuals and their spatial coordinates. Moreover, the clusters were in partial agreement with the AMOVA results, as locations in each cluster shared low ΦPT values; and highest ΦPT values were between locations that were assigned to other clusters, with the exception of locations Panguilemu and Colin, which shared low ΦPT values. AMOVA has the clear disadvantage of having to define populations a priori, thus significance of values may change depending on a priori grouping. In contrast, Bayesian methods have the advantage of inferring populations based on the frequencies of the alleles (Bolstad, Reference Bolstad2004). Thus, E. lanigerum populations seem to consist of four distinct clusters. ΦPT values between populations revealed considerable genetic differentiation, which was correlated with geographical distance between sampling sites.
An important difference with the results reported from South Africa was the significant IBD found in the Chilean populations. A smaller spatial scale used in South Africa (approx. 10–200 km), with a relative isolation of the fruit production areas in the Western Cape, as well as the absence of wild hosts for E. lanigerum, could explain this result. On the contrary, apple growing areas in Chile are located almost continuously along the central valley, flanked by the coastal and Andes ranges (Gwynne, Reference Gwynne1999). Furthermore, domestic culturing of apple is a widespread practice in the rural Chilean landscape (Gwynne, Reference Gwynne1999), and trees are usually maintained without insecticide treatments and act as ‘stepping stones’ for the dispersal of alates of E. lanigerum. The recent spread of modern fruticulture in Chile (the last 50 years for export-oriented production) and the introduction of E. lanigerum to the southern cone of America at the middle of the 19th century (Artigas, Reference Artigas1994) could also explain the differences reported with South Africa.
Another explanation for the differences found in the genetic structure of E. lanigerum could be attributed to the molecular markers used (i.e. AFLP in South Africa and ISSR in Chile). However, both are dominant markers with high reliability and should not produce different significant results (Wolfe et al., Reference Wolfe, Xiang and Kephart1998; Abbot, Reference Abbot2001; Nybom, Reference Nybom2004). Simultaneous results have been published only for plant species, with no major difference between the conclusions obtained (Nybom, Reference Nybom2004; Gao et al., Reference Gao, Zhang, Qi, Zhang, Wang and Song2006), therefore showing the usefulness of these markers.
Barriers to gene flow
Clearly the most important parameter affecting gene flow seems to be distance. However, several geographical structures separate the clusters when placed on the map (fig. 3). Some main rivers and mountains effectively separate all clusters. Locations within clusters presented rivers but not mountains with the exception of cluster one (fig. 3). All locations on cluster one were isolated from the other surrounding locations by these putative barriers. As it has been suggested that E. lanigerum is mainly dispersed with the wind and with rootstocks, this would explain why some main rivers and mountains could isolate populations. The most geographically isolated locations happened to be in cluster one. Individuals here could be brought to apple orchards with the rootstocks, suggesting a similar origin and, as they are isolated, limited or no flow with other populations from other clusters, might have maintained these populations with no or little change.
The Claro River separates cluster two, from the other clusters; this river is a canyon-like river with a higher north edge (DGA, 1998). As winds move predominantly in a south–north direction during summer and spring (Santibáñez, Reference Santibáñez1993) and rivers in Chile cut the landscape in a west-east direction (Solervicens, Reference Solervicens, Simonetti, Arroyo, Spotorno and Lozada1995), aphids carried by the wind would not reach the north edge. On the other hand, canyon-like rivers generate wind flows of there own, which could disperse aphids, impeding movement to the north.
Interestingly, other important rivers that were within genetical clusters were not found as barriers. This was the case of the Teno and Tinguiririca rivers within cluster two. This could be due to the fact that these rivers are not canyon-like rivers and are quite wide with very variable flow from season to season (DGA, 1998). It remains unanswered why some geographical structures that are expected to affect aphid population connectivity do not do so.
Although landscape genetics are rarely used in pest management, our results suggest that area-wide management programs can use this type of information in order to inform management decisions, identifying the source of insect spread and the possible barriers to further dispersal. For example, eradication of a close and small genetic population with limited flow with other areas, such as Panguilemo (cluster four), should be feasible.
Acknowledgements
The author would like to acknowledge the helpful comments from the anonymous reviewers and Wilson Barros and Cristián Muñoz for information of orchards and help collecting aphids from the different locations. Research was funded by Programa Bicentenario de Ciencia y Tecnología, Conicyt, Chile and the International Foundation for Science through a grant to Dr Blas Lavandero. Dr Claudio C. Ramírez and Dr Eduardo Fuentes-Contreras would like to acknowledge Anillo-PBCT AC38 for partial financial support.