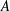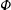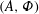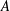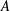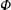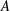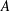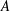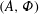1 Introduction
Spatial and temporal growth of small-amplitude perturbations represent important pathways towards dissipation, and subsequently mixing, for internal gravity waves in the atmosphere, ocean and planetary systems. Moreover, wave instabilities are potentially relevant for understanding the internal wave spectra observed in the ocean (Garrett & Munk Reference Garrett and Munk1975). A myriad of linear instabilities have previously been identified in internal waves of various spatial profiles, summaries of which can be found in Lombard & Riley (Reference Lombard and Riley1996), Sonmor & Klaassen (Reference Sonmor and Klaassen1997), Staquet & Sommeria (Reference Staquet and Sommeria2002) and Dauxois et al. (Reference Dauxois, Joubaud, Odier and Venaille2018).
Heuristic arguments and approximations based on static vertical profiles have been useful in identifying certain instabilities in large-amplitude internal waves (Fritts & Yuan Reference Fritts and Yuan1989; Thorpe Reference Thorpe1994), although they are also known to ignore important dynamical effects (Hines Reference Hines1971). By contrast, Floquet theory fully incorporates, and takes advantage of, the spatial and temporal periodicity of plane internal waves while placing no restriction on the amplitude (Mied Reference Mied1976; Drazin Reference Drazin1977; Klostermeyer Reference Klostermeyer1982). Additionally, Floquet theory makes no assumptions on the spatial scale of the perturbations, although it relies on the assumption of small-amplitude perturbations, and requires the truncation of an infinite sum in its solution, with the required number of terms being greater for larger internal wave amplitudes (Sonmor & Klaassen Reference Sonmor and Klaassen1997). For certain large-amplitude internal waves, the required number of terms in the Floquet sum can be several hundred, thus significantly increasing the computational requirement to solve the resulting eigenvalue problem for a given perturbation wave vector. Furthermore, the solution form in Floquet theory, as assumed in Sonmor & Klaassen (Reference Sonmor and Klaassen1997), is not applicable if the temporal or spatial periodicity of the internal wave field does not hold, e.g. a plane internal wave with steady background shear or an internal wave beam.
Using Floquet theory alongside an energy budget analysis, Lombard & Riley (Reference Lombard and Riley1996) calculated and characterised two-dimensional (2-D) and three-dimensional (3-D) instabilities of finite amplitude internal gravity waves. Lombard & Riley (Reference Lombard and Riley1996) concluded that small-amplitude plane internal waves can succumb to 2-D instabilities related to second-order wave–wave interactions, and that large-amplitude plane internal waves are also prone to 3-D instabilities that may be related to higher-order resonant interactions. Using a similar approach, Sonmor & Klaassen (Reference Sonmor and Klaassen1997) showed that the dominant linear instabilities in large-amplitude plane internal waves can be traced back to resonant instabilities at small amplitude. These resonant wave–wave interactions, which underlie the instabilities of large-amplitude internal waves observed by Lombard & Riley (Reference Lombard and Riley1996) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997), comprise the formation of a resonant wave triad between the primary internal wave and two perturbation waves. The particular class of triads corresponding to small-scale perturbations propagating at half the temporal frequency of the primary wave is known as parametric subharmonic instability (PSI) (McEwan & Robinson Reference Mcewan and Robinson1975), and has been the subject of several experimental (Bourget et al. Reference Bourget, Dauxois, Joubaud and Odier2013) and numerical (Koudella & Staquet Reference Koudella and Staquet2006) studies. The potential for PSI to serve as a mechanism that can transfer energy from large to small scales has made them the subject of studies focusing on oceanic phenomena (McComas & Bretherton Reference Mccomas and Bretherton1977; MacKinnon & Winters Reference MacKinnon and Winters2005). Apart from PSI, higher-order resonant interactions that lead to the growth of shear-aligned perturbations at a frequency that is half of an integer multiple of the primary wave frequency have also been studied (Sonmor & Klaassen Reference Sonmor and Klaassen1996). As we will show, the local stability approach that we employ in this paper recovers some well-established features of PSI and higher-order resonance occurring for small-amplitude internal waves.
The local stability equations (Lifschitz & Hameiri Reference Lifschitz and Hameiri1991), which are a set of ordinary differential equations governing the evolution of perturbation amplitude and wave vector on fluid particle trajectories in the base flow, are restricted to perturbations whose spatial scales are small relative to the base flow length scale. Being much simpler to solve than the corresponding linear stability equations that govern perturbations of arbitrary spatial scales, the local stability equations have proven to be very useful in identifying and analysing short-wavelength instabilities in steady but strongly non-parallel flows such as a vortex. Local stability studies have focused on the centrifugal (Sipp & Jacquin Reference Sipp and Jacquin2000; Nagarathinam, Sameen & Mathur Reference Nagarathinam, Sameen and Mathur2015), elliptic (Bayly Reference Bayly1986) and hyperbolic (Leblanc Reference Leblanc1997) instabilities in a number of idealized vortex models that incorporate the effects of background rotation (Godeferd, Cambon & Leblanc Reference Godeferd, Cambon and Leblanc2001), stratification (Miyazaki & Fukumoto Reference Miyazaki and Fukumoto1992) or a combination of these factors (Miyazaki Reference Miyazaki1993). The local stability approach has also been applied to unsteady vortex models (Bayly, Holm & Lifschitz Reference Bayly, Holm and Lifschitz1996). Moreover, the instabilities of vortical or tidal motions of stratified fluids have been shown, using local stability theory, to resonantly excite internal gravity waves (Miyazaki & Fukumoto Reference Miyazaki and Fukumoto1992; Le Reun, Favier & Le Bars Reference Le Reun, Favier and Le Bars2018). The correspondence between the local and global (normal mode) stability approaches, however, remains an intriguing question, although some studies (Sipp & Jacquin Reference Sipp and Jacquin2000; Mathur et al. Reference Mathur, Ortiz, Dubos and Chomaz2014) have reported on this aspect for the centrifugal instability; local stability studies of numerically simulated 2-D vortex flows have also performed some comparisons with the growth rates obtained from global stability analyses (Gallaire, Marquillie & Ehrenstein Reference Gallaire, Marquillie and Ehrenstein2007; Aravind, Mathur & Dubos Reference Aravind, Mathur and Dubos2017). Recent local stability studies of geophysical flows have helped identify small-scale instabilities of Gerstner’s waves (Leblanc Reference Leblanc2004), equatorially trapped waves (Constantin & Germain Reference Constantin and Germain2013) and edge waves on a sloping beach (Ionescu-Kruse Reference Ionescu-Kruse2014, Reference Ionescu-Kruse2015).
In this paper, we elucidate the various small-scale 2-D and 3-D linear instabilities of a plane internal gravity wave using the local stability approach. In doing so, we demonstrate the local stability approach to be a physically insightful and computationally efficient tool to study internal waves in various settings. It is worth highlighting that it is a priori unknown which instabilities present in a global stability approach, like the Floquet theory of Mied (Reference Mied1976) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997), may be captured in our local stability analysis. As we will show, the local stability approach recovers established results of small-scale internal wave instabilities, and sheds light on previously unexplored 3-D instabilities.
The paper is organized as follows. Section 2 presents a description of the base flow, and the local stability equations that govern the evolution of small-scale perturbations of plane internal waves. In § 3, we present our calculations and results spanning a large range of non-dimensional wave amplitudes and orientation angles, and offer comparisons with previous literature. A geophysical application of the local stability approach is presented in § 4. Finally, a summary of our results followed by conclusions and suggestions for future work are presented in § 5.
2 Theory
We consider an unbounded, non-rotating, uniformly stratified fluid of constant buoyancy frequency
![]() $N$
. The total velocity
$N$
. The total velocity
![]() $\boldsymbol{U}$
, pressure
$\boldsymbol{U}$
, pressure
![]() $P$
and buoyancy
$P$
and buoyancy
![]() $B$
fields are a superposition of small-amplitude, short-wavelength perturbations onto an internal wave base flow:
$B$
fields are a superposition of small-amplitude, short-wavelength perturbations onto an internal wave base flow:
where
![]() $\bar{\bar{\unicode[STIX]{x1D70C}}}(z)=\unicode[STIX]{x1D70C}_{0}-(\unicode[STIX]{x1D70C}_{0}/g)N^{2}z$
is the stable background linear density stratification;
$\bar{\bar{\unicode[STIX]{x1D70C}}}(z)=\unicode[STIX]{x1D70C}_{0}-(\unicode[STIX]{x1D70C}_{0}/g)N^{2}z$
is the stable background linear density stratification;
![]() $\bar{\bar{b}}=(\bar{\bar{\unicode[STIX]{x1D70C}}}/\unicode[STIX]{x1D70C}_{0})g$
is the background buoyancy field;
$\bar{\bar{b}}=(\bar{\bar{\unicode[STIX]{x1D70C}}}/\unicode[STIX]{x1D70C}_{0})g$
is the background buoyancy field;
![]() $\unicode[STIX]{x1D70C}_{0}$
is a reference density;
$\unicode[STIX]{x1D70C}_{0}$
is a reference density;
![]() $\bar{\boldsymbol{u}}$
,
$\bar{\boldsymbol{u}}$
,
![]() $\bar{p}$
and
$\bar{p}$
and
![]() $\bar{b}$
are the velocity, pressure and buoyancy fields of the internal wave, respectively, (
$\bar{b}$
are the velocity, pressure and buoyancy fields of the internal wave, respectively, (
![]() $\boldsymbol{u}^{\prime }$
,
$\boldsymbol{u}^{\prime }$
,
![]() $p^{\prime }$
, and
$p^{\prime }$
, and
![]() $b^{\prime }$
are the corresponding perturbation fields); and
$b^{\prime }$
are the corresponding perturbation fields); and
![]() $\boldsymbol{g}=-g\hat{\boldsymbol{e}}_{z}$
is gravity. The momentum, incompressibility and mass conservation equations – under the inviscid, non-diffusive, Boussinesq approximations – are, respectively,
$\boldsymbol{g}=-g\hat{\boldsymbol{e}}_{z}$
is gravity. The momentum, incompressibility and mass conservation equations – under the inviscid, non-diffusive, Boussinesq approximations – are, respectively,
The base flow is described by a 2-D plane internal gravity wave:
subject to the dispersion relation:
where
![]() $\bar{\unicode[STIX]{x1D713}}$
is the streamfunction of the velocity field
$\bar{\unicode[STIX]{x1D713}}$
is the streamfunction of the velocity field
![]() $\bar{\boldsymbol{u}}=(-\bar{\unicode[STIX]{x1D713}}_{z},0,\bar{\unicode[STIX]{x1D713}}_{x})$
,
$\bar{\boldsymbol{u}}=(-\bar{\unicode[STIX]{x1D713}}_{z},0,\bar{\unicode[STIX]{x1D713}}_{x})$
,
![]() $\unicode[STIX]{x1D6F9}$
is the streamfunction amplitude,
$\unicode[STIX]{x1D6F9}$
is the streamfunction amplitude,
![]() $\boldsymbol{x}=(x,y,z)$
is the spatial coordinate,
$\boldsymbol{x}=(x,y,z)$
is the spatial coordinate,
![]() $\boldsymbol{k}=(k,0,m)$
is the wave vector,
$\boldsymbol{k}=(k,0,m)$
is the wave vector,
![]() $t$
is time,
$t$
is time,
![]() $\unicode[STIX]{x1D714}$
is the wave frequency and
$\unicode[STIX]{x1D714}$
is the wave frequency and
![]() $\unicode[STIX]{x1D6F7}$
is the inclination angle of the wave vector
$\unicode[STIX]{x1D6F7}$
is the inclination angle of the wave vector
![]() $\boldsymbol{k}$
to the horizontal
$\boldsymbol{k}$
to the horizontal
![]() $x$
-axis (or alternatively, the inclination of the constant phase lines to the vertical
$x$
-axis (or alternatively, the inclination of the constant phase lines to the vertical
![]() $z$
-axis), as shown in figure 1. We note that (2.7a–c
) are solutions to the linearised and fully nonlinear version of (2.4)–(2.6), and that equations (2.7b,c
) follow from the linearised forms of (2.4) and (2.5), respectively (see Tabaei & Akylas Reference Tabaei and Akylas2003, § 2).
$z$
-axis), as shown in figure 1. We note that (2.7a–c
) are solutions to the linearised and fully nonlinear version of (2.4)–(2.6), and that equations (2.7b,c
) follow from the linearised forms of (2.4) and (2.5), respectively (see Tabaei & Akylas Reference Tabaei and Akylas2003, § 2).
Using (2.8) to compute the group velocity vector
![]() $\boldsymbol{c}_{g}=(\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D714},0,\unicode[STIX]{x2202}_{m}\unicode[STIX]{x1D714})$
, one finds that as
$\boldsymbol{c}_{g}=(\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D714},0,\unicode[STIX]{x2202}_{m}\unicode[STIX]{x1D714})$
, one finds that as
![]() $\unicode[STIX]{x1D6F7}$
, and thus
$\unicode[STIX]{x1D6F7}$
, and thus
![]() $\boldsymbol{k}$
, approach the
$\boldsymbol{k}$
, approach the
![]() $x$
-axis,
$x$
-axis,
![]() $\boldsymbol{c}_{g}$
approaches the
$\boldsymbol{c}_{g}$
approaches the
![]() $z$
-axis by virtue of
$z$
-axis by virtue of
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{c}_{g}$
being orthogonal (see Kundu, Cohen & Dowling Reference Kundu, Cohen and Dowling2012, § 7.8). As a result, the internal wave energy propagates at a steep (shallow) angle for small (large)
$\boldsymbol{c}_{g}$
being orthogonal (see Kundu, Cohen & Dowling Reference Kundu, Cohen and Dowling2012, § 7.8). As a result, the internal wave energy propagates at a steep (shallow) angle for small (large)
![]() $\unicode[STIX]{x1D6F7}$
. Figure 1 illustrates the internal wave base flow and relevant system parameters.
$\unicode[STIX]{x1D6F7}$
. Figure 1 illustrates the internal wave base flow and relevant system parameters.

Figure 1. An illustration of the base flow
![]() $\bar{\unicode[STIX]{x1D713}}$
: a plane internal gravity wave in the
$\bar{\unicode[STIX]{x1D713}}$
: a plane internal gravity wave in the
![]() $(x,z)$
-plane. The initial wave vector
$(x,z)$
-plane. The initial wave vector
![]() $\unicode[STIX]{x1D73F}_{0}$
of the perturbation that is superposed onto the base flow makes an angle
$\unicode[STIX]{x1D73F}_{0}$
of the perturbation that is superposed onto the base flow makes an angle
![]() $\unicode[STIX]{x1D703}_{0}$
with its projection on the
$\unicode[STIX]{x1D703}_{0}$
with its projection on the
![]() $(x,z)$
-plane, and its projection on the
$(x,z)$
-plane, and its projection on the
![]() $(x,z)$
-plane makes an angle
$(x,z)$
-plane makes an angle
![]() $\unicode[STIX]{x1D719}_{0}$
with the
$\unicode[STIX]{x1D719}_{0}$
with the
![]() $x$
-axis. The angle
$x$
-axis. The angle
![]() $\unicode[STIX]{x1D6F7}$
is the inclination angle of the base flow wave vector (group velocity vector) relative to the
$\unicode[STIX]{x1D6F7}$
is the inclination angle of the base flow wave vector (group velocity vector) relative to the
![]() $x$
-axis (
$x$
-axis (
![]() $z$
-axis).
$z$
-axis).
Choosing
![]() $N^{-1}$
and
$N^{-1}$
and
![]() $|\boldsymbol{k}|^{-1}$
as representative time and length scales, respectively, we write the following dimensionless parameters to characterise the base flow:
$|\boldsymbol{k}|^{-1}$
as representative time and length scales, respectively, we write the following dimensionless parameters to characterise the base flow:
where
![]() $A$
is the dimensionless net-velocity amplitude of the base flow and
$A$
is the dimensionless net-velocity amplitude of the base flow and
![]() $\unicode[STIX]{x1D6F7}$
is a measure of the base flow orientation. We introduce a metric of isopycnal steepness defined as
$\unicode[STIX]{x1D6F7}$
is a measure of the base flow orientation. We introduce a metric of isopycnal steepness defined as
where
![]() $\text{max}(\bar{u})$
is the maximum horizontal velocity of the base flow and
$\text{max}(\bar{u})$
is the maximum horizontal velocity of the base flow and
![]() $c_{x}=\unicode[STIX]{x1D714}/k$
is the horizontal phase velocity. The condition
$c_{x}=\unicode[STIX]{x1D714}/k$
is the horizontal phase velocity. The condition
![]() $s>1$
is sufficient for the existence of at least one time instance during the internal wave period when overturned isopycnals occur, i.e.
$s>1$
is sufficient for the existence of at least one time instance during the internal wave period when overturned isopycnals occur, i.e.
![]() $\unicode[STIX]{x2202}_{z}(\bar{\bar{\unicode[STIX]{x1D70C}}}+\bar{\unicode[STIX]{x1D70C}})>0$
. The characteristics of such locally overturned regions are known to be related to internal wave breaking (Thorpe Reference Thorpe1994).
$\unicode[STIX]{x2202}_{z}(\bar{\bar{\unicode[STIX]{x1D70C}}}+\bar{\unicode[STIX]{x1D70C}})>0$
. The characteristics of such locally overturned regions are known to be related to internal wave breaking (Thorpe Reference Thorpe1994).
Following Lifschitz & Hameiri (Reference Lifschitz and Hameiri1991), we write the short-wavelength perturbations, which we superimpose onto the base flow, in the Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) form:
where
![]() $\boldsymbol{a}(\boldsymbol{x},t)$
,
$\boldsymbol{a}(\boldsymbol{x},t)$
,
![]() $p(\boldsymbol{x},t)$
and
$p(\boldsymbol{x},t)$
and
![]() $b(\boldsymbol{x},t)$
are, respectively, the complex leading order velocity, pressure and buoyancy perturbation amplitudes,
$b(\boldsymbol{x},t)$
are, respectively, the complex leading order velocity, pressure and buoyancy perturbation amplitudes,
![]() $\unicode[STIX]{x1D6E9}(\boldsymbol{x},t)$
is a real-valued phase function,
$\unicode[STIX]{x1D6E9}(\boldsymbol{x},t)$
is a real-valued phase function,
![]() $0<\unicode[STIX]{x1D700}\ll 1$
is the parameter reflecting the length scale ratio of the perturbation to the base flow and
$0<\unicode[STIX]{x1D700}\ll 1$
is the parameter reflecting the length scale ratio of the perturbation to the base flow and
![]() $\unicode[STIX]{x1D73F}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D700}$
is the perturbation wave vector. Substituting (2.11) into (2.4)–(2.6) and retaining
$\unicode[STIX]{x1D73F}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D700}$
is the perturbation wave vector. Substituting (2.11) into (2.4)–(2.6) and retaining
![]() $O(\unicode[STIX]{x1D700}^{-1})$
and
$O(\unicode[STIX]{x1D700}^{-1})$
and
![]() $O(\unicode[STIX]{x1D700}^{0})$
terms yields the following equations governing the evolution of the perturbation wave vector
$O(\unicode[STIX]{x1D700}^{0})$
terms yields the following equations governing the evolution of the perturbation wave vector
![]() $\unicode[STIX]{x1D73F}$
and the leading order perturbation amplitudes
$\unicode[STIX]{x1D73F}$
and the leading order perturbation amplitudes
![]() $(\boldsymbol{a},b)$
(Miyazaki & Fukumoto Reference Miyazaki and Fukumoto1992):
$(\boldsymbol{a},b)$
(Miyazaki & Fukumoto Reference Miyazaki and Fukumoto1992):
where
![]() $\text{d}/\text{d}t=\unicode[STIX]{x2202}_{t}+\bar{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the material time derivative with respect to the base flow
$\text{d}/\text{d}t=\unicode[STIX]{x2202}_{t}+\bar{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the material time derivative with respect to the base flow
![]() $\bar{\boldsymbol{u}}$
. The local stability equations, (2.12)–(2.14), are, therefore, ordinary differential equations to be solved on fluid particle trajectories in the base flow. We will hereafter be working in a dimensionless framework, using
$\bar{\boldsymbol{u}}$
. The local stability equations, (2.12)–(2.14), are, therefore, ordinary differential equations to be solved on fluid particle trajectories in the base flow. We will hereafter be working in a dimensionless framework, using
![]() $|\boldsymbol{k}|^{-1}$
,
$|\boldsymbol{k}|^{-1}$
,
![]() $N^{-1}$
and
$N^{-1}$
and
![]() $N^{2}|\boldsymbol{k}|^{-1}$
as the length, time and buoyancy scales, respectively.
$N^{2}|\boldsymbol{k}|^{-1}$
as the length, time and buoyancy scales, respectively.
Fluid particle trajectories
![]() $\bar{\boldsymbol{x}}(t)=(\bar{x},0,\bar{z})$
in the base flow are given by
$\bar{\boldsymbol{x}}(t)=(\bar{x},0,\bar{z})$
in the base flow are given by
where
![]() $\boldsymbol{x}_{0}=(x_{0},0,z_{0})$
is the initial particle position at
$\boldsymbol{x}_{0}=(x_{0},0,z_{0})$
is the initial particle position at
![]() $t=0$
and
$t=0$
and
![]() $\unicode[STIX]{x1D717}_{0}=\cos \unicode[STIX]{x1D6F7}x_{0}+\sin \unicode[STIX]{x1D6F7}z_{0}$
. With no loss of generality, we assume
$\unicode[STIX]{x1D717}_{0}=\cos \unicode[STIX]{x1D6F7}x_{0}+\sin \unicode[STIX]{x1D6F7}z_{0}$
. With no loss of generality, we assume
![]() $(x_{0},z_{0})=(0,0)$
, as all trajectories on the
$(x_{0},z_{0})=(0,0)$
, as all trajectories on the
![]() $(x,z)$
-plane are equivalent for a plane wave. All fluid particle trajectories, irrespective of initial location, are periodic in time, i.e.
$(x,z)$
-plane are equivalent for a plane wave. All fluid particle trajectories, irrespective of initial location, are periodic in time, i.e.
![]() $\bar{\boldsymbol{x}}(t=2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7})=\bar{\boldsymbol{x}}(t=0)$
.
$\bar{\boldsymbol{x}}(t=2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7})=\bar{\boldsymbol{x}}(t=0)$
.
Since the local stability equations (2.12)–(2.14) are linear in
![]() $\unicode[STIX]{x1D73F}$
, it suffices to consider only initial perturbation wave vectors of unit magnitude:
$\unicode[STIX]{x1D73F}$
, it suffices to consider only initial perturbation wave vectors of unit magnitude:
where
![]() $\unicode[STIX]{x1D703}_{0}$
is the angle made by
$\unicode[STIX]{x1D703}_{0}$
is the angle made by
![]() $\unicode[STIX]{x1D73F}_{0}$
with its projection on the
$\unicode[STIX]{x1D73F}_{0}$
with its projection on the
![]() $(x,z)$
-plane, and
$(x,z)$
-plane, and
![]() $\unicode[STIX]{x1D719}_{0}$
is the angle that the projection of
$\unicode[STIX]{x1D719}_{0}$
is the angle that the projection of
![]() $\unicode[STIX]{x1D73F}_{0}$
on the
$\unicode[STIX]{x1D73F}_{0}$
on the
![]() $(x,z)$
-plane makes with the
$(x,z)$
-plane makes with the
![]() $x$
axis (see figure 1);
$x$
axis (see figure 1);
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
corresponds to 2-D perturbations and any
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
corresponds to 2-D perturbations and any
![]() $\unicode[STIX]{x1D703}_{0}>0^{\circ }$
corresponds to 3-D perturbations. The limit
$\unicode[STIX]{x1D703}_{0}>0^{\circ }$
corresponds to 3-D perturbations. The limit
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
represents a wave vector aligned entirely along the
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
represents a wave vector aligned entirely along the
![]() $y$
axis, i.e. purely transverse perturbations, where the value of
$y$
axis, i.e. purely transverse perturbations, where the value of
![]() $\unicode[STIX]{x1D719}_{0}$
is irrelevant. Equation (2.12), subject to the initial condition (2.16), is solved for the perturbation wave vector to give
$\unicode[STIX]{x1D719}_{0}$
is irrelevant. Equation (2.12), subject to the initial condition (2.16), is solved for the perturbation wave vector to give
where
![]() $\unicode[STIX]{x1D705}_{0,x}$
and
$\unicode[STIX]{x1D705}_{0,x}$
and
![]() $\unicode[STIX]{x1D705}_{0,z}$
are the
$\unicode[STIX]{x1D705}_{0,z}$
are the
![]() $x$
and
$x$
and
![]() $z$
components of the initial perturbation wave vector
$z$
components of the initial perturbation wave vector
![]() $\unicode[STIX]{x1D73F}_{0}$
, respectively. For all
$\unicode[STIX]{x1D73F}_{0}$
, respectively. For all
![]() $(A,\unicode[STIX]{x1D6F7})$
, every
$(A,\unicode[STIX]{x1D6F7})$
, every
![]() $\unicode[STIX]{x1D73F}$
specified by an initial condition
$\unicode[STIX]{x1D73F}$
specified by an initial condition
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
in the range
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
in the range
![]() $[0^{\circ },360^{\circ }]\times [-90^{\circ },90^{\circ }]$
is periodic over one internal wave time period. Thus, the growth rate associated with every
$[0^{\circ },360^{\circ }]\times [-90^{\circ },90^{\circ }]$
is periodic over one internal wave time period. Thus, the growth rate associated with every
![]() $\unicode[STIX]{x1D73F}_{0}$
is computed following the approach of Mathur et al. (Reference Mathur, Ortiz, Dubos and Chomaz2014).
$\unicode[STIX]{x1D73F}_{0}$
is computed following the approach of Mathur et al. (Reference Mathur, Ortiz, Dubos and Chomaz2014).
A fourth-order Runge–Kutta scheme is used to numerically solve (2.13) and (2.14), for
![]() $\unicode[STIX]{x1D73F}$
spanning various
$\unicode[STIX]{x1D73F}$
spanning various
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
, along
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
, along
![]() $\bar{\boldsymbol{x}}$
(with a temporal resolution such that one internal wave period is represented using
$\bar{\boldsymbol{x}}$
(with a temporal resolution such that one internal wave period is represented using
![]() $500$
points). We use four different initial condition vectors of the form
$500$
points). We use four different initial condition vectors of the form
![]() $\boldsymbol{c}_{0}=[a_{x,0}\,\,a_{y,0}\,\,a_{z,0}\,\,b_{0}]$
such that the initial condition matrix,
$\boldsymbol{c}_{0}=[a_{x,0}\,\,a_{y,0}\,\,a_{z,0}\,\,b_{0}]$
such that the initial condition matrix,
![]() $[\boldsymbol{c}_{0,1};\,\,\boldsymbol{c}_{0,2};\,\,\boldsymbol{c}_{0,3};\,\,\boldsymbol{c}_{0,4}]$
, is equal to the identity matrix. Thus, for each
$[\boldsymbol{c}_{0,1};\,\,\boldsymbol{c}_{0,2};\,\,\boldsymbol{c}_{0,3};\,\,\boldsymbol{c}_{0,4}]$
, is equal to the identity matrix. Thus, for each
![]() $\boldsymbol{c}_{0}$
, we numerically obtain amplitude vectors at
$\boldsymbol{c}_{0}$
, we numerically obtain amplitude vectors at
![]() $t=2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7}$
as
$t=2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7}$
as
![]() $\boldsymbol{c}_{f,1}=[a_{x,1}\,\,a_{y,1}\,\,a_{z,1}\,\,b_{1}]$
,
$\boldsymbol{c}_{f,1}=[a_{x,1}\,\,a_{y,1}\,\,a_{z,1}\,\,b_{1}]$
,
![]() $\boldsymbol{c}_{f,2}=[a_{x,2}\,\,a_{y,2}\,\,a_{z,2}\,\,b_{2}]$
,
$\boldsymbol{c}_{f,2}=[a_{x,2}\,\,a_{y,2}\,\,a_{z,2}\,\,b_{2}]$
,
![]() $\boldsymbol{c}_{f,3}=[a_{x,3}\,\,a_{y,3}\,\,a_{z,3}\,\,b_{3}]$
, and
$\boldsymbol{c}_{f,3}=[a_{x,3}\,\,a_{y,3}\,\,a_{z,3}\,\,b_{3}]$
, and
![]() $\boldsymbol{c}_{f,4}=[a_{x,4}\,\,a_{y,4}\,\,a_{z,4}\,\,b_{4}]$
. The instability growth rates are then calculated as (Chicone Reference Chicone2000)
$\boldsymbol{c}_{f,4}=[a_{x,4}\,\,a_{y,4}\,\,a_{z,4}\,\,b_{4}]$
. The instability growth rates are then calculated as (Chicone Reference Chicone2000)
where
![]() $\unicode[STIX]{x1D648}=[\boldsymbol{c}_{f,1};\,\,\boldsymbol{c}_{f,2};\,\,\boldsymbol{c}_{f,3};\,\,\boldsymbol{c}_{f,4}]$
. The growth rate
$\unicode[STIX]{x1D648}=[\boldsymbol{c}_{f,1};\,\,\boldsymbol{c}_{f,2};\,\,\boldsymbol{c}_{f,3};\,\,\boldsymbol{c}_{f,4}]$
. The growth rate
![]() $\unicode[STIX]{x1D70E}$
is periodic over
$\unicode[STIX]{x1D70E}$
is periodic over
![]() $\unicode[STIX]{x1D719}_{0}\in [0^{\circ },180^{\circ }]$
and symmetric about
$\unicode[STIX]{x1D719}_{0}\in [0^{\circ },180^{\circ }]$
and symmetric about
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
; our subsequent analysis of
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
; our subsequent analysis of
![]() $\unicode[STIX]{x1D70E}$
is, therefore, presented over
$\unicode[STIX]{x1D70E}$
is, therefore, presented over
![]() $\unicode[STIX]{x1D719}_{0}\in [0^{\circ },180^{\circ }]$
and
$\unicode[STIX]{x1D719}_{0}\in [0^{\circ },180^{\circ }]$
and
![]() $\unicode[STIX]{x1D703}_{0}\in [0^{\circ },90^{\circ }]$
. We moreover note that
$\unicode[STIX]{x1D703}_{0}\in [0^{\circ },90^{\circ }]$
. We moreover note that
![]() $\unicode[STIX]{x1D70E}$
is dimensionless, with a growth rate scale of
$\unicode[STIX]{x1D70E}$
is dimensionless, with a growth rate scale of
![]() $N$
.
$N$
.
3 Results
3.1 Instability growth rates
In figure 2, we present the growth rate
![]() $\unicode[STIX]{x1D70E}$
(2.18) over the
$\unicode[STIX]{x1D70E}$
(2.18) over the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for nine different pairs of base flow parameters
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for nine different pairs of base flow parameters
![]() $(A,\unicode[STIX]{x1D6F7})$
. As noted in § 2, the growth rates are periodic in
$(A,\unicode[STIX]{x1D6F7})$
. As noted in § 2, the growth rates are periodic in
![]() $\unicode[STIX]{x1D719}_{0}$
over
$\unicode[STIX]{x1D719}_{0}$
over
![]() $[0^{\circ },180^{\circ }]$
and symmetric about
$[0^{\circ },180^{\circ }]$
and symmetric about
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
. In figure 2, the internal wave base flow progresses from steep (
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
. In figure 2, the internal wave base flow progresses from steep (
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
) in the leftmost column to shallow (
$\unicode[STIX]{x1D6F7}=15^{\circ }$
) in the leftmost column to shallow (
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
) in the rightmost column, and from small-amplitude (
$\unicode[STIX]{x1D6F7}=75^{\circ }$
) in the rightmost column, and from small-amplitude (
![]() $A=0.1$
) in the top row to large-amplitude (
$A=0.1$
) in the top row to large-amplitude (
![]() $A=10$
) in the bottom row.
$A=10$
) in the bottom row.
For
![]() $(A,\unicode[STIX]{x1D6F7})=(0.1,15^{\circ })$
, i.e. small-amplitude, steep internal waves (figure 2
a), we observe, in the limit of 2-D perturbations (
$(A,\unicode[STIX]{x1D6F7})=(0.1,15^{\circ })$
, i.e. small-amplitude, steep internal waves (figure 2
a), we observe, in the limit of 2-D perturbations (
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
), two thin instability peaks centred at
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
), two thin instability peaks centred at
![]() $\unicode[STIX]{x1D719}_{0}=61^{\circ }$
and
$\unicode[STIX]{x1D719}_{0}=61^{\circ }$
and
![]() $\unicode[STIX]{x1D719}_{0}=119^{\circ }$
. These instability peaks extend towards regions of 3-D perturbations (
$\unicode[STIX]{x1D719}_{0}=119^{\circ }$
. These instability peaks extend towards regions of 3-D perturbations (
![]() $\unicode[STIX]{x1D703}_{0}>0^{\circ }$
) to form two instability ridges on the
$\unicode[STIX]{x1D703}_{0}>0^{\circ }$
) to form two instability ridges on the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane; the two instability ridges, labelled I and II in figure 2(a), seem to have similar maximum growth rates, both of which occur on the
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane; the two instability ridges, labelled I and II in figure 2(a), seem to have similar maximum growth rates, both of which occur on the
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis. Significantly, the growth rates on the
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis. Significantly, the growth rates on the
![]() $\unicode[STIX]{x1D703}_{0}>0^{\circ }$
portions of the ridges are comparable to those on the
$\unicode[STIX]{x1D703}_{0}>0^{\circ }$
portions of the ridges are comparable to those on the
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis, suggesting that a continuous range of perturbation wave vectors on these ridges are of similar growth rates. It is also noteworthy that the variation of
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis, suggesting that a continuous range of perturbation wave vectors on these ridges are of similar growth rates. It is also noteworthy that the variation of
![]() $\unicode[STIX]{x1D70E}$
with
$\unicode[STIX]{x1D70E}$
with
![]() $\unicode[STIX]{x1D703}_{0}$
on ridges I and II is different, with ridge II retaining larger values of
$\unicode[STIX]{x1D703}_{0}$
on ridges I and II is different, with ridge II retaining larger values of
![]() $\unicode[STIX]{x1D70E}$
up to larger
$\unicode[STIX]{x1D70E}$
up to larger
![]() $\unicode[STIX]{x1D703}_{0}$
. As
$\unicode[STIX]{x1D703}_{0}$
. As
![]() $\unicode[STIX]{x1D703}_{0}$
approaches a threshold value of
$\unicode[STIX]{x1D703}_{0}$
approaches a threshold value of
![]() $29^{\circ }$
, the two instability ridges approach each other; above the threshold
$29^{\circ }$
, the two instability ridges approach each other; above the threshold
![]() $\unicode[STIX]{x1D703}_{0}$
, ridges I and II vanish. As
$\unicode[STIX]{x1D703}_{0}$
, ridges I and II vanish. As
![]() $\unicode[STIX]{x1D703}_{0}$
increases towards even larger values, a third, notably weaker, thin instability ridge appears (labelled III in figure 2
a). Ridge III seems to extend all the way to
$\unicode[STIX]{x1D703}_{0}$
increases towards even larger values, a third, notably weaker, thin instability ridge appears (labelled III in figure 2
a). Ridge III seems to extend all the way to
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
, the axis of 2-D perturbations. Interestingly, ridge III becomes aligned with
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
, the axis of 2-D perturbations. Interestingly, ridge III becomes aligned with
![]() $\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
(vertical dotted lines in figure 2), indicating the emergence of shear-aligned instabilities as the ridge approaches the
$\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
(vertical dotted lines in figure 2), indicating the emergence of shear-aligned instabilities as the ridge approaches the
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis. The existence of distinct instability bands in an otherwise stable landscape suggests the occurrence of select resonant wave–wave interactions in the small
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis. The existence of distinct instability bands in an otherwise stable landscape suggests the occurrence of select resonant wave–wave interactions in the small
![]() $s$
limit, which we discuss further in §§ 3.2–3.4.
$s$
limit, which we discuss further in §§ 3.2–3.4.

Figure 2. Growth rate,
![]() $\unicode[STIX]{x1D70E}$
, presented as a function of
$\unicode[STIX]{x1D70E}$
, presented as a function of
![]() $\unicode[STIX]{x1D719}_{0}$
and
$\unicode[STIX]{x1D719}_{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
for
$\unicode[STIX]{x1D703}_{0}$
for
![]() $A=0.1$
,
$A=0.1$
,
![]() $1$
,
$1$
,
![]() $10$
(top, middle and bottom rows, respectively), and
$10$
(top, middle and bottom rows, respectively), and
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
,
$\unicode[STIX]{x1D6F7}=15^{\circ }$
,
![]() $45^{\circ }$
,
$45^{\circ }$
,
![]() $75^{\circ }$
(left, middle and right columns, respectively). Stable regions of the
$75^{\circ }$
(left, middle and right columns, respectively). Stable regions of the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane where
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane where
![]() $\unicode[STIX]{x1D70E}<10^{-10}$
have been coloured white. The dotted vertical lines in each panel denote
$\unicode[STIX]{x1D70E}<10^{-10}$
have been coloured white. The dotted vertical lines in each panel denote
![]() $\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
.
At a moderate internal wave angle, i.e.
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
, as shown in figure 2(b), we similarly observe only three thin instability ridges over a
$\unicode[STIX]{x1D6F7}=45^{\circ }$
, as shown in figure 2(b), we similarly observe only three thin instability ridges over a
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane that is mostly stable. The range of 3-D wave vectors to which ridges I and II extend is smaller when compared with the case of
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane that is mostly stable. The range of 3-D wave vectors to which ridges I and II extend is smaller when compared with the case of
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
in figure 2(a). Ridge I appears to be noticeably stronger than ridge II in figure 2(b). Moreover, a third instability ridge is also identified in figure 2(b), although it is nearly indiscernible given its relatively weak growth rates. For a shallow propagating internal wave, as shown in figure 2(c) for
$\unicode[STIX]{x1D6F7}=15^{\circ }$
in figure 2(a). Ridge I appears to be noticeably stronger than ridge II in figure 2(b). Moreover, a third instability ridge is also identified in figure 2(b), although it is nearly indiscernible given its relatively weak growth rates. For a shallow propagating internal wave, as shown in figure 2(c) for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
, only three ridges are faintly visible due to the growth rates being an order of magnitude weaker than their
$\unicode[STIX]{x1D6F7}=75^{\circ }$
, only three ridges are faintly visible due to the growth rates being an order of magnitude weaker than their
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
and
$\unicode[STIX]{x1D6F7}=15^{\circ }$
and
![]() $45^{\circ }$
counterparts, and for the range of
$45^{\circ }$
counterparts, and for the range of
![]() $\unicode[STIX]{x1D703}_{0}$
to which they extend being notably limited.
$\unicode[STIX]{x1D703}_{0}$
to which they extend being notably limited.
For the moderate-amplitude, steep-propagation case of
![]() $(A,\unicode[STIX]{x1D6F7})=(1,15^{\circ })$
(figure 2
d), the growth rate distribution is qualitatively similar to that of figure 2(a), but with wider regions of the
$(A,\unicode[STIX]{x1D6F7})=(1,15^{\circ })$
(figure 2
d), the growth rate distribution is qualitatively similar to that of figure 2(a), but with wider regions of the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane that are unstable. The difference between regions I and II is more dramatic than what is observed at small-amplitude (figure 2
a). Moreover, region III (which was a ridge in figure 2
a) contains growth rate magnitudes comparable to that of regions I and II. The larger instability regions on the
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane that are unstable. The difference between regions I and II is more dramatic than what is observed at small-amplitude (figure 2
a). Moreover, region III (which was a ridge in figure 2
a) contains growth rate magnitudes comparable to that of regions I and II. The larger instability regions on the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane imply that there is now a wider, continuous range of perturbation wave vectors whose growth rates are of comparable magnitude. At an even larger value of
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane imply that there is now a wider, continuous range of perturbation wave vectors whose growth rates are of comparable magnitude. At an even larger value of
![]() $A=10$
(figure 2
g), nearly the entire
$A=10$
(figure 2
g), nearly the entire
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane is unstable, with a fourth region – narrowly separated from region III – that encompasses purely transverse (
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane is unstable, with a fourth region – narrowly separated from region III – that encompasses purely transverse (
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
) perturbations (which was not the case for weaker amplitude internal waves in figure 2
a,d). As in figure 2(a), the outer boundary of region III in both figure 2(d,g) aligns with
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
) perturbations (which was not the case for weaker amplitude internal waves in figure 2
a,d). As in figure 2(a), the outer boundary of region III in both figure 2(d,g) aligns with
![]() $\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
(shear-aligned perturbations) as
$\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
(shear-aligned perturbations) as
![]() $\unicode[STIX]{x1D703}_{0}\rightarrow 0^{\circ }$
.
$\unicode[STIX]{x1D703}_{0}\rightarrow 0^{\circ }$
.
At a moderate-amplitude and intermediate internal wave angle, i.e.
![]() $(A,\unicode[STIX]{x1D6F7})=(1,45^{\circ })$
(figure 2
e), the instability islands cover a large part of the
$(A,\unicode[STIX]{x1D6F7})=(1,45^{\circ })$
(figure 2
e), the instability islands cover a large part of the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane, but are nestled among a still sizeable region of stability. When compared with figure 2(b,e) has an additional region of instability (region IV) close to the
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane, but are nestled among a still sizeable region of stability. When compared with figure 2(b,e) has an additional region of instability (region IV) close to the
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis, apart from the fact that the original instability regions from
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis, apart from the fact that the original instability regions from
![]() $A=0.1$
have become wider and stronger for
$A=0.1$
have become wider and stronger for
![]() $A=1$
. Similar to what is seen in figure 2(d,g), as
$A=1$
. Similar to what is seen in figure 2(d,g), as
![]() $A$
increases to
$A$
increases to
![]() $10$
for
$10$
for
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
(see figure 2
h), the entire
$\unicode[STIX]{x1D6F7}=45^{\circ }$
(see figure 2
h), the entire
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane becomes effectively unstable. Strikingly, there are at least two more separate instability regions for
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane becomes effectively unstable. Strikingly, there are at least two more separate instability regions for
![]() $A=10$
(figure 2
h) when compared with
$A=10$
(figure 2
h) when compared with
![]() $A=1$
(figure 2
e). The largest growth rate for
$A=1$
(figure 2
e). The largest growth rate for
![]() $(A,\unicode[STIX]{x1D6F7})=(10,45^{\circ })$
occurs for purely transverse perturbations (
$(A,\unicode[STIX]{x1D6F7})=(10,45^{\circ })$
occurs for purely transverse perturbations (
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
). There is, however, a ridge-like feature spanning nearly all of
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
). There is, however, a ridge-like feature spanning nearly all of
![]() $\unicode[STIX]{x1D703}_{0}$
along
$\unicode[STIX]{x1D703}_{0}$
along
![]() $\unicode[STIX]{x1D719}_{0}\approx 45^{\circ }$
, on which the growth rate is quite close to the maximum growth rate (which occurs on
$\unicode[STIX]{x1D719}_{0}\approx 45^{\circ }$
, on which the growth rate is quite close to the maximum growth rate (which occurs on
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
). Interestingly, the perturbation wave vectors corresponding to this near-vertical ridge are shear-aligned, i.e.
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
). Interestingly, the perturbation wave vectors corresponding to this near-vertical ridge are shear-aligned, i.e.
![]() $\unicode[STIX]{x1D719}_{0}\approx \unicode[STIX]{x1D6F7}$
, in the
$\unicode[STIX]{x1D719}_{0}\approx \unicode[STIX]{x1D6F7}$
, in the
![]() $(x,z)$
-plane of the base flow.
$(x,z)$
-plane of the base flow.
In the shallow internal wave regime of
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
, the instability landscape of moderate amplitude internal waves of
$\unicode[STIX]{x1D6F7}=75^{\circ }$
, the instability landscape of moderate amplitude internal waves of
![]() $A=1$
are characterised by an array of several relatively thin unstable ridges, as shown in figure 2(f). We recall that only three instability ridges are discernible at
$A=1$
are characterised by an array of several relatively thin unstable ridges, as shown in figure 2(f). We recall that only three instability ridges are discernible at
![]() $A=0.1$
in figure 2(c). As the internal wave amplitude increases to
$A=0.1$
in figure 2(c). As the internal wave amplitude increases to
![]() $A=10$
(figure 2
i), the instability landscape changes significantly. The unstable ridges in figure 2(f) all seem to widen such that the entire
$A=10$
(figure 2
i), the instability landscape changes significantly. The unstable ridges in figure 2(f) all seem to widen such that the entire
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane, except for a small patch around
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane, except for a small patch around
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})=(75^{\circ },0^{\circ })$
, is unstable. Remarkably, there is now a vertical ridge (spanning the entire
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})=(75^{\circ },0^{\circ })$
, is unstable. Remarkably, there is now a vertical ridge (spanning the entire
![]() $\unicode[STIX]{x1D703}_{0}$
range of
$\unicode[STIX]{x1D703}_{0}$
range of
![]() $0^{\circ }\leqslant \unicode[STIX]{x1D703}_{0}\leqslant 90^{\circ }$
) at
$0^{\circ }\leqslant \unicode[STIX]{x1D703}_{0}\leqslant 90^{\circ }$
) at
![]() $\unicode[STIX]{x1D719}_{0}=75^{\circ }$
along which the growth rate is large and nearly uniform. The overall maximum growth rate in figure 2(i) still occurs on
$\unicode[STIX]{x1D719}_{0}=75^{\circ }$
along which the growth rate is large and nearly uniform. The overall maximum growth rate in figure 2(i) still occurs on
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
although the shear-aligned wave vectors on the vertical ridge are not far behind. Furthermore, at
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
although the shear-aligned wave vectors on the vertical ridge are not far behind. Furthermore, at
![]() $A=10$
, the maximum growth rates at
$A=10$
, the maximum growth rates at
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
are now comparable in magnitude to the growth rates at
$\unicode[STIX]{x1D6F7}=75^{\circ }$
are now comparable in magnitude to the growth rates at
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
and
$\unicode[STIX]{x1D6F7}=45^{\circ }$
and
![]() $15^{\circ }$
, suggesting that the dependence of maximum growth rate on
$15^{\circ }$
, suggesting that the dependence of maximum growth rate on
![]() $\unicode[STIX]{x1D6F7}$
is weaker at larger amplitudes.
$\unicode[STIX]{x1D6F7}$
is weaker at larger amplitudes.
Some of the distinct instability ridges seen across
![]() $\unicode[STIX]{x1D6F7}$
for
$\unicode[STIX]{x1D6F7}$
for
![]() $A=1$
in figure 2(d–f) appear to be amplified extensions of the thin instability ridges observed at
$A=1$
in figure 2(d–f) appear to be amplified extensions of the thin instability ridges observed at
![]() $A=0.1$
in figure 2(a–c). For example, the first three instability regions (I, II and III) in figure 2(d,e) clearly have thinner, weaker counterparts in figure 2(a,b). Similarly, the broad and barely separated regions of instability in figure 2(g–i) at
$A=0.1$
in figure 2(a–c). For example, the first three instability regions (I, II and III) in figure 2(d,e) clearly have thinner, weaker counterparts in figure 2(a,b). Similarly, the broad and barely separated regions of instability in figure 2(g–i) at
![]() $A=10$
seem to be extensions of the
$A=10$
seem to be extensions of the
![]() $A=1$
unstable regions in figure 2(d–f), but not necessarily with one-to-one correspondence between scenarios of the same
$A=1$
unstable regions in figure 2(d–f), but not necessarily with one-to-one correspondence between scenarios of the same
![]() $\unicode[STIX]{x1D6F7}$
. For example, the fourth instability region in figure 2(g) does not have a counterpart in figure 2(d). Additionally, the number of seemingly separate instability regions in figure 2(h) is larger than the number in figure 2(e). The unstable regions I–III at
$\unicode[STIX]{x1D6F7}$
. For example, the fourth instability region in figure 2(g) does not have a counterpart in figure 2(d). Additionally, the number of seemingly separate instability regions in figure 2(h) is larger than the number in figure 2(e). The unstable regions I–III at
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
,
$\unicode[STIX]{x1D6F7}=15^{\circ }$
,
![]() $45^{\circ }$
and
$45^{\circ }$
and
![]() $75^{\circ }$
for
$75^{\circ }$
for
![]() $A=0.1$
(in figure 2), suggest that the instabilities occurring at large
$A=0.1$
(in figure 2), suggest that the instabilities occurring at large
![]() $A$
may be linked to instabilities at small
$A$
may be linked to instabilities at small
![]() $A$
, in line with Klostermeyer (Reference Klostermeyer1991), who proposed a connection between small
$A$
, in line with Klostermeyer (Reference Klostermeyer1991), who proposed a connection between small
![]() $A$
resonances and all instability modes at all internal wave angles. Sonmor & Klaassen (Reference Sonmor and Klaassen1997) reaffirmed the conjecture of Klostermeyer (Reference Klostermeyer1991) by concluding that there exist no instabilities in finite-amplitude plane internal waves that cannot be traced back to resonant instabilities at small
$A$
resonances and all instability modes at all internal wave angles. Sonmor & Klaassen (Reference Sonmor and Klaassen1997) reaffirmed the conjecture of Klostermeyer (Reference Klostermeyer1991) by concluding that there exist no instabilities in finite-amplitude plane internal waves that cannot be traced back to resonant instabilities at small
![]() $A$
. The connection between small
$A$
. The connection between small
![]() $A$
resonances and finite
$A$
resonances and finite
![]() $A$
instabilities is addressed more rigorously in §§ 3.4 and 3.5.
$A$
instabilities is addressed more rigorously in §§ 3.4 and 3.5.
3.2 Two-dimensional PSI
In the limit of 2-D perturbations, i.e.
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
and small
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
and small
![]() $A$
, the local stability approach shows the existence of two distinct values of
$A$
, the local stability approach shows the existence of two distinct values of
![]() $\unicode[STIX]{x1D719}_{0}$
at which thin instability peaks are present (figure 2
a–c). In this section, we verify that these peaks arise from a resonant wave triad, and proceed to establish correspondence with existing results on 2-D PSI. Furthermore, the local stability approach facilitates an investigation of how 2-D PSI continuously extends towards large internal wave amplitudes as well as 3-D perturbations (we discuss the latter in § 3.3).
$\unicode[STIX]{x1D719}_{0}$
at which thin instability peaks are present (figure 2
a–c). In this section, we verify that these peaks arise from a resonant wave triad, and proceed to establish correspondence with existing results on 2-D PSI. Furthermore, the local stability approach facilitates an investigation of how 2-D PSI continuously extends towards large internal wave amplitudes as well as 3-D perturbations (we discuss the latter in § 3.3).
Resonant triad interaction (RTI) represents a mechanism by which a pair of subharmonic or superharmonic internal waves extract energy from a primary internal wave through the formation of a resonant triad (Mied Reference Mied1976). Such a resonant triad is formed when the spatial and temporal resonant conditions are satisfied:
and
where the internal wave
![]() $(\boldsymbol{k},\unicode[STIX]{x1D714})$
resonantly interacts with the internal waves
$(\boldsymbol{k},\unicode[STIX]{x1D714})$
resonantly interacts with the internal waves
![]() $(\boldsymbol{k}_{1},\unicode[STIX]{x1D714}_{1})$
and
$(\boldsymbol{k}_{1},\unicode[STIX]{x1D714}_{1})$
and
![]() $(\boldsymbol{k}_{2},\unicode[STIX]{x1D714}_{2})$
, and
$(\boldsymbol{k}_{2},\unicode[STIX]{x1D714}_{2})$
, and
![]() $n$
is any positive integer (Hasselmann Reference Hasselmann1967; Drazin Reference Drazin1977). In the context of RTI,
$n$
is any positive integer (Hasselmann Reference Hasselmann1967; Drazin Reference Drazin1977). In the context of RTI,
![]() $(\boldsymbol{k},\unicode[STIX]{x1D714})$
denote the primary wave properties presented in (2.7), the subscripts
$(\boldsymbol{k},\unicode[STIX]{x1D714})$
denote the primary wave properties presented in (2.7), the subscripts
![]() $1$
and
$1$
and
![]() $2$
denote subharmonic daughter waves and
$2$
denote subharmonic daughter waves and
![]() $n+1$
is the order of the resonance. In this section and the next (§ 3.3), we will focus on second-order wave interactions, which take place for
$n+1$
is the order of the resonance. In this section and the next (§ 3.3), we will focus on second-order wave interactions, which take place for
![]() $n=1$
; higher order resonances (
$n=1$
; higher order resonances (
![]() $n>1$
) are discussed in § 3.4.
$n>1$
) are discussed in § 3.4.
To illustrate the main features of 2-D RTI, i.e. resonant triads formed in the plane of the primary wave, we begin by considering an arbitrary pair of daughter waves,
![]() $(\boldsymbol{k}_{1},\unicode[STIX]{x1D714}_{1})$
and
$(\boldsymbol{k}_{1},\unicode[STIX]{x1D714}_{1})$
and
![]() $(\boldsymbol{k}_{2},\unicode[STIX]{x1D714}_{2})$
, for a given primary wave
$(\boldsymbol{k}_{2},\unicode[STIX]{x1D714}_{2})$
, for a given primary wave
![]() $(\boldsymbol{k},\unicode[STIX]{x1D714})$
. The conditions (3.1) and (3.2) with
$(\boldsymbol{k},\unicode[STIX]{x1D714})$
. The conditions (3.1) and (3.2) with
![]() $n=1$
, together with the dispersion relation (2.8) for all three waves, can be solved to obtain a relation between
$n=1$
, together with the dispersion relation (2.8) for all three waves, can be solved to obtain a relation between
![]() $m_{1}$
and
$m_{1}$
and
![]() $k_{1}$
, where
$k_{1}$
, where
![]() $\boldsymbol{k}_{1}=(k_{1},0,m_{1})$
(see Bourget et al.
Reference Bourget, Dauxois, Joubaud and Odier2013, equation (3.29)). A plot of
$\boldsymbol{k}_{1}=(k_{1},0,m_{1})$
(see Bourget et al.
Reference Bourget, Dauxois, Joubaud and Odier2013, equation (3.29)). A plot of
![]() $m_{1}$
(normalised by the primary vertical wavenumber
$m_{1}$
(normalised by the primary vertical wavenumber
![]() $m$
) as a function of
$m$
) as a function of
![]() $k_{1}$
(normalised by the primary horizontal wavenumber
$k_{1}$
(normalised by the primary horizontal wavenumber
![]() $k$
) is shown in figure 3(a). Any point on this resonance curve describes the tip of
$k$
) is shown in figure 3(a). Any point on this resonance curve describes the tip of
![]() $\boldsymbol{k}_{1}$
, which when subtracted from the primary wave vector
$\boldsymbol{k}_{1}$
, which when subtracted from the primary wave vector
![]() $\boldsymbol{k}$
– located at
$\boldsymbol{k}$
– located at
![]() $(1,1)$
in figure 3(a) – will yield the
$(1,1)$
in figure 3(a) – will yield the
![]() $\boldsymbol{k}_{2}$
that completes the resonant triad (Phillips Reference Phillips1977). An example resonant triad is presented in figure 3(a).
$\boldsymbol{k}_{2}$
that completes the resonant triad (Phillips Reference Phillips1977). An example resonant triad is presented in figure 3(a).

Figure 3. (a) The
![]() $\boldsymbol{k}_{1}$
resonance curve (solid black line) for a primary wave
$\boldsymbol{k}_{1}$
resonance curve (solid black line) for a primary wave
![]() $\boldsymbol{k}=(k,0,m)$
(depicted by the arrow starting at the origin and ending at point
$\boldsymbol{k}=(k,0,m)$
(depicted by the arrow starting at the origin and ending at point
![]() $(1,1)$
) obtained from the solution to the set of equations comprising the resonant conditions (3.1) and (3.2) (for
$(1,1)$
) obtained from the solution to the set of equations comprising the resonant conditions (3.1) and (3.2) (for
![]() $n=1$
) and the dispersion relation (2.8). Superposed onto the resonance curve is a representative PSI resonant triad:
$n=1$
) and the dispersion relation (2.8). Superposed onto the resonance curve is a representative PSI resonant triad:
![]() $\boldsymbol{k}$
(——),
$\boldsymbol{k}$
(——),
![]() $\boldsymbol{k}_{1}$
(— ⋅ —), and
$\boldsymbol{k}_{1}$
(— ⋅ —), and
![]() $\boldsymbol{k}_{2}$
(
$\boldsymbol{k}_{2}$
(
![]() $\cdots$
). (b) The instability growth rates (solid line), as derived by Koudella & Staquet (Reference Koudella and Staquet2006), corresponding to the resonance curve in panel (a) for
$\cdots$
). (b) The instability growth rates (solid line), as derived by Koudella & Staquet (Reference Koudella and Staquet2006), corresponding to the resonance curve in panel (a) for
![]() $(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
. The asymptotic values of the growth rate in the PSI limit for branch-A and branch-B (denoted by ○ and ▵, respectively), as derived by Sonmor & Klaassen (Reference Sonmor and Klaassen1997), are consistent with Koudella & Staquet (Reference Koudella and Staquet2006).
$(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
. The asymptotic values of the growth rate in the PSI limit for branch-A and branch-B (denoted by ○ and ▵, respectively), as derived by Sonmor & Klaassen (Reference Sonmor and Klaassen1997), are consistent with Koudella & Staquet (Reference Koudella and Staquet2006).
Of particular relevance to our study is the limit where the magnitudes of
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
are significantly larger than
$\boldsymbol{k}_{2}$
are significantly larger than
![]() $\boldsymbol{k}$
, which translates to short-wavelength perturbations (i.e. daughter waves) relative to the base flow (i.e. primary wave). In this limit (
$\boldsymbol{k}$
, which translates to short-wavelength perturbations (i.e. daughter waves) relative to the base flow (i.e. primary wave). In this limit (
![]() $|k_{1}|\rightarrow \infty$
and
$|k_{1}|\rightarrow \infty$
and
![]() $\boldsymbol{k}_{1}$
lying on the resonance curve in figure 3
a),
$\boldsymbol{k}_{1}$
lying on the resonance curve in figure 3
a),
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
become increasingly anti-parallel, and both
$\boldsymbol{k}_{2}$
become increasingly anti-parallel, and both
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{2}$
approach
$\unicode[STIX]{x1D714}_{2}$
approach
![]() $\unicode[STIX]{x1D714}/2$
. The class of resonant triads characterised by long, anti-parallel perturbation wave vectors with frequencies that are half the primary wave frequency is referred to as PSI (McComas & Bretherton Reference Mccomas and Bretherton1977; Dauxois et al.
Reference Dauxois, Joubaud, Odier and Venaille2018).
$\unicode[STIX]{x1D714}/2$
. The class of resonant triads characterised by long, anti-parallel perturbation wave vectors with frequencies that are half the primary wave frequency is referred to as PSI (McComas & Bretherton Reference Mccomas and Bretherton1977; Dauxois et al.
Reference Dauxois, Joubaud, Odier and Venaille2018).
Since the local stability approach and PSI both concern small-scale perturbations, we proceed to investigate the extent to which the local stability approach recovers 2-D PSI characteristics, i.e. the daughter wave vectors and associated growth rates. We focus on the case presented in figure 2(b), i.e.
![]() $(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
, which corresponds to an isopycnal steepness of
$(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
, which corresponds to an isopycnal steepness of
![]() $s\approx 0.07$
. For 2-D perturbations (
$s\approx 0.07$
. For 2-D perturbations (
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
), the local stability approach identifies instabilities at
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
), the local stability approach identifies instabilities at
![]() $\unicode[STIX]{x1D719}_{0,1}\approx 69^{\circ }$
and
$\unicode[STIX]{x1D719}_{0,1}\approx 69^{\circ }$
and
![]() $\unicode[STIX]{x1D719}_{0,3}\approx 111^{\circ }$
, and (by virtue of the periodicity of
$\unicode[STIX]{x1D719}_{0,3}\approx 111^{\circ }$
, and (by virtue of the periodicity of
![]() $\unicode[STIX]{x1D70E}$
with
$\unicode[STIX]{x1D70E}$
with
![]() $\unicode[STIX]{x1D719}_{0}$
) at
$\unicode[STIX]{x1D719}_{0}$
) at
![]() $\unicode[STIX]{x1D719}_{0,2}=\unicode[STIX]{x1D719}_{0,1}+180^{\circ }$
and
$\unicode[STIX]{x1D719}_{0,2}=\unicode[STIX]{x1D719}_{0,1}+180^{\circ }$
and
![]() $\unicode[STIX]{x1D719}_{0,4}=\unicode[STIX]{x1D719}_{0,3}+180^{\circ }$
. The wave vectors
$\unicode[STIX]{x1D719}_{0,4}=\unicode[STIX]{x1D719}_{0,3}+180^{\circ }$
. The wave vectors
![]() $\unicode[STIX]{x1D73F}_{0,1}=\unicode[STIX]{x1D73F}_{0}(\unicode[STIX]{x1D719}_{0,1},\unicode[STIX]{x1D703}_{0}=0^{\circ })$
and
$\unicode[STIX]{x1D73F}_{0,1}=\unicode[STIX]{x1D73F}_{0}(\unicode[STIX]{x1D719}_{0,1},\unicode[STIX]{x1D703}_{0}=0^{\circ })$
and
![]() $\unicode[STIX]{x1D73F}_{0,2}=\unicode[STIX]{x1D73F}_{0}(\unicode[STIX]{x1D719}_{0,2},\unicode[STIX]{x1D703}_{0}=0^{\circ })$
, together with the base flow wave vector
$\unicode[STIX]{x1D73F}_{0,2}=\unicode[STIX]{x1D73F}_{0}(\unicode[STIX]{x1D719}_{0,2},\unicode[STIX]{x1D703}_{0}=0^{\circ })$
, together with the base flow wave vector
![]() $\boldsymbol{k}$
, satisfy the spatial triadic resonance condition (3.1) as
$\boldsymbol{k}$
, satisfy the spatial triadic resonance condition (3.1) as
where
![]() $\unicode[STIX]{x1D73F}_{0,1}$
and
$\unicode[STIX]{x1D73F}_{0,1}$
and
![]() $\unicode[STIX]{x1D73F}_{0,2}$
are anti-parallel to each other, and represent wave vectors of much larger magnitude than the base flow wave vector due to the short-wavelength approximation. Thus, the wave vectors
$\unicode[STIX]{x1D73F}_{0,2}$
are anti-parallel to each other, and represent wave vectors of much larger magnitude than the base flow wave vector due to the short-wavelength approximation. Thus, the wave vectors
![]() $\unicode[STIX]{x1D73F}_{0,1}$
and
$\unicode[STIX]{x1D73F}_{0,1}$
and
![]() $\unicode[STIX]{x1D73F}_{0,2}$
are consistent with the daughter wave vectors in the PSI limit shown in figure 3(a).
$\unicode[STIX]{x1D73F}_{0,2}$
are consistent with the daughter wave vectors in the PSI limit shown in figure 3(a).
If
![]() $\unicode[STIX]{x1D73F}_{0,1}$
and
$\unicode[STIX]{x1D73F}_{0,1}$
and
![]() $\unicode[STIX]{x1D73F}_{0,2}$
are to represent internal wave vectors, then the corresponding frequencies based on the dispersion relation should be
$\unicode[STIX]{x1D73F}_{0,2}$
are to represent internal wave vectors, then the corresponding frequencies based on the dispersion relation should be
![]() $\unicode[STIX]{x1D714}_{1}/N=\cos \unicode[STIX]{x1D719}_{0,1}\approx 0.36$
and
$\unicode[STIX]{x1D714}_{1}/N=\cos \unicode[STIX]{x1D719}_{0,1}\approx 0.36$
and
![]() $\unicode[STIX]{x1D714}_{2}/N=-\text{cos}\,\unicode[STIX]{x1D719}_{0,2}\approx 0.36$
, both of which equal approximately half of the base flow wave frequency
$\unicode[STIX]{x1D714}_{2}/N=-\text{cos}\,\unicode[STIX]{x1D719}_{0,2}\approx 0.36$
, both of which equal approximately half of the base flow wave frequency
![]() $\unicode[STIX]{x1D714}/N=\cos \unicode[STIX]{x1D6F7}\approx 0.71$
. Given that the local stability framework allows the perturbation wave vectors to evolve in time, we verify that the PSI triadic resonance conditions are satisfied over the entire time period
$\unicode[STIX]{x1D714}/N=\cos \unicode[STIX]{x1D6F7}\approx 0.71$
. Given that the local stability framework allows the perturbation wave vectors to evolve in time, we verify that the PSI triadic resonance conditions are satisfied over the entire time period
![]() $0\leqslant t\cos \unicode[STIX]{x1D6F7}<2\unicode[STIX]{x03C0}$
by computing
$0\leqslant t\cos \unicode[STIX]{x1D6F7}<2\unicode[STIX]{x03C0}$
by computing
![]() $\unicode[STIX]{x1D73F}_{0,1}(t)$
and
$\unicode[STIX]{x1D73F}_{0,1}(t)$
and
![]() $\unicode[STIX]{x1D73F}_{0,2}(t)$
via (2.17) and confirming them to be effectively constant in time, with
$\unicode[STIX]{x1D73F}_{0,2}(t)$
via (2.17) and confirming them to be effectively constant in time, with
![]() ${\lesssim}5\,\%$
variation (the variation decreases as
${\lesssim}5\,\%$
variation (the variation decreases as
![]() $A$
decreases). We have thus established that the internal waves at the unstable wave vectors
$A$
decreases). We have thus established that the internal waves at the unstable wave vectors
![]() $\unicode[STIX]{x1D73F}_{0,1}$
and
$\unicode[STIX]{x1D73F}_{0,1}$
and
![]() $\unicode[STIX]{x1D73F}_{0,2}$
from the local stability approach indeed satisfy the classical PSI triadic resonance conditions with the base flow wave vector. A similar calculation reveals that the internal waves at the unstable wave vectors
$\unicode[STIX]{x1D73F}_{0,2}$
from the local stability approach indeed satisfy the classical PSI triadic resonance conditions with the base flow wave vector. A similar calculation reveals that the internal waves at the unstable wave vectors
![]() $\unicode[STIX]{x1D73F}_{0,3}$
and
$\unicode[STIX]{x1D73F}_{0,3}$
and
![]() $\unicode[STIX]{x1D73F}_{0,4}$
are also in PSI triadic resonance with
$\unicode[STIX]{x1D73F}_{0,4}$
are also in PSI triadic resonance with
![]() $\boldsymbol{k}$
. In summary, each of the two pairs of unstable 2-D perturbation wave vectors from the local stability approach represent a daughter wave pair that is in PSI resonance with
$\boldsymbol{k}$
. In summary, each of the two pairs of unstable 2-D perturbation wave vectors from the local stability approach represent a daughter wave pair that is in PSI resonance with
![]() $\boldsymbol{k}$
. We proceed to investigate the growth rate at these unstable wave vectors.
$\boldsymbol{k}$
. We proceed to investigate the growth rate at these unstable wave vectors.
For small isopycnal steepness (
![]() $s\ll 1$
) of the primary wave, the growth rate corresponding to any resonant triad in the plane of the primary wave is (Koudella & Staquet Reference Koudella and Staquet2006, § 4.3.1)
$s\ll 1$
) of the primary wave, the growth rate corresponding to any resonant triad in the plane of the primary wave is (Koudella & Staquet Reference Koudella and Staquet2006, § 4.3.1)
where
the subscripts
![]() $p,q,r=1,2,3$
form a circular permutation, with
$p,q,r=1,2,3$
form a circular permutation, with
![]() $1$
and
$1$
and
![]() $2$
denoting the daughter waves and
$2$
denoting the daughter waves and
![]() $3$
denoting the primary wave.
$3$
denoting the primary wave.
Figure 3(b) shows
![]() $\unicode[STIX]{x1D70E}_{\text{KS}}$
as a function of
$\unicode[STIX]{x1D70E}_{\text{KS}}$
as a function of
![]() $k_{1}/k$
, from which we see that the growth rate approaches two different asymptotic values at the PSI limits
$k_{1}/k$
, from which we see that the growth rate approaches two different asymptotic values at the PSI limits
![]() $k_{1}\rightarrow \pm \infty$
. The larger asymptote (corresponding to the maximum PSI growth rate) occurs as
$k_{1}\rightarrow \pm \infty$
. The larger asymptote (corresponding to the maximum PSI growth rate) occurs as
![]() $k_{1}\rightarrow \infty$
, and is referred to as branch-A PSI. The smaller asymptote occurs in the limit
$k_{1}\rightarrow \infty$
, and is referred to as branch-A PSI. The smaller asymptote occurs in the limit
![]() $k_{1}\rightarrow -\infty$
, and is referred to as branch-B PSI. The growth rates in these two limits are (Sonmor & Klaassen Reference Sonmor and Klaassen1997, § 3):
$k_{1}\rightarrow -\infty$
, and is referred to as branch-B PSI. The growth rates in these two limits are (Sonmor & Klaassen Reference Sonmor and Klaassen1997, § 3):
where the upper and lower signs correspond to branch-A and -B, respectively (in figure 3(b) we confirm that
![]() $\unicode[STIX]{x1D70E}_{\text{KS}}$
approaches
$\unicode[STIX]{x1D70E}_{\text{KS}}$
approaches
![]() $\unicode[STIX]{x1D70E}_{\text{SK}}$
at the PSI limits). We denote the 2-D PSI growth rates in (3.6) associated with branch-A and branch-B as
$\unicode[STIX]{x1D70E}_{\text{SK}}$
at the PSI limits). We denote the 2-D PSI growth rates in (3.6) associated with branch-A and branch-B as
![]() $\unicode[STIX]{x1D70E}_{A}$
and
$\unicode[STIX]{x1D70E}_{A}$
and
![]() $\unicode[STIX]{x1D70E}_{B}$
, respectively.
$\unicode[STIX]{x1D70E}_{B}$
, respectively.
We find, for
![]() $(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
, the local stability growth rates to be
$(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
, the local stability growth rates to be
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,1},\unicode[STIX]{x1D703}_{0}=0^{\circ })=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,2},\unicode[STIX]{x1D703}_{0}=0^{\circ })=0.01970$
, which is within
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,1},\unicode[STIX]{x1D703}_{0}=0^{\circ })=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,2},\unicode[STIX]{x1D703}_{0}=0^{\circ })=0.01970$
, which is within
![]() $0.002\,\%$
of
$0.002\,\%$
of
![]() $\unicode[STIX]{x1D70E}_{A}=0.01966$
. Similarly,
$\unicode[STIX]{x1D70E}_{A}=0.01966$
. Similarly,
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,3},\unicode[STIX]{x1D703}_{0}=0^{\circ })=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,4},\unicode[STIX]{x1D703}_{0}=0^{\circ })=0.01349$
, which is within
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,3},\unicode[STIX]{x1D703}_{0}=0^{\circ })=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0,4},\unicode[STIX]{x1D703}_{0}=0^{\circ })=0.01349$
, which is within
![]() $0.006\,\%$
of
$0.006\,\%$
of
![]() $\unicode[STIX]{x1D70E}_{B}=0.01341$
. Summarising our investigations at other
$\unicode[STIX]{x1D70E}_{B}=0.01341$
. Summarising our investigations at other
![]() $\unicode[STIX]{x1D6F7}$
, we conclude that the local stability approach, for small
$\unicode[STIX]{x1D6F7}$
, we conclude that the local stability approach, for small
![]() $A$
internal waves and 2-D perturbations, recovers sharp instability peaks at
$A$
internal waves and 2-D perturbations, recovers sharp instability peaks at
![]() $\unicode[STIX]{x1D719}_{0,1}=\cos ^{-1}(\cos \unicode[STIX]{x1D6F7}/2)$
and
$\unicode[STIX]{x1D719}_{0,1}=\cos ^{-1}(\cos \unicode[STIX]{x1D6F7}/2)$
and
![]() $\unicode[STIX]{x1D719}_{0,2}=\unicode[STIX]{x1D719}_{0,1}+180^{\circ }$
, the growth rates at which match with that of branch-A PSI. The local stability approach also recovers sharp instability peaks at
$\unicode[STIX]{x1D719}_{0,2}=\unicode[STIX]{x1D719}_{0,1}+180^{\circ }$
, the growth rates at which match with that of branch-A PSI. The local stability approach also recovers sharp instability peaks at
![]() $\unicode[STIX]{x1D719}_{0,3}=\cos ^{-1}(-\text{cos}\,\unicode[STIX]{x1D6F7}/2)$
and
$\unicode[STIX]{x1D719}_{0,3}=\cos ^{-1}(-\text{cos}\,\unicode[STIX]{x1D6F7}/2)$
and
![]() $\unicode[STIX]{x1D719}_{0,4}=\unicode[STIX]{x1D719}_{0,3}+180^{\circ }$
, the growth rates at which match with that of branch-B PSI. We now perform a more comprehensive comparison of 2-D PSI growth rates derived by Sonmor & Klaassen (Reference Sonmor and Klaassen1997) (
$\unicode[STIX]{x1D719}_{0,4}=\unicode[STIX]{x1D719}_{0,3}+180^{\circ }$
, the growth rates at which match with that of branch-B PSI. We now perform a more comprehensive comparison of 2-D PSI growth rates derived by Sonmor & Klaassen (Reference Sonmor and Klaassen1997) (
![]() $\unicode[STIX]{x1D70E}_{A}$
and
$\unicode[STIX]{x1D70E}_{A}$
and
![]() $\unicode[STIX]{x1D70E}_{B}$
) and our local stability approach (
$\unicode[STIX]{x1D70E}_{B}$
) and our local stability approach (
![]() $\unicode[STIX]{x1D70E}_{A}^{L}$
and
$\unicode[STIX]{x1D70E}_{A}^{L}$
and
![]() $\unicode[STIX]{x1D70E}_{B}^{L}$
).
$\unicode[STIX]{x1D70E}_{B}^{L}$
).

Figure 4. 2-D PSI growth rates (a–c) and corresponding wave vector orientations (d–f) presented as a function of
![]() $A$
for
$A$
for
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
,
$\unicode[STIX]{x1D6F7}=15^{\circ }$
,
![]() $45^{\circ }$
and
$45^{\circ }$
and
![]() $75^{\circ }$
(left, middle and right columns, respectively). The solid and dashed lines in panels (a–c), respectively, denote the branch-A and branch-B PSI growth rates derived by Sonmor & Klaassen (Reference Sonmor and Klaassen1997) in (3.6); the solid and dashed lines in panels (d–f) denote the corresponding perturbation wave vector orientations given by
$75^{\circ }$
(left, middle and right columns, respectively). The solid and dashed lines in panels (a–c), respectively, denote the branch-A and branch-B PSI growth rates derived by Sonmor & Klaassen (Reference Sonmor and Klaassen1997) in (3.6); the solid and dashed lines in panels (d–f) denote the corresponding perturbation wave vector orientations given by
![]() $\cos ^{-1}(\pm \cos \unicode[STIX]{x1D6F7}/2)$
. Our local stability results are denoted by ○ and ▵ for branch-A and branch-B PSI, respectively. The vertical lines associated with our results in panels (d–f) denote the width of the PSI peaks, with the colour intensity indicating the growth rates normalised by the corresponding growth rates plotted in panels (a–c). The value
$\cos ^{-1}(\pm \cos \unicode[STIX]{x1D6F7}/2)$
. Our local stability results are denoted by ○ and ▵ for branch-A and branch-B PSI, respectively. The vertical lines associated with our results in panels (d–f) denote the width of the PSI peaks, with the colour intensity indicating the growth rates normalised by the corresponding growth rates plotted in panels (a–c). The value
![]() $s=0.1$
is indicated in each panel by a dotted vertical line, indicating the upper limit of the small
$s=0.1$
is indicated in each panel by a dotted vertical line, indicating the upper limit of the small
![]() $s$
regime.
$s$
regime.
For a given
![]() $(A,\unicode[STIX]{x1D6F7})$
, we calculate the maximum growth rate
$(A,\unicode[STIX]{x1D6F7})$
, we calculate the maximum growth rate
![]() $\unicode[STIX]{x1D70E}_{A}^{L}$
within the instability peak associated with
$\unicode[STIX]{x1D70E}_{A}^{L}$
within the instability peak associated with
![]() $\unicode[STIX]{x1D719}_{0,1}=\cos ^{-1}(\cos \unicode[STIX]{x1D6F7}/2)$
for 2-D perturbations (
$\unicode[STIX]{x1D719}_{0,1}=\cos ^{-1}(\cos \unicode[STIX]{x1D6F7}/2)$
for 2-D perturbations (
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
); the corresponding location of locally maximum growth rate is denoted
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
); the corresponding location of locally maximum growth rate is denoted
![]() $\unicode[STIX]{x1D719}_{0,1}^{\ast }$
, which equals
$\unicode[STIX]{x1D719}_{0,1}^{\ast }$
, which equals
![]() $\unicode[STIX]{x1D719}_{0,1}$
only for sufficiently small
$\unicode[STIX]{x1D719}_{0,1}$
only for sufficiently small
![]() $A$
since the peaks around
$A$
since the peaks around
![]() $\unicode[STIX]{x1D719}_{0,1}$
(and
$\unicode[STIX]{x1D719}_{0,1}$
(and
![]() $\unicode[STIX]{x1D719}_{0,3}$
) expand into finite-width instability regions as
$\unicode[STIX]{x1D719}_{0,3}$
) expand into finite-width instability regions as
![]() $A$
increases. Similarly, the maximum growth rate within the instability peak around
$A$
increases. Similarly, the maximum growth rate within the instability peak around
![]() $\unicode[STIX]{x1D719}_{0,3}=\cos ^{-1}(-\text{cos}\,\unicode[STIX]{x1D6F7}/2)$
is denoted as
$\unicode[STIX]{x1D719}_{0,3}=\cos ^{-1}(-\text{cos}\,\unicode[STIX]{x1D6F7}/2)$
is denoted as
![]() $\unicode[STIX]{x1D70E}_{B}^{L}$
, and the corresponding location of locally maximum growth rate is
$\unicode[STIX]{x1D70E}_{B}^{L}$
, and the corresponding location of locally maximum growth rate is
![]() $\unicode[STIX]{x1D719}_{0,3}^{\ast }$
. In the top row of figure 4, we plot
$\unicode[STIX]{x1D719}_{0,3}^{\ast }$
. In the top row of figure 4, we plot
![]() $\unicode[STIX]{x1D70E}_{A}^{L}$
and
$\unicode[STIX]{x1D70E}_{A}^{L}$
and
![]() $\unicode[STIX]{x1D70E}_{B}^{L}$
as a function of
$\unicode[STIX]{x1D70E}_{B}^{L}$
as a function of
![]() $A$
for three different internal wave orientations (
$A$
for three different internal wave orientations (
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
,
$\unicode[STIX]{x1D6F7}=15^{\circ }$
,
![]() $45^{\circ }$
, and
$45^{\circ }$
, and
![]() $75^{\circ }$
in figure 4
a–c, respectively). For all three
$75^{\circ }$
in figure 4
a–c, respectively). For all three
![]() $\unicode[STIX]{x1D6F7}$
, there is excellent quantitative agreement between
$\unicode[STIX]{x1D6F7}$
, there is excellent quantitative agreement between
![]() $\unicode[STIX]{x1D70E}_{A,B}^{L}$
(denoted by ○ and ▵ for branch-A and -B, respectively) and the
$\unicode[STIX]{x1D70E}_{A,B}^{L}$
(denoted by ○ and ▵ for branch-A and -B, respectively) and the
![]() $\unicode[STIX]{x1D70E}_{A,B}$
growth rates of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) (denoted by solid and dashed lines for branch-A and -B, respectively) for
$\unicode[STIX]{x1D70E}_{A,B}$
growth rates of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) (denoted by solid and dashed lines for branch-A and -B, respectively) for
![]() $s<0.1$
(
$s<0.1$
(
![]() $s=0.1$
is indicated by the vertical dotted lines in all panels of figure 4). The bottom row of figure 4 shows the variation of
$s=0.1$
is indicated by the vertical dotted lines in all panels of figure 4). The bottom row of figure 4 shows the variation of
![]() $\unicode[STIX]{x1D719}_{0,1}^{\ast }$
and
$\unicode[STIX]{x1D719}_{0,1}^{\ast }$
and
![]() $\unicode[STIX]{x1D719}_{0,3}^{\ast }$
with
$\unicode[STIX]{x1D719}_{0,3}^{\ast }$
with
![]() $A$
, which are in excellent agreement with
$A$
, which are in excellent agreement with
![]() $\unicode[STIX]{x1D719}_{0,1}$
and
$\unicode[STIX]{x1D719}_{0,1}$
and
![]() $\unicode[STIX]{x1D719}_{0,3}$
, respectively, for
$\unicode[STIX]{x1D719}_{0,3}$
, respectively, for
![]() $s<0.1$
. Also shown in the bottom row of figure 4 (using vertical bars) are the widths, along
$s<0.1$
. Also shown in the bottom row of figure 4 (using vertical bars) are the widths, along
![]() $\unicode[STIX]{x1D719}_{0}$
of the corresponding instability regions; the widths remain close to zero for
$\unicode[STIX]{x1D719}_{0}$
of the corresponding instability regions; the widths remain close to zero for
![]() $s<0.1$
at all
$s<0.1$
at all
![]() $\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}$
.
As
![]() $A$
, and thus
$A$
, and thus
![]() $s$
, increases, there is a noticeable deviation of the local stability growth rates from the PSI growth rates of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) (top row of figure 4). Around
$s$
, increases, there is a noticeable deviation of the local stability growth rates from the PSI growth rates of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) (top row of figure 4). Around
![]() $s\approx 0.5$
, PSI theory breaks down regardless of the specific
$s\approx 0.5$
, PSI theory breaks down regardless of the specific
![]() $A$
and
$A$
and
![]() $\unicode[STIX]{x1D6F7}$
values. For each
$\unicode[STIX]{x1D6F7}$
values. For each
![]() $\unicode[STIX]{x1D6F7}$
, in the large
$\unicode[STIX]{x1D6F7}$
, in the large
![]() $A$
limit,
$A$
limit,
![]() $\unicode[STIX]{x1D70E}_{A}^{L}$
and
$\unicode[STIX]{x1D70E}_{A}^{L}$
and
![]() $\unicode[STIX]{x1D70E}_{B}^{L}$
converge and saturate at
$\unicode[STIX]{x1D70E}_{B}^{L}$
converge and saturate at
![]() ${\approx}1$
, which, in dimensional time, corresponds to a growth rate of
${\approx}1$
, which, in dimensional time, corresponds to a growth rate of
![]() ${\approx}N$
. In summary, branch-A PSI dominates branch-B PSI at small
${\approx}N$
. In summary, branch-A PSI dominates branch-B PSI at small
![]() $A$
, but the growth rates of both branches converge to a similar value at large
$A$
, but the growth rates of both branches converge to a similar value at large
![]() $A$
. We note that the intriguing convergence of the local stability PSI growth rates in the large
$A$
. We note that the intriguing convergence of the local stability PSI growth rates in the large
![]() $A$
limit revealed by the local stability approach is beyond the scope of classical PSI theories. We further note that as
$A$
limit revealed by the local stability approach is beyond the scope of classical PSI theories. We further note that as
![]() $A$
increases, the unstable perturbation wave vectors initialised at
$A$
increases, the unstable perturbation wave vectors initialised at
![]() $\unicode[STIX]{x1D73F}_{0}(\unicode[STIX]{x1D719}_{0,1-4}^{\ast },\unicode[STIX]{x1D703}_{0}=0^{\circ })$
begin to substantially evolve along the base flow fluid particle trajectories and can no longer be classified as internal waves.
$\unicode[STIX]{x1D73F}_{0}(\unicode[STIX]{x1D719}_{0,1-4}^{\ast },\unicode[STIX]{x1D703}_{0}=0^{\circ })$
begin to substantially evolve along the base flow fluid particle trajectories and can no longer be classified as internal waves.
For
![]() $s>0.1$
,
$s>0.1$
,
![]() $\unicode[STIX]{x1D719}_{0,1}^{\ast }$
and
$\unicode[STIX]{x1D719}_{0,1}^{\ast }$
and
![]() $\unicode[STIX]{x1D719}_{0,3}^{\ast }$
deviate noticeably from the branch-A and -B PSI theoretical estimates
$\unicode[STIX]{x1D719}_{0,3}^{\ast }$
deviate noticeably from the branch-A and -B PSI theoretical estimates
![]() $\unicode[STIX]{x1D719}_{0,1}$
and
$\unicode[STIX]{x1D719}_{0,1}$
and
![]() $\unicode[STIX]{x1D719}_{0,3}$
, respectively. As
$\unicode[STIX]{x1D719}_{0,3}$
, respectively. As
![]() $\unicode[STIX]{x1D6F7}$
increases, however, the deviations of
$\unicode[STIX]{x1D6F7}$
increases, however, the deviations of
![]() $\unicode[STIX]{x1D719}_{0,1}^{\ast }$
from
$\unicode[STIX]{x1D719}_{0,1}^{\ast }$
from
![]() $\unicode[STIX]{x1D719}_{0,1}$
decrease, while the deviations of
$\unicode[STIX]{x1D719}_{0,1}$
decrease, while the deviations of
![]() $\unicode[STIX]{x1D719}_{0,3}^{\ast }$
from
$\unicode[STIX]{x1D719}_{0,3}^{\ast }$
from
![]() $\unicode[STIX]{x1D719}_{0,3}$
increase (for
$\unicode[STIX]{x1D719}_{0,3}$
increase (for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
,
$\unicode[STIX]{x1D6F7}=75^{\circ }$
,
![]() $\unicode[STIX]{x1D719}_{0,1}^{\ast }\approx \unicode[STIX]{x1D719}_{0,1}$
even at large
$\unicode[STIX]{x1D719}_{0,1}^{\ast }\approx \unicode[STIX]{x1D719}_{0,1}$
even at large
![]() $A$
). We note that the branch-A (
$A$
). We note that the branch-A (
![]() $\unicode[STIX]{x1D719}_{0,1}^{\ast }$
) and branch-B (
$\unicode[STIX]{x1D719}_{0,1}^{\ast }$
) and branch-B (
![]() $\unicode[STIX]{x1D719}_{0,3}^{\ast }$
) instabilities become anti-parallel to each other at large
$\unicode[STIX]{x1D719}_{0,3}^{\ast }$
) instabilities become anti-parallel to each other at large
![]() $A$
(i.e. separated by
$A$
(i.e. separated by
![]() $180^{\circ }$
), consistent with
$180^{\circ }$
), consistent with
![]() $\unicode[STIX]{x1D70E}_{A}^{L}$
and
$\unicode[STIX]{x1D70E}_{A}^{L}$
and
![]() $\unicode[STIX]{x1D70E}_{B}^{L}$
converging at large
$\unicode[STIX]{x1D70E}_{B}^{L}$
converging at large
![]() $A$
. As wave steepness increases (or as
$A$
. As wave steepness increases (or as
![]() $A$
increases for fixed
$A$
increases for fixed
![]() $\unicode[STIX]{x1D6F7}$
), the branch-A peak gradually widens, although, for large
$\unicode[STIX]{x1D6F7}$
), the branch-A peak gradually widens, although, for large
![]() $\unicode[STIX]{x1D6F7}$
, the width of the peak is quite small even at large
$\unicode[STIX]{x1D6F7}$
, the width of the peak is quite small even at large
![]() $A$
. The width of the branch-B peak increases with
$A$
. The width of the branch-B peak increases with
![]() $A$
as well, with the increase being larger than that of branch-A; for
$A$
as well, with the increase being larger than that of branch-A; for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
(figure 4
f), the width of the branch-B peaks becomes very large, spanning
$\unicode[STIX]{x1D6F7}=75^{\circ }$
(figure 4
f), the width of the branch-B peaks becomes very large, spanning
![]() $90^{\circ }\lesssim \unicode[STIX]{x1D719}_{0}\lesssim 250^{\circ }$
at large
$90^{\circ }\lesssim \unicode[STIX]{x1D719}_{0}\lesssim 250^{\circ }$
at large
![]() $A$
. The wider PSI peaks at large
$A$
. The wider PSI peaks at large
![]() $A$
indicate a larger range of instability, as we have seen in figure 2.
$A$
indicate a larger range of instability, as we have seen in figure 2.
3.3 Three-dimensional PSI
The instability ridges for
![]() $(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
(figure 2
b), at
$(A,\unicode[STIX]{x1D6F7})=(0.1,45^{\circ })$
(figure 2
b), at
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
, comprise branch-A (
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
, comprise branch-A (
![]() $\unicode[STIX]{x1D719}_{0,1}\approx 69^{\circ }$
and
$\unicode[STIX]{x1D719}_{0,1}\approx 69^{\circ }$
and
![]() $\unicode[STIX]{x1D719}_{0,2}=\unicode[STIX]{x1D719}_{0,1}+180^{\circ }$
) and branch-B (
$\unicode[STIX]{x1D719}_{0,2}=\unicode[STIX]{x1D719}_{0,1}+180^{\circ }$
) and branch-B (
![]() $\unicode[STIX]{x1D719}_{0,3}\approx 111^{\circ }$
and
$\unicode[STIX]{x1D719}_{0,3}\approx 111^{\circ }$
and
![]() $\unicode[STIX]{x1D719}_{0,4}=\unicode[STIX]{x1D719}_{0,3}+180^{\circ }$
) PSI peaks. The extension of these peaks towards 3-D perturbation wave vectors, i.e.
$\unicode[STIX]{x1D719}_{0,4}=\unicode[STIX]{x1D719}_{0,3}+180^{\circ }$
) PSI peaks. The extension of these peaks towards 3-D perturbation wave vectors, i.e.
![]() $\unicode[STIX]{x1D703}_{0}>0^{\circ }$
, suggests the existence of 3-D PSI. To confirm this, we first compute
$\unicode[STIX]{x1D703}_{0}>0^{\circ }$
, suggests the existence of 3-D PSI. To confirm this, we first compute
![]() $\unicode[STIX]{x1D70E}$
over the
$\unicode[STIX]{x1D70E}$
over the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for
![]() $A=0.01$
and various values of
$A=0.01$
and various values of
![]() $\unicode[STIX]{x1D6F7}$
in the small
$\unicode[STIX]{x1D6F7}$
in the small
![]() $s$
regime, and then trace the instability ridges that emerge from the
$s$
regime, and then trace the instability ridges that emerge from the
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis (figure 5
a–c). The 3-D perturbation wave vectors corresponding to these traces satisfy the spatial resonant condition,
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis (figure 5
a–c). The 3-D perturbation wave vectors corresponding to these traces satisfy the spatial resonant condition,
along the curves in figure 5(a–c) (we recall from § 2 that
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0}+180^{\circ },\unicode[STIX]{x1D703}_{0})$
and
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0}+180^{\circ },\unicode[STIX]{x1D703}_{0})$
and
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0},\pm \unicode[STIX]{x1D703}_{0})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0},\mp \unicode[STIX]{x1D703}_{0})$
). The equal and opposite wave vector components in
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0},\pm \unicode[STIX]{x1D703}_{0})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{0},\mp \unicode[STIX]{x1D703}_{0})$
). The equal and opposite wave vector components in
![]() $y$
for the two daughter waves in (3.7) are a consequence of the primary wave vector
$y$
for the two daughter waves in (3.7) are a consequence of the primary wave vector
![]() $\boldsymbol{k}$
being entirely in the
$\boldsymbol{k}$
being entirely in the
![]() $(x,z)$
-plane.
$(x,z)$
-plane.
Requiring the two daughter waves in (3.7) to satisfy the 3-D internal wave dispersion relation,
(where
![]() $\boldsymbol{k}_{xy}=(k,\ell ,0)$
is the wave vector projected onto the
$\boldsymbol{k}_{xy}=(k,\ell ,0)$
is the wave vector projected onto the
![]() $xy$
-plane), and the temporal resonance condition in (3.2) for
$xy$
-plane), and the temporal resonance condition in (3.2) for
![]() $n=1$
yields the relation
$n=1$
yields the relation
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}=\cos ^{-1}\left(\pm \sqrt{\frac{1}{4}\frac{\cos ^{2}\unicode[STIX]{x1D6F7}}{\cos ^{2}\unicode[STIX]{x1D703}_{0}}-\tan ^{2}\unicode[STIX]{x1D703}_{0}}\right)\quad \text{for }|\unicode[STIX]{x1D703}_{0}|\leqslant \sin ^{-1}\left(\frac{|\text{cos}\,\unicode[STIX]{x1D6F7}|}{2}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}=\cos ^{-1}\left(\pm \sqrt{\frac{1}{4}\frac{\cos ^{2}\unicode[STIX]{x1D6F7}}{\cos ^{2}\unicode[STIX]{x1D703}_{0}}-\tan ^{2}\unicode[STIX]{x1D703}_{0}}\right)\quad \text{for }|\unicode[STIX]{x1D703}_{0}|\leqslant \sin ^{-1}\left(\frac{|\text{cos}\,\unicode[STIX]{x1D6F7}|}{2}\right), & & \displaystyle\end{eqnarray}$$
with the daughter waves at frequency
![]() $\unicode[STIX]{x1D714}/2$
. In figure 5(a–c), we superpose points corresponding to (3.9) onto the instability traces; the excellent agreement confirms that the temporal resonant condition is satisfied by the 3-D perturbation wave vectors that comprise each trace. Furthermore, we verify that the perturbation wave vectors on these instability traces are effectively invariant in time, with
$\unicode[STIX]{x1D714}/2$
. In figure 5(a–c), we superpose points corresponding to (3.9) onto the instability traces; the excellent agreement confirms that the temporal resonant condition is satisfied by the 3-D perturbation wave vectors that comprise each trace. Furthermore, we verify that the perturbation wave vectors on these instability traces are effectively invariant in time, with
![]() ${\lesssim}1.5\,\%$
variation over
${\lesssim}1.5\,\%$
variation over
![]() $0\leqslant t<2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7}$
. In summary, the perturbation wave vectors
$0\leqslant t<2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7}$
. In summary, the perturbation wave vectors
![]() $\unicode[STIX]{x1D73F}(\unicode[STIX]{x1D719}_{0},\pm \unicode[STIX]{x1D703}_{0})$
and
$\unicode[STIX]{x1D73F}(\unicode[STIX]{x1D719}_{0},\pm \unicode[STIX]{x1D703}_{0})$
and
![]() $\unicode[STIX]{x1D73F}(\unicode[STIX]{x1D719}_{0}+180^{\circ },\mp \unicode[STIX]{x1D703}_{0})$
are in 3-D PSI triadic resonance with the primary wave vector
$\unicode[STIX]{x1D73F}(\unicode[STIX]{x1D719}_{0}+180^{\circ },\mp \unicode[STIX]{x1D703}_{0})$
are in 3-D PSI triadic resonance with the primary wave vector
![]() $\boldsymbol{k}$
, where
$\boldsymbol{k}$
, where
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
is any point on the curves shown in figure 5(a–c).
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
is any point on the curves shown in figure 5(a–c).

Figure 5. Traces of 3-D PSI ridges in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane (a–c), and corresponding growth rates (d–f) for a base flow of
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane (a–c), and corresponding growth rates (d–f) for a base flow of
![]() $A=10^{-2}$
and
$A=10^{-2}$
and
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
,
$\unicode[STIX]{x1D6F7}=15^{\circ }$
,
![]() $45^{\circ }$
,
$45^{\circ }$
,
![]() $75^{\circ }$
(left, middle and right columns, respectively); the corresponding isopycnal steepnesses are, respectively,
$75^{\circ }$
(left, middle and right columns, respectively); the corresponding isopycnal steepnesses are, respectively,
![]() $s\approx 0.003$
,
$s\approx 0.003$
,
![]() $0.007$
and
$0.007$
and
![]() $0.01$
. The trace segments associated with branch-A and branch-B PSI are denoted by the solid and dash-dotted lines, respectively. Superposed onto panels (a–c) are discrete points of (3.9) (denoted by the circle markers), and the threshold values of
$0.01$
. The trace segments associated with branch-A and branch-B PSI are denoted by the solid and dash-dotted lines, respectively. Superposed onto panels (a–c) are discrete points of (3.9) (denoted by the circle markers), and the threshold values of
![]() $\unicode[STIX]{x1D703}_{0}$
(denoted by the asterisk markers).
$\unicode[STIX]{x1D703}_{0}$
(denoted by the asterisk markers).
Having confirmed that the instability ridges that exist at small
![]() $s$
are indeed a 3-D manifestation of PSI, we proceed to elucidate the growth rate variation along the curves in figure 5(a–c). Each ridge has a point at which the growth rate approaches zero, which we use to separate the trace into two segments, branches-A and -B, based on which 2-D PSI branch the segment is on at
$s$
are indeed a 3-D manifestation of PSI, we proceed to elucidate the growth rate variation along the curves in figure 5(a–c). Each ridge has a point at which the growth rate approaches zero, which we use to separate the trace into two segments, branches-A and -B, based on which 2-D PSI branch the segment is on at
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
(ridges I and II in figure 2
a, respectively). The growth rates corresponding to each trace are presented in figure 5(d–f). For 2-D perturbation wave vectors (
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
(ridges I and II in figure 2
a, respectively). The growth rates corresponding to each trace are presented in figure 5(d–f). For 2-D perturbation wave vectors (
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
), the maximum growth rate corresponds to branch-A regardless of
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
), the maximum growth rate corresponds to branch-A regardless of
![]() $\unicode[STIX]{x1D6F7}$
. For
$\unicode[STIX]{x1D6F7}$
. For
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
in figure 5(d), however, branch-B is dominant for practically the entire range of
$\unicode[STIX]{x1D6F7}=15^{\circ }$
in figure 5(d), however, branch-B is dominant for practically the entire range of
![]() $\unicode[STIX]{x1D703}_{0}>0^{\circ }$
. Moreover, for both
$\unicode[STIX]{x1D703}_{0}>0^{\circ }$
. Moreover, for both
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
and
$\unicode[STIX]{x1D6F7}=15^{\circ }$
and
![]() $75^{\circ }$
(figure 5
d,f, respectively), the maximum branch-B growth rate is comparable to the maximum branch-A growth rate. Looking at 2-D PSI alone for
$75^{\circ }$
(figure 5
d,f, respectively), the maximum branch-B growth rate is comparable to the maximum branch-A growth rate. Looking at 2-D PSI alone for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
, one would conclude that branch-A clearly dominates branch-B; in 3-D, however, the maximum branch-B growth rate is almost as strong as branch-A is in two dimensions.
$\unicode[STIX]{x1D6F7}=75^{\circ }$
, one would conclude that branch-A clearly dominates branch-B; in 3-D, however, the maximum branch-B growth rate is almost as strong as branch-A is in two dimensions.
As
![]() $\unicode[STIX]{x1D6F7}$
increases, we observe five general features of 3-D PSI: (i) the range, in
$\unicode[STIX]{x1D6F7}$
increases, we observe five general features of 3-D PSI: (i) the range, in
![]() $\unicode[STIX]{x1D719}_{0}$
, of PSI decreases; (ii) the range, in
$\unicode[STIX]{x1D719}_{0}$
, of PSI decreases; (ii) the range, in
![]() $\unicode[STIX]{x1D703}_{0}$
, of branch-A (solid line in figure 5) shortens; (iii) the branch-B growth rate curve evolves from one that is monotonically decreasing to one that increases and achieves a maximum growth rate in the vicinity of the threshold
$\unicode[STIX]{x1D703}_{0}$
, of branch-A (solid line in figure 5) shortens; (iii) the branch-B growth rate curve evolves from one that is monotonically decreasing to one that increases and achieves a maximum growth rate in the vicinity of the threshold
![]() $\unicode[STIX]{x1D703}_{0}$
(asterisk marker in figure 5
a–c); (iv) the overall magnitudes of
$\unicode[STIX]{x1D703}_{0}$
(asterisk marker in figure 5
a–c); (iv) the overall magnitudes of
![]() $\unicode[STIX]{x1D70E}$
decrease; and (v) the threshold value of
$\unicode[STIX]{x1D70E}$
decrease; and (v) the threshold value of
![]() $\unicode[STIX]{x1D703}_{0}$
decreases substantially, thereby restricting the three-dimensionality of the resonant wave interaction between the 3-D perturbation wave vectors and the internal wave base flow.
$\unicode[STIX]{x1D703}_{0}$
decreases substantially, thereby restricting the three-dimensionality of the resonant wave interaction between the 3-D perturbation wave vectors and the internal wave base flow.
3.4 Higher-order resonances
To understand the origin of various large
![]() $A$
instabilities, we plot, in figure 6, the growth rates in the
$A$
instabilities, we plot, in figure 6, the growth rates in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
$\unicode[STIX]{x1D6F7}=15^{\circ }$
![]() $45^{\circ }$
, and
$45^{\circ }$
, and
![]() $75^{\circ }$
for three base flow amplitudes that reasonably span the transition from small to large
$75^{\circ }$
for three base flow amplitudes that reasonably span the transition from small to large
![]() $A$
:
$A$
:
![]() $A=0.3$
,
$A=0.3$
,
![]() $0.5$
and
$0.5$
and
![]() $0.7$
. Moreover, we superpose on figure 6 the contours along which the corresponding perturbation wave vectors are in second- or higher-order triadic resonance with the primary wave, i.e. equation (3.9) modified to include any order of resonance (
$0.7$
. Moreover, we superpose on figure 6 the contours along which the corresponding perturbation wave vectors are in second- or higher-order triadic resonance with the primary wave, i.e. equation (3.9) modified to include any order of resonance (
![]() $n\geqslant 1$
):
$n\geqslant 1$
):
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}=\cos ^{-1}\left(\pm \sqrt{\frac{n^{2}}{4}\frac{\cos ^{2}\unicode[STIX]{x1D6F7}}{\cos ^{2}\unicode[STIX]{x1D703}_{0}}-\tan ^{2}\unicode[STIX]{x1D703}_{0}}\right)\quad \text{for }|\unicode[STIX]{x1D703}_{0}|\leqslant \sin ^{-1}\left(\frac{n}{2}|\text{cos}\,\unicode[STIX]{x1D6F7}|\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}=\cos ^{-1}\left(\pm \sqrt{\frac{n^{2}}{4}\frac{\cos ^{2}\unicode[STIX]{x1D6F7}}{\cos ^{2}\unicode[STIX]{x1D703}_{0}}-\tan ^{2}\unicode[STIX]{x1D703}_{0}}\right)\quad \text{for }|\unicode[STIX]{x1D703}_{0}|\leqslant \sin ^{-1}\left(\frac{n}{2}|\text{cos}\,\unicode[STIX]{x1D6F7}|\right), & & \displaystyle\end{eqnarray}$$
where the daughter waves are now at frequency
![]() $n\unicode[STIX]{x1D714}/2$
. The second-order (
$n\unicode[STIX]{x1D714}/2$
. The second-order (
![]() $n=1$
) resonance contour is closest to the
$n=1$
) resonance contour is closest to the
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
-axis; as
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
-axis; as
![]() $n$
increases, the higher-order resonance curves expand outwards and approach the
$n$
increases, the higher-order resonance curves expand outwards and approach the
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis. As
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis. As
![]() $\unicode[STIX]{x1D6F7}$
increases, the frequency
$\unicode[STIX]{x1D6F7}$
increases, the frequency
![]() $\unicode[STIX]{x1D714}/N$
decreases [see (2.8)], which, in turn, allows for a greater number of higher-harmonics (i.e.
$\unicode[STIX]{x1D714}/N$
decreases [see (2.8)], which, in turn, allows for a greater number of higher-harmonics (i.e.
![]() $n$
) to fit within the internal wave passband
$n$
) to fit within the internal wave passband
![]() $0<n\unicode[STIX]{x1D714}/2<N$
. From (3.10), the highest possible order of resonance is specified by
$0<n\unicode[STIX]{x1D714}/2<N$
. From (3.10), the highest possible order of resonance is specified by
![]() $n=2$
for
$n=2$
for
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
and
$\unicode[STIX]{x1D6F7}=15^{\circ }$
and
![]() $45^{\circ }$
, and
$45^{\circ }$
, and
![]() $n=7$
for
$n=7$
for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
. Interestingly, for quasi-2-D perturbations (
$\unicode[STIX]{x1D6F7}=75^{\circ }$
. Interestingly, for quasi-2-D perturbations (
![]() $\unicode[STIX]{x1D703}_{0}\approx 0^{\circ }$
), (3.10) simplifies to
$\unicode[STIX]{x1D703}_{0}\approx 0^{\circ }$
), (3.10) simplifies to
![]() $\unicode[STIX]{x1D719}_{0}\approx \unicode[STIX]{x1D6F7}$
(i.e. perturbations that are shear aligned) for
$\unicode[STIX]{x1D719}_{0}\approx \unicode[STIX]{x1D6F7}$
(i.e. perturbations that are shear aligned) for
![]() $n=2$
(third-order resonance). This explains the orientation of ridge III near the
$n=2$
(third-order resonance). This explains the orientation of ridge III near the
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis in figure 2(a,b) given that ridge III corresponds to third-order resonance, as we will show below.
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
axis in figure 2(a,b) given that ridge III corresponds to third-order resonance, as we will show below.

Figure 6. Growth rate,
![]() $\unicode[STIX]{x1D70E}$
, in the
$\unicode[STIX]{x1D70E}$
, in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
,
$\unicode[STIX]{x1D6F7}=15^{\circ }$
,
![]() $45^{\circ }$
and
$45^{\circ }$
and
![]() $75^{\circ }$
(left, middle and right columns, respectively) for
$75^{\circ }$
(left, middle and right columns, respectively) for
![]() $A=0.3$
,
$A=0.3$
,
![]() $0.5$
and
$0.5$
and
![]() $0.7$
(top, middle and bottom rows, respectively). Superposed onto each panel are the higher-order resonance curves (dashed lines) given by (3.10); the innermost curve corresponds to
$0.7$
(top, middle and bottom rows, respectively). Superposed onto each panel are the higher-order resonance curves (dashed lines) given by (3.10); the innermost curve corresponds to
![]() $n=1$
, with
$n=1$
, with
![]() $n$
incrementally increasing outwards. Stable regions of the
$n$
incrementally increasing outwards. Stable regions of the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane where
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane where
![]() $\unicode[STIX]{x1D70E}<10^{-10}$
have been coloured white.
$\unicode[STIX]{x1D70E}<10^{-10}$
have been coloured white.
For
![]() $(A,\unicode[STIX]{x1D6F7})=(0.3,15^{\circ })$
(figure 6
a), the instability ridges are of finite width. The
$(A,\unicode[STIX]{x1D6F7})=(0.3,15^{\circ })$
(figure 6
a), the instability ridges are of finite width. The
![]() $n=1$
resonance contour overlaps with its corresponding instability ridges I and II, as was reported in § 3.3. In contrast, the
$n=1$
resonance contour overlaps with its corresponding instability ridges I and II, as was reported in § 3.3. In contrast, the
![]() $n=2$
resonance contour does not necessarily capture the most unstable locations within the corresponding instability region. Instead, the
$n=2$
resonance contour does not necessarily capture the most unstable locations within the corresponding instability region. Instead, the
![]() $n=2$
contour accurately captures the upper boundary of instability region III. As
$n=2$
contour accurately captures the upper boundary of instability region III. As
![]() $A$
decreases, however, the instability region III of
$A$
decreases, however, the instability region III of
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
becomes progressively thinner (and weaker) and overlaps with the
$\unicode[STIX]{x1D6F7}=15^{\circ }$
becomes progressively thinner (and weaker) and overlaps with the
![]() $n=2$
resonance contour. For
$n=2$
resonance contour. For
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
and
$\unicode[STIX]{x1D6F7}=45^{\circ }$
and
![]() $75^{\circ }$
(figure 6
b,c, respectively), the theoretical resonance curves nicely capture all of the instability ridges, although the ridges are very thin and weak for
$75^{\circ }$
(figure 6
b,c, respectively), the theoretical resonance curves nicely capture all of the instability ridges, although the ridges are very thin and weak for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
.
$\unicode[STIX]{x1D6F7}=75^{\circ }$
.
Slightly increasing
![]() $A$
to
$A$
to
![]() $0.5$
(figure 6
d–f) yields results similar to
$0.5$
(figure 6
d–f) yields results similar to
![]() $A=0.3$
. At
$A=0.3$
. At
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
, a deviation from theoretical resonance happens in the form of a widening of the instability ridges, although the signature of the higher-order resonance curves are still clearly present. The upper boundary of instability region III is still nicely captured by the
$\unicode[STIX]{x1D6F7}=15^{\circ }$
, a deviation from theoretical resonance happens in the form of a widening of the instability ridges, although the signature of the higher-order resonance curves are still clearly present. The upper boundary of instability region III is still nicely captured by the
![]() $n=2$
contour. Deviation of the instability ridges from higher-order resonance curves is notable at
$n=2$
contour. Deviation of the instability ridges from higher-order resonance curves is notable at
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
, although there is overlap near
$\unicode[STIX]{x1D6F7}=75^{\circ }$
, although there is overlap near
![]() $\unicode[STIX]{x1D719}_{0}=90^{\circ }$
. The deviations taking place for
$\unicode[STIX]{x1D719}_{0}=90^{\circ }$
. The deviations taking place for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
are unsurprising given that
$\unicode[STIX]{x1D6F7}=75^{\circ }$
are unsurprising given that
![]() $s$
increases with
$s$
increases with
![]() $\unicode[STIX]{x1D6F7}$
, and we expect deviations to occur beyond the PSI regime for large
$\unicode[STIX]{x1D6F7}$
, and we expect deviations to occur beyond the PSI regime for large
![]() $s$
. Interestingly, a new instability region appears in the vicinity of the
$s$
. Interestingly, a new instability region appears in the vicinity of the
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis for
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis for
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
(figure 6
e), and it seems to have no corresponding theoretical resonance contour in its neighbourhood. We investigate this new instability region in § 3.5.
$\unicode[STIX]{x1D6F7}=45^{\circ }$
(figure 6
e), and it seems to have no corresponding theoretical resonance contour in its neighbourhood. We investigate this new instability region in § 3.5.
The results for
![]() $A=0.7$
depict a departure from alignment between the instability ridges and the higher-order resonance curves. Either the instability ridges widen substantially to cover a larger band of the
$A=0.7$
depict a departure from alignment between the instability ridges and the higher-order resonance curves. Either the instability ridges widen substantially to cover a larger band of the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane (as for
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane (as for
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
and
$\unicode[STIX]{x1D6F7}=15^{\circ }$
and
![]() $45^{\circ }$
in figure 6
g,h, respectively), or they remain relatively thin but completely fall out of alignment and into a non-trivial pattern (as for
$45^{\circ }$
in figure 6
g,h, respectively), or they remain relatively thin but completely fall out of alignment and into a non-trivial pattern (as for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
in figure 6
i). What is most striking, however, is the connection observed between the instability ridges and the higher-order resonance curves for small
$\unicode[STIX]{x1D6F7}=75^{\circ }$
in figure 6
i). What is most striking, however, is the connection observed between the instability ridges and the higher-order resonance curves for small
![]() $A$
and the persistence of that connection as
$A$
and the persistence of that connection as
![]() $A$
increases. It appears that many features of the instability landscape, especially those corresponding to the maximum growth rates, originate from higher-order resonances in the small
$A$
increases. It appears that many features of the instability landscape, especially those corresponding to the maximum growth rates, originate from higher-order resonances in the small
![]() $A$
regime, a result that is consistent with the conclusions of Klostermeyer (Reference Klostermeyer1991) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997).
$A$
regime, a result that is consistent with the conclusions of Klostermeyer (Reference Klostermeyer1991) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997).
3.5 Transverse instabilities
In figure 6(e,h), we note the existence of an instability region near
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
that is seemingly independent of the higher-order resonance curves. Equation (3.10) informs us that the higher-order resonance curves approach the
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
that is seemingly independent of the higher-order resonance curves. Equation (3.10) informs us that the higher-order resonance curves approach the
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis as
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis as
![]() $\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
. The appearance of the instability region at and around
$\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
. The appearance of the instability region at and around
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
for
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
for
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
(figure 6
e,h), and its absence for
$\unicode[STIX]{x1D6F7}=45^{\circ }$
(figure 6
e,h), and its absence for
![]() $\unicode[STIX]{x1D6F7}=15^{\circ }$
(figure 6
d,g) and
$\unicode[STIX]{x1D6F7}=15^{\circ }$
(figure 6
d,g) and
![]() $75^{\circ }$
(figure 6
f,i), suggests that the transverse
$75^{\circ }$
(figure 6
f,i), suggests that the transverse
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
instability is unrelated to higher-order resonances. We note that the perturbation wave vector giving rise to the purely transverse instability is normal to the plane of the base flow, and thus invariant in time [by virtue of (2.12)].
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
instability is unrelated to higher-order resonances. We note that the perturbation wave vector giving rise to the purely transverse instability is normal to the plane of the base flow, and thus invariant in time [by virtue of (2.12)].

Figure 7. (a) Growth rate as a function of
![]() $(A,\unicode[STIX]{x1D6F7})$
for
$(A,\unicode[STIX]{x1D6F7})$
for
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
(
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
(
![]() $\unicode[STIX]{x1D719}_{0}$
is arbitrarily set to
$\unicode[STIX]{x1D719}_{0}$
is arbitrarily set to
![]() $0^{\circ }$
). Stable regions of the
$0^{\circ }$
). Stable regions of the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane where
$(A,\unicode[STIX]{x1D6F7})$
-plane where
![]() $\unicode[STIX]{x1D70E}<10^{-10}$
has been coloured white. The origin of the largest instability tongue at
$\unicode[STIX]{x1D70E}<10^{-10}$
has been coloured white. The origin of the largest instability tongue at
![]() $A=0$
, which occurs at
$A=0$
, which occurs at
![]() $\unicode[STIX]{x1D6F7}_{1}\approx 48^{\circ }$
, is marked by the left-most vertical dotted line. Additional tongues occur at half-integer multiples of
$\unicode[STIX]{x1D6F7}_{1}\approx 48^{\circ }$
, is marked by the left-most vertical dotted line. Additional tongues occur at half-integer multiples of
![]() $\sec \unicode[STIX]{x1D6F7}_{1}$
, as shown in panel (b). The threshold for gravitational stability, (3.14), is denoted by the dashed line, and the modified gravitational stability threshold, (3.15), is denoted by the dash-dotted line.
$\sec \unicode[STIX]{x1D6F7}_{1}$
, as shown in panel (b). The threshold for gravitational stability, (3.14), is denoted by the dashed line, and the modified gravitational stability threshold, (3.15), is denoted by the dash-dotted line.
To better understand this transverse instability, we plot the growth rate for
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
(and
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
(and
![]() $\unicode[STIX]{x1D719}_{0}$
arbitrarily set to
$\unicode[STIX]{x1D719}_{0}$
arbitrarily set to
![]() $0^{\circ }$
) as a function of
$0^{\circ }$
) as a function of
![]() $(A,\unicode[STIX]{x1D6F7})$
in figure 7. Interestingly, there are distinct instability tongues spanning the
$(A,\unicode[STIX]{x1D6F7})$
in figure 7. Interestingly, there are distinct instability tongues spanning the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane. These tongues seem to originate at specific points along the
$(A,\unicode[STIX]{x1D6F7})$
-plane. These tongues seem to originate at specific points along the
![]() $\unicode[STIX]{x1D6F7}$
-axis at
$\unicode[STIX]{x1D6F7}$
-axis at
![]() $A=0$
, where the growth rates are infinitesimal. Substituting purely transverse perturbations (
$A=0$
, where the growth rates are infinitesimal. Substituting purely transverse perturbations (
![]() $\unicode[STIX]{x1D73F}_{0}=\hat{\boldsymbol{e}}_{y}$
) into equations (2.13) and (2.14) yields a set of coupled ordinary differential equations for
$\unicode[STIX]{x1D73F}_{0}=\hat{\boldsymbol{e}}_{y}$
) into equations (2.13) and (2.14) yields a set of coupled ordinary differential equations for
![]() $a_{x}$
and
$a_{x}$
and
![]() $a_{z}$
:
$a_{z}$
:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}^{2}a_{x}}{\text{d}t^{2}}+A\cos ^{2}\unicode[STIX]{x1D6F7}\sin \unicode[STIX]{x1D6F7}\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)a_{x}\nonumber\\ \displaystyle & & \displaystyle \quad =-A\sin ^{2}\unicode[STIX]{x1D6F7}\cos \unicode[STIX]{x1D6F7}\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)a_{z}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,A\sin \unicode[STIX]{x1D6F7}\cos (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)\left(\cos \unicode[STIX]{x1D6F7}\frac{\text{d}a_{x}}{\text{d}t}+\sin \unicode[STIX]{x1D6F7}\frac{\text{d}a_{z}}{\text{d}t}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}^{2}a_{x}}{\text{d}t^{2}}+A\cos ^{2}\unicode[STIX]{x1D6F7}\sin \unicode[STIX]{x1D6F7}\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)a_{x}\nonumber\\ \displaystyle & & \displaystyle \quad =-A\sin ^{2}\unicode[STIX]{x1D6F7}\cos \unicode[STIX]{x1D6F7}\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)a_{z}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,A\sin \unicode[STIX]{x1D6F7}\cos (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)\left(\cos \unicode[STIX]{x1D6F7}\frac{\text{d}a_{x}}{\text{d}t}+\sin \unicode[STIX]{x1D6F7}\frac{\text{d}a_{z}}{\text{d}t}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}^{2}a_{z}}{\text{d}t^{2}}+[1-A\sin \unicode[STIX]{x1D6F7}(1+\cos ^{2}\unicode[STIX]{x1D6F7})\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)]a_{z}\nonumber\\ \displaystyle & & \displaystyle \quad =A(\cos ^{3}\unicode[STIX]{x1D6F7}+\cos \unicode[STIX]{x1D6F7})\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)a_{x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,A\cos \unicode[STIX]{x1D6F7}\cos (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)\left(\cos \unicode[STIX]{x1D6F7}\frac{\text{d}a_{x}}{\text{d}t}+\sin \unicode[STIX]{x1D6F7}\frac{\text{d}a_{z}}{\text{d}t}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}^{2}a_{z}}{\text{d}t^{2}}+[1-A\sin \unicode[STIX]{x1D6F7}(1+\cos ^{2}\unicode[STIX]{x1D6F7})\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)]a_{z}\nonumber\\ \displaystyle & & \displaystyle \quad =A(\cos ^{3}\unicode[STIX]{x1D6F7}+\cos \unicode[STIX]{x1D6F7})\sin (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)a_{x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,A\cos \unicode[STIX]{x1D6F7}\cos (\unicode[STIX]{x1D717}_{0}-\cos \unicode[STIX]{x1D6F7}t)\left(\cos \unicode[STIX]{x1D6F7}\frac{\text{d}a_{x}}{\text{d}t}+\sin \unicode[STIX]{x1D6F7}\frac{\text{d}a_{z}}{\text{d}t}\right).\end{eqnarray}$$
After neglecting the forcing and damping terms on the right-hand side of (3.12), we obtain a Mathieu-like equation for
![]() $a_{z}$
which describes a parametrically forced system that has instability tongues in the
$a_{z}$
which describes a parametrically forced system that has instability tongues in the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane corresponding to regions of parametric resonance. These tongues originate at
$(A,\unicode[STIX]{x1D6F7})$
-plane corresponding to regions of parametric resonance. These tongues originate at
![]() $A=0$
from the following points (Bender & Orszag Reference Bender and Orszag1999, chap. 11.4):
$A=0$
from the following points (Bender & Orszag Reference Bender and Orszag1999, chap. 11.4):
The points given by (3.13), which are denoted by vertical dotted lines in figure 7, accurately predict the points along the
![]() $\unicode[STIX]{x1D6F7}$
-axis from which the tongues emanate. As
$\unicode[STIX]{x1D6F7}$
-axis from which the tongues emanate. As
![]() $A$
increases, the points widen into instability regions with finite and increasing growth rates. We do observe, however, a detachment of the tongues (especially for large
$A$
increases, the points widen into instability regions with finite and increasing growth rates. We do observe, however, a detachment of the tongues (especially for large
![]() $\unicode[STIX]{x1D6F7}$
) from the
$\unicode[STIX]{x1D6F7}$
) from the
![]() $A=0$
axis, which we attribute to the damping and forcing terms in the right-hand side of (3.11) and (3.12) (Nayfeh & Mook Reference Nayfeh and Mook1995, chap. 1.5).
$A=0$
axis, which we attribute to the damping and forcing terms in the right-hand side of (3.11) and (3.12) (Nayfeh & Mook Reference Nayfeh and Mook1995, chap. 1.5).
The first tongue originating at
![]() $\unicode[STIX]{x1D6F7}_{1}\approx 48^{\circ }$
spans the largest region of the
$\unicode[STIX]{x1D6F7}_{1}\approx 48^{\circ }$
spans the largest region of the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane, and the bulk of the tongue appears to take form at relatively smaller values of
$(A,\unicode[STIX]{x1D6F7})$
-plane, and the bulk of the tongue appears to take form at relatively smaller values of
![]() $A$
. It is this tongue that we observe in figure 6(e) at
$A$
. It is this tongue that we observe in figure 6(e) at
![]() $(A,\unicode[STIX]{x1D6F7})=(0.5,45^{\circ })$
; the other tongues at larger
$(A,\unicode[STIX]{x1D6F7})=(0.5,45^{\circ })$
; the other tongues at larger
![]() $\unicode[STIX]{x1D6F7}$
have not taken form by
$\unicode[STIX]{x1D6F7}$
have not taken form by
![]() $A=0.5$
, which explains the absence of a transverse instability in figure 6(f) at
$A=0.5$
, which explains the absence of a transverse instability in figure 6(f) at
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
. We note that it is the peculiar shape of the instability tongues (the inclined upper boundary in particular) that accounts for
$\unicode[STIX]{x1D6F7}=75^{\circ }$
. We note that it is the peculiar shape of the instability tongues (the inclined upper boundary in particular) that accounts for
![]() $(A,\unicode[STIX]{x1D6F7})=(1,45^{\circ })$
having no purely transverse instabilities (figure 2
e), in contrast to smaller
$(A,\unicode[STIX]{x1D6F7})=(1,45^{\circ })$
having no purely transverse instabilities (figure 2
e), in contrast to smaller
![]() $A=0.5$
and
$A=0.5$
and
![]() $0.7$
for
$0.7$
for
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
(figure 6
e,h) having purely transverse instabilities. Another consequence of the non-trivial formation of transverse instabilities is region IV in figure 2(e). Although it has detached from the
$\unicode[STIX]{x1D6F7}=45^{\circ }$
(figure 6
e,h) having purely transverse instabilities. Another consequence of the non-trivial formation of transverse instabilities is region IV in figure 2(e). Although it has detached from the
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis, region IV is an extension of the transverse instability seen at smaller
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis, region IV is an extension of the transverse instability seen at smaller
![]() $A$
in figure 6(h). (For
$A$
in figure 6(h). (For
![]() $\unicode[STIX]{x1D6F7}=45^{\circ }$
, we observe the detachment of region IV from the
$\unicode[STIX]{x1D6F7}=45^{\circ }$
, we observe the detachment of region IV from the
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis at some
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
axis at some
![]() $A$
in
$A$
in
![]() $0.95<A<0.96$
.)
$0.95<A<0.96$
.)
The density of tongues grows as
![]() $\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
and remapping the growth rates to the
$\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
and remapping the growth rates to the
![]() $(A,\sec \unicode[STIX]{x1D6F7})$
-plane better reveals the formation of instability tongues (figure 7
b). We superpose on each plot in figure 7 the threshold amplitude below which statically unstable layers do not occur at any time during the internal wave period:
$(A,\sec \unicode[STIX]{x1D6F7})$
-plane better reveals the formation of instability tongues (figure 7
b). We superpose on each plot in figure 7 the threshold amplitude below which statically unstable layers do not occur at any time during the internal wave period:
where
![]() $\bar{\bar{\unicode[STIX]{x1D70C}}}(z)$
is the background density stratification and
$\bar{\bar{\unicode[STIX]{x1D70C}}}(z)$
is the background density stratification and
![]() $\bar{\unicode[STIX]{x1D70C}}(\boldsymbol{x},t)$
is the density field of the internal wave base flow. The minimum
$\bar{\unicode[STIX]{x1D70C}}(\boldsymbol{x},t)$
is the density field of the internal wave base flow. The minimum
![]() $A$
at which the instability tongues form increases with
$A$
at which the instability tongues form increases with
![]() $\unicode[STIX]{x1D6F7}$
and appears to approach the gravitational stability curve (dashed line in figure 7) at large
$\unicode[STIX]{x1D6F7}$
and appears to approach the gravitational stability curve (dashed line in figure 7) at large
![]() $\unicode[STIX]{x1D6F7}$
. The region above the gravitational stability curve is largely unstable, although thin bands of stability separate the unstable tongues.
$\unicode[STIX]{x1D6F7}$
. The region above the gravitational stability curve is largely unstable, although thin bands of stability separate the unstable tongues.
Without parametric pumping (i.e. the time dependency in the coefficient of
![]() $a_{z}$
), equation (3.12), with the right-hand side set to zero, would have neutrally stable oscillatory solutions if
$a_{z}$
), equation (3.12), with the right-hand side set to zero, would have neutrally stable oscillatory solutions if
which appears to be a slightly modified version of the static gravitational stability criterion (3.14). The inclusion of parametric pumping, however, allows for unstable solutions (i.e. parametric resonance) – even if the coefficient of
![]() $a_{z}$
is positive over the entirety of the forcing period – provided that the pumping occurs at half-integer multiples of the natural period of the system (3.13). In an effort to separate the influence of parametric pumping on wave stability, we identify, in (3.15), a heuristic measure of stability by requiring the coefficient of
$a_{z}$
is positive over the entirety of the forcing period – provided that the pumping occurs at half-integer multiples of the natural period of the system (3.13). In an effort to separate the influence of parametric pumping on wave stability, we identify, in (3.15), a heuristic measure of stability by requiring the coefficient of
![]() $a_{z}$
in (3.12) to be positive at all times. The criterion in (3.15), which is plotted as a dash-dotted curve in figure 7, adequately separates the bulk of the instability tongues from the stems connecting them to
$a_{z}$
in (3.12) to be positive at all times. The criterion in (3.15), which is plotted as a dash-dotted curve in figure 7, adequately separates the bulk of the instability tongues from the stems connecting them to
![]() $A=0$
. The region above (3.15) in figure 7 is overwhelmingly unstable due to both parametric and gravitational-like instability given that the coefficient of
$A=0$
. The region above (3.15) in figure 7 is overwhelmingly unstable due to both parametric and gravitational-like instability given that the coefficient of
![]() $a_{z}$
in the left-hand side of (3.12) is negative for a substantial portion of the wave period; the thin instability stems below (3.15) exist entirely due to parametric resonance.
$a_{z}$
in the left-hand side of (3.12) is negative for a substantial portion of the wave period; the thin instability stems below (3.15) exist entirely due to parametric resonance.
Although the transverse instability regions and other instability ridges seen in figure 6 both originate at small
![]() $A$
, the former arises from parametric resonance and the latter from RTI. The instabilities associated with transverse perturbations, therefore, offer another mechanism, separate from RTI, by which large
$A$
, the former arises from parametric resonance and the latter from RTI. The instabilities associated with transverse perturbations, therefore, offer another mechanism, separate from RTI, by which large
![]() $A$
instabilities can form. Our findings remain in line with the position of Klostermeyer (Reference Klostermeyer1991) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997), who conclude that all large
$A$
instabilities can form. Our findings remain in line with the position of Klostermeyer (Reference Klostermeyer1991) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997), who conclude that all large
![]() $A$
instabilities are linked to small
$A$
instabilities are linked to small
![]() $A$
resonances.
$A$
resonances.
3.6 Dominant instability modes
To identify the dominant instability mode for a given
![]() $(A,\unicode[STIX]{x1D6F7})$
, we calculate
$(A,\unicode[STIX]{x1D6F7})$
, we calculate
![]() $\unicode[STIX]{x1D70E}$
over the entire
$\unicode[STIX]{x1D70E}$
over the entire
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane and then select the maximum growth rate, which we denote
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane and then select the maximum growth rate, which we denote
![]() $\unicode[STIX]{x1D70E}^{\ast }$
. The corresponding
$\unicode[STIX]{x1D70E}^{\ast }$
. The corresponding
![]() $\unicode[STIX]{x1D719}_{0}$
and
$\unicode[STIX]{x1D719}_{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
of
$\unicode[STIX]{x1D703}_{0}$
of
![]() $\unicode[STIX]{x1D70E}^{\ast }$
, denoted
$\unicode[STIX]{x1D70E}^{\ast }$
, denoted
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }$
and
$\unicode[STIX]{x1D719}_{0}^{\ast }$
and
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
, respectively, reflect the initial wave vector orientation of the most unstable perturbation. Figures 8(a)–8(c), respectively, plot
$\unicode[STIX]{x1D703}_{0}^{\ast }$
, respectively, reflect the initial wave vector orientation of the most unstable perturbation. Figures 8(a)–8(c), respectively, plot
![]() $\unicode[STIX]{x1D70E}^{\ast }$
,
$\unicode[STIX]{x1D70E}^{\ast }$
,
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
and
$\unicode[STIX]{x1D703}_{0}^{\ast }$
and
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }$
over a range of base flow parameters
$\unicode[STIX]{x1D719}_{0}^{\ast }$
over a range of base flow parameters
![]() $(A,\unicode[STIX]{x1D6F7})$
. Moreover, we derive from figure 8 a regime diagram for the various dominant instability modes, which we present in figure 9. We superpose on each plot in figures 8 and 9 the boundary below which the gravitational stability criterion given by (3.14) is satisfied (dashed line), and the boundary below which the classical shear stability criterion is satisfied (dotted line):
$(A,\unicode[STIX]{x1D6F7})$
. Moreover, we derive from figure 8 a regime diagram for the various dominant instability modes, which we present in figure 9. We superpose on each plot in figures 8 and 9 the boundary below which the gravitational stability criterion given by (3.14) is satisfied (dashed line), and the boundary below which the classical shear stability criterion is satisfied (dotted line):
where
![]() $Ri=N^{2}/(\text{d}\bar{u}/\text{d}z)^{2}$
is the instantaneous Richardson number associated with the base flow without accounting for the unsteady density gradients associated with the internal wave. We note that (3.14) represents the stability criterion for a steady, one-dimensional (1-D), vertical density gradient with no shear flow; similarly, (3.16) is strictly valid only for 1-D shear and density profiles along the direction of gravity. Despite their limitations, (3.14) and (3.16) do provide points of reference for evaluating the relevance of classical gravitational and shear instability criteria to the emergence of various instabilities in the local stability approach. Interestingly, if we include the unsteady density gradients associated with the internal wave base flow in the definition of the Richardson number, i.e.
$Ri=N^{2}/(\text{d}\bar{u}/\text{d}z)^{2}$
is the instantaneous Richardson number associated with the base flow without accounting for the unsteady density gradients associated with the internal wave. We note that (3.14) represents the stability criterion for a steady, one-dimensional (1-D), vertical density gradient with no shear flow; similarly, (3.16) is strictly valid only for 1-D shear and density profiles along the direction of gravity. Despite their limitations, (3.14) and (3.16) do provide points of reference for evaluating the relevance of classical gravitational and shear instability criteria to the emergence of various instabilities in the local stability approach. Interestingly, if we include the unsteady density gradients associated with the internal wave base flow in the definition of the Richardson number, i.e.
![]() $Ri=(N^{2}-(g/\unicode[STIX]{x1D70C}_{0})\,\text{d}\bar{\unicode[STIX]{x1D70C}}/\text{d}z)/(\text{d}\bar{u}/\text{d}z)^{2}$
, then the boundary given by
$Ri=(N^{2}-(g/\unicode[STIX]{x1D70C}_{0})\,\text{d}\bar{\unicode[STIX]{x1D70C}}/\text{d}z)/(\text{d}\bar{u}/\text{d}z)^{2}$
, then the boundary given by
![]() $\min _{0\leqslant t<2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7}}Ri>1/4$
coincides with the gravitational stability boundary in (3.14).
$\min _{0\leqslant t<2\unicode[STIX]{x03C0}/\cos \unicode[STIX]{x1D6F7}}Ri>1/4$
coincides with the gravitational stability boundary in (3.14).

Figure 8. (a) Maximum growth rate,
![]() $\unicode[STIX]{x1D70E}^{\ast }$
, as a function of
$\unicode[STIX]{x1D70E}^{\ast }$
, as a function of
![]() $A$
and
$A$
and
![]() $\unicode[STIX]{x1D6F7}$
, and the corresponding perturbation wave vector orientations (b)
$\unicode[STIX]{x1D6F7}$
, and the corresponding perturbation wave vector orientations (b)
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
and (c)
$\unicode[STIX]{x1D703}_{0}^{\ast }$
and (c)
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }$
. The dashed (– –) and dotted (
$\unicode[STIX]{x1D719}_{0}^{\ast }$
. The dashed (– –) and dotted (
![]() $\cdots$
) lines denote threshold boundaries of gravitational and shear stability, respectively.
$\cdots$
) lines denote threshold boundaries of gravitational and shear stability, respectively.

Figure 9. Regime diagram indicating the dependence of the dominant instability mode on the base flow orientation,
![]() $\unicode[STIX]{x1D6F7}$
, and amplitude,
$\unicode[STIX]{x1D6F7}$
, and amplitude,
![]() $A$
. The thresholds for gravitational and shear stability are denoted by the dashed (– –) and dotted (
$A$
. The thresholds for gravitational and shear stability are denoted by the dashed (– –) and dotted (
![]() $\cdots$
) lines, respectively.
$\cdots$
) lines, respectively.
In general,
![]() $\unicode[STIX]{x1D70E}^{\ast }$
monotonically increases with
$\unicode[STIX]{x1D70E}^{\ast }$
monotonically increases with
![]() $A$
for a given
$A$
for a given
![]() $\unicode[STIX]{x1D6F7}$
. For a given
$\unicode[STIX]{x1D6F7}$
. For a given
![]() $A$
, however,
$A$
, however,
![]() $\unicode[STIX]{x1D70E}^{\ast }$
decreases with
$\unicode[STIX]{x1D70E}^{\ast }$
decreases with
![]() $\unicode[STIX]{x1D6F7}$
for
$\unicode[STIX]{x1D6F7}$
for
![]() $A\ll 10$
because the dominant instability in that regime is PSI (as discussed below and shown in figure 9), for which we know that
$A\ll 10$
because the dominant instability in that regime is PSI (as discussed below and shown in figure 9), for which we know that
![]() $\unicode[STIX]{x1D70E}_{A}$
decreases with
$\unicode[STIX]{x1D70E}_{A}$
decreases with
![]() $\unicode[STIX]{x1D6F7}$
(as shown in figure 4
a–c). For
$\unicode[STIX]{x1D6F7}$
(as shown in figure 4
a–c). For
![]() $A\gtrsim 10$
,
$A\gtrsim 10$
,
![]() $\unicode[STIX]{x1D70E}^{\ast }$
decreases with
$\unicode[STIX]{x1D70E}^{\ast }$
decreases with
![]() $\unicode[STIX]{x1D6F7}$
below some
$\unicode[STIX]{x1D6F7}$
below some
![]() $\unicode[STIX]{x1D6F7}$
value, past which
$\unicode[STIX]{x1D6F7}$
value, past which
![]() $\unicode[STIX]{x1D70E}^{\ast }$
abruptly begins to increase. This dual-behaviour of
$\unicode[STIX]{x1D70E}^{\ast }$
abruptly begins to increase. This dual-behaviour of
![]() $\unicode[STIX]{x1D70E}^{\ast }$
for
$\unicode[STIX]{x1D70E}^{\ast }$
for
![]() $A\gtrsim 10$
is linked to a transition of the dominant instability mode, as discussed later in this section.
$A\gtrsim 10$
is linked to a transition of the dominant instability mode, as discussed later in this section.
The corresponding
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
values, shown in figure 8(b), clearly indicate a number of distinct regimes of the dominant instability mode. Up to
$\unicode[STIX]{x1D703}_{0}^{\ast }$
values, shown in figure 8(b), clearly indicate a number of distinct regimes of the dominant instability mode. Up to
![]() $A\sim 1$
, the dominant instability is 2-D by virtue of the perturbation wave vectors having
$A\sim 1$
, the dominant instability is 2-D by virtue of the perturbation wave vectors having
![]() $\unicode[STIX]{x1D703}_{0}=0^{\circ }$
. As we have shown in § 3.2, the dominant instability mode for small
$\unicode[STIX]{x1D703}_{0}=0^{\circ }$
. As we have shown in § 3.2, the dominant instability mode for small
![]() $A$
and 2-D perturbations is 2-D PSI. As further evidence, we note that the corresponding
$A$
and 2-D perturbations is 2-D PSI. As further evidence, we note that the corresponding
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }$
values in this regime (shown in figure 8
c) are independent of
$\unicode[STIX]{x1D719}_{0}^{\ast }$
values in this regime (shown in figure 8
c) are independent of
![]() $A$
and approach
$A$
and approach
![]() $90^{\circ }$
as
$90^{\circ }$
as
![]() $\unicode[STIX]{x1D6F7}$
increases, both of which are in agreement with the behaviour of branch-A PSI in figure 4(d–f). The boundary for classical shear stability (dotted line in figures 8 and 9) appears to nicely delineate this limit of the PSI regime for sufficiently large
$\unicode[STIX]{x1D6F7}$
increases, both of which are in agreement with the behaviour of branch-A PSI in figure 4(d–f). The boundary for classical shear stability (dotted line in figures 8 and 9) appears to nicely delineate this limit of the PSI regime for sufficiently large
![]() $\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}$
.
Beyond the upper boundary of the 2-D PSI regime, there is another distinct regime where
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
is close to
$\unicode[STIX]{x1D703}_{0}^{\ast }$
is close to
![]() $90^{\circ }$
(figure 8
b), which corresponds to a dominant mode that is transverse to the base flow. This 3-D instability dominates for large
$90^{\circ }$
(figure 8
b), which corresponds to a dominant mode that is transverse to the base flow. This 3-D instability dominates for large
![]() $A$
, with the threshold in
$A$
, with the threshold in
![]() $A$
decreasing as
$A$
decreasing as
![]() $\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
. We note that there are only certain points in this regime where
$\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
. We note that there are only certain points in this regime where
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
is precisely
$\unicode[STIX]{x1D703}_{0}^{\ast }$
is precisely
![]() $90^{\circ }$
; the mean and standard deviation of
$90^{\circ }$
; the mean and standard deviation of
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
are approximately
$\unicode[STIX]{x1D703}_{0}^{\ast }$
are approximately
![]() $81^{\circ }$
and
$81^{\circ }$
and
![]() $6.5^{\circ }$
, respectively. In figure 7, we see that the instability tongues for purely transverse perturbations are separated by thin stability bands along the
$6.5^{\circ }$
, respectively. In figure 7, we see that the instability tongues for purely transverse perturbations are separated by thin stability bands along the
![]() $\unicode[STIX]{x1D6F7}$
axis at large
$\unicode[STIX]{x1D6F7}$
axis at large
![]() $A$
. The transverse dominant instability mode may, therefore, be slightly offset from
$A$
. The transverse dominant instability mode may, therefore, be slightly offset from
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }=90^{\circ }$
, as we see in figure 8(b), due to the presence of these thin stability bands. Despite transverse perturbations having the maximum growth rate in the
$\unicode[STIX]{x1D703}_{0}^{\ast }=90^{\circ }$
, as we see in figure 8(b), due to the presence of these thin stability bands. Despite transverse perturbations having the maximum growth rate in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane at large
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane at large
![]() $A$
, we recall that there are instabilities spanning nearly the entire range of
$A$
, we recall that there are instabilities spanning nearly the entire range of
![]() $\unicode[STIX]{x1D703}_{0}$
at
$\unicode[STIX]{x1D703}_{0}$
at
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }\approx \unicode[STIX]{x1D6F7}$
with growth rates close to
$\unicode[STIX]{x1D719}_{0}^{\ast }\approx \unicode[STIX]{x1D6F7}$
with growth rates close to
![]() $\unicode[STIX]{x1D70E}^{\ast }$
(see, for example, figure 2
i).
$\unicode[STIX]{x1D70E}^{\ast }$
(see, for example, figure 2
i).
Sandwiched between the distinct 3-D transverse and 2-D PSI regimes are two intermediary regimes: one where the dominant perturbation wave vector is effectively 2-D and shear-aligned, and another regime where the perturbation wave vector is 3-D over a range of oblique angles. We identify the shear-aligned regime as one where
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }$
is within
$\unicode[STIX]{x1D719}_{0}^{\ast }$
is within
![]() $15^{\circ }$
of
$15^{\circ }$
of
![]() $\unicode[STIX]{x1D6F7}$
and is thus aligned with the direction of shear in the base flow. Moreover, the corresponding
$\unicode[STIX]{x1D6F7}$
and is thus aligned with the direction of shear in the base flow. Moreover, the corresponding
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
values are all less than
$\unicode[STIX]{x1D703}_{0}^{\ast }$
values are all less than
![]() $15^{\circ }$
, which translates to perturbation wave vectors that are effectively two-dimensional. From figures 8(c) and 9, we can see that the shear-aligned regime hugs the lower boundary of the 3-D transverse regime and, for small
$15^{\circ }$
, which translates to perturbation wave vectors that are effectively two-dimensional. From figures 8(c) and 9, we can see that the shear-aligned regime hugs the lower boundary of the 3-D transverse regime and, for small
![]() $A$
and large
$A$
and large
![]() $\unicode[STIX]{x1D6F7}$
, overlaps with the 2-D PSI regime. The overlap of the shear-aligned and 2-D PSI regimes is to be expected since the
$\unicode[STIX]{x1D6F7}$
, overlaps with the 2-D PSI regime. The overlap of the shear-aligned and 2-D PSI regimes is to be expected since the
![]() $\unicode[STIX]{x1D719}_{0}$
values for branch-A PSI approach
$\unicode[STIX]{x1D719}_{0}$
values for branch-A PSI approach
![]() $90^{\circ }$
as
$90^{\circ }$
as
![]() $\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
(as can be seen in figure 4
d–f). The lower boundary of the non-PSI shear-aligned regime is nicely captured by the shear stability curve, as shown in figure 9.
$\unicode[STIX]{x1D6F7}\rightarrow 90^{\circ }$
(as can be seen in figure 4
d–f). The lower boundary of the non-PSI shear-aligned regime is nicely captured by the shear stability curve, as shown in figure 9.
The classical shear stability curve nicely separates the shear-aligned regime from the remaining regime, which is located below the shear stability curve and above the 2-D PSI regime. This regime corresponds to perturbation wave vectors with oblique 3-D
![]() $\unicode[STIX]{x1D703}_{0}^{\ast }$
(
$\unicode[STIX]{x1D703}_{0}^{\ast }$
(
![]() $40^{\circ }\lesssim \unicode[STIX]{x1D703}_{0}^{\ast }\lesssim 50^{\circ }$
) and a range of
$40^{\circ }\lesssim \unicode[STIX]{x1D703}_{0}^{\ast }\lesssim 50^{\circ }$
) and a range of
![]() $\unicode[STIX]{x1D719}_{0}^{\ast }$
that is strongly dependent on
$\unicode[STIX]{x1D719}_{0}^{\ast }$
that is strongly dependent on
![]() $A$
and
$A$
and
![]() $\unicode[STIX]{x1D6F7}$
. Interestingly, this 3-D oblique regime is situated between two regimes that are predominantly two-dimensional.
$\unicode[STIX]{x1D6F7}$
. Interestingly, this 3-D oblique regime is situated between two regimes that are predominantly two-dimensional.
Figure 9 presents a summary diagram of the four dominant instability regimes (listed in increasing
![]() $A$
): 2-D PSI, 3-D oblique, quasi-2-D shear-aligned, and 3-D transverse (with the quasi-2-D shear-aligned and 2-D PSI regimes overlapping for
$A$
): 2-D PSI, 3-D oblique, quasi-2-D shear-aligned, and 3-D transverse (with the quasi-2-D shear-aligned and 2-D PSI regimes overlapping for
![]() $\unicode[STIX]{x1D6F7}>70^{\circ }$
). The shear stability curve separates the 2-D PSI and 3-D oblique regimes from the quasi-2-D shear-aligned and 3-D transverse regimes. Given how our calculations are restricted to small-scale instabilities, it is only our 2-D branch-A PSI regime, at small
$\unicode[STIX]{x1D6F7}>70^{\circ }$
). The shear stability curve separates the 2-D PSI and 3-D oblique regimes from the quasi-2-D shear-aligned and 3-D transverse regimes. Given how our calculations are restricted to small-scale instabilities, it is only our 2-D branch-A PSI regime, at small
![]() $A$
, that is in agreement with the dominant instability regime diagram of Sonmor & Klaassen (Reference Sonmor and Klaassen1997, figure 22); both of our studies also recover a shear-aligned regime, but the shear-aligned regime of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) overlaps with our 3-D transverse regime in the
$A$
, that is in agreement with the dominant instability regime diagram of Sonmor & Klaassen (Reference Sonmor and Klaassen1997, figure 22); both of our studies also recover a shear-aligned regime, but the shear-aligned regime of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) overlaps with our 3-D transverse regime in the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane. A more quantitative comparison of the other regimes in figure 22 of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) are precluded because they are derived from finite-scale instabilities, which are beyond the scope of the local stability approach.
$(A,\unicode[STIX]{x1D6F7})$
-plane. A more quantitative comparison of the other regimes in figure 22 of Sonmor & Klaassen (Reference Sonmor and Klaassen1997) are precluded because they are derived from finite-scale instabilities, which are beyond the scope of the local stability approach.
4 Geophysical application
To estimate the instability regimes in which oceanic internal waves could lie, we consider parameter values that are representative of the region around the Kaena ridge near the Hawaiian islands, known to be a location for enhanced internal tide generation (Rudnick et al. Reference Rudnick, Boyd, Brainard, Carter, Egbert, Gregg, Holloway, Klymak, Kunze, Lee, Levine, Luther, Martin, Merrifield, Moum, Nash, Pinkel, Rainville and Sanford2003).
Internal tides occur predominantly at the semi-diurnal frequency of
![]() $\unicode[STIX]{x1D714}\approx 1.4\times 10^{-4}~\text{rad}~\text{s}^{-1}$
, and a typical stratification profile in the region shows a value of
$\unicode[STIX]{x1D714}\approx 1.4\times 10^{-4}~\text{rad}~\text{s}^{-1}$
, and a typical stratification profile in the region shows a value of
![]() $N\approx 7.6\times 10^{-4}~\text{rad}~\text{s}^{-1}$
in the deep ocean, where the stratification is effectively uniform (Echeverri & Peacock Reference Echeverri and Peacock2010). Neglecting background rotation, these values of
$N\approx 7.6\times 10^{-4}~\text{rad}~\text{s}^{-1}$
in the deep ocean, where the stratification is effectively uniform (Echeverri & Peacock Reference Echeverri and Peacock2010). Neglecting background rotation, these values of
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $N$
correspond to
$N$
correspond to
![]() $\unicode[STIX]{x1D6F7}\approx 79.4^{\circ }$
(2.8) in the deep ocean. For a given barotropic velocity amplitude
$\unicode[STIX]{x1D6F7}\approx 79.4^{\circ }$
(2.8) in the deep ocean. For a given barotropic velocity amplitude
![]() $U$
, linear models of internal tide generation at the Kaena ridge predict that the internal tide horizontal velocities are of the order of
$U$
, linear models of internal tide generation at the Kaena ridge predict that the internal tide horizontal velocities are of the order of
![]() $10U$
and the horizontal length-scale of the internal tides are
$10U$
and the horizontal length-scale of the internal tides are
![]() ${\approx}25~\text{km}$
(Echeverri & Peacock Reference Echeverri and Peacock2010; Mathur, Carter & Peacock Reference Mathur, Carter and Peacock2016). Assuming
${\approx}25~\text{km}$
(Echeverri & Peacock Reference Echeverri and Peacock2010; Mathur, Carter & Peacock Reference Mathur, Carter and Peacock2016). Assuming
![]() $U\approx 2~\text{cm}~\text{s}^{-1}$
, a resulting estimate for
$U\approx 2~\text{cm}~\text{s}^{-1}$
, a resulting estimate for
![]() $A$
is
$A$
is
![]() $0.37$
(2.9). We note, however, that the uncertainties in
$0.37$
(2.9). We note, however, that the uncertainties in
![]() $U$
and the length scale of the internal tides introduce significant uncertainty into our estimate for
$U$
and the length scale of the internal tides introduce significant uncertainty into our estimate for
![]() $A$
.
$A$
.
For values of
![]() $(A,\unicode[STIX]{x1D6F7})$
around
$(A,\unicode[STIX]{x1D6F7})$
around
![]() $(0.37,79.4^{\circ })$
, figure 9 identifies the dominant instability mode to be 2-D PSI, with the growth rate distribution on the
$(0.37,79.4^{\circ })$
, figure 9 identifies the dominant instability mode to be 2-D PSI, with the growth rate distribution on the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane resembling the instability ridges shown in figure 6(c). From figure 8(a), we find the corresponding maximum growth rate to be approximately
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane resembling the instability ridges shown in figure 6(c). From figure 8(a), we find the corresponding maximum growth rate to be approximately
![]() $0.017$
, which is
$0.017$
, which is
![]() ${\approx}10\,\%$
of the internal wave frequency
${\approx}10\,\%$
of the internal wave frequency
![]() $\cos \unicode[STIX]{x1D6F7}$
, i.e. the rate of energy extraction from the primary plane wave could occur on a time scale that is
$\cos \unicode[STIX]{x1D6F7}$
, i.e. the rate of energy extraction from the primary plane wave could occur on a time scale that is
![]() ${\approx}10$
times longer than the internal tide time period. Moreover, for values of
${\approx}10$
times longer than the internal tide time period. Moreover, for values of
![]() $\unicode[STIX]{x1D6F7}$
as large as
$\unicode[STIX]{x1D6F7}$
as large as
![]() $79.4^{\circ }$
, a number of higher-order resonances are possible (as shown in figure 6(c,f) for
$79.4^{\circ }$
, a number of higher-order resonances are possible (as shown in figure 6(c,f) for
![]() $\unicode[STIX]{x1D6F7}=75^{\circ }$
), which have finite growth rates that can possibly give rise to further redistribution of internal wave energy. We note that, apart from the uncertainties in the estimate of
$\unicode[STIX]{x1D6F7}=75^{\circ }$
), which have finite growth rates that can possibly give rise to further redistribution of internal wave energy. We note that, apart from the uncertainties in the estimate of
![]() $A$
and
$A$
and
![]() $\unicode[STIX]{x1D6F7}$
, the exclusion of background rotation from our calculations could also affect the accuracy of our conclusions regarding the Kaena ridge. Nonetheless, the identification of 2-D PSI as the dominant instability mode is consistent with the observations of Alford et al. (Reference Alford, MacKinnon, Zhao, Pinkel, Klymak and Peacock2007) near the Hawaiian ridge.
$\unicode[STIX]{x1D6F7}$
, the exclusion of background rotation from our calculations could also affect the accuracy of our conclusions regarding the Kaena ridge. Nonetheless, the identification of 2-D PSI as the dominant instability mode is consistent with the observations of Alford et al. (Reference Alford, MacKinnon, Zhao, Pinkel, Klymak and Peacock2007) near the Hawaiian ridge.
Viscous effects, which have thus far been absent in our study, are likely to have an effect on the local instabilities. Assuming weak viscous effects, i.e.
![]() $\unicode[STIX]{x1D708}\sim O(\unicode[STIX]{x1D700}^{2})$
[where
$\unicode[STIX]{x1D708}\sim O(\unicode[STIX]{x1D700}^{2})$
[where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
![]() $\unicode[STIX]{x1D700}$
is the short-wavelength parameter introduced in (2.11)], the viscous correction to the inviscid growth rates is given by (Landman & Saffman Reference Landman and Saffman1987):
$\unicode[STIX]{x1D700}$
is the short-wavelength parameter introduced in (2.11)], the viscous correction to the inviscid growth rates is given by (Landman & Saffman Reference Landman and Saffman1987):
where
![]() $T$
is the time period of the fluid particle trajectory on which the local stability equations are solved. In non-dimensional terms,
$T$
is the time period of the fluid particle trajectory on which the local stability equations are solved. In non-dimensional terms,
![]() $\unicode[STIX]{x1D708}$
would be replaced by the inverse of the appropriately defined Reynolds number, which in our study is
$\unicode[STIX]{x1D708}$
would be replaced by the inverse of the appropriately defined Reynolds number, which in our study is
![]() $Re=N/(\unicode[STIX]{x1D708}|\boldsymbol{k}|^{2})$
.
$Re=N/(\unicode[STIX]{x1D708}|\boldsymbol{k}|^{2})$
.
We assume an initial perturbation wave vector of the form in (2.16), but with its magnitude
![]() $\unicode[STIX]{x1D705}_{0}$
not necessarily restricted to unity. Using the closed form expression in (2.17) for the evolution of
$\unicode[STIX]{x1D705}_{0}$
not necessarily restricted to unity. Using the closed form expression in (2.17) for the evolution of
![]() $\unicode[STIX]{x1D73F}$
, the viscous correction to the inviscid growth rate is analytically evaluated to give
$\unicode[STIX]{x1D73F}$
, the viscous correction to the inviscid growth rate is analytically evaluated to give
where
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D708}}$
is the viscous growth rate,
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D708}}$
is the viscous growth rate,
![]() $\unicode[STIX]{x1D70E}$
is the numerically calculated inviscid local instability growth rate and
$\unicode[STIX]{x1D70E}$
is the numerically calculated inviscid local instability growth rate and
![]() $\tilde{\unicode[STIX]{x1D705}}_{0}=|\boldsymbol{k}|\unicode[STIX]{x1D705}_{0}$
is the dimensional magnitude of the initial perturbation wave vector. We recall that
$\tilde{\unicode[STIX]{x1D705}}_{0}=|\boldsymbol{k}|\unicode[STIX]{x1D705}_{0}$
is the dimensional magnitude of the initial perturbation wave vector. We recall that
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D708}}$
are non-dimensional, with
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D708}}$
are non-dimensional, with
![]() $N^{-1}$
used as the time scale.
$N^{-1}$
used as the time scale.
Using the expression in (4.2), we write the threshold wavenumber
above which viscous effects completely suppress the inviscid instability of growth rate
![]() $\unicode[STIX]{x1D70E}$
. Correspondingly,
$\unicode[STIX]{x1D70E}$
. Correspondingly,
![]() $\tilde{\unicode[STIX]{x1D706}}_{0}=2\unicode[STIX]{x03C0}/\tilde{\unicode[STIX]{x1D705}}_{0}$
is the shortest dimensional wavelength for which viscous effects do not completely suppress the inviscid instability; the horizontal and vertical wavelengths are
$\tilde{\unicode[STIX]{x1D706}}_{0}=2\unicode[STIX]{x03C0}/\tilde{\unicode[STIX]{x1D705}}_{0}$
is the shortest dimensional wavelength for which viscous effects do not completely suppress the inviscid instability; the horizontal and vertical wavelengths are
![]() $\tilde{\unicode[STIX]{x1D706}}_{0,x}=2\unicode[STIX]{x03C0}/(\tilde{\unicode[STIX]{x1D705}}_{0}|\text{cos}\,\unicode[STIX]{x1D703}_{0}\cos \unicode[STIX]{x1D719}_{0}|)$
and
$\tilde{\unicode[STIX]{x1D706}}_{0,x}=2\unicode[STIX]{x03C0}/(\tilde{\unicode[STIX]{x1D705}}_{0}|\text{cos}\,\unicode[STIX]{x1D703}_{0}\cos \unicode[STIX]{x1D719}_{0}|)$
and
![]() $\tilde{\unicode[STIX]{x1D706}}_{0,z}=2\unicode[STIX]{x03C0}/(\tilde{\unicode[STIX]{x1D705}}_{0}|\text{cos}\,\unicode[STIX]{x1D703}_{0}\sin \unicode[STIX]{x1D719}_{0}|)$
. Interestingly, (4.3) simplifies to
$\tilde{\unicode[STIX]{x1D706}}_{0,z}=2\unicode[STIX]{x03C0}/(\tilde{\unicode[STIX]{x1D705}}_{0}|\text{cos}\,\unicode[STIX]{x1D703}_{0}\sin \unicode[STIX]{x1D719}_{0}|)$
. Interestingly, (4.3) simplifies to
![]() $\tilde{\unicode[STIX]{x1D705}}_{0}^{T}=\sqrt{\unicode[STIX]{x1D70E}N/\unicode[STIX]{x1D708}}$
in the limit of either
$\tilde{\unicode[STIX]{x1D705}}_{0}^{T}=\sqrt{\unicode[STIX]{x1D70E}N/\unicode[STIX]{x1D708}}$
in the limit of either
![]() $\unicode[STIX]{x1D703}_{0}=90^{\circ }$
(purely transverse perturbations) or
$\unicode[STIX]{x1D703}_{0}=90^{\circ }$
(purely transverse perturbations) or
![]() $\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
(shear-aligned perturbations).
$\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D6F7}$
(shear-aligned perturbations).
As discussed earlier in this section,
![]() $(A,\unicode[STIX]{x1D6F7})\approx (0.37,79.4^{\circ })$
in the Kaena ridge region and the resulting maximum
$(A,\unicode[STIX]{x1D6F7})\approx (0.37,79.4^{\circ })$
in the Kaena ridge region and the resulting maximum
![]() $\unicode[STIX]{x1D70E}\approx 0.017$
occurs at
$\unicode[STIX]{x1D70E}\approx 0.017$
occurs at
![]() $(\unicode[STIX]{x1D719}_{0}^{\ast },\unicode[STIX]{x1D703}_{0}^{\ast })\approx (85.1^{\circ },0^{\circ })$
. These values, along with
$(\unicode[STIX]{x1D719}_{0}^{\ast },\unicode[STIX]{x1D703}_{0}^{\ast })\approx (85.1^{\circ },0^{\circ })$
. These values, along with
![]() $N\approx 7.6\times 10^{-4}~\text{rad}~\text{s}^{-1}$
and
$N\approx 7.6\times 10^{-4}~\text{rad}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, are substituted into (4.3) to give
$\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, are substituted into (4.3) to give
![]() $\tilde{\unicode[STIX]{x1D706}}_{0}\approx 1.8~\text{m}$
,
$\tilde{\unicode[STIX]{x1D706}}_{0}\approx 1.8~\text{m}$
,
![]() $\tilde{\unicode[STIX]{x1D706}}_{0,x}\approx 20.7~\text{m}$
,
$\tilde{\unicode[STIX]{x1D706}}_{0,x}\approx 20.7~\text{m}$
,
![]() $\tilde{\unicode[STIX]{x1D706}}_{0,z}\approx 1.8~\text{m}$
, suggesting that the small-scale instability predicted by the local stability framework would indeed occur for short-wavelength perturbations since the internal tide length scales are at least an order of magnitude larger than these cut-off wavelengths. Even if the effective kinematic viscosity is increased to
$\tilde{\unicode[STIX]{x1D706}}_{0,z}\approx 1.8~\text{m}$
, suggesting that the small-scale instability predicted by the local stability framework would indeed occur for short-wavelength perturbations since the internal tide length scales are at least an order of magnitude larger than these cut-off wavelengths. Even if the effective kinematic viscosity is increased to
![]() $\unicode[STIX]{x1D708}\sim 10^{-4}~\text{m}^{2}~\text{s}^{-1}$
(by small-scale turbulence, for example), the cut-off wavelengths only increase by a factor of
$\unicode[STIX]{x1D708}\sim 10^{-4}~\text{m}^{2}~\text{s}^{-1}$
(by small-scale turbulence, for example), the cut-off wavelengths only increase by a factor of
![]() $10$
and still remain relatively small. For
$10$
and still remain relatively small. For
![]() $(A,\unicode[STIX]{x1D6F7})\approx (0.37,79.4^{\circ })$
, there is also a local maximum of
$(A,\unicode[STIX]{x1D6F7})\approx (0.37,79.4^{\circ })$
, there is also a local maximum of
![]() $\unicode[STIX]{x1D70E}\approx 0.01$
at
$\unicode[STIX]{x1D70E}\approx 0.01$
at
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})\approx (91.3^{\circ },5^{\circ })$
. With
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})\approx (91.3^{\circ },5^{\circ })$
. With
![]() $N=7.6\times 10^{-4}~\text{rad}~\text{s}^{-1}$
and
$N=7.6\times 10^{-4}~\text{rad}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, the cut-off wavelengths are
$\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, the cut-off wavelengths are
![]() $\tilde{\unicode[STIX]{x1D706}}_{0}\approx 2.4~\text{m}$
,
$\tilde{\unicode[STIX]{x1D706}}_{0}\approx 2.4~\text{m}$
,
![]() $\tilde{\unicode[STIX]{x1D706}}_{0,x}\approx 105~\text{m}$
and
$\tilde{\unicode[STIX]{x1D706}}_{0,x}\approx 105~\text{m}$
and
![]() $\tilde{\unicode[STIX]{x1D706}}_{0,z}\approx 2.4~\text{m}$
. Again, with an enhanced effective diffusivity of
$\tilde{\unicode[STIX]{x1D706}}_{0,z}\approx 2.4~\text{m}$
. Again, with an enhanced effective diffusivity of
![]() $\unicode[STIX]{x1D708}=10^{-4}~\text{m}^{2}~\text{s}^{-1}$
, these cut-off wavelengths increase by a factor of
$\unicode[STIX]{x1D708}=10^{-4}~\text{m}^{2}~\text{s}^{-1}$
, these cut-off wavelengths increase by a factor of
![]() $10$
and are still well below internal tide length scales. While viscous effects would suppress the inviscid instabilities at sufficiently small perturbation length scales, it seems unlikely that they would significantly affect the dominant local instabilities under typical oceanic conditions of strong internal tide generation.
$10$
and are still well below internal tide length scales. While viscous effects would suppress the inviscid instabilities at sufficiently small perturbation length scales, it seems unlikely that they would significantly affect the dominant local instabilities under typical oceanic conditions of strong internal tide generation.
5 Summary and conclusions
We have applied the local stability approach to gain insights into 3-D, small-scale, linear instabilities of plane internal gravity waves. The short-wavelength approximation reduces the linearised perturbation equations to a set of ordinary differential equations governing the evolution of the perturbation wave vector and leading-order perturbation amplitude along fluid particle trajectories in the plane internal wave. The resulting local stability equations are computationally inexpensive to solve, and hence allow us to obtain detailed plots of growth rates as a function of the coordinates characterising the initial perturbation wave vector,
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
. We subsequently extend our calculations to a continuous range of
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
. We subsequently extend our calculations to a continuous range of
![]() $(A,\unicode[STIX]{x1D6F7})$
, parameters which, respectively, characterise the amplitude and orientation of the plane internal wave. It is noteworthy that the extent to which the local stability approach recovers existing knowledge of plane internal wave instabilities was a priori unknown. An important outcome of this paper is, therefore, the demonstration of quantitative agreement between the local and global stability approaches (in the appropriate limit of small-scale perturbations) for a plane internal wave.
$(A,\unicode[STIX]{x1D6F7})$
, parameters which, respectively, characterise the amplitude and orientation of the plane internal wave. It is noteworthy that the extent to which the local stability approach recovers existing knowledge of plane internal wave instabilities was a priori unknown. An important outcome of this paper is, therefore, the demonstration of quantitative agreement between the local and global stability approaches (in the appropriate limit of small-scale perturbations) for a plane internal wave.
Small
![]() $A$
internal waves are characterised by thin instability ridges in the
$A$
internal waves are characterised by thin instability ridges in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane. The number of such ridges seemed to generally increase with
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane. The number of such ridges seemed to generally increase with
![]() $\unicode[STIX]{x1D6F7}$
, i.e. shallow internal waves correspond to the presence of more instability ridges. At moderate
$\unicode[STIX]{x1D6F7}$
, i.e. shallow internal waves correspond to the presence of more instability ridges. At moderate
![]() $A$
, the weak, thin instability ridges from small
$A$
, the weak, thin instability ridges from small
![]() $A$
evolve into stronger, wider instability regions. For a given
$A$
evolve into stronger, wider instability regions. For a given
![]() $\unicode[STIX]{x1D6F7}$
, we also observe newer instability regions emerge in the neighbourhood of purely transverse perturbations at moderate
$\unicode[STIX]{x1D6F7}$
, we also observe newer instability regions emerge in the neighbourhood of purely transverse perturbations at moderate
![]() $A$
. At sufficiently large
$A$
. At sufficiently large
![]() $A$
, purely transverse instability seems to become dominant at all
$A$
, purely transverse instability seems to become dominant at all
![]() $\unicode[STIX]{x1D6F7}$
, although shear-aligned perturbations spanning some or all of
$\unicode[STIX]{x1D6F7}$
, although shear-aligned perturbations spanning some or all of
![]() $\unicode[STIX]{x1D703}_{0}$
are not far behind in growth rate. For small
$\unicode[STIX]{x1D703}_{0}$
are not far behind in growth rate. For small
![]() $A$
and 2-D perturbations, we showed that the two instability ridges recover the well-known PSI branch-A and -B characteristics, including both the secondary wave vectors and the growth rate magnitudes; at sufficiently large
$A$
and 2-D perturbations, we showed that the two instability ridges recover the well-known PSI branch-A and -B characteristics, including both the secondary wave vectors and the growth rate magnitudes; at sufficiently large
![]() $A$
, the growth rates of the two PSI branches become equally strong, and the ridges become significantly wider in the range of unstable wave vectors. It is noteworthy that the local stability approach requires no additional assumptions to capture the large amplitude extension of 2-D PSI. Three-dimensional manifestations of branch-A and branch-B PSI were then highlighted, an aspect that is potentially important in the ocean and the atmosphere. At small
$A$
, the growth rates of the two PSI branches become equally strong, and the ridges become significantly wider in the range of unstable wave vectors. It is noteworthy that the local stability approach requires no additional assumptions to capture the large amplitude extension of 2-D PSI. Three-dimensional manifestations of branch-A and branch-B PSI were then highlighted, an aspect that is potentially important in the ocean and the atmosphere. At small
![]() $A$
, while branch-A 2-D PSI is dominant, we showed that the 3-D extension of both branch-A and -B may have similar growth rates; for branch-B, the 3-D perturbations are sometimes more unstable than their 2-D counterparts.
$A$
, while branch-A 2-D PSI is dominant, we showed that the 3-D extension of both branch-A and -B may have similar growth rates; for branch-B, the 3-D perturbations are sometimes more unstable than their 2-D counterparts.
We then proceeded to show that the remaining unstable ridges in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for small
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane for small
![]() $A$
are also manifestations of unstable resonant triads, but of higher-order RTI. The PSI and higher-order resonances at small
$A$
are also manifestations of unstable resonant triads, but of higher-order RTI. The PSI and higher-order resonances at small
![]() $A$
were shown to continuously evolve into complex instability regions in the
$A$
were shown to continuously evolve into complex instability regions in the
![]() $(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane at moderate and large
$(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D703}_{0})$
-plane at moderate and large
![]() $A$
. A notable exception was an instability region encompassing (or located close to) the axis of purely transverse perturbations
$A$
. A notable exception was an instability region encompassing (or located close to) the axis of purely transverse perturbations
![]() $(\unicode[STIX]{x1D703}_{0}=90^{\circ })$
, which had no apparent connection to triadic resonance of any order. A detailed investigation of purely transverse instabilities showed that a parametric resonance mechanism results in instabilities at specific
$(\unicode[STIX]{x1D703}_{0}=90^{\circ })$
, which had no apparent connection to triadic resonance of any order. A detailed investigation of purely transverse instabilities showed that a parametric resonance mechanism results in instabilities at specific
![]() $\unicode[STIX]{x1D6F7}$
at small
$\unicode[STIX]{x1D6F7}$
at small
![]() $A$
. The parametric resonance regions were then shown to expand into instability tongues as
$A$
. The parametric resonance regions were then shown to expand into instability tongues as
![]() $A$
increased, nearly occupying the entire range of
$A$
increased, nearly occupying the entire range of
![]() $\unicode[STIX]{x1D6F7}$
for
$\unicode[STIX]{x1D6F7}$
for
![]() $A>2$
. A modified form of the classical gravitational instability criterion was then shown to accurately capture the threshold amplitude above which the transverse instability regions encompass large portions of the
$A>2$
. A modified form of the classical gravitational instability criterion was then shown to accurately capture the threshold amplitude above which the transverse instability regions encompass large portions of the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane.
$(A,\unicode[STIX]{x1D6F7})$
-plane.
Subsequently, we investigated the dominant instability for any
![]() $(A,\unicode[STIX]{x1D6F7})$
, although our earlier results suggest that an identification of a unique dominant instability mode may potentially ignore, particularly at large
$(A,\unicode[STIX]{x1D6F7})$
, although our earlier results suggest that an identification of a unique dominant instability mode may potentially ignore, particularly at large
![]() $A$
, several other perturbation wave vectors that have quantitatively similar growth rates to the dominant instability. The local stability approach identifies four distinct dominant instability regimes in the
$A$
, several other perturbation wave vectors that have quantitatively similar growth rates to the dominant instability. The local stability approach identifies four distinct dominant instability regimes in the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane: 2-D PSI, 3-D oblique, quasi-2-D shear-aligned and 3-D transverse.
$(A,\unicode[STIX]{x1D6F7})$
-plane: 2-D PSI, 3-D oblique, quasi-2-D shear-aligned and 3-D transverse.
The relevance of classical gravitational instability (i.e. the appearance of statically unstable layers) and shear instability (
![]() $Ri<1/4$
) were then addressed by plotting the corresponding curves in the
$Ri<1/4$
) were then addressed by plotting the corresponding curves in the
![]() $(A,\unicode[STIX]{x1D6F7})$
-plane of the dominant instability mode regime diagram. The gravitational instability criterion reasonably serves the purpose of identifying when 2-D PSI ceases to be the dominant instability mode, except for steep internal waves. Similarly, the classical shear instability criterion seems to somewhat delineate the regions of 3-D oblique and quasi-2-D shear-aligned dominant instabilities. For any given
$(A,\unicode[STIX]{x1D6F7})$
-plane of the dominant instability mode regime diagram. The gravitational instability criterion reasonably serves the purpose of identifying when 2-D PSI ceases to be the dominant instability mode, except for steep internal waves. Similarly, the classical shear instability criterion seems to somewhat delineate the regions of 3-D oblique and quasi-2-D shear-aligned dominant instabilities. For any given
![]() $\unicode[STIX]{x1D6F7}$
, at sufficiently large
$\unicode[STIX]{x1D6F7}$
, at sufficiently large
![]() $A$
, a transverse instability that arises from a combination of parametric resonance and gravitational-like instability becomes dominant, although non-transverse shear-aligned perturbations are strongly unstable as well. In summary, while the classical instability criteria based on idealized, 1-D base flow profiles have some role in understanding the regions of various instability mechanisms, the use of
$A$
, a transverse instability that arises from a combination of parametric resonance and gravitational-like instability becomes dominant, although non-transverse shear-aligned perturbations are strongly unstable as well. In summary, while the classical instability criteria based on idealized, 1-D base flow profiles have some role in understanding the regions of various instability mechanisms, the use of
![]() $Ri<1/4$
criterion as a signature of turbulence in an internal wave dominated flow field represents an over simplification. In actuality, the scope of 3-D small-scale instabilities in an internal wave field is rather complex, as demonstrated by figure 9. The fact that flows in the ocean and atmosphere are by nature three-dimensional further underscores the importance of understanding the behaviour of 3-D instabilities. Typical values of oceanic parameters from the Kaena ridge suggest that 2-D PSI may be dominant, but is present alongside other 3-D instabilities. We conclude by quantitatively estimating the role of weak viscous effects in suppressing the inviscid instabilities derived from the local stability framework.
$Ri<1/4$
criterion as a signature of turbulence in an internal wave dominated flow field represents an over simplification. In actuality, the scope of 3-D small-scale instabilities in an internal wave field is rather complex, as demonstrated by figure 9. The fact that flows in the ocean and atmosphere are by nature three-dimensional further underscores the importance of understanding the behaviour of 3-D instabilities. Typical values of oceanic parameters from the Kaena ridge suggest that 2-D PSI may be dominant, but is present alongside other 3-D instabilities. We conclude by quantitatively estimating the role of weak viscous effects in suppressing the inviscid instabilities derived from the local stability framework.
Typical studies concerning the estimation of RTI characteristics involve a two-step procedure: (i) the identification of all wave vectors that are in triadic resonance with a given primary wave field and (ii) the derivation of evolution equations (based on weakly nonlinear expansions) that are then solved by analytical or numerical means. In a uniform stratification, the identification of all possible resonant triads that contain the primary wave involves simultaneously solving the spatial and temporal resonance conditions, along with the dispersion relation for the secondary waves. In a non-uniform stratification, however, even the identification of resonant triads for a plane wave or mode is in itself a complex task (e.g. Varma & Mathur Reference Varma and Mathur2017) since there is no unique vertical wavenumber associated with the wave field, contrary to the case of a plane wave or mode in a uniform stratification. Moreover, theoretical studies are often restricted to specific resonant triads, like 2-D PSI (where the daughter waves have half the primary wave frequency), which imposes the dominant instability mechanism in the problem formulation. Even if the dominant resonant triad is correctly selected for the problem at hand, we have shown that the most-unstable perturbation wave vectors are not necessarily in exact triadic resonance with the primary wave, but offset from theoretical RTI contours.
The local stability approach circumvents the two-step procedure described in the previous paragraph and instead provides a direct growth rate estimate associated with all possible perturbation wave vectors for a given base flow internal wave; the approach is not necessarily restricted to perturbations that are in triadic resonance with the primary wave. The Floquet solution form used by Mied (Reference Mied1976) and Sonmor & Klaassen (Reference Sonmor and Klaassen1997) does achieve the same goal of providing growth rate estimates for all perturbation wave vectors, but it is restricted to spatially and temporally periodic primary wave fields. It is possible, however, to account for spatial non-periodicity in the Floquet solution by methods discussed by Kataoka & Akylas (Reference Kataoka and Akylas2013, § 2), albeit at significantly higher computational cost than for spatially periodic waves. Unless additional assumptions are made, like long-wavelength perturbations in Kataoka & Akylas (Reference Kataoka and Akylas2013), the Floquet problem requires an infinite series be truncated to a finite number of modes. In contrast to Floquet theory, the local stability approach is computationally efficient – even for large-amplitude internal waves and 3-D perturbations – and does not require spatial periodicity of the primary wave field. Local stability may, therefore, offer an alternative approach to interpreting both resonant and non-resonant instabilities in various settings studied by laboratory experiments, numerical simulations and field studies. In fact, the local stability approach could even identify specific regions conducive to instabilities in a spatially non-uniform internal wave field. For example, the generation of higher harmonics or subharmonics when an internal wave beam impinges on a pycnocline (Mercier et al. Reference Mercier, Mathur, Gostiaux, Gerkema, Magalhães, Da Silva and Dauxois2012; Gayen & Sarkar Reference Gayen and Sarkar2013) can be the result of an instability on the underlying linear wave field.
The local stability approach does have its limits, however. Our study is restricted to short-wavelength perturbations of an internal wave, which is a reasonable assumption for geophysical flows, but not so for laboratory experiments. Moreover, the local stability approach requires periodic particle trajectories and wave vectors; the relevance of non-periodic fluid particle trajectories and wave vectors remains largely unexplored. Even for periodic wave vectors, the physical interpretation of an evolving, non-constant wave vector along the fluid particle trajectories, and hence the construction of an equivalent global eigenmode, remains unclear. Finally, the incorporation of finite-wavenumber effects (Bayly Reference Bayly1986) in the local stability approach remains an important step in making it more representative of realistic settings and establishing a connection with the global stability approach.
A natural extension of our study would be to incorporate the effects of background rotation. One could also investigate if the local stability approach recovers, and provides additional insight into, the instabilities that are attributed to the finite-width feature of internal wave beams (Karimi & Akylas Reference Karimi and Akylas2014; Dauxois et al. Reference Dauxois, Joubaud, Odier and Venaille2018). It would also be worthwhile to consider the effects of background shear and individual or combinations of internal wave modes. Finally, the local stability approach may motivate targeted 3-D direct numerical simulations to investigate the actual path towards turbulence, dissipation and mixing depending on the dominant linear instability mode.
Acknowledgements
The authors thank the American Physical Society, the Indo-U.S. Science and Technology Forum, and the Indian Ministry of Earth Sciences (Monsoon Mission grant no. MM/2014/IND-002) for funding the visits of S.J.G. to IIT Madras, Chennai, India.