1. Introduction
The study of Rao, Narasimha & Narayanan (Reference Rao, Narasimha and Narayanan1971) first illustrated the coupling between large and small scales in a turbulent flow through investigation of the bursting phenomenon in a turbulent boundary layer. This has led to an increased interest in the coupling between these inner and outer scales in wall bounded flows in more recent years, with Hutchins & Marusic (Reference Hutchins and Marusic2007) proposing a modulation of the small near-wall structures by the larger outer structures.
The comprehensive study of Bandyopadhyay & Hussain (Reference Bandyopadhyay and Hussain1984) was the first to extend this idea of an interaction between the large and small scales in a number of different shear flows, including both wall bounded and free shear flows. Through examination of short-time correlations between the low-pass filtered time series of data from hot-wire experiments and the envelope of the small-scale (high-pass filtered) component the authors were able to demonstrate a significant degree of coupling between the scales across all shear flows. The coupling between the scales was observed to be maximised when the high-frequency and low-frequency signals were concurrent. Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013) laid the theoretical framework for the ‘quasisteady’ description of the inner–outer modulation in turbulent boundary layers, further suggesting that concurrent modulation effects are of great significance in turbulent flows.
While a large proportion of the work investigating scale interactions in turbulent flows has concentrated on wall bounded flows, some significant progress has been made by looking at free shear flows through the prism of large-eddy-simulation subgrid-scale (SGS) models. For example, Meneveau (Reference Meneveau1994) took single-point measurements in grid turbulence to compute joint moments between real (measured) SGS stresses and large-scale (filtered) velocity fluctuations. This was extended by O’Neil & Meneveau (Reference O’Neil and Meneveau1997), who showed that large-scale organised structures within a turbulent free shear flow impact the statistical distribution of small-scale (SGS) velocity gradient quantities, such as the dissipation rate. The study of Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) presented evidence for the concurrent interaction between large-scale velocity fluctuations in a fully developed turbulent mixing layer and the ‘roughness’ of the fine-scale turbulence. Due to intrinsic experimental uncertainties, analogues to dissipation, namely
![]() ${\it\epsilon}\sim {\it\nu}(u_{S}/{\it\lambda})^{2}$
and
${\it\epsilon}\sim {\it\nu}(u_{S}/{\it\lambda})^{2}$
and
![]() ${\it\epsilon}\sim {\it\sigma}_{u_{S}}$
, in which
${\it\epsilon}\sim {\it\sigma}_{u_{S}}$
, in which
![]() ${\it\lambda}$
is the Taylor microscale,
${\it\lambda}$
is the Taylor microscale,
![]() ${\it\epsilon}$
is the rate of dissipation (of turbulent kinetic energy),
${\it\epsilon}$
is the rate of dissipation (of turbulent kinetic energy),
![]() ${\it\nu}$
is the kinematic viscosity,
${\it\nu}$
is the kinematic viscosity,
![]() $u_{S}$
the small-scale content of the velocity fluctuations and
$u_{S}$
the small-scale content of the velocity fluctuations and
![]() ${\it\sigma}_{u_{S}}$
is the variance of the small-scale fluctuations, were used to identify the modulation of small-scale dissipation by large-scale fluctuations. In this paper we thus choose to examine a direct numerical simulation (DNS) dataset in order to directly observe the modulation of dissipation by large-scale velocity fluctuations without recourse to dissipation analogues.
${\it\sigma}_{u_{S}}$
is the variance of the small-scale fluctuations, were used to identify the modulation of small-scale dissipation by large-scale fluctuations. In this paper we thus choose to examine a direct numerical simulation (DNS) dataset in order to directly observe the modulation of dissipation by large-scale velocity fluctuations without recourse to dissipation analogues.
2. Data
The data are identical to those used by Buxton, Laizet & Ganapathisubramani (Reference Buxton, Laizet and Ganapathisubramani2011) in the developed far-field region of a turbulent planar mixing layer that closely matches the experimental dataset of Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014). The mixing layer is produced by means of a DNS of two flows of different free stream velocities,
![]() $U_{1}$
and
$U_{1}$
and
![]() $U_{2}$
in the ratio
$U_{2}$
in the ratio
![]() $U_{1}/U_{2}=2$
, either side of a splitter plate of thickness
$U_{1}/U_{2}=2$
, either side of a splitter plate of thickness
![]() $h$
to which a wedge of angle 4° is appended to produce a sharp trailing edge. The computational domain
$h$
to which a wedge of angle 4° is appended to produce a sharp trailing edge. The computational domain
![]() $(L_{x}\times L_{y}\times L_{z})=(230.4h\times 48h\times 28.8h)$
is discretised onto a Cartesian mesh that is stretched in the cross-stream (
$(L_{x}\times L_{y}\times L_{z})=(230.4h\times 48h\times 28.8h)$
is discretised onto a Cartesian mesh that is stretched in the cross-stream (
![]() $y$
) direction of
$y$
) direction of
![]() $(2049\times 513\times 256)$
mesh nodes. The stretching of the mesh in the cross-stream direction leads to a minimal mesh size of
$(2049\times 513\times 256)$
mesh nodes. The stretching of the mesh in the cross-stream direction leads to a minimal mesh size of
![]() ${\rm\Delta}y\approx 0.03h$
. The time step,
${\rm\Delta}y\approx 0.03h$
. The time step,
![]() ${\rm\Delta}t=0.05h/U_{c}$
, in which
${\rm\Delta}t=0.05h/U_{c}$
, in which
![]() $U_{c}=(U_{1}+U_{2})/2$
is the mean convection velocity, is low enough to satisfy the Courant–Friedrichs–Lewy condition, ensuring temporal stability of the simulation.
$U_{c}=(U_{1}+U_{2})/2$
is the mean convection velocity, is low enough to satisfy the Courant–Friedrichs–Lewy condition, ensuring temporal stability of the simulation.
The code ‘incompact3d’ is used to solve the incompressible non-dimensionalised Navier–Stokes equations. Details on the numerical schemes for this code can be found in Laizet & Lamballais (Reference Laizet and Lamballais2009). The boundary conditions are inflow/outflow in the streamwise direction (velocity boundary conditions of the Dirichlet type), free slip in the cross-stream direction at
![]() $y=\pm L_{y}/2$
and periodic in the spanwise direction at
$y=\pm L_{y}/2$
and periodic in the spanwise direction at
![]() $z=\pm L_{z}/2$
. The pressure mesh is staggered from the velocity mesh to avoid spurious pressure oscillations. Using the concept of modified wavenumber, the divergence-free condition is ensured up to the machine accuracy.
$z=\pm L_{z}/2$
. The pressure mesh is staggered from the velocity mesh to avoid spurious pressure oscillations. Using the concept of modified wavenumber, the divergence-free condition is ensured up to the machine accuracy.
A subdomain that consisted of the final
![]() $301\,(\times 512\times 256)$
mesh nodes in the streamwise,
$301\,(\times 512\times 256)$
mesh nodes in the streamwise,
![]() $x$
, direction was isolated at three time steps that were sufficiently well spaced in time to ensure statistical independence from one another and stored. The subdomain is in the far field of the mixing layer in which the turbulence is fully developed with self-similar mean velocity profiles throughout, with all subsequent data and analyses presented in this paper coming from this subdomain. A threshold based on enstrophy was devised to discriminate between the turbulent and potential flow within the subdomain. Only data points for which
$x$
, direction was isolated at three time steps that were sufficiently well spaced in time to ensure statistical independence from one another and stored. The subdomain is in the far field of the mixing layer in which the turbulence is fully developed with self-similar mean velocity profiles throughout, with all subsequent data and analyses presented in this paper coming from this subdomain. A threshold based on enstrophy was devised to discriminate between the turbulent and potential flow within the subdomain. Only data points for which
![]() ${\it\omega}^{2}>0.025\langle {\it\omega}^{2}\rangle (t)$
are included in the statistics presented in this paper, in which
${\it\omega}^{2}>0.025\langle {\it\omega}^{2}\rangle (t)$
are included in the statistics presented in this paper, in which
![]() $\langle {\it\omega}^{2}\rangle (t)$
is the mean enstrophy for each stored time step, accounting for some 30 % of the original data. Within this region of the flow the centreline Reynolds number based on the Taylor microscale is
$\langle {\it\omega}^{2}\rangle (t)$
is the mean enstrophy for each stored time step, accounting for some 30 % of the original data. Within this region of the flow the centreline Reynolds number based on the Taylor microscale is
![]() $\mathit{Re}_{{\it\lambda}}\approx 220$
, which approximates the experimental mixing layer data of Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) (
$\mathit{Re}_{{\it\lambda}}\approx 220$
, which approximates the experimental mixing layer data of Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) (
![]() $\mathit{Re}_{{\it\lambda}}\approx 260$
at the centreline).
$\mathit{Re}_{{\it\lambda}}\approx 260$
at the centreline).
3. Filtering
In order to observe the modulation of the small-scale velocity gradient phenomena by the concurrent large-scale velocity fluctuations it is necessary to filter the data. Throughout this paper the velocity field is filtered with a sharp spectral cutoff filter, implemented in three dimensions such that
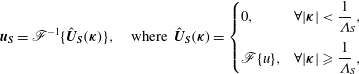 $$\begin{eqnarray}\boldsymbol{u}_{\boldsymbol{S}}=\mathscr{F}^{-1}\{\hat{\boldsymbol{U}}_{\boldsymbol{ S}}({\bf\kappa})\},\quad \text{where }\hat{\boldsymbol{U}}_{\boldsymbol{S}}({\bf\kappa})=\left\{\begin{array}{@{}ll@{}}0, & \forall \displaystyle |{\bf\kappa}|<\frac{1}{{\it\Lambda}}_{\!S},\\ \mathscr{F}\{u\}, & \forall \displaystyle |{\bf\kappa}|\geqslant \frac{1}{{\it\Lambda}}_{\!S},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}_{\boldsymbol{S}}=\mathscr{F}^{-1}\{\hat{\boldsymbol{U}}_{\boldsymbol{ S}}({\bf\kappa})\},\quad \text{where }\hat{\boldsymbol{U}}_{\boldsymbol{S}}({\bf\kappa})=\left\{\begin{array}{@{}ll@{}}0, & \forall \displaystyle |{\bf\kappa}|<\frac{1}{{\it\Lambda}}_{\!S},\\ \mathscr{F}\{u\}, & \forall \displaystyle |{\bf\kappa}|\geqslant \frac{1}{{\it\Lambda}}_{\!S},\end{array}\right.\end{eqnarray}$$
in which
![]() $\mathscr{F}$
denotes the three-dimensional Fourier transform operator,
$\mathscr{F}$
denotes the three-dimensional Fourier transform operator,
![]() ${\bf\kappa}$
is a three-dimensional wavenumber vector and
${\bf\kappa}$
is a three-dimensional wavenumber vector and
![]() ${\it\Lambda}_{S}$
is the filter length that defines the small scales. It should be noted that the definition of the wavenumber neglects the factor of
${\it\Lambda}_{S}$
is the filter length that defines the small scales. It should be noted that the definition of the wavenumber neglects the factor of
![]() $2{\rm\pi}$
for simplicity. Since the original simulation was run on a gird that was stretched in the
$2{\rm\pi}$
for simplicity. Since the original simulation was run on a gird that was stretched in the
![]() $y$
direction the data were interpolated onto a uniform grid in which
$y$
direction the data were interpolated onto a uniform grid in which
![]() ${\rm\Delta}y={\rm\Delta}x~(={\rm\Delta}z)$
prior to the implementation of the sharp spectral cutoff filter. The filter lengths are visualised in figure 1, which shows the dissipation spectrum for the central part of the mixing layer in which the enstrophy threshold is met. The dashed lines represent filter lengths of
${\rm\Delta}y={\rm\Delta}x~(={\rm\Delta}z)$
prior to the implementation of the sharp spectral cutoff filter. The filter lengths are visualised in figure 1, which shows the dissipation spectrum for the central part of the mixing layer in which the enstrophy threshold is met. The dashed lines represent filter lengths of
![]() ${\it\Lambda}_{S}={\it\lambda},2{\it\lambda},3{\it\lambda}$
and
${\it\Lambda}_{S}={\it\lambda},2{\it\lambda},3{\it\lambda}$
and
![]() $4{\it\lambda}$
, where
$4{\it\lambda}$
, where
![]() ${\it\lambda}$
is the Taylor microscale, and thus
${\it\lambda}$
is the Taylor microscale, and thus
![]() $\boldsymbol{u}_{\boldsymbol{S}}$
contains content to the right-hand side of these dashed lines. The large-scale velocity field is similarly defined as
$\boldsymbol{u}_{\boldsymbol{S}}$
contains content to the right-hand side of these dashed lines. The large-scale velocity field is similarly defined as
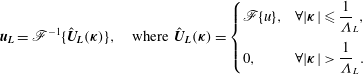 $$\begin{eqnarray}\boldsymbol{u}_{\boldsymbol{L}}=\mathscr{F}^{-1}\{\hat{\boldsymbol{U}}_{\boldsymbol{ L}}({\bf\kappa})\},\quad \text{where }\hat{\boldsymbol{U}}_{\boldsymbol{L}}({\bf\kappa})=\left\{\begin{array}{@{}ll@{}}\mathscr{F}\{u\}, & \forall \displaystyle |{\bf\kappa}|\leqslant \frac{1}{{\it\Lambda}}_{L},\\ 0, & \forall \displaystyle |{\bf\kappa}|>\frac{1}{{\it\Lambda}}_{L}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}_{\boldsymbol{L}}=\mathscr{F}^{-1}\{\hat{\boldsymbol{U}}_{\boldsymbol{ L}}({\bf\kappa})\},\quad \text{where }\hat{\boldsymbol{U}}_{\boldsymbol{L}}({\bf\kappa})=\left\{\begin{array}{@{}ll@{}}\mathscr{F}\{u\}, & \forall \displaystyle |{\bf\kappa}|\leqslant \frac{1}{{\it\Lambda}}_{L},\\ 0, & \forall \displaystyle |{\bf\kappa}|>\frac{1}{{\it\Lambda}}_{L}.\end{array}\right.\end{eqnarray}$$
It should be noted that in the subsequent analysis
![]() ${\it\Lambda}_{S}$
does not necessarily equal
${\it\Lambda}_{S}$
does not necessarily equal
![]() ${\it\Lambda}_{L}$
and thus modulations across a ‘gap’ in wavenumber space are presented. The small-scale velocity gradient field,
${\it\Lambda}_{L}$
and thus modulations across a ‘gap’ in wavenumber space are presented. The small-scale velocity gradient field,
![]() $(\partial \boldsymbol{u}_{\boldsymbol{S}}/\partial \boldsymbol{x})(\boldsymbol{x},t)$
, is then numerically computed by fitting sixth-order Lagrange interpolating polynomials through the small-scale velocity field in the
$(\partial \boldsymbol{u}_{\boldsymbol{S}}/\partial \boldsymbol{x})(\boldsymbol{x},t)$
, is then numerically computed by fitting sixth-order Lagrange interpolating polynomials through the small-scale velocity field in the
![]() $Ox,Oy$
and
$Ox,Oy$
and
![]() $Oz$
directions and calculating the tangent to these polynomials at
$Oz$
directions and calculating the tangent to these polynomials at
![]() $\boldsymbol{x}$
.
$\boldsymbol{x}$
.

Figure 1. One-dimensional dissipation spectrum for the region of the mixing layer fulfilling the minimum enstrophy threshold. From left to right the dashed lines mark the cutoff filter lengths of
![]() ${\it\kappa}_{1}{\it\lambda}=1/4$
,
${\it\kappa}_{1}{\it\lambda}=1/4$
,
![]() ${\it\kappa}_{1}{\it\lambda}=1/3$
,
${\it\kappa}_{1}{\it\lambda}=1/3$
,
![]() ${\it\kappa}_{1}{\it\lambda}=1/2$
and
${\it\kappa}_{1}{\it\lambda}=1/2$
and
![]() ${\it\kappa}_{1}{\it\lambda}=1$
respectively.
${\it\kappa}_{1}{\it\lambda}=1$
respectively.
With regards to the velocity gradient tensor, the generalised topology of a turbulent flow can be shown to depend solely on the second and third invariants,
![]() $Q$
and
$Q$
and
![]() $R$
respectively, of this tensor (Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990). Further, the joint probability density function (p.d.f.) between
$R$
respectively, of this tensor (Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990). Further, the joint probability density function (p.d.f.) between
![]() $Q$
and
$Q$
and
![]() $R$
is known to take a characteristic ‘tear-drop’ shape for a number of fully developed turbulent flows such that it is considered a universal aspect of fine-scale turbulence. The discriminant,
$R$
is known to take a characteristic ‘tear-drop’ shape for a number of fully developed turbulent flows such that it is considered a universal aspect of fine-scale turbulence. The discriminant,
![]() ${\it\Delta}=Q^{3}+(27/4)R^{2}$
for an incompressible flow, separates purely real (straining) from complex (swirling) states of the flow (Perry & Chong Reference Perry and Chong1994) and is known to act as an attractor, leading to the so-called ‘Viellefosse tail’ (Vieillefosse Reference Vieillefosse1982) in the lower right-hand quadrant. The effect of filtering the velocity fields at various values of
${\it\Delta}=Q^{3}+(27/4)R^{2}$
for an incompressible flow, separates purely real (straining) from complex (swirling) states of the flow (Perry & Chong Reference Perry and Chong1994) and is known to act as an attractor, leading to the so-called ‘Viellefosse tail’ (Vieillefosse Reference Vieillefosse1982) in the lower right-hand quadrant. The effect of filtering the velocity fields at various values of
![]() ${\it\Lambda}_{S}$
is thus illustrated in figure 2, which shows the joint p.d.f.s between
${\it\Lambda}_{S}$
is thus illustrated in figure 2, which shows the joint p.d.f.s between
![]() $Q$
and
$Q$
and
![]() $R$
for the small-scale velocity gradient fields filtered at various length scales. The classical ‘tear-drop’ shape can be seen to develop as the filter length is increased from
$R$
for the small-scale velocity gradient fields filtered at various length scales. The classical ‘tear-drop’ shape can be seen to develop as the filter length is increased from
![]() ${\it\Lambda}_{S}={\it\lambda}$
(a) to
${\it\Lambda}_{S}={\it\lambda}$
(a) to
![]() ${\it\Lambda}_{S}=4{\it\lambda}$
(d). In particular, the filling out of the ‘Vieillefosse tail’ and the upper left quadrant (defined by
${\it\Lambda}_{S}=4{\it\lambda}$
(d). In particular, the filling out of the ‘Vieillefosse tail’ and the upper left quadrant (defined by
![]() ${\it\Delta}>0;R<0$
), which Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2010) showed to be where enstrophy amplification (
${\it\Delta}>0;R<0$
), which Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2010) showed to be where enstrophy amplification (
![]() ${\it\Omega}={\it\omega}_{i}\unicode[STIX]{x1D634}_{ij}{\it\omega}_{j}>0$
) is dominant, is observed as
${\it\Omega}={\it\omega}_{i}\unicode[STIX]{x1D634}_{ij}{\it\omega}_{j}>0$
) is dominant, is observed as
![]() ${\it\Lambda}_{S}$
is increased. Contrastingly, for the smallest filter length,
${\it\Lambda}_{S}$
is increased. Contrastingly, for the smallest filter length,
![]() ${\it\Lambda}_{S}={\it\lambda}$
, which can be seen to correspond to a wavenumber that is greater than that for the peak of the dissipation spectrum in figure 1, a classical ‘tear-drop’ shape is not present. Neither the ‘Vieillefosse tail’ nor the upper left-hand quadrant is observed to be well developed, and its shape resembles that produced from within the turbulence production region of the turbulence generating grids of Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2014) and the transitional boundary layer data of Elsinga et al. (Reference Elsinga, Poelma, Schröder, Geisler, Scarano and Westerweel2012) and G. Elsinga (private communication). In both of these flows there are few length scales present, which is mimicked in the case of
${\it\Lambda}_{S}={\it\lambda}$
, which can be seen to correspond to a wavenumber that is greater than that for the peak of the dissipation spectrum in figure 1, a classical ‘tear-drop’ shape is not present. Neither the ‘Vieillefosse tail’ nor the upper left-hand quadrant is observed to be well developed, and its shape resembles that produced from within the turbulence production region of the turbulence generating grids of Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2014) and the transitional boundary layer data of Elsinga et al. (Reference Elsinga, Poelma, Schröder, Geisler, Scarano and Westerweel2012) and G. Elsinga (private communication). In both of these flows there are few length scales present, which is mimicked in the case of
![]() ${\it\Lambda}_{S}={\it\lambda}$
of figure 2(a). The ‘tear-drop’ shape of the
${\it\Lambda}_{S}={\it\lambda}$
of figure 2(a). The ‘tear-drop’ shape of the
![]() $Q{-}R$
joint p.d.f. thus appears to be driven by the presence of a broad range of scales in the inertial range as opposed to simply the dissipative scales. Qualitatively, this can be linked to the conditional mean trajectories of
$Q{-}R$
joint p.d.f. thus appears to be driven by the presence of a broad range of scales in the inertial range as opposed to simply the dissipative scales. Qualitatively, this can be linked to the conditional mean trajectories of
![]() $Q$
and
$Q$
and
![]() $R$
presented in a turbulent boundary layer from the study of Atkinson et al. (Reference Atkinson, Chumakov, Bermejo-Moreno and Soria2012). It is shown that in the viscous and buffer layers, in which the range of scales is small, there is an attraction to smaller gradients at the origin (
$R$
presented in a turbulent boundary layer from the study of Atkinson et al. (Reference Atkinson, Chumakov, Bermejo-Moreno and Soria2012). It is shown that in the viscous and buffer layers, in which the range of scales is small, there is an attraction to smaller gradients at the origin (
![]() $Q=R=0$
) in time, whereas in the log and outer layers these trajectories ‘fill out’ the upper left-hand quadrant and are attracted to the ‘Vieillefosse tail’. This is explained by a smaller contribution from the viscous diffusion term in the dynamics of the velocity gradient tensor.
$Q=R=0$
) in time, whereas in the log and outer layers these trajectories ‘fill out’ the upper left-hand quadrant and are attracted to the ‘Vieillefosse tail’. This is explained by a smaller contribution from the viscous diffusion term in the dynamics of the velocity gradient tensor.

Figure 2. Joint p.d.f.s between
![]() $Q$
and
$Q$
and
![]() $R$
for the high-pass filtered (in wavenumber space) velocity gradient fields in which
$R$
for the high-pass filtered (in wavenumber space) velocity gradient fields in which
![]() ${\it\Lambda}_{S}=$
(a)
${\it\Lambda}_{S}=$
(a)
![]() ${\it\lambda}$
, (b)
${\it\lambda}$
, (b)
![]() $2{\it\lambda}$
, (c)
$2{\it\lambda}$
, (c)
![]() $3{\it\lambda}$
and (d)
$3{\it\lambda}$
and (d)
![]() $4{\it\lambda}$
. Contour levels are logarithmically spaced from
$4{\it\lambda}$
. Contour levels are logarithmically spaced from
![]() $10^{-5.6}$
to
$10^{-5.6}$
to
![]() $10^{-1}$
.
$10^{-1}$
.
4. Results and discussion
Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) proposed a convective mechanism for the modulation of the ‘roughness’ of the small-scale turbulence by the large-scale velocity fluctuations. For a developed turbulent free shear flow the peak ensemble averaged Reynolds stresses are observed on the centreline and thus a positive cross-stream (
![]() $v$
) fluctuation will on average convect a fluid element of ‘rougher’ turbulence towards the high-speed side of the mixing layer. Due to the non-negativity of the mean turbulent kinetic energy (TKE) production term for a nominally two-dimensional free shear flow,
$v$
) fluctuation will on average convect a fluid element of ‘rougher’ turbulence towards the high-speed side of the mixing layer. Due to the non-negativity of the mean turbulent kinetic energy (TKE) production term for a nominally two-dimensional free shear flow,
![]() $\mathscr{P}=-\langle uv\rangle (\partial \overline{U}/\partial y)$
, a positive
$\mathscr{P}=-\langle uv\rangle (\partial \overline{U}/\partial y)$
, a positive
![]() $v$
fluctuation is inversely correlated with a negative
$v$
fluctuation is inversely correlated with a negative
![]() $u$
fluctuation, explaining their finding that ‘rougher’ small-scale turbulence is found concurrently to negative
$u$
fluctuation, explaining their finding that ‘rougher’ small-scale turbulence is found concurrently to negative
![]() $u$
fluctuations. Additional evidence for this convective modulation hypothesis is presented in figure 3(a), which shows the p.d.f.s of
$u$
fluctuations. Additional evidence for this convective modulation hypothesis is presented in figure 3(a), which shows the p.d.f.s of
![]() $u_{S}$
conditioned on the sign of
$u_{S}$
conditioned on the sign of
![]() $u_{L}$
for the case in which
$u_{L}$
for the case in which
![]() ${\it\Lambda}_{S}={\it\Lambda}_{L}=2{\it\lambda}$
in the low-speed side of the mixing layer, i.e.
${\it\Lambda}_{S}={\it\Lambda}_{L}=2{\it\lambda}$
in the low-speed side of the mixing layer, i.e.
![]() $y<0$
. It can be seen that the p.d.f. conditioned on
$y<0$
. It can be seen that the p.d.f. conditioned on
![]() $u_{L}\geqslant 0$
has a lower modal peak and broader tails, indicating an increase in small-scale turbulent activity concurrent to positive
$u_{L}\geqslant 0$
has a lower modal peak and broader tails, indicating an increase in small-scale turbulent activity concurrent to positive
![]() $u_{L}$
fluctuations. These are correlated to a negative (downward)
$u_{L}$
fluctuations. These are correlated to a negative (downward)
![]() $v_{L}$
fluctuation, which is the opposite finding to Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) for the high-speed side of the mixing layer, as required by the proposed convective mechanism. It should be noted that all subsequent results are derived from the low-speed side of the mixing layer for consistency with figure 3(a).
$v_{L}$
fluctuation, which is the opposite finding to Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) for the high-speed side of the mixing layer, as required by the proposed convective mechanism. It should be noted that all subsequent results are derived from the low-speed side of the mixing layer for consistency with figure 3(a).

Figure 3. The p.d.f.s of (a)
![]() $u_{S}$
fluctuations, (b) dissipation, (c) enstrophy and (d) the enstrophy amplification term conditioned on
$u_{S}$
fluctuations, (b) dissipation, (c) enstrophy and (d) the enstrophy amplification term conditioned on
![]() $u_{L}\geqslant 0$
(solid lines) and
$u_{L}\geqslant 0$
(solid lines) and
![]() $u_{L}<0$
(dashed lines) for
$u_{L}<0$
(dashed lines) for
![]() ${\it\Lambda}_{S}={\it\Lambda}_{L}=2{\it\lambda}$
.
${\it\Lambda}_{S}={\it\Lambda}_{L}=2{\it\lambda}$
.
Figure 3(b–d) shows the p.d.f.s of small-scale dissipation (
![]() ${\it\epsilon}_{S}$
), enstrophy (
${\it\epsilon}_{S}$
), enstrophy (
![]() ${{\it\omega}_{S}}^{2}$
) and the enstrophy amplification term (
${{\it\omega}_{S}}^{2}$
) and the enstrophy amplification term (
![]() ${\it\Omega}_{S}={\it\omega}_{i}\unicode[STIX]{x1D634}_{ij}{\it\omega}_{j}$
), in which
${\it\Omega}_{S}={\it\omega}_{i}\unicode[STIX]{x1D634}_{ij}{\it\omega}_{j}$
), in which
![]() $\unicode[STIX]{x1D634}_{ij}$
represents the fluctuating strain-rate tensor,
$\unicode[STIX]{x1D634}_{ij}$
represents the fluctuating strain-rate tensor,
![]() $\unicode[STIX]{x1D634}_{ij}=(\partial u_{S,i}/\partial x_{j}+\partial u_{S,j}/\partial x_{i})/2$
, conditioned on the sign of
$\unicode[STIX]{x1D634}_{ij}=(\partial u_{S,i}/\partial x_{j}+\partial u_{S,j}/\partial x_{i})/2$
, conditioned on the sign of
![]() $u_{L}$
. Whereas Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) were able to show that the small-scale turbulence is modulated to be ‘rougher’ via a dissipation analogue, it is clear that the p.d.f.s
$u_{L}$
. Whereas Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) were able to show that the small-scale turbulence is modulated to be ‘rougher’ via a dissipation analogue, it is clear that the p.d.f.s
![]() ${\it\epsilon}_{S},{{\it\omega}_{S}}^{2}$
and
${\it\epsilon}_{S},{{\it\omega}_{S}}^{2}$
and
![]() ${\it\Omega}_{S}$
all have more extensive tails when conditioned on positive
${\it\Omega}_{S}$
all have more extensive tails when conditioned on positive
![]() $u_{L}$
than negative
$u_{L}$
than negative
![]() $u_{L}$
. Interestingly, it can be observed that both the enstrophy attenuating (
$u_{L}$
. Interestingly, it can be observed that both the enstrophy attenuating (
![]() ${\it\Omega}_{S}<0$
) and the enstrophy amplifying (
${\it\Omega}_{S}<0$
) and the enstrophy amplifying (
![]() ${\it\Omega}_{S}>0$
) tails are enhanced by concurrent positive
${\it\Omega}_{S}>0$
) tails are enhanced by concurrent positive
![]() $u_{L}$
fluctuations.
$u_{L}$
fluctuations.
The difference between the two conditional p.d.f.s in figure 3 can be quantified by means of the Kullback–Leibler divergence (KLD) (Kullback & Leibler Reference Kullback and Leibler1951). The KLD is a non-negative non-symmetric measurement of the difference between two probability density functions and is defined as
in which
![]() $a(X)$
and
$a(X)$
and
![]() $b(X)$
are probability density functions of a fluctuating variable
$b(X)$
are probability density functions of a fluctuating variable
![]() $X$
(
$X$
(
![]() $D_{KL}(A\Vert B)=0$
only if the distributions
$D_{KL}(A\Vert B)=0$
only if the distributions
![]() $A$
and
$A$
and
![]() $B$
are identical). The KLD originates from information theory and is asymmetric, such that
$B$
are identical). The KLD originates from information theory and is asymmetric, such that
![]() $D_{KL}(A\Vert B)\neq D_{KL}(B\Vert A)$
. The divergence
$D_{KL}(A\Vert B)\neq D_{KL}(B\Vert A)$
. The divergence
![]() $D_{KL}(A\Vert B)$
can be thought of as the loss of information/power as a hypothesised distribution
$D_{KL}(A\Vert B)$
can be thought of as the loss of information/power as a hypothesised distribution
![]() $A$
is misspecified as
$A$
is misspecified as
![]() $B$
(Eguchi & Copas Reference Eguchi and Copas2006). We may thus quantify the difference between the p.d.f.s of figure 3 conditioned on the sign of the large-scale velocity fluctuations, and hence the magnitude of the scale modulation, through the KLD. The advantage of using the KLD to quantify the difference between the two conditional p.d.f.s is that it is based around the log likelihood ratio
$B$
(Eguchi & Copas Reference Eguchi and Copas2006). We may thus quantify the difference between the p.d.f.s of figure 3 conditioned on the sign of the large-scale velocity fluctuations, and hence the magnitude of the scale modulation, through the KLD. The advantage of using the KLD to quantify the difference between the two conditional p.d.f.s is that it is based around the log likelihood ratio
![]() $\ln [a(X)/b(X)]$
. As can be seen in figure 3, the high-magnitude intermittent dissipation/enstrophy events are more than three orders of magnitude less probable than the modal events, and it is important to ensure that this is factored into the quantification of the scale modulation, particularly so for higher Reynolds number turbulent flows in which the intermittency is larger. The notation
$\ln [a(X)/b(X)]$
. As can be seen in figure 3, the high-magnitude intermittent dissipation/enstrophy events are more than three orders of magnitude less probable than the modal events, and it is important to ensure that this is factored into the quantification of the scale modulation, particularly so for higher Reynolds number turbulent flows in which the intermittency is larger. The notation
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
denotes the KLD for the p.d.f. of quantity
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
denotes the KLD for the p.d.f. of quantity
![]() $X_{S}$
(which may be
$X_{S}$
(which may be
![]() $u_{S},{\it\epsilon}_{S},{{\it\omega}_{S}}^{2},{\it\Omega}_{S}$
, etc.) conditioned on positive large-scale velocity fluctuations to that conditioned on negative large-scale velocity fluctuations. Thus, a larger value of
$u_{S},{\it\epsilon}_{S},{{\it\omega}_{S}}^{2},{\it\Omega}_{S}$
, etc.) conditioned on positive large-scale velocity fluctuations to that conditioned on negative large-scale velocity fluctuations. Thus, a larger value of
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
is indicative of a more significant modulation effect and will, in general, be a function of both
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
is indicative of a more significant modulation effect and will, in general, be a function of both
![]() ${\it\Lambda}_{S}$
and
${\it\Lambda}_{S}$
and
![]() ${\it\Lambda}_{L}$
. In practice, of course, an integration from
${\it\Lambda}_{L}$
. In practice, of course, an integration from
![]() $-\infty$
to
$-\infty$
to
![]() $\infty$
is not possible, hence the p.d.f.s of figure 3 are truncated, neglecting
$\infty$
is not possible, hence the p.d.f.s of figure 3 are truncated, neglecting
![]() ${<}1\,\%$
of the data at the extremities of the tails. The two discrete p.d.f.s are then sampled at the same values of
${<}1\,\%$
of the data at the extremities of the tails. The two discrete p.d.f.s are then sampled at the same values of
![]() $X_{S}$
, and thus the integral of (4.1) is evaluated numerically over the truncated range of
$X_{S}$
, and thus the integral of (4.1) is evaluated numerically over the truncated range of
![]() $X_{S}$
. Eight hundred bins were used to formulate the p.d.f.s, which was observed to make the computation of
$X_{S}$
. Eight hundred bins were used to formulate the p.d.f.s, which was observed to make the computation of
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
insensitive to the resolution of the p.d.f.s/statistical convergence, and the truncation was chosen such that the computation of
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
insensitive to the resolution of the p.d.f.s/statistical convergence, and the truncation was chosen such that the computation of
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
was also observed to be insensitive to this choice. This validation is not presented for brevity.
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
was also observed to be insensitive to this choice. This validation is not presented for brevity.

Figure 4. The Kullback–Leibler divergence,
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
, for
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
, for
![]() $X_{S}=u_{S}$
(a),
$X_{S}=u_{S}$
(a),
![]() ${\it\epsilon}_{S}$
(b),
${\it\epsilon}_{S}$
(b),
![]() ${{\it\omega}_{S}}^{2}$
(c) and
${{\it\omega}_{S}}^{2}$
(c) and
![]() ${\it\Omega}_{S}$
(d) for
${\it\Omega}_{S}$
(d) for
![]() $1\leqslant {\it\Lambda}_{L}/{\it\lambda}\leqslant 18$
. It should be noted that
$1\leqslant {\it\Lambda}_{L}/{\it\lambda}\leqslant 18$
. It should be noted that
![]() $D_{KL}({{\it\omega}_{S}}^{2},u_{L}^{+}\Vert u_{L}^{-})$
and
$D_{KL}({{\it\omega}_{S}}^{2},u_{L}^{+}\Vert u_{L}^{-})$
and
![]() $D_{KL}({\it\Omega}_{S},u_{L}^{+}\Vert u_{L}^{-})$
for
$D_{KL}({\it\Omega}_{S},u_{L}^{+}\Vert u_{L}^{-})$
for
![]() ${\it\Lambda}_{S}={\it\lambda}$
are plotted as a solid line and dashed line respectively in (b) to indicate their relative magnitudes.
${\it\Lambda}_{S}={\it\lambda}$
are plotted as a solid line and dashed line respectively in (b) to indicate their relative magnitudes.
Figure 4 presents
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
for
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
for
![]() $X_{S}=u_{S}$
(a),
$X_{S}=u_{S}$
(a),
![]() ${\it\epsilon}_{S}$
(b),
${\it\epsilon}_{S}$
(b),
![]() ${{\it\omega}_{S}}^{2}$
(c) and
${{\it\omega}_{S}}^{2}$
(c) and
![]() ${\it\Omega}_{S}$
(d) for
${\it\Omega}_{S}$
(d) for
![]() $1\leqslant {\it\Lambda}_{L}/{\it\lambda}\leqslant 18$
. This range is limited to preserve the Nyquist sampling theorem in the cross-stream,
$1\leqslant {\it\Lambda}_{L}/{\it\lambda}\leqslant 18$
. This range is limited to preserve the Nyquist sampling theorem in the cross-stream,
![]() $y$
, direction for the implementation of the sharp spectral cutoff filter. Thus, it can be seen that there is a difference between the p.d.f.s conditioned on positive large-scale fluctuations and negative large-scale fluctuations for all four small-scale quantities presented in figure 4 up to
$y$
, direction for the implementation of the sharp spectral cutoff filter. Thus, it can be seen that there is a difference between the p.d.f.s conditioned on positive large-scale fluctuations and negative large-scale fluctuations for all four small-scale quantities presented in figure 4 up to
![]() ${\it\Lambda}_{L}=18{\it\lambda}$
and for all four values of
${\it\Lambda}_{L}=18{\it\lambda}$
and for all four values of
![]() ${\it\Lambda}_{S}$
tested. This is indicative of a scale modulation that is non-local in wavenumber space in which even very-large-scale (purely inertial) fluctuations modulate the concurrent small-scale behaviour. This modulation decays with
${\it\Lambda}_{S}$
tested. This is indicative of a scale modulation that is non-local in wavenumber space in which even very-large-scale (purely inertial) fluctuations modulate the concurrent small-scale behaviour. This modulation decays with
![]() ${\it\Lambda}_{L}$
, from a peak value at approximately
${\it\Lambda}_{L}$
, from a peak value at approximately
![]() ${\it\Lambda}_{L}\approx 3{\it\lambda}$
, regardless of
${\it\Lambda}_{L}\approx 3{\it\lambda}$
, regardless of
![]() ${\it\Lambda}_{S}$
, but is present nonetheless at large values of
${\it\Lambda}_{S}$
, but is present nonetheless at large values of
![]() ${\it\Lambda}_{L}$
.
${\it\Lambda}_{L}$
.
Since the constituent p.d.f.s are conditioned on the large-scale velocity fluctuations figure 4(a) is presented only for the cases of
![]() ${\it\Lambda}_{L}>{\it\Lambda}_{S}$
. The modulation effect is seen to be greater as
${\it\Lambda}_{L}>{\it\Lambda}_{S}$
. The modulation effect is seen to be greater as
![]() ${\it\Lambda}_{S}$
is increased for smaller values of
${\it\Lambda}_{S}$
is increased for smaller values of
![]() ${\it\Lambda}_{L}$
. This is intuitive, since one is effectively closing the ‘gap’ in wavenumber space by increasing
${\it\Lambda}_{L}$
. This is intuitive, since one is effectively closing the ‘gap’ in wavenumber space by increasing
![]() ${\it\Lambda}_{S}$
for a given
${\it\Lambda}_{S}$
for a given
![]() ${\it\Lambda}_{L}$
. However, for
${\it\Lambda}_{L}$
. However, for
![]() ${\it\Lambda}_{S}\geqslant 2{\it\lambda}$
it can be observed that the KLD plots effectively merge at a value of
${\it\Lambda}_{S}\geqslant 2{\it\lambda}$
it can be observed that the KLD plots effectively merge at a value of
![]() ${\it\Lambda}_{L}\approx 6.5{\it\lambda}$
before collapsing. This scale modulation by large/very large scales is thus observed to depend not upon the ‘gap’ in wavenumber space but on the physical size of the large/very large scales themselves. Thus, there is an apparent physical significance attributable to the length scale
${\it\Lambda}_{L}\approx 6.5{\it\lambda}$
before collapsing. This scale modulation by large/very large scales is thus observed to depend not upon the ‘gap’ in wavenumber space but on the physical size of the large/very large scales themselves. Thus, there is an apparent physical significance attributable to the length scale
![]() ${\it\Lambda}\approx 6.5{\it\lambda}$
after which ‘local’ (in wavenumber space) effects become important in the modulation of small velocity fluctuations by concurrent large ones, which shall be discussed in the paragraph below.
${\it\Lambda}\approx 6.5{\it\lambda}$
after which ‘local’ (in wavenumber space) effects become important in the modulation of small velocity fluctuations by concurrent large ones, which shall be discussed in the paragraph below.
The KLD for
![]() ${\it\Lambda}_{S}={\it\lambda}$
displays qualitatively different behaviour from the other three, with a much flatter decay than for the other three over low and intermediate values of
${\it\Lambda}_{S}={\it\lambda}$
displays qualitatively different behaviour from the other three, with a much flatter decay than for the other three over low and intermediate values of
![]() ${\it\Lambda}_{L}$
. Figure 2 shows that when
${\it\Lambda}_{L}$
. Figure 2 shows that when
![]() ${\it\Lambda}_{S}={\it\lambda}$
the exaggerated ‘tear-drop’ shape of the
${\it\Lambda}_{S}={\it\lambda}$
the exaggerated ‘tear-drop’ shape of the
![]() $Q$
–
$Q$
–
![]() $R$
joint p.d.f. is not observed, whereas it is (to varying extents) for
$R$
joint p.d.f. is not observed, whereas it is (to varying extents) for
![]() ${\it\Lambda}_{L}\geqslant 2{\it\lambda}$
. These velocity fluctuations can thus be considered to consist almost entirely of dissipative scale fluctuations. The merger with the other
${\it\Lambda}_{L}\geqslant 2{\it\lambda}$
. These velocity fluctuations can thus be considered to consist almost entirely of dissipative scale fluctuations. The merger with the other
![]() $D_{KL}(u_{S},u_{L}^{+}\Vert u_{L}^{-})$
curves is now observed to take place at
$D_{KL}(u_{S},u_{L}^{+}\Vert u_{L}^{-})$
curves is now observed to take place at
![]() ${\it\Lambda}_{L}\approx 13{\it\lambda}$
, which is close to a subharmonic value to that for the other merger point. It is additionally observed that for low values of
${\it\Lambda}_{L}\approx 13{\it\lambda}$
, which is close to a subharmonic value to that for the other merger point. It is additionally observed that for low values of
![]() ${\it\Lambda}_{L}$
there are two distinct regions,
${\it\Lambda}_{L}$
there are two distinct regions,
![]() ${\it\lambda}\lesssim {\it\Lambda}_{L}\lesssim 3.5{\it\lambda}$
and
${\it\lambda}\lesssim {\it\Lambda}_{L}\lesssim 3.5{\it\lambda}$
and
![]() $4{\it\lambda}\lesssim {\it\Lambda}_{L}\lesssim 6.5{\it\lambda}$
, over which the KLD is observed to increase with
$4{\it\lambda}\lesssim {\it\Lambda}_{L}\lesssim 6.5{\it\lambda}$
, over which the KLD is observed to increase with
![]() ${\it\Lambda}_{L}$
before then falling away rapidly. The second of these rapid drop-offs coincides with the merger point at
${\it\Lambda}_{L}$
before then falling away rapidly. The second of these rapid drop-offs coincides with the merger point at
![]() ${\it\Lambda}_{L}\approx 6.5{\it\lambda}$
. It is difficult to apportion a physical significance to a length scale of
${\it\Lambda}_{L}\approx 6.5{\it\lambda}$
. It is difficult to apportion a physical significance to a length scale of
![]() $13{\it\lambda}$
(and harmonic at
$13{\it\lambda}$
(and harmonic at
![]() $6.5{\it\lambda}$
). While an insufficient number of time steps of the data were stored to accurately compute the integral length scale at this point of the flow, a coarse estimate based on an exponential fit to the longitudinal correlation function suggests that
$6.5{\it\lambda}$
). While an insufficient number of time steps of the data were stored to accurately compute the integral length scale at this point of the flow, a coarse estimate based on an exponential fit to the longitudinal correlation function suggests that
![]() $L\approx 13{\it\lambda}$
is in the right ‘ball park’. This is in agreement with the data of Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) when adjusted for the lower
$L\approx 13{\it\lambda}$
is in the right ‘ball park’. This is in agreement with the data of Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) when adjusted for the lower
![]() $\mathit{Re}_{{\it\lambda}}$
. It thus appears that the scale modulation effect for velocity fluctuations may be driven by the integral scale streamwise rollers that are present in a turbulent mixing layer, linking the convective scale interaction mechanism with the eddy structure of the flow, although this conclusion should be treated with some caution.
$\mathit{Re}_{{\it\lambda}}$
. It thus appears that the scale modulation effect for velocity fluctuations may be driven by the integral scale streamwise rollers that are present in a turbulent mixing layer, linking the convective scale interaction mechanism with the eddy structure of the flow, although this conclusion should be treated with some caution.
Some other general observations from the figure may be made. First, it can be seen that the magnitude of the modulation is greater for the small-scale velocity gradient quantities (b–d) than for the small-scale velocity fluctuations (a) for smaller values of
![]() ${\it\Lambda}_{L}$
. This is, however, observed to converge as
${\it\Lambda}_{L}$
. This is, however, observed to converge as
![]() ${\it\Lambda}_{L}\rightarrow 18{\it\lambda}$
, as the modulation effect diminishes across the large gap in wavenumber space. It should be noted that the
${\it\Lambda}_{L}\rightarrow 18{\it\lambda}$
, as the modulation effect diminishes across the large gap in wavenumber space. It should be noted that the
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
curves for various values of
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
curves for various values of
![]() ${\it\Lambda}_{S}$
do not collapse for velocity gradient quantities, unlike those for velocity fluctuations. Additionally, the decay in
${\it\Lambda}_{S}$
do not collapse for velocity gradient quantities, unlike those for velocity fluctuations. Additionally, the decay in
![]() $D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
with
$D_{KL}(X_{S},u_{L}^{+}\Vert u_{L}^{-})$
with
![]() ${\it\Lambda}_{L}$
is not observed to be smooth but has three small, but distinct, local peaks at
${\it\Lambda}_{L}$
is not observed to be smooth but has three small, but distinct, local peaks at
![]() ${\it\Lambda}_{L}\approx 3.5{\it\lambda}$
,
${\it\Lambda}_{L}\approx 3.5{\it\lambda}$
,
![]() ${\it\lambda}_{L}\approx 6.5{\it\lambda}$
and
${\it\lambda}_{L}\approx 6.5{\it\lambda}$
and
![]() ${\it\Lambda}_{L}\approx 13{\it\lambda}$
. These correspond to the merger points for the
${\it\Lambda}_{L}\approx 13{\it\lambda}$
. These correspond to the merger points for the
![]() $D_{KL}(u_{S},u_{L}^{+}\Vert u_{L}^{-})$
curves of figure 4(a) and are linked to the streamwise integral length scale. Finally, it can be seen for all cases that there is a significant increase in the scale modulation effect as
$D_{KL}(u_{S},u_{L}^{+}\Vert u_{L}^{-})$
curves of figure 4(a) and are linked to the streamwise integral length scale. Finally, it can be seen for all cases that there is a significant increase in the scale modulation effect as
![]() ${\it\Lambda}_{S}$
is increased from
${\it\Lambda}_{S}$
is increased from
![]() ${\it\lambda}$
to
${\it\lambda}$
to
![]() $2{\it\lambda}$
. This corresponds to the cutoff wavenumber moving from below the peak of the dissipation spectrum to the peak value in figure 1. As
$2{\it\lambda}$
. This corresponds to the cutoff wavenumber moving from below the peak of the dissipation spectrum to the peak value in figure 1. As
![]() ${\it\Lambda}_{S}$
is increased further the modulation effect varies according to
${\it\Lambda}_{S}$
is increased further the modulation effect varies according to
![]() $X_{S}$
, which is discussed further below.
$X_{S}$
, which is discussed further below.
The largest modulation effect is present for
![]() $X_{S}={\it\epsilon}_{S}$
. Figure 4(b) shows the KLD for the dissipation, enstrophy and enstrophy amplification term for
$X_{S}={\it\epsilon}_{S}$
. Figure 4(b) shows the KLD for the dissipation, enstrophy and enstrophy amplification term for
![]() ${\it\Lambda}_{S}={\it\lambda}$
on the same axes for comparison. It can be seen that
${\it\Lambda}_{S}={\it\lambda}$
on the same axes for comparison. It can be seen that
![]() $D_{KL}({\it\epsilon}_{S},u_{L}^{+}\Vert u_{L}^{-})$
is consistently approximately 1.5 times
$D_{KL}({\it\epsilon}_{S},u_{L}^{+}\Vert u_{L}^{-})$
is consistently approximately 1.5 times
![]() $D_{KL}({{\it\omega}_{S}}^{2},u_{L}^{+}\Vert u_{L}^{-})$
, the solid line of figure 4(b), across the entire range of
$D_{KL}({{\it\omega}_{S}}^{2},u_{L}^{+}\Vert u_{L}^{-})$
, the solid line of figure 4(b), across the entire range of
![]() ${\it\Lambda}_{L}$
. The scale modulation of rotation is thus significantly less than that of the strain rate, i.e. the symmetric part of the velocity gradient tensor is more sensitive to concurrent velocity fluctuations than the skew-symmetric part. This is reinforced by the observation that
${\it\Lambda}_{L}$
. The scale modulation of rotation is thus significantly less than that of the strain rate, i.e. the symmetric part of the velocity gradient tensor is more sensitive to concurrent velocity fluctuations than the skew-symmetric part. This is reinforced by the observation that
![]() $D_{KL}({\it\Omega}_{S},u_{L}^{+}\Vert u_{L}^{-})$
, the dashed line in figure 4(b), is intermediate between those for dissipation and enstrophy. von Kármán (Reference von Kármán1937) first identified
$D_{KL}({\it\Omega}_{S},u_{L}^{+}\Vert u_{L}^{-})$
, the dashed line in figure 4(b), is intermediate between those for dissipation and enstrophy. von Kármán (Reference von Kármán1937) first identified
![]() ${\it\Omega}_{S}={\it\omega}_{i}\unicode[STIX]{x1D634}_{ij}{\it\omega}_{j}$
as the inviscid source/sink term in the enstrophy equation as the interaction between rotation and strain rate. It is thus revealed that the scale modulation of this quantity is intermediate between those for rotation and strain rate.
${\it\Omega}_{S}={\it\omega}_{i}\unicode[STIX]{x1D634}_{ij}{\it\omega}_{j}$
as the inviscid source/sink term in the enstrophy equation as the interaction between rotation and strain rate. It is thus revealed that the scale modulation of this quantity is intermediate between those for rotation and strain rate.
Additionally, the increase in modulation effect, for
![]() ${\it\Lambda}_{L}\lesssim 10{\it\lambda}$
at least, as
${\it\Lambda}_{L}\lesssim 10{\it\lambda}$
at least, as
![]() ${\it\Lambda}_{S}$
is increased from
${\it\Lambda}_{S}$
is increased from
![]() ${\it\lambda}$
to
${\it\lambda}$
to
![]() $2{\it\lambda}$
is greater for dissipation (b) than for enstrophy (c). This may be linked to the finding of figure 2, that as the definition of
$2{\it\lambda}$
is greater for dissipation (b) than for enstrophy (c). This may be linked to the finding of figure 2, that as the definition of
![]() ${\it\Lambda}_{S}$
is broadened the ‘Vieillefosse tail’ is the region that is significantly extended, which is strain-rate (dissipation) dominated. However, while the modulation effect is observed to increase further as
${\it\Lambda}_{S}$
is broadened the ‘Vieillefosse tail’ is the region that is significantly extended, which is strain-rate (dissipation) dominated. However, while the modulation effect is observed to increase further as
![]() ${\it\Lambda}_{S}$
is increased from
${\it\Lambda}_{S}$
is increased from
![]() $2{\it\lambda}$
to
$2{\it\lambda}$
to
![]() $3{\it\lambda}$
for dissipation (b) this is not the case for enstrophy (c). At the largest value of
$3{\it\lambda}$
for dissipation (b) this is not the case for enstrophy (c). At the largest value of
![]() ${\it\Lambda}_{S}=4{\it\lambda}$
the modulation effect is similar to that for
${\it\Lambda}_{S}=4{\it\lambda}$
the modulation effect is similar to that for
![]() ${\it\Lambda}_{S}=3{\it\lambda}$
for dissipation but has decayed significantly for enstrophy. In particular, it can be seen that at lower values of
${\it\Lambda}_{S}=3{\it\lambda}$
for dissipation but has decayed significantly for enstrophy. In particular, it can be seen that at lower values of
![]() ${\it\Lambda}_{L}$
,
${\it\Lambda}_{L}$
,
![]() $D_{KL}({{\it\omega}_{S}}^{2},u_{L}^{+}\Vert u_{L}^{-})$
computed from
$D_{KL}({{\it\omega}_{S}}^{2},u_{L}^{+}\Vert u_{L}^{-})$
computed from
![]() ${\it\Lambda}_{S}=4{\it\lambda}$
is lower than both
${\it\Lambda}_{S}=4{\it\lambda}$
is lower than both
![]() ${\it\Lambda}_{S}=3{\it\lambda}$
and
${\it\Lambda}_{S}=3{\it\lambda}$
and
![]() ${\it\Lambda}_{S}=2{\it\lambda}$
, while at the highest values of
${\it\Lambda}_{S}=2{\it\lambda}$
, while at the highest values of
![]() ${\it\Lambda}_{L}$
, the modulation effect is smaller for
${\it\Lambda}_{L}$
, the modulation effect is smaller for
![]() ${\it\Lambda}_{S}=4{\it\lambda}$
than any other values. Exactly the same trend is followed in (d) for
${\it\Lambda}_{S}=4{\it\lambda}$
than any other values. Exactly the same trend is followed in (d) for
![]() $D_{KL}({\it\Omega}_{S},u_{L}^{+}\Vert u_{L}^{-})$
. Contrastingly, the scale modulation for dissipation increases up to
$D_{KL}({\it\Omega}_{S},u_{L}^{+}\Vert u_{L}^{-})$
. Contrastingly, the scale modulation for dissipation increases up to
![]() ${\it\Lambda}_{S}=3{\it\lambda}$
and remains unchanged for
${\it\Lambda}_{S}=3{\it\lambda}$
and remains unchanged for
![]() ${\it\Lambda}_{S}=4{\it\lambda}$
. This is in contrast to the modulation of the velocity fluctuations (figure 4
a), in which (at low
${\it\Lambda}_{S}=4{\it\lambda}$
. This is in contrast to the modulation of the velocity fluctuations (figure 4
a), in which (at low
![]() ${\it\Lambda}_{L}$
) the modulation effect is observed to increase monotonically as
${\it\Lambda}_{L}$
) the modulation effect is observed to increase monotonically as
![]() ${\it\Lambda}_{S}$
is increased.
${\it\Lambda}_{S}$
is increased.

Figure 5. Instantaneous visualisation of high-enstrophy
![]() $({{\it\omega}_{S}}^{2})$
‘worms’ concurrent to
$({{\it\omega}_{S}}^{2})$
‘worms’ concurrent to
![]() $u_{L}/U_{c}=0.1$
(red) and
$u_{L}/U_{c}=0.1$
(red) and
![]() $u_{L}/U_{c}=-0.1$
(blue) isosurfaces for the low-speed side of the mixing layer. In this case
$u_{L}/U_{c}=-0.1$
(blue) isosurfaces for the low-speed side of the mixing layer. In this case
![]() ${\it\Lambda}_{S}={\it\Lambda}_{L}=3{\it\lambda}$
.
${\it\Lambda}_{S}={\it\Lambda}_{L}=3{\it\lambda}$
.
5. Conclusions
The hypothesised convective scale modulation mechanism presented in Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) is lent further credence in this paper. A concurrent scale modulation of the small-scale velocity fluctuations, and importantly velocity gradient quantities, is observed in which positive
![]() $u_{L}$
fluctuations contain ‘rougher’ small-scale turbulence with more intermittent dissipation, enstrophy and enstrophy amplification in the low-speed side of a mixing layer. This scale modulation is observed to occur when the small scales, defined by a sharp cutoff wavenumber, consist entirely of dissipative motions as well as inertial motions. It is visualised in figure 5, which illustrates the ‘worm-like’ structures of high enstrophy, which are widely reported in the literature (e.g. Kerr Reference Kerr1985), concurrent to isosurfaces of
$u_{L}$
fluctuations contain ‘rougher’ small-scale turbulence with more intermittent dissipation, enstrophy and enstrophy amplification in the low-speed side of a mixing layer. This scale modulation is observed to occur when the small scales, defined by a sharp cutoff wavenumber, consist entirely of dissipative motions as well as inertial motions. It is visualised in figure 5, which illustrates the ‘worm-like’ structures of high enstrophy, which are widely reported in the literature (e.g. Kerr Reference Kerr1985), concurrent to isosurfaces of
![]() $u_{L}/U_{c}=\pm 0.1$
. The positive velocity fluctuations (red isosurfaces) are clearly more densely populated with the high-enstrophy ‘worms’ than the negative fluctuations (blue isosurfaces).
$u_{L}/U_{c}=\pm 0.1$
. The positive velocity fluctuations (red isosurfaces) are clearly more densely populated with the high-enstrophy ‘worms’ than the negative fluctuations (blue isosurfaces).
The scale modulation peaks when the cutoff is close to the peak of the dissipation spectrum in which the characteristic ‘tear-drop’ shaped joint p.d.f. between the second and third invariants of the velocity gradient tensor begins to take shape, namely the extended ‘Vieillefosse tail’ and enhanced contribution from the primarily enstrophy amplifying sector. The ‘tear-drop’ shape itself is only produced when a significant range of scales is present, beyond merely the dissipative range. The scale modulation effect is shown to be non-local in the sense that very-large-scale velocity fluctuations alter the distribution of concurrent small-scale velocity and velocity gradient quantities across a large ‘gap’ in wavenumber space. The modulation of small-scale velocity fluctuations by very large scales collapses below a certain wavenumber definition for these large scales, whereas this collapse is not observed for velocity gradient quantities. The sign of the large-scale velocity fluctuations is also observed to modulate the small-scale velocity gradient quantities, with a peak modulation length scale observed to be
![]() ${\it\Lambda}_{L}\approx 3{\it\lambda}$
, regardless of how the small scales are defined. Further, the modulation of strain (dissipation) is observed to be more significant than that of rotation (enstrophy), with vortex stretching intermediate between the two, as illustrated in figure 4(b). As the definition of the small scales is broadened, including a greater contribution to the total dissipation, the modulation effect increases up to a point. This is observed to lie between
${\it\Lambda}_{L}\approx 3{\it\lambda}$
, regardless of how the small scales are defined. Further, the modulation of strain (dissipation) is observed to be more significant than that of rotation (enstrophy), with vortex stretching intermediate between the two, as illustrated in figure 4(b). As the definition of the small scales is broadened, including a greater contribution to the total dissipation, the modulation effect increases up to a point. This is observed to lie between
![]() $3{\it\lambda}$
and
$3{\it\lambda}$
and
![]() $4{\it\lambda}$
for dissipation and somewhat smaller than this for enstrophy and enstrophy amplification, after which the modulation effect diminishes. This is not observed for the modulation of small-scale velocity fluctuations, which is observed to increase monotonically (over the range of
$4{\it\lambda}$
for dissipation and somewhat smaller than this for enstrophy and enstrophy amplification, after which the modulation effect diminishes. This is not observed for the modulation of small-scale velocity fluctuations, which is observed to increase monotonically (over the range of
![]() ${\it\Lambda}_{S}$
tested) as the definition of the small scales is broadened. The modulation effect is observed to spike when the large scales are harmonics of the integral length scale, linking this mechanism to the large-scale rollers that are present in turbulent shear flows. It can thus be postulated that the convective mechanism for scale interaction is driven by the large-scale engulfment of regions of high small-scale activity, close to the peak Reynolds stress location, which are then transported in the cross-stream direction.
${\it\Lambda}_{S}$
tested) as the definition of the small scales is broadened. The modulation effect is observed to spike when the large scales are harmonics of the integral length scale, linking this mechanism to the large-scale rollers that are present in turbulent shear flows. It can thus be postulated that the convective mechanism for scale interaction is driven by the large-scale engulfment of regions of high small-scale activity, close to the peak Reynolds stress location, which are then transported in the cross-stream direction.
Acknowledgements
The author would like to acknowledge EPSRC for the provision of computational time on HECToR through the Resource Allocation Panel, Dr S. Laizet for his role in simulating the data and Mr M. Chamand for fruitful discussions on scale interactions.








