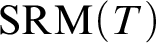1 Introduction
The countable models of uncountably categorical theories were characterized by Baldwin and Lachlan [Reference Baldwin and Lachlan7] as being completely determined by a single dimension. Thus these models are very well understood model-theoretically. We seek to also understand them recursion-theoretically. A fundamental question is which of these models have recursive presentations.
From Baldwin and Lachlan’s characterization in terms of dimensions, the countable models of any uncountably categorical but not countably categorical theory form an elementary chain
![]() $M_0\prec M_1\prec M_2\prec \cdots \prec M_\omega $
. For such a theory T, the Spectrum of Recursive Models of T (
$M_0\prec M_1\prec M_2\prec \cdots \prec M_\omega $
. For such a theory T, the Spectrum of Recursive Models of T (
![]() $ \operatorname {\mathrm {SRM}}(T)$
) is the set of i so that
$ \operatorname {\mathrm {SRM}}(T)$
) is the set of i so that
![]() $M_i$
has a recursive presentation. The spectrum problem asks which subsets of
$M_i$
has a recursive presentation. The spectrum problem asks which subsets of
![]() $\omega +1$
appear as
$\omega +1$
appear as
![]() $ \operatorname {\mathrm {SRM}}(T)$
for some theory T.
$ \operatorname {\mathrm {SRM}}(T)$
for some theory T.
The following theorem summarizes all the positive results currently known about the existence of spectra.
Theorem 1.1. The following are spectra of recursive models of strongly minimal theories:
-
•
 $\emptyset $
,
$\emptyset $
, -
•
 $[0,\omega ]$
, i.e.,
$[0,\omega ]$
, i.e.,
 $\omega +1$
,
$\omega +1$
, -
•
 $\{0\}$
(Goncharov [Reference Gončarov8]),
$\{0\}$
(Goncharov [Reference Gončarov8]), -
•
 $[0,n]$
, i.e.,
$[0,n]$
, i.e.,
 $\{0,\ldots n\}$
, for any
$\{0,\ldots n\}$
, for any
 $n \in \omega $
(Kudaibergenov [Reference Kudaĭbergenov17]),
$n \in \omega $
(Kudaibergenov [Reference Kudaĭbergenov17]), -
•
 $[0,\omega )$
, i.e.,
$[0,\omega )$
, i.e.,
 $\omega $
(Khoussainov/Nies/Shore [Reference Khoussainov, Nies and Shore15]),
$\omega $
(Khoussainov/Nies/Shore [Reference Khoussainov, Nies and Shore15]), -
•
 $[1,\omega ]$
, i.e.,
$[1,\omega ]$
, i.e.,
 $(\omega +1)\smallsetminus \{0\}$
(Khoussainov/Nies/Shore [Reference Khoussainov, Nies and Shore15], see also [Reference Khoussainov, Semukhin and Stephan16]),
$(\omega +1)\smallsetminus \{0\}$
(Khoussainov/Nies/Shore [Reference Khoussainov, Nies and Shore15], see also [Reference Khoussainov, Semukhin and Stephan16]), -
•
 $\{1\}$
(Nies [Reference Nies18]),
$\{1\}$
(Nies [Reference Nies18]), -
•
 $[1,\alpha )$
for any
$[1,\alpha )$
for any
 $\alpha \in [2,\omega ]$
(Nies/Hirschfeldt, see Nies [Reference Nies18, p. 314]),
$\alpha \in [2,\omega ]$
(Nies/Hirschfeldt, see Nies [Reference Nies18, p. 314]), -
•
 $\{\omega \}$
(Hirschfeldt/Khoussainov/Semukhin [Reference Hirschfeldt, Khoussainov and Semukhin10]),
$\{\omega \}$
(Hirschfeldt/Khoussainov/Semukhin [Reference Hirschfeldt, Khoussainov and Semukhin10]), -
•
 $\{0,\omega \}$
(Andrews [Reference Andrews6]).
$\{0,\omega \}$
(Andrews [Reference Andrews6]).
While relatively few sets are known to be spectra, the only known upper bound on all spectra is that every spectrum must be
 $\Sigma ^0_{\omega +3}$
, and for a model complete theory,
$\Sigma ^0_{\omega +3}$
, and for a model complete theory,
![]() $ \operatorname {\mathrm {SRM}}(T)$
is
$ \operatorname {\mathrm {SRM}}(T)$
is
![]() $\Sigma ^0_4$
[Reference Nies18].
$\Sigma ^0_4$
[Reference Nies18].
In the hopes of coming to a better understanding of possible spectra, a few approaches have been taken, including: Focusing on the strongly minimal theories, focusing on theories with particular geometric properties, and focusing on theories in languages with finite signatures. In these cases, we have better characterizations of the possible spectra.
By “particular geometric properties,” we refer to the Zilber trichotomy: Zilber conjectured that every strongly minimal theory is either disintegrated (
 $ \operatorname {\mathrm {acl}}(A)=\bigcup _{a\in A} \operatorname {\mathrm {acl}}(a)$
) or locally modular (after adding one constant, we get
$ \operatorname {\mathrm {acl}}(A)=\bigcup _{a\in A} \operatorname {\mathrm {acl}}(a)$
) or locally modular (after adding one constant, we get
![]() $\dim (A\cup B)=\dim (A)+\dim (B)-\dim (A\cap B)$
for any finite-dimensional closed sets A and B) or is field-like (there is an interpretable an infinite field with no definable sets on it aside from the ones definable in the field itself).
$\dim (A\cup B)=\dim (A)+\dim (B)-\dim (A\cap B)$
for any finite-dimensional closed sets A and B) or is field-like (there is an interpretable an infinite field with no definable sets on it aside from the ones definable in the field itself).
Under such assumptions, we can completely characterize the possible spectra:
Theorem 1.2 (Andrews–Medvedev [Reference Andrews and Medvedev3])
If T is disintegrated strongly minimal and the language has a finite signature, then
![]() $ \operatorname {\mathrm {SRM}}(T)=\emptyset ,\{0\},$
or
$ \operatorname {\mathrm {SRM}}(T)=\emptyset ,\{0\},$
or
![]() $[0,\omega ]$
.
$[0,\omega ]$
.
By Herwig–Lempp–Ziegler [Reference Herwig, Lempp and Ziegler11], all three of these cases are in fact spectra of disintegrated theories in languages with finite signature.
Theorem 1.3 (Andrews–Medvedev [Reference Andrews and Medvedev3])
If T is a modular strongly minimal theory expanding a group in a language with finite signature, then
![]() $ \operatorname {\mathrm {SRM}}(T)=\emptyset ,\{0\},$
or
$ \operatorname {\mathrm {SRM}}(T)=\emptyset ,\{0\},$
or
![]() $[0,\omega ]$
.
$[0,\omega ]$
.
If T is a field-like strongly minimal theory expanding a field in a language with finite signature, then
![]() $ \operatorname {\mathrm {SRM}}(T)= [0,\omega ]$
.
$ \operatorname {\mathrm {SRM}}(T)= [0,\omega ]$
.
Thus, in each prototypical case of the Zilber trichotomy, if the language has a finite signature, then there are very few possible spectra. In particular, either all or no models of positive dimension have recursive presentations.
Hrushovski [Reference Hrushovski13] showed that the Zilber conjecture is false and produced a new class of strongly minimal sets, all of which have a geometric property called flatness. Formally, flatness is defined below, but intuitively it describes dimension as being purely combinatorial in a way that allows for no algebraic rules (such as associativity of a group operation) to hold:
Definition 1.4. A theory is flat if whenever
![]() $\{E_i \mid i\in I\}$
is a finite collection of finite-dimensional closed sets, and s ranges over the subsets of I, we have
$\{E_i \mid i\in I\}$
is a finite collection of finite-dimensional closed sets, and s ranges over the subsets of I, we have
 $\Sigma _{s}{(-1)}^{\lvert s\rvert }\dim (E_s)\leq 0$
.
$\Sigma _{s}{(-1)}^{\lvert s\rvert }\dim (E_s)\leq 0$
.
Andrews [Reference Andrews5, Reference Andrews6] showed that
![]() $[0,n]$
,
$[0,n]$
,
![]() $[0,\omega )$
, and
$[0,\omega )$
, and
![]() $\{\omega \}$
are spectra of recursive models of flat strongly minimal theories in languages with finite signature. Thus, it is possible for a strongly minimal theory in a finite language to have some positive-dimensional models be recursive and others not.
$\{\omega \}$
are spectra of recursive models of flat strongly minimal theories in languages with finite signature. Thus, it is possible for a strongly minimal theory in a finite language to have some positive-dimensional models be recursive and others not.
In this paper, we present another schema of spectra of a flat strongly minimal theory in a language with finite signature:
![]() $[0,n]\cup \{\omega \}$
$[0,n]\cup \{\omega \}$
We also point out the most important technical innovation in this paper. For the general technique, we code extra relations in a structure by the number of extensions of a certain type over a base. That is, in the amalgamation, we allow more or fewer occurrences of a certain extension in order to code information. This only successfully codes that information if a tuple will have the maximal number of extensions allowed. In condition (3”) on page 32, we see that if the base is strong enough, then it has the maximal number of realizations, but there is much room for exceptions. In the previous uses of this technique [Reference Andrews5, Reference Andrews6], there were two different tricks used to avoid these exceptions, but one only works if the size of the base of the extension is at most one more than the dimension of the prime model and the other only works if we have a bound on the size of the extensions that we will need. Neither can work in our current setting, and they are both fragile methods. In §3 we present the correct solution for this problem: We present a collection of “unblockable” extensions which for any base whatsoever in any Hrushovski construction must have the maximal possible number of extensions. This tool should make any combination of recursion theory with Hrushovski constructions far easier in the future.
A different approach to recursion-theoretically understanding strongly minimal theories is to consider the relative complexity of models. That is, if one model of a theory T is recursive, how difficult can it be to compute the other models of T? In the case of a disintegrated theory, every other model must be recursive in
![]() $\mathbf {0}''$
[Reference Goncharov, Harizanov, Laskowski, Lempp and McCoy9] and there is a theory where
$\mathbf {0}''$
[Reference Goncharov, Harizanov, Laskowski, Lempp and McCoy9] and there is a theory where
![]() $\mathbf {0}''$
is needed to compute the other models [Reference Khoussainov, Laskowski, Lempp and Solomon14]. In general, the degrees which compute every countable model of a strongly minimal theory which has a recursive model are exactly the degrees which are high over
$\mathbf {0}''$
is needed to compute the other models [Reference Khoussainov, Laskowski, Lempp and Solomon14]. In general, the degrees which compute every countable model of a strongly minimal theory which has a recursive model are exactly the degrees which are high over
![]() $\mathbf {0}''$
[Reference Andrews and Knight1, Reference Andrews, Lempp and Schweber2]. That is, exactly the degrees
$\mathbf {0}''$
[Reference Andrews and Knight1, Reference Andrews, Lempp and Schweber2]. That is, exactly the degrees
![]() $\mathbf {d}$
so that
$\mathbf {d}$
so that
![]() $\mathbf {d}>\mathbf {0}''$
and
$\mathbf {d}>\mathbf {0}''$
and
![]() $\mathbf {d}'\geq \mathbf {0}^{(4)}$
.
$\mathbf {d}'\geq \mathbf {0}^{(4)}$
.
2 Background
2.1 Notation
We write
![]() $\exists ^{k}\bar {x} \phi (\bar {x})$
to mean that there are at least k disjoint tuples
$\exists ^{k}\bar {x} \phi (\bar {x})$
to mean that there are at least k disjoint tuples
![]() $\bar {x}$
which satisfy
$\bar {x}$
which satisfy
![]() $\phi $
.
$\phi $
.
2.2 Hrushovski constructions in infinite languages where
 $\mu $
depends on the self-sufficient closure
$\mu $
depends on the self-sufficient closure
Fix
![]() $\mathcal {L}$
a relational language with the relations indexed by a (finite or not) initial segment of
$\mathcal {L}$
a relational language with the relations indexed by a (finite or not) initial segment of
![]() $\omega $
. We will enforce in our construction that each relation is symmetric (if we do not do this, the same construction works with no changes—this is purely a stylistic choice).
$\omega $
. We will enforce in our construction that each relation is symmetric (if we do not do this, the same construction works with no changes—this is purely a stylistic choice).
The following definitions and lemmas are standard to all Hrushovski constructions.
Definition 2.1. The pre-dimension function on
![]() $\mathcal {L}$
-structures is the function
$\mathcal {L}$
-structures is the function
![]() $\delta $
from finite
$\delta $
from finite
![]() $\mathcal {L}$
-structures to
$\mathcal {L}$
-structures to
![]() $\mathbb {Z}\cup \{-\infty \}$
so that
$\mathbb {Z}\cup \{-\infty \}$
so that
![]() $\delta (A)=\lvert A\rvert -\Sigma _{R\in \mathcal {L}}\#R(A)$
. Here
$\delta (A)=\lvert A\rvert -\Sigma _{R\in \mathcal {L}}\#R(A)$
. Here
![]() $\#R(A)$
counts the number of occurrences of the relations on A (counting
$\#R(A)$
counts the number of occurrences of the relations on A (counting
![]() $R(\bar {a})$
together with
$R(\bar {a})$
together with
![]() $R(\sigma (\bar {a}))$
as a single relation for all permutations
$R(\sigma (\bar {a}))$
as a single relation for all permutations
![]() $\sigma $
).
$\sigma $
).
For
![]() $A, B\subseteq C$
with
$A, B\subseteq C$
with
![]() $A,B$
finite:
$A,B$
finite:
-
• We write
 $\delta (B/A)=\delta (A\cup B)-\delta (A)$
.
$\delta (B/A)=\delta (A\cup B)-\delta (A)$
. -
• We define
 $\delta (A,C)=\inf \{\delta (D)\mid A\subseteq D\subseteq C, D\text { finite}\}$
.
$\delta (A,C)=\inf \{\delta (D)\mid A\subseteq D\subseteq C, D\text { finite}\}$
. -
• We say A is strong (also called self-sufficient) in C, written
 $A\leq C$
, if
$A\leq C$
, if
 $\delta (A)=\delta (A,C)$
.
$\delta (A)=\delta (A,C)$
. -
• We say B is simply algebraic over A if
 $A\cap B=\emptyset $
,
$A\cap B=\emptyset $
,
 $A\leq A\cup B$
,
$A\leq A\cup B$
,
 $\delta (B/A)=0$
, and there is no proper non-empty subset
$\delta (B/A)=0$
, and there is no proper non-empty subset
 $B'$
of B so that
$B'$
of B so that
 $\delta (B'/A)=0$
.
$\delta (B'/A)=0$
. -
• We say B is minimally simply algebraic over A if B is simply algebraic over A and A is minimal so that B is simply algebraic over A.
-
• If
 $A\subseteq B$
and
$A\subseteq B$
and
 $B\smallsetminus A$
is (minimally) simply algebraic over A, then we say
$B\smallsetminus A$
is (minimally) simply algebraic over A, then we say
 $A\subseteq B$
(or
$A\subseteq B$
(or
 $B/A$
) is a (minimally) simply algebraic extension.
$B/A$
) is a (minimally) simply algebraic extension.
Let
![]() $\mathcal {C}_0$
be the collection of
$\mathcal {C}_0$
be the collection of
![]() $\mathcal {L}$
-structures C so that
$\mathcal {L}$
-structures C so that
![]() $\delta (A)\geq 0$
for every finite
$\delta (A)\geq 0$
for every finite
![]() $A\subseteq C$
.
$A\subseteq C$
.
Observation 2.2. For
![]() $A,B$
finite subsets of an
$A,B$
finite subsets of an
![]() $\mathcal {L}$
-structure C,
$\mathcal {L}$
-structure C,
with equality if and only if there are no relations holding between A and B other than those inside A or those inside B. In this case, we say A and B are freely joined over
![]() $A\cap B$
and we write
$A\cap B$
and we write
![]() $A\cup B = A\oplus _{A\cap B}B$
.
$A\cup B = A\oplus _{A\cap B}B$
.
Proof This is just inclusion–exclusion on the number of relations holding in
![]() $A\cup B$
.⊣
$A\cup B$
.⊣
The following two lemmas capture some basic facts about the notion of strong substructure.
Lemma 2.3. If
![]() $A\leq B$
, then for any
$A\leq B$
, then for any
![]() $X\subseteq B$
,
$X\subseteq B$
,
![]() $\delta (X\cap A)\leq \delta (X)$
.
$\delta (X\cap A)\leq \delta (X)$
.
If
![]() $A\leq B\leq C$
, then
$A\leq B\leq C$
, then
![]() $A\leq C$
.
$A\leq C$
.
Proof Suppose
![]() $A\leq B$
. Then
$A\leq B$
. Then
![]() $\delta (A)\leq \delta (X\cup A)\leq \delta (X)+\delta (A)-\delta (X\cap A)$
. Thus,
$\delta (A)\leq \delta (X\cup A)\leq \delta (X)+\delta (A)-\delta (X\cap A)$
. Thus,
![]() $\delta (X\cap A)\leq \delta (X)$
.
$\delta (X\cap A)\leq \delta (X)$
.
Now suppose
![]() $A\leq B\leq C$
. Let
$A\leq B\leq C$
. Let
![]() $A\subseteq X\subseteq C$
. Then
$A\subseteq X\subseteq C$
. Then
![]() $\delta (X\cap B)\leq \delta (X)$
since
$\delta (X\cap B)\leq \delta (X)$
since
![]() $B\leq C$
, and
$B\leq C$
, and
![]() $\delta (A)=\delta (X\cap B\cap A)\leq \delta (X\cap B)$
since
$\delta (A)=\delta (X\cap B\cap A)\leq \delta (X\cap B)$
since
![]() $A\leq B$
. So,
$A\leq B$
. So,
![]() $\delta (A)\leq \delta (X)$
.⊣
$\delta (A)\leq \delta (X)$
.⊣
Lemma 2.4. Suppose
![]() $X\leq C$
and
$X\leq C$
and
![]() $Y,Z\subseteq C$
are distinct, simply algebraic over X. Then Y and Z are disjoint.
$Y,Z\subseteq C$
are distinct, simply algebraic over X. Then Y and Z are disjoint.
Proof Since
![]() $\delta (X\cup Y \cup Z)\leq \delta (X\cup Y)+\delta (X\cup Z)-\delta (X\cup (Y\cap Z))$
, we can subtract
$\delta (X\cup Y \cup Z)\leq \delta (X\cup Y)+\delta (X\cup Z)-\delta (X\cup (Y\cap Z))$
, we can subtract
![]() $\delta (X)$
from both sides and see that
$\delta (X)$
from both sides and see that
![]() $\delta (Y\cup Z/X)\leq \delta (Y/X)+\delta (Z/X)-\delta (Y\cap Z/X)=-\delta (Y\cap Z/X)$
. Since Y and Z are simply algebraic over X, either
$\delta (Y\cup Z/X)\leq \delta (Y/X)+\delta (Z/X)-\delta (Y\cap Z/X)=-\delta (Y\cap Z/X)$
. Since Y and Z are simply algebraic over X, either
![]() $Y\cap Z=\emptyset $
or
$Y\cap Z=\emptyset $
or
![]() $\delta (Y\cap Z/X)>0$
. But since
$\delta (Y\cap Z/X)>0$
. But since
![]() $X\leq C$
,
$X\leq C$
,
![]() $0\leq \delta (Y\cup Z/X)=-\delta (Y\cap Z/X)$
. So Y and Z are disjoint.⊣
$0\leq \delta (Y\cup Z/X)=-\delta (Y\cap Z/X)$
. So Y and Z are disjoint.⊣
Definition 2.5. For
![]() $C\in \mathcal {C}_0$
and
$C\in \mathcal {C}_0$
and
![]() $A\subseteq C$
finite, the self-sufficient closure of A is the smallest set X so that
$A\subseteq C$
finite, the self-sufficient closure of A is the smallest set X so that
![]() $A\subseteq X\leq C$
.
$A\subseteq X\leq C$
.
Lemma 2.6. For any finite
![]() $A\subseteq C\in \mathcal {C}_0$
, the self-sufficient closure exists, is unique, and is finite.
$A\subseteq C\in \mathcal {C}_0$
, the self-sufficient closure exists, is unique, and is finite.
Proof Take
![]() $X\supseteq A$
with minimal
$X\supseteq A$
with minimal
![]() $\delta (X)$
and take X minimal as such (i.e., it has no proper subset containing A with the same value of
$\delta (X)$
and take X minimal as such (i.e., it has no proper subset containing A with the same value of
![]() $\delta $
). The minimality of
$\delta $
). The minimality of
![]() $\delta (X)$
implies that
$\delta (X)$
implies that
![]() $X\leq C$
. Suppose X were not unique, then there would be another such set
$X\leq C$
. Suppose X were not unique, then there would be another such set
![]() $Y\supseteq A$
with
$Y\supseteq A$
with
![]() $\delta (Y)=\delta (X)$
. Then
$\delta (Y)=\delta (X)$
. Then
![]() $\delta (X\cup Y)\leq \delta (X)+\delta (Y)-\delta (X\cap Y)<\delta (Y)=\delta (X)$
by minimality of the set X. But this would contradict the minimality of
$\delta (X\cup Y)\leq \delta (X)+\delta (Y)-\delta (X\cap Y)<\delta (Y)=\delta (X)$
by minimality of the set X. But this would contradict the minimality of
![]() $\delta (X)$
.⊣
$\delta (X)$
.⊣
The following definitions are necessary to do the Hrushovski construction with an infinite signature. We will build our theory by using an infinite signature and then taking a reduct to a finite sub-signature.
Definition 2.7. For any
![]() $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
![]() $\bar {a},\bar {b}\subseteq C$
, the relative quantifier-free type of
$\bar {a},\bar {b}\subseteq C$
, the relative quantifier-free type of
![]() $\bar {b}$
over
$\bar {b}$
over
![]() $\bar {a}$
, written
$\bar {a}$
, written
 $ \operatorname {\mathrm {tp_{r.q.f.}}}(\bar {b}/\bar {a})$
, is the set of formulas
$ \operatorname {\mathrm {tp_{r.q.f.}}}(\bar {b}/\bar {a})$
, is the set of formulas
 $\{R(\bar {x}_i,\bar {y}_i)\mid (\bar {b}_i\bar {a}_i)\subseteq (\bar {b}\cup \bar {a})^{ \operatorname {\mathrm {arity}}(R)}\smallsetminus \bar {a}^{ \operatorname {\mathrm {arity}}(R)}, R\in \mathcal {L}, C\models R(\bar {b}_i,\bar {a}_i) \}$
.
$\{R(\bar {x}_i,\bar {y}_i)\mid (\bar {b}_i\bar {a}_i)\subseteq (\bar {b}\cup \bar {a})^{ \operatorname {\mathrm {arity}}(R)}\smallsetminus \bar {a}^{ \operatorname {\mathrm {arity}}(R)}, R\in \mathcal {L}, C\models R(\bar {b}_i,\bar {a}_i) \}$
.
Fix
![]() $\mu (A,B,m)$
to be a function that takes in pairs of
$\mu (A,B,m)$
to be a function that takes in pairs of
![]() $\mathcal {L}$
-structures so that
$\mathcal {L}$
-structures so that
![]() $A\subset B$
is a minimally simply algebraic extension, and a number
$A\subset B$
is a minimally simply algebraic extension, and a number
![]() $m\in \omega \cup \{\infty \}$
, and
$m\in \omega \cup \{\infty \}$
, and
![]() $\mu $
outputs a number in
$\mu $
outputs a number in
![]() $\omega $
so that
$\omega $
so that
![]() $\mu (A,B,m)\geq \delta (A)$
.
$\mu (A,B,m)\geq \delta (A)$
.
We also require
![]() $\mu $
to satisfy: For every relative quantifier-free type
$\mu $
to satisfy: For every relative quantifier-free type
![]() $\Psi $
of a minimally simply algebraic extension, there is a finite sublanguage
$\Psi $
of a minimally simply algebraic extension, there is a finite sublanguage
![]() $\mathcal {L}'\subseteq \mathcal {L}$
so that
$\mathcal {L}'\subseteq \mathcal {L}$
so that
 $ \operatorname {\mathrm {tp}}_{q.f.}(A)\vert \mathcal {L}'= \operatorname {\mathrm {tp}}_{q.f.}(A')\vert \mathcal {L}'$
and
$ \operatorname {\mathrm {tp}}_{q.f.}(A)\vert \mathcal {L}'= \operatorname {\mathrm {tp}}_{q.f.}(A')\vert \mathcal {L}'$
and
![]() $ \operatorname {\mathrm {tp_{r.q.f.}}}(B/A)= \operatorname {\mathrm {tp_{r.q.f.}}}(B'/A')=\Psi $
implies
$ \operatorname {\mathrm {tp_{r.q.f.}}}(B/A)= \operatorname {\mathrm {tp_{r.q.f.}}}(B'/A')=\Psi $
implies
![]() $\mu (A,B,m)=\mu (A',B',m)$
. Further, for every
$\mu (A,B,m)=\mu (A',B',m)$
. Further, for every
![]() $A,B$
, we must have
$A,B$
, we must have
![]() $\lim _{m\rightarrow \infty } \mu (A,B,m)=\mu (A,B,\infty )$
.
$\lim _{m\rightarrow \infty } \mu (A,B,m)=\mu (A,B,\infty )$
.
For any
![]() $A\subseteq C$
, we let
$A\subseteq C$
, we let
![]() $g_C(A)$
be the least m so that there exists an
$g_C(A)$
be the least m so that there exists an
![]() $X\subseteq C$
so that
$X\subseteq C$
so that
![]() $A\not \leq X$
which is witnessed by using only the first m relations in the language
$A\not \leq X$
which is witnessed by using only the first m relations in the language
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\lvert X\rvert \leq \lvert A\rvert +m$
. If there is no such m, then
$\lvert X\rvert \leq \lvert A\rvert +m$
. If there is no such m, then
![]() $A\leq C$
and we let
$A\leq C$
and we let
![]() $g_C(A)=\infty $
.
$g_C(A)=\infty $
.
We have chosen to present the definition of
![]() $\mu $
in terms of an extension
$\mu $
in terms of an extension
![]() $A\subseteq B$
. For
$A\subseteq B$
. For
![]() $A,B\subseteq C$
with
$A,B\subseteq C$
with
![]() $A,B$
finite, if B is minimally simply algebraic over A (in particular, B is disjoint from A), then we also write
$A,B$
finite, if B is minimally simply algebraic over A (in particular, B is disjoint from A), then we also write
![]() $\mu (A,B,m)$
for
$\mu (A,B,m)$
for
![]() $\mu (A,A\cup B, m)$
.
$\mu (A,A\cup B, m)$
.
The following observation is a critical fact about how the function g behaves.
Observation 2.8. If
![]() $A\subseteq B\leq C$
, then
$A\subseteq B\leq C$
, then
![]() $g_B(A)=g_C(A)$
.
$g_B(A)=g_C(A)$
.
Proof That
![]() $g_C(A)\leq g_B(A)$
is immediate since any
$g_C(A)\leq g_B(A)$
is immediate since any
![]() $X\subseteq B$
so that
$X\subseteq B$
so that
![]() $A\subseteq X$
and
$A\subseteq X$
and
![]() $\delta (X)<\delta (A)$
is also a subset of C. Suppose
$\delta (X)<\delta (A)$
is also a subset of C. Suppose
![]() $X\subseteq C$
is so that
$X\subseteq C$
is so that
![]() $A\subseteq X$
and
$A\subseteq X$
and
![]() $\mathcal {L}_0\subseteq \mathcal {L}$
is a sublanguage so that restricting to this sublanguage,
$\mathcal {L}_0\subseteq \mathcal {L}$
is a sublanguage so that restricting to this sublanguage,
![]() $\delta (X\vert \mathcal {L}_0)<\delta (A\vert \mathcal {L}_0)$
. Then
$\delta (X\vert \mathcal {L}_0)<\delta (A\vert \mathcal {L}_0)$
. Then
![]() $\delta (X\cap B)\leq \delta (X)< \delta (A)$
, so in the same sublanguage, B contains a set no larger than X witnessing that A is not strong. So
$\delta (X\cap B)\leq \delta (X)< \delta (A)$
, so in the same sublanguage, B contains a set no larger than X witnessing that A is not strong. So
![]() $g_B(A)\leq g_C(A)$
.⊣
$g_B(A)\leq g_C(A)$
.⊣
Definition 2.9. Let Y and X be finite
![]() $\mathcal {L}$
-structures so that Y is minimally simply algebraic over X.
$\mathcal {L}$
-structures so that Y is minimally simply algebraic over X.
We define
![]() $\mathcal {L}_{Y/X}$
to be the finite collection of symbols occurring in
$\mathcal {L}_{Y/X}$
to be the finite collection of symbols occurring in
![]() $ \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
.
$ \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
.
Suppose B and A are finite
![]() $\mathcal {L}$
-structures such that
$\mathcal {L}$
-structures such that
![]() $ \operatorname {\mathrm {tp_{r.q.f.}}}(B/A) \supseteq \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
and
$ \operatorname {\mathrm {tp_{r.q.f.}}}(B/A) \supseteq \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
and
 $ \operatorname {\mathrm {tp}}_{q.f.}(X)= \operatorname {\mathrm {tp}}_{q.f.}(A)$
, then we say the extension B over A is of the form of Y over X.
$ \operatorname {\mathrm {tp}}_{q.f.}(X)= \operatorname {\mathrm {tp}}_{q.f.}(A)$
, then we say the extension B over A is of the form of Y over X.
Definition 2.10. Let
![]() $\mathcal {C}_{\mu }$
be the collection of finite
$\mathcal {C}_{\mu }$
be the collection of finite
![]() $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
![]() $C \in \mathcal {C}_0$
that satisfy:
$C \in \mathcal {C}_0$
that satisfy:
Suppose
![]() $A,B^1,\ldots ,B^r$
are disjoint subsets of C so that each
$A,B^1,\ldots ,B^r$
are disjoint subsets of C so that each
![]() $B^i/A$
is of the form of
$B^i/A$
is of the form of
![]() $Y/X$
, then
$Y/X$
, then
![]() $r\leq \mu (X,Y,g_C(A))$
.
$r\leq \mu (X,Y,g_C(A))$
.
For any
![]() $\forall $
-axiomatizable elementary property
$\forall $
-axiomatizable elementary property
![]() $\zeta $
which is preserved by free joins, let
$\zeta $
which is preserved by free joins, let
![]() $\mathcal {C}_{\mu }^{\zeta }$
be the collection of
$\mathcal {C}_{\mu }^{\zeta }$
be the collection of
![]() $C\in \mathcal {C}_{\mu }$
so that
$C\in \mathcal {C}_{\mu }$
so that
![]() $\mathcal {C}\models \zeta $
.
$\mathcal {C}\models \zeta $
.
Note that for trivial
![]() $\zeta $
,
$\zeta $
,
 $\mathcal {C}_{\mu }^\zeta = \mathcal {C}_{\mu }$
.
$\mathcal {C}_{\mu }^\zeta = \mathcal {C}_{\mu }$
.
In most uses of the amalgamation method, we use the class
![]() $\mathcal {C}_{\mu }$
, but it requires very little extra work to include the generality of working with
$\mathcal {C}_{\mu }$
, but it requires very little extra work to include the generality of working with
![]() $\mathcal {C}_{\mu }^\zeta $
and it will make our construction of a strongly minimal theory T with
$\mathcal {C}_{\mu }^\zeta $
and it will make our construction of a strongly minimal theory T with
![]() $ \operatorname {\mathrm {SRM}}(T)=[0,n]\cup \{\omega \}$
slightly cleaner.
$ \operatorname {\mathrm {SRM}}(T)=[0,n]\cup \{\omega \}$
slightly cleaner.
Observation 2.11. Fix
![]() $Y/X$
a minimally simply algebraic extension. There is a first-order formula which is true in any
$Y/X$
a minimally simply algebraic extension. There is a first-order formula which is true in any
 $C\in \mathcal {C}^\zeta _\mu $
and implies that C does not contain disjoint subsets
$C\in \mathcal {C}^\zeta _\mu $
and implies that C does not contain disjoint subsets
![]() $A,B^1,\ldots ,B^r$
of the form of
$A,B^1,\ldots ,B^r$
of the form of
![]() $Y/X$
with
$Y/X$
with
![]() $r>\mu (X,Y,g_C(A))$
.
$r>\mu (X,Y,g_C(A))$
.
Proof Let
![]() $\mathcal {L}'$
be the finite sublanguage of
$\mathcal {L}'$
be the finite sublanguage of
![]() $\mathcal {L}$
guaranteed in Definition 2.7, and let m be an integer so that
$\mathcal {L}$
guaranteed in Definition 2.7, and let m be an integer so that
![]() $\mu (X,Y,k)=\mu (X,Y,\infty )$
for any
$\mu (X,Y,k)=\mu (X,Y,\infty )$
for any
![]() $k\geq m$
.
$k\geq m$
.
Let
![]() $\rho (A)$
say that
$\rho (A)$
say that
![]() $A\vert \mathcal {L}'\cong X\vert \mathcal {L}'$
. For each
$A\vert \mathcal {L}'\cong X\vert \mathcal {L}'$
. For each
![]() $k\in \omega $
, let
$k\in \omega $
, let
![]() $\psi _k(A,C^1,\ldots C^k)$
say that the sets are disjoint, and that
$\psi _k(A,C^1,\ldots C^k)$
say that the sets are disjoint, and that
![]() $ \operatorname {\mathrm {tp_{r.q.f.}}}(C^j/A)\supseteq \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
for each j. For each
$ \operatorname {\mathrm {tp_{r.q.f.}}}(C^j/A)\supseteq \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
for each j. For each
![]() $l\leq m$
, let
$l\leq m$
, let
![]() $\phi _l$
say that
$\phi _l$
say that
![]() $g_C(A)=l$
. Finally, let
$g_C(A)=l$
. Finally, let
![]() $\theta $
be the formula which says
$\theta $
be the formula which says
![]() $\forall A$
, if
$\forall A$
, if
![]() $\rho (A)$
holds, then
$\rho (A)$
holds, then
 $$\begin{align*}\bigvee_{l<m}\left( \phi_l(A)\wedge \neg \exists Z \psi_{\mu(X,Y,l)+1}(A,Z)\right)\vee \left(\bigwedge_{l<m}\neg \phi_l(A)\wedge \neg \exists Z \psi_{\mu(X,Y,\infty)+1}(A,Z)\right). \end{align*}$$
$$\begin{align*}\bigvee_{l<m}\left( \phi_l(A)\wedge \neg \exists Z \psi_{\mu(X,Y,l)+1}(A,Z)\right)\vee \left(\bigwedge_{l<m}\neg \phi_l(A)\wedge \neg \exists Z \psi_{\mu(X,Y,\infty)+1}(A,Z)\right). \end{align*}$$
Let
![]() $\Omega $
be the collection of all the extensions
$\Omega $
be the collection of all the extensions
![]() $Y'/X'$
so that
$Y'/X'$
so that
![]() $ \operatorname {\mathrm {tp_{r.q.f.}}}(Y'/X')= \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
and
$ \operatorname {\mathrm {tp_{r.q.f.}}}(Y'/X')= \operatorname {\mathrm {tp_{r.q.f.}}}(Y/X)$
and
![]() $X'\vert \mathcal {L}'\cong X\vert \mathcal {L}'$
. Then
$X'\vert \mathcal {L}'\cong X\vert \mathcal {L}'$
. Then
![]() $\theta $
says that the
$\theta $
says that the
![]() $\mu $
-bound is obeyed for each extension in
$\mu $
-bound is obeyed for each extension in
![]() $\Omega $
. Thus
$\Omega $
. Thus
![]() $\theta $
is true in every
$\theta $
is true in every
 $C\in \mathcal {C}^\zeta _{\mu }$
and implies that C respects the
$C\in \mathcal {C}^\zeta _{\mu }$
and implies that C respects the
![]() $\mu $
-bound for
$\mu $
-bound for
![]() $Y/X$
.⊣
$Y/X$
.⊣
The following observation follows directly from the definition of being of the form of
![]() $Y/X$
.
$Y/X$
.
Observation 2.12. Let
![]() $A\subseteq B$
be finite
$A\subseteq B$
be finite
![]() $\mathcal {L}$
-structures. Let
$\mathcal {L}$
-structures. Let
![]() $A'\subseteq B'$
be formed by removing some occurrence
$A'\subseteq B'$
be formed by removing some occurrence
![]() $R(\bar {b})$
of some relation R from B. If
$R(\bar {b})$
of some relation R from B. If
![]() $B'/A'$
is of the form of
$B'/A'$
is of the form of
![]() $Y/X$
, then either
$Y/X$
, then either
![]() $B/A$
is of the form of
$B/A$
is of the form of
![]() $Y/X$
or
$Y/X$
or
![]() $\bar {b}\subseteq A$
.
$\bar {b}\subseteq A$
.
The following three Lemmas allow us to perform “strong amalgamation” on the class
![]() $\mathcal {C}^\zeta _{\mu }$
, which will lead to a generic structure. The theory of this generic will be our strongly minimal theory.
$\mathcal {C}^\zeta _{\mu }$
, which will lead to a generic structure. The theory of this generic will be our strongly minimal theory.
Lemma 2.13. Suppose
![]() $A,B_1,B_2\in \mathcal {C}_0$
,
$A,B_1,B_2\in \mathcal {C}_0$
,
![]() $A=B_1\cap B_2$
, and
$A=B_1\cap B_2$
, and
![]() $A\leq B_1$
. Let
$A\leq B_1$
. Let
![]() $E=B_1\oplus _A B_2$
. Suppose
$E=B_1\oplus _A B_2$
. Suppose
![]() $F,C^1,\ldots, C^r$
are disjoint substructures of E such that each
$F,C^1,\ldots, C^r$
are disjoint substructures of E such that each
![]() $C^i$
is minimally simply algebraic over F. Then one of the following holds:
$C^i$
is minimally simply algebraic over F. Then one of the following holds:
-
• One of the
 $C^i$
is contained in
$C^i$
is contained in
 $B_1\smallsetminus A$
and
$B_1\smallsetminus A$
and
 $F\subseteq A$
.
$F\subseteq A$
. -
•
 $F\cup \bigcup _{i\leq r} C^i$
is contained either entirely in
$F\cup \bigcup _{i\leq r} C^i$
is contained either entirely in
 $B_1$
or entirely in
$B_1$
or entirely in
 $B_2$
.
$B_2$
. -
•
 $r\leq \delta (F).$
$r\leq \delta (F).$
-
• For one
 $C^i$
, setting
$C^i$
, setting
 $Z=(F\cap A)\cup (C^i\cap B_2)$
,
$Z=(F\cap A)\cup (C^i\cap B_2)$
,
 $\delta (Z/Z\cap A)<0$
. Further, one of the
$\delta (Z/Z\cap A)<0$
. Further, one of the
 $C^j$
is entirely contained in
$C^j$
is entirely contained in
 $B_1\smallsetminus A$
. (Note that this cannot happen if
$B_1\smallsetminus A$
. (Note that this cannot happen if
 $A\leq B_2$
.)
$A\leq B_2$
.)
Proof A careful reading of Lemma 3 of [Reference Hrushovski13] will show that this is what is proved there. The full proof appears as Lemma 42 in [Reference Andrews4].⊣
Lemma 2.14 (Algebraic Amalgamation Lemma)
Suppose
![]() $A=B_1\cap B_2$
,
$A=B_1\cap B_2$
,
 $A,B_1,B_2\in \mathcal {C}^\zeta _\mu $
, and
$A,B_1,B_2\in \mathcal {C}^\zeta _\mu $
, and
![]() $B_1\smallsetminus A$
is simply algebraic over A. Let E be the free-join of
$B_1\smallsetminus A$
is simply algebraic over A. Let E be the free-join of
![]() $B_1$
with
$B_1$
with
![]() $B_2$
over A. Then
$B_2$
over A. Then
 $E\in \mathcal {C}^\zeta _\mu $
unless one of the following holds:
$E\in \mathcal {C}^\zeta _\mu $
unless one of the following holds:
-
(1)
 $B_1\smallsetminus A$
is minimally simply algebraic over
$B_1\smallsetminus A$
is minimally simply algebraic over
 $F\subseteq A$
and there are
$F\subseteq A$
and there are
 $\mu (F, B_1\smallsetminus A, g_{B_2}(F))$
disjoint extensions over F of the form of
$\mu (F, B_1\smallsetminus A, g_{B_2}(F))$
disjoint extensions over F of the form of
 $B_1\smallsetminus A$
over F.
$B_1\smallsetminus A$
over F. -
(2) There is a set
 $Y\subseteq B_2$
with
$Y\subseteq B_2$
with
 $\lvert Y\rvert \leq \lvert B_1\smallsetminus A\rvert $
so that
$\lvert Y\rvert \leq \lvert B_1\smallsetminus A\rvert $
so that
 $\delta (Y\vert \mathcal {L}_{B_1/A}/A\vert \mathcal {L}_{B_1/A})<0$
.
$\delta (Y\vert \mathcal {L}_{B_1/A}/A\vert \mathcal {L}_{B_1/A})<0$
. -
(3) There is a minimally simply algebraic extension
 $Y/X$
and a set
$Y/X$
and a set
 $F\subseteq B_1$
and
$F\subseteq B_1$
and
 $C\subseteq B_1$
of the form of
$C\subseteq B_1$
of the form of
 $Y/X$
so that
$Y/X$
so that
 $\mu (X,Y,g_{E}(F))<\mu (X,Y,g_{B_1}(F))$
.
$\mu (X,Y,g_{E}(F))<\mu (X,Y,g_{B_1}(F))$
.
Proof It is immediate that
![]() $E\models \zeta $
because
$E\models \zeta $
because
![]() $\zeta $
is preserved under free joins. Let
$\zeta $
is preserved under free joins. Let
![]() $X\subseteq E$
. Then
$X\subseteq E$
. Then
![]() $\delta (X)=\delta (X\cap B_1)+\delta (X\cap B_2)-\delta (X\cap A)\geq \delta (X\cap B_2)\geq 0$
, since X is the free-join of
$\delta (X)=\delta (X\cap B_1)+\delta (X\cap B_2)-\delta (X\cap A)\geq \delta (X\cap B_2)\geq 0$
, since X is the free-join of
![]() $X\cap B_1$
with
$X\cap B_1$
with
![]() $X\cap B_2$
over
$X\cap B_2$
over
![]() $X\cap A$
and
$X\cap A$
and
![]() $A\leq B_1$
. Thus
$A\leq B_1$
. Thus
![]() $E\in \mathcal {C}_0$
.
$E\in \mathcal {C}_0$
.
Suppose that
![]() $Y/X$
is a minimally simply algebraic extension, and
$Y/X$
is a minimally simply algebraic extension, and
![]() $F,C^1,\ldots ,C^r$
are disjoint subsets of E so that each
$F,C^1,\ldots ,C^r$
are disjoint subsets of E so that each
![]() $C^i/F$
is of the form of
$C^i/F$
is of the form of
![]() $Y/X$
. We restrict E to
$Y/X$
. We restrict E to
![]() $\mathcal {L}_{Y/X}$
for all tuples outside of F.
$\mathcal {L}_{Y/X}$
for all tuples outside of F.
By Lemma 2.13, there are four cases to consider:
-
• One of the
 $C^i$
is contained in
$C^i$
is contained in
 $B_1\smallsetminus A$
and
$B_1\smallsetminus A$
and
 $F\subseteq A$
. Since
$F\subseteq A$
. Since
 $B_1\smallsetminus A$
is simply algebraic over A, we have that
$B_1\smallsetminus A$
is simply algebraic over A, we have that
 $C^i=B_1\smallsetminus A$
. In this case, we have that r is at most one more than the number of disjoint extensions over F of the form of
$C^i=B_1\smallsetminus A$
. In this case, we have that r is at most one more than the number of disjoint extensions over F of the form of
 $Y/X$
in
$Y/X$
in
 $B_2$
. Since
$B_2$
. Since
 $B_2\leq E$
, Observation 2.8 shows that
$B_2\leq E$
, Observation 2.8 shows that
 $g_{B_2}(F)=g_{E}(F)$
. So, if
$g_{B_2}(F)=g_{E}(F)$
. So, if
 $r>\mu (X, Y,g_E(F))$
, then in
$r>\mu (X, Y,g_E(F))$
, then in
 $B_2$
we already have
$B_2$
we already have
 $g_{B_2}(F)$
disjoint extensions over F of the form of
$g_{B_2}(F)$
disjoint extensions over F of the form of
 $Y/X$
. Since
$Y/X$
. Since
 $B_1\smallsetminus A/F$
is minimally simply algebraic and of the form of
$B_1\smallsetminus A/F$
is minimally simply algebraic and of the form of
 $Y/X$
, each of these extensions is of the form of
$Y/X$
, each of these extensions is of the form of
 $B_1\smallsetminus A/F$
. Thus we have (2.14) above.
$B_1\smallsetminus A/F$
. Thus we have (2.14) above. -
•
 $F\cup \bigcup _{i\leq r}C^i$
is entirely contained in
$F\cup \bigcup _{i\leq r}C^i$
is entirely contained in
 $B_1$
or
$B_1$
or
 $B_2$
. If it’s contained in
$B_2$
. If it’s contained in
 $B_2$
, then since
$B_2$
, then since
 $B_2\in \mathcal {C}_\mu $
and
$B_2\in \mathcal {C}_\mu $
and
 $B_2\leq E$
, we see that
$B_2\leq E$
, we see that
 $r\leq \mu (X,Y,g_{B_2}(F))=\mu (X,Y,g_{E}(F))$
. If it’s contained in
$r\leq \mu (X,Y,g_{B_2}(F))=\mu (X,Y,g_{E}(F))$
. If it’s contained in
 $B_1$
, then since
$B_1$
, then since
 $B_1\in \mathcal {C}_\mu $
, we have that
$B_1\in \mathcal {C}_\mu $
, we have that
 $r\leq \mu (X,Y,g_{B_1}(F))$
. Either
$r\leq \mu (X,Y,g_{B_1}(F))$
. Either
 $r\leq \mu (X,Y,g_{B_1}(F))\leq \mu (X,Y,g_{E}(F))$
or we are in case (2.14) above.
$r\leq \mu (X,Y,g_{B_1}(F))\leq \mu (X,Y,g_{E}(F))$
or we are in case (2.14) above. -
•
 $r\leq \delta (F)$
. Then it’s automatic that
$r\leq \delta (F)$
. Then it’s automatic that
 $r\leq \mu (X,Y,g_E(F))$
as
$r\leq \mu (X,Y,g_E(F))$
as
 $\mu (X,Y,m)$
is always
$\mu (X,Y,m)$
is always
 $\geq \delta (X)=\delta (F)$
.
$\geq \delta (X)=\delta (F)$
. -
• For one
 $C^i$
, setting
$C^i$
, setting
 $Z=(F\cap A)\cup (C^i\cap B_2)$
, we see
$Z=(F\cap A)\cup (C^i\cap B_2)$
, we see
 $\delta (Z/Z\cap A)<0$
. Let
$\delta (Z/Z\cap A)<0$
. Let
 $Y=Z\smallsetminus A$
. Then
$Y=Z\smallsetminus A$
. Then
 $\delta (Y/A)<0$
. Further, one of the
$\delta (Y/A)<0$
. Further, one of the
 $C^j$
is contained in
$C^j$
is contained in
 $B_1\smallsetminus A$
, so
$B_1\smallsetminus A$
, so
 $\lvert Y\rvert \leq \lvert C^i\cap B_2\rvert \leq \lvert B_1\smallsetminus A\rvert $
. Since one of the
$\lvert Y\rvert \leq \lvert C^i\cap B_2\rvert \leq \lvert B_1\smallsetminus A\rvert $
. Since one of the
 $C^j$
is contained in
$C^j$
is contained in
 $B_1\smallsetminus A$
, all of the relations between the set Y and A which were retained when we took the reduct above are in
$B_1\smallsetminus A$
, all of the relations between the set Y and A which were retained when we took the reduct above are in
 $\mathcal {L}_{B_1/A}$
, so
$\mathcal {L}_{B_1/A}$
, so
 $\delta (Y\vert \mathcal {L}_{B_1/A}/A\vert \mathcal {L}_{B_1/A})<0$
. Thus, case (2.14) holds.⊣
$\delta (Y\vert \mathcal {L}_{B_1/A}/A\vert \mathcal {L}_{B_1/A})<0$
. Thus, case (2.14) holds.⊣
Lemma 2.15 (Strong Amalgamation Lemma)
Suppose
 $A,B_1,B_2\in \mathcal {C}^\zeta _\mu $
and
$A,B_1,B_2\in \mathcal {C}^\zeta _\mu $
and
![]() $A\leq B_i$
for
$A\leq B_i$
for
![]() $i=1,2$
. Then there exists a
$i=1,2$
. Then there exists a
 $D\in \mathcal {C}^\zeta _\mu $
so that
$D\in \mathcal {C}^\zeta _\mu $
so that
![]() $B_2\leq D$
and a
$B_2\leq D$
and a
![]() $g:B_1\rightarrow D$
so that g is the identity map on A and
$g:B_1\rightarrow D$
so that g is the identity map on A and
![]() $g(B_1)\leq D$
.
$g(B_1)\leq D$
.
Proof We may assume that there is no
![]() $B'$
so that
$B'$
so that
![]() $A\leq B'\leq B_1$
as otherwise we can first amalgamate this
$A\leq B'\leq B_1$
as otherwise we can first amalgamate this
![]() $B'$
with
$B'$
with
![]() $B_2$
over A. Thus, either
$B_2$
over A. Thus, either
![]() $B_1$
is
$B_1$
is
![]() $A\cup \{x\}$
where x is unrelated to any element in A or
$A\cup \{x\}$
where x is unrelated to any element in A or
![]() $B_1$
is simply algebraic over A, say minimally simply algebraic over
$B_1$
is simply algebraic over A, say minimally simply algebraic over
![]() $F\subseteq A$
. In the first case, the free-join suffices. In the second case, the free-join works unless one of the three conditions enumerated in the Algebraic Amalgamation Lemma holds. The second and third cannot hold, because
$F\subseteq A$
. In the first case, the free-join suffices. In the second case, the free-join works unless one of the three conditions enumerated in the Algebraic Amalgamation Lemma holds. The second and third cannot hold, because
![]() $A\leq B_2$
. Thus we can assume that
$A\leq B_2$
. Thus we can assume that
![]() $B_1\smallsetminus A$
is minimally simply algebraic over
$B_1\smallsetminus A$
is minimally simply algebraic over
![]() $F\subseteq A$
and that in
$F\subseteq A$
and that in
![]() $B_2$
there are
$B_2$
there are
![]() $C^1,\ldots C^{r}$
which are
$C^1,\ldots C^{r}$
which are
![]() $\mu (F,B_1\smallsetminus A,g_{B_2}(F))$
disjoint extensions of the form of
$\mu (F,B_1\smallsetminus A,g_{B_2}(F))$
disjoint extensions of the form of
![]() $B_1\smallsetminus A/F$
. Since
$B_1\smallsetminus A/F$
. Since
![]() $A\leq B_1$
and
$A\leq B_1$
and
![]() $A\leq B_2$
, we have
$A\leq B_2$
, we have
![]() $g_A(F)=g_{B_1}(F)=g_{B_2}(F)$
. Thus, it cannot be that all of these
$g_A(F)=g_{B_1}(F)=g_{B_2}(F)$
. Thus, it cannot be that all of these
![]() $C^j$
are contained in A, since then
$C^j$
are contained in A, since then
![]() $B_1$
would have violated the
$B_1$
would have violated the
![]() $\mu $
-bound. Without loss of generality,
$\mu $
-bound. Without loss of generality,
![]() $C^1\not \subseteq A$
.
$C^1\not \subseteq A$
.
![]() $C^1$
cannot be partially in A since
$C^1$
cannot be partially in A since
![]() $A\leq B_2$
. Thus
$A\leq B_2$
. Thus
![]() $C^1\subseteq B_2\smallsetminus A$
. Since
$C^1\subseteq B_2\smallsetminus A$
. Since
![]() $A\leq B_2$
, there are no extra relations in
$A\leq B_2$
, there are no extra relations in
 $ \operatorname {\mathrm {tp_{r.q.f.}}}(C^1/A)$
other than those in
$ \operatorname {\mathrm {tp_{r.q.f.}}}(C^1/A)$
other than those in
![]() $ \operatorname {\mathrm {tp_{r.q.f.}}}(B_1\smallsetminus A/F)$
, and
$ \operatorname {\mathrm {tp_{r.q.f.}}}(B_1\smallsetminus A/F)$
, and
![]() $A\cup C^1\leq B_2$
. Thus, we can form g by sending
$A\cup C^1\leq B_2$
. Thus, we can form g by sending
![]() $B_1\smallsetminus A$
to
$B_1\smallsetminus A$
to
![]() $C^1$
over A.⊣
$C^1$
over A.⊣
Using the Strong Amalgamation Lemma, we build a generic model
![]() $\mathcal {M}$
. We discuss its theory in the next subsection.
$\mathcal {M}$
. We discuss its theory in the next subsection.
2.3 The theory of the generic
Using the Strong Amalgamation Lemma, via a Fraïssé-style construction, we get a model
 $\mathcal {M}:=\mathcal {M}^\zeta _\mu $
(if
$\mathcal {M}:=\mathcal {M}^\zeta _\mu $
(if
![]() $\zeta $
is trivial, we write
$\zeta $
is trivial, we write
![]() $\mathcal {M}=\mathcal {M}_{\mu }$
) which satisfies the following three properties:
$\mathcal {M}=\mathcal {M}_{\mu }$
) which satisfies the following three properties:
-
(1)
 $\mathcal {M}$
is countable.
$\mathcal {M}$
is countable. -
(2) If
 $A\leq \mathcal {M}$
is finite, then
$A\leq \mathcal {M}$
is finite, then
 $A\in \mathcal {C}^\zeta _\mu $
.
$A\in \mathcal {C}^\zeta _\mu $
. -
(3) Suppose
 $B\leq \mathcal {M}$
,
$B\leq \mathcal {M}$
,
 $B\leq C$
, and
$B\leq C$
, and
 $C\in \mathcal {C}^\zeta _\mu $
. Then there exists an embedding
$C\in \mathcal {C}^\zeta _\mu $
. Then there exists an embedding
 $f:C\rightarrow \mathcal {M}$
which is the identity on B and
$f:C\rightarrow \mathcal {M}$
which is the identity on B and
 $f(C)\leq \mathcal {M}$
.
$f(C)\leq \mathcal {M}$
.
By a standard back-and-forth on strong substructures, these three properties characterize
![]() $\mathcal {M}$
up to isomorphism. We want to show that
$\mathcal {M}$
up to isomorphism. We want to show that
![]() $\mathcal {M}$
is saturated by showing that any countable elementary extension of
$\mathcal {M}$
is saturated by showing that any countable elementary extension of
![]() $\mathcal {M}$
is isomorphic to
$\mathcal {M}$
is isomorphic to
![]() $\mathcal {M}$
. To do so, we must check that these properties are elementary. We consider the properties:
$\mathcal {M}$
. To do so, we must check that these properties are elementary. We consider the properties:
-
(2’) This is broken down into three statements:
-
a)
 $\mathcal {M}\models \zeta $
.
$\mathcal {M}\models \zeta $
. -
b)
 $\delta (A)\geq 0$
for every finite
$\delta (A)\geq 0$
for every finite
 $A\subseteq \mathcal {M}$
.
$A\subseteq \mathcal {M}$
. -
c) If
 $F,C^1,\ldots C^r$
are disjoint subsets of
$F,C^1,\ldots C^r$
are disjoint subsets of
 $\mathcal {M}$
and each
$\mathcal {M}$
and each
 $C^i/F$
is of the form of
$C^i/F$
is of the form of
 $Y/X$
. Then
$Y/X$
. Then
 $r\leq \mu (X,Y,g_{\mathcal {M}}(F))$
.
$r\leq \mu (X,Y,g_{\mathcal {M}}(F))$
.
-
-
(3’) There is an infinite set
 $I\subseteq \mathcal {M}$
on which no relation holds and every finite
$I\subseteq \mathcal {M}$
on which no relation holds and every finite
 $A\subset I$
is strong in
$A\subset I$
is strong in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(3”) Suppose
 $B\subseteq \mathcal {M}$
,
$B\subseteq \mathcal {M}$
,
 $B\leq C$
,
$B\leq C$
,
 $C\in \mathcal {C}^\zeta _\mu $
, and
$C\in \mathcal {C}^\zeta _\mu $
, and
 $C\smallsetminus B$
is simply algebraic over B, say minimally simply algebraic over
$C\smallsetminus B$
is simply algebraic over B, say minimally simply algebraic over
 $F\subseteq B$
. Suppose that there is no
$F\subseteq B$
. Suppose that there is no
 $Y\subseteq \mathcal {M}$
such that
$Y\subseteq \mathcal {M}$
such that
 $\delta (Y\vert \mathcal {L}_{C/B}/B\vert \mathcal {L}_{C/B})<0$
and
$\delta (Y\vert \mathcal {L}_{C/B}/B\vert \mathcal {L}_{C/B})<0$
and
 $\lvert Y\rvert \leq \lvert C\smallsetminus B\rvert $
. Further suppose that there is no minimally simply algebraic extension
$\lvert Y\rvert \leq \lvert C\smallsetminus B\rvert $
. Further suppose that there is no minimally simply algebraic extension
 $H/G$
and sets
$H/G$
and sets
 $H',G'\subseteq C$
of the form of
$H',G'\subseteq C$
of the form of
 $H/G$
so that
$H/G$
so that
 $\mu (G,H,g_{C}(G))\neq \mu (G,H,g_{\mathcal {M}\oplus _B C}(G))$
. Then there are
$\mu (G,H,g_{C}(G))\neq \mu (G,H,g_{\mathcal {M}\oplus _B C}(G))$
. Then there are
 $\mu (F, C\smallsetminus B, g_{\mathcal {M}}(F))$
disjoint extensions over F of the form of
$\mu (F, C\smallsetminus B, g_{\mathcal {M}}(F))$
disjoint extensions over F of the form of
 $C\smallsetminus B$
over F in
$C\smallsetminus B$
over F in
 $\mathcal {M}$
.
$\mathcal {M}$
.
Lemma 2.16. (1)–(3) are equivalent to (1), (2’), (3’), (3”).
Proof Suppose (1)–(3) are true. To see (2’)(a) holds, since
![]() $\zeta $
is universal it suffices to check that
$\zeta $
is universal it suffices to check that
![]() $\zeta $
holds on every finite substructure of
$\zeta $
holds on every finite substructure of
![]() $\mathcal {M}$
. Every finite
$\mathcal {M}$
. Every finite
![]() $A\subseteq \mathcal {M}$
is contained in its finite self-sufficient closure C, which is strong in
$A\subseteq \mathcal {M}$
is contained in its finite self-sufficient closure C, which is strong in
![]() $\mathcal {M}$
. As
$\mathcal {M}$
. As
 $C\in \mathcal {C}_\mu ^\zeta $
by (2), we have
$C\in \mathcal {C}_\mu ^\zeta $
by (2), we have
![]() $C\models \zeta $
and thus
$C\models \zeta $
and thus
![]() $A\models \zeta $
. Similarly by
$A\models \zeta $
. Similarly by
 $C\in \mathcal {C}_\mu ^\zeta $
, (2’)(b) holds on A. Finally, to see (2’)(c), let
$C\in \mathcal {C}_\mu ^\zeta $
, (2’)(b) holds on A. Finally, to see (2’)(c), let
 $A=F\cup \bigcup _{i\leq r}C^i$
and again consider the self-sufficient closure C of A. Then since
$A=F\cup \bigcup _{i\leq r}C^i$
and again consider the self-sufficient closure C of A. Then since
 $C\in \mathcal {C}_\mu ^\zeta $
by (2), we have that
$C\in \mathcal {C}_\mu ^\zeta $
by (2), we have that
![]() $r\leq \mu (X,Y,g_{C}(F))$
, but
$r\leq \mu (X,Y,g_{C}(F))$
, but
![]() $g_C(F)=g_{\mathcal {M}}(F)$
because
$g_C(F)=g_{\mathcal {M}}(F)$
because
![]() $C\leq \mathcal {M}$
. This shows that (2’) holds. (3’) and (3”) hold similarly by applying the algebraic amalgamation lemma, i.e., the algebraic amalgamation lemma shows that it would keep us in
$C\leq \mathcal {M}$
. This shows that (2’) holds. (3’) and (3”) hold similarly by applying the algebraic amalgamation lemma, i.e., the algebraic amalgamation lemma shows that it would keep us in
![]() $\mathcal {C}^\zeta _\mu $
to have these sets, and property (3) then gives us the needed sets inside
$\mathcal {C}^\zeta _\mu $
to have these sets, and property (3) then gives us the needed sets inside
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Now we suppose (1),(2’),(3’),(3”). Suppose
![]() $C\leq \mathcal {M}$
. Then for any set
$C\leq \mathcal {M}$
. Then for any set
![]() $A\subseteq C$
, we have
$A\subseteq C$
, we have
![]() $g_C(A)=g_{\mathcal {M}}(A)$
. Thus condition (2’) ensures that
$g_C(A)=g_{\mathcal {M}}(A)$
. Thus condition (2’) ensures that
 $C\in \mathcal {C}^\zeta _\mu $
, so (2) holds. Property (3) follows from (3’) and (3”) exactly as the strong amalgamation lemma follows from the algebraic amalgamation lemma.⊣
$C\in \mathcal {C}^\zeta _\mu $
, so (2) holds. Property (3) follows from (3’) and (3”) exactly as the strong amalgamation lemma follows from the algebraic amalgamation lemma.⊣
Lemma 2.17. Conditions (2’),(3”) are elementary schemata, i.e., there is a set of sentences
![]() $\Psi $
so that
$\Psi $
so that
![]() $M\models \Psi $
if and only if M satisfies the conditions. Furthermore,
$M\models \Psi $
if and only if M satisfies the conditions. Furthermore,
![]() $\Psi $
can be chosen to be a set of
$\Psi $
can be chosen to be a set of
![]() $\forall \exists $
-sentences.
$\forall \exists $
-sentences.
Condition (3’) is preserved in elementary extensions or substructures containing I. That is, if
![]() $I\subseteq M\preceq N$
, then I satisfies the condition in M if and only if it satisfies the condition in N.
$I\subseteq M\preceq N$
, then I satisfies the condition in M if and only if it satisfies the condition in N.
Proof The first two conditions in (2’) are easy to see are elementary. For the third, we use the formulas from Observation 2.11. Carefully examining the formula
![]() $\theta $
produced in Observation 2.11, one can see they are equivalent to
$\theta $
produced in Observation 2.11, one can see they are equivalent to
![]() $\forall \exists $
formulas. Alternatively, to see that (2’) is equivalent to a collection of
$\forall \exists $
formulas. Alternatively, to see that (2’) is equivalent to a collection of
![]() $\forall \exists $
-sentences, it suffices to see that it is preserved in unions of chains. Suppose
$\forall \exists $
-sentences, it suffices to see that it is preserved in unions of chains. Suppose
![]() $M_0\subseteq M_1\subseteq \cdots \subseteq \bigcup _i M_i=N$
are so that each
$M_0\subseteq M_1\subseteq \cdots \subseteq \bigcup _i M_i=N$
are so that each
![]() $M_i$
satisfies (2’). Note that
$M_i$
satisfies (2’). Note that
![]() $\lim _i g_{M_i}(A)=g_N(A)$
for every
$\lim _i g_{M_i}(A)=g_N(A)$
for every
![]() $A\subseteq N$
. Suppose there are
$A\subseteq N$
. Suppose there are
![]() $F,C^1,\ldots, C^r$
disjoint subsets of N and each extension
$F,C^1,\ldots, C^r$
disjoint subsets of N and each extension
![]() $C^j/F$
is of the form of
$C^j/F$
is of the form of
![]() $Y/X$
. Then take i large enough that
$Y/X$
. Then take i large enough that
![]() $M_i$
contains
$M_i$
contains
![]() $F\cup \bigcup _i C^i$
and
$F\cup \bigcup _i C^i$
and
![]() $g_{M_i}(A)=g_{N}(A)$
. Then since
$g_{M_i}(A)=g_{N}(A)$
. Then since
![]() $M_i$
satisfies (2’), we see that
$M_i$
satisfies (2’), we see that
![]() $r\leq \mu (X,Y,g_{M_i}(A))=\mu (X,Y,g_N(A))$
.
$r\leq \mu (X,Y,g_{M_i}(A))=\mu (X,Y,g_N(A))$
.
For (3’), it suffices to note that a finite set being strong in the structure is defined by an infinite schema of universal sentences.
For (3”), the fact that it is first-order to determine the value of
![]() $\mu (X,Y,m)$
(as in Observation 2.11) and that it is first-order to be strong enough so that
$\mu (X,Y,m)$
(as in Observation 2.11) and that it is first-order to be strong enough so that
![]() $\mu (G,H,g_C(G))=\mu (G,H,g_{M\oplus _B C}(G))$
suffices to make this first order. Let us see that it is preserved in unions of chains. Again suppose that
$\mu (G,H,g_C(G))=\mu (G,H,g_{M\oplus _B C}(G))$
suffices to make this first order. Let us see that it is preserved in unions of chains. Again suppose that
![]() $M_0\subseteq M_1\subseteq \cdots \subseteq \bigcup _i M_i=N$
and each
$M_0\subseteq M_1\subseteq \cdots \subseteq \bigcup _i M_i=N$
and each
![]() $M_i$
satisfies (3”). Let
$M_i$
satisfies (3”). Let
![]() $B\subseteq N$
,
$B\subseteq N$
,
 $B,C\in \mathcal {C}^\zeta _\mu $
be as in the hypothesis of (3”). If B is strong enough in N that there is no Y with
$B,C\in \mathcal {C}^\zeta _\mu $
be as in the hypothesis of (3”). If B is strong enough in N that there is no Y with
![]() $\lvert Y\rvert <\lvert C\smallsetminus B\rvert $
and
$\lvert Y\rvert <\lvert C\smallsetminus B\rvert $
and
 $\delta (Y\vert \mathcal {L}_{C/B}/B\vert \mathcal {L}_{C/B})<0$
, then this is true in every
$\delta (Y\vert \mathcal {L}_{C/B}/B\vert \mathcal {L}_{C/B})<0$
, then this is true in every
![]() $M_i$
which contains B as the non-existence of this Y is a universal condition. Similarly, since for every
$M_i$
which contains B as the non-existence of this Y is a universal condition. Similarly, since for every
![]() $A\subseteq N$
, we have that
$A\subseteq N$
, we have that
![]() $\lim _i g_{M_i}(A)=g_N(A)$
, and
$\lim _i g_{M_i}(A)=g_N(A)$
, and
![]() $M_i\leq M_i\oplus _B C$
and
$M_i\leq M_i\oplus _B C$
and
![]() $N\leq N\oplus _B C$
, we also have that
$N\leq N\oplus _B C$
, we also have that
![]() $\lim _i g_{M_i\oplus _B C}(A)=g_{N\oplus _B C}(A)$
. Thus if there is no
$\lim _i g_{M_i\oplus _B C}(A)=g_{N\oplus _B C}(A)$
. Thus if there is no
![]() $H/G$
an extension in C so that
$H/G$
an extension in C so that
![]() $\mu (G,H,g_C(G))\neq \mu (G,H,g_{N\oplus _B C}(G))$
, then the same is true in
$\mu (G,H,g_C(G))\neq \mu (G,H,g_{N\oplus _B C}(G))$
, then the same is true in
![]() $M_i$
for any large enough
$M_i$
for any large enough
![]() $M_i$
. Thus, in a large enough
$M_i$
. Thus, in a large enough
![]() $M_i$
, we must have
$M_i$
, we must have
![]() $\mu (F,C\smallsetminus B,g_{M_i}(F))=\mu (F,C\smallsetminus B,g_{N}(F))$
disjoint extensions over F of the form of
$\mu (F,C\smallsetminus B,g_{M_i}(F))=\mu (F,C\smallsetminus B,g_{N}(F))$
disjoint extensions over F of the form of
![]() $C\smallsetminus B$
over F. Thus, we have these extensions in N as well.⊣
$C\smallsetminus B$
over F. Thus, we have these extensions in N as well.⊣
Lemma 2.18.
![]() $\mathcal {M} $
is saturated.
$\mathcal {M} $
is saturated.
Proof Since any countable elementary extension of
![]() $\mathcal {M}$
is isomorphic with
$\mathcal {M}$
is isomorphic with
![]() $\mathcal {M}$
, we see that there are only countably many m-types in
$\mathcal {M}$
, we see that there are only countably many m-types in
![]() $\text {Th} (\mathcal {M})$
for each m. Thus, there is some countable saturated model of the theory of
$\text {Th} (\mathcal {M})$
for each m. Thus, there is some countable saturated model of the theory of
![]() $\mathcal {M}$
. But this, being an elementary extension of
$\mathcal {M}$
. But this, being an elementary extension of
![]() $\mathcal {M}$
, is isomorphic with
$\mathcal {M}$
, is isomorphic with
![]() $\mathcal {M}$
.⊣
$\mathcal {M}$
.⊣
Next we want to describe algebraicity inside
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Definition 2.19. For any finite set
![]() $A\subset \mathcal {M}$
, we define
$A\subset \mathcal {M}$
, we define
![]() $d(A)=\delta (A,\mathcal {M})$
. Recall,
$d(A)=\delta (A,\mathcal {M})$
. Recall,
![]() $\delta (A,\mathcal {M})=\min \{\delta (C)\mid A\subseteq C\subset \mathcal {M}, C \text {finite}\}$
.
$\delta (A,\mathcal {M})=\min \{\delta (C)\mid A\subseteq C\subset \mathcal {M}, C \text {finite}\}$
.
Lemma 2.20. If
![]() $d(\{x\}\cup A)=d(A)+1=d(\{y\}\cup A)$
, then
$d(\{x\}\cup A)=d(A)+1=d(\{y\}\cup A)$
, then
![]() $(\mathcal {M},Ax)\cong _A (\mathcal {M},Ay)$
.
$(\mathcal {M},Ax)\cong _A (\mathcal {M},Ay)$
.
Proof Let B be the self-sufficient closure of A, so
![]() $\delta (B)=d(A)$
. Then
$\delta (B)=d(A)$
. Then
![]() $B\leq \mathcal {M}$
. Thus
$B\leq \mathcal {M}$
. Thus
![]() $\{x\}\cup B\leq \mathcal {M}$
and
$\{x\}\cup B\leq \mathcal {M}$
and
![]() $\{y\}\cup B\leq \mathcal {M}$
. Using property (3) and a back-and-forth along strong substructures, we see that
$\{y\}\cup B\leq \mathcal {M}$
. Using property (3) and a back-and-forth along strong substructures, we see that
![]() $(\mathcal {M},Bx)\cong _B (\mathcal {M},By)$
, which implies the needed isomorphism.⊣
$(\mathcal {M},Bx)\cong _B (\mathcal {M},By)$
, which implies the needed isomorphism.⊣
Lemma 2.21. If
![]() $d(\{x\}\cup A)=d(A)$
, then
$d(\{x\}\cup A)=d(A)$
, then
![]() $x\in \operatorname {\mathrm {acl}}(A)$
.
$x\in \operatorname {\mathrm {acl}}(A)$
.
Proof Suppose
![]() $d(\{x\}\cup A)=d(A)$
. Let B be the self-sufficient closure of A, so
$d(\{x\}\cup A)=d(A)$
. Let B be the self-sufficient closure of A, so
![]() $\delta (B)=d(A)$
. Lemma 2.6 shows that B is algebraic over A.
$\delta (B)=d(A)$
. Lemma 2.6 shows that B is algebraic over A.
Now we show that
![]() $x\in \operatorname {\mathrm {acl}}(B)$
, which suffices since
$x\in \operatorname {\mathrm {acl}}(B)$
, which suffices since
![]() $B\subseteq \operatorname {\mathrm {acl}}(A)$
. Fix E to be a set so that
$B\subseteq \operatorname {\mathrm {acl}}(A)$
. Fix E to be a set so that
![]() $\delta (E)=d(\lbrace x \rbrace \cup A)=d(A)$
and
$\delta (E)=d(\lbrace x \rbrace \cup A)=d(A)$
and
![]() $\lbrace x \rbrace \cup A\subseteq E$
. Then
$\lbrace x \rbrace \cup A\subseteq E$
. Then
![]() $\delta (E\cup B)\leq \delta (E)+\delta (B)-\delta (E\cap B)$
. If E does not contain B, then
$\delta (E\cup B)\leq \delta (E)+\delta (B)-\delta (E\cap B)$
. If E does not contain B, then
![]() $\delta (E\cap B)>\delta (B)$
by minimality of B. Then
$\delta (E\cap B)>\delta (B)$
by minimality of B. Then
![]() $\delta (E\cup B)<\delta (E)=d(A)$
, a contradiction. So E contains B.
$\delta (E\cup B)<\delta (E)=d(A)$
, a contradiction. So E contains B.
Take a sequence of extensions
![]() $B=B_0\subset B_1\subset \cdots B_n=E$
with each
$B=B_0\subset B_1\subset \cdots B_n=E$
with each
![]() $B_{i+1}$
chosen to be minimal containing
$B_{i+1}$
chosen to be minimal containing
![]() $B_i$
contained in E with
$B_i$
contained in E with
![]() $\delta (B_{i+1})=d(A)$
. It follows from
$\delta (B_{i+1})=d(A)$
. It follows from
![]() $\delta (B_{i})=d(A)$
that each
$\delta (B_{i})=d(A)$
that each
![]() $B_i\leq \mathcal {M}$
. Then
$B_i\leq \mathcal {M}$
. Then
![]() $B_{i+1}$
is a simply algebraic extension over
$B_{i+1}$
is a simply algebraic extension over
![]() $B_i$
. Thus, the
$B_i$
. Thus, the
![]() $\mu $
-bound ensures that there are not infinitely many extensions over
$\mu $
-bound ensures that there are not infinitely many extensions over
![]() $B_i$
which are disjoint and of the form of
$B_i$
which are disjoint and of the form of
![]() $B_{i+1}/B_i$
, and Lemma 2.4 shows that any two extensions of the form of
$B_{i+1}/B_i$
, and Lemma 2.4 shows that any two extensions of the form of
![]() $B_{i+1}/B_i$
must be disjoint. Thus
$B_{i+1}/B_i$
must be disjoint. Thus
![]() $B_{i+1}$
is algebraic over
$B_{i+1}$
is algebraic over
![]() $B_i$
. Conclude that E is algebraic over B.⊣
$B_i$
. Conclude that E is algebraic over B.⊣
Corollary 2.22.
![]() $\text {Th} (\mathcal {M})$
is strongly minimal.
$\text {Th} (\mathcal {M})$
is strongly minimal.
Proof In the previous two lemmas, we saw that over any set there is a unique non-algebraic type realized in
![]() $\mathcal {M}$
. Since
$\mathcal {M}$
. Since
![]() $\mathcal {M}$
is saturated, this implies that
$\mathcal {M}$
is saturated, this implies that
![]() $\text {Th} (\mathcal {M})$
is strongly minimal.⊣
$\text {Th} (\mathcal {M})$
is strongly minimal.⊣
Lemma 2.23. The axioms stating the model is infinite, (2’) and (3”) axiomatize
 $\text {Th} (\mathcal {M}^\zeta _\mu )$
. Thus,
$\text {Th} (\mathcal {M}^\zeta _\mu )$
. Thus,
 $\text {Th} (\mathcal {M}^\zeta _\mu )$
is model complete.
$\text {Th} (\mathcal {M}^\zeta _\mu )$
is model complete.
Proof Observe that Lemma 2.21 holds for any model satisfying (2’). Let N be infinite and satisfy (2’) and (3”). Let
![]() $N'\succeq N$
contain a countable indiscernible sequence
$N'\succeq N$
contain a countable indiscernible sequence
![]() $I=(x_i)_{i\in \omega }$
. We observe that
$I=(x_i)_{i\in \omega }$
. We observe that
![]() $d(\{x_i\mid i<k\})=k$
. Were this not the case, then we would have some
$d(\{x_i\mid i<k\})=k$
. Were this not the case, then we would have some
![]() $x_i\in \operatorname {\mathrm {acl}}(\{x_j\mid j<i\})$
by Lemma 2.21, which cannot happen by indiscernibility. Thus every finite initial subsequence of I, and thus every finite subsequence of I is strong in
$x_i\in \operatorname {\mathrm {acl}}(\{x_j\mid j<i\})$
by Lemma 2.21, which cannot happen by indiscernibility. Thus every finite initial subsequence of I, and thus every finite subsequence of I is strong in
![]() $N'$
. Let
$N'$
. Let
![]() $M\preceq N'$
be countable and contain I. Then M satisfies (1), (2’), (3’), and (3”), with (3’) witnessed by I. Thus
$M\preceq N'$
be countable and contain I. Then M satisfies (1), (2’), (3’), and (3”), with (3’) witnessed by I. Thus
 $M\cong \mathcal {M}_\mu ^\zeta $
by Lemma 2.16. So
$M\cong \mathcal {M}_\mu ^\zeta $
by Lemma 2.16. So
 $N\models \text {Th} (\mathcal {M}_\mu ^\zeta )$
.
$N\models \text {Th} (\mathcal {M}_\mu ^\zeta )$
.
By Lindström’s test [Reference Hodges12, 8.3.4] and Lemmas 2.17 and 2.22,
 $\text {Th} (\mathcal {M}^\zeta _\mu )$
is model complete.⊣
$\text {Th} (\mathcal {M}^\zeta _\mu )$
is model complete.⊣
Corollary 2.24. T is flat and non-disintegrated.
Proof As in [Reference Hrushovski13, Lemma 15], the geometry associated to any hypergraph via the d function is flat. Lemmas 2.20 and 2.21 show that d is the dimension function of the acl-geometry in
![]() $\mathcal {M}$
.⊣
$\mathcal {M}$
.⊣
3 Technical amalgamation facts
In this section, we gather some facts about amalgamation that will be important in our particular construction of the theory whose spectrum of recursive models is
![]() $[0,n]\cup \{\omega \}$
. In our language, we will have a ternary relation symbol. Thus below we will discuss hypergraphs with a ternary edge.
$[0,n]\cup \{\omega \}$
. In our language, we will have a ternary relation symbol. Thus below we will discuss hypergraphs with a ternary edge.
In the course of our construction, we will need two facts that this section will provide. Firstly, we will need, at one point in the construction of the recursive saturated model, to cause the dimension of a tuple to decrease while staying in the amalgamation class. In Corollary 3.9, we will do this by extending a finite structure in a non-strong way. Usually, Hrushovski amalgamation constructions only allow for strong amalgamations at any stage in the construction, so this requires some separate considerations, which we do in this section. Secondly, we will need a collection of extensions that are guaranteed to have the maximal possible number of occurrences over any base. We will call these unblockable extensions, and we show they exist in Corollary 3.18.
For the remainder of this section, we will work with
![]() $\mathcal {C}_{\mu }$
. While it will be true that all of the particular structures that we mention in this section will satisfy the formula
$\mathcal {C}_{\mu }$
. While it will be true that all of the particular structures that we mention in this section will satisfy the formula
![]() $\zeta $
that we use in our construction, we focus on only
$\zeta $
that we use in our construction, we focus on only
![]() $\mathcal {C}_{\mu }$
in this section for the sake of generality and re-usability of these results. It is immediate that if the particular structures mentioned in this section satisfy
$\mathcal {C}_{\mu }$
in this section for the sake of generality and re-usability of these results. It is immediate that if the particular structures mentioned in this section satisfy
![]() $\zeta $
, then our results in this section about
$\zeta $
, then our results in this section about
![]() $\mathcal {C}_{\mu }$
also hold for
$\mathcal {C}_{\mu }$
also hold for
![]() $\mathcal {C}^\zeta _{\mu }$
.
$\mathcal {C}^\zeta _{\mu }$
.
We implicitly assume that
![]() $\mathcal {L}$
has a ternary relation symbol R, and that the isomorphism type of three elements with a unique ternary edge is an element of
$\mathcal {L}$
has a ternary relation symbol R, and that the isomorphism type of three elements with a unique ternary edge is an element of
![]() $\mathcal {C}_\mu $
.
$\mathcal {C}_\mu $
.
Remark. In this section we do not use that
![]() $\mu (A,B,m)\geq \delta (A)$
. Rather, we only use that
$\mu (A,B,m)\geq \delta (A)$
. Rather, we only use that
![]() $\mu $
is such that
$\mu $
is such that
![]() $\mathcal {C}_\mu $
satisfies the Strong Amalgamation Lemma.
$\mathcal {C}_\mu $
satisfies the Strong Amalgamation Lemma.
3.1 Dropping dimensions
We introduce a particular type of extension B over A with
![]() $\delta (B/A)=-1$
. We will use this below to decrease dimension by adding extensions of this type over particular tuples in our constructed structure.
$\delta (B/A)=-1$
. We will use this below to decrease dimension by adding extensions of this type over particular tuples in our constructed structure.
Definition 3.1. For
![]() $t>k\geq 2$
, let
$t>k\geq 2$
, let
![]() $A=\lbrace a_1,\dots , a_k, g,h \rbrace $
. For every
$A=\lbrace a_1,\dots , a_k, g,h \rbrace $
. For every
![]() $l>k$
, by
$l>k$
, by
![]() $a_l$
we mean
$a_l$
we mean
![]() $a_i$
where
$a_i$
where
![]() $i\equiv _k l$
and
$i\equiv _k l$
and
![]() $1\leq i\leq k$
. Let
$1\leq i\leq k$
. Let
![]() $B=B_1\cup B_2$
where
$B=B_1\cup B_2$
where
![]() $B_1 = \lbrace b_1,\dots , b_{t}, b_{t+1} \rbrace $
,
$B_1 = \lbrace b_1,\dots , b_{t}, b_{t+1} \rbrace $
,
![]() $B_2 = \lbrace b_{t+1},\dots , b_{2t}, b_1 \rbrace $
and let
$B_2 = \lbrace b_{t+1},\dots , b_{2t}, b_1 \rbrace $
and let
![]() $R = R_1\cup R_2\cup R_3$
where
$R = R_1\cup R_2\cup R_3$
where
 $$ \begin{align*} R_1 &= \{(b_i,a_i,b_{i+1}) \mid 0< i \leq t\}, \\ R_2 &= \{(b_i,a_i,b_{i+1}) \mid t< i< 2t\} \cup\lbrace (b_{2t}, g, b_1) \rbrace, \\ R_3 &= \lbrace (b_1,h,b_{t+1}) \rbrace. \end{align*} $$
$$ \begin{align*} R_1 &= \{(b_i,a_i,b_{i+1}) \mid 0< i \leq t\}, \\ R_2 &= \{(b_i,a_i,b_{i+1}) \mid t< i< 2t\} \cup\lbrace (b_{2t}, g, b_1) \rbrace, \\ R_3 &= \lbrace (b_1,h,b_{t+1}) \rbrace. \end{align*} $$
Let
![]() $D_t$
be the hypergraph with vertex set
$D_t$
be the hypergraph with vertex set
![]() $A\cup B$
and edge set R.
$A\cup B$
and edge set R.
Here we classify the extensions
![]() $B_0$
over
$B_0$
over
![]() $A_0$
with
$A_0$
with
![]() $\delta (B_0/A_0)\leq 0$
where
$\delta (B_0/A_0)\leq 0$
where
![]() $B_0\subseteq B$
and
$B_0\subseteq B$
and
![]() $A_0\subseteq A$
.
$A_0\subseteq A$
.
Lemma 3.2. If
![]() $A_0\subseteq A$
,
$A_0\subseteq A$
,
![]() $\emptyset \neq B_0\subseteq B$
are such that
$\emptyset \neq B_0\subseteq B$
are such that
![]() $\delta (B_0/A_0)\leq 0$
, then at least one of the following holds:
$\delta (B_0/A_0)\leq 0$
, then at least one of the following holds:
-
(1)
 $A_0 \supseteq A\smallsetminus \lbrace h \rbrace $
and
$A_0 \supseteq A\smallsetminus \lbrace h \rbrace $
and
 $B_0 = B$
,
$B_0 = B$
, -
(2)
 $A_0 \supseteq A\smallsetminus \lbrace g \rbrace $
and
$A_0 \supseteq A\smallsetminus \lbrace g \rbrace $
and
 $B_0 \supseteq B_1$
,
$B_0 \supseteq B_1$
, -
(3)
 $A_0 = A$
and
$A_0 = A$
and
 $B_0 \supseteq B_2$
.
$B_0 \supseteq B_2$
.
Moreover, if
![]() $\delta (B_0/A_0)<0$
, then
$\delta (B_0/A_0)<0$
, then
![]() $A_0=A$
and
$A_0=A$
and
![]() $B_0 = B$
.
$B_0 = B$
.
Proof Since we are trying to show that
![]() $B_0$
is large (i.e., contains either B,
$B_0$
is large (i.e., contains either B,
![]() $B_1$
or
$B_1$
or
![]() $B_2$
, depending on the case), we can assume that there is no proper subset
$B_2$
, depending on the case), we can assume that there is no proper subset
![]() $B_0^{\prime }\subset B_0$
which has
$B_0^{\prime }\subset B_0$
which has
![]() $\delta (B_0^{\prime }/A_0)\leq 0$
. For every
$\delta (B_0^{\prime }/A_0)\leq 0$
. For every
![]() $b_i\in B$
clearly
$b_i\in B$
clearly
![]() $\delta (b_i/A_0) = 1$
, so
$\delta (b_i/A_0) = 1$
, so
![]() $|B_0|>1$
. Then for every
$|B_0|>1$
. Then for every
![]() $b_i\in B_0$
, the element
$b_i\in B_0$
, the element
![]() $b_i$
must appear in at least two relations in
$b_i$
must appear in at least two relations in
![]() $A_0\cup B_0$
or else
$A_0\cup B_0$
or else
![]() $B_0\smallsetminus \lbrace b_i \rbrace $
contradicts the minimality of
$B_0\smallsetminus \lbrace b_i \rbrace $
contradicts the minimality of
![]() $B_0$
. Now, for every
$B_0$
. Now, for every
![]() $i\notin \lbrace 1,t+1 \rbrace $
, if
$i\notin \lbrace 1,t+1 \rbrace $
, if
![]() $b_i\in B_0$
, then
$b_i\in B_0$
, then
![]() $(b_{i-1},a_{i-1},b_i)$
,
$(b_{i-1},a_{i-1},b_i)$
,
![]() $(b_i,a_i,b_{i+1})$
are edges in
$(b_i,a_i,b_{i+1})$
are edges in
![]() $A_0\cup B_0$
(if
$A_0\cup B_0$
(if
![]() $i=2t$
, then take
$i=2t$
, then take
![]() $a_i = g$
and
$a_i = g$
and
![]() $b_{i+1} = b_1$
). For
$b_{i+1} = b_1$
). For
![]() $i\in \lbrace 1,t+1 \rbrace $
, if
$i\in \lbrace 1,t+1 \rbrace $
, if
![]() $b_i\in B_0$
, then at least one of
$b_i\in B_0$
, then at least one of
![]() $b_{i-1}$
,
$b_{i-1}$
,
![]() $b_{i+1}$
(for
$b_{i+1}$
(for
![]() $i=1$
, take
$i=1$
, take
![]() $b_{i-1}$
to be
$b_{i-1}$
to be
![]() $b_{2t}$
) must be an element of
$b_{2t}$
) must be an element of
![]() $B_0$
. Hence,
$B_0$
. Hence,
![]() $R[A_0\cup B_0]$
, the restriction of R to
$R[A_0\cup B_0]$
, the restriction of R to
![]() $A_0\cup B_0$
, must contain at least one of
$A_0\cup B_0$
, must contain at least one of
![]() $R_1$
,
$R_1$
,
![]() $R_2$
. In particular,
$R_2$
. In particular,
![]() $b_1,b_{2t}\in B_0$
. Since
$b_1,b_{2t}\in B_0$
. Since
![]() $t\geq k+1$
, also in any case
$t\geq k+1$
, also in any case
![]() $A\smallsetminus \lbrace g,h \rbrace \subseteq A_0$
. Furthermore, if
$A\smallsetminus \lbrace g,h \rbrace \subseteq A_0$
. Furthermore, if
![]() $R_2\subseteq R[A_0\cup B_0]$
, then also
$R_2\subseteq R[A_0\cup B_0]$
, then also
![]() $g\in A_0$
. I.e., if
$g\in A_0$
. I.e., if
![]() $g\notin A_0$
, then
$g\notin A_0$
, then
![]() $R_1\subseteq R[A_0\cup B_0]$
.
$R_1\subseteq R[A_0\cup B_0]$
.
If
![]() $h\notin A_0$
, then as
$h\notin A_0$
, then as
![]() $b_1\in B_0$
and
$b_1\in B_0$
and
![]() $b_1$
must appear in two relation, we have
$b_1$
must appear in two relation, we have
![]() $b_2,b_{2t}\in B_0$
, and consequently
$b_2,b_{2t}\in B_0$
, and consequently
![]() $R_1,R_2\subseteq R[A_0\cup B_0]$
. This is case (1), so we may assume
$R_1,R_2\subseteq R[A_0\cup B_0]$
. This is case (1), so we may assume
![]() $h\in A_0$
. Now, if
$h\in A_0$
. Now, if
![]() $g\notin A_0$
, then as we’ve seen we must be in case (2). Finally, assume we are not in cases (1) or (2), in particular
$g\notin A_0$
, then as we’ve seen we must be in case (2). Finally, assume we are not in cases (1) or (2), in particular
![]() $A=A_0$
. Since
$A=A_0$
. Since
![]() $B_1\nsubseteq B_0$
, also
$B_1\nsubseteq B_0$
, also
![]() $R_1\nsubseteq R[A_0\cup B_0]$
. Then
$R_1\nsubseteq R[A_0\cup B_0]$
. Then
![]() $R_2\subseteq R[A_0\cup B_0]$
and we are in case (3).
$R_2\subseteq R[A_0\cup B_0]$
and we are in case (3).
Now for the additional part, assume instead that
![]() $B_0$
is minimal such that
$B_0$
is minimal such that
![]() $\delta (B_0/A_0)< 0 $
. Again, if
$\delta (B_0/A_0)< 0 $
. Again, if
![]() $b_i\in B_0$
then it must appear in at least two relations in
$b_i\in B_0$
then it must appear in at least two relations in
![]() $R[A_0\cup B_0]$
. By what we’ve shown, for some
$R[A_0\cup B_0]$
. By what we’ve shown, for some
![]() $i\in \lbrace 1,2 \rbrace $
,
$i\in \lbrace 1,2 \rbrace $
,
![]() $B_i\subseteq B_0$
. Observe that
$B_i\subseteq B_0$
. Observe that
![]() $\delta (B_i/A_0)\geq \delta (B_i/A) = 0$
, so there exists
$\delta (B_i/A_0)\geq \delta (B_i/A) = 0$
, so there exists
![]() $b_j\in B_0\smallsetminus B_i$
. As before, this implies that also
$b_j\in B_0\smallsetminus B_i$
. As before, this implies that also
![]() $B_{3-i}\subseteq B_0$
, i.e.,
$B_{3-i}\subseteq B_0$
, i.e.,
![]() $B_0 = B$
. A short check yields that for any
$B_0 = B$
. A short check yields that for any
![]() $A\smallsetminus \lbrace g,h \rbrace \subseteq X \subset A$
, we have
$A\smallsetminus \lbrace g,h \rbrace \subseteq X \subset A$
, we have
![]() $\delta (B/X)\geq 0$
. So
$\delta (B/X)\geq 0$
. So
![]() $A_0=A$
and indeed
$A_0=A$
and indeed
![]() $\delta (B/A) < 0$
.⊣
$\delta (B/A) < 0$
.⊣
Now we show that
![]() $D_t$
is in
$D_t$
is in
![]() $\mathcal {C}_{\mu }$
. All we are assuming about
$\mathcal {C}_{\mu }$
. All we are assuming about
![]() $\mu $
is that the isomorphism type of three elements with a unique ternary edge is an element of
$\mu $
is that the isomorphism type of three elements with a unique ternary edge is an element of
![]() $\mathcal {C}_{\mu }$
.
$\mathcal {C}_{\mu }$
.
Lemma 3.3.
![]() $D_t\in \mathcal {C}_{\mu }$
.
$D_t\in \mathcal {C}_{\mu }$
.
Proof First we show that no subset of
![]() $D_t$
has
$D_t$
has
![]() $\delta (X)<2$
unless
$\delta (X)<2$
unless
![]() $\lvert X\rvert \leq 1$
. Assume to the contrary that
$\lvert X\rvert \leq 1$
. Assume to the contrary that
![]() $|X|\geq 2$
,
$|X|\geq 2$
,
![]() $\delta (X) < 2$
. Then there must be edges in X, hence
$\delta (X) < 2$
. Then there must be edges in X, hence
![]() $X\cap A$
and
$X\cap A$
and
![]() $X\cap B$
are non-empty.
$X\cap B$
are non-empty.
![]() $\delta (D_t)> 1$
, so
$\delta (D_t)> 1$
, so
![]() $X\neq D_t$
. Then by Lemma 3.2,
$X\neq D_t$
. Then by Lemma 3.2,
![]() $\delta (X\cap B/X\cap A) \geq 0$
. So,
$\delta (X\cap B/X\cap A) \geq 0$
. So,
![]() $1-\delta (X\cap A) \geq \delta (X)-\delta (X\cap A)\geq 0$
which means we must have
$1-\delta (X\cap A) \geq \delta (X)-\delta (X\cap A)\geq 0$
which means we must have
![]() $1\geq \delta (X\cap A) =|X\cap A|\geq 1$
since there are no relations holding in the set A. But then again by Lemma 3.2,
$1\geq \delta (X\cap A) =|X\cap A|\geq 1$
since there are no relations holding in the set A. But then again by Lemma 3.2,
![]() $\delta (X)>\delta (X\cap A) = 1$
in contradiction to
$\delta (X)>\delta (X\cap A) = 1$
in contradiction to
![]() $\delta (X)<2$
.
$\delta (X)<2$
.
We show
![]() $D_t$
embeds strongly into
$D_t$
embeds strongly into
![]() $\mathcal {M}_\mu $
. Embed
$\mathcal {M}_\mu $
. Embed
![]() $\lbrace a_1,\dots , a_k, b_1 \rbrace $
onto an independent subset of
$\lbrace a_1,\dots , a_k, b_1 \rbrace $
onto an independent subset of
![]() $\mathcal {M}_\mu $
. Because the isomorphism type of a ternary edge is in
$\mathcal {M}_\mu $
. Because the isomorphism type of a ternary edge is in
![]() $\mathcal {C}_\mu $
, by genericity of
$\mathcal {C}_\mu $
, by genericity of
![]() $\mathcal {M}_\mu $
, any two independent points extend to an edge. Embed
$\mathcal {M}_\mu $
, any two independent points extend to an edge. Embed
![]() $b_2$
onto an extension of
$b_2$
onto an extension of
![]() $b_{1}, a_1$
to an edge. Now embed
$b_{1}, a_1$
to an edge. Now embed
![]() $b_3$
onto an extension of
$b_3$
onto an extension of
![]() $b_2, a_2$
to an edge. Continue in this manner until
$b_2, a_2$
to an edge. Continue in this manner until
![]() $b_{2t}$
has been embedded. Now embed g onto an extension of
$b_{2t}$
has been embedded. Now embed g onto an extension of
![]() $b_{2t}, b_1$
to an edge and h onto an extension of
$b_{2t}, b_1$
to an edge and h onto an extension of
![]() $b_1, b_{t+1}$
to an edge. Observe that each embedded point must be new. Now, since
$b_1, b_{t+1}$
to an edge. Observe that each embedded point must be new. Now, since
![]() $D_t\leq \mathcal {M}_{\mu }$
, we have
$D_t\leq \mathcal {M}_{\mu }$
, we have
![]() $D_t\in \mathcal {C}_{\mu }$
by property (2) of
$D_t\in \mathcal {C}_{\mu }$
by property (2) of
![]() $\mathcal {M}_{\mu }$
.⊣
$\mathcal {M}_{\mu }$
.⊣
Observation 3.4. Let C be minimally simply algebraic over F. From the definition of a minimally simply algebraic extension, it follows that every element of F appears in at least one edge in
![]() $F\cup C$
that is not an edge of F, and every element of C appears in at least two edges in
$F\cup C$
that is not an edge of F, and every element of C appears in at least two edges in
![]() $F\cup C$
(unless
$F\cup C$
(unless
![]() $\lvert C\rvert =1$
).
$\lvert C\rvert =1$
).
Observation 3.5. Suppose
![]() $E=B_1\oplus _A B_2$
where every point in
$E=B_1\oplus _A B_2$
where every point in
![]() $B_1\smallsetminus A$
appears in at most k edges in
$B_1\smallsetminus A$
appears in at most k edges in
![]() $B_1$
. Let
$B_1$
. Let
![]() $F, C^1,\dots , C^r\subseteq E$
be disjoint such that each
$F, C^1,\dots , C^r\subseteq E$
be disjoint such that each
![]() $C^i/F$
is a minimally simply algebraic extension. If
$C^i/F$
is a minimally simply algebraic extension. If
![]() $F\nsubseteq B_2$
, then it is immediate from Observation 3.4 that
$F\nsubseteq B_2$
, then it is immediate from Observation 3.4 that
![]() $r\leq k$
.
$r\leq k$
.
Definition 3.6. Say that
![]() $\mu $
is k-permissive if
$\mu $
is k-permissive if
![]() $\mu (A,B,m)\geq k$
whenever B is minimally simply algebraic over A and
$\mu (A,B,m)\geq k$
whenever B is minimally simply algebraic over A and
![]() $m\in \omega \cup \{\infty \} $
.
$m\in \omega \cup \{\infty \} $
.
Lemma 3.7. Suppose
![]() $\mu $
is 3-permissive and
$\mu $
is 3-permissive and
![]() $M\in \mathcal {C}_{\mu }$
. Fix
$M\in \mathcal {C}_{\mu }$
. Fix
![]() $\bar {c}\in M^{k+2}$
with
$\bar {c}\in M^{k+2}$
with
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $\delta (\bar {c},M)>0$
. Label
$\delta (\bar {c},M)>0$
. Label
![]() $\bar {c}=(a_1,\ldots , a_k,g,h)$
. For each t, let
$\bar {c}=(a_1,\ldots , a_k,g,h)$
. For each t, let
![]() $E_t$
be the free join of M and
$E_t$
be the free join of M and
![]() $D_t$
over
$D_t$
over
![]() $\bar {c}$
. Then
$\bar {c}$
. Then
![]() $E_t\in \mathcal {C}_\mu $
for all large enough t.
$E_t\in \mathcal {C}_\mu $
for all large enough t.
Proof We start with the following claim:
Claim. If
![]() $A\subseteq M$
and
$A\subseteq M$
and
![]() $Z\subseteq E_t$
contains A such that
$Z\subseteq E_t$
contains A such that
![]() $\delta (Z/A)<0$
, then either
$\delta (Z/A)<0$
, then either
![]() $\delta (Z\cap M/A)<0$
or
$\delta (Z\cap M/A)<0$
or
![]() $|Z\cap (D_t\smallsetminus \bar {c})|\geq t$
.
$|Z\cap (D_t\smallsetminus \bar {c})|\geq t$
.
Proof Using
![]() $\delta (Z)=\delta (Z\cap M)+\delta (Z\cap D_t)-\delta (Z\cap \bar {c})$
, we subtract
$\delta (Z)=\delta (Z\cap M)+\delta (Z\cap D_t)-\delta (Z\cap \bar {c})$
, we subtract
![]() $\delta (A)$
from both sides and combine with
$\delta (A)$
from both sides and combine with
![]() $\delta (Z\cap D_t)-\delta (Z\cap \bar {c})=\delta (Z\cap D_t/Z\cap \bar {c})$
to see
$\delta (Z\cap D_t)-\delta (Z\cap \bar {c})=\delta (Z\cap D_t/Z\cap \bar {c})$
to see
![]() $0> \delta (Z/A)=\delta (Z\cap M/A)+\delta (Z\cap D_t/Z\cap \bar {c})$
. Thus, either
$0> \delta (Z/A)=\delta (Z\cap M/A)+\delta (Z\cap D_t/Z\cap \bar {c})$
. Thus, either
![]() $\delta (Z\cap M/A)<0$
or
$\delta (Z\cap M/A)<0$
or
![]() $\delta (Z\cap D_t/Z\cap \bar {c})<0$
. In the latter case, Lemma 3.2 shows that
$\delta (Z\cap D_t/Z\cap \bar {c})<0$
. In the latter case, Lemma 3.2 shows that
![]() $|Z\cap (D_t\smallsetminus \bar {c})|\geq t$
.⊣
$|Z\cap (D_t\smallsetminus \bar {c})|\geq t$
.⊣
Choose
![]() $t>|M|$
greater than the index of any relation symbol appearing in M, in particular greater than
$t>|M|$
greater than the index of any relation symbol appearing in M, in particular greater than
![]() $\max \{g_M(A) \mid A\not \leq M\}$
, and also large enough so that for every
$\max \{g_M(A) \mid A\not \leq M\}$
, and also large enough so that for every
![]() $A, B\subseteq M$
such that
$A, B\subseteq M$
such that
![]() $B/A$
is of the form of an extension
$B/A$
is of the form of an extension
![]() $Y/X$
,
$Y/X$
,
![]() $\mu (X,Y,m) = \mu (X,Y,\infty )$
for every
$\mu (X,Y,m) = \mu (X,Y,\infty )$
for every
![]() $m\geq t$
. Denote
$m\geq t$
. Denote
![]() $E:=E_t$
. By the claim, this guarantees that for any
$E:=E_t$
. By the claim, this guarantees that for any
![]() $A\subseteq M$
, if
$A\subseteq M$
, if
![]() $A\not \leq M$
, then
$A\not \leq M$
, then
![]() $g_E(A) = g_M(A)$
. If
$g_E(A) = g_M(A)$
. If
![]() $A\leq M$
, then
$A\leq M$
, then
![]() $\mu (A,B,g_E(A)) = \mu (A,B,\infty )$
whenever
$\mu (A,B,g_E(A)) = \mu (A,B,\infty )$
whenever
![]() $B\subseteq M$
is minimally simply algebraic over A. In any case, whenever
$B\subseteq M$
is minimally simply algebraic over A. In any case, whenever
![]() $A,B\subseteq M$
are such that
$A,B\subseteq M$
are such that
![]() $A/B$
is of the form of an extension
$A/B$
is of the form of an extension
![]() $Y/X$
, then
$Y/X$
, then
![]() $\mu (X,Y,g_E(A)) = \mu (X,Y, g_M(A))$
.
$\mu (X,Y,g_E(A)) = \mu (X,Y, g_M(A))$
.
Now assume for a contradiction that
![]() $F, C^1,\dots , C^r\subseteq E$
are disjoint such that each
$F, C^1,\dots , C^r\subseteq E$
are disjoint such that each
![]() $C^i/F$
is of the form of a minimally simply algebraic extension
$C^i/F$
is of the form of a minimally simply algebraic extension
![]() $Y/X$
, and
$Y/X$
, and
![]() $r>\mu (X, Y, g_E(F))$
. By construction, every point in
$r>\mu (X, Y, g_E(F))$
. By construction, every point in
![]() $D_t\smallsetminus X$
is in at most three relations in
$D_t\smallsetminus X$
is in at most three relations in
![]() $E_t$
, so 3-permissiveness and Observation 3.5 imply
$E_t$
, so 3-permissiveness and Observation 3.5 imply
![]() $F\subseteq M$
. By what we’ve shown, at most
$F\subseteq M$
. By what we’ve shown, at most
![]() $\mu (X, Y, g_E(F)) = \mu (X, Y, g_M(F))$
of the
$\mu (X, Y, g_E(F)) = \mu (X, Y, g_M(F))$
of the
![]() $C^i$
are contained in M. Without loss of generality assume
$C^i$
are contained in M. Without loss of generality assume
![]() $C^1\nsubseteq M$
. Then by
$C^1\nsubseteq M$
. Then by
![]() $\delta (C^1\cap D_t/F\cup (C^1\cap M)) \leq 0$
, Lemma 3.2 implies
$\delta (C^1\cap D_t/F\cup (C^1\cap M)) \leq 0$
, Lemma 3.2 implies
![]() $|C^1|> t> |M|$
and so none of the
$|C^1|> t> |M|$
and so none of the
![]() $C^i$
can be fully contained in M. Using the same reasoning for
$C^i$
can be fully contained in M. Using the same reasoning for
![]() $\delta (C^2/F\cup (C^2\cap M))\leq 0$
, again by Lemma 3.2, we see that
$\delta (C^2/F\cup (C^2\cap M))\leq 0$
, again by Lemma 3.2, we see that
![]() $C_1$
and
$C_1$
and
![]() $C_2$
intersect inside
$C_2$
intersect inside
![]() $D_t$
, in contradiction.⊣
$D_t$
, in contradiction.⊣
Lemma 3.8. Let M,
![]() $\bar {c}$
and
$\bar {c}$
and
![]() $E_t$
be as in the lemma above and let
$E_t$
be as in the lemma above and let
![]() $X\subseteq M$
. Then
$X\subseteq M$
. Then
![]() $\delta (X, E_t) = \delta (X, M)$
, unless there is some
$\delta (X, E_t) = \delta (X, M)$
, unless there is some
![]() $Y\subseteq M$
containing
$Y\subseteq M$
containing
![]() $\bar {c}\cup X$
with
$\bar {c}\cup X$
with
![]() $\delta (Y) = \delta (X, M)$
, in which case
$\delta (Y) = \delta (X, M)$
, in which case
![]() $\delta (X, E_t) = \delta (X, M)-1$
.
$\delta (X, E_t) = \delta (X, M)-1$
.
Proof Clearly
![]() $\delta (X, E_t) \leq \delta (X, M)$
. Let
$\delta (X, E_t) \leq \delta (X, M)$
. Let
![]() $X\subseteq Z\subseteq E_t$
, then
$X\subseteq Z\subseteq E_t$
, then
The first summand is at least
![]() $\delta (X, M)$
and the second summand is at least
$\delta (X, M)$
and the second summand is at least
![]() $-1$
. Thus, to witness
$-1$
. Thus, to witness
![]() $\delta (X,E_t)< \delta (X,M)$
, we must have that
$\delta (X,E_t)< \delta (X,M)$
, we must have that
![]() $\delta (Z\cap M)=\delta (X, M)$
and
$\delta (Z\cap M)=\delta (X, M)$
and
![]() $\delta (Z\cap D_t/Z\cap F) = {-}1$
. By Lemma 3.2, this means
$\delta (Z\cap D_t/Z\cap F) = {-}1$
. By Lemma 3.2, this means
![]() $D_t\subseteq Z$
, and in particular
$D_t\subseteq Z$
, and in particular
![]() $\bar {c}\subseteq Z\cap M$
. Conversely, if Y such as in the statement exists then
$\bar {c}\subseteq Z\cap M$
. Conversely, if Y such as in the statement exists then
![]() $Y\cup D_t$
witnesses
$Y\cup D_t$
witnesses
![]() $\delta (X,E_t) \leq \delta (X,M)-1$
.⊣
$\delta (X,E_t) \leq \delta (X,M)-1$
.⊣
Corollary 3.9. Let
![]() $\mu $
be 3-permissive, and
$\mu $
be 3-permissive, and
![]() $A\in \mathcal {C}_{\mu }$
,
$A\in \mathcal {C}_{\mu }$
,
![]() $\bar {b}\in A$
so that
$\bar {b}\in A$
so that
![]() $\delta (\bar {b},A)>0$
. Then there exists
$\delta (\bar {b},A)>0$
. Then there exists
![]() $B\in \mathcal {C}_{\mu }$
containing A so that for every
$B\in \mathcal {C}_{\mu }$
containing A so that for every
![]() $X\subseteq A$
,
$X\subseteq A$
,
![]() $\delta (X,B)=\delta (X,A)$
unless there is
$\delta (X,B)=\delta (X,A)$
unless there is
![]() $Y\supseteq X$
so that
$Y\supseteq X$
so that
![]() $\delta (Y)=\delta (X,A)$
and
$\delta (Y)=\delta (X,A)$
and
![]() $\bar {b}\in Y$
, in which case
$\bar {b}\in Y$
, in which case
![]() $\delta (X,B)=\delta (X,A)-1$
.
$\delta (X,B)=\delta (X,A)-1$
.
Proof If
![]() $|\bar {b}|\geq 4$
, then by labeling
$|\bar {b}|\geq 4$
, then by labeling
 $\bar {b} = (a_1,\dots , a_{|\bar {b}|-2}, g,h)$
Lemma 3.7 and Lemma 3.8 give us the desired B.
$\bar {b} = (a_1,\dots , a_{|\bar {b}|-2}, g,h)$
Lemma 3.7 and Lemma 3.8 give us the desired B.
Otherwise, construct
![]() $M'$
by adding new points
$M'$
by adding new points
![]() $p_1,\dots , p_{4-|b|}$
to M and no new edges. Let
$p_1,\dots , p_{4-|b|}$
to M and no new edges. Let
![]() $\bar {b}'$
be the concatenation of
$\bar {b}'$
be the concatenation of
![]() $\bar {b}$
with
$\bar {b}$
with
 $(p_1,\dots, p_{4-|\bar {b}|})$
. Now apply the above to M and
$(p_1,\dots, p_{4-|\bar {b}|})$
. Now apply the above to M and
![]() $\bar {b}'$
consecutively
$\bar {b}'$
consecutively
![]() $5-|b|$
times. To use Lemma 3.8 note that after the penultimate application, every set containing
$5-|b|$
times. To use Lemma 3.8 note that after the penultimate application, every set containing
![]() $\bar {b}$
can be extended to a set containing
$\bar {b}$
can be extended to a set containing
![]() $\bar {b}'$
without changing its
$\bar {b}'$
without changing its
![]() $\delta $
value.⊣
$\delta $
value.⊣
3.2 Unblockability
Definition 3.10. We say that a minimally simply algebraic extension
![]() $X\subseteq Y$
is k-unblockable if for any k-permissive
$X\subseteq Y$
is k-unblockable if for any k-permissive
![]() $\mu $
, if
$\mu $
, if
![]() $Y\in C_\mu $
then for any
$Y\in C_\mu $
then for any
![]() $X\subseteq Z\in C_\mu $
, either
$X\subseteq Z\in C_\mu $
, either
![]() $Y\oplus _X Z\in C_\mu $
or Z already contains
$Y\oplus _X Z\in C_\mu $
or Z already contains
![]() $\mu (X,Y,g_Z(X))$
disjoint extensions of the form of
$\mu (X,Y,g_Z(X))$
disjoint extensions of the form of
![]() $Y/X$
over X.
$Y/X$
over X.
Observation 3.11. A minimally simply algebraic extension
![]() $X\subseteq Y$
is k-unblockable if and only if for any k-permissive
$X\subseteq Y$
is k-unblockable if and only if for any k-permissive
![]() $\mu $
, if
$\mu $
, if
![]() $Y\in \mathcal {C}_\mu $
and
$Y\in \mathcal {C}_\mu $
and
![]() $M\equiv \mathcal {M}_\mu $
then for any
$M\equiv \mathcal {M}_\mu $
then for any
![]() $Z\cong X$
in M, M contains
$Z\cong X$
in M, M contains
![]() $\mu (X,Y,g_M(Z))$
disjoint extensions over Z each of the form of
$\mu (X,Y,g_M(Z))$
disjoint extensions over Z each of the form of
![]() $Y/X$
.
$Y/X$
.
We now endeavor to show that over any size of a base, there is an infinite recursive sequence of 3-unblockable extensions. Further, under the assumption of 3-permissiveness, each of these extensions is in
![]() $\mathcal {C}_{\mu }$
.
$\mathcal {C}_{\mu }$
.
Lemma 3.12. If
![]() $A\subseteq B$
is a minimally simply algebraic extension such that each element in
$A\subseteq B$
is a minimally simply algebraic extension such that each element in
![]() $B\smallsetminus A$
appears in at most k edges in B, then
$B\smallsetminus A$
appears in at most k edges in B, then
![]() $A\subseteq B$
is k-unblockable.
$A\subseteq B$
is k-unblockable.
Proof Let
![]() $\mu $
be k-permissive such that
$\mu $
be k-permissive such that
![]() $B\in \mathcal {C}_\mu $
, let
$B\in \mathcal {C}_\mu $
, let
![]() $Z\in \mathcal {C}_\mu $
contain A, and let
$Z\in \mathcal {C}_\mu $
contain A, and let
![]() $E=B\oplus _A Z$
. Suppose
$E=B\oplus _A Z$
. Suppose
![]() $F,C^1,\ldots, C^r$
are disjoint extensions of the form of a minimally simply algebraic extension
$F,C^1,\ldots, C^r$
are disjoint extensions of the form of a minimally simply algebraic extension
![]() $Y/X$
with
$Y/X$
with
![]() $r>\mu (X,Y,g_{E}(F))$
. By k-permissiveness of
$r>\mu (X,Y,g_{E}(F))$
. By k-permissiveness of
![]() $\mu $
, we have
$\mu $
, we have
![]() $r>k$
. Thus, by Observation 3.5 it must be that
$r>k$
. Thus, by Observation 3.5 it must be that
![]() $F\subseteq Z$
. Now we observe that every
$F\subseteq Z$
. Now we observe that every
![]() $C^i$
is either contained in
$C^i$
is either contained in
![]() $B\smallsetminus A$
or is contained in Z, for if it were partially but not totally in
$B\smallsetminus A$
or is contained in Z, for if it were partially but not totally in
![]() $B\smallsetminus A$
, then we would have
$B\smallsetminus A$
, then we would have
![]() $\delta (C^i/Z)<0$
showing that
$\delta (C^i/Z)<0$
showing that
![]() $Z\not \leq E$
, which is a contradiction. So, either
$Z\not \leq E$
, which is a contradiction. So, either
 $F\cup \bigcup _{i\leq r}C^i\subseteq Z$
or one of the
$F\cup \bigcup _{i\leq r}C^i\subseteq Z$
or one of the
![]() $C^i$
is contained in
$C^i$
is contained in
![]() $B\smallsetminus A$
, which implies that
$B\smallsetminus A$
, which implies that
![]() $F\subseteq A$
. Since B is minimally simply algebraic over A, this implies
$F\subseteq A$
. Since B is minimally simply algebraic over A, this implies
![]() $C^i=B\smallsetminus A$
and
$C^i=B\smallsetminus A$
and
![]() $F=A$
. So, we conclude that there are already
$F=A$
. So, we conclude that there are already
![]() $\mu (X,Y,g_{E}(F))=\mu (X,Y,g_M(F))$
disjoint extensions of the form
$\mu (X,Y,g_{E}(F))=\mu (X,Y,g_M(F))$
disjoint extensions of the form
![]() $Y/X$
over F in M.⊣
$Y/X$
over F in M.⊣
Lemma 3.13. There are infinitely many 2-unblockable minimally simply algebraic extensions over a set of size at least 3. Moreover, these extensions are in
![]() $\mathcal {C}_\mu $
.
$\mathcal {C}_\mu $
.
Proof We define a sequence of 2-unblockables over
 $\hat {A} = \lbrace a_1,\dots , a_k,g \rbrace $
, where
$\hat {A} = \lbrace a_1,\dots , a_k,g \rbrace $
, where
![]() $k\geq 2$
and all the elements of
$k\geq 2$
and all the elements of
![]() $\hat {A}$
are distinct. For every
$\hat {A}$
are distinct. For every
![]() $l>k$
, by
$l>k$
, by
![]() $a_l$
we mean
$a_l$
we mean
![]() $a_i$
where
$a_i$
where
![]() $i\equiv _k l$
,
$i\equiv _k l$
,
![]() $1\leq i\leq k$
. Let
$1\leq i\leq k$
. Let
![]() $B=\lbrace b_1,\dots , b_{2t} \rbrace $
be new elements, where
$B=\lbrace b_1,\dots , b_{2t} \rbrace $
be new elements, where
![]() $t>k+1$
is arbitrary. Define
$t>k+1$
is arbitrary. Define
![]() $\hat {D}_t$
to be the hypergraph whose set of edges is
$\hat {D}_t$
to be the hypergraph whose set of edges is
Observe that
![]() $\hat {D}_t$
is in fact
$\hat {D}_t$
is in fact
![]() $D_t\smallsetminus \{h\}$
, so
$D_t\smallsetminus \{h\}$
, so
![]() $\hat {D}_t\leq D_t$
. Lemma 3.3 says that
$\hat {D}_t\leq D_t$
. Lemma 3.3 says that
![]() $D_t\in \mathcal {C}_\mu $
, thus
$D_t\in \mathcal {C}_\mu $
, thus
 $\hat {D}_t\in \mathcal {C}_{\mu }$
as well.
$\hat {D}_t\in \mathcal {C}_{\mu }$
as well.
There is a clear bijection between elements of B and edges in R, so
![]() $\delta (B/A) = 0$
. By Lemma 3.2, there are no
$\delta (B/A) = 0$
. By Lemma 3.2, there are no
![]() $A_0\subseteq \hat {A}$
,
$A_0\subseteq \hat {A}$
,
![]() $\emptyset \neq B_0\subset B$
such that
$\emptyset \neq B_0\subset B$
such that
![]() $\delta (B_0/A_0) \leq 0$
, so B is minimally simply algebraic over A. Finally, 2-unblockability is immediate by Lemma 3.12.⊣
$\delta (B_0/A_0) \leq 0$
, so B is minimally simply algebraic over A. Finally, 2-unblockability is immediate by Lemma 3.12.⊣
Next, we will give constructions for infinitely many 3-unblockable extensions over sets of size
![]() $0$
,
$0$
,
![]() $1$
, or
$1$
, or
![]() $2$
.
$2$
.
Definition 3.14. For
![]() $k\geq 3$
define on the set of vertices
$k\geq 3$
define on the set of vertices
![]() $\lbrace a_1,\dots , a_k \rbrace $
the following isomorphism types of minimal simple algebraicities:
$\lbrace a_1,\dots , a_k \rbrace $
the following isomorphism types of minimal simple algebraicities:
-
• the ternary k-path
 $P_k$
whose set of edges is and whose base is
$P_k$
whose set of edges is and whose base is $$\begin{align*}\{\lbrace a_i,a_{i+1},a_{i+2} \rbrace \mid 1\leq i \leq k-2\} \end{align*}$$
$$\begin{align*}\{\lbrace a_i,a_{i+1},a_{i+2} \rbrace \mid 1\leq i \leq k-2\} \end{align*}$$
 $\lbrace a_1, a_k \rbrace $
$\lbrace a_1, a_k \rbrace $
-
• the ternary closed- k-path
 $H_k$
whose set of edges is and whose base is the singleton
$H_k$
whose set of edges is and whose base is the singleton $$\begin{align*}\{\lbrace a_i,a_{i+1},a_{i+2} \rbrace \mid 1\leq i \leq k-2\}\cup\lbrace \lbrace a_{k-1},a_k,a_1 \rbrace \rbrace \end{align*}$$
$$\begin{align*}\{\lbrace a_i,a_{i+1},a_{i+2} \rbrace \mid 1\leq i \leq k-2\}\cup\lbrace \lbrace a_{k-1},a_k,a_1 \rbrace \rbrace \end{align*}$$
 $\lbrace a_1 \rbrace $
$\lbrace a_1 \rbrace $
-
• the ternary k-loop
 $L_k$
whose set of edges is and whose base is
$L_k$
whose set of edges is and whose base is $$\begin{align*}\{\lbrace a_i,a_{i+1},a_{i+2} \rbrace \mid 1\leq i \leq k-2\}\cup\lbrace \lbrace a_{k-1},a_k,a_1 \rbrace,\lbrace a_k,a_1,a_2 \rbrace \rbrace \end{align*}$$
$$\begin{align*}\{\lbrace a_i,a_{i+1},a_{i+2} \rbrace \mid 1\leq i \leq k-2\}\cup\lbrace \lbrace a_{k-1},a_k,a_1 \rbrace,\lbrace a_k,a_1,a_2 \rbrace \rbrace \end{align*}$$
 $\emptyset $
$\emptyset $
Call any of these hypergraphs a generalized path.
Lemma 3.15. Every generalized path B over its base A is 3-unblockable.
Proof By Lemma 3.12 we only need to show that B is minimally simply algebraic over A. To see this, let
![]() $\emptyset \neq X\subset B$
and observe that there are strictly more elements in
$\emptyset \neq X\subset B$
and observe that there are strictly more elements in
![]() $X\smallsetminus A$
than there are edges in X.⊣
$X\smallsetminus A$
than there are edges in X.⊣
Lemma 3.16. If A is a generalized path of size k and
![]() $F\cup C\subset A$
are such that C is minimally simply algebraic over F, then
$F\cup C\subset A$
are such that C is minimally simply algebraic over F, then
![]() $C\cup F\cong P_l$
for some
$C\cup F\cong P_l$
for some
![]() $l\leq k$
, where F is the pair of end-points of the path.
$l\leq k$
, where F is the pair of end-points of the path.
Consequently, if
![]() $C/F$
is of the form of a minimally simply algebraic extension
$C/F$
is of the form of a minimally simply algebraic extension
![]() $Y/X$
, then there can be at most one other extension in A of the form of
$Y/X$
, then there can be at most one other extension in A of the form of
![]() $Y/X$
, and that is only in the cases that
$Y/X$
, and that is only in the cases that
![]() $A=L_{2l-2}$
, or
$A=L_{2l-2}$
, or
![]() $F\cup C$
is an edge, i.e.,
$F\cup C$
is an edge, i.e.,
![]() $F\cup C \cong P_3$
.
$F\cup C \cong P_3$
.
Proof If
![]() $|C|=1$
, then
$|C|=1$
, then
![]() $C\cup F$
is an edge, i.e., isomorphic to
$C\cup F$
is an edge, i.e., isomorphic to
![]() $P_3$
. Otherwise, each
$P_3$
. Otherwise, each
![]() $a_i\in C$
must appear in at least two edges in
$a_i\in C$
must appear in at least two edges in
![]() $C\cup F$
, hence
$C\cup F$
, hence
![]() $a_{i-1},a_{i+1}\in C\cup F$
. Proceeding this way in both directions, since by assumption
$a_{i-1},a_{i+1}\in C\cup F$
. Proceeding this way in both directions, since by assumption
![]() $F\cup C\neq A$
, we find
$F\cup C\neq A$
, we find
![]() $a_m, a_M\in F$
distinct such that
$a_m, a_M\in F$
distinct such that
![]() $a_j\in C$
for every
$a_j\in C$
for every
![]() $m<j<M$
(where if
$m<j<M$
(where if
![]() $j>k$
we replace it with
$j>k$
we replace it with
![]() $j-k$
). By definition of minimal simple algebraicity, these are exactly the points in
$j-k$
). By definition of minimal simple algebraicity, these are exactly the points in
![]() $F\cup C$
, with
$F\cup C$
, with
![]() $F=\lbrace a_m, a_M \rbrace $
.⊣
$F=\lbrace a_m, a_M \rbrace $
.⊣
Corollary 3.17. If
![]() $\mu $
is 2-permissive, then
$\mu $
is 2-permissive, then
![]() $\mathcal {C}_\mu $
contains all generalized paths.
$\mathcal {C}_\mu $
contains all generalized paths.
Now Lemma 3.13, Lemma 3.15, and Corollary 3.17 together yield:
Corollary 3.18. There exists a recursive sequence of 3-unblockable extensions
![]() $X_{k,l}\subseteq Y_{k,l}$
with each
$X_{k,l}\subseteq Y_{k,l}$
with each
![]() $X_{k,l}$
having size k. Further, if
$X_{k,l}$
having size k. Further, if
![]() $\mu $
is 3-permissive, then
$\mu $
is 3-permissive, then
![]() $Y_{k,l}\in \mathcal {C}_{\mu }$
for every
$Y_{k,l}\in \mathcal {C}_{\mu }$
for every
![]() $k,l$
.
$k,l$
.
4 Constructing
 $T$
$T$
In this section, we construct a theory
![]() $T:=T_{S_1}$
which is determined by a given r.e. set
$T:=T_{S_1}$
which is determined by a given r.e. set
![]() $S_1$
. For any
$S_1$
. For any
![]() $A\subseteq \omega $
, we denote by
$A\subseteq \omega $
, we denote by
![]() $A^{[i]}$
the ith column of A, i.e.,
$A^{[i]}$
the ith column of A, i.e.,
![]() $A^{[i]} = \lbrace j\mid \langle i, j \rangle \in A \rbrace $
. For the sake of uniformity of notation below, we assume that for every i, there are at least two numbers in
$A^{[i]} = \lbrace j\mid \langle i, j \rangle \in A \rbrace $
. For the sake of uniformity of notation below, we assume that for every i, there are at least two numbers in
 $S_1^{[i]}$
. For any r.e. set
$S_1^{[i]}$
. For any r.e. set
![]() $S_1$
, this construction will produce a strongly minimal theory T. In the next section, we will show that this theory T (for any r.e. set
$S_1$
, this construction will produce a strongly minimal theory T. In the next section, we will show that this theory T (for any r.e. set
![]() $S_1$
) is so that
$S_1$
) is so that
![]() $ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
.
$ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
.
Given the r.e. set
![]() $S_1$
, we define
$S_1$
, we define
![]() $S_0$
to the be the r.e. set which in each column
$S_0$
to the be the r.e. set which in each column
 $S_0^{[i]}$
contains all elements of
$S_0^{[i]}$
contains all elements of
 $S_1^{[i]}$
except the last two enumerated into
$S_1^{[i]}$
except the last two enumerated into
 $S_1^{[i]}$
. We assume that for each i,
$S_1^{[i]}$
. We assume that for each i,
 $S_1^{[i]}$
contains at least two elements (and the particular choice of
$S_1^{[i]}$
contains at least two elements (and the particular choice of
![]() $S_1$
we make below will have this property), so if
$S_1$
we make below will have this property), so if
 $S_1^{[i]}$
is not infinite, then
$S_1^{[i]}$
is not infinite, then
![]() $S_1$
contains exactly two elements in the ith column which are not in
$S_1$
contains exactly two elements in the ith column which are not in
![]() $S_0$
, which we call
$S_0$
, which we call
![]() $\langle i, j_0\rangle , \langle i, j_1\rangle $
, where
$\langle i, j_0\rangle , \langle i, j_1\rangle $
, where
![]() $\langle i,j_0\rangle $
enters
$\langle i,j_0\rangle $
enters
![]() $S_1$
first. Otherwise,
$S_1$
first. Otherwise,
 $S_1^{[i]}$
is infinite and
$S_1^{[i]}$
is infinite and
 $S_1^{[i]}= S_0^{[i]}$
. In this case, the first two cases of the definition of
$S_1^{[i]}= S_0^{[i]}$
. In this case, the first two cases of the definition of
![]() $\mu $
below simply cannot hold since
$\mu $
below simply cannot hold since
![]() $\langle i,j_0\rangle $
and
$\langle i,j_0\rangle $
and
![]() $\langle i,j_1\rangle $
are not defined.
$\langle i,j_1\rangle $
are not defined.
Let
![]() $\mathcal {L}=\{R\}$
and
$\mathcal {L}=\{R\}$
and
![]() $\mathcal {L}'=\{R\}\cup \{R_m\mid m\in \omega \}$
where R is a ternary relation symbol and each
$\mathcal {L}'=\{R\}\cup \{R_m\mid m\in \omega \}$
where R is a ternary relation symbol and each
![]() $R_m$
is
$R_m$
is
![]() $n+2$
-ary (the same n as in
$n+2$
-ary (the same n as in
![]() $[0,n]\cup \lbrace \omega \rbrace $
).
$[0,n]\cup \lbrace \omega \rbrace $
).
The outline of our construction is as follows: We first construct a theory
![]() $\hat {T}$
in the language
$\hat {T}$
in the language
 $\hat {\mathcal {L}}=\{R\}\cup \{R_i\mid S_1^{[i]}\neq S_0^{[i]}\}$
via an amalgamation construction. We will then let T be the reduct to the language
$\hat {\mathcal {L}}=\{R\}\cup \{R_i\mid S_1^{[i]}\neq S_0^{[i]}\}$
via an amalgamation construction. We will then let T be the reduct to the language
![]() $\mathcal {L}$
. We will choose
$\mathcal {L}$
. We will choose
![]() $\mu $
so that
$\mu $
so that
![]() $\hat {T}$
is a definitional expansion of T. In particular, if
$\hat {T}$
is a definitional expansion of T. In particular, if
![]() $R_i$
holds on a tuple
$R_i$
holds on a tuple
![]() $\bar {a}$
, then
$\bar {a}$
, then
![]() $\mu $
will allow extra extensions of some form over
$\mu $
will allow extra extensions of some form over
![]() $\bar {a}$
.
$\bar {a}$
.
In building the recursive model
![]() $\mathcal {M}$
of dimension
$\mathcal {M}$
of dimension
![]() $\leq n$
or
$\leq n$
or
![]() $\omega $
, we work with the language
$\omega $
, we work with the language
![]() $\mathcal {L}'$
and construct a model
$\mathcal {L}'$
and construct a model
![]() $\mathcal {M}'$
so that
$\mathcal {M}'$
so that
![]() $\mathcal {M}=\mathcal {M}'\vert \mathcal {L}$
. This is necessary since
$\mathcal {M}=\mathcal {M}'\vert \mathcal {L}$
. This is necessary since
![]() $\hat {\mathcal {L}}$
is not recursive, so we don’t know which relations are the important ones to consider. When we see a relation
$\hat {\mathcal {L}}$
is not recursive, so we don’t know which relations are the important ones to consider. When we see a relation
![]() $R_i$
holding on a tuple, we are unsure if
$R_i$
holding on a tuple, we are unsure if
![]() $R_i\in \hat {\mathcal {L}}$
, so the
$R_i\in \hat {\mathcal {L}}$
, so the
![]() $\delta $
-function might give a smaller value in
$\delta $
-function might give a smaller value in
![]() $\mathcal {M}'$
than the correct dimension of the set in
$\mathcal {M}'$
than the correct dimension of the set in
![]() $\mathcal {M}$
. Thus the dimension of
$\mathcal {M}$
. Thus the dimension of
![]() $\mathcal {M}$
could be larger than the dimension of
$\mathcal {M}$
could be larger than the dimension of
![]() $\mathcal {M}'$
. This poses no problem for the construction of the saturated model, since
$\mathcal {M}'$
. This poses no problem for the construction of the saturated model, since
![]() $\dim (\mathcal {M})\geq \dim (\mathcal {M}')=\omega $
ensures that
$\dim (\mathcal {M})\geq \dim (\mathcal {M}')=\omega $
ensures that
![]() $\mathcal {M}$
is saturated. But this poses a problem for constructing the recursive finite-dimensional models.
$\mathcal {M}$
is saturated. But this poses a problem for constructing the recursive finite-dimensional models.
This is precisely the difficulty which we will use to ensure that
![]() $ \operatorname {\mathrm {SRM}}(T)\cap [n+1,\omega )=\emptyset $
. In particular, if the enemy attempts to construct a model of dimension
$ \operatorname {\mathrm {SRM}}(T)\cap [n+1,\omega )=\emptyset $
. In particular, if the enemy attempts to construct a model of dimension
![]() $k>n$
with basis
$k>n$
with basis
![]() $\bar {b}$
, we will find some element c so that
$\bar {b}$
, we will find some element c so that
![]() $c\notin \operatorname {\mathrm {acl}}(\bar {b})$
. In particular, this c will be some element which appears to satisfy a relation
$c\notin \operatorname {\mathrm {acl}}(\bar {b})$
. In particular, this c will be some element which appears to satisfy a relation
![]() $R_i(\bar {b}_0,c)$
for
$R_i(\bar {b}_0,c)$
for
![]() $\bar {b}_0\subseteq \bar {b}$
of length
$\bar {b}_0\subseteq \bar {b}$
of length
![]() $n+1$
and
$n+1$
and
 $R_i\notin \hat {\mathcal {L}}$
.
$R_i\notin \hat {\mathcal {L}}$
.
We choose
![]() $\mu $
to specifically help the recursive construction of models of dimension
$\mu $
to specifically help the recursive construction of models of dimension
![]() $\leq n$
in a way that does not help finite-dimensional models of larger dimension. In particular, we need a way to remove
$\leq n$
in a way that does not help finite-dimensional models of larger dimension. In particular, we need a way to remove
![]() $R_i(\bar {a})$
from a tuple
$R_i(\bar {a})$
from a tuple
![]() $\bar {a}$
if we suspect that
$\bar {a}$
if we suspect that
 $R_i\notin \hat {\mathcal {L}}$
. We will do this by defining
$R_i\notin \hat {\mathcal {L}}$
. We will do this by defining
![]() $\mu $
so that having
$\mu $
so that having
![]() $g_C(\bar {a})$
small enough will allow an extra extension of some form over
$g_C(\bar {a})$
small enough will allow an extra extension of some form over
![]() $\bar {a}$
in C. So there are two reasons a tuple might get an extra extension of this form: Either
$\bar {a}$
in C. So there are two reasons a tuple might get an extra extension of this form: Either
![]() $R_i(\bar {a})$
holds or
$R_i(\bar {a})$
holds or
![]() $g_C(\bar {a})$
is small enough. So if
$g_C(\bar {a})$
is small enough. So if
![]() $g_C(\bar {a})$
is small enough we can remove the relation
$g_C(\bar {a})$
is small enough we can remove the relation
![]() $R_i(\bar {a})$
. We will ensure models of dimension
$R_i(\bar {a})$
. We will ensure models of dimension
![]() $\leq n$
always have the opportunity to remove relations
$\leq n$
always have the opportunity to remove relations
![]() $R_i$
for
$R_i$
for
 $R_i\notin \hat {\mathcal {L}}$
, which we will be able to do since every
$R_i\notin \hat {\mathcal {L}}$
, which we will be able to do since every
![]() $n+2$
-tuple on which
$n+2$
-tuple on which
![]() $R_i$
holds will have a finite g-value, but models of higher dimension will not have this opportunity.
$R_i$
holds will have a finite g-value, but models of higher dimension will not have this opportunity.
Definition 4.1. We say that a relation symbol
![]() $R_i$
is “limited away” if
$R_i$
is “limited away” if
 $S_0^{[i]}=S_1^{[i]}$
.
$S_0^{[i]}=S_1^{[i]}$
.
Let
 $\hat {\mathcal {L}}=\{R\}\cup \{R_i\mid R_i\text { is not limited away}\}$
.
$\hat {\mathcal {L}}=\{R\}\cup \{R_i\mid R_i\text { is not limited away}\}$
.
We fix
![]() $\zeta $
to say that no relation holds on a subtuple of one where another relation holds (i.e., for each
$\zeta $
to say that no relation holds on a subtuple of one where another relation holds (i.e., for each
![]() $U\neq V\in \hat {\mathcal {L}}$
, if
$U\neq V\in \hat {\mathcal {L}}$
, if
![]() $U(\bar {x})$
and
$U(\bar {x})$
and
![]() $\bar {y}\subseteq \bar {x}$
, then
$\bar {y}\subseteq \bar {x}$
, then
![]() $\neg V(\bar {y})$
holds). Note that
$\neg V(\bar {y})$
holds). Note that
![]() $\zeta $
holds on each of the particular structures mentioned in §3, as each of those use only the single ternary relation symbol R, thus the results about
$\zeta $
holds on each of the particular structures mentioned in §3, as each of those use only the single ternary relation symbol R, thus the results about
![]() $\mathcal {C}_{\mu }$
in §3 hold for
$\mathcal {C}_{\mu }$
in §3 hold for
![]() $\mathcal {C}_{\mu }^\zeta $
as well. Enumerate the relative quantifier-free types of infinitely many 3-unblockable extensions as built in §3.2 over a set of size
$\mathcal {C}_{\mu }^\zeta $
as well. Enumerate the relative quantifier-free types of infinitely many 3-unblockable extensions as built in §3.2 over a set of size
![]() $n+2$
:
$n+2$
:
![]() $\langle \Omega _i\mid i\in \omega \rangle $
. Note that these use only the relation symbol R.
$\langle \Omega _i\mid i\in \omega \rangle $
. Note that these use only the relation symbol R.
We fix the function
![]() $\mu $
defined as follows:
$\mu $
defined as follows:
 $$\begin{align*}\mu(A,B,m)= \begin{cases} \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j_0\rangle }\text{-extension and}\ R_i(A),\\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j_1\rangle }\text{-extension,}\ R_i(A), \\ & \text{ and}\ m\geq \langle i,j_1\rangle, \\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j\rangle }\text{-extension,}\ \langle i,j\rangle\in S_0,\\ \lvert A\rvert+3 &\text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\mu(A,B,m)= \begin{cases} \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j_0\rangle }\text{-extension and}\ R_i(A),\\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j_1\rangle }\text{-extension,}\ R_i(A), \\ & \text{ and}\ m\geq \langle i,j_1\rangle, \\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j\rangle }\text{-extension,}\ \langle i,j\rangle\in S_0,\\ \lvert A\rvert+3 &\text{ otherwise.} \end{cases} \end{align*}$$
Observation 4.2.
![]() $\mu $
is 3-permissive, so each
$\mu $
is 3-permissive, so each
![]() $\Omega $
-extension occurs the
$\Omega $
-extension occurs the
![]() $\mu $
-maximal number of times over any subset of a model of
$\mu $
-maximal number of times over any subset of a model of
 $\text {Th} (\mathcal {M}_\mu ^\zeta )$
.
$\text {Th} (\mathcal {M}_\mu ^\zeta )$
.
Let
![]() $\hat {\mathcal {C}}$
be the class of
$\hat {\mathcal {C}}$
be the class of
![]() $\hat {\mathcal {L}}$
-structures
$\hat {\mathcal {L}}$
-structures
![]() $\mathcal {C}_\mu ^\zeta $
, and let
$\mathcal {C}_\mu ^\zeta $
, and let
![]() $\mathcal {M}$
be the generic built from
$\mathcal {M}$
be the generic built from
![]() $\hat {\mathcal {C}}$
. Let
$\hat {\mathcal {C}}$
. Let
![]() $\hat {T}$
be the theory of
$\hat {T}$
be the theory of
![]() $\hat {\mathcal {M}}$
. Let
$\hat {\mathcal {M}}$
. Let
![]() $\mathcal {M}$
be the reduct of
$\mathcal {M}$
be the reduct of
![]() $\hat {\mathcal {M}}$
to the language
$\hat {\mathcal {M}}$
to the language
![]() $\mathcal {L}$
, and let T be the theory of
$\mathcal {L}$
, and let T be the theory of
![]() $\mathcal {M}$
. It follows from the general construction that both
$\mathcal {M}$
. It follows from the general construction that both
![]() $\hat {T}$
and T are strongly minimal theories.
$\hat {T}$
and T are strongly minimal theories.
Lemma 4.3. Let
![]() $R_i$
be a relation symbol which is not limited away, i.e.,
$R_i$
be a relation symbol which is not limited away, i.e.,
![]() $R_i\in \hat {\mathcal {L}}$
. Then
$R_i\in \hat {\mathcal {L}}$
. Then
 $\hat {T}\models R_i(\bar {x})\leftrightarrow \exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
.
$\hat {T}\models R_i(\bar {x})\leftrightarrow \exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
.
Thus
![]() $\hat {\mathcal {M}}$
is a definitional expansion of
$\hat {\mathcal {M}}$
is a definitional expansion of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof We first verify the leftward direction. In the definition of
![]() $\mu $
, we see that
$\mu $
, we see that
 $$\begin{align*}\mu(A,B,m)= \begin{cases} \lvert A\rvert+4=n+6 &\text{ if}\ R_i(A),\\ \lvert A\rvert+3=n+5 &\text{ otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\mu(A,B,m)= \begin{cases} \lvert A\rvert+4=n+6 &\text{ if}\ R_i(A),\\ \lvert A\rvert+3=n+5 &\text{ otherwise,} \end{cases} \end{align*}$$
where
 $ \operatorname {\mathrm {tp_{r.q.f.}}}(B/A)=\Omega _{\langle i,j_0\rangle }$
. Thus, if
$ \operatorname {\mathrm {tp_{r.q.f.}}}(B/A)=\Omega _{\langle i,j_0\rangle }$
. Thus, if
![]() $\neg R_i(A)$
, then
$\neg R_i(A)$
, then
![]() $\mu $
enforces that
$\mu $
enforces that
 $\neg \exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
.
$\neg \exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
.
If
![]() $R_i(\bar {x})$
holds, then since
$R_i(\bar {x})$
holds, then since
![]() $\Omega _{\langle i,j_0\rangle }$
is a 3-unblockable extension, in any model of
$\Omega _{\langle i,j_0\rangle }$
is a 3-unblockable extension, in any model of
![]() $\hat {T}$
, we have the maximal number of allowed extensions over any set, so we must have
$\hat {T}$
, we have the maximal number of allowed extensions over any set, so we must have
 $\exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
.⊣
$\exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
.⊣
Lemma 4.4. Let
![]() $R_i\in \hat {\mathcal {L}}$
. For every
$R_i\in \hat {\mathcal {L}}$
. For every
![]() $\bar {x}$
of size
$\bar {x}$
of size
![]() $n+1$
containing no tuple on which R holds, there are exactly
$n+1$
containing no tuple on which R holds, there are exactly
![]() $n+4$
elements y so that
$n+4$
elements y so that
 $\hat {\mathcal {M}}\models R_i(\bar {x},y)$
.
$\hat {\mathcal {M}}\models R_i(\bar {x},y)$
.
Proof We apply property (3”) of any model of
![]() $\hat {T}$
. Let
$\hat {T}$
. Let
![]() $B=\bar {x}$
and
$B=\bar {x}$
and
![]() $C=\bar {x}y$
with the relative quantifier-free type consisting of the single relation
$C=\bar {x}y$
with the relative quantifier-free type consisting of the single relation
![]() $R_i(\bar {x},y)$
. This is easily seen to be in
$R_i(\bar {x},y)$
. This is easily seen to be in
![]() $\mathcal {C}^\zeta _{\mu }$
. Clearly, since
$\mathcal {C}^\zeta _{\mu }$
. Clearly, since
![]() $R_i$
is a symmetric
$R_i$
is a symmetric
![]() $n+2$
-ary relation, there is no set Y with
$n+2$
-ary relation, there is no set Y with
![]() $\lvert Y\rvert \leq |C\smallsetminus B|= 1$
so that
$\lvert Y\rvert \leq |C\smallsetminus B|= 1$
so that
![]() $\delta (Y\vert \{R_i\}/A\vert \{R_i\})<0$
. Let
$\delta (Y\vert \{R_i\}/A\vert \{R_i\})<0$
. Let
![]() $H',G'\subseteq C$
be of the form of a minimally simply algebraic
$H',G'\subseteq C$
be of the form of a minimally simply algebraic
![]() $H/G$
. Since the only relation that holds on C is the single relation
$H/G$
. Since the only relation that holds on C is the single relation
![]() $R_i(\bar {x}y)$
, we must have
$R_i(\bar {x}y)$
, we must have
![]() $H'$
is a singleton and
$H'$
is a singleton and
![]() $G'$
is the remainder. So,
$G'$
is the remainder. So,
![]() $H/G$
is not an
$H/G$
is not an
![]() $\Omega _i$
-extension for any i and
$\Omega _i$
-extension for any i and
![]() $\mu (G,H,g_C(G))=\mu (G,H,g_{\mathcal {M}\oplus _B C}(G))=\lvert G\rvert +3$
. So (3”) guarantees that there are
$\mu (G,H,g_C(G))=\mu (G,H,g_{\mathcal {M}\oplus _B C}(G))=\lvert G\rvert +3$
. So (3”) guarantees that there are
![]() $\mu (\bar {x},\bar {x}y,g_{\mathcal {M}}(\bar {x}))=n+4$
realizations of this relative quantifier-free type over
$\mu (\bar {x},\bar {x}y,g_{\mathcal {M}}(\bar {x}))=n+4$
realizations of this relative quantifier-free type over
![]() $\bar {x}$
.
$\bar {x}$
.
Corollary 4.5. Each relation
![]() $R_i$
is both existentially and universally definable in
$R_i$
is both existentially and universally definable in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof That
![]() $R_i$
is existentially definable in
$R_i$
is existentially definable in
![]() $\mathcal {M}$
follows from Lemma 4.3. Also,
$\mathcal {M}$
follows from Lemma 4.3. Also,
 $\neg R_i(\bar {x},y)\leftrightarrow \exists ^{n+4}z (R_i(\bar {x},z)\wedge z\neq y)\vee \bigvee _{u,v,w\in \bar {x}} R(u,v,w)$
gives an existential definition of
$\neg R_i(\bar {x},y)\leftrightarrow \exists ^{n+4}z (R_i(\bar {x},z)\wedge z\neq y)\vee \bigvee _{u,v,w\in \bar {x}} R(u,v,w)$
gives an existential definition of
![]() $\neg R_i$
.⊣
$\neg R_i$
.⊣
Corollary 4.6. T is model complete.
Proof Let
![]() $\phi $
be an existential formula in
$\phi $
be an existential formula in
![]() $\hat {\mathcal {L}}$
written in prenex normal form. Then
$\hat {\mathcal {L}}$
written in prenex normal form. Then
![]() $\phi = \exists \bar {z} \bigvee \bigwedge Q(\bar {x})$
where
$\phi = \exists \bar {z} \bigvee \bigwedge Q(\bar {x})$
where
![]() $Q(\bar {x})$
is one of
$Q(\bar {x})$
is one of
![]() $R(\bar {x}),\neg R(\bar {x}), R_i(\bar {x}),\neg R_i(\bar {x})$
. If
$R(\bar {x}),\neg R(\bar {x}), R_i(\bar {x}),\neg R_i(\bar {x})$
. If
![]() $Q=R_i(\bar {x})$
, then we replace
$Q=R_i(\bar {x})$
, then we replace
![]() $R_i$
by the existential formula in the language
$R_i$
by the existential formula in the language
![]() $\mathcal {L}=\{R\}$
which defines
$\mathcal {L}=\{R\}$
which defines
![]() $R_i$
. If
$R_i$
. If
![]() $Q=\neg R_i(\bar {x})$
, we replace
$Q=\neg R_i(\bar {x})$
, we replace
![]() $R_i$
by the universal formula in the language
$R_i$
by the universal formula in the language
![]() $\mathcal {L}$
which defines
$\mathcal {L}$
which defines
![]() $R_i$
. As such, we see that every existential
$R_i$
. As such, we see that every existential
![]() $\hat {\mathcal {L}}$
-formula is equivalent in
$\hat {\mathcal {L}}$
-formula is equivalent in
![]() $\hat {T}$
to an existential
$\hat {T}$
to an existential
![]() $\mathcal {L}$
-formula. Model-completeness of
$\mathcal {L}$
-formula. Model-completeness of
![]() $\hat {T}$
follows from Lemma 2.23 and shows that every
$\hat {T}$
follows from Lemma 2.23 and shows that every
![]() $\hat {\mathcal {L}}$
-formula is equivalent over
$\hat {\mathcal {L}}$
-formula is equivalent over
![]() $\hat {T}$
to an existential
$\hat {T}$
to an existential
![]() $\hat {\mathcal {L}}$
-formula, thus every formula is equivalent over
$\hat {\mathcal {L}}$
-formula, thus every formula is equivalent over
![]() $\hat {T}$
to an existential
$\hat {T}$
to an existential
![]() $\mathcal {L}$
-formula. So every
$\mathcal {L}$
-formula. So every
![]() $\mathcal {L}$
-formula is equivalent over T to an existential
$\mathcal {L}$
-formula is equivalent over T to an existential
![]() $\mathcal {L}$
-formula.⊣
$\mathcal {L}$
-formula.⊣
Lemma 4.7. T is flat and not disintegrated.
Proof
![]() $\hat {T}$
is a definitional expansion of T, thus
$\hat {T}$
is a definitional expansion of T, thus
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\hat {\mathcal {M}}$
have the same acl-geometry. By Corollary 2.24, the acl-geometry of T is flat. To see that this geometry is non-disintegrated, consider
$\hat {\mathcal {M}}$
have the same acl-geometry. By Corollary 2.24, the acl-geometry of T is flat. To see that this geometry is non-disintegrated, consider
![]() $\lbrace a,b,c \rbrace \leq \mathcal {M}$
such that
$\lbrace a,b,c \rbrace \leq \mathcal {M}$
such that
![]() $\mathcal {M}\models R(a,b,c)$
and R is the only relation holding on
$\mathcal {M}\models R(a,b,c)$
and R is the only relation holding on
![]() $\lbrace a,b,c \rbrace $
. Then
$\lbrace a,b,c \rbrace $
. Then
![]() $c\in \operatorname {\mathrm {acl}}(ab)$
but
$c\in \operatorname {\mathrm {acl}}(ab)$
but
![]() $c\notin \operatorname {\mathrm {acl}}(a)\cup \operatorname {\mathrm {acl}}(b)$
.⊣
$c\notin \operatorname {\mathrm {acl}}(a)\cup \operatorname {\mathrm {acl}}(b)$
.⊣
5 Building the recursive models of T
In this section, we construct a recursive copy of
![]() $\mathcal {M}$
, the saturated model of T. We will show that the l-dimensional submodels of
$\mathcal {M}$
, the saturated model of T. We will show that the l-dimensional submodels of
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $l\leq n$
are r.e. subsets, thus
$l\leq n$
are r.e. subsets, thus
![]() $ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
. In the next section, we will choose
$ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
. In the next section, we will choose
![]() $S_1$
to ensure that there are no other recursive models. We will have
$S_1$
to ensure that there are no other recursive models. We will have
![]() $S_1$
be the increasing union of the sets
$S_1$
be the increasing union of the sets
![]() $\{S_{1,s} \mid s\in \omega \}$
. In our enumeration of S, we take
$\{S_{1,s} \mid s\in \omega \}$
. In our enumeration of S, we take
![]() $\lvert S_{1,s+1}\smallsetminus S_{1,s}\rvert =1$
, so for each column i and
$\lvert S_{1,s+1}\smallsetminus S_{1,s}\rvert =1$
, so for each column i and
![]() $s\in \omega $
, the set
$s\in \omega $
, the set
 $S_{1,s}^{[i]}$
is finite.
$S_{1,s}^{[i]}$
is finite.
We will construct a copy of
![]() $\mathcal {M}$
where we also give uniformly
$\mathcal {M}$
where we also give uniformly
![]() $\Pi ^0_1$
sets which are to represent the relations
$\Pi ^0_1$
sets which are to represent the relations
![]() $R_i$
. Thus, we may say we remove a relation
$R_i$
. Thus, we may say we remove a relation
![]() $R_i$
from a tuple
$R_i$
from a tuple
![]() $\bar {a}$
.
$\bar {a}$
.
We construct the model in stages as usual by amalgamation:
![]() $N_0\subseteq N_1\subseteq N_2\subseteq \cdots \subseteq \bigcup _i N_i=\mathcal {N}$
. Note that
$N_0\subseteq N_1\subseteq N_2\subseteq \cdots \subseteq \bigcup _i N_i=\mathcal {N}$
. Note that
![]() $N_{s-1}$
may have a relation
$N_{s-1}$
may have a relation
![]() $R_i$
hold on a tuple whereas
$R_i$
hold on a tuple whereas
![]() $N_s$
removes that relation, but in the relation R, they are substructures. As usual, we say that a relation
$N_s$
removes that relation, but in the relation R, they are substructures. As usual, we say that a relation
![]() $R_i(\bar {a})$
holds in
$R_i(\bar {a})$
holds in
![]() $\mathcal {N}$
if it holds on every structure in the chain where
$\mathcal {N}$
if it holds on every structure in the chain where
![]() $\bar {a}\subseteq N_i$
. We will ensure that for any tuple
$\bar {a}\subseteq N_i$
. We will ensure that for any tuple
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $N_k$
,
$N_k$
,
![]() $\delta (\bar {a},N_k)=\delta (\bar {a},N_{k+1})$
. Furthermore, we will ensure that for every tuple
$\delta (\bar {a},N_k)=\delta (\bar {a},N_{k+1})$
. Furthermore, we will ensure that for every tuple
![]() $\bar {a}$
, there is some k so that the self-sufficient closure of
$\bar {a}$
, there is some k so that the self-sufficient closure of
![]() $\bar {a}$
is the same (both in set and isomorphism-type) in every
$\bar {a}$
is the same (both in set and isomorphism-type) in every
![]() $N_l$
for
$N_l$
for
![]() $l\geq k$
.
$l\geq k$
.
At stage s, we consider the language
![]() $\mathcal {L}_s=\{R\}\cup \{R_i\mid i<s\}$
. For every
$\mathcal {L}_s=\{R\}\cup \{R_i\mid i<s\}$
. For every
![]() $i\leq s$
, we let
$i\leq s$
, we let
![]() $\langle i,j^s_0\rangle , \langle i,j^s_1\rangle $
be the unique elements in the ith column of
$\langle i,j^s_0\rangle , \langle i,j^s_1\rangle $
be the unique elements in the ith column of
![]() $S_{1,s}\smallsetminus S_{0,s}$
where
$S_{1,s}\smallsetminus S_{0,s}$
where
![]() $\langle i,j^s_0\rangle $
entered
$\langle i,j^s_0\rangle $
entered
![]() $S_1$
first, and we let
$S_1$
first, and we let
 $$\begin{align*}\mu_s(A,B,m)= \begin{cases} \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j^s_0\rangle }\text{-extension and}\ R_i(A),\\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j^s_1\rangle }\text{-extension,}\ R_i(A), \\ & \text{ and}\ m\geq \langle i,j^s_1\rangle, \\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j\rangle }\text{-extension,}\ \langle i,j\rangle\in S_{0,s}\\ \lvert A\rvert+3 &\text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\mu_s(A,B,m)= \begin{cases} \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j^s_0\rangle }\text{-extension and}\ R_i(A),\\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j^s_1\rangle }\text{-extension,}\ R_i(A), \\ & \text{ and}\ m\geq \langle i,j^s_1\rangle, \\ \lvert A\rvert+4 &\text{ if}\ B/A\ \text{is an}\ \Omega_{\langle i,j\rangle }\text{-extension,}\ \langle i,j\rangle\in S_{0,s}\\ \lvert A\rvert+3 &\text{ otherwise.} \end{cases} \end{align*}$$
Let
![]() $\mathcal {C}_s$
be the amalgamation class defined by this function
$\mathcal {C}_s$
be the amalgamation class defined by this function
![]() $\mu _s$
and
$\mu _s$
and
![]() $\zeta $
(as defined below 4.1). We enumerate the amalgamation requirements for
$\zeta $
(as defined below 4.1). We enumerate the amalgamation requirements for
![]() $\mathcal {C}_s$
. A requirement is of the form: If
$\mathcal {C}_s$
. A requirement is of the form: If
![]() $A\leq \mathcal {N}$
and
$A\leq \mathcal {N}$
and
![]() $A\leq B\in \mathcal {C}_s$
, then there is an
$A\leq B\in \mathcal {C}_s$
, then there is an
![]() $f:B\rightarrow \mathcal {N}$
which is the identity on A so that
$f:B\rightarrow \mathcal {N}$
which is the identity on A so that
![]() $f(B)\leq \mathcal {N}$
. We do this so that the order between two requirements which exist in
$f(B)\leq \mathcal {N}$
. We do this so that the order between two requirements which exist in
![]() $\mathcal {C}_s$
is preserved when considered in
$\mathcal {C}_s$
is preserved when considered in
![]() $\mathcal {C}_{s+1}$
and all new requirements from
$\mathcal {C}_{s+1}$
and all new requirements from
![]() $\mathcal {C}_{s+1}$
appear after all requirements for amalgamations from
$\mathcal {C}_{s+1}$
appear after all requirements for amalgamations from
![]() $\mathcal {C}_s$
of sets of size
$\mathcal {C}_s$
of sets of size
![]() $\leq s$
on the first
$\leq s$
on the first
![]() $\leq s$
elements (i.e., the base is among the first s elements of
$\leq s$
elements (i.e., the base is among the first s elements of
![]() $\omega $
and the extension over the base is by at most s new elements.). This ensures that every requirement in the full language is considered from some stage onward.
$\omega $
and the extension over the base is by at most s new elements.). This ensures that every requirement in the full language is considered from some stage onward.
Now we describe the times when we might remove an occurrence of a relation.
Definition 5.1. In a structure C, we say an occurrence of a relation
![]() $R_i(\bar {a})$
is defunct at stage s if
$R_i(\bar {a})$
is defunct at stage s if
![]() $g_C(\bar {a})<\langle i, j_1^s\rangle $
.
$g_C(\bar {a})<\langle i, j_1^s\rangle $
.
In the definition of
![]() $\mu _s$
above, note that defunct relations are precisely the occurrences of
$\mu _s$
above, note that defunct relations are precisely the occurrences of
![]() $R_i(\bar {a})$
which do not allow
$R_i(\bar {a})$
which do not allow
 $\lvert \bar {a}\rvert +4 \Omega _{\langle i,j^s_1\rangle }$
-extensions over
$\lvert \bar {a}\rvert +4 \Omega _{\langle i,j^s_1\rangle }$
-extensions over
![]() $\bar {a}$
. If
$\bar {a}$
. If
![]() $R_i(\bar {a})$
is defunct at stage s and then another number gets enumerated into
$R_i(\bar {a})$
is defunct at stage s and then another number gets enumerated into
 $S_1^{[i]}$
, then nothing will prevent us from removing the relation
$S_1^{[i]}$
, then nothing will prevent us from removing the relation
![]() $R_i$
from the tuple
$R_i$
from the tuple
![]() $\bar {a}$
, with respect to future
$\bar {a}$
, with respect to future
![]() $\mu $
values, as seen in Lemma 5.3.
$\mu $
values, as seen in Lemma 5.3.
The following will be useful in the construction as we move from one stage to the next:
Lemma 5.2.
![]() $\mathcal {C}_{s-1}\subseteq \mathcal {C}_s$
.
$\mathcal {C}_{s-1}\subseteq \mathcal {C}_s$
.
Proof By inspecting the definitions of
![]() $\mu _s$
, we see that
$\mu _s$
, we see that
![]() $\mu _{s-1}\leq \mu _s$
. This is because
$\mu _{s-1}\leq \mu _s$
. This is because
![]() $\langle i,j^{s-1}_1\rangle $
is either
$\langle i,j^{s-1}_1\rangle $
is either
![]() $\langle i,j^{s}_1\rangle $
or
$\langle i,j^{s}_1\rangle $
or
![]() $\langle i,j^s_0\rangle $
and
$\langle i,j^s_0\rangle $
and
![]() $\mu _s$
can only increase by this. Similarly,
$\mu _s$
can only increase by this. Similarly,
 $\langle i,j^{s-1}_0\rangle $
is either
$\langle i,j^{s-1}_0\rangle $
is either
![]() $\langle i,j^{s}_0\rangle $
or this number enters
$\langle i,j^{s}_0\rangle $
or this number enters
![]() $S_0$
. Thus
$S_0$
. Thus
![]() $\mathcal {C}_{s-1}\subseteq \mathcal {C}_s$
.⊣
$\mathcal {C}_{s-1}\subseteq \mathcal {C}_s$
.⊣
Construction. At stage s of the construction, we have built
![]() $N_{s-1}\in \mathcal {C}_{s-1}$
and we will construct
$N_{s-1}\in \mathcal {C}_{s-1}$
and we will construct
![]() $N_s\in \mathcal {C}_s$
:
$N_s\in \mathcal {C}_s$
:
We first do the clean-up phase: Let i be the unique number so that something is enumerated into
 $S_1^{[i]}$
at stage s. Let
$S_1^{[i]}$
at stage s. Let
![]() $\bar {a}$
be the smallest tuple (under a fixed ordering of
$\bar {a}$
be the smallest tuple (under a fixed ordering of
![]() $\omega ^{n+2}$
of order type
$\omega ^{n+2}$
of order type
![]() $\omega $
) on which
$\omega $
) on which
![]() $N_{s-1}$
has a defunct relation
$N_{s-1}$
has a defunct relation
![]() $R_i(\bar {a})$
at stage
$R_i(\bar {a})$
at stage
![]() $s-1$
. We will now remove
$s-1$
. We will now remove
![]() $R_i$
from the tuple
$R_i$
from the tuple
![]() $\bar {a}$
and replace it with an extension involving only R so that we maintain dimensions:
$\bar {a}$
and replace it with an extension involving only R so that we maintain dimensions:
Lemma 5.3. If
![]() $A\in \mathcal {C}_{s-1}$
and
$A\in \mathcal {C}_{s-1}$
and
![]() $R_i(\bar {a})$
is a defunct relation at stage
$R_i(\bar {a})$
is a defunct relation at stage
![]() $s-1$
, then let
$s-1$
, then let
![]() $A_0$
be the result of removing
$A_0$
be the result of removing
![]() $R_i(\bar {a})$
from A. Then there is an
$R_i(\bar {a})$
from A. Then there is an
![]() $A'\in \mathcal {C}_{s}$
containing
$A'\in \mathcal {C}_{s}$
containing
![]() $A_0$
so that for every
$A_0$
so that for every
![]() $X\subseteq A$
,
$X\subseteq A$
,
![]() $\delta (X,A)=\delta (X,A')$
and the only relation occurring on
$\delta (X,A)=\delta (X,A')$
and the only relation occurring on
![]() $A'$
outside of
$A'$
outside of
![]() $A_0$
is the relation R.
$A_0$
is the relation R.
Proof We first observe that
![]() $A_0\in \mathcal {C}_{s}$
. Removing relations certainly does not cause the
$A_0\in \mathcal {C}_{s}$
. Removing relations certainly does not cause the
![]() $\delta $
-value of any set to drop below
$\delta $
-value of any set to drop below
![]() $0$
or make the structure fail to satisfy
$0$
or make the structure fail to satisfy
![]() $\zeta $
. So, we need only check that
$\zeta $
. So, we need only check that
![]() $A_0$
satisfies the
$A_0$
satisfies the
![]() $\mu _s$
-bound. Suppose
$\mu _s$
-bound. Suppose
![]() $F,C^1,\ldots C^r$
are disjoint subsets of
$F,C^1,\ldots C^r$
are disjoint subsets of
![]() $A_0$
and each
$A_0$
and each
![]() $C^i/F$
is of the form of
$C^i/F$
is of the form of
![]() $Y/X$
. Then by Observation 2.12, either these sets are each of the form of
$Y/X$
. Then by Observation 2.12, either these sets are each of the form of
![]() $Y/X$
in A or else the relation removed is in F. In the former case, using Lemma 5.2 we know that
$Y/X$
in A or else the relation removed is in F. In the former case, using Lemma 5.2 we know that
![]() $r\leq \mu _s(X,Y,g_A(F))$
, and
$r\leq \mu _s(X,Y,g_A(F))$
, and
![]() $g_{A_0}(F)\geq g_A(F)$
. Since our
$g_{A_0}(F)\geq g_A(F)$
. Since our
![]() $\mu _s$
is non-decreasing in the last coordinate, we see
$\mu _s$
is non-decreasing in the last coordinate, we see
![]() $r\leq \mu _s(X,Y,g_{A_0}(F))$
.
$r\leq \mu _s(X,Y,g_{A_0}(F))$
.
Now we suppose the removed relation is in F. Let
![]() $Y'/X'$
be the minimally simply algebraic extension we get by adding the removed relation in F to X (so each
$Y'/X'$
be the minimally simply algebraic extension we get by adding the removed relation in F to X (so each
![]() $C^r/F$
is of the form of
$C^r/F$
is of the form of
![]() $Y'/X'$
in A). We have
$Y'/X'$
in A). We have
![]() $g_{A}(F)=g_{A_0}(F)$
since no relations outside of F have been removed. Unless
$g_{A}(F)=g_{A_0}(F)$
since no relations outside of F have been removed. Unless
![]() $Y'/X'$
is an
$Y'/X'$
is an
 $\Omega _{\langle i,j^{s}_0\rangle }$
- or
$\Omega _{\langle i,j^{s}_0\rangle }$
- or
![]() $\Omega _{\langle i,j^{s}_1\rangle }$
-extension, we have
$\Omega _{\langle i,j^{s}_1\rangle }$
-extension, we have
![]() $r\leq \mu _s(X',Y',g_A(F))=\mu _s(X,Y,g_{A_0}(F))$
.
$r\leq \mu _s(X',Y',g_A(F))=\mu _s(X,Y,g_{A_0}(F))$
.
So, now we consider the critical case where
![]() $R_i(\bar {a})$
is the removed relation and the extensions
$R_i(\bar {a})$
is the removed relation and the extensions
![]() $C^1,\ldots , C^r$
are
$C^1,\ldots , C^r$
are
 $\Omega _{\langle i,j^s_0\rangle }$
- or
$\Omega _{\langle i,j^s_0\rangle }$
- or
![]() $\Omega _{\langle i,j^s_1\rangle }$
-extensions over the base
$\Omega _{\langle i,j^s_1\rangle }$
-extensions over the base
![]() $\bar {a}$
. For
$\bar {a}$
. For
 $\Omega _{\langle i,j^s_0\rangle }$
, since
$\Omega _{\langle i,j^s_0\rangle }$
, since
![]() $R_i(\bar {a})$
is defunct, there can only be
$R_i(\bar {a})$
is defunct, there can only be
 $n+5\ \ \Omega _{\langle i,j^{s-1}_1\rangle }=\Omega _{\langle i,j^{s}_0\rangle }$
-extensions in A, thus in
$n+5\ \ \Omega _{\langle i,j^{s-1}_1\rangle }=\Omega _{\langle i,j^{s}_0\rangle }$
-extensions in A, thus in
![]() $A_0$
. Thus, there are
$A_0$
. Thus, there are
![]() $\leq \mu _s$
-many even without
$\leq \mu _s$
-many even without
![]() $R_i(\bar {a})$
. For
$R_i(\bar {a})$
. For
![]() $\Omega _{\langle i,j^s_1\rangle }$
, since
$\Omega _{\langle i,j^s_1\rangle }$
, since
![]() $\mu _{s-1}$
allowed only
$\mu _{s-1}$
allowed only
![]() $n+5\ \ \Omega _{\langle i, j^s_1\rangle }$
-extensions over any base (in the fourth case of the definition of
$n+5\ \ \Omega _{\langle i, j^s_1\rangle }$
-extensions over any base (in the fourth case of the definition of
![]() $\mu _{s-1}$
), the
$\mu _{s-1}$
), the
![]() $\mu _s$
-bound is satisfied. In any case,
$\mu _s$
-bound is satisfied. In any case,
![]() $F,C^1,\ldots C^r$
does not violate the
$F,C^1,\ldots C^r$
does not violate the
![]() $\mu _s$
-bound.
$\mu _s$
-bound.
Now, we apply Corollary 3.9 to add an extension to
![]() $A_0$
to see that there is an
$A_0$
to see that there is an
![]() $A'$
as needed: Corollary 3.9 guarantees that, for an arbitrary
$A'$
as needed: Corollary 3.9 guarantees that, for an arbitrary
![]() $Z_0\subseteq A_0$
,
$Z_0\subseteq A_0$
,
![]() $\delta (Z_0,A')=\delta (Z_0,A_0)$
unless there is a
$\delta (Z_0,A')=\delta (Z_0,A_0)$
unless there is a
![]() $Y_0\supseteq Z_0$
witnessing
$Y_0\supseteq Z_0$
witnessing
![]() $\delta (Z_0,A_0)$
with
$\delta (Z_0,A_0)$
with
![]() $\bar {a}\in Y$
, in which case
$\bar {a}\in Y$
, in which case
![]() $\delta (Z_0,A')=\delta (Z_0,A_0)-1$
. Letting Z represent the set
$\delta (Z_0,A')=\delta (Z_0,A_0)-1$
. Letting Z represent the set
![]() $Z_0$
in A, obtained by adding the removed relation
$Z_0$
in A, obtained by adding the removed relation
![]() $R_i(\bar {a})$
, we wish to show that
$R_i(\bar {a})$
, we wish to show that
![]() $\delta (Z_0, A') =\delta (Z,A)$
. If there is a
$\delta (Z_0, A') =\delta (Z,A)$
. If there is a
![]() $Y_0\supseteq Z_0$
as described above, letting
$Y_0\supseteq Z_0$
as described above, letting
![]() $Y\supseteq Z$
be obtained from Y be adding the removed relation, we have
$Y\supseteq Z$
be obtained from Y be adding the removed relation, we have
![]() $\delta (Y)=\delta (Y_0)-1$
, so
$\delta (Y)=\delta (Y_0)-1$
, so
![]() $\delta (Z,A)=\delta (Z_0,A_0)-1 = \delta (Z_0,A')$
. If no such
$\delta (Z,A)=\delta (Z_0,A_0)-1 = \delta (Z_0,A')$
. If no such
![]() $Y_0$
exists, then clearly
$Y_0$
exists, then clearly
![]() $\delta (Z,A) = \delta (Z_0,A_0) = \delta (Z_0,A')$
. Putting these facts together, we see that in each case,
$\delta (Z,A) = \delta (Z_0,A_0) = \delta (Z_0,A')$
. Putting these facts together, we see that in each case,
![]() $\delta (Z,A)=\delta (Z_0,A')$
.⊣
$\delta (Z,A)=\delta (Z_0,A')$
.⊣
By applying this Lemma to the defunct relation
![]() $R_i(\bar {a})$
we produce a structure
$R_i(\bar {a})$
we produce a structure
![]() $N_{s-1}^{\prime }$
which is in
$N_{s-1}^{\prime }$
which is in
![]() $\mathcal {C}_{s}$
. Then, we satisfy the first s amalgamation requirements. To do this, we use the strong amalgamation lemma for the class
$\mathcal {C}_{s}$
. Then, we satisfy the first s amalgamation requirements. To do this, we use the strong amalgamation lemma for the class
![]() $\mathcal {C}_s$
to construct
$\mathcal {C}_s$
to construct
![]() $N_s\in \mathcal {C}_s$
which satisfies the first s amalgamation requirements. This defines
$N_s\in \mathcal {C}_s$
which satisfies the first s amalgamation requirements. This defines
![]() $N_{s}$
and the stage is done.
$N_{s}$
and the stage is done.
Observation 5.4.
![]() $N_s\in \mathcal {C}_s$
, thus we have maintained the inductive hypothesis for the next stage.
$N_s\in \mathcal {C}_s$
, thus we have maintained the inductive hypothesis for the next stage.
Thus we have described the construction of a structure
![]() $\mathcal {N}$
. We will show below that
$\mathcal {N}$
. We will show below that
![]() $\mathcal {N}\vert \mathcal {L}$
is a recursive presentation of the saturated model of T. From this, we will also produce recursive presentations of the models of dimension
$\mathcal {N}\vert \mathcal {L}$
is a recursive presentation of the saturated model of T. From this, we will also produce recursive presentations of the models of dimension
![]() $\leq n$
.
$\leq n$
.
Verification. We now show that
![]() $\mathcal {N}\vert \mathcal {L}\cong \mathcal {M}$
.
$\mathcal {N}\vert \mathcal {L}\cong \mathcal {M}$
.
Lemma 5.5. For
![]() $R_i\in \hat {\mathcal {L}}$
,
$R_i\in \hat {\mathcal {L}}$
,
 $\mathcal {N}\models R_i(\bar {x})\leftrightarrow \exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
$\mathcal {N}\models R_i(\bar {x})\leftrightarrow \exists ^{n+6}\bar {y}\,\Omega _{\langle i,j_0\rangle }(\bar {x},\bar {y})$
Proof Since
![]() $R_i$
is a
$R_i$
is a
![]() $\Pi ^0_1$
predicate on
$\Pi ^0_1$
predicate on
![]() $\mathcal {N}$
, if
$\mathcal {N}$
, if
![]() $\mathcal {N}\models R_i(\bar {x})$
, then it does so from the first stage that
$\mathcal {N}\models R_i(\bar {x})$
, then it does so from the first stage that
![]() $\bar {x}$
is first constructed. Thus, at every stage s once
$\bar {x}$
is first constructed. Thus, at every stage s once
![]() $\langle i,j^s_0\rangle = \langle i,j_0\rangle $
, we have
$\langle i,j^s_0\rangle = \langle i,j_0\rangle $
, we have
![]() $\mu _s(\bar {x},Y,g_{N_s}(\bar {x}))=n+6$
where
$\mu _s(\bar {x},Y,g_{N_s}(\bar {x}))=n+6$
where
 $ \operatorname {\mathrm {tp_{r.q.f.}}}(Y/\bar {x})=\Omega _{\langle i,j_0\rangle }$
. Since
$ \operatorname {\mathrm {tp_{r.q.f.}}}(Y/\bar {x})=\Omega _{\langle i,j_0\rangle }$
. Since
![]() $\Omega _{\langle i,j_0\rangle }$
is 3-unblockable, we know that at some stage, when all the appropriate amalgamation requirements have been taken care of, we get
$\Omega _{\langle i,j_0\rangle }$
is 3-unblockable, we know that at some stage, when all the appropriate amalgamation requirements have been taken care of, we get
![]() $n+6$
many disjoint extensions of this form. But this is realized by the relation R alone, so once it is satisfied, it is permanently satisfied inside
$n+6$
many disjoint extensions of this form. But this is realized by the relation R alone, so once it is satisfied, it is permanently satisfied inside
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
Suppose
![]() $\neg R_i(\bar {x})$
holds in
$\neg R_i(\bar {x})$
holds in
![]() $\mathcal {N}$
. Then this is seen from some s onward since
$\mathcal {N}$
. Then this is seen from some s onward since
![]() $R_i$
is a
$R_i$
is a
![]() $\Pi ^0_1$
relation in
$\Pi ^0_1$
relation in
![]() $\mathcal {N}$
. Since each
$\mathcal {N}$
. Since each
![]() $N_s\in \mathcal {C}_s$
, we see that at no stage
$N_s\in \mathcal {C}_s$
, we see that at no stage
![]() $\geq s$
can we have
$\geq s$
can we have
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j_0\rangle }$
-extensions over
$\Omega _{\langle i,j_0\rangle }$
-extensions over
![]() $\bar {x}$
, thus in the limit we do not have
$\bar {x}$
, thus in the limit we do not have
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j_0\rangle }$
-extensions over
$\Omega _{\langle i,j_0\rangle }$
-extensions over
![]() $\bar {x}$
.⊣
$\bar {x}$
.⊣
We define
![]() $\hat {\mathcal {N}}$
to be the definitional expansion of
$\hat {\mathcal {N}}$
to be the definitional expansion of
![]() $\mathcal {N}\vert \mathcal {L}$
to the language
$\mathcal {N}\vert \mathcal {L}$
to the language
![]() $\hat {\mathcal {L}}$
given by Lemma 5.5. It now suffices to show that
$\hat {\mathcal {L}}$
given by Lemma 5.5. It now suffices to show that
![]() $\hat {\mathcal {N}}$
satisfies the properties of the generic of the class
$\hat {\mathcal {N}}$
satisfies the properties of the generic of the class
![]() $\hat {\mathcal {C}}$
defined above. This proves that
$\hat {\mathcal {C}}$
defined above. This proves that
![]() $\hat {\mathcal {N}}\cong \hat {\mathcal {M}}$
, so
$\hat {\mathcal {N}}\cong \hat {\mathcal {M}}$
, so
 $\mathcal {N}\vert \mathcal {L} = \hat {\mathcal {N}}\vert \mathcal {L}\cong \hat {\mathcal {M}}\vert \mathcal {L} = \mathcal {M}$
.
$\mathcal {N}\vert \mathcal {L} = \hat {\mathcal {N}}\vert \mathcal {L}\cong \hat {\mathcal {M}}\vert \mathcal {L} = \mathcal {M}$
.
Note that for
 $R_i\notin \hat {\mathcal {L}}$
, we may very well have
$R_i\notin \hat {\mathcal {L}}$
, we may very well have
![]() $R_i(\bar {a})$
holding in
$R_i(\bar {a})$
holding in
![]() $\mathcal {N}$
, but this will not be seen in
$\mathcal {N}$
, but this will not be seen in
![]() $\mathcal {N}\vert \mathcal {L}$
or in
$\mathcal {N}\vert \mathcal {L}$
or in
![]() $\hat {\mathcal {N}}$
.
$\hat {\mathcal {N}}$
.
Lemma 5.6. For every
![]() $\bar {a}\in \mathcal {N}$
, there is some k so that the self-sufficient closure of
$\bar {a}\in \mathcal {N}$
, there is some k so that the self-sufficient closure of
![]() $\bar {a}$
is the same in every
$\bar {a}$
is the same in every
![]() $N_l$
with
$N_l$
with
![]() $l\geq k$
.
$l\geq k$
.
Proof The self-sufficient closure of
![]() $\bar {a}$
may change because some defunct relation
$\bar {a}$
may change because some defunct relation
![]() $R_i$
in the self-sufficient closure is removed. At that point, we add more elements and occurrences of the relation R so that the predimension of
$R_i$
in the self-sufficient closure is removed. At that point, we add more elements and occurrences of the relation R so that the predimension of
![]() $\bar {a}$
is made the same in
$\bar {a}$
is made the same in
![]() $N_{s}$
as in
$N_{s}$
as in
![]() $N_{s-1}$
. In doing so, the self-sufficient closure may have grown, but the total number of occurrences of relations other than R on the self-sufficient closure has decreased. This can happen only finitely often.⊣
$N_{s-1}$
. In doing so, the self-sufficient closure may have grown, but the total number of occurrences of relations other than R on the self-sufficient closure has decreased. This can happen only finitely often.⊣
Lemma 5.7. Let A be an
![]() $\hat {\mathcal {L}}$
-structure. Then
$\hat {\mathcal {L}}$
-structure. Then
![]() $A\in \hat {\mathcal {C}}$
if and only if
$A\in \hat {\mathcal {C}}$
if and only if
![]() $A\in \mathcal {C}_s$
for all sufficiently large s.
$A\in \mathcal {C}_s$
for all sufficiently large s.
Proof Let s be any stage large enough that for every relation
![]() $R_i\in \hat {\mathcal {L}}$
which occurs in A,
$R_i\in \hat {\mathcal {L}}$
which occurs in A,
 $S_1^{[i]}$
is enumerated by stage s. It suffices to show that
$S_1^{[i]}$
is enumerated by stage s. It suffices to show that
![]() $A\in \hat {\mathcal {C}}$
if and only if
$A\in \hat {\mathcal {C}}$
if and only if
![]() $A\in \mathcal {C}_s$
. Suppose
$A\in \mathcal {C}_s$
. Suppose
 $A\notin \hat {\mathcal {C}}$
. This could happen if some set has
$A\notin \hat {\mathcal {C}}$
. This could happen if some set has
![]() $\delta (X)<0$
or violates
$\delta (X)<0$
or violates
![]() $\zeta $
, which certainly ensures that
$\zeta $
, which certainly ensures that
![]() $A\notin \mathcal {C}_s$
, or if A violates the
$A\notin \mathcal {C}_s$
, or if A violates the
![]() $\mu $
-bound. But
$\mu $
-bound. But
![]() $\mu =\mu _s$
for any extension involving only the relations that occur in A, so this implies
$\mu =\mu _s$
for any extension involving only the relations that occur in A, so this implies
![]() $A\notin \mathcal {C}_s$
. The same argument shows the implication the other way.⊣
$A\notin \mathcal {C}_s$
. The same argument shows the implication the other way.⊣
Lemma 5.8.
![]() $\hat {\mathcal {N}}$
is a generic model for the class
$\hat {\mathcal {N}}$
is a generic model for the class
![]() $\hat {\mathcal {C}}$
.
$\hat {\mathcal {C}}$
.
Proof We need to verify the three facts:
-
(1)
 $\hat {\mathcal {N}}$
is countable.
$\hat {\mathcal {N}}$
is countable. -
(2) If
 $A\leq \hat {\mathcal {N}}$
is finite, then
$A\leq \hat {\mathcal {N}}$
is finite, then
 $A\in \hat {\mathcal {C}}$
.
$A\in \hat {\mathcal {C}}$
. -
(3) Suppose
 $A\leq \hat {\mathcal {N}}$
and
$A\leq \hat {\mathcal {N}}$
and
 $A\leq B\in \hat {\mathcal {C}}$
, then there is an embedding
$A\leq B\in \hat {\mathcal {C}}$
, then there is an embedding
 $f:B\rightarrow \hat {\mathcal {N}}$
so that
$f:B\rightarrow \hat {\mathcal {N}}$
so that
 $f(B)\leq \hat {\mathcal {N}}$
and f is the identity on A.
$f(B)\leq \hat {\mathcal {N}}$
and f is the identity on A.
The first here is trivial, since
![]() $\hat {\mathcal {N}}$
is a definitional expansion of a countable structure
$\hat {\mathcal {N}}$
is a definitional expansion of a countable structure
![]() $\mathcal {N}\vert \mathcal {L}$
, so it is countable. Given
$\mathcal {N}\vert \mathcal {L}$
, so it is countable. Given
![]() $A\leq \hat {\mathcal {N}}$
,
$A\leq \hat {\mathcal {N}}$
,
![]() $A\leq N_s$
and thus is in
$A\leq N_s$
and thus is in
![]() $\mathcal {C}_s$
for all sufficiently large s, by Lemma 5.6. Thus by Lemma 5.7,
$\mathcal {C}_s$
for all sufficiently large s, by Lemma 5.6. Thus by Lemma 5.7,
![]() $A\in \hat {\mathcal {C}}$
.
$A\in \hat {\mathcal {C}}$
.
Lastly, consider
![]() $A\leq \hat {\mathcal {N}}$
and
$A\leq \hat {\mathcal {N}}$
and
![]() $A\leq B\in \hat {\mathcal {C}}$
. Let s be large enough that
$A\leq B\in \hat {\mathcal {C}}$
. Let s be large enough that
![]() $A,B\in \mathcal {C}_t$
for every
$A,B\in \mathcal {C}_t$
for every
![]() $t\geq s$
. Further, let s be large enough that
$t\geq s$
. Further, let s be large enough that
![]() $A\leq N_t$
for all
$A\leq N_t$
for all
![]() $t\geq s$
. Further, let s be large enough that we consider the amalgamation requirement to build this B. Further, let s be large enough that
$t\geq s$
. Further, let s be large enough that we consider the amalgamation requirement to build this B. Further, let s be large enough that
 $S_{1,s}^{[i]}=S_1^{[i]}$
for every
$S_{1,s}^{[i]}=S_1^{[i]}$
for every
![]() $R_i\in \hat {\mathcal {L}}$
occurring inside B. Then in
$R_i\in \hat {\mathcal {L}}$
occurring inside B. Then in
![]() $N_s$
, we have the embedding
$N_s$
, we have the embedding
![]() $f:B\rightarrow N_s$
so that
$f:B\rightarrow N_s$
so that
![]() $f(B)\leq N_s$
and f is the identity on A. Further, since no element is ever enumerated into
$f(B)\leq N_s$
and f is the identity on A. Further, since no element is ever enumerated into
 $S_1^{[i]}$
, we cannot ever remove any
$S_1^{[i]}$
, we cannot ever remove any
![]() $R_i$
-relations occurring in B. It suffices to see that
$R_i$
-relations occurring in B. It suffices to see that
![]() $f(B)\leq N_t$
for every
$f(B)\leq N_t$
for every
![]() $t>s$
. This follows from the following claim:
$t>s$
. This follows from the following claim:
Claim. If
![]() $X\leq N_s$
and no relation inside X is ever removed, then
$X\leq N_s$
and no relation inside X is ever removed, then
![]() $X\leq N_t$
for every
$X\leq N_t$
for every
![]() $t>s$
.
$t>s$
.
Proof We proceed by induction. This is true for
![]() $t=s$
. For every
$t=s$
. For every
![]() $t\geq s$
, the
$t\geq s$
, the
![]() $\delta $
-value of X as a substructure of
$\delta $
-value of X as a substructure of
![]() $N_t$
is the same, since no relation is ever removed from X. Thus, we will unambiguously write
$N_t$
is the same, since no relation is ever removed from X. Thus, we will unambiguously write
![]() $\delta (X)$
which does not depend on stage.
$\delta (X)$
which does not depend on stage.
When we pass from
![]() $N_{t-1}$
to
$N_{t-1}$
to
![]() $N_{t-1}^{\prime }$
we ensured by adding elements and occurrences of R that we have maintained dimension (i.e.,
$N_{t-1}^{\prime }$
we ensured by adding elements and occurrences of R that we have maintained dimension (i.e.,
![]() $\delta (A,N_{t-1})=\delta (A,N_{t-1}^{\prime })$
for every
$\delta (A,N_{t-1})=\delta (A,N_{t-1}^{\prime })$
for every
![]() $A\subseteq N_{t-1}$
), so
$A\subseteq N_{t-1}$
), so
![]() $\delta (X)=\delta (X,N_{t-1})=\delta (X,N_{t-1}^{\prime })$
and thus
$\delta (X)=\delta (X,N_{t-1})=\delta (X,N_{t-1}^{\prime })$
and thus
![]() $X\leq N_{t-1}^{\prime }$
. Lastly, to go from
$X\leq N_{t-1}^{\prime }$
. Lastly, to go from
![]() $N_{t-1}^{\prime }$
to
$N_{t-1}^{\prime }$
to
![]() $N_t$
, we use strong amalgamation, so
$N_t$
, we use strong amalgamation, so
![]() $X\leq N_{t-1}^{\prime }\leq N_t$
.⊣
$X\leq N_{t-1}^{\prime }\leq N_t$
.⊣
Thus,
![]() $\mathcal {N}\vert \mathcal {L}$
is a recursive copy of the saturated model of T.⊣
$\mathcal {N}\vert \mathcal {L}$
is a recursive copy of the saturated model of T.⊣
Lemma 5.9. If
![]() $\bar {a}$
is an independent set in
$\bar {a}$
is an independent set in
![]() $\hat {\mathcal {N}}$
of size
$\hat {\mathcal {N}}$
of size
![]() $\leq n$
, then
$\leq n$
, then
![]() $ \operatorname {\mathrm {acl}}(\bar {a})$
is a
$ \operatorname {\mathrm {acl}}(\bar {a})$
is a
![]() $\Sigma ^0_1$
subset of
$\Sigma ^0_1$
subset of
![]() $\hat {\mathcal {N}}$
.
$\hat {\mathcal {N}}$
.
Proof Let X be the set of elements which ever appear to be in
![]() $ \operatorname {\mathrm {acl}}(\bar {a})$
. That is, we say x is enumerated into X at stage s if there is some
$ \operatorname {\mathrm {acl}}(\bar {a})$
. That is, we say x is enumerated into X at stage s if there is some
![]() $Y\subseteq N_s$
so that
$Y\subseteq N_s$
so that
![]() $\bar {a}\leq Y$
,
$\bar {a}\leq Y$
,
![]() $b\in Y$
, and
$b\in Y$
, and
![]() $\delta (Y/\bar {a})=0$
. It is clear that
$\delta (Y/\bar {a})=0$
. It is clear that
![]() $ \operatorname {\mathrm {acl}}(\bar {a})\subseteq X$
since for any
$ \operatorname {\mathrm {acl}}(\bar {a})\subseteq X$
since for any
![]() $x\in \operatorname {\mathrm {acl}}(\bar {a})$
, such a Y must exist in
$x\in \operatorname {\mathrm {acl}}(\bar {a})$
, such a Y must exist in
![]() $\mathcal {N}$
, thus in every large enough
$\mathcal {N}$
, thus in every large enough
![]() $N_s$
. Also, X is
$N_s$
. Also, X is
![]() $\Sigma ^0_1$
. The fear is that since some relations
$\Sigma ^0_1$
. The fear is that since some relations
![]() $R_i$
get removed either due to being limited away (i.e.,
$R_i$
get removed either due to being limited away (i.e.,
 $R_i\notin \hat {\mathcal {L}}$
) or in the clean-up phase, X may contain some elements that are not actually algebraic over
$R_i\notin \hat {\mathcal {L}}$
) or in the clean-up phase, X may contain some elements that are not actually algebraic over
![]() $\bar {a}$
.
$\bar {a}$
.
Fix
![]() $b\in X$
. It enters X because we see some Y in
$b\in X$
. It enters X because we see some Y in
![]() $N_s$
containing
$N_s$
containing
![]() $\bar {a}\cup \{b\}$
so that
$\bar {a}\cup \{b\}$
so that
![]() $\delta (Y/\bar {a})=0$
. Any removed relation in the clean-up phase is immediately replaced by an R-witnessed dimension drop which maintains
$\delta (Y/\bar {a})=0$
. Any removed relation in the clean-up phase is immediately replaced by an R-witnessed dimension drop which maintains
![]() $\delta $
. Thus, for every
$\delta $
. Thus, for every
![]() $t>s$
,
$t>s$
,
![]() $\delta (Y,N_t)=\delta (Y,N_s)$
, thus there is always some
$\delta (Y,N_t)=\delta (Y,N_s)$
, thus there is always some
![]() $Y'\subseteq N_t$
containing Y with
$Y'\subseteq N_t$
containing Y with
![]() $\delta (Y')\leq \lvert \bar {a}\rvert $
. Let Z be the self-sufficient closure of
$\delta (Y')\leq \lvert \bar {a}\rvert $
. Let Z be the self-sufficient closure of
![]() $\bar {a}b$
in
$\bar {a}b$
in
![]() $N_t$
for all sufficiently large t. We must have
$N_t$
for all sufficiently large t. We must have
![]() $\delta (Z)= \lvert \bar {a}\rvert $
, since
$\delta (Z)= \lvert \bar {a}\rvert $
, since
![]() $\delta (Z)=\delta (\bar {a}b,N_t)= \lvert \bar {a}\rvert $
. To see that
$\delta (Z)=\delta (\bar {a}b,N_t)= \lvert \bar {a}\rvert $
. To see that
![]() $b\in \operatorname {\mathrm {acl}}(\bar {a})$
witnessed by Z, we need only argue that each relation appearing in Z is in
$b\in \operatorname {\mathrm {acl}}(\bar {a})$
witnessed by Z, we need only argue that each relation appearing in Z is in
![]() $\hat {L}$
. Were it true that
$\hat {L}$
. Were it true that
![]() $R_i(\bar {z})$
holds in Z and
$R_i(\bar {z})$
holds in Z and
 $R_i\notin \hat {\mathcal {L}}$
, then from some stage onwards the relation
$R_i\notin \hat {\mathcal {L}}$
, then from some stage onwards the relation
![]() $R_i(\bar {z})$
would become defunct. This is because
$R_i(\bar {z})$
would become defunct. This is because
![]() $R_i(\bar {z})$
implies
$R_i(\bar {z})$
implies
![]() $\delta (\bar {z})=\lvert \bar {z}\rvert -1=n+1$
yet
$\delta (\bar {z})=\lvert \bar {z}\rvert -1=n+1$
yet
![]() $\delta (Z) = |\bar {a}|\leq n$
, so
$\delta (Z) = |\bar {a}|\leq n$
, so
![]() $g_{N_t}(\bar {z})$
is finite. But if
$g_{N_t}(\bar {z})$
is finite. But if
![]() $R_i(\bar {z})$
were to become defunct from some stage onwards, then it would eventually be removed.Footnote
1
But removing
$R_i(\bar {z})$
were to become defunct from some stage onwards, then it would eventually be removed.Footnote
1
But removing
![]() $R_i(\bar {z})$
would change the self-sufficient closure of
$R_i(\bar {z})$
would change the self-sufficient closure of
![]() $\bar {a}b$
, contrary to the definition of Z. Thus,
$\bar {a}b$
, contrary to the definition of Z. Thus,
![]() $b\in \operatorname {\mathrm {acl}}(\bar {a})$
in
$b\in \operatorname {\mathrm {acl}}(\bar {a})$
in
![]() $\hat {\mathcal {N}}$
.⊣
$\hat {\mathcal {N}}$
.⊣
Corollary 5.10. We conclude that
![]() $ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
.
$ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
.
Proof It is a standard fact that if
![]() $\mathcal {B}$
is any recursive structure and
$\mathcal {B}$
is any recursive structure and
![]() $\mathcal {A}$
is a recursively enumerable subset of
$\mathcal {A}$
is a recursively enumerable subset of
![]() $\mathcal {B}$
, then
$\mathcal {B}$
, then
![]() $\mathcal {A}$
has a recursive presentation.
$\mathcal {A}$
has a recursive presentation.
Since the k-dimensional model of T is
![]() $ \operatorname {\mathrm {acl}}(\bar {a})$
for an independent tuple in
$ \operatorname {\mathrm {acl}}(\bar {a})$
for an independent tuple in
![]() $\hat {\mathcal {N}}$
of size k and
$\hat {\mathcal {N}}$
of size k and
![]() $\mathcal {N}$
is recursive and infinite-dimensional, we conclude that
$\mathcal {N}$
is recursive and infinite-dimensional, we conclude that
![]() $ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
.⊣
$ \operatorname {\mathrm {SRM}}(T)\supseteq [0,n]\cup \{\omega \}$
.⊣
6 Defeating other models
Next we ensure that
![]() $[n+1,\omega )\cap \operatorname {\mathrm {SRM}}(T)=\emptyset $
. We do this by enumerating
$[n+1,\omega )\cap \operatorname {\mathrm {SRM}}(T)=\emptyset $
. We do this by enumerating
![]() $S_1$
appropriately. We will describe how numbers enter
$S_1$
appropriately. We will describe how numbers enter
 $S_1^{[i]}$
and we will note that we enumerate this column in order. In particular, at stage s, if we put anything into this column, we will put s into
$S_1^{[i]}$
and we will note that we enumerate this column in order. In particular, at stage s, if we put anything into this column, we will put s into
 $S_1^{[i]}$
, and thus this is the largest number to enter this column. Even though in the construction of the recursive models, we assumed that
$S_1^{[i]}$
, and thus this is the largest number to enter this column. Even though in the construction of the recursive models, we assumed that
![]() $\lvert S_{1,s+1}\smallsetminus S_{1,s}\rvert =1$
for all s, we will not be careful in this below, as any enumeration of an infinite
$\lvert S_{1,s+1}\smallsetminus S_{1,s}\rvert =1$
for all s, we will not be careful in this below, as any enumeration of an infinite
![]() $\Sigma ^0_1$
-set can be altered to give one enumerating the set in the same order and enumerating exactly one element per stage.
$\Sigma ^0_1$
-set can be altered to give one enumerating the set in the same order and enumerating exactly one element per stage.
Let
![]() $B_i,\bar {b}_i$
be the ith pair consisting of a partial recursive atomic diagram of an
$B_i,\bar {b}_i$
be the ith pair consisting of a partial recursive atomic diagram of an
![]() $\mathcal {L}$
-structure along with a finite tuple of size at least
$\mathcal {L}$
-structure along with a finite tuple of size at least
![]() $n+1$
given by canonical index. We next describe a strategy to enumerate the ith column of
$n+1$
given by canonical index. We next describe a strategy to enumerate the ith column of
![]() $S_1$
so that either
$S_1$
so that either
![]() $B_i\not \models T$
or
$B_i\not \models T$
or
![]() $\bar {b}_i$
is not a basis for
$\bar {b}_i$
is not a basis for
![]() $B_i$
. These strategies are put together into a construction by running the first s of these strategies in order at each stage s. At stage s, for
$B_i$
. These strategies are put together into a construction by running the first s of these strategies in order at each stage s. At stage s, for
![]() $\bar {c}\in B_i$
we say that
$\bar {c}\in B_i$
we say that
![]() $R_i(\bar {c})$
holds if there is some
$R_i(\bar {c})$
holds if there is some
![]() $\langle i,j\rangle \in S_{1,s}\smallsetminus S_{0,s}$
so that
$\langle i,j\rangle \in S_{1,s}\smallsetminus S_{0,s}$
so that
 $\exists ^{n+6} \Omega _{\langle i,j\rangle }$
-extensions over
$\exists ^{n+6} \Omega _{\langle i,j\rangle }$
-extensions over
![]() $\bar {c}$
.
$\bar {c}$
.
We do this as follows:
Step 0: Let
![]() $\bar {b}$
consist of the first
$\bar {b}$
consist of the first
![]() $n+1$
elements of
$n+1$
elements of
![]() $\bar {b}_i$
. Enumerate
$\bar {b}_i$
. Enumerate
![]() $\langle i,0\rangle , \langle i,1\rangle $
into
$\langle i,0\rangle , \langle i,1\rangle $
into
![]() $S_1$
. Wait until a stage where we see some element c so that
$S_1$
. Wait until a stage where we see some element c so that
![]() $R_i(\bar {b},c)$
holds.
$R_i(\bar {b},c)$
holds.
Step 1: Let
![]() $j^s_0<j^s_1$
and
$j^s_0<j^s_1$
and
 $\{j^s_0,j^s_1 \}=(S_{1,s}^{[i]}\smallsetminus S_{0,s}^{[i]})$
at stage s. When we first come to this step, we define the set of obstructions to moving to the next step. If we see a set
$\{j^s_0,j^s_1 \}=(S_{1,s}^{[i]}\smallsetminus S_{0,s}^{[i]})$
at stage s. When we first come to this step, we define the set of obstructions to moving to the next step. If we see a set
![]() $Y\subseteq B_i$
and enough relations hold on Y so that
$Y\subseteq B_i$
and enough relations hold on Y so that
![]() $\delta (Y)<\lvert \bar {b}_i\rvert $
and
$\delta (Y)<\lvert \bar {b}_i\rvert $
and
![]() $\bar {b}_i\subseteq Y$
, then we call Y an obstruction to moving to the next step.
$\bar {b}_i\subseteq Y$
, then we call Y an obstruction to moving to the next step.
If
 $S_1^{[i']}$
enumerates a number after the stage when we entered this step, we call the relation symbol
$S_1^{[i']}$
enumerates a number after the stage when we entered this step, we call the relation symbol
![]() $R_{i'}$
suspicious (i.e., we suspect it might limit away). At each stage t, we let
$R_{i'}$
suspicious (i.e., we suspect it might limit away). At each stage t, we let
![]() $\mathcal {L}_t$
be the set of non-suspicious relation symbols. We define
$\mathcal {L}_t$
be the set of non-suspicious relation symbols. We define
![]() for any Y to be
for any Y to be
![]() $\lvert Y\rvert -\Sigma _{Q\in \mathcal {L}_t}\#Q(Y)$
. If at some stage t we see
$\lvert Y\rvert -\Sigma _{Q\in \mathcal {L}_t}\#Q(Y)$
. If at some stage t we see
![]() , then we say the obstruction Y has been removed.
, then we say the obstruction Y has been removed.
We say that the requirement is ready for the next step if
![]() $\bar {b}c$
has
$\bar {b}c$
has
![]() $n+6$
-many
$n+6$
-many
 $\Omega _{\langle i,j^s_0\rangle }$
and
$\Omega _{\langle i,j^s_0\rangle }$
and
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j^s_1\rangle }$
-extensions and all obstructions have been removed. Wait until the requirement is ready for the next step. At that point, go to step 2.
$\Omega _{\langle i,j^s_1\rangle }$
-extensions and all obstructions have been removed. Wait until the requirement is ready for the next step. At that point, go to step 2.
Step 2: Put
![]() $\langle i,s\rangle $
(s is the current stage) into
$\langle i,s\rangle $
(s is the current stage) into
![]() $S_{1,s}$
. Note that this enumerates
$S_{1,s}$
. Note that this enumerates
 $\langle i,j^{s-1}_0\rangle $
into
$\langle i,j^{s-1}_0\rangle $
into
![]() $S_{0,s}$
. Return to Step 1.
$S_{0,s}$
. Return to Step 1.
Lemma 6.1.
![]() $[n+1,\omega )\cap \operatorname {\mathrm {SRM}}(T)=\emptyset $
.
$[n+1,\omega )\cap \operatorname {\mathrm {SRM}}(T)=\emptyset $
.
Proof We check that no
![]() $B_i,\bar {b}_i$
can be a recursive model of T with basis
$B_i,\bar {b}_i$
can be a recursive model of T with basis
![]() $\bar {b}_i$
.
$\bar {b}_i$
.
If we never leave step 0, then
 $S_1^{[i]}$
is finite, hence
$S_1^{[i]}$
is finite, hence
![]() $R_i\in \hat {\mathcal {L}}$
. By Lemma 4.4, clearly
$R_i\in \hat {\mathcal {L}}$
. By Lemma 4.4, clearly
![]() $B_i\not \models T$
. So we may assume we have reached step 1 at some stage. Observe that in every subsequent stage, we have
$B_i\not \models T$
. So we may assume we have reached step 1 at some stage. Observe that in every subsequent stage, we have
![]() $R_i(\bar {b}c)$
holding. This is because we only enumerate a number into
$R_i(\bar {b}c)$
holding. This is because we only enumerate a number into
 $S_{1,s}^{[i]}$
if we have both
$S_{1,s}^{[i]}$
if we have both
![]() $n+6$
-many
$n+6$
-many
 $\Omega _{\langle i,j^{s-1}_0\rangle }$
and
$\Omega _{\langle i,j^{s-1}_0\rangle }$
and
![]() $n+6$
-many
$n+6$
-many
 $\Omega _{\langle i,j^{s-1}_1\rangle }$
-extensions over
$\Omega _{\langle i,j^{s-1}_1\rangle }$
-extensions over
![]() $\bar {b}c$
. Recall that
$\bar {b}c$
. Recall that
 $\Omega _{\langle i,j^{s-1}_1\rangle }$
only uses R, thus even after enumerating
$\Omega _{\langle i,j^{s-1}_1\rangle }$
only uses R, thus even after enumerating
 $\langle i,j^{s-1}_0\rangle $
into
$\langle i,j^{s-1}_0\rangle $
into
![]() $S_0$
, we still have
$S_0$
, we still have
![]() $n+6$
-many
$n+6$
-many
 $\Omega _{\langle i,j^{s-1}_1\rangle }=\Omega _{\langle i,j^s_0\rangle }$
-extensions over
$\Omega _{\langle i,j^{s-1}_1\rangle }=\Omega _{\langle i,j^s_0\rangle }$
-extensions over
![]() $\bar {b}c$
, so
$\bar {b}c$
, so
![]() $R_i(\bar {b}c)$
still holds.
$R_i(\bar {b}c)$
still holds.
There are two possible outcomes to the strategy to defeat
![]() $B_i,\bar {b}_i$
: Either we go through step 2 finitely or infinitely often.
$B_i,\bar {b}_i$
: Either we go through step 2 finitely or infinitely often.
If we go through step 2 finitely often, then
![]() $R_i\in \hat {\mathcal {L}}$
and we must get stuck in step 1. This is either because of a non-removed obstruction, in which case
$R_i\in \hat {\mathcal {L}}$
and we must get stuck in step 1. This is either because of a non-removed obstruction, in which case
![]() $\delta (\bar {b}, B_i)<\lvert \bar {b}\rvert $
or we never have both
$\delta (\bar {b}, B_i)<\lvert \bar {b}\rvert $
or we never have both
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j_0\rangle }$
and
$\Omega _{\langle i,j_0\rangle }$
and
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j_1\rangle }$
-extensions over
$\Omega _{\langle i,j_1\rangle }$
-extensions over
![]() $\bar {b}c$
. The first option means
$\bar {b}c$
. The first option means
![]() $\bar {B}_i$
is not a basis, so we may assume it is false, implying
$\bar {B}_i$
is not a basis, so we may assume it is false, implying
![]() $\bar {b}c\leq B_i$
. By (3”) and choice of
$\bar {b}c\leq B_i$
. By (3”) and choice of
![]() $\mu $
, since
$\mu $
, since
![]() $\bar {b}c\leq B_i$
, all of these
$\bar {b}c\leq B_i$
, all of these
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j_0\rangle }$
and
$\Omega _{\langle i,j_0\rangle }$
and
![]() $n+6$
-many
$n+6$
-many
![]() $\Omega _{\langle i,j_1\rangle }$
-extensions over
$\Omega _{\langle i,j_1\rangle }$
-extensions over
![]() $\bar {b}c$
should exist. Thus,
$\bar {b}c$
should exist. Thus,
![]() $B_i$
cannot model T.
$B_i$
cannot model T.
In the infinite outcome, we argue that if
![]() $B_i\models T$
and
$B_i\models T$
and
![]() $\bar {b}_i$
is independent in
$\bar {b}_i$
is independent in
![]() $B_i$
, then
$B_i$
, then
![]() $c\notin \operatorname {\mathrm {acl}}(\bar {b}_i)$
. Suppose otherwise that
$c\notin \operatorname {\mathrm {acl}}(\bar {b}_i)$
. Suppose otherwise that
![]() $B_i\models T$
and
$B_i\models T$
and
![]() $\bar {b}_i$
is independent and there is some Y containing
$\bar {b}_i$
is independent and there is some Y containing
![]() $\bar {b}_ic$
and
$\bar {b}_ic$
and
![]() $\delta (Y)=\lvert \bar {b}_i\rvert $
. Recall
$\delta (Y)=\lvert \bar {b}_i\rvert $
. Recall
![]() $\delta $
is calculated in the language
$\delta $
is calculated in the language
![]() $\hat {\mathcal {L}}$
, which in this case does not include
$\hat {\mathcal {L}}$
, which in this case does not include
![]() $R_i$
. Thus, when we also consider the relation
$R_i$
. Thus, when we also consider the relation
![]() $R_i(\bar {b}c)$
, from some stage onward this Y forms an obstruction that is never removed. So, we get stuck in step 1 contradicting that we are in the infinite outcome. Thus, under the infinite outcome, if
$R_i(\bar {b}c)$
, from some stage onward this Y forms an obstruction that is never removed. So, we get stuck in step 1 contradicting that we are in the infinite outcome. Thus, under the infinite outcome, if
![]() $B_i\models T$
and
$B_i\models T$
and
![]() $\bar {b}_i$
is independent, then
$\bar {b}_i$
is independent, then
![]() $c\notin \operatorname {\mathrm {acl}}(\bar {b}_i)$
, contradicting that
$c\notin \operatorname {\mathrm {acl}}(\bar {b}_i)$
, contradicting that
![]() $\bar {b}$
is a basis for
$\bar {b}$
is a basis for
![]() $B_i$
.⊣
$B_i$
.⊣
Theorem 6.2.
T is a strongly minimal, flat, non-disintegrated, model complete theory in a language with finite signature, and
![]() $ \operatorname {\mathrm {SRM}}(T)=[0,n]\cup \{\omega \}$
.
$ \operatorname {\mathrm {SRM}}(T)=[0,n]\cup \{\omega \}$
.
Proof The theory T is in the language
![]() $\mathcal {L}$
which has the finite signature
$\mathcal {L}$
which has the finite signature
![]() $\{R\}$
. In the previous lemma, we showed that
$\{R\}$
. In the previous lemma, we showed that
![]() $[n+1,\omega )\cap \operatorname {\mathrm {SRM}}(T)=\emptyset $
. In Corollary 5.10, we showed that
$[n+1,\omega )\cap \operatorname {\mathrm {SRM}}(T)=\emptyset $
. In Corollary 5.10, we showed that
![]() $[0,n]\cup \{\omega \}\subseteq \operatorname {\mathrm {SRM}}(T)$
. Thus
$[0,n]\cup \{\omega \}\subseteq \operatorname {\mathrm {SRM}}(T)$
. Thus
![]() $ \operatorname {\mathrm {SRM}}(T)=[0,n]\cup \{\omega \}$
. In Corollary 2.22, we showed
$ \operatorname {\mathrm {SRM}}(T)=[0,n]\cup \{\omega \}$
. In Corollary 2.22, we showed
![]() $\hat {T}$
is strongly minimal, which implies T is strongly minimal. In Corollary 4.6 we showed T is model complete. In Lemma 4.7 we showed that T is flat and non-disintegrated.⊣
$\hat {T}$
is strongly minimal, which implies T is strongly minimal. In Corollary 4.6 we showed T is model complete. In Lemma 4.7 we showed that T is flat and non-disintegrated.⊣
Acknowledgments
Uri Andrews was partially supported by NSF grant DMS-1600228.