1. Introduction
In the past few decades, optimal reinsurance problems for various risk models have attracted the attention of a large number of scholars in actuarial sciences area, and the technique of stochastic control theory and the corresponding Hamilton–Jacobi–Bellman (HJB) equation are widely used to cope with these problems. See, for example, Browne (Reference Browne1995), Schmidli (2001, Reference Schmidli2002), Promislow & Young (Reference Promislow and Young2005), Bai et al. (Reference Bai, Cai and Zhou2013), Liang & Bayraktar (Reference Liang and Bayraktar2014), Liang & Yuen (Reference Liang and Yuen2016) and Bi et al. (Reference Bi, Liang and Xu2016). The main popular criteria include maximising the expected utility of the terminal wealth, minimising the probability of ruin of the insurer and so on.
Our paper falls naturally within the area of optimally controlling wealth to reach a goal, which is an important research topic. It began with the seminal work of Dubins & Savage (Reference Dubins and Savage1976 [1965]), and continued with the work of Pestien & Sudderth (Reference Pestien and Sudderth1985), Sudderth et al. (Reference Sudderth, William and Ananda1989), Browne (1997, 1999a, Reference Browne1999b ), Young (Reference Young2004), Moore et al. (Reference Moore, Kristen and Young2006), Wang & Young (2012a, Reference Wang and Young2012b ) and Yener (Reference Yener2015). A typical problem considered in this research area is to control a process to minimise the probability of ruin. See, for example, Promislow & Young (Reference Promislow and Young2005) found the optimal investment and quota-share reinsurance strategies to minimise the probability of ruin of an insurer who faces a claim process that follows Brownian motion with drift. Bayraktar & Young (Reference Bayraktar and Young2008) considered the minimum probability of ruin when an agent’s rate of consumption is ratcheted; i.e., it forms a non-decreasing process. Azcue & Muler (Reference Azcue and Muler2013) also studied the minimum probability of ruin, assuming that the decision-maker can invest dynamically part of the reserve in an asset that has a positive fixed return. Bäuerle & Bayraktar (Reference Bäuerle and Bayraktar2014) obtained that the optimal investment strategy to minimise the probability of ruin is the one that maximises the ratio of drift of a diffusion divided to its volatility squared, which was also shown in Pestien & Sudderth (Reference Pestien and Sudderth1985).
Drawdown, measuring the decline of portfolio value from its historic high-water mark, is a frequently quoted risk metric to evaluate the performance of portfolio managers in the fund management industry. A significant drawdown not only leads to large portfolio losses but may also trigger a long-term recession. It is also considered as a key determinant of sustainable investments since investors tend to overestimate their tolerance to risk. Besides, investors prefer to assess their investment success by comparing their current portfolio value to the historical maximum value. Therefore, portfolio managers have strong incentives to adopt strategies with low drawdown risks. Recently, Angoshtari et al. (Reference Angoshtari, Bayraktar and Young2016a ) investigated the minimum drawdown probability problem over an infinite-time horizon and showed that the optimal strategy which minimises the probability of ruin also minimises the probability of drawdown if drawdown does not happen. Besides, Chen et al.(Reference Chen, Landriault, Li and Li2015) and Angoshtari et al. (Reference Angoshtari, Bayraktar and Young2016b ) both studied a lifetime investment problem aiming at minimising the risk of drawdown occurrence. They found that the optimal strategy for a random (or finite) maturity setting such as lifetime drawdown is very different from that of the corresponding ruin problem. We can see other works involving drawdown such as Grossman & Zhou (Reference Grossman and Zhou1993), Cvitanić & Karatzas (Reference Cvitanić and Karatzas1995) and Elie & Touzi (Reference Elie and Touzi2008) for early references.
Even though lots of literature on optimal reinsurance problems in controlling wealth to reach a goal has been worked out, there are still many aspects being worthily further explored. For example, most of the literature about reinsurance optimisation is based on independent aggregate claims. However, in practice, insurance businesses are usually dependent in some way. A typical example is that an earthquake, hurricane or tsunami often leads to various kinds of insurance claims such as death claims, medical claims and household claims. That is to say, a single event generates claims from different lines of insurance. To depict such a dependence structure among several classes of insurance business, the so-called common shock risk model may be of some practical relevance. Research on risk models with dependent risk is increasing rapidly in recent years. See, for example, Wang (Reference Wang1998), and Yuen et al. (2002, Reference Yuen, Guo and Wu2006). Meanwhile, some researchers are devoted to solving the problem of optimal reinsurance. Bai et al. (Reference Bai, Cai and Zhou2013) sought the optimal excess of loss reinsurance to minimise the ruin probability for the diffusion approximation risk model. Liang & Yuen (Reference Liang and Yuen2016) adopted the variance premium principle to study the optimal proportional reinsurance problem for both the compound Poisson risk model and the diffusion approximation risk model. Yuen et al. (Reference Yuen, Liang and Zhou2015) extended the work of Liang & Yuen (Reference Liang and Yuen2016) to the case with the reinsurance premium calculated by the expected value principle and to the model with two or more classes of dependent risks. Liang et al. (Reference Liang, Bi, Yuen and Zhang2016) also studied the optimal reinsurance–investment problems in a financial market with jump-diffusion risky asset, where the insurance risk model is modulated by a compound Poisson process, and the two jump number processes are correlated by a common shock. However, among these papers with common shock dependence, few of them are related to the problem of minimising the probability of drawdown.
As we know, with drawdown, the decision-maker wants to choose the optimal strategy which minimises the probability that the value of the surplus process reaches some fixed proportion, say α∈[0,1), of its maximum value to date. Naturally, it seems more reasonable for insurers to bear drawdown than ruin, where the wealth drops below a fix level, such as 0. It is obvious that, when α=0, minimising the probability of drawdown is equal to minimising the probability of ruin. Therefore, in our paper, we consider the optimal proportional reinsurance problem in a risk model with two dependent classes of insurance business in two different cases, where the criterion is minimising the probability of drawdown. In the first case, the level we set is a fixed one. Based on the method of maximising the ratio of drift of the surplus process divided to its volatility squared in Bäuerle & Bayraktar (Reference Bäuerle and Bayraktar2014), we obtain the optimal results. In the second case, the level is not necessarily a fixed one, then the method mentioned above does not apply. Thus, following the analysis of Chen et al. (Reference Chen, Landriault, Li and Li2015) and Angoshtari et al. (2016a, 2016 Reference Angoshtari, Bayraktar and Youngb ), we use the technique of stochastic control theory and the corresponding HJB equation to tackle the optimisation problem. In particular, since we constrain the reinsurance proportion in the interval [0,1] for each case, the optimisation problems are discussed in three different situations, which makes the problem more challenging. By some interesting analytic technique, we obtain the explicit solutions for the optimal proportional reinsurance strategy and the minimum probability of drawdown, which strongly depend on the value of the surplus wealth. In addition, we come to the conclusion that the optimal proportional reinsurance strategy for the drawdown problem coincides with the one for the ruin problem if drawdown does not happen. Moreover, we can see that, for the optimisation problem with common shock dependent risk model, the way of solving the HJB equation to gain the optimal results is relatively easier than the way of maximising the ratio of the drift of the surplus process to its volatility squared, but the latter makes the analysis of the constrained control variables more convenient.
The remainder of this paper is organised as follows. In section 2, the model and the optimisation problem are presented. With constraint on the reinsurance strategy, explicit expressions of the optimal strategy and the corresponding minimum probability of drawdown are obtained in sections 3 and 4. In section 5, we present some numerical examples which show the impact of some model parameters on the optimal results. Finally, we conclude the paper in section 6.
2. Model and Problem Formulation
Suppose that an insurance company has two dependent classes of insurance business such as motor and life insurance. Let {X i , i≥1} be the claim size random variables for the first class following a common distribution F X (x) with F X (x)=0 for x≤0, and 0<F X (x)≤1 for x>0; and {Y i , i≥1} be the claim size random variables for the second class following a common distribution F Y (y) with F Y (y)=0 for y≤0, 0<F Y (y)≤1 for y>0. Then, the aggregate claims process generated from these two classes of business is given by
where N i (t)+N(t) (i=1, 2) is the claim number process for class i (i=1, 2), and N 1(t), N 2(t) and N(t) are three independent Poisson processes with parameters λ 1, λ 2 and λ, respectively. Assume that X i and Y i are independent claim size random variables, and that they are independent of N 1(t), N 2(t) and N(t). It is obvious that the dependence of the two classes of business is due to a common shock governed by the counting process N(t).
We allow the insurance company to continuously reinsure a fraction of its claim with the retention levels q 1(⋅)∈[0,1] and q 2(⋅)∈[0,1] for X i and Y i , respectively, and the reinsurance premium rate at time t is δ(q 1(⋅), q 2(⋅)). Let {U t , t≥0} denote the associated surplus process, i.e., U t is the surplus of the insurer at time t under the strategy (q 1(U t ), q 2(U t )). This controlled surplus process can be given by
where the constant c is the premium rate. Moreover, from Grandell (Reference Grandell1991), we know that the Brownian motion risk model given by
with a
1=(λ
1+λ)E(X) and
![]() $b_{1}^{2} {\equals}\left( {\lambda _{1} {\plus}\lambda } \right)E\left( {X^{2} } \right)$
can be seen as a diffusion approximation to the compound Poisson process S
1(t). Similarly,
$b_{1}^{2} {\equals}\left( {\lambda _{1} {\plus}\lambda } \right)E\left( {X^{2} } \right)$
can be seen as a diffusion approximation to the compound Poisson process S
1(t). Similarly,
with a
2=(λ
2 + λ)E(Y) and
![]() $b_{2}^{2} {\equals}\left( {\lambda _{2} {\plus}\lambda } \right)E\left( {Y^{2} } \right)$
can be treated as a diffusion approximation to the compound Poisson process S
2(t). Here, B
1t
and B
2t
are standard Brownian motions with the correlation coefficient
$b_{2}^{2} {\equals}\left( {\lambda _{2} {\plus}\lambda } \right)E\left( {Y^{2} } \right)$
can be treated as a diffusion approximation to the compound Poisson process S
2(t). Here, B
1t
and B
2t
are standard Brownian motions with the correlation coefficient
Thus, E[B 1t B 2t ]=ρt. With expected value principle:
and the reinsurance premium rate at time t is
where θ i (i=1, 2) and η i (i=1, 2) are the insurer’s and reinsurer’s safety loading of the two classes of the insurance business, respectively. Without loss of generality, we assume that η i ≥θ i , and η i >θ i holds at least for one i (i=1,2), otherwise the problem becomes trivial.
Replace S
i
(t)(i=1, 2) by
![]() $\hat{S}_{i} (t){\rm }(i{\equals}1,2)$
in (2.1). Furthermore, we assume that the insurer is allowed to invest all its surplus in a risk-free asset (bond or bank account) with interest rate r. Then the process evolves as
$\hat{S}_{i} (t){\rm }(i{\equals}1,2)$
in (2.1). Furthermore, we assume that the insurer is allowed to invest all its surplus in a risk-free asset (bond or bank account) with interest rate r. Then the process evolves as
 $$\eqalignno{ d\hat{U}_{t} {\equals} & \left[ {r\hat{U}_{t} {\plus}a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} q_{1} \left( {\hat{U}_{t} } \right)} \right)} \right.\left. {{\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} q_{2} \left( {\hat{U}_{t} } \right)} \right)} \right]dt \cr & {\rm }{\plus} b_{1} q_{1} \left( {\hat{U}_{t} } \right)dB_{{1t}} {\plus}b_{2} q_{2} \left( {\hat{U}_{t} } \right)dB_{{2t}} $$
$$\eqalignno{ d\hat{U}_{t} {\equals} & \left[ {r\hat{U}_{t} {\plus}a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} q_{1} \left( {\hat{U}_{t} } \right)} \right)} \right.\left. {{\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} q_{2} \left( {\hat{U}_{t} } \right)} \right)} \right]dt \cr & {\rm }{\plus} b_{1} q_{1} \left( {\hat{U}_{t} } \right)dB_{{1t}} {\plus}b_{2} q_{2} \left( {\hat{U}_{t} } \right)dB_{{2t}} $$
or equivalently:
 $$\eqalignno{ d\hat{U}_{t} {\equals} & \left[ {r\hat{U}_{t} {\plus}a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} q_{1} \left( {\hat{U}_{t} } \right)} \right){\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} q_{2} \left( {\hat{U}_{t} } \right)} \right)} \right]dt \cr & {\rm }{\plus} \sqrt {b_{1}^{2} q_{1}^{2} \left( {\hat{U}_{t} } \right){\plus}b_{2}^{2} q_{2}^{2} \left( {\hat{U}_{t} } \right){\plus}2b_{1} b_{2} q_{1} \left( {\hat{U}_{t} } \right)q_{2} \left( {\hat{U}_{t} } \right)\rho } dB_{t} $$
$$\eqalignno{ d\hat{U}_{t} {\equals} & \left[ {r\hat{U}_{t} {\plus}a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} q_{1} \left( {\hat{U}_{t} } \right)} \right){\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} q_{2} \left( {\hat{U}_{t} } \right)} \right)} \right]dt \cr & {\rm }{\plus} \sqrt {b_{1}^{2} q_{1}^{2} \left( {\hat{U}_{t} } \right){\plus}b_{2}^{2} q_{2}^{2} \left( {\hat{U}_{t} } \right){\plus}2b_{1} b_{2} q_{1} \left( {\hat{U}_{t} } \right)q_{2} \left( {\hat{U}_{t} } \right)\rho } dB_{t} $$
with
![]() $\hat{U}_{0} {\equals}u$
and
$\hat{U}_{0} {\equals}u$
and
![]() $B_{t} $
is a standard Brownian motion. The similar model has also been studied in the literature; see, for example, Yuen et al. (Reference Yuen, Liang and Zhou2015), Liang & Yuen (Reference Liang and Yuen2016), Bi et al. (Reference Bi, Liang and Xu2016) and the references therein.
$B_{t} $
is a standard Brownian motion. The similar model has also been studied in the literature; see, for example, Yuen et al. (Reference Yuen, Liang and Zhou2015), Liang & Yuen (Reference Liang and Yuen2016), Bi et al. (Reference Bi, Liang and Xu2016) and the references therein.
Define the maximum surplus value M t at time t by
where M 0=m>0. Note that we allow the surplus process to have a financial past, and that m is no less than the initial surplus u by definition. We mean that when the value of the surplus process reaches α∈[0,1) times its maximum value, then drawdown occurs. Define the corresponding hitting time by
We can see that, if α=0, then we are in the case of minimising the probability of ruin for the fixed ruin level 0. Besides, if the value of the investment fund is big enough, say, at least
then the insurer can transfer all the risk, and the surplus value will never decrease, i.e., drawdown cannot occur in this case. We generalise from this case in the following Remark 2.1.
Remark 2.1. Throughout this paper, we know there exists a unique
such that
and
If
![]() $\hat{U}_{0} {\equals}u\geq u_{s} $
, then we can set
$\hat{U}_{0} {\equals}u\geq u_{s} $
, then we can set
![]() $q_{1}^{{\rm {\asterisk}}} (\hat{U}_{t} ){\equals}0$
,
$q_{1}^{{\rm {\asterisk}}} (\hat{U}_{t} ){\equals}0$
,
![]() $q_{2}^{{\rm {\asterisk}}} (\hat{U}_{t} ){\equals}0$
for all t≥0, which implies
$q_{2}^{{\rm {\asterisk}}} (\hat{U}_{t} ){\equals}0$
for all t≥0, which implies
Under this reinsurance strategy, the value of the surplus process is non-decreasing, so drawdown will never occur. For this reason, we call u s safe level as defined in Angoshtari et al. (Reference Angoshtari, Bayraktar and Young2016a ).
In the following definition, we give the admissible set of
![]() $$\left( {q_{1} \left( {\hat{U}_{t} } \right),q_{2} \left( {\hat{U}_{t} } \right)} \right)$$
.
$$\left( {q_{1} \left( {\hat{U}_{t} } \right),q_{2} \left( {\hat{U}_{t} } \right)} \right)$$
.
Definition 2.1 Let
![]() $(\Omega ,{\cal F},{\cal P})$
be a probability space equipped with a complete filtration
$(\Omega ,{\cal F},{\cal P})$
be a probability space equipped with a complete filtration
![]() ${\cal F}_{t} $
which is generated by
${\cal F}_{t} $
which is generated by
![]() $\hat{U}_{s} \left( {0\leq s\leq t} \right)$
. A strategy
$\hat{U}_{s} \left( {0\leq s\leq t} \right)$
. A strategy
![]() $$\left( {q_{1} \left( {\hat{U}_{t} } \right),q_{2} \left( {\hat{U}_{t} } \right)} \right)$$
is said to be admissible if the following conditions are satisfied:
$$\left( {q_{1} \left( {\hat{U}_{t} } \right),q_{2} \left( {\hat{U}_{t} } \right)} \right)$$
is said to be admissible if the following conditions are satisfied:
(a)
 $\left( {q_{1} \left( {\hat{U}_{t} } \right),q_{2} \left( {\hat{U}_{t} } \right)} \right)$
is
$\left( {q_{1} \left( {\hat{U}_{t} } \right),q_{2} \left( {\hat{U}_{t} } \right)} \right)$
is
 ${\cal F}_{t} $
-progressively measurable;
${\cal F}_{t} $
-progressively measurable;(b)
 $q_{i} \left( {\hat{U}_{t} } \right)\in[0,1]$
for i=1, 2;
$q_{i} \left( {\hat{U}_{t} } \right)\in[0,1]$
for i=1, 2;(c) Equation (2.2) for
 $\hat{U}_{t} $
has a unique strong solution.
$\hat{U}_{t} $
has a unique strong solution.
The set of all admissible strategies is denoted by
![]() ${\cal D}$
.
${\cal D}$
.
Now assume that the insurer is interested in minimising the probability of drawdown, we denote the minimum probability of drawdown by ϕ(u, m), which depends on the initial surplus u and the maximum (past) value m. Specifically, ϕ is the minimum probability of τ α <∞, thus, we derive the objective function
Here, P
u,m
and E
u,m
denote the probability and expectation, respectively, conditional on
![]() $\hat{U}_{0} {\equals}u$
and
$\hat{U}_{0} {\equals}u$
and
![]() $M_{0} {\equals}m$
. Then, the corresponding value function is given by
$M_{0} {\equals}m$
. Then, the corresponding value function is given by
3. Minimising the Probability of Drawdown When m≥u s
We first consider the case for which m≥u
s
. Note that if αm>u
s
, then the probability of drawdown ϕ(u,m)=1 for all u≤αm, and when u≤αm, we have u>u
s
, then according to Remark 2.1, the value of the surplus will consistently increase, and thus the probability of drawdown ϕ(u,m)=0 for all u >αm. In the following context, we shall investigate the case of αm≤u
s
in detail. When
![]() $\hat{U}_{0} {\equals}u\geq u_{s} $
, the drawdown is impossible; and when
$\hat{U}_{0} {\equals}u\geq u_{s} $
, the drawdown is impossible; and when
![]() $\hat{U}_{0} {\equals}u\leq \alpha m$
, then the drawdown has occurred and the game is over. Therefore, we assume that
$\hat{U}_{0} {\equals}u\leq \alpha m$
, then the drawdown has occurred and the game is over. Therefore, we assume that
![]() $\hat{U}_{0} {\equals}u\in[\alpha m,u_{s} ]$
.
$\hat{U}_{0} {\equals}u\in[\alpha m,u_{s} ]$
.
![]() $\hat{U}_{0} {\equals}u\leq u_{s} $
implies that either
$\hat{U}_{0} {\equals}u\leq u_{s} $
implies that either
![]() $\hat{U}_{t} \,\lt\,u_{s} $
almost surely, for all t≥0, or
$\hat{U}_{t} \,\lt\,u_{s} $
almost surely, for all t≥0, or
![]() $\hat{U}_{t} {\equals}u_{s} $
for some t>0. Since
$\hat{U}_{t} {\equals}u_{s} $
for some t>0. Since
![]() $m\geq u_{s} $
, M
t
=m holds almost surely for all t≥0. Therefore, avoiding drawdown is equivalent to avoiding ruin with a (fixed) ruin level of αm.
$m\geq u_{s} $
, M
t
=m holds almost surely for all t≥0. Therefore, avoiding drawdown is equivalent to avoiding ruin with a (fixed) ruin level of αm.
From Bäuerle & Bayraktar (Reference Bäuerle and Bayraktar2014), we can see that the optimal proportional reinsurance strategy with no constraint is the one that maximises the ratio of the drift of the surplus process to its volatility squared in (2.2). Thus, when the arguments u and m indicate the initial surplus and the maximum (past) value, respectively, the Proposition 3.1 can be derived.
Proposition 3.1. If m≥u s , the optimal proportional reinsurance strategy with no constraint is
 $$ \scale98% { \left\{ \matrix{ \hat{q}_{1} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{2} \eta _{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr \hat{q}_{2} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr} \right.$$
$$ \scale98% { \left\{ \matrix{ \hat{q}_{1} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{2} \eta _{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr \hat{q}_{2} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr} \right.$$
in which Δ1 and Δ2 are defined by
Proof. From (2.2), we denote the ratio of the drift to its volatility squared by ξ(u), thus we have
Differentiating ξ(u) with respect to q 1(u) and q 2(u), respectively, we have
 $$ \scale98% { \left\{ \matrix{ a_{1} \eta _{1} \left( {b_{1}^{2} \hat{q}_{1}^{2} \left( u \right){\plus}b_{2}^{2} \hat{q}_{2}^{2} \left( u \right){\plus}2b_{1} b_{2} \hat{q}_{1} \left( u \right)\hat{q}_{2} \left( u \right)\rho } \right) \hfill \cr {\minus}\left[ {a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} \hat{q}_{1} \left( u \right)} \right){\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} \hat{q}_{2} \left( u \right)} \right){\plus}ru} \right]\left( {2\hat{q}_{1} \left( u \right)b_{1}^{2} {\plus}2\hat{q}_{2} \left( u \right)b_{1} b_{2} \rho } \right){\equals}0 \hfill \cr a_{2} \eta _{2} \left( {b_{1}^{2} \hat{q}_{1}^{2} \left( u \right){\plus}b_{2}^{2} \hat{q}_{2}^{2} \left( u \right){\plus}2b_{1} b_{2} \hat{q}_{1} \left( u \right)\hat{q}_{2} \left( u \right)\rho } \right) \hfill \cr {\minus}\left[ {a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} \hat{q}_{1} \left( u \right)} \right){\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} \hat{q}_{2} \left( u \right)} \right){\plus}ru} \right]\left( {2\hat{q}_{2} \left( u \right)b_{2}^{2} {\plus}2\hat{q}_{1} \left( u \right)b_{1} b_{2} \rho } \right){\equals}0 \hfill \cr} \right.$$
$$ \scale98% { \left\{ \matrix{ a_{1} \eta _{1} \left( {b_{1}^{2} \hat{q}_{1}^{2} \left( u \right){\plus}b_{2}^{2} \hat{q}_{2}^{2} \left( u \right){\plus}2b_{1} b_{2} \hat{q}_{1} \left( u \right)\hat{q}_{2} \left( u \right)\rho } \right) \hfill \cr {\minus}\left[ {a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} \hat{q}_{1} \left( u \right)} \right){\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} \hat{q}_{2} \left( u \right)} \right){\plus}ru} \right]\left( {2\hat{q}_{1} \left( u \right)b_{1}^{2} {\plus}2\hat{q}_{2} \left( u \right)b_{1} b_{2} \rho } \right){\equals}0 \hfill \cr a_{2} \eta _{2} \left( {b_{1}^{2} \hat{q}_{1}^{2} \left( u \right){\plus}b_{2}^{2} \hat{q}_{2}^{2} \left( u \right){\plus}2b_{1} b_{2} \hat{q}_{1} \left( u \right)\hat{q}_{2} \left( u \right)\rho } \right) \hfill \cr {\minus}\left[ {a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} \hat{q}_{1} \left( u \right)} \right){\plus}a_{2} \left( {\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} \hat{q}_{2} \left( u \right)} \right){\plus}ru} \right]\left( {2\hat{q}_{2} \left( u \right)b_{2}^{2} {\plus}2\hat{q}_{1} \left( u \right)b_{1} b_{2} \rho } \right){\equals}0 \hfill \cr} \right.$$
Solving these equations yields the solution (3.1).
On the other hand, by the technique of stochastic control theory and the corresponding HJB equation, we can also get the candidate optimiser (see e.g., (4.3)) along the same lines in section 4, which is exactly the same as the one in (3.1). Therefore, we can directly come to the conclusion that the solution given by (3.1) is indeed the optimal proportional reinsurance strategy for the case with no constraint.□
From Bäuerle & Bayraktar (Reference Bäuerle and Bayraktar2014, theorem 4.1) and Karatzas & Shreve(Reference Karatzas and Shreve1991: 339), we have the following lemma.
Lemma 3.1. Let ξ(⋅) be given in (3.3), in which the reinsurance strategy is the optimal one. Then, the minimum probability of ruin is given by
where g is defined by
Note that g in (3.4) is the scale function associated with the diffusion process in (2.2).
Next, we shall focus on discussing the optimal reinsurance strategy which minimises the probability of drawdown when m≥u s .
Because of the constraints of
![]() $\left( {q_{1}^{{\rm {\asterisk}}} \left( u \right),q_{2}^{{\rm {\asterisk}}} \left( u \right)} \right)$
and the result of
$\left( {q_{1}^{{\rm {\asterisk}}} \left( u \right),q_{2}^{{\rm {\asterisk}}} \left( u \right)} \right)$
and the result of
![]() $${{{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } \mathord{\left/ {\vphantom {{{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } {{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} {\equals}{1 \over {\rho ^{2} }}\,\gt\,1}}} \right. \kern-\nulldelimiterspace} {{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} {\equals}{1 \over {\rho ^{2} }}\,\gt\,1}}$$
, to get the optimal strategy and the minimum probability of drawdown, we need to discuss the following three cases:
$${{{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } \mathord{\left/ {\vphantom {{{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } {{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} {\equals}{1 \over {\rho ^{2} }}\,\gt\,1}}} \right. \kern-\nulldelimiterspace} {{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} {\equals}{1 \over {\rho ^{2} }}\,\gt\,1}}$$
, to get the optimal strategy and the minimum probability of drawdown, we need to discuss the following three cases:
 $$\left\{ {\matrix{ {{\rm Case}\quad 1\,\colon\,\quad {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } & {\left( {{\rm i}{\rm .e}{\rm .,}\hat{q}_{1} \left( u \right)\,\gt\,0,\hat{q}_{2} \left( u \right)\,\gt\,0} \right)} \cr \hskip-38pt {{\rm Case}\quad 2\,\colon\,\quad \eta _{1} \leq {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} } & {\left( {{\rm i}{\rm .e}{\rm .,}\hat{q}_{1} \left( u \right)\leq 0,\hat{q}_{2} \left( u \right)\,\gt\,0} \right)} \cr \hskip-38pt {{\rm Case}\quad 3\,\colon\,\quad \eta _{1} \geq {{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } & {\left( {{\rm i}{\rm .e}{\rm .,}\hat{q}_{1} \left( u \right)\,\gt\,0,\hat{q}_{2} \left( u \right)\leq 0} \right)} \cr } } \right.$$
$$\left\{ {\matrix{ {{\rm Case}\quad 1\,\colon\,\quad {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } & {\left( {{\rm i}{\rm .e}{\rm .,}\hat{q}_{1} \left( u \right)\,\gt\,0,\hat{q}_{2} \left( u \right)\,\gt\,0} \right)} \cr \hskip-38pt {{\rm Case}\quad 2\,\colon\,\quad \eta _{1} \leq {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} } & {\left( {{\rm i}{\rm .e}{\rm .,}\hat{q}_{1} \left( u \right)\leq 0,\hat{q}_{2} \left( u \right)\,\gt\,0} \right)} \cr \hskip-38pt {{\rm Case}\quad 3\,\colon\,\quad \eta _{1} \geq {{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} } & {\left( {{\rm i}{\rm .e}{\rm .,}\hat{q}_{1} \left( u \right)\,\gt\,0,\hat{q}_{2} \left( u \right)\leq 0} \right)} \cr } } \right.$$
Since the proof of Case 3 is similar to Case 2, in the following context, we just need to present the proof of Case 1 and Case 2 in detail.
Case 1:
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
In this case,
![]() $\hat{q}_{1} (u)\,\gt\,0$
and
$\hat{q}_{1} (u)\,\gt\,0$
and
![]() $\hat{q}_{2} (u)\,\gt\,0$
. Let
$\hat{q}_{2} (u)\,\gt\,0$
. Let
 $$\left\{ \matrix{ u_{1} {\equals}{1 \over r}\left[ {{{{\rm \Delta }_{2} } \over {2\left( {a_{2} {\rm \eta }_{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)}}{\minus}{\rm \Delta }_{1} } \right] \hfill \cr u_{2} {\equals}{1 \over r}\left[ {{{{\rm \Delta }_{2} } \over {2\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)}}{\minus}{\rm \Delta }_{1} } \right] \hfill \cr} \right.$$
$$\left\{ \matrix{ u_{1} {\equals}{1 \over r}\left[ {{{{\rm \Delta }_{2} } \over {2\left( {a_{2} {\rm \eta }_{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)}}{\minus}{\rm \Delta }_{1} } \right] \hfill \cr u_{2} {\equals}{1 \over r}\left[ {{{{\rm \Delta }_{2} } \over {2\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)}}{\minus}{\rm \Delta }_{1} } \right] \hfill \cr} \right.$$
It’s easy to see that
![]() $\hat{q}_{1} (u_{1} ){\equals}1$
,
$\hat{q}_{1} (u_{1} ){\equals}1$
,
![]() $\hat{q}_{2} (u_{2} ){\equals}1$
.
$\hat{q}_{2} (u_{2} ){\equals}1$
.
For convenience, we assume that u
1<u
2 as similar results can be obtained for u
1>u
2. From (3.1), we can see that
![]() $\hat{q}_{1} (u)$
,
$\hat{q}_{1} (u)$
,
![]() $\hat{q}_{2} (u)$
are decreasing functions w.r.t. u. Thus, when u
2≤u≤u
s
, we have
$\hat{q}_{2} (u)$
are decreasing functions w.r.t. u. Thus, when u
2≤u≤u
s
, we have
![]() $0\leq \hat{q}_{1} (u)\,\lt\,1$
,
$0\leq \hat{q}_{1} (u)\,\lt\,1$
,
![]() $0\leq \hat{q}_{2} (u)\leq 1$
, and hence
$0\leq \hat{q}_{2} (u)\leq 1$
, and hence
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{1} (u)$
,
$q_{1}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{1} (u)$
,
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{2} (u)$
. One can show that, under this optimal reinsurance strategy given in (3.1), we have
$q_{2}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{2} (u)$
. One can show that, under this optimal reinsurance strategy given in (3.1), we have
On the other hand, when
![]() $u\leq u_{2} $
, we obtain
$u\leq u_{2} $
, we obtain
![]() $\hat{q}_{2} (u)\geq 1$
. Then we have to choose
$\hat{q}_{2} (u)\geq 1$
. Then we have to choose
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
. Inserting
$q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
. Inserting
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
into (3.3) and maximising the ratio of the drift of the surplus process to its volatility squared, we can get
$q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
into (3.3) and maximising the ratio of the drift of the surplus process to its volatility squared, we can get
in which A, B, C are defined by
 $$\left\{ \matrix{ A{\equals}{\minus}{{a_{1}^{2} \eta _{1}^{2} } \over {2b_{1}^{2} }} \hfill \cr B{\equals}a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\minus}{{\rho b_{2} \eta _{1} } \over {b_{1} }}} \right){\plus}a_{2} \theta _{2} \hfill \cr C{\equals}{1 \over 2}b_{2}^{2} \left( {1{\minus}\rho ^{2} } \right) \hfill \cr} \right.$$
$$\left\{ \matrix{ A{\equals}{\minus}{{a_{1}^{2} \eta _{1}^{2} } \over {2b_{1}^{2} }} \hfill \cr B{\equals}a_{1} \left( {\theta _{1} {\minus}\eta _{1} {\minus}{{\rho b_{2} \eta _{1} } \over {b_{1} }}} \right){\plus}a_{2} \theta _{2} \hfill \cr C{\equals}{1 \over 2}b_{2}^{2} \left( {1{\minus}\rho ^{2} } \right) \hfill \cr} \right.$$
From (3.6), we know that
![]() $\tilde{q}_{1} (u)$
is also a decreasing function w.r.t. u and when
$\tilde{q}_{1} (u)$
is also a decreasing function w.r.t. u and when
we have
![]() $\tilde{q}_{1} (\tilde{u}_{1} ){\equals}1$
. Before we continue our analysis on the optimal results with constraint, we present the following Lemma first.
$\tilde{q}_{1} (\tilde{u}_{1} ){\equals}1$
. Before we continue our analysis on the optimal results with constraint, we present the following Lemma first.
Lemma 3.2. Under the assumption of
![]() $u_{1} \,\lt\,u_{2} $
, we have
$u_{1} \,\lt\,u_{2} $
, we have
![]() $\tilde{u}_{1} \,\lt\,u_{2} $
.
$\tilde{u}_{1} \,\lt\,u_{2} $
.
Proof. Note that
 $$\eqalignno{ u_{2} {\minus}\tilde{u}_{1} {\equals} & {1 \over r}\left[ {{{{\rm \Delta }_{2} } \over {2\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)}}{\minus}{\rm \Delta }_{1} } \right]{\minus}{1 \over r}\left[ {{{a_{1} \eta _{1} \left( {b_{2}^{2} {\minus}b_{1}^{2} } \right)} \over {2\left( {b_{1}^{2} {\plus}b_{1} b_{2} \rho } \right)}}{\minus}\left( {{\rm \Delta }_{1} {\plus}a_{2} \eta _{2} } \right)} \right] \cr {\equals} & {{b_{1}^{4} a_{2}^{2} \eta _{2}^{2} {\plus}b_{1}^{3} b_{2} \rho a_{2}^{2} \eta _{2}^{2} {\plus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho {\minus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{2} b_{2}^{2} } \over {2r\left( {b_{1}^{2} {\plus}b_{1} b_{2} \rho } \right)\left( {a_{2} \eta _{2} b_{1}^{2} {\minus}a_{1} \eta _{1} \rho b_{1} b_{2} } \right)}} $$
$$\eqalignno{ u_{2} {\minus}\tilde{u}_{1} {\equals} & {1 \over r}\left[ {{{{\rm \Delta }_{2} } \over {2\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)}}{\minus}{\rm \Delta }_{1} } \right]{\minus}{1 \over r}\left[ {{{a_{1} \eta _{1} \left( {b_{2}^{2} {\minus}b_{1}^{2} } \right)} \over {2\left( {b_{1}^{2} {\plus}b_{1} b_{2} \rho } \right)}}{\minus}\left( {{\rm \Delta }_{1} {\plus}a_{2} \eta _{2} } \right)} \right] \cr {\equals} & {{b_{1}^{4} a_{2}^{2} \eta _{2}^{2} {\plus}b_{1}^{3} b_{2} \rho a_{2}^{2} \eta _{2}^{2} {\plus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho {\minus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{2} b_{2}^{2} } \over {2r\left( {b_{1}^{2} {\plus}b_{1} b_{2} \rho } \right)\left( {a_{2} \eta _{2} b_{1}^{2} {\minus}a_{1} \eta _{1} \rho b_{1} b_{2} } \right)}} $$
Because of the assumption of u 1<u 2, we have
then,
 $$ \eqalignno{ & {\rm }b_{1}^{4} a_{2}^{2} \eta _{2}^{2} {\plus}b_{1}^{3} b_{2} \rho a_{2}^{2} \eta _{2}^{2} {\plus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho {\minus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{2} b_{2}^{2} \cr & \,\gt\,b_{1}^{2} \left( {a_{1} \eta _{1} b_{2}^{2} {\plus}a_{1} \eta _{1} \rho b_{1} b_{2} } \right){\plus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho {\minus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{2} b_{2}^{2} \cr & {\equals}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\plus}a_{1} \eta _{1} a_{2} \eta _{2} b_{1}^{3} b_{2} \rho {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho \cr & \,\gt\,a_{1} \eta _{1} b_{1}^{2} \left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} \rho b_{1} b_{2} } \right){\minus}a_{1} \eta _{1} b_{1}^{2} \left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} \rho b_{1} b_{2} } \right) {\equals}0 $$
$$ \eqalignno{ & {\rm }b_{1}^{4} a_{2}^{2} \eta _{2}^{2} {\plus}b_{1}^{3} b_{2} \rho a_{2}^{2} \eta _{2}^{2} {\plus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho {\minus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{2} b_{2}^{2} \cr & \,\gt\,b_{1}^{2} \left( {a_{1} \eta _{1} b_{2}^{2} {\plus}a_{1} \eta _{1} \rho b_{1} b_{2} } \right){\plus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho {\minus}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{2} b_{2}^{2} \cr & {\equals}a_{1} a_{2} \eta _{1} \eta _{2} b_{1}^{4} {\minus}b_{1}^{2} b_{2}^{2} a_{1}^{2} \eta _{1}^{2} {\plus}a_{1} \eta _{1} a_{2} \eta _{2} b_{1}^{3} b_{2} \rho {\minus}a_{1}^{2} \eta _{1}^{2} b_{1}^{3} b_{2} \rho \cr & \,\gt\,a_{1} \eta _{1} b_{1}^{2} \left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} \rho b_{1} b_{2} } \right){\minus}a_{1} \eta _{1} b_{1}^{2} \left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} \rho b_{1} b_{2} } \right) {\equals}0 $$
In Case 1, it’s clear that
then we have
![]() $\tilde{u}_{1} \,\lt\,u_{2} .$
□
$\tilde{u}_{1} \,\lt\,u_{2} .$
□
Therefore, when
![]() $\tilde{u}_{1} \leq u\leq u_{2} $
, we have
$\tilde{u}_{1} \leq u\leq u_{2} $
, we have
![]() $0\,\lt\,\tilde{q}_{1} (u)\leq 1$
, thus
$0\,\lt\,\tilde{q}_{1} (u)\leq 1$
, thus
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}\tilde{q}_{1} (u)$
. Under the optimal reinsurance strategy of
$q_{1}^{{\rm {\asterisk}}} (u){\equals}\tilde{q}_{1} (u)$
. Under the optimal reinsurance strategy of
![]() $(q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)){\equals}(\tilde{q}_{1} (u),1)$
, it follows that
$(q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)){\equals}(\tilde{q}_{1} (u),1)$
, it follows that
 $$\xi _{{12}} (u){\equals}{{\mu \left( {u,q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)} \over {\sigma ^{2} \left( {u,q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)}}{\equals}{{{\minus}2A\sqrt {\left( {B{\plus}ru} \right)^{2} {\minus}4AC} } \over {\left[ {{\minus}(B{\plus}ru){\plus}\sqrt {\left( {B{\plus}ru} \right)^{2} {\minus}4AC} } \right]^{2} {\minus}4AC}}$$
$$\xi _{{12}} (u){\equals}{{\mu \left( {u,q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)} \over {\sigma ^{2} \left( {u,q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)}}{\equals}{{{\minus}2A\sqrt {\left( {B{\plus}ru} \right)^{2} {\minus}4AC} } \over {\left[ {{\minus}(B{\plus}ru){\plus}\sqrt {\left( {B{\plus}ru} \right)^{2} {\minus}4AC} } \right]^{2} {\minus}4AC}}$$
Finally, when
![]() $\alpha m\leq u\leq \tilde{u}_{1} $
, we have to choose
$\alpha m\leq u\leq \tilde{u}_{1} $
, we have to choose
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}1$
and
$q_{1}^{{\rm {\asterisk}}} (u){\equals}1$
and
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
. Inserting
$q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
. Inserting
![]() $\left( {q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)} \right){\equals}\left( {1,1} \right)$
into (3.3), and we obtain
$\left( {q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)} \right){\equals}\left( {1,1} \right)$
into (3.3), and we obtain
To summarise, we give the optimal reinsurance strategy and the corresponding minimum probability of drawdown for the case of m≥u
s
with
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
in Theorem 3.1.
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
in Theorem 3.1.
Theorem 3.1. Suppose that
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let Δ1, Δ2 be given in (3.2), A,B,C be given in (3.7), and ξ
11(u),ξ
12(u),ξ
13(u) be given in (3.5), (3.8), (3.9), respectively. Then, for any u∈[αm,u
s
], the minimum probability of drawdown for the surplus process (2.2) is
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let Δ1, Δ2 be given in (3.2), A,B,C be given in (3.7), and ξ
11(u),ξ
12(u),ξ
13(u) be given in (3.5), (3.8), (3.9), respectively. Then, for any u∈[αm,u
s
], the minimum probability of drawdown for the surplus process (2.2) is
 $$\phi (u,m){\equals}\left\{ {\matrix{ {1{\minus}{{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,m)}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {1{\minus}{{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,m)}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {1{\minus}{{g_{{13}} (u,m)} \over {g_{{13}} (u_{s} ,m)}},} & {{\rm max}(\alpha m,u_{2} )\leq u\leq u_{s} } \cr } } \right.$$
$$\phi (u,m){\equals}\left\{ {\matrix{ {1{\minus}{{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,m)}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {1{\minus}{{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,m)}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {1{\minus}{{g_{{13}} (u,m)} \over {g_{{13}} (u_{s} ,m)}},} & {{\rm max}(\alpha m,u_{2} )\leq u\leq u_{s} } \cr } } \right.$$
and the optimal reinsurance strategy is
 $$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}\left\{ {\matrix{ {\left( {1,1} \right),}\hfill & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {(\tilde{q}_{1} (u),1),}\hfill & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {(\hat{q}_{1} (u),\hat{q}_{2} (u)),} & {{\rm max}(\alpha m,u_{2} )\leq u\leq u_{s} } \cr } } \right.$$
$$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}\left\{ {\matrix{ {\left( {1,1} \right),}\hfill & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {(\tilde{q}_{1} (u),1),}\hfill & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {(\hat{q}_{1} (u),\hat{q}_{2} (u)),} & {{\rm max}(\alpha m,u_{2} )\leq u\leq u_{s} } \cr } } \right.$$
in which g 1i (u,m) (i=1,2,3) are defined by
 $$\eqalignno{ \scale98% \left\{ \matrix{ g_{{11}} (u,m){\equals}{\int}_{\alpha m}^u {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{13}} (w)dw} {\rm \ztbnd }} \right\}dy,\hfill \cr g_{{12}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{13}} (w)dw} } \right\}dy\hfill \cr \hskip45pt {\plus}{\int}_{\alpha m\vee\tilde{u}_{1} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {\xi _{{13}} (w){\plus}} {\int}_{\alpha m\vee\tilde{u}_{1} }^y {\xi _{{12}} (w)} } \right)dw} \right\}dy \hfill\cr g_{{13}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{13}} (w)dw} {\rm \ztbnd }} \right\}dy \hfill\cr \hskip45pt {\plus}{\int}_{\alpha m\vee\tilde{u}_{1} }^{\alpha m\vee u_{2} } {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {\xi _{{13}} (w){\plus}} {\int}_{\alpha m\vee\tilde{u}_{1} }^y {\xi _{{12}} (w)} } \right)dw} \right\}dy \hfill\cr \hskip45pt {\plus}{\int}_{\alpha m\vee u_{2} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee u_{1} } {\xi _{{13}} (w)} {\plus}{\int}_{\alpha m\vee\tilde{u}_{1} }^{\alpha m\vee u_{2} } {\xi _{{12}} (w){\plus}} {\int}_{\alpha m\vee u_{2} }^y {\xi _{{11}} (w)} } \right)dw} \right\}dy $$
$$\eqalignno{ \scale98% \left\{ \matrix{ g_{{11}} (u,m){\equals}{\int}_{\alpha m}^u {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{13}} (w)dw} {\rm \ztbnd }} \right\}dy,\hfill \cr g_{{12}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{13}} (w)dw} } \right\}dy\hfill \cr \hskip45pt {\plus}{\int}_{\alpha m\vee\tilde{u}_{1} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {\xi _{{13}} (w){\plus}} {\int}_{\alpha m\vee\tilde{u}_{1} }^y {\xi _{{12}} (w)} } \right)dw} \right\}dy \hfill\cr g_{{13}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{13}} (w)dw} {\rm \ztbnd }} \right\}dy \hfill\cr \hskip45pt {\plus}{\int}_{\alpha m\vee\tilde{u}_{1} }^{\alpha m\vee u_{2} } {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee\tilde{u}_{1} } {\xi _{{13}} (w){\plus}} {\int}_{\alpha m\vee\tilde{u}_{1} }^y {\xi _{{12}} (w)} } \right)dw} \right\}dy \hfill\cr \hskip45pt {\plus}{\int}_{\alpha m\vee u_{2} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee u_{1} } {\xi _{{13}} (w)} {\plus}{\int}_{\alpha m\vee\tilde{u}_{1} }^{\alpha m\vee u_{2} } {\xi _{{12}} (w){\plus}} {\int}_{\alpha m\vee u_{2} }^y {\xi _{{11}} (w)} } \right)dw} \right\}dy $$
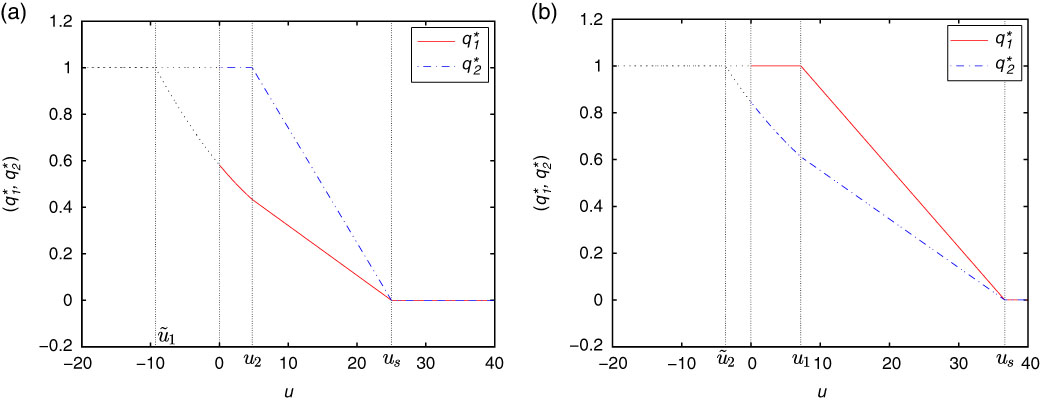
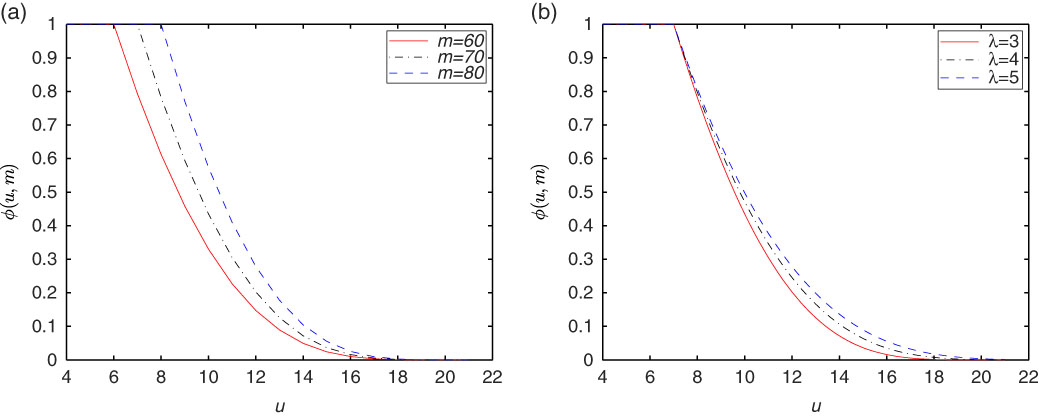
Remark 3.1. We can see that ϕ(⋅,m) is a non-increasing and continuous function, which satisfies the following boundary conditions: ϕ(αm,m)=1, ϕ(u s ,m)=0. Furthermore, note that u s is a constant and g 13(u s ,m) is finite. Indeed, the integrand in the expression for g 13 is bounded by 1, then we can get g 13(u s ,m)≤u s −αm<∞. In addition, we know g(u,m) defined in (3.4) is non-decreasing, thus, g 11 and g 12 are also finite
Remark 3.2. Note that the relationship between αm and
![]() $\tilde{u}_{1} (u_{2} )$
is uncertain. Since we are only interested in u∈[αm,u
s
], the notations of
$\tilde{u}_{1} (u_{2} )$
is uncertain. Since we are only interested in u∈[αm,u
s
], the notations of
![]() ${\rm max}(\alpha m,\tilde{u}_{1} )$
and
${\rm max}(\alpha m,\tilde{u}_{1} )$
and
![]() ${\rm max}(\alpha m,u_{2} )$
are used in the expressions for the optimal results. In this sense, the optimal reinsurance strategy depends on the values of α and m. This remark is also applicable for the following theorems.
${\rm max}(\alpha m,u_{2} )$
are used in the expressions for the optimal results. In this sense, the optimal reinsurance strategy depends on the values of α and m. This remark is also applicable for the following theorems.
By the same way, we can get the optimal results for the other two cases as follows:
Case 2:
![]() $\eta _{1} \leq {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
.
$\eta _{1} \leq {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
.
In this case,
![]() $\hat{q}_{1} (u)\leq 0$
,
$\hat{q}_{1} (u)\leq 0$
,
![]() $\hat{q}_{2} (u)\,\gt\,0$
. Then we have to choose
$\hat{q}_{2} (u)\,\gt\,0$
. Then we have to choose
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}0$
, and thus we derive the minimiser
$q_{1}^{{\rm {\asterisk}}} (u){\equals}0$
, and thus we derive the minimiser
Let
it is easy to see that
![]() $\bar{q}_{2} (u_{2}^{{\rm '}} ){\equals}1$
.
$\bar{q}_{2} (u_{2}^{{\rm '}} ){\equals}1$
.
In particular, when
![]() $u_{2}^{{\rm '}} \leq u\leq u_{s} $
, we have
$u_{2}^{{\rm '}} \leq u\leq u_{s} $
, we have
![]() $0\leq \bar{q}_{2} (u)\leq 1$
, then it follows that
$0\leq \bar{q}_{2} (u)\leq 1$
, then it follows that
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}\bar{q}_{2} (u)$
. Under the optimal reinsurance strategy
$q_{2}^{{\rm {\asterisk}}} (u){\equals}\bar{q}_{2} (u)$
. Under the optimal reinsurance strategy
![]() $\left( {q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)} \right){\equals}\left( {0,\bar{q}_{2} (u)} \right)$
, we have
$\left( {q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)} \right){\equals}\left( {0,\bar{q}_{2} (u)} \right)$
, we have
However, when
![]() $\alpha m\leq u\leq u_{2}^{{\rm '}} $
, we have
$\alpha m\leq u\leq u_{2}^{{\rm '}} $
, we have
![]() $\bar{q}_{2} (u)\geq 1$
, thus we have to choose
$\bar{q}_{2} (u)\geq 1$
, thus we have to choose
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
, and then we obtain
$q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
, and then we obtain
Therefore, we have the following theorem:
Theorem 3.2. Suppose that
![]() $\eta _{1} \,\lt\,{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
. Let Δ1 and Δ2 be given in (3.2), and ξ
21(u),ξ
22(u) be given in (3.13), (3.14), respectively. Then, for any u∈[αm,u
s
], the minimum probability of drawdown for the surplus process (2.2) is
$\eta _{1} \,\lt\,{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
. Let Δ1 and Δ2 be given in (3.2), and ξ
21(u),ξ
22(u) be given in (3.13), (3.14), respectively. Then, for any u∈[αm,u
s
], the minimum probability of drawdown for the surplus process (2.2) is
and the optimal reinsurance strategy is
in which g 2i (u,m)(i=1,2) are defined by
 $$\left\{ \matrix{ g_{{21}} (u,m){\equals}{\int}_{\alpha m}^u {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{22}} (w)dw} } \right\}dy, \hfill \cr g_{{22}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee u_{2}^{{\rm '}} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{22}} (w)dw} } \right\}dy \hfill \cr {\plus}{\int}_{\alpha m\vee u_{2}^{{\rm '}} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee u_{2}^{{\rm '}} } {\xi _{{22}} (w)} {\plus}{\int}_{\alpha m\vee u_{2}^{{\rm '}} }^y {\xi _{{21}} (w)} } \right)dw} \right\}dy \hfill \cr} \right.$$
$$\left\{ \matrix{ g_{{21}} (u,m){\equals}{\int}_{\alpha m}^u {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{22}} (w)dw} } \right\}dy, \hfill \cr g_{{22}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee u_{2}^{{\rm '}} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{22}} (w)dw} } \right\}dy \hfill \cr {\plus}{\int}_{\alpha m\vee u_{2}^{{\rm '}} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee u_{2}^{{\rm '}} } {\xi _{{22}} (w)} {\plus}{\int}_{\alpha m\vee u_{2}^{{\rm '}} }^y {\xi _{{21}} (w)} } \right)dw} \right\}dy \hfill \cr} \right.$$
We can see that ϕ(u,m) in this case also satisfies the properties in Remark 3.1.
Case 3:
![]() $\eta _{1} \geq {{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
$\eta _{1} \geq {{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
In this case,
![]() $\hat{q}_{1} (u)\,\gt\,0$
,
$\hat{q}_{1} (u)\,\gt\,0$
,
![]() $\hat{q}_{2} (u)\leq 0$
. Along the same lines in Case 2, we can get the following result:
$\hat{q}_{2} (u)\leq 0$
. Along the same lines in Case 2, we can get the following result:
Theorem 3.3. Suppose that
![]() $\eta _{1} \,\gt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let Δ1 and Δ2 be given in (3.2). Then, for any u∈[αm,u
s
], the minimum probability of drawdown for the surplus process (2.2) is
$\eta _{1} \,\gt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let Δ1 and Δ2 be given in (3.2). Then, for any u∈[αm,u
s
], the minimum probability of drawdown for the surplus process (2.2) is
and the optimal reinsurance strategy is
in which g 3i (u,m)(i=1,2) are defined by
 $$\left\{ \matrix{ g_{{31}} (u,m){\equals}{\int}_{\alpha m}^u {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{32}} (w)dw} {\rm \ztbnd }} \right\}dy, \hfill \cr g_{{32}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee u_{1}^{{\rm '}} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{32}} (w)dw} {\rm \ztbnd }} \right\}dy \hfill \cr \hskip45pt {\plus}{\int}_{\alpha m\vee u_{1}^{{\rm '}} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee u_{1}^{{\rm '}} } {\xi _{{32}} (w){\plus}} {\int}_{\alpha m\vee u_{1}^{{\rm '}} }^y {\xi _{{31}} (w)} {\rm \ztbnd }} \right)dw} \right\}dy \hfill \cr} \right.$$
$$\left\{ \matrix{ g_{{31}} (u,m){\equals}{\int}_{\alpha m}^u {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{32}} (w)dw} {\rm \ztbnd }} \right\}dy, \hfill \cr g_{{32}} (u,m){\equals}{\int}_{\alpha m}^{\alpha m\vee u_{1}^{{\rm '}} } {{\rm exp}} \left\{ {{\minus}2{\int}_{\alpha m}^y {\xi _{{32}} (w)dw} {\rm \ztbnd }} \right\}dy \hfill \cr \hskip45pt {\plus}{\int}_{\alpha m\vee u_{1}^{{\rm '}} }^u {{\rm exp}} \left\{ {{\minus}2\left( {{\int}_{\alpha m}^{\alpha m\vee u_{1}^{{\rm '}} } {\xi _{{32}} (w){\plus}} {\int}_{\alpha m\vee u_{1}^{{\rm '}} }^y {\xi _{{31}} (w)} {\rm \ztbnd }} \right)dw} \right\}dy \hfill \cr} \right.$$
and ξ
3i
(i=1,2),
![]() $u_{1}^{{\rm '}} $
and
$u_{1}^{{\rm '}} $
and
![]() $\bar{q}_{1} (u)$
are given by
$\bar{q}_{1} (u)$
are given by
 $$\left\{ {\matrix{ {\xi _{{31}} (u){\equals}{\minus}{{a_{1}^{2} \eta _{1}^{2} } \over {4b_{1}^{2} \left( {{\rm \Delta }_{1} {\plus}ru} \right)}}} \cr {\xi _{{32}} (u){\equals}{\minus}{{{\rm \Delta }_{1} {\plus}a_{1} \eta _{1} {\plus}ru} \over {b_{1}^{2} }}} \cr \hskip35pt {u_{1}^{{\rm '}} {\equals}{1 \over {2r}}\left( {{\minus}a_{1} \eta _{1} {\minus}2{\rm \Delta }_{1} } \right)} \cr \hskip-9pt {\bar{q}_{1} (u){\equals}{{{\minus}2({\rm \Delta }_{1} {\plus}ru)} \over {a_{2} \eta _{2} }}} \cr } } \right.$$
$$\left\{ {\matrix{ {\xi _{{31}} (u){\equals}{\minus}{{a_{1}^{2} \eta _{1}^{2} } \over {4b_{1}^{2} \left( {{\rm \Delta }_{1} {\plus}ru} \right)}}} \cr {\xi _{{32}} (u){\equals}{\minus}{{{\rm \Delta }_{1} {\plus}a_{1} \eta _{1} {\plus}ru} \over {b_{1}^{2} }}} \cr \hskip35pt {u_{1}^{{\rm '}} {\equals}{1 \over {2r}}\left( {{\minus}a_{1} \eta _{1} {\minus}2{\rm \Delta }_{1} } \right)} \cr \hskip-9pt {\bar{q}_{1} (u){\equals}{{{\minus}2({\rm \Delta }_{1} {\plus}ru)} \over {a_{2} \eta _{2} }}} \cr } } \right.$$
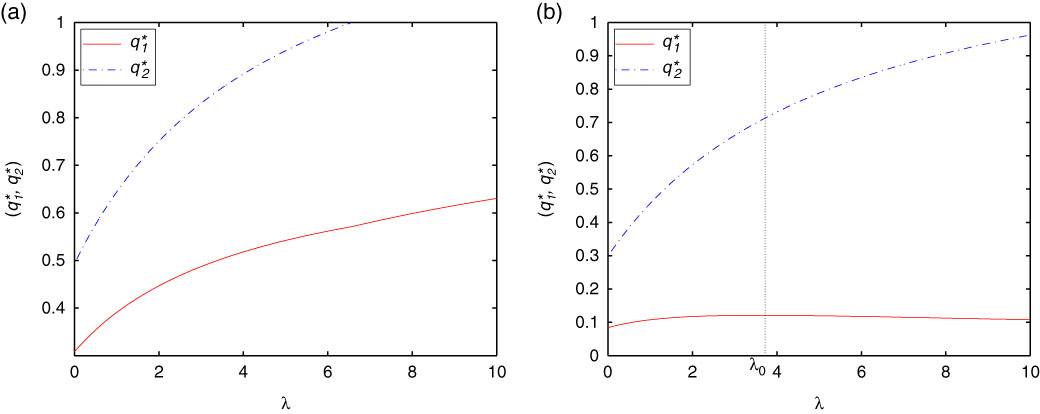
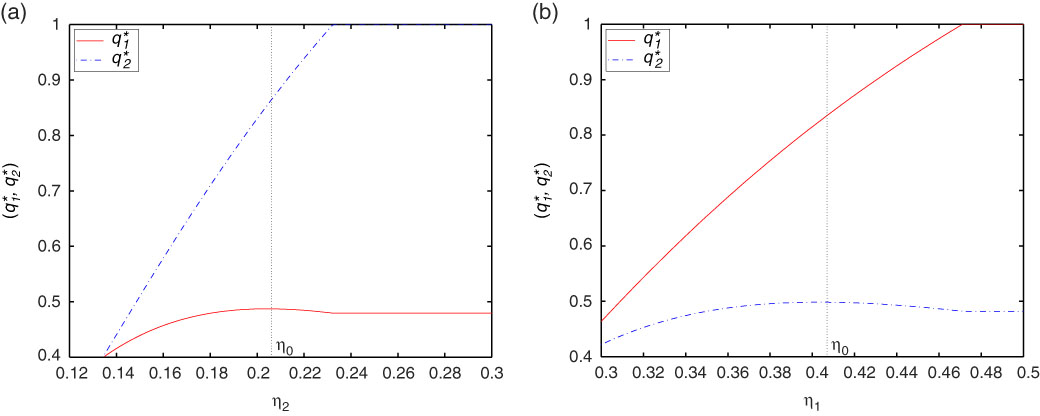
Remark 3.3. We can see clearly that the optimal proportional reinsurance strategies given by Theorems 3.1–3.3 are strongly depend on the value of surplus u. Besides, if α=0 in Theorems 3.1–3.3, then we are in the case of minimising the probability of ruin for the fix level 0, and the corresponding optimal results can be derived directly. Moreover, as the wealth increases towards u s , the optimal reinsurance proportion approaches 0. It makes sense because when the value of the surplus increases, the insurer can transfer all the risk to reinsurer, and thus the wealth will never decrease, then drawdown cannot happen.
4. Minimising the Probability of Drawdown When m<u s
In the previous section, we show the minimum probability of drawdown and the corresponding optimal strategy for the case of m≥u s . In this section, we will consider the same problem for the case of m<u s . Since M t can be larger than m, i.e., the level that we set is not necessarily a fixed one, the special method in Bäuerle & Bayraktar (Reference Bäuerle and Bayraktar2014) does not apply anymore. Therefore, following the analysis of Chen et al. (Reference Chen, Landriault, Li and Li2015) and Angoshtari et al. (2016a, 2016 Reference Angoshtari, Bayraktar and Youngb ), we use the technique of stochastic control theory and the corresponding HJB equation to tackle the optimal problem.
Again, we only need to consider function f on the domain
![]() ${\cal O}\,\colon\,{\equals}\{ (u,m)\in(R^{{\plus}} )^{2} \,\colon\,\alpha m\leq u\leq m,m\,\lt\,u_{s} \} $
. Let C
2,1 denote the space of f(u,m) such that f and its partial derivatives f
u
, f
uu
, f
m
are continuous on
${\cal O}\,\colon\,{\equals}\{ (u,m)\in(R^{{\plus}} )^{2} \,\colon\,\alpha m\leq u\leq m,m\,\lt\,u_{s} \} $
. Let C
2,1 denote the space of f(u,m) such that f and its partial derivatives f
u
, f
uu
, f
m
are continuous on
![]() ${\cal O}$
. It follows from the standard arguments that if the value function ϕ(u,m)∈C
2,1, then ϕ satisfies the following HJB equation:
${\cal O}$
. It follows from the standard arguments that if the value function ϕ(u,m)∈C
2,1, then ϕ satisfies the following HJB equation:
where
 $$\eqalignno{ {\cal A}^{{q_{1} q_{2} }} \phi (u,m){\equals} & \left[ {ru{\plus}a_{1} (\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} q_{1} (u)){\plus}a_{2} (\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} q_{2} (u))} \right]\phi _{u} \cr {\rm }{\plus} & {1 \over 2}\left( {q_{1}^{2} (u)b_{1}^{2} {\plus}q_{2}^{2} (u)b_{2}^{2} {\plus}2\rho b_{1} b_{2} q_{1} (u)q_{2} (u)} \right)\phi _{{uu}} $$
$$\eqalignno{ {\cal A}^{{q_{1} q_{2} }} \phi (u,m){\equals} & \left[ {ru{\plus}a_{1} (\theta _{1} {\minus}\eta _{1} {\plus}\eta _{1} q_{1} (u)){\plus}a_{2} (\theta _{2} {\minus}\eta _{2} {\plus}\eta _{2} q_{2} (u))} \right]\phi _{u} \cr {\rm }{\plus} & {1 \over 2}\left( {q_{1}^{2} (u)b_{1}^{2} {\plus}q_{2}^{2} (u)b_{2}^{2} {\plus}2\rho b_{1} b_{2} q_{1} (u)q_{2} (u)} \right)\phi _{{uu}} $$
Applying the method of Angoshtari et al. (Reference Angoshtari, Bayraktar and Young2016a ), we can get the following Verification Theorem.
Theorem 4.1. (Verification Theorem): Suppose that
![]() $h\,\colon\,{\cal O}\to R$
is a bounded, continuous function, which satisfies the following condition:
$h\,\colon\,{\cal O}\to R$
is a bounded, continuous function, which satisfies the following condition:
(i) h(⋅,m)∈C 2(αm,m) is a non-increasing convex function,
(ii) h(u,⋅) is continuously differentiable, except possibly at u s ,
(iii) h m (m,m)≥0 if m<u s ,
(iv) h(αm,m)=1,
(v) h(u s ,m)=0 if m≥u s ,
(vi)
 ${\cal A}^{{q_{1} ,q_{2} }} h\geq 0$
for all
${\cal A}^{{q_{1} ,q_{2} }} h\geq 0$
for all
 $q_{1} ,q_{2} \in{\cal D}$
.
$q_{1} ,q_{2} \in{\cal D}$
.
Then, h(u,m)≤ϕ(u,m) on
![]() ${\cal O}$
. Furthermore, suppose that the function h satisfies the conditions mentioned above in such a way that conditions (iii) and (vi) hold with equality for some admissible strategy
${\cal O}$
. Furthermore, suppose that the function h satisfies the conditions mentioned above in such a way that conditions (iii) and (vi) hold with equality for some admissible strategy
![]() $(q_{1}^{{\rm {\asterisk}}} (u)$
,
$(q_{1}^{{\rm {\asterisk}}} (u)$
,
![]() $q_{2}^{{\rm {\asterisk}}} (u))$
, which is defined in feedback form
$q_{2}^{{\rm {\asterisk}}} (u))$
, which is defined in feedback form
![]() $(q_{1}^{{\rm {\asterisk}}} (\hat{U}_{t} ),q_{2}^{{\rm {\asterisk}}} (\hat{U}_{t} ))$
. Then, we have h(u,m)=ϕ(u,m) on
$(q_{1}^{{\rm {\asterisk}}} (\hat{U}_{t} ),q_{2}^{{\rm {\asterisk}}} (\hat{U}_{t} ))$
. Then, we have h(u,m)=ϕ(u,m) on
![]() ${\cal O}$
, and
${\cal O}$
, and
![]() $(q_{1}^{{\rm {\asterisk}}} (u)$
,
$(q_{1}^{{\rm {\asterisk}}} (u)$
,
![]() $q_{2}^{{\rm {\asterisk}}} (u))$
is the optimal reinsurance strategy.
$q_{2}^{{\rm {\asterisk}}} (u))$
is the optimal reinsurance strategy.
For convenience, we denote
Differentiating
![]() $\hat{f}(q_{1} (u),q_{2} (u))$
w.r.t q
i
(u) (i=1,2) yields
$\hat{f}(q_{1} (u),q_{2} (u))$
w.r.t q
i
(u) (i=1,2) yields
 $$\left\{ \matrix{ {{\partial ^{2} \hat{f}} \over {\partial q_{1}^{2} (u)}}{\equals}b_{1}^{2} h_{{uu}} ,{\rm }{{\partial ^{2} \hat{f}} \over {\partial q_{2}^{2} (u)}}{\equals}b_{2}^{2} h_{{uu}} \hfill \cr {{\partial ^{2} \hat{f}} \over {\partial q_{1} (u)\partial q_{2} (u)}}{\equals}\rho b_{1} b_{2} h_{{uu}} \hfill \cr} \right.$$
$$\left\{ \matrix{ {{\partial ^{2} \hat{f}} \over {\partial q_{1}^{2} (u)}}{\equals}b_{1}^{2} h_{{uu}} ,{\rm }{{\partial ^{2} \hat{f}} \over {\partial q_{2}^{2} (u)}}{\equals}b_{2}^{2} h_{{uu}} \hfill \cr {{\partial ^{2} \hat{f}} \over {\partial q_{1} (u)\partial q_{2} (u)}}{\equals}\rho b_{1} b_{2} h_{{uu}} \hfill \cr} \right.$$
It is not difficult to see that the Hessian matrix of
![]() $\hat{f}$
is positive definite, and thus
$\hat{f}$
is positive definite, and thus
![]() $\hat{f}(q_{1} (u),q_{2} (u))$
is a convex function with respect to q
i
(u) (i=1,2). Therefore, the minimiser of
$\hat{f}(q_{1} (u),q_{2} (u))$
is a convex function with respect to q
i
(u) (i=1,2). Therefore, the minimiser of
![]() $\hat{f}(q_{1} (u),q_{2} (u))$
is obtained at
$\hat{f}(q_{1} (u),q_{2} (u))$
is obtained at
 $$\left\{ \matrix{ \hat{q}_{1} (u){\equals}{{\rho b_{1} b_{2} a_{2} \eta _{2} {\minus}b_{2}^{2} a_{1} \eta _{1} } \over {b_{1}^{2} b_{2}^{2} \left( {1{\minus}\rho ^{2} } \right)}}{{h_{u} } \over {h_{{uu}} }} \hfill \cr \hat{q}_{2} (u){\equals}{{\rho b_{1} b_{2} a_{1} \eta _{1} {\minus}b_{1}^{2} a_{2} \eta _{2} } \over {b_{1}^{2} b_{2}^{2} \left( {1{\minus}\rho ^{2} } \right)}}{{h_{u} } \over {h_{{uu}} }} \hfill \cr} \right.$$
$$\left\{ \matrix{ \hat{q}_{1} (u){\equals}{{\rho b_{1} b_{2} a_{2} \eta _{2} {\minus}b_{2}^{2} a_{1} \eta _{1} } \over {b_{1}^{2} b_{2}^{2} \left( {1{\minus}\rho ^{2} } \right)}}{{h_{u} } \over {h_{{uu}} }} \hfill \cr \hat{q}_{2} (u){\equals}{{\rho b_{1} b_{2} a_{1} \eta _{1} {\minus}b_{1}^{2} a_{2} \eta _{2} } \over {b_{1}^{2} b_{2}^{2} \left( {1{\minus}\rho ^{2} } \right)}}{{h_{u} } \over {h_{{uu}} }} \hfill \cr} \right.$$
If Theorem 4.1 (1) holds, we must have
![]() ${{h_{u} } \over {h_{{uu}} }}\leq 0$
. Because of the constraints of
${{h_{u} } \over {h_{{uu}} }}\leq 0$
. Because of the constraints of
![]() $(q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} )$
and the result of
$(q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} )$
and the result of
![]() ${{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} \,/\,{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} {\equals}{1 \over {\rho ^{2} }}\,\gt\,1$
, we also need to discuss the three cases mentioned in the previous section.
${{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} \,/\,{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} {\equals}{1 \over {\rho ^{2} }}\,\gt\,1$
, we also need to discuss the three cases mentioned in the previous section.
Case 1:
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
In this case,
![]() $\hat{q}_{1} (u)\,\gt\,0$
,
$\hat{q}_{1} (u)\,\gt\,0$
,
![]() $\hat{q}_{2} (u)\,\gt\,0$
. If
$\hat{q}_{2} (u)\,\gt\,0$
. If
![]() $0\leq \hat{q}_{1} (u)\leq 1$
and
$0\leq \hat{q}_{1} (u)\leq 1$
and
![]() $0\leq \hat{q}_{2} (u)\leq 1$
hold, then
$0\leq \hat{q}_{2} (u)\leq 1$
hold, then
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{1} (u)$
,
$q_{1}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{1} (u)$
,
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{2} (u)$
. Inserting
$q_{2}^{{\rm {\asterisk}}} (u){\equals}\hat{q}_{2} (u)$
. Inserting
![]() $\left( {q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)} \right){\equals}\left( {\hat{q}_{1} (u),\hat{q}_{2} (u)} \right)$
into (4.1) and putting
$\left( {q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)} \right){\equals}\left( {\hat{q}_{1} (u),\hat{q}_{2} (u)} \right)$
into (4.1) and putting
![]() ${\cal A}^{{q_{1} ,q_{2} }} h(u,m){\equals}0$
, we obtain
${\cal A}^{{q_{1} ,q_{2} }} h(u,m){\equals}0$
, we obtain
in which ξ
11(u) is defined by (3.5). Substituting
![]() ${{h_{u} } \over {h_{{uu}} }}$
back into (4.2), then we have
${{h_{u} } \over {h_{{uu}} }}$
back into (4.2), then we have
 $$\left\{ \matrix{ \hat{q}_{1} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{2} \eta _{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr \hat{q}_{2} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr} \right.$$
$$\left\{ \matrix{ \hat{q}_{1} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{2} \eta _{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr \hat{q}_{2} (u){\equals}{{2\left[ {{\rm \Delta }_{1} {\plus}ru} \right]\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr} \right.$$
which is identical to (3.1) and satisfies
![]() $\hat{q}_{1} (u_{1} ){\equals}1$
and
$\hat{q}_{1} (u_{1} ){\equals}1$
and
![]() $\hat{q}_{2} (u_{2} ){\equals}1$
.
$\hat{q}_{2} (u_{2} ){\equals}1$
.
Here, we also suppose that u
1<u
2. Along the same lines, we can get the results for u
1>u
2. Thus, when
![]() $0\leq \hat{q}_{1} (u)\leq 1$
,
$0\leq \hat{q}_{1} (u)\leq 1$
,
![]() $0\leq \hat{q}_{2} (u)\leq 1$
, we have u
2≤u≤u
s
. On the other hand, if
$0\leq \hat{q}_{2} (u)\leq 1$
, we have u
2≤u≤u
s
. On the other hand, if
![]() $0\leq \hat{q}_{1} (u)\leq 1$
and
$0\leq \hat{q}_{1} (u)\leq 1$
and
![]() $\hat{q}_{2} (u)\,\gt\,1$
, then we have to choose
$\hat{q}_{2} (u)\,\gt\,1$
, then we have to choose
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
, and derive the minimiser
$q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
, and derive the minimiser
Therefore, when
![]() $0\leq \tilde{q}_{1} (u)\leq 1$
, we have
$0\leq \tilde{q}_{1} (u)\leq 1$
, we have
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}\tilde{q}_{1} (u)$
,
$q_{1}^{{\rm {\asterisk}}} (u){\equals}\tilde{q}_{1} (u)$
,
![]() $q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
. Substituting them into (4.1) and letting
$q_{2}^{{\rm {\asterisk}}} (u){\equals}1$
. Substituting them into (4.1) and letting
![]() ${\cal A}h(u,m){\equals}0$
, we get
${\cal A}h(u,m){\equals}0$
, we get
in which ξ 12(u) is defined by (3.8). Then it is easy to show that
Under the assumption of u
1<u
2, we come to the conclusion that
![]() $\tilde{u}_{1} \leq u\,\lt\,u_{2} $
when
$\tilde{u}_{1} \leq u\,\lt\,u_{2} $
when
![]() $0\leq \tilde{q}_{1} (u)\leq 1$
holds. Finally, if
$0\leq \tilde{q}_{1} (u)\leq 1$
holds. Finally, if
![]() $\tilde{q}_{1} (u)\,\gt\,1$
, then we have to choose
$\tilde{q}_{1} (u)\,\gt\,1$
, then we have to choose
![]() $q_{1}^{{\rm {\asterisk}}} (u){\equals}1$
. Inserting
$q_{1}^{{\rm {\asterisk}}} (u){\equals}1$
. Inserting
![]() $(q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)){\equals}(1,1)$
into (4.1) yields
$(q_{1}^{{\rm {\asterisk}}} (u),q_{2}^{{\rm {\asterisk}}} (u)){\equals}(1,1)$
into (4.1) yields
in which ξ
13(u) is defined by (3.9). In this case, we can get
![]() $\alpha m\leq u\,\lt\,\tilde{u}_{1} $
. It is clear that the optimal reinsurance strategy in this case equals to the one when m≥u
s
.
$\alpha m\leq u\,\lt\,\tilde{u}_{1} $
. It is clear that the optimal reinsurance strategy in this case equals to the one when m≥u
s
.
Now considering the following boundary-value problem, we wish to find a solution at which a certain function is minimised according to Theorem 4.1. When αm≤u≤m≤u s , we have
 $$\left\{ \matrix{ {{h_{u} } \over {h_{{uu}} }}{\equals}{\minus}{1 \over {2\xi (u)}} \hfill \cr h(u_{s} ,u_{s} ){\equals}0,h_{m} (m,m){\equals}0 \hfill \cr h(\alpha m,m){\equals}1 \hfill \cr} \right.$$
$$\left\{ \matrix{ {{h_{u} } \over {h_{{uu}} }}{\equals}{\minus}{1 \over {2\xi (u)}} \hfill \cr h(u_{s} ,u_{s} ){\equals}0,h_{m} (m,m){\equals}0 \hfill \cr h(\alpha m,m){\equals}1 \hfill \cr} \right.$$
We first present the solution of (4.4) for m∈[max(αm,u
2),u
s
) in the next proposition, the solutions for the other two cases of
![]() $m\in[{\rm max}(\alpha m,\tilde{u}_{1} ),{\rm max}(\alpha m,u_{2} ))$
and
$m\in[{\rm max}(\alpha m,\tilde{u}_{1} ),{\rm max}(\alpha m,u_{2} ))$
and
![]() $m\in[\alpha m,{\rm max}(\alpha m,\tilde{u}_{1} ))$
can be derived by the same way.
$m\in[\alpha m,{\rm max}(\alpha m,\tilde{u}_{1} ))$
can be derived by the same way.
Proposition 4.1. When
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
, the solution of (4.4) on {(u,m)∈(R
+)2: αm≤u≤m, max(αm,u
2)≤m<u
s
} is given by
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
, the solution of (4.4) on {(u,m)∈(R
+)2: αm≤u≤m, max(αm,u
2)≤m<u
s
} is given by
 $$h(u,m){\equals}\left\{ {\matrix{ {1{\minus}{\rm exp}\left\{ {{\int}_m^{u_{s} } {{\minus}f_{{13}} (y)dy} } \right\} \cdot {{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \hfill \cr {1{\minus}{\rm exp}\left\{ {{\int}_m^{u_{s} } {{\minus}f_{{13}} (y)dy} } \right\} \cdot {{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {1{\minus}{\rm exp}\left\{ {{\int}_m^{u_{s} } {{\minus}f_{{13}} (y)dy} } \right\} \cdot {{g_{{13}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,u_{2} )\leq u\leq m\,\lt\,u_{s} }\hfill \cr } } \right.$$
$$h(u,m){\equals}\left\{ {\matrix{ {1{\minus}{\rm exp}\left\{ {{\int}_m^{u_{s} } {{\minus}f_{{13}} (y)dy} } \right\} \cdot {{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \hfill \cr {1{\minus}{\rm exp}\left\{ {{\int}_m^{u_{s} } {{\minus}f_{{13}} (y)dy} } \right\} \cdot {{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {1{\minus}{\rm exp}\left\{ {{\int}_m^{u_{s} } {{\minus}f_{{13}} (y)dy} } \right\} \cdot {{g_{{13}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,u_{2} )\leq u\leq m\,\lt\,u_{s} }\hfill \cr } } \right.$$
in which g 1i (i=1,2,3) are given in (3.10), and f 13 is defined by
 $$f_{{13}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{13}} (y,y)}}{\minus}2\xi _{{11}} (\alpha y)} \right],} & {{\rm if}\,u_{2} \,\lt\,\alpha m} \hfill \cr {\alpha \left[ {{1 \over {g_{{13}} (y,y)}}{\minus}2\xi _{{12}} (\alpha y)} \right],} & {{\rm if}\,\tilde{u}_{1} \leq \alpha m\leq u_{2} } \cr {\alpha \left[ {{1 \over {g_{{13}} (y,y)}}{\minus}2\xi _{{13}} ({\rm \alpha }y)} \right],} & {{\rm if}\,\alpha m\,\lt\,\tilde{u}_{1} } \hfill \cr } } \right.$$
$$f_{{13}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{13}} (y,y)}}{\minus}2\xi _{{11}} (\alpha y)} \right],} & {{\rm if}\,u_{2} \,\lt\,\alpha m} \hfill \cr {\alpha \left[ {{1 \over {g_{{13}} (y,y)}}{\minus}2\xi _{{12}} (\alpha y)} \right],} & {{\rm if}\,\tilde{u}_{1} \leq \alpha m\leq u_{2} } \cr {\alpha \left[ {{1 \over {g_{{13}} (y,y)}}{\minus}2\xi _{{13}} ({\rm \alpha }y)} \right],} & {{\rm if}\,\alpha m\,\lt\,\tilde{u}_{1} } \hfill \cr } } \right.$$
Proof. Because of h in (4.4) satisfying the differential equation as well as the boundary conditions, taking the integral of h u over [αm,u], we get
where g(u,m) is given in (3.4) and c 1(m) is a function of m to be determined.
Differentiating h w.r.t m, it follows that
Next, we discuss the solution on cases. When max(αm,u 2)≤u≤m≤u s , we have
with
Since h m (m,m)=0, one can show that
with f 13 given by (4.5). It then follows that
According to the continuity of h, the result for the other two cases, i.e.,
![]() ${\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )$
and
${\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )$
and
![]() $\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )$
, can be obtained along the same lines. We complete the proof.□
$\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )$
, can be obtained along the same lines. We complete the proof.□
Combining the results of Theorem 4.1 and Proposition 4.1, we get the following theorem:
Theorem 4.2. Suppose that
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let g
1i
(i=1,2,3) be given in (3.10) and f
13 be given in (4.5). Then,
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let g
1i
(i=1,2,3) be given in (3.10) and f
13 be given in (4.5). Then,
(i) if
 ${\rm max}(\alpha m, \tilde{u}_{2} )\leq m\,\lt\, u_{s} $
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
${\rm max}(\alpha m, \tilde{u}_{2} )\leq m\,\lt\, u_{s} $
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
 $$\phi (u,m){\equals}\left\{ {\matrix{ {1{\minus}k_{{13}} (m) \cdot {{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {1{\minus}k_{{13}} (m) \cdot {{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {1{\minus}k_{{13}} (m) \cdot {{g_{{13}} (u,{\rm m})} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,u_{2} )\leq u\leq m\,\lt\,u_{s} } \cr } } \right.$$
$$\phi (u,m){\equals}\left\{ {\matrix{ {1{\minus}k_{{13}} (m) \cdot {{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {1{\minus}k_{{13}} (m) \cdot {{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {1{\minus}k_{{13}} (m) \cdot {{g_{{13}} (u,{\rm m})} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,u_{2} )\leq u\leq m\,\lt\,u_{s} } \cr } } \right.$$
in which
(ii) if
 ${\rm max}\,(\alpha m,\,\tilde {u} _{1})\le m \,\lt\, {\rm max}(\alpha m,\tilde{u}_{2} )$
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given byin which
${\rm max}\,(\alpha m,\,\tilde {u} _{1})\le m \,\lt\, {\rm max}(\alpha m,\tilde{u}_{2} )$
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given byin which $$\phi (u,m){\equals}\left\{ {\matrix{ {1{\minus}k_{{12}} (m) \cdot {{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {1{\minus}k_{{12}} (m) \cdot {{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\leq m\,\lt\,u_{2} } \cr } } \right.$$
(4.6)with
$$\phi (u,m){\equals}\left\{ {\matrix{ {1{\minus}k_{{12}} (m) \cdot {{g_{{11}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {\alpha m\leq u\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {1{\minus}k_{{12}} (m) \cdot {{g_{{12}} (u,m)} \over {g_{{13}} (u_{s} ,u_{s} )}},} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\leq m\,\lt\,u_{2} } \cr } } \right.$$
(4.6)with $$k_{{12}} (m){\equals}{\rm exp}\left\{ {\left( {{\int}_m^{u_{2} } {{\minus}f_{{12}} (y){\minus}} {\int}_{u_{2} }^{u_{s} } {f_{{13}} (y)} } \right)dy} \right\}$$
$$k_{{12}} (m){\equals}{\rm exp}\left\{ {\left( {{\int}_m^{u_{2} } {{\minus}f_{{12}} (y){\minus}} {\int}_{u_{2} }^{u_{s} } {f_{{13}} (y)} } \right)dy} \right\}$$
 $$f_{{12}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{12}} (y,y)}}{\minus}2\xi _{{12}} (\alpha y)} \right],} & {{\rm if}\,\tilde{u}_{1} \leq \alpha m} \cr {\alpha \left[ {{1 \over {g_{{12}} (y,y)}}{\minus}2\xi _{{13}} (\alpha y)} \right],} & {{\rm if}\,\alpha m\,\lt\,\tilde{u}_{1} } \cr } } \right.$$
$$f_{{12}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{12}} (y,y)}}{\minus}2\xi _{{12}} (\alpha y)} \right],} & {{\rm if}\,\tilde{u}_{1} \leq \alpha m} \cr {\alpha \left[ {{1 \over {g_{{12}} (y,y)}}{\minus}2\xi _{{13}} (\alpha y)} \right],} & {{\rm if}\,\alpha m\,\lt\,\tilde{u}_{1} } \cr } } \right.$$
(iii) if αm≤m<max(
 $\alpha m,\tilde{u}_{1} $
), for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
$\alpha m,\tilde{u}_{1} $
), for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
in which
with
Also, the corresponding optimal reinsurance strategy has the form
 $$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}\left\{ {\matrix{ {\left( {1,1} \right),} & {\alpha m\leq u\leq m\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {(\tilde{q}_{1} (u),1),} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\leq m\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {(\hat{q}_{1} (u),\hat{q}_{2} (u)),} & {{\rm max}(\alpha m,u_{2} )\leq u\leq m\,\lt\,u_{s} } \cr } } \right.$$
$$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}\left\{ {\matrix{ {\left( {1,1} \right),} & {\alpha m\leq u\leq m\,\lt\,{\rm max}(\alpha m,\tilde{u}_{1} )} \cr {(\tilde{q}_{1} (u),1),} & {{\rm max}(\alpha m,\tilde{u}_{1} )\leq u\leq m\,\lt\,{\rm max}(\alpha m,u_{2} )} \cr {(\hat{q}_{1} (u),\hat{q}_{2} (u)),} & {{\rm max}(\alpha m,u_{2} )\leq u\leq m\,\lt\,u_{s} } \cr } } \right.$$
Proof. Given the results of Proposition 4.1, it is not difficult to see that h satisfies Conditions (iv), (v) and (vi) of Theorem 4.1. Besides, in Appendix A, we prove that h(u,m) is a non-increasing convex function in u but an increasing function in m. The only item remaining to show is that h as well as its derivatives w.r.t. u and m is continuous at
![]() $u{\equals}\tilde{u}_{1} $
, u=u
2,
$u{\equals}\tilde{u}_{1} $
, u=u
2,
![]() $m{\equals}\tilde{u}_{1} $
and m=u
2. We give the proof of these properties in Appendix B. Then, h also satisfies Conditions (i), (ii) and (iii). Therefore, we have ϕ=h with the optimal reinsurance strategy
$m{\equals}\tilde{u}_{1} $
and m=u
2. We give the proof of these properties in Appendix B. Then, h also satisfies Conditions (i), (ii) and (iii). Therefore, we have ϕ=h with the optimal reinsurance strategy
![]() $\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)$
given in (4.8).□
$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)$
given in (4.8).□
Case 2:
![]() $\eta _{1} \leq {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
.
$\eta _{1} \leq {{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
.
In this case,
![]() $\hat{q}_{1} (u)\leq 0$
,
$\hat{q}_{1} (u)\leq 0$
,
![]() $\hat{q}_{2} (u)\,\gt\,0$
. The analysis is similar to Case 1, thus we give the following theorem directly:
$\hat{q}_{2} (u)\,\gt\,0$
. The analysis is similar to Case 1, thus we give the following theorem directly:
Theorem 4.3. Suppose that
![]() $\eta _{1} \,\lt\,{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
. Let g
2i
(i=1,2) be given in (3.15),
$\eta _{1} \,\lt\,{{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} $
. Let g
2i
(i=1,2) be given in (3.15),
![]() $\bar{q}_{2} (u)$
be given in (3.11),
$\bar{q}_{2} (u)$
be given in (3.11),
![]() $u_{2}^{'} $
be given in (3.12), and ξ
3i
(i=1,2) be given in (3.13) and (3.14), respectively. Then, (i) if
$u_{2}^{'} $
be given in (3.12), and ξ
3i
(i=1,2) be given in (3.13) and (3.14), respectively. Then, (i) if
![]() ${\rm max}(\alpha m,u_{2}^{{\rm '}} )\leq m\,\lt\,u_{s} $
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
${\rm max}(\alpha m,u_{2}^{{\rm '}} )\leq m\,\lt\,u_{s} $
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
in which
with
 $$f_{{22}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{22}} (y,y)}}{\minus}2\xi _{{21}} (\alpha y)} \right],} & {{\rm if}\,u_{2}^{{\rm '}} \leq \alpha m} \cr {\alpha \left[ {{1 \over {g_{{22}} (y,y)}}{\minus}2\xi _{{22}} (\alpha y)} \right],} & {{\rm if}\,\alpha m\,\lt\,u_{2}^{{\rm '}} } \cr } } \right.$$
$$f_{{22}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{22}} (y,y)}}{\minus}2\xi _{{21}} (\alpha y)} \right],} & {{\rm if}\,u_{2}^{{\rm '}} \leq \alpha m} \cr {\alpha \left[ {{1 \over {g_{{22}} (y,y)}}{\minus}2\xi _{{22}} (\alpha y)} \right],} & {{\rm if}\,\alpha m\,\lt\,u_{2}^{{\rm '}} } \cr } } \right.$$
(ii) if
![]() $\alpha m\leq m\,\lt\,{\rm max}(\alpha m,u_{2}^{{\rm '}} )$
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
$\alpha m\leq m\,\lt\,{\rm max}(\alpha m,u_{2}^{{\rm '}} )$
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is given by
in which
with
Also, the optimal reinsurance strategy is
Proof. The proof is similar to Theorem 4.2, thus, we omit the details here.□
Case 3:
![]() $\eta _{1} \geq {{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
$\eta _{1} \geq {{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
In this case,
![]() $\hat{q}_{1} (u)\,\gt\,0$
,
$\hat{q}_{1} (u)\,\gt\,0$
,
![]() $\hat{q}_{2} (u)\leq 0$
. Then we can get the following result:
$\hat{q}_{2} (u)\leq 0$
. Then we can get the following result:
Theorem 4.4. Suppose that
![]() $\eta _{1} \,\gt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let g
3i
(i=1,2) be given in (3.16), ξ
3i
(i=1,2),
$\eta _{1} \,\gt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
. Let g
3i
(i=1,2) be given in (3.16), ξ
3i
(i=1,2),
![]() $u_{1}^{'} $
and
$u_{1}^{'} $
and
![]() $\bar{q}_{1} (u)$
be given in (3.17). Then,
$\bar{q}_{1} (u)$
be given in (3.17). Then,
(i) if
 ${\rm max}(\alpha m,u_{1}^{'} )\leq m\,\lt\,u_{s} $
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is
${\rm max}(\alpha m,u_{1}^{'} )\leq m\,\lt\,u_{s} $
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is
in which
with
 $$f_{{32}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{32}} (y,y)}}{\minus}2\xi _{{31}} (\alpha y)} \right],} & {{\rm if}\,u_{1}^{{\rm '}} \leq \alpha m} \cr {\alpha \left[ {{1 \over {g_{{32}} (y,y)}}{\minus}2\xi _{{32}} (\alpha y)} \right],} & {{\rm if}\,\alpha m\leq u_{1}^{{\rm '}} } \cr } } \right.$$
$$f_{{32}} (y){\equals}\left\{ {\matrix{ {\alpha \left[ {{1 \over {g_{{32}} (y,y)}}{\minus}2\xi _{{31}} (\alpha y)} \right],} & {{\rm if}\,u_{1}^{{\rm '}} \leq \alpha m} \cr {\alpha \left[ {{1 \over {g_{{32}} (y,y)}}{\minus}2\xi _{{32}} (\alpha y)} \right],} & {{\rm if}\,\alpha m\leq u_{1}^{{\rm '}} } \cr } } \right.$$
(ii) if
 $\alpha m\leq m\,\lt\,{\rm max}(\alpha m,u_{1}^{'} )$
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is
$\alpha m\leq m\,\lt\,{\rm max}(\alpha m,u_{1}^{'} )$
, for any u∈[αm,m], the minimum probability of drawdown for the surplus process (2.2) is
in which
with
Also, the optimal reinsurance strategy is
Remark 4.1. Comparing the expressions of the optimal reinsurance strategies in sections 3 and 4, it is not difficult to find that the optimal drawdown policy follows the optimal ruin policy until drawdown happens. In fact, we can see from Hipp & Taksar (Reference Hipp and Taksar2010: 246–247) that if the HJB equation in our paper remains the same, the optimal strategy is only determined by the drift and the volatility of the controlled process. Therefore, as was mentioned in remark 3.2 of Angoshtari et al. (2016 Reference Angoshtari, Bayraktar and Younga ), we can also conclude that the same reinsurance strategy minimises the expectation of any function that is non-increasing in the minimum surplus value or non-decreasing in the maximum surplus value. The changes only happen in the boundary conditions. Besides, we can see that, the calculation with the method in section 4 to derive the optimal strategy is relatively easier than the one in section 3 when our surplus comes down to the process with common shock dependence, but the latter facilitates the discussion of the constrained control variables in section 4.
In the following proposition, we investigate the behaviour of the process U t in a special case. We find that the optimal reinsurance strategy will never achieve the safe level u s with positive probability before reaching the (moving) lower bound αm.
Proposition 4.2. Assume that the inequality
![]() $\tilde{u}_{1} \,\lt\,u_{2} \,\lt\,\alpha m$
holds in Case 1. Let
$\tilde{u}_{1} \,\lt\,u_{2} \,\lt\,\alpha m$
holds in Case 1. Let
![]() $U^{{\asterisk}} $
be the optimal controlled wealth starting at u,
$U^{{\asterisk}} $
be the optimal controlled wealth starting at u,
![]() $\tau _{s}^{{\asterisk}} \,\colon\,{\equals}{\rm inf}\{ t\geq 0\,\colon\,\hat{U}^{{\asterisk}} (t)\geq u_{s} \} $
and
$\tau _{s}^{{\asterisk}} \,\colon\,{\equals}{\rm inf}\{ t\geq 0\,\colon\,\hat{U}^{{\asterisk}} (t)\geq u_{s} \} $
and
![]() $\tau _{\alpha }^{{\asterisk}} \,\colon\, {\equals}{\rm inf}\{ t\geq 0\,\colon\,\hat{U}^{{\asterisk}} (t)\leq \alpha m\} $
be the corresponding hitting times. Then
$\tau _{\alpha }^{{\asterisk}} \,\colon\, {\equals}{\rm inf}\{ t\geq 0\,\colon\,\hat{U}^{{\asterisk}} (t)\leq \alpha m\} $
be the corresponding hitting times. Then
![]() $P\left( {\tau _{s}^{{\asterisk}} \,\lt\,\tau _{\alpha }^{{\asterisk}} } \right){\equals}0$
.
$P\left( {\tau _{s}^{{\asterisk}} \,\lt\,\tau _{\alpha }^{{\asterisk}} } \right){\equals}0$
.
Proof. Since we are only interested in whether the safe level can be reached before drawdown, we may extend the domain of
![]() $(q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} )$
to ℝ and set
$(q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} )$
to ℝ and set
 $$\left\{ \matrix{ q_{1}^{{\rm {\asterisk}}} (u){\equals}{{[{\rm \Delta }_{1} {\plus}ru]\left( {a_{2} \eta _{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr q_{2}^{{\rm {\asterisk}}} (u){\equals}{{[{\rm \Delta }_{1} {\plus}ru]\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr} \right.$$
$$\left\{ \matrix{ q_{1}^{{\rm {\asterisk}}} (u){\equals}{{[{\rm \Delta }_{1} {\plus}ru]\left( {a_{2} \eta _{2} \rho b_{1} b_{2} {\minus}a_{1} \eta _{1} b_{2}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr q_{2}^{{\rm {\asterisk}}} (u){\equals}{{[{\rm \Delta }_{1} {\plus}ru]\left( {a_{1} \eta _{1} \rho b_{1} b_{2} {\minus}a_{2} \eta _{2} b_{1}^{2} } \right)} \over {{\rm \Delta }_{2} }} \hfill \cr} \right.$$
for u<αm. Define
and
Let
be the scale function, and
Now we want to show that v(−∞,m)=v(u s ,m)=∞.
Note that b(u)=0 for u<αm, then
![]() $$p({\minus}\infty){\equals}{\int}_{\alpha m}^{{\minus}\infty} {1dy{\equals}{\minus}\infty} $$
. It follows from (5.74) of Karatzas & Shreve (Reference Karatzas and Shreve1991: 348) that v(−∞,m)=∞. Besides, when
$$p({\minus}\infty){\equals}{\int}_{\alpha m}^{{\minus}\infty} {1dy{\equals}{\minus}\infty} $$
. It follows from (5.74) of Karatzas & Shreve (Reference Karatzas and Shreve1991: 348) that v(−∞,m)=∞. Besides, when
![]() $\tilde{u}_{1} \,\lt\,u_{2} \,\lt\,\alpha m$
, it is not difficult to find that
$\tilde{u}_{1} \,\lt\,u_{2} \,\lt\,\alpha m$
, it is not difficult to find that
![]() $\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}\left( {\hat{q}_{1} ,\hat{q}_{2} } \right)$
for any u∈[αm,u
s
], thus
$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}\left( {\hat{q}_{1} ,\hat{q}_{2} } \right)$
for any u∈[αm,u
s
], thus
Let
then we have
 $$\eqalignno{ p(u_{s} ){\minus} p(x) & {\equals}{\int}_x^{u_{s} } {{\rm exp}} \left\{ {{\int}_{\alpha m}^y {{d \over {z{\minus}u_{s} }}dz} } \right\}dy \cr & {\equals} {1 \over {d{\plus}1}}{{(u_{s} {\minus}x)^{{d{\plus}1}} } \over {(u_{s} {\minus}\alpha m)^{d} }} $$
$$\eqalignno{ p(u_{s} ){\minus} p(x) & {\equals}{\int}_x^{u_{s} } {{\rm exp}} \left\{ {{\int}_{\alpha m}^y {{d \over {z{\minus}u_{s} }}dz} } \right\}dy \cr & {\equals} {1 \over {d{\plus}1}}{{(u_{s} {\minus}x)^{{d{\plus}1}} } \over {(u_{s} {\minus}\alpha m)^{d} }} $$
and
Therefore, we can see that
 $$\eqalignno{ v(u_{s} ,m){\equals} & {\int}_{\alpha m}^{u_{s} } {(p(u_{s} ){\minus}p(x))} {2 \over {p^{{\rm '}} (x)s^{2} (x)}}dx \cr {\equals} & {d \over {r(d{\plus}1)}}{\int}_{\alpha m}^{u_{s} } {{1 \over {(u_{s} {\minus}x)}}dx{\equals}\infty} $$
$$\eqalignno{ v(u_{s} ,m){\equals} & {\int}_{\alpha m}^{u_{s} } {(p(u_{s} ){\minus}p(x))} {2 \over {p^{{\rm '}} (x)s^{2} (x)}}dx \cr {\equals} & {d \over {r(d{\plus}1)}}{\int}_{\alpha m}^{u_{s} } {{1 \over {(u_{s} {\minus}x)}}dx{\equals}\infty} $$
Then it follows from Feller’s test for explosions (Theorem 5.5.29 of Karatzas & Shreve, Reference Karatzas and Shreve1991: 348) that
![]() $P(\tau _{s}^{{\rm {\asterisk}}} \,\lt\,\tau _{\alpha }^{{\rm {\asterisk}}} ){\equals}0$
.□
$P(\tau _{s}^{{\rm {\asterisk}}} \,\lt\,\tau _{\alpha }^{{\rm {\asterisk}}} ){\equals}0$
.□
Remark 4.2. Note that when the surplus gets closer to the safe level u s , both the drift and volatility of the optimally controlled surplus process approach to 0. Thus, it is reasonable to expect that the safe level might not be reachable, which has been confirmed in Proposition 4.2.
Let
![]() $\tau {\equals}\tau _{\alpha }^{{\rm {\asterisk}}} \wedge\tau _{s}^{{\rm {\asterisk}}} $
denote the first hitting time of αm and u
s
when the initial surplus u lies in (αm,u
s
). From proposition 5.5.32 of Karatzas & Shreve (Reference Karatzas and Shreve1991: 350) and the result of v(u
s
,m)=∞, we can derive that 0<P(τ<∞)<1. Furthermore, in combination with the Proposition 4.2, we can see that either drawdown occurs with probability ϕ(u,m)=P(τ<∞) or the optimal controlled surplus value lies strictly between αm and u
s
, for all time, with probability of 1−ϕ(u,m). The similar conclusion is also derived in Angoshtari et al.(2016
Reference Angoshtari, Bayraktar and Younga
).
$\tau {\equals}\tau _{\alpha }^{{\rm {\asterisk}}} \wedge\tau _{s}^{{\rm {\asterisk}}} $
denote the first hitting time of αm and u
s
when the initial surplus u lies in (αm,u
s
). From proposition 5.5.32 of Karatzas & Shreve (Reference Karatzas and Shreve1991: 350) and the result of v(u
s
,m)=∞, we can derive that 0<P(τ<∞)<1. Furthermore, in combination with the Proposition 4.2, we can see that either drawdown occurs with probability ϕ(u,m)=P(τ<∞) or the optimal controlled surplus value lies strictly between αm and u
s
, for all time, with probability of 1−ϕ(u,m). The similar conclusion is also derived in Angoshtari et al.(2016
Reference Angoshtari, Bayraktar and Younga
).
5. Numerical Examples
In this section, we assume that the insurer has two lines of business: one is heavy-tailed risk, and the other is light-tailed risk. Let
Then we have
![]() $E(X){\equals}{1 \over 2}$
,
$E(X){\equals}{1 \over 2}$
,
![]() $E(Y){\equals}{1 \over 2}$
, E(X
2)=1,
$E(Y){\equals}{1 \over 2}$
, E(X
2)=1,
![]() $E(Y^{2} ){\equals}{1 \over 2}$
. In the following examples, we perform five examples to show the effect of different parameters on the optimal results. In these examples, we only consider the case of
$E(Y^{2} ){\equals}{1 \over 2}$
. In the following examples, we perform five examples to show the effect of different parameters on the optimal results. In these examples, we only consider the case of
![]() ${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
${{a_{2} \rho b_{1} } \over {a_{1} b_{2} }}\eta _{2} \,\lt\,\eta _{1} \,\lt\,{{a_{2} b_{1} } \over {a_{1} \rho b_{2} }}\eta _{2} $
.
Example 5.1. In this example, we set r=0.03, λ=3, λ 1=4, λ 2=5 and θ 1=θ 2=0.12. The results are shown in Figure 1.
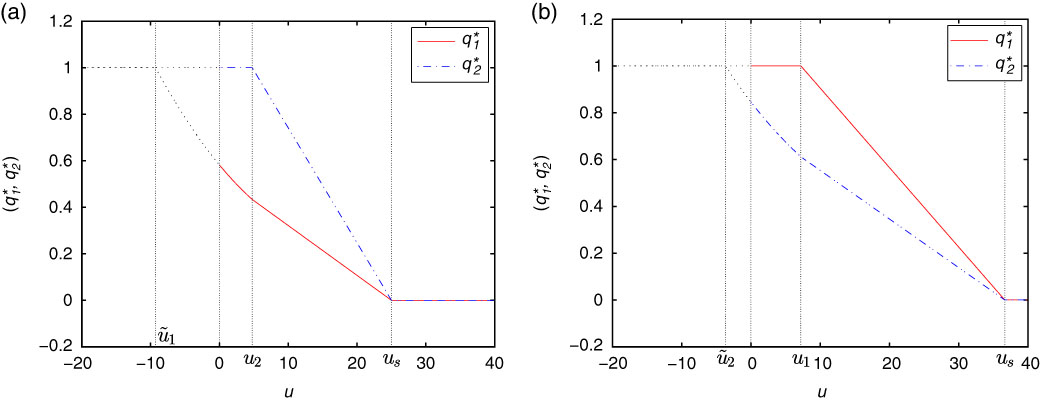
Figure 1 The influence of u on the optimal reinsurance strategy.
From Figure 1, we can see that the optimal reinsurance strategy
![]() $\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)$
decreases as u increases. It is to be expected, since, according to (3.1) and (3.6), we can prove that
$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right)$
decreases as u increases. It is to be expected, since, according to (3.1) and (3.6), we can prove that
![]() $q_{1}^{{\rm {\asterisk}}} $
and
$q_{1}^{{\rm {\asterisk}}} $
and
![]() $q_{2}^{{\rm {\asterisk}}} $
are decreasing and continuous functions w.r.t. u. Furthermore, we can observe from Figure 1(a) that
$q_{2}^{{\rm {\asterisk}}} $
are decreasing and continuous functions w.r.t. u. Furthermore, we can observe from Figure 1(a) that
![]() $q_{1}^{{\rm {\asterisk}}} $
is always less than
$q_{1}^{{\rm {\asterisk}}} $
is always less than
![]() $q_{2}^{{\rm {\asterisk}}} $
when the two lines have the same safety loading for insurer as well as for reinsurer, say, η
1=η
2=0.22. It is also natural consequence since the insurer always tries to keep a smaller retention level for the heavy-tailed risk business. However, when the reinsurer’s safety loading in the first line is much larger than the one in the second, say, η
1=0.4 and η
2=0.15, it is reasonable for the insurer to keep a smaller retention level for the cheaper one (see Figure 1(b)).
$q_{2}^{{\rm {\asterisk}}} $
when the two lines have the same safety loading for insurer as well as for reinsurer, say, η
1=η
2=0.22. It is also natural consequence since the insurer always tries to keep a smaller retention level for the heavy-tailed risk business. However, when the reinsurer’s safety loading in the first line is much larger than the one in the second, say, η
1=0.4 and η
2=0.15, it is reasonable for the insurer to keep a smaller retention level for the cheaper one (see Figure 1(b)).
Example 5.2. In this example, we set α=0.1, r=0.03, λ 1=4, λ 2=5, θ 1=θ 2=0.12 and η 1=η 2=0.22. The results are shown in Figure 2.
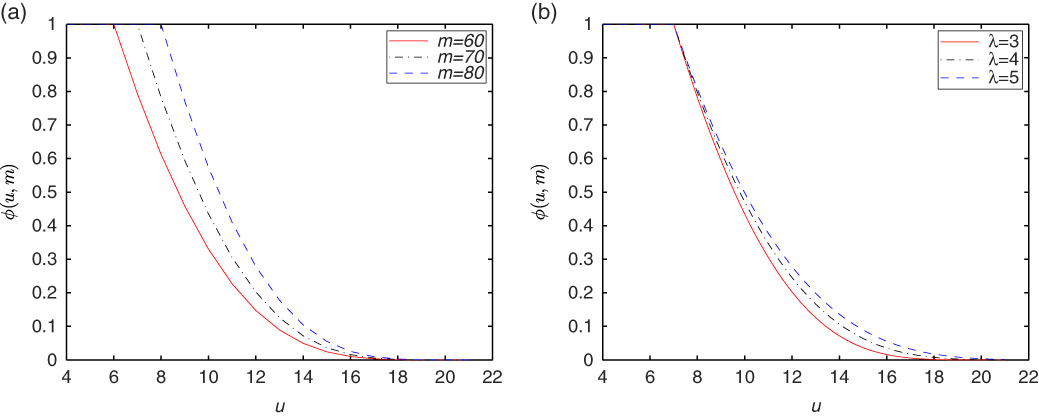
Figure 2 The influence of m and λ on the minimum probability of drawdown.
Figure 2 shows that the minimum probability of drawdown ϕ(u,m) satisfies the boundary conditions: ϕ(am,m)=1 and ϕ(u s ,m)=0. Besides, we can see that ϕ(u,m) is a decreasing function w.r.t. u but an increasing function w.r.t. m and λ. They are natural consequences, since, when the value of the surplus increases toward u s , the insurer can transfer all the risk to reinsurer, and thus the wealth will never decrease, then drawdown cannot happen. However, the drawdown level increases as the maximum (past) value m increases (See Figure 2(a)), and a greater value of λ means a greater value of expected claim number as well as safe level, which both could make drawdown more likely (See Figure 2(b)).
Example 5.3. In this example, we set r=0.03, λ 1=4, λ 2=5, θ 1=0.1 and θ 2=0.12. The results are shown in Figure 3.
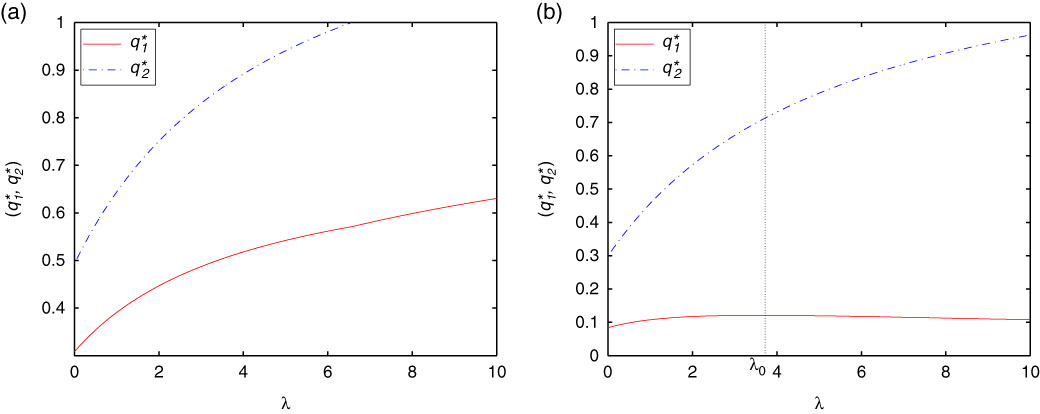
Figure 3 The influence of λ on the optimal reinsurance strategy.
From Figure 3(a) with η
1=0.25 and η
2=0.2, we can see that the optimal reinsurance strategy increases when λ increases, which implies that even though the greater value of λ means a greater value of expected claim number, the insurer still chooses to retain a larger share of each claim because of the expensive reinsurance cost. However, when the reinsurance premium is small enough, the insurer would rather retain a less share of the claim when the expected claim number becomes larger. This kind of property is shown in Figure 3(b) with η
1=0.14 and η
2=0.25, where a greater value of λ(>λ
0) yields a less value of the optimal reinsurance strategy
![]() $q_{1}^{{\rm {\asterisk}}} $
. Besides, it is not difficult to see that the optimal reinsurance strategy
$q_{1}^{{\rm {\asterisk}}} $
. Besides, it is not difficult to see that the optimal reinsurance strategy
![]() $q_{2}^{{\rm {\asterisk}}} $
in Figure 3(a) increases faster than the one in Figure 3(b) when λ increases, which shows once more that the reinsurer’s safety loading has a direct impact on the optimal reinsurance strategy.
$q_{2}^{{\rm {\asterisk}}} $
in Figure 3(a) increases faster than the one in Figure 3(b) when λ increases, which shows once more that the reinsurer’s safety loading has a direct impact on the optimal reinsurance strategy.
Example 5.4. In this example, we set r=0.03, λ=2, λ 2=7 and θ 1=θ 2=0.1. The results are shown in Figure 4.
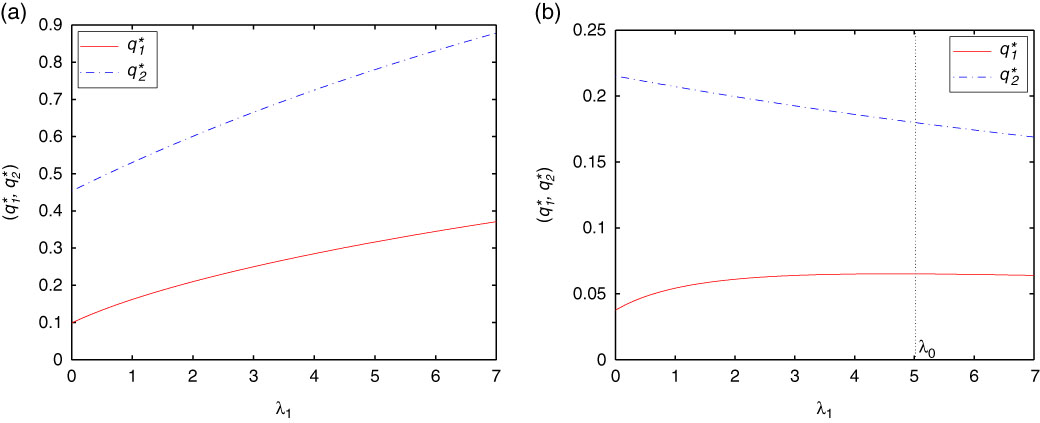
Figure 4 The influence of λ 1 on the optimal reinsurance strategy.
From Figure 4(a) with η
1=0.21 and η
2=0.23, we can see that a greater value of λ
1 yields greater values of the optimal reinsurance strategy
![]() $q_{1}^{{\rm {\asterisk}}} $
and
$q_{1}^{{\rm {\asterisk}}} $
and
![]() ${\rm q}_{2}^{{\rm {\asterisk}}} $
. It makes sense because the reinsurance premium is much more expensive in this case, the insurer would rather retain a larger share of each claim even though a greater value of λ
1 implies a larger insurance risk. However, when the reinsurer’s safety loading is small enough, say η
1=0.1 and η
2=0.12 as in Figure 4(b), to reduce the risk, the insurer tends to purchase more reinsurance for class 2 because of the cheap reinsurance premium. Meanwhile, since
${\rm q}_{2}^{{\rm {\asterisk}}} $
. It makes sense because the reinsurance premium is much more expensive in this case, the insurer would rather retain a larger share of each claim even though a greater value of λ
1 implies a larger insurance risk. However, when the reinsurer’s safety loading is small enough, say η
1=0.1 and η
2=0.12 as in Figure 4(b), to reduce the risk, the insurer tends to purchase more reinsurance for class 2 because of the cheap reinsurance premium. Meanwhile, since
![]() $q_{1}^{{\rm {\asterisk}}} $
is much more sensitive to λ
1 than
$q_{1}^{{\rm {\asterisk}}} $
is much more sensitive to λ
1 than
![]() $q_{2}^{{\rm {\asterisk}}} $
, there is a trade-off in allowing q
1 to increase or decrease. When λ
1 is not large enough, say λ
1<λ
0, the insurer prefers to retain a greater share of each claim as λ
1 increases, which could help increase the premium income. However, a greater value of λ
1 also implies a larger insurance risk, when λ
1 is large enough, say λ
1>λ
0, the insurer needs to reduce the risk of its insurance portfolios by transferring more risk to the reinsurer.
$q_{2}^{{\rm {\asterisk}}} $
, there is a trade-off in allowing q
1 to increase or decrease. When λ
1 is not large enough, say λ
1<λ
0, the insurer prefers to retain a greater share of each claim as λ
1 increases, which could help increase the premium income. However, a greater value of λ
1 also implies a larger insurance risk, when λ
1 is large enough, say λ
1>λ
0, the insurer needs to reduce the risk of its insurance portfolios by transferring more risk to the reinsurer.
Example 5.5. In this example, we set r=0.03, λ=3, λ 1=4, λ 2=5, θ 1=0.1 and θ 2=0.12. The results are shown in Figure 5.
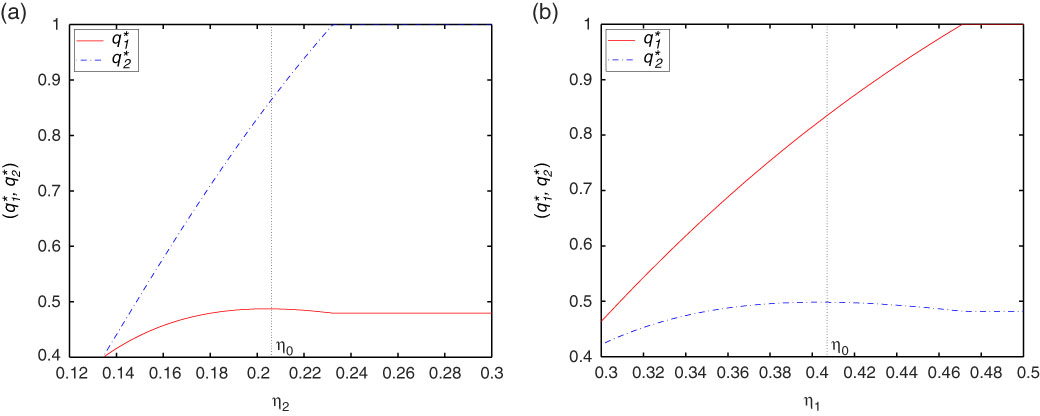
Figure 5 The influence of η 1 and η 2 on the optimal reinsurance strategy.
Figure 5 further investigates the influence of the reinsurer’s safety loadings, i.e., η
1 and η
2 on optimal reinsurance strategy. It is easy to see that a greater value of η
i
(i=1,2) yields a greater value of
![]() $q_{i}^{{\rm {\asterisk}}} (i{\equals}1,2)$
, which illustrates the intuitive observation that if the reinsurance premium increases, the insurer would rather retain a greater share of each claim by purchasing less reinsurance. We also see that as the value of η
1(η
2) increases, the retention level of the other class first increases and then decreases after reaching a certain level (say, η
0). These observations are kind of reasonable. When the company keep buying less and less reinsurance for one class, it eventually needs to reduce the risk of its insurance portfolios by buying a bit more reinsurance for another class.
$q_{i}^{{\rm {\asterisk}}} (i{\equals}1,2)$
, which illustrates the intuitive observation that if the reinsurance premium increases, the insurer would rather retain a greater share of each claim by purchasing less reinsurance. We also see that as the value of η
1(η
2) increases, the retention level of the other class first increases and then decreases after reaching a certain level (say, η
0). These observations are kind of reasonable. When the company keep buying less and less reinsurance for one class, it eventually needs to reduce the risk of its insurance portfolios by buying a bit more reinsurance for another class.
6. Conclusion
We first recap the main results of this paper. From an insurer’s point of view, we consider the optimal proportional reinsurance problem to minimise the probability of drawdown in a diffusion approximation risk model where the aggregate claim processes are correlated by a common shock. Based on the method of maximising the ratio of drift of a diffusion divided to its volatility squared, and the technique of stochastic control theory and the corresponding HJB equation, we investigate the optimal results in the cases of m≥u s and m<u s . Furthermore, in each case, we constrain the reinsurance proportion in the interval [0,1], which makes the optimisation problems being discussed in three different situations. The explicit expressions of the optimal proportional reinsurance strategy and the minimum probability of drawdown are derived, which strongly depend on the value of the surplus u, as well as the two important parameters of drawdown α and m.
For the further research, there are still several interesting problems that deserve investigation. First, one may take the life time of individual τ d into consideration so as to investigate the problem of optimal insurance which minimises the probability of lifetime drawdown. Second, we can generalise the model to the one that insurers can invest their wealth not only in risk-free bond but also in risky assets. Note that if the process of risky assets is independent of the claim process, we can obtain the optimal results by the same way as in our paper. However, if the assumption of independence is removed, the problem will become more complex. Third, the problem of minimising the probability of drawdown in our risk model can be extended to the more general objective function, such as minimising the expectation of any function which is non-increasing with respect to the minimum surplus value or non-decreasing with respect to the maximum surplus value. Fourth, under the criterion of minimising the probability of drawdown, we can also consider the optimal proportional reinsurance strategy in a risk model with multiple dependent classes of insurance business. All of these problems will be more challenging, but also more meaningful and realistic to be discussed, and they are our future research work directions.
Acknowledgements
The authors would like to thank the anonymous referees for their careful reading and helpful comments on an earlier version of this paper, which led to a considerable improvement of the presentation of the work. This research was supported by the National Natural Science Foundation of China (Grant No. 11471165) and Jiangsu Natural Science Foundation (Grant No. BK20141442).
Appendix A: Proof of Monotonicity and Convexity of h
Note that when u
2≤u≤m<u
s
and the inequality
![]() $\alpha m\,\lt\,\tilde{u}_{1} \,\lt\,u_{2} $
holds, we have
$\alpha m\,\lt\,\tilde{u}_{1} \,\lt\,u_{2} $
holds, we have
in which
with
It then follows that
 $$\eqalignno{ h_{m} (u,m){\equals} & {\minus}{{k_{{13}} (m)} \over {g_{{13}} (u_{s} ,u_{s} )}} \cdot \left[ {f_{{13}} (m)g_{{13}} (u,m){\minus}\alpha \xi _{{13}} (\alpha m)g_{{13}} (u,m){\minus}\alpha } \right] \cr {\equals} & {{\alpha \cdot k_{{13}} (m)} \over {g_{{13}} (u_{s} ,u_{s} )}} \cdot \left[ {1{\minus}{{g_{{13}} (u,m)} \over {g_{{13}} (m,m)}}} \right]\geq 0 $$
$$\eqalignno{ h_{m} (u,m){\equals} & {\minus}{{k_{{13}} (m)} \over {g_{{13}} (u_{s} ,u_{s} )}} \cdot \left[ {f_{{13}} (m)g_{{13}} (u,m){\minus}\alpha \xi _{{13}} (\alpha m)g_{{13}} (u,m){\minus}\alpha } \right] \cr {\equals} & {{\alpha \cdot k_{{13}} (m)} \over {g_{{13}} (u_{s} ,u_{s} )}} \cdot \left[ {1{\minus}{{g_{{13}} (u,m)} \over {g_{{13}} (m,m)}}} \right]\geq 0 $$
It is not difficult to see that h m (m,m)=0 for u=m.
Differentiating g 13 with respect to u yields
and
Thus, we have h u <0 and h uu >0. Along the same lines, we can get the same results for other cases. Therefore, we conclude that h(u,m) is a non-increasing convex function with respect to the surplus wealth u but a non-decreasing function with respect to the maximum (past) value m.
Appendix B: Proof of Continuity of h, h u , h uu and h m
The continuity of h is obviously satisfied, thus we only need to prove that its partial derivatives h
u
, h
uu
and h
m
are also continuous. To keep things simple, we assume that the equality
![]() $\alpha m\,\lt\,\tilde{u}_{1} \,\lt\,u_{2} $
holds. We only present the proof for the case of m∈[u
2,u
s
). The proofs for
$\alpha m\,\lt\,\tilde{u}_{1} \,\lt\,u_{2} $
holds. We only present the proof for the case of m∈[u
2,u
s
). The proofs for
![]() $m\in[\tilde{u}_{1} ,u_{2} )$
and
$m\in[\tilde{u}_{1} ,u_{2} )$
and
![]() $m\in[\alpha m,\tilde{u}_{1} )$
can be derived similarly.
$m\in[\alpha m,\tilde{u}_{1} )$
can be derived similarly.
When
![]() $\alpha m\leq u\,\lt\,\tilde{u}_{1} $
, we have
$\alpha m\leq u\,\lt\,\tilde{u}_{1} $
, we have
and
When
![]() $\tilde{u}_{1} \leq u\,\lt\,u_{2} \leq m$
, it follows that
$\tilde{u}_{1} \leq u\,\lt\,u_{2} \leq m$
, it follows that
and
We can see from (4.8) that
![]() $\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}(1,1)$
for
$\left( {q_{1}^{{\rm {\asterisk}}} ,q_{2}^{{\rm {\asterisk}}} } \right){\equals}(1,1)$
for
![]() $u{\equals}\tilde{u}_{1} $
, and thus
$u{\equals}\tilde{u}_{1} $
, and thus
Therefore, it is not difficult to find that the partial derivatives h
u
and h
uu
are continuous at
![]() $u{\equals}\tilde{u}_{1} $
. By the same way, we can also prove that h
u
and h
uu
are continuous at u=u
2.
$u{\equals}\tilde{u}_{1} $
. By the same way, we can also prove that h
u
and h
uu
are continuous at u=u
2.
Next, we show the continuity of ϕ
m
at
![]() $m{\equals}\tilde{u}_{1} $
. Since
$m{\equals}\tilde{u}_{1} $
. Since
for
![]() $\alpha m\leq u\leq m\leq \tilde{u}_{1} $
, and
$\alpha m\leq u\leq m\leq \tilde{u}_{1} $
, and
for
![]() $\tilde{u}_{1} \leq u\leq m\leq u_{2} $
, then according to (4.6) and (4.7), it is obvious that
$\tilde{u}_{1} \leq u\leq m\leq u_{2} $
, then according to (4.6) and (4.7), it is obvious that
![]() $k_{{11}} (\tilde{u}_{1} ){\equals}k_{{12}} (\tilde{u}_{1} )$
and
$k_{{11}} (\tilde{u}_{1} ){\equals}k_{{12}} (\tilde{u}_{1} )$
and
![]() $k_{{11}}^{{\rm '}} (\tilde{u}_{1} ){\equals}k_{{12}}^{{\rm '}} (\tilde{u}_{1} )$
. Besides, because of
$k_{{11}}^{{\rm '}} (\tilde{u}_{1} ){\equals}k_{{12}}^{{\rm '}} (\tilde{u}_{1} )$
. Besides, because of
then we have
Thus, it is clear that ϕ
m
is continuous at
![]() $m{\equals}\tilde{u}_{1} $
. Along the same lines, we can also prove the continuity of h
m
at u=u
2. Therefore, we conclude that h as well as its partial derivatives h
u
, h
uu
and h
m
is continuous.
$m{\equals}\tilde{u}_{1} $
. Along the same lines, we can also prove the continuity of h
m
at u=u
2. Therefore, we conclude that h as well as its partial derivatives h
u
, h
uu
and h
m
is continuous.