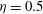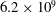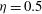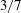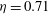1 Introduction
The paradigmatic Taylor–Couette (TC) flow has long been a flow configuration of great interest to fluid dynamicists. It consists of flow between two coaxial cylinders that can rotate independently (see figure 1). This system has been used extensively as a model in fluid physics because it is a closed system, has a relatively simple geometry and therefore has multiple symmetries. After early investigations (Couette Reference Couette1890; Mallock Reference Mallock1896; Taylor Reference Taylor1923), Wendt (Reference Wendt1933) started studying turbulence in this system. For a further historical overview, the reader is referred to Donnelly (Reference Donnelly1991). For a review on TC flow at the onset of instabilities and slightly above, see Fardin, Perge & Taberlet (Reference Fardin, Perge and Taberlet2014). The state of the art of high-Reynolds-number TC turbulence is treated by Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016).
The two geometrical control parameters of TC flow are the ratio
![]() ${\it\eta}$
of the inner and outer cylinder radii and the aspect ratio
${\it\eta}$
of the inner and outer cylinder radii and the aspect ratio
![]() ${\it\Gamma}=L/d$
, where
${\it\Gamma}=L/d$
, where
![]() $d$
is the gap width and
$d$
is the gap width and
![]() $L$
is the height of the cylinders. In this work we use a small radius ratio of
$L$
is the height of the cylinders. In this work we use a small radius ratio of
![]() ${\it\eta}=0.5$
, corresponding to a relatively wide gap. The vast majority of existing work (see overview by Dubrulle et al. (Reference Dubrulle, Dauchot, Daviaud, Longgaretti, Richard and Zahn2005) and review by Grossmann et al. (Reference Grossmann, Lohse and Sun2016)) focuses on a radius ratio of 0.71 or higher. Lower-
${\it\eta}=0.5$
, corresponding to a relatively wide gap. The vast majority of existing work (see overview by Dubrulle et al. (Reference Dubrulle, Dauchot, Daviaud, Longgaretti, Richard and Zahn2005) and review by Grossmann et al. (Reference Grossmann, Lohse and Sun2016)) focuses on a radius ratio of 0.71 or higher. Lower-
![]() ${\it\eta}$
experiments concern the Rayleigh-stable regime (Ji et al.
Reference Ji, Burin, Schartman and Goodman2006), mean flow and turbulence characteristics (van Hout & Katz Reference van Hout and Katz2011) and global torque measurements (Merbold, Brauckmann & Egbers Reference Merbold, Brauckmann and Egbers2013). In addition, numerical work has been done for
${\it\eta}$
experiments concern the Rayleigh-stable regime (Ji et al.
Reference Ji, Burin, Schartman and Goodman2006), mean flow and turbulence characteristics (van Hout & Katz Reference van Hout and Katz2011) and global torque measurements (Merbold, Brauckmann & Egbers Reference Merbold, Brauckmann and Egbers2013). In addition, numerical work has been done for
![]() ${\it\eta}=0.5$
(Dong Reference Dong2007; Chouippe et al.
Reference Chouippe, Climent, Legendre and Gabillet2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
). The radius ratio is a key control parameter (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007) in TC flow, and it has been found that a low-radius-ratio TC system behaves differently compared to higher-
${\it\eta}=0.5$
(Dong Reference Dong2007; Chouippe et al.
Reference Chouippe, Climent, Legendre and Gabillet2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
). The radius ratio is a key control parameter (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007) in TC flow, and it has been found that a low-radius-ratio TC system behaves differently compared to higher-
![]() ${\it\eta}$
set-ups in several aspects, which will be outlined below. The underlying reason for the different behaviour is the strong boundary layer asymmetry. Because the ratio of inner and outer boundary layer thicknesses scales as
${\it\eta}$
set-ups in several aspects, which will be outlined below. The underlying reason for the different behaviour is the strong boundary layer asymmetry. Because the ratio of inner and outer boundary layer thicknesses scales as
![]() ${\it\eta}^{3}$
(Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007), a strong asymmetry between the inner and outer boundary layers exists for small radius ratio.
${\it\eta}^{3}$
(Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007), a strong asymmetry between the inner and outer boundary layers exists for small radius ratio.

Figure 1. (a) Schematic of the vertical cross-section of the TC set-up, showing the horizontal laser sheet, which is imaged from above through the transparent top plate. The laser can be traversed vertically. (b) Horizontal cross-section of the set-up. The shaded red rectangle represents the typical field of view.
As dimensionless control parameters of the system, we use the (negative) rotation ratio
![]() $a=-{\it\omega}_{o}/{\it\omega}_{i}$
and the Taylor number (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007):
$a=-{\it\omega}_{o}/{\it\omega}_{i}$
and the Taylor number (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007):
where
![]() ${\it\omega}_{i,o}$
are the angular velocities of the inner and outer cylinders,
${\it\omega}_{i,o}$
are the angular velocities of the inner and outer cylinders,
![]() $r_{i,o}$
are the inner and outer cylinder radii,
$r_{i,o}$
are the inner and outer cylinder radii,
![]() ${\it\eta}=r_{i}/r_{o}$
is the radius ratio, and
${\it\eta}=r_{i}/r_{o}$
is the radius ratio, and
![]() ${\it\nu}$
is the kinematic viscosity. The driving of the system can also be described by the shear Reynolds number (Dubrulle et al.
Reference Dubrulle, Dauchot, Daviaud, Longgaretti, Richard and Zahn2005):
${\it\nu}$
is the kinematic viscosity. The driving of the system can also be described by the shear Reynolds number (Dubrulle et al.
Reference Dubrulle, Dauchot, Daviaud, Longgaretti, Richard and Zahn2005):
for which
![]() $Re_{S}\propto Ta^{1/2}$
.
$Re_{S}\propto Ta^{1/2}$
.
When increasing the driving strength (i.e. the Taylor number), TC flow first gradually undergoes a transition from a purely azimuthal, laminar state to a state where the bulk becomes turbulent while the boundary layers still remain laminar. The latter state is called the classical turbulent regime (Grossmann & Lohse Reference Grossmann and Lohse2000). By further increasing
![]() $Ta$
, the ultimate turbulent regime (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2011; He et al.
Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers2012) is reached, in which also the boundary layers are turbulent. The signature of these turbulent boundary layers are logarithmic velocity profiles, which have recently been found for a radius ratio of
$Ta$
, the ultimate turbulent regime (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2011; He et al.
Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers2012) is reached, in which also the boundary layers are turbulent. The signature of these turbulent boundary layers are logarithmic velocity profiles, which have recently been found for a radius ratio of
![]() ${\it\eta}=0.716$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) and for
${\it\eta}=0.716$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) and for
![]() ${\it\eta}=0.909$
(Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016). Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2014) have derived theoretical velocity profiles, and found that the angular velocity profile follows a log law more closely than the azimuthal velocity profile, an effect that is more pronounced with the stronger asymmetry for smaller
${\it\eta}=0.909$
(Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016). Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2014) have derived theoretical velocity profiles, and found that the angular velocity profile follows a log law more closely than the azimuthal velocity profile, an effect that is more pronounced with the stronger asymmetry for smaller
![]() ${\it\eta}$
. In § 3.1 we set out to investigate the correspondence of experimentally measured angular and azimuthal velocity profiles to a log law for
${\it\eta}$
. In § 3.1 we set out to investigate the correspondence of experimentally measured angular and azimuthal velocity profiles to a log law for
![]() ${\it\eta}=0.5$
and Taylor numbers up to
${\it\eta}=0.5$
and Taylor numbers up to
![]() $6.2\times 10^{9}$
at the onset of the ultimate turbulent regime. Furthermore, the velocity profiles are compared to existing experimental and numerical work.
$6.2\times 10^{9}$
at the onset of the ultimate turbulent regime. Furthermore, the velocity profiles are compared to existing experimental and numerical work.
In addition to affecting the velocity profiles, the radius ratio strongly influences the transitional Taylor number for the ultimate regime (Ravelet, Delfos & Westerweel Reference Ravelet, Delfos and Westerweel2010; Merbold et al.
Reference Merbold, Brauckmann and Egbers2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, Huisman, Jannink, van Gils, Verzicco, Grossmann, Sun and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
c
). For
![]() ${\it\eta}=0.5$
the ultimate regime does not start before
${\it\eta}=0.5$
the ultimate regime does not start before
![]() $Ta=10^{10}$
(Merbold et al.
Reference Merbold, Brauckmann and Egbers2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
), whereas the transition for a higher radius ratio of
$Ta=10^{10}$
(Merbold et al.
Reference Merbold, Brauckmann and Egbers2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
), whereas the transition for a higher radius ratio of
![]() ${\it\eta}=0.71$
already occurs at
${\it\eta}=0.71$
already occurs at
![]() $Ta=5\times 10^{8}$
(van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
). Very different scaling of the angular momentum transfer and the ‘wind’ in the gap with the driving parameter
$Ta=5\times 10^{8}$
(van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
). Very different scaling of the angular momentum transfer and the ‘wind’ in the gap with the driving parameter
![]() $Ta$
exist for the classical and ultimate regimes (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2011). The degree of turbulence of the wind in the gap of the cylinders, which measures the strength of the secondary flows
$Ta$
exist for the classical and ultimate regimes (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2011). The degree of turbulence of the wind in the gap of the cylinders, which measures the strength of the secondary flows
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{z}$
, can be characterised by the wind Reynolds number. We use the standard deviation of the radial velocity
$u_{z}$
, can be characterised by the wind Reynolds number. We use the standard deviation of the radial velocity
![]() ${\it\sigma}(u_{r})$
to quantify the wind Reynolds number,
${\it\sigma}(u_{r})$
to quantify the wind Reynolds number,
with the gap width
![]() $d=r_{o}-r_{i}$
. The late onset of the ultimate regime for
$d=r_{o}-r_{i}$
. The late onset of the ultimate regime for
![]() ${\it\eta}=0.5$
gives us the opportunity to analyse the scaling of the wind Reynolds number with Taylor numbers in the classical TC regime, up to the onset of the ultimate regime, and to compare it with theoretical predictions (§ 3.2). Furthermore, a similar analysis is performed on the standard deviation of the azimuthal velocity, leading to a scaling of the turbulence intensity, which is compared to that in Rayleigh–Bénard convection.
${\it\eta}=0.5$
gives us the opportunity to analyse the scaling of the wind Reynolds number with Taylor numbers in the classical TC regime, up to the onset of the ultimate regime, and to compare it with theoretical predictions (§ 3.2). Furthermore, a similar analysis is performed on the standard deviation of the azimuthal velocity, leading to a scaling of the turbulence intensity, which is compared to that in Rayleigh–Bénard convection.
Another area where the influence of the radius ratio is apparent is the angular momentum transport through the gap. This transport is a key response parameter of the system and is directly connected to the torque required to maintain constant cylinder velocities (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). The radius ratio strongly influences the rotation ratio for which optimal momentum transport occurs (van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013; Merbold et al.
Reference Merbold, Brauckmann and Egbers2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, Huisman, Jannink, van Gils, Verzicco, Grossmann, Sun and Lohse2014a
; Brauckmann, Salewski & Eckhardt Reference Brauckmann, Salewski and Eckhardt2016). For example, the optimal momentum transport occurs at
![]() $a_{opt}\approx 0.33$
for
$a_{opt}\approx 0.33$
for
![]() ${\it\eta}=0.714$
(van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012) whereas it is
${\it\eta}=0.714$
(van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012) whereas it is
![]() $a_{opt}\approx 0.20$
for
$a_{opt}\approx 0.20$
for
![]() ${\it\eta}=0.5$
(Merbold et al.
Reference Merbold, Brauckmann and Egbers2013).
${\it\eta}=0.5$
(Merbold et al.
Reference Merbold, Brauckmann and Egbers2013).
Roll structures play an important role in the momentum transport in the TC system (Fenstermacher, Swinney & Gollub Reference Fenstermacher, Swinney and Gollub1979; Andereck, Liu & Swinney Reference Andereck, Liu and Swinney1986; Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
). With increasing Taylor number, the system undergoes transitions from a purely laminar state to having steady coherent Taylor vortices, to having modulated wavy Taylor vortices, which eventually evolve into chaotic turbulent Taylor vortices (Lewis & Swinney Reference Lewis and Swinney1999). But even in the ultimate regime, for some
![]() $a>0$
, it was found that remnants of these rolls are present in time-averaged quantities (Tokgoz et al.
Reference Tokgoz, Elsinga, Delfos and Westerweel2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
), whereas for
$a>0$
, it was found that remnants of these rolls are present in time-averaged quantities (Tokgoz et al.
Reference Tokgoz, Elsinga, Delfos and Westerweel2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
), whereas for
![]() $a=0$
(pure inner cylinder rotation) these rolls vanish for large Taylor number (Lathrop, Fineberg & Swinney Reference Lathrop, Fineberg and Swinney1992). In § 3.3 we will characterise the roll structures for
$a=0$
(pure inner cylinder rotation) these rolls vanish for large Taylor number (Lathrop, Fineberg & Swinney Reference Lathrop, Fineberg and Swinney1992). In § 3.3 we will characterise the roll structures for
![]() ${\it\eta}=0.5$
at both pure inner cylinder rotation
${\it\eta}=0.5$
at both pure inner cylinder rotation
![]() $a=0$
and slight counter-rotation
$a=0$
and slight counter-rotation
![]() $a=0.2$
, at which optimal transport occurs.
$a=0.2$
, at which optimal transport occurs.
It was recently proposed that the logarithmic velocity profiles in ultimate TC flow are triggered by turbulent plume ejection (Ahlers, Bodenschatz & He Reference Ahlers, Bodenschatz and He2014; Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b ; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015), which in turn is regulated by the relative strength of the axial and radial mean flows. Using time-resolved azimuthal and radial velocity field measurements at several heights in the set-up, we will investigate the connection between the roll structures that generate strong radial and axial flows, and the turbulent plumes that emanate from either the inner or outer cylinder (§ 3.4). Furthermore, in § 3.5 we will quantify how these plumes affect the logarithmic nature of the velocity profiles.
2 Set-up and explored parameter space
2.1 Set-up
The experiments were carried out in the Cottbus Taylor–Couette Facility (Merbold, Fischer & Egbers Reference Merbold, Fischer and Egbers2011; Merbold et al.
Reference Merbold, Brauckmann and Egbers2013). The inner and outer cylinder radii are
![]() $r_{i}=35.0\pm 0.2~\text{mm}$
and
$r_{i}=35.0\pm 0.2~\text{mm}$
and
![]() $r_{o}=70.0\pm 0.2~\text{mm}$
, respectively, and the height of the set-up is
$r_{o}=70.0\pm 0.2~\text{mm}$
, respectively, and the height of the set-up is
![]() $L=700~\text{mm}$
. This gives a radius ratio of
$L=700~\text{mm}$
. This gives a radius ratio of
![]() ${\it\eta}=0.5$
and an aspect ratio of
${\it\eta}=0.5$
and an aspect ratio of
![]() ${\it\Gamma}=20$
. This aspect ratio is sufficiently large so that we do not expect the endwalls to significantly affect the velocity in the bulk (van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Paoletti et al.
Reference Paoletti, van Gils, Dubrulle, Sun, Lohse and Lathrop2012). The cylindricities of the cylinders that were used are 0.4 mm and 0.3 mm for the inner and outer cylinders, respectively. The maximum rotation rates are 5 Hz for both the inner and outer cylinders.
${\it\Gamma}=20$
. This aspect ratio is sufficiently large so that we do not expect the endwalls to significantly affect the velocity in the bulk (van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Paoletti et al.
Reference Paoletti, van Gils, Dubrulle, Sun, Lohse and Lathrop2012). The cylindricities of the cylinders that were used are 0.4 mm and 0.3 mm for the inner and outer cylinders, respectively. The maximum rotation rates are 5 Hz for both the inner and outer cylinders.

Figure 2. The explored parameter space. The Taylor number (
![]() $Ta$
) is varied for inner cylinder rotation (
$Ta$
) is varied for inner cylinder rotation (
![]() $a=0$
), and axial scans have been performed for (negative) rotation ratios
$a=0$
), and axial scans have been performed for (negative) rotation ratios
![]() $a=0$
and
$a=0$
and
![]() $a=0.2$
.
$a=0.2$
.
The end plates rotate with the outer cylinder. The outer cylinder and the top plate are transparent, making the set-up ideally suited to be used in combination with particle image velocimetry (PIV). A high-resolution PIV camera (LaVision Imager sCMOS) with a resolution of
![]() $2560\times 2160$
pixels and a frame rate of 50 Hz is installed above the top end plate, pointing downwards. Water is used as the working fluid (
$2560\times 2160$
pixels and a frame rate of 50 Hz is installed above the top end plate, pointing downwards. Water is used as the working fluid (
![]() $20\,^{\circ }\text{C}$
,
$20\,^{\circ }\text{C}$
,
![]() ${\it\nu}=1.0\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
). The water contains fluorescent particles (Dantec Dynamics, PMMA-RhB,
${\it\nu}=1.0\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
). The water contains fluorescent particles (Dantec Dynamics, PMMA-RhB,
![]() $1{-}20~{\rm\mu}\text{m}$
) with a maximum Stokes number of
$1{-}20~{\rm\mu}\text{m}$
) with a maximum Stokes number of
![]() $St={\it\tau}_{p}/{\it\tau}_{{\it\eta}}\approx 10^{-4}\ll 1$
, which means that they faithfully follow the flow and can be considered as tracer particles. The flow is illuminated by a horizontal light sheet from a high-powered pulsed Nd:YLF dual-cavity laser (Litron LDY303HE). Because of the high-resolution PIV camera, very high-resolution measurements of the flow fields can be achieved. The imaging of the full width of the gap combined with a vector grid of
$St={\it\tau}_{p}/{\it\tau}_{{\it\eta}}\approx 10^{-4}\ll 1$
, which means that they faithfully follow the flow and can be considered as tracer particles. The flow is illuminated by a horizontal light sheet from a high-powered pulsed Nd:YLF dual-cavity laser (Litron LDY303HE). Because of the high-resolution PIV camera, very high-resolution measurements of the flow fields can be achieved. The imaging of the full width of the gap combined with a vector grid of
![]() $16\times 16$
pixels with 50 % overlap results in a velocity vector spacing of 0.13 mm. The PIV system is operated in dual frame mode, allowing for an inter-frame time
$16\times 16$
pixels with 50 % overlap results in a velocity vector spacing of 0.13 mm. The PIV system is operated in dual frame mode, allowing for an inter-frame time
![]() ${\rm\Delta}t$
smaller than the inverse frame rate. The PIV image pairs are processed using LaVision DaVis software, after which the flow fields are transformed to the radial velocity
${\rm\Delta}t$
smaller than the inverse frame rate. The PIV image pairs are processed using LaVision DaVis software, after which the flow fields are transformed to the radial velocity
![]() $u_{r}({\it\theta},r,z,t)$
and the azimuthal velocity
$u_{r}({\it\theta},r,z,t)$
and the azimuthal velocity
![]() $u_{{\it\theta}}({\it\theta},r,z,t)$
.
$u_{{\it\theta}}({\it\theta},r,z,t)$
.
2.2 Explored parameter space
The parameter space that was explored for this work is shown in figure 2. The first set of measurements that is treated here consists of varying the Taylor number between
![]() $Ta=5.8\times 10^{7}$
and
$Ta=5.8\times 10^{7}$
and
![]() $Ta=6.2\times 10^{9}$
(corresponding to a shear Reynolds number of
$Ta=6.2\times 10^{9}$
(corresponding to a shear Reynolds number of
![]() $Re_{S}=6.0\times 10^{3}$
–
$Re_{S}=6.0\times 10^{3}$
–
![]() $6.2\times 10^{4}$
) for inner cylinder rotation only (
$6.2\times 10^{4}$
) for inner cylinder rotation only (
![]() $a=0$
) at mid-height (
$a=0$
) at mid-height (
![]() $h=0.5L$
). These measurements were performed as a single continuous experiment; the cylinder velocity was increased slowly between experiments, and before each measurement approximately 10 min were taken to give the flow ample time to stabilise. Each measurement in this set consists of 10 000 PIV image pairs, which were recorded at 25 frames per second (f.p.s.). This corresponds to 235 and 2418 cylinder revolutions for
$h=0.5L$
). These measurements were performed as a single continuous experiment; the cylinder velocity was increased slowly between experiments, and before each measurement approximately 10 min were taken to give the flow ample time to stabilise. Each measurement in this set consists of 10 000 PIV image pairs, which were recorded at 25 frames per second (f.p.s.). This corresponds to 235 and 2418 cylinder revolutions for
![]() $Ta=5.8\times 10^{7}$
and
$Ta=5.8\times 10^{7}$
and
![]() $Ta=6.2\times 10^{9}$
, respectively.
$Ta=6.2\times 10^{9}$
, respectively.
In addition to investigating the Taylor-number dependence, the height of the laser sheet was varied to characterise the axial dependence of the flow field. At 13 different heights with 7.5 mm spacing, 5000 image pairs of the velocity field were recorded. This was done at
![]() $Ta=4.2\times 10^{9}$
for both pure inner cylinder rotation and optimal (Merbold et al.
Reference Merbold, Brauckmann and Egbers2013) counter-rotation
$Ta=4.2\times 10^{9}$
for both pure inner cylinder rotation and optimal (Merbold et al.
Reference Merbold, Brauckmann and Egbers2013) counter-rotation
![]() $a=0.2$
.
$a=0.2$
.

Figure 3. Overview of the flow profiles for varying Taylor number with pure inner cylinder rotation
![]() $a=0$
at mid-height
$a=0$
at mid-height
![]() $h/L=0.5$
. (a) Snapshot of the flow field for
$h/L=0.5$
. (a) Snapshot of the flow field for
![]() $Ta=6.2\times 10^{9}$
. The colours and lengths of the arrows indicate the norm of the velocity
$Ta=6.2\times 10^{9}$
. The colours and lengths of the arrows indicate the norm of the velocity
![]() $|\tilde{\boldsymbol{u}}|$
. (c) Averaged flow field over 10 000 PIV image pairs at
$|\tilde{\boldsymbol{u}}|$
. (c) Averaged flow field over 10 000 PIV image pairs at
![]() $Ta=6.2\times 10^{9}$
. (b) Radial velocity profiles across the gap of the TC apparatus, normalised by the inner cylinder velocity. For lower Taylor numbers, there is still a strong radial flow, which can be attributed to the presence of Taylor vortices. (d) Azimuthal velocity profiles normalised by the inner cylinder velocity. For increasing Taylor number, the profiles become flatter and the boundary layers steeper. (e,f) Magnification of the azimuthal velocity profiles in (d) close to the cylinders.
$Ta=6.2\times 10^{9}$
. (b) Radial velocity profiles across the gap of the TC apparatus, normalised by the inner cylinder velocity. For lower Taylor numbers, there is still a strong radial flow, which can be attributed to the presence of Taylor vortices. (d) Azimuthal velocity profiles normalised by the inner cylinder velocity. For increasing Taylor number, the profiles become flatter and the boundary layers steeper. (e,f) Magnification of the azimuthal velocity profiles in (d) close to the cylinders.

Figure 4. Velocity profiles for inner cylinder rotation
![]() $a=0$
and varying Taylor number. See main text for the definitions of
$a=0$
and varying Taylor number. See main text for the definitions of
![]() $u^{+}$
,
$u^{+}$
,
![]() ${\it\omega}^{+}$
and
${\it\omega}^{+}$
and
![]() $y^{+}$
. (a) Azimuthal velocity profiles near the inner cylinder (
$y^{+}$
. (a) Azimuthal velocity profiles near the inner cylinder (
![]() $\tilde{r}\in [0,1/2]$
). (b) Azimuthal velocity profiles near the outer cylinder (
$\tilde{r}\in [0,1/2]$
). (b) Azimuthal velocity profiles near the outer cylinder (
![]() $\tilde{r}\in [1/2,1]$
). (c) Angular velocity profiles near the inner cylinder (
$\tilde{r}\in [1/2,1]$
). (c) Angular velocity profiles near the inner cylinder (
![]() $\tilde{r}\in [0,1/2]$
). (d) Angular velocity profiles near the outer cylinder (
$\tilde{r}\in [0,1/2]$
). (d) Angular velocity profiles near the outer cylinder (
![]() $\tilde{r}\in [1/2,1]$
). All panels include the logarithmic law of the wall from Prandtl and von Kármán,
$\tilde{r}\in [1/2,1]$
). All panels include the logarithmic law of the wall from Prandtl and von Kármán,
![]() $u^{+}=1/{\it\kappa}\ln y^{+}+B$
, with the typical values of
$u^{+}=1/{\it\kappa}\ln y^{+}+B$
, with the typical values of
![]() ${\it\kappa}=0.40$
and
${\it\kappa}=0.40$
and
![]() $B=5.2$
(see Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) and references therein), the viscous sublayer
$B=5.2$
(see Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) and references therein), the viscous sublayer
![]() $u^{+}=y^{+}$
, direct numerical simulation data from Chouippe et al. (Reference Chouippe, Climent, Legendre and Gabillet2014), Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) at
$u^{+}=y^{+}$
, direct numerical simulation data from Chouippe et al. (Reference Chouippe, Climent, Legendre and Gabillet2014), Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) at
![]() ${\it\eta}=0.5$
, and measurement data from Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) at
${\it\eta}=0.5$
, and measurement data from Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) at
![]() ${\it\eta}=0.716$
.
${\it\eta}=0.716$
.
3 Results
3.1 Azimuthal and angular velocity profiles
In this part the properties of flow profiles for varying Taylor number will be investigated. An example of an instantaneous flow field is shown in figure 3(a), while the averaged field is shown in figure 3(c). In figure 3(b) the normalised radial velocity
![]() $\tilde{u} _{r}=u_{r}/u_{{\it\theta}}(r_{i})$
versus the dimensionless gap position
$\tilde{u} _{r}=u_{r}/u_{{\it\theta}}(r_{i})$
versus the dimensionless gap position
![]() $\tilde{r}=(r-r_{i})/(r_{o}-r_{i})$
is shown, from which it is apparent that, at this specific axial position (mid-height), a significant mean radial flow still exists for the lower Taylor numbers up to approximately
$\tilde{r}=(r-r_{i})/(r_{o}-r_{i})$
is shown, from which it is apparent that, at this specific axial position (mid-height), a significant mean radial flow still exists for the lower Taylor numbers up to approximately
![]() $10^{9}$
. These are Taylor vortices, which at
$10^{9}$
. These are Taylor vortices, which at
![]() $a=0$
disappear for higher Taylor numbers (Lathrop et al.
Reference Lathrop, Fineberg and Swinney1992). With increasing Taylor number, the azimuthal velocity profile in the bulk becomes flatter (figure 3
d–f), but it is still apparent that the strong curvature of a radius ratio of
$a=0$
disappear for higher Taylor numbers (Lathrop et al.
Reference Lathrop, Fineberg and Swinney1992). With increasing Taylor number, the azimuthal velocity profile in the bulk becomes flatter (figure 3
d–f), but it is still apparent that the strong curvature of a radius ratio of
![]() ${\it\eta}=0.5$
creates a significant asymmetry between the inner and outer boundary layers.
${\it\eta}=0.5$
creates a significant asymmetry between the inner and outer boundary layers.
In figure 4, profiles up to the middle of the gap are shown, normalised to the wall-normal distance
![]() $y^{+}$
from both the inner and outer cylinders, and to the azimuthal velocity
$y^{+}$
from both the inner and outer cylinders, and to the azimuthal velocity
![]() $u^{+}$
(figure 4
a,b) and angular velocity
$u^{+}$
(figure 4
a,b) and angular velocity
![]() ${\it\omega}^{+}$
(figure 4
c,d). The wall-normal distance, azimuthal velocity and angular velocity for the inner cylinder are defined as
${\it\omega}^{+}$
(figure 4
c,d). The wall-normal distance, azimuthal velocity and angular velocity for the inner cylinder are defined as
As the driving is increased, the profiles slowly approach the Prandtl–von Kármán log law, although at these Taylor numbers the log layer is not yet fully developed. For comparison, profiles at higher Taylor numbers and aspect ratio of
![]() ${\it\eta}=0.716$
from Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) are also plotted. The data show good agreement with direct numerical simulations (DNS) at the same radius ratio
${\it\eta}=0.716$
from Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) are also plotted. The data show good agreement with direct numerical simulations (DNS) at the same radius ratio
![]() ${\it\eta}=0.5$
from Chouippe et al. (Reference Chouippe, Climent, Legendre and Gabillet2014) at
${\it\eta}=0.5$
from Chouippe et al. (Reference Chouippe, Climent, Legendre and Gabillet2014) at
![]() $Ta=1.8\times 10^{8}$
, Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
) at
$Ta=1.8\times 10^{8}$
, Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
) at
![]() $Ta=1.0\times 10^{9}$
and
$Ta=1.0\times 10^{9}$
and
![]() $Ta=1.0\times 10^{10}$
, and Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) at
$Ta=1.0\times 10^{10}$
, and Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) at
![]() $Ta=1.1\times 10^{11}$
.
$Ta=1.1\times 10^{11}$
.
When comparing the azimuthal velocity
![]() $u^{+}$
to the angular velocity
$u^{+}$
to the angular velocity
![]() ${\it\omega}^{+}$
, i.e. figure 4(a) to 4(c) and figure 4(b) to 4(d), it can be seen that the angular velocity profiles curve upwards more compared to the azimuthal ones. This is consistent with the theoretical argument of Grossmann et al. (Reference Grossmann, Lohse and Sun2014) that the angular velocity profile
${\it\omega}^{+}$
, i.e. figure 4(a) to 4(c) and figure 4(b) to 4(d), it can be seen that the angular velocity profiles curve upwards more compared to the azimuthal ones. This is consistent with the theoretical argument of Grossmann et al. (Reference Grossmann, Lohse and Sun2014) that the angular velocity profile
![]() ${\it\omega}^{+}$
is closer to a log law than the azimuthal velocity profile
${\it\omega}^{+}$
is closer to a log law than the azimuthal velocity profile
![]() $u^{+}$
. The effect is much more pronounced for the smaller
$u^{+}$
. The effect is much more pronounced for the smaller
![]() ${\it\eta}=0.5$
here as compared to the
${\it\eta}=0.5$
here as compared to the
![]() ${\it\eta}=0.716$
from Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013). Note that, for example, the lower-Taylor-number
${\it\eta}=0.716$
from Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013). Note that, for example, the lower-Taylor-number
![]() $u^{+}$
profiles at
$u^{+}$
profiles at
![]() ${\it\eta}=0.716$
are above the profiles measured here, but that they cross when represented as
${\it\eta}=0.716$
are above the profiles measured here, but that they cross when represented as
![]() ${\it\omega}^{+}$
. This clearly shows the influence of the large curvature for small-radius-ratio TC set-ups.
${\it\omega}^{+}$
. This clearly shows the influence of the large curvature for small-radius-ratio TC set-ups.

Figure 5. The scaling of the wind Reynolds number
![]() $Re_{w}$
and turbulence intensity
$Re_{w}$
and turbulence intensity
![]() $I$
with Taylor number for inner cylinder rotation
$I$
with Taylor number for inner cylinder rotation
![]() $a=0$
. (a,b) The standard deviation of the radial velocity (a) and azimuthal velocity (b) over 10 000 frames (400 s) and the azimuthal direction, normalised by the inner cylinder velocity, as a function of the normalised radial position. This corresponds to the turbulence intensity
$a=0$
. (a,b) The standard deviation of the radial velocity (a) and azimuthal velocity (b) over 10 000 frames (400 s) and the azimuthal direction, normalised by the inner cylinder velocity, as a function of the normalised radial position. This corresponds to the turbulence intensity
![]() $I$
in the case of the azimuthal velocity. See the legend in figures 3 or 4 for the values of the Taylor numbers. The three areas A (
$I$
in the case of the azimuthal velocity. See the legend in figures 3 or 4 for the values of the Taylor numbers. The three areas A (
![]() $\tilde{r}\in [1/8,3/8]$
), B (
$\tilde{r}\in [1/8,3/8]$
), B (
![]() $\tilde{r}\in [3/8,5/8]$
) and C (
$\tilde{r}\in [3/8,5/8]$
) and C (
![]() $\tilde{r}\in [5/8,7/8]$
) indicate regions over which
$\tilde{r}\in [5/8,7/8]$
) indicate regions over which
![]() ${\it\sigma}$
is averaged for (c–e). The black dots represent the position of the start of the outer layers at
${\it\sigma}$
is averaged for (c–e). The black dots represent the position of the start of the outer layers at
![]() $y^{+}=50$
. (c) Plot showing
$y^{+}=50$
. (c) Plot showing
![]() $Re_{w}$
versus
$Re_{w}$
versus
![]() $Ta$
averaged over
$Ta$
averaged over
![]() $\tilde{r}$
values corresponding to regions A, B, C and all three combined (
$\tilde{r}$
values corresponding to regions A, B, C and all three combined (
![]() $\tilde{r}\in [1/8,7/8]$
). In addition, data from Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) at
$\tilde{r}\in [1/8,7/8]$
). In addition, data from Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) at
![]() ${\it\eta}=0.716$
with their fit are shown, which are fully in the ultimate turbulent regime. These data use the equivalent to area B for averaging. (d) Turbulence intensity
${\it\eta}=0.716$
with their fit are shown, which are fully in the ultimate turbulent regime. These data use the equivalent to area B for averaging. (d) Turbulence intensity
![]() $I$
versus
$I$
versus
![]() $Ta$
averaged over the same regions as before. The fits are
$Ta$
averaged over the same regions as before. The fits are
![]() $I=0.27Ta^{-0.066}$
for area A,
$I=0.27Ta^{-0.066}$
for area A,
![]() $I=0.33Ta^{-0.076}$
for area B,
$I=0.33Ta^{-0.076}$
for area B,
![]() $I=0.41Ta^{-0.098}$
for area C and
$I=0.41Ta^{-0.098}$
for area C and
![]() $I=0.32Ta^{-0.079}$
for the three areas combined. (e) Data in (c) compensated by
$I=0.32Ta^{-0.079}$
for the three areas combined. (e) Data in (c) compensated by
![]() $Ta^{3/7}$
. The fits are
$Ta^{3/7}$
. The fits are
![]() $Re_{w}=0.162Ta^{0.434}$
for area A,
$Re_{w}=0.162Ta^{0.434}$
for area A,
![]() $Re_{w}=0.193Ta^{0.424}$
for area B,
$Re_{w}=0.193Ta^{0.424}$
for area B,
![]() $Re_{w}=0.240Ta^{0.402}$
for area C and
$Re_{w}=0.240Ta^{0.402}$
for area C and
![]() $Re_{w}=0.192Ta^{0.421}$
for the three areas combined. The standard errors of the fitted exponents are 0.007, 0.007, 0.005 and 0.005, respectively.
$Re_{w}=0.192Ta^{0.421}$
for the three areas combined. The standard errors of the fitted exponents are 0.007, 0.007, 0.005 and 0.005, respectively.
3.2 Wind Reynolds number and turbulence intensity
In the analogy between TC and Rayleigh–Bénard flow, the unifying theory of Grossmann & Lohse (Reference Grossmann and Lohse2000) predicts that the wind Reynolds number in the classical turbulent regime scales as
In contrast, in the ultimate turbulent regime, the scaling was predicted to be
![]() $Re_{w}\propto Ta^{1/2}$
(Grossmann & Lohse Reference Grossmann and Lohse2011), which was confirmed experimentally by Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) for TC flow with
$Re_{w}\propto Ta^{1/2}$
(Grossmann & Lohse Reference Grossmann and Lohse2011), which was confirmed experimentally by Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) for TC flow with
![]() ${\it\eta}=0.716$
for
${\it\eta}=0.716$
for
![]() $Ta$
up to
$Ta$
up to
![]() $6.2\times 10^{12}$
.
$6.2\times 10^{12}$
.
The highest Taylor number we achieve in the present measurements is
![]() $Ta=6.2\times 10^{9}$
, which for
$Ta=6.2\times 10^{9}$
, which for
![]() ${\it\eta}=0.5$
with the higher transitional Taylor number of
${\it\eta}=0.5$
with the higher transitional Taylor number of
![]() $Ta=10^{10}$
(Merbold et al.
Reference Merbold, Brauckmann and Egbers2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
) implies that we are in the classical turbulent regime. Therefore we expect the theoretically predicted
$Ta=10^{10}$
(Merbold et al.
Reference Merbold, Brauckmann and Egbers2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
) implies that we are in the classical turbulent regime. Therefore we expect the theoretically predicted
![]() $3/7$
scaling to hold. This classical scaling was measured in Rayleigh–Bénard convection (He et al.
Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers2012), but to our knowledge has not yet been confirmed for TC flow.
$3/7$
scaling to hold. This classical scaling was measured in Rayleigh–Bénard convection (He et al.
Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers2012), but to our knowledge has not yet been confirmed for TC flow.
The wind Reynolds number
![]() $Re_{w}$
is extracted from the velocity field
$Re_{w}$
is extracted from the velocity field
![]() $u_{r}({\it\theta},r,z,t)$
by calculating the standard deviation
$u_{r}({\it\theta},r,z,t)$
by calculating the standard deviation
![]() ${\it\sigma}(u_{r}(r,{\it\theta},t))$
over time and the azimuthal direction, which is then averaged over a certain range in the gap (see figure 5). When looking at the shape of the
${\it\sigma}(u_{r}(r,{\it\theta},t))$
over time and the azimuthal direction, which is then averaged over a certain range in the gap (see figure 5). When looking at the shape of the
![]() $\tilde{r}$
dependence of
$\tilde{r}$
dependence of
![]() ${\it\sigma}(u_{r})$
in figure 5(a), it is apparent that an asymmetry is present. The fluctuations exhibit a maximum around a quarter of the gap width away from the inner cylinder. It is likely that the strong curvature of the
${\it\sigma}(u_{r})$
in figure 5(a), it is apparent that an asymmetry is present. The fluctuations exhibit a maximum around a quarter of the gap width away from the inner cylinder. It is likely that the strong curvature of the
![]() ${\it\eta}=0.5$
set-up causes this asymmetry. Calculating the wind Reynolds number thus comes with an arbitrariness in the area to choose for averaging the profile of
${\it\eta}=0.5$
set-up causes this asymmetry. Calculating the wind Reynolds number thus comes with an arbitrariness in the area to choose for averaging the profile of
![]() ${\it\sigma}(r)$
, although excluding the boundary layers is reasonable because the interest lies in the convective bulk transport, as opposed to the diffusive transport in the boundary layers. The dependence of
${\it\sigma}(r)$
, although excluding the boundary layers is reasonable because the interest lies in the convective bulk transport, as opposed to the diffusive transport in the boundary layers. The dependence of
![]() $Re_{w}(Ta)$
is shown in figure 5(c) for different regions of averaging. Region B lies within the outer layer of both the inner and outer cylinders for all Taylor numbers.
$Re_{w}(Ta)$
is shown in figure 5(c) for different regions of averaging. Region B lies within the outer layer of both the inner and outer cylinders for all Taylor numbers.
From figure 5(e) it can be seen that a clear power-law scaling is present, with an exponent that ranges from 0.402 to 0.434, depending on the region of averaging. The scaling in regions A, B and A + B + C is consistent with the theoretically predicted classical regime scaling of
![]() $3/7\approx 0.429$
(Grossmann & Lohse Reference Grossmann and Lohse2000) within the experimental uncertainties.
$3/7\approx 0.429$
(Grossmann & Lohse Reference Grossmann and Lohse2000) within the experimental uncertainties.
A similar analysis is performed on the azimuthal velocity instead of the radial velocity, as shown in figure 5(b,d). Again, the difference of the shearing velocity (
![]() $u_{i}-u_{o}$
), which in the case of
$u_{i}-u_{o}$
), which in the case of
![]() $a=0$
simplifies to
$a=0$
simplifies to
![]() $u_{i}$
, is used to normalise the standard deviation. This results in a turbulence intensity
$u_{i}$
, is used to normalise the standard deviation. This results in a turbulence intensity
![]() $I={\it\sigma}(u_{{\it\theta}})/u_{i}$
, analogous to the turbulence intensity defined in Rayleigh–Bénard convection. The difference in rotation velocities of TC flow is analogous to the temperature difference in Rayleigh–Bénard convection (Grossmann & Lohse Reference Grossmann and Lohse2000). We find that the turbulence intensity has maxima in both the boundary layers, similar to the findings of Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013), and a relatively flat region in the bulk. The turbulence intensity
$I={\it\sigma}(u_{{\it\theta}})/u_{i}$
, analogous to the turbulence intensity defined in Rayleigh–Bénard convection. The difference in rotation velocities of TC flow is analogous to the temperature difference in Rayleigh–Bénard convection (Grossmann & Lohse Reference Grossmann and Lohse2000). We find that the turbulence intensity has maxima in both the boundary layers, similar to the findings of Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013), and a relatively flat region in the bulk. The turbulence intensity
![]() $I(r)$
is averaged over the same regions as in figure 5(a) and shows negative scaling:
$I(r)$
is averaged over the same regions as in figure 5(a) and shows negative scaling:
![]() $I\propto Ta^{{\it\gamma}}$
with
$I\propto Ta^{{\it\gamma}}$
with
![]() $-0.1<{\it\gamma}<-0.07$
, depending on the region of averaging. This result is in rough agreement with the findings in Rayleigh–Bénard flow (Shang, Tong & Xia Reference Shang, Tong and Xia2008; Lakkaraju et al.
Reference Lakkaraju, Stevens, Verzicco, Grossmann, Prosperetti, Sun and Lohse2012), where the authors found a scaling exponent of
$-0.1<{\it\gamma}<-0.07$
, depending on the region of averaging. This result is in rough agreement with the findings in Rayleigh–Bénard flow (Shang, Tong & Xia Reference Shang, Tong and Xia2008; Lakkaraju et al.
Reference Lakkaraju, Stevens, Verzicco, Grossmann, Prosperetti, Sun and Lohse2012), where the authors found a scaling exponent of
![]() $-0.2<{\it\gamma}_{RB}<-0.1$
in the classical regime, depending on the Rayleigh number and the location of the temperature measurements. It is expected that
$-0.2<{\it\gamma}_{RB}<-0.1$
in the classical regime, depending on the Rayleigh number and the location of the temperature measurements. It is expected that
![]() ${\it\gamma}\rightarrow 0$
for
${\it\gamma}\rightarrow 0$
for
![]() $Re\rightarrow \infty$
, possibly explaining the higher exponent measured here because of a more turbulent system. Additionally, TC flow, with its curved boundaries, might have a fundamentally different scaling exponent.
$Re\rightarrow \infty$
, possibly explaining the higher exponent measured here because of a more turbulent system. Additionally, TC flow, with its curved boundaries, might have a fundamentally different scaling exponent.

Figure 6. Dependence of flow profiles on axial position for rotation ratios
![]() $a=0$
(a,b,e,f) and
$a=0$
(a,b,e,f) and
![]() $a=0.2$
(c,d,g,h) for
$a=0.2$
(c,d,g,h) for
![]() $Ta=4.2\times 10^{9}$
. The normalised radial velocity is
$Ta=4.2\times 10^{9}$
. The normalised radial velocity is
![]() $\tilde{u} _{r}=u_{r}(r)/(u_{i}-u_{o})$
and the azimuthal velocity is
$\tilde{u} _{r}=u_{r}(r)/(u_{i}-u_{o})$
and the azimuthal velocity is
![]() $\tilde{u} _{{\it\theta}}=(u_{{\it\theta}}(r)-u_{o})/(u_{i}-u_{o})$
. The data are represented in a colour map (a–d) and as profiles in (e–h).
$\tilde{u} _{{\it\theta}}=(u_{{\it\theta}}(r)-u_{o})/(u_{i}-u_{o})$
. The data are represented in a colour map (a–d) and as profiles in (e–h).
3.3 Roll structures
The phenomena of roll structures, turbulent plumes and logarithmic velocity profiles in TC flow are intimately connected (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
c
). We will first show an example of roll structures that are observed in TC flow. Flow profiles at several heights for both
![]() $a=0$
and
$a=0$
and
![]() $a=0.2$
are measured, allowing us to visualise roll structures as shown in figure 6. At this reasonably high Taylor number of
$a=0.2$
are measured, allowing us to visualise roll structures as shown in figure 6. At this reasonably high Taylor number of
![]() $Ta=4.2\times 10^{9}$
, no clear roll structures exist for inner cylinder rotation only. The radial velocity shows some very faint indications of rolls, with a maximum value of
$Ta=4.2\times 10^{9}$
, no clear roll structures exist for inner cylinder rotation only. The radial velocity shows some very faint indications of rolls, with a maximum value of
![]() $\tilde{u} _{r}=0.01$
in the centre of the gap. In contrast, in the case of counter-rotation (
$\tilde{u} _{r}=0.01$
in the centre of the gap. In contrast, in the case of counter-rotation (
![]() $a=0.2$
), very strong roll structures can be seen. The fact that there are strong rolls at optimal counter-rotation and no clear structures at inner cylinder rotation only is corroborated by recent work for higher radius ratio (Tokgoz et al.
Reference Tokgoz, Elsinga, Delfos and Westerweel2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
).
$a=0.2$
), very strong roll structures can be seen. The fact that there are strong rolls at optimal counter-rotation and no clear structures at inner cylinder rotation only is corroborated by recent work for higher radius ratio (Tokgoz et al.
Reference Tokgoz, Elsinga, Delfos and Westerweel2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
).
In the radial flow between two rolls at approximately
![]() $h/L=0.50$
to
$h/L=0.50$
to
![]() $h/L=0.52$
, there is very strong outwards radial flow (see figure 6
c). Specifically, the height
$h/L=0.52$
, there is very strong outwards radial flow (see figure 6
c). Specifically, the height
![]() $0.52L$
corresponds to the bottom of a roll, while
$0.52L$
corresponds to the bottom of a roll, while
![]() $0.50L$
corresponds to the top of the roll below. Exactly in between the rolls at
$0.50L$
corresponds to the top of the roll below. Exactly in between the rolls at
![]() $0.51L$
, the radial flow surprisingly exhibits a local minimum. One might a priori expect symmetry around mid-height (
$0.51L$
, the radial flow surprisingly exhibits a local minimum. One might a priori expect symmetry around mid-height (
![]() $0.50L$
) instead of at
$0.50L$
) instead of at
![]() $0.51L$
as observed. However, symmetry breaking of large-scale turbulent flow structures in symmetrical set-ups has been observed before, not only in TC flow (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016), but also in von Kármán flow (López-Caballero & Burguete Reference López-Caballero and Burguete2013). In figure 6(d,h) it can be seen that, in the case of positive (outward) radial flow, the inner cylinder velocity is advected outwards, shifting the profiles upwards at the inner half of the gap. For negative (inward) radial flow, the profiles shift downwards in the outer half of the gap. In summary, the roll structures are represented by a large secondary flow of
$0.51L$
as observed. However, symmetry breaking of large-scale turbulent flow structures in symmetrical set-ups has been observed before, not only in TC flow (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016), but also in von Kármán flow (López-Caballero & Burguete Reference López-Caballero and Burguete2013). In figure 6(d,h) it can be seen that, in the case of positive (outward) radial flow, the inner cylinder velocity is advected outwards, shifting the profiles upwards at the inner half of the gap. For negative (inward) radial flow, the profiles shift downwards in the outer half of the gap. In summary, the roll structures are represented by a large secondary flow of
![]() $u_{r}$
, which advects velocity from the cylinders and changes the azimuthal velocity profiles. In the following two subsections we will elaborate on the characteristics of turbulent plumes and their effect on the velocity profiles.
$u_{r}$
, which advects velocity from the cylinders and changes the azimuthal velocity profiles. In the following two subsections we will elaborate on the characteristics of turbulent plumes and their effect on the velocity profiles.
3.4 Turbulent plumes
In turbulent TC flow, structures detach from the boundary layers, called herring-bone streaks (Dong Reference Dong2007) or velocity plumes (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
), in correspondence to the thermal plumes in the analogous turbulent Rayleigh–Bénard convection. These plumes in TC flow are large-scale spatial and temporal fluctuations in the velocity fields that detach from either the inner or outer cylinder and advect velocity from the respective cylinder. Because of the sufficiently high frame rate of 25 f.p.s. and large amount of data recorded in our experiments, these plumes can be resolved in time, and the typical velocity can be extracted. We are interested in understanding how these plumes are affected by roll structures and whether some scaling relation exists for the typical plume velocity as a function of the driving parameter
![]() $Ta$
.
$Ta$
.

Figure 7. Overview of turbulent burst velocity depending on axial position, for both pure inner cylinder rotation
![]() $a=0$
(a–f) and counter-rotation of
$a=0$
(a–f) and counter-rotation of
![]() $a=0.2$
(g–l), at
$a=0.2$
(g–l), at
![]() $Ta=4.2\times 10^{9}$
. The radial velocity dependence is shown in (a,c,d,g,i,j) and the azimuthal velocity in (b,e,f,h,k,l). (a,b,g,h) Example of the radial and azimuthal velocity as a function of the normalised gap distance and time for the axial position of
$Ta=4.2\times 10^{9}$
. The radial velocity dependence is shown in (a,c,d,g,i,j) and the azimuthal velocity in (b,e,f,h,k,l). (a,b,g,h) Example of the radial and azimuthal velocity as a function of the normalised gap distance and time for the axial position of
![]() $0.50L$
. Only 10 s of the total 200 s per experiment are shown for clarity. Diagonal lines with a positive (negative) slope correspond to plumes coming from the inner (outer) cylinder. The extracted plume velocity (see text for method) is shown as a black line. (c,e,i,k) As above, for every height normalised by the total height of the cylinder
$0.50L$
. Only 10 s of the total 200 s per experiment are shown for clarity. Diagonal lines with a positive (negative) slope correspond to plumes coming from the inner (outer) cylinder. The extracted plume velocity (see text for method) is shown as a black line. (c,e,i,k) As above, for every height normalised by the total height of the cylinder
![]() $L$
. (d,f,j,l) The inverse of the resulting normalised burst velocity. For
$L$
. (d,f,j,l) The inverse of the resulting normalised burst velocity. For
![]() $a=0$
the inner cylinder velocity is
$a=0$
the inner cylinder velocity is
![]() $1.1~\text{m}~\text{s}^{-1}$
and for
$1.1~\text{m}~\text{s}^{-1}$
and for
![]() $a=0.2$
the inner and outer cylinder velocities are
$a=0.2$
the inner and outer cylinder velocities are
![]() $0.91~\text{m}~\text{s}^{-1}$
and
$0.91~\text{m}~\text{s}^{-1}$
and
![]() $-0.36~\text{m}~\text{s}^{-1}$
, respectively. The error bars show the width of the test function at 0.95 times the peak value.
$-0.36~\text{m}~\text{s}^{-1}$
, respectively. The error bars show the width of the test function at 0.95 times the peak value.
The time dependence of the profiles of the azimuthal and radial velocity can be represented by the spatio-temporal fields
![]() $u_{r}(r,t)$
and
$u_{r}(r,t)$
and
![]() $u_{{\it\theta}}(r,t)$
, with the value of the velocities represented by a colour map, as shown in figure 7(a), for example. In this way, structures or fluctuations of the profiles that propagate inwards or outwards become visible as diagonal lines. It has to be stressed that these diagonals do not represent a non-zero mean radial flow, but only the fluctuations on these profiles that travel outwards or inwards. In order to assign a velocity to these plumes, we employ an analysis that is based on applying the following affine shearing transformation to the functions
$u_{{\it\theta}}(r,t)$
, with the value of the velocities represented by a colour map, as shown in figure 7(a), for example. In this way, structures or fluctuations of the profiles that propagate inwards or outwards become visible as diagonal lines. It has to be stressed that these diagonals do not represent a non-zero mean radial flow, but only the fluctuations on these profiles that travel outwards or inwards. In order to assign a velocity to these plumes, we employ an analysis that is based on applying the following affine shearing transformation to the functions
![]() $u_{r}(r,t)$
and
$u_{r}(r,t)$
and
![]() $u_{{\it\theta}}(r,t)$
:
$u_{{\it\theta}}(r,t)$
:
with
![]() $\tilde{r}=(r-r_{i})/d$
, gap width
$\tilde{r}=(r-r_{i})/d$
, gap width
![]() $d$
and plume velocity
$d$
and plume velocity
![]() $v_{b}$
. For a certain amount of shearing, the plumes that were represented by diagonal lines become vertical lines. To find this optimal value of shearing, we postulate that, when averaging the sheared function over
$v_{b}$
. For a certain amount of shearing, the plumes that were represented by diagonal lines become vertical lines. To find this optimal value of shearing, we postulate that, when averaging the sheared function over
![]() $\tilde{r}$
, the standard deviation of the resulting time signal has a maximum as a function of the shearing value. At this optimal shearing, the plumes are represented by narrow peaks in the time signal, creating a high standard deviation. Using a golden section search algorithm (Kiefer Reference Kiefer1953), the optimal shearing value is found, which corresponds to the characteristic plume velocity
$\tilde{r}$
, the standard deviation of the resulting time signal has a maximum as a function of the shearing value. At this optimal shearing, the plumes are represented by narrow peaks in the time signal, creating a high standard deviation. Using a golden section search algorithm (Kiefer Reference Kiefer1953), the optimal shearing value is found, which corresponds to the characteristic plume velocity
![]() $v_{b}$
. Note that plumes can go both inwards and outwards and that this
$v_{b}$
. Note that plumes can go both inwards and outwards and that this
![]() $v_{b}$
corresponds to the ‘strongest’ plume direction, not necessarily to the mean plume velocity.
$v_{b}$
corresponds to the ‘strongest’ plume direction, not necessarily to the mean plume velocity.
The dependence of the plume velocity on the axial position and the rotation ratio is shown in figure 7. Again, for inner cylinder rotation only (
![]() $a=0$
), no height dependence can be seen. The fluctuations on the radial velocity are moving outwards with a velocity
$a=0$
), no height dependence can be seen. The fluctuations on the radial velocity are moving outwards with a velocity
![]() $v_{b}/(u_{i}-u_{o})=0.25\pm 0.02$
(
$v_{b}/(u_{i}-u_{o})=0.25\pm 0.02$
(
![]() $u_{o}=0$
,
$u_{o}=0$
,
![]() $2{\it\sigma}$
error). When the azimuthal velocity is considered, the picture looks different. Crossing diagonal lines can be seen, meaning that plumes emit from both the inner and outer cylinders. A maximum was found for inward plumes with an average velocity of
$2{\it\sigma}$
error). When the azimuthal velocity is considered, the picture looks different. Crossing diagonal lines can be seen, meaning that plumes emit from both the inner and outer cylinders. A maximum was found for inward plumes with an average velocity of
![]() $v_{b}/(u_{i}-u_{o})=-0.20\pm 0.02$
. The velocity of these plumes is of the same order, but it remains to be explained why the main plume direction is different for the two velocity components.
$v_{b}/(u_{i}-u_{o})=-0.20\pm 0.02$
. The velocity of these plumes is of the same order, but it remains to be explained why the main plume direction is different for the two velocity components.
For counter-rotation (
![]() $a=0.2$
), the bottom half of figure 7 clearly indicates that roll structures are present. There is a correspondence between the sign of the mean radial velocity and the direction of these turbulent plumes, coming from either the inner or outer cylinder – compare figure 6(c) with figure 7(i,k). For both velocity components, the direction of the plumes corresponds to the direction of the mean radial velocity. The mean radial velocity forces the plumes strongly in the inward or outward direction, also typically creating a higher plume velocity than for the
$a=0.2$
), the bottom half of figure 7 clearly indicates that roll structures are present. There is a correspondence between the sign of the mean radial velocity and the direction of these turbulent plumes, coming from either the inner or outer cylinder – compare figure 6(c) with figure 7(i,k). For both velocity components, the direction of the plumes corresponds to the direction of the mean radial velocity. The mean radial velocity forces the plumes strongly in the inward or outward direction, also typically creating a higher plume velocity than for the
![]() $a=0$
case. Whereas for the
$a=0$
case. Whereas for the
![]() $a=0$
case there was some ambiguity in the direction of the plumes for the azimuthal velocity, for
$a=0$
case there was some ambiguity in the direction of the plumes for the azimuthal velocity, for
![]() $a=0.2$
it exactly follows the roll structure. When looking at the radial velocity, the inward plumes are less pronounced than the outward ones, likely due to a tendency for the
$a=0.2$
it exactly follows the roll structure. When looking at the radial velocity, the inward plumes are less pronounced than the outward ones, likely due to a tendency for the
![]() $u_{r}$
plumes to flow outwards, as could be seen for the
$u_{r}$
plumes to flow outwards, as could be seen for the
![]() $a=0$
case.
$a=0$
case.
In addition to the dependence on the axial position and the rotation ratio, in figure 8 the dependence of the plume velocity on the driving parameter
![]() $Ta$
is shown. With increasing driving strength, the velocity of the plumes also increases. When the plume velocity is normalised by
$Ta$
is shown. With increasing driving strength, the velocity of the plumes also increases. When the plume velocity is normalised by
![]() $(u_{i}-u_{o})$
, it is however nearly constant over two decades of
$(u_{i}-u_{o})$
, it is however nearly constant over two decades of
![]() $Ta$
.
$Ta$
.

Figure 9. Angular velocity profile dependence on mean radial flow for counter-rotation
![]() $a=0.2$
and
$a=0.2$
and
![]() $Ta=4.2\times 10^{9}$
at varying axial positions (data from figure 6
h). (a) Angular velocity profiles near the inner cylinder (
$Ta=4.2\times 10^{9}$
at varying axial positions (data from figure 6
h). (a) Angular velocity profiles near the inner cylinder (
![]() $\tilde{r}\in [0,1/2]$
). The angular velocity
$\tilde{r}\in [0,1/2]$
). The angular velocity
![]() ${\it\omega}^{+}$
and wall-normal distance
${\it\omega}^{+}$
and wall-normal distance
![]() $y^{+}$
are defined in the caption of figure 4, the colours and line styles of the profiles correspond to those in figure 6. The grey area is the fitting domain
$y^{+}$
are defined in the caption of figure 4, the colours and line styles of the profiles correspond to those in figure 6. The grey area is the fitting domain
![]() $y^{+}\in [50,800]$
, chosen to encompass the start of the outer region up to mid-gap for both inner and outer cylinders. (b) Angular velocity profiles near the outer cylinder (
$y^{+}\in [50,800]$
, chosen to encompass the start of the outer region up to mid-gap for both inner and outer cylinders. (b) Angular velocity profiles near the outer cylinder (
![]() $\tilde{r}\in [1/2,1]$
). (c) Normalised radial velocity
$\tilde{r}\in [1/2,1]$
). (c) Normalised radial velocity
![]() $\tilde{u} _{r}$
as in figure 6(g). (d) The von Kármán constant
$\tilde{u} _{r}$
as in figure 6(g). (d) The von Kármán constant
![]() ${\it\kappa}_{{\it\omega}}$
found by fitting
${\it\kappa}_{{\it\omega}}$
found by fitting
![]() ${\it\omega}^{+}=1/{\it\kappa}_{{\it\omega}}\ln y^{+}+B$
for
${\it\omega}^{+}=1/{\it\kappa}_{{\it\omega}}\ln y^{+}+B$
for
![]() $y^{+}\in [50,800]$
near the inner (IC) and outer (OC) cylinder. The horizontal axis shows the normalised wall-normal velocity, equal to
$y^{+}\in [50,800]$
near the inner (IC) and outer (OC) cylinder. The horizontal axis shows the normalised wall-normal velocity, equal to
![]() $\tilde{u} _{r}$
and
$\tilde{u} _{r}$
and
![]() $-\tilde{u} _{r}$
for the IC and OC, respectively, averaged over
$-\tilde{u} _{r}$
for the IC and OC, respectively, averaged over
![]() $\tilde{r}\in [1/4,3/4]$
. The error bars have a total length of four times the standard error of the fit. (e) The standard error of the fitting parameter
$\tilde{r}\in [1/4,3/4]$
. The error bars have a total length of four times the standard error of the fit. (e) The standard error of the fitting parameter
![]() ${\it\kappa}_{{\it\omega}}$
.
${\it\kappa}_{{\it\omega}}$
.
3.5 Logarithmic velocity profiles
It has been proposed that the logarithmic temperature profiles in Rayleigh–Bénard convection and logarithmic velocity profiles in TC flow are triggered by plume ejection (Ahlers et al. Reference Ahlers, Bodenschatz and He2014; Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b ; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015). These authors also support the notion that parts of the boundary layer can be turbulent, while others are not, and that the transition to the ultimate regime entails plume emission from the full extent of the boundary layer.
We will now further investigate the effect of the plumes on the logarithmic nature of the velocity profiles. As we have seen before, the roll structure that appears for counter-rotation of
![]() $a=0.2$
provides strong mean radial flows, which cause plume emission away from either the inner or outer cylinder.
$a=0.2$
provides strong mean radial flows, which cause plume emission away from either the inner or outer cylinder.
In figure 9(a) the angular velocity at the inner cylinder is shown. It can be seen that there is a significant variation in the shape of the profiles, and that profiles at the axial positions where a strong positive radial flow exists (top lines in figure 9 c) follow the shape of a logarithmic law more closely. This effect is even stronger at the outer cylinder in figure 9(b), where profiles at an axial position with negative radial flow, so a flow away from the outer cylinder, correspond best to a log law.
To quantify this phenomenon, the velocity profiles are fitted with the modified (Grossmann et al.
Reference Grossmann, Lohse and Sun2014) Prandtl–von Kármán law of the wall:
![]() ${\it\omega}^{+}=1/{\it\kappa}_{{\it\omega}}\ln y^{+}+B$
, with both
${\it\omega}^{+}=1/{\it\kappa}_{{\it\omega}}\ln y^{+}+B$
, with both
![]() ${\it\kappa}_{{\it\omega}}$
and
${\it\kappa}_{{\it\omega}}$
and
![]() $B$
as fitting parameters. We quantify the deviation from a log profile by the standard error of the fitting parameter
$B$
as fitting parameters. We quantify the deviation from a log profile by the standard error of the fitting parameter
![]() ${\it\sigma}({\it\kappa}_{{\it\omega}})$
. A small value of
${\it\sigma}({\it\kappa}_{{\it\omega}})$
. A small value of
![]() ${\it\sigma}({\it\kappa}_{{\it\omega}})$
corresponds to a profile that closely follows a log law. In figure 9(d) it can be seen that, for a mean wall-normal velocity away from the cylinder (positive
${\it\sigma}({\it\kappa}_{{\it\omega}})$
corresponds to a profile that closely follows a log law. In figure 9(d) it can be seen that, for a mean wall-normal velocity away from the cylinder (positive
![]() $\langle \tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\rangle$
), the value of
$\langle \tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\rangle$
), the value of
![]() ${\it\kappa}_{{\it\omega}}$
more closely approaches the known classical value of 0.40. Additionally, the error of the fit is much smaller for positive values of the outward wall-normal velocity as compared to negative values. This means that, for regions with strong radial flow away from a cylinder surface, the velocity profiles follow a log law more closely. In the previous section it was found that, at these regions, plumes are emitted from the cylinder surface. We therefore postulate that turbulent plumes are responsible for logarithmic boundary layers. This is in line with results from DNS (van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
).
${\it\kappa}_{{\it\omega}}$
more closely approaches the known classical value of 0.40. Additionally, the error of the fit is much smaller for positive values of the outward wall-normal velocity as compared to negative values. This means that, for regions with strong radial flow away from a cylinder surface, the velocity profiles follow a log law more closely. In the previous section it was found that, at these regions, plumes are emitted from the cylinder surface. We therefore postulate that turbulent plumes are responsible for logarithmic boundary layers. This is in line with results from DNS (van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
).
4 Conclusions
In this work, we measured velocity profiles, the wind Reynolds number and characteristics of turbulent plumes in TC flow for a radius ratio of 0.5 and Taylor number of up to
![]() $6.2\times 10^{9}$
. The flow profiles show Taylor vortices for a Taylor number smaller than
$6.2\times 10^{9}$
. The flow profiles show Taylor vortices for a Taylor number smaller than
![]() $Ta\approx 10^{9}$
. The normalised profiles approach the Prandtl–von Kármán log law, although at the highest
$Ta\approx 10^{9}$
. The normalised profiles approach the Prandtl–von Kármán log law, although at the highest
![]() $Ta=6.2\times 10^{9}$
the log layer is not yet fully developed. They are in good agreement with DNS data from other work (Chouippe et al.
Reference Chouippe, Climent, Legendre and Gabillet2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
; Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016). Owing to the strong curvature of this
$Ta=6.2\times 10^{9}$
the log layer is not yet fully developed. They are in good agreement with DNS data from other work (Chouippe et al.
Reference Chouippe, Climent, Legendre and Gabillet2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
; Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016). Owing to the strong curvature of this
![]() ${\it\eta}=0.5$
set-up, a large difference between the azimuthal velocity
${\it\eta}=0.5$
set-up, a large difference between the azimuthal velocity
![]() $u^{+}$
and the angular velocity
$u^{+}$
and the angular velocity
![]() ${\it\omega}^{+}$
arises. The angular velocity
${\it\omega}^{+}$
arises. The angular velocity
![]() ${\it\omega}^{+}$
resembles a log law more closely, as suggested by Grossmann et al. (Reference Grossmann, Lohse and Sun2014), based on their Navier–Stokes based theoretical considerations.
${\it\omega}^{+}$
resembles a log law more closely, as suggested by Grossmann et al. (Reference Grossmann, Lohse and Sun2014), based on their Navier–Stokes based theoretical considerations.
Because of the late onset of the ultimate regime for
![]() ${\it\eta}=0.5$
, the measurements with
${\it\eta}=0.5$
, the measurements with
![]() $Ta$
up to
$Ta$
up to
![]() $6.2\times 10^{9}$
are in the classical turbulent regime. For the first time, the wind Reynolds number has been measured in the classical regime of TC flow, and it indeed follows the theoretically predicted classical scaling of
$6.2\times 10^{9}$
are in the classical turbulent regime. For the first time, the wind Reynolds number has been measured in the classical regime of TC flow, and it indeed follows the theoretically predicted classical scaling of
![]() $Re_{w}\propto Ta^{3/7}$
. The scaling of the turbulence intensity was found to be
$Re_{w}\propto Ta^{3/7}$
. The scaling of the turbulence intensity was found to be
![]() $I\propto Ta^{{\it\gamma}}$
with
$I\propto Ta^{{\it\gamma}}$
with
![]() $-0.1<{\it\gamma}<-0.07$
, depending on the position in the gap.
$-0.1<{\it\gamma}<-0.07$
, depending on the position in the gap.
Moreover, we focused on the interplay between rolls, turbulent plumes and logarithmic velocity profiles. At a strong driving of
![]() $Ta=4.2\times 10^{9}$
, no significant coherent structures exist for pure inner cylinder rotation, but roll structures appear for counter-rotation at
$Ta=4.2\times 10^{9}$
, no significant coherent structures exist for pure inner cylinder rotation, but roll structures appear for counter-rotation at
![]() $a=-{\it\omega}_{o}/{\it\omega}_{i}=0.2$
. This behaviour has been observed previously for different values of
$a=-{\it\omega}_{o}/{\it\omega}_{i}=0.2$
. This behaviour has been observed previously for different values of
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $Ta$
, and shows the important part that rolls play in momentum transfer between the two cylinders.
$Ta$
, and shows the important part that rolls play in momentum transfer between the two cylinders.
For inner cylinder rotation only, strong outward plumes are visible in the radial velocity. In the azimuthal velocity, the plumes mainly go inwards. The exact mechanism causing this difference is yet to be elucidated. For counter-rotation, the roll structures strongly influence the direction of the plumes. There is a direct correspondence between the direction of the mean radial flow and the direction of the plumes at a certain position. The plume velocity in the radial flow profiles increases with Taylor number, and has an approximately constant value of one-quarter of the inner cylinder velocity for pure inner cylinder rotation.
Lastly, by quantifying the correspondence of the angular velocity profiles to a log law for several axial positions, it was found that, in regions with strong radial flow away from a cylinder surface, plumes will emit from that cylinder, which in turn create logarithmic boundary layers.
This work confirms predictions about velocity profiles and the scaling of the wind Reynolds number and sheds new light on the characteristics and the role of plumes in TC flow for a radius ratio
![]() ${\it\eta}=0.5$
, and hopefully will spark further research into these intricate phenomena.
${\it\eta}=0.5$
, and hopefully will spark further research into these intricate phenomena.
Acknowledgements
We thank the technicians of the Department of Aerodynamics and Fluid Mechanics at the BTU for their technical support. This work was financially supported by the European High-Performance Infrastructures in Turbulence (EuHIT), COST Action MP1305, a European Research Council (ERC) Advanced Grant, and the Simon Stevin Prize of the Technology Foundation STW of The Netherlands. C.E. and S.M. acknowledge the financial support of DFG (FOR 118, EG 100/15-2).