2.1 Properties of the Reynolds shear stress

Multiplying the MMB-$\unicode[STIX]{x1D719}$ equation (2.6b) by $r^{2}$, simple mathematical manipulation gives

(2.7)$$\begin{eqnarray}0={\displaystyle \frac{\text{d}}{\text{d}r}}\left(r^{2}\unicode[STIX]{x1D708}\left({\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\right)\right)+{\displaystyle \frac{\text{d}(r^{2}R_{r\unicode[STIX]{x1D719}})}{\text{d}r}}.\end{eqnarray}$$

Equation (2.7) is equivalent to (9.2.1.) in Townsend (Reference Townsend1980), and is also essentially the same as (3.3) in Eckhardt, Grossmann & Lohse (Reference Eckhardt, Grossmann and Lohse2007).

In a fully developed turbulent TCF, the moment of the viscous shear stress is

(2.8)$$\begin{eqnarray}M_{visc}=2\unicode[STIX]{x03C0}rL\unicode[STIX]{x1D70F}_{r\unicode[STIX]{x1D719}}r=(2\unicode[STIX]{x03C0}L\unicode[STIX]{x1D70C})r^{2}\unicode[STIX]{x1D708}\left({\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\right),\end{eqnarray}$$

and the moment of the Reynolds shear stress is

(2.9)$$\begin{eqnarray}M_{turb}=2\unicode[STIX]{x03C0}rL\unicode[STIX]{x1D70C}R_{r\unicode[STIX]{x1D719}}r=(2\unicode[STIX]{x03C0}L\unicode[STIX]{x1D70C})r^{2}R_{r\unicode[STIX]{x1D719}}.\end{eqnarray}$$

Hence, equation (2.7) can be presented in the form of moment as

(2.10)$$\begin{eqnarray}0={\displaystyle \frac{\text{d}M_{visc}}{\text{d}r}}+{\displaystyle \frac{\text{d}M_{turb}}{\text{d}r}}.\end{eqnarray}$$

Integrating the mean momentum equation (2.7) or (2.10) in the wall-normal direction from the inner cylinder and applying boundary conditions yields

(2.11)$$\begin{eqnarray}r^{2}\unicode[STIX]{x1D708}\left({\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\right)+r^{2}R_{r\unicode[STIX]{x1D719}}=r^{2}\unicode[STIX]{x1D708}\left({\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\right)\Big|_{r=r_{i}}+(r^{2}R_{r\unicode[STIX]{x1D719}})\big|_{r=ri}=-r_{i}^{2}u_{\unicode[STIX]{x1D70F},i}^{2}.\end{eqnarray}$$

Note that the Reynolds shear stress at the inner cylinder is zero for a turbulent TCF with smooth walls. As mentioned in the previous section, the coordinate system is set up such that the mean azimuthal velocity gradient and the Reynolds shear stress are both negative. Thus, the total moment is also negative. Equation (2.11) is equivalent to (9.2.2) in Townsend (Reference Townsend1980), and is also essentially the same as the identity equation (3.4) in Eckhardt et al. (Reference Eckhardt, Grossmann and Lohse2007). Townsend (Reference Townsend1980) interpreted equation (2.11) as follows: ‘the sum of the ‘couples’ transmitted by viscous and turbulent stress across surfaces of constant radius is independent of the radius’. Eckhardt et al. (Reference Eckhardt, Grossmann and Lohse2007) called the constant the angular velocity current. Here, a simple interpretation of (2.11) is that the total moment (per $2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}L$), viscous plus turbulent $M_{visc}+M_{turb}$, is a constant, independent of the radial location. The constancy of (2.11) has been used as a consistency check for DNS simulations, as by Dong (Reference Dong2008).

To establish a turbulent plane Couette flow, one can move the top plate only, or the bottom plate only or move both plates in the same direction or opposite direction. However, the total shear stress, viscous plus turbulent $\unicode[STIX]{x1D70F}_{wu}+R_{wu}$, is always a constant across the channel, regardless of how the top and bottom plates are being moved. Similarly, equation (2.11) also indicates that the total moment in a turbulent TCF is always a constant, regardless of $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}$ or how the inner and outer cylinders are being rotated.

In turbulent channel or boundary layer flows, viscous shear stress peaks at the wall and decreases rapidly away from the wall. In a turbulent TCF, the moment of viscous shear stress also peaks at the wall and decreases rapidly along the wall-normal direction. Away from the wall, the viscous term in the integrated MMB-$\unicode[STIX]{x1D719}$ (2.11) becomes negligible and the Reynolds shear stress can be approximated as

(2.12)$$\begin{eqnarray}R_{r\unicode[STIX]{x1D719}}\approx -{\displaystyle \frac{r_{i}^{2}}{r^{2}}}u_{\unicode[STIX]{x1D70F},i}^{2}.\quad \text{Core Region}\end{eqnarray}$$

Hence, Reynolds shear stress in the core of a highly turbulent TCF decreases in a $1/r^{2}$ fashion along the radial direction.

Following the convention commonly followed for turbulent wall-bounded flows, the Reynolds shear stress normalized by $u_{\unicode[STIX]{x1D70F},i}^{2}$ is denoted as $R_{r\unicode[STIX]{x1D719}}^{+}=R_{r\unicode[STIX]{x1D719}}/u_{\unicode[STIX]{x1D70F},i}^{2}$. Equation (2.12) in the non-dimensional form can be presented as

(2.13a)$$\begin{eqnarray}\displaystyle & \displaystyle R_{r\unicode[STIX]{x1D719}}^{+}\approx -\left({\displaystyle \frac{r_{i}}{r}}\right)^{2}=-\left({\displaystyle \frac{1}{1+{\displaystyle \frac{\unicode[STIX]{x1D6FF}}{r_{i}}}z^{-}}}\right)^{2}=-\left({\displaystyle \frac{1-A_{t}}{1-A_{t}+A_{t}z^{-}}}\right)^{2}, & \displaystyle\end{eqnarray}$$

(2.13b)$$\begin{eqnarray}\displaystyle & \displaystyle \text{or}\quad \left({\displaystyle \frac{r}{r_{i}}}\right)^{2}R_{r\unicode[STIX]{x1D719}}^{+}\approx -1. & \displaystyle\end{eqnarray}$$

$z^{-}$

$A_{t}$

(2.14a)$$\begin{eqnarray}\displaystyle & \displaystyle z^{-}\stackrel{\text{def}}{=}{\displaystyle \frac{r-r_{i}}{0.5(r_{o}-r_{i})}}={\displaystyle \frac{r-r_{i}}{\unicode[STIX]{x1D6FF}}}; & \displaystyle\end{eqnarray}$$

(2.14b)$$\begin{eqnarray}\displaystyle & \displaystyle A_{t}\stackrel{\text{def}}{=}{\displaystyle \frac{\unicode[STIX]{x1D6FF}}{r_{ctr}}}={\displaystyle \frac{0.5(r_{o}-r_{i})}{0.5(r_{o}+r_{i})}}. & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D702}$

$\unicode[STIX]{x1D702}$

$z^{-}$

$r-r_{i}$

$\unicode[STIX]{x1D6FF}$

The definition of $A_{t}$ in (2.14b) is analogous to the Atwood number used in the study of hydrodynamic instability in density stratified flows, such as Rayleigh–Taylor instability (Glimm et al. Reference Glimm, Grove, Li, Oh and Sharp2001; Livescu et al. Reference Livescu, Ristorcelli, Gore, Dean, Cabot and Cook2009; Wei & Livescu Reference Wei and Livescu2012), see appendix A. In the present work, therefore, this non-dimensional number is called a geometry Atwood number.

Figure 2. (a) Reynolds shear stress in a Taylor–Couette flow. The curve is (2.13a). Data are from DNS of Dong (Reference Dong2008), with $r_{i}/r_{o}=0.5$ or $A_{t}=1/3$. (b) $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ versus the wall-normal distance scaled by the TCF gap half-width $z^{-}$. The PCF data are from DNS of Kawamura, Abe & Shingai (Reference Kawamura, Abe and Shingai2000) at $Re_{\unicode[STIX]{x1D70F}}=181$.

The approximate equation (2.13a) for the Reynolds shear stress is compared with DNS data of Dong (Reference Dong2008) in figure 2. The DNS is for the same gap geometry with $A_{t}=1/3$, and four different Reynolds numbers. At $Re_{\unicode[STIX]{x1D70F},i}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}=32.7$, the Reynolds shear stress profile in the core of the gap deviates from (2.13a), because at such a low Reynolds number, turbulence is still not well established and the viscous shear stress is not negligible in the outer layer. However, at higher Reynolds numbers, $Re_{\unicode[STIX]{x1D70F},i}>74$, DNS data of Reynolds shear stress in the core of the gap agree well with (2.13a), supporting the validity of the analysis.

In figure 2(b), the approximate equation (2.13b) is compared with the DNS data of TCF; the Reynolds shear stress in a turbulent PCF is also plotted. The PCF data are from Kawamura’s group at $Re_{\unicode[STIX]{x1D70F}}=181.3$ (Kawamura et al. Reference Kawamura, Abe and Shingai2000; Shingai, Kawamura & Matsuo Reference Shingai, Kawamura, Matsuo and Dopazo2000; Tsukahara, Kawamura & Shingai Reference Tsukahara, Kawamura and Shingai2006). Figure 2(b) displays the resemblance between the turbulent TCF and PCF, and in particular in the inner half next to the inner cylinder. Near the outer cylinder, $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ is different from the Reynolds shear stress in a turbulent plane Couette flow, but the difference becomes smaller as the Reynolds number increases.

In a turbulent plane Couette flow, the Reynolds shear stress is symmetric about the gap centreline, with a peak at the middle. In a turbulent TCF, the mid-gap is located at $r_{ctr}=0.5(r_{i}+r_{0})$, and its Reynolds shear stress can be approximated as

(2.15)$$\begin{eqnarray}R_{r\unicode[STIX]{x1D719}}|_{ctr}\approx -\left({\displaystyle \frac{r_{i}}{0.5(r_{i}+r_{o})}}\right)^{2}u_{\unicode[STIX]{x1D70F},i}^{2}=-(1-A_{t})^{2}u_{\unicode[STIX]{x1D70F},i}^{2}.\end{eqnarray}$$

Hence, the magnitude of the Reynolds shear stress at the mid-gap of a turbulent TCF is always smaller than $u_{\unicode[STIX]{x1D70F},i}^{2}$ or $|R_{r\unicode[STIX]{x1D719}}^{+}|\leqslant 1$. As the geometry Atwood number approaches zero $A_{t}\rightarrow 0$ or the small-gap limit, the Reynolds shear stress at the mid-gap approaches the kinematic wall shear stress at the inner cylinder $|R_{r\unicode[STIX]{x1D719}}|_{ctr}\approx u_{\unicode[STIX]{x1D70F},i}^{2}$, and the turbulent TCF becomes similar to a turbulent plane Couette flow. However, at a large geometry Atwood number $A_{t}\rightarrow 1$, the magnitude of the Reynolds shear stress is much smaller than $u_{\unicode[STIX]{x1D70F},i}^{2}$ or $|R_{r\unicode[STIX]{x1D719}}^{+}|\ll 1$, as shown figure 3(a).

Figure 3. Effects of geometry Atwood number $A_{t}$ on the shape of Reynolds shear stress in TCF. (a) $-R_{r\unicode[STIX]{x1D719}}^{+}$ versus $z^{-}$. The curve is the approximate equation (2.13a). Data for $A_{t}=0.333$ are from DNS of Dong (Reference Dong2008). Data for $A_{t}=0.43$, $0.54$ and $0.667$ are from DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018). (b) $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ versus $z^{-}$. For comparison, Reynolds shear stress of a plane Couette flow is also presented. The data are from DNS of Kawamura’s group $Re_{\unicode[STIX]{x1D70F}}=181.3$ (Kawamura et al. Reference Kawamura, Abe and Shingai2000; Shingai et al. Reference Shingai, Kawamura, Matsuo and Dopazo2000; Tsukahara et al. Reference Tsukahara, Kawamura and Shingai2006).

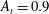The effect of the geometry Atwood number $A_{t}$ on the Reynolds shear stress is displayed in figure 3. The approximate equation (2.13a) is compared with DNS data of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) for three geometry Atwood numbers: $A_{t}=0.43$, $0.54$, $0.667$. Also shown are the DNS data of Dong (Reference Dong2008) for $A_{t}=0.333$. Curves at $A_{t}=0.1$ and $A_{t}=0.9$ are plotted to illustrate the trend at low and high geometry Atwood numbers. As $A_{t}$ approaches zero, the shape of the Reynolds shear stress becomes similar to that of a turbulent plane Couette flow. On the other hand, as $A_{t}$ approaches $1$, Reynolds shear stress is very small, except within a thin layer next to the inner cylinder.

Figure 3(b) shows that $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ in the inner half of a turbulent TCF resembles the shape of the Reynolds shear stress in a turbulent plane Couette flow, even at large geometry Atwood numbers. However, in the outer half, $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ in a turbulent TCF is lower than the Reynolds shear stress in a turbulent plane Couette flow. The difference becomes smaller as the Atwood number decreases.

In a turbulent TCF, the peak Reynolds shear stress always occurs in the inner half (next to the inner cylinder), as shown in figures 2 and 3. The peak location depends on the Reynolds number and the geometry Atwood number. In figure 4(a), the peak Reynolds shear stress location $z_{max}^{-}$ is plotted versus the Reynolds number. DNS data of TCF for $A_{t}=0.333$ are from independent studies by Dong (Reference Dong2008) (open circles in the figure) and Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) (filled circles). DNS data at $A_{t}=0.667$ are from DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018). At the same Reynolds number, the peak Reynolds shear stress location moves closer to the inner cylinder as the geometry Atwood number increases. For the same geometry Atwood number, the peak location moves closer to the inner cylinder as the Reynolds number increases.

Figure 4. Peak Reynolds shear stress location. (a) Effect of Reynolds number. Open circles are DNS of TCF by Dong (Reference Dong2008) for $A_{t}=0.333$, and filled circles are DNS of TCF by Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) for $A_{t}=0.333$ and $A_{t}=0.668$. DNS data of turbulent plane Poiseuille flow (PPF) are from three independent groups: Kawamura’s group (Kawamura et al. Reference Kawamura, Abe and Shingai2000; Abe, Kawamura & Matsuo Reference Abe, Kawamura and Matsuo2001), Moser’s group (Lee & Moser Reference Lee and Moser2015) and Pirozzoli’s group (Pirozzoli, Bernardini & Orlandi Reference Pirozzoli, Bernardini and Orlandi2016). (b) Effect of geometry Atwood number. Note that inset is plotted in linear–linear axes. Data are from DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018).

In a pressure-driven turbulent channel or pipe flow or a shear-driven turbulent flow over a flat plate, the peak Reynolds shear stress location is a geometric mean of the inner and outer length scales $z_{max}\sim \sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}}$ or $z_{max}^{-}\sim 1/\sqrt{Re_{\unicode[STIX]{x1D70F}}}$ (see Long & Chen Reference Long and Chen1981; Afzal Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and McMurtry2005). For comparison, therefore, DNS data for a pressure-driven channel flow are also plotted in figure 4(a). The presently available TCF data seem to follow a trend similar to those in a pressure-driven turbulent channel flow. In other words, the peak Reynolds shear stress location in a turbulent TCF also occurs at the meso length scale $\sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F},i}}$. However, the Reynolds numbers of the TCF data used in the present work are low to moderate, and the trend at high Reynolds numbers remains to be investigated.

The effect of the geometry Atwood number $A_{t}$ on the peak location of the Reynolds shear stress is shown in figure 4(b). The DNS data are from Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) for four geometry Atwood numbers $A_{t}=0.333$, $0.43$, $0.54$, $0.667$. The data are for two Reynolds numbers $Re_{i}=2\unicode[STIX]{x1D6FF}r_{i}\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D708}=500$ and $4000$. The corresponding friction Reynolds numbers are listed in table 1. Data for $z_{max}^{-}$ at $Re_{i}=4000$ are smaller than those at $Re_{i}=500$, showing the effect of Reynolds number as presented in figure 4(a).

Table 1. Parameters of DNS by Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018), shown in figure 4(b).

As shown in figure 3(a), the peak Reynolds shear stress location $z_{max}^{-}$ becomes smaller with increasing $A_{t}$, meaning that the peak Reynolds shear stress location moves closer to the inner cylinder. (In a turbulent TCF, the peak Reynolds shear stress will never occur in the outer half of the gap, regardless of the Reynolds number, $A_{t}$, or rotation ratio.) The presently available DNS data are limited to moderate geometry Atwood numbers, so the functional dependence at $A_{t}\rightarrow 0$ or $A_{t}\rightarrow 1$ is not clear at this time. Based on the DNS data at moderate $A_{t}$, however, geometry Atwood number dependencies can be approximated by a simple power law of $z_{max}^{-}\sim f(Re)/A_{t}$. The peak Reynolds shear stress location $z_{max}^{-}$ is bounded between $0$ and $1$, and the inset of figure 4(b) indicates that this power law cannot be extrapolated to the $A_{t}\rightarrow 0$ limit. An asymptotic analysis might uncover the functional dependence at the small and large Atwood number limits.

Next, the MMB-$\unicode[STIX]{x1D719}$ equation will be rearranged and integrated to reveal properties of the turbulent Coriolis force.

2.2 Property of the turbulent Coriolis force

In previous studies of turbulent TCF, the properties of the turbulent Coriolis force have not been clear. Here, properties of the turbulent Coriolis force are revealed directly from the mean momentum balance equation.

The viscous force in the MMB-$\unicode[STIX]{x1D719}$ (2.6b) is written as a function of the mean azimuthal velocity, but it can be written in more than one form, as shown in appendix B. For example, the MMB-$\unicode[STIX]{x1D719}$ equation can also be written as

(2.16)$$\begin{eqnarray}0=\unicode[STIX]{x1D708}{\displaystyle \frac{\text{d}}{\text{d}r}}\left({\displaystyle \frac{1}{r}}{\displaystyle \frac{\text{d}(rU_{\unicode[STIX]{x1D719}})}{\text{d}r}}\right)+{\displaystyle \frac{\text{d}R_{r\unicode[STIX]{x1D719}}}{\text{d}r}}+{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}}{r}}.\end{eqnarray}$$

Integrating the MMB-$\unicode[STIX]{x1D719}$ (2.16) along the radial direction from the inner cylinder to the outer cylinder yields

(2.17)$$\begin{eqnarray}\int _{r_{i}}^{r_{o}}{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}}{r}}\,\text{d}r=\left\{\unicode[STIX]{x1D708}{\displaystyle \frac{1}{r}}{\displaystyle \frac{\text{d}(rU_{\unicode[STIX]{x1D719}})}{\text{d}r}}\right\}\Big|_{r_{i}}-\left\{\unicode[STIX]{x1D708}{\displaystyle \frac{1}{r}}{\displaystyle \frac{\text{d}(rU_{\unicode[STIX]{x1D719}})}{\text{d}r}}\right\}\Big|_{r_{o}}+R_{r\unicode[STIX]{x1D719}}|_{r_{i}}-R_{r\unicode[STIX]{x1D719}}|_{r_{o}}.\end{eqnarray}$$

For a turbulent TCF with smooth walls, the Reynolds shear stress $R_{r\unicode[STIX]{x1D719}}$ is zero at both the inner and outer cylinders: $R_{r\unicode[STIX]{x1D719}}|_{r_{i}}=0$ and $R_{r\unicode[STIX]{x1D719}}|_{r_{o}}=0$. The first two terms on the right side of (2.17) can be arranged as

(2.18a)$$\begin{eqnarray}\displaystyle & \displaystyle \left\{\unicode[STIX]{x1D708}{\displaystyle \frac{1}{r}}{\displaystyle \frac{\text{d}(rU_{\unicode[STIX]{x1D719}})}{\text{d}r}}\right\}\Big|_{r_{i}}=\unicode[STIX]{x1D708}\Big\{{\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}+{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\Big\}\Big|_{r=r_{i}}=\unicode[STIX]{x1D708}\Big\{{\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}+2{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\Big\}\Big|_{r=r_{i}}, & \displaystyle\end{eqnarray}$$

(2.18b)$$\begin{eqnarray}\displaystyle & \displaystyle \left\{\unicode[STIX]{x1D708}{\displaystyle \frac{1}{r}}{\displaystyle \frac{\text{d}(rU_{\unicode[STIX]{x1D719}})}{\text{d}r}}\right\}\Big|_{r_{o}}=\unicode[STIX]{x1D708}\Big\{{\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}+{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\Big\}\Big|_{r=r_{o}}=\unicode[STIX]{x1D708}\Big\{{\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}}{\text{d}r}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}+2{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{r}}\Big\}\Big|_{r=r_{o}}. & \displaystyle\end{eqnarray}$$

$(U_{\unicode[STIX]{x1D719}}/r)_{r=r_{i}}=\unicode[STIX]{x1D6FA}_{i}$

$(U_{\unicode[STIX]{x1D719}}/r)_{r=r_{o}}=\unicode[STIX]{x1D6FA}_{o}$

$\text{d}U_{\unicode[STIX]{x1D719}}/\text{d}r$

$\unicode[STIX]{x1D708}(\text{d}U_{\unicode[STIX]{x1D719}}/\text{d}r-U_{\unicode[STIX]{x1D719}}/r)_{r=r_{i}}=-u_{\unicode[STIX]{x1D70F},i}^{2}$

$\unicode[STIX]{x1D708}(\text{d}U_{\unicode[STIX]{x1D719}}/\text{d}r-U_{\unicode[STIX]{x1D719}}/r)_{r=r_{o}}=-u_{\unicode[STIX]{x1D70F},o}^{2}$

Figure 5. Verification of the global integral equation (2.20) for the turbulent Coriolis force against DNS data. Parameters for the DNS data of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) are listed in table 1, and the TCF is counter-rotating with $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}=-1/\unicode[STIX]{x1D6F1}_{r}=-(1+A_{t})/(1-A_{t})$. $\text{TKT}$$(500)$ refers to the data of Tanaka et al. at $\mathit{Re}_{i}=500$, and $\text{TKT}$$(4000)$ at $\mathit{Re}_{i}=4000$. DNS of Dong (Reference Dong2007) was for fixed outer cylinder or $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}=\infty$, $Re_{i}=8000$, $Re_{\unicode[STIX]{x1D70F},i}=225$ and $A_{t}=0.333$. The cross symbols are the right side of (2.20). The dashed curve is the first part on the right side of (2.20).

Substituting the boundary condition (2.18a) and (2.18b) and the boundary conditions for $R_{r\unicode[STIX]{x1D719}}$, the global integral equation (2.17) of the turbulent Coriolis force can be written as

(2.19)$$\begin{eqnarray}\int _{r_{i}}^{r_{o}}{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}}{r}}\,\text{d}r=\{u_{\unicode[STIX]{x1D70F},o}^{2}-u_{\unicode[STIX]{x1D70F},i}^{2}\}-\{2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}_{o}-2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}_{i}\}.\end{eqnarray}$$

Thus, the global integral of the turbulent Coriolis force depends on the wall shear stresses at the inner and outer cylinders, as well as the rotation speeds of the inner and outer cylinders.

Normalizing equation (2.19) by $u_{\unicode[STIX]{x1D70F},i}^{2}$, the global integral of the turbulent Coriolis force can be expressed as

(2.20)$$\begin{eqnarray}\int _{r_{i}}^{r_{o}}{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}^{+}}{r}}\,\text{d}r=\left[\left({\displaystyle \frac{1-A_{t}}{1+A_{t}}}\right)^{2}-1\right]-\left({\displaystyle \frac{1+A_{t}}{1-A_{t}}}-1\right)\left({\displaystyle \frac{1}{\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}}}-1\right){\displaystyle \frac{U_{\unicode[STIX]{x1D719},i}^{+}}{Re_{\unicode[STIX]{x1D70F},i}}},\end{eqnarray}$$

where $U_{\unicode[STIX]{x1D719},i}^{+}=U_{\unicode[STIX]{x1D719},i}/u_{\unicode[STIX]{x1D70F},i}$ is the inner cylinder’s azimuthal velocity normalized by the friction velocity at the inner cylinder. Equation (2.20) indicates that the global integral of the turbulent Coriolis force depends on the gap geometry $A_{t}$, rotation ratio $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}$, Reynolds number $Re_{\unicode[STIX]{x1D70F},i}$ and $U_{\unicode[STIX]{x1D719},i}^{+}$.

The global integral equation (2.20) for the turbulent Coriolis force is verified by DNS data in figure 5. As shown in figure 5, the integrated $\int _{r_{i}}^{r_{o}}(2R_{r\unicode[STIX]{x1D719}}^{+}/r)\,\text{d}r$ (open square or circle) agrees well with the analytical solution (X in the figure). Note that the turbulent Coriolis force is negative in the coordinate system, and a negative sign is multiplied to both sides of (2.20) in figure 5.

In general, $U_{\unicode[STIX]{x1D719},i}^{+}/Re_{\unicode[STIX]{x1D70F},i}$ becomes smaller as the Reynolds number increases. Thus, at high Reynolds numbers, the last part on the right side of (2.20) becomes less important, and the global integral can be approximated by the first part only, represented by the dashed curve in figure 5. The DNS data of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) at $Re_{i}=500$ deviate from the dashed curve as shown in figure 5, meaning that rotation ratio is important in the global integral of the turbulent Coriolis force. At a higher Reynolds number of $Re_{i}=4000$, the DNS data of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) move closer to the dashed curve, especially for small Atwood numbers.

Table 2. The global integral of the turbulent Coriolis force for limiting cases.

Using (2.20), the global integral of the turbulent Coriolis force under four limiting cases is determined and listed in table 2. For the limiting case of a small gap ($r_{i}\approx r_{o}$ or $A_{t}\rightarrow 0$), the global integral of the turbulent Coriolis force approaches zero, meaning that the Coriolis force is not important for a small-gap TCF. In other words, in the limit of $A_{t}\rightarrow 0$, a turbulent TCF becomes a turbulent plane Couette flow. On the other hand, for a turbulent TCF with a large gap or $A_{t}\rightarrow 1$, the effect of rotation ratio can become significant because $(1+A_{t})/(1-A_{t})$ approaches infinity. At the large-gap limit (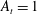$A_{t}=1$), the global integral of the turbulent Coriolis force $\int _{r_{i}}^{r_{o}}(2R_{r\unicode[STIX]{x1D719}}^{+}/r)\,\text{d}r$ approaches $-1$ or $\int _{r_{i}}^{r_{o}}(2R_{r\unicode[STIX]{x1D719}}/r)\,\text{d}r$ approaches $-u_{\unicode[STIX]{x1D70F},i}^{2}$.

For the case of only the outer cylinder rotating ($\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}=0$), the last part in (2.20) is zero because the azimuthal velocity of the inner cylinder is zero or $U_{\unicode[STIX]{x1D719},i}^{+}=0$. For the case of inner cylinder rotating only ($\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}=\infty$), the term $(1/\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}-1)$ in (2.20) becomes $-1$.

3.1 Layer structure of a turbulent TCF

One way to describe the layered structure of a turbulent flow is through the characteristic of the force balance in the mean momentum balance equation. This approach has been used to reveal the layer structure in pressure- or shear-driven turbulent wall-bounded flows (Wei et al. Reference Wei, Fife, Klewicki and McMurtry2005; Klewicki et al. Reference Klewicki, Fife, Wei and McMurtry2007). A similar approach has been applied to uncover the layer structure of passive scalar transport in a turbulent channel flow (Wei Reference Wei2018) and buoyancy-driven turbulent flow and heat transfer in a differentially heated vertical channel (Wei Reference Wei2019).

Figure 6. Three forces in the MMB-$\unicode[STIX]{x1D719}$ (2.6b). The data are from the DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018). The case is a counter-rotating TCF with $r_{i}/r_{0}=0.5$ or $A_{t}=1/3$. The Reynolds number of the simulation is $(2\unicode[STIX]{x1D6FF}r_{i}|\unicode[STIX]{x1D6FA}_{i}|)/\unicode[STIX]{x1D708}=(2\unicode[STIX]{x1D6FF}r_{o}|\unicode[STIX]{x1D6FA}_{o}|)/\unicode[STIX]{x1D708}=4000.$ The corresponding friction Reynolds numbers are $Re_{\unicode[STIX]{x1D70F},i}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}\approx 165$ and $Re_{\unicode[STIX]{x1D70F},o}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},o}/\unicode[STIX]{x1D708}\approx 82$. The magnitudes of the forces are not shown in the figure, for they depend on the method of normalization.

For a turbulent TCF, the typical shapes of the three forces in the MMB-$\unicode[STIX]{x1D719}$ (2.6b) are illustrated in figure 6. The magnitudes of the forces are not shown in the figure, for they depend on the method of normalization, but the shapes and relative magnitudes do not depend on the normalization. Adjacent to the inner cylinder, the viscous force is positive, or a driving force, and the turbulent force is negative, or a drag force. The directions of the forces are reversed adjacent to the outer cylinder, where the turbulent force is a driving force and the viscous force is a drag force.

Starting from zero at the inner cylinder wall, the viscous force rises sharply to a peak value, then decreases sharply away from the wall. In the meantime, the Reynolds shear force starts from zero at the inner cylinder and decreases sharply to a minimum, then rises sharply away from the inner cylinder. Adjacent to the inner cylinder the force balance is between the viscous force and the Reynolds shear force. In the core of the gap, the viscous force is essentially zero and the Reynolds shear force is positive, but the magnitude is much smaller than that adjacent to the inner cylinder. Approaching the outer cylinder, the force balance is again balanced by the viscous force and Reynolds shear force. Thus, the force balance in the MMB-$\unicode[STIX]{x1D719}$ (2.6b) undergoes a series of transitions at the intersections of the different layers.

One way to assess the contributions of different forces to the balance of the MMB-$\unicode[STIX]{x1D719}$ (2.6b) is by plotting the ratio of two forces (Wei et al. Reference Wei, Fife, Klewicki and McMurtry2005; Klewicki et al. Reference Klewicki, Fife, Wei and McMurtry2007; Wei Reference Wei2018, Reference Wei2019). The ratio between the viscous force and the turbulent force $F_{visc}/F_{turb}$ in a TCF is shown in figure 7(a). For comparison, the force ratio $F_{visc}/F_{turb}$ in a pressure-driven turbulent channel flow is shown figure 7(b).

Figure 7. (a) Ratio between the viscous force and Reynolds shear force $F_{visc}/F_{turb}$ in the MMB-$\unicode[STIX]{x1D719}$ (2.6b) for a TCF. Data are from DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) for $r_{i}/r_{o}=0.5$ ($A_{t}=0.33$) and $(r_{o}-r_{i})r_{i}|\unicode[STIX]{x1D6FA}_{i}|/\unicode[STIX]{x1D708}=500$ and $4000$. (b) Ratio of $F_{visc}/F_{turb}$ in a pressure-driven plane channel flow. Here $z$ is the wall-normal distance, and $\unicode[STIX]{x1D6FF}$ is the channel half-width. Data are from DNS by Kawamura’s group (Kawamura et al. Reference Kawamura, Abe and Shingai2000; Shingai et al. Reference Shingai, Kawamura, Matsuo and Dopazo2000; Tsukahara et al. Reference Tsukahara, Kawamura and Shingai2006).

In a pressure-driven turbulent channel flow, the Reynolds shear force is zero near the channel wall, where the force balance is between the pressure force and the viscous force. Thus, the force ratio $F_{visc}/F_{turb}$ in a turbulent channel flow starts from a large negative value at the channel wall. In a turbulent TCF, the turbulent Coriolis force is zero near the inner cylinder, where the force balance is between the viscous force and Reynolds shear force. Thus, the force ratio $F_{visc}/F_{turb}$ in a turbulent TCF is $-1$ at the inner cylinder. At sufficiently high Reynolds numbers, the inner half of a TCF exhibits a structure similar to that in the lower or upper half of a turbulent channel flow. The flow structure in a turbulent channel flow is symmetric about the channel centreline, but the flow structure in a TCF is not symmetric, because the friction velocity at the inner cylinder is different from that at the outer cylinder.

Based on the characteristics of the force ratio presented in figure 7, the inner half of a turbulent TCF can be divided into at least three layers:

1. (i) Layer I, an inner layer where the force balance is between the viscous force and the Reynolds shear force: $|F_{visc}|\approx |F_{turb}|$.

2. (ii) Layer II, a meso layer centred around the peak Reynolds shear stress location.

3. (iii) Layer III, an outer layer where the viscous force is negligible and the force balance is between the Reynolds shear force and the turbulent Coriolis force: $|F_{cori}|\approx |F_{turb}|$.

The three-layer structure for the inner half of a turbulent TCF is sketched in figure 8.

Figure 8. Sketch of the layer structure in the inner half of a turbulent TCF. The data points are from DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018) for $\mathit{Re}_{i}=4000$ and $A_{t}=0.333$ ($\mathit{Re}_{\unicode[STIX]{x1D70F},i}=164.6$).

We note that the DNS data used in this work are limited to relatively moderate Reynolds number. In particular, the friction Reynolds number for the outer half of a TCF, $Re_{\unicode[STIX]{x1D70F},o}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},o}/\unicode[STIX]{x1D708}$, is small. Thus, for the two cases shown in figure 7(a) the friction Reynolds numbers for the outer half are $Re_{\unicode[STIX]{x1D70F},o}=16.5$, and $82.5$. In the DNS of Tanaka et al. (Reference Tanaka, Kawata and Tsukahara2018), the lowest Reynolds number case, $Re_{\unicode[STIX]{x1D70F},i}=33$ and $Re_{\unicode[STIX]{x1D70F},o}=16.5$, has not achieved a fully developed turbulent state yet, and the flow in the outer half is more laminar like. For their highest Reynolds number case of $Re_{\unicode[STIX]{x1D70F},i}=165$ and $Re_{\unicode[STIX]{x1D70F},o}=82.5$, the inner half displays a well-established three-layer structure, but the layer structure of the outer half is very different.

The thickness of Layers I, II and III will depend on the Reynolds number, the geometry Atwood number and likely the rotation ratio $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}$. More DNS data are required to determine the thickness and the dependencies on the controlling non-dimensional numbers.

3.2 Scaling for Layer $\text{III}$ of the inner half

In the outer Layer III shown in figure 8, a natural length scale for the spatial variation in the radial direction $\text{d}r$ is the gap half-width, $l_{ref}=\unicode[STIX]{x1D6FF}$. A reasonable length scale for the radial location is the mid-gap location $r_{ref}=r_{ctr}=0.5(r_{i}+r_{o})$. The friction velocity $u_{\unicode[STIX]{x1D70F},i}$ is used as a reference velocity scale $U_{\unicode[STIX]{x1D719},ref}=u_{\unicode[STIX]{x1D70F},i}$, as in pressure- or shear-driven turbulent wall-bounded flows. The Reynolds shear stress at the TCF mid-gap is used as a reference scale for the Reynolds shear stress $R_{r\unicode[STIX]{x1D719},ref}=|R_{r\unicode[STIX]{x1D719}}|_{ctr}$. The scaled variables for Layer III are denoted as follows

(3.4a-e)$$\begin{eqnarray}z^{-}\stackrel{\text{def}}{=}{\displaystyle \frac{r-r_{_{i}}}{\unicode[STIX]{x1D6FF}}};\quad \text{d}z^{-}\stackrel{\text{def}}{=}{\displaystyle \frac{\text{d}r}{\unicode[STIX]{x1D6FF}}};\quad r^{\ast }\stackrel{\text{def}}{=}{\displaystyle \frac{r}{r_{ctr}}};\quad U_{\unicode[STIX]{x1D719}}^{+}\stackrel{\text{def}}{=}{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{u_{\unicode[STIX]{x1D70F},i}}};\quad R_{r\unicode[STIX]{x1D719}}^{\ast }\stackrel{\text{def}}{=}{\displaystyle \frac{R_{r\unicode[STIX]{x1D719}}}{|R_{r\unicode[STIX]{x1D719}}|_{ctr}}}.\end{eqnarray}$$

Substituting the outer-scaled variables into (3.3), the outer-scaled MMB-$\unicode[STIX]{x1D719}$ equation can be presented as

(3.5)$$\begin{eqnarray}0=\left[{\displaystyle \frac{u_{\unicode[STIX]{x1D70F},i}^{2}}{|R_{r\unicode[STIX]{x1D719}}|_{ctr}}}{\displaystyle \frac{1}{\mathit{Re}_{\unicode[STIX]{x1D70F},i}}}\right]{\displaystyle \frac{\text{d}}{\text{d}z^{-}}}\left({\displaystyle \frac{1}{r^{\ast }}}{\displaystyle \frac{\text{d}}{\text{d}z^{-}}}(r^{\ast }U_{\unicode[STIX]{x1D719}}^{+})\right)+{\displaystyle \frac{\text{d}R_{r\unicode[STIX]{x1D719}}^{\ast }}{\text{d}z^{-}}}+A_{t}{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}^{\ast }}{r^{\ast }}}.\end{eqnarray}$$

For a small gap with $r_{i}\approx r_{o}$ or $A_{t}\approx 0$, $|R_{r\unicode[STIX]{x1D719}}|_{ctr}\approx u_{\unicode[STIX]{x1D70F},i}^{2}$ as shown above. Hence, a proper outer scaling for a turbulent TCF at small geometry Atwood number is

(3.6)$$\begin{eqnarray}0=\left[{\displaystyle \frac{1}{\mathit{Re}_{\unicode[STIX]{x1D70F},i}}}\right]{\displaystyle \frac{\text{d}}{\text{d}z^{-}}}\left({\displaystyle \frac{1}{r^{\ast }}}{\displaystyle \frac{\text{d}}{\text{d}z^{-}}}(r^{\ast }U_{\unicode[STIX]{x1D719}}^{+})\right)+{\displaystyle \frac{\text{d}R_{r\unicode[STIX]{x1D719}}^{+}}{\text{d}z^{-}}}+A_{t}{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}^{+}}{r^{\ast }}}.\end{eqnarray}$$

This outer-scaled MMB-$\unicode[STIX]{x1D719}$ equation involves two non-dimensional numbers: $A_{t}$ and a friction Reynolds number $Re_{\unicode[STIX]{x1D70F},i}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}$. An advantage of using 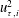$u_{\unicode[STIX]{x1D70F},i}^{2}$ instead of $|R_{r\unicode[STIX]{x1D719}}|_{ctr}$, from a practical perspective, is that $u_{\unicode[STIX]{x1D70F},i}$ can be directly obtained from the measurement of the mean torque at either the inner cylinder or the outer cylinder. Based on dimensional analysis, $|R_{r\unicode[STIX]{x1D719}}|_{ctr}$ is a function of $A_{t}$ and $Re_{\unicode[STIX]{x1D70F},i}$ and $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}$. Therefore, for simplicity, $u_{\unicode[STIX]{x1D70F},i}^{2}$ will be used as a reference scale for the Reynolds shear stress, even when $|R_{r\unicode[STIX]{x1D719}}|_{ctr}$ is much smaller than $u_{\unicode[STIX]{x1D70F},i}^{2}$, when $A_{t}$ is not small.

Figure 9. Mean azimuthal velocity in outer scaling. Data are from DNS of Dong (Reference Dong2008) with $A_{t}=1/3$. (a) $U_{\unicode[STIX]{x1D719}}^{+}$ versus $z^{-}$. (b) $r^{\ast }U_{\unicode[STIX]{x1D719}}^{+}$ versus $z^{-}$. PCF data are from DNS of Kawamura et al. (Reference Kawamura, Abe and Shingai2000) at $Re_{\unicode[STIX]{x1D70F}}=181$. PPF data are from Moser, Kim & Mansour (Reference Moser, Kim and Mansour1999) at $Re_{\unicode[STIX]{x1D70F}}=180$.

Figure 9 presents the DNS data of the mean azimuthal velocity for the same $A_{t}$ and $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FA}}$, but different Reynolds numbers. In figure 9(a), the DNS data are presented as the inner-scaled mean azimuthal velocity $U_{\unicode[STIX]{x1D719}}^{+}$ versus the outer-scaled wall-normal distance $z^{-}$. In figure 9(b), the DNS data are presented as the normalized angular momentum $r^{\ast }U_{\unicode[STIX]{x1D719}}^{+}$ versus the outer-scaled wall-normal distance $z^{-}$. Figure 9 shows that the data at $Re_{\unicode[STIX]{x1D70F},i}=33$ deviate from the higher Reynolds number data. This deviation is the low Reynolds number effect, as in canonical turbulent channel or pipe flows (Tennekes & Lumley Reference Tennekes and Lumley1972).

In a turbulent plane Couette flow or a turbulent plane Poiseuille flow, the coordinate system is typically set up so the mean velocity at the wall is $0$ and the scaling of the mean velocity for the outer layer is usually the so-called mean velocity deficit: $U_{ctr}-U$. In a TCF, the mean azimuthal velocity at the inner cylinder is usually set as $U_{\unicode[STIX]{x1D719},i}=r_{i}\unicode[STIX]{x1D6FA}_{i}$. Hence, the profile of $U_{\unicode[STIX]{x1D719}}$ in a TCF is analogous to the mean velocity deficit in a plane Couette flow. For comparison, the mean velocity deficit $U_{ctr}^{+}-U^{+}$ for a pressure-driven turbulent channel flow and a turbulent plane Couette flow are also presented in figure 9.

In figure 9, the mean velocity deficits for PCF and PPF are multiplied by an empirical factor of $1/3$, to demonstrate the similar trend between TCF and PCF or PPF. The multiplying factor is related to the pre-factor in the viscous force term in (3.5): $u_{\unicode[STIX]{x1D70F},i}^{2}/|R_{r\unicode[STIX]{x1D719}}|_{ctr}\approx 1/(1-A_{t})^{2}\geqslant 1$. Compared with PCF or PPF, the core region of a turbulent TCF is better mixed and the mean velocity gradient is smaller. For a small Atwood number $A_{t}\rightarrow 0$, the mean azimuthal velocity in a turbulent TCF will approach the mean velocity deficit in a turbulent plane Couette flow.

In a pressure-driven turbulent channel flow, the mean velocity is symmetric about the channel centreline. In a shear-driven turbulent plane Couette flow, on the other hand, the mean velocity is anti-symmetric about the channel centreline. In either case, the mean velocity deficit will be exactly zero at the channel centreline $z^{-}=1$. Notably, in a turbulent TCF, the mean flow is not anti-symmetric about the mid-gap. As shown in figure 9, $U_{\unicode[STIX]{x1D719}}$ in general is not zero at $z^{-}=1$.

In pressure- or shear-driven turbulent wall-bounded flows, the Reynolds shear stress profiles from different Reynolds numbers collapse well (see Pope Reference Pope2001), and as shown in figure 2, $R_{r\unicode[STIX]{x1D719}}^{+}$ from different Reynolds numbers also collapse reasonably well versus $z^{-}$ for a turbulent TCF. The outer layer scaling for a turbulent TCF and pressure- or shear-driven turbulent wall-bounded flows are similar.

3.3 Scaling for Layer I of the inner half

In Layer I of the inner half shown in figure 8, the force balance is between the viscous force and the Reynolds shear force, similar to the inner layer in a pressure-driven turbulent channel or pipe flow. The mean azimuthal velocity will be scaled by $u_{\unicode[STIX]{x1D70F},i}$, and the Reynolds shear stress will also be scaled by $u_{\unicode[STIX]{x1D70F},i}^{2}$. The distance from the wall $z=r-r_{i}$ will be scaled by the viscous length scale $\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F},i}$. The inner scaled variables are denoted as

(3.7a-e)$$\begin{eqnarray}z=r-r_{i};\quad \text{d}z^{+}\stackrel{\text{def}}{=}{\displaystyle \frac{\text{d}r}{\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F},i}}};\quad U_{\unicode[STIX]{x1D719}}^{+}\stackrel{\text{def}}{=}{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}}{u_{\unicode[STIX]{x1D70F},i}}};\quad R_{r\unicode[STIX]{x1D719}}^{+}\stackrel{\text{def}}{=}{\displaystyle \frac{R_{r\unicode[STIX]{x1D719}}}{u_{\unicode[STIX]{x1D70F},i}^{2}}};\quad r^{\ast }\stackrel{\text{def}}{=}{\displaystyle \frac{r}{r_{ctr}}}.\end{eqnarray}$$

Substituting the inner-scaled variables into (3.3), the inner-scaled MMB-$\unicode[STIX]{x1D719}$ equation can be expressed as

(3.8)$$\begin{eqnarray}0={\displaystyle \frac{\text{d}}{\text{d}z^{+}}}\left({\displaystyle \frac{1}{r^{\ast }}}{\displaystyle \frac{\text{d}}{\text{d}z^{+}}}(r^{\ast }U_{\unicode[STIX]{x1D719}}^{+})\right)+{\displaystyle \frac{\text{d}R_{r\unicode[STIX]{x1D719}}^{+}}{\text{d}z^{+}}}+{\displaystyle \frac{A_{t}}{\mathit{Re}_{\unicode[STIX]{x1D70F},i}}}{\displaystyle \frac{2R_{r\unicode[STIX]{x1D719}}^{+}}{r^{\ast }}}.\end{eqnarray}$$

The inner-scaled mean azimuthal velocity profiles are presented in figure 10(a). The data are presented as the difference between the mean azimuthal velocity and the inner cylinder velocity (the data are from the DNS of Dong (Reference Dong2008) for four Reynolds numbers). For comparison, the mean streamwise velocity in a turbulent plane Poiseuille flow and a turbulent plane Couette flow are also presented. As Reynolds number increases, the mean velocity $U^{+}$ in PPF or PCF exhibits a layer with a logarithmic-like growth. The so-called log layer extends outwards as the Reynolds number increases. The mean relative velocity $U_{\unicode[STIX]{x1D719},i}^{+}-U_{\unicode[STIX]{x1D719}}^{+}$ in a turbulent TCF also exhibits a logarithmic-like growth away from the inner cylinder, but the additive constant in the logarithmic function varies with the Reynolds number, as shown in figure 10(a).

In figure 10(b), the relative angular momentum is plotted as the form in (3.8). DNS data from different Reynolds numbers but the same $A_{t}$ are seen to collapse reasonably well in the inner region. The relative angular momentum $r^{\ast }(U_{\unicode[STIX]{x1D719},i}^{+}-U_{\unicode[STIX]{x1D719}}^{+})$, for $A_{t}=1/3$, is below the mean velocity profile in a turbulent PPF or PCF. At the small-gap limit or $A_{t}\rightarrow 0$, the relative angular momentum $r^{\ast }(U_{\unicode[STIX]{x1D719},i}^{+}-U_{\unicode[STIX]{x1D719}}^{+})$ in a turbulent TCF will approach the mean velocity distribution of a turbulent channel or Couette flow. On the other hand, for the large-gap limit, the relative angular momentum will become even smaller, as indicated by the arrow for $A_{t}$. For a fixed $A_{t}$, the relative angular momentum also exhibits a layer with a logarithmic-like growth, and this log layer extends outwards as the Reynolds number increases, indicated by the arrow for $\mathit{Re}$. More DNS simulations are required to study the effect of Atwood number, Reynolds number and rotation ratio.

Figure 10. Scaling of the mean azimuthal velocity for Layer I of inner half. (a) Inner-scaled mean azimuthal velocity relative to the inner cylinder velocity versus the inner-scaled wall-normal distance $z^{+}$. (b) Inner-scaled mean angular momentum versus $z^{+}$. Data are from DNS of Dong (Reference Dong2008) for $A_{t}=1/3$. For comparison, DNS data of turbulent plane Couette flow at $Re_{\unicode[STIX]{x1D70F}}=181$ by Kawamura et al. (Reference Kawamura, Abe and Shingai2000), and DNS data of turbulent channel flow at two Reynolds numbers $Re_{\unicode[STIX]{x1D70F}}=180$ and $590$ by Moser et al. (Reference Moser, Kim and Mansour1999) are also plotted.

Note that the boundary condition at the inner cylinder wall can be presented as

(3.9)$$\begin{eqnarray}\left|{\displaystyle \frac{\text{d}U_{\unicode[STIX]{x1D719}}^{+}}{\text{d}z^{+}}}\right|_{r=r_{i}}-{\displaystyle \frac{U_{\unicode[STIX]{x1D719}}^{+}|_{r=r_{i}}}{\left({\displaystyle \frac{1}{A_{t}}}-1\right)Re_{\unicode[STIX]{x1D70F},i}}}\bigg|=1.\end{eqnarray}$$

If $U_{\unicode[STIX]{x1D719}}^{+}|_{r=r_{i}}=0$ (inner cylinder fixed, outer cylinder rotating), the inner-scaled mean azimuthal velocity gradient is $1$, similar to that in a turbulent channel or Couette flow. However, if the inner cylinder is not fixed, the inner-scaled mean azimuthal velocity gradient at the wall will be smaller than $1$. The difference is minor for small Atwood numbers and/or high Reynolds numbers. This explains why the TCF data in figure 10(a) are slightly below the curve of $U^{+}=z^{+}$ (dashed curve in the figure).

DNS data for the inner scaling of the Reynolds shear stress are presented in figure 11. For the same $A_{t}$ and rotation ratio, the inner-scaled Reynolds shear stress profiles from different Reynolds numbers collapse reasonable well in the inner layer. For comparison, the Reynolds shear stress for a turbulent channel flow at $Re_{\unicode[STIX]{x1D70F}}=180$ is shown in figure 11(a). The inner-scaled Reynolds shear stress in a turbulent TCF displays a trend in Layer I that is similar to the Layer I of a pressure-driven turbulent channel flow.

In figure 11(b), the DNS data of $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ in a TCF are plotted, along with the Reynolds shear stress for a turbulent plane Couette flow at $Re_{\unicode[STIX]{x1D70F}}=181$. The inner-scaled Reynolds shear stress data for TCF at different Reynolds numbers collapse reasonably well. The deviation at $Re_{\unicode[STIX]{x1D70F},i}=33$ is caused by the low Reynolds number effect.

Figure 11. Scaling of the Reynolds shear stress for the inner layer. (a) $-R_{r\unicode[STIX]{x1D719}}^{+}$ versus $z^{+}$. The TCF data are from DNS of Dong (Reference Dong2008) with counter-rotating cylinder and $A_{t}=0.333$. The turbulent plane channel flow data are from DNS of Moser et al. (Reference Moser, Kim and Mansour1999) at $\mathit{Re}_{\unicode[STIX]{x1D70F}}=180$. (b) $-(r/r_{i})^{2}R_{r\unicode[STIX]{x1D719}}^{+}$ versus $z^{+}$. The turbulent plane Couette data are from DNS of Kawamura et al. (Reference Kawamura, Abe and Shingai2000) at $Re_{\unicode[STIX]{x1D70F}}=181$.