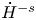1. Introduction
A fluid-mechanical theory for two-phase mixtures of fluids faces a well-known mathematical difficulty: the movement of the interfaces is naturally amenable to a Lagrangian description, while the bulk fluid flow is usually considered in the Eulerian framework [Reference Feireisl, Petzeltova, Rocca and Schimperna10]. Recently, the phase-field methods, or sometimes called the diffuse interface approaches, has been introduced to overcome this difficulty by postulating the existence of a ‘diffuse’ interface spread over a possibly narrow region covering the ‘real’ sharp interface boundary. Now, these models become one of the major tools to study a variety of interfacial phenomena. As the underlying physical problem still conceptually consists of sharp interfaces, the dynamics of the phase variable remains to a considerable extent purely fictitious [Reference Feireisl, Petzeltova, Rocca and Schimperna10]. Typically, different variants of Allen–Cahn, Cahn–Hilliard or other types of dynamics were used to describe the models, see previous studies [Reference Anderson, McFadden and Wheeler1, Reference Gurti, Polignone and Vinals14, Reference Liu, Shen and Yang20, Reference Lowengrub and Truskinovsky21] for example.
One of the well-known diffuse interface model for two-phase flow is the coupled Navier–Stokes/Allen–Cahn system. In this model, the interfaces between the phases are assumed to be of ‘diffuse’ nature, that is, sharp interfaces are replaced by narrow transition layers. These regions are located by a phase field variable ![]() $\chi$ governed by the Allen–Cahn equation, while the dynamics are described by the Navier–Stokes equations. In [Reference Blesgen2], Blesgen proposed this model and developed a thermodynamically and mechanically consistent set of partial differential equations extending the Navier–Stokes equations to a compressible binary Allen–Cahn mixture. As Blesgen [Reference Blesgen2] has pointed out before, the Navier–Stokes–Allen–Cahn model can be seen as a first step towards incorporating transport mechanism into the description of phase-formation processes.
$\chi$ governed by the Allen–Cahn equation, while the dynamics are described by the Navier–Stokes equations. In [Reference Blesgen2], Blesgen proposed this model and developed a thermodynamically and mechanically consistent set of partial differential equations extending the Navier–Stokes equations to a compressible binary Allen–Cahn mixture. As Blesgen [Reference Blesgen2] has pointed out before, the Navier–Stokes–Allen–Cahn model can be seen as a first step towards incorporating transport mechanism into the description of phase-formation processes.
During the past few years, many authors studied the properties of solutions for the incompressible Navier–Stokes system with matched density. For example, Favre and Schimperna [Reference Favre and Schimperna9] considered the existence of weak solution in three-dimensional (3D) and well-posedness of strong solution in two-dimensional (2D), Xu et al. [Reference Xu, Zhao and Liu29] studied the existence of axisymmetric solutions, Zhao et al. [Reference Zhao, Guo and Huang31] studied the vanishing viscosity limit, Gal and Grasselli [Reference Gal and Grasselli11, Reference Gal and Grasselli12] considered the asymptotic behaviour and attractors. For the system based on the incompressible Navier–Stokes system with different densities, Li et al. [Reference Li and Huang18, Reference Li, Ding and Huang19] studied the local well-posedness and blow-up criterion of strong solutions. Moreover, by using an energetic variational approach, Jiang et al. [Reference Jiang, Li and Liu15] derived a different model of Navier–Stokes–Allen–Cahn, then proved the existence of weak solutions in 3D, the well-posedness of strong solutions in 2D, and studied the long-time behaviour of the strong solutions.
As far as we know, there are also some classical results are available for the initial-boundary value problem of compressible Navier–Stokes–Allen–Cahn system. In [Reference Feireisl, Petzeltova, Rocca and Schimperna10], for the initial-boundary value problem of 3D compressible model, by using Faedo–Galerkin approximation, Feireisl et al. proved the existence of global-in-time weak solutions without any restriction on the size of initial data for the exponent of pressure ![]() $\gamma >6$. This result was extended to
$\gamma >6$. This result was extended to ![]() $\gamma >2$ in Chen et al. [Reference Chen, Wen and Zhu4]. Moreover, supposed that the boundary conditions of the model are of mixed type (Neumann–Dirichlet) and may be nonhomogeneous, the density is Hölder continuous for instance, Kotschote [Reference Kotschote17] established the local well-posedness of solutions for sufficiently smooth data, in a general
$\gamma >2$ in Chen et al. [Reference Chen, Wen and Zhu4]. Moreover, supposed that the boundary conditions of the model are of mixed type (Neumann–Dirichlet) and may be nonhomogeneous, the density is Hölder continuous for instance, Kotschote [Reference Kotschote17] established the local well-posedness of solutions for sufficiently smooth data, in a general ![]() $C^2$ bounded domain of
$C^2$ bounded domain of ![]() $\mathbb {R}^n$ (
$\mathbb {R}^n$ (![]() $n\geq 1$). Ding et al. [Reference Ding, Li and Luo5, Reference Ding, Li and Tang6] proved the existence and uniqueness of global classical solution, the existence of weak solutions and the existence of unique global strong solution of the initial-boundary value problem of one-dimensional (1D) compressible Navier–Stokes–Allen–Cahn systems for the initial data without vacuum states. Recently, Zhu and his authors [Reference Luo, Yin and Zhu22, Reference Yin and Zhu30] paid their attention to the large time behaviour of solutions for the Cauchy problem and inflow problem of 1D compressible Navier–Stokes–Allen–Cahn equations, respectively. In [Reference Luo, Yin and Zhu22], Luo, Yin and Zhu proved that the solutions to the Cauchy problem of 1D compressible Navier–Stokes/Allen–Cahn system tend time-asymptotically to the rarefaction wave, where the strength of the rarefaction wave is not required to be small. In addition, for the inflow problem of 1D compressible Navier–Stokes/Allen–Cahn system, Yin and Zhu [Reference Yin and Zhu30] analysed the large-time behaviour of the solution, proved the existence of the stationary solution and the asymptotic stability of the nonlinear wave. However, to our knowledge, there's no result on the Cauchy problem for the 3D compressible Navier–Stokes–Allen–Cahn system.
$n\geq 1$). Ding et al. [Reference Ding, Li and Luo5, Reference Ding, Li and Tang6] proved the existence and uniqueness of global classical solution, the existence of weak solutions and the existence of unique global strong solution of the initial-boundary value problem of one-dimensional (1D) compressible Navier–Stokes–Allen–Cahn systems for the initial data without vacuum states. Recently, Zhu and his authors [Reference Luo, Yin and Zhu22, Reference Yin and Zhu30] paid their attention to the large time behaviour of solutions for the Cauchy problem and inflow problem of 1D compressible Navier–Stokes–Allen–Cahn equations, respectively. In [Reference Luo, Yin and Zhu22], Luo, Yin and Zhu proved that the solutions to the Cauchy problem of 1D compressible Navier–Stokes/Allen–Cahn system tend time-asymptotically to the rarefaction wave, where the strength of the rarefaction wave is not required to be small. In addition, for the inflow problem of 1D compressible Navier–Stokes/Allen–Cahn system, Yin and Zhu [Reference Yin and Zhu30] analysed the large-time behaviour of the solution, proved the existence of the stationary solution and the asymptotic stability of the nonlinear wave. However, to our knowledge, there's no result on the Cauchy problem for the 3D compressible Navier–Stokes–Allen–Cahn system.
In this paper, we consider the Cauchy problem of 3D compressible Navier–Stokes–Allen–Cahn equations [Reference Blesgen2, Reference Kotschote17, Reference Witterstein28]
 \begin{equation} \left\{\begin{array}{@{}l} \rho_t+\nabla\cdot(\rho u)=0,\\ \partial_t(\rho u)+\nabla\cdot(\rho u\otimes u)+\nabla p-\mu\Delta u-(\mu+\lambda)\nabla\text{div}\,u\\ \qquad\qquad\qquad={-}\ell\nabla\cdot\left(\nabla\chi\otimes\nabla\chi={-}\dfrac{|\nabla\chi|^2}2 \mathbb{I}_3\right),\\ \partial_t(\rho\chi)+\text{div}(\rho\chi u)={-}\omega, \\ \rho\omega={-}\ell\Delta\chi+\rho\dfrac{\partial\Phi(\rho,\chi)}{\partial\chi},\\ (\rho,u,\chi)|_{t=0}=(\rho_0,u_0,\chi_0), \end{array} \right. \end{equation}
\begin{equation} \left\{\begin{array}{@{}l} \rho_t+\nabla\cdot(\rho u)=0,\\ \partial_t(\rho u)+\nabla\cdot(\rho u\otimes u)+\nabla p-\mu\Delta u-(\mu+\lambda)\nabla\text{div}\,u\\ \qquad\qquad\qquad={-}\ell\nabla\cdot\left(\nabla\chi\otimes\nabla\chi={-}\dfrac{|\nabla\chi|^2}2 \mathbb{I}_3\right),\\ \partial_t(\rho\chi)+\text{div}(\rho\chi u)={-}\omega, \\ \rho\omega={-}\ell\Delta\chi+\rho\dfrac{\partial\Phi(\rho,\chi)}{\partial\chi},\\ (\rho,u,\chi)|_{t=0}=(\rho_0,u_0,\chi_0), \end{array} \right. \end{equation}
where ![]() $\rho$ denotes the total fluid density,
$\rho$ denotes the total fluid density, ![]() $u$ implies the mean velocity of the fluid mixture,
$u$ implies the mean velocity of the fluid mixture, ![]() $\chi$ is the concentration of one selected constituent and the pressure
$\chi$ is the concentration of one selected constituent and the pressure ![]() $p=p(\rho )$ is a smooth function in a neighbourhood of
$p=p(\rho )$ is a smooth function in a neighbourhood of ![]() $1$ with
$1$ with ![]() $p'(1)=1$, respectively. Moreover,
$p'(1)=1$, respectively. Moreover, ![]() $\omega$ is the chemical potential and
$\omega$ is the chemical potential and ![]() $\mathbb {I}_3$ denotes a
$\mathbb {I}_3$ denotes a ![]() $3\times 3$ identity matrix.
$3\times 3$ identity matrix. ![]() $\mu$ and
$\mu$ and ![]() $\lambda$ are two viscosity coefficients, which satisfy
$\lambda$ are two viscosity coefficients, which satisfy
The specific free energy ![]() $f(\rho ,\chi )$ can be defined as
$f(\rho ,\chi )$ can be defined as
where ![]() $\gamma >1$ is the adiabatic constant and the constant
$\gamma >1$ is the adiabatic constant and the constant ![]() $\sqrt {\ell }$ denotes the thickness of the interfacial region. In this paper, we take
$\sqrt {\ell }$ denotes the thickness of the interfacial region. In this paper, we take
For simplicity, we let ![]() $\ell \equiv 1$ throughout the rest of this paper.
$\ell \equiv 1$ throughout the rest of this paper.
Notation 1.1 In the following, we use ![]() $H^k(\mathbb {R}^3$
$H^k(\mathbb {R}^3$ ![]() $(k\in \mathbb {R})$ to denote the usual Sobolev spaces with norm
$(k\in \mathbb {R})$ to denote the usual Sobolev spaces with norm ![]() $\|\cdot \|_{H^s}$ and
$\|\cdot \|_{H^s}$ and ![]() $L^p(\mathbb {R}^3)$,
$L^p(\mathbb {R}^3)$, ![]() $1\leq p\leq \infty$ to denote the usual
$1\leq p\leq \infty$ to denote the usual ![]() $L^p$ spaces with norm
$L^p$ spaces with norm ![]() $\|\cdot \|_{L^p}$. We also introduce the homogeneous negative index Sobolev space
$\|\cdot \|_{L^p}$. We also introduce the homogeneous negative index Sobolev space ![]() $\dot {H}^{-s}(\mathbb {R}^3)$:
$\dot {H}^{-s}(\mathbb {R}^3)$:
endowed with the norm ![]() $\|f\|_{\dot {H}^{-s}}:=\||\xi |^{-s}\hat {f}(\xi )\|_{L^2}$. The symbol
$\|f\|_{\dot {H}^{-s}}:=\||\xi |^{-s}\hat {f}(\xi )\|_{L^2}$. The symbol ![]() $\nabla ^l$ with an integer
$\nabla ^l$ with an integer ![]() $l\geq 0$ stands for the usual spatial derivatives of order
$l\geq 0$ stands for the usual spatial derivatives of order ![]() $l$. For instance, define
$l$. For instance, define
If ![]() $l<0$ or
$l<0$ or ![]() $l$ is not a positive integer,
$l$ is not a positive integer, ![]() $\nabla ^l$ stands for
$\nabla ^l$ stands for ![]() $\Lambda ^l$ defined by
$\Lambda ^l$ defined by
where ![]() $\hat {f}$ is the Fourier transform of
$\hat {f}$ is the Fourier transform of ![]() $f$ (see [Reference Grafakos13]). Moreover, we use the notation
$f$ (see [Reference Grafakos13]). Moreover, we use the notation ![]() $A\lesssim B$ to mean that
$A\lesssim B$ to mean that ![]() $A\leq cB$ for a universal constant
$A\leq cB$ for a universal constant ![]() $c>0$ that only depends on the parameters coming from the problem and the indexes
$c>0$ that only depends on the parameters coming from the problem and the indexes ![]() $N$ and
$N$ and ![]() $s$ coming from the regularity on the data.
$s$ coming from the regularity on the data.
For this system, we first show the local well-posedness in the following lemma.
Lemma 1.1 Let the initial data![]() $(\varrho _0,u_0, \chi _0)\in H^3(\mathbb {R}^3)\times H^3(\mathbb {R}^3)\times H^{4}(\mathbb {R}^3)$. Then there exit positive constants
$(\varrho _0,u_0, \chi _0)\in H^3(\mathbb {R}^3)\times H^3(\mathbb {R}^3)\times H^{4}(\mathbb {R}^3)$. Then there exit positive constants ![]() $\nu _0>0$ and
$\nu _0>0$ and ![]() $T>0$ depending only on
$T>0$ depending only on ![]() $\|(\varrho _0,u_0, \chi _0,\nabla \chi _0)\|_{H^3}$ such that the system (1.4) has a unique solution
$\|(\varrho _0,u_0, \chi _0,\nabla \chi _0)\|_{H^3}$ such that the system (1.4) has a unique solution
satisfying
 \begin{align*}
&\|(\varrho,u,\chi,\nabla\chi)(t)\|_{H^3}, \left(\nu_0\int_0^t\|\nabla(u,\chi,\nabla\chi)(\tau)\|_{H^3}^2\,{\rm d}\tau\right)^{1/2}\\
&\quad \leq
C(\|(\varrho_0,u_0,\chi_0,\nabla\chi_0)\|_{H^3}),\quad\forall
t\in[0,T]. \end{align*}
\begin{align*}
&\|(\varrho,u,\chi,\nabla\chi)(t)\|_{H^3}, \left(\nu_0\int_0^t\|\nabla(u,\chi,\nabla\chi)(\tau)\|_{H^3}^2\,{\rm d}\tau\right)^{1/2}\\
&\quad \leq
C(\|(\varrho_0,u_0,\chi_0,\nabla\chi_0)\|_{H^3}),\quad\forall
t\in[0,T]. \end{align*}
Lemma 1.1 can be proved by using the Banach fixed point theorem. One will sketch the proof in the second part of § 2.
Next, denote ![]() $\varrho =\rho -1$, rewrite (1.1) in the perturbation form as
$\varrho =\rho -1$, rewrite (1.1) in the perturbation form as
 \begin{equation}
\left\{\begin{array}{@{}l}
\varrho_t+\text{div}\,u={-}\varrho\text{div}\,u-u\cdot\nabla\varrho,\\
u_t-\mu\Delta u-(\mu+\lambda)\nabla\text{div}\,u+\nabla\varrho\\
\quad ={-}u\cdot\nabla u-h(\varrho)(\mu\Delta u+(\mu+\lambda)\nabla\text{div}\,u)\\
\qquad\,-g(\varrho)\nabla\varrho-\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\dfrac{|\nabla\chi|^2}2
\mathbb{I}_3\right),\\
\chi_t-\Delta\chi ={-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi),\\
(\varrho,u,\chi)|_{t=0}=(\varrho_0,u_0,\chi_0)=(\rho_0-1,u_0,\chi_0),
\end{array} \right.
\end{equation}
\begin{equation}
\left\{\begin{array}{@{}l}
\varrho_t+\text{div}\,u={-}\varrho\text{div}\,u-u\cdot\nabla\varrho,\\
u_t-\mu\Delta u-(\mu+\lambda)\nabla\text{div}\,u+\nabla\varrho\\
\quad ={-}u\cdot\nabla u-h(\varrho)(\mu\Delta u+(\mu+\lambda)\nabla\text{div}\,u)\\
\qquad\,-g(\varrho)\nabla\varrho-\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\dfrac{|\nabla\chi|^2}2
\mathbb{I}_3\right),\\
\chi_t-\Delta\chi ={-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi),\\
(\varrho,u,\chi)|_{t=0}=(\varrho_0,u_0,\chi_0)=(\rho_0-1,u_0,\chi_0),
\end{array} \right.
\end{equation}where
The main purpose of this paper is to study the small initial data global well-posedness and optimal decay estimates of strong solutions for system (1.1) in the whole space ![]() $\mathbb {R}^3$. We use a general energy method, Kato–Ponce inequality and the Gagliardo–Nirenberg interpolation techniques to obtain the global well-posedness and the optimal time-decay rates of the solution to system (1.1) when the initial data are sufficiently small.
$\mathbb {R}^3$. We use a general energy method, Kato–Ponce inequality and the Gagliardo–Nirenberg interpolation techniques to obtain the global well-posedness and the optimal time-decay rates of the solution to system (1.1) when the initial data are sufficiently small.
Next, one state the global well-posedness and decay estimates of solutions for system (1.4):
Theorem 1.1 Let ![]() $N\geq 3$, assume that
$N\geq 3$, assume that ![]() $(\varrho _0,u_0, \chi _0)\in H^N(\mathbb {R}^3)\times H^N(\mathbb {R}^3)\times H^{N+1}(\mathbb {R}^3)$, and there exists a constant
$(\varrho _0,u_0, \chi _0)\in H^N(\mathbb {R}^3)\times H^N(\mathbb {R}^3)\times H^{N+1}(\mathbb {R}^3)$, and there exists a constant ![]() $\delta _0>0$ such that if
$\delta _0>0$ such that if
then there exists a unique global solution ![]() $(\varrho ,u,\chi )$ satisfying that for all
$(\varrho ,u,\chi )$ satisfying that for all ![]() $t\geq 0$,
$t\geq 0$,
 \begin{align}
&\|\varrho(t)\|_{H^N}^2+\|u(t)\|_{H^N}^2+\|
\chi\|_{H^N}^2+\|\nabla \chi\|_{H^N}^2\nonumber\\
&\quad+\int_0^t(\|\nabla
u(s)\|_{H^N}^2+\|\chi\|_{H^N}^2+\|\nabla
\chi\|_{H^N}^2)\,{\rm d}s\nonumber\\ &\qquad\leq
C(\|\varrho_0\|_{H^N}^2+\|u_0\|_{H^N}^2+\|
\chi_0\|_{H^N}^2+\| \nabla\chi_0\|_{H^N}^2).
\end{align}
\begin{align}
&\|\varrho(t)\|_{H^N}^2+\|u(t)\|_{H^N}^2+\|
\chi\|_{H^N}^2+\|\nabla \chi\|_{H^N}^2\nonumber\\
&\quad+\int_0^t(\|\nabla
u(s)\|_{H^N}^2+\|\chi\|_{H^N}^2+\|\nabla
\chi\|_{H^N}^2)\,{\rm d}s\nonumber\\ &\qquad\leq
C(\|\varrho_0\|_{H^N}^2+\|u_0\|_{H^N}^2+\|
\chi_0\|_{H^N}^2+\| \nabla\chi_0\|_{H^N}^2).
\end{align}
If further, ![]() $(\varrho , u_0, \chi _0,\nabla \chi _0)\in \dot {H}^{-s}(\mathbb {R}^3)$ for some
$(\varrho , u_0, \chi _0,\nabla \chi _0)\in \dot {H}^{-s}(\mathbb {R}^3)$ for some ![]() $s\in [0,\frac {3}{2})$, then for all
$s\in [0,\frac {3}{2})$, then for all ![]() $t\geq 0$,
$t\geq 0$,
and
 \begin{align} &\|\nabla^l\varrho(t)\|_{H^{N-l}}+\|\nabla^lu(t)\|_{H^{N-l}}+\|\nabla^l \chi(t)\|_{H^{N-l}}\nonumber\\ &\quad+ \|\nabla^{l+1} \chi(t)\|_{H^{N-l}}\leq C(1+t)^{-({l+1})/2},\quad\text{for}\ l=0,1,\ldots, N-1. \end{align}
\begin{align} &\|\nabla^l\varrho(t)\|_{H^{N-l}}+\|\nabla^lu(t)\|_{H^{N-l}}+\|\nabla^l \chi(t)\|_{H^{N-l}}\nonumber\\ &\quad+ \|\nabla^{l+1} \chi(t)\|_{H^{N-l}}\leq C(1+t)^{-({l+1})/2},\quad\text{for}\ l=0,1,\ldots, N-1. \end{align} Note that the Hardy–Littlewood-Sobolev theorem implies that for ![]() $p\in (1,2]$,
$p\in (1,2]$, ![]() $L^{p}(\mathbb {R}^3)\subset \dot {H}^{-s}(\mathbb {R}^3)$ with
$L^{p}(\mathbb {R}^3)\subset \dot {H}^{-s}(\mathbb {R}^3)$ with ![]() $s=3(\frac {1}{p}-\frac {1}{2})\in [0,\frac {3}{2})$. Then, on the basis of theorem 1.1, we easily obtain the following corollary of the optimal decay estimates.
$s=3(\frac {1}{p}-\frac {1}{2})\in [0,\frac {3}{2})$. Then, on the basis of theorem 1.1, we easily obtain the following corollary of the optimal decay estimates.
Corollary 1.1 Under the assumptions of theorem 1.1, if we replace the ![]() $\dot {H}^{-s}(\mathbb {R}^3)$ assumption by
$\dot {H}^{-s}(\mathbb {R}^3)$ assumption by
then the following decay estimate holds:
 \begin{align}
&\|\nabla^l\varrho(t)\|_{H^{N-l}}+\|\nabla^lu(t)\|_{H^{N-l}}+\|\nabla^l
\chi(t)\|_{H^{N-l}}+\|\nabla^{l+1}
\chi(t)\|_{H^{N-l}}\nonumber\\ &\quad \leq
C(1+t)^{-\left[{3}/{2}\left({1}/{p}
-{1}/{2}\right)+{l}/{2}\right]},\quad\text{for}\
l=0,1,\ldots, N-1.
\end{align}
\begin{align}
&\|\nabla^l\varrho(t)\|_{H^{N-l}}+\|\nabla^lu(t)\|_{H^{N-l}}+\|\nabla^l
\chi(t)\|_{H^{N-l}}+\|\nabla^{l+1}
\chi(t)\|_{H^{N-l}}\nonumber\\ &\quad \leq
C(1+t)^{-\left[{3}/{2}\left({1}/{p}
-{1}/{2}\right)+{l}/{2}\right]},\quad\text{for}\
l=0,1,\ldots, N-1.
\end{align}Remark 1.1 The compressible Hall-magnetohydrodynamics system [Reference Fan, Alsaedi, Hayat, Nakamura and Zhou7] has the following form:
 \begin{equation} \left\{\begin{array}{@{}l} \rho_t+\text{div}(\rho u)=0,\\ (\rho u)_t+\text{div}(\rho u\otimes u)+\nabla p-\mu\Delta u-(\lambda+\mu)\nabla\text{div}\,u=(\nabla\times b)\times b,\\ b_t+\nabla\times(b\times u)+\nabla\times\left(\dfrac{(\nabla\times b)\times b}{\rho}\right)=\Delta b,\\ \text{div}\,b=0,\\ (\rho,u,b)|_{t=0}=(\rho_0,u_0,b_0), \end{array} \right. \end{equation}
\begin{equation} \left\{\begin{array}{@{}l} \rho_t+\text{div}(\rho u)=0,\\ (\rho u)_t+\text{div}(\rho u\otimes u)+\nabla p-\mu\Delta u-(\lambda+\mu)\nabla\text{div}\,u=(\nabla\times b)\times b,\\ b_t+\nabla\times(b\times u)+\nabla\times\left(\dfrac{(\nabla\times b)\times b}{\rho}\right)=\Delta b,\\ \text{div}\,b=0,\\ (\rho,u,b)|_{t=0}=(\rho_0,u_0,b_0), \end{array} \right. \end{equation}
where ![]() $\rho$ is the density of the fluid,
$\rho$ is the density of the fluid, ![]() $u$ is the fluid velocity field and
$u$ is the fluid velocity field and ![]() $b$ is the magnetic field. In [Reference Fan, Alsaedi, Hayat, Nakamura and Zhou7], the authors considered the local well-posedness, small initial data global well-posedness and large time behaviour of strong solutions for system (1.10). It is worth pointing out that the structures of systems (1.1) and (1.10) are different. Especially, the principle part of (1.10)
$b$ is the magnetic field. In [Reference Fan, Alsaedi, Hayat, Nakamura and Zhou7], the authors considered the local well-posedness, small initial data global well-posedness and large time behaviour of strong solutions for system (1.10). It is worth pointing out that the structures of systems (1.1) and (1.10) are different. Especially, the principle part of (1.10)![]() $_3$ is a linear term
$_3$ is a linear term ![]() $-\Delta b$, however, it is a nonlinear function
$-\Delta b$, however, it is a nonlinear function ![]() $-({\ell }/{\rho })\Delta \chi$ in (1.1)
$-({\ell }/{\rho })\Delta \chi$ in (1.1)![]() $_3$. One can't use the tools of the dissipative equation with linear principle part to study the properties of this equation. Here, we borrow a linear term from the right-hand side of (1.1)
$_3$. One can't use the tools of the dissipative equation with linear principle part to study the properties of this equation. Here, we borrow a linear term from the right-hand side of (1.1)![]() $_3$, rewrite this equation as a second-order PDE
$_3$, rewrite this equation as a second-order PDE
where ![]() $\varrho =\rho -1$,
$\varrho =\rho -1$, ![]() $\phi (\varrho )=1/{(\varrho +1)}$ and
$\phi (\varrho )=1/{(\varrho +1)}$ and ![]() $\varphi (\varrho )=({\varrho (\varrho +2)})/({(\varrho +1)^2})$. It is worth pointing out that there exists a linear principle part
$\varphi (\varrho )=({\varrho (\varrho +2)})/({(\varrho +1)^2})$. It is worth pointing out that there exists a linear principle part ![]() $-\Delta \chi$ in (1.11). Then, by using the pure energy method, one can obtain suitable energy estimates. Moreover, the right-hand term of system (1.1)
$-\Delta \chi$ in (1.11). Then, by using the pure energy method, one can obtain suitable energy estimates. Moreover, the right-hand term of system (1.1)![]() $_2$ is different from system (1.10)
$_2$ is different from system (1.10)![]() $_2$. One can use the usual Sobolev embedding inequality, Kato–Ponce inequality together with the Gagliardo–Nirenberg interpolation techniques to deal with this term.
$_2$. One can use the usual Sobolev embedding inequality, Kato–Ponce inequality together with the Gagliardo–Nirenberg interpolation techniques to deal with this term.
Remark 1.2 There are some classical results on the initial-boundary value problem of compressible Navier–Stokes–Allen–Cahn equations in bounded domains, for example [Reference Chen and Guo3, Reference Ding, Li and Luo5, Reference Ding, Li and Tang6, Reference Fan and Li8, Reference Kotschote17, Reference Song, Zhang and Wang24] and references therein. However, only a few results related to the Cauchy problem. In terms of well-posedness of compressible Navier–Stokes–Allen–Cahn equations on bounded domains, the known constructions make use of some compactness properties in an essential manner, and more specifically of the compact Sobolev embeddings. However, if we consider the equations in the whole space, such properties are no longer valid, it is more difficult to obtain suitable a priori estimates to develop a general theory of well-posedness. In this paper, we adopt the Gagliardo–Nirenberg inequality in ![]() $\mathbb {R}^3$ (lemma 2.2), negative Sobolev norm estimates and pure energy method, overcome this difficulty, obtain the global well-posedness and the decay rate of higher-order derivatives of strong solutions. We remark that since the decay estimate is same as the heat equation, it is optimal.
$\mathbb {R}^3$ (lemma 2.2), negative Sobolev norm estimates and pure energy method, overcome this difficulty, obtain the global well-posedness and the decay rate of higher-order derivatives of strong solutions. We remark that since the decay estimate is same as the heat equation, it is optimal.
The structure of this paper is organized as follows. In § 2, we introduce some preliminary results and give a brief proof on the local well-posedness. Section 3 is devoted to establish some refined energy estimates for the solution. In § 4, we derive the evolution of the negative Sobolev norms of the solution. Finally, the proof of theorem 1.1 is postponed in § 5.
2. Preliminaries
2.1 Useful inequalities
In this section, we introduce some helpful results in ![]() $\mathbb {R}^3$.
$\mathbb {R}^3$.
First of all, the following Kato–Ponce inequality is of great importance in our paper.
Lemma 2.1 [Reference Kato and Ponce16]
Let ![]() $1< p<\infty$,
$1< p<\infty$, ![]() $s>0$. There exists a positive constant
$s>0$. There exists a positive constant ![]() $C$ such that
$C$ such that
where ![]() $p_2,q_2\in (1,\infty )$ satisfying
$p_2,q_2\in (1,\infty )$ satisfying ![]() $\frac 1p=\frac 1{p_1}+\frac 1{p_2}=\frac 1{q_1}+\frac 1{q_2}$.
$\frac 1p=\frac 1{p_1}+\frac 1{p_2}=\frac 1{q_1}+\frac 1{q_2}$.
The following Gagliardo–Nirenberg inequality in ![]() $\mathbb {R}^3$ was proved in [Reference Nirenberg23].
$\mathbb {R}^3$ was proved in [Reference Nirenberg23].
Lemma 2.2 [Reference Nirenberg23]
Let ![]() $0\leq m,\alpha \leq l$, then we have
$0\leq m,\alpha \leq l$, then we have
where ![]() $\theta \in [0,1]$ and
$\theta \in [0,1]$ and ![]() $\alpha$ satisfies
$\alpha$ satisfies
Here, when ![]() $p=\infty$, we require that
$p=\infty$, we require that ![]() $0<\theta <1$.
$0<\theta <1$.
We recall the following commutator estimate:
Lemma 2.3 [Reference Wang26]
Let ![]() $m\geq 1$ be an integer and define the commutator
$m\geq 1$ be an integer and define the commutator
Then, the following inequality holds:
where ![]() $p,~p_2,~p_3\in (1,\infty )$ and
$p,~p_2,~p_3\in (1,\infty )$ and ![]() $\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}=\frac {1}{p_3}+\frac {1}{p_4}.$
$\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}=\frac {1}{p_3}+\frac {1}{p_4}.$
Wang [Reference Wang26], Wei, Li and Yao [Reference Wei, Li and Yao27] introduced the following result:
Lemma 2.4 Suppose that ![]() $\|\varrho \|_{L^{\infty }}\leq 1$ and
$\|\varrho \|_{L^{\infty }}\leq 1$ and ![]() $p>1$. Let
$p>1$. Let ![]() $f(\varrho )$ be a smooth function of
$f(\varrho )$ be a smooth function of ![]() $\varrho$ with bounded derivatives of any order, then for any integer
$\varrho$ with bounded derivatives of any order, then for any integer ![]() $n\geq 1$, the following inequality holds:
$n\geq 1$, the following inequality holds:
We also introduce the Hardy–Littlewood–Sobolev theorem, which implies the following ![]() $L^p$ type inequality.
$L^p$ type inequality.
Lemma 2.5 [Reference Grafakos13, Reference Stein25]
Let ![]() $0\leq s<\frac {3}{2}$,
$0\leq s<\frac {3}{2}$, ![]() $1< p\leq 2$ and
$1< p\leq 2$ and ![]() $\frac {1}{2}+\frac {s}{3}=\frac {1}{p}$, then
$\frac {1}{2}+\frac {s}{3}=\frac {1}{p}$, then
The special Sobolev interpolation lemma will be used in the proof of theorem 1.1.
Lemma 2.6 [Reference Stein25, Reference Wang26]
Let ![]() $s,k\geq 0$ and
$s,k\geq 0$ and ![]() $l\geq 0$, then
$l\geq 0$, then
2.2 Local well-posedness
In the following, we give a brief proof of lemma 1.1 on the local well-posedness of system (1.1), which is similar to the arguments in [Reference Fan, Alsaedi, Hayat, Nakamura and Zhou7]. For completeness, we outline the proof here.
First, consider the following system
 \begin{equation}
\left\{\begin{array}{@{}l} \rho_t+\nabla\cdot(\rho
\tilde{u})=0,\\ \partial_t(\rho u)+\nabla\cdot(\rho
\tilde{u}\otimes u)+\nabla p=\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u\\
\quad -\,\ell\nabla\cdot\left(\nabla\chi\otimes\nabla\chi-\dfrac{|\nabla\chi|^2}2
\mathbb{I}_3\right),\\
\partial_t(\rho\chi)+\text{div}(\rho\chi
\tilde{u})={-}\omega, \\
\rho\omega={-}\ell\Delta\chi+\dfrac{\rho}{\ell}[(\tilde{\chi})^2-1]\chi
,\\ (\rho,u,\chi)|_{t=0}=(\rho_0,u_0,\chi_0),
\end{array} \right.
\end{equation}
\begin{equation}
\left\{\begin{array}{@{}l} \rho_t+\nabla\cdot(\rho
\tilde{u})=0,\\ \partial_t(\rho u)+\nabla\cdot(\rho
\tilde{u}\otimes u)+\nabla p=\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u\\
\quad -\,\ell\nabla\cdot\left(\nabla\chi\otimes\nabla\chi-\dfrac{|\nabla\chi|^2}2
\mathbb{I}_3\right),\\
\partial_t(\rho\chi)+\text{div}(\rho\chi
\tilde{u})={-}\omega, \\
\rho\omega={-}\ell\Delta\chi+\dfrac{\rho}{\ell}[(\tilde{\chi})^2-1]\chi
,\\ (\rho,u,\chi)|_{t=0}=(\rho_0,u_0,\chi_0),
\end{array} \right.
\end{equation}
where ![]() $(\tilde {u},\tilde {\varphi })\in R_T^*$ are known functions with
$(\tilde {u},\tilde {\varphi })\in R_T^*$ are known functions with ![]() $(\tilde {u},\tilde {\varphi })(x,0)=(u_0,\varphi _0)$ and
$(\tilde {u},\tilde {\varphi })(x,0)=(u_0,\varphi _0)$ and
 \[ R^*_T=\left\{v\in
H^3|\sup_{0\leq t\leq T }\|v\|^2_{H^3}+\int_0^{T }\|\nabla
v\|_{H^3}^2\,{\rm d}s\leq R\right\}, \]
\[ R^*_T=\left\{v\in
H^3|\sup_{0\leq t\leq T }\|v\|^2_{H^3}+\int_0^{T }\|\nabla
v\|_{H^3}^2\,{\rm d}s\leq R\right\}, \]
where ![]() $R>1$ and
$R>1$ and ![]() $T>0$ will be decided later.
$T>0$ will be decided later.
Note that (2.9)![]() $_1$ is linear with regular
$_1$ is linear with regular ![]() $\tilde {u}$. The existence and uniqueness are well-known and we also have
$\tilde {u}$. The existence and uniqueness are well-known and we also have
Then, if ![]() $T$ is suitably small, we can obtain the estimates for
$T$ is suitably small, we can obtain the estimates for ![]() $\rho$. Next, taking advantage of the estimate for
$\rho$. Next, taking advantage of the estimate for ![]() $\rho$ and the classical theory of linear parabolic system, one can get the existence and uniqueness of
$\rho$ and the classical theory of linear parabolic system, one can get the existence and uniqueness of ![]() $(u,\varphi ,\nabla \varphi )$ by (2.9)
$(u,\varphi ,\nabla \varphi )$ by (2.9)![]() $_2$–(2.9)
$_2$–(2.9)![]() $_4$.
$_4$.
Define a fixed point map ![]() $F:(\tilde {u},\tilde {\varphi },\tilde {\nabla \varphi })\in R_T^*\times R_T^*\times R_T^*\rightarrow (u,\varphi ,\nabla \varphi )$. We will prove that the map
$F:(\tilde {u},\tilde {\varphi },\tilde {\nabla \varphi })\in R_T^*\times R_T^*\times R_T^*\rightarrow (u,\varphi ,\nabla \varphi )$. We will prove that the map ![]() $F$ mapping
$F$ mapping ![]() $R_T^*\times R_T^*\times R_T^*$ into itself for suitable constant
$R_T^*\times R_T^*\times R_T^*$ into itself for suitable constant ![]() $R$ and small time
$R$ and small time ![]() $T$ and
$T$ and ![]() $F$ is a contraction mapping on
$F$ is a contraction mapping on ![]() $R_T^*\times R_T^*\times R_T^*$. Thus,
$R_T^*\times R_T^*\times R_T^*$. Thus, ![]() $F$ has a unique fixed point in
$F$ has a unique fixed point in ![]() $R_T^*\times R_T^*\times R_T^*$ and prove the local well-posedness result.
$R_T^*\times R_T^*\times R_T^*$ and prove the local well-posedness result.
First, in order to prove ![]() $F$ mapping
$F$ mapping ![]() $R_T^*\times R_T^*\times R_T^*$ into itself, one need to establish some a priori estimates on
$R_T^*\times R_T^*\times R_T^*$ into itself, one need to establish some a priori estimates on ![]() $(u,\varphi ,\nabla \varphi )$. In fact, simple calculations show that
$(u,\varphi ,\nabla \varphi )$. In fact, simple calculations show that
for sufficiently small ![]() $T\in (0, 1]$, and thus
$T\in (0, 1]$, and thus ![]() $F$ maps
$F$ maps ![]() $R_T^*\times R_T^*\times R_T^*$ into
$R_T^*\times R_T^*\times R_T^*$ into ![]() $R_T^*\times R_T^*\times R_T^*$.
$R_T^*\times R_T^*\times R_T^*$.
Second, in order to show ![]() $F$ is contracted in the sense of weaker norm, one suppose that
$F$ is contracted in the sense of weaker norm, one suppose that ![]() $(\rho _i,u_i,\varphi _i,)$
$(\rho _i,u_i,\varphi _i,)$ ![]() $(i=1,2)$ are the solutions to system (2.9) corresponding to
$(i=1,2)$ are the solutions to system (2.9) corresponding to ![]() $(\tilde {u}_i,\tilde {\varphi }_i)$. Denote
$(\tilde {u}_i,\tilde {\varphi }_i)$. Denote
We obtain
 \begin{equation} \left\{\begin{array}{l} \rho_t+\nabla\cdot(\rho \tilde{u}_1)={-}\nabla\cdot(\rho_2\tilde{u}),\\ \rho_1\partial_tu+\rho_1\tilde{u}_1\cdot\nabla u+\nabla(p(\rho_1)-p(\rho_2))-\mu\Delta u-(\lambda+\mu)\nabla\nabla\cdot u\\ \quad={-}\rho\partial_tu_2-(\rho_1\tilde{u}-\rho_2\tilde{u}_2)\cdot\nabla u_2-\ell \nabla\cdot\left(\nabla\chi_1\otimes\nabla\chi_1-\dfrac{|\nabla\chi_1|^2}2 \mathbb{I}_3\right)\\ \qquad p+\ell \nabla\cdot\left(\nabla\chi_2\otimes\nabla\chi_2-\dfrac{|\nabla\chi_2|^2}2 \mathbb{I}_3\right),\\ \rho_1\partial_t\chi+\rho\partial_t\chi_2+\nabla\cdot(\rho\chi_1\tilde{u}_1+\rho_2\chi\tilde{u}_1+\rho_2\chi_2\tilde{u})={-}\omega,\\ \rho_1\omega+\rho\omega_2={-}\ell\Delta\chi+\dfrac1{\ell}\rho(\tilde{\chi}_1+1)(\tilde{\chi}_1-1)\chi_1+\dfrac1{\ell}\rho_2(\tilde{\chi} +1)(\tilde{\chi}_1-1)\chi_1\\ p+\dfrac1{\ell}\rho_2(\tilde{\chi}_2+1)(\tilde{\chi}-1)\chi_1+\dfrac1{\ell}\rho_2(\tilde{\chi}_2+1)(\tilde{\chi}_2-1)\chi_2. \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \rho_t+\nabla\cdot(\rho \tilde{u}_1)={-}\nabla\cdot(\rho_2\tilde{u}),\\ \rho_1\partial_tu+\rho_1\tilde{u}_1\cdot\nabla u+\nabla(p(\rho_1)-p(\rho_2))-\mu\Delta u-(\lambda+\mu)\nabla\nabla\cdot u\\ \quad={-}\rho\partial_tu_2-(\rho_1\tilde{u}-\rho_2\tilde{u}_2)\cdot\nabla u_2-\ell \nabla\cdot\left(\nabla\chi_1\otimes\nabla\chi_1-\dfrac{|\nabla\chi_1|^2}2 \mathbb{I}_3\right)\\ \qquad p+\ell \nabla\cdot\left(\nabla\chi_2\otimes\nabla\chi_2-\dfrac{|\nabla\chi_2|^2}2 \mathbb{I}_3\right),\\ \rho_1\partial_t\chi+\rho\partial_t\chi_2+\nabla\cdot(\rho\chi_1\tilde{u}_1+\rho_2\chi\tilde{u}_1+\rho_2\chi_2\tilde{u})={-}\omega,\\ \rho_1\omega+\rho\omega_2={-}\ell\Delta\chi+\dfrac1{\ell}\rho(\tilde{\chi}_1+1)(\tilde{\chi}_1-1)\chi_1+\dfrac1{\ell}\rho_2(\tilde{\chi} +1)(\tilde{\chi}_1-1)\chi_1\\ p+\dfrac1{\ell}\rho_2(\tilde{\chi}_2+1)(\tilde{\chi}-1)\chi_1+\dfrac1{\ell}\rho_2(\tilde{\chi}_2+1)(\tilde{\chi}_2-1)\chi_2. \end{array}\right. \end{equation}
Testing (2.10)![]() $_1$, (2.10)
$_1$, (2.10)![]() $_2$ by
$_2$ by ![]() $\rho$,
$\rho$, ![]() $u$, testing (2.10)
$u$, testing (2.10)![]() $_3$ by
$_3$ by ![]() $\varphi$ and
$\varphi$ and ![]() $\Delta \varphi$ respectively, after simple calculations, one obtains
$\Delta \varphi$ respectively, after simple calculations, one obtains
 \begin{align*} &\|F(\tilde{u}_1,\tilde{\varphi}_1,\tilde{\nabla\varphi}_1)-F(\tilde{u}_2,\tilde{\varphi}_2,\tilde{\nabla\varphi}_2)\|_{L^2(0,T;H^1)}\\ &\quad\leq \theta\|(\tilde{u}_1-\tilde{u}_2,\tilde{\varphi}_1-\tilde{\varphi}_2,\nabla\tilde{\varphi}_1-\nabla\tilde{\varphi}_2\|_{L^2(0,T;H^1)}, \end{align*}
\begin{align*} &\|F(\tilde{u}_1,\tilde{\varphi}_1,\tilde{\nabla\varphi}_1)-F(\tilde{u}_2,\tilde{\varphi}_2,\tilde{\nabla\varphi}_2)\|_{L^2(0,T;H^1)}\\ &\quad\leq \theta\|(\tilde{u}_1-\tilde{u}_2,\tilde{\varphi}_1-\tilde{\varphi}_2,\nabla\tilde{\varphi}_1-\nabla\tilde{\varphi}_2\|_{L^2(0,T;H^1)}, \end{align*}
where ![]() $\theta \in (0,1)$ is a constant and
$\theta \in (0,1)$ is a constant and ![]() $T\in (0,1]$ is a small time. The above inequality implies that
$T\in (0,1]$ is a small time. The above inequality implies that ![]() $F$ is contracted in the sense of weaker norm.
$F$ is contracted in the sense of weaker norm.
Next, by using Banach fixed point theorem, we complete the proof of lemma 1.1.
3. Energy estimates
In this section, we derive the a priori energy estimates for system (1.4). Suppose that there exists a small positive constant ![]() $\delta >0$ such that
$\delta >0$ such that
which, together with Sobolev's inequality, yields directly
Simple calculations show that
and
Next, we establish the following energy estimates including ![]() $\varrho$,
$\varrho$, ![]() $u$ and
$u$ and ![]() $\chi$ themselves.
$\chi$ themselves.
Lemma 3.1 If ![]() $\sqrt {\mathcal {E}_0^3(t)}\leq \delta$, then for
$\sqrt {\mathcal {E}_0^3(t)}\leq \delta$, then for ![]() $k=0,1,\ldots , N-1$, we have
$k=0,1,\ldots , N-1$, we have
 \begin{align} &\frac{{\rm d}}{{\rm d}t}(\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{ L^2}^2)\nonumber\\ &\quad+C(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\nabla\chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim (\delta+\delta^3)(\|\nabla^{k +1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\nabla\chi\|_{L^2}^2). \end{align}
\begin{align} &\frac{{\rm d}}{{\rm d}t}(\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{ L^2}^2)\nonumber\\ &\quad+C(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\nabla\chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim (\delta+\delta^3)(\|\nabla^{k +1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\nabla\chi\|_{L^2}^2). \end{align}Proof. Taking ![]() $k$-th spatial derivatives to (1.1)
$k$-th spatial derivatives to (1.1)![]() $_1$, (1.1)
$_1$, (1.1)![]() $_2$ and (1.1)
$_2$ and (1.1)![]() $_3$,
$_3$, ![]() $k+1$th spatial derivatives to (1.1)
$k+1$th spatial derivatives to (1.1)![]() $_3$, multiplying the resulting identities by
$_3$, multiplying the resulting identities by ![]() $\nabla ^k\varrho$,
$\nabla ^k\varrho$, ![]() $\nabla ^ku$,
$\nabla ^ku$, ![]() $\nabla ^k\chi$ and
$\nabla ^k\chi$ and ![]() $\nabla ^{k+1}\chi$ respectively, summing up and then integrating over
$\nabla ^{k+1}\chi$ respectively, summing up and then integrating over ![]() $\mathbb {R}^3$, we derive that
$\mathbb {R}^3$, we derive that
 \begin{align}
&\frac{1}{2}\frac{{\rm d}}{{\rm
d}t}\int_{\mathbb{R}^3}(|\nabla^k\varrho|^2+|\nabla^ku|^2+|\nabla^k\chi|^2+|\nabla^{k+1}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad+\int_{\mathbb{R}^3}(|\nabla^{k+1}u|^2+|\nabla^{k+1}\chi|^2+|\nabla^{k+2}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad\quad=\int_{\mathbb{R}^3}\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2\mathbb{I}_3\right)}
\nabla^k(-\varrho\text{div}\,u-u\cdot\nabla\varrho)\cdot\nabla^k\varrho\right.\nonumber\\
&\quad \qquad -\nabla^k\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2\mathbb{I}_3\right)}u\cdot\nabla u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)\right.\nonumber\\
&\quad\quad\quad\left.\left.+\,g(\varrho)\nabla\varrho+\phi(\varrho)\text{div}
\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\cdot\nabla^ku \right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^k\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)
\right)\cdot\nabla^k\chi \right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^{k+1}\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)\right)\cdot\nabla^{k+1}\chi\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2\mathbb{I}_3\right)}\right]{\rm
d}x\nonumber\\ &\quad\quad=\sum_{i=1}^{12}I_i.
\end{align}
\begin{align}
&\frac{1}{2}\frac{{\rm d}}{{\rm
d}t}\int_{\mathbb{R}^3}(|\nabla^k\varrho|^2+|\nabla^ku|^2+|\nabla^k\chi|^2+|\nabla^{k+1}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad+\int_{\mathbb{R}^3}(|\nabla^{k+1}u|^2+|\nabla^{k+1}\chi|^2+|\nabla^{k+2}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad\quad=\int_{\mathbb{R}^3}\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2\mathbb{I}_3\right)}
\nabla^k(-\varrho\text{div}\,u-u\cdot\nabla\varrho)\cdot\nabla^k\varrho\right.\nonumber\\
&\quad \qquad -\nabla^k\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2\mathbb{I}_3\right)}u\cdot\nabla u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)\right.\nonumber\\
&\quad\quad\quad\left.\left.+\,g(\varrho)\nabla\varrho+\phi(\varrho)\text{div}
\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\cdot\nabla^ku \right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^k\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)
\right)\cdot\nabla^k\chi \right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^{k+1}\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)\right)\cdot\nabla^{k+1}\chi\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2\mathbb{I}_3\right)}\right]{\rm
d}x\nonumber\\ &\quad\quad=\sum_{i=1}^{12}I_i.
\end{align}
The right-hand side terms of (3.5) will be estimated one by one in the following. The main idea is that we will carefully interpolate the spatial derivatives between the higher-order derivatives and the lower-order derivatives to bound these nonlinear terms by the right-hand side of (3.4). First, for ![]() $I_1$, by using Kato–Ponce inequality (lemma 2.1), Gagliardo–Nirenberg inequality (lemma 2.2) and Sobolev embedding theorem, we can estimate as
$I_1$, by using Kato–Ponce inequality (lemma 2.1), Gagliardo–Nirenberg inequality (lemma 2.2) and Sobolev embedding theorem, we can estimate as
 \begin{align}
I_1&\lesssim\|\nabla^k\varrho\|_{L^6}\|\nabla^k(\varrho\nabla\cdot
u)\|_{L^{6/5}}\lesssim
\|\nabla^k\varrho\|_{L^6}(\|\nabla^k\varrho\|_{L^3}\|\nabla
u\|_{L^2}+\|\varrho\|_{L^3}\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}\varrho\|_{L^2}\left(\|\nabla^{k+1}\varrho\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}\varrho\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\notag\\
&\quad \times \Lambda^{1/2}u\|_{L^2}^{k/{(k+1/2)}}\|\nabla^{k+1}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}
\left.+\vphantom{\nabla^{k+1}\varrho\|_{L^2}^{{k}/{(k+1/2)}}}\|\Lambda^{1/2}\varrho\|_{L^2}\|\nabla^{k+1}u\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}\varrho\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}).
\end{align}
\begin{align}
I_1&\lesssim\|\nabla^k\varrho\|_{L^6}\|\nabla^k(\varrho\nabla\cdot
u)\|_{L^{6/5}}\lesssim
\|\nabla^k\varrho\|_{L^6}(\|\nabla^k\varrho\|_{L^3}\|\nabla
u\|_{L^2}+\|\varrho\|_{L^3}\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}\varrho\|_{L^2}\left(\|\nabla^{k+1}\varrho\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}\varrho\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\notag\\
&\quad \times \Lambda^{1/2}u\|_{L^2}^{k/{(k+1/2)}}\|\nabla^{k+1}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}
\left.+\vphantom{\nabla^{k+1}\varrho\|_{L^2}^{{k}/{(k+1/2)}}}\|\Lambda^{1/2}\varrho\|_{L^2}\|\nabla^{k+1}u\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}\varrho\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}).
\end{align}
Similarly, by using Kato–Ponce inequality (lemma 2.1), Gagliardo–Nirenberg inequality (lemma 2.2) and Sobolev embedding theorem again, we estimate the terms ![]() $I_2$ and
$I_2$ and ![]() $I_3$ as
$I_3$ as
 \begin{align}
I_2&\lesssim\|\nabla^k\varrho\|_{L^6}\|\nabla^k(u\cdot\nabla\varrho)\|_{L^{6/5}}\lesssim\|\nabla^k\varrho\|_{L^6}(\|\nabla^ku\|_{L^3}\|\nabla\varrho\|_{L^2}+\|u\|_{L^3}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}\varrho\|_{L^2}\left(\|\nabla^{k+1}u\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times\left.
\Lambda^{1/2}\varrho\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}\varrho\|_{L^2}^{{(1/2)}/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}\varrho\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}),
\end{align}
\begin{align}
I_2&\lesssim\|\nabla^k\varrho\|_{L^6}\|\nabla^k(u\cdot\nabla\varrho)\|_{L^{6/5}}\lesssim\|\nabla^k\varrho\|_{L^6}(\|\nabla^ku\|_{L^3}\|\nabla\varrho\|_{L^2}+\|u\|_{L^3}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}\varrho\|_{L^2}\left(\|\nabla^{k+1}u\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times\left.
\Lambda^{1/2}\varrho\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}\varrho\|_{L^2}^{{(1/2)}/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}\varrho\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}),
\end{align}and
 \begin{align}
I_3&\lesssim\|\nabla^k u\|_{L^6}\|\nabla^k(u\cdot\nabla
u)\|_{L^{6/5}}\lesssim \|\nabla^k
u\|_{L^6}(\|\nabla^ku\|_{L^3}\|\nabla
u\|_{L^2}+\|u\|_{L^3}\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}u\|_{L^2}\left(\|\nabla^{k+1}u\|_{L^2}^{
k/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times \left.\Lambda^{1/2}u\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+1}u\|_{L^2}\right)\nonumber\\
&\lesssim\|\Lambda^{1/2}u\|_{L^2}
\|\nabla^{k+1}u\|_{L^2}\lesssim \delta
\|\nabla^{k+1}u\|_{L^2}.
\end{align}
\begin{align}
I_3&\lesssim\|\nabla^k u\|_{L^6}\|\nabla^k(u\cdot\nabla
u)\|_{L^{6/5}}\lesssim \|\nabla^k
u\|_{L^6}(\|\nabla^ku\|_{L^3}\|\nabla
u\|_{L^2}+\|u\|_{L^3}\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}u\|_{L^2}\left(\|\nabla^{k+1}u\|_{L^2}^{
k/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times \left.\Lambda^{1/2}u\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+1}u\|_{L^2}\right)\nonumber\\
&\lesssim\|\Lambda^{1/2}u\|_{L^2}
\|\nabla^{k+1}u\|_{L^2}\lesssim \delta
\|\nabla^{k+1}u\|_{L^2}.
\end{align}
Next, for the term ![]() $I_4$, we do the approximation to simplify the presentations by
$I_4$, we do the approximation to simplify the presentations by
If ![]() $k=0$, on the basis of the fact (3.2), Hölder's together with Sobolev embedding theorem, we deduce that
$k=0$, on the basis of the fact (3.2), Hölder's together with Sobolev embedding theorem, we deduce that
 \begin{align} I_4&\approx{-}\int_{\mathbb{R}^3}h(\varrho)\nabla^2u\cdot u\,{\rm d}x\lesssim \|\nabla h(\varrho)\|_{L^2}\|\nabla u\|_{L^3}\|u\|_{L^6}+\|\varrho\|_{L^{\infty}}\|\nabla u\|_{L^2}\|\nabla u\|_{L^2}\nonumber\\ &\lesssim(\|\nabla u\|_{L^3}+\|\varrho\|_{L^{\infty}})(\|\nabla\varrho\|_{L^2}^2+\|\nabla u\|_{L^2}^2)\nonumber\\ &\lesssim(\|\Lambda^{3/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2})(\|\nabla\varrho\|_{L^2}^2+\|\nabla u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla\varrho\|_{L^2}^2+\|\nabla u\|_{L^2}^2). \end{align}
\begin{align} I_4&\approx{-}\int_{\mathbb{R}^3}h(\varrho)\nabla^2u\cdot u\,{\rm d}x\lesssim \|\nabla h(\varrho)\|_{L^2}\|\nabla u\|_{L^3}\|u\|_{L^6}+\|\varrho\|_{L^{\infty}}\|\nabla u\|_{L^2}\|\nabla u\|_{L^2}\nonumber\\ &\lesssim(\|\nabla u\|_{L^3}+\|\varrho\|_{L^{\infty}})(\|\nabla\varrho\|_{L^2}^2+\|\nabla u\|_{L^2}^2)\nonumber\\ &\lesssim(\|\Lambda^{3/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2})(\|\nabla\varrho\|_{L^2}^2+\|\nabla u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla\varrho\|_{L^2}^2+\|\nabla u\|_{L^2}^2). \end{align}
If ![]() $k=1$, by the fact (3.2), integrating by parts, one obtains
$k=1$, by the fact (3.2), integrating by parts, one obtains
 \begin{align} I_4&\approx{-}\int_{\mathbb{R}^3}\nabla[h(\varrho)\nabla^2u]\cdot \nabla u\,{\rm d}x\approx \int_{\mathbb{R}^3}h(\varrho)|\nabla^2u|^2\,{\rm d}x\nonumber\\ &\lesssim \|h(\varrho)\|_{L^{\infty}}\|\nabla^2u\|_{L^2}^2\lesssim \|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^2u\|_{L^2}^2 \lesssim \delta\|\nabla^2u\|_{L^2}^2. \end{align}
\begin{align} I_4&\approx{-}\int_{\mathbb{R}^3}\nabla[h(\varrho)\nabla^2u]\cdot \nabla u\,{\rm d}x\approx \int_{\mathbb{R}^3}h(\varrho)|\nabla^2u|^2\,{\rm d}x\nonumber\\ &\lesssim \|h(\varrho)\|_{L^{\infty}}\|\nabla^2u\|_{L^2}^2\lesssim \|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^2u\|_{L^2}^2 \lesssim \delta\|\nabla^2u\|_{L^2}^2. \end{align}
If ![]() $k\geq 2$, by using Hölder's inequality, lemmas 2.1 and 2.4 and Sobolev embedding theorem, we deduce that
$k\geq 2$, by using Hölder's inequality, lemmas 2.1 and 2.4 and Sobolev embedding theorem, we deduce that
 \begin{align}
I_4&\lesssim\|\nabla^{k+1}
u\|_{L^2}\|\nabla^{k-1}[h(\varrho)\nabla^2u]\|_{L^{2}}\nonumber\\
&\lesssim\|\nabla^{k+1}u\|_{L^2}(\|\nabla^k\varrho\|_{L^2}\|\Lambda^{5/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}u\|_{L^2}\left(\|\nabla^{k+1}\varrho\|_{L^2}^{{(k-3/2)}/{(k-1/2)}}\|\Lambda^{3/2}\varrho\|_{L^2}^{1/{(k-1/2)}}\|\nabla^{k+1}u\|_{L^2}^{1/{(k-1/2)}}\|\right.\nonumber\\
&\quad\times\left.\Lambda^{3/2}u\|_{L^2}^{{(k-3/2)}/{(k-1/2)}}
+\vphantom{\nabla^{k+1}\varrho\|_{L^2}^{{(k-3/2)}/{(k-1/2)}}}\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^{k+1}u\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{3/2}\varrho\|_{L^2}+\|\Lambda^{3/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}+\|\Delta\varrho\|_{L^2})(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|^2_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|^2_{L^2}).
\end{align}
\begin{align}
I_4&\lesssim\|\nabla^{k+1}
u\|_{L^2}\|\nabla^{k-1}[h(\varrho)\nabla^2u]\|_{L^{2}}\nonumber\\
&\lesssim\|\nabla^{k+1}u\|_{L^2}(\|\nabla^k\varrho\|_{L^2}\|\Lambda^{5/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}u\|_{L^2}\left(\|\nabla^{k+1}\varrho\|_{L^2}^{{(k-3/2)}/{(k-1/2)}}\|\Lambda^{3/2}\varrho\|_{L^2}^{1/{(k-1/2)}}\|\nabla^{k+1}u\|_{L^2}^{1/{(k-1/2)}}\|\right.\nonumber\\
&\quad\times\left.\Lambda^{3/2}u\|_{L^2}^{{(k-3/2)}/{(k-1/2)}}
+\vphantom{\nabla^{k+1}\varrho\|_{L^2}^{{(k-3/2)}/{(k-1/2)}}}\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^{k+1}u\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{3/2}\varrho\|_{L^2}+\|\Lambda^{3/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}+\|\Delta\varrho\|_{L^2})(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|^2_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|^2_{L^2}).
\end{align}
Moreover, applying lemma 2.4, Hölder's inequality, the Kato–Ponce inequality (lemma 2.1) together with Sobolev embedding theorem, the term ![]() $I_5$ can be bounded as
$I_5$ can be bounded as
 \begin{align}
I_5&={-}\int_{\mathbb{R}^3}\nabla^k(g(\varrho)\nabla\varrho)\cdot\nabla^k
u\,{\rm
d}x\lesssim\|\nabla^ku\|_{L^3}\|\nabla^k(g(\varrho)\nabla\varrho)\|_{L^{3/2}}\nonumber\\
&\lesssim\|\nabla^ku\|_{L^3}(\|\nabla^kg(\varrho)\|_{L^6}\|\nabla\varrho\|_{L^2}+\|g(\varrho)\|_{L^6}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\
&\lesssim\left(\|\nabla^{k+1}u\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\right)\notag\\
&\quad \times \left(\|\nabla^{k+1}
\varrho \|_{L^2} \|\Lambda^{1/2}\varrho\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}\varrho\|_{L^2}^{{(1/2)}/{(k+1/2)}}
\right)\nonumber\\ &\lesssim
(\|\Lambda^{1/2}\varrho\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})
(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2)\nonumber\\
&\lesssim \delta
(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2).
\end{align}
\begin{align}
I_5&={-}\int_{\mathbb{R}^3}\nabla^k(g(\varrho)\nabla\varrho)\cdot\nabla^k
u\,{\rm
d}x\lesssim\|\nabla^ku\|_{L^3}\|\nabla^k(g(\varrho)\nabla\varrho)\|_{L^{3/2}}\nonumber\\
&\lesssim\|\nabla^ku\|_{L^3}(\|\nabla^kg(\varrho)\|_{L^6}\|\nabla\varrho\|_{L^2}+\|g(\varrho)\|_{L^6}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\
&\lesssim\left(\|\nabla^{k+1}u\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\right)\notag\\
&\quad \times \left(\|\nabla^{k+1}
\varrho \|_{L^2} \|\Lambda^{1/2}\varrho\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}\varrho\|_{L^2}^{{(1/2)}/{(k+1/2)}}
\right)\nonumber\\ &\lesssim
(\|\Lambda^{1/2}\varrho\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})
(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2)\nonumber\\
&\lesssim \delta
(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2).
\end{align}
For the term ![]() $I_6$, since
$I_6$, since ![]() $|\phi (\varrho )|\leq C$, by using lemmas 2.4 and 2.1 and Sobolev embedding theorem, we have
$|\phi (\varrho )|\leq C$, by using lemmas 2.4 and 2.1 and Sobolev embedding theorem, we have
 \begin{align} I_6&\lesssim\|\nabla^k u\|_{L^6}\left\|\nabla^k\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\right\|_{L^{6/5}}\nonumber\\ &\lesssim\|\nabla^{k+1}u\|_{L^2} \|\phi(\varrho)\|_{L^{\infty}}\left\|\nabla^k\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right\|_{L^{6/5}}\nonumber\\ &\quad+\|\nabla^{k+1}u\|_{L^2}\|\nabla^k\phi(\varrho)\|_{L^6}\left\| \text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right\|_{L^{3/2}}\nonumber\\ &\lesssim\|\nabla^{k+1}u\|_{L^2} \|\nabla\chi\|_{L^3}\|\nabla^{k+1}\nabla \chi\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}\|\nabla^k\varrho\|_{L^6}\|\nabla\chi\|_{L^3}\|\nabla^2\chi\|_{L^3}\nonumber\\ &\lesssim\delta^2(\|\nabla^{k+1}u\|_{L^2}^2+ \|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2). \end{align}
\begin{align} I_6&\lesssim\|\nabla^k u\|_{L^6}\left\|\nabla^k\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\right\|_{L^{6/5}}\nonumber\\ &\lesssim\|\nabla^{k+1}u\|_{L^2} \|\phi(\varrho)\|_{L^{\infty}}\left\|\nabla^k\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right\|_{L^{6/5}}\nonumber\\ &\quad+\|\nabla^{k+1}u\|_{L^2}\|\nabla^k\phi(\varrho)\|_{L^6}\left\| \text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right\|_{L^{3/2}}\nonumber\\ &\lesssim\|\nabla^{k+1}u\|_{L^2} \|\nabla\chi\|_{L^3}\|\nabla^{k+1}\nabla \chi\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}\|\nabla^k\varrho\|_{L^6}\|\nabla\chi\|_{L^3}\|\nabla^2\chi\|_{L^3}\nonumber\\ &\lesssim\delta^2(\|\nabla^{k+1}u\|_{L^2}^2+ \|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2). \end{align}
Using Kato–Ponce inequality (lemma 2.1), Gagliardo–Nirenberg inequality (lemma 2.2) and Sobolev embedding theorem, we can estimate ![]() $I_7$ as
$I_7$ as
 \begin{align} I_7&={-}
\int_{\mathbb{R}^3}\nabla^k(u\nabla\cdot \chi)\cdot\nabla^k\chi\,{\rm d}x\nonumber\\
&\lesssim\|\nabla^k\chi\|_{L^6}\|\nabla^k(u\nabla\cdot
\chi)\|_{L^{6/5}}\nonumber\\
&\lesssim\|\nabla^k\chi\|_{L^6}(\|\nabla^ku\|_{L^3}\|\nabla\chi\|_{L^2}+\|u\|_{L^3}\|\nabla^{k+1}\chi\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}\chi\|_{L^2}\left(\|\nabla^{k+1}u\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times \left.\Lambda^{1/2}\chi\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}\chi\|_{L^2}^{{(1/2)}/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+1}\chi\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}u\|_{L^2}+\|\Lambda^{1/2}\chi\|_{L^2})(\|\nabla^{k+1}\chi\|_{L^2}+\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}\chi\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}).
\end{align}
\begin{align} I_7&={-}
\int_{\mathbb{R}^3}\nabla^k(u\nabla\cdot \chi)\cdot\nabla^k\chi\,{\rm d}x\nonumber\\
&\lesssim\|\nabla^k\chi\|_{L^6}\|\nabla^k(u\nabla\cdot
\chi)\|_{L^{6/5}}\nonumber\\
&\lesssim\|\nabla^k\chi\|_{L^6}(\|\nabla^ku\|_{L^3}\|\nabla\chi\|_{L^2}+\|u\|_{L^3}\|\nabla^{k+1}\chi\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+1}\chi\|_{L^2}\left(\|\nabla^{k+1}u\|_{L^2}^{{k}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{{(1/2)}/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times \left.\Lambda^{1/2}\chi\|_{L^2}^{
k/{(k+1/2)}}\|\nabla^{k+1}\chi\|_{L^2}^{{(1/2)}/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+1}\chi\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}u\|_{L^2}+\|\Lambda^{1/2}\chi\|_{L^2})(\|\nabla^{k+1}\chi\|_{L^2}+\|\nabla^{k+1}u\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+1}\chi\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}).
\end{align}
For ![]() $I_8$, if
$I_8$, if ![]() $k=0$, Hölder's inequality and Sobolev embedding theorem imply
$k=0$, Hölder's inequality and Sobolev embedding theorem imply
 \begin{align} I_8&\approx{-}\int_{\mathbb{R}^3}\varphi(\varrho)\cdot\nabla^2\chi\cdot \chi\,{\rm d}x\nonumber\\ &\lesssim \|\nabla \varphi(\varrho)\|_{L^2}\|\nabla \chi\|_{L^3}\|\chi\|_{L^6}+\|\varrho\|_{L^6}\|\nabla \chi\|_{L^{\infty}}\|\nabla \chi\|_{L^2}\nonumber\\ &\lesssim\delta(\|\nabla\varrho\|_{L^2}^2+\|\nabla\chi\|_{L^2}^2). \end{align}
\begin{align} I_8&\approx{-}\int_{\mathbb{R}^3}\varphi(\varrho)\cdot\nabla^2\chi\cdot \chi\,{\rm d}x\nonumber\\ &\lesssim \|\nabla \varphi(\varrho)\|_{L^2}\|\nabla \chi\|_{L^3}\|\chi\|_{L^6}+\|\varrho\|_{L^6}\|\nabla \chi\|_{L^{\infty}}\|\nabla \chi\|_{L^2}\nonumber\\ &\lesssim\delta(\|\nabla\varrho\|_{L^2}^2+\|\nabla\chi\|_{L^2}^2). \end{align}
On the other hand, if ![]() $k\geq 1$, employing the Leibniz formula and Hölder's inequality, we arrive at
$k\geq 1$, employing the Leibniz formula and Hölder's inequality, we arrive at
 \begin{align} I_8&={-}\int_{\mathbb{R}^3}\nabla^{k-1}[\varphi(\varrho)\nabla^2\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &={-}\sum_{l=0}^{k-1}C_{k-1}^l\int_{\mathbb{R}^3}\nabla^{k-1-l} \varphi(\varrho)\cdot\nabla^{l}\nabla^2\chi\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim \sum_{l=0}^{[{k}/{2}]-1}C_{k-1}^l\|\nabla^{l+2}\chi \|_{L^3}\|\nabla^{k-l-1}\varphi(\varrho)\|_{L^6}\|\nabla^{k+1}\chi \|_{L^2}\nonumber\\ &\quad+\sum_{l=[k/2]}^{k-2}C_{k-1}^l\|\nabla^{l+2}\chi \|_{L^6}\|\nabla^{k-1-l}\varphi(\varrho)\|_{L^3} \|\nabla^{k+1}\chi \|_{L^2}\nonumber\\ &\quad+\underbrace{\int_{\mathbb{R}^3}|\varphi(\varrho)||\nabla^{k+1}\chi |^2{\rm d}x}_{l=k-1}. \end{align}
\begin{align} I_8&={-}\int_{\mathbb{R}^3}\nabla^{k-1}[\varphi(\varrho)\nabla^2\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &={-}\sum_{l=0}^{k-1}C_{k-1}^l\int_{\mathbb{R}^3}\nabla^{k-1-l} \varphi(\varrho)\cdot\nabla^{l}\nabla^2\chi\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim \sum_{l=0}^{[{k}/{2}]-1}C_{k-1}^l\|\nabla^{l+2}\chi \|_{L^3}\|\nabla^{k-l-1}\varphi(\varrho)\|_{L^6}\|\nabla^{k+1}\chi \|_{L^2}\nonumber\\ &\quad+\sum_{l=[k/2]}^{k-2}C_{k-1}^l\|\nabla^{l+2}\chi \|_{L^6}\|\nabla^{k-1-l}\varphi(\varrho)\|_{L^3} \|\nabla^{k+1}\chi \|_{L^2}\nonumber\\ &\quad+\underbrace{\int_{\mathbb{R}^3}|\varphi(\varrho)||\nabla^{k+1}\chi |^2{\rm d}x}_{l=k-1}. \end{align}Gagliardo–Nirenberg's inequality (lemma 2.2) implies that
 \begin{align}
&\sum_{l=0}^{[{k}/{2}]-1}C_{k-1}^l\|\nabla^{l+2}\chi
\|_{L^3}\|\nabla^{k-l-1}\varphi(\varrho)\|_{L^6}\|\nabla^{k+1}\chi
\|_{L^2}\nonumber\\
&\quad \lesssim\sum_{l=0}^{[{k}/{2}]-1}\|\nabla^{\alpha}\chi
\|_{L^2}^{1-({(l+1)}/{(k+1)})}\|\nabla^{k+1}\chi
\|_{L^2}^{{(l+1)}/{(k+1)}}\|\varrho\|_{L^2}^{{(l+1)}/{(k+1)}}\|\nonumber\\
&\qquad \times \nabla^{k+1}\varrho\|_{L^2}^{1-({(l+1)}/{(k+1)})}
\|\nabla^{k+1}u\|_{L^2}\nonumber\\
&\quad \lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}^2
+\|\nabla^{k+1}\chi \|_{L^2}^2),
\end{align}
\begin{align}
&\sum_{l=0}^{[{k}/{2}]-1}C_{k-1}^l\|\nabla^{l+2}\chi
\|_{L^3}\|\nabla^{k-l-1}\varphi(\varrho)\|_{L^6}\|\nabla^{k+1}\chi
\|_{L^2}\nonumber\\
&\quad \lesssim\sum_{l=0}^{[{k}/{2}]-1}\|\nabla^{\alpha}\chi
\|_{L^2}^{1-({(l+1)}/{(k+1)})}\|\nabla^{k+1}\chi
\|_{L^2}^{{(l+1)}/{(k+1)}}\|\varrho\|_{L^2}^{{(l+1)}/{(k+1)}}\|\nonumber\\
&\qquad \times \nabla^{k+1}\varrho\|_{L^2}^{1-({(l+1)}/{(k+1)})}
\|\nabla^{k+1}u\|_{L^2}\nonumber\\
&\quad \lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}^2
+\|\nabla^{k+1}\chi \|_{L^2}^2),
\end{align}
where ![]() $\alpha$ satisfies
$\alpha$ satisfies
that is
Moreover, also by Gagliardo–Nirenberg's inequality (lemma 2.2), we derive that
 \begin{align}
&\sum_{l=[k/2]}^{k-2}C_{k-1}^l\|\nabla^{l+2}\chi
\|_{L^6}\|\nabla^{k-1-l}\varphi(\varrho)\|_{L^3}
\|\nabla^{k+1}\chi \|_{L^2}\nonumber\\
&\quad\lesssim\sum_{l=[k/2]}^{k-2}\| \chi
\|_{L^2}^{1-({(l+3)}/{(k+1)})}\|\nabla^{k+1}\chi
\|_{L^2}^{{(l+3)}/{(k+1)}}\|\nabla^{\alpha}\varrho\|_{L^2}^{{(l+3)}/{(k+1)}}\|\notag\\
&\qquad \times \nabla^{k+1}\varrho\|_{L^2}^{1-({(l+3)}/{(k+1)})}\|\nabla^{k+1}\chi
\|_{L^2}\nonumber\\
&\quad\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}^2
+\|\nabla^{k+1}\chi \|_{L^2}^2 ),
\end{align}
\begin{align}
&\sum_{l=[k/2]}^{k-2}C_{k-1}^l\|\nabla^{l+2}\chi
\|_{L^6}\|\nabla^{k-1-l}\varphi(\varrho)\|_{L^3}
\|\nabla^{k+1}\chi \|_{L^2}\nonumber\\
&\quad\lesssim\sum_{l=[k/2]}^{k-2}\| \chi
\|_{L^2}^{1-({(l+3)}/{(k+1)})}\|\nabla^{k+1}\chi
\|_{L^2}^{{(l+3)}/{(k+1)}}\|\nabla^{\alpha}\varrho\|_{L^2}^{{(l+3)}/{(k+1)}}\|\notag\\
&\qquad \times \nabla^{k+1}\varrho\|_{L^2}^{1-({(l+3)}/{(k+1)})}\|\nabla^{k+1}\chi
\|_{L^2}\nonumber\\
&\quad\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}^2
+\|\nabla^{k+1}\chi \|_{L^2}^2 ),
\end{align}
where ![]() $\alpha$ satisfies
$\alpha$ satisfies
that is
For the last term of the right-hand side of (3.17), we have
Combining (3.16)–(3.20) together, we easily obtain
Note that ![]() $I_9$ satisfies
$I_9$ satisfies
 \begin{align}
I_9&={-}\int_{\mathbb{R}^3}\nabla^k[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^k\chi\,{\rm
d}x\nonumber\\ &\lesssim\left(\|\nabla^k[\phi(\varrho)
\chi^3 ]\|_{L^{6/5}}+\|\nabla^k[\phi(\varrho) \chi
]\|_{L^{6/5}}\right)\|\nabla^k\chi\|_{L^6}\nonumber\\
&\lesssim(\|\phi(\varrho)\|_{L^3}\|\nabla^k \chi^3
\|_{L^2}+\|\chi^2
\|_{L^6}\|\chi\|_{L^2}\|\nabla^k\phi(\varrho)\|_{L^6} \notag\\
&\quad +\|\nabla^k[\phi(\varrho) \chi
]\|_{L^{6/5}})\|\nabla^{k+1}\chi\|_{L^2}\nonumber\\
&\lesssim(I_{91}+I_{92}+I_{93})\|\nabla^{k+1}\chi\|_{L^2},
\end{align}
\begin{align}
I_9&={-}\int_{\mathbb{R}^3}\nabla^k[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^k\chi\,{\rm
d}x\nonumber\\ &\lesssim\left(\|\nabla^k[\phi(\varrho)
\chi^3 ]\|_{L^{6/5}}+\|\nabla^k[\phi(\varrho) \chi
]\|_{L^{6/5}}\right)\|\nabla^k\chi\|_{L^6}\nonumber\\
&\lesssim(\|\phi(\varrho)\|_{L^3}\|\nabla^k \chi^3
\|_{L^2}+\|\chi^2
\|_{L^6}\|\chi\|_{L^2}\|\nabla^k\phi(\varrho)\|_{L^6} \notag\\
&\quad +\|\nabla^k[\phi(\varrho) \chi
]\|_{L^{6/5}})\|\nabla^{k+1}\chi\|_{L^2}\nonumber\\
&\lesssim(I_{91}+I_{92}+I_{93})\|\nabla^{k+1}\chi\|_{L^2},
\end{align}
where we have used Hölder's inequality and Kato–Ponce inequality (lemma 2.1) in (3.22). Next, we first estimate ![]() $I_{91}$–
$I_{91}$–![]() $I_{92}$ term by term:
$I_{92}$ term by term:
 \begin{align} I_{91} &\lesssim\|\varrho\|_{L^3}\|\chi\|^2_{L^6}\|\nabla^k\chi\|_{L^6}\nonumber\\ &\lesssim\|\Lambda^{1/2}\varrho\|_{L^2}\|\nabla\chi\|_{L^2}^2\|\nabla^{k+1}\chi\|_{L^2}\lesssim\delta^3\|\nabla^{k+1}\chi\|_{L^2}, \end{align}
\begin{align} I_{91} &\lesssim\|\varrho\|_{L^3}\|\chi\|^2_{L^6}\|\nabla^k\chi\|_{L^6}\nonumber\\ &\lesssim\|\Lambda^{1/2}\varrho\|_{L^2}\|\nabla\chi\|_{L^2}^2\|\nabla^{k+1}\chi\|_{L^2}\lesssim\delta^3\|\nabla^{k+1}\chi\|_{L^2}, \end{align}and
 \begin{align} I_{92} &\lesssim\|\varrho\|_{L^\infty}\|\chi\|_{L^6}\|\chi\|_{L^2}\|\nabla^k\varrho\|_{L^6}\nonumber\\ &\lesssim\|\nabla\varrho\|_{L^2}^{1/2}\|\nabla^2\varrho\|_{L^2}^{1/2}\|\nabla\chi\|_{L^2}\|\chi\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim\delta^3\|\nabla^{k+1}\varrho\|_{L^2}. \end{align}
\begin{align} I_{92} &\lesssim\|\varrho\|_{L^\infty}\|\chi\|_{L^6}\|\chi\|_{L^2}\|\nabla^k\varrho\|_{L^6}\nonumber\\ &\lesssim\|\nabla\varrho\|_{L^2}^{1/2}\|\nabla^2\varrho\|_{L^2}^{1/2}\|\nabla\chi\|_{L^2}\|\chi\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim\delta^3\|\nabla^{k+1}\varrho\|_{L^2}. \end{align}
Since ![]() $\phi (\varrho )=1/{(\varrho +1)}$, we obtain
$\phi (\varrho )=1/{(\varrho +1)}$, we obtain ![]() $\zeta (\varrho ):=\sqrt {\phi (\varrho )}=1/{\sqrt {(\varrho +1)}}$. It is easy to see that
$\zeta (\varrho ):=\sqrt {\phi (\varrho )}=1/{\sqrt {(\varrho +1)}}$. It is easy to see that ![]() $\zeta (\varrho )$ is a smooth function of
$\zeta (\varrho )$ is a smooth function of ![]() $\varrho$ with bounded derivatives of any order. Hence, lemma 2.4 holds for
$\varrho$ with bounded derivatives of any order. Hence, lemma 2.4 holds for ![]() $\zeta (\varrho )$. By using Sobolev embedding theorem and Kato–Ponce inequality, we have
$\zeta (\varrho )$. By using Sobolev embedding theorem and Kato–Ponce inequality, we have
 \begin{align} I_{93}&=\|\nabla^k[\phi(\varrho) \chi ]\|_{L^{6/5}}=\|\nabla^k[\zeta(\varrho)\zeta(\varrho)\chi ]\|_{L^{6/5}}\nonumber\\ &\lesssim\|\zeta(\varrho)\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\chi\|_{L^6}+\|\chi\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\zeta(\varrho)\|_{L^6}\nonumber\\ &\lesssim\|\varrho\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+1}\chi\|_{L^2}+\|\chi\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim \delta^2 (\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}\chi\|_{L^2}). \end{align}
\begin{align} I_{93}&=\|\nabla^k[\phi(\varrho) \chi ]\|_{L^{6/5}}=\|\nabla^k[\zeta(\varrho)\zeta(\varrho)\chi ]\|_{L^{6/5}}\nonumber\\ &\lesssim\|\zeta(\varrho)\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\chi\|_{L^6}+\|\chi\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\zeta(\varrho)\|_{L^6}\nonumber\\ &\lesssim\|\varrho\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+1}\chi\|_{L^2}+\|\chi\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim \delta^2 (\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+1}\chi\|_{L^2}). \end{align}Combining (3.23)–(3.25) together, we derive that
The term ![]() $I_{10}$ satisfies
$I_{10}$ satisfies
 \begin{align} I_{10}&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[u\cdot\nabla\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+1}\chi\|_{L^6}\|\nabla^{k+1}[u\cdot\nabla\chi]\|_{L^{6/5}}\nonumber\\ &\lesssim\|\nabla^{k+1}\chi\|_{L^6}(\|\nabla^{k+1}u\|_{L^2}\|\nabla\chi\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+1}\nabla\chi\|_{L^2})\nonumber\\ &\lesssim(\|\nabla\chi\|_{L^3}+\|u\|_{L^3})(\|\nabla^{k+1}\nabla\chi\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+1}\nabla\chi\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2), \end{align}
\begin{align} I_{10}&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[u\cdot\nabla\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+1}\chi\|_{L^6}\|\nabla^{k+1}[u\cdot\nabla\chi]\|_{L^{6/5}}\nonumber\\ &\lesssim\|\nabla^{k+1}\chi\|_{L^6}(\|\nabla^{k+1}u\|_{L^2}\|\nabla\chi\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+1}\nabla\chi\|_{L^2})\nonumber\\ &\lesssim(\|\nabla\chi\|_{L^3}+\|u\|_{L^3})(\|\nabla^{k+1}\nabla\chi\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+1}\nabla\chi\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2), \end{align}
where we have used Kato–Ponce inequality (lemma 2.1) and Sobolev embedding theorem in (3.27). Similar to (3.27), ![]() $I_{11}$ and
$I_{11}$ and ![]() $I_{12}$ can be bounded as
$I_{12}$ can be bounded as
 \begin{align} I_{11}&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}\|\nabla^k[\varphi(\varrho)\Delta\chi]\|_{L^2}\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\varphi(\varrho)\|_{L^{\infty}}\|\nabla^k\Delta\chi\|_{L^2}+\|\Delta\chi\|_{L^{3}}\|\nabla^k\varphi(\varrho)\|_{L^6})\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\nabla\varrho\|_{L^{2}}^{1/2}\|\nabla^2\varrho\|_{L^{2}}^{1/2}\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla^3\chi\|_{L^2}^{1/2}\|\nabla^2\chi\|_{L^2}^{1/2}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2), \end{align}
\begin{align} I_{11}&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}\|\nabla^k[\varphi(\varrho)\Delta\chi]\|_{L^2}\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\varphi(\varrho)\|_{L^{\infty}}\|\nabla^k\Delta\chi\|_{L^2}+\|\Delta\chi\|_{L^{3}}\|\nabla^k\varphi(\varrho)\|_{L^6})\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\nabla\varrho\|_{L^{2}}^{1/2}\|\nabla^2\varrho\|_{L^{2}}^{1/2}\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla^3\chi\|_{L^2}^{1/2}\|\nabla^2\chi\|_{L^2}^{1/2}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2), \end{align}and
 \begin{align} I_{12}&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\nabla^k[\phi(\varrho) \chi^3 ]\|_{L^2}+\|\nabla^k[\phi(\varrho) \chi ]\|_{L^2})\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\phi(\varrho)\|_{L^{\infty}}\|\nabla^k\chi^3\|_{L^2}+\|\chi^3 \|_{L^{3}}\|\nabla^k\phi(\varrho)\|_{L^6}\nonumber\\ &\quad+\|\zeta(\varrho)\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\chi\|_{L^6}+\|\chi\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\zeta(\varrho)\|_{L^6}). \end{align}
\begin{align} I_{12}&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\nabla^k[\phi(\varrho) \chi^3 ]\|_{L^2}+\|\nabla^k[\phi(\varrho) \chi ]\|_{L^2})\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\phi(\varrho)\|_{L^{\infty}}\|\nabla^k\chi^3\|_{L^2}+\|\chi^3 \|_{L^{3}}\|\nabla^k\phi(\varrho)\|_{L^6}\nonumber\\ &\quad+\|\zeta(\varrho)\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\chi\|_{L^6}+\|\chi\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^k\zeta(\varrho)\|_{L^6}). \end{align}It then follows from (3.23) that
Adding (3.29) and (3.30) together gives
 \begin{align} I_{12}&\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\phi(\varrho)\|_{L^{\infty}}\delta^2\|\nabla^{k+2}\chi\|_{L^2} +(\|\chi\|_{L^{9}}^3+\|\chi\|_{L^{3}})\|\nabla^{k+1} \varrho \|_{L^2})\nonumber\\ &\lesssim\left(\delta^3+\delta\right)(\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+1} \varrho \|_{L^2}^2). \end{align}
\begin{align} I_{12}&\lesssim\|\nabla^{k+2}\chi\|_{L^2}(\|\phi(\varrho)\|_{L^{\infty}}\delta^2\|\nabla^{k+2}\chi\|_{L^2} +(\|\chi\|_{L^{9}}^3+\|\chi\|_{L^{3}})\|\nabla^{k+1} \varrho \|_{L^2})\nonumber\\ &\lesssim\left(\delta^3+\delta\right)(\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+1} \varrho \|_{L^2}^2). \end{align}
Summing up the estimates for ![]() $I_1$–
$I_1$–![]() $I_{12}$, we deduce (3.4), this yields the desired result.
$I_{12}$, we deduce (3.4), this yields the desired result.
We also need to derive the second type of energy estimates excluding ![]() $\varrho$,
$\varrho$, ![]() $u$ and
$u$ and ![]() $\chi$ themselves.
$\chi$ themselves.
Lemma 3.2 If ![]() $\sqrt {\mathcal {E}_0^3(t)}\leq \delta$. Then, for
$\sqrt {\mathcal {E}_0^3(t)}\leq \delta$. Then, for ![]() $k=0,1,\ldots ,N-1$, the following inequality holds:
$k=0,1,\ldots ,N-1$, the following inequality holds:
 \begin{align} &\frac{{\rm d}}{{\rm d}t}(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\nabla\chi\|_{L^2}^2)\nonumber\\ &\quad+C(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+2}\nabla\chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim(\delta^3+\delta)(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+2}\nabla\chi\|_{L^2}^2). \end{align}
\begin{align} &\frac{{\rm d}}{{\rm d}t}(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+1}\nabla\chi\|_{L^2}^2)\nonumber\\ &\quad+C(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+2}\nabla\chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim(\delta^3+\delta)(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+2}\nabla\chi\|_{L^2}^2). \end{align}Proof. Taking ![]() $k+1$th spatial derivatives to (1.1)
$k+1$th spatial derivatives to (1.1)![]() $_1$, (1.1)
$_1$, (1.1)![]() $_2$ and (1.1)
$_2$ and (1.1)![]() $_3$,
$_3$, ![]() $k+2$th spatial derivatives to (1.1)
$k+2$th spatial derivatives to (1.1)![]() $_3$, multiplying the resulting identities by
$_3$, multiplying the resulting identities by ![]() $\nabla ^{k+1}\varrho$,
$\nabla ^{k+1}\varrho$, ![]() $\nabla ^{k+1}u$,
$\nabla ^{k+1}u$, ![]() $\nabla ^{k+1}\chi$ and
$\nabla ^{k+1}\chi$ and ![]() $\nabla ^{k+2}\chi$ respectively, summing up and then integrating over
$\nabla ^{k+2}\chi$ respectively, summing up and then integrating over ![]() $\mathbb {R}^3$ by parts, we derive that
$\mathbb {R}^3$ by parts, we derive that
 \begin{align}
&\frac12\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}(|\nabla^{k+1}\varrho|^2+|\nabla^{k+1}u|^2+|\nabla^{k+1}\chi|^2+|\nabla^{k+2}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad+\int_{\mathbb{R}^3}(|\nabla^{k+2}u|^2+|\nabla^{k+2}\chi|^2+|\nabla^{k+3}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad\quad=\int_{\mathbb{R}^3}\left[\nabla^{k+1}(-\varrho\text{div}\,u-u\cdot\nabla\varrho)\cdot\nabla^{k+1}\varrho
\right.\nonumber\\
&\quad\quad\quad\left.-\nabla^{k+1}\left[u\cdot\nabla
u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\quad\quad\quad\left.\left.+\,\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]
\cdot\nabla^{k+1}u\right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^{k+1}\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)
\right)\cdot\nabla^{k+1}\chi\right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^{k+2}\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)\right)\cdot\nabla^{k+2}\chi\right]{\rm
d}x\nonumber\\ &\quad\quad=\sum_{i=1}^{12}K_i.
\end{align}
\begin{align}
&\frac12\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}(|\nabla^{k+1}\varrho|^2+|\nabla^{k+1}u|^2+|\nabla^{k+1}\chi|^2+|\nabla^{k+2}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad+\int_{\mathbb{R}^3}(|\nabla^{k+2}u|^2+|\nabla^{k+2}\chi|^2+|\nabla^{k+3}\chi|^2)\,{\rm
d}x\nonumber\\
&\quad\quad=\int_{\mathbb{R}^3}\left[\nabla^{k+1}(-\varrho\text{div}\,u-u\cdot\nabla\varrho)\cdot\nabla^{k+1}\varrho
\right.\nonumber\\
&\quad\quad\quad\left.-\nabla^{k+1}\left[u\cdot\nabla
u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\quad\quad\quad\left.\left.+\,\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]
\cdot\nabla^{k+1}u\right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^{k+1}\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)
\right)\cdot\nabla^{k+1}\chi\right.\nonumber\\
&\quad\quad\quad\left.+\,\nabla^{k+2}\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)\right)\cdot\nabla^{k+2}\chi\right]{\rm
d}x\nonumber\\ &\quad\quad=\sum_{i=1}^{12}K_i.
\end{align}
We will estimate the term ![]() $K_1$–
$K_1$–![]() $K_{11}$ on the right-hand side of (3.33) one by one. First, through Hölder's inequality and lemma 2.1, we arrive at
$K_{11}$ on the right-hand side of (3.33) one by one. First, through Hölder's inequality and lemma 2.1, we arrive at
 \begin{align} K_1&={-} \int_{\mathbb{R}^3}\nabla^{k+1}(\varrho\text{div}\,u)\cdot\nabla^{k+1}\varrho\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+1}\varrho\|_{L^2}\|\nabla^{k+1}(\varrho\nabla\cdot u)\|_{L^2}\nonumber\\ &\lesssim\|\nabla^{k+1}\varrho\|_{L^2}(\|\nabla^{k+1}\varrho\|_{L^2}\|\nabla u\|_{L^{\infty}}+\|\varrho\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2})\nonumber\\ &\lesssim(\|\nabla u\|_{L^{\infty}}+\|\varrho\|_{L^{\infty}})(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2). \end{align}
\begin{align} K_1&={-} \int_{\mathbb{R}^3}\nabla^{k+1}(\varrho\text{div}\,u)\cdot\nabla^{k+1}\varrho\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+1}\varrho\|_{L^2}\|\nabla^{k+1}(\varrho\nabla\cdot u)\|_{L^2}\nonumber\\ &\lesssim\|\nabla^{k+1}\varrho\|_{L^2}(\|\nabla^{k+1}\varrho\|_{L^2}\|\nabla u\|_{L^{\infty}}+\|\varrho\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2})\nonumber\\ &\lesssim(\|\nabla u\|_{L^{\infty}}+\|\varrho\|_{L^{\infty}})(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+1}\varrho\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2). \end{align}
Next, for the term ![]() $J_2$, we utilize the commutator notation (2.4) to rewrite it, then integrate by part and use Sobolev's inequality, obtain the following inequality:
$J_2$, we utilize the commutator notation (2.4) to rewrite it, then integrate by part and use Sobolev's inequality, obtain the following inequality:
 \begin{align} K_2&={-}
\int_{\mathbb{R}^3}\nabla^{k+1}(u\cdot\nabla\varrho)\cdot\nabla^{k+1}\varrho\,{\rm
d}x\nonumber\\
&={-}\int_{\mathbb{R}^3}(u\cdot\nabla\nabla^{k+1}\varrho+[\nabla^{k+1},u]\cdot\nabla\varrho)\nabla^{k+1}\varrho\,{\rm
d}x\nonumber\\
&={-}\int_{\mathbb{R}^3}u\cdot\nabla\frac{|\nabla^{k+1}\varrho|^2}2\,{\rm
d}x\notag\\
&\quad +(\|\nabla
u\|_{L^{\infty}}\|\nabla^k\nabla\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}\|\nabla\varrho\|_{L^{\infty}})\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&=\frac12\int_{\mathbb{R}^3}\nabla\cdot
u|\nabla^{k+1}\varrho|^2\,{\rm d}x\notag\\
&\quad +(\|\nabla
u\|_{L^{\infty}}\|\nabla^k\nabla\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}\|\nabla\varrho\|_{L^{\infty}})\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&\lesssim\|\nabla
u\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|^2_{L^2}+(\|\nabla
u\|_{L^{\infty}}+\|\nabla\varrho\|_{L^{\infty}})\|\nabla^{k+1}\varrho\|_{L^2}^2\nonumber\\
&\lesssim\delta\|\nabla^{k+1}\varrho\|^2_{L^2}.
\end{align}
\begin{align} K_2&={-}
\int_{\mathbb{R}^3}\nabla^{k+1}(u\cdot\nabla\varrho)\cdot\nabla^{k+1}\varrho\,{\rm
d}x\nonumber\\
&={-}\int_{\mathbb{R}^3}(u\cdot\nabla\nabla^{k+1}\varrho+[\nabla^{k+1},u]\cdot\nabla\varrho)\nabla^{k+1}\varrho\,{\rm
d}x\nonumber\\
&={-}\int_{\mathbb{R}^3}u\cdot\nabla\frac{|\nabla^{k+1}\varrho|^2}2\,{\rm
d}x\notag\\
&\quad +(\|\nabla
u\|_{L^{\infty}}\|\nabla^k\nabla\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}\|\nabla\varrho\|_{L^{\infty}})\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&=\frac12\int_{\mathbb{R}^3}\nabla\cdot
u|\nabla^{k+1}\varrho|^2\,{\rm d}x\notag\\
&\quad +(\|\nabla
u\|_{L^{\infty}}\|\nabla^k\nabla\varrho\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}\|\nabla\varrho\|_{L^{\infty}})\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&\lesssim\|\nabla
u\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|^2_{L^2}+(\|\nabla
u\|_{L^{\infty}}+\|\nabla\varrho\|_{L^{\infty}})\|\nabla^{k+1}\varrho\|_{L^2}^2\nonumber\\
&\lesssim\delta\|\nabla^{k+1}\varrho\|^2_{L^2}.
\end{align}
Integrating by parts, applying Hölder's inequality, Kato–Ponce inequality (lemma 2.1), Gagliardo–Nirenberg inequality (lemma 2.2) and Sobolev embedding theorem, one estimates ![]() $K_3$–
$K_3$–![]() $K_8$ as
$K_8$ as
 \begin{align}
K_3&={-}\int_{\mathbb{R}^3}\nabla^{k+1}(u\cdot\nabla
u)\cdot\nabla^{k+1}u\,{\rm d}x\nonumber\\
&=\int_{\mathbb{R}^3}\nabla^k(u\cdot\nabla
u)\cdot\nabla^{k+2}u\,{\rm d}x\nonumber\\ &\lesssim
\|\nabla^{k+2}u\|_{L^2}\|\nabla^{k}(u\cdot\nabla
u)\|_{L^2}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^ku\|_{L^6}\|\nabla
u\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+1}u\|_{L^6})\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}\left(\|\nabla^{k+2}u\|_{L^2}^{{(k-1/2)}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{1/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times \left. \Lambda^{1/2}u\|_{L^2}^{{(k-1/2)}/{(k+1/2)}}\|\nabla^{k+2}u\|_{L^2}^{1/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+2}u\|_{L^2}\right)\nonumber\\
&\lesssim\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+2}u\|_{L^2}^2\lesssim\delta\|\nabla^{k+2}u\|_{L^2}^2,
\end{align}
\begin{align}
K_3&={-}\int_{\mathbb{R}^3}\nabla^{k+1}(u\cdot\nabla
u)\cdot\nabla^{k+1}u\,{\rm d}x\nonumber\\
&=\int_{\mathbb{R}^3}\nabla^k(u\cdot\nabla
u)\cdot\nabla^{k+2}u\,{\rm d}x\nonumber\\ &\lesssim
\|\nabla^{k+2}u\|_{L^2}\|\nabla^{k}(u\cdot\nabla
u)\|_{L^2}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^ku\|_{L^6}\|\nabla
u\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+1}u\|_{L^6})\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}\left(\|\nabla^{k+2}u\|_{L^2}^{{(k-1/2)}/{(k+1/2)}}\|\Lambda^{1/2}u\|_{L^2}^{1/{(k+1/2)}}\|\right.\nonumber\\
&\quad\times \left. \Lambda^{1/2}u\|_{L^2}^{{(k-1/2)}/{(k+1/2)}}\|\nabla^{k+2}u\|_{L^2}^{1/{(k+1/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+2}u\|_{L^2}\right)\nonumber\\
&\lesssim\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+2}u\|_{L^2}^2\lesssim\delta\|\nabla^{k+2}u\|_{L^2}^2,
\end{align} \begin{align}
K_4&\approx{-}\int_{\mathbb{R}^3}\nabla^{k+1}[h(\varrho)\nabla^2u]\cdot\nabla^{k+1}u\,{\rm
d}x\nonumber\\
&\approx\int_{\mathbb{R}^3}\nabla^{k}[h(\varrho)\nabla^2u]\cdot\nabla^{k+2}u\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}\|\nabla^k[h(\varrho)\nabla^2u]\|_{L^2}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^kh(\varrho)\|_{L^6}\|\nabla^2u\|_{L^3}+\|h(\varrho)\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^{k+1}\varrho
\|_{L^2}\|\nabla^{5/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}
\|\nabla^{k+2}u\|_{L^2})\nonumber\\
&\lesssim(\|\nabla^{5/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}+\|\Delta\varrho\|_{L^2})(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2)\nonumber\\
&\lesssim\delta(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2),
\end{align}
\begin{align}
K_4&\approx{-}\int_{\mathbb{R}^3}\nabla^{k+1}[h(\varrho)\nabla^2u]\cdot\nabla^{k+1}u\,{\rm
d}x\nonumber\\
&\approx\int_{\mathbb{R}^3}\nabla^{k}[h(\varrho)\nabla^2u]\cdot\nabla^{k+2}u\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}\|\nabla^k[h(\varrho)\nabla^2u]\|_{L^2}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^kh(\varrho)\|_{L^6}\|\nabla^2u\|_{L^3}+\|h(\varrho)\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^{k+1}\varrho
\|_{L^2}\|\nabla^{5/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}
\|\nabla^{k+2}u\|_{L^2})\nonumber\\
&\lesssim(\|\nabla^{5/2}u\|_{L^2}+\|\nabla\varrho\|_{L^2}+\|\Delta\varrho\|_{L^2})(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2)\nonumber\\
&\lesssim\delta(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2),
\end{align} \begin{align} K_5&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[g(\varrho )\nabla\varrho]\cdot\nabla^{k+1}u\,{\rm d}x\nonumber\\ &=\int_{\mathbb{R}^3}\nabla^{k}[g(\varrho)\nabla\varrho]\cdot\nabla^{k+2}u\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^kg(\varrho)\|_{L^6}\|\nabla\varrho\|_{L^3}+\|g(\varrho)\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\ &\lesssim\|\nabla^{k+2}u\|_{L^2}(\| \nabla^{k+1}\varrho \|_{L^2}\|\Lambda^{3/2}\varrho\|_{L^2}+\| \nabla\varrho \|_{L^2}^{1/2}\| \Delta\varrho \|_{L^2}^{1/2}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\ &\lesssim(\|\Lambda^{3/2}\varrho\|_{L^2}+\| \nabla\varrho \|_{L^2}+\| \Delta\varrho \|_{L^2})(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2 \|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2 \|_{L^2}^2), \end{align}
\begin{align} K_5&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[g(\varrho )\nabla\varrho]\cdot\nabla^{k+1}u\,{\rm d}x\nonumber\\ &=\int_{\mathbb{R}^3}\nabla^{k}[g(\varrho)\nabla\varrho]\cdot\nabla^{k+2}u\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}u\|_{L^2}(\|\nabla^kg(\varrho)\|_{L^6}\|\nabla\varrho\|_{L^3}+\|g(\varrho)\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\ &\lesssim\|\nabla^{k+2}u\|_{L^2}(\| \nabla^{k+1}\varrho \|_{L^2}\|\Lambda^{3/2}\varrho\|_{L^2}+\| \nabla\varrho \|_{L^2}^{1/2}\| \Delta\varrho \|_{L^2}^{1/2}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\ &\lesssim(\|\Lambda^{3/2}\varrho\|_{L^2}+\| \nabla\varrho \|_{L^2}+\| \Delta\varrho \|_{L^2})(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2 \|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2 \|_{L^2}^2), \end{align} \begin{align}
K_6&=\int_{\mathbb{R}^3}\nabla^{k+1}\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\cdot\nabla^{k+1}u\,{\rm d}x\nonumber\\
&\lesssim\|\nabla^{k+2} u\|_{L^2}\left\|\nabla^{k }\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\right\|_{L^{2}}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2} \|\phi(\varrho)\|_{L^{\infty}}\left\|\nabla^{k
}\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right\|_{L^{2}}\nonumber\\
&\quad+\|\nabla^{k+2}u\|_{L^2}\|\nabla^{k
}\phi(\varrho)\|_{L^6}\left\|
\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right\|_{L^{3}}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}\|\varrho\|_{L^{\infty}}\|\nabla\chi\|_{L^3}\|\nabla^{k+2}
\chi\|_{L^2}+\|\nabla^{k+2}u\|_{L^2}\|\notag\\
&\quad \times \nabla^{k+1}\varrho\|_{L^2}\|\nabla\chi\|_{L^6}\|\nabla^2\chi\|_{L^6}\nonumber\\
&\lesssim\delta^2(\|\nabla^{k+2}u\|_{L^2}^2+
\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+2}\varrho\|_{L^2}^2),
\end{align}
\begin{align}
K_6&=\int_{\mathbb{R}^3}\nabla^{k+1}\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\cdot\nabla^{k+1}u\,{\rm d}x\nonumber\\
&\lesssim\|\nabla^{k+2} u\|_{L^2}\left\|\nabla^{k }\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\right\|_{L^{2}}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2} \|\phi(\varrho)\|_{L^{\infty}}\left\|\nabla^{k
}\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right\|_{L^{2}}\nonumber\\
&\quad+\|\nabla^{k+2}u\|_{L^2}\|\nabla^{k
}\phi(\varrho)\|_{L^6}\left\|
\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right\|_{L^{3}}\nonumber\\
&\lesssim\|\nabla^{k+2}u\|_{L^2}\|\varrho\|_{L^{\infty}}\|\nabla\chi\|_{L^3}\|\nabla^{k+2}
\chi\|_{L^2}+\|\nabla^{k+2}u\|_{L^2}\|\notag\\
&\quad \times \nabla^{k+1}\varrho\|_{L^2}\|\nabla\chi\|_{L^6}\|\nabla^2\chi\|_{L^6}\nonumber\\
&\lesssim\delta^2(\|\nabla^{k+2}u\|_{L^2}^2+
\|\nabla^{k+1}\chi\|_{L^2}^2+\|\nabla^{k+2}\varrho\|_{L^2}^2),
\end{align} \begin{align}
K_7&={-}\int_{\mathbb{R}^3}\nabla^{k+1}(u\cdot\nabla\chi)\cdot\nabla^{k+1}\chi\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+1}\chi\|_{L^6}\|\nabla^{k+1}(u\cdot\nabla\chi)\|_{L^{6/5}}\nonumber\\
&\lesssim\|\nabla^{k+2}
\chi\|_{L^2}(\|\nabla^{k+1}u\|_{L^2}\|\nabla\chi\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+1}\nabla\chi\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+2}
\chi\|_{L^2}\left(\|\nabla^{k+2}u\|_{L^2}^{{(k+1/2)}/{(k+3/2)}}\|
\Lambda^{1/2}u\|_{L^2}^{1/{(k+3/2)}}\|\right.\nonumber\\
&\quad\times \left.\nabla^{k+2}\chi\|_{L^2}^{{1}/{(k+3/2)}}\|
\Lambda^{1/2}\chi\|_{L^2}^{{(k+1/2)}/{(k+3/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+2}\chi
\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}\chi\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+1}\nabla\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)\nonumber\\
&\lesssim\delta(\|\nabla^{k+2}
\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2),
\end{align}
\begin{align}
K_7&={-}\int_{\mathbb{R}^3}\nabla^{k+1}(u\cdot\nabla\chi)\cdot\nabla^{k+1}\chi\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+1}\chi\|_{L^6}\|\nabla^{k+1}(u\cdot\nabla\chi)\|_{L^{6/5}}\nonumber\\
&\lesssim\|\nabla^{k+2}
\chi\|_{L^2}(\|\nabla^{k+1}u\|_{L^2}\|\nabla\chi\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+1}\nabla\chi\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+2}
\chi\|_{L^2}\left(\|\nabla^{k+2}u\|_{L^2}^{{(k+1/2)}/{(k+3/2)}}\|
\Lambda^{1/2}u\|_{L^2}^{1/{(k+3/2)}}\|\right.\nonumber\\
&\quad\times \left.\nabla^{k+2}\chi\|_{L^2}^{{1}/{(k+3/2)}}\|
\Lambda^{1/2}\chi\|_{L^2}^{{(k+1/2)}/{(k+3/2)}}
+\|\Lambda^{1/2}u\|_{L^2}\|\nabla^{k+2}\chi
\|_{L^2}\right)\nonumber\\
&\lesssim(\|\Lambda^{1/2}\chi\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+1}\nabla\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)\nonumber\\
&\lesssim\delta(\|\nabla^{k+2}
\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2),
\end{align}and
 \begin{align} K_8&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim \|\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\|_{L^{6/5}}\|\nabla^{k+1}\chi\|_{L^6}\nonumber\\ &\lesssim(\|\varphi(\varrho)\|_{L^3}\|\nabla^{k+1}\Delta\chi\|_{L^2}+\|\Delta\chi\|_{L^3}\|\nabla^{k+1}\varphi(\varrho)\|_{L^2})\|\nabla^{k+2}\chi\|_{L^2}\nonumber\\ &\lesssim(\|\varrho\|_{L^3}\|\nabla^{k+3}\chi\|_{L^2}+\|\nabla^2\chi\|_{L^3}\|\nabla^{k+1}\varrho\|_{L^2})\|\nabla^{k+2}\chi\|_{L^2}\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+3}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2 ). \end{align}
\begin{align} K_8&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim \|\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\|_{L^{6/5}}\|\nabla^{k+1}\chi\|_{L^6}\nonumber\\ &\lesssim(\|\varphi(\varrho)\|_{L^3}\|\nabla^{k+1}\Delta\chi\|_{L^2}+\|\Delta\chi\|_{L^3}\|\nabla^{k+1}\varphi(\varrho)\|_{L^2})\|\nabla^{k+2}\chi\|_{L^2}\nonumber\\ &\lesssim(\|\varrho\|_{L^3}\|\nabla^{k+3}\chi\|_{L^2}+\|\nabla^2\chi\|_{L^3}\|\nabla^{k+1}\varrho\|_{L^2})\|\nabla^{k+2}\chi\|_{L^2}\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}\chi\|_{L^2}^2+\|\nabla^{k+3}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2 ). \end{align}
Next, we consider the term ![]() $K_9$. Hölder's inequality implies that
$K_9$. Hölder's inequality implies that
 \begin{align} K_9&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim(\|\nabla^{k+1}[\phi(\varrho) \chi^3 ]\|_{L^{6/5}}+\|\nabla^{k+1}[\zeta(\varrho)\zeta(\varrho) \chi ]\|_{L^{6/5}})\|\nabla^{k+1}\chi\|_{L^6}\nonumber\\ &=:(K_{91}+K_{92})\|\nabla^{k+2}\chi\|_{L^2}. \end{align}
\begin{align} K_9&={-}\int_{\mathbb{R}^3}\nabla^{k+1}[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^{k+1}\chi\,{\rm d}x\nonumber\\ &\lesssim(\|\nabla^{k+1}[\phi(\varrho) \chi^3 ]\|_{L^{6/5}}+\|\nabla^{k+1}[\zeta(\varrho)\zeta(\varrho) \chi ]\|_{L^{6/5}})\|\nabla^{k+1}\chi\|_{L^6}\nonumber\\ &=:(K_{91}+K_{92})\|\nabla^{k+2}\chi\|_{L^2}. \end{align}By using Kato–Ponce inequality of lemma 2.1 and Sobolev embedding theorem, we arrive at
 \begin{align} K_{91}&=\|\nabla^{k+1}[\phi(\varrho) \chi^3 ]\|_{L^{6/5}}\nonumber\\ &\lesssim \|\phi(\varrho)\|_{L^3}\|\nabla^{k+1} \chi^3 \|_{L^2}+\|\chi^3 \|_{L^3}\|\nabla^{k+1}\phi(\varrho)\|_{L^2}\nonumber\\ &\lesssim \|\phi(\varrho)\|_{L^3}\|\chi\|_{L^6}^2\|\nabla^{k+1}\chi\|_{L^6}+\|\chi\|_{L^\infty}\|\chi\|_{L^6}^2\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim \|\Lambda^{1/2}\varrho\|_{L^2}\|\nabla\chi\|^2_{L^2}\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla\chi\|_{L^2}^{1/2}\|\Delta\chi\|_{L^2}^{1/2}\|\nabla\chi\|_{L^2}^2\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim\delta^3(\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla^{k+1}\varrho\|_{L^2}). \end{align}
\begin{align} K_{91}&=\|\nabla^{k+1}[\phi(\varrho) \chi^3 ]\|_{L^{6/5}}\nonumber\\ &\lesssim \|\phi(\varrho)\|_{L^3}\|\nabla^{k+1} \chi^3 \|_{L^2}+\|\chi^3 \|_{L^3}\|\nabla^{k+1}\phi(\varrho)\|_{L^2}\nonumber\\ &\lesssim \|\phi(\varrho)\|_{L^3}\|\chi\|_{L^6}^2\|\nabla^{k+1}\chi\|_{L^6}+\|\chi\|_{L^\infty}\|\chi\|_{L^6}^2\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim \|\Lambda^{1/2}\varrho\|_{L^2}\|\nabla\chi\|^2_{L^2}\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla\chi\|_{L^2}^{1/2}\|\Delta\chi\|_{L^2}^{1/2}\|\nabla\chi\|_{L^2}^2\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim\delta^3(\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla^{k+1}\varrho\|_{L^2}). \end{align}
Moreover, the term ![]() $K_{92}$ can be bounded as
$K_{92}$ can be bounded as
 \begin{align} K_{92}&=\|\nabla^{k+1}[\phi(\varrho) \chi ]\|_{L^{6/5}}=\|\nabla^{k+1}[\zeta(\varrho)\zeta(\varrho)\chi ]\|_{L^{6/5}}\nonumber\\ &\lesssim\|\zeta(\varrho)\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^{k+1}\chi\|_{L^6}+\|\chi\|_{L^6}\|\zeta(\varrho)\|_{L^6}\|\nabla^{k+1}\zeta(\varrho)\|_{L^2}\nonumber\\ &\lesssim\|\varrho\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla\chi\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim \delta^2 (\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+2}\chi\|_{L^2}). \end{align}
\begin{align} K_{92}&=\|\nabla^{k+1}[\phi(\varrho) \chi ]\|_{L^{6/5}}=\|\nabla^{k+1}[\zeta(\varrho)\zeta(\varrho)\chi ]\|_{L^{6/5}}\nonumber\\ &\lesssim\|\zeta(\varrho)\|_{L^2}\|\zeta(\varrho)\|_{L^6}\|\nabla^{k+1}\chi\|_{L^6}+\|\chi\|_{L^6}\|\zeta(\varrho)\|_{L^6}\|\nabla^{k+1}\zeta(\varrho)\|_{L^2}\nonumber\\ &\lesssim\|\varrho\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+2}\chi\|_{L^2}+\|\nabla\chi\|_{L^2}\|\nabla\varrho\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim \delta^2 (\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla^{k+2}\chi\|_{L^2}). \end{align}Combining (3.43)–(3.44) together, we derive that
Next, employing Hölder's inequality, Kato–Ponce inequality of lemma 2.1 and Sobolev embedding theorem, we estimate the term ![]() $K_{10}$ as
$K_{10}$ as
 \begin{align} K_{10}&={-}\int_{\mathbb{R}^3}\nabla^{k+2}[u\cdot\nabla\chi]\cdot\nabla^{k+2}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^6}\|\nabla^{k+2}(u\cdot\nabla\chi)\|_{L^{6/5}}\nonumber\\ &\lesssim\|\nabla^{k+2}\nabla\chi\|_{L^2}(\|\nabla^{k+2}u\|_{L^2}\|\nabla\chi\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+2}\nabla\chi\|_{L^2})\nonumber\\ &\lesssim(\|\Lambda^{3/2}\chi\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+2}\nabla\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}\nabla\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2). \end{align}
\begin{align} K_{10}&={-}\int_{\mathbb{R}^3}\nabla^{k+2}[u\cdot\nabla\chi]\cdot\nabla^{k+2}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\nabla^{k+2}\chi\|_{L^6}\|\nabla^{k+2}(u\cdot\nabla\chi)\|_{L^{6/5}}\nonumber\\ &\lesssim\|\nabla^{k+2}\nabla\chi\|_{L^2}(\|\nabla^{k+2}u\|_{L^2}\|\nabla\chi\|_{L^3}+\|u\|_{L^3}\|\nabla^{k+2}\nabla\chi\|_{L^2})\nonumber\\ &\lesssim(\|\Lambda^{3/2}\chi\|_{L^2}+\|\Lambda^{1/2}u\|_{L^2})(\|\nabla^{k+2}\nabla\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)\nonumber\\ &\lesssim\delta(\|\nabla^{k+2}\nabla\chi\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2). \end{align}Using Hölder's inequality, Kato–Ponce inequality, Gagliardo–Nirenberg inequality together with Sobolev embedding theorem again, we have
 \begin{align}
K_{11}&={-}\int_{\mathbb{R}^3}\nabla^{k+2}[\varphi(\varrho)\Delta\chi]\cdot\nabla^{k+2}\chi\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}\|\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\|_{L^2}\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\varphi(\varrho)\|_{L^{\infty}}\|\nabla^{k+1}\Delta\chi\|_{L^2}+\|\Delta\chi\|_{L^{\infty}}\|\nabla^{k+1}\varphi(\varrho)\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\nabla\varrho\|_{L^{2}}^{1/2}\|\nabla^2\varrho\|_{L^{2}}^{1/2}\|\nabla^{k+3}\chi\|_{L^2}\nonumber\\
&\quad +\|\nabla^3\chi\|_{L^2}^{1/2}\|\nabla^3\nabla\chi\|_{L^2}^{1/2}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+3}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2),
\end{align}
\begin{align}
K_{11}&={-}\int_{\mathbb{R}^3}\nabla^{k+2}[\varphi(\varrho)\Delta\chi]\cdot\nabla^{k+2}\chi\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}\|\nabla^{k+1}[\varphi(\varrho)\Delta\chi]\|_{L^2}\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\varphi(\varrho)\|_{L^{\infty}}\|\nabla^{k+1}\Delta\chi\|_{L^2}+\|\Delta\chi\|_{L^{\infty}}\|\nabla^{k+1}\varphi(\varrho)\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\nabla\varrho\|_{L^{2}}^{1/2}\|\nabla^2\varrho\|_{L^{2}}^{1/2}\|\nabla^{k+3}\chi\|_{L^2}\nonumber\\
&\quad +\|\nabla^3\chi\|_{L^2}^{1/2}\|\nabla^3\nabla\chi\|_{L^2}^{1/2}\|\nabla^{k+1}\varrho\|_{L^2})\nonumber\\
&\lesssim\delta(\|\nabla^{k+3}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2),
\end{align}and
 \begin{align}
K_{12}&={-}\int_{\mathbb{R}^3}\nabla^{k+2}[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^{k+2}\chi\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\nabla^{k+1}[\phi(\varrho)
\chi^3
]\|_{L^2}+\|\nabla^{k+1}[\zeta(\varrho)\zeta(\varrho) \chi
]\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\phi(\varrho)\|_{L^{\infty}}\|\chi\|^2_{L^6}\|\nabla^{k+1}
\chi \|_{L^6}+\|
\chi\|_{L^{\infty}}\|\nabla^{k+1}\phi(\varrho)\|_{L^2}\nonumber\\
&\quad+\|\zeta(\varrho)\|_{L^6}^2\|\nabla^{k+1}\chi\|_{L^6}+\|\zeta(\varrho)\|_{L^\infty}\|\chi\|_{L^\infty}\|\nabla^{k+1}\zeta(\varrho)\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\nabla\varrho
\|_{L^{2}}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla\chi\|^2_{L^2}\|\nabla^{k+1}\chi
\|_{L^6}\nonumber\\ &\quad +\| \nabla\chi\|_{L^{2}}^{1/2}\|
\Delta\chi\|_{L^{2}}^{1/2}\|\nabla^{k+1} \varrho
\|_{L^2}+\|\nabla\varrho
\|_{L^2}^2\|\nabla^{k+2}\chi\|_{L^2}\nonumber\\
&\quad+\|
\nabla\chi\|_{L^{2}}^{1/2}\|
\Delta\chi\|_{L^{2}}^{1/2}\|\nabla^{k+1} \varrho
\|_{L^2})\nonumber\\
&\lesssim\left(\delta^3+\delta\right)(\|\nabla^{k+3}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho
\|_{L^2}^2).
\end{align}
\begin{align}
K_{12}&={-}\int_{\mathbb{R}^3}\nabla^{k+2}[\phi(\varrho)(\chi^3-\chi)]\cdot\nabla^{k+2}\chi\,{\rm
d}x\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\nabla^{k+1}[\phi(\varrho)
\chi^3
]\|_{L^2}+\|\nabla^{k+1}[\zeta(\varrho)\zeta(\varrho) \chi
]\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\phi(\varrho)\|_{L^{\infty}}\|\chi\|^2_{L^6}\|\nabla^{k+1}
\chi \|_{L^6}+\|
\chi\|_{L^{\infty}}\|\nabla^{k+1}\phi(\varrho)\|_{L^2}\nonumber\\
&\quad+\|\zeta(\varrho)\|_{L^6}^2\|\nabla^{k+1}\chi\|_{L^6}+\|\zeta(\varrho)\|_{L^\infty}\|\chi\|_{L^\infty}\|\nabla^{k+1}\zeta(\varrho)\|_{L^2})\nonumber\\
&\lesssim\|\nabla^{k+3}\chi\|_{L^2}(\|\nabla\varrho
\|_{L^{2}}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla\chi\|^2_{L^2}\|\nabla^{k+1}\chi
\|_{L^6}\nonumber\\ &\quad +\| \nabla\chi\|_{L^{2}}^{1/2}\|
\Delta\chi\|_{L^{2}}^{1/2}\|\nabla^{k+1} \varrho
\|_{L^2}+\|\nabla\varrho
\|_{L^2}^2\|\nabla^{k+2}\chi\|_{L^2}\nonumber\\
&\quad+\|
\nabla\chi\|_{L^{2}}^{1/2}\|
\Delta\chi\|_{L^{2}}^{1/2}\|\nabla^{k+1} \varrho
\|_{L^2})\nonumber\\
&\lesssim\left(\delta^3+\delta\right)(\|\nabla^{k+3}\chi\|_{L^2}^2+\|\nabla^{k+1}\varrho
\|_{L^2}^2).
\end{align}
Summing up the estimates for ![]() $K_1$–
$K_1$–![]() $K_{12}$, we deduce (3.32), this yields the desired result.
$K_{12}$, we deduce (3.32), this yields the desired result.
The following lemma provides the dissipation estimate for ![]() $\varrho$.
$\varrho$.
Lemma 3.3 If ![]() $\sqrt {\mathcal {E}_0^3(t)}<\delta$, then for
$\sqrt {\mathcal {E}_0^3(t)}<\delta$, then for ![]() $k=0,1,\ldots ,N-1$, we have
$k=0,1,\ldots ,N-1$, we have
Proof. Applying ![]() $\nabla ^k$ to (1.4)
$\nabla ^k$ to (1.4)![]() $_2$, multiplying
$_2$, multiplying ![]() $\nabla \nabla ^k\varrho$, integrating over
$\nabla \nabla ^k\varrho$, integrating over ![]() $\mathbb {R}^3$ by parts, it yields that
$\mathbb {R}^3$ by parts, it yields that
 \begin{align}
\int_{\mathbb{R}^3}|\nabla^{k+1}\varrho|^2\,{\rm
d}x&\leq{-}\int_{\mathbb{R}^3}\nabla^ku_t\cdot\nabla\nabla^k\varrho\,{\rm
d}x+C\|\nabla^{k+2}u\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&\quad+\left\|\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)}\nabla^k\left[u\cdot\nabla
u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\left.\left.\quad +\,\psi(\varrho)\text{div}
\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\right\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}.
\end{align}
\begin{align}
\int_{\mathbb{R}^3}|\nabla^{k+1}\varrho|^2\,{\rm
d}x&\leq{-}\int_{\mathbb{R}^3}\nabla^ku_t\cdot\nabla\nabla^k\varrho\,{\rm
d}x+C\|\nabla^{k+2}u\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&\quad+\left\|\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)}\nabla^k\left[u\cdot\nabla
u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\left.\left.\quad +\,\psi(\varrho)\text{div}
\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\right\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}.
\end{align}
For the first term of the right-hand side of (3.50), using (1.4)![]() $_1$, integrating by parts for both the
$_1$, integrating by parts for both the ![]() $t$ and
$t$ and ![]() $x$ variables, one obtains
$x$ variables, one obtains
 \begin{align} &-\int_{\mathbb{R}^3}\nabla^ku_t\cdot\nabla\nabla^k\varrho\,{\rm d}x\nonumber\\ &\quad={-}\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}\nabla^ku \cdot\nabla\nabla^k\varrho\,{\rm d}x-\int_{\mathbb{R}^3}\nabla^k\text{div}\,u\cdot\nabla^k\varrho_t\,{\rm d}x\nonumber\\ &\quad={-}\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}\nabla^ku \cdot\nabla\nabla^k\varrho\,{\rm d}x+\|\nabla^k\text{div}\,u\|_{L^2}^2+\int_{\mathbb{R}^3}\nabla^k\text{div}\,u\cdot\nabla^k\text{div}(\varrho u)\,{\rm d}x. \end{align}
\begin{align} &-\int_{\mathbb{R}^3}\nabla^ku_t\cdot\nabla\nabla^k\varrho\,{\rm d}x\nonumber\\ &\quad={-}\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}\nabla^ku \cdot\nabla\nabla^k\varrho\,{\rm d}x-\int_{\mathbb{R}^3}\nabla^k\text{div}\,u\cdot\nabla^k\varrho_t\,{\rm d}x\nonumber\\ &\quad={-}\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}\nabla^ku \cdot\nabla\nabla^k\varrho\,{\rm d}x+\|\nabla^k\text{div}\,u\|_{L^2}^2+\int_{\mathbb{R}^3}\nabla^k\text{div}\,u\cdot\nabla^k\text{div}(\varrho u)\,{\rm d}x. \end{align}Employing Hölder's inequality, Kato–Ponce inequality and Sobolev embedding theorem, we obtain
 \begin{align} &\int_{\mathbb{R}^3}\nabla^k\text{div}\,u\cdot\nabla^k\text{div}(\varrho u)\,{\rm d}x\nonumber\\ &\quad\lesssim\|\nabla^{k+1}u\|_{L^2}(\|\nabla^{k+1}\varrho\|_{L^2}\|u\|_{L^\infty}+\|\varrho\|_{L^\infty}\|\nabla^{k+1}u\|_{L^2})\nonumber\\ &\quad\lesssim\|\nabla^{k+1}u\|_{L^2}(\|\nabla^{k+1}\varrho\|_{L^2}\|\nabla u\|_{L^2}^{1/2}\|\Delta u\|_{L^2}^{1/2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^{k+1}u\|_{L^2})\nonumber\\ &\quad\lesssim(\|\nabla u\|_{L^2}+\|\Delta u\|_{L^2}+\|\nabla\varrho\|_{L^2}+\|\Delta\varrho\|_{L^2})(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2)\nonumber\\ &\quad\lesssim\delta(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2). \end{align}
\begin{align} &\int_{\mathbb{R}^3}\nabla^k\text{div}\,u\cdot\nabla^k\text{div}(\varrho u)\,{\rm d}x\nonumber\\ &\quad\lesssim\|\nabla^{k+1}u\|_{L^2}(\|\nabla^{k+1}\varrho\|_{L^2}\|u\|_{L^\infty}+\|\varrho\|_{L^\infty}\|\nabla^{k+1}u\|_{L^2})\nonumber\\ &\quad\lesssim\|\nabla^{k+1}u\|_{L^2}(\|\nabla^{k+1}\varrho\|_{L^2}\|\nabla u\|_{L^2}^{1/2}\|\Delta u\|_{L^2}^{1/2}+\|\nabla\varrho\|_{L^2}^{1/2}\|\Delta\varrho\|_{L^2}^{1/2}\|\nabla^{k+1}u\|_{L^2})\nonumber\\ &\quad\lesssim(\|\nabla u\|_{L^2}+\|\Delta u\|_{L^2}+\|\nabla\varrho\|_{L^2}+\|\Delta\varrho\|_{L^2})(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2)\nonumber\\ &\quad\lesssim\delta(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+1}\varrho\|_{L^2}^2). \end{align}It then follows from (3.51) and (3.52) that
 \begin{align} &-\int_{\mathbb{R}^3}\nabla^ku_t\cdot\nabla\nabla^k\varrho\,{\rm d}x\nonumber\\ &\quad\leq{-}\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}\nabla^ku \cdot\nabla\nabla^k\varrho\,{\rm d}x+C(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)+C\delta\|\nabla^{k+1}\varrho\|_{L^2}^2. \end{align}
\begin{align} &-\int_{\mathbb{R}^3}\nabla^ku_t\cdot\nabla\nabla^k\varrho\,{\rm d}x\nonumber\\ &\quad\leq{-}\frac{{\rm d}}{{\rm d}t}\int_{\mathbb{R}^3}\nabla^ku \cdot\nabla\nabla^k\varrho\,{\rm d}x+C(\|\nabla^{k+1}u\|_{L^2}^2+\|\nabla^{k+2}u\|_{L^2}^2)+C\delta\|\nabla^{k+1}\varrho\|_{L^2}^2. \end{align}Next, one need to estimate the last term of the right-hand side of (3.50). Note that
 \begin{align} \|\nabla^k(u\cdot\nabla u)\|_{L^2}&\lesssim\|u\|_{L^3}\|\nabla^{k+1}u\|_{L^6}+\|\nabla u\|_{L^3}\|\nabla^ku\|_{L^6}\nonumber\\ &\lesssim(\|\Lambda^{1/2}u\|_{L^2}+\|\Lambda^{3/2}u\|_{L^2})(\|\nabla^{k+1}u\|_{L^2}+\|\nabla^{k+2}u\|_{L^2})\nonumber\\ &\lesssim\delta(\|\nabla^{k+1}u\|_{L^2}+\|\nabla^{k+2}u\|_{L^2}). \end{align}
\begin{align} \|\nabla^k(u\cdot\nabla u)\|_{L^2}&\lesssim\|u\|_{L^3}\|\nabla^{k+1}u\|_{L^6}+\|\nabla u\|_{L^3}\|\nabla^ku\|_{L^6}\nonumber\\ &\lesssim(\|\Lambda^{1/2}u\|_{L^2}+\|\Lambda^{3/2}u\|_{L^2})(\|\nabla^{k+1}u\|_{L^2}+\|\nabla^{k+2}u\|_{L^2})\nonumber\\ &\lesssim\delta(\|\nabla^{k+1}u\|_{L^2}+\|\nabla^{k+2}u\|_{L^2}). \end{align}We also have
 \begin{align} &\|\nabla^k[h(\varrho)(\mu\Delta u+(\mu+\lambda)\nabla\text{div}\,u)]\|_{L^2}\nonumber\\ &\quad\approx\|\nabla^k(h(\varrho)\nabla^2 u\|_{L^2}\nonumber\\ &\quad\lesssim\|h(\varrho)\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2}+\|\nabla^2u\|_{L^3}\|\nabla^kh(\varrho)\|_{L^6}\nonumber\\ &\quad\lesssim\|\varrho\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2}+\|\nabla^2u\|_{L^3}\|\nabla^{k+1}\varrho \|_{L^2}\nonumber\\ &\quad\lesssim\delta(\|\nabla^{k+2}u\|_{L^2}+\|\nabla^{k+1}\varrho \|_{L^2}), \end{align}
\begin{align} &\|\nabla^k[h(\varrho)(\mu\Delta u+(\mu+\lambda)\nabla\text{div}\,u)]\|_{L^2}\nonumber\\ &\quad\approx\|\nabla^k(h(\varrho)\nabla^2 u\|_{L^2}\nonumber\\ &\quad\lesssim\|h(\varrho)\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2}+\|\nabla^2u\|_{L^3}\|\nabla^kh(\varrho)\|_{L^6}\nonumber\\ &\quad\lesssim\|\varrho\|_{L^{\infty}}\|\nabla^{k+2}u\|_{L^2}+\|\nabla^2u\|_{L^3}\|\nabla^{k+1}\varrho \|_{L^2}\nonumber\\ &\quad\lesssim\delta(\|\nabla^{k+2}u\|_{L^2}+\|\nabla^{k+1}\varrho \|_{L^2}), \end{align}and
 \begin{align} \|\nabla^k(g(\varrho)\nabla\varrho)\|_{L^2}&\lesssim \|g(\varrho)\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla\varrho\|_{L^3}\|\nabla^kg(\varrho)\|_{L^6}\nonumber\\ &\lesssim\|\varrho\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla\varrho\|_{L^3}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim\delta \|\nabla^{k+1}\varrho \|_{L^2}. \end{align}
\begin{align} \|\nabla^k(g(\varrho)\nabla\varrho)\|_{L^2}&\lesssim \|g(\varrho)\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla\varrho\|_{L^3}\|\nabla^kg(\varrho)\|_{L^6}\nonumber\\ &\lesssim\|\varrho\|_{L^{\infty}}\|\nabla^{k+1}\varrho\|_{L^2}+\|\nabla\varrho\|_{L^3}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\lesssim\delta \|\nabla^{k+1}\varrho \|_{L^2}. \end{align}Moreover, Kato–Ponce inequality of lemma 2.1 and Sobolev inequality of lemma 2.2 imply that
 \begin{align} &\left\|\nabla^k\left[\psi(\varrho)\text{div} \left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\right\|_{L^2}\nonumber\\ &\quad\lesssim\|\psi(\varrho)\|_{L^3}\left\|\nabla^k \text{div} \left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right) \right\|_{L^6}\nonumber\\ &\quad\quad+\left\| \text{div} \left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right\|_{L^3}\|\nabla^k\psi(\varrho)\|_{L^6}\nonumber\\ &\quad\approx\|\psi(\varrho)\|_{L^3} \|\nabla^{k+1}|\nabla\chi|^2 \|_{L^6}+ \||\nabla\chi||\nabla^2\chi|\|_{L^3}\|\nabla^k\psi(\varrho) \|_{L^6}\nonumber\\ &\quad\lesssim\|\varrho\|_{L^3}\|\nabla\chi\|_{L^{\infty}}\|\nabla^{k+2}\nabla\chi\|_{L^2}+\|\nabla\chi\|_{L^6}\|\nabla^2\chi\|_{L^6}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\quad\lesssim\delta^3(\|\nabla^{k+1}\varrho \|_{L^2}+\|\nabla^{k+2}\nabla\chi\|_{L^2}). \end{align}
\begin{align} &\left\|\nabla^k\left[\psi(\varrho)\text{div} \left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\right\|_{L^2}\nonumber\\ &\quad\lesssim\|\psi(\varrho)\|_{L^3}\left\|\nabla^k \text{div} \left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right) \right\|_{L^6}\nonumber\\ &\quad\quad+\left\| \text{div} \left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right\|_{L^3}\|\nabla^k\psi(\varrho)\|_{L^6}\nonumber\\ &\quad\approx\|\psi(\varrho)\|_{L^3} \|\nabla^{k+1}|\nabla\chi|^2 \|_{L^6}+ \||\nabla\chi||\nabla^2\chi|\|_{L^3}\|\nabla^k\psi(\varrho) \|_{L^6}\nonumber\\ &\quad\lesssim\|\varrho\|_{L^3}\|\nabla\chi\|_{L^{\infty}}\|\nabla^{k+2}\nabla\chi\|_{L^2}+\|\nabla\chi\|_{L^6}\|\nabla^2\chi\|_{L^6}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\ &\quad\lesssim\delta^3(\|\nabla^{k+1}\varrho \|_{L^2}+\|\nabla^{k+2}\nabla\chi\|_{L^2}). \end{align}Combining (3.54)–(3.57) together, we easily obtain
 \begin{align}
&\left\|\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)}\nabla^k\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)}u\cdot\nabla u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\quad\left.\left.+\,\psi(\varrho)\text{div}
\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\right\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&\quad\quad\lesssim(\delta^3+\delta)(\|\nabla^{k+1}\varrho
\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}+\|\nabla^{k+2}u\|_{L^2}+\|\nabla^{k+2}\nabla\chi\|_{L^2}).
\end{align}
\begin{align}
&\left\|\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)}\nabla^k\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)}u\cdot\nabla u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\quad\left.\left.+\,\psi(\varrho)\text{div}
\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2
\mathbb{I}_3\right)\right]\right\|_{L^2}\|\nabla^{k+1}\varrho\|_{L^2}\nonumber\\
&\quad\quad\lesssim(\delta^3+\delta)(\|\nabla^{k+1}\varrho
\|_{L^2}+\|\nabla^{k+1}u\|_{L^2}+\|\nabla^{k+2}u\|_{L^2}+\|\nabla^{k+2}\nabla\chi\|_{L^2}).
\end{align}
Plugging the estimates (3.53) and (3.58) into (3.50), by using Cauchy's inequality and the smallness of ![]() $\delta$, we then complete the proof of lemma 3.3.
$\delta$, we then complete the proof of lemma 3.3.
4. Negative Sobolev estimates
In this section, we derive the evolution of the negative Sobolev norms of the solution.
Lemma 4.1 If ![]() $\sqrt {\mathcal {E}_0^3(t)}\leq \delta$. Then for
$\sqrt {\mathcal {E}_0^3(t)}\leq \delta$. Then for ![]() $s\in [0,\frac 12]$, we have
$s\in [0,\frac 12]$, we have
 \begin{align}
&\frac{{\rm d}}{{\rm
d}t}(\|\Lambda^{{-}s}\varrho\|_{L^2}^2+\|\Lambda^{{-}s}u\|_{L^2}^2+\|\Lambda^{{-}s}\chi\|_{L^2}^2+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}^2)\nonumber\\
&\quad+C(\|\nabla\Lambda^{{-}s}u\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2)\nonumber\\
&\quad\quad\lesssim(\|\varrho\|_{H^2}^2+\|\nabla
u\|_{H^1}^2+\|\nabla\chi\|_{H^3}^2)(\|\Lambda^{{-}s}\varrho\|_{L^2}
+\|\Lambda^{{-}s}u\|_{L^2}\notag\\
&\qquad \quad +\,\|\Lambda^{{-}s}\chi\|_{L^2}
+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}).
\end{align}
\begin{align}
&\frac{{\rm d}}{{\rm
d}t}(\|\Lambda^{{-}s}\varrho\|_{L^2}^2+\|\Lambda^{{-}s}u\|_{L^2}^2+\|\Lambda^{{-}s}\chi\|_{L^2}^2+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}^2)\nonumber\\
&\quad+C(\|\nabla\Lambda^{{-}s}u\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2)\nonumber\\
&\quad\quad\lesssim(\|\varrho\|_{H^2}^2+\|\nabla
u\|_{H^1}^2+\|\nabla\chi\|_{H^3}^2)(\|\Lambda^{{-}s}\varrho\|_{L^2}
+\|\Lambda^{{-}s}u\|_{L^2}\notag\\
&\qquad \quad +\,\|\Lambda^{{-}s}\chi\|_{L^2}
+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}).
\end{align}
Moreover, for ![]() $s\in (\frac 12,\frac 32)$, we have
$s\in (\frac 12,\frac 32)$, we have
 \begin{align}
&\frac{{\rm d}}{{\rm
d}t}(\|\Lambda^{{-}s}\varrho\|_{L^2}^2+\|\Lambda^{{-}s}u\|_{L^2}^2+\|\Lambda^{{-}s}\chi\|_{L^2}^2+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}^2)\nonumber\\
&\quad+C(\|\nabla\Lambda^{{-}s}u\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2)\nonumber\\
&\quad\quad\lesssim\left[\|(\varrho,u,\chi,\nabla\chi)\|_{L^2}^{s-1/2}(\|\varrho\|_{H^2}
+\|\nabla u\|_{H^1} +\|\nabla\chi\|_{H^1}
+\|\nabla^2\chi\|_{H^1} )^{5/2-s}\right.\nonumber\\
&\quad\quad\quad\left.+\,(\|\nabla\varrho\|_{H^1}^2+\|\Delta\chi\|_{L^2}^2)\right]\nonumber\\
&\quad\quad\quad\times(\|\Lambda^{{-}s}\varrho\|_{L^2}
+\|\Lambda^{{-}s}u\|_{L^2} +\|\Lambda^{{-}s}\chi\|_{L^2}
+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}).
\end{align}
\begin{align}
&\frac{{\rm d}}{{\rm
d}t}(\|\Lambda^{{-}s}\varrho\|_{L^2}^2+\|\Lambda^{{-}s}u\|_{L^2}^2+\|\Lambda^{{-}s}\chi\|_{L^2}^2+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}^2)\nonumber\\
&\quad+C(\|\nabla\Lambda^{{-}s}u\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2+\|\nabla\Lambda^{{-}s}\chi\|_{L^2}^2)\nonumber\\
&\quad\quad\lesssim\left[\|(\varrho,u,\chi,\nabla\chi)\|_{L^2}^{s-1/2}(\|\varrho\|_{H^2}
+\|\nabla u\|_{H^1} +\|\nabla\chi\|_{H^1}
+\|\nabla^2\chi\|_{H^1} )^{5/2-s}\right.\nonumber\\
&\quad\quad\quad\left.+\,(\|\nabla\varrho\|_{H^1}^2+\|\Delta\chi\|_{L^2}^2)\right]\nonumber\\
&\quad\quad\quad\times(\|\Lambda^{{-}s}\varrho\|_{L^2}
+\|\Lambda^{{-}s}u\|_{L^2} +\|\Lambda^{{-}s}\chi\|_{L^2}
+\|\Lambda^{{-}s}\nabla\chi\|_{L^2}).
\end{align}Proof. Applying ![]() $\Lambda ^{-s}$ to (1.4)
$\Lambda ^{-s}$ to (1.4)![]() $_1$, (1.4
$_1$, (1.4![]() $_2$ and (1.4)
$_2$ and (1.4)![]() $_3$,
$_3$, ![]() $\Lambda ^{-s}\nabla$ to (1.4)
$\Lambda ^{-s}\nabla$ to (1.4)![]() $_3$, multiplying the resulting identities by
$_3$, multiplying the resulting identities by ![]() $\Lambda ^{-s}\varrho$,
$\Lambda ^{-s}\varrho$, ![]() $\Lambda ^{-s}u$,
$\Lambda ^{-s}u$, ![]() $\Lambda ^{-s}\chi$ and
$\Lambda ^{-s}\chi$ and ![]() $\Lambda ^{-s}\nabla \chi$, respectively, summing up and then integrating by parts, we deduce that
$\Lambda ^{-s}\nabla \chi$, respectively, summing up and then integrating by parts, we deduce that
 \begin{align}
&\frac12\frac{{\rm d}}{{\rm
d}t}\int_{\mathbb{R}^3}(|\Lambda^{{-}s}\varrho|^2+|\Lambda^{{-}s}u|^2+|\Lambda^{{-}s}\chi|^2+|\Lambda^{{-}s}\nabla\chi|^2)\,{\rm
d}x\nonumber\\
&\quad\quad+\int_{\mathbb{R}^3}(|\Lambda^{{-}s}\nabla
u|^2+|\Lambda^{{-}s}\nabla \chi|^2+|\Lambda^{{-}s}\nabla
^2\chi|^2)\,{\rm d}x\nonumber\\
&\quad=\int_{\mathbb{R}^3}\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)}\Lambda^{{-}s}
(-\varrho\text{div}\,u-u\cdot\nabla\varrho)\cdot\Lambda^{{-}s}
\varrho \right.\nonumber\\ &\quad\quad\left.-\,\Lambda^{{-}s}
\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)}u\cdot\nabla u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\quad\quad\left.\left.+\,\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\cdot\Lambda^{{-}s}u
\right.\nonumber\\ &\quad\quad\left.+\,\Lambda^{{-}s}
\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)
\right)\cdot\Lambda^{{-}s} \chi \right.\nonumber\\
&\quad\quad\left.+\,\Lambda^{{-}s}
\nabla\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)\right)\cdot\Lambda^{{-}s}
\nabla\chi\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)}\right]{\rm d}x\nonumber\\
&\quad=\sum_{i=1}^{12}J_i.
\end{align}
\begin{align}
&\frac12\frac{{\rm d}}{{\rm
d}t}\int_{\mathbb{R}^3}(|\Lambda^{{-}s}\varrho|^2+|\Lambda^{{-}s}u|^2+|\Lambda^{{-}s}\chi|^2+|\Lambda^{{-}s}\nabla\chi|^2)\,{\rm
d}x\nonumber\\
&\quad\quad+\int_{\mathbb{R}^3}(|\Lambda^{{-}s}\nabla
u|^2+|\Lambda^{{-}s}\nabla \chi|^2+|\Lambda^{{-}s}\nabla
^2\chi|^2)\,{\rm d}x\nonumber\\
&\quad=\int_{\mathbb{R}^3}\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)}\Lambda^{{-}s}
(-\varrho\text{div}\,u-u\cdot\nabla\varrho)\cdot\Lambda^{{-}s}
\varrho \right.\nonumber\\ &\quad\quad\left.-\,\Lambda^{{-}s}
\left[\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)}u\cdot\nabla u+h(\varrho)(\mu\Delta
u+(\mu+\lambda)\nabla\text{div}\,u)+g(\varrho)\nabla\varrho\right.\right.\nonumber\\
&\quad\quad\left.\left.+\,\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\cdot\Lambda^{{-}s}u
\right.\nonumber\\ &\quad\quad\left.+\,\Lambda^{{-}s}
\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)
\right)\cdot\Lambda^{{-}s} \chi \right.\nonumber\\
&\quad\quad\left.+\,\Lambda^{{-}s}
\nabla\left({-}u\cdot\nabla\chi-\varphi(\varrho)\Delta\chi-\phi(\varrho)(\chi^3-\chi)\right)\cdot\Lambda^{{-}s}
\nabla\chi\vphantom{\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)}\right]{\rm d}x\nonumber\\
&\quad=\sum_{i=1}^{12}J_i.
\end{align}
The main tool to estimate the nonlinear terms in the right-hand side of (4.3) is the estimate in lemma 2.5. This forces us to require that ![]() $s\in (0,\frac 32)$. If
$s\in (0,\frac 32)$. If ![]() $s\in (0,\frac 12]$, we easily obtain
$s\in (0,\frac 12]$, we easily obtain ![]() $\frac 12+\frac s3<1$ and
$\frac 12+\frac s3<1$ and ![]() $\frac 3s\geq 6$. Then, applying lemmas 2.5, 2.2 together with Hölder's and Young's inequalities, it yields that
$\frac 3s\geq 6$. Then, applying lemmas 2.5, 2.2 together with Hölder's and Young's inequalities, it yields that
 \begin{align} J_1&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(\varrho\nabla\cdot u)\Lambda^{{-}s}\varrho\,{\rm d}x\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(\varrho\nabla\cdot u)\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\nabla\cdot u\|_{L^{1/{(1/2+ s/3)}}}\lesssim \|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\|_{L^{3/s}}\|\nabla u\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla u\|_{L^2}\lesssim (\|\nabla \varrho\|_{H^1}^2+\|\nabla u\|_{L^2}^2)\|\Lambda^{{-}s}\varrho\|_{L^2}. \end{align}
\begin{align} J_1&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(\varrho\nabla\cdot u)\Lambda^{{-}s}\varrho\,{\rm d}x\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(\varrho\nabla\cdot u)\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\nabla\cdot u\|_{L^{1/{(1/2+ s/3)}}}\lesssim \|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\|_{L^{3/s}}\|\nabla u\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla u\|_{L^2}\lesssim (\|\nabla \varrho\|_{H^1}^2+\|\nabla u\|_{L^2}^2)\|\Lambda^{{-}s}\varrho\|_{L^2}. \end{align}
Similarly, by using lemmas 2.5 and 2.2 together with Hölder's and Young's inequalities, the term ![]() $J_2$-
$J_2$-![]() $J_{12}$ can be bound by
$J_{12}$ can be bound by
 \begin{align} J_2&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(u\cdot\nabla\varrho)\Lambda^{{-}s}\varrho\,{\rm d}x\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla\varrho )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|u\cdot\nabla\varrho \|_{L^{1/{(1/2+ s/3)}}}\lesssim \|\Lambda^{{-}s}\varrho\|_{L^2}\|u\|_{L^{3/s}}\|\nabla \varrho\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\nabla u\|_{L^2}^{1/2+s}\|\nabla^2u\|_{L^2}^{1/2-s}\|\nabla \varrho\|_{L^2}\nonumber\\ &\lesssim(\|\nabla u\|_{H^1}^2+\|\nabla \varrho\|_{L^2}^2)\|\Lambda^{{-}s}\varrho\|_{L^2}, \end{align}
\begin{align} J_2&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(u\cdot\nabla\varrho)\Lambda^{{-}s}\varrho\,{\rm d}x\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla\varrho )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|u\cdot\nabla\varrho \|_{L^{1/{(1/2+ s/3)}}}\lesssim \|\Lambda^{{-}s}\varrho\|_{L^2}\|u\|_{L^{3/s}}\|\nabla \varrho\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\nabla u\|_{L^2}^{1/2+s}\|\nabla^2u\|_{L^2}^{1/2-s}\|\nabla \varrho\|_{L^2}\nonumber\\ &\lesssim(\|\nabla u\|_{H^1}^2+\|\nabla \varrho\|_{L^2}^2)\|\Lambda^{{-}s}\varrho\|_{L^2}, \end{align} \begin{align} J_3&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(u\cdot\nabla u )\Lambda^{{-}s}u\,{\rm d}x\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla u )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|u\cdot\nabla u \|_{L^{1/{(1/2+s/3)}}}\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|u\|_{L^{3/s}}\|\nabla u\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\nabla u\|_{L^2}^{1/2+s}\|\nabla^2u\|_{L^2}^{1/2-s}\|\nabla u\|_{L^2}\lesssim \|\nabla u\|_{H^1}^2 \|\Lambda^{{-}s}u\|_{L^2}, \end{align}
\begin{align} J_3&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(u\cdot\nabla u )\Lambda^{{-}s}u\,{\rm d}x\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla u )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|u\cdot\nabla u \|_{L^{1/{(1/2+s/3)}}}\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|u\|_{L^{3/s}}\|\nabla u\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\nabla u\|_{L^2}^{1/2+s}\|\nabla^2u\|_{L^2}^{1/2-s}\|\nabla u\|_{L^2}\lesssim \|\nabla u\|_{H^1}^2 \|\Lambda^{{-}s}u\|_{L^2}, \end{align} \begin{align} J_4&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u) )\Lambda^{{-}s}u\,{\rm d}x\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u) )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u)\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|h(\varrho)\|_{L^{3/s}}\|\Delta u\|_{L^2}\notag\\ & \lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\nabla \varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla^2 u\|_{L^2}\nonumber\\ &\lesssim(\|\nabla \varrho\|_{H^1}^2+\|\nabla^2 u\|_{L^2}^2)\|\Lambda^{{-}s}u\|_{L^2}, \end{align}
\begin{align} J_4&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u) )\Lambda^{{-}s}u\,{\rm d}x\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u) )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u)\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|h(\varrho)\|_{L^{3/s}}\|\Delta u\|_{L^2}\notag\\ & \lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\nabla \varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla^2 u\|_{L^2}\nonumber\\ &\lesssim(\|\nabla \varrho\|_{H^1}^2+\|\nabla^2 u\|_{L^2}^2)\|\Lambda^{{-}s}u\|_{L^2}, \end{align} \begin{align} J_5&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(g(\varrho)\nabla\varrho)\Lambda^{{-}s}u\,{\rm d}x\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(g(\varrho)\nabla\varrho )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| g(\varrho)\nabla\varrho \|_{L^{1/{(1/2+s/3)}}}\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|g(\varrho)\|_{L^{3/s}}\|\nabla\varrho\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| \nabla \varrho \|_{L^2}^{1/2+s}\| \nabla^2\varrho \|_{L^2}^{1/2-s}\|\nabla\varrho\|_{L^2}\lesssim \|\nabla \varrho\|_{H^1}^2 \|\Lambda^{{-}s}u\|_{L^2}, \end{align}
\begin{align} J_5&={-}\int_{\mathbb{R}^3}\Lambda^{{-}s}(g(\varrho)\nabla\varrho)\Lambda^{{-}s}u\,{\rm d}x\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(g(\varrho)\nabla\varrho )\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| g(\varrho)\nabla\varrho \|_{L^{1/{(1/2+s/3)}}}\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|g(\varrho)\|_{L^{3/s}}\|\nabla\varrho\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| \nabla \varrho \|_{L^2}^{1/2+s}\| \nabla^2\varrho \|_{L^2}^{1/2-s}\|\nabla\varrho\|_{L^2}\lesssim \|\nabla \varrho\|_{H^1}^2 \|\Lambda^{{-}s}u\|_{L^2}, \end{align} \begin{align} J_6&=\int_{\mathbb{R}^3}\Lambda^{{-}s}\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\cdot\Lambda^{{-}s}u\,{\rm d}x\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}[\phi(\varrho)|\nabla\chi||\nabla^2\chi|]\|_{L^2}\lesssim \|\Lambda^{{-}s}u\|_{L^2}\|\phi(\varrho)|\nabla\chi||\nabla^2\chi|\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\||\nabla\chi||\nabla^2\chi|\|_{L^{1/{(1/2+s/3)}}}\lesssim \|\nabla\chi\|_{L^{3/s}}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}\nonumber\\ &\lesssim\|\nabla^2\chi\|_{L^2}^{1/2-s}\|\nabla^3\chi\|_{L^2}^{1/2+s}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}\notag\\ &\lesssim(\|\nabla^2\chi\|_{L^2}^2+\|\nabla ^3\chi\|_{L^2}^2)\|\Lambda^{{-}s}u\|_{L^2}, \end{align}
\begin{align} J_6&=\int_{\mathbb{R}^3}\Lambda^{{-}s}\left[\phi(\varrho)\text{div}\left(\nabla\chi\otimes\nabla\chi-\frac{|\nabla\chi|^2}2 \mathbb{I}_3\right)\right]\cdot\Lambda^{{-}s}u\,{\rm d}x\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}[\phi(\varrho)|\nabla\chi||\nabla^2\chi|]\|_{L^2}\lesssim \|\Lambda^{{-}s}u\|_{L^2}\|\phi(\varrho)|\nabla\chi||\nabla^2\chi|\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\||\nabla\chi||\nabla^2\chi|\|_{L^{1/{(1/2+s/3)}}}\lesssim \|\nabla\chi\|_{L^{3/s}}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}\nonumber\\ &\lesssim\|\nabla^2\chi\|_{L^2}^{1/2-s}\|\nabla^3\chi\|_{L^2}^{1/2+s}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}\notag\\ &\lesssim(\|\nabla^2\chi\|_{L^2}^2+\|\nabla ^3\chi\|_{L^2}^2)\|\Lambda^{{-}s}u\|_{L^2}, \end{align} \begin{align} J_7&\lesssim\|\Lambda^{{-}s}\chi \|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla\chi)\|_{L^2}\lesssim \|\Lambda^{{-}s}\chi \|_{L^2}\|u\cdot\nabla\chi\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi \|_{L^2}\|u\|_{L^{\frac 3s}}\|\nabla\chi\|_{L^{2}}\lesssim\|\nabla u\|_{L^2}^{1/2-s}\|\nabla^2u\|_{L^2}^{1/2+s}\|\nabla \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla u\|_{L^2}^2+\|\nabla^2u\|_{L^2}^2+\|\nabla \chi\|_{L^2}^2)\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align}
\begin{align} J_7&\lesssim\|\Lambda^{{-}s}\chi \|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla\chi)\|_{L^2}\lesssim \|\Lambda^{{-}s}\chi \|_{L^2}\|u\cdot\nabla\chi\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi \|_{L^2}\|u\|_{L^{\frac 3s}}\|\nabla\chi\|_{L^{2}}\lesssim\|\nabla u\|_{L^2}^{1/2-s}\|\nabla^2u\|_{L^2}^{1/2+s}\|\nabla \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla u\|_{L^2}^2+\|\nabla^2u\|_{L^2}^2+\|\nabla \chi\|_{L^2}^2)\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align} \begin{align} J_8&=\int_{\mathbb{R}^3}\Lambda^{{-}s}(\varphi(\varrho)\Delta\chi)\cdot\Lambda^{{-}s}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\|\Lambda^{{-}s}(\varphi(\varrho)\Delta\chi)\|_{L^2}\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\Delta\chi\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\|_{L^{3/s}}\|\Delta\chi\|_{L^{2}} \lesssim\|\nabla \varrho\|_{L^2}^{1/2-s}\|\nabla^2\varrho\|_{L^2}^{1/2+s}\|\Delta \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla \varrho\|_{L^2}^2+\|\nabla^2\varrho \|_{L^2}^2+\|\nabla^2 \chi\|_{L^2}^2)\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align}
\begin{align} J_8&=\int_{\mathbb{R}^3}\Lambda^{{-}s}(\varphi(\varrho)\Delta\chi)\cdot\Lambda^{{-}s}\chi\,{\rm d}x\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\|\Lambda^{{-}s}(\varphi(\varrho)\Delta\chi)\|_{L^2}\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\Delta\chi\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\|_{L^{3/s}}\|\Delta\chi\|_{L^{2}} \lesssim\|\nabla \varrho\|_{L^2}^{1/2-s}\|\nabla^2\varrho\|_{L^2}^{1/2+s}\|\Delta \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla \varrho\|_{L^2}^2+\|\nabla^2\varrho \|_{L^2}^2+\|\nabla^2 \chi\|_{L^2}^2)\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align} \begin{align} J_9&\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}(\|\Lambda^{{-}s}(\phi(\varrho) \chi^3 \|_{L^2}+\|\Lambda^{{-}s}(\zeta(\varrho)\zeta(\varrho) \chi\|_{L^2})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\left(\|\phi(\varrho) \chi^3\|_{L^{1/{(1/2+s/3)}}}+\|\zeta(\varrho)\zeta(\varrho) \chi \|_{L^{1/{(1/2+s/3)}}}\right)\nonumber\\ &\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\left(\|\phi(\varrho)\|_{L^{\infty}}\|\chi \|_{L^{\infty}} \|\chi \|_{L^{2}} \| \chi \|_{L^{3/s}}+\|\zeta(\varrho)\|_{L^{3/s}}\|\zeta(\varrho)\|_{L^\infty}\| \chi \|_{L^2}\right)\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\left(\|\nabla\chi \|_{L^{2}}^{1/2} \|\Delta\chi \|_{L^{2}}^{1/2}\|\chi \|_{L^{2}}\| \nabla\chi\|_{L^2}^{1/2-s}\|\nabla^2\chi\|_{L^2}^{1/2+s}\right.\nonumber\\ &\left.\quad +\,\| \nabla\varrho\|_{L^2}^{1/2-s}\|\nabla^2\varrho\|_{L^2}^{1/2+s}\|\nabla\varrho \|_{L^{2}}^{1/2} \|\Delta\varrho \|_{L^{2}}^{1/2}\|\chi \|_{L^{2}}\right)\nonumber\\ &\lesssim(\delta +1)(\| \nabla \varrho\|_{L^2}^2+\| \Delta \varrho\|_{L^2}^2+\|\nabla^2\chi \|_{L^2}^2 +\| \nabla \chi\|_{L^2}^2)\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align}
\begin{align} J_9&\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}(\|\Lambda^{{-}s}(\phi(\varrho) \chi^3 \|_{L^2}+\|\Lambda^{{-}s}(\zeta(\varrho)\zeta(\varrho) \chi\|_{L^2})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\left(\|\phi(\varrho) \chi^3\|_{L^{1/{(1/2+s/3)}}}+\|\zeta(\varrho)\zeta(\varrho) \chi \|_{L^{1/{(1/2+s/3)}}}\right)\nonumber\\ &\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\left(\|\phi(\varrho)\|_{L^{\infty}}\|\chi \|_{L^{\infty}} \|\chi \|_{L^{2}} \| \chi \|_{L^{3/s}}+\|\zeta(\varrho)\|_{L^{3/s}}\|\zeta(\varrho)\|_{L^\infty}\| \chi \|_{L^2}\right)\nonumber\\ &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\left(\|\nabla\chi \|_{L^{2}}^{1/2} \|\Delta\chi \|_{L^{2}}^{1/2}\|\chi \|_{L^{2}}\| \nabla\chi\|_{L^2}^{1/2-s}\|\nabla^2\chi\|_{L^2}^{1/2+s}\right.\nonumber\\ &\left.\quad +\,\| \nabla\varrho\|_{L^2}^{1/2-s}\|\nabla^2\varrho\|_{L^2}^{1/2+s}\|\nabla\varrho \|_{L^{2}}^{1/2} \|\Delta\varrho \|_{L^{2}}^{1/2}\|\chi \|_{L^{2}}\right)\nonumber\\ &\lesssim(\delta +1)(\| \nabla \varrho\|_{L^2}^2+\| \Delta \varrho\|_{L^2}^2+\|\nabla^2\chi \|_{L^2}^2 +\| \nabla \chi\|_{L^2}^2)\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align} \begin{align} J_{10}&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\|\Lambda^{{-}s}(\nabla u\cdot\nabla\chi+u\cdot\nabla^2\chi)\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla u\cdot\nabla\chi\|_{L^{1/{(1/2+s/3)}}}+\|u\cdot\nabla^2\chi\|_{L^{1/{(1/2+s/3)}}})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla\chi\|_{L^{3/s}}\|\nabla u\|_{L^2}+\|\nabla^2\chi\|_{L^2}\|u\|_{L^{3/s}})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla^2\chi\|_{L^{2}}^{1/2+s}\|\nabla^3\chi\|_{L^2}^{1/2-s}\|\nabla u\|_{L^2}\notag\\ &\quad +\,\|\nabla^2\chi\|_{L^2}\|\nabla u\|_{L^{2}}^{1/2+s}\|\nabla^2u\|_{L^2}^{1/2-s})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla^2\chi\|_{L^2}^2+\|\nabla^3\chi\|_{L^2}^2+\|\nabla u\|_{L^2}^2+\|\nabla^2u\|_{L^2}^2), \end{align}
\begin{align} J_{10}&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\|\Lambda^{{-}s}(\nabla u\cdot\nabla\chi+u\cdot\nabla^2\chi)\|_{L^2}\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla u\cdot\nabla\chi\|_{L^{1/{(1/2+s/3)}}}+\|u\cdot\nabla^2\chi\|_{L^{1/{(1/2+s/3)}}})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla\chi\|_{L^{3/s}}\|\nabla u\|_{L^2}+\|\nabla^2\chi\|_{L^2}\|u\|_{L^{3/s}})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla^2\chi\|_{L^{2}}^{1/2+s}\|\nabla^3\chi\|_{L^2}^{1/2-s}\|\nabla u\|_{L^2}\notag\\ &\quad +\,\|\nabla^2\chi\|_{L^2}\|\nabla u\|_{L^{2}}^{1/2+s}\|\nabla^2u\|_{L^2}^{1/2-s})\nonumber\\ &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla^2\chi\|_{L^2}^2+\|\nabla^3\chi\|_{L^2}^2+\|\nabla u\|_{L^2}^2+\|\nabla^2u\|_{L^2}^2), \end{align} \begin{align} J_{11}&\lesssim\|\Lambda^{{-}s}(\varphi(\varrho)\nabla^3\chi+\varphi'(\varrho)\nabla\varrho\nabla^2\chi)\|_{L^2}\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\varphi(\varrho)\nabla^3\chi\|_{L^{1/{(1/2+s/3)}}}+\|\varphi'(\varrho)\nabla\varrho\nabla^2\chi\|_{L^{1/{(1/2+s/3)}}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla^3\chi\|_{L^2}\|\varrho\|_{L^{3/s}}+\|\nabla\varrho\|_{L^2}\|\nabla^2\chi\|_{L^{3/s}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla^3\chi\|_{L^2}\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\notag\\ &\quad +\,\|\nabla\varrho\|_{L^2}\|\nabla^3\chi\|^{1/2+s}_{L^{2}}\|\nabla^4\chi\|^{1/2-s}_{L^{2}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla^3\chi\|_{L^2}^2+\|\nabla\varrho\|_{L^2}^2+\|\nabla^2\varrho\|_{L^2}^2+\|\nabla^4\chi\|_{L^2}^2)\|\Lambda^{{-}s}\nabla\chi\|_{L^2}, \end{align}
\begin{align} J_{11}&\lesssim\|\Lambda^{{-}s}(\varphi(\varrho)\nabla^3\chi+\varphi'(\varrho)\nabla\varrho\nabla^2\chi)\|_{L^2}\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\varphi(\varrho)\nabla^3\chi\|_{L^{1/{(1/2+s/3)}}}+\|\varphi'(\varrho)\nabla\varrho\nabla^2\chi\|_{L^{1/{(1/2+s/3)}}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla^3\chi\|_{L^2}\|\varrho\|_{L^{3/s}}+\|\nabla\varrho\|_{L^2}\|\nabla^2\chi\|_{L^{3/s}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla^3\chi\|_{L^2}\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\notag\\ &\quad +\,\|\nabla\varrho\|_{L^2}\|\nabla^3\chi\|^{1/2+s}_{L^{2}}\|\nabla^4\chi\|^{1/2-s}_{L^{2}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\ &\lesssim(\|\nabla^3\chi\|_{L^2}^2+\|\nabla\varrho\|_{L^2}^2+\|\nabla^2\varrho\|_{L^2}^2+\|\nabla^4\chi\|_{L^2}^2)\|\Lambda^{{-}s}\nabla\chi\|_{L^2}, \end{align}and
 \begin{align}
J_{12}&=\int_{\mathbb{R}^3}\Lambda^{{-}s}[\phi'(\varrho)\nabla\varrho(\chi^3-\chi)+\phi(\varrho)(3\chi^2-1)\nabla\chi]\cdot\Lambda^{{-}s}\nabla\chi\,{\rm d}x\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left(\|\phi'(\varrho)\nabla\varrho
\chi^3 \|_{L^{1/{(1/2+3/s)}}}+\|\phi'(\varrho)\nabla\varrho \chi \|_{L^{1/{(1/2+3/s)}}}\right.\nonumber\\
&\quad\left.+\,\|\phi(\varrho) \chi^2
\nabla\chi\|_{L^{1/{(1/2+s/3)}}}+\|\zeta(\varrho)\zeta(\varrho)
\nabla\chi\|_{L^{1/{(1/2+s/3)}}}\right)\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left( \|\chi
\|_{L^{\infty}}^2\|\nabla\varrho\|_{L^2}\|\nabla\chi\|_{L^2}^{1/2+s}\|\nabla^2\chi\|_{L^2}^{1/2-s}\right.\notag\\
&\quad +\,\|\nabla\varrho\|_{L^2}\|\nabla\chi\|_{L^2}^{1/2+s}\|\nabla^2\chi\|_{L^2}^{1/2-s}\nonumber\\
&\left.\quad +\,\| \chi
\|_{L^{\infty}}^2\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla\chi\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla\chi\|_{L^2}\right)\nonumber\\
&\lesssim(1+\delta^2)\|\Lambda^{{-}s}\nabla\chi\|_{L^2}
(|\nabla\varrho\|_{L^2}^2+\|\nabla\chi\|_{L^2}^2+\|\nabla^2\chi\|_{L^2}^2+\|\nabla^2\varrho\|_{L^2}^2).
\end{align}
\begin{align}
J_{12}&=\int_{\mathbb{R}^3}\Lambda^{{-}s}[\phi'(\varrho)\nabla\varrho(\chi^3-\chi)+\phi(\varrho)(3\chi^2-1)\nabla\chi]\cdot\Lambda^{{-}s}\nabla\chi\,{\rm d}x\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left(\|\phi'(\varrho)\nabla\varrho
\chi^3 \|_{L^{1/{(1/2+3/s)}}}+\|\phi'(\varrho)\nabla\varrho \chi \|_{L^{1/{(1/2+3/s)}}}\right.\nonumber\\
&\quad\left.+\,\|\phi(\varrho) \chi^2
\nabla\chi\|_{L^{1/{(1/2+s/3)}}}+\|\zeta(\varrho)\zeta(\varrho)
\nabla\chi\|_{L^{1/{(1/2+s/3)}}}\right)\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left( \|\chi
\|_{L^{\infty}}^2\|\nabla\varrho\|_{L^2}\|\nabla\chi\|_{L^2}^{1/2+s}\|\nabla^2\chi\|_{L^2}^{1/2-s}\right.\notag\\
&\quad +\,\|\nabla\varrho\|_{L^2}\|\nabla\chi\|_{L^2}^{1/2+s}\|\nabla^2\chi\|_{L^2}^{1/2-s}\nonumber\\
&\left.\quad +\,\| \chi
\|_{L^{\infty}}^2\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla\chi\|_{L^2}+\|\nabla\varrho\|_{L^2}^{1/2+s}\|\nabla^2\varrho\|_{L^2}^{1/2-s}\|\nabla\chi\|_{L^2}\right)\nonumber\\
&\lesssim(1+\delta^2)\|\Lambda^{{-}s}\nabla\chi\|_{L^2}
(|\nabla\varrho\|_{L^2}^2+\|\nabla\chi\|_{L^2}^2+\|\nabla^2\chi\|_{L^2}^2+\|\nabla^2\varrho\|_{L^2}^2).
\end{align}Plugging the estimates (4.4)–(4.15) into (4.3), we obtain (4.1).
Next, if ![]() $s\in (\frac 12,\frac 32)$, we can estimate
$s\in (\frac 12,\frac 32)$, we can estimate ![]() $J_1$–
$J_1$–![]() $J_{12}$ in a different way. Since
$J_{12}$ in a different way. Since ![]() $s\in (\frac 12,\frac 32)$, itis easy to see that
$s\in (\frac 12,\frac 32)$, itis easy to see that ![]() $\frac 12+\frac s3<1$ and
$\frac 12+\frac s3<1$ and ![]() $2<\frac 3s<6$. Then, lemmas 2.5 and 2.2 implies that
$2<\frac 3s<6$. Then, lemmas 2.5 and 2.2 implies that
 \begin{align} J_1&\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(\varrho\nabla\cdot u)\|_{L^2}\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\nabla\cdot u\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim \|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\|_{L^{\frac 3s}}\|\nabla u\|_{L^2}\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\| \varrho\|_{L^2}^{s-1/2 }\|\nabla \varrho\|_{L^2}^{3/2-s}\|\nabla u\|_{L^2}. \end{align}
\begin{align} J_1&\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(\varrho\nabla\cdot u)\|_{L^2}\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\nabla\cdot u\|_{L^{1/{(1/2+s/3)}}}\nonumber\\ &\lesssim \|\Lambda^{{-}s}\varrho\|_{L^2}\|\varrho\|_{L^{\frac 3s}}\|\nabla u\|_{L^2}\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\| \varrho\|_{L^2}^{s-1/2 }\|\nabla \varrho\|_{L^2}^{3/2-s}\|\nabla u\|_{L^2}. \end{align}
Similarly, by using lemmas 2.5 and 2.2, the term ![]() $J_2$–
$J_2$–![]() $J_{12}$ can be bound by
$J_{12}$ can be bound by
 \begin{align} J_2&\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla\varrho )\|_{L^2}\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|u\|_{L^{3/s}}\|\nabla \varrho\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\| u\|_{L^2}^{s-1/2}\|\nabla u\|_{L^2}^{3/2-s}\|\nabla \varrho\|_{L^2}, \end{align}
\begin{align} J_2&\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla\varrho )\|_{L^2}\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\|u\|_{L^{3/s}}\|\nabla \varrho\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\varrho\|_{L^2}\| u\|_{L^2}^{s-1/2}\|\nabla u\|_{L^2}^{3/2-s}\|\nabla \varrho\|_{L^2}, \end{align} \begin{align} J_3 &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla u )\|_{L^2} \lesssim \|\Lambda^{{-}s} u\|_{L^2}\|u\|_{L^{3/s}}\|\nabla u\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| u\|_{L^2}^{s-1/2}\|\nabla u\|_{L^2}^{3/2-s}\|\nabla u\|_{L^2}, \end{align}
\begin{align} J_3 &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(u\cdot\nabla u )\|_{L^2} \lesssim \|\Lambda^{{-}s} u\|_{L^2}\|u\|_{L^{3/s}}\|\nabla u\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| u\|_{L^2}^{s-1/2}\|\nabla u\|_{L^2}^{3/2-s}\|\nabla u\|_{L^2}, \end{align} \begin{align} J_4&\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u) )\|_{L^2}\nonumber\\[2pt] &\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|h(\varrho)\|_{L^{3/s}}\|\Delta u\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| \varrho\|_{L^2}^{s-1/2}\|\nabla \varrho\|_{L^2}^{3/2-s}\|\nabla^2 u\|_{L^2}, \end{align}
\begin{align} J_4&\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(h(\varrho)(\nu\Delta u+(\nu+\eta)\nabla\text{div}\,u) )\|_{L^2}\nonumber\\[2pt] &\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|h(\varrho)\|_{L^{3/s}}\|\Delta u\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\| \varrho\|_{L^2}^{s-1/2}\|\nabla \varrho\|_{L^2}^{3/2-s}\|\nabla^2 u\|_{L^2}, \end{align} \begin{align} J_5&\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(g(\varrho)\nabla\varrho )\|_{L^2}\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|g(\varrho)\|_{L^{3/s}}\|\nabla\varrho\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\varrho \|_{L^2}^{s-1/2 }\| \nabla \varrho \|_{L^2}^{3/2-s}\|\nabla\varrho\|_{L^2}, \end{align}
\begin{align} J_5&\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\Lambda^{{-}s}(g(\varrho)\nabla\varrho )\|_{L^2}\lesssim \|\Lambda^{{-}s} u\|_{L^2}\|g(\varrho)\|_{L^{3/s}}\|\nabla\varrho\|_{L^2}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}u\|_{L^2}\|\varrho \|_{L^2}^{s-1/2 }\| \nabla \varrho \|_{L^2}^{3/2-s}\|\nabla\varrho\|_{L^2}, \end{align} \begin{align} J_6&\lesssim\|\Lambda^{{-}s}u\|_{L^2}\||\nabla\chi||\nabla^2\chi|\|_{L^{1/{(1/2+s/3)}}}\lesssim \|\nabla\chi\|_{L^{3/s}}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}\nonumber\\[2pt] &\lesssim\|\nabla \chi\|_{L^2}^{s-1/2}\|\nabla^2\chi\|_{L^2}^{3/2-s}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}, \end{align}
\begin{align} J_6&\lesssim\|\Lambda^{{-}s}u\|_{L^2}\||\nabla\chi||\nabla^2\chi|\|_{L^{1/{(1/2+s/3)}}}\lesssim \|\nabla\chi\|_{L^{3/s}}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}\nonumber\\[2pt] &\lesssim\|\nabla \chi\|_{L^2}^{s-1/2}\|\nabla^2\chi\|_{L^2}^{3/2-s}\|\nabla^2\chi\|_{L^2}\|\Lambda^{{-}s}u\|_{L^2}, \end{align} \begin{align} J_7&\lesssim \|\Lambda^{{-}s}\chi \|_{L^2}\|u\cdot\nabla\chi\|_{L^{1/{(1/2+s/3)}}}\lesssim \|\Lambda^{{-}s}\chi \|_{L^2}\|u\|_{L^{3/s}}\|\nabla\chi\|_{L^{2}}\nonumber\\[2pt] &\lesssim\|u\|_{L^2}^{s-1/2 }\|\nabla u\|_{L^2}^{3/2-s}\|\nabla \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align}
\begin{align} J_7&\lesssim \|\Lambda^{{-}s}\chi \|_{L^2}\|u\cdot\nabla\chi\|_{L^{1/{(1/2+s/3)}}}\lesssim \|\Lambda^{{-}s}\chi \|_{L^2}\|u\|_{L^{3/s}}\|\nabla\chi\|_{L^{2}}\nonumber\\[2pt] &\lesssim\|u\|_{L^2}^{s-1/2 }\|\nabla u\|_{L^2}^{3/2-s}\|\nabla \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align} \begin{align} J_8&\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\Delta\chi\|_{L^{1/{(1/2+s/3)}}}\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\|_{L^{3/s}}\|\Delta\chi\|_{L^{2}}\nonumber\\[2pt] &\lesssim\|\varrho\|_{L^2}^{s-1/2 }\|\nabla \varrho\|_{L^2}^{3/2-s}\|\Delta \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align}
\begin{align} J_8&\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\Delta\chi\|_{L^{1/{(1/2+s/3)}}}\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\|\varphi(\varrho)\|_{L^{3/s}}\|\Delta\chi\|_{L^{2}}\nonumber\\[2pt] &\lesssim\|\varrho\|_{L^2}^{s-1/2 }\|\nabla \varrho\|_{L^2}^{3/2-s}\|\Delta \chi\|_{L^2}\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align} \begin{align} J_9&\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\phi(\varrho)(\chi^3-\chi) \|_{L^{1/{(1/2+s/3)}}}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\|\phi(\varrho)\|_{L^{2}}(\|\chi \|_{L^{\infty}}^2+1)\|\chi \|_{L^{3/s}}\nonumber\\[2pt] &\lesssim\| \varrho\|_{L^2}(\|\chi \|_{L^{\infty}}^2+1) \| \chi\|_{L^2}^{s-1/2 }\|\nabla \chi\|_{L^2}^{3/2-s}\|\Lambda^{{-}s}\chi\|_{L^2}\nonumber\\[2pt] &\lesssim(\delta^2+1)\| \varrho\|_{L^2}\|\chi\|_{L^2}^{s-1/2 }\|\nabla \chi\|_{L^2}^{3/2-s}\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align}
\begin{align} J_9&\lesssim \|\Lambda^{{-}s}\chi\|_{L^2}\|\phi(\varrho)(\chi^3-\chi) \|_{L^{1/{(1/2+s/3)}}}\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\chi\|_{L^2}\|\phi(\varrho)\|_{L^{2}}(\|\chi \|_{L^{\infty}}^2+1)\|\chi \|_{L^{3/s}}\nonumber\\[2pt] &\lesssim\| \varrho\|_{L^2}(\|\chi \|_{L^{\infty}}^2+1) \| \chi\|_{L^2}^{s-1/2 }\|\nabla \chi\|_{L^2}^{3/2-s}\|\Lambda^{{-}s}\chi\|_{L^2}\nonumber\\[2pt] &\lesssim(\delta^2+1)\| \varrho\|_{L^2}\|\chi\|_{L^2}^{s-1/2 }\|\nabla \chi\|_{L^2}^{3/2-s}\|\Lambda^{{-}s}\chi\|_{L^2}, \end{align} \begin{align} J_{10}&\lesssim \|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla u\cdot\nabla\chi\|_{L^{1/{(1/2+ s/3)}}}+\|u\cdot\nabla^2\chi\|_{L^{1/{(1/2+ s/3)}}})\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla\chi\|_{L^{3/s}}\|\nabla u\|_{L^2}+\|\nabla^2\chi\|_{L^2}\|u\|_{L^{3/s}})\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla \chi\|_{L^{2}}^{s-1/2}\|\nabla^2\chi\|_{L^2}^{3/2-s}\|\nabla u\|_{L^2}\notag\\[2pt] &\quad +\|\nabla^2\chi\|_{L^2}\| u\|_{L^{2}}^{s-1/2 }\|\nabla u\|_{L^2}^{3/2-s}), \end{align}
\begin{align} J_{10}&\lesssim \|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla u\cdot\nabla\chi\|_{L^{1/{(1/2+ s/3)}}}+\|u\cdot\nabla^2\chi\|_{L^{1/{(1/2+ s/3)}}})\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla\chi\|_{L^{3/s}}\|\nabla u\|_{L^2}+\|\nabla^2\chi\|_{L^2}\|u\|_{L^{3/s}})\nonumber\\[2pt] &\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}(\|\nabla \chi\|_{L^{2}}^{s-1/2}\|\nabla^2\chi\|_{L^2}^{3/2-s}\|\nabla u\|_{L^2}\notag\\[2pt] &\quad +\|\nabla^2\chi\|_{L^2}\| u\|_{L^{2}}^{s-1/2 }\|\nabla u\|_{L^2}^{3/2-s}), \end{align} \begin{align} J_{11}&\lesssim(\|\varphi(\varrho)\nabla^3\chi\|_{L^{1/{(1/2+ s/3)}}}+\| \nabla\varrho\nabla^2\chi\|_{L^{1/{(1/2+ s/3)}}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\[2pt] &\lesssim(\|\nabla^3\chi\|_{L^2}\|\varrho\|_{L^{ 3/s}}+\|\nabla\varrho\|_{L^{3/s}}\|\nabla^2\chi\|_{L^{2}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\[2pt] &\lesssim(\|\nabla^3\chi\|_{L^2}\| \varrho\|_{L^2}^{s-1/2 }\|\nabla \varrho\|_{L^2}^{3/2-s}\notag\\[2pt] &\quad +\|\nabla^2\chi\|_{L^{2}}\|\nabla\varrho\|_{L^2}^{s-1/2} \|\nabla^2\varrho\|^{3/2-s}_{L^{2}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}, \end{align}
\begin{align} J_{11}&\lesssim(\|\varphi(\varrho)\nabla^3\chi\|_{L^{1/{(1/2+ s/3)}}}+\| \nabla\varrho\nabla^2\chi\|_{L^{1/{(1/2+ s/3)}}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\[2pt] &\lesssim(\|\nabla^3\chi\|_{L^2}\|\varrho\|_{L^{ 3/s}}+\|\nabla\varrho\|_{L^{3/s}}\|\nabla^2\chi\|_{L^{2}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\nonumber\\[2pt] &\lesssim(\|\nabla^3\chi\|_{L^2}\| \varrho\|_{L^2}^{s-1/2 }\|\nabla \varrho\|_{L^2}^{3/2-s}\notag\\[2pt] &\quad +\|\nabla^2\chi\|_{L^{2}}\|\nabla\varrho\|_{L^2}^{s-1/2} \|\nabla^2\varrho\|^{3/2-s}_{L^{2}})\|\Lambda^{{-}s}\nabla\chi\|_{L^2}, \end{align}and
 \begin{align}
J_{12}&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left(\|\phi'(\varrho)\nabla\varrho
(\chi^3-\chi)\|_{L^{1/{(1/2+
3/s)}}}+\|\phi(\varrho)(3\chi^2-1)\nabla\chi\|_{L^{1/{(1/2+
s/3)}}}\right)\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left(\|\phi'(\varrho)\|_{L^{\infty}}(1+\|\chi
\|_{L^{\infty}}^2)\|\nabla\varrho\|_{L^2}\|\chi\|_{L^{3/s}}\right.\nonumber\\
&\quad\left.+\,(1+\|\chi
\|_{L^{\infty}}^2)\|\varrho\|_{L^{3/s}}\|\nabla\chi\|_{L^2}\right)\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left( (1+\|\chi
\|_{L^{\infty}}^2)\|\nabla\varrho\|_{L^2}\|
\chi\|_{L^2}^{s-1/2}\|\nabla\chi\|_{L^2}^{3/2-s}\right.\nonumber\\
&\quad\left.+\,(1+\|\chi \|_{L^{\infty}}^2)\|
\varrho\|_{L^2}^{s-1/2}\|\nabla
\varrho\|_{L^2}^{3/2-s}\|\nabla\chi\|_{L^2}\right)\nonumber\\
&\lesssim(1+\delta^2)\|\Lambda^{{-}s}\nabla\chi\|_{L^2}
\left( \|\nabla\varrho\|_{L^2}\|
\chi\|_{L^2}^{s-1/2}\|\nabla\chi\|_{L^2}^{3/2-s}\right.\notag\\
&\quad +\left. \| \varrho\|_{L^2}^{s-1/2}\|\nabla \varrho\|_{L^2}^{3/2-s}\|\nabla\chi\|_{L^2}\right). \end{align}
\begin{align}
J_{12}&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left(\|\phi'(\varrho)\nabla\varrho
(\chi^3-\chi)\|_{L^{1/{(1/2+
3/s)}}}+\|\phi(\varrho)(3\chi^2-1)\nabla\chi\|_{L^{1/{(1/2+
s/3)}}}\right)\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left(\|\phi'(\varrho)\|_{L^{\infty}}(1+\|\chi
\|_{L^{\infty}}^2)\|\nabla\varrho\|_{L^2}\|\chi\|_{L^{3/s}}\right.\nonumber\\
&\quad\left.+\,(1+\|\chi
\|_{L^{\infty}}^2)\|\varrho\|_{L^{3/s}}\|\nabla\chi\|_{L^2}\right)\nonumber\\
&\lesssim\|\Lambda^{{-}s}\nabla\chi\|_{L^2}\left( (1+\|\chi
\|_{L^{\infty}}^2)\|\nabla\varrho\|_{L^2}\|
\chi\|_{L^2}^{s-1/2}\|\nabla\chi\|_{L^2}^{3/2-s}\right.\nonumber\\
&\quad\left.+\,(1+\|\chi \|_{L^{\infty}}^2)\|
\varrho\|_{L^2}^{s-1/2}\|\nabla
\varrho\|_{L^2}^{3/2-s}\|\nabla\chi\|_{L^2}\right)\nonumber\\
&\lesssim(1+\delta^2)\|\Lambda^{{-}s}\nabla\chi\|_{L^2}
\left( \|\nabla\varrho\|_{L^2}\|
\chi\|_{L^2}^{s-1/2}\|\nabla\chi\|_{L^2}^{3/2-s}\right.\notag\\
&\quad +\left. \| \varrho\|_{L^2}^{s-1/2}\|\nabla \varrho\|_{L^2}^{3/2-s}\|\nabla\chi\|_{L^2}\right). \end{align}Plugging the estimates (4.16)–(4.27) into (4.3), we obtain (4.2). Hence, the proof is complete.
5. Proof of theorem 1.1
We first close the energy estimates at each ![]() $l$-th level in our weaker sense. Suppose that
$l$-th level in our weaker sense. Suppose that ![]() $N\geq 3$ and
$N\geq 3$ and ![]() $0\leq l\leq m-1$ with
$0\leq l\leq m-1$ with ![]() $1\leq m\leq N$. Summing up the estimates (3.4) from
$1\leq m\leq N$. Summing up the estimates (3.4) from ![]() $k=l$ to
$k=l$ to ![]() $m-1$, since
$m-1$, since ![]() $\sqrt {\mathcal {E}_0^3(t)}\leq \delta$ is sufficiently small, we arrive at
$\sqrt {\mathcal {E}_0^3(t)}\leq \delta$ is sufficiently small, we arrive at
 \begin{align}
&\frac{{\rm d}}{{\rm d}t}\sum_{l\leq k\leq m-1}
(\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{
L^2}^2)\nonumber\\ &\quad+\,C \sum_{l+1\leq k\leq
m}(\|\nabla^{k }u\|_{L^2}^2+\|\nabla^{k
}\chi\|_{L^2}^2+\|\nabla^{k+1} \chi\|_{L^2}^2)\nonumber\\
&\quad\quad\lesssim (\delta^3+\delta) \sum_{l+1\leq k\leq
m}\left( \|\nabla^{k }\varrho\|_{L^2}^2+\|\nabla^{k
}u\|_{L^2}^2+\|\nabla^{k }\chi\|_{L^2}^2+\|\nabla^{k+1}
\chi\|_{L^2}^2\right).
\end{align}
\begin{align}
&\frac{{\rm d}}{{\rm d}t}\sum_{l\leq k\leq m-1}
(\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{
L^2}^2)\nonumber\\ &\quad+\,C \sum_{l+1\leq k\leq
m}(\|\nabla^{k }u\|_{L^2}^2+\|\nabla^{k
}\chi\|_{L^2}^2+\|\nabla^{k+1} \chi\|_{L^2}^2)\nonumber\\
&\quad\quad\lesssim (\delta^3+\delta) \sum_{l+1\leq k\leq
m}\left( \|\nabla^{k }\varrho\|_{L^2}^2+\|\nabla^{k
}u\|_{L^2}^2+\|\nabla^{k }\chi\|_{L^2}^2+\|\nabla^{k+1}
\chi\|_{L^2}^2\right).
\end{align}
Moreover, let ![]() $k=m-1$ in the estimates (3.32). Hence
$k=m-1$ in the estimates (3.32). Hence
 \begin{align} &\frac{{\rm d}}{{\rm d}t}(\|\nabla^m\varrho\|_{L^2}^2+\|\nabla^mu\|_{L^2}^2+\|\nabla^m\chi\|_{L^2}^2+\|\nabla^{m+1}\chi\|_{L^2}^2)\nonumber\\ &\quad+C(\|\nabla^{m+1}u\|_{L^2}^2+\|\nabla^{m+1}\chi\|_{L^2}^2+\|\nabla^{m+2}\chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim (\delta^3+\delta)(\|\nabla^m\varrho\|_{L^2}^2+\|\nabla^{m+1}u\|_{L^2}^2+\|\nabla^{m+1}\chi\|_{L^2}^2+\|\nabla^{m+2}\chi\|_{L^2}^2). \end{align}
\begin{align} &\frac{{\rm d}}{{\rm d}t}(\|\nabla^m\varrho\|_{L^2}^2+\|\nabla^mu\|_{L^2}^2+\|\nabla^m\chi\|_{L^2}^2+\|\nabla^{m+1}\chi\|_{L^2}^2)\nonumber\\ &\quad+C(\|\nabla^{m+1}u\|_{L^2}^2+\|\nabla^{m+1}\chi\|_{L^2}^2+\|\nabla^{m+2}\chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim (\delta^3+\delta)(\|\nabla^m\varrho\|_{L^2}^2+\|\nabla^{m+1}u\|_{L^2}^2+\|\nabla^{m+1}\chi\|_{L^2}^2+\|\nabla^{m+2}\chi\|_{L^2}^2). \end{align}Combining (5.1) and (5.2) together gives
 \begin{align} &\frac{{\rm d}}{{\rm d}t}\sum_{l\leq k\leq m} (\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{ L^2}^2)\nonumber\\ &\quad+C_1 \sum_{l+1\leq k\leq m+1}(\|\nabla^{k }u\|_{L^2}^2+\|\nabla^{k }\chi\|_{L^2}^2+\|\nabla^{k+1} \chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim C_2(\delta^3+\delta) \sum_{l+1\leq k\leq m} \|\nabla^{k }\varrho\|_{L^2}^2. \end{align}
\begin{align} &\frac{{\rm d}}{{\rm d}t}\sum_{l\leq k\leq m} (\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{ L^2}^2)\nonumber\\ &\quad+C_1 \sum_{l+1\leq k\leq m+1}(\|\nabla^{k }u\|_{L^2}^2+\|\nabla^{k }\chi\|_{L^2}^2+\|\nabla^{k+1} \chi\|_{L^2}^2)\nonumber\\ &\quad\quad\lesssim C_2(\delta^3+\delta) \sum_{l+1\leq k\leq m} \|\nabla^{k }\varrho\|_{L^2}^2. \end{align}
Summing up the estimates (3.49) from ![]() $k=l$ to
$k=l$ to ![]() $m-1$, we obtain
$m-1$, we obtain
 \begin{align} &\frac{{\rm d}}{{\rm d}t}\sum_{l\leq k\leq m-1}\int_{\mathbb{R}^3}\nabla^ku\cdot\nabla^{k+1}\varrho\,{\rm d}x+C_3\sum_{l+1\leq k\leq m}\|\nabla^k\varrho\|_{L^2}^2\nonumber\\ &\quad\lesssim C_4\left(\sum_{l+1\leq k\leq m+1}\|\nabla^{k}u\|_{L^2}^2+\sum_{l+2\leq k\leq m+1}\|\nabla^{k} \nabla\chi\|_{L^2}^2\right). \end{align}
\begin{align} &\frac{{\rm d}}{{\rm d}t}\sum_{l\leq k\leq m-1}\int_{\mathbb{R}^3}\nabla^ku\cdot\nabla^{k+1}\varrho\,{\rm d}x+C_3\sum_{l+1\leq k\leq m}\|\nabla^k\varrho\|_{L^2}^2\nonumber\\ &\quad\lesssim C_4\left(\sum_{l+1\leq k\leq m+1}\|\nabla^{k}u\|_{L^2}^2+\sum_{l+2\leq k\leq m+1}\|\nabla^{k} \nabla\chi\|_{L^2}^2\right). \end{align}
Multiplying (5.4) by ![]() $C_5\equiv 2C_2\delta (\delta ^2+1)/C_3$, adding the resulting inequality with (5.1), since
$C_5\equiv 2C_2\delta (\delta ^2+1)/C_3$, adding the resulting inequality with (5.1), since ![]() $\delta >0$ is sufficiently small, we deduce that there exists a positive constant
$\delta >0$ is sufficiently small, we deduce that there exists a positive constant ![]() $C_6$ such that for
$C_6$ such that for ![]() $0\leq l\leq m-1$,
$0\leq l\leq m-1$,
 \begin{align}
&\frac{{\rm d}}{{\rm d}t}\left\{\sum_{l\leq k\leq m}
(\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{
L^2}^2)\right.\nonumber\\ &\quad\left.+\,C_5\sum_{l\leq k\leq
m-1}\int_{\mathbb{R}^3}\nabla^ku\cdot\nabla^{k+1}\varrho\,{\rm
d}x\right\}\nonumber\\ &\quad+C_6\left\{\sum_{l+1\leq k\leq
m}\|\nabla^{k}\varrho\|_{L^2}^2+\sum_{l+1\leq k\leq
m+1}(\|\nabla^{k}u\|_{L^2}^2+\|\nabla^{k}\chi\|_{L^2}^2+\|\nabla^{k}
\nabla\chi\|_{L^2}^2\right\}\nonumber\\ &\quad\quad\leq0.
\end{align}
\begin{align}
&\frac{{\rm d}}{{\rm d}t}\left\{\sum_{l\leq k\leq m}
(\|\nabla^k\varrho\|_{L^2}^2+\|\nabla^ku\|_{L^2}^2+\|\nabla^k\chi\|_{L^2}^2+\|\nabla^k\nabla\chi\|_{
L^2}^2)\right.\nonumber\\ &\quad\left.+\,C_5\sum_{l\leq k\leq
m-1}\int_{\mathbb{R}^3}\nabla^ku\cdot\nabla^{k+1}\varrho\,{\rm
d}x\right\}\nonumber\\ &\quad+C_6\left\{\sum_{l+1\leq k\leq
m}\|\nabla^{k}\varrho\|_{L^2}^2+\sum_{l+1\leq k\leq
m+1}(\|\nabla^{k}u\|_{L^2}^2+\|\nabla^{k}\chi\|_{L^2}^2+\|\nabla^{k}
\nabla\chi\|_{L^2}^2\right\}\nonumber\\ &\quad\quad\leq0.
\end{align}
Define ![]() $\mathcal {E}_l^m(t)$ to be
$\mathcal {E}_l^m(t)$ to be ![]() $1/{C_6}$ times the expression under the time derivative in (5.5). It is easy to see that since
$1/{C_6}$ times the expression under the time derivative in (5.5). It is easy to see that since ![]() $\delta >0$ is so small,
$\delta >0$ is so small, ![]() $\mathcal {E}_l^m(t)$ is equivalent to
$\mathcal {E}_l^m(t)$ is equivalent to
Then, (5.5) can be rewritten as that for ![]() $0\leq l\leq m-1$,
$0\leq l\leq m-1$,
Taking ![]() $l=0$ and
$l=0$ and ![]() $m=3$ in (5.6), integrating directly in time, it yields that
$m=3$ in (5.6), integrating directly in time, it yields that
 \begin{align} &\|\varrho\|_{H^3}^2+\|u\|_{H^3}^2+\|\chi\|_{H^3}^3+\|\nabla\chi\|_{H^3}^2\lesssim\mathcal{E}_0^3(0)\nonumber\\ &\quad\lesssim\|\varrho_0\|_{H^3}^2+\|u_0\|_{H^3}^2+\|\chi_0\|_{H^3}^3+\|\nabla\chi_0\|_{H^3}^2. \end{align}
\begin{align} &\|\varrho\|_{H^3}^2+\|u\|_{H^3}^2+\|\chi\|_{H^3}^3+\|\nabla\chi\|_{H^3}^2\lesssim\mathcal{E}_0^3(0)\nonumber\\ &\quad\lesssim\|\varrho_0\|_{H^3}^2+\|u_0\|_{H^3}^2+\|\chi_0\|_{H^3}^3+\|\nabla\chi_0\|_{H^3}^2. \end{align}
Then, by a standard continuity argument, this closes the a priori estimates (3.1) if at the initial time we assume that ![]() $\|\varrho _0\|_{H^3}^2 +\|u_0\|_{H^3}^2+\|\chi _0\|_{H^3}^3+\|\nabla \chi _0\|_{H^3}^2\leq \delta _0$ is sufficiently small. This in turn allows us to take
$\|\varrho _0\|_{H^3}^2 +\|u_0\|_{H^3}^2+\|\chi _0\|_{H^3}^3+\|\nabla \chi _0\|_{H^3}^2\leq \delta _0$ is sufficiently small. This in turn allows us to take ![]() $l=0$ and
$l=0$ and ![]() $m=N$ in (5.6), and then integrate it directly in time to obtain (1.6).
$m=N$ in (5.6), and then integrate it directly in time to obtain (1.6).
Next, we prove the decay rate of solutions for ![]() $s\in [0,\frac 12]$. Define
$s\in [0,\frac 12]$. Define
Then, integrating in time (4.1), by the bound (1.6), we derive that
 \begin{align} \mathcal{E}_{{-}s}(t)&\leq\mathcal{E}_{{-}s}(0)+C\int_0^t(\|\varrho\|_{H^2}^2+\|\nabla u\|_{H^1}^2+\|\nabla\chi\|_{H^3}^2)\sqrt{\mathcal{E}_{{-}s}(\tau)}\,{\rm d}\tau\nonumber\\ &\leq C_0\left(1+\sup_{0\leq\tau\leq t}\sqrt{\mathcal{E}_{{-}s}(\tau)} \right), \end{align}
\begin{align} \mathcal{E}_{{-}s}(t)&\leq\mathcal{E}_{{-}s}(0)+C\int_0^t(\|\varrho\|_{H^2}^2+\|\nabla u\|_{H^1}^2+\|\nabla\chi\|_{H^3}^2)\sqrt{\mathcal{E}_{{-}s}(\tau)}\,{\rm d}\tau\nonumber\\ &\leq C_0\left(1+\sup_{0\leq\tau\leq t}\sqrt{\mathcal{E}_{{-}s}(\tau)} \right), \end{align}
which implies (1.7) for ![]() $s\in [0,\frac 12]$, that is
$s\in [0,\frac 12]$, that is
Moreover, if ![]() $l=1,2,\ldots ,N-1$, we may use lemma 2.6 to have
$l=1,2,\ldots ,N-1$, we may use lemma 2.6 to have
Then, by this facts and (5.9), we get
Thus, for ![]() $1=1,2,\ldots ,N-1$,
$1=1,2,\ldots ,N-1$,
Thus, we deduce from (5.6) with ![]() $m=N$ the following inequality
$m=N$ the following inequality
which implies
Hence, (1.7) holds.
On the other hand, the arguments for ![]() $s\in [0,\frac 12]$ cannot be applied to
$s\in [0,\frac 12]$ cannot be applied to ![]() $s\in (\frac 12,\frac 32)$. However, observing that
$s\in (\frac 12,\frac 32)$. However, observing that ![]() $\varrho _0,u_0,\chi _0,\nabla \chi _0\in \dot {H}^{-(1/2)}$ hold since
$\varrho _0,u_0,\chi _0,\nabla \chi _0\in \dot {H}^{-(1/2)}$ hold since ![]() $\dot {H}^{-s}\bigcap L^2\subset \dot {H}^{-s'}$ for any
$\dot {H}^{-s}\bigcap L^2\subset \dot {H}^{-s'}$ for any ![]() $s'\in [0,s]$, we can deduce from what we have proved for (1.7)–(1.8) with
$s'\in [0,s]$, we can deduce from what we have proved for (1.7)–(1.8) with ![]() $s=\frac 12$ that the following estimate holds for l = 0,1, … , N − 1:
$s=\frac 12$ that the following estimate holds for l = 0,1, … , N − 1:
Therefore, we deduce from (4.2) that for ![]() $s\in (\frac 12,\frac 32)$,
$s\in (\frac 12,\frac 32)$,
 \begin{align}
\mathcal{E}_{{-}s}(t)&\leq\mathcal{E}_{{-}s}(0)+C\int_0^t(\|\nabla\varrho\|_{H^1}^2+\|\Delta\chi\|^2_{L^2})\sqrt{\mathcal{E}_{{-}s}(\tau)}\,{\rm
d}\tau\nonumber\\
&\quad+C\int_0^t\|(\varrho,u,\chi,\nabla\chi)\|_{L^2}^{s-1/2}(\|\varrho\|_{H^2}
+\|\nabla u\|_{H^1} \notag\\
&\quad
+\|\nabla\chi\|_{H^1}+\|\nabla^2\chi\|_{H^1} )^{5/2-s}
\sqrt{\mathcal{E}_{{-}s}(\tau)}\,{\rm d}\tau\nonumber\\
&\leq C+C\sup_{0\leq\tau\leq
t}\sqrt{\mathcal{E}_{{-}s}(\tau)}+C\int_0^t(1+\tau)^{-(7/4)-(
s/2)}\,{\rm d}\tau\sup_{\tau\in[0,t]}
\sqrt{\mathcal{E}_{{-}s}(\tau)}\nonumber\\ &\lesssim
1+\sup_{\tau\in[0,t]} \sqrt{\mathcal{E}_{{-}s}(\tau)},
\end{align}
\begin{align}
\mathcal{E}_{{-}s}(t)&\leq\mathcal{E}_{{-}s}(0)+C\int_0^t(\|\nabla\varrho\|_{H^1}^2+\|\Delta\chi\|^2_{L^2})\sqrt{\mathcal{E}_{{-}s}(\tau)}\,{\rm
d}\tau\nonumber\\
&\quad+C\int_0^t\|(\varrho,u,\chi,\nabla\chi)\|_{L^2}^{s-1/2}(\|\varrho\|_{H^2}
+\|\nabla u\|_{H^1} \notag\\
&\quad
+\|\nabla\chi\|_{H^1}+\|\nabla^2\chi\|_{H^1} )^{5/2-s}
\sqrt{\mathcal{E}_{{-}s}(\tau)}\,{\rm d}\tau\nonumber\\
&\leq C+C\sup_{0\leq\tau\leq
t}\sqrt{\mathcal{E}_{{-}s}(\tau)}+C\int_0^t(1+\tau)^{-(7/4)-(
s/2)}\,{\rm d}\tau\sup_{\tau\in[0,t]}
\sqrt{\mathcal{E}_{{-}s}(\tau)}\nonumber\\ &\lesssim
1+\sup_{\tau\in[0,t]} \sqrt{\mathcal{E}_{{-}s}(\tau)},
\end{align}
which implies that (1.7) holds for ![]() $s\in (\frac 12,\frac 32)$, i.e.
$s\in (\frac 12,\frac 32)$, i.e.
Since we have proved (5.15), we may repeat the arguments leading to (1.8) for ![]() $s\in [0,\frac 12]$ to prove that they also hold for
$s\in [0,\frac 12]$ to prove that they also hold for ![]() $s\in (\frac 12,\frac 32)$. Therefore, the proof of theorem 1.1 is complete.
$s\in (\frac 12,\frac 32)$. Therefore, the proof of theorem 1.1 is complete.
Acknowledgements
This paper was supported by the Fundamental Research Funds for the Central Universities (grant N2005031). The author thanks the anonymous referees for his(her) profitable suggestions. Moreover, the author also thank Prof. Yong Zhou and Prof. Hao Wu for their encourage and guidance.