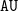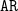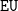1. Introduction
Propositional Dynamic Logic (PDL), cf. Fischer and Ladner (Reference Fischer and Ladner1979) or Harel et al. (Reference Harel, Kozen and Tiuryn2000, Chap. 5), and Computation Tree Logic (CTL), cf. Clarke and Emerson (Reference Clarke and Emerson1982) or Emerson and Halpern (Reference Emerson and Halpern1985), are proposed as specification formalisms. However, these logics were shown to be unable to express fairness, cf. Harel and Sherman (Reference Harel and Sherman1982) for PDL and Emerson and Halpern (Reference Emerson and Halpern1986), Thm. 7 or Clarke and Draghicescu (Reference Clarke and Draghicescu1989) for CTL. Here, fairness means the existence of a path on that a certain proposition holds infinitely often, cf. Lamport (Reference Lamport1980). By contrast, some extensions of PDL and CTL can express fairness, cf. Streett (Reference Streett1981) for PDL and Emerson and Halpern (Reference Emerson and Halpern1986) for CTL.
In essence, the semantics of CTL comprises a path quantifier and a temporal quantifier along the path. Axelsson et al. (Reference Axelsson, Hague, Kreutzer, Lange and Latte2010a, b) incorporate ideas from PDL into CTL. Basically, the domain of the temporal quantifier is refined from the set of all times to a syntax-given set of times. In this way, the obtained logic (XCTL) can express, for instance, that a path exists on which a certain formula holds at all even times. Because the quantifier pattern remains unchanged, the logic is expected to not express fairness either. However, the proof in Reference Axelsson, Hague, Kreutzer, Lange and LatteAxelsson et al. (2010b , Claim 2 in the proof to Lem. 4.3) is faulty. Footnote 1
This article provides a unified proof that neither PDL, CTL, nor XCTL captures fairness. A second aspect concerns the universal path quantifiers.
Fairness depends on a single path. Accordingly, universal path quantifiers should not assist any formula in expressing fairness. The inexpressiveness results by Emerson and Halpern (Reference Emerson and Halpern1986, Thm. 7), Harel and Sherman (Reference Harel and Sherman1982), and by Clarke and Draghicescu (Reference Clarke and Draghicescu1989), Thm. 3 are not stated for arbitrary universal path quantifiers because the results regard negation-closed logics. As an example, we consider the two formulae
\begin{equation} \vartheta_1 \enspace:=\enspace \mathtt{E}\, \mathord{\mathtt{t\!t}} \mathbin{ ^{}\mathtt{U} ^{}} p \qquad\text{and}\qquad \vartheta_2 \enspace:=\enspace \mathtt{E}\, \mathord{\mathtt{t\!t}} \mathbin{ ^{}\mathtt{U} ^{}} (p \wedge \neg\mathtt{E}\mathtt{GF}\, p)\end{equation}
where p is some proposition,
$\mathtt{E}\, \mathord{\mathtt{t\!t}} \mathbin{ ^{}\mathtt{U} ^{}} \psi$
states that a vertex is reachable at which
$\psi$
holds, and
$\mathtt{E}\mathtt{GF}\, p$
stands for p-fairness. Neither
$\vartheta_1$
nor
$\vartheta_2$
is equivalent to p-fairness. More precisely, the linear loop-free structure on that p holds only at the root is a model of both formulae but is p-unfair. The formula
$\vartheta_1$
belongs to CTL and is expressible in PDL. The subformula
$\mathtt{E}\mathtt{GF}\, p$
places
$\vartheta_2$
outside of CTL and PDL. Hence, the three cited proofs can handle
$\vartheta_1$
but not
$\vartheta_2$
. Nevertheless, the last two proofs can be adjusted. Basically, it is sufficient to decompose equivalences into implications according to the polarity of the subformulae, similar to the pair (18) and (19) in lem:strInv. Such an adjustment cannot be taken for granted, cf. Bojańczyk (Reference Bojańczyk2008) for a peculiar case. For instance, Demri et al. (Reference Demri, Goranko and Lange2016, Thm. 10.3.7) simplify the proof by Emerson and Halpern (Reference Emerson and Halpern1986, Thm. 7) but the younger proof applies its induction hypothesis bidirectionally. Hence, a polarity-based decomposition cannot adjust this proof.
Section 3 defines a plain branching-time logic with the said logics as its sublogics. Theorem 20 in Section 4 is the main result. As a consequence, the mentioned sublogics are uniformly proven unable to express fairness. Section 6 addresses an extension of Section 4.
2. Notations
Ordinal numbers are understood in the sense of von Neumann. In particular, the set of natural numbers is written as
$\omega$
, and each number is the set of all smaller numbers. For example,
$$\omega + 1 = \{ 0,1, \ldots ,\omega \} $$
and
$$c \setminus a = \{ b{\rm{ }}|a \le b < c\} $$
.
Let
$\langle {\;},{\;} \rangle$
be a bijection from
$\omega \times \omega$
to
$\omega$
such that
$a \leq \langle {a},{b} \rangle$
for all
$a,b\in\omega$
. For instance, Cantor suggests
$\langle {a},{b} \rangle := (a+b)(a+b+1)/2+a$
.
A function and its graph are considered as interchangeable. The image of a function f is written as
$\mathsf{img}(f)$
.
3. A Unified Branching-Time Logic
3.1 Syntax
Let
$\mathbb{P}$
denote a non-empty set of propositions. The set
$\mathbb{F}$
of formulae is the least fixed point (Phillips Reference Phillips1992, Subsec. 3.1) for the following rules.
\begin{align} \notag \mathbb{F} \quad\ni\quad \psi &::= p \enspace\mid\enspace \neg \psi \enspace\mid\enspace \psi \vee \psi \enspace\mid\enspace \mathtt{E} L\\ \notag p & \in \mathbb{P}\\ L &\subseteq \boldsymbol\omega \to \Psi \end{align}
\begin{align} \boldsymbol{\Psi} &\text{is}\quad \text{a finite set of objects named} \psi \end{align}
The variables
$\varphi$
,
$\alpha$
, and
$\varepsilon$
refer to formulae. An entity L generated by (2) is a language of infinite words. Its alphabet
$\Sigma(L) := \bigcup \{ \mathsf{img}(w) \mathrel| w \in L \}$
is finite due to (3). In formulae, parentheses may be inserted to improve readability.
3.2 Semantics
A structure is a quadruple
$(V, E, \ell, r)$
that consists of a set V of vertices, a set E of edges as a subset of
$V \times V$
such that each
$v \in V$
has a
$w \in V$
with
$(v,w) \in E$
, a labelling function
$\ell$
in
$V \to 2^\mathbb{P}$
, and a root r in V. For such a structure
$\mathcal S$
, the root is changed to s by
$\mathcal S \mathbin{\mathsf{@}} s$
. A path
$\pi$
is a function in
$\omega \to V$
such that
$\pi(0) = r$
and
$(\pi(i), \pi(i{+}1)) \in E$
for all
$i\in\omega$
. Whether a structure
$\mathcal S$
is a model of a formula
$\varphi$
, written as
$\mathcal S \models \varphi$
, is defined as follows.
For a chosen pair in the last clause, its components are called witnessing path and witnessing word.
Two structures
$\mathcal S_1$
and
$\mathcal S_2$
are 0-bisimilar, written as
$\mathcal S_1 \mathrel{\approx_0} \mathcal S_2$
, iff each proposition p fulfils
$\mathcal S_1 \models p$
iff
$\mathcal S_2 \models p$
. Two formulae are equivalent iff they have the same models.
3.3 Abbreviations
Boolean values and operations are available by the usual abbreviations
$\mathord{\mathtt{t\!t}} := p \vee \neg p$
for some
$p \in \mathbb{P}$
and
$\psi_0 \wedge \psi_1 := \neg(\neg\psi_0 \vee \neg\psi_1)$
. A disjunction
$\psi_0 \vee \psi_1$
could have been alternatively defined as
$\mathtt{E} \{ z_0, z_1 \}$
where, for both
$j\in2$
, the word
$z_j$
is constantly true, e.g.
$\neg\mathtt{E}\emptyset$
, but is
$\psi_j$
at 0. For concise definitions in Subsection 3.4, disjunctions are first-class citizens, though.
The
$\mathtt{EU}$
-,
$\mathtt{EG}$
-,
$\mathtt{EX}$
-,
$\mathtt{ER}$
-constructors from CTL can be imitated and generalised. For
$\alpha, \varepsilon \in \mathbb{F}$
and for
$A, E \subseteq \omega$
, the languages
and
\begin{align} \mathopen{\mathtt{G}^{A}} \alpha \enspace:=\enspace & \big\{ z \;\big|\; \text{each $n\in\omega$ fulfils $z(n) = \alpha$ if $n \in A$ and $z(n) = \mathord{\mathtt{t\!t}}$ otherwise}\big\}\end{align}
are defined as subsets of
$\omega \to \{\mathord{\mathtt{t\!t}}, \alpha, \varepsilon\}$
and of
$\omega \to \{\mathord{\mathtt{t\!t}}, \alpha\}$
, respectively. For convenience,
\begin{align} \mathopen{\mathtt{X}} \varepsilon \enspace&:=\enspace \mathord{\mathtt{t\!t}} \mathbin{ ^{\emptyset}\mathtt{U} ^{\{1\}}} \varepsilon \end{align}
and
\begin{align} \varepsilon \mathbin{ ^{E}\mathtt{R} ^{A}} \alpha \quad&:=\quad \mathopen{\mathtt{G}^{A}} \alpha\enspace\cup\enspace \alpha \mathbin{ ^{A}\mathtt{U} ^{E \cap A}} (\varepsilon\wedge\alpha)\enspace\cup\enspace \alpha \mathbin{ ^{A}\mathtt{U} ^{E \setminus A}} \varepsilon \,\text.\end{align}
The sets A and E restrict the temporal quantifiers. For instance,
$\mathtt{E}\mathopen{\mathtt{G}^{\{2t \,\mathrel|\, t \in \omega\}}} \varphi$
asks for a path on that the formula
$\varphi$
holds at all even times while odd times are unspecified. The standard constructors appear when
$A=E=\omega$
. The setting (7) rests on the corresponding decomposition of
$\mathtt{ER}$
-formulae for CTL, cf. Emerson and Halpern (Reference Emerson and Halpern1985, proof of Thm. 8.4) or Demri et al. (Reference Demri, Goranko and Lange2016, dual of Lem. 7.1.2).
Example 1. Let
$\varphi$
be a formula. The formula
\begin{align*} \notag \mathtt{AGF}\, \varphi \quad&:=\quad \neg \mathtt{E} \mathord{\mathtt{t\!t}} \mathbin{ ^{\omega}\mathtt{U} ^{\omega}} \big( \mathtt{E} \neg\mathord{\mathtt{t\!t}} \mathbin{ ^{\omega}\mathtt{R} ^{\omega}} \neg \varphi \big) \end{align*}
asserts that
$\varphi$
holds infinitely often on every path. With the language
\begin{align} \mathtt{GF}\, \varphi \quad&:=\quad \big\{ z \colon \omega \to \{\mathord{\mathtt{t\!t}},\varphi\} \;\big|\; \text{$z(i)=\varphi$ for infinitely many $i\in\omega$} \big\} \end{align}
the dual formula
$\mathtt{E}\mathtt{GF}\, \varphi$
asserts that
$\varphi$
holds infinitely often on some path.
Definition 2. (Fairness) Let
$\varphi$
be a formula. A structure is
$\varphi$
/fair iff it is a model of
$\mathtt{E}\mathtt{GF}\,\varphi$
.
Remark 4. Each proof that is cited in Section 1 shows that a pair of two structures cannot be distinguished by some PDL- or CTL-formulae. However,
$\mathtt{E}\mathopen{\mathtt{G}^{\{2t \,\mathrel|\, t\in\omega\}}}p$
distinguishes the pairs by Emerson and Halpern (1986, Thm. 7) and
$\mathtt{E}\mathopen{\mathtt{G}^{\{2t \,\mathrel|\, t\in\omega\}}} \neg p$
the pair by Clarke and Draghicescu (1989, Sec. 4). Both formulae are handled by Theorem 20.
3.4 Sublogics
Definition 5. The sets of negative and positive subformulae of a formula
$\varphi$
are the smallest sets
$\mathsf{subf}_{-1}(\varphi)$
and
$\mathsf{subf}_1(\varphi)$
that fulfil for both signs
$s \in \{-1,1\}$
-
$\varphi \in \mathsf{subf}_1(\varphi)$
, -
$\neg\psi \in \mathsf{subf}_s(\varphi)$
implies
$\psi \in \mathsf{subf}_{-s}(\varphi)$
,
-
$\psi_0 \vee \psi_1 \in \mathsf{subf}_s(\varphi)$
implies
$\{\psi_0,\psi_1\} \subseteq \mathsf{subf}_s(\varphi)$
, and
-
$\mathtt{E} L \in \mathsf{subf}_s(\varphi)$
implies
$\Sigma(L) \subseteq \mathsf{subf}_s(\varphi)$
.
Definition 6. Let
$S \subseteq \{-1,1\}$
be a set of signs. Its set of languages in a formula is
\begin{equation*} \mathsf{lngs}_S(\varphi) \quad:=\quad \{ L \mathrel| \mathtt{E} L \in \mathsf{subf}_s(\varphi) \text{ for some } s \in S \} \,\text. \end{equation*}
Restrictions on
$\mathbb{F}$
through
$\mathsf{lngs}$
reveal various branching-time logics. Prominently, CTL is just
\begin{equation} \big\{ \varphi \in \mathbb{F} \;\big|\; \text{each $L \in \mathsf{lngs}_{\{-1,1\}}(\varphi)$ has the shape of (6) or of (4) or (7) for} \, A = E= \omega \big\}.\end{equation}
Example 7. In continuation of Example 1, the formula
$\mathtt{AGF}\, \varphi$
belongs to CTL but
$\mathtt{E} \mathtt{GF}\, \varphi$
does not. Because any restriction of negative
$\mathtt{E}$
-constructors is irrelevant for Theorem 20, we drop those constraints and obtain the larger logic
\begin{align} & \big\{ \varphi \in \mathbb{F} \;\big|\; \text{each $L \in \mathsf{lngs}_{\{1\}}(\varphi)$ has the shape of (6) or of (4) or (7) for} \, A = E = \omega \big\}. \end{align}
In other words, negative
$\mathtt{E}$
-constructors are entirely unrestricted and may quantify along a path freely. A variant is
\begin{align} & \big\{ \varphi \in \mathbb{F} \;\big|\; \text{each $L \in \mathsf{lngs}_{\{1\}}(\varphi)$ has the shape of (4) or (7)} \big\} \end{align}
which allows to customise the range of the temporal quantifiers on both sides of an
$\mathbin{ ^{}\mathtt{U} ^{}}$
and a
$\mathbin{ ^{}\mathtt{R} ^{}}$
. The logic subsumes limited variants (Axelsson et al. Reference Axelsson, Hague, Kreutzer, Lange and Latte2010a; b) that allow the customisation on the right side of
$\mathbin{ ^{}\mathtt{U} ^{}}$
and
$\mathbin{ ^{}\mathtt{R} ^{}}$
only. Similarly,
\begin{align} & \big\{ \varphi \in \mathbb{F} \;\big|\; \text{each $z \in \textstyle\bigcup\mathsf{lngs}_{\{1\}}(\varphi)$ fulfils $z(i)=\mathord{\mathtt{t\!t}}$ for almost all $i\in\omega$ } \big\}\end{align}
captures reachability and thus subsumes PDL and its nonregular extensions (Harel et al. Reference Harel, Kozen and Tiuryn2000, Chap. 5 and 9). All stated subsumptions ignore edge labels or understand them as encoded by propositions, cf. De Nicola and Vaandrager (Reference De Nicola and Vaandrager1990). In particular, Theorem 20 disregards edge labels.
4. Inexpressiveness of Fairness
To reveal fairness as inexpressible, a fair structure and a bunch of unfair structures are proven as indistinguishable, cf. Theorem 20 with its elaboration in Section 4.1. Finally, Subsection 4.2 applies Theorem 20 to the logics from Subsection 3.4.
4.1 Indistinguishable structures
Assumption 8. Until the end of this subsection, we let p be a proposition and let
$\vartheta$
be an arbitrary formula such that
$\bigcup\mathsf{lngs}_{\{1\}}(\vartheta)$
is a countable set of words.
In Definition 15, we shall construct a set
$\{ \mathcal T_k \mathrel| k\in\omega+1 \}$
of structures. The structure
$\mathcal T_\omega$
is p-fair while
$\mathcal T_k$
is not for any
$k\in\omega$
, cf. Lemma 16.
Lemma 19 demonstrates that both kinds of structures are indistinguishable. The crucial cases are the
$\mathtt{E}$
-subformulae of
$\vartheta$
. Positive
$\mathtt{E}$
-subformulae shall transfer from the p-fair structure
$\mathcal T_\omega$
to a p-unfair structure
$\mathcal T_k$
for
$k \in \omega$
. The direction of negative
$\mathtt{E}$
-subformulae is reverse.
In a first approximation, each structure is linear. Along the sole path in the structure
$\mathcal T_\omega$
, the proposition p is placed infinitely often but sparsely. The places are enumerated by the function T, as determined by Definition 11 with Lemma 10. The vertices for p are so seldom that, for each possible witnessing word of each positive
$\mathtt{E}$
-subformulae, each asked formula is also asked at a vertex for
$\neg p$
. Hence, some suffix of the witnessing word can cope with only
$\neg p$
. Along the corresponding suffix of the path, the proposition p can be erased stealthily, cf. the proof of Lemma 18. The modification for the k-th suffix yields the p-unfair structure
$\mathcal T_k$
. So far, the backbone of
$\mathcal T_k$
for
$k\in\omega+1$
is described.
The other direction has to convey a negative
$\mathtt{E}$
-subformula from
$\mathcal T_k$
for
$k\in\omega$
to
$\mathcal T_\omega$
. In such a formula
$\mathtt{E} L$
, the language L is not captured by Assumption 8. As a compensation, we attach for each
$\mathtt{E}$
-subformula a p-unfair model to
$\mathcal T_\omega$
to capture any witnessing path from the p-unfair structure
$\mathcal T_k$
, cf. Lemma 17. Back to the first direction, witnessing paths in
$\mathcal T_\omega$
can enter the now attached structures. Thus, these structures are also attached to
$\mathcal T_k$
for each
$k\in\omega$
. All in all, we collected all ingredients for Definition 15.
The just drafted diagonalisation against positive
$\mathtt{E}$
-subformulae requires that the set of all possible witnessing words is enumerable, cf. Assumption 8 and Definition 9
Definition 9. We fix an arbitrary enumeration
$Z \colon \omega \to (\omega \to \mathbb{F})$
of all words in
$\bigcup\mathsf{lngs}_{\{1\}}(\vartheta)$
.
Lemma 10. There exists a function
$T \colon \omega \to \omega$
such that all
$n \in \omega$
meet the condition
Proof. An induction on n constructs T(n) and entails that
$n \leq T(n)$
as a support. Given n, the values
$t_0$
and i exist. Because
$t_0 \leq \langle {t_0},{i} \rangle = n \leq T(n)$
, the set
$X := \{ \; z(t-t_0) \; \mathrel| \; T(n) < t \in \omega \; \}$
is well defined and not empty. As z is a word, the set is finite. Hence, the conditions
\begin{equation*} \min\{ \; t \; \mathrel| \; z(t-t_0)=x \text{ and } T(n) < t \in \omega \; \}\enspace<\enspace T(n+1) \qquad \text{for each $x \in X$} \end{equation*}
characterise
$T(n+1)$
completely. As a by-product,
$n \leq T(n) < T(n+1)$
.
Definition 11. Henceforth, an arbitrary function provided by Lemma 10 is designated as T.
Definition 12. (Default Unfair Models) For each formula,
$\varphi$
let
$\mathcal U_\varphi = (V_\varphi, E_\varphi, \ell_\varphi, r_\varphi)$
be some model of
$\varphi \wedge \neg\mathtt{E}\mathtt{GF}\, p$
if existing and an arbitrary model of
$\neg\mathtt{E}\mathtt{GF}\, p$
otherwise. We consider their sets of vertices as pairwise disjoint and disjoint from
$\omega$
.
Attaching a structure to another structure can change the modelled formulae at the shared root. As Lemma 17 bridges from an attached structure to the entire structure, Definition 15 filters each
$\mathtt{E}$
-subformula of
$\vartheta$
by the formulae that can be asked at a root.
Definition 13. The filtering of a language L by a formula
$\psi$
is
$ L \mathbin{\downarrow} \psi \; := \; \{ z \in L \mathrel| z(0) = \psi \} $
.
Definition 14.
$\mathtt{E}$
-subformulae of
$\vartheta$
are split by their first letter through
\begin{equation*} \Xi \quad:=\quad \big\{\; \mathtt{E} (L \mathbin{\downarrow} \psi) \;\;\big|\;\; \mathtt{E} L \in \mathsf{subf}_{-1}(\vartheta) \cup \mathsf{subf}_1(\vartheta) \text{ and } \psi \in \Sigma(L) \;\big\} \,\text. \end{equation*}
Definition 15. (Sample Structures) Let
$k \in \omega+1$
. The structure
$\mathcal T_k$
is the quadruple
$(V, E, \ell, 0)$
where the set V of vertices is
\begin{alignat*}{2} &\bigcup_{\xi\in\Xi} V_\xi &\quad\cup\quad &\omega \,\text, \end{alignat*}
the set E of edges is
\begin{alignat*}{2} &\bigcup_{\xi\in\Xi} E_\xi &\quad\cup\quad &\bigcup_{\xi\in\Xi} \big\{\; (t,s) \;\;\big|\;\; t\in\omega \text{ and } (r_\xi,s) \in E_\xi \;\big\} \quad\cup\quad \{\; (t,t+1) \;\mathrel|\; t\in\omega \;\} \,\text,\end{alignat*}
and the labelling function
$\ell$
is
\begin{alignat*}{2} &\bigcup_{\xi\in\Xi} \ell_\xi &\quad\cup\quad &\big\{\; \big(t,\{ p \mathrel| t \in \mathsf{img}(T) \cap k \}\big) \;\;\big|\;\; t\in\omega \; \big\} \,\text. \end{alignat*}
Figure 1 sketches the structure
$\mathcal T_k$
. Basically,
$\mathcal T_k$
is linear where at each vertex t the structure
$\mathcal U_\xi$
is attached for all
$\xi \in \Xi$
. Along the linear basis, the places for the proposition p are determined by
$\mathsf{img}(T)$
until k. For
$k \in \omega+1$
and
$t \in \omega$
, the backbone of
$\mathcal T_k \mathbin{\mathsf{@}} t$
is the path
$\{ (i,t+i) \mathrel| i\in\omega \}$
, that is, the t-th suffix of the underlying linear structure.
Figure 1. The structure
$\mathcal T_k$
where
$k \in \omega+1$
.
Lemma 16. Let
$k \in \omega+1$
and
$t \in \omega$
. Then,
$\mathcal T_k \mathbin{\mathsf{@}} t \models \mathtt{E}\mathtt{GF}\, p$
iff
$k = \omega$
.
Proof. The function T is unbounded. On the backbone of
$\mathcal T_k \mathbin{\mathsf{@}} t$
, the set of p-labelled vertices is
$\mathsf{img}(T) \cap k \setminus t$
. Its cardinality is infinite iff
$k = \omega$
. Because each attached structure
$\mathcal U_\xi$
for
$\xi\in\Xi$
is a model of
$\neg\mathtt{E}\mathtt{GF}\, p$
, any witnessing path for
$\mathcal T_k \mathbin{\mathsf{@}} t \models \mathtt{E}\mathtt{GF}\, p$
sits on the backbone.
As tools for the proof of Lemma 19 later, Lemma 17 basically exchanges a p-unfair model of an
$\mathtt{E}$
-subformula for a p-fair model, and Lemma 18 shows that each witnessing word from Z can be misled by some p-unfair structure.
Lemma 17. Let
$k \in \omega+1$
, let
$t\in\omega$
, and let
$\xi \in \Xi$
of the shape
$\mathtt{E}(L \mathbin{\downarrow} \psi)$
. If
$\xi \wedge \neg\mathtt{E}\mathtt{GF}\, p$
has a model and
$\mathcal T_k \mathbin{\mathsf{@}} t \models \psi$
then
$\mathcal T_k \mathbin{\mathsf{@}} t \models \xi$
.
Proof. A witness for
$\mathcal U_\xi \models \xi$
is adjusted to a witness for
$\mathcal T_k \mathbin{\mathsf{@}} t \models \xi$
. The first vertex of the witnessing path is replaced with t while the witnessing word remains. The adjustment is sound. First,
$\mathcal U_\xi$
is a model of
$\psi$
because any word in
$L \mathbin{\downarrow} \psi$
begins with
$\psi$
. Second,
$\mathcal T_k \mathbin{\mathsf{@}} t$
is also a model of
$\psi$
by assumption. Third,
$\mathcal U_\xi$
is a substructure of
$\mathcal T_k \mathbin{\mathsf{@}} t$
and no edge in
$\mathcal T_k \mathbin{\mathsf{@}} t$
leaves this substructure.
In Lemma 18, the line (15) switches a p-fair model of an
$\mathtt{E}$
-formula to a p-unfair model if the witnessing word is captured by the enumeration Z. The premise (14) is provided by the induction hypothesis when (15) is applied in the proof of Lemma 19.
Lemma 18. Let
$t_0, i \in \omega$
. Set
$c := T\big(\langle {t_0},{i} \rangle+1\big) + 1$
and
$z := Z(i)$
. If
\begin{align} \mathcal T_\omega \mathbin{\mathsf{@}} t_1 \enspace\models\enspace \psi \quad&\text{implies}\quad \mathcal T_c \mathbin{\mathsf{@}} t_2 \enspace\models\enspace \psi \end{align}
for all
$\psi \in \Sigma(\{ z \})$
and for all pairs
$t_1, t_2 \in \omega$
such that
$\mathcal T_\omega \mathbin{\mathsf{@}} t_1 \mathrel{\approx_0} \mathcal T_c \mathbin{\mathsf{@}} t_2$
, then
\begin{align} \mathcal T_\omega \mathbin{\mathsf{@}} t_0 \enspace\models\enspace \mathtt{E}\{ z \} \quad&\text{implies}\quad \mathcal T_c \mathbin{\mathsf{@}} t_0 \enspace\models\enspace \mathtt{E}\{ z \} \,\text. \end{align}
Proof. Let
$\pi$
be a witnessing path for
$\mathcal T_\omega \mathbin{\mathsf{@}} t_0 \models \mathtt{E}\{ z \}$
. We take this path for
$\mathcal T_c \mathbin{\mathsf{@}} t_0 \models \mathtt{E}\{ z \}$
. Because the structures that are attached to the backbone are shared among
$\mathcal T_\omega \mathbin{\mathsf{@}} t_0$
and
$\mathcal T_c \mathbin{\mathsf{@}} t_0$
, it remains to consider the backbone. So, let
$t_2$
be a vertex of
$\pi$
on the backbone. As the backbone is linear,
\begin{equation*} \mathcal T_\omega \mathbin{\mathsf{@}} t_2 \enspace\models\enspace \psi \enspace:=\enspace z(t_2-t_0) \,\text. \end{equation*}
Next, we show that
\begin{equation} \mathcal T_\omega \mathbin{\mathsf{@}} t_1 \enspace\models\enspace \psi \quad\text{and}\quad \mathcal T_\omega \mathbin{\mathsf{@}} t_1 \enspace\mathrel{\approx_0}\enspace \mathcal T_c \mathbin{\mathsf{@}} t_2 \quad\text{for some $t_1 \in \omega$} \end{equation}
because this property together with (14) entails that
$\mathcal T_c \mathbin{\mathsf{@}} t_2 \models \psi$
and complete the proof.
Case:
$t_2 < c$
. We take
$t_2$
as
$t_1$
. In particular, Definition 15 ensures the second part of (16) because
$t_1 \in \omega$
on the backbone and because
$t_2 \in c$
in this case.
Case:
$c \leq t_2$
. The condition (13) for
$n := \langle {t_0},{i} \rangle$
yields a
$t_1$
such that
\begin{equation} T(n) \enspace<\enspace t_1 \enspace<\enspace T(n+1) \quad\text{and}\quad z(t_1-t_0) \enspace=\enspace \psi \,\text. \end{equation}
Because the first conjunct implies
$t_1 \leq t_2$
in this case,
$t_1$
also refers to the backbone. Hence, the second conjunct in (17) shows that
$\mathcal T_\omega \mathbin{\mathsf{@}} t_1 \models \psi$
. The second part of (16) is a consequence of Definition 15 for the following reason. First,
$\mathcal T_\omega \mathbin{\mathsf{@}} t_1 \models \neg p$
due to the first conjunct in (17). Second,
$\mathcal T_c \mathbin{\mathsf{@}} t_2 \models \neg p$
because
$t_2 \notin c$
in this case.
Lemma 19. Each formula
$\varphi$
fulfils
\begin{align} \varphi \in \mathsf{subf}_1(\vartheta) \enspace\text{and}\enspace \mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \models \varphi \quad&\text{imply}\quad \mathcal T_{k}\phantom\omega \mathbin{\mathsf{@}} t_{k}\phantom\omega \models \varphi \end{align}
and
\begin{align} \varphi \in \mathsf{subf}_{-1}(\vartheta) \enspace\text{and}\enspace \mathcal T_{k}\phantom\omega \mathbin{\mathsf{@}} t_{k}\phantom\omega \models \varphi \quad&\text{imply}\quad \mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \models \varphi \end{align}
for all
$k \in \omega$
, and all pairs
$t_k, t_\omega \in \omega$
such that
$\mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \; \mathrel{\approx_0} \; \mathcal T_k \mathbin{\mathsf{@}} t_k$
.
Proof. Induction on
$\varphi$
. A proposition is handled by the definition of
$\mathrel{\approx_0}$
. The induction hypothesis yields negation and disjunction where a negation swaps between (18) and (19). So, let
$\varphi$
be
$\mathtt{E} L$
for some language L.
Case: the premises of (19) hold. Let z be a witnessing word for
$\mathcal T_k \mathbin{\mathsf{@}} t_k \models \varphi$
. Hence,
\begin{equation} \phantom{ \enspace \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace z(0)} \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace z(0) \quad\text{and}\quad \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace \mathtt{E}\big( L \mathbin{\downarrow} z(0) \big) \enspace=:\enspace\xi \,\text. \phantom{ \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace\mathtt{E}\big( L \mathbin{\downarrow} z(0) \big) \enspace=:\enspace\xi \,\text. \enspace } \end{equation}
The induction hypothesis for the first conjunct and Lemma 16 for the second conjunct entail that
\begin{equation*} \phantom{ \enspace \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace z(0)} \mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \enspace\models\enspace z(0) \quad\text{and}\quad \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace \xi \wedge \neg\mathtt{E}\mathtt{GF}\, p \,\text. \phantom{ \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace\mathtt{E}\big( L \mathbin{\downarrow} z(0) \big) \enspace=:\enspace\xi \,\text. \enspace } \end{equation*}
Because
$\xi \in \Xi$
, Lemma 17 combines both parts to
$\mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \models \xi$
. Finally, as the semantics of
$\mathtt{E}$
is monotone in the language,
$\mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \models \varphi$
.
Case: the premises of (18) hold. Let z be a witnessing word for
$\mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \models \varphi$
. As
$z \in L$
and
$L \in \mathsf{lngs}_{\{1\}}(\vartheta)$
, Definition 9 yields an
$i \in \omega$
such that
$Z(i) = z$
. Thus,
\begin{equation*} \phantom{ \enspace \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace z(0)} \mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \enspace\models\enspace z(0) \quad\text{and}\quad \mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \enspace\models\enspace \mathtt{E}\{z\} \,\text. \phantom{ \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace\mathtt{E}\big( L \mathbin{\downarrow} z(0) \big) \enspace=:\enspace\xi \,\text. \enspace } \end{equation*}
Because the induction hypothesis supplies the premise (14) of Lemma 18, the implication (15) affects the second conjunct. As the semantics of
$\mathtt{E}$
is monotone in the language,
\begin{equation*} \phantom{ \enspace \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace z(0)} \mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \enspace\models\enspace z(0) \quad\text{and}\quad \mathcal T_c \mathbin{\mathsf{@}} t_\omega \enspace\models\enspace \mathtt{E}\big( L \mathbin{\downarrow} z(0) \big) \enspace=:\enspace \xi \phantom{ \mathcal T_k \mathbin{\mathsf{@}} t_k \enspace\models\enspace\mathtt{E}\big( L \mathbin{\downarrow} z(0) \big) \enspace=:\enspace\xi \,\text. \enspace } \end{equation*}
for some
$c \in \omega$
. This situation reminds of (20). The reasoning there results in
$\mathcal T_k \mathbin{\mathsf{@}} t_k \models \varphi$
here.
The scope of Assumption 8 ends here.
4.2 Consequences
Theorem 20. Let p be a proposition, and let
$\vartheta$
be a formula. If
$\bigcup\mathsf{lngs}_{\{1\}}(\vartheta)$
is a countable set of words then
$\vartheta$
is not equivalent to
$\mathtt{E}\mathtt{GF}\, p$
.
Proof. Assumption 8 is fulfilled. We consider Lemma 19 for
$\varphi := \vartheta$
,
$k := 1$
, and
$t_k := 0 =: t_\omega$
. In particular,
$\mathcal T_\omega \mathbin{\mathsf{@}} t_\omega \mathrel{\approx_0} \mathcal T_k \mathbin{\mathsf{@}} t_k$
due to Definition 15. The implication (18) and Lemma 16 reject an equivalence of
$\vartheta$
and
$\mathtt{E}\mathtt{GF}\, p$
.
The language
$\mathtt{GF}\, p$
is uncountable. Consequently, Theorem 20 also shows that
$\mathtt{E} L$
is not equivalent to
$\mathtt{E}\mathtt{GF}\, p$
when L is only a countable subset of
$\mathtt{GF}\, p$
.
Corollary 21. Let p be a proposition. The logics in (10), (11), and (12) do not contain any formula that is equivalent to
$\mathtt{E}\mathtt{GF}\, p$
.
For example, Corollary 21 handles both formulae from (1). They belong to (10) although the second formula hosts
$\mathtt{E}\mathtt{GF}\, p$
as a negative subformula.
Given the subsumptions between logics in Subsection 3.4, Corollary 21 remedies the faulty argument in Axelsson et al. (2010 b, Lem. 4.3) and reproves the results by Emerson and Halpern (Reference Emerson and Halpern1986, Thm. 7) on CTL and by Harel and Sherman (Reference Harel and Sherman1982) on PDL.
Corollary 22. Let p be a proposition. Neither CTL, XCTL, PDL nor its nonregular extensions contain any formula that is equivalent to
$\mathtt{E}\mathtt{GF}\, p$
.
5. Remark on Unfair Models
The proofs by Harel and Sherman (Reference Harel and Sherman1982) and by Emerson and Halpern (Reference Emerson and Halpern1986, Thm. 7) as well as the proof here attach some unfair structures to a fair structure. The cited proofs construct each attached unfair structure explicitly as an open box. By contrast, Definition 12 picks unfair structures and attach them as closed boxes.
The closed-box principle can simplify the definition of structures and shorten argumentations. An example is the proof by Emerson and Halpern that CTL cannot express p-fairness. Figure 2 depicts a pair of a p-fair structure
$\mathcal S^+_\vartheta$
and a p-unfair structure
$\mathcal S^-_\vartheta$
for a CTL-formula
$\vartheta$
. However, this formula cannot distinguish between both structures. In fact, an induction yields
\begin{equation} \mathcal S^+_\vartheta \mathbin{\mathsf{@}} v \models \varphi \quad\text{iff}\quad \mathcal S^-_\vartheta \mathbin{\mathsf{@}} v \models \varphi\end{equation}
for both
$v \in 2$
and each subformula
$\varphi$
of
$\vartheta$
. The transfer of a witnessing path from
$\mathcal S^+_\vartheta$
to
$\mathcal S^-_\vartheta$
basically tightens the cycle
$0 {\rightarrow} 1 {\rightarrow} 0$
to the loop
$0 {\rightarrow} 0$
and possibly redirects the edge
$0 {\rightarrow} 1$
to
$0 {\rightarrow} r_{\varepsilon}$
if a formula
$\mathtt{E}\, \alpha \mathbin{ ^{}\mathtt{U} ^{}} \varepsilon$
is considered and
$\mathcal S^-_\vartheta \mathbin{\mathsf{@}} 1 \models \varepsilon$
.
Figure 2. The structures
$\mathcal S^+_\vartheta$
and
$\mathcal S^-_\vartheta$
for a CTL-formula
$\vartheta$
. Both differ in the edge
$0 {\rightarrow} 1$
.
Looking back to the introduction, the previous argument can be expanded to any formula
$\vartheta$
from (10). For this purpose, the equivalence (21) is split by the polarity of
$\varphi$
similar to (18) and (19).
6. Extension
Theorem 20 requires any language L to be countable if
$\mathtt{E} L$
is a positive subformula. This constraint cannot be relaxed from “countable” to “uncountable” as the opponent language
$\mathtt{GF}\, p$
is already uncountable. Hence, the cardinality is a border between unfairness and fairness.
Harel and Sherman (Reference Harel and Sherman1982) prove that a certain extension of PDL cannot express fairness. Basically, this extension allows languages of finite-state automata that regard each infinite run as accepting. An instance is the uncountable language
$\{\psi_0, \psi_1\}^\omega$
for two different formulae
$\psi_0$
and
$\psi_1$
. Nevertheless, this class of languages is tame through its pumping property (Harel and Sherman Reference Harel and Sherman1982, case “
$loop(\alpha)$
” in the proof of Lemma 7): each suffix s of each word in such a language admits two finite words x and y such that the length of xy is language-specifically bounded, xy is a prefix of s, and s can be replaced with
$xy^\omega$
. Such languages can be incorporated into Subsection 4.1 with ease. First, the enumeration Z has to list those languages as well. Second, (13) is expanded such that if n refers to such a language then
$T(n+1)-T(n)$
exceeds the language-specific bound. Third, Lemma 18 has to be adjusted. The line (15) was formulated with a singleton language just for simplicity. Now, the pumping property requires to mention the entire language because the witnessing word will be replaced.
7. Conclusion
Theorem 20 draws the line between unfairness and fairness at the level of cardinality for positive
$\mathtt{E}$
-subformulae. In particular, the rigidity of the temporal constructors
$\mathtt{EU}$
,
$\mathtt{EG}$
, … alone cannot be hold responsible for unfairness. In truth, their implicit countability is responsible. On the other hand, Theorem 20 additionally reveals that negative
$\mathtt{E}$
-subformulae have no impact on fairness.
Acknowledgements
The article in hand is dedicated to Martin Hofmann. I am deeply grateful for many years of delightful discussions, his keen perception, scientific inspiration, permissive supervisions, and much more.
We met at his seminar about “proofs from <sc>the book</sc>” for the first time. So, I like to continue the tradition of short stories proofs. When we were discussing my PhD project on CTL years later, he objected that CTL is rather weak and advertised more goal-driven formal systems. Along these lines, this contribution has two ingredients: shortness and expressiveness.
As words fail me, I just want to say: Martin, thank you! In the same year of the seminar, you also gave a lecture on “efficient algorithms” and offered some challenging exercises. The bottle of “corona extra” beer that you rewarded is still adorning my home and is a precious reminder for me.
