1. INTRODUCTION
With the advent of high-power lasers, theoretical as well as experimental investigations of nonlinear interaction of intense laser beams with plasmas are gaining much interest among researchers due to its widespread importance in a number of novel applications, including laser-driven particle accelerators (Tajima & Dawson, Reference Tajima and Dawson1979; Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Mangles et al., Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick2004), inertial confinement fusion (Deutsch et al., Reference Deutsch, Furukawa, Mima, Murakami and Nishihara1996; Hora, Reference Hora2007), X-ray lasers (Amendt et al., Reference Amendt, Eder and Wilks1991), harmonic generation (Sturrock et al., Reference Sturrock, Ball and Baldwin1965; Bulanov et al., Reference Bulanov, Naumova and Pegoraro1994; Lichters et al., Reference Lichters, Vehn and Pukhov1996; Willes et al., Reference Willes, Robinson and Melrose1996; Dromey et al., Reference Dromey, Adams, Horlein, Nomura, Rykovanov, Carroll, Foster, Kar, Markey, McKenna, Neely, Geissler, Tsakiris and Zepf2009), etc. Propagation of laser beams through plasmas up to several Rayleigh lengths is an important prerequisite for successful realization of all these applications. During the propagation of intense laser beams through plasmas many nonlinear effects such as filamentation of laser beam, self-phase modulation, group velocity dispersion, relativistic self-focusing, etc. come into the picture. It is therefore essential to investigate some of these effects for the in-depth understanding of laser–plasma interaction physics.
The inertial confinement fusion programs led to construction of lasers capable of reaching intensities over the range 1018–1020 W/cm2. When such a highly intense laser beam propagates through the plasma, the quiver velocity of plasma electrons becomes comparable to that of light in the vacuum, causing significant increase in their mass. Owing to the spatial intensity distribution of the laser beam along its wavefront, electrons will experience mass change according to their radial position. The mass change will translate into modification of dielectric properties of plasma due to which the plasma behave like a convex lens leading to self-focusing of the laser beam.
Harmonic generation of electromagnetic radiations in the laser-produced plasmas has become an important field of research due to its number of applications. The process of higher harmonic generation has strong influence on the nature of propagation of laser beams through plasmas. It allows the penetration of laser power to overdense regions and hence is a promising diagnostic tool for obtaining information of plasma parameters such as local electron density, electrical conductivity, opacity, expansion velocity, as reviewed by Teubner and Gibbon (Reference Teubner and Gibbon2009). Harmonic generation can also be used to detect the presence of large electrical and magnetic fields, plasma waves, and the electron transport inside the target with the help of interferometry or absorption spectroscopy. The second-harmonic generation is used to track the passage of high-intensity laser pulses through underdense plasma targets and also provides information about linear mode conversion of the laser beam into plasma wave near the critical layer (Stamper et al., Reference Stamper, Lehmberg, Schmitt, Herbst, Young, Gardner and Obenshain1985). Owing to their high penetrating power, harmonic radiations also find applications in material and biological imaging.
Being already in an ionized state, the plasma is capable of handling very high electric fields and hence, offers a promising medium for producing higher harmonic radiations. There are a number of mechanisms through which one can generate higher harmonics of laser beams in plasmas. These mechanisms include resonance absorption (Erokhin et al., Reference Erokhin, Zakharov and Moiseev1969), parametric instabilities (Bobin, Reference Bobin1985), transverse density gradients associated with light filaments (Stamper et al., Reference Stamper, Lehmberg, Schmitt, Herbst, Young, Gardner and Obenshain1985), ionization fronts (Brunel, Reference Brunel1990), and photon acceleration (Wilks et al., Reference Wilks, Dawson, Mori, Katsouleas and Jones1989), through plasma wave excitation (Sodha et al., Reference Sodha, Sharma, Tewari, Sharma and Kaushik1978; Parashar & Pandey, Reference Parashar and Pandey1992; Singh & Walia, Reference Singh and Walia2011a, Reference Singh and Waliab). In the case of second-harmonic generation, the main mechanism is excitation of the electron plasma wave at pump frequency that interacts with the pump beam to produce its second harmonics.
Harmonic generation in the laser–plasma interaction has been investigated extensively both experimentally as well as theoretically by a number of workers (Kant et al., Reference Kant and Sharma2004a, Reference Kant and Sharmab, Reference Kant, Gupta and Suk2011, Reference Kant, Gupta and Suk2012; Singh & Gupta, Reference Singh and Gupta2015; Verma et al., Reference Verma, Agrawal and Jha2015). Burnett et al. (Reference Burnett, Baldis, Richardson and Enright1977) observed harmonics up to 11th from planar solid targets. Carman et al. (Reference Carman, Forslund and Kindel1981a) observed harmonic orders up to 27, and then 49 in a second experiment (Carman et al., Reference Carman, Rhodes and Benjamin1981b). Hora and Ghatak (Reference Hora and Ghatak1985) derived and evaluated the second-harmonic resonance for perpendicular incidence at four times the critical density. Kant et al. (Reference Kant and Sharma2004a, Reference Kant and Sharmab) investigated the second-harmonic generation of short laser pulse in the plasma by taking into consideration the effect of pulse slippage. Kaur et al. (Reference Kaur, Sharma and Salih2009) investigated the resonant second-harmonic generation of Gaussian laser beam in collisional magnetoplasma. Agarwal et al. (Reference Agarwal, Pandey and Sharma2001) studied the resonant second-harmonic generation of a millimeter wave in plasma in the presence of magnetic wiggler. The wiggler provides an additional momentum for the generation of harmonic photon. Singh et al. investigated the effect of self-focusing of the Gaussian laser beam on second-harmonic generation in collisional (Singh & Walia, Reference Singh and Walia2011a), collisionless (Singh & Walia, Reference Singh and Walia2011b), and relativistic (Singh & Walia, Reference Singh and Walia2013) plasmas using the moment theory approach (Lam et al., Reference Lam, Lippmann and Tappert1975, Reference Lam, Lippmann and Tappert1977). Jha & Aggarwal (Reference Jha and Aggarwal2014) investigated the second-harmonic generation of p-polarized laser beam in underdense plasma.
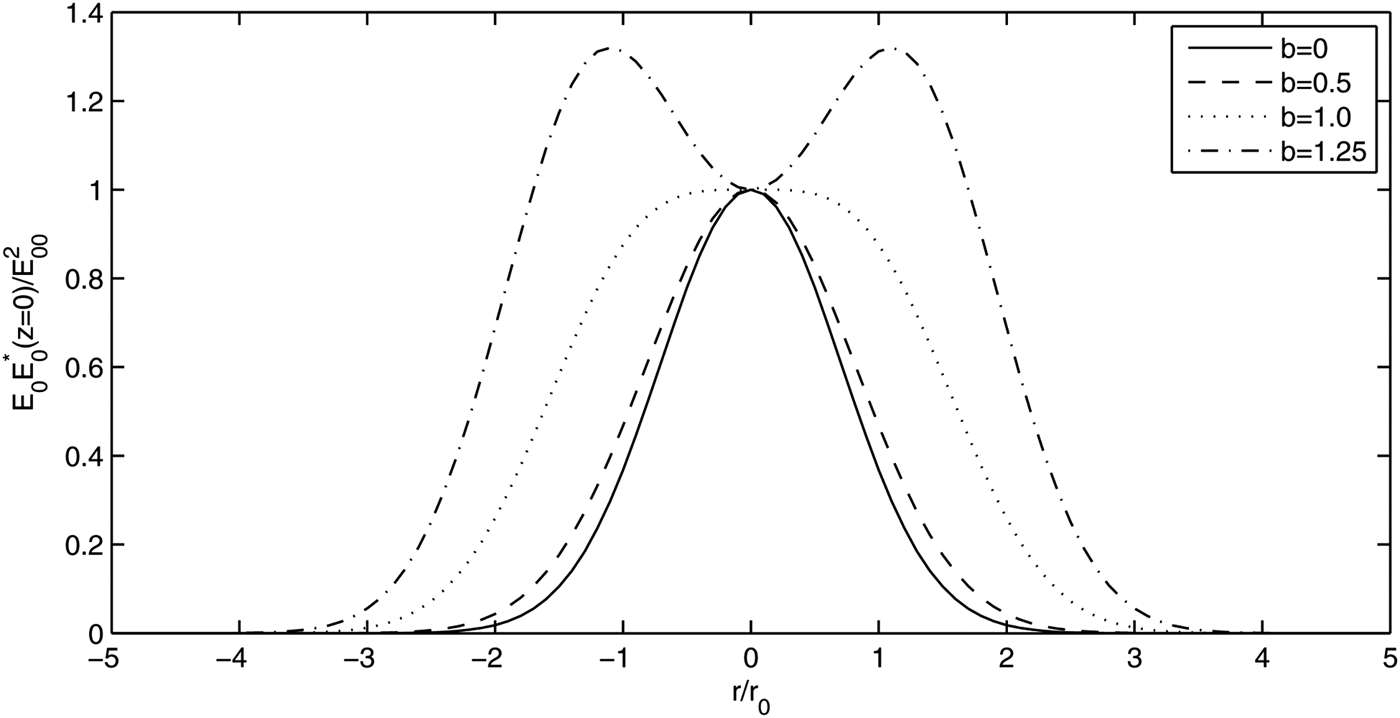
Laser beams with different intensity profiles behave differently in plasmas (Nanda et al., Reference Nanda, Kant and Wani2013). Literature review reveals the fact that most of the theoretical investigations on second-harmonic generation have been carried out under the assumption of uniform laser beam or laser beams having Gaussian distribution of intensity along their wavefronts. In contrast to this picture, a new class of laser beams known as cosh-Gaussian (ChG) laser beams has become the center of attraction to researchers because these beams possess high-power and low divergence in comparison to Gaussian beams. Recently in some publications (Patil et al., Reference Patil, Takale, Navare, Fulari and Dongare2012; Nanda & Kant, Reference Nanda and Kant2014), self-focusing of ChG laser beams has been reported with the help of the paraxial theory. The paraxial theory being local in character overemphasizes the field close to the beam axis. In ChG laser beams, most of the energy is concentrated in the off-axial region of wavefront as compared to the axial region. Moreover, for decentered parameter b > 1 of the ChG laser beam, maximum intensity appears in the outer lobes of the wavefront as compared to the intensity on the axis of the laser beam (cf. Fig. 1). In view of this, it is not appropriate to the Taylor expand nonlinear part of the dielectric function about the axis of ChG laser beam. To overcome this major drawback the moment theory has been used for the analysis of propagation characteristics of ChG laser beam in which the entire nonlinear part of the dielectric function is taken into consideration. The aim of this paper is to investigate, for the first time, the effect of relativistic self-focusing of the ChG laser beam in plasma and its effect on the second-harmonic generation.
Fig. 1. Variation of the normalized intensity 
$\left( {{E_0}.E_0^{\ast} {\vert_{z = 0}}/E_{00}^2} \right)$ with normalized radial distance r/r 0 for different values of b viz. b = 0, 0.5, 1.0, 1.25
The systematic organization of this paper is as follows:
In Section 2, the differential equation describing the evolution of spot size of the laser beam with distance of propagation has been derived. In Section 3, the conditions for uniform wave-guide propagation of the laser beam have been obtained. Section 4 describes the generation of electron plasma wave (EPW) at pump frequency, and in Section 5 the equation for conversion efficiency of the second harmonics has been obtained. Lastly in Section 6, the detailed discussion of the results obtained has been presented.
2. EVOLUTION OF SPOT SIZE OF LASER BEAM
Consider the propagation of an intense, circularly polarized laser beam having an electric field vector
$${\bf E}(r,z,t) = {E_0}(r,z){\kern 1pt} {e^{\iota ({{\rm \omega} _0}t - {k_0}z)}}({{\bf e}_x} + \iota {{\bf e}_y})$$through an underdense plasma having the dielectric constant
$${\rm \epsilon} = 1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2}},$$where ex and ey are the unit vectors along the x- and y-axes, respectively, E 0(r,z) is the slowly varying complex amplitude of the electric field of the laser beam and
$${\rm \omega} _{\rm p}^2 = \displaystyle{{4{\rm \pi} {e^2}{n_0}} \over m}$$is the plasma frequency in the presence of laser beam; n 0 is the electron density; e and m, respectively, are the charge and effective mass of the electron.
Owing to the circular polarization of the field of laser beam, the plasma electrons move along the circular orbits with frequency ω0 and due to high field associated with the laser beam the quiver speed of the electrons becomes comparable to that of light in the vacuum. Hence, the effective mass m of the electrons in Eq. (3) gets replaced by m 0γ, where m 0 is the rest mass of the electrons and γ is the relativistic Lorentz factor. Following Akhiezer and Polovin (Reference Akhiezer and Polovin1956), at equilibrium
$$ - e{E_0} = mv{{\rm \omega }_0}$$from which we get
$${\rm \gamma} = (1 + {\rm \beta} {E_0}E_0^{\ast} {)^{1/2}},$$where
$${\rm \beta} = \displaystyle{{{e^2}} \over {m_0^2 {c^2}{\rm \omega} _0^2}} $$is the coefficient of the relativistic nonlinearity. Hence, the effective dielectric function of the plasma can be written as
$${\rm \epsilon} = 1 - \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} _0^2}} {(1 + {\rm \beta} {E_0}E_0^{\ast} )^{ - 1/2}},$$where
$${\rm \omega} _{{\rm p}0}^2 = \displaystyle{{4{\rm \pi} {e^2}{n_0}} \over {{m_0}}}$$is the plasma frequency in the absence of laser beam. Equation (6) can be written as
$${\rm \epsilon} = {{\rm \epsilon} _0} + {\rm \phi} ({E_0}E_0^{\ast} ),$$where
$${{\rm \epsilon} _0} = 1 - \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} _0^2}} $$is the linear part of the dielectric function, and
$${\rm \phi} ({E_0}E_0^{\ast} ) = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} _0^2}} \left( {1 - \displaystyle{1 \over {\rm \gamma}}} \right)$$is the nonlinear dielectric response of the plasma to the field of incident laser beam.
The electric field vector E of the laser beam satisfy the electromagnetic wave equation
$${\nabla ^2}{\bf E} - \nabla (\nabla. {\bf E}) + \displaystyle{{{\rm \omega} _0^2} \over {{c^2}}}{\rm \epsilon} {\bf E} = 0.$$ Even, if E has the longitudinal components, the polarization term 
$\nabla (\nabla. {\bf E})$ of Eq. (11) can be neglected provided 
${c^2}/{\rm \omega} _0^2 \left\vert {(1/{\rm \varepsilon} ){\nabla ^2}\ln {\rm \epsilon}} \right\vert{\rm \ll} 1$. This will be valid if 
${\nabla _ \bot }\left( {(1/{\rm \epsilon }){\nabla _ \bot }{\rm \epsilon }} \right) \ll k_0^2 ,$ that is, the transverse gradient of the dielectric function is smaller as compared with the laser wavelength which implies that either the transverse dielectric variation is weak or the plasma is significantly underdense. We need only to stress that Eq. (11) is the nonlinear wave equation, since ε depends on field amplitude E 0 via Eq. (6). Under this approximation, Eq. (11) can be written as
$$\iota \displaystyle{{d{E_0}} \over {dz}} = \displaystyle{1 \over {2{k_0}}}\nabla _ \bot ^2 {E_0} + \displaystyle{{{k_0}} \over {2{{\rm \varepsilon} _0}}}{\rm \phi} ({E_0}E_0^{\ast} ){E_0}.$$In deriving Eq. (12), the term d 2E 0/dz 2 has been neglected under the assumption that the wave-amplitude scale length along the longitudinal direction is much larger as compared to the characteristic scale in the transverse direction. Equation (12) is the well-known nonlinear Schrödinger wave equation and possesses a number of conserved quantities due to its symmetry properties. Among them two most important are:
$${I_0} = \int_0^{2{\rm \pi}} \int_0^\infty {E_0}E_0^{\ast} rdrd{\rm \theta,} $$
$${I_2} = \int_0^{2{\rm \pi}} \int_0^\infty \displaystyle{1 \over {2k_0^2}} ( \vert {\nabla _ \bot} {E_0}{ \vert ^2} - F)rdrd{\rm \theta}, $$where
$$F({E_0}E_0^{\ast} ) = \displaystyle{1 \over {2{{\rm \epsilon} _0}}}\int_0^{{E_0}E_0^{\ast}} {\rm \phi} ({E_0}E_0^{\ast} )d({E_0}E_0^{\ast} ).$$The first invariant I 0, which is a consequence of Gauge invariance, is merely a statement of conservation of energy of the laser beam and second invariant I 2 relates the wavefront curvature of the laser beam to plasma nonlinearity.
Now, from the definition of the second-order spatial moment of intensity distribution of the laser beam along its wave front, the mean-square radius of the laser beam is given by
$$\langle {R^2}(z)\rangle = \displaystyle{1 \over {{I_0}}}\int_0^{2{\rm \pi}} \int_0^\infty {r^2}{E_0}E_0^{\ast} rdrd{\rm \theta}. $$Following the procedure of Lam et al. (Reference Lam, Lippmann and Tappert1975, Reference Lam, Lippmann and Tappert1977), we get the following quasi-optic equation governing the evolution of mean-square radius of the laser beam with the distance of propagation.
$$\displaystyle{{{d^2}\langle {R^2}\rangle} \over {d{z^2}}} = \displaystyle{{4{I_2}} \over {{I_0}}} - \displaystyle{4 \over {{I_0}}}\int_0^{2{\rm \pi}} \int_0^\infty Q({E_0}E_0^{\ast} )rdrd{\rm \theta}, $$where
$$Q({E_0}E_0^{\ast} ) = \left[ {\displaystyle{{{E_0}E_0^{\ast} {\rm \phi} ({E_0}E_0^{\ast} )} \over {2{{\rm \epsilon} _0}}} - 2F({E_0}E_0^{\ast} )} \right].$$The intensity distribution of ChG laser beam along its wave front, at the plane of incidence (z = 0) is given by (Lu et al., Reference Lu, Ma and Zhang1999; Konar et al., Reference Konar, Mishra and Jana2007; Patil et al., Reference Patil, Takale, Navare, Fulari and Dongare2012)
$${E_0}E_0^{\ast} = E_{00}^2 {e^{ - {r^2}/r_0^2}} \mathop {\cosh} \nolimits^2 \left( {\displaystyle{b \over {{r_0}}}r} \right),$$where r 0 is the spot size of the laser beam at z = 0, E 00 is the axial amplitude of the electric field of the laser beam, b/r 0 is the parameter associated with the cosh function, also called Cosh factor. For b = 0, the intensity distribution attains the usual Gaussian distribution. Equation (18) can be written as
$${E_0}E_0^{\ast} = \displaystyle{{{E_{00}}} \over 4}{e^{{{\rm b}^2}}}\left[ {{e^{ - {{\left( {(r/{r_0}) + b} \right)}^2}}} + {e^{ - {{\left( {(r/{r_0}) - b} \right)}^2}}} + 2{e^{ - \left( {({r^2}/r_0^2 ) + {b^2}} \right)}}} \right],$$which implies that the ChG beam can be produced simply in the laboratory by superposition of two decentered Gaussian beams with same spot size and in phase, whose centers are located at the positions (b/2, 0) and (−b/2, 0), respectively.
For z > 0, energy-conserving ansatz for the intensity distribution of ChG laser beam propagating along the z-axis is given by
$${E_0}E_0^{\ast } = \displaystyle{{E_{00}^2 } \over {{\,f^2}}}{e^{ - {r^2}/r_0^2 {\,f^2}}}\mathop {\cosh }\nolimits^2 \left( {\displaystyle{b \over {{r_0}f}}r} \right),$$
where r 0f is the instantaneous spot size of the laser beam. Hence, the function f is termed as the dimensionless beam width parameter which is measure of both axial intensity and spot size of the laser beam. Using Eqs (10), (15), (16), and (19) in Eq. (17) we get the following differential equation governing the evolution of spot size of ChG laser beam with dimensionless distance of propagation 
$\left(\xi = z/{k_0}{r_0^2}\right)$.
$$\eqalign{\displaystyle{{{d^2}f} \over {d{\xi ^2}}} + \displaystyle{1 \over f}{\left( {\displaystyle{{df} \over {d\xi}}} \right)^2} & = \left( {\displaystyle{{1 + {e^{ - {b^2}}}(1 - {b^2})} \over {2(1 + {b^2})}}} \right)\displaystyle{1 \over {{\,f^3}}} - \left( {\displaystyle{{{e^{ - {b^2}}}} \over {1 + {b^2}}}} \right) \cr & \quad\times \left( {\displaystyle{{{\rm \beta} E_{00}^2} \over {{\,f^2}}}} \right) \left( {\displaystyle{{{\rm \omega} _{{\rm p}0}^2 r_0^2} \over {{c^2}}}} \right) ({T_1} - b{T_2}),}$$where
$${T_1} = \int_0^\infty {x^3}{\left\{ {1 + \displaystyle{{{\rm \beta} E_{00}^2} \over {{\,f^2}}}{e^{ - {x^2}}}{\rm cos}{{\rm h}^2}(bx)} \right\}^{ - 3/2}}{e^{ - 2{x^2}}}{\rm cos}{{\rm h}^4}(bx)dr,$$
$${T_2} = \int_0^\infty {x^2}{e^{ - 2{x^2}}}{\left\{ {1 + \displaystyle{{{\rm \beta} E_{00}^2} \over {{\,f^2}}}{e^{ - {x^2}}}{\rm cos}{{\rm h}^2}(bx)} \right\}^{ - 3/2}}{\rm cos}{{\rm h}^3}(bx){\rm sinh}(bx)dr,$$
$$x = \displaystyle{r \over {{r_0}f}}.$$For an initially plane wavefront, Eq. (20) is subjected to the boundary conditions f = 1 and df/dξ = 0 at ξ = 0.
3. UNIFORM WAVEGUIDE PROPAGATION
For an initially plane wavefront f = 1 and df/dξ = 0 at ξ = 0, the condition d 2f/dξ2 = 0 leads to the propagation of the ChG beam in uniform waveguide mode. The condition under which this occurs is termed as critical condition. By substituting df/dξ = d 2f/dξ2 = 0 into Eq. (20), we obtain the following relation between the dimensionless equilibrium beam width r e = ωp0r 0/c and critical beam intensity 
${\rm \beta} E_{00}^2 $$
$${r_{\rm e}} = {\left( {\displaystyle{{1 - {b^2} + {e^{{b^2}}}} \over {4{\rm \beta }E_{00}^2 }}} \right)^{1/2}}\displaystyle{1 \over {\sqrt {T_1^{\prime} - bT_2^{\prime} } }}, $$where
$${r_{\rm e}} = \displaystyle{{{{\rm \omega} _{{\rm p}0}}{r_0}} \over c},$$
$$T_1^{\prime} = \int_0^\infty {x^3}{\left\{ {1 + {\rm \beta }E_{00}^2 {e^{ - {x^2}}}{\rm cos}{{\rm h}^2}(bx)} \right\}^{ - 3/2}}{e^{ - 2{x^2}}}{\rm cos}{{\rm h}^4}(bx)dr,$$
$$T_2{\prime} = \int_0^\infty {x^2}{e^{ - 2{x^2}}}{\left\{ {1 + {\rm \beta }E_{00}^2 {e^{ - {x^2}}}{\rm cos}{{\rm h}^2}(bx)} \right\}^{ - 3/2}}{\rm cos}{{\rm h}^3}(bx){\rm sinh}(bx)dr.$$ Equation (21) can be depicted on the (
${\rm \beta} E_{00}^2 $, r e) plane and is generally referred to as the critical power curve or, simply the critical curve. If the initial value of 
${\rm \beta} E_{00}^2 $ and r e of the laser beam are such that the point (
${\rm \beta} E_{00}^2 $, r e) lies on the critical curve, then the value of d 2f/dξ2 will vanish at ξ = 0. Since the initial value of df/dξ (in the case of plane wavefront) is zero, the value of df/dξ continues to be zero as the beam propagates through the plasma. Hence, the value of f, which is unity (=1) at ξ = 0, will remain unchanged. The beam thus propagates without any change in its width. This regime is known as uniform waveguide propagation.
If the point (
${\rm \beta} E_{00}^2 $, r e), corresponding to initial normalized beam intensity and beam radius, lies below the critical curve, then d 2f/dξ2 >0 and hence the spot size of the laser beam increases as it propagates through the plasma; whereas if the point (
${\rm \beta} E_{00}^2 $, r e) lie above the critical curve, then d 2f/dξ2 <0 and hence the spot size of the laser beam decreases with the distance of propagation.
4. PLASMA WAVE GENERATION
In the dynamics of excitation of EPW, it must be mentioned here that the contribution of ions is negligible because they only provide a static positive background, that is, only plasma electrons are responsible for the excitation of EPW. The background plasma density is modified via relativistic electron mass variation. Therefore, the amplitude of the EPW that depends on the background electron density gets strongly coupled to the laser beam.
The generated EPW is governed by the equation of continuity, equation of motion, equation of state, and Poisson's equation
$$\displaystyle{{\partial n} \over {\partial t}} + \nabla (nv) = 0,$$
$$\displaystyle{{\partial (nv)} \over {\partial t}} + \nabla (n{v^2}) + \displaystyle{1 \over m}\nabla {P_{\rm e}} + \displaystyle{{neE} \over m} = 0,$$
$$\displaystyle{{{P_{\rm e}}} \over {{n^3}}} = {\rm constant,}$$
$$\nabla E = 4{\rm \pi} (Z{N_{{\rm 0i}}} - n)e,$$where n is the total electron density, that is, sum of the equilibrium plasma density and density perturbation associated with EPW, E is the sum of electric field vectors of the laser beam and self-consistent field associated with plasma wave, v is the velocity of electron fluid, P e is the hydrodynamic pressure of the electron fluid, Z is the charge state of ions. Using the linear perturbation theory it can be shown that the plasma wave is governed by
$$ - {\rm \omega }_0^2 {n^{\prime}} + v_{{\rm th}}^2 {\nabla ^2}{n^{\prime}} + {\rm \omega }_{\rm p}^2 {n^{\prime}} = \displaystyle{e \over m}{n_0}\nabla {E_0},$$
where 
$v_{{\rm th}}^2 = 2{K_0}{T_0}/{m_0}$ is the thermal velocity of electrons and n′ is the density perturbation associated with the plasma wave.
Taking
$${n^{\prime}} = {n_1}{e^{\iota ({k_0}z - {{\rm \omega} _0}t)}},$$we get the following source term for the second-harmonic generation
$$\eqalign{{n_1} & = \displaystyle{{e{n_0}} \over m}\displaystyle{{{E_{00}}} \over f}\displaystyle{{{e^{ - {r^2}/2r_0^2 {\,f^2}}}} \over {({\rm \omega} _0^2 - k_0^2 v_{{\rm th}}^2 - {\rm \omega} _{\rm p}^2 )}} \cr &\quad \times \left\{ {\displaystyle{r \over {r_0^2 {\,f^2}}} - \displaystyle{b \over {{r_0}f}}{\rm tanh}\left( {\displaystyle{b \over {{r_0}f}}r} \right)} \right\}{\rm cos}{{\rm h}^2}\left( {\displaystyle{b \over {{r_0}f}}r} \right),}$$where n 1(r, z) is the amplitude of the plasma wave.
5. SECOND-HARMONIC GENERATION
The wave equation governing the electric field E 2 of the second harmonic is given by (Singh et al., Reference Singh and Walia2011a, Reference Singh and Waliab, Reference Singh and Walia2013)
$${\nabla ^2}{{\bf E}_2} + \displaystyle{{{\rm \omega} _2^2} \over {{c^2}}}{{\rm \epsilon} _2}({{\rm \omega} _2}){{\bf E}_2} = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{c^2}}}\displaystyle{{{n_1}} \over {{n_0}}}{{\bf E}_0},$$where ω2 = 2ω0 is the frequency of the second harmonic and ε2 is the effective dielectric constant at second-harmonic frequency. From the above equation we get the expression for field E 2 of second harmonic as
$${E_2} = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{c^2}}}\displaystyle{{{n_1}} \over {{n_0}}}\displaystyle{{{E_0}} \over {(k_2^2 - 4k_0^2 )}}.$$Now the second-harmonic power can be written as
$${P_2} = \int_0^{2{\rm \pi}} \int_0^\infty {E_2}E_2^{\ast} rdrd{\rm \theta} $$also the power of the initial pump beam is given by
$${P_0} = \int_0^{2{\rm \pi}} \int_0^\infty {E_0}E_0^{\ast} rdrd{\rm \theta}. $$Defining the second-harmonic yield as
$${Y_2} = \displaystyle{{{P_2}} \over {{P_0}}},$$
$${Y_2} = \displaystyle{2 \over 9}\left( {\displaystyle{{{\rm \omega} _0^2 r_0^2} \over {{c^2}}}} \right)\left( {\displaystyle{{{\rm \beta} E_{00}^2} \over {{\,f^4}}}} \right){e^{ - {b^2}}}H,$$where
$$H = \int_0^\infty {{e^{ - 2{x^2}}}} \displaystyle{{{{(x - b{\rm tanh}(bx))}^2}{\rm cos}{{\rm h}^4}(bx)} \over \matrix{\left\{ {\displaystyle{{\omega _0^2 r_0^2 } \over {{c^2}}} - {{\rm \epsilon }_0}\displaystyle{{v_{{\rm th}}^2 } \over {{c^2}}}\displaystyle{{\omega _0^2 r_0^2 } \over {{c^2}}} - \displaystyle{{\omega _{{\rm p}0}^2 r_0^2 } \over {{c^2}}}} \right. \hfill \cr\times {\left. {\left( {1 + \displaystyle{{\beta E_{00}^2 } \over {{\,f^2}}}{e^{ - {x^2}}}{\rm cos}{{\rm h}^2}(bx)} \right)^{-1/2}} \right\}^2}\hfill} }dx. $$6. DISCUSSION
Equations (20) and (32) respectively describe the variation of dimensionless beam width parameter f and the conversion efficiency η2% of second harmonics of an intense ChG laser beam with dimensionless distance of propagation ξ, in an underdense plasma. These equations have been solved numerically for the following critical set of laser–plasma parameters:
ω0 = 1.78 × 1015 rad/s, λ = 1.06 µm, r 0 = µm, and equilibrium plasma temperature T 0 = 106 K to analyze the effect of decentered parameter, intensity of laser beam as well as plasma density on relativistic self-focusing, and further its effect on conversion efficiency η2% of second harmonics.
It is further mentioned that the right-hand side of Eq. (20) contains several terms, each representing some physical mechanism responsible for the evolution of beam during its propagation through plasma. First term on the right-hand side has its origin in the Laplacian (
$\nabla _ \bot ^2 $) in the nonlinear Schrödinger wave Eq. (12) and is responsible for diffraction divergence of the laser beam as it propagates through the medium, whereas the second term that arises under the effect of relativistic nonlinearity, is responsible for the convergence of the beam due to nonlinear refraction. This nonlinear term opposes the phenomenon of diffraction and depending on its numerical value as compared with the diffractive term, one can observe focusing/defocusing of the laser beam. It is the relative competition of various terms that ultimately determines the fate of spot size of the laser beam.
Figure 1 illustrates the normalized intensity profile 
$({E_0}.E_0^{\ast} {\vert_{z = 0}}/E_{00}^2 )$ versus r/r 0 of ChG laser beam for different values of decentered parameter b. For b = 0, the intensity profile of the ChG beam is similar to the Gaussian distribution and with increasing b (=0.5, 1.0) the profile becomes flat-topped. Moreover, with further increase in b (=1.25) a central dip appears in the intensity profile. Hence, it is observed from Figure 1 that with a suitable choice of decentered parameter b the intensity profile of ChG beam resembles to that of Gaussian, flat-topped, and dark hollow Gaussian laser beams.
Figure 2 illustrates normalized intensity of the ChG laser beam with normalized distance of propagation ξ and normalized radial distance r/r 0 for different values of decentered parameter b = 0, 0.50, 1.0, 1.50, respectively, in the absence of nonlinear refraction. The plots in Figure 2 depict that with an increase in the value of decentered parameter b the vacuum diffraction of the ChG laser beam decreases. This is solely due to the fact that for a given spot size r 0, the ChG laser beam with larger value of b possesses larger root mean square (r.m.s) beam width and hence diffract less, which supports the results of Konar et al. (Reference Konar, Mishra and Jana2007).
Fig. 2. Variation of the normalized laser beam intensity with normalized distance of propagation ξ and radial distance r/r 0, in the absence of nonlinear refraction, at different values of decentered parameter, (a) b = 0, (b) b = 0.50, (c) b = 1.0, and (d) b = 1.50, respectively.
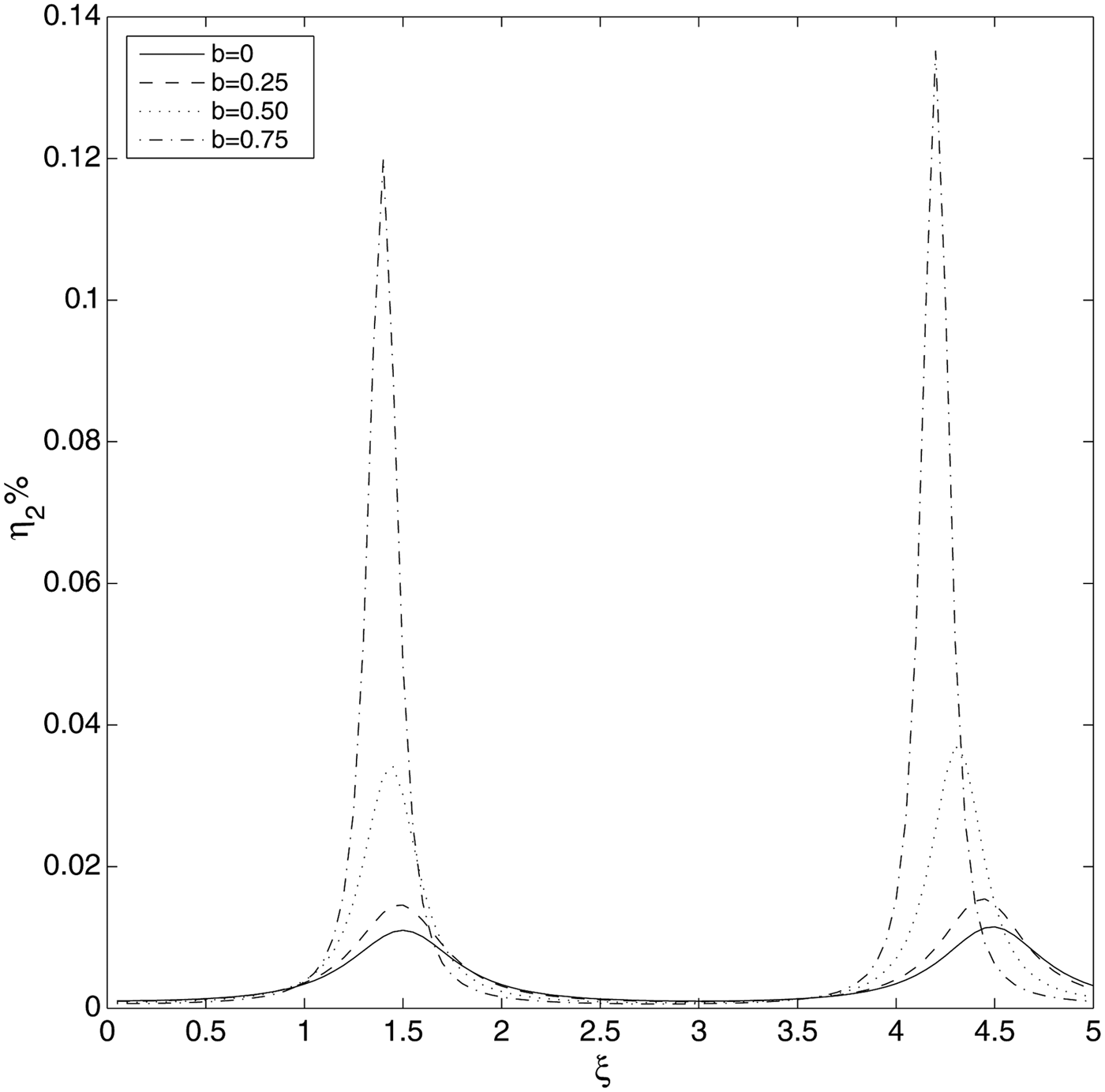
Figures 3 and 4 show normalized intensity of the ChG laser beam in the plasma with normalized distance of propagation ξ and normalized radial distance r/r 0. It is observed that as the laser beam propagates through the plasma it gets filamented due to laser–plasma coupling through relativistic nonlinearity of electron mass. Figure 3 shows the generated filaments of the laser beam by taking fixed values of plasma density 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12.0$, laser intensity 
${\rm \beta} E_{00}^2 = 3.0,$ and varying decentered parameter b = 0, 0.25, 0.50, 0.75. The plots in Figure 3(a)–(d) depict that an increase in the value of decentered parameter b from 0 toward 1 leads to enhanced localization of the filaments, that is, the generated filaments become more and more intense with an increase in the value of decentered parameter. This is due to the fact that for 0 < b < 1 the intensity profile of the ChG laser beam resembles to that of flat-topped beam (cf. Fig. 1) as a result of which nonlinear refraction of most of the transverse part of the wavefront of the laser beam opposes the diffraction divergence. Hence, an increase in the value of b from 0 to 1 leads to localization of laser filaments. Hence, it is concluded from the present analysis that as we increase the value of decentered parameter for 0 ≤ b < 1 the refractive term in Eq. (20) dominates the diffractive term and the refractive term is more pronounced in the case of flat-topped laser beams as compared to that of Gaussian beams. Figure 4 shows the generated filaments of the laser beam by taking fixed values of plasma density 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12.0$, laser intensity 
${\rm \beta} E_{00}^2 = 3.0,$ and varying decentered parameter b = 1.0, 1.25, 1.50, 1.75. The plots in Figures 4(a)–(d) depict that for b > 1, with an increase in the value of b localization of the filaments decreases. It is observed from Figure 4 that as the value of decentered parameter b increases from 1 onwards up to 1.50, the diffractive term relatively dominates the refractive term but still maintaining the focusing character of the laser beam. As the value of b becomes more than 1.50 (or b > 1.50) the diffractive term completely dominates over the refractive term leading to complete defocusing of the laser beam.
Fig. 3. Variation of the normalized laser beam intensity with normalized distance of propagation ξ and radial distance r/r 0, keeping (ωp0r 0/c)2 = 12, 
${\rm \beta} E_{00}^2 = 3$ fixed and at different values of decentered parameter, (a) b = 0, (b) b = 0.25, (c) b = 0.50, (d) b = 0.75, respectively.
Fig. 4. Variation of the normalized laser beam intensity with normalized distance of propagation ξ and radial distance r/r 0, keeping (ωp0r 0/c)2 = 12, 
${\rm \beta} E_{00}^2 = 3$ fixed and at different values of decentered parameter, (a) b = 1.0, (b) b = 1.25, (c) b = 1.50, and (d) b = 1.75, respectively.
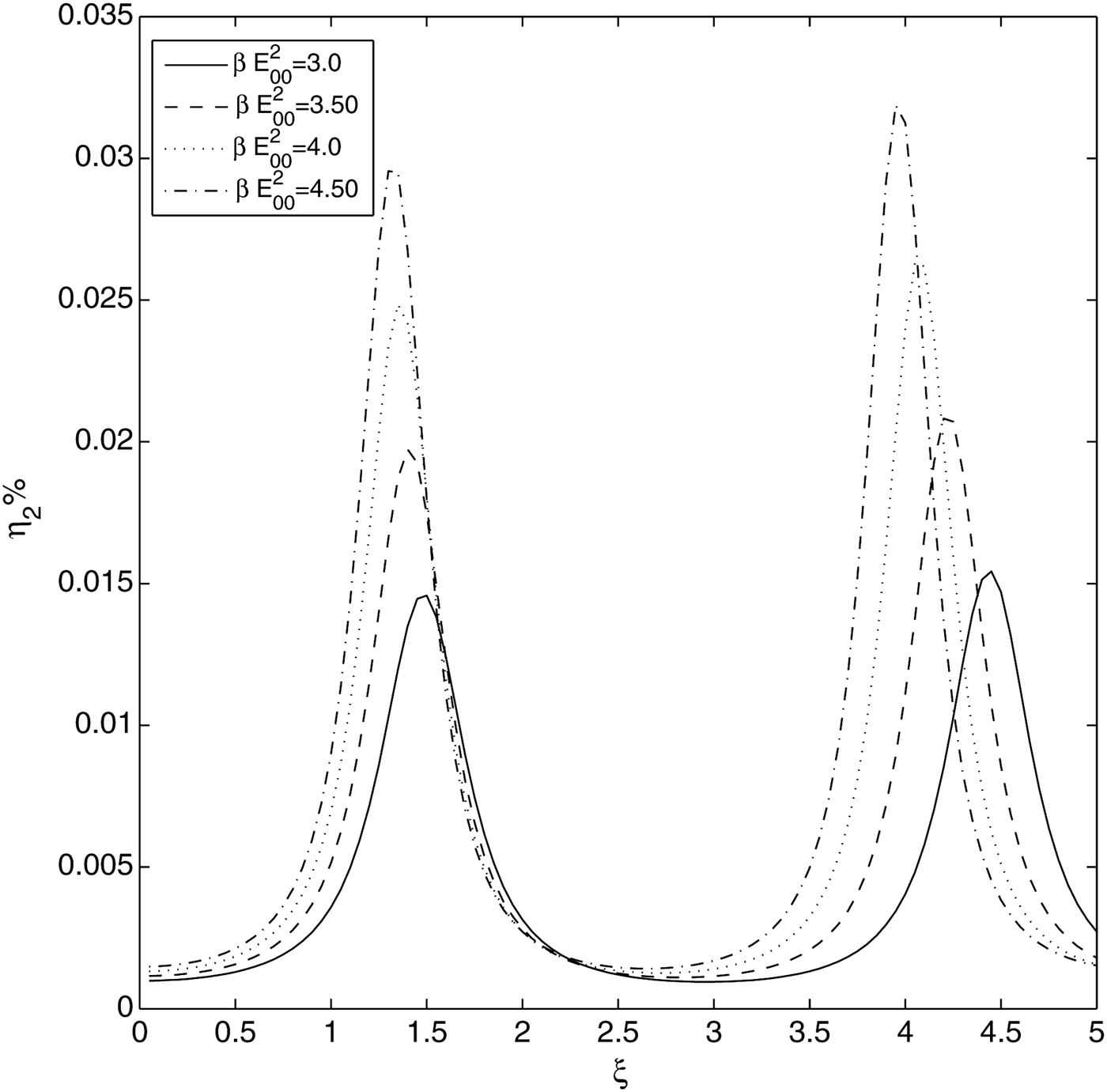
Figure 5 shows the normalized intensity of the ChG laser beam in the plasma with normalized distance of propagation ξ and normalized radial distance r/r 0 for fixed values of decentered parameter b = 0.25, plasma density 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12,$ and at varying values of laser intensity 
${\rm \beta} E_{00}^2 = 3.0,3.50,4.0,4.50$. It is observed from Figure 5 that an increase in the laser intensity leads to enhanced intensity of the laser filaments. This is due to the fact that with an increase in the laser intensity the relativistic nonlinearity of electron mass also increases which leads to enhanced focusing of the laser beam.
Fig. 5. Variation of the normalized laser beam intensity with normalized distance of propagation ξ and radial distance r/r 0, keeping (ωp0r 0/c)2 = 12, b = 0.25 fixed and at different laser beam intensities, (a) 
${\rm \beta} E_{00}^2 = 3.0$, (b) 
${\rm \beta} E_{00}^2 = 3.50$, (c) 
${\rm \beta} E_{00}^2 = 4.0$, and (d) 
${\rm \beta} E_{00}^2 = 4.50$, respectively.
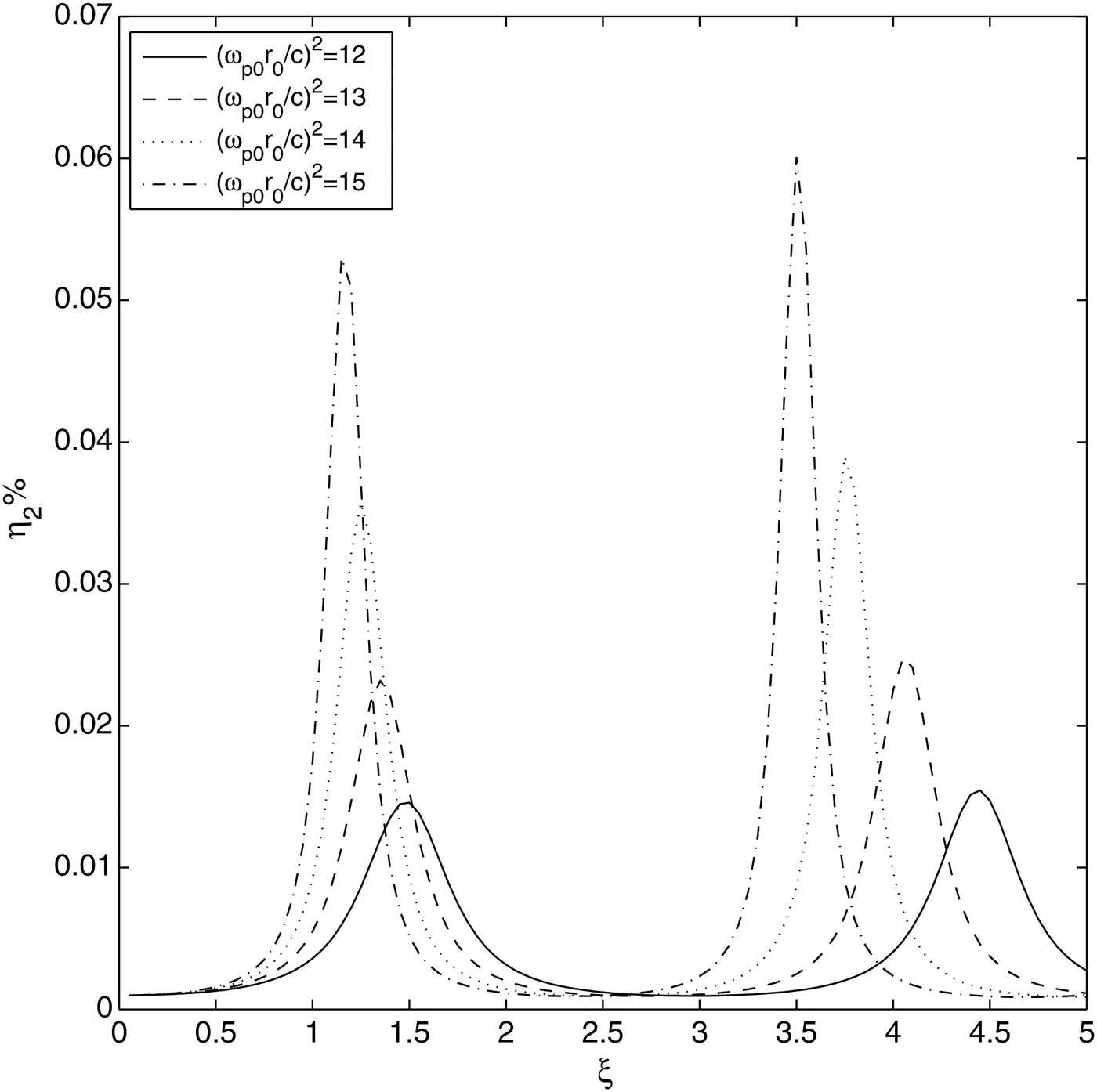
Figure 6 shows the normalized intensity of the ChG laser beam in the plasma with normalized distance of propagation ξ and normalized radial distance r/r 0 for fixed values of decentered parameter b = 0.25, laser intensity 
${\rm \beta} E_{00}^2 = 3.0,$ and at varying values of plasma density 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12,13,14,15$. It is observed from Figure 6 that an increase in the plasma density leads to increase in the intensity of laser filaments. This is due to the fact that with an increase in plasma density the number of electrons contributing to self-focusing of the laser beam also increases.
Fig. 6. Variation of the normalized laser beam intensity with normalized distance of propagation ξ and radial distance r/r 0, keeping 
${\rm \beta} E_{00}^2 = 3.0$, b = 0.25 fixed and at different plasma densities, (a) (ωp0r 0/c)2 = 12.0, (b) (ωp0r 0/c)2 = 13.0, (c) (ωp0r 0/c)2 = 14.0, and (d) (ωp0r 0/c)2 = 15.0, respectively.
Figure 7 describes the variation of equilibrium beam width r e against the normalized intensity 
${\rm \beta} E_{00}^2 $ for different values of decentered parameter b viz. b = 0, 0.50, 0.75, 1.0. It is observed from Figure 7 that for uniform waveguide propagation of ChG laser beam corresponding to the fixed value of equilibrium beam radius r e, low-power lasers are required as we increase the value of decentered parameter for 0 ≤ b < 1. So it is obvious from Figure 7 that highest laser power is required for the Gaussian laser beam to propagate in the uniform waveguide mode. Therefore, it is concluded that the flat-topped laser beams are more suitable for propagation in uniform waveguide mode at lowest laser power.
Fig. 7. Variation of the equilibrium beam width r e against the normalized intensity 
${\rm \beta} E_{00}^2 $ for different values of decentered parameter b viz. b = 0, 0.50, 0.75, 1.0.
Figures 8 and 9 describe the variation of the second-harmonic conversion efficiency η2% against normalized distance of propagation ξ for fixed laser intensity 
${\rm \beta} E_{00}^2 = 3.0$, plasma density 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12.0,$ and at varying values of the decentered parameter b = 0, 0.25, 0.50, 0.75 and 1.0, 1.25, 1.50, 1.75, respectively. It is seen that the conversion efficiency η2% of the second harmonic oscillates as the laser beam propagates through the plasma and maximum conversion efficiency occurs at the focal regions. This is due to the fact that intensity gradients are very steep in the focal regions and hence, the plasma wave gets localized in these regions and consequently, the second-harmonic conversion efficiency is also more in these regions. The plots in Figures 8 and 9 depict that as the value of decentered parameter b increases from 0 to 1 there is substantial increase in the conversion efficiency η2% of the second harmonics and with further increase of b from 1 onwards there is decrease in the conversion efficiency. This is due to the sensitiveness of conversion efficiency to the extent of localization of laser filaments. Greater is the localization of laser filaments, higher is the transverse density gradient in the focal region and hence higher is the harmonic yield and vice versa.
Fig. 8. Variation of the second-harmonic conversion efficiency η2% against the normalized distance of propagation ξ for different values of decentered parameter b viz. b = 0, 0.25, 0.50, 0.75 at fixed laser intensity 
${\rm \beta} E_{00}^2 = 3.0$ and plasma density (ωp0r 0/c)2 = 12.
Fig. 9. Variation of the second-harmonic conversion efficiency η2% against the normalized distance of propagation ξ for different values of decentered parameter b viz. b = 1.0, 1.25, 1.50, 1.75 at fixed laser intensity 
${\rm \beta} E_{00}^2 = 3.0$ and plasma density (ωp0r 0/c)2 = 12.
Figure 10 describes the variation of the second-harmonic conversion efficiency η2% against the normalized distance of propagation ξ for fixed values of decentered parameter b = 0.25, plasma density 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12.0,$ and at varying values of laser intensity 
${\rm \beta} E_{00}^2 = 3.0,3.50,4.0,4.50$. It is observed that with an increase in the intensity of the laser beam there is an increase in the conversion efficiency η2%. This is due to the fact that the increase in the intensity of the incident laser beam enhances the intensity of laser filaments which further enhances the second-harmonic conversion efficiency η2%.
Fig. 10. Variation of the second-harmonic conversion efficiency η2% against the normalized distance of propagation ξ for different laser intensities 
${\rm \beta} E_{00}^2 = 3.0,3.50,4.0,4.50$ at fixed decentered parameter b = 0.25 and plasma density (ωp0r 0/c)2 = 12.
Figure 11 describes the variation of the second-harmonic conversion efficiency η2% against the normalized distance of propagation ξ for fixed values of decentered parameter b = 0.25, laser intensity 
${\rm \beta} E_{00}^2 = 3.0,$ and at varying values of plasma density viz. 
${\rm \omega} _{{\rm p}0}^2 r_0^2 /{c^2} = 12,13,14,15$. It is observed that with an increase in the plasma density there is an increase in the second-harmonic conversion efficiency η2%. This is due to the fact that an increase in plasma density leads to the enhanced intensity of laser filaments and therefore the transverse density gradient becomes very steep in the focal region, which leads to an increase in the amplitude of the plasma wave and hence the conversion efficiency η2%.
Fig. 11. Variation of the second-harmonic conversion efficiency η2% against the normalized distance of propagation ξ for different plasma densities (ωp0r 0/c)2 = 12.0, 13.0, 14.0, 15.0 at fixed decentered parameter b = 0.25 and laser intensity 
${\rm \beta} E_{00}^2 = 3.0$.
7. CONCLUSIONS
The present work delineates the effect of relativistic self-focusing of an intense ChG laser beam on the second-harmonic generation in underdense plasmas. Following important conclusions have been drawn from the present analysis:
• With an increase in decentered parameter for 0 ≤ b ≤ 1, there is an increase in extent of self-focusing of the laser beam as well as of harmonic yield.
• With an increase in decentered parameter for b > 1, there is a decrease in extent of self-focusing of the laser beam as well as of harmonic yield.
These results are relevant to various contexts of laser–plasma interaction physics. Besides its obvious relevance to the inertial confinement fusion, these results can also be helpful in other applications requiring laser beams with localized energy. The present results may serve as a guide for both experimental and theoretical investigations of laser–plasma interactions.
ACKNOWLEDGMENT
The authors are grateful to the Ministry of Human Resources and Development of India for providing financial assistance for carrying out this work.
