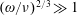1 Introduction
The Kennel & Engelmann (Reference Kennel and Engelmann1966) quasilinear operator used to simulate radio frequency (rf) heating and current drive in tokamaks has a velocity space diffusivity proportional to a delta function at the wave–particle resonances associated with Landau and Doppler shifts. To deal with this awkward feature the quasilinear operator is normally assumed to be valid in tokamak geometry so that its transit or bounce average may be employed (Eriksson et al. Reference Eriksson, Mantsinen, Hellsten and Carlsson1999; Jaeger et al. Reference Jaeger, Harvey, Berry, Myra, Dumont, Phillips, Smithe, Barrett, Batchelor and Bonoli2006; Lee et al. Reference Lee, Wright, Bertelli, Jaeger, Valeo, Harvey and Bonoli2017), even though it was originally derived in a constant magnetic field. Recently a rigorous high frequency gyrokinetic derivation of the quasilinear operator in tokamak geometry (Catto, Lee & Ram Reference Catto, Lee and Ram2017) has been performed to provide further justification for this approach even when magnetic drifts must be retained. Nevertheless, in the absence of transit averaging the troublesome delta function, now associated with the magnetic drift as well as Doppler and Landau shifted resonances, remains.
One possible way to remove this singular behaviour is via collisions, which are normally dismissed as unimportant because the wave frequency 
$\unicode[STIX]{x1D714}$ is so large compared to the collision frequency 
$\unicode[STIX]{x1D708}$. However, phenomenological collision models that attempt to decorrelate wave–particle interactions more strongly than a simple Krook model (Catto & Myra Reference Catto and Myra1992; Lamalle Reference Lamalle1997) rely on transit averaging as well as uncorrelated sequential passes through resonance. Here, however, a collisional boundary layer treatment of the resonant particle interactions, as employed by Johnston (Reference Johnston1971) and in more detail by Auerbach (Reference Auerbach1977), is demonstrated to dramatically enhance the role of collisions. The boundary layer procedure increases the effective collision frequency by 
$(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708})^{2/3}\gg 1$, even without recourse to transit averaging. Unlike the steady state applied rf case, these earlier efforts focused on Landau damping and bump on tail stability by allowing an imaginary part in the frequency. They did not consider magnetized plasmas and the quasilinear (QL) operator that is the main focus herein. The collisional boundary layer behaviour is shown to be fully consistent with the delta function approximation, while allowing it to be replaced in the QL operator in a non-singular manner.
The collisional boundary layer procedure considered here provides an estimate of when the rf wave amplitude becomes large enough that a quasilinear treatment of rf begins to fail. As might be expected, the estimate indicates this failure typically does not begin to occur until the unperturbed distribution function becomes appreciably distorted from Maxwellian, suggesting a possible explanation as to why quasilinear theory has been rather successful in describing rf heating and current drive. The failure of QL theory may also indicate the need to more accurately consider the onset of stochastic behaviour if the rf perturbs the resonant particle trajectories in a wider boundary layer as the electric field strength increases (Becoulet, Gambier & Samain Reference Becoulet, Gambier and Samain1991).
In § 2 a streamlined derivation of the quasilinear operator of Kennel & Engelmann (Reference Kennel and Engelmann1966) is presented to introduce notation and clarify the origin of the resonant particle delta function. This derivation is just the constant magnetic field limit of the procedure used in Catto et al. (Reference Catto, Lee and Ram2017). Section 3 resolves the singular behaviour of the resonant particles by performing a collisional boundary layer analysis for the particles participating in the wave–particle interaction. This boundary layer analysis of the linear response properly accounts for the collisional interaction time of the resonant particles with the wave. It is a magnetized plasma variation of the treatments of Johnston (Reference Johnston1971) and Auerbach (Reference Auerbach1977) allowing a Doppler modified Landau resonance for an applied rf wave field. The QL operator of Kennel & Engelmann (Reference Kennel and Engelmann1966) is generalized to retain collisional boundary layer effects so that the delta function no longer appears but the entropy production principle is preserved. The section closes with estimates of the physics associated with the collisional boundary layer interpretation of quasilinear theory. A brief discussion of the results follows in § 4. Justification for using a pitch angle scattering collision operator is presented in appendix A, while appendix B suggests the existence of a collisional boundary layer in tokamaks for correlated resonant kicks.
2 Quasilinear theory in uniformly magnetized plasma
2.1 Formulation and notation
To illustrate and evaluate the role of collisions in disrupting resonant particles interacting with applied rf waves, a cylindrical plasma aligned with a constant magnetic field 
$B$,
$$\begin{eqnarray}\boldsymbol{B}=B\boldsymbol{z},\end{eqnarray}$$ is considered for simplicity, with 
$\boldsymbol{z}$ a unit vector along the axis of the cylinder of length 
$L_{0}$. The other cylindrical spatial variables are the radius 
$r$ and the cylindrical angle variable 
$\unicode[STIX]{x1D717}$, having the orthonormal unit vectors 
$\unicode[STIX]{x1D735}r$ and 
$r\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}$ satisfying 
$r\unicode[STIX]{x1D735}r\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D717}=\boldsymbol{z}$.
Denoting the applied electric and magnetic fields by 
$\boldsymbol{e}$ and 
$\boldsymbol{b}$, respectively, then the resulting perturbed acceleration is
$$\begin{eqnarray}\boldsymbol{a}=(Ze/M)(\boldsymbol{e}+c^{-1}\boldsymbol{v}\times \boldsymbol{b}),\end{eqnarray}$$ with 
$Z$ and 
$M$ the charge number and mass of the species, 
$e$ the charge on a proton and 
$c$ the speed of light. Then the full kinetic equation is written as
$$\begin{eqnarray}\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f+(\boldsymbol{a}+\unicode[STIX]{x1D6FA}\boldsymbol{v}\times \boldsymbol{z})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}}f=C\{f\},\end{eqnarray}$$ with 
$\unicode[STIX]{x1D6FA}=ZeB/Mc$ the species gyrofrequency and 
$C$ the full collision operator.
Writing
$$\begin{eqnarray}f=f_{0}+f_{1}+\cdots\end{eqnarray}$$ with 
$f_{1}\ll f_{0}$, 
$f_{0}$ is assumed to contain only slow radial and temporal variation and no 
$\unicode[STIX]{x1D717}$, 
$z$, or gyrophase, 
$\unicode[STIX]{x1D711}$, dependence: 
$f_{0}=f_{0}(r,v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E},t)$, where 
$v=|\boldsymbol{v}|$ is the speed, 
$\unicode[STIX]{x1D707}=v_{\bot }^{2}/2B$ is the magnetic moment, 
$\unicode[STIX]{x1D70E}=v_{\Vert }/|v_{\Vert }|$ and
$$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{v}_{\bot }+v_{\Vert }\boldsymbol{z}=v_{\bot }(\cos \unicode[STIX]{x1D711}\unicode[STIX]{x1D735}r+r\sin \unicode[STIX]{x1D711}\unicode[STIX]{x1D735}\unicode[STIX]{x1D717})+v_{\Vert }\boldsymbol{z}.\end{eqnarray}$$ A combined coarse grain average and gyroaverage is used to remove any fast time and spatial dependence from any quantity 
$A$,
$$\begin{eqnarray}\langle A\rangle _{cg}=\frac{1}{2T}\int _{t-T}^{t+T}\text{d}\unicode[STIX]{x1D70F}\frac{1}{2\unicode[STIX]{x0394}}\int _{r-\unicode[STIX]{x0394}}^{r+\unicode[STIX]{x0394}}\text{d}r^{\prime }\frac{1}{2L_{0}}\int _{z-L}^{z+L}\text{d}z^{\prime }A,\end{eqnarray}$$ where the integrals over 
$\unicode[STIX]{x1D717}$ and 
$z$ remove the poloidal mode number (
$m$) and parallel wavenumber (
$k_{\Vert }$) variation. The integral over 
$\unicode[STIX]{x1D70F}$ removes fast time variation by taking 
$\unicode[STIX]{x1D714}^{-1}\ll T\ll \unicode[STIX]{x1D708}_{\text{eff}}^{-1}$, and the integral over radius 
$r$ removes rapid radial variation by assuming 
$\unicode[STIX]{x1D706}_{\text{rf}}^{\text{radial}}\ll \unicode[STIX]{x1D6E5}\ll a$, with 
$\unicode[STIX]{x1D708}_{\text{eff}}$ and 
$\unicode[STIX]{x1D714}$ being the effective collision frequency and typical rf wave frequency, respectively, and 
$a$ and 
$\unicode[STIX]{x1D706}_{\text{rf}}^{\text{radial}}$ being the minor radius and the typical radial wavelength of the rf wave, respectively.
These scale separation assumptions result in 
$f_{0}$ satisfying the QL equation
$$\begin{eqnarray}\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}t=C\{f_{0}\}+Q\{f_{0}\},\end{eqnarray}$$ with the QL operator 
$Q$ defined as
$$\begin{eqnarray}Q\{f_{0}\}=-\langle \boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{1}\rangle _{cg}=-\langle \unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }(\boldsymbol{a}f_{1})\rangle _{cg}.\end{eqnarray}$$2.2 Gyrokinetic solution for perturbed distribution function
The equation for the perturbed distribution function 
$f_{1}$ is
$$\begin{eqnarray}\unicode[STIX]{x2202}f_{1}/\unicode[STIX]{x2202}t+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{1}+(Ze/Mc)\boldsymbol{v}\times \boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{1}=-\boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{0}+C\{f_{1}\},\end{eqnarray}$$ where the nonlinear term 
$\boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{1}$ is always neglected as small in QL treatments, and normally collisions are ignored as well, except possibly for resolving singularities that arise from wave–particle resonances. In the next section it will be shown that a more sophisticated collisional boundary layer model leads to a more satisfying and complete description.
To extract the non-resonant portion of the perturbed distribution function, define
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}t}-\frac{Zev_{\Vert }}{MB}\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{z}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}},\end{eqnarray}$$as in Catto et al. (Reference Catto, Lee and Ram2017), and use Faraday’s law,
$$\begin{eqnarray}c\unicode[STIX]{x1D735}\times \boldsymbol{e}=-\unicode[STIX]{x2202}\boldsymbol{b}/\unicode[STIX]{x2202}t,\end{eqnarray}$$to write
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{a}}{\unicode[STIX]{x2202}t}=\frac{Ze}{M}\left[\frac{\unicode[STIX]{x2202}\boldsymbol{e}}{\unicode[STIX]{x2202}t}-\boldsymbol{v}\times (\unicode[STIX]{x1D735}\times \boldsymbol{e})\right]=\frac{Ze}{M}\left(\frac{\unicode[STIX]{x2202}\boldsymbol{e}}{\unicode[STIX]{x2202}t}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{e}-\unicode[STIX]{x1D735}\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{v}\right)\end{eqnarray}$$to obtain the more convenient form
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}t^{2}}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D6FA}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}\nonumber\\ \displaystyle & & \displaystyle \quad =C\left\{\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x1D700}_{\Vert }v_{\Vert }}{B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right\}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D73A}}{\unicode[STIX]{x2202}t}\boldsymbol{\cdot }\boldsymbol{v}\left(\frac{1}{v}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{1}{B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D73A}}{\unicode[STIX]{x2202}z}\boldsymbol{\cdot }\boldsymbol{v}\frac{v_{\Vert }}{B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}},\quad\end{eqnarray}$$where
$$\begin{eqnarray}\unicode[STIX]{x1D73A}=\frac{Ze}{M}\boldsymbol{e}\quad \text{and}\quad \unicode[STIX]{x1D700}_{\Vert }=\frac{Ze}{M}e_{\Vert }=\frac{Ze}{M}\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{z}.\end{eqnarray}$$ To solve the linear equation it is convenient to use the gyrokinetic variables 
$\boldsymbol{R},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D711}$ of Catto (Reference Catto1978), Lee, Myra & Catto (Reference Lee, Myra and Catto1983) and Parra & Catto (Reference Parra and Catto2008), where
$$\begin{eqnarray}\boldsymbol{R}=\boldsymbol{r}+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{z}.\end{eqnarray}$$ Using 
$\boldsymbol{v}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{R}+\unicode[STIX]{x1D6FA}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}\boldsymbol{R}=0$ and 
$f_{0}$ a slow function of 
$r$, the kinetic equation becomes
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}t^{2}}+v_{\Vert }\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}z\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}\unicode[STIX]{x2202}t}=C\left\{\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x1D700}_{\Vert }v_{\Vert }}{B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right\}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D73A}}{\unicode[STIX]{x2202}t}\boldsymbol{\cdot }\boldsymbol{v}\left(\frac{1}{v}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{1}{B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D73A}}{\unicode[STIX]{x2202}z}\boldsymbol{\cdot }\boldsymbol{v}\frac{v_{\Vert }}{B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}},\end{eqnarray}$$ with 
$h=h(\boldsymbol{R},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711},t)$, but 
$\unicode[STIX]{x1D73A}=\unicode[STIX]{x1D73A}(\boldsymbol{r},t)$. The distinction between 
$\boldsymbol{R}$ (the guiding centre location) and 
$\boldsymbol{r}$ (the particle location) will lead to the usual Bessel function modifications.
Fourier decomposing the applied electric field 
$\boldsymbol{e}$ in space, and considering only a single wave frequency 
$\unicode[STIX]{x1D714}$ for simplicity, gives
$$\begin{eqnarray}\boldsymbol{e}=\boldsymbol{e}(\boldsymbol{r},t)=\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\mathop{\sum }_{k}\boldsymbol{e}_{k}\text{e}^{\text{i}k_{\Vert }z+\text{i}m\unicode[STIX]{x1D717}+\text{i}S(r)},\end{eqnarray}$$ with 
$S$ the eikonal defined such that 
$\unicode[STIX]{x1D735}S=(\unicode[STIX]{x2202}S/\unicode[STIX]{x2202}r)\unicode[STIX]{x1D735}r=\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}r=\unicode[STIX]{x1D73F}$, and
$$\begin{eqnarray}\boldsymbol{k}=\unicode[STIX]{x1D73F}+m\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}+k_{\Vert }\boldsymbol{z}=\boldsymbol{k}_{\bot }+k_{\Vert }\boldsymbol{z}=k_{\bot }(\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D735}r+r\sin \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D735}\unicode[STIX]{x1D717})+k_{\Vert }\boldsymbol{z}.\end{eqnarray}$$ As 
$h$ depends on gyrophase and 
$\boldsymbol{R}$, rather than 
$\boldsymbol{r}$, the form
$$\begin{eqnarray}h=h(\boldsymbol{R},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711},t)=\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\mathop{\sum }_{k,p}h_{p}\,\text{e}^{\text{i}k_{\Vert }z+\text{i}S(R)+\text{i}m\unicode[STIX]{x1D6E9}-\text{i}p\unicode[STIX]{x1D711}},\end{eqnarray}$$is employed with
$$\begin{eqnarray}\displaystyle & \displaystyle R=r+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r=r+r\,\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D717}+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}=\unicode[STIX]{x1D717}-r^{-1}\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r, & \displaystyle\end{eqnarray}$$ where Taylor expanding 
$S$ gives
$$\begin{eqnarray}S(R)=S(r)+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\unicode[STIX]{x1D73F}+\cdots \,.\end{eqnarray}$$Retaining the distinction between drift kinetic and gyrokinetic variables in exponentials, the preceding yields the alternate and useful form
$$\begin{eqnarray}\boldsymbol{e}=\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\mathop{\sum }_{k}\boldsymbol{e}_{k}\text{e}^{\text{i}k_{\Vert }z+\text{i}m\unicode[STIX]{x1D6E9}+\text{i}S(R)-\text{i}L},\end{eqnarray}$$where
$$\begin{eqnarray}L\equiv \unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\boldsymbol{k}=(k_{\bot }v_{\bot }/\unicode[STIX]{x1D6FA})\sin (\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FC}).\end{eqnarray}$$Using the preceding harmonic forms and Bessel generating function
$$\begin{eqnarray}\text{e}^{-\text{i}L}=\text{e}^{-\text{i}\unicode[STIX]{x1D702}\sin (\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FC})}=\mathop{\sum }_{p}\text{e}^{-\text{i}p(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FC})}J_{p}(\unicode[STIX]{x1D702}),\end{eqnarray}$$ where 
$\unicode[STIX]{x1D702}=k_{\bot }v_{\bot }/\unicode[STIX]{x1D6FA}$, leads to the equation
$$\begin{eqnarray}\displaystyle \text{i}\mathop{\sum }_{p}\text{e}^{-\text{i}p\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })h_{p} & = & \displaystyle \mathop{\sum }_{p}\text{e}^{-\text{i}p(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FC})}(\unicode[STIX]{x1D73A}_{k}\boldsymbol{\cdot }\boldsymbol{z}v_{\Vert }+\unicode[STIX]{x1D73A}_{p}\boldsymbol{\cdot }\boldsymbol{v}_{\bot })\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{1}{v}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{(\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert })}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right]J_{p}(\unicode[STIX]{x1D702}),\end{eqnarray}$$ where collisions are normally replaced by causality to use 
$\text{Im}\,\unicode[STIX]{x1D714}>0$.
Solving by multiplying by 
$\text{e}^{\text{i}p^{\prime }\unicode[STIX]{x1D711}}$ and gyroaveraging yields the solution
$$\begin{eqnarray}h_{p}=\frac{W_{p,k}}{\text{i}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })},\end{eqnarray}$$with notation essentially the same as (Catto et al. Reference Catto, Lee and Ram2017)
$$\begin{eqnarray}W_{p,k}=\text{e}^{\text{i}p\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D73A}_{k}\boldsymbol{\cdot }[\boldsymbol{z}v_{\Vert }J_{p}(\unicode[STIX]{x1D702})+\boldsymbol{e}_{\bot p}v_{\bot }]\left[\frac{1}{v}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{(\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert })}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right],\end{eqnarray}$$and
$$\begin{eqnarray}\boldsymbol{e}_{\bot p}=\frac{1}{k_{\bot }}\left[\boldsymbol{k}_{\bot }\frac{p}{\unicode[STIX]{x1D702}}J_{p}(\unicode[STIX]{x1D702})+\text{i}\boldsymbol{z}\times \boldsymbol{k}\frac{\unicode[STIX]{x2202}J_{p}(\unicode[STIX]{x1D702})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right].\end{eqnarray}$$2.3 Standard quasilinear operator form
To form the QL operator, use of 
$\text{Im}\,\unicode[STIX]{x1D714}>0$ resolves the singularity to give
$$\begin{eqnarray}\frac{1}{\text{i}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })}\rightarrow -\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert }),\end{eqnarray}$$and the usual approximation used to derive the QL operator, namely
$$\begin{eqnarray}h_{p}\rightarrow -\unicode[STIX]{x03C0}W_{p,k}\text{e}^{\text{i}L}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert }),\end{eqnarray}$$ where the exponential factor 
$\text{e}^{\text{i}L}$ is inserted as 
$h$ in the QL operator must be rewritten in the drift kinetic variable 
$\boldsymbol{r}$ (rather that the gyrokinetic variable 
$\boldsymbol{R}$) to perform the coarse grain average. Therefore, using
$$\begin{eqnarray}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{R}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{z}\boldsymbol{\cdot }\boldsymbol{k}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}+L,\end{eqnarray}$$leads to
$$\begin{eqnarray}h(\boldsymbol{R},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711},t)=\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\mathop{\sum }_{k,p}h_{p}\,\text{e}^{\text{i}k_{\Vert }z+\text{i}S(r)+\text{i}m\unicode[STIX]{x1D717}-\text{i}p\unicode[STIX]{x1D711}+\text{i}L}.\end{eqnarray}$$ Next, the delta function is used to simplify 
$W_{p,k}$ in the QL operator to
$$\begin{eqnarray}W_{p,k}\rightarrow \text{e}^{\text{i}p\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D73A}_{k}\boldsymbol{\cdot }[\boldsymbol{z}v_{\Vert }J_{p}(\unicode[STIX]{x1D702})+\boldsymbol{e}_{\bot p}v_{\bot }]\left(\frac{1}{v}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{p\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right).\end{eqnarray}$$ Then, as the difference between 
$f_{1}$ and 
$h$ is independent of gyrophase to lowest order,
$$\begin{eqnarray}f_{1}=h+\frac{\text{i}Zev_{\Vert }}{M\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}e_{\Vert },\end{eqnarray}$$ and 
$\oint \text{d}\unicode[STIX]{x1D711}\boldsymbol{v}_{\bot }=0$, it is seen that
$$\begin{eqnarray}\langle \unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }[\boldsymbol{a}(f_{1}-h)]\rangle _{cg}=\frac{v_{\Vert }\unicode[STIX]{x2202}}{v\unicode[STIX]{x2202}v}\left\langle \frac{(f_{1}-h)\unicode[STIX]{x1D700}_{\Vert }v_{\Vert }}{v_{\Vert }}\right\rangle _{cg}+\frac{v_{\Vert }\unicode[STIX]{x2202}}{v\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\left\langle \frac{v(f_{1}-h)}{Bv_{\Vert }}\unicode[STIX]{x1D73A}\boldsymbol{\cdot }\boldsymbol{v}_{\bot }\right\rangle _{cg}=0,\end{eqnarray}$$ where 
$\unicode[STIX]{x1D735}_{v}\unicode[STIX]{x1D711}=v_{\bot }^{-2}\boldsymbol{z}\times \boldsymbol{v}$ is used to obtain 
$\unicode[STIX]{x1D735}_{v}v\times \unicode[STIX]{x1D735}_{v}\unicode[STIX]{x1D707}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}\unicode[STIX]{x1D711}=1/vB$. Therefore, only
$$\begin{eqnarray}Q\{f_{0}\}=-\frac{v_{\Vert }}{v}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}\left(\frac{1}{v_{\Vert }}\langle h\unicode[STIX]{x1D73A}\boldsymbol{\cdot }\boldsymbol{v}\rangle _{cg}\right)-\frac{v_{\Vert }\unicode[STIX]{x2202}}{Bv\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\left(\frac{v}{v_{\Vert }}\langle h\unicode[STIX]{x1D73A}\boldsymbol{\cdot }\boldsymbol{v}_{\bot }\rangle _{cg}\right)\end{eqnarray}$$need be considered.
Using the preceding yields
$$\begin{eqnarray}\oint \frac{\text{d}\unicode[STIX]{x1D711}}{2\unicode[STIX]{x03C0}}\text{e}^{\text{i}L-\text{i}p(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FC})}=J_{p}(\unicode[STIX]{x1D702}),\end{eqnarray}$$and
$$\begin{eqnarray}\oint \frac{\text{d}\unicode[STIX]{x1D711}}{2\unicode[STIX]{x03C0}v_{\bot }}\boldsymbol{v}_{\bot }\text{e}^{\text{i}L-\text{i}p(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FC})}=\boldsymbol{e}_{\bot p}^{\ast },\end{eqnarray}$$ with 
$\ast$ denoting complex conjugate. Then for harmonic fields,
$$\begin{eqnarray}\langle \unicode[STIX]{x1D73A}\unicode[STIX]{x1D73A}\rangle _{cg}=\frac{1}{4}\mathop{\sum }_{k}(\unicode[STIX]{x1D73A}_{k}\unicode[STIX]{x1D73A}_{k}^{\ast }+\unicode[STIX]{x1D73A}_{k}^{\ast }\unicode[STIX]{x1D73A}_{k}),\end{eqnarray}$$leading to
$$\begin{eqnarray}\langle h\,\unicode[STIX]{x1D73A}\boldsymbol{\cdot }\boldsymbol{v}_{\bot }\rangle _{cg}=-\frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FA}}{2\unicode[STIX]{x1D714}v}\mathop{\sum }_{k,p}p\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })|\unicode[STIX]{x1D73A}_{k}\boldsymbol{\cdot }[\boldsymbol{z}v_{\Vert }J_{p}(\unicode[STIX]{x1D702})+\boldsymbol{e}_{\bot p}v_{\bot }]|^{2}\left(\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{p\unicode[STIX]{x1D6FA}v}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right),\end{eqnarray}$$ where the 
$\langle \ldots \rangle _{cg}$ replaces the double sum over 
$k$ and 
$k^{\prime }$ with a single sum over 
$k$ by introducing the Kronecker delta function 
$\unicode[STIX]{x1D6FF}_{k^{\prime }k}$.
Combining the preceding results, the final form for the QL operator is
$$\begin{eqnarray}Q\{f_{0}\}=\mathop{\sum }_{p}\frac{v_{\Vert }}{v}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}+\frac{p\unicode[STIX]{x1D6FA}v}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right)\left[D\frac{v}{v_{\Vert }}\left(\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{p\unicode[STIX]{x1D6FA}v}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right)\right],\end{eqnarray}$$with
$$\begin{eqnarray}D=\frac{\unicode[STIX]{x03C0}Z^{2}e^{2}}{2M^{2}v^{2}}\mathop{\sum }_{k}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })|\boldsymbol{e}_{m}\boldsymbol{\cdot }[\boldsymbol{z}v_{\Vert }J_{p}(\unicode[STIX]{x1D702})+\boldsymbol{e}_{\bot p}v_{\bot }]|^{2},\end{eqnarray}$$a manifestly positive diffusivity. The preceding QL operator is exactly the same as the Kennel–Englemann (Reference Kennel and Engelmann1966) result, but a gyrokinetic formulation is used to streamline the derivation, as in the full toroidal version by Catto et al. (Reference Catto, Lee and Ram2017).
Multiplying 
$Q$ by 
$\ell nf_{0}$ and integrating over all velocity space (using 
$\text{d}^{3}v\rightarrow 2\unicode[STIX]{x03C0}vB\,\text{d}v\,\text{d}\unicode[STIX]{x1D707}/|v_{\Vert }|$) yields negative definite entropy production as required,
$$\begin{eqnarray}\int \text{d}^{3}v\ell nf_{0}Q\{f_{0}\}=-\int \text{d}^{3}v\mathop{\sum }_{\unicode[STIX]{x1D714},p}\frac{D}{f_{0}}\left|\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{p\unicode[STIX]{x1D6FA}v}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right|^{2}\leqslant 0.\end{eqnarray}$$ Reverting to cylindrical velocity space variables 
$v_{\bot }$, 
$v_{\Vert }$, and 
$\unicode[STIX]{x1D711}$ the quasilinear operator in vector form is
$$\begin{eqnarray}Q\{f_{0}\}=\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }(\overset{\leftrightarrow }{D}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{0}),\end{eqnarray}$$with
$$\begin{eqnarray}\overset{\leftrightarrow }{D}=D_{\Vert }\boldsymbol{z}\boldsymbol{z}+v_{\bot }^{-2}D_{\bot }\boldsymbol{v}_{\bot }\boldsymbol{v}_{\bot }+v_{\bot }^{-1}D_{\times }(\boldsymbol{z}\boldsymbol{v}_{\bot }+\boldsymbol{v}_{\bot }\boldsymbol{z}),\end{eqnarray}$$where the various diffusivities are defined as
$$\begin{eqnarray}\displaystyle & \displaystyle D_{\Vert }=\mathop{\sum }_{\unicode[STIX]{x1D714},p}\left(1-\frac{p\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}}\right)^{2}\frac{v^{2}}{v_{\Vert }^{2}}D, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{\bot }=\mathop{\sum }_{\unicode[STIX]{x1D714},p}\left(\frac{p\unicode[STIX]{x1D6FA}v}{\unicode[STIX]{x1D714}v_{\bot }}\right)^{2}D, & \displaystyle\end{eqnarray}$$and
$$\begin{eqnarray}D_{\times }=\mathop{\sum }_{\unicode[STIX]{x1D714},p}\frac{p\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}}\left(1-\frac{p\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}}\right)\frac{v^{2}}{v_{\Vert }v_{\bot }}D.\end{eqnarray}$$ For simulations allowing 
$Q\sim C$, the delta function is typically removed by assuming the preceding form remains valid in toroidal geometry and then averaging trapped particles over a full bounce and passing particles over a poloidal transit.
The next section demonstrates that a collisional boundary layer treatment leads to the replacement of the delta function with an integral representation dependent on the collisional physics disrupting the wave–resonant particle resonance, so transit averaging is no longer needed.
3 Collisional boundary layer reformulation of quasilinear theory
3.1 Collisional boundary layer model for resonant particles
Normally collisions are ignored in QL theory except when used to resolve singularities in the same manner as causality. However, collisions are diffusive and thereby introduce a narrow boundary layer in which wave–particle resonances are disrupted as will be shown next. Assuming the boundary layer is narrow, only diffusive scattering need be retained as it disrupts the resonant interaction. As shown in appendix A for a general non-isotropic distribution function, pitch angle scattering is normally the dominant collisional process of interest. As a result, the following linearized pitch angle scattering collision operator replacement is appropriate,
$$\begin{eqnarray}C\{h\}\rightarrow \unicode[STIX]{x1D708}(v)L\{h\},\end{eqnarray}$$ where the pitch angle variable is 
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x1D707}B/v^{2}=v_{\bot }^{2}/v^{2}=1-v_{\Vert }^{2}/v^{2}=1-\unicode[STIX]{x1D709}^{2}$, and for a narrow boundary layer in 
$\unicode[STIX]{x1D706}$ or 
$\unicode[STIX]{x1D709}=v_{\Vert }/v$,
$$\begin{eqnarray}\displaystyle L\{h\} & = & \displaystyle \unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }[(v^{2}\overset{\leftrightarrow }{I}-\boldsymbol{v}\boldsymbol{v})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}h]=\frac{4v_{\Vert }}{v^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}\left(\unicode[STIX]{x1D706}v_{\Vert }\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}\right)\nonumber\\ \displaystyle & = & \displaystyle v\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v_{\Vert }}\left(\frac{v_{\bot }^{2}}{v}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}v_{\Vert }}\right)\simeq v_{\bot }^{2}\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}v_{\Vert }^{2}}=(1-\unicode[STIX]{x1D709}^{2})\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{2}},\end{eqnarray}$$ where the last four forms are in 
$\unicode[STIX]{x1D706}$, 
$v$; 
$v_{\Vert }$, 
$v$; 
$v_{\Vert }$, 
$v$; and 
$\unicode[STIX]{x1D709}$, 
$v$ variables, respectively. Appendix A gives expressions for the collision frequency 
$\unicode[STIX]{x1D708}(v)$ for lower hybrid current drive and minority heating.
Using the boundary layer collision operator in the particularly convenient form
$$\begin{eqnarray}C\{h\}\simeq \unicode[STIX]{x1D708}v_{\bot }^{2}\unicode[STIX]{x2202}^{2}h/\unicode[STIX]{x2202}v_{\Vert }^{2},\end{eqnarray}$$ with the 
$C\{v_{\Vert }\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D707}\}$ term ignored as smaller by a boundary layer width, the equation to be solved in gyrokinetic variables is
$$\begin{eqnarray}\text{i}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })h_{p}+\unicode[STIX]{x1D708}v_{\bot }^{2}\frac{\unicode[STIX]{x2202}^{2}h_{p}}{\unicode[STIX]{x2202}v_{\Vert }^{2}}=W_{p,k}.\end{eqnarray}$$Notice that spatial variation has no effect on broadening the resonance. This statement is true even in the presence of parallel gradients as shown in appendix B for successive correlated passes through resonance.
To solve for 
$h$, let
$$\begin{eqnarray}s=(k_{\Vert }/v_{\bot }^{2}\unicode[STIX]{x1D708})^{1/3}[v_{\Vert }-(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA})/k_{\Vert }],\end{eqnarray}$$to obtain
$$\begin{eqnarray}\unicode[STIX]{x2202}^{2}h_{p}/\unicode[STIX]{x2202}s^{2}-\text{i}sh_{p}=(k_{\Vert }^{2}v_{\bot }^{2}\unicode[STIX]{x1D708})^{-1/3}W_{p,k}.\end{eqnarray}$$ The solution vanishing as 
$s\rightarrow \pm \infty$ (Su & Oberman Reference Su and Oberman1968) is
$$\begin{eqnarray}h_{p}=-\frac{W_{p,k}}{(k_{\Vert }^{2}v_{\bot }^{2}\unicode[STIX]{x1D708})^{1/3}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\,\text{e}^{-\text{i}s\,\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}^{3}/3}\underset{s\rightarrow \pm \infty }{\rightarrow }\frac{W_{p,k}}{\text{i}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })}.\end{eqnarray}$$ The preceding solution means that to account for the collisional boundary layer physics 
$[\text{i}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })]^{-1}\rightarrow -\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })$, should be replaced by
$$\begin{eqnarray}\frac{1}{\text{i}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })}\rightarrow -\frac{\displaystyle \int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\text{e}^{-\text{i}s\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}^{3}/3}}{(k_{\Vert }^{2}v_{\bot }^{2}\unicode[STIX]{x1D708})^{1/3}}.\end{eqnarray}$$Plots of the real and imaginary parts of the integral in (3.8) are given in figure 1 of Auerbach (Reference Auerbach1977), where collisional boundary layer effects were considered in great detail for the unmagnetized Landau limit.
To use the preceding result in the QL diffusivity the following replacement is required:
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })\rightarrow \text{Re}\left[(k_{\Vert }^{2}v_{\bot }^{2}\unicode[STIX]{x1D708})^{-1/3}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\,\text{e}^{-\text{i}s\,\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}^{3}/3}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =(k_{\Vert }^{2}v_{\bot }^{2}\unicode[STIX]{x1D708})^{-1/3}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\,\text{e}^{-\unicode[STIX]{x1D70F}^{3}/3}\cos (s\unicode[STIX]{x1D70F}).\end{eqnarray}$$Therefore, with the boundary layer physics included, the QL diffusivity becomes
$$\begin{eqnarray}D=\frac{Z^{2}e^{2}}{2M^{2}v^{2}}\mathop{\sum }_{k}|\boldsymbol{e}_{k}\boldsymbol{\cdot }[\boldsymbol{z}v_{\Vert }J_{p}(w)+\boldsymbol{e}_{\bot p}v_{\bot }]|^{2}(k_{\Vert }^{2}v_{\bot }^{2}\unicode[STIX]{x1D708})^{-1/3}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\,\text{e}^{-\unicode[STIX]{x1D70F}^{3}/3}\cos (s\unicode[STIX]{x1D70F}),\end{eqnarray}$$ where 
$D$ maintains non-negative entropy production as required because of the integration over velocity space in (2.44). The integral in (3.10), and therefore 
$D$, is not manifestly positive. However, it has the required delta function behaviour as indicated by the real part of (3.8) for 
$\unicode[STIX]{x1D714}\gg \unicode[STIX]{x1D708}$. Auerbach (Reference Auerbach1977) gives a plot of the real and imaginary parts of the integral in his figure 1. The integral in (3.10) is the negative of the imaginary part plotted there and displays the required behaviour. The same replacement can also be used in the general tokamak geometry result for 
$D$ in Catto et al. (Reference Catto, Lee and Ram2017) provided the argument of the delta function and then 
$s$ is generalized to include the magnetic drift velocity, 
$\boldsymbol{v}_{d}$,
$$\begin{eqnarray}s=(k_{\Vert }/v_{\bot }^{2}\unicode[STIX]{x1D708})^{1/3}[v_{\Vert }-(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{v}_{d})/k_{\Vert }].\end{eqnarray}$$The preceding collisional boundary layer analysis associated with the resonant particles demonstrates that the delta function in the quasilinear operator is actually the limiting form of some unspecified physical process. Its more precise form depends on the details of the relevant physics disrupting the unperturbed resonant particle trajectories.
Another possible disruptive mechanism is resonant particles moving in a wave. Then stochastic separatrix crossings associated with wave trapping and detrapping may occur as resonant interactions are tuned and detuned. If stochasticity leads to a shorter wave–particle interaction time than collisions, then presumably the delta function must become the limit of a different functional form representing the physics linked to the stochastically smeared separatrix between trapped and detrapped trajectories. A Monte Carlo scheme introducing stochastic kicks into the quasilinear operator (Johnson, Hellsten & Eriksson Reference Johnson, Hellsten and Eriksson2006) might provide further insight.
The brief subsection that follows summarizes the collisional boundary layer physics in a phenomenological way. It assumes collisions are disrupting the wave–particle interactions and that a narrow collisional boundary layer forms as evaluated in this section. It gives estimates of when unperturbed trajectories are applicable, and suggests that the quasilinear operator begins to fail once it becomes large enough to cause substantial distortions from a Maxwellian.
3.2 Phenomenological estimates for the collisional boundary layer model
The physics of the collisional boundary layer model can be summarized by first estimating the dimensionless velocity space width of the resonant interaction. Using (3.4) and (2.27), the width 
$w\equiv (\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })/\unicode[STIX]{x1D714}$ is estimated from
$$\begin{eqnarray}\unicode[STIX]{x1D714}wh_{p}\equiv (\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })h_{p}\sim \unicode[STIX]{x1D708}v_{\bot }^{2}\unicode[STIX]{x2202}^{2}h_{p}/\unicode[STIX]{x2202}v_{\Vert }^{2}\sim \unicode[STIX]{x1D708}h_{p}/w^{2},\end{eqnarray}$$to find
$$\begin{eqnarray}w\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{1/3},\end{eqnarray}$$indicating an effective collision frequency of
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\text{eff}}\sim \unicode[STIX]{x1D708}/w^{2}\sim \unicode[STIX]{x1D708}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708})^{2/3}\gg \unicode[STIX]{x1D708},\end{eqnarray}$$and an effective wave–particle collision time of
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\text{int}}\sim 1/\unicode[STIX]{x1D708}_{\text{eff}}\sim 1/\unicode[STIX]{x1D714}w\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{2/3}/\unicode[STIX]{x1D708}\ll 1/\unicode[STIX]{x1D708}.\end{eqnarray}$$ Defining the quiver speed 
$v_{\text{quiv}}$ as
$$\begin{eqnarray}v_{\text{quiv}}\equiv Ze|\boldsymbol{e}|/M\unicode[STIX]{x1D714},\end{eqnarray}$$ then balancing the first term on the left with the right side of (3.4) gives 
$\unicode[STIX]{x1D714}wh_{p}\sim W_{p,k}$ or
$$\begin{eqnarray}h_{p}/f_{0}\sim v_{\text{quiv}}/v_{\text{th}}w\sim (v_{\text{quiv}}/v_{\text{th}})(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708})^{1/3}\ll 1,\end{eqnarray}$$ where 
$v_{\text{th}}\sim (T/M)^{1/2}$ is the thermal speed of the species. Also, recalling (2.30) and (3.12) and using 
$s\sim 1$ in (3.8), leads to the estimate 
$(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })^{-1}\sim \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })\sim 1/\unicode[STIX]{x1D714}w$, giving the QL diffusivity estimate of
$$\begin{eqnarray}D\sim Z^{2}e^{2}|\boldsymbol{e}_{m}\,|^{2}/M^{2}\unicode[STIX]{x1D714}w\sim \unicode[STIX]{x1D714}v_{\text{quiv}}^{2}/w.\end{eqnarray}$$ To ignore the nonlinear term 
$\boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}h_{p}$ in the perturbed equation requires assuming
$$\begin{eqnarray}\unicode[STIX]{x1D714}wh_{p}\sim (\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}-k_{\Vert }v_{\Vert })h_{p}\gg \boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}h_{p}\sim (v_{\text{quiv}}\unicode[STIX]{x1D714}h_{p}/v_{\text{th}}w).\end{eqnarray}$$Consequently, the unperturbed trajectory, collisional boundary layer treatment of quasilinear theory assumes
$$\begin{eqnarray}v_{\text{quiv}}/v_{\text{th}}\ll w^{2}\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{2/3}\ll 1.\end{eqnarray}$$ Notice that (3.20) is consistent with the assumption that 
$\boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}h_{p}\ll \boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{0}$ or 
$h_{p}\ll wf_{0}$ if
$$\begin{eqnarray}h_{p}/f_{0}\sim (v_{\text{quiv}}/v_{\text{th}})(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708})^{1/3}\ll w\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{1/3}\ll 1.\end{eqnarray}$$The preceding are important restrictions. In particular QL theory assumes (3.21) holds.
As no resonant behaviour occurs in the unperturbed equation, 
$Q\{f_{0}\}\sim Df_{0}/v_{\text{th}}^{2}$ and 
$C\{f_{0}\}\sim \unicode[STIX]{x1D708}f_{0}$. Therefore, 
$f_{0}$ departs appreciably from Maxwellian when 
$Q\{f_{0}\}\sim C\{f_{0}\}$, or
$$\begin{eqnarray}Df_{0}\sim \unicode[STIX]{x1D708}v_{\text{th}}^{2}\,f_{0},\end{eqnarray}$$giving
$$\begin{eqnarray}(v_{\text{quiv}}/v_{\text{th}})^{2}\sim \unicode[STIX]{x1D708}w/\unicode[STIX]{x1D714}\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{4/3}.\end{eqnarray}$$ Comparing (3.21) and (3.23) suggests the collisional boundary layer treatment of quasilinear theory begins to fail just as it becomes most interesting. Consequently, the non-Maxwellian features in the unperturbed distribution function 
$f_{0}$ may not be reliably found by a QL treatment of lower hybrid current drive or minority heating. For both these processes it is the tail particles that matter, although it is difficult to refine the estimate for the minorities due to their extended energetic and anisotropic tail.
However, the preceding estimates can be improved slightly for lower hybrid current drive (LHCD) by considering tail electrons with speeds about three times the electron thermal speed, 
$v_{\text{tail}}\sim 3v_{e}$. Using appendix A, the collision frequency of these faster electrons is reduced
$$\begin{eqnarray}\unicode[STIX]{x1D708}\sim \unicode[STIX]{x1D708}_{ee}(v_{e}/v_{\text{tail}})^{3},\end{eqnarray}$$and the extended tail suggests the estimates
$$\begin{eqnarray}\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}v_{\Vert }\sim f_{0}/v_{\text{tail}},\end{eqnarray}$$and
$$\begin{eqnarray}\unicode[STIX]{x2202}h_{p}/\unicode[STIX]{x2202}v_{\Vert }\sim h_{p}/v_{\text{tail}},\end{eqnarray}$$ as 
$W_{p,k}\sim (\unicode[STIX]{x1D700}_{\Vert }v_{\Vert }/v)\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}v\sim \unicode[STIX]{x1D700}_{\Vert }f_{0}/v_{\text{tail}}$. In this LHCD case the reduced collision frequency narrows the boundary layer further and the altered estimate of (3.12) gives a width
$$\begin{eqnarray}w\sim (\unicode[STIX]{x1D708}_{ee}/\unicode[STIX]{x1D714})^{1/3}(v_{e}/v_{\text{tail}})^{5/3},\end{eqnarray}$$ in place of (3.13). The effective collision frequency now becomes 
$\unicode[STIX]{x1D708}_{\text{eff}}\sim (\unicode[STIX]{x1D708}/w^{2})(v_{e}/v_{\text{tail}})^{2}$, reducing (3.14) to
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\text{eff}}\sim \unicode[STIX]{x1D708}_{ee}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}_{ee})^{2/3}(v_{e}/v_{\text{tail}})^{5/3}.\end{eqnarray}$$ Balancing 
$\unicode[STIX]{x1D714}wh_{p}\sim W_{p,k}$ replaces (3.17) with the more restrictive condition
$$\begin{eqnarray}h_{p}/f_{0}\sim v_{\text{quiv}}/v_{\text{tail}}w\sim (v_{\text{quiv}}/v_{e})(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}_{ee})^{1/3}(v_{\text{tail}}/v_{e})^{2/3}\ll 1.\end{eqnarray}$$ Ignoring the nonlinear term by assuming 
$\boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}h_{p}\ll \boldsymbol{a}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{0}$ or 
$h_{p}/f_{0}\ll w$, now requires
$$\begin{eqnarray}h_{p}/wf_{0}\sim (v_{\text{quiv}}/v_{e})(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}_{ee})^{2/3}(v_{\text{tail}}/v_{e})^{7/3}\ll 1,\end{eqnarray}$$ instead of the less restrictive condition of (3.20) and (3.21). Finally, using 
$Q\{f_{0}\}\sim Df_{0}/v_{\text{tail}}^{2}$, and (A 4) to estimate 
$C\{f_{0}\}\sim \unicode[STIX]{x1D708}_{ee}(v_{e}/v_{\text{tail}})^{3}f_{0}$, as electron drag dominates at high speeds, then 
$f_{0}$ departs appreciably from Maxwellian when 
$Q\{f_{0}\}\sim C\{f_{0}\}$, or
$$\begin{eqnarray}h_{p}/wf_{0}\sim (v_{\text{quiv}}/v_{e})(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}_{ee})^{2/3}(v_{\text{tail}}/v_{e})^{7/3}\sim (v_{\text{tail}}/v_{e})\gg 1.\end{eqnarray}$$Combining (3.30) and (3.31) more strongly suggests that the QL treatment of LHCD fails when it is most interesting. The preceding estimates imply that the non-Maxwellian electron tail features are not being reliably found by a QL treatment of LHCD.
4 Summary
The collisional boundary layer associated with resonant wave–particle interactions is investigated to demonstrate that it gives a deeper and more complete interpretation of quasilinear theory and the delta function appearing in the Kennel & Engelmann (Reference Kennel and Engelmann1966) operator. The balance between particles resonating with the wave and collisions, allows a narrow collisional boundary layer to form that is shown to be fully consistent with the collisionless form of the Kennel–Englemann quasilinear operator. Similar ‘plateau’ behaviour occurs whenever collisions enter to resolve a singularity as in the plateau regime of neoclassical theory (see, for example, p. 291 of Hinton & Hazeltine (Reference Hinton and Hazeltine1976)) and the superbanana plateau regime of ripple transport (for example, see section 5 of Catto (Reference Catto2019)).
The collisional boundary layer enhances the collisions to give an effective collision frequency of 
$\unicode[STIX]{x1D708}_{\text{eff}}\sim \unicode[STIX]{x1D708}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708})^{2/3}\gg \unicode[STIX]{x1D708}$. The quasilinear operator remains fully self-consistent provided the applied rf amplitude remains small enough that the quiver speed, 
$v_{\text{quiv}}=Ze|\boldsymbol{e}|/M\unicode[STIX]{x1D714}$, divided by the thermal speed, 
$v_{\text{th}}$, satisfies 
$v_{\text{quiv}}/v_{\text{th}}\ll (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{2/3}\ll 1$. However, once the applied wave amplitude becomes large enough that 
$v_{\text{quiv}}/v_{\text{th}}\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{2/3}$, a collisional boundary layer justification of the Kennel–Engelmann (Reference Kennel and Engelmann1966) quasilinear operator becomes inadequate. In particular, the collisional boundary layer treatment suggests that quasilinear theory is failing for both lower hybrid current drive and minority heating once the departure from Maxwellian become significant.
Acknowledgements
Work supported by the US Department of Energy grants DE-FG02-91ER-54109 at MIT. P.J.C. is grateful for insightful conversations and interactions with Professors A. Schekochihin and F. Parra of Oxford University at the 12th plasma Kinetics Working Group Meeting at the Wolfgang Pauli Institute in Vienna workshop in 2019, for motivating discussions with L. Tolman and Drs P. Bonoli and J. Wright, and clarifying and enlightening consultations with Dr A. Ram at the PSFC. Finally, the helpful suggestions of the referees are very much appreciated.
Appendix A. Boundary layer collision operator
Quasilinear diffusion can become strong enough that it significantly distorts the high speed tail of the electron and/or minority ion distribution functions away from Maxwellian. To obtain a reasonable approximation to the collision operator for the boundary layer particles, only the diffusive portion of the full (unlinearized) Fokker–Planck collision operator,
$$\begin{eqnarray}C^{b\ell }\{f\}\simeq \sum ^{\prime }\frac{2\unicode[STIX]{x03C0}(ZZ^{\prime }e^{2})^{2}\ell n\unicode[STIX]{x1D6EC}}{M^{2}}\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }\left\{\left[\int \text{d}^{3}v^{\prime }f^{\prime }g^{-3}(g^{2}\overset{\leftrightarrow }{I}-\boldsymbol{g}\boldsymbol{g})\right]\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f\right\},\end{eqnarray}$$ need be retained, where 
$\boldsymbol{g}=\boldsymbol{v}-\boldsymbol{v}^{\prime }$, the sum 
$\sum ^{\prime }$ is over all relevant species including self-collisions if needed, and 
$\ell n\unicode[STIX]{x1D6EC}$ is the Coulomb logarithm. For tail particles colliding with slower thermal particles and for self-collisions of tail particles with the thermal particles, 
$|\boldsymbol{v}|\gg |\boldsymbol{v}^{\prime }|$ may be assumed to obtain 
$\boldsymbol{g}\simeq \boldsymbol{v}$, and thereby find
$$\begin{eqnarray}C^{b\ell }\{f\}\simeq \sum ^{\prime }\frac{2\unicode[STIX]{x03C0}(ZZ^{\prime }e^{2})^{2}n^{\prime }\ell n\unicode[STIX]{x1D6EC}}{M^{2}v^{3}}\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }[(v^{2}\overset{\leftrightarrow }{I}-\boldsymbol{v}\boldsymbol{v})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f],\end{eqnarray}$$ as in (3.2), where 
$n^{\prime }=\int \text{d}^{3}v^{\prime }f^{\prime }$ is the density of the species that are summed over.
The two non-Maxwellian cases of most interest are minority heating and lower hybrid current drive. Before giving the boundary layer forms for these two cases it is convenient to define the electron and ion thermal speeds, 
$v_{e}=\sqrt{2T_{e}/m}$ and 
$v_{i}=\sqrt{2T_{i}/M}$, and like collision frequencies, 
$\unicode[STIX]{x1D708}_{ee}=4\sqrt{2\unicode[STIX]{x03C0}}\,e^{4}n_{e}\ell n\unicode[STIX]{x1D6EC}/3m^{1/2}T_{e}^{3/2}$ and 
$\unicode[STIX]{x1D708}_{ii}=4\sqrt{\unicode[STIX]{x03C0}}\,Z^{4}e^{4}n_{i}\ell n\unicode[STIX]{x1D6EC}/3M^{1/2}T_{i}^{3/2}$.
Then for lower hybrid current drive (
$Z\rightarrow -1$, 
$M\rightarrow m$, 
$Z^{\prime }\rightarrow Z_{i}~\& ~-1$, 
$n^{\prime }\rightarrow n_{i}~\& ~n_{e}$) the boundary layer form of the collision operator with both electron–ion and electron–electron collisions is
$$\begin{eqnarray}C_{LH}^{b\ell }\{f_{e}\}=\frac{3\sqrt{\unicode[STIX]{x03C0}}(1+Z_{\text{eff}})v_{e}^{3}\unicode[STIX]{x1D708}_{ee}}{8v^{3}}\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }[(v^{2}\overset{\leftrightarrow }{I}-\boldsymbol{v}\boldsymbol{v})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{e}],\end{eqnarray}$$ with 
$Z_{\text{eff}}=\sum _{i}Z_{i}^{2}n_{i}/n_{e}$ and 
$\sum _{i}$ a sum over all the background ion species. In the boundary layer it is not necessary to retain the term that restores momentum conservation for like collisions. Normally 
$v_{\Vert }\simeq 3v_{e}$ are the electrons of interest for lower hybrid current drive. The unperturbed electron distribution function will also be acted on by drag. As a result, the following must be added to (A 3)
$$\begin{eqnarray}C_{\text{drag}}^{b\ell }\{f_{0}\}=\frac{3\sqrt{\unicode[STIX]{x03C0}}v_{e}^{3}\unicode[STIX]{x1D708}_{ee}}{4}\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }(v^{-3}\boldsymbol{v}f_{e})=\frac{3\sqrt{\unicode[STIX]{x03C0}}v_{e}^{3}\unicode[STIX]{x1D708}_{ee}}{4v^{2}}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}.\end{eqnarray}$$ For minority (subscript 
$m$) heating (
$Z\rightarrow Z_{m}$, 
$M\rightarrow M_{m}$, 
$Z^{\prime }\rightarrow Z_{i}$, 
$n^{\prime }\rightarrow n_{i}$)
$$\begin{eqnarray}C_{\min }^{b\ell }\{f_{m}\}=\frac{3\sqrt{2\unicode[STIX]{x03C0}}Z_{m}^{2}}{8M_{m}^{2}v^{3}}\mathop{\sum }_{i}\left(\frac{M_{i}^{2}v_{i}^{3}\unicode[STIX]{x1D708}_{ii}}{Z_{i}^{2}}\right)\unicode[STIX]{x1D735}_{v}\boldsymbol{\cdot }[(v^{2}\overset{\leftrightarrow }{I}-\boldsymbol{v}\boldsymbol{v})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{v}f_{m}],\end{eqnarray}$$where electron drag and ion drag are negligible in the boundary layer. Again, electron drag must be kept for the unperturbed minority distribution function by adding (A 4) to (A 5).
Appendix B. Collisional boundary layer in tokamak geometry
In tokamak geometry the linearized kinetic equation that replaces (3.4) is
$$\begin{eqnarray}\frac{v_{\Vert }}{qR}\frac{\unicode[STIX]{x2202}h_{p}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-\text{i}\left[\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6E9})+\frac{(n-q^{-1}m)v_{\Vert }(\unicode[STIX]{x1D6E9})}{R}\right]h_{p}-\unicode[STIX]{x1D708}v_{\bot }^{2}\frac{\unicode[STIX]{x2202}^{2}h_{p}}{\unicode[STIX]{x2202}v_{\Vert }^{2}}=-\mathop{\sum }_{m^{\prime }}\text{e}^{\text{i}(m^{\prime }-m)\unicode[STIX]{x1D6E9}}W_{p,m^{\prime }},\end{eqnarray}$$ where for a tokamak magnetic field 
$\boldsymbol{B}=B\boldsymbol{b}=I\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}+\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$, and the Fourier form
$$\begin{eqnarray}\boldsymbol{e}(\boldsymbol{r},t)=\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\mathop{\sum }_{m}\boldsymbol{e}_{m}\text{e}^{\text{i}n\unicode[STIX]{x1D701}-\text{i}m\unicode[STIX]{x1D717}+\text{i}S(\unicode[STIX]{x1D713})}\end{eqnarray}$$is employed, along with the ansatz
$$\begin{eqnarray}h(\boldsymbol{R},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E},t)=\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\,\mathop{\sum }_{p}h_{p}(\unicode[STIX]{x1D6E9},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E})\text{e}^{\text{i}nZ+\text{i}S(\unicode[STIX]{x1D6F9})-\text{i}m\unicode[STIX]{x1D6E9}-\text{i}p\unicode[STIX]{x1D711}}.\end{eqnarray}$$ Here, 
$\unicode[STIX]{x1D717}$ and 
$\unicode[STIX]{x1D701}$ are the poloidal and toroidal angles and 
$\unicode[STIX]{x1D713}$ the poloidal flux function, with 
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D713}+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$, 
$\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D717}+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}$ and 
$Z=\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FA}^{-1}\boldsymbol{v}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$, their gyrokinetic counterparts. To simplify the presentation, drift effects are ignored and 
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}\simeq B/qR$ is employed. The definition of 
$W_{p,m}$ is now as in Catto et al. (Reference Catto, Lee and Ram2017) without drifts,
$$\begin{eqnarray}W_{p,m}=\text{e}^{\text{i}p\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D73A}_{m}\boldsymbol{\cdot }[\boldsymbol{b}v_{\Vert }J_{p}(\unicode[STIX]{x1D702})+\boldsymbol{e}_{\bot p}v_{\bot }]\left[\frac{1}{v}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\frac{(\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert })}{\unicode[STIX]{x1D714}B}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right],\end{eqnarray}$$where
$$\begin{eqnarray}\boldsymbol{e}_{\bot p}=\frac{1}{k_{\bot }}\left[\boldsymbol{k}_{\bot }\frac{p}{\unicode[STIX]{x1D702}}J_{p}(\unicode[STIX]{x1D702})+\text{i}\boldsymbol{b}\times \boldsymbol{k}\frac{\unicode[STIX]{x2202}J_{p}(\unicode[STIX]{x1D702})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right].\end{eqnarray}$$ Defining 
$k_{\Vert }=(qn-m)/qR$, gives
$$\begin{eqnarray}\frac{v_{\Vert }}{qR}\frac{\unicode[STIX]{x2202}h_{p}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-\text{i}[\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6E9})-k_{\Vert }v_{\Vert }(\unicode[STIX]{x1D6E9})]h_{p}-\unicode[STIX]{x1D708}v_{\bot }^{2}\frac{\unicode[STIX]{x2202}^{2}h_{p}}{\unicode[STIX]{x2202}v_{\Vert }^{2}}=-\mathop{\sum }_{m^{\prime }}\text{e}^{\text{i}(m^{\prime }-m)\unicode[STIX]{x1D6E9}}W_{p,m^{\prime }},\end{eqnarray}$$where for resonant particles and weak collisions the second and third terms on the left are small giving the lowest-order result
$$\begin{eqnarray}\frac{v_{\Vert }}{qR}\frac{\unicode[STIX]{x2202}h_{p}^{(0)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}=0,\end{eqnarray}$$ with 
$h_{p}=h_{p}^{(0)}+h_{p}^{(1)}+\cdots \,$ and 
$h_{p}^{(0)}\gg h_{p}^{(1)}$. Consequently, 
$h_{p}$ is slow function of 
$\unicode[STIX]{x1D6E9}$. To next order
$$\begin{eqnarray}\frac{v_{\Vert }}{qR}\frac{\unicode[STIX]{x2202}h_{p}^{(1)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-\text{i}[\unicode[STIX]{x1D714}-p\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6E9})-k_{\Vert }v_{\Vert }(\unicode[STIX]{x1D6E9})]h_{p}^{(0)}-\unicode[STIX]{x1D708}v_{\bot }^{2}\frac{\unicode[STIX]{x2202}^{2}h_{p}^{(0)}}{\unicode[STIX]{x2202}v_{\Vert }^{2}}=-\mathop{\sum }_{m^{\prime }}\text{e}^{\text{i}(m^{\prime }-m)\unicode[STIX]{x1D6E9}}W_{p,m^{\prime }}.\end{eqnarray}$$Assuming successive correlated passes through resonance, transit averaging over a full bounce for the trapped and a single poloidal circuit for the passing to annihilate the streaming term using
$$\begin{eqnarray}\overline{(\ldots )}=\oint \text{d}\unicode[STIX]{x1D70F}(\ldots )\left/\oint \text{d}\unicode[STIX]{x1D70F}\right.,\end{eqnarray}$$with
$$\begin{eqnarray}\text{d}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70F})/\text{d}\unicode[STIX]{x1D70F}=v_{\Vert }(\unicode[STIX]{x1D70F})/qR,\end{eqnarray}$$leaves
$$\begin{eqnarray}\text{i}[\unicode[STIX]{x1D714}-p\overline{\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6E9})}-k_{\Vert }\overline{v_{\Vert }(\unicode[STIX]{x1D6E9})}]h_{p}^{(0)}+\unicode[STIX]{x1D708}v_{\bot }^{2}\frac{\unicode[STIX]{x2202}^{2}h_{p}^{(0)}}{\unicode[STIX]{x2202}v_{\Vert }^{2}}=\mathop{\sum }_{m^{\prime }}\overline{\text{e}^{\text{i}(m^{\prime }-m)\unicode[STIX]{x1D6E9}}W_{p,m^{\prime }}},\end{eqnarray}$$ where for the trapped 
$\overline{v_{\Vert }(\unicode[STIX]{x1D6E9})}=0$. The preceding equation is of the same form as (3.4). Therefore, a collisional boundary layer is expected to exist about the resonance 
$\unicode[STIX]{x1D714}-p\overline{\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6E9})}-k_{\Vert }\overline{v_{\Vert }(\unicode[STIX]{x1D6E9})}=0$ even in the presence of the parallel gradients that are inherent to a tokamak. However, in this case as particles go out of resonance they are replaced by new particles, while in the uniform field case the same particles tend to stay in resonance.
Even though the resonance location depends on poloidal angle in (B 11), it is only the velocity space diffusion that broadens the resonance as in (3.4).
