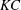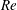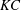1. Introduction
1.1. Motivation and objectives
Sinusoidally oscillatory flow around a circular cylinder has been studied extensively for decades owing to its relevance to engineering applications, such as wave loads on cylindrical marine structures (Maull & Milliner Reference Maull and Milliner1978; Bearman et al. Reference Bearman, Downie, Graham and Obasaju1985; Williamson Reference Williamson1985; Obasaju, Bearman & Graham Reference Obasaju, Bearman and Graham1988; Sarpkaya Reference Sarpkaya2002; Saghafian et al. Reference Saghafian, Stansby, Saidi and Apsley2003) and the rich physics displayed by the flow, especially at relatively low oscillation amplitude and frequency (Honji Reference Honji1981; Tatsuno & Bearman Reference Tatsuno and Bearman1990; Dütsch et al. Reference Dütsch, Durst, Becker and Lienhart1998; Elston, Blackburn & Sheridan Reference Elston, Blackburn and Sheridan2006; An, Cheng & Zhao Reference An, Cheng and Zhao2011). In contrast, oscillatory flow around multiple cylinders has not attracted the attention that this interesting problem deserves. Owing to functional requirements, multiple cylinders are commonly arranged in groups in many offshore engineering applications, where the structures are routinely exposed to oscillatory flow induced by waves. For example, a tension leg platform or a semisubmersible platform often has four columns that are spaced at around three to four diameters apart. The riser systems of floating offshore platforms often comprise closely spaced multiple pipes. The case of four cylinders in a square arrangement is unique in terms of the flow characteristics that it displays. This is because it includes a pair of tandem cylinders in a side-by-side arrangement, as well as two pairs of staggered cylinders, such that both wake and proximity interferences may occur.
Steady flow around multiple structures has attracted significant research attention because of the diversity of fluid forces and flow features in this case. For example, it has been observed that, when two or more circular cylinders are arranged close to each other in a steady flow, proximity and wake interferences lead to repulsive forces and biased vortex shedding (Zdravkovich Reference Zdravkovich1987; Hu & Zhou Reference Hu and Zhou2008). Oscillatory flow around multiple cylinders is expected to exhibit similar responses to these types of interference. However, our understanding is limited by the scarcity of research on the subject. This motivates the present study of oscillatory flow around four cylinders in a square arrangement, as shown in figure 1.
Figure 1. Schematic representation of the four-circular-cylinder system. The cylinders are represented by four circles 1–4 in a clockwise direction.
Oscillatory flow around a circular cylinder is mainly governed by two dimensionless parameters, namely the Keulegan–Carpenter number
$\mathit{KC}$
and the Reynolds number
$\mathit{Re}$
. These are conventionally defined as
$$\begin{eqnarray}\mathit{KC}=\frac{U_{m}T}{D}\quad \text{and}\quad \mathit{Re}=\frac{U_{m}D}{{\it\nu}},\end{eqnarray}$$
where
$D$
is the diameter of the cylinder,
${\it\nu}$
is the kinematic viscosity of the fluid, and
$U_{m}$
and
$T$
are the amplitude and period of the velocity oscillation, respectively. The ratio of
$\mathit{Re}$
and
$\mathit{KC}$
, known as the frequency parameter or Stokes number (
${\it\beta}=D^{2}/{\it\nu}T$
), is also often referred to in the literature. For oscillatory flow around a four-cylinder array, flow features are also affected by the gap ratio, which is defined as the ratio of gap distance,
$L$
, to the cylinder diameter (see figure 1),
$$\begin{eqnarray}G=\frac{L}{D}.\end{eqnarray}$$
It should be pointed out that the flow is also dependent on the angle between the direction of the oscillatory flow and the cylinder array. However, this effect is not investigated in the present study. The main aim of the present work is to investigate the oscillatory flow features around four circular cylinders arranged in an in-line square arrangement, as shown in figure 1. The study focuses on comparatively small
$\mathit{KC}$
and
$\mathit{Re}$
conditions in the range
$\mathit{KC}\in [1,12]$
and
$\mathit{Re}\in [20,200]$
, at a gap ratio ranging from 0.5 to 4.
1.2. Previous studies
At low
$\mathit{KC}$
and
$\mathit{Re}$
values, oscillatory flow around a single cylinder may present four kinds of two-dimensional (2D) symmetries (Elston, Sheridan & Blackburn Reference Elston, Sheridan and Blackburn2004; Elston et al.
Reference Elston, Blackburn and Sheridan2006): one reflection symmetry about the axis of oscillation,
$K_{x}$
, and two spatio-temporal symmetries,
$H_{1}$
and
$H_{2}$
, along with a ‘basic state’, where all of these three symmetries are preserved. By introducing an oscillatory flow in the
$y$
direction,
$U_{y}(t)=U_{m}\sin (2{\rm\pi}t/T)$
, the symmetry patterns identified for oscillatory flow around a single cylinder can be represented through the vorticity component in the axial direction,
${\it\omega}_{z}$
, as
$$\begin{eqnarray}\displaystyle K_{x}:\quad {\it\omega}_{z}(x,y,t) & = & \displaystyle {\it\omega}_{z}(-x,y,t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{1}:\quad {\it\omega}_{z}(x,y,t) & = & \displaystyle -{\it\omega}_{z}(x,-y,t+T/2),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{2}:\quad {\it\omega}_{z}(x,y,t) & = & \displaystyle {\it\omega}_{z}(-x,-y,t+T/2),\end{eqnarray}$$
${\it\omega}_{z}$
is determined as the curl of velocity vector
$\boldsymbol{U}=(U_{x},U_{y})$
, 
$$\begin{eqnarray}{\it\omega}_{z}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{U}\left(\frac{D}{U_{m}}\right).\end{eqnarray}$$
These symmetries are illustrated in figure 2 based on the present numerical results at
$\mathit{KC}=11$
and
$\mathit{Re}=60$
, 80 and 100, respectively. It is noted that both
$H_{1}$
and
$H_{2}$
are preserved in the
$K_{x}$
symmetry. It was also observed by Elston et al. (Reference Elston, Blackburn and Sheridan2006) that the
$K_{x}$
symmetry in the cross-sectional flow fields around a single oscillatory cylinder is identical to the basic state with full symmetry.
Figure 2. The three symmetries
$K_{x}$
,
$H_{1}$
and
$H_{2}$
of the
$z$
-vorticity component for oscillating flow around a fixed circular cylinder at
$\mathit{KC}=11$
: (a)
$K_{x}$
at
$\mathit{Re}=60$
, along with the coordinate system; (b)
$H_{1}$
at
$\mathit{Re}=80$
; and (c)
$H_{2}$
at
$\mathit{Re}=100$
. Instantaneous vorticity contours are obtained from 2D direct numerical simulation at 100th oscillation. The continuous contours denote positive vorticity, whereas dotted ones are for negative vorticity, with cutoff level
${\it\Omega}=\pm 0.1$
. The inlet oscillatory flow is in the vertical direction.
Comprehensive flow features induced by sinusoidal oscillations of a circular cylinder in an otherwise stationary fluid at low
$\mathit{KC}$
and low
${\it\beta}$
were experimentally identified by Tatsuno & Bearman (Reference Tatsuno and Bearman1990). Eight flow regimes were classified within
$1.6\leqslant \mathit{KC}\leqslant 15$
and
$5\leqslant {\it\beta}\leqslant 160$
. The flow regime map in the range of
$\mathit{KC}\leqslant 12$
and
$\mathit{Re}\leqslant 400$
is reproduced for the convenience of discussion in figure 3 as a function of
$\mathit{KC}$
and
$\mathit{Re}$
. Among the flow regimes, flows in regimes A and
$\text{A}^{\ast }$
are 2D and symmetric to the direction of motion, with vortex shedding occurring in regime A but not in
$\text{A}^{\ast }$
. Regime B features the so called ‘streaked flow’ along the axis of the cylinder, which is composed of equally spaced streaks of mushroom-shape flow structures (Honji Reference Honji1981). Although regime B flows are three-dimensional (3D), cross-sectional flows (in the
$x{-}y$
plane) preserve
$K_{x}$
symmetry (Elston et al.
Reference Elston, Blackburn and Sheridan2006). Flows in regimes C–G are apparently 3D and also break the 2D
$K_{x}$
symmetry. A key observation in regime C is that the vortex does not synchronize with the oscillation period; rather, it is rearranged into large vortices with a secondary period before emanating in the direction of motion. The transverse vortex streets are found in regimes D and E, where vortices are obliquely convected to one side of the axis of oscillation. Irregular switching of the convection direction is evolved in regime E. Diagonal double-pair vortices feature in regime F. The
$H_{1}$
symmetry is largely preserved while
$K_{x}$
and
$H_{2}$
symmetries are broken in regimes C, D and E. The
$H_{2}$
symmetry is roughly preserved, but
$K_{x}$
and
$H_{1}$
symmetries are broken in regime F. The flow field in regime G breaks all the
$K_{x}$
,
$H_{1}$
and
$H_{2}$
symmetric patterns, is chaotic and characterized by a circulatory flow streaming and irregular 3D flow structures.
Figure 3. Flow regimes reproduced from Tatsuno & Bearman (Reference Tatsuno and Bearman1990): regime A, symmetric with vortex shedding, 2D; A
$^{\ast }$
, symmetric and attached, 2D; B, longitudinal vortices, 3D streaked flow; C, rearrangement of large vortices, 3D; D, transverse street, 3D; E, transverse street with irregular switching, 3D; F, diagonal double pair, 3D; and G, circulatory flow streaming that intermittently changes directions, 3D.
Many experimental and numerical studies have been carried out within the parameter ranges covered in the map of regimes shown in figure 3. Some of these studies are summarized in table 1. Where they were not provided in the original study, the flow regimes listed in table 1 were estimated based on the ranges of
$\mathit{KC}$
and
${\it\beta}$
. A significant amount of knowledge has been gained through these studies, which has been reviewed by Bearman (Reference Bearman1984) and Elston et al. (Reference Elston, Blackburn and Sheridan2006) and thus is not repeated here. Only those numerical studies that are closely relevant to the present study are briefly reviewed. It has been generally accepted that 2D numerical models are able to predict oscillatory flow features under a reasonably wide range of flow regimes, including the regimes that harbour 3D flows. By solving the 2D Navier–Stokes (NS) equations, Justesen (Reference Justesen1991) found that the simulated oscillatory flow structures around a cylinder were in good agreement with those observed in experimental flow visualizations at about
${\it\beta}\leqslant 250$
with small
$\mathit{KC}$
numbers. The calculated drag and inertia coefficients for
${\it\beta}=196$
, 483 and 1035 and
$0<\mathit{KC}<26$
were found to agree with the experimental data well. Lin, Bearman & Graham (Reference Lin, Bearman and Graham1996) investigated oscillatory flow around a circular cylinder at a fixed
${\it\beta}=76$
using a 2D discrete vortex method. It was reported that all major vortex-shedding regimes that were observed in the experiments at
$\mathit{KC}$
values up to 30 were well reproduced by the numerical simulation. Dütsch et al. (Reference Dütsch, Durst, Becker and Lienhart1998) reproduced regimes A, E and F by 2D simulations, and reported a good comparison of drag and inertia coefficients with experimental data at
${\it\beta}=35$
(see figure 3) and
$\mathit{KC}\leqslant 15$
. Nehari, Armenio & Ballio (Reference Nehari, Armenio and Ballio2004) compared the 2D and 3D numerical results in regimes D and F. It was found that the in-line force component (in the direction of oscillatory flow) is only weakly affected by the 3D effect. It was also found that most of the cross-sectional vortex streets are induced by 2D instabilities and can be reproduced by pure 2D simulations. The numerical results obtained from 2D numerical studies appear to suggest that three-dimensionality has limited effects on the principal cross-sectional flow features and the in-line force at relative low
$\mathit{KC}$
and
${\it\beta}$
values.
Table 1. A brief summary of reviewed studies of oscillatory flow around a circular cylinder. The last column was estimated based on
$\mathit{KC}$
and
${\it\beta}$
provided, if not specifically mentioned in the original paper.
Studies on oscillatory flow around two or more cylinders have not been documented extensively in the literature, and some available experimental and numerical investigations are summarized in table 2. The alignment angle
${\it\alpha}$
listed in table 2 is the angle between the flow and the line joining cylinder centres. Williamson (Reference Williamson1985) carried out an experimental study to investigate the synchronization of vortex shedding of two oscillatory cylinders in still fluid and measured the forces on the cylinders. Uzunoğlu et al. (Reference Uzunoğlu, Tan and Price2001) investigated the flow fields and force coefficients for two cylinders in the side-by-side and tandem configurations. It is only recently that oscillatory flow around two or four cylinders has attracted reasonable research interest, mainly based on 2D numerical models. Chern et al. (Reference Chern, Rajesh Kanna, Lu, Cheng and Chang2010) and Chern, Shiu & Horng (Reference Chern, Shiu and Horng2013) simulated oscillatory flow past two side-by-side square cylinders and four circular cylinders in staggered and in-line arrangements, respectively. It was found that the gap flow between the cylinders has a significant effect on the flow field and hydrodynamic forces on the cylinders. Yang et al. (Reference Yang, Cheng, An, Bassom and Zhao2013) investigated oscillatory flow around a pair of cylinders of unequal diameters based on a 2D model. The influence of gap ratio and positional angle on the flow field and hydrodynamic forces were investigated. By solving the 2D NS equations using a finite-element method, Zhao & Cheng (Reference Zhao and Cheng2014) investigated oscillatory flow around a two-cylinder system in both side-by-side and tandem arrangements at Reynolds numbers 150 and 100. They identified several flow regimes based on combinations of the flow regimes observed around a single cylinder, as well as some new flow features, such as gap vortex shedding (GVS), where the vortices only shed from the gap side of the system. So far, there has not been a systematic study on flow regimes around four cylinders, to the authors’ knowledge.
Table 2. Selected studies of oscillatory flow around multiple cylinders.
In the present study, a 2D numerical model is employed to investigate oscillatory flow regimes around a four-cylinder array in the parameter range of
$\mathit{KC}\in [1,12]$
and
$\mathit{Re}\in [20,200]$
with a
$\mathit{KC}$
increment of 1 and an
$\mathit{Re}$
increment of 20. It is expected that the 2D model is sufficient to reveal the occurrence of various flow regimes that are related to the 2D instabilities (Nehari et al.
Reference Nehari, Armenio and Ballio2004), and this is also tested by a brief comparison of the 2D and 3D numerical results in the present study.
The remainder of the paper is organized in the following manner. In § 2, the governing equations, numerical model and model validation exercises are introduced, while § 3 presents the flow regime classifications. Drag and inertia coefficients are discussed in § 4, along with a brief analysis on wall vorticity. Finally, major conclusions are drawn in § 5. In the Appendix we provide further validation of the numerical model.
2. Numerical method and model validation
2.1. Numerical model
Oscillatory flow around the four-cylinder array shown in figure 1 is simulated by solving the 2D NS equations. The dimensionless form of the 2D NS equations for incompressible flow in the Cartesian coordinate system can be expressed as (An et al. Reference An, Cheng and Zhao2011)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\mathit{KC}}\frac{\partial U_{x}}{\partial t}+U_{x}\frac{\partial U_{x}}{\partial x}+U_{y}\frac{\partial U_{x}}{\partial y}+\frac{\partial p}{\partial x}=\frac{1}{\mathit{Re}}\left(\frac{\partial ^{2}U_{x}}{\partial x^{2}}+\frac{\partial ^{2}U_{x}}{\partial y^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\mathit{KC}}\frac{\partial U_{y}}{\partial t}+U_{x}\frac{\partial U_{y}}{\partial x}+U_{y}\frac{\partial U_{y}}{\partial y}+\frac{\partial p}{\partial y}=\frac{1}{\mathit{Re}}\left(\frac{\partial ^{2}U_{y}}{\partial x^{2}}+\frac{\partial ^{2}U_{y}}{\partial y^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial U_{x}}{\partial x}+\frac{\partial U_{y}}{\partial y}=0, & \displaystyle\end{eqnarray}$$
$U_{x}$
and
$U_{y}$
are the velocity components in the
$x$
and
$y$
directions, respectively,
$t$
is time and
$p$
is pressure. The finite-volume method is used and pressure–velocity coupling is achieved following the pressure implicit with splitting of operators (PISO) method. The convection terms are discretized using the Gauss cubic scheme, while the Laplacian and pressure terms in the momentum equations are discretized using the Gauss linear scheme. The Euler implicit scheme is adopted for the temporal discretization. The NS equations are solved using the Open-source Field Operation and Manipulation (OpenFOAM®) C
$++$
libraries, which is an open-source computational fluid dynamics (CFD) package developed by OpenCFD Ltd.
A rectangular computational domain, as shown in figure 4(a), is employed in this study, with the cylinder array being placed at the centre of the domain. The initial values for flow velocity and pressure in the whole domain are set to zero. Flow velocity and pressure boundary conditions on the bottom boundary are specified as
$$\begin{eqnarray}\displaystyle & \displaystyle U_{y}(t)=U_{m}\sin \!\left(\frac{2{\rm\pi}}{T}t\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & U_{x}(t)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial p}{\partial y}=U_{m}\frac{2{\rm\pi}}{T}\cos \!\left(\frac{2{\rm\pi}}{T}t\right). & \displaystyle\end{eqnarray}$$
Figure 4. Schematic representation of (a) the computational domain and (b) the mesh distribution around a single cylinder.
At the top boundary, the velocity gradients in the
$y$
direction and the pressure are set to zero. The symmetry boundary condition is applied at the two lateral boundaries that are parallel to the flow directions and the no-slip boundary condition is adopted on the cylinder surfaces.
2.2. Mesh dependence check
The present numerical model is validated extensively against experimental and numerical results for oscillatory flow around a single cylinder. First of all, suitable domain and mesh sizes are determined through a domain and mesh size dependence check. Then the numerically determined force coefficients, velocity distributions and flow regimes are compared with published results. The detailed validation checks are reported in this subsection and in the Appendix.
The computational domain size and mesh dependence checks are carried out against oscillatory flow around a circular cylinder at
$(\mathit{Re},\mathit{KC})=(100,5)$
, where independent experimental and numerical results are available. Figure 4(b) illustrates a typical mesh distribution around the cylinder. Five meshes (as detailed in table 3) with cell counts ranging from 41 948 to 186 264 corresponding to domain size of
$32D\times 58D$
and
$100D\times 100D$
, respectively, are generated by changing the mesh distribution around the cylinder surface, in both the radial and circumferential directions, and also in the far field The calculated drag and inertia coefficients,
$C_{D}$
and
$C_{M}$
, are compared with available data in table 3.
$C_{D}$
and
$C_{M}$
are derived through the least-squares regression analysis of the in-line force on the cylinder based on the Morison equation (Morison, Johnson, & Schaaf Reference Morison, Johnson and Schaaf1950),
$$\begin{eqnarray}F_{y}=\frac{1}{2}{\it\rho}DC_{D}|U_{y}(t)|U_{y}(t)+{\it\rho}\frac{{\rm\pi}D^{2}}{4}C_{M}\frac{\text{d}U_{y}(t)}{\text{d}t},\end{eqnarray}$$
where
$F_{y}$
is the force on the cylinder in the in-line direction and is obtained by integrating the pressure and shear stress along the cylinder surface, and
${\it\rho}$
is the density of the fluid. It can be seen that, despite the large differences in the domain and mesh sizes, the predicted
$C_{D}$
and
$C_{M}$
are almost identical, suggesting that the numerical results are independent of the domain and mesh sizes in the range employed here. Even mesh 1, with the coarsest mesh on the smallest computational domain of the tested cases, is sufficient for the case
$(\mathit{Re},\mathit{KC})=(100,5)$
.
$C_{D}$
and
$C_{M}$
showed less than 2 % difference from those predicted by previous 2D and 3D numerical studies, confirming that three-dimensionality in the flow is weak. The mesh and domain size adequacy is also checked for the most extreme case covered in this study at
$(\mathit{Re},\mathit{KC})=(200,12)$
and the results are shown in table 4. Again, good convergence is observed.
Table 3. Influence of the computational domain and mesh sizes on
$C_{D}$
and
$C_{M}$
for a single cylinder in oscillatory flow at
$(\mathit{Re},\mathit{KC})=(100,5)$
. Here
$N_{v}$
is total mesh number; and
$N_{c}$
is mesh number attached to the cylinder surface.
Table 4. Mesh-independent study at
$\mathit{Re}=200$
,
$\mathit{KC}=12$
.
Although all the meshes tested in table 3 have been demonstrated to be sufficient for the flow condition around a single cylinder, the relatively fine mesh 4 with a large domain size is mostly chosen in the simulations for the four-cylinder array. It is considered, first of all, that the large domain size of
$100D\times 100D$
is well suited for the planned simulations with the increased blockage ratio. Secondly, the fine mesh in mesh 4, with the number of cells being more than four times that of mesh 1, is needed to resolve the fine flow structures in the gaps. Mesh 4, which has a minimum non-dimensional distance of
$y^{+}=0.03$
for the largest
$\mathit{Re}$
considered in this study (
$y^{+}=u_{f}{\it\Delta}/{\it\nu}$
, where
$u_{f}$
is the friction velocity and
${\it\Delta}$
is the size of the first layer next to the cylinder surface), is considered to be sufficiently fine for all the cases in this study.
Figure 5. Simulated flow patterns represented by streaklines in different flow regimes for oscillatory flow past a single cylinder, generated by releasing massless particles around the cylinder surface. The background dashed square is 2D in size. The inlet oscillatory flow is in the vertical direction.
The predicted flow regimes agree qualitatively with those reported by Tatsuno & Bearman (Reference Tatsuno and Bearman1990). Six selected cases representing the flow regimes
$\text{A}^{\ast }$
, A, C, D, E and F are visualized through streaklines in figure 5. The streaklines are generated by releasing massless particles at 100 points around the cylinder surface with a frequency eight times the oscillatory flow frequency. Care is taken in generating the streaklines to make sure that the choice of the number of points around the cylinder and the frequency of particle release does not affect the visualization of the flow fields. The massless fluid particles are released from the cylinder surface after the simulations become fully established, generally after
$t=90T$
.
In regime A
$^{\ast }$
, the fluid particles are transported away from the cylinder surface symmetrically along the axis of flow oscillation without vortex shedding. The flow patterns in regime A are similar to those observed in regime A
$^{\ast }$
except that vortex shedding is detected. Regimes A
$^{\ast }$
and A can be classified as the reflection symmetry,
$K_{x}$
. The rearrangement of large vortices in regime C and transverse vortex shedding (Vpattern) in regimes D and E belong to the spatio-temporal symmetry
$H_{1}$
. Regime F falls into the
$H_{2}$
symmetry pattern, with two branches of the vortex streets being diagonally aligned on opposite sides of the cylinder.
More model validations are presented in the Appendix and these tests demonstrate that the present numerical model is capable of predicting the force coefficients, velocity distribution and flow patterns of oscillatory flow past a single cylinder within
$\mathit{KC}\in [1,12]$
and
$\mathit{Re}\in [20,200]$
. In the remaining part of this paper, we will simulate oscillatory flow around a four-cylinder array in a square arrangement.
3. Flow regimes around the cylinder array
A number of flow patterns are observed around a four-cylinder array for
$0.5\leqslant G\leqslant 4$
,
$20\leqslant \mathit{Re}\leqslant 200$
and
$1\leqslant \mathit{KC}\leqslant 12$
. While a few of the observed flow patterns resemble the flow fields around a single cylinder in many respects, a number of new flow structures induced by the interactions of shear layers/vortices from individual cylinders are discovered and classified. Instead of creating new names for the flow features around the four-cylinder array, we prefer to classify the flow regimes by adopting and combining names established for the flow regimes and symmetry patterns by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) and Elston et al. (Reference Elston, Blackburn and Sheridan2006).
The flow regimes for gap ratios
$G=0.5$
, 1, 2 and 4 are mapped out on the
$\mathit{Re}{-}\mathit{KC}$
plane in figure 6, along with the symmetry patterns that describe the flow fields as a whole. The reflection symmetry and two spatio-temporal symmetries are labelled as
$K_{x}$
,
$H_{1}$
and
$H_{2}$
, respectively, while symmetry breaking is labelled
$N$
, i.e. no symmetry could be found. The areas at the bottom left corner enclosed by the dark dash-dotted lines (labelled
$K_{x}$
) and the figure frame boundaries in figure 6 belong to
$K_{x}$
symmetry, while the areas beyond the lines labelled
$N$
at the top right corners of figure 6(b–d) belong to the symmetry-breaking regime
$N$
. Regime
$H_{1}$
flows are only observed at the smallest gap ratio of
$G=0.5$
in an area enclosed by the
$K_{x}$
line,
$H_{1}$
line and the top and right figure frame. Regime
$H_{2}$
flows are found at three larger gap ratios in the
$\mathit{Re}{-}\mathit{KC}$
plane in figure 6(b–d); they fall into an area between
$K_{x}$
and
$N$
and are labelled
$H_{2}$
directly on the corresponding points. The boundaries of flow regimes for a single cylinder in oscillatory flow are also included as light dashed lines in figure 6 for the purpose of comparison.
Figure 6. Classifications of flow regimes of oscillating flow around four circular cylinders in an in-line square arrangement: (a) gap ratio
$G=0.5$
; (b)
$G=1$
; (c)
$G=2$
; (d)
$G=4$
. Here,
$K_{x}$
,
$H_{1}$
and
$H_{2}$
are the 2D symmetry states explained in § 1.2;
$N$
denotes that none of the symmetries were found, i.e. the state of symmetry breaking;
$\cdots \cdots$
, marginal lines for basic state within
$K_{x}$
symmetry where both
$H_{1}$
and
$H_{2}$
are preserved; grey dashed lines, the boundary regimes found by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) for a single cylinder.
In the
$K_{x}$
domain, the flow regimes around the cylinders are named based on the flow regimes identified by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) for a single cylinder. For instance, regime 4A indicates four individual regime A flows, with little influence from flows induced elsewhere in the array. The structure of the flow in each regime will be explained in the following subsections.
3.1.
$K_{x}$
symmetry
It is observed that the upper
$K_{x}$
regime boundary lines for
$G=0.5$
and 1 are located at the top right corners of figure 6(a,b) and are far different from the boundary lines dividing flow regimes A and D for a single cylinder. The reason for the dominance of regime
$K_{x}$
at low gap ratios is twofold. Firstly, oscillatory flow around the four-cylinder array at small gap ratios behaves in a similar way to oscillatory flow around a single cylinder with a large effective cylinder diameter. A large effective cylinder diameter corresponds to a small effective
$\mathit{KC}$
number, which shifts the
$K_{x}$
regime boundary to the bottom right and also suggests a more stable flow based on the flow regime chart (in the
${\it\beta}{-}\mathit{KC}$
plane) reported by Tatsuno & Bearman (Reference Tatsuno and Bearman1990).
Figure 7. Contours of jet-like flow along with the streamlines at
$(G,\mathit{Re},\mathit{KC})=(0.5,120,8)$
. The inlet oscillatory flow is in the vertical direction.
Figure 8. Measured velocity in the oscillation direction at selected probes compared to the inlet velocity for cases of
$(\mathit{Re},\mathit{KC})=(120,8)$
at
$t=98T{-}99T$
. (a) For
$G=0.5$
: — ⋅ —, probe 1; - - - -, probe 2;
$\cdots \cdots$
, probe 3; ——, inlet. (b) For probe 1: — ⋅ —,
$G=0.5$
; - - - -,
$G=1$
;
$\cdots \cdots$
,
$G=2$
; ——,
$G=\infty$
.
Secondly, the jet-like flow through the cylinder gaps in the oscillation direction plays an important role in maintaining the
$K_{x}$
symmetry. Oscillatory flow structures are examined to illustrate this point further. Figure 7 shows the contours of
$U_{y}$
together with a few illustrative streamlines at eight instants with a time interval of
$T/8$
in an oscillation period at
$(G,\mathit{Re},\mathit{KC})=(0.5,120,8)$
. A jet-like flow pattern is observed through the gap between two cylinder columns in all instants except for the two instants when the flow changes its direction, as seen from the upright streamlines. Figure 8(a) shows the measured velocity at three locations along the oscillation direction in the gap (probes 1 and 3 bisect the faces of the square normal to the flow, while probe 2 is at the origin of coordinates), together with the ambient flow velocity imposed at the inlet of the computational domain. From the velocity contours and the measured velocity at the probe locations, it is observed that: (i) the velocity magnitudes at the three probe locations are about twice the ambient velocity at the inlet of the computational domain; (ii) there are phase differences between the ambient velocity and the velocities measured at the three probe locations; (iii) the phase differences between the ambient flow and flow at probes 1 and 3 are somewhat larger than those between the ambient flow and the flow at probe 2, while the velocities at all three probe locations reach their peaks at almost the same time; and (iv) the duration of the flow acceleration phase at probe 2 is shorter than the duration of the deceleration phase at the same location.
Explanations of all these observations are proposed. The large velocity magnitudes at the three probe locations are due to the blockage effects of the structure. The phase differences between the ambient velocity and the velocity measured at the three probe locations are the direct results of wall boundary layers around the cylinder surfaces. The larger phase differences between the ambient flow and the flow at probes 1 and 3 and that between the ambient flow and the flow at probe 2 are because the former are closer to the cylinder surface. The closer to the wall boundary, the larger is the expected phase angle difference (based on the Stokes boundary layer solution). The shorter duration of the acceleration phase at probe 2 is mainly caused by the combined effects of the phase difference between the velocity at probe 2 and probe 1 (and 3) at small velocity magnitudes and the continuity constraint of the strong jet flow through the cylinder gaps at large velocity magnitudes. This forces the velocity at probe 2 to reach its peak value at approximately the same time as the velocities at probes 1 and 3 reach their peak values. The strong jet-like flow through the gap forms a distinct separation of the left two cylinders from their right counterparts and decreases the chance of vortex and/or shear layer interactions between the flows around the left and right columns of cylinders. Therefore it plays a significant role in stabilizing the flow field in the
$K_{x}$
symmetry. We call this flow feature at low gap ratios the ‘stabilization effect’, since it provides stability to the flow in the streamwise (oscillation) direction.
The stabilization effect weakens with increasing
$G$
and/or
$\mathit{Re}$
, where vortices start to be shed alternatively from the inner sides of the cylinders. Figure 8(b) shows the variation of fluid velocity over an oscillation period at probe 1 for four gap ratios at
$(\mathit{Re},\mathit{KC})=(120,8)$
. It is seen that the differences in both the magnitude and the phase angle between the velocity at probe 1 and the ambient velocity at the inlet gradually diminish with increasing gap distance.
At
$G=2$
and 4, on the other hand, the increase in gap ratio leads to an increase in individual flow behaviour around the four cylinders, and more vortex interactions. Referring to figure 6, much of the
$\mathit{Re}{-}\mathit{KC}$
plane at
$G=2$
and 4 is dominated by asymmetric flow fields (regime
$N$
), because the symmetric pattern is simply not easy to achieve with independent vortex shedding from all of the four structures.
Owing to the interaction of flow fields from each of the four cylinders, six types of
$K_{x}$
symmetry are observed and are labelled 2(A
$^{\ast }$
-A
$^{\ast }$
), 2(A-A), 4A
$^{\ast }$
, 4A, 2(A-D) and 4D. Each of these symmetric patterns is explained below.
3.1.1. Regimes 2(A
$^{\ast }$
-A
$^{\ast }$
) and 2(A-A)
In regimes 2(A
$^{\ast }$
-A
$^{\ast }$
) and 2(A-A), the left and right columns of two cylinders behave like two elongated structures in a side-by-side configuration. The flow fields around both of the elongated structures fall into regime A
$^{\ast }$
or A at small values of
$\mathit{KC}$
and
$\mathit{Re}$
. Vorticity
$({\it\omega}_{z})$
contours and streaklines of a typical regime 2(A
$^{\ast }$
-A
$^{\ast }$
) flow with
$(G,\mathit{Re},\mathit{KC})=(1,20,5)$
and of a typical 2(A-A) flow with
$(G,\mathit{Re},\mathit{KC})=(1,80,5)$
in one vortex shedding period are shown in figures 9 and 10, respectively. The massless particles released from different cylinders are denoted by different colours to visualize the mixing of particles as a consequence of flow interference. It is seen that the shear layers from each of the two elongated pairs are merged together for most of an oscillation period, but are divided after flow reversal when the velocity of the fluid is relatively low, i.e. at
$t=99+{\textstyle \frac{1}{8}}T$
and
$+{\textstyle \frac{5}{8}}T$
. The vorticity strengths at the outer sides of the array are considerably lower than those on the inner sides. The strong flow through the streamwise gap is an obvious feature of regime 2(A
$^{\ast }$
-A
$^{\ast }$
) and 2(A-A) flows. A similar feature of vortex shedding from the gap observed in figure 10 was also reported in oscillatory flow around two side-by-side cylinders by Zhao & Cheng (Reference Zhao and Cheng2014) and named GVS. Since weak vortex shedding is also observed from the outsides of the four-cylinder array, we named this regime 2(A-A).
Figure 9. An example of flow in regime 2(A
$^{\ast }$
-A
$^{\ast }$
) in the
$K_{x}$
symmetry zone at
$(G,\mathit{Re},\mathit{KC})=(1,20,5)$
for oscillatory flow around four circular cylinders in an in-line square arrangement. The flow field is illustrated by eight instantaneous vorticity contours at one oscillation period and by the massless particles advected from the surfaces of each cylinder with different colours. The continuous contours denote positive vorticity, whereas dotted ones are for negative vorticity, with cutoff level
${\it\Omega}=\pm 0.1$
. The inlet oscillatory flow is in the vertical direction.
Figure 10. An example of oscillatory flow field in regime 2(A-A) in the
$K_{x}$
symmetry zone at
$(G,\mathit{Re},\mathit{KC})=(1,80,5)$
.
The resemblance of the oscillatory flow features around a four-cylinder array at small gap ratios to those of a single cylinder is illustrated and explained with the aid of flow visualization in figure 10. If we view the four-cylinder array as a single object represented by the shaded square shown at instant
$100T$
, paying attention to those large merged vortices away from the cylinders and ignoring the fine vortices close to the cylinder surfaces, then the flow field around the four-cylinder array is nothing but a regime A flow around a single cylinder, where vortices
$\text{A}_{1}$
and
$\text{A}_{2}$
and vortices
$\text{B}_{1}$
and
$\text{B}_{2}$
are shed from the sides of the square. Therefore, as a whole, the flow in regime 2(A-A) around four cylinders can be likened to regime A of the single-cylinder case with a larger equivalent diameter. From the illustrations of streaklines in figures 9 and 10, on the other hand, regimes 2(A
$^{\ast }$
-A
$^{\ast }$
) and 2(A-A) are very similar to those of regime A
$^{\ast }$
and A observed in figure 5, despite the difference in the flow field close to the cylinder surfaces. The fine-scale vortices near the cylinder surfaces are mostly generated through the gaps and are quickly merged with surrounding large vortices or simply dissipated, resembling flow features around a porous structure. At low and medium gap ratios, the flow fields around the four-cylinder array are characterized by the coexistence of influences from both individual cylinders and the cylinder array as a whole.
Regimes 2(A
$^{\ast }$
-A
$^{\ast }$
) and 2(A-A) dominate the
$\mathit{Re}{-}\mathit{KC}$
parameter plane shown in figure 6 for gap ratios of 0.5 and 1, but this dominance weakens with increasing gap ratio and mostly disappears at a gap ratio of 4.
3.1.2. Regimes 4A
$^{\ast }$
and 4A
The regimes 4A
$^{\ast }$
and 4A occupy a large part of the
$\mathit{Re}{-}\mathit{KC}$
parameter plane at gap ratios of 2 and 4 as shown in figure 6. Regime 4A
$^{\ast }$
and 4A flows comprise regime A
$^{\ast }$
and A fluid flows around each of the four circular cylinders, respectively. A typical regime 4A flow with
$(G,\mathit{Re},\mathit{KC})=(2,80,5)$
is visualized in figure 11 through four snapshots in an oscillation period, together with the streakline flow pattern. In one oscillation period, a pair of counter-rotating vortices are generated at each side of an individual cylinder and this is distinctly different from regime 2(A-A) flows, where the vortex shedding in the transverse gaps is largely suppressed. The vortices shed in the transverse gaps in regime 4A tend to be convected out sideways from the area enclosed by the cylinders, where the fluid particles form a ‘mushroom’ shape on each side of the transverse gap. Each ‘mushroom’-shaped flow pattern comprises two circulation zones, as represented by two arrows in figure 11. It is seen that each of these circulation zones corresponds to another circulation zone in the inner space surrounded by the four circular cylinders. These circulation zones are the direct result of vortex shedding and interaction of vortices shed in the transverse gaps.
Figure 11. An example of oscillatory flow field in regime 4A in the
$K_{x}$
symmetry zone at
$(G,\mathit{Re},\mathit{KC})=(2,80,5)$
.
With increasing
$\mathit{KC}$
and/or
$\mathit{Re}$
, stronger vortices are found in both streamwise and transverse directions, and therefore the convection of fluid particles in these directions is stronger, leading to increasingly complex streaming flow patterns. Figure 12 shows an example at
$(G,\mathit{Re},\mathit{KC})=(2,200,5)$
, which has a higher value of
$\mathit{Re}$
than the case shown in figure 11 but identical values of
$G$
and
$\mathit{KC}$
. Stronger vortices and longer wakes are observed around each of the four cylinders. This suggests that vortex interactions between any two adjacent cylinders become more vigorous at
$\mathit{Re}=200$
. The strong interactions between the wakes around the top two and bottom two cylinders, respectively, lead to four enlarged circulation zones, which replace the mushroom-type flow in figure 11. The limited gap space between cylinders 1 and 2 (also between cylinders 3 and 4) allows vortices to be shed from the gap sides but forces them to be convected horizontally outwards. It is interesting to observe that the convection of vortices behind the cylinder columns in the
$+y$
direction is weaker than that in the
$-y$
direction, resulting in a smaller wake area in the top than in the bottom, which corresponds to the inclined transverse-gap flow towards the
$+y$
direction. This flow feature can be clearly observed from the streakline patterns shown in figure 12. It is also observed that only a few fluid particles released from cylinder 2 and cylinder 3 are convected in the
$+y$
direction. Most of these particles are trapped and circulated in the inner side circulation zones and are eventually convected out sideways.
Figure 12. An example of oscillatory flow field in regime 4A in the
$K_{x}$
symmetry zone at
$(G,\mathit{Re},\mathit{KC})=(2,200,5)$
.
Figure 13. Steady streaming velocity from averaged flow fields in 10 oscillation periods at
$(G,\mathit{Re},\mathit{KC})=(2,200,5)$
: (a) velocity profile
$\bar{U}_{x}/U_{m}$
along
$x=3.5D$
; (b) velocity contour with streamlines.
To investigate the transverse mass convection observed in figure 12, the steady streaming velocity is obtained by averaging flow velocities over 10 consecutive oscillation periods, as given in figure 13. The temporal mean velocity profile along a vertical line
$2D$
away from cylinders 3 and 4, as presented in figure 13(a), demonstrates that the transverse mass convection observed in figure 12 is indeed due to the large horizontal velocities directed away from the cylinder array. The magnitude of the mass convection velocity observed in the gap between cylinders 3 and 4 can be much larger than
$0.2U_{m}$
, as given in figure 13(b).
Similar to its counterpart in regime A for the single cylinder, the convection of fluid particles in regime 4A does not change its direction once the asymmetry pattern about the
$x$
axis has been developed. Figure 14 shows the time histories of the lift coefficient imposed by the flow fields shown in figure 12, which is defined as
$F_{L}=F_{x}/(0.5{\it\rho}U_{m}^{2})$
, with
$F_{x}$
being the force in the
$x$
direction. Only plots for the left pair of cylinders (1 and 2) are given because of the symmetric pattern. It is readily seen that
$F_{L}$
is quite stable over the time period of the simulation, suggesting a stable flow mode.
Figure 14. Time history of lift force coefficients on two chosen cylinders at
$(G,\mathit{Re},\mathit{KC})=(2,200,5)$
.
Regimes 4A
$^{\ast }$
and 4A generally occur at smaller
$\mathit{KC}$
values than those of regimes 2(A
$^{\ast }$
-A
$^{\ast }$
) or 2(A-A). No regime 4A
$^{\ast }$
or 4A is found at
$G=0.5$
, and they seem to be a common feature at large gap ratios.
3.1.3. Regime 2(A-D)
Regime 2(A-D) flows generally develop at relatively larger gap ratios with slightly higher
$\mathit{KC}$
values than regime 4A, as shown in figure 6. Several cases of regime 2(A-D) flows are presented within the zone of
$K_{x}$
symmetry. A flow in this regime, as the name suggests, has characteristics of both single-cylinder regimes A and D. Figure 15 shows a typical regime 2(A-D) flow at
$(G,\mathit{Re},\mathit{KC})=(4,140,6)$
, with vorticity contours in four equally spaced instants of time in an oscillation period and flow streaklines generated using the data in 10 periods.
Figure 15. An example of oscillatory flow field in regime 2(A-D) in the
$K_{x}$
symmetry at
$(G,\mathit{Re},\mathit{KC})=(4,140,6)$
.
The vortices shed from the inner sides of cylinders 2 and 3 are considerably stronger than those shed from the outer sides in each half-period. Consequently, the fluid mass is obliquely convected to the outer sides of oscillation and the flow field is classified as regime D. The flow fields around the two bottom cylinders are similar to those around the two top cylinders in figure 12 at regime 4A but with slightly more complex features. The fluid mass is not convected sideways through the horizontal gaps as shown in figure 15, but instead two large circulation zones are formed in the streamwise gap. This is believed to be due to the strong interactions between the shed vortices as a result of increased gap space and the blockage of the inclined vortex streets from the top cylinders. The collisions of the streaklines from the top and bottom cylinders as indicated by the arrow S in figure 15 result in three convectional paths of fluid mass indicated by arrows
$\text{S}_{1}$
,
$\text{S}_{2}$
and
$\text{S}_{3}$
. The movement of fluid mass accompanying the vortices generated from the two bottom cylinders is complex but is highly influenced by the jet flow and thus falls into flow regime A. Since the flow fields around the right-hand two cylinders are actually a reflection of what occurs on the left, this regime is named 2(A-D). With several circulation zones, regime 2(A-D) presents perfect
$K_{x}$
symmetry.
The flow structure observed in figure 15 is unstable, as demonstrated by the lift coefficient along with the flow fields shown in figure 16. The time histories of the lift coefficient on cylinders 1 exhibit five distinct time zones (I–V) and each of the time zones corresponds to an evolving stage of the flow field as shown in figure 16(b). The flow around each of the four cylinders initially appears to be in regime D over a long time in zone I. In time zones II and III, the vortices shed from the two bottom cylinders gradually move closer to the streamwise gap and the flow develops into a regime 2(A-D). Meanwhile, the direction of the mean lift and the magnitude of the lift change several times, but the flow field continues to exhibit
$K_{x}$
symmetry. However, regime 2(A-D) can be stable, as shown in figure 16(c), where the time histories of the lift force for cylinders 1 and 2 at
$(G,\mathit{Re},\mathit{KC})=(1,140,5)$
remain regular and repeatable over the entire simulation period, indicating that the flow pattern remains stable in
$K_{x}$
symmetry. An obvious beating characteristic of lift is found in the time history for small gap ratios (figure 16
c), but the beating characteristic at large gap ratios is not as significant (figure 16
a). This beating feature is due to the impingement of vortices shed from its neighbouring cylinder in the same column and is one of the common features for cylinder arrays with small gap ratios.
Figure 16. Time history of lift force coefficients on two chosen cylinders and the flow fields for regime 2(A-D): (a) lift force coefficients for case of figure 15 at regime 2(A-D); (b) flow fields of different zones as listed in (a); and (c) lift force coefficients for the case of
$(G,\mathit{Re},\mathit{KC})=(1,140,5)$
at regime 2(A-D).
Regime 2(A-D) flows only occur at several specific values of
$(G,\mathit{Re},\mathit{KC})$
and it can be deemed a transitional regime between regimes 4A and 4D.
3.1.4. Regime 4D
Regime 4D flows generally develop at relatively larger gap ratios with slightly higher
$\mathit{KC}$
values than those of regime 2(A-D) flows, as given in figure 6. The regime D flow around a single cylinder shows
$H_{1}$
symmetry. However, the regime 4D around the four-cylinder array, where a regime D flow occurs around each of the four cylinders, is found in
$K_{x}$
symmetry.
One of the prominent features of a regime 4D flow is that vortices shed from each cylinder clearly deviate from the direction of flow oscillation, and tend to be convected transversely. Figure 17 shows the flow patterns at various stages in an oscillation period in regime 4D at
$(G,\mathit{Re},\mathit{KC})=(2,120,7)$
, together with the streakline pattern of the flow. Owing to the fact that stronger vortices are developed on the inner sides of cylinders than on the outer sides, and also due to the weakening of the stabilization effect, the shed vortices from each cylinder tend to move diagonally. As indicated by the ellipses at
$t=+{\textstyle \frac{2}{4}}T$
and
$+{\textstyle \frac{4}{4}}T$
, when the flow oscillates upwards, three vortices are developed around each cylinder, with a pair of counter-rotating vortices along the inner sides and a single vortex along the outer sides of the cylinders. However, when the flow reverses, only a pair of vortices is shed along the inner sides of the cylinders. Hence, the flow fields are asymmetric with respect to the
$x$
axis and the fluid mass is convected downwards. Vortices around cylinders 1 and 2 (also around 3 and 4) appear to be similar, but, because the movement of vortices in the transverse gaps is constricted by the space, the fluid mass convected from the top two cylinders is forced to circulate around the bottom two cylinders and then convected obliquely by the vortices developed from the two bottom cylinders.
Figure 17. An example of oscillatory flow field in regime 4D in the
$K_{x}$
symmetry zone at
$(G,\mathit{Re},\mathit{KC})=(2,120,7)$
.
Figure 18 illustrates the features of regime 4D flows when the flow fields are symmetric to the
$x$
axis at
$(G,\mathit{Re},\mathit{KC})=(2,160,6)$
. It is seen that vigorous vortex pairing and merging take place in this case. For convenience, at
$t=99+{\textstyle \frac{1}{4}}T$
, the three vortices surrounding cylinder 1 are named
$\text{A}_{1}^{\mathit{o}}$
,
$\text{B}_{1}^{\mathit{o}}$
and
$\text{C}_{1}^{\mathit{o}}$
, where ‘
$o$
’ denotes the vertices generated from the last oscillation period. With increasing velocity in the
$+y$
direction, a new positive vortex named
$\text{N}_{1}^{+}$
is generated from the surface of cylinder 1. Vortex
$\text{N}_{1}^{+}$
breaks
$\text{B}_{1}^{\mathit{o}}$
into two parts, i.e.
$\text{B}_{1-\mathit{p}1}^{\mathit{o}}$
and
$\text{B}_{1-\mathit{p}2}^{\mathit{o}}$
, as
$\text{B}_{1}^{\mathit{o}}$
moves upwards along with the flow. Vortex
$\text{N}_{1}^{+}$
starts to merge with
$\text{A}_{1}^{\mathit{o}}$
and
$\text{C}_{1}^{\mathit{o}}$
at
$+{\textstyle \frac{2}{4}}T$
and a long positive vortex that wraps around the inner side of cylinder 1 is formed before
$+{\textstyle \frac{3}{4}}T$
. At the same time, a new negative vortex, named
$\text{N}_{1}^{-}$
, starts to emerge from the cylinder surface. The
$\text{N}_{1}^{-}$
gradually grows in strength and cuts the positive vortex generated at
$+{\textstyle \frac{3}{4}}T$
into two new vortices,
$\text{A}_{1}^{n}$
and
$\text{C}_{1}^{n}$
, which replace the vortex
$\text{A}_{1}^{\mathit{o}}$
and
$\text{C}_{1}^{\mathit{o}}$
. Meanwhile,
$\text{N}_{1}^{-}$
,
$\text{B}_{1-\mathit{p}1}^{\mathit{o}}$
and
$\text{B}_{1-\mathit{p}2}^{\mathit{o}}$
begin to combine and eventually generate vortex
$\text{B}_{1}^{n}$
at the start of the next period of oscillation. It is also observed at
$+{\textstyle \frac{4}{4}}T$
that part of
$\text{B}_{1-\mathit{p}2}^{\mathit{o}}$
is merged upwards into the sideways vortex generated from cylinder 2; while vortex
$\text{C}_{1}^{\mathit{o}}$
also attracts vortices from cylinder 2 at
$+{\textstyle \frac{2}{4}}T$
. Except for the interaction just described, the individual regime D flows around each of the cylinders in the array do not interact with each other actively, and much of the merging and pairing of vortices occurs among vortices from the same cylinder. Even when no vortex merging takes place, vortex interactions in the confined space between the transverse gaps are quite visible.
Figure 18. An example of flow field in regime 4D in the
$K_{x}$
symmetry zone at
$(G,\mathit{Re},\mathit{KC})=(2,160,6)$
.
One difference between the regime 4D flows shown in figures 17 and 18 is that the flow field maintains all three symmetries in figure 18. Both types of regime 4D flow are stable, as evidenced by the time history of lift (not shown here), mainly due to a mechanism that is similar to the stable sideways convection of fluid particles in regime D for a single cylinder.
The steady streaming velocity fields for the case shown in figure 18 are given in figure 19(a,b), which show, respectively, the streaming velocity profile along
$x=3.5D$
and the contour of streaming
$\bar{U}_{x}/U_{m}$
along with the streamlines. The cylinder array seems to attract fluid mass from an even larger area than the case in figure 13, since all streamlines above the top two cylinders and below the bottom two cylinders are attracted towards the cylinder array and are directed away horizontally from the transverse gaps.
Figure 19. Steady streaming velocity averaged from flow fields in 10 oscillation periods at
$(G,\mathit{Re},\mathit{KC})=(2,160,6)$
: (a) velocity profile
$\bar{U}_{x}/U_{m}$
along
$x=3.5D$
; (b) velocity contour with streamlines.
Regime 4D is only found at large gap ratios (
$G=2$
and 4 in the present study) and occupies an area in the
$\mathit{Re}{-}\mathit{KC}$
plane where regime D would normally occur for a single-cylinder case. It involves vigorous vortex interactions, which result in complex flow features.
3.1.5. Comparisons of the
$K_{x}$
symmetries
One of the interesting features for oscillatory flow around the four-cylinder array is that both
$H_{1}$
and
$H_{2}$
are frequently broken within
$K_{x}$
zones near the boundary line, as shown in figure 6, for example, the cases in regimes 2(A-D), 4D and even regime 4A. This is different from the
$K_{x}$
symmetry for a single cylinder, where both
$H_{1}$
and
$H_{2}$
symmetry are satisfied within the
$K_{x}$
regime.
For a single cylinder, it has been demonstrated that as soon as the 2D
$K_{x}$
symmetry is broken, 3D secondary instabilities will develop, such as flow changing from regime A to D (Nehari et al.
Reference Nehari, Armenio and Ballio2004; Elston et al.
Reference Elston, Blackburn and Sheridan2006). This leads to an interesting scenario, in that 2D simulations can be used to predict the boundary line in the
$\mathit{Re}{-}\mathit{KC}$
plane beyond which 3D instabilities occur. In the four-cylinder case considered in the present study, it is expected that the onset of 3D instabilities will occur within the zone of
$K_{x}$
symmetry rather than on the boundary, especially at large gap ratios, because the
$K_{x}$
symmetry around the four-cylinder array is not a basic state as that in the single-cylinder case where both
$H_{1}$
and
$H_{2}$
are satisfied.
For this reason, a boundary line (dotted) is interpolated at each gap ratio in figure 6 to distinguish the zone of the basic state of
$K_{x}$
from the rest of
$K_{x}$
symmetry. At
$G=0.5$
, the basic state boundary overlaps the
$K_{x}$
boundary line. At
$G=1$
,
$H_{1}$
and
$H_{2}$
symmetries are broken only at several cases –
$(\mathit{Re},\mathit{KC})=(200,4)$
and
$(\mathit{Re},\mathit{KC})=(140{-}160,5)$
– where
$K_{x}$
symmetry is still observed. At those two small gap ratios, both
$H_{1}$
and
$H_{2}$
are satisfied in large parts of the
$K_{x}$
symmetry regime. This is because the flow around the cylinder array behaves similarly to that around a single cylinder and fine flow details around each cylinder have limited effect on the overall behaviour of the flow.
In contrast, the boundary lines for the basic state at two large gap ratios deviate noticeably from the
$K_{x}$
boundary lines and are close to the boundary lines of regime A for the single-cylinder case. The flow regimes 2(A-D) and 4D for the four-cylinder array generally fall between the boundaries of the basic state and
$K_{x}$
symmetry regime and thus into an area where regime D would normally occur for a single cylinder. At those gap ratios, flow features around individual cylinders become important and the
$H_{2}$
symmetry is broken beyond the basic state lines within the
$K_{x}$
regime simply because the
$H_{2}$
symmetry for a single cylinder is broken in regime D. The
$K_{x}$
symmetry occurs beyond basic state lines because the interaction between the flows around the two cylinder columns is normally weak, inducing a flow field around one cylinder column that is the mirror image of the other.
3.2.
$H_{1}$
symmetry (regime D)
The
$H_{1}$
symmetry flow for the four-cylinder array is observed at low gap ratios and relatively high
$\mathit{KC}$
and
$\mathit{Re}$
, as seen from figure 20 at
$(G,\mathit{Re},\mathit{KC})=(0.5,200,9)$
. Figure 20 is deliberately arranged such that the flow features in the top row are
$H_{1}$
symmetric with respect to those in the bottom row. It is seen that vortices are shed both from the streamwise gaps and from the outside of the cylinder array every oscillation half-period. The generation of a vortex named
$\text{A}^{\mathit{o}}$
at
$t=99+{\textstyle \frac{1}{8}}T$
is chosen to explain how vortices are shed, interact and pair in this regime. At
${\textstyle \frac{2}{8}}T$
, three new vortices named
$\text{A}_{\mathit{p}1}^{n}$
,
$\text{A}_{\mathit{p}2}^{n}$
and
$\text{A}_{\mathit{p}3}^{n}$
are shed from the gap and the outer sides of the cylinder array. The strengths of those vortices are comparable (with those from the gap being slightly larger), unlike those in
$K_{x}$
symmetry. The small vortices of the same sign shed from the gap and from the outer sides of the cylinders quickly merge before being convected further from the cylinder array. The convection process of these vortices can be observed from the flow fields at
${\textstyle \frac{3}{8}}T{-}{\textstyle \frac{6}{8}}T$
. Vortices
$\text{A}_{\mathit{p}1}^{n}$
,
$\text{A}_{\mathit{p}2}^{n}$
and
$\text{A}_{\mathit{p}3}^{n}$
are fully merged at
${\textstyle \frac{7}{8}}T$
and a new large vortex
$\text{A}^{n}$
is formed at
${\textstyle \frac{8}{8}}T$
. The generation of other large vortex cores is similar to the process just described. The large vortices generated are convected obliquely to one side of the axis of oscillation, in the same manner as those observed in regime D in figure 5. The streaklines on the right-hand side of figure 20 show similarities to those in regime D for a single cylinder. Therefore, the resultant flow field falls into the
$H_{1}$
symmetry and this kind of
$H_{1}$
symmetric flow around the four cylinders is named regime D, as in figure 6(a). It is easily seen that at
$G=0.5$
,
$H_{1}$
symmetry occurs because the four cylinders behave similarly to a porous single structure, with fine-scale vortices being shed from different parts of this porous structure, but those of the same sign quickly merged to a single core. The vortices shed from the gap are significant but do not dominate the flow field, so fluid mass is obliquely convected with the merged cores.
Figure 20. The
$H_{1}$
symmetric flow for four circular cylinders in oscillatory flow at
$(G,\mathit{Re},\mathit{KC})=(0.5,200,9)$
.
Figure 21. The
$H_{2}$
symmetry resulting from severe boundary layer and vortex interactions at
$(G,\mathit{Re},\mathit{KC})=(1,180,5)$
.
Similar to regime D for a single cylinder, the convection of fluid particles in
$H_{1}$
symmetry for the four-cylinder array is consistently inclined to one direction. We extended the simulation at
$(G,\mathit{Re},\mathit{KC})=(0.5,200,5)$
for up to 280 cycles, and the inclination direction was maintained for the entire period of the simulation.
It is worth pointing out that
$H_{1}$
symmetry for the four-cylinder array only occurs at the lowest gap ratio in this work. It is also observed from figure 6 that the flow regime transits directly from regime
$K_{x}$
to regime
$N$
or regime
$H_{2}$
at gap ratios of 1, 2 and 4, without
$H_{1}$
symmetry flow. The reason is that, in the four-cylinder array, the flow structures around the left and right columns of cylinders are almost identical due to the existence of a jet-like flow in the streamwise gaps. The
$H_{1}$
symmetry can be observed around individual cylinders in regimes 2(A-D) and 4D, but, as a whole, these regimes represent a
$K_{x}$
symmetry.
3.3.
$H_{2}$
symmetry
The
$H_{2}$
symmetry flow occurs in a narrow area of the
$\mathit{Re}{-}\mathit{KC}$
plane for
$G=1$
, 2 and 4, as shown in figure 6. There are two types of
$H_{2}$
symmetry for the four-cylinder array investigated. The first one is due to vigorous boundary layer and vortex interactions at small gap ratios and the other features to gentle wake interactions.
Figure 21 shows consecutive stages of flow development over an oscillation period for the first type of
$H_{2}$
symmetry at
$(G,\mathit{Re},\mathit{KC})=(1,180,5)$
, along with the streakline. The process of vortex development and shedding can be clearly observed from the four snapshots. The snapshots with a half-period time difference have
$H_{2}$
symmetry. Unlike the cases with
$K_{x}$
symmetry, the vortices in the streamwise gaps start to be shed unevenly from, for instance, the inner sides of cylinders 2 and 3. So the flow fields close to the cylinders are quite chaotic, with many fine-scale vortices being shed, combined and dissipated. However, overall, these fine-scale vortices are evenly arranged in a regular pattern with
$H_{2}$
symmetry. It is interesting to see that two large vortices of the same sign are developed in the far field shown in figure 21.
Figure 22 gives another example of the first type of
$H_{2}$
symmetry resulting from vigorous vortex interactions at
$(G,\mathit{Re},\mathit{KC})=(2,100,10)$
. The shear layer interaction in this case is not as significant as that shown in figure 21, and vortex merging occurs comparatively far from the cylinder surfaces. The merged vortex cores are convected in the oscillation direction and are roughly
$H_{2}$
symmetric, but the vortex cores in the
$+y$
direction appear to be slightly larger and closer to each other than those in the
$-y$
direction. The merged vortices are staggered at each side in a way resembling the Kármán vortex street. The flow fields in figure 22 show a quasi-periodic state when they are convected away from the cylinder surfaces, with a secondary frequency that is clearly different from the velocity oscillation frequency. This is similar to regime C for a single cylinder as experimentally observed by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) and numerically reproduced by Elston et al. (Reference Elston, Blackburn and Sheridan2006). One primary difference is that regime C is in
$H_{1}$
symmetry, but here the flow field is in
$H_{2}$
symmetry.
Figure 22. The
$H_{2}$
symmetry flow resulting from severe vortex interactions at
$(G,\mathit{Re},\mathit{KC})=(2,100,10)$
.
Figure 23 illustrates the second type of
$H_{2}$
symmetry for the cylinder array at
$(G,\mathit{Re},\mathit{KC})=(4,120,8)$
, where the shear layer and vortex interactions are less intensive than those shown in figures 21 and 22, as observed from the mixture of particles from different cylinders as they are convected away. It is seen that the convection of vortices generated around cylinders 2 and 4 is relatively constrained while those from cylinders 1 and 3 move further away from the cylinder surfaces. The vorticity contours illustrate that the merging of vortices from different cylinders only occurs in the transverse gaps. Similar to the behaviour observed in figure 21, the two large vortex cores away from the cylinder surface tend to rotate in the same direction. The fluid mass around cylinder 4 is partially forced to circulate around the cylinder itself and is partially convected upwards before it is attracted by the vortex developed on cylinder 3 and then convected upwards along with the vortex shed from cylinder 3. Fluid mass from cylinder 2 is transported downwards in the same way. Similar movements of mass and vortices from cylinders 2 and 4 can also be found in regime 4D.
Figure 23. The
$H_{2}$
symmetry resulting from gentle vortex interactions at
$(G,\mathit{Re},\mathit{KC})=(4,120,8)$
.
The
$H_{2}$
symmetry involves flow field interactions among the four cylinders and occurs only at a few cases near the symmetry-breaking boundary lines. The flow features in the
$H_{2}$
symmetry are quite spectacular, owing to the wake and proximity interferences in the cylinder array. It is noted that none of the
$H_{2}$
flows, except two cases at
$G=1$
, are strictly in
$H_{2}$
symmetry, especially close to the cylinder surfaces where vortex interaction is strong. Unlike those in the single-cylinder case, the
$H_{2}$
symmetry in the four-cylinder case is weakly stable.
3.4. Symmetry breaking
In a large area at the top right corner of the
$\mathit{Re}{-}\mathit{KC}$
plane with gap ratios of 1, 2 and 4 in figure 6, none of the symmetry patterns discussed above is observed. The flow falling into this area is classified as regime
$N$
. The cross-sectional flow fields in regime
$N$
tend to be chaotic and correspond to those in regime G of a single cylinder. However, the flow mechanisms responsible for those flow features are different. Regime G flow for a single circular cylinder is generated by strong three-dimensionality at larger
$\mathit{Re}$
values than those of regime
$N$
flows for the four-cylinder array. On the other hand, regime
$N$
flows are mainly attributed to the results of the interactions among the individual shear layers and vortices shed from each cylinder in the array and also to the weak three-dimensionality of the wake flow, as discussed further in the next section.
Much of the flow field beyond the
$N$
-line shown in figure 6 cannot be classified easily. However, for the cases where
$\mathit{KC}$
and
$\mathit{Re}$
are close to or on the border of regime
$N$
, the flow is usually in a transitional breaking pattern from symmetry to asymmetry. Several interesting symmetry-breaking flows are given in figure 24 by streaklines and the instant vorticity contours. Figure 24(a) shows a symmetry-breaking case from regime D at
$(G,\mathit{Re},\mathit{KC})=(0.5,200,11)$
where streaklines and the wake in the
$-y$
axis direction hook more towards the
$x$
axis than those in the
$+y$
direction, leading to an asymmetric pattern. The symmetry-breaking flows from regime 4A and 4D are shown in figure 24(b,c). The streakline pattern in the
$-y$
direction illustrated in figure 24(b) resembles a ‘fishtail’ shape. From a comparison of figures 24(c) and 18, it may be seen that the transverse convection of fluid mass by vortices generated from the right-hand two cylinders is broken, while the flow field around the two left cylinders is kept. The flow fields of figure 24(c) are found to be sensitive to both the computational domain and the length of simulations. A developed chaotic flow field is shown in figure 24(d), where no symmetric pattern could be observed around any individual cylinder or the cylinder array as a whole.
Figure 24. Symmetry breaking for oscillating flow around four circular cylinders and regime
$N$
: (a) symmetry breaking from regime D (
$H_{1}$
symmetry), for
$(G,\mathit{Re},\mathit{KC})=(0.5,200,11)$
; (b) from regime 4D,
$K_{x}$
symmetry, for
$(G,\mathit{Re},\mathit{KC})=(2,200,6)$
; (c) from regime 4D,
$K_{x}$
symmetry, for
$(G,\mathit{Re},\mathit{KC})=(2,180,7)$
; (d) regime
$N$
, for
$(G,\mathit{Re},\mathit{KC})=(4,180,9)$
. Panels are not to scale and the dashed squares are 2D in size.
Symmetry breaking for a single cylinder, which leads to regime G, can only evolve from
$H_{1}$
and
$H_{2}$
symmetries In contrast, symmetry breaking in the four-cylinder array (regime
$N$
) can evolve directly from
$K_{x}$
symmetry.
3.5. 3D effects on onset of symmetry breaking
It has been demonstrated in a steady current that the existence of an additional cylinder in close proximity has a tendency to suppress or enhance the three-dimensionality of the flow, depending on the distance between the cylinders (Papaioannou et al.
Reference Papaioannou, Yue, Triantafyllou and Karniadakis2006; Carmo, Meneghini & Sherwin Reference Carmo, Meneghini and Sherwin2010). Although the range of
$\mathit{KC}$
and
$\mathit{Re}$
was carefully selected to avoid 3D flow regimes, 3D effects are likely to occur within the parameter space covered in this study, especially in areas outside and just within the symmetric regimes. To investigate the possible effect of the three-dimensionality on the onset of symmetry-breaking regime
$N$
, a limited number of 3D simulations close to the symmetry-breaking boundaries were carried out. They are listed in table 5, along with the reasons for choosing these cases. These simulations are based on the coarsest mesh 1 in table 3, where a spanwise length of
$10D$
is used, with 100 layers of the 2D mesh.
Figure 25. Flow features revealed by instantaneous isosurface of
${\it\omega}_{z}=\pm 0.5$
from 3D simulation (represented by two different colours, with the lighter one denoting negative): (a) case I at
$Ut/D=72.5$
; (b) case II at 33.625; (c) case III at 27.125; and (d) case IV at 33.75. Inlet oscillatory flow is in the
$y$
direction.
Table 5. 3D simulations for selected cases.
Three-dimensionality affects the flow field differently for different cases. The isosurfaces of spanwise vorticity (
${\it\omega}_{z}$
) at a time instant are shown in figure 25. The high repeatability of hydrodynamic forces over many cycles is considered as evidence for a saturated simulation. Obvious three-dimensionality is observed in cases I and III, while organized spanwise repetitions are observed for cases II and IV. The cross-sectional flow fields at selected heights are compared with the corresponding 2D simulation results in figure 26 for cases I–III. As for case IV, the sectional flow fields are very similar to those in figure 12 obtained by 2D simulation, although changes along spanwise directions are noted. A number of observations are made from the limited number of 3D simulations. First of all, the three-dimensionality does not appear to affect the onset of symmetry-breaking regime
$N$
based on these three cases located close to the symmetry-breaking boundaries. The
$K_{x}$
symmetry is clearly observed from the 3D results and the 2D simulation reasonably reproduces the main cross-sectional flow features for cases II and IV. It is also seen that, despite the strong three-dimensionality, the cross-sectional flows of case III generally retain
$H_{1}$
symmetry. The case III flow can still be classified as regime D, although a direction change of transverse wakes is observed along the spanwise direction of the cylinder array. Secondly, the symmetry-breaking case I flow shows the strongest three-dimensionality among the four 3D cases and is still classified as symmetry-breaking flow. Significant differences in wake flow structure exist between the cross-sectional flows themselves and also between the 3D and 2D simulations; however, some major flow structures are less influenced by the 3D instability. Thirdly, the flows outside the symmetry-breaking regime (cases II–IV) show relatively weak three-dimensionality and can be classified based on 2D simulation results.
Figure 26. Comparison on the cross-sectional flow fields between 3D and 2D (bottom row) simulations. Inlet oscillatory flow is in the horizontal direction.
Figure 27. The change of vorticity on cylinder surfaces with gap distances at
$(\mathit{Re},\mathit{KC})=(160,5)$
. (a)–(e) Plots of
${\it\omega}_{z}$
on the wall of cylinder 4: (a) single cylinder (
$G=\infty$
), regime A; (b)
$G=0.5$
, regime D; (c)
$G=1$
, regime 2(A-D); (d)
$G=2$
, regime 4A; and (e)
$G=4$
, regime 4A. ( f,g) Comparison of the squared integration of
${\it\omega}_{z}$
on cylinders 2 and 4 respectively: - - - -, single total; — ⋅ —, single
$0{-}{\rm\pi}$
; — ⋅ ⋅ —, single
${\rm\pi}{-}2{\rm\pi}$
; ——, individual cylinder total; ○, individual cylinder outer sidewall; ●, individual cylinder inner sidewall.
4. Quantifications on the flow fields
4.1. Vorticity on the wall
As discussed from the above analysis, the oscillatory flow field around the four-cylinder array displays great diversity and complexity, which makes meaningful quantitative analyses more difficult. Nonetheless, the non-dimensional vorticity on the cylinder surface of selected cylinders in an oscillation period at
$(\mathit{Re},\mathit{KC})=(160,5)$
of the cylinder array cases are compared with that of a single-cylinder case in figure 27. One prominent observation is that the maximum vorticity on the inner side surface is consistently larger than that on the outer side surface for the cylinder array, and the difference between the vorticity on the inner and outer side surfaces appears to be dependent on the gap ratio. Another interesting feature is that, when the flows around individual cylinders are in the same regimes, such as at
$G=0.5$
, 2 and 4, the vorticity generated in the first half-period and the second half-period are quite close but not identical, especially on the inner surface of the cylinders. It is speculated that the slight difference in the vorticity generated in the two half-periods contributes to the asymmetric flow features observed in the oscillatory direction, such as that shown in figure 12. A noticeable difference between the two half-periods on the wall vorticity is found at
$G=1$
, where cylinder 3 is in regime D and cylinder 4 is in regime A. Figure 27( f,g) also illustrates the enstrophy integrated around the wall (inner sidewall, outer sidewall and the total, respectively) of two diagonal cylinders in an oscillation period, which is defined as
$$\begin{eqnarray}{\it\varepsilon}=\int _{T}\int _{{\it\Omega}}({\it\omega}_{z})^{2}\text{d}V\text{d}t,\end{eqnarray}$$
where
${\it\Omega}$
represents the cell volumes surrounding the cylinder. On cylinders 2 and 4, less than 5 % difference is found in the total enstrophy at
$G=0.5$
and 1, and the difference is negligible at
$G=2$
and 4. The total enstrophy on both cylinders 2 and 4 is smaller than that of the single cylinder for all gap ratios. The enstrophy on the inner sidewall at
$G=0.5$
and 1 is larger than that on half of the single cylinder, and becomes almost identical to that on half of the single cylinder at
$G=2$
and 4. The enstrophy on the outer sidewall is significantly smaller than that on half of the single cylinder.
4.2. Force coefficients
Hydrodynamic forces on the cylinder array are investigated and the total force coefficients are illustrated as a function of
$\mathit{KC}$
and
$\mathit{Re}$
in figure 28. The total in-line forces
$F_{y,T}$
are calculated by integrating the pressure and shear stress on the surfaces of all four cylinders. To facilitate the comparison with forces on a single cylinder, the total in-line force was divided by the number of cylinders before it was expressed as in (2.7). Thus, the total drag and inertia force coefficients are defined as
$$\begin{eqnarray}\frac{F_{y,T}}{4}=\frac{1}{2}{\it\rho}DC_{D,T}|U_{y}(t)|U_{y}(t)+{\it\rho}\frac{{\rm\pi}D^{2}}{4}C_{M,T}\frac{\text{d}U_{y}(t)}{\text{d}t},\end{eqnarray}$$
where
$C_{D,T}$
and
$C_{M,T}$
are the total drag and inertia force coefficients for the four-cylinder array, respectively.
$C_{D,T}$
and
$C_{M,T}$
are presented here for a medium gap ratio (
$G=1$
, figure 28
c,d) and a large gap ratio (
$G=4$
, figure 28
e, f), along with those of a single cylinder (figure 28
a,b) under the same flow conditions.
Figure 28. Comparison of drag and inertia coefficients for four circular cylinders in an in-line square arrangement with gap ratio of 1 and 4 with those of a single cylinder in the same flow condition: (a)
$C_{D}$
, single cylinder; (b)
$C_{M}$
, single cylinder; (c)
$C_{D,T}$
,
$G=1$
; (d)
$C_{M,T}$
,
$G=1$
; (e)
$C_{D,T}$
,
$G=4$
; ( f)
$C_{M,T}$
,
$G=4$
.
For a single cylinder,
$C_{D}$
generally decreases with increasing
$\mathit{Re}$
and
$\mathit{KC}$
, with much steeper gradients at low
$\mathit{KC}$
and
$\mathit{Re}$
than that at high
$\mathit{KC}$
and
$\mathit{Re}$
, as indicated by the density of the contour lines. On the other hand,
$C_{M}$
exhibits much more intricate features. For regimes A
$^{\ast }$
and A (refer to figure 32),
$C_{M}$
is diagonally distributed in a trend of increase in step with the increase of
$\mathit{KC}$
, and a decreasing trend with increasing
$\mathit{Re}$
. However, for regime F, the coefficient is in a pattern of reverse-diagonal distribution compared with those of regimes A
$^{\ast }$
and A. At the interface between those two areas of diagonally distributed
$C_{M}$
, regimes D and E present very irregular patterns in
$C_{M}$
distribution.
For the four cylinders at
$G=1$
,
$C_{D,T}$
at small
$\mathit{Re}$
shares the same pattern of distribution as that of a single cylinder where the contour lines are diagonally distributed. Large differences are observed beyond
$\mathit{Re}\geqslant 100$
, especially at the high end of the
$\mathit{Re}$
range (
$\mathit{KC}=5{-}6$
), where an
$H_{2}$
symmetric pattern is found in the flow patterns. Overall,
$C_{D,T}$
is larger than that of a single cylinder at low
$\mathit{KC}$
but smaller at high
$\mathit{KC}$
, and it is more evenly distributed. The large area of sparse contour lines at high
$\mathit{Re}$
for a single cylinder almost disappears in the four-cylinder case, except in a small region where
$H_{2}$
symmetry occurs.
$C_{M,T}$
at
$G=1$
across the map is similar to that of the single-cylinder case at regimes A
$^{\ast }$
and A, and the reverse-diagonal distribution of
$C_{M}$
at large
$\mathit{KC}$
values is not observed in
$C_{M,T}$
.
The total drag and inertia coefficients at
$G=4$
are very similar to those on a single cylinder, not only in distribution, but also in magnitude (only
$C_{M,T}$
is smaller). For instance, the drag shows similar contour lines with mild slopes at high
$\mathit{Re}$
but steep slopes at low
$\mathit{Re}$
; in addition, the distribution of
$C_{M,T}$
shows two zones of diagonally distributed contours and an irregular pattern in the area where presumably regime D and E would occur if there were only one cylinder.
To summarize, the drag distribution at
$G=1$
overall resembles an area at low
$\mathit{KC}$
of the single-cylinder case, because the cylinder array behaves as a single structure. This is consistent with the flow features observed in figure 6. At large gap ratios, such as at
$G=4$
, the drag distribution is almost equivalent to that of a single cylinder. Although the flow fields around a four-cylinder array at this gap distance are much different from those around a single cylinder, the in-line forces are less affected.
The total lift coefficients (
$C_{L,T}$
) from two selected gap ratios are presented in figure 29, which is defined as
$$\begin{eqnarray}\frac{F_{x,T}}{4}=\frac{1}{2}C_{L,T}{\it\rho}DU_{m}^{2},\end{eqnarray}$$
where
$F_{x,T}$
is the total lift force on all cylinders. It is evident that, in zones of
$K_{x}$
symmetry,
$C_{L,T}$
is zero, because the lift forces on the left pair and right pair are equal but with opposite signs. Whenever the flow regime breaks the
$K_{x}$
symmetry, the asymmetric flow fields (with respect to the
$x$
axis) leads to a non-zero total lift coefficient. This is why the contour lines of
$C_{L,T}$
are very similar to the regime boundary lines seen in figure 6. It seems the lift coefficient experiences a dramatic rise with increasing
$\mathit{Re}$
in both
$H_{2}$
and
$N$
regimes, consistent with the increasingly chaotic flow fields.
Figure 29. Lift force coefficients (
$C_{L,T}$
) for four circular cylinders in an in-line square arrangement with gap ratio of 1 and 4: (a)
$C_{L,T}$
,
$G=1$
; (b)
$C_{L,T}$
,
$G=4$
.
5. Conclusions
The flow structures around four circular cylinders in an in-line square arrangement induced by sinusoidally oscillatory flow were numerically investigated. Two-dimensional simulations were carried out at relatively low frequencies and amplitudes of oscillations within
$\mathit{KC}\in [1,12]$
and
$\mathit{Re}\in [20,200]$
. The flow fields around the four-cylinder array are composed of many combinations of established flow regimes around a single cylinder identified by previous studies. These combinations show an even more captivating set of flow patterns around four circular cylinders than those which occur around a single cylinder. The flow features are classified into six types of reflection symmetry with respect to the axis of oscillation, two types of spatio-temporal symmetry and a series of symmetry-breaking flow patterns, which are mapped out in the
$\mathit{Re}{-}\mathit{KC}$
plane. The reflection symmetry with respect to the axis of oscillation dominates the maps of flow regimes, especially at low gap distances, owing to the stabilization effect induced by the jet-like flow through the gap formed by cylinder columns that are parallel to the direction of flow oscillation. In general, at small gap distances, the four structures behave as a single porous body, and therefore the flow fields resemble those around a single cylinder. With increasing gap distance, the individual flow behaviour around each cylinder in the array starts to influence the overall flow patterns, and thus the flow shows a variety of symmetry patterns as a result of vortex interactions from each cylinder, though the symmetric patterns are also found to be prone to asymmetry. It is also found that three-dimensionality of the flow does not appear to significantly influence the cross-sectional flow fields or the onset of the symmetry-breaking regime. The drag force coefficient of the four cylinders as a whole at low gap distance shows a trend of variation similar to an area at low
$\mathit{KC}$
of the single-cylinder case, but gradually changes to the same pattern with increasing distance between the cylinders. The drag force seems to be less influenced than the flow fields at large gap distances. The lift coefficient is zero for the cylinder array at the reflection symmetry regimes, and experiences a dramatic increase with
$\mathit{KC}$
and
$\mathit{Re}$
once the symmetry of the flow is broken.
Acknowledgements
This work was supported by Australian Research Council Discovery Grant (Project ID: DP110105171) and by iVEC through the use of advanced computing resources (Epic and Magnus supercomputers). F.T. would like to acknowledge the support of the Australian Government and the University of Western Australia by providing SIRF, UIS and Completion scholarships for a doctoral degree.
Appendix. Further model validations
The predicted velocity distributions around a single cylinder are compared with the experimental data of Dütsch et al. (Reference Dütsch, Durst, Becker and Lienhart1998) for
$(\mathit{Re},\mathit{KC})=(100,5)$
in figure 30. Since the tests were carried out with an oscillatory cylinder in still water, the present data were converted into those in the coordinate system used in Dütsch et al. (Reference Dütsch, Durst, Becker and Lienhart1998) to facilitate the comparison, detailed in the caption of figure 30. The calculated velocity profiles along four straight lines of
${\it\xi}/D=-0.6$
, 0, 0.6 and 1.2 at two phase angles of
${\it\psi}=180^{\circ }$
and 330° are compared with the experimental data. The comparison suggests that the numerical results agree well with the measured data. The predicted velocity profiles are also compared with the numerical results reported by Zhao & Cheng (Reference Zhao and Cheng2014), and the predicted velocity profiles from the two numerical simulations match exactly.
Figure 30. Comparison between the present results (lines) of velocity components and the experimental data (symbols) by Dütsch et al. (Reference Dütsch, Durst, Becker and Lienhart1998) for
$\mathit{KC}=5$
,
${\it\beta}=20$
: ▫ / ——,
${\it\xi}/D=-0.6$
; ▵ / - - - -,
${\it\xi}/D=0.0$
; ♢ / — ⋅ —,
${\it\xi}/D=0.6$
; ○ / — ⋅ ⋅ —,
${\it\xi}/D=1.2$
. Since in the study by Dütsch et al. (Reference Dütsch, Durst, Becker and Lienhart1998) the cylinder was forced to oscillate in otherwise still water, while in the present study the cylinder was kept still, the coordinates and velocity were transformed through:
${\it\xi}=y+A\sin ({\it\psi})$
,
${\it\psi}={\it\varphi}-90^{\circ }$
,
$u_{a}=U_{y}(t)-U_{m}\sin ({\it\varphi})$
and
$v_{a}=U_{x}(t)$
, where
${\it\xi}$
,
${\it\psi}$
,
$u_{a}$
and
$v_{a}$
are the vertical coordinate, the phase angle, the velocity in the vertical direction and the velocity in the horizontal direction, respectively, and correspondingly,
$y$
,
${\it\varphi}$
,
$U_{y}$
and
$U_{x}$
are those parameters in the present study;
$A$
is the amplitude of the movement in the experimental study, and
$U_{m}$
is the maximum velocity in the present study.
The predicted drag and inertia coefficients at
${\it\beta}=35$
are compared with those reported by Kuehtz (Reference Kuehtz1996) and Dütsch et al. (Reference Dütsch, Durst, Becker and Lienhart1998) in figure 31. Both drag and inertia coefficients derived from the numerical results are found to be in good agreement with the published data. The drag coefficient decreases monotonically with increasing
$\mathit{KC}$
before
$\mathit{KC}=4$
, then it stays almost constant until
$\mathit{KC}=16$
. On the other hand,
$C_{M}$
does not show much change before
$\mathit{KC}=7$
, followed by a sudden reduction until
$\mathit{KC}=16$
. It is also observed that the numerical results agree with experimental data slightly better at low
$\mathit{KC}~({\leqslant}6)$
than at high
$\mathit{KC}$
values, probably due to the occurrence of 3D flow at high
$\mathit{KC}$
values.
Figure 31. Comparison of in-line force coefficients at
${\it\beta}=35$
: (a) drag coefficient; (b) inertia coefficient.
The oscillatory flow regimes identified by the present numerical model based on mesh 2 for a single cylinder are shown and compared with those reported by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) in figure 32. The dashed lines shown in figure 32 are the regime boundaries, based on Tatsuno & Bearman (Reference Tatsuno and Bearman1990), and the letters denote results from the present study. Letter A marks the location where the highest
$\mathit{Re}$
is detected for regime A at a constant
$\mathit{KC}$
, while all other letters indicate the location of the smallest
$\mathit{Re}$
detected for the corresponding regimes at constant
$\mathit{KC}$
values. It is seen that all the flow regimes are captured at the same corresponding areas as identified by Tatsuno & Bearman (Reference Tatsuno and Bearman1990). Although the flows in regimes C, D, E and F are 3D, they are successfully captured by the present 2D model. This supports the conclusion by Nehari et al. (Reference Nehari, Armenio and Ballio2004) that the three-dimensionality of the flow has a negligible effect on the cross-sectional flow features of oscillatory flow around a circular cylinder.
Figure 32. Comparison on flow regimes around a single cylinder identified by the present study and by Tatsuno & Bearman (Reference Tatsuno and Bearman1990).
It should be noted, however, that the regime B flow, which is often observed in the range
$\mathit{Re}>180$
and
$2<\mathit{KC}<4.5$
and was first reported by Honji (Reference Honji1981), corresponds to the onset of 3D instability. The cross-sectional flow fields in regime B are similar to those in regime A
$^{\ast }$
or A. Therefore, regime B cannot be distinguished from regimes A
$^{\ast }$
and A based on 2D simulations. Partly for this reason,
$\mathit{Re}$
is limited to approximately 200 in the present study.
