2. PLASMA GENERATION/ANNIHILATION

Consider the propagation of a high intensity laser pulse along the z′ axis through a neutral gas with atomic density n ₀; the circularly polarized electric field vector for the electromagnetic (em) pulse can be written as

(1)$${\bi E}\lpar r\comma \; z^{\prime}\comma \; t\rpar = A\lpar r\comma \; z^{\prime}\comma \; t\rpar \lpar \hat x + i\hat y\rpar exp\lsqb i\lpar kz^{\prime} - {\rm \omega} t\rpar \rsqb\comma$$

where A(r,z′,t) is the complex amplitude of the electric field while ω and k refer to the frequency and wave number associated with the em laser pulse.

This analysis takes into account the situation where the plasma is maintained through the tunnel ionization of the gas by a high intensity em laser pulse (DHGPs or Gaussian intensity profile) and electron ion recombination. Following earlier investigations (Gildenburg et al., Reference Gildenburg, Kim, Krupnov, Semenov, Sergeev and Zharova1993; Liu & Tripathi, Reference Liu and Tripathi2000), the evolution of the plasma density (n _e) in the presence of em field can be expressed as

(2)$$\partial n_e /\partial t = {\rm \beta} _a \lpar n_0 - n_e \rpar - {\rm \alpha} _a n_e^2\comma$$

where β_a refers to the rate of tunnel ionization of neutral gas (Liu & Tripathi, Reference Liu and Tripathi2000), α_a[=α₀ (300/T _e)^κcm ³/s] is the recombination coefficient of plasma electrons and ions (Gurevich, Reference Gurevich1978), α₀ and κ are the constants and T _e is the electron temperature.

The first term on the right-hand side refers to the generation of electrons due to ionization of neutral species while the newly added second term corresponds to the depletion of plasma electrons on account of electron/ ion recombination. Following β_a have been given for DC field by Landau and Lifshitz (Reference Landau and Lifshitz1978) and for AC field by Keldysh (Reference Keldysh1965) (later modified rate is ADK rate); Gildenberg et al. (Reference Gildenburg, Kim, Krupnov, Semenov, Sergeev and Zharova1993) have used a simplified version. In this analysis the authors have used a simpler expression, used in many investigations (Liu & Tripathi, Reference Liu and Tripathi2000; Verma & Sharma, Reference Verma and Sharma2011), can be expressed as

(3)$${\rm \beta} _a = s\lpar \left\vert {\bi E} \right\vert /E_A \rpar ^{1/2} exp\lpar \!\!- E_A /\left\vert {\bi E} \right\vert \rpar \comma$$

where s = (π/2)^1/2$\lpar I_0 /\hbar \rpar \comma \; E_A = \lpar 4/3\rpar \sqrt {2m_e } I_0^{3/2} /e\hbar $ is the characteristic atomic field, I ₀ is the ionization potential of the neutral species, m _e is the mass of the electron, $\hbar = \lpar h/2{\rm \pi} \rpar $, h is the Planck's constant and eis the electronic charge.

3. PULSE PROPAGATION: DARK HOLLOW GAUSSIAN PULSE

The initial (i.e., at z′ = 0) complex amplitude of the DHGP can be expressed as

(4)$$A\lpar r\comma \; 0\comma \; t\rpar = A_0 \lpar r^2 /2r_0^2 \rpar ^n exp\lpar \!\!- r^2 /2r_0^2 \rpar exp\lpar \!\!- t^2 /2{\rm \tau} _p^2 \rpar \comma$$

where r ₀ and τ_p are the beam (in space) and pulse (in time) widths, respectively, n is the order of the DHGP and a positive integer, characterizing the shape of the pulse and position of its maximum intensity; the maximum of |A| exists at r = r _max = r ₀(2n)^1/2.

The em field associated with the pulse in the plasma is characterized by the dispersion relation, i.e., ω² = (c ²k ² + ω_p²), where ω_p represents the plasma frequency, k = (ω/c)ε₀^1/2, ε₀ is the dielectric function corresponding to the maximum electric field on the wavefront of the pulse and c refers to speed of light in vacuum.

The propagation of the em pulse in the plasma can be described by the wave equation. Utilizing Jeffreys-Wentzel–Kramers–Brillouin approximation (under which ∂²A/∂z ² is neglected considering A to be a slowly varying function of z) the electric field vector (Eq. (1)) satisfies the nonlinear Schrödinger wave equation (NLSE) as follows (Sharma et al., Reference Sharma, Borhanian and Kourakis2009)

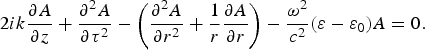(5)$$2ik\displaystyle{{\partial A} \over {\partial z}} + \displaystyle{{\partial ^2 A} \over {\partial {\rm \tau} ^2 }} - \left({\displaystyle{{\partial ^2 A} \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A} \over {\partial r}}} \right)- \displaystyle{{{\rm \omega} _{}^2 } \over {c^2 }}\lpar {\rm \varepsilon} - {\rm \varepsilon} _0 \rpar A = 0.$$

In writing the above equation, the relation z′ = z and τ = (ct − z) is used. The second and third terms in the above equation represents the group velocity dispersion (GVD) and diffraction terms respectively; the manifestation of these terms in the plasma nonlinearity (viz. last term), leads to the phenomena of pulse compression and transverse focusing respectively. The nonlinearity in the plasma arises due to non-uniformity in the irradiance distribution in the spatial/ transient pulse profile, which is basically caused due to modification in the electron density. The solution of Eq. (5) can be expressed as

(6)$${\bi A}\lpar r\comma \; z\comma \; {\rm \tau} \rpar = A_0 \lpar r\comma \; z\comma \; t\rpar exp\lsqb \!\!- ikS\lpar r\comma \; z\comma \; {\rm \tau} \rpar \rsqb \comma$$

where A ₀ and S represents DHGP amplitude and eikonal respectively and are real quantities; the eikonal describes the curvature of the em pulse wavefront while the amplitude square i.e. A ₀² characterizes the intensity profile.

Substituting for A from Eq. (6) in Eq. (5) and separating the real and imaginary parts, one obtains

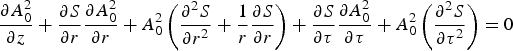(7a)$$\displaystyle{{\partial A_0^2 } \over {\partial z}} + \displaystyle{{\partial S} \over {\partial r}}\displaystyle{{\partial A_0^2 } \over {\partial r}} + A_0^2 \left({\displaystyle{{\partial ^2 S} \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right)+ \displaystyle{{\partial S} \over {\partial {\rm \tau} }}\displaystyle{{\partial A_0^2 } \over {\partial {\rm \tau} }} + A_0^2 \left({\displaystyle{{\partial ^2 S} \over {\partial {\rm \tau} ^2 }}} \right)= 0$$

and

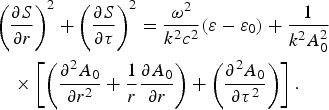(7b)$$\eqalign{&\left({\displaystyle{{\partial S} \over {\partial r}}} \right)^2 + \left({\displaystyle{{\partial S} \over {\partial {\rm \tau} }}} \right)^2 = \displaystyle{{{\rm \omega} _{}^2 } \over {k^2 c^2 }}\lpar {\rm \varepsilon} - {\rm \varepsilon} _0 \rpar + \displaystyle{1 \over {k^2 A_0^2 }}\cr & \quad \times \left[{\left({\displaystyle{{\partial ^2 A_0 } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_0 } \over {\partial r}}} \right)+ \left({\displaystyle{{\partial ^2 A_0 } \over {\partial {\rm \tau} ^2 }}} \right)} \right].}$$

To proceed further a paraxial like approach (Misra & Mishra, Reference Misra and Mishra2009) analogous to paraxial approximation is adopted where the coordinate system is transformed from (r,z,τ) to (η,z,τ) space such that

(8)$${\rm \eta} = \left[{\lpar r/r_0 f\rpar - \sqrt {2n} } \right]$$

r ₀f(z) is the width of the beam and $r = r_0 f\sqrt {2n}$ represents the position of the maximum irradiance on the DHGP wavefront as it advances in the plasma. Since the irradiance of the HGP is maximum at $r = r_0 f\sqrt {2n}$ and τ = 0; the expansion of the expressions for the relevant parameters around $r_0 f\sqrt {2n} $ and τ = 0 are certainly justified in the paraxial like approximation; for n = 0 (Gaussian beam), the expansion is made (like wise) around r = τ= 0 (as usual). Like the paraxial theory, the present analysis is strictly applicable when ${\rm \eta} \lt \!\!\lt \sqrt {2n} $. Utilizing the transformation (i.e., Eq. 8), Eqs. (7a) and (7b) reduce to

(9a)$$\eqalign{& \left({\displaystyle{{\partial A_0^2 } \over {\partial z}} - \displaystyle{{\lpar \sqrt {2n} + {\rm \eta} \rpar } \over f}\displaystyle{{\partial f} \over {\partial z}}\displaystyle{{\partial A_0^2 } \over {\partial {\rm \eta} }}} \right) + \displaystyle{1 \over {r_0^2 f^2 }}\displaystyle{{\partial S} \over {\partial {\rm \eta} }}\displaystyle{{\partial A_0^2 } \over {\partial {\rm \eta} }}\cr & \quad + \displaystyle{{A_0^2 } \over {r_0^2 f^2 }}\left({\displaystyle{{\partial ^2 S} \over {\partial {\rm \eta} ^2 }} + \displaystyle{1 \over {\lpar \sqrt {2n} + {\rm \eta} \rpar }}\displaystyle{{\partial S} \over {\partial {\rm \eta} }}} \right)+ \displaystyle{{\partial S} \over {\partial {\rm \tau} }}\displaystyle{{\partial A_0^2 } \over {\partial {\rm \tau} }} \cr &\quad + A_0^2 \left({\displaystyle{{\partial ^2 S} \over {\partial {\rm \tau} ^2 }}} \right)= 0}$$

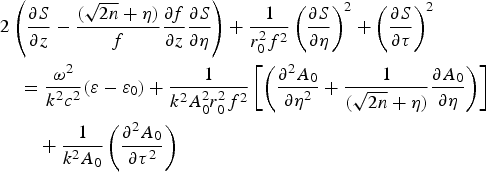(9b)$$\eqalign{&2\left({\displaystyle{{\partial S} \over {\partial z}} - \displaystyle{{\lpar \sqrt {2n} + {\rm \eta} \rpar } \over f} \displaystyle{{\partial f} \over {\partial z}}\displaystyle{{\partial S} \over {\partial {\rm \eta} }}} \right)+ \displaystyle{1 \over {r_0^2 f^2 }}\left({\displaystyle{{\partial S} \over {\partial {\rm \eta} }}} \right)^2 + \left({\displaystyle{{\partial S} \over {\partial {\rm \tau} }}} \right)^2 \cr & \quad = \displaystyle{{{\rm \omega} ^2 } \over {k^2 c^2 }}\lpar {\rm \varepsilon} - {\rm \varepsilon} _0 \rpar + \displaystyle{1 \over {k^2 A_0^2 r_0^2 f^2 }}\left[{\left({\displaystyle{{\partial ^2 A_0 } \over {\partial {\rm \eta} ^2 }} + \displaystyle{1 \over {\lpar \sqrt {2n} + {\rm \eta} \rpar }}\displaystyle{{\partial A_0 } \over {\partial {\rm \eta} }}} \right)} \right]\cr & \qquad + \displaystyle{1 \over {k^2 A_0 }}\left({\displaystyle{{\partial ^2 A_0 } \over {\partial {\rm \tau} ^2 }}} \right)}$$

In the paraxial like approximation, the solution of Eq. (9a) can be chosen as,

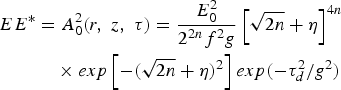(10a)$$\eqalign{ EE^ {\ast} &= A_0^2 \lpar r\comma \; z\comma \; {\rm \tau} \rpar = \displaystyle{{E_0^2 } \over {2^{2n} f^2g}}\left[{\sqrt {2n} + {\rm \eta} } \right]^{4n} \cr & \quad \times exp\left[{ - \lpar \sqrt {2n} + {\rm \eta} \rpar ^2 } \right]exp\lpar - {\rm \tau} _d^2 /g^2 \rpar }$$

and

(10b)$$\eqalign {& S\lpar r\comma \; z\comma \; {\rm \tau} \rpar = \lpar \sqrt {2n} + {\rm \eta} \rpar ^2 \lpar r_0^2 f/2\rpar \lpar df/dz\rpar + \lpar {\rm \tau} ^2 /2g\rpar \lpar dg/dz\rpar + {\rm \varphi} \lpar z\rpar }\comma$$

where the beam (f) and pulse width (g) parameters characterize the modification of the pulse profile in space and time as the pulse advances through the plasma, τ_L(=cτ_p) refers to the pulse length and τ_d = τ/τ_L.

The first two terms in Eq. (10b) refer to the spherical curvature of the DHGP while φ is the phase describing the departure from the spherical nature. It is necessary to mention that the choice of solutions for A ₀² and S are consistent with set of Eqs. (9). In the paraxial like approach the effective dielectric function ε(η,z,τ) around the maximum (i.e., η = 0 and τ = 0) can be expressed as

(11)$${\rm \varepsilon} \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = {\rm \varepsilon} _0 \lpar z\rpar - {\rm \eta} ^2 {\rm \varepsilon} _{\rm \eta} \lpar z\rpar - {\rm \tau} _d^2 {\rm \varepsilon} _{\rm \tau} \lpar z\rpar \comma$$

where ε₀ (z) is the abbreviated form of ε (z,η = 0,τ = 0).

On substituting for A ₀², S and ε in Eq. (9) and equating the coefficients of η² and τ_d² on both sides of the resulting equation one obtains

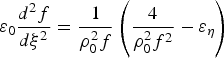(12a)$${\rm \varepsilon} _0 \displaystyle{{d^2 f} \over {d{\rm \xi} ^2 }} = \displaystyle{1 \over {{\rm \rho} _0^2 f}}\left({\displaystyle{4 \over {{\rm \rho} _0^2 f^2 }} - {\rm \varepsilon} _{\rm \eta} } \right)$$

and

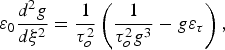(12b)$${\rm \varepsilon} _0 \displaystyle{{d^2g} \over {d{\rm \xi} ^2 }} = \displaystyle{1 \over {{\rm \tau} _o^2 }}\left({\displaystyle{1 \over {{\rm \tau} _o^2g^3 }} - g{\rm \varepsilon} _{\rm \tau} } \right)\comma$$

where τ_o = (τ_Lω/c) = τ_p ω, ρ₀ = (r ₀ ω/c) and ξ (= zω/c).

The above coupled equations (i.e., Eqs. 12) describe the evolution of spatial and temporal envelopes as the pulse propagates in the plasma where the processes of self focusing and compression are simultaneously operative. It is necessary to point out that the equations for f and g are based on the assumption that the pulse profile remains unaltered as it propagates in the plasma; this is consistent with the irradiance profile (as evinced from Eq. 9a). It may be noted that left hand side of Eq. (9b) has a term proportional to η with coefficient [∝ f(∂²f/∂z ²)] but none in the right hand side. This leads to (∂²f/∂z ²) = 0 and an erroneous result that the beam width parameter (f) is independent of plasma nonlinearity and remains unaltered as it traverses through the plasma. Since this is an absurd solution for f hence not considered in the further analysis and treated as redundant.

In case of Gaussian pulse the intensity maximum is exhibited at r = 0; following the earlier analyses based on paraxial approach, the coupled differential equations describing the pulse width parameters in space (f _o) and time (g _o) corresponding to Gaussian wavefront can be expressed as (Sharma et al., Reference Sharma, Borhanian and Kourakis2009)

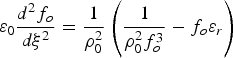(13a)$${\rm \varepsilon} _0 \displaystyle{{d^2 f_o } \over {d{\rm \xi} ^2 }} = \displaystyle{1 \over {{\rm \rho} _0^2 }}\left({\displaystyle{1 \over {{\rm \rho} _0^2 f_o^3 }} - f_o {\rm \varepsilon} _r } \right)$$

and

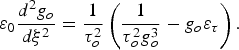(13b)$${\rm \varepsilon} _0 \displaystyle{{d^2 g_o } \over {d{\rm \xi} ^2 }} = \displaystyle{1 \over {{\rm \tau} _o^2 }}\left({\displaystyle{1 \over {{\rm \tau} _o^2 g_o^3 }} - g_o {\rm \varepsilon} _{\rm \tau} } \right).$$

The above equations (Eqs. 13) characterizing f _o and g _o are consistent with the irradiance profile

(14a)$$A_0^2 = \lpar E_0^2 /f_o^2 g_o \rpar exp\lpar \!- r_d^2 /f_o^2 \rpar exp\lpar \!- {\rm \tau} _d^2 /g_o^2 \rpar$$

with

$$\eqalign{\varepsilon (r,z,\tau ) &= \varepsilon _0 (z) - r_d^2 \varepsilon _r (z) - \tau _d^2 \varepsilon _\tau (z), \cr r_d & = (r/r_0 ) \;{\rm and} \;\varepsilon _0 (z)=\varepsilon (z,r = 0,\tau = 0).}$$

Using the appropriate expression for ε corresponding to plasma generated through tunnel ionization of the gas and suitable choice of gas/pulse parameters in addition to initial boundary conditions (corresponding to plane wavefront of the pulse at z = 0) viz. f(0) = g(0) = 1 and f′(0) = g′(0) = 0, the set of Eqs. (12 & 13) can be numerically solved to evaluate the beam (f) and pulse (g) width parameters as a function of the propagation distance ξ; the knowledge of f and g leads to the information about spatio-temporal evolution of pulse profile as it propagates in the plasma.

4. EVALUATION OF NONLINEAR PERMITTIVITY (DIELECTRIC FUNCTION)

Following earlier analyses (Borisov et al., Reference Borisov, Borovisiky, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992; Brandi et al., Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993), the effective dielectric function of the plasma characterized by simultaneously operative relativistic and ponderomotive effects, can be expressed as

(15)$${\rm \varepsilon} \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = \left[{1 - \lpar 4{\rm \pi} e^2 /{\rm \gamma} m_e {\rm \omega} ^2 \rpar n_e \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar - \lpar c^2 /{\rm \omega} ^2 \rpar \nabla \lpar \nabla {\rm \gamma} /{\rm \gamma} \rpar } \right]\comma$$

where γ [= (1 + a _o²)^1/2] is the relativistic factor, a _o = (e/m _ecω)E = α (E/E _A) and α = (eE _A/m _e cω).

Specifically, the expressions for dielectric function corresponding to DHGPs and Gaussian pulses respectively can be written as

(15a)$${\rm \varepsilon} \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = \left[{1 - \lpar 4{\rm \pi} e^2 /{\rm \gamma} m_e {\rm \omega} ^2 \rpar n_e \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar - \lpar 1/{\rm \rho} _0^2 f^2 \rpar \partial _{\rm \eta} \lpar \partial _{\rm \eta} {\rm \gamma} /{\rm \gamma} \rpar } \right]$$

and

(15b)$${\rm \varepsilon} \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = \left[{1 - \lpar 4{\rm \pi} e^2 /{\rm \gamma} m_e {\rm \omega} ^2 \rpar n_e \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar - \lpar r_0^2 /{\rm \rho} _0^2 \rpar \partial _r \lpar \partial _r {\rm \gamma} /{\rm \gamma} \rpar } \right]$$

Case-1: For Dark Hollow Gaussian Pulses

Utilizing the paraxial like approach n _e, β_a and γ can be expanded around the intensity maximum (i.e., η = 0 and τ = 0) and can be expressed as

(16a)$$n_e \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = n_{e0} \lpar z\rpar - {\rm \eta} ^2 n_{e{\rm \eta} } \lpar z\rpar - {\rm \tau} _d^2 n_{e{\rm \tau} } \lpar z\rpar \comma$$

(16b)$${\rm \beta} _a \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = {\rm \beta} _0 \lpar z\rpar - {\rm \eta} ^2 {\rm \beta} _{\rm \eta} \lpar z\rpar - {\rm \tau} _d^2 {\rm \beta} _{\rm \tau} \lpar z\rpar$$

and

(16c)$${\rm \gamma} \lpar {\rm \eta} \comma \; z\comma \; {\rm \tau} \rpar = {\rm \gamma} _0 \lpar z\rpar - {\rm \eta} ^2 {\rm \gamma} _{\rm \eta} \lpar z\rpar - {\rm \tau} _d^2 {\rm \gamma} _{\rm \tau} \lpar z\rpar .$$

Substituting for $n_e $ and β_a in Eq. (2) and equating the coefficients of η⁰, η² and τ_d² on both sides of the resulting equation yields

(17a)$$n_{e0} = \lsqb \!\!- {\rm \beta} _0 + \lpar {\rm \beta} _0^2 + 4{\rm \beta} _0 {\rm \alpha} _a n_0 \rpar ^{1/2} \rsqb /2{\rm \alpha} _a\comma$$

(17b)$$n_{e{\rm \eta} } = \lsqb {\rm \beta} _{\rm \eta} \lpar n_0 - n_{e0} \rpar /\lpar {\rm \beta} _0 + 2{\rm \alpha} _a n_{e0} \rpar \rsqb$$

and

(17c)$$n_{e{\rm \tau} } = \lsqb {\rm \beta} _{\rm \tau} \lpar n_0 - n_{e0} \rpar /\lpar {\rm \beta} _0 + 2{\rm \alpha} _a n_{e0} \rpar \rsqb .$$

The coefficients (β₀, β_η and β_τ) occurring in the definition of β_a can be obtained by substituting the DHGP field profile in Eq. (3) and equating the coefficients of η⁰, η² and τ_d² by using definition of β_a from Eq. (16b). Using Eq. (10a) the DHGP amplitude profile under paraxial like approximation can be expressed as

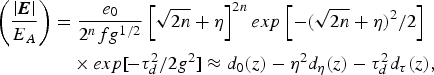(18a)$$\eqalign{ \left({\displaystyle{{\left\vert {\bi E} \right\vert } \over {E_A }}} \right)&= \displaystyle{{e_0 } \over {2^n fg^{1/2} }}\left[{\sqrt {2n} + {\rm \eta} } \right]^{2n} exp\left[{ - \lpar \sqrt {2n} + {\rm \eta} \rpar ^2 /2} \right]\cr & \quad \times exp\lsqb \!- {\rm \tau} _d^2 /2g^2 \rsqb \approx d_0 \lpar z\rpar - {\rm \eta} ^2 d_{\rm \eta} \lpar z\rpar - {\rm \tau} _d^2 d_{\rm \tau} \lpar z\rpar \comma }$$

where

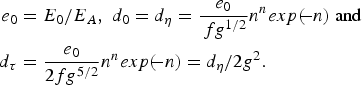(18b)$$\eqalign{ e_0 &= E_0 /E_A \comma \; d_0 = d_{\rm \eta} = \displaystyle{{e_0 } \over {\,fg^{1/2} }}n^n exp\lpar \!\!- n\rpar\ {\rm and}\cr d_{\rm \tau} & = \displaystyle{{e_0 } \over {2fg^{5/2} }}n^n exp\lpar \!\!- n\rpar = d_{\rm \eta} /2g^2.}$$

This leads to β₀ = sd ₀^1/2exp[−(1/d ₀)], β_η = (β₀/2)[1 + (2/d ₀)] and β_τ = (β₀ /4g ² )[1 + (2/d ₀)].

Further using the definition of γ [=(1 + a _o²)^1/2], the coefficients (γ₀, γ_η and γ_τ) can be expressed as

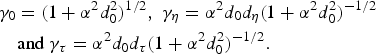$$\eqalign{& {\rm \gamma} _0 = \lpar 1 + {\rm \alpha} ^2 d_0^2 \rpar ^{1/2}\comma \; {\rm \gamma} _{\rm \eta} = {\rm \alpha} ^2 d_0 d_{\rm \eta} \lpar 1 + {\rm \alpha} ^2 d_0^2 \rpar ^{ - 1/2} \cr & \quad {\rm and}\ {\rm \gamma} _{\rm \tau} = {\rm \alpha} ^2 d_0 d_{\rm \tau} \lpar 1 + {\rm \alpha} ^2 d_0^2 \rpar ^{ - 1/2}.}$$

Finally, substituting for n _e, ε and γ from Eqs. (16 & 11) in Eq. (15a) and equating the coefficient of η⁰, η² and τ_d² from both sides in resulting equation one easily gets

(19a)$${\rm \varepsilon} _0 \lpar z\rpar = \left[{1 - \lpar 4{\rm \pi} e^2 /{\rm \gamma} _0 m_e {\rm \omega} ^2 \rpar n_{e0} } \right]+ \lpar 2/{\rm \rho} _0^2 f^2 \rpar \lpar {\rm \gamma} _{\rm \eta} /{\rm \gamma} _0 \rpar \comma$$

(19b)$${\rm \varepsilon} _{\rm \eta} \lpar z\rpar = \lpar 4{\rm \pi} e^2 /{\rm \gamma} _0 m_e {\rm \omega} ^2 \rpar \left[{\lpar n_{e0} {\rm \gamma} _{\rm \eta} /{\rm \gamma} _0 \rpar - n_{e{\rm \eta} } } \right]- \lpar 6/{\rm \rho} _0^2 f^2 \rpar \lpar {\rm \gamma} _{\rm \eta} /{\rm \gamma} _0 \rpar ^2$$

and

(19c)$${\rm \varepsilon} _{\rm \tau} \lpar z\rpar = \lpar 4{\rm \pi} e^2 /{\rm \gamma} _0 m_e {\rm \omega} ^2 \rpar \left[{\lpar n_{e0} {\rm \gamma} _{\rm \tau} /{\rm \gamma} _0 \rpar - n_{e{\rm \tau} } } \right]- \lpar 2/{\rm \rho} _0^2 f^2 \rpar \lpar {\rm \gamma} _{\rm \eta} {\rm \gamma} _{\rm \tau} /{\rm \gamma} _0^2 \rpar .$$

Case-2: For Gaussian Pulses

The expressions derived for the coefficients of n _e in Eq. (17) are equally applicable for the Gaussian pulses provided n _e/β_a are expanded around r = 0 and τ = 0 under paraxial approximation and the subsequent coefficients of n _e/β_a corresponding to Gaussian profile are used in place of DHGP profile coefficients.

For Gaussian pulses, the field amplitude profile (Eq. 14) can be expressed as

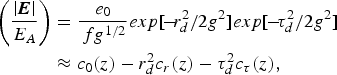(20a)$$\eqalign{ \left({\displaystyle{{\left\vert {\bi E} \right\vert } \over {E_A }}} \right)&= \displaystyle{{e_0 } \over {\,fg^{1/2} }}exp\lsqb \! -\! r_d^2 /2g^2 \rsqb exp\lsqb \!-\! {\rm \tau} _d^2 /2g^2 \rsqb \cr & \approx c_0 \lpar z\rpar - r_d^2 c_r \lpar z\rpar - {\rm \tau} _d^2 c_{\rm \tau} \lpar z\rpar \comma}$$

where

(20b)$$c_0 = \lpar e_0 /fg^{1/2} \rpar \comma \; c_r = \lpar c_0 /2f^2 \rpar\ {\rm and}\ c_{\rm \tau} = \lpar c_0 /2g^2 \rpar .$$

Consequently, following the approach similar to that in case of DHGP, the components of the ionization coefficient (β₀, β_r and β_τ) and relativistic factor (γ₀, γ_r and γ_τ) for the Gaussian pulse can be expressed as

β₀ = sc₀^1/2exp[−(1/c ₀)], β_r = (β₀/4f ²)[1 + (2/c ₀)], β_τ = (β₀/4g ²)[1 + (2/c ₀)], γ₀ = (1 + α²c ₀²)^1/2, γ_r = α²c ₀c _r(1 + α²c ₀²)^−1/2 and γτ = α²c ₀cτ(1 + α²c ₀²)^−1/2.

Further utilizing the definition of n _e/ε/γ in paraxial regime (i.e., expansion around r,τ = 0), the components of the dielectric function (i.e., Eq. 15b) for Gaussian pulse can be expressed as

(21a)$${\rm \varepsilon} _0 \lpar z\rpar = \left[{1 - \lpar 4{\rm \pi} e^2 /{\rm \gamma} _0 m_e {\rm \omega} ^2 \rpar n_{e0} } \right]+ \lpar 2/{\rm \rho} _0^2 \rpar \lpar {\rm \gamma} _r /{\rm \gamma} _0 \rpar \comma$$

(21b)$${\rm \varepsilon} _r \lpar z\rpar = \lpar 4{\rm \pi} e^2 /{\rm \gamma} _0 m_e {\rm \omega} ^2 \rpar \left[{\lpar n_{e0} {\rm \gamma} _r /{\rm \gamma} _0 \rpar - n_{er} } \right]- \lpar 6/{\rm \rho} _0^2 \rpar \lpar {\rm \gamma} _r /{\rm \gamma} _0 \rpar ^2$$

and

(21c)$${\rm \varepsilon} _{\rm \tau} \lpar z\rpar = \lpar 4{\rm \pi} e^2 /{\rm \gamma} _0 m_e {\rm \omega} ^2 \rpar \left[{\lpar n_{e0} {\rm \gamma} _{\rm \tau} /{\rm \gamma} _0 \rpar - n_{e{\rm \tau} } } \right]- \lpar 2/{\rm \rho} _0^2 \rpar \lpar {\rm \gamma} _r {\rm \gamma} _{\rm \tau} /{\rm \gamma} _0^2 \rpar .$$

5. NUMERICAL RESULTS AND DISCUSSION

This analysis brings out the spatiotemporal dynamics of a finite duration pico-second (ps) intense hollow Gaussian/ Gaussian laser pulse as it advances through a tunnel ionized gas; in this process the phenomena of transverse self focusing and pulse compression are explored. In contrast to earlier investigations this analysis takes account of electron ion recombination in addition to the neutral atom ionization in plasmas. This process (i.e. electron-ion recombination) was ignored in earlier analyses; hence the plasma density kept on increasing due to ionization which leads to decrease in the dielectric function.

In general in the absence of recombination, the nonuniform transverse intensity distribution of the laser pulse causes nonuniform tunnel ionization of the gas resulting in nonuniformity in the refractive index over its wavefront with a minimum at the axis (irradiance maximum); this in addition to diffraction leads to the divergence of the laser and the laser intensity falls off as it propagates in the plasma, i.e., the pulse suffers steady divergence. Intuitively, the inclusion of recombination term may lead to a balance between gas ionization and recombination processes and thus to the steady state situation, characterized by a saturating nonlinear dielectric function which takes finite value, usually larger than the case when it was ignored. In case of nonuniform laser intensity distribution in the transverse plane the recombination effect should be larger on the axis of intensity maximum and decrease radially; this modifies the refractive index in the same way. Hence the manifestation of nonuniform radial intensity profile of the pulse with gas ionization/ recombination processes in addition to relativistic mass correction and ponderomotive effects, results in modification in the background electron density in the transverse plane; this modifies the intensity profile of the wavefront of the pulse in a way that enhances the nonlinear dielectric function and hence the nonlinear propagation characteristics. The nonlinear pulse dynamics and its space-time evolution are described by a set of coupled equations (i.e., Eqs. 12 & 13) where the nonlinearity is triggered by modification in the electron density via the dielectric function (Eqs. 19 & 21). It is also interesting to notice that due to weaker diffraction, the central shadow off axis (higher order hollow Gaussian) pulses shows smaller divergence as compared to the same for Gaussian pulses; thus the DHGPs can be utilized to achieve enhanced energy transport in the plasma. To describe the dynamics of DHG (or Gaussian) pulse, Paraxial like (or paraxial) approach has been adopted which is applicable within the finite region characterized by ${\rm \eta} \ll \sqrt {2n}$ (or r _d ≪ 1) and τ_d ≪ 1, around the axis of maximum pulse intensity and valid throughout the pulse dynamics as it propagate in the plasma. In this limit all the relevant parameters have been expanded upto quadratic terms (first order in η² (r _d²) and τ_d²) only in the vicinity of η = r _d = 0 = τ_d and higher order terms are ignored. It is evident from Eq. (9a) that the nature of the pulse profile (i.e. hollow Gaussian/Gaussian) remains unchanged as it traverse in the plasma and this is a natural consequence of paraxial approximation; the numerical results obtained are based on this paraxial formalism.

For a numerical appreciation of the analysis the following standard set of parameters corresponding to Neon gas (Liu & Tripathi, Reference Liu and Tripathi2000; Biondi & Brown, Reference Biondi and Brown1949) have been used for the computations; the effect of various parameters has been studied by varying one parameter and keeping others the same.

n ₀ = 10²⁰cm ⁻³, e ₀ = (E ₀/E _A) = 1/2 and 1/3 corresponding to peak pulse intensity I _p ≈ 1.52 × 10¹⁶ (a ₀ ≈ 1.05) and ≈ 6.75 × 10¹⁵W/cm ² (a ₀ ≈ 0.7) respectively, τ_p = 10ps, α₀ = 2.2 × 10⁻⁶cm ³ sec⁻¹ (corresponding to Neon gas [48]), I ₀ = 21.5eV, κ = 1.0, T _e0 = 1eV, λ = 10μm, ω = 27πc/λ, r ₀ = 10λ, c = 3 × 10⁸m/sec and e = 1.6 × 10⁻¹⁹.

Using the above set of parameters and initial boundary conditions (corresponding to plane wavefront of the pulse at z = 0) viz. f(0) = g(0) = 1 and f′(0) = g′(0) = 0, the set of Eqs. (12 & 13) can numerically be solved to evaluate the pulse compression parameters, describing the pulse width in space (f) and time (g) as a function of propagation distance (ξ); the knowledge of f and g leads to the information about space-time evolution of pulse profile as it advances through the plasma. Further for the illustration purpose normalized irradiance of the pulse is defined as ς_a = A ₀²(z)/A ₀²(0) while the normalized axial irradiance corresponding to η = 0,τ = 0 is given by ς_ao[=(1/f ²g)].

The set of Figure 1 illustrates the dependence of the normalized axial irradiance ς_ao[=(1/f ²g)] on the dimensionless distance of propagation (ξ) for various plasma/pulse parameters as DHGPs advances through the plasma. One of the common features is that the pulse exhibits three regime propagation characteristics (Sodha et al., Reference Sodha, Mishra and Misra2009a) viz. self focusing, oscillatory divergence and steady divergence, in the vicinity of the irradiance maximum. The effect of inclusion of electron ion recombination (characterized by the parameter α₀) on the propagation of zero (Gaussian, broken lines) and first order DHGPs (i.e. n = 1, solid lines) has been displayed in Figures 1 and 2 respectively. It may however be emphasized that electrons and ions of a gas at a given electron temperature will have a unique recombination coefficient; the parameter α₀ has been varied only to evaluate the importance of the recombination coefficient in focusing as a part of the parametric analysis. The figures indicate that in the absence of recombination (corresponding to black color lines) the Gaussian pulse exhibits steady divergence while DHGPs undergo oscillatory defocusing; nevertheless it can be seen from the figures that the inclusion of electron-ion recombination drives the system to the focusing regime and the effect is more pronounced with increasing recombination coefficient. The figure suggests that both the Gaussian and DHG pulses undergo periodic self focusing with increasing magnitude of the recombination coefficient; this leads to the enhancement in axial irradiance and hence enhanced energy localization as these pulses propagate through the tunnel ionized gas plasmas. The evolution of axial irradiance of the pulse for the propagation of different order DHGPs has been illustrated in Figure 3; it is noticed that the pulse shifts from oscillatory focusing to oscillatory divergence regime with increasing order of DHGP while the Gaussian pulse in the oscillatory divergence regime. It is necessary to point out that the space-time evolution of the em pulse field is sensitive to the choice of magnitude and profile of the intensity pattern and that they evolve differently depending on pulse/plasma parameters. The effect of pulse length (τ_p) on the axial irradiance of the first order DHGP as it advances through the plasma has been illustrated in Figure 4; it is seen that the oscillations in ς_ao become symmetrical while the focusing slightly decreases with increasing pulse width. This nature can be attributed to the fact that longer pulses drive the plasma to the steady state where the pulse dynamics is primarily governed by space profile only and temporal evolution becomes insignificant. Further it is also noticed that the focusing length increases with increasing the pulse duration.

Fig. 1. (Color online) Dependence of normalized axial irradiance ς_ao[=(1/f ²g)] of the Gaussian pulse on the normalized propagation distance of (ξ) for e ₀ = (1/3) and standard set of parameters as stated in the text; black, brown, green, red, and blue color lines correspond to recombination coefficients α₀ = 0, 10⁻⁷, 10⁻⁶, 10⁻⁵ and 10⁻⁴ cm³s⁻¹, respectively.

Fig. 2. (Color online) Dependence of normalized axial irradiance ς_ao of the first order DHGP on the normalized propagation distance (ξ) for e ₀ = (1/2) and standard set of parameters as stated in the text; black, green, red, and blue color lines correspond to recombination coefficients α₀ = 0, 10⁻⁷, 10⁻⁶ and 10⁻⁵cm³s⁻¹, respectively.

Fig. 3. (Color online) Dependence of normalized axial irradiance ς_ao of the DHGP and Gaussian pulse on normalized propagation distance of (ξ) for e ₀ = (1/2) and standard set of parameters as stated in the text; blue, red, and green color lines correspond to DHGP of the order n = 1, 2 and 3, respectively, while black line refers to Gaussian pulse (n = 0).

Fig. 4. (Color online) Dependence of normalized axial irradiance ς_ao of the first order DHGP (solid lines) and Gaussian pulse (broken lines) on normalized propagation distance of (ξ) for e ₀ = (1/2) and standard set of parameters as stated in the text; blue, red, green, and black color lines correspond to pulse length τ_p= 0.05, 0.1, 1.0 and 10 ps, respectively.

The set of Figure 5 display the spatiotemporal evolution of the normalized irradiance (ς_a) of different order DHGPs at different distances of propagation in a tunnel ionized gas plasma; the dynamics of the pulse can be understood in terms of the mutual collective effect of transverse and longitudinal evolution of laser field leading to compression in space (transverse self-focusing, f) and time (longitudinal pulse compression, g). Figure 5a clearly indicates the broadening of the pulse width in space i.e., the divergence of Gaussian profile pulse (i.e. n = 0) as it advances through the plasma while DHGPs displays the pulse compression in time and space resulting in larger axial intensity. Further it is also seen that the two lobes (characterizing the dipole potential associated with DHGPs) oscillate about the central axis as the pulse propagate through the plasma and lead to convergence of intensity maxima (merging) of DHG pulse about central axis r = 0; this nature has been displayed in Figure 5b for the first order DHGP (i.e. n = 1). It is necessary to point out that the em pulse compression/rarefaction effects displayed in the simulation results in its space/time evolution, are the consequence of modification in pulse width in space (r = r ₀f) and time (τ = τ₀g) as it advances through the plasma; however this does not distort the nature of the pulse profile and the pulse retains its characteristic profile (i.e. hollow Gaussian or Gaussian) throughout the propagation in the vicinity of paraxial approximation. Further, it should be emphasized that the numerical results displayed are consistent with a particular set of parameters; however various features and effects can be explored by suitable choice of physical pulse/plasma parameters.

Fig. 5. (Color online) (A) Demonstration of spatiotemporal evolution of normalized irradiance ς_a[=A ₀² (z)/A ₀² (0)] of the Gaussian pulse (n = 0) and various order DHGPs (n = 1 and 2), as a function of normalized propagation distance (ξ) for the standard set of parameters as stated in the text with e ₀ = (1/3) and τ_p = 10ps; here R(=r/r ₀) and T(=τ/τ_L) while side bar represents the irradiance magnitude of the color index. (B) Demonstration of spatiotemporal evolution of normalized irradiance ς_a of the first order DHGP (n = 1), as a function of normalized propagation distance (ξ) for the standard set of parameters as stated in the text with e ₀ = (1/3) and τ_p = 1 ps; here R(=r/r ₀) and T(=τ/τ_L)$ while side bar represents the irradiance magnitude of the color index.