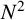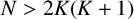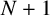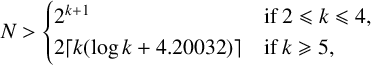1 Introduction
An
![]() $N \times N$
matrix
$N \times N$
matrix
![]() ${\mathbf Z} = (z_{i,j})_{1 \leqslant i,j \leqslant N}$
is a magic square of order N if the sums of the entries in each of its rows, columns and two main diagonals are equal. Given
${\mathbf Z} = (z_{i,j})_{1 \leqslant i,j \leqslant N}$
is a magic square of order N if the sums of the entries in each of its rows, columns and two main diagonals are equal. Given
![]() $K \geqslant 2$
, we say a matrix
$K \geqslant 2$
, we say a matrix
![]() ${\mathbf Z} \in {\mathbb Z}^{N \times N}$
is a K-multimagic square of order N, or an
${\mathbf Z} \in {\mathbb Z}^{N \times N}$
is a K-multimagic square of order N, or an
![]() $\textbf {MMS}(K,N)$
for short, if the matrices
$\textbf {MMS}(K,N)$
for short, if the matrices
remain magic squares for
![]() $1 \leqslant k \leqslant K$
. Here, we expand on our previous investigation [Reference Flores5], where we saw that given any
$1 \leqslant k \leqslant K$
. Here, we expand on our previous investigation [Reference Flores5], where we saw that given any
![]() $K \geqslant 2$
and
$K \geqslant 2$
and
![]() $N \in {\mathbb N}$
, there exists many trivial examples of
$N \in {\mathbb N}$
, there exists many trivial examples of
![]() $\textbf {MMS}(K,N)$
using at most N distinct integers. Given K, we previously focused on the problem of finding a lower bound for N such that there exists an
$\textbf {MMS}(K,N)$
using at most N distinct integers. Given K, we previously focused on the problem of finding a lower bound for N such that there exists an
![]() $\textbf {MMS}(K,N)$
using
$\textbf {MMS}(K,N)$
using
![]() $N+1$
or more digits. Via the circle method, we proved in [Reference Flores5] that
$N+1$
or more digits. Via the circle method, we proved in [Reference Flores5] that
![]() $N>2K{(K+1)}$
is a suitable lower bound on N for this problem.
$N>2K{(K+1)}$
is a suitable lower bound on N for this problem.
However, this may not be satisfactory for those familiar with magic squares as the typical parlance usually refers to magic squares with any repeated entries as trivial. A more satisfactory result would be to determine a lower bound on N in terms of K for which there exists an
![]() $\textbf {MMS}(K,N)$
with distinct entries.
$\textbf {MMS}(K,N)$
with distinct entries.
This question has been considered in the past by several authors (see [Reference Boyer1, Reference Derksen, Eggermont and van den Essen4, Reference Trump9–Reference Zhang, Chen and Li11]) via constructive methods. We give a brief overview of the best known results in Table 1. The curious reader is encouraged to read the introductions of both [Reference Flores5, Reference Rome and Yamagishi7] for more information on the history of magic squares.
Table 1 Best known results for K-multimagic squares.

Although the circle method tells us there exists an
![]() $\textbf {MMS}(K,N)$
with at least N distinct entries when
$\textbf {MMS}(K,N)$
with at least N distinct entries when
![]() $N> 2K(K+1)$
, it could be the case that to establish the existence of an
$N> 2K(K+1)$
, it could be the case that to establish the existence of an
![]() $\textbf {MMS}(K,N)$
with all distinct entries, we may require N to be even larger relative to
$\textbf {MMS}(K,N)$
with all distinct entries, we may require N to be even larger relative to
![]() $2K(K+1)$
. This difficulty may be seen in the recent work by Rome and Yamagishi [Reference Rome and Yamagishi7], where they tackle the simpler problem of showing the existence of magic squares of distinct kth powers. Via the techniques in [Reference Rome and Yamagishi7], one may obtain an asymptotic formula for the cardinality of the subset of
$2K(K+1)$
. This difficulty may be seen in the recent work by Rome and Yamagishi [Reference Rome and Yamagishi7], where they tackle the simpler problem of showing the existence of magic squares of distinct kth powers. Via the techniques in [Reference Rome and Yamagishi7], one may obtain an asymptotic formula for the cardinality of the subset of
![]() $N \times N$
magic squares of kth powers (with potential repeats) as soon as
$N \times N$
magic squares of kth powers (with potential repeats) as soon as
 $$ \begin{align*} N \geqslant \begin{cases} 2^{k+2}+\Delta & \text{if}\ 2 \leqslant k \leqslant 4, \\ 4 \lceil k (\log k + 4.20032) \rceil+\Delta & \text{if}\ 5 \leqslant k, \end{cases} \end{align*} $$
$$ \begin{align*} N \geqslant \begin{cases} 2^{k+2}+\Delta & \text{if}\ 2 \leqslant k \leqslant 4, \\ 4 \lceil k (\log k + 4.20032) \rceil+\Delta & \text{if}\ 5 \leqslant k, \end{cases} \end{align*} $$
with
![]() $\Delta = 12$
. However, Rome and Yamagishi end up requiring
$\Delta = 12$
. However, Rome and Yamagishi end up requiring
![]() $\Delta = 20$
to ensure that all entries of these magic squares are distinct kth powers. To understand why this increase in N is required in [Reference Rome and Yamagishi7], we first need to establish the notion of a partitionable matrix.
$\Delta = 20$
to ensure that all entries of these magic squares are distinct kth powers. To understand why this increase in N is required in [Reference Rome and Yamagishi7], we first need to establish the notion of a partitionable matrix.
Definition 1.1. We say a matrix
![]() $C= [{\mathbf c}_1,{\mathbf c}_2,\ldots ,{\mathbf c}_{rn}]$
of dimensions
$C= [{\mathbf c}_1,{\mathbf c}_2,\ldots ,{\mathbf c}_{rn}]$
of dimensions
![]() $r \times rn$
is partitionable if there exist disjoint sets
$r \times rn$
is partitionable if there exist disjoint sets
![]() $J_l \subset \{1,2,\ldots ,rn\}$
of size r for
$J_l \subset \{1,2,\ldots ,rn\}$
of size r for
![]() $1 \leqslant j \leqslant n$
satisfying
$1 \leqslant j \leqslant n$
satisfying
where
![]() $C_J$
denotes the submatrix of C consisting of columns indexed by J.
$C_J$
denotes the submatrix of C consisting of columns indexed by J.
Upon examination of the methods used in [Reference Rome and Yamagishi7], one sees that N is required to be slightly larger because of the difficulty of finding a large enough partitionable submatrix for the family of coefficient matrices associated with magic squares with particular repeated entries.
In [Reference Flores5], we define the notion of a matrix dominating a function as follows.
Definition 1.2. We say that a matrix
![]() $C \in {\mathbb C}^{r \times s}$
dominates a function
$C \in {\mathbb C}^{r \times s}$
dominates a function
![]() $f:{\mathbb N} \to {\mathbb R}^+$
if for all
$f:{\mathbb N} \to {\mathbb R}^+$
if for all
![]() $J \subset \{1, \ldots , s\}$
,
$J \subset \{1, \ldots , s\}$
,
where
![]() $C_J = [{\mathbf c}_j]_{j \in J}$
.
$C_J = [{\mathbf c}_j]_{j \in J}$
.
Then, by [Reference Low, Pitman and Wolff6, Lemma 1], if a matrix C dominates a certain function, we obtain information regarding its partitionable submatrices. This allows us to circumvent several difficulties encountered in [Reference Rome and Yamagishi7] and prove the following result.
Theorem 1.3. Given
![]() $K \geqslant 2$
, there exist infinitely many
$K \geqslant 2$
, there exist infinitely many
![]() $\mathbf {MMS}(K,N)$
consisting of
$\mathbf {MMS}(K,N)$
consisting of
![]() $N^2$
distinct integers as soon as
$N^2$
distinct integers as soon as
![]() $N>2K(K+1)$
.
$N>2K(K+1)$
.
It is important to note here that our lower bound on N remains unchanged. Additionally, just as in [Reference Flores5], one may easily obtain the following result via the Green–Tao theorem.
Corollary 1.4. Given
![]() $K \geqslant 2$
, there exist infinitely many
$K \geqslant 2$
, there exist infinitely many
![]() $\mathbf {MMS}(K,N)$
consisting of
$\mathbf {MMS}(K,N)$
consisting of
![]() $N^2$
distinct prime numbers as soon as
$N^2$
distinct prime numbers as soon as
![]() $N>2K(K+1)$
.
$N>2K(K+1)$
.
Finally, we present an analogous argument for finding magic squares of distinct kth powers. This approach uses the notion of our matrix of coefficients dominating a particular function, allowing us to establish the following result.
Theorem 1.5. Given
![]() $k \geqslant 2$
, there exist infinitely many
$k \geqslant 2$
, there exist infinitely many
![]() $N \times N$
magic squares of distinct kth powers as soon as
$N \times N$
magic squares of distinct kth powers as soon as
 $$ \begin{align*}N> \begin{cases} 2^{k+1} & \text{if}\ 2 \leqslant k \leqslant 4, \\ 2 \lceil k(\log k + 4.20032) \rceil & \text{if}\ k \geqslant 5. \end{cases}\end{align*} $$
$$ \begin{align*}N> \begin{cases} 2^{k+1} & \text{if}\ 2 \leqslant k \leqslant 4, \\ 2 \lceil k(\log k + 4.20032) \rceil & \text{if}\ k \geqslant 5. \end{cases}\end{align*} $$
This improves the recent result of Rome and Yamagishi [Reference Rome and Yamagishi7]. It is worth noting, just as Rome and Yamagishi did in [Reference Rome and Yamagishi8], that Theorem 1.5 is not entirely optimal for
![]() $4 \leqslant k \leqslant 20$
, we simply choose this representation of our theorem for convenience (see the introduction of [Reference Rome and Yamagishi7] for more detail).
$4 \leqslant k \leqslant 20$
, we simply choose this representation of our theorem for convenience (see the introduction of [Reference Rome and Yamagishi7] for more detail).
Remark 1.6. The application of the circle method to this problem has been part of the mathematical folklore for at least 30 years, with discussions dating back to the early 90s in talks by Bremner (see [Reference Bremner2, Reference Bremner3]). The recent breakthrough in this area lies in achieving a refined understanding of the coefficient matrix associated with the magic square system. Viewing a matrix as dominating a function appears to be the appropriate perspective, as it provides insight into the partitionability of submatrices.
2 Finding solutions of additive systems with distinct entries
Our basic parameter, P, is always assumed to be a large positive integer. Whenever
![]() $\varepsilon $
appears in a statement, either implicitly or explicitly, we assert that the statement holds for every
$\varepsilon $
appears in a statement, either implicitly or explicitly, we assert that the statement holds for every
![]() $\varepsilon>0$
. Implicit constants in Vinogradov’s notation
$\varepsilon>0$
. Implicit constants in Vinogradov’s notation
![]() $\ll $
and
$\ll $
and
![]() $\gg $
may depend on
$\gg $
may depend on
![]() $\varepsilon $
, r, s, k, K and the elements of the matrix C.
$\varepsilon $
, r, s, k, K and the elements of the matrix C.
Let
![]() $C =[{\mathbf c}_1,\ldots ,{\mathbf c}_s]= (c_{i,j})_{\substack {1 \leqslant i \leqslant r \\ 1 \leqslant j \leqslant s}} \in {\mathbb Z}^{r \times s}$
be given, and consider the diagonal system
$C =[{\mathbf c}_1,\ldots ,{\mathbf c}_s]= (c_{i,j})_{\substack {1 \leqslant i \leqslant r \\ 1 \leqslant j \leqslant s}} \in {\mathbb Z}^{r \times s}$
be given, and consider the diagonal system
 $$ \begin{align} \sum_{1 \leqslant j \leqslant s}c_{i,j}x_j^k = 0, \quad 1 \leqslant i \leqslant r. \end{align} $$
$$ \begin{align} \sum_{1 \leqslant j \leqslant s}c_{i,j}x_j^k = 0, \quad 1 \leqslant i \leqslant r. \end{align} $$
We define
![]() $S_k(P;C)$
to be the set of solutions
$S_k(P;C)$
to be the set of solutions
![]() ${\mathbf x} \in {\mathbb Z}^s$
to (2.1), where
${\mathbf x} \in {\mathbb Z}^s$
to (2.1), where
![]() $\max _{j}|x_j| \leqslant P$
. Given
$\max _{j}|x_j| \leqslant P$
. Given
![]() $i, j$
with
$i, j$
with
![]() $1 \leqslant i< j \leqslant s$
, it is not difficult to see that
$1 \leqslant i< j \leqslant s$
, it is not difficult to see that
where
![]() $C^{(i,j)}$
is the matrix obtained by substituting the ith column of C with
$C^{(i,j)}$
is the matrix obtained by substituting the ith column of C with
![]() ${\mathbf c}_{i}+{\mathbf c}_{j}$
and deleting the jth column of C.
${\mathbf c}_{i}+{\mathbf c}_{j}$
and deleting the jth column of C.
Thus, if
![]() $S^*_k(P;C)$
denotes the subset of
$S^*_k(P;C)$
denotes the subset of
![]() $S_k(P;C)$
with distinct entries,
$S_k(P;C)$
with distinct entries,

Separately, one may deduce from [Reference Flores5, Lemma 3.4] and [Reference Low, Pitman and Wolff6, Lemma 1] the following result.
Lemma 2.1. Let
![]() $K \geqslant 2$
and
$K \geqslant 2$
and
![]() $C \in {\mathbb Z}^{r \times s}$
with
$C \in {\mathbb Z}^{r \times s}$
with
![]() $s \geqslant rK(K+1)$
. If C contains a partitionable submatrix of size
$s \geqslant rK(K+1)$
. If C contains a partitionable submatrix of size
![]() $r \times rK(K+1)$
, then one has the bound
$r \times rK(K+1)$
, then one has the bound
for any
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
If C dominates the function
then, for
![]() $1 \leqslant i <j \leqslant s$
, the matrix
$1 \leqslant i <j \leqslant s$
, the matrix
![]() $C^{(i,j)}$
contains a submatrix of C of size
$C^{(i,j)}$
contains a submatrix of C of size
![]() $r \times (s-2)$
. By [Reference Low, Pitman and Wolff6, Lemma 1], this matrix contains a partitionable submatrix of size
$r \times (s-2)$
. By [Reference Low, Pitman and Wolff6, Lemma 1], this matrix contains a partitionable submatrix of size
![]() $r \times r \lfloor {(s-2)}/{r} \rfloor .$
Combining this with (2.2), Lemma 2.1 and [Reference Flores5, Theorem 2.2], we deduce the following general result.
$r \times r \lfloor {(s-2)}/{r} \rfloor .$
Combining this with (2.2), Lemma 2.1 and [Reference Flores5, Theorem 2.2], we deduce the following general result.
Lemma 2.2. Let
![]() $K \geqslant 2$
and suppose that
$K \geqslant 2$
and suppose that
![]() $C \in {\mathbb Z}^{r \times s}$
satisfies
$C \in {\mathbb Z}^{r \times s}$
satisfies
![]() $s \geqslant rK(K+1)+2$
. If C dominates the function
$s \geqslant rK(K+1)+2$
. If C dominates the function
then
where
![]() $\sigma _K(C) \geqslant 0$
is a real number depending only on K and C. Additionally,
$\sigma _K(C) \geqslant 0$
is a real number depending only on K and C. Additionally,
![]() ${\sigma _K(C)> 0}$
if there exist nonsingular real and p-adic simultaneous solutions to the system (2.1) for
${\sigma _K(C)> 0}$
if there exist nonsingular real and p-adic simultaneous solutions to the system (2.1) for
![]() $1 \leqslant k \leqslant K$
.
$1 \leqslant k \leqslant K$
.
3 K-multimagic squares with distinct entries
A matrix
![]() ${\mathbf Z} = (z_{i,j})_{\substack {1 \leqslant i,j \leqslant N}}$
is an
${\mathbf Z} = (z_{i,j})_{\substack {1 \leqslant i,j \leqslant N}}$
is an
![]() $\textbf {MMS}(K,N)$
if and only if, for all k with
$\textbf {MMS}(K,N)$
if and only if, for all k with
![]() $1 \leqslant k \leqslant K$
, it satisfies the simultaneous conditions
$1 \leqslant k \leqslant K$
, it satisfies the simultaneous conditions
 $$ \begin{align} \sum_{1 \leqslant j \leqslant N} z_{i,j}^{k} = \sum_{1 \leqslant j \leqslant N} z_{j,N-j+1}^{k} \quad \text{for } 1 \leqslant i \leqslant N. \end{align} $$
$$ \begin{align} \sum_{1 \leqslant j \leqslant N} z_{i,j}^{k} = \sum_{1 \leqslant j \leqslant N} z_{j,N-j+1}^{k} \quad \text{for } 1 \leqslant i \leqslant N. \end{align} $$
One may wonder if these equations are equivalent to those of an
![]() $\textbf {MMS}(K,N)$
. Indeed, at a first glance, it does not seem clear that the main diagonal and anti-diagonal are equal. One can show that this is implied by simply summing over all j in (3.1) and noting that this is equal to summing over all i in (3.2). Upon dividing out a factor of N, one deduces that (3.1) and (3.2) imply
$\textbf {MMS}(K,N)$
. Indeed, at a first glance, it does not seem clear that the main diagonal and anti-diagonal are equal. One can show that this is implied by simply summing over all j in (3.1) and noting that this is equal to summing over all i in (3.2). Upon dividing out a factor of N, one deduces that (3.1) and (3.2) imply
 $$ \begin{align*}\sum_{1 \leqslant i \leqslant N} z_{i,i}^{k} = \sum_{1 \leqslant j \leqslant N} z_{j,N-j+1}^{k}.\end{align*} $$
$$ \begin{align*}\sum_{1 \leqslant i \leqslant N} z_{i,i}^{k} = \sum_{1 \leqslant j \leqslant N} z_{j,N-j+1}^{k}.\end{align*} $$
Before we construct a matrix corresponding to this system, we must first establish some notational shorthand. Let
![]() $\mathbf {1}_n$
denote an n-dimensional vector of all ones and
$\mathbf {1}_n$
denote an n-dimensional vector of all ones and
![]() $\mathbf {0}_n$
an n-dimensional vector of all zeros. Let
$\mathbf {0}_n$
an n-dimensional vector of all zeros. Let
![]() ${\mathbf e}_n(m)$
denote the mth standard basis vector of dimension n. For a fixed N, we define
${\mathbf e}_n(m)$
denote the mth standard basis vector of dimension n. For a fixed N, we define
and
For each
![]() $(i,j) \in ([1,N] \cap {\mathbb Z})^2$
, we define the
$(i,j) \in ([1,N] \cap {\mathbb Z})^2$
, we define the
![]() $2N$
-dimensional vectors
$2N$
-dimensional vectors
 $$ \begin{align*}{\mathbf d}_{i,j} = \begin{cases} ({\mathbf e}_N(i)-\mathbf{1_N},{\mathbf e}_N(j) - \mathbf{1_N}) & \mbox{for } (i,j) \in D_1(N) \cap D_2(N), \\ ({\mathbf e}_N(i)-\mathbf{1_N},{\mathbf e}_N(j)) & \mbox{for } (i,j) \in D_1(N) \backslash D_2(N), \\ ({\mathbf e}_N(i),{\mathbf e}_N(j) - \mathbf{1_N}) & \mbox{for } (i,j) \in D_2(N) \backslash D_1(N), \\ ({\mathbf e}_N(i),{\mathbf e}_N(j)) & \text{otherwise.} \\ \end{cases}\end{align*} $$
$$ \begin{align*}{\mathbf d}_{i,j} = \begin{cases} ({\mathbf e}_N(i)-\mathbf{1_N},{\mathbf e}_N(j) - \mathbf{1_N}) & \mbox{for } (i,j) \in D_1(N) \cap D_2(N), \\ ({\mathbf e}_N(i)-\mathbf{1_N},{\mathbf e}_N(j)) & \mbox{for } (i,j) \in D_1(N) \backslash D_2(N), \\ ({\mathbf e}_N(i),{\mathbf e}_N(j) - \mathbf{1_N}) & \mbox{for } (i,j) \in D_2(N) \backslash D_1(N), \\ ({\mathbf e}_N(i),{\mathbf e}_N(j)) & \text{otherwise.} \\ \end{cases}\end{align*} $$
Let
![]() $\phi : [1,N^2] \cap {\mathbb Z} \to ([1,N] \cap {\mathbb Z})^2$
be any fixed bijection. Then, the
$\phi : [1,N^2] \cap {\mathbb Z} \to ([1,N] \cap {\mathbb Z})^2$
be any fixed bijection. Then, the
![]() $2N \times N^2$
matrix,
$2N \times N^2$
matrix,
corresponds to the system defined by (3.1) and (3.2) up to some arbitrary relabelling of variables defined by the bijection
![]() $\phi $
. We now establish that one may apply Lemma 2.2 with
$\phi $
. We now establish that one may apply Lemma 2.2 with
![]() $C=C_N^{\text {magic}}$
.
$C=C_N^{\text {magic}}$
.
Lemma 3.1. For
![]() $N \geqslant 4$
, the matrix
$N \geqslant 4$
, the matrix
![]() $C_N^{\mathrm {\scriptsize magic}}$
dominates the function
$C_N^{\mathrm {\scriptsize magic}}$
dominates the function
with
![]() $s = N^2$
and
$s = N^2$
and
![]() $r=2N$
.
$r=2N$
.
Proof. We show in [Reference Flores5, Section 4] that
![]() $C_N^{\text {magic}}$
satisfies the rank condition
$C_N^{\text {magic}}$
satisfies the rank condition
 $$ \begin{align*}\text{rank} \,((C_N^{\text{magic}})_J) \geqslant \begin{cases} \lceil 2 \sqrt{|J|} \rceil-1 & \text{if }1 \leqslant |J| \leqslant N(N-1)-1, \\ |J|-N^2+3N-1 & \text{if }N(N-1)-1 \leqslant |J| \leqslant N(N-1)+1, \\ 2N & \text{if }N(N-1)+1 \leqslant |J| \leqslant N^2, \end{cases} \end{align*} $$
$$ \begin{align*}\text{rank} \,((C_N^{\text{magic}})_J) \geqslant \begin{cases} \lceil 2 \sqrt{|J|} \rceil-1 & \text{if }1 \leqslant |J| \leqslant N(N-1)-1, \\ |J|-N^2+3N-1 & \text{if }N(N-1)-1 \leqslant |J| \leqslant N(N-1)+1, \\ 2N & \text{if }N(N-1)+1 \leqslant |J| \leqslant N^2, \end{cases} \end{align*} $$
when
![]() $|J| \neq (N-1)^2+1$
and
$|J| \neq (N-1)^2+1$
and
when
![]() $|J|= (N-1)^2+1$
. Given this, if
$|J|= (N-1)^2+1$
. Given this, if
![]() $|J|> N(N-1)$
, trivially,
$|J|> N(N-1)$
, trivially,
Let us now focus on the case in which N is even and
![]() $|J| \leqslant N(N-1)$
. When N is even, one may show that
$|J| \leqslant N(N-1)$
. When N is even, one may show that
 $$ \begin{align*}F(x) = \begin{cases} \dfrac{2x}{N} & \text{if}\ 0 \leqslant x \leqslant N(N-1), \\[6pt] \dfrac{2x-4}{N-2}-4 & \text{if}\ N(N-1) \leqslant x. \end{cases}\end{align*} $$
$$ \begin{align*}F(x) = \begin{cases} \dfrac{2x}{N} & \text{if}\ 0 \leqslant x \leqslant N(N-1), \\[6pt] \dfrac{2x-4}{N-2}-4 & \text{if}\ N(N-1) \leqslant x. \end{cases}\end{align*} $$
Thus, if
![]() $N(N-1)-1 \leqslant |J| \leqslant N(N-1)$
,
$N(N-1)-1 \leqslant |J| \leqslant N(N-1)$
,
Let us now suppose that
![]() $1 \leqslant |J| < N(N-1)-1$
and
$1 \leqslant |J| < N(N-1)-1$
and
![]() $|J| \neq (N-1)^2+1$
. Similarly, in this range,
$|J| \neq (N-1)^2+1$
. Similarly, in this range,
Let us now consider the case
![]() $|J| = (N-1)^2+1$
. Since
$|J| = (N-1)^2+1$
. Since
![]() $N \geqslant 4$
,
$N \geqslant 4$
,
The case in which N is odd may be established in a similar fashion.
By Lemma 2.2 and using the existence of nonsingular solutions to the magic square system proved in [Reference Flores5], we deduce the following asymptotic formula.
Theorem 3.2. For
![]() $K \geqslant 2$
and
$K \geqslant 2$
and
![]() $N> 2K(K+1)$
, let
$N> 2K(K+1)$
, let
![]() $M^*_{K,N}(P)$
denote the number of
MMS
$M^*_{K,N}(P)$
denote the number of
MMS
![]() $(K,N)$
consisting of
$(K,N)$
consisting of
![]() $N^2$
distinct integers bounded in absolute value by P. Then, there exists a constant
$N^2$
distinct integers bounded in absolute value by P. Then, there exists a constant
![]() $c> 0$
for which one has the asymptotic formula
$c> 0$
for which one has the asymptotic formula
This immediately implies Theorem 1.3.
4 Magic squares of distinct kth powers
Let us now consider the problem of showing the existence of magic squares of distinct kth powers. One may repeat the arguments of Rome and Yamagishi [Reference Rome and Yamagishi7], where instead of requiring a lower bound on the size of the largest partitionable submatrix, we assume that the matrix of coefficients dominates the function
It is clear that all arguments of [Reference Rome and Yamagishi7] follow from this assumption by [Reference Low, Pitman and Wolff6, Lemma 1], assuming
![]() $ \lfloor {(s-2)}/{r} \rfloor $
is large enough in terms of k. How large this term needs to be, as seen in Lemma 2.1, is directly determined by when one can establish a mean value estimate of the type
$ \lfloor {(s-2)}/{r} \rfloor $
is large enough in terms of k. How large this term needs to be, as seen in Lemma 2.1, is directly determined by when one can establish a mean value estimate of the type

where A is the set from which the solutions may come. Then, by a direct analogue of the arguments in Section 2, we obtain a version of [Reference Rome and Yamagishi7, Theorem 1.4] which provides an asymptotic for the number of solutions with distinct entries.
Lemma 4.1. Let
![]() $k \geqslant 2$
and
$k \geqslant 2$
and
![]() $C \in {\mathbb Z}^{r \times s}$
, where
$C \in {\mathbb Z}^{r \times s}$
, where
![]() $s \geqslant r \min \{2^{k},k(k+1)\} +2$
. If C dominates the function
$s \geqslant r \min \{2^{k},k(k+1)\} +2$
. If C dominates the function
then
where
![]() $\sigma _k(C) \geqslant 0$
is a real number depending only on k and C. Additionally,
$\sigma _k(C) \geqslant 0$
is a real number depending only on k and C. Additionally,
![]() $\sigma _k(C)> 0$
if there exist nonsingular real and p-adic solutions to the system (2.1).
$\sigma _k(C)> 0$
if there exist nonsingular real and p-adic solutions to the system (2.1).
Let
Then, the same may be done to obtain an analogue of [Reference Rome and Yamagishi7, Theorem 1.5], which provides an asymptotic for the number of smooth solutions with distinct entries.
Lemma 4.2. Let
![]() $k \geqslant 2$
and
$k \geqslant 2$
and
![]() $C \in {\mathbb Z}^{r \times s}$
, where
$C \in {\mathbb Z}^{r \times s}$
, where
![]() $s \geqslant r \lceil k(\log k + 4.20032) \rceil +2$
. If C dominates the function
$s \geqslant r \lceil k(\log k + 4.20032) \rceil +2$
. If C dominates the function
then, providing
![]() $\eta>0$
is sufficiently small in terms of
$\eta>0$
is sufficiently small in terms of
![]() $s,r,k$
and C,
$s,r,k$
and C,
where
![]() $\sigma _k(C)$
is the same quantity as in Lemma 4.1 and
$\sigma _k(C)$
is the same quantity as in Lemma 4.1 and
![]() $c(\eta )>0$
depends only on
$c(\eta )>0$
depends only on
![]() $\eta $
.
$\eta $
.
Applying Lemmas 4.1 and 4.2 with
![]() $C = C_N^{\text {magic}}$
and noting that the analysis in [Reference Flores5, Section 5] implies
$C = C_N^{\text {magic}}$
and noting that the analysis in [Reference Flores5, Section 5] implies
![]() $\sigma _k(C_N^{\text {magic}})$
is positive, we deduce Theorem 1.5.
$\sigma _k(C_N^{\text {magic}})$
is positive, we deduce Theorem 1.5.
Acknowledgements
The author expresses profound gratitude to Trevor Wooley for his invaluable mentorship over the past five years and for highlighting Andrew Bremner’s talks from the 1990s. Thanks are also extended to Nick Rome and Shuntaro Yamagishi for their insightful and collegial discussions on this problem. Finally, the author is grateful to the referee for helpful comments.