Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T06:56:17.196Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-phase modulation of a laser in self created plasma channel

Published online by Cambridge University Press:  12 March 2009

A. Panwar  and
A.K. Sharma
A. Panwar*
Affiliation:
Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi, India
A.K. Sharma
Affiliation:
Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi, India
*
Address correspondence and reprint requests to: Anuraj Panwar, Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi-110016, India. E-mail: anurajpanwar@rediffmail.com
Rights & Permissions [Opens in a new window]

Abstract

An analytical formalism of self focusing and self-phase modulation of an intense short pulse laser in a plasma due to relativistic and ponderomotive nonlinearities is developed. In the paraxial ray approximation, the pulse retains its Gaussian radial profile, however, its spot size varies with the distance of propagation in a periodic manner. It is influenced by self focusing. The frequency of the laser undergoes red shift. For a tanhyperbolic temporal profile of pulse, the red-shift is maximum at the foot of the pulse and decreases slowly as one goes to higher and higher intensity portions. The effect of ponderomotive nonlinearity is very significant in this respect. The maximum downshift occurs at a distance at which the laser acquires a minimum spot size. With retarded time normalized axial intensity increases more at z ~ Rd and the radial intensity is also more narrowly peaked at z ~ Rd, where Rd = 2π r02/λ is the Rayleigh length, r0 and λ are the spot size and wavelength of the laser pulse respectively.

Keywords

Self-focusingSelf-phase modulationRelativistic mass nonlinearityPonderomotive nonlinearity
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 2 , June 2009 , pp. 249 - 253
Copyright
Copyright © Cambridge University Press 2009

1. INTRODUCTION

Self-phase-modulation (SPM) of laser is an important nonlinear process in a variety of media with intensity dependent index of refraction. Max et al. (Reference Max, Arons and Bruce Langdon1974) observed the nonlinear frequency shift of a strong electromagnetic wave in plasma, due to weak relativistic effects. Yablonovitch (Reference Yablonovitch1974a, Reference Yablonovitch1974b) investigated SPM and short pulse generation from laser breakdown plasmas. Tsintsadze et al. (Reference Tsintsadze, Tskhakaya and Stenflo1979) obtained the generalized dispersion relation for modulational instabilities due to relativistic electron mass variations. The SPM is accompanied by self focusing/defocusing of the laser beams and is significantly modified by those effects. Gill and Saini (Reference Gill and Saini2007) observed the enhancement of Raman scattering in collisional plasma by the interaction of rippled laser beam with upper hybrid mode and also observed the focusing of the upper hybrid wave. Willi et al. (Reference Willi, Toncian, Borghesi, Fuchs, D'Humieres, Antici, Audebert, Brambrink, Cecchetti, Pipahl and Romagnani2007) presented a novel technique for focusing and energy selection of MeV protons by employing a hollow micro-cylinder, which irradiated at the outer wall by a high intensity ultra-short laser pulse. Purohit et al. (Reference Purohit, Chauhan and Sharma2008) studied the excitation of an upper hybrid wave by a relativistic laser beam in the presence of perpendicular static magnetic field and also introduced the relativistic electron mass nonlinearity as well as relativistic self-focusing effect. Liu and Tripathi (Reference Liu and Tripathi2000) have developed an unified formalism of SPM and self defocusing in a tunnel ionizing plasma. The self defocusing limits the frequency upshift of the laser. Liu and Tripathi (Reference Liu and Tripathi2001) studied the frequency downshift of a Gaussian beam due to relativistic self focusing of the laser.

Watts et al. (Reference Watts, Zepf, Clark, Tatarakis, Krushelnik, Dangor, Alott, Clarke, Neely and Norreys2002) observed the relativistic SPM in the interaction of a high-intensity laser pulse (1 ps, 1.053 µm, 80 J) with the plasma. Singh et al. (Reference Singh, Konar and Sharma2001) observed the resonant cross modulation of two laser beams in a semiconductor slab. Saini and Gill (Reference Saini and Gill2006) studied the self focusing and SPM of an elliptic Gaussian laser beam in collisionless magnetized plasma, by using the variational approach considering the effects of nonlinearity and diffraction. Gupta and Suk (Reference Gupta and Suk2007) obtained the electron acceleration by two crossing chirped lasers of same amplitude and frequency, at an arbitrary angle, and causing modulation of laser intensity. Recently, Nickles et al. (Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007) experimentally observed the interactions of a laser pulse at intensities above 1019 W/cm2, and covered the rear and front side acceleration mechanisms, particle dynamics inside the dense target, proton source characteristics, strong modulations in proton and deuteron emission spectra, and generation of quasi-monoenergetic deuteron bursts.

Liu and Jetendra (Reference Liu and Jetendra2006) studied the self-defocusing/focusing of a right circularly polarized laser, in a preexisting density channel, and studied the effect of ponderomotive force driven plasma wave on the growth of modulational instability. Borghesi et al. (Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007) studied the probing technique to provide the maps of impulsive electrostatic fields with high spatial and temporal resolution by the high-intensity laser matter interactions. The dynamics of ponderomotive channeling in underdense plasmas is also observed by the processes of Debye sheath formation and MeV ion front expansion at the rear of laser-irradiated thin metallic foils. Hafizi et al. (Reference Hafizi, Tang, Sprangle and Hubbard2000) studied the relativistic focusing and ponderomotive channeling of intense laser beams—ponderomotive channeling modified the effective potential of the laser spot size—and obtained the envelope equation by using the source-dependent expansion method with Laguerre-Gaussian Eigen functions. Experimental observations of relativistic focusing and ponderomotive channeling have been reported in the literature (Faenov et al., Reference Faenov, Magunov, Pikuz, Skobelev, Gasilov, Stagira, Calegari, Nisoli, De Silvestri, Poletto, Villoresi and Andreev2007; Torrisi et al., Reference Torrisi, Margarone, Laska, Krasa, Velyhan, Pfeifer, Ullschmied and Ryc2008; Chessa et al., Reference Chessa, Mora and Antonsen1998; Sun et al., Reference Sun, Ott, Lee and Guzdar1987; Kurki-Suonio et al., Reference Kurki-Suonio, Morrison and Tajima1989; Borisov et al., Reference Borisov, Borovskiy, Korobkin, Prokhovrov, Rdodes and Shiryaev1990, Reference Borisov, Borovskiy, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992a, Reference Borisov, Borovskiy, Korobkin, Prokhorov, Shiryaev, Shi, Luk, Mcpherson, Solem, Boyer and Rhodes1992b; Konar & Manoj, Reference Konar and Manoj2005; Abramyan et al., Reference Abramyan, Litvak, Mironov and Sergeev1992; Chen & Sudan, Reference Chen and Sudan1993; Annou et al., Reference Annou, Tripathi and Srivastava1996; Tzeng & Mori, Reference Tzeng and Mori1998; Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Louis-Jacquet, Malka and Miquel1995).

In this paper, we study the effect of self focusing on SPM of a laser pulse in self-channeled plasma. The self focusing, caused by relativistic mass shift as well as radial ponderomotive force, modifies the electron density. In Section 2, we obtain the nonlinear current density due to a high power laser. In Section 3, we drive coupled equations for amplitude and phase of the laser pulse. In Section 4, we solve these equations in near-axis approximation and by expanding the Eikonal up to second order in radial coordinates r.

2. NONLINEAR CURRENT DENSITY

Consider the propagation of a laser pulse in a plasma of electron density n 00 along the z-axis. At z = 0, the electric field of the laser is

(1)
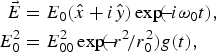
\eqalignno{\vec {E}&= E_0 \lpar \hat x + i \hat y\rpar \exp\!\lpar \!\!- \! i{\rm \omega}_0 t\rpar \comma \; \cr E_0^2 &= E_{00}^2 \exp \!\lpar\!\! -\! r^2\!/r_0^2\rpar g\lpar t\rpar \comma \;}

where g(t) is the temporal shape of the pulse For z > 0, we may write,

(2)
\vec {E} = A\lpar \hat x + i\hat y\rpar \exp\! \lpar\!\! -\! i{\rm \phi}\rpar \comma \;

where A(t, z, r) is the complex amplitude, φ (t, z) is the fast phase of the wave, and one may take ω = ∂φ/∂t and k = −∂φ/∂z.

The laser pulse imparts an oscillatory velocity to the electrons,

(3)
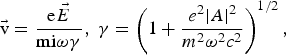
{{\rm \vec v}}={{\rm e}{\vec E} \over {\rm mi}{{\rm \omega}{ \rm \gamma}}}\comma \; \gamma = \left(1 + {e^2 \vert A \vert^2 \over m^2 {\rm \omega}^2 c^2}\right)^{1/2}\comma \;

where −e and m are the electronic charge and mass, respectively, and c is the velocity of light in vacuum. It also exerts a relativistic ponderomotive force on the electrons $\vec F_p = e{\rm \nabla \phi}_p$,

(4)
{\rm \phi}_p = - {mc^2 \over e}\lpar {\rm \gamma} - 1\rpar \approx - {e\left\vert A \right\vert^2 \over m{\rm \gamma {\rm \omega}}^2}\comma \; \quad \hbox{for } \lpar eA/m{\rm \omega} c\rpar \lt 1.

The ponderomotive force expels the electrons away from the region of higher electric field, while the ions remain stationary due to their heavy mass. On the time scale longer than the electron plasma period and shorter than the ion plasma period (ωp−1 < t < ωpi−1), one may take the static space charge potential, caused by the displacement of electrons, φs ≈ −φp. Using this in the Poisson equation, ∇2φs = 4π e(n e − n i), we get

(5)
n_e = n_0^0 - {\rm \nabla}^2 {\rm \phi}_p /4{\rm\pi e}.

The nonlinear electron current density at the frequency of the laser can now be written as,

(6)
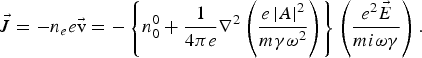
\vec J=- n_e e{{\rm \vec v}}=- \left\{{n_0^0+{1 \over {4{\rm \pi} e}}{\rm \nabla}^2 \left({{{e\left\vert A \right\vert ^2 } \over {m{{\rm \gamma} {\rm \omega}}^2}}} \right)} \right\}\left({{{e^2 \vec E} \over {mi{{\rm \omega} \rm \gamma} }}} \right).

3. COUPLED EQUATIONS FOR AMPLITUDE AND PHASE

The wave equation governing the propagation of the laser in underdense plasma is

(7)
{\rm \nabla}^2 \vec E - {\rm \nabla} \lpar {\rm \nabla} . \vec E\rpar - \lpar 1/c^2\rpar \lpar {\rm \partial}^2 \vec E/{\rm \partial} t^2\rpar = \lpar 4{\rm \pi} /c^2 \rpar \lpar {\rm \partial} \vec J/{\rm \partial} t\rpar .

We get

(8)
{\rm \nabla}^2 \vec E - {{{\rm \omega}_p^2 } \over {{\rm \gamma} c^2 }}\vec E - {e \over {m{\rm \gamma} c^2 }}{\rm \nabla}^2 \left({{{e\left\vert A \right\vert ^2 } \over {m{\rm \gamma {\rm \omega}}^2 }}} \right)\vec E - {1 \over {c^2 }}{{{\rm \partial} ^2 \vec E} \over {{\rm \partial} t^2 }}=0\comma

where ωp2 = (4πn 00e 2/m) is the plasma frequency. The second term on left-hand-side arises due to relativistic mass variation and the third is due to the ponderomotive force.

On substituting $\vec E$ from Eq. (2) in the wave equation and assuming the wave amplitude A to be a slowly varying function of t and z (Wentzel-Kramer-Brillouin approximation) we obtain,

(9)
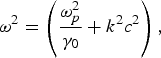
{\rm \omega}^2 = \left({{{{\rm \omega}_p^2 } \over {{\rm \gamma}_0}}+k^2 c^2} \right)\comma
(10)
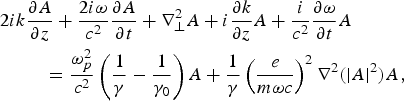
\eqalignno{2ik & {{{\rm \partial} A} \over {{\rm \partial} z}} +{{2i{\rm \omega}} \over {c^2 }}{{{\rm \partial} A} \over {{\rm \partial} t}}+{\rm \nabla}_\bot ^2 A+i{{{\rm \partial} k} \over {{\rm \partial} z}}A+{i \over {c^2 }}{{{{\rm \partial}{\rm \omega}}} \over {{\rm \partial} t}}A\cr &\quad ={{{\rm \omega}_p^2 } \over {c^2 }}\left({{1 \over {\rm \gamma}} - {1 \over {{\rm \gamma}_0 }}} \right)A+{1 \over {\rm \gamma} }\left({{e \over {m{\rm \omega} c}}} \right)^2 {\rm \nabla}^2 \lpar \left\vert A \right\vert^2 \rpar A\comma}

where γ0 = γ at r = 0.

Differentiating Eq. (9) with respect to t by use of ∂k/∂t = −∂ω/∂z,

(11)
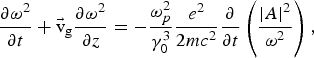
{{{{\rm \partial} {\rm \omega}}^2 } \over {{\rm \partial} t}}+{{\rm \vec v}}_{{\rm g}} {{{{\rm \partial}{\rm \omega}}^2 } \over {{\rm \partial} z}}=- {{{\rm \omega}_p^2 } \over {{\rm \gamma}_0^3 }}{{e^2} \over {2mc^2 }}{{\rm \partial} \over {{\rm \partial} t}}\left({{{\left\vert A \right\vert^2 } \over {{\rm \omega}^2 }}} \right)\comma

where ${{\rm \vec v}}_{{\rm g}}=c\lpar 1 - {\rm \omega}_p^2 / {\rm \omega}^2 {\rm \gamma}_0\rpar $ is the group velocity.

We define a function F = (ω/ω0)1/2A, t / = t − z/c and z / = z, Eqs (10) and (11) become

(12)
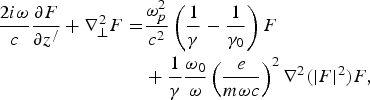
\eqalign{{{2i{\rm \omega}} \over c}{{{\rm \partial} F} \over {{\rm \partial} z^/ }}+{\rm \nabla}_{\rm \bot}^2 F= & {{{\rm \omega}_p^2 } \over {c^2 }}\left({{1 \over {\rm \gamma}} - {1 \over {{\rm \gamma}_0 }}} \right)F \cr & +{1 \over {\rm \gamma}}{{{\rm \omega}_0 } \over {\rm \omega}}\left({{e \over {m{\rm \omega} c}}} \right)^2 {\rm \nabla}^2 \lpar \left\vert F \right\vert^2\rpar F\comma}

and

(13)
{{{{\rm \partial} {\rm \omega}}^2 } \over {{\rm \partial} z^/ }}={{{\rm \omega}_p^2 } \over {{\rm \gamma}_0^2}}{{e^2 } \over {2\, m{\rm \omega}_0^2 c^2 }}{{\rm \partial} \over {{\rm \partial} t^/ }}\left({{{\left\vert F \right\vert ^2 } \over {\lpar {\rm \omega} / {\rm \omega}_0\rpar ^3 }}} \right).

We may write F = F 0 exp(iS), where F 0 (t /, z /, r) and S(t /, z /, r) are real and separate the real and the imaginary parts of Eq. (11),

(14)
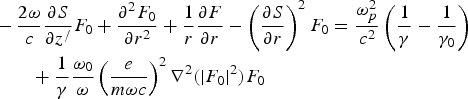
\eqalignno{&- {{2{\rm \omega} } \over c}{{{\rm \partial} S} \over {{\rm \partial} z^/ }}F_0+{{{\rm \partial}^2 F_0 } \over {{\rm \partial} r^2 }}+{1 \over r}{{{\rm \partial} F} \over {{\rm \partial} r}} - \left({{{{\rm \partial} S} \over {{\rm \partial} r}}} \right)^2 F_0={{{\rm \omega} _p^2 } \over {c^2 }}\left({{1 \over {\rm \gamma}} - {1 \over {{\rm \gamma}_0 }}} \right)\cr &\qquad +{1 \over {\rm \gamma}}{{{\rm \omega}_0 } \over {\rm \omega}}\left({{e \over {m{\rm \omega} c}}} \right)^2 {\rm \nabla}^2 \lpar \left\vert {F_0 } \right\vert^2 \rpar F_0}

and

(15)
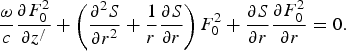
{{\rm \omega} \over c}{{{\rm \partial} F_0^2 } \over {{\rm \partial} z^/ }}+\left({{{{\rm \partial}^2 S} \over {{\rm \partial} r^2 }}+{1 \over r}{{{\rm \partial} S} \over {{\rm \partial} r}}} \right)F_0^2+{{{\rm \partial} S} \over {{\rm \partial} r}}{{{\rm \partial} F_0^2 } \over {{\rm \partial} r}}=0.

Equations (13), (14), and (15) are the coupled phase and amplitude equations.

4. FREQUENCY DOWN SHIFT

We solve Eqs (14) and (15) by expanding S as S = S 0 + S 2r 2/r 02 and introducing a function f(z /) such that S 2 = (ωr 02/2c)(1/f)(∂f/∂z /). Then Eq. (15), for an initially Gaussian profile of laser intensity, gives

(16)
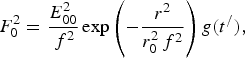
F_0^2 = {{E_{00}^2 } \over {\,f^2 }}\exp \left({ - {{r^2 } \over {r_0^2\, f^2 }}} \right)g\lpar t^/ \rpar \comma

where (r 0f) is the modified radius of the laser beam and the beam width parameter f has implicit dependence on t /.

Using Eq. (16) in Eq. (14) and collecting the coefficient of r 2, we obtain

(17)
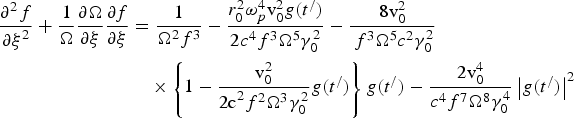
\eqalignno{{{{\rm \partial}^2 f} \over {{\rm \partial \xi}^2 }} + {1 \over {\rm \Omega}}{{{\rm \partial \Omega}} \over {{\rm \partial \xi}}}{{{\rm \partial} f} \over {{\rm \partial \xi}}}& ={1 \over {{\rm \Omega}^2 f^3 }} - {{r_0^2 {\rm \omega}_p^4 {{\rm v}}_{{\rm 0}}^{{\rm 2}} g\lpar t^/ \rpar } \over {2c^4 f^3 \Omega^5 {\rm \gamma}_0^2 }} - {{8{{\rm v}}_{{\rm 0}}^{{\rm 2}} } \over {\,f^3 {\rm \Omega}^5 c^2 {\rm \gamma}_0^2}} \cr &\quad \times \left\{{1 - {{{{\rm v}}_{{\rm 0}}^{{\rm 2}} } \over {{{\rm 2c}}^{{\rm 2}} f^2 {\rm \Omega}^3 {\rm \gamma}_0^2 }}g\lpar t^/ \rpar } \right\}g\lpar t^/ \rpar - {{2{{\rm v}}_{{\rm 0}}^{{\rm 4}} } \over {c^4 f^7 {\rm \Omega}^8 {\rm \gamma}_0^4 }}\left\vert {g\lpar t^/ \rpar } \right\vert ^2}
(18)
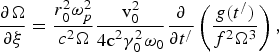
\eqalignno{{{{\rm \partial \Omega}} \over {{\rm \partial \xi}}} &= {{r_0^2 {\rm \omega}_p^2 } \over {c^2 {\rm \Omega}}}{{{{\rm v}}_{{\rm 0}}^{{\rm 2}} } \over {{{\rm 4c}}^{{\rm 2}} {\rm \gamma}_{{\rm 0}}^{{\rm 2}} {\rm \omega}_0 }}{{\rm \partial} \over {{\rm \partial} t^/ }}\left({{{g\lpar t^/ \rpar } \over {f^2 {\rm \Omega}^3}}} \right)\comma}

where v0/c = eE 00/mω0c is the normalized oscillatory velocity and ξ = z //R d, Ω = ω/ω0, R d = (ω0/c)r 02.

The boundary conditions at ξ = 0 for an initially plane wavefront are f = 1, ∂f/∂ξ = 0, Ω = 1, and S 0 = 0. The first term on the right-hand-side of Eq. (17) represents the diffraction divergence, the second term gives the beam convergence due to relativistic mass non-linearity, whereas the third and forth terms describe the convergence due to ponderomotive nonlinearity. We choose the temporal profile g(t /) = tanh (t //τ) for t / > 0 and zero otherwise, where τ is the pulse rise time, and solve the coupled Eqs (17) and (18) numerically for the parameters: r 0ωp/c = 5, ω0τ = 40, v0/c = 1, γ0 = √2, T ≅ (t − z/c)/τ = 0 − 3, z/R d = 0 − 3.

Figure 1 shows the variation of the beam width parameter f with the normalized distance of propagation ξ. At T = 0, f increases monotonically with ξ due to diffraction. At higher T, the nonlinear convergence exceeds the diffraction divergence, and f decreases with ξ, i.e., focusing occurs. After certain distance, the electrons are significantly depleted from the axial region, and the nonlinear convergence weakens. At a certain value of ξ, the beam starts to diverge due to the predominance of diffraction divergence. As the beam acquires a large spot size, the nonlinear convergence again predominates beyond ξ = 0.7. Figure 2 shows the frequency of the laser pulse as a function of retarded time T at z/R d = 1. The front of pulse undergoes frequency downshift at T = 0. With increasing T, ω/ω0 increases monotonically and attains a saturation value. In the simultaneous presence of relativistic mass nonlinearity and ponderomotive nonlinearity, self focusing is stronger; hence red shift remains fairly constant with retarded time throughout the channel. Figure 3 shows the variation of the normalized axial intensity |E|r=02/E 002 as a function of T at z = R d and z = 0. At z = 0, the normalized axial intensity remains tanh (T) with retarded time, but at z = R d due to periodic self focusing, it deviates from tanh (T) and increases monotonically with the retarded time. For the normalized retarded time T = 1.5, the variation of the radial intensity |E|2/|E|r=02 with (r/r 0) at z = R d and z = 0 is shown in Figure 4. Due to periodic self focusing, the radial intensity is also more narrowly peaked at z ~ R d than at z = 0, but its shape remains Gaussian at z = R d and z = 0.

Fig. 1. (Color online) Beam-width parameter f as a function of normalized propagation distance ξ = z/R d at T = 0,1,2,3, where τ is the pulse rise time. The parameters are r 0ωp/c = 5, ω0τ = 40 and v0/c = 1.

Fig. 2. Normalized frequency of laser as a function of the retarded time T ≅ (t − z/c)/τ at z/R d = 1. The other parameters are the same as in Figure 1.

Fig. 3. Normalized axial intensity |E|r=02/E 002 plotted as a function of retarded time T at z = 0, R d. The other parameters are the same as in Figure 1.

Fig. 4. Radial intensity profile |E|2/E r=02 at z = 0 and z = R d for (t − z/c)/τ = 1.5. The other parameters are the same as in Figure 1.

5. DISCUSSION

A fast rising laser pulse, with tanhyperbolic temporal profile and Gaussian radial profile, propagating through preformed plasma undergoes downshift in frequency. Maximum downshift occurs at t / = (t − z/vg) ~ 0, i.e., at the foot of the pulse. However, self focusing significantly modifies the temporal profile of the pulse, hence influences the frequency shift. When relativistic mass nonlinearity alone is considered, the frequency shift diminishes as one approaches the higher intensity of the pulse. With the inclusion of ponderomotive nonlinearity the frequency downshift continues to be significant up to longer times due to the temporal variation of electron density in the axial regions. Normalized axial intensity deviates from tanh (T) form. The deviation increases with retarded time and is maximum at z ~ R d (Fig. 3).

References

REFERENCES

Annou, R., Tripathi, V.K. & Srivastava, M.P. (1996). Plasma channel formation by short pulse laser. Phys. Plasma 3, 1356–1359.CrossRefGoogle Scholar
Abramyan, L.A., Litvak, A.G., Mironov, V.A. & Sergeev, A.M. (1992). Self-focusing and relativistic waveguiding of an ultrashort laser pulse in a plasma. Sov. Phys. JETP 75, 978.Google Scholar
Borisov, A.B., Borovskiy, A.V., Korobkin, V.V., Prokhovrov, A.M., Rdodes, C.K. & Shiryaev, O.B. (1990). Stabilization of relativistic self focusing of intense subpicosecond ultraviolet pulses in plasma. Phys. Rev. Lett. 65, 1753–1756.CrossRefGoogle Scholar
Borisov, A.B., Borovskiy, A.V., Shiryaev, O.B., Korobkin, V.V., Prokhorov, A.M., Solem, J.C., Luk, T.S., Boyer, K. & Rhodes, C.K. (1992 a). Relativistic and charge-displacement self channeling of intense ultrashort laser pulses in plasmas. Phys. Rev. A 45, 5830–5845.CrossRefGoogle ScholarPubMed
Borisov, A.B., Borovskiy, A.V., Korobkin, V.V., Prokhorov, A.M., Shiryaev, O.B., Shi, X.M., Luk, T.S., Mcpherson, A., Solem, J.C., Boyer, K. & Rhodes, C.K. (1992 b). Observation of relativistic and charge-displacement self-channeling of intense subpicosecond ultraviolet (248 nm) radiation in plasmas. Phys. Rev. Lett. 68, 2309–2312.CrossRefGoogle ScholarPubMed
Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C.A., Fuchs, J., Galimberti, M., Gizzi, L.A., Grismayer, T., Lyseikina, T., Jung, R., Macchi, A., Mora, P., Osterholtz, J., Schiavi, A. & Willi, O. (2007). Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25, 161–167.CrossRefGoogle Scholar
Chessa, P., Mora, P. & Antonsen, T.M. (1998). Numerical simulation of short laser pulse relativistic self-focusing in underdense plasma. Phys. Plasma 5, 3451–3458.CrossRefGoogle Scholar
Chen, X.L. & Sudan, R.N. (1993). Necessary and sufficient conditions for self-focusing of short ultraintense laser pulse in underdense plasma. Phys. Rev. Lett. 70, 2082–2085.CrossRefGoogle ScholarPubMed
Faenov, A.Y., Magunov, A.I., Pikuz, T.A., Skobelev, I.Y., Gasilov, S.V., Stagira, S., Calegari, F., Nisoli, M., De Silvestri, S., Poletto, L., Villoresi, P. & Andreev, A.A. (2007). X-ray spectroscopy observation of fast ions generation in plasma produced by short low-contrast laser pulse irradiation of solid targets. Laser Part. Beams 25, 267–275.CrossRefGoogle Scholar
Gill, T.S. & Saini, N.S. (2007). Nonlinear interaction of a rippled laser beam with an electrostatic upper hybrid wave in collisional plasma. Laser Part. Beams 25, 283–293.CrossRefGoogle Scholar
Gupta, D.N. & Suk, H. (2007). Electron acceleration to high energy by using two chirped lasers. Laser Part. Beams 25, 31–36.CrossRefGoogle Scholar
Hafizi, B., Tang, A., Sprangle, P. & Hubbard, R.F. (2000). Relativistic focusing and ponderomotive channeling of intense laser beams. Phys. Rev. E. 62, 4120–4125.CrossRefGoogle ScholarPubMed
Konar, S. & Manoj, M. (2005). Effect of higher order nonlinearities on induced focusing and on the conversion of circular Gaussian laser beams into elliptic Gaussian laser beam. J. Opt. A: Pure Appl. Opt. 7, 576.CrossRefGoogle Scholar
Kurki-Suonio, T., Morrison, P.J. & Tajima, T. (1989). Self-focusing of an optical beam in a plasma. Phys. Rev. A 40, 3230–3239.CrossRefGoogle ScholarPubMed
Liu, C.S. & Jetendra, P. (2006). Modulational instability of a self-guided laser in a magnetized plasma channel. IEEE Trans. Plasma Sci. 34, 2561.CrossRefGoogle Scholar
Liu, C.S. & Tripathi, V.K. (2001). Self focusing and frequency broadening of an intense short-pulse laser in plasma. J. Opt. Soc. Am. A. 18, 1714–1718.CrossRefGoogle Scholar
Liu, C.S. & Tripathi, V.K. (2000). Laser frequency upshift, self-defocusing, and ring formation in tunnel ionizing gases and plasmas. Phys. Plasma 7, 4360–4363.CrossRefGoogle Scholar
Max, C.E., Arons, J. & Bruce Langdon, A. (1974). Self modulation and self focusing of electromagnetic waves in plasmas. Phys. Rev. Lett. 33, 209–212.CrossRefGoogle Scholar
Monot, P., Auguste, T., Gibbon, P., Jakober, F., Mainfray, G., Dulieu, A., Louis-Jacquet, , Malka, M.G. & Miquel, J.L. (1995). Experimental demonstration of relativistic self-channeling of a multiterawatt laser pulse in an underdense plasma. Phys. Rev. Lett. 74, 2953–2956.CrossRefGoogle Scholar
Nickles, P.V., Ter-Avetisyan, S., Schnuerer, M., Sokollik, T., Sandner, W., Schreiber, J., Hilscher, D., Jahnke, U., Andreev, A. & Tikhonchuk, V. (2007). Review of ultrafast ion acceleration experiments in laser plasma at Max Born Institute. Laser Part. Beams 25, 347–364.CrossRefGoogle Scholar
Purohit, G., Chauhan, P.K. & Sharma, R.P. (2008). Excitation of an upper hybrid wave by a high power laser beam in plasma. Laser Part. Beams 26, 61–67.CrossRefGoogle Scholar
Saini, N.S. & Gill, T.S. (2006). Self-focusing and self-phase modulation of an elliptic Gaussian laser beam in collisionless magnetoplasma. Laser Part. Beams 24, 447–453.CrossRefGoogle Scholar
Singh, L., Konar, S. & Sharma, A.K. (2001). Resonant cross modulation of laser beams in a semiconductor slab. J. Phys. D: Appl. Phys. 34, 2237.CrossRefGoogle Scholar
Sun, G.Z., Ott, E., Lee, Y.C. & Guzdar, P. (1987). Self-focusing short of intense pulses in plasmas. Phys. Fluids 30, 526–532.CrossRefGoogle Scholar
Torrisi, L., Margarone, D., Laska, L., Krasa, J., Velyhan, A., Pfeifer, M., Ullschmied, J. & Ryc, L. (2008). Self-focusing effect in Au-target induced by high power pulsed laser at PALS. Laser Part. Beams 26, 379–387.CrossRefGoogle Scholar
Tsintsadze, N.L., Tskhakaya, D.D. & Stenflo, L. (1979). Modulational instabilities due to relativistic electron mass variations. Phys. Lett. A 72, 115–116.CrossRefGoogle Scholar
Tzeng, K.C. & Mori, W.B. (1998). Suppression of electron ponderomotive blowout and relativistic self-focusing by the occurrence of Raman scattering and plasma heating. Phys. Rev. Lett. 81, 104–107.CrossRefGoogle Scholar
Watts, I., Zepf, M., Clark, L., Tatarakis, M., Krushelnik, K., Dangor, A.E., Alott, R., Clarke, J., Neely, D. & Norreys, P.N. (2002). Measurement of relativistic self-phase modulation in plasma. Phys. Rev. E, Stat. Phys. Plasma Fluids Relat. Interdiscip. Top. 66, 036409-1/036409-6.Google ScholarPubMed
Willi, O., Toncian, T., Borghesi, M., Fuchs, J., D'Humieres, E., Antici, P., Audebert, P., Brambrink, E., Cecchetti, C., Pipahl, A. & Romagnani, L. (2007). Laser triggered micro-lens for focusing and energy selection of MeV protons. Laser Part. Beams 25, 71–77.CrossRefGoogle Scholar
Yablonovitch, E. (1974 a). Self-phase modulation of light in a laser-breakdown plasma. Phys. Rev. Lett. 32, 1101–1104.CrossRefGoogle Scholar
Yablonovitch, E. (1974 b). Self-phase modulation and short-pulse generation from laser-breakdown plasmas. Phys. Rev. A 10, 1888–1895.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) Beam-width parameter f as a function of normalized propagation distance ξ = z/Rd at T = 0,1,2,3, where τ is the pulse rise time. The parameters are r0ωp/c = 5, ω0τ = 40 and v0/c = 1.

Figure 1

Fig. 2. Normalized frequency of laser as a function of the retarded time T ≅ (t − z/c)/τ at z/Rd = 1. The other parameters are the same as in Figure 1.

Figure 2

Fig. 3. Normalized axial intensity |E|r=02/E002 plotted as a function of retarded time T at z = 0, Rd. The other parameters are the same as in Figure 1.

Figure 3

Fig. 4. Radial intensity profile |E|2/Er=02 at z = 0 and z = Rd for (t − z/c)/τ = 1.5. The other parameters are the same as in Figure 1.