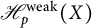1 Introduction
Throughout the paper, X will always be a complex Banach space. Let
$\mathcal {D}(X)$
be the space of Dirichlet series
$\sum _{n\geq 1}x_nn^{-s}$
with
$\{x_n\}_{n\geq 1}\subset X$
that converge at some point
$s_0\in \mathbb {C}$
, and let
$\mathcal {P}(X)$
be the space of X-valued Dirichlet polynomials
$\sum _{n=1}^Nx_nn^{-s}$
. In the case
$X=\mathbb {C}$
, we will write
$\mathcal {D}$
instead of
$\mathcal {D}(\mathbb {C})$
. Recently, the study of functional-analytic aspects of the theory of (vector-valued) Dirichlet series has attracted great attention; see [Reference Bonet5, Reference Carando, Defant and Sevilla-Peris7–Reference Carando, Marceca, Scotti and Tradacete10, Reference Defant, García, Maestre and Pérez-García13, Reference Defant and Pérez15–Reference Defant, Schwarting and Sevilla-Peris17] and the references therein. In this note, we are going to investigate the properties of Volterra operators between some Hardy spaces of vector-valued Dirichlet series.
To clarify the definition of Hardy spaces of vector-valued Dirichlet series, we need the following notions (see for instance [Reference Defant, García, Maestre and Sevilla-Peris14, Reference Defant and Pérez15]). We denote by
$\mathbb {T}^{\infty }$
the infinite-dimensional complex polytorus carrying a normalized Haar measure
$m_{\infty }$
that coincides with the product of the normalized Lebesgue measure m on the unit circle
$\mathbb {T}\subset \mathbb {C}$
. Given
$1\leq p<\infty $
, let
$L_p(\mathbb {T}^{\infty },X)$
be the space of p-Bochner integrable functions
$F:\mathbb {T}^{\infty }\to X$
with respect to the Haar measure
$m_{\infty }$
. For any multi-index
$\nu =(\nu _1,\dots ,\nu _n,0,\dots )\in \mathbb {Z}^{(\infty )}$
(the set of eventually null sequences of integers) the
$\nu $
th Fourier coefficient
$\widehat {F}(\nu )$
of
$F\in L_1(\mathbb {T}^{\infty },X)$
is given by
$$\begin{align*}\widehat{F}(\nu):=\int_{\mathbb{T}^{\infty}}F(z)z^{-\nu}dm_{\infty}(z).\end{align*}$$
For
$1\leq p<\infty $
, the Hardy space
$H_p(\mathbb {T}^{\infty },X)$
is defined as the closed subspace of
$L_p(\mathbb {T}^{\infty },X)$
consisting of those functions F with
$\widehat {F}(\nu )=0$
for all
$\nu \in \mathbb {Z}^{(\infty )}\setminus \mathbb {N}_0^{(\infty )}$
, where
$\mathbb {N}_0^{(\infty )}$
denotes the set of
$\nu $
’s in
$\mathbb {Z}^{(\infty )}$
with
$\nu _j\in \mathbb {N}_0:=\mathbb {N}\cup \{0\}$
for all j.
Let
$\mathfrak {p}=\{\mathfrak {p}_j\}_{j\geq 1}$
be the increasing sequence of prime numbers. Given
$\nu \in \mathbb {Z}^{(\infty )}$
, we write
$\mathfrak {p}^{\nu }:=\mathfrak {p}_1^{\nu _1}\mathfrak {p}_2^{\nu _2}\cdots $
. By the fundamental theorem of arithmetic, for any
$n\in \mathbb {N}$
there exists a unique multi-index
$\nu (n)\in \mathbb {N}_0^{(\infty )}$
such that
$n=\mathfrak {p}^{\nu (n)}$
. Recall that every
$F\in L_1(\mathbb {T}^{\infty },X)$
is uniquely determined by its Fourier coefficients
$\{\widehat {F}(\nu )\}_{\nu \in \mathbb {Z}^{(\infty )}}$
. Consequently, for every
$F\in H_1(\mathbb {T}^{\infty },X)$
we may define its Bohr transform
$\mathfrak {B}(F)$
as the following X-valued Dirichlet series:
$$\begin{align*}\mathfrak{B}(F)(s):=\sum_{n=1}^{\infty}\widehat{F}\big(\nu(n)\big)n^{-s}.\end{align*}$$
Then the Hardy space
$\mathscr {H}_p(X)$
of X-valued Dirichlet series is defined as the image of
$H_p(\mathbb {T}^{\infty },X)$
under the Bohr transform
$\mathfrak {B}$
, endowed with the norm
$$\begin{align*}\|f\|_{\mathscr{H}_p(X)}:=\left\|\mathfrak{B}^{-1}(f)\right\|_{H_p(\mathbb{T}^{\infty},X)},\quad f\in\mathscr{H}_p(X).\end{align*}$$
As before, for the case
$X=\mathbb {C}$
, the corresponding spaces are denoted by
$H_p(\mathbb {T}^{\infty })$
and
$\mathscr {H}_p$
, respectively. This scale of Hardy spaces of Dirichlet series was introduced in [Reference Bayart2, Reference Hedenmalm, Lindqvist and Seip20] for scalar-valued Dirichlet series, and in [Reference Carando, Defant and Sevilla-Peris7] for Dirichlet series with values in a Banach space. We refer to [Reference Defant, García, Maestre and Sevilla-Peris14, Reference Queffélec and Queffélec28] for more information.
We will also consider some larger Hardy spaces of vector-valued Dirichlet series. Given
$u\in \mathbb {C}$
and
$f\in \mathcal {D}(X)$
, let
$f_u$
denote the translation of f by u, i.e.,
${f_u(\cdot ):=f(\cdot +u)}$
. For
$1\leq p<\infty $
, the Hardy space
$\mathscr {H}^+_p(X)$
, introduced in [Reference Defant and Pérez15], consists of
$f\in \mathcal {D}(X)$
such that
$f_{\sigma }\in \mathscr {H}_p(X)$
for any
$\sigma>0$
and
$$\begin{align*}\|f\|_{\mathscr{H}^+_p(X)}:=\sup_{\sigma>0}\|f_{\sigma}\|_{\mathscr{H}_p(X)}<\infty.\end{align*}$$
It was shown in [Reference Defant and Pérez15, Theorems 2.1 and 5.4] that
$\mathscr {H}_p(X)$
is isometrically embedded into
$\mathscr {H}^+_p(X)$
, and
$\mathscr {H}_p(X)=\mathscr {H}^+_p(X)$
if and only if X has the analytic Radon–Nikodým property. For
$1\leq p<\infty $
, let
$\mathscr {H}^{\text {weak}}_p(X)$
be the weak version of Hardy space of Dirichlet series in
$\mathcal {D}(X)$
. More precisely, the space
$\mathscr {H}^{\text {weak}}_p(X)$
consists of Dirichlet series
$f\in \mathcal {D}(X)$
such that
$x^*\circ f\in \mathscr {H}_p$
for every
$x^*\in X^*$
and
$$\begin{align*}\|f\|_{\mathscr{H}^{\text{weak}}_p(X)}:=\sup_{x^*\in B_{X^*}}\|x^*\circ f\|_{\mathscr{H}_p}<\infty,\end{align*}$$
where
$B_{X^*}$
is the closed unit ball of
$X^*$
. As far as we know, the space
$\mathscr {H}^{\text {weak}}_p(X)$
has not been documented in the literature yet. It is clear that
$\mathscr {H}^+_p(X)\subset \mathscr {H}^{\text {weak}}_p(X)$
. Moreover, by considering Dirichlet series supported on a single prime number and applying [Reference Laitila22, Example 15], one can conclude that
$\mathscr {H}^+_p(X)\subsetneq \mathscr {H}^{\text {weak}}_p(X)$
and
$\|\cdot \|_{\mathscr {H}^{\text {weak}}_p(X)}$
is not equivalent to
$\|\cdot \|_{\mathscr {H}^+_p(X)}$
on
$\mathscr {H}^+_p(X)$
if X is infinite-dimensional (see also [Reference Freniche, García-Vázquez and Rodríguez-Piazza19, Reference Laitila and Tylli23]).
Given
$g\in \mathcal {D}$
, the Volterra operator
$T_g$
is defined for
$f\in \mathcal {D}(X)$
by
$$\begin{align*}T_gf(s):=-\int_s^{+\infty}f(u)g'(u)du,\end{align*}$$
where
$\Re s$
is large enough. This operator was first introduced by Pommerenke [Reference Pommerenke27] in the setting of analytic functions on the unit disk
$\mathbb {D}$
of
$\mathbb {C}$
. The Dirichlet series analogue was defined by Brevig, Perfekt, and Seip [Reference Brevig, Perfekt and Seip6]. In their work, they gave some necessary and sufficient conditions for the boundedness of
$T_g$
acting on the Hardy spaces
$\mathscr {H}_p$
. Motivated by this, and in view of the fact that
$\mathscr {H}^+_p(X)$
and
$\mathscr {H}^{\text {weak}}_p(X)$
are essentially different spaces for any infinite-dimensional Banach space X, we here investigate the Volterra operators
$T_g$
that are bounded from
$\mathscr {H}^{\text {weak}}_p(X)$
to
$\mathscr {H}^+_p(X)$
. This problem was initially considered by Laitila, Tylli, and Wang [Reference Laitila, Tylli and Wang24] for composition operators in the setting of Hardy and Bergman spaces of vector-valued analytic functions on
$\mathbb {D}$
. Later on, Chen and Wang [Reference Chen and Wang11] characterized the Volterra operators that are bounded from weak to strong Hardy (and Bergman) spaces of vector-valued analytic functions on
$\mathbb {D}$
.
To state our main result, we need the notion of uniform PL-convexity of a complex Banach space (see [Reference Davis, Garling and Tomczak-Jaegermann12]). For
$1\leq p<\infty $
, the modulus of PL-convexity
$\delta ^X_p(\epsilon )$
(
$\epsilon>0$
) of the space X is defined by
$$\begin{align*}\delta^X_p(\epsilon):=\inf\left\{\left(\int_{\mathbb{T}}\|x+\xi y\|^pdm(\xi)\right)^{1/p}-1:x,y\in X,\ \|x\|_X=1,\ \|y\|_X=\epsilon\right\}.\end{align*}$$
The space X is said to be uniformly PL-convex if
$\delta ^X_1(\epsilon )>0$
for all
$\epsilon>0$
, and for
$2\leq p<\infty $
, X is said to be p-uniformly PL-convex if there exists
$C>0$
such that
$\delta ^X_p(\epsilon )\geq C\epsilon ^p$
for all
$\epsilon>0$
. It is well-known (see [Reference Davis, Garling and Tomczak-Jaegermann12, p. 117] or [Reference Blasco and Pavlović4, p. 750]) that X is p-uniformly PL-convex if and only if there exists
$C>0$
such that
$$\begin{align*}\int_{\mathbb{T}}\|x+\xi y\|^p_Xdm(\xi)\geq\|x\|^p_X+C\|y\|^p_X,\quad \forall x,y\in X.\end{align*}$$
For
$1\leq p<\infty $
, let
$H_p(\mathbb {D},X)$
be the Hardy space consisting of X-valued analytic functions f on the unit disk
$\mathbb {D}$
such that
$$\begin{align*}\|f\|_{H_p(\mathbb{D},X)}:=\sup_{0<r<1}\left(\int_{\mathbb{T}}\|f(r\xi)\|^p_Xdm(\xi)\right)^{1/p}<\infty.\end{align*}$$
The corresponding weak version
$H^{\text {weak}}_p(\mathbb {D},X)$
can be defined as before. It was shown in [Reference Chen and Wang11, Remark 3.7] that for
$2\leq p<\infty $
and any infinite-dimensional p-uniformly PL-convex space X, the boundedness of Volterra operators from
$H^{\text {weak}}_p(\mathbb {D},X)$
to
$H_p(\mathbb {D},X)$
is related to the membership of Schatten p-class of Volterra operators on the Hardy space
$H_2(\mathbb {D})$
. Here and in the sequel,
$H_p(\mathbb {D})$
denotes the classical Hardy space over
$\mathbb {D}$
. On the other hand, Brevig, Perfekt, and Seip [Reference Brevig, Perfekt and Seip6, Theorem 7.2] proved that there is no nontrivial Volterra operator
$T_g$
in the Schatten class
$S_p(\mathscr {H}_2)$
for all
$0<p<\infty $
. Based on the aforementioned results, we may conjecture that for
$2\leq p<\infty $
and any infinite-dimensional p-uniformly PL-convex space X, there is no nontrivial bounded Volterra operator
$T_g$
from
$\mathscr {H}^{\text {weak}}_p(X)$
to
$\mathscr {H}^+_p(X)$
. Our main result establishes that this is the case.
Theorem 1.1 Let
$2\leq p<\infty $
,
$g\in \mathcal {D}$
, and let X be infinite-dimensional and p-uniformly PL-convex. If
$T_g:\mathscr {H}_p^{\text {weak}}(X)\to \mathscr {H}_p^+(X)$
is bounded, then g is constant.
In order to prove the above theorem, we need to estimate the norm of
$f\in \mathscr {H}^+_p(X)$
from below via its derivative
$f'$
. A classical result of this style is the Littlewood–Paley inequality (see [Reference Littlewood and Paley26] or [Reference Jevtić, Vukotić and Arsenović21, Theorem 4.4.4]), which indicates that if
$2\leq p<\infty $
, then there exists
$C>0$
such that for any
$f\in H_p(\mathbb {D})$
,
$$\begin{align*}\|f\|_{H_p(\mathbb{D})}\geq\left(|f(0)|^p+C\int_{\mathbb{D}}|f'(\xi)|^p(1-|\xi|^2)^{p-1}dA(\xi)\right)^{1/p},\end{align*}$$
where
$dA$
is the Lebesgue measure on
$\mathbb {C}$
normalized so that
$A(\mathbb {D})=1$
. Vector-valued versions of Littlewood–Paley theory have been considered by several authors for various reasons. In particular, Blasco and Pavlović [Reference Blasco and Pavlović4] proved that for
$2\leq p<\infty $
, the Banach space X is p-uniformly PL-convex if and only if there exists
$C>0$
such that for every
$f\in H_p(\mathbb {D},X)$
,
$$ \begin{align} \|f\|_{H_p(\mathbb{D},X)}\geq\left(\|f(0)\|^p_X+C\int_{\mathbb{D}}\|f'(\xi)\|^p_X(1-|\xi|^2)^{p-1}dA(\xi)\right)^{1/p}. \end{align} $$
Based on this inequality, we can establish the following Littlewood–Paley inequality for vector-valued Dirichlet series, which plays an essential role in the proof of Theorem 1.1.
Theorem 1.2 Let
$2\leq p<\infty $
and X be a p-uniformly PL-convex space. Then there exists
$C>0$
such that for any
$f\in \mathscr {H}^+_p(X)$
,
$$\begin{align*}\|f(+\infty)\|_X+\left(\int_0^{+\infty}\|f^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma\right)^{1/p}\leq C\|f\|_{\mathscr{H}^+_p(X)}.\end{align*}$$
For any
$\alpha>-1$
and
$1\leq p<\infty $
, we define the McCarthy–Dirichlet space
$\mathscr {D}^p_{\alpha }(X)$
of X-valued Dirichlet series as the completion of
$\mathcal {P}(X)$
with respect to the norm
$$\begin{align*}\|P\|_{\mathscr{D}^p_{\alpha}(X)}:=\|P(+\infty)\|_X+\left(\int_0^{+\infty}\|P^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{\alpha}d\sigma\right)^{1/p}, \quad P\in\mathcal{P}(X).\end{align*}$$
Then Theorem 1.2 can be restated as follows: if
$2\leq p<\infty $
and X is a p-uniformly PL-convex Banach space, then we have the bounded inclusion
$$\begin{align*}\mathscr{H}^+_p(X)\subset\mathscr{D}^p_{p-1}(X).\end{align*}$$
This can be compared with the inclusion between classical Hardy and Dirichlet spaces over the unit disk.
Remark 1.3 Since every Hilbert space is
$2$
-uniformly PL-convex (and consequently, p-uniformly PL-convex for all
$2\leq p<\infty $
), Theorem 1.2 is valid for every Hilbert space X. In particular, it is valid for the scalar case.
Theorems 1.1 and 1.2 are proven in Section 2. We also give two generalizations of Theorem 1.2 in the end of Section 2. Finally, in Section 3, some remarks regarding the Littlewood–Paley inequalities for the case
$1<p\leq 2$
are given.
Throughout the paper, the letter C always denotes a positive constant whose value is not essential and may change from one occurrence to the next. We also write
$A\lesssim B$
or
$B\gtrsim A$
if
$A\leq CB$
for some inessential constant
$C>0$
. For a Dirichlet series
$f(s)=\sum _{n=1}^{\infty }x_nn^{-s}$
, we always use
$f(+\infty )$
to denote
$x_1$
.
2 Proofs of Theorems 1.1 and 1.2
In this section, we are going to prove Theorems 1.1 and 1.2. Before proceeding, we introduce some auxiliary results.
We first explain more about the definition of the Hardy spaces
$\mathscr {H}_p(X)$
. Due to the definition, a Dirichlet series
$f(s)=\sum _{n=1}^{\infty }x_nn^{-s}$
belongs to
$\mathscr {H}_p(X)$
if and only if there exists
$F\in H_p(\mathbb {T}^{\infty },X)$
such that
$\widehat {F}\big (\nu (n)\big )=x_n$
for every
$n\in \mathbb {N}$
. In this case, one has
$\|f\|_{\mathscr {H}_p(X)}=\|F\|_{H_p(\mathbb {T}^{\infty },X)}$
. In particular, for any Dirichlet polynomial
$P(s)=\sum _{n=1}^Nx_nn^{-s}$
,
$\mathfrak {B}^{-1}(P)(z)=\sum _{n=1}^Nx_nz^{\nu (n)}$
, and
$$ \begin{align} \|P\|_{\mathscr{H}_p(X)}=\left(\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^Nx_nz^{\nu(n)}\right\|^p_Xdm_{\infty}(z)\right)^{1/p}. \end{align} $$
It is clear that for
$1\leq p<\infty $
the Bohr transform
$\mathfrak {B}$
is an isometric isomorphism from
$H_p(\mathbb {T}^{\infty },X)$
onto
$\mathscr {H}_p(X)$
. There are two elementary consequences of this fact.
-
(i) The coefficients of a Dirichlet series
$f\in \mathscr {H}_p(X)$
are bounded by
$\|f\|_{\mathscr {H}_p(X)}$
. Consequently, if we use
$c_n(f)$
to denote the nth Dirichlet coefficient of
$f\in \mathcal {D}(X)$
, then the convergence
$f_j\to f$
in
$\mathscr {H}_p(X)$
implies the convergence
$c_n(f_j)\to c_n(f)$
in X for every
$n\in \mathbb {N}$
. -
(ii) The set
$\mathcal {P}(X)$
of Dirichlet polynomials is dense in
$\mathscr {H}_p(X)$
for
$1\leq p<\infty $
(see [Reference Defant, García, Maestre and Sevilla-Peris14, Proposition 24.6]).
The following lemma concerns the horizontal translation of Dirichlet series in Hardy spaces, which can be found in [Reference Defant and Pérez15, Proposition 2.3].
Lemma 2.1 Suppose
$1\leq p<\infty $
and
$f\in \mathscr {H}_p(X)$
. Then for any
$\sigma>0$
,
$f_{\sigma }\in \mathscr {H}_p(X)$
. Moreover, the function
$\sigma \mapsto \|f_{\sigma }\|_{\mathscr {H}_p(X)}$
is decreasing on
$[0,\infty )$
.
For any
$P(s)=\sum _{n=1}^Nx_nn^{-s}$
in
$\mathcal {P}(X)$
and
$w\in \mathbb {T}^{\infty }$
, write
$$\begin{align*}P_w(s):=\sum_{n=1}^Nx_nw^{\nu(n)}n^{-s}.\end{align*}$$
Recall that
$\nu (n)\in \mathbb {N}_0^{(\infty )}$
is the multi-index such that
$n=\mathfrak {p}^{\nu (n)}$
. The following lemma is an immediate consequence of the rotation invariance of the measure
$m_{\infty }$
and (2.1). Nevertheless, we include a proof here for the convenience of the reader.
Lemma 2.2 Let
$1\leq p<\infty $
and
$P\in \mathcal {P}(X)$
. Then for any
$s=\sigma +it\in \mathbb {C}$
,
$$\begin{align*}\int_{\mathbb{T}^{\infty}}\|P_w(s)\|^p_Xdm_{\infty}(w)=\|P_{\sigma}\|^p_{\mathscr{H}_p(X)}.\end{align*}$$
Proof By the rotation invariance of the measure
$m_{\infty }$
,
$$ \begin{align*} \int_{\mathbb{T}^{\infty}}\|P_w(s)\|^p_Xdm_{\infty}(w)&=\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^Nx_nn^{-\sigma-it}w^{\nu(n)}\right\|_X^pdm_{\infty}(w)\\ &=\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^Nx_nn^{-\sigma}z^{\nu(n)}\right\|_X^pdm_{\infty}(z)\\ &=\|P_{\sigma}\|^p_{\mathscr{H}_p(X)}, \end{align*} $$
where the last equality is due to (2.1).
Given
$N\in \mathbb {N}$
, let
$S_N$
be the partial sum operator defined by
$$\begin{align*}S_N\left(\sum_{n=1}^{\infty}x_nn^{-s}\right):=\sum_{n=1}^{N}x_nn^{-s}.\end{align*}$$
The estimates of the operators
$S_N$
are crucial for the modern theory of Dirichlet series. It was proved in [Reference Defant and Pérez15, Theorem 3.2] that there exists
$C>0$
such that for every
$N\in \mathbb {N}$
and every
$1\leq p<\infty $
,
$$ \begin{align} \|S_N\|_{\mathscr{H}^+_p(X)\to\mathscr{H}^+_p(X)}\leq C\log N. \end{align} $$
Based on the above estimate, we can establish the following proposition on derivatives of Dirichlet series in Hardy spaces.
Proposition 2.3 Let
$1\leq p<\infty $
. Then for any
$\sigma>0$
and
$f\in \mathscr {H}^+_p(X)$
,
$f^{\prime }_{\sigma }\in \mathscr {H}_p(X)$
.
Proof Fix
$\sigma>0$
, and suppose that
$f(s)=\sum _{n=1}^{\infty }x_nn^{-s}$
belongs to
$\mathscr {H}^+_p(X)$
. Then for any
$2\leq N<M$
, Abel’s summation formula yields that
$$ \begin{align*} \sum_{n=N}^{M}x_nn^{-(s+\frac{\sigma}{2})}\log n =&\sum_{n=N}^{M-1}\left(\sum_{k=1}^nx_kk^{-s}\right)\left(n^{-\frac{\sigma}{2}}\log n-(n+1)^{-\frac{\sigma}{2}}\log(n+1)\right)\\ &+\left(\sum_{k=1}^Mx_kk^{-s}\right)M^{-\frac{\sigma}{2}}\log M-\left(\sum_{k=1}^{N-1}x_kk^{-s}\right)N^{-\frac{\sigma}{2}}\log N. \end{align*} $$
Taking norms and using (2.2), we obtain that
$$ \begin{align*} &\left\|\sum_{n=N}^{M}x_nn^{-(s+\frac{\sigma}{2})}\log n\right\|_{\mathscr{H}^+_p(X)}\\ &\ \lesssim\sum_{n=N}^{M-1}\log n\left|n^{-\frac{\sigma}{2}}\log n-(n+1)^{-\frac{\sigma}{2}}\log(n+1)\right| +M^{-\frac{\sigma}{2}}\log^2M+N^{-\frac{\sigma}{2}}\log^2N\\ &\ \lesssim\sum_{n=N}^{M-1}n^{-\frac{\sigma}{2}-1}\log^2n+M^{-\frac{\sigma}{2}}\log^2M+N^{-\frac{\sigma}{2}}\log^2N\to0 \end{align*} $$
as
$N,M\to \infty $
. Therefore, there exists
$g\in \mathscr {H}^+_p(X)$
such that
$$\begin{align*}\sum_{n=2}^{N}x_nn^{-(\cdot+\frac{\sigma}{2})}\log n\to g(\cdot)\end{align*}$$
in
$\mathscr {H}^+_p(X)$
as
$N\to \infty $
. Consequently,
$$\begin{align*}\sum_{n=2}^{N}x_nn^{-(\cdot+\sigma)}\log n\to g_{\sigma/2}(\cdot)\end{align*}$$
in
$\mathscr {H}_p(X)$
as
$N\to \infty $
. Comparing the Dirichlet coefficients and using the consequence (i) at the beginning of this section, we finally conclude that
$f^{\prime }_{\sigma }=-g_{\sigma /2}\in \mathscr {H}_p(X)$
.
We are now ready to prove Theorem 1.2.
Proof of Theorem 1.2
For
$\eta>0$
, let
$\phi _{\eta }:\mathbb {D}\to \mathbb {C}_0$
be the Cayley transform defined by
$$\begin{align*}\phi_{\eta}(\xi)=\eta\frac{1+\xi}{1-\xi},\quad \xi\in\mathbb{D},\end{align*}$$
where
$\mathbb {C}_0:=\{s\in \mathbb {C}:\Re s>0\}$
. Then for any
$P\in \mathcal {P}(X)$
and
$w\in \mathbb {T}^{\infty }$
, noting that
$P_w\circ \phi _{\eta }\in H_p(\mathbb {D},X)$
since it is bounded on
$\mathbb {D}$
, we may apply (1.1) to the function
$P_w\circ \phi _{\eta }$
to obtain that
$$\begin{align*}\|P_w(\eta)\|^p_X+C\int_{\mathbb{D}}\|(P_w\circ\phi_{\eta})'(\xi)\|_X^p(1-|\xi|^2)^{p-1}dA(\xi)\leq\|P_w\circ\phi_{\eta}\|^p_{H_p(\mathbb{D},X)}.\end{align*}$$
Using the change of variables
$s=\sigma +it=\phi _{\eta }(\xi )$
, we get
$$ \begin{align*} &\int_{\mathbb{D}}\|(P_w\circ\phi_{\eta})'(\xi)\|_X^p(1-|\xi|^2)^{p-1}dA(\xi)\\ &\ \ =\int_{\mathbb{D}}\|P^{\prime}_w(\phi_{\eta}(\xi))\|^p_X|\phi^{\prime}_{\eta}(\xi)|^p(1-|\xi|^2)^{p-1}dA(\xi)\\ &\ \ =\int_{\mathbb{C}_0}\|P^{\prime}_w(s)\|^p_X|\phi^{\prime}_{\eta}(\phi^{-1}_{\eta}(s))|^{p-2}(1-|\phi^{-1}_{\eta}(s)|^2)^{p-1}dA(s)\\ &\ \ =\int_{\mathbb{C}_0}\|P^{\prime}_w(s)\|^p_X\left(\frac{2\eta}{\left|1-\frac{s-\eta}{s+\eta}\right|{}^2}\right)^{p-2} \left(1-\left|\frac{s-\eta}{s+\eta}\right|{}^2\right)^{p-1}dA(s)\\ &\ \ =2^p\int_0^{+\infty}\int_{\mathbb{R}}\|P^{\prime}_w(\sigma+it)\|^p_X\frac{\sigma^{p-1}\eta}{(\sigma+\eta)^2+t^2}dtd\sigma. \end{align*} $$
Therefore, we have establish that
$$ \begin{align} \|P_w(\eta)\|^p_X+C\int_0^{+\infty}\int_{\mathbb{R}}\|P^{\prime}_w(\sigma+it)\|^p_X\frac{\sigma^{p-1}\eta}{(\sigma+\eta)^2+t^2}dtd\sigma \leq\|P_w\circ\phi_{\eta}\|^p_{H_p(\mathbb{D},X)}. \end{align} $$
Integrating on both sides with respect to w on
$\mathbb {T}^{\infty }$
, the left hand side of (2.3) gives, using both Fubini’s theorem and Lemma 2.2,
$$ \begin{align} &\int_{\mathbb{T}^{\infty}}\left(\|P_w(\eta)\|^p_X+ C\int_0^{+\infty}\int_{\mathbb{R}}\|P^{\prime}_w(\sigma+it)\|^p_X\frac{\sigma^{p-1}\eta}{(\sigma+\eta)^2+t^2}dtd\sigma\right)dm_{\infty}(w)\nonumber\\ &\ \ =\|P_{\eta}\|^p_{\mathscr{H}_p(X)}+C\int_0^{+\infty}\int_{\mathbb{R}}\|P^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)} \frac{\sigma^{p-1}\eta}{(\sigma+\eta)^2+t^2}dtd\sigma\nonumber\\ &\ \ =\|P_{\eta}\|^p_{\mathscr{H}_p(X)}+C\int_0^{+\infty}\|P^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\frac{\sigma^{p-1}\eta}{\sigma+\eta}d\sigma, \end{align} $$
where in the last identity we have used that
$\frac {\sigma +\eta }{\pi ((\sigma +\eta )^2+t^2)}dt$
is a probability measure on
$\mathbb {R}$
. Regarding the right hand side of (2.3), recalling the definition of
$H_p(\mathbb {D},X)$
, applying first Fatou’s lemma, then Fubini’s theorem, and finally Lemma 2.2, we find that
$$ \begin{align*} \int_{\mathbb{T}^{\infty}}\|P_w\circ\phi_{\eta}\|^p_{H_p(\mathbb{D},X)}dm_{\infty}(w) &=\int_{\mathbb{T}^{\infty}}\lim_{r\to1^-}\int_{\mathbb{T}}\left\|P_w(\phi_{\eta}(r\zeta))\right\|^p_Xdm(\zeta)dm_{\infty}(w)\\ &\leq\liminf_{r\to1^-}\int_{\mathbb{T}^{\infty}}\int_{\mathbb{T}}\|P_w(\phi_{\eta}(r\zeta))\|^p_{X}dm(\zeta)dm_{\infty}(w)\\ &=\liminf_{r\to1^-}\int_{\mathbb{T}}\int_{\mathbb{T}^{\infty}}\|P_w(\phi_{\eta}(r\zeta))\|^p_{X}dm_{\infty}(w)dm(\zeta)\\ &=\liminf_{r\to1^-}\int_{\mathbb{T}}\Big\|P\Big(\cdot+\Re(\phi_{\eta}(r\zeta))\Big)\Big\|^p_{\mathscr{H}_p(X)}dm(\zeta). \end{align*} $$
Now, thanks to Lemma 2.1, we conclude that
$$\begin{align*}\int_{\mathbb{T}^{\infty}}\|P_w\circ\phi_{\eta}\|^p_{H_p(\mathbb{D},X)}dm_{\infty}(w) \leq\liminf_{r\to1^-}\int_{\mathbb{T}}\Big\|P\Big(\cdot+\Re(\phi_{\eta}(r\zeta))\Big)\Big\|^p_{\mathscr{H}_p(X)}dm(\zeta) \leq\|P\|^p_{\mathscr{H}_p(X)}.\end{align*}$$
Putting this estimate together with (2.4) gives
$$\begin{align*}\|P_{\eta}\|^p_{\mathscr{H}_p(X)}+C\int_0^{+\infty}\|P^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\frac{\sigma^{p-1}\eta}{\sigma+\eta}d\sigma\leq\|P\|^p_{\mathscr{H}_p(X)}.\end{align*}$$
Letting
$\eta \to +\infty $
and using Lebesgue’s dominated convergence theorem, we obtain that
$$ \begin{align} \|P(+\infty)\|^p_{X}+C\int_0^{+\infty}\|P^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma\leq\|P\|^p_{\mathscr{H}_p(X)}. \end{align} $$
Recall that the McCarthy–Dirichlet space
$\mathscr {D}^p_{p-1}(X)$
is the completion of
$\mathcal {P}(X)$
with respect to the norm
$$\begin{align*}\|Q\|_{\mathscr{D}^p_{p-1}(X)}:=\|Q(+\infty)\|_X+\left(\int_0^{+\infty}\|Q^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma\right)^{1/p}, \quad Q\in\mathcal{P}(X).\end{align*}$$
Since Dirichlet polynomials are dense in
$\mathscr {H}_p(X)$
, it follows from (2.5) that the identity operator extends to a bounded operator from
$\mathscr {H}_p(X)$
into
$\mathscr {D}^p_{p-1}(X)$
. Consequently, there exists
$C>0$
such that for any
$g\in \mathscr {H}_p(X)$
,
$$ \begin{align} \|g(+\infty)\|^p_X+\int_0^{+\infty}\|g^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma\leq C\|g\|^p_{\mathscr{H}_p(X)}. \end{align} $$
Suppose now that
$f\in \mathscr {H}^+_p(X)$
. Then for any
$\delta>0$
,
$f_{\delta }\in \mathscr {H}_p(X)$
and by Proposition 2.3,
$f^{\prime }_{\delta }\in \mathscr {H}_p(X)$
. Applying (2.6) to the Dirichlet series
$f_{\delta }$
yields that
$$\begin{align*}\|f(+\infty)\|^p_X+\int_0^{+\infty}\|f^{\prime}_{\delta+\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma \leq C\|f_{\delta}\|^p_{\mathscr{H}_p(X)}\leq C\|f\|^p_{\mathscr{H}^+_p(X)}.\end{align*}$$
In view of Lemma 2.1, we may let
$\delta \to 0$
and use Lebesgue’s monotone convergence theorem to conclude that
$$\begin{align*}\|f(+\infty)\|^p_X+\int_0^{+\infty}\|f^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma\leq C\|f\|^p_{\mathscr{H}^+_p(X)},\end{align*}$$
which finishes the proof.
To establish Theorem 1.1, we need some more auxiliary results. The following Dvoretzky theorem can be found in [Reference Diestel, Jarchow and Tonge18, Chapter 19].
Theorem 2.4 For any
$N\in \mathbb {N}$
and
$\epsilon>0$
there is
$c(N,\epsilon )\in \mathbb {N}$
so that for any Banach space X of dimension at least
$c(N,\epsilon )$
, there is a linear embedding
$E_N:l^N_2\to X$
so that
$$ \begin{align} (1+\epsilon)^{-1}\biggl(\sum_{n=1}^N|a_n|^2\biggr)^{1/2}\leq\biggl\|\sum_{n=1}^Na_nE_Nv_n\biggr\|_X \leq\biggl(\sum_{n=1}^N|a_n|^2\biggr)^{1/2} \end{align} $$
for any
$a_1,\dots ,a_N\in \mathbb {C}$
. Here
$(v_1,\dots ,v_N)$
is some fixed orthonormal basis of
$l^N_2$
.
Recall that a sequence
$\{\lambda _n\}_{n\geq 1}$
of complex numbers is completely multiplicative if
$\lambda _{mn}=\lambda _m\lambda _n$
for all
$m,n\in \mathbb {N}$
. For
$1\leq p,q<\infty $
, a sequence
$\{\lambda _n\}_{n\geq 1}$
is said to be a multiplier from
$\mathscr {H}_p$
to
$\mathscr {H}_q$
if
$\sum _{n=1}^{\infty }\lambda _na_nn^{-s}\in \mathscr {H}_q$
for each
$f(s)=\sum _{n=1}^{\infty }a_nn^{-s}$
in
$\mathscr {H}_p$
. Note that by the closed graph theorem, if
$\{\lambda _n\}_{n\geq 1}$
is a multiplier from
$\mathscr {H}_p$
to
$\mathscr {H}_q$
, then there exists
$C>0$
such that for any
$f(s)=\sum _{n=1}^{\infty }a_nn^{-s}$
in
$\mathscr {H}_p$
,
$$\begin{align*}\left\|\sum_{n=1}^{\infty}\lambda_na_nn^{-s}\right\|_{\mathscr{H}_q}\leq C\left\|\sum_{n=1}^{\infty}a_nn^{-s}\right\|_{\mathscr{H}_p}.\end{align*}$$
The following lemma is due to Bayart [Reference Bayart3], which can be proved by using Weissler’s hypercontractive inequality of the Poisson kernels [Reference Weissler29] and Minkowski’s inequality; see [Reference Bayart2, Theorem 9].
Lemma 2.5 Let
$1\leq p\leq q<\infty $
and
$\{\lambda _n\}_{n\geq 1}$
be a completely multiplicative sequence of positive numbers such that
$\lambda _{\mathfrak {p}_j}\leq \sqrt {p/q}$
for each
$j\geq 1$
. Then
$\{\lambda _n\}_{n\geq 1}$
is a multiplier from
$\mathscr {H}_p$
to
$\mathscr {H}_q$
. Moreover, the operator induced by
$\{\lambda _n\}_{n\geq 1}$
is a contraction from
$\mathscr {H}_p$
into
$\mathscr {H}_q$
.
We also need the following lemma.
Lemma 2.6 Let
$1\leq p<\infty $
. Suppose that
$f(s)=\sum _{n=1}^Nx_nn^{-s}$
belongs to
$\mathcal {P}(X)$
, and
$g(s)=\sum _{n=1}^{\infty }b_nn^{-s}$
belongs to
$\mathscr {H}_p$
. Then
$fg\in \mathscr {H}_p(X)$
and
$\mathfrak {B}^{-1}(fg)=\mathfrak {B}^{-1}(f)\mathfrak {B}^{-1}(g)$
.
Proof Write
$F=\mathfrak {B}^{-1}(f)$
and
$G=\mathfrak {B}^{-1}(g)$
. Then it is clear that
$FG\in H_p(\mathbb {T}^{\infty },X)$
. Moreover,
$$\begin{align*}F(z)=\sum_{n=1}^Nx_nz^{\nu(n)},\quad z\in\mathbb{T}^{\infty},\end{align*}$$
and for any
$n\in \mathbb {N}$
,
$\widehat {G}\big (\nu (n)\big )=b_n$
. We now calculate the
$\nu $
th Fourier coefficient of
$FG$
for
$\nu \in \mathbb {N}_0^{(\infty )}$
. Bearing in mind that
$G\in H_p(\mathbb {T}^{\infty })$
, we have
$$ \begin{align*} \widehat{FG}(\nu)&=\int_{\mathbb{T}^{\infty}}(FG)(z)z^{-\nu}dm_{\infty}(z)\\ &=\int_{\mathbb{T}^{\infty}}F(z)G(z)z^{-\nu}dm_{\infty}(z)\\ &=\sum_{n=1}^{N}x_n\int_{\mathbb{T}^{\infty}}G(z)z^{-(\nu-\nu(n))}dm_{\infty}(z)\\ &=\sum_{\substack{n|\mathfrak{p}^{\nu}\\1\leq n\leq N}}x_n\widehat{G}\big(\nu-\nu(n)\big). \end{align*} $$
On the other hand, it is easy to see that the lth Dirichlet coefficient
$c_l(fg)$
of
$fg$
is given by
$$\begin{align*}c_l(fg)=\sum_{\substack{n|l\\1\leq n\leq N}}x_nb_{l/n}.\end{align*}$$
Therefore, noting that
$\widehat {G}(\nu (n))=b_n$
, we obtain that
$\widehat {FG}\big (\nu (l)\big )=c_l(fg)$
for any
$l\in \mathbb {N}$
, which implies that
$\mathfrak {B}(FG)=fg$
and
$fg\in \mathscr {H}_p(X)$
.
We are now in a position to prove Theorem 1.1.
Proof of Theorem 1.1
Suppose that
$T_g:\mathscr {H}_p^{\text {weak}}(X)\to \mathscr {H}_p^+(X)$
is bounded. Then it is easy to see that
$g\in \mathscr {H}_p$
since
$T_g1=g-g(+\infty )$
. Consequently, by Proposition 2.3,
$g^{\prime }_{\sigma }\in \mathscr {H}_p$
for any
$\sigma>0$
. We will complete the proof by showing
$\|g^{\prime }_{1/2}\|_{\mathscr {H}_p}=0$
.
Let
$N\in \mathbb {N}$
and
$\epsilon>0$
. According to Theorem 2.4, we may fix a linear embedding
$E_N:l^N_2\to X$
such that (2.7) holds. Put
$x^{(N)}_n=E_Nv_n$
for
$n=1,2,\dots ,N$
, and let
$\lambda _n=\left (2p^{-1}\right )^{\frac {\Omega (n)}{2}}$
for
$n\geq 1$
, where
$\Omega (n)$
is the number of prime factors of n, counted with multiplicity. Then
$\{\lambda _n\}_{n\geq 1}$
is completely multiplicative and
$\lambda _{\mathfrak {p}_j}=\sqrt {2/p}$
for each
$j\geq 1$
. Define the X-valued Dirichlet polynomial
$f_N$
by
$$\begin{align*}f_N(s)=\sum_{n=1}^N\lambda_nx^{(N)}_nn^{-s}=E_N\left(\sum_{n=1}^N\lambda_nv_nn^{-s}\right).\end{align*}$$
Then by Lemma 2.5,
$$ \begin{align*} \|f_N\|_{\mathscr{H}^{\text{weak}}_p(X)}&=\sup_{x^*\in B_{X^*}}\|x^*\circ f_N\|_{\mathscr{H}_p}\\ &=\sup_{x^*\in B_{X^*}}\left\|\sum_{n=1}^N\lambda_nx^*\left(x^{(N)}_n\right)n^{-s}\right\|_{\mathscr{H}_p}\\ &\leq\sup_{x^*\in B_{X^*}}\left\|\sum_{n=1}^Nx^*\left(x^{(N)}_n\right)n^{-s}\right\|_{\mathscr{H}_2}\\ &=\sup_{x^*\in B_{X^*}}\left(\sum_{n=1}^N\left|\left(E^*_Nx^*\right)(v_n)\right|{}^2\right)^{1/2}\\ &=\sup_{x^*\in B_{X^*}}\left\|E_N^*x^*\right\|_{l^N_2}\\ &\leq1, \end{align*} $$
where we have used the facts that
$(v_1,\dots ,v_N)$
is an orthonormal basis of
$l^N_2$
and
$\|E_N\|_{l^N_2\to X}\leq 1$
due to (2.7). Hence it follows from Theorem 1.2 and Lemma 2.6 that
$$ \begin{align*} \|T_g\|^p &\geq\|T_gf_N\|^p_{\mathscr{H}^+_p(X)}\\ &\gtrsim\int_0^{+\infty}\|(f_N)_{\sigma}g^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(X)}\sigma^{p-1}d\sigma\\ &=\int_0^{+\infty}\left\|\mathfrak{B}^{-1}\Big((f_N)_{\sigma}g^{\prime}_{\sigma}\Big)\right\|^p_{H_p(\mathbb{T}^{\infty},X)}\sigma^{p-1}d\sigma\\ &=\int_0^{+\infty}\left\|\mathfrak{B}^{-1}\Big((f_N)_{\sigma}\Big)\mathfrak{B}^{-1}(g^{\prime}_{\sigma})\right\|^p_{H_p(\mathbb{T}^{\infty},X)}\sigma^{p-1}d\sigma\\ &=\int_0^{+\infty}\sigma^{p-1}\int_{\mathbb{T}^{\infty}}\left\|\mathfrak{B}^{-1}\Big((f_N)_{\sigma}\Big)(z)\right\|^p_X|\mathfrak{B}^{-1}(g^{\prime}_{\sigma})(z)|^pdm_{\infty}(z)d\sigma. \end{align*} $$
Note that for any
$z\in \mathbb {T}^{\infty }$
, it follows from (2.7) that
$$ \begin{align*} \left\|\mathfrak{B}^{-1}\Big((f_N)_{\sigma}\Big)(z)\right\|_X&=\left\|\sum_{n=1}^{N}\lambda_nn^{-\sigma}z^{\nu(n)}E_Nv_n\right\|_X\\ &\gtrsim\left(\sum_{n=1}^N(2p^{-1})^{\Omega(n)}n^{-2\sigma}\right)^{1/2}\\ &\gtrsim\left(\sum_{1\leq j\leq\pi(N)}\mathfrak{p}_j^{-2\sigma}\right)^{1/2}, \end{align*} $$
where
$\pi (N)$
denotes the number of primes less than or equal to N. Therefore, we may apply Lemma 2.1 to obtain that
$$ \begin{align*} \|T_g\|^p &\gtrsim\int_0^{+\infty}\left(\left(\sum_{1\leq j\leq\pi(N)}\mathfrak{p}_j^{-2\sigma}\right)^{p/2}\sigma^{p-1} \int_{\mathbb{T}^{\infty}}|\mathfrak{B}^{-1}(g^{\prime}_{\sigma})(z)|^pdm_{\infty}(z)\right)d\sigma\\ &\geq\int_0^{1/2}\|g^{\prime}_{\sigma}\|^p_{\mathscr{H}_p}\left(\sum_{1\leq j\leq\pi(N)}\mathfrak{p}_j^{-2\sigma}\right)^{p/2}\sigma^{p-1}d\sigma\\ &\gtrsim\|g^{\prime}_{1/2}\|^p_{\mathscr{H}_p}\left(\sum_{1\leq j\leq\pi(N)}\mathfrak{p}_j^{-1}\right)^{p/2}. \end{align*} $$
Since
$N\in \mathbb {N}$
is arbitrary and
$\sum _{j=1}^{\infty }\mathfrak {p}_j^{-1}=\infty $
, we conclude that
$\|g^{\prime }_{1/2}\|_{\mathscr {H}_p}=0$
, which finishes the proof.
We end this section with two generalizations of Theorem 1.2. The following corollary concerns
$f\in \mathscr {H}^+_q(X)$
with p-uniformly PL-convex space X, where
$p\geq \max \{2,q\}$
.
Corollary 2.7 Let
$2\leq p<\infty $
,
$1\leq q\leq p$
, and let X be a p-uniformly PL-convex space. Then there exists
$C>0$
such that for any
$f\in \mathscr {H}^+_q(X)$
,
$$\begin{align*}\|f(+\infty)\|_X+\left(\int_0^{+\infty}\|f^{\prime}_{\sigma}\|^p_{\mathscr{H}_q(X)}\sigma^{p-1}d\sigma\right)^{1/p}\leq C\|f\|_{\mathscr{H}^+_q(X)}.\end{align*}$$
Proof Let
$P(s)=\sum _{n=1}^{N}x_nn^{-s}$
belong to
$\mathcal {P}(X)$
. Define
$$\begin{align*}h(u,s):=P_u(s)=\sum_{n=1}^{N}x_nn^{-s}n^{-u},\quad u\in\mathbb{C}_0.\end{align*}$$
Applying first [Reference Defant and Pérez15, Theorem 2.1] and then (2.1) twice, we obtain that
$$ \begin{align*} \|h\|^p_{\mathscr{H}^+_p(\mathscr{H}_q(X))} &=\|h\|^p_{\mathscr{H}_p(\mathscr{H}_q(X))}\\ &=\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^{N}(x_nn^{-s})z^{\nu(n)}\right\|^p_{\mathscr{H}_q(X)}dm_{\infty}(z)\\ &=\int_{\mathbb{T}^{\infty}}\left(\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^{N}x_nz^{\nu(n)}w^{\nu(n)}\right\|^q_X dm_{\infty}(w)\right)^{p/q}dm_{\infty}(z), \end{align*} $$
which, by the rotation invariance of
$m_{\infty }$
, yields
$$ \begin{align*} \|h\|^p_{\mathscr{H}^+_p(\mathscr{H}_q(X))} &=\int_{\mathbb{T}^{\infty}}\left(\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^{N}x_nz^{\nu(n)}w^{\nu(n)}\right\|^q_X dm_{\infty}(w)\right)^{p/q}dm_{\infty}(z)\\ &=\left(\int_{\mathbb{T}^{\infty}}\left\|\sum_{n=1}^{N}x_nw^{\nu(n)}\right\|^q_Xdm_{\infty}(w)\right)^{p/q}. \end{align*} $$
Then, using (2.1) again, we establish that
$$\begin{align*}\|h\|^p_{\mathscr{H}^+_p(\mathscr{H}_q(X))}=\|P\|^p_{\mathscr{H}_q(X)}.\end{align*}$$
It follows from [Reference Davis, Garling and Tomczak-Jaegermann12, Theorem 4.1] that
$L_q(\mathbb {T}^{\infty },X)$
is p-uniformly PL-convex, which implies that
$\mathscr {H}_q(X)$
is p-uniformly PL-convex. Therefore, we may apply Theorem 1.2 to obtain that
$$ \begin{align*} \|h(+\infty)\|_{\mathscr{H}_q(X)}+\left(\int_0^{+\infty}\|h^{\prime}_{\sigma}\|^p_{\mathscr{H}_p(\mathscr{H}_q(X))}\sigma^{p-1}d\sigma\right)^{1/p}\\ \leq C\|h\|_{\mathscr{H}^+_p(\mathscr{H}_q(X))}=C\|P\|_{\mathscr{H}_q(X)}. \end{align*} $$
It is clear that
$\|h(+\infty )\|_{\mathscr {H}_q(X)}=\|P(+\infty )\|_{X}$
. Moreover, using again both (2.1) and the rotation invariance as above gives that
$\|h^{\prime }_{\sigma }\|^p_{\mathscr {H}_p(\mathscr {H}_q(X))}=\|P^{\prime }_{\sigma }\|^p_{\mathscr {H}_q(X)}$
for any
$\sigma>0$
. Consequently,
$$\begin{align*}\|P(+\infty)\|_{X}+\left(\int_0^{+\infty}\|P^{\prime}_{\sigma}\|^p_{\mathscr{H}_q(X)}\sigma^{p-1}d\sigma\right)^{1/p}\leq C\|P\|_{\mathscr{H}_q(X)}.\end{align*}$$
Arguing as in the proof of Theorem 1.2, we can establish the desired result.
The following theorem concerns
$f\in \mathscr {H}^+_q(X)$
with p-uniformly PL-convex space X, where
$2\leq p\leq q$
.
Theorem 2.8 Let
$2\leq p\leq q<\infty $
, and let X be p-uniformly PL-convex. Then there exists
$C>0$
such that for any
$f\in \mathscr {H}^+_q(X)$
,
$$ \begin{align*} \|f(+\infty)\|_X+\left(\int_0^{+\infty}\int_{\mathbb{T}^{\infty}}\left\|\mathfrak{B}^{-1}(f^{\prime}_{\sigma})(z)\right\|^p_X \left\|\mathfrak{B}^{-1}(f_{\sigma})(z)\right\|^{q-p}_Xdm_{\infty}(z)\sigma^{p-1}d\sigma\right)^{1/q}\\ \leq C\|f\|_{\mathscr{H}^+_q(X)}. \end{align*} $$
Proof If
$f\in \mathscr {H}^+_q(X)$
, then, for any
$\sigma>0$
, by Proposition 2.3,
$f^{\prime }_{\sigma }\in \mathscr {H}_q(X)$
. Also, by definition,
$f_{\sigma }\in \mathscr {H}_q(X)$
for all
$\sigma>0$
. Hence both
$\mathfrak {B}^{-1}(f_{\sigma })$
and
$\mathfrak {B}^{-1}(f^{\prime }_{\sigma })$
are well-defined.
Using [Reference Blasco and Pavlović4, Theorem 2.6] instead of (1.1), and arguing as in the proof of Theorem 1.2, we obtain that for any
$g\in \mathscr {H}_q(X)$
,
$$ \begin{align} \nonumber\|g(+\infty)\|^q_X+\int_0^{+\infty}\sigma^{p-1}\int_{\mathbb{T}^{\infty}}\left\|\mathfrak{B}^{-1}(g^{\prime}_{\sigma})\right\|^p_X \left\|\mathfrak{B}^{-1}(g_{\sigma})\right\|^{q-p}_Xdm_{\infty}d\sigma\\ \leq C\|g\|^q_{\mathscr{H}_q(X)}. \end{align} $$
Suppose now
$f\in \mathscr {H}^+_q(X)$
. Then for any
$\delta>0$
, applying (2.8) to
$f_{\delta }$
yields that
$$ \begin{align*} \|f(+\infty)\|^q_X+\int_0^{+\infty}\sigma^{p-1}\int_{\mathbb{T}^{\infty}}\left\|\mathfrak{B}^{-1}(f^{\prime}_{\sigma+\delta})\right\|^p_X \left\|\mathfrak{B}^{-1}(f_{\sigma+\delta})\right\|^{q-p}_Xdm_{\infty}d\sigma\\ \leq C\|f\|^q_{\mathscr{H}^+_q(X)}. \end{align*} $$
Equivalently,
where 
is the characteristic function of
$[\delta ,+\infty )$
. Since the above inequality holds for any
$\delta>0$
, letting
$\delta \to 0$
and using Fatou’s lemma, we conclude the desired result.
3 Concluding remarks
In the case
$1\leq p\leq 2$
, the following Littlewood–Paley inequality for scalar-valued analytic functions on the unit disk
$\mathbb {D}$
is well-known (see [Reference Littlewood and Paley26] or [Reference Jevtić, Vukotić and Arsenović21, Theorem 4.4.4]):
$$ \begin{align} \|f\|_{H_p(\mathbb{D})}\leq|f(0)|+C\left(\int_{\mathbb{D}}|f'(\xi)|^p(1-|\xi|^2)^{p-1}dA(\xi)\right)^{1/p}. \end{align} $$
This inequality should be understood as follows: if the integral at the right-hand side is finite, then
$f\in H_p(\mathbb {D})$
and the norm of f is less than or equal to the quantity at the right-hand side. However, if the integral is infinite, then nothing can be said about f. Based on (3.1), we can use the same method as in the proof of Theorem 1.2 to establish the following Littlewood–Paley inequality for scalar-valued Dirichlet series.
Theorem 3.1 Let
$1\leq p\leq 2$
and
$f\in \mathcal {D}$
. If for any
$\sigma>0$
,
$f^{\prime }_{\sigma }\in \mathscr {H}_p$
, and
$$\begin{align*}\int_0^{+\infty}\|f^{\prime}_{\sigma}\|^p_{\mathscr{H}_p}\sigma^{p-1}d\sigma<\infty,\end{align*}$$
then
$f\in \mathscr {H}_p$
. Moreover, there exists some constant
$C>0$
, independent of f, such that
$$\begin{align*}\|f\|_{\mathscr{H}_p}\leq |f(+\infty)|+C\left(\int_0^{+\infty}\|f^{\prime}_{\sigma}\|^p_{\mathscr{H}_p}\sigma^{p-1}d\sigma\right)^{1/p}.\end{align*}$$
In other words, if
$1\leq p\leq 2$
, then
$\mathscr {D}^p_{p-1}\subset \mathscr {H}_p$
, and the inclusion is bounded.
In order to establish the vector-valued version of the above theorem, one need to find the vector-valued version of (3.1). For harmonic functions on
$\mathbb {D}$
with values in a real, p-uniformly smooth Banach space, this was done in [Reference Avetisyan, Djordjević and Pavlović1]. Therefore, it is reasonable to guess that, for analytic functions on
$\mathbb {D}$
with values in a complex Banach space, the inequality of the form (3.1) is related to some complex smoothness. However, to the best of our knowledge, we cannot find any references devoted to the notion of complex smoothness of Banach spaces. Here we are going to make some elementary attempts on this direction. Motivated by the modulus of smoothness of a real Banach space (see [Reference Lindenstrauss and Tzafriri25, Definition 1.e.1]), we define the modulus of PL-smoothness
$\rho _1^X(\tau )$
(
$\tau>0$
) of a complex Banach space X as follows:
$$\begin{align*}\rho_1^X(\tau):=\sup\left\{\int_{\mathbb{T}}\|x+\xi y\|_Xdm(\xi)-1:x,y\in X,\ \|x\|_X=1,\ \|y\|_X=\tau\right\}.\end{align*}$$
The Banach space X is said to be uniformly PL-smooth if
$\lim _{\tau \to 0}\rho ^X_1(\tau )/\tau =0$
, and for
$1<p\leq 2$
, X is said to be p-uniformly PL-smooth if there exists
$C>0$
such that
$\rho ^X_1(\tau )\leq C\tau ^p$
for
$\tau>0$
. For any
$1<p\leq 2$
, it is not difficult to see that if there exists
$C>0$
such that for any X-valued analytic function f on
$\mathbb {D}$
,
$$\begin{align*}\|f\|_{H_p(\mathbb{D},X)}\leq\left(\|f(0)\|^p_X+C\int_{\mathbb{D}}\|f'(\xi)\|^p_{X}(1-|\xi|^2)^{p-1}dA(\xi)\right)^{1/p},\end{align*}$$
then X is p-uniformly PL-smooth. In order to establish the reverse implication, one need to consider the dual relation between uniform PL-smoothness and uniform PL-convexity (see [Reference Lindenstrauss and Tzafriri25, Proposition 1.e.2] for the dual relation in real Banach spaces). This is of independent interest and is worthy to be investigated further.
Acknowledgements
The author would like to thank the referee for his/her valuable comments and suggestions which improved the final version of presentation.
