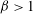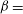1 Background
The groundbreaking effort of Velikhov (Reference Velikhov1959) and the pioneering work of Balbus & Hawley (Reference Balbus and Hawley1991) has led to a generally accepted explanation that the magnetorotational instability (MRI) is responsible for the existence of turbulence in accretion disks and provides a possible anomalous transport mechanism for particle accretion by compact astrophysical objects while angular momentum is transport outward. Cylindrical numerical simulations retaining the drive for magnetorotational instability indicate that the flow in the washer-shaped disk becomes turbulent with angular momentum redistribution (Hawley & Balbus Reference Hawley and Balbus1991). Later simulations observed turbulent angular momentum distribution by continuing to omit the vertical component of gravity and neglecting pressure and density gradients (Hawley, Gammie & Balbus Reference Hawley, Gammie and Balbus1995). These early analytic results focused on the incompressible limit and the early simulation of Hawley & Balbus (Reference Hawley and Balbus1991) indicated insensitivity to compressibility. Even more recent simulations (Stone, Pringle & Begelman Reference Stone, Pringle and Begelman1999; Stone & Pringle Reference Stone and Pringle2001) apply a vertical magnetic field to the polytropic (or adiabatic) hydrodynamic equilibrium of Papaloizou & Pringle (Reference Papaloizou and Pringle1984). Other treatments exist (Ogilvie Reference Ogilvie1998), but most treatments seem to assume strict Keplerian motion by which we mean the gravitational and centrifugal forces are in exact balance at the equatorial plane. When this assumption is removed, recent stratified shearing box simulations exhibit some sensitivity to compressibility (McNally & Pessah Reference McNally and Pessah2015). Here we assume a magnetized equilibrium and allow for general compressibility, more general rotational motion allowing an imbalance between the gravitational and centrifugal forces, and a fully self-consistent equilibrium with density variation. We find that all these ingredients are important in the overall stability threshold. However, when the motion is strictly Keplerian we show that both compressibility and density variation effects are absent, but departures from an axial magnetic field provide further destabilization. Interestingly, in the non-gravitational, axial magnetic field limit of Velikhov (Reference Velikhov1959) we find that density gradient effects are always present for a careful treatment of compressibility.
The MRI is thought to play a role in the formation of stars (Stone et al. Reference Stone, Gammie, Balbus, Hawley, Mannings, Boss and Russell2000), the production of X-rays in neutron star and black hole systems (Blaes Reference Blaes, Menard, Pelletier, Beskin and Dalibard2004) and the creation of gamma-ray bursts (Wheeler Reference Wheeler2004). Local numerical investigations indicate that the magnetorotational instability allows mass to be accreted by the central compact object while angular momentum is transported radially outwards (Hawley et al. Reference Hawley, Gammie and Balbus1995; Hawley, Gammie & Balbus Reference Hawley, Gammie and Balbus1996; Stone et al. Reference Stone, Hawley, Gammie and Balbus1996) and that the instability might result in a magnetohydrodynamic (MHD) accretion disk dynamo generating a self-sustaining magnetic field. A possible implication is that a re-examination of stability for a fully self-consistent rotating and magnetized global gravitational equilibrium with compressibility and density gradient effects retained is a natural and needed step.
The lack of a fully self-consistent magnetized three-dimensional equilibrium in the presence of gravity is a shortcoming of previous work that can now be better addressed thanks to the self-similar equilibrium model recently formulated by Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015) and solved analytically and numerically by Catto, Pusztai & Krasheninnikov (Reference Catto, Pusztai and Krasheninnikov2015). This global equilibrium model allows, but does not require, strict Keplerian motion in the equatorial plane. It fully retains the imbalance between the cylindrical centrifugal force and the central gravitational force that makes disk equilibria possible for some parameter ranges. Moreover, the condition for unstable modes to fit in the plasma disk results in the disk width entering the condition for instability. Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) have shown numerically that the
![]() $\unicode[STIX]{x1D6FD}\ll 1$
equilibria found analytically by Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015) actually require a toroidal magnetic field as well. However, in the more interesting
$\unicode[STIX]{x1D6FD}\ll 1$
equilibria found analytically by Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015) actually require a toroidal magnetic field as well. However, in the more interesting
![]() $\unicode[STIX]{x1D6FD}>1$
limit, both numerical and analytic equilibrium solutions are found without a toroidal magnetic field. The work herein only considers magnetorotational stability in this zero toroidal magnetic field limit, since retaining it substantially complicates the analysis.
$\unicode[STIX]{x1D6FD}>1$
limit, both numerical and analytic equilibrium solutions are found without a toroidal magnetic field. The work herein only considers magnetorotational stability in this zero toroidal magnetic field limit, since retaining it substantially complicates the analysis.
In the following sections we re-consider ideal magnetohyrodynamic magnetorotational stability. We begin by briefly summarizing in § 2 the axisymmetric equilibrium equations for a general poloidal magnetic field satisfying the constraints imposed by the kinetic equation for a drifting Maxwellian (Hinton & Wong Reference Hinton and Wong1985; Catto, Bernstein & Tessarotto Reference Catto, Bernstein and Tessarotto1987; Helander Reference Helander2014). In § 3 we then derive the linearized equations for an arbitrary axisymmetric perturbation in a hot, compressible, finite
![]() $\unicode[STIX]{x1D6FD}$
, magnetized plasma rotating in a gravitational field. We then investigate the general magnetorotational stability condition for arbitrary
$\unicode[STIX]{x1D6FD}$
, magnetized plasma rotating in a gravitational field. We then investigate the general magnetorotational stability condition for arbitrary
![]() $\unicode[STIX]{x1D6FD}$
when the magnetic field is assumed axial. The results without gravity in § 4 are consistent with Velikhov (Reference Velikhov1959), and the eikonal results of §§ 5 and 6 with gravity reduce to Balbus & Hawley (Reference Balbus and Hawley1991) in the strict Keplerian limit. The Velikhov case without gravity is considered to illustrate our analysis technique in the simplest possible limit and to contrast its differences with the gravitational cases that follow. A self-consistent equilibrium without gravity (Catto & Krasheninnikov Reference Catto and Krasheninnikov2015) allows us to make a further connection to the seminal work of Velikhov (Reference Velikhov1959) in the unbounded plasma limit (most of Velikhov’s analysis is for plasma bounded by two rotating cylindrical surfaces). Unlike Velikhov, we allow compressibility and radial density variation. To make further connections to the insightful astrophysical work of Balbus & Hawley (Reference Balbus and Hawley1991) we retain compressibility and density gradient effects when the rotation is not strictly Keplerian as both impact the stability threshold. Moreover, we also apply our stability results to the self-consistent magnetized gravitational equilibrium recently found by Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) In this case we account for the thinness of the self-consistent plasma disk width when
$\unicode[STIX]{x1D6FD}$
when the magnetic field is assumed axial. The results without gravity in § 4 are consistent with Velikhov (Reference Velikhov1959), and the eikonal results of §§ 5 and 6 with gravity reduce to Balbus & Hawley (Reference Balbus and Hawley1991) in the strict Keplerian limit. The Velikhov case without gravity is considered to illustrate our analysis technique in the simplest possible limit and to contrast its differences with the gravitational cases that follow. A self-consistent equilibrium without gravity (Catto & Krasheninnikov Reference Catto and Krasheninnikov2015) allows us to make a further connection to the seminal work of Velikhov (Reference Velikhov1959) in the unbounded plasma limit (most of Velikhov’s analysis is for plasma bounded by two rotating cylindrical surfaces). Unlike Velikhov, we allow compressibility and radial density variation. To make further connections to the insightful astrophysical work of Balbus & Hawley (Reference Balbus and Hawley1991) we retain compressibility and density gradient effects when the rotation is not strictly Keplerian as both impact the stability threshold. Moreover, we also apply our stability results to the self-consistent magnetized gravitational equilibrium recently found by Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) In this case we account for the thinness of the self-consistent plasma disk width when
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. In § 7 and the appendix we consider the stability of arbitrary
$\unicode[STIX]{x1D6FD}\gg 1$
. In § 7 and the appendix we consider the stability of arbitrary
![]() $\unicode[STIX]{x1D6FD}$
non-axial, magnetic field equilibria.
$\unicode[STIX]{x1D6FD}$
non-axial, magnetic field equilibria.
2 Equilibrium
We consider the stability of a hot, axisymmetric magnetized plasma rotating toroidally in a gravitational field. We assume the unperturbed axisymmetric magnetic field,
![]() $\boldsymbol{B}_{0}$
, has no toroidal component so we can write
$\boldsymbol{B}_{0}$
, has no toroidal component so we can write
where
![]() $\unicode[STIX]{x1D701}$
is the toroidal angle and
$\unicode[STIX]{x1D701}$
is the toroidal angle and
![]() $\unicode[STIX]{x1D713}_{0}$
is the unperturbed poloidal flux function. The unperturbed velocity
$\unicode[STIX]{x1D713}_{0}$
is the unperturbed poloidal flux function. The unperturbed velocity
![]() $\boldsymbol{V}_{0}$
must be toroidal to satisfy the constraints (
$\boldsymbol{V}_{0}$
must be toroidal to satisfy the constraints (
![]() $\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{V}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
and
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{V}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
and
![]() $\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T_{0}=0$
) imposed on a drifting Maxwellian solution in an axisymmetric system by the gyro-averaged kinetic equation in the presence of Coulomb collisions (Hinton & Wong Reference Hinton and Wong1985; Catto et al.
Reference Catto, Bernstein and Tessarotto1987; Helander Reference Helander2014):
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T_{0}=0$
) imposed on a drifting Maxwellian solution in an axisymmetric system by the gyro-averaged kinetic equation in the presence of Coulomb collisions (Hinton & Wong Reference Hinton and Wong1985; Catto et al.
Reference Catto, Bernstein and Tessarotto1987; Helander Reference Helander2014):
where the toroidal rotation frequency
![]() $\unicode[STIX]{x1D6FA}$
is related to the electrostatic potential
$\unicode[STIX]{x1D6FA}$
is related to the electrostatic potential
![]() $\unicode[STIX]{x1D6F7}_{0}$
by
$\unicode[STIX]{x1D6F7}_{0}$
by
![]() $\unicode[STIX]{x1D6FA}=c\,\text{d}\unicode[STIX]{x1D6F7}_{0}/\text{d}\unicode[STIX]{x1D713}_{0}$
with the electric field given by
$\unicode[STIX]{x1D6FA}=c\,\text{d}\unicode[STIX]{x1D6F7}_{0}/\text{d}\unicode[STIX]{x1D713}_{0}$
with the electric field given by
![]() $\boldsymbol{E}_{0}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\,\text{d}\unicode[STIX]{x1D6F7}_{0}/\text{d}\unicode[STIX]{x1D713}_{0}$
,
$\boldsymbol{E}_{0}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\,\text{d}\unicode[STIX]{x1D6F7}_{0}/\text{d}\unicode[STIX]{x1D713}_{0}$
,
![]() $R$
the cylindrical radius from the axis of symmetry and
$R$
the cylindrical radius from the axis of symmetry and
![]() $c$
the speed of light. We have used
$c$
the speed of light. We have used
![]() $c\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}=\boldsymbol{V}_{0}\times \boldsymbol{B}_{0}$
and
$c\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}=\boldsymbol{V}_{0}\times \boldsymbol{B}_{0}$
and
![]() $\boldsymbol{B}_{o}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}=0$
to find that the electrostatic potential
$\boldsymbol{B}_{o}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}=0$
to find that the electrostatic potential
![]() $\unicode[STIX]{x1D6F7}_{0}$
, and therefore
$\unicode[STIX]{x1D6F7}_{0}$
, and therefore
![]() $\unicode[STIX]{x1D6FA}$
, must be a flux function to lowest order. The ideal gas relation between the total unperturbed pressure
$\unicode[STIX]{x1D6FA}$
, must be a flux function to lowest order. The ideal gas relation between the total unperturbed pressure
![]() $p_{0}$
and the ion density
$p_{0}$
and the ion density
![]() $n_{0},p_{0}=n_{0}(T_{0i}+ZT_{0e})=2n_{0}T_{0}$
, defines the effective temperature
$n_{0},p_{0}=n_{0}(T_{0i}+ZT_{0e})=2n_{0}T_{0}$
, defines the effective temperature
![]() $T_{0}$
, with
$T_{0}$
, with
![]() $T_{0i}$
and
$T_{0i}$
and
![]() $T_{0e}$
the unperturbed ion and electron temperatures.
$T_{0e}$
the unperturbed ion and electron temperatures.
We write the gravitational potential
![]() $G$
as
$G$
as
with
![]() $G_{0}$
the gravitational constant,
$G_{0}$
the gravitational constant,
![]() $r$
the spherical radius and
$r$
the spherical radius and
![]() $M_{0}$
the mass of the astrophysical body that is assumed to be a massive localized source centred at
$M_{0}$
the mass of the astrophysical body that is assumed to be a massive localized source centred at
![]() $r=0$
, such that
$r=0$
, such that
![]() $R=r$
sin
$R=r$
sin
![]() $\unicode[STIX]{x1D717}$
with
$\unicode[STIX]{x1D717}$
with
![]() $\unicode[STIX]{x1D717}$
the angle from the axis of symmetry. We define our spherical and cylindrical coordinates to satisfy
$\unicode[STIX]{x1D717}$
the angle from the axis of symmetry. We define our spherical and cylindrical coordinates to satisfy
![]() $r\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}=R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \unicode[STIX]{x1D735}r$
and
$r\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}=R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \unicode[STIX]{x1D735}r$
and
![]() $\unicode[STIX]{x1D735}z=R\unicode[STIX]{x1D735}R\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D735}z=R\unicode[STIX]{x1D735}R\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
.
The hot magnetized plasma must adjust its flux surfaces to satisfy Ampere’s law and total momentum balance under the influence of the attractive force of gravity and the outward centrifugal and plasma pressure forces:
where
![]() $M$
is the mass of the plasma ions and the plasma is quasi-neutral (
$M$
is the mass of the plasma ions and the plasma is quasi-neutral (
![]() $Zn_{0}=n_{0e}=\text{electron}$
density, with
$Zn_{0}=n_{0e}=\text{electron}$
density, with
![]() $Z$
the charge number of the ions). Importantly, the density must satisfy total parallel momentum balance
$Z$
the charge number of the ions). Importantly, the density must satisfy total parallel momentum balance
with both
![]() $T_{0}$
and the unperturbed normalizing density
$T_{0}$
and the unperturbed normalizing density
![]() $\unicode[STIX]{x1D702}_{0}$
(which we refer to as the psuedo-density to distinguish it from
$\unicode[STIX]{x1D702}_{0}$
(which we refer to as the psuedo-density to distinguish it from
![]() $n_{0}$
) flux functions,
$n_{0}$
) flux functions,
and
![]() $\ell n$
the natural logarithm. The density and pseudo-density are related by a poloidally varying Maxwell–Boltzmann exponential factor
$\ell n$
the natural logarithm. The density and pseudo-density are related by a poloidally varying Maxwell–Boltzmann exponential factor
![]() $\unicode[STIX]{x1D705}_{0}$
that conveniently accounts for the mismatch between the centrifugal and gravitational potentials
$\unicode[STIX]{x1D705}_{0}$
that conveniently accounts for the mismatch between the centrifugal and gravitational potentials
The parallel momentum constraint determines
![]() $\unicode[STIX]{x1D705}_{0}$
within a flux function that can be set to zero by absorbing it into the pseudo-density
$\unicode[STIX]{x1D705}_{0}$
within a flux function that can be set to zero by absorbing it into the pseudo-density
![]() $\unicode[STIX]{x1D702}_{0}$
. As a result, (2.5) and (2.7) yield
$\unicode[STIX]{x1D702}_{0}$
. As a result, (2.5) and (2.7) yield
showing that the flux surfaces and poloidal variation of the density in the plasma pressure must adjust to maintain parallel force balance between the inward central gravitational force and the outward cylindrical rotation.
The preceding constraints differ from a true hydrodynamic equilibrium. For a drifting Maxwellian to satisfy the Boltzmann equation, constant
![]() $T_{0},\unicode[STIX]{x1D6FA}$
and
$T_{0},\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D702}_{0}$
are required in the Maxwell–Boltzmann density relation
$\unicode[STIX]{x1D702}_{0}$
are required in the Maxwell–Boltzmann density relation
![]() $n_{0}=\unicode[STIX]{x1D702}_{0}\exp [(M/2T_{0})(\unicode[STIX]{x1D6FA}^{2}R^{2}-2G)]$
. If we allow
$n_{0}=\unicode[STIX]{x1D702}_{0}\exp [(M/2T_{0})(\unicode[STIX]{x1D6FA}^{2}R^{2}-2G)]$
. If we allow
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
, using
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
, using
![]() $\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D735}G=0$
in the momentum conservation,
$\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D735}G=0$
in the momentum conservation,
![]() $n_{0}^{-1}\unicode[STIX]{x1D735}p_{0}=M(\unicode[STIX]{x1D735}G-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)$
, gives
$n_{0}^{-1}\unicode[STIX]{x1D735}p_{0}=M(\unicode[STIX]{x1D735}G-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)$
, gives
![]() $\unicode[STIX]{x1D735}n_{0}\times \unicode[STIX]{x1D735}T_{0}=0$
. However, we desire a solution with
$\unicode[STIX]{x1D735}n_{0}\times \unicode[STIX]{x1D735}T_{0}=0$
. However, we desire a solution with
![]() $n_{0}=n_{0}(R,z)$
, so we need to keep
$n_{0}=n_{0}(R,z)$
, so we need to keep
![]() $T_{0}$
constant. Keeping
$T_{0}$
constant. Keeping
![]() $\unicode[STIX]{x1D702}_{0}$
constant, then
$\unicode[STIX]{x1D702}_{0}$
constant, then
![]() $n_{0}=\unicode[STIX]{x1D702}_{0}\exp [(M/T_{0})(\int \text{d}R\,\unicode[STIX]{x1D6FA}^{2}R-G)]$
. Then
$n_{0}=\unicode[STIX]{x1D702}_{0}\exp [(M/T_{0})(\int \text{d}R\,\unicode[STIX]{x1D6FA}^{2}R-G)]$
. Then
![]() $f$
or example, angular momentum can be preserved by assuming constant
$f$
or example, angular momentum can be preserved by assuming constant
![]() $\unicode[STIX]{x1D6FA}R^{2}$
, to obtain
$\unicode[STIX]{x1D6FA}R^{2}$
, to obtain
![]() $n_{0}=\unicode[STIX]{x1D702}_{0}\exp [-(M/2T_{0})(\unicode[STIX]{x1D6FA}^{2}R^{2}+2G)]$
. Perhaps, more interestingly, assuming
$n_{0}=\unicode[STIX]{x1D702}_{0}\exp [-(M/2T_{0})(\unicode[STIX]{x1D6FA}^{2}R^{2}+2G)]$
. Perhaps, more interestingly, assuming
![]() $\unicode[STIX]{x1D6FA}^{2}R^{3}=MM_{0}G_{0}$
and defining
$\unicode[STIX]{x1D6FA}^{2}R^{3}=MM_{0}G_{0}$
and defining
![]() $2g=MM_{0}G_{0}/T_{0}R_{0}$
, with
$2g=MM_{0}G_{0}/T_{0}R_{0}$
, with
![]() $R_{0}$
an arbitrary equatorial plane reference location, gives
$R_{0}$
an arbitrary equatorial plane reference location, gives
![]() $n_{0}=\unicode[STIX]{x1D702}_{0}\exp \{-2g[(R_{0}/R)-(R_{0}/r)]\}$
, with
$n_{0}=\unicode[STIX]{x1D702}_{0}\exp \{-2g[(R_{0}/R)-(R_{0}/r)]\}$
, with
![]() $r>R$
so that
$r>R$
so that
![]() $n_{0}/\unicode[STIX]{x1D702}_{0}<1$
. Notice that
$n_{0}/\unicode[STIX]{x1D702}_{0}<1$
. Notice that
![]() $n_{0}(r=R)=\unicode[STIX]{x1D702}_{0}$
is the density at the equatorial plane, and that for
$n_{0}(r=R)=\unicode[STIX]{x1D702}_{0}$
is the density at the equatorial plane, and that for
![]() $g\gg 1$
a thin plasma disk occurs.
$g\gg 1$
a thin plasma disk occurs.
The
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}$
and
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}$
and
![]() $\unicode[STIX]{x1D735}r$
components of Ampere’s law,
$\unicode[STIX]{x1D735}r$
components of Ampere’s law,
![]() $c\unicode[STIX]{x1D735}\times \boldsymbol{B}_{0}=4\unicode[STIX]{x03C0}\boldsymbol{J}_{0}$
, require
$c\unicode[STIX]{x1D735}\times \boldsymbol{B}_{0}=4\unicode[STIX]{x03C0}\boldsymbol{J}_{0}$
, require
![]() $\boldsymbol{J}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}=0$
and
$\boldsymbol{J}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}=0$
and
![]() $\boldsymbol{J}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r=0$
giving
$\boldsymbol{J}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r=0$
giving
![]() $\boldsymbol{J}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
. As a result, there is unperturbed current only in the toroidal direction
$\boldsymbol{J}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
. As a result, there is unperturbed current only in the toroidal direction
The toroidal component of Ampere’s law gives the Grad–Shafranov equation,
that must be solved to find the equilibrium flux surfaces.
3 Linearized equations
Linear stability is normally examined by perturbing about a presumed equilibrium to find the conditions for instability. However, a self-consistent equilibrium normally imposes additional constraints that can determine whether these unstable conditions are accessible. Consequently, the actual stability of a system can only be determined for a fully self-consistent equilibrium. Said another way, we want to avoid instability being an artefact of perturbing around a state that has not fully relaxed to a self-consistent magnetized equilibrium. Consequently, we perturb about an equilibrium satisfying (2.5) and (2.10)
We investigate the stability of our axisymmetric equilibrium to axisymmetric ideal MHD perturbations with adiabatic index
![]() $\unicode[STIX]{x1D6FE}=5/3$
. We denote linearized quantities by a subscript ‘1’ except for
$\unicode[STIX]{x1D6FE}=5/3$
. We denote linearized quantities by a subscript ‘1’ except for
![]() $B_{\unicode[STIX]{x1D701}}$
, the toroidal component of the perturbed magnetic field
$B_{\unicode[STIX]{x1D701}}$
, the toroidal component of the perturbed magnetic field
![]() $\boldsymbol{B}_{1}$
, and the displacement vector
$\boldsymbol{B}_{1}$
, and the displacement vector
![]() $\unicode[STIX]{x1D743}$
, which is related to the perturbed velocity
$\unicode[STIX]{x1D743}$
, which is related to the perturbed velocity
![]() $\boldsymbol{V}_{1}$
by
$\boldsymbol{V}_{1}$
by
The total (unperturbed plus perturbed) conservation of number and energy equations,
are then conveniently used to obtain the perturbed density and pressure,
![]() $n_{1}$
and
$n_{1}$
and
![]() $p_{1}$
, as
$p_{1}$
, as
since
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{V}_{0}=0=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n_{1}\boldsymbol{V}_{0})=\boldsymbol{V}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{1}$
. The unperturbed particle and energy conservation equations are satisfied by the unperturbed flow so there is no need to assume an unperturbed adiabatic or polytropic relation between the unperturbed density and pressure. If
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{V}_{0}=0=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n_{1}\boldsymbol{V}_{0})=\boldsymbol{V}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{1}$
. The unperturbed particle and energy conservation equations are satisfied by the unperturbed flow so there is no need to assume an unperturbed adiabatic or polytropic relation between the unperturbed density and pressure. If
![]() $n_{1}$
and
$n_{1}$
and
![]() $p_{1}$
are combined to eliminate
$p_{1}$
are combined to eliminate
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
the result is the entropy constraint,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
the result is the entropy constraint,
which differs in form from Balbus & Hawley (Reference Balbus and Hawley1991) who are missing the perturbed pressure term in their equations (2.2h) and (2.3a). They also employ incompressibility by using their equation (2.3c).
We desire to find a set of three equations in which only the three components of the displacement enter, as in ideal MHD without an unperturbed flow. To begin, we consider Faraday’s law for ideal MHD,
![]() $\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t=-c\unicode[STIX]{x1D735}\times \boldsymbol{E}=\unicode[STIX]{x1D735}\times (\boldsymbol{V}\times \boldsymbol{B})$
. Linearization gives the equation for the perturbed magnetic field
$\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t=-c\unicode[STIX]{x1D735}\times \boldsymbol{E}=\unicode[STIX]{x1D735}\times (\boldsymbol{V}\times \boldsymbol{B})$
. Linearization gives the equation for the perturbed magnetic field
![]() $\boldsymbol{B}_{1}$
to be
$\boldsymbol{B}_{1}$
to be
The
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
component of (3.5) gives the equation for
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
component of (3.5) gives the equation for
![]() $B_{\unicode[STIX]{x1D701}}\equiv R\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
to be
$B_{\unicode[STIX]{x1D701}}\equiv R\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
to be
where
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\,\equiv \,R\unicode[STIX]{x1D743}\!\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
, and we have used
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\,\equiv \,R\unicode[STIX]{x1D743}\!\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
, and we have used
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\boldsymbol{B}_{0}\,=\,0\,=\!\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\boldsymbol{B}_{1}\,=\,0\,=\!\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\boldsymbol{V}_{0}\,=\,0\,=\!\boldsymbol{V}_{0}\!\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\boldsymbol{B}_{1}\!\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})$
. For the poloidal components of Faraday’s law we use (3.5) to form the equation for
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\boldsymbol{B}_{0}\,=\,0\,=\!\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\boldsymbol{B}_{1}\,=\,0\,=\!\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\boldsymbol{V}_{0}\,=\,0\,=\!\boldsymbol{V}_{0}\!\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\boldsymbol{B}_{1}\!\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})$
. For the poloidal components of Faraday’s law we use (3.5) to form the equation for
![]() $\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q$
, where
$\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q$
, where
![]() $Q$
is an arbitrary axisymmetric scalar function so that
$Q$
is an arbitrary axisymmetric scalar function so that
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q=0$
. Taking advantage of axisymmetry Faraday’s law gives the simple result
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q=0$
. Taking advantage of axisymmetry Faraday’s law gives the simple result
Using
![]() $Q=\unicode[STIX]{x1D713}_{0}$
, the preceding gives
$Q=\unicode[STIX]{x1D713}_{0}$
, the preceding gives
![]() $\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}=\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})$
. Axisymmetry and
$\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}=\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})$
. Axisymmetry and
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}_{1}=0$
mean we can write
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}_{1}=0$
mean we can write
with
![]() $\unicode[STIX]{x1D713}_{1}$
the perturbed flux function defined so that
$\unicode[STIX]{x1D713}_{1}$
the perturbed flux function defined so that
![]() $\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{1}=0$
. Consequently,
$\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{1}=0$
. Consequently,
![]() $\unicode[STIX]{x1D713}_{1}=-\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}$
and we may write
$\unicode[STIX]{x1D713}_{1}=-\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}$
and we may write
Then we can form
![]() $R^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \boldsymbol{B}_{1}=-\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})$
and
$R^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \boldsymbol{B}_{1}=-\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})$
and
Finally, we turn our attention to the linearization of the momentum conservation equation,
To carry out the linearization we use
and
as well as axisymmetry. We obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t^{2}}+\unicode[STIX]{x1D6FA}R^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}(\unicode[STIX]{x1D6FA}R^{2})\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}-\unicode[STIX]{x1D6FA}R(\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\unicode[STIX]{x1D735}R\,+\,\unicode[STIX]{x1D735}R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{n_{1}}{n_{0}}\left(\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\,-\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r\right)=-\frac{\unicode[STIX]{x1D735}p_{1}}{Mn_{0}}-\frac{J_{0}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})}{cMn_{0}R}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(RB_{\unicode[STIX]{x1D701}})}{4\unicode[STIX]{x03C0}Mn_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t^{2}}+\unicode[STIX]{x1D6FA}R^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}(\unicode[STIX]{x1D6FA}R^{2})\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}-\unicode[STIX]{x1D6FA}R(\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\unicode[STIX]{x1D735}R\,+\,\unicode[STIX]{x1D735}R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{n_{1}}{n_{0}}\left(\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\,-\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r\right)=-\frac{\unicode[STIX]{x1D735}p_{1}}{Mn_{0}}-\frac{J_{0}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})}{cMn_{0}R}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(RB_{\unicode[STIX]{x1D701}})}{4\unicode[STIX]{x03C0}Mn_{0}}.\end{eqnarray}$$
Recalling (3.3) and (3.10) we see that a time derivative of (3.16) will result in an equation in which only the three components of the displacement enter.
The preceding observation leads us to taking a time derivative of the
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
component of (3.16) and inserting (3.10) yields a form in which only the displacement enters
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
component of (3.16) and inserting (3.10) yields a form in which only the displacement enters
Using parallel and radial pressure balance allows us to rewrite equation (3.16) and then dot it by
![]() $\boldsymbol{B}_{0}$
to obtain a second component, namely
$\boldsymbol{B}_{0}$
to obtain a second component, namely
where using that the unperturbed current density is azimuthal we find
![]() $\unicode[STIX]{x1D735}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{B}_{0}$
, giving
$\unicode[STIX]{x1D735}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{B}_{0}$
, giving
with
![]() $\boldsymbol{U}$
an arbitrary vector.
$\boldsymbol{U}$
an arbitrary vector.
For the final component we use
![]() $0=\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times (\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D735}Q)=\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}Q\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}Q$
to form the
$0=\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times (\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D735}Q)=\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}Q\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}Q$
to form the
![]() $\unicode[STIX]{x1D735}Q$
component of the momentum equation by noting that
$\unicode[STIX]{x1D735}Q$
component of the momentum equation by noting that
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}Q=R^{-1}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D735}R\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q$
. The result is
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}Q=R^{-1}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\,\unicode[STIX]{x1D735}R\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q$
. The result is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D735}R-\frac{n_{1}}{n_{0}}\left(\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R-\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r\right)+\frac{\unicode[STIX]{x1D735}p_{1}}{Mn_{0}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{J_{0}\unicode[STIX]{x1D735}Q\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})}{cMn_{0}R}+\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q}{4\unicode[STIX]{x03C0}Mn_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[R^{-2}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D735}R-\frac{n_{1}}{n_{0}}\left(\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R-\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r\right)+\frac{\unicode[STIX]{x1D735}p_{1}}{Mn_{0}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{J_{0}\unicode[STIX]{x1D735}Q\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})}{cMn_{0}R}+\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}Q}{4\unicode[STIX]{x03C0}Mn_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[R^{-2}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})].\end{eqnarray}$$
Equations (3.17), (3.18) and (3.20) are the key equations we will make use of to obtain our stability condition. It has only been necessary to take the extra time derivative when forming (3.17).
Only the displacement enters in equations (3.18) and (3.20), since
![]() $n_{1}$
and
$n_{1}$
and
![]() $p_{1}$
are known in terms of
$p_{1}$
are known in terms of
![]() $\unicode[STIX]{x1D743}$
. Equations (3.16)–(3.20), with (3.3) inserted, are the key equations for the three displacement components from the momentum equation. They are given in vector forms to allow us to work in any axisymmetric coordinate system we desire.
$\unicode[STIX]{x1D743}$
. Equations (3.16)–(3.20), with (3.3) inserted, are the key equations for the three displacement components from the momentum equation. They are given in vector forms to allow us to work in any axisymmetric coordinate system we desire.
4 Cylindrically symmetric magnetic field in the absence of gravity
 $(G=0)$
$(G=0)$
To illustrate the subtleties of retaining compressibility and unperturbed radial variation in a self-consistent equilibrium it is informative to first consider the simplest limit of rotation in an axial magnetic field without gravity (
![]() $G=0$
) or any unperturbed axial variation. In this limit the equilibrium magnetic field
$G=0$
) or any unperturbed axial variation. In this limit the equilibrium magnetic field
![]() $\boldsymbol{B}_{0}$
is axial and of the form
$\boldsymbol{B}_{0}$
is axial and of the form
with
![]() $\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x1D713}_{0}(R)$
and
$\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x1D713}_{0}(R)$
and
![]() $RB_{0}=\text{d}\unicode[STIX]{x1D713}_{0}/\text{d}R$
. In this cylindrical geometry limit
$RB_{0}=\text{d}\unicode[STIX]{x1D713}_{0}/\text{d}R$
. In this cylindrical geometry limit
![]() $\boldsymbol{J}_{0}\times \boldsymbol{B}_{0}=J_{0}B_{0}\unicode[STIX]{x1D735}R$
so equilibrium pressure balance has only the
$\boldsymbol{J}_{0}\times \boldsymbol{B}_{0}=J_{0}B_{0}\unicode[STIX]{x1D735}R$
so equilibrium pressure balance has only the
![]() $\unicode[STIX]{x1D735}R$
component
$\unicode[STIX]{x1D735}R$
component
and
![]() $T_{0},p_{0}$
and
$T_{0},p_{0}$
and
![]() $n_{0}$
depend only on
$n_{0}$
depend only on
![]() $R$
since the equilibrium has no axial variation.
$R$
since the equilibrium has no axial variation.
Defining the Alfvén speed by
the equation for (3.17) becomes
where we now write the displacement as
![]() $\unicode[STIX]{x1D743}=\unicode[STIX]{x1D709}_{R}\unicode[STIX]{x1D735}R+\unicode[STIX]{x1D709}_{z}\unicode[STIX]{x1D735}z+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
. We may use
$\unicode[STIX]{x1D743}=\unicode[STIX]{x1D709}_{R}\unicode[STIX]{x1D735}R+\unicode[STIX]{x1D709}_{z}\unicode[STIX]{x1D735}z+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$
. We may use
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
because
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
because
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D713}_{0})$
.
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D713}_{0})$
.
To get the remaining components we use the parallel or
![]() $Q=z$
form of (3.20) to find the
$Q=z$
form of (3.20) to find the
![]() $\unicode[STIX]{x1D709}_{z}$
equation and then insert
$\unicode[STIX]{x1D709}_{z}$
equation and then insert
![]() $p_{1}$
and use unperturbed pressure balance to find
$p_{1}$
and use unperturbed pressure balance to find
where
and
The last equation for
![]() $\unicode[STIX]{x1D709}_{R}$
follows by using
$\unicode[STIX]{x1D709}_{R}$
follows by using
![]() $Q=R$
in (3.20) and then substituting in
$Q=R$
in (3.20) and then substituting in
![]() $n_{1}$
and
$n_{1}$
and
![]() $p_{1}$
from (3.3) to obtain
$p_{1}$
from (3.3) to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{R}}{\unicode[STIX]{x2202}t^{2}}-2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}+R\unicode[STIX]{x1D6FA}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{z}}{\unicode[STIX]{x2202}z}-R\unicode[STIX]{x1D709}_{R}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]+v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{R}}{\unicode[STIX]{x2202}z^{2}}+\frac{\unicode[STIX]{x1D6FE}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\frac{p_{0}}{M}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{R}}{\unicode[STIX]{x2202}t^{2}}-2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}+R\unicode[STIX]{x1D6FA}^{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{z}}{\unicode[STIX]{x2202}z}-R\unicode[STIX]{x1D709}_{R}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]+v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{R}}{\unicode[STIX]{x2202}z^{2}}+\frac{\unicode[STIX]{x1D6FE}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\frac{p_{0}}{M}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}\right),\end{eqnarray}$$
where we eliminate
![]() $\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}R$
by using unperturbed pressure balance.
$\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}R$
by using unperturbed pressure balance.
The preceding two equations (4.5) and (4.9), along with (4.4) for
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
are the general set of equations for a cylindrically symmetric magnetic field configuration with no axial variation in the absence of gravity. The final forms of the equations for
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
are the general set of equations for a cylindrically symmetric magnetic field configuration with no axial variation in the absence of gravity. The final forms of the equations for
![]() $\unicode[STIX]{x1D709}_{R}$
and
$\unicode[STIX]{x1D709}_{R}$
and
![]() $\unicode[STIX]{x1D709}_{z}$
allow us to be sure that we are carefully treating all terms in
$\unicode[STIX]{x1D709}_{z}$
allow us to be sure that we are carefully treating all terms in
![]() $n_{1}$
and
$n_{1}$
and
![]() $p_{1}$
.
$p_{1}$
.
To simplify the description we Fourier transform in
![]() $z$
and seek solutions harmonic in time by assuming
$z$
and seek solutions harmonic in time by assuming
We obtain the three equations for the three components of the displacement
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\right)\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\text{i}k_{z}\left[R\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{z}-\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\right)\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\text{i}k_{z}\left[R\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{z}-\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})\right].\end{eqnarray}$$
First, eliminating
![]() $\unicode[STIX]{x1D709}_{z}$
by substituting (4.12) into (4.13) gives
$\unicode[STIX]{x1D709}_{z}$
by substituting (4.12) into (4.13) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\right)\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\frac{k_{z}^{2}}{n_{0}c_{S}^{2}}\left(R\unicode[STIX]{x1D6FA}^{2}-c_{S}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right)\left\{\frac{n_{0}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\left[R\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{R}+\frac{c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\right)\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\frac{k_{z}^{2}}{n_{0}c_{S}^{2}}\left(R\unicode[STIX]{x1D6FA}^{2}-c_{S}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right)\left\{\frac{n_{0}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\left[R\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{R}+\frac{c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Then eliminating
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
from the preceding by using (4.11) gives the full radial differential equation for
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
from the preceding by using (4.11) gives the full radial differential equation for
![]() $\unicode[STIX]{x1D709}_{R}$
to be
$\unicode[STIX]{x1D709}_{R}$
to be
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-\frac{R}{n_{0}}\frac{\unicode[STIX]{x2202}(n_{0}\unicode[STIX]{x1D6FA}^{2})}{\unicode[STIX]{x2202}R}-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}\right]\unicode[STIX]{x1D709}_{R}+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{k_{z}^{2}R^{2}\unicode[STIX]{x1D6FA}^{4}\unicode[STIX]{x1D709}_{R}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\,-\frac{\unicode[STIX]{x1D714}^{2}R\unicode[STIX]{x1D709}_{R}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right]-\frac{\unicode[STIX]{x1D714}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}R^{-1}\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})/\unicode[STIX]{x2202}R}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-\frac{R}{n_{0}}\frac{\unicode[STIX]{x2202}(n_{0}\unicode[STIX]{x1D6FA}^{2})}{\unicode[STIX]{x2202}R}-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}\right]\unicode[STIX]{x1D709}_{R}+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{k_{z}^{2}R^{2}\unicode[STIX]{x1D6FA}^{4}\unicode[STIX]{x1D709}_{R}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\,-\frac{\unicode[STIX]{x1D714}^{2}R\unicode[STIX]{x1D709}_{R}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right]-\frac{\unicode[STIX]{x1D714}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}R^{-1}\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})/\unicode[STIX]{x2202}R}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right],\end{eqnarray}$$
where we have combined the
![]() $n_{0}c_{S}^{2}\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})/\unicode[STIX]{x2202}R$
terms to exactly cancel some first derivatives of
$n_{0}c_{S}^{2}\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})/\unicode[STIX]{x2202}R$
terms to exactly cancel some first derivatives of
![]() $R\unicode[STIX]{x1D709}_{R}$
terms. Equation (4.15) is the generalization of the radial differential form of Velikhov (Reference Velikhov1959) to retain compressibility. Its solution for a self-consistent equilibrium with the appropriate boundary conditions will give the exact eigenfrequencies, eigenfunctions and stability threshold condition. To retain Alfvén and sound waves and their coupling it allows
$R\unicode[STIX]{x1D709}_{R}$
terms. Equation (4.15) is the generalization of the radial differential form of Velikhov (Reference Velikhov1959) to retain compressibility. Its solution for a self-consistent equilibrium with the appropriate boundary conditions will give the exact eigenfrequencies, eigenfunctions and stability threshold condition. To retain Alfvén and sound waves and their coupling it allows
![]() $k_{z}^{2}c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\sim k_{z}^{2}v_{A}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
,
$k_{z}^{2}c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\sim k_{z}^{2}v_{A}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
,
![]() $k_{z}^{2}R^{2}\sim 1$
, and
$k_{z}^{2}R^{2}\sim 1$
, and
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}R\sim 1/R$
. These orderings will be further verified shortly when we consider the integral constraint associated with the self-adjoint form (4.15).
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}R\sim 1/R$
. These orderings will be further verified shortly when we consider the integral constraint associated with the self-adjoint form (4.15).
To perform a Wentzel–Kramers–Brillouin (WKB) analysis we must assume
so that
![]() $k_{R}^{2}R^{2}\gg 1$
, where
$k_{R}^{2}R^{2}\gg 1$
, where
![]() $\unicode[STIX]{x1D709}_{R}\propto \text{e}^{\text{i}\int \text{d}R\,k_{R}}$
. To allow
$\unicode[STIX]{x1D709}_{R}\propto \text{e}^{\text{i}\int \text{d}R\,k_{R}}$
. To allow
![]() $k_{z}^{2}R^{2}\gtrsim 1$
and correctly treat marginal stability, we order
$k_{z}^{2}R^{2}\gtrsim 1$
and correctly treat marginal stability, we order
and thereby assume
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. The geometric optics dispersion relation allowing
$\unicode[STIX]{x1D6FD}\gg 1$
. The geometric optics dispersion relation allowing
![]() $k_{R}^{2}\gtrsim k_{z}^{2}$
is then
$k_{R}^{2}\gtrsim k_{z}^{2}$
is then
where
![]() $k^{2}=k_{z}^{2}+k_{R}^{2}$
. All terms in (4.18) are allowed to be the same order. Notice that at marginality (
$k^{2}=k_{z}^{2}+k_{R}^{2}$
. All terms in (4.18) are allowed to be the same order. Notice that at marginality (
![]() $\unicode[STIX]{x1D714}^{2}\rightarrow 0$
) equation (4.18) recovers a radial density gradient term as well as the usual rotation frequency gradient
$\unicode[STIX]{x1D714}^{2}\rightarrow 0$
) equation (4.18) recovers a radial density gradient term as well as the usual rotation frequency gradient
Marginal stability is most easily determined graphically from (4.18) by examining the behaviour near
![]() $\unicode[STIX]{x1D714}^{2}=0$
. The instability window for this new result is larger than if we had assumed strict incompressibility (
$\unicode[STIX]{x1D714}^{2}=0$
. The instability window for this new result is larger than if we had assumed strict incompressibility (
![]() $c_{S}^{2}\rightarrow \infty$
). Also, (4.19) does not assume constant
$c_{S}^{2}\rightarrow \infty$
). Also, (4.19) does not assume constant
![]() $n_{0}$
as in Velikhov (Reference Velikhov1959) or
$n_{0}$
as in Velikhov (Reference Velikhov1959) or
![]() $\unicode[STIX]{x1D6FA}^{2}\propto R^{-3}$
.
$\unicode[STIX]{x1D6FA}^{2}\propto R^{-3}$
.
In the hydrodynamic limit (
![]() $v_{A}^{2}\equiv 0$
), WKB still requires
$v_{A}^{2}\equiv 0$
), WKB still requires
![]() $k_{R}R\gg 1$
, but in (4.15) we can allow
$k_{R}R\gg 1$
, but in (4.15) we can allow
![]() $c_{S}^{2}/R^{2}\sim k_{z}^{2}c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\sim R^{2}\unicode[STIX]{x1D6FA}^{4}/c_{S}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
to find
$c_{S}^{2}/R^{2}\sim k_{z}^{2}c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\sim R^{2}\unicode[STIX]{x1D6FA}^{4}/c_{S}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
to find
![]() $\unicode[STIX]{x1D714}^{2}k^{2}k_{z}^{-2}=R^{-3}n_{0}^{-1}\unicode[STIX]{x2202}(n_{0}\unicode[STIX]{x1D6FA}^{2}R^{4})/\unicode[STIX]{x2202}R-R^{2}\unicode[STIX]{x1D6FA}^{4}/\,c_{S}^{2}$
when
$\unicode[STIX]{x1D714}^{2}k^{2}k_{z}^{-2}=R^{-3}n_{0}^{-1}\unicode[STIX]{x2202}(n_{0}\unicode[STIX]{x1D6FA}^{2}R^{4})/\unicode[STIX]{x2202}R-R^{2}\unicode[STIX]{x1D6FA}^{4}/\,c_{S}^{2}$
when
![]() $\unicode[STIX]{x1D714}^{2}\ll k_{z}^{2}\,c_{S}^{2}$
. For a hydrodynamic equilibrium at constant
$\unicode[STIX]{x1D714}^{2}\ll k_{z}^{2}\,c_{S}^{2}$
. For a hydrodynamic equilibrium at constant
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
![]() $T_{0}$
and
$T_{0}$
and
![]() $\unicode[STIX]{x1D702}_{0}$
stability is assured. In fact, for
$\unicode[STIX]{x1D702}_{0}$
stability is assured. In fact, for
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
and constant
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}(R)$
and constant
![]() $T_{0}$
and
$T_{0}$
and
![]() $\unicode[STIX]{x1D702}_{0}$
, an inviscid Couette flow instability requires
$\unicode[STIX]{x1D702}_{0}$
, an inviscid Couette flow instability requires
![]() $-R\unicode[STIX]{x1D6FA}^{-2}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}/\unicode[STIX]{x2202}R>4+(\unicode[STIX]{x1D6FE}-1)M\unicode[STIX]{x1D6FA}^{2}R^{2}/\unicode[STIX]{x1D6FE}T_{0}$
, since in the fluid limit
$-R\unicode[STIX]{x1D6FA}^{-2}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}/\unicode[STIX]{x2202}R>4+(\unicode[STIX]{x1D6FE}-1)M\unicode[STIX]{x1D6FA}^{2}R^{2}/\unicode[STIX]{x1D6FE}T_{0}$
, since in the fluid limit
![]() $c_{S}^{2}\rightarrow \unicode[STIX]{x1D6FE}T_{0}/M$
and
$c_{S}^{2}\rightarrow \unicode[STIX]{x1D6FE}T_{0}/M$
and
![]() $\unicode[STIX]{x1D6FE}\rightarrow 5/3$
.
$\unicode[STIX]{x1D6FE}\rightarrow 5/3$
.
The preceding results are consistent with the following integral constraint obtained by multiplying (4.15) by
![]() $n_{0}R\unicode[STIX]{x1D709}_{R}^{\ast }$
:
$n_{0}R\unicode[STIX]{x1D709}_{R}^{\ast }$
:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }\text{d}R\,n_{0}|\unicode[STIX]{x1D709}_{R}^{2}|\left\{\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-\frac{R}{n_{0}}\frac{\unicode[STIX]{x2202}(n_{0}\unicode[STIX]{x1D6FA}^{2})}{\unicode[STIX]{x2202}R}-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.-\,\frac{k_{z}^{2}R^{2}\unicode[STIX]{x1D6FA}^{4}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\,+\frac{k_{z}^{2}R}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}\unicode[STIX]{x1D6FA}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }\text{d}R\frac{n_{0}}{R}\left[v_{A}^{2}+\frac{\unicode[STIX]{x1D714}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right]\left|\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right|^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }\text{d}R\,n_{0}|\unicode[STIX]{x1D709}_{R}^{2}|\left\{\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-\frac{R}{n_{0}}\frac{\unicode[STIX]{x2202}(n_{0}\unicode[STIX]{x1D6FA}^{2})}{\unicode[STIX]{x2202}R}-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.-\,\frac{k_{z}^{2}R^{2}\unicode[STIX]{x1D6FA}^{4}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\,+\frac{k_{z}^{2}R}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}\unicode[STIX]{x1D6FA}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }\text{d}R\frac{n_{0}}{R}\left[v_{A}^{2}+\frac{\unicode[STIX]{x1D714}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\right]\left|\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right|^{2},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D709}_{R}^{\ast }$
is the complex conjugate of
$\unicode[STIX]{x1D709}_{R}^{\ast }$
is the complex conjugate of
![]() $\unicode[STIX]{x1D709}_{R}$
and we assume the total derivative terms vanish at
$\unicode[STIX]{x1D709}_{R}$
and we assume the total derivative terms vanish at
![]() $R=0$
and infinity. At marginality this gives the threshold constraint
$R=0$
and infinity. At marginality this gives the threshold constraint
These integral constraints are consistent with the WKB dispersion relation, stability threshold condition, and our orderings, and remain valid even when geometric optics fails for
![]() $\unicode[STIX]{x1D6FD}\lesssim 1$
so that the full differential equation (4.15) must be solved. Indeed, (4.21) indicates there are no other unstable modes besides the MRI. At marginality (4.15) becomes
$\unicode[STIX]{x1D6FD}\lesssim 1$
so that the full differential equation (4.15) must be solved. Indeed, (4.21) indicates there are no other unstable modes besides the MRI. At marginality (4.15) becomes
which is consistent with our WKB treatment. We can see from (4.20) to (4.22) that we need to order
![]() $k_{z}^{2}c_{S}^{2}\sim R^{2}\unicode[STIX]{x1D6FA}^{4}/c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\,\sim k_{R}^{2}v_{A}^{2}\gtrsim k_{z}^{2}v_{A}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
for
$k_{z}^{2}c_{S}^{2}\sim R^{2}\unicode[STIX]{x1D6FA}^{4}/c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\,\sim k_{R}^{2}v_{A}^{2}\gtrsim k_{z}^{2}v_{A}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
for
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. These orderings based on the cylindrical limit provide much of the basis for the orderings in limits with gravity.
$\unicode[STIX]{x1D6FD}\gg 1$
. These orderings based on the cylindrical limit provide much of the basis for the orderings in limits with gravity.
The Velikhov (Reference Velikhov1959) condition for marginality (
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
) is obtained from
$\unicode[STIX]{x1D714}\rightarrow 0$
) is obtained from
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\text{i}k_{z}\left[R\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{z}-\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\text{i}k_{z}\left[R\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{z}-\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})\right].\end{eqnarray}$$
Inserting (4.23) into (4.25) leaves (4.24) and the radial momentum balance equation
Then eliminating
![]() $\unicode[STIX]{x1D709}_{z}$
by inserting (4.24) into (4.26) yields (4.19). To recover the incompressible limit we see that a careful treatment of the
$\unicode[STIX]{x1D709}_{z}$
by inserting (4.24) into (4.26) yields (4.19). To recover the incompressible limit we see that a careful treatment of the
![]() $c_{S}^{2}\rightarrow \infty$
terms is required.
$c_{S}^{2}\rightarrow \infty$
terms is required.
4.1 Self-consistent equilibrium for an axial magnetic field without gravity
For the exact self-similar equilibrium solution of Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015)
where
![]() $\unicode[STIX]{x1D707}=\cos \unicode[STIX]{x1D717},C$
is a constant and
$\unicode[STIX]{x1D707}=\cos \unicode[STIX]{x1D717},C$
is a constant and
![]() $\unicode[STIX]{x1D6FC}$
is an eigenvalue determined by solving the nonlinear Grad–Shafranov equation for
$\unicode[STIX]{x1D6FC}$
is an eigenvalue determined by solving the nonlinear Grad–Shafranov equation for
![]() $H$
. The density, temperature and rotation are of the form
$H$
. The density, temperature and rotation are of the form
![]() $n_{0}\propto R^{-2\unicode[STIX]{x1D6FC}-3}$
,
$n_{0}\propto R^{-2\unicode[STIX]{x1D6FC}-3}$
,
![]() $T_{0}\propto R^{-1}$
and
$T_{0}\propto R^{-1}$
and
![]() $\unicode[STIX]{x1D6FA}\propto R^{-3/2}$
, and the solution of the Grad–Shafranov equation requires
$\unicode[STIX]{x1D6FA}\propto R^{-3/2}$
, and the solution of the Grad–Shafranov equation requires
![]() $\unicode[STIX]{x1D6FC}$
to satisfy
$\unicode[STIX]{x1D6FC}$
to satisfy
For
![]() $\unicode[STIX]{x1D6FC}+2<0$
the axial magnetic field of this equilibrium model increases away from the axis of symmetry for instability. Using the preceding gives
$\unicode[STIX]{x1D6FC}+2<0$
the axial magnetic field of this equilibrium model increases away from the axis of symmetry for instability. Using the preceding gives
Then for
![]() $\unicode[STIX]{x1D6FD}\gg 1$
, inserting (4.29) our condition for instability for this self-consistent equilibrium becomes
$\unicode[STIX]{x1D6FD}\gg 1$
, inserting (4.29) our condition for instability for this self-consistent equilibrium becomes
where we must keep
![]() $k_{R}^{2}R^{2}\gg 1$
to satisfy our geometric optics treatment in the radial direction. Therefore, compressibility stabilizes the MRI for all wavelengths when
$k_{R}^{2}R^{2}\gg 1$
to satisfy our geometric optics treatment in the radial direction. Therefore, compressibility stabilizes the MRI for all wavelengths when
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}>2\unicode[STIX]{x1D6FA}^{2}R^{2}/3v_{A}^{2}\gg 1$
. Also, density variation is stabilizing since it results in the standard Balbus & Hawley (Reference Balbus and Hawley1991) result
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}>2\unicode[STIX]{x1D6FA}^{2}R^{2}/3v_{A}^{2}\gg 1$
. Also, density variation is stabilizing since it results in the standard Balbus & Hawley (Reference Balbus and Hawley1991) result
![]() $k^{2}v_{A}^{2}/3\unicode[STIX]{x1D6FA}^{2}$
being replaced by
$k^{2}v_{A}^{2}/3\unicode[STIX]{x1D6FA}^{2}$
being replaced by
![]() $k^{2}v_{A}^{2}/2\unicode[STIX]{x1D6FA}^{2}$
. It is interesting to notice that the compressibility effects hidden in the self-consistent variation of
$k^{2}v_{A}^{2}/2\unicode[STIX]{x1D6FA}^{2}$
. It is interesting to notice that the compressibility effects hidden in the self-consistent variation of
![]() $n\unicode[STIX]{x1D6FA}^{2}$
from (4.29) give rise to an implicit stabilizing compressibility effect larger than the explicit destabilizing one in (4.19).
$n\unicode[STIX]{x1D6FA}^{2}$
from (4.29) give rise to an implicit stabilizing compressibility effect larger than the explicit destabilizing one in (4.19).
Our incompressible condition for instability
![]() $2\unicode[STIX]{x1D6FA}^{2}>k^{2}v_{A}^{2}$
is consistent with the findings of Velikhov (Reference Velikhov1959) who worked in the
$2\unicode[STIX]{x1D6FA}^{2}>k^{2}v_{A}^{2}$
is consistent with the findings of Velikhov (Reference Velikhov1959) who worked in the
![]() $\unicode[STIX]{x1D6FD}\gg 1$
limit by assuming
$\unicode[STIX]{x1D6FD}\gg 1$
limit by assuming
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}=0$
so that
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}=0$
so that
![]() $c_{S}^{2}\rightarrow \infty$
. In the absence of an azimuthal unperturbed magnetic field he considered the full radial eigenvalue problem. However, he only mentions in passing ‘the flow near a cylinder rotating in an unbounded medium’ as his work focused on plasma being driven unstable between two concentric rotating cylinders. In the unbounded limit Velikhov’s quasi-classical calculation for a radial mode number of 10 at the end of his section 2 estimated magnetic fields
$c_{S}^{2}\rightarrow \infty$
. In the absence of an azimuthal unperturbed magnetic field he considered the full radial eigenvalue problem. However, he only mentions in passing ‘the flow near a cylinder rotating in an unbounded medium’ as his work focused on plasma being driven unstable between two concentric rotating cylinders. In the unbounded limit Velikhov’s quasi-classical calculation for a radial mode number of 10 at the end of his section 2 estimated magnetic fields
![]() $B_{0}<(4\unicode[STIX]{x03C0}Mn_{0})^{1/2}\unicode[STIX]{x1D6FA}R/18$
as being unstable – a condition in rough agreement with our result of
$B_{0}<(4\unicode[STIX]{x03C0}Mn_{0})^{1/2}\unicode[STIX]{x1D6FA}R/18$
as being unstable – a condition in rough agreement with our result of
![]() $2\unicode[STIX]{x1D6FA}^{2}>k_{R}^{2}v_{A}^{2}$
for
$2\unicode[STIX]{x1D6FA}^{2}>k_{R}^{2}v_{A}^{2}$
for
![]() $k_{R}R=10$
when
$k_{R}R=10$
when
![]() $3c_{S}^{2}\gg \unicode[STIX]{x1D6FA}^{2}R^{2}$
.
$3c_{S}^{2}\gg \unicode[STIX]{x1D6FA}^{2}R^{2}$
.
5 Axial magnetic field with gravity and strict Keplerian rotation
In this strict Keplerian limit in which the equilibrium magnetic field
![]() $\boldsymbol{B}_{0}$
is axial and any unperturbed axial variation caused by the imbalance of the centrifugal and gravitational forces ignored, the calculation of the previous section can be repeated by keeping gravity in the radial and axial pressure balance conditions. We order
$\boldsymbol{B}_{0}$
is axial and any unperturbed axial variation caused by the imbalance of the centrifugal and gravitational forces ignored, the calculation of the previous section can be repeated by keeping gravity in the radial and axial pressure balance conditions. We order
![]() $c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
so that we can consider the thin disk limit
$c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
so that we can consider the thin disk limit
![]() $c_{S}^{2}\ll \unicode[STIX]{x1D6FA}^{2}R^{2}$
, as well as the extended, non-disk global equilibrium that exist more generally (Catto et al.
Reference Catto, Pusztai and Krasheninnikov2015).
$c_{S}^{2}\ll \unicode[STIX]{x1D6FA}^{2}R^{2}$
, as well as the extended, non-disk global equilibrium that exist more generally (Catto et al.
Reference Catto, Pusztai and Krasheninnikov2015).
We first obtain the equations for general Keplerian rotation by letting
![]() $\unicode[STIX]{x1D6FA}^{2}\rightarrow \unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3}$
in (4.12) and (4.13) except in the
$\unicode[STIX]{x1D6FA}^{2}\rightarrow \unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3}$
in (4.12) and (4.13) except in the
![]() $2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
term in (4.13). No changes are needed in (4.11). The equations for the components of the displacement then become
$2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
term in (4.13). No changes are needed in (4.11). The equations for the components of the displacement then become
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})\,\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\frac{\text{i}k_{z}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})+\text{i}k_{z}R(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})\unicode[STIX]{x1D709}_{z}-\unicode[STIX]{x1D709}_{R}R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})\,\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\frac{\text{i}k_{z}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})+\text{i}k_{z}R(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})\unicode[STIX]{x1D709}_{z}-\unicode[STIX]{x1D709}_{R}R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Next we assume strict Keplerian rotation by using
![]() $\unicode[STIX]{x1D6FA}^{2}=M_{0}G_{0}r^{-3}$
in (5.2) and (5.3). Again, eliminating
$\unicode[STIX]{x1D6FA}^{2}=M_{0}G_{0}r^{-3}$
in (5.2) and (5.3). Again, eliminating
![]() $\unicode[STIX]{x1D709}_{z}$
first gives
$\unicode[STIX]{x1D709}_{z}$
first gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\frac{k_{z}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{4}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\frac{k_{z}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{4}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right].\end{eqnarray}$$
Then, eliminating
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
gives the radial eigenvalue equation
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
gives the radial eigenvalue equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}-R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\right]\,\unicode[STIX]{x1D709}_{R}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D714}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}-R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}\right]\,\unicode[STIX]{x1D709}_{R}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D714}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]=0.\end{eqnarray}$$
Solving by geometric optics (
![]() $k_{R}^{2}R^{2}\gg 1$
) the dispersion relation that results is
$k_{R}^{2}R^{2}\gg 1$
) the dispersion relation that results is
where
![]() $k^{2}=k_{z}^{2}+k_{R}^{2}$
. We allow
$k^{2}=k_{z}^{2}+k_{R}^{2}$
. We allow
![]() $k_{z}^{2}c_{S}^{2}\,\sim R^{2}\unicode[STIX]{x1D6FA}^{4}/c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\sim k_{R}^{2}v_{A}^{2}\gtrsim k_{z}^{2}v_{A}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
and
$k_{z}^{2}c_{S}^{2}\,\sim R^{2}\unicode[STIX]{x1D6FA}^{4}/c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}\sim k_{R}^{2}v_{A}^{2}\gtrsim k_{z}^{2}v_{A}^{2}\gtrsim \unicode[STIX]{x1D714}^{2}$
and
![]() $k_{z}^{2}R^{2}\gtrsim 1$
, and note that
$k_{z}^{2}R^{2}\gtrsim 1$
, and note that
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. Graphically, (5.6) gives magnetorotational (or equivalently, magnetogravitational) instability to be the standard result of Balbus & Hawley (Reference Balbus and Hawley1991),
$\unicode[STIX]{x1D6FD}\gg 1$
. Graphically, (5.6) gives magnetorotational (or equivalently, magnetogravitational) instability to be the standard result of Balbus & Hawley (Reference Balbus and Hawley1991),
where for Keplerian rotation
![]() $-R\unicode[STIX]{x1D6FA}^{-2}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}/\unicode[STIX]{x2202}R=3$
. The preceding is in agreement with Balbus & Hawley (Reference Balbus and Hawley1991) provided their small
$-R\unicode[STIX]{x1D6FA}^{-2}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}/\unicode[STIX]{x2202}R=3$
. The preceding is in agreement with Balbus & Hawley (Reference Balbus and Hawley1991) provided their small
![]() $\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}R$
and
$\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}R$
and
![]() $\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}z$
terms are ignored. In Hawley et al. (Reference Hawley, Gammie and Balbus1995) the entropy equation is corrected to be consistent with energy conservation (recall our entropy equation after (3.2)). Condition (5.7) gives the MRI as
$\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}z$
terms are ignored. In Hawley et al. (Reference Hawley, Gammie and Balbus1995) the entropy equation is corrected to be consistent with energy conservation (recall our entropy equation after (3.2)). Condition (5.7) gives the MRI as
![]() $B_{0}\rightarrow 0$
. Stability may be possible for strong magnetic fields since
$B_{0}\rightarrow 0$
. Stability may be possible for strong magnetic fields since
![]() $k_{R}^{2}R^{2}\lesssim 1$
gives
$k_{R}^{2}R^{2}\lesssim 1$
gives
![]() $3\unicode[STIX]{x1D6FA}^{2}R^{2}/v_{A}^{2}\lesssim 1$
, implying
$3\unicode[STIX]{x1D6FA}^{2}R^{2}/v_{A}^{2}\lesssim 1$
, implying
![]() $\unicode[STIX]{x1D6FD}\lesssim 2c_{S}^{2}/3\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}\sim 1$
for our
$\unicode[STIX]{x1D6FD}\lesssim 2c_{S}^{2}/3\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}\sim 1$
for our
![]() $c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
ordering. Interestingly, in the hydrodynamic limit (
$c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
ordering. Interestingly, in the hydrodynamic limit (
![]() $v_{A}^{2}\equiv 0$
) if
$v_{A}^{2}\equiv 0$
) if
![]() $\unicode[STIX]{x1D714}^{2}\ll k_{z}^{2}c_{S}^{2}$
, (5.4) reduces to
$\unicode[STIX]{x1D714}^{2}\ll k_{z}^{2}c_{S}^{2}$
, (5.4) reduces to
![]() $\unicode[STIX]{x1D714}^{2}k^{2}k_{z}^{-2}=R^{-3}\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FA}^{2}R^{4})/\unicode[STIX]{x2202}R$
.
$\unicode[STIX]{x1D714}^{2}k^{2}k_{z}^{-2}=R^{-3}\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FA}^{2}R^{4})/\unicode[STIX]{x2202}R$
.
This strict Keplerian case is the one that the insightful physical interpretation by Balbus (Reference Balbus2006) of masses attached by springs is most appropriate. The bare bones strict Keplerian WKB treatment reduces (5.1)–(5.3) to
and
from which we obtain
where we can now use
![]() $k_{z}^{2}c_{S}^{2}\gg \unicode[STIX]{x1D714}^{2}$
to further simplify the last term to obtain (5.6). If we simply want to get the MRI threshold (
$k_{z}^{2}c_{S}^{2}\gg \unicode[STIX]{x1D714}^{2}$
to further simplify the last term to obtain (5.6). If we simply want to get the MRI threshold (
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
) we may assume incompressibility in (5.9) to remove the
$\unicode[STIX]{x1D714}\rightarrow 0$
) we may assume incompressibility in (5.9) to remove the
![]() $c_{S}^{2}$
terms in (5.10) to obtain
$c_{S}^{2}$
terms in (5.10) to obtain
and
The only non-Alfvénic term is from the inertial term
![]() $2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
in (5.13) since (5.12) is from the right side of (3.17). The simple toroidal momentum conservation equation of (5.12) is recovered from the vanishing of the toroidal component of the perturbed magnetic field for a frozen-in flow, (3.6), or equivalently, the vanishing of the perturbed radial current density,
$2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
in (5.13) since (5.12) is from the right side of (3.17). The simple toroidal momentum conservation equation of (5.12) is recovered from the vanishing of the toroidal component of the perturbed magnetic field for a frozen-in flow, (3.6), or equivalently, the vanishing of the perturbed radial current density,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{B}_{1}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})=0$
. Equation (5.13) is radial momentum balance between the inertial term and
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{B}_{1}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})=0$
. Equation (5.13) is radial momentum balance between the inertial term and
![]() $\boldsymbol{J}\times \boldsymbol{B}$
force to lowest order:
$\boldsymbol{J}\times \boldsymbol{B}$
force to lowest order:
Equations (5.12) and (5.13) are the ones for which the Balbus (Reference Balbus2006) physical interpretation is valid. For a marginally unstable mode
![]() $\unicode[STIX]{x1D714}\rightarrow \text{i}\,\text{Im}\,\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D714}\rightarrow \text{i}\,\text{Im}\,\unicode[STIX]{x1D714}$
with
![]() $\text{Im}\,\unicode[STIX]{x1D714}>0$
we see from (5.12) that
$\text{Im}\,\unicode[STIX]{x1D714}>0$
we see from (5.12) that
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\rightarrow 3\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{R}/2\,\text{Im}\,\unicode[STIX]{x1D714}$
, where Im denotes the imaginary part. Using
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\rightarrow 3\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{R}/2\,\text{Im}\,\unicode[STIX]{x1D714}$
, where Im denotes the imaginary part. Using
![]() $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{R}/\unicode[STIX]{x2202}R^{2}\rightarrow -k_{R}^{2}\unicode[STIX]{x1D709}_{R}$
in (5.13) gives
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{R}/\unicode[STIX]{x2202}R^{2}\rightarrow -k_{R}^{2}\unicode[STIX]{x1D709}_{R}$
in (5.13) gives
![]() $\unicode[STIX]{x1D709}_{R}\rightarrow 2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\text{Im}\,\unicode[STIX]{x1D714}/k_{R}^{2}v_{A}^{2}$
, where the signs of two displacements
$\unicode[STIX]{x1D709}_{R}\rightarrow 2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\text{Im}\,\unicode[STIX]{x1D714}/k_{R}^{2}v_{A}^{2}$
, where the signs of two displacements
![]() $\unicode[STIX]{x1D709}_{R}$
and
$\unicode[STIX]{x1D709}_{R}$
and
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
are seen to be the same. Therefore, two incremental axisymmetric toroidal mass rings stacked one above the other with oppositely directed initial radial displacements rotate toroidally in opposite directions and continue to separate radially due to the MRI. Noticing
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
are seen to be the same. Therefore, two incremental axisymmetric toroidal mass rings stacked one above the other with oppositely directed initial radial displacements rotate toroidally in opposite directions and continue to separate radially due to the MRI. Noticing
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\text{Im}\,\unicode[STIX]{x1D714}\rightarrow -R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\boldsymbol{V}_{1}$
, the upper mass ring with an initial radial perturbation
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\text{Im}\,\unicode[STIX]{x1D714}\rightarrow -R\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\boldsymbol{\cdot }\boldsymbol{V}_{1}$
, the upper mass ring with an initial radial perturbation
![]() $\unicode[STIX]{x1D709}_{R}>0$
slows (
$\unicode[STIX]{x1D709}_{R}>0$
slows (
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}>0$
) when moved outward, thereby decreasing its angular rotation frequency (
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}>0$
) when moved outward, thereby decreasing its angular rotation frequency (
![]() $\unicode[STIX]{x1D6FA}\propto R^{-3/2}$
) and increasing its angular momentum (
$\unicode[STIX]{x1D6FA}\propto R^{-3/2}$
) and increasing its angular momentum (
![]() $\unicode[STIX]{x1D6FA}R^{2}\propto R^{1/2}$
). Similarly, the initial
$\unicode[STIX]{x1D6FA}R^{2}\propto R^{1/2}$
). Similarly, the initial
![]() $\unicode[STIX]{x1D709}_{R}<0$
radial perturbation of the lower mass ring increases its angular rotation frequency (
$\unicode[STIX]{x1D709}_{R}<0$
radial perturbation of the lower mass ring increases its angular rotation frequency (
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}<0$
) as it moves inward, causing its angular momentum to drop. In the unstable limit, the tension of the frozen-in magnetic field lines resists any decrease (or increase) in angular rotation frequency of the upper (lower) ring by a positive (negative) torque that increases its angular momentum, thereby moving the ring to still larger (smaller)
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}<0$
) as it moves inward, causing its angular momentum to drop. In the unstable limit, the tension of the frozen-in magnetic field lines resists any decrease (or increase) in angular rotation frequency of the upper (lower) ring by a positive (negative) torque that increases its angular momentum, thereby moving the ring to still larger (smaller)
![]() $R$
and further lowering (raising) its angular frequency. As a result, the upper mass ring continues to move to a larger radius, thereby lowering its angular frequency, while the lower mass ring moves to smaller radii in an attempt to gain angular frequency. The presence of a magnetic field importantly changes the azimuthal component (3.17) of the conservation of angular momentum equation. In the absence of a magnetic field only the left side of (3.17) enters and acts to try to keep the angular momentum
$R$
and further lowering (raising) its angular frequency. As a result, the upper mass ring continues to move to a larger radius, thereby lowering its angular frequency, while the lower mass ring moves to smaller radii in an attempt to gain angular frequency. The presence of a magnetic field importantly changes the azimuthal component (3.17) of the conservation of angular momentum equation. In the absence of a magnetic field only the left side of (3.17) enters and acts to try to keep the angular momentum
![]() $\unicode[STIX]{x1D6FA}R^{2}$
constant. If a magnetic field is present then field line bending dominates at marginality and tries to keep the angular frequency
$\unicode[STIX]{x1D6FA}R^{2}$
constant. If a magnetic field is present then field line bending dominates at marginality and tries to keep the angular frequency
![]() $\unicode[STIX]{x1D6FA}$
fixed.
$\unicode[STIX]{x1D6FA}$
fixed.
5.1 Self-consistent strict Keplerian equilibrium for an axial magnetic field
In the strict Keplerian limit, Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) obtain
![]() $\unicode[STIX]{x1D6FD}>1$
analytic and numerical results with the equatorial plane plasma density increasing linearly with
$\unicode[STIX]{x1D6FD}>1$
analytic and numerical results with the equatorial plane plasma density increasing linearly with
![]() $R$
for a thin equatorial plane disk when
$R$
for a thin equatorial plane disk when
![]() $M\unicode[STIX]{x1D6FA}^{2}R^{2}/4T=M_{0}G_{0}M/4TR\gg 1$
. In this case the disk width
$M\unicode[STIX]{x1D6FA}^{2}R^{2}/4T=M_{0}G_{0}M/4TR\gg 1$
. In this case the disk width
![]() $\unicode[STIX]{x1D6E5}$
is given by
$\unicode[STIX]{x1D6E5}$
is given by
![]() $\unicode[STIX]{x1D6E5}/R=2T^{1/2}/M^{1/2}\unicode[STIX]{x1D6FA}R\ll 1$
. Perturbation wavelengths in the
$\unicode[STIX]{x1D6E5}/R=2T^{1/2}/M^{1/2}\unicode[STIX]{x1D6FA}R\ll 1$
. Perturbation wavelengths in the
![]() $z$
direction are limited to the disk width and therefore must satisfy
$z$
direction are limited to the disk width and therefore must satisfy
![]() $k_{z}\unicode[STIX]{x1D6E5}>2\unicode[STIX]{x03C0}$
, while our eikonal treatment requires
$k_{z}\unicode[STIX]{x1D6E5}>2\unicode[STIX]{x03C0}$
, while our eikonal treatment requires
![]() $k_{R}^{2}R^{2}\gg 1$
. Assuming
$k_{R}^{2}R^{2}\gg 1$
. Assuming
![]() $k_{R}^{2}>k_{z}^{2}$
in the condition for instability requires
$k_{R}^{2}>k_{z}^{2}$
in the condition for instability requires
![]() $3\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FA}^{2}R^{2}/2c_{S}^{2}>k_{R}^{2}R^{2}>k_{z}^{2}R^{2}>4\unicode[STIX]{x03C0}^{2}R^{2}/\unicode[STIX]{x1D6E5}^{2}=2\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}/c_{S}^{2}$
or
$3\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FA}^{2}R^{2}/2c_{S}^{2}>k_{R}^{2}R^{2}>k_{z}^{2}R^{2}>4\unicode[STIX]{x03C0}^{2}R^{2}/\unicode[STIX]{x1D6E5}^{2}=2\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}/c_{S}^{2}$
or
Therefore, the high
![]() $\unicode[STIX]{x1D6FD}$
ordering is appropriate with large
$\unicode[STIX]{x1D6FD}$
ordering is appropriate with large
![]() $\unicode[STIX]{x1D6FD}$
needed for instability as might be expected. Moreover, thin disk equilibria exist for the self-similar equilibria of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) in the strict Keplerian limit when
$\unicode[STIX]{x1D6FD}$
needed for instability as might be expected. Moreover, thin disk equilibria exist for the self-similar equilibria of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) in the strict Keplerian limit when
![]() $H\simeq (1-\unicode[STIX]{x1D707}^{2})^{-\unicode[STIX]{x1D6FC}/3}$
inside the thin disk, transitions to
$H\simeq (1-\unicode[STIX]{x1D707}^{2})^{-\unicode[STIX]{x1D6FC}/3}$
inside the thin disk, transitions to
![]() $H\simeq (1-\unicode[STIX]{x1D707}^{2})^{-\unicode[STIX]{x1D6FC}/2}$
outside the disk and
$H\simeq (1-\unicode[STIX]{x1D707}^{2})^{-\unicode[STIX]{x1D6FC}/2}$
outside the disk and
![]() $\unicode[STIX]{x1D6FC}\approx -2$
. Global extended or non-disk strict Keplerian self-similar solutions are found when
$\unicode[STIX]{x1D6FC}\approx -2$
. Global extended or non-disk strict Keplerian self-similar solutions are found when
![]() $M\unicode[STIX]{x1D6FA}^{2}R^{2}/4T=M_{0}G_{0}M/4TR\lesssim 1$
.
$M\unicode[STIX]{x1D6FA}^{2}R^{2}/4T=M_{0}G_{0}M/4TR\lesssim 1$
.
The preceding treatment might be viewed as somewhat unsatisfactory since we seem to have assumed
![]() $\unicode[STIX]{x1D6FA}^{2}=M_{0}G_{0}r^{-3}$
for all
$\unicode[STIX]{x1D6FA}^{2}=M_{0}G_{0}r^{-3}$
for all
![]() $z$
. To counter the imbalance between the centrifugal and gravitational forces the density must depend on
$z$
. To counter the imbalance between the centrifugal and gravitational forces the density must depend on
![]() $z$
and satisfy parallel pressure balance. Consequently, in the next section we justify the preceding limit by extending the analysis of (5.1)–(5.3) to a fully self-consistent configuration allowing
$z$
and satisfy parallel pressure balance. Consequently, in the next section we justify the preceding limit by extending the analysis of (5.1)–(5.3) to a fully self-consistent configuration allowing
![]() $z$
variation without assuming strict Keplerian rotation.
$z$
variation without assuming strict Keplerian rotation.
6 Axial magnetic field with gravity for general rotation
When the equilibrium magnetic field is axial as in (4.1) and unperturbed axial variation of the plasma density retained, the calculation of the previous sections can be repeated for general Keplerian motion by using a geometric optics approach in the
![]() $z$
direction that seeks solutions of the form
$z$
direction that seeks solutions of the form
![]() $\unicode[STIX]{x1D743}\propto \text{e}^{-\text{i}\unicode[STIX]{x1D714}t+\text{i}k_{z}z}$
. The equations obtained are identical to (5.1)–(5.3) which retain gravity in the radial and axial pressure balance conditions. Parallel momentum balance accounts for the difference between
$\unicode[STIX]{x1D743}\propto \text{e}^{-\text{i}\unicode[STIX]{x1D714}t+\text{i}k_{z}z}$
. The equations obtained are identical to (5.1)–(5.3) which retain gravity in the radial and axial pressure balance conditions. Parallel momentum balance accounts for the difference between
![]() $\unicode[STIX]{x1D6FA}^{2}R^{2}$
and
$\unicode[STIX]{x1D6FA}^{2}R^{2}$
and
![]() $M_{0}G_{0}/r$
and results in the unperturbed pressure gradient term in (3.18). The axial eikonal treatment then requires
$M_{0}G_{0}/r$
and results in the unperturbed pressure gradient term in (3.18). The axial eikonal treatment then requires
![]() $n_{1}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}\ll n_{0}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{1}$
or
$n_{1}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}\ll n_{0}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{1}$
or
![]() $k_{z}\unicode[STIX]{x1D6E5}\gg 1$
, with
$k_{z}\unicode[STIX]{x1D6E5}\gg 1$
, with
![]() $\unicode[STIX]{x1D6E5}$
the disk thickness.
$\unicode[STIX]{x1D6E5}$
the disk thickness.
For the general Keplerian case self-similar solutions are found to exist when
![]() $\unicode[STIX]{x1D6FA}^{2}R^{2}\geqslant M_{0}G_{0}/R$
in the equatorial plane, but not for
$\unicode[STIX]{x1D6FA}^{2}R^{2}\geqslant M_{0}G_{0}/R$
in the equatorial plane, but not for
![]() $\unicode[STIX]{x1D6FA}^{2}R^{2}<M_{0}G_{0}/R$
as gravity is so strong it cannot be balanced by the centrifugal force. In this general Keplerian limit thin disk equilibria require
$\unicode[STIX]{x1D6FA}^{2}R^{2}<M_{0}G_{0}/R$
as gravity is so strong it cannot be balanced by the centrifugal force. In this general Keplerian limit thin disk equilibria require
![]() $M_{0}G_{0}M\,/4TR\gg 1$
, but when
$M_{0}G_{0}M\,/4TR\gg 1$
, but when
![]() $\unicode[STIX]{x1D6FA}^{2}R^{2}>M_{0}G_{0}/R$
the Maxwell–Boltzmann behaviour of the density as given by (2.7) only seems to allow thin disks with
$\unicode[STIX]{x1D6FA}^{2}R^{2}>M_{0}G_{0}/R$
the Maxwell–Boltzmann behaviour of the density as given by (2.7) only seems to allow thin disks with
![]() $\unicode[STIX]{x1D6FD}\gg 1$
in the strict Keplerian limit
$\unicode[STIX]{x1D6FD}\gg 1$
in the strict Keplerian limit
![]() $\unicode[STIX]{x1D6FA}^{2}R^{2}=M_{0}G_{0}/R$
(Catto et al.
Reference Catto, Pusztai and Krasheninnikov2015). We continue to order
$\unicode[STIX]{x1D6FA}^{2}R^{2}=M_{0}G_{0}/R$
(Catto et al.
Reference Catto, Pusztai and Krasheninnikov2015). We continue to order
![]() $c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
to be able to treat the thin disks of the strict Keplerian limit as well as the global solutions of more general Keplerian motion.
$c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
to be able to treat the thin disks of the strict Keplerian limit as well as the global solutions of more general Keplerian motion.
Eliminating
![]() $\unicode[STIX]{x1D709}_{z}$
by inserting (5.2) into (5.3) gives
$\unicode[STIX]{x1D709}_{z}$
by inserting (5.2) into (5.3) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)\right]\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]=2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\frac{1}{n_{0}}\left[\frac{R}{c_{S}^{2}}\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right]\qquad \nonumber\\ \displaystyle & & \displaystyle \quad \times \,\left\{\frac{n_{0}k_{z}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\left[R\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)\unicode[STIX]{x1D709}_{R}+\frac{c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)\right]\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]=2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}+\frac{1}{n_{0}}\left[\frac{R}{c_{S}^{2}}\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right]\qquad \nonumber\\ \displaystyle & & \displaystyle \quad \times \,\left\{\frac{n_{0}k_{z}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\left[R\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)\unicode[STIX]{x1D709}_{R}+\frac{c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\right\}.\end{eqnarray}$$
Then using (5.1) to eliminate
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
from (6.1) gives the radial differential equation
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
from (6.1) gives the radial differential equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\frac{M_{0}G_{0}}{r^{3}}\right)\right]\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\quad \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{R}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}+\frac{1}{n_{0}}\left[\frac{R}{c_{S}^{2}}\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\frac{n_{0}k_{z}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\left[R\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)\unicode[STIX]{x1D709}_{R}+\frac{c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2}-R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\frac{M_{0}G_{0}}{r^{3}}\right)\right]\unicode[STIX]{x1D709}_{R}+\frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\,(R\unicode[STIX]{x1D709}_{R})\right]\quad \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{R}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}+\frac{1}{n_{0}}\left[\frac{R}{c_{S}^{2}}\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left\{\frac{n_{0}k_{z}^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}c_{S}^{2})}\left[R\left(\unicode[STIX]{x1D6FA}^{2}-\frac{M_{0}G_{0}}{r^{3}}\right)\unicode[STIX]{x1D709}_{R}+\frac{c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]\right\}.\end{eqnarray}$$
Equation (6.2) is the radial differential equation for general rotation in an axial magnetic field for the MRI instability when an axial eikonal treatment is employed.
We seek a WKB, geometric optics or eikonal radial solution by using
![]() $\unicode[STIX]{x1D709}_{R}\propto \text{e}^{\text{i}\int k_{R}\,\text{d}R}$
and
$\unicode[STIX]{x1D709}_{R}\propto \text{e}^{\text{i}\int k_{R}\,\text{d}R}$
and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{R}/\unicode[STIX]{x2202}R=\text{i}k_{R}\unicode[STIX]{x1D709}_{R}$
with
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{R}/\unicode[STIX]{x2202}R=\text{i}k_{R}\unicode[STIX]{x1D709}_{R}$
with
by allowing
![]() $k_{z}^{2}R^{2}\gtrsim 1$
and
$k_{z}^{2}R^{2}\gtrsim 1$
and
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. From (6.2) we obtain the dispersion relation
$\unicode[STIX]{x1D6FD}\gg 1$
. From (6.2) we obtain the dispersion relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle k^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\frac{M_{0}G_{0}}{r^{3}}\right)+\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}-\frac{\unicode[STIX]{x1D714}^{2}k_{R}^{2}}{k_{z}^{2}}-\frac{R^{2}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})^{2}}{c_{S}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{R}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}[n_{0}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})]=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle k^{2}v_{A}^{2}+R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left(\frac{M_{0}G_{0}}{r^{3}}\right)+\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{z}^{2}v_{A}^{2})}-\frac{\unicode[STIX]{x1D714}^{2}k_{R}^{2}}{k_{z}^{2}}-\frac{R^{2}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})^{2}}{c_{S}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{R}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}[n_{0}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})]=0,\end{eqnarray}$$
where
![]() $k^{2}=k_{z}^{2}+k_{R}^{2}$
. Graphically, the behaviour near
$k^{2}=k_{z}^{2}+k_{R}^{2}$
. Graphically, the behaviour near
![]() $\unicode[STIX]{x1D714}^{2}=0$
gives gravitational magnetorotational instability when
$\unicode[STIX]{x1D714}^{2}=0$
gives gravitational magnetorotational instability when
Clearly, the preceding reduces to the Velikhov (Reference Velikhov1959) result (4.18) in the absence of gravity and the Balbus & Hawley (Reference Balbus and Hawley1991) result (5.7) when
![]() $\unicode[STIX]{x1D6FA}^{2}=M_{0}G_{0}r^{-3}$
. More importantly, it is clear that unless the motion is strictly Keplerian, compressibility and density gradient effects will impact the stability threshold.
$\unicode[STIX]{x1D6FA}^{2}=M_{0}G_{0}r^{-3}$
. More importantly, it is clear that unless the motion is strictly Keplerian, compressibility and density gradient effects will impact the stability threshold.
For a hydrodynamic equilibrium (
![]() $v_{A}^{2}=0$
), equation (6.2) yields the dispersion relation
$v_{A}^{2}=0$
), equation (6.2) yields the dispersion relation
For strict Keplerian motion we see that instability occurs whenever angular momentum decreases with radius.
We can interpret (6.6) by first considering radial force balance for two adjacent, axisymmetric, incompressible plasma rings (
![]() $j=1,2$
) near the equatorial plane with radius
$j=1,2$
) near the equatorial plane with radius
![]() $R_{j}$
, plasma mass density
$R_{j}$
, plasma mass density
![]() $Mn_{j}=\unicode[STIX]{x1D70C}_{j}$
, rotation frequency
$Mn_{j}=\unicode[STIX]{x1D70C}_{j}$
, rotation frequency
![]() $\unicode[STIX]{x1D6FA}_{j}$
and pressure
$\unicode[STIX]{x1D6FA}_{j}$
and pressure
![]() $p_{j}$
:
$p_{j}$
:
If the first ring is displaced outward to the location of the second ring (
![]() $R_{1}\rightarrow R_{2}>R_{1}$
and
$R_{1}\rightarrow R_{2}>R_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{1}\rightarrow \unicode[STIX]{x1D70C}_{1}$
), the frozen-in magnetic field lines moves with it. Therefore, the ring continues to rotate at the original angular frequency
$\unicode[STIX]{x1D70C}_{1}\rightarrow \unicode[STIX]{x1D70C}_{1}$
), the frozen-in magnetic field lines moves with it. Therefore, the ring continues to rotate at the original angular frequency
![]() $\unicode[STIX]{x1D6FA}_{1}$
of these frozen in field lines. Consequently, the resulting torques due to field line bending act on the first ring to keep its angular frequency fixed while its fluid element is moved (
$\unicode[STIX]{x1D6FA}_{1}$
of these frozen in field lines. Consequently, the resulting torques due to field line bending act on the first ring to keep its angular frequency fixed while its fluid element is moved (
![]() $\unicode[STIX]{x1D6FA}_{1}\rightarrow \unicode[STIX]{x1D6FA}_{1}$
), as pointed out by Velikhov (Reference Velikhov1959) and Balbus & Hawley (Reference Balbus and Hawley1991). After being displaced the first ring is acted on by the pressure difference across its new location
$\unicode[STIX]{x1D6FA}_{1}\rightarrow \unicode[STIX]{x1D6FA}_{1}$
), as pointed out by Velikhov (Reference Velikhov1959) and Balbus & Hawley (Reference Balbus and Hawley1991). After being displaced the first ring is acted on by the pressure difference across its new location
![]() $\unicode[STIX]{x2202}p_{2}/\unicode[STIX]{x2202}R$
. However, force balance is no longer satisfied as a restoring force
$\unicode[STIX]{x2202}p_{2}/\unicode[STIX]{x2202}R$
. However, force balance is no longer satisfied as a restoring force
![]() $\unicode[STIX]{x0394}F$
arises due to its movement:
$\unicode[STIX]{x0394}F$
arises due to its movement:
Subtracting force balance for the initial second ring from the preceding expression gives
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}F & = & \displaystyle \unicode[STIX]{x1D70C}_{1}(\unicode[STIX]{x1D6FA}_{1}^{2}R_{2}-M_{0}G_{0}/R_{1}^{2})-\unicode[STIX]{x1D70C}_{2}(\unicode[STIX]{x1D6FA}_{2}^{2}R_{2}-M_{0}G_{0}/R_{2}^{2})\nonumber\\ \displaystyle & = & \displaystyle -\left[\unicode[STIX]{x1D70C}R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D6FA}^{2}R-M_{0}G_{0}/R^{2})\right](R_{2}-R_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}F & = & \displaystyle \unicode[STIX]{x1D70C}_{1}(\unicode[STIX]{x1D6FA}_{1}^{2}R_{2}-M_{0}G_{0}/R_{1}^{2})-\unicode[STIX]{x1D70C}_{2}(\unicode[STIX]{x1D6FA}_{2}^{2}R_{2}-M_{0}G_{0}/R_{2}^{2})\nonumber\\ \displaystyle & = & \displaystyle -\left[\unicode[STIX]{x1D70C}R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D6FA}^{2}R-M_{0}G_{0}/R^{2})\right](R_{2}-R_{1}).\end{eqnarray}$$
If
![]() $\unicode[STIX]{x0394}F<0$
, then the new plasma pressure difference across the displaced ring returns it to its original location. If instead,
$\unicode[STIX]{x0394}F<0$
, then the new plasma pressure difference across the displaced ring returns it to its original location. If instead,
![]() $\unicode[STIX]{x0394}F>0$
then the plasma pressure across the ring is too small to prevent the displaced ring from continuing to move outward. Therefore, in agreement with (6.6) the incompressible instability condition is
$\unicode[STIX]{x0394}F>0$
then the plasma pressure across the ring is too small to prevent the displaced ring from continuing to move outward. Therefore, in agreement with (6.6) the incompressible instability condition is
To get the marginal stability condition in general rotation case we need only combine the following
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
versions of (5.1)–(5.3):
$\unicode[STIX]{x1D714}\rightarrow 0$
versions of (5.1)–(5.3):
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]=2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\frac{\text{i}k_{z}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{i}k_{z}R(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})\unicode[STIX]{x1D709}_{z}-\unicode[STIX]{x1D709}_{R}R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{n_{0}c_{S}^{2}}{R}\frac{\unicode[STIX]{x2202}(R\unicode[STIX]{x1D709}_{R})}{\unicode[STIX]{x2202}R}\right]+\frac{v_{A}^{2}}{B_{0}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\left[\frac{B_{0}^{2}}{R}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(R\unicode[STIX]{x1D709}_{R})\right]=2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\frac{\text{i}k_{z}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(n_{0}c_{S}^{2}\unicode[STIX]{x1D709}_{z})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{i}k_{z}R(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3})\unicode[STIX]{x1D709}_{z}-\unicode[STIX]{x1D709}_{R}R\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}r^{-3}).\end{eqnarray}$$
Of course these equations are more complicated than (5.12) and (5.13) because compressibility effects must be retained when
![]() $\unicode[STIX]{x1D6FA}^{2}\neq M_{0}G_{0}r^{-3}$
.
$\unicode[STIX]{x1D6FA}^{2}\neq M_{0}G_{0}r^{-3}$
.
6.1 Self-consistent equilibrium in an axial magnetic field with gravity at
 $\unicode[STIX]{x1D6FD}\gg 1$
$\unicode[STIX]{x1D6FD}\gg 1$
We consider the limit of the self-consistent equilibrium of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) with
![]() $B_{0}$
axial,
$B_{0}$
axial,
![]() $\unicode[STIX]{x1D6FA}^{2}\propto R^{-3},T_{0}\propto R^{-1}$
and axial pressure balance in the vicinity of the equatorial plane requiring
$\unicode[STIX]{x1D6FA}^{2}\propto R^{-3},T_{0}\propto R^{-1}$
and axial pressure balance in the vicinity of the equatorial plane requiring
with
![]() $\bar{p}_{0}$
a constant and
$\bar{p}_{0}$
a constant and
![]() $\unicode[STIX]{x1D6E5}/R=2(TR/MM_{0}G_{0})^{1/2}$
. In this limit the motion cannot be strictly Keplerian since
$\unicode[STIX]{x1D6E5}/R=2(TR/MM_{0}G_{0})^{1/2}$
. In this limit the motion cannot be strictly Keplerian since
![]() $\unicode[STIX]{x1D6FA}^{2}>M_{0}G_{0}R^{-3}$
is required to find a solution. Also, disk formation is unlikely for the nearly axial equilibrium solutions found as
$\unicode[STIX]{x1D6FA}^{2}>M_{0}G_{0}R^{-3}$
is required to find a solution. Also, disk formation is unlikely for the nearly axial equilibrium solutions found as
![]() $\unicode[STIX]{x1D6FD}$
is required to be extremely large:
$\unicode[STIX]{x1D6FD}$
is required to be extremely large:
![]() $\unicode[STIX]{x1D6FD}\gg [\unicode[STIX]{x1D6FA}^{2}/(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}R^{-3})]^{2}\text{e}^{-3(R/\unicode[STIX]{x1D6E5})^{2}}$
. Taking
$\unicode[STIX]{x1D6FD}\gg [\unicode[STIX]{x1D6FA}^{2}/(\unicode[STIX]{x1D6FA}^{2}-M_{0}G_{0}R^{-3})]^{2}\text{e}^{-3(R/\unicode[STIX]{x1D6E5})^{2}}$
. Taking
![]() $\unicode[STIX]{x1D6E5}/R\sim 1$
, we can use
$\unicode[STIX]{x1D6E5}/R\sim 1$
, we can use
![]() $n_{0}\propto R$
to find
$n_{0}\propto R$
to find
![]() $R\unicode[STIX]{x2202}n_{0}/\unicode[STIX]{x2202}R\simeq R$
. In addition, we have
$R\unicode[STIX]{x2202}n_{0}/\unicode[STIX]{x2202}R\simeq R$
. In addition, we have
![]() $R\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}/\unicode[STIX]{x2202}R=-3\unicode[STIX]{x1D6FA}^{2}$
so that using (6.6) and
$R\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}^{2}/\unicode[STIX]{x2202}R=-3\unicode[STIX]{x1D6FA}^{2}$
so that using (6.6) and
![]() $k_{R}^{2}R^{2}\gg 1$
for
$k_{R}^{2}R^{2}\gg 1$
for
![]() $\unicode[STIX]{x1D6FD}\gg 1$
gives instability when
$\unicode[STIX]{x1D6FD}\gg 1$
gives instability when
where
![]() $\unicode[STIX]{x1D6FD}\gg 2c_{S}^{2}/\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}$
. Consequently, the departure from strict Keplerian rotation increases the size of the instability window when
$\unicode[STIX]{x1D6FD}\gg 2c_{S}^{2}/\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}$
. Consequently, the departure from strict Keplerian rotation increases the size of the instability window when
and decreases it otherwise. The smallest non-disk window of instability occurs in the Velikhov limit (4.24) when
![]() $\unicode[STIX]{x1D6FA}^{2}R^{2}/c_{S}^{2}\ll 1$
and
$\unicode[STIX]{x1D6FA}^{2}R^{2}/c_{S}^{2}\ll 1$
and
![]() $M_{0}G_{0}/\unicode[STIX]{x1D6FA}^{2}r^{3}\ll 1$
. Stability may only be possible for strong magnetic fields when WKB fails (
$M_{0}G_{0}/\unicode[STIX]{x1D6FA}^{2}r^{3}\ll 1$
. Stability may only be possible for strong magnetic fields when WKB fails (
![]() $k^{2}R^{2}\lesssim 1$
) and
$k^{2}R^{2}\lesssim 1$
) and
implying
![]() $\unicode[STIX]{x1D6FD}\lesssim 2c_{S}^{2}/3\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}\sim 1$
for our
$\unicode[STIX]{x1D6FD}\lesssim 2c_{S}^{2}/3\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FA}^{2}R^{2}\sim 1$
for our
![]() $c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
and
$c_{S}^{2}\sim \unicode[STIX]{x1D6FA}^{2}R^{2}$
and
![]() $M_{0}G_{0}/\,\unicode[STIX]{x1D6FA}^{2}r^{3}\sim 1$
ordering.
$M_{0}G_{0}/\,\unicode[STIX]{x1D6FA}^{2}r^{3}\sim 1$
ordering.
Often the magnetic field is not cylindrically symmetric so the self-similar form of (4.14),
![]() $\unicode[STIX]{x1D713}_{0}=CH(\cos \unicode[STIX]{x1D717})/r^{\unicode[STIX]{x1D6FC}}$
, allows solutions away from
$\unicode[STIX]{x1D713}_{0}=CH(\cos \unicode[STIX]{x1D717})/r^{\unicode[STIX]{x1D6FC}}$
, allows solutions away from
![]() $\unicode[STIX]{x1D6FC}\approx -2$
(see figures 1, 3 and 4 of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015), for example, where
$\unicode[STIX]{x1D6FC}\approx -2$
(see figures 1, 3 and 4 of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015), for example, where
![]() $\unicode[STIX]{x1D6FC}\approx -3,-4$
and
$\unicode[STIX]{x1D6FC}\approx -3,-4$
and
![]() $-6$
respectively). For smooth, slowly varying departures from cylindrical symmetry for which the radial magnetic field component is sufficiently weak, (6.16) can be generalized slightly by using
$-6$
respectively). For smooth, slowly varying departures from cylindrical symmetry for which the radial magnetic field component is sufficiently weak, (6.16) can be generalized slightly by using
![]() $n_{0}\propto R^{-2\unicode[STIX]{x1D6FC}-3}$
. In such cases
$n_{0}\propto R^{-2\unicode[STIX]{x1D6FC}-3}$
. In such cases
with
![]() $\unicode[STIX]{x1D6FC}\leqslant -2$
an eigenvalue determined by solving the self-similar form of the Grad–Shafranov equation, and where
$\unicode[STIX]{x1D6FC}\leqslant -2$
an eigenvalue determined by solving the self-similar form of the Grad–Shafranov equation, and where
![]() $\unicode[STIX]{x1D6FC}=-2$
corresponds to the cylindrically symmetric limit. When
$\unicode[STIX]{x1D6FC}=-2$
corresponds to the cylindrically symmetric limit. When
![]() $\unicode[STIX]{x1D6FC}<-2$
, stronger density variation further narrows the instability window; however, once
$\unicode[STIX]{x1D6FC}<-2$
, stronger density variation further narrows the instability window; however, once
![]() $|\unicode[STIX]{x1D6FC}|$
becomes too large the radial magnetic field may no longer be negligible.
$|\unicode[STIX]{x1D6FC}|$
becomes too large the radial magnetic field may no longer be negligible.
It is important to realize that equilibrium solutions can be found for
![]() $\unicode[STIX]{x1D6FD}\gg 1$
and
$\unicode[STIX]{x1D6FD}\gg 1$
and
![]() $\unicode[STIX]{x1D6FA}^{2}>M_{0}G_{0}R^{-3}$
with very strong departures from cylindrical symmetry (see figures 2 and 5 of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) for examples). The general, but rather complicated, magnetorotational stability treatment in the next section is intended to deal these and other non-cylindrically symmetric equilibrium solutions for which the radial magnetic field cannot be ignored.
$\unicode[STIX]{x1D6FA}^{2}>M_{0}G_{0}R^{-3}$
with very strong departures from cylindrical symmetry (see figures 2 and 5 of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) for examples). The general, but rather complicated, magnetorotational stability treatment in the next section is intended to deal these and other non-cylindrically symmetric equilibrium solutions for which the radial magnetic field cannot be ignored.
7 Stability in a general poloidal magnetic field for
 $\unicode[STIX]{x1D6FD}>1$
$\unicode[STIX]{x1D6FD}>1$
In a strong gravitational field at high
![]() $\unicode[STIX]{x1D6FD}$
, the magnetic field is comparatively weak. The rotating frozen-in plasma is more easily distorted, with the field lines bulging outward substantially and the possibility of quite substantial departures from cylindrical symmetry.
$\unicode[STIX]{x1D6FD}$
, the magnetic field is comparatively weak. The rotating frozen-in plasma is more easily distorted, with the field lines bulging outward substantially and the possibility of quite substantial departures from cylindrical symmetry.
To perform the stability analysis for an arbitrary axisymmetric poloidal magnetic field it is convenient to use the azimuthal, parallel and
![]() $Q=\unicode[STIX]{x1D713}_{0}$
components of the
$Q=\unicode[STIX]{x1D713}_{0}$
components of the
![]() $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t^{2}$
equation:
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t^{2}$
equation:
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D735}R-\frac{n_{1}}{n_{0}}\left(\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R-\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r\right)+\frac{\unicode[STIX]{x1D735}p_{1}}{Mn_{0}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \quad =v_{A}^{2}R^{2}\left[\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})\right]\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+v_{A}^{2}R^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[R^{-2}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D743}}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D735}R-\frac{n_{1}}{n_{0}}\left(\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R-\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r\right)+\frac{\unicode[STIX]{x1D735}p_{1}}{Mn_{0}}\right]\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \quad =v_{A}^{2}R^{2}\left[\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})\right]\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+v_{A}^{2}R^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }[R^{-2}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})],\end{eqnarray}$$
where to remove
![]() $J_{0}$
in the last equation we used the Grad–Shafranov equation
$J_{0}$
in the last equation we used the Grad–Shafranov equation
To complete the description we only need
![]() $n_{1}$
and
$n_{1}$
and
![]() $p_{1}$
as given in § 3.
$p_{1}$
as given in § 3.
For the general analysis we write
and
Using the preceding, the equations for
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
and
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
and
![]() $\unicode[STIX]{x1D709}_{\Vert }$
become
$\unicode[STIX]{x1D709}_{\Vert }$
become
and, after using the Grad–Shafranov equation and inserting
![]() $p_{1}$
and
$p_{1}$
and
![]() $n_{1}$
,
$n_{1}$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\Vert }}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}B_{0R}B_{0}^{-1}-\frac{\unicode[STIX]{x1D6FE}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743})}{Mn_{0}B_{0}}-\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0})}{Mn_{0}B_{0}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D709}_{||}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(n_{0}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0})}{Mn_{0}^{2}B_{0}^{2}}=-\frac{\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}}{Mn_{0}^{2}B_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{n_{0}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,R^{-2}B_{0}^{-3}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }[M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R]\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\Vert }}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}B_{0R}B_{0}^{-1}-\frac{\unicode[STIX]{x1D6FE}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743})}{Mn_{0}B_{0}}-\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x2202}p_{0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0})}{Mn_{0}B_{0}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D709}_{||}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(n_{0}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0})}{Mn_{0}^{2}B_{0}^{2}}=-\frac{\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}}{Mn_{0}^{2}B_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{n_{0}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,R^{-2}B_{0}^{-3}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }[M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R]\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}},\end{eqnarray}$$
where
and
Inserting
![]() $p_{1}$
and
$p_{1}$
and
![]() $n_{1}$
and using
$n_{1}$
and using
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{R^{2}B_{0}^{2}}{Mn_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}p_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\right)=-R^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{R^{2}B_{0}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}n_{0}}{R^{2}B_{0}^{2}}\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{R^{2}B_{0}^{2}}{Mn_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}p_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\right)=-R^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{R^{2}B_{0}^{2}}{n_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}n_{0}}{R^{2}B_{0}^{2}}\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right],\end{eqnarray}$$
we obtain a convenient form for the third equation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}RB_{0z}-\frac{R^{2}B_{0}^{2}}{Mn_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\unicode[STIX]{x1D6FE}p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}+\unicode[STIX]{x1D709}_{\Vert }B_{0}^{-1}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(n_{0}^{-1}\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743})\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,n_{0}^{-1}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}n_{0}}{R^{2}B_{0}^{2}}\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =v_{A}^{2}R^{2}\left[\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}}\right)-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}t^{2}}-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}RB_{0z}-\frac{R^{2}B_{0}^{2}}{Mn_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\unicode[STIX]{x1D6FE}p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}+\unicode[STIX]{x1D709}_{\Vert }B_{0}^{-1}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(n_{0}^{-1}\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743})\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,n_{0}^{-1}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}n_{0}}{R^{2}B_{0}^{2}}\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =v_{A}^{2}R^{2}\left[\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}}\right)-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where in the axial magnetic field limit
Using
to simplify further gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}t^{2}}\,-\frac{R^{2}B_{0}^{2}}{Mn_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\unicode[STIX]{x1D6FE}p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}+\unicode[STIX]{x1D709}_{\Vert }B_{0}^{-1}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}B_{0}^{-1}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{R^{2}B_{0}}\right]-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}RB_{0z}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\left[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}B_{0}^{-1}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(B_{0}^{-1}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+n_{0}^{-1}\boldsymbol{B}_{0}\,\boldsymbol{\cdot }\unicode[STIX]{x1D735}(B_{0}^{-1}n_{0}\unicode[STIX]{x1D709}_{\Vert })\right]\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \,\,=v_{A}^{2}R^{2}\left[\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}}\right)-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}t^{2}}\,-\frac{R^{2}B_{0}^{2}}{Mn_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\unicode[STIX]{x1D6FE}p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}+\unicode[STIX]{x1D709}_{\Vert }B_{0}^{-1}\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}B_{0}^{-1}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{R^{2}B_{0}}\right]-2\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D6FA}RB_{0z}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\left[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}B_{0}^{-1}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(B_{0}^{-1}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+n_{0}^{-1}\boldsymbol{B}_{0}\,\boldsymbol{\cdot }\unicode[STIX]{x1D735}(B_{0}^{-1}n_{0}\unicode[STIX]{x1D709}_{\Vert })\right]\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \,\,=v_{A}^{2}R^{2}\left[\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}}\right)-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where in the axial magnetic field limit
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(B_{0}^{-1}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})\rightarrow 0$
.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(B_{0}^{-1}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})\rightarrow 0$
.
The three equations (7.8), (7.9) and (7.16) are the most general forms of our equations for the three components of the displacement
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
,
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
,
![]() $\unicode[STIX]{x1D709}_{\Vert }$
and
$\unicode[STIX]{x1D709}_{\Vert }$
and
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
. They are the full ideal MHD representation for the magneto-rotational instability for axisymmetric perturbations to a self-consistent axisymmetric magnetic field having both radial and axial components at high
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
. They are the full ideal MHD representation for the magneto-rotational instability for axisymmetric perturbations to a self-consistent axisymmetric magnetic field having both radial and axial components at high
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
Our three displacement equations are now in the desired form to begin to employ the eikonal approximation by assuming
with
![]() $S$
independent of
$S$
independent of
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $k_{\unicode[STIX]{x1D713}}=\unicode[STIX]{x2202}S/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
, and the wave vector assumed to be slowly varying. As in earlier sections we only perform the eikonal treatment in the parallel direction to start. We need to be careful with
$k_{\unicode[STIX]{x1D713}}=\unicode[STIX]{x2202}S/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
, and the wave vector assumed to be slowly varying. As in earlier sections we only perform the eikonal treatment in the parallel direction to start. We need to be careful with
![]() $\unicode[STIX]{x1D713}_{0}$
derivatives in
$\unicode[STIX]{x1D713}_{0}$
derivatives in
![]() $c_{S}^{2}$
terms as before, but we also want to retain departures from cylindrical symmetry for the magnetic field.
$c_{S}^{2}$
terms as before, but we also want to retain departures from cylindrical symmetry for the magnetic field.
For a general poloidal magnetic field we assume
![]() $k_{\bot }^{2}R^{2}\gg 1$
and
$k_{\bot }^{2}R^{2}\gg 1$
and
![]() $k_{\Vert }^{2}R^{2}\gtrsim 1$
and
$k_{\Vert }^{2}R^{2}\gtrsim 1$
and
![]() $\unicode[STIX]{x1D6FD}\gg 1$
and use
$\unicode[STIX]{x1D6FD}\gg 1$
and use
![]() $k^{2}=k_{\Vert }^{2}+k_{\bot }^{2}$
. We assume small wavelengths parallel unperturbed magnetic field,
$k^{2}=k_{\Vert }^{2}+k_{\bot }^{2}$
. We assume small wavelengths parallel unperturbed magnetic field,
so that
and recall
![]() $\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\text{d}\unicode[STIX]{x1D6FA}/\text{d}\unicode[STIX]{x1D713}_{0})=0$
. Then the
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\text{d}\unicode[STIX]{x1D6FA}/\text{d}\unicode[STIX]{x1D713}_{0})=0$
. Then the
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
equation gives
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
equation gives
The
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
equation contains
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
equation contains
![]() $\unicode[STIX]{x1D709}_{\Vert }$
dependence which accounts for a new non-axial field effect.
$\unicode[STIX]{x1D709}_{\Vert }$
dependence which accounts for a new non-axial field effect.
Using the eikonal approximation on the equation for
![]() $\unicode[STIX]{x1D709}_{\Vert }$
and neglecting the small terms already noted we obtain
$\unicode[STIX]{x1D709}_{\Vert }$
and neglecting the small terms already noted we obtain
where once again all components of the displacement enter. In the
![]() $\unicode[STIX]{x1D709}_{\Vert }$
equation we have been careful to retain seemingly small terms. We will eventually find that the
$\unicode[STIX]{x1D709}_{\Vert }$
equation we have been careful to retain seemingly small terms. We will eventually find that the
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
terms will cancel exactly and the remaining large
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
terms will cancel exactly and the remaining large
![]() $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}$
term will enter with a small coefficient at marginality (
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}$
term will enter with a small coefficient at marginality (
![]() $\unicode[STIX]{x1D714}^{2}\rightarrow 0$
) as in earlier sections. For this reason we must retain
$\unicode[STIX]{x1D714}^{2}\rightarrow 0$
) as in earlier sections. For this reason we must retain
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r\,-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)$
, as well as
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r\,-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)$
, as well as
![]() $c_{S}^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})$
.
$c_{S}^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})$
.
For the third equation we use
for
![]() $v_{A}^{2}$
terms, but we again keep seemingly small terms to carefully deal with the later cancelation in
$v_{A}^{2}$
terms, but we again keep seemingly small terms to carefully deal with the later cancelation in
![]() $c_{S}^{2}$
terms:
$c_{S}^{2}$
terms:
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{B_{0}^{2}R^{2}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \,\,=2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\text{i}k_{\Vert }\left[\unicode[STIX]{x1D709}_{\Vert }\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}(p_{0}\unicode[STIX]{x1D709}_{\Vert })\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{B_{0}^{2}R^{2}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \,\,=2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}-\text{i}k_{\Vert }\left[\unicode[STIX]{x1D709}_{\Vert }\left(\frac{M_{0}G_{0}}{r^{2}}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}(p_{0}\unicode[STIX]{x1D709}_{\Vert })\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where to combine terms we use
We retain all the
![]() $\unicode[STIX]{x1D709}_{\Vert }$
terms because of the cancelation that will occur as already noted.
$\unicode[STIX]{x1D709}_{\Vert }$
terms because of the cancelation that will occur as already noted.
To highlight a new effect due to the non-axial magnetic fields we consider marginality (
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
) for strict Keplerian rotation (
$\unicode[STIX]{x1D714}\rightarrow 0$
) for strict Keplerian rotation (
![]() $M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}$
), to reduce these equations to
$M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}$
), to reduce these equations to
and
Combining to eliminate
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
and
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
and
![]() $\unicode[STIX]{x1D709}_{\Vert }$
and using the radial eikonal form instability occurs if
$\unicode[STIX]{x1D709}_{\Vert }$
and using the radial eikonal form instability occurs if
The new term that appears in the preceding is always destabilizing when
![]() $k_{\Vert }^{-1}k_{\bot }B_{0R}B_{0z}^{-1}<0$
and accounts for non-axial magnetic field effects. Moreover, instability occurs for
$k_{\Vert }^{-1}k_{\bot }B_{0R}B_{0z}^{-1}<0$
and accounts for non-axial magnetic field effects. Moreover, instability occurs for
![]() $\text{d}\unicode[STIX]{x1D6FA}^{2}/\text{d}\unicode[STIX]{x1D713}_{0}>0$
when
$\text{d}\unicode[STIX]{x1D6FA}^{2}/\text{d}\unicode[STIX]{x1D713}_{0}>0$
when
![]() $k_{\Vert }^{-1}k_{\bot }B_{0R}B_{0z}^{-1}>1$
, a new limit not previously noted.
$k_{\Vert }^{-1}k_{\bot }B_{0R}B_{0z}^{-1}>1$
, a new limit not previously noted.
The eikonal treatment for the general axisymmetric poloidal magnetic field case is quite complex so the details are relegated to the appendix A. The general condition for instability is found from
![]() $\unicode[STIX]{x1D714}^{2}=0$
to be
$\unicode[STIX]{x1D714}^{2}=0$
to be
 $$\begin{eqnarray}\displaystyle k^{2}v_{A}^{2} & {<} & \displaystyle \frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}c_{S}^{2}}-\left(B_{0z}-\frac{k_{\bot }}{k_{\Vert }}B_{0R}\right)R^{2}\frac{\text{d}\unicode[STIX]{x1D6FA}^{2}}{\text{d}\unicode[STIX]{x1D713}_{0}}\nonumber\\ \displaystyle & & \displaystyle +\,(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\frac{\unicode[STIX]{x2202}n_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k^{2}v_{A}^{2} & {<} & \displaystyle \frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}c_{S}^{2}}-\left(B_{0z}-\frac{k_{\bot }}{k_{\Vert }}B_{0R}\right)R^{2}\frac{\text{d}\unicode[STIX]{x1D6FA}^{2}}{\text{d}\unicode[STIX]{x1D713}_{0}}\nonumber\\ \displaystyle & & \displaystyle +\,(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\frac{\unicode[STIX]{x2202}n_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}=R^{2}B_{0}^{2}\unicode[STIX]{x2202}n_{0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
. For our ordering
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}=R^{2}B_{0}^{2}\unicode[STIX]{x2202}n_{0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
. For our ordering
![]() $(k_{\bot }/k_{\Vert })^{2}\gg 1$
, making the new non-axial magnetic field term potentially important when
$(k_{\bot }/k_{\Vert })^{2}\gg 1$
, making the new non-axial magnetic field term potentially important when
![]() $|k_{\bot }B_{0R}|\gtrsim |k_{\Vert }|B_{0z}$
. The preceding is our most general expression for gravitational magnetorotational instability. Once again strict Keplerian motion removes compressibility and density gradient effects.
$|k_{\bot }B_{0R}|\gtrsim |k_{\Vert }|B_{0z}$
. The preceding is our most general expression for gravitational magnetorotational instability. Once again strict Keplerian motion removes compressibility and density gradient effects.
8 Discussion and conclusions
We have re-examined magnetorotational stability with and without gravity by retaining compressibility and density variation, and allowing general axisymmetric poloidal magnetic fields in fully self-consistent equilibria. Within the limitations of a geometric optics or eikonal analysis, we have obtained general expressions for the stability threshold, which is found to have a different form in the absence of gravity than in the presence of strict Keplerian motion, as can be seen by comparing (4.19) and (5.7). Further subtle and important modifications arise when gravity is present if the rotation frequency is general as can be seen by the appearance of compressibility and density gradient terms in (6.6). For the
![]() $\unicode[STIX]{x1D6FD}\gg 1$
equilibria of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) with rotation stronger than Keplerian these compressibility and density gradient effects become important as seen by (6.16). Interestingly, the incompressible limit without gravity, but with density variation is unstable for the model equilibrium of Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015) for a geometric optics approach when
$\unicode[STIX]{x1D6FD}\gg 1$
equilibria of Catto et al. (Reference Catto, Pusztai and Krasheninnikov2015) with rotation stronger than Keplerian these compressibility and density gradient effects become important as seen by (6.16). Interestingly, the incompressible limit without gravity, but with density variation is unstable for the model equilibrium of Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015) for a geometric optics approach when
![]() $2\unicode[STIX]{x1D6FA}^{2}>k^{2}v_{A}^{2}$
. However, in the strict Keplerian limit of Balbus & Hawley (Reference Balbus and Hawley1991), compressibility and density variation do not matter and
$2\unicode[STIX]{x1D6FA}^{2}>k^{2}v_{A}^{2}$
. However, in the strict Keplerian limit of Balbus & Hawley (Reference Balbus and Hawley1991), compressibility and density variation do not matter and
![]() $3\unicode[STIX]{x1D6FA}^{2}>k^{2}v_{A}^{2}$
is required for instability.
$3\unicode[STIX]{x1D6FA}^{2}>k^{2}v_{A}^{2}$
is required for instability.
In the absence of gravity our WKB results are consistent with the unbounded medium case of Velikhov (Reference Velikhov1959) in the incompressible limit he considered. Our general compressibility results modify his results and are illustrated by applying them to the self-consistent equilibrium of Catto & Krasheninnikov (Reference Catto and Krasheninnikov2015). This analysis highlights the need to treat the radial WKB analysis carefully to fully retain compressibility and radial density variation as well as the radial variation of the rotation frequency. Compressibility is found to completely stabilize the Velikhov (Reference Velikhov1959) limit when
![]() $3c_{S}^{2}/\unicode[STIX]{x1D6FA}^{2}R^{2}<1$
. However, when
$3c_{S}^{2}/\unicode[STIX]{x1D6FA}^{2}R^{2}<1$
. However, when
![]() $3c_{S}^{2}/\unicode[STIX]{x1D6FA}^{2}R^{2}>1$
instability occurs when
$3c_{S}^{2}/\unicode[STIX]{x1D6FA}^{2}R^{2}>1$
instability occurs when
thereby requiring
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. The self-similar equilibrium for this case without gravity has a magnetic field strength that increases with radius as in most of the cases with gravity.
$\unicode[STIX]{x1D6FD}\gg 1$
. The self-similar equilibrium for this case without gravity has a magnetic field strength that increases with radius as in most of the cases with gravity.
In the presence of gravity our results are in agreement with Balbus & Hawley (Reference Balbus and Hawley1991) and Hawley et al. (Reference Hawley, Gammie and Balbus1995) for strict Keplerian motion, but there are subtle and significant differences whenever there are departures from strict Keplerian motion or non-axial magnetic field effects. Departure from strict Keplerian motion gives rise to compressibility and density gradient effects in our cylindrically symmetric and general axisymmetric magnetic field treatments for
![]() $\unicode[STIX]{x1D6FD}>1$
. These extensions allow us to obtain a general threshold for gravitational magnetorotational instability in thermal magnetized plasmas. The results depend explicitly on gravity, compressibility, and density variation as well as rotation frequency. In the presence of a sufficiently strong radial magnetic field at
$\unicode[STIX]{x1D6FD}>1$
. These extensions allow us to obtain a general threshold for gravitational magnetorotational instability in thermal magnetized plasmas. The results depend explicitly on gravity, compressibility, and density variation as well as rotation frequency. In the presence of a sufficiently strong radial magnetic field at
![]() $\unicode[STIX]{x1D6FD}>1$
, the radial component of the magnetic field provides further destabilization based on (7.33), and the density gradient term depends on axial as well as radial gradients.
$\unicode[STIX]{x1D6FD}>1$
, the radial component of the magnetic field provides further destabilization based on (7.33), and the density gradient term depends on axial as well as radial gradients.
In the strict Keplerian limit these compressibility and density gradient effects vanish. For an axial magnetic field the disk width
![]() $\unicode[STIX]{x1D6E5}$
is given by
$\unicode[STIX]{x1D6E5}$
is given by
![]() $\unicode[STIX]{x1D6E5}/R=2T^{1/2}/M^{1/2}\unicode[STIX]{x1D6FA}R\ll 1$
, limiting perturbation wavelengths in the
$\unicode[STIX]{x1D6E5}/R=2T^{1/2}/M^{1/2}\unicode[STIX]{x1D6FA}R\ll 1$
, limiting perturbation wavelengths in the
![]() $z$
direction. Then, for
$z$
direction. Then, for
![]() $k_{z}\unicode[STIX]{x1D6E5}>2\unicode[STIX]{x03C0}$
and
$k_{z}\unicode[STIX]{x1D6E5}>2\unicode[STIX]{x03C0}$
and
![]() $k_{R}^{2}R^{2}\gg 1$
, the instability requires large
$k_{R}^{2}R^{2}\gg 1$
, the instability requires large
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
This limit is the case for which Balbus’ (Reference Balbus2006) intuitive physical picture of masses attached by springs is most appropriate.
Whether instability is responsible for shedding excess momentum in an accretion disk is unclear, of course, based on a linear eikonal analysis of axisymmetric perturbations. The nonlinear evolution will have to be determined by sophisticated nonlinear global simulations, presumably requiring full kinetic simulations with dissipation. Clearly much work remains if speculation is to be converted to substance To do so requires using fully self-consistent global magnetized equilibria when performing global simulations allowing non-axisymmetric fluctuations
Acknowledgements
P.J.C. thanks Merton College and Peierls Centre for Theoretical Physics at Oxford for rekindling interest in this problem. He is particularly grateful and indebted to A. Schekochihin of Merton College at Oxford who made his visit possible and provided incomparable hospitality. P.J.C. also thanks his colleague N. Loureiro for informative discussions. Work supported by the US Department of Energy grants at DE-FG02-91ER-54109 at MIT and DE-FG02-04ER54739 at UCSD.
Appendix A. General poloidal field case
Equations (7.24) to (7.27) can be combined to obtain the general eikonal stability condition. We first eliminate
![]() $\unicode[STIX]{x1D709}_{\Vert }$
from the
$\unicode[STIX]{x1D709}_{\Vert }$
from the
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
equation to obtain
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
equation to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\unicode[STIX]{x1D714}\left[\!(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}}{B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\!\right]\!\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}=[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})(R\,\text{d}\unicode[STIX]{x1D6FA}/\text{d}\unicode[STIX]{x1D713}_{0})+2\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}R^{-1}B_{0}^{-2}B_{0z}]\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \,\,+\frac{2\text{i}k_{\Vert }\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}B_{0R}}{B_{0}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\,\boldsymbol{\cdot }\,(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)-c_{S}^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\unicode[STIX]{x1D714}\left[\!(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}}{B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\!\right]\!\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}=[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})(R\,\text{d}\unicode[STIX]{x1D6FA}/\text{d}\unicode[STIX]{x1D713}_{0})+2\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}R^{-1}B_{0}^{-2}B_{0z}]\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \,\,+\frac{2\text{i}k_{\Vert }\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}B_{0R}}{B_{0}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\,\boldsymbol{\cdot }\,(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)-c_{S}^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Eliminating
![]() $\unicode[STIX]{x1D709}_{\Vert }$
from the
$\unicode[STIX]{x1D709}_{\Vert }$
from the
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
equation we find
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
equation we find
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{B_{0}^{2}R^{2}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right]-2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle =+\,k_{\Vert }R^{2}B_{0}^{2}p_{0}^{-1}\left[R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+c_{S}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\right]\left\{\frac{2\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}p_{0}B_{0R}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{B_{0}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad \!+\,\frac{k_{\Vert }p_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\,\boldsymbol{\cdot }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}-c_{S}^{2}\unicode[STIX]{x1D735}\,\boldsymbol{\cdot }\,(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})]\!\right\}\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{B_{0}^{2}R^{2}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right]-2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle =+\,k_{\Vert }R^{2}B_{0}^{2}p_{0}^{-1}\left[R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+c_{S}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\right]\left\{\frac{2\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}p_{0}B_{0R}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{B_{0}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad \!+\,\frac{k_{\Vert }p_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\,\boldsymbol{\cdot }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}-c_{S}^{2}\unicode[STIX]{x1D735}\,\boldsymbol{\cdot }\,(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})]\!\right\}\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Next, we may use
for the
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
terms in this last equation, since cancelation of
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
terms in this last equation, since cancelation of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
terms is not an issue. Doing so we obtain
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
terms is not an issue. Doing so we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{B_{0}^{2}R^{2}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right]-2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2k_{\Vert }c_{S}^{2}R^{2}B_{0}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,k_{\Vert }R^{2}B_{0}^{2}p_{0}^{-1}\left[R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+c_{S}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \!\left\{\!\frac{k_{\Vert }p_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}-c_{S}^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})]\!\right\}\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{B_{0}^{2}R^{2}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\right)\right]-2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2k_{\Vert }c_{S}^{2}R^{2}B_{0}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,k_{\Vert }R^{2}B_{0}^{2}p_{0}^{-1}\left[R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}+c_{S}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \!\left\{\!\frac{k_{\Vert }p_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}[\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}-c_{S}^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}R^{-2}B_{0}^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})]\!\right\}\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Combining
![]() $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}$
terms and cancelling the
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}$
terms and cancelling the
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
terms in the
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}$
terms in the
![]() $c_{S}^{2}$
terms leaves
$c_{S}^{2}$
terms leaves
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{\unicode[STIX]{x1D714}^{2}c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[\frac{p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}B_{0}^{-2}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{p_{0}k_{\Vert }^{2}c_{S}^{2}}{R^{2}B_{0}^{2}}\left[\frac{(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{p_{0}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{k_{\Vert }^{2}[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}+2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{2k_{\Vert }c_{S}^{2}R^{2}B_{0}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{||}^{2}c_{S}^{2})}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}+R^{2}B_{0}^{2}v_{A}^{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}^{2}}+\frac{\unicode[STIX]{x1D714}^{2}c_{S}^{2}R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left[\frac{p_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}B_{0}^{-2}R^{-2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0})}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}\frac{p_{0}k_{\Vert }^{2}c_{S}^{2}}{R^{2}B_{0}^{2}}\left[\frac{(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{p_{0}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{k_{\Vert }^{2}[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{R^{2}B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}+2\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}RB_{0z}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{2k_{\Vert }c_{S}^{2}R^{2}B_{0}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{||}^{2}c_{S}^{2})}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}},\end{eqnarray}$$
where we use
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\frac{p_{0}Q}{R^{2}B_{0}^{2}}\right)-Q\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{R^{2}B_{0}^{2}}\right)=\frac{1}{p_{0}B_{0}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{p_{0}Q}{R^{2}B_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{Q}{B_{0}}\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{R^{2}B_{0}}\right)=-\frac{p_{0}Q^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{p_{0}Q}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{R^{2}B_{0}^{2}}{p_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}\left(\frac{p_{0}Q}{R^{2}B_{0}^{2}}\right)-Q\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{R^{2}B_{0}^{2}}\right)=\frac{1}{p_{0}B_{0}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{p_{0}Q}{R^{2}B_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{Q}{B_{0}}\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{R^{2}B_{0}}\right)=-\frac{p_{0}Q^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{p_{0}Q}\right).\end{eqnarray}$$
Notice that within the eikonal approximation it is tempting to assume
however, at marginality (
![]() $\unicode[STIX]{x1D714}^{2}\rightarrow 0$
) this large term becomes unimportant so we have been extra careful to retain the next largest terms.
$\unicode[STIX]{x1D714}^{2}\rightarrow 0$
) this large term becomes unimportant so we have been extra careful to retain the next largest terms.
Inserting
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
in its lowest order form
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}$
in its lowest order form
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\unicode[STIX]{x1D714}\left[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}}{B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})R\,\frac{\text{d}\unicode[STIX]{x1D6FA}}{\text{d}\unicode[STIX]{x1D713}_{0}}+\frac{2\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}B_{0z}}{RB_{0}^{2}}\right]\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}-\frac{2\text{i}k_{\Vert }c_{S}^{2}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}B_{0R}}{B_{0}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\unicode[STIX]{x1D714}\left[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})-\frac{4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}}{B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})R\,\frac{\text{d}\unicode[STIX]{x1D6FA}}{\text{d}\unicode[STIX]{x1D713}_{0}}+\frac{2\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}B_{0z}}{RB_{0}^{2}}\right]\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}-\frac{2\text{i}k_{\Vert }c_{S}^{2}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}B_{0R}}{B_{0}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}},\end{eqnarray}$$
into the preceding equation for
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
we can finally use the remaining eikonal approximation
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
we can finally use the remaining eikonal approximation
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}=\text{i}k_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
to obtain the full stability relation
$\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}=\text{i}k_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$
to obtain the full stability relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D714}^{2}-k^{2}v_{A}^{2}-\frac{\unicode[STIX]{x1D714}^{2}k_{\bot }^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}=\frac{k_{\Vert }^{2}[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\nonumber\\ \displaystyle & & \displaystyle \!\!\quad -\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\;\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \!\!\quad -\,\frac{p_{0}k_{\Vert }^{2}c_{S}^{2}}{R^{2}B_{0}^{2}}\!\left[\frac{(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\left[\frac{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{p_{0}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\,\boldsymbol{\cdot }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}\!\right]\nonumber\\ \displaystyle & & \displaystyle \!\!\quad +\!\left[B_{0z}+\frac{k_{\Vert }k_{\bot }c_{S}^{2}\,B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\!\frac{\left\{\!(\unicode[STIX]{x1D714}^{2}-k_{||}^{2}v_{A}^{2})(R^{2}\,\text{d}\unicode[STIX]{x1D6FA}^{2}/\text{d}\unicode[STIX]{x1D713}_{0})+4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0}^{-2}\left[B_{0z}+\displaystyle \frac{k_{\Vert }k_{\bot }c_{S}^{2}B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\!\right\}}{\{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})-[4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}/(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})B_{0}^{2}]\}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D714}^{2}-k^{2}v_{A}^{2}-\frac{\unicode[STIX]{x1D714}^{2}k_{\bot }^{2}c_{S}^{2}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}=\frac{k_{\Vert }^{2}[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\nonumber\\ \displaystyle & & \displaystyle \!\!\quad -\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\;\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]}\right\}\nonumber\\ \displaystyle & & \displaystyle \!\!\quad -\,\frac{p_{0}k_{\Vert }^{2}c_{S}^{2}}{R^{2}B_{0}^{2}}\!\left[\frac{(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]^{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\!\left[\frac{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}{p_{0}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\,\boldsymbol{\cdot }\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}}\!\right]\nonumber\\ \displaystyle & & \displaystyle \!\!\quad +\!\left[B_{0z}+\frac{k_{\Vert }k_{\bot }c_{S}^{2}\,B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\!\frac{\left\{\!(\unicode[STIX]{x1D714}^{2}-k_{||}^{2}v_{A}^{2})(R^{2}\,\text{d}\unicode[STIX]{x1D6FA}^{2}/\text{d}\unicode[STIX]{x1D713}_{0})+4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0}^{-2}\left[B_{0z}+\displaystyle \frac{k_{\Vert }k_{\bot }c_{S}^{2}B_{0R}}{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})}\right]\!\right\}}{\{(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})-[4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}/(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}c_{S}^{2})B_{0}^{2}]\}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where we have used
![]() $k_{\bot }=k_{\unicode[STIX]{x1D713}}RB_{0}$
and
$k_{\bot }=k_{\unicode[STIX]{x1D713}}RB_{0}$
and
![]() $k^{2}=k_{\Vert }^{2}+k_{\bot }^{2}\simeq k_{\bot }^{2}$
. Discarding small terms leaves
$k^{2}=k_{\Vert }^{2}+k_{\bot }^{2}\simeq k_{\bot }^{2}$
. Discarding small terms leaves
 $$\begin{eqnarray}\displaystyle & & \displaystyle k^{2}v_{A}^{2}-\frac{\unicode[STIX]{x1D714}^{2}k_{\bot }^{2}}{k_{\Vert }^{2}}\,=\,\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}c_{S}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}}{n_{0}R^{2}B_{0}^{2}}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[B_{0z}-\frac{k_{\bot }\,B_{0R}}{k_{\Vert }}\right]\frac{\left\{\!(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})(R^{2}\,\text{d}\unicode[STIX]{x1D6FA}^{2}/\text{d}\unicode[STIX]{x1D713}_{0})+4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0}^{-2}\left[B_{0z}-\displaystyle \frac{k_{\bot }\,B_{0R}}{k_{\Vert }}\right]\!\right\}}{[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})+(4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}/k_{\Vert }^{2}c_{S}^{2}B_{0}^{2})]}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle k^{2}v_{A}^{2}-\frac{\unicode[STIX]{x1D714}^{2}k_{\bot }^{2}}{k_{\Vert }^{2}}\,=\,\frac{[(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}]^{2}}{R^{2}B_{0}^{2}c_{S}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}}{n_{0}R^{2}B_{0}^{2}}(M_{0}G_{0}r^{-2}\unicode[STIX]{x1D735}r-\unicode[STIX]{x1D6FA}^{2}R\unicode[STIX]{x1D735}R)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}_{0}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[B_{0z}-\frac{k_{\bot }\,B_{0R}}{k_{\Vert }}\right]\frac{\left\{\!(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})(R^{2}\,\text{d}\unicode[STIX]{x1D6FA}^{2}/\text{d}\unicode[STIX]{x1D713}_{0})+4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0}^{-2}\left[B_{0z}-\displaystyle \frac{k_{\bot }\,B_{0R}}{k_{\Vert }}\right]\!\right\}}{[(\unicode[STIX]{x1D714}^{2}-k_{\Vert }^{2}v_{A}^{2})+(4\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FA}^{2}B_{0R}^{2}/k_{\Vert }^{2}c_{S}^{2}B_{0}^{2})]}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$