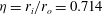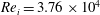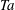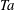1 Introduction
Non-smooth surfaces exist everywhere in nature, and many engineering applications need to deal with rough boundaries. The question of how local wall roughness affects global transport properties dates back to the pioneering study by Nikuradse (Reference Nikuradse1933) in pipe flow. Nikuradse performed experiments on pipes with sand glued to the wall as densely as possible. The measurements of the friction coefficient
![]() $C_{f}={\it\tau}/({\it\rho}U^{2}/2)$
, where
$C_{f}={\it\tau}/({\it\rho}U^{2}/2)$
, where
![]() ${\it\tau}$
is the surfaced averaged friction stress,
${\it\tau}$
is the surfaced averaged friction stress,
![]() ${\it\rho}$
the fluid density and
${\it\rho}$
the fluid density and
![]() $U$
the mean flow velocity, show that roughness has little impact in the laminar regime, but after increasing the Reynolds number
$U$
the mean flow velocity, show that roughness has little impact in the laminar regime, but after increasing the Reynolds number
![]() $Re$
, the friction factor turns upwards and reaches an asymptote. At the highest
$Re$
, the friction factor turns upwards and reaches an asymptote. At the highest
![]() $Re$
, the friction factor becomes independent of
$Re$
, the friction factor becomes independent of
![]() $Re$
. Nikuradse then explained that, in the smooth case, the viscous sublayer depth depends on
$Re$
. Nikuradse then explained that, in the smooth case, the viscous sublayer depth depends on
![]() $Re$
, and hence the friction factor. However, by introducing roughness, the viscous sublayer decreases down to the roughness scale, where the friction factor becomes independent of
$Re$
, and hence the friction factor. However, by introducing roughness, the viscous sublayer decreases down to the roughness scale, where the friction factor becomes independent of
![]() $Re$
. Since then, there have been many studies concerning flow in pipes with surface roughness (see Jimenez (Reference Jimenez2004) for a review).
$Re$
. Since then, there have been many studies concerning flow in pipes with surface roughness (see Jimenez (Reference Jimenez2004) for a review).
In general, studying the effect of a change of the boundary conditions at the wall will lead to a better understanding of the bulk–boundary layer (BL) interaction and the flow transport properties which are closely connected therewith. Next to pipe flow, the canonical systems in turbulent flows are Rayleigh–Bénard (RB) flow, in which a fluid is driven by the temperature difference between the hot bottom plate and cold top plate, and Taylor–Couette (TC) flow, in which a fluid is confined between two independently rotating coaxial cylinders. Both flows have been well studied and show rich patterns with smooth walls (see Ahlers, Grossmann & Lohse (Reference Ahlers, Grossmann and Lohse2009) for a comprehensive review on RB flow and Fardin, Perge & Taberlet (Reference Fardin, Perge and Taberlet2014); Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016) on TC flow). Eckhardt, Grossmann & Lohse (Reference Eckhardt, Grossmann and Lohse2007a ,Reference Eckhardt, Grossmann and Lohse b ) showed that pipe, RB and TC flows are analogous to each other. Because of the close analogy, a better understanding of TC flow will lead to a more profound insight also in RB and pipe flow, and vice versa.
The temperature difference between the top and bottom plate in RB flow is analogous to different rotation rates of the inner and outer cylinders in TC flow. The rotation difference in TC flow is non-dimensionally characterized by the Taylor number
![]() $Ta$
, which is analogous to the dimensionless temperature difference in RB flow, i.e. the Rayleigh number
$Ta$
, which is analogous to the dimensionless temperature difference in RB flow, i.e. the Rayleigh number
![]() $Ra$
. For TC flow, the global transport property is expressed as the dimensionless torque
$Ra$
. For TC flow, the global transport property is expressed as the dimensionless torque
![]() $Nu_{{\it\omega}}$
, which is analogous to the dimensionless heat flux in RB flow, i.e. the Nusselt number
$Nu_{{\it\omega}}$
, which is analogous to the dimensionless heat flux in RB flow, i.e. the Nusselt number
![]() $Nu$
. In TC flow, when the driving force
$Nu$
. In TC flow, when the driving force
![]() $Ta$
is small, both the BL and the bulk are of laminar type. When increasing
$Ta$
is small, both the BL and the bulk are of laminar type. When increasing
![]() $Ta$
, first the bulk becomes turbulent, and finally also the BLs (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
). This state is the so-called ‘ultimate’ regime. The ultimate regime is relevant not only conceptually (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001), but also because many applications in nature and engineering are within that regime. For TC flow, the BL transition was first found by Lathrop, Fineberg & Swinney (Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
) and Lewis & Swinney (Reference Lewis and Swinney1999), though they did not relate it to the ‘ultimate’ regime. Later, van Gils et al. (Reference van Gils, Huisman, Bruggert, Sun and Lohse2011), Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012, Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
) put it into this conceptual framework. In RB turbulence, the ultimate regime was experimentally found by He et al. (Reference He, Funfschilling, Bodenschatz and Ahlers2012a
,Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers
b
). In both RB and TC turbulence, the ultimate regime scalings, namely
$Ta$
, first the bulk becomes turbulent, and finally also the BLs (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
). This state is the so-called ‘ultimate’ regime. The ultimate regime is relevant not only conceptually (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001), but also because many applications in nature and engineering are within that regime. For TC flow, the BL transition was first found by Lathrop, Fineberg & Swinney (Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
) and Lewis & Swinney (Reference Lewis and Swinney1999), though they did not relate it to the ‘ultimate’ regime. Later, van Gils et al. (Reference van Gils, Huisman, Bruggert, Sun and Lohse2011), Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012, Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
) put it into this conceptual framework. In RB turbulence, the ultimate regime was experimentally found by He et al. (Reference He, Funfschilling, Bodenschatz and Ahlers2012a
,Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers
b
). In both RB and TC turbulence, the ultimate regime scalings, namely
![]() $Nu\sim Ra^{{\it\beta}}$
in RB flow and
$Nu\sim Ra^{{\it\beta}}$
in RB flow and
![]() $Nu_{{\it\omega}}\sim Ta^{{\it\beta}}$
in TC flow, have an effective exponent of
$Nu_{{\it\omega}}\sim Ta^{{\it\beta}}$
in TC flow, have an effective exponent of
![]() ${\it\beta}\approx 0.38{-}0.40$
, originating from
${\it\beta}\approx 0.38{-}0.40$
, originating from
![]() $1/2$
(Kraichnan Reference Kraichnan1962) and logarithmic corrections (Grossmann & Lohse Reference Grossmann and Lohse2011, Reference Grossmann and Lohse2012).
$1/2$
(Kraichnan Reference Kraichnan1962) and logarithmic corrections (Grossmann & Lohse Reference Grossmann and Lohse2011, Reference Grossmann and Lohse2012).
For RB flow with roughness, various different effective scaling laws relating heat transport to the driving, written in the form
![]() $Nu=ARa^{{\it\beta}}$
, were suggested. When the height of roughness
$Nu=ARa^{{\it\beta}}$
, were suggested. When the height of roughness
![]() ${\it\delta}$
is larger than the thermal BL thickness
${\it\delta}$
is larger than the thermal BL thickness
![]() ${\it\lambda}_{{\it\theta}}\simeq L/(2Nu)$
, where
${\it\lambda}_{{\it\theta}}\simeq L/(2Nu)$
, where
![]() $L$
is the distance between two plates, Shen, Tong & Xia (Reference Shen, Tong and Xia1996) found that the prefactor
$L$
is the distance between two plates, Shen, Tong & Xia (Reference Shen, Tong and Xia1996) found that the prefactor
![]() $A$
increased by 20 %, whereas the exponent
$A$
increased by 20 %, whereas the exponent
![]() ${\it\beta}$
did not change on using rough surfaces made of regularly spaced pyramids. Later, by using the same facility, but a different pyramid height (9 mm compared to 3.2 mm in Shen et al. (Reference Shen, Tong and Xia1996)), Du & Tong (Reference Du and Tong2000) measured the increase of
${\it\beta}$
did not change on using rough surfaces made of regularly spaced pyramids. Later, by using the same facility, but a different pyramid height (9 mm compared to 3.2 mm in Shen et al. (Reference Shen, Tong and Xia1996)), Du & Tong (Reference Du and Tong2000) measured the increase of
![]() $A$
to be as much as 76 % and the exponent
$A$
to be as much as 76 % and the exponent
![]() ${\it\beta}$
again stayed the same. Based on flow visualization, Du & Tong (Reference Du and Tong2000) concluded that the enhancement of heat transport is due to plume ejection from the tip of the pyramids. Also Ciliberto & Laroche (Reference Ciliberto and Laroche1999) found that
${\it\beta}$
again stayed the same. Based on flow visualization, Du & Tong (Reference Du and Tong2000) concluded that the enhancement of heat transport is due to plume ejection from the tip of the pyramids. Also Ciliberto & Laroche (Reference Ciliberto and Laroche1999) found that
![]() ${\it\beta}$
was unaffected but, more surprisingly,
${\it\beta}$
was unaffected but, more surprisingly,
![]() $A$
decreased when
$A$
decreased when
![]() ${\it\lambda}_{{\it\theta}}<{\it\delta}$
. In another experiment, which used pyramid roughness, by Qiu, Xia & Tong (Reference Qiu, Xia and Tong2005), both
${\it\lambda}_{{\it\theta}}<{\it\delta}$
. In another experiment, which used pyramid roughness, by Qiu, Xia & Tong (Reference Qiu, Xia and Tong2005), both
![]() $A$
and
$A$
and
![]() ${\it\beta}$
were found to increase and the new
${\it\beta}$
were found to increase and the new
![]() ${\it\beta}$
with roughness was 0.35. Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) found
${\it\beta}$
with roughness was 0.35. Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) found
![]() ${\it\beta}\approx 0.35$
with roughness on both the lower and upper plates. In contrast, Stringano, Pascazio & Verzicco (Reference Stringano, Pascazio and Verzicco2006), who numerically investigated RB convection over grooved plates, showed that the secondary vortex inside the grooves would lift up the BL and help the plumes detach from the tip, which is consistent with the result of Du & Tong (Reference Du and Tong2000). Both
${\it\beta}\approx 0.35$
with roughness on both the lower and upper plates. In contrast, Stringano, Pascazio & Verzicco (Reference Stringano, Pascazio and Verzicco2006), who numerically investigated RB convection over grooved plates, showed that the secondary vortex inside the grooves would lift up the BL and help the plumes detach from the tip, which is consistent with the result of Du & Tong (Reference Du and Tong2000). Both
![]() $A$
and
$A$
and
![]() ${\it\beta}$
increased and
${\it\beta}$
increased and
![]() ${\it\beta}$
changed to approximately 0.37. By implementing V-shaped axis-symmetrical roughness both on the sidewalls and horizontal plates, Roche et al. (Reference Roche, Castaing, Chabaud and Hébral2001) obtained an increase of
${\it\beta}$
changed to approximately 0.37. By implementing V-shaped axis-symmetrical roughness both on the sidewalls and horizontal plates, Roche et al. (Reference Roche, Castaing, Chabaud and Hébral2001) obtained an increase of
![]() ${\it\beta}$
to approximately 0.51, which was interpreted as triggering the ultimate region
${\it\beta}$
to approximately 0.51, which was interpreted as triggering the ultimate region
![]() $1/2$
law without the logarithmic correction proposed by Kraichnan (Reference Kraichnan1962), after
$1/2$
law without the logarithmic correction proposed by Kraichnan (Reference Kraichnan1962), after
![]() ${\it\lambda}_{{\it\theta}}$
drops below the roughness height. They concluded that the roughness imposes a new length scale on the thermal BLs. They argued that the sublayer thickness would be fixed by the roughness such that the logarithmic correction would become irrelevant. Ahlers et al. (Reference Ahlers, Grossmann and Lohse2009) pointed out that the
${\it\lambda}_{{\it\theta}}$
drops below the roughness height. They concluded that the roughness imposes a new length scale on the thermal BLs. They argued that the sublayer thickness would be fixed by the roughness such that the logarithmic correction would become irrelevant. Ahlers et al. (Reference Ahlers, Grossmann and Lohse2009) pointed out that the
![]() $1/2$
scaling observed might possibly be due to a crossover between rough surfaces from a regime with a groove depth less than the BL thickness to a regime where the groove depth is larger than the BL thickness. Tisserand et al. (Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chillà2011) postulated that, if this interpretation was correct, then the
$1/2$
scaling observed might possibly be due to a crossover between rough surfaces from a regime with a groove depth less than the BL thickness to a regime where the groove depth is larger than the BL thickness. Tisserand et al. (Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chillà2011) postulated that, if this interpretation was correct, then the
![]() ${\it\beta}=1/2$
behaviour of RB flow with roughness would be fortuitous. Salort et al. (Reference Salort, Liot, Rusaouen, Seychelles, Tisserand, Creyssels, Castaing and Chillà2014) further showed that, in their model,
${\it\beta}=1/2$
behaviour of RB flow with roughness would be fortuitous. Salort et al. (Reference Salort, Liot, Rusaouen, Seychelles, Tisserand, Creyssels, Castaing and Chillà2014) further showed that, in their model,
![]() ${\it\beta}$
could range from 0.38 to 0.5, depending on the extent of instability of the BL. Clearly, more work is needed to resolve this issue.
${\it\beta}$
could range from 0.38 to 0.5, depending on the extent of instability of the BL. Clearly, more work is needed to resolve this issue.
We now come to TC flow with roughness, the subject of the present study, for which studies are less common. Cadot et al. (Reference Cadot, Couder, Daerr, Douady and Tsinober1997) performed experiments with equidistant ribs on both the inner and the outer surface. These ribs were straight and parallel to the axis of the cylinders. With smooth boundaries, the dissipation in the boundary is dominant and the drag coefficient decreases with increasing
![]() $Re$
. However, with rough walls, Cadot et al. (Reference Cadot, Couder, Daerr, Douady and Tsinober1997) argued that the dissipation in the BLs is no longer dominant, due to the extra dissipation in the bulk. In that regime the global drag coefficient becomes constant with increasing
$Re$
. However, with rough walls, Cadot et al. (Reference Cadot, Couder, Daerr, Douady and Tsinober1997) argued that the dissipation in the BLs is no longer dominant, due to the extra dissipation in the bulk. In that regime the global drag coefficient becomes constant with increasing
![]() $Re$
. Inspired by this work, van den Berg et al. (Reference van den Berg, Doering, Lohse and Lathrop2003) performed further experiments with the same style of roughness. They reported results for the four cases of two smooth walls, smooth-inner/rough-outer, rough-outer/smooth-inner, and two rough walls. The data were interpreted within the Grossmann–Lohse (GL) theory (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2002). The flow was found to change from BL dominant to bulk dominant. In the case with two rough walls, the drag coefficient is again found to be independent of
$Re$
. Inspired by this work, van den Berg et al. (Reference van den Berg, Doering, Lohse and Lathrop2003) performed further experiments with the same style of roughness. They reported results for the four cases of two smooth walls, smooth-inner/rough-outer, rough-outer/smooth-inner, and two rough walls. The data were interpreted within the Grossmann–Lohse (GL) theory (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2002). The flow was found to change from BL dominant to bulk dominant. In the case with two rough walls, the drag coefficient is again found to be independent of
![]() $Re$
. The phenomenon of drag saturation with increasing
$Re$
. The phenomenon of drag saturation with increasing
![]() $Re$
is very similar to that found by Nikuradse (Reference Nikuradse1933) in his rough pipe experiments.
$Re$
is very similar to that found by Nikuradse (Reference Nikuradse1933) in his rough pipe experiments.
We stress that there are usually two different types of wall roughness. In the first type the roughness is arranged in such a way as to impede the mean flow. We call this ‘perpendicular roughness’. This kind of roughness element seems to be a more efficient generator of skin friction than smooth walls (Jimenez Reference Jimenez2004). The studies of Cadot et al. (Reference Cadot, Couder, Daerr, Douady and Tsinober1997) and van den Berg et al. (Reference van den Berg, Doering, Lohse and Lathrop2003) can both be included in this category. The other possibility is to arrange the roughness aligned with the mean flow, i.e. ‘parallel roughness’. A well-documented example is the flow over riblets (Choi, Moin & Kim Reference Choi, Moin and Kim1993; Chu & Karniadakis Reference Chu and Karniadakis1993). Under specific circumstances they decrease drag by 6 % (Choi et al. Reference Choi, Moin and Kim1993). Many different kinds of roughness can be formed by combining these two approaches.

Figure 1. Schematic view of the Taylor–Couette system and the groove geometry. (a) Three-dimensional view. The inner cylinder with radius
![]() $r_{i}$
is rotating with angular velocity
$r_{i}$
is rotating with angular velocity
![]() ${\it\omega}_{i}$
. The outer cylinder with radius
${\it\omega}_{i}$
. The outer cylinder with radius
![]() $r_{o}$
is at rest. (b) Cross-section view of the gap between the cylinders:
$r_{o}$
is at rest. (b) Cross-section view of the gap between the cylinders:
![]() $d=r_{o}-r_{i}$
. The length scale of the grooves is
$d=r_{o}-r_{i}$
. The length scale of the grooves is
![]() ${\it\delta}$
.
${\it\delta}$
.
Inspired by the above studies, especially the similarities between pipe, RB and TC flow, we study how the
![]() $Nu_{{\it\omega}}$
versus
$Nu_{{\it\omega}}$
versus
![]() $Ta$
scaling and the corresponding flow structure behave with roughness in TC. In the present study, we perform direct numerical simulation (DNS) of TC flow with grooved walls. Because the grooves are quite large compared to the viscous scale, we avoid calling them roughness, similar to Stringano et al. (Reference Stringano, Pascazio and Verzicco2006). The grooves implemented here are V-shaped obstacles attached to the wall with a tip angle of 90° and axisymmetric to the axis of cylinder. This arrangement of grooves is categorized as parallel roughness. A schematic view of the structure is shown in figure 1. Note that the rough element type in this study is similar to the one used in Stringano et al. (Reference Stringano, Pascazio and Verzicco2006), but different from the one used in Shen et al. (Reference Shen, Tong and Xia1996) and Du & Tong (Reference Du and Tong2000), in which pyramid structures were used.
$Ta$
scaling and the corresponding flow structure behave with roughness in TC. In the present study, we perform direct numerical simulation (DNS) of TC flow with grooved walls. Because the grooves are quite large compared to the viscous scale, we avoid calling them roughness, similar to Stringano et al. (Reference Stringano, Pascazio and Verzicco2006). The grooves implemented here are V-shaped obstacles attached to the wall with a tip angle of 90° and axisymmetric to the axis of cylinder. This arrangement of grooves is categorized as parallel roughness. A schematic view of the structure is shown in figure 1. Note that the rough element type in this study is similar to the one used in Stringano et al. (Reference Stringano, Pascazio and Verzicco2006), but different from the one used in Shen et al. (Reference Shen, Tong and Xia1996) and Du & Tong (Reference Du and Tong2000), in which pyramid structures were used.
Our motivations are as follows: (i) DNS provides us with the ability to reproduce all the details of the flow field which are unavailable in experiments, and therefore enables us to reveal the connection between the effective scaling laws for the torque, the boundary layer, and the flow structures. (ii) We want to answer the question whether, with parallel roughness, the ultimate regime effective scaling exponent
![]() ${\it\beta}$
would change, or whether it stays the same as in the smooth case, namely
${\it\beta}$
would change, or whether it stays the same as in the smooth case, namely
![]() ${\it\beta}=0.38$
in the relevant
${\it\beta}=0.38$
in the relevant
![]() $Ta$
regime.
$Ta$
regime.
The manuscript is organized as follows. In § 2, we describe the numerical methods and parameter settings. In § 3, we show the effective scaling laws between the Nusselt number and Taylor number in smooth and grooved cases. In § 4, it is shown how grooves change the flow structure. Section 5 presents the boundary layer dynamics with grooves. Finally, conclusions are drawn in § 6.
2 Numerical settings
2.1 Parameter descriptions
In the present study, the outer cylinder is stationary and only the inner cylinder is rotating and thus driving the flow. The flow is bounded by two lateral grooved walls cylinders with no-slip boundary conditions. The lower and upper surfaces are replaced by axially periodic boundary conditions and therefore do not include the effects of end walls unavoidably present in TC experiments. The grooves of the lateral walls are V-shaped, with a tip angle of 90° and a height
![]() ${\it\delta}$
(figure 1).
${\it\delta}$
(figure 1).
![]() $r_{i}$
and
$r_{i}$
and
![]() $r_{o}$
are the base radii of the inner and the outer cylinder without grooves, respectively. The valley-to-valley distance
$r_{o}$
are the base radii of the inner and the outer cylinder without grooves, respectively. The valley-to-valley distance
![]() $d=r_{o}-r_{i}$
is used to non-dimensionalize all lengths and the base velocity of the inner cylinder
$d=r_{o}-r_{i}$
is used to non-dimensionalize all lengths and the base velocity of the inner cylinder
![]() $U=r_{i}{\it\omega}_{i}$
for normalizing velocities, where
$U=r_{i}{\it\omega}_{i}$
for normalizing velocities, where
![]() ${\it\omega}_{i}$
is the angular velocity of the inner cylinder. The inner grooves rotate with the inner cylinder, and thus have constant angular velocity. This means that the azimuthal velocity at the tip of the groove is slightly larger by a factor of
${\it\omega}_{i}$
is the angular velocity of the inner cylinder. The inner grooves rotate with the inner cylinder, and thus have constant angular velocity. This means that the azimuthal velocity at the tip of the groove is slightly larger by a factor of
![]() $(r_{i}+{\it\delta})/r_{i}$
than the velocity at the valley of the inner cylinder. The geometry of the system is fixed at a specific radius ratio
$(r_{i}+{\it\delta})/r_{i}$
than the velocity at the valley of the inner cylinder. The geometry of the system is fixed at a specific radius ratio
![]() ${\it\eta}=r_{i}/r_{o}=0.714$
. The reasons for keeping the outer cylinder stationary and choosing such a radius ratio are because they are close to the previous experimental and numerical studies (Lathrop et al.
Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
; Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012, Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
), so that we can make direct comparisons with those results. We define the dimensionless radial coordinate as
${\it\eta}=r_{i}/r_{o}=0.714$
. The reasons for keeping the outer cylinder stationary and choosing such a radius ratio are because they are close to the previous experimental and numerical studies (Lathrop et al.
Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
; Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012, Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
), so that we can make direct comparisons with those results. We define the dimensionless radial coordinate as
![]() $y=(r-r_{i})/d$
, so that it ranges from 0 at the inner cylinder to 1 at the outer cylinder. Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
) showed that a rotational symmetry of order six does not change the flow statistics for
$y=(r-r_{i})/d$
, so that it ranges from 0 at the inner cylinder to 1 at the outer cylinder. Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
) showed that a rotational symmetry of order six does not change the flow statistics for
![]() ${\it\eta}=0.714$
. We follow their approach and choose this value to reduce the number of grids and the computational cost. The aspect ratio
${\it\eta}=0.714$
. We follow their approach and choose this value to reduce the number of grids and the computational cost. The aspect ratio
![]() ${\it\Gamma}$
is chosen to be
${\it\Gamma}$
is chosen to be
![]() ${\it\Gamma}=L/d=2{\rm\pi}/3=2.094$
(Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
), where
${\it\Gamma}=L/d=2{\rm\pi}/3=2.094$
(Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
), where
![]() $L$
is the axial domain length. In this way one pair of Taylor vortices can be sustained in our DNS. The dimensionless torque is defined in the form
$L$
is the axial domain length. In this way one pair of Taylor vortices can be sustained in our DNS. The dimensionless torque is defined in the form
![]() $Nu_{{\it\omega}}=T/T_{pa}$
, where
$Nu_{{\it\omega}}=T/T_{pa}$
, where
![]() $T_{pa}$
is the torque of the purely azimuthal laminar state without grooves.
$T_{pa}$
is the torque of the purely azimuthal laminar state without grooves.
The motion of the fluid is governed by the incompressible Navier–Stokes equations
where
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
are the fluid velocity and pressure, respectively.
$p$
are the fluid velocity and pressure, respectively.
![]() $f({\it\eta})$
is a geometrical factor which is in the form
$f({\it\eta})$
is a geometrical factor which is in the form
The
![]() $Ta$
number, in the absence of outer cylinder rotation, is written as
$Ta$
number, in the absence of outer cylinder rotation, is written as
where
![]() ${\it\nu}$
is the kinematic viscosity of the fluid.
${\it\nu}$
is the kinematic viscosity of the fluid.
An alternative way to determine the system by using the inner cylinder Reynolds number
![]() $Re_{i}=r_{i}{\it\omega}_{i}d/{\it\nu}$
, rather than the
$Re_{i}=r_{i}{\it\omega}_{i}d/{\it\nu}$
, rather than the
![]() $Ta$
number, is suggested in the work of Lathrop et al. (Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
), Lewis & Swinney (Reference Lewis and Swinney1999). Note that these two definitions can be easily translated into each other using the relation
$Ta$
number, is suggested in the work of Lathrop et al. (Reference Lathrop, Fineberg and Swinney1992a
,Reference Lathrop, Fineberg and Swinney
b
), Lewis & Swinney (Reference Lewis and Swinney1999). Note that these two definitions can be easily translated into each other using the relation
2.2 Numerical method
A second-order finite difference code is employed for the present research, which is written in cylindrical coordinates and discretized on a staggered mesh. Details of the base code can be found in Verzicco & Orlandi (Reference Verzicco and Orlandi1996) and van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015a ). The code has been extensively validated in Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a ,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse b ). Time marching is performed by a third-order Runge–Kutta scheme and the fractional step is used for the pressure–momentum coupling, in combination with a semi-implicit scheme for viscous terms. To achieve large-scale computation, a hybrid MPI-pencil and OpenMP decomposition is used to parallelize the code.
An immersed boundary (IB) technique (Fadlun et al.
Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) has been implemented into the code in order to deal with grooves on the surfaces of both cylinders. The main idea of the IB method is to add a body force term
![]() $\boldsymbol{f}$
to the momentum equation (2.1), mimicking the boundary effect, to enforce in this way the desired velocity on the boundary, so that a regular non-body fitted mesh can be used. The information transfer between boundaries and nearby meshes is performed by means of interpolation. The advantage of the IB method is immediate: flow bounded by arbitrary complex geometry can be easily solved on a very simple mesh with an additional body force. This IB method has already been validated in a variety of contexts (Fadlun et al.
Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006). For more details on the implementation, accuracy and application of the IB method, we refer the reader to Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) and Mittal & Iaccarino (Reference Mittal and Iaccarino2005).
$\boldsymbol{f}$
to the momentum equation (2.1), mimicking the boundary effect, to enforce in this way the desired velocity on the boundary, so that a regular non-body fitted mesh can be used. The information transfer between boundaries and nearby meshes is performed by means of interpolation. The advantage of the IB method is immediate: flow bounded by arbitrary complex geometry can be easily solved on a very simple mesh with an additional body force. This IB method has already been validated in a variety of contexts (Fadlun et al.
Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006). For more details on the implementation, accuracy and application of the IB method, we refer the reader to Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) and Mittal & Iaccarino (Reference Mittal and Iaccarino2005).
In order to guarantee the proper resolution, we proceed as follows. The mean angular velocity current
![]() $J^{{\it\omega}}$
, defined by
$J^{{\it\omega}}$
, defined by
is strictly conserved along the radius
![]() $r$
(Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007b
). In this equation,
$r$
(Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007b
). In this equation,
![]() $u_{r}$
denotes the radial velocity component and
$u_{r}$
denotes the radial velocity component and
![]() ${\it\omega}$
the angular velocity. On the one hand,
${\it\omega}$
the angular velocity. On the one hand,
![]() $J^{{\it\omega}}$
is related to the torque
$J^{{\it\omega}}$
is related to the torque
![]() $T$
by
$T$
by
![]() $T/(2{\rm\pi}L{\it\rho}_{f})=J^{{\it\omega}}$
, where
$T/(2{\rm\pi}L{\it\rho}_{f})=J^{{\it\omega}}$
, where
![]() ${\it\rho}_{f}$
is the fluid density. On the other hand,
${\it\rho}_{f}$
is the fluid density. On the other hand,
![]() $J^{{\it\omega}}$
can also be related to
$J^{{\it\omega}}$
can also be related to
![]() $Nu_{{\it\omega}}$
as
$Nu_{{\it\omega}}$
as
![]() $Nu_{{\it\omega}}=T/T_{pa}=J^{{\it\omega}}/J_{0}^{{\it\omega}}$
, in which
$Nu_{{\it\omega}}=T/T_{pa}=J^{{\it\omega}}/J_{0}^{{\it\omega}}$
, in which
![]() $J_{0}^{{\it\omega}}$
is the angular velocity current of the purely azimuthal state without grooves.
$J_{0}^{{\it\omega}}$
is the angular velocity current of the purely azimuthal state without grooves.
![]() $\langle \cdots \,\rangle _{A,t}$
represents averages over a cylindrical surface at radius
$\langle \cdots \,\rangle _{A,t}$
represents averages over a cylindrical surface at radius
![]() $r$
and over time. Numerically,
$r$
and over time. Numerically,
![]() $J^{{\it\omega}}$
will deviate slightly from being constant due to numerical errors. To quantify this difference, we define
$J^{{\it\omega}}$
will deviate slightly from being constant due to numerical errors. To quantify this difference, we define
where the maximum and minimum are determined over all
![]() $r$
, which is chosen to be within the range
$r$
, which is chosen to be within the range
![]() $r_{i}+{\it\delta}\leqslant r\leqslant r_{o}-{\it\delta}$
because of the influences of the grooves. As illustrated by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013),
$r_{i}+{\it\delta}\leqslant r\leqslant r_{o}-{\it\delta}$
because of the influences of the grooves. As illustrated by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013),
![]() ${\it\Delta}_{J}\leqslant 0.01$
is a very strict requirement for the meshes. We make sure that all of our simulations meet this criterion (see table 1). An additional issue on resolution within the near-wall region by using the IB method is that grooves do not coincide with the coordinate lines. This results in a finer mesh in the radial and axial directions. Compared to the case without grooves at the same
${\it\Delta}_{J}\leqslant 0.01$
is a very strict requirement for the meshes. We make sure that all of our simulations meet this criterion (see table 1). An additional issue on resolution within the near-wall region by using the IB method is that grooves do not coincide with the coordinate lines. This results in a finer mesh in the radial and axial directions. Compared to the case without grooves at the same
![]() $Ta$
number, the number of grids increases by at least by a factor of four. Figure 2 shows an example of the mesh in the meridional plane.
$Ta$
number, the number of grids increases by at least by a factor of four. Figure 2 shows an example of the mesh in the meridional plane.

Figure 2. An example of the mesh used in our simulations in the meridional plane with radial grids and axial grids of
![]() $N_{r}\times N_{z}=160\times 512$
. (a) Whole surface. (b) Enlargement of the region near the grooves. A more refined mesh is needed near the tip of the grooves. Note that the grid resolution in the axial direction is much higher than the one used in Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013), Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
) because here we have to implement the IB method.
$N_{r}\times N_{z}=160\times 512$
. (a) Whole surface. (b) Enlargement of the region near the grooves. A more refined mesh is needed near the tip of the grooves. Note that the grid resolution in the axial direction is much higher than the one used in Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013), Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
) because here we have to implement the IB method.
Table 1. Values of the control parameters and the numerical results of the simulations. Three series of different groove height are presented. In each series, we vary
![]() $Ta$
, and thus
$Ta$
, and thus
![]() $Re_{i}$
. The fourth column shows the number of grids used in the azimuthal (
$Re_{i}$
. The fourth column shows the number of grids used in the azimuthal (
![]() $N_{{\it\theta}}$
), radial (
$N_{{\it\theta}}$
), radial (
![]() $N_{r}$
) and axial direction (
$N_{r}$
) and axial direction (
![]() $N_{z}$
). The fifth column shows the dimensionless torque,
$N_{z}$
). The fifth column shows the dimensionless torque,
![]() $Nu_{{\it\omega}}$
. The last column shows the criteria of resolution we choose, i.e. angular velocity current difference along the radius
$Nu_{{\it\omega}}$
. The last column shows the criteria of resolution we choose, i.e. angular velocity current difference along the radius
![]() $J_{{\it\omega}}$
. All of the simulations were run in a reduced geometry with
$J_{{\it\omega}}$
. All of the simulations were run in a reduced geometry with
![]() $L=2{\rm\pi}/3$
and a rotation symmetry of the order 6. The corresponding cases at the same
$L=2{\rm\pi}/3$
and a rotation symmetry of the order 6. The corresponding cases at the same
![]() $Ta$
without grooves (with smooth cylinders) can be found in Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013), Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
).
$Ta$
without grooves (with smooth cylinders) can be found in Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013), Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
).

2.3 Explored phase space
Inspired by the literature on RB flow with roughness (Shen et al.
Reference Shen, Tong and Xia1996; Du & Tong Reference Du and Tong2000), in which it was found that the heat flux increase can not be explained solely by the increase of surface area, three different groove heights with the same total area in each series, i.e.
![]() ${\it\delta}=0.052d$
,
${\it\delta}=0.052d$
,
![]() ${\it\delta}=0.105d$
and
${\it\delta}=0.105d$
and
![]() ${\it\delta}=0.209d$
, corresponding to 20, 10 and 5 grooves on both surfaces of cylinder, were analysed. In each series with the same groove height,
${\it\delta}=0.209d$
, corresponding to 20, 10 and 5 grooves on both surfaces of cylinder, were analysed. In each series with the same groove height,
![]() $Ta$
is varied from
$Ta$
is varied from
![]() $10^{5}$
to
$10^{5}$
to
![]() $10^{9}$
. We then directly compare our results with our previous simulations by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
), as well as experiments by Lewis & Swinney (Reference Lewis and Swinney1999), all without grooves. The details of all simulations are given in table 1.
$10^{9}$
. We then directly compare our results with our previous simulations by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
), as well as experiments by Lewis & Swinney (Reference Lewis and Swinney1999), all without grooves. The details of all simulations are given in table 1.
3 Global response: dimensionless torque
As mentioned above, the global response of transport of the TC system can be expressed as the torque which is required to keep the inner cylinder at a fixed angular velocity. To investigate the effect of the grooved walls, in this section, the dimensionless torque
![]() $Nu_{{\it\omega}}$
is presented as a function of
$Nu_{{\it\omega}}$
is presented as a function of
![]() $Ta$
, i.e.
$Ta$
, i.e.
![]() $Nu_{{\it\omega}}=ATa^{{\it\beta}}$
, with grooved walls, in comparison with the results for smooth walls.
$Nu_{{\it\omega}}=ATa^{{\it\beta}}$
, with grooved walls, in comparison with the results for smooth walls.

Figure 3. (a) Nusselt number as function of
![]() $Ta$
for
$Ta$
for
![]() ${\it\eta}=0.714$
. The data are from experiments and numerical simulations:
${\it\eta}=0.714$
. The data are from experiments and numerical simulations:
![]() $\cdots \,$
, smooth walls experiments by Lewis & Swinney (Reference Lewis and Swinney1999); ○, smooth walls simulations by Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2013); ▫, smooth walls simulations by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
); ▵, grooved walls simulations with
$\cdots \,$
, smooth walls experiments by Lewis & Swinney (Reference Lewis and Swinney1999); ○, smooth walls simulations by Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2013); ▫, smooth walls simulations by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
); ▵, grooved walls simulations with
![]() ${\it\delta}=0.052d$
in the present study; ♢, grooved walls simulations with
${\it\delta}=0.052d$
in the present study; ♢, grooved walls simulations with
![]() ${\it\delta}=0.105d$
in the present study; ◃, grooved walls simulations with
${\it\delta}=0.105d$
in the present study; ◃, grooved walls simulations with
![]() ${\it\delta}=0.209d$
in the present study. Dashed line and dotted dashed line show the
${\it\delta}=0.209d$
in the present study. Dashed line and dotted dashed line show the
![]() $1/3$
and the 0.38 slope. Two arrows indicate
$1/3$
and the 0.38 slope. Two arrows indicate
![]() $Ta=4.77\times 10^{7}$
and
$Ta=4.77\times 10^{7}$
and
![]() $Ta=9.85\times 10^{8}$
in the
$Ta=9.85\times 10^{8}$
in the
![]() ${\it\delta}=0.105d$
series. The former
${\it\delta}=0.105d$
series. The former
![]() $Ta$
is in the regime where the scaling slope is larger than 0.38 and the latter is in the regime where the slope saturates back to 0.38. These two cases are used in the main text as examples to show why
$Ta$
is in the regime where the scaling slope is larger than 0.38 and the latter is in the regime where the slope saturates back to 0.38. These two cases are used in the main text as examples to show why
![]() $Nu_{{\it\omega}}$
is increased and why the scaling slope is changed. (b) The same as (a), but now the Nusselt number is scaled with
$Nu_{{\it\omega}}$
is increased and why the scaling slope is changed. (b) The same as (a), but now the Nusselt number is scaled with
![]() $Ta^{-1/3}$
. (c) The same as (a), now with the Nusselt number scaled with
$Ta^{-1/3}$
. (c) The same as (a), now with the Nusselt number scaled with
![]() $Ta^{-1/2}$
. The arrows show the positions where the local
$Ta^{-1/2}$
. The arrows show the positions where the local
![]() $1/2$
law can be seen. (d) The same as (a), now with the Nusselt number scaled with
$1/2$
law can be seen. (d) The same as (a), now with the Nusselt number scaled with
![]() $Ta^{-0.38}$
.
$Ta^{-0.38}$
.
Figure 3 shows
![]() $Nu_{{\it\omega}}$
with increasing
$Nu_{{\it\omega}}$
with increasing
![]() $Ta$
for smooth cases and grooved cases with three series of different groove heights. For the smooth TC flow, from
$Ta$
for smooth cases and grooved cases with three series of different groove heights. For the smooth TC flow, from
![]() $Ta=2.5\times 10^{5}$
up to
$Ta=2.5\times 10^{5}$
up to
![]() $Ta=3\times 10^{6}$
, an effective scaling law of
$Ta=3\times 10^{6}$
, an effective scaling law of
![]() $Nu_{{\it\omega}}\sim Ta^{1/3}$
is found, which is associated with the laminar Taylor vortices. Between
$Nu_{{\it\omega}}\sim Ta^{1/3}$
is found, which is associated with the laminar Taylor vortices. Between
![]() $Ta=3\times 10^{6}$
and
$Ta=3\times 10^{6}$
and
![]() $Ta=2\times 10^{8}$
, there is a transitional region in which first the bulk becomes turbulent, and then the boundary layers also become gradually turbulent (see the gradually growing turbulent BL in Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
)). When
$Ta=2\times 10^{8}$
, there is a transitional region in which first the bulk becomes turbulent, and then the boundary layers also become gradually turbulent (see the gradually growing turbulent BL in Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
)). When
![]() $Ta$
is even larger, the flow is fully turbulent, in both the bulk and boundary layer, and the so-called ‘ultimate’ regime appears, with an effective scaling law close to
$Ta$
is even larger, the flow is fully turbulent, in both the bulk and boundary layer, and the so-called ‘ultimate’ regime appears, with an effective scaling law close to
![]() $Nu_{{\it\omega}}\sim Ta^{0.38}$
(Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
).
$Nu_{{\it\omega}}\sim Ta^{0.38}$
(Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
).
The situation is more complicated for the grooved TC flow. As shown in figure 3, for the case of
![]() ${\it\delta}=0.052d$
, three different scaling laws are found with increasing
${\it\delta}=0.052d$
, three different scaling laws are found with increasing
![]() $Ta$
: at the early stage, the effective scaling follows the same
$Ta$
: at the early stage, the effective scaling follows the same
![]() $Nu_{{\it\omega}}\sim Ta^{1/3}$
, as long as
$Nu_{{\it\omega}}\sim Ta^{1/3}$
, as long as
![]() $Ta$
is smaller than a threshold Taylor number
$Ta$
is smaller than a threshold Taylor number
![]() $Ta_{th}$
, at which the effective scaling exponent
$Ta_{th}$
, at which the effective scaling exponent
![]() ${\it\beta}$
in the grooved cases starts to deviate from the smooth cases. Once
${\it\beta}$
in the grooved cases starts to deviate from the smooth cases. Once
![]() $Ta>Ta_{th}$
,
$Ta>Ta_{th}$
,
![]() $Nu_{{\it\omega}}$
for the grooved wall cases increases with a steeper exponent
$Nu_{{\it\omega}}$
for the grooved wall cases increases with a steeper exponent
![]() ${\it\beta}$
than for the smooth wall counterpart. The exponent
${\it\beta}$
than for the smooth wall counterpart. The exponent
![]() ${\it\beta}$
can locally be
${\it\beta}$
can locally be
![]() $1/2$
for this region. However, further increasing
$1/2$
for this region. However, further increasing
![]() $Ta$
leads to a saturation to the ultimate regime effective scaling
$Ta$
leads to a saturation to the ultimate regime effective scaling
![]() $Nu_{{\it\omega}}\sim Ta^{0.38}$
, as already seen for smooth walls, but with a larger prefactor. This means that the influence of the grooves on the effective scaling exponent becomes weaker with increasing
$Nu_{{\it\omega}}\sim Ta^{0.38}$
, as already seen for smooth walls, but with a larger prefactor. This means that the influence of the grooves on the effective scaling exponent becomes weaker with increasing
![]() $Ta$
.
$Ta$
.
Note that
![]() $Nu_{{\it\omega}}$
does not always increase after
$Nu_{{\it\omega}}$
does not always increase after
![]() $Ta$
exceeds the threshold
$Ta$
exceeds the threshold
![]() $Ta_{th}$
. For the case of
$Ta_{th}$
. For the case of
![]() ${\it\delta}=0.105d$
, at
${\it\delta}=0.105d$
, at
![]() $Ta<Ta_{th}$
, the relations between
$Ta<Ta_{th}$
, the relations between
![]() $Nu_{{\it\omega}}$
and
$Nu_{{\it\omega}}$
and
![]() $Ta$
of smooth and grooved cases still follow the same route. But, after
$Ta$
of smooth and grooved cases still follow the same route. But, after
![]() $Ta>Ta_{th}$
, there is a region where
$Ta>Ta_{th}$
, there is a region where
![]() $Nu_{{\it\omega}}$
decreases. The largest decrease is 5 % and occurs at
$Nu_{{\it\omega}}$
decreases. The largest decrease is 5 % and occurs at
![]() $Ta=1.0\times 10^{7}$
. The mechanism will be shown and explained in detail in § 4. This can be related to channel flow in which Choi et al. (Reference Choi, Moin and Kim1993) also found drag reduction in a specific range of
$Ta=1.0\times 10^{7}$
. The mechanism will be shown and explained in detail in § 4. This can be related to channel flow in which Choi et al. (Reference Choi, Moin and Kim1993) also found drag reduction in a specific range of
![]() $Re$
. With a further increase in
$Re$
. With a further increase in
![]() $Ta$
, when
$Ta$
, when
![]() $Ta>2.5\times 10^{7}$
, the exponent
$Ta>2.5\times 10^{7}$
, the exponent
![]() ${\it\beta}$
starts to increase and can locally be as steep as
${\it\beta}$
starts to increase and can locally be as steep as
![]() $1/2$
. Again, after that, the effective scaling saturates once
$1/2$
. Again, after that, the effective scaling saturates once
![]() $Ta$
is large enough.
$Ta$
is large enough.

Figure 4. Friction factor
![]() $C_{f}=2{\rm\pi}Nu_{{\it\omega}}J_{0}^{{\it\omega}}{\it\nu}^{-2}/Re_{i}^{2}$
as a function of the inner cylinder Reynolds number
$C_{f}=2{\rm\pi}Nu_{{\it\omega}}J_{0}^{{\it\omega}}{\it\nu}^{-2}/Re_{i}^{2}$
as a function of the inner cylinder Reynolds number
![]() $Re_{i}$
. ▫, smooth walls simulations by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
); ▵, grooved walls simulations with
$Re_{i}$
. ▫, smooth walls simulations by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
); ▵, grooved walls simulations with
![]() ${\it\delta}=0.052d$
; ♢, grooved walls simulations with
${\it\delta}=0.052d$
; ♢, grooved walls simulations with
![]() ${\it\delta}=0.105d$
; ◃, grooved walls simulations with
${\it\delta}=0.105d$
; ◃, grooved walls simulations with
![]() ${\it\delta}=0.209d$
.
${\it\delta}=0.209d$
.
For
![]() ${\it\delta}=0.209d$
, the threshold
${\it\delta}=0.209d$
, the threshold
![]() $Ta_{th}$
is at approximately
$Ta_{th}$
is at approximately
![]() $Ta=1.0\times 10^{5}$
. After a small range of steep regime in which the slope is larger than 0.38, we find only an upward shift of
$Ta=1.0\times 10^{5}$
. After a small range of steep regime in which the slope is larger than 0.38, we find only an upward shift of
![]() $Nu_{{\it\omega}}$
. The effective scaling law does not change much, either in the laminar or in the turbulent region. This suggests that these massive grooves cannot shift the transition to the ultimate regime to even smaller value of
$Nu_{{\it\omega}}$
. The effective scaling law does not change much, either in the laminar or in the turbulent region. This suggests that these massive grooves cannot shift the transition to the ultimate regime to even smaller value of
![]() $Ta$
.
$Ta$
.
At given
![]() $Ta$
, we find that a larger groove height causes a more profound increase of
$Ta$
, we find that a larger groove height causes a more profound increase of
![]() $Nu_{{\it\omega}}$
. For example, after saturation, for the cases of
$Nu_{{\it\omega}}$
. For example, after saturation, for the cases of
![]() ${\it\delta}=0.052d$
,
${\it\delta}=0.052d$
,
![]() ${\it\delta}=0.105d$
and
${\it\delta}=0.105d$
and
![]() ${\it\delta}=0.209d$
,
${\it\delta}=0.209d$
,
![]() $Nu_{{\it\omega}}$
increases by 41 %, 58 % and 68 %, respectively. The enhanced transport in TC flow with grooved walls therefore cannot be solely ascribed to the surface area increase; it is rather the local flow dynamics near the grooves which enhances the transport. In the following sections we will look into the flow details to explore the mechanism of
$Nu_{{\it\omega}}$
increases by 41 %, 58 % and 68 %, respectively. The enhanced transport in TC flow with grooved walls therefore cannot be solely ascribed to the surface area increase; it is rather the local flow dynamics near the grooves which enhances the transport. In the following sections we will look into the flow details to explore the mechanism of
![]() $Nu_{{\it\omega}}$
increase which goes beyond the pure increase of surface area by the grooves. Note that the behaviour of
$Nu_{{\it\omega}}$
increase which goes beyond the pure increase of surface area by the grooves. Note that the behaviour of
![]() $Nu_{{\it\omega}}$
versus
$Nu_{{\it\omega}}$
versus
![]() $Ta$
can also be expressed in terms of the friction factor
$Ta$
can also be expressed in terms of the friction factor
as a function of the inner cylinder Reynolds number
![]() $Re_{i}$
, which is shown in figure 4. From this definition, we find that once the local scaling exponent between
$Re_{i}$
, which is shown in figure 4. From this definition, we find that once the local scaling exponent between
![]() $Nu_{{\it\omega}}$
and
$Nu_{{\it\omega}}$
and
![]() $Ta$
equals
$Ta$
equals
![]() $1/2$
, a plateau can be found in the
$1/2$
, a plateau can be found in the
![]() $C_{f}$
versus
$C_{f}$
versus
![]() $Re_{i}$
relation.
$Re_{i}$
relation.
It is a common finding that, in RB flow, the surface roughness becomes active only when the thermal boundary layer is thinner than a characteristic roughness height (Shen et al.
Reference Shen, Tong and Xia1996; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006). Similar to this, we also want to stress that, in TC flow with grooves, the effect of grooves on
![]() $Nu_{{\it\omega}}$
can only be seen when the BL thickness
$Nu_{{\it\omega}}$
can only be seen when the BL thickness
![]() ${\it\lambda}$
becomes less than the groove height
${\it\lambda}$
becomes less than the groove height
![]() ${\it\delta}$
. At small
${\it\delta}$
. At small
![]() $Ta$
, the BL is very thick, and thus the grooves are buried under the BL and the fluid cannot feel their influence. At large
$Ta$
, the BL is very thick, and thus the grooves are buried under the BL and the fluid cannot feel their influence. At large
![]() $Ta$
, the BL becomes thinner than the grooves, and thus they strongly affect the BL dynamics and thereby alter the transport properties. At this critical value
$Ta$
, the BL becomes thinner than the grooves, and thus they strongly affect the BL dynamics and thereby alter the transport properties. At this critical value
![]() $Ta_{th}$
, the BL thickness equals the groove height. The averaged BL thickness
$Ta_{th}$
, the BL thickness equals the groove height. The averaged BL thickness
![]() ${\it\lambda}$
in TC flow can be estimated by
${\it\lambda}$
in TC flow can be estimated by
![]() ${\it\lambda}\simeq d{\it\sigma}/(2Nu_{{\it\omega}})$
(Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013), where
${\it\lambda}\simeq d{\it\sigma}/(2Nu_{{\it\omega}})$
(Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013), where
![]() ${\it\sigma}$
is defined as
${\it\sigma}$
is defined as
![]() ${\it\sigma}=[(r_{i}+r_{o})/(2\sqrt{r_{o}r_{i}})]^{4}$
. Indeed, our simulations show that
${\it\sigma}=[(r_{i}+r_{o})/(2\sqrt{r_{o}r_{i}})]^{4}$
. Indeed, our simulations show that
![]() $Nu_{{\it\omega}}$
starts to change once the boundary layer thickness becomes smaller than the groove height. As shown in figure 5, for cases of
$Nu_{{\it\omega}}$
starts to change once the boundary layer thickness becomes smaller than the groove height. As shown in figure 5, for cases of
![]() ${\it\delta}=0.209d$
,
${\it\delta}=0.209d$
,
![]() ${\it\delta}=0.105d$
and
${\it\delta}=0.105d$
and
![]() ${\it\delta}=0.502d$
, we have
${\it\delta}=0.502d$
, we have
![]() $Ta_{th}\simeq 1.0\times 10^{5}$
,
$Ta_{th}\simeq 1.0\times 10^{5}$
,
![]() $Ta_{th}\simeq 2.8\times 10^{6}$
and
$Ta_{th}\simeq 2.8\times 10^{6}$
and
![]() $Ta_{th}\simeq 9.0\times 10^{7}$
, respectively. Also from figure 3 it is found that there are sharp transitions for
$Ta_{th}\simeq 9.0\times 10^{7}$
, respectively. Also from figure 3 it is found that there are sharp transitions for
![]() $Nu_{{\it\omega}}$
at these points.
$Nu_{{\it\omega}}$
at these points.

Figure 5. Comparison between boundary layer thickness
![]() ${\it\lambda}$
and groove height
${\it\lambda}$
and groove height
![]() ${\it\delta}$
. The solid line denotes the averaged boundary layer thickness estimated by
${\it\delta}$
. The solid line denotes the averaged boundary layer thickness estimated by
![]() ${\it\lambda}\simeq d{\it\sigma}/(2Nu_{{\it\omega}})$
(Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013). Each triangle symbol shows the value of
${\it\lambda}\simeq d{\it\sigma}/(2Nu_{{\it\omega}})$
(Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013). Each triangle symbol shows the value of
![]() $Ta$
at which the groove height equals the boundary layer thickness.
$Ta$
at which the groove height equals the boundary layer thickness.
We stress that the local exponent
![]() ${\it\beta}\approx 1/2$
we have found in figure 3 (see the arrows) is not the ultimate region scaling without logarithmic correction, but just a crossover between a regime where the groove depth is less than the BL thickness and a regime where the groove depth is larger than the BL thickness. Hence it is fortuitous to find this
${\it\beta}\approx 1/2$
we have found in figure 3 (see the arrows) is not the ultimate region scaling without logarithmic correction, but just a crossover between a regime where the groove depth is less than the BL thickness and a regime where the groove depth is larger than the BL thickness. Hence it is fortuitous to find this
![]() $1/2$
exponent in TC flow with grooves. Note that in pipe flow (Nikuradse Reference Nikuradse1933) and TC flow with perpendicular roughness (van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003) the situation is different. In both cases, the roughness is orthogonal to the flow direction and the main flow is impeded by the roughness. The transfer of momentum from the fluid to the wall is accomplished by the drag on the roughness elements, which at high
$1/2$
exponent in TC flow with grooves. Note that in pipe flow (Nikuradse Reference Nikuradse1933) and TC flow with perpendicular roughness (van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003) the situation is different. In both cases, the roughness is orthogonal to the flow direction and the main flow is impeded by the roughness. The transfer of momentum from the fluid to the wall is accomplished by the drag on the roughness elements, which at high
![]() $Re$
is predominantly by pressure forces, rather than by viscous stresses. A new length scale of the groove height is thus implemented into the system and the drag is independent of
$Re$
is predominantly by pressure forces, rather than by viscous stresses. A new length scale of the groove height is thus implemented into the system and the drag is independent of
![]() $Re$
at high
$Re$
at high
![]() $Re$
(Pope Reference Pope2002). In contrast, in our current simulations with grooves, these are aligned with the flow direction. As a result, the grooves do not play an immediate role in generating drag, and there is no new length scale to be implemented into the BL. With increasing
$Re$
(Pope Reference Pope2002). In contrast, in our current simulations with grooves, these are aligned with the flow direction. As a result, the grooves do not play an immediate role in generating drag, and there is no new length scale to be implemented into the BL. With increasing
![]() $Ta$
, the viscous stresses still dominate the drag. Therefore, the exponent
$Ta$
, the viscous stresses still dominate the drag. Therefore, the exponent
![]() ${\it\beta}$
saturates to the same value as for the smooth case at larger
${\it\beta}$
saturates to the same value as for the smooth case at larger
![]() $Ta$
. It is important to note that, in RB flow, the large-scale flow fluctuates, and so it always sees the roughness as small obstacles generating direct drag. This aspect is different from TC flow. However, drag in TC flow is caused by the wall shear rate of the azimuthal velocity. This is analogous to the wall gradient of the temperature in RB flow, not to the drag caused by the velocity field.
$Ta$
. It is important to note that, in RB flow, the large-scale flow fluctuates, and so it always sees the roughness as small obstacles generating direct drag. This aspect is different from TC flow. However, drag in TC flow is caused by the wall shear rate of the azimuthal velocity. This is analogous to the wall gradient of the temperature in RB flow, not to the drag caused by the velocity field.
From the above findings, we summarize that, compared to smooth cases, in grooved wall TC flow there are three different characteristic regimes. First, when
![]() $Ta<Ta_{th}$
, smooth and groove cases show the same behaviour. Second, when
$Ta<Ta_{th}$
, smooth and groove cases show the same behaviour. Second, when
![]() $Ta>Ta_{th}$
, the scaling exponent
$Ta>Ta_{th}$
, the scaling exponent
![]() ${\it\beta}$
increases to be locally as large as
${\it\beta}$
increases to be locally as large as
![]() $1/2$
. Third, when
$1/2$
. Third, when
![]() $Ta$
is large enough, there is a saturation regime in which the exponent
$Ta$
is large enough, there is a saturation regime in which the exponent
![]() ${\it\beta}$
saturates back to the ultimate region effective scaling law 0.38, but the prefactor of
${\it\beta}$
saturates back to the ultimate region effective scaling law 0.38, but the prefactor of
![]() $Nu_{{\it\omega}}$
is increased by a substantial margin.
$Nu_{{\it\omega}}$
is increased by a substantial margin.

Figure 6. Tip-to-tip Nusselt number as a function of the tip-to-tip Taylor number scale with
![]() $Ta^{tt-0.38}$
for
$Ta^{tt-0.38}$
for
![]() ${\it\eta}=0.714$
. ▵, grooved walls simulations with
${\it\eta}=0.714$
. ▵, grooved walls simulations with
![]() ${\it\delta}=0.052d$
; ♢, grooved walls simulations with
${\it\delta}=0.052d$
; ♢, grooved walls simulations with
![]() ${\it\delta}=0.105d$
; ◃, grooved walls simulations with
${\it\delta}=0.105d$
; ◃, grooved walls simulations with
![]() ${\it\delta}=0.209d$
. Comparing this figure with figure 3(d), we find no change in the scaling exponent.
${\it\delta}=0.209d$
. Comparing this figure with figure 3(d), we find no change in the scaling exponent.
So far, the
![]() $Ta$
and
$Ta$
and
![]() $Nu_{{\it\omega}}$
depicted here are both based on the base-to-base distance
$Nu_{{\it\omega}}$
depicted here are both based on the base-to-base distance
![]() $d$
. The usage of
$d$
. The usage of
![]() $d$
follows the convention of RB studies (Du & Tong Reference Du and Tong2000; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006). This choice, however, is quite arbitrary, because
$d$
follows the convention of RB studies (Du & Tong Reference Du and Tong2000; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006). This choice, however, is quite arbitrary, because
![]() $d$
is only one possibility for the reference length. The tip-to-tip distance could also be selected to non-dimensionalize
$d$
is only one possibility for the reference length. The tip-to-tip distance could also be selected to non-dimensionalize
![]() $Ta$
and
$Ta$
and
![]() $Nu_{{\it\omega}}$
. Such a definition would then lead to the tip-to-tip Taylor number
$Nu_{{\it\omega}}$
. Such a definition would then lead to the tip-to-tip Taylor number
![]() $Ta^{tt}=Ta(d-2{\it\delta})^{2}/d^{2}$
and Nusselt number
$Ta^{tt}=Ta(d-2{\it\delta})^{2}/d^{2}$
and Nusselt number
![]() $Nu_{{\it\omega}}^{tt}=Nu_{{\it\omega}}(d-2{\it\delta})r_{i}^{2}r_{o}^{2}/[d(r_{i}+{\it\delta})^{2}(r_{o}-{\it\delta})^{2}]$
. In figure 6, we show
$Nu_{{\it\omega}}^{tt}=Nu_{{\it\omega}}(d-2{\it\delta})r_{i}^{2}r_{o}^{2}/[d(r_{i}+{\it\delta})^{2}(r_{o}-{\it\delta})^{2}]$
. In figure 6, we show
![]() $Nu_{{\it\omega}}^{tt}$
as a function of
$Nu_{{\it\omega}}^{tt}$
as a function of
![]() $Ta^{tt}$
. Despite the grooves being quite high in our simulations, different choices of the characteristic length scale do not affect the effective power laws, but only the exact values of the transitional
$Ta^{tt}$
. Despite the grooves being quite high in our simulations, different choices of the characteristic length scale do not affect the effective power laws, but only the exact values of the transitional
![]() $Ta$
numbers. Therefore, it is a reasonable choice that we only use
$Ta$
numbers. Therefore, it is a reasonable choice that we only use
![]() $d$
as the reference length scale. If the system reached the ultimate state, one would expect that the transport of torque should be the same, i.e. the
$d$
as the reference length scale. If the system reached the ultimate state, one would expect that the transport of torque should be the same, i.e. the
![]() $Nu_{{\it\omega}}$
versus
$Nu_{{\it\omega}}$
versus
![]() $Ta$
relation should be the same as that for the smooth case. When deducing the surface area increase, in our current simulations of
$Ta$
relation should be the same as that for the smooth case. When deducing the surface area increase, in our current simulations of
![]() ${\it\delta}=0.052d$
,
${\it\delta}=0.052d$
,
![]() ${\it\delta}=0.105d$
and
${\it\delta}=0.105d$
and
![]() ${\it\delta}=0.209d$
,
${\it\delta}=0.209d$
,
![]() $Nu_{{\it\omega}}$
increases by
$Nu_{{\it\omega}}$
increases by
![]() $-1\,\%$
, 12 % and 18 % compared to the smooth case, respectively. We expect that these differences become smaller and smaller with increasing
$-1\,\%$
, 12 % and 18 % compared to the smooth case, respectively. We expect that these differences become smaller and smaller with increasing
![]() $Ta$
. Simulations with higher
$Ta$
. Simulations with higher
![]() $Ta$
are required to resolve this question.
$Ta$
are required to resolve this question.
4 Flow structures
In order to find the mechanism behind the
![]() $Nu_{{\it\omega}}$
increase, in this section, visualizations of the flow in the bulk and the grooves are shown to compare the grooved and smooth cases. Figure 7 shows three contour plots of the instantaneous azimuthal velocity
$Nu_{{\it\omega}}$
increase, in this section, visualizations of the flow in the bulk and the grooves are shown to compare the grooved and smooth cases. Figure 7 shows three contour plots of the instantaneous azimuthal velocity
![]() $u_{{\it\theta}}$
in the meridional plane for the smooth and the
$u_{{\it\theta}}$
in the meridional plane for the smooth and the
![]() ${\it\delta}=0.052d$
and
${\it\delta}=0.052d$
and
![]() ${\it\delta}=0.105d$
cases at
${\it\delta}=0.105d$
cases at
![]() $Ta=4.77\times 10^{7}$
. Figure 7(a) shows the flow in the transition region where the laminar zones in the BL coexist with turbulent, plume-ejecting areas. These plumes are associated with the axial and radial structure which is induced by the Taylor vortices. Plumes are ejected from preferential positions where there are adverse pressure gradients such that detachment from the BL is supported. In figure 7(b), where
$Ta=4.77\times 10^{7}$
. Figure 7(a) shows the flow in the transition region where the laminar zones in the BL coexist with turbulent, plume-ejecting areas. These plumes are associated with the axial and radial structure which is induced by the Taylor vortices. Plumes are ejected from preferential positions where there are adverse pressure gradients such that detachment from the BL is supported. In figure 7(b), where
![]() ${\it\delta}=0.052d$
,
${\it\delta}=0.052d$
,
![]() $Ta$
is still smaller than
$Ta$
is still smaller than
![]() $Ta_{th}$
, which also means that the grooves are still buried within the BL and hence the effect of the grooves is very small. This is the reason why obvious differences cannot be distinguished between figure 7(a) and (b). However, for figure 7(c), where
$Ta_{th}$
, which also means that the grooves are still buried within the BL and hence the effect of the grooves is very small. This is the reason why obvious differences cannot be distinguished between figure 7(a) and (b). However, for figure 7(c), where
![]() ${\it\delta}=0.105d$
,
${\it\delta}=0.105d$
,
![]() $Ta>Ta_{th}$
and the power law between
$Ta>Ta_{th}$
and the power law between
![]() $Nu_{{\it\omega}}$
and
$Nu_{{\it\omega}}$
and
![]() $Ta$
, which can be seen from figure 3, is in the steep regime. We find that plumes are ejected from all the tips of the grooves. It is interesting to note that, for the smooth case, the plumes are ejected only from some specific regions, while for the grooved case, plumes are detached from nearly all the tips of the grooves. Because more plumes are ejected compared to the smooth case,
$Ta$
, which can be seen from figure 3, is in the steep regime. We find that plumes are ejected from all the tips of the grooves. It is interesting to note that, for the smooth case, the plumes are ejected only from some specific regions, while for the grooved case, plumes are detached from nearly all the tips of the grooves. Because more plumes are ejected compared to the smooth case,
![]() $Nu_{{\it\omega}}$
is greatly enhanced, and the larger exponent
$Nu_{{\it\omega}}$
is greatly enhanced, and the larger exponent
![]() ${\it\beta}$
regime can be seen in figure 3.
${\it\beta}$
regime can be seen in figure 3.

Figure 7. Contour plots of the instantaneous azimuthal velocity field
![]() $u_{{\it\theta}}$
for (a) the smooth, (b) the
$u_{{\it\theta}}$
for (a) the smooth, (b) the
![]() ${\it\delta}=0.052d$
, and (c) the
${\it\delta}=0.052d$
, and (c) the
![]() ${\it\delta}=0.105d$
cases at
${\it\delta}=0.105d$
cases at
![]() $Ta=4.77\times 10^{7}$
. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). In the smooth case, the flow is in the transition region where the laminar regions in the boundary layer coexist with turbulent, plume-ejecting areas. In (b), the boundary layer is still thicker than the groove, and therefore no evident difference can be distinguished between (a) and (b). For (c), the boundary layer is thinner than the grooves and plumes are ejected from all tips of the grooves.
$Ta=4.77\times 10^{7}$
. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). In the smooth case, the flow is in the transition region where the laminar regions in the boundary layer coexist with turbulent, plume-ejecting areas. In (b), the boundary layer is still thicker than the groove, and therefore no evident difference can be distinguished between (a) and (b). For (c), the boundary layer is thinner than the grooves and plumes are ejected from all tips of the grooves.

Figure 8. Contour plots of the instantaneous azimuthal velocity field
![]() $u_{{\it\theta}}$
for (a) the smooth, (b) the
$u_{{\it\theta}}$
for (a) the smooth, (b) the
![]() ${\it\delta}=0.052d$
, and (c) the
${\it\delta}=0.052d$
, and (c) the
![]() ${\it\delta}=0.105d$
cases at
${\it\delta}=0.105d$
cases at
![]() $Ta=9.75\times 10^{8}$
. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). In the smooth case, the flow is in the fully turbulent region where the bulk and boundary both become turbulent. Due to the decrease of wall pressure gradient in the axial direction, plumes are ejected from more places compared to
$Ta=9.75\times 10^{8}$
. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). In the smooth case, the flow is in the fully turbulent region where the bulk and boundary both become turbulent. Due to the decrease of wall pressure gradient in the axial direction, plumes are ejected from more places compared to
![]() $Ta=4.77\times 10^{7}$
. In (b) and (c), where
$Ta=4.77\times 10^{7}$
. In (b) and (c), where
![]() $Ta>Ta_{th}$
, plumes are ejected from the tips, and these plumes all show preferential directions which follow the Taylor vortices.
$Ta>Ta_{th}$
, plumes are ejected from the tips, and these plumes all show preferential directions which follow the Taylor vortices.
Figure 8 shows three contour plots of the instantaneous azimuthal velocity
![]() $u_{{\it\theta}}$
in the meridional plane for the smooth, and the
$u_{{\it\theta}}$
in the meridional plane for the smooth, and the
![]() ${\it\delta}=0.052d$
and
${\it\delta}=0.052d$
and
![]() ${\it\delta}=0.105d$
cases at
${\it\delta}=0.105d$
cases at
![]() $Ta=9.75\times 10^{8}$
. Figure 8(a) shows the flow in the fully turbulent region. Due to the decrease in the wall pressure gradient in the axial direction, plumes are ejected from more places compared to
$Ta=9.75\times 10^{8}$
. Figure 8(a) shows the flow in the fully turbulent region. Due to the decrease in the wall pressure gradient in the axial direction, plumes are ejected from more places compared to
![]() $Ta=4.77\times 10^{7}$
. For figure 8(b), where
$Ta=4.77\times 10^{7}$
. For figure 8(b), where
![]() ${\it\delta}=0.052d$
, we have
${\it\delta}=0.052d$
, we have
![]() $Ta>Ta_{th}$
, and thus we can see that more plumes are ejected due to the existence of grooves. The groove tips are the preferential places for these ejections. In figure 8(c), for the case of
$Ta>Ta_{th}$
, and thus we can see that more plumes are ejected due to the existence of grooves. The groove tips are the preferential places for these ejections. In figure 8(c), for the case of
![]() ${\it\delta}=0.105d$
, compared to the smooth case, plumes are still ejected from the tips of grooves, but near the valleys there are spots where plumes grow. The difference in the number of plumes between the grooved and smooth cases reduces with increasing
${\it\delta}=0.105d$
, compared to the smooth case, plumes are still ejected from the tips of grooves, but near the valleys there are spots where plumes grow. The difference in the number of plumes between the grooved and smooth cases reduces with increasing
![]() $Ta$
. This maybe another reason why the
$Ta$
. This maybe another reason why the
![]() $Nu_{{\it\omega}}$
versus
$Nu_{{\it\omega}}$
versus
![]() $Ta$
scaling saturates at high
$Ta$
scaling saturates at high
![]() $Ta$
. In addition, we note that these plumes have different directions of movement, either to the top or bottom. It is interesting to find that these plumes follow the direction of Taylor vortices, which also means that Taylor vortices still exist even if there are grooves. This behaviour can be explained by the association between the large-scale Taylor vortices and the secondary vortices inside the grooves, which we will show in the following paragraphs.
$Ta$
. In addition, we note that these plumes have different directions of movement, either to the top or bottom. It is interesting to find that these plumes follow the direction of Taylor vortices, which also means that Taylor vortices still exist even if there are grooves. This behaviour can be explained by the association between the large-scale Taylor vortices and the secondary vortices inside the grooves, which we will show in the following paragraphs.
One may argue that plumes may only be emitted at some points of the groove tips. This, however, is not the case. Figure 9 shows contour plots of the instantaneous azimuthal velocity
![]() $u_{{\it\theta}}$
of the smooth and
$u_{{\it\theta}}$
of the smooth and
![]() ${\it\delta}=0.105d$
cases for Taylor number
${\it\delta}=0.105d$
cases for Taylor number
![]() $Ta=9.75\times 10^{8}$
at constant radius cuts. In figure 9(a), at wall distance
$Ta=9.75\times 10^{8}$
at constant radius cuts. In figure 9(a), at wall distance
![]() $y=(r-r_{i})/d=4\times 10^{-3}$
, the flow is in the BL and herring-bone streaks can be seen due to the boundary layer instability. While, in figure 9(b), at wall distance
$y=(r-r_{i})/d=4\times 10^{-3}$
, the flow is in the BL and herring-bone streaks can be seen due to the boundary layer instability. While, in figure 9(b), at wall distance
![]() $y=(r-r_{i})/d=0.106$
or wall distance in terms of the tip of grooves
$y=(r-r_{i})/d=0.106$
or wall distance in terms of the tip of grooves
![]() $y^{\prime }=(r-r_{i}-{\it\delta})/d=1\times 10^{-3}$
, the flow is very close to the tips of the grooves, high-speed plumes (shown in red) can be identified almost everywhere near the tips of the grooves. It is also seen from this panel that evidence of large-scale vortices can be identified between high-speed regions where there are large zones of low speed. This is because in these regions flows are driven by Taylor rolls and move from the outer to the inner cylinder or vice versa. In addition, the flow is statistically homogeneous in the
$y^{\prime }=(r-r_{i}-{\it\delta})/d=1\times 10^{-3}$
, the flow is very close to the tips of the grooves, high-speed plumes (shown in red) can be identified almost everywhere near the tips of the grooves. It is also seen from this panel that evidence of large-scale vortices can be identified between high-speed regions where there are large zones of low speed. This is because in these regions flows are driven by Taylor rolls and move from the outer to the inner cylinder or vice versa. In addition, the flow is statistically homogeneous in the
![]() ${\it\theta}$
direction. Both panels can serve as a confirmation of this assumption.
${\it\theta}$
direction. Both panels can serve as a confirmation of this assumption.

Figure 9. Contour plots of the instantaneous azimuthal velocity
![]() $u_{{\it\theta}}({\it\theta},z)$
for Taylor number
$u_{{\it\theta}}({\it\theta},z)$
for Taylor number
![]() $Ta=9.75\times 10^{8}$
at constant radius cuts. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). (a) The smooth case at fixed wall distance
$Ta=9.75\times 10^{8}$
at constant radius cuts. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). (a) The smooth case at fixed wall distance
![]() $y=(r-r_{i})/d=4\times 10^{-3}$
. (b) The
$y=(r-r_{i})/d=4\times 10^{-3}$
. (b) The
![]() ${\it\delta}=0.105d$
case at fixed wall distance in terms of the tip of grooves
${\it\delta}=0.105d$
case at fixed wall distance in terms of the tip of grooves
![]() $y^{\prime }=(r-r_{i}-{\it\delta})/d=1\times 10^{-3}$
. (a) Shows the herring-bone streaks in the boundary layer while (b) shows plumes being ejected homogeneously along the azimuthal direction.
$y^{\prime }=(r-r_{i}-{\it\delta})/d=1\times 10^{-3}$
. (a) Shows the herring-bone streaks in the boundary layer while (b) shows plumes being ejected homogeneously along the azimuthal direction.

Figure 10. Enlargement of the near-wall region for contour plots of the instantaneous azimuthal velocity
![]() $u_{{\it\theta}}$
superposed with instantaneous velocity vectors in the meridional plane at
$u_{{\it\theta}}$
superposed with instantaneous velocity vectors in the meridional plane at
![]() $Ta=9.75\times 10^{8}$
. (a) The smooth case, (b) the
$Ta=9.75\times 10^{8}$
. (a) The smooth case, (b) the
![]() ${\it\delta}=0.105d$
case. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). The velocity vectors are formed by the axial and radial velocity on the surface. For the smooth case in (a), the plumes are induced by the acceleration of radial flow. Then vortex rings are formed. For the grooved configuration in (b), the axial flow drives the secondary vortex inside the grooves. At the same time the interaction between the secondary vortex and the Taylor rolls causes the detachment of the boundary layer from the tips of the grooves. The detached azimuthal flow then develops into a plume.
${\it\delta}=0.105d$
case. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). The velocity vectors are formed by the axial and radial velocity on the surface. For the smooth case in (a), the plumes are induced by the acceleration of radial flow. Then vortex rings are formed. For the grooved configuration in (b), the axial flow drives the secondary vortex inside the grooves. At the same time the interaction between the secondary vortex and the Taylor rolls causes the detachment of the boundary layer from the tips of the grooves. The detached azimuthal flow then develops into a plume.
We now discuss why plumes are preferentially ejected from the tips of the grooves. Figure 10 shows the contour plots of the instantaneous azimuthal velocity
![]() $u_{{\it\theta}}$
, which are enlargements of the plume-detaching region of figure 8, superposed by instantaneous velocity vectors in the meridional plane. Figure 8(a) shows how plumes detach from the wall of the inner cylinder. A radial pressure gradient accelerates the fluid in the central part of the plume. The sudden acceleration generates secondary vorticity close to the plume, deforming the plume into a mushroom shape. However, for the grooved case, the situation is completely different. The axial pressure gradient favours the Taylor vortex propelling a secondary vortex inside the grooves. This secondary vortex has the opposite direction compared to the large-scale Taylor vortex. The interaction between the Taylor vortex and the secondary vortex causes the detachment of the BL from the tips of the grooves into the bulk, and hence forms a plume. Then the plumes are dissipated into the large-scale Taylor rolls. These phenomena are clearly seen in figure 8(b). We note that it is very similar to the famous ‘lid-driven-cavity’ flow – however, it is the Taylor roll that drives the flow in the grooves. Although in RB flows the mechanism for large-scale rolls is different from TC flow, similar thermal plumes are also found to be ejected from the tips of roughness elements there (Du & Tong Reference Du and Tong2000; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006).
$u_{{\it\theta}}$
, which are enlargements of the plume-detaching region of figure 8, superposed by instantaneous velocity vectors in the meridional plane. Figure 8(a) shows how plumes detach from the wall of the inner cylinder. A radial pressure gradient accelerates the fluid in the central part of the plume. The sudden acceleration generates secondary vorticity close to the plume, deforming the plume into a mushroom shape. However, for the grooved case, the situation is completely different. The axial pressure gradient favours the Taylor vortex propelling a secondary vortex inside the grooves. This secondary vortex has the opposite direction compared to the large-scale Taylor vortex. The interaction between the Taylor vortex and the secondary vortex causes the detachment of the BL from the tips of the grooves into the bulk, and hence forms a plume. Then the plumes are dissipated into the large-scale Taylor rolls. These phenomena are clearly seen in figure 8(b). We note that it is very similar to the famous ‘lid-driven-cavity’ flow – however, it is the Taylor roll that drives the flow in the grooves. Although in RB flows the mechanism for large-scale rolls is different from TC flow, similar thermal plumes are also found to be ejected from the tips of roughness elements there (Du & Tong Reference Du and Tong2000; Stringano et al.
Reference Stringano, Pascazio and Verzicco2006).

Figure 11. Contour plots of the time- and azimuthally averaged correlation
![]() $r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}$
at
$r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}$
at
![]() $Ta=9.75\times 10^{8}$
. (a) The smooth case, (b) the
$Ta=9.75\times 10^{8}$
. (a) The smooth case, (b) the
![]() ${\it\delta}=0.105d$
case. The correlation has been normalized according to
${\it\delta}=0.105d$
case. The correlation has been normalized according to
![]() $r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}/(J_{0}^{{\it\omega}}Nu_{{\it\omega}})$
. The red colour represents the largest value while the blue colour represents the smallest value. It can be seen from the comparison that the interaction between the secondary vortices inside the grooves and large-scale Taylor rolls enhances the convective part of the transport in the near-tip regions.
$r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}/(J_{0}^{{\it\omega}}Nu_{{\it\omega}})$
. The red colour represents the largest value while the blue colour represents the smallest value. It can be seen from the comparison that the interaction between the secondary vortices inside the grooves and large-scale Taylor rolls enhances the convective part of the transport in the near-tip regions.
It can be seen from figure 10 how plumes enhance
![]() $Nu_{{\it\omega}}$
as well. From the definition of angular velocity current
$Nu_{{\it\omega}}$
as well. From the definition of angular velocity current
![]() $J_{{\it\omega}}$
(equation (2.1)), it is known that
$J_{{\it\omega}}$
(equation (2.1)), it is known that
![]() $Nu_{{\it\omega}}$
consists of two parts: convective and conductive contributions. The convective contribution is proportional to the correlation
$Nu_{{\it\omega}}$
consists of two parts: convective and conductive contributions. The convective contribution is proportional to the correlation
![]() $r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}$
. The interaction between the secondary vortex inside the grooves and the Taylor vortex first induces a radial velocity at the tips, then lifts the BL. The geometrically induced radial flow separation, together with the BL detachment, greatly enhances the convective part of the Nusselt number. As evidence of this, in figure 11, a comparison of the correlation
$r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}$
. The interaction between the secondary vortex inside the grooves and the Taylor vortex first induces a radial velocity at the tips, then lifts the BL. The geometrically induced radial flow separation, together with the BL detachment, greatly enhances the convective part of the Nusselt number. As evidence of this, in figure 11, a comparison of the correlation
![]() $r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}$
at the same
$r^{3}\langle u_{r}{\it\omega}\rangle _{A,t}$
at the same
![]() $Ta=9.75\times 10^{8}$
between the smooth and
$Ta=9.75\times 10^{8}$
between the smooth and
![]() ${\it\delta}=0.105d$
cases is performed. From figure 11(b), it is seen that the BL is thin enough for the grooves to protrude from it, so that, in this case, the interaction of the secondary vortex inside the grooves with the Taylor rolls contributes to the total angular momentum transport, while the additional activity in the near-tip region determines the extra transport increase. In other words, the grooves enhance plume generation and allow the plumes to be ejected towards the Taylor rolls. The combined mechanisms then increase the convective part of torque transport.
${\it\delta}=0.105d$
cases is performed. From figure 11(b), it is seen that the BL is thin enough for the grooves to protrude from it, so that, in this case, the interaction of the secondary vortex inside the grooves with the Taylor rolls contributes to the total angular momentum transport, while the additional activity in the near-tip region determines the extra transport increase. In other words, the grooves enhance plume generation and allow the plumes to be ejected towards the Taylor rolls. The combined mechanisms then increase the convective part of torque transport.

Figure 12. Contour plots of the time- and azimuthally averaged azimuthal velocity
![]() $\langle u_{{\it\theta}}\rangle _{{\it\theta},t}$
superposed by time- and azimuthally averaged velocity vectors in the meridional plane at
$\langle u_{{\it\theta}}\rangle _{{\it\theta},t}$
superposed by time- and azimuthally averaged velocity vectors in the meridional plane at
![]() $Ta=9.75\times 10^{8}$
. (a) The smooth case, (b) the
$Ta=9.75\times 10^{8}$
. (a) The smooth case, (b) the
![]() ${\it\delta}=0.105d$
case. The colour scale goes from azimuthal velocity 0.3 (blue) to 0.7 (red). It can be seen from the comparison that the interaction between the secondary vortices inside the grooves and large-scale Taylor rolls favours the circulation of Taylor rolls, and hence we get enhanced transport.
${\it\delta}=0.105d$
case. The colour scale goes from azimuthal velocity 0.3 (blue) to 0.7 (red). It can be seen from the comparison that the interaction between the secondary vortices inside the grooves and large-scale Taylor rolls favours the circulation of Taylor rolls, and hence we get enhanced transport.
From another point of view, we have mentioned before that large-scale Taylor vortices still exist in grooved TC flow. In figure 12, time-averaged azimuthal velocity contour plots with superposed velocity vectors are presented for the smooth and the
![]() ${\it\delta}=0.105d$
configurations at
${\it\delta}=0.105d$
configurations at
![]() $Ta=9.75\times 10^{8}$
. Figure 12(a) corresponds to a flow field in the ultimate regime. The Taylor roll is still present, but weaker, and plumes are ejected from many places on the surface. As a comparison, in figure 12(b) it is seen that the large-scale Taylor roll interacts with the secondary vortex inside the grooves, and therefore we conclude that, because of these grooves, on one hand, the Taylor roll induces recirculation inside the grooves, and at the same time the secondary vortex also favours the flow of Taylor rolls more effectively than the smooth case. We define a wind Reynolds number as
$Ta=9.75\times 10^{8}$
. Figure 12(a) corresponds to a flow field in the ultimate regime. The Taylor roll is still present, but weaker, and plumes are ejected from many places on the surface. As a comparison, in figure 12(b) it is seen that the large-scale Taylor roll interacts with the secondary vortex inside the grooves, and therefore we conclude that, because of these grooves, on one hand, the Taylor roll induces recirculation inside the grooves, and at the same time the secondary vortex also favours the flow of Taylor rolls more effectively than the smooth case. We define a wind Reynolds number as
![]() $Re_{w}={\it\sigma}(u_{r})d/{\it\nu}$
, where
$Re_{w}={\it\sigma}(u_{r})d/{\it\nu}$
, where
![]() ${\it\sigma}(u_{r})$
is the standard deviation of the radial velocity. For this figure, we find
${\it\sigma}(u_{r})$
is the standard deviation of the radial velocity. For this figure, we find
![]() $Re_{w}(\text{grooved})=1.12Re_{w}(\text{smooth})$
. In this case the presence of grooves generally leads to a stronger Taylor roll, which also contributes to the convective part of torque transport.
$Re_{w}(\text{grooved})=1.12Re_{w}(\text{smooth})$
. In this case the presence of grooves generally leads to a stronger Taylor roll, which also contributes to the convective part of torque transport.

Figure 13. Contour plots of the time- and azimuthally averaged azimuthal velocity
![]() $\langle u_{{\it\theta}}\rangle _{{\it\theta},t}$
superposed by time- and azimuthally averaged velocity vectors in the meridional plane at
$\langle u_{{\it\theta}}\rangle _{{\it\theta},t}$
superposed by time- and azimuthally averaged velocity vectors in the meridional plane at
![]() $Ta=9.52\times 10^{6}$
. (a) The smooth case, (b) the
$Ta=9.52\times 10^{6}$
. (a) The smooth case, (b) the
![]() ${\it\delta}=0.105d$
case. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). Comparing the two panels, no evident secondary vortices can be identified inside the grooves, which serve only as obstacles to the Taylor rolls. This is the reason why in some cases we find that
${\it\delta}=0.105d$
case. The colour scale goes from azimuthal velocity 0 (blue) to 1 (red). Comparing the two panels, no evident secondary vortices can be identified inside the grooves, which serve only as obstacles to the Taylor rolls. This is the reason why in some cases we find that
![]() $Nu_{{\it\omega}}$
is decreased.
$Nu_{{\it\omega}}$
is decreased.
If, in contrast, the fluctuation of the Taylor roll is not strong enough to induce the secondary vortex inside the grooves, then stagnant flow inside the grooves could not favour the Taylor vortices. Oppositely, the grooves impede the circulation of Taylor rolls when the rolls flow past the grooves. In figure 13, a time-averaged azimuthal velocity contour plot with superposed velocity vectors is presented for the
![]() ${\it\delta}=0.105d$
configuration at
${\it\delta}=0.105d$
configuration at
![]() $Ta=9.52\times 10^{6}$
. No evident secondary vortices can be seen inside the grooves. Also, no large separation of Taylor rolls can be identified and these grooves serve only as obstacles to hinder the flow from crossing them. For this figure, we find
$Ta=9.52\times 10^{6}$
. No evident secondary vortices can be seen inside the grooves. Also, no large separation of Taylor rolls can be identified and these grooves serve only as obstacles to hinder the flow from crossing them. For this figure, we find
![]() $Re_{w}(\text{grooved})=0.84Re_{w}(\text{smooth})$
. As a result, weaker Taylor vortices reduce the radial angular velocity transport, and
$Re_{w}(\text{grooved})=0.84Re_{w}(\text{smooth})$
. As a result, weaker Taylor vortices reduce the radial angular velocity transport, and
![]() $Nu_{{\it\omega}}$
is decreased.
$Nu_{{\it\omega}}$
is decreased.

Figure 14. Enlargement of the near-wall region for contour plots of the instantaneous streamwise vorticity field superposed with instantaneous velocity vectors in the meridional plane at
![]() $Ta=9.52\times 10^{6}$
(a) and
$Ta=9.52\times 10^{6}$
(a) and
![]() $Ta=9.75\times 10^{8}$
(b) with
$Ta=9.75\times 10^{8}$
(b) with
![]() ${\it\delta}=0.105d$
. The black arrows show the velocity vectors in the plane. Blue denotes a negative streamwise vorticity and red a positive streamwise vorticity.
${\it\delta}=0.105d$
. The black arrows show the velocity vectors in the plane. Blue denotes a negative streamwise vorticity and red a positive streamwise vorticity.
In the above paragraphs, we discussed how grooves affect the bulk flow and the convective part of
![]() $Nu_{{\it\omega}}$
. Because of the conservation of angular velocity current
$Nu_{{\it\omega}}$
. Because of the conservation of angular velocity current
![]() $J^{{\it\omega}}$
along the radius, the grooves will also have an impact on the wall turbulence structure and wall shear rate. To further illustrate the mechanism increasing or decreasing
$J^{{\it\omega}}$
along the radius, the grooves will also have an impact on the wall turbulence structure and wall shear rate. To further illustrate the mechanism increasing or decreasing
![]() $Nu_{{\it\omega}}$
, here we include a snapshot of the instantaneous streamwise (azimuthal) vorticity field, as shown in figure 14 for
$Nu_{{\it\omega}}$
, here we include a snapshot of the instantaneous streamwise (azimuthal) vorticity field, as shown in figure 14 for
![]() $Ta=9.52\times 10^{6}$
and
$Ta=9.52\times 10^{6}$
and
![]() $Ta=9.75\times 10^{8}$
with
$Ta=9.75\times 10^{8}$
with
![]() ${\it\delta}=0.105d$
. This figure shows the streamwise vorticity field superposed by the velocity vectors in the plane. At
${\it\delta}=0.105d$
. This figure shows the streamwise vorticity field superposed by the velocity vectors in the plane. At
![]() $Ta=9.52\times 10^{6}$
, there is almost no secondary vortex between the grooves, and only at the tips of the grooves do we see the streamwise vortices which are caused by flow separation there. At
$Ta=9.52\times 10^{6}$
, there is almost no secondary vortex between the grooves, and only at the tips of the grooves do we see the streamwise vortices which are caused by flow separation there. At
![]() $Ta=9.75\times 10^{8}$
, the secondary vortex is much stronger compared to that of the
$Ta=9.75\times 10^{8}$
, the secondary vortex is much stronger compared to that of the
![]() $Ta=9.52\times 10^{6}$
case. Between groove tips, almost all surface areas of grooves are exposed to the sweep motion that streamwise vorticity (secondary vortex) induces. The stronger the secondary vortex, the greater the surface area exposed to the sweep motion it induces, and hence the higher the shear rate of azimuthal velocity. We refer later, in figures 21 and 22, to how secondary vortices gradually occupy the entire region between grooves, and hence increase the shear rate not only at the tips, but also in the valleys, with increasing
$Ta=9.52\times 10^{6}$
case. Between groove tips, almost all surface areas of grooves are exposed to the sweep motion that streamwise vorticity (secondary vortex) induces. The stronger the secondary vortex, the greater the surface area exposed to the sweep motion it induces, and hence the higher the shear rate of azimuthal velocity. We refer later, in figures 21 and 22, to how secondary vortices gradually occupy the entire region between grooves, and hence increase the shear rate not only at the tips, but also in the valleys, with increasing
![]() $Re$
.
$Re$
.

Figure 15. Wall shear rate
![]() $\partial u_{{\it\theta}}/\partial r$
averaged in time, azimuthally, and over ten grooves for the
$\partial u_{{\it\theta}}/\partial r$
averaged in time, azimuthally, and over ten grooves for the
![]() ${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
![]() $Ta=9.52\times 10^{6}$
; (b)
$Ta=9.52\times 10^{6}$
; (b)
![]() $Ta=9.75\times 10^{8}$
. The solid lines denote the grooved case and the dashed line the averaged wall shear rate for the smooth case at the same
$Ta=9.75\times 10^{8}$
. The solid lines denote the grooved case and the dashed line the averaged wall shear rate for the smooth case at the same
![]() $Ta$
.
$Ta$
.
We now turn to discussing how the secondary vortices are related to the wall shear rate of the azimuthal velocity, and hence
![]() $Nu_{{\it\omega}}$
. In figure 15, we show the azimuthal shear rate averaged in time, azimuthally, and over ten grooves at two different Taylor numbers
$Nu_{{\it\omega}}$
. In figure 15, we show the azimuthal shear rate averaged in time, azimuthally, and over ten grooves at two different Taylor numbers
![]() $Ta=9.52\times 10^{6}$
and
$Ta=9.52\times 10^{6}$
and
![]() $Ta=9.75\times 10^{8}$
, compared with the results in the smooth case. At
$Ta=9.75\times 10^{8}$
, compared with the results in the smooth case. At
![]() $Ta=9.52\times 10^{6}$
, without secondary vortices, only the tips of the grooves are exposed to the shear of the Taylor rolls, and the shear rate decays very quickly to zero from the tips to the valleys of the grooves. There is just a small region close to the groove tip where the shear rate is larger than that in the smooth case. That is why the torque is reduced. However, at
$Ta=9.52\times 10^{6}$
, without secondary vortices, only the tips of the grooves are exposed to the shear of the Taylor rolls, and the shear rate decays very quickly to zero from the tips to the valleys of the grooves. There is just a small region close to the groove tip where the shear rate is larger than that in the smooth case. That is why the torque is reduced. However, at
![]() $Ta=9.75\times 10^{8}$
, with strong secondary vortices, the strong mixing effect causes almost the entire surface area to be exposed equally to the high shear rate. Only very close to the valley, can one find that the shear rate is smaller than its smooth counterpart. That is why the torque is enhanced. The mechanism proposed here is similar to that in channel flow with riblets, where the location of quasistreamwise vortices is changed by the size of the grooves, and thus turbulence drag increases or decreases according to the groove size (Choi et al.
Reference Choi, Moin and Kim1993). However, we observe only very few cases at one groove height
$Ta=9.75\times 10^{8}$
, with strong secondary vortices, the strong mixing effect causes almost the entire surface area to be exposed equally to the high shear rate. Only very close to the valley, can one find that the shear rate is smaller than its smooth counterpart. That is why the torque is enhanced. The mechanism proposed here is similar to that in channel flow with riblets, where the location of quasistreamwise vortices is changed by the size of the grooves, and thus turbulence drag increases or decreases according to the groove size (Choi et al.
Reference Choi, Moin and Kim1993). However, we observe only very few cases at one groove height
![]() $0.1d$
with
$0.1d$
with
![]() $Ta$
number of approximately
$Ta$
number of approximately
![]() $10^{7}$
where torque is reduced. At this
$10^{7}$
where torque is reduced. At this
![]() $Ta$
, the flow is not fully turbulent, and we would restrict our analysis to specific cases. Indeed, more work is needed to explore whether drag reduction is possible for fully turbulent TC flow.
$Ta$
, the flow is not fully turbulent, and we would restrict our analysis to specific cases. Indeed, more work is needed to explore whether drag reduction is possible for fully turbulent TC flow.

Figure 16. Averaged azimuthal velocity profile along a radius for the smooth and the
![]() ${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
![]() $Ta=4.77\times 10^{7}$
; (b)
$Ta=4.77\times 10^{7}$
; (b)
![]() $Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profile for the smooth case. The dashed line denotes the grooved case profile over time, azimuth and ten valleys, while the dot-dashed line denotes time, azimuth and ten tips, respectively.
$Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profile for the smooth case. The dashed line denotes the grooved case profile over time, azimuth and ten valleys, while the dot-dashed line denotes time, azimuth and ten tips, respectively.
5 Boundary layer dynamics
In this section we focus on the question of how exactly the grooves modify the BL dynamics. Figure 16 shows the mean velocity profiles in the smooth and in the
![]() ${\it\delta}=0.105d$
configuration at
${\it\delta}=0.105d$
configuration at
![]() $Ta=4.77\times 10^{7}$
and at
$Ta=4.77\times 10^{7}$
and at
![]() $Ta=9.75\times 10^{8}$
. At the smaller
$Ta=9.75\times 10^{8}$
. At the smaller
![]() $Ta$
the scaling slope is larger than the effective ultimate regime scaling 0.38, while at the larger
$Ta$
the scaling slope is larger than the effective ultimate regime scaling 0.38, while at the larger
![]() $Ta$
the effective scaling saturates back to 0.38. By choosing these two
$Ta$
the effective scaling saturates back to 0.38. By choosing these two
![]() $Ta$
, we can thus directly compare the BL differences between these two regimes. It is seen from this figure that the bulk velocity increases in the presence of wall roughness, i.e. the influence of the wall roughness penetrates well into the bulk region of the flow, because of the conservation of the angular velocity current
$Ta$
, we can thus directly compare the BL differences between these two regimes. It is seen from this figure that the bulk velocity increases in the presence of wall roughness, i.e. the influence of the wall roughness penetrates well into the bulk region of the flow, because of the conservation of the angular velocity current
![]() $J^{{\it\omega}}=r^{3}(\langle u_{r}{\it\omega}\rangle _{A,t}-{\it\nu}\partial _{r}\langle {\it\omega}\rangle _{A,t})$
along the radius. Figure 17 shows an enlarged region of figure 16 near the wall of the inner cylinder. The velocity profile for the smooth case is time-, azimuthally, and axially averaged, while for the grooved case it is time- and azimuthally averaged for ten different tip points and valley points of the grooves. For the smooth case, the velocity profile indicates that, due to turbulent mixing induced by the Taylor rolls, the azimuthal velocity is uniform in the bulk region and the velocity gradient across the radius is concentrated in thin boundary layers. With increasing
$J^{{\it\omega}}=r^{3}(\langle u_{r}{\it\omega}\rangle _{A,t}-{\it\nu}\partial _{r}\langle {\it\omega}\rangle _{A,t})$
along the radius. Figure 17 shows an enlarged region of figure 16 near the wall of the inner cylinder. The velocity profile for the smooth case is time-, azimuthally, and axially averaged, while for the grooved case it is time- and azimuthally averaged for ten different tip points and valley points of the grooves. For the smooth case, the velocity profile indicates that, due to turbulent mixing induced by the Taylor rolls, the azimuthal velocity is uniform in the bulk region and the velocity gradient across the radius is concentrated in thin boundary layers. With increasing
![]() $Ta$
, the BL becomes thinner and the velocity gradient becomes steeper, as expected. Correspondingly, the azimuthal velocity profile in the bulk becomes flatter and the bulk is more extended towards the walls.
$Ta$
, the BL becomes thinner and the velocity gradient becomes steeper, as expected. Correspondingly, the azimuthal velocity profile in the bulk becomes flatter and the bulk is more extended towards the walls.

Figure 17. A close look at the near inner cylinder region for the averaged azimuthal velocity profile of the smooth and the
![]() ${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
![]() $Ta=4.77\times 10^{7}$
; (b)
$Ta=4.77\times 10^{7}$
; (b)
![]() $Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profile for the smooth case. The dashed line denotes the grooved case profile over time, azimuth and ten valleys, while the dot-dashed line denotes time, azimuth and ten tips, respectively. Note that
$Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profile for the smooth case. The dashed line denotes the grooved case profile over time, azimuth and ten valleys, while the dot-dashed line denotes time, azimuth and ten tips, respectively. Note that
![]() ${\it\zeta}=y-{\it\delta}/d$
is the horizontal distance from the solid surface.
${\it\zeta}=y-{\it\delta}/d$
is the horizontal distance from the solid surface.
Similar features also apply to TC flow with grooves, but at the same time it also shows some interesting characteristic differences. For the grooved case at
![]() $Ta=4.77\times 10^{7}$
, the velocity gradient is larger at the tip of the groove, while it attains the minimum value at the valley. This is because the flow trapped inside the groove is viscosity dominated and the secondary vortex is very weak. In comparison, at
$Ta=4.77\times 10^{7}$
, the velocity gradient is larger at the tip of the groove, while it attains the minimum value at the valley. This is because the flow trapped inside the groove is viscosity dominated and the secondary vortex is very weak. In comparison, at
![]() $Ta=9.75\times 10^{8}$
, the secondary vortex inside the groove is strengthened significantly. The strong secondary vortex fully mixes the flow inside the grooves, and even a flat small bulk region can be seen. At the same time, the BL thickness at the valley is greatly decreased as a result of the extension of the secondary vortex. Because the secondary vortex must flow smoothly over the valley, where it is singular, the BL is thicker in the valley as compared to at the tip. We expect the difference of the BL thickness between the tip and valley point to become smaller and smaller on increasing the
$Ta=9.75\times 10^{8}$
, the secondary vortex inside the groove is strengthened significantly. The strong secondary vortex fully mixes the flow inside the grooves, and even a flat small bulk region can be seen. At the same time, the BL thickness at the valley is greatly decreased as a result of the extension of the secondary vortex. Because the secondary vortex must flow smoothly over the valley, where it is singular, the BL is thicker in the valley as compared to at the tip. We expect the difference of the BL thickness between the tip and valley point to become smaller and smaller on increasing the
![]() $Ta$
. The asymmetry of the BL at the inner and outer surfaces is caused by the curvature of the cylinders, and also depends on the strength of the Taylor rolls, as has been detailed in Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
).
$Ta$
. The asymmetry of the BL at the inner and outer surfaces is caused by the curvature of the cylinders, and also depends on the strength of the Taylor rolls, as has been detailed in Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
).

Figure 18. Velocity profiles of the smooth and the
![]() ${\it\delta}=0.105d$
case non-dimensionalized by friction velocity and wall distance at
${\it\delta}=0.105d$
case non-dimensionalized by friction velocity and wall distance at
![]() $Ta=9.75\times 10^{8}$
. The ten red and ten green lines represent the non-dimensionalized azimuthal velocity
$Ta=9.75\times 10^{8}$
. The ten red and ten green lines represent the non-dimensionalized azimuthal velocity
![]() $u^{+}=(U-\langle u_{{\it\theta}}\rangle _{{\it\theta},t})/u_{\ast }$
over ten valleys and ten tips for the grooved case, which show different interactions with the Taylor rolls. The local friction velocity is defined as
$u^{+}=(U-\langle u_{{\it\theta}}\rangle _{{\it\theta},t})/u_{\ast }$
over ten valleys and ten tips for the grooved case, which show different interactions with the Taylor rolls. The local friction velocity is defined as
![]() $u_{\ast }=({\it\nu}\langle \partial _{r}u_{{\it\theta}}(r_{i})\rangle _{t,{\it\theta}})^{1/2}$
, with
$u_{\ast }=({\it\nu}\langle \partial _{r}u_{{\it\theta}}(r_{i})\rangle _{t,{\it\theta}})^{1/2}$
, with
![]() $\partial _{r}$
the derivative normal to the wall, where
$\partial _{r}$
the derivative normal to the wall, where
![]() $y^{+}$
is the non-dimensional wall distance
$y^{+}$
is the non-dimensional wall distance
![]() $y^{+}=(r-r_{i})u_{\ast }/{\it\nu}$
for valleys and
$y^{+}=(r-r_{i})u_{\ast }/{\it\nu}$
for valleys and
![]() $y^{+}=(r-r_{i}-{\it\delta})u_{\ast }/{\it\nu}$
for tips in wall units. The blue line shows the averaged mean velocity profile for the smooth case at the same
$y^{+}=(r-r_{i}-{\it\delta})u_{\ast }/{\it\nu}$
for tips in wall units. The blue line shows the averaged mean velocity profile for the smooth case at the same
![]() $Ta$
. In the smooth case, we also average over the axial direction. That is, replacing
$Ta$
. In the smooth case, we also average over the axial direction. That is, replacing
![]() $\langle \cdots \rangle _{{\it\theta},t}$
by
$\langle \cdots \rangle _{{\it\theta},t}$
by
![]() $\langle \cdots \rangle _{{\it\theta},t,z}$
in the above definitions, with the wall distance being the same as the one used for the valleys. The dashed lines show the relationships
$\langle \cdots \rangle _{{\it\theta},t,z}$
in the above definitions, with the wall distance being the same as the one used for the valleys. The dashed lines show the relationships
![]() $u^{+}=y^{+}$
and
$u^{+}=y^{+}$
and
![]() $u^{+}=2.5\ln \,(y^{+})+5.2$
.
$u^{+}=2.5\ln \,(y^{+})+5.2$
.
The distinctive feature for the ultimate regime is the turbulent BL. For wall distances much larger than the internal length scale and much smaller than the outer length scale, the mean velocity profile has a logarithmic dependence on the distance to the wall. It has been shown in many canonical flows, such as pipe, channel and BL flow, that logarithmic velocity profiles exist. We refer the reader to the reviews by Marusic et al. (Reference Marusic, Mckeon, Monkewitz, Nagib, Smits and Sreenivasan2010) and Smits, McKeon & Marusic (Reference Smits, Mckeon and Marusic2011) for a detailed introduction. Figure 18 presents the non-dimensionalized azimuthal velocity
![]() $u^{+}=(U-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}})/u_{\ast }$
on tips and valleys as a function of the wall distance
$u^{+}=(U-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}})/u_{\ast }$
on tips and valleys as a function of the wall distance
![]() $y^{+}$
for the inner cylinder boundary layer at
$y^{+}$
for the inner cylinder boundary layer at
![]() $Ta=9.75\times 10^{8}$
for the grooved case. We define
$Ta=9.75\times 10^{8}$
for the grooved case. We define
![]() $u_{\ast }$
, the local friction velocity, as
$u_{\ast }$
, the local friction velocity, as
![]() $u_{\ast }=({\it\nu}\langle \partial _{r}u_{{\it\theta}}(r_{i})\rangle _{t,{\it\theta}})^{1/2}$
for valleys and tips, with
$u_{\ast }=({\it\nu}\langle \partial _{r}u_{{\it\theta}}(r_{i})\rangle _{t,{\it\theta}})^{1/2}$
for valleys and tips, with
![]() $\partial _{r}$
the derivative normal to the wall and
$\partial _{r}$
the derivative normal to the wall and
![]() $y^{+}$
the non-dimensional wall distance, given by
$y^{+}$
the non-dimensional wall distance, given by
![]() $y^{+}=(r-r_{i})u_{\ast }/{\it\nu}$
for valleys and
$y^{+}=(r-r_{i})u_{\ast }/{\it\nu}$
for valleys and
![]() $y^{+}=(r-r_{i}-{\it\delta})u_{\ast }/{\it\nu}$
for tips in terms of wall units. As a comparison, in figure 18 we also plot the averaged mean velocity profile for the smooth case at the same
$y^{+}=(r-r_{i}-{\it\delta})u_{\ast }/{\it\nu}$
for tips in terms of wall units. As a comparison, in figure 18 we also plot the averaged mean velocity profile for the smooth case at the same
![]() $Ta$
. That is, by replacing
$Ta$
. That is, by replacing
![]() $\langle \cdots \rangle _{t,{\it\theta}}$
with
$\langle \cdots \rangle _{t,{\it\theta}}$
with
![]() $\langle \cdots \rangle _{t,{\it\theta},z}$
in the above definitions, with the wall distance the same as the one used for valleys. In the smooth case, the mean velocity profile is first linear in the viscous region, then after a buffer region becomes logarithmic. For the grooved case, significant downward shifts in the log-law are obtained near the tips, whereas significant upward shifts are obtained near the valleys. Because of the strong plume ejection, all tips of grooves show logarithmic behaviour in the boundary layer, in accordance with the findings by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
) and van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015b
), which show that the BL is turbulent at the place where plumes are ejected. The implication is that a specific layout of grooves with tips could locally induce turbulent BLs at specific points. Meanwhile, because Taylor rolls still exist, the plumes have to follow the direction of the Taylor rolls, which results in the different velocity profile slopes for the logarithmic region at different tips (also see figure 12
b). In the valley, as described before, the BL is thicker than at the tip, so that the flow is more viscosity dominated. It is interesting to note that the velocity profiles nearly overlap in the valleys. This indicates that different secondary vortices at different heights are homogeneous.
$\langle \cdots \rangle _{t,{\it\theta},z}$
in the above definitions, with the wall distance the same as the one used for valleys. In the smooth case, the mean velocity profile is first linear in the viscous region, then after a buffer region becomes logarithmic. For the grooved case, significant downward shifts in the log-law are obtained near the tips, whereas significant upward shifts are obtained near the valleys. Because of the strong plume ejection, all tips of grooves show logarithmic behaviour in the boundary layer, in accordance with the findings by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
) and van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015b
), which show that the BL is turbulent at the place where plumes are ejected. The implication is that a specific layout of grooves with tips could locally induce turbulent BLs at specific points. Meanwhile, because Taylor rolls still exist, the plumes have to follow the direction of the Taylor rolls, which results in the different velocity profile slopes for the logarithmic region at different tips (also see figure 12
b). In the valley, as described before, the BL is thicker than at the tip, so that the flow is more viscosity dominated. It is interesting to note that the velocity profiles nearly overlap in the valleys. This indicates that different secondary vortices at different heights are homogeneous.

Figure 19. Root mean square azimuthal velocity profile of the smooth and the
![]() ${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
${\it\delta}=0.105d$
case at two different Taylor numbers: (a)
![]() $Ta=4.77\times 10^{7}$
; (b)
$Ta=4.77\times 10^{7}$
; (b)
![]() $Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profile for the smooth case. The dashed line denotes the grooved case profile for valleys, while the dot-dashed denotes the profile above tips. The r.m.s. velocity for the smooth case is defined as
$Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profile for the smooth case. The dashed line denotes the grooved case profile for valleys, while the dot-dashed denotes the profile above tips. The r.m.s. velocity for the smooth case is defined as
![]() $(u_{{\it\theta}})_{rms}=(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta},z}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta},z}^{2})^{1/2}$
, while for grooved case it is defined as
$(u_{{\it\theta}})_{rms}=(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta},z}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta},z}^{2})^{1/2}$
, while for grooved case it is defined as
![]() $(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta}}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}}^{2})^{1/2}$
and then averaged over ten different tips or valleys.
$(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta}}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}}^{2})^{1/2}$
and then averaged over ten different tips or valleys.

Figure 20. A close look at the root mean square azimuthal velocity profile of the smooth and the
![]() ${\it\delta}=0.105d$
case in the near-wall region at two different Taylor numbers: (a)
${\it\delta}=0.105d$
case in the near-wall region at two different Taylor numbers: (a)
![]() $Ta=4.77\times 10^{7}$
; (b)
$Ta=4.77\times 10^{7}$
; (b)
![]() $Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profiles for the smooth case. The dashed line denotes the grooved case profile for valleys, while the dot-dashed denotes the profile above the tips. The r.m.s. velocity for the smooth case is defined as
$Ta=9.75\times 10^{8}$
. The solid line shows the time-, azimuthally and axially averaged velocity profiles for the smooth case. The dashed line denotes the grooved case profile for valleys, while the dot-dashed denotes the profile above the tips. The r.m.s. velocity for the smooth case is defined as
![]() $(u_{{\it\theta}})_{rms}=(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta},z}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta},z}^{2})^{1/2}$
, while for grooved case it is defined as
$(u_{{\it\theta}})_{rms}=(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta},z}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta},z}^{2})^{1/2}$
, while for grooved case it is defined as
![]() $(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta}}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}}^{2})^{1/2}$
and then averaged over ten different tips or valleys. Note that
$(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta}}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}}^{2})^{1/2}$
and then averaged over ten different tips or valleys. Note that
![]() ${\it\zeta}=y-{\it\delta}/d$
is the horizontal distance from the solid surface.
${\it\zeta}=y-{\it\delta}/d$
is the horizontal distance from the solid surface.
The grooves not only influence the mean velocity, but also the fluctuations. Figure 19 shows the root mean square (r.m.s.) azimuthal velocity profiles in the smooth and the
![]() ${\it\delta}=0.105d$
configuration at
${\it\delta}=0.105d$
configuration at
![]() $Ta=4.77\times 10^{7}$
and at
$Ta=4.77\times 10^{7}$
and at
![]() $Ta=9.75\times 10^{8}$
. Figure 20 shows an enlarged region of figure 19 near the wall of the inner cylinder. The r.m.s. velocity for the smooth case is defined as
$Ta=9.75\times 10^{8}$
. Figure 20 shows an enlarged region of figure 19 near the wall of the inner cylinder. The r.m.s. velocity for the smooth case is defined as
![]() $(u_{{\it\theta}})_{rms}=(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta},z}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta},z}^{2})^{1/2}$
, while for the grooved case it is defined as
$(u_{{\it\theta}})_{rms}=(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta},z}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta},z}^{2})^{1/2}$
, while for the grooved case it is defined as
![]() $(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta}}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}}^{2})^{1/2}$
, averaged over different tips or valleys. For the smooth case, there is only one peak of the r.m.s. velocity, which is associated with the enhanced fluctuation in the buffer layer. With increasing
$(\langle u_{{\it\theta}}^{2}\rangle _{t,{\it\theta}}-\langle u_{{\it\theta}}\rangle _{t,{\it\theta}}^{2})^{1/2}$
, averaged over different tips or valleys. For the smooth case, there is only one peak of the r.m.s. velocity, which is associated with the enhanced fluctuation in the buffer layer. With increasing
![]() $Ta$
, as the turbulent intensity becomes larger and the BL becomes thinner, and, as expected, the peak is shifted to the inner cylinder and the r.m.s. is larger.
$Ta$
, as the turbulent intensity becomes larger and the BL becomes thinner, and, as expected, the peak is shifted to the inner cylinder and the r.m.s. is larger.
For the grooved case with
![]() $Ta=4.77\times 10^{7}$
, at the tips of the grooves, the position where the peak occurs is also shifted to the inner cylinder and the r.m.s. velocity is larger. In the valley, we see two different peaks of the r.m.s. velocity. One close to the wall and one close to the bulk. The near-wall peak is associated with the buffer layer and the other peak is associated with the shear layer between the secondary vortex and the Taylor roll. The secondary vortex is located between these two peaks. Because the flow inside the groove is viscosity dominated and laminar, the position of this peak is far away from the wall and the intensity is less than in the shear layer. At
$Ta=4.77\times 10^{7}$
, at the tips of the grooves, the position where the peak occurs is also shifted to the inner cylinder and the r.m.s. velocity is larger. In the valley, we see two different peaks of the r.m.s. velocity. One close to the wall and one close to the bulk. The near-wall peak is associated with the buffer layer and the other peak is associated with the shear layer between the secondary vortex and the Taylor roll. The secondary vortex is located between these two peaks. Because the flow inside the groove is viscosity dominated and laminar, the position of this peak is far away from the wall and the intensity is less than in the shear layer. At
![]() $Ta=9.75\times 10^{8}$
, the secondary vortex becomes stronger and extends closer towards the wall, as illustrated before. As a result, the BL becomes thinner and shifts closer to the wall; at the same time, the intensity of fluctuation becomes higher than the shear layer.
$Ta=9.75\times 10^{8}$
, the secondary vortex becomes stronger and extends closer towards the wall, as illustrated before. As a result, the BL becomes thinner and shifts closer to the wall; at the same time, the intensity of fluctuation becomes higher than the shear layer.

Figure 21. The positions of the peaks of the r.m.s. azimuthal velocity profile near the inner cylinder for the
![]() ${\it\delta}=0.105d$
cases averaged in time, azimuth and over ten grooves at two different Taylor numbers: (a)
${\it\delta}=0.105d$
cases averaged in time, azimuth and over ten grooves at two different Taylor numbers: (a)
![]() $Ta=4.77\times 10^{7}$
; (b)
$Ta=4.77\times 10^{7}$
; (b)
![]() $Ta=9.75\times 10^{8}$
. The red points are the positions of these peaks. We average over ten grooves. Abbreviations: BL
$Ta=9.75\times 10^{8}$
. The red points are the positions of these peaks. We average over ten grooves. Abbreviations: BL
![]() $=$
boundary layer, SV
$=$
boundary layer, SV
![]() $=$
secondary vortex.
$=$
secondary vortex.
Figure 21 shows the positions where the peaks of the r.m.s. azimuthal velocity profiles close to the inner cylinder occur for
![]() $Ta=4.77\times 10^{7}$
and for
$Ta=4.77\times 10^{7}$
and for
![]() $Ta=9.75\times 10^{8}$
, both for the
$Ta=9.75\times 10^{8}$
, both for the
![]() ${\it\delta}=0.105d$
case. The profiles were averaged in the azimuthal direction, in time and over the ten grooves. Although other definitions are possible, inspired by the work of Stringano et al. (Reference Stringano, Pascazio and Verzicco2006), we define the near-wall peak of the r.m.s. velocity profile as the thickness of the boundary layer. This enables us to separate the flow domain into three zones. Between the wall and the near-wall peak is the BL layer zone. Between the two peaks is the secondary vortex zone, and beyond is the bulk zone. From the comparison between these two panels, it is seen that, with increasing
${\it\delta}=0.105d$
case. The profiles were averaged in the azimuthal direction, in time and over the ten grooves. Although other definitions are possible, inspired by the work of Stringano et al. (Reference Stringano, Pascazio and Verzicco2006), we define the near-wall peak of the r.m.s. velocity profile as the thickness of the boundary layer. This enables us to separate the flow domain into three zones. Between the wall and the near-wall peak is the BL layer zone. Between the two peaks is the secondary vortex zone, and beyond is the bulk zone. From the comparison between these two panels, it is seen that, with increasing
![]() $Ta$
, the BL inside the groove becomes thinner and more uniformly distributed along the surface of the groove. This indicates that, at high
$Ta$
, the BL inside the groove becomes thinner and more uniformly distributed along the surface of the groove. This indicates that, at high
![]() $Ta$
, the azimuthal velocity can not feel the effect of the grooves, and thus forms the uniformly thick BL, just as in the smooth case. As an indication of the growing strength of the secondary vortices, in figure 22 we show the distance between the peaks of the r.m.s. azimuthal velocity in the groove valley as a function of
$Ta$
, the azimuthal velocity can not feel the effect of the grooves, and thus forms the uniformly thick BL, just as in the smooth case. As an indication of the growing strength of the secondary vortices, in figure 22 we show the distance between the peaks of the r.m.s. azimuthal velocity in the groove valley as a function of
![]() $Ta$
for the
$Ta$
for the
![]() ${\it\delta}=0.105d$
case. It is found that the size of the secondary vortex saturates to
${\it\delta}=0.105d$
case. It is found that the size of the secondary vortex saturates to
![]() $0.11d$
.
$0.11d$
.

Figure 22. Distance
![]() $l/d$
between the peaks of the root mean square azimuthal velocity in the groove valley as a function of
$l/d$
between the peaks of the root mean square azimuthal velocity in the groove valley as a function of
![]() $Ta$
for the
$Ta$
for the
![]() ${\it\delta}=0.105d$
cases.
${\it\delta}=0.105d$
cases.

Figure 23. Energy dissipation rate
![]() ${\it\epsilon}_{u}={\it\nu}\langle ({\rm\nabla}\boldsymbol{u})^{2}\rangle _{t,{\it\theta},z}$
along the radius for the
${\it\epsilon}_{u}={\it\nu}\langle ({\rm\nabla}\boldsymbol{u})^{2}\rangle _{t,{\it\theta},z}$
along the radius for the
![]() ${\it\delta}=0.105d$
series. It was averaged in time, azimuth and height at two different
${\it\delta}=0.105d$
series. It was averaged in time, azimuth and height at two different
![]() $Ta$
: (a)
$Ta$
: (a)
![]() $Ta=4.77\times 10^{7}$
; (b)
$Ta=4.77\times 10^{7}$
; (b)
![]() $Ta=9.75\times 10^{8}$
.
$Ta=9.75\times 10^{8}$
.
Finally, to shed further light on why the effective scaling is larger than 0.38 at
![]() $Ta=4.77\times 10^{7}$
and saturates back to 0.38 at
$Ta=4.77\times 10^{7}$
and saturates back to 0.38 at
![]() $Ta=9.75\times 10^{8}$
for the
$Ta=9.75\times 10^{8}$
for the
![]() ${\it\delta}=0.105d$
series, we compare the energy dissipation rate
${\it\delta}=0.105d$
series, we compare the energy dissipation rate
![]() ${\it\epsilon}_{u}={\it\nu}\langle ({\rm\nabla}\boldsymbol{u})^{2}\rangle _{t,{\it\theta},z}$
along the radius, as shown in figure 23. According to Grossmann & Lohse (Reference Grossmann and Lohse2011), the logarithmic correction, which originates from the turbulent boundary layer, leads to an effective scaling of 0.38. Even in the fully turbulent regime in which we are, the boundary layer effects still play a major role in determining the scaling exponent. Only asymptotically, will the
${\it\epsilon}_{u}={\it\nu}\langle ({\rm\nabla}\boldsymbol{u})^{2}\rangle _{t,{\it\theta},z}$
along the radius, as shown in figure 23. According to Grossmann & Lohse (Reference Grossmann and Lohse2011), the logarithmic correction, which originates from the turbulent boundary layer, leads to an effective scaling of 0.38. Even in the fully turbulent regime in which we are, the boundary layer effects still play a major role in determining the scaling exponent. Only asymptotically, will the
![]() $Nu$
versus
$Nu$
versus
![]() $Ta$
scaling exponent go to
$Ta$
scaling exponent go to
![]() $1/2$
, but we are far away from this exponent in any experiment. At
$1/2$
, but we are far away from this exponent in any experiment. At
![]() $Ta=9.75\times 10^{8}$
, because the BL inside the groove becomes more similar to the smooth case, the contribution of the BL to the energy dissipation returns. As a result, the logarithmic correction to the scaling law occurs. At
$Ta=9.75\times 10^{8}$
, because the BL inside the groove becomes more similar to the smooth case, the contribution of the BL to the energy dissipation returns. As a result, the logarithmic correction to the scaling law occurs. At
![]() $Ta=4.77\times 10^{7}$
, the BL inside the groove is thick and laminar; however, this is not the smooth laminar BL where there is a steep shear layer very close to the wall which contributes significantly to the dissipation. In this case, the shear is very small in the valley region, but large around the tip (see figures 15 and 16). It is clearly seen that the shear rate in the region between the grooves is much less than that of the smooth case. Thus, it is reasonable that the dissipation from the BL contributes less and it is bulk dominant. We estimate the dissipation contributed from BL and bulk at two values of Taylor number from figure 23. At
$Ta=4.77\times 10^{7}$
, the BL inside the groove is thick and laminar; however, this is not the smooth laminar BL where there is a steep shear layer very close to the wall which contributes significantly to the dissipation. In this case, the shear is very small in the valley region, but large around the tip (see figures 15 and 16). It is clearly seen that the shear rate in the region between the grooves is much less than that of the smooth case. Thus, it is reasonable that the dissipation from the BL contributes less and it is bulk dominant. We estimate the dissipation contributed from BL and bulk at two values of Taylor number from figure 23. At
![]() $Ta=4.77\times 10^{7}$
, the region below the groove height contributes 49 % of the total dissipation while the bulk contributes 51 %. In contrast, at
$Ta=4.77\times 10^{7}$
, the region below the groove height contributes 49 % of the total dissipation while the bulk contributes 51 %. In contrast, at
![]() $Ta=9.75\times 10^{8}$
, the region below the groove height contributes 65 % of the total dissipation while the bulk contributes 35 %. Therefore, according to the GL theory (Grossmann & Lohse Reference Grossmann and Lohse2000), in the regime close to
$Ta=9.75\times 10^{8}$
, the region below the groove height contributes 65 % of the total dissipation while the bulk contributes 35 %. Therefore, according to the GL theory (Grossmann & Lohse Reference Grossmann and Lohse2000), in the regime close to
![]() $Ta=4.77\times 10^{7}$
, where it is more bulk dominant, the local effective scaling exponent is larger than 0.38.
$Ta=4.77\times 10^{7}$
, where it is more bulk dominant, the local effective scaling exponent is larger than 0.38.
6 Conclusions
In this study, direct numerical simulations are conducted to explore Taylor–Couette flow in the presence of grooved walls. Numerical results corresponding to Taylor numbers up to
![]() $Ta=2.15\times 10^{9}$
are presented for three different sizes of groove, namely
$Ta=2.15\times 10^{9}$
are presented for three different sizes of groove, namely
![]() ${\it\delta}=0.052d$
,
${\it\delta}=0.052d$
,
![]() ${\it\delta}=0.105d$
and
${\it\delta}=0.105d$
and
![]() ${\it\delta}=0.209d$
, at a radius ratio
${\it\delta}=0.209d$
, at a radius ratio
![]() ${\it\eta}=0.714$
.
${\it\eta}=0.714$
.
We find three different characteristic regimes, reflected in different effective scaling laws between
![]() $Nu_{{\it\omega}}$
and
$Nu_{{\it\omega}}$
and
![]() $Ta$
. First, when
$Ta$
. First, when
![]() $Ta<Ta_{th}$
, i.e. when the boundary layer thickness is larger than the height of the grooves, there is an overlap regime in which smooth and groove cases show the same behaviour. Second, when
$Ta<Ta_{th}$
, i.e. when the boundary layer thickness is larger than the height of the grooves, there is an overlap regime in which smooth and groove cases show the same behaviour. Second, when
![]() $Ta>Ta_{th}$
, i.e. when the boundary layer thickness is less than the groove height, there is a steep-slope regime in which the power-law exponent between
$Ta>Ta_{th}$
, i.e. when the boundary layer thickness is less than the groove height, there is a steep-slope regime in which the power-law exponent between
![]() $Nu_{{\it\omega}}$
and
$Nu_{{\it\omega}}$
and
![]() $Ta$
becomes larger than the ultimate region effective scaling of 0.38. Third, when
$Ta$
becomes larger than the ultimate region effective scaling of 0.38. Third, when
![]() $Ta$
is large enough, there is a saturation regime in which the effective scaling law saturates back to 0.38. It is found that, even after saturation, the slope is the same as for the smooth case, and the absolute value of torque is increased beyond the ratio of the surface area increase between grooved and smooth walls.
$Ta$
is large enough, there is a saturation regime in which the effective scaling law saturates back to 0.38. It is found that, even after saturation, the slope is the same as for the smooth case, and the absolute value of torque is increased beyond the ratio of the surface area increase between grooved and smooth walls.
The visualization of the flow structure shows that the enhanced transport is caused by plume ejection from the tips of the grooves. First, the axial flow induces secondary vortices inside the grooves. Second, the interaction between the secondary vortices and the Taylor vortices facilitates flow separation on the tips. Third, this flow separation causes the boundary layer to detach into the bulk, and thus the boundary layer flow forms plumes and follows the preferential direction of Taylor vortices. Finally, the combination of plumes and flow separation greatly strengthens the convective part of
![]() $Nu_{{\it\omega}}$
. In particular, there is a possibility that the torque can become smaller when there are no plumes ejected from the tips of the grooves and the grooves impede the Taylor rolls. Another interesting feature revealed from visualizations is that large-scale Taylor vortices still survive in the presence of the grooves. This is because the induced secondary vortices inside the grooves also favour the circulation of the Taylor rolls.
$Nu_{{\it\omega}}$
. In particular, there is a possibility that the torque can become smaller when there are no plumes ejected from the tips of the grooves and the grooves impede the Taylor rolls. Another interesting feature revealed from visualizations is that large-scale Taylor vortices still survive in the presence of the grooves. This is because the induced secondary vortices inside the grooves also favour the circulation of the Taylor rolls.
With increasing
![]() $Ta$
, the intensity of the secondary vortex inside the grooves is strengthened. The boundary layer thickness in the valley is decreased and more uniformly distributed along the surface of the groove. A small flat bulk region for the mean velocity profile can be seen inside the grooves. At high
$Ta$
, the intensity of the secondary vortex inside the grooves is strengthened. The boundary layer thickness in the valley is decreased and more uniformly distributed along the surface of the groove. A small flat bulk region for the mean velocity profile can be seen inside the grooves. At high
![]() $Ta$
, the azimuthal velocity cannot feel the effect of the grooves, and thus forms the uniformly thick BL, just as the smooth case. As to the fluctuation, it is found that, on the tips of the grooves, there is only one peak for the root mean square azimuthal velocity, while in the valley there are two peaks. The first peak is associated with the BL near the valley, and the second peak with the shear layer between the secondary vortices and the Taylor vortices. We found that the steep-slope regime is more bulk dominant, and therefore the effective scaling slope is larger, while in the saturation regime, the boundary layer contribution reoccurs, and hence the scaling slope saturates.
$Ta$
, the azimuthal velocity cannot feel the effect of the grooves, and thus forms the uniformly thick BL, just as the smooth case. As to the fluctuation, it is found that, on the tips of the grooves, there is only one peak for the root mean square azimuthal velocity, while in the valley there are two peaks. The first peak is associated with the BL near the valley, and the second peak with the shear layer between the secondary vortices and the Taylor vortices. We found that the steep-slope regime is more bulk dominant, and therefore the effective scaling slope is larger, while in the saturation regime, the boundary layer contribution reoccurs, and hence the scaling slope saturates.
Our ambition is to further understand plume-triggered transitions. Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a
) and van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015b
) have shown that in smooth TC and RB flows the transition to the ultimate regime can be triggered by plumes because the regions of BLs where the plumes are ejected become turbulent. On the one hand, we would like to study whether in the grooved case the turbulent boundary layer can not only be formed on the tips of grooves, but for much larger
![]() $Ta$
also inside the grooves, and thus lead to the ultimate regime. On the other hand, grooves can be used to manipulate the plumes because they are ejected from the tips of the grooves. If we implemented more and more grooves, and made the tips sharp enough such that there were more and more tips where plumes could be ejected, the ultimate regime could possibly be achieved at a much smaller
$Ta$
also inside the grooves, and thus lead to the ultimate regime. On the other hand, grooves can be used to manipulate the plumes because they are ejected from the tips of the grooves. If we implemented more and more grooves, and made the tips sharp enough such that there were more and more tips where plumes could be ejected, the ultimate regime could possibly be achieved at a much smaller
![]() $Ta$
.
$Ta$
.
Acknowledgements
This work is sponsored by the Foundation for Fundamental Research on Matter (FOM), which is a part of the Netherlands Organisation for Scientific Research (NWO). The authors would like to thank C. Sun, E. P. van der Poel and Y. Yang for many valuable discussions and the Dutch Supercomputing Consortium SurfSARA for the allocation of computing time.