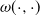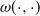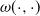1. Introduction
As a natural generalization of a Lévy process, a continuous-time Markov additive process (MAP) has various applications in the fields of risk theory, financial mathematics, environmental problems, queueing, and so forth (see, e.g., [Reference Asmussen2], [Reference Breuer5], [Reference D’Auria, Ivanovs, Kella and Mandjes6], [Reference Dieker and Mandjes7], [Reference Ivanovs and Mandjes13]). Informally speaking, a MAP can be viewed as a Lévy process in a Markov environment whose characteristic function depends on the state of the current environment, with possible jumps at the times of transition between states. This structure of a MAP enriches its modelling possibilities in consideration of seasonality of prices, recurring patterns of activity, burst arrivals, or occurrence of events in phases. Throughout this article, we will consider a bivariate MAP 
$(X,J)=\{(X_t,J_t)\}_{t\ge0}$
such that X is a real-valued càdlàg (right-continuous with left limits) process and J is a right-continuous jump process with a finite state space 
$E = \lbrace 1,2,...,N\rbrace$
to capture the states of the environment.
In the application of stochastic processes in insurance and finance, an important role is played by exit problems, which focus on the behavior of the process across some specified interval (possibly unbounded). Quantities of interest include the so-called first passage time (or first exit time), the level of the process right before or after exiting (which could be calculated directly from the resolvent (or potential) measures at killing), and the occupation time (the total time spent in a certain interval before exiting). For example, in ruin theory, the classical time to ruin is defined as the first time that a surplus process exits from the interval (0, 
$+\infty$
). In the event of ruin, the surplus prior to ruin and the deficit at ruin are the two important quantities by which to measure the company’s economic cost. In the theory of exit problems under a spectrally negative Lévy process (with downward jumps only), it is well known that the results are (semi-)explicitly expressed in terms of so-called scale functions. Such representations offer a convenient way to analyze the properties of exit problems by examining the characteristics of scale functions. For more details, we refer interested readers to [Reference Kyprianou19]. In the MAP framework, we can also find such representations by means of a nontrivial generalization. In this case, one needs to work with matrix-valued functions, called scale matrices, as an analogue for scale functions. The definitions and properties of scale matrices are presented in Section 2; see also [Reference Ivanovs and Palmowski15] and [Reference Ivanovs16] for more results on this topic.
This paper solves exit problems for a spectrally negative MAP which is exponentially killed with a bivariate killing intensity 
$\omega(\cdot,\cdot)$
dependent on the present states of the process and the environment. We use the expression ‘
$\omega$
-killing’ for such a killing feature, which could be interpreted as a (state- and/or level-dependent) Laplace argument, a discount factor, a bankruptcy rate, or the weight for occupation time in different contexts. To formulate our problems mathematically, let us first introduce the first passage times:
\begin{equation*}\tau_{x}^{+} = \inf \lbrace t > 0 \,:\, X_t \geq x \rbrace,\qquad\tau_{x}^{-} = \inf \lbrace t > 0 \,:\, X_t
< x \rbrace.\end{equation*}
Then we assume that 
$\omega\,:\, E \times \mathbb{R} \rightarrow \mathbb{R}^{+}$
is a bounded, nonnegative measurable function, and for any given 
$i \in E$
, 
$\omega(i,x) = \omega_i(x)$
. One of the main interests of this paper is to derive closed-form formulas for occupation times (up to some exit times), weighted by the omega function. More specifically, for 
$d\leq x\leq c$
and 
$1\le i,j \le N$
, we are interested in the expectation matrices whose (i, j)-th elements are, respectively,
\begin{equation}\hspace*{-4pt}\mathbb{E}_{x} \left[e^{-\int_0^{\tau_c^+}\omega_{J_s}(X_s)ds}, \tau_c^+<\tau_d^-, J_{\tau_c^+}=j | J_0 = i \right]\end{equation}
and
\begin{equation}\mathbb{E}_{x} \left[e^{-\int_0^{\tau_d^-}\omega_{J_s}(X_s)ds},\tau_d^-
< \tau_c^+, J_{\tau_d^-}=j | J_0 = i \right].\end{equation}
Recently, Li and Palmowski [Reference Li and Palmowski22] investigated such 
$\omega$
-killed exit identities and resolvents for a general (reflected) spectrally negative Lévy process. They obtained representations of exit problems in terms of new 
$\omega$
-scale functions, which are generalizations of the classical scale functions. Similarly, in our article we describe exit problems in terms of 
$\omega$
-scale matrices, denoted by 
$\mathcal{W}^{(\omega)}$
and 
$\mathcal{Z}^{(\omega)}$
, which are generalizations of classical scale matrices. In the particular case of constant killing intensity 
$\omega$
, our results are consistent with the traditional (two-sided) exit identities (and resolvents) obtained in [Reference Ivanovs and Palmowski15] and [Reference Ivanovs16]. Moreover, it is shown that these new generalized scale matrices satisfy certain integral equations.
There is a long list of potential areas where (1.1) and (1.2) can be applied. Here we would like to mention two practical examples of the use of (1.1), which will also demonstrate the different interpretations of 
$\omega$
-killing. These two examples also motivate the discussions in Sections 4 and 5.
From one point of view, we can consider 
$\omega$
as a weight function to describe a sophisticated discount structure, which is essential in financial mathematics. For instance, one is interested in the present value of a $1 payment made at the time of the surplus reaching level c (e.g., in the situation of performance-dependent payoff). When 
$\omega(i,x) = \delta>0$
, we have only one single discount factor. However, with the general 
$\omega$
-killing feature, one can capture dynamic discount rates to reflect economic environment changes in the whole path of the additive process up to a certain stopping time. This is consistent with the practice that the discount rate (or interest rate) varies with environment states. A company’s surplus level could also be used as an indication of the economic environment. For illustration purposes, we will present as examples some natural choices of 
$\omega$
, such as a (level-dependent) step function and a constant state-dependent function, under a Markov-modulated Brownian motion risk process. We will show how to identify the 
$\omega$
-scale matrices using differential equations. Numerical examples are also provided by making use of Ivanov’s Mathematica package [Reference Ivanovs17].
The second example is an application in ruin theory. The traditional definition of bankruptcy occurs at the time to ruin (namely the first time that the surplus level drops below level zero). However, bankruptcy can be defined in different ways to allow for the company’s self-recovery within a certain grace period. One research direction is omega ruin time, proposed in [Reference Albrecher, Gerber and Shiu1] and [Reference Gerber, Shiu and Yang11], where bankruptcy occurs either when the process crosses a pre-defined threshold level or with intensity 
$\omega$
when the process stays in the red zone. Then the expectation (1.1) is interpreted as the probability of the surplus reaching level c before bankruptcy (or omega ruin). More details are provided in Section 4. In this setting, our general results can be directly applied to derive the value function of discounted dividend payments up to omega ruin time under a barrier strategy. Our contribution lies in the fact that this is the first time that omega ruin time has been investigated for a modulated process. As the surplus process evolves in a Markovian environment, it offers more flexibility for describing various business cycles. In other words, this model takes into account two sources of risk: claims risk and regime-switching risk.
The paper is organized as follows. Section 2 recalls some basic definitions and properties of MAPs, and formally introduces the bivariate 
$\omega$
-function. In Section 3, we present the definitions of 
$\omega$
-scale matrices, making use of which we derive the explicit expressions for our main results, including the one-sided and two-sided exit problems. Moreover, we analyze the respective 
$\omega$
-killed resolvents, which can be used for further development of the theory (e.g. the surplus prior to ruin and deficit at ruin in the Omega model). Section 4 applies the main results to find the value function for dividends paid until ruin under the Omega model. Section 5 is dedicated to the analysis of some particular examples of the omega function. Further numerical computations are performed. Finally, for conciseness and completeness, we postpone to Appendix A the proofs of the existence and invertibility of 
$\omega$
-killed scale matrices, and to Appendix B some proofs (of one lemma and one corollary) related to the main results.
2. Preliminaries
A Markov additive process (MAP) is defined as follows. Let 
$(\Omega,\mathcal{F},\mathbb{F}, \mathbb{P})$
be a filtered probability space, with filtration 
$\mathbb{F} = \lbrace \mathcal{F}_t \,:\, t \geq 0 \rbrace$
which satisfies the usual conditions. We say that a bivariate process (X, J) is a MAP if, given 
$\lbrace J_t = i \rbrace$
for 
$i\in E$
, the vector 
$(X_{t+s}-X_{t},J_{t+s})$
is independent of 
$\mathcal{F}_t$
and has the same law as 
$(X_s - X_0, J_s)$
given 
$\lbrace J_0 = i \rbrace$
for all 
$s,t \geq 0$
and 
$i \in E$
. Usually, X is called an additive component and J is a background process representing the environment. Moreover, every MAP has the following important representation. It is straightforward from the definition that J forms a Markov chain. Furthermore, the process X evolves as some Lévy process 
$X^{i}$
when J is in state i. In addition, when J transits to state 
$j \neq i$
, the process X jumps according to the distribution of the random variable 
$U_{ij}$
, where 
$i,j \in E$
. All these components are assumed to be independent. The above structure explains why the other name for a MAP is ‘Markov-modulated Lévy process’. In particular, when J lives on a single state, X reduces to a Lévy process. Throughout this paper we assume that the process X has no positive jumps; thus 
$X^i$
is a spectrally negative Lévy process and 
$U_{ij} \leq 0$
almost surely (for every 
$i,j \in E$
). We exclude the case when X has monotone paths. We further assume that J is an irreducible Markov chain, with 
${\textit{\textbf{Q}}}$
being its transition probability matrix and 
$\boldsymbol{\pi}$
being its unique stationary vector.
Here are some basic characteristics and properties of MAPs. Let 
$\textbf{F}(\alpha)$
be the matrix analogue of the Laplace exponent of the spectrally negative Lévy process: it satisfies
\begin{equation*}\mathbb{E}\left( e^{\alpha X_t}, J_t=j|J_0=i\right)=\left(e^{\textbf{F}(\alpha)t} \right)_{ij} \quad \mbox{for}\quad \alpha \geq 0.\end{equation*}
It has an explicit representation, namely
\begin{equation*}\textbf{F}(\alpha)=\mbox{diag}(\psi_1(\alpha),...,\psi_N(\alpha))+{\textit{\textbf{Q}}}\circ \mathbb{E}(e^{\alpha U_{ij}}),\end{equation*}
where 
$\psi_{i}(\cdot)$
is the Laplace exponent of the Lévy process 
$X^{i}$
(i.e., 
$\mathbb{E}( e^{\alpha X^i_t})=e^{\psi_{i}(\alpha)t}$
), and 
${\textit{\textbf{A}}} \circ {\textit{\textbf{B}}}=(a_{ij}b_{ij})$
stands for the entrywise (Hadamard) matrix product. Note that 
$\textbf{F}(0)$
is the transition rate matrix of J, and hence a MAP is non-defective if and only if 
${\textbf{F}}(0) \vec{1}= \vec{{0}}$
, where 
$\vec{{0}}$
and 
$\vec{1}$
denote the (column) vectors of 0s and 1s respectively (whereas the identity and the zero matrices are denoted by 
$\textbf{I}$
and 
$\textbf{0}$
respectively). Throughout this article, the law of (X, J) such that 
$X_0 = x$
and 
$J_0 = i$
is denoted by 
$\mathbb{P}_{x,i}$
and its expectation by 
$\mathbb{E}_{x,i}$
. We will also use equivalently 
$\mathbb{E}_x[\cdot| J_0 = i]$
for 
$\mathbb{E}_{x,i}[\cdot]$
to emphasize the starting state. When 
$x =0$
, we will write 
$\mathbb{P}(\cdot|J_0 = i)$
and 
$\mathbb{E}[\cdot|J_0 =i]$
respectively. For a stopping time 
$\kappa$
, the notation 
$\mathbb{E}_x[\cdot,J_{\kappa}|J_0]$
is used to denote an 
$N \times N$
matrix whose (i, j) entry equals 
$\mathbb{E}_{x}[\cdot, J_{\kappa} = j|J_0=i]$
.
In the study of exit problems of spectrally negative MAPs, an essential role is played by the so-called scale matrices, which are defined analogously to the scale functions of spectrally negative Lévy processes. From Kyprianou and Palmowski [Reference Kyprianou and Palmowski21], for 
$q \geq 0$
, there exists a continuous, invertible matrix function 
$\textbf{W}^{(q)}\,:\,[0,\infty) \rightarrow \mathbb{R}^{N \times N}$
such that for all 
$0 \leq x \leq a$
,
\begin{equation}\mathbb{E}_x \Bigl[ e^{-q \tau_a^{+}}, \tau_a^{+}
< \tau_0^{-}, J_{\tau_{a}^{+}}|J_0\Bigr] = \textbf{W}^{(q)}(x)\textbf{W}^{(q)}(a)^{-1}.\end{equation}
Moreover, Ivanovs [Reference Ivanovs14] and Ivanovs and Palmowski [Reference Ivanovs and Palmowski15] showed that 
$\textbf{W}^{(q)}$
can be characterized by
\begin{equation}\widetilde{\textbf{W}}^{(q)}(\alpha)=\left( \textbf{F}(\alpha)-q\textbf{I}\right)^{-1} \quad \mbox{for large enough}\ \alpha,\end{equation}
where 
$\widetilde{f}(\alpha)= \int_0^{\infty} e^{-\alpha x} f(x) dx$
denotes the Laplace transform of the (matrix) function f. Furthermore, the domain of 
$\textbf{W}^{(q)}$
can be extended to the negative half line by taking 
$\textbf{W}^{(q)}(x) = \textbf{0}$
for 
$x < 0$
. The basis of the above transform is a probabilistic construction of the scale matrix 
$\textbf{W}^{(q)}$
, which involves the first hitting time at level x and can be written as
\begin{equation*} \textbf{W}^{(q)}(x)= e^{-\boldsymbol{\Lambda}^q x} \textbf{L}^{q}(x),\end{equation*}
with 
$\boldsymbol{\Lambda}^q$
being the transition rate matrix of the Markov chain 
$\{J_{\tau_x^+}\}_{x\geq 0}$
. In other words, one has 
$\mathbb{P}(\tau_x^+<\mbox{e}_q, J_{\tau_x^+})=e^{\boldsymbol{\Lambda}^q x}$
with 
$\mbox{e}_q$
being an independent exponential random variable of rate 
$q > 0$
. Moreover, 
$\textbf{L}^q(x)$
denotes a matrix of expected occupation times at 0 up to the first passage time over x. In addition, the matrix 
$\textbf{L}^q\,:\!=\textbf{L}^q(\infty)$
is the expected occupation density at 0. It is known that 
$\textbf{L}^q$
has finite entries and is invertible unless the process is non-defective and 
$\boldsymbol{\pi}\mathbb{E}[X_1, J_1|J_0]\vec{1}=0$
(see [Reference Ivanovs and Palmowski15). Hence, we have
\begin{equation}\lim_{x \to \infty}e^{\boldsymbol{\Lambda}^q x}\textbf{W}^{(q)}(x)=\lim_{x \to \infty}\textbf{W}^{(q)}(x) e^{\textbf{R}^q x}=\textbf{L}^{q},\end{equation}
where the matrix 
$\textbf{R}^q\,:\!=\left(\textbf{L}^{q}\right)^{-1}\boldsymbol{\Lambda}^q \textbf{L}^{q}.$
Moreover, it is easy to see that the limit 
$\lim_{a \to \infty}\textbf{W}^{(q)}(a)^{-1}=\textbf{0}$
, since the expectation (2.1) tends to 
$\textbf{0}$
when 
$a \to \infty$
; therefore, from the above argument,
\begin{equation*} \lim_{x \to \infty}e^{\boldsymbol{\Lambda}^q x}= \lim_{x \to \infty}\textbf{W}^{(q)}(x)^{-1}\textbf{L}^{q}(x)=\textbf{0}.\end{equation*}
The second scale matrix 
$\textbf{Z}^{(q)}$
is then defined through the 
$\textbf{W}^{(q)}$
matrix function:
\begin{equation*}\textbf{Z}^{(q)}(x)=\textbf{I}-\int_0^{x}\textbf{W}^{(q)}(y)dy \; (\textbf{F}(0)-q\textbf{I}).\end{equation*}
Note that 
$\textbf{Z}^{(q)}(x)$
is continuous in x with 
$\textbf{Z}^{(q)}(0)=\textbf{I}$
. Furthermore,
\begin{equation*} \lim_{x \to \infty}e^{\boldsymbol{\Lambda}^q x}\textbf{Z}^{(q)}(x)=\int_0^{\infty} e^{\boldsymbol{\Lambda}^q z} dz\textbf{L}^{q} \; (q\textbf{I}-\textbf{F}(0)).\end{equation*}
Remark 2.1. In the cases without exponential killing (
$q=0$
), the superscript q will be omitted in the quantities mentioned above, which will be written as 
$\textbf{W}(x), \textbf{Z}(x), \textbf{L}(x), \boldsymbol{\Lambda}$
, etc.
For more details about scale matrices, we refer the reader to [Reference Ivanovs and Palmowski15], [Reference Ivanovs16].
Definition 2.1. Let 
$\omega \,:\, E \times \mathbb{R} \rightarrow \mathbb{R}^{+}$
be a function defined as 
$\omega(i,x) = \omega_{i}(x)$
, where for a fixed 
$i \in E$
, 
$\omega_i \,:\, \mathbb{R} \rightarrow \mathbb{R}^{+}$
is a bounded, nonnegative measurable function, and let its values form the matrix 
$\boldsymbol{\omega}(x)\,:\!=\mbox{diag}(\omega_1(x),...,\omega_N(x))$
. Let 
$\lambda>0$
be an upper bound of 
$|\omega_i(x)|$
on 
$[0,\infty)$
for all 
$i \in E$
.
Further discussions of applications with some particular choices of 
$\omega$
will be presented in Section 5.
3. Main results
3.1 Omega-scale matrices
Before presenting our main results, we shall devote a little time to establishing some necessary notation. Our main aim is to represent fluctuation identities for MAPs with 
$\omega$
-killing in terms of new 
$\omega$
-scale matrices defined as the unique solutions to the following equations:
\begin{align}\mathcal{W}^{(\omega)}(x)&=\textbf{W}(x)+ \textbf{W}*\left(\boldsymbol{\omega}\mathcal{W}^{(\omega)}\right)(x),\\[4pt] \mathcal{Z}^{(\omega)}(x)&=\textbf{I}+ \textbf{W}*\left(\boldsymbol{\omega}\mathcal{Z}^{(\omega)}\right)(x),\nonumber \end{align}
where 
$f*g(x)= \int_0^{x} f(x-y) g(y) dy$
denotes the convolution of two matrix functions f and g. The following lemma shows that the above 
$\omega$
-scale matrices 
$\mathcal{W}^{(\omega)}$
and 
$\mathcal{Z}^{(\omega)}$
are well-defined and exist uniquely (see Appendix A.1 for the proof).
Lemma 3.1. For every 
$i,j \in E$
, let us assume that 
${h}_{ij}$
is a locally bounded function and 
$\omega_i$
is a bounded function on 
$\mathbb{R}$
. There exists a unique solution to the following equation:
\begin{equation}\textbf{H}(x)=\textbf{h}(x)+\textbf{W}*\left( \boldsymbol{\omega}\textbf{H}\right)(x),\end{equation}
where 
$\textbf{H}(x)=\textbf{h}(x)$
for 
$x<0$
. Furthermore, for any fixed 
$\delta>0$
, 
$\textbf{H}$
satisfies (3.2) if and only if 
$\textbf{H}$
satisfies
\begin{equation}\textbf{H}(x)=\textbf{h}_{\delta}(x)+ \textbf{W}^{(\delta)}*\left((\boldsymbol{\omega}-\delta\textbf{I})\textbf{H}\right)(x), \end{equation}
where 
$\textbf{h}_{\delta}(x)=\textbf{h}(x)+\delta \textbf{W}^{(\delta)}*\textbf{h}(x)$
.
We further introduce more general scale matrices 
$\mathcal{W}^{(\omega)}(x,y)$
and 
$\mathcal{Z}^{(\omega)}(x,y)$
to allow shifting:
\begin{align}\mathcal{W}^{(\omega)}(x,y)&=\textbf{W}(x-y)+\int_{y}^{x} \textbf{W}(x-z) \boldsymbol{\omega}(z)\mathcal{W}^{(\omega)}(z,y)dz, \end{align}
\begin{align}\mathcal{Z}^{(\omega)}(x,y)&=\textbf{I}+\int_{y}^{x} \textbf{W}(x-z)\boldsymbol{\omega}(z)\mathcal{Z}^{(\omega)}(z,y)dz. \end{align}
Also note that 
$\mathcal{W}^{(\omega)}(x,0)=\mathcal{W}^{(\omega)}(x)$
, 
$\mathcal{Z}^{(\omega)}(x,0)=\mathcal{Z}^{(\omega)}(x)$
,
\begin{equation}\mathcal{W}^{(\omega^*)}(x-y)=\mathcal{W}^{(\omega)}(x,y),\quad \mbox{and}\quad \mathcal{Z}^{(\omega^*)}(x-y)=\mathcal{Z}^{(\omega)}(x,y), \end{equation}
with 
$\omega^*(\cdot,z)=\omega(\cdot,z+y)$
.
Based on the fact that 
$ \textbf{W}^{(\delta)}- \textbf{W}= \delta \textbf{W}^{(\delta)}* \textbf{W}$
and 
$ \textbf{Z}^{(\delta)}- \textbf{Z}=\delta \textbf{W}^{(\delta)}* \textbf{Z}$
, it is easy to check that
\begin{align}\mathcal{W}^{(\omega)}(x,y)&=\textbf{W}^{(\delta)}(x-y)+\int_{y}^{x} \textbf{W}^{(\delta)}(x-z) (\boldsymbol{\omega}(z)-\delta\textbf{I})\mathcal{W}^{(\omega)}(z,y)dz, \end{align}
\begin{align*}\mathcal{Z}^{(\omega)}(x,y)&=\textbf{Z}^{(\delta)}(x-y)+\int_{y}^{x} \textbf{W}^{(\delta)}(x-z)(\boldsymbol{\omega}(z)-\delta\textbf{I})\mathcal{Z}^{(\omega)}(z,y)dz. \end{align*}
To solve the one-sided upward problem (i.e. to get Corollary 3.1(i)), we have to assume additionally that
\begin{equation}\omega_i(x) \equiv \beta \geq 0 \quad \mbox{for all } x\leq 0 \mbox{ and } i \in E.\end{equation}
Hence we define a matrix function 
$\mathcal{H}^{(\omega)}$
which satisfies the following integral equation:
\begin{equation}\mathcal{H}^{(\omega)}(x)= e^{-\textbf{R}^{\beta}x}+\int_{0}^{x} \textbf{W}^{(\beta)}(x-z) (\boldsymbol{\omega}(z)-\beta\textbf{I})\mathcal{H}^{(\omega)}(z)dz.\end{equation}
3.2. Exit problems and resolvents
In this section, we establish our main results concerning fluctuation identities and resolvents for spectrally negative 
$\omega$
-killed MAPs.
Theorem 3.1. (Two-sided exit problem)
For the invertible matrix functions 
$\mathcal{W}^{(\omega)}$
and 
$\mathcal{Z}^{(\omega)}$
given in (3.4) and (3.5) respectively, the following hold.
(i) For
$d \leq x \leq c$
,
\begin{equation*}\textbf{A}^{(\omega)}_d(x,c)\,:\!=\mathbb{E}_{x} \left[e^{-\int_0^{\tau_c^+}\omega_{J_s}(X_s)ds}, \tau_c^+<\tau_d^-, J_{\tau_c^+}|J_0 \right]=\mathcal{W}^{(\omega)}(x,d) \mathcal{W}^{(\omega)}(c,d)^{-1}.\end{equation*}
(ii) For
$d \leq x \leq c$
,
\begin{align*}\textbf{B}^{(\omega)}_d(x,c)&\,:\!=\mathbb{E}_{x} \left[e^{-\int_0^{\tau_d^-}\omega_{J_s}(X_s)ds},\tau_d^-
< \tau_c^+, J_{\tau_d^-}|J_0 \right]\\&\ =\mathcal{Z}^{(\omega)}(x,d)-\mathcal{W}^{(\omega)}(x,d) \mathcal{W}^{(\omega)}(c,d)^{-1}\mathcal{Z}^{(\omega)}(c,d).\end{align*}
Proof of Theorem 3.1 Part (i). In what follows, we prove the case of 
$d=0$
, and then the general result holds true using the shifting argument as well as the identity (3.6). First, applying the strong Markov property of X at 
$\tau_y^+$
and using the fact that X has no positive jumps, we get that
\begin{equation}\textbf{A}^{(\omega)}(x,z)=\textbf{A}^{(\omega)}(x,y)\textbf{A}^{(\omega)}(y,z) \end{equation}
for all 
$0 \le x\le y\le z$
.
Following an argument similar to that of Li and Palmowski [Reference Li and Palmowski22], we recall that 
$\lambda>0$
is an arbitrary upper bound of 
$\omega_i(x)$
(for all 
$x \in \mathbb{R}$
and 
$1\le i \le N$
). Let 
$\Psi=\{\Psi_{t},t\ge 0\}$
be a Poisson point process with a characteristic measure 
$\mu(dt,dy)=\lambda dt \; \frac{1}{\lambda}1_{\{[0,\lambda]\}}(y)dy$
. Hence 
$\Psi=\{(T_k,M_k),k=1,2,\dots\}$
is a doubly stochastic marked Poisson process with jump intensity 
$\lambda$
, jumps epochs 
$T_k$
and marks 
$M_k$
being uniformly distributed on 
$[0,\lambda]$
. Moreover, we construct 
$\Psi$
to be independent of X. Therefore, for 
$T^{\omega}\,:\!=\inf{\{T_k>0\,:\, M_k < \omega_{J_{T_k}}(X_{T_k}); \mbox{ for } k \geq 1 \}}$
, we have
\begin{align*}A_{ij}^{(\omega)}(x,c)&= \mathbb{P}_{x,i}\left( \tau_c^+< \tau_0^- \wedge T^{\omega}, J_{\tau_c^+}=j \right)\\&= \mathbb{P} _{x,i}\left(\#_{k} \{ M_{k}<\omega_{J_{T_k}} (X_{T_{k}} ) \mbox{ for } T_{k}< \tau_c^+ ,\tau_c^+<\tau_0^- , J_{\tau_c^+}=j \}=0 \right)\!.\end{align*}
In this case, there are the following two scenarios: either there is no 
$T_k$
which occurs before reaching level c, or the first jump time 
$T_1$
occurs in state m and the process renews from state m. Hence
\begin{align*}A_{ij}^{(\omega)}(x,c)&= \mathbb{P} _{x,i}(T_1>\tau_c^+, \tau_c^+<\tau_0^-, J_{\tau_c^+}=j)\\&\quad +\sum_{m=1}^{N}\mathbb{E}_{x,i} \left[ A_{mj}^{(\omega)}(X_{T_1},c), T_1<\tau_c^+\wedge \tau_0^-, M_1>\omega_m(X_{T_1}), J_{T_1}=m \right]\\&=\mathbb{E} _{x,i}[e^{-\lambda \tau_c^+};\, \tau_c^+<\tau_0^-, J_{\tau_c^+}=j]\\&\quad +\int_0^{\infty} \sum_{m=1}^{N} \mathbb{E}_{x,i} \left[ X_{T_1}\in dy, T_1<\tau_c^+\wedge \tau_0^-, J_{T_1}=m \right] \frac{\lambda-\omega_m(y)}{\lambda}A_{mj}^{(\omega)}(y,c),\end{align*}
which is equivalent to
\begin{align}\textbf{A}^{(\omega)}(x,c) &=\mathbb{E} _{x}[e^{-\lambda \tau_c^+}, \tau_c^+<\tau_0^-, J_{\tau_c^+}]\nonumber\\
&\quad +\int_0^{c}\mathbb{E}_{x} \left[ X_{T_1}\in dy, T_1<\tau_c^+\wedge \tau_0^-, J_{T_1} \right]\frac{1}{\lambda} \left( \lambda\textbf{I}-\boldsymbol{\omega}(y) \right)\textbf{A}^{(\omega)}(y,c), \end{align}
where 
$\mathbb{E} _{x}[e^{-\lambda \tau_c^+}, \tau_c^+<\tau_0^-, J_{\tau_c^+}]=\textbf{W}^{(\lambda)}(x)\textbf{W}^{(\lambda)}(c)^{-1}$
and
\begin{align*}&\frac{1}{\lambda}\mathbb{E}_{x} \left[ X_{T_1}\in dy, T_1<\tau_c^+\wedge \tau_0^-, J_{T_1} \right]=\left(\textbf{W}^{(\lambda)}(x)\textbf{W}^{(\lambda)}(c)^{-1}\textbf{W}^{(\lambda)}(c-y)- \textbf{W}^{(\lambda)}(x-y)\right) dy\end{align*}
are given in Ivanovs and Palmowski [Reference Ivanovs and Palmowski15] and Ivanovs [Reference Ivanovs16], respectively. After some rearrangement of (3.11) together with the relation (3.10), we have
\begin{align}&\left(\textbf{I}+\int_0^{x} \textbf{W}^{(\lambda)}(x-y) \left( \lambda\textbf{I}-\boldsymbol{\omega}(y) \right)\textbf{A}^{(\omega)}(y,x)dy\right)\textbf{A}^{(\omega)}(x,c)\nonumber\\ &=\textbf{W}^{(\lambda)}(x)\textbf{W}^{(\lambda)}(c)^{-1}\left( \textbf{I}+\int_0^{c}\textbf{W}^{(\lambda)}(c-y)\left( \lambda\textbf{I}-\boldsymbol{\omega}(y) \right)\textbf{A}^{(\omega)}(y,c)dy\right)\!.\end{align}
By defining
\begin{equation}\mathcal{W}^{(\omega)}(x)^{-1}\,:\!=\textbf{W}^{(\lambda)}(x)^{-1}\left(\textbf{I}+\int_0^{x} \textbf{W}^{(\lambda)}(x-y) \left( \lambda\textbf{I}-\boldsymbol{\omega}(y) \right)\textbf{A}^{(\omega)}(y,x)dy\right)\!, \end{equation}
we obtain the required identity
\begin{equation*}\textbf{A}^{(\omega)}(x,c)=\mathcal{W}^{(\omega)}(x)\mathcal{W}^{(\omega)}(c)^{-1}.\end{equation*}
The proof of the invertibility of the matrix 
$\mathcal{W}^{(\omega)}(x)^{-1}$
is deferred to Appendix A.2.
After making the replacement 
$\textbf{A}^{(\omega)}(y,x)=\mathcal{W}^{(\omega)}(y)\mathcal{W}^{(\omega)}(x)^{-1}$
in (3.13), we have
\begin{align*}\textbf{W}^{(\lambda)}(x)&=\left(\textbf{I}+\int_0^{x}\textbf{W}^{(\lambda)}(x-y) \left( \lambda\textbf{I}-\boldsymbol{\omega}(y) \right)\textbf{A}^{(\omega)}(y,x)dy\right)\mathcal{W}^{(\omega)}(x)\\ &= \mathcal{W}^{(\omega)}(x)+\int_0^{x} \textbf{W}^{(\lambda)}(x-y) \left( \lambda\textbf{I}-\boldsymbol{\omega}(y) \right)\mathcal{W}^{(\omega)}(y)dy.\end{align*}
Now using the identity 
$\textbf{W}^{(\delta)}-\textbf{W}=\delta\textbf{W}* \textbf{W} ^{(\delta)},$
it is easy to show that
\begin{align*}\mathcal{W}^{(\omega)}(x)=\textbf{W}(x)+\int_0^{x}\textbf{W}(x-y) \boldsymbol{\omega}(y)\mathcal{W}^{(\omega)}(y)\;dy,\end{align*}
which completes the proof of Part (i) of the theorem.
We need to pause for some preparation before we move to the proof of Part (ii). Let 
$\{(X_t,J_t)\}_{t\ge 0 }$
be a MAP with lifetime 
$\xi$
, and with transition probabilities and q-resolvent measures given respectively by
\begin{equation*}Q_{t,ij} \,f_j(x)=\mathbb{E}_{x,i}\left[\,f_j(X_t), t
< \xi, J_t=j \right]\end{equation*}
and
\begin{equation*}K^{(q)}_{ij} f_j(x)= \int_0^{\infty} e^{-qt} Q_{t,ij}\,f_j(x) dt,\end{equation*}
where 
$\{f_j\}_{j=1}^N$
is a set of nonnegative, bounded, continuous functions on 
$\mathbb{R}$
such that 
$\sup_{i,j} K^{(0)}_{ij}f_j(x)<\infty$
. Then the 
$\omega$
-type resolvent 
${K}^{(\omega)}_{ij}$
is defined by
\begin{equation*}K^{(\omega)}_{ij} f_j(x)\,:\!=\int_0^{\infty} Q_{t,ij}^{(\omega)}\, f_j(x)dt,\end{equation*}
where
\begin{equation*}Q_{t,ij}^{(\omega)}\,f_j(x)\,:\!=\mathbb{E}_{x,i} \left[ \exp\left ( -\int_0^{t} \omega_{J_s} (X_s) ds\right) f_{j}(X_t);\,t<\xi, J_{t}=j \right].\end{equation*}
The next lemma is a helpful tool used below to get the representation of the matrix 
$\textbf{B}^{(\omega)}(x,c)$
. Its proof is postponed to Appendix B, since the arguments tend to be technical.
Lemma 3.2. The matrix 
$\textbf{K}^{(\omega)}{\textit{\textbf{f}}}(x)=\{K^{(\omega)}_{ij} f_j(x)\}_{i,j=1}^N$
satisfies the following equality:
\begin{equation*}\textbf{K}^{(\omega)} {\textit{\textbf{f}}}(x)= \textbf{K}^{(0)}\left ( {\textit{\textbf{f}}} - \boldsymbol{\omega}\textbf{K}^{(\omega)}{\textit{\textbf{f}}}\right)(x),\end{equation*}
where 
${\textit{\textbf{f}}}={diag}(\,f_1,...,f_N)$
.
Now we can continue the proof of Theorem 3.1 as follows.
Proof of Theorem 3.1Part (ii). Again we prove the case of 
$d=0$
, and then the general result holds true using the shifting argument as well as the identity (3.6).
For 
$i,j \in E$
, define
\begin{equation}B_{ij}^{(\omega)}(x)\,:\!=\lim_{c\rightarrow\infty}B_{ij}^{(\omega)}(x,c)=\mathbb{E}_{x,i} \left[e^{-\int_0^{\tau_0^-}\omega_{J_s}(X_s)ds},\tau_0^-
< \infty, J_{\tau_0^-}=j \right]. \end{equation}
Note that for any 
$i,j \in E$
and 
$x,c \in \mathbb{R}$
such that 
$x<c$
, the matrix function 
$B_{ij}^{(\omega)}(x,c)$
is monotone in c, and it is bounded by 
$0 \leq B_{ij}^{(\omega)}(x,c)\leq \mathbb{P}_{x,i} \left(\tau_0^- < \tau_c^+, J_{\tau_0^-}=j\right)\leq 1$
, so the limit in (3.14) exists and is finite. The strong Markov property and spectral negativity of X give that
\begin{equation}\textbf{B}^{(\omega)}(x,c)=\textbf{B}^{(\omega)}(x)-\textbf{A}^{(\omega)}(x,c)\textbf{B}^{(\omega)}(c).\end{equation}
To identify 
$\textbf{B}^{(\omega)}(x)$
, we use Lemma 3.2 with 
$\xi=\tau_0^-$
and 
${\textit{\textbf{f}}}(\cdot)=\boldsymbol{\omega}(\cdot)$
. This implies that
\begin{align} \textbf{I}(x)-\textbf{B}^{(\omega)}(x)&= \mathbb{E}_{x} \left[ \int_0^{\tau_0^-} \omega_{J_t}(X_t) \exp\left( -\int_0^t \omega_{J_s}(X_s) ds\right)dt, t<\tau_0^-, J_{t}\right]\nonumber\\
&= \int_0^{\infty}\mathbb{E}_{x} \left[ \omega_{J_t}(X_t) \exp\left( -\int_0^t \omega_{J_s}(X_s) ds\right)\!, t<\tau_0^- ,J_{t}\right]dt\nonumber\\&=\int_0^{\infty} \left( \textbf{W}(x)e^{\textbf{R}y}-\textbf{W}(x-y) \right) \left [ \boldsymbol{\omega}(y)-\boldsymbol{\omega}(\textbf{I}-\textbf{B}^{(\omega)})(y)\right]dy,\end{align}
where the potential measure
\begin{equation*}\textbf{K}^{(0)} \left(1\hspace{-2.2mm}{1}_{(0,\infty)}(X_t \in dy)\right)(x)={\textit{\textbf{U}}}_{(0,\infty)}(x,dy)=\left( \textbf{W}(x)e^{\textbf{R} y}-\textbf{W}(x-y) \right)dy\end{equation*}
was obtained in [Reference Ivanovs16] with 
$\textbf{R}=\textbf{R}^0$
. We may rewrite (3.16) as
\begin{equation}\textbf{B}^{(\omega)}(x)=\textbf{I}(x)- \textbf{W}(x) \textbf{C}_{B^{(\omega)}} +\int_0^{x} \textbf{W}(x-y)\boldsymbol{ \omega}(y)\textbf{B}^{(\omega)}(y)dy,\end{equation}
where
\begin{equation} \textbf{C}_{B^{(\omega)}}=\int_0^{\infty} e^{\textbf{R}y}\boldsymbol{\omega}(y)\textbf{B}^{(\omega)}(y)dy.\end{equation}
Note that 
$0\leq B^{(\omega)}_{ij}(y)\leq 1$
, and recall that 
$0\leq \omega_i(x)\leq\lambda$
. Hence the last increment on the right-hand side of Equation (3.17) is finite, so that the matrix 
$\textbf{C}_{B^{(\omega)}}$
is well-defined and finite. From the definitions of 
$\omega$
-scale matrices we have
\begin{equation}\textbf{B}^{(\omega)}(x)=\mathcal{Z}^{(\omega)}(x)-\mathcal{W}^{(\omega)}(x)\textbf{C}_{B^{(\omega)}}.\end{equation}
Equation (3.15) completes the proof.
Remark 3.1. When 
$d=0$
, we use the simplified notation 
$\textbf{A}^{(\omega)}(x,c)\,:\!=\textbf{A}^{(\omega)}_0(x,c)$
and 
$\textbf{B}^{(\omega)}(x,c)\,:\!=\textbf{B}^{(\omega)}_0(x,c)$
.
Now, taking the limits as 
$d \to -\infty$
and 
$c \to \infty$
(as well as 
$d=0$
) in Theorem 3.1 Parts (i) and (ii) respectively, we obtain the following corollary regarding the one-sided exit problem. A detailed proof is given in Appendix B.
Corollary 3.1. (One-sided exit problem)
(i) Under the assumption (3.8), for
$ x \leq c$
,
where the invertible matrix function
\begin{equation*}\mathbb{E}_{x} \left[e^{-\int_0^{\tau_c^+}\omega_{J_s}(X_s)ds}, \tau_c^+<\infty, J_{\tau_c^+}|J_0 \right]=\mathcal{H}^{(\omega)}(x) \mathcal{H}^{(\omega)}(c)^{-1},\end{equation*}
$\mathcal{H}^{(\omega)}$
is given in (3.9).(ii) For
$x \geq 0 $
and
$\lambda>0$
,
where the matrix
\begin{equation*}\mathbb{E}_{x} \left[e^{-\int_0^{\tau_0^-}\omega_{J_s}(X_s)ds},\tau_0^-
< \infty, J_{\tau_0^-}|J_0 \right]=\mathcal{Z}^{(\omega)}(x)- \mathcal{W}^{(\omega)}(x)\textbf{C}_{\mathcal{W}(\infty)^{-1}\mathcal{Z}(\infty)},\end{equation*}
exists and has finite entries.
\begin{equation*} \textbf{C}_{\mathcal{W}(\infty)^{-1}\mathcal{Z}(\infty)}\,:\!= \lim_{c \to \infty} \mathcal{W}^{(\omega)}(c)^{-1}\mathcal{Z}^{(\omega)}(c)\end{equation*}
Next, we present the representations of four 
$\omega$
-type resolvents. These types of identities usually are used to describe the position of a Lévy process right before exit from some interval or half-line based on a so-called compensation formula; see [Reference Kyprianou20, Chap. 5] for details.
Theorem 3.2. (Resolvents.)
(i) For
$d\le x \leq c$
,
\begin{align*}{\textit{\textbf{U}}}^{(\omega)}_{(d,c)}(x,dy)&\,:\!=\int_0^{\infty} \mathbb{E}_{x}\left[\exp\left( -\int_0^{t} \omega_{J_s}(X_s)ds \right)\!, X_t\in dy, t<\tau_d^- \wedge\tau_c^+, J_t|J_0 \right] dt\\&\ = \left ( \mathcal{W}^{(\omega)}(x,d) \mathcal{W}^{(\omega)}(c,d)^{-1} \mathcal{W}^{(\omega)}(c,y)-\mathcal{W}^{(\omega)}(x,y)\right) dy.\end{align*}
(ii) For
$ x \geq 0$
and
$\lambda>0$
,
where
\begin{align*}{\textit{\textbf{U}}}^{(\omega)}_{(0,\infty)}(x,dy)&\,:\!=\int_0^{\infty} \mathbb{E}_{x}\left[\exp\left( -\int_0^{t} \omega_{J_s}(X_s)ds \right)\!, X_t\in dy, t<\tau_0^-, J_t|J_0 \right] dt\\&\ = \left ( \mathcal{W}^{(\omega)}(x) \textbf{C}_{\mathcal{W}(\infty)^{-1}\mathcal{W}(\infty)}(y) -\mathcal{W}^{(\omega)}(x,y)\right) dy,\end{align*}
is a well-defined and finite matrix.
\begin{equation*}\textbf{C}_{\mathcal{W}(\infty)^{-1}\mathcal{W}(\infty)}(y)\,:\!=\lim_{c \to \infty} \mathcal{W}^{(\omega)}(c)^{-1}\mathcal{W}^{(\omega)}(c,y)\end{equation*}
(iii) For
$ x,y\le c$
,
\begin{align*}{\textit{\textbf{U}}}^{(\omega)}_{({-}\infty,c)}(x,dy)&\,:\!=\int_0^{\infty} \mathbb{E}_{x}\left[\exp\left( -\int_0^{t} \omega_{J_s}(X_s)ds \right)\!, X_t\in dy, t
< \tau_c^+, J_t|J_0 \right] dt\\&= \left ( \mathcal{H}^{(\omega)}(x) \mathcal{H}^{(\omega)}(c)^{-1} \mathcal{W}^{(\omega)}(c,y)-\mathcal{W}^{(\omega)}(x,y)\right) dy.\end{align*}
(iv) For
$x \in \mathbb{R}$
,
where the matrix
\begin{align*}{\textit{\textbf{U}}}^{(\omega)}_{({-}\infty,\infty)}(x,dy)&\,:\!=\int_0^{\infty} \mathbb{E}_{x}\left[\exp\left( -\int_0^{t} \omega_{J_s}(X_s)ds \right)\!, X_t\in dy, J_t|J_0 \right] dt\\&= \left ( \mathcal{H}^{(\omega)}(x) \textbf{C}_{\mathcal{H}(\infty)^{-1}\mathcal{W}(\infty)}(y)-\mathcal{W}^{(\omega)}(x,y)\right) dy,\end{align*}
$\textbf{C}_{\mathcal{H}(\infty)^{-1}\mathcal{W}(\infty)}= \lim_{c \to \infty} \mathcal{H}^{(\omega)}(c)^{-1}\mathcal{W}^{(\omega)}(c,y)$
exists and has finite entries.
Proof of Part (i). Using Lemma 3.2, we have
\begin{align}{\textit{\textbf{U}}}^{(\omega)}_{(d,c)}{\,\textit{\textbf{f}}}(x)&\,:\!=\int_0^{\infty} \mathbb{E}_{x}\left[\,f_{J_t}(X_t)\exp\left( -\int_0^{t} \omega_{J_s}(X_s)ds \right)\!, t<\tau_d^- \wedge \tau_c^+, J_t|J_0 \right] dt\\
&=\int_d^{c} {\textit{\textbf{U}}}_{(d,c)}(x,dy) \left ( {\textit{\textbf{f}}}(y)-\boldsymbol{\omega}(y){\textit{\textbf{U}}}_{(d,c)}^{(\omega)}{\,\textit{\textbf{f}}}(y) \right)\!, \nonumber\end{align}
where 
${\textit{\textbf{U}}}_{(d,c)}(x,dy)$
is the potential measure of the MAP without 
$\omega$
-killing, as given in Theorem 1 of Ivanovs [Reference Ivanovs16]:
\begin{equation*}{\textit{\textbf{U}}}_{(d,c)}(x,dy)=\left( \textbf{W}(x-d)\textbf{W}(c-d)^{-1}\textbf{W}(c-y)-\textbf{W}(x-y) \right)dy.\end{equation*}
Hence we can rewrite Equation (3.20) as
\begin{equation*}{\textit{\textbf{U}}}^{(\omega)}_{(d,c)}{\,\textit{\textbf{f}}}(x)= \textbf{W}(x-d) \textbf{C}_U -\int_d^x \textbf{W}(x-y){\,\textit{\textbf{f}}}(y) dy+\int_d^x \textbf{W}(x-y) \boldsymbol{\omega}(y){\textit{\textbf{U}}}_{(d,c)}^{(\omega)}{\,\textit{\textbf{f}}}(y)dy,\end{equation*}
where 
$\textbf{C}_U=\int_d^c \textbf{W}(c-d)^{-1}\textbf{W}(c-y) \left ( {\,\textit{\textbf{f}}}(y)- \boldsymbol{\omega}(y){\textit{\textbf{U}}}_{(d,c)}^{(\omega)}{\,\textit{\textbf{f}}}(y) \right)dy.$
Multiplying Equation (3.4) by 
$\textbf{C}_U$
gives that
\begin{equation*}\mathcal{W}^{(\omega)}(x,d)\textbf{C}_U =\textbf{W}(x-d)\textbf{C}_U+\int_d^{x} \textbf{W}(x-y)\boldsymbol{\omega}(y)\mathcal{W}^{(\omega)}(y,d)\textbf{C}_U dy.\end{equation*}
Defining the operator 
$\mathcal{R}^{(\omega)} {\,\textit{\textbf{f}}}(x)\,:\!=\int_d^{x}\mathcal{W}^{(\omega)}(x,y){\,\textit{\textbf{f}}}(y)dy$
, we obtain
\begin{equation*}\mathcal{R}^{(\omega)} {\textit{\textbf{f}}}(x)=\int_d^x \textbf{W}(x-y){\,\textit{\textbf{f}}}(y) dy+\int_{d}^{x} \textbf{W}(x-y)\boldsymbol{\omega}(y)\mathcal{R}^{(\omega)} {\textit{\textbf{f}}}(y) dy.\end{equation*}
Therefore, by the uniqueness property in Lemma 3.1, we have
\begin{equation*}{\textit{\textbf{U}}}_{(d,c)}^{(\omega)}{\,\textit{\textbf{f}}}(x)=\mathcal{W}^{(\omega)}(x,d)\textbf{C}_U-\mathcal{R}^{(\omega)} {\textit{\textbf{f}}}(x).\end{equation*}
To find the constant matrix 
$\textbf{C}_U$
, we use the boundary condition 
${\textit{\textbf{U}}}^{(\omega)}_{(d,c)}{\,\textit{\textbf{f}}}(c)=0$
. One completes the proof by denoting the density of 
${\textit{\textbf{U}}}^{(\omega)}_{(d,c)}{\,\textit{\textbf{f}}}(x)$
as 
${\textit{\textbf{U}}}^{(\omega)}_{(d,c)}(x,dy)$
.
Proof of Part (ii). This identity follows directly from Theorem 3.2(i) by taking the limit and using (2.3) together with the dominated convergence theorem.
Proof of Part (iii). The formula follows by taking the limit as 
$d \to -\infty$
in Theorem 3.2(i) and then using (B.3).
Proof of Part (iv). This identity follows from Theorem 3.2(iii) by taking the limit as 
$c \to \infty$
. Since 
$\mathcal{H}^{(\omega)}(c)^{-1}\mathcal{W}^{(\omega)}(c,y)$
is monotonic in c, the result holds.
4. Dividends in the omega ruin model
In this section, we demonstrate one application of the previously obtained results to the dividend problem. The optimal dividend problem has been widespread in the field of applied mathematics since De Finetti [Reference De Finetti10], who was the first to introduce the dividend model in risk theory. In his work, it was proved that, under the rule of maximizing the expected discounted dividends before the classical ruin time, the optimal strategy is the barrier strategy described as follows. For a fixed level 
$c > 0$
, whenever the surplus process reaches this level, one reflects the process and pays all excess above c as dividends. In the literature, there is a rich set of articles studying this problem in the continuous-time framework; see, e.g., Loeffen [Reference Loeffen23], Loeffen and Renaud [Reference Loeffen and Renaud24], and Avram et al. [Reference Avram, Palmowski and Pistorius3], where the value function of the barrier strategy and the optimal barrier level were described in terms of scale functions.
In this paper, we assume that the company’s reserve process is governed by a MAP (X, J). We consider a dividend barrier strategy (at c) and define the cumulative dividends paid up to time t as follows:
\begin{equation*} L_t^c = \sup_{s \leq t}[X_s - c]\vee 0.\end{equation*}
With the barrier dividend strategy, we work with the regulated process
\begin{equation*}U_t^c=X_t-L_t^c.\end{equation*}
Moreover, we assume that this company pays dividends according to the barrier strategy until omega ruin time, defined as
\begin{equation*}\tau_{\omega}^d=\inf\{t\ge 0\,:\, \int_0^{t}\omega_{J_s}(U_s^c) ds>\mbox{e}_1 \mbox{ or } U^{c}_t <-d\},\end{equation*}
where 
$\mbox{e}_1$
is an independent exponential random variable (with mean 1), and a fixed level 
$-d \leq 0$
is a threshold. For all 
$i \in E$
and for 
$-d\leq x \leq 0$
, the (typically decreasing) function 
$\omega_i(x) \geq 0$
can be interpreted as a bankruptcy rate. Thus ruin can occur in two situations. The first is the situation when the process crosses a fixed level 
$-d\leq 0$
(for 
$d =0$
we have a case of classical ruin time). The second possibility is when bankruptcy happens in the so-called ‘red zone’ (i.e. when the surplus process is in 
$[-d,0]$
), and the intensity of this bankruptcy is a function of the current level of the additive regulated component 
$U^c$
and the Markov chain J. In other words, whenever the regulated surplus equals x for 
$x\le 0$
, the probability of bankruptcy within an infinitesimal time dt is 
$\omega_{J_t}(x)dt$
. (For more details related to the omega ruin time, we refer the reader to [Reference Gerber, Shiu and Yang11] and [Reference Li and Palmowski22].) Furthermore, when the regulated surplus process 
$U_t^c$
is positive, the omega function is interpreted only as a path-dependent discount factor, and it does not apply for the definition of the omega ruin time. In the following theorem, we examine the case of 
$d=0$
; we then consider a general d in the corollary.
Theorem 4.1. Assume that dividends are discounted at a constant force of interest 
$\delta>0$
, and 
$d=0$
. The expected discounted present value of the dividends paid before omega ruin (
$\tau_{\omega}\,:\!=\tau_{\omega}^0$
) under a constant dividend barrier c is given by
\begin{equation*}\begin{split}\textbf{v}_c(x)\,:\!&= \mathbb{E}_x\left[ \int_0^{\tau_{\omega}} e^{-\delta t} dL_t, J_{\tau_{\omega}}| J_0\right]=\begin{cases} \mathcal{W}^{(\delta+\omega)}(x)\mathcal{W}^{(\delta+\omega)\prime}(c)^{-1} & \mbox{for} \quad 0
< x \leq c, \\ (x-c) + \mathcal{W}^{(\delta+\omega)}(c)\mathcal{W}^{(\delta+\omega)\prime}(c)^{-1} & \mbox{for} \quad x > c, \end{cases}\end{split}\end{equation*}
where the invertible matrix function 
$\mathcal{W}^{(\delta+\omega)\prime}(c)$
is given by
\begin{equation*}\mathcal{W}^{(\delta+\omega)\prime}(c)=\textbf{W}^{\prime}(c)+\int_0^c \textbf{W}^{\prime}(c-y)(\boldsymbol{\omega}(y)+\delta\textbf{I})\mathcal{W}^{(\delta+\omega)}(y) dy+\textbf{W}(0)(\boldsymbol{\omega}(c)+\delta\textbf{I})\mathcal{W}^{(\delta+\omega)}(c). \end{equation*}
Proof. We start with the case 
$0 < x \leq c$
. Conditioning on reaching the level c first, we have
\begin{equation*}\textbf{v}_c(x)=\textbf{A}^{(\omega)}(x,c)\textbf{v}_c(c)=\mathcal{W}^{(\delta+\omega)}(x)\mathcal{W}^{(\delta+\omega)}(c)^{-1}\textbf{v}_c(c).\end{equation*}
As a first step, we will find a lower bound for 
$\textbf{v}_c(c)$
. For 
$m\in \mathbb{N}$
, suppose that the dividend is not paid until reaching the level 
$c+\frac{1}{m}$
:
\begin{align*}\textbf{v}_c (c) & \ge \ \mathbb{E}_c\left [e^{-\int_0^{\tau_{c+1/m}^{+}}(\delta\,{+}\,\omega_{J_s}(X_s))ds} , \tau_{c+\frac{1}{m}}^+<\tau_0^{-}, J_{\tau_{c+\frac{1}{m}}^{+}}|J_{0} \right] \textbf{v}_c\left(c+\frac{1}{m}\right)\\ &= \mathbb{E}_c\left [e^{-\int_0^{\tau_{c+1/m}^{+}}(\delta\,{+}\,\omega_{J_s}(X_s))ds} , \tau_{c+\frac{1}{m}}^+<\tau_0^{-}, J_{\tau_{c+\frac{1}{m}}^{+}}|J_{0}\right]\left ( \textbf{v}_c(c)+\frac{1}{m}\textbf{I}\right)\!,\end{align*}
where the last equality is due to the dividend of 
$\frac{1}{m}$
paid immediately and the fact that the drop in surplus will not cause a state transition.
On the other hand, an upper bound can be found as
\begin{align*}\textbf{v}_c (c) \leq & \ \mathbb{E}_c\left [e^{-\int_0^{\tau_{c+1/m}^{+}}(\delta\,{+}\,\omega_{J_s}(X_s))ds} , \tau_{c+\frac{1}{m}}^+<\tau_0^{-}, J_{\tau_{c+\frac{1}{m}}^{+}}|J_0 \right] \left( \textbf{v}_c(c)+\frac{1}{m}\textbf{I}\right)\\& +\frac{1}{m}\mathbb{E}_{c}\left[ \int_0^{\tau_{c+1/m}^{+}} e^{-\delta t} dt \ e^{-\int_0^{\tau_{c+1/m}^{+}}\omega_{J_s}(X_s)ds} , \tau_{c+\frac{1}{m}}^{+}<\tau_0^- , J_{\tau_0^-} | J_0\right]\\&+\mathbb{E}_{c}\left[ \int_0^{\tau_{\omega}} e^{-\delta t} dL_{t}^c, \tau_{\omega} <\tau_{c+\frac{1}{m}}^{+} , J_{\tau_{\omega}} | J_0\right],\end{align*}
where 
$L_t^{c}$
will be bounded by 
$\frac{1}{m}$
for the process from level c to level 
$c+\frac{1}{m}$
; i.e.,
\begin{equation*}\mathbb{E}_{c}\left[ \int_0^{\tau_{\omega}} e^{-\delta t} dL_{t}^c, \tau_{\omega} <\tau_{c+\frac{1}{m}}^{+} , J_{\tau_{\omega}} | J_0\right] \le \frac{1}{m} \mathbb{P}_c\left (\tau_{\omega} <\tau_{c+\frac{1}{m}}^{+} , J_{\tau_{\omega}}| J_0\right)\!.\end{equation*}
Note that as 
$m\rightarrow \infty$
, the following two quantities approach 
$ \textbf{0}$
:
\begin{equation*}\lim_{m\rightarrow \infty} \mathbb{E}_{c}\left[ \int_0^{\tau_{c+1/m}^{+}} e^{-\delta t} dt\ e^{-\int_0^{\tau_{c+1/m}^{+}}\omega_{J_s}(X_s)ds} , \tau_{c+\frac{1}{m}}^{+}<\tau_0^- , J_{\tau_0^-} | J_0\right]= \textbf{0}\end{equation*}
and
\begin{equation*}\lim_{m\rightarrow \infty} \mathbb{P}_c\left (\tau_{\omega} <\tau_{c+\frac{1}{m}}^{+} , J_{\tau_{\omega}} | J_0\right) =\textbf{0}.\end{equation*}
See Renaud and Zhou [Reference Renaud and Zhou25] and Czarna et al. [Reference Czarna, Li, Palmowski and Zhao9] for more details.
Therefore, by matching the upper and lower bounds, we have
\begin{align*}\textbf{v}_c (c)& = \mathbb{E}_c\left [e^{-\int_0^{\tau_{c+1/m}^{+}}(\delta+\omega_{J_s}(X_s))ds} , \tau_{c+\frac{1}{m}}^+<\tau_0^{-}, J_{\tau_{c+\frac{1}{m}}^{+}}|J_0 \right]\left( \textbf{v}_c(c)+\frac{1}{m}\textbf{I}\right)+o\left(\frac{1}{m}\right)\\&= \mathcal{W}^{(\delta+\omega)}(c)\mathcal{W}^{(\delta+\omega)}\left(c+\frac{1}{m}\right)^{-1} \left( \textbf{v}_c(c)+\frac{1}{m}\textbf{I}\right)+o\left(\frac{1}{m}\right)\!,\end{align*}
and hence, after some rearrangement,
\begin{equation*}\left( \frac{ \mathcal{W}^{(\delta+\omega)}(c+\frac{1}{m}) - \mathcal{W}^{(\delta+\omega)}(c) }{1/m} \right)\mathcal{W}^{(\delta+\omega)}(c)^{-1} \textbf{v}_c (c)=\textbf{I}+ o\left(\frac{1}{m}\right)\!.\end{equation*}
Letting 
$m\rightarrow\infty$
, it turns out that
\begin{equation*} \mathcal{W}^{(\delta+\omega)\prime}(c) \mathcal{W}^{(\delta+\omega)}(c)^{-1} \textbf{v}_c (c)=\textbf{I},\end{equation*}
where the matrix
\begin{equation*}\mathcal{W}^{(\delta+\omega)\prime}(c)=\textbf{W}^{\prime}(c)+\int_0^c \textbf{W}^{\prime}(c-y)({\omega}(y)+\delta\textbf{I})\mathcal{W}^{(\delta+\omega)}(y) dy+\textbf{W}(0)({\omega}(c)+\delta\textbf{I})\mathcal{W}^{(\delta+\omega)}(c) \end{equation*}
is well-defined since the scale matrix 
$\textbf{W}$
is almost everywhere differentiable (see [Reference Kyprianou and Palmowski21]). Furthermore, one can observe that, from the representation (A.5), the above matrix is invertible for any 
$c > 0$
, and then 
$ \textbf{v}_c (c)= \mathcal{W}^{(\delta+\omega)}(c)\mathcal{W}^{(\delta+\omega)\prime}(c)^{-1} .$
To end this proof, note that for 
$x > c$
, one is immediately paying a dividend of size 
$x-c$
(and this will not cause a state transition); therefore
\begin{equation*}\textbf{v}_c(x) = (x-c) + \textbf{v}_c(c) = (x-c)+ \mathcal{W}^{(\delta+\omega)}(c)\mathcal{W}^{(\delta+\omega)\prime}(c)^{-1}.\end{equation*}
Applying the shifting argument to Theorem 4.1, we have the representation of the value function for a general 
$d \ge 0$
.
Corollary 4.1. For 
$\delta>0$
, the expected present value of the dividend paid before omega ruin (
$\tau_{\omega}^d$
) under a constant dividend barrier c is
\begin{equation*}\begin{split}\textbf{v}^d_c(x)\,&:\!= \mathbb{E}_x\left[ \int_0^{\tau_{\omega}^d} e^{-\delta t} dL_t, J_{\tau_{\omega}^d}| J_0\right]\\ &= \begin{cases} \mathcal{W}^{(\delta+\omega)}(x,-d)\mathcal{W}^{(\delta+\omega)\prime}(c,-d)^{-1} & \quad \mbox{for} \quad -d
< x \leq c, \\ (x-c) + \mathcal{W}^{(\delta+\omega)}(c,-d)\mathcal{W}^{(\delta+\omega)\prime}(c,-d)^{-1} &\quad \mbox{for} \quad x > c, \end{cases}\end{split}\end{equation*}
for the invertible matrix
\begin{align*}\mathcal{W}^{(\delta+\omega)\prime}(c,-d)&=\textbf{W}^{\prime}(c+d)+\int_{-d}^c \textbf{W}^{\prime}(c-y)({\omega}(y)+\delta\textbf{I})\mathcal{W}^{(\delta+\omega)}(y,-d) dy \\&\quad +\textbf{W}(0)({\omega}(c)+\delta\textbf{I})\mathcal{W}^{(\delta+\omega)}(c,-d).\end{align*}
5. Examples
This section aims to demonstrate some explicit examples of 
$\omega$
-scale matrices when the function 
$\omega$
is specified. We would like to present relations between 
$\mathcal{W}^{(\omega)}$
and 
$\textbf{W}^{(q)}$
, for some 
$q \geq 0$
, as well as numerical examples which provide a better understanding of the nature of the matrix-valued functions explored. We will start with a short analysis of 
$\textbf{W}^{(q)}$
for Markov-modulated Brownian motion (MMBM), since this will be a base model for more complicated scale matrices.
5.1. Markov-modulated Brownian motion and its scale matrix
In this subsection, we will consider a particular case where (X, J) is a Markov-modulated Brownian motion. Some essential relations are derived for later use in the subsequent examples. Let 
$X_i$
be a Brownian motion with variance 
$\sigma_i^2>0$
and drift 
$\mu_i$
for all 
$i \in E$
. Further denote 
$\boldsymbol{\sigma}$
and 
$\boldsymbol{\mu}$
as the (column) vectors of 
$\sigma_i$
and 
$\mu_i$
, and 
$\Delta_{\textit{\textbf{v}}}$
as the diagonal matrix with 
${\textit{\textbf{v}}}$
on the diagonal. Then the matrix Laplace exponent 
${\textit{\textbf{F}}}(s)$
is given by
\begin{equation*}{\textit{\textbf{F}}}(s)=\frac{1}{2}\Delta_{\boldsymbol{\sigma}}^2 s^2 +\Delta_{\boldsymbol{\mu}}s +{\textit{\textbf{Q}}}.\end{equation*}
Outside of the case when 
${\kappa} \,:\!= \boldsymbol{\pi} \boldsymbol{\mu} = 0$
and 
$q =0$
, Ivanovs [Reference Ivanovs12] performs the representation of the q-scale matrix
\begin{equation}\textbf{W}^{(q)}(x)=\left( e^{-\boldsymbol{\Lambda}^{+}_q x}-e^{\boldsymbol{\Lambda}^{-}_q x}\right)\boldsymbol{\Xi}_q,\end{equation}
where 
$\boldsymbol{\Xi}_q^{-1}=-\frac{1}{2} \Delta_{\boldsymbol{\sigma}}^2(\boldsymbol{\Lambda}_{q}^{+} +\boldsymbol{\Lambda}_{q}^{-})$
and 
$\boldsymbol{\Lambda}^{\pm}_q$
are the (unique) right solutions to the matrix integral equation 
${\textit{\textbf{F}}}(\mp\boldsymbol{\Lambda}^{\pm}_q)=\textbf{0}$
; that is,
\begin{equation}\Delta_{\frac{\boldsymbol{\sigma}^2}{2}}(\boldsymbol{\Lambda}^{\pm}_q)^{2} \mp \Delta_{\boldsymbol{\mu}}\boldsymbol{\Lambda}^{\pm}_q + \Bigl({\textit{\textbf{Q}}} - q \textbf{I}\Bigr) = \boldsymbol{0}.\end{equation}
In the next lemma, we present relations between 
$\boldsymbol{\Lambda}_{q}^{+}$
and 
$\boldsymbol{\Lambda}_{q}^{-}$
.
Lemma 5.1. For 
$q \geq 0$
, we have
\begin{equation}\Delta_{\frac{2 \boldsymbol{\mu}}{\boldsymbol{\sigma}^2}} = \boldsymbol{\Lambda}_{q}^{+} - {\textit{\textbf{C}}}_{q}, \quad{\textit{\textbf{C}}}_{q}\boldsymbol{\Lambda}_{q}^{+} = \Delta_{\frac{2}{\boldsymbol{\sigma}^{2}}}\Bigl[-{\textit{\textbf{Q}}} + q \textbf{\textit{I}}\Bigr]\end{equation}
and
\begin{equation}\Delta_{\frac{2 \boldsymbol{\mu}}{\boldsymbol{\sigma}^2}} = {\textit{\textbf{D}}}_{q} - \boldsymbol{\Lambda}^{-}_{q}, \quad {\textit{\textbf{D}}}_{q}\boldsymbol{\Lambda}^{-}_{q} = \Delta_{\frac{2}{\sigma^2}}\Bigl[-{\textit{\textbf{Q}}} + q \textbf{\textit{I}}\Bigr],\end{equation}
where
\begin{equation*} {\textit{\textbf{C}}}_{q} = (\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-})\boldsymbol{\Lambda}_{q}^{-}(\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-})^{-1},\quad{\textit{\textbf{D}}}_{q} = \Bigl(\boldsymbol{\Lambda}^{+}_{q} + \boldsymbol{\Lambda}^{-}_{q}\Bigr)\boldsymbol{\Lambda}^{+}_{q}\Bigl(\boldsymbol{\Lambda}^{+}_{q} + \boldsymbol{\Lambda}^{-}_{q}\Bigr)^{-1}.\end{equation*}
Proof. Using the equations (5.2) all together, one can obtain
\begin{equation*} \Delta_{\frac{\boldsymbol{\sigma}^2}{2}}\Bigl( (\boldsymbol{\Lambda}_{q}^{+})^{2} - (\boldsymbol{\Lambda}_{q}^{-})^{2}\Bigr) =\Delta_{\boldsymbol{\mu}}\Bigl(\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-} \Bigr);\end{equation*}
hence, using 
$(\boldsymbol{\Lambda}_{q}^{+})^{2} - (\boldsymbol{\Lambda}_{q}^{-})^{2}=\boldsymbol{\Lambda}_{q}^{+}(\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-})-(\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-})\boldsymbol{\Lambda}_{q}^{-}$
, we have
\begin{equation*} \begin{split}\Delta_{\frac{2 \boldsymbol{\mu}}{\boldsymbol{\sigma}^{2}}} &= \Bigl( (\boldsymbol{\Lambda}_{q}^{+})^{2} - (\boldsymbol{\Lambda}_{q}^{-})^{2}\Bigr)\Bigl(\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-}\Bigr)^{-1}= \boldsymbol{\Lambda}_{q}^{+} - {\textit{\textbf{C}}}_{q}.\end{split}\end{equation*}
Now, the above relationship together with (5.2) gives that
\begin{equation*} {\textit{\textbf{C}}}_{q}\boldsymbol{\Lambda}_{q}^{+} = \Delta_{\frac{2}{\boldsymbol{\sigma}^{2}}}\Bigl[-{\textit{\textbf{Q}}} + q \textbf{I}\Bigr].\end{equation*}
The remaining part of the proof can be done in a similar way by using
\begin{equation*}(\boldsymbol{\Lambda}_{q}^{+})^2 - (\boldsymbol{\Lambda}_{q}^{-})^2 = (\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-})\boldsymbol{\Lambda}_{q}^{+} - \boldsymbol{\Lambda}_{q}^{-}(\boldsymbol{\Lambda}_{q}^{+}+\boldsymbol{\Lambda}_{q}^{-}).\end{equation*}
In the special case of 
$q = 0$
we will write 
$\boldsymbol{\Lambda}^{+}$
, 
$\boldsymbol{\Lambda}^{-}$
, 
${\textit{\textbf{C}}}$
and 
${\textit{\textbf{D}}}$
for 
$\boldsymbol{\Lambda}^{+}_{0}$
, 
$\boldsymbol{\Lambda}^{-}_{0}$
, 
${\textit{\textbf{C}}}_{0}$
and 
${\textit{\textbf{D}}}_{0}$
, respectively.
Note that if (X, J) is a MMBM with one single state (i.e. one-dimensional Brownian motion), we have, for 
$q\ge 0$
,
\begin{equation*}\boldsymbol{\Lambda}_q^+= -\rho_2, \quad \boldsymbol{\Lambda}_q^-=-\rho_1,\end{equation*}
where 
$\rho_1-\rho_2=\frac{2\mu}{\sigma^2}$
and 
$\rho_1 + \rho_2 = \frac{2\sqrt{\mu^2+2q\sigma^2}}{\sigma^2}$
. In general, for MMBM, we can only calculate explicit analytical formulas for 
$\textbf{W}^{(q)}(x)$
, 
$\boldsymbol{\Lambda}^{+}_{q},$
and 
$\boldsymbol{\Lambda}^{-}_q$
in some special cases. For instance, consider the following parameters: 
$q > 0$
,
\begin{equation}\Delta_{\boldsymbol{\sigma}} = \left( \begin{array}{c@{\quad}c} \sigma_{1} & 0\\ 0 & \sigma_{2} \end{array}\right)\!, \quad \Delta_{\boldsymbol{\mu}} = \left(\begin{array}{c@{\quad}c} 0&0 \\0&0 \end{array}\right)\!, \quad \mbox{and} \quad{\textit{\textbf{Q}}} = \left(\begin{array}{c@{\quad}c} -q_{11}& q_{11} \\ q_{22}& -q_{22}\end{array}\right) \end{equation}
with 
$\sigma_{1}$
, 
$\sigma_{2}$
, 
$q_{11}$
, 
$q_{22} \in \mathbb{R}_{+} $
. Then the matrix 
${\textit{\textbf{F}}}(s) - q\textbf{I}$
is of the form
\begin{equation*} {\textit{\textbf{F}}}(s)-q\textbf{I} = \left(\begin{array}{c@{\quad}c} \frac{\sigma_{1}^2}{2}s^2 - q_{11} - q & q_{11} \\ q_{22} & \frac{\sigma_2^2}{2}s^2 -q_{22} -q\end{array}\right)\!.\end{equation*}
Therefore, inversion of the Laplace transform (2.2) with respect to s gives
\begin{align} \textbf{W}^{(q)}(x) &=\left(\begin{array}{cc} 2(q_{22}+q)-\alpha_2^2 \sigma_2^2 & 2 q_{11}\\[10pt] 2 q_{22} & 2(q_{11}+q)-\alpha_2^2 \sigma_1^2 \end{array}\right)\frac{e^{\alpha_2 x}-e^{-\alpha_2 x}}{(\alpha_1^2-\alpha_2^2)\alpha_2\sigma_1^2\sigma_2^2} \\[10pt]&\quad -\left(\begin{array}{cc} 2(q_{22}+q)-\alpha_{1}^2 \sigma_2^2 & 2 q_{11} \\[10pt] 2 q_{22} &2(q_{11}+q)-\alpha_1^2 \sigma_1^2 \end{array}\right)\frac{e^{\alpha_{1} x} - e^{- \alpha_{1} x}}{(\alpha_1^2-\alpha_2^2)\alpha_1 \sigma_1^2 \sigma_2^2},\end{align}
where
\begin{align*} \alpha_1 &= \frac{\sqrt{M_{q}+\sqrt{(M_q)^2 - 4\sigma_1^2\sigma_2^2K_q}}}{\sigma_1 \sigma_2},\quad \alpha_2 = \frac{\sqrt{M_q-\sqrt{(M_q)^2 - 4\sigma_1^2\sigma_2^2K_q}}}{\sigma_1 \sigma_2},\\ M_{q}&=\sigma_1^2(q_{22}+q)+\sigma_2^2(q_{11}+q), \quad K_{q}=(q_{11}+q_{22}+q)q.\end{align*}
Likewise, one can find the representation formulas for 
$\boldsymbol{\Lambda}_{q}^{+}$
and 
$\boldsymbol{\Lambda}_{q}^{-}$
. First, note that 
$\boldsymbol{\Lambda}_{q}^{+} = \boldsymbol{\Lambda}_{q}^{-}$
thanks to the assumption of 
$\mu_{1} = \mu_{2} = 0$
and Equation (5.2); thus (5.3) becomes
\begin{equation*} (\boldsymbol{\Lambda}_{q}^{+})^2 = \Delta_{\frac{2}{\boldsymbol{\sigma}^2}}\Bigl[-{\textit{\textbf{Q}}} + q\textbf{I}\Bigr].\end{equation*}
Since 
$-\alpha_1$
and 
$-\alpha_2$
are eigenvalues of 
$\boldsymbol{\Lambda}_{q}^{+}$
, after some basic algebra one finds that
\begin{equation*} \boldsymbol{\Lambda}_{q}^{+} = \boldsymbol{\Lambda}_{q}^{-} = \left( \begin{array}{cc} \frac{-\sqrt{2\sigma_2^2(\alpha_1+\alpha_2)^2(q_{11}+q)-4q_{11}q_{22}}}{\sigma_1 \sigma_2} & \frac{2 q_{11}}{\sigma_1^2} \\[10pt] \frac{2 q_{22}}{\sigma_2^2} & \frac{-\sqrt{2\sigma_1^2 (\alpha_1+\alpha_2)^2(q_{22}+q)- 4 q_{11}q_{22}}}{\sigma_1 \sigma_2 }\end{array}\right) \frac{1}{\alpha_1+\alpha_2}.\end{equation*}
5.2 Constant state-dependent discount rates
Consider the special case where 
$\omega_i(x)\equiv \omega_i$
is a constant for all 
$x \in \mathbb{R}$
and 
$i \in E$
. Therefore the discounting structure depends on the state of the chain J alone. In this case, we have the following proposition.
Proposition 5.1. Let 
$\omega_i(x)\equiv \omega_i$
for all 
$x \in \mathbb{R}$
and 
$i \in E$
. The 
$\omega$
-scale matrix has the Laplace transform
\begin{equation*}\widetilde{\mathcal{W}}^{(\omega)}(s)=(\textbf{F}(s)-\boldsymbol{\omega})^{-1}.\end{equation*}
Proof. Taking the Laplace transform on both sides of (3.1), we have
\begin{equation*}\widetilde{\mathcal{W}}^{(\omega)}(s)=\widetilde{\textbf{W}}(s)+\widetilde{\textbf{W}}(s)\boldsymbol{\omega}\widetilde{\mathcal{W}}^{(\omega)}(s),\end{equation*}
which gives
\begin{equation*}\widetilde{\mathcal{W}}^{(\omega)}(s)=\left(\textbf{I}- \widetilde{\textbf{W}}(s)\boldsymbol{\omega}\right)^{-1} \widetilde{\textbf{W}}(s)=(\textbf{F}(s)-\boldsymbol{\omega})^{-1}.\end{equation*}
As an example of such an 
$\omega$
-scale matrix, we take again the model of MMBM with the following parameters: 
$ \omega_{1}(x) = \omega_{1}$
, 
$\omega_{2}(x) = \omega_{2}$
, and 
$\Delta_{\boldsymbol{\sigma}}$
, 
$\Delta_{\boldsymbol{\mu}}$
and 
${\textit{\textbf{Q}}}$
are as given in (5.5).
One can use the inverse of the Laplace transform to get that
\begin{align*}\mathcal{W}^{(\omega)}(x) &= \left(\begin{array}{cc} 2(q_{22}+\omega_2)-\alpha_2^2\sigma_2^2 & 2q_{11} \\ 2q_{22} & 2(q_{11}+\omega_1) - \alpha_2^2\sigma_1^2 \end{array}\right)\frac{e^{\alpha_2 x}-e^{-\alpha_2 x}}{(\alpha_1^2-\alpha_2^2)\alpha_2 \sigma_1^2 \sigma_2^2} \\[10pt]&\quad- \left(\begin{array}{cc} 2(q_{22}+q_2)-\alpha_1^2\sigma_2^2 & 2q_{11} \\ 2q_{22} & 2(q_{11}+\delta_1) - \alpha_1^2 \sigma_1^2\end{array}\right) \frac{e^{\alpha_1 x } - e^{-\alpha_1 x}}{(\alpha_1^2-\alpha_2^2)\alpha_1 \sigma_1^2 \sigma_2^2},\end{align*}
where
\begin{equation*} \begin{split}& \alpha_1 = \frac{\sqrt{M_{\omega} + \sqrt{(M_{\omega})^2- 4\sigma_1^2\sigma_2^2 K_{\omega}}}}{\sigma_1 \sigma_2}, \quad \alpha_2 = \frac{\sqrt{M_{\omega} - \sqrt{(M_{\omega})^2- 4\sigma_1^2\sigma_2^2 K_{\omega}}}}{\sigma_1 \sigma_2},\\&\hspace*{-4pt} M_{\omega}=\sigma_1^2(q_{22}+\omega_2) + \sigma_2^2(q_{11}+\omega_1), \quad K_{\omega}=q_{11}\omega_2+\omega_1q_{22} + \omega_1\omega_2.\end{split}\end{equation*}
Note that for 
$\omega_1=\omega_2=q$
, this result is consistent with the previous result for the (q)-scale matrix 
$\textbf{W}^{(q)}$
in (5.6).
5.3 Step
$\omega$
-scale matrix
In this example, we consider the omega function as a positive step function which depends only on the position of the process X. Such an assumption is motivated by the situation where a company has a discount structure which depends on its current financial status (or which is used as an indication of the economic environment). Li and Palmowski [Reference Li and Palmowski22] showed that, in the case of spectrally negative Lévy processes, such 
$\omega$
-scale functions have a recurrent nature. The same observation holds true for MAPs.
Proposition 5.2. Assume that the omega function is of the form
\begin{equation} \omega(i,x)\,:\!=\omega(x)=p_0+\sum_{j=1}^n(p_j-p_{j-1})1_{\{x>x_j\}} \quad \mbox{ for all i} \in E,\end{equation}
where 
$n \in \mathbb{N}$
, 
$\{p_j\}_{j=0}^n$
is a fixed sequence, and 
$\{x_j\}_{j=1}^n$
is an increasing sequence dividing 
$\mathbb{R}$
into 
$(n+1)$
parts. Then the omega matrix 
$\mathcal{W}^{(\omega)}(x,y)$
satisfies
\begin{equation*}\mathcal{W}^{(\omega)}(x,y)=\mathcal{W}_n^{(\omega)}(x,y)\end{equation*}
for 
$x>y$
, where 
$\mathcal{W}_n^{(\omega)}(x,y)$
is defined recursively as follows:
\begin{equation*}\mathcal{W}_{k+1}^{(\omega)}(x,y)=\mathcal{W}_{k}^{(\omega)}(x,y)+(p_{k+1}-p_{k})\int_{x_{k+1}}^{x} \textbf{W}^{(p_{k+1})}(x-z)\mathcal{W}_k^{(\omega)}(z,y)dz\end{equation*}
for 
$x>x_{k+1}$
and 
$k=1, \ldots, n-1$
, with 
$\mathcal{W}_0^{(\omega)}(x,y)=\textbf{W}^{(p_0)}(x-y).$
Proof. Define 
$\omega^{(k)}(x)\,:\!=p_0+\sum_{j=1}^k(p_j-p_{j-1})1_{\{x>x_j\}}$
, with 
$\omega^{(0)}(x)=p_0$
. From Equation (3.7), we get that
\begin{equation}\mathcal{W}^{(\omega)}_{k}(x,y)=\textbf{W}^{(p_{k+1})}(x-y)+\int_{y}^{x} (\omega^{(k)}(z)-p_{k+1})\textbf{W}^{(p_{k+1})}(x-z)\mathcal{W}_k^{(\omega)}(z,y)dz \end{equation}
and
\begin{equation}\mathcal{W}^{(\omega)}_{k+1}(x,y)=\textbf{W}^{(p_{k+1})}(x-y)+\int_{y}^{x} (\omega^{(k+1)}(z)-p_{k+1})\textbf{W}^{(p_{k+1})}(x-z)\mathcal{W}_{k+1}^{(\omega)}(z,y)dz. \end{equation}
Note that 
$\omega^{(k+1)}(z)-p_{k+1}=0$
for 
$z>{x_{k+1}}$
and 
$\omega^{(k+1)}(z)=\omega^{(k)}(z)$
for 
$z\le x_{k+1}$
. Thus, from Lemma 3.1, we have
\begin{equation*}\mathcal{W}^{(\omega)}_{k+1}(x,y)=\mathcal{W}^{(\omega)}_{k}(x,y)\end{equation*}
for 
$x\le x_{k+1}$
. Equation (5.8) can be rewritten as
\begin{align*}\mathcal{W}^{(\omega)}_{k+1}(x,y)&=\textbf{W}^{(p_{k+1})}(x-y)+\int_{y}^{x_k} (\omega^{(k+1)}(z)-p_{k+1})\textbf{W}^{(p_{k+1})}(x-z)\mathcal{W}_{k+1}^{(\omega)}(z,y)dz\\&=\textbf{W}^{(p_{k+1})}(x-y)+\int_{y}^{x_k} (\omega^{(k)}(z)-p_{k+1})\textbf{W}^{(p_{k+1})}(x-z)\mathcal{W}_{k+1}^{(\omega)}(z,y)dz\\&=\mathcal{W}^{(\omega)}_{k}(x,y)-\int_{x_k}^{x} (\omega^{(k)}(z)-p_{k+1})\textbf{W}^{(p_{k+1})}(x-z)\mathcal{W}_k^{(\omega)}(z,y)dz,\end{align*}
where the last step uses (5.7). The proof is completed by noticing that 
$\omega^{(k)}(z)-p_{k+1}=p_{k}-p_{k+1}$
for 
$z>x_{k+1}$
.
Note also that similar considerations will lead to the same result for the second 
$\omega$
-scale matrix 
$\mathcal{Z}^{(\omega)}$
.
In the next proposition, we will compute the matrix 
$\mathcal{W}^{(\omega)}$
for one particular case.
Proposition 5.3. Let (X, J) be a Markov-modulated Brownian motion with 
$\mu_i \in \mathbb{R}$
and 
$\sigma_{i}^2 > 0$
for all 
$i \in E$
. Assume that 
$n=1$
, 
$\lbrace p_{j} \rbrace_{j=0}^{n} = \lbrace p_{0},p_{1}\rbrace$
, and 
$\lbrace x_{j} \rbrace_{j = 1}^{n} = \lbrace x_{1} \rbrace$
, with 
$p_0,p_1,x_1$
being positive numbers. Then for 
$x \leq x_1$
,
\begin{equation}\mathcal{W}^{(\omega)}(x,y) = \textbf{W}^{(p_0)}(x-y),\end{equation}
and for 
$x > x_1$
,
\begin{align*}\mathcal{W}^{(\omega)} (x,y) &= \Bigl(e^{-\boldsymbol{\Lambda}^{+}_{p_{1}}(x-x_{1})}\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1}\boldsymbol{\Lambda}^{-}_{p_{1}} + e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-x_{1})}\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1} \boldsymbol{\Lambda}^{+}_{p_{1}}\Bigr) \\&\cdot \textbf{W}^{(p_{0})}(x_{1}-y) - \textbf{W}^{(p_{1})}(x-x_{1})\Delta_{\frac{\sigma^2}{2}}\textbf{W}^{(p_{0})'}(x_{1}-y).\end{align*}
Proof. Note that the case 
$x \leq x_{1}$
is a straightforward conclusion from Proposition 5.2. For 
$x > x_{1}$
, from Proposition 5.2 and Equation (5.1), we have
\begin{align}\mathcal{W}_{1}(x,y) &= \mathcal{W}_{0}(x,y) + (p_{1}-p_{0})\int_{x_{1}}^{x} \textbf{W}^{(p_{1})}(x-z)\mathcal{W}_{0}(z,y)dz\nonumber\\&= \textbf{W}^{(p_{0})}(x-y) + (p_{1}-p_{0})\int_{x_{1}}^{x}\Bigl(e^{-\boldsymbol{\Lambda}^{+}_{p_{1}} (x-z)}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(z-y)}\nonumber \end{align}
\begin{align} &- e^{-\boldsymbol{\Lambda}^{+}_{p_{1}}(x-z)}\Xi_{p_{1}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}} (z-y)} - e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-z)}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(z-y)} + e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-z)}\Xi_{p_{1}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(z-y)}\Bigr)dz \;\Xi_{p_{0}}.\end{align}
We start by identifying the following integral appearing in (5.9):
\begin{equation}\int_{x_{1}}^{x} \Bigl(e^{-\boldsymbol{\Lambda}^{+}_{p_{1}} (x-z)}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(z-y)}\Bigr)dz.\end{equation}
Consider (5.10) as a function 
$M_{1}\,:\,A \rightarrow \mathbb{R}^{N \times N}$
, where
\begin{equation} A = \lbrace (x,y) \,:\, x \geq x_{1}, x> y\rbrace,\end{equation}
and N is the size of the matrix 
$\textbf{W}^{(p_{0})}$
. Then
\begin{equation*}\begin{split} M_{1}(x,y) &= \int_{x_{1}}^{x} \Bigl(e^{-\boldsymbol{\Lambda}^{+}_{p_{1}} (x-z)}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(z-y)}\Bigr)dz= e^{-\boldsymbol{\Lambda}^{+}_{p_{1}} x}\int_{x_{1}}^{x} \Bigl(e^{\boldsymbol{\Lambda}^{+}_{p_{1}} z}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}z}\Bigr)dz \ e^{\boldsymbol{\Lambda}^{+}_{p_{0}}y}.\end{split}\end{equation*}
Let
\begin{equation*} K_{1}(x)\,:\!=M_{1}(x,x_{1}) = \int_{x_{1}}^{x} \Bigl(e^{-\boldsymbol{\Lambda}^{+}_{p_{1}} (x-z)}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(z-x_{1})}\Bigr)dz.\end{equation*}
The derivative of 
$K_{1}(x)$
is equal to
\begin{equation}K^{\prime}_{1}(x) = -\boldsymbol{\Lambda}^{+}_{p_{1}} K_{1}(x) + \Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}} (x-x_{1})},\end{equation}
with the boundary condition 
$K_{1}(x_{1}) = \boldsymbol{0}$
. We will prove that the solution of the above differential equation is of the form
\begin{equation}K_{1}(x) = {\textit{\textbf{C}}}e^{-\boldsymbol{\Lambda}^{+}_{p_0}(x-x_{1})} - e^{-\boldsymbol{\Lambda}^{+}_{p_1}(x-x_{1})}{\textit{\textbf{C}}},\end{equation}
where 
${\textit{\textbf{C}}}$
is some constant matrix. To do this, we need to verify our guess for 
$K_1(x)$
by plugging it into (5.11). After some calculation one can prove that (5.12) is indeed the solution if the following equation holds true:
\begin{equation}\boldsymbol{\Lambda}^{+}_{p_{1}}{\textit{\textbf{C}}} - {\textit{\textbf{C}}} \boldsymbol{\Lambda}^{+}_{p_{0}} =\Xi_{p_{1}}.\end{equation}
The above equality is an example of the well-known Sylvester equation. To solve equations of this type, one usually needs to rely on numerical methods. However, in this case, one can find a formula for 
${\textit{\textbf{C}}}$
via guess-and-check:
\begin{equation} {\textit{\textbf{C}}} = -\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1} \Bigl(\boldsymbol{\Lambda}^{+}_{p_{0}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)\cdot \frac{1}{p_{1}-p_{0}}.\end{equation}
Indeed, plugging this back into (5.13), one can verify the equivalence of both sides.
Therefore, 
$K_1(x)$
as defined in (5.12) (with constant matrix 
${\textit{\textbf{C}}}$
given in (5.14)) is a solution to the differential equation (5.11). It is now straightforward to check the expression for 
$M_{1}(x,y)$
; i.e.,
\begin{equation*} M_{1}(x,y) = {\textit{\textbf{C}}} e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(x-y)} - e^{-\boldsymbol{\Lambda}^{+}_{p_{1}}(x-x_{1})}{\textit{\textbf{C}}} e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(x_{1}-y)}.\end{equation*}
Following similar reasoning as for the derivation of 
$M_{1}$
, one can determine the other integrals appearing in (5.9), namely
\begin{equation*}\begin{split} & M_{2}(x,y) = \int_{x_{1}}^{x} e^{-\boldsymbol{\Lambda}^{+}_{p_{1}}(x-z)}\Xi_{p_{1}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(z-y)}dz = {\textit{\textbf{D}}} e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(x-y)} - e^{-\boldsymbol{\Lambda}^{+}_{p_{1}}(x-x_{1})}{\textit{\textbf{D}}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(x_{1}-y)}, \\&M_{3}(x,y) = \int_{x_{1}}^{x} e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-z)}\Xi_{p_{1}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(z-y)}dz= {\textit{\textbf{E}}} e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(x-y)} - e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-x_{1})}{\textit{\textbf{E}}}e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(x_{1}-y)}, \\&M_{4}(x,y) = \int_{x_{1}}^{x} e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-z)}\Xi_{p_{1}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(z-y)}dz={\textit{\textbf{F}}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}} (x-y)} - e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-x_{1})}{\,\textit{\textbf{F}}}e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(x_{1}-y)},\end{split}\end{equation*}
where the matrices 
${\textit{\textbf{C}}},{\textit{\textbf{D}}},{\textit{\textbf{E}}},{\textit{\textbf{F}}}$
are given by
\begin{align*}{\textit{\textbf{C}}} &= -\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}} + \boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1}\Bigl(\boldsymbol{\Lambda}^{+}_{p_{0}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)\cdot \frac{1}{p_{1}-p_{0}}, \\{\textit{\textbf{D}}} &= \Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}} + \boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1}\Bigl(\boldsymbol{\Lambda}^{-}_{p_{0}}-\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)\cdot \frac{1}{p_{1}-p_{0}},\displaybreak\\ {\textit{\textbf{E}}} &= -\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}} + \boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1}\Bigl(\boldsymbol{\Lambda}^{+}_{p_{0}}-\boldsymbol{\Lambda}^{+}_{p_{1}}\Bigr)\cdot \frac{1}{p_{1}-p_{0}},\\ {\textit{\textbf{F}}} &= \Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}} + \boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1}\Bigl(\boldsymbol{\Lambda}^{-}_{p_{0}}+\boldsymbol{\Lambda}^{+}_{p_{1}}\Bigr)\cdot \frac{1}{p_{1}-p_{0}}.\end{align*}
Plugging these back into (5.9), we have, for 
$x > x_{1}$
,
\begin{align*}\mathcal{W}_{1}^{(\omega)}(x,y) &= \Bigl(e^{-\boldsymbol{\Lambda}^{+}_{p_{0}}(x-y)}-e^{\boldsymbol{\Lambda}^{-}_{p_{0}}(x-y)}\Bigr)\Xi_{p_{0}}\\&\quad + (p_{1}-p_{0})\Bigl(M_{1}(x,y)-M_{2}(x,y) - M_{3}(x,y)+ M_{4}(x,y)\Bigr) \Xi_{p_{0}} \\&=\Bigl[e^{-\boldsymbol{\Lambda}^{+}_{p_{1}}(x-x_{1})}\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1}\boldsymbol{\Lambda}^{-}_{p_{1}}+ e^{\boldsymbol{\Lambda}^{-}_{p_{1}}(x-x_{1})}\Bigl(\boldsymbol{\Lambda}^{+}_{p_{1}}+\boldsymbol{\Lambda}^{-}_{p_{1}}\Bigr)^{-1} \boldsymbol{\Lambda}^{+}_{p_{1}}\Bigr] \\& \cdot \textbf{W}^{(p_{0})}(x_{1}-y)- \textbf{W}^{(p_{1})}(x-x_{1})\Delta_{\frac{\sigma^2}{2}}\textbf{W}^{(p_{0})\prime}(x_{1}-y),\end{align*}
which completes the proof of this proposition. Note that the uniqueness of this result is a straightforward conclusion from Lemma 3.1.
Remark 5.1. In general, if we choose to divide 
$\mathbb{R}$
into more intervals, a similar idea could be adopted for computing the 
$\omega$
-scale matrix.
5.4 Omega model
In Section 4, we examined an (omega) dividend problem in the general Markov additive model, where the formula for the value function was derived in terms of the 
$\omega$
-scale matrix. In this subsection, we will revisit this problem under MMBM and for a specific choice of omega function:
\begin{equation*}\omega_i(x) \,:\!= \omega(x)=\Bigl (\gamma_0+\gamma_1(x+d) \Bigr)1_{\{{-}d\le x\le 0\}} \quad \mbox{for all } i \in E,\end{equation*}
where 
$\gamma_0>0$
and 
$\gamma_1<0$
are constants such that the omega function is decreasing in x. A similar model for a Lévy risk process was analyzed in Li and Palmowski [Reference Li and Palmowski22].
Let us fix a constant force of interest 
$\delta \geq 0$
. Using (3.4) one can obtain that 
$\mathcal{W}^{(\omega + \delta)}$
satisfies the following equation: for 
$x\in [-d,0]$
,
\begin{align*}\mathcal{W}^{(\omega+\delta)}(x,-d)&=\textbf{W}(x+d)+\int_{-d}^{x} (\omega(z)+\delta)\textbf{W}(x-z)\mathcal{W}^{(\omega)}(z,-d)dz\\&=\textbf{W}(x+d)+\int_{0}^{x+d} (\omega(y-d)+\delta)\textbf{W}(x+d-y)\mathcal{W}^{(\omega)}(y-d,-d)dy \\&=\textbf{W}^{(\gamma_0 +\delta)}(x+d)+ \gamma_1 \int_{0}^{x+d}y\textbf{W}^{(\gamma_0 + \delta)}(x+d-y)\mathcal{W}^{(\omega)}(y-d,-d)dy. \end{align*}
Now, let 
$z=x+d\ge 0$
and
\begin{align}{\textit{\textbf{G}}}(z)\,:\!=\mathcal{W}^{(\omega + \delta)}(z-d,-d)=\mathcal{W}^{(\omega + \delta)}(x,-d).\end{align}
Then we can rewrite the equation for 
$\mathcal{W}^{(\omega + \delta)}$
as
\begin{equation*}{\textit{\textbf{G}}}(z) = \textbf{W}^{( \gamma_0 + \delta)}(z) + \gamma_1 \int_{0}^{z} y \textbf{W}^{(\gamma_0 + \delta)}(z-y){\textit{\textbf{G}}}(y)dy.\end{equation*}
From (5.1), we obtain the following for 
$\textbf{W}^{( \gamma_0 + \delta)}$
:
\begin{equation}\Bigl(\frac{d}{dz} - {\textit{\textbf{C}}}_{\gamma_{0}+\delta}\Bigr) \Bigl(\frac{d}{dz} + \Lambda_{\gamma_{0}+\delta}^{+}\Bigr) \textbf{W}^{(\gamma_0 + \delta)}(z) = \boldsymbol{0},\end{equation}
where 
${\textit{\textbf{C}}}_{\gamma_{0}+\delta} = (\boldsymbol{\Lambda}_{\gamma_{0}}^{+}d + \boldsymbol{\Lambda}_{\gamma_{0}}^{-}d)\boldsymbol{\Lambda}_{\gamma_{0}}^{-}d(\boldsymbol{\Lambda}_{\gamma_{0}}^{+}d+\boldsymbol{\Lambda}_{\gamma_{0}}^{-}d)^{-1}$
.
Based on (5.15), for 
$z \in [0,d]$
(or equivalently for 
$x \in [-d,0]$
) we have
\begin{equation}\Bigl(\frac{d}{dz} - {\textit{\textbf{C}}}_{\gamma_{0}+\delta}\Bigr) \Bigl(\frac{d}{dz} + \Lambda_{\gamma_{0}+\delta}^{+}\Bigr){\textit{\textbf{G}}}(z) = \gamma_{1}z\Delta_{\frac{2}{ \boldsymbol{\sigma}^{2}}}{\textit{\textbf{G}}}(z)\end{equation}
with the boundary conditions 
${\textit{\textbf{G}}}(0) = \boldsymbol{0}$
and 
$\boldsymbol{G^{\prime}}(0) = \Delta_{\frac{2}{\boldsymbol{\sigma}^{2}}}$
.
Let us rewrite the above differential matrix equation in the following form:
\begin{equation*}{\textit{\textbf{G}}}^{\prime \prime}(z) + \Bigl(\boldsymbol{\Lambda}_{\gamma_{0}}^{+}d - C_{\gamma_{0}+\delta}\Bigr){\textit{\textbf{G}}}^{\prime}(z) - \Bigl({\textit{\textbf{C}}}_{\gamma_{0}+\delta}\boldsymbol{\Lambda}_{\gamma_{0}}^{+}d + 2\gamma_{1}z\Delta_{1 / \boldsymbol{\sigma}^{2}}\Bigr){\textit{\textbf{G}}}(z) = \boldsymbol{0},\end{equation*}
which, by (5.3), can be simplified to
\begin{equation*}\Delta_{\frac{\boldsymbol{\sigma}^2}{2}}{\textit{\textbf{G}}}^{\prime \prime}(z) + \Delta_{\boldsymbol{\mu}}{\textit{\textbf{G}}}^{\prime}(z) + {\textit{\textbf{Q}}}{\textit{\textbf{G}}}(z) - (\omega_1(z)+\delta){\textit{\textbf{G}}}(z) = \boldsymbol{0}, \quad \mbox{for } z \in [0,d].\end{equation*}
Now we will treat the case of 
$z \geq d$
(or equivalently 
$x \geq 0$
). We first rewrite the formula
\begin{equation*}\mathcal{W}^{(\omega + \delta)}(x;\,{-}d) = \textbf{W}(x+d) + \int_{0}^{x+d}\omega(y-d)\textbf{W}(x+d-y)\mathcal{W}^{(\omega + \delta)}(y-d;-d)dy \quad \mbox{for } x\geq 0,\end{equation*}
in terms of the matrix 
${\textit{\textbf{G}}}(z)$
with 
$z \geq d$
:
\begin{equation*} {\textit{\textbf{G}}}(z) = \textbf{W}(z) + \int_{0}^{d}(\delta+ (\gamma_0 + \gamma_1 y))\textbf{W}(z-y){\textit{\textbf{G}}}(y)dy + \delta \int_{d}^{z} \textbf{W}(z-y) {\textit{\textbf{G}}}(y) dy.\end{equation*}
Similarly to (5.16) and (5.17), we have, respectively,
\begin{equation*} \Bigl(\frac{d}{dz}- {\textit{\textbf{C}}}\Bigr)\Bigl(\frac{d}{dz} + \boldsymbol{\Lambda}^{+}\Bigr)\textbf{W}(z) = \boldsymbol{0}\end{equation*}
and
\begin{equation*}\Bigl(\frac{d}{dz}- {\textit{\textbf{C}}}\Bigr)\Bigl(\frac{d}{dz} + \boldsymbol{\Lambda}^{+}\Bigr){\textit{\textbf{G}}}(z) = \delta \Delta_{\frac{2}{\boldsymbol{\sigma}^2}}{\textit{\textbf{G}}}(z) \quad \mbox{for } z \geq d,\end{equation*}
where 
${\textit{\textbf{C}}} = (\boldsymbol{\Lambda}^{+} + \boldsymbol{\Lambda}^{-})\boldsymbol{\Lambda}^{-}(\boldsymbol{\Lambda}^{+}+\boldsymbol{\Lambda}^{-})^{-1}$
. Using (5.3) with 
$q = 0$
, one can get that
\begin{equation*}\Delta_{\frac{\boldsymbol{\sigma}^2}{2}}{\textit{\textbf{G}}}^{\prime \prime}(z) + \Delta_{\boldsymbol{\mu}}{\textit{\textbf{G}}}^{\prime}(z) + {\textit{\textbf{Q}}}{\textit{\textbf{G}}}(z) - \delta{\textit{\textbf{G}}}(z) = \boldsymbol{0} \quad \mbox{for } z > d.\end{equation*}
Summarizing, 
${\textit{\textbf{G}}}(z)$
satisfies the following differential equations:
\begin{equation*} \begin{array}{r@{\quad}l} \Delta_{\frac{\boldsymbol{\sigma}^2}{2}}{\textit{\textbf{G}}}^{\prime \prime}(z) + \Delta_{\boldsymbol{\mu}}{\textit{\textbf{G}}}^{\prime}(z) + {\textit{\textbf{Q}}}{\textit{\textbf{G}}}(z) - (\omega_1(z)+\delta) {\textit{\textbf{G}}}(z) = \boldsymbol{0}& \mbox{for}\ z \in [0,d],\\ \Delta_{\frac{\boldsymbol{\sigma}^2}{2}}{\textit{\textbf{G}}}^{\prime \prime}(z) + \Delta_{\boldsymbol{\mu}}{\textit{\textbf{G}}}^{\prime}(z) + {\textit{\textbf{Q}}}{\textit{\textbf{G}}}(z) - \delta {\textit{\textbf{G}}}(z)= \boldsymbol{0} & \mbox{for}\ z>d,\end{array}\end{equation*}
with the boundary conditions 
${\textit{\textbf{G}}}(0) = \boldsymbol{0}$
and 
${\textit{\textbf{G}}}^{\prime}(0) = \Delta_{\frac{2}{\boldsymbol{\sigma^2}}}$
.
Therefore, from (5.15), for 
$x \in [-d,0]$
we obtain
\begin{equation*} \Delta_{\frac{\boldsymbol{\sigma}^2}{2}}\mathcal{W}^{(\omega + \delta)\prime \prime}(x,-d) + \Delta_{\boldsymbol{\mu}}\mathcal{W}^{(\omega +\delta)\prime}(x,-d)-((\omega(x+d)+\delta){\textit{\textbf{I}}}-{\textit{\textbf{Q}}})\mathcal{W}^{(\omega + \delta)}(x,-d)=\boldsymbol{0},\end{equation*}
and for 
$x > 0$
,
\begin{equation*} \Delta_{\frac{\boldsymbol{\sigma}^2}{2}}\mathcal{W}^{(\omega + \delta)\prime \prime}(x,-d) + \Delta_{\boldsymbol{\mu}}\mathcal{W}^{(\omega +\delta)\prime}(x,-d)-(\delta{\textit{\textbf{I}}}-{\textit{\textbf{Q}}})\mathcal{W}^{(\omega + \delta)}(x,-d)=\boldsymbol{0},\end{equation*}
with the boundary conditions 
$\mathcal{W}^{(\omega + \delta)} ({-}d,-d) = \boldsymbol{0}$
and 
$\mathcal{W}^{(\omega+\delta)\prime}({-}d,-d) = \Delta_{\frac{2}{\boldsymbol{\sigma}^{2}}}$
.
Before we proceed to the numerical example, we recall that N is the cardinality of the state space E, and 
$\mathcal{W}^{(\omega + \delta)}$
maps 
$\mathbb{R}$
into 
$\mathbb{R}^{N\times N}$
. Thus, one can see that the differential equations for 
$\mathcal{W}^{(\omega+\delta)}$
can be treated as a (2
$\times$
N)th-order system of second-order initial-value problems. As usual in such a setting, one can introduce new unknown functions as derivatives of the remaining functions. Thus we obtain a (4
$\times$
N)th-order system of first-order initial-value problems, for which there exist rich collections of iterative algorithms. Let us focus on uniqueness and existence in the general case. Specifically, recall that every mth-order system of first-order initial-value problems can be written in the form
\begin{equation*} \frac{dy_i}{dt} = g_i(t,y_1,y_2,...,y_m),\end{equation*}
where for each 
$i \in \lbrace 1,2,...,m\rbrace$
, 
$g_i$
is assumed to be defined on some set
\begin{equation*}D_i = \lbrace (t,y_1,...,y_m)\,{:}\,a \leq t \leq b , -\infty < y_k
< \infty, \forall k = 1,2,...,m \rbrace.\end{equation*}
Then the system has a unique solution 
$y_1(t),y_2(t),...,y_m(t)$
for 
$a \leq t \leq b$
if all 
$g_i$
are continuous on 
$D_i$
and satisfy a Lipschitz condition with respect to 
$(y_1,y_2,...,y_m)$
.
Figure 1. Entries of 
$\omega$
-scale matrix function 
$\mathcal{W}^{(\omega+\delta)}$
In the framework of this section, we choose 
$a = -d$
and 
$b = t_{max}$
as an upper limit of our approximation. It is also clear that if we choose 
$\omega$
to be continuous, then the above sufficient condition holds true. For illustration, given the parameters
\begin{equation*} \begin{split}&\Delta_{\boldsymbol{\sigma}} = \left(\begin{array}{c@{\quad}c} 1.2 & 0 \\ 0 & 2 \end{array}\right)\!, \quad\Delta_{\boldsymbol{\mu}} = \left(\begin{array}{c@{\quad}c} 1.75 & 0 \\ 0 & 1.25 \end{array}\right)\!, \quad{\textit{\textbf{Q}}} = \left(\begin{array}{c@{\quad}c} -0.4 & 0.4 \\ 0.2 & -0.2 \end{array}\right)\!,\\[10pt]& \gamma_0 = 0.5,\quad \gamma_1 = -0.1, \quad d = 5, \quad t_{max} = 10 \quad \mbox{ and } \quad \delta = 0.04,\end{split}\end{equation*}
Figure 1 shows the entries of the numerical approximations of the matrix function 
$\mathcal{W}^{(\omega + \delta)}$
. We see that the main difference between the classical scale matrix and the 
$\omega$
-scale matrix is the fact that here we have nonzero values in the interval 
$({-}d,0]$
.
Practical applications of our models and results will rely heavily on numerical evaluation. For instance, one can use the numerical approach presented here to approximate the value function of the dividend strategy in the Omega model. Moreover, one can produce similar experiments for different choices of 
$\omega$
to capture different discount structures or bankruptcy rates depending on the context; this will bring 
$\omega$
-scale matrices closer to our intuition.
Appendix A. The existence and invertibility of
$\omega$
-scale matrices
A.1. Proof of Lemma 3.1 for the existence of
$\omega$
-scale matrices
Proof. To prove the uniqueness of the solution, we will show that 
$\textbf{H}(x)=\textbf{0}$
is the only solution to
\begin{equation}\textbf{H}(x)=\int_0^{x}\textbf{W}(x-y)\boldsymbol{\omega}(y)\textbf{H}(y)dy. \end{equation}
Taking the Laplace transform on both sides of (A.1) (with an argument 
$s_0$
), we get
\begin{equation*}\widetilde{\textbf{H}}(s_0) = \widetilde{\textbf{W}}(s_0)\ \widetilde{\boldsymbol{\omega} \textbf{H}}(s_0).\end{equation*}
Recall that 
$\lambda$
is an upper bound of 
$|\omega_i(y)|$
on 
$[0,\infty)$
for all 
$i \in E$
. Using (2.2), we obtain that the matrix norm of 
$\widetilde{\textbf{H}}(s_0) $
fulfills the inequality
\begin{equation}\lVert \widetilde {\textbf{H}}(s_0) \rVert \le \lambda \lVert \widetilde {\textbf{W}}(s_0) \rVert \lVert \widetilde {\textbf{H}}(s_0) \rVert=\lambda \lVert {\textbf{F}}^{-1}(s_0) \rVert \lVert \widetilde {\textbf{H}}(s_0) \rVert. \end{equation}
Next we will show that there exists 
$s_0$
such that
\begin{equation} \lVert {\textbf{F}}(s) ^{-1}\rVert
< \frac{1}{2\lambda} \qquad \mbox{ for all}\ s\ge s_0. \end{equation}
To do so, we recall the expression for 
$\textbf{F}(\alpha)$
:
\begin{equation*}\textbf{F}(\alpha)=\mbox{diag}(\psi_1(\alpha),\dots,\psi_N(\alpha) )+{\textit{\textbf{Q}}}\circ \mathbb{E}(e^{\alpha U_{ij}}).\end{equation*}
Observe that its diagonal goes to infinity as 
$\alpha$
goes to infinity, and each element (entrywise) away from the diagonal is bounded by the (fixed) 
$q_{ij}$
.
We now prove, using an induction argument with respect to the dimension of 
$\textbf{F}(\alpha)$
, that
\begin{equation*}{\textbf{F}}(\alpha)^{-1} \rightarrow \textbf{0} \mbox{ as } \alpha \rightarrow \infty. \end{equation*}
Define a series of sub-matrices of 
$\textbf{F}(\alpha)$
, for 
$m=1,2,\ldots, N$
:
\begin{equation*}\textbf{F}_{m}(\alpha)^{-1}\,:\!=\textbf{F}(\alpha)^{-1}_{m\times m}=\left(\left \{F_{ij}(\alpha)\right\}_{i,j=1}^m\right)^{-1}.\end{equation*}
In what follows, we will show that
\begin{equation}{\textbf{F}}_m^{-1}(\alpha) \rightarrow \textbf{0}_{m\times m},\mbox{ as } \alpha \rightarrow \infty. \end{equation}
Clearly, 
$\textbf{F}_{N}(\alpha)^{-1}=\textbf{F}(\alpha)^{-1}$
.
When 
$m=1$
, 
$\textbf{F}_{1}(\alpha)^{-1}=\frac{1}{\psi_1(s_0)+q_{11}}$
, which makes (A.4) hold obviously, and 
$s_0$
in (A.3) is chosen so that 
$\frac{1}{\psi_1(s_0)+q_{11}} < \frac{1}{2\lambda}$
. Assume (A.4) holds for the dimension 
$m=k-1$
. Then in the dimension 
$m=k$
, we have
\begin{align*}\textbf{F}_{k}(\alpha)^{-1}&= \begin{pmatrix} \textbf{A} &\quad \textbf{B}\\ \textbf{C} &\quad \textbf{D} \end{pmatrix}^{-1},\end{align*}
where
\begin{equation*}\textbf{A}_{(k-1)\times (k-1)}=\textbf{F}_{k-1}(\alpha),\end{equation*}
\begin{equation*}\textbf{B}_{(k-1)\times 1}=(q_{1 k} \mathbb{E}(e^{\alpha U_{1k}}), \ldots, q_{(k-1) k} \mathbb{E}(e^{\alpha U_{(k-1)k}}))^T,\end{equation*}
\begin{equation*}\hspace*{-5pt}\textbf{C}_{1\times(k-1)}= (q_{ k1} \mathbb{E}(e^{\alpha U_{k1}}), \ldots, q_{k(k-1) } \mathbb{E}(e^{\alpha U_{k(k-1)}})),\end{equation*}
and
\begin{equation*}\textbf{D}_{1\times1}=\psi_k(\alpha)-q_{kk}.\end{equation*}
Using the formula for the inverse of the block matrix
\begin{equation*} \begin{pmatrix} \textbf{A} &\quad \textbf{B}\\ \textbf{C} &\quad \textbf{D}\\ \end{pmatrix}^{-1} = \left(\begin{array}{c@{\quad}c} \textbf{A}^{-1}+\textbf{A}^{-1}\textbf{B}(\textbf{D}-\textbf{C}\textbf{A}^{-1}\textbf{B})^{-1}\textbf{C}\textbf{A}^{-1} & -\textbf{A}^{-1}\textbf{B}(\textbf{D}-\textbf{C}\textbf{A}^{-1}\textbf{B})^{-1}\\[2pt] -(\textbf{D}-\textbf{C}\textbf{A}^{-1}\textbf{B})^{-1}\textbf{C}\textbf{A}^{-1} & (\textbf{D}-\textbf{C}\textbf{A}^{-1}\textbf{B})^{-1} \end{array}\right),\end{equation*}
it is easy to see that each block in 
$\textbf{F}_{k}(\alpha)^{-1}$
goes to 
$\textbf{0}$
as 
$\alpha\rightarrow \infty$
, since
\begin{equation*}\textbf{A}^{-1}=\textbf{F}_{k-1}(\alpha)^{-1}\rightarrow \textbf{0}_{(k-1)\times(k-1)},\end{equation*}
\begin{equation*}(\textbf{D}-\textbf{C}\textbf{A}^{-1}\textbf{B})^{-1}=\frac{1}{\psi_k(\alpha)-q_{kk}-\textbf{C}\textbf{A}^{-1}\textbf{B}} \rightarrow 0,\end{equation*}
and 
$\textbf{B}$
, 
$\textbf{C}$
have bounded (nonnegative) elements. This completes the proof of (A.3).
Plugging (A.3) into (A.2) gives
\begin{equation*}\lVert \widetilde {\textbf{H}}(s_0) \rVert =0; \mbox{ i.e. } \textbf{H}(x)=\textbf{0},\end{equation*}
which completes the proof of the uniqueness of the solution to Equation (3.2).
To prove the existence of a solution to Equation (3.2), we construct a series of matrices 
$\{\textbf{H}_m\}$
which converge to the unique solution. Define the operator 
$\mathcal{G}$
on a matrix as follows: for 
$z>0$
,
\begin{equation*}\mathcal{G}\widetilde{\textbf{K}}(z)=\int_0^{\infty} e^{-zx}\int_0^{x} e^{-s_0(x-y)}\textbf{W}(x-y) \boldsymbol{\omega}(y)\textbf{K}(y)dydx= \widetilde {\textbf{W}}(s_0+z)\ \widetilde {\boldsymbol{\omega} \textbf{K}}(z) ,\end{equation*}
\begin{equation*}\mathcal{G}^{(m+1)} \widetilde{\textbf{K}}(z) =\mathcal{G} (\mathcal{G}^{(m)})\widetilde{\textbf{K}}(z),\end{equation*}
\begin{equation*}\widetilde{\textbf{H}}_0(z)=\int_{0}^{\infty} e^{-zx}e^{-s_0x}\textbf{h}(x)dx=\widetilde{\textbf{h}}_0(s_0+z), \qquad \widetilde{\textbf{H}}_{m+1}(z)=\widetilde{\textbf{H}}_0(z)+\mathcal{G}\widetilde{\textbf{H}}_m(z).\end{equation*}
Then 
$\mathcal{G}$
is a linear operator such that 
$\lVert\mathcal{G}\widetilde{\textbf{K}}(z) \rVert < \frac{1}{2}\lVert \widetilde{\textbf{K}}(z) \rVert $
for 
$z>0$
. Therefore, for 
$m>l$
, we have
\begin{equation*}\lVert \widetilde{\textbf{H}}_m(z) - \widetilde{\textbf{H}}_l(z) \rVert = \lVert \sum_{k=l+1}^{m}\mathcal{G}^{(k)}\widetilde{\textbf{H}}_0(z) \rVert
< 2^{-l} \lVert \widetilde{\textbf{H}}_0(z) \rVert,\end{equation*}
which means 
$\{\widetilde{\textbf{H}}_{m}(z),z>0\}_{m \ge 0}$
forms a Cauchy sequence (entrywise) that admits a limit 
$\widetilde{\mathfrak{H}}(z)$
for any 
$z>0$
satisfying
\begin{equation*}\widetilde{\mathfrak{H}}(z)=\widetilde{\textbf{H}}_0(z)+\mathcal{G}\widetilde{\mathfrak{H}}(z)=\widetilde{\textbf{h}}_0(s_0+z)+ \widetilde {\textbf{W}}(s_0+z)\ \widetilde {\boldsymbol{\omega} \mathfrak{H}}(z).\end{equation*}
Using the uniqueness of the Laplace transform, we have
\begin{equation*}{\mathfrak{H}}(x)=e^{-s_0x}{\textbf{h}}_0(x)+ \int_0^{x} e^{-s_0(x-y)}\textbf{W}(x-y)\boldsymbol{ \omega}(y)\mathfrak{H}(y)dy,\end{equation*}
which shows that 
$\textbf{H}(x)=e^{s_0x}{\mathfrak{H}}(x)$
is a solution to (3.2).
As for the second statement in this lemma, we see that if 
$\textbf{H}$
satisfies (3.3), then by letting 
$\delta=0$
, we obtain (3.2) immediately. Now we only need to show that if 
$\textbf{H}$
is a solution to (3.2), it is also a solution to (3.3). We convolute both sides of (3.2) with 
$\delta \textbf{W}^{(\delta)}$
(on the left):
\begin{align*}\delta \textbf{W}^{(\delta)}* \textbf{H}(x)&=\delta \textbf{W}^{(\delta)}*\textbf{h}(x)+\delta \textbf{W}^{(\delta)}* \textbf{W} *(\boldsymbol{\omega}\textbf{H})(x)=\delta \textbf{W}^{(\delta)}*\textbf{h}(x)+( \textbf{W}^{(\delta)}- \textbf{W})*(\boldsymbol{\omega}\textbf{H})(x),\end{align*}
where the last step uses the identity 
$ \textbf{W}^{(\delta)}- \textbf{W}= \delta \textbf{W}^{(\delta)}* \textbf{W}$
(which can be easily seen from the Laplace transform). Therefore,
\begin{equation*}\textbf{H}(x)=\textbf{h}(x)+\delta \textbf{W}^{(\delta)}*\textbf{h}(x)+ \textbf{W}^{(\delta)}* ((\boldsymbol{\omega}-\delta\textbf{I})\textbf{H})(x),\end{equation*}
which completes the proof.
A.2. Proof of the invertibility of
$\omega$
-scale matrices
Proposition A.1. The matrix 
$\mathcal{W}^{(\omega)}(x)^{-1}$
is invertible for any 
$x > 0$
.
Proof. From (3.13), one can see that it is enough to prove that the matrix
\begin{equation*}\textbf{P}(x)\,:\!= \textbf{I}+\int_0^{x} \textbf{W}^{(\lambda)}(x-y) \left( \lambda\textbf{I}-\boldsymbol{\omega}(y)\right)\textbf{A}^{(\omega)}(y,x)dy\end{equation*}
is invertible for every 
$x\geq 0$
. Using an argument similar to that of [Reference Kyprianou and Palmowski21], note that for each 
$y > 0$
there exists some 
$N \times N$
sub-stochastic invertible intensity matrix 
$\boldsymbol{\Lambda}^{\omega, *}(y)$
such that
\begin{equation}\mathbb{P}_x\left( \tau_c^+
< \tau_0^- \wedge T^{\omega}, J_{\tau_c^+}| J_0 \right)= \exp\left(\int_x^c \boldsymbol{\Lambda}^{\omega, *}(y)\; dy\right)\!.\end{equation}
This observation implies that the matrix 
$\textbf{A}^{(\omega)}(x,c)$
is invertible for any 
$x,c \in \mathbb{R}_{+}$
such that 
$0<x\leq c$
. The matrix 
$\textbf{A}^{(\omega)}(x,c)$
is also continuous (entrywise) with respect to c. Now, assume that there exists 
$c>0$
such that matrix 
$\textbf{P}(x)$
is invertible for some 
$0<x<c$
and is singular for 
$x=c$
. Then from the relation (3.12) we get a contradiction, because the left-hand side of it is invertible (as a product of invertible matrices) and the right-hand side is singular from the assumption. Hence only two scenarios are possible: the matrix 
$\textbf{P}(x)$
is invertible for all 
$x > 0$
, or it is singular for all 
$x> 0$
. Finally, since 
$\textbf{P}(0)=\textbf{I}$
and 
$\textbf{P}(x)$
is continuous in 
$x \geq 0$
, we obtain that 
$\textbf{P}(x)$
must be invertible for all 
$x\geq 0$
.
Appendix B. Proofs of additional facts
Here are the proofs of Lemma 3.2 and Corollary 3.1.
B.1. Proof of Lemma 3.2
Proof. As before, without loss of generality, we assume that 
$\omega_i(x)$
is bounded by some 
$\lambda>0$
for all 
$x \in \mathbb{R}$
and 
$i \in E$
. The finiteness of 
$K^{(\omega)}_{ij} f_j(x)$
comes from the fact that 
$K^{(\omega)}_{ij} f_j(x)<K^{(0)}_{ij} f_j(x)$
for all 
$1\le i \le N$
. Using arguments similar to those in the proof of Theorem 3.1(i), we have
\begin{align*}&Q_{t,ij}^{(\omega)} f_j(x)\\&= \mathbb{E}_{x,i}\left [ f_{J_t}(X_t);\, t
< \xi \mbox{ and } M_k> \omega_{J_{T_k}}(X_{T_k}) \mbox{ for all }T_k<t, J_{t}=j\right]\\&= \mathbb{E}_{x,i}\left [ f_{J_t}(X_t);\, t
< \xi, T_1>t, J_{t}=j\right]+\sum_{l=1}^{N} \int_0^{t} \mathbb{E}_{x,i}\left [ Q_{t-s,lj}^{(\omega)} \,f_j(X_s), M_1> \omega_{l}(X_{s}), J_s=l\right] \mathbb{P}(T_1 \in ds) \\&= \mathbb{E}_{x,i}\left [ e^{-\lambda t}f_{j}(X_t);\, t
< \xi, J_t=j\right]+\sum_{l=1}^{N} \int_0^{t} \mathbb{E}_{x,i}\left [ (\lambda -\omega_l (X_s))Q_{t-s,lj}^{(\omega)} \,f_j(X_s), J_s=l\right] e^{-\lambda s}ds \\&= Q_{t,ij}^{(\lambda)} \,f_{j}(x)+ \sum_{l=1}^{N}\int_0^{t} Q_{s,il}^{(\lambda)} \left ((\lambda-\omega_l)Q_{t-s,lj}^{(\omega)} \,f_j\right)(x)ds.\end{align*}
Note that the superscript 
$\lambda$
denotes a counterpart of fixed 
$\omega_i(x)\equiv\lambda$
. Equivalently, in matrix form, we have
\begin{equation*}{\textit{\textbf{Q}}}_{t}^{(\omega)} {\textit{\textbf{f}}}(x)= {\textit{\textbf{Q}}}_t^{(\lambda)}{\,\textit{\textbf{f}}}(x)+ \int_0^{t} {\textit{\textbf{Q}}}_s^{(\lambda)}\left((\lambda\textbf{I}-\boldsymbol{\omega}){\textit{\textbf{Q}}}_{t-s}^{(\omega)}\,{\textit{\textbf{f}}}\right)(x) ds,\end{equation*}
where by matrix compounding we mean 
$\left (\textbf{A}(\textbf{B})(x)\right)_{ij}=\sum_{m=1}^N A_{im} B_{mj}(x)$
. Thus,
\begin{equation}\textbf{K}^{(\omega)}{\textit{\textbf{f}}}(x)=\int_0^{\infty} {\textit{\textbf{Q}}}_{t}^{(\omega)} {\textit{\textbf{f}}}(x)dt=\textbf{K}^{(\lambda)}{\textit{\textbf{f}}}(x)+ \textbf{K}^{(\lambda)}\left((\lambda\textbf{I}-\boldsymbol{\omega})\textbf{K}^{(\omega)}{\textit{\textbf{f}}}\right)(x). \end{equation}
Using the resolvent identity 
$\lambda \textbf{K}^{(0)}(\textbf{K}^{(\lambda)})= \textbf{K}^{(0)}- \textbf{K}^{(\lambda)}$
, we have
\begin{align}\lambda \textbf{K}^{(0)} \left(\textbf{K}^{(\omega)}\,{\textit{\textbf{f}}} \right) (x)=(\textbf{K}^{(0)}- \textbf{K}^{(\lambda)}){\textit{\textbf{f}}}(x)+ (\textbf{K}^{(0)}- \textbf{K}^{(\lambda)}) \left((\lambda\textbf{I}-\boldsymbol{\omega})\textbf{K}^{(\omega)}{\textit{\textbf{f}}}\right)(x).\end{align}
B.2. Proof of Corollary 3.1
Proof of Part (i). First we will prove that
\begin{equation}\lim_{d \to -\infty} \mathcal{W}^{(\omega)}(x,d) \mathcal{W}^{(\omega)}(c,d)^{-1}= \mathcal{H}^{(\omega)}(x)\mathcal{H}^{(\omega)}(c)^{-1}.\end{equation}
Then the result will follow from Theorem 3.1(i). Recall that for 
$x\geq d$
and any fixed 
$\beta \geq 0$
we have
\begin{equation*}\mathcal{W}^{(\omega)}(x,d)=\textbf{W}^{(\beta)}(x-d)+\int_{0}^{x} \textbf{W}^{(\beta)}(x-z) (\boldsymbol{\omega}(z)- \beta \textbf{I})\mathcal{W}^{(\omega)}(z,d)dz. \end{equation*}
Moreover, for 
$x=0$
,
\begin{equation*} \mathcal{W}^{(\omega)}(0,d)e^{-\textbf{R}^{\beta}d}= \textbf{W}^{(\beta)}({-}d) e^{-\textbf{R}^{\beta}d}.\end{equation*}
Hence from (2.3) we have
\begin{equation*}\lim_{d \to -\infty}\mathcal{W}^{(\omega)}(0,d)e^{-\textbf{R}^{\beta}d}=\lim_{d \to -\infty}\textbf{W}^{(\beta)}({-}d)e^{-\textbf{R}^{\beta}d}= \textbf{L}^{\boldsymbol\beta} . \end{equation*}
From Theorem 3.1(i), for 
$x>0$
,
\begin{equation*}\mathbb{E}\left[e^{-\int_0^{\tau_x^+}\omega_{J_s}(X_s)ds}, \tau_x^+<\tau_d^-, J_{\tau_x^+}|J_0 \right]\mathcal{W}^{(\omega)}(x,d)= \mathcal{W}^{(\omega)}(0,d).\end{equation*}
Since the above expectation is increasing with respect to d, the following limit is well-defined and finite for every 
$x>d$
:
\begin{align*}&\lim_{d \to -\infty} \mathbb{E}\left[e^{-\int_0^{\tau_x^+}\omega_{J_s}(X_s)ds}, \tau_x^+<\tau_d^-, J_{\tau_x^+}|J_0 \right] \mathcal{W}^{(\omega)}(x,d)e^{-\textbf{R}^{\beta}d}\\&=\mathbb{E}\left[e^{-\int_0^{\tau_x^+}\omega_{J_s}(X_s)ds}, \tau_x^+<\infty, J_{\tau_x^+}|J_0 \right]\lim_{d \to -\infty}\mathcal{W}^{(\omega)}(x,d)e^{-\textbf{R}^{\beta}d}=\textbf{L}^{\boldsymbol\beta}.\end{align*}
Note also that, since the matrix 
$\textbf{L}^{\boldsymbol\beta}$
is invertible (as was noted above Equation (2.3)), from the above equation it follows that the matrix 
$\lim_{d \to -\infty}\mathcal{W}^{(\omega)}(x,d)e^{-\textbf{R}^{\beta}d}$
is also invertible. Taking
\begin{equation*}\mathcal{H}^{(\omega)}(x)\,:\!=\lim_{d \to -\infty} \mathcal{W}^{(\omega)}(x,d) e^{-\textbf{R}^{\beta}d} (\textbf{L}^{\boldsymbol\beta})^{-1}\end{equation*}
completes the proof of the first part of the corollary. To show that the above-defined 
$\mathcal{H}^{(\omega)}(x)$
satisfies (3.9), note that
\begin{equation*} \mathcal{W}^{(\omega)}(x,d) e^{-\textbf{R}^{\beta}d}=\left(\textbf{W}^{(\beta)}(x-d)+\int_{0}^{x}\textbf{W}^{(\beta)}(x-z) (\boldsymbol{\omega}(z)- \beta \textbf{I})\mathcal{W}^{(\omega)}(z,d)dz \right) e^{-\textbf{R}^{\beta}d}. \end{equation*}
Then take the limit as 
$d \to -\infty$
and apply the dominated convergence theorem; the result follows.
Proof of Part (ii). The proof follows from taking the limit (3.13), which exists and is finite. Moreover, the limit
\begin{equation*}\lim_{c \to \infty} \mathcal{W}^{(\omega)}(c)^{-1}\mathcal{Z}^{(\omega)}(c)=\textbf{C}_{\mathcal{W}(\infty)^{-1}\mathcal{Z}(\infty)}=\textbf{C}_{B^{(\omega)}} \end{equation*}
is finite by (3.17). This completes the proof.
Acknowledgements
This work was partially supported by the National Science Centre Grant No. 2015/19/D/ST1/01182, the National Science Centre Grant No. 2015/17/B/ST1/01102, the National Science Centre Grant No. 2016/23/B/HS4/00566, and a start-up grant from Western University. The authors are thankful to the anonymous referees and the associate editor for their valuable suggestions, which improved the quality of the article.
