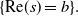1. Introduction
Semi-Markov processes (SMPs) are widely used to describe the passage of a stochastic system through its states. The generality of the SMP model is such that it has found application in widely diverging subjects such as reliability theory, queueing theory, as well as in multistate survival analysis [Reference Lagakos, Sommer and Zelen15]. In such applications, it is often the transient behaviour of the SMP which is of interest, as reflected in the survival and density/mass function of the random variable X defined as a first-passage time from one state to some other states. For example, in reliability theory, if X is the first-passage time to a subset of failed states, then
$S(t)=\mathbb{P}(X\geq t)$
is the reliability function for the system. In multistate survival analysis, if X is the lifetime of a patient, then it is modelled as the first-passage time of an SMP through multiple clinical states to a fatal state or a collection of such states.
Asymptotic expansions for the survival and density/mass functions of the first-passage time X have been proposed in the author’s previous work in [Reference Butler4, Reference Butler5]. The leading terms in these expansions assume the form of a gamma survival/density function in continuous time and a discrete gamma in integer time. This paper provides the fundamental requirements that a finite-state SMP must satisfy in order for these expansions to be valid, as explained in more detail below. The expansions are determined from the moment generating function (MGF)
$\mathcal{M}(s)$
of X, which, subject to mild conditions, is shown to be convergent on
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b\}$
for
$b>0.$
In continuous time, it was shown in [Reference Butler5] that if the MGF
$\mathcal{M}$
has a simple pole at
$b>0$
and this pole is dominant in the sense that
$\mathcal{M}$
is analytic on
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b+\varepsilon\,=\!:\,b^{+}\}\backslash\{b\}$
for some
$\varepsilon>0,$
then, subject to certain other technical conditions, the survival S(t) and density f(t) for X have Exponential (b) residue expansions of the form
\begin{equation}S(t)=e^{-bt}\frac{-\beta_{-1}}{b}+o\big(e^{-b^{+}t}\big), \qquad f(t)=e^{-bt}({-}\beta_{-1})+o\big(e^{-b^{+}t}\big), \qquad t\rightarrow \infty, \end{equation}
where
$\beta_{-1}=\text{Res}\{\mathcal{M}(s),b\}$
is the residue of the simple pole at b.
In the current work, we show these expansions apply to first-passage distributions in SMPs whose relevant transient states form an irreducible class (in which all states communicate). The expansions apply to first passage from one state to a new state (Section 3.1.1, Theorem 1), to first passage to a subset of new states (Section 4.1), and to first return to a starting state (Section 4.2.2, Theorem 3). The two keys to showing this are Proposition 3 (Section 3.1), which proves that b is a simple pole when transient states are irreducible, and Proposition 4, (Section 3.1) which proves that b is a dominant pole.
In integer time, comparable Geometric
$\big(e^{-b}\big)$
residue expansions for the survival
$S(n)\,:\!=\,\mathbb{P}(X\geq n)$
and mass function
$p(n)=\mathbb{P}(X=n)$
were developed in [Reference Butler6]. These expansions are given by
\begin{equation}S(n)=e^{-bn}\frac{-\beta_{-1}}{1-e^{-b}}+o\big(e^{-b^{+}n}\big), \qquad p(n)=e^{-bn}({-}\beta_{-1})+o\big(e^{-b^{+}n}\big), \qquad n\rightarrow \infty, \end{equation}
and were shown to hold under much the same conditions: that b is a simple dominant pole of
$\mathcal{M}$
, but also that p(n) is aperiodic and non-degenerate.
In the current paper we show that the expansions in (2) apply to first-passage distributions of SMPs when the relevant transient states form an irreducible class. In integer time, Proposition 3 (Section 3.1) proves that b is a simple pole and, subject to additional aperiodic and non-degenerate requirements on the holding-time distributions in states, Propositions 4–5 (Section 3.1) prove that b is also a dominant pole. Thus these expansions apply to first passage to a new state (Section 3.1.1, Theorem 1), to a subset of new states (Section 4.1), and to first return to a starting state (Section 4.2.2, Theorem 3).
To avoid a proliferation of notation, we use S as a survival function in both continuous and integer time; the argument t or n distinguishes the context. We continue this use of notation for other functions. For example, the leading expansion terms in (1) and (2) are defined as
$S_{1}(t)$
and
$S_{1}(n)$
respectively, even though they are different functions in continuous and integer time.
The residue expansions in (1) and (2) mimic those which may be obtained in finite-state Markov processes in which the leading term is the inversion of the dominant term in a partial-fraction expansion of the rational MGF
$\mathcal{M}$
for a phase-type distribution. In both continuous-time Markov chains (CTMCs) and discrete-time Markov chains (DTMCs), the Perron–Frobenius theory for the infinitesimal generator matrix
$\textbf{Q}$
and the transition probability matrix
$\textbf{P}$
ensure that b is a dominant pole.
The necessity that b is a dominant pole in these two classes of time-homogeneous Markov processes does not carry over to the greater generality of SMPs or to time-heterogeneous Markov processes. Consider a two-state SMP in which the process starts in the working state 1 and goes directly to the failed state
$2.$
This is also a Markov process but is time-heterogeneous unless the holding time in state 1 is exponential. Taking the holding time in state 1 to have density
$f(t)=2e^{-t}(t-\sin t)$
for
$t>0,$
its MGF is
$\mathcal{M}(s)=2(1-s)^{-2}(1+i-s)^{-1}(1-i-s)^{-1}$
with a 2-pole at 1 and simple poles
$1\pm i.$
The pole at 1 contributes the
$O(te^{-t})$
term in the density, while the simple poles add an
$O(e^{-t})$
term. Following O’Cinneide [Reference O’Cinneide19], we do not say that 1 is a dominant pole, and according to Theorem 1.1 of his paper, the density f(t) does not represent a phase-type distribution and is oscillatory with frequency
$2\pi$
into its infinite tail.
There are two main contributions of this paper. First, we identify irreducibility of the transitional states in the sojourn as the main fundamental condition to ensure that the residue expansions in (1) and (2) apply with relative errors of exponentially small order. The means for showing this is to prove that such irreducibility and other conditions lead to a first-passage MGF
$\mathcal{M}$
whose convergence bound b is a positive and simple dominant pole. This then ensures the non-oscillatory exponential/geometric expansions in (1) and (2). These results are proved by applying Perron–Frobenius theory to the Laplace–Stieltjes transform of the semi-Markov kernel.
The second main contribution is to develop some of the author’s more informal results in [Reference Butler1, Reference Butler3] and provide a more mathematically rigorous basis for them as given in Propositions 2–5. These results are needed to formally prove that the convergence bound b is a positive, simple, and dominant pole of the SMP, thus facilitating the main results of the paper.
1.1. Implications, extensions, and background
The similarity of the expansions for Markov processes and SMPs reinforces the insensitivity properties pertaining to SMPs discussed by Tijms in [Reference Tijms23, Section 5.4]. Tijms’s discussion centres on stationary SMPs and notes the insensitivity of the stationary distribution to details of the holding-time distributions for the SMP (they depend only the individual mean holding times). The insensitivity property here applies to the transient behaviour within arbitrary SMPs (stationary or transient) and may be stated as follows. Any two processes, whether Markov or semi-Markov, will exhibit the same first-passage behaviour to order
$o\big(e^{-b^{+}t}\big)$
or
$o\big(e^{-b^{+}n}\big)$
if their first-passage MGFs share a common convergence bound
$b>0$
as a simple dominant pole with the same residue
$\beta_{-1}<0.$
The distributional details of the individual holding-time distributions matter only insofar as they end up summarised in the specific values for b and
$\beta_{-1}.$
Perhaps this helps to explain why Markov processes can be useful for applications in which holding times are known not to be memoryless and independent of the destination state but rather to reflect the properties of an SMP.
If all relevant transient states are progressive, so they cannot be returned to upon exit, then first passage in a finite-state process must necessarily occur in a bounded number of steps using a bounded count of distinct pathways. Expansions for first passage in these settings are detailed in Theorem 5 of Section 7.7 in the supplementary material and have leading terms which are of Gamma
$(\mathfrak{m},b)$
or Discrete Gamma
$(\mathfrak{m},b)$
form.
When relevant transient states for first passage are both progressive and irreducible, expansions as in (1) and (2) are given in Theorem 2 (Section 3.3.1). The same sort of expansions hold for first-return distributions as noted in Theorem 4 (Section 4.2.3). The form of these expansions is largely due to the presence of an irreducible class of states which allows for an unbounded number of steps as well as a countably infinite number of distinct pathways for passage. The unbounded nature of indefinitely feeding back amongst the relevant transient states is reflected in the value of
$b>0$
, which we interpret as the asymptotic hazard rate for exit from the irreducible class; see Section 3.1.4 for details.
Developing such expansions relies on working with a tractable form for the first-passage MGFs. This entails using the cofactor ratio in (4), which was first developed in [Reference Butler1] and is summarised in [Reference Butler3, Chapter 13]. Previous derivations of such MGFs can be found in the development of Mason’s loop-sum rule [Reference Mason17, Reference Mason18] in electrical engineering, which is a ratio of sums expressed in terms of all feedback loops involved in first passage. Also, Pyke [Reference Pyke21] and Howard ([Reference Howard13], [Reference Howard14, Sections 10.10, 11.11]) gave a representation for the first-passage MGF as an entry in the matrix computation in (5). That these two other formulas agree with (4) was shown in [Reference Butler2].
To develop the residue expansions above, new results must be shown to hold for the cofactor expression in (4) for the first-passage MGF. First we prove in Proposition 2 (Section 2.4) that it can be analytically continued beyond its convergence domain. Furthermore, in the same proposition we prove that an equivalent expression in (9), which expresses the MGF as the sum over all distinct pathways, may also be analytically continued. These new results facilitate the proof for the residue expansions, which are based upon using Cauchy’s residue theorem.
The presence of multiple relevant irreducible classes complicates the nature of the pole b, as discussed in Section 5. Examples using identical irreducible subsystems which exist in parallel or in series connections lead to b as either a simple pole or as a 2-pole, respectively.
Two numerical examples in Section 6 demonstrate that the expansions achieve substantially greater accuracy than ordinary saddlepoint approximations. In the continuous-time example, exact computations used to check this accuracy rely on inverting the MGF by numerically integrating along the path of steepest descent, which asymptotically takes the bearing
$\theta=0.$
Inversion using vertical contour integration with bearing
$\theta=\pi/2$
and inside the convergence domain lacks sufficient accuracy to assess expansion accuracy. Above the 75th percentile, the expansions can replace exact computation in these models and potentially in other SMP models.
The paper does not address SMPs with countably infinite state spaces unless first passage only depends on a finite portion of the state space. For example, in a birth–death process on
$\{0,1,\ldots\},$
the results apply to first passage from
$0\rightarrow m$
, but not to first return to
$0.$
The conditional MGF for the latter sojourn time X given
$X<\infty$
has convergence domain
$\{s\in\mathbb{C}\,:-\infty<\text{Re}(s)\leq b\}$
, where b is not a pole but rather a branch point of the square root function.
The residue expansions do not apply to SMPs with heavy-tailed holding-time distributions whose MGFs have convergence regions
$\text{Re}(s)\leq0.$
The cofactor rules for the first-passage MGF
$\mathcal{F}_{1N}$
in (4) and first-return MGF
$\mathcal{F}_{11}$
in (25) are still valid with convergence domain
$\text{Re}(s)\leq0$
, and this leads to two options for inversion. Either one uses saddlepoint approximation if the first-passage MGF is steep at
$s=0$
(a sufficient condition is that
$\mathcal{F}_{1N}^{\prime}(s)\uparrow\infty$
as
$s\uparrow0),$
or else one uses numerical inversion, which is best implemented by following a path of steepest descent from the negative real axis.
2. Notation and basic properties for a semi-Markov process
A finite m-state SMP is characterised by its
$m\times m$
semi-Markov kernel matrix
$\big\{p_{ij}G_{ij}(t)\,:\,i,j\in\mathbb{I}_{m}\big\}$
, where
$\mathbb{I}_{m}=\{1,\ldots,m\}$
is the state space. Row i of this matrix is a vector of sub-distributions which characterises the process for exiting from state i as a competing risk situation. Transition is to state j with probability
$p_{ij}$
and, with destination j ensured, the holding time in state i has distribution
$G_{ij}.$
Any distributional consideration of two or more successive state transitions entails convolving sets of sub-distributions in the time domain. The even more complicated analysis of a sojourn through
$\mathbb{I}_{m}$
becomes quite intractable unless these convolutions are considered in terms of their Laplace–Stieltjes transforms, i.e.
\begin{equation*}\mathcal{T}_{ij}(s)=p_{ij}\int_{0}^{\infty}e^{st}dG_{ij}(t)=p_{ij}\mathcal{M}_{ij}(s),\qquad i,j\in\mathbb{I}_{m}.\end{equation*}
The pair (i, j) is a branch, and the transform
$\mathcal{T}_{ij}(s)$
is referred to as a (branch) transmittance and is defined as the product of a transition probability and an MGF. Suppose the convergence domain for
$\mathcal{M}_{ij}(s)$
is either
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b_{ij}\}$
or
$\{s\in\mathbb{C}\,:\,\text{Re}(s)\leq b_{ij}\}$
for
$b_{ij}>0.$
If
$p_{ij}=0$
it is convenient for notational purposes to assume that
$b_{ij}=\infty.$
With the set of possible branches with
$p_{ij}>0,$
we suppose in the continuous-time setting that the distributions
$\{G_{ij}(t)\,:\,p_{ij}>0\}$
in the semi-Markov kernel matrix admit density functions
$\{g_{ij}(t)\,:\,p_{ij}>0\}$
for which the inversion formula applies to
$\{\mathcal{M}_{ij}(s)\,:\,p_{ij}>0\}.$
Minimal assumptions for this to hold are that
$\{g_{ij}(t)\,:$
$p_{ij}>0\}$
are locally of bounded variation for all values of
$t>0;$
see [Reference Doetsch11, Theorem 24.3].
The Laplace–Stieltjes transform of the semi-Markov kernel is the
$m\times m$
matrix function
\begin{equation*}\textbf{T}(s)=\big\{\mathcal{T}_{ij}(s)\big\}=\big\{p_{ij}\big\}\odot\big\{\mathcal{M}_{ij}(s)\big\}\,:\!=\,\textbf{P}\odot\textbf{M}(s),\end{equation*}
which also characterises the SMP. The matrix
$\textbf{T}(s)$
is the one-step transmittance matrix of the SMP and is the Hadamard product of the transition probability matrix
$\textbf{P}$
and
$\textbf{M}(s)$
. The importance of
$\textbf{T}(s)$
as compared to the semi-Markov kernel is that it provides a direct means by which sojourn times over state space
$\mathbb{I}_{m}$
can be analysed and approximated either by residue expansions or saddlepoint approximations. We refer to the DTMC with transition probability matrix
$\textbf{P}$
as the jump chain for the SMP.
2.1. First-passage distributions to a new state
For any two states in
$\mathbb{I}_{m},$
the probability of first passage from one state to the other and the associated sojourn-time MGF can be written explicitly in terms of the transmittance matrix
$\textbf{T}(s).$
For notational convenience and without loss in generality, suppose the sojourn time X starts in state 1 at time zero and stops upon entering state m. The distribution of X has first-passage transmittance defined as
\begin{equation}f_{1m}\mathcal{F}_{1m}(s)=\mathbb{E}\Big(e^{sX}1_{\{X<\infty\}}\Big), \end{equation}
where
$f_{1m}=\mathbb{P}(X<\infty)$
is the probability of first passage from
$1\rightarrow m\neq1$
and
$\mathcal{F}_{1m}(s)$
is the conditional MGF of X given
$\{X<\infty\},$
i.e. the MGF for sojourn time. In [Reference Butler1] it is shown that the transmittance (3) is determined from
$\textbf{T}(s)$
as
\begin{equation}f_{1m}\mathcal{F}_{1m}(s)=\frac{(m,1)\text{ cofactor of }\textbf{I}_{m}-\textbf{T}(s)}{(m,m)\text{ cofactor of }\textbf{I}_{m}-\textbf{T}(s)}\,:\!=\,\frac{({-}1)^{m+1}|\boldsymbol{\Psi}_{m;\,1}(s)|}{\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|},\end{equation}
where
$|\boldsymbol{\Psi}_{m;\,1}(s)|$
and
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|$
are the (m, 1) and (m, m) minors of
$\textbf{I}_{m}-\textbf{T}(s)$
and
$\textbf{I}_{m}$
is an
$m\times m$
identity matrix.
Historically, an expression for
$f_{1m}\mathcal{F}_{1m}(s)$
was first derived by Mason [Reference Mason17, Reference Mason18] in terms of a ‘loop-sum formula’ used to determine the transfer function connected with complex feedback control systems; see [Reference Phillips and Harbor20]. The loop-sum formula is equivalent to a ratio of the non-zero permutation sums of the cofactors involved in (4), as shown in [Reference Butler2]. Later, Pyke (in [Reference Pyke21, Theorem 4.2]) and Howard (in [Reference Howard13] and [Reference Howard14, Sections 10.10, 11.11]) showed that
$f_{1m}\mathcal{F}_{1m}(s)$
is the (1,m) entry of the matrix
\begin{equation}\textbf{T}(s)\left\{ \textbf{I}_{m}-\textbf{T}(s)\right\} ^{-1}\left(\left[ \left\{ \textbf{I}_{m}-\textbf{T}(s)\right\} ^{-1}\right]_{d}\right) ^{-1}, \qquad \text{Re}(s)\leq0, \end{equation}
where the operation
$\left[ \textbf{A}\right] _{d}$
preserves the diagonal entries of
$\textbf{A}$
and sets off-diagonal entries to
$0.$
The equivalence of (5) to (4) was shown in [Reference Butler2]. Neither Mason’s loop-sum formula nor (5) lends itself to dealing with the nature of the convergence bound b for
$\mathcal{F}_{1m}$
or with computational efficiency when
$\textbf{T}(s)$
reflects complicated state transitions and/or large m.
2.2. Relevant states and convergence domain
The expression (4) requires that all relevant states to the sojourn
$1\rightarrow m$
are included in the state space
$\mathbb{I}_{m}$
of the SMP. For numerical stability, it is also best that only such states are included. A state is not relevant to passage
$1\rightarrow m$
if it is not 1 or m and cannot possibly be a transient intermediate state during the sojourn. For example, any absorbing states or absorbing irreducible classes of states which block the passage
$1\rightarrow m$
are not relevant and are presumed not to be in
$\mathbb{I}_{m}.$
The existence of such non-relevant absorbing states accessible from state 1 ensures that row sums for
$\textbf{P}$
are not all 1 and that
$f_{1m}<1$
when
$\mathbb{I}_{m}=\{$
relevant states for
$1\rightarrow m\}$
. Throughout, we make the following non-restrictive assumption concerning the SMPs considered:
$(\mathcal{R}_{1\rightarrow m})$
The finite state space
$\mathbb{I}_{m}$
consists of exactly those states that are relevant to passage
$1\rightarrow m.$
Without further assumptions, the general convergence domain for (4) is
$\{s\in\mathbb{C}\,:\,\text{Re}(s)\leq0\}.$
With the assumption
$\mathcal{CD}_{1\rightarrow m}$
below, concerning the components of
$\boldsymbol{\Psi}_{m;\,1}$
and
$\boldsymbol{\Psi}_{m;\,m},$
the convergence domain is
$\{\text{Re}(s)<b\}$
where
$b>0$
is the smallest positive zero of
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|.$
Proof of this result is contained in Proposition 2 below. The assumption
$\mathcal{CD}_{1\rightarrow m}$
is as follows:
$(\mathcal{CD}_{1\rightarrow m})$
The convergence domains for
$\big\{\mathcal{M}_{ij}(s)\,:\,(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}\big\},$
in the first
$m-1$
rows of
$\textbf{M}(s)$
take the form
$({-}\infty,b_{ij})$
or
$({-}\infty,b_{ij}]$
with
$\min_{(i,\,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}}b_{ij}>0$
(assuming
$b_{ij}=\infty$
when
$p_{ij}=0$
).
If
$\mathbb{I}_{m}$
includes all relevant states of the SMP and at least one non-relevant state, then (4) continues to hold except at
$s=0.$
This is now formalised, with the proof given in Section 7.1 of the supplementary material.
Proposition 1. (Non-relevant states.) Suppose
$\mathcal{CD}_{1\rightarrow m}$
holds but
$\mathcal{R}_{1\rightarrow m}$
does not, and there is at least one non-relevant state in
$\mathbb{I}_{m}.$
Then
$f_{1m}\mathcal{F}_{1m}(s)$
in the expression (4) has a removable singularity at
$s=0.$
The order of the singularity, or the number of derivatives needed with l’Hôpital’s rule to find the limit as
$s\rightarrow 0$
, is the number of irreducible and absorbing subchains for the non-relevant states in
$\mathbb{I}_{m}.$
Assuming
$\mathcal{R}_{1\rightarrow m}$
and restricting
$\mathbb{I}_{m}$
to relevant states is necessary for numerical stability in the computation of (4) near
$s=0.$
Furthermore, it allows for explicit evaluation of (4) at
$s=0$
to determine
$f_{1m}$
as
\begin{equation*}f_{1m}=f_{1m}\mathcal{F}_{1m}(0)=\frac{({-}1)^{m+1}|\boldsymbol{\Psi}_{m;\,1}(0)|}{|\boldsymbol{\Psi}_{m;\,m}(0)|}\leq1\end{equation*}
without having to use l’Hôpital’s rule.
2.3. Compound distributional representation
Additional insight into the form of
$\mathcal{F}_{1m}(s)$
in (4) has recently been provided in [Reference Butler4, Proposition 3, Section 7], where it is characterised as a compound distribution. Assuming passage from
$1\rightarrow m$
occurs, then the sojourn time X is the compound distribution
\begin{equation}X|\{X<\infty\}\,\overset{D}{=}\,\sum_{i=1}^{m-1}\sum_{j=1}^{m}1\big\{N_{ij}\geq1\big\}\sum_{k=1}^{N_{ij}}H_{ijk}. \end{equation}
Here,
$N_{ij}$
counts the number of transitions
$i\rightarrow j$
in the jump chain for the SMP during its sojourn, and
$\big\{H_{ijk}\,:\,k\geq1\big\}$
are independent and identically distributed as
$G_{ij}.$
Thus, the (i, j)th term on the right-hand side is the total time spent in state i before passing to j during the sojourn. The joint conditional probability generating function (PGF) of
$\textbf{N}=\big\{ N_{ij}\,:\,(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}\big\}$
for the jump chain is
\begin{equation}\mathcal{P}(\textbf{Z}_{m;}\,|\,X<\infty)\,:\!=\,\mathbb{E}\!\left( \prod_{i\in\mathbb{I}_{m-1}}\prod_{j\in\mathbb{I}_{m}}z_{ij}^{N_{ij}}|\,X<\infty\right) =\frac{(m,1)\text{ cofactor of }\textbf{I}_{m}-\textbf{P}\odot\textbf{Z}}{(m,m)\text{ cofactor of }\textbf{I}_{m}-\textbf{P}\odot\textbf{Z}}, \end{equation}
where
$\textbf{Z}=\{z_{ij}\,:\,i,j\in\mathbb{I}_{m}\}$
is
$m\times m,$
and
$\textbf{Z}_{m;}$
is
$\textbf{Z}$
with its last row removed. The choice of notation
$\textbf{Z}_{m;}$
reflects the fact that the right-hand side of (7) does not depend on the last row of
$\textbf{Z}$
, despite its appearance there. The matrix
$\textbf{Z}_{m;}$
with index pairs in
$\mathbb{I}_{m-1}\times\mathbb{I}_{m}$
could be further limited by eliminating those pairs whose transition probabilities
$p_{ij}=0$
; however, doing so would create a notational quagmire which we avoid. As it stands, (7) is correct, since
$N_{ij}=0$
with probability 1 (w.p. 1) when
$p_{ij}=0$
, so that (7) embodies the full generality of the joint PGF during first passage from
$1\rightarrow m.$
The cofactor expression (4) for
$\mathcal{F}_{1m}(s)$
may be interpreted as the compound MGF
$\mathcal{P}\{\textbf{M}_{m;}\,(s)\textbf{|}X<\infty\textbf{\}}$
for the compound distribution in (6), where
$\textbf{M}_{m;}\,(s)$
is
$\textbf{M}(s)$
with its last row removed.
2.3.1. Convergence domain
The convergence domain in
$\mathbb{R}^{(m-1)\times m}$
for
$\mathcal{P}\big(\textbf{Z}_{m;}|\,X<\infty\big)$
in (7) is
$\mathfrak{O}$
defined as the largest connected neighbourhood of
$\textbf{0}\in\mathbb{R}^{(m-1)\times m}$
(
$\text{lcn}_{\textbf{0}})$
for which
$\big\Vert\lambda_{1}\big({\tilde{\textbf{P}}}\odot\textbf{Z}\big)\big\Vert \lt 1$
, where
${\tilde{\textbf{P}}}$
is
$\textbf{P}$
with its mth row replaced by zeros,
$\lambda_{1}({\cdot})$
denotes the eigenvalue of largest modulus for the matrix argument, and
${\Vert\cdot\Vert}$
denotes the complex norm. We write this as
\begin{equation}\mathfrak{O}=\text{lcn}_{\textbf{0}}\!\left\{ \textbf{Z}_{m;}\in\mathbb{R}^{(m-1)\times m}\,:\,\big\Vert\lambda_{1}\big({\tilde{\textbf{P}}}\odot\textbf{Z}\big)\big\Vert \lt 1\right\} . \end{equation}
Let
$\mathbb{Z}^{2}=\big\{(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}\,:\,p_{ij}=0\big\}$
with complement
$\mathbb{\bar{Z}}^{2}=\mathbb{I}_{m-1}\times\mathbb{I}_{m}\backslash\mathbb{Z}^{2}.$
If
$(i,j)\in\mathbb{Z}^{2}$
, then the corresponding factor
$z_{ij}$
in
$\textbf{Z}_{m;}$
has convergence domain
$\mathbb{R}$
, and
$\lambda_{1}\big({\tilde{\textbf{P}}}\odot\textbf{Z}\big)$
is constant with a change in
$z_{ij}.$
For components
$(i,j)\in\mathbb{\bar{Z}}^{2},$
if all such components in
$\mathbb{\bar{Z}}^{2}$
are non-negative, then
$\lambda_{1}({\tilde{\textbf{P}}}\odot\textbf{Z)}$
is real, non-negative, and non-decreasing in each such
$z_{ij}$
; see Section 7.2 of the supplementary material. Thus, with each component of
$\textbf{Z}_{m;}$
ranging over (0,1],
\begin{equation*}\lambda_{1}\big({\tilde{\textbf{P}}}\odot\textbf{Z}\big)\leq\lambda_{1}\big({\tilde{\textbf{P}}}\odot\textbf{11}^{T}\big)=\lambda_{1}\big({\tilde{\textbf{P}}}\big)=\lambda_{1}\big(\textbf{P}_{m;\,m}\big)<1, \qquad \textbf{Z}\in\lbrack 0,1]^{m\times m},\end{equation*}
where
$\textbf{P}_{m;\,m}$
is
$\textbf{P}$
without its mth row and mth column. To show the last inequality, consider the case when the subset of states
$\mathbb{I}_{m-1}$
has one or more irreducible classes. Then
$\lambda_{1}\big(\textbf{P}_{m;\,m}\big)$
is the Perron–Frobenius eigenvalue for one of these subblocks, all of which are
${<}1$
owing to the removal of the mth column; see Section 7.2 of the supplementary material for more details. Thus
$\lambda_{1}\big(\textbf{P}_{m;\,m}\big)<1$
and
$\mathfrak{O}$
includes the unit square
$[0,1]^{(m-1)\times m}$
in its interior. Alternatively, if all states in
$\mathbb{I}_{m-1}$
are progressive and not repeatable, then
$\lambda_{1}\big(\textbf{P}_{m;\,m}\big)=0$
, so
$\mathfrak{O}=\mathbb{R}^{(m-1)\times m}.$
Convergence in the square
$[0,1]^{(m-1)\times m}$
may be expanded to convergence in
$[-1,1]^{(m-1)\times m}.$
Since
$\mathcal{P}$
is a PGF, we have for any real-valued
$\textbf{Z}_{m;}$
that
$|\mathcal{P}(\textbf{Z}_{m;}\,|\,X<\infty)|\leq\mathcal{P}(\Vert{\textbf{Z}}_{m;}\,\Vert\,|\,X \lt \infty),$
where
${\Vert{\textbf{Z}}}_{m;}\,\Vert$
denotes the
$(m-1)\times m$
matrix of componentwise moduli. Thus,
$\mathfrak{O}\supset\{\textbf{Z}_{m;}\in[-1,1]^{(m-1)\times m}\}.$
The convergence domain in
$\mathbb{R}$
for
$\mathcal{F}_{1m}(s)$
expressed as the compound MGF in (4) is the largest neighbourhood of 0 in which
$\lambda_{1}\big\{{\tilde{\textbf{P}}}\odot\textbf{M}(s)\big\}<1$
or
\begin{equation*}\text{lcn}_{0}\big[ s\in\mathbb{R}\,:\,\lambda_{1}\big\{{\tilde{\textbf{P}}}\odot\textbf{M}(s)\big\}<1\big] =\{s<b\}.\end{equation*}
Subject to the conditions
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}$
, b is the smallest positive zero of
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|$
if
$\mathbb{I}_{m-1}$
contains at least one irreducible subset of states; this follows from Perron–Frobenius theory as shown in Section 7.2 of the supplementary material. If all states in
$\mathbb{I}_{m-1}$
are progressive states, then
$b=\min\big\{b_{ij}\,:\,i\in\mathbb{I}_{m-1},j\in\mathbb{I}_{m}\backslash\{1\}\big\}$
. The value
$s=0$
is in the interior of this set and
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|>0$
for
$s\leq0.$
Thus,
$b>0$
and the first-passage distribution has all its moments.
2.4. As a countably infinite mixture summing over all distinct pathways
The first-passage distribution with MGF
$\mathcal{F}_{1m}(s)$
may also be represented as a countably infinite mixture distribution using the total probability formula. The mixing components represent distinct pathways from
$1\rightarrow m$
, and these components are products of one-step transmittances along the distinct pathways. More specifically, let
$\mathfrak{P=\{p\}}$
denote the countably infinite collection of distinct finite-step pathways for first passage from
$1\rightarrow m$
, and let
$T_{\mathfrak{p}}(s)$
be the transmittance of pathway
$\mathfrak{p}$
, defined as the product of all one-step transmittances along that pathway. For example, if
$\mathfrak{p}$
is the pathway
$1\rightarrow 2\rightarrow m$
, then
$\mathcal{T}_{\mathfrak{p}}(s)=\mathcal{T}_{12}(s)\mathcal{T}_{2m}(s).$
Proposition 2. (Sum over all distinct pathways.) Under the conditions
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}$
, the cofactor expression for
$f_{1m}\mathcal{F}_{1m}(s)$
given in (4) agrees with the sum over all distinct pathways as expressed in (9) on the convergence domain
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b\}$
where b is the smallest positive zero of
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|$
:
\begin{equation}f_{1m}\mathcal{F}_{1m}(s)=\sum_{\mathfrak{p\in P}}\mathcal{T}_{\mathfrak{p}}(s), \qquad \text{Re}(s)<b. \end{equation}
In the analytic continuation of
$f_{1m}\mathcal{F}_{1m}(s)$
given by
$\{\text{Re}(s)\geq b\},$
the identity (9) continues to hold on
\begin{equation}\mathfrak{R}=\left\{ s\in\mathbb{C}\,:\,\text{Re}(s)\geq b\text{ and }\max_{(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}\,:\,p_{ij}>0}\Vert\mathcal{M}_{ij}(s)\Vert<1\right\} . \end{equation}
The representation of the first-passage transmittance as the sum in (9) over all distinct pathways was first considered in [Reference Butler2], which showed directly that the right side of (9) takes the very compact form given in (4) for
$\{\text{Re}(s)<b\}$
but not for
$s\in\mathfrak{R}.$
We provide a different formal proof of (9), as well as the extension of the identity (9) to the set
$\mathfrak{R}$
, in Section 7.3 of the supplementary material. This extension to
$\mathfrak{R}$
is fundamental and needed to derive the expansions in Theorem 1 using Cauchy’s deformation theorem. Further discussion of such passage-time distributions is found in [Reference Butler1] and [Reference Butler3, Chapter 13].
3. Asymptotic expansions for first-passage distributions
Expansions for such distributions will be provided in three common settings: when all transient states form an irreducible class (and therefore communicate), when such states are progressive and no state may be repeated, and when transient states have both progressive states and an irreducible block. For all settings, the conditions needed for valid expansions are simple and quite weak.
3.1. Relevant states form an irreducible class
Consider SMPs in which all states in
$\mathbb{I}_{m-1}$
communicate to form an irreducible class. The transient states in
$\mathbb{I}_{m-1}$
may be reentered an indefinite number of times, but the process is certain to either arrive at state m or leave
$\mathbb{I}_{m}$
altogether (without arriving at m) in finite time with a finite number of steps. Practical examples for such settings have been given in [Reference Butler1] and [Reference Butler3, Chapters 13–15].
Let
$b_{\mathcal{I}}=\min_{(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m-1}}b_{ij},$
define
$\mathcal{L}=\big\{(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m-1}\,:\,b_{ij}=b_{\mathcal{I}}\big\}$
, and let
$b_{\min}=\min_{(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}}b_{ij}.$
The next result has a long and rather difficult proof, given in Section 7.4 of the supplementary material.
Proposition 3. (Simple pole b.) Consider a continuous- or integer-time SMP satisfying the conditions
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}.$
Let the transient states
$\mathbb{I}_{m-1}$
form an irreducible class. With the additional conditions
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow m}$
below,
$\mathcal{F}_{1m}(s)$
has convergence bound b such that
$b<b_{\min}$
and b is a simple pole of
$\mathcal{F}_{1m}(s)$
:
$(\mathcal{L}_{\text{reg}})$
For some branch
$\mathfrak{b}\in\mathcal{L},$
the convergence domain for
$\mathcal{M}_{\mathfrak{b}}(s)$
is regular, i.e. it is the open set
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b_{\mathcal{I}}\}.$
$(\mathcal{FS}_{\rightarrow m})$
We have
$b<\min_{i\in\mathbb{I}_{m-1}}b_{im},$
where
$\{b_{im}\}$
are the convergence bounds for MGFs of the final step into state m.
In the majority of applications, all components of
$\textbf{M}_{m;}\,(s)$
are regular, so that both
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{CD}_{1\rightarrow m}$
hold. Since the condition
$\mathcal{R}_{1\rightarrow m}$
is without loss in generality, the conditions of Proposition 3 are minimal and simple: that transient states
$\mathbb{I}_{m-1}$
form an irreducible class and the necessary condition
$\mathcal{FS}_{\rightarrow m}$
holds.
The bound
$b_{\min}$
for b is often quite crude, as b is typically much closer to
$0.$
A value
$b_{1}>0$
is an upper bound for b if the smallest row sum of
$\textbf{T}_{m;\,m}(b_{1})$
exceeds
$1.$
This result follows from the fact that b solves
$0=|\boldsymbol{\Psi}_{m;\,m}(b)|=|\textbf{I}_{m-1}-\textbf{T}_{m;\,m}(b)|$
, so that 1 is the Perron–Frobenius eigenvalue for
$\textbf{T}_{m;\,m}(b).$
By Corollary 1 to Theorem 1.5 in [Reference Seneta22], if the smallest row sum of
$\textbf{T}_{m;\,m}(b_{1})$
exceeds 1, then
$\textbf{T}_{m;\,m}(b_{1})$
has a Perron–Frobenius eigenvalue larger than 1, and hence
$b<b_{1}.$
The value b is therefore close to 0, since all row sums of
$\textbf{T}_{m;\,m}(0)=\textbf{P}_{m;\,m}$
are typically close to
$1.$
The generality of Proposition 3 allows
$\textbf{M}_{m;}\,(s)$
to have non-regular components. For example,
$\mathcal{M}_{ij}(s)$
can have convergence region
$({-}\infty,b_{ij}],$
as would occur with an inverse Gaussian MGF, if
$(i,j)\in(\mathbb{I}_{m-1}\times\mathbb{I}_{m})\backslash\mathcal{L}.$
The result does not specify what happens if all members of
$\mathcal{L}$
are non-regular. Indeed,
$b<b_{\min}$
may very well still hold (see the example in Section 6.1), since
$\mathcal{L}_{\text{reg}}$
is not a necessary condition; only
$\mathcal{FS}_{\rightarrow m}$
is necessary. Neither condition is necessary for the convergence bound b to be a simple pole.
An important consequence of Propositions 2 and 3 is that the cofactor ratio in (4) provides an explicit expression for the analytic continuation of
$\mathcal{F}_{1m}(s)$
just across its convergence boundary
$\{s\in\mathbb{C}\,:\,\text{Re}(s)=b\}$
, as stated in the next proposition. The somewhat involved proof is given in Section 7.5 of the supplementary material. Propositions 2–5 together lead to simple asymptotic expansions of exponential/geometric form for first-passage survival and density functions, as given further below in Theorem 1.
Proposition 4. (Dominant pole b.) Assume
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}$
, that the transient states
$\mathbb{I}_{m-1}$
form an irreducible class, and either that
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow m}$
hold or else that the conclusions of Proposition 3 hold. Then b is a dominant pole as detailed in the following two cases:
Continuous time. Apart from the pole at b,
$\mathcal{F}_{1m}$
can be analytically continued to
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b+\varepsilon_{0}\}\backslash\{b\}$
using the expression (4) for some
$\varepsilon_{0}>0.$
Integer time. Suppose
$|\boldsymbol{\Psi}_{m;\,m}(b+iy)|\neq0$
for
$0\neq y\in({-}\pi,\pi].$
Then, apart from the pole at b,
$\mathcal{F}_{1m}$
can be analytically continued into the principal convergence domain
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b+\varepsilon_{0},$
$-\pi<\text{Im}(s)\leq\pi\}\backslash\{b\}$
using the expression (4) for some
$\varepsilon_{0}>0.$
Assuming the conclusions of Proposition 3 rather than their sufficient conditions
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow m}$
widens the applicability of Proposition 4. This happens for the example in Section 6.1 where the condition
$\mathcal{L}_{\text{reg}}$
fails but its conclusions hold.
In the CTMC setting, the same result forms part of a characterisation for the class of phase-type distributions as shown by O’Cinneide [Reference O’Cinneide19, Theorem 1.1]. He showed that the dominance of the pole b is a necessary and sufficient condition for the distribution to be of phase type. Thus the result above extends the necessity part of this result to a general class of continuous-time SMPs.
In integer time, this result cannot hold with the same generality since the first-passage mass function could be d-periodic. We say the mass function
$\{p(n)\,:\,n\geq0\}$
is aperiodic if
$1=\gcd\{n_{2}-n_{1}\,:\,p(n_{1})>0<p(n_{2})$
and
$n_{2}>n_{1}\},$
where
$\gcd$
indicates the greatest common divisor. With periodicity, the simple pole at b is replicated by an additional
$d-1$
simple poles equally spaced along the vertical line
$\{b+iy\,:\,0\neq y\in({-}\pi,\pi]\}.$
For example, with
$p=2,$
$b+i\pi$
is also a simple pole.
If the first-passage mass function is aperiodic, then it remains unclear whether or not multiple poles can occur along this vertical line, and that is the reason for the extra condition in Proposition 4. In the much simpler DTMC setting, if the class
$\mathbb{I}_{m-1}$
is aperiodic, then the first-passage mass function must be aperiodic and its MGF must have a dominant pole at b. This follows from the Perron–Frobenius theory of [Reference Seneta22, Theorem 1.1] as applied to the primitive matrix
$\textbf{P}_{m;\,m}$
in the expression
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|=|\textbf{I}_{m-1}-\textbf{P}_{m;\,m}e^{s}|;$
see Section 3.4.2 and Corollary 3 for further consideration. Along the same lines, [Reference O’Cinneide19, Theorem 1.2] showed that this dominance characterises phase-type distributions of the type we consider here for DTMCs, in which the relevant states form an irreducible class.
In practice, it is perhaps simplest to just check for no zeros of
$|\boldsymbol{\Psi}_{m;\,m}(b+iy)|$
for
$y\in(0,\pi]$
along the upper half of the convergence boundary, since the lower half assumes complex conjugate values for
$|\boldsymbol{\Psi}_{m;\,m}(b-iy)|.$
Checking for zeros is unnecessary when the sufficient condition of the next proposition holds. The proof is in Section 7.5.2 of the supplementary material.
Proposition 5. (Alternative conditions in integer time for a dominant pole b.) The non-degenerate and aperiodic condition
$\mathcal{ND}\hbox{-}\mathcal{A}_{1\rightarrow m}$
below suffices for guaranteeing that
$|\boldsymbol{\Psi}_{m;\,m}(b+iy)|\neq0$
for
$0\neq y\in({-}\pi,\pi]$
:
$\big(\mathcal{ND}-\mathcal{A}_{1\rightarrow m}\big)$
In integer time, the one-step mass functions for transitions from
$\mathbb{I}_{m-1}\rightarrow \mathbb{I}_{m}$
are non-degenerate and aperiodic.
The condition
$\mathcal{ND}\hbox{-}\mathcal{A}_{1\rightarrow m}$
is violated by a DTMC in which all one-step mass functions are degenerate at
$1.$
3.1.1. Residue expansions
The expansions in Theorem 1 below apply to the conditional distribution of the first-passage time X given
$X<\infty.$
This conditional distribution is a proper distribution which sums to 1 and has MGF
$\mathcal{F}_{1m}(s).$
The theorem applies when X has either a non-defective distribution with
$f_{1m}=\mathbb{P}\{X=\infty\}=0$
or a defective distribution with
$f_{1m}>0.$
The distribution is defective if the process may be diverted into a non-relevant state not in
$\mathbb{I}_{m-1}$
, thus preempting passage
$1\rightarrow m.$
This occurs when the row sums of
$\textbf{P}_{m;}$
are not all
$1.$
For integer-time SMPs, the geometric expansions and their errors hold under minimal assumptions. For continuous-time SMPs, exponential expansions with errors are given, but they require some additional weak assumptions. One such assumption concerns a blockade
$\mathcal{B}$
for passage
$1\rightarrow m$
in
$\mathbb{I}_{m}$
, which is defined as a minimal set of branches or transition steps from
$\mathbb{I}_{m-1}\rightarrow \mathbb{I}_{m}$
which, when removed, prohibits passage from
$1\rightarrow m.$
Another assumption concerns an unbounded-step blockade
$\mathcal{B}_{U}$
for passage
$1\rightarrow m$
, which is a minimal set of branches from
$\mathbb{I}_{m-1}\rightarrow \mathbb{I}_{m}$
which, when removed, prohibits passage from
$1\rightarrow m$
using an unbounded number of steps; for such a blockade, it suffices to remove enough branches so that all feedback loops in
$\mathbb{I}_{m-1}$
are broken. The proofs are long and involved and therefore given in Section 7.6 of the supplementary material.
Theorem 1. (Geometric and exponential expansions.) Suppose that the conditions
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}$
hold and that the transient states
$\mathbb{I}_{m-1}$
form an irreducible class. Also suppose either the conditions
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow m}$
used in Proposition 3 or else the conclusions of Proposition 3 that
$b<b_{\min}$
is a simple pole of
$\mathcal{F}_{1m}(s).$
Denote by
$\beta_{-1}=\text{Res}\{\mathcal{F}_{1m}(s);\,b\}$
the residue of
$\mathcal{F}_{1m}(s)$
at b, which takes the form
\begin{equation}\beta_{-1}=\frac{\left| \boldsymbol{\Psi}_{m;\,m}\!\left( 0\right) \right|}{\left| \boldsymbol{\Psi}_{m;\,1}\!\left( 0\right) \right| }\frac{\left|\boldsymbol{\Psi}_{m;\,1}\!\left( b\right) \right| }{\text{tr}\left[\text{adj}\{\boldsymbol{\Psi}_{m;\,m}\!\left( b\right) \}\boldsymbol{\Psi}_{m;\,m}^{\prime}\!\left( b\right) \right] }. \end{equation}
Here,
$\text{adj}\{\cdot\}$
denotes the
$(m-1)\times(m-1)$
adjoint of the matrix argument, and
$\boldsymbol{\Psi}_{m;\,m}^{\prime}\!\left( b\right) =d\boldsymbol{\Psi}_{m;\,m}(s)/ds|_{s=b}.$
Integer time. Subject to the additional integer-time conditions in either Proposition 4 or Proposition 5, the first-passage survival and mass functions of
$X|X<\infty$
have Geometric
$\big(e^{-b}\big)$
tail expansions as
$n\rightarrow \infty$
given by
\begin{align}S(n) & \,:\!=\,\mathbb{P}(X\geq n|X<\infty)=S_{1}(n)+R_{1}^{S}(n)\,:\!=\,e^{-bn}\frac{-\beta_{-1}}{1-e^{-b}}+R_{1}^{S}(n),\nonumber\\\rule[-0.09in]{0in}{0.27in}p(n) & \,:\!=\,\mathbb{P}(X=n|X<\infty)=p_{1}(n)+R_{1}(n)\,:\!=\,e^{-bn}({-}\beta_{-1})+R_{1}(n). \end{align}
The mass function error
$R_{1}(n)$
in (12) is
\begin{equation}R_{1}(n)\,:\!=\,e^{-b^{+}n}\frac{1}{2\pi}\int_{-\pi}^{\pi}\mathcal{F}_{1m}(b^{+}+iy)e^{-iyn}dy=o\big(e^{-b^{+}n}\big),\qquad n\rightarrow \infty, \end{equation}
where
$b^{+}=b+\varepsilon$
for sufficiently small
$\varepsilon>0.$
The survival function error
$R_{1}^{S}(n)$
is the same integral with the additional integrand factor
$\big(1-e^{-b^{+}-iy}\big)^{-1}.$
Continuous time. Subject to the additional blockade assumption
$\mathcal{B}_{1\rightarrow m}$
below, the first-passage survival function for
$X|X<\infty$
has an Exponential (b) tail expansion given by
\begin{equation}S(t)=S_{1}(t)+R_{1}^{S}(t)\,:\!=\,e^{-bt}\frac{-\beta_{-1}}{b}+R_{1}^{S}(t),\end{equation}
where
$\beta_{-1}$
is the residue in (11). The error is
\begin{equation}R_{1}^{S}(t)\,:\!=\,e^{-b^{+}t}\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{\mathcal{F}_{1m}(b^{+}+iy)}{b^{+}+iy}e^{-iyt}dy=o\big(e^{-b^{+}t}\big),\qquad t\rightarrow \infty. \end{equation}
The condition
$\mathcal{B}_{1\rightarrow m}$
is as follows:
$(\mathcal{B}_{1\rightarrow m})$
A blockade
$\mathcal{B}\subset\mathbb{I}_{m-1}\times\mathbb{I}_{m}$
for passage
$1\rightarrow m$
exists such that each member
$(i,j)\in\mathcal{B}$
has
$\left\| \mathcal{M}_{ij}(b^{+}+iy)\right\| ^{q}$
integrable in y for a sufficiently large
$q=q(i,j)\geq1.$
Subject to the assumptions
$\mathcal{BTV}_{1\rightarrow m}$
,
$\mathcal{ZD}_{1\rightarrow m}$
, and
$\mathcal{UB}_{1\rightarrow m}$
below, the first-passage density function has expansion
\begin{equation}\rule[-0.09in]{0in}{0.27in}f(t)=f_{1}(t)+R_{1}(t)\,:\!=\,e^{-bt}({-}\beta_{-1})+R_{1}(t), \end{equation}
with error
$R_{1}(t)=o\big(e^{-b^{+}t}\big)$
as in (15) but without the factor
$b^{+}+iy$
in the denominator of the integrand:
$(\mathcal{BTV}_{1\rightarrow m})$
A blockade
$\mathcal{B}\subset\mathbb{I}_{m-1}\times\mathbb{I}_{m}$
for passage
$1\rightarrow m$
exists such that each member
$(i,j)\in\mathcal{B}$
has one-step transition density
$g_{ij}(t)$
with finite total variation.
$(\mathcal{ZD}_{1\rightarrow m})$
We have
$e^{b^{+}t}g_{ij}(t)\rightarrow 0$
as
$t\rightarrow \infty$
for all
$(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}.$
$(\mathcal{UB}_{1\rightarrow m})$
An unbounded-step blockade
$\mathcal{B}_{U}\subseteq\mathbb{I}_{m-1}\times\mathbb{I}_{m-1}$
exists such that each member
$(i,j)\in\mathcal{B}_{U}\subseteq\mathbb{I}_{m-1}\times\mathbb{I}_{m-1}$
has
$\left\| \mathcal{M}_{ij}(b^{+}+iy)\right\| ^{q}$
integrable in y for sufficiently large
$q=q(i,j)\geq1.$
In integer time when
$\mathcal{F}_{1m}$
is periodic, expansions of order
$o\big(e^{-b^{+}n}\big)$
can be obtained if the single-term expansions in (12) are replaced with multiple-term expansions which capture the residues of all poles on the boundary
$\{s=b+iy\,:\,\text{Im}(y)\in({-}\pi,\pi]\};$
see [Reference Butler6, Section 9.4].
In continuous time, the ‘smoothness’ assumptions
$\mathcal{B}_{1\rightarrow m}$
and
$\mathcal{UB}_{1\rightarrow m}$
apply to powers of
$\mathcal{M}_{ij}(b^{+}+iy)$
, which is the characteristic function for the tilted density
$e^{b^{+}t}g_{ij}(t).$
These conditions imply that its q(i, j)-fold convolution leads to a bounded and continuous density [Reference Feller12, Section XV.3, Theorem 33]. Such assumptions allow, for example,
$g_{ij}$
to be Gamma
$(a_{ij},b_{ij})$
for any
$a_{ij}>0$
, including unbounded/discontinuous densities with
$0<a_{ij}\leq1.$
However, for density expansions, blockades satisfying
$\mathcal{BTV}_{1\rightarrow m}$
must exclude transitions with unbounded gamma densities and
$a_{ij}<1.$
The condition
$\mathcal{ZD}_{1\rightarrow m}$
is very weak, since a density
$g_{ij}$
which violates it would have to be quite ‘lumpy’ into its infinite tail, given that
$b^{+}<b_{ij}.$
A variety of other conditions which commonly hold could have been used in place of
$\mathcal{ZD}_{1\rightarrow m}$
and
$\mathcal{UB}_{1\rightarrow m}$
to get the density expansions of Theorem 1. Corollary 1 formalises one such result, motivated by the fact that, like the conditions
$\mathcal{ZD}_{1\rightarrow m}$
and
$\mathcal{UB}_{1\rightarrow m},$
the conditions apply to the class of CTMCs. A proof is given in Section 7.6.2 of the supplementary material.
Corollary 1. (Alternate conditions for density expansions.) The conclusions concerning the density expansion of Theorem 1 continue to hold if the conditions
$\mathcal{ZD}_{1\rightarrow m}$
and
$\mathcal{UB}_{1\rightarrow m}$
are replaced with
$\mathcal{ONE}_{1\rightarrow m}$
and
$\mathcal{MIN}_{1\rightarrow m}$
below:
$(\mathcal{ONE}_{1\rightarrow m})$
If
$p_{1m}>0,$
then there exists
$T_{0}$
such that
$\int_{-\infty}^{\infty}\mathcal{M}_{1m}(b^{+}+iy)e^{-ity}dy$
is uniformly integrable for
$t>T_{0}.$
$(\mathcal{MIN}_{1\rightarrow m})$
Apart from a one-step passage, if the minimum number of steps for passage
$1\rightarrow m$
is
$q\geq2$
steps, then assume
$\left\|\mathcal{M}_{ij}(b^{+}+iy)\right\| ^{q}$
is integrable in y for all
$(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}.$
3.1.2. Applicability to Markov chains
If an SMP is a DTMC or a conservative CTMC, then to apply Theorem 1 the following assumptions are made: only relevant states are considered
$(\mathcal{R}_{1\rightarrow m})$
, and the transient states of
$\mathbb{I}_{m-1}$
form an irreducible class. The conditions
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow m}$
of Proposition 3 hold automatically. The other assumptions depend upon whether time is continuous or integer-valued.
In conservative CTMCs, denote the exit rate from relevant state i by
$-q_{ii}>0$
, so that
$\mathcal{M}_{ij}(s)=(1+s/q_{ii})^{-1}.$
This ensures that all conditions of Theorem 1 and Corollary 1 hold. Thus, the survival and density expansions in (14) and (16) hold. In the condition
$\mathcal{ONE}_{1\rightarrow m},$
the uniform integrability of the exponential MGF
$\mathcal{M}_{1m}$
follows from using an integration-by-parts argument while the condition
$\mathcal{MIN}_{1\rightarrow m}$
holds with
$q=2.$
For DTMCs, the condition
$\mathcal{ND}-\mathcal{A}_{1\rightarrow m}$
is violated since each one-step distribution is degenerate at
$1.$
However,
$\mathcal{ND}-\mathcal{A}_{1\rightarrow m}$
holds when
$p_{ii}>0$
for all
$i\in\{1,\ldots,m-1\}$
if the process is reformulated so that all one-step feedback transitions are removed. This alternative reformulation, for first-passage purposes, is the Markov process in which one-step return to state i is not allowed and exit from state i to a different state
$j\neq i$
has a Geometric
$(p_{ii})$
holding time with transition probability
$p_{ij}/(1-p_{ii})$
. It is in this form that Theorem 1 applies to a DTMC.
If a DTMC is aperiodic (a single
$p_{ii}>0$
ensures this), then [Reference O’Cinneide19, Theorem 1.2] showed that
$\mathcal{F}_{1m}$
must have a simple real-valued dominant pole on its convergence boundary since it represents a phase-type distribution. See Section 4.4.2 for more discussion of DTMCs.
In both DTMCs and CTMCs the expansions of Theorem 1 are well established, since PGF
$\mathcal{F}_{1m}(\ln s)$
and MGF
$\mathcal{F}_{1m}(s)$
respectively are rational and the expansions follow directly from their partial-fraction expansions. The importance of Theorem 1 is that it rather applies to SMPs whose transmittance matrix
$\textbf{T}$
consists of non-rational one-step MGFs.
3.1.3. Relationship to literature
The expansions in Theorem 1 were first developed in [4, Section 7] and were derived using proofs with stronger and different conditions. These proofs used Darboux’s theorem in integer time and the Ikehara–Wiener Tauberian theorem in continuous time, with both of these theories finding their origins in analytic number theory. This previous work, however, was limited to providing only the expansion orders as
$o\big(e^{-bn}\big)$
and
$o\big(e^{-bt}\big)$
, whereas Theorem 1 provides explicit integral-form error terms for
$R_{1}(n),$
$R_{1}^{S}(n),$
$R_{1}(t),$
and
$R_{1}^{S}(t)$
which have these asymptotic orders. As will be seen in Section 6.2, this explicit integral form allows these errors to be approximated by using saddlepoint methods. This then improves the expansions by allowing additive saddlepoint corrections as described in [Reference Butler5, Section 2.4] and [Reference Butler6, Section 3].
The development here goes beyond that of [Reference Butler4, Section 7] by basing assumptions on more fundamental properties of the SMP. In this previous work, b was assumed to be a simple pole, whereas in Proposition 3 this property is proved and follows from the more basic assumption that the states in
$\mathbb{I}_{m-1}$
are irreducible. Also, in previous work,
$\mathcal{F}_{1m}$
was only shown to be analytically extendable to
$\{\text{Re}(s)\leq b\}\backslash\{b\}$
, whereas in Proposition 4 it is shown to be analytically extendable to
$\{\text{Re}(s)<b+\varepsilon_{0}\}\backslash\{b\}$
for some
$\varepsilon_{0}>0.$
This may seem to be a minor extension, but it is crucially needed in order to use Cauchy’s deformation theorem in deriving the results of Theorem 1. Finally, the conditions placed on the one-step densities
$\{g_{ij}(t)\}$
to get a first-passage density expansion are weaker than the Tauberian-type conditions in [Reference Butler4], which require that tilted versions of these densities are ultimately monotone decreasing for large t.
3.1.4. The asymptotic hazard rate for exit from the class
$\mathbb{I}_{m-1}$
From Theorem 1, the asymptotic hazard rate for the sojourn from
$1\rightarrow m,$
which reflects the tail of the distribution of
$\mathcal{F}_{1m},$
is
$b>0$
in continuous time and
$1-e^{-b}$
in integer time and is consistent with the findings in [Reference Butler4, Theorems 1–2]. No finite-step or finite-time aspect of the transient process determines the value of b. Its value is associated with a sojourn that maintains itself in perpetual transience by continuing to feed back within the class
$\mathbb{I}_{m-1}.$
Thus the value b is characterised only by the transitional properties within the class
$\mathbb{I}_{m-1}$
, and this is reflected in its value as the smallest positive root of
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|.$
It is therefore natural to refer to b as the asymptotic hazard rate for exit from the irreducible class
$\mathbb{I}_{m-1}.$
3.2. All relevant states are progressive
We now consider the case in which the transient states of
$\mathbb{I}_{m-1}$
are progressive, so these states can only be entered a single time during a sojourn. This means self-looping is not allowed, so
$p_{ii}=0$
for all
$i\in\mathbb{I}_{m-1}.$
When this occurs, the denominator factor for
$\mathcal{F}_{1m}$
is
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|\equiv1$
for all s. To show this, order the states in
$\mathbb{I}_{m-1}$
in such a way that if transition
$i\rightarrow j$
is possible in a single step then
$i<j.$
The resulting matrix
$\textbf{T}_{m;\,m}(s)$
has zeros in all entries on or below its diagonal. Thus,
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|=|\textbf{I}_{m-1}-\textbf{T}_{m;\,m}(s)|=1$
and, from (4),
\begin{equation}\mathcal{F}_{1m}(s)=({-}1)^{m+1}|\boldsymbol{\Psi}_{m;\,1}(s)|. \end{equation}
The non-zero portion of the permutation sum of the cofactor in (17) enumerates all possible disjoint pathways that the sojourn can take from
$1\rightarrow m.$
Thus the distribution of X is a finite mixture/convolution distribution. The sojourn-time MGF
$\mathcal{F}_{1m}(s)$
has convergence domain
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b\}$
or
$\{s\in\mathbb{C}\,:\,\text{Re}(s)\leq b\}$
with
$0<b=\min\big\{b_{ij}\,:\,(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m},$
$i<j\big\}.$
Let
$\mathcal{L}=\big\{(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m},$
$i<j\,:\,b_{ij}=b\big\}$
denote the set of one-step branches with b as the common convergence bound.
Asymptotic expansions continue to hold in both integer and continuous time, but now
$\mathcal{F}_{1m}$
shares the same convergence domain as the one-step MGFs in
$\mathcal{L}.$
Since its convergence domain is no longer a proper subset of the domains for all the one-step components of
$\boldsymbol{\Psi}_{m;\,1}(s),$
different assumptions are needed to obtain the expansions, and these concern the analytic continuations of one-step MGFs in
$\mathcal{L}$
as specified in Theorem 5. The proof is in Section 7.7 of the supplementary material.
3.3. Relevant states are progressive and irreducible
Suppose an SMP consists of both transient states in
$\mathcal{T}$
and a single irreducible subchain
$\mathcal{J}$
with a stationary distribution. If states 1 and m are both in
$\mathcal{T}$
$(\mathcal{J})$
, then the other states in
$\mathcal{J}$
$(\mathcal{T})$
are not relevant to first passage
$1\rightarrow m$
, so
$\mathbb{I}_{m-1}$
comprises only the relevant states in
$\mathcal{T}$
$(\mathcal{J}).$
This leaves the case
$1\in\mathcal{T}$
and
$m\in\mathcal{J}$
where the relevant states for passage are those relevant from
$\mathcal{T}\cup\mathcal{J}.$
Not all states in
$\mathcal{J}\backslash\{m\}$
are necessarily relevant, as those reachable only after passing through state m are not relevant to the first passage.
In all three settings above, if state m is removed from the relevant class, then
$\mathbb{I}_{m-1}$
consists entirely of transient states, but there may be
$0,1,2,\ldots,m-2$
irreducible subclasses. (There are
$m-2$
such classes when exit from each of the states
$2,\ldots,m-2$
is return to that same state or else direct passage to state
$m).$
The next subsection deals with the most common situation, in which there is a single irreducible subclass in
$\mathbb{I}_{m-1}.$
3.3.1. Relevant states are progressive with one irreducible subclass
Consider the general class of SMPs in which the states in
$\mathbb{I}_{m-1}$
may be partitioned into a progressive class
$\mathcal{P}$
of size p and a single irreducible subclass
$\mathcal{I}$
of size
$I=m-1-p.$
The designation of
$\mathcal{I}$
as irreducible simply means that
$\textbf{P}_{\mathcal{II}},$
the
$\mathcal{I}\times\mathcal{I}$
subblock of
$\textbf{P,}$
satisfies the condition that
$\textbf{P}_{\mathcal{II}}^{n}>\textbf{0}$
componentwise for some n.
Upon distinguishing two classes
$\mathcal{P}$
and
$\mathcal{I}$
of relevant states, it becomes necessary to distinguish those progressive states
$\mathcal{P}^{1}\subseteq\mathcal{P}$
that can be realised before entering into
$\mathcal{I}$
and those
$\mathcal{P}^{2}\subseteq\mathcal{P}$
realised after leaving
$\mathcal{I}.$
The two subsets are disjoint since any state which could be entered both before and after
$\mathcal{I}$
would not be progressive.
There are two possible models, determined by whether
$1\in\mathcal{I}$
or
$1\in\mathcal{P}^{1}.$
The two models use state decompositions
$\mathbb{I}_{m-1}=\mathcal{I\cup P}^{2}$
and
$\mathbb{I}_{m-1}=\mathcal{P}^{1}\cup\mathcal{I\cup P}^{2}$
, respectively. We assume the latter, which includes the former by taking
$\mathcal{P}^{1}=\emptyset.$
Thus, Proposition 6 and Theorem 2, stated below, apply to both settings, where
$\mathcal{P}^{1}=\emptyset$
means the rows and columns for
$\mathcal{P}^{1}$
are not in the matrices
$\boldsymbol{\Psi}_{m;\,m}(s)$
and
$\boldsymbol{\Psi}_{m;\,1}(s).$
Within this general class structure for
$\mathbb{I}_{m-1}$
and subject to mild conditions, exponential and geometric asymptotic expansions hold for the first-passage distribution from
$1\rightarrow m$
which reflect the asymptotic hazard rate b associated with the irreducible subset
$\mathcal{I}$
. To show this, order the
$p_{i}$
states in
$\mathcal{P}^{i}$
so the
$\mathcal{P}^{i}\times\mathcal{P}^{i}$
block of
$\textbf{T}(s),$
denoted by
$\textbf{T}_{\mathcal{P}^{i}\mathcal{P}^{i}}(s),$
consists of zeros on and below its diagonal. The smallest positive value of b that solves
\begin{align}0 & =\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|=\left| \left(\begin{array}[c]{c@{\quad}c@{\quad}c}\rule[-0.07in]{0in}{0.24in}\textbf{I}_{p_{1}}-\textbf{T}_{\mathcal{P}^{1}\mathcal{P}^{1}}(s) & -\textbf{T}_{\mathcal{P}^{1}\mathcal{I}}(s) &-\textbf{T}_{\mathcal{P}^{1}\mathcal{P}^{2}}(s)\\\rule[-0.07in]{0in}{0.24in}\textbf{0} & \textbf{I}_{I}-\textbf{T}_{\mathcal{II}}(s) & -\textbf{T}_{\mathcal{IP}^{2}}(s)\\\rule[-0.07in]{0in}{0.24in}\textbf{0} & \textbf{0} & \textbf{I}_{p_{2}}-\textbf{T}_{\mathcal{P}^{2}\mathcal{P}^{2}}(s)\end{array}\right) \right| \nonumber\\& =\rule[-0.1in]{0in}{0.28in}\left| \textbf{I}_{I}-\textbf{T}_{\mathcal{II}}(s)\right| \end{align}
is the asymptotic hazard rate for the class
$\mathcal{I}$
.
The following results extend Propositions 2–4 to deal with this more general class of SMPs.
Proposition 6. (Sum over all distinct pathways, simple dominant pole b.) Suppose that the conditions
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}$
hold and that the relevant set
$\mathbb{I}_{m-1}$
for passage
$1\rightarrow m$
can be partitioned into a progressive class
$\mathcal{P=P}^{1}\cup\mathcal{P}^{2}$
and an irreducible class
$\mathcal{I}.$
Let
$b>0$
be the asymptotic hazard rate for the irreducible class
$\mathcal{I}$
defined as the smallest positive root of (18). Then the following hold:
(A) The conclusions of Proposition 2 apply to
$f_{1m}\mathcal{F}_{1m}(s),$
as given in (4). This concerns the agreement of (4) with the expression (9), as the sum of transmittances over all distinct pathways from
$1\rightarrow m,$
on the convergence domain
$\{\text{Re}(s)<b\}$
, as well as its agreement with (9) on its analytic continuation to
$\mathfrak{R\subset}\{\text{Re}(s)\geq b\}$
as defined in (10).
(B) With the additional assumptions
$\mathcal{LI}_{\text{reg}}$
and
$\mathcal{PIFS}_{\rightarrow m}$
given below, the conclusions of Proposition 3 hold, so
$b<b_{\min}\,:\!=\,\min\{b_{ij}:$
$(i,j)\in\mathbb{I}_{m-1}\times\mathbb{I}_{m}\}$
and b is a simple pole of
$\mathcal{F}_{1m}$
:
$(\mathcal{LI}_{\text{reg}})$
Take
$b_{\mathcal{I}}=\min\{b_{ij}\,:\,(i,j)\in\mathcal{I\times I\}}$
and
$\mathcal{L}=\{(i,j)\in\mathcal{I\times I}\,:\,b_{ij}=b_{\mathcal{I}}\}.$
For some branch
$\mathfrak{b}\in\mathcal{L},$
the convergence domain for
$\mathcal{M}_{\mathfrak{b}}(s)$
is regular, i.e. it is the open set
$\{s\in\mathbb{C}\,:\,\text{Re}(s)<b_{\mathcal{I}}\}.$
$(\mathcal{PIFS}_{\rightarrow m})$
We have
$b<\min_{(i,j)\in\mathcal{W}}b_{ij}$
where
$\mathcal{W}=(\mathcal{P}^{1}\times\mathbb{I}_{m})\cup\left[ (\mathcal{I\cup P}^{2})\times(\mathcal{P}^{2}\cup\{m\})\right] .$
(C) Assume the conditions
$\mathcal{LI}_{\text{reg}}$
and
$\mathcal{PIFS}_{\rightarrow m}$
above or else the conclusions of part B. Then, in continuous time, b is a dominant pole, in that an
$\varepsilon_{0}>0$
exists such that
$\mathcal{F}_{1m}$
can be analytically extended to
$\{\text{Re}(s)<b+\varepsilon_{0}\}\backslash\{b\}$
using (4). In integer time, the same conclusions hold with analytic continuation to the principal convergence region if one of these conditions holds: either (i)
$|\boldsymbol{\Psi}_{\mathcal{II}}(s)|\,:\!=\,|\textbf{I}_{I}-\mathcal{P}_{\mathcal{II}}(s)|$
has a unique zero at b along
$\{b+iy\,:\,y\in({-}\pi,\pi]\}$
, or else (ii)
$\mathcal{ND}-\mathcal{A}_{1\rightarrow m}$
holds, as stated in Proposition 5.
The proofs are given in Section 7.8 of the supplementary material. The proof of 3C requires proving that
$({-}1)^{m+1}|\boldsymbol{\Psi}_{m;\,1}(b)|>0.$
The argument for this differs from the simpler setting of Proposition 3 and requires a long and quite difficult argument.
Proposition 6 sets the stage for developing the expansions and conclusions of Theorem 1 but with the class of transient relevant states expanded so that
$\mathbb{I}_{m-1}=\mathcal{P}\cup\mathcal{I}$
rather than just
$\mathcal{I}.$
The proof for Theorem 2 follow the same arguments as those used in Theorem 1 and Corollary 1. The residue has a slightly different form due to the identity in (18).
Theorem 2. (Expansions with progressive states and a single irreducible subclass.) Suppose that the conditions
$\mathcal{R}_{1\rightarrow m}$
and
$\mathcal{CD}_{1\rightarrow m}$
hold and that the relevant states
$\mathbb{I}_{m-1}$
for passage
$1\rightarrow m$
can be partitioned into a progressive class
$\mathcal{P=P}^{1}\cup\mathcal{P}^{2}$
and a single irreducible class
$\mathcal{I}.$
Furthermore, assume the conditions
$\mathcal{LI}_{\text{reg}}$
and
$\mathcal{PIFS}_{\rightarrow m}$
in Proposition 6B, or else assume
$b<b_{\min}$
and b is a simple pole. Denote the residue of
$\mathcal{F}_{1m}(s)$
at b by
\begin{equation}\beta_{-1}=\frac{\left| \boldsymbol{\Psi}_{\mathcal{II}}(0)\right| }{\left|\boldsymbol{\Psi}_{m;\,1}\!\left( 0\right) \right| }\frac{\left| \boldsymbol{\Psi}_{m;\,1}\!\left( b\right) \right| }{\text{tr}[\text{adj}\{\boldsymbol{\Psi}_{\mathcal{II}}\!\left( b\right) \}\boldsymbol{\Psi}_{\mathcal{II}}^{\prime}\!\left( b\right) ]}, \end{equation}
where
$\boldsymbol{\Psi}_{\mathcal{II}}(s)=\textbf{I}_{I}-\textbf{T}_{\mathcal{II}}\!\left( s\right) .$
Integer time. With the additional integer-time conditions of Proposition 6C, the mass and survival function expansions of Theorem 1 hold with residue
$\beta_{-1}$
as in (19).
Continuous time. The survival function expansion in Theorem 1 holds with residue (19) subject to the condition
$\mathcal{B}_{1\rightarrow m}$
of Theorem 1. The density function expansion holds subject to the conditions
$\mathcal{BTV}_{1\rightarrow m}$
and
$\mathcal{ZD}_{1\rightarrow m}$
of Theorem 1 and
$\mathcal{UBI}_{1\rightarrow m}$
below:
$(\mathcal{UBI}_{1\rightarrow m})$
An unbounded-step blockage
$\mathcal{B}_{U}\subset\mathcal{I}\times\mathcal{I}$
exists such that for all
$(i,j)\in\mathcal{B}_{U},$
$\Vert\mathcal{M}_{ij}(b^{+}+iy)\Vert^{q}$
is integrable in y for a sufficiently large
$q=q(i,j)\geq1.$
The density function expansion holds if the conditions
$\mathcal{ZD}_{1\rightarrow m}$
and
$\mathcal{UBI}_{1\rightarrow m}$
are replaced with the alternative conditions
$\mathcal{ONE}_{1\rightarrow m}$
and
$\mathcal{MIN}_{1\rightarrow m}$
from Corollary 1.
3.4. First passage in Markov processes
The conclusions of Theorems 1, 2, and 5 apply to CTMCs, and it is perhaps useful to see how the established results for phase-type distributions relate to such SMP results as given in Corollaries 2 and 3 below. We continue to assume the condition
$\mathcal{R}_{1\rightarrow m}$
, so
$\mathbb{I}_{m}$
consists of exactly those states relevant to first passage
$1\rightarrow m.$
3.4.1. Continuous-time Markov chains
Let
$\textbf{Q}=\{q_{ij}\}$
denote the
$m\times m$
infinitesimal generator or intensity matrix of a CTMC, and suppose the chain is conservative with
$q_{ij}\geq0$
and
$q_{ii}<0$
with
$q_{ii}\leq-q_{i\cdot}=-\sum_{j\neq i}q_{ij}.$
Strict inequality
$q_{ii}<-q_{i\cdot}$
occurs if state i can lead to a non-relevant state. The relationship between
$\textbf{Q}$
and the transmittance
$\textbf{T}(s)$
is
\begin{equation*}\textbf{T}(s)=\textbf{W}(s)\textbf{P},\end{equation*}
where
$\textbf{W}(s)=$
$\text{diag}\{(1+s/q_{ii})^{-1}\,:\,i=1,\ldots,m\}$
contains the MGFs of Exponential
$({-}q_{ii})$
holding times, and
$\textbf{P}=(p_{ij})$
is the transition probability matrix of the jump chain with
\begin{equation*}p_{ij}=\left\{\begin{array}[c]{l@{\quad}l@{\quad}l}q_{ij}/({-}q_{ii}) & \text{if} & i\neq j,\\0 & \text{if} & i=j.\end{array}\right.\end{equation*}
Suppose relevant states
$\mathbb{I}_{m-1}=\mathcal{P}\cup\mathcal{I}$
with progressive states
$\mathcal{P=P}^{1}\cup\mathcal{P}^{2}$
and irreducible states
$\mathcal{I}$
. Exact first-passage density and survival functions conditional on a finite passage time are derived in Section 7.9 of the supplementary material as
\begin{equation}S(t)=\frac{\boldsymbol{\xi}_{1}^{T}{\exp}\big(\textbf{Q}_{m;\,m}t\big)\textbf{Q}_{m;\,m}^{-1}\textbf{q}_{m}}{\boldsymbol{\xi}_{1}^{T}\textbf{Q}_{m;\,m}^{-1}\textbf{q}_{m}}, \qquad \qquad
\textbf{}f(t)=\frac{\boldsymbol{\xi}_{1}^{T}{\exp}\big(\textbf{Q}_{m;\,m}t\big)\textbf{q}_{m}}{-\boldsymbol{\xi}_{1}^{T}\textbf{Q}_{m;\,m}^{-1}\textbf{q}_{m}}, \end{equation}
where
$\boldsymbol{\xi}_{1}^{T}$
is a
$1\times(m-1)$
indicator of state 1,
$\textbf{q}_{m}=(q_{1m},\ldots,q_{m-1,m})^{T}$
, and
\begin{equation*}\textbf{Q}_{m;\,m}=\left(\begin{array}[c]{c@{\quad}c@{\quad}c}\rule[-0.07in]{0in}{0.24in}\textbf{Q}_{\mathcal{P}^{1}\mathcal{P}^{1}} &\textbf{Q}_{\mathcal{P}^{1}\mathcal{I}} & \textbf{Q}_{\mathcal{P}^{1}\mathcal{P}^{2}}\\\rule[-0.07in]{0in}{0.24in}\textbf{0} & \textbf{Q}_{\mathcal{II}} &\textbf{Q}_{\mathcal{IP}^{2}}\\\rule[-0.07in]{0in}{0.24in}\textbf{0} & \textbf{0} & \textbf{Q}_{\mathcal{P}^{2}\mathcal{P}^{2}}\end{array}\right) ,\end{equation*}
where
$\textbf{Q}_{\mathcal{II}}$
is the intensity matrix for the block of irreducible transient states, etc. States in
$\mathcal{P}^{1}$
and
$\mathcal{P}^{2}$
are ordered so
$\textbf{Q}_{\mathcal{P}^{1}\mathcal{P}^{1}}$
and
$\textbf{Q}_{\mathcal{P}^{2}\mathcal{P}^{2}}$
have zeros below the diagonal. Let
$b>0$
be the eigenvalue of
$-\textbf{Q}_{\mathcal{II}}$
with smallest real part (which is necessarily positive).
Corollary 2. (Continuous-time conservative Markov chain.) For the chain as described above, suppose
$b<b_{\mathcal{P}}\,:\!=\,\min\{-q_{ii}\,:\,i\in\mathcal{P}^{1}\cup\mathcal{P}^{2}\}$
so that b is the eigenvalue of
$-\textbf{Q}_{m;\,m}$
with the smallest real part. Then the expansions of Theorem 2 apply so that
\begin{equation}S(t)=e^{-bt}\frac{-\beta_{-1}}{b}+o\big(e^{-b^{+}t}\big)\qquad \text{and}\qquad f(t)=e^{-bt}({-}\beta_{-1})+o\big(e^{-b^{+}t}\big), \end{equation}
where
$\beta_{-1}=\text{Res}\{\mathcal{F}_{1m}(s);\,b\},$
$b<b^{+}<b_{2}=\min\!\left[ \big\{\text{Re}(\lambda_{j})\,:\,j\geq2\big\},b_{\mathcal{P}}\right] ,$
and
$\big\{\lambda_{j}\,:\,j\geq2\big\}$
are the non-dominant eigenvalues of
$-\textbf{Q}_{\mathcal{II}}.$
The derivation of Corollary 2 is given in Section 7.9 of the supplementary material. The residue computation for
$\beta_{-1},$
as it relates to the dominant eigenvectors of
$\textbf{Q}_{m;\,m},$
is given in Equation (50) in the supplementary material.
3.4.2. Discrete-time Markov chains
Similarly, suppose the relevant states of a DTMC are
$\mathbb{I}_{m-1}\mathcal{=P}^{1}\cup\mathcal{I\cup P}^{2}.$
Here, we change the definition of a progressive state to allow it to have self-loops. We say state
$i\in\mathcal{P}$
is ‘progressive’ if it can be exited only once to a different state, thus allowing
$p_{ii}>0.$
Also suppose
$\mathcal{I}$
is an irreducible aperiodic class of size I. The transmittance for the chain is
$\textbf{P}_{m;\,m}e^{s}.$
The smallest positive solution to
\begin{equation}0=\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|=\prod_{i\in\mathcal{P}^{1}\mathcal{\cup P}^{2}}\big(1-p_{ii}e^{s}\big)\times\big|\textbf{I}_{I}-\textbf{P}_{\mathcal{II}}e^{s}\big|\end{equation}
determines b, the edge of the convergence domain. We suppose
$b=-\ln\lambda_{1}$
where
$\lambda_{1}>0$
is the Perron–Frobenius eigenvalue of
$\textbf{P}_{\mathcal{II}}.$
We know that
$\lambda_{1}\in(0,1)$
since at least one row sum of
$\textbf{P}_{m;\,m}$
is strictly
$<1.$
Exact expressions for the conditional first-passage survival and mass functions given finite passage time are derived in Section 7.10.1 of the supplementary material as
\begin{equation}S(n)=\frac{\boldsymbol{\xi}_{1}^{T}(\textbf{I}_{m-1}-\textbf{P}_{m;\,m})^{-1}\textbf{P}_{m;\,m}^{n-1}\textbf{p}_{m}}{\boldsymbol{\xi}_{1}^{T}(\textbf{I}_{m-1}-\textbf{P}_{m;\,m})^{-1}\textbf{p}_{m}}, \qquad \textbf{}p(n)=\frac{\boldsymbol{\xi}_{1}^{T}\textbf{P}_{m;\,m}^{n-1}\textbf{p}_{m}}{\boldsymbol{\xi}_{1}^{T}(\textbf{I}_{m-1}-\textbf{P}_{m;\,m})^{-1}\textbf{p}_{m}}, \qquad\textbf{}n\geq1, \end{equation}
where
$\textbf{p}_{m}=(p_{1m},\ldots,p_{m-1,m})$
.
Corollary 3. (Discrete-time Markov chain.) For the chain described above, let
$\mathcal{I}$
be an irreducible aperiodic class with
$b<b_{\mathcal{P}}\,:\!=\,\min_{\{i\in\mathcal{P}^{1}\mathcal{\cup P}^{2}\,:\,p_{ii}>0\}}({-}\ln p_{ii}).$
Then expansions for S(n) and p(n) in (23) are
\begin{equation}S(n)=e^{-bn}\frac{-\beta_{-1}}{1-e^{-b}}+o\big(e^{-b^{+}n}\big)\qquad \text{and}\qquad p(n)=e^{-bn}({-}\beta_{-1})+o\big(e^{-b^{+}n}\big) \end{equation}
for
$b<b^{+}<b_{2},$
where
$\beta_{-1}=\text{Res}\{\mathcal{F}_{1m}(s);\,b\}$
and
$b_{2}=\min\!\left[ \{\text{Re}({-}\ln\lambda_{j})\,:\,j\geq2\},b_{\mathcal{P}}\right] ,$
where
$\{\lambda_{j}\,:\,j\geq2\}$
are the non-dominant eigenvalues of
$P_{\mathcal{II}}.$
For the same chain as described above, if
$\mathcal{I}$
is instead periodic with period
$d\geq2,$
then
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|$
has d equally spaced zeros on the boundary
$\{s\in\mathbb{C}\,:\,\text{Re}(s)=b\}$
of the convergence domain for
$\mathcal{F}_{1m}.$
The other
$d-1$
zeros contribute additional terms of order
$O\big(e^{-bt}\big)$
to those given in (24).
Proof of Corollary 3 is given in Section 7.10 of the supplementary material. The residue
$\beta_{-1}$
is expressed in terms of the dominant eigenvalue and eigenvectors of
$\textbf{P}_{m;\,m}$
in Equation (52) in the supplementary material.
Of course, in all of these Markov settings, the expansions have already been well established, since MGF
$\mathcal{F}_{1m}(s)$
and PGF
$\mathcal{F}_{1m}(\ln s)$
respectively are rational and the expansions follow directly from their partial-fraction expansions. The importance of Theorems 1, 2, and 5, however, is their applicability to SMPs without rational transmittance matrices
$\textbf{T}(s)\textbf{.}$
What Theorems 1, 2, and 5 also demonstrate is an insensitivity property such as that discussed in [Reference Tijms23, Section 5.4]: SMPs in general exhibit the same sort of exponential/geometric tail behaviour as occurs with phase-type distributions of Markov processes.
4. Additional sojourn types with poles
Other types of sojourns, which might at first seem different from the first-passage context
$1\rightarrow m\neq1,$
are essentially related, and theorems from Section 3 with some modifications can be applied as discussed below.
4.1. First passage to a subset of states
First-passage sojourns from
$1\rightarrow \mathcal{D}$
where
$\mathcal{D}$
includes two or more states of an SMP are equivalent to first passages to a lumped state m constructed from
$\mathcal{D}.$
Suppose relevant state space
$\mathbb{I}_{m-1}\cup\mathcal{D}$
for passage
$1\rightarrow \mathcal{D}$
where
$\mathbb{I}_{m-1}=\{1,\ldots,m-1\}.$
Let m be the lumped state for
$\mathcal{D}$
such that one-step passage from
$i\in\mathbb{I}_{m-1}$
to m has transmittance
$\mathcal{T}_{i\cdot}(s)=\sum_{j\in\mathcal{D}}\mathcal{T}_{ij}(s).$
In this setup, the first-passage transmittance from
$1\rightarrow \mathcal{D}$
is just the first-passage transmittance from
$1\rightarrow m$
as treated in Section 3 by using the cofactor rule in (4). The only modifications are to the last column of the
$m\times m$
matrix
$\textbf{T}(s),$
which is now
$\big\{\mathcal{T}_{1\cdot}(s),\ldots,\mathcal{T}_{m-1,\cdot}(s),\ast\big\}^{T}$
, where
$\ast$
indicates that the last component is not used in the cofactor rule.
4.2. First return to state 1
Let X be the first-return time to state 1 when the process enters state 1 at time
$0.$
The transmittance
$\mathbb{E}\big(e^{sX}1_{\{X<\infty\}}\big)$
for first return
$1\rightarrow 1$
is given in [Reference Butler3, Section 13.2.6] as
\begin{equation}f_{11}\mathcal{F}_{11}(s)=1-\frac{|\textbf{I}_{m}-\textbf{T}(s)|}{|\boldsymbol{\Psi}_{11}(s)|}, \end{equation}
where
$|\boldsymbol{\Psi}_{11}(s)|$
is the (1,1) minor of
$\textbf{I}_{m}-\textbf{T}(s).$
Assume
$\mathcal{R}_{1\rightarrow 1}$
or that
$\mathbb{I}_{m}=\{1,\ldots,m\}$
contains all relevant states and no non-relevant states for the sojourn
$1\rightarrow 1.$
A cofactor expansion of
$|\textbf{I}_{m}-\textbf{T}(s)|$
along its first row corresponds to a one-step argument and gives
\begin{align}f_{11}\mathcal{F}_{11}(s) & =1-\left[ 1-\mathcal{T}_{11}(s)+\sum_{j=2}^{m}({-}1)^{1+j}\{-\mathcal{T}_{1j}(s)\}\frac{|\boldsymbol{\Psi}_{1j}(s)|}{|\boldsymbol{\Psi}_{11}(s)|}\right] \nonumber\\& =\mathcal{T}_{11}(s)+\sum_{j=2}^{m}\mathcal{T}_{1j}(s)f_{j1}\mathcal{F}_{j1}(s), \end{align}
where
$f_{j1}\mathcal{F}_{j1}(s)$
is the first-passage transmittance from state
$j\neq1$
to 1 in (4). This relationship embodies the one-step argument and naturally leads to a characterisation of the distribution of
$X|X<\infty$
as a finite-mixture distribution in which
\begin{equation*}X|X<\infty=\left\{\begin{array}[c]{l@{\quad}c@{\quad}l}H_{11} & \text{w.p.} & p_{11}/f_{11},\\[3pt]H_{1j}+X_{j1} & \text{w.p.} & p_{1j}f_{j1}/f_{11},\quad j\geq2,\end{array}\right.\end{equation*}
where
$H_{1j}$
has MGF
$\mathcal{M}_{1j}$
, the first-passage random variable
$X_{j1}$
has MGF
$\mathcal{F}_{j1},$
and all random variables are mutually independent. The first-return probability
$f_{11}=p_{11}+\sum_{j=2}^{m}p_{1j}f_{j1}$
is the expression (26) evaluated at
$s=0.$
Note that if
$\mathbb{I}_{m}$
is irreducible and
$\textbf{P}$
has row sums which are all 1, then
$|\textbf{I}_{m}-\textbf{T}(0)|=0$
, so
$f_{11}=1.$
4.2.1. Other relevant states are progressive
If all states in
$\mathbb{I}_{m\backslash1}=\{2,\ldots,m\}$
are progressive (but state 1 is not), then
$|\boldsymbol{\Psi}_{11}(s)|=1$
and the non-zero terms in the permutation sum for
$1-|\textbf{I}_{m}-\textbf{T}(s)|$
enumerate all distinct first-return pathways. In this case, a result like Theorem 5 in Section 7.7 of the supplementary material can be stated to provide integer- and continuous-time expansions. Such a result requires the assumption
$\mathcal{CD}_{1\rightarrow 1}$
, which is the same as
$\mathcal{CD}_{1\rightarrow m}$
but now applies to all one-step MGFs in
$\textbf{T}(s).$
The assumptions
$\mathcal{AC}_{\mathcal{L}}$
and
$\mathcal{ZM}_{\mathcal{L}}$
are needed but now apply to a new
$\mathcal{L}=\{(i,j)\in\mathbb{I}_{m}\times\mathbb{I}_{m}\,:\,b_{ij}=b\}$
where
$b=\min_{(i,j)\in\mathbb{I}_{m}\times\mathbb{I}_{m}}b_{ij}.$
For density expansions, the comparable assumptions
$\mathcal{BTV}_{1\rightarrow 1},$
$\mathcal{ONE}_{1\rightarrow 1},$
and
$\mathcal{MIN}_{1\rightarrow 1}$
pertaining to passage
$1\rightarrow 1$
rather than their counterpart
$1\rightarrow m\neq1$
must also hold.
4.2.2. Other relevant states are irreducible
Alternatively, if states in
$\mathbb{I}_{m\backslash1}$
form an irreducible class, then expansions analogous to those in Theorem 1 hold for first return to state 1, as now formalised. Proof is in Section 7.11 of the supplementary material. Suppose
$b>0$
is the smallest positive zero of
$|\boldsymbol{\Psi}_{11}(s)|.$
Let
$b_{\min}=\min_{(i,j)\in\mathbb{I}_{m}\times\mathbb{I}_{m}}b_{ij},$
$\ b_{\mathcal{I}}=\min_{(i,j)\in\mathbb{I}_{m\backslash1}\times\mathbb{I}_{m\backslash1}}b_{ij},$
and
$\mathcal{L}=\{(i,j)\in\mathbb{I}_{m\backslash1}\times\mathbb{I}_{m\backslash1}\,:\,b_{ij}=b_{\mathcal{I}}\}.$
Here, let
$\mathcal{L}_{\text{reg}}$
impose regularity on some
$\mathcal{M}_{ij}(s)$
for which
$(i,j)\in\mathcal{L},$
and let
$\mathcal{FS}_{\rightarrow 1}$
denote the assumption that
$b<\min\{b_{ij}\,:\,i=1$
or
$j=1\}.$
Theorem 3. (First-return expansions with irreducible states.) Suppose that the conditions
$\mathcal{R}_{1\rightarrow 1}$
and
$\mathcal{CD}_{1\rightarrow 1}$
hold and that
$\mathbb{I}_{m\backslash1}$
forms an irreducible class. Additionally, assume
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow 1}$
hold. Denote by
$\beta_{-1}=\text{Res}\{\mathcal{F}_{11}(s);\,b\}$
the residue of
$\mathcal{F}_{11}$
at b, which takes the form
\begin{equation}\beta_{-1}=\frac{-1}{f_{11}}\frac{|\textbf{I}_{m}-\textbf{T}(b)|}{\text{tr}\left[ \text{adj}\{\boldsymbol{\Psi}_{11}(b)\}\boldsymbol{\Psi}_{11}^{\prime}(b)\right] }<0, \end{equation}
where
$f_{11}=p_{11}+\sum_{j=2}^{m}p_{1j}({-}1)^{j+1}|\boldsymbol{\Psi}_{1j}(0)|/|\boldsymbol{\Psi}_{11}(0)|.$
Integer or continuous time. Then
$b<b_{\min}$
and b is a simple pole.
Integer time. In this setting, suppose the additional condition that either
$|\boldsymbol{\Psi}_{11}(s)|$
has a unique zero at b on
$\{b+iy\,:\,y\in({-}\pi,\pi]\}$
or else
$\mathcal{ND}-\mathcal{A}_{1\rightarrow 1}$
holds (which is the condition
$\mathcal{ND}-\mathcal{A}_{1\rightarrow m}$
but now pertaining to all one-step transitions from
$\mathbb{I}_{m}$
to
$\mathbb{I}_{m})$
. Then b is a dominant pole. Also, the conditional first-return survival and mass functions and error expressions take the form in Theorem 1 using the residue
$\beta_{-1}$
in (27).
Continuous time. Then the simple pole b is a dominant pole.
Additionally, suppose
$\mathcal{B}_{1\rightarrow 1}$
(which places absolute integrability conditions like those in
$\mathcal{B}_{1\rightarrow m}$
on MGFs forming a blockade for passage
$1\rightarrow 1).$
Then the conditional first-return survival function has an expansion and error expression as given in Theorem 1 using the residue (27).
Suppose
$\mathcal{BTV}_{1\rightarrow 1}$
holds and either conditions
$\mathcal{ZD}_{1\rightarrow 1}$
and
$\mathcal{UB}_{1\rightarrow 1}$
(as in Theorem 2
) or else
$\mathcal{ONE}_{1\rightarrow 1}$
and
$\mathcal{MIN}_{1\rightarrow 1}$
(as in Corollary 1
) hold. Then the conditional first-return density expansion and error expression are as given in Theorem 1 using residue (27).
In Theorem 3, the assumptions
$\mathcal{L}_{\text{reg}}$
and
$\mathcal{FS}_{\rightarrow 1}$
ensure that
$b<b_{\min}$
and b is a simple pole. The additional results in both integer time and continuous time also hold if we instead choose to assume that
$b<b_{\min}$
and b is a simple pole.
4.2.3. Other relevant states are progressive and irreducible
If states in
$\mathbb{I}_{m\backslash1}=\mathcal{P}^{1}\cup\mathcal{P}^{2}\cup\mathcal{I}$
are both progressive
$(\mathcal{P}^{1}\cup\mathcal{P}^{2})$
and irreducible
$(\mathcal{I})$
, as introduced for Theorem 2, an analogue of Theorem 2 holds for first return to state 1. Suppose
$b>0$
is now the smallest positive zero of
$|\boldsymbol{\Psi}_{\mathcal{II}}(s)|$
and the asymptotic hazard rate for the irreducible set
$\mathcal{I}.$
In this context, set
$b_{\min}=\min\{b_{ij}\,:\,(i,j)\in\mathbb{I}_{m}\times\mathbb{I}_{m}\},$
$b_{\mathcal{I}}=\min\{(i,j)\in\mathcal{I\times I}\}$
, and
$\mathcal{LI}=\{(i,j)\in\mathcal{I\times I}\,:\,b_{ij}=b_{\mathcal{I}}\}.$
The condition
$\mathcal{LI}_{\text{reg}}$
requires that
$\mathcal{M}_{ij}$
is regular for some
$(i,j)\in\mathcal{LI}.$
Also suppose the condition
$\mathcal{PIFS}_{\rightarrow 1}$
, which requires
\begin{equation*}b<\min\!\left[ b_{ij}\,:\,(i,j)\in\{i=1\text{ or }j=1\}\cup\left( \mathcal{P}^{1}\times\mathbb{I}_{m\backslash1}\right) \cup\left\{ \left(\mathcal{I\cup\mathcal{P}}^{2}\right) \times\mathcal{P}^{2}\right\} \right].\end{equation*}
Theorem 4. (First-return expansions with progressive states and one irreducible class.) Assume
$\mathcal{R}_{1\rightarrow 1}$
and
$\mathcal{CD}_{1\rightarrow 1}$
and suppose
$\mathbb{I}_{m\backslash1}$
partitions so that
$\mathbb{I}_{m\backslash1}=\mathcal{P}^{1}\cup\mathcal{P}^{2}\cup\mathcal{I},$
where
$\mathcal{P}^{1}$
and
$\mathcal{P}^{2}$
are progressive states before and after entering
$\mathcal{I},$
where
$\mathcal{I}$
is an irreducible class. Also, assume the conditions
$\mathcal{LI}_{\text{reg}}$
and
$\mathcal{PIFS}_{\rightarrow 1}.$
Denote by
$\beta_{-1}=\text{Res}\big\{\mathcal{F}_{11}(s);\,b\big\}$
the residue of
$\mathcal{F}_{11}$
at b, which takes the form
\begin{equation}\beta_{-1}=\text{Res}\{\mathcal{F}_{11}(s);\,b\}=\frac{-1}{f_{11}}\frac{|\textbf{I}_{m}-\textbf{T}(b)|}{\text{tr}\left[\text{adj}\{\boldsymbol{\Psi}_{\mathcal{II}}(b)\}\boldsymbol{\Psi}_{\mathcal{II}}^{\prime}(b)\right] }<0, \end{equation}
where
$f_{11}=p_{11}+\sum_{j=2}^{m}p_{1j}({-}1)^{j+1}|\boldsymbol{\Psi}_{1j}(0)|/|\boldsymbol{\Psi}_{\mathcal{II}}(0)|.$
Integer or continuous time. Then
$b<b_{\min}$
and b is a simple pole.
Integer time. In this setting, suppose the additional condition that either
$|\boldsymbol{\Psi}_{\mathcal{II}}(s)|$
has a unique zero at b on
$\{b+iy\,:\,y\in({-}\pi,\pi]\}$
or else
$\mathcal{ND}-\mathcal{A}_{1\rightarrow 1}$
holds. Then b is a dominant pole. Furthermore, the expansions for the conditional survival and mass function are as given in Theorem 1 using the residue (28).
Continuous time. Then the simple pole
$b>0$
is also a dominant pole.
Additionally, suppose
$\mathcal{B}_{1\rightarrow 1}.$
Then the conditional survival function for the first return has an expansion and error expression as given in Theorem 1 using the residue (28).
Suppose the condition
$\mathcal{BTV}_{1\rightarrow 1}$
holds, and either
$\mathcal{ZD}_{1\rightarrow 1},$
and
$\mathcal{UBI}_{1\rightarrow 1}$
hold (as in Theorem 2
), or else
$\mathcal{ONE}_{1\rightarrow 1}$
and
$\mathcal{MIN}_{1\rightarrow 1}$
hold as in Corollary 1. Then the conditional density expansion and error expression for the first return are as given in Theorem 1 using the residue (28).
The last results of Theorem 4 stated under the categories of integer time and continuous time also hold if we assume that
$b<b_{\min}$
and b is a simple pole.
5. Sojourns with two or more relevant irreducible classes
If the relevant state space consists of a progressive class and two or more irreducible classes, then the conclusions of Theorems 2 and 4 may continue to apply as concerns first-passage distributions from
$1\rightarrow m$
and
$1\rightarrow 1$
, but under revised conditions.
These conditions for first passage
$1\rightarrow m$
can get very complicated even for the setting
$\mathbb{I}_{m-1}\mathcal{=P\cup I}_{1}\cup\mathcal{I}_{2}$
with two irreducible classes. The conditions depend on what transitions are possible amongst the classes
$\mathcal{P},$
$\mathcal{I}_{1},$
and
$\mathcal{I}_{2}.$
If
$\overset{c}{\rightarrow }$
indicates the presence of one-directional communication between subsets of states, then we may have
$\mathcal{I}_{1}\overset{c}{\rightarrow }\mathcal{I}_{2}$
or
$\mathcal{I}_{2}\overset{c}{\rightarrow }\mathcal{I}_{1}$
, but not both, since the two classes are disjoint irreducible classes. If we allow
$\mathcal{I}_{1}\overset{c}{\rightarrow }\mathcal{I}_{2},$
then
$\mathcal{P}$
can be partitioned into three progressive classes
$\mathcal{P=P}^{1,2}\cup\mathcal{P}^{2\backslash1}\cup\mathcal{P}^{\backslash2}$
characterised by state transition orderings such that
$1\in\mathcal{P}^{1,2}\overset{c}{\rightarrow }\mathcal{I}_{1}\overset{c}{\rightarrow }\mathcal{P}^{2\backslash1}\overset{c}{\rightarrow }\mathcal{I}_{2}\overset{c}{\rightarrow }\mathcal{P}^{\backslash2}\rightarrow \{m\}.$
Additional ordering of states within the three sets
$\mathcal{P}^{1,2},$
$\mathcal{P}^{2\backslash1},$
and
$\mathcal{P}^{\backslash2}$
according to the
$\overset{c}{\rightarrow }$
relation leads to an expression for
$\textbf{T}(s)$
in block form which has zero blocks below the diagonal blocks. Thus,
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|=|\boldsymbol{\Psi}_{\mathcal{I}_{1}\mathcal{I}_{1}}(s)|\times|\boldsymbol{\Psi}_{\mathcal{I}_{2}\mathcal{I}_{2}}(s)|.$
If the asymptotic hazard rate for
$\mathcal{I}_{2}$
is
$b>0$
and strictly smaller than that for
$\mathcal{I}_{1}$
(the case when they are equal is discussed below), then b is a simple zero of
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|$
and the conclusions of Theorems 2 and 4 follow subject to the following conditions in both integer and continuous time:
$\mathcal{R}_{1\rightarrow m}$
;
$\mathcal{CD}_{1\rightarrow m}$
; a suitably modified
$\mathcal{LI}_{2\text{reg}}$
to account for feedback within
$\mathcal{I}_{2}\rightarrow \mathcal{I}_{2}$
; and
$\mathcal{PIFS}_{\rightarrow m}$
, which accounts for transitions involving progressive states. One must also assume that
$|\boldsymbol{\Psi}_{m;\,1}(b)|\neq0$
, which is no longer guaranteed from the composition of
$\mathbb{I}_{m-1}.$
Then, in integer time, the expansions of Theorem 1 hold if
$|\boldsymbol{\Psi}_{m;\,m}(b+iy)|$
has no further zeros for
$0\neq y\in({-}\pi,\pi]$
or else
$\mathcal{ND}-\mathcal{A}_{1\rightarrow m}$
holds. In continuous time, the survival expansion holds subject to
$\mathcal{B}_{1\rightarrow m}$
, and the density expansion holds with
$\mathcal{BTV}_{1\rightarrow m},$
$\mathcal{ZD}_{1\rightarrow m},$
and
$\mathcal{UBI}_{1\rightarrow m},$
where the last assumption must account for infinite-step pathways in
$\mathcal{I}_{1}\cup\mathcal{I}_{2}.$
In the setting for first return to state 1, only minor modifications to these conditions are needed to make them relevant for
$1\rightarrow 1$
passage. A simple pole still occurs at
$b>0$
, and the numerator value
$|\textbf{I}_{m}-\textbf{T}(b\textbf{)|}<0$
is ensured.
One notable class of SMP examples violates the conditions above. Suppose
$\mathcal{I}_{1}$
and
$\mathcal{I}_{2}$
represent identical subsystems, so that
$\textbf{T}_{\mathcal{I}_{1}\mathcal{I}_{1}}(s)\equiv\textbf{T}_{\mathcal{I}_{2}\mathcal{I}_{2}}(s).$
Assume these subsystems are connected in series so that
$\mathcal{P}^{1,2}\overset{c}{\rightarrow }\mathcal{I}_{1}\overset{c}{\rightarrow }\mathcal{I}_{2}\overset{c}{\rightarrow }m$
. In this case, the two irreducible classes have the same asymptotic hazard rate, and so b is a 2-zero of
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|.$
Typically in this setting
$|\boldsymbol{\Psi}_{m;\,1}(b)|\neq0$
, so that b becomes a 2-pole for
$\mathcal{F}_{1m}(s).$
This leads to a Gamma (2,b) or a Discrete Gamma (2, b) tail with an expansion of the type given in Theorem 5 of the supplementary material.
Another class of examples connects these identical subsystems in parallel, as occurs when there are redundant subsystems in place. In this context,
$\mathcal{P}^{1,2}\overset{c}{\rightarrow }\mathcal{I}_{1}\overset{c}{\rightarrow }m$
and
$\mathcal{P}^{1,2}\overset{c}{\rightarrow }\mathcal{I}_{2}\overset{c}{\rightarrow }m$
are parallel pathways with no communication between
$\mathcal{I}_{1}$
and
$\mathcal{I}_{2}.$
Again
$\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|=|\boldsymbol{\Psi}_{\mathcal{I}_{1}\mathcal{I}_{1}}(s)|\times|\boldsymbol{\Psi}_{\mathcal{I}_{2}\mathcal{I}_{2}}(s)|$
and b is a 2-zero. However, in this setting
$|\boldsymbol{\Psi}_{m;\,1}(b)|=0$
and b can be shown to be a 1-zero of the numerator. Hence, b is a simple pole, and an expansion as in Theorem 1 exists but with the alternative residue computation
\begin{align*}\beta_{-1} & =\text{Res}\{\mathcal{F}_{1m}(s);\,b\}=\frac{1}{f_{1m}}\frac{\left. \partial|\boldsymbol{\Psi}_{m;\,1}(s)|/\partial s\right| _{s=b}}{\left. \partial^{2}\big|\boldsymbol{\Psi}_{m;\,m}(s)\big|/\partial s^{2}\right|_{s=b}/2}\\[4pt]& =\frac{2}{f_{1m}}\frac{\text{tr}\left[ \text{adj}\big\{\boldsymbol{\Psi}_{m;\,1}(b)\big\}\boldsymbol{\Psi}_{m;\,1}^{\prime}(b)\right]}{\text{tr}\left[ \text{adj}\big\{\boldsymbol{\Psi}_{m;\,m}(b)\big\}\boldsymbol{\Psi}_{m;\,m}^{\prime\prime}(b)+\text{Dadj}\big\{\boldsymbol{\Psi}_{m;\,m}(b)\big\}\boldsymbol{\Psi}_{m;\,m}^{\prime}(b)\right] },\end{align*}
where
$\text{Dadj}\{\boldsymbol{\Psi}_{m;\,m}(s)\}=\partial\text{adj}\{\boldsymbol{\Psi}_{m;\,m}(s)\}/\partial s$
is
$(m-1)\times(m-1)$
and has components which are computed as derivatives of determinants.
6. Numerical examples
6.1. Reliability system
A system consists of four components, each of which has an Exponential
$(1/4)$
failure time. Let components 1–3 be repairable, but not component 4. The system ultimately fails at time X which is the time of failure of component 4. Let all failure and repair times be independent, and suppose the repair times for components
$i=1,2,3$
are Inverse Gaussian
$\big(\mu_{i},\sigma_{i}^{2}\big)$
with mean
$\mu_{i}$
and variance
$\sigma_{i}^{2}$
, so the process is semi-Markov.
The SMP can be modelled with five states, of which 0 indicates that the system is working and
$i\in\{1,\ldots,4\}$
indicates that component i has failed. The exit time from the working state 0 is Exponential
$(1).$
The MGF for an inverse Gaussian
$\big(\mu_{i},\sigma_{i}^{2}\big)$
distribution is
\begin{equation*}\mathcal{N}_{i}(s)=\exp\!\left[ \frac{\mu_{i}^{2}}{\sigma_{i}^{2}}\left\{1-\sqrt{1-2s\sigma_{i}^{2}/\mu_{i}}\right\} \right], \qquad \text{Re}(s)\leq\frac{\mu_{i}}{2\sigma_{i}^{2}},\end{equation*}
so that the first-passage MGF from
$0\rightarrow 4$
from (4) becomes
\begin{equation}\mathcal{F}(s)=\frac{1/4(1-s)^{-1}}{1-1/4(1-s)^{-1}\sum_{i=1}^{3}\mathcal{N}_{i}(s)}=\frac{1/4}{1-s-1/4\sum_{i=1}^{3}\mathcal{N}_{i}(s)}.\end{equation}
The middle expression in (29) demonstrates that there is some discretion in our characterisation of the SMP in terms of the choice of states for expressing system failure. We can eliminate states 1–3 and consider a two-state SMP in which states 1 and 2 are respectively the working and failed system states. This has SMP transmittance matrix
\begin{equation*}\textbf{T}(s)=\left(\begin{array}[c]{c@{\quad}c}\rule[-0.07in]{0in}{0.24in}1/4\,(1-s)^{-1}\sum_{i=1}^{3}\mathcal{N}_{i}(s) &1/4\,(1-s)^{-1}\\\rule[-0.07in]{0in}{0.24in}0 & 0\end{array}\right),\end{equation*}
and system failure time is the first-passage time from
$1\rightarrow 2$
for
$\textbf{T}(s)$
, which gives the same MGF as in (29).
As a numerical example, suppose the Inverse Gaussian
$\big(\mu_{i},\sigma_{i}^{2}\big)$
repair times have
$\big(\mu_{i},\sigma_{i}^{2}\big)=(1/2,1/2),$
(1,1), and
$(2,2).$
Then for the two-state SMP,
$b_{11}=1/2$
and
$b_{12}=1$
, and the condition
$\mathcal{L}_{\text{reg}}$
of Proposition 3 does not hold. Despite this, the conclusions of Proposition 3 still hold, and the MGF
$\mathcal{F}(s)$
has a simple pole at
$b=0.1228$
, which is the asymptotic failure rate of
$\{1\}$
for the two-state model or for
$\mathcal{I}=\{0, 1, 2, 3\}$
in the five-state model. The MGF also has branch points at
$1/2$
and
$\infty$
and simple poles at
$2.305\pm0.089i.$
The accuracy of the survival and density expansions for time to failure in Theorem 1 is compared to that of ‘exact’ and saddlepoint computations in Table 1. The survival saddlepoint approximation
$\hat{S}(t)$
is the approximation of Lugannani and Rice [Reference Lugannani and Rice16] given in [Reference Butler3, Section 1.2.1], and the saddlepoint density approximation
$\hat{f}(t)$
is the standard one in [Reference Butler3, Section 1.1.2]. The residue expansions are more accurate than the saddlepoint approximations for all values of t except at
$t=5$
near the median, where
$\hat{S}(5)$
is more accurate than
$S_{1}(5).$
The greater accuracy of
$S_{1}$
and
$f_{1}$
is quite dramatic, and these expansions provide close to exact computations for many practical purposes.
Table 1. Exact survival and density values S(t) and f(t) are compared with expansion values
$S_{1}(t)$
and
$f_{1}(t)$
as well as saddlepoint approximations
$\hat{S}(t)$
and
$\hat{f}(t)$
for
$t=5,$
10, 20, 40, and
$80.$
A bold digit denotes the last digit which agrees with exact computation when both are rounded. Percentage relative errors (
$\%$
rel. err.)
$100\{S_{1}(t)/S(t)-1\}$
for the approximations are provided.
As
$t\rightarrow \infty,$
the relative error of
$S_{1}(t)$
and
$f_{1}(t)$
must approach 0, and this can be seen in the table. The saddlepoint approximations have the property that
\begin{equation}100\left\{ \frac{\hat{S}(t)}{S(t)}-1\right\} \rightarrow \frac{\Gamma(1)}{\hat{\Gamma}(1)}-1\simeq8.444\%\leftarrow100\left\{ \frac{\hat{f}(t)}{f(t)}-1\right\}, \qquad t\rightarrow \infty. \end{equation}
These limits hold since the two-state SMP satisfies Corollary 4 in [Reference Butler and Wood8, Section 4.1.2], which establishes the limiting relative error for such saddlepoint approximations when used in conjunction with the cofactor rule of (4). At
$t=80$
the relative error for the saddlepoint density is
$8.480\%$
and close to the limit
$8.444\%$
with clear evidence of convergence. The table shows much slower convergence in relative error for the Lugannani–Rice approximation, an observation that was also noted in [Reference Butler and Wood8, Section 6.1, Ex.8, and Section 6.1, Ex.1].
Not only are the expansions more accurate than the saddlepoint approximations, they also provide simpler and more useful expressions for later computation, which take the form
\begin{align}S_{1}(t) & =0.912\,902\,842\,295\,\exp\!\left({-}0.122\,770\,963\,311\,290\,t\right),\nonumber\\f_{1}(t) & =0.112\,077\,961\,358\,\exp\!\left({-}0.122\,770\,963\,311\,290\,t\right) . \end{align}
An approximate reliability function for the system is explicit in (31) and when inverted gives an explicit expression for quantile computation. Such simplicity is not possible using saddlepoint approximations since each value of t requires root-finding to solve for its saddlepoint.
For statistical inference in stochastic modelling settings in which the likelihood is intractable, the density expression
$f_{1}$
provides a useful and easily computed expression for likelihood computation. Suppose the system parameter
$\theta$
concerning the transmittance
$\textbf{T}(s;\,\theta)$
is unknown and the data
$\{t_{i}\}$
consist of overall times to system failure. To make inferences about a hypothesised value
$\theta$
, the intractable likelihood
$\prod_{i}f(t_{i};\,\theta)$
can be approximated quite simply by the expansion product
$\prod_{i}f_{1}(t_{i};\,\theta)$
with convergence bound b and its residue as functions of
$\theta.$
Computation of the saddlepoint product
$\prod_{i}\hat{f}(t_{i};\,\theta)$
is much more difficult and plagued by the need to computed a saddlepoint for each
$t_{i}$
as a function of
$\theta.$
6.1.1. Inversion formulas and integration paths
The exact computations in Table 1 were performed using numerical contour integration that roughly follows the path of steepest descent. Before considering this, we first show why inversion should not be performed staying in the convergence domain for
$\mathcal{F}.$
The discussion below applies to quite a few applications in which the cofactor rule in (4) is inverted.
Inside the convergence domain. From the inversion formula, f(t) may be written as
\begin{equation}f(t)=\frac{1}{2\pi i}\int_{\varepsilon-i\infty}^{\varepsilon+i\infty}\mathcal{F}(s)e^{-ts}ds=\frac{e^{-\varepsilon t}}{\pi}\int_{0}^{\infty}\text{Re}\left\{ \mathcal{F}(\varepsilon+iy)e^{-ity}\right\} dy\end{equation}
for any
$\varepsilon\in(0,b).$
Quite often when using the cofactor rule in (4), the integrand in (32) is not absolutely integrable, and we show this for the reliability example. In (29), note that
$\left\|\mathcal{N}_{i}(\varepsilon+iy)\right\| \rightarrow 0$
as
$y\rightarrow \infty$
since
$\varepsilon+iy$
is in the convergence domain of
$\mathcal{N}_{i}$
. Thus,
$\mathcal{F}(\varepsilon+iy)\sim(1-\varepsilon-iy)^{-1}/4$
as
$y\rightarrow \infty$
, and
\begin{equation}\text{Re}\left\{ \mathcal{F}(\varepsilon+iy)e^{-ity}\right\}\sim\frac{1}{4}\text{Re}\!\left( \frac{e^{-ity}}{1-\varepsilon-iy}\right) =\frac{{\sin}(ty)}{4y}+O\big(y^{-2}\big). \end{equation}
The right side of (33) is not absolutely integrable in y and is only conditionally integrable. For large y, half the absolute value of the right side of (33) is a lower bound for the absolute value of the left side. Thus, by the comparison theorem for integrals, the integrand in (32) is not absolutely integrable.
The inversion for S(t) uses (32) but with the additional term
$1/(\varepsilon+iy)$
inside the curly braces. Thus,
\begin{equation}\text{Re}\left\{ \frac{\mathcal{F}(\varepsilon+iy)}{\varepsilon+iy}e^{-ity}\right\} \sim\frac{{\cos}(ty)}{4y^{2}}+O\big(y^{-3}\big). \end{equation}
The integrand on the left of (34) is absolutely integrable by the same argument: take twice the right-hand side of (34) as an upper bound and apply the comparison test for integrals. Thus, accuracy using vertical contour inversion for S(t) with absolute integrability fares only slightly better than for f(t).
Considerable computational time was used to numerically integrate accurately along the vertical line
$\{b/4+iy\,:\,y>0\}$
inside the convergence domain up to
$y=500.$
The line segment was broken into 30 pieces with each piece requiring about 45 seconds of CPU time to achieve desired error bounds. For S(5) this resulted in accuracy to 8 significant digits. In the computation of f(5), integration was extended up to
$y=1000$
and led to accuracy to only 4 significant digits for
$f(5).$
Computation of the integrand order at
$b/4+500i$
and
$b/4+1000i$
for the two inversions S(5) and f(5) were
$O(10^{-7})$
and
$O(10^{-5})$
respectively, in line with the reported accuracy. Based on the accuracy of the expansions shown in Table 1, this is less than the accuracy of
$S_{1}$
and
$f_{1}$
for values
$t\geq10$
and above the 75th percentile of the distribution.
Path of steepest descent. We first determine the ultimate direction of steepest descent. Taking
$s=re^{i\theta}$
and letting
$r\rightarrow \infty,$
we have
$\Vert\mathcal{N}_{j}\big(re^{i\theta}\big)\Vert=O\big(e^{-c_{j}\sqrt{r}}\big)$
for some
$c_{j}>0$
,
$j = 1, 2, 3$
, when
$\theta\neq0.$
Thus,
$\mathcal{F}(s)\sim(1-s)^{-1}/4$
and the steepest descent path ends up roughly following the steepest descent path for an Exponential (1) MGF. This would start at say
$b/4$
and bend clockwise into its analytic continuation to asymptotically approach the horizontal line
$y=\pi i.$
Accordingly, our integration started at
$y=b/4$
and proceeded vertically to
$b/4+i\pi$
, then followed a horizontal line out to
$b/4+50+i\pi$
. This is less than 10% and 5%, respectively, of the numerical effort used above for vertical contour integration inside the convergence domain to determine S(5) and f(5). We say ‘less than’ because the integrand was not as ill-behaved as with the vertical contour, so segments typically took less that 45 seconds each. Changes to the exact path were implemented to check accuracy and led to the same computational values when computed to the 30 digits of floating point accuracy used when performing Maple computations. At
$y=b/4+50+i\pi,$
the values of the integrands were of order
$O(10^{-115})$
and
$O(10^{-113})$
for S(5) and f(5), suggesting accuracy close to the 30 digits used in the computations.
6.2. Community bicycles
Suppose community bicycles are available at two locations, 1 and 2, in a small town. When rider usage ends, the bicycles must be returned to one of these two locations. Consider a new bicycle which starts in location 1 and moves amongst the locations until it is stolen either by a user or from a user, whereupon it arrives at the new location
$3.$
The duration of community usage of the bicycle X is the first-passage time from
$1\rightarrow 3$
and is measured in integer time. Usage times for individual riders clearly depend upon both the location at which usage starts and the intended destination of the rider/thief. Thus the process which describes the bicycle’s location is best modelled as an integer-time SMP.
Let the SMP model have three states, and take all one-step MGFs as Poisson
$(\lambda)$
restricted to
$\{1,2,\ldots\}$
with MGF
$\mathcal{N}(s;\,\lambda)=\{\exp(\lambda e^{s})-1\}/(e^{\lambda}-1).$
Assume the transmittance matrix is
\begin{equation*}\textbf{T}(s)=\left(\begin{array}[c]{c@{\quad}c@{\quad}c}0.7\,\mathcal{N}(s;\,2) & 0.2\,\mathcal{N}(s;\,2) &0.1\,\mathcal{N}(s;\,1)\\[3pt]0.65\,\mathcal{N}(s;\,11) & 0.3\,\mathcal{N}(s;\,3) &0.05\,\mathcal{N}(s;\,9)\\[3pt]0 &0 & 0 \end{array}\right)\end{equation*}
and the initial state is
$1.$
From the jump chain, the mean number of visits to locations 1 and 2 before passage to 3 is computed as
$(1,0)\big\{\textbf{I}_{2}-\textbf{T}_{\mathbb{I}_{2}\mathbb{I}_{2}}(0)\big\}^{-1}=\big(7\frac{7}{9},4\frac{4}{9}\big)$
, so the bicycle averages
$12\frac{2}{9}$
usages before its theft. The mean and standard deviation of the first-passage time are computed from derivatives of
$\mathcal{F}_{13}$
as
$59.64$
and
$70.26$
respectively.
Since
$\mathcal{N}(s;\,\lambda)$
is an entire function, all singularities of
$\mathcal{F}_{13}$
must be zeros of its denominator. This leads to simple poles at
$b=0.0138\,091$
and
$b_{2}=0.171\,477.$
First-order expansions
$S_{1}(n)$
and
$p_{1}(n)$
using the pole b are provided in Table 2 below for
$n=35,$
85, 200, and
$400.$
The arguments leading to the first-order expansions also allow second-order expansions
$S_{2}(n)$
and
$p_{2}(n)$
, which make additional use of the pole
$b_{2}$
as described in [Reference Butler6, Section 2.3]. These expressions are easily computed as
\begin{equation*}S_{2}\!\left( n\right) =e^{-bn}\frac{-\beta_{-1}}{1-e^{-b}}+e^{-b_{2}n}\frac{-(\beta_{2})_{-1}}{1-e^{-b_{2}}}, \qquad p_{2}\!\left( n\right)=e^{-bn}({-}\beta_{-1})+e^{-b_{2}n}\{-(\beta_{2})_{-1}\},\end{equation*}
where the first terms in the expressions are
$S_{1}\!\left( n\right) $
and
$p_{1}\!\left( n\right)$
, and
$(\beta_{2})_{-1}=\text{Res}\big\{\mathcal{F}_{13}(s),b_{2}\big\}.$
The first-order expansions may also be improved by using the corrected values
$S_{1}\!\left( n\right) +\hat{R}_{1}^{S}(n)$
and
$p_{1}\!\left( n\right)+\hat{R}_{1}(n),$
where
$\hat{R}_{1}^{S}(n)$
and
$\hat{R}_{1}(n)$
are saddlepoint approximations for expansion errors
$R_{1}^{S}(n)$
and
$R_{1}(n)$
represented in terms of the contour integral in (13) of Theorem 1. To get these approximations, we deform the error contour integrals to pass through saddlepoints lying on the real axis in
$(b,b_{2})$
as described in [Reference Butler6, Section 3]. For example, consider
$n=35.$
In the integral expression for
$R_{1}(35)$
there are two saddlepoints for its integrand in
$(b,b_{2})$
, given as
$\hat{s}_{1}=0.07946$
and
$\hat{s}_{2}=0.1340.$
The saddlepoint at
$\hat{s}_{1}$
has steepest descent paths in horizontal directions 0 and
$\pi$
, while
$\hat{s}_{2}$
has steepest descent directions
$\pm\pi/2.$
Figure 1 shows this saddlepoint geometry in terms of the plot of the inversion integrand
$\mathcal{F}_{13}(s)e^{-35s}$
for p(35) over
$s\in(0.01,0.21).$
The vertical lines locate the poles at
$s=b$
and
$b_{2}.$
The graph is flat at
$\hat{s}_{1}=0.079$
and
$\hat{s}_{2}=0.134$
, so these are critical values and hence saddlepoints. The concave shape at
$\hat{s}_{1}$
means that this saddlepoint has steepest descent directions 0 and
$\pi.$
The convex shape at
$\hat{s}_{2}$
means the steepest descent directions are perpendicular in directions
$\pm\pi/2$
(this follows since both saddlepoints are simple with non-zero second derivatives for
$\mathcal{F}_{13}(s)e^{-35s}$
at these points). The geometry is the same for all values of n with roughly the same saddlepoint values.
Figure 1. Plot of
$\mathcal{F}_{13}(s)e^{-35s}$
for
$s\in(0,0.21).$
Vertical lines locate poles at
$b=0.014$
and
$b_{2}=0.171.$
Saddlepoints are critical values of the graph at
$\hat{s}_{1}=0.079$
and
$\hat{s}_{2}=0.134$
.
The saddlepoint
$\hat{s}_{2}$
and not
$\hat{s}_{1}$
is the appropriate choice of saddlepoint for use in the approximation
$\hat{R}_{1}(n)$
, as has been discussed in [Reference Butler5, Sections 2.5 and 3.2.1]. The appropriate expressions for
$\hat{R}_{1}(n)$
and
$\hat{R}_{1}^{S}(n)$
are given in [Reference Butler6, Section 3] with
$\hat{R}_{1}^{S}(n)$
using a slightly different saddlepoint from
$\hat{s}_{2}.$
Table 2. Exact values of survival and mass functions S(n) and p(n) are compared with first-order expansion values
$S_{1}(n)$
and
$p_{1}(n)$
as well as second-order expansion values
$S_{2}(n)$
and
$p_{2}(n).$
First-order expansion errors
$R_{1}^{S}(n)$
and
$R_{1}(n)$
along with their saddlepoint approximations
$\hat{R}_{1}^{S}(n)$
and
$\hat {R}_{1}(n)$
are shown, together with first-order expansions corrected by these error approximations, denoted by
$S_{1}(n)+\hat{R}_{1}^{S}(n)$
and
$p_{1}(n)+\hat{R}_{1}(n).$
The standard saddlepoint approximations
$\hat{S}_{1}(n)\textit{,}$
$\hat{S}_{2}(n),$
and
$\hat{p}(n)$
are described in the text.
A comparison of approximation procedures in Table 2 confirms all the conclusions determined from the previous example. From Table 2 with
$n=35$
and
$n=85$
, and below the 75th percentile, the second-order expansions are most accurate; they are followed closely by the saddlepoint-corrected first-order expansions and then by the first-order expansions, the latter being entirely adequate for most applications. At the 95th percentile with
$n=200$
and above, the first-order approximations achieve the same very high accuracy as the second-order expansions and the saddlepoint-corrected first-order expansions. This may in part be explained by the asymptotic nature of the approximations as
$n\rightarrow \infty.$
Conventional saddlepoint methods for S(n) and p(n) are less accurate than first-order expansions for all values of n displayed. For the survival S(n), these approximations are denoted by
$\hat{S}_{1}(n)$
and
$\hat{S}_{2}(n)$
and are the continuity-corrected approximations suggested in [Reference Daniels10, Section 6] and described in detail as
$\widehat{\Pr}_{1}$
and
$\widehat{\Pr}_{2}$
in [Reference Butler3, Section 1.2.3]. The mass function approximation
$\hat{p}(n)$
is the standard approximation given in [Reference Butler3, Section 1.1.5]. The limiting relative errors of
$\hat{S}_{1}(n),$
$\hat{S}_{2}(n),$
and
$\hat{p}(n)$
are given in (30), and the error for
$\hat{p}(400)$
reflects such convergence. That such convergence should hold follows from [Reference Butler and Wood8, Section 6, Corollary 8 and Theorem 7(a)].
For integer-time distributions, the computation of exact values is considerably easier, since the inversion contour is now finite over
$\{\varepsilon+iy\,:\,y\in({-}\pi,\pi)\}$
for
$\varepsilon>0$
and integration can be reduced to the positive half. To achieve sufficient accuracy when determining the accuracy of the approximations, each numerical inversion required several minutes for smaller n and perhaps a minute for larger
$n.$
Acknowledgements
The author is grateful to two referees who provided helpful comments.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/apr.2022.4.
