Introduction
A shape grammar is a formal rewriting system for producing languages of shapes (Stiny & Gips, Reference Stiny, Gips and Freiman1972; Stiny, Reference Stiny1980). A shape grammar is typically specified to consist of a set of productions, or shape rules, operating over a vocabulary of (terminal) spatial elements and a vocabulary of (non-terminal) symbols or markers, for example, labels, and to include an initial shape as the starting point in the productive (generative) process (Stiny, Reference Stiny1980; Yue & Krishnamurti, Reference Yue and Krishnamurti2013). Then, a shape is defined as any composition of spatial elements and, optionally, symbols from the respective vocabularies. A shape rule is commonly expressed in the form a→b, with both a and b constituting shapes, such that the application of the rule to a shape s under a (similarity) transformation t yields the shape s − t(a) + t(b), with the condition that t(a) ≤ s. The left-hand side of the rule, a, must necessarily be non-zero, that is, non-empty, otherwise the transformation t is indeterminate. The language defined by a shape grammar is the set of shapes generated by the grammar that do not contain any non-terminal symbols.
Grammar formalisms for design come in a large variety, requiring different representations of the entities being generated, and different interpretative mechanisms for this generation. Shape grammars also come in a variety of forms, even if less broadly. Most examples of shape grammars rely on labeled shapes, a combination of line segments and labeled points (in two dimensions) (Stiny, Reference Stiny1980). Stiny (Reference Stiny1992) proposes numeric weights as attributes to denote line thicknesses or surface tones. Knight (Reference Knight1989, Reference Knight1993) considers a variety of qualitative aspects of design, such as color, as shape attributes. Stiny (Reference Stiny1981) also proposes to augment a shape grammar with a description function in order to enable the construction of verbal descriptions of designs. Note that shape attributes may be considered to form part of the terminal vocabulary of the shape grammar.
Implementing a shape grammar interpreter requires implementing the part relationship for shapes – with or without attributes – the operations of sum and difference on shapes, and solving the matching problem, that is, identifying under which transformation a rule may apply to a given shape. Beirão (Reference Beirão2012, pp. 228–236) offers a survey of (implementations of) shape grammar interpreters, and must conclude that they have common limitations. Many of them compute only on two-dimensional (2D) shapes; and most do not apply sub-shape detection and therefore do not support emergence; also, “very few shape grammar interpreters allow for the implementation of rules operating with symbols” (Beirão, Reference Beirão2012, p. 235), never mind other attributes or a description function.
In this paper, we address the problem of developing an implementation of a shape grammar interpreter supporting varying shape grammar formalisms, by focusing on the procedural abstraction of operations underlying parallel and compound shape grammars. We review the literature on parallel and compound shape grammars (sections “Parallel and compound shape grammars” and “Shape algebras”) and propose an algebraic treatment of shape grammar representations and their operations (section “Algebraic abstractions”). This algebraic treatment facilitates a modular approach, based on a similarity between algebraic abstraction and procedural abstraction (Frank, Reference Frank, Freksa and Mark1999). We emphasize the algebraic derivation of shape algebras from partial algebras operating on spatial elements (section “Deriving algebras from two-sorted partial algebras”) and of combinations of basic shape algebras with attribute algebras (section “Deriving augmented shape algebras”) as novel contributions to the shape algebra theory. We consider practical limitations on algebraic compositions of basic shape algebras with attribute algebras (section “Algebraic compositions”) and address the complication of efficiently resolving the matching problem for parallel and compound shape grammars when the particular compound algebra underlying the shape grammar is not known in advance (section “The matching problem”).
Parallel and compound shape grammars
Originally, a parallel shape grammar was defined by Stiny (Reference Stiny1975, p. 37) and Gips (Reference Gips1975, p. 7) as a shape grammar intended to be used in the parallel generation of shapes, that is, “whenever a shape rule is used, it is applied simultaneously to every part of the shape to which it is applicable” (Gips, Reference Gips1975, p. 7; Stiny, Reference Stiny1975, p. 37). This is in contrast to the more common serial application of shape rules, where at each step of the generation, a shape rule is applied to only one part of a shape. However, more recently, the term parallel (shape) grammar has been adopted in the context of parallel computations on multiple descriptions.
Li (Reference Li1999) defines a parallel grammar as a grammar operating on different descriptions with the objective to resolve parametric dependencies. For example, consider a shape grammar generating a plan where the number of rooms is dependent on the selection of rules applied. In this process, it is almost impossible to constrain the boundaries of the plan at the same time, as this would require the room sizes to be made dependent on the total number of rooms, which is only known at the end of the production process. Instead, Li (Reference Li1999) suggests adopting (at least) two descriptions, the first one a diagram with the number of rooms as (an) independent parameter(s), and the second one the plan with the room sizes as dependent parameters (of the number of rooms). By staging the production of the diagram before the production of the plan, the assignment of values to the dependent parameters can be postponed until after the assignment of values to the independent parameters. Figure 1 illustrates a single diagram production rule (Li, Reference Li1999), embedding line segments and markers, and labels/descriptions as attributes.

Fig. 1. A diagram production rule adding two bays at a time (after Li, Reference Li1999: 266).
Duarte (Reference Duarte2001) defines a parallel grammar as separating different representations or aspects of a design into different computations that interact with each other. Specifically, Duarte (Reference Duarte2001, Reference Duarte2005) considers a discursive (parallel) grammar incorporating a shape grammar and a description grammar – as well as a set of heuristics, where the latter is intended to constrain the rules that are applicable at each step of the design generation. While the shape grammar operates on shapes and the description grammar on textual (including numeric) descriptions, their rules are commonly coupled, with the description rule part constraining the shape rule part. This combination of a shape grammar and a description grammar follows Stiny's (Reference Stiny1981) definition of a description function to augment a shape grammar in order to construct design descriptions. Where Stiny (Reference Stiny1981) considers a description function as made up of functions, with each function assigned to a shape rule and computing in parallel to the shape rule, Duarte instead denotes the functions as description rules and the description function as a description grammar. Otherwise, these operate in exactly the same way and with the same intention. In fact, although Stiny nowhere adopts the term parallel grammar in this sense, Knight (Reference Knight1999, Reference Knight2003a) explicitly attributes the concept to Stiny (Reference Stiny1981). Knight (Reference Knight2003a) also offers a definition of a parallel grammar as “a network of two or more grammars that operate simultaneously”.
Admittedly, Li (Reference Li1999) and Knight's (Reference Knight2003a; also, Duarte Reference Duarte2001) interpretations are not unequivocal. Following Stiny's (Reference Stiny1990) definition of a design as “an element in an n-ary relation among drawings, other kinds of descriptions, and correlative devices as needed,” Li (Reference Li2001, Reference Li and Gero2004) considers seven drawings (from plan diagram to plan, section, and elevation) and nine descriptions (specifying measures of width, depth, and height, among others), in his specification of a shape grammar for (teaching) the architectural style of the Yingzao fashi. However, he considers only four grammar components to define his parallel grammar, corresponding to four stages in the production (Li, Reference Li1999). However, in Knight's (Reference Knight2003a) parallel grammar interpretation of Stiny's (Reference Stiny1981) example, the two grammar components of the parallel grammar – the shape grammar and the description function – apply hand in hand: “the rules of a parallel grammar may be linked so that the application of a rule in one grammar triggers the application of one or more rules in other grammars” (Knight, Reference Knight2003a). In fact, Knight (Reference Knight2003a) suggests the same interpretation for Li's (Reference Li2001, Reference Li and Gero2004) grammar, with each drawing and description specifying a component grammar in the parallel grammar, for each stage. Duarte (Reference Duarte2001) takes a similar position when describing his discursive grammar applied to the houses designed by the architect Alvaro Siza at Malagueira. Even though, strictly speaking, he only refers to two grammars – a shape grammar and a description grammar – he specifically acknowledges that both grammars include several sub-grammars. “These sub-grammars correspond to viewpoints in the shape grammar (e.g., first-floor plan), and to features in the description grammar (e.g., morphology)” (Duarte, Reference Duarte2001). Viewpoints define separate drawings (sketches, plans, elevation, envelope, etc.) while features specify individual descriptions. Figure 2 shows a rule from Duarte's Malagueira grammar including views relating to the envelope (walls; W), spaces (rooms; R), first-floor plan (F 1), second-floor plan (F 2), and descriptions (D). These views embed line segments, plane segments, volume segments, or descriptions, and weights (gray scales, dashed strokes) and descriptions (labels) as attributes.
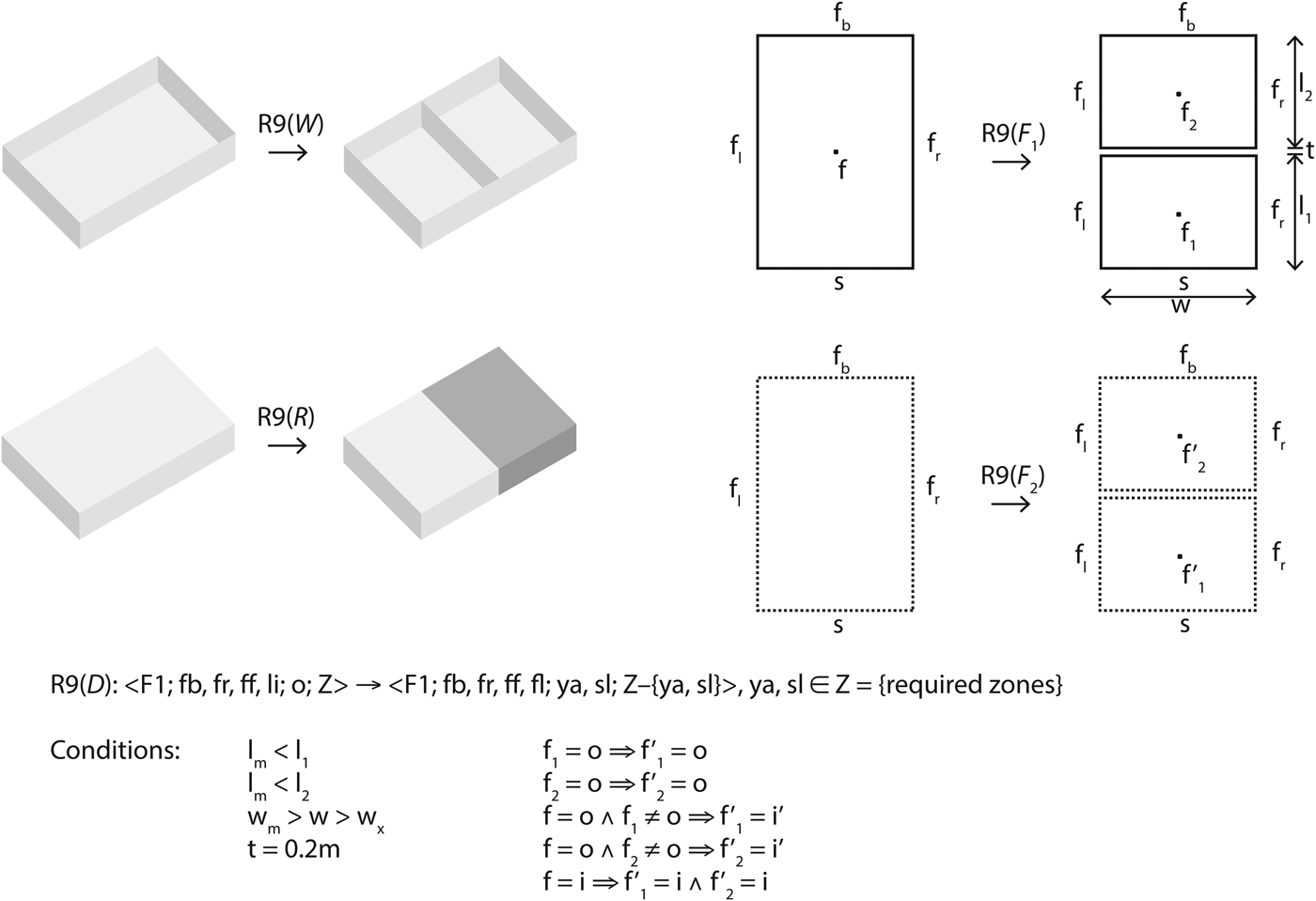
Fig. 2. Rule dissecting an outside zone into yard and sleeping zones (after Duarte, Reference Duarte2005: 359).
When the rules of a parallel grammar are linked, the linked rules can be expressed as one compound rule (Knight, Reference Knight2003a). Therefore, some authors consider compound grammars as an alternative term to parallel grammars, though others adopt the term compound grammars also to denote compositions of grammars that do not operate in parallel. For example, Beirão (Reference Beirão2012) uses the term compound grammar to denote a composition of several discursive grammars, where each discursive grammar formalizes a so-called urban induction pattern, encoding a typical urban design operation or design move. Knight (Reference Knight2004), instead, suggests a distinction between synchronized and a-synchronized parallel grammars, where the latter allows for sequential production stages as proposed by Li (Reference Li1999, Reference Li2001).
Shape algebras
While Stiny avoids the term parallel grammar when referring to parallel computations, he does emphasize parallel computations in multiple algebras. For example, when a rule applies to a shape composed of points and line segments, though the rule may require both one and more points and one or more line segments to be present within a prescribed spatial relationship, the rule computes with points and line segments in parallel. The overall shape rule computation actually combines two computations – one with shapes of line segments and one with shapes of points – “that are carried out in parallel and influence one another mutually” (Stiny, Reference Stiny1990).
Points and line segments, and by extension other spatial elements, can be considered to adhere to an algebra [specifically, a generalized Boolean algebra (Krstic, Reference Krstic1999)] that is ordered by a part relation (“≤”) and closed under the operations of sum (“+”), product (“·”), and difference (“−”), as well as relevant transformations. For example, points may belong to the algebra U 02 and line segments to the algebra U 12 [in two dimensions (2D)] (Stiny, Reference Stiny1992); U ij denotes the algebra of rectilinear spatial elements of dimension i, for example, 0 for points, 1 for line segments, 2 for plane segments, embedded in a space with dimension j, for example, 1D, 2D, 3D. Stiny (Reference Stiny1992) extends the notion of algebras to shapes with attributes: labeled points belong to the algebra V 02, while weighted line segments belong to the algebra W 12. Then, shapes of line segments and labeled points can be said to belong to an algebra that is the direct product of the algebras U 12 and V 02, U 12 × V 02. Consequently, a shape rule applying to shapes of line segments and labeled points can be considered to combine two shape rules, one in U 12 applying to line segments and one in V 02 applying to labeled points.
Any selection of shape algebras, including labeled and weighted shape algebras, can be combined using the direct product into a compound algebra of compound shapes that are made up of a mix of various spatial elements, and optionally augmented with labels or weights. Chase (Reference Chase1999) notes that “this is common in maps, as map features may be distinguished by different element types (for example, lines representing roads, points representing cities), or labels used to distinguish elements with the same basic geometry but different semantics (e.g., lines can represent roads and rivers)”. Examples in architectural representation abound as well. Compound shapes may be expressed in unions of the sets that form shapes from different algebras, with the understanding that basic and augmented spatial elements only interact if they are of the same kind (same dimension and attribute kind, if any), and are independent otherwise (Stiny, Reference Stiny1992).
Embedding spaces
Whereas we consider shape algebras U ij specifying rectilinear spatial elements of dimension i within an (embedding – as opposed to visual –) space of dimension j, the specification of the dimension of the space is often omitted, assuming that the actual dimension, for example, 2D or 3D, is unimportant within the context or, otherwise, can be construed from the context. While there is little issue with the assumption itself, the implicit attention to the dimension of the space hides the fact that, irrespective of the dimension, shape algebras may operate in the same space or in different spaces. Jowers and Earl (Reference Jowers and Earl2015) recognize that a (basic) shape algebra is not only dependent on the representation of the shape, but also on the space and the set of transformations used. At a minimum, shape algebras operating in the same space compute under the same transformations, while shape algebras operating in different spaces may use different transformations. For example, in the case of a drawing of line segments and labeled points, the segments and points operate in the same (2D or 3D) Euclidean space and transformations of shapes of line segments and shapes of labeled points necessarily need to go hand in hand. Instead, when shape algebras operate in a different space (or drawing), transformations may differ.
Stiny (Reference Stiny1992) shows an example where a series of cubes is described separately in plan – presented in the algebra U 12, in a front elevation with line weights decreasing as the edges of cubes recede – presented in the algebra W 12, and in a side elevation as an arrangement of shaded areas that decrease in weight as the faces of cubes advance – in the algebra W 22. For each drawing, the grammar considers three rules, an initialization rule, a rule to add a cube to the series – decreasing in size geometrically at a specified rate – and a finalization rule. Figure 3 shows Stiny's rule(s) adding a cube to the series in plan, front, and side elevation view. The three views embed points, line segments, and plane segments, and weights (line thicknesses and surface tones) and descriptions (labels) as attributes. Note that the weights themselves are also governed by descriptions.

Fig. 3. Rule adding a cube in plan, front, and side elevation view (after Stiny, Reference Stiny1992: 425–426)
Although the dimension of the spaces is two for all three drawings, plan, front elevation, and side elevation, the three drawings define three separate spaces. The respective rules compute in parallel, however, under different transformations. Only if the algebras are defined in three dimensions, that is, U 13, W 13, and W 23, can the algebras be selected to operate in the same 3D space and a single transformation be determined that applies to all rules in parallel. Such a solution may not always be applicable, as when working with diagrams and sketches, next to other drawings, such as plans, elevations, and even 3D models (e.g., Li, Reference Li1999).
Knight (Reference Knight2003b; see also, Krstic, Reference Krstic and Gero2012) therefore distinguishes an operation of sum of algebras from the operation of direct product on algebras. Whereas the latter allows algebras to operate in different spaces, the former requires algebras to be specified in the same space. Space is however only part of the picture; the allowable transformations matter separately as well.
Allowable transformations
Ultimately, and especially from an implementation point of view, whether algebras operate in the same space or in different spaces can be merely a visualization issue, the most important issue being whether they adopt the same or different transformations. Knight (Reference Knight2003a) even gives the following example of the component rules of a compound rule as being defined to operate in the same space: “the rules of color grammars as defined by Knight (Reference Knight1989) are compound rules with three components defined in the same 2D or 3D space: a shape component, a label component, and a color field component”. This is not entirely true; while shapes, labels, and color fields may be visually represented in the same space, they inhabit completely different spaces. A shape component exists in a 2D or 3D space, a label component inhabits a quasi-alphanumeric space, and a color field component a color space. If they would be defined – other than visualized – in the same space, then the same types of (e.g., geometric) transformations would apply to them.
Firstly, it is important to note that space is not just defined by its dimension. Jowers and Earl (Reference Jowers and Earl2015) provide an example of a 2D conic space (Fig. 4), rather than the traditional 2D Euclidean space. In a 2D conic space, line segments may become circular, elliptic, or parabolic arc segments under rotation, whereas in Euclidean space, line segments, circular, elliptic, and parabolic arc segments are all distinct under similarity transformations. This example also emphasizes the importance of the allowable transformations. If we allow affine transformations in Euclidean space, then circular arc segments can be transformed into elliptic arc segments and vice versa. Under projective transformations, circular arc segments can even be transformed into parabolic arc segments and vice versa. Nonetheless, from an implementation point of view, we can consider the shape algebras of circular, elliptic, and parabolic arc segments as distinct – or consider circular arcs as a subset of elliptic arcs, with both distinct from parabolic arcs – and consider an algebra of conic line segments as an algebraic composition under sum of all these algebras together with the shape algebra of line segments. Transformations – and spaces – that may result in interalgebra exchanges of spatial elements may then be considered separately as part of the matching mechanism.

Fig. 4. Rotation of a line segment in a 2D conic space (after Jowers & Earl, Reference Jowers and Earl2015: 959).
Secondly, Krstic (Reference Krstic1999) points out that even if algebras operate in different spaces and allow for different sets of transformations, these sets of allowable transformations may not necessarily be independent, but may actually be related via some mapping. For example, in the case of Stiny's (Reference Stiny1992) series of cubes described in plan, front elevation, and side elevation, it may be possible to conceive of these three descriptions as projections of a 3D series of cubes, with transformations in each drawing or algebra, mapped to a single, if hypothetical, 3D transformation. However, from an implementation point of view, it may be easier to consider this mapping only implicit rather than explicit; that is, the allowable transformations for each algebra may be considered independent if only the author of the shape rules carefully considers the relationships between the three drawings, as Stiny (Reference Stiny1992) does. Krstic (Reference Krstic1999) instead offers examples where labels or descriptions change with geometric transformations. For example, building elevation labels, for example, indicating north, east, south, or west elevations may change when the building plan is rotated. Though perfectly acceptable, the problem from an implementation point of view is that such mappings are specific and cannot easily be generalized. As such, we largely ignore transformations from here on and, instead, refer to Krstic (Reference Krstic and Gero2012) for a treatment of transformations in the context of shape algebras.
Algebraic abstractions
The notion of compound shapes, as resulting from compound algebras defined by the sum or direct product of basic shape algebras, is useful for a modular (or procedural) implementation of a shape grammar interpreter (e.g., Frank, Reference Frank, Freksa and Mark1999). Each basic shape algebra can define a single module (or a class in an object-oriented programming paradigm), and modules can be combined to define compound algebras, facilitating a variety of shape grammar formalisms.
The algebra's signature specifies the operations of the algebra, at a minimum, the operations of sum (“+”), product (“·”), and difference (“−”). The allowable transformations can be considered external to the algebra, as part of the signature or as part of the algebra's carrier, that is, the set of elements of the algebra (Krstic, Reference Krstic1999; Reference Krstic and Gero2012). The part relation (“≤”) is not an operation of the algebra but can be expressed in terms of the operation of product: t(a) ≤ s ⇔ t(a) s = t(a). From a modular implementation point of view, the algebra's signature contributes to the module's interface (the class methods in object-oriented programming), but the interface can be extended to include, among others, the part relation. Nevertheless, having a (even partially) uniform interface, that is, sharing the same class methods, greatly eases the implementation of a general shape grammar interpreter.
Unfortunately, as Knight (Reference Knight2003b) acknowledges, “the algebras that designers use, informally or formally, are many”. Beyond labels and weights, shapes can be augmented with attributes of any kind: “aesthetic, formal, functional, structural, and so on. For example, points can have diameters, lines can have thicknesses, planes can have colors, solids can have materials” (Knight, Reference Knight2003b) (see also Fig. 1 through Fig. 3). “The only condition is that the operators of any shape algebra are defined on all its elementary objects, are recursively applicable, and are closed” (Yue & Krishnamurti, Reference Yue and Krishnamurti2013). Fortunately, the notion of an algebra as derived from existing algebras can be extended to shapes augmented with attributes, for example, of labeled points (Stouffs, Reference Stouffs2008). Defining an algebra for labels is straightforward. Similar to points, a label can be said to be part of another label only if these are identical. Then, the operations of sum, product, and difference correspond to the set operations of union, intersection, and difference. Labels may not exhibit any allowable transformations, unless we consider, for example, case transformations. However, the operations of sum and direct product on algebras do not support an attribute behavior, and it is not straightforward to consider an alternative operation on algebras. Krstic (Reference Krstic1999) offers an unintentional hint.
Krstic (Reference Krstic1999) notes the difference between an algebra of (maximal) spatial elements and an algebra of shapes, shapes referring to collections of spatial elements. The former is a partial algebra as the operations of sum, product, and difference are not closed. The sum of two spatial elements is a spatial element only if the two elements overlap or are both parts of another spatial element and have boundaries that overlap. In general, the operations of sum, product, and difference on spatial elements are only defined if the spatial elements exist in the same subspace, where the dimension of the subspace equals the dimension of the spatial elements. For example, two line segments must be part of the same infinite line, two plane segments of the same infinite plane, and two volumes of the same 3D hyperplane. This subspace is denoted as the carrier of the spatial element, but in order to avoid any confusion with the carrier of an algebra, we instead refer to the descriptor of the subspace. Krishnamurti (Reference Krishnamurti1992) adopts the functional co to denote when two spatial elements of the same type share the same descriptor: “two points can combine when they are co-incident; two lines can combine when they are co-linear; two planes can combine when they are co-planar; and so on. Two spatial elements that share the same co-descriptor are referred to as co-equal” (Krishnamurti, Reference Krishnamurti1992). Then, the operations of sum, product, and difference on spatial elements are defined only if the spatial elements are co-equal. Note from above that, in and of itself, it is not a sufficient condition for the operations to be closed (Table 1).
Table 1. The “sum” of two line segments may or may not be a line segment, that is, the operation of sum on line segments may or may not be closed

Having established the difference, Krstic (Reference Krstic1999) goes on to focus solely on shape algebras. However, it is possible to derive shape algebras from partial algebras of spatial or other elements in a general way (Fig. 5). First, let us assume a two-sorted partial algebra with carrier {A, ℘(A)} and signature including operations of combine, common, and complement on members of A. We consider a two-sorted algebra because we want the operations of combine, common, and complement to extend upon the respective operations of sum, product, and difference, and at the same time be closed for co-equal (spatial) elements. For example, the combination of two co-equal spatial elements that do not have overlapping boundaries is the set of the two spatial elements (e.g., Table 1). Thus, each of the operations of combine, common, and complement takes as argument two (co-equal) elements of A and returns an element of ℘(A), the set of all subsets of A (Table 1). We then derive shape and attribute algebras from two-sorted partial algebras and algebras for shapes augmented with attributes from the combination of a two-sorted partial algebra and an attribute algebra (Fig. 5). We use the term augmented shape algebra to denote an algebra for shapes (of a single type of spatial elements) augmented with attributes (also of a single kind) in order to distinguish it from general compound (shape) algebras (which may include algebraic compositions under the direct product or sum). Figure 5 shows two variants: the structure on the left distinguishes basic shape algebras and basic attribute algebras. This is the standard view, in which shapes are paramount and shapes can be differentiated into attributes. This is also the view we will conform to in this section. The structure on the right, instead, follows the definition of sortal structures and grammars (Stouffs et al., Reference Stouffs, Krishnamurti and Park2007) where no explicit distinction is made between shape and attribute algebras and shape algebras can serve as attribute algebras and vice versa. From an application point of view, we prefer this second view (see “Algebraic compositions” section).

Fig. 5. Dependency structure underlying the construction of (compound) shape algebras (two variants). Basic (shape and attribute) algebras can be defined from two-sorted partial algebras. Augmented shape algebras are defined from a two-sorted partial (shape) algebra and a basic attribute algebra. Compound shape algebras combine basic and/or augmented shape algebras under the direct product.
Deriving algebras from two-sorted partial algebras
To derive a shape algebra from this two-sorted partial algebra, we need to distinguish the desired behavior. Each behavior results in a different derivation. Fortunately, we can reuse behaviors for different kinds of spatial or other elements. The simplest behavior is a discrete behavior, applying to both points and labels.
An algebra with carrier ℘(A) and signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”) can be defined for a discrete behavior as follows:
 $$\eqalign{& \forall \,X,\,Y \in \wp \,(A) \Rightarrow \cr & \quad X + Y = X \cup Y \cr & \quad X \cdot Y = X \cap Y \cr & \quad X - Y = X\backslash Y \cr & \quad r\,{\rm (}X{\rm )} = X.} $$
$$\eqalign{& \forall \,X,\,Y \in \wp \,(A) \Rightarrow \cr & \quad X + Y = X \cup Y \cr & \quad X \cdot Y = X \cap Y \cr & \quad X - Y = X\backslash Y \cr & \quad r\,{\rm (}X{\rm )} = X.} $$In a discrete behavior, the operations of sum, product, and difference correspond to the normal set operations of union, intersection, and difference. The reduce operation reduces any set to a set of maximal elements (Krishnamurti, Reference Krishnamurti1992). Under a discrete behavior, any set is maximal because any duplicates are automatically removed. The algebras U 0 (shapes of points; we omit the dimension of the space for simplicity) and L, sets of labels, can be defined in this way (Table 2). Note that descriptions, from an algebraic point of view, behave exactly as labels, and thus, the algebra D of sets of descriptions can be defined in this way as well.
Table 2. Algebraic operations of sum, product, and the difference for points (U 0), labels (L), and numeric weights (N)

Before we address other spatial elements, let us first consider a behavior for weights (e.g., line thicknesses or surface tones), as is apparent from drawings on paper – a single line drawn multiple times, each time with a different thickness, appears as if it were drawn once with the largest thickness, even though it assumes the same line with other thicknesses (Stiny, Reference Stiny1992).
An algebra with carrier ℘1(A), the set of all singleton subsets of A, and signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”) can be defined for an ordinal behavior, applying to weights, in terms of the two-sorted partial algebra with carrier {A, ℘(A)} and signature including the operations of combine, common, and complement, as follows:
 $$\eqalign{& \forall \,(x),\,(y) \in \wp _1\,(A) \Rightarrow \cr & \quad {\rm (}x{\rm )} + {\rm (}y{\rm )} = \hbox{combine}\,{\rm (}x,\,y{\rm )} \cr & \quad (x) \cdot (y) = \hbox{common}\,{\rm (}x,\,y{\rm )} \cr & \quad (x) - (y) = \hbox{complement}\,{\rm (}x,\,y{\rm )} \cr & \quad r\,(\{ x\} {\rm )} = {\rm \{} x{\rm \}} .} $$
$$\eqalign{& \forall \,(x),\,(y) \in \wp _1\,(A) \Rightarrow \cr & \quad {\rm (}x{\rm )} + {\rm (}y{\rm )} = \hbox{combine}\,{\rm (}x,\,y{\rm )} \cr & \quad (x) \cdot (y) = \hbox{common}\,{\rm (}x,\,y{\rm )} \cr & \quad (x) - (y) = \hbox{complement}\,{\rm (}x,\,y{\rm )} \cr & \quad r\,(\{ x\} {\rm )} = {\rm \{} x{\rm \}} .} $$For weights, we know that the result of the operations of combine, common, and complement on two singleton weights is always a singleton weight. We use this knowledge to define the operations of sum, product, and difference in terms of the operations of combine, common, and complement. Again, the reduce operation results in the argument (singleton) set itself. The algebra N of singletons of numeric weights can be defined in this way. Table 2 illustrates the algebra N if combine (x, y) ≡ max (x, y), common (x, y) ≡ min (x, y), and complement (x, y) ≡ x − y (i.e., arithmetic difference) as suggested by Stiny (Reference Stiny1992).
Deriving a shape algebra for spatial elements other than points from a two-sorted partial algebra is a little bit more complicated because of the need to consider co-equal shapes. We take a two-step approach. First, we derive a sub-algebra for co-equal shapes of spatial elements, next we define a shape algebra for a single type of spatial elements from this sub-algebra (Table 3).
Table 3. Dependencies underlying the construction of shape algebras from sub-algebras for co-equal shapes and two-sorted partial algebras of spatial elements

A sub-algebra with carrier ℘(A) and signature including sum, product, difference, and reduce can be defined for an areal behavior as follows:
 $$\eqalign{& \forall \,X,\,Y \in \wp \,(A):\,\,\forall \,x \in \,X,\,\forall \,y \in Y,\,\hbox{co}(x) = \hbox{co}(y) \Rightarrow \cr & \quad \hbox{sum}\,{\rm (}X,\,Y{\rm )} = \hbox{construct}\,(\hbox{outside}\, (b\, (X{\rm )},\,Y )\,\cup \cr &\qquad \hbox{outside}\, (b\, (Y ),\,X)\, \cup \,\hbox{same - side}\, (b\, (X),\,b\, (Y))) \cr & \quad \hbox{product}\, (X,\,Y) = \hbox{construct}\,(\hbox{inside}\, (b\, (X),\,Y)\, \cup \cr &\qquad \hbox{inside}\, (b\, (Y),\,X)\, \cup \,\hbox{same - side}\, (b\, (X),\,b (Y))) \cr & \quad \hbox{difference}\, (X,\,Y) = \hbox{construct}\,(\hbox{outside}\, (b\, (X),\,Y)\, \cup \,\cr & \qquad \hbox{inside} (b\, (Y),\,X)\, \cup \,\hbox{opposite - side}\, (b\, (X),\,b\, (Y))) \cr & \quad \hbox{reduce}\, (X) = \hbox{sum}\, ((x),\,\hbox{reduce}\, (X\backslash x))\,\qquad\hbox{if}\,\,\exists \,x \in X \cr &\qquad \emptyset \qquad \qquad \qquad \qquad \hbox{otherwise.}} $$
$$\eqalign{& \forall \,X,\,Y \in \wp \,(A):\,\,\forall \,x \in \,X,\,\forall \,y \in Y,\,\hbox{co}(x) = \hbox{co}(y) \Rightarrow \cr & \quad \hbox{sum}\,{\rm (}X,\,Y{\rm )} = \hbox{construct}\,(\hbox{outside}\, (b\, (X{\rm )},\,Y )\,\cup \cr &\qquad \hbox{outside}\, (b\, (Y ),\,X)\, \cup \,\hbox{same - side}\, (b\, (X),\,b\, (Y))) \cr & \quad \hbox{product}\, (X,\,Y) = \hbox{construct}\,(\hbox{inside}\, (b\, (X),\,Y)\, \cup \cr &\qquad \hbox{inside}\, (b\, (Y),\,X)\, \cup \,\hbox{same - side}\, (b\, (X),\,b (Y))) \cr & \quad \hbox{difference}\, (X,\,Y) = \hbox{construct}\,(\hbox{outside}\, (b\, (X),\,Y)\, \cup \,\cr & \qquad \hbox{inside} (b\, (Y),\,X)\, \cup \,\hbox{opposite - side}\, (b\, (X),\,b\, (Y))) \cr & \quad \hbox{reduce}\, (X) = \hbox{sum}\, ((x),\,\hbox{reduce}\, (X\backslash x))\,\qquad\hbox{if}\,\,\exists \,x \in X \cr &\qquad \emptyset \qquad \qquad \qquad \qquad \hbox{otherwise.}} $$Instead of comparing the shape operands for coequality, it is checked that all spatial elements are co-equal, that is, share the same (co-)descriptor (“co”). Then, the operations can be expressed in terms of the boundaries (“b”) of each (co-equal) shape (Krishnamurti & Stouffs, Reference Krishnamurti and Stouffs2004; Stouffs & Krishnamurti, Reference Stouffs and Krishnamurti2006). Specifically, “outside(b(X), Y)” returns the collection of boundaries of shape X that lie outside of shape Y. Similarly, “inside(b(Y), X)” returns the collection of boundaries of shape Y that lie inside of shape X. “same-side(b(X), b(Y))” denotes the collection of boundaries that belong to both shapes X and Y, and where the interiors of the respective shapes lie on the same side of the boundary, and “opposite-side(b(X), b(Y))” denotes the collection of boundaries that belong to both shapes X and Y, and where the interiors of the respective shapes lie on opposite sides of the boundary. Then, the boundary of the shape resulting from the co-sum operation is formed by the “outside(b(X), Y)”, “outside(b(Y), X)”, and “same-side(b(X), b(Y))” collections, and the shape can be constructed from the union of these collections. The product and difference operations are similarly defined (Table 4). In the case of the reduce operation, each spatial element in the shape is summed with the reduced remainder of the shape. From an implementation point of view, this recursive definition of reduce is certainly not the most efficient; actually, the same can be said about the other operations – the classification of boundary segments with respect to another shape can be computed once for all of the classes inside, outside, same-side, and opposite-side. Obviously, these definitions only serve as abstractions of the actual procedures, we refer to Stouffs and Krishnamurti (Reference Stouffs and Krishnamurti2006) for actual, and efficient, algorithms.
Table 4. Classified boundary segments that make up the shape resulting from a shape operation

Then, a shape algebra with carrier ℘(A) and signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”) can be defined for an areal behavior, applying to line segments, plane segments, and volumes, in terms of the sub-algebra with carrier ℘(A) and signature sum, product, difference, and reduce, as follows:
 $$\eqalign{& \forall \,X,\,Y \in \wp \,(A) \Rightarrow \cr & \quad X + Y = r\,(X \cup Y) \cr &\quad X \cdot Y = \cup _{\rm c}\hbox{product}\,(\{ x \in X:\,\hbox{co(}x) = c\}, \cr &\qquad \{ y \in Y:\,\hbox{co(}y) = c\}) \cr & \quad X - Y = \cup _{\rm c}\{ x \in X:\,\hbox{co(}x) = c \wedge \neg \exists \,y \in Y:\,\hbox{co(}y) = c\} \cup \cr & \cup_{\rm c} \hbox{difference}\,(\{ x \in X:\,\hbox{co(}x) = c\}, \{ y \in Y:\,\hbox{co(}y) = c\}) \cr & \quad r (X) = \cup _{\rm c}\hbox{reduce} \; (\{ x \in X:\,\hbox{co(}x) = c\}).} $$
$$\eqalign{& \forall \,X,\,Y \in \wp \,(A) \Rightarrow \cr & \quad X + Y = r\,(X \cup Y) \cr &\quad X \cdot Y = \cup _{\rm c}\hbox{product}\,(\{ x \in X:\,\hbox{co(}x) = c\}, \cr &\qquad \{ y \in Y:\,\hbox{co(}y) = c\}) \cr & \quad X - Y = \cup _{\rm c}\{ x \in X:\,\hbox{co(}x) = c \wedge \neg \exists \,y \in Y:\,\hbox{co(}y) = c\} \cup \cr & \cup_{\rm c} \hbox{difference}\,(\{ x \in X:\,\hbox{co(}x) = c\}, \{ y \in Y:\,\hbox{co(}y) = c\}) \cr & \quad r (X) = \cup _{\rm c}\hbox{reduce} \; (\{ x \in X:\,\hbox{co(}x) = c\}).} $$The operations of product, difference, and reduce are expressed directly in terms of the similar operations on the respective sub-shapes of co-equal spatial elements. In the case of complement, shapes of co-equal spatial elements from X for which there exists no (co-equal) shape in Y also form part of the result. A similar approach can be taken for the operation of sum; however, for simplicity, we prefer to express the operation of sum in terms of the operation of reducing (“r”) on the combined sets of spatial elements. Note that the algebras U 1 (shapes of line segments), U 2 (shapes of plane segments), and U 3 (shapes of volumes) can all be defined in this way (Table 5).
Table 5. Algebraic operations of sum, product, and difference for plane segments (U 2) and volumes (U 3)

We should note that while an areal behavior applies to shapes of line segments as well, from an implementation point of view, it is more efficient to define an interval behavior for shapes of line segments. Additionally, while these behaviors cover shapes of different kinds of spatial elements and sets of labels and singletons of weights, other behaviors can be identified to apply to other kinds of attributes, for example, for material rankings (Knight, Reference Knight1993). Instead, we continue with the derivation of compositions of algebras under the direct product.
Deriving algebras with sum and direct product
The operations of sum and direct product apply to all algebras that share the same signature, specifically, the algebras U 0, U 1, U 2, U 3, L, D, and N we have previously defined. We address some implications of this in the section Algebraic Compositions. Here, we define an (shape) algebra with carrier ℘(A) × ℘(B) and signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”) in terms of the (shape) algebras with carriers ℘(A) and ℘(B) and identical signatures, as follows:
 $$\eqalign{& \forall (A_{\rm 1},\,B_{\rm 1}),\,(A_{\rm 2},\,B_{\rm 2}) \in \wp (A) \times \wp (B) \Rightarrow \cr & \quad (A_{\rm 1},B_{\rm 1}) + (A_{\rm 2},B_{\rm 2}) = (A_{\rm 1} + A_{\rm 2},\,B_{\rm 1} + B_{\rm 2}) \cr & \quad (A_{\rm 1},\,B_{\rm 1}) \cdot (A_{\rm 2},\,B_{\rm 2}) = (A_{\rm 1} \cdot A_{\rm 2},\,B_{\rm 1} \cdot B_{\rm 2}) \cr & \quad (A_{\rm 1},\,B_{\rm 1}) - (A_{\rm 2},\,B_{\rm 2}) = (A_{\rm 1} - A_{\rm 2},\,B_{\rm 1} - B_{\rm 2}) \cr & \quad r (A_{\rm 1},B_{\rm 1}) = (r (A_{\rm 1}),\,r (B_{\rm 1})).} $$
$$\eqalign{& \forall (A_{\rm 1},\,B_{\rm 1}),\,(A_{\rm 2},\,B_{\rm 2}) \in \wp (A) \times \wp (B) \Rightarrow \cr & \quad (A_{\rm 1},B_{\rm 1}) + (A_{\rm 2},B_{\rm 2}) = (A_{\rm 1} + A_{\rm 2},\,B_{\rm 1} + B_{\rm 2}) \cr & \quad (A_{\rm 1},\,B_{\rm 1}) \cdot (A_{\rm 2},\,B_{\rm 2}) = (A_{\rm 1} \cdot A_{\rm 2},\,B_{\rm 1} \cdot B_{\rm 2}) \cr & \quad (A_{\rm 1},\,B_{\rm 1}) - (A_{\rm 2},\,B_{\rm 2}) = (A_{\rm 1} - A_{\rm 2},\,B_{\rm 1} - B_{\rm 2}) \cr & \quad r (A_{\rm 1},B_{\rm 1}) = (r (A_{\rm 1}),\,r (B_{\rm 1})).} $$An algebra of shapes of points and line segments, U 0 + U 1, and an algebra of shapes of line segments and sets of descriptions, U 1 × D, among others, can be defined in this way. We do not distinguish algebraic derivations under sum or direct product, the distinction only relates to the (embedding) space(s) and the allowable transformations, neither of which is considered here. As we have mentioned before, for algebraic compositions under the direct product – and sum – shape rules and the operations of sum, product, and difference (and reduce) operate in parallel on the various component algebras.
Deriving augmented shape algebras
Next, we can tackle the issue of an algebra for shapes augmented with attributes. When defining the augmented shape algebra, rather than referring to a shape algebra and an attribute algebra (e.g., L or N), we instead refer to the partial algebra for the spatial elements, just as we define the shape algebra from the partial algebra of its spatial elements. That is, we derive the operational behavior of an augmented shape algebra from the behaviors of the partial algebra of spatial elements and the algebra of attribute elements. For example, consider two co-equal line segments that overlap. Without attributes, these combine into a single line segment. With attributes, they combine only if they share the same attributes or, otherwise, if the segments are identical. In the latter case, the attributes combine. Otherwise, different segments (or parts thereof) necessarily have different attributes and need to be represented separately (Table 6). The behavior of the attribute elements, for each of the different line segments (or parts thereof), however remains the same.
Table 6. Two spatial elements (line segments) combine depending on whether their attributes combine

An algebra with carrier ℘[A × ℘(B)] and signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”) can be defined for a discrete behavior, in terms of the (attribute) algebra ℘(B) with signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”), as follows:
 $$\eqalign{& \forall \,X,\,Y \in \wp \,[A \times \wp (B)] \Rightarrow \cr & \quad X + Y = \{ (x,\,B_x + B_y):\,(x,\,B_x) \in X \wedge (x,\,B_y) \in Y\}\cup \cr & \quad \quad \quad \{ (x,\,B_x):\,(x,B_x) \in X \wedge \neg \exists (x,B_y) \in Y\} \cup \cr & \quad \quad \quad \{ (y,\,B_y):\,(y,\,B_y) \in Y \wedge \neg \exists (y,\,B_x) \in X\} \cr & \quad X \cdot Y = \{ (x,\,B_x \cdot B_y):\,(x,\,B_x) \in X \wedge (x,\,B_y) \in Y\} \cr & \quad X - Y = \{ (x,\,B_x - B_y):\,(x,\,B_x) \in X \wedge (x,\,B_y) \in Y\} \cup \cr & \quad \quad \quad \{ (x,\,B_x):\,(x,\,B_x) \in X \wedge \neg \exists (x,\,B_y) \in Y\} \cr & \quad r (X) = \{ (x,\,B_x)\} + r[\hbox{X}\backslash (x,\,B_x)]\,\qquad \hbox{if}\,\,\exists (x,\,B_x) \in X \cr & \quad\qquad \emptyset \qquad \qquad \qquad \hbox{otherwise.}} $$
$$\eqalign{& \forall \,X,\,Y \in \wp \,[A \times \wp (B)] \Rightarrow \cr & \quad X + Y = \{ (x,\,B_x + B_y):\,(x,\,B_x) \in X \wedge (x,\,B_y) \in Y\}\cup \cr & \quad \quad \quad \{ (x,\,B_x):\,(x,B_x) \in X \wedge \neg \exists (x,B_y) \in Y\} \cup \cr & \quad \quad \quad \{ (y,\,B_y):\,(y,\,B_y) \in Y \wedge \neg \exists (y,\,B_x) \in X\} \cr & \quad X \cdot Y = \{ (x,\,B_x \cdot B_y):\,(x,\,B_x) \in X \wedge (x,\,B_y) \in Y\} \cr & \quad X - Y = \{ (x,\,B_x - B_y):\,(x,\,B_x) \in X \wedge (x,\,B_y) \in Y\} \cup \cr & \quad \quad \quad \{ (x,\,B_x):\,(x,\,B_x) \in X \wedge \neg \exists (x,\,B_y) \in Y\} \cr & \quad r (X) = \{ (x,\,B_x)\} + r[\hbox{X}\backslash (x,\,B_x)]\,\qquad \hbox{if}\,\,\exists (x,\,B_x) \in X \cr & \quad\qquad \emptyset \qquad \qquad \qquad \hbox{otherwise.}} $$Comparing this to the discrete behavior for a non-augmented shape algebra, we observe that for the operations of sum, product, and difference, if a spatial element is shared between both (augmented) shapes, we combine both attributes of the spatial element under the same operation. In the case of the operations of sum and difference, we may need to add spatial elements, with their original attribute, that belong to one augmented shape but not the other. We express the operation of reducing in terms of the operation of sum for the same algebra. An algebra of shapes of labeled points, V 0, or shapes of weighted points, W 0, with the weights representing gray scales or diameters, can be defined in this way (Table 7).
Table 7. Algebraic operations of sum, product, and difference for labeled points (V 0) and weighted line segments (W 1)

Having established an augmented shape algebra for points, a demonstration of an augmented shape algebra for other spatial elements, using the areal behavior, remains. In fact, where the shape algebra for an areal behavior is expressed in terms of the sub-algebra for co-equal shapes, we can define a sub-algebra for co-equal augmented shapes and retain the definition for the shape algebra as a definition for the augmented shape algebra as well. The only difficulty is the use of the (co-)descriptor function (“co”) on elements of the shape algebra. However, if we overload the function “co” to accept augmented spatial elements, that is, elements with attributes, then there is no issue.
A sub-algebra with carrier ℘(A × ℘(B)) and signature including sum, product, difference, and reduce can be defined for an areal behavior, in terms of the two-sorted partial algebra with carrier {A, ℘(A)} and signature including the operations of combine, common, and complement, and the (attribute) algebra ℘(B) with signature including sum (“+”), product (“·”), difference (“−”), and reduce (“r”), as follows:
 $$\eqalign{& \forall X,Y \in \wp (A \times \wp (B)):\forall (x,\,B_x) \in X,\,\forall (y,\,B_y) \in Y,\cr &\quad \hbox{co(}x) = \hbox{co(}y) \Rightarrow\cr & \quad \hbox{sum}\, (X,\,Y) = \hbox{consolidate}\,(\hbox{common-with-sum}\, (X,Y) \cup \cr & \quad \hbox{remainder}\, (X,\,Y) \cup \hbox{remainder}\, (Y,X)) \cr & \quad \hbox{product}\, (X,\,Y) = \hbox{consolidate(} \cr &\quad {\rm common} \hbox{-} {\rm with}\hbox{-}{\rm product}\, (X,\,Y)) \cr & \quad \hbox{difference}\, (X,\,Y) = \hbox{consolidate(}\, \cr & \quad {\rm common \hbox{-} with \hbox{-} difference}\, (X,\,Y) \cup\cr &\quad \hbox{remainder}\, (X,\,Y)) \cr & \quad \hbox{reduce}\, (X) = \cr &\quad \hbox{sum}\,(\{ (x,\,B_x)\}, \hbox{reduce}\,(X\backslash (x,\,B_x)))\,\quad \hbox{if}\,\,\exists \,(x,\,B_x) \in X \cr & \quad \qquad \emptyset \qquad \qquad \qquad \hbox{otherwise.}}$$
$$\eqalign{& \forall X,Y \in \wp (A \times \wp (B)):\forall (x,\,B_x) \in X,\,\forall (y,\,B_y) \in Y,\cr &\quad \hbox{co(}x) = \hbox{co(}y) \Rightarrow\cr & \quad \hbox{sum}\, (X,\,Y) = \hbox{consolidate}\,(\hbox{common-with-sum}\, (X,Y) \cup \cr & \quad \hbox{remainder}\, (X,\,Y) \cup \hbox{remainder}\, (Y,X)) \cr & \quad \hbox{product}\, (X,\,Y) = \hbox{consolidate(} \cr &\quad {\rm common} \hbox{-} {\rm with}\hbox{-}{\rm product}\, (X,\,Y)) \cr & \quad \hbox{difference}\, (X,\,Y) = \hbox{consolidate(}\, \cr & \quad {\rm common \hbox{-} with \hbox{-} difference}\, (X,\,Y) \cup\cr &\quad \hbox{remainder}\, (X,\,Y)) \cr & \quad \hbox{reduce}\, (X) = \cr &\quad \hbox{sum}\,(\{ (x,\,B_x)\}, \hbox{reduce}\,(X\backslash (x,\,B_x)))\,\quad \hbox{if}\,\,\exists \,(x,\,B_x) \in X \cr & \quad \qquad \emptyset \qquad \qquad \qquad \hbox{otherwise.}}$$We cannot simply determine a resulting shape – from one of the operations of sum, product, and difference – from the classification of the boundaries of both (co-equal) shapes in their entirety. Instead, we need to apply the classification and construction to each pair of spatial elements from the respective shapes, in order to be able to assign the appropriate attributes – as defined by the operation of sum, product, or difference applied to the respective attributes of the spatial elements. Basically, we split any overlapping spatial elements into their common parts and the remaining complement parts. For each common part, we combine the attributes under the respective operation of sum, product, or difference. This is expressed by the helper functions “common-with-sum”, “common-with-product”, and “common-with-difference”; these return the common shape of two co-equal spatial elements, with as attribute, respectively, the sum, product, and difference of the respective attributes (see below for their specification). Any complement part that forms part of the result naturally retains its attribute; the helper function “remainder” returns the complement shape of a spatial element with respect to a co-equal shape, with as attribute the original attribute of the spatial element. Finally, we combine any parts that end up having the same attribute. The helper function “consolidate” is a variant of the operation of reducing (for a co-equal shape) that assumes that none of the spatial elements overlap, though they may share boundaries. It recursively tries to find two spatial elements that share a boundary and also share the same attribute(s), in which case it combines both elements into a single element.
 $$\eqalign{& {\rm common \hbox{-} with \hbox{-} sum}\, (X,Y) = \cup _x \cup _y\{ (z,\,B_x + B_y): \cr & \quad (x,\,B_x) \in X \wedge (y,\,B_y) \in Y \wedge z \in \hbox{common}\, (x,\,y)\} \cr &{\rm common \hbox{-} with \hbox{-} product}\, (X,\,Y) = \cup _x \cup _y\{ (z,\,B_x \cdot B_y): \cr & \quad (x,\,B_x) \in X \wedge (y,\,B_y) \in Y \wedge z \in \hbox{common}\, (x,\,y)\} \cr & {\rm common \hbox{-} with \hbox{-} difference}\, (X,\,Y) = \cup _x \cup _y\{ (z,B_x - B_y): \cr & \quad {\rm} (x,B_x) \in X \wedge (y,B_{\scriptstyle y \hfill \atop \scriptstyle \hfill}) \in Y \wedge z \in \hbox{common}\, (x,\,y)\} \cr & \hbox{remainder}\, (X,\,Y) = \cup _x\{ (z,\,B_x):(x,\,B_x) \in X \wedge \cr & \quad z \in \hbox{difference}\, (\{ x\}, \,Y)\} \cr & \hbox{consolidate}\, (X) = \cr & \quad \hbox{consolidate}\,(\{ (z,\,B_x)\} \cup X\backslash {\rm} \{ (x,\,B_x),(y,\,B_x)\}) \cr & \quad\quad \hbox{if}\,\exists \,(x,\,B_x) \in X \wedge (y,\,B_x) \in X: x \ne y \wedge \cr & \quad \ \{ z\} = \hbox{combine}\, (x,\,y) \cr & \quad X \qquad \hbox{otherwise}{\rm.}} $$
$$\eqalign{& {\rm common \hbox{-} with \hbox{-} sum}\, (X,Y) = \cup _x \cup _y\{ (z,\,B_x + B_y): \cr & \quad (x,\,B_x) \in X \wedge (y,\,B_y) \in Y \wedge z \in \hbox{common}\, (x,\,y)\} \cr &{\rm common \hbox{-} with \hbox{-} product}\, (X,\,Y) = \cup _x \cup _y\{ (z,\,B_x \cdot B_y): \cr & \quad (x,\,B_x) \in X \wedge (y,\,B_y) \in Y \wedge z \in \hbox{common}\, (x,\,y)\} \cr & {\rm common \hbox{-} with \hbox{-} difference}\, (X,\,Y) = \cup _x \cup _y\{ (z,B_x - B_y): \cr & \quad {\rm} (x,B_x) \in X \wedge (y,B_{\scriptstyle y \hfill \atop \scriptstyle \hfill}) \in Y \wedge z \in \hbox{common}\, (x,\,y)\} \cr & \hbox{remainder}\, (X,\,Y) = \cup _x\{ (z,\,B_x):(x,\,B_x) \in X \wedge \cr & \quad z \in \hbox{difference}\, (\{ x\}, \,Y)\} \cr & \hbox{consolidate}\, (X) = \cr & \quad \hbox{consolidate}\,(\{ (z,\,B_x)\} \cup X\backslash {\rm} \{ (x,\,B_x),(y,\,B_x)\}) \cr & \quad\quad \hbox{if}\,\exists \,(x,\,B_x) \in X \wedge (y,\,B_x) \in X: x \ne y \wedge \cr & \quad \ \{ z\} = \hbox{combine}\, (x,\,y) \cr & \quad X \qquad \hbox{otherwise}{\rm.}} $$An algebra of shapes of weighted line segments, W 1, or shapes of labeled plane segments, V 2, among others, can be defined in this way (Table 7).
Algebraic compositions
We have adopted a constructive, algebraic approach to defining shape algebras and compound (shape) algebras (Fig. 5). This allows for a variety of algebras to be defined from an array of basic (partial) algebras of spatial and other elements. For example, we can define an algebra of shapes of line segments and labeled points, U 1 + V 0, from basic partial algebras of points, line segments, and labels. We can extend this notation to the definition of augmented (shape) algebras, considering an operation of attribution, denoted with the operator “∧”, as in V 0 = U 0 ∧ L and W 1 = U 1 ∧ N. Note that this is not formally correct; while the operations of sum and direct product operate on two algebras, the operation of attribution combines a two-sorted partial algebra with an algebra. Nevertheless, for the sake of simplicity and readability, we adopt the notation above. Having established this notation, let us assess the generality of the adopted approach, starting with augmented (shape) algebras.
Attribution
The derivation of augmented (shape) algebras distinguishes between shape algebras and attribute algebras. However, considering that shape and attribute algebras may share the same behavior, and no conditions have been specified on the behavior of the attribute algebra component of the augmented (shape) algebra, the derivations above equally apply to augmented algebras where the base component is a two-sorted partial algebra for, for example, labels, and the attribute algebra is a shape algebra. Thus, we can conceivably write L ∧ U 0, an algebra for sets of labels with points as attributes. In fact, any two-sorted partial algebra can be considered as a base component and any basic algebra as attribute algebra, allowing for combinations of shapes and non-geometric attributes, non-geometric elements and shape attributes, shapes and shape attributes, and non-geometric elements and non-geometric attributes (see Fig. 5, right). For example, Stouffs et al. (Reference Stouffs, Krishnamurti and Park2007) consider algebras of shapes as attribute algebras, with the base algebra defined as an algebra of labels, for example, L ∧ U 3. As an example, the primary information target of a planner of embedded sensors is the building slab for the sensor to be embedded, for example, represented as a label identifying the slab, while the shape of the slab is also required, but only as an attribute to the label. While visual calculating (Stiny, Reference Stiny2006) is a powerful paradigm for design, design actions also move beyond the visual, requiring alternative design representations that primarily target non-spatial data elements. A truly algebraic approach to representing design data enables such flexibility. For example, consider the algebra D of sets of descriptions. While most authors consider descriptions parallel to drawings, for example, U 1 × D, Beirão (Reference Beirão2012) considers descriptions as attributes to spatial objects, allowing for objects to refer to alternate, though similar, descriptions, thus, U 1 ∧ D.
Returning to the derivation of augmented algebras, admittedly, we did not specify an augmented algebra for an ordinal behavior. This, however, can be easily done and we leave it as an exercise to the reader. Similarly, other behaviors can also be considered, such as an enumerative behavior allowing for Knight's (Reference Knight1989, Reference Knight1993) color grammars. Knight (Reference Knight1993) considers explicit rankings for colors, materials, or other qualitative aspects of design. Alternatively, we can consider a behavior for colors based on a method to combine RGB or HSV color values and determine the common and complement value of one color with respect to another. Whichever approach we adopt to represent colors, once we have defined a basic algebra of sets of colors, C, we can define an algebra of shapes of colored plane segments as U 2 ∧ C.
One step further, the derivation of augmented algebras does not restrict the attribute component to only basic algebras. Any algebra ℘(B) with signature including sum, product, difference, and reduce can serve as attribute component, including both augmented and compound algebras. As such, we can define an attribute algebra as the sum of two basic attribute algebras, for instance, U 0 ∧ (L + N) defines an algebra of shapes of points with both labels and weights (e.g., diameters or gray scales) as attributes. Intuitively, we can consider the operation of sum to distribute over the operation of attribution, that is, U 0 ∧ (L + N) = (U 0 ∧ L) + (U 0 ∧ N) = V 0 + W 0, combining points with labels and points with weights.
A hierarchical modus operandi
Considering these extensions, it is useful to further explore how the different operations on algebras – direct product, sum, and attribution – may combine to define compound algebras, and thus, shape grammars. From an algebraic point of view, the base component of an augmented algebra should always be a two-sorted partial algebra, and therefore, we restrict the base operand under attribution to a basic algebra. That is, we never write (U 0 + U 1) ∧ L but, instead, always (U 0 ∧ L) + (U 1 ∧ L). Secondly, though operations of sum and the direct product could be mixed indiscriminately from an algebraic point of view, conceptually, we may choose to restrict the use of the direct product to the first – outer – compositional layer (Fig. 6). That is, we take the point of view that each (compound) algebra under the operation of direct product represents a different drawing or information view and that all the information within the same drawing or view (corresponding to different component algebras within a composition under sum) adopts a single set of allowable transformations for rule application. The opposite, an algebra that is composed under direct product and itself takes part in a composition under sum is not feasible; it is impossible to determine which transformation(s) applies over the composition under sum, since at least one component – the composition under direct product – is unequivocal on the transformation(s) to apply. Obviously, when we write L + N or U 1 + D, clearly, we are not assuming that labels and weights populate the same space or, similarly, for line segments and descriptions, nor that their respective sets of allowable transformations necessarily must be related via some mapping. Within a single set of allowable transformations for rule application, subsets of allowable transformations can be identified for different algebras. In fact, even if neither labels nor weights allow any transformations, we can consider them under the operation of sum. The operation of sum simply implies that if two algebras allow for the same set of transformations, for example, similarity transformations for geometric elements, including points, lines segments, and plane segments, they must share the same transformation – under rule application. Otherwise, they can simply operate in parallel under different transformations, or none at all.

Fig. 6. A hierarchical modus operandi for the three operations on algebras, direct product (“×”), sum (“+”), and attribution (“∧”). Basic algebras are indicated with a black core; ellipses mark undeveloped branches that are, each, similar to the developed branch for the same operation (as illustrated with a miniature expansion); each developed branch indicates its potential cardinality.
The same applies for attribute shape algebras. Referring once again to the example of the embedded sensor view presented by Stouffs et al. (Reference Stouffs, Krishnamurti and Park2007), a more extensive information list required by the embedded sensor planner includes the target slab, represented as a label or description, its shape, represented as a volume in U 33, its material type, again represented as a label or description, and its location, represented as a point in U 03. The corresponding algebra for this view may be defined as L ∧ U 33 ∧ L ∧ U 03. Although the algebras U 33 and U 03 are related through attribution, rather than the sum, they should still be considered as using the same space, not just from a dimensional point of view. In this example, it makes perfect sense that the shape and location of the slabs are subject to the same transformation.
Thus, if the first – outer – compositional layer is specified under the operation of the direct product, its components can be algebraic compositions under sum, augmented algebras and/or basic algebras, together defining a second compositional layer (Fig. 6). Compositions under sum are themselves made up of augmented algebras and/or basic algebras; while, augmented algebras are considered – informally – as compositions of a basic algebra as a base and either a composition under sum, an augmented algebra, or a basic algebra as an attribute (Fig. 6). Some implications of this hierarchical modus operandi are discussed below.
Though the definition of a compound algebra under sum or direct product (5) is strictly speaking non-commutative, intuitively, and from an implementation point of view, it makes more sense to consider the operations of sum and direct product on algebras as both commutative and associative, for example, for an algebra of shapes of labeled points and line segments, V 0 + U 1 = U 1 + V 0, and for an algebra of shapes of labeled points, weighted line segments, and plane segments, V 0 + (W 1 + U 2) = (V 0 + W 1) + U 2 = V 0 + W 1 + U 2. Hereto, we can consider a canonical ordering of the component algebras within a composition under sum or direct product. On the other hand, the operation of attribution on algebras is, obviously, non-commutative and, considering that the base is in fact defined as a two-sorted partial algebra, non-associative. Given a basic algebra of sets of colors, C, we might conceive of an algebra U 0 ∧ L ∧ C. This should always be interpreted as U 0 ∧ (L ∧ C), that is, an algebra of points, where each point has one or more labels and each label has a color specified. If we want colors to be applied to points instead, we can write U 0 ∧ (L + C), and if we want colors to be applied to both points and labels, we must write U 0 ∧ [(L ∧ C) + C]. As a consequence of the latter, the points might exhibit different colors than the points’ labels. Any constraints relating the labels’ colors to the points’ colors would have to be specified outside of the algebraic composition, for example, in the shape rules and initial shape. We already considered the operation of sum to distribute over the operation of attribution, that is, U 0 ∧ (L + N) = (U 0 ∧ L) + (U 0 ∧ N) = V 0 + W 0, combining points with labels and points with weights. Considering the hierarchical modus operandi, other distributive rules do not apply.
Finally, let us revisit Stiny's (Reference Stiny1992) example describing a series of cubes separately in the plan, in front elevation, and in side elevation. While the resulting shapes are presented in the algebras U 12, W 12, and W 22, respectively, the shape rules additionally make use of labeled points – and line segments in the case of the side elevation – to constrain rule application. That is, the shape rules are presented in the algebras U 12 + V 02, W 12 + V 02, and W 22 + U 12 + V 02, respectively. Considering that Stiny (Reference Stiny1992) only considers the operation of direct product on algebras, he poses the question whether to write (U 12 × V 02) × (W 12 × V 02) × (W 22 × U 12 × V 02) – with or without parentheses – or to simplify this as U 12 × V 02 × W 12 × W 22. However, when we distinguish the operations of sum and direct product on algebras and adopt the operation of direct product exclusively to combine different drawings or information views, the question is no longer pertinent and the only appropriate representation is the compound algebra (U 12 + V 02) × (W 12 + V 02) × (W 22 + U 12 + V 02). Here the parentheses are only added for readability.
The matching problem
One consequence of supporting a wide variety of algebraic compositions within a single shape grammar interpreter is that the process of determining the applicable transformation(s) for shape rule application is further complicated from what was already far from straightforward. Recall that a shape rule a→b applies to a shape s if there exists a (similarity) transformation t such that t(a) ≤ s. Let us assume we have a shape rule defined over an algebraic composition under sum and attribution. Obviously, if the algebraic composition is defined under the direct product, we can split the problem into a few smaller problems, one for each algebraic component under the direct product, as the operation of direct product assumes each component to apply under a different transformation.
Krishnamurti and Stouffs (Reference Krishnamurti and Stouffs1997) consider all possible cases of applicable similarity transformations for shapes in the algebra U 0 + U 1 + U 2 + U 3, or any other combination of U 0, U 1, U 2, and/or U 3 under sum. These include both determinate, resulting in a finite number of possible transformations, and indeterminate, allowing for an infinite number of possible transformations, cases, based on the process of identifying and constructing distinguishable elements – that is, spatial elements (points, lines, or planes) the properties of which (with respect to the original shape) are preserved under the part relation and (similarity) transformations. They also allude to the fact that these spatial elements may have attributes assigned.
However, from an implementation point of view, whether spatial elements have attributes and the kind of attributes can make an important difference in the efficiency of the matching algorithm. After all, it is not just important to find all possible transformations under which the left-hand side of a shape rule is a part of a given shape s, this should also be done efficiently within a reasonable time frame. For instance, labeled points are often considered in shape grammars in order to reduce the number of possible ways – that is, transformations – under which a rule may apply to a given shape. Labeled points are particularly appropriate for this as both labels and points adhere to a discrete behavior. As labels only match if they are identical, labeled points only match if they have identical labels. Furthermore, three non-collinear distinguishable points – additional distinguishable points can be constructed as the intersection points of two lines, or a line and a plane, or two lines of intersection of corresponding planes, or as the feet of the common perpendicular of two skew lines – is the only possible determinate case in three dimensions. As such, considering labeled points not only reduces the number of possible transformations, labeled points can also be considered preferential in the process of determining distinguishable elements in order to address the matching problem.
In general, we may conclude that both a basic algebra's behavior and the allowable transformations for the algebra contribute to the preferential applicability of this particular basic algebra in the process of determining applicable transformations for shape rule application. Thus, we can prioritize the basic algebras that participate in an algebraic composition under sum and attribution for their role in the process of determining applicable transformations based on these two characteristics. We suggest a classification of basic algebras based on their behavioral specification into four classes: discrete, linear, planar, and spatial. These may be assigned consecutive numeric values, such as 0, 1, 2, and 3, respectively. Obviously, both points (U 0) and labels (L), as well as (textual) descriptions (D) adhere to the discrete class. Other spatial and non-spatial elements that can be classified as discrete are circles, ellipses, infinite lines, numeric labels, images, dates, enumerative values, etc. Line segments (U 1) and weights (N) form part of the linear class, as do any other elements that adhere to a linear dimension, such as, circular arcs and elliptical arcs, but also time periods and, potentially, colors (C). Whether colors are classified as linear or, instead, spatial, is dependent on their exact behavioral specification. Classifying colors as linear reflects on Knight's (Reference Knight1993) adoption of notions of transparency, opacity, and ranking to regulate the behavior of colors on interacting areas or volumes. Finally, plane segments (U 2) and volumes (U 3) are classified as planar and spatial, respectively.
Additionally, we suggest a classification of allowable transformations by their degrees-of-freedom. Similarity transformations demonstrate seven degrees-of-freedom: three translational, three rotational, and one (uniform) scaling. These can apply to all spatial elements. Most other basic algebras do not allow for any transformations, the corresponding degrees-of-freedom is therefore zero. However, if case transformations would be considered for labels, the degrees-of-freedom could be specified as one. This is also the case for descriptions, even if case transformations for descriptions are not considered. Description rules (or a description function, Stiny, Reference Stiny1981) allow for parameters to be specified in the left-hand side of the rule, thereby allowing for more than an exact match. Such necessitates a degrees-of-freedom of at least one. Considering these classifications of behavioral specifications and allowable transformations, a simple prioritization of basic algebras in the process of determining applicable transformations can be based on adding both values, the numeric value of the behavioral class and the degrees-of-freedom, together. In addition, if relevant, the algebraic operation under which the basic algebra forms part of the overall algebraic composition, that is, sum or attribution, can be considered as an additional prioritization factor.
For example, an algebra of labeled points and line segments distinguishes three basic algebras: labels, points, and line segments. Points and labels are classified as discrete, with value 0, while line segments belong to the linear class, with value 1. Labels may not allow for any transformations, specifying the degrees-of-freedom as 0; whereas points and line segments, under similarity transformations, have 7 degrees of freedom. Adding the classification value and the degrees-of-freedom results in prioritization values of 0, 7, and 8 for labels, points, and line segments, respectively. Thus, when determining potential matches, we can first look for different labels on the left-hand side of the shape rule. Obviously, if all points share the same label, there is little benefit in considering the labels and the problem remains to identify three distinguishable points. Assuming there are (at least) three distinguishable (labeled) points in the left-hand side of the shape rule and n distinguishable (labeled) points in the shape under rule application, the number of combinations of points matching the three selected points from the left-hand side equals ![]() $\left( \matrix{ n \cr 3} \right) = \displaystyle{n! \over 3!(n - 3)!} = (1/6)n\,(n - 1)\,(n - 2) = O\,(n^3)$. This assumes all points share the same label or no label at all. However, if there are three (or more) distinct labels in the left-hand side of the shape rule, we can classify the points by their label and select just one point per label. Assuming an equal distribution of the labeled points over the three distinct labels in the shape under rule application, the number of combinations of points matching the three selected points equals
$\left( \matrix{ n \cr 3} \right) = \displaystyle{n! \over 3!(n - 3)!} = (1/6)n\,(n - 1)\,(n - 2) = O\,(n^3)$. This assumes all points share the same label or no label at all. However, if there are three (or more) distinct labels in the left-hand side of the shape rule, we can classify the points by their label and select just one point per label. Assuming an equal distribution of the labeled points over the three distinct labels in the shape under rule application, the number of combinations of points matching the three selected points equals ![]() $3\left(\matrix{n/3 \cr 1} \right) = \displaystyle{3\,(n/3)! \over 1!((n/3) - 1)!} = n$. We only need to consider each point once. Note that this holds even if the labeled points are not evenly distributed per label. Thus, the presence of three distinct labels reduces the number of combinations from O(n 3) to O(n). Similarly, if there are only two distinct labels, the number of combinations is reduced to O(n 2), which is potentially still an important improvement. Note that this applies as well for labeled line segments, with distinguishable points (e.g., intersection points) classified by the label. Obviously, considering that points have a lower prioritization value than line segments, 7 versus 8, gives preference to labeled points over labeled line segments. Similarly, if we assume an algebra of labeled points and line segments as well as labels, U 0 ∧ L + U 1 + L, we must prioritize between the two basic algebras of labels. Considering that one instance stands on its own under the operation of sum, while the other is part of an augmented algebra (under attribution), the latter receives higher priority among the two. That is perfectly logical; while the attribute labels constrain the similarity transformations over points and line segments, the other labels can only serve to constrain transformations over labels, if any.
$3\left(\matrix{n/3 \cr 1} \right) = \displaystyle{3\,(n/3)! \over 1!((n/3) - 1)!} = n$. We only need to consider each point once. Note that this holds even if the labeled points are not evenly distributed per label. Thus, the presence of three distinct labels reduces the number of combinations from O(n 3) to O(n). Similarly, if there are only two distinct labels, the number of combinations is reduced to O(n 2), which is potentially still an important improvement. Note that this applies as well for labeled line segments, with distinguishable points (e.g., intersection points) classified by the label. Obviously, considering that points have a lower prioritization value than line segments, 7 versus 8, gives preference to labeled points over labeled line segments. Similarly, if we assume an algebra of labeled points and line segments as well as labels, U 0 ∧ L + U 1 + L, we must prioritize between the two basic algebras of labels. Considering that one instance stands on its own under the operation of sum, while the other is part of an augmented algebra (under attribution), the latter receives higher priority among the two. That is perfectly logical; while the attribute labels constrain the similarity transformations over points and line segments, the other labels can only serve to constrain transformations over labels, if any.
Discussion
The above is certainly not the only complication with respect to implementing a shape grammar interpreter supporting a wide variety of compositions of basic algebras under the operations of direct product, sum, and attribution. A number of authors of description grammars consider parallel descriptions, specifying interdependencies between these parallel descriptions or between (textual) descriptions and shape descriptions. Specifically, Li (Reference Li2001) considers description rules referencing the current value of other, parallel, descriptions, in the specification of the right-hand side of the description rule. For example, having one description count the number of rafters, another description describes the disposition of the beams, including the resulting number of rafters. Others, similarly, consider description rules referencing other parallel descriptions. Aside from referring to the entire description value, these may include only a specific entity, where the entity in question is identified by a parameter in a parallel description rule that, otherwise, may leave this other description unchanged, or they may require the parallel shape rule to provide specific values, for example, referring to dimensions within a shape or shape rule. In such cases, the timing of the resolution of the rules may be important in order to ensure that the information from one description, shape, or rule may be available to another rule. Alternatively, the resolution process could be split into two phases, a first phase in which dependencies are identified and stored, and a second phase in which these dependencies are revisited and resolved. Of course, circular dependencies must be avoided any time.
Conclusion
We presented an algebraic approach to describing compound shapes that includes the definition of non-spatial algebras and the combination of shape algebras and non-spatial algebras under an operation of attribution. This algebraic abstraction serves as a procedural abstraction for the modular implementation of a general shape grammar interpreter. We have extended the algebraic approach to the operation of sum, as compared with direct product, reflecting on whether shape algebras adhere to the same or different transformations under rule application, although we limited this to capturing the limitations that may be placed on algebraic compositions in light of practical applications and their implementation. The main contributions of this paper are the algebraic derivation of shape algebras from partial algebras operating on spatial elements as well as of combinations of basic shape algebras with attribute algebras. We have also identified practical limitations on algebraic compositions of basic shape algebras with attribute algebras and proposed prioritizing basic algebras with respect to solving the matching problem for parallel and compound shape grammars efficiently.
Acknowledgments
The author would like to thank Ramesh Krishnamurti for his insightful feedback on an earlier version of the paper. They would also like to thank the reviewers for their comments and feedback. This work received some funding support from Singapore MOE's AcRF start-up grant, WBS R-295-000-129-133.
Rudi Stouffs is an Associate Professor in the Department of Architecture at the National University of Singapore, and Guest Associate Professor at the Chair of Design Informatics at the Delft University of Technology. He holds an MS in architectural engineering from the Vrije Universiteit Brussel, an MS in computational design, and a PhD in architecture from Carnegie Mellon University. He has held previous appointments at the School of Architecture at Carnegie Mellon University, the Chair for Architecture and CAAD at ETH Zurich, and the Chair of Design Informatics at TU Delft. His research interests include computational issues of description, modeling, and representation for design, mainly in the areas of shape recognition and generation, and building/city information modeling and analysis.















