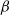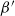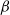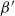1. Introduction
Random tessellations in Euclidean space are among the most central objects studied in stochastic geometry. Their analysis is motivated by their rich inner mathematical structures, but in equal measure also by the wide range of applications in which they arise. For example, tessellations, and especially triangulations of a space, play a prominent role in finite element methods in numerical analysis, for example in computer vision, material science, ecology, chemistry, astrophysics, machine learning, network modelling, and computational geometry; we refer the reader to the monographs [Reference Aurenhammer, Klein and Lee1, Reference Blaszczyszyn, Haenggi, Keeler and Mukherjee3, Reference Cheng, Dey and Shewchuk7, Reference Edelsbrunner8, Reference Haenggi12, Reference Lo23, Reference MØller26, Reference Okabe, Boots, Sugihara and Chiu27, Reference Preparata and Shamos28, Reference Schneider and Weil31, Reference Stoyan, Kendall and Mecke33] as well as the references cited therein for an extensive overview. However, there are very few mathematically tractable models for which rigorous results are available and which do not require an analysis purely by computer simulations. Among these models are the Poisson–Voronoi tessellations and their duals, the Poisson–Delaunay tessellations. Their construction can be described as follows. Given a stationary Poisson point process X in
![]() ${\mathbb{R}}^{d-1}$
, we define for any point
${\mathbb{R}}^{d-1}$
, we define for any point
![]() $v\in X$
the Voronoi cell C(v, X) of v as
$v\in X$
the Voronoi cell C(v, X) of v as
that is, C(v, X) contains all points that are closer to v than to any other point from X. In applications, C(v, X) might represent the domain of influence of a point v, for example the area in a communication network that a base station placed at v may cover. All such Voronoi cells are random convex polytopes, and the collection of all Voronoi cells is the Poisson–Voronoi tessellation of
![]() ${\mathbb{R}}^{d-1}$
. To define the dual tessellation we say that the convex hull
${\mathbb{R}}^{d-1}$
. To define the dual tessellation we say that the convex hull
![]() ${\textrm{conv}}(v_1,\ldots,v_d)$
of d distinct points from X is a Delaunay simplex provided that X has no points in the interior of the ball containing
${\textrm{conv}}(v_1,\ldots,v_d)$
of d distinct points from X is a Delaunay simplex provided that X has no points in the interior of the ball containing
![]() $v_1,\ldots,v_d$
on its boundary. The collection of all Delaunay simplices is what is known as the Poisson–Delaunay tessellation. It is easy to observe that
$v_1,\ldots,v_d$
on its boundary. The collection of all Delaunay simplices is what is known as the Poisson–Delaunay tessellation. It is easy to observe that
![]() ${\textrm{conv}}(v_1,\ldots,v_d)$
is a Delaunay simplex if and only if the Voronoi cells of the points
${\textrm{conv}}(v_1,\ldots,v_d)$
is a Delaunay simplex if and only if the Voronoi cells of the points
![]() $v_1,\ldots,v_d$
meet at a common point, which is then the center of the circumscribed sphere of the simplex.
$v_1,\ldots,v_d$
meet at a common point, which is then the center of the circumscribed sphere of the simplex.
It is the purpose of this series of papers to introduce and to initiate a systematic study of a generalization of Poisson–Delaunay tessellations, the so-called
![]() $\beta$
-Delaunay tessellations, denoted by
$\beta$
-Delaunay tessellations, denoted by
![]() ${\mathcal{D}}_\beta$
. This is a one-parametric family of random tessellations of
${\mathcal{D}}_\beta$
. This is a one-parametric family of random tessellations of
![]() ${\mathbb{R}}^{d-1}$
, where the parameter
${\mathbb{R}}^{d-1}$
, where the parameter
![]() $\beta$
satisfies
$\beta$
satisfies
![]() $-1<\beta<\infty$
. We will also introduce the dual tessellations of
$-1<\beta<\infty$
. We will also introduce the dual tessellations of
![]() ${\mathcal{D}}_\beta$
, which are denoted by
${\mathcal{D}}_\beta$
, which are denoted by
![]() ${\mathcal{V}}_\beta$
and called the
${\mathcal{V}}_\beta$
and called the
![]() $\beta$
-Voronoi tessellations. The classical Poisson–Delaunay and Poisson–Voronoi tessellations arise as the limiting cases of these tessellations when
$\beta$
-Voronoi tessellations. The classical Poisson–Delaunay and Poisson–Voronoi tessellations arise as the limiting cases of these tessellations when
![]() $\beta\to -1$
.
$\beta\to -1$
.
As for the classical Poisson–Delaunay tessellation, the construction of the
![]() $\beta$
-Delaunay tessellation is based on a Poisson point process as well. However, while the Poisson point process for the Poisson–Delaunay tessellation is located in
$\beta$
-Delaunay tessellation is based on a Poisson point process as well. However, while the Poisson point process for the Poisson–Delaunay tessellation is located in
![]() ${\mathbb{R}}^{d-1}$
, for the
${\mathbb{R}}^{d-1}$
, for the
![]() $\beta$
-Delaunay tessellation we start with a Poisson point process
$\beta$
-Delaunay tessellation we start with a Poisson point process
![]() $\eta_{\beta}$
in the product space
$\eta_{\beta}$
in the product space
![]() ${\mathbb{R}}^{d-1}\times [0,\infty)$
whose intensity measure has the form
${\mathbb{R}}^{d-1}\times [0,\infty)$
whose intensity measure has the form
![]() $\text{const}\cdot h^\beta\,\textrm{d} v\textrm{d} h$
, where
$\text{const}\cdot h^\beta\,\textrm{d} v\textrm{d} h$
, where
![]() $v\in{\mathbb{R}}^{d-1}$
stands for the spatial coordinate and
$v\in{\mathbb{R}}^{d-1}$
stands for the spatial coordinate and
![]() $h>0$
for the height coordinate of a point
$h>0$
for the height coordinate of a point
![]() $x=(v,h)\in{\mathbb{R}}^{d-1}\times [0,\infty)$
. A realization of this Poisson point process for
$x=(v,h)\in{\mathbb{R}}^{d-1}\times [0,\infty)$
. A realization of this Poisson point process for
![]() $d=3$
is shown in the left panel of Figure 1. In the next step, we construct the paraboloid hull process associated with
$d=3$
is shown in the left panel of Figure 1. In the next step, we construct the paraboloid hull process associated with
![]() $\eta_{\beta}$
. This is a particular germ–grain process with paraboloid grains which in stochastic geometry was introduced by Schreiber and Yukich [Reference Schreiber and Yukich32], and was further developed in Calka, Schreiber and Yukich [Reference Calka, Schreiber and Yukich5] and Calka and Yukich [Reference Calka and Yukich6] in order to study the asymptotic geometry of random convex hulls near their boundary. We shall use the same paraboloid hull process to construct a random tessellation
$\eta_{\beta}$
. This is a particular germ–grain process with paraboloid grains which in stochastic geometry was introduced by Schreiber and Yukich [Reference Schreiber and Yukich32], and was further developed in Calka, Schreiber and Yukich [Reference Calka, Schreiber and Yukich5] and Calka and Yukich [Reference Calka and Yukich6] in order to study the asymptotic geometry of random convex hulls near their boundary. We shall use the same paraboloid hull process to construct a random tessellation
![]() ${\mathcal{D}}_\beta$
of
${\mathcal{D}}_\beta$
of
![]() ${\mathbb{R}}^{d-1}$
with only simplicial cells as follows. Given d points
${\mathbb{R}}^{d-1}$
with only simplicial cells as follows. Given d points
![]() $x_1=(v_1,h_1),\ldots,x_d=(v_d,h_d)$
of
$x_1=(v_1,h_1),\ldots,x_d=(v_d,h_d)$
of
![]() $\eta_\beta$
with affinely independent spatial coordinates
$\eta_\beta$
with affinely independent spatial coordinates
![]() $v_1,\ldots,v_d$
, there is a unique shift of the standard downward paraboloid
$v_1,\ldots,v_d$
, there is a unique shift of the standard downward paraboloid
containing
![]() $x_1,\ldots,x_d$
on its boundary. We declare
$x_1,\ldots,x_d$
on its boundary. We declare
![]() ${\textrm{conv}}(v_1,\ldots,v_d)$
to be a
${\textrm{conv}}(v_1,\ldots,v_d)$
to be a
![]() $\beta$
-Delaunay simplex in
$\beta$
-Delaunay simplex in
![]() ${\mathbb{R}}^{d-1}$
if and only if the interior of the downward paraboloid determined by
${\mathbb{R}}^{d-1}$
if and only if the interior of the downward paraboloid determined by
![]() $x_1,\ldots,x_d$
is void of points of
$x_1,\ldots,x_d$
is void of points of
![]() $\eta_{\beta}$
. The collection of all
$\eta_{\beta}$
. The collection of all
![]() $\beta$
-Delaunay simplices is called the
$\beta$
-Delaunay simplices is called the
![]() $\beta$
-Delaunay tessellation of
$\beta$
-Delaunay tessellation of
![]() ${\mathbb{R}}^{d-1}$
. Two realizations of the paraboloid hull process in the case
${\mathbb{R}}^{d-1}$
. Two realizations of the paraboloid hull process in the case
![]() $d=2$
are shown in Figure 2. It should be mentioned at this point that one can alternatively think of
$d=2$
are shown in Figure 2. It should be mentioned at this point that one can alternatively think of
![]() ${\mathcal{D}}_{\beta}$
as the dual to the Laguerre diagram
${\mathcal{D}}_{\beta}$
as the dual to the Laguerre diagram
![]() ${\mathcal{V}}_\beta$
of
${\mathcal{V}}_\beta$
of
![]() $\eta_{\beta}$
, where each point
$\eta_{\beta}$
, where each point
![]() $x=(v,h)\in\eta_{\beta}$
represents a sphere with center v and (imaginary) radius
$x=(v,h)\in\eta_{\beta}$
represents a sphere with center v and (imaginary) radius
![]() $\sqrt{-h}$
; see Section 3.2 for more details. We will call
$\sqrt{-h}$
; see Section 3.2 for more details. We will call
![]() ${\mathcal{V}}_\beta$
the
${\mathcal{V}}_\beta$
the
![]() $\beta$
-Voronoi tessellation. The tessellations
$\beta$
-Voronoi tessellation. The tessellations
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{V}}_\beta$
are dual to each other in the following sense. A simplex
${\mathcal{V}}_\beta$
are dual to each other in the following sense. A simplex
![]() ${\textrm{conv}}(v_1,\ldots,v_d)$
is a cell of the
${\textrm{conv}}(v_1,\ldots,v_d)$
is a cell of the
![]() $\beta$
-Delaunay tessellation if and only if the cells generated by
$\beta$
-Delaunay tessellation if and only if the cells generated by
![]() $x_1,\ldots,x_d$
in the
$x_1,\ldots,x_d$
in the
![]() $\beta$
-Voronoi tessellation are non-empty and meet at a common point. The two constructions of the
$\beta$
-Voronoi tessellation are non-empty and meet at a common point. The two constructions of the
![]() $\beta$
-Delaunay tessellation are equivalent, and each of them plays a role in the study of the properties of
$\beta$
-Delaunay tessellation are equivalent, and each of them plays a role in the study of the properties of
![]() ${\mathcal{D}}_{\beta}$
.
${\mathcal{D}}_{\beta}$
.

Figure 1. Poisson point processes in
![]() ${\mathbb{R}}^d$
with
${\mathbb{R}}^d$
with
![]() $d=3$
used to construct the tessellations on the plane. Left:
$d=3$
used to construct the tessellations on the plane. Left:
![]() $\eta_\beta$
with
$\eta_\beta$
with
![]() $\beta=2$
. Right:
$\beta=2$
. Right:
![]() $\eta^{\prime}_\beta$
with
$\eta^{\prime}_\beta$
with
![]() $\beta=3$
. The plane
$\beta=3$
. The plane
![]() $h=0$
in which the tessellation is constructed is shown in yellow.
$h=0$
in which the tessellation is constructed is shown in yellow.

Figure 2. Construction of the
![]() $\beta$
-Delaunay tessellation
$\beta$
-Delaunay tessellation
![]() ${\mathcal{D}}_\beta$
for
${\mathcal{D}}_\beta$
for
![]() $d=2$
. The figure shows the Poisson point process
$d=2$
. The figure shows the Poisson point process
![]() $\eta_{\beta}$
and the corresponding paraboloid hull. Top:
$\eta_{\beta}$
and the corresponding paraboloid hull. Top:
![]() $\beta=0$
. Bottom:
$\beta=0$
. Bottom:
![]() $\beta=2$
. Points on the horizontal axis are the vertices of the
$\beta=2$
. Points on the horizontal axis are the vertices of the
![]() $\beta$
-Delaunay tessellation of
$\beta$
-Delaunay tessellation of
![]() ${\mathbb{R}}$
.
${\mathbb{R}}$
.
Let us present a simple description of the
![]() $\beta$
-Voronoi tessellation
$\beta$
-Voronoi tessellation
![]() ${\mathcal{V}}_\beta$
. Imagine that each atom
${\mathcal{V}}_\beta$
. Imagine that each atom
![]() $x=(v,h)\in {\mathbb{R}}^{d-1}\times [0,\infty)$
of the Poisson point process
$x=(v,h)\in {\mathbb{R}}^{d-1}\times [0,\infty)$
of the Poisson point process
![]() $\eta_\beta$
gives rise to a crystallization process in
$\eta_\beta$
gives rise to a crystallization process in
![]() ${\mathbb{R}}^{d-1}$
which starts at the spatial position
${\mathbb{R}}^{d-1}$
which starts at the spatial position
![]() $v\in {\mathbb{R}}^{d-1}$
at time
$v\in {\mathbb{R}}^{d-1}$
at time
![]() $h>0$
. The speed of the crystallization process is not constant and is assumed to be such that the process reaches a point
$h>0$
. The speed of the crystallization process is not constant and is assumed to be such that the process reaches a point
![]() $w\in {\mathbb{R}}^d$
at time
$w\in {\mathbb{R}}^d$
at time
![]() $h + \|w-v\|^2$
. Then, the cell generated by (v, h) is just the set of all points
$h + \|w-v\|^2$
. Then, the cell generated by (v, h) is just the set of all points
![]() $w\in {\mathbb{R}}^{d-1}$
that are reached by the crystallization process started at (v, h) not later than by a crystallization process started at any other point (v
′, h
′). It should be emphasized that the cell may be empty and that in the case when it is non-empty, it need not contain the point v (which is different from the case of the classical Poisson–Voronoi tessellation). The set of cells with non-empty interior forms the
$w\in {\mathbb{R}}^{d-1}$
that are reached by the crystallization process started at (v, h) not later than by a crystallization process started at any other point (v
′, h
′). It should be emphasized that the cell may be empty and that in the case when it is non-empty, it need not contain the point v (which is different from the case of the classical Poisson–Voronoi tessellation). The set of cells with non-empty interior forms the
![]() $\beta$
-Voronoi tessellation
$\beta$
-Voronoi tessellation
![]() ${\mathcal{V}}_\beta$
.
${\mathcal{V}}_\beta$
.
The goal of the present paper (which is the first in a series of papers) is to show that these constructions do indeed lead to well-defined stationary random tessellations of
![]() ${\mathbb{R}}^{d-1}$
, and to study their geometric properties. Moreover, and in parallel to the construction of the
${\mathbb{R}}^{d-1}$
, and to study their geometric properties. Moreover, and in parallel to the construction of the
![]() $\beta$
-Delaunay tessellation, we introduce the concept of a
$\beta$
-Delaunay tessellation, we introduce the concept of a
![]() $\beta^{\prime}$
-Delaunay tessellation
$\beta^{\prime}$
-Delaunay tessellation
![]() ${\mathcal{D}}^{\prime}_{\beta}$
${\mathcal{D}}^{\prime}_{\beta}$
![]() $\big($
together with its dual
$\big($
together with its dual
![]() $\beta^{\prime}$
-Voronoi tessellation
$\beta^{\prime}$
-Voronoi tessellation
![]() ${\mathcal{V}}^{\prime}_\beta\big)$
, whose construction is based on a Poisson point process
${\mathcal{V}}^{\prime}_\beta\big)$
, whose construction is based on a Poisson point process
![]() $\eta^{\prime}_\beta$
on the product space
$\eta^{\prime}_\beta$
on the product space
![]() ${\mathbb{R}}^{d-1}\times ({-}\infty,0)$
with intensity measure
${\mathbb{R}}^{d-1}\times ({-}\infty,0)$
with intensity measure
![]() $\text{const}\cdot ({-}h)^{-\beta}\,\textrm{d} v\textrm{d} h$
for
$\text{const}\cdot ({-}h)^{-\beta}\,\textrm{d} v\textrm{d} h$
for
![]() $\beta>(d+1)/2$
. A realization of the Poisson point process
$\beta>(d+1)/2$
. A realization of the Poisson point process
![]() $\eta^{\prime}_\beta$
for
$\eta^{\prime}_\beta$
for
![]() $d=3$
is shown in the right panel of Figure 1, while the paraboloid hull process in the case
$d=3$
is shown in the right panel of Figure 1, while the paraboloid hull process in the case
![]() $d=2$
is shown in Figure 3.
$d=2$
is shown in Figure 3.

Figure 3. Construction of the
![]() $\beta^{\prime}$
-Delaunay tessellation
$\beta^{\prime}$
-Delaunay tessellation
![]() ${\mathcal{D}}^{\prime}_\beta$
for
${\mathcal{D}}^{\prime}_\beta$
for
![]() $d=2$
. The figure shows the Poisson point process
$d=2$
. The figure shows the Poisson point process
![]() $\eta^{\prime}_{\beta}$
and the corresponding paraboloid hull. Top:
$\eta^{\prime}_{\beta}$
and the corresponding paraboloid hull. Top:
![]() $\beta=2$
, bottom:
$\beta=2$
, bottom:
![]() $\beta=3$
.
$\beta=3$
.
Whenever possible, we will develop our results for both random tessellation models,
![]() $\beta$
and
$\beta$
and
![]() $\beta^{\prime}$
, in parallel. In particular, we are interested in what is known as the typical cell of
$\beta^{\prime}$
, in parallel. In particular, we are interested in what is known as the typical cell of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}^{\prime}_\beta$
. Intuitively, one can think of such a cell as a randomly chosen cell, which is selected independently of its size and shape. More generally, we shall study volume-power-weighted typical cells, where the weight is a certain power
${\mathcal{D}}^{\prime}_\beta$
. Intuitively, one can think of such a cell as a randomly chosen cell, which is selected independently of its size and shape. More generally, we shall study volume-power-weighted typical cells, where the weight is a certain power
![]() $\nu$
of the volume. One of our main contributions is Theorem 1, which gives a precise distributional characterization of the weighted typical cell of
$\nu$
of the volume. One of our main contributions is Theorem 1, which gives a precise distributional characterization of the weighted typical cell of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}^{\prime}_\beta$
. In particular, we will prove that the weighted typical cell of
${\mathcal{D}}^{\prime}_\beta$
. In particular, we will prove that the weighted typical cell of
![]() ${\mathcal{D}}_\beta$
(respectively,
${\mathcal{D}}_\beta$
(respectively,
![]() ${\mathcal{D}}^{\prime}_\beta$
) is a randomly rescaled volume-power-weighted
${\mathcal{D}}^{\prime}_\beta$
) is a randomly rescaled volume-power-weighted
![]() $\beta$
-simplex (respectively,
$\beta$
-simplex (respectively,
![]() $\beta^{\prime}$
-simplex) (see Remark 5), which also explains the names of the models. Very remarkably, this provides a new link between the
$\beta^{\prime}$
-simplex) (see Remark 5), which also explains the names of the models. Very remarkably, this provides a new link between the
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^{\prime}$
-Delaunay tessellations and the classes of
$\beta^{\prime}$
-Delaunay tessellations and the classes of
![]() $\beta$
-polytopes and
$\beta$
-polytopes and
![]() $\beta^{\prime}$
-polytopes, which has recently been under intensive investigation; see, for example, [Reference Grote, Kabluchko and Thäle10, Reference Kabluchko14, Reference Kabluchko, Temesvari and Thäle15, Reference Kabluchko, Thäle and Zaporozhets17], and also Remark 8 below. This opens a way to study the geometry and the combinatorial properties of the typical cells of
$\beta^{\prime}$
-polytopes, which has recently been under intensive investigation; see, for example, [Reference Grote, Kabluchko and Thäle10, Reference Kabluchko14, Reference Kabluchko, Temesvari and Thäle15, Reference Kabluchko, Thäle and Zaporozhets17], and also Remark 8 below. This opens a way to study the geometry and the combinatorial properties of the typical cells of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}^{\prime}_\beta$
. Among our results are explicit formulas for the moments of the volume as well as probabilistic representations in terms of independent gamma- and beta-distributed random variables. We also compute explicitly the j-face intensities and determine the expected angle sums of weighted typical cells.
${\mathcal{D}}^{\prime}_\beta$
. Among our results are explicit formulas for the moments of the volume as well as probabilistic representations in terms of independent gamma- and beta-distributed random variables. We also compute explicitly the j-face intensities and determine the expected angle sums of weighted typical cells.
Finally, we prove that, as
![]() $\beta\to\infty$
, the expected angle sums of the volume-power-weighted typical cells tend to those of a regular simplex in
$\beta\to\infty$
, the expected angle sums of the volume-power-weighted typical cells tend to those of a regular simplex in
![]() ${\mathbb{R}}^{d-1}$
. We will pick up this topic in detail in Part II of this series of papers, where we describe the common limiting tessellation
${\mathbb{R}}^{d-1}$
. We will pick up this topic in detail in Part II of this series of papers, where we describe the common limiting tessellation
![]() ${\mathcal{D}}\,:\!=\,{\mathcal{D}}_{\infty}$
of
${\mathcal{D}}\,:\!=\,{\mathcal{D}}_{\infty}$
of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}^{\prime}_\beta$
, as
${\mathcal{D}}^{\prime}_\beta$
, as
![]() $\beta\to\infty$
, after suitable rescaling. This will provide an explanation of the limit behavior of the expected angle sums just described. In Part III we will prove various high-dimensional limit theorems for the volume of weighted typical cells in
$\beta\to\infty$
, after suitable rescaling. This will provide an explanation of the limit behavior of the expected angle sums just described. In Part III we will prove various high-dimensional limit theorems for the volume of weighted typical cells in
![]() ${\mathcal{D}}_\beta$
,
${\mathcal{D}}_\beta$
,
![]() ${\mathcal{D}}^{\prime}_\beta$
, and
${\mathcal{D}}^{\prime}_\beta$
, and
![]() ${\mathcal{D}}$
, that is, limit theorems where
${\mathcal{D}}$
, that is, limit theorems where
![]() $d\to\infty$
(potentially in a coupled way with other parameters). We will also describe there the shape of large weighted typical cells in the spirit of Kendall’s problem, generalizing thereby results of Hug and Schneider [Reference Hug and Schneider13] on the classical Poisson–Delaunay tessellation. Finally, in Part IV we study mixing properties of the tessellations
$d\to\infty$
(potentially in a coupled way with other parameters). We will also describe there the shape of large weighted typical cells in the spirit of Kendall’s problem, generalizing thereby results of Hug and Schneider [Reference Hug and Schneider13] on the classical Poisson–Delaunay tessellation. Finally, in Part IV we study mixing properties of the tessellations
![]() ${\mathcal{D}}_\beta$
,
${\mathcal{D}}_\beta$
,
![]() ${\mathcal{D}}^{\prime}_\beta$
, and
${\mathcal{D}}^{\prime}_\beta$
, and
![]() ${\mathcal{D}}$
, and as a consequence we derive central limit theorems for the number of k-dimensional faces of
${\mathcal{D}}$
, and as a consequence we derive central limit theorems for the number of k-dimensional faces of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}$
in a growing window.
${\mathcal{D}}$
in a growing window.
The remaining parts of this text are structured as follows. In Section 2 we recall the necessary notions and notation from random tessellation and point process theory, which are used throughout the paper. The detailed construction of
![]() $\beta$
-Delaunay tessellations is presented in Section 3. The explicit distributions of their volume-power-weighted typical cells is the content of Section 4. These results are used in Section 5 to derive explicit formulas and probabilistic representations for the moments of the volume of such cells. The final Section 6 discusses expected angle sums of weighted typical cells as well as formulas for face intensities.
$\beta$
-Delaunay tessellations is presented in Section 3. The explicit distributions of their volume-power-weighted typical cells is the content of Section 4. These results are used in Section 5 to derive explicit formulas and probabilistic representations for the moments of the volume of such cells. The final Section 6 discusses expected angle sums of weighted typical cells as well as formulas for face intensities.
2. Preliminaries
2.1. Frequently used notation
Let
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $A\subset{\mathbb{R}}^d$
. We denote by
$A\subset{\mathbb{R}}^d$
. We denote by
![]() ${\rm int}\,A$
the interior of A and by
${\rm int}\,A$
the interior of A and by
![]() $\partial A$
its boundary. A centered closed Euclidean ball in
$\partial A$
its boundary. A centered closed Euclidean ball in
![]() ${\mathbb{R}}^d$
with radius
${\mathbb{R}}^d$
with radius
![]() $r>0$
is denoted by
$r>0$
is denoted by
![]() ${\mathbb{B}}_r^d$
, and we put
${\mathbb{B}}_r^d$
, and we put
![]() ${\mathbb{B}}^d\,:\!=\,{\mathbb{B}}_1^d$
. The volume of
${\mathbb{B}}^d\,:\!=\,{\mathbb{B}}_1^d$
. The volume of
![]() ${\mathbb{B}}^d$
is given by
${\mathbb{B}}^d$
is given by
By
![]() $\sigma_{d-1}$
we denote the spherical Lebesgue measure on the
$\sigma_{d-1}$
we denote the spherical Lebesgue measure on the
![]() $(d-1)$
-dimensional unit sphere
$(d-1)$
-dimensional unit sphere
![]() ${\mathbb{S}}^{d-1}=\partial {\mathbb{B}}^d$
, normalized in such a way that
${\mathbb{S}}^{d-1}=\partial {\mathbb{B}}^d$
, normalized in such a way that
 \begin{equation*}\omega_d\,:\!=\,\sigma_{d-1}\big({\mathbb{S}}^{d-1}\big)=\frac{2\pi^{\frac{d}{2}}}{\Gamma\!\left({\frac{d}{2}}\right)}.\end{equation*}
\begin{equation*}\omega_d\,:\!=\,\sigma_{d-1}\big({\mathbb{S}}^{d-1}\big)=\frac{2\pi^{\frac{d}{2}}}{\Gamma\!\left({\frac{d}{2}}\right)}.\end{equation*}
Given a set
![]() $C\subset {\mathbb{R}}^{d-1}$
, we denote by
$C\subset {\mathbb{R}}^{d-1}$
, we denote by
![]() ${\textrm{conv}}(C)$
its convex hull. For points
${\textrm{conv}}(C)$
its convex hull. For points
![]() $v_0,\ldots,v_k\in{\mathbb{R}}^{d-1}$
we write
$v_0,\ldots,v_k\in{\mathbb{R}}^{d-1}$
we write
![]() ${\textrm{aff}}(v_0,\ldots,v_k)$
for the affine hull of
${\textrm{aff}}(v_0,\ldots,v_k)$
for the affine hull of
![]() $v_0,\ldots,v_k$
, which is an at most k-dimensional affine subspace of
$v_0,\ldots,v_k$
, which is an at most k-dimensional affine subspace of
![]() ${\mathbb{R}}^{d-1}$
,
${\mathbb{R}}^{d-1}$
,
![]() $k\in\{0,1,\ldots,d-1\}$
.
$k\in\{0,1,\ldots,d-1\}$
.
In what follows we shall represent points
![]() $x\in{\mathbb{R}}^d$
in the form
$x\in{\mathbb{R}}^d$
in the form
![]() $x=(v,h)$
with
$x=(v,h)$
with
![]() $v\in{\mathbb{R}}^{d-1}$
(called the spatial coordinate) and
$v\in{\mathbb{R}}^{d-1}$
(called the spatial coordinate) and
![]() $h\in{\mathbb{R}}$
(called the height, weight, or time coordinate).
$h\in{\mathbb{R}}$
(called the height, weight, or time coordinate).
We will often use the following notation. Let
![]() $\Pi$
(respectively,
$\Pi$
(respectively,
![]() $\Pi^+$
) be the standard downward (respectively, upward) paraboloid, defined as
$\Pi^+$
) be the standard downward (respectively, upward) paraboloid, defined as
 \begin{align*}\Pi&\,:\!=\,\big\{\big(v^{\prime},h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, h^{\prime}=-\|v^{\prime}\|^2\big\},\\\Pi^+&\,:\!=\,\big\{\big(v^{\prime},h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, h^{\prime}=\|v^{\prime}\|^2\big\}.\end{align*}
\begin{align*}\Pi&\,:\!=\,\big\{\big(v^{\prime},h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, h^{\prime}=-\|v^{\prime}\|^2\big\},\\\Pi^+&\,:\!=\,\big\{\big(v^{\prime},h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, h^{\prime}=\|v^{\prime}\|^2\big\}.\end{align*}
Further, let
![]() $\Pi_{x}$
be the translation of
$\Pi_{x}$
be the translation of
![]() $\Pi$
by a vector
$\Pi$
by a vector
![]() $x\,:\!=\,(v,h)\in{\mathbb{R}}^d$
, that is,
$x\,:\!=\,(v,h)\in{\mathbb{R}}^d$
, that is,
Moreover, given a set
![]() $A\subset {\mathbb{R}}^d$
, we define the hypograph and the epigraph of A as
$A\subset {\mathbb{R}}^d$
, we define the hypograph and the epigraph of A as
 \begin{align*}A^{\downarrow}&\,:\!=\,\big\{\big(v,h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, (v,h) \in A \text{ for some } h\ge h^{\prime}\big\},\\A^{\uparrow}&\,:\!=\,\big\{\big(v,h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, (v,h) \in A \text{ for some } h\leq h^{\prime}\big\}.\end{align*}
\begin{align*}A^{\downarrow}&\,:\!=\,\big\{\big(v,h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, (v,h) \in A \text{ for some } h\ge h^{\prime}\big\},\\A^{\uparrow}&\,:\!=\,\big\{\big(v,h^{\prime}\big)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}\,:\, (v,h) \in A \text{ for some } h\leq h^{\prime}\big\}.\end{align*}
The point x is the apex of the paraboloid
![]() $\Pi_x$
, and we write
$\Pi_x$
, and we write
![]() ${\textrm{apex}}\Pi^{\downarrow}_x={\textrm{apex}}\Pi_x\,:\!=\,x.$
${\textrm{apex}}\Pi^{\downarrow}_x={\textrm{apex}}\Pi_x\,:\!=\,x.$
2.2. (Poisson) point processes
Let
![]() $({\mathbb{X}},{\mathcal{X}})$
be a measurable space supplied with a
$({\mathbb{X}},{\mathcal{X}})$
be a measurable space supplied with a
![]() $\sigma$
-finite measure
$\sigma$
-finite measure
![]() $\mu$
. By
$\mu$
. By
![]() ${\textsf{N}}({\mathbb{X}})$
we denote the space of
${\textsf{N}}({\mathbb{X}})$
we denote the space of
![]() $\sigma$
-finite counting measures on
$\sigma$
-finite counting measures on
![]() ${\mathbb{X}}$
. The
${\mathbb{X}}$
. The
![]() $\sigma$
-field
$\sigma$
-field
![]() ${\mathcal{N}}({\mathbb{X}})$
is defined as the smallest
${\mathcal{N}}({\mathbb{X}})$
is defined as the smallest
![]() $\sigma$
-field on
$\sigma$
-field on
![]() ${\textsf{N}}({\mathbb{X}})$
such that the evaluation mappings
${\textsf{N}}({\mathbb{X}})$
such that the evaluation mappings
![]() $\xi\mapsto\xi(B)$
,
$\xi\mapsto\xi(B)$
,
![]() $B\in{\mathcal{X}}$
,
$B\in{\mathcal{X}}$
,
![]() $\xi\in{\textsf{N}}({\mathbb{X}})$
are measurable. A point process on
$\xi\in{\textsf{N}}({\mathbb{X}})$
are measurable. A point process on
![]() ${\mathbb{X}}$
is a measurable mapping with values in
${\mathbb{X}}$
is a measurable mapping with values in
![]() ${\textsf{N}}({\mathbb{X}})$
defined over some fixed probability space
${\textsf{N}}({\mathbb{X}})$
defined over some fixed probability space
![]() $(\Omega,{\mathcal{A}},{\mathbb{P}})$
. By a Poisson point process
$(\Omega,{\mathcal{A}},{\mathbb{P}})$
. By a Poisson point process
![]() $\eta$
on
$\eta$
on
![]() ${\mathbb{X}}$
with intensity measure
${\mathbb{X}}$
with intensity measure
![]() $\mu$
we understand a point process with the following two properties:
$\mu$
we understand a point process with the following two properties:
-
(i) for any
 $B\in{\mathcal{X}}$
, the random variable
$B\in{\mathcal{X}}$
, the random variable
 $\eta(B)$
is Poisson distributed with mean
$\eta(B)$
is Poisson distributed with mean
 $\mu(B)$
;
$\mu(B)$
; -
(ii) for any
 $n\in{\mathbb{N}}$
and pairwise disjoint sets
$n\in{\mathbb{N}}$
and pairwise disjoint sets
 $B_1,\ldots,B_n\in{\mathcal{X}}$
, the random variables
$B_1,\ldots,B_n\in{\mathcal{X}}$
, the random variables
 $\eta(B_1),\ldots,\eta(B_n)$
are independent.
$\eta(B_1),\ldots,\eta(B_n)$
are independent.
We refer the reader to [Reference Last and Penrose20, Reference Schneider and Weil31] for the existence and construction of Poisson point processes and for further details.
2.3. Tessellations
In this subsection we recall the concept of a random tessellation and include a brief overview of its basic properties. For more detailed discussion we refer the reader to [Reference Schneider and Weil31, Chapter 10]. Roughly speaking, a tessellation (or a mosaic) is a system of polytopes that cover the whole space and have disjoint interiors. We fix a space dimension
![]() $d\geq 2$
. Since the tessellations we construct in Section 3 are driven by a Poisson point process in
$d\geq 2$
. Since the tessellations we construct in Section 3 are driven by a Poisson point process in
![]() ${\mathbb{R}}^d$
and induce a tessellation in
${\mathbb{R}}^d$
and induce a tessellation in
![]() ${\mathbb{R}}^{d-1}$
, we consider this set-up in what follows.
${\mathbb{R}}^{d-1}$
, we consider this set-up in what follows.
Definition 1. A tessellation M in
![]() ${\mathbb{R}}^{d-1}$
is a countable system of subsets of
${\mathbb{R}}^{d-1}$
is a countable system of subsets of
![]() ${\mathbb{R}}^{d-1}$
satisfying the following conditions:
${\mathbb{R}}^{d-1}$
satisfying the following conditions:
-
1. M is a locally finite system of non-empty closed sets, where local finiteness means that every bounded subset of
 ${\mathbb{R}}^{d-1}$
intersects only finitely many sets from M;
${\mathbb{R}}^{d-1}$
intersects only finitely many sets from M; -
2. the sets
 $m\in M$
are compact and convex, and they have interior points;
$m\in M$
are compact and convex, and they have interior points; -
3. the sets of M cover the space, meaning that
 \begin{equation*}\bigcup\limits_{m\in M}m={\mathbb{R}}^{d-1};\end{equation*}
\begin{equation*}\bigcup\limits_{m\in M}m={\mathbb{R}}^{d-1};\end{equation*}
-
4. if
 $m_1,m_2\in M$
and
$m_1,m_2\in M$
and
 $m_1\neq m_2$
, then
$m_1\neq m_2$
, then
 $\operatorname{int} m_1\cap \operatorname{int} m_2=\varnothing$
.
$\operatorname{int} m_1\cap \operatorname{int} m_2=\varnothing$
.
The elements of M are called cells of M, and they are convex polytopes by [Reference Schneider and Weil31, Lemma 10.1.1]. Given a polytope P, for
![]() $k\in\{0,1,\ldots,d-1\}$
we denote by
$k\in\{0,1,\ldots,d-1\}$
we denote by
![]() ${\mathcal{F}}_k(P)$
the set of its k-dimensional faces, and we let
${\mathcal{F}}_k(P)$
the set of its k-dimensional faces, and we let
![]() ${\mathcal{F}}(P):\!=\,\bigcup_{k=0}^{d-1}{\mathcal{F}}_{k}(P)$
. A tessellation M is called face-to-face if for all
${\mathcal{F}}(P):\!=\,\bigcup_{k=0}^{d-1}{\mathcal{F}}_{k}(P)$
. A tessellation M is called face-to-face if for all
![]() $P_1,P_2\in M$
we have
$P_1,P_2\in M$
we have
A face-to-face tessellation in
![]() ${\mathbb{R}}^{d-1}$
is called normal if each k-dimensional face of the tessellation is contained in precisely
${\mathbb{R}}^{d-1}$
is called normal if each k-dimensional face of the tessellation is contained in precisely
![]() $d-k$
cells for all
$d-k$
cells for all
![]() $k\in\{0,1,\ldots,d-2\}$
. We denote by
$k\in\{0,1,\ldots,d-2\}$
. We denote by
![]() ${\mathbb{M}}$
the set of all face-to-face tessellations in
${\mathbb{M}}$
the set of all face-to-face tessellations in
![]() ${\mathbb{R}}^{d-1}$
. By a random tessellation in
${\mathbb{R}}^{d-1}$
. By a random tessellation in
![]() ${\mathbb{R}}^{d-1}$
we understand a particle process X in
${\mathbb{R}}^{d-1}$
we understand a particle process X in
![]() ${\mathbb{R}}^{d-1}$
(in the usual sense of stochastic geometry; see [Reference Schneider and Weil31]) satisfying
${\mathbb{R}}^{d-1}$
(in the usual sense of stochastic geometry; see [Reference Schneider and Weil31]) satisfying
![]() $X\in{\mathbb{M}}$
almost surely. Implicitly, we assume here and for the rest of this paper that all the random objects we consider are defined on a probability space
$X\in{\mathbb{M}}$
almost surely. Implicitly, we assume here and for the rest of this paper that all the random objects we consider are defined on a probability space
![]() $(\Omega,{\mathcal{A}},{\mathbb{P}})$
.
$(\Omega,{\mathcal{A}},{\mathbb{P}})$
.
3. Construction of
 $\beta^{(^{\prime})}$
-Voronoi and
$\beta^{(^{\prime})}$
-Voronoi and
 $\beta^{(^{\prime})}$
-Delaunay tessellations
$\beta^{(^{\prime})}$
-Delaunay tessellations
3.1. Underlying point processes
Let us start by defining the
![]() $\beta$
- or
$\beta$
- or
![]() $\beta^{\prime}$
-Voronoi tessellation and its dual, the
$\beta^{\prime}$
-Voronoi tessellation and its dual, the
![]() $\beta$
- or
$\beta$
- or
![]() $\beta^{\prime}$
-Delaunay tessellation. We will give two alternative definitions using the concept of Laguerre tessellations and the notion of paraboloid hull processes introduced by Schreiber and Yukich [Reference Schreiber and Yukich32], Calka, Schreiber and Yukich [Reference Calka, Schreiber and Yukich5], and Calka and Yukich [Reference Calka and Yukich6]. As an underlying process for the
$\beta^{\prime}$
-Delaunay tessellation. We will give two alternative definitions using the concept of Laguerre tessellations and the notion of paraboloid hull processes introduced by Schreiber and Yukich [Reference Schreiber and Yukich32], Calka, Schreiber and Yukich [Reference Calka, Schreiber and Yukich5], and Calka and Yukich [Reference Calka and Yukich6]. As an underlying process for the
![]() $\beta$
-Voronoi and the
$\beta$
-Voronoi and the
![]() $\beta$
-Delaunay tessellations we consider a space–time Poisson point process
$\beta$
-Delaunay tessellations we consider a space–time Poisson point process
![]() $\eta=\eta_{\beta}$
in
$\eta=\eta_{\beta}$
in
![]() ${\mathbb{R}}^{d-1}\times {\mathbb{R}}_{+}$
, where
${\mathbb{R}}^{d-1}\times {\mathbb{R}}_{+}$
, where
![]() ${\mathbb{R}}_{+}\,:\!=\,[0,+\infty)$
denotes the set of non-negative real numbers, with intensity measure having density
${\mathbb{R}}_{+}\,:\!=\,[0,+\infty)$
denotes the set of non-negative real numbers, with intensity measure having density
 \begin{equation}(x,h)\mapsto\gamma\,c_{d,\beta} \cdot h^{\beta},\qquad c_{d,\beta}\,:\!=\,\frac{\Gamma\!\left({\frac{d}{2}}+\beta+1\right)}{\pi^{\frac{d}{2}}\Gamma(\beta+1)},\qquad \gamma > 0,\,\beta>-1,\end{equation}
\begin{equation}(x,h)\mapsto\gamma\,c_{d,\beta} \cdot h^{\beta},\qquad c_{d,\beta}\,:\!=\,\frac{\Gamma\!\left({\frac{d}{2}}+\beta+1\right)}{\pi^{\frac{d}{2}}\Gamma(\beta+1)},\qquad \gamma > 0,\,\beta>-1,\end{equation}
with respect to the Lebesgue measure on
![]() ${\mathbb{R}}^{d-1}\times {\mathbb{R}}_{+}$
. Here,
${\mathbb{R}}^{d-1}\times {\mathbb{R}}_{+}$
. Here,
![]() $\gamma>0$
is the intensity parameter (which will usually be suppressed in our notation),
$\gamma>0$
is the intensity parameter (which will usually be suppressed in our notation),
![]() $\beta>-1$
is the shape parameter, and the normalizing constant
$\beta>-1$
is the shape parameter, and the normalizing constant
![]() $c_{d,\beta}$
has been introduced to simplify some of the computations below. See Figure 1 (left panel) and Figure 2 for realizations of these point processes with
$c_{d,\beta}$
has been introduced to simplify some of the computations below. See Figure 1 (left panel) and Figure 2 for realizations of these point processes with
![]() $d=3$
and
$d=3$
and
![]() $d=2$
, respectively.
$d=2$
, respectively.
For the
![]() $\beta^{\prime}$
-Voronoi and the
$\beta^{\prime}$
-Voronoi and the
![]() $\beta^{\prime}$
-Delaunay tessellations we consider a space–time Poisson point process
$\beta^{\prime}$
-Delaunay tessellations we consider a space–time Poisson point process
![]() $\eta^{\prime}=\eta^{\prime}_{\beta}$
in
$\eta^{\prime}=\eta^{\prime}_{\beta}$
in
![]() ${\mathbb{R}}^{d-1}\times{\mathbb{R}}_{-}^*$
, where
${\mathbb{R}}^{d-1}\times{\mathbb{R}}_{-}^*$
, where
![]() ${\mathbb{R}}_{-}^*\,:\!=\,({-}\infty,0)$
denotes the set of negative real numbers, with intensity measure having density
${\mathbb{R}}_{-}^*\,:\!=\,({-}\infty,0)$
denotes the set of negative real numbers, with intensity measure having density
with respect to the Lebesgue measure on
![]() ${\mathbb{R}}^{d-1}\times{\mathbb{R}}_{-}^*$
. Again,
${\mathbb{R}}^{d-1}\times{\mathbb{R}}_{-}^*$
. Again,
![]() $\gamma>0$
and
$\gamma>0$
and
![]() $\beta>(d+1)/2$
are the parameters of the process. See Figure 1 (right panel) and Figure 3 for realizations of
$\beta>(d+1)/2$
are the parameters of the process. See Figure 1 (right panel) and Figure 3 for realizations of
![]() $\eta^{\prime}_{\beta}$
with
$\eta^{\prime}_{\beta}$
with
![]() $d=3$
and
$d=3$
and
![]() $d=2$
, respectively.
$d=2$
, respectively.
As we will see later, the
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^{\prime}$
-tessellations can often be treated in a unified way. To make this explicit and in order to shorten and simplify the presentation of the paper, we introduce the following variable notation. We put
$\beta^{\prime}$
-tessellations can often be treated in a unified way. To make this explicit and in order to shorten and simplify the presentation of the paper, we introduce the following variable notation. We put
![]() $\kappa\,:\!=\,1$
if the
$\kappa\,:\!=\,1$
if the
![]() $\beta$
model is being considered and
$\beta$
model is being considered and
![]() $\kappa\,:\!=\,-1$
if we are working with the
$\kappa\,:\!=\,-1$
if we are working with the
![]() $\beta^{\prime}$
model. Moreover, throughout the paper we will use almost the same notation for
$\beta^{\prime}$
model. Moreover, throughout the paper we will use almost the same notation for
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^{\prime}$
-tessellations, the only difference being the use of the symbol
$\beta^{\prime}$
-tessellations, the only difference being the use of the symbol
![]() $\prime$
in the case of the
$\prime$
in the case of the
![]() $\beta^{\prime}$
model. When the formulas for the
$\beta^{\prime}$
model. When the formulas for the
![]() $\beta$
and
$\beta$
and
![]() $\beta^{\prime}$
model are close enough to be joined into one expression, we will indicate this by
$\beta^{\prime}$
model are close enough to be joined into one expression, we will indicate this by
![]() $\!\!\!\!\phantom{x}^{(\prime)}$
, meaning that this sign should be omitted when a
$\!\!\!\!\phantom{x}^{(\prime)}$
, meaning that this sign should be omitted when a
![]() $\beta$
model is being considered.
$\beta$
model is being considered.
Using the convention just introduced, we can consistently represent the density of the Poisson point process
![]() $\eta^{(^{\prime})}$
on
$\eta^{(^{\prime})}$
on
![]() ${\mathbb{R}}^{d-1}\times{\mathbb{R}}$
as
${\mathbb{R}}^{d-1}\times{\mathbb{R}}$
as
with
![]() $\beta>-1$
for the
$\beta>-1$
for the
![]() $\beta$
model and
$\beta$
model and
![]() $\beta>(d+1)/2$
for the
$\beta>(d+1)/2$
for the
![]() $\beta^{\prime}$
model.
$\beta^{\prime}$
model.
3.2. General Laguerre diagrams
Let us start by defining a Laguerre tessellation, which can be considered as a generalized (or weighted) version of a classical Voronoi tessellation. For two points
![]() $v,w \in {\mathbb{R}}^{d-1}$
and
$v,w \in {\mathbb{R}}^{d-1}$
and
![]() $h\in{\mathbb{R}}$
we define the power of w with respect to the pair (v, h) as
$h\in{\mathbb{R}}$
we define the power of w with respect to the pair (v, h) as
In this situation h is referred to as the weight of the point v. A closely related concept is known from elementary geometry, where for
![]() $h < 0$
the value
$h < 0$
the value
![]() ${\textrm{pow}}(w, (v, h))$
describes the square length of the tangent through a point w at a circle with radius
${\textrm{pow}}(w, (v, h))$
describes the square length of the tangent through a point w at a circle with radius
![]() $\sqrt{-h}$
around v.
$\sqrt{-h}$
around v.
Let X be a countable set of marked points of the form (v, h) in
![]() ${\mathbb{R}}^{d-1}\times {\mathbb{R}}$
. Then the Laguerre cell of
${\mathbb{R}}^{d-1}\times {\mathbb{R}}$
. Then the Laguerre cell of
![]() $(v,h)\in X$
is defined as
$(v,h)\in X$
is defined as
Let us mention an intuitive interpretation of the notions introduced above in terms of a crystallization process. Imagine that
![]() $v\in {\mathbb{R}}^{d-1}$
denotes a point at which a certain crystallization process starts at time
$v\in {\mathbb{R}}^{d-1}$
denotes a point at which a certain crystallization process starts at time
![]() $h\in{\mathbb{R}}$
. Then X is a collection of centers of crystallization together with the corresponding initial times. Suppose further that after a crystallization process has started at some point
$h\in{\mathbb{R}}$
. Then X is a collection of centers of crystallization together with the corresponding initial times. Suppose further that after a crystallization process has started at some point
![]() $v\in{\mathbb{R}}^{d-1}$
, it needs time
$v\in{\mathbb{R}}^{d-1}$
, it needs time
![]() $R^2$
to cover a ball of radius
$R^2$
to cover a ball of radius
![]() $R>0$
around v. In particular, the spreading speed of the crystallization is non-constant and decreases with time. Then
$R>0$
around v. In particular, the spreading speed of the crystallization is non-constant and decreases with time. Then
![]() ${\textrm{pow}}(w,(v,h))$
is just the time at which the point w is covered by the crystallization process that started at (v, h). Moreover, the Laguerre cell of (v, h) is just the crystal with ‘center’ v, that is, the set of points which are covered by the crystallization process that started at (v, h) before they are covered by any other crystallization process. It should be pointed out that in our model we assume that crystallization starts at the point
${\textrm{pow}}(w,(v,h))$
is just the time at which the point w is covered by the crystallization process that started at (v, h). Moreover, the Laguerre cell of (v, h) is just the crystal with ‘center’ v, that is, the set of points which are covered by the crystallization process that started at (v, h) before they are covered by any other crystallization process. It should be pointed out that in our model we assume that crystallization starts at the point
![]() $(v,h)\in X$
even if this point has already been covered by another crystallization process which started earlier.
$(v,h)\in X$
even if this point has already been covered by another crystallization process which started earlier.
Note that Laguerre cells can have vanishing topological interior and that in our case most of them will actually be empty. The collection of all Laguerre cells of X which have non-vanishing topological interior is called the Laguerre diagram:
Also, let us emphasize that the Laguerre cell generated by (v, h), even if it is non-empty, need not contain the point v. Indeed, the cell of (v, h) does not contain v if at time h the point v has been already covered by a crystallization process that started at some other point
![]() $(v^{\prime},h^{\prime})\neq (v,h)$
.
$(v^{\prime},h^{\prime})\neq (v,h)$
.
Laguerre diagrams play an important role in computational geometry, where it is more common to use the following interpretation of
![]() ${\mathcal{L}}(X)$
as a vertical projection of a d-dimensional polyhedral set to
${\mathcal{L}}(X)$
as a vertical projection of a d-dimensional polyhedral set to
![]() ${\mathbb{R}}^{d-1}$
; see [Reference Boissonnat and Yvinec4, Chapters 17--18]. Assuming that
${\mathbb{R}}^{d-1}$
; see [Reference Boissonnat and Yvinec4, Chapters 17--18]. Assuming that
![]() $h=-r^2$
for some complex number
$h=-r^2$
for some complex number
![]() $r\in\mathbb{C}$
, to every point
$r\in\mathbb{C}$
, to every point
![]() $(v,-r^2)\in X$
we assign a
$(v,-r^2)\in X$
we assign a
![]() $(d-2)$
-dimensional sphere
$(d-2)$
-dimensional sphere
![]() $S(v,r)\subset {\mathbb{R}}^{d-1}$
with center
$S(v,r)\subset {\mathbb{R}}^{d-1}$
with center
![]() $v\in{\mathbb{R}}^{d-1}$
and (potentially imaginary) radius r. Two spheres
$v\in{\mathbb{R}}^{d-1}$
and (potentially imaginary) radius r. Two spheres
![]() $S(v_1,r_1)$
and
$S(v_1,r_1)$
and
![]() $S(v_2,r_2)$
are orthogonal if
$S(v_2,r_2)$
are orthogonal if
![]() $\|v_1-v_2\|^2=r_1^2+r_2^2$
or, equivalently,
$\|v_1-v_2\|^2=r_1^2+r_2^2$
or, equivalently,
![]() ${\textrm{pow}}(v_2,(v_1,-r_1^2))=r_2^2$
. Thus, for a point
${\textrm{pow}}(v_2,(v_1,-r_1^2))=r_2^2$
. Thus, for a point
![]() $w\in{\mathbb{R}}^{d-1}$
, the value
$w\in{\mathbb{R}}^{d-1}$
, the value
![]() ${\textrm{pow}}\big(w,(v,-r^2)\big)$
is the squared radius of the sphere centered at w and orthogonal to S(v, r). Consider the transformation
${\textrm{pow}}\big(w,(v,-r^2)\big)$
is the squared radius of the sphere centered at w and orthogonal to S(v, r). Consider the transformation
![]() $\phi\,:\, S(v,r)\mapsto (v,\|v\|^2-r^2)$
that maps
$\phi\,:\, S(v,r)\mapsto (v,\|v\|^2-r^2)$
that maps
![]() $(d-2)$
-dimensional spheres to points in
$(d-2)$
-dimensional spheres to points in
![]() ${\mathbb{R}}^{d}$
. Considering a point
${\mathbb{R}}^{d}$
. Considering a point
![]() $w\in{\mathbb{R}}^{d-1}$
as a sphere of zero radius, the above transformation maps
$w\in{\mathbb{R}}^{d-1}$
as a sphere of zero radius, the above transformation maps
![]() ${\mathbb{R}}^{d-1}$
to the standard upward paraboloid
${\mathbb{R}}^{d-1}$
to the standard upward paraboloid
![]() $\Pi^+$
in
$\Pi^+$
in
![]() ${\mathbb{R}}^{d}$
. Moreover, each vertical line in
${\mathbb{R}}^{d}$
. Moreover, each vertical line in
![]() ${\mathbb{R}}^{d}$
passing through (v,0) represents the set of spheres centered at v, and real spheres are mapped to points below
${\mathbb{R}}^{d}$
passing through (v,0) represents the set of spheres centered at v, and real spheres are mapped to points below
![]() $\Pi^+$
, while imaginary spheres correspond to points above
$\Pi^+$
, while imaginary spheres correspond to points above
![]() $\Pi^+$
. Treating the paraboloid
$\Pi^+$
. Treating the paraboloid
![]() $\Pi^+$
as a quadric, for each point
$\Pi^+$
as a quadric, for each point
![]() $x\in{\mathbb{R}}^{d}$
we can define the polar hyperplane
$x\in{\mathbb{R}}^{d}$
we can define the polar hyperplane
![]() $x^o$
of x with respect to
$x^o$
of x with respect to
![]() $\Pi^+$
. Then [Reference Boissonnat and Yvinec4, Lemma 17.2.1] implies that the set of spheres orthogonal to a given sphere S(v, r) is mapped by
$\Pi^+$
. Then [Reference Boissonnat and Yvinec4, Lemma 17.2.1] implies that the set of spheres orthogonal to a given sphere S(v, r) is mapped by
![]() $\phi$
to
$\phi$
to
![]() $\phi(S(v,r))^o$
. Moreover, [Reference Boissonnat and Yvinec4, Lemma 17.2.3] shows that
$\phi(S(v,r))^o$
. Moreover, [Reference Boissonnat and Yvinec4, Lemma 17.2.3] shows that
![]() ${\textrm{pow}}\big(w,(v,-r^2)\big)$
is the signed vertical distance between the point
${\textrm{pow}}\big(w,(v,-r^2)\big)$
is the signed vertical distance between the point
![]() $\phi(w)$
and the hyperplane
$\phi(w)$
and the hyperplane
![]() $\phi(S(v,r))^o$
, i.e. the difference of the dth coordinates of
$\phi(S(v,r))^o$
, i.e. the difference of the dth coordinates of
![]() $\phi(w)$
and the unique point
$\phi(w)$
and the unique point
![]() $y\in\phi(S(v,r))^o$
with
$y\in\phi(S(v,r))^o$
with
![]() $(y_1,\ldots,y_{d-1})=w$
. Using this interpretation and writing
$(y_1,\ldots,y_{d-1})=w$
. Using this interpretation and writing
it is clear that the Laguerre diagram
![]() ${\mathcal{L}}(X)$
arises as the vertical projection (setting the dth coordinate to zero) of the boundary of P(X) to
${\mathcal{L}}(X)$
arises as the vertical projection (setting the dth coordinate to zero) of the boundary of P(X) to
![]() ${\mathbb{R}}^{d-1}$
. Thus, each non-empty Laguerre cell is a vertical projection of a face of P(X). For a more detailed overview of the above interpretation we refer the reader to [Reference Boissonnat and Yvinec4, Chapters 17--18].
${\mathbb{R}}^{d-1}$
. Thus, each non-empty Laguerre cell is a vertical projection of a face of P(X). For a more detailed overview of the above interpretation we refer the reader to [Reference Boissonnat and Yvinec4, Chapters 17--18].
3.3. Random Laguerre tessellations
It should be mentioned that a Laguerre diagram is not necessarily a tessellation, at least as long as we do not impose additional assumptions on the geometric properties of the set X. We also note that the case when all weights are equal corresponds to the case of the classical Voronoi tessellation. The first formal description of geometric properties of the set X ensuring that the Laguerre diagram
![]() ${\mathcal{L}}(X)$
becomes a tessellation is due to Schlottmann [Reference Schlottmann29], and a thorough investigation of the case when all weights are negative has been made by Lautensack and Zuyev [Reference Lautensack21, Reference Lautensack and Zuyev22]. In our situation we are interested in the cases of positive, negative, and general weights
${\mathcal{L}}(X)$
becomes a tessellation is due to Schlottmann [Reference Schlottmann29], and a thorough investigation of the case when all weights are negative has been made by Lautensack and Zuyev [Reference Lautensack21, Reference Lautensack and Zuyev22]. In our situation we are interested in the cases of positive, negative, and general weights
![]() $h\in{\mathbb{R}}$
. More precisely, and in view of the applications in Part II of this series of papers, we consider a point process
$h\in{\mathbb{R}}$
. More precisely, and in view of the applications in Part II of this series of papers, we consider a point process
![]() $\xi$
in
$\xi$
in
![]() ${\mathbb{R}}^{d-1}\times E$
, where
${\mathbb{R}}^{d-1}\times E$
, where
![]() $E\subset {\mathbb{R}}$
is a possibly unbounded interval, satisfying the following properties:
$E\subset {\mathbb{R}}$
is a possibly unbounded interval, satisfying the following properties:
-
(P1) For every
 $(w,t)\in{\mathbb{R}}^{d-1}\times E$
, there are almost surely only finitely many
$(w,t)\in{\mathbb{R}}^{d-1}\times E$
, there are almost surely only finitely many
 $(v,h)\in\xi$
satisfying In words, at the time when a crystallization process starts at some (w, t), the point w has already been reached by at most finitely many crystallization processes.
$(v,h)\in\xi$
satisfying In words, at the time when a crystallization process starts at some (w, t), the point w has already been reached by at most finitely many crystallization processes. \begin{equation*}{\textrm{pow}}(w,(v,h)) = \|w-v\|^2+h \leq t.\end{equation*}
\begin{equation*}{\textrm{pow}}(w,(v,h)) = \|w-v\|^2+h \leq t.\end{equation*}
-
(P2) With probability 1 we have
 \begin{equation*}{\textrm{conv}}(v\,:\, (v,h)\in\xi)={\mathbb{R}}^{d-1}.\end{equation*}
\begin{equation*}{\textrm{conv}}(v\,:\, (v,h)\in\xi)={\mathbb{R}}^{d-1}.\end{equation*}
-
(P3) With probability 1, no
 $d+1$
points
$d+1$
points
 $(v_0,h_0),\ldots, (v_d,h_d)$
from
$(v_0,h_0),\ldots, (v_d,h_d)$
from
 $\xi$
lie on the same downward paraboloid of the form with
$\xi$
lie on the same downward paraboloid of the form with \begin{equation*} \big\{(v,h)\in {\mathbb{R}}^{d-1}\times E\,:\, \|v - w\|^2 + h = t\big\} \end{equation*}
\begin{equation*} \big\{(v,h)\in {\mathbb{R}}^{d-1}\times E\,:\, \|v - w\|^2 + h = t\big\} \end{equation*}
 $(w,t)\in{\mathbb{R}}^{d-1}\times E$
. In words, with probability 1 it is not possible that
$(w,t)\in{\mathbb{R}}^{d-1}\times E$
. In words, with probability 1 it is not possible that
 $d+1$
crystallization processes reach the same point in space simultaneously.
$d+1$
crystallization processes reach the same point in space simultaneously.
In the following two lemmas we prove that the Laguerre diagram constructed on the Poisson point process
![]() $\xi$
is a random face-to-face normal tessellation in
$\xi$
is a random face-to-face normal tessellation in
![]() ${\mathbb{R}}^{d-1}$
.
${\mathbb{R}}^{d-1}$
.
Lemma 1. Let
![]() $\xi$
be a point process satisfying Properties (P1) and (P2). Then
$\xi$
be a point process satisfying Properties (P1) and (P2). Then
![]() ${\mathcal{L}}(\xi)$
is a random face-to-face tessellation in
${\mathcal{L}}(\xi)$
is a random face-to-face tessellation in
![]() ${\mathbb{R}}^{d-1}$
.
${\mathbb{R}}^{d-1}$
.
Proof. The proof follows directly from [Reference Schlottmann29, Proposition 1]. In this context, it should be noted that in [Reference Schlottmann29] the function
was considered. However, this does not influence the proof, and in this paper we prefer to use the function
![]() ${\textrm{pow}}(\,\cdot\,)$
, which is more convenient for our purposes.
${\textrm{pow}}(\,\cdot\,)$
, which is more convenient for our purposes.
Lemma 2. Let
![]() $\xi$
be a point process satisfying Properties (P1)–(P3). Then the random tessellation
$\xi$
be a point process satisfying Properties (P1)–(P3). Then the random tessellation
![]() ${\mathcal{L}}(\xi)$
is normal with probability 1.
${\mathcal{L}}(\xi)$
is normal with probability 1.
Proof. The statement follows directly from the interpretation of the Laguerre diagram
![]() ${\mathcal{L}}(\xi)$
as the boundary of the polyhedral set
${\mathcal{L}}(\xi)$
as the boundary of the polyhedral set
![]() $P(\xi)$
. Let
$P(\xi)$
. Let
![]() $\xi^{\prime}$
be the image of the point process
$\xi^{\prime}$
be the image of the point process
![]() $\xi$
under the transformation
$\xi$
under the transformation
![]() $(v,h)\mapsto \big(v,\|v\|^2+h\big)$
. Property (P3) is equivalent to the fact that with probability 1 no
$(v,h)\mapsto \big(v,\|v\|^2+h\big)$
. Property (P3) is equivalent to the fact that with probability 1 no
![]() $d+1$
points
$d+1$
points
![]() $(w_0,s_0),\ldots, (w_d,s_d)$
from
$(w_0,s_0),\ldots, (w_d,s_d)$
from
![]() $\xi^{\prime}$
lie on the same hyperplane in
$\xi^{\prime}$
lie on the same hyperplane in
![]() ${\mathbb{R}}^{d}$
. From this it also follows that for any
${\mathbb{R}}^{d}$
. From this it also follows that for any
![]() $k=1,\ldots, d$
, with probability 1 no
$k=1,\ldots, d$
, with probability 1 no
![]() $k+1$
points
$k+1$
points
![]() $(w_0,s_0),\ldots, (w_k,s_k)$
lie on the same
$(w_0,s_0),\ldots, (w_k,s_k)$
lie on the same
![]() $(k-1)$
-dimensional hyperplane. Thus, using polarity with respect to the paraboloid
$(k-1)$
-dimensional hyperplane. Thus, using polarity with respect to the paraboloid
![]() $\Pi^+$
, we conclude that any
$\Pi^+$
, we conclude that any
![]() $(d-k)$
-dimensional face of
$(d-k)$
-dimensional face of
![]() $P(\xi)$
,
$P(\xi)$
,
![]() $k=1,\ldots,d$
, is contained in exactly k facets, which implies the normality of
$k=1,\ldots,d$
, is contained in exactly k facets, which implies the normality of
![]() ${\mathcal{L}}(\xi)$
.
${\mathcal{L}}(\xi)$
.
Remark 1. It is easy to see that if the point process
![]() $\xi$
satisfies Properties (P1)–(P3), then with probability 1 there is no non-empty Laguerre cell with vanishing interior. To see this, we again use the correspondence between the Laguerre tessellation
$\xi$
satisfies Properties (P1)–(P3), then with probability 1 there is no non-empty Laguerre cell with vanishing interior. To see this, we again use the correspondence between the Laguerre tessellation
![]() ${\mathcal{L}}(\xi)$
and the boundary of
${\mathcal{L}}(\xi)$
and the boundary of
![]() $P(\xi)$
. First of all we note that every Laguerre cell with vanishing interior corresponds to a face
$P(\xi)$
. First of all we note that every Laguerre cell with vanishing interior corresponds to a face
![]() $F$
of
$F$
of
![]() $P(\xi)$
with dimension
$P(\xi)$
with dimension
![]() $k\leq d-2$
. Thus, there are at least
$k\leq d-2$
. Thus, there are at least
![]() $d-k$
facets of
$d-k$
facets of
![]() $P(\xi)$
containing
$P(\xi)$
containing
![]() $F$
, and hence, using the polarity relation between hyperplanes with respect to the paraboloid
$F$
, and hence, using the polarity relation between hyperplanes with respect to the paraboloid
![]() $\Pi^+$
, there are at least
$\Pi^+$
, there are at least
![]() $d-k+1$
points in
$d-k+1$
points in
![]() $\xi^{\prime}$
lying on the same
$\xi^{\prime}$
lying on the same
![]() $(d-1-k)$
-dimensional hyperplane. According to (P3) this happens with probability 0.
$(d-1-k)$
-dimensional hyperplane. According to (P3) this happens with probability 0.
3.4. Definition of
 $\beta^{(^{\prime})}$
-Voronoi tessellations
$\beta^{(^{\prime})}$
-Voronoi tessellations
The
![]() $\beta^{(^{\prime})}$
-Voronoi tessellations we are interested in are defined as random Laguerre tessellations driven by the Poisson point processes
$\beta^{(^{\prime})}$
-Voronoi tessellations we are interested in are defined as random Laguerre tessellations driven by the Poisson point processes
![]() $\eta_\beta$
and
$\eta_\beta$
and
![]() $\eta^{\prime}_\beta$
with intensities given by (3.1) and (3.2).
$\eta^{\prime}_\beta$
with intensities given by (3.1) and (3.2).
Lemma 3. The point processes
![]() $\eta_\beta$
for
$\eta_\beta$
for
![]() $\beta>-1$
and
$\beta>-1$
and
![]() $\eta^{\prime}_\beta$
for
$\eta^{\prime}_\beta$
for
![]() $\beta>(d+1)/2$
satisfy Properties (P1)–(P3) with
$\beta>(d+1)/2$
satisfy Properties (P1)–(P3) with
![]() $E=[0,\infty)$
in the
$E=[0,\infty)$
in the
![]() $\beta$
case and
$\beta$
case and
![]() $E= ({-}\infty,0)$
in the
$E= ({-}\infty,0)$
in the
![]() $\beta^{\prime}$
case.
$\beta^{\prime}$
case.
Proof. Property (P2) holds because the projections of the Poisson point processes
![]() $\eta_\beta$
and
$\eta_\beta$
and
![]() $\eta_\beta^\prime$
to the space component
$\eta_\beta^\prime$
to the space component
![]() ${\mathbb{R}}^{d-1}$
are everywhere dense sets, with probability 1. Indeed, the integrals of the intensities of these processes over any set of the form
${\mathbb{R}}^{d-1}$
are everywhere dense sets, with probability 1. Indeed, the integrals of the intensities of these processes over any set of the form
![]() $B\times {\mathbb{R}}$
, where
$B\times {\mathbb{R}}$
, where
![]() $B\subset {\mathbb{R}}^{d-1}$
is a non-empty ball, are infinite, which means that infinitely many points project to B almost surely.
$B\subset {\mathbb{R}}^{d-1}$
is a non-empty ball, are infinite, which means that infinitely many points project to B almost surely.
Property (P3) holds for any Poisson point process
![]() $\eta$
in
$\eta$
in
![]() ${\mathbb{R}}^{d-1}\times E$
whose intensity measure
${\mathbb{R}}^{d-1}\times E$
whose intensity measure
![]() $\Theta_{\eta}$
is absolutely continuous with respect to the Lebesgue measure with density
$\Theta_{\eta}$
is absolutely continuous with respect to the Lebesgue measure with density
![]() $\varrho$
, say (see, for example, [Reference MØller26, Proposition 4.1.2] for a closely related result in the setting of a stationary Poisson point process). Let us verify (P3) by applying the multivariate Mecke formula [Reference Schneider and Weil31, Corollary 3.2.3]. Write
$\varrho$
, say (see, for example, [Reference MØller26, Proposition 4.1.2] for a closely related result in the setting of a stationary Poisson point process). Let us verify (P3) by applying the multivariate Mecke formula [Reference Schneider and Weil31, Corollary 3.2.3]. Write
![]() $\eta_{\neq}^{d+1}$
for the set of
$\eta_{\neq}^{d+1}$
for the set of
![]() $(d+1)$
-tuples of distinct points of
$(d+1)$
-tuples of distinct points of
![]() $\eta$
and
$\eta$
and
![]() $\Pi(x_1,\ldots,x_d)$
for the unique downward paraboloid on which the points
$\Pi(x_1,\ldots,x_d)$
for the unique downward paraboloid on which the points
![]() $x_1,\ldots,x_d\in{\mathbb{R}}^d$
lie. With this notation we have that
$x_1,\ldots,x_d\in{\mathbb{R}}^d$
lie. With this notation we have that
 \begin{align*}{\mathbb{E}}&\sum_{(x_1,\ldots,x_{d+1})\in \eta^{d+1}_{\neq}}\textbf{1}\big(x_1,\ldots,x_{d+1}\text{ lie on the same paraboloid}\big)\\&=\frac{1}{(d+1)!}\int_{{\mathbb{R}}^{d-1}}\ldots \int_{{\mathbb{R}}^{d-1}}\int_{E}\ldots \int_{E}\;\;\prod_{i=1}^{d}\varrho(h_i,v_i){\rm d} v_1\ldots {\rm d} v_{d}\,{\rm d} h_1\ldots {\rm d} h_{d}\\&\quad \times \int_{{\mathbb{R}}^{d-1}}\int _{E} \textbf{1}\big(\big(v_{d+1}, h_{d+1}\big)\in\Pi\big(\big(v_1,h_1\big),\ldots,\big(v_d,h_d\big)\big)\big)\varrho\big(h_{d+1},v_{d+1}\big){\rm d} v_{d+1}\,{\rm d} h_{d+1} = 0,\end{align*}
\begin{align*}{\mathbb{E}}&\sum_{(x_1,\ldots,x_{d+1})\in \eta^{d+1}_{\neq}}\textbf{1}\big(x_1,\ldots,x_{d+1}\text{ lie on the same paraboloid}\big)\\&=\frac{1}{(d+1)!}\int_{{\mathbb{R}}^{d-1}}\ldots \int_{{\mathbb{R}}^{d-1}}\int_{E}\ldots \int_{E}\;\;\prod_{i=1}^{d}\varrho(h_i,v_i){\rm d} v_1\ldots {\rm d} v_{d}\,{\rm d} h_1\ldots {\rm d} h_{d}\\&\quad \times \int_{{\mathbb{R}}^{d-1}}\int _{E} \textbf{1}\big(\big(v_{d+1}, h_{d+1}\big)\in\Pi\big(\big(v_1,h_1\big),\ldots,\big(v_d,h_d\big)\big)\big)\varrho\big(h_{d+1},v_{d+1}\big){\rm d} v_{d+1}\,{\rm d} h_{d+1} = 0,\end{align*}
since the inner integral is equal to 0.
Verification of Property (P1) requires additional computations. To consider the case of
![]() $\eta_\beta$
, fix
$\eta_\beta$
, fix
![]() $w\in{\mathbb{R}}^{d-1}$
and
$w\in{\mathbb{R}}^{d-1}$
and
![]() $t>0$
. The inequalities in (P1) describe the bounded domain
$t>0$
. The inequalities in (P1) describe the bounded domain
lying below the paraboloid
![]() $h = t-\|v-w\|^2$
and above the hyperplane
$h = t-\|v-w\|^2$
and above the hyperplane
![]() $h=0$
. Since the intensity measure of the Poisson point process
$h=0$
. Since the intensity measure of the Poisson point process
![]() $\eta_\beta$
is locally integrable because of the condition
$\eta_\beta$
is locally integrable because of the condition
![]() $\beta>-1$
, there are only finitely many points (v, h) of
$\beta>-1$
, there are only finitely many points (v, h) of
![]() $\eta_\beta$
in D, and Property (P1) holds.
$\eta_\beta$
in D, and Property (P1) holds.
In order to check (P1) for
![]() $\eta^{\prime}_\beta$
, we fix
$\eta^{\prime}_\beta$
, we fix
![]() $w\in{\mathbb{R}}^{d-1}$
and
$w\in{\mathbb{R}}^{d-1}$
and
![]() $t<0$
. We need to show that the downward paraboloid
$t<0$
. We need to show that the downward paraboloid
contains only finitely many points of
![]() $\eta_\beta^\prime$
almost surely. Using the stationarity of the process
$\eta_\beta^\prime$
almost surely. Using the stationarity of the process
![]() $\eta_\beta^\prime$
in the space coordinate, we can put
$\eta_\beta^\prime$
in the space coordinate, we can put
![]() $w=0$
without loss of generality. The expected number of points of
$w=0$
without loss of generality. The expected number of points of
![]() $\eta_\beta^\prime$
in D is then given by
$\eta_\beta^\prime$
in D is then given by
 \begin{align*}{\mathbb{E}} \sum_{(v,h)\in\eta^{\prime}_\beta} \textbf{1}\big(\|v\|^2+h\leq t\big)&=\gamma\,c_{d,\beta}^{\prime}\int_{{\mathbb{R}}^{d-1}}\int_{0}^\infty \textbf{1}\big(\|v\|^2-s\leq t\big) s^{-\beta}{\rm d} s\,{\rm d} v\\&=\frac{\gamma\,c_{d,\beta}^{\prime}}{1-\beta}\int_{{\mathbb{R}}^{d-1}} \big(\|v\|^2 + |t|\big)^{1-\beta} {\rm d} v\\&=\frac{\gamma \, c_{d,\beta}^{\prime}}{1-\beta}\,(d-1)\kappa_{d-1}\int_0^\infty\big(r^2+|t|\big)^{1-\beta}r^{d-2}\,\textrm{d} r\\&=\frac{\gamma \, c_{d,\beta}^{\prime}}{(1-\beta)c_{d-1,\beta-1}^{\prime}}|t|^{\frac{d+1-2\beta}{2}}<\infty,\end{align*}
\begin{align*}{\mathbb{E}} \sum_{(v,h)\in\eta^{\prime}_\beta} \textbf{1}\big(\|v\|^2+h\leq t\big)&=\gamma\,c_{d,\beta}^{\prime}\int_{{\mathbb{R}}^{d-1}}\int_{0}^\infty \textbf{1}\big(\|v\|^2-s\leq t\big) s^{-\beta}{\rm d} s\,{\rm d} v\\&=\frac{\gamma\,c_{d,\beta}^{\prime}}{1-\beta}\int_{{\mathbb{R}}^{d-1}} \big(\|v\|^2 + |t|\big)^{1-\beta} {\rm d} v\\&=\frac{\gamma \, c_{d,\beta}^{\prime}}{1-\beta}\,(d-1)\kappa_{d-1}\int_0^\infty\big(r^2+|t|\big)^{1-\beta}r^{d-2}\,\textrm{d} r\\&=\frac{\gamma \, c_{d,\beta}^{\prime}}{(1-\beta)c_{d-1,\beta-1}^{\prime}}|t|^{\frac{d+1-2\beta}{2}}<\infty,\end{align*}
where we have introduced spherical coordinates in
![]() ${\mathbb{R}}^{d-1}$
, applied the definition of the constants
${\mathbb{R}}^{d-1}$
, applied the definition of the constants
![]() $\kappa_{d-1}$
and
$\kappa_{d-1}$
and
![]() $c_{d-1,\beta-1}^{\prime}$
, and used the condition that
$c_{d-1,\beta-1}^{\prime}$
, and used the condition that
![]() $\beta> (d+1)/2$
to ensure the finiteness of the integral over
$\beta> (d+1)/2$
to ensure the finiteness of the integral over
![]() ${\mathbb{R}}^{d-1}$
. This completes the proof.
${\mathbb{R}}^{d-1}$
. This completes the proof.
Summarizing, we conclude that the Laguerre tessellations
![]() ${\mathcal{L}}(\eta_\beta)$
and
${\mathcal{L}}(\eta_\beta)$
and
![]() ${\mathcal{L}}(\eta^{\prime}_\beta)$
are with probability 1 stationary and normal random tessellations in
${\mathcal{L}}(\eta^{\prime}_\beta)$
are with probability 1 stationary and normal random tessellations in
![]() ${\mathbb{R}}^{d-1}$
. We can thus state the following definition.
${\mathbb{R}}^{d-1}$
. We can thus state the following definition.
Definition 2. The random tessellation
![]() ${\mathcal{V}}_\beta\,:\!=\,{\mathcal{L}}(\eta_\beta)$
is called the
${\mathcal{V}}_\beta\,:\!=\,{\mathcal{L}}(\eta_\beta)$
is called the
![]() $\beta$
-Voronoi tessellation and the random tessellation
$\beta$
-Voronoi tessellation and the random tessellation
![]() ${\mathcal{V}}^{\prime}_\beta\,:\!=\,{\mathcal{L}}(\eta^{\prime}_\beta)$
is called the
${\mathcal{V}}^{\prime}_\beta\,:\!=\,{\mathcal{L}}(\eta^{\prime}_\beta)$
is called the
![]() $\beta^{\prime}$
-Voronoi tessellation in
$\beta^{\prime}$
-Voronoi tessellation in
![]() ${\mathbb{R}}^{d-1}$
.
${\mathbb{R}}^{d-1}$
.
Let us emphasize that even though the Poisson point processes
![]() $\eta_\beta$
$\eta_\beta$
![]() $\big($
respectively
$\big($
respectively
![]() $\eta^{\prime}_{\beta}\big)$
are actually well-defined on
$\eta^{\prime}_{\beta}\big)$
are actually well-defined on
![]() ${\mathbb{R}}^{d-1}\times (0,\infty)$
(respectively
${\mathbb{R}}^{d-1}\times (0,\infty)$
(respectively
![]() ${\mathbb{R}}^{d-1}\times ({-}\infty,0)$
) for every
${\mathbb{R}}^{d-1}\times ({-}\infty,0)$
) for every
![]() $\beta\in {\mathbb{R}}$
, the corresponding tessellations are well-defined only under the conditions
$\beta\in {\mathbb{R}}$
, the corresponding tessellations are well-defined only under the conditions
![]() $\beta>-1$
(respectively
$\beta>-1$
(respectively
![]() $\beta>(d+1)/2$
) (because otherwise Property (P1) is not satisfied).
$\beta>(d+1)/2$
) (because otherwise Property (P1) is not satisfied).
Remark 2. We would like to stress the fact that what we call the
![]() $\beta$
-Voronoi tessellation is not a Voronoi tessellation in the classical sense; see [Reference Boissonnat and Yvinec4]. However, the
$\beta$
-Voronoi tessellation is not a Voronoi tessellation in the classical sense; see [Reference Boissonnat and Yvinec4]. However, the
![]() $\beta$
-Voronoi tessellation is a deformation of a Voronoi tessellation, because it converges to the latter as
$\beta$
-Voronoi tessellation is a deformation of a Voronoi tessellation, because it converges to the latter as
![]() $\beta\to -1$
. The situation is similar for the
$\beta\to -1$
. The situation is similar for the
![]() $\beta$
-Delaunay tessellation defined in the next section, which is a deformation of a Delaunay tessellation and converges to it as
$\beta$
-Delaunay tessellation defined in the next section, which is a deformation of a Delaunay tessellation and converges to it as
![]() $\beta\to -1$
.
$\beta\to -1$
.
3.5. Definition of
 $\beta^{(^{\prime})}$
-Delaunay tessellations
$\beta^{(^{\prime})}$
-Delaunay tessellations
Given a Laguerre diagram
![]() ${\mathcal{L}}(\xi)$
we can associate to it a so-called dual Laguerre diagram
${\mathcal{L}}(\xi)$
we can associate to it a so-called dual Laguerre diagram
![]() ${\mathcal{L}}^*(\xi)$
, which can be defined in the same spirit as a classical Delaunay diagram for a given Voronoi construction. Let
${\mathcal{L}}^*(\xi)$
, which can be defined in the same spirit as a classical Delaunay diagram for a given Voronoi construction. Let
![]() $\xi$
be a Poisson point process in
$\xi$
be a Poisson point process in
![]() ${\mathbb{R}}^{d-1}\times E$
,
${\mathbb{R}}^{d-1}\times E$
,
![]() $E\subset {\mathbb{R}}$
satisfying Properties (P1)–(P3). Then
$E\subset {\mathbb{R}}$
satisfying Properties (P1)–(P3). Then
![]() ${\mathcal{L}}(\xi)$
is a random normal face-to-face tessellation and we denote by
${\mathcal{L}}(\xi)$
is a random normal face-to-face tessellation and we denote by
![]() ${\mathcal{F}}_0({\mathcal{L}}(\xi))$
the set of its vertices. Further, given a point
${\mathcal{F}}_0({\mathcal{L}}(\xi))$
the set of its vertices. Further, given a point
![]() $z\in {\mathcal{F}}_0({\mathcal{L}}(\xi))$
we construct a Delaunay cell
$z\in {\mathcal{F}}_0({\mathcal{L}}(\xi))$
we construct a Delaunay cell
![]() $D(z,\xi)$
as a convex hull of those v for which
$D(z,\xi)$
as a convex hull of those v for which
![]() $(v,h)\in\xi$
and
$(v,h)\in\xi$
and
![]() $z\in C((v,h),\xi)$
, namely
$z\in C((v,h),\xi)$
, namely
Since the tessellation
![]() ${\mathcal{L}}(\xi)$
is normal with probability 1, for every vertex
${\mathcal{L}}(\xi)$
is normal with probability 1, for every vertex
![]() $z\in {\mathcal{F}}_0({\mathcal{L}}(\xi))$
there exist exactly d points
$z\in {\mathcal{F}}_0({\mathcal{L}}(\xi))$
there exist exactly d points
![]() $x_1,\ldots, x_d$
of
$x_1,\ldots, x_d$
of
![]() $\xi$
such that the corresponding cells
$\xi$
such that the corresponding cells
![]() $C(x_1,\xi),\dots, C(x_d,\xi)$
of the Laguerre tessellation
$C(x_1,\xi),\dots, C(x_d,\xi)$
of the Laguerre tessellation
![]() ${\mathcal{L}}(\xi)$
contain z. Thus,
${\mathcal{L}}(\xi)$
contain z. Thus,
![]() $D(z,\xi)$
is a simplex with probability 1. We define the dual Laguerre diagram
$D(z,\xi)$
is a simplex with probability 1. We define the dual Laguerre diagram
![]() ${\mathcal{L}}^*(\xi)$
as the collection of all Delaunay simplices
${\mathcal{L}}^*(\xi)$
as the collection of all Delaunay simplices
From the above construction it follows that for any
![]() $z\in {\mathcal{F}}_0({\mathcal{L}}(\xi))$
there exists a number
$z\in {\mathcal{F}}_0({\mathcal{L}}(\xi))$
there exists a number
![]() $K_{z}\in{\mathbb{R}}$
such that with probability 1 there exist exactly d points
$K_{z}\in{\mathbb{R}}$
such that with probability 1 there exist exactly d points
![]() $(v_1,h_1),\ldots, (v_d,h_d)$
of
$(v_1,h_1),\ldots, (v_d,h_d)$
of
![]() $\xi$
with
$\xi$
with
and there is no
![]() $(v,h)\in\xi$
with
$(v,h)\in\xi$
with
![]() ${\textrm{pow}}(z,(v,h))<K_{z}$
. Consider the set
${\textrm{pow}}(z,(v,h))<K_{z}$
. Consider the set
It turns out that the dual Laguerre diagram
![]() ${\mathcal{L}}^*(\xi)$
is a Laguerre diagram constructed for the set
${\mathcal{L}}^*(\xi)$
is a Laguerre diagram constructed for the set
![]() $\xi^*$
and that
$\xi^*$
and that
![]() $\xi^*$
satisfies Properties (P1) and (P2) if
$\xi^*$
satisfies Properties (P1) and (P2) if
![]() $\xi$
satisfies them (for the proof of these facts see [Reference Schlottmann29, Proposition 2]). Thus, by Lemma 3 we conclude that
$\xi$
satisfies them (for the proof of these facts see [Reference Schlottmann29, Proposition 2]). Thus, by Lemma 3 we conclude that
![]() ${\mathcal{L}}^*(\xi)={\mathcal{L}}(\xi^*)$
is a random face-to-face simplicial tessellation.
${\mathcal{L}}^*(\xi)={\mathcal{L}}(\xi^*)$
is a random face-to-face simplicial tessellation.
As for the usual Laguerre diagram
![]() ${\mathcal{L}}(X)$
, where X is some countable set, there is an alternative construction of the dual Laguerre diagram
${\mathcal{L}}(X)$
, where X is some countable set, there is an alternative construction of the dual Laguerre diagram
![]() ${\mathcal{L}}^*(X)$
, which is more common in computational geometry; see [Reference Boissonnat and Yvinec4, Chapters 17--18]. It can be described as follows. Interpreting points of
${\mathcal{L}}^*(X)$
, which is more common in computational geometry; see [Reference Boissonnat and Yvinec4, Chapters 17--18]. It can be described as follows. Interpreting points of
![]() $(v,h)\in X$
as spheres with center v and radius
$(v,h)\in X$
as spheres with center v and radius
![]() $\sqrt{-h}\in\mathbb{C}$
, and applying the transformation
$\sqrt{-h}\in\mathbb{C}$
, and applying the transformation
![]() $\phi$
introduced in Section 3.2, we obtain a set of points
$\phi$
introduced in Section 3.2, we obtain a set of points
![]() $X^{\prime}\,:\!=\,\big\{\big(v,\|v\|^2+h\big)\,:\, (v,h)\in X\big\}$
in
$X^{\prime}\,:\!=\,\big\{\big(v,\|v\|^2+h\big)\,:\, (v,h)\in X\big\}$
in
![]() ${\mathbb{R}}^{d}$
. Then the dual Laguerre diagram
${\mathbb{R}}^{d}$
. Then the dual Laguerre diagram
![]() ${\mathcal{L}}^*(X)$
is the vertical projection along the dth coordinate of the boundary of the polyhedral set
${\mathcal{L}}^*(X)$
is the vertical projection along the dth coordinate of the boundary of the polyhedral set
![]() $P^*(X^{\prime})\,:\!=\,{\textrm{conv}}(X^{\prime})^{\uparrow}$
. It is also common in computational geometry to call
$P^*(X^{\prime})\,:\!=\,{\textrm{conv}}(X^{\prime})^{\uparrow}$
. It is also common in computational geometry to call
![]() ${\mathcal{L}}^*(X)$
a ‘regular triangulation’.
${\mathcal{L}}^*(X)$
a ‘regular triangulation’.
We will be interested in the case when
![]() $\xi$
is one of the Poisson point processes
$\xi$
is one of the Poisson point processes
![]() $\eta_\beta$
or
$\eta_\beta$
or
![]() $\eta_{\beta}^\prime$
.
$\eta_{\beta}^\prime$
.
Definition 3. The random tessellation
![]() ${\mathcal{D}}_\beta\,:\!=\,{\mathcal{L}}^*(\eta_{\beta})$
is called the
${\mathcal{D}}_\beta\,:\!=\,{\mathcal{L}}^*(\eta_{\beta})$
is called the
![]() $\beta$
-Delaunay tessellation in
$\beta$
-Delaunay tessellation in
![]() ${\mathbb{R}}^{d-1}$
, while the random tessellation
${\mathbb{R}}^{d-1}$
, while the random tessellation
![]() ${\mathcal{D}}^{\prime}_\beta\,:\!=\,{\mathcal{L}}^*\big(\eta^{\prime}_{\beta}\big)$
is called the
${\mathcal{D}}^{\prime}_\beta\,:\!=\,{\mathcal{L}}^*\big(\eta^{\prime}_{\beta}\big)$
is called the
![]() $\beta^{\prime}$
-Delaunay tessellation in
$\beta^{\prime}$
-Delaunay tessellation in
![]() ${\mathbb{R}}^{d-1}$
. For the realization of the tessellation
${\mathbb{R}}^{d-1}$
. For the realization of the tessellation
![]() ${\mathcal{D}}_{\beta}$
in dimension 2, see Figure 4, and for
${\mathcal{D}}_{\beta}$
in dimension 2, see Figure 4, and for
![]() ${{\mathcal{D}}^{\prime}}_{\!\!\beta}$
in dimension 2 see Figure 5.
${{\mathcal{D}}^{\prime}}_{\!\!\beta}$
in dimension 2 see Figure 5.

Figure 4. Realization of
![]() $\beta$
-Delaunay tessellation in
$\beta$
-Delaunay tessellation in
![]() ${\mathbb{R}}^2$
. Left:
${\mathbb{R}}^2$
. Left:
![]() $\beta=5$
. Right:
$\beta=5$
. Right:
![]() $\beta=15$
. The pictures above were created with the help of the Computational Geometry Algorithms Library (CGAL) [34].
$\beta=15$
. The pictures above were created with the help of the Computational Geometry Algorithms Library (CGAL) [34].

Figure 5. Realization of
![]() $\beta^{^{\prime}}$
-Delaunay tessellation in
$\beta^{^{\prime}}$
-Delaunay tessellation in
![]() ${\mathbb{R}}^2$
. Left:
${\mathbb{R}}^2$
. Left:
![]() $\beta=2.1$
. Right:
$\beta=2.1$
. Right:
![]() $\beta=2.5$
. The pictures above were created with the help of CGAL [34].
$\beta=2.5$
. The pictures above were created with the help of CGAL [34].
3.6. Paraboloid hull process
The paraboloid hull process was first introduced in [Reference Calka, Schreiber and Yukich5, Reference Schreiber and Yukich32] in order to study the asymptotic geometry of the convex hull of Poisson point processes in the unit ball. It is designed to exhibit properties analogous to those of convex polytopes, with the paraboloids playing the role of hyperplanes, the spatial coordinates v playing the role of spherical coordinates, and the height coordinates h playing the role of the radial coordinate. The numerous properties of the paraboloid hull process, which are analogous to standard statements of convex geometry, have been developed in [Reference Calka, Schreiber and Yukich5, Section 3], and we refer the reader to this paper for further information and background material. At this point let us mention, without making the statement precise or proving it, that the
![]() $\beta$
-Delaunay tessellation we are interested in describes the local asymptotic structure (near the boundary of the unit sphere) of the so-called beta random polytope [Reference Kabluchko, Thäle and Zaporozhets17] in the d-dimensional unit ball generated by n points, as
$\beta$
-Delaunay tessellation we are interested in describes the local asymptotic structure (near the boundary of the unit sphere) of the so-called beta random polytope [Reference Kabluchko, Thäle and Zaporozhets17] in the d-dimensional unit ball generated by n points, as
![]() $n\to\infty$
. After rescaling, the unit sphere looks locally like
$n\to\infty$
. After rescaling, the unit sphere looks locally like
![]() ${\mathbb{R}}^{d-1}$
, while the boundary of the beta random polytope (projected to the sphere) looks locally like the
${\mathbb{R}}^{d-1}$
, while the boundary of the beta random polytope (projected to the sphere) looks locally like the
![]() $\beta$
-Delaunay tessellation.
$\beta$
-Delaunay tessellation.
The idea is that the shifts of the hypographs of the standard paraboloid
![]() $\Pi^{\downarrow}$
are, in some sense, analogous to the half-spaces in
$\Pi^{\downarrow}$
are, in some sense, analogous to the half-spaces in
![]() ${\mathbb{R}}^{d}$
not containing the origin 0 in their boundary. For any collection
${\mathbb{R}}^{d}$
not containing the origin 0 in their boundary. For any collection
![]() $x_1\,:\!=\,(v_1,h_1),\ldots,x_k\,:\!=\,(v_k,h_k)$
of
$x_1\,:\!=\,(v_1,h_1),\ldots,x_k\,:\!=\,(v_k,h_k)$
of
![]() $k\leq d$
points in
$k\leq d$
points in
![]() ${\mathbb{R}}^{d-1}\times{\mathbb{R}}$
with affinely independent coordinates
${\mathbb{R}}^{d-1}\times{\mathbb{R}}$
with affinely independent coordinates
![]() $v_1,\ldots,v_k$
, we define
$v_1,\ldots,v_k$
, we define
![]() $\Pi(x_1,\ldots,x_k)$
as the intersection of
$\Pi(x_1,\ldots,x_k)$
as the intersection of
![]() ${\textrm{aff}}(v_1,\ldots,v_k)\times{\mathbb{R}}$
with a translation of
${\textrm{aff}}(v_1,\ldots,v_k)\times{\mathbb{R}}$
with a translation of
![]() $\Pi$
containing all of the points
$\Pi$
containing all of the points
![]() $x_1,\ldots,x_k$
. It should be noted that the set
$x_1,\ldots,x_k$
. It should be noted that the set
![]() $\Pi(x_1,\ldots,x_k)$
is well-defined, although for
$\Pi(x_1,\ldots,x_k)$
is well-defined, although for
![]() $k<d$
the translation of
$k<d$
the translation of
![]() $\Pi$
containing all
$\Pi$
containing all
![]() $x_1,\ldots,x_k$
is not unique. Nevertheless, for
$x_1,\ldots,x_k$
is not unique. Nevertheless, for
![]() $k=d$
and all tuples
$k=d$
and all tuples
![]() $x_1,\ldots,x_d$
with affinely independent spatial coordinates
$x_1,\ldots,x_d$
with affinely independent spatial coordinates
![]() $v_1,\ldots,v_d$
, such a translation is unique. Then we define
$v_1,\ldots,v_d$
, such a translation is unique. Then we define
![]() $\Pi[x_1,\ldots,x_k]$
as
$\Pi[x_1,\ldots,x_k]$
as
We will say that a set
![]() $A\subset {\mathbb{R}}^d$
has the paraboloid convexity property if for each
$A\subset {\mathbb{R}}^d$
has the paraboloid convexity property if for each
![]() $y_1,y_2\in A$
we have
$y_1,y_2\in A$
we have
![]() $\Pi[y_1,y_2]\subset A$
. Clearly,
$\Pi[y_1,y_2]\subset A$
. Clearly,
![]() $\Pi[x_1,\ldots,x_k]$
is the smallest set containing
$\Pi[x_1,\ldots,x_k]$
is the smallest set containing
![]() $x_1,\ldots,x_k$
and having the paraboloid convexity property. Next, we say the set
$x_1,\ldots,x_k$
and having the paraboloid convexity property. Next, we say the set
![]() $A\subset {\mathbb{R}}^d$
is upwards paraboloid convex if and only if A has the paraboloid convexity property and if for each
$A\subset {\mathbb{R}}^d$
is upwards paraboloid convex if and only if A has the paraboloid convexity property and if for each
![]() $x=(v,h)\in A$
we have
$x=(v,h)\in A$
we have
![]() $\{x\}^{\uparrow}\subset A$
.
$\{x\}^{\uparrow}\subset A$
.
Finally, given a locally finite point set
![]() $X\subset{\mathbb{R}}^d$
, we define its paraboloid hull
$X\subset{\mathbb{R}}^d$
, we define its paraboloid hull
![]() $\Phi(X)$
to be the smallest upwards paraboloid convex set containing X. In particular, given a Poisson point process
$\Phi(X)$
to be the smallest upwards paraboloid convex set containing X. In particular, given a Poisson point process
![]() $\xi$
in
$\xi$
in
![]() ${\mathbb{R}}^{d-1}\times E$
,
${\mathbb{R}}^{d-1}\times E$
,
![]() $E\subset{\mathbb{R}}$
, we define the paraboloid hull process
$E\subset{\mathbb{R}}$
, we define the paraboloid hull process
![]() $\Phi(\xi)$
in
$\Phi(\xi)$
in
![]() ${\mathbb{R}}^{d-1}\times E$
as the paraboloid hull of
${\mathbb{R}}^{d-1}\times E$
as the paraboloid hull of
![]() $\xi$
.
$\xi$
.
Using arguments analogous to those of [Reference Calka, Schreiber and Yukich5, Lemma 3.1], it is easy to derive an alternative and more convenient way to represent
![]() $\Phi(\xi)$
; namely, with probability 1 we have that
$\Phi(\xi)$
; namely, with probability 1 we have that
where
![]() $\xi_{\neq}^d$
is the collection of all d-tuples of distinct points of
$\xi_{\neq}^d$
is the collection of all d-tuples of distinct points of
![]() $\xi$
.
$\xi$
.
For
![]() $(x_1,\ldots,x_d)\in\xi_{\neq}^d$
, the set
$(x_1,\ldots,x_d)\in\xi_{\neq}^d$
, the set
![]() $\Pi[x_1,\ldots,x_d]$
is called a paraboloid sub-facet of
$\Pi[x_1,\ldots,x_d]$
is called a paraboloid sub-facet of
![]() $\Phi(\xi)$
if
$\Phi(\xi)$
if
![]() $\Pi[x_1,\ldots,x_d] \subset\partial \Phi(\xi)$
. Two paraboloid sub-facets
$\Pi[x_1,\ldots,x_d] \subset\partial \Phi(\xi)$
. Two paraboloid sub-facets
![]() $\Pi[x_1,\ldots,x_d]$
and
$\Pi[x_1,\ldots,x_d]$
and
![]() $\Pi[y_1,\ldots,y_d]$
are called co-paraboloid provided that
$\Pi[y_1,\ldots,y_d]$
are called co-paraboloid provided that
![]() $\Pi(x_1,\ldots,x_d)=\Pi(y_1,\ldots,y_d)$
, and by paraboloid facet of
$\Pi(x_1,\ldots,x_d)=\Pi(y_1,\ldots,y_d)$
, and by paraboloid facet of
![]() $\Phi(\xi)$
we understand a collection of co-paraboloid sub-facets. Since
$\Phi(\xi)$
we understand a collection of co-paraboloid sub-facets. Since
![]() $\xi$
is a Poisson point process, each paraboloid facet of
$\xi$
is a Poisson point process, each paraboloid facet of
![]() $\Phi(\xi)$
with probability 1 consists of exactly one sub-facet. Thus we can say that
$\Phi(\xi)$
with probability 1 consists of exactly one sub-facet. Thus we can say that
![]() $\Pi[x_1,\ldots,x_d]$
is a paraboloid facet of
$\Pi[x_1,\ldots,x_d]$
is a paraboloid facet of
![]() $\Phi(\xi)$
if and only if
$\Phi(\xi)$
if and only if
![]() $\xi \cap \left(\Pi(x_1,\ldots,x_d)\right)^{\downarrow}=\{x_1,\ldots, x_d\}$
.
$\xi \cap \left(\Pi(x_1,\ldots,x_d)\right)^{\downarrow}=\{x_1,\ldots, x_d\}$
.
Using the paraboloid hull processes
![]() $\Phi(\xi)$
, we now construct a diagram
$\Phi(\xi)$
, we now construct a diagram
![]() ${\mathcal{D}}(\xi)$
on
${\mathcal{D}}(\xi)$
on
![]() ${\mathbb{R}}^{d-1}$
in the following way: for any collection
${\mathbb{R}}^{d-1}$
in the following way: for any collection
![]() $x_1\,:\!=\,(v_1,h_1),\ldots,x_d\,:\!=\,(v_d,h_d)$
of pairwise distinct points from
$x_1\,:\!=\,(v_1,h_1),\ldots,x_d\,:\!=\,(v_d,h_d)$
of pairwise distinct points from
![]() $\xi$
, we say that the simplex
$\xi$
, we say that the simplex
![]() ${\textrm{conv}}(v_1,\ldots,v_d)$
belongs to
${\textrm{conv}}(v_1,\ldots,v_d)$
belongs to
![]() ${\mathcal{D}}(\xi)$
if and only if
${\mathcal{D}}(\xi)$
if and only if
![]() $\Pi[x_1,\ldots,x_k]$
is a paraboloid facet of
$\Pi[x_1,\ldots,x_k]$
is a paraboloid facet of
![]() $\Phi(\xi)$
. Thus, if
$\Phi(\xi)$
. Thus, if
![]() $\xi$
satisfies Properties (P1)–(P3), then
$\xi$
satisfies Properties (P1)–(P3), then
![]() ${\mathcal{D}}(\xi)={\mathcal{L}}^{*}(\xi)$
is a random simplicial tessellation.
${\mathcal{D}}(\xi)={\mathcal{L}}^{*}(\xi)$
is a random simplicial tessellation.
It is clear now that the tessellations
![]() ${\mathcal{D}}(\eta_{\beta})$
and
${\mathcal{D}}(\eta_{\beta})$
and
![]() ${\mathcal{D}}(\eta^{\prime}_{\beta})$
coincide with
${\mathcal{D}}(\eta^{\prime}_{\beta})$
coincide with
![]() $\beta$
–Delaunay and
$\beta$
–Delaunay and
![]() $\beta^{\prime}$
–Delaunay tessellations (respectively), defined in the previous subsection.
$\beta^{\prime}$
–Delaunay tessellations (respectively), defined in the previous subsection.
4. Weighted typical cells in
 $\beta$
- and
$\beta$
- and
 $\beta^{\prime}$
-Delaunay tessellations
$\beta^{\prime}$
-Delaunay tessellations
4.1. Definition of the
 $\nu$
-weighted typical cell
$\nu$
-weighted typical cell
In this section we derive an explicit representation of the distribution of typical cells in a
![]() $\beta$
-Delaunay tessellation
$\beta$
-Delaunay tessellation
![]() ${\mathcal{D}}_\beta$
with parameter
${\mathcal{D}}_\beta$
with parameter
![]() $\beta > -1$
and a
$\beta > -1$
and a
![]() $\beta^{\prime}$
-Delaunay tessellation
$\beta^{\prime}$
-Delaunay tessellation
![]() ${\mathcal{D}}^{\prime}_\beta$
with parameter
${\mathcal{D}}^{\prime}_\beta$
with parameter
![]() $\beta > (d+1)/2$
as described in the previous sections, and, more generally, of the distribution of typical cells weighted by the
$\beta > (d+1)/2$
as described in the previous sections, and, more generally, of the distribution of typical cells weighted by the
![]() $\nu$
th power of their volume, with
$\nu$
th power of their volume, with
![]() $\nu\ge-1$
. On the intuitive level, the construction presented below can be understood as follows. Consider the collection of all cells of
$\nu\ge-1$
. On the intuitive level, the construction presented below can be understood as follows. Consider the collection of all cells of
![]() ${\mathcal{D}}_\beta$
or
${\mathcal{D}}_\beta$
or
![]() ${\mathcal{D}}^{\prime}_\beta$
and assign to each cell a weight equal to the
${\mathcal{D}}^{\prime}_\beta$
and assign to each cell a weight equal to the
![]() $\nu$
th power of its volume. Then pick one cell at random, where the probability of picking a given cell is proportional to the
$\nu$
th power of its volume. Then pick one cell at random, where the probability of picking a given cell is proportional to the
![]() $\nu$
th power of its volume. The resulting random simplex is denoted by
$\nu$
th power of its volume. The resulting random simplex is denoted by
![]() $Z_{\beta,\nu}$
$Z_{\beta,\nu}$
![]() $\big($
respectively,
$\big($
respectively,
![]() $Z_{\beta,\nu}^\prime\big)$
, and its probability distribution on the space of compact convex subsets of
$Z_{\beta,\nu}^\prime\big)$
, and its probability distribution on the space of compact convex subsets of
![]() ${\mathbb{R}}^{d-1}$
is denoted by
${\mathbb{R}}^{d-1}$
is denoted by
![]() ${\mathbb{P}}_{\beta,\nu}$
${\mathbb{P}}_{\beta,\nu}$
![]() $\big($
respectively,
$\big($
respectively,
![]() ${\mathbb{P}}_{\beta,\nu}^\prime\big)$
. Since the number of cells in the tessellation is infinite, some work is necessary to define these objects in a mathematically rigorous way. The reader should keep in mind the following two important special cases:
${\mathbb{P}}_{\beta,\nu}^\prime\big)$
. Since the number of cells in the tessellation is infinite, some work is necessary to define these objects in a mathematically rigorous way. The reader should keep in mind the following two important special cases:
-
(i)
 $\nu=0$
:
$\nu=0$
:
 $Z_{\beta,0}$
$Z_{\beta,0}$
 $\big($
respectively,
$\big($
respectively,
 $Z_{\beta,0}^{\prime}\big)$
coincides with the classical typical cell of
$Z_{\beta,0}^{\prime}\big)$
coincides with the classical typical cell of
 ${\mathcal{D}}_\beta$
${\mathcal{D}}_\beta$
 $\big($
respectively,
$\big($
respectively,
 ${\mathcal{D}}_\beta^{\prime}\big)$
;
${\mathcal{D}}_\beta^{\prime}\big)$
; -
(ii)
 $\nu=1$
:
$\nu=1$
:
 $Z_{\beta,1}$
$Z_{\beta,1}$
 $\big($
respectively,
$\big($
respectively,
 $Z_{\beta,1}^{\prime}\big)$
coincides with the volume-weighted typical cell of
$Z_{\beta,1}^{\prime}\big)$
coincides with the volume-weighted typical cell of
 ${\mathcal{D}}_\beta$
${\mathcal{D}}_\beta$
 $\big($
respectively,
$\big($
respectively,
 ${\mathcal{D}}_\beta^{\prime}\big)$
(which has the same distribution as the almost surely unique cell containing the origin, up to translation; see Theorem 10.4.1 in [Reference Schneider and Weil31]).
${\mathcal{D}}_\beta^{\prime}\big)$
(which has the same distribution as the almost surely unique cell containing the origin, up to translation; see Theorem 10.4.1 in [Reference Schneider and Weil31]).
To formally present the definition of volume-power-weighted typical cells, we use the concept of generalized center functions and Palm calculus for marked point processes as outlined in [Reference Schneider and Weil31, p.116] and [Reference Schneider and Weil30, Section 4.3]. Following the arguments from Subsection 3.3 and Subsection 3.6, a random tessellation
![]() ${\mathcal{D}}(\xi)$
, where
${\mathcal{D}}(\xi)$
, where
![]() $\xi$
is a point process in
$\xi$
is a point process in
![]() ${\mathbb{R}}^{d-1}\times E$
,
${\mathbb{R}}^{d-1}\times E$
,
![]() $E\subset {\mathbb{R}}$
satisfying (P1)–(P3), coincides with the Laguerre tessellation of the random set
$E\subset {\mathbb{R}}$
satisfying (P1)–(P3), coincides with the Laguerre tessellation of the random set
![]() $\xi^*$
described by (3.3). In this section we additionally assume that
$\xi^*$
described by (3.3). In this section we additionally assume that
![]() $\xi$
is stationary with respect to the shifts of the
$\xi$
is stationary with respect to the shifts of the
![]() ${\mathbb{R}}^{d-1}$
-component, which implies stationarity of the tessellation
${\mathbb{R}}^{d-1}$
-component, which implies stationarity of the tessellation
![]() ${\mathcal{D}}(\xi)$
. Observe that
${\mathcal{D}}(\xi)$
. Observe that
![]() $\xi^*$
can alternatively be described via the set of apexes of paraboloid facets of the paraboloid hull process
$\xi^*$
can alternatively be described via the set of apexes of paraboloid facets of the paraboloid hull process
![]() $\Phi(\xi)$
; that is,
$\Phi(\xi)$
; that is,
Let
![]() ${\mathcal{C}}^{\prime}$
denote the space of non-empty compact subsets of
${\mathcal{C}}^{\prime}$
denote the space of non-empty compact subsets of
![]() ${\mathbb{R}}^{d-1}$
endowed with the usual Hausdorff metric and the corresponding Borel
${\mathbb{R}}^{d-1}$
endowed with the usual Hausdorff metric and the corresponding Borel
![]() $\sigma$
-field
$\sigma$
-field
![]() ${\mathcal{B}}({\mathcal{C}}^{\prime})$
. The random tessellation
${\mathcal{B}}({\mathcal{C}}^{\prime})$
. The random tessellation
![]() ${\mathcal{D}}(\xi)$
(which is defined as a random subset of
${\mathcal{D}}(\xi)$
(which is defined as a random subset of
![]() ${\mathcal{C}}^{\prime}$
) can be identified with the particle process
${\mathcal{C}}^{\prime}$
) can be identified with the particle process
![]() $\sum_{c\in{\mathcal{D}}(\xi)}\delta_c$
; see [Reference Schneider and Weil31, Chapter 4]. Formally, this is a simple point process on
$\sum_{c\in{\mathcal{D}}(\xi)}\delta_c$
; see [Reference Schneider and Weil31, Chapter 4]. Formally, this is a simple point process on
![]() ${\mathcal{C}}^{\prime}$
, or equivalently, a random element in the space
${\mathcal{C}}^{\prime}$
, or equivalently, a random element in the space
![]() ${\textsf{N}}_s({\mathcal{C}}^{\prime})$
of
${\textsf{N}}_s({\mathcal{C}}^{\prime})$
of
![]() $\sigma$
-finite simple counting measures on
$\sigma$
-finite simple counting measures on
![]() ${\mathcal{C}}^{\prime}$
(a counting measure
${\mathcal{C}}^{\prime}$
(a counting measure
![]() $\zeta$
on
$\zeta$
on
![]() ${\mathcal{C}}^{\prime}$
is simple if
${\mathcal{C}}^{\prime}$
is simple if
![]() $\zeta(\{K\})\in\{0,1\}$
for all
$\zeta(\{K\})\in\{0,1\}$
for all
![]() $K\in{\mathcal{C}}^{\prime}$
). Next, we define the measurable set
$K\in{\mathcal{C}}^{\prime}$
). Next, we define the measurable set
![]() ${\mathcal{C}}^{\prime}\circ{\textsf{N}}({\mathcal{C}}^{\prime})\,:\!=\,\{(K,\zeta)\in{\mathcal{C}}^{\prime} \times {\textsf{N}}_s({\mathcal{C}}^{\prime})\,:\,K\in\zeta\}$
and recall that a generalized center function is any Borel-measurable map
${\mathcal{C}}^{\prime}\circ{\textsf{N}}({\mathcal{C}}^{\prime})\,:\!=\,\{(K,\zeta)\in{\mathcal{C}}^{\prime} \times {\textsf{N}}_s({\mathcal{C}}^{\prime})\,:\,K\in\zeta\}$
and recall that a generalized center function is any Borel-measurable map
![]() $z\,:\,{\mathcal{C}}^{\prime}\circ{\textsf{N}}({\mathcal{C}}^{\prime})\to{\mathbb{R}}^{d-1}$
such that
$z\,:\,{\mathcal{C}}^{\prime}\circ{\textsf{N}}({\mathcal{C}}^{\prime})\to{\mathbb{R}}^{d-1}$
such that
![]() $z(K+t, \zeta+t) = z(K,\zeta)+t$
for every
$z(K+t, \zeta+t) = z(K,\zeta)+t$
for every
![]() $t\in{\mathbb{R}}^{d-1}$
and
$t\in{\mathbb{R}}^{d-1}$
and
![]() $(K,\zeta)\in{\mathcal{C}}^{\prime}\circ{\textsf{N}}({\mathcal{C}}^{\prime})$
. In our case we take
$(K,\zeta)\in{\mathcal{C}}^{\prime}\circ{\textsf{N}}({\mathcal{C}}^{\prime})$
. In our case we take
 \begin{equation*}z(K,\zeta)\,:\!=\,\begin{cases}v & \text{if } K=C\big((v,h), \xi^*\big),\,\zeta ={{\mathcal{D}}}(\xi),\\[4pt]0 & \text{otherwise},\end{cases}\end{equation*}
\begin{equation*}z(K,\zeta)\,:\!=\,\begin{cases}v & \text{if } K=C\big((v,h), \xi^*\big),\,\zeta ={{\mathcal{D}}}(\xi),\\[4pt]0 & \text{otherwise},\end{cases}\end{equation*}
where we recall that
![]() $C\big((v,h), \xi^*\big)$
is the Laguerre cell of
$C\big((v,h), \xi^*\big)$
is the Laguerre cell of
![]() $(v,h)\in \xi^*$
.
$(v,h)\in \xi^*$
.
Next we consider the random marked point process
![]() $\mu_{\xi}$
on
$\mu_{\xi}$
on
![]() ${\mathbb{R}}^{d-1}$
with mark space
${\mathbb{R}}^{d-1}$
with mark space
![]() ${\mathcal{C}}^{\prime}$
, formed as follows:
${\mathcal{C}}^{\prime}$
, formed as follows:
It is evident from the construction that the point process
![]() $\mu_{\xi}$
is stationary and that the intensity measure
$\mu_{\xi}$
is stationary and that the intensity measure
![]() $\Theta$
of
$\Theta$
of
![]() $\mu_{\xi}$
is locally finite. Thus, according to [Reference Schneider and Weil31, Theorem 3.5.1] it admits the decomposition
$\mu_{\xi}$
is locally finite. Thus, according to [Reference Schneider and Weil31, Theorem 3.5.1] it admits the decomposition
where
![]() $0<\lambda<\infty$
,
$0<\lambda<\infty$
,
![]() ${\rm Leb}\big({\mathbb{R}}^{d-1}\big)$
is the Lebesgue measure on
${\rm Leb}\big({\mathbb{R}}^{d-1}\big)$
is the Lebesgue measure on
![]() ${\mathbb{R}}^{d-1}$
, and
${\mathbb{R}}^{d-1}$
, and
![]() ${\mathbb{P}}_{\xi,0}$
is a probability measure on
${\mathbb{P}}_{\xi,0}$
is a probability measure on
![]() ${\mathcal{C}}^{\prime}$
, the so-called mark distribution of
${\mathcal{C}}^{\prime}$
, the so-called mark distribution of
![]() $\mu_{\xi}$
. By [Reference Schneider and Weil31, p.84] it can be represented as
$\mu_{\xi}$
. By [Reference Schneider and Weil31, p.84] it can be represented as
where
![]() $[0,1]^{d-1}$
denotes the
$[0,1]^{d-1}$
denotes the
![]() $(d-1)$
-dimensional unit cube. The probability measure
$(d-1)$
-dimensional unit cube. The probability measure
![]() ${\mathbb{P}}_{\xi,0}$
describes the mark attached to the typical point of
${\mathbb{P}}_{\xi,0}$
describes the mark attached to the typical point of
![]() $\mu_{\xi}$
, that is, the typical cell of the tessellation
$\mu_{\xi}$
, that is, the typical cell of the tessellation
![]() ${\mathcal{D}}(\xi)$
. This motivates the following definition.
${\mathcal{D}}(\xi)$
. This motivates the following definition.
For a given
![]() $\nu$
we define a probability measure
$\nu$
we define a probability measure
![]() ${\mathbb{P}}_{\xi,\nu}$
on
${\mathbb{P}}_{\xi,\nu}$
on
![]() ${\mathcal{C}}^{\prime}$
by
${\mathcal{C}}^{\prime}$
by
for
![]() $A\in {\mathcal{B}}({\mathcal{C}}^{\prime})$
, where
$A\in {\mathcal{B}}({\mathcal{C}}^{\prime})$
, where
![]() $\lambda_{\xi,\nu}$
is the normalizing constant given by
$\lambda_{\xi,\nu}$
is the normalizing constant given by
It should be mentioned that for some values of
![]() $\nu$
the value
$\nu$
the value
![]() $\lambda_{\xi,\nu}$
can be equal to infinity. This is the reason why for any point process
$\lambda_{\xi,\nu}$
can be equal to infinity. This is the reason why for any point process
![]() $\xi$
one needs to specify possible values of
$\xi$
one needs to specify possible values of
![]() $\nu$
.
$\nu$
.
Definition 4. A random simplex
![]() $Z_{\beta,\nu}$
, where
$Z_{\beta,\nu}$
, where
![]() $\nu \ge -1$
and
$\nu \ge -1$
and
![]() $\beta>-1$
, with distribution
$\beta>-1$
, with distribution
![]() ${\mathbb{P}}_{\beta,\nu}\,:\!=\,{\mathbb{P}}_{\eta_\beta,\nu}$
is the
${\mathbb{P}}_{\beta,\nu}\,:\!=\,{\mathbb{P}}_{\eta_\beta,\nu}$
is the
![]() $\textrm{Vol}^{\nu}$
-weighted (or just
$\textrm{Vol}^{\nu}$
-weighted (or just
![]() $\nu$
-weighted) typical cell of the
$\nu$
-weighted) typical cell of the
![]() $\beta$
-Delaunay tessellation
$\beta$
-Delaunay tessellation
![]() ${\mathcal{D}}_\beta$
.
${\mathcal{D}}_\beta$
.
Definition 5. A random simplex
![]() $Z_{\beta,\nu}^{\prime}$
, where
$Z_{\beta,\nu}^{\prime}$
, where
![]() $\beta>(d+1)/2$
and
$\beta>(d+1)/2$
and
![]() $2\beta - d>\nu\ge -1$
, with distribution
$2\beta - d>\nu\ge -1$
, with distribution
![]() ${\mathbb{P}}_{\beta,\nu}^{\prime}\,:\!=\,{\mathbb{P}}_{\eta_\beta^{\prime},\nu}$
is the
${\mathbb{P}}_{\beta,\nu}^{\prime}\,:\!=\,{\mathbb{P}}_{\eta_\beta^{\prime},\nu}$
is the
![]() $\textrm{Vol}^{\nu}$
-weighted typical cell of the
$\textrm{Vol}^{\nu}$
-weighted typical cell of the
![]() $\beta^{\prime}$
-Delaunay tessellation
$\beta^{\prime}$
-Delaunay tessellation
![]() ${\mathcal{D}}^{\prime}_\beta$
.
${\mathcal{D}}^{\prime}_\beta$
.
Remark 3. That the constants
![]() $\lambda_{\beta,\nu}\,:\!=\,\lambda_{\eta_{\beta},\nu}$
and
$\lambda_{\beta,\nu}\,:\!=\,\lambda_{\eta_{\beta},\nu}$
and
![]() $\lambda^{\prime}_{\beta,\nu}\,:\!=\,\lambda_{\eta_{\beta}^{\prime},\nu}$
are in fact finite for the ranges of d,
$\lambda^{\prime}_{\beta,\nu}\,:\!=\,\lambda_{\eta_{\beta}^{\prime},\nu}$
are in fact finite for the ranges of d,
![]() $\beta$
, and
$\beta$
, and
![]() $\nu$
mentioned in the previous definition will be established in the proof of Theorem 1.
$\nu$
mentioned in the previous definition will be established in the proof of Theorem 1.
Remark 4. We also conjecture that it is possible to enlarge the diapason of possible values for the parameter
![]() $\nu$
to
$\nu$
to
![]() $\nu>-2$
.
$\nu>-2$
.
4.2. Stochastic representation of the
 $\nu$
-weighted typical cell
$\nu$
-weighted typical cell
After having introduced the concept of weighted typical cells, we are now going to develop an explicit description of their distributions. In fact, the following theorem may be considered our main contribution in this paper, since it is the principal device on which most of the results in this part, as well as in Parts II and III of this series of papers, are based. To present it, let us recall our convention that
![]() $\kappa=1$
if we consider the
$\kappa=1$
if we consider the
![]() $\beta$
model and that
$\beta$
model and that
![]() $\kappa=-1$
in the case of the
$\kappa=-1$
in the case of the
![]() $\beta^{\prime}$
model.
$\beta^{\prime}$
model.
Theorem 1. Fix
![]() $d\geq 2$
,
$d\geq 2$
,
![]() $\nu\ge-1$
, and
$\nu\ge-1$
, and
![]() $\beta>-1$
for the
$\beta>-1$
for the
![]() $\beta$
model, or
$\beta$
model, or
![]() $2\beta - d>\nu\ge -1$
,
$2\beta - d>\nu\ge -1$
,
![]() $\beta>(d+1)/2$
for the
$\beta>(d+1)/2$
for the
![]() $\beta^{\prime}$
model. Then for any Borel set
$\beta^{\prime}$
model. Then for any Borel set
![]() $A\subset {\mathcal{C}}^{\prime}$
we have that
$A\subset {\mathcal{C}}^{\prime}$
we have that
 \begin{align*}{\mathbb{P}}_{\beta,\nu}^{(\prime)}(A)&=\alpha_{d,\beta,\nu}^{(\prime)}\int_{\big({\mathbb{R}}^{d-1}\big)^d}{\rm d} y_1\ldots {\rm d} y_d \int_{0}^{\infty}{\rm d} r\,\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d)) r^{2\kappa d\beta+d^2+\nu(d-1)}\notag\\&\quad \times e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa\beta}}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big),\end{align*}
\begin{align*}{\mathbb{P}}_{\beta,\nu}^{(\prime)}(A)&=\alpha_{d,\beta,\nu}^{(\prime)}\int_{\big({\mathbb{R}}^{d-1}\big)^d}{\rm d} y_1\ldots {\rm d} y_d \int_{0}^{\infty}{\rm d} r\,\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d)) r^{2\kappa d\beta+d^2+\nu(d-1)}\notag\\&\quad \times e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa\beta}}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big),\end{align*}
where
![]() $\Delta_{d-1}(y_1,\ldots,y_d)$
is the volume of
$\Delta_{d-1}(y_1,\ldots,y_d)$
is the volume of
![]() ${\textrm{conv}}(y_1,\ldots,y_d)$
, and
${\textrm{conv}}(y_1,\ldots,y_d)$
, and
![]() $\alpha_{d,\beta,\nu}$
,
$\alpha_{d,\beta,\nu}$
,
![]() $\alpha^{\prime}_{d,\beta,\nu}$
,
$\alpha^{\prime}_{d,\beta,\nu}$
,
![]() $m_{d,\beta}$
, and
$m_{d,\beta}$
, and
![]() $m^{\prime}_{d,\beta}$
are constants given by
$m^{\prime}_{d,\beta}$
are constants given by
 \begin{align}\alpha_{d,\beta,\nu}&=\pi^{\frac{d(d-1)}{2}}\frac{(d-1)!^{\nu+1}(d+1+2\beta)\Gamma\Big(\frac{d(d+\nu+2\beta)-\nu+1}{2}\Big)}{\Gamma\big(\frac{d(d+\nu+2\beta)}{2}+1\big)\Gamma\Big(d+\frac{(\nu-1)(d-1)}{d+2\beta+1}\Big)}\frac{\Gamma\big(\frac{d+\nu}{2}+\beta+1\big)^d}{\Gamma(\beta+1)^d}\notag\\[5pt]&\quad \times\Bigg(\frac{\gamma\,\Gamma\big({\frac{d}{2}}+\beta+1\big)}{\sqrt{\pi}\Gamma\big(\frac{d+1}{2}+\beta+1\big)}\Bigg)^{d+\frac{(\nu-1)(d-1)}{d+2\beta+1}}\prod\limits_{i=1}^{d-1}\frac{\Gamma\big(\frac{i}{2}\big)}{\Gamma\big({i+\nu+1\over 2}\big)},\end{align}
\begin{align}\alpha_{d,\beta,\nu}&=\pi^{\frac{d(d-1)}{2}}\frac{(d-1)!^{\nu+1}(d+1+2\beta)\Gamma\Big(\frac{d(d+\nu+2\beta)-\nu+1}{2}\Big)}{\Gamma\big(\frac{d(d+\nu+2\beta)}{2}+1\big)\Gamma\Big(d+\frac{(\nu-1)(d-1)}{d+2\beta+1}\Big)}\frac{\Gamma\big(\frac{d+\nu}{2}+\beta+1\big)^d}{\Gamma(\beta+1)^d}\notag\\[5pt]&\quad \times\Bigg(\frac{\gamma\,\Gamma\big({\frac{d}{2}}+\beta+1\big)}{\sqrt{\pi}\Gamma\big(\frac{d+1}{2}+\beta+1\big)}\Bigg)^{d+\frac{(\nu-1)(d-1)}{d+2\beta+1}}\prod\limits_{i=1}^{d-1}\frac{\Gamma\big(\frac{i}{2}\big)}{\Gamma\big({i+\nu+1\over 2}\big)},\end{align}
 \begin{align}\alpha^{\prime}_{d,\beta,\nu}&=\pi^{\frac{d(d-1)}{2}}\frac{(d-1)!^{\nu+1}(d+1-2\beta)\Gamma\Big(\frac{d(2\beta-d-\nu)}{2}\Big)}{\Gamma\Big(\frac{d(2\beta-d-\nu)+\nu+1}{2}\Big)\Gamma\Big(d+\frac{(\nu-1)(d-1)}{d-2\beta+1}\Big)}\frac{\Gamma(\beta)^d}{\Gamma\Big(\beta-\frac{d+\nu}{2}\Big)^d}\notag\\[5pt]&\quad \times\Bigg({\gamma\,\Gamma\big(\beta-\frac{d+1}{2}\big)\over \sqrt{\pi}\Gamma\big(\beta-{\frac{d}{2}}\big)}\Bigg)^{d+{(\nu-1)(d-1)\over d-2\beta+1}}\prod_{i=1}^{d-1}{\Gamma\big({i\over 2}\big)\over \Gamma\Big({i+\nu+1\over 2}\Big)}.\qquad\qquad\quad\end{align}
\begin{align}\alpha^{\prime}_{d,\beta,\nu}&=\pi^{\frac{d(d-1)}{2}}\frac{(d-1)!^{\nu+1}(d+1-2\beta)\Gamma\Big(\frac{d(2\beta-d-\nu)}{2}\Big)}{\Gamma\Big(\frac{d(2\beta-d-\nu)+\nu+1}{2}\Big)\Gamma\Big(d+\frac{(\nu-1)(d-1)}{d-2\beta+1}\Big)}\frac{\Gamma(\beta)^d}{\Gamma\Big(\beta-\frac{d+\nu}{2}\Big)^d}\notag\\[5pt]&\quad \times\Bigg({\gamma\,\Gamma\big(\beta-\frac{d+1}{2}\big)\over \sqrt{\pi}\Gamma\big(\beta-{\frac{d}{2}}\big)}\Bigg)^{d+{(\nu-1)(d-1)\over d-2\beta+1}}\prod_{i=1}^{d-1}{\Gamma\big({i\over 2}\big)\over \Gamma\Big({i+\nu+1\over 2}\Big)}.\qquad\qquad\quad\end{align}
Remark 5. In more probabilistic terms, the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta$
-Delaunay tessellation
$\beta$
-Delaunay tessellation
![]() ${\mathcal{D}}_\beta$
has the same distribution as the random simplex
${\mathcal{D}}_\beta$
has the same distribution as the random simplex
![]() ${\textrm{conv}}(RY_1,\ldots,RY_d)$
, where
${\textrm{conv}}(RY_1,\ldots,RY_d)$
, where
-
(a) R is a random variable whose density is proportional to
 $r^{2d\beta+d^2+\nu(d-1)}e^{-m_{d,\beta} r^{d+1+2\beta}}$
on
$r^{2d\beta+d^2+\nu(d-1)}e^{-m_{d,\beta} r^{d+1+2\beta}}$
on
 $(0,\infty)$
;
$(0,\infty)$
; -
(b)
 $(Y_1,\ldots,Y_d)$
are d random points in the unit ball
$(Y_1,\ldots,Y_d)$
are d random points in the unit ball
 ${\mathbb{B}}^{d-1}$
whose joint density is proportional to
${\mathbb{B}}^{d-1}$
whose joint density is proportional to  \begin{equation*}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1} \prod\limits_{i=1}^d\big(1-\|y_i\|^2\big)^{\beta},\qquad y_1\in {\mathbb{B}}^{d-1},\ldots, y_d\in {\mathbb{B}}^{d-1};\end{equation*}
\begin{equation*}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1} \prod\limits_{i=1}^d\big(1-\|y_i\|^2\big)^{\beta},\qquad y_1\in {\mathbb{B}}^{d-1},\ldots, y_d\in {\mathbb{B}}^{d-1};\end{equation*}
-
(c) R is independent of
 $(Y_1,\ldots,Y_d)$
.
$(Y_1,\ldots,Y_d)$
.
In other words this means that the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta$
-Delaunay tessellation coincides in distribution with the randomly rescaled
$\beta$
-Delaunay tessellation coincides in distribution with the randomly rescaled
![]() $(\nu+1)$
-volume-weighted
$(\nu+1)$
-volume-weighted
![]() $\beta$
-simplex
$\beta$
-simplex
![]() ${\textrm{conv}}(Y_1,\ldots,Y_d)$
.
${\textrm{conv}}(Y_1,\ldots,Y_d)$
.
In the same way, the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta^{\prime}$
-Delaunay tessellation
$\beta^{\prime}$
-Delaunay tessellation
![]() ${\mathcal{D}}^{\prime}_\beta$
has the same distribution as the random simplex
${\mathcal{D}}^{\prime}_\beta$
has the same distribution as the random simplex
![]() ${\textrm{conv}}(RY_1,\ldots,RY_d)$
, where
${\textrm{conv}}(RY_1,\ldots,RY_d)$
, where
-
(a′) R is a random variable whose density is proportional to
 $r^{-2d\beta+d^2+\nu(d-1)}e^{-m^{\prime}_{d,\beta} r^{d+1-2\beta}}$
on
$r^{-2d\beta+d^2+\nu(d-1)}e^{-m^{\prime}_{d,\beta} r^{d+1-2\beta}}$
on
 $(0,\infty)$
;
$(0,\infty)$
; -
(b′)
 $(Y_1,\ldots,Y_d)$
are d random points in
$(Y_1,\ldots,Y_d)$
are d random points in
 ${\mathbb{R}}^{d-1}$
whose joint density is proportional to
${\mathbb{R}}^{d-1}$
whose joint density is proportional to  \begin{equation*}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1} \prod\limits_{i=1}^d\big(1+\|y_i\|^2\big)^{-\beta},\qquad y_1\in {\mathbb{R}}^{d-1},\ldots, y_d\in {\mathbb{R}}^{d-1};\end{equation*}
\begin{equation*}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1} \prod\limits_{i=1}^d\big(1+\|y_i\|^2\big)^{-\beta},\qquad y_1\in {\mathbb{R}}^{d-1},\ldots, y_d\in {\mathbb{R}}^{d-1};\end{equation*}
-
(c′) R is independent of
 $(Y_1,\ldots,Y_d)$
.
$(Y_1,\ldots,Y_d)$
.
Alternatively we say that the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta^{\prime}$
-Delaunay tessellation coincides in distribution with the randomly rescaled
$\beta^{\prime}$
-Delaunay tessellation coincides in distribution with the randomly rescaled
![]() $(\nu+1)$
-volume-weighted
$(\nu+1)$
-volume-weighted
![]() $\beta^{\prime}$
-simplex
$\beta^{\prime}$
-simplex
![]() ${\textrm{conv}}(Y^{\prime}_1,\ldots,Y^{\prime}_d)$
.
${\textrm{conv}}(Y^{\prime}_1,\ldots,Y^{\prime}_d)$
.
Exact formulas for the constants needed to normalize the density of
![]() $(Y_1,\ldots,Y_d)$
appearing in (b) and (b
$(Y_1,\ldots,Y_d)$
appearing in (b) and (b
![]() $^\prime$
) will be given in (4.9) and (4.10).
$^\prime$
) will be given in (4.9) and (4.10).
Remark 6. Let us point out that in the limiting case
![]() $\beta\to -1$
the beta distribution with density
$\beta\to -1$
the beta distribution with density
![]() $c_{d-1,\beta}\big(1-\|x\|^2\big)^{\beta}\textbf{1}_{{\mathbb{B}}^{d-1}}(x)$
weakly converges to the uniform distribution on the unit sphere
$c_{d-1,\beta}\big(1-\|x\|^2\big)^{\beta}\textbf{1}_{{\mathbb{B}}^{d-1}}(x)$
weakly converges to the uniform distribution on the unit sphere
![]() ${\mathbb{S}}^{d-2}$
, denoted by
${\mathbb{S}}^{d-2}$
, denoted by
![]() $\sigma_{d-2}$
. Thus,
$\sigma_{d-2}$
. Thus,
![]() ${\mathbb{P}}_{\beta,\nu}$
for fixed
${\mathbb{P}}_{\beta,\nu}$
for fixed
![]() $\nu\ge-1$
and
$\nu\ge-1$
and
![]() $\gamma>0$
weakly converges to a probability measure
$\gamma>0$
weakly converges to a probability measure
![]() ${\mathbb{P}}_{-1,\nu}$
with
${\mathbb{P}}_{-1,\nu}$
with
 \begin{align*}{\mathbb{P}}_{-1,\nu}(A)&=\alpha^{*}_{d,\nu}\int_{({\mathbb{S}}^{d-2})^d} \sigma_{d-2}({\rm d} u_1)\ldots \sigma_{d-2}({\rm d} u_d) \int_{0}^{\infty}{\rm d} r\,\textbf{1}_A({\textrm{conv}}(ru_1,\ldots,ru_d))\\&\quad \times r^{d^2-2d+\nu(d-1)}e^{-\frac{2\gamma\kappa_{d-1}}{\omega_d} r^{d-1}} (\Delta_{d-1}(u_1,\ldots,u_d))^{\nu+1},\end{align*}
\begin{align*}{\mathbb{P}}_{-1,\nu}(A)&=\alpha^{*}_{d,\nu}\int_{({\mathbb{S}}^{d-2})^d} \sigma_{d-2}({\rm d} u_1)\ldots \sigma_{d-2}({\rm d} u_d) \int_{0}^{\infty}{\rm d} r\,\textbf{1}_A({\textrm{conv}}(ru_1,\ldots,ru_d))\\&\quad \times r^{d^2-2d+\nu(d-1)}e^{-\frac{2\gamma\kappa_{d-1}}{\omega_d} r^{d-1}} (\Delta_{d-1}(u_1,\ldots,u_d))^{\nu+1},\end{align*}
where
 \begin{align*}\alpha^{*}_{d,\nu}&=\big(2\gamma \omega_d^{-1}\big)^{d+\nu-1}{(d-1)(d-1)!^{\nu+1}\pi^{(\nu-1)(d-1)\over 2}\over 2^d \Gamma(d+\nu-1)}{\Gamma\big({(d+\nu-1)(d-1)\over 2}\big)\over \Gamma\big({d(d+\nu-2)\over 2}+1\big)}\\&\quad \times{\Gamma\big({d+\nu\over 2}\big)^d\over \Gamma\big(\frac{d+1}{2}\big)^{d+\nu-1}}\prod\limits_{i=1}^{d-1}{\Gamma\big({i\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)}.\end{align*}
\begin{align*}\alpha^{*}_{d,\nu}&=\big(2\gamma \omega_d^{-1}\big)^{d+\nu-1}{(d-1)(d-1)!^{\nu+1}\pi^{(\nu-1)(d-1)\over 2}\over 2^d \Gamma(d+\nu-1)}{\Gamma\big({(d+\nu-1)(d-1)\over 2}\big)\over \Gamma\big({d(d+\nu-2)\over 2}+1\big)}\\&\quad \times{\Gamma\big({d+\nu\over 2}\big)^d\over \Gamma\big(\frac{d+1}{2}\big)^{d+\nu-1}}\prod\limits_{i=1}^{d-1}{\Gamma\big({i\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)}.\end{align*}
This coincides with the formula for the distribution of the
![]() $\nu$
-weighted typical cell of a Poisson–Delaunay tessellation in
$\nu$
-weighted typical cell of a Poisson–Delaunay tessellation in
![]() ${\mathbb{R}}^{d-1}$
corresponding to the intensity
${\mathbb{R}}^{d-1}$
corresponding to the intensity
![]() $2\gamma\omega_d^{-1}$
of the underlying Poisson point process; see [Reference Gusakova and Thäle11, Theorem 2.3] for general
$2\gamma\omega_d^{-1}$
of the underlying Poisson point process; see [Reference Gusakova and Thäle11, Theorem 2.3] for general
![]() $\nu$
and [Reference MØller25] or [Reference MØller26, Proposition 4.3.1] for the case
$\nu$
and [Reference MØller25] or [Reference MØller26, Proposition 4.3.1] for the case
![]() $\nu=0$
.
$\nu=0$
.
Remark 7. It should be mentioned that in the case of the classical Poisson–Delaunay and Poisson–Voronoi tessellations many more results regarding the distribution of typical cells and faces are available. For example, in [Reference Mecke and Muche24, Lemma 1] a precise measure-theoretic description of the Palm distribution of the original Poisson point process with respect to the vertex process of the Poisson–Voronoi tessellation is given. It characterizes the distribution of the Poisson–Delaunay tessellation around its typical cell. A further generalization, providing an explicit description of the Palm distribution of the Poisson–Voronoi tessellation around a uniform random point on the typical k-face, is obtained in [Reference Baumstark and Last2].
In our situation it is also possible to characterize the Palm distribution of
![]() $\eta_{\beta}$
and
$\eta_{\beta}$
and
![]() $\eta^{\prime}_{\beta}$
with respect to the vertex process of the
$\eta^{\prime}_{\beta}$
with respect to the vertex process of the
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^{\prime}$
-Voronoi tessellations, respectively, in the spirit of [Reference Mecke and Muche24, Lemma 1]. To formulate the corresponding result, let
$\beta^{\prime}$
-Voronoi tessellations, respectively, in the spirit of [Reference Mecke and Muche24, Lemma 1]. To formulate the corresponding result, let
![]() $G=\big\{g_w\,:\,w\in{\mathbb{R}}^{d-1}\big\}$
be the group of translations acting on
$G=\big\{g_w\,:\,w\in{\mathbb{R}}^{d-1}\big\}$
be the group of translations acting on
![]() ${\mathbb{R}}^{d-1}\times{\mathbb{R}}$
by shifts in the spatial coordinate
${\mathbb{R}}^{d-1}\times{\mathbb{R}}$
by shifts in the spatial coordinate
![]() $\big($
the
$\big($
the
![]() ${\mathbb{R}}^{d-1}$
-coordinate
${\mathbb{R}}^{d-1}$
-coordinate
![]() $\big)$
; that is,
$\big)$
; that is,
![]() $g_w(v,h)\,:\!=\,(v+w,h)$
for
$g_w(v,h)\,:\!=\,(v+w,h)$
for
![]() $(v,h)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}$
,
$(v,h)\in{\mathbb{R}}^{d-1}\times{\mathbb{R}}$
,
![]() $w\in{\mathbb{R}}^{d-1}$
. Next, we denote by
$w\in{\mathbb{R}}^{d-1}$
. Next, we denote by
 \begin{equation*} \chi_{\beta}^{(^{\prime})}\,:\!=\,\chi\big(\eta_{\beta}^{(^{\prime})}\big) =\sum\limits_{v\in {\mathcal{F}}_0\big({\mathcal{V}}^{(^{\prime})}_{\beta}\big)}\delta_v \end{equation*}
\begin{equation*} \chi_{\beta}^{(^{\prime})}\,:\!=\,\chi\big(\eta_{\beta}^{(^{\prime})}\big) =\sum\limits_{v\in {\mathcal{F}}_0\big({\mathcal{V}}^{(^{\prime})}_{\beta}\big)}\delta_v \end{equation*}
the point process of vertices of the
![]() $\beta^{(^{\prime})}$
-Voronoi tessellation
$\beta^{(^{\prime})}$
-Voronoi tessellation
![]() ${\mathcal{V}}^{(^{\prime})}_{\beta}$
. According to the properties of the Poisson point process
${\mathcal{V}}^{(^{\prime})}_{\beta}$
. According to the properties of the Poisson point process
![]() $\eta^{(^{\prime})}_{\beta}$
, the pair
$\eta^{(^{\prime})}_{\beta}$
, the pair
![]() $\left(\chi_{\beta}^{(^{\prime})}, \eta^{(^{\prime})}_{\beta}\right)$
is jointly G-stationary. This allows us to define the Palm distribution
$\left(\chi_{\beta}^{(^{\prime})}, \eta^{(^{\prime})}_{\beta}\right)$
is jointly G-stationary. This allows us to define the Palm distribution
![]() ${\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}$
of
${\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}$
of
![]() $\eta^{(^{\prime})}_{\beta}$
with respect to
$\eta^{(^{\prime})}_{\beta}$
with respect to
![]() $\chi_{\beta}^{(^{\prime})}$
as
$\chi_{\beta}^{(^{\prime})}$
as
 \begin{equation*} {\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}(A)\,:\!=\,{1\over \gamma_0}{\mathbb{E}} \sum_{v\in\chi_{\beta}^{(^{\prime})}} {\textbf{1}}(v \in [0,1]^{d-1}, g_{-v}\eta^{(^{\prime})}_{\beta} \in A), \qquad \qquad A\in{\mathcal{N}}\big({\mathbb{R}}^d\big), \end{equation*}
\begin{equation*} {\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}(A)\,:\!=\,{1\over \gamma_0}{\mathbb{E}} \sum_{v\in\chi_{\beta}^{(^{\prime})}} {\textbf{1}}(v \in [0,1]^{d-1}, g_{-v}\eta^{(^{\prime})}_{\beta} \in A), \qquad \qquad A\in{\mathcal{N}}\big({\mathbb{R}}^d\big), \end{equation*}
where
![]() $\gamma_0\,:\!=\,\gamma_0\big({\mathcal{V}}^{(^{\prime})}_{\beta}\big)$
is the intensity of the vertices of
$\gamma_0\,:\!=\,\gamma_0\big({\mathcal{V}}^{(^{\prime})}_{\beta}\big)$
is the intensity of the vertices of
![]() $\beta^{(^{\prime})}$
-Voronoi tessellation, whose exact value can be derived from the results of Subsection 6.3; see [Reference Kallenberg19, Section 7.2].
$\beta^{(^{\prime})}$
-Voronoi tessellation, whose exact value can be derived from the results of Subsection 6.3; see [Reference Kallenberg19, Section 7.2].
Given a point set X, let us denote by
![]() $\Pi^{\downarrow}(X)$
the shift of the standard downward paraboloid
$\Pi^{\downarrow}(X)$
the shift of the standard downward paraboloid
![]() $\Pi_{(0,a)}^{\downarrow}$
along the height (time) coordinate, such that
$\Pi_{(0,a)}^{\downarrow}$
along the height (time) coordinate, such that
![]() $\Pi_{(0,a)}^{\downarrow}$
does not contain any points from X in its interior and that for any
$\Pi_{(0,a)}^{\downarrow}$
does not contain any points from X in its interior and that for any
![]() $b>a$
we have
$b>a$
we have
![]() $\operatorname{int}\Pi_{(0,b)}^{\downarrow}\cap X\neq \emptyset$
. Now, if
$\operatorname{int}\Pi_{(0,b)}^{\downarrow}\cap X\neq \emptyset$
. Now, if
![]() ${\mathbb{P}}_{\beta^{(^{\prime})}}$
denotes the distribution of the Poisson point process
${\mathbb{P}}_{\beta^{(^{\prime})}}$
denotes the distribution of the Poisson point process
![]() $\eta_{\beta}^{(^{\prime})}$
, then for any measurable function
$\eta_{\beta}^{(^{\prime})}$
, then for any measurable function
![]() $u\,:\,{\textsf{N}}\big({\mathbb{R}}^d\big)\to[0,\infty)$
we have that
$u\,:\,{\textsf{N}}\big({\mathbb{R}}^d\big)\to[0,\infty)$
we have that
 \begin{align*} \int_{{\textsf{N}}\big({\mathbb{R}}^d\big)}&u(\varphi){\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}(\textrm{d}\varphi)\\ &=\int_{{\textsf{N}}\big({\mathbb{R}}^d\big)}\int_{{\textsf{N}}\big({\mathbb{R}}^d\big)}u\big(\big(\varphi_1\cap \Pi^{\downarrow}(\varphi_1)\big)\cup(\varphi_2\cap (\Pi^{\downarrow}(\varphi_1))^{c})\big){\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}(\textrm{d}\varphi_1){\mathbb{P}}_{\beta^{(^{\prime})}}(\textrm{d}\varphi_2). \end{align*}
\begin{align*} \int_{{\textsf{N}}\big({\mathbb{R}}^d\big)}&u(\varphi){\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}(\textrm{d}\varphi)\\ &=\int_{{\textsf{N}}\big({\mathbb{R}}^d\big)}\int_{{\textsf{N}}\big({\mathbb{R}}^d\big)}u\big(\big(\varphi_1\cap \Pi^{\downarrow}(\varphi_1)\big)\cup(\varphi_2\cap (\Pi^{\downarrow}(\varphi_1))^{c})\big){\mathbb{P}}_{\beta^{(^{\prime})}}^{0,\chi}(\textrm{d}\varphi_1){\mathbb{P}}_{\beta^{(^{\prime})}}(\textrm{d}\varphi_2). \end{align*}
This identity explains what the
![]() $\beta^{(^{\prime})}$
-Delaunay tessellation looks like in a neighborhood of the typical cell. Namely, it is generated by a Poisson point process which is restricted to the complement of the paraboloid defining the typical cell and which is unaffected by the shape of the typical cell. The proof of this formula is a straightforward modification of the proof of Lemma 1 in [Reference Mecke and Muche24], and we omit the details here in order to keep our presentation short.
$\beta^{(^{\prime})}$
-Delaunay tessellation looks like in a neighborhood of the typical cell. Namely, it is generated by a Poisson point process which is restricted to the complement of the paraboloid defining the typical cell and which is unaffected by the shape of the typical cell. The proof of this formula is a straightforward modification of the proof of Lemma 1 in [Reference Mecke and Muche24], and we omit the details here in order to keep our presentation short.
Remark 8. There exists an interesting and very useful connection between the boundary of the convex hull generated by a Poisson point process inside the unit ball, and the boundary of the paraboloid hull process. It was shown in [Reference Calka, Schreiber and Yukich5] that by applying a particular scaling transformation, the boundary of the convex hull can be mapped into a random surface, which locally converges to the boundary of the paraboloid hull process as the intensity of the underlying Poisson point process tends to infinity. This fact proved to be very useful for investigation of the local properties of the convex hull of Poisson point processes.
In our case, the Poisson point process with intensity measure having density
generates a convex hull, whose boundary will converge after a suitable transformation locally, as
![]() $\gamma\to\infty$
, to the boundary of paraboloid hull process
$\gamma\to\infty$
, to the boundary of paraboloid hull process
![]() $\Phi(\eta_{\beta})$
. This is evidence that there exists a way to build a bridge between
$\Phi(\eta_{\beta})$
. This is evidence that there exists a way to build a bridge between
![]() $\beta$
-polytopes and
$\beta$
-polytopes and
![]() $\beta$
-Delaunay tessellations. In particular, the
$\beta$
-Delaunay tessellations. In particular, the
![]() $\beta$
-Delaunay tessellation describes the local limit of
$\beta$
-Delaunay tessellation describes the local limit of
![]() $\beta$
-polytopes as the number of generating points tends to infinity.
$\beta$
-polytopes as the number of generating points tends to infinity.
Proof of Theorem 1. Let us recall that for any collection of points
with affinely independent spatial coordinates
![]() $v_i$
, we denote by
$v_i$
, we denote by
![]() $\Pi^{\downarrow}(x_1,\ldots,x_d)$
the unique translation of the standard downward paraboloid
$\Pi^{\downarrow}(x_1,\ldots,x_d)$
the unique translation of the standard downward paraboloid
![]() $\Pi^\downarrow$
containing
$\Pi^\downarrow$
containing
![]() $x_1,\ldots,x_d$
on its boundary. If
$x_1,\ldots,x_d$
on its boundary. If
![]() $x_1,\ldots,x_d$
are distinct points of the Poisson point process
$x_1,\ldots,x_d$
are distinct points of the Poisson point process
![]() $\eta_\beta^{(^{\prime})}$
, then the simplex
$\eta_\beta^{(^{\prime})}$
, then the simplex
![]() $K \,:\!=\, {\textrm{conv}}(v_1,\ldots,v_d)$
belongs to the tessellation
$K \,:\!=\, {\textrm{conv}}(v_1,\ldots,v_d)$
belongs to the tessellation
![]() ${\mathcal{D}}_\beta^{(^{\prime})}$
if and only if
${\mathcal{D}}_\beta^{(^{\prime})}$
if and only if
![]() $\operatorname{int}\big(\Pi^{\downarrow}(x_1,\ldots,x_d)\big)\cap\eta_\beta^{(^{\prime})}=\varnothing$
, that is, if there are no points of
$\operatorname{int}\big(\Pi^{\downarrow}(x_1,\ldots,x_d)\big)\cap\eta_\beta^{(^{\prime})}=\varnothing$
, that is, if there are no points of
![]() $\eta_\beta^{(^{\prime})}$
strictly inside
$\eta_\beta^{(^{\prime})}$
strictly inside
![]() $\Pi^{\downarrow}(x_1,\ldots,x_d)$
. Let us denote the apex of the paraboloid
$\Pi^{\downarrow}(x_1,\ldots,x_d)$
. Let us denote the apex of the paraboloid
![]() $\Pi^{\downarrow}(x_1,\ldots,x_d)$
by
$\Pi^{\downarrow}(x_1,\ldots,x_d)$
by
![]() $(w,t)\in {\mathbb{R}}^{d-1} \times {\mathbb{R}}$
. We then have
$(w,t)\in {\mathbb{R}}^{d-1} \times {\mathbb{R}}$
. We then have
As the center of the simplex
![]() ${\textrm{conv}}(v_1,\ldots,v_d)$
we choose the point w and therefore put
${\textrm{conv}}(v_1,\ldots,v_d)$
we choose the point w and therefore put
We are now ready to begin the essential part of the proof of Theorem 1. Fix some Borel set
![]() $A\subset {\mathcal{C}}^{\prime}$
. From (4.1) and the definition of the generalized center function for the tessellation
$A\subset {\mathcal{C}}^{\prime}$
. From (4.1) and the definition of the generalized center function for the tessellation
![]() ${\mathcal{D}}_\beta^{(^{\prime})}$
, we get
${\mathcal{D}}_\beta^{(^{\prime})}$
, we get
 \begin{align*}S_{\eta_\beta^{(^{\prime})}}(A)&\,:\!=\, {\mathbb{E}}\sum_{(v,M)\in \mu_{\eta_\beta^{(^{\prime})}}}\textbf{1}_A(M)\textbf{1}_{[0,1]^{d-1}}(v)(\textrm{Vol}(M))^{\nu}\\&={1\over d!}\,{\mathbb{E}}\sum\limits_{(x_1,\ldots,x_d)\in \big(\eta_\beta^{(^{\prime})}\big)_{\neq}^d}\textbf{1}_A({\textrm{conv}}(v_1,\ldots,v_d)-z(x_1,\ldots,x_d))\\&\quad \times \textbf{1}_{[0,1]^{d-1}}(z(x_1,\ldots,x_d))\textbf{1}\!\left\{\operatorname{int} (\Pi^{\downarrow}(x_1,\ldots,x_d))\cap\eta_\beta^{(^{\prime})}=\varnothing\right\}\\&\quad \times \Delta_{d-1}(v_1,\ldots,v_d)^{\nu}.\end{align*}
\begin{align*}S_{\eta_\beta^{(^{\prime})}}(A)&\,:\!=\, {\mathbb{E}}\sum_{(v,M)\in \mu_{\eta_\beta^{(^{\prime})}}}\textbf{1}_A(M)\textbf{1}_{[0,1]^{d-1}}(v)(\textrm{Vol}(M))^{\nu}\\&={1\over d!}\,{\mathbb{E}}\sum\limits_{(x_1,\ldots,x_d)\in \big(\eta_\beta^{(^{\prime})}\big)_{\neq}^d}\textbf{1}_A({\textrm{conv}}(v_1,\ldots,v_d)-z(x_1,\ldots,x_d))\\&\quad \times \textbf{1}_{[0,1]^{d-1}}(z(x_1,\ldots,x_d))\textbf{1}\!\left\{\operatorname{int} (\Pi^{\downarrow}(x_1,\ldots,x_d))\cap\eta_\beta^{(^{\prime})}=\varnothing\right\}\\&\quad \times \Delta_{d-1}(v_1,\ldots,v_d)^{\nu}.\end{align*}
Here,
![]() $\big(\eta_\beta^{(^{\prime})}\big)_{\neq}^d$
denotes the collection of all tuples of the form
$\big(\eta_\beta^{(^{\prime})}\big)_{\neq}^d$
denotes the collection of all tuples of the form
![]() $(x_1,\ldots,x_d)$
consisting of pairwise distinct points
$(x_1,\ldots,x_d)$
consisting of pairwise distinct points
![]() $x_1,\ldots,x_d$
of the Poisson point process
$x_1,\ldots,x_d$
of the Poisson point process
![]() $\eta_\beta^{(^{\prime})}$
. We write
$\eta_\beta^{(^{\prime})}$
. We write
![]() $S_{\beta}(A)\,:\!=\,S_{\eta_{\beta}}(A)$
and
$S_{\beta}(A)\,:\!=\,S_{\eta_{\beta}}(A)$
and
![]() $S_{\beta}^{\prime}(A)\,:\!=\,S_{\eta_{\beta}^{\prime}}(A)$
. Note that
$S_{\beta}^{\prime}(A)\,:\!=\,S_{\eta_{\beta}^{\prime}}(A)$
. Note that
![]() $S_{\beta}^{(\prime)}(A)$
is in fact the same as
$S_{\beta}^{(\prime)}(A)$
is in fact the same as
![]() $\lambda_{\beta,\nu}^{(\prime)}\,{\mathbb{P}}_{\beta,\nu}^{(\prime)}(A)$
, but since at the present moment we do not know whether the normalizing constants
$\lambda_{\beta,\nu}^{(\prime)}\,{\mathbb{P}}_{\beta,\nu}^{(\prime)}(A)$
, but since at the present moment we do not know whether the normalizing constants
![]() $\lambda_{\beta,\nu}$
and
$\lambda_{\beta,\nu}$
and
![]() $\lambda_{\beta,\nu}^{\prime}$
, given by (4.2), are finite, we prefer to use the notation
$\lambda_{\beta,\nu}^{\prime}$
, given by (4.2), are finite, we prefer to use the notation
![]() $S_{\beta}^{(\prime)}(A)$
. Applying the multivariate Mecke formula [Reference Schneider and Weil31, Corollary 3.2.3] to the Poisson point process
$S_{\beta}^{(\prime)}(A)$
. Applying the multivariate Mecke formula [Reference Schneider and Weil31, Corollary 3.2.3] to the Poisson point process
![]() $\eta_{\beta}^{(\prime)}$
and taking into account (3.1) and (3.2), we obtain
$\eta_{\beta}^{(\prime)}$
and taking into account (3.1) and (3.2), we obtain
 \begin{align}S_{\beta}^{(\prime)}(A)&={\gamma^d \big(c^{(\prime)}_{d,\beta}\big)^d\over d!}\int_{{\mathbb{R}}^{d-1}} {\rm d} v_1 \, \ldots \, \int_{{\mathbb{R}}^{d-1}} {\rm d} v_d\,\int_{0}^{\infty}{\rm d} h_1\, \ldots \, \int_{0}^{\infty} {\rm d} h_d \,\notag\\[4pt]&\qquad \phantom{\times} \textbf{1}_A\big({\textrm{conv}}(v_1,\ldots,v_d)-z\big(\tilde x_1,\ldots,\tilde x_d\big)\big)\notag\\[4pt]&\quad \times \textbf{1}_{[0,1]^{d-1}}\big(z\big(\tilde x_1,\ldots,\tilde x_d\big)\big){\mathbb{P}}\left(\operatorname{int} (\Pi^{\downarrow}\big(\tilde x_1,\ldots,\tilde x_d\big))\cap \eta_{\beta}^{(\prime)}=\varnothing\right)\notag\\[4pt]&\quad \times h_1^{\kappa\beta}\ldots h_d^{\kappa\beta}\,\Delta_{d-1}(v_1,\ldots,v_d)^{\nu},\end{align}
\begin{align}S_{\beta}^{(\prime)}(A)&={\gamma^d \big(c^{(\prime)}_{d,\beta}\big)^d\over d!}\int_{{\mathbb{R}}^{d-1}} {\rm d} v_1 \, \ldots \, \int_{{\mathbb{R}}^{d-1}} {\rm d} v_d\,\int_{0}^{\infty}{\rm d} h_1\, \ldots \, \int_{0}^{\infty} {\rm d} h_d \,\notag\\[4pt]&\qquad \phantom{\times} \textbf{1}_A\big({\textrm{conv}}(v_1,\ldots,v_d)-z\big(\tilde x_1,\ldots,\tilde x_d\big)\big)\notag\\[4pt]&\quad \times \textbf{1}_{[0,1]^{d-1}}\big(z\big(\tilde x_1,\ldots,\tilde x_d\big)\big){\mathbb{P}}\left(\operatorname{int} (\Pi^{\downarrow}\big(\tilde x_1,\ldots,\tilde x_d\big))\cap \eta_{\beta}^{(\prime)}=\varnothing\right)\notag\\[4pt]&\quad \times h_1^{\kappa\beta}\ldots h_d^{\kappa\beta}\,\Delta_{d-1}(v_1,\ldots,v_d)^{\nu},\end{align}
where
![]() $\tilde x_i = (v_i, \kappa h_i)$
for
$\tilde x_i = (v_i, \kappa h_i)$
for
![]() $i=1,\ldots,d$
. In the above integral, we are going to pass from integration over the variables
$i=1,\ldots,d$
. In the above integral, we are going to pass from integration over the variables
![]() $(v_1,\ldots,v_d,h_1,\ldots,h_d)\in \big({\mathbb{R}}^{d-1}\big)^d \times\big({\mathbb{R}}_{+}^*\big)^d$
, where
$(v_1,\ldots,v_d,h_1,\ldots,h_d)\in \big({\mathbb{R}}^{d-1}\big)^d \times\big({\mathbb{R}}_{+}^*\big)^d$
, where
![]() ${\mathbb{R}}_+^*=(0,\infty)$
, to integration over certain new variables
${\mathbb{R}}_+^*=(0,\infty)$
, to integration over certain new variables
![]() $(w,r,y_1,\ldots,y_d)\in {\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\times\left({\mathbb{R}}^{d-1}\right)^d$
introduced as follows. Take some tuple
$(w,r,y_1,\ldots,y_d)\in {\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\times\left({\mathbb{R}}^{d-1}\right)^d$
introduced as follows. Take some tuple
![]() $(v_1,\ldots,v_d,h_1,\ldots,h_d)\in \big({\mathbb{R}}^{d-1}\big)^d \times\big({\mathbb{R}}_{+}^*\big)^d$
and assume that
$(v_1,\ldots,v_d,h_1,\ldots,h_d)\in \big({\mathbb{R}}^{d-1}\big)^d \times\big({\mathbb{R}}_{+}^*\big)^d$
and assume that
![]() $v_1,\ldots,v_d$
are affinely independent. Denote the apex of the unique downward paraboloid
$v_1,\ldots,v_d$
are affinely independent. Denote the apex of the unique downward paraboloid
![]() $\Pi^\downarrow\big(\tilde x_1,\ldots,\tilde x_d\big)$
whose boundary passes through the points
$\Pi^\downarrow\big(\tilde x_1,\ldots,\tilde x_d\big)$
whose boundary passes through the points
![]() $(v_1,\kappa h_1),\ldots,(v_d,\kappa h_d)$
by
$(v_1,\kappa h_1),\ldots,(v_d,\kappa h_d)$
by
![]() $(w,\kappa r^2)\in {\mathbb{R}}^{d-1} \times {\mathbb{R}}$
, and note that
$(w,\kappa r^2)\in {\mathbb{R}}^{d-1} \times {\mathbb{R}}$
, and note that
![]() $w= z\big(\tilde x_1,\ldots,\tilde x_d\big)$
. Observe that in the
$w= z\big(\tilde x_1,\ldots,\tilde x_d\big)$
. Observe that in the
![]() $\beta^{\prime}$
case the second coordinate of the apex can be positive, but since such a downward paraboloid contains infinitely many points of the Poisson point process
$\beta^{\prime}$
case the second coordinate of the apex can be positive, but since such a downward paraboloid contains infinitely many points of the Poisson point process
![]() $\eta_\beta^{\prime}$
$\eta_\beta^{\prime}$
![]() $\big($
because any point (w, 0) with vanishing second coordinate is an accumulation point for the atoms of
$\big($
because any point (w, 0) with vanishing second coordinate is an accumulation point for the atoms of
![]() $\eta_{\beta}^{\prime}\big)$
, we can ignore this possibility in the following. We can write
$\eta_{\beta}^{\prime}\big)$
, we can ignore this possibility in the following. We can write
![]() $v_i = w + ry_i$
with some uniquely defined and pairwise distinct
$v_i = w + ry_i$
with some uniquely defined and pairwise distinct
![]() $y_1,\ldots,y_d\in {\mathbb{R}}^{d-1}$
. The condition that the boundary of the paraboloid passes through the point
$y_1,\ldots,y_d\in {\mathbb{R}}^{d-1}$
. The condition that the boundary of the paraboloid passes through the point
![]() $(v_i,\kappa h_i)$
reads as
$(v_i,\kappa h_i)$
reads as
![]() $\kappa r^2 - \|v_i-w\|^2 = \kappa h_i$
, or
$\kappa r^2 - \|v_i-w\|^2 = \kappa h_i$
, or
![]() $h_i = r^2 (1-\kappa\|y_i\|^2)$
. In the
$h_i = r^2 (1-\kappa\|y_i\|^2)$
. In the
![]() $\beta$
case it follows that
$\beta$
case it follows that
![]() $y_1,\ldots,y_d \in {\mathbb{B}}^{d-1}$
. Let us therefore introduce the transformation
$y_1,\ldots,y_d \in {\mathbb{B}}^{d-1}$
. Let us therefore introduce the transformation
![]() $T\,:\,{\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\times\left({\mathbb{B}}^{d-1}\right)^d\rightarrow\left({\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\right)^d$
(in the
$T\,:\,{\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\times\left({\mathbb{B}}^{d-1}\right)^d\rightarrow\left({\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\right)^d$
(in the
![]() $\beta$
case) or
$\beta$
case) or
![]() $T\,:\,{\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\times\left({\mathbb{R}}^{d-1}\right)^d\rightarrow\left({\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\right)^d$
(in the
$T\,:\,{\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\times\left({\mathbb{R}}^{d-1}\right)^d\rightarrow\left({\mathbb{R}}^{d-1}\times{\mathbb{R}}_{+}^*\right)^d$
(in the
![]() $\beta^{\prime}$
case), defined as
$\beta^{\prime}$
case), defined as
This transformation is bijective (up to sets of Lebesgue measure zero and provided that in the
![]() $\beta^{\prime}$
case we agree to exclude from the image set all combinations
$\beta^{\prime}$
case we agree to exclude from the image set all combinations
![]() $(v_1,h_1,\ldots,v_d,h_d)$
which lead to a paraboloid whose apex has positive height). The absolute value of the Jacobian of T is the absolute value of the determinant of the block matrix
$(v_1,h_1,\ldots,v_d,h_d)$
which lead to a paraboloid whose apex has positive height). The absolute value of the Jacobian of T is the absolute value of the determinant of the block matrix
 \begin{equation*}J(T)\,:\!=\,\left|\begin{matrix}E_{d-1} & \quad y_1 & \quad rE_{d-1} & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad 2r\big(1-\kappa\|y_1\|^2\big) & \quad -2r^2\kappa y_1^{\top} & \quad 0 & \quad \dots & \quad 0\\[4pt]E_{d-1} & \quad y_2 & \quad 0 & \quad rE_{d-1} & \quad \dots & \quad 0\\[4pt]0 & \quad 2r\big(1-\kappa\|y_2\|^2\big) & \quad 0 & \quad -2r^2\kappa y_2^{\top} & \quad \dots & \quad 0\\[4pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]E_{d-1} & \quad y_d & \quad 0 & \quad 0 & \quad \dots & \quad rE_{d-1}\\[4pt]0 & \quad 2r\big(1-\kappa\|y_d\|^2\big) & \quad 0 & \quad 0 & \quad \dots & \quad -2r^2\kappa y_d^{\top}\\[4pt]\end{matrix}\right|,\end{equation*}
\begin{equation*}J(T)\,:\!=\,\left|\begin{matrix}E_{d-1} & \quad y_1 & \quad rE_{d-1} & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad 2r\big(1-\kappa\|y_1\|^2\big) & \quad -2r^2\kappa y_1^{\top} & \quad 0 & \quad \dots & \quad 0\\[4pt]E_{d-1} & \quad y_2 & \quad 0 & \quad rE_{d-1} & \quad \dots & \quad 0\\[4pt]0 & \quad 2r\big(1-\kappa\|y_2\|^2\big) & \quad 0 & \quad -2r^2\kappa y_2^{\top} & \quad \dots & \quad 0\\[4pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]E_{d-1} & \quad y_d & \quad 0 & \quad 0 & \quad \dots & \quad rE_{d-1}\\[4pt]0 & \quad 2r\big(1-\kappa\|y_d\|^2\big) & \quad 0 & \quad 0 & \quad \dots & \quad -2r^2\kappa y_d^{\top}\\[4pt]\end{matrix}\right|,\end{equation*}
where
![]() $E_{k}$
is the
$E_{k}$
is the
![]() $k\times k$
unit matrix, the vectors
$k\times k$
unit matrix, the vectors
![]() $y_1,\ldots,y_d$
are considered to be column vectors, and
$y_1,\ldots,y_d$
are considered to be column vectors, and
![]() $|M|$
stands for the absolute value of the determinant of the matrix M. We can compute J(T) as follows:
$|M|$
stands for the absolute value of the determinant of the matrix M. We can compute J(T) as follows:
 \begin{align*}{J(T)\over2^dr^{d^2}}& =\left|\begin{matrix}E_{d-1} & \quad y_1 & \quad E_{d-1} & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad 1-\kappa\|y_1\|^2 & \quad -\kappa y_1^{\top} & \quad 0 & \quad \dots & \quad 0\\[4pt]E_{d-1} & \quad y_2 & \quad 0 & \quad E_{d-1} & \quad \dots & \quad 0\\[4pt]0 & \quad 1-\kappa\|y_2\|^2 & \quad 0 & \quad -\kappa y_2^{\top} & \quad \dots & \quad 0\\[4pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]E_{d-1} & \quad y_d & \quad 0 & \quad 0 & \quad \dots & \quad E_{d-1}\\[4pt]0 & \quad 1-\kappa\|y_d\|^2 & \quad 0 & \quad 0 & \quad \dots & \quad -\kappa y_d^{\top}\\[4pt]\end{matrix}\right|\\[11pt]& =\left|\begin{matrix}0 & \quad 0 & \quad E_{d-1} & \quad 0 & \quad \dots & \quad 0\\[4pt]\kappa y_1^{\top} & \quad 1 & \quad -\kappa y_1^{\top} & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad 0 & \quad 0 & \quad E_{d-1} & \quad \dots & \quad 0\\[4pt]\kappa y_2^{\top} & \quad 1 & \quad 0 & \quad -\kappa y_2^{\top} & \quad \dots & \quad 0\\[4pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]0 & \quad 0 & \quad 0 & \quad 0 & \quad \dots & \quad E_{d-1}\\[4pt]\kappa y_d^{\top} & \quad 1 & \quad 0 & \quad 0 & \quad \dots & \quad -\kappa y_d^{\top}\\[4pt]\end{matrix}\right|=\big|\kappa^d\big|\,\left|\begin{matrix}0 & \quad E_{d(d-1)}\\[4pt]\begin{matrix}y_1^{\top} & \quad 1 \\[4pt]\vdots & \quad \vdots\\[4pt]y_d^{\top} & \quad 1\\[4pt]\end{matrix} & \quad \Large{{\textbf{0}}} \\[4pt]\end{matrix}\right|=\left|\begin{matrix}1 & \quad \ldots & \quad 1\\[4pt]y_1 & \quad \ldots & \quad y_d \\[4pt]\end{matrix}\right|.\end{align*}
\begin{align*}{J(T)\over2^dr^{d^2}}& =\left|\begin{matrix}E_{d-1} & \quad y_1 & \quad E_{d-1} & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad 1-\kappa\|y_1\|^2 & \quad -\kappa y_1^{\top} & \quad 0 & \quad \dots & \quad 0\\[4pt]E_{d-1} & \quad y_2 & \quad 0 & \quad E_{d-1} & \quad \dots & \quad 0\\[4pt]0 & \quad 1-\kappa\|y_2\|^2 & \quad 0 & \quad -\kappa y_2^{\top} & \quad \dots & \quad 0\\[4pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]E_{d-1} & \quad y_d & \quad 0 & \quad 0 & \quad \dots & \quad E_{d-1}\\[4pt]0 & \quad 1-\kappa\|y_d\|^2 & \quad 0 & \quad 0 & \quad \dots & \quad -\kappa y_d^{\top}\\[4pt]\end{matrix}\right|\\[11pt]& =\left|\begin{matrix}0 & \quad 0 & \quad E_{d-1} & \quad 0 & \quad \dots & \quad 0\\[4pt]\kappa y_1^{\top} & \quad 1 & \quad -\kappa y_1^{\top} & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad 0 & \quad 0 & \quad E_{d-1} & \quad \dots & \quad 0\\[4pt]\kappa y_2^{\top} & \quad 1 & \quad 0 & \quad -\kappa y_2^{\top} & \quad \dots & \quad 0\\[4pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]0 & \quad 0 & \quad 0 & \quad 0 & \quad \dots & \quad E_{d-1}\\[4pt]\kappa y_d^{\top} & \quad 1 & \quad 0 & \quad 0 & \quad \dots & \quad -\kappa y_d^{\top}\\[4pt]\end{matrix}\right|=\big|\kappa^d\big|\,\left|\begin{matrix}0 & \quad E_{d(d-1)}\\[4pt]\begin{matrix}y_1^{\top} & \quad 1 \\[4pt]\vdots & \quad \vdots\\[4pt]y_d^{\top} & \quad 1\\[4pt]\end{matrix} & \quad \Large{{\textbf{0}}} \\[4pt]\end{matrix}\right|=\left|\begin{matrix}1 & \quad \ldots & \quad 1\\[4pt]y_1 & \quad \ldots & \quad y_d \\[4pt]\end{matrix}\right|.\end{align*}
Thus,
![]() $J(T)=2^dr^{d^2}(d-1)! \Delta_{d-1}(y_1,\ldots,y_d)$
. Applying the transformation T in (4.6), we derive
$J(T)=2^dr^{d^2}(d-1)! \Delta_{d-1}(y_1,\ldots,y_d)$
. Applying the transformation T in (4.6), we derive
 \begin{align}S_{\beta}^{(\prime)}(A)&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d}\int_{{\mathbb{R}}^{d-1}}{\rm d} y_1\, \ldots\, \int_{{\mathbb{R}}^{d-1}}{\rm d} y_d\, \int_{{\mathbb{R}}^{d-1}} {\rm d} w\, \int_{0}^{\infty}{\rm d} r\notag\\&\quad\times\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d)) \textbf{1}_{[0,1]^{d-1}}(w)r^{2\kappa d\beta+d^2+\nu(d-1)}\notag\\&\quad\times{\mathbb{P}}\Big(\big\{(v,\kappa h)\in{\mathbb{R}}^{d-1}\times \kappa {\mathbb{R}}_{+}^*\,:\, \kappa h<-\|v-w\|^2+\kappa r^2\big\}\cap \eta_{\beta}^{(\prime)}=\varnothing\Big)\notag\\&\quad\times \Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big).\end{align}
\begin{align}S_{\beta}^{(\prime)}(A)&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d}\int_{{\mathbb{R}}^{d-1}}{\rm d} y_1\, \ldots\, \int_{{\mathbb{R}}^{d-1}}{\rm d} y_d\, \int_{{\mathbb{R}}^{d-1}} {\rm d} w\, \int_{0}^{\infty}{\rm d} r\notag\\&\quad\times\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d)) \textbf{1}_{[0,1]^{d-1}}(w)r^{2\kappa d\beta+d^2+\nu(d-1)}\notag\\&\quad\times{\mathbb{P}}\Big(\big\{(v,\kappa h)\in{\mathbb{R}}^{d-1}\times \kappa {\mathbb{R}}_{+}^*\,:\, \kappa h<-\|v-w\|^2+\kappa r^2\big\}\cap \eta_{\beta}^{(\prime)}=\varnothing\Big)\notag\\&\quad\times \Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big).\end{align}
Now using the stationarity of the Poisson point processes
![]() $\eta_\beta$
and
$\eta_\beta$
and
![]() $\eta_\beta^{\prime}$
with respect to the v-coordinate, we conclude that, for any
$\eta_\beta^{\prime}$
with respect to the v-coordinate, we conclude that, for any
![]() $w\in{\mathbb{R}}^{d-1}$
,
$w\in{\mathbb{R}}^{d-1}$
,
 \begin{align*}P^{(\prime)} &\,:\!=\,{\mathbb{P}}\left(\big\{(v,\kappa h)\in{\mathbb{R}}^{d-1}\times \kappa {\mathbb{R}}_{+}^*\,:\, \kappa h<-\|v-w\|^2+\kappa r^2\big\}\cap \eta_{\beta}^{(\prime)}=\varnothing\right)\\&={\mathbb{P}}\left(\big\{(v,\kappa h)\in{\mathbb{R}}^{d-1}\times \kappa {\mathbb{R}}_{+}^*\,:\, \kappa h<-\|v\|^2+\kappa r^2\big\}\cap \eta_{\beta}^{(\prime)}=\varnothing\right)\\&=\exp\bigg({-}\gamma c^{(\prime)}_{d,\beta}\int_{0}^{\infty}\int_{{\mathbb{R}}^{d-1}}\textbf{1}\big(\kappa h<-\|v\|^2+\kappa r^2\big)h^{\kappa \beta}{\rm d} v\,{\rm d} h\bigg).\end{align*}
\begin{align*}P^{(\prime)} &\,:\!=\,{\mathbb{P}}\left(\big\{(v,\kappa h)\in{\mathbb{R}}^{d-1}\times \kappa {\mathbb{R}}_{+}^*\,:\, \kappa h<-\|v-w\|^2+\kappa r^2\big\}\cap \eta_{\beta}^{(\prime)}=\varnothing\right)\\&={\mathbb{P}}\left(\big\{(v,\kappa h)\in{\mathbb{R}}^{d-1}\times \kappa {\mathbb{R}}_{+}^*\,:\, \kappa h<-\|v\|^2+\kappa r^2\big\}\cap \eta_{\beta}^{(\prime)}=\varnothing\right)\\&=\exp\bigg({-}\gamma c^{(\prime)}_{d,\beta}\int_{0}^{\infty}\int_{{\mathbb{R}}^{d-1}}\textbf{1}\big(\kappa h<-\|v\|^2+\kappa r^2\big)h^{\kappa \beta}{\rm d} v\,{\rm d} h\bigg).\end{align*}
For the further computations we need to distinguish the
![]() $\beta$
case and the
$\beta$
case and the
![]() $\beta^{\prime}$
case. For the
$\beta^{\prime}$
case. For the
![]() $\beta$
model we have
$\beta$
model we have
 \begin{align*}P&\,:\!=\,\exp\!\Bigg({-}\gamma c_{d,\beta}\int_{0}^{r^2}\int_{\big\{v\,:\, \|v\|\leq \big(r^2-h\big)^{1/2}\big\}}h^{\beta}{\rm d} v\,{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c_{d,\beta}\int_{0}^{r^2}\big(r^2-h\big)^{{d-1\over 2}}h^{\beta}{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c_{d,\beta}r^{d+1+2\beta}\int_{0}^{1}\big(1-h^{\prime}\big)^{{d-1\over 2}}h^{\prime \beta}{\rm d} h^{\prime}\Bigg)\\&=\exp\!\left({-}m_{d,\beta} r^{d+1+2\beta}\right),\end{align*}
\begin{align*}P&\,:\!=\,\exp\!\Bigg({-}\gamma c_{d,\beta}\int_{0}^{r^2}\int_{\big\{v\,:\, \|v\|\leq \big(r^2-h\big)^{1/2}\big\}}h^{\beta}{\rm d} v\,{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c_{d,\beta}\int_{0}^{r^2}\big(r^2-h\big)^{{d-1\over 2}}h^{\beta}{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c_{d,\beta}r^{d+1+2\beta}\int_{0}^{1}\big(1-h^{\prime}\big)^{{d-1\over 2}}h^{\prime \beta}{\rm d} h^{\prime}\Bigg)\\&=\exp\!\left({-}m_{d,\beta} r^{d+1+2\beta}\right),\end{align*}
where
![]() $m_{d,\beta}={\gamma c_{d,\beta}\over \pi c_{d+1,\beta}}$
. For the
$m_{d,\beta}={\gamma c_{d,\beta}\over \pi c_{d+1,\beta}}$
. For the
![]() $\beta^{\prime}$
model we obtain
$\beta^{\prime}$
model we obtain
 \begin{align*}P^{\prime}&\,:\!=\,\exp\!\Bigg({-}\gamma c^{\prime}_{d,\beta}\int_{r^2}^{\infty}\int_{\big\{v\,:\, \|v\|\leq \big(h-r^2\big)^{1/2}\big\}}h^{-\beta}{\rm d} v\,{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c^{\prime}_{d,\beta}\int_{r^2}^{\infty}\big(h-r^2\big)^{{d-1\over 2}}h^{-\beta}{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c^{\prime}_{d,\beta}r^{d+1-2\beta}\int_{0}^{1}\big(1-h^{\prime}\big)^{{d-1\over 2}}h^{\prime\beta-(d+1)/2-1}{\rm d} h^{\prime}\Bigg)\\&=\exp\!\left({-}m^{\prime}_{d,\beta} r^{d+1-2\beta}\right),\end{align*}
\begin{align*}P^{\prime}&\,:\!=\,\exp\!\Bigg({-}\gamma c^{\prime}_{d,\beta}\int_{r^2}^{\infty}\int_{\big\{v\,:\, \|v\|\leq \big(h-r^2\big)^{1/2}\big\}}h^{-\beta}{\rm d} v\,{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c^{\prime}_{d,\beta}\int_{r^2}^{\infty}\big(h-r^2\big)^{{d-1\over 2}}h^{-\beta}{\rm d} h\Bigg)\\&=\exp\!\Bigg({-}\gamma \kappa_{d-1}c^{\prime}_{d,\beta}r^{d+1-2\beta}\int_{0}^{1}\big(1-h^{\prime}\big)^{{d-1\over 2}}h^{\prime\beta-(d+1)/2-1}{\rm d} h^{\prime}\Bigg)\\&=\exp\!\left({-}m^{\prime}_{d,\beta} r^{d+1-2\beta}\right),\end{align*}
with
![]() $m^{\prime}_{d,\beta}={\gamma c^{\prime}_{d,\beta}\over \pi c^{\prime}_{d+1,\beta}}$
. Substituting this into (4.7) leads to
$m^{\prime}_{d,\beta}={\gamma c^{\prime}_{d,\beta}\over \pi c^{\prime}_{d+1,\beta}}$
. Substituting this into (4.7) leads to
 \begin{align}S_{\beta}^{(\prime)}(A)&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d}\int_{{\mathbb{R}}^{d-1}}{\rm d} y_1\, \ldots\, \int_{{\mathbb{R}}^{d-1}} {\rm d} y_d\, \int_{0}^{\infty} {\rm d} r\,\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d))\notag\\&\quad \times r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa \beta}}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\notag\\&\quad \times \prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big).\end{align}
\begin{align}S_{\beta}^{(\prime)}(A)&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d}\int_{{\mathbb{R}}^{d-1}}{\rm d} y_1\, \ldots\, \int_{{\mathbb{R}}^{d-1}} {\rm d} y_d\, \int_{0}^{\infty} {\rm d} r\,\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d))\notag\\&\quad \times r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa \beta}}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\notag\\&\quad \times \prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big).\end{align}
We are now in position to determine the normalizing constants
![]() $\lambda_{\beta,\nu}$
and
$\lambda_{\beta,\nu}$
and
![]() $\lambda_{\beta,\nu}^{\prime}$
from (4.2). To this end, we plug
$\lambda_{\beta,\nu}^{\prime}$
from (4.2). To this end, we plug
![]() $A={\mathcal{C}}^{\prime}$
$A={\mathcal{C}}^{\prime}$
![]() $\big($
the set of non-empty compact subsets of
$\big($
the set of non-empty compact subsets of
![]() ${\mathbb{R}}^{d-1}\big)$
into the expression (4.8) for
${\mathbb{R}}^{d-1}\big)$
into the expression (4.8) for
![]() $S_\beta^{(\prime)}$
. Doing this and using the substitution
$S_\beta^{(\prime)}$
. Doing this and using the substitution
![]() $s=m^{(\prime)}_{d,\beta} r^{d+1+2\kappa \beta}$
, we obtain
$s=m^{(\prime)}_{d,\beta} r^{d+1+2\kappa \beta}$
, we obtain
 \begin{align*}\lambda_{\beta,\nu}^{(\prime)}&=S_{\beta}^{(\prime)}({\mathcal{C}}^{\prime})\\&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d}\int_{\big({\mathbb{R}}^{d-1}\big)^d}\int_{0}^{\infty} r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa \beta}}\\&\quad \times \Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} r\,{\rm d} y_1\ldots {\rm d} y_d\end{align*}
\begin{align*}\lambda_{\beta,\nu}^{(\prime)}&=S_{\beta}^{(\prime)}({\mathcal{C}}^{\prime})\\&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d}\int_{\big({\mathbb{R}}^{d-1}\big)^d}\int_{0}^{\infty} r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa \beta}}\\&\quad \times \Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} r\,{\rm d} y_1\ldots {\rm d} y_d\end{align*}
 \begin{align*}&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d(d+1+2\kappa \beta)}\Big(m^{(\prime)}_{d,\beta}\Big)^{-d-{(\nu-1)(d-1)\over d+2\kappa \beta+1}}\int_{0}^{\infty} s^{d+{(\nu-1)(d-1)\over d+2\kappa\beta+1}-1}e^{-s}{\rm d} s\\&\quad \times\int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d\\&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\Gamma\big(d+{(\nu-1)(d-1)\over d+2\kappa\beta+1}\big)\over d(d+1+2\kappa\beta)}\Big(m^{(\prime)}_{d,\beta}\Big)^{-d-{(\nu-1)(d-1)\over d+2\kappa \beta+1}}\\&\quad \times\int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d.\end{align*}
\begin{align*}&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\over d(d+1+2\kappa \beta)}\Big(m^{(\prime)}_{d,\beta}\Big)^{-d-{(\nu-1)(d-1)\over d+2\kappa \beta+1}}\int_{0}^{\infty} s^{d+{(\nu-1)(d-1)\over d+2\kappa\beta+1}-1}e^{-s}{\rm d} s\\&\quad \times\int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d\\&={\Big(2\gamma\,c^{(\prime)}_{d,\beta}\Big)^d\Gamma\big(d+{(\nu-1)(d-1)\over d+2\kappa\beta+1}\big)\over d(d+1+2\kappa\beta)}\Big(m^{(\prime)}_{d,\beta}\Big)^{-d-{(\nu-1)(d-1)\over d+2\kappa \beta+1}}\\&\quad \times\int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d.\end{align*}
The last integral (which is finite for
![]() $\nu\ge-1$
) is equal—up to a constant—to the
$\nu\ge-1$
) is equal—up to a constant—to the
![]() $(\nu+1)$
th moment of the volume of a random simplex with vertices having a
$(\nu+1)$
th moment of the volume of a random simplex with vertices having a
![]() $\beta$
- or
$\beta$
- or
![]() $\beta^{\prime}$
-distribution. The exact values are calculated in [Reference Grote, Kabluchko and Thäle10, Theorem 2.3] or [Reference Kabluchko, Temesvari and Thäle15, Proposition 2.8] and are given (in the cases
$\beta^{\prime}$
-distribution. The exact values are calculated in [Reference Grote, Kabluchko and Thäle10, Theorem 2.3] or [Reference Kabluchko, Temesvari and Thäle15, Proposition 2.8] and are given (in the cases
![]() $\kappa=+1$
and
$\kappa=+1$
and
![]() $\kappa=-1$
) as follows:
$\kappa=-1$
) as follows:
 \begin{align}&\int_{\big({\mathbb{B}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod\limits_{i=1}^d\big(1-\|y_i\|^2\big)^{\beta}{\rm d} y_1\ldots {\rm d} y_d \notag\\&={1\over (d-1)!^{\nu+1}c_{d-1,\beta}^d}{\Gamma\Big(\frac{d+1}{2}+\beta\Big)^d\over \Gamma\Big({d+\nu\over 2}+\beta+1\Big)^d}{\Gamma\Big({d(d+\nu+2\beta)\over 2} +1\Big)\over \Gamma\Big({d(d+\nu+2\beta)-\nu +1 \over 2}\Big)}\prod\limits_{i=1}^{d-1} {\Gamma\big({i+\nu+1\over 2}\big)\over \Gamma\big({i\over 2}\big)},\end{align}
\begin{align}&\int_{\big({\mathbb{B}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod\limits_{i=1}^d\big(1-\|y_i\|^2\big)^{\beta}{\rm d} y_1\ldots {\rm d} y_d \notag\\&={1\over (d-1)!^{\nu+1}c_{d-1,\beta}^d}{\Gamma\Big(\frac{d+1}{2}+\beta\Big)^d\over \Gamma\Big({d+\nu\over 2}+\beta+1\Big)^d}{\Gamma\Big({d(d+\nu+2\beta)\over 2} +1\Big)\over \Gamma\Big({d(d+\nu+2\beta)-\nu +1 \over 2}\Big)}\prod\limits_{i=1}^{d-1} {\Gamma\big({i+\nu+1\over 2}\big)\over \Gamma\big({i\over 2}\big)},\end{align}
 \begin{align}&\int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod\limits_{i=1}^d\big(1+\|y_i\|^2\big)^{-\beta}{\rm d} y_1\ldots {\rm d} y_d \notag\\&={1\over (d-1)!^{\nu+1}\big(c^{\prime}_{d-1,\beta}\big)^d}{\Gamma\Big({d(2\beta-d-\nu)+\nu+1\over 2}\Big)\over\Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)}{\Gamma\Big(\beta-{d+\nu\over 2}\Big)^d\over\Gamma\Big(\beta-{d-1\over 2}\Big)^d}\prod_{i=1}^{d-1}{\Gamma\Big({i+\nu+1\over 2}\Big)\over\Gamma\Big({i\over 2}\Big)}.\end{align}
\begin{align}&\int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod\limits_{i=1}^d\big(1+\|y_i\|^2\big)^{-\beta}{\rm d} y_1\ldots {\rm d} y_d \notag\\&={1\over (d-1)!^{\nu+1}\big(c^{\prime}_{d-1,\beta}\big)^d}{\Gamma\Big({d(2\beta-d-\nu)+\nu+1\over 2}\Big)\over\Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)}{\Gamma\Big(\beta-{d+\nu\over 2}\Big)^d\over\Gamma\Big(\beta-{d-1\over 2}\Big)^d}\prod_{i=1}^{d-1}{\Gamma\Big({i+\nu+1\over 2}\Big)\over\Gamma\Big({i\over 2}\Big)}.\end{align}
We have thus shown that
 \begin{align*}\lambda_{\beta,\nu}&={\Gamma\Big(d+{(\nu-1)(d-1)\over d+2\beta+1}\Big)m_{d,\beta}^{-d-{(\nu-1)(d-1)\over d+2 \beta+1}}\over d(d+1+2\beta)(d-1)!^{\nu+1}}\Bigg({2\gamma\,c_{d,\beta}\Gamma\big(\frac{d+1}{2}+\beta\big)\over c_{d-1,\beta}\Gamma\big({d+\nu\over 2}+\beta+1\big)}\Bigg)^d\\&\quad \times{\Gamma\Big({d(d+\nu+2\beta)\over 2} +1\Big)\over \Gamma\Big({d(d+\nu+2\beta)-\nu +1 \over 2}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({i+\nu+1\over 2}\Big)\over \Gamma\Big({i\over 2}\Big)},\end{align*}
\begin{align*}\lambda_{\beta,\nu}&={\Gamma\Big(d+{(\nu-1)(d-1)\over d+2\beta+1}\Big)m_{d,\beta}^{-d-{(\nu-1)(d-1)\over d+2 \beta+1}}\over d(d+1+2\beta)(d-1)!^{\nu+1}}\Bigg({2\gamma\,c_{d,\beta}\Gamma\big(\frac{d+1}{2}+\beta\big)\over c_{d-1,\beta}\Gamma\big({d+\nu\over 2}+\beta+1\big)}\Bigg)^d\\&\quad \times{\Gamma\Big({d(d+\nu+2\beta)\over 2} +1\Big)\over \Gamma\Big({d(d+\nu+2\beta)-\nu +1 \over 2}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({i+\nu+1\over 2}\Big)\over \Gamma\Big({i\over 2}\Big)},\end{align*}
 \begin{align*}\lambda^{\prime}_{\beta,\nu}&={\Gamma\Big(d+{(\nu-1)(d-1)\over d-2\beta+1}\Big)\Big(m^{\prime}_{d,\beta}\Big)^{-d-{(\nu-1)(d-1)\over d-2 \beta+1}}\over d(d+1-2\beta)(d-1)!^{\nu+1}}\Bigg({2\gamma\,c^{\prime}_{d,\beta}\Gamma\big(\beta-{d+\nu\over 2}\big)\over c^{\prime}_{d-1,\beta}\Gamma\big(\beta-{d-1\over 2}\big)}\Bigg)^d\\&\quad \times{\Gamma\Big({d(2\beta-d-\nu)+\nu+1\over 2}\Big)\over\Gamma\Big({d(2\beta-d\nu\over 2}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\big({i+\nu+1\over 2}\big)\over \Gamma\big({i\over 2}\big)}.\end{align*}
\begin{align*}\lambda^{\prime}_{\beta,\nu}&={\Gamma\Big(d+{(\nu-1)(d-1)\over d-2\beta+1}\Big)\Big(m^{\prime}_{d,\beta}\Big)^{-d-{(\nu-1)(d-1)\over d-2 \beta+1}}\over d(d+1-2\beta)(d-1)!^{\nu+1}}\Bigg({2\gamma\,c^{\prime}_{d,\beta}\Gamma\big(\beta-{d+\nu\over 2}\big)\over c^{\prime}_{d-1,\beta}\Gamma\big(\beta-{d-1\over 2}\big)}\Bigg)^d\\&\quad \times{\Gamma\Big({d(2\beta-d-\nu)+\nu+1\over 2}\Big)\over\Gamma\Big({d(2\beta-d\nu\over 2}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\big({i+\nu+1\over 2}\big)\over \Gamma\big({i\over 2}\big)}.\end{align*}
In particular, this implies that
![]() $\lambda_{\beta,\nu}, \lambda^{\prime}_{\beta,\nu}<\infty$
provided
$\lambda_{\beta,\nu}, \lambda^{\prime}_{\beta,\nu}<\infty$
provided
![]() $\nu \geq -1$
in the
$\nu \geq -1$
in the
![]() $\beta$
case and
$\beta$
case and
![]() $2\beta-d>\nu \geq -1$
in the
$2\beta-d>\nu \geq -1$
in the
![]() $\beta^{\prime}$
case. From (4.8) we conclude
$\beta^{\prime}$
case. From (4.8) we conclude
 \begin{align*}{\mathbb{P}}^{(\prime)}_{\beta,\nu}(A)=\frac{S_{\beta}^{(\prime)}}{\lambda_{\beta,\nu}^{(\prime)}}&=\alpha^{(\prime)}_{d,\beta,\nu}\int_{\big({\mathbb{R}}^{d-1}\big)^d}{\rm d} y_1\ldots {\rm d} y_d \, \int_{0}^{\infty}{\rm d} r\notag\\&\quad \times\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d)) r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta}r^{d+1+2\kappa\beta}} \notag\\&\quad \times\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big),\end{align*}
\begin{align*}{\mathbb{P}}^{(\prime)}_{\beta,\nu}(A)=\frac{S_{\beta}^{(\prime)}}{\lambda_{\beta,\nu}^{(\prime)}}&=\alpha^{(\prime)}_{d,\beta,\nu}\int_{\big({\mathbb{R}}^{d-1}\big)^d}{\rm d} y_1\ldots {\rm d} y_d \, \int_{0}^{\infty}{\rm d} r\notag\\&\quad \times\textbf{1}_A({\textrm{conv}}(ry_1,\ldots,ry_d)) r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta}r^{d+1+2\kappa\beta}} \notag\\&\quad \times\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big),\end{align*}
with
![]() $\alpha_{d,\beta,\nu}$
and
$\alpha_{d,\beta,\nu}$
and
![]() $\alpha^{\prime}_{d,\beta,\nu}$
given by (4.4) and (4.5) respectively. This completes the argument.
$\alpha^{\prime}_{d,\beta,\nu}$
given by (4.4) and (4.5) respectively. This completes the argument.
5. The volume of weighted typical cells
5.1. Moment formulas
In this section we apply Theorem 1 to compute all moments of the random variables
![]() ${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
and
${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
and
![]() ${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
. These explicit formulas will be the basis of some of the results in Part III of this series of papers. In particular, they generalize the moment formulas in [Reference Gusakova and Thäle11] for weighted typical cells in classical Poisson–Delaunay tessellations.
${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
. These explicit formulas will be the basis of some of the results in Part III of this series of papers. In particular, they generalize the moment formulas in [Reference Gusakova and Thäle11] for weighted typical cells in classical Poisson–Delaunay tessellations.
Theorem 2. Let
![]() $Z_{\beta,\nu}$
be the
$Z_{\beta,\nu}$
be the
![]() $\nu$
-weighted typical cell of a
$\nu$
-weighted typical cell of a
![]() $\beta$
-Delaunay tessellation with
$\beta$
-Delaunay tessellation with
![]() $\beta\geq -1$
and
$\beta\geq -1$
and
![]() $\nu\ge-1$
, and let
$\nu\ge-1$
, and let
![]() $Z^{\prime}_{\beta,\nu}$
be the
$Z^{\prime}_{\beta,\nu}$
be the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta^{\prime}$
-Delaunay tessellation with
$\beta^{\prime}$
-Delaunay tessellation with
![]() $\beta> (d+1)/2$
and
$\beta> (d+1)/2$
and
![]() $2\beta - d>\nu\ge-1$
. Then, for any
$2\beta - d>\nu\ge-1$
. Then, for any
![]() $s>-\nu-1$
, we have
$s>-\nu-1$
, we have
 \begin{align*}{\mathbb{E}}\ &{\textrm{Vol}}\big(Z_{\beta,\nu}\big)^s = {1\over (d-1)!^s}\bigg({ \sqrt{\pi}\Gamma\big(\frac{d+1}{2}+\beta+1\big)\over \gamma\Gamma\big({\frac{d}{2}}+\beta+1\big)}\bigg)^{{s(d-1)\over d+2\beta+1}}{\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}\Big)\over\Gamma\Big({d(d+2\beta)+(\nu+s)(d-1)+1\over 2}\Big)}\\&\times{\Gamma\Big({d+\nu\over 2}+\beta +1\Big)^d\over\Gamma\Big({d+\nu+s\over 2}+\beta +1\Big)^d}{\Gamma\Big({d(d+\nu+s +2\beta)\over 2}+1\Big)\over\Gamma\Big({d(d+\nu +2\beta)\over 2}+1\Big)}{\Gamma\Big(d+{(\nu+s-1)(d-1)\over d+2\beta+1}\Big)\over\Gamma\Big(d+{(\nu-1)(d-1)\over d+2\beta+1}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\big({i+\nu+s+1\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)},\end{align*}
\begin{align*}{\mathbb{E}}\ &{\textrm{Vol}}\big(Z_{\beta,\nu}\big)^s = {1\over (d-1)!^s}\bigg({ \sqrt{\pi}\Gamma\big(\frac{d+1}{2}+\beta+1\big)\over \gamma\Gamma\big({\frac{d}{2}}+\beta+1\big)}\bigg)^{{s(d-1)\over d+2\beta+1}}{\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}\Big)\over\Gamma\Big({d(d+2\beta)+(\nu+s)(d-1)+1\over 2}\Big)}\\&\times{\Gamma\Big({d+\nu\over 2}+\beta +1\Big)^d\over\Gamma\Big({d+\nu+s\over 2}+\beta +1\Big)^d}{\Gamma\Big({d(d+\nu+s +2\beta)\over 2}+1\Big)\over\Gamma\Big({d(d+\nu +2\beta)\over 2}+1\Big)}{\Gamma\Big(d+{(\nu+s-1)(d-1)\over d+2\beta+1}\Big)\over\Gamma\Big(d+{(\nu-1)(d-1)\over d+2\beta+1}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\big({i+\nu+s+1\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)},\end{align*}
and for any
![]() $2\beta -d-\nu>s>-\nu-1$
we have
$2\beta -d-\nu>s>-\nu-1$
we have
 \begin{align*}{\mathbb{E}}\ {\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)^s & = {1\over (d-1)!^s}\bigg({ \sqrt{\pi}\Gamma\big(\beta -{\frac{d}{2}}\big)\over \gamma\Gamma\big(\beta-\frac{d+1}{2}\big)}\bigg)^{{s(d-1)\over d-2\beta+1}}{\Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)\over\Gamma\Big({d(2\beta-d-\nu-s)\over 2}\Big)}{\Gamma\big(\beta -{d+\nu+s\over 2}\big)^d\over\Gamma\big(\beta -{d+\nu\over 2}\big)^d}\\&\quad \times{\Gamma\Big({d(2\beta-d)-(\nu+s)(d-1)+1\over 2}\Big)\over\Gamma\Big({d(2\beta-d)-\nu(d-1)+1\over 2}\Big)}{\Gamma\Big(d+{(\nu+s-1)(d-1)\over d-2\beta+1}\Big)\over\Gamma\Big(d+{(\nu-1)(d-1)\over d-2\beta+1}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({i+\nu+s+1\over 2}\Big)\over \Gamma\Big({i+\nu+1\over 2}\Big)}.\end{align*}
\begin{align*}{\mathbb{E}}\ {\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)^s & = {1\over (d-1)!^s}\bigg({ \sqrt{\pi}\Gamma\big(\beta -{\frac{d}{2}}\big)\over \gamma\Gamma\big(\beta-\frac{d+1}{2}\big)}\bigg)^{{s(d-1)\over d-2\beta+1}}{\Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)\over\Gamma\Big({d(2\beta-d-\nu-s)\over 2}\Big)}{\Gamma\big(\beta -{d+\nu+s\over 2}\big)^d\over\Gamma\big(\beta -{d+\nu\over 2}\big)^d}\\&\quad \times{\Gamma\Big({d(2\beta-d)-(\nu+s)(d-1)+1\over 2}\Big)\over\Gamma\Big({d(2\beta-d)-\nu(d-1)+1\over 2}\Big)}{\Gamma\Big(d+{(\nu+s-1)(d-1)\over d-2\beta+1}\Big)\over\Gamma\Big(d+{(\nu-1)(d-1)\over d-2\beta+1}\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({i+\nu+s+1\over 2}\Big)\over \Gamma\Big({i+\nu+1\over 2}\Big)}.\end{align*}
Proof. Applying Theorem 1 we get
 \begin{align*}{\mathbb{E}}\ \textrm{Vol}\Big(Z^{(\prime)}_{\beta,\nu}\Big)^s &= \alpha_{d,\beta,\nu}^{(\prime)}\int_{\big({\mathbb{R}}^{d-1}\big)^d}{\rm d} y_1\ldots {\rm d} y_d \, \int_{0}^{\infty}{\rm d} r\\&\quad \times \textrm{Vol}({\textrm{conv}}(ry_1,\ldots,ry_d))^s r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa\beta}}\\&\quad \times\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big).\end{align*}
\begin{align*}{\mathbb{E}}\ \textrm{Vol}\Big(Z^{(\prime)}_{\beta,\nu}\Big)^s &= \alpha_{d,\beta,\nu}^{(\prime)}\int_{\big({\mathbb{R}}^{d-1}\big)^d}{\rm d} y_1\ldots {\rm d} y_d \, \int_{0}^{\infty}{\rm d} r\\&\quad \times \textrm{Vol}({\textrm{conv}}(ry_1,\ldots,ry_d))^s r^{2\kappa d\beta+d^2+\nu(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa\beta}}\\&\quad \times\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big).\end{align*}
Then from Fubini’s theorem we obtain
 \begin{align*}{\mathbb{E}}\ \textrm{Vol}\Big(Z^{(\prime)}_{\beta,\nu}\Big)^s &= \alpha_{d,\beta,\nu}^{(\prime)}\int_{0}^{\infty}r^{2\kappa d\beta+d^2+\nu(d-1)+s(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa\beta}}\,{\rm d} r\\&\quad\times \int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1+s}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\\&\qquad \times \textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d\\&=\alpha_{d,\beta,\nu}^{(\prime)}{\Gamma\Big(d+{(\nu-1)(d-1)\over d+2\kappa\beta+1}+{s(d-1)\over d+2\kappa\beta+1}\Big)\over (d+1+2\kappa\beta)}\Big(m_{d,\beta}^{(\prime)}\Big)^{-d-{(\nu-1)(d-1)\over d+2\kappa\beta+1}-{s(d-1)\over d+2\kappa\beta+1}}\\&\quad\times \int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1+s}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\\&\qquad \times \textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d.\end{align*}
\begin{align*}{\mathbb{E}}\ \textrm{Vol}\Big(Z^{(\prime)}_{\beta,\nu}\Big)^s &= \alpha_{d,\beta,\nu}^{(\prime)}\int_{0}^{\infty}r^{2\kappa d\beta+d^2+\nu(d-1)+s(d-1)}e^{-m^{(\prime)}_{d,\beta} r^{d+1+2\kappa\beta}}\,{\rm d} r\\&\quad\times \int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1+s}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\\&\qquad \times \textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d\\&=\alpha_{d,\beta,\nu}^{(\prime)}{\Gamma\Big(d+{(\nu-1)(d-1)\over d+2\kappa\beta+1}+{s(d-1)\over d+2\kappa\beta+1}\Big)\over (d+1+2\kappa\beta)}\Big(m_{d,\beta}^{(\prime)}\Big)^{-d-{(\nu-1)(d-1)\over d+2\kappa\beta+1}-{s(d-1)\over d+2\kappa\beta+1}}\\&\quad\times \int_{\big({\mathbb{R}}^{d-1}\big)^d}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1+s}\prod_{i=1}^d\big(1-\kappa\|y_i\|^2\big)^{\kappa\beta}\\&\qquad \times \textbf{1}\big(1-\kappa\|y_i\|^2\ge 0\big){\rm d} y_1\ldots {\rm d} y_d.\end{align*}
Finally, using (4.9), (4.10), and the definition of the constants
![]() $\alpha_{\beta,d,\nu}$
,
$\alpha_{\beta,d,\nu}$
,
![]() $\alpha^{\prime}_{\beta,d,\nu}$
,
$\alpha^{\prime}_{\beta,d,\nu}$
,
![]() $m_{d,\beta}$
, and
$m_{d,\beta}$
, and
![]() $m^{\prime}_{d,\beta}$
, we complete the proof.
$m^{\prime}_{d,\beta}$
, we complete the proof.
5.2. Probabilistic representations
Based on the formulas for the moments of the volume of the random simplices
![]() $Z_{\beta, \nu}$
and
$Z_{\beta, \nu}$
and
![]() $Z_{\beta, \nu}^{\prime}$
, we can obtain probabilistic representations for the random variables
$Z_{\beta, \nu}^{\prime}$
, we can obtain probabilistic representations for the random variables
![]() ${\textrm{Vol}}\big(Z_{\beta,\nu}\big)^2$
and
${\textrm{Vol}}\big(Z_{\beta,\nu}\big)^2$
and
![]() ${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)^2$
, which are similar in spirit to the ones for Gaussian or beta random simplices [Reference Grote, Kabluchko and Thäle10, Reference Gusakova and Thäle11].
${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)^2$
, which are similar in spirit to the ones for Gaussian or beta random simplices [Reference Grote, Kabluchko and Thäle10, Reference Gusakova and Thäle11].
Let us first recall some standard distributions. A random variable has a gamma distribution with shape
![]() $\alpha\in(0,\infty)$
and rate
$\alpha\in(0,\infty)$
and rate
![]() $\lambda \in(0,\infty)$
if its density function is given by
$\lambda \in(0,\infty)$
if its density function is given by
A random variable has a beta distribution with shape parameters
![]() $\alpha_1, \alpha_2\in(0,\infty)$
if its density function is given by
$\alpha_1, \alpha_2\in(0,\infty)$
if its density function is given by
A random variable has a beta-prime distribution with shape parameters
![]() $\alpha_1, \alpha_2\in(0,\infty)$
if its density function is given by
$\alpha_1, \alpha_2\in(0,\infty)$
if its density function is given by
We will use the notation
![]() $\xi\sim {\textrm{Gamma}}(\alpha,\lambda)$
,
$\xi\sim {\textrm{Gamma}}(\alpha,\lambda)$
,
![]() $\xi\sim {\textrm{Beta}}(\alpha,\beta)$
, and
$\xi\sim {\textrm{Beta}}(\alpha,\beta)$
, and
![]() $\xi\sim {\textrm{Beta}}^{\prime}(\alpha,\beta)$
to indicate that the random variable
$\xi\sim {\textrm{Beta}}^{\prime}(\alpha,\beta)$
to indicate that the random variable
![]() $\xi$
has a gamma distribution with shape
$\xi$
has a gamma distribution with shape
![]() $\alpha$
and rate
$\alpha$
and rate
![]() $\lambda$
, a beta distribution with shape parameters
$\lambda$
, a beta distribution with shape parameters
![]() $\alpha_1, \alpha_2$
, or a beta-prime distribution with shape parameters
$\alpha_1, \alpha_2$
, or a beta-prime distribution with shape parameters
![]() $\alpha_1, \alpha_2$
, respectively. Moreover,
$\alpha_1, \alpha_2$
, respectively. Moreover,
![]() $\xi\overset{D}{=}\xi^{\prime}$
will indicate that two random variables
$\xi\overset{D}{=}\xi^{\prime}$
will indicate that two random variables
![]() $\xi$
and
$\xi$
and
![]() $\xi^{\prime}$
have the same distribution.
$\xi^{\prime}$
have the same distribution.
Theorem 3. The following assertions hold:
-
(a) for
 $\beta\geq -1$
,
$\beta\geq -1$
,
 $\nu\ge-1$
,
$\nu\ge-1$
,
 $d\geq 2$
, one has that (5.1)
$d\geq 2$
, one has that (5.1) \begin{align}\xi(1-\xi)^{d-1}\left((d-1)!{\textrm{Vol}}\big(Z_{\beta,\nu}\big)\right)^2&\overset{D}{=} \bigg({\rho\over m_{\beta,d}}\bigg)^{{2(d-1)\over d+2\beta+1}}(1-\eta)^{d-1}\prod\limits_{i=1}^{d-1}\xi_i,\end{align}
\begin{align}\xi(1-\xi)^{d-1}\left((d-1)!{\textrm{Vol}}\big(Z_{\beta,\nu}\big)\right)^2&\overset{D}{=} \bigg({\rho\over m_{\beta,d}}\bigg)^{{2(d-1)\over d+2\beta+1}}(1-\eta)^{d-1}\prod\limits_{i=1}^{d-1}\xi_i,\end{align}
-
(b) and for
 $\beta> (d+1)/2$
,
$\beta> (d+1)/2$
,
 $2\beta - d>\nu\ge -1$
,
$2\beta - d>\nu\ge -1$
,
 $d\geq 2$
, one has that (5.2)
$d\geq 2$
, one has that (5.2) \begin{align}\big(1+\eta^{\prime}\big)^{d-1}\Big((d-1)!\textrm{Vol}\Big(Z^{\prime}_{\beta,\nu}\Big)\Big)^2&\overset{D}{=} \bigg({\rho^{\prime}\over m_{\beta,d}^{\prime}}\bigg)^{{2(d-1)\over d-2\beta+1}}(\xi^{\prime})^{-1}\big(1+\xi^{\prime}\big)^{d}\prod\limits_{i=1}^{d-1}\xi^{\prime}_i,\end{align}
\begin{align}\big(1+\eta^{\prime}\big)^{d-1}\Big((d-1)!\textrm{Vol}\Big(Z^{\prime}_{\beta,\nu}\Big)\Big)^2&\overset{D}{=} \bigg({\rho^{\prime}\over m_{\beta,d}^{\prime}}\bigg)^{{2(d-1)\over d-2\beta+1}}(\xi^{\prime})^{-1}\big(1+\xi^{\prime}\big)^{d}\prod\limits_{i=1}^{d-1}\xi^{\prime}_i,\end{align}
where
and
for
![]() $i\in\{1,\ldots,d-1\}$
, are independent random variables, independent of
$i\in\{1,\ldots,d-1\}$
, are independent random variables, independent of
![]() ${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
and
${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
and
![]() ${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
, and where
${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
, and where
![]() $m_{\beta,d}$
,
$m_{\beta,d}$
,
![]() $m_{\beta,d}^{\prime}$
are defined in (4.3).
$m_{\beta,d}^{\prime}$
are defined in (4.3).
Remark 9. The equality (5.1) generalizes [Reference Gusakova and Thäle11, Theorem 2.6] for
![]() $\beta=-1$
to general values of
$\beta=-1$
to general values of
![]() $\beta\geq -1$
and [Reference Grote, Kabluchko and Thäle10, Theorem 2.5(b)] for
$\beta\geq -1$
and [Reference Grote, Kabluchko and Thäle10, Theorem 2.5(b)] for
![]() $\nu = -1$
to general
$\nu = -1$
to general
![]() $\nu \ge -1$
. The equality (5.2) generalizes [Reference Grote, Kabluchko and Thäle10, Theorem 2.5(c)] for
$\nu \ge -1$
. The equality (5.2) generalizes [Reference Grote, Kabluchko and Thäle10, Theorem 2.5(c)] for
![]() $\nu = -1$
to general
$\nu = -1$
to general
![]() $2\beta - d>\nu\ge-1$
.
$2\beta - d>\nu\ge-1$
.
Proof. First of all let us recall that for
![]() $\xi_i$
with
$\xi_i$
with
![]() $s>-{\nu+1\over 2}$
and for
$s>-{\nu+1\over 2}$
and for
![]() $\xi^{\prime}_i$
with
$\xi^{\prime}_i$
with
![]() $-{\nu+1\over 2}< s< \beta -{d+\nu\over 2}$
we have
$-{\nu+1\over 2}< s< \beta -{d+\nu\over 2}$
we have
 \begin{equation*}{\mathbb{E}}\big[\xi_i^{s}\big]={\Gamma\Big({d+\nu\over 2}+\beta+1\Big)\Gamma\Big({i+\nu+1\over 2}+s\Big)\over \Gamma\Big({i+\nu+1\over 2}\Big)\Gamma\Big({d+\nu\over 2}+\beta+1+s\Big)},\qquad {\mathbb{E}}\big[\big(\xi_i^{\prime}\big)^{s}\big]={\Gamma\big(\beta-{d+\nu\over 2}-s\big)\Gamma\big({i+\nu+1\over 2}+s\big)\over \Gamma\big(\beta-{d+\nu\over 2}\big)\Gamma\big({i+\nu+1\over 2}\big)},\end{equation*}
\begin{equation*}{\mathbb{E}}\big[\xi_i^{s}\big]={\Gamma\Big({d+\nu\over 2}+\beta+1\Big)\Gamma\Big({i+\nu+1\over 2}+s\Big)\over \Gamma\Big({i+\nu+1\over 2}\Big)\Gamma\Big({d+\nu\over 2}+\beta+1+s\Big)},\qquad {\mathbb{E}}\big[\big(\xi_i^{\prime}\big)^{s}\big]={\Gamma\big(\beta-{d+\nu\over 2}-s\big)\Gamma\big({i+\nu+1\over 2}+s\big)\over \Gamma\big(\beta-{d+\nu\over 2}\big)\Gamma\big({i+\nu+1\over 2}\big)},\end{equation*}
respectively, and for
![]() $\rho$
and
$\rho$
and
![]() $\rho^{\prime}$
with
$\rho^{\prime}$
with
![]() $s>0$
we have
$s>0$
we have
 \begin{equation*}{\mathbb{E}}\Big[\rho^{{2s(d-1)\over d+2\beta+1}}\Big]={\Gamma\Big(d+{(\nu-1)(d-1)+2s(d-1)\over d+2\beta+1}\Big)\over \Gamma\Big(d+{(\nu-1)(d-1)\over d+2\beta+1}\Big)},\qquad {\mathbb{E}}\Big[(\rho^{\prime})^{{2s(d-1)\over d-2\beta+1}}\Big]={\Gamma\Big(d+{(\nu-1)(d-1)+2s(d-1)\over d-2\beta+1}\Big)\over \Gamma\Big(d+{(\nu-1)(d-1)\over d-2\beta+1}\Big)},\end{equation*}
\begin{equation*}{\mathbb{E}}\Big[\rho^{{2s(d-1)\over d+2\beta+1}}\Big]={\Gamma\Big(d+{(\nu-1)(d-1)+2s(d-1)\over d+2\beta+1}\Big)\over \Gamma\Big(d+{(\nu-1)(d-1)\over d+2\beta+1}\Big)},\qquad {\mathbb{E}}\Big[(\rho^{\prime})^{{2s(d-1)\over d-2\beta+1}}\Big]={\Gamma\Big(d+{(\nu-1)(d-1)+2s(d-1)\over d-2\beta+1}\Big)\over \Gamma\Big(d+{(\nu-1)(d-1)\over d-2\beta+1}\Big)},\end{equation*}
respectively. Moreover, for
![]() $s>-{\nu+1\over 2}$
we compute that
$s>-{\nu+1\over 2}$
we compute that
 \begin{equation*}{\mathbb{E}}\Big[\xi^{s}(1-\xi)^{(d-1)s}\Big]={\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}+s(d-1)\Big)\Gamma\Big({d+\nu\over 2}+\beta+1+s\Big)\Gamma\Big({d(d+2\beta+\nu)\over 2}+1\Big)\over\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}\Big)\Gamma\Big({d+\nu\over 2}+\beta+1\Big)\Gamma\Big({d(d+2\beta+\nu)\over 2}+1+sd\Big)}\end{equation*}
\begin{equation*}{\mathbb{E}}\Big[\xi^{s}(1-\xi)^{(d-1)s}\Big]={\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}+s(d-1)\Big)\Gamma\Big({d+\nu\over 2}+\beta+1+s\Big)\Gamma\Big({d(d+2\beta+\nu)\over 2}+1\Big)\over\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}\Big)\Gamma\Big({d+\nu\over 2}+\beta+1\Big)\Gamma\Big({d(d+2\beta+\nu)\over 2}+1+sd\Big)}\end{equation*}
and
 \begin{equation*}{\mathbb{E}}\big[(1-\eta)^{(d-1)s}\big]={\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}\Big)\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}+s(d-1)\Big)\over\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}+s(d-1)\Big)\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}\Big)}.\end{equation*}
\begin{equation*}{\mathbb{E}}\big[(1-\eta)^{(d-1)s}\big]={\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}\Big)\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}+s(d-1)\Big)\over\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}+s(d-1)\Big)\Gamma\Big({(d-1)(d+\nu+2\beta)\over 2}\Big)}.\end{equation*}
Combining this with Theorem 2 we conclude that, for all
![]() $s>-{\nu+1\over 2}$
,
$s>-{\nu+1\over 2}$
,
 \begin{equation*}(d-1)!^{2s}\,{\mathbb{E}}\Big[\xi^{s}(1-\xi)^{(d-1)s}\,{\textrm{Vol}}\big(Z_{\beta,\nu}\big)^{2s}\Big]=m_{\beta,d}^{-{2s(d-1)\over d+2\beta+1}}{\mathbb{E}}\Bigg[\rho^{{2s(d-1)\over d+2\beta+1}}(1-\eta)^{(d-1)s}\prod\limits_{i=1}^{d-1}\xi_i^s\Bigg],\end{equation*}
\begin{equation*}(d-1)!^{2s}\,{\mathbb{E}}\Big[\xi^{s}(1-\xi)^{(d-1)s}\,{\textrm{Vol}}\big(Z_{\beta,\nu}\big)^{2s}\Big]=m_{\beta,d}^{-{2s(d-1)\over d+2\beta+1}}{\mathbb{E}}\Bigg[\rho^{{2s(d-1)\over d+2\beta+1}}(1-\eta)^{(d-1)s}\prod\limits_{i=1}^{d-1}\xi_i^s\Bigg],\end{equation*}
which finishes the proof of (5.1). Analogously, for
![]() $-{\nu+1\over 2}< s< \beta -{d+\nu\over 2}$
we have
$-{\nu+1\over 2}< s< \beta -{d+\nu\over 2}$
we have
 \begin{equation*}{\mathbb{E}}\Big[(\xi^{\prime})^{-s}\big(1+\xi^{\prime}\big)^{ds}\Big]={\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}-s(d-1)\Big)\Gamma\Big(\beta-{d+\nu\over 2}-s\Big)\Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)\over\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}\Big)\Gamma\Big(\beta-{d+\nu\over 2}\Big)\Gamma\Big({d(2\beta-d-\nu)\over 2}-sd\Big)}\end{equation*}
\begin{equation*}{\mathbb{E}}\Big[(\xi^{\prime})^{-s}\big(1+\xi^{\prime}\big)^{ds}\Big]={\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}-s(d-1)\Big)\Gamma\Big(\beta-{d+\nu\over 2}-s\Big)\Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)\over\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}\Big)\Gamma\Big(\beta-{d+\nu\over 2}\Big)\Gamma\Big({d(2\beta-d-\nu)\over 2}-sd\Big)}\end{equation*}
and
 \begin{equation*}{\mathbb{E}}\Big[\big(1+\eta^{\prime}\big)^{(d-1)s}\Big]={\Gamma\Big({d(2\beta-d)-\nu(d-1)+1\over 2}\Big)\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}-s(d-1)\Big)\over\Gamma\Big({d(2\beta-d)-\nu(d-1)+1\over 2}+s(d-1)\Big)\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}\Big)}.\end{equation*}
\begin{equation*}{\mathbb{E}}\Big[\big(1+\eta^{\prime}\big)^{(d-1)s}\Big]={\Gamma\Big({d(2\beta-d)-\nu(d-1)+1\over 2}\Big)\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}-s(d-1)\Big)\over\Gamma\Big({d(2\beta-d)-\nu(d-1)+1\over 2}+s(d-1)\Big)\Gamma\Big({(d-1)(2\beta-d-\nu)\over 2}\Big)}.\end{equation*}
By Theorem 2, for all
![]() $-{\nu+1\over 2}< s< \beta -{d+\nu\over 2}$
we obtain
$-{\nu+1\over 2}< s< \beta -{d+\nu\over 2}$
we obtain
 \begin{align*}(d-1)!^{2s}\,&{\mathbb{E}}\Big[\big(1+\eta^{\prime}\big)^{(d-1)s}\,{\textrm{Vol}}\big(Z_{\beta,\nu}^{\prime}\big)^{2s}\Big]\\&=\big(m_{\beta,d}^{\prime}\big)^{-{2s(d-1)\over d-2\beta+1}}{\mathbb{E}}\Bigg[\rho^{{2s(d-1)\over d-2\beta+1}}(\xi^{\prime})^{-s}\big(1+\xi^{\prime}\big)^{ds}\prod\limits_{i=1}^{d-1}(\xi_i^{\prime})^s\Bigg],\end{align*}
\begin{align*}(d-1)!^{2s}\,&{\mathbb{E}}\Big[\big(1+\eta^{\prime}\big)^{(d-1)s}\,{\textrm{Vol}}\big(Z_{\beta,\nu}^{\prime}\big)^{2s}\Big]\\&=\big(m_{\beta,d}^{\prime}\big)^{-{2s(d-1)\over d-2\beta+1}}{\mathbb{E}}\Bigg[\rho^{{2s(d-1)\over d-2\beta+1}}(\xi^{\prime})^{-s}\big(1+\xi^{\prime}\big)^{ds}\prod\limits_{i=1}^{d-1}(\xi_i^{\prime})^s\Bigg],\end{align*}
and (5.2) follows.
The next result specifies, for integer values of
![]() $\nu$
, the connection between the distributions of
$\nu$
, the connection between the distributions of
![]() ${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
and
${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
and
![]() ${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
and those of the volume of a
${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
and those of the volume of a
![]() $\beta$
-simplex and the volume of a
$\beta$
-simplex and the volume of a
![]() $\beta^{\prime}$
-simplex as studied in [Reference Grote, Kabluchko and Thäle10], respectively.
$\beta^{\prime}$
-simplex as studied in [Reference Grote, Kabluchko and Thäle10], respectively.
Proposition 1.
-
(a) For
 $d\geq 2$
,
$d\geq 2$
,
 $\beta\geq -1$
and integers
$\beta\geq -1$
and integers
 $\nu\geq -1$
we have where
$\nu\geq -1$
we have where \begin{equation*}(1-\xi)^{d-1}\,{\textrm{Vol}}\big(Z_{\beta,\nu}\big)^2\overset{D}{=} (m_{\beta,d}^{-1}\,\rho)^{{2(d-1)\over d+2\beta+1}}\textrm{Vol}\left({\textrm{conv}}(X_0,\ldots, X_{d-1})\right)^2,\end{equation*}
\begin{equation*}(1-\xi)^{d-1}\,{\textrm{Vol}}\big(Z_{\beta,\nu}\big)^2\overset{D}{=} (m_{\beta,d}^{-1}\,\rho)^{{2(d-1)\over d+2\beta+1}}\textrm{Vol}\left({\textrm{conv}}(X_0,\ldots, X_{d-1})\right)^2,\end{equation*}
 $X_0,\ldots, X_{d-1}$
are independent and identically distributed (i.i.d.) random points in
$X_0,\ldots, X_{d-1}$
are independent and identically distributed (i.i.d.) random points in
 ${\mathbb{B}}^{d+\nu}$
whose distribution has density
${\mathbb{B}}^{d+\nu}$
whose distribution has density  \begin{equation*}c_{d+\nu,\beta}(1-\|x\|)^{\beta},\qquad x\in{\mathbb{B}}^{d+\nu},\end{equation*}
is independent of
\begin{equation*}c_{d+\nu,\beta}(1-\|x\|)^{\beta},\qquad x\in{\mathbb{B}}^{d+\nu},\end{equation*}
is independent of \begin{equation*}\xi\sim{\textrm{Beta}}\Big({\nu+1\over 2}, {d(d+2\beta)+\nu(d-1)+1\over 2}\Big)\end{equation*}
\begin{equation*}\xi\sim{\textrm{Beta}}\Big({\nu+1\over 2}, {d(d+2\beta)+\nu(d-1)+1\over 2}\Big)\end{equation*}
 ${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
, and is independent of
${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
, and is independent of \begin{equation*}\rho\sim{\textrm{Gamma}}\Big(d+{(\nu-1)(d-1)\over d+2\beta+1},1\Big)\end{equation*}
\begin{equation*}\rho\sim{\textrm{Gamma}}\Big(d+{(\nu-1)(d-1)\over d+2\beta+1},1\Big)\end{equation*}
 $X_0,\ldots, X_{d-1}$
.
$X_0,\ldots, X_{d-1}$
.
-
(b) For
 $d\geq 2$
,
$d\geq 2$
,
 $\beta> (d+1)/2$
and integers
$\beta> (d+1)/2$
and integers
 $2\beta - d>\nu\ge -1$
we have where
$2\beta - d>\nu\ge -1$
we have where \begin{equation*}\big(1+\xi^{\prime}\big)^{d-1}\,{\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)^2\overset{D}{=} \big(\big(m_{\beta,d}^{\prime}\big)^{-1}\,\rho^{\prime}\big)^{{2(d-1)\over d-2\beta+1}}\,{\textrm{Vol}}\big({\textrm{conv}}\big(X^{\prime}_0,\ldots, X^{\prime}_{d-1}\big)\big)^2,\end{equation*}
\begin{equation*}\big(1+\xi^{\prime}\big)^{d-1}\,{\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)^2\overset{D}{=} \big(\big(m_{\beta,d}^{\prime}\big)^{-1}\,\rho^{\prime}\big)^{{2(d-1)\over d-2\beta+1}}\,{\textrm{Vol}}\big({\textrm{conv}}\big(X^{\prime}_0,\ldots, X^{\prime}_{d-1}\big)\big)^2,\end{equation*}
 $X^{\prime}_0,\ldots, X^{\prime}_{d-1}$
are i.i.d. random points in
$X^{\prime}_0,\ldots, X^{\prime}_{d-1}$
are i.i.d. random points in
 ${\mathbb{R}}^{d+\nu}$
whose distribution has density
${\mathbb{R}}^{d+\nu}$
whose distribution has density  \begin{equation*}c^{\prime}_{d+\nu,\beta}(1+\|x\|)^{-\beta},\qquad x\in{\mathbb{R}}^{d+\nu},\end{equation*}
is independent of
\begin{equation*}c^{\prime}_{d+\nu,\beta}(1+\|x\|)^{-\beta},\qquad x\in{\mathbb{R}}^{d+\nu},\end{equation*}
is independent of \begin{equation*}\xi^{\prime}\sim{\textrm{Beta}}^{\prime}\Big({\nu+1\over 2}, {d(2\beta - d -\nu)\over 2}\Big)\end{equation*}
\begin{equation*}\xi^{\prime}\sim{\textrm{Beta}}^{\prime}\Big({\nu+1\over 2}, {d(2\beta - d -\nu)\over 2}\Big)\end{equation*}
 ${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
, and is independent of
${\textrm{Vol}}\big(Z^{\prime}_{\beta,\nu}\big)$
, and is independent of \begin{equation*}\rho^{\prime}\sim{\textrm{Gamma}}\Big(d+{(\nu-1)(d-1)\over d-2\beta+1},1\Big)\end{equation*}
\begin{equation*}\rho^{\prime}\sim{\textrm{Gamma}}\Big(d+{(\nu-1)(d-1)\over d-2\beta+1},1\Big)\end{equation*}
 $X^{\prime}_0,\ldots, X^{\prime}_{d-1}$
.
$X^{\prime}_0,\ldots, X^{\prime}_{d-1}$
.
Proof. From [Reference Grote, Kabluchko and Thäle10, Theorem 2.3(b)] we have
 \begin{align*}(d-1)!^{2s}&{\mathbb{E}}\big[\textrm{Vol}\left({\textrm{conv}}(X_0,\ldots, X_{d-1})\right)^{2s}\big]\\&={\Gamma({d+2\beta+\nu+2\over 2})^d\over \Gamma\Big({d+2\beta+\nu+2\over 2}+s\Big)^{d}}{\Gamma\Big({d(d+2\beta+\nu)+2\over 2}+ds\Big)\over \Gamma\Big({d(d+\beta+\nu)+2\over 2}+(d-1)s\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({\nu+1+i\over 2}+s\Big)\over\Gamma\Big({\nu+1+i\over 2}\Big)}\end{align*}
\begin{align*}(d-1)!^{2s}&{\mathbb{E}}\big[\textrm{Vol}\left({\textrm{conv}}(X_0,\ldots, X_{d-1})\right)^{2s}\big]\\&={\Gamma({d+2\beta+\nu+2\over 2})^d\over \Gamma\Big({d+2\beta+\nu+2\over 2}+s\Big)^{d}}{\Gamma\Big({d(d+2\beta+\nu)+2\over 2}+ds\Big)\over \Gamma\Big({d(d+\beta+\nu)+2\over 2}+(d-1)s\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({\nu+1+i\over 2}+s\Big)\over\Gamma\Big({\nu+1+i\over 2}\Big)}\end{align*}
for any
![]() $\beta-{d+\nu\over 2}>s>0$
. Using the equality
$\beta-{d+\nu\over 2}>s>0$
. Using the equality
 \begin{align*}{\mathbb{E}}\big[(1-\xi)^{(d-1)s}\big]&={\Gamma\Big({d(d+2\beta+\nu)\over 2}+1\Big)\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}+(d-1)s\Big)\over \Gamma\Big({d(d+2\beta+\nu)\over 2}+1+(d-1)s\Big)\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}\Big)}\end{align*}
\begin{align*}{\mathbb{E}}\big[(1-\xi)^{(d-1)s}\big]&={\Gamma\Big({d(d+2\beta+\nu)\over 2}+1\Big)\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}+(d-1)s\Big)\over \Gamma\Big({d(d+2\beta+\nu)\over 2}+1+(d-1)s\Big)\Gamma\Big({d(d+2\beta)+\nu(d-1)+1\over 2}\Big)}\end{align*}
and combining this with Theorem 2, we conclude that, for all
![]() $\beta-{d+\nu\over 2}>s>0$
,
$\beta-{d+\nu\over 2}>s>0$
,
and (a) is proven. Analogously, from [Reference Grote, Kabluchko and Thäle10, Theorem 2.3(b)--(c)] we have
 \begin{align*}&(d-1)!^{2s}{\mathbb{E}}\Big[{\textrm{Vol}}\big({\textrm{conv}}\big(X^{\prime}_0,\ldots, X^{\prime}_{d-1}\big)\big)^{2s}\Big]\\&\qquad \qquad ={\Gamma\Big(\beta-{d+\nu\over 2}-s\Big)^d\over \Gamma\Big(\beta-{d+\nu\over 2}\Big)^{d}}{\Gamma\Big({d(2\beta-d-\nu)\over 2}-(d-1)s\Big)\over \Gamma\Big({d(2\beta-d-\nu)\over 2}-ds\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({\nu+1+i\over 2}+s\Big)\over\Gamma\Big({\nu+1+i\over 2}\Big)},\end{align*}
\begin{align*}&(d-1)!^{2s}{\mathbb{E}}\Big[{\textrm{Vol}}\big({\textrm{conv}}\big(X^{\prime}_0,\ldots, X^{\prime}_{d-1}\big)\big)^{2s}\Big]\\&\qquad \qquad ={\Gamma\Big(\beta-{d+\nu\over 2}-s\Big)^d\over \Gamma\Big(\beta-{d+\nu\over 2}\Big)^{d}}{\Gamma\Big({d(2\beta-d-\nu)\over 2}-(d-1)s\Big)\over \Gamma\Big({d(2\beta-d-\nu)\over 2}-ds\Big)}\prod\limits_{i=1}^{d-1}{\Gamma\Big({\nu+1+i\over 2}+s\Big)\over\Gamma\Big({\nu+1+i\over 2}\Big)},\end{align*}
and using the fact that
 \begin{equation*}{\mathbb{E}}\Big[\big(1+\xi^{\prime}\big)^{(d-1)s}\Big]={\Gamma\Big({d(2\beta-d-\nu)\over 2}-(d-1)s\Big)\Gamma\Big({d(2\beta - d)-\nu(d-1)+1\over 2}\Big)\over \Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)\Gamma\Big({d(2\beta - d)-\nu(d-1)+1\over 2}-s(d-1)\Big)},\end{equation*}
\begin{equation*}{\mathbb{E}}\Big[\big(1+\xi^{\prime}\big)^{(d-1)s}\Big]={\Gamma\Big({d(2\beta-d-\nu)\over 2}-(d-1)s\Big)\Gamma\Big({d(2\beta - d)-\nu(d-1)+1\over 2}\Big)\over \Gamma\Big({d(2\beta-d-\nu)\over 2}\Big)\Gamma\Big({d(2\beta - d)-\nu(d-1)+1\over 2}-s(d-1)\Big)},\end{equation*}
together with Theorem 2, we have for all
![]() $s>0$
$s>0$
which finishes the proof of (b) and of the theorem.
Remark 10. The formula for
![]() ${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
is the extension of [Reference Gusakova and Thäle11, Proposition 2.8] to general
${\textrm{Vol}}\big(Z_{\beta,\nu}\big)$
is the extension of [Reference Gusakova and Thäle11, Proposition 2.8] to general
![]() $\beta\geq -1$
.
$\beta\geq -1$
.
Remark 11. In [Reference Grote, Kabluchko and Thäle10, Theorem 2.7] it is shown that the random variable
![]() $\xi$
(respectively,
$\xi$
(respectively,
![]() $\xi^{\prime}$
) in the previous proposition is equal in distribution to the squared distance from the origin to the
$\xi^{\prime}$
) in the previous proposition is equal in distribution to the squared distance from the origin to the
![]() $(d-1)$
-dimensional affine subspace spanned by the random vectors
$(d-1)$
-dimensional affine subspace spanned by the random vectors
![]() $X_0,\ldots, X_{d-1}$
$X_0,\ldots, X_{d-1}$
![]() $\big($
respectively,
$\big($
respectively,
![]() $X^{\prime}_0,\ldots, X^{\prime}_{d-1}\big)$
.
$X^{\prime}_0,\ldots, X^{\prime}_{d-1}\big)$
.
6. Angle sums and face intensities
The aim of this section is to compute the intensity of j-dimensional faces in the
![]() $\beta$
-Delaunay tessellations
$\beta$
-Delaunay tessellations
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}_{\beta}^\prime$
, for all
${\mathcal{D}}_{\beta}^\prime$
, for all
![]() $j\in \{0,\ldots,d-1\}$
. Intuitively, the face intensities can be understood as follows. In a stationary random tessellation
$j\in \{0,\ldots,d-1\}$
. Intuitively, the face intensities can be understood as follows. In a stationary random tessellation
![]() $\mathcal T$
, the expected number of j-dimensional faces in a large cube of volume V is asymptotically equivalent to
$\mathcal T$
, the expected number of j-dimensional faces in a large cube of volume V is asymptotically equivalent to
![]() $\gamma_j(\mathcal T)V$
, as
$\gamma_j(\mathcal T)V$
, as
![]() $V\to\infty$
, for a certain constant
$V\to\infty$
, for a certain constant
![]() $\gamma_j(\mathcal T)$
, called the intensity of j-dimensional faces of
$\gamma_j(\mathcal T)$
, called the intensity of j-dimensional faces of
![]() $\mathcal T$
. A precise definition, using Palm calculus, will be given below. To evaluate these constants for the tessellations
$\mathcal T$
. A precise definition, using Palm calculus, will be given below. To evaluate these constants for the tessellations
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}_{\beta}^\prime$
, we will first compute the expected angle sums of the volume-power-weighted typical cells of
${\mathcal{D}}_{\beta}^\prime$
, we will first compute the expected angle sums of the volume-power-weighted typical cells of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}_{\beta}^\prime$
.
${\mathcal{D}}_{\beta}^\prime$
.
6.1. Expected angle sums of weighted typical cells
Let us recall that
![]() $Z_{\beta,\nu}$
and
$Z_{\beta,\nu}$
and
![]() $Z_{\beta,\nu}^\prime$
denote the typical cells of
$Z_{\beta,\nu}^\prime$
denote the typical cells of
![]() ${\mathcal{D}}_\beta$
and
${\mathcal{D}}_\beta$
and
![]() ${\mathcal{D}}_{\beta}^\prime$
weighted by the
${\mathcal{D}}_{\beta}^\prime$
weighted by the
![]() $\nu$
th power of their volume. Our aim is to compute the expected angle sums of these random simplices. First we need to introduce the necessary notation.
$\nu$
th power of their volume. Our aim is to compute the expected angle sums of these random simplices. First we need to introduce the necessary notation.
Given a simplex
![]() $T \,:\!=\, {\textrm{conv}}(Z_1,\ldots,Z_d) \subset {\mathbb{R}}^{d-1}$
, we denote by
$T \,:\!=\, {\textrm{conv}}(Z_1,\ldots,Z_d) \subset {\mathbb{R}}^{d-1}$
, we denote by
![]() $\sigma_k(T)$
the sum of internal angles of T at all its k-vertex faces of the form
$\sigma_k(T)$
the sum of internal angles of T at all its k-vertex faces of the form
![]() ${\textrm{conv}}\big(Z_{i_1},\ldots, Z_{i_k}\big)$
; that is,
${\textrm{conv}}\big(Z_{i_1},\ldots, Z_{i_k}\big)$
; that is,
 \begin{equation*}\sigma_k(T) = \sum_{\substack{1\leq i_1<\ldots< i_k\leq d\\F \,:=\, {\textrm{conv}}\big(Z_{i_1},\ldots,Z_{i_k}\big)}} \beta(F,T), \qquad k\in \{1,\ldots,d\}.\end{equation*}
\begin{equation*}\sigma_k(T) = \sum_{\substack{1\leq i_1<\ldots< i_k\leq d\\F \,:=\, {\textrm{conv}}\big(Z_{i_1},\ldots,Z_{i_k}\big)}} \beta(F,T), \qquad k\in \{1,\ldots,d\}.\end{equation*}
Here,
![]() $\beta(F,T)$
is the internal angle of T at its face F, normalized in such a way that the angle of the full space is 1; see [Reference Schneider and Weil31, p.458]. If
$\beta(F,T)$
is the internal angle of T at its face F, normalized in such a way that the angle of the full space is 1; see [Reference Schneider and Weil31, p.458]. If
![]() $Z_1,\ldots,Z_d$
are d i.i.d. random points in
$Z_1,\ldots,Z_d$
are d i.i.d. random points in
![]() ${\mathbb{B}}^{d-1}$
distributed according to the beta density
${\mathbb{B}}^{d-1}$
distributed according to the beta density
then
![]() ${\textrm{conv}}(Z_1,\ldots,Z_d)$
is called the
${\textrm{conv}}(Z_1,\ldots,Z_d)$
is called the
![]() $\beta$
-simplex with parameter
$\beta$
-simplex with parameter
![]() $\beta>-1$
. The
$\beta>-1$
. The
![]() $\beta$
-simplex with parameter
$\beta$
-simplex with parameter
![]() $\beta=-1$
is defined as
$\beta=-1$
is defined as
![]() ${\textrm{conv}}(Z_1,\ldots,Z_d)$
, where
${\textrm{conv}}(Z_1,\ldots,Z_d)$
, where
![]() $Z_1,\ldots,Z_d$
are i.i.d. uniform on the unit sphere
$Z_1,\ldots,Z_d$
are i.i.d. uniform on the unit sphere
![]() ${\mathbb{S}}^{d-2}$
. The expected angle sums of these simplices, denoted by
${\mathbb{S}}^{d-2}$
. The expected angle sums of these simplices, denoted by
are computed in [Reference Kabluchko14]; see Theorem 1.2 and the discussion thereafter. According to this formula, we have
 \begin{align}\mathbb J_{d,k}\left(\frac{\alpha-d+1}{2}\right)&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha d}2} (\cosh u)^{-\alpha d - 2}\notag\\&\quad \times\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha-1}{2}} (\cosh v)^{\alpha}{\rm d} v \right)^{d-k} {\rm d} u\end{align}
\begin{align}\mathbb J_{d,k}\left(\frac{\alpha-d+1}{2}\right)&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha d}2} (\cosh u)^{-\alpha d - 2}\notag\\&\quad \times\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha-1}{2}} (\cosh v)^{\alpha}{\rm d} v \right)^{d-k} {\rm d} u\end{align}
for all
![]() $d\geq 3$
,
$d\geq 3$
,
![]() $k\in \{1,\ldots,d\}$
, and
$k\in \{1,\ldots,d\}$
, and
![]() $\alpha \geq d-3$
, where
$\alpha \geq d-3$
, where
 \begin{equation*}c_{\gamma} \,:\!=\, c_{1,\gamma} = \frac{ \Gamma\!\left(\gamma + \frac{3}{2} \right) }{ \sqrt \pi\, \Gamma (\gamma+1)}, \qquad \gamma>-1.\end{equation*}
\begin{equation*}c_{\gamma} \,:\!=\, c_{1,\gamma} = \frac{ \Gamma\!\left(\gamma + \frac{3}{2} \right) }{ \sqrt \pi\, \Gamma (\gamma+1)}, \qquad \gamma>-1.\end{equation*}
Similarly, let
![]() $Z_1^\prime,\ldots,Z_d^\prime$
be d i.i.d. random points in
$Z_1^\prime,\ldots,Z_d^\prime$
be d i.i.d. random points in
![]() ${\mathbb{R}}^{d-1}$
distributed according to the beta-prime density
${\mathbb{R}}^{d-1}$
distributed according to the beta-prime density
Then
![]() ${\textrm{conv}}\big(Z_1^\prime,\ldots,Z_d^\prime\big)$
is called the
${\textrm{conv}}\big(Z_1^\prime,\ldots,Z_d^\prime\big)$
is called the
![]() $\beta^{\prime}$
-simplex with parameter
$\beta^{\prime}$
-simplex with parameter
![]() $\beta> \frac{d-1}{2}$
. The expected angle sums of the
$\beta> \frac{d-1}{2}$
. The expected angle sums of the
![]() $\beta^{\prime}$
-simplices, denoted by
$\beta^{\prime}$
-simplices, denoted by
are computed in [Reference Kabluchko14] (see Theorem 1.7 and the discussion thereafter):
 \begin{align*}\mathbb J_{d,k}^\prime\left(\frac{\alpha+d-1}{2}\right)&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha d}2}^\prime (\cosh u)^{-(\alpha d - 1)}\\&\quad \times\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha+1}{2}}^\prime (\cosh v)^{\alpha-1}{\rm d} v \right)^{d-k} {\rm d} u\end{align*}
\begin{align*}\mathbb J_{d,k}^\prime\left(\frac{\alpha+d-1}{2}\right)&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha d}2}^\prime (\cosh u)^{-(\alpha d - 1)}\\&\quad \times\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha+1}{2}}^\prime (\cosh v)^{\alpha-1}{\rm d} v \right)^{d-k} {\rm d} u\end{align*}
for all
![]() $d\in{\mathbb{N}}$
,
$d\in{\mathbb{N}}$
,
![]() $k\in \{1,\ldots,d\}$
, and for all
$k\in \{1,\ldots,d\}$
, and for all
![]() $\alpha >0$
such that
$\alpha >0$
such that
![]() $\alpha d >1$
. Here,
$\alpha d >1$
. Here,
 \begin{equation*}c_{\gamma}^\prime \,:\!=\, c_{1,\gamma}^\prime = \frac{ \Gamma (\gamma) }{ \sqrt \pi\, \Gamma\!\left(\gamma - \frac 12\right)}, \qquad \gamma > \frac 12.\end{equation*}
\begin{equation*}c_{\gamma}^\prime \,:\!=\, c_{1,\gamma}^\prime = \frac{ \Gamma (\gamma) }{ \sqrt \pi\, \Gamma\!\left(\gamma - \frac 12\right)}, \qquad \gamma > \frac 12.\end{equation*}
We are now going to state a formula for the expected angle sums of the typical cells
![]() $Z_{\beta,\nu}$
and
$Z_{\beta,\nu}$
and
![]() $Z_{\beta,\nu}^\prime$
. Note that we include the case of
$Z_{\beta,\nu}^\prime$
. Note that we include the case of
![]() $Z_{-1,\nu}$
, which is interpreted as the
$Z_{-1,\nu}$
, which is interpreted as the
![]() $\nu$
-weighted typical cell in the classical Poisson–Delaunay tessellation; see Remark 6.
$\nu$
-weighted typical cell in the classical Poisson–Delaunay tessellation; see Remark 6.
Theorem 4. Let
![]() $Z_{\beta,\nu}$
be the
$Z_{\beta,\nu}$
be the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta$
-Delaunay tessellation with
$\beta$
-Delaunay tessellation with
![]() $\beta\geq -1$
and integer
$\beta\geq -1$
and integer
![]() $\nu\ge -1$
. Also, let
$\nu\ge -1$
. Also, let
![]() $Z_{\beta,\nu}^\prime$
be the
$Z_{\beta,\nu}^\prime$
be the
![]() $\nu$
-weighted typical cell of the
$\nu$
-weighted typical cell of the
![]() $\beta^\prime$
-Delaunay tessellation with
$\beta^\prime$
-Delaunay tessellation with
![]() $\beta > (d+1)/2$
and integer
$\beta > (d+1)/2$
and integer
![]() $\nu$
such that
$\nu$
such that
![]() $2\beta-d > \nu \ge-1$
. Then, for all
$2\beta-d > \nu \ge-1$
. Then, for all
![]() $k\in \{1,\ldots,d\}$
,
$k\in \{1,\ldots,d\}$
,
 \begin{align*}{\mathbb{E}} \sigma_k\big(Z_{\beta,\nu}\big)&=\mathbb J_{d,k}\left(\beta + \frac {\nu+1} 2\right)\\&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha d}2} (\cosh u)^{-\alpha d - 2}\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha-1}{2}} (\cosh v)^{\alpha}{\rm d} v \right)^{d-k} {\rm d} u,\\{\mathbb{E}} \sigma_k\big(Z_{\beta,\nu}^\prime\big)&=\mathbb J_{d,k}^\prime\left(\beta - \frac {\nu+1} 2\right)\\&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha^\prime d}2}^\prime (\cosh u)^{-(\alpha^\prime d - 1)}\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha^\prime-1}{2}}^\prime (\cosh v)^{\alpha^\prime-1}{\rm d} v \right)^{d-k} {\rm d} u,\end{align*}
\begin{align*}{\mathbb{E}} \sigma_k\big(Z_{\beta,\nu}\big)&=\mathbb J_{d,k}\left(\beta + \frac {\nu+1} 2\right)\\&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha d}2} (\cosh u)^{-\alpha d - 2}\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha-1}{2}} (\cosh v)^{\alpha}{\rm d} v \right)^{d-k} {\rm d} u,\\{\mathbb{E}} \sigma_k\big(Z_{\beta,\nu}^\prime\big)&=\mathbb J_{d,k}^\prime\left(\beta - \frac {\nu+1} 2\right)\\&=\binom dk \int_{-\infty}^{+\infty} c_{\frac{\alpha^\prime d}2}^\prime (\cosh u)^{-(\alpha^\prime d - 1)}\left(\frac 12 + 1 \int_0^u c_{\frac{\alpha^\prime-1}{2}}^\prime (\cosh v)^{\alpha^\prime-1}{\rm d} v \right)^{d-k} {\rm d} u,\end{align*}
where
![]() $\alpha = 2\beta + \nu + d$
and
$\alpha = 2\beta + \nu + d$
and
![]() $\alpha^{\prime} = 2\beta - \nu - d$
.
$\alpha^{\prime} = 2\beta - \nu - d$
.
Proof. We consider the
![]() $\beta$
-Delaunay case. First, let
$\beta$
-Delaunay case. First, let
![]() $\beta>-1$
. Since rescaling does not change angle sums, it follows from Remark 5 that
$\beta>-1$
. Since rescaling does not change angle sums, it follows from Remark 5 that
where
![]() $(Y_1,\ldots,Y_d)$
are d random points in the unit ball
$(Y_1,\ldots,Y_d)$
are d random points in the unit ball
![]() ${\mathbb{B}}^{d-1}$
whose joint density is proportional to
${\mathbb{B}}^{d-1}$
whose joint density is proportional to
 \begin{equation*}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1} \, \prod\limits_{i=1}^d\big(1-\|y_i\|^2\big)^{\beta},\qquad y_1\in {\mathbb{B}}^{d-1},\ldots,y_d\in {\mathbb{B}}^{d-1}.\end{equation*}
\begin{equation*}\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1} \, \prod\limits_{i=1}^d\big(1-\|y_i\|^2\big)^{\beta},\qquad y_1\in {\mathbb{B}}^{d-1},\ldots,y_d\in {\mathbb{B}}^{d-1}.\end{equation*}
On the other hand, let
![]() $Y_1^*,\ldots,Y_d^*$
be d i.i.d. random points in
$Y_1^*,\ldots,Y_d^*$
be d i.i.d. random points in
![]() ${\mathbb{B}}^{d-1}$
with joint density proportional to
${\mathbb{B}}^{d-1}$
with joint density proportional to
 \begin{equation*}\prod\limits_{i=1}^d\big(1-\|y_i^*\|^2\big)^{\beta+ \frac {\nu+1} 2}.\end{equation*}
\begin{equation*}\prod\limits_{i=1}^d\big(1-\|y_i^*\|^2\big)^{\beta+ \frac {\nu+1} 2}.\end{equation*}
By Remark 4.2 of [Reference Kabluchko, Thäle and Zaporozhets17], we have
The expected angle sums of
![]() ${\textrm{conv}}\big(Y_1^*,\ldots,Y_d^*\big)$
are
${\textrm{conv}}\big(Y_1^*,\ldots,Y_d^*\big)$
are
which is given by (6.1) with
![]() $\alpha = 2\beta + \nu + d$
. Taking everything together proves the theorem in the
$\alpha = 2\beta + \nu + d$
. Taking everything together proves the theorem in the
![]() $\beta$
-Delaunay case with
$\beta$
-Delaunay case with
![]() $\beta>-1$
.
$\beta>-1$
.
For the
![]() $\beta$
-Delaunay case with
$\beta$
-Delaunay case with
![]() $\beta=-1$
(where
$\beta=-1$
(where
![]() $Z_{-1,\nu}$
is interpreted as the
$Z_{-1,\nu}$
is interpreted as the
![]() $\nu$
-weighted cell in the classical Poisson–Delaunay tessellation), the starting point is Remark 6, which implies that
$\nu$
-weighted cell in the classical Poisson–Delaunay tessellation), the starting point is Remark 6, which implies that
where
![]() $(Y_1,\ldots,Y_d)$
are d random points in the unit sphere
$(Y_1,\ldots,Y_d)$
are d random points in the unit sphere
![]() ${\mathbb{S}}^{d-2}$
whose joint probability law is proportional to
${\mathbb{S}}^{d-2}$
whose joint probability law is proportional to
The rest of the proof is similar to the case
![]() $\beta>-1$
. The
$\beta>-1$
. The
![]() $\beta^\prime$
case is similar as well.
$\beta^\prime$
case is similar as well.
We stated Theorem 4 for integer
![]() $\nu$
only because this assumption is required by the method of proof of Remark 4.2 in [Reference Kabluchko, Thäle and Zaporozhets17]. Specializing Theorem 4 to
$\nu$
only because this assumption is required by the method of proof of Remark 4.2 in [Reference Kabluchko, Thäle and Zaporozhets17]. Specializing Theorem 4 to
![]() $\nu=0$
(respectively,
$\nu=0$
(respectively,
![]() $\nu=1$
), we obtain the expected angle sums of the typical cell (respectively, the cell containing the origin) of the
$\nu=1$
), we obtain the expected angle sums of the typical cell (respectively, the cell containing the origin) of the
![]() $\beta$
-Delaunay tessellation, for
$\beta$
-Delaunay tessellation, for
![]() $\beta\geq -1$
. For the typical cell (
$\beta\geq -1$
. For the typical cell (
![]() $\nu=0$
) of the classical Poisson–Delaunay tessellation in
$\nu=0$
) of the classical Poisson–Delaunay tessellation in
![]() ${\mathbb{R}}^{d-1}$
(corresponding to
${\mathbb{R}}^{d-1}$
(corresponding to
![]() $\beta=-1$
), the angle sum is given by
$\beta=-1$
), the angle sum is given by
Applying to the quantity on the right-hand side Theorem 1.3 of [Reference Kabluchko14], we arrive at the following result.
Theorem 5. Let
![]() $Z=Z_{-1,0}$
be the typical cell of the classical Poisson–Delaunay tessellation
$Z=Z_{-1,0}$
be the typical cell of the classical Poisson–Delaunay tessellation
![]() ${\mathcal{D}}_{-1}$
in
${\mathcal{D}}_{-1}$
in
![]() ${\mathbb{R}}^{d-1}$
. Then, for all
${\mathbb{R}}^{d-1}$
. Then, for all
![]() $k\in \{1,\ldots,d\}$
such that
$k\in \{1,\ldots,d\}$
such that
![]() $(d-1)(k-1)$
is even, we have
$(d-1)(k-1)$
is even, we have
 \begin{equation*}{\mathbb{E}} \sigma_{k}(Z) =\binom{d}{k} \left(\frac{\Gamma\big(\frac{d}{2}\big)}{\sqrt{\pi}\, \Gamma\big(\frac{d-1}{2}\big)}\right)^{d-k} \cdot \frac{\sqrt \pi\, \Gamma\Big(\frac{(d-1)^2+2}{2}\Big) }{\Gamma\Big(\frac{(d-1)^2+1}{2}\Big)}\cdot \mathop{\textrm{Res}}\nolimits\limits_{x=0} \left[\frac{\Big(\int_{0}^x (\!\sin y)^{d-2} {\rm d} y\Big)^{d-k}}{(\!\sin x)^{(d-1)^2+1}}\right].\end{equation*}
\begin{equation*}{\mathbb{E}} \sigma_{k}(Z) =\binom{d}{k} \left(\frac{\Gamma\big(\frac{d}{2}\big)}{\sqrt{\pi}\, \Gamma\big(\frac{d-1}{2}\big)}\right)^{d-k} \cdot \frac{\sqrt \pi\, \Gamma\Big(\frac{(d-1)^2+2}{2}\Big) }{\Gamma\Big(\frac{(d-1)^2+1}{2}\Big)}\cdot \mathop{\textrm{Res}}\nolimits\limits_{x=0} \left[\frac{\Big(\int_{0}^x (\!\sin y)^{d-2} {\rm d} y\Big)^{d-k}}{(\!\sin x)^{(d-1)^2+1}}\right].\end{equation*}
In the case when both d and k are even, Proposition 1.4 of [Reference Kabluchko14] yields a formula for
![]() ${\mathbb{E}} \sigma_k(Z)$
which is more complicated than the one given in Theorem 5.
${\mathbb{E}} \sigma_k(Z)$
which is more complicated than the one given in Theorem 5.
6.2. Behavior of
 $\beta$
-Delaunay cells and their expected angle sums as
$\beta$
-Delaunay cells and their expected angle sums as
 $\beta\to\infty$
$\beta\to\infty$
Figure 6 shows the numerical values for the expected angle sums
![]() ${\mathbb{E}}\sigma_1\big(Z_{\beta,\nu}\big)$
of the
${\mathbb{E}}\sigma_1\big(Z_{\beta,\nu}\big)$
of the
![]() $\nu$
-weighted typical
$\nu$
-weighted typical
![]() $\beta$
-Delaunay simplex in
$\beta$
-Delaunay simplex in
![]() ${\mathbb{R}}^{d-1}$
for
${\mathbb{R}}^{d-1}$
for
![]() $\beta\in\{-1,0,\ldots,20\}$
, with
$\beta\in\{-1,0,\ldots,20\}$
, with
![]() $\nu=0$
and
$\nu=0$
and
![]() $d=4$
. It suggests that, as
$d=4$
. It suggests that, as
![]() $\beta$
grows,
$\beta$
grows,
![]() ${\mathbb{E}}\sigma_1\big(Z_{\beta,\nu}\big)$
approaches the value
${\mathbb{E}}\sigma_1\big(Z_{\beta,\nu}\big)$
approaches the value
![]() ${3\over \pi} \arccos \frac 13 -1\approx 0.1755$
, which is the angle sum
${3\over \pi} \arccos \frac 13 -1\approx 0.1755$
, which is the angle sum
![]() $\sigma_1(\Sigma_3)$
of a regular simplex
$\sigma_1(\Sigma_3)$
of a regular simplex
![]() $\Sigma_3$
in
$\Sigma_3$
in
![]() ${\mathbb{R}}^3$
. The next proposition confirms this conjecture in full generality, that is, for general dimensions d, weights
${\mathbb{R}}^3$
. The next proposition confirms this conjecture in full generality, that is, for general dimensions d, weights
![]() $\nu$
, and
$\nu$
, and
![]() $k\in\{1,\ldots,d\}$
. Moreover, it states that the weak limit of
$k\in\{1,\ldots,d\}$
. Moreover, it states that the weak limit of
![]() $Z_{\beta,\nu}$
as
$Z_{\beta,\nu}$
as
![]() $\beta\to\infty$
is the volume-weighted Gaussian simplex whose angle sums, by coincidence, are the same as for the regular simplex. We will come back to this behavior in Part II of this series of papers, where we shall describe the limit of the whole
$\beta\to\infty$
is the volume-weighted Gaussian simplex whose angle sums, by coincidence, are the same as for the regular simplex. We will come back to this behavior in Part II of this series of papers, where we shall describe the limit of the whole
![]() $\beta$
-Delaunay tessellations as
$\beta$
-Delaunay tessellations as
![]() $\beta\to\infty$
.
$\beta\to\infty$
.

Figure 6. Numerical values for the expected angle sums
![]() ${\mathbb{E}}\sigma_k(Z_{\beta,\nu})$
of the
${\mathbb{E}}\sigma_k(Z_{\beta,\nu})$
of the
![]() $\nu$
-weighted typical Delaunay simplex in
$\nu$
-weighted typical Delaunay simplex in
![]() ${\mathbb{R}}^{d-1}$
with
${\mathbb{R}}^{d-1}$
with
![]() $\beta\in\{-1,0,\ldots,20\}$
,
$\beta\in\{-1,0,\ldots,20\}$
,
![]() $\nu=0$
,
$\nu=0$
,
![]() $d=4$
, and
$d=4$
, and
![]() $k=1$
. The corresponding angle sum of a regular simplex is
$k=1$
. The corresponding angle sum of a regular simplex is
![]() $\frac 3 \pi \arccos \frac 13 -1\approx 0.1755$
.
$\frac 3 \pi \arccos \frac 13 -1\approx 0.1755$
.
Proposition 2. Fix
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $\nu>-1$
. Then, as
$\nu>-1$
. Then, as
![]() $\beta\to\infty$
, the distribution of
$\beta\to\infty$
, the distribution of
![]() $\sqrt{2\beta}\, Z_{\beta,\nu}$
, as well as that of
$\sqrt{2\beta}\, Z_{\beta,\nu}$
, as well as that of
![]() $\sqrt{2\beta}\, Z_{\beta,\nu}^\prime$
, converges weakly on the space
$\sqrt{2\beta}\, Z_{\beta,\nu}^\prime$
, converges weakly on the space
![]() $\mathcal C^{\prime}$
to the distribution of the volume-power-weighted Gaussian random simplex
$\mathcal C^{\prime}$
to the distribution of the volume-power-weighted Gaussian random simplex
![]() ${\textrm{conv}}(G_1,\ldots, G_d)$
, where
${\textrm{conv}}(G_1,\ldots, G_d)$
, where
![]() $(G_1,\ldots,G_d)$
are d random points in
$(G_1,\ldots,G_d)$
are d random points in
![]() ${\mathbb{R}}^{d-1}$
with the joint density given by
${\mathbb{R}}^{d-1}$
with the joint density given by
 \begin{equation*}\frac{(d-1)!^{\nu+1}}{ d^{\frac{\nu+1}2} 2^{(\nu+1)(d-1)/2}}\left(\prod\limits_{i=1}^{d-1} {\Gamma\big({i\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)}\right)\Delta_{d-1}(g_1,\ldots,g_d)^{\nu+1}\!\left(\frac {1}{\sqrt{2\pi}}\right)^{d(d-1)} \prod_{i=1}^d e^{-\|g_i\|^2/2},\end{equation*}
\begin{equation*}\frac{(d-1)!^{\nu+1}}{ d^{\frac{\nu+1}2} 2^{(\nu+1)(d-1)/2}}\left(\prod\limits_{i=1}^{d-1} {\Gamma\big({i\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)}\right)\Delta_{d-1}(g_1,\ldots,g_d)^{\nu+1}\!\left(\frac {1}{\sqrt{2\pi}}\right)^{d(d-1)} \prod_{i=1}^d e^{-\|g_i\|^2/2},\end{equation*}
for
![]() $g_1\in{\mathbb{R}}^{d-1},\ldots,g_d\in{\mathbb{R}}^{d-1}$
. Also, if
$g_1\in{\mathbb{R}}^{d-1},\ldots,g_d\in{\mathbb{R}}^{d-1}$
. Also, if
![]() $\nu\ge-1$
is an integer, then for all
$\nu\ge-1$
is an integer, then for all
![]() $k\in\{1,\ldots,d\}$
one has that
$k\in\{1,\ldots,d\}$
one has that
where
![]() $\Sigma_{d-1}$
stands for a regular simplex with d vertices in
$\Sigma_{d-1}$
stands for a regular simplex with d vertices in
![]() ${\mathbb{R}}^{d-1}$
.
${\mathbb{R}}^{d-1}$
.
Proof. For concreteness, we consider the
![]() $\beta$
case. From Remark 5 and Equation (4.9) we know that
$\beta$
case. From Remark 5 and Equation (4.9) we know that
![]() $Z_{\beta,\nu}$
has the same distribution as the random simplex
$Z_{\beta,\nu}$
has the same distribution as the random simplex
![]() ${\textrm{conv}}(RY_1,\ldots,RY_d)$
, where
${\textrm{conv}}(RY_1,\ldots,RY_d)$
, where
-
(a) R is a random variable with density proportional to
 $r^{2d\beta+d^2+\nu(d-1)}e^{-m_{d,\beta}r^{d+1+2\beta}}$
,
$r^{2d\beta+d^2+\nu(d-1)}e^{-m_{d,\beta}r^{d+1+2\beta}}$
,
 $r\in(0,\infty)$
,
$r\in(0,\infty)$
, -
(b)
 $Y_1,\ldots,Y_d$
are random vectors with joint density equal to and
$Y_1,\ldots,Y_d$
are random vectors with joint density equal to and \begin{align*}f(y_1,&\ldots,y_d) \\&\,:\!=\, \left({1\over (d-1)!^{\nu+1}c_{d-1,\beta}^d}{\Gamma\Big(\frac{d+1}{2}+\beta\Big)^d\over \Gamma\Big({d+\nu\over 2}+\beta+1\Big)^d}{\Gamma\Big({d(d+\nu+2\beta)\over 2} +1\Big)\over \Gamma\Big({d(d+\nu+2\beta)-\nu +1 \over 2}\Big)}\prod\limits_{i=1}^{d-1} {\Gamma\Big({i+\nu+1\over 2}\Big)\over \Gamma\big({i\over 2}\big)}\right)^{-1}\\&\qquad \times\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\|y_i\|^2\big)^\beta,\qquad y_1\in{\mathbb{B}}^{d-1},\ldots,y_d\in{\mathbb{B}}^{d-1},\end{align*}
\begin{align*}f(y_1,&\ldots,y_d) \\&\,:\!=\, \left({1\over (d-1)!^{\nu+1}c_{d-1,\beta}^d}{\Gamma\Big(\frac{d+1}{2}+\beta\Big)^d\over \Gamma\Big({d+\nu\over 2}+\beta+1\Big)^d}{\Gamma\Big({d(d+\nu+2\beta)\over 2} +1\Big)\over \Gamma\Big({d(d+\nu+2\beta)-\nu +1 \over 2}\Big)}\prod\limits_{i=1}^{d-1} {\Gamma\Big({i+\nu+1\over 2}\Big)\over \Gamma\big({i\over 2}\big)}\right)^{-1}\\&\qquad \times\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\prod_{i=1}^d\big(1-\|y_i\|^2\big)^\beta,\qquad y_1\in{\mathbb{B}}^{d-1},\ldots,y_d\in{\mathbb{B}}^{d-1},\end{align*}
-
(c) R is independent from
 $(Y_1,\ldots,Y_d)$
.
$(Y_1,\ldots,Y_d)$
.
Let us first show that
![]() $R\to 1$
in probability, as
$R\to 1$
in probability, as
![]() $\beta\to\infty$
. Define
$\beta\to\infty$
. Define
let
![]() $Z\sim\Gamma(\alpha,1)$
, and observe that R and
$Z\sim\Gamma(\alpha,1)$
, and observe that R and
![]() $\big(m_{d,\beta}^{-1}Z\big)^{1/(d+1+2\beta)}$
are identically distributed. We thus compute that
$\big(m_{d,\beta}^{-1}Z\big)^{1/(d+1+2\beta)}$
are identically distributed. We thus compute that
 \begin{align*}{\mathbb{E}}[R] &= {1\over m_{d,\beta}^{1/(d+1+2\beta)}}{\mathbb{E}}\big[Z^{1/(d+1+2\beta)}\big] \\[3pt]&=m_{d,\beta}^{-1/(d+1+2\beta)}{1\over\Gamma(\alpha)}\int_0^\infty z^{1/(d+1+2\beta)}z^{\alpha-1}e^{-z}\,\textrm{d} z\\[3pt]&= \Bigg({2\sqrt{\pi}\Gamma\big({\frac{d}{2}}+\beta+{3\over 2}\big)\over\Gamma\big({\frac{d}{2}}+\beta+1\big)}\Bigg)^{1\over d+1+2\beta}{\Gamma\big(\alpha+{1\over d+1+2\beta}\big)\over \Gamma(\alpha)}=1+O\big(\beta^{-1}\log\beta\big)\end{align*}
\begin{align*}{\mathbb{E}}[R] &= {1\over m_{d,\beta}^{1/(d+1+2\beta)}}{\mathbb{E}}\big[Z^{1/(d+1+2\beta)}\big] \\[3pt]&=m_{d,\beta}^{-1/(d+1+2\beta)}{1\over\Gamma(\alpha)}\int_0^\infty z^{1/(d+1+2\beta)}z^{\alpha-1}e^{-z}\,\textrm{d} z\\[3pt]&= \Bigg({2\sqrt{\pi}\Gamma\big({\frac{d}{2}}+\beta+{3\over 2}\big)\over\Gamma\big({\frac{d}{2}}+\beta+1\big)}\Bigg)^{1\over d+1+2\beta}{\Gamma\big(\alpha+{1\over d+1+2\beta}\big)\over \Gamma(\alpha)}=1+O\big(\beta^{-1}\log\beta\big)\end{align*}
and, similarly,
 \begin{align*}{\mathbb{V}}[R]&= \Bigg({2\sqrt{\pi}\Gamma\big({\frac{d}{2}}+\beta+{3\over 2}\big)\over\Gamma\big({\frac{d}{2}}+\beta+1\big)}\Bigg)^{2\over d+1+2\beta}\Bigg({\Gamma\Big(\alpha+{2\over d+1+2\beta}\Big)\over \Gamma(\alpha)}-{\Gamma\Big(\alpha+{1\over d+1+2\beta}\Big)^2\over \Gamma(\alpha)^2}\Bigg)\\&={\psi^{(1)}(d+1)\over 4\beta^2}+O\big(\beta^{-3}\big)\end{align*}
\begin{align*}{\mathbb{V}}[R]&= \Bigg({2\sqrt{\pi}\Gamma\big({\frac{d}{2}}+\beta+{3\over 2}\big)\over\Gamma\big({\frac{d}{2}}+\beta+1\big)}\Bigg)^{2\over d+1+2\beta}\Bigg({\Gamma\Big(\alpha+{2\over d+1+2\beta}\Big)\over \Gamma(\alpha)}-{\Gamma\Big(\alpha+{1\over d+1+2\beta}\Big)^2\over \Gamma(\alpha)^2}\Bigg)\\&={\psi^{(1)}(d+1)\over 4\beta^2}+O\big(\beta^{-3}\big)\end{align*}
as
![]() $\beta\to\infty$
, by a multiple application of the asymptotic expansion of the gamma function (here,
$\beta\to\infty$
, by a multiple application of the asymptotic expansion of the gamma function (here,
![]() $\psi^{(1)}$
stands for the first polygamma function, that is, the first derivative of
$\psi^{(1)}$
stands for the first polygamma function, that is, the first derivative of
![]() $\ln\Gamma(x)$
). As a consequence, using Chebyshev’s inequality we have that, for any
$\ln\Gamma(x)$
). As a consequence, using Chebyshev’s inequality we have that, for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
as
![]() $\beta\to\infty$
. In other words,
$\beta\to\infty$
. In other words,
![]() $R-{\mathbb{E}}[R]$
converges to zero in probability as
$R-{\mathbb{E}}[R]$
converges to zero in probability as
![]() $\beta\to\infty$
. Since
$\beta\to\infty$
. Since
![]() ${\mathbb{E}}[R]\to 1$
, we also have that R converges in probability to the constant random variable 1, as
${\mathbb{E}}[R]\to 1$
, we also have that R converges in probability to the constant random variable 1, as
![]() $\beta\to\infty$
, by Slutsky’s theorem.
$\beta\to\infty$
, by Slutsky’s theorem.
Next, we claim that
![]() $\sqrt{2\beta}(Y_1,\ldots,Y_d)$
converges in distribution, as
$\sqrt{2\beta}(Y_1,\ldots,Y_d)$
converges in distribution, as
![]() $\beta\to\infty$
, to a d-tuple
$\beta\to\infty$
, to a d-tuple
![]() $(G_1,\ldots,G_d)$
of random vectors in
$(G_1,\ldots,G_d)$
of random vectors in
![]() ${\mathbb{R}}^{d-1}$
with a certain joint density which we will compute. Indeed, the density of
${\mathbb{R}}^{d-1}$
with a certain joint density which we will compute. Indeed, the density of
![]() $\sqrt{2\beta}(Y_1,\ldots,Y_d)$
is given by
$\sqrt{2\beta}(Y_1,\ldots,Y_d)$
is given by
We now let
![]() $\beta\to\infty$
. Using that
$\beta\to\infty$
. Using that
![]() $\big(1-\|y\|^2/(2\beta)\big)^\beta\to e^{-\|y\|^2/2}$
and the standard asymptotics
$\big(1-\|y\|^2/(2\beta)\big)^\beta\to e^{-\|y\|^2/2}$
and the standard asymptotics
![]() $\Gamma(\beta + c_1)/\Gamma(\beta+c_2) \sim \beta^{c_1-c_2}$
, we obtain that the above density converges pointwise to
$\Gamma(\beta + c_1)/\Gamma(\beta+c_2) \sim \beta^{c_1-c_2}$
, we obtain that the above density converges pointwise to
 \begin{equation*}\frac{(d-1)!^{\nu+1}}{ d^{\frac{\nu+1}2} 2^{(\nu+1)(d-1)/2}}\left(\prod\limits_{i=1}^{d-1} {\Gamma\big({i\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)}\right)\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\left(\frac {1}{\sqrt{2\pi}}\right)^{d(d-1)} \prod_{i=1}^d e^{-\|y_i\|^2/2}.\end{equation*}
\begin{equation*}\frac{(d-1)!^{\nu+1}}{ d^{\frac{\nu+1}2} 2^{(\nu+1)(d-1)/2}}\left(\prod\limits_{i=1}^{d-1} {\Gamma\big({i\over 2}\big)\over \Gamma\big({i+\nu+1\over 2}\big)}\right)\Delta_{d-1}(y_1,\ldots,y_d)^{\nu+1}\left(\frac {1}{\sqrt{2\pi}}\right)^{d(d-1)} \prod_{i=1}^d e^{-\|y_i\|^2/2}.\end{equation*}
By Scheffé’s lemma, the tuple
![]() $\sqrt{2\beta}(Y_1,\ldots,Y_d)$
converges weakly to the tuple
$\sqrt{2\beta}(Y_1,\ldots,Y_d)$
converges weakly to the tuple
![]() $(G_1,\ldots,G_d)$
with the above joint density. A related result without the volume-power weighting can be found in Lemma 1.1 in [Reference Kabluchko, Thäle and Zaporozhets17].
$(G_1,\ldots,G_d)$
with the above joint density. A related result without the volume-power weighting can be found in Lemma 1.1 in [Reference Kabluchko, Thäle and Zaporozhets17].
Now, again using Slutsky’s theorem together with the continuous mapping theorem, we conclude that, as
![]() $\beta\to\infty$
, the random simplex
$\beta\to\infty$
, the random simplex
converges in distribution (on the space of convex bodies in
![]() ${\mathbb{R}}^{d-1}$
supplied with the Hausdorff distance) to a weighted Gaussian simplex
${\mathbb{R}}^{d-1}$
supplied with the Hausdorff distance) to a weighted Gaussian simplex
![]() ${\textrm{conv}}(G_1,\ldots,G_d)$
; the continuity of the map involved is guaranteed by [Reference Schneider and Weil31, Theorem 12.3.5]. Using once again the continuous mapping theorem, this implies that, as
${\textrm{conv}}(G_1,\ldots,G_d)$
; the continuity of the map involved is guaranteed by [Reference Schneider and Weil31, Theorem 12.3.5]. Using once again the continuous mapping theorem, this implies that, as
![]() $\beta\to\infty$
,
$\beta\to\infty$
,
for all
![]() $k\in\{1,\ldots,d\}$
, since angle sums are invariant under rescaling. As they are also bounded, the sequence of random variables
$k\in\{1,\ldots,d\}$
, since angle sums are invariant under rescaling. As they are also bounded, the sequence of random variables
![]() $\sigma_k\big(\sqrt{2\beta}Z_{\beta,\nu}\big)$
,
$\sigma_k\big(\sqrt{2\beta}Z_{\beta,\nu}\big)$
,
![]() $\beta>-1$
, is uniformly integrable, and we have that
$\beta>-1$
, is uniformly integrable, and we have that
However, by taking the limit as
![]() $\beta\to\infty$
in [Reference Kabluchko, Thäle and Zaporozhets17, Remark 4.2], we have that the expected angle sum of the weighted Gaussian simplex
$\beta\to\infty$
in [Reference Kabluchko, Thäle and Zaporozhets17, Remark 4.2], we have that the expected angle sum of the weighted Gaussian simplex
![]() ${\textrm{conv}}(G_1,\ldots,G_d)$
coincides with the expected angle sum of a standard (unweighted) Gaussian simplex
${\textrm{conv}}(G_1,\ldots,G_d)$
coincides with the expected angle sum of a standard (unweighted) Gaussian simplex
![]() ${\textrm{conv}}(N_1,\ldots,N_d)$
, where
${\textrm{conv}}(N_1,\ldots,N_d)$
, where
![]() $N_1,\ldots,N_d$
are i.i.d. standard Gaussian random vectors in
$N_1,\ldots,N_d$
are i.i.d. standard Gaussian random vectors in
![]() ${\mathbb{R}}^{d-1}$
. Finally, let
${\mathbb{R}}^{d-1}$
. Finally, let
![]() $\Sigma_{d-1}$
be a regular simplex in
$\Sigma_{d-1}$
be a regular simplex in
![]() ${\mathbb{R}}^{d-1}$
and recall from [Reference Götze, Kabluchko and Zaporozhets9, Reference Kabluchko and Zaporozhets18] that the expected angle sum
${\mathbb{R}}^{d-1}$
and recall from [Reference Götze, Kabluchko and Zaporozhets9, Reference Kabluchko and Zaporozhets18] that the expected angle sum
![]() ${\mathbb{E}}[\sigma_k({\textrm{conv}}(N_1,\ldots,N_d))]$
coincides with
${\mathbb{E}}[\sigma_k({\textrm{conv}}(N_1,\ldots,N_d))]$
coincides with
![]() $\sigma_k(\Sigma_{d-1})$
. We have thus shown that
$\sigma_k(\Sigma_{d-1})$
. We have thus shown that
 \begin{align*}\lim_{\beta\to\infty}{\mathbb{E}}\sigma_k\big(Z_{\beta,\nu}\big) &=\lim_{\beta\to\infty}{\mathbb{E}}\big[\sigma_k\big(\sqrt{2\beta}Z_{\beta,\nu}\big)\big] \\&= {\mathbb{E}}\big[\sigma_k\big({\textrm{conv}}(G_1,\ldots,G_d)\big)\big]\\&= {\mathbb{E}}\big[\sigma_k\big({\textrm{conv}}(N_1,\ldots,N_d)\big)\big]\\&= \sigma_k\big(\Sigma_{d-1}\big),\end{align*}
\begin{align*}\lim_{\beta\to\infty}{\mathbb{E}}\sigma_k\big(Z_{\beta,\nu}\big) &=\lim_{\beta\to\infty}{\mathbb{E}}\big[\sigma_k\big(\sqrt{2\beta}Z_{\beta,\nu}\big)\big] \\&= {\mathbb{E}}\big[\sigma_k\big({\textrm{conv}}(G_1,\ldots,G_d)\big)\big]\\&= {\mathbb{E}}\big[\sigma_k\big({\textrm{conv}}(N_1,\ldots,N_d)\big)\big]\\&= \sigma_k\big(\Sigma_{d-1}\big),\end{align*}
and the proof is complete.
6.3. Face intensities in
 $\beta$
-tessellations
$\beta$
-tessellations
Given a stationary tessellation
![]() ${\mathcal{T}}$
on
${\mathcal{T}}$
on
![]() ${\mathbb{R}}^{d-1}$
, one can introduce the notion of face intensities for faces of all dimensions
${\mathbb{R}}^{d-1}$
, one can introduce the notion of face intensities for faces of all dimensions
![]() $j\in\{0,\ldots, d-1\}$
as follows (see [Reference Schneider and Weil31, p. 450 and Section 4.1]). Fix some center function
$j\in\{0,\ldots, d-1\}$
as follows (see [Reference Schneider and Weil31, p. 450 and Section 4.1]). Fix some center function
![]() $z\,:\,{\mathcal{C}}^{\prime} \to {\mathbb{R}}^{d-1}$
. Let
$z\,:\,{\mathcal{C}}^{\prime} \to {\mathbb{R}}^{d-1}$
. Let
![]() ${\mathcal{F}}_{j}({\mathcal{T}})$
be the set of all j-dimensional faces of the cells of the tessellation
${\mathcal{F}}_{j}({\mathcal{T}})$
be the set of all j-dimensional faces of the cells of the tessellation
![]() ${\mathcal{T}}$
. By convention, each face is counted once even if it is a face of two or more cells. Consider the point process
${\mathcal{T}}$
. By convention, each face is counted once even if it is a face of two or more cells. Consider the point process
on
![]() ${\mathbb{R}}^{d-1}$
and note that it is stationary because the center function is required to be translation-invariant. The intensity of j-dimensional cells of
${\mathbb{R}}^{d-1}$
and note that it is stationary because the center function is required to be translation-invariant. The intensity of j-dimensional cells of
![]() ${\mathcal{T}}$
is just the intensity of this point process, that is,
${\mathcal{T}}$
is just the intensity of this point process, that is,
In the next theorem we compute the cell intensities in the
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^\prime$
-Delaunay tessellations
$\beta^\prime$
-Delaunay tessellations
![]() ${\mathcal{D}}_{\beta}$
and
${\mathcal{D}}_{\beta}$
and
![]() ${\mathcal{D}}_\beta^\prime$
on
${\mathcal{D}}_\beta^\prime$
on
![]() ${\mathbb{R}}^{d-1}$
.
${\mathbb{R}}^{d-1}$
.
Theorem 6. For all
![]() $j\in\{0,\ldots, d-1\}$
and
$j\in\{0,\ldots, d-1\}$
and
![]() $\beta\geq -1$
(in the
$\beta\geq -1$
(in the
![]() $\beta$
case) or
$\beta$
case) or
![]() $\beta>(d+1)/2$
(in the
$\beta>(d+1)/2$
(in the
![]() $\beta^\prime$
case), we have
$\beta^\prime$
case), we have
 \begin{equation*}\gamma_j\big({\mathcal{D}}_{\beta}\big) = \frac {\mathbb J_{d,j+1}\!\left(\beta + \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}\big)},\qquad \gamma_j\big({\mathcal{D}}_{\beta}^\prime\big) = \frac {\mathbb J_{d,j+1}^\prime\left(\beta - \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}^\prime\big)},\end{equation*}
\begin{equation*}\gamma_j\big({\mathcal{D}}_{\beta}\big) = \frac {\mathbb J_{d,j+1}\!\left(\beta + \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}\big)},\qquad \gamma_j\big({\mathcal{D}}_{\beta}^\prime\big) = \frac {\mathbb J_{d,j+1}^\prime\left(\beta - \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}^\prime\big)},\end{equation*}
where
![]() ${\mathbb{E}}\ \textrm{Vol} \Big(Z_{\beta,0}^{(\prime)}\Big)$
is as in Theorem 2 and
${\mathbb{E}}\ \textrm{Vol} \Big(Z_{\beta,0}^{(\prime)}\Big)$
is as in Theorem 2 and
 \begin{align*}\mathbb J_{d,j+1}\!\left(\beta + \frac {1} 2\right)&=\binom d{j+1} \int_{-\infty}^{+\infty} c_{\frac{(2\beta + d) d}2} (\cosh u)^{- (2\beta + d) d - 2}\\&\quad\times\left(\frac 12 + 1 \int_0^u c_{\frac{2\beta + d - 1}{2}} (\cosh v)^{2\beta + d}{\rm d} v \right)^{d-j-1} {\rm d} u,\\\mathbb J_{d,j+1}^\prime\!\left(\beta - \frac {1} 2\right)&=\binom d{j+1} \int_{-\infty}^{+\infty} c_{\frac{(2\beta-d) d}2}^\prime (\cosh u)^{-(2\beta-d) d + 1}\\&\quad\times\left(\frac 12 + 1 \int_0^u c_{\frac{2\beta - d - 1}{2}}^\prime (\cosh v)^{2\beta-d-1}{\rm d} v \right)^{d-j-1} {\rm d} u.\end{align*}
\begin{align*}\mathbb J_{d,j+1}\!\left(\beta + \frac {1} 2\right)&=\binom d{j+1} \int_{-\infty}^{+\infty} c_{\frac{(2\beta + d) d}2} (\cosh u)^{- (2\beta + d) d - 2}\\&\quad\times\left(\frac 12 + 1 \int_0^u c_{\frac{2\beta + d - 1}{2}} (\cosh v)^{2\beta + d}{\rm d} v \right)^{d-j-1} {\rm d} u,\\\mathbb J_{d,j+1}^\prime\!\left(\beta - \frac {1} 2\right)&=\binom d{j+1} \int_{-\infty}^{+\infty} c_{\frac{(2\beta-d) d}2}^\prime (\cosh u)^{-(2\beta-d) d + 1}\\&\quad\times\left(\frac 12 + 1 \int_0^u c_{\frac{2\beta - d - 1}{2}}^\prime (\cosh v)^{2\beta-d-1}{\rm d} v \right)^{d-j-1} {\rm d} u.\end{align*}
Proof. For concreteness, we consider the
![]() $\beta$
case. According to Theorem 10.1.3 of [Reference Schneider and Weil31], the cell intensities of
$\beta$
case. According to Theorem 10.1.3 of [Reference Schneider and Weil31], the cell intensities of
![]() ${\mathcal{D}}_{\beta}$
satisfy
${\mathcal{D}}_{\beta}$
satisfy
where
![]() $Z_{\beta,0}$
is the typical cell of the tessellation
$Z_{\beta,0}$
is the typical cell of the tessellation
![]() ${\mathcal{D}}_{\beta}$
(that is, a random simplex distributed according to
${\mathcal{D}}_{\beta}$
(that is, a random simplex distributed according to
![]() ${\mathbb{P}}_{\beta,0}$
). The intensity of the cells of maximal dimension
${\mathbb{P}}_{\beta,0}$
). The intensity of the cells of maximal dimension
![]() $d-1$
is known to satisfy
$d-1$
is known to satisfy
see [Reference Schneider and Weil31, Equation (10.4)]. On the other hand, by Theorem 4,
and the same theorem yields also an explicit expression for
![]() $\mathbb J_{d,j+1}\big(\beta + \frac {1} 2\big)$
. Taking these three equations together completes the proof in the
$\mathbb J_{d,j+1}\big(\beta + \frac {1} 2\big)$
. Taking these three equations together completes the proof in the
![]() $\beta$
case. The
$\beta$
case. The
![]() $\beta^\prime$
case is similar.
$\beta^\prime$
case is similar.
Using duality, we can also compute the face intensities of the
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^\prime$
-Voronoi tessellations.
$\beta^\prime$
-Voronoi tessellations.
Proposition 3. The face intensities of
![]() ${\mathcal{D}}_{\beta}^{(\prime)}$
and
${\mathcal{D}}_{\beta}^{(\prime)}$
and
![]() ${\mathcal{V}}_{\beta}^{(\prime)}$
are related via
${\mathcal{V}}_{\beta}^{(\prime)}$
are related via
Proof. Since the
![]() $\beta^{(^{\prime})}$
-Voronoi tessellation
$\beta^{(^{\prime})}$
-Voronoi tessellation
![]() ${\mathcal{V}}_{\beta}^{(\prime)}$
is dual to the
${\mathcal{V}}_{\beta}^{(\prime)}$
is dual to the
![]() $\beta^{(\prime)}$
-Delaunay tessellation
$\beta^{(\prime)}$
-Delaunay tessellation
![]() ${\mathcal{D}}_{\beta}^{(\prime)}$
, each
${\mathcal{D}}_{\beta}^{(\prime)}$
, each
![]() $(k-1)$
-dimensional face of
$(k-1)$
-dimensional face of
![]() ${\mathcal{D}}_\beta^{(\prime)}$
corresponds to a
${\mathcal{D}}_\beta^{(\prime)}$
corresponds to a
![]() $(d-k)$
-dimensional face of
$(d-k)$
-dimensional face of
![]() ${\mathcal{V}}_\beta^{(^{\prime})}$
, and the claim follows.
${\mathcal{V}}_\beta^{(^{\prime})}$
, and the claim follows.
6.4. Expected face numbers of the typical
 $\beta$
-Voronoi cell
$\beta$
-Voronoi cell
In the next theorem we compute the expected
f
-vector of the typical cell of the
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^\prime$
-Voronoi tessellations
$\beta^\prime$
-Voronoi tessellations
![]() ${\mathcal{V}}_{\beta}$
and
${\mathcal{V}}_{\beta}$
and
![]() ${\mathcal{V}}_\beta^\prime$
.
${\mathcal{V}}_\beta^\prime$
.
Theorem 7. Let
![]() $Y_{\beta}^{(\prime)}$
be the typical cell of the
$Y_{\beta}^{(\prime)}$
be the typical cell of the
![]() $\beta^{(\prime)}$
-Voronoi tessellation
$\beta^{(\prime)}$
-Voronoi tessellation
![]() ${\mathcal{V}}_{\beta}^{(\prime)}$
in
${\mathcal{V}}_{\beta}^{(\prime)}$
in
![]() ${\mathbb{R}}^{d-1}$
, where, as usual,
${\mathbb{R}}^{d-1}$
, where, as usual,
![]() $\beta \geq -1$
in the
$\beta \geq -1$
in the
![]() $\beta$
case and
$\beta$
case and
![]() $\beta>(d+1)/2$
in the
$\beta>(d+1)/2$
in the
![]() $\beta^\prime$
case. Then, for all
$\beta^\prime$
case. Then, for all
![]() $k\in \{1,\ldots,d\}$
,
$k\in \{1,\ldots,d\}$
,
 \begin{equation*}{\mathbb{E}} f_{d-k}(Y_{\beta}) = k \gamma_{k-1} ({\mathcal{D}}_\beta) = \frac {k \mathbb J_{d,k}\!\left(\beta + \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}\big)},\quad{\mathbb{E}} f_{d-k}(Y_{\beta}^\prime) = k \gamma_{k-1} ({\mathcal{D}}_\beta^\prime) = \frac {k \mathbb J_{d,k}^\prime\left(\beta - \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}^\prime\big)}.\end{equation*}
\begin{equation*}{\mathbb{E}} f_{d-k}(Y_{\beta}) = k \gamma_{k-1} ({\mathcal{D}}_\beta) = \frac {k \mathbb J_{d,k}\!\left(\beta + \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}\big)},\quad{\mathbb{E}} f_{d-k}(Y_{\beta}^\prime) = k \gamma_{k-1} ({\mathcal{D}}_\beta^\prime) = \frac {k \mathbb J_{d,k}^\prime\left(\beta - \frac {1} 2\right)} {{\mathbb{E}}\ {\textrm{Vol}}\big(Z_{\beta,0}^\prime\big)}.\end{equation*}
Proof. Let us consider the
![]() $\beta$
case. Note that the
$\beta$
case. Note that the
![]() $\beta$
-Voronoi tessellation
$\beta$
-Voronoi tessellation
![]() ${\mathcal{V}}_\beta$
is normal by Theorem 10.2.3 of [Reference Schneider and Weil31] (for
${\mathcal{V}}_\beta$
is normal by Theorem 10.2.3 of [Reference Schneider and Weil31] (for
![]() $\beta=-1$
) or by Lemmas 2 and 3 (for
$\beta=-1$
) or by Lemmas 2 and 3 (for
![]() $\beta>-1$
). Hence, Theorem 10.1.2 of [Reference Schneider and Weil31] implies that
$\beta>-1$
). Hence, Theorem 10.1.2 of [Reference Schneider and Weil31] implies that
By Proposition 3, we also have
![]() $\gamma_{k-1}\big({\mathcal{D}}_{\beta}\big) = \gamma_{d-k}({\mathcal{V}}_{\beta})$
. Taking these equalities together and recalling Theorem 6 yields the claim in the
$\gamma_{k-1}\big({\mathcal{D}}_{\beta}\big) = \gamma_{d-k}({\mathcal{V}}_{\beta})$
. Taking these equalities together and recalling Theorem 6 yields the claim in the
![]() $\beta$
case. The
$\beta$
case. The
![]() $\beta^\prime$
case is similar.
$\beta^\prime$
case is similar.
Remark 12. For
![]() $\beta=-1$
,
$\beta=-1$
,
![]() $Y_{-1}$
is the typical cell in the classical Poisson–Voronoi tessellation in
$Y_{-1}$
is the typical cell in the classical Poisson–Voronoi tessellation in
![]() ${\mathbb{R}}^{d-1}$
. The expected f-vector of
${\mathbb{R}}^{d-1}$
. The expected f-vector of
![]() $Y_{-1}$
was determined in [Reference Kabluchko14, Theorem 2.8], where
$Y_{-1}$
was determined in [Reference Kabluchko14, Theorem 2.8], where
![]() $Y_{-1}$
was denoted by
$Y_{-1}$
was denoted by
![]() ${\mathcal{V}}_{d-1}$
. In [Reference Kabluchko, Thäle and Zaporozhets17], we showed that the expected f-vector of
${\mathcal{V}}_{d-1}$
. In [Reference Kabluchko, Thäle and Zaporozhets17], we showed that the expected f-vector of
![]() $Y_{-1}$
is related to the angle sums of
$Y_{-1}$
is related to the angle sums of
![]() $\beta^\prime$
-simplices, whereas the above theorem expresses it in terms of the values
$\beta^\prime$
-simplices, whereas the above theorem expresses it in terms of the values
![]() $\mathbb J_{d,k}\big({-}\frac {1} 2\big)$
originating from
$\mathbb J_{d,k}\big({-}\frac {1} 2\big)$
originating from
![]() $\beta$
-simplices. For the typical Voronoi cell on the sphere, there also exist similar representations in terms of both
$\beta$
-simplices. For the typical Voronoi cell on the sphere, there also exist similar representations in terms of both
![]() $\beta$
- and
$\beta$
- and
![]() $\beta^\prime$
-simplices [Reference Kabluchko and Thäle16].
$\beta^\prime$
-simplices [Reference Kabluchko and Thäle16].
Acknowledgements
We thank the referees for their careful reading and their comments, which helped to significantly improve the paper. In particular, we are grateful to the referee who suggested an alternative proof of Lemma 2 which is more elegant than the original one. We would like to thank Claudia Redenbach (Kaiserslautern) for pointing us to the CGAL Project, which we used to create the simulations shown in Figure 4 and Figure 5.
Funding information
A. G. was partially supported by the Deutsche Forschungsgemeinschaft (DFG) via RTG 2131, High-Dimensional Phenomena in Probability—Fluctuations and Discontinuity. Z. K. and C. T. were supported by the DFG priority program SPP 2265, Random Geometric Systems.A. G. and Z. K. were supported by the DFG under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics—Geometry—Structure.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.