1. INTRODUCTION
Electron acceleration by interaction of high-intensity laser pulse with plasma is of great interest because of its tremendous applicability in fundamental research and industrial use. There are several mechanisms for laser-driven electron acceleration, such as direct laser acceleration and acceleration by ponderomotive force of laser-induced in various forms (Tajima & Dawson, Reference Tajima and Dawson1979; Khachatryan, Reference Khachatryan2002). The ponderomotive force accelerates the electron or excites a large amplitude plasma wave that can accelerate electrons indirectly. Many schemes of particle acceleration have been proposed since long-time back and recent developments are also there in the acceleration process. Optical mixing of laser light in a plasma and electron acceleration by relativistic electron plasma waves has been studied by Ebrahim in (Reference Ebrahim1994). Pukhov (Reference Pukhov2004) investigated the particle acceleration process in relativistic laser channels; multi-GeV energy gain in a plasma wakefield accelerator and low-energy spread electron bunches (100 MeV–1 GeV) from laser wakefield acceleration has been studied by Hogan et al. (Reference Hogan, Barnes, Clayton, Decker, Emma, Huang, Iverson, Johnson, Joshi, Katsouleas, Krejcik, Lu, Marsh, Mori, Nuggl, Connel, Oz, Siemann and Walz2005), Robinson (Reference Robinson2006), etc. over the last decade. Kinetic modeling of intense short laser pulses propagating in plasmas as well as the ponderomotive effects on electron acceleration by plasma wave by short pulse lasers has been studied by Mora and Antonsen (Reference Mora and Antonsen1997) and Liu and Tripathi (Reference Liu and Tripathi2005). Ponderomotive acceleration of electron by a self-focused laser pulse has been studied by Singh et al. (Reference Singh, Sharma and Tripathi2010). The interaction of arbitrarily polarized laser pulse with a tenuous plasma in the acceleration process has been studied by Sazergari et al. (Reference Sazergari, Muizale and Shokui2006). Numerical study has been carried out from much earlier times. Hartemann et al. (Reference Hartemann, Fochs, Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995) studied the nonlinear ponderomotive scattering of relativistic electrons by intense laser field at focus in vacuum by employing one-dimensional (1D) plane wave pulse and 2D Gaussian pulses. Later, Pukhov and Vehn (Reference Pukhov and Vehn1999) in their three-dimensional particle-in-cell (3D-PIC) simulation of intense short laser pulse interaction with plasma have observed the strong flow of relativistic electrons axially, moving with the laser pulse and generating 100 MG azimuthal magnetic field. The electron energies are far in excess of ponderomotive potential energy and the acceleration is a consequence of direct exchange of energy between electron and laser via betatron resonance phenomenon. Later in the same year Gahn (Reference Gahn1999) experimentally observed generation of multi-MeV electron beam by direct laser acceleration in high-density plasma channels. Tsakiris et al. (Reference Tsakiris, Gahn and Tripathi2000) developed an analytical theory and a fully relativistic 3D single-particle code for direct laser acceleration of electron in radial electrical and azimuthal magnetic fields. Effect on an axial magnetic field and ion space charge on laser beat wave acceleration and a surfatron acceleration of electron has been studied by Prasad et al. (Reference Prasad, Singh and Tripathi2009). Tanimoto (Reference Tanimoto2003) studied the effect of self-induced azimuthal magnetic field on the direct electron acceleration by laser with stochastic phase disturbance. They found that apart from beam collimation electrons are accelerated to ultrahigh energies that are greater than the ponderomotive energy and that the acceleration is enhanced by increasing the strength of magnetic field. Liu et al. (Reference Liu, He and Chen2004) showed that the electron acceleration depends on laser intensity and the ratio of cyclotron frequency to laser frequency. Yu et al. (Reference Yu, Chen, Yu, Qian, Lu and Koyama2002) examined similar configuration using linearly polarized laser. They have obtained electron acceleration to relativistic energies using weak magnetic field. The dependence of high-energy electron generation on the pulse duration of a high-intensity LFEX laser was experimentally investigated by Kojima (Reference Kojima2016).
For plasma where the density is quite high and the de-Broglie thermal wavelength associated with the charge particle, that is,
${\rm \lambda} _{\rm B} = \hbar /2{\rm \pi} mk_{\rm B} T$
approaches the electron Fermi wavelength λFe and exceeds the electron Debye radius
${\rm \lambda} _{{\rm De}} ({\rm viz.,} {\rm \lambda} _{\rm B} \sim {\rm \lambda} _{{\rm Fe}} \gt {\rm \lambda} _{{\rm De}} ),$
the quantum effects become important. Furthermore, the quantum effects associated with the strong density correlation start playing a significant role when λB becomes of the same order or larger than the average inter-particle distance
$(\sim n_0^{ - 1{\rm /}3} )$
, that is,
$n_0 {\rm \lambda} _{\rm B}^{\rm 3} \ge 1$
hold in degenerate plasma. However, the other condition for degeneracy is that the Fermi temperture T
F, which is related to the equilibrium density n
0 of the charged particles must be greater than the thermal temperture T of the system. The high-density, low-temperature quantum Fermi plasma is significantly different from the low-density, high-temperature ‘classical plasma’ obeying Maxwell–Boltzmann distribution. Over the last decade, there has been a growing interest in investigating new aspects of dense quantum plasmas by developing the quantum hydrodynamic (QHD) equations (Gardner & Ringhofer, Reference Gardner and Ringhofer1996). The QHD equations are useful for studying numerous collective effects (Shukla & Eliasson, Reference Shukla and Eliasson2006) involving different quantum forces. Haas et al. (Reference Haas, Manfredi and Feix2000) presented a quantum multistream model by using a nonlinear system and derived the dispersion relations for one and two-stream plasma instability. Later, Anderson (Reference Anderson2002) examined the statistical behavior of quantum plasma. Propagation of short-wavelength electromagnetic waves through magnetized quantum plasmas have been studied (Shokari et al., Reference Shokari, Khorashady and Pramana2003; Shukla, Reference Shukla2006; Ali, Reference Ali2006). The instabilities arising in quantum plasmas have also been studied (Ludin, Reference Ludin2007; Bret, Reference Bret2008). Possibilities of magnetic field generation by ponderomotive force of electromagnetic waves in dense plasma has been explored (Shukla et al., Reference Shukla, Shukla and Stenflo2010; Kumar & Tewari, Reference Kumar and Tewari2012). Recently, it has been shown that the quantum effects can be important even in the classical regime (Opher et al., Reference Opher, Silva and Dauger2001; Brodin et al., Reference Brodin, Marklund and Manfredi2008).
In the present work, we focus on the recently developed QHD model (Shukla & Eliasson, Reference Shukla and Eliasson2006; Haas et al. Reference Haas, Manfredi and Feix2000). The QHD model consists of a set of equations describing the transport of charge density, momentum (including the Bohm potential) and energy in a charged particle system interacting through a self-consistent electrostatic potential. QHD is a macroscopic model and application is limited to those systems that are large compared with Fermi length of the species in the system. The advantages of the QHD model over kinetic descriptions are its numerical efficiency, the direct use of the macroscopic variables of interest such as momentum and energy and the easy way the boundary conditions are implemented.
In this paper, we have examined the possibilities of electron acceleration by a circularly polarized laser pulse in magnetized quantum plasma. The basic mechanism involves acceleration of electron by the axial gradient in the ponderomotive potential of the laser. The ponderomotive force of the laser is resonantly enhanced when Doppler-shifted laser frequency equals the cyclotron frequency. Such a study has not been reported in literatures so far.
2. THEORETICAL FORMULATION
Consider the propagation of a right circularly polarized laser pulse in quantum plasma in the direction of the static axial magnetic field
$b_0 \hat z.$
The laser fields being (Sharma & Tripathi, Reference Sharma and Tripathi2009)
$$\eqalign{E_x & = A\left( {t - \displaystyle{z \over {{\rm \eta} _{\rm g} c}}} \right)\exp \left[ { - i{\rm \omega} \left( {t - \displaystyle{{{\rm \eta} z} \over c}} \right)} \right],\quad E_y = iE_x ; \cr B_y = & \left[ {{\rm \eta} A + i\displaystyle{{(1 - {\rm \eta} {\rm \eta} _{\rm g} )} \over {{\rm \eta} _{\rm g} {\rm \omega}}} \displaystyle{{\partial A} \over {\partial t}}} \right] \exp \left[ { - i{\rm \omega} \left( {t - \displaystyle{{{\rm \eta} z} \over c}} \right)} \right],\quad B_x = iB_y ;} $$
where A for a Gaussian pulse is given by
$$A^2 = A_0^2 \exp \left[ {\displaystyle{{ - (t - z/{\rm \eta} _{\rm g} c - t_0 )^2} \over {{\rm \tau} ^2}}} \right],$$
${\rm \eta} _{\rm g} c = {\rm \eta} c/[1 + {\rm \omega} _{\rm p}^{\rm 2} {\rm \omega} _{\rm b} /2{\rm \omega} ({\rm \omega} - {\rm \omega} _{\rm b} )^2 {\rm ]}$
is the group velocity of laser pulse; τ is the laser pulse duration,
${\rm \eta} = {\rm [}1 - {\rm \omega} _{\rm p}^{\rm 2} /$
${\rm \omega} ({\rm \omega} - {\rm \omega} _{\rm b} ){\rm ]}^{1/2} $
is the refractive index of plasma; ωp is the electron plasma frequency; ωb = eb
0/mc is the cyclotron frequency; −e is the electronic charge; m is the rest mass of electron; and c is the speed of light. The refractive index is crucially dependent on the static magnetic field, through the term (ω − ωb). This is due to the fact that the static magnetic field tends to rotate the electron. The laser field also rotates the electron, and hence at resonance (ω = ωb), the two rotation frequencies resonate resulting in considerable enhancement in electron response and hence the refractive index.
The QHD equations (Jung, Reference Jung2013; Li et al., Reference Li, Wu, Yang and Chu2014; Seadway, Reference Seadway2014; Wallin et al., Reference Wallin, Zamanian and Brodin2014) governing the motion of electron in the presence of laser field and the static magnetic field are given by
$$\eqalign{& \vec F = \displaystyle{{d\vec p} \over {dt}} = - e\vec E - \displaystyle{e \over {{\rm \gamma} mc}}(\vec p \times \vec B) - \displaystyle{{v_{\rm F}^{\rm 2}} \over {3n_0^2}} \displaystyle{{\nabla n^3} \over n} \cr & \qquad + \displaystyle{{\hbar ^2} \over {2m_{\rm e}}} \nabla \left( {\displaystyle{1 \over {\sqrt n}} \nabla ^2 \sqrt n} \right)} $$
and the continuity equation
$$\displaystyle{{\partial n} \over {\partial t}} + \nabla. \left( {\displaystyle{{n\vec p} \over {{\rm \gamma} m}}} \right) = 0,$$
where n = (n
0 + n
(1)) is the electron density, m is the electron's rest mass,
$\hbar $
is the Planck's constant divided by 2π, and
$v_{\rm F} = [\hbar /m)(3{\rm \pi} ^2 n)^{1/3} ]$
is the Fermi velocity. The third term on the right-hand side of Eq. (1) denotes the Fermi electron pressure
$(P = mv_{\rm F}^{\rm 2} n^3 /3n_0^3 )$
. The fourth term is the quantum Bohm force and is due to the quantum corrections in the density fluctuation. The classical equation may be recovered in the limit of
$\hbar = 0$
. The ponderomotive force of the high-frequency laser pulse drives longitudinal waves with a frequency much smaller than ω, but fast enough for the dynamics to take place on the electron time scale. The ions form a neutralizing background in the dense plasma. Perturbatively expanding Eqs. (1) and (2) for first order of the electromagnetic field, we get
$$\eqalign{ \displaystyle{{d\vec p^{\,(1)}} \over {dt}} &= - e\vec E^{(1)} - \displaystyle{e \over {{\rm \gamma} _0 mc}}\left[ {\vec B^{(0)} \times \vec p^{\,(1)}} \right] - \displaystyle{{v_{\rm F}^{\rm 2}} \over {n_0}} \nabla n^{(1)} \cr & \quad + \displaystyle{{\hbar ^2} \over {4m^2}} \left( {\displaystyle{1 \over {n_0}} \nabla (\nabla ^2 n^{(1)} )} \right),}$$
$$\displaystyle{{\partial n^{(1)}} \over {\partial t}} + \displaystyle{{n_0} \over {{\rm \gamma} _0 m}}(\nabla. \vec p^{\,(1)} ) = 0,$$
where, p (1) is the quiver momentum. The fourth term of Eq. (3a) has been obtained by using perturbative expansion (Cao & Ren, Reference Cao and Ren2008)
$$\eqalign{\nabla \left( {\displaystyle{1 \over {\sqrt n}} \nabla ^2 \sqrt n} \right) = & \displaystyle{1 \over {n_0}} \left[ {\displaystyle{1 \over 2}\nabla \nabla ^2 n^{(1)} - \displaystyle{1 \over {2n_0}} \nabla n^{(1)} \nabla ^2 n_0} \right. \cr & - \displaystyle{1 \over {4n_0}} \nabla (2\nabla n_0. \nabla n^{(1)} ) + \displaystyle{1 \over {4n_0 ^2}} n^{^{(1)}} \nabla (\nabla n_0 )^2 \cr & + \displaystyle{1 \over {2n_0^2}} (\nabla n_0 )^2 \nabla n^{(1)} + \displaystyle{1 \over {n_0^2}} (\nabla n_0. \nabla n^{(1)} )\nabla n_0 \cr &{\hskip2pt} \left. { - \displaystyle{1 \over {n_0^3}} (\nabla n_{\rm 0} )^2 n^{(1)} \nabla n_0} \right].} $$
Thus, the electron motion in the presence of laser and guiding magnetic fields is described by
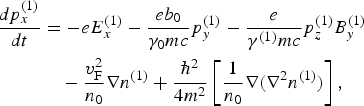$$\eqalign{ \displaystyle{{dp_x^{(1)}} \over {dt}} &= - eE_x^{(1)} - \displaystyle{{eb_0} \over {{\rm \gamma} _0 mc}}p_y^{(1)} - \displaystyle{e \over {{\rm \gamma} ^{(1)} mc}}p_z^{(1)} B_y^{(1)} \cr & \quad - \displaystyle{{v_{\rm F}^{\rm 2}} \over {n_0}} \nabla n^{(1)} + \displaystyle{\hbar^2\over {4m^2}} \left[ {\displaystyle{1 \over {n_0}} \nabla (\nabla ^2 n^{(1)} )} \right],}$$
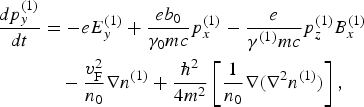$$\eqalign{ \displaystyle{{dp_y^{(1)}} \over {dt}} &= - eE_y^{(1)} + \displaystyle{{eb_0} \over {{\rm \gamma} _0 mc}}p_x^{(1)} - \displaystyle{e \over {{\rm \gamma} ^{(1)} mc}}p_z^{(1)} B_x^{(1)} \cr & \quad - \displaystyle{{v_{\rm F}^{\rm 2}} \over {n_0}} \nabla n^{(1)} + \displaystyle{{\hbar^2} \over {4m^2}} \left[ {\displaystyle{1 \over {n_0}} \nabla (\nabla ^2 n^{(1)} )} \right],} $$
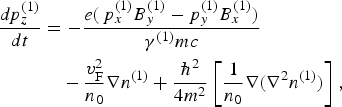$$\eqalign{ \displaystyle{{dp_z^{(1)}} \over {dt}} &= - \displaystyle{{e(\,p_x^{(1)} B_y^{(1)} - p_y^{(1)} B_x^{(1)} )} \over {{\rm \gamma} ^{(1)} mc}} \cr & \quad - \displaystyle{{v_{\rm F}^2} \over {n_0}} \nabla n^{(1)} + \displaystyle{{\hbar ^2} \over {4m^2}} \left[ {\displaystyle{1 \over {n_0}} \nabla (\nabla ^2 n^{(1)} )} \right],}$$
where
${\rm \gamma} ^{(1)} = (1 + (\,p_x^{(1)2} /m^{2} c^{2} ) + (\,p_y^{(1)2} /m^{2} c^{2} ) + (\,p_z^{(1)2} /$
$m^2 c^2 ))^{1/2} $
. Assuming the perturbed density to vary as n
(1) = n
1 (t − (z/ηg
c))exp [− iω (t − (ηz/c))] and simultaneously solving Eqs. (4a) and (4b), we get the transverse momentum as
$$p_x^{(1)} = ({\rm \beta} + n_1 {\rm \beta} _{\rm q} )\left( {t - \displaystyle{z \over {{\rm \eta} _{\rm g} c}}} \right)\exp \left[ { - i{\rm \omega} \left( {t - \displaystyle{{{\rm \eta} z} \over c}} \right)} \right],$$
$$p_y^{(1)} = ip_x^{(1)}, $$
where
$$\eqalign{{\rm \beta} = & - \displaystyle{{e(\partial A/\partial t)} \over {{\rm \omega} _{\rm b}^{\rm 2} [({\rm \omega} /{\rm \omega} _{\rm b} )(1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} )) - (1/{\rm \gamma} _0 )]^2}} \left[ \left( {1 - \displaystyle{{P_z {\rm \eta}} \over {{\rm \gamma} ^{(1)}}}} \right)^2 \right. \cr &\quad \left. - \displaystyle{{{\rm \omega} _{\rm b} P_z (1 - {\rm \eta} {\rm \eta} _{\rm g} )} \over {{\rm \eta} _{\rm g} {\rm \omega} {\rm \gamma} ^{(1) 2}}} \right] + \displaystyle{{eA(1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} ))} \over {i{\rm \omega} _{\rm b} [({\rm \omega} /{\rm \omega} _{\rm b} )1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} ) - (1/{\rm \gamma} _0 )]}} \cr &\quad + \displaystyle{{eA{\rm \omega} _{\rm b} (1 - (P_z /{\rm \eta} _{\rm g} {\rm \gamma} ^{(1)} ))(1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} ))} \over {{\rm \omega} _{\rm b}^{\rm 3} {\rm \gamma} ^{(1)2} [({\rm \omega} /{\rm \omega} _{\rm b} )1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} ) - (1/{\rm \gamma} _0 )]^3}} \displaystyle{{d{\rm \gamma} ^{(1)}} \over {dt}},} $$
$$\eqalign{{\rm \beta} _{\rm q} = & \displaystyle{{eA(1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} ))} \over {i{\rm \omega} _{\rm b} [({\rm \omega} /{\rm \omega} _{\rm b} )(1 - (P_z {\rm \eta} /{\rm \gamma} ^{(1)} )) - (1/{\rm \gamma} _0 )]}} \cr & \left[ {\displaystyle{{v_{\rm F}^{\rm 2}} \over {n_0 c}}\left\{ {\displaystyle{1 \over {{\rm \eta} _{\rm g}}} - i{\rm \omega} {\rm \eta} \left( {t - \displaystyle{z \over {{\rm \eta} _{\rm g} c}}} \right)} \right\}} \right. \cr & \left. { + \displaystyle{{\hbar ^2} \over {4m^2 n_0}} \displaystyle{{{\rm \omega} ^2 {\rm \eta} ^2} \over {c^3}} \left\{ {\displaystyle{3 \over {{\rm \eta} _{\rm g}}} - i\left( {t - \displaystyle{z \over {{\rm \eta} _{\rm g} c}}} \right)} \right\}} \right],} $$
and
$$P_z = \displaystyle{{\,p_z^{(1)}} \over {mc}}.$$
The perturbed electron density is obtained with the help of Eq. (3b) on substituting the relevant quantities
$$\eqalign{ n^{(1)} &= - \displaystyle{\matrix{(n_0({\rm \beta} + i{\rm \beta} )/{\rm \gamma} _0m) \cr (i{\rm \omega} {\rm \eta} {\rm \eta} _{\rm g}(t - (z/{\rm \eta} _{\rm g}c)) - 1)(t - (z/{\rm \eta} _{\rm g}c)) } \over \matrix{{\rm \gamma} _0{\rm \eta} _{\rm g}mc\left\{ {1 - i{\rm \omega} (t - (z/{\rm \eta} _{\rm g}c)) + (n_0({\rm \beta} _{\rm q} + i{\rm \beta} _{\rm q})} \right. \cr \left. {(i{\rm \omega} {\rm \eta} {\rm \eta} _{\rm g}(t - (z/{\rm \eta} _{\rm g}c)) - 1)/{\rm \gamma} _0{\rm \eta} _{\rm g}mc)} \right\} } } \cr & \qquad \exp \left[ { - i{\rm \omega} \left( {t - \displaystyle{{{\rm \eta} z} \over c}} \right)} \right].} $$
The energy exchange is governed by the relation,
$$\eqalign{ \displaystyle{{d{\rm \gamma} ^{(2)}} \over {dt}} &= \displaystyle{e \over {m^2 c^2 {\rm \gamma} _0}} \{ ({\rm \beta} + n_1 {\rm \beta} _{\rm q} ) + i({\rm \beta} + n_1 {\rm \beta} _{\rm q} )\} \cr & \quad A_0 \left( {t - \displaystyle{z \over {{\rm \eta} _{\rm g} c}}} \right)^2 \left\{ {\exp \left[ { - i{\rm \omega} \left( {t - \displaystyle{{{\rm \eta} z} \over c}} \right)} \right]} \right\}^2.} $$
From the above equation, it is clear that the energy exchange is critically dependent on the static magnetic field. The magnetic field tends to rotate the electrons about the line of force in the right-handed sense at the cyclotron frequency. The right circularly polarized wave also rotates the electrons in the clockwise direction at the frequency ω. Hence, resonance occurs at ω = ωb resulting in energy gain enhancement.
In our analysis, we consider the parameter values as in (Misra et al., Reference Misra, Bhowmik and Shukla2009), that is, the particle density to be of the order of 1034 m−3. Such a density regime is relevant for dense plasma environments (including outer layers of astrophysical plasmas, such as neutron stars and white dwarfs) (Ali et al., Reference Ali, Maslam, Shukla and Schilickeiser2007). In this regime, the particle Fermi velocity becomes less than the speed of light c in vacuum and the Fermi screening length is greater than the average particle distance, a condition for the collective quantum effects in plasmas to be important. It has been reported that for intense laser–solid density plasma interaction experiments and for the next generation of laser-based plasma compression experiments, the electron number density n 0 can vary between 1030 and 1034 m−3 (Harding & Lai, Reference Harding and Lai2006; Shukla & Eliassion, Reference Shukla and Eliassion2007; Sharma & Tripathi, Reference Sharma and Tripathi2009; Zhu & Ji, Reference Zhu and Ji2012) and v F/c is in the range 0.005 → 0.25 (Wang et al., Reference Wang, Shukla and Eliassion2013).
Figure 1, shows the variation of normalized group velocity of the laser pulse ηgwith normalized plasma frequency (ωp/ω) for ω = 0.5ωb. It is observed that the group velocity decreases with increase in plasma frequency. It is seen that ηg initially drops sharply with (ωp/ω) , but afterwards this decrease is at a slower pace. In Fig. 2, the variation of normalized group velocity with (ω/ωb) for ωp/ω = 0.3 has been studied. It is observed that the group velocity ηg ≈ c, except on and near resonance (ω = ωb).
Fig. 1. Variation of ηg with ωp/ω for ω = 0.5ωb.
Fig. 2. Variation of ηg with ω/ωb for ωp = 0.3ω.
We have numerically solved Eq. (7) to investigate the electron dynamics for different values of plasma density, ratio of laser frequency to electron cyclotron frequency (ω/ωb), normalized laser amplitude and the static magnetic field. In Figures 3 and 4, the electron energy γ as a function of ξ( = t − ηz/c) have been plotted for A
0 = 0.2 and 0.8, respectively. The energy gain is increased due to increase in normalized laser amplitude. Higher electron energy can be achieved by increasing the laser field amplitude. As far as the effect of plasma frequency on electron is concerned, both the refractive index and group velocity of the laser pulse are functions of plasma frequency. Their values (η and ηg) increase with decrease in ωp. The energy gain of electron will be optimum near resonance. The variation of energy gain with normalized frequency (ω/ωb) has been shown in Figure 5. The energy gain increases with increase in ω/ωb. Near resonance, at ω/ωb ≃ 0.9, the group velocity is found to be
$\sim 0.20c,$
while at ω/ωb ≃ 0.4, the group velocity has a larger value
$(\sim 0.94c)$
, even then the gain is larger near resonance. This is due to the fact that the magnetic field of the laser, which is responsible for the ponderomotive force is significantly reduced at lower values of group velocity [α(1 − ηη
g)]. Electron attains maximum acceleration near the normalized Doppler-shifted cyclotron resonance
$([{\rm \omega} (1 - P_z {\rm \eta} /{\rm \gamma} ^{(1)} )/$
${\rm \omega} _b - 1/{\rm \gamma} _0 ]\sim 0)$
. Also at, ω/ωb ≃ 0.4,
$([{\rm \omega} (1 - P_z {\rm \eta} /{\rm \gamma} ^{(1)} )/$
${\rm \omega} _{\rm b} - {1 / {{\rm \gamma} _0}} ]\sim 0.42)$
remains aways from the resonance values, that is, zero hence electron gain less energy. At resonance the energy gain becomes infinity and the theory breaks down. After resonance, for ω/ωb > 1, the term [ω(1 − P
z
η/γ
(1))/ωb − 1/γ
0] increases and consequently the electron can gain higher energy.
Fig. 3. Variation of γ with ξ for A 0 = 0.2, n 0 = 1034 m−3, ωp = 0.3ω, ω = 0.5ωb.
Fig. 4. Variation of γ with ξ for A 0 = 0.8, n 0 = 1034 m−3, ωp = 0.3ω, ω = 0.5ωb.
Fig. 5. Variation of γ with ω/ωb for A 0 = 0.2, z = −6, n 0 = 1034 m−3.
Figure 6 depicts the variation of electron energy with ξ for A
0 = 0.6. The dashed line shows the variation as per the QHD model, while the solid line denotes the trend for a non-QHD setting (at
$\hbar = 0$
). It is found that the quantum effects damp the electron energy by about 14%. This damping is due to the diffraction induced by quantum effects.
Fig. 6. Variation of γ with ξ for A 0 = 0.6, n 0 = 1034 m−3, ωp = 0.3ω, ω = 0.5ωb.
3. DISCUSSION
A detailed theory for particle acceleration by the non-stationary ponderomotive force of a large-amplitude circularly polarized electromagnetic wave in a very dense, magnetized quantum plasma has been presented. The effects associated with the Fermi pressure and the Bohm potential have been incorporated. The ponderomotive acceleration of electrons by a Gaussian laser pulse is significantly affected by the presence of a magnetic field. An electron gains energy during the rising part of the laser pulse and loses during the trailing part. The quantum diffraction effects also play a crucial role by modifying the energy exchange rate. The non-stationary radiation pressure creates a slowely varying electric fields and current, which contributes to ponderomotive acceleration. The non-oscillatory quantum terms are embedded in βq. When ω < ωb, the first-order velocity due to the laser is very small as the resonance condition is not satisfied and hence the ponderomotive force produced is also insignificant. For ω > ωb, the pondermotive force produced is significant and considerable acceleration of electrons can be obtained in this regime. In practical applications, the ponderomotively accelerated ultrahigh energy electrons in the rising part of the pulse can be easily extracted by impinging the pulse into a solid target or through an overdense plasma seperator (Yu et al., Reference Yu, Bychenkov, Senyoku, Yu, Sheng and Mima2000; Miyauchi et al., Reference Miyauchi, Miyazaki, Sakai, Kawata, Kong, Andreev and Kikuchi2004). The pulse will then be reflected and the high-energy electrons are released into the target without suffering any deceleration. The electron energy is reduced by nearly 8% due to the quantum diffraction effects. This can be compensated by further increasing the strength of the applied magnetic field. The present study has relevance to the environment of dense astrophysical plasmas, quantum free-electron lasers, as well as to the next generation of intense laser–solid density plasma interaction experiments.
