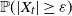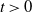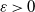1. Introduction and motivations
The law of any Lévy process X is the convolution between a Gaussian process, the martingale M describing its small jumps, and a compound Poisson process. For most Lévy processes, a closed-form expression for the law of its increments is not known. The core of the problem lies in computing the distribution of the small jumps. This technical limitation makes both inference and simulation difficult for Lévy processes. To cope with this shortcoming it is usual to approximate a general Lévy process X by a family of compound Poisson processes, by ignoring the jumps smaller than some level
$\varepsilon$
. Also, when the Lévy measure is of infinite variation, solutions that consist in approximating the law of
$M_t$
with a Gaussian distribution are motivated by [Reference Gnedenko and Kolmogorov10] (see also [Reference Cont and Tankov6], [Reference Cohen and Rosinski5], or [Reference Carpentier, Duval and Mariucci4]). This type of approximation is of interest as both Gaussian and compound Poisson processes are well understood, in terms of both continuous and discrete observations. The same cannot be said for the small jumps, which remain complex objects, difficult to manipulate.
To quantify the precision of such approximations, it becomes crucially important to have a sharp control of quantities such as
$\mathbb P\big(|X_t|>\varepsilon\big)$
and
$\mathbb{P}(|M_t|>\varepsilon)$
. This control, besides being interesting in itself, is sometimes required, for instance, to get Monte Carlo approximates of functionals of Lévy processes or to study non-asymptotic risk bounds for estimators of the Lévy density from discrete observations of X (see [Reference Figueroa-López and Houdré9] or [Reference Duval and Mariucci7]). This has important consequences in various fields of application where Lévy processes are commonly used to describe real-life phenomena. The literature on the applications of Lévy processes is abundant, ranging from finance, biology, geophysics, and neuroscience, to name but a few fields. In this respect, we will limit ourselves to mentioning [Reference Barndorff-Nielsen, Mikosch and Resnick2] and the references therein.
Formally, a Lévy process X is characterized by its Lévy triplet
$\big(b,\Sigma^{2},\nu\big)$
, where
$b\in\mathbb{R}$
,
$\Sigma\ge 0$
, and
$\nu$
is a Borel measure on
$\mathbb{R}$
such that
$\nu(\{0\})=0$
and
$\int_{\mathbb{R}}\big(y^2\wedge 1\big)\nu(d y)<\infty.$
The Lévy–Itô decomposition (see [Reference Bertoin3]) allows one to write a Lévy process X of Lévy triplet
$\big(b,\Sigma^{2},\nu\big)$
as the sum of four independent Lévy processes, as follows: for all
$t\ge0$
,
\begin{align} X_t&=tb+\Sigma W_{t}+\lim_{\eta\to 0}\Bigg(\sum_{s\leq t}\Delta X_s\mathbf{1}_{(\eta,1]}(|\Delta X_s|)-t\int_{\eta<|x|\leq 1}x\nu(d x)\Bigg) + \sum_{s\leq t}\Delta X_s\mathbf{1}_{(1,\infty)}(|\Delta X_s|)\nonumber \\
&\,=\!:\, tb+\Sigma W_{t}+M_t+Z_t,\end{align}
where
$\Delta X_r$
denotes the jump at time r of the càdlàg process X :
$\Delta X_r=X_r-\lim_{s\uparrow r} X_s. $
The first term is a deterministic drift, W is a standard Brownian motion which is pathwise continuous, and M and Z compose the discontinuous jump part of X. The process M is a centered martingale gathering the small jumps, i.e. the jumps of size smaller than 1, and it has Lévy measure
$\mathbf{1}_{|x|\leq 1}\nu$
. The process Z, on the other hand, is a compound Poisson process gathering jumps larger than 1 in absolute value; it has Lévy measure
$\mathbf{1}_{|x|> 1}\nu$
. In the sequel we let
$(b,\Sigma)=(\gamma_\nu,0)$
with
\begin{equation*}\gamma_\nu\,:\!=\,\begin{cases}\int_{|x|\leq1 }x\nu(dx) & \mbox{if }\int_{|x|\leq 1}|x|\nu(dx)<\infty, \\[5pt]
0 & \mbox{if } \int_{|x|\leq 1}|x|\nu(dx)=\infty. \end{cases}\end{equation*}
The choice
$\Sigma=0$
has been made to avoid too cumbersome proofs. A discussion about the general case is postponed to Section 2.5. Then, we rewrite (1) as
\begin{equation}X_t=t b(\varepsilon) + M_t(\varepsilon)+ Z_t(\varepsilon),\quad \forall 1\ge \varepsilon>0,\end{equation}
where
\begin{equation*}b(\varepsilon)\,:\!=\,\begin{cases}\,\ \ \int_{|x|\leq \varepsilon } x\nu(dx)\quad &\text{if}\quad \int_{|x|\leq 1}|x|\nu(dx)<\infty,\\[5pt]
-\int_{\varepsilon\leq |x|\leq 1} x\nu(dx)\quad &\text{if}\quad \int_{|x|\leq 1}|x|\nu(dx)=\infty; \end{cases}\end{equation*}
$M(\varepsilon)=(M_t(\varepsilon))_{t\geq 0}$
is a Lévy process accounting for the centered jumps of X with size smaller than
$\varepsilon$
, i.e.
\begin{equation*}M_t(\varepsilon)=\lim_{\eta\to 0} \Bigg(\sum_{s\leq t} \Delta X_s\mathbf{1}_{\eta<|\Delta X_s|\leq \varepsilon}-t\int_{\eta<|x|\leq \varepsilon} x\nu(dx)\Bigg);\end{equation*}
and
$Z(\varepsilon)=(Z_t(\varepsilon))_{t\geq 0}$
is a compound Poisson process of the form
\begin{equation*}Z_t(\varepsilon)\,:\!=\,\sum_{i=1}^{N_t(\varepsilon)} Y_i^{(\varepsilon)},\end{equation*}
where
$N(\varepsilon)=(N_t(\varepsilon))_{t\geq 0}$
is a Poisson process of intensity
$\lambda_\varepsilon\,:\!=\,\int_{|x|> \varepsilon} \nu(dx)$
independent of the sequence of independent and identically distributed random variables
$\big(Y_i^{(\varepsilon)}\big)_{i\geq 1}$
with common law
$\nu_{|_{\mathbb{R}\setminus[{-}\varepsilon,\varepsilon]}}/\lambda_\varepsilon$
. In the sequel we use the notation
$a\wedge b=\min(a,b)$
and
$a\vee b=\max(a,b)$
.
A first well-known result (see e.g. [Reference Bertoin3, Section I.5] or [Reference Rüschendorf and Woerner16, Corollary 3]) relates the Lévy measure to the limit of
$\mathbb{P}(|X_{t}|\ge \varepsilon)$
as
$t\to 0$
as follows.
Lemma 1. Let X be a Lévy process with Lévy measure
$\nu$
. For all
$\varepsilon>0$
it holds that
\begin{equation*}\lim_{t\to0}\frac{ \mathbb{P}(|X_t|\geq \varepsilon)}{t}=\int_{\mathbb{R}\setminus[{-}\varepsilon,\varepsilon]} \nu(dy).\end{equation*}
In particular, this leads to
$\lim_{t\to0}\frac1t{\mathbb{P}(|M_t(\varepsilon)|\geq\varepsilon)}=0$
and
$\lim_{t\to0}\frac1t{\mathbb{P}(|tb(\varepsilon)+M_t(\varepsilon)|\geq}$
$\varepsilon)=0.$
Lemma 1 suggests that
$\mathbb{P}(|X_{t}|\ge \varepsilon)\asymp \lambda_{\varepsilon}t$
‘for t small enough’; however, it gives no information on how small t should be, on the size of the error term
$\mathbb{P}(|X_{t}|\ge \varepsilon)- \lambda_{\varepsilon}t$
, or on what happens if
$\varepsilon$
becomes small. Of course,
$ \mathbb{P}(|X_t|\geq \varepsilon)$
and
$\mathbb{P}(|M_t(\varepsilon)|\geq\varepsilon)$
can be controlled with elementary inequalities, such as the Markov inequality, but this often leads to suboptimal results. Indeed, the Markov inequality gives
$\mathbb{P}(M_t(\varepsilon)>\varepsilon)\leq t\sigma^2(\varepsilon)\varepsilon^{-2},$
if we denote by
$\sigma^2(\varepsilon)\,:\!=\,\int_{-\varepsilon}^\varepsilon x^2\nu(dx)$
the variance of
$M_{1}(\varepsilon)$
, whereas a sharper result can be achieved using the Chernov inequality, as follows.
Lemma 2. For any
$\varepsilon\in(0,1]$
,
$t>0$
and
$x>0$
, it holds that
\begin{align*}\mathbb{P}(|M_t(\varepsilon)|>x)&\leq 2 e^{\frac{x}{\varepsilon}}\bigg(\frac{t\sigma^2(\varepsilon)}{x\varepsilon+t\sigma^2(\varepsilon)}\bigg)^{\frac{x\varepsilon+t\sigma^2(\varepsilon)}{\varepsilon^2}}.\end{align*}
Moreover, if
$t\sigma^2(\varepsilon)\varepsilon^{-2}\leq 1$
, this leads to
\begin{align}\mathbb{P}(M_t(\varepsilon)>x)&\leq \bigg(\frac{e\sigma^2(\varepsilon)}{\varepsilon^2}\bigg)^{\frac{x}{\varepsilon}} e^{e^{-1}}t^{\frac{x}{\varepsilon}} \ \ and \ \ \mathbb{P}(M_t(\varepsilon)\leq -x)\leq \bigg(\frac{e\sigma^2(\varepsilon)}{\varepsilon^2}\bigg)^{\frac{x}{\varepsilon}} e^{e^{-1}}t^{\frac{x}{\varepsilon}}.\end{align}
Lemma 2 is a modification of [Reference Figueroa-López and Houdré9, Remark 3.1]; its proof is postponed to Appendix A. A similar result can also be obtained using martingale arguments (see [Reference Dzhaparidze and Van Zanten8, Theorem 4.1]). Again, Lemma 2 is suboptimal, as it does not allow us to derive that
$\lim_{t\to0}{\mathbb{P}(M_t(\varepsilon)\geq\varepsilon)}/{t}=0.$
If we want to be more precise about the behavior for
$t\to 0$
, we need additional assumptions.
The study of the behavior at small times of the transition density of a Lévy process goes back to [Reference Léandre, Azéma, Mayer and Yor12] (see also [Reference Ishikawa11]) and is carried out in the real case in [Reference Picard14], which is also interested in the behavior of the supremum of this quantity and its derivatives. For the cumulative distribution function, expansions of order 2 for
$\mathbb{P}(X_{t}\ge y),$
for fixed y and t going to 0, are given in [Reference Marchal13] in the particular cases where X is the sum of a compound Poisson process and either a Brownian motion or an
$\alpha$
-stable process.
The most complete results can be found in [Reference Figueroa-López and Houdré9] (see also [Reference Barndorff-Nielsen and Hubalek1]), which, for general Lévy processes, establishes asymptotic expansions at any order of
$\mathbb{P}(X_{t}\ge y)$
, for fixed y bounded away from 0 and
$t\to0$
. In particular, [Reference Figueroa-López and Houdré9] proves that
$d_2(y) = \lim_{t\to0} \frac1t\big(\frac1t\mathbb{P}(X_{t}>y)-\nu((y,\infty))\big)$
exists, when the Lévy density f is bounded outside the interval
$[{-}\eta,\eta]$
,
$0<\eta<y/2\wedge 1$
, and either f is
$C^{1}$
in a neighborhood of y, or f is continuous in a neighborhood of y, of bounded variation, and
$\Sigma=0$
(defined as in (1)). This is an asymptotic result; therefore, it provides no information on how small t should be for the approximation of
$\mathbb{P}(X_{t}>y)-t\nu((y,\infty))$
by
$d_{2}(y)t^{2}$
to be accurate. Moreover, even though an explicit characterization of
$d_2(y)$
is given, this does not translate to a readily understandable dependency on y.
Our main contribution is a non-asymptotic control of
$\mathbb{P}(|X_{t}|\ge \varepsilon)$
, which is valid for any
$\varepsilon>0$
and any
$0<t<t_{0}(\varepsilon)$
. A considerable effort has been made to make the dependency on
$\varepsilon$
explicit, both in
$t_{0}(\varepsilon)$
and in the final bound. Concerning the hypotheses on the Lévy density f, in the finite-variation case we do not require any continuity, but only that it is bounded from above by an
$\alpha$
-stable-like density in a neighborhood of 0; see the definition on the class
${\mathscr{L}}_{{\rm K},\alpha}$
below. In the setting of infinite variation, we distinguish between two cases: when f is also Lipschitz continuous in a neighborhood of
$\varepsilon$
(a similar condition to that of [Reference Figueroa-López and Houdré9]), we find a non-asymptotic bound of the order of
$t^2$
. We also analyze the case where the continuity hypothesis on f is dropped. Then the order in t of the non-asymptotic bound deteriorates to
$t^{1 + 1/\alpha}$
,
$1 \leq \alpha < 2$
. This is not an artifact of the proof, as an example in [Reference Marchal13] indicates.
Section 2 gathers the main results of the paper. We begin by defining the classes of Lévy densities that we consider. On these classes we provide a non-asymptotic control of
$\mathbb{P}(|M_{t}(\varepsilon)|\ge \varepsilon)$
and
$\mathbb{P}(|X_{t}|\ge \varepsilon)$
. We consider separately finite-variation Lévy processes and infinite-variation Lévy processes, for which we detail only the symmetric case. In both cases our results permit us to recover Lemma 1. We compare our results to examples for which the quantity
$\mathbb{P}(|X_{t}|\ge \varepsilon)$
is known. The case of the small jumps is treated separately as an intermediate step to the general case (see Theorems 1 and 3). We think that these results are of independent interest and provide new insight into the process of the small jumps. Section 2 ends with a discussion on the validity of the results in presence of a Brownian component. Section 3 gathers the proofs of the main results, whereas in Appendix A all auxiliary results are established and the computations of the examples are carried out. Our proofs are elementary and self-contained, and they do not rely on the use of the infinitesimal generator.
2. Non-asymptotic expansions
In the sequel, let
$\nu$
be a Lévy measure that is absolutely continuous with respect to the Lebesgue measure, and denote by
$f=\frac{d\nu}{dx}$
its density. Letting
$\alpha\in(0,2)$
and K be positive constants, define the classes of functions
\begin{align*}{\mathscr{L}}_{{\rm K},\alpha}&\,:\!=\,\Bigg\{f \,:\, f(x)\leq \frac{{\rm K}}{|x|^{1+\alpha}},\quad \forall |x|\leq 2\Bigg\},\quad {\mathscr{L}}_{{\rm K}}\,:\!=\,\Bigg\{f \,:\, \sup_{|x|\geq 1}|f(x)|\leq {\rm K}\Bigg\}.\end{align*}
A Lévy density f belongs to the class
${\mathscr{L}}_{{\rm K}}$
,
${\rm K}>0$
, if it is bounded outside a neighborhood of the origin. It belongs to
${\mathscr{L}}_{{\rm K},\alpha}$
,
${\rm K}>0$
and
$\alpha>0$
, if
$\sup_{x\in[{-}2,2]}f(x)|x|^{1+\alpha}\le {\rm K}$
. In particular
${\mathscr{L}}_{{\rm K},\alpha}$
contains any
$\tilde\alpha$
-stable Lévy density such that
$\tilde\alpha\le\alpha$
. We stress that no lower-bound condition is required for the Lévy density. In this paper we consider only Lévy measures in these classes, the assumptions above being crucial in our proofs. However, we emphasize that the results recalled in Lemmas 1 and 2 hold true for any Lévy process, without any assumption on the Lévy measure.
2.1. Finite-variation Lévy processes
We state two non-asymptotic results offering a control of the distribution function of a finite-variation Lévy process.
Theorem 1. Let
$\varepsilon\in(0,1]$
and let f be a Lévy density such that for
$\alpha\in(0,1)$
and
${\rm K}>0$
it holds that
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
. Then there exists a constant
$ {\rm C}_1 >0$
, depending only on
$\alpha$
, such that
\begin{equation*}\mathbb{P}(|tb(\varepsilon)+M_t(\varepsilon)|\geq \varepsilon)\leq 2t^2 {\rm K}^2 {\rm C}_1 \varepsilon^{-2\alpha},\quad \forall \ 0<t\leq \frac{(1-\alpha)\varepsilon^{\alpha}}{{\rm K}4^{1+\alpha}} .\end{equation*}
If, in addition, f is a symmetric function, then there exists a constant
${\rm C}_2 >0$
, depending only on
$\alpha$
, such that
\begin{equation*}\mathbb{P}(|M_t(\varepsilon)|\geq \varepsilon)\leq 2t^2 {\rm K}^2 {\rm C}_2 \varepsilon^{-2\alpha},\quad \forall \ 0<t\leq \frac{\varepsilon^\alpha(2-\alpha)}{{\rm K}2^{\alpha+1}} .\end{equation*}
Explicit formulas for the constants
$ {\rm C}_1$
and
$ {\rm C}_2$
are given in (21) and (22), respectively.
Theorem 1 highlights how likely the process of the jumps smaller than
$\varepsilon$
is to present excursions larger than their size
$\varepsilon$
in a time interval of length t. When we are dealing with a discretized trajectory of a Lévy process, this provides relevant information on the contribution of the small jumps to the value of the observed increment. The following result generalizes Theorem 1 to any Lévy process with a Lévy density in
${\mathscr{L}}_{{\rm K},\alpha}$
,
$\alpha\in(0,1)$
, or in
${\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
if
$\varepsilon>1$
. In particular it permits us to derive an order of the rate of convergence in Lemma 1.
Theorem 2. Let
$X_t=\sum_{s\leq t} \Delta X_s$
be a finite-variation Lévy process with Lévy density f. Then the following hold:
-
If
$\varepsilon\in(0,1]$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, then for all
$0<t< (1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)}$
it holds that
where
\begin{equation*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|\leq t^2{\rm K}^2\varepsilon^{-2\alpha}\big( 2{\rm C_1}+ {\rm D}_1\big)+t^2{\rm K}\lambda_\varepsilon\varepsilon^{-\alpha} {\rm D}_2+2t^2\lambda_\varepsilon^2,\end{equation*}
$\rm C_1$
,
$\rm D_1$
, and
$\rm D_2$
depend only on
$\alpha$
and are defined in (21) and (41).
-
If
$\varepsilon>1$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, then for all
$0<t<(1-\alpha)(5{\rm K})^{-1}\wedge(1-\alpha) K^{-1} 4^{-1-\alpha}$
it holds that
where
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|&\leq 2{\rm K}^2t^2 \big(\tilde{\rm D}_1+ {\rm C_1}\big)+2t^2\lambda_1^2\\ &\quad+2{\rm K}^2t^2\bigg(\frac{4}{2-\alpha}(\varepsilon-3/2-t|b(1)|)\mathbf{1}_{\varepsilon>3/2+t|b(1)|}\Big)\\&\quad +{\rm K}t^2\bigg(4\times 5^{\alpha}\mathbf{1}_{1<\varepsilon<1+2t|b(1)|}+\frac{8}{5}+\frac32\lambda_2+\frac{4\lambda_1}{2-\alpha}\bigg),\end{align*}
$\rm C_1$
and
$\tilde{\rm D}_1$
depend only on
$\alpha$
and are defined in (21) and (49).
If in addition we suppose that
$\nu$
is a symmetric measure, then we have the following:
-
If
$\varepsilon\in(0,1]$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, then for any
$0<t<\varepsilon^\alpha$
$(2-\alpha){\rm K}^{-1}2^{-\alpha-1}$
it holds that
where
\begin{equation*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|\leq 2t^2{\rm K}^2\varepsilon^{-2\alpha}({\rm C_2}+{\rm D_3})+\frac{{\rm K}t^2}{2(2-\alpha)}\big(\lambda_\varepsilon \varepsilon^{-\alpha}+4\lambda_{2\varepsilon} \varepsilon^{-\alpha}\big)+2t^2\lambda_\varepsilon^2,\end{equation*}
$\rm C_2$
and
$\rm D_3$
depend only on
$\alpha$
and are defined in (22) and (50).
-
If
$\varepsilon>1$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, then for any
$0<t<$
$(2-\alpha){\rm K}^{-1}2^{-\alpha-1}$
it holds that
where
\begin{equation*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|\leq 2t^2{\rm K}^2{\rm C_2}+\frac{{\rm K}t^2}{2-\alpha}\bigg(\lambda_1 2^{-\alpha}+\frac{4K}{\alpha(1-\alpha)}+\lambda_{1+\varepsilon} \bigg)+2t^2\lambda_1^2,\end{equation*}
$\rm C_2$
is defined in (22).
The results of Theorems 1 and 2 are non-asymptotic. If we apply Theorem 2 to a Lévy process X whose Lévy measure
$\nu$
is concentrated on
$[{-}\varepsilon,\varepsilon]$
, for
$\varepsilon\in(0,1]$
, we recover the result of Theorem 1 up to the constant
${\rm D}_{1}$
, as in that case
$\lambda_{\varepsilon}=0$
. However, Theorem is not a corollary of Theorem 2, as the proof of the latter uses Theorem 1.
These results show that for a finite-variation Lévy process whose Lévy density lies in
${\mathscr{L}}_{{\rm K},\alpha}$
, for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, the discrepancy between
$\mathbb{P}(|X_{t}|>\varepsilon)$
and
$\lambda_{\varepsilon}t$
is in
$t^{2}$
. Moreover, as the role of the cutoff
$\varepsilon$
is made explicit in the upper bound, it is possible to measure the accuracy of this approximation when
$\varepsilon$
gets small. Then, the rate of the upper bound is—up to a constant—in
$t^{2}\big(\varepsilon^{-2\alpha}\vee\lambda_{\varepsilon}\varepsilon^{-\alpha}\vee \lambda_{\varepsilon}^{2}\big)$
. For example, for an
$\alpha$
-stable process with
$\alpha\in(0,1)$
, this order simplifies to
$t^{2}\lambda_{\varepsilon}^{2}.$
2.2. Symmetric infinite-variation Lévy processes
We generalize Theorems 1 and 2 to symmetric infinite-variation Lévy processes whose Lévy density lies in
${\mathscr{L}}_{{\rm K},\alpha},\ \alpha\in[1,2)$
and
${\rm K}>0$
.
Theorem 3. Let
$\varepsilon\in(0,1]$
and
$0<t<(\varepsilon/2)^\alpha(1\land ((2-\alpha)/2{\rm K}))$
. Let f be a symmetric Lévy density such that for
$\alpha\in[1,2)$
,
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
. Then there exists a constant
$ {\rm E}_{1}>0$
, depending only on
$\alpha$
(see (30)), such that
\begin{align*}\mathbb{P}(|M_t(\varepsilon)|\geq \varepsilon)&\leq\frac{2^{2+\alpha}{\rm K} t^{1+1/\alpha}}{\varepsilon^{1+\alpha}}\bigg(1+\frac{4{\rm K}}{\alpha(2-\alpha)(\alpha-1)}\bigg)+ 2t^2 {\rm K}^2 {\rm E}_{1} \varepsilon^{-2\alpha}, \quad \alpha\in(1,2),\\[5pt]
\mathbb{P}\big(M_t(\varepsilon)\geq \varepsilon\big)&\leq \frac{4t^2{\rm K}^2}{\varepsilon^2}\bigg(e^{2+1/e}+ \frac{38}{9}\bigg)+\frac{4{\rm K} t^2}{\varepsilon^2}+\frac{16{\rm K}^2}{\varepsilon^2}t^2 \ln\Big(\frac{\varepsilon}{2t}\Big), \quad \alpha=1.\end{align*}
Theorem 4. Let f be a symmetric Lévy density and
$f\in {\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
for some
$\alpha\in[1,2)$
and
${\rm K}>0$
. Then, for all
$0<t<((\varepsilon\wedge1)/2)^\alpha\big(1\land ((2-\alpha)/2{\rm K})\big)$
,
$\varepsilon>0$
, it holds that
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-&\lambda_\varepsilon t|\leq {\rm G}_{1}\frac{t^{1+1/\alpha}}{(\varepsilon\wedge 1)^{1+\alpha}}+{\rm G}_{2}\frac{t^{2}}{(\varepsilon\wedge 1)^{2\alpha}}+\frac{5{\rm K}}{2-\alpha}\frac{t^{2}\lambda_{1}}{(\varepsilon\wedge1)^2}+\frac{4{\rm K}^{2}t^{2}\varepsilon}{2-\alpha}\mathbf{1}_{\varepsilon>2} \\
&\quad+{\rm K}^2t^{2}\mathbf{1}_{\alpha=1}\bigg(8\bigg(2\mathbf{1}_{\varepsilon>1}\mathbf{1}_{t/C<1\wedge (\varepsilon-1)}\ln\bigg(\frac{C(1\wedge|\varepsilon-1|)}{t}\bigg)+\ln\bigg(\frac{C\rho}{t}\bigg)\bigg)\frac{1}{\varepsilon\wedge 1} \\
&\quad+\frac{32}{(\varepsilon\wedge 1)^2} \ln\bigg(\frac{\varepsilon\wedge 1}{2t}\bigg)\bigg)+2\lambda_{\varepsilon\wedge1}^{2}t^{2},\end{align*}
where
$C\,:\!=\,\big(1\wedge\big((2-\alpha)/2{\rm K} \big)\big)^{1/\alpha}$
and
${\rm G}_{1}$
and
${\rm G}_{2}$
are positive constants, depending only on K and
$\alpha$
, defined in (31).
Compared to Theorems 1 and 2, the rates of Theorems 3 and 4 are slower, as
$t^{2}\le t^{1+1/\alpha}$
for
$\alpha\in(1,2)$
. Nevertheless, the rate
$t^{1+1/\alpha}$
of Theorems 3 and 4 seems optimal. Indeed, as shown in [Reference Figueroa-López and Houdré9, Remark 3.5] (see also [Reference Marchal13]), it is possible to build a discontinuous Lévy measure f as the sum of an
$\alpha$
-stable Lévy process and a compound Poisson process presenting a discontinuity at
$\varepsilon$
that lies in
${\mathscr{L}}_{{\rm K},\alpha}$
and attains this rate
$t^{1+1/\alpha}$
. Adding a regularity assumption on f in a neighborhood of
$\varepsilon$
, it is possible to have a finer bound in
$t^{2}$
, as established in the following result.
Theorem 5. Let f be a symmetric Lévy density such that
$f\in {\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in[1,2)$
and
${\rm K}>0$
. Let
$\varepsilon>0$
and assume that f is
${\rm K}(\varepsilon\wedge 1)^{-(2+\alpha)}$
-Lipschitz on the interval
$((3/4(\varepsilon\wedge1),2\varepsilon-3/4(\varepsilon\wedge1))$
. For all
\begin{equation*}0<t\leq \frac{(2-\alpha)(1\wedge\varepsilon)^\alpha}{2^{1+\alpha}{\rm K}},\end{equation*}
it holds that
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|&\leq t^2{\rm K}^2 \big( \big({\rm F}_{1}\varepsilon^{-2\alpha}+\lambda_1\varepsilon^{-\alpha}{\rm F}_2\big) \mathbf{1}_{0<\varepsilon\leq 1}+\big(\varepsilon^2{\rm F}_3 +{\rm F}_{4}\big)\mathbf{1}_{\varepsilon>1} \big) \\&\quad +4t^2\lambda_1^2 +\frac{t^4 {\rm K}^4 {\rm F}_5}{(\varepsilon\wedge 1)^{4\alpha}},\end{align*}
where
${\rm F}_1,\dots, {\rm F}_5$
are universal positive constants, depending only on
$\alpha$
, defined in (32).
First, note that any Lévy density f that can be written as
$L(x)/x^{1+\alpha}$
for
$x\in[{-}2,2]\setminus \{0\}$
, where L is differentiable and bounded, with bounded derivative, and
$\alpha\in[1,2)$
, satisfies the assumptions of Theorem 5. Moreover, under the latter assumption, the application of Theorem 5 to a Lévy process X whose Lévy density f is concentrated on
$[{-}\varepsilon,\varepsilon]$
,
$\varepsilon\in(0,1],$
leads to a finer rate than that of Theorem 3, namely,
\begin{align*}\mathbb{P}\big(|M_t(\varepsilon)|>\varepsilon\big)&\leq t^2{\rm K}^2 \big({\rm F}_{1}\varepsilon^{-2\alpha}+\lambda_1\varepsilon^{-\alpha}{\rm F}_2\big) +4t^2\lambda_1^2+\frac{t^4 {\rm K}^4 {\rm F}_5}{(\varepsilon\wedge 1)^{4\alpha}}.\end{align*}
2.3. Discussion
The results of Theorems 1–5 are non-asymptotic and show the impact of the cutoff
$\varepsilon$
in the constants. In particular they permit us to recover, for every fixed
$\varepsilon>0$
, on the classes considered, the result of Lemma 1 with
$t\to0$
.
Optimality of the results. The rates of Theorems 1, 2, and 5 are of the form
$t^{2}(\varepsilon\wedge 1)^{-2\alpha}$
, up to a constant depending on K and
$\alpha$
. This quantity is optimal in t on the classes considered, in the sense that the rate in t cannot be improved under the general assumptions of these theorems. Indeed, in Section 2.4 we show that for compound Poisson processes, for which explicit calculations can be performed and which are included in
$\mathscr{L}_{{\rm K},\alpha}$
for all
$\alpha\in(0,2),$
examples can be built attaining this rate. As already highlighted, the rate of Theorem 3 is also optimal when considered in this general setting. The dependency on
$\varepsilon$
of the constant
$\varepsilon^{-2\alpha}$
also appears to be the right one, since, for an
$\alpha$
-stable process, it holds that
$\lambda_{\varepsilon}=O(\varepsilon^{-\alpha})$
. Therefore, in general it is not possible to improve the rates derived in these theorems, even though we stress that this might be possible in specific examples (see the Cauchy process in Section 2.4).
Strategy of the proofs. All the proofs are self-contained; they rely on the decomposition (2), which holds for any Lévy process and any level
$\varepsilon>0$
, and on Lemma 2. More precisely, to establish Theorems 2 and 4, we consider the decomposition (2), and decomposing on the values of the Poisson process
$N(\varepsilon)$
leads to
\begin{align} |\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|&\leq \mathbb{P}(|tb(\varepsilon)+M_t(\varepsilon)|>\varepsilon) )\nonumber\\
&+\lambda_\varepsilon t|\mathbb{P}(|tb(\varepsilon+M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|>\varepsilon) e^{-\lambda_\varepsilon t}-1\big|+\mathbb{P}\big(N_{t}(\varepsilon)\ge 2\big).\end{align}
The last term raises no difficulty as
$\mathbb{P}\big(N_{t}(\varepsilon)\ge 2\big)=O\big(\lambda_{\varepsilon}^{2}t^{2}\big)$
. The first term is treated in Theorems 1 and 3, which are established using the decomposition (2) at level
$\varepsilon/2$
and Lemma 2. The proof of Theorem 1 is made particularly technical by the presence of the drift term
$b(\varepsilon)$
. This is why, in the infinite-variation counterpart Theorem 3, we specialize to the symmetric case, so that
$b(\varepsilon)=0$
. Finally, to prove Theorems 2 and 5 (resp. Theorem 4) it remains to show that
$\mathbb{P}\big(\big|tb(\varepsilon)+M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|\leq\varepsilon\big)=O\big(t\lambda_\varepsilon\big)$
$\big(\textrm{resp.}\ O_{\varepsilon}\big(t^{1/\alpha}\big)\big)$
, which corresponds to proving that
$|\mathbb{P}\big(\big|tb(\varepsilon)+M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|>\varepsilon\big) e^{-\lambda_\varepsilon t}-1|=O\big(\lambda_\varepsilon t\big)$
$\big(\textrm{resp.}\ O_{\varepsilon}\big(t^{1/\alpha}\big)\big)$
.
For this term, the cases of finite-variation (Theorem 2) and infinite-variation (Theorems 4 and 5) Lévy processes essentially differ. For finite-variation Lévy processes,
$\alpha\in(0,1)$
, the result
$\mathbb{P}\big(\big|tb(\varepsilon)+M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|\leq\varepsilon\big)=O\big(t\lambda_\varepsilon\big)$
holds true, and a main difficulty here lies in the management of the drift, which can be nonzero. For infinite-variation Lévy processes,
$\alpha\in[1,2)$
, this result is not true in general. For instance, consider the case of a Cauchy process X and fixed
$\varepsilon$
. The Cauchy process has a Lévy density
$(\pi x^{2})^{-1}\mathbf{1}_{\mathbb{R}\setminus\{0\}}$
and is therefore in
${\mathscr{L}}_{1/\pi,1}\cap{\mathscr{L}}_{1/\pi}$
and is
$\pi^{-1}2^{7}3^{-3}(\varepsilon\wedge 1)^{-3}$
-Lipschitz on the interval
$((3/4(\varepsilon\wedge1),$
$2\varepsilon-3/4(\varepsilon\wedge1))$
for all
$\varepsilon>0$
. Theorems 3, 4, and 5 thus apply. For this example, direct calculations allow one to show that
$|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|=O\big(\lambda_\varepsilon^3 t^3\big)$
(see Section 2.4); however,
$\lim_{t\to 0}\frac1t{\mathbb{P}\big(\big|tb(\varepsilon)+M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|\leq\varepsilon\big)}=\infty$
, implying that
$\mathbb{P}\big(\big|tb(\varepsilon)+M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|\leq\varepsilon\big)=O\big(t\lambda_\varepsilon\big)$
cannot hold. Indeed, since the Lévy measure is symmetric, it leads to
$b(\varepsilon)=0$
and
\begin{equation*}\mathbb{P}\big(\big|M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|\leq \varepsilon\big)=\frac{1}{\lambda_\varepsilon}\int_{-\infty}^{-\varepsilon}\mathbb{P}\big(|M_t(\varepsilon)+z|\leq\varepsilon\big) \frac{dz}{\pi z^2}+\frac{1}{\lambda_\varepsilon}\int_{\varepsilon}^{\infty}\mathbb{P}\big(|M_t(\varepsilon)+z|\leq\varepsilon\big) \frac{dz}{\pi z^2}.\end{equation*}
Fatou’s lemma, together with the fact that
\begin{equation*}\lim_{t\to 0}\frac{\mathbb{P}(M_t(\varepsilon)\in A)}{t}=\nu_\varepsilon(A),\end{equation*}
$\nu_\varepsilon=\nu\mathbf{1}_{|x|\leq \varepsilon}$
, and f is symmetric, gives
\begin{align*}\lambda_\varepsilon \liminf_{t\to 0} \frac{\mathbb{P}\big(\big|M_t(\varepsilon)+Y_1^{(\varepsilon)}\big|\leq \varepsilon\big)}{t}&\geq \bigg(\int_{-\infty}^{-\varepsilon}+\int_{\varepsilon}^\infty\bigg)\liminf_{t\to 0}\frac{\mathbb{P}\big(M_t(\varepsilon)\in({-}\varepsilon-z,\varepsilon-z)\big)}{t}\frac{dz}{\pi z^2}\\[3pt]
&\ge\int_{\varepsilon}^\infty \nu_\varepsilon(z-\varepsilon,z+\varepsilon)\nu(dz)=\int_{\varepsilon}^{2\varepsilon} \nu_\varepsilon(z-\varepsilon,\varepsilon)\nu(dz)\\[3pt]
&=\frac{1}{\pi^{2}}\int_{\varepsilon}^{2\varepsilon} \frac{2\varepsilon-z}{\varepsilon(z-\varepsilon)}\frac{dz}{z^2}=\infty.\end{align*}
We derive that the decomposition (4) that leads to Theorem 2,
$\alpha\in(0,1)$
, does not permit one to obtain optimal results for
$\alpha\in[1,2)$
such as Theorem 5. These are instead obtained by firstly adding a regularity assumption in a neighborhood of
$\varepsilon$
and secondly modifying the decomposition (4), considering a cutoff level
$\varepsilon^{\prime}<\varepsilon$
, for example
$\varepsilon^{\prime}=3\varepsilon/4$
(see Lemmas 5 and 6 below).
Generalizing the results of Theorems 3, 4, and 5 to non-symmetric Lévy processes is possible at the expense of more cumbersome proofs and modifying the conditions on t. To exemplify this point, consider the proof of Theorem 1, for which a comparison between the non-symmetric and the symmetric case is possible, as we propose an alternative compact proof in the symmetric case.
2.4. Examples
We consider four examples of Lévy processes for whose laws explicit formulas are available. This permits us to conduct direct computations and expansions for the marginal laws and to compare them with the previous results. Let us stress that even in these cases where the law of the process is known, we do not know the law of the process corresponding to its small jumps. Besides the compound Poisson process, it is hard to propose examples to compare with Theorems 1 and 3. Finally, we present a non-asymptotic control of the marginal law of
$\alpha$
-stable-type processes. Proofs are postponed to Section A.7.
-
1. Let X be a compound Poisson process. Then, for any
$\varepsilon>0$
,
as
\begin{equation*}\big|\mathbb{P}(|X_{t}|>{\varepsilon})-\lambda_{\varepsilon}t \big| = O_{\varepsilon}\big(t^2\big)\quad\text{and}\quad \mathbb{P}(|M_{t}(\varepsilon\wedge 1)+tb(\varepsilon\wedge 1)|>{\varepsilon\wedge 1}) = O_{\varepsilon}\big(t^2\big),\end{equation*}
$t\to 0$
. It is possible to build examples for which these rates are sharp (see Section A.7).
-
2. Let X be a gamma process of parameter (1,1), that is, a finite-variation Lévy process with Lévy density
and
\begin{equation*}f(x)=\frac{e^{-x}}{x}\mathbf{1}_{(0,\infty)}(x), \qquad \lambda_\varepsilon=\int_\varepsilon^\infty \frac{e^{-x}}{x}dx,\end{equation*}
where
\begin{equation*}\mathbb{P}(|X_{t}|>\varepsilon)=\mathbb{P}(X_t>\varepsilon)=\int_\varepsilon^\infty \frac{x^{t-1}}{\Gamma(t)}e^{-x}dx,\quad \forall \varepsilon>0,\end{equation*}
$\Gamma(t)$
denotes the
$\Gamma$
function, i.e.
$\Gamma(t)=\int_{0}^\infty x^{t-1}e^{-x}dx$
. Then
$\big|\mathbb{P}(X_{t}>{\varepsilon})-\lambda_{\varepsilon}t \big| = O_{\varepsilon}\big(t^2\big),$
as
$t\to 0.$
-
3. Cauchy processes. Let X be a 1-stable Lévy process with
Then
\begin{equation*}f(x)=\frac{1}{\pi x^2}\mathbf{1}_{\mathbb{R}\setminus \{0\}}\quad \text{ and }\quad \mathbb{P}\big(|X_t|>\varepsilon\big)=2\int_{\frac{\varepsilon}{t}}^{\infty}\frac{dx}{\pi(x^2+1)},\quad \forall\varepsilon>0.\end{equation*}
(5)For this example, the bound of Theorem 5 is suboptimal. However, it is hopeless to try to improve Theorem 5 relying on the same strategy of proof, i.e. using compound Poisson approximations, and a different approach should be considered.
\begin{equation} \big|\mathbb{P}\big(|X_t|>\varepsilon\big)-t\lambda_\varepsilon\big|=O_{\varepsilon}\big(t^3\big),\quad \text{ as }t\to 0.\end{equation}
-
4.
$\alpha$
-stable-type processes. Results for the cumulative distribution function for
$\alpha$
-stable processes were already known (see e.g. [Reference Marchal13]). The following result is a generalization to any Lévy process whose Lévy measure behaves as an
$\alpha$
-stable process in a neighborhood of the origin, such as a tempered stable Lévy process (see e.g. [Reference Cont and Tankov6, Section 4.2] or [Reference Rosiński15]). This result is a consequence of Theorems 2, 4, and 5, observing that, under the assumptions of Corollary 1,
for
\begin{align*}2{\rm K} _{1}\varepsilon^{-\alpha}/\alpha\le\lambda_{\varepsilon,1}\le 2{\rm K} _{2}\varepsilon^{-\alpha}/\alpha,\quad\varepsilon^\alpha\leq \frac{2{\rm K} _2}{\alpha\lambda_{\varepsilon,1}},\quad \text{and}\quad \varepsilon^{-\alpha}\leq \frac{\alpha\lambda_{\varepsilon}}{2{\rm K} _1},\end{align*}
$\lambda_{\varepsilon,1}$
defined as in Section 3.1.
Corollary 1. Let X be a symmetric Lévy process with a Lévy density f. Suppose there exist
$\alpha\in(0,2)$
,
${\rm K}_1>0$
, and
${\rm K}_2>0$
such that
${\rm K}_1|x|^{-(1+\alpha)}\leq |f(x)|\leq {\rm K}_2|x|^{-(1+\alpha)}$
, for all
$0<|x|\leq 2$
. Let
$\varepsilon\in(0,1]$
and
$t>0$
. We have the following:
-
If
$\alpha\in(0,1)$
, there exists a constant
$\mathbf A_{{\rm K}_1,{\rm K}_2,\alpha} >0$
, depending only on
${\rm K}_1$
,
${\rm K}_2$
, and
$\alpha$
, such that
\begin{equation*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|\leq \mathbf A_{{\rm K}_1,{\rm K}_2,\alpha} t^2\lambda_\varepsilon^2,\quad \forall \ t\lambda_\varepsilon\leq 2^{-\alpha}(2-\alpha)\alpha^{-1}.\end{equation*}
-
If
$\alpha\in [1,2)$
and
$f\in {\mathscr{L}}_{{\rm K}_2}$
, there exist two constants
$\mathbf B_{{\rm K}_1,{\rm K}_2,\alpha} >0$
and
$\tilde B$
, depending only on
${\rm K}_1$
,
${\rm K}_2$
, and
$\alpha$
, such that for any
$\ t\lambda_\varepsilon\leq 2^{1-\alpha}{\rm K}_2(1\wedge(2-\alpha)/2{\rm K} _2)\alpha^{-1}$
, it holds that
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|\leq \mathbf B_{{\rm K}_1,{\rm K}_2,\alpha} t^{1+1/\alpha}\lambda_\varepsilon^{1+1/\alpha}\bigg(\mathbf{1}_{\alpha\in(1,2)}+\ln\bigg(\frac{\tilde B}{\lambda_\varepsilon t}\bigg)\mathbf{1}_{\alpha=1}\bigg).\end{align*}
-
If
$\alpha\in [1,2)$
and f is globally
${\rm K}\varepsilon^{-(2+\alpha)}$
-Lipschitz on the interval
$((3/4\varepsilon,2\varepsilon-3/4\varepsilon)$
, there exists a constant
$\mathbf C_{{\rm K}_1,{\rm K}_2,\alpha} >0$
, depending only on
${\rm K}_1$
,
${\rm K}_2$
, and
$\alpha$
, such that
\begin{equation*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|\leq \mathbf C_{{\rm K}_1,{\rm K}_2,\alpha} t^2 \lambda_\varepsilon^2,\quad \forall \ t\lambda_\varepsilon\leq 2^{-\alpha}(2-\alpha)\alpha^{-1}.\end{equation*}
2.5. Extension
A natural question is whether the above results hold true for general Lévy processes, that is in presence of a Gaussian part,
$\Sigma>0$
in (1). The answer is essentially positive, but to avoid cumbersome proofs we have chosen to take
$\Sigma=0$
. If
$\Sigma >0$
, the proofs can be adapted following the same steps as in Section 3, replacing
$M_{t}(\varepsilon)$
with
$\Sigma W_{t}+M_{t}(\varepsilon)$
, to yield similar results to those presented in Section 2.
More precisely, in order to mimic what is done in Section 3 for pure jump Lévy processes, we need to generalize Lemma 2. Adapting its proof, we obtain the following result. For any
$\varepsilon\in(0,1]$
,
$t>0$
, and
$x>0$
, it holds that
\begin{equation*}\mathbb{P}\big(\Sigma W_t+M_t(\varepsilon)>x\big)\leq e^{\frac{x}{\varepsilon}}\bigg(\frac{t\sigma^2(\varepsilon)}{x\varepsilon+t\sigma^2(\varepsilon)}\bigg)^{\frac{x\varepsilon+t\sigma^2(\varepsilon)}{\varepsilon^2}}\exp\bigg({t\frac{\Sigma^2}{2\varepsilon^2} \ln^2\bigg(1+\frac{x\varepsilon}{t\sigma^2(\varepsilon)}\bigg)}\bigg).\end{equation*}
In particular, using that
$u\mapsto u\ln^{2}(1+1/u)$
is bounded by 1 for
$u>0$
, we observe that the additional term
\begin{equation*}e^{t\frac{\Sigma^2}{2\varepsilon^2} \ln^2\Big(1+\frac{x\varepsilon}{t\sigma^2(\varepsilon)}\Big)}\le e^{\frac{\Sigma^{2}x}{2\varepsilon\sigma^{2}(\varepsilon)}}\end{equation*}
is bounded.
Similarly, it is possible to have a more general drift b in the triplet (see (1)). Proofs can be adapted at the cost of a more stringent condition on t. Indeed, the condition on t in the above theorems ensures that
$tb(\varepsilon)\le \varepsilon/2$
; a similar condition should be satisfied in presence of a general drift b.
3. Proofs
3.1. Preliminaries
Assume
$b\ge a>0$
, and define
$\lambda_{a}\,:\!=\,\int_{|x|>a}f(x)dx$
and
$\lambda_{a,b}\,:\!=\,\int_{b>|x|>a}f(x)dx$
, with the convention
$\lambda_{a,a}=0.$
Recall that
$\sigma^{2}(a)\,:\!=\,\int_{0<|x|<a}x^{2}f(x)dx$
, and for finite-variation processes the drift is denoted by
$b(a)\,:\!=\,\int_{0< |x|<a}xf(x)dx$
. Furthermore, we write
$Y^{(a)}$
(resp.
$Y^{(a,b)}$
) for a random variable with density
$f\mathbf{1}_{({-}a,a)^{c}}/\lambda_{a}$
(resp.
$f\mathbf{1}_{[{-}b,-a]\cup[a,b]}/\lambda_{a,b}$
). With this notation, following (2), consider the independent decomposition which plays an essential role in the sequel: for all
$t>0$
,
\begin{align}M_t(\varepsilon)=M_t(\eta)+Z_t(\eta,\varepsilon)-t\big(b(\varepsilon)-b(\eta)\big), \quad \forall\ 0<\eta
< \varepsilon\leq 1,\end{align}
where
$Z_t(\eta,\varepsilon)=\sum_{i=1}^{N_{t}(\eta,\varepsilon)}Y_{i}^{(\eta,\varepsilon)}$
,
$N(\eta,\varepsilon)$
being a Poisson process of intensity
$\lambda_{\eta,\varepsilon}$
independent of
$\Big(Y_{i}^{(\eta,\varepsilon)}\Big)$
. Therefore, for all
$0<x\leq \delta$
and
$t>0$
it holds that
\begin{align}\mathbb{P}(N_t(x,\delta)\geq 1)\leq \lambda_{x,\delta} t \quad \text{ and }\quad \mathbb{P}(N_t(x,\delta)\geq 2)\leq (\lambda_{x,\delta} t )^2.\end{align}
In the sequel we make intensive use of the following inequalities. For any
$0<x\le y\leq 2$
and f in
${\mathscr{L}}_{{\rm K},\alpha}$
, it holds that
\begin{align}\frac{\sigma^{2}(x)}{x^{2}}&=\frac{\int_{-x}^x u^2 f(u)du}{x^2}\leq \frac{2{\rm K} }{2-\alpha} x^{-\alpha},\end{align}
\begin{align}\lambda_{x,y}&= \int_{y>|u|>x} f(u)du \leq \frac{2{\rm K} }{\alpha} \big(x^{-\alpha}-y^{-\alpha}\big),\end{align}
\begin{align}\lambda_{x,y}&= \int_{y>|u|>x} f(u)du \leq \frac{2{\rm K} }{\alpha} x^{-\alpha},\end{align}
\begin{align} b(x)&= \int_{|u|\leq x} uf(u)du \leq \frac{2{\rm K} }{1-\alpha} x^{1-\alpha}, \quad {\text{ if } \alpha\in(0,1)}.\end{align}
3.2. Proof of Theorem 1
First, note that
\begin{equation*}\mathbb{P}(|tb(\varepsilon)+M_{t}(\varepsilon)|> \varepsilon)=\mathbb{P}(tb(\varepsilon)+M_{t}(\varepsilon)> \varepsilon)+\mathbb{P}(tb(\varepsilon)+M_{t}(\varepsilon)<- \varepsilon).\end{equation*}
We consider only the term
$\mathbb{P}(tb(\varepsilon)+M_{t}(\varepsilon)> \varepsilon)$
, as
$\mathbb{P}(tb(\varepsilon)+M_{t}(\varepsilon)<- \varepsilon)$
can be treated analogously. Define
\begin{equation*}\eta\,:\!=\,\sup \bigg\{\frac{\varepsilon}{4}\leq u<\varepsilon:\ u\leq \frac{\varepsilon-t\int_{-u}^u x f(x)dx}{2},t\lambda_{\varepsilon/8,u}<1\bigg\}.\end{equation*}
Observe that if
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
,
${\rm K}>0$
,
$\alpha\in(0,1)$
,
$\varepsilon\in(0,1]$
, and
$0<t\leq (1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)}$
, then the set
\begin{equation*}A_{\varepsilon,t}\,:\!=\,\bigg\{\frac{\varepsilon}{4}\leq u<\varepsilon:\ u\leq \frac{\varepsilon-tb(u)}{2},t\lambda_{\varepsilon/8,u}<1\bigg\}\end{equation*}
is not empty, as
$\varepsilon/4\in A_{\varepsilon,t}$
and
$t\lambda_{\varepsilon/8,\varepsilon/4}\le (1-\alpha)(2^\alpha-1)/(2\alpha)<1$
, using (9).
By means of (6) and the definition of
$b(\cdot)$
, we have
\begin{align}\mathbb{P}(t&b(\varepsilon)+M_{t}(\varepsilon)> \varepsilon)=\mathbb{P}\big(M_{t}(\eta)+Z_{t}(\eta,\varepsilon)> \varepsilon-tb(\eta)\big)\nonumber \\
&\leq \mathbb{P}(M_t(\eta)>\varepsilon-tb(\eta))+\lambda_{\eta,\varepsilon}t \mathbb{P}\Big(M_t(\eta)+Y_{1}^{(\eta,\varepsilon)}>\varepsilon-tb(\eta)\Big)+ \mathbb{P}\big(N_t(\eta,\varepsilon)\geq 2\big) ,\end{align}
where we decomposed on the values of the Poisson process
$N(\eta,\varepsilon)$
. Using (7), we have
$\mathbb{P}\big(N_{t}(\eta,\varepsilon)\geq 2\big)\leq (\lambda_{\eta,\varepsilon}t)^{2}$
. We thus only have to control the first and second summands in (12). For the first one, we apply Lemma 2, using that
$t\leq (1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)}$
implies that
$t\sigma^2(x)x^{-2}\leq 1$
for all
$x\in[\varepsilon/4,\varepsilon]$
. From the definition of
$\eta$
and (3) it follows that
\begin{align*}\mathbb{P}(M_{t}(\eta)>\varepsilon-tb(\eta))&\le \mathbb{P}(M_{t}(\eta)>2\eta)\leq \bigg(\frac{e\sigma^2(\eta)}{4\eta^2}\bigg)^{2} e^{e^{-1}}t^{2}.\end{align*}
Hence, using (8) and the fact that
$\eta\geq \varepsilon/4$
and
$4^{2\alpha-1}e^{2+1/e}(2-\alpha)^{-2}\le 4e^{2+1/e}$
, we have
\begin{align}\mathbb{P}(M_{t}(\eta)>\varepsilon-tb(\eta))&\leq 4e^{2+1/e} t^2 {\rm K}^2 \varepsilon^{-2\alpha}.\end{align}
For the second term in (12), set
$\varepsilon^{\prime}\,:\!=\,\varepsilon-tb(\eta)$
and notice that
$\varepsilon^{\prime}\geq \varepsilon/2$
. It holds that
\begin{align*}\lambda_{\eta,\varepsilon}&\mathbb{P}\Big(M_t(\eta)+Y_{1}^{(\eta,\varepsilon)}>\varepsilon^{\prime}\Big)=\int_{\eta<|y|<\varepsilon}\mathbb{P}\big(M_t(\eta)>\varepsilon^{\prime}-y\big) f(y)dy\\
&\leq \mathbb{P}\big(M_t(\eta)>\varepsilon^{\prime}+\eta\big)\int_{-\varepsilon}^{-\eta} f(x)dx+\int_{\eta<y<\varepsilon}\mathbb{P}\big(M_t(\eta)>\varepsilon^{\prime}-y\big) f(y)dy\,=\!:\, T_1+T_2.\end{align*}
From
$\varepsilon^{\prime}>0$
it follows that
$ \mathbb{P}\big(M_t(\eta)>\varepsilon^{\prime}+\eta)\leq \mathbb{P}\big(M_t(\eta)>\eta)$
. The Markov inequality and (8), combined with the fact that
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
and
$\eta\ge\varepsilon/4$
, yield
\begin{align*}T_1&\leq 2{\rm K}^2 t\eta^{-\alpha}(2-\alpha)^{-1}\int_{\eta}^\varepsilon|x|^{-(1+\alpha)}dx\leq \frac{2{\rm K}^2}{\alpha(2-\alpha)} \eta^{-2\alpha} t\leq t{\rm K}^2 \varepsilon^{-2\alpha} \mathbf C_{1,\alpha}\end{align*}
\begin{align}\mbox{with }\mathbf C_{1,\alpha}\,:\!=\, \frac{2^{1+4\alpha}}{\alpha(2-\alpha)}.\end{align}
To treat the term
$T_2$
we suppose that
$b(\eta)\geq0$
; the case
$b(\eta)<0$
is handled similarly. After a change of variable, we obtain
\begin{align*}T_2 & =\int_{-tb(\eta)}^{\varepsilon^{\prime}-\eta} \mathbb{P}\big(M_t(\eta) >x\big) f\big(\varepsilon^{\prime}-x\big)dx\leq \int_{-tb(\eta)}^{0} f\big(\varepsilon^{\prime}-x\big)dx+\int_{0}^{\eta/2} \mathbb{P}\big(M_t(\eta) >x\big) f\big(\varepsilon^{\prime}-x\big)dx\\
&\quad+\int_{\eta/2}^{\eta} \mathbb{P}\big(M_t(\eta) >x\big) f\big(\varepsilon^{\prime}-x\big)dx+\int_{\eta}^{\varepsilon^{\prime}-\eta} \mathbb{P}\big(M_t(\eta) >x\big) f\big(\varepsilon^{\prime}-x\big)dx \\
&\,=\!:\,T_{2,1}+T_{2,2}+T_{2,3}+T_{2,4}.\end{align*}
First observe that for
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
and
$\varepsilon^{\prime}\ge\varepsilon/2$
we get
\begin{equation*}f\big(\varepsilon^{\prime}-x\big)\leq \frac{{\rm K}}{|\varepsilon^{\prime}-x|^{1+\alpha}}\leq {\rm K}(\varepsilon^{\prime})^{-(1+\alpha)}\le {\rm K} 2^{1+\alpha}\varepsilon^{-(1+\alpha)},\quad \forall x\in[{-}tb(\eta),0].\end{equation*}
Furthermore, using that
$b(\eta)\leq 2{\rm K} (1-\alpha)^{-1} \eta^{1-\alpha}\leq 2{\rm K} (1-\alpha)^{-1} \varepsilon^{1-\alpha}$
, we conclude that
\begin{equation}T_{2,1}\leq \frac{2^{2+\alpha}t{\rm K}^2}{1-\alpha}\varepsilon^{-2\alpha}.\end{equation}
Next we consider
$T_{2,2}$
. By (6), for any
$\tilde x\in(0,\eta)$
, we write
$M_t(\eta) =M_t(\tilde x)+Z_t(\tilde x,\eta)-t(b(\eta)-b(\tilde x))$
. Observe that, as
$0<t\leq (1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)}$
, it holds that
$2{\rm K}t\eta^{1-\alpha} (1-\alpha)^{-1}\leq \eta/2$
. Consider
$x\in(2{\rm K}t\eta^{1-\alpha} (1-\alpha)^{-1},\eta/2)$
and set
$\tilde x\,:\!=\,x-2{\rm K}t\eta^{1-\alpha} (1-\alpha)^{-1}$
. Using that
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
we have
\begin{equation*}|b(\eta)-b(\tilde x)|=\bigg|\int_{|u|\in[\tilde x,\eta]} u f(u)du\bigg|\leq 2{\rm K} \eta^{1-\alpha}(1-\alpha)^{-1},\end{equation*}
from which we derive that
$\mathbb{P}(M_t(\tilde x) >x+t(b(\eta)-b(\tilde x)))\leq \mathbb{P}(M_t(\tilde x)>\tilde x)$
. It follows that for
$x\in(2{\rm K}t\eta^{1-\alpha} (1-\alpha)^{-1},\eta/2)$
we may write, decomposing on the values of
$N(\tilde x,\eta)$
,
\begin{align*} \mathbb{P}\big(M_t(\eta) >x\big)&= \mathbb{P}\big(M_t(\tilde x)+Z_t(\tilde x,\eta) >x+t(b(\eta)-b(\tilde x))\big) \\ &\leq \mathbb{P}\big(M_t(\tilde x) >\tilde x\big)+\mathbb{P}(N_t(\tilde x,\eta)\geq 1)\\ &\leq t\frac{2{\rm K} }{2-\alpha}(\tilde x)^{-\alpha} +t\lambda_{\tilde x,\eta}\leq \frac{2{\rm K}t (\tilde x)^{-\alpha}(2+\alpha)}{\alpha(2-\alpha)}, \end{align*}
where, in the second-to-last inequality, we used the Markov inequality and (8), and in the last inequality we used (7) and (10). Consequently, using that
$\eta\le\varepsilon$
and noticing that
$3/8\varepsilon\leq \varepsilon^{\prime}-x\leq 1$
for all
$x\in(0,\eta/2)$
, we derive
\begin{align}T_{2,2}&\leq \int_0^{\frac{2{\rm K}t\eta^{1-\alpha}}{ 1-\alpha}}f\big(\varepsilon^{\prime}-x\big)dx+ \frac{2(2+\alpha){\rm K}t }{\alpha(2-\alpha)}\int_{\frac{2{\rm K}t\eta^{1-\alpha}}{ 1-\alpha}}^{\eta/2} \bigg(x-\frac{2{\rm K}t\eta^{1-\alpha}}{ 1-\alpha}\bigg)^{-\alpha}f\big(\varepsilon^{\prime}-x\big)dx\nonumber\\
&\leq \frac{2{\rm K}^2t\varepsilon^{-2\alpha}}{ 1-\alpha}\bigg(\frac{8}{3}\bigg)^{1+\alpha}+ \frac{2(2+\alpha){\rm K}^2t }{2^{1-\alpha}\alpha(2-\alpha)(1-\alpha)}\bigg( \frac{8}{3}\bigg)^{1+\alpha} \varepsilon^{-2\alpha}\nonumber\\
&= \frac{2{\rm K}^2t\varepsilon^{-2\alpha}}{ 1-\alpha}\bigg(\frac{8}{3}\bigg)^{1+\alpha}\bigg(1+\frac{2+\alpha}{2^{1-\alpha} \alpha(2-\alpha)}\bigg).\end{align}
To treat the term
$T_{2,3}$
we proceed analogously. Let
$x\in[\eta/2,\eta]$
and
$\tilde Z_t(x,\eta)$
be a centered version of
$Z_t(x,\eta)$
, that is,
\begin{equation*}\tilde Z_t(x,\eta)=\sum_{i=1}^{N_t(x,\eta)}\Big(Y_i^{(x,\eta)}-\mathbb{E}[Y_i^{(x,\eta)}]\Big).\end{equation*}
In particular, by the definition of
$\eta$
, it follows that
$t\lambda_{x,\eta}<1$
and Lemma 7 applies. On the one hand we derive that
\begin{align*} \big|&\mathbb{P}\big(M_t(x)+Z_t(x,\eta)-\mathbb{E}\big[Z_t(x,\eta)\big] >x\big)-\mathbb{P}\big(M_t(x)+\tilde Z_t(x,\eta) >x\big)\big|\\
&\leq 2t\lambda_{x,\eta}\Big|\mathbb{E}\Big[Y_1^{(x,\eta)}\Big]\Big|\sup_{|y|\in[x,\eta]}\big|f(y)/\lambda_{x,\eta}|\leq t{\rm K} 2^{2+\alpha}\eta^{-(1+\alpha)}\int_{x<|u|<\eta}\frac{\eta f(u)}{\lambda_{x,\eta}} du\leq 2^{2+\alpha}t{\rm K} \eta^{-\alpha}, \end{align*}
where we used that
$f\in {\mathscr{L}}_{{\rm K},\alpha}$
. On the other hand, we have that
\begin{align*} \mathbb{P}\big(M_t(x)+\tilde Z_t(x,\eta) >x\big)&\leq \mathbb{P}\big(M_t(x) >x\big)+ \mathbb{P}\big(N_t(x,\eta) \geq 1\big)\leq \frac{10{\rm K}t x^{-\alpha}}{\alpha(2-\alpha)}\leq \frac{20{\rm K}t \eta^{-\alpha}}{\alpha(2-\alpha)}, \end{align*}
where we used the Markov inequality, (8), (7), (10), and that
$x>\eta/2$
. Finally, by the triangle inequality and using that
$\varepsilon^{\prime}-\eta\geq \eta\geq \varepsilon/4$
and
$\mathbb{E}[Z_t(x,\eta)]=t(b(\eta)-b(x))$
, we deduce that
\begin{align}T_{2,3}&\leq \frac{28{\rm K}t \eta^{-\alpha}}{\alpha(2-\alpha)}\int_{\eta/2}^\eta f\big(\varepsilon^{\prime}-x\big)dx\leq \frac{28{\rm K}^2t \eta^{-\alpha}(\varepsilon^{\prime}-\eta)^{-\alpha}}{\alpha^2(2-\alpha)}\leq \frac{28\times 4^{2\alpha}{\rm K}^2t \varepsilon^{-2\alpha}}{\alpha^2(2-\alpha)}.\end{align}
Then, for the term
$T_{2,4}$
, the Markov inequality and (8), for any
$x\in[\eta,\varepsilon^{\prime}-\eta]$
, lead to
\begin{equation*}\mathbb{P}(M_t(\eta)>x)\leq \frac{2{\rm K} }{2-\alpha}\eta^{-\alpha}t. \end{equation*}
Therefore, using that
$\varepsilon^{\prime}-\eta\geq \eta\geq \varepsilon/4$
, we get
\begin{align}T_{2,4}&\leq \frac{2{\rm K} }{2-\alpha}\eta^{-\alpha}t \int_\eta^{\varepsilon^{\prime}-\eta}f\big(\varepsilon^{\prime}-x\big)dx\leq \frac{2{\rm K}^2}{(2-\alpha)\alpha}\eta^{-2\alpha}t\leq \frac{2^{1+4\alpha}{\rm K}^2}{\alpha(2-\alpha)}\varepsilon^{-2\alpha}t.\end{align}
Gathering Equations (15), (16), (17), and (18) yields
\begin{align}T_2&\leq t{\rm K}^2 \varepsilon^{-2\alpha} \mathbf C_{2,\alpha},\end{align}
with
\begin{align*}\mathbf C_{2,\alpha}=\bigg(\frac{2^{2+\alpha}}{1-\alpha}+\frac{ 2^{4\alpha+3}(2^{1-\alpha}\alpha(2-\alpha)+2+\alpha)}{\alpha(2-\alpha)(1-\alpha)3^{1+\alpha}}+\frac{28\times 4^{2\alpha}}{\alpha^2(2-\alpha)}+\frac{2^{1+4\alpha}}{\alpha(2-\alpha)}\bigg).\end{align*}
Combining (14) and (19), we conclude that if
$b(\eta)\geq 0$
, then
\begin{equation}\lambda_{\eta,\varepsilon}t\mathbb{P}\Big(M_t(\eta)+Y_{1}^{(\eta,\varepsilon)}>\varepsilon^{\prime}\Big)\leq t^2{\rm K}^2 \varepsilon^{-2\alpha} (\mathbf C_{1,\alpha}+\mathbf C_{2,\alpha}).\end{equation}
The case
$b(\eta)<0$
is treated similarly and therefore not detailed here. Inserting in (12) Equations (13), (10), and (20), we conclude that
\begin{equation}\mathbb{P}(tb(\varepsilon)+M_t(\varepsilon)>\varepsilon)\leq t^2 {\rm K}^2\varepsilon^{-2\alpha} \big(4e^{2+1/e}+64\alpha^{-2}+\mathbf C_{1,\alpha}+\mathbf C_{2,\alpha}\big)\,=\!:\, t^2 {\rm K}^2\varepsilon^{-2\alpha} \mathbf {\rm C}_1,\end{equation}
as desired.
For a symmetric Lévy measure, the above computations can be simplified. In this case
$b(\varepsilon)=0$
and one can directly take
$\eta=\varepsilon/2$
in the previous lines. More precisely, it holds that
\begin{align*}\mathbb{P}\big(M_t(\varepsilon)>\varepsilon\big)\leq \mathbb{P}\big(M_t(\varepsilon/2)>\varepsilon\big)+\big(t \lambda_{\varepsilon/2,\varepsilon}\big)^2+ t \lambda_{\varepsilon/2,\varepsilon}\mathbb{P}\Big(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\varepsilon)}>\varepsilon\Big).\end{align*}
To control the first two summands, use Lemma 2
$\big(\textrm{using} \, \textrm{that} \, 4t\sigma^2(\varepsilon/2)\leq \varepsilon^2\big)$
and (10). It follows that
\begin{align*}\mathbb{P}(M_t(\varepsilon/2)>\varepsilon)&\leq t^2 \varepsilon^{-2\alpha}K^2 e^{2+1/e} \frac{4^{1+\alpha}}{(2-\alpha)^2},\\
(t \lambda_{\varepsilon/2,\varepsilon})^2&\leq t^2 \varepsilon^{-2\alpha}K^2 \frac{4^{1+\alpha}}{\alpha^2}.\end{align*}
To treat the last term we proceed as follows:
\begin{align*}\lambda_{\varepsilon/2,\varepsilon}&\mathbb{P}(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\varepsilon)}>\varepsilon)=\int_{\varepsilon/2}^\varepsilon +\int_{-\varepsilon}^{-\varepsilon/2} \mathbb{P}(M_t(\varepsilon/2)>\varepsilon-z)f(z) dz\\
&\leq \int_{\varepsilon/2}^\varepsilon \big(\mathbb{P}(M_t(\varepsilon-z)>\varepsilon-z) +t\lambda_{\varepsilon-z,\varepsilon/2}\big) f(z) dz+\frac{\mathbb{P}(M_t(\varepsilon/2)>\varepsilon3/2)}{2}\lambda_{\varepsilon/2,\varepsilon}\\
&\leq t \int_{\varepsilon/2}^\varepsilon \bigg(\frac{\sigma^2(\varepsilon-z)}{(\varepsilon-z)^2} +\lambda_{\varepsilon-z,\varepsilon/2}\bigg) f(z) dz+\frac{\mathbb{P}(M_t(\varepsilon/2)>\varepsilon3/2)}{2}\lambda_{\varepsilon/2,\varepsilon}\\
&\leq \frac{4^{1+\alpha} t{\rm K}^2\varepsilon^{-2\alpha}}{\alpha(1-\alpha)(2-\alpha)}+\frac{\mathbb{P}(M_t(\varepsilon/2)>\varepsilon3/2)}{2}\lambda_{\varepsilon/2,\varepsilon},\end{align*}
where in the last inequality we used (8) and (10). The term
$\mathbb{P}(M_t(\varepsilon/2)>\varepsilon3/2)$
is controlled by applying Lemma 2, using that
$4t\sigma^2(\varepsilon/2)\leq \varepsilon^2$
. By means of (8) it follows that
\begin{equation*}\frac{\mathbb{P}(M_t(\varepsilon/2)>\varepsilon3/2)}{2}\leq \frac{t^2 \varepsilon^{-2\alpha} K^2 e^{3+1/e}2^{1+2\alpha}}{(2-\alpha)^2}.\end{equation*}
Collecting all the pieces together, one derives the following result: for all
$t>0$
such that
$t\leq \varepsilon^\alpha(2-\alpha){\rm K}^{-1}2^{-\alpha-1}$
(implying that
$t\lambda_{\varepsilon/2,\varepsilon}\leq 1$
), it holds that
$\mathbb{P}(M_t(\varepsilon)>\varepsilon)\leq t^2\varepsilon^{-2\alpha}{\rm K}^2 {\rm C}_2,$
where
\begin{equation}{\rm C}_2\,:\!=\, \frac{2^{2\alpha+1} e^{2+1/e}(2+e)}{(2-\alpha)^2}+\frac{4^{1+\alpha}}{\alpha(1-\alpha)(2-\alpha)}+\frac{4^{1+\alpha}}{\alpha^2}.\end{equation}
3.3. Proof of Theorem 2
To prove Theorem 2 we first introduce an auxiliary result.
Lemma 3. Let f be a Lévy density and
$\varepsilon>0$
. Set
$\rho\,:\!=\,\varepsilon\wedge 1$
and
$Q\,:\!=\,|\lambda_\rho t \mathbb{P}\big(\big|M_t(\rho)+tb(\rho)+Y_1^{(\rho)}\big|>\varepsilon\big)-\lambda_\varepsilon t |.$
Then the following hold:
-
If
$\varepsilon\in(0,1]$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, then
where
\begin{equation*}Q\leq t^{2}({\rm K}^2{\rm D}_1\varepsilon^{-2\alpha}+{\rm K}\lambda_\varepsilon\varepsilon^{-\alpha}{\rm D}_2),\quad \forall\ 0<t
< (1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)},\end{equation*}
$\rm D_1$
and
$\rm D_2$
are defined as in (41).
-
If
$\varepsilon>1$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, then for all
$0<t<(1-\alpha)(5{\rm K})^{-1}$
it holds that for
$\tilde{\rm D}_1$
as defined in (49),
\begin{align*}Q&\leq 2{\rm K}^2t^2\Big(\tilde{\rm D}_1+\frac{4}{2-\alpha}(\varepsilon-3/2-t|b(1)|)\mathbf{1}_{\varepsilon>3/2+t|b(1)|}\Big)\\&\quad +{\rm K}t^2\bigg(4\times 5^{\alpha}\mathbf{1}_{1<\varepsilon<1+2t|b(1)|}+\frac{8}{5}+3\lambda_2+\frac{4\lambda_1}{2-\alpha}\bigg).\end{align*}
If in addition we suppose that
$\nu$
is a symmetric measure, then the following hold:
-
If
$\varepsilon\in(0,1]$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, it holds that
where
\begin{equation*}Q\leq \frac{t^2{\rm K} }{2(2-\alpha)}\big(\lambda_\varepsilon \varepsilon^{-\alpha}+4\lambda_{2\varepsilon} \varepsilon^{-\alpha}\big)+2t^2{\rm K}^2{\rm D_3} \varepsilon^{-2\alpha},\quad \forall \ t>0,\end{equation*}
${\rm D_3}$
is defined as in (50).
-
If
$\varepsilon>1$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
for some
$\alpha\in(0,1)$
and
${\rm K}>0$
, it holds that
\begin{equation*}Q\leq \frac{t^2{\rm K} }{2-\alpha}\bigg(\lambda_1 2^{-\alpha}+\frac{4{\rm K}}{\alpha(1-\alpha)}+\lambda_{1+\varepsilon} \bigg),\quad \forall\ t>0.\end{equation*}
Proof of Theorem 2
. Using the decomposition
$X_t=M_t(\rho)+tb(\rho)+Z_t(\rho)$
,
$\rho=\varepsilon\wedge 1$
, we derive, decomposing on the Poisson process
$N(\rho)$
, that
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|&= \bigg|\mathbb{P}\big(\big|M_t(\rho)+tb(\rho)\big|>\varepsilon\big)e^{-\lambda_\rho t}+\lambda_\rho t \mathbb{P}\Big(\big|M_t(\rho)+tb(\rho)+Y_1^{(\rho)}\big|>\varepsilon\Big) e^{-\lambda_\rho t}\\
&\quad -\lambda_\varepsilon t + \sum_{n=2}^\infty\mathbb{P}\Bigg(\Bigg|M_t(\rho)+tb(\rho)+\sum_{i=1}^{n}Y_i^{(\rho)}\Bigg|>\varepsilon\Bigg)\mathbb{P}(N_t(\rho)=n)\bigg|\\
&\leq \mathbb{P}(|M_t(\rho)+tb(\rho)|>\rho)+|\lambda_\rho t \mathbb{P}\Big(\big|M_t(\rho)+tb(\rho)+Y_1^{(\rho)}\big|>\varepsilon\Big)-\lambda_\varepsilon t |\\
&\quad + \lambda_\rho t \big(1-e^{-\lambda_\rho t}\big) + \mathbb{P}\big(N_t(\rho)\geq 2\big)\\
&:\!=\,I_{1}+I_{2}+I_{3}+I_{4}.\end{align*}
The term
$I_{1}$
is controlled with Theorem 1,
$I_{2}$
with Lemma 3; for
$I_{3}$
use that
$1-e^{-x}\leq x$
for all
$x>0$
to get
$I_{3}\leq \lambda_{\rho}^{2}t^{2}$
; and finally, it follows from an argument similar to (7) that
$I_{4}=\mathbb{P}(N_{t}(\rho)\geq 2)\leq \lambda_{\rho}^{2}t^{2}$
(as
$1-e^{-x}-xe^{-x}\leq x^2$
for all
$x>0$
).
3.4. Proof of Theorem 3
As
$\nu$
is symmetric it holds that
$\mathbb{P}(|M_t(\varepsilon)|\geq \varepsilon)=2\mathbb{P}\big(M_t(\varepsilon)\geq \varepsilon\big)$
. Using the same reasoning as in the proof of Theorem 1, we get
\begin{equation}\mathbb{P}\big(M_t(\varepsilon)\geq \varepsilon\big)\leq \mathbb{P}\big(M_t(\varepsilon/2)\geq \varepsilon\big)+t\lambda_{\varepsilon/2,\varepsilon} \mathbb{P}\Big(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\varepsilon)}\geq \varepsilon\Big)+\big(t\lambda_{\varepsilon/2,\varepsilon}\big)^2.\end{equation}
By means of Lemma 2 together with (8), we get that
\begin{equation}\mathbb{P}\big(M_t(\varepsilon/2)\geq \varepsilon\big)\leq t^2 \frac{4^{1+\alpha}{\rm K}^2e^{2+1/e}}{(2-\alpha)^2\varepsilon^{2\alpha}},\end{equation}
and, using (10), that
\begin{equation}\big(t\lambda_{\varepsilon/2,\varepsilon}\big)^2\leq \frac{t^2 {\rm K}^2 4^{1+\alpha}}{\alpha^2\varepsilon^{2\alpha}}.\end{equation}
Finally, using the symmetry of
$\nu$
, we have that
\begin{align*} \lambda_{\varepsilon/2,\varepsilon}&\mathbb{P}\Big(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\varepsilon)}\geq \varepsilon\Big) =\int_{\varepsilon/2}^\varepsilon \big( \mathbb{P}(M_t(\varepsilon/2)\geq \varepsilon -z)+ \mathbb{P}(M_t(\varepsilon/2)\geq \varepsilon +z)\big)f(z)dz\nonumber \\ &\leq \int_{\varepsilon/2}^\varepsilon \mathbb{P}(M_t(\varepsilon/2)\geq \varepsilon -z)f(z)dz+ \frac{ \mathbb{P}(M_t(\varepsilon/2)\geq \varepsilon3/2)}{2} \lambda_{\varepsilon/2,\varepsilon} \,=\!:\,T_1+T_2.\nonumber\end{align*}
To control the term
$T_1$
, observe that
\begin{align*}T_1&=\int_0^{t^{1/\alpha}} \mathbb{P}(M_t(\varepsilon/2)\geq z) f(\varepsilon-z) dz+\int_{t^{1/\alpha}}^{\varepsilon/2} \mathbb{P}(M_t(\varepsilon/2)\geq z) f(\varepsilon-z) dz\\&\leq \frac{{\rm K}t^{1/\alpha}}{(\varepsilon-t^{1/\alpha})^{1+\alpha}}+\frac{2^{1+\alpha}{\rm K}}{\varepsilon^{1+\alpha}}\int_{t^{1/\alpha}}^{\varepsilon/2} \mathbb{P}(M_t(\varepsilon/2)\geq z) dz.\end{align*}
Next, for
$z\in (t^{1/\alpha},\varepsilon/2)$
, the decomposition
$M_t(\varepsilon/2)=M_t(z)+Z_t(z,\varepsilon/2)$
, Equation (7), the Markov inequality, and (8) lead to
\begin{align*} \mathbb{P}(M_t(\varepsilon/2)\geq z)& \leq \mathbb{P}(M_t(z)\geq z)+ t\lambda_{z,\varepsilon/2}\leq \frac{t\sigma^2(z)}{z^2} +2t {\rm K}\int_{z}^{\varepsilon/2} \frac{dx}{x^{1+\alpha}}\leq 2{\rm K} t z^{-\alpha}\bigg(\frac{1}{2-\alpha}+\frac{1}{\alpha}\bigg).\end{align*}
Therefore, for any
$\alpha\in(1,2)$
,
\begin{equation*}\int_{t^{1/\alpha}}^{\varepsilon/2} \mathbb{P}(M_t(\varepsilon/2)\geq z) dz\leq \frac{4{\rm K} t^{\frac{1}{\alpha}}}{\alpha(2-\alpha)(\alpha-1)}; \end{equation*}
then, using that
$\varepsilon-t^{1/\alpha}\geq \varepsilon/2$
, we derive that
\begin{align}T_1\leq \frac{2^{1+\alpha}{\rm K} t^{1/\alpha}}{\varepsilon^{1+\alpha}}\bigg(1+\frac{4{\rm K}}{\alpha(2-\alpha)(\alpha-1)}\bigg),\quad \alpha\in(1,2).\end{align}
If, instead,
$\alpha=1$
, we get
\begin{align}T_1\leq \frac{4{\rm K} t}{\varepsilon^2}+\frac{16{\rm K}^2}{\varepsilon^2}t \ln\Big(\frac{\varepsilon}{2t}\Big).\end{align}
To control the term
$T_2$
we use once again the Markov inequality together with (8) and (10) to obtain
\begin{align}T_2&\leq\frac{t\sigma^2(\varepsilon/2)}{9(\varepsilon/2)^2}\frac{\lambda_{\varepsilon/2,\varepsilon}}{2}\leq \frac{2^{2\alpha+1}{\rm K}^2 t}{9\alpha(2-\alpha)\varepsilon^{2\alpha}}, \quad \alpha\in[1,2).\end{align}
Gathering (26) and (28) we have, for
$\alpha\in(1,2)$
,
\begin{align} \lambda_{\varepsilon/2,\varepsilon}\mathbb{P}\Big(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\varepsilon)}\geq \varepsilon\Big)\leq \frac{2^{1+\alpha}{\rm K} t^{1/\alpha}}{\varepsilon^{1+\alpha}}\bigg(1+\frac{4{\rm K}}{\alpha(2-\alpha)(\alpha-1)}\bigg)+ \frac{2^{2\alpha+1}{\rm K}^2 t}{9\alpha(2-\alpha)\varepsilon^{2\alpha}}.\end{align}
Combining (23) with (24), (25), and (29), we conclude that for all
$\alpha\in(1,2)$
it holds that
\begin{align*}\mathbb{P}\big(M_t(\varepsilon)\geq \varepsilon\big)\leq \frac{t^2{\rm K}^2}{\varepsilon^{2\alpha}}{\rm E}_{1}+\frac{2^{1+\alpha}{\rm K} t^{1+1/\alpha}}{\varepsilon^{1+\alpha}}\bigg(1+\frac{4{\rm K}}{\alpha(2-\alpha)(\alpha-1)}\bigg),\end{align*}
with
\begin{align}{\rm E}_{1}\,:\!=\,\bigg(\frac{4e^{2+1/e}}{(2-\alpha)^2}+\frac{4^{1+\alpha}}{\alpha^2}+\frac{2^{2\alpha+1}}{9\alpha(2-\alpha)}\bigg).\end{align}
If, instead,
$\alpha=1$
, then using (27) we have
\begin{align*}\mathbb{P}\big(M_t(\varepsilon)\geq \varepsilon\big)\leq \frac{4t^2{\rm K}^2}{\varepsilon^2}\bigg(e^{2+1/e}+ \frac{38}{9}\bigg)+\frac{4{\rm K} t^2}{\varepsilon^2}+\frac{16{\rm K}^2}{\varepsilon^2}t^2 \ln\Big(\frac{\varepsilon}{2t}\Big).\end{align*}
This concludes the proof.
3.5. Proof of Theorem 4
Lemma 4. Let f be a symmetric Lévy density such that
$f\in {\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
for some
$\alpha\in[1,2)$
and
${\rm K}>0$
. Let
$\varepsilon>0$
and set
$\rho=\varepsilon\wedge1$
. Then, for all
$0<t<((\varepsilon{\wedge 1})/2)^\alpha\big(1\land ((2-\alpha)/2{\rm K} )\big)$
, it holds that
\begin{align*}&\big|\lambda_\rho t \mathbb{P}\Big(|M_t(\rho)+Y_1^{(\rho)}|>\varepsilon\Big)-\lambda_\varepsilon t \big| \leq{\rm L}_{1}\frac{t^{1+1/\alpha}}{(\varepsilon\wedge 1)^{1+\alpha}}+\frac{8{\rm K}^{2}}{\alpha(2-\alpha)}\frac{t^{2}}{(\varepsilon\wedge 1)^{2\alpha}}+\frac{5{\rm K}}{2-\alpha}\frac{t^{2}\lambda_{1}}{(\varepsilon\wedge1)^2}\\&\quad+\frac{4{\rm K}^{2}t^{2}}{2-\alpha}\varepsilon\mathbf{1}_{\varepsilon>2} +8{\rm K}^2t^{2}\mathbf{1}_{\alpha=1}\bigg(2\mathbf{1}_{\varepsilon>1}\mathbf{1}_{t/C<1\wedge (\varepsilon-1)}\ln\Big(\frac{C(1\wedge|\varepsilon-1|)}{t}\Big)+\ln\Big(\frac{C\rho}{t}\Big)\bigg)\frac{1}{\varepsilon\wedge 1}, \end{align*}
where
$C\,:\!=\,\big(1\wedge\big((2-\alpha)/2{\rm K} \big)\big)^{1/\alpha}$
and
${\rm L}_{1}$
is defined in (68).
Proof of Theorem 4. The result follows from Theorem 3 and Lemma 4 using the decomposition
\begin{align*}|\mathbb{P}&(|X_t|>\varepsilon)-\lambda_\varepsilon t|\leq \mathbb{P}(|M_t(\rho)|>\rho)+|\lambda_\rho t \mathbb{P}\big(\big|M_t(\rho)+Y_1^{(\rho)}\big|>\varepsilon\big)-\lambda_\varepsilon t |+2\lambda_\rho^2t^2\\
&\leq{\rm G}_{1}\frac{t^{1+1/\alpha}}{(\varepsilon\wedge 1)^{1+\alpha}}+{\rm G}_{2}\frac{t^{2}}{(\varepsilon\wedge 1)^{2\alpha}}+\frac{5{\rm K}}{2-\alpha}\frac{t^{2}\lambda_{1}}{(\varepsilon\wedge1)^2}+\frac{4{\rm K}^{2}t^{2}}{2-\alpha}\varepsilon\mathbf{1}_{\varepsilon>2} \\
&\quad+{\rm K}^2t^{2}\mathbf{1}_{\alpha=1}\bigg(8\bigg(2\mathbf{1}_{\varepsilon>1}\mathbf{1}_{t/C<1\wedge (\varepsilon-1)}\ln\bigg(\frac{C(1\wedge|\varepsilon-1|)}{t}\bigg)+\ln\bigg(\frac{C\rho}{t}\bigg)\bigg)\frac{1}{\varepsilon\wedge 1} \\
&\quad+\frac{32}{(\varepsilon\wedge 1)^2} \ln\bigg(\frac{\varepsilon\wedge 1}{2t}\bigg)\bigg)+2\lambda_{\varepsilon\wedge1}^{2}t^{2},\end{align*}
with
$\rho\,:\!=\,\varepsilon\wedge 1$
and
\begin{align}{\rm G}_{1}&={\rm L}_{1}+\mathbf{1}_{\alpha\in(1,2)}{2^{2+\alpha}{\rm K} }\bigg(1+\frac{{\rm K}}{\alpha(2-\alpha)(\alpha-1)}\bigg)+\mathbf{1}_{\alpha=1}\bigg( {8{\rm K}^2}\bigg(e^{2+1/e}+ \frac{38}{9}\bigg)+{8{\rm K} }\bigg),\\
{\rm G}_{2}&=\frac{8{\rm K}^{2}}{\alpha(2-\alpha)}+{\rm K}^2 {\rm E}_{1}\mathbf{1}_{\alpha\in(1,2)}.\nonumber\end{align}
3.6. Proof of Theorem 5
We first introduce two auxiliary lemmas whose proofs can be found in the appendix.
Lemma 5. Let f be a symmetric Lévy density such that
$f\in {\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in[1,2)$
and
${\rm K}>0$
. Let
$\varepsilon\in(0,1]$
. Then there exist three positive constants
${\rm H}_1$
,
${\rm H}_2$
, and
${\rm H}_3$
, dependent only on
$\alpha$
, such that for all
\begin{equation*}0<t\leq \frac{(2-\alpha)\varepsilon^\alpha}{2^{1+\alpha}{\rm K}},\end{equation*}
it holds that
\begin{align*}\frac{\mathbb{P}(|M_t(3\varepsilon/4)|>\varepsilon)}{2}\leq \frac{{\rm K}^2t^2{\rm H}_1}{\varepsilon^{2\alpha}}+ t^2 \varepsilon^{-2\alpha}{\rm K}^2 {\rm H}_2\mathbf{1}_{\alpha\in(1,2)}+\frac{t^4 {\rm K}^4 {\rm H}_3}{\varepsilon^{4\alpha}}+\frac{32 {\rm K}^2 t^2}{\varepsilon^2} \ln(2)\mathbf{1}_{\alpha=1}.\end{align*}
For explicit formulas for
${\rm H}_1,\ {\rm H}_{2}$
, and
${\rm H}_3$
, see (53) and (58).
Lemma 6. Let f be a symmetric Lévy density f in
$ {\mathscr{L}}_{{\rm K},\alpha}$
for some
$\alpha\in[1,2)$
and
${\rm K}>0$
. Let
$\varepsilon>0$
, set
$\rho=3/4(\varepsilon\wedge1)$
, and assume that f is
${\rm K}(\varepsilon\wedge 1)^{-(2+\alpha)}$
-Lipschitz on the interval
$((3/4(\varepsilon\wedge1),2\varepsilon-3/4(\varepsilon\wedge1))$
. Then for all
$t>0$
it holds that
\begin{align*}\big|\lambda_\rho t \mathbb{P}\Big(\Big|M_t(\rho)+Y_1^{(\rho)}\Big|>\varepsilon\Big)-\lambda_\varepsilon t \big|&\leq {\rm K}^2 t^2\Big({\rm H}_4 \varepsilon^{-2\alpha} \mathbf{1}_{0<\varepsilon\leq 1}+ \varepsilon^{2}{\rm H}_5 \mathbf{1}_{\varepsilon>1}\Big) +{\rm H}_6{\rm K} t^2\lambda_{1}(\varepsilon\wedge1)^{-\alpha},\end{align*}
where
${\rm H}_4,\ {\rm H}_5$
, and
${\rm H}_{6}$
are positive universal constants, depending only on
$\alpha$
, defined in (67).
Proof of Theorem 5. Let
$\rho\,:\!=\,3/4(\varepsilon\wedge1)$
; using (2) at the point
$\rho$
and
$\mathbb{P}(|M_t(\rho)|>\varepsilon)\le\mathbb{P}(|M_t(\rho)|>1\wedge\varepsilon)$
, we derive
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big)-\lambda_\varepsilon t|&\leq \mathbb{P}(|M_t(\rho)|>1\wedge\varepsilon)+|\lambda_\rho t \mathbb{P}\Big(\Big|M_t(\rho)+Y_1^{(\rho)}\Big|>\varepsilon\Big)\\
&\quad-\lambda_\varepsilon t | + \lambda_\rho t \big(1-e^{-\lambda_\rho t}\big) + \mathbb{P}\big(N_t(\rho)\geq 2\big)\\
:&=I_{1}+I_{2}+I_{3}+I_{4}.\end{align*}
By Lemma 5 and Lemma 6 it follows that
\begin{align*}I_1&\leq \frac{2{\rm K}^2t^2{\rm H}_1}{(\varepsilon\wedge 1)^{2\alpha}}+ 2t^2 (\varepsilon\wedge 1)^{-2\alpha}{\rm K}^2 {\rm H}_2\mathbf{1}_{\alpha\in(1,2)}+\frac{2t^4 {\rm K}^4 {\rm H}_3}{(\varepsilon\wedge 1)^{4\alpha}}+\frac{64 {\rm K}^2 t^2}{(\varepsilon\wedge 1)^2} \ln(2)\mathbf{1}_{\alpha=1},\\I_2&\leq {\rm K}^2 t^2\big({\rm H}_4 \varepsilon^{-2\alpha} \mathbf{1}_{0<\varepsilon\leq 1}+ \varepsilon^{2}{\rm H}_5 \mathbf{1}_{\varepsilon>1}\big) +{\rm H}_6{\rm K} t^2\lambda_{1}(\varepsilon\wedge1)^{-\alpha}.\end{align*}
Furthermore, by (7) and (9), it holds that
\begin{align*}I_3+I_4&\leq 2(\lambda_\rho t)^2=2 t^2 (\lambda_{\rho,1}+\lambda_1)^2\leq 4 t^2 (\lambda_{\rho,1})^2+ 4t^2 \lambda_1^2\\
&\leq \frac{16t^2K^2}{\alpha^2} \bigg(\bigg(\frac{4}{3}\bigg)^\alpha(\varepsilon\wedge 1)^{-\alpha}-1\bigg)^2+ 4t^2 \lambda_1^2.\end{align*}
Therefore
\begin{align*}|\mathbb{P}\big(|X_t|>\varepsilon\big) &-\lambda_\varepsilon t| \leq t^2{\rm K}^2 \big( \big({\rm F}_{1}\varepsilon^{-2\alpha}+\lambda_1\varepsilon^{-\alpha}{\rm F}_2\big) \mathbf{1}_{0<\varepsilon\leq 1}\\
& +(\varepsilon^2{\rm F}_3 +{\rm F}_{4})\mathbf{1}_{\varepsilon>1} \big) +t^4 {\rm K}^4 {\rm F}_5(\varepsilon\wedge 1)^{-4\alpha}+4t^2\lambda_1^2,\end{align*}
with
${\rm F}_{2}={\frac{{\rm H}_{6}}{{\rm K}}} $
,
${\rm F}_{3}={\rm H}_{5}$
,
${\rm F}_{5}=2{\rm H}_{3} $
, and
\begin{align}{\rm F}_{1}&\,:\!=\,2{\rm H}_1+2{\rm H}_2\mathbf{1}_{\alpha\in(1,2)}+{\rm H}_4+64\ln(2)\mathbf{1}_{\alpha=1}+\frac{16(4/3)^{2\alpha}}{\alpha^2},\nonumber\\{\rm F}_{4}&\,:\!=\,2{\rm H}_1+2{\rm H}_2\mathbf{1}_{\alpha\in(1,2)}+64\ln(2)\mathbf{1}_{\alpha=1}+{\frac{16}{\alpha^2}},\end{align}
where in defining
${\rm F}_{4}$
we used that
$((4/3)^\alpha-1)^2\leq 1$
.
Appendix A. Technical lemmas and additional proofs
A.1. Proof of Lemma 2
For any
$u>0$
we have that
\begin{equation*}\mathbb{E}\big[e^{u M_t(\varepsilon)}\big]\leq \exp\bigg(t\int (e^{u|y|}-u|y|-1)\nu_\varepsilon(dy) \bigg).\end{equation*}
Therefore, using that
$\int |y|^k\nu_\varepsilon(dy)\leq \varepsilon^{k-2}\sigma^2(\varepsilon)$
for all
$k\geq 2$
, we have
\begin{align}\mathbb{P}(M_t(\varepsilon)>x)&\leq \exp\bigg({-}ux+t\int (e^{u|y|}-u|y|-1)\nu_\varepsilon(dy)\bigg)\nonumber \\
&\leq \exp\bigg(\frac{u^2 t\sigma^2(\varepsilon)}{2}-ux +t \sigma^2(\varepsilon)\sum_{k=3}^\infty \frac{u^k\varepsilon^{k-2}}{k!}\bigg)\nonumber\\
&=\exp\bigg({-}ux +t \frac{\sigma^2(\varepsilon)}{\varepsilon^2}(e^{u\varepsilon}-1-u\varepsilon)\bigg).\end{align}
Substituting
\begin{equation*}u^*=\frac{1}{\varepsilon}\ln\bigg(1+\frac{x\varepsilon}{t\sigma^2(\varepsilon)}\bigg)\end{equation*}
in (33), we find that
\begin{equation*}\mathbb{P}(M_t(\varepsilon)>x)\leq e^{\frac{x}{\varepsilon}}\bigg(\frac{t\sigma^2(\varepsilon)}{x\varepsilon+t\sigma^2(\varepsilon)}\bigg)^{\frac{x\varepsilon+t\sigma^2(\varepsilon)}{\varepsilon^2}},\end{equation*}
as claimed. To derive (3), we use that
$u^{-u}\leq e^{e^{-1}}$
for all
$u> 0$
. Indeed, set
\begin{equation*}u=\frac{x\varepsilon+t\sigma^2(\varepsilon)}{\varepsilon^2}\end{equation*}
and notice that
\begin{align*}\bigg(\frac{t\sigma^2(\varepsilon)}{x\varepsilon+t\sigma^2(\varepsilon)}\bigg)^{\frac{x\varepsilon+t\sigma^2(\varepsilon)}{\varepsilon^2}}&=\bigg(\frac{t\sigma^2(\varepsilon)}{\varepsilon^2}\bigg)^u u^{-u}\leq e^{e^{-1}} \bigg(\frac{t\sigma^2(\varepsilon)}{\varepsilon^2}\bigg)^{\frac{x\varepsilon+t\sigma^2(\varepsilon)}{\varepsilon^2}}.\end{align*}
The first part of Equation (3) then follows under the assumption
$t\sigma^2(\varepsilon)\varepsilon^{-2}\leq 1$
. Analogous arguments, with
$M_t(\varepsilon)$
replaced by
$-M_t(\varepsilon)$
, allow us to deduce the right-hand part of Equation (3).
A.2. Proof of Lemma 3
First, we consider the general case where
$\nu$
is not symmetric. We control the quantity
$J=\lambda_\rho\mathbb{P}\big(\big|M_t(\rho)+tb(\rho)+Y_1^{(\rho)}\big|>\varepsilon\big)-\lambda_\varepsilon$
as
$Q=|J|t$
. It holds that
\begin{align}J&=\int_\rho^\infty \big(\mathbb{P}(M_t(\rho)+tb(\rho)<-\varepsilon-z) f(z)+\mathbb{P}(M_t(\rho)+tb(\rho)>\varepsilon+z) f({-}z)\big)dz\nonumber\\&\quad -\int_\varepsilon^\infty \big(\mathbb{P}(M_t(\rho)+tb(\rho)\leq \varepsilon-z)f(z)+\mathbb{P}(M_t(\rho)+tb(\rho)>z-\varepsilon)f({-}z)\big)dz\nonumber\\&\quad+\int_{\rho}^\varepsilon \big(\mathbb{P}(M_t(\rho)+tb(\rho)> \varepsilon-z)f(z)+\mathbb{P}(M_t(\rho)+tb(\rho)<-\varepsilon+z)f({-}z)\big)dz\nonumber\\&\,=\!:\,R-S+T. \end{align}
Recall
$\rho=\varepsilon\wedge1$
; both assumptions on t ensure that
$t|b(\rho)|\leq \rho/2$
, and thus
\begin{align*}R\leq \int_\rho^\infty \big(\mathbb{P}(M_t(\rho)<-\rho) f(z)+\mathbb{P}(M_t(\rho)>\rho) f({-}z)\big)dz.\end{align*}
By means of the Markov inequality and (8) we then derive
\begin{equation}|R|\leq \frac{2{\rm K} }{2-\alpha}t \lambda_\rho \rho^{-\alpha}.\end{equation}
To treat the terms S and T we distinguish the cases
$\varepsilon\in(0,1]$
and
$\varepsilon>1$
. Moreover, we restrict to the case
$b(\rho)\geq 0$
; the case
$b(\rho)<0$
can be obtained similarly and leads to the same result. Decompose
$S\,:\!=\,S_{1}+S_{2}$
, where
\begin{align*}S_{1}+S_{2}=\int_{-tb(\rho)}^\infty \mathbb{P}(M_t(\rho)> x)f({-}\varepsilon-tb(\rho)-x)dx+ \int_{tb(\rho)}^{\infty} \mathbb{P}(M_t(\rho)\leq -x)f(x+\varepsilon-tb(\rho))dx.\end{align*}
We detail only the computations for the term
$S_1$
, those for the term
$S_2$
being analogous.
Case
$\varepsilon\in(0,1]:$
In this case,
$\rho=\varepsilon$
, and it holds that
\begin{align*}|S_1|&\leq\int_{-tb(\varepsilon)}^{tb(\varepsilon)}f({-}\varepsilon-tb(\varepsilon)-x)dx+\int_{t b(\varepsilon)}^{\varepsilon/2}\mathbb{P}( M_t(\varepsilon)> x)f({-}\varepsilon-tb(\varepsilon)-x)dx\\&\quad +\int_{\varepsilon/2}^\varepsilon\mathbb{P}( M_t(\varepsilon)> x)f({-}\varepsilon-tb(\varepsilon)-x)dx+\int_{\varepsilon}^\infty\mathbb{P}( M_t(\varepsilon)> x)f({-}\varepsilon-tb(\varepsilon)-x)dx\\&=S_{1,1}+S_{1,2}+S_{1,3}+S_{1,4}.\end{align*}
From the fact that
$f\in{\mathscr{L}}_{{\rm K},\alpha} $
and (11), it follows that
\begin{align}S_{1,1}&\leq 2{\rm K}tb(\varepsilon) \varepsilon^{-(1+\alpha)}\leq \frac{4{\rm K}^2t\varepsilon^{-2\alpha}}{1-\alpha}.\end{align}
To control the term
$S_{1,2}$
we proceed as for the control of the term
$T_{2,1}$
in the proof of Theorem 1. Observe that
$0<t\leq (1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)}$
implies
$2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1}<\varepsilon/2$
. Let
$x\in(2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1},\varepsilon/2)$
and set
$\tilde x\,:\!=\,x-2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1}$
. In particular we can write
$M_t(\varepsilon)=M_t(\tilde x)+Z_t(\tilde x, \varepsilon)-t(b(\varepsilon)-b(\tilde x))$
. From the assumption
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
it also follows that
$|b(\varepsilon)-b(\tilde x)|\leq 2{\rm K} \varepsilon^{1-\alpha}(1-\alpha)^{-1}$
, and so
\begin{equation*}\mathbb{P}(M_t(\tilde x) >x+t(b(\varepsilon)-b(\tilde x)))\leq \mathbb{P}(M_t(\tilde x)>\tilde x).\end{equation*}
Therefore, for all
$x\in(2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1},\varepsilon/2)$
, the Markov inequality and (8) lead to
\begin{align*}\mathbb{P}(M_t(\varepsilon)>x)&\leq \mathbb{P}(M_t(\tilde x) >x+t(b(\varepsilon)-b(\tilde x)))+\mathbb{P}(N_t(\tilde x,\varepsilon)\geq 1)\leq \mathbb{P}(M_t(\tilde x)>\tilde x)+t \lambda_{\tilde x,\varepsilon}\\&\leq \frac{2(2+\alpha){\rm K}t \tilde x^{-\alpha}}{\alpha(2-\alpha)}.\end{align*}
Furthermore, by means of (11),
$t|b(\varepsilon)|\leq2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1}$
, and
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
, we get
\begin{equation*}\int_{tb(\varepsilon)}^{2{\rm K} /(1-\alpha)t\varepsilon^{1-\alpha} }f({-}\varepsilon-tb(\varepsilon)-x)dx\leq \int_{0}^{2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1}}f({-}\varepsilon-tb(\varepsilon)-x)dx \leq \frac{2{\rm K}^2}{1-\alpha}t\varepsilon^{-2\alpha}\end{equation*}
and
\begin{align*}\int_{ \frac{2}{1-\alpha}{\rm K}t\varepsilon^{1-\alpha}}^{\varepsilon/2}\tilde x^{-\alpha}f({-}\varepsilon-tb(\varepsilon)-x)dx&\le\frac{ {\rm K}}{\varepsilon^{1+\alpha}}\int_{\frac{2}{1-\alpha}{\rm K}t\varepsilon^{1-\alpha}}^{\varepsilon/2} \Big(x-2{\rm K}t\varepsilon^{1-\alpha} (1-\alpha)^{-1}\Big)^{-\alpha}dx\\&\le \frac{{\rm K}}{1-\alpha}\varepsilon^{-2\alpha}.\end{align*}
We derive that
\begin{align}S_{1,2}\leq\frac{2{\rm K}^2}{1-\alpha}t\varepsilon^{-2\alpha}+ \frac{2(2+\alpha){\rm K}^{2}}{\alpha(2-\alpha)(1-\alpha)}t \varepsilon^{-2\alpha}.\end{align}
To treat the term
$S_{1,3}$
we notice that, for any
$t\in(0,(1-\alpha) {\rm K}^{-1} \varepsilon^{\alpha}4^{-(1+\alpha)})$
and
$x\in[\varepsilon/2,\varepsilon]$
, we have that
$t\lambda_{x,\varepsilon}\leq 1$
, and hence, by Lemma 7, we derive that for all
$x\in[\varepsilon/2,\varepsilon]$
,
\begin{align*}\mathbb{P}\big(M_t(\varepsilon)>x\big)\leq \mathbb{P}\big(M_t(x) +\tilde Z_t(x,\varepsilon)>x\big) +2t\varepsilon \sup_{|y|\in[x,\varepsilon]} f(y),\end{align*}
where
\begin{equation*}\tilde Z_t(x,\varepsilon)\,:\!=\,\sum_{i=1}^{N_t(x,\eta)}\Big(Y_i^{(x,\eta)}-\mathbb{E}\Big[Y_i^{(x,\eta)}\Big]\Big).\end{equation*}
Then, using (7), the Markov inequality, (8), and (10), we get
\begin{align*} \mathbb{P}(M_t(x) +\tilde Z_t(x,\varepsilon)>x)\leq \mathbb{P}(M_t(x)>x)+\mathbb{P}(N_{t}(x,\varepsilon)\geq1)\leq \frac{2(2+\alpha){\rm K}tx^{-\alpha}}{(2-\alpha)\alpha}.\end{align*}
Moreover, the fact that
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
implies
$ \sup_{|y|\in[x,\varepsilon]} f(y)\leq {\rm K} x^{-(1+\alpha)}\leq {\rm K} 2^{1+\alpha} \varepsilon^{-(1+\alpha)}$
for
$x\in[\varepsilon/2,\varepsilon]$
and so we deduce that
\begin{align*}\mathbb{P}(M_t(\varepsilon)>x)\leq2^{\alpha+1} {\rm K}t\varepsilon^{-\alpha}\bigg(2+\frac{2+\alpha}{(2-\alpha)\alpha}\bigg).\end{align*}
Combining this with
$ \int_{\varepsilon/2}^{\varepsilon} f({-}\varepsilon-tb(\varepsilon)-x)dx\leq \lambda_\varepsilon$
, we obtain
\begin{align}S_{1,3}\leq\lambda_\varepsilon2^{\alpha+1} {\rm K}t\varepsilon^{-\alpha}\bigg(2+\frac{2+\alpha}{(2-\alpha)\alpha}\bigg).\end{align}
Finally, for the term
$S_{1,4}$
we have that
\begin{align*}S_{1,4}\leq \mathbb{P}(M_t(\varepsilon)>\varepsilon)\int_{-\infty}^{-2\varepsilon-tb(\varepsilon)} f(x)dx\leq \mathbb{P}(M_t(\varepsilon)>\varepsilon) \lambda_\varepsilon.\end{align*}
From the Markov inequality and (8) we then derive
\begin{equation}S_{1,4}\leq \frac{2{\rm K} }{2-\alpha}t \lambda_\varepsilon \varepsilon^{-\alpha}.\end{equation}
Combining (36), (37), (38), and (39) yields
\begin{align*} |S_1|&\leq\frac{ 2{\rm K}^2}{1-\alpha}t\varepsilon^{-2\alpha}\bigg(3+\frac{2+\alpha}{\alpha(2-\alpha)}\bigg)+ 2{\rm K}t\varepsilon^{-\alpha}\lambda_\varepsilon\bigg(1+2^\alpha\bigg(2+\frac{2+\alpha}{\alpha(2-\alpha)}\bigg)\bigg). \end{align*}
The term
$S_2$
can be controlled in a similar way; in particular it holds that
\begin{align}|-S|\leq \frac{ 4{\rm K}^2}{1-\alpha}t\varepsilon^{-2\alpha}\bigg(3+\frac{2+\alpha}{\alpha(2-\alpha)}\bigg)+ 4{\rm K}t\varepsilon^{-\alpha}\lambda_\varepsilon\bigg(1+2^\alpha\bigg(2+\frac{2+\alpha}{\alpha(2-\alpha)}\bigg)\bigg). \end{align}
Finally, we observe that when
$\varepsilon\in(0,1]$
the term T is identically zero.
Gathering Equations (34), (35), and (40), we conclude that for
$\varepsilon\in(0,1]$
,
\begin{align*} |\lambda_\varepsilon t \mathbb{P}\Big(|M_t(\varepsilon)+tb(\varepsilon)+Y_1^{(\varepsilon)}|>\varepsilon\Big)-\lambda_\varepsilon t |&\leq t^{2}\big({\rm K}^2{\rm D}_1\varepsilon^{-2\alpha}+{\rm K}\lambda_\varepsilon\varepsilon^{-\alpha} {\rm D}_2\big), \end{align*}
where
\begin{align} {\rm D}_1&\,:\!=\,\frac{4}{1-\alpha}\bigg(3+\frac{2+\alpha}{\alpha(2-\alpha)}\bigg)\quad \text{ and }\quad {\rm D}_2\,:\!=\,4\Big(\frac{1}{2-\alpha}+1+2^\alpha\Big(2+\frac{2+\alpha}{\alpha(2-\alpha)}\Big)\Big). \end{align}
Case
$\varepsilon>1:$
In this case
$\rho=1$
, and using that
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap{\mathscr{L}}_{{\rm K}}$
we readily derive
\begin{align}S_1\leq 2{\rm K}tb(1)+{\rm K}\bigg(\int_{tb(1)}^{1/2}+\int_{1/2}^\infty \mathbb{P}(M_t(1)>x)dx\bigg)\,=\!:\,\tilde S_{1,1}+\tilde S_{1,2}+\tilde S_{1,3}.\end{align}
The term
$\tilde S_{1,2}$
is the analogue of
$S_{1,2}$
above. Observe that under the assumptions
$0<t\leq (1-\alpha) (5{\rm K})^{-1}$
and
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
, we get
$t|b(1)|\leq 1/2$
. For any
$x\in (2{\rm K}t(1-\alpha)^{-1},1/2)$
, set
$\hat x\,:\!=\, x-2{\rm K}t(1-\alpha)^{-1}.$
The same reasoning as for the term
$S_{1,2}$
allows us to conclude that, for any
$x\in \big(2{\rm K}t(1-\alpha)^{-1},1/2\big)$
,
\begin{align}\mathbb{P}(M_t(1)>x)\leq \mathbb{P}(M_t(\hat x)>\hat x)+t(\lambda_{\hat x,2}+\lambda_2)\leq \frac{4}{(2-\alpha)\alpha}{\rm K}t \hat x^{-\alpha} +t\lambda_2,\end{align}
where in the last inequality we used the fact that
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
together with the Markov inequality, (8), and (10). Therefore, from (43) and using again that
$f\in{\mathscr{L}}_{{\rm K}}$
, we get
\begin{align}\tilde S_{1,2}&\leq {\rm K}t\bigg(\frac{2{\rm K} }{1-\alpha}-b(1)\bigg)+\frac{4{\rm K}^2t}{\alpha(2-\alpha)}\int_{2{\rm K}t(1-\alpha)^{-1}}^{1/2} \bigg(x-\frac{2{\rm K}t}{1-\alpha}\bigg)^{-\alpha}dx+\frac{t{\rm K}\lambda_2}{2}\nonumber\\[4pt]
&\leq {\rm K}t\bigg(\frac{2{\rm K} }{1-\alpha}-b(1)\bigg)+\frac{4 {\rm K}^2t}{\alpha(2-\alpha)(1-\alpha)}+\frac{t{\rm K}\lambda_2}{2}.\end{align}
Furthermore, by the Markov inequality and (8), we deduce that
\begin{align}\tilde S_{1,3}\leq \frac{4{\rm K}^2t}{2-\alpha}.\end{align}
Gathering (42), (44), and (45), we conclude that
\begin{align*}S_1&\leq 2{\rm K}tb(1)+{\rm K}t\bigg(\frac{2{\rm K} }{1-\alpha}-b(1)\bigg)+\frac{8 {\rm K}^2t}{\alpha(2-\alpha)(1-\alpha)}+\frac{t{\rm K}\lambda_2}{2}.\end{align*}
Thus the term S in (34) can be bounded by
\begin{align}|S|\leq 4{\rm K}tb(1)+2{\rm K}t\bigg(\frac{2{\rm K} }{1-\alpha}-b(1)\bigg)+\frac{16 {\rm K}^2t}{\alpha(2-\alpha)(1-\alpha)}+t{\rm K}\lambda_2.\end{align}
By means of (35), the term R in (34) is bounded by
\begin{align}|R|\leq \frac{2{\rm K}t\lambda_1}{2-\alpha}.\end{align}
To control J it remains to control the term T in (34). We provide an upper bound for
\begin{equation*}T_1\,:\!=\,\int_1^\varepsilon \mathbb{P}(M_t(1)+tb(1)>\varepsilon-z)f(z)dz=\int_{-tb(1)}^{\varepsilon-1-tb(1)}\mathbb{P}(M_{t}(1)\ge x)f(\varepsilon-x-tb(1))dx;\end{equation*}
the control of the quantity
$\int_1^\varepsilon\mathbb{P}(M_t(1)+tb(1)<-\varepsilon+z)f({-}z)\big)dz$
can be treated similarly. We have, using
$t|b(1)|\le 1/2$
, that
\begin{align*}T_{1}&=\mathbf{1}_{\varepsilon\ge 1+2tb(1)}\Bigg(\int_{-tb(1)}^{tb(1)}+\int_{tb(1)}^{1/2\wedge(\varepsilon-1-tb(1))}+\int_{1/2\wedge(\varepsilon-1-tb(1))}^{\varepsilon-1-tb(1))}\mathbb{P}(M_{t}(1)\ge x)f(\varepsilon-x-tb(1))dx\Bigg)\\
&\quad + \mathbf{1}_{1<\varepsilon<1+2tb(1)}\int_{-tb(1)}^{tb(1)}\mathbb{P}(M_{t}(1)\ge x)f(\varepsilon-x-tb(1))dx =T_{1,1}+T_{1,2}.\end{align*}
For
$f\in{\mathscr{L}}_{{\rm K}}$
, recalling the definition of
$\tilde S_{1,2}$
given in (42) and that we assumed
$b(1)\geq0$
, for
$\varepsilon\geq 1+2tb(1)$
we write
\begin{align*}T_{1,1}&\leq 2{\rm K}tb(1)+ {\rm K}\int_{tb(1)}^{1/2\wedge (\varepsilon-1-tb(1))}\mathbb{P}(M_t(1)>y)dy+{\rm K}\int_{1/2\wedge (\varepsilon-1-tb(1))}^{\varepsilon-1-tb(1)}\mathbb{P}(M_t(1)>y)dy\\
&\leq {\rm K}\Big(2tb(1)+\tilde S_{1,2}+\mathbb{P}(M_t(1)>1/2)(\varepsilon-3/2-tb(1))\mathbf{1}_{1/2<\varepsilon-1-tb(1)}\Big)\\
&\leq {\rm K}t\bigg(2b(1)+\frac{2{\rm K} }{1-\alpha}+\frac{4 {\rm K}}{\alpha(2-\alpha)(1-\alpha)}+\frac{\lambda_2}{2}+\frac{8{\rm K}}{2-\alpha}(\varepsilon-3/2-tb(1))\mathbf{1}_{\varepsilon>3/2+tb(1)}\bigg),\end{align*}
where we used (44), the Markov inequality, and (8). For the term
$T_{1,2}$
, using
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
together with (11) and the assumption
$t<(1-\alpha)(5{\rm K})^{-1}$
, we get
\begin{equation*}T_{1,2}\leq 2{\rm K}tb(1)(\varepsilon-2tb(1))^{-1-\alpha}\mathbf{1}_{1<\varepsilon<1+2tb(1)}\leq 4{\rm K}t5^{\alpha}\mathbf{1}_{1<\varepsilon<1+2tb(1)}.\end{equation*}
This implies that
\begin{align}T\leq {\rm K}t&\Bigg(\mathbf{1}_{\varepsilon\ge 1+2t|b(1)|}\bigg(\frac{6{\rm K}}{1-\alpha}+\frac{4 {\rm K}}{\alpha(2-\alpha)(1-\alpha)}+\frac{\lambda_2}{2}\nonumber\\
&+\frac{8{\rm K}}{2-\alpha}(\varepsilon-3/2-t|b(1)|)\mathbf{1}_{3/2+t|b(1)|<\varepsilon}\bigg)+ 5^{\alpha}4\mathbf{1}_{1<\varepsilon<1+2t|b(1)|}\Bigg).\end{align}
Combining (34), (46), (47), and (48), and using (10), we conclude that, for any
$\varepsilon>1$
,
$0<t< (1-\alpha)(5{\rm K})^{-1}$
, and
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap{\mathscr{L}}_{{\rm K}}$
, using
$t|b(1)|\le 1/2$
, we have
\begin{align*}J&\leq 2{\rm K}^2t \Big(\tilde{\rm D}_1+\frac{4}{2-\alpha}(\varepsilon-3/2-t|b(1)|)\mathbf{1}_{3/2+t|b(1)|<\varepsilon}\Big) \\&\quad+{\rm K}t\bigg(4\times 5^{\alpha}\mathbf{1}_{1<\varepsilon<1+2t|b(1)|}+\frac{8}{5}+3\lambda_2+\frac{4\lambda_1}{2-\alpha}\bigg),\end{align*}
where we used the notation
\begin{equation}\tilde{\rm D}_1\,:\!=\,\frac{5}{1-\alpha}+\frac{10}{\alpha(2-\alpha)(1-\alpha)}.\end{equation}
Case
$\nu$
symmetric and
$\varepsilon>0:$
In the case where
$\nu$
is symmetric the proof can be simplified. Since
$b(\rho)\equiv0$
,
$M_t(\rho)=M_t(x)+Z_t(x,\rho)$
for all
$x\in(0,\rho)$
,
$t>0$
, and it holds that
\begin{align*} \lambda_\rho &\mathbb{P}(|M_t(\rho)+Y_1^{(\rho)}|>\varepsilon)-\lambda_\varepsilon =2\Bigg(\int_\rho^\infty \big(\mathbb{P}(M_t(\rho)>\varepsilon+z)-\mathbb{P}(M_t(\rho)<\varepsilon-z)\big)f(z)dz\Bigg)\\
&\leq \lambda_\rho \mathbb{P}(M_t(\rho)>2\rho)+2\Bigg(\int_0^\rho \mathbb{P}(M_t(\rho)>x) f(x+\varepsilon)dx+\mathbb{P}(M_t(\rho)>\rho)\int_{\rho}^\infty f(x+\varepsilon)dx\Bigg). \end{align*}
By the same arguments as those used to treat the term
$S_{1,2}$
above, one finds that for any
$x\in(0,\varepsilon)$
and
$t>0$
,
\begin{equation*}\mathbb{P}(M_t(\rho)>x)\leq \frac{2(2+\alpha){\rm K} tx^{-\alpha}}{\alpha(2-\alpha)}.\end{equation*}
Therefore, by the Markov inequality, (8), and the fact that
$f\in{\mathscr{L}}_{{\rm K},\alpha}$
, we conclude that for all
$\varepsilon\in(0,1)$
and
$t>0$
,
\begin{equation*}\Big| \lambda_\rho \mathbb{P}\Big(\Big|M_t(\rho)+Y_1^{(\rho)}\Big|>\varepsilon\Big)-\lambda_\varepsilon|\leq \frac{t{\rm K}}{2(2-\alpha)}\big(\lambda_\varepsilon \varepsilon^{-\alpha}+4\lambda_{2\varepsilon} \varepsilon^{-\alpha}\big)+2t{\rm K}^2{\rm D_2}\varepsilon^{-2\alpha},\end{equation*}
with
\begin{equation}{ \rm D}_3\,:\!=\,\frac{2(2+\alpha)}{(2-\alpha)\alpha(1-\alpha)}. \end{equation}
If instead
$\varepsilon>1$
, then assuming in addition that
$f\in {\mathscr{L}}_{{\rm K}}$
, we derive
\begin{equation*}\Big| \lambda_1 \mathbb{P}\Big(\Big|M_t(1)+Y_1^{(1)}\Big|>\varepsilon\Big)-\lambda_\varepsilon\Big|\leq \frac{t{\rm K}}{2-\alpha}\bigg(\lambda_1 2^{-\alpha}+\frac{4{\rm K}}{\alpha(1-\alpha)}+\lambda_{1+\varepsilon} \bigg).\end{equation*}
This concludes the proof.
A.3. Proof of Lemma 5
First, by the symmetry of
$\nu$
, it holds that
$\mathbb{P}(|M_t(\rho)|>\varepsilon)=2\mathbb{P}(M_t(\rho)>\varepsilon)$
, where we write
$\rho\,:\!=\,3\varepsilon/4$
. Since
$\varepsilon/2<\rho<\varepsilon$
together with (6) and (7), we obtain
\begin{align}\mathbb{P}\big(M_t(\rho)>\varepsilon\big)\leq \mathbb{P}\big(M_t(\varepsilon/2)>\varepsilon\big)+t\lambda_{\varepsilon/2,\rho}\mathbb{P}\Big(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\rho)}>\varepsilon\Big)+\big(t\lambda_{\varepsilon/2,\rho}\big)^2.\end{align}
Applying the second part of Lemma 2 and using (8), we derive
\begin{align}\mathbb{P}\big(M_t(\varepsilon/2)>\varepsilon\big)+\big(t\lambda_{\varepsilon/2,\rho}\big)^2\leq {\rm K}^2t^2\varepsilon^{-2\alpha}{\rm H}_1,\end{align}
with
\begin{equation}{\rm H}_1\,:\!=\,4^{1+\alpha}\bigg( \frac{e^{2+1/e}}{(2-\alpha)^2}+\frac{1}{\alpha^2}\bigg).\end{equation}
Using again the symmetry of
$\nu$
we can establish
\begin{align}\lambda_{\varepsilon/2,\rho}\mathbb{P}\Big(&M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\rho)}>\varepsilon\Big)\nonumber\\
&=\int_{\varepsilon/4}^{\varepsilon/2} \mathbb{P}\big(M_t(\varepsilon/2)>y\big) f(\varepsilon-y)dy+\int_{\varepsilon/2}^\rho \mathbb{P}\big(M_t(\varepsilon/2)>\varepsilon+y\big)f(y)dy\nonumber \\
&\leq \int_{\varepsilon/4}^{\varepsilon/2} \mathbb{P}\big(M_t(\varepsilon/2)>y\big) f(\varepsilon-y)dy+ \mathbb{P}\big(M_t(\varepsilon/2)>3/2\varepsilon\big)\frac{\lambda_{\varepsilon/2,\rho}}{2}\nonumber\\
&\,=\!:\,T_1+T_2.\end{align}
Applying (6), (7), the Markov inequality, and (8), for any
$y\in (\varepsilon/4,\varepsilon/2)$
we have
\begin{align*}\mathbb{P}\big(M_t(\varepsilon/2)>y\big)&\leq \mathbb{P}(M_t(y)>y)+t\lambda_{y,\varepsilon/2}\leq \frac{4{\rm K}t y^{-\alpha}}{\alpha(2-\alpha)}.\end{align*}
It follows that
\begin{align}T_1&\leq \frac{4{\rm K}t }{\alpha(2-\alpha)} \int_{\varepsilon/4}^{\varepsilon/2} y^{-\alpha} f(\varepsilon-y)dy\leq \frac{2^{3+\alpha}{\rm K}^2t }{\alpha(2-\alpha)\varepsilon^{1+\alpha}}\bigg(\frac{(\varepsilon/4)^{1-\alpha}}{(\alpha-1)}\mathbf{1}_{\alpha\in(1,2)}+\ln(2)\mathbf{1}_{\alpha=1}\bigg).\end{align}
Furthermore, note that Lemma 2 applies as
\begin{equation*}t\leq \frac{(2-\alpha)\varepsilon^\alpha}{2^{1+\alpha}{\rm K}}\end{equation*}
implies
$4t\sigma^2(\varepsilon/2)\varepsilon^{-2}\leq 1$
. Together with (8), this gives
\begin{align}T_2&\leq \frac{t^32^{3(1+\alpha)}e^{3+1/e} {\rm K}^4 }{\alpha(2-\alpha)^3\varepsilon^{4\alpha}}.\end{align}
From (54), (55), and (56), we obtain that
\begin{align}\lambda_{\varepsilon/2,\rho}\mathbb{P}\Big(M_t(\varepsilon/2)+Y_1^{(\varepsilon/2,\rho)}>\varepsilon\Big)\leq &t \varepsilon^{-2\alpha}{\rm K}^2 {\rm H}_2\mathbf{1}_{\alpha\in(1,2)}+\frac{t^3 {\rm K}^4 {\rm H}_3}{\varepsilon^{4\alpha}}+\frac{16 {\rm K}^2 t}{\varepsilon^2} \ln(2)\mathbf{1}_{\alpha=1},\end{align}
with
\begin{align} {\rm H}_2&\,:\!=\,\frac{2^{1+3\alpha}}{\alpha(2-\alpha)(\alpha-1)} \quad \text{ and } \quad {\rm H}_3\,:\!=\,\frac{2^{3(1+\alpha)}e^{3+1/e} }{\alpha(2-\alpha)^3}.\end{align}
Finally, gathering (51), (52), and (57), we derive
\begin{equation*}\mathbb{P}(M_t(\rho)>\varepsilon)\leq {\rm K}^2t^2\varepsilon^{-2\alpha}{\rm H}_1+ t^2 \varepsilon^{-2\alpha}{\rm K}^2 {\rm H}_2\mathbf{1}_{\alpha\in(1,2)}+\frac{t^4 {\rm K}^4 {\rm H}_3}{\varepsilon^{4\alpha}}+\frac{16 {\rm K}^2 t^2}{\varepsilon^2} \ln(2)\mathbf{1}_{\alpha=1}.\end{equation*}
A.4. Proof of Lemma 6
Using that
$\nu$
is symmetric gives
\begin{equation*}\lambda_\rho \mathbb{P}\Big(|M_t(\rho)+Y_1^{(\rho)}|>\varepsilon\Big)=2\int_\rho^\infty \big(\mathbb{P}(M_t(\rho)>\varepsilon-z)+\mathbb{P}(M_t(\rho)>\varepsilon+z)\big)\nu(dz).\end{equation*}
Moreover, since
$\rho<\varepsilon,$
and using again the symmetry, we obtain
\begin{align}\nonumber \lambda_\rho t \mathbb{P}(|M_t(\rho)+Y_1^{(\rho)}|>\varepsilon)&-\lambda_\varepsilon t \nonumber\\
=&2t\bigg[ \int_\rho^\varepsilon \mathbb{P}(M_t(\rho)>\varepsilon-z)\nu(dz)-\int_\varepsilon^\infty \mathbb{P}(M_t(\rho)\leq \varepsilon-z)\nu(dz)\bigg]\nonumber \\
&\quad +2t\int^\infty_{\rho}\mathbb{P}(M_t(\rho)>\varepsilon+z)\nu(dz)\,=\!:\,2t (R_1+R_2).\end{align}
We begin by controlling the term
$R_1$
. Recalling that
$\rho=3/4(\varepsilon\wedge 1)$
and setting
$\eta\,:\!=\,\varepsilon-3/4(\varepsilon\wedge1)$
, we have
\begin{align*}\int_\rho^\varepsilon \mathbb{P}(M_t(\rho)>\varepsilon-z)\nu(dz) &=\int_0^{ \eta}\mathbb{P}(M_t(\rho)>x)f(\varepsilon-x)dx,\\\int_\varepsilon^\infty \mathbb{P}(M_t(\rho)\leq \varepsilon-z)\nu(dz) &=\int_\varepsilon^\infty \mathbb{P}(M_t(\rho)> z-\varepsilon)\nu(dz)\\&=\int_0^\infty \mathbb{P}(M_t(\rho)> x)f(\varepsilon+x)dx,\end{align*}
where we used the symmetry of
$\nu$
in the second line. The triangle inequality gives
\begin{align}|R_1|&\leq \bigg|\int_0^{ \eta}\mathbb{P}(M_t(\rho)>x)(f(\varepsilon-x)-f(\varepsilon+x))dx\bigg|+\bigg|\int_{\eta}^\infty \mathbb{P}( M_t(\rho)> x)f(\varepsilon+x)dx\bigg|\nonumber\\&\,=\!:\,R_{1,1}+R_{1,2}.\end{align}
Therefore, by (6), (7), the Markov inequality, (8), and the fact that f is
${\rm K}(\varepsilon\wedge 1)^{-(2+\alpha)}$
-Lipschitz on the interval
$\big(3/4(\varepsilon\wedge 1),2\varepsilon-3/4(\varepsilon\wedge 1)\big)$
, it follows that
\begin{align}R_{1,1}&\leq 2{\rm K} (\varepsilon\wedge 1)^{-(2+\alpha)}\Bigg[\mathbf{1}_{0<\varepsilon\leq 1}\int_0^{\varepsilon/4}(\mathbb{P}(M_t(x)>x)+t\lambda_{x,3/4\varepsilon})xdx\nonumber \\
& +\mathbf{1}_{\varepsilon> 1}\int_0^{(\varepsilon-3/4)\wedge 3/4}(\mathbb{P}(M_t(x)>x)+t\lambda_{x,3/4})xdx\nonumber\\
&+\mathbf{1}_{\varepsilon> 1}\mathbb{P}(M_t(3/4)>3/4)\int_{(\varepsilon-3/4)\wedge3/4}^{\varepsilon-3/4}xdx\Bigg]\nonumber\\
\leq& \frac{8t{\rm K}^2(\varepsilon\wedge 1)^{-(2+\alpha)}}{\alpha(2-\alpha)}\Bigg(\mathbf{1}_{0<\varepsilon\leq 1}\int_0^{\varepsilon/4}\frac{dx}{x^{\alpha-1}}+\mathbf{1}_{\varepsilon> 1}\int_0^{(\varepsilon-3/4)\wedge 3/4}\frac{dx}{x^{\alpha-1}}\Bigg)\nonumber\\
&+\mathbf{1}_{\varepsilon\geq 3/2}\frac{4^{1+\alpha}3^{-\alpha}{\rm K}^2t\varepsilon^2}{2-\alpha}\nonumber\\
&\leq\frac{2^{2\alpha-1}}{\alpha(2-\alpha)^{2}}{\rm K}^{2}t\varepsilon^{-2\alpha}\mathbf{1}_{0<\varepsilon\le1}+\frac{8t{\rm K}^{2}}{\alpha(2-\alpha)^{2}}(\varepsilon-3/4)^{2-\alpha}\mathbf{1}_{1<\varepsilon\le3/2}+\frac{4^{1+\alpha}\varepsilon^{2}{\rm K}^{2}t}{3^{\alpha}(2-\alpha)}\mathbf{1}_{\varepsilon>3/2}.\end{align}
Concerning the term
$R_{1,2}$
, we have
\begin{align}R_{1,2}&\leq \mathbf{1}_{0<\varepsilon\leq 1}\Bigg(\int_{\varepsilon/4}^{\varepsilon3/4}\mathbb{P}(M_{t}(\varepsilon3/4)>x)f(x+\varepsilon)dx+\mathbb{P}(M_{t}(\varepsilon3/4)>\varepsilon3/4)\int_{\varepsilon3/4}^{\infty} f(x+\varepsilon)dx\Bigg) \nonumber \\
&\quad +\mathbf{1}_{1< \varepsilon<3/2}\Bigg(\int_{\varepsilon-3/4}^{3/4}\mathbb{P}(M_{t}(3/4)>x)f(x+\varepsilon)dx+ \mathbb{P}(M_{t}(3/4)>3/4)\int_{3/4}^{\infty}f(x+\varepsilon)dx\Bigg) \nonumber \\
&\quad +\mathbf{1}_{ \varepsilon\geq 3/2} \mathbb{P}(M_t(3/4)>3/4)\int_{\varepsilon-3/4}^\infty f(x+\varepsilon)dx.\end{align}
Using (6), (7), the Markov inequality, (8), and (10), we get
\begin{align}\mathbb{P}(M_{t}(\varepsilon3/4)>x)&\leq \mathbb{P}(M_{t}(x/2)>x)+t\lambda_{x/2,\varepsilon3/4}\leq \frac{2^{2+\alpha}{\rm K}tx^{-\alpha}}{\alpha(2-\alpha)} ,\quad \forall x\le \frac{3\varepsilon}{2}, \ \varepsilon<1, \nonumber\\\mathbb{P}\big(M_{t}(3/4)&>3/4(\varepsilon\wedge 1)\big)\leq t{\rm K}\frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}(\varepsilon\wedge 1)^{-\alpha}. \end{align}
Therefore, from (62), (63), and (10), using the fact that
$f\in {\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
, we derive
\begin{align}R_{1,2}&\leq \mathbf{1}_{0<\varepsilon\leq 1} \Bigg(t{\rm K}^2\varepsilon^{-2\alpha}\Big(\frac{2^{3\alpha}}{\alpha(\alpha-1)(2-\alpha)}+\frac{2^{4\alpha+1}}{21^{\alpha}\alpha(2-\alpha)}\Big)+t{\rm K}\varepsilon^{-\alpha}\lambda_{1}\frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}\Bigg)\nonumber \\[4pt]
&\quad+\mathbf{1}_{1< \varepsilon<3/2}t{\rm K}\Bigg(\frac{2^{3\alpha}M}{\alpha(\alpha-1)(2-\alpha)}+\frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}\lambda_{7/4}\Bigg)+\mathbf{1}_{ \varepsilon\geq 3/2} t{\rm K}\lambda_{9/4}\frac{2(4/3)^\alpha}{2-\alpha}.\end{align}
Gathering Equations (60), (61), and (64), we get
\begin{align}R_{1}&\leq \mathbf{1}_{0<\varepsilon\leq 1} \Bigg(t{\rm K}^2\varepsilon^{-2\alpha}\bigg(\frac{2^{2\alpha-1}}{\alpha(2-\alpha)^{2}}+\frac{2^{3\alpha}}{\alpha(\alpha-1)(2-\alpha)}+\frac{2^{4\alpha+1}}{21^{\alpha}\alpha(2-\alpha)}\bigg)+t{\rm K}\varepsilon^{-\alpha}\lambda_{1}\frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}\Bigg)\nonumber \\[3pt]
&\quad+\mathbf{1}_{1< \varepsilon<3/2}t{\rm K}\Bigg( \frac{8{\rm K}}{\alpha(2-\alpha)^{2}}(\varepsilon-3/4)^{2-\alpha}+\frac{2^{3\alpha}{\rm K}}{\alpha(\alpha-1)(2-\alpha)}+\frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}\lambda_{7/4}\Bigg)\\[3pt]
&\quad+\mathbf{1}_{ \varepsilon\geq 3/2}\bigg(\frac{4^{1+\alpha}\varepsilon^{2}{\rm K}^{2}t}{3^{\alpha}(2-\alpha)}+ t{\rm K}\lambda_{9/4}\frac{2(4/3)^\alpha}{2-\alpha}\bigg).\nonumber\end{align}
To complete the proof it remains to control the term
$R_2$
in (59). The Markov inequality, (8), the symmetry of
$\nu$
, and the fact that
$\rho>1/2(\varepsilon\wedge1)$
yield
\begin{align}R_2&\leq \frac{\mathbb{P}(M_t(\rho)>\rho)}{2}(\lambda_{\rho,1}+\lambda_1)\leq \frac{2^{\alpha}{\rm K}t(1\wedge\varepsilon)^{-\alpha}}{2-\alpha}\big(2^{\alpha+1}{\rm K}(1\wedge\varepsilon)^{-\alpha}\alpha^{-1}+\lambda_1\big).\end{align}
Therefore, from (59), (65), and (66), we conclude that
\begin{align*}\Big|\lambda_\rho t \mathbb{P}\Big(|M_t(\rho)+Y_1^{(\rho)}|>\varepsilon\Big)-\lambda_\varepsilon t \Big|&\leq {\rm K}^2 t^2\big({\rm H}_4 \varepsilon^{-2\alpha} \mathbf{1}_{0<\varepsilon\leq 1}+ \varepsilon^{2}{\rm H}_5 \mathbf{1}_{\varepsilon>1}\big) +{\rm H}_6{\rm K} t^2\lambda_{1}(\varepsilon\wedge1)^{-\alpha} ,\end{align*}
where
${\rm H}_4,\ {\rm H}_5$
, and
${\rm H}_{6}$
are positive universal constants, depending only on
$\alpha$
, defined as follows:
\begin{align}{\rm H}_4&\,:\!=\,\frac{2^{2\alpha-1}}{\alpha(2-\alpha)^{2}}+\frac{2^{3\alpha}}{\alpha(\alpha-1)(2-\alpha)}+\frac{2^{4\alpha+1}}{21^{\alpha}\alpha(2-\alpha)}+\frac{2^{2\alpha+2}}{\alpha(2-\alpha)},\nonumber\\[3pt]
\quad {\rm H}_5&\,:\!=\,\bigg( \frac{8(3/4)^{2-\alpha}}{\alpha(2-\alpha)^{2}}++\frac{2^{3\alpha}}{\alpha(\alpha-1)(2-\alpha)}\bigg)\mathbf{1}_{1<\varepsilon<3/2}+\frac{4^{1+\alpha}}{3^{\alpha}(2-\alpha)}\mathbf{1}_{\varepsilon\ge3/2},\\[3pt]
{\rm H}_6&\,:\!=\, \mathbf{1}_{0<\varepsilon\leq 1} \frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}+\mathbf{1}_{1< \varepsilon<3/2}\frac{2^{2\alpha+1}}{3^{\alpha}(2-\alpha)}+\mathbf{1}_{ \varepsilon\geq 3/2}\frac{2(4/3)^\alpha}{2-\alpha}. \nonumber\end{align}
A.5. Proof of Lemma 4
The decomposition (59) as in the proof of Lemma 6 in
$\lambda_\rho t \mathbb{P}(|M_t(\rho)+Y_1^{(\rho)}|>\varepsilon)-\lambda_\varepsilon t\,=\!:\,2t (R_1+R_2)$
still holds with
\begin{align*}|R_2|\leq t{\rm K} \mathbf{1}_{0<\varepsilon\leq 1}\bigg(\frac{{\rm K}\varepsilon^{-2\alpha}}{\alpha(2-\alpha)}+\frac{\varepsilon^{-\alpha}\lambda_1}{2(2-\alpha)}\bigg)+t{\rm K}\frac{\mathbf{1}_{\varepsilon>1}\lambda_1}{(2-\alpha)(\varepsilon+1)^2}.\end{align*}
Set
$C=\big(1\wedge\big((2-\alpha)/2{\rm K} \big)\big)^{1/\alpha}$
and note that
$C(\varepsilon\wedge 1)/2>t^{1/\alpha}$
. Using the symmetry of f we get
\begin{align*}|R_1|&\leq \int_0^{t^{1/\alpha}/C}\big( f(y+\varepsilon)+2\mathbf{1}_{\varepsilon>1}f(\varepsilon-y)\big)dy +\int_{t^{1/\alpha}/C}^{\rho}\big(\mathbb{P}(M_t(y)>y)+t\lambda_{y,\rho}\big)f(\varepsilon+y)dy\\
&\quad+\mathbb{P}(M_t(\rho)>\rho)\int_\rho^\infty f(y+\varepsilon)dy\\
&\quad +\mathbf{1}_{\varepsilon>1}\Bigg(\mathbf{1}_{t^{1/\alpha}/C<1\wedge(\varepsilon-1)}\int_{t^{1/\alpha}/C}^{1\wedge(\varepsilon-1)}\big(\mathbb{P}(M_t(y)>y)\\
& \quad +t\lambda_{y,1}\big)f(\varepsilon-y)dy+2\mathbb{P}\big(M_t(1)>1\big)\int_{1\wedge(\varepsilon-1)}^{\varepsilon-1} f(\varepsilon-y)dy\Bigg).\end{align*}
Next, as
$f\in{\mathscr{L}}_{{\rm K},\alpha}\cap {\mathscr{L}}_{{\rm K}}$
, it follows from Equations (6), (7), (8), and (10) and the Markov inequality that
\begin{align*}|R_1|&\leq \frac{{\rm K} t^{1/\alpha}}{C}\bigg(\frac{1}{(\varepsilon\wedge 1)^{1+\alpha}}+\frac{2\mathbf{1}_{\varepsilon>1}}{(\varepsilon-t^{1/\alpha}/C)\wedge 1}\bigg) +\frac{2{\rm K}t}{2-\alpha}\bigg( \rho^{-\alpha}\bigg({\rm K}\alpha^{-1}(\rho+\varepsilon)^{-\alpha}+\frac{\lambda_1}{2}\bigg)\\[3pt]
&\quad +{\rm K}\mathbf{1}_{\varepsilon>2}(\varepsilon-2)\bigg) +\frac{4{\rm K}^2 t^{1/\alpha}C^{\alpha-1}\mathbf{1}_{\alpha\in(1,2)}}{\alpha(2-\alpha)(\alpha-1)}\bigg(\frac{1}{(\varepsilon+t^{1/\alpha}/C)\wedge 1}+\frac{\mathbf{1}_{\varepsilon>1}}{(\varepsilon-t^{1/\alpha}/C)\wedge 1}\bigg)\\[3pt]
&\quad +4{\rm K}^2t\mathbf{1}_{\alpha=1}\bigg(\ln\bigg(\frac{C(1\wedge|\varepsilon-1|)}{t}\bigg)\frac{\mathbf{1}_{\varepsilon>1}}{(\varepsilon-t/C)\wedge 1}+\ln\bigg(\frac{C\rho}{t}\bigg)\frac{1}{(\varepsilon+t/C)\wedge 1}\bigg)\\[3pt]
&\leq \frac{{\rm K} t^{1/\alpha}}{C}\bigg(\frac{1}{(\varepsilon\wedge 1)^{1+\alpha}}+\frac{2}{\varepsilon\wedge 1}\bigg)+\frac{2{\rm K}t}{2-\alpha}\bigg(K\alpha^{-1}(\varepsilon\wedge1)^{-2\alpha}+\frac{\lambda_1(\varepsilon\wedge 1)^{-\alpha}}{2}+{\rm K}\mathbf{1}_{\varepsilon>2}\varepsilon\bigg)\\[3pt]
&+ \frac{12{\rm K}^2 t^{1/\alpha}C^{\alpha-1}\mathbf{1}_{\alpha\in(1,2)}}{\alpha(2-\alpha)(\alpha-1)}\frac{1}{\varepsilon\wedge 1} + \frac{4 K^2t \mathbf{1}_{\alpha=1}}{\varepsilon\wedge 1}\bigg(2\mathbf{1}_{\varepsilon>1}\mathbf{1}_{t/C<1\wedge (\varepsilon-1)}\ln\Big(\frac{C(1\wedge|\varepsilon-1|)}{t}\Big)\\
& \quad +\ln\bigg(\frac{C\rho}{t}\bigg)\bigg),\end{align*}
with the convention that
$0\ln 0=0$
. Therefore, we get
\begin{align*} \Big|&\lambda_\rho t \mathbb{P}\Big(|M_t(\rho)+Y_1^{(\rho)}\Big|>\varepsilon\Big)-\lambda_\varepsilon t|\leq{\rm L}_{1}\frac{t^{1+1/\alpha}}{(\varepsilon\wedge 1)^{1+\alpha}}+\frac{8{\rm K}^{2}}{\alpha(2-\alpha)}\frac{t^{2}}{(\varepsilon\wedge 1)^{2\alpha}}+\frac{5{\rm K}}{2-\alpha}\frac{t^{2}\lambda_{1}}{(\varepsilon\wedge1)^2}\\
&\quad +\frac{4{\rm K}^{2}t^{2}}{2-\alpha}\varepsilon\mathbf{1}_{\varepsilon>2}+8{\rm K}^2t^{2}\mathbf{1}_{\alpha=1}\bigg(2\mathbf{1}_{\varepsilon>1}\mathbf{1}_{t/C<1\wedge (\varepsilon-1)}\ln\Big(\frac{C(1\wedge|\varepsilon-1|)}{t}\Big)+\ln\bigg(\frac{C\rho}{t}\bigg)\bigg)\frac{1}{\varepsilon\wedge 1}, \end{align*}
where
\begin{align}{\rm L}_{1}&=\frac{2{\rm K} }{C}+\frac{4{\rm K}}{C}+\frac{24{\rm K}^2 C^{\alpha-1}\mathbf{1}_{\alpha\in(1,2)}}{\alpha(2-\alpha)(\alpha-1)}.\end{align}
A.6. A result for compound Poisson processes
Lemma 7. Let N be a Poisson random variable with mean
$0<\lambda\leq 1$
and
$(Y_i)_{i\geq 0}$
a sequence of independent and identically distributed random variables independent of N with bounded density g (with respect to the Lebesgue measure). Furthermore, let M be any random variable independent of
$\big(N,(Y_i)_{i\geq 0}\big)$
. Then, for all
$x\in\mathbb{R}$
,
\begin{align*}\Bigg|\mathbb{P}\Bigg(M+\sum_{i=1}^NY_i-\mathbb{E}\Bigg[\sum_{i=1}^NY_i\Bigg]>x\Bigg)-\mathbb{P}\Bigg(M+\sum_{i=1}^N(Y_i-\mathbb{E}[Y_i])>x\Bigg)\Bigg|\leq 2\lambda e^{-\lambda} |\mathbb{E}[Y_1]| \|g\|_{\infty}.\end{align*}
Proof. Note that
\begin{align*} &\Bigg|\mathbb{P}\Bigg(\sum_{i=1}^NY_i-\mathbb{E}\Bigg[\sum_{i=1}^NY_i\Bigg]>x\Bigg)-\mathbb{P}\Bigg(\sum_{i=1}^N(Y_i-\mathbb{E}[Y_i])>x\Bigg)\Bigg|\leq \|g\|_{\infty}|\mathbb{E}[Y_1] |\mathbb{E}[|N-\lambda|].\end{align*}
Observe that, for
$\lambda\leq1$
, it holds that
$\mathbb{E}[|N-\lambda|]=2\lambda e^{-\lambda}.$
We conclude the proof by observing that for any real random variable
$Z_1$
independent of
$Z_2$
and
$Z_3$
and any
$z\in\mathbb{R}$
, it holds that
$|\mathbb{P}(Z_1+Z_2>z)-\mathbb{P}(Z_1+Z_3>z)|\leq\sup_{x\in\mathbb{R}} |\mathbb{P}(Z_2>x)-\mathbb{P}(Z_3>x)|.$
A.7. Proofs of the examples
-
1. Compound Poisson processes. Let X be a compound Poisson process with intensity
$\lambda=\nu(\mathbb{R})<\infty$
and jump density
$f/\lambda$
. Write
$X_t=\sum_{i=1}^{N_t} Y_i$
. For any
$\varepsilon>0$
, it holds that
Using
\begin{align*}\mathbb{P}\big(|X_t|>\varepsilon\big)&=t\lambda_{\varepsilon} e^{-\lambda t}+\sum_{n=2}^\infty \mathbb{P}\Bigg(\Bigg|\sum_{i=1}^nY_i\Bigg|>\varepsilon\Bigg)\mathbb{P}(N_t=n).\end{align*}
$\mathbb{P}(N_{t}\ge 2)=O(t^{2})$
we obtain
$|\mathbb{P}\big(|X_t|>\varepsilon\big)-t\lambda_\varepsilon|=O(t^2),$
as
$t\to0.$
For f a Lévy density such that
$f=f\mathbf{1}_{[\varepsilon,\infty)}$
, it holds that
$\lambda=\lambda_{\varepsilon}$
, and later computations simplify to
In that case, the rate is exactly of the order of
\begin{equation*}\mathbb{P}(|X_{t}|>\varepsilon)=\mathbb{P}(N_{t}\ge 1)=1-e^{-\lambda_{\varepsilon}t}=\lambda_{\varepsilon}t-t^{2}\sum_{k\ge 2}t^{k-2}({-}\lambda_{\varepsilon})^{k}/k!.\end{equation*}
$t^{2}$
. Next, considering the small jumps, it holds for
$\varepsilon\in(0,1]$
that
$tb(\varepsilon)+M_{t}(\varepsilon)=\sum_{i=1}^{N_{t}^{(0,\varepsilon)}}Y_{i}^{(0,\varepsilon)}$
, and using (7),
This is exactly of order
\begin{equation*}\mathbb{P}(|tb(\varepsilon)+M_{t}(\varepsilon)|\ge \varepsilon)=\sum_{k=2}^{\infty}\mathbb{P}(N_{t}^{(0,\varepsilon)}=k)\mathbb{P}\Bigg(\Bigg|\sum_{i=1}^{k}Y^{(0,\varepsilon)}_{i}\Bigg|\ge \varepsilon\Bigg)\le t^{2}(\lambda-\lambda_{\varepsilon})^{2}.\end{equation*}
$t ^{2}$
for any Lévy density such that
$f=f\mathbf{1}_{[3\varepsilon/4,\infty)}$
.
-
2. Gamma processes. Set
$\Gamma(t,\varepsilon)=\int_\varepsilon^\infty x^{t-1}e^{-x}dx$
, so that
$\Gamma(t,0) = \Gamma(t)$
. Using that
$\Gamma(t,\varepsilon)$
is analytic, we can write
(69)As
\begin{align} \bigg|\lambda_{\varepsilon}-\frac{\mathbb{P}(X_{t}>\varepsilon)}{t}\bigg| &=\frac{1}{\Delta\Gamma(t)}\bigg|\Delta\Gamma(t,0)\Gamma(0,\varepsilon) - \sum_{k=0}^\infty \frac{\Delta^k}{k!} \bigg\{\frac{\partial^k}{\partial t^k}\Gamma(t,\varepsilon)\bigg|_{t=0}\bigg\}\bigg| \nonumber\\
&\leq\Gamma(0,\varepsilon)\bigg|\frac{1-t\Gamma(t,0)}{t\Gamma(t)}\bigg|+\bigg|\frac{1}{t\Gamma(t)}\sum_{k=1}^\infty \frac{t^k}{k!} \bigg\{\frac{\partial^k}{\partial t^k}\Gamma(t,\varepsilon)\bigg|_{t=0}\bigg\}\bigg|. \end{align}
$\Gamma(t,0)$
is a meromorphic function with a simple pole at 0 and residue 1, there exists a sequence
$(a_k)_{k\geq 0}$
such that
Therefore,
\begin{equation*}\Gamma(t)=\frac{1}{t}+\sum_{k=0}^\infty a_kt^k.\end{equation*}
and
\begin{equation*} 1-t\Gamma(t,0)=t\sum_{k=0}^\infty a_kt^k,\end{equation*}
Let us now study the term
\begin{equation*}\frac{1-t\Gamma(t)}{t\Gamma(t)}=\frac{t\sum_{k=0}^\infty a_kt^k}{1+t\sum_{k=0}^\infty a_kt^k} = O(t),\quad \text{as }t\to 0.\end{equation*}
We have
\begin{equation*}\sum_{k=1}^\infty \frac{t^k}{k!} \big(\frac{\partial^k}{\partial t^k}\Gamma(t,\varepsilon)\big)\big|_{t=0}.\end{equation*}
Let
\begin{align}\bigg|\frac{\partial^k}{\partial t^k}\Gamma(t,\varepsilon)\bigg|_{t=0}\bigg| &\leq \bigg|e^{-1}\int_\varepsilon^1x^{-1}(\ln(x))^kdx\bigg| + \bigg|\int_{1}^\infty e^{-x}(\ln(x))^kdx\bigg| \nonumber \\
&=e^{-1}\frac{|\ln(\varepsilon)|^{k+1}}{k+1}+\int_{1}^\infty e^{-x}(\ln(x))^kdx. \nonumber\end{align}
$x_0$
be the largest real number such that
This equation has two solutions if and only if
\begin{equation*}e^{\frac{x_0}{2}}=(\ln(x_0))^k.\end{equation*}
$k\geq6$
. If no such point exists, take
$x_0 = 1$
. Then
where we used the inequality
\begin{align*} \int_{1}^\infty e^{-x}(\ln(x))^kdx&\leq \int_1^{x_0}\!e^{-x}(\ln(x))^kdx+\int_{x_0}^\infty\! e^{-\frac{x}{2}}dx\leq (\ln(x_0))^k \big(e^{-1}-e^{-x_0}\big)+2e^{-\frac{x_0}{2}}\\ &\leq e^{\frac{x_0}{2}-1} + e^{-\frac{x_0}{2}} \leq k^k+1,\end{align*}
$x_0 < 2k \ln k$
, for each integer k. Summing up, we get
In the last two steps, we have used first that
\begin{align*} \bigg|\sum_{k=1}^\infty \frac{t^k}{k!} \bigg\{\frac{\partial^k}{\partial t}&\Gamma(t,\varepsilon) \bigg|_{t=0} \bigg\}\bigg|\leq e^{-1}\sum_{k=1}^\infty \frac{t^k}{k!}\frac{|\ln(\varepsilon)|^{k+1}}{k+1}+\sum_{k=1}^5 2e^{-\frac{1}{2}}\frac{t^k}{k!} + \sum_{k=6}^\infty \frac{t^k}{k!} (k^k+1)\\
&\leq |\ln(\varepsilon)|\big[e^{t|\ln(\varepsilon)|}-1\big]+\sum_{k=6}^\infty \frac{t^{\frac{k}{2}}}{k!}\bigg(\frac{k}{e}\bigg)^k + O(t)\leq (\ln(\varepsilon))^2t + O(t).\end{align*}
$t < e^{-2}$
and then the Stirling approximation formula to deduce that the last remaining sum is
$O(t^3)$
. Clearly, the factor
$\frac{1}{t\Gamma(t)}\sim 1$
, as
$t\to0$
, in (69) does not change the asymptotic. Finally we derive that
as desired.
\begin{equation*}\big|t\lambda_{\varepsilon} -\mathbb{P}(X_t>\varepsilon)\Big| = O\big(t^2\big),\quad \text{as }t\to 0,\end{equation*}
-
3. Cauchy processes. Observe that
$\lambda_\varepsilon=\frac{2}{\pi \varepsilon}$
and
Hence, to prove (5), it is enough to show that
\begin{equation*}\mathbb{P}\big(|X_t|>\varepsilon\big)=\frac{2}{\pi}\left(\frac{\pi}{2}-\arctan\left(\frac{\varepsilon}{t}\right)\right).\end{equation*}
(70)Set
\begin{equation}\lim_{t\to 0}\frac{2}{\pi}\bigg|\frac{\varepsilon^3}{t^3}\bigg(\frac{\pi}{2}-\arctan\Big(\frac{\varepsilon}{t}\Big)\bigg)-\frac{\varepsilon^2}{t^2}\bigg|<\infty.\end{equation}
$y=\frac{t}{\varepsilon}$
; we compute the limit in (70) by means of de l’Hôpital’s rule:
\begin{align*} \frac{2}{\pi}\lim_{y\to 0}\bigg|\frac{1}{y^3}\bigg(\frac{\pi}{2}-\arctan\Big(\frac{1}{y}\Big)\bigg)-\frac{1}{y^2}\bigg|&= \frac{2}{\pi}\lim_{y\to 0}\bigg|\frac{\frac{\pi}{2}-\arctan\Big(\frac{1}{y}\Big)-y}{y^3}\bigg|\\ &=\lim_{y\to 0}\frac{y^2}{(1+y^2)3\pi y^2}<\infty.\end{align*}
Acknowledgements
E. Mariucci would like to thank Francesco Caravenna, Jean Jacod, and Markus Reiß for several enlightening discussions which initially motivated the underlying research of this paper. In addition, the authors are very grateful to the two anonymous referees for their detailed and constructive comments on the paper.
Funding information
The work of E. Mariucci was partially funded by the Federal Ministry for Education and Research through the sponsorship provided by the Alexander von Humboldt Foundation, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—314838170, GRK 2297 MathCoRe, and by DFG SFB1294/1–318763901.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.
