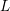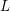Let 
$B_{n}$ be the braid group with standard generators 
$\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n-1}$. We denote the closure of a braid 
$\unicode[STIX]{x1D6FD}\in B_{n}$ by 
$\widehat{\unicode[STIX]{x1D6FD}}\subset S^{3}$. For an oriented link 
$L\subset S^{3}$, let 
$\mathbf{B}\mathbf{r}_{n}(L)=\{\unicode[STIX]{x1D6FD}\in B_{n}\mid \widehat{\unicode[STIX]{x1D6FD}}=L\}$ be the set of 
$n$-braids whose closures are 
$L$.
The set 
$\mathbf{B}\mathbf{r}_{n}(L)$ may contain infinitely many mutually nonconjugate braids. However, Birman and Menasco proved a remarkable (non)finiteness theorem [Reference Birman and MenascoBM]: 
$\mathbf{B}\mathbf{r}_{n}(L)$ modulo the exchange move 
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}_{n-1}^{-1}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{n-1}\leftrightarrow \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}_{n-1}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{n-1}^{-1}$ (
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in B_{n-1}$; see Figure 1(i)) has only finitely many conjugacy classes. In particular, when 
$\mathbf{B}\mathbf{r}_{n}(L)$ does not contain a braid admitting an exchange move, 
$\mathbf{B}\mathbf{r}_{n}(L)$ contains only finitely many conjugacy classes.
We ask the converseFootnote 1: Does 
$\mathbf{B}\mathbf{r}_{n}(L)$contain infinitely many mutually nonconjugate braids if 
$\mathbf{B}\mathbf{r}_{n}(L)$contains a braid admitting an exchange move?
This question was studied in [Reference Shinjo and StoimenowSS, Reference ShinjoSh, Reference StoimenowSt1, Reference StoimenowSt2] where it was shown that under some additional and technical assumptions, iterations of exchange moves indeed produce infinitely many nonconjugate braids.
In this note, we give a simpler and shorter proof of infiniteness under the weakest assumption. We use a formulation of iterations of exchange moves following [Reference Shinjo and StoimenowSS].
Definition 1. We say that an 
$n$-braid 
$\unicode[STIX]{x1D6FD}$admits an exchange move if one can write 
$\unicode[STIX]{x1D6FD}=AB$ for 
$A\in \langle \unicode[STIX]{x1D70E}_{1}^{\pm 1},\ldots ,\unicode[STIX]{x1D70E}_{n-2}^{\pm 1}\rangle$ and 
$B\in \langle \unicode[STIX]{x1D70E}_{2}^{\pm 1},\ldots ,\unicode[STIX]{x1D70E}_{n-1}^{\pm 1}\rangle$.
For 
$k\in \mathbb{Z}$ and an 
$n$-braid 
$\unicode[STIX]{x1D6FD}=AB$ admitting an exchange move, the 
$k$-iterated exchange move of 
$\unicode[STIX]{x1D6FD}=AB$ is the braid 
$\text{ex}^{k}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70F}^{k}A\unicode[STIX]{x1D70F}^{-k}B$, where 
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70E}_{2}\cdots \unicode[STIX]{x1D70E}_{n-2})^{n-2}\in B_{n}$. We say that an (iterated) exchange move is degenerate if 
$A\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}A$ or 
$B\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}B$. Otherwise, an (iterated) exchange move is nondegenerate.
Figure 1. (i) Exchange move for (closed) braids. (ii) Realization of the move 
$\unicode[STIX]{x1D6FD}=AB\rightarrow \text{ex}^{1}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70F}A\unicode[STIX]{x1D70F}^{-1}B$ by exchange move and conjugation. (The figure illustrates the 
$n=4$ case.) Here 
$=$ and 
$\cong$ denote the identity and conjugation in the braid group, respectively. At 
$(\ast 1)$, we use the relation 
$(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\cdots \unicode[STIX]{x1D70E}_{n-2})(\unicode[STIX]{x1D70E}_{n-2}\cdots \unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1})=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}^{-1}$ and at 
$(\ast 2)$, we use the relation 
$A\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}A$ since 
$\unicode[STIX]{x1D6FF}$ is the full twist of 
$(n-1)$ strands.
A 
$k$-iterated exchange move is attained by repeating an exchange move 
$|k|$ times (see Figure 1(ii)) so the closures of 
$\unicode[STIX]{x1D6FD}$ and 
$\text{ex}^{k}(\unicode[STIX]{x1D6FD})$ represent the same link. A degenerate exchange move obviously preserves the conjugacy classes. Our main theorem shows that, except in trivial cases, iterated exchange moves always produce infinitely many mutually nonconjugate braids.
We identify the braid group 
$B_{n}$ with the mapping class group 
$MCG(D_{n})$ of the 
$n$-punctured disk 
$D_{n}$. Let 
$\text{ent}(\unicode[STIX]{x1D6FD})$ be the topological entropy of 
$\unicode[STIX]{x1D6FD}$, the infimum of the topological entropy of homeomorphisms that represent 
$\unicode[STIX]{x1D6FD}$.
Theorem 2. If 
$\unicode[STIX]{x1D6FD}\in \mathbf{B}\mathbf{r}_{n}(L)$ admits a nondegenerate exchange move, then the set 
$\{\text{ent}(\text{ex}^{k}(\unicode[STIX]{x1D6FD}))\mid k\in \mathbb{Z}\}$ is unbounded. In particular, the set 
$\{\text{ex}^{k}(\unicode[STIX]{x1D6FD})\mid k\in \mathbb{Z}\}\subset \mathbf{B}\mathbf{r}_{n}(L)$ contains infinitely many distinct conjugacy classes.
Let 
$S$ be a closed orientable surface minus finitely many open disks and puncture points in its interior. A simple closed curve 
$c$ in 
$S$ is essential if 
$c$ is neither boundary parallel nor surrounds a single puncture. We denote by 
$T_{c}$ the Dehn twist along 
$c$. A family of essential simple closed curves 
$\{c_{1},\ldots ,c_{N}\}$fills 
$S$ if 
$\max i(c,c_{i})\neq 0$ for any essential simple closed curve 
$c$, where 
$i(c,c^{\prime })$ denotes the geometric intersection number. Our proof is based on the following theorem of Fathi [Reference FathiFa, Theorem 7.9].
Theorem 3. Let 
$f\in MCG(S)$ and 
$c_{1},\ldots ,c_{N}$ be essential simple closed curves in 
$S$. Assume the following.
(i) The set of curves
$\{c_{1},\ldots ,c_{N}\}$ fills $S$.(ii)
$i(c_{i},c_{i+1})\neq 0$ for $i=1,\ldots ,N-1$ and $i(c_{N},c_{1})\neq 0$.
Then for given 
$R>0$, there is 
$k=k(R)>0$ such that 
$T_{c_{1}}^{n_{1}}T_{c_{2}}^{n_{2}}\cdots T_{c_{N}}^{n_{N}}f$ is pseudo-Anosov whose dilatation is 
${>}R$ whenever 
$|n_{i}|>k$ for all 
$i$.
Remark. Although the statements and assumptions of Theorem 3 are slightly different, Theorem 3 follows from the proof of [Reference FathiFa, Theorem 7.9]. First, assumptions (i) and (ii) allow us to apply an interpolation inequality [Reference FathiFa, Theorem 7.4]. Second, to get the dilatation bound, we take a choice of 
$\unicode[STIX]{x1D700}>0$ on page 149 of the proof of [Reference FathiFa, Theorem 7.9] as 
$\unicode[STIX]{x1D700}=(K^{2}R^{2l-1})^{-1}$ instead of 
$(2K^{2})^{-1}$ as in the original argument. Then the same argument gives the desired dilatation bound.
Proof of Theorem 2.
The braid 
$\unicode[STIX]{x1D70F}$ in the iterated exchange move corresponds to the Dehn twist 
$T_{c}$ along the simple closed curve 
$c$ surrounding punctures 2 through 
$n-2$. The nondegeneracy assumption is equivalent to saying that 
$A(c)\neq c$ and 
$B(c)\neq c$.
For 
$i>0$, let 
$c_{2i}=\unicode[STIX]{x1D6FD}^{i-1}(A(c))=(AB)^{i-1}A(c)$ and 
$c_{2i-1}=\unicode[STIX]{x1D6FD}^{i-1}(c)=(AB)^{i-1}(c)$. Thus 
$\{c_{1},c_{2},c_{3},c_{4},\ldots \}=\{c,A(c),\unicode[STIX]{x1D6FD}(c),\unicode[STIX]{x1D6FD}(A(c)),\ldots \}$. Since 
$fT_{C}=T_{f(C)}f$ for 
$f\in MCG(D_{n})$, for 
$N>0$ we have
$$\begin{eqnarray}\displaystyle \text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N} & = & \displaystyle (T_{c}^{k}AT_{c}^{-k}B)\cdots (T_{c}^{k}AT_{c}^{-k}B)(T_{c}^{k}AT_{c}^{-k}B)\nonumber\\ \displaystyle & = & \displaystyle (T_{c}^{k}T_{A(c)}^{-k}AB)\cdots (T_{c}^{k}T_{A(c)}^{-k}AB)(T_{c}^{k}T_{A(c)}^{-k}AB)\nonumber\\ \displaystyle & = & \displaystyle (T_{c}^{k}T_{A(c)}^{-k}AB)\cdots (T_{c}^{k}T_{A(c)}^{-k}T_{AB(c)}^{k}T_{ABA(c)}^{-k}(AB)^{2})\nonumber\\ \displaystyle & = & \displaystyle \cdots \nonumber\\ \displaystyle & = & \displaystyle T_{c_{1}}^{k}T_{c_{2}}^{-k}\cdots T_{c_{2N-1}}^{k}T_{c_{2N}}^{-k}\unicode[STIX]{x1D6FD}^{N}.\nonumber\end{eqnarray}$$ We equip a complete hyperbolic metric (of finite area) on 
$D_{n}$ and take 
$c_{i}$ as a closed geodesic. Let 
$S$ be the smallest complete geodesic subsurface of 
$D_{n}$ that contains 
$\{c_{1},c_{2},c_{3},c_{4},\ldots \}$. Then for sufficiently large 
$M$, the set of curves 
$\{c_{1},c_{2},\ldots ,c_{M}\}$ fills 
$S$. By the nondegeneracy assumption, 
$S$ contains 
$\unicode[STIX]{x2202}D_{n}$ in its boundary.
Claim 1. 
$\unicode[STIX]{x1D6FD}$ preserves the subsurface 
$S$ setwise. In particular, the restriction 
$\text{ex}^{k}(\unicode[STIX]{x1D6FD})|_{S}\in MCG(S)$ is well defined for all 
$k$.
Proof of Claim 1.
If 
$S=D_{n}$, then it is obvious, and so we assume that 
$S\neq D_{n}$. Then 
$C=\unicode[STIX]{x2202}S\setminus \unicode[STIX]{x2202}D_{n}$ is a nonempty multicurve. If 
$\unicode[STIX]{x1D6FD}(S)\neq S$, then 
$\unicode[STIX]{x1D6FD}^{-1}(S)\neq S$ and 
$i(\unicode[STIX]{x1D6FD}^{-1}(C),C)\neq 0$. Since 
$\{c_{1},c_{2},\ldots ,c_{M}\}$ fills 
$S$, this means 
$i(\unicode[STIX]{x1D6FD}^{-1}(C),c_{i})=i(C,\unicode[STIX]{x1D6FD}(c_{i}))=i(C,c_{i+2})\neq 0$ for some 
$i$. This is a contradiction since 
$i(C,c_{i+2})=0$ by definition.◻
Claim 2. There exists 
$N\geqslant M$ such that 
$i(c_{1},c_{2N})\neq 0$.
Proof of Claim 2.
Assume to the contrary that 
$i(c_{1},c_{2N})=0$ for all 
$N\geqslant M$. Let 
$S^{\prime }$ be the smallest geodesic subsurface of 
$S$ that contains 
$\{c_{2M},c_{2(M+1)},\ldots \}=\{c_{2M},\unicode[STIX]{x1D6FD}(c_{2M}),\unicode[STIX]{x1D6FD}^{2}(c_{2M}),\ldots \}$. By the same argument as Claim 1, 
$\unicode[STIX]{x1D6FD}$ preserves 
$S^{\prime }$, and 
$i(c,c^{\prime })=0$ for every curve 
$c^{\prime }\subset S^{\prime }$. Then 
$\unicode[STIX]{x1D6FD}^{-2(M-1)}(c_{2M})=A(c)\subset S^{\prime }$, so 
$i(c,A(c))=0$. This contradicts the nondegeneracy assumption.◻
By the nondegeneracy assumption, 
$i(c_{i},c_{i+1})\neq 0$ for every 
$i>0$. Thus by Claim 2, there is 
$N>0$ such that
$$\begin{eqnarray}\text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N}|_{S}=T_{c_{1}}^{k}T_{c_{2}}^{-k}\cdots T_{c_{2N-1}}^{k}T_{c_{2N}}^{-k}\unicode[STIX]{x1D6FD}^{N}|_{S}\in MCG(S)\end{eqnarray}$$ satisfies the assumptions of Theorem 3. Hence for any given 
$R>0$, whenever 
$|k|$ is sufficiently large, 
$\text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N}|_{S}$ is pseudo-Anosov whose dilatation 
$\unicode[STIX]{x1D706}(\text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N}|_{S})$ is 
${>}R$. Since
$$\begin{eqnarray}\displaystyle \text{ent}(\text{ex}^{k}(\unicode[STIX]{x1D6FD})) & =\frac{\text{ent}(\text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N})}{N}\geqslant \frac{\text{ent}(\text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N}|_{S})}{N}=\frac{\log \unicode[STIX]{x1D706}(\text{ex}^{k}(\unicode[STIX]{x1D6FD})^{N}|_{S})}{N}\geqslant \frac{\log R}{N}, & \displaystyle \nonumber\end{eqnarray}$$ the set 
$\{\text{ent}(\text{ex}^{k}(\unicode[STIX]{x1D6FD}))\mid k\in \mathbb{Z}\}$ is unbounded.◻
Our proof shows that as 
$k$ increases, a nondegenerate 
$k$-iterated exchange move increases the entropy, the complexity of dynamics, as long as 
$k$ is sufficiently large. Since the core of Birman–Menasco’s proof of the (non)finiteness theorem is to reduce the complexity (the number of singular points) of a braid foliation corresponding to a Seifert surface, it is natural to expect relations between the entropy and braid foliation.
Question 1. If a braid 
$\unicode[STIX]{x1D6FD}$ is obtained from 
$\unicode[STIX]{x1D6FD}^{\prime }$ by an exchange move reducing the complexity of braid foliation, then is 
$\text{ent}(\unicode[STIX]{x1D6FD})\leqslant \text{ent}(\unicode[STIX]{x1D6FD}^{\prime })$?
Acknowledgments
The author is partially supported by JSPS KAKENHI Grant Numbers 19K03490 and 16H02145. This research was supported in part by funding from the Simons Foundation and the Centre de Recherches Mathématiques, through the Simons-CRM scholar-in-residence program. Finally, the author thanks the referee for many helpful suggestions and comments.
