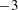1 Introduction
It is well known that multi-dimensional detonations exhibit a characteristic cellular pattern on their fronts, as they propagate in a reactive medium. This cell pattern is associated with wave interactions whose directions are predominantly transverse to the direction of flow. At each transverse wave collision, whose natural spacing is of the order of 100 ideal, and steady, induction-zone lengths (Fickett & Davis Reference Fickett and Davis1979), a new cell is formed as triple points are reflected from each other. This process is illustrated in figure 1. The triple point is a key feature of detonation waves. It is the location where three principal shock waves meet: the transverse wave, the Mach stem and incident shock. The latter two are both associated with the front of the wave as indicated in figure 1. Furthermore, these wave interactions, or cell patterns, are generally classified as having either a regular structure or an irregular structure.

Figure 1. Sketch showing a triple-point collision process. Various waves indicated are the incident shocks (I), Mach shocks (M) and transverse shocks (T). The extents of the turbulent reaction zones are also shown (R).
Regular detonations exhibit very structured-looking fish-scale patterns with consistent, and repeating, cell sizes (Strehlow Reference Strehlow1968; Austin Reference Austin2003; Pintgen et al.
Reference Pintgen, Eckett, Austin and Shepherd2003). In general, regular detonations are associated with fuel mixtures having low activation energies (Strehlow Reference Strehlow1968). Typical examples are
![]() $\text{H}_{2}+\text{O}_{2}$
(pure hydrogen–oxygen) and
$\text{H}_{2}+\text{O}_{2}$
(pure hydrogen–oxygen) and
![]() $\text{C}_{2}\text{H}_{2}+\text{O}_{2}$
(acetylene–oxygen). Owing to the relatively low activation energies, regular mixtures typically have little variation of ignition delays for the reactive gas mixture that passes through the wave front structure. For this reason, it is generally believed that the principal ignition mechanism is by adiabatic shock compression (Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). This was shown to be the case for regular detonations where the structure is well predicted by considering only the ignition delay history of a shocked particle, where transport mechanisms have been neglected (Edwards & Jones Reference Edwards and Jones1978). For irregular mixtures, many experiments (Strehlow Reference Strehlow1968; Subbotin Reference Subbotin1975; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005; Kiyanda & Higgins Reference Kiyanda and Higgins2013) have shown that a very different cell pattern exists. Typically, irregular mixtures correspond to hydrocarbon fuels with oxygen or air. These mixtures tend to exhibit much more stochastic-looking cell structures. The cell sizes are much more variable, and sometimes contain what appear to be cells within cells: a smaller cell structure within a much larger, and more prominent, cell structure. Furthermore, a number of experiments have shown the wave front to be highly turbulent, often giving rise to shocked unburned pockets of reactive fuel in its wake (Subbotin Reference Subbotin1975; Oran et al.
Reference Oran, Young, Boris and Picone1982; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005; Kiyanda & Higgins Reference Kiyanda and Higgins2013). An example experiment (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007) for an irregular detonation wave, involving methane–oxygen, is shown in figure 2. In this figure, the turbulent structure is illustrated via schlieren photography. In figure 2, each notable feature is also illustrated and labelled in a supplemental sketch. These features include the various shock wave dynamics, shear layers and triple points. Of particular interest is the presence of the unburned fuel pockets in the wake, also shown in figure 2. Such pockets contain fine-scale corrugations on their edges due to turbulence, where burning occurs.
$\text{C}_{2}\text{H}_{2}+\text{O}_{2}$
(acetylene–oxygen). Owing to the relatively low activation energies, regular mixtures typically have little variation of ignition delays for the reactive gas mixture that passes through the wave front structure. For this reason, it is generally believed that the principal ignition mechanism is by adiabatic shock compression (Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). This was shown to be the case for regular detonations where the structure is well predicted by considering only the ignition delay history of a shocked particle, where transport mechanisms have been neglected (Edwards & Jones Reference Edwards and Jones1978). For irregular mixtures, many experiments (Strehlow Reference Strehlow1968; Subbotin Reference Subbotin1975; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005; Kiyanda & Higgins Reference Kiyanda and Higgins2013) have shown that a very different cell pattern exists. Typically, irregular mixtures correspond to hydrocarbon fuels with oxygen or air. These mixtures tend to exhibit much more stochastic-looking cell structures. The cell sizes are much more variable, and sometimes contain what appear to be cells within cells: a smaller cell structure within a much larger, and more prominent, cell structure. Furthermore, a number of experiments have shown the wave front to be highly turbulent, often giving rise to shocked unburned pockets of reactive fuel in its wake (Subbotin Reference Subbotin1975; Oran et al.
Reference Oran, Young, Boris and Picone1982; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005; Kiyanda & Higgins Reference Kiyanda and Higgins2013). An example experiment (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007) for an irregular detonation wave, involving methane–oxygen, is shown in figure 2. In this figure, the turbulent structure is illustrated via schlieren photography. In figure 2, each notable feature is also illustrated and labelled in a supplemental sketch. These features include the various shock wave dynamics, shear layers and triple points. Of particular interest is the presence of the unburned fuel pockets in the wake, also shown in figure 2. Such pockets contain fine-scale corrugations on their edges due to turbulence, where burning occurs.

Figure 2. Detonation structure for
![]() $\text{CH}_{4}+2\text{O}_{2}$
, initially at
$\text{CH}_{4}+2\text{O}_{2}$
, initially at
![]() $\hat{p}_{o}=3.4$
kPa: (a) a schlieren photograph and (b) the corresponding explanatory sketch (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007).
$\hat{p}_{o}=3.4$
kPa: (a) a schlieren photograph and (b) the corresponding explanatory sketch (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007).
Irregular mixtures, which have higher activation energies, exhibit a much larger variation of shock-induced ignition delays, for unburned fuel passing through the wave structure, compared to regular detonations. Furthermore, experiments reveal that the pockets of gas in the wake burn up relatively quickly, orders of magnitude faster than expected from diffusionless ignition (Radulescu et al. Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005, Reference Radulescu, Sharpe, Law and Lee2007; Kiyanda & Higgins Reference Kiyanda and Higgins2013). As a result, the Zel’dovich–von Neumann–Doring (ZND) model (Fickett & Davis Reference Fickett and Davis1979) does not predict well the structure behind the incident and Mach shocks (Radulescu et al. Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). This suggests that any unburned pockets in the wake of irregular mixtures burn through turbulent mixing with product gases, and not by shock compression alone. Currently, it is not yet understood how the burning rate of these pockets affects the cell pattern observed on the wave front, and is the principal topic investigated in this study. One hypothesis proposes that, as energy is released from the burning of unreacted fuel mixture pockets, pressure pulses can reach and perturb the leading shock, thus influencing the overall structure to generate new cells (Oran et al. Reference Oran, Young, Boris and Picone1982). Such pressure pulses are able to reach the detonation front since the unreacted pockets lie within the hydrodynamic structure of the detonation, between the leading front and its trailing average sonic surface (Radulescu et al. Reference Radulescu, Sharpe, Law and Lee2007). Furthermore, the triple point appears to play a major role affecting the dynamics of how these pockets burn out. Not only is the triple point a source of high temperature and pressure due to shock compression from multiple waves, but it is also a source of enhanced turbulent mixing. The triple point has been shown to give rise to a shear layer in its wake that is susceptible to the Kelvin–Helmholtz (KH) instability and forward jetting (Massa, Austin & Jackson Reference Massa, Austin and Jackson2007; Mach & Radulescu Reference Mach and Radulescu2011; Bhattacharjee Reference Bhattacharjee2013). This shear layer thus acts to enhance mixing between burned product gases with unburned pockets, and therefore acts to increase reaction rates. Therefore, to gain further insight on irregular detonation propagation, it is important to correctly model this hybrid ignition regime, where both turbulent mixing and compression ignition are important.
To date, numerical investigations have been able to show that, with sufficient resolution, mildly irregular detonation structures are recovered quite well by solving Euler’s equations of fluid motion (Gamezo, Desbordes & Oran Reference Gamezo, Desbordes and Oran1999; Sharpe Reference Sharpe2001; Cael et al. Reference Cael, Ng, Bates, Nikiforakis and Short2009), which do not account for turbulent mixing or molecular diffusion. More recent numerical investigations, however, have attempted the same approach for modelling highly irregular mixtures, with much higher activation energies, but with limited success (Radulescu et al. Reference Radulescu, Sharpe, Law and Lee2007). Although such attempts have provided some insight into the roles that shock compression or turbulent motions may have on detonation propagation, the solutions obtained were subject to changes in resolution and did not converge to unique solutions (Radulescu et al. Reference Radulescu, Sharpe, Law and Lee2007). Furthermore, such investigations have confirmed that very long induction times exist, of the order of 100 times longer than observed experimentally, and that unburned pockets burn out much more rapidly through numerical diffusion. Some recent modelling attempts through direct numerical simulation (DNS) of the Navier–Stokes (NS) equations address this problem by attempting to resolve the full spectrum of scales present, including molecular diffusion effects. Unfortunately, such investigations (Gamezo et al. Reference Gamezo, Vasil’ev, Khokhlov and Oran2000; Mahmoudi et al. Reference Mahmoudi, Karimi, Deiterding and Emami2014) have revealed that practically attainable resolutions, in full-scale two-dimensional problems, are insufficient to capture the correct reaction rates of unburned pockets. Thus, full-scale DNS is currently limited to providing insight only on single isolated events, such as triple-point collisions (Ziegler et al. Reference Ziegler, Deiterding, Shepherd and Pullin2011; Lau-Chapdelaine & Radulescu Reference Lau-Chapdelaine and Radulescu2016). Furthermore, turbulence inherently contains three-dimensional effects. It is well known that the dissipation of turbulent motions, the Kolmogorov energy cascade, depends intimately on the ability of vortices to stretch in the third dimension. For this reason, two-dimensional flows tend to experience more backscatter, and hence produce larger-scale fluid motions, compared to realistic three-dimensional flows (Kraichnan Reference Kraichnan1967; Leith Reference Leith1968; Batchelor Reference Batchelor1969). In order to address these fundamental shortcomings associated with Euler simulations or DNS, a reasonable compromise between accuracy of solution and resolvability is to employ large-eddy simulation (LES). For LES, the large-scale fluid motions, governed by the NS equations, are solved directly using numerical methods. The unresolved microscale turbulence is then modelled as a supplement to the large-scale numerical solutions. Recent studies (Gottiparthi et al. Reference Gottiparthi, Genin, Srinivasan and Menon2009; Mahmoudi et al. Reference Mahmoudi, Karimi, Deiterding and Emami2014) have demonstrated that LES can be used to provide insight on the subgrid turbulent mixing effects that contribute to the highly irregular detonation reaction rate. Full closure to the reaction rate, however, remains difficult, as it is typically obtained by assuming either instantaneous mixing or reaction at the subgrid scale. Owing to the difficulties associated with each of these strategies, adequate resolution of the reaction rate of fuel following the wake of a detonation wave remains problematic. All of this previous work clearly highlights the need to isolate and resolve turbulent mixing and combustion rates in mixtures prone to irregular structures.
An alternative LES methodology that shows promise at capturing and resolving mixing rates in detonation propagation problems is the linear eddy model for large-eddy simulation (LEM-LES) (Menon & Kerstein Reference Menon and Kerstein2011). In the past, LEM-LES has been successfully applied to model weakly compressible turbulent premixed and non-premixed flames (Menon & Calhoon Reference Menon and Calhoon1996; Chakravarthy & Menon Reference Chakravarthy and Menon2000). The method is therefore adaptable to a range of combustion regimes. Furthermore, the method has also been successfully applied to model supersonic inert mixing layers (Sankaran & Menon Reference Sankaran and Menon2005). Only recently has the methodology been applied to treat, simultaneously, highly compressible and reactive flows that involve very rapid transients in pressure and energy (Maxwell et al. Reference Maxwell, Falle, Sharpe and Radulescu2015; Maxwell Reference Maxwell2016). It has thus been termed compressible LEM-LES (CLEM-LES). In the CLEM-LES context, the subgrid is treated as a one-dimensional sample of a diffusion–reaction system within each multi-dimensional LES cell. This reduces the expense of solving a complete multi-dimensional problem through DNS while preserving microscale hotspots and their physical effects on ignition. Thus, the model provides high-resolution closure for the unresolved chemical reaction terms in the governing, LES-filtered, reactive NS equations. A principal advantage of this methodology is the ability to treat flows where chemical reactions and microscale mixing occur on the same scales, without the need to provide compromising assumptions on the reaction rate.
In the current work, experiments and numerical simulations have been conducted in order to identify, qualitatively and quantitatively, the flow instabilities that lead to turbulence in the wake of an irregular detonation wave. Moreover, the effect that turbulent mixing has on the burning rates of unburned pockets of reactive gas in the wake of such detonations has been studied. Particular focus has been placed on investigating the impact that such turbulent burning of pockets has on local wave velocities, observed cell patterns and overall wave structure. From the physical experiments, useful quantitative statistical properties of the wave front (i.e. wave velocity distributions) have been obtained, which are intended to serve as validation criteria for numerical strategies applied to highly compressible combustion problems involving detonations. To complement this experimental work, numerical simulations have been conducted, using the CLEM-LES strategy (Maxwell Reference Maxwell2016), in order to examine the effect that turbulent fluctuations have on the resulting flow-field evolution, through varying turbulence intensities of the flow. This was achieved through calibration of a single tuning parameter, as will be discussed later in the paper. As such, the numerical simulations have been validated to the experiments accordingly. Further validation has also been made through comparison to similar experiments (Kiyanda & Higgins Reference Kiyanda and Higgins2013), which have also investigated irregular detonation propagation in methane–oxygen.
The paper is organized as follows. First, the experimental work is presented in § 2, which includes the methodology and also qualitative and quantitative results. Section 3 presents the strategy and formulation adopted to reconstruct, numerically, the observed experimental flow field. Section 4 then presents the results obtained through numerical simulation. Next, § 5 offers a discussion on the findings from both experiments and numerical simulations and provides further analysis. Finally, conclusions are presented in § 6.
2 Experiments
2.1 Methodology
For the experiments conducted in this study, a shock tube technique is used, as illustrated in figure 3. The shock tube is 3 m in total length and has a rectangular cross-section whose height is
![]() ${\hat{H}}=203$
mm by
${\hat{H}}=203$
mm by
![]() $\hat{d}=19$
mm wide. The narrowness of its cross-section in one direction allows one to establish detonations whose cellular structure is essentially two-dimensional, permitting comparison with two-dimensional simulations. The experimental set-up consists of a test section where a methane–oxygen mixture (
$\hat{d}=19$
mm wide. The narrowness of its cross-section in one direction allows one to establish detonations whose cellular structure is essentially two-dimensional, permitting comparison with two-dimensional simulations. The experimental set-up consists of a test section where a methane–oxygen mixture (
![]() $\text{CH}_{4}+\text{2O}_{2}$
) was filled to the desired pressure of
$\text{CH}_{4}+\text{2O}_{2}$
) was filled to the desired pressure of
![]() $\hat{p}=3.5\pm 0.1$
kPa. Such a low pressure has been chosen to allow the formation of cells larger than the channel thickness, in order to obtain mainly two-dimensional structures. Furthermore, this pressure is consistent with previous investigations (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007; Kiyanda & Higgins Reference Kiyanda and Higgins2013), to provide useful comparison. This test section was separated from a driver section by an
$\hat{p}=3.5\pm 0.1$
kPa. Such a low pressure has been chosen to allow the formation of cells larger than the channel thickness, in order to obtain mainly two-dimensional structures. Furthermore, this pressure is consistent with previous investigations (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007; Kiyanda & Higgins Reference Kiyanda and Higgins2013), to provide useful comparison. This test section was separated from a driver section by an
![]() $80~\unicode[STIX]{x03BC}\text{m}$
thick plastic diaphragm, which contained acetylene–oxygen (
$80~\unicode[STIX]{x03BC}\text{m}$
thick plastic diaphragm, which contained acetylene–oxygen (
![]() $\text{C}_{2}\text{H}_{2}+\text{2.5O}_{2}$
) at
$\text{C}_{2}\text{H}_{2}+\text{2.5O}_{2}$
) at
![]() $\hat{p}\sim 20$
kPa. A detonation was first initiated in the driver section by a capacitor discharge, delivering
$\hat{p}\sim 20$
kPa. A detonation was first initiated in the driver section by a capacitor discharge, delivering
![]() ${\sim}1$
kJ in less than
${\sim}1$
kJ in less than
![]() $2~\unicode[STIX]{x03BC}\text{s}$
, to a spark plug located at the end wall, as shown in figure 3. This application of a driver section was necessary to ensure that a detonation wave propagates through the test section, which is difficult to initiate directly at such a low pressure. Prior to conducting the experiment, each chamber was evacuated below 80 Pa before it was filled with the respective gas. To capture the resulting flow-field evolution, a high-speed camera (Phantom V1210) was used to take schlieren photographs, an imaging technique that uses refraction of light in a fluid to capture density gradients (Settles Reference Settles2001), with a frame rate of 77 108 frames per second. The schlieren system uses 12 inch field mirrors and a continuous high-intensity light-emitting diode (LED) light source. This permits velocimetry of the various shock speeds in the flow field with
$2~\unicode[STIX]{x03BC}\text{s}$
, to a spark plug located at the end wall, as shown in figure 3. This application of a driver section was necessary to ensure that a detonation wave propagates through the test section, which is difficult to initiate directly at such a low pressure. Prior to conducting the experiment, each chamber was evacuated below 80 Pa before it was filled with the respective gas. To capture the resulting flow-field evolution, a high-speed camera (Phantom V1210) was used to take schlieren photographs, an imaging technique that uses refraction of light in a fluid to capture density gradients (Settles Reference Settles2001), with a frame rate of 77 108 frames per second. The schlieren system uses 12 inch field mirrors and a continuous high-intensity light-emitting diode (LED) light source. This permits velocimetry of the various shock speeds in the flow field with
![]() ${\sim}10~\unicode[STIX]{x03BC}\text{s}$
time resolution. Further details on the experiments can be found in Bhattacharjee (Reference Bhattacharjee2013).
${\sim}10~\unicode[STIX]{x03BC}\text{s}$
time resolution. Further details on the experiments can be found in Bhattacharjee (Reference Bhattacharjee2013).

Figure 3. Shock tube set-up for the detonation propagation experiment in
![]() $\text{CH}_{4}+\text{2O}_{2}$
, initially at
$\text{CH}_{4}+\text{2O}_{2}$
, initially at
![]() $\hat{p}_{o}=3.5~\text{kPa}$
.
$\hat{p}_{o}=3.5~\text{kPa}$
.

Figure 4. Detonation flow evolution for
![]() $\text{CH}_{4}+\text{2O}_{2}$
, initially at
$\text{CH}_{4}+\text{2O}_{2}$
, initially at
![]() $\hat{p}_{o}=3.5~\text{kPa}$
, obtained for successive frames,
$\hat{p}_{o}=3.5~\text{kPa}$
, obtained for successive frames,
![]() $11~\unicode[STIX]{x03BC}\text{s}$
apart (Bhattacharjee Reference Bhattacharjee2013). Various features of interest are indicated: the incident and Mach shocks, triple points, decoupled reaction zone (pocket of unreacted gas) and shear layers where KH instability is present.
$11~\unicode[STIX]{x03BC}\text{s}$
apart (Bhattacharjee Reference Bhattacharjee2013). Various features of interest are indicated: the incident and Mach shocks, triple points, decoupled reaction zone (pocket of unreacted gas) and shear layers where KH instability is present.
2.2 Qualitative observations
In figure 4, an example flow evolution of a detonation in
![]() $\text{CH}_{4}+\text{2O}_{2}$
at
$\text{CH}_{4}+\text{2O}_{2}$
at
![]() $\hat{p}=3.5\pm 0.1~\text{kPa}$
is shown. This figure shows a sequence of schlieren images, at
$\hat{p}=3.5\pm 0.1~\text{kPa}$
is shown. This figure shows a sequence of schlieren images, at
![]() $11~\unicode[STIX]{x03BC}\text{s}$
intervals, where various features are observed. These features include the incident and Mach shocks and triple points, previously indicated in figure 1. In the sequence of images presented, the reaction zone behind the incident shock, labelled in figure 4(d), is decoupled from the shock wave. This is observed by a thick region between the smooth shock and the textured region where turbulent burning occurs. This decoupling between the shock and reaction zone can be seen to give rise to a pocket of unburned gas behind the triple-point collision process, as observed in figure 4(e–i). Furthermore, shear layers are observed behind the triple-point trajectories, which give rise to KH instability. These hydrodynamic instabilities are further disrupted and thus enhanced by the passage of transverse shock waves, also originating from the triple point. Finally, behind the newly formed Mach shocks, following the triple-point collisions, the wave appears overdriven, as observed by a close coupling between the reaction zone and leading shock wave in figure 4(k).
$11~\unicode[STIX]{x03BC}\text{s}$
intervals, where various features are observed. These features include the incident and Mach shocks and triple points, previously indicated in figure 1. In the sequence of images presented, the reaction zone behind the incident shock, labelled in figure 4(d), is decoupled from the shock wave. This is observed by a thick region between the smooth shock and the textured region where turbulent burning occurs. This decoupling between the shock and reaction zone can be seen to give rise to a pocket of unburned gas behind the triple-point collision process, as observed in figure 4(e–i). Furthermore, shear layers are observed behind the triple-point trajectories, which give rise to KH instability. These hydrodynamic instabilities are further disrupted and thus enhanced by the passage of transverse shock waves, also originating from the triple point. Finally, behind the newly formed Mach shocks, following the triple-point collisions, the wave appears overdriven, as observed by a close coupling between the reaction zone and leading shock wave in figure 4(k).
In figure 5, a repeated experiment at the same conditions reveals a very different cell pattern on the wave front. Thus the wave structure appears stochastic, reflecting the highly irregular nature of detonations in methane–oxygen. Thus, it is of particular interest to examine how turbulent mixing, driven through turbulent instabilities and velocity fluctuations, can impact the overall cell structure and propagation characteristics of a detonation wave.

Figure 5. Another detonation flow evolution for
![]() $\text{CH}_{4}+\text{2O}_{2}$
, initially at
$\text{CH}_{4}+\text{2O}_{2}$
, initially at
![]() $\hat{p}_{o}=3.5~\text{kPa}$
, also obtained for successive frames (
$\hat{p}_{o}=3.5~\text{kPa}$
, also obtained for successive frames (
![]() $a2$
–
$a2$
–
![]() $c2$
),
$c2$
),
![]() $11~\unicode[STIX]{x03BC}\text{s}$
apart (Bhattacharjee Reference Bhattacharjee2013). In this experiment, a different cell pattern compared to figure 4 (shown here in frames
$11~\unicode[STIX]{x03BC}\text{s}$
apart (Bhattacharjee Reference Bhattacharjee2013). In this experiment, a different cell pattern compared to figure 4 (shown here in frames
![]() $a1$
–
$a1$
–
![]() $c1$
) is observed on the wave front.
$c1$
) is observed on the wave front.

Figure 6. P.d.f. of a detonation wave, for
![]() $H=20$
(203 mm), having a certain velocity (
$H=20$
(203 mm), having a certain velocity (
![]() $D/D_{avg}$
) at any given moment and location (this study). Also shown is a p.d.f. compiled from Kiyanda & Higgins (Reference Kiyanda and Higgins2013) for
$D/D_{avg}$
) at any given moment and location (this study). Also shown is a p.d.f. compiled from Kiyanda & Higgins (Reference Kiyanda and Higgins2013) for
![]() $H=10$
(100 mm). Note that
$H=10$
(100 mm). Note that
![]() $D_{avg}=5.19$
(
$D_{avg}=5.19$
(
![]() $1850~\text{m}~\text{s}^{-1}$
) for
$1850~\text{m}~\text{s}^{-1}$
) for
![]() $H=20$
and
$H=20$
and
![]() $D_{avg}=5.53$
(
$D_{avg}=5.53$
(
![]() $1970~\text{m}~\text{s}^{-1}$
) for
$1970~\text{m}~\text{s}^{-1}$
) for
![]() $H=10$
. The theoretical CJ value is
$H=10$
. The theoretical CJ value is
![]() $D_{CJ}=6.30$
(
$D_{CJ}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
).
$2240~\text{m}~\text{s}^{-1}$
).
2.3 Statistical analysis: velocity of the wave
Four different experiments were conducted at the same conditions. In order to obtain useful quantitative data, and to gain insight into the observed flow-field patterns, velocimetry of the wave was performed on all images obtained from all experiments. A probability density function (p.d.f.) of wave velocities was constructed and is shown in figure 6. This figure shows the probability of the wave having a certain velocity at any random time and location. The wave speeds expected on the detonation front (
![]() $D$
) are normalized by the averaged propagation speed, which for this study was found to be
$D$
) are normalized by the averaged propagation speed, which for this study was found to be
![]() $D_{avg}=5.19$
(
$D_{avg}=5.19$
(
![]() $1850~\text{m}~\text{s}^{-1}$
). It is noted that an average velocity deficit exists compared to the theoretical Chapman–Jouguet (CJ) value of
$1850~\text{m}~\text{s}^{-1}$
). It is noted that an average velocity deficit exists compared to the theoretical Chapman–Jouguet (CJ) value of
![]() $D_{CJ}=6.30$
(
$D_{CJ}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
), owing to mass divergence from the flow to the boundary layers found on the glass walls of the channel (Fay Reference Fay1959). To measure the wave speed, at any given location on the shock, the distance the shock travels, along its normal vector, to the next intersecting shock location in the subsequent schlieren image is divided by the time in between images (
$2240~\text{m}~\text{s}^{-1}$
), owing to mass divergence from the flow to the boundary layers found on the glass walls of the channel (Fay Reference Fay1959). To measure the wave speed, at any given location on the shock, the distance the shock travels, along its normal vector, to the next intersecting shock location in the subsequent schlieren image is divided by the time in between images (
![]() $11~\unicode[STIX]{x03BC}\text{s}$
). A total of 6651 velocity measurements were collected using this procedure. The p.d.f. was then evaluated at
$11~\unicode[STIX]{x03BC}\text{s}$
). A total of 6651 velocity measurements were collected using this procedure. The p.d.f. was then evaluated at
![]() $\unicode[STIX]{x1D6FF}D=0.2$
intervals. Also shown in figure 6, for comparison, is a p.d.f. obtained from experimental data provided in Kiyanda & Higgins (Reference Kiyanda and Higgins2013) for an experiment at the same conditions, but for half of the channel height (
$\unicode[STIX]{x1D6FF}D=0.2$
intervals. Also shown in figure 6, for comparison, is a p.d.f. obtained from experimental data provided in Kiyanda & Higgins (Reference Kiyanda and Higgins2013) for an experiment at the same conditions, but for half of the channel height (
![]() ${\hat{H}}=100$
mm). Here, 37 velocity data points are available, along the channel walls, to construct the p.d.f. from one entire cell cycle. For this experiment,
${\hat{H}}=100$
mm). Here, 37 velocity data points are available, along the channel walls, to construct the p.d.f. from one entire cell cycle. For this experiment,
![]() $D_{avg}=5.53$
(
$D_{avg}=5.53$
(
![]() $1970~\text{m}~\text{s}^{-1}$
).
$1970~\text{m}~\text{s}^{-1}$
).
Two principal observations are made. First, for this study the most probable wave speed favoured is
![]() $(D/D_{avg})=0.93\pm 0.04$
with a peak p.d.f. value of 3.3. This implies that the detonation tends to favour a greater chance of having wave speeds below the average propagation speed value, i.e. when
$(D/D_{avg})=0.93\pm 0.04$
with a peak p.d.f. value of 3.3. This implies that the detonation tends to favour a greater chance of having wave speeds below the average propagation speed value, i.e. when
![]() $(D/D_{avg})<1$
. This observation was also made previously for irregular detonation wave propagation, through statistical analysis, in several studies (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007; Shepherd Reference Shepherd2009; Mevel et al.
Reference Mevel, Davidenko, Lafosse, Chaumeix, Dupre, Paillard and Shepherd2015). Since the wave spends more time below CJ velocities, most of the unburned gas that is shocked by the wave front has a lower post-shock temperature, and thus a much longer ignition delay compared to the ZND model. For this reason, and owing to very strong unsteady expansion effects (Lundstrom & Oppenheim Reference Lundstrom and Oppenheim1969; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005; Kiyanda & Higgins Reference Kiyanda and Higgins2013), unburned pockets of gas are able to form in the wake, which eventually burn up through turbulent mixing. This burning through turbulent mixing is believed to be a very important mechanism that allows irregular detonations to sustain propagation (Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005, Reference Radulescu, Sharpe, Law and Lee2007; Borzou & Radulescu Reference Borzou and Radulescu2016). The second observation made is that the p.d.f. has a decaying behaviour, where the probability of the wave speed exhibits an approximate power-law dependence on wave speeds above the favoured value. From the experiments conducted here, the p.d.f. was found to be well predicted by
$(D/D_{avg})<1$
. This observation was also made previously for irregular detonation wave propagation, through statistical analysis, in several studies (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007; Shepherd Reference Shepherd2009; Mevel et al.
Reference Mevel, Davidenko, Lafosse, Chaumeix, Dupre, Paillard and Shepherd2015). Since the wave spends more time below CJ velocities, most of the unburned gas that is shocked by the wave front has a lower post-shock temperature, and thus a much longer ignition delay compared to the ZND model. For this reason, and owing to very strong unsteady expansion effects (Lundstrom & Oppenheim Reference Lundstrom and Oppenheim1969; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005; Kiyanda & Higgins Reference Kiyanda and Higgins2013), unburned pockets of gas are able to form in the wake, which eventually burn up through turbulent mixing. This burning through turbulent mixing is believed to be a very important mechanism that allows irregular detonations to sustain propagation (Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005, Reference Radulescu, Sharpe, Law and Lee2007; Borzou & Radulescu Reference Borzou and Radulescu2016). The second observation made is that the p.d.f. has a decaying behaviour, where the probability of the wave speed exhibits an approximate power-law dependence on wave speeds above the favoured value. From the experiments conducted here, the p.d.f. was found to be well predicted by
![]() $\text{p.d.f.}=2.6(D/D_{avg})^{-4.0}$
. A similar power-law correlation was also observed by Radulescu et al. (Reference Radulescu, Sharpe, Law and Lee2007) from high-resolution Euler simulations, who found a
$\text{p.d.f.}=2.6(D/D_{avg})^{-4.0}$
. A similar power-law correlation was also observed by Radulescu et al. (Reference Radulescu, Sharpe, Law and Lee2007) from high-resolution Euler simulations, who found a
![]() $-3$
power-law dependence of the p.d.f. on detonation velocity. When compared to existing experimental data (Kiyanda & Higgins Reference Kiyanda and Higgins2013), whose p.d.f. correlation was found to be
$-3$
power-law dependence of the p.d.f. on detonation velocity. When compared to existing experimental data (Kiyanda & Higgins Reference Kiyanda and Higgins2013), whose p.d.f. correlation was found to be
![]() $\text{p.d.f.}=1.9(D/D_{avg})^{-4.7}$
, very close agreement is observed, despite propagation through a channel with only half the height (
$\text{p.d.f.}=1.9(D/D_{avg})^{-4.7}$
, very close agreement is observed, despite propagation through a channel with only half the height (
![]() $H$
). In Kiyanda & Higgins (Reference Kiyanda and Higgins2013), the most probable wave speed favoured is
$H$
). In Kiyanda & Higgins (Reference Kiyanda and Higgins2013), the most probable wave speed favoured is
![]() $(D/D_{avg})=0.814\pm 0.005$
with a peak p.d.f. value of 6.15.
$(D/D_{avg})=0.814\pm 0.005$
with a peak p.d.f. value of 6.15.
2.4 Rate of burning of fuel pockets in the wake
For the detonation wave, shown previously in figure 4, it is of particular interest to estimate the rate at which burning of the pockets of unreacted gas occurs. Upon isolating a single pocket surface, starting with figure 4(g), an approximate method to estimate the turbulent flame speed is to consider the pocket’s size, and how long it takes to be consumed. For this method, the pocket’s volume (
![]() $\hat{V}$
) and surface area (
$\hat{V}$
) and surface area (
![]() $\hat{A}_{s}$
) are estimated from the figure by tracing the pocket shape with a linear spline, multiplied by the channel depth in the third dimension. In this regard, the reader is cautioned that the extent of the structures based on the schlieren image is sensitive to the experimental set-up, for which the sensitivity has not been quantified. For this particular pocket, the characteristic length of the pocket is estimated as
$\hat{A}_{s}$
) are estimated from the figure by tracing the pocket shape with a linear spline, multiplied by the channel depth in the third dimension. In this regard, the reader is cautioned that the extent of the structures based on the schlieren image is sensitive to the experimental set-up, for which the sensitivity has not been quantified. For this particular pocket, the characteristic length of the pocket is estimated as
![]() $\hat{L}=\hat{V}/\hat{A}_{s}=5.30$
mm, where
$\hat{L}=\hat{V}/\hat{A}_{s}=5.30$
mm, where
![]() $\hat{V}=36\,000~\text{mm}^{3}$
and
$\hat{V}=36\,000~\text{mm}^{3}$
and
![]() $\hat{A}_{s}=6800~\text{mm}^{2}$
. From this moment, it takes the pocket four frames (
$\hat{A}_{s}=6800~\text{mm}^{2}$
. From this moment, it takes the pocket four frames (
![]() $44~\unicode[STIX]{x03BC}\text{s}$
) to become fully consumed. Thus, the turbulent flame speed, from experiment, is
$44~\unicode[STIX]{x03BC}\text{s}$
) to become fully consumed. Thus, the turbulent flame speed, from experiment, is
![]() ${\hat{S}}_{t}\approx \hat{L}/\unicode[STIX]{x0394}\hat{t}=120~\text{m}~\text{s}^{-1}$
. To compare with the local laminar flame speed, post-shock conditions are considered for a shock travelling at 70 % the theoretical CJ speed for the given quiescent mixture. This particular state of reference (70 % CJ) has been chosen since wave velocity deficits of 20–30 % have been found in the current experiment to exist near the end of the cell cycle during propagation. Furthermore, this state is representative of the pockets of unreacted gas, which form in regions where the shock strength is weaker. The velocity deficits, near the end of the cell cycle, give rise to a significant increase in ignition delay by several orders of magnitude (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007), thus allowing the pocket to decouple from the wave front. Then, by considering realistic chemistry using Cantera libraries (Goodwin, Moffat & Speth Reference Goodwin, Moffat and Speth2016) and the GRI-3.0 detailed kinetic mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016), the state properties of the unburned pocket, and the laminar flame speed are obtained prior to autoignition of the pocket. In this case,
${\hat{S}}_{t}\approx \hat{L}/\unicode[STIX]{x0394}\hat{t}=120~\text{m}~\text{s}^{-1}$
. To compare with the local laminar flame speed, post-shock conditions are considered for a shock travelling at 70 % the theoretical CJ speed for the given quiescent mixture. This particular state of reference (70 % CJ) has been chosen since wave velocity deficits of 20–30 % have been found in the current experiment to exist near the end of the cell cycle during propagation. Furthermore, this state is representative of the pockets of unreacted gas, which form in regions where the shock strength is weaker. The velocity deficits, near the end of the cell cycle, give rise to a significant increase in ignition delay by several orders of magnitude (Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007), thus allowing the pocket to decouple from the wave front. Then, by considering realistic chemistry using Cantera libraries (Goodwin, Moffat & Speth Reference Goodwin, Moffat and Speth2016) and the GRI-3.0 detailed kinetic mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016), the state properties of the unburned pocket, and the laminar flame speed are obtained prior to autoignition of the pocket. In this case,
![]() ${\hat{S}}_{L,\,70\,\%\,CJ}=16.4~\text{m}~\text{s}^{-1}$
. Thus, the turbulent flame speed is found to be approximately seven times larger than the laminar flame speed, i.e.
${\hat{S}}_{L,\,70\,\%\,CJ}=16.4~\text{m}~\text{s}^{-1}$
. Thus, the turbulent flame speed is found to be approximately seven times larger than the laminar flame speed, i.e.
![]() ${\hat{S}}_{t}/{\hat{S}}_{L}\approx 7.3$
.
${\hat{S}}_{t}/{\hat{S}}_{L}\approx 7.3$
.
3 Numerical reconstruction of the flow field
3.1 Overview
In order to reconstruct the flow-field evolution observed experimentally, LEM-LES (Menon & Kerstein Reference Menon and Kerstein2011) has been applied. In this approach, solutions to the governing NS equations were obtained at two different scales; the supergrid and the subgrid scales. On the large scales, the governing LES equations are obtained in the usual manner by filtering the NS equations to some attainable scale. Subgrid contributions are then accounted for through the appropriate closure model. For LEM-LES, the closure model is a self-contained one-dimensional diffusion–reaction system within each LES cell. This strategy has proven to be effective for both non-premixed (McMurtry, Menon & Kerstein Reference McMurtry, Menon and Kerstein1992; Menon et al. Reference Menon, McMurtry, Kerstein and Chen1994; Menon & Calhoon Reference Menon and Calhoon1996) and premixed (Menon & Kerstein Reference Menon and Kerstein1992; Menon et al. Reference Menon, Patrick, McMurtry and Kerstein1993; Calhoon, Menon & Goldin Reference Calhoon, Menon and Goldin1995; Calhoon & Menon Reference Calhoon and Menon1996; Smith & Menon Reference Smith and Menon1996, Reference Smith and Menon1997; Chakravarthy & Menon Reference Chakravarthy and Menon2000; Porumbel Reference Porumbel2006) combustion applications. The LES formulation adopted here largely follows previous LEM-LES implementations (Smith & Menon Reference Smith and Menon1997; Sankaran Reference Sankaran2003; Menon & Kerstein Reference Menon and Kerstein2011) with a few differences in formulation and implementation. The most significant and novel contribution to the advancement of the LEM-LES strategy is the treatment of pressure on the subgrid, and its influence on reaction rates, which allows for adequate closure of the reaction rate in the presence of shocks and strong expansions that evolve on the supergrid.
A significant realization of this methodology is that information regarding local hotspots and contact surfaces on the molecular level are accounted for and resolved. This subgrid modelling strategy thus provides high-resolution closure to the filtered reaction rate on the large scales. Furthermore, to simulate the effect of turbulent mixing at the subgrid scale, the one-dimensional flow fields are randomly ‘stirred’ by linear eddies according to a p.d.f. (Kerstein Reference Kerstein1991a ). The effect of the resulting compressive strain on the flow field, due to the presence of the random subgrid eddies, is to reproduce the turbulent diffusivity on the small scales, based on local properties of the flow on the large scales. The principal advantage of this modelling strategy is that restrictive assumptions, such as infinitely fast mixing or chemical reactions, are not required.
Finally, adaptive mesh refinement (AMR) is applied to the supergrid, providing increased efficiency in obtaining solutions by computing high-resolution solutions only in the regions of interest. In this section, the strategy formulation is first summarized for both the supergrid and subgrid scales, respectively in §§ 3.2 and 3.3. Then, the simulation set-up, including initial and boundary conditions, and also the numerical parameters are presented in § 3.5. Finally, results of the simulation are provided in § 4. Specific details of the CLEM-LES strategy, including procedural algorithms, numerical methods and limitations, are given in Maxwell (Reference Maxwell2016).
3.2 The filtered large-eddy simulation equations
For flows that are highly transient, turbulent, compressible and involve rapid combustion chemistry, the gas-dynamic evolution is governed by the compressible NS equations. In order to address the difficulty of resolving the full spectrum of length scales resulting from the presence of large flow velocities with high Mach numbers (
![]() $M_{a}$
) and Reynolds numbers (
$M_{a}$
) and Reynolds numbers (
![]() $\mathit{Re}$
), the unresolved scales of the governing equations are filtered and modelled through the LES approach. In this respect, rapid transients and fluid motions are captured on the large scales, while the small-scale contributions are modelled through source terms. The LES-filtered conservation equations for mass, momentum and energy (sensible plus kinetic) of a calorically perfect reactive fluid system are given below in (3.1)–(3.3), respectively. Here, a linear eddy viscosity model (Pope Reference Pope2000) and gradient-driven turbulent heat diffusion hypothesis (Poinsot & Veynante Reference Poinsot and Veynante2005; Combest, Ramachandran & Dudukovic Reference Combest, Ramachandran and Dudukovic2011) have been applied to describe the inert effect of velocity fluctuations on the flow field in terms of a turbulent kinematic viscosity,
$\mathit{Re}$
), the unresolved scales of the governing equations are filtered and modelled through the LES approach. In this respect, rapid transients and fluid motions are captured on the large scales, while the small-scale contributions are modelled through source terms. The LES-filtered conservation equations for mass, momentum and energy (sensible plus kinetic) of a calorically perfect reactive fluid system are given below in (3.1)–(3.3), respectively. Here, a linear eddy viscosity model (Pope Reference Pope2000) and gradient-driven turbulent heat diffusion hypothesis (Poinsot & Veynante Reference Poinsot and Veynante2005; Combest, Ramachandran & Dudukovic Reference Combest, Ramachandran and Dudukovic2011) have been applied to describe the inert effect of velocity fluctuations on the flow field in terms of a turbulent kinematic viscosity,
![]() $\unicode[STIX]{x1D708}_{t}$
. The set of equations are further supplemented by a one-equation localized kinetic energy model (LKM) (Schumann Reference Schumann1975; Chakravarthy & Menon Reference Chakravarthy and Menon2001) to describe the diffusion, advection, production and dissipation of the subgrid kinetic energy (
$\unicode[STIX]{x1D708}_{t}$
. The set of equations are further supplemented by a one-equation localized kinetic energy model (LKM) (Schumann Reference Schumann1975; Chakravarthy & Menon Reference Chakravarthy and Menon2001) to describe the diffusion, advection, production and dissipation of the subgrid kinetic energy (
![]() $k^{sgs}$
) associated with subgrid velocity fluctuations in the flow; see (3.4). Finally, the equations of state are given by (3.5). It should be noted that the equations are given in non-dimensional form where the various gas properties are normalized by the reference quiescent state. Favre-averaged filtering is achieved by letting
$k^{sgs}$
) associated with subgrid velocity fluctuations in the flow; see (3.4). Finally, the equations of state are given by (3.5). It should be noted that the equations are given in non-dimensional form where the various gas properties are normalized by the reference quiescent state. Favre-averaged filtering is achieved by letting
![]() $\tilde{f}=\overline{\unicode[STIX]{x1D70C}f}/\bar{\unicode[STIX]{x1D70C}}$
, where
$\tilde{f}=\overline{\unicode[STIX]{x1D70C}f}/\bar{\unicode[STIX]{x1D70C}}$
, where
![]() $f$
represents one of the many state variables. Here
$f$
represents one of the many state variables. Here
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $p$
,
$p$
,
![]() $e$
,
$e$
,
![]() $T$
and
$T$
and
![]() $\boldsymbol{u}$
refer to density, pressure, specific sensible plus kinetic energy, temperature and velocity vector, respectively. Other usual properties to note are the heat release
$\boldsymbol{u}$
refer to density, pressure, specific sensible plus kinetic energy, temperature and velocity vector, respectively. Other usual properties to note are the heat release
![]() $Q$
, the ratio of specific heats
$Q$
, the ratio of specific heats
![]() $\unicode[STIX]{x1D6FE}$
, the kinematic viscosity
$\unicode[STIX]{x1D6FE}$
, the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
, the resolved shear stress tensor
$\unicode[STIX]{x1D708}$
, the resolved shear stress tensor
![]() $\bar{\bar{\unicode[STIX]{x1D749}}}$
, and the Prandtl number
$\bar{\bar{\unicode[STIX]{x1D749}}}$
, and the Prandtl number
![]() $\mathit{Pr}$
:
$\mathit{Pr}$
:
Above, the various state variables have been normalized such that
where the subscript ‘
![]() $o$
’ refers to the reference state, the hat superscript refers to a dimensional quantity,
$o$
’ refers to the reference state, the hat superscript refers to a dimensional quantity,
![]() $\unicode[STIX]{x1D644}$
is the identity matrix,
$\unicode[STIX]{x1D644}$
is the identity matrix,
![]() $c$
is the speed of sound, and
$c$
is the speed of sound, and
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
is a reference length scale. This reference length scale is taken as the theoretical half-reaction length associated with the steady ZND solution for a detonation wave propagating in the quiescent reference fluid. In the equation set above, the subgrid kinetic energy,
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
is a reference length scale. This reference length scale is taken as the theoretical half-reaction length associated with the steady ZND solution for a detonation wave propagating in the quiescent reference fluid. In the equation set above, the subgrid kinetic energy,
![]() $k^{sgs}$
, is produced at the same rate as the large-scale turbulent motions are dissipated, on the supergrid, through the turbulent kinematic viscosity. Hence, the rate of production of subgrid kinetic energy is given by
$k^{sgs}$
, is produced at the same rate as the large-scale turbulent motions are dissipated, on the supergrid, through the turbulent kinematic viscosity. Hence, the rate of production of subgrid kinetic energy is given by
and the dissipation rate is modelled as
Finally, a Smagorinsky-type model is applied to link the turbulent kinematic viscosity to the unresolved velocity fluctuations (Pope Reference Pope2000), and thus the subgrid kinetic energy, through
Here,
![]() $C_{\unicode[STIX]{x1D705}}$
is the Kolmogorov constant, a model parameter that requires calibration. Typically,
$C_{\unicode[STIX]{x1D705}}$
is the Kolmogorov constant, a model parameter that requires calibration. Typically,
![]() $C_{\unicode[STIX]{x1D705}}$
is estimated from experiments to be
$C_{\unicode[STIX]{x1D705}}$
is estimated from experiments to be
![]() ${\sim}1.5$
; however, published values range anywhere from 1.2 to 4 (Chasnov Reference Chasnov1991). Also found in (3.8) and (3.9) is the LES filter size,
${\sim}1.5$
; however, published values range anywhere from 1.2 to 4 (Chasnov Reference Chasnov1991). Also found in (3.8) and (3.9) is the LES filter size,
![]() $\bar{\unicode[STIX]{x1D6E5}}$
. For simplicity, it is assumed that
$\bar{\unicode[STIX]{x1D6E5}}$
. For simplicity, it is assumed that
![]() $\bar{\unicode[STIX]{x1D6E5}}=b$
, where
$\bar{\unicode[STIX]{x1D6E5}}=b$
, where
![]() $b$
is the minimum grid spacing. It is noted, however, that this assumption may introduce errors at fine–coarse cell interfaces when coupled with AMR (Pope Reference Pope2004; Vanella, Piomelli & Balaras Reference Vanella, Piomelli and Balaras2008). Since the bulk of the subgrid kinetic energy is generated and dissipated in regions containing shock waves, which are refined to the highest level, it is believed that such fine–coarse interface errors will not affect the solution outcome. Finally, to close the conservation of energy equation (3.3), the heat release term,
$b$
is the minimum grid spacing. It is noted, however, that this assumption may introduce errors at fine–coarse cell interfaces when coupled with AMR (Pope Reference Pope2004; Vanella, Piomelli & Balaras Reference Vanella, Piomelli and Balaras2008). Since the bulk of the subgrid kinetic energy is generated and dissipated in regions containing shock waves, which are refined to the highest level, it is believed that such fine–coarse interface errors will not affect the solution outcome. Finally, to close the conservation of energy equation (3.3), the heat release term,
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}$
, requires closure. This is done through the application of the CLEM subgrid within each LES cell.
$\overline{\dot{\unicode[STIX]{x1D714}}}$
, requires closure. This is done through the application of the CLEM subgrid within each LES cell.
3.3 The CLEM subgrid model
For the CLEM subgrid modelling strategy, the small-scale mixing and chemical reactions are solved separately from the large-scale pressure evolution. The present implementation of the LEM strategy, introduced by Kerstein (Reference Kerstein1988, Reference Kerstein1989, Reference Kerstein1990, Reference Kerstein1991a
,Reference Kerstein
b
, Reference Kerstein1992a
,Reference Kerstein
b
), differs from previous subgrid formulations for LES (McMurtry et al.
Reference McMurtry, Menon and Kerstein1992; Menon et al.
Reference Menon, Patrick, McMurtry and Kerstein1993; Calhoon & Menon Reference Calhoon and Menon1996; Menon & Calhoon Reference Menon and Calhoon1996; Mathey & Chollet Reference Mathey, Chollet, Galperin and Orszag1997; Sankaran Reference Sankaran2003; Porumbel Reference Porumbel2006; Menon & Kerstein Reference Menon and Kerstein2011) by ensuring appropriate coupling of the pressure and energy fields on both scales. More specifically, the supergrid simulation, (3.1)–(3.4), provides the local rates of change of pressure to the subgrid (i.e. the pressure evolution), while the subgrid model is then applied to simulate the small-scale molecular mixing and chemical reactions, which thus provides
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}$
to the supergrid as a source term. Thus, the sole purpose of the subgrid simulation is to provide closure to
$\overline{\dot{\unicode[STIX]{x1D714}}}$
to the supergrid as a source term. Thus, the sole purpose of the subgrid simulation is to provide closure to
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}$
in (3.3).
$\overline{\dot{\unicode[STIX]{x1D714}}}$
in (3.3).
Here, the subgrid model is a one-dimensional representation of the flow field within each supergrid cell whose orientation is aligned in the direction of local flow. Furthermore, the subgrid simulation is only applied to the finest cells on the AMR-enabled supergrid. Thus, each supergrid cell on the finest grid level, which requires closure, contains one subgrid domain. To formally derive the subgrid model, presented below, the low-Mach-number approximation (Paolucci Reference Paolucci1982) is applied to the governing NS equations. In this approximation, pressure gradients are locally neglected within the small scales of each supergrid cell. This effectively assumes that pressure waves travel much faster than the physical expansion or contraction of the local fluid relative to its convective motion (Maxwell et al. Reference Maxwell, Falle, Sharpe and Radulescu2015).
Furthermore, the chemistry has been simplified by assuming that reactants form products according to a single-step global reaction with no intermediate reactions:
![]() $\text{reactants}\rightarrow \text{products}$
directly and irreversibly. In reality, the reaction rate (
$\text{reactants}\rightarrow \text{products}$
directly and irreversibly. In reality, the reaction rate (
![]() $\dot{\unicode[STIX]{x1D714}}$
) is governed by chemistry involving multiple reactions between multiple species. This requires significant computational overhead due to the requirement to account for hundreds, or thousands, of equations and reactions in reactive flows. Thus, for the subgrid system, the resulting conservations of enthalpy and reactant mass, along particle paths, are expressed in non-dimensional form as
$\dot{\unicode[STIX]{x1D714}}$
) is governed by chemistry involving multiple reactions between multiple species. This requires significant computational overhead due to the requirement to account for hundreds, or thousands, of equations and reactions in reactive flows. Thus, for the subgrid system, the resulting conservations of enthalpy and reactant mass, along particle paths, are expressed in non-dimensional form as
 $$\begin{eqnarray}\displaystyle & \displaystyle \underbrace{\unicode[STIX]{x1D70C}\frac{\text{D}T}{\text{D}t}}_{\substack{ \mathit{rate~of~change} \\ \mathit{of~enthalpy~along} \\ \mathit{a~particle~path}}}-\underbrace{\left(\frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}}\right){\dot{p}}}_{\substack{ \mathit{rate~of~change~of} \\ \mathit{energy~due~to~local} \\ \mathit{pressure~changes}}}-\underbrace{\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}m}\left(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}m}\right)}_{\substack{ \mathit{heat~diffusion} \\ \mathit{to~neighbouring} \\ \mathit{fluid~elements}}}=-\underbrace{\left(\frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}}\right)Q\dot{\unicode[STIX]{x1D714}}}_{\mathit{heat~release}}+\,\dot{F_{T}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \underbrace{\unicode[STIX]{x1D70C}\frac{\text{D}T}{\text{D}t}}_{\substack{ \mathit{rate~of~change} \\ \mathit{of~enthalpy~along} \\ \mathit{a~particle~path}}}-\underbrace{\left(\frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}}\right){\dot{p}}}_{\substack{ \mathit{rate~of~change~of} \\ \mathit{energy~due~to~local} \\ \mathit{pressure~changes}}}-\underbrace{\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}m}\left(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}m}\right)}_{\substack{ \mathit{heat~diffusion} \\ \mathit{to~neighbouring} \\ \mathit{fluid~elements}}}=-\underbrace{\left(\frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}}\right)Q\dot{\unicode[STIX]{x1D714}}}_{\mathit{heat~release}}+\,\dot{F_{T}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \underbrace{\unicode[STIX]{x1D70C}\frac{\text{D}Y}{\text{D}t}}_{\substack{ \mathit{rate~of~change~of} \\ \mathit{reactant~density~along} \\ \mathit{a~particle~path}}}-\underbrace{\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}m}\left(\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x1D6FC}}{Le}\frac{\unicode[STIX]{x2202}Y}{\unicode[STIX]{x2202}m}\right)}_{\substack{ \mathit{reactant~diffusion} \\ \mathit{ to~neighbouring } \\ \mathit{fluid~elements}}}=\dot{\unicode[STIX]{x1D714}}+\dot{F_{Y}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \underbrace{\unicode[STIX]{x1D70C}\frac{\text{D}Y}{\text{D}t}}_{\substack{ \mathit{rate~of~change~of} \\ \mathit{reactant~density~along} \\ \mathit{a~particle~path}}}-\underbrace{\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}m}\left(\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x1D6FC}}{Le}\frac{\unicode[STIX]{x2202}Y}{\unicode[STIX]{x2202}m}\right)}_{\substack{ \mathit{reactant~diffusion} \\ \mathit{ to~neighbouring } \\ \mathit{fluid~elements}}}=\dot{\unicode[STIX]{x1D714}}+\dot{F_{Y}}, & \displaystyle\end{eqnarray}$$
where
![]() $Y$
is defined as the reactant mass fraction. In this formulation, the material derivative has been applied, where
$Y$
is defined as the reactant mass fraction. In this formulation, the material derivative has been applied, where
![]() $\text{D}\unicode[STIX]{x1D719}/\text{D}t=\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}t+u(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}x)$
. Also,
$\text{D}\unicode[STIX]{x1D719}/\text{D}t=\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}t+u(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}x)$
. Also,
![]() $m$
is a one-dimensional mass-weighted Lagrangian coordinate whose transformation to Cartesian spatial coordinates is given by
$m$
is a one-dimensional mass-weighted Lagrangian coordinate whose transformation to Cartesian spatial coordinates is given by
Then, for the one-step global reaction mechanism, which considers a single premixed reactant, with mass fraction
![]() $Y$
, products are formed according to the single-step Arrhenius expression (Williams Reference Williams1985):
$Y$
, products are formed according to the single-step Arrhenius expression (Williams Reference Williams1985):
where
![]() $E_{a}$
is the non-dimensional activation energy of the reactant mixture. Here, the activation energy (
$E_{a}$
is the non-dimensional activation energy of the reactant mixture. Here, the activation energy (
![]() $\hat{E_{a}}$
), heat release (
$\hat{E_{a}}$
), heat release (
![]() $\hat{Q}$
) and pre-exponential factor (
$\hat{Q}$
) and pre-exponential factor (
![]() $\hat{A}$
) are normalized according to
$\hat{A}$
) are normalized according to
Furthermore, it is useful to define the following transport relationships in order to relate viscosity to heat and mass diffusion in terms of Reynolds (
![]() $\mathit{Re}$
), Prandtl (
$\mathit{Re}$
), Prandtl (
![]() $\mathit{Pr}$
), Schmidt (
$\mathit{Pr}$
), Schmidt (
![]() $Sc$
) and Lewis numbers (
$Sc$
) and Lewis numbers (
![]() $Le$
):
$Le$
):
The source terms,
![]() $\dot{F_{T}}$
and
$\dot{F_{T}}$
and
![]() $\dot{F_{Y}}$
, in (3.10) and (3.11) do not take on any specific values, but rather account for the effect of turbulence on the subgrid in the form of random ‘stirring’ events (Kerstein Reference Kerstein1991a
). These ‘stirring’ events are implemented as a series of random instantaneous remapping procedures on the subgrid. The remapping procedure is designed to simulate the effect that a multi-dimensional eddy would have on a one-dimensional sample of the flow field. In order to achieve this, a triplet map is implemented, as detailed by Kerstein (Reference Kerstein1991a
). Functionally, the application of these ‘stirring’ events depends on the local turbulent diffusivity (or viscosity), which in turn depends on local velocity fluctuations through the subgrid kinetic energy,
$\dot{F_{Y}}$
, in (3.10) and (3.11) do not take on any specific values, but rather account for the effect of turbulence on the subgrid in the form of random ‘stirring’ events (Kerstein Reference Kerstein1991a
). These ‘stirring’ events are implemented as a series of random instantaneous remapping procedures on the subgrid. The remapping procedure is designed to simulate the effect that a multi-dimensional eddy would have on a one-dimensional sample of the flow field. In order to achieve this, a triplet map is implemented, as detailed by Kerstein (Reference Kerstein1991a
). Functionally, the application of these ‘stirring’ events depends on the local turbulent diffusivity (or viscosity), which in turn depends on local velocity fluctuations through the subgrid kinetic energy,
![]() $k^{sgs}$
. Finally, the source term involving
$k^{sgs}$
. Finally, the source term involving
![]() ${\dot{p}}$
accounts for enthalpy changes that arise from local temporal changes in pressure, which is obtained from the supergrid simulation.
${\dot{p}}$
accounts for enthalpy changes that arise from local temporal changes in pressure, which is obtained from the supergrid simulation.
3.4 Numerical implementation
In order to solve the system of equations (3.1)–(3.4), a numerical framework developed by Mantis Numerics is employed. The compressible flow solver uses a second-order-accurate exact Godunov solver (Richtmyer & Morton Reference Richtmyer and Morton1967; Falle Reference Falle1991), which features a symmetric monotonized central flux limiter (van Leer Reference van Leer1977) to treat the convection terms. The diffusive terms are handled explicitly in time using the forward Euler method, and spatially discretized using second-order-accurate central differences (Tannehill, Anderson & Pletcher Reference Tannehill, Anderson and Pletcher1997). Structured Cartesian grids are applied in order to take advantage of AMR (Falle & Giddings Reference Falle and Giddings1993) for increased efficiency. It should be noted, however, that the application of LEM-LES may not necessarily be limited to structured Cartesian grids (Cannon et al.
Reference Cannon, Adumitroaie, McDaniel and Smith2001). In this work, AMR is implemented only on the supergrid, equations (3.1)–(3.4). Specifically, the supergrid is refined, on a per-cell basis, in regions where the density or reactant mass (
![]() $\bar{\unicode[STIX]{x1D70C}}$
or
$\bar{\unicode[STIX]{x1D70C}}$
or
![]() $\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}$
) changes by more than 0.1 % locally between existing grid levels. Furthermore, when a cell is flagged as ‘bad’, or needing refinement, this badness is diffused by approximately 5–10 cells in each direction on the current grid level. For the purpose of refinement, the Favre-averaged reactant mass,
$\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}$
) changes by more than 0.1 % locally between existing grid levels. Furthermore, when a cell is flagged as ‘bad’, or needing refinement, this badness is diffused by approximately 5–10 cells in each direction on the current grid level. For the purpose of refinement, the Favre-averaged reactant mass,
![]() $\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}$
, is obtained from information stored entirely on the subgrid, through
$\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}$
, is obtained from information stored entirely on the subgrid, through
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}=\frac{\displaystyle \mathop{\sum }_{i=1}^{N}m_{i}Y_{i}}{V_{cell}},\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}=\frac{\displaystyle \mathop{\sum }_{i=1}^{N}m_{i}Y_{i}}{V_{cell}},\end{eqnarray}$$
where
![]() $m$
and
$m$
and
![]() $Y$
refer to the mass and reactant mass fraction, respectively, of each
$Y$
refer to the mass and reactant mass fraction, respectively, of each
![]() $i$
th subgrid element within the LES cell, and
$i$
th subgrid element within the LES cell, and
![]() $V_{cell}$
is the LES cell volume. The supergrid is also refined in the presence of shocked and unburned reactant (i.e.
$V_{cell}$
is the LES cell volume. The supergrid is also refined in the presence of shocked and unburned reactant (i.e.
![]() $\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}>0$
and
$\bar{\unicode[STIX]{x1D70C}}{\tilde{Y}}>0$
and
![]() $\bar{\unicode[STIX]{x1D70C}}>1.1$
). Furthermore, the subgrid model is only active on the finest cells of the supergrid system, and not the coarsest and intermediate grid levels. AMR is not applied to the subgrid domains. For newly refined supergrid cells, and thus newly created LEM subgrid domains, the initial values of
$\bar{\unicode[STIX]{x1D70C}}>1.1$
). Furthermore, the subgrid model is only active on the finest cells of the supergrid system, and not the coarsest and intermediate grid levels. AMR is not applied to the subgrid domains. For newly refined supergrid cells, and thus newly created LEM subgrid domains, the initial values of
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $T$
take on those of the supergrid, and
$T$
take on those of the supergrid, and
![]() $Y=1$
.
$Y=1$
.
To solve the subgrid system of equations (3.10) and (3.11), operator splitting (Leveque Reference Leveque2002) is applied to treat the various terms. First, the enthalpy contribution due to pressure changes is applied to each LEM element through the source term
![]() ${\dot{p}}$
, as detailed in Maxwell (Reference Maxwell2016). Then, the diffusion terms are solved in the same manner as the supergrid diffusion terms: explicitly in time using the forward Euler method, and spatially discretized using second-order-accurate central differences (Tannehill et al.
Reference Tannehill, Anderson and Pletcher1997). This is done for successive and sufficiently small subgrid time steps (
${\dot{p}}$
, as detailed in Maxwell (Reference Maxwell2016). Then, the diffusion terms are solved in the same manner as the supergrid diffusion terms: explicitly in time using the forward Euler method, and spatially discretized using second-order-accurate central differences (Tannehill et al.
Reference Tannehill, Anderson and Pletcher1997). This is done for successive and sufficiently small subgrid time steps (
![]() $\unicode[STIX]{x0394}t_{diff}$
) in order to satisfy either the Courant–Friedrichs–Lewy (CFL) stability criterion associated with the explicit diffusion operation, or the time at which the stirring event occurs, whichever is smaller. Then, the reaction terms are solved, implicitly, for the same time step,
$\unicode[STIX]{x0394}t_{diff}$
) in order to satisfy either the Courant–Friedrichs–Lewy (CFL) stability criterion associated with the explicit diffusion operation, or the time at which the stirring event occurs, whichever is smaller. Then, the reaction terms are solved, implicitly, for the same time step,
![]() $\unicode[STIX]{x0394}t_{diff}$
, using the backward Euler method (Tannehill et al.
Reference Tannehill, Anderson and Pletcher1997).
$\unicode[STIX]{x0394}t_{diff}$
, using the backward Euler method (Tannehill et al.
Reference Tannehill, Anderson and Pletcher1997).
Procedurally, the supergrid system of equations (3.1)–(3.4) is solved first for one global time step (
![]() $\unicode[STIX]{x0394}t$
) without chemical reaction by letting
$\unicode[STIX]{x0394}t$
) without chemical reaction by letting
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}=0$
. This provides
$\overline{\dot{\unicode[STIX]{x1D714}}}=0$
. This provides
![]() ${\dot{p}}$
to the subgrid system, (3.10) and (3.11), which is then simulated in each refined supergrid cell for the same
${\dot{p}}$
to the subgrid system, (3.10) and (3.11), which is then simulated in each refined supergrid cell for the same
![]() $\unicode[STIX]{x0394}t$
. Zero-gradient boundary conditions are assumed for the LEM domains during this process. This provides the exact
$\unicode[STIX]{x0394}t$
. Zero-gradient boundary conditions are assumed for the LEM domains during this process. This provides the exact
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}$
contribution, which is then accounted for in (3.3). Finally, once the LEM domains evolve across each supergrid time step (
$\overline{\dot{\unicode[STIX]{x1D714}}}$
contribution, which is then accounted for in (3.3). Finally, once the LEM domains evolve across each supergrid time step (
![]() $\unicode[STIX]{x0394}t$
), large-scale advection of LEM elements is handled by transferring elements to or from neighbouring cells through a splicing procedure detailed in Sankaran (Reference Sankaran2003). This is easily implemented and satisfies the basic mass conservation requirement since the mass flux (
$\unicode[STIX]{x0394}t$
), large-scale advection of LEM elements is handled by transferring elements to or from neighbouring cells through a splicing procedure detailed in Sankaran (Reference Sankaran2003). This is easily implemented and satisfies the basic mass conservation requirement since the mass flux (
![]() $\bar{\unicode[STIX]{x1D70C}}\tilde{\boldsymbol{u}}$
) across each LES cell face is known. More specific details on the procedure, methodology, algorithms and model derivation are found in Maxwell (Reference Maxwell2016).
$\bar{\unicode[STIX]{x1D70C}}\tilde{\boldsymbol{u}}$
) across each LES cell face is known. More specific details on the procedure, methodology, algorithms and model derivation are found in Maxwell (Reference Maxwell2016).

Figure 7. Initial and boundary conditions for the two-dimensional planar detonation propagation experiment (not to scale). Note that
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}=9.68$
mm.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}=9.68$
mm.
3.5 Numerical domain and model parameters
A schematic showing the set-up for the numerical domain is shown in figure 7. In all simulations, the total domain length is 900 half reaction lengths (
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
) long, which is sufficient to allow adequate sampling and analysis of the detonation structure beyond the time it takes for the CJ speed to be recovered. A domain height of
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
) long, which is sufficient to allow adequate sampling and analysis of the detonation structure beyond the time it takes for the CJ speed to be recovered. A domain height of
![]() $20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
corresponds to the experiments in § 2, while a height of
$20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
corresponds to the experiments in § 2, while a height of
![]() $10\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
corresponds to the experiments of Kiyanda & Higgins (Reference Kiyanda and Higgins2013). For the wall boundary, shown in figure 7,
$10\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
corresponds to the experiments of Kiyanda & Higgins (Reference Kiyanda and Higgins2013). For the wall boundary, shown in figure 7,
![]() $u=v=k^{sgs}=0$
and the normal gradients of all remaining variables are zero. For the symmetry boundary condition, only the normal velocity component is taken as zero. Thus
$u=v=k^{sgs}=0$
and the normal gradients of all remaining variables are zero. For the symmetry boundary condition, only the normal velocity component is taken as zero. Thus
![]() $v=0$
, while the normal gradients of all other variables are also zero. Finally, the zero-gradient boundary condition assumes that all normal gradients for all variables are zero. To initiate the planar detonation wave, an initially overdriven ZND profile is initialized in the first
$v=0$
, while the normal gradients of all other variables are also zero. Finally, the zero-gradient boundary condition assumes that all normal gradients for all variables are zero. To initiate the planar detonation wave, an initially overdriven ZND profile is initialized in the first
![]() $20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
lengths of the computational domain. The initial ZND profile corresponds to an overdriven detonation by 10 % or 20 % in order to overcome start-up errors associated with the initially sharp discontinuity at the shock. A section ahead of the ZND profile,
$20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
lengths of the computational domain. The initial ZND profile corresponds to an overdriven detonation by 10 % or 20 % in order to overcome start-up errors associated with the initially sharp discontinuity at the shock. A section ahead of the ZND profile,
![]() $4\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
long, contains random perturbations to the quiescent density field. This allows for the two-dimensional cellular structure to develop further down the channel. Finally, the resulting expansion wave which originates from the wall boundary acts to decelerate the wave from its overdriven state to the theoretical CJ speed (Fickett & Davis Reference Fickett and Davis1979). Formally, the initial conditions for
$4\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
long, contains random perturbations to the quiescent density field. This allows for the two-dimensional cellular structure to develop further down the channel. Finally, the resulting expansion wave which originates from the wall boundary acts to decelerate the wave from its overdriven state to the theoretical CJ speed (Fickett & Davis Reference Fickett and Davis1979). Formally, the initial conditions for
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $u$
,
$u$
,
![]() $p$
and
$p$
and
![]() $Y$
are given according to
$Y$
are given according to
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}(x,y,0)=\left\{\begin{array}{@{}ll@{}}\text{ZND solution} & \text{if}~x<0,\\ 1.25-0.5n & \text{if}~0\leqslant x\leqslant 4,\\ 1 & \text{otherwise},\end{array}\right. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}(x,y,0)=\left\{\begin{array}{@{}ll@{}}\text{ZND solution} & \text{if}~x<0,\\ 1.25-0.5n & \text{if}~0\leqslant x\leqslant 4,\\ 1 & \text{otherwise},\end{array}\right. & \displaystyle\end{eqnarray}$$
Next, in order to determine the required model parameters that mimic the experimental premixed methane–oxygen mixtures, from § 2 and Kiyanda & Higgins (Reference Kiyanda and Higgins2013), the various dimensional and non-dimensional properties were obtained using the procedure detailed in Maxwell (Reference Maxwell2016). To summarize the procedure, the global activation energy, heat release, post-shock flame speed and the ZND structure (Fickett & Davis Reference Fickett and Davis1979) are first obtained using the Cantera libraries (Goodwin et al.
Reference Goodwin, Moffat and Speth2016) for realistic chemistry with the GRI-3.0 detailed kinetic mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016). The pre-exponential factor,
![]() $A$
, and diffusion coefficients are then chosen such that the one-step model reproduces the correct half reaction length,
$A$
, and diffusion coefficients are then chosen such that the one-step model reproduces the correct half reaction length,
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, and also the correct laminar premixed flame speed at post-shock conditions, prior to autoignition, for a shock travelling at 70 % the theoretical CJ speed for the given quiescent mixture. This particular state of reference (70 % CJ) was previously chosen in order to evaluate the laminar flame speed of unburned pockets of gas in § 2.4. The various dimensional and corresponding non-dimensional parameters relevant to the one-step combustion model are given in table 1.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, and also the correct laminar premixed flame speed at post-shock conditions, prior to autoignition, for a shock travelling at 70 % the theoretical CJ speed for the given quiescent mixture. This particular state of reference (70 % CJ) was previously chosen in order to evaluate the laminar flame speed of unburned pockets of gas in § 2.4. The various dimensional and corresponding non-dimensional parameters relevant to the one-step combustion model are given in table 1.
Table 1. Dimensional and non-dimensional fluid properties, and model parameters, for methane–oxygen combustion at
![]() $\hat{T}_{o}=300$
K and
$\hat{T}_{o}=300$
K and
![]() $\hat{p}_{o}=3500$
Pa.
$\hat{p}_{o}=3500$
Pa.

4 Simulation results
4.1 Preliminary simulation results
Here, a CLEM-LES simulation was conducted for a
![]() $C_{\unicode[STIX]{x1D705}}$
value of 1.5 to illustrate the solution. The maximum resolution of the supergrid was set to
$C_{\unicode[STIX]{x1D705}}$
value of 1.5 to illustrate the solution. The maximum resolution of the supergrid was set to
![]() $b=1/32$
(32 cells per
$b=1/32$
(32 cells per
![]() $\hat{\unicode[STIX]{x1D706}}_{1/2}$
), while the number of subgrid elements within each LES cell was set to
$\hat{\unicode[STIX]{x1D706}}_{1/2}$
), while the number of subgrid elements within each LES cell was set to
![]() $N=16$
. For the AMR implementation, the base grid (G1) has a resolution of
$N=16$
. For the AMR implementation, the base grid (G1) has a resolution of
![]() $b_{G1}=1$
with five additional levels of refinement for a total of six grid levels on the supergrid. Also, the domain height for this simulation was
$b_{G1}=1$
with five additional levels of refinement for a total of six grid levels on the supergrid. Also, the domain height for this simulation was
![]() $H=20$
, consistent with the experiments in § 2. In the simulation, the wave was allowed to travel approximately
$H=20$
, consistent with the experiments in § 2. In the simulation, the wave was allowed to travel approximately
![]() ${\sim}850\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
downstream, which was found to be sufficient to allow the wave to reach a quasi-steady state, in terms of velocity and exhibited cell patterns. Snapshots of the density and temperature fields of the wave, for a particular instant in time near the end of the channel, are shown in figure 8. This particular figure shows that a very irregular pattern emerges on the front. Clearly, there is one large cell that spans half of the domain height, and several much smaller cells above it. Also shown in the figure is the formation of a typical unburned pocket of reactive gas that appears in the wake. Such pockets are much more cool and dense compared to the surrounding burned products. Also, to complement figure 8, the corresponding grid topology, which indicates the locations of each grid level (G) in a portion of the flow field, is shown in figure 9 for the same instant in time. From this figure, it can be verified that the reaction zone is always refined to the finest level, G6 in this case.
${\sim}850\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
downstream, which was found to be sufficient to allow the wave to reach a quasi-steady state, in terms of velocity and exhibited cell patterns. Snapshots of the density and temperature fields of the wave, for a particular instant in time near the end of the channel, are shown in figure 8. This particular figure shows that a very irregular pattern emerges on the front. Clearly, there is one large cell that spans half of the domain height, and several much smaller cells above it. Also shown in the figure is the formation of a typical unburned pocket of reactive gas that appears in the wake. Such pockets are much more cool and dense compared to the surrounding burned products. Also, to complement figure 8, the corresponding grid topology, which indicates the locations of each grid level (G) in a portion of the flow field, is shown in figure 9 for the same instant in time. From this figure, it can be verified that the reaction zone is always refined to the finest level, G6 in this case.

Figure 8. Density (a) and temperature (b) fields for the CLEM-LES with
![]() $C_{\unicode[STIX]{x1D705}}=1.5$
. This preliminary result shows the irregular cellular pattern that emerges on the detonation front, and the occasional formation of unburned pockets of reactive gas that appear in the wake. Note that density, temperature, and distance are normalized by
$C_{\unicode[STIX]{x1D705}}=1.5$
. This preliminary result shows the irregular cellular pattern that emerges on the detonation front, and the occasional formation of unburned pockets of reactive gas that appear in the wake. Note that density, temperature, and distance are normalized by
![]() $\hat{\unicode[STIX]{x1D70C}}_{o}$
,
$\hat{\unicode[STIX]{x1D70C}}_{o}$
,
![]() $\unicode[STIX]{x1D6FE}\hat{T}_{o}$
, and
$\unicode[STIX]{x1D6FE}\hat{T}_{o}$
, and
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, respectively.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, respectively.

Figure 9. Grid topology (a) and corresponding density field (b) for a portion of the CLEM-LES simulation shown in figure 8. Also shown are the locations of the various grid levels (G2–G6). Note that the base grid G1 is always refined to at least grid level G2, everywhere.
To gain insight on how these cells evolve as the wave propagates through the channel, a numerical soot foil was obtained by integrating the local vorticity
![]() $\unicode[STIX]{x1D6FA}(x,y)$
throughout the duration of the simulation, locally at each spatial location, given by
$\unicode[STIX]{x1D6FA}(x,y)$
throughout the duration of the simulation, locally at each spatial location, given by
Figure 10 shows a portion of the numerical soot foil obtained for a later portion of the channel, for
![]() $700<x<800$
. This particular portion is shown because it highlights, in detail, the complex nature of the cellular pattern that emerges. In figure 10, the streak marks follow paths of large vorticity associated with triple-point trajectories. Clearly, there are several different cell sizes observed. These range from as large as the domain height,
$700<x<800$
. This particular portion is shown because it highlights, in detail, the complex nature of the cellular pattern that emerges. In figure 10, the streak marks follow paths of large vorticity associated with triple-point trajectories. Clearly, there are several different cell sizes observed. These range from as large as the domain height,
![]() $H$
, to cells as small as
$H$
, to cells as small as
![]() ${\sim}H/4$
. Furthermore, there does not appear to be any coherent pattern to the appearance of smaller cells in the presence of larger, more prominent, ones. Also, the triple-point paths, given by the streaks on the image, do not follow perfectly straight lines, or at consistent angles. Sometimes these triple-point paths curve more than others in a very irregular manner. Thus, it is of interest to determine how turbulence intensity, a function of
${\sim}H/4$
. Furthermore, there does not appear to be any coherent pattern to the appearance of smaller cells in the presence of larger, more prominent, ones. Also, the triple-point paths, given by the streaks on the image, do not follow perfectly straight lines, or at consistent angles. Sometimes these triple-point paths curve more than others in a very irregular manner. Thus, it is of interest to determine how turbulence intensity, a function of
![]() $C_{\unicode[STIX]{x1D705}}$
, might affect the qualitative features discussed above. Of particular interest is the distance it takes for pockets of unreacted gas to burn up, i.e. the reaction zone thickness. Also, it is of interest to determine how turbulence affects the overall flow field at the wave front, the formation and burnout of the unreacted pockets of gas, and also the cell patterns that emerge. Capturing such features, numerically, will serve to validate the strategy with experiments in § 2, and also those of Kiyanda & Higgins (Reference Kiyanda and Higgins2013).
$C_{\unicode[STIX]{x1D705}}$
, might affect the qualitative features discussed above. Of particular interest is the distance it takes for pockets of unreacted gas to burn up, i.e. the reaction zone thickness. Also, it is of interest to determine how turbulence affects the overall flow field at the wave front, the formation and burnout of the unreacted pockets of gas, and also the cell patterns that emerge. Capturing such features, numerically, will serve to validate the strategy with experiments in § 2, and also those of Kiyanda & Higgins (Reference Kiyanda and Higgins2013).
Finally, figure 11 shows the
![]() $x$
velocity of the detonation wave as a function of time, measured along the bottom wall at
$x$
velocity of the detonation wave as a function of time, measured along the bottom wall at
![]() $y=0$
. Initially, the wave is clearly overdriven above the theoretical CJ value. However, after
$y=0$
. Initially, the wave is clearly overdriven above the theoretical CJ value. However, after
![]() $t>55$
, sufficient time has passed to allow the detonation wave to decelerate from the overdriven state and reach velocities closer to the CJ speed. In fact, beyond
$t>55$
, sufficient time has passed to allow the detonation wave to decelerate from the overdriven state and reach velocities closer to the CJ speed. In fact, beyond
![]() $t>55$
, the averaged speed of the wave was
$t>55$
, the averaged speed of the wave was
![]() $D=6.35$
(
$D=6.35$
(
![]() $2260~\text{m}~\text{s}^{-1}$
), within 1 % error of the CJ value of
$2260~\text{m}~\text{s}^{-1}$
), within 1 % error of the CJ value of
![]() $D_{CJ}=6.30$
(
$D_{CJ}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
). Clearly, in figure 11, the velocity peaks and valleys also appear very irregular in nature, with no coherent pattern. These velocity measurements correspond to cells that form along the wall. In fact, the maxima correspond to the start of each cell cycle observed along the bottom wall, where triple-point collisions occur. The minima represent the end of the cell cycle where the velocity has decayed below the CJ value. Although the cell cycles appear random, much like the cells shown in the numerical soot foil of figure 10, it is of particular interest to determine how the wave velocities are statistically distributed on the wave front, given the turbulence intensity (
$2240~\text{m}~\text{s}^{-1}$
). Clearly, in figure 11, the velocity peaks and valleys also appear very irregular in nature, with no coherent pattern. These velocity measurements correspond to cells that form along the wall. In fact, the maxima correspond to the start of each cell cycle observed along the bottom wall, where triple-point collisions occur. The minima represent the end of the cell cycle where the velocity has decayed below the CJ value. Although the cell cycles appear random, much like the cells shown in the numerical soot foil of figure 10, it is of particular interest to determine how the wave velocities are statistically distributed on the wave front, given the turbulence intensity (
![]() $C_{\unicode[STIX]{x1D705}}$
). Furthermore, it is of prime importance to compare such a velocity distribution with available experimental data obtained in this study and also in Kiyanda & Higgins (Reference Kiyanda and Higgins2013), for the purpose of CLEM-LES validation.
$C_{\unicode[STIX]{x1D705}}$
). Furthermore, it is of prime importance to compare such a velocity distribution with available experimental data obtained in this study and also in Kiyanda & Higgins (Reference Kiyanda and Higgins2013), for the purpose of CLEM-LES validation.

Figure 10. Portion of the numerical soot foil obtained for the CLEM-LES with
![]() $C_{\unicode[STIX]{x1D705}}=1.5$
. The streak marks show the paths of high vorticity associated with triple-point trajectories. Note that distances are normalized by
$C_{\unicode[STIX]{x1D705}}=1.5$
. The streak marks show the paths of high vorticity associated with triple-point trajectories. Note that distances are normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.

Figure 11. The
![]() $x$
velocity of detonation for
$x$
velocity of detonation for
![]() $C_{\unicode[STIX]{x1D705}}=1.5$
and
$C_{\unicode[STIX]{x1D705}}=1.5$
and
![]() $b=1/32$
as a function of time, measured along the bottom wall at
$b=1/32$
as a function of time, measured along the bottom wall at
![]() $y=0$
. Note that
$y=0$
. Note that
![]() $D$
and
$D$
and
![]() $t$
are normalized by
$t$
are normalized by
![]() $\hat{D}_{CJ}$
and (
$\hat{D}_{CJ}$
and (
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}/{\hat{c}}_{o}$
), respectively.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}/{\hat{c}}_{o}$
), respectively.

Figure 12. Numerical soot foils for
![]() $C_{\unicode[STIX]{x1D705}}=1.5$
at various resolutions,
$C_{\unicode[STIX]{x1D705}}=1.5$
at various resolutions,
![]() $b$
(all with
$b$
(all with
![]() $N=16$
elements per LES cell). Note that distance
$N=16$
elements per LES cell). Note that distance
![]() $x$
is normalized by
$x$
is normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
4.2 Grid convergence study
Prior to investigating the effect of turbulent mixing rates on the detonation propagation characteristics, it is important to first determine a sufficient resolution which resolves both the reaction rate and qualitative features of the cellular structure. For this resolution study, the domain height is kept constant at
![]() $H=20$
. Also,
$H=20$
. Also,
![]() $C_{\unicode[STIX]{x1D705}}=1.5$
is specified for the CLEM-LES simulations, and the number of subgrid elements within each LES cell is held constant at
$C_{\unicode[STIX]{x1D705}}=1.5$
is specified for the CLEM-LES simulations, and the number of subgrid elements within each LES cell is held constant at
![]() $N=16$
. Only the supergrid resolution,
$N=16$
. Only the supergrid resolution,
![]() $b$
, is varied. This value for
$b$
, is varied. This value for
![]() $N$
was found, in previous work (Maxwell et al.
Reference Maxwell, Falle, Sharpe and Radulescu2015), to be sufficient at capturing stirring events and eddy–flame interactions on the subgrid, while optimizing computational efficiency associated with the method. Also, it is worth noting here that at
$N$
was found, in previous work (Maxwell et al.
Reference Maxwell, Falle, Sharpe and Radulescu2015), to be sufficient at capturing stirring events and eddy–flame interactions on the subgrid, while optimizing computational efficiency associated with the method. Also, it is worth noting here that at
![]() $b=1/32$
resolution with
$b=1/32$
resolution with
![]() $N=16$
, the laminar flame speed is fully resolved in one dimension; see Maxwell et al. (Reference Maxwell, Falle, Sharpe and Radulescu2015) for details.
$N=16$
, the laminar flame speed is fully resolved in one dimension; see Maxwell et al. (Reference Maxwell, Falle, Sharpe and Radulescu2015) for details.
First, to assess the qualitative behaviour of resolution on the inherent cellular instability of the wave front, numerical soot foils were obtained for each simulation and compared in figure 12. For all resolutions, the simulations are run up to
![]() $t=127.5$
. As observed in figure 12, the lowest resolution,
$t=127.5$
. As observed in figure 12, the lowest resolution,
![]() $b=1/4$
, produces only large cells whose size appears to be mode-locked by the channel height. Furthermore, the cells at this resolution exhibit a very regular self-repeating pattern. As the resolution is increased to
$b=1/4$
, produces only large cells whose size appears to be mode-locked by the channel height. Furthermore, the cells at this resolution exhibit a very regular self-repeating pattern. As the resolution is increased to
![]() $b=1/8$
, the detonation wave continues to exhibit large cells of the order of the domain height. However, the cells at this resolution appear to be slightly irregular in size and shape. Also, the appearance of smaller cells within the larger cell structure is observed starting around
$b=1/8$
, the detonation wave continues to exhibit large cells of the order of the domain height. However, the cells at this resolution appear to be slightly irregular in size and shape. Also, the appearance of smaller cells within the larger cell structure is observed starting around
![]() $x\sim 550$
. For
$x\sim 550$
. For
![]() $b=1/16$
, the cell sizes appear much smaller and even more irregular. Also, there appears to be much more variation in cell sizes observed throughout the channel. For example, at
$b=1/16$
, the cell sizes appear much smaller and even more irregular. Also, there appears to be much more variation in cell sizes observed throughout the channel. For example, at
![]() $x\sim 200$
there are approximately four cells spanning the domain height. At
$x\sim 200$
there are approximately four cells spanning the domain height. At
![]() $x\sim 400$
, the cells are intermittently much larger, with approximately one cell spanning the domain height. At
$x\sim 400$
, the cells are intermittently much larger, with approximately one cell spanning the domain height. At
![]() $x\sim 500$
there are two cells across the domain height. At
$x\sim 500$
there are two cells across the domain height. At
![]() $x\sim 700$
, the cell size increases to one cell across the domain height. Then, at
$x\sim 700$
, the cell size increases to one cell across the domain height. Then, at
![]() $x\sim 800$
there are once again approximately two cells spanning the domain height. For the higher resolutions,
$x\sim 800$
there are once again approximately two cells spanning the domain height. For the higher resolutions,
![]() $b=1/32$
and
$b=1/32$
and
![]() $b=1/64$
, the same stochastic cell size behaviour is observed as the
$b=1/64$
, the same stochastic cell size behaviour is observed as the
![]() $b=1/8$
case. For these two higher-resolution cases, however, the pattern appears even more irregular than the
$b=1/8$
case. For these two higher-resolution cases, however, the pattern appears even more irregular than the
![]() $b=1/8$
case. In fact, the
$b=1/8$
case. In fact, the
![]() $b=1/32$
and
$b=1/32$
and
![]() $b=1/64$
cases are qualitatively similar to each other in terms of observed cell sizes, pattern behaviour and irregularity.
$b=1/64$
cases are qualitatively similar to each other in terms of observed cell sizes, pattern behaviour and irregularity.
To effectively quantify the average rate at which reactant was consumed behind the leading shock wave, at any given instant in time, the average distance for the reactant to be consumed behind the leading shock wave was measured. This was indicative of the time it takes for the reactant burn up behind the leading shock. To measure this average reaction zone thickness, a Favre averaging technique in spatial slices on the supergrid,
![]() $\text{d}x$
, was applied to give a mass-weighted average reactant and density profile along the channel length for any given time. This procedure was previously applied in Radulescu et al. (Reference Radulescu, Sharpe, Law and Lee2007). Formally, the Favre-averaged reactant profile is given by the expression
$\text{d}x$
, was applied to give a mass-weighted average reactant and density profile along the channel length for any given time. This procedure was previously applied in Radulescu et al. (Reference Radulescu, Sharpe, Law and Lee2007). Formally, the Favre-averaged reactant profile is given by the expression
 $$\begin{eqnarray}{\tilde{Y}}(x,t)=\frac{\displaystyle \int _{y=0}^{H}\bar{\unicode[STIX]{x1D70C}}(x,y,t){\tilde{Y}}(x,y,t)\,\text{d}y}{\displaystyle \int _{y=0}^{H}\bar{\unicode[STIX]{x1D70C}}(x,y,t)\,\text{d}y},\end{eqnarray}$$
$$\begin{eqnarray}{\tilde{Y}}(x,t)=\frac{\displaystyle \int _{y=0}^{H}\bar{\unicode[STIX]{x1D70C}}(x,y,t){\tilde{Y}}(x,y,t)\,\text{d}y}{\displaystyle \int _{y=0}^{H}\bar{\unicode[STIX]{x1D70C}}(x,y,t)\,\text{d}y},\end{eqnarray}$$
where the average density profile, in
![]() $x$
, is found by
$x$
, is found by
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}(x,t)=\frac{\displaystyle \int _{y=0}^{H}\bar{\unicode[STIX]{x1D70C}}(x,y,t)\,\text{d}y}{H}.\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}(x,t)=\frac{\displaystyle \int _{y=0}^{H}\bar{\unicode[STIX]{x1D70C}}(x,y,t)\,\text{d}y}{H}.\end{eqnarray}$$
Finally, the Favre-averaged mass fractions are ensemble-averaged for
![]() $k=50$
random instants in time. Thus,
$k=50$
random instants in time. Thus,
 $$\begin{eqnarray}{\tilde{Y}}(x-x_{s})=\frac{\displaystyle \mathop{\sum }_{i=0}^{k}{\tilde{Y}}(x-x_{s},t_{i})}{k}.\end{eqnarray}$$
$$\begin{eqnarray}{\tilde{Y}}(x-x_{s})=\frac{\displaystyle \mathop{\sum }_{i=0}^{k}{\tilde{Y}}(x-x_{s},t_{i})}{k}.\end{eqnarray}$$
Here
![]() $x_{s}$
was the location of the shock wave determined by the location where the right-most maximum gradients in the spatially averaged density occur. Also, the sample slices for which averaging is done is taken as the minimum supergrid resolution size,
$x_{s}$
was the location of the shock wave determined by the location where the right-most maximum gradients in the spatially averaged density occur. Also, the sample slices for which averaging is done is taken as the minimum supergrid resolution size,
![]() $\text{d}x=b$
. Finally, it should be noted that this ensemble averaging only considers profiles when
$\text{d}x=b$
. Finally, it should be noted that this ensemble averaging only considers profiles when
![]() $t>40$
. This was done to allow sufficient time for the detonation wave to decelerate from the overdriven state and reach its self-sustained equilibrium structure.
$t>40$
. This was done to allow sufficient time for the detonation wave to decelerate from the overdriven state and reach its self-sustained equilibrium structure.

Figure 13. Effect of resolution on average reactant profiles for (a) the CLEM-LES compared to (b) Euler methods. Note that distances
![]() $x$
and
$x$
and
![]() $x_{s}$
are normalized by
$x_{s}$
are normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.

Figure 14. Effect of resolution on the mean reaction zone thickness (
![]() $\unicode[STIX]{x1D6E5}_{R}$
) for CLEM-LES compared to Euler methods. The error bars indicate the standard deviation in
$\unicode[STIX]{x1D6E5}_{R}$
) for CLEM-LES compared to Euler methods. The error bars indicate the standard deviation in
![]() $\unicode[STIX]{x1D6E5}_{R}$
for each simulation. Note that
$\unicode[STIX]{x1D6E5}_{R}$
for each simulation. Note that
![]() $\unicode[STIX]{x1D6E5}_{R}$
is normalized by
$\unicode[STIX]{x1D6E5}_{R}$
is normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
In figure 13(a), the average profiles obtained for
![]() ${\tilde{Y}}(x-x_{s})$
are presented for the CLEM-LES at various resolutions. For the CLEM-LES, it can clearly be seen that the average rate of depletion of
${\tilde{Y}}(x-x_{s})$
are presented for the CLEM-LES at various resolutions. For the CLEM-LES, it can clearly be seen that the average rate of depletion of
![]() ${\tilde{Y}}(x-x_{s})$
behind the shock wave does not vary significantly across the range of resolutions tested. In fact, all of the simulations appear to consume 90 % of the reactant within the same average distance,
${\tilde{Y}}(x-x_{s})$
behind the shock wave does not vary significantly across the range of resolutions tested. In fact, all of the simulations appear to consume 90 % of the reactant within the same average distance,
![]() ${\sim}5\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
. Only the highest resolutions,
${\sim}5\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
. Only the highest resolutions,
![]() $b=1/32$
and
$b=1/32$
and
![]() $b=1/64$
, develop fluctuations in reactant mass fractions when
$b=1/64$
, develop fluctuations in reactant mass fractions when
![]() ${\tilde{Y}}(x-x_{s})<10\,\%$
, and thus have a slightly lengthened structure compared to lower-resolution cases. These fluctuations are believed to arise due to unresolved sampling of high-frequency statistics sufficiently far from the leading shock wave. For the low-resolution cases, even though the same reaction zone thickness is captured, these high-frequency instabilities are effectively filtered out. This suggests that the reaction rate, in general, is not very sensitive to resolution. However, the irregular propagation behaviour and fine-scale qualitative observations are sensitive to resolution. To compare the performance of the CLEM-LES with the traditional use of Euler simulations, figure 13(b) shows the average reactant profiles for
${\tilde{Y}}(x-x_{s})<10\,\%$
, and thus have a slightly lengthened structure compared to lower-resolution cases. These fluctuations are believed to arise due to unresolved sampling of high-frequency statistics sufficiently far from the leading shock wave. For the low-resolution cases, even though the same reaction zone thickness is captured, these high-frequency instabilities are effectively filtered out. This suggests that the reaction rate, in general, is not very sensitive to resolution. However, the irregular propagation behaviour and fine-scale qualitative observations are sensitive to resolution. To compare the performance of the CLEM-LES with the traditional use of Euler simulations, figure 13(b) shows the average reactant profiles for
![]() ${\tilde{Y}}(x-x_{s})$
using the Euler method across the range of resolutions from
${\tilde{Y}}(x-x_{s})$
using the Euler method across the range of resolutions from
![]() $b=1/4$
to
$b=1/4$
to
![]() $b=1/128$
. It should be noted here that the Euler simulations adopt the same second-order-accurate exact Godunov solver that was applied to the advection terms on the CLEM-LES supergrid (Falle Reference Falle1991). Clearly, the Euler method does not provide any convergence of the solution with increased resolution. This can be observed by the lengthening of the structure, or distance it takes for reactant to become consumed, as the resolution increases. To quantify the reaction zone thickness of the structure of each simulation, the thickness,
$b=1/128$
. It should be noted here that the Euler simulations adopt the same second-order-accurate exact Godunov solver that was applied to the advection terms on the CLEM-LES supergrid (Falle Reference Falle1991). Clearly, the Euler method does not provide any convergence of the solution with increased resolution. This can be observed by the lengthening of the structure, or distance it takes for reactant to become consumed, as the resolution increases. To quantify the reaction zone thickness of the structure of each simulation, the thickness,
![]() $\unicode[STIX]{x1D6E5}_{R}$
, is arbitrarily taken as the distance from the shock location, at
$\unicode[STIX]{x1D6E5}_{R}$
, is arbitrarily taken as the distance from the shock location, at
![]() $x=x_{s}$
, to the position where
$x=x_{s}$
, to the position where
![]() ${\tilde{Y}}(x-x_{s})<2\,\%$
. Figure 14 shows that, across the range of resolutions, the average reaction zone thickness for the CLEM-LES is not very sensitive to resolution, whereas the Euler method clearly shows an increase in average thickness as resolution increases. Figure 14 also shows the range of reaction zone thickness observed throughout the random sampling process. The error bars thus serve as the variation in thickness for the 50 random samples used in the ensemble averaging process of each simulation. Clearly, the Euler method yields an increasing variation in thickness as the resolution is increased. Also, at high resolutions,
${\tilde{Y}}(x-x_{s})<2\,\%$
. Figure 14 shows that, across the range of resolutions, the average reaction zone thickness for the CLEM-LES is not very sensitive to resolution, whereas the Euler method clearly shows an increase in average thickness as resolution increases. Figure 14 also shows the range of reaction zone thickness observed throughout the random sampling process. The error bars thus serve as the variation in thickness for the 50 random samples used in the ensemble averaging process of each simulation. Clearly, the Euler method yields an increasing variation in thickness as the resolution is increased. Also, at high resolutions,
![]() $b\geqslant 1/64$
, the Euler method yields a larger, and more stochastic, range in thickness compared to the CLEM-LES. The CLEM-LES, on the other hand, appears to converge to a statistically consistent range of thickness observed with each random sample. This can be seen for
$b\geqslant 1/64$
, the Euler method yields a larger, and more stochastic, range in thickness compared to the CLEM-LES. The CLEM-LES, on the other hand, appears to converge to a statistically consistent range of thickness observed with each random sample. This can be seen for
![]() $b=1/32$
and
$b=1/32$
and
![]() $b=1/64$
where the reaction zone thickness is found to vary stochastically between
$b=1/64$
where the reaction zone thickness is found to vary stochastically between
![]() $\unicode[STIX]{x1D6E5}_{R}=3-16\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
for both resolutions. Furthermore, the average thickness for the CLEM-LES remains consistent around
$\unicode[STIX]{x1D6E5}_{R}=3-16\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
for both resolutions. Furthermore, the average thickness for the CLEM-LES remains consistent around
![]() $\unicode[STIX]{x1D6E5}_{R}=6-9\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
for all resolutions.
$\unicode[STIX]{x1D6E5}_{R}=6-9\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
for all resolutions.
To summarize the findings in this section, a resolution of
![]() $b=1/32$
has been demonstrated to sufficiently resolve and capture the structure size, high-frequency instabilities exhibited through cell patterns and overall propagation behaviour. Thus,
$b=1/32$
has been demonstrated to sufficiently resolve and capture the structure size, high-frequency instabilities exhibited through cell patterns and overall propagation behaviour. Thus,
![]() $b=1/32$
is the resolution used throughout the remainder of the paper.
$b=1/32$
is the resolution used throughout the remainder of the paper.
4.3 Effect of the Kolmogorov parameter (
 $C_{k}$
)
$C_{k}$
)
In order to investigate the role of turbulent mixing rates on the detonation front cellular patterns, burning rates and irregularity, the parameter
![]() $C_{\unicode[STIX]{x1D705}}$
has been varied. This was done using a maximum supergrid resolution of
$C_{\unicode[STIX]{x1D705}}$
has been varied. This was done using a maximum supergrid resolution of
![]() $b=1/32$
with
$b=1/32$
with
![]() $N=16$
subgrid elements within each supergrid cell. As before, to achieve this resolution on the supergrid, the base grid (G1) has a resolution of
$N=16$
subgrid elements within each supergrid cell. As before, to achieve this resolution on the supergrid, the base grid (G1) has a resolution of
![]() $b_{G1}=1$
with five additional levels of refinement. It should also be noted that a formal grid resolution study for each
$b_{G1}=1$
with five additional levels of refinement. It should also be noted that a formal grid resolution study for each
![]() $C_{\unicode[STIX]{x1D705}}$
was not conducted here. In the previous section, this particular resolution and AMR configuration were found to be adequate to resolve the qualitative features associated with cell sizes and patterns and irregularity. Furthermore, this resolution was found to give converged burning rates behind the shock, which was measured quantitatively by considering the size of the observed reaction zone thickness (
$C_{\unicode[STIX]{x1D705}}$
was not conducted here. In the previous section, this particular resolution and AMR configuration were found to be adequate to resolve the qualitative features associated with cell sizes and patterns and irregularity. Furthermore, this resolution was found to give converged burning rates behind the shock, which was measured quantitatively by considering the size of the observed reaction zone thickness (
![]() $\unicode[STIX]{x1D6E5}_{R}$
). Also, the one-dimensional laminar flame speed is resolved at this resolution. As discussed previously, in § 3.2, the turbulent viscosity and dissipation rates,
$\unicode[STIX]{x1D6E5}_{R}$
). Also, the one-dimensional laminar flame speed is resolved at this resolution. As discussed previously, in § 3.2, the turbulent viscosity and dissipation rates,
![]() $\unicode[STIX]{x1D708}_{t}$
and
$\unicode[STIX]{x1D708}_{t}$
and
![]() $\unicode[STIX]{x1D716}$
, are both functions of
$\unicode[STIX]{x1D716}$
, are both functions of
![]() $C_{\unicode[STIX]{x1D705}}$
, which are consequently functions of
$C_{\unicode[STIX]{x1D705}}$
, which are consequently functions of
![]() $k^{sgs}$
. Thus turbulent mixing rates, and hence combustion rates, are expected to be influenced by changes in
$k^{sgs}$
. Thus turbulent mixing rates, and hence combustion rates, are expected to be influenced by changes in
![]() $C_{\unicode[STIX]{x1D705}}$
. For the numerical experiment in this section,
$C_{\unicode[STIX]{x1D705}}$
. For the numerical experiment in this section,
![]() $C_{\unicode[STIX]{x1D705}}$
has been varied from 1.2 to 10.0. As was done in the previous section, the qualitative features are compared using numerically obtained soot foil images. The domain height for all simulations in this section have once again been kept constant at
$C_{\unicode[STIX]{x1D705}}$
has been varied from 1.2 to 10.0. As was done in the previous section, the qualitative features are compared using numerically obtained soot foil images. The domain height for all simulations in this section have once again been kept constant at
![]() $H=20$
. Also, the average reaction zone thickness has been collected for each simulation.
$H=20$
. Also, the average reaction zone thickness has been collected for each simulation.
First, numerically obtained soot foils are shown in figure 15 for the range of
![]() $C_{\unicode[STIX]{x1D705}}$
values investigated (1.2–10). Also, the CLEM-LES soot foil images are compared against the Euler simulation, which also has a resolution of 32 cells per half reaction length. Clearly the Euler simulation exhibits much smaller cells compared to all of the CLEM-LES soot foil images. For the CLEM-LES at
$C_{\unicode[STIX]{x1D705}}$
values investigated (1.2–10). Also, the CLEM-LES soot foil images are compared against the Euler simulation, which also has a resolution of 32 cells per half reaction length. Clearly the Euler simulation exhibits much smaller cells compared to all of the CLEM-LES soot foil images. For the CLEM-LES at
![]() $C_{\unicode[STIX]{x1D705}}=1.2$
, in figure 15, the cells are still fairly small compared to the channel height, but there is some irregularity to the pattern observed. As
$C_{\unicode[STIX]{x1D705}}=1.2$
, in figure 15, the cells are still fairly small compared to the channel height, but there is some irregularity to the pattern observed. As
![]() $C_{\unicode[STIX]{x1D705}}$
is increased, the observed cell sizes also increase. For
$C_{\unicode[STIX]{x1D705}}$
is increased, the observed cell sizes also increase. For
![]() $C_{\unicode[STIX]{x1D705}}=3.0{-}4.0$
it is observed that the range of cell sizes spans from three cells to one cell per channel height, intermittently, throughout the simulations. As
$C_{\unicode[STIX]{x1D705}}=3.0{-}4.0$
it is observed that the range of cell sizes spans from three cells to one cell per channel height, intermittently, throughout the simulations. As
![]() $C_{\unicode[STIX]{x1D705}}$
is increased beyond 6.7, the cells become even larger, with an observed range of two cells to half a cell per channel height.
$C_{\unicode[STIX]{x1D705}}$
is increased beyond 6.7, the cells become even larger, with an observed range of two cells to half a cell per channel height.

Figure 15. Numerical soot foils for various
![]() $C_{\unicode[STIX]{x1D705}}$
values and an Euler simulation (all with resolution of
$C_{\unicode[STIX]{x1D705}}$
values and an Euler simulation (all with resolution of
![]() $b=1/32$
and, for the LES, a further
$b=1/32$
and, for the LES, a further
![]() $N=16$
elements per supergrid cell). Note that distance
$N=16$
elements per supergrid cell). Note that distance
![]() $x$
is normalized by
$x$
is normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
Next, in figure 16, the average reactant profiles are compared for the range of
![]() $C_{\unicode[STIX]{x1D705}}$
values using the procedure described in the previous section. Also, the simulations are compared to the Euler simulation with the same resolution as the CLEM-LES supergrid. Clearly, as
$C_{\unicode[STIX]{x1D705}}$
values using the procedure described in the previous section. Also, the simulations are compared to the Euler simulation with the same resolution as the CLEM-LES supergrid. Clearly, as
![]() $C_{\unicode[STIX]{x1D705}}$
increases, not only does the cell size increase, but the average reaction zone thickness of the detonation wave also increases. This observation on reaction zone thickness is made by considering the distance it takes for
$C_{\unicode[STIX]{x1D705}}$
increases, not only does the cell size increase, but the average reaction zone thickness of the detonation wave also increases. This observation on reaction zone thickness is made by considering the distance it takes for
![]() ${\tilde{Y}}(x-x_{s})\rightarrow 0$
. Furthermore, this relation between the cell size and the reaction zone thickness is consistent with earlier correlations, as reported by Lee (Reference Lee1984). In this sense, as
${\tilde{Y}}(x-x_{s})\rightarrow 0$
. Furthermore, this relation between the cell size and the reaction zone thickness is consistent with earlier correlations, as reported by Lee (Reference Lee1984). In this sense, as
![]() $C_{\unicode[STIX]{x1D705}}$
increases,
$C_{\unicode[STIX]{x1D705}}$
increases,
![]() $\unicode[STIX]{x1D6E5}_{R}$
increases, which consequently exhibits larger cell sizes. On the other hand, the Euler method at the same resolution, which is subject to a large amount of numerical diffusion, burns fuel at a much quicker rate than all of the CLEM-LES simulations. It is noted that, although the Euler simulations and CLEM-LES have the same numerical diffusion on the supergrid, where the pressure evolution is solved for both strategies, the CLEM-LES has much better closure of the reaction rate since the higher-resolution subgrid itself has much less numerical diffusion that contributes to mixing and chemical reaction. Finally, owing to the sensitivity of the reaction zone thickness (
$\unicode[STIX]{x1D6E5}_{R}$
increases, which consequently exhibits larger cell sizes. On the other hand, the Euler method at the same resolution, which is subject to a large amount of numerical diffusion, burns fuel at a much quicker rate than all of the CLEM-LES simulations. It is noted that, although the Euler simulations and CLEM-LES have the same numerical diffusion on the supergrid, where the pressure evolution is solved for both strategies, the CLEM-LES has much better closure of the reaction rate since the higher-resolution subgrid itself has much less numerical diffusion that contributes to mixing and chemical reaction. Finally, owing to the sensitivity of the reaction zone thickness (
![]() $\unicode[STIX]{x1D6E5}_{R}$
), and consequently the cell size, to turbulent fluctuations, this permits us to fit the Kolmogorov parameter (
$\unicode[STIX]{x1D6E5}_{R}$
), and consequently the cell size, to turbulent fluctuations, this permits us to fit the Kolmogorov parameter (
![]() $C_{\unicode[STIX]{x1D705}}$
) against experimental observations.
$C_{\unicode[STIX]{x1D705}}$
) against experimental observations.

Figure 16. Effect of turbulent intensity (through
![]() $C_{\unicode[STIX]{x1D705}}$
) on average reactant profiles for the CLEM-LES (all with resolution
$C_{\unicode[STIX]{x1D705}}$
) on average reactant profiles for the CLEM-LES (all with resolution
![]() $b=1/32$
and
$b=1/32$
and
![]() $N=16$
elements per LES cell). Also shown is the average reactant profile obtained from the Euler method at
$N=16$
elements per LES cell). Also shown is the average reactant profile obtained from the Euler method at
![]() $b=1/32$
resolution. Note that distances
$b=1/32$
resolution. Note that distances
![]() $x$
and
$x$
and
![]() $x_{s}$
are normalized by
$x_{s}$
are normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.

Figure 17. (a) Numerical density evolution for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs (this study) of a detonation triple-point collision process. The time between images is
$C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs (this study) of a detonation triple-point collision process. The time between images is
![]() $\unicode[STIX]{x0394}t=0.425$
(
$\unicode[STIX]{x0394}t=0.425$
(
![]() $11.53~\unicode[STIX]{x03BC}\text{s}$
). The remaining sequence of images is continued in figure 18.
$11.53~\unicode[STIX]{x03BC}\text{s}$
). The remaining sequence of images is continued in figure 18.

Figure 18. Continuation of figure 17. (a) Numerical density evolution for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs of a detonation triple-point collision process.
$C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs of a detonation triple-point collision process.

Figure 19. Comparison of experiments and the CLEM-LES with
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
, both showing an instant where stochastic behaviour is observed such that a different cell pattern is observed compared to figure 17.
$C_{\unicode[STIX]{x1D705}}=6.7$
, both showing an instant where stochastic behaviour is observed such that a different cell pattern is observed compared to figure 17.
5 Discussion
5.1 Qualitative comparison of the flow evolution with experiments
A visual comparison of a flow field, obtained through resolved LES and the corresponding experiment of § 2, is shown in figures 17 and 18 for an instant where a triple-point collision occurs for a detonation whose cell size is comparable to the channel height. For the LES, the density evolution is shown for various instants of the collision process for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
. This value of
$C_{\unicode[STIX]{x1D705}}=6.7$
. This value of
![]() $C_{\unicode[STIX]{x1D705}}$
was found to produce cell sizes and overall qualitative behaviour comparable to experimental observation. Here, the channel height is kept at
$C_{\unicode[STIX]{x1D705}}$
was found to produce cell sizes and overall qualitative behaviour comparable to experimental observation. Here, the channel height is kept at
![]() $H=20$
. For the experiment, schlieren images of each corresponding instant are obtained from high-speed photography and are also shown in figures 17 and 18. For comparison, many features are noted (1–7). In figure 17, feature 1 is a Mach shock with a turbulent reaction zone that follows closely. In both the simulation and the experiment, the reaction zone is slightly decoupled from the shock owing to local unsteadiness of the wave front. This can be seen by the thickening of the shocked unburned gas region as time evolves. In the LES, however, this wave appears to be more irregular, containing what appears to be a smaller and less pronounced cell structure (cells within cells). It should be noted that experimental observations, of § 2, report a very stochastic nature of the propagating wave. In this sense, random bifurcations on wave fronts and changes in cell patterns are expected. In some cases much smaller cells are observed experimentally and numerically for the same quiescent conditions and numerical parameters; see figure 19. Feature 2 in figure 17 is a completely decoupled incident shock reaction zone, as can be seen by the large region of dense unburned gas. As the two triple points approach each other, transverse shock waves compress this gas further. At the focal point of the collision, owing to the increased pressure and temperature, the unburned pocket (2) ignites very rapidly. This ‘explosion’, denoted by feature 3, drives transverse shock waves and a strong Mach shock forward coupled with very rapid burning. Feature 4 is a pocket of unburned gas that is not ignited by compression associated with the original Mach shocks (feature 1). Instead, these pockets mix and burn, on their surfaces, along turbulent shear layers. Owing to shock compression associated with the passage of transverse shock waves, these shear layers experience increased burning rates through turbulent mixing of the burned and unburned gases via Richtmyer–Meshkov instability. These transverse shocks, labelled as feature 5 in figure 18, originate from feature 3. Feature 6 in figure 18 is a new pocket of unburned gas that forms along slip lines associated with the collision process. In fact, the formation of such pockets, in this manner, is typical of irregular detonation propagation (Subbotin Reference Subbotin1975; Oran et al.
Reference Oran, Young, Boris and Picone1982; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005, Reference Radulescu, Sharpe, Law and Lee2007; Kiyanda & Higgins Reference Kiyanda and Higgins2013). Finally, feature 7 in figure 18 is a bifurcation observed on the Mach shock of feature 3, owing to the unstable nature of methane–air detonations. This bifurcation also occurs in the experiment but is less pronounced. Although features 1–7 are captured by the LES, a key difference is observed in the burning rate behind the Mach shock originating from feature 3. In the simulation, the size of this region grows slightly faster compared to experiment, owing to the lower detonation velocity reported in § 2.3.
$H=20$
. For the experiment, schlieren images of each corresponding instant are obtained from high-speed photography and are also shown in figures 17 and 18. For comparison, many features are noted (1–7). In figure 17, feature 1 is a Mach shock with a turbulent reaction zone that follows closely. In both the simulation and the experiment, the reaction zone is slightly decoupled from the shock owing to local unsteadiness of the wave front. This can be seen by the thickening of the shocked unburned gas region as time evolves. In the LES, however, this wave appears to be more irregular, containing what appears to be a smaller and less pronounced cell structure (cells within cells). It should be noted that experimental observations, of § 2, report a very stochastic nature of the propagating wave. In this sense, random bifurcations on wave fronts and changes in cell patterns are expected. In some cases much smaller cells are observed experimentally and numerically for the same quiescent conditions and numerical parameters; see figure 19. Feature 2 in figure 17 is a completely decoupled incident shock reaction zone, as can be seen by the large region of dense unburned gas. As the two triple points approach each other, transverse shock waves compress this gas further. At the focal point of the collision, owing to the increased pressure and temperature, the unburned pocket (2) ignites very rapidly. This ‘explosion’, denoted by feature 3, drives transverse shock waves and a strong Mach shock forward coupled with very rapid burning. Feature 4 is a pocket of unburned gas that is not ignited by compression associated with the original Mach shocks (feature 1). Instead, these pockets mix and burn, on their surfaces, along turbulent shear layers. Owing to shock compression associated with the passage of transverse shock waves, these shear layers experience increased burning rates through turbulent mixing of the burned and unburned gases via Richtmyer–Meshkov instability. These transverse shocks, labelled as feature 5 in figure 18, originate from feature 3. Feature 6 in figure 18 is a new pocket of unburned gas that forms along slip lines associated with the collision process. In fact, the formation of such pockets, in this manner, is typical of irregular detonation propagation (Subbotin Reference Subbotin1975; Oran et al.
Reference Oran, Young, Boris and Picone1982; Austin Reference Austin2003; Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005, Reference Radulescu, Sharpe, Law and Lee2007; Kiyanda & Higgins Reference Kiyanda and Higgins2013). Finally, feature 7 in figure 18 is a bifurcation observed on the Mach shock of feature 3, owing to the unstable nature of methane–air detonations. This bifurcation also occurs in the experiment but is less pronounced. Although features 1–7 are captured by the LES, a key difference is observed in the burning rate behind the Mach shock originating from feature 3. In the simulation, the size of this region grows slightly faster compared to experiment, owing to the lower detonation velocity reported in § 2.3.

Figure 20. (a) Numerical density evolution for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs (Kiyanda & Higgins Reference Kiyanda and Higgins2013) of an irregular detonation propagation in a channel. The time between images is
$C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs (Kiyanda & Higgins Reference Kiyanda and Higgins2013) of an irregular detonation propagation in a channel. The time between images is
![]() $\unicode[STIX]{x0394}t=0.37$
(
$\unicode[STIX]{x0394}t=0.37$
(
![]() $10.0~\unicode[STIX]{x03BC}\text{s}$
). The remaining sequence of images is continued in figure 21.
$10.0~\unicode[STIX]{x03BC}\text{s}$
). The remaining sequence of images is continued in figure 21.

Figure 21. Continuation of figure 20. (a) Numerical density evolution for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs (Kiyanda & Higgins Reference Kiyanda and Higgins2013) of an irregular detonation propagation in a channel. The time between images is
$C_{\unicode[STIX]{x1D705}}=6.7$
and (b) the corresponding experimental schlieren photographs (Kiyanda & Higgins Reference Kiyanda and Higgins2013) of an irregular detonation propagation in a channel. The time between images is
![]() $\unicode[STIX]{x0394}t=0.37$
(
$\unicode[STIX]{x0394}t=0.37$
(
![]() $10.0~\unicode[STIX]{x03BC}\text{s}$
).
$10.0~\unicode[STIX]{x03BC}\text{s}$
).
To further compare the performance of the LES with available experimental data (Kiyanda & Higgins Reference Kiyanda and Higgins2013), the simulation was repeated with a channel height of
![]() $H=10$
. Both the density evolution from the numerical simulation and the corresponding instants obtained in the experiment through schlieren photography are shown in figures 20 and 21. In this case, all model parameters, including
$H=10$
. Both the density evolution from the numerical simulation and the corresponding instants obtained in the experiment through schlieren photography are shown in figures 20 and 21. In this case, all model parameters, including
![]() $C_{\unicode[STIX]{x1D705}}$
, are consistent with the previous simulation, except that the reduced channel height permits only half a cell to form. Thus the cell pattern is effectively influenced by the channel walls, or mode-locked into a cell size which corresponds roughly to twice the channel height. In this case, only a single transverse wave is observed. Again, for qualitative comparison, many features (1–7) are noted in figures 20 and 21. Feature 1 in figure 20 is the incident shock wave and decoupled reaction zone, as observed by the region of very dense, shocked and unburned fuel following the shock. From the top wall of the channel, feature 2 is a Mach stem, which initially results from a transverse wave collision with the wall. As observed in figure 17, this Mach stem travels faster than the incident wave, owing to the wave collision process. Feature 3 in figure 20 is a pocket of dense unburned fuel in the wake of the wave, which is consumed by a surface turbulent flame. Furthermore, consumption rates would be enhanced by Richtmyer–Meshkov instability associated with the transverse shock wave, feature 4. In fact, this region burns out only slightly faster than the observed experimental rate. In the experiment, the pocket burns up completely within seven frames (
$C_{\unicode[STIX]{x1D705}}$
, are consistent with the previous simulation, except that the reduced channel height permits only half a cell to form. Thus the cell pattern is effectively influenced by the channel walls, or mode-locked into a cell size which corresponds roughly to twice the channel height. In this case, only a single transverse wave is observed. Again, for qualitative comparison, many features (1–7) are noted in figures 20 and 21. Feature 1 in figure 20 is the incident shock wave and decoupled reaction zone, as observed by the region of very dense, shocked and unburned fuel following the shock. From the top wall of the channel, feature 2 is a Mach stem, which initially results from a transverse wave collision with the wall. As observed in figure 17, this Mach stem travels faster than the incident wave, owing to the wave collision process. Feature 3 in figure 20 is a pocket of dense unburned fuel in the wake of the wave, which is consumed by a surface turbulent flame. Furthermore, consumption rates would be enhanced by Richtmyer–Meshkov instability associated with the transverse shock wave, feature 4. In fact, this region burns out only slightly faster than the observed experimental rate. In the experiment, the pocket burns up completely within seven frames (
![]() $70~\unicode[STIX]{x03BC}\text{s}$
), while the simulation burns up completely within five frames (
$70~\unicode[STIX]{x03BC}\text{s}$
), while the simulation burns up completely within five frames (
![]() $50~\unicode[STIX]{x03BC}\text{s}$
). Using the method described in § 2.4, the turbulent flame speed of this experiment is found to be
$50~\unicode[STIX]{x03BC}\text{s}$
). Using the method described in § 2.4, the turbulent flame speed of this experiment is found to be
![]() ${\hat{S}}_{t}/{\hat{S}}_{L}\approx 6.6$
(
${\hat{S}}_{t}/{\hat{S}}_{L}\approx 6.6$
(
![]() ${\hat{S}}_{t}\approx 110~\text{m}~\text{s}^{-1}$
). This is comparable to the experimental flame speed found in the current study, § 2, where
${\hat{S}}_{t}\approx 110~\text{m}~\text{s}^{-1}$
). This is comparable to the experimental flame speed found in the current study, § 2, where
![]() ${\hat{S}}_{t}/{\hat{S}}_{L}\approx 7.3$
(
${\hat{S}}_{t}/{\hat{S}}_{L}\approx 7.3$
(
![]() ${\hat{S}}_{t}\approx 120~\text{m}~\text{s}^{-1}$
). Feature 5 in figure 20 is a hotspot that forms behind a bifurcation of the Mach shock and is only clearly visible in the numerical simulation. This bifurcation of the Mach stem near the triple point was also observed in the previous comparison to experiment (figure 17). As the Mach stem, feature 1, continues to evolve, the combustion zone becomes further decoupled from the shock, as observed by an increased thickness of dense unburned fuel behind the shock. Furthermore, a new pocket of dense unburned fuel forms in the wake of the triple-point path, denoted by feature 6 in figure 21. This pocket is initially consumed from its edges via turbulent flame. The passage of the reflected transverse shock wave, feature 7, further contributes to turbulent mixing through Richtmyer–Meshkov instability.
${\hat{S}}_{t}\approx 120~\text{m}~\text{s}^{-1}$
). Feature 5 in figure 20 is a hotspot that forms behind a bifurcation of the Mach shock and is only clearly visible in the numerical simulation. This bifurcation of the Mach stem near the triple point was also observed in the previous comparison to experiment (figure 17). As the Mach stem, feature 1, continues to evolve, the combustion zone becomes further decoupled from the shock, as observed by an increased thickness of dense unburned fuel behind the shock. Furthermore, a new pocket of dense unburned fuel forms in the wake of the triple-point path, denoted by feature 6 in figure 21. This pocket is initially consumed from its edges via turbulent flame. The passage of the reflected transverse shock wave, feature 7, further contributes to turbulent mixing through Richtmyer–Meshkov instability.
Finally, for the
![]() $H=10$
simulation, figure 22 shows how the instantaneous reaction rate obtained numerically compares with the corresponding experimental photographs of Kiyanda & Higgins (Reference Kiyanda and Higgins2013), which recorded the self-luminosity signal. In figure 22, the instantaneous rate of reaction,
$H=10$
simulation, figure 22 shows how the instantaneous reaction rate obtained numerically compares with the corresponding experimental photographs of Kiyanda & Higgins (Reference Kiyanda and Higgins2013), which recorded the self-luminosity signal. In figure 22, the instantaneous rate of reaction,
![]() $\dot{\unicode[STIX]{x1D714}}$
, is superimposed onto two consecutive density evolution plots to show where chemical reactions are occurring, and the intensity. In both the experiment and the simulation, chemical reactions appear to be very intense behind the Mach shock, where short ignition delays are expected due to the overdriven shock. Also, combustion of the unburned gas pockets also becomes intensified with passage of the transverse shock wave. Finally, for the unburned pockets of gas, the chemical reactions occur predominantly on the surfaces, and not uniformly throughout. This suggests that turbulent mixing is the dominant mechanism through which the unburned pockets are consumed. It is therefore of particular interest to quantify the turbulent mixing rates and determine their impact on burnout rates of the pockets. Furthermore, it is of interest to determine the overall impact such burning has on the observed structure and cell pattern of the detonation wave.
$\dot{\unicode[STIX]{x1D714}}$
, is superimposed onto two consecutive density evolution plots to show where chemical reactions are occurring, and the intensity. In both the experiment and the simulation, chemical reactions appear to be very intense behind the Mach shock, where short ignition delays are expected due to the overdriven shock. Also, combustion of the unburned gas pockets also becomes intensified with passage of the transverse shock wave. Finally, for the unburned pockets of gas, the chemical reactions occur predominantly on the surfaces, and not uniformly throughout. This suggests that turbulent mixing is the dominant mechanism through which the unburned pockets are consumed. It is therefore of particular interest to quantify the turbulent mixing rates and determine their impact on burnout rates of the pockets. Furthermore, it is of interest to determine the overall impact such burning has on the observed structure and cell pattern of the detonation wave.

Figure 22. (a) Numerical density evolution with superimposed chemical reaction rate (
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}$
), shown in red, and (b) the corresponding experimental self-luminous images (Kiyanda & Higgins Reference Kiyanda and Higgins2013). The time between images is
$\overline{\dot{\unicode[STIX]{x1D714}}}$
), shown in red, and (b) the corresponding experimental self-luminous images (Kiyanda & Higgins Reference Kiyanda and Higgins2013). The time between images is
![]() $\unicode[STIX]{x0394}t=0.74$
(
$\unicode[STIX]{x0394}t=0.74$
(
![]() $20.0~\unicode[STIX]{x03BC}\text{s}$
).
$20.0~\unicode[STIX]{x03BC}\text{s}$
).
5.2 Quantitative analysis: turbulent flame speeds
For the detonation simulations presented in § 5.1, where
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
for both
$C_{\unicode[STIX]{x1D705}}=6.7$
for both
![]() $H=10$
and
$H=10$
and
![]() $H=20$
, it is of particular interest to estimate and compare the turbulent flame speed at which the pockets of unreacted gas, labelled as feature 4 in figure 17 and as feature 3 in figure 20, burn up. In contrast to the experiments, the turbulent flame speed of the pockets in the simulations is readily available by considering the rates at which reactant mass is consumed within the one-dimensional ‘samples’ of the CLEM subgrid. For the pockets, the local turbulent flame speeds are estimated from
$H=20$
, it is of particular interest to estimate and compare the turbulent flame speed at which the pockets of unreacted gas, labelled as feature 4 in figure 17 and as feature 3 in figure 20, burn up. In contrast to the experiments, the turbulent flame speed of the pockets in the simulations is readily available by considering the rates at which reactant mass is consumed within the one-dimensional ‘samples’ of the CLEM subgrid. For the pockets, the local turbulent flame speeds are estimated from
where
![]() ${\dot{m}}$
is the instantaneous rate of reactant mass consumption,
${\dot{m}}$
is the instantaneous rate of reactant mass consumption,
![]() $\unicode[STIX]{x1D70C}_{u}$
is the density of the upstream unburned reactant, located to within
$\unicode[STIX]{x1D70C}_{u}$
is the density of the upstream unburned reactant, located to within
![]() $0.5\unicode[STIX]{x1D6E5}_{1/2}$
, and
$0.5\unicode[STIX]{x1D6E5}_{1/2}$
, and
![]() $A_{c}$
is the cross-sectional area through which the flame propagates against the unburned reactant within each ‘sample’. In this case,
$A_{c}$
is the cross-sectional area through which the flame propagates against the unburned reactant within each ‘sample’. In this case,
![]() $A_{c}$
is known and constant for all CLEM domains. In this approach, mass is conserved since the burning rate is balanced by the mass flow rate of unburned reactant. Furthermore, this method was previously applied to calculate turbulent flame speeds in a stand-alone one-dimensional CLEM subgrid formulation (Maxwell et al.
Reference Maxwell, Falle, Sharpe and Radulescu2015). Finally, the global turbulent flame speed is obtained by ensemble averaging the flame speeds on the pocket surface in both space and time. Thus
$A_{c}$
is known and constant for all CLEM domains. In this approach, mass is conserved since the burning rate is balanced by the mass flow rate of unburned reactant. Furthermore, this method was previously applied to calculate turbulent flame speeds in a stand-alone one-dimensional CLEM subgrid formulation (Maxwell et al.
Reference Maxwell, Falle, Sharpe and Radulescu2015). Finally, the global turbulent flame speed is obtained by ensemble averaging the flame speeds on the pocket surface in both space and time. Thus
where
![]() $n$
is the number of samples acquired on the pocket surface.
$n$
is the number of samples acquired on the pocket surface.
Using this method, the turbulent flame speeds of the unburned pockets are found to be
![]() $S_{t}/S_{L}=3.74$
(
$S_{t}/S_{L}=3.74$
(
![]() ${\hat{S}}_{t}=61.3~\text{m}~\text{s}^{-1}$
) and
${\hat{S}}_{t}=61.3~\text{m}~\text{s}^{-1}$
) and
![]() $S_{t}/S_{L}=3.63$
(
$S_{t}/S_{L}=3.63$
(
![]() ${\hat{S}}_{t}=59.5~\text{m}~\text{s}^{-1}$
) for the
${\hat{S}}_{t}=59.5~\text{m}~\text{s}^{-1}$
) for the
![]() $H=20$
and
$H=20$
and
![]() $H=10$
simulations, respectively. These values differ, by a factor of 2, from those found experimentally, which were
$H=10$
simulations, respectively. These values differ, by a factor of 2, from those found experimentally, which were
![]() $S_{t}/S_{L}\approx 7.3$
(
$S_{t}/S_{L}\approx 7.3$
(
![]() ${\hat{S}}_{t}=120~\text{m}~\text{s}^{-1}$
) and
${\hat{S}}_{t}=120~\text{m}~\text{s}^{-1}$
) and
![]() $S_{t}/S_{L}\approx 6.6$
(
$S_{t}/S_{L}\approx 6.6$
(
![]() ${\hat{S}}_{t}\approx 110~\text{m}~\text{s}^{-1}$
) for
${\hat{S}}_{t}\approx 110~\text{m}~\text{s}^{-1}$
) for
![]() $H=20$
and
$H=20$
and
![]() $H=10$
, respectively. The difference in simulation values from the experimental ones are noted in the difficulties of evaluating the true volume and surface area solely from schlieren images in the experiments. The simulation and experiment, however, both predict turbulent flame speeds of roughly half an order to one order of magnitude of the turbulent flame speed.
$H=10$
, respectively. The difference in simulation values from the experimental ones are noted in the difficulties of evaluating the true volume and surface area solely from schlieren images in the experiments. The simulation and experiment, however, both predict turbulent flame speeds of roughly half an order to one order of magnitude of the turbulent flame speed.
To gain further insight into the effect of local turbulent mixing rates on turbulent flame speeds, it is possible to obtain average turbulent flame speeds for given ranges of turbulence intensity values,
![]() $u^{\prime }$
, since the subgrid kinetic energy is known. In fact, the turbulence intensity is simply
$u^{\prime }$
, since the subgrid kinetic energy is known. In fact, the turbulence intensity is simply
Figure 23 shows the average turbulent flame speeds,
![]() $S_{t}/S_{L}$
, in the wake of the simulated detonations according to their turbulence intensities,
$S_{t}/S_{L}$
, in the wake of the simulated detonations according to their turbulence intensities,
![]() $u^{\prime }/S_{L}$
. For each value of
$u^{\prime }/S_{L}$
. For each value of
![]() $u^{\prime }/S_{L}$
, the flame speeds are averaged within intervals of
$u^{\prime }/S_{L}$
, the flame speeds are averaged within intervals of
![]() $u^{\prime }/S_{L}\pm 0.5$
. Also shown in figure 23 are fan-stirred bomb experiment measurements of Abdel-Gayed, Al-Khishali & Bradley (Reference Abdel-Gayed, Al-Khishali and Bradley1984) for stoichiometric methane–air mixtures at atmospheric pressures. Clearly, the simulation exhibits larger average turbulent flame speeds in regions of higher turbulence intensity. In fact, much like the experiments of Abdel-Gayed et al. (Reference Abdel-Gayed, Al-Khishali and Bradley1984),
$u^{\prime }/S_{L}\pm 0.5$
. Also shown in figure 23 are fan-stirred bomb experiment measurements of Abdel-Gayed, Al-Khishali & Bradley (Reference Abdel-Gayed, Al-Khishali and Bradley1984) for stoichiometric methane–air mixtures at atmospheric pressures. Clearly, the simulation exhibits larger average turbulent flame speeds in regions of higher turbulence intensity. In fact, much like the experiments of Abdel-Gayed et al. (Reference Abdel-Gayed, Al-Khishali and Bradley1984),
![]() $S_{t}/S_{L}$
appears to increase proportionally with
$S_{t}/S_{L}$
appears to increase proportionally with
![]() $u^{\prime }/S_{L}$
. Turbulence intensities were not recorded above the values shown in figure 23, as such high-velocity fluctuations have not had sufficient time to develop on the pocket surfaces. For the turbulence intensities observed, the results are in good agreement with the experiments.
$u^{\prime }/S_{L}$
. Turbulence intensities were not recorded above the values shown in figure 23, as such high-velocity fluctuations have not had sufficient time to develop on the pocket surfaces. For the turbulence intensities observed, the results are in good agreement with the experiments.

Figure 23. Average turbulent flame speeds (
![]() $S_{t}/S_{L}$
) versus turbulent intensities (
$S_{t}/S_{L}$
) versus turbulent intensities (
![]() $u^{\prime }/S_{L}$
), obtained from simulation and compared to experiments of Abdel-Gayed et al. (Reference Abdel-Gayed, Al-Khishali and Bradley1984).
$u^{\prime }/S_{L}$
), obtained from simulation and compared to experiments of Abdel-Gayed et al. (Reference Abdel-Gayed, Al-Khishali and Bradley1984).
5.3 Quantitative analysis: the reaction zone and hydrodynamic thickness
In order to determine the effect that turbulent mixing intensity has on the reaction zone thickness, the average thickness of the structure (
![]() $\unicode[STIX]{x1D6E5}_{R}$
) has been measured for various
$\unicode[STIX]{x1D6E5}_{R}$
) has been measured for various
![]() $C_{\unicode[STIX]{x1D705}}$
values for the domain height of
$C_{\unicode[STIX]{x1D705}}$
values for the domain height of
![]() $H=20$
. This was achieved by following the procedure to generate the Favre-averaged reactant profiles in figure 16. Figure 24 thus shows the reaction zone thickness (
$H=20$
. This was achieved by following the procedure to generate the Favre-averaged reactant profiles in figure 16. Figure 24 thus shows the reaction zone thickness (
![]() $\unicode[STIX]{x1D6E5}_{R}$
), defined here as the distance from the shock wave,
$\unicode[STIX]{x1D6E5}_{R}$
), defined here as the distance from the shock wave,
![]() $x=x_{s}$
, to where
$x=x_{s}$
, to where
![]() ${\tilde{Y}}(x)<2\,\%$
, as a function of
${\tilde{Y}}(x)<2\,\%$
, as a function of
![]() $C_{\unicode[STIX]{x1D705}}$
. Clearly, there is an increasing trend in thickness with
$C_{\unicode[STIX]{x1D705}}$
. Clearly, there is an increasing trend in thickness with
![]() $C_{\unicode[STIX]{x1D705}}$
. In fact, the thickness appears to increase linearly with
$C_{\unicode[STIX]{x1D705}}$
. In fact, the thickness appears to increase linearly with
![]() $C_{\unicode[STIX]{x1D705}}$
for the range of values simulated here. A line of best fit (obtained from linear regression of each data point),
$C_{\unicode[STIX]{x1D705}}$
for the range of values simulated here. A line of best fit (obtained from linear regression of each data point),
![]() $\unicode[STIX]{x1D6E5}_{R}=1.19C_{\unicode[STIX]{x1D705}}+4.49$
, is also indicated in figure 24. Also shown are error bars indicating the standard deviation of thickness for each value of
$\unicode[STIX]{x1D6E5}_{R}=1.19C_{\unicode[STIX]{x1D705}}+4.49$
, is also indicated in figure 24. Also shown are error bars indicating the standard deviation of thickness for each value of
![]() $C_{\unicode[STIX]{x1D705}}$
.
$C_{\unicode[STIX]{x1D705}}$
.

Figure 24. Effect of turbulence intensity (through
![]() $C_{\unicode[STIX]{x1D705}}$
) on the mean reaction zone thickness (
$C_{\unicode[STIX]{x1D705}}$
) on the mean reaction zone thickness (
![]() $\unicode[STIX]{x1D6E5}_{R}$
) for the CLEM-LES (all with resolution
$\unicode[STIX]{x1D6E5}_{R}$
) for the CLEM-LES (all with resolution
![]() $b=1/32$
and
$b=1/32$
and
![]() $N=16$
elements per LES cell). The error bars indicate the standard deviation in
$N=16$
elements per LES cell). The error bars indicate the standard deviation in
![]() $\unicode[STIX]{x1D6E5}_{R}$
for each simulation. Note that
$\unicode[STIX]{x1D6E5}_{R}$
for each simulation. Note that
![]() $\unicode[STIX]{x1D6E5}_{R}$
is normalized by
$\unicode[STIX]{x1D6E5}_{R}$
is normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.

Figure 25. Schlieren photograph (this study), which shows that pockets of unburned gas can take up to
![]() ${\sim}9\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
behind the leading shock to burn up.
${\sim}9\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
behind the leading shock to burn up.
To quantitatively compare the CLEM-LES to experimental observations in terms of the reaction zone thickness, or distance it takes for the pockets of unburned gas to burn, results from § 4.3 are considered. In figure 24, it was observed that the average reaction zone thickness captured by all values of
![]() $C_{\unicode[STIX]{x1D705}}$
, for
$C_{\unicode[STIX]{x1D705}}$
, for
![]() $H=20$
, was in the range
$H=20$
, was in the range
![]() $5<\unicode[STIX]{x1D6E5}_{R}<17$
. More specifically, for
$5<\unicode[STIX]{x1D6E5}_{R}<17$
. More specifically, for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $C_{\unicode[STIX]{x1D705}}=10.0$
, the average thickness was found to be
$C_{\unicode[STIX]{x1D705}}=10.0$
, the average thickness was found to be
![]() $\unicode[STIX]{x1D6E5}_{R}=13.0$
and
$\unicode[STIX]{x1D6E5}_{R}=13.0$
and
![]() $\unicode[STIX]{x1D6E5}_{R}=16.2$
, respectively. These computed average thicknesses are much higher than previous reports of burnout distances of
$\unicode[STIX]{x1D6E5}_{R}=16.2$
, respectively. These computed average thicknesses are much higher than previous reports of burnout distances of
![]() ${\sim}(4{-}6)\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
(Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007), which were measured from Euler simulations with significant numerical viscosity. Upon close inspection, however, of the experimental images shown in § 2, burnout distances were estimated to be as high as
${\sim}(4{-}6)\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
(Radulescu et al.
Reference Radulescu, Sharpe, Law and Lee2007), which were measured from Euler simulations with significant numerical viscosity. Upon close inspection, however, of the experimental images shown in § 2, burnout distances were estimated to be as high as
![]() ${\sim}9\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, as can be seen in figure 25. Thus, compared to the experiment in figure 25,
${\sim}9\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, as can be seen in figure 25. Thus, compared to the experiment in figure 25,
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
yields an error of
$C_{\unicode[STIX]{x1D705}}=6.7$
yields an error of
![]() ${\sim}44\,\%$
, while
${\sim}44\,\%$
, while
![]() $C_{\unicode[STIX]{x1D705}}=10.0$
yields an error of
$C_{\unicode[STIX]{x1D705}}=10.0$
yields an error of
![]() ${\sim}80\,\%$
. Despite these large errors, however, it should be noted that the simulations for
${\sim}80\,\%$
. Despite these large errors, however, it should be noted that the simulations for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $C_{\unicode[STIX]{x1D705}}=10.0$
have standard deviations of
$C_{\unicode[STIX]{x1D705}}=10.0$
have standard deviations of
![]() $\unicode[STIX]{x1D6E5}_{R}\pm 6.4$
and
$\unicode[STIX]{x1D6E5}_{R}\pm 6.4$
and
![]() $\unicode[STIX]{x1D6E5}_{R}\pm 5.7$
, respectively. Thus, a large range of possible expected thicknesses lie anywhere from
$\unicode[STIX]{x1D6E5}_{R}\pm 5.7$
, respectively. Thus, a large range of possible expected thicknesses lie anywhere from
![]() $6.6<\unicode[STIX]{x1D6E5}_{R}<22$
. Furthermore, the current experiments, which are stochastic in nature, have not quantified the probability and variance of the reaction zone thickness that are possible during propagation.
$6.6<\unicode[STIX]{x1D6E5}_{R}<22$
. Furthermore, the current experiments, which are stochastic in nature, have not quantified the probability and variance of the reaction zone thickness that are possible during propagation.
Finally, the reaction zone thickness has been well correlated with the detonation cell size, where chemical reactions are completed roughly within one cell cycle (Lee Reference Lee1984). From figure 15, the cell size
![]() $\unicode[STIX]{x1D706}\approx 10$
when
$\unicode[STIX]{x1D706}\approx 10$
when
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
. This compares well with the average reaction zone thickness,
$C_{\unicode[STIX]{x1D705}}=6.7$
. This compares well with the average reaction zone thickness,
![]() $\unicode[STIX]{x1D6E5}_{R}=13.0$
. Furthermore, the entire hydrodynamic thickness of the wave (
$\unicode[STIX]{x1D6E5}_{R}=13.0$
. Furthermore, the entire hydrodynamic thickness of the wave (
![]() $\unicode[STIX]{x1D6E5}_{H}$
), or distance from the leading shock to the trailing sonic plane (or CJ state), is also well correlated with the cell size:
$\unicode[STIX]{x1D6E5}_{H}$
), or distance from the leading shock to the trailing sonic plane (or CJ state), is also well correlated with the cell size:
![]() $\unicode[STIX]{x1D6E5}_{H}=6.5\unicode[STIX]{x1D706}$
(Lee Reference Lee1984). In figure 26, the ensemble space- and time-averaged pressure profile for
$\unicode[STIX]{x1D6E5}_{H}=6.5\unicode[STIX]{x1D706}$
(Lee Reference Lee1984). In figure 26, the ensemble space- and time-averaged pressure profile for
![]() $\bar{p}(x)$
is presented for the
$\bar{p}(x)$
is presented for the
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $H=20$
case and compared to the ZND solution for
$H=20$
case and compared to the ZND solution for
![]() $p(x)$
. For this case, it takes approximately
$p(x)$
. For this case, it takes approximately
![]() ${\sim}50\unicode[STIX]{x1D6E5}_{1/2}$
for the pressure to reach the CJ solution state, which corresponds to the sonic plane in the wake of the wave. This is consistent with findings in Lee & Radulescu (Reference Lee and Radulescu2005) for highly unstable detonations involving methane at similar conditions. Furthermore, since
${\sim}50\unicode[STIX]{x1D6E5}_{1/2}$
for the pressure to reach the CJ solution state, which corresponds to the sonic plane in the wake of the wave. This is consistent with findings in Lee & Radulescu (Reference Lee and Radulescu2005) for highly unstable detonations involving methane at similar conditions. Furthermore, since
![]() $\unicode[STIX]{x1D706}\approx 10$
for
$\unicode[STIX]{x1D706}\approx 10$
for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
, then
$C_{\unicode[STIX]{x1D705}}=6.7$
, then
![]() $\unicode[STIX]{x1D6E5}_{H}\approx 5\unicode[STIX]{x1D706}$
. This result is of the same order as that reported by Lee (Reference Lee1984) from previous experimental correlations. To summarize the findings here, increasing the value of
$\unicode[STIX]{x1D6E5}_{H}\approx 5\unicode[STIX]{x1D706}$
. This result is of the same order as that reported by Lee (Reference Lee1984) from previous experimental correlations. To summarize the findings here, increasing the value of
![]() $C_{\unicode[STIX]{x1D705}}$
was found to generate a larger reaction zone thickness. This, in turn, is believed to lead to an increased hydrodynamic thickness and cell size, due to their dependence on the reaction zone thickness.
$C_{\unicode[STIX]{x1D705}}$
was found to generate a larger reaction zone thickness. This, in turn, is believed to lead to an increased hydrodynamic thickness and cell size, due to their dependence on the reaction zone thickness.

Figure 26. Ensemble space- and time-averaged pressure profile (
![]() $\bar{p}(x)$
) for the
$\bar{p}(x)$
) for the
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $H=20$
simulation and compared to the ZND solution for
$H=20$
simulation and compared to the ZND solution for
![]() $p(x)$
. Note that distances
$p(x)$
. Note that distances
![]() $x$
and
$x$
and
![]() $x_{s}$
are normalized by
$x_{s}$
are normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
. The pressure
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
. The pressure
![]() $p$
is normalized by
$p$
is normalized by
![]() $\unicode[STIX]{x1D6FE}p_{o}$
.
$\unicode[STIX]{x1D6FE}p_{o}$
.
5.4 Qualitative comparison of cell patterns with experiments
To further compare the CLEM-LES with experiment, in terms of cell patterns and irregularity, numerically obtained soot foils for both
![]() $H=10$
and
$H=10$
and
![]() $H=20$
at
$H=20$
at
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
were compared to those obtained experimentally for
$C_{\unicode[STIX]{x1D705}}=6.7$
were compared to those obtained experimentally for
![]() $\text{CH}_{4}+2\text{O}_{2}$
at
$\text{CH}_{4}+2\text{O}_{2}$
at
![]() $\hat{p}_{o}=3.5$
kPa, courtesy of Radulescu et al. (Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005), and
$\hat{p}_{o}=3.5$
kPa, courtesy of Radulescu et al. (Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005), and
![]() $\text{CH}_{4}+2\text{O}_{2}+0.2\text{air}$
at
$\text{CH}_{4}+2\text{O}_{2}+0.2\text{air}$
at
![]() $\hat{p}_{o}=11$
kPa (Austin Reference Austin2003). For
$\hat{p}_{o}=11$
kPa (Austin Reference Austin2003). For
![]() $H=20$
, the numerical soot foil, presented in figure 27, corresponds exactly to the soot foil image of figure 15 for
$H=20$
, the numerical soot foil, presented in figure 27, corresponds exactly to the soot foil image of figure 15 for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
. Although the experimental soot foil, also shown in figure 27, was obtained for a smaller channel height (127 mm) and also for a much higher pressure, the two are comparable in terms of scaling through the half reaction length. For the experiment (Austin Reference Austin2003),
$C_{\unicode[STIX]{x1D705}}=6.7$
. Although the experimental soot foil, also shown in figure 27, was obtained for a smaller channel height (127 mm) and also for a much higher pressure, the two are comparable in terms of scaling through the half reaction length. For the experiment (Austin Reference Austin2003),
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}=5.1$
mm. This value was obtained in this study using the Cantera libraries (Goodwin et al.
Reference Goodwin, Moffat and Speth2016) and the GRI-3.0 detailed kinetic mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016), consistent with the procedure in Maxwell (Reference Maxwell2016). Thus, the experimental soot foil was estimated to be
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}=5.1$
mm. This value was obtained in this study using the Cantera libraries (Goodwin et al.
Reference Goodwin, Moffat and Speth2016) and the GRI-3.0 detailed kinetic mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016), consistent with the procedure in Maxwell (Reference Maxwell2016). Thus, the experimental soot foil was estimated to be
![]() ${\sim}25\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
high. This is comparable to the simulation, whose domain is
${\sim}25\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
high. This is comparable to the simulation, whose domain is
![]() $20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
in height. In the portion of the numerical soot foil presented in figure 27, the overall cell size and pattern match well to the experiment. In the experiment, however, a very distinct substructure was observed. This was observed by the presence of much smaller cells within the larger and more predominant cell structure. Although such a fine substructure is not so obvious in the simulation, there are still some streaks on the numerical soot foil, which are indicative of triple-point paths associated with cell bifurcations. The lack of detailed substructure in the simulation could be an artifact of the supergrid resolution, differences in mixture properties, or most likely associated with the limitation of the one-step model in capturing the very short-duration energy release of methane combustion and the associated instabilities that exist on that finer small scale. Furthermore, it is likely that, at the resolution presented here, 32 grids per
$20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
in height. In the portion of the numerical soot foil presented in figure 27, the overall cell size and pattern match well to the experiment. In the experiment, however, a very distinct substructure was observed. This was observed by the presence of much smaller cells within the larger and more predominant cell structure. Although such a fine substructure is not so obvious in the simulation, there are still some streaks on the numerical soot foil, which are indicative of triple-point paths associated with cell bifurcations. The lack of detailed substructure in the simulation could be an artifact of the supergrid resolution, differences in mixture properties, or most likely associated with the limitation of the one-step model in capturing the very short-duration energy release of methane combustion and the associated instabilities that exist on that finer small scale. Furthermore, it is likely that, at the resolution presented here, 32 grids per
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, the fine details associated with the expected substructure have effectively been filtered out. It is noted that higher-resolution simulations were not conducted for
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
, the fine details associated with the expected substructure have effectively been filtered out. It is noted that higher-resolution simulations were not conducted for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
. Despite this lack of fine-scale detail for the substructure, the overall cell behaviour and irregularity are captured well by the simulation.
$C_{\unicode[STIX]{x1D705}}=6.7$
. Despite this lack of fine-scale detail for the substructure, the overall cell behaviour and irregularity are captured well by the simulation.

Figure 27. (a) Numerical soot foil obtained for the CLEM-LES with
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $H=20$
compared with (b) an experimental soot foil for
$H=20$
compared with (b) an experimental soot foil for
![]() $\text{CH}_{4}+2\text{O}_{2}+0.2\text{air}$
at
$\text{CH}_{4}+2\text{O}_{2}+0.2\text{air}$
at
![]() $\hat{p}_{o}=11~\text{kPa}$
(Austin Reference Austin2003). Note that the channel height for the experiment is
$\hat{p}_{o}=11~\text{kPa}$
(Austin Reference Austin2003). Note that the channel height for the experiment is
![]() ${\sim}25\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
(127 mm), while the simulation is
${\sim}25\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
(127 mm), while the simulation is
![]() $20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
(203 mm).
$20\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
(203 mm).
For
![]() $H=10$
, figure 28 shows numerical soot foils obtained for two different portions of the numerical domain and compares them to soot foils of experiments conducted in Radulescu et al. (Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). Here, the experimental soot foils were obtained using the same experimental apparatus as described in Kiyanda & Higgins (Reference Kiyanda and Higgins2013). For both experimental soot foils, the numerical simulation captures well the cell size behaviour and irregularity. In general the channel height allows only half a cell to form. The cells, however, occasionally bifurcate, giving rise to the formation of cells of the order of the channel height. This behaviour can be observed in the bottom frames of figure 28. Finally, it is noted that a prominent substructure was not observed experimentally or numerically for
$H=10$
, figure 28 shows numerical soot foils obtained for two different portions of the numerical domain and compares them to soot foils of experiments conducted in Radulescu et al. (Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). Here, the experimental soot foils were obtained using the same experimental apparatus as described in Kiyanda & Higgins (Reference Kiyanda and Higgins2013). For both experimental soot foils, the numerical simulation captures well the cell size behaviour and irregularity. In general the channel height allows only half a cell to form. The cells, however, occasionally bifurcate, giving rise to the formation of cells of the order of the channel height. This behaviour can be observed in the bottom frames of figure 28. Finally, it is noted that a prominent substructure was not observed experimentally or numerically for
![]() $H=10$
, as was observed experimentally in figure 27. This could be attributed to differences in the mixture or conditions (i.e. the pressure) at which tests were performed.
$H=10$
, as was observed experimentally in figure 27. This could be attributed to differences in the mixture or conditions (i.e. the pressure) at which tests were performed.

Figure 28. Numerical soot foils obtained for the CLEM-LES with
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $H=10$
compared with two experimental soot foils for
$H=10$
compared with two experimental soot foils for
![]() $\text{CH}_{4}+2\text{O}_{2}$
at
$\text{CH}_{4}+2\text{O}_{2}$
at
![]() $\hat{p}_{o}=3.5~\text{kPa}$
, courtesy of M. Radulescu. Note that the channel height for the experiment is also
$\hat{p}_{o}=3.5~\text{kPa}$
, courtesy of M. Radulescu. Note that the channel height for the experiment is also
![]() $10\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$10\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
5.5 Quantitative analysis: velocity of the wave
To gain insight into why increasing
![]() $C_{\unicode[STIX]{x1D705}}$
has the effect of generating larger hydrodynamic structures, the subgrid kinetic energy associated with random velocity fluctuations (
$C_{\unicode[STIX]{x1D705}}$
has the effect of generating larger hydrodynamic structures, the subgrid kinetic energy associated with random velocity fluctuations (
![]() $k^{sgs}$
) is Favre- and ensemble-averaged for each
$k^{sgs}$
) is Favre- and ensemble-averaged for each
![]() $C_{\unicode[STIX]{x1D705}}$
case using the same procedure as was done for the reactant profiles, i.e. equations (4.2)–(4.4). The averaged profiles obtained for
$C_{\unicode[STIX]{x1D705}}$
case using the same procedure as was done for the reactant profiles, i.e. equations (4.2)–(4.4). The averaged profiles obtained for
![]() $k^{sgs}$
at various values of
$k^{sgs}$
at various values of
![]() $C_{\unicode[STIX]{x1D705}}$
are thus shown in figure 29. The principal observation made here is that, as
$C_{\unicode[STIX]{x1D705}}$
are thus shown in figure 29. The principal observation made here is that, as
![]() $C_{\unicode[STIX]{x1D705}}$
is increased, more subgrid kinetic energy is generated. This is not surprising since
$C_{\unicode[STIX]{x1D705}}$
is increased, more subgrid kinetic energy is generated. This is not surprising since
![]() $k^{sgs}$
is a function of
$k^{sgs}$
is a function of
![]() $C_{\unicode[STIX]{x1D705}}$
, as demonstrated in Maxwell (Reference Maxwell2016). This increase in
$C_{\unicode[STIX]{x1D705}}$
, as demonstrated in Maxwell (Reference Maxwell2016). This increase in
![]() $k^{sgs}$
with
$k^{sgs}$
with
![]() $C_{\unicode[STIX]{x1D705}}$
thus generates more frequent stirring events on the CLEM subgrid, and therefore faster burning rates on pocket surfaces. Despite this faster mixing and burning, larger pockets of unburned gas are able to form in the wake. This suggests that an overall velocity deficit develops on the wave front, allowing for increased ignition delays.
$C_{\unicode[STIX]{x1D705}}$
thus generates more frequent stirring events on the CLEM subgrid, and therefore faster burning rates on pocket surfaces. Despite this faster mixing and burning, larger pockets of unburned gas are able to form in the wake. This suggests that an overall velocity deficit develops on the wave front, allowing for increased ignition delays.

Figure 29. Effect of
![]() $C_{\unicode[STIX]{x1D705}}$
on the averaged subgrid kinetic energy (
$C_{\unicode[STIX]{x1D705}}$
on the averaged subgrid kinetic energy (
![]() $k^{sgs}$
) profile for the CLEM-LES. Note that distances
$k^{sgs}$
) profile for the CLEM-LES. Note that distances
![]() $x$
and
$x$
and
![]() $x_{s}$
are normalized by
$x_{s}$
are normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
To quantify the statistical distribution of velocities experienced by the wave front, and how such a distribution was affected by
![]() $C_{\unicode[STIX]{x1D705}}$
, p.d.f.s were constructed from the numerical simulations and are shown in figures 30 and 31 for
$C_{\unicode[STIX]{x1D705}}$
, p.d.f.s were constructed from the numerical simulations and are shown in figures 30 and 31 for
![]() $H=20$
and
$H=20$
and
![]() $H=10$
, respectively. Also shown in these figures are the experimental p.d.f.s previously shown in figure 6. To construct the p.d.f.s from the numerical simulations, velocity measurements were taken on the top and bottom walls for a total of 500 data points in each simulation. The p.d.f.s were then evaluated at
$H=10$
, respectively. Also shown in these figures are the experimental p.d.f.s previously shown in figure 6. To construct the p.d.f.s from the numerical simulations, velocity measurements were taken on the top and bottom walls for a total of 500 data points in each simulation. The p.d.f.s were then evaluated at
![]() $D\pm 0.5$
intervals and normalized by
$D\pm 0.5$
intervals and normalized by
![]() $D_{avg}$
accordingly. For the CLEM-LES, conducted at various
$D_{avg}$
accordingly. For the CLEM-LES, conducted at various
![]() $C_{\unicode[STIX]{x1D705}}$
values, and also an Euler simulation at the same supergrid resolution (
$C_{\unicode[STIX]{x1D705}}$
values, and also an Euler simulation at the same supergrid resolution (
![]() $b=1/32$
), the average propagation speed is always within 1 % error of the CJ value, where
$b=1/32$
), the average propagation speed is always within 1 % error of the CJ value, where
![]() $D_{CJ}=6.30$
(
$D_{CJ}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
).
$2240~\text{m}~\text{s}^{-1}$
).

Figure 30. The p.d.f. of a detonation wave, in a channel with
![]() $H=20$
, having a certain velocity (
$H=20$
, having a certain velocity (
![]() $D/D_{avg}$
) at any given moment and location. Also shown is a p.d.f. compiled from experiments (this study). Note that
$D/D_{avg}$
) at any given moment and location. Also shown is a p.d.f. compiled from experiments (this study). Note that
![]() $D_{avg}=5.19$
(
$D_{avg}=5.19$
(
![]() $1850~\text{m}~\text{s}^{-1}$
) for the experiment and
$1850~\text{m}~\text{s}^{-1}$
) for the experiment and
![]() $D_{avg}=6.30$
(
$D_{avg}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
) for the simulations.
$2240~\text{m}~\text{s}^{-1}$
) for the simulations.

Figure 31. The p.d.f. of a detonation wave, in a channel with
![]() $H=10$
, having a certain velocity (
$H=10$
, having a certain velocity (
![]() $D/D_{avg}$
) at any given moment and location. Also shown is a p.d.f. compiled from Kiyanda & Higgins (Reference Kiyanda and Higgins2013). Note that
$D/D_{avg}$
) at any given moment and location. Also shown is a p.d.f. compiled from Kiyanda & Higgins (Reference Kiyanda and Higgins2013). Note that
![]() $D_{avg}=5.53$
(
$D_{avg}=5.53$
(
![]() $1970~\text{m}~\text{s}^{-1}$
) for the experiment and
$1970~\text{m}~\text{s}^{-1}$
) for the experiment and
![]() $D_{avg}=6.30$
(
$D_{avg}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
) for the simulations.
$2240~\text{m}~\text{s}^{-1}$
) for the simulations.
Clearly, from figures 30 and 31, as
![]() $C_{\unicode[STIX]{x1D705}}$
increases, the likelihood or probability of the detonation wave to travel at speeds below the average CJ value also increases. This is especially true for
$C_{\unicode[STIX]{x1D705}}$
increases, the likelihood or probability of the detonation wave to travel at speeds below the average CJ value also increases. This is especially true for
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
. At these high values of
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
. At these high values of
![]() $C_{\unicode[STIX]{x1D705}}$
, the detonation tends to favour a greater chance of having wave speeds below the average propagation speed value, i.e. when
$C_{\unicode[STIX]{x1D705}}$
, the detonation tends to favour a greater chance of having wave speeds below the average propagation speed value, i.e. when
![]() $(D/D_{avg})<1$
. Conversely, at lower values of
$(D/D_{avg})<1$
. Conversely, at lower values of
![]() $C_{\unicode[STIX]{x1D705}}$
, and the Euler simulation, velocities above the average propagation speed are favoured. This would lead to much shorter ignition delays, thus explaining the relatively quick burning times associated with the observed shortened reaction zone thickness, previously shown in figure 24. For higher
$C_{\unicode[STIX]{x1D705}}$
, and the Euler simulation, velocities above the average propagation speed are favoured. This would lead to much shorter ignition delays, thus explaining the relatively quick burning times associated with the observed shortened reaction zone thickness, previously shown in figure 24. For higher
![]() $C_{\unicode[STIX]{x1D705}}$
values, since the wave spends more time at below CJ velocities, most of the unburned gas that is shocked by the wave front has a much longer ignition delay compared to the ZND model. For this reason, unburned pockets of gas are able to form in the wake, which eventually burn up through turbulent mixing. This favouring of velocities below the average propagation speed thus lengthens the overall hydrodynamic structure of the wave. Consequently, the cells also increase in size and become more irregular in appearance, as observed in the cell patterns of figure 15. Since higher
$C_{\unicode[STIX]{x1D705}}$
values, since the wave spends more time at below CJ velocities, most of the unburned gas that is shocked by the wave front has a much longer ignition delay compared to the ZND model. For this reason, unburned pockets of gas are able to form in the wake, which eventually burn up through turbulent mixing. This favouring of velocities below the average propagation speed thus lengthens the overall hydrodynamic structure of the wave. Consequently, the cells also increase in size and become more irregular in appearance, as observed in the cell patterns of figure 15. Since higher
![]() $C_{\unicode[STIX]{x1D705}}$
values inherently generate more random fluctuations, the cell irregularity would also be expected to increase.
$C_{\unicode[STIX]{x1D705}}$
values inherently generate more random fluctuations, the cell irregularity would also be expected to increase.
In general, the p.d.f.s collected for
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
compared well to experiments, in terms of the most probable velocity expected on the wave front. The experiments and the simulations, for
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
compared well to experiments, in terms of the most probable velocity expected on the wave front. The experiments and the simulations, for
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
, both show that the most probable velocity on the wave front, at any given instant or location, is actually below the average propagation value,
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
, both show that the most probable velocity on the wave front, at any given instant or location, is actually below the average propagation value,
![]() $(D/D_{avg})<1$
. The simulations for
$(D/D_{avg})<1$
. The simulations for
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
also reproduce well the decaying behaviour of the wave velocity, where the probability of the wave speed exhibits a power-law dependence on wave speeds above the favoured value. For
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
also reproduce well the decaying behaviour of the wave velocity, where the probability of the wave speed exhibits a power-law dependence on wave speeds above the favoured value. For
![]() $H=20$
, although the numerical simulations for
$H=20$
, although the numerical simulations for
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
do not collapse onto this correlation, the same decaying trend is observed. For
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
do not collapse onto this correlation, the same decaying trend is observed. For
![]() $H=20$
, the most probable wave speed favoured, experimentally, is
$H=20$
, the most probable wave speed favoured, experimentally, is
![]() $(D/D_{avg})=0.93\pm 0.04$
with a peak p.d.f. value of 3.3. For the simulation at
$(D/D_{avg})=0.93\pm 0.04$
with a peak p.d.f. value of 3.3. For the simulation at
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
, the most probable velocity was
$C_{\unicode[STIX]{x1D705}}=6.7$
, the most probable velocity was
![]() $(D/D_{avg})=0.96\pm 0.04$
with a peak p.d.f. value of 1.74. This favoured velocity value has 8.6 % error compared to experiment. For
$(D/D_{avg})=0.96\pm 0.04$
with a peak p.d.f. value of 1.74. This favoured velocity value has 8.6 % error compared to experiment. For
![]() $C_{\unicode[STIX]{x1D705}}=10.0$
, the most probable velocity was
$C_{\unicode[STIX]{x1D705}}=10.0$
, the most probable velocity was
![]() $(D/D_{avg})=0.85\pm 0.04$
with a peak p.d.f. value of 2.25. This agrees well for the favoured velocity value, with only 3.2 % error. Despite this, however, the range of expected velocities on the wave front is much larger in the simulations compared to experiment. These differences in peak p.d.f. values and expected ranges of velocities are believed to be influenced by several factors. First, the numerical simulations do not account for energy losses that are present in the experiments. Therefore, the detonation, in the simulations, has higher velocities. Furthermore, cell patterns for a channel height of
$(D/D_{avg})=0.85\pm 0.04$
with a peak p.d.f. value of 2.25. This agrees well for the favoured velocity value, with only 3.2 % error. Despite this, however, the range of expected velocities on the wave front is much larger in the simulations compared to experiment. These differences in peak p.d.f. values and expected ranges of velocities are believed to be influenced by several factors. First, the numerical simulations do not account for energy losses that are present in the experiments. Therefore, the detonation, in the simulations, has higher velocities. Furthermore, cell patterns for a channel height of
![]() $H=20$
are very stochastic and irregular. The experimental p.d.f. in figure 30 was compiled for only four different experiments. It is likely that many more experiments are required in order to capture the events in the tails of the p.d.f., beyond the velocity limits currently obtained. Finally, velocity measurements are captured experimentally every
$H=20$
are very stochastic and irregular. The experimental p.d.f. in figure 30 was compiled for only four different experiments. It is likely that many more experiments are required in order to capture the events in the tails of the p.d.f., beyond the velocity limits currently obtained. Finally, velocity measurements are captured experimentally every
![]() $11.53~\unicode[STIX]{x03BC}\text{s}$
, which may filter out any high-speed and short-lived velocity fluctuations, which may occur beyond the current p.d.f. limits. It is likely that, in reality, the experimental p.d.f. should have a larger range with a smaller peak p.d.f. value. Despite the differences in p.d.f. values between experiment and simulation, it should be noted that
$11.53~\unicode[STIX]{x03BC}\text{s}$
, which may filter out any high-speed and short-lived velocity fluctuations, which may occur beyond the current p.d.f. limits. It is likely that, in reality, the experimental p.d.f. should have a larger range with a smaller peak p.d.f. value. Despite the differences in p.d.f. values between experiment and simulation, it should be noted that
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
does much better at capturing the peak value location
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
does much better at capturing the peak value location
![]() $(D/D_{avg})$
compared to Euler or low-value
$(D/D_{avg})$
compared to Euler or low-value
![]() $C_{\unicode[STIX]{x1D705}}$
simulations. This location, when
$C_{\unicode[STIX]{x1D705}}$
simulations. This location, when
![]() $(D/D_{avg})<1$
, is the key feature that influences pocket formation, and thus increased hydrodynamic thickness, owing to increased ignition delays at most locations on the wave front.
$(D/D_{avg})<1$
, is the key feature that influences pocket formation, and thus increased hydrodynamic thickness, owing to increased ignition delays at most locations on the wave front.
For
![]() $H=10$
, much better agreement with experiment is observed when
$H=10$
, much better agreement with experiment is observed when
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
. The most probable wave speed favoured, experimentally (Kiyanda & Higgins Reference Kiyanda and Higgins2013), is
$C_{\unicode[STIX]{x1D705}}=6.7$
. The most probable wave speed favoured, experimentally (Kiyanda & Higgins Reference Kiyanda and Higgins2013), is
![]() $(D/D_{avg})=0.814\pm 0.005$
with a peak p.d.f. value of 6.15. In this case, the simulation at
$(D/D_{avg})=0.814\pm 0.005$
with a peak p.d.f. value of 6.15. In this case, the simulation at
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
has a favoured velocity of
$C_{\unicode[STIX]{x1D705}}=6.7$
has a favoured velocity of
![]() $(D/D_{avg})=0.84\pm 0.04$
with a peak p.d.f. value of 2.55. This also agrees well for the favoured velocity value, with only 1.0 % error. This better agreement can probably be attributed to the fact that a domain height of
$(D/D_{avg})=0.84\pm 0.04$
with a peak p.d.f. value of 2.55. This also agrees well for the favoured velocity value, with only 1.0 % error. This better agreement can probably be attributed to the fact that a domain height of
![]() $H=10$
effectively mode-locks the detonation in such a way that much less variation in cell size was observed. This was seen in the soot foils presented in figure 28. Clearly, the analysis conducted here supports the need to calibrate
$H=10$
effectively mode-locks the detonation in such a way that much less variation in cell size was observed. This was seen in the soot foils presented in figure 28. Clearly, the analysis conducted here supports the need to calibrate
![]() $C_{\unicode[STIX]{x1D705}}$
in order to ensure the correct velocity probability trend and qualitative features are obtained numerically.
$C_{\unicode[STIX]{x1D705}}$
in order to ensure the correct velocity probability trend and qualitative features are obtained numerically.

Figure 32. Numerical soot foils obtained for the 3D CLEM-LES for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $H=10$
.
$H=10$
.
5.6 Three-dimensional effects and the validity of the two-dimensional LES approach
Finally, in order to further validate the two-dimensional (2D) numerical results obtained throughout this work, a thin-channel three-dimensional (3D) simulation has been conducted for the
![]() $H=10$
case, with
$H=10$
case, with
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and a domain width of
$C_{\unicode[STIX]{x1D705}}=6.7$
and a domain width of
![]() $2\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
. This corresponds roughly to the experimental set-up of Kiyanda & Higgins (Reference Kiyanda and Higgins2013). The grid resolution used for the 3D simulation was
$2\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
. This corresponds roughly to the experimental set-up of Kiyanda & Higgins (Reference Kiyanda and Higgins2013). The grid resolution used for the 3D simulation was
![]() $b=1/16$
with
$b=1/16$
with
![]() $N=16$
subgrid elements within each cell. Figure 32 shows a portion of soot foils which were obtained on the side and top walls of the domain. More specifically, these are obtained at
$N=16$
subgrid elements within each cell. Figure 32 shows a portion of soot foils which were obtained on the side and top walls of the domain. More specifically, these are obtained at
![]() $z=0$
in the
$z=0$
in the
![]() $x{-}y$
plane and
$x{-}y$
plane and
![]() $y=10$
in the
$y=10$
in the
![]() $x{-}z$
plane, respectively. Here,
$x{-}z$
plane, respectively. Here,
![]() $x$
is the direction along the channel length,
$x$
is the direction along the channel length,
![]() $y$
is along the channel height and
$y$
is along the channel height and
![]() $z$
is along the channel width. Upon comparing the sidewall soot foil with that of the 2D LES simulation in figure 28, the cell size obtained is comparable. In both the 2D and 3D simulations, the resulting cell size is one-half cell per channel height throughout most of the domain. Furthermore, the soot foil obtained in the 3D simulation does not exhibit a visible substructure, as was the case for the 2D simulation in figure 28. Finally, the vorticity streaks on the top wall soot foil suggest the resulting cell pattern is predominantly 2D for the thin channel.
$z$
is along the channel width. Upon comparing the sidewall soot foil with that of the 2D LES simulation in figure 28, the cell size obtained is comparable. In both the 2D and 3D simulations, the resulting cell size is one-half cell per channel height throughout most of the domain. Furthermore, the soot foil obtained in the 3D simulation does not exhibit a visible substructure, as was the case for the 2D simulation in figure 28. Finally, the vorticity streaks on the top wall soot foil suggest the resulting cell pattern is predominantly 2D for the thin channel.

Figure 33. Profile sections of density extracted in the
![]() $x{-}y$
,
$x{-}y$
,
![]() $z{-}y$
and
$z{-}y$
and
![]() $x{-}z$
planes for the 3D CLEM-LES.
$x{-}z$
planes for the 3D CLEM-LES.

Figure 34. Average reactant profiles for both 2D and 3D CLEM-LES. Note that distances
![]() $x$
and
$x$
and
![]() $x_{s}$
are normalized by
$x_{s}$
are normalized by
![]() $\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
$\hat{\unicode[STIX]{x1D6E5}}_{1/2}$
.
To further investigate the resulting flow pattern of the 3D simulation, various sections of density profiles are extracted in the
![]() $x{-}y$
,
$x{-}y$
,
![]() $z{-}y$
and
$z{-}y$
and
![]() $x{-}z$
planes for a single instant in time and presented in figure 33. This was done for an instant in time just before a triple point reflects on the top wall, where a pocket of unburned gas has nearly formed in the wake of the wave. In three sections taken in the
$x{-}z$
planes for a single instant in time and presented in figure 33. This was done for an instant in time just before a triple point reflects on the top wall, where a pocket of unburned gas has nearly formed in the wake of the wave. In three sections taken in the
![]() $x{-}y$
plane, at
$x{-}y$
plane, at
![]() $z=0.25$
,
$z=0.25$
,
![]() $z=1.0$
and
$z=1.0$
and
![]() $z=1.75$
, it is clear that the dense pocket of unreacted gas does not have a uniform shape along the width of the channel. Upon investigating the sections along various
$z=1.75$
, it is clear that the dense pocket of unreacted gas does not have a uniform shape along the width of the channel. Upon investigating the sections along various
![]() $x$
locations in the
$x$
locations in the
![]() $z{-}y$
plane and
$z{-}y$
plane and
![]() $y$
locations in the
$y$
locations in the
![]() $x{-}z$
plane, it is clear that the burning of the pocket of unreacted gas indeed occurs in all three dimensions. The presence of unburned gas, however, varies much more significantly in the
$x{-}z$
plane, it is clear that the burning of the pocket of unreacted gas indeed occurs in all three dimensions. The presence of unburned gas, however, varies much more significantly in the
![]() $x$
and
$x$
and
![]() $y$
directions compared to the channel width in the
$y$
directions compared to the channel width in the
![]() $z$
direction. Significant burn-up along the channel width is only observed in frames where the remaining pocket is nearly consumed, sufficiently far from the leading shock. This can be seen in frames in the
$z$
direction. Significant burn-up along the channel width is only observed in frames where the remaining pocket is nearly consumed, sufficiently far from the leading shock. This can be seen in frames in the
![]() $z{-}y$
plane for
$z{-}y$
plane for
![]() $x\leqslant 734.5$
and the
$x\leqslant 734.5$
and the
![]() $x{-}z$
plane for
$x{-}z$
plane for
![]() $y\leqslant 5.5$
. Finally, despite the non-uniformities in the pocket shape observed across the channel width, and the three-dimensional structure of the pocket burnout, the positions of the incident and Mach shocks remain uniform throughout the channel width.
$y\leqslant 5.5$
. Finally, despite the non-uniformities in the pocket shape observed across the channel width, and the three-dimensional structure of the pocket burnout, the positions of the incident and Mach shocks remain uniform throughout the channel width.
To further compare the 2D and 3D simulations, in terms of the rate at which the unreacted gas is consumed, the Favre-averaged reactant profiles are presented in figure 34. It is clear that the reactant profiles of the 3D simulation match closely the profiles obtained from the 2D simulation for
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
. In fact, both the 2D and 3D simulations have an average hydrodynamic thickness of
$C_{\unicode[STIX]{x1D705}}=6.7$
. In fact, both the 2D and 3D simulations have an average hydrodynamic thickness of
![]() $\unicode[STIX]{x1D6E5}_{R}=8.2$
with standard deviations of
$\unicode[STIX]{x1D6E5}_{R}=8.2$
with standard deviations of
![]() $\unicode[STIX]{x1D6E5}_{R}\pm 2.7$
and
$\unicode[STIX]{x1D6E5}_{R}\pm 2.7$
and
![]() $\unicode[STIX]{x1D6E5}_{R}\pm 2.0$
, respectively. To further compare 2D and 3D simulation results, the p.d.f.s of wave propagation velocity for both simulations are presented in figure 35, and compared to the experiment (Kiyanda & Higgins Reference Kiyanda and Higgins2013). It is clear that the 2D and 3D simulations both exhibit a similar p.d.f. trend. The 3D simulation however favours a slightly higher velocity
$\unicode[STIX]{x1D6E5}_{R}\pm 2.0$
, respectively. To further compare 2D and 3D simulation results, the p.d.f.s of wave propagation velocity for both simulations are presented in figure 35, and compared to the experiment (Kiyanda & Higgins Reference Kiyanda and Higgins2013). It is clear that the 2D and 3D simulations both exhibit a similar p.d.f. trend. The 3D simulation however favours a slightly higher velocity
![]() $(D/D_{avg})=0.87\pm 0.04$
with a peak p.d.f. value of 3.30 compared with the 2D simulation which favoured a velocity of
$(D/D_{avg})=0.87\pm 0.04$
with a peak p.d.f. value of 3.30 compared with the 2D simulation which favoured a velocity of
![]() $(D/D_{avg})=0.84\pm 0.04$
and a peak p.d.f. value of 2.55. The two results, however, are within measurement error of each other. Since these peak p.d.f. locations are below
$(D/D_{avg})=0.84\pm 0.04$
and a peak p.d.f. value of 2.55. The two results, however, are within measurement error of each other. Since these peak p.d.f. locations are below
![]() $(D/D_{avg})<1$
, as was observed in the experiment, pockets of unburned fuel are able to form in the wake, owing to increased ignition delays at most locations on the wave front, thus lengthening the hydrodynamic structure as observed in figure 34. The results presented in figures 34 and 35 suggest that, despite the 3D nature of local burning on unburned pocket surfaces, the use of 2D LES is justified for flows with high aspect ratios, where cell sizes are sufficiently large in height compared to their channel width. This can be attributed to the large-scale flow patterns, which are predominantly 2D. Furthermore, the use of 2D LES, in this study, is further justified by the fact that the LEM subgrid accounts for the small-scale 3D shear instabilities, on the unburned gas pocket surfaces, through the stirring terms,
$(D/D_{avg})<1$
, as was observed in the experiment, pockets of unburned fuel are able to form in the wake, owing to increased ignition delays at most locations on the wave front, thus lengthening the hydrodynamic structure as observed in figure 34. The results presented in figures 34 and 35 suggest that, despite the 3D nature of local burning on unburned pocket surfaces, the use of 2D LES is justified for flows with high aspect ratios, where cell sizes are sufficiently large in height compared to their channel width. This can be attributed to the large-scale flow patterns, which are predominantly 2D. Furthermore, the use of 2D LES, in this study, is further justified by the fact that the LEM subgrid accounts for the small-scale 3D shear instabilities, on the unburned gas pocket surfaces, through the stirring terms,
![]() $\dot{F_{T}}$
and
$\dot{F_{T}}$
and
![]() $\dot{F_{Y}}$
, in (3.10) and (3.11) (Kerstein Reference Kerstein1991a
). To this effect, the LEM subgrid simulates 3D isotropic turbulent mixing according to the large-scale flow conditions. The principal caveat here is that, owing to the low-Mach-number approximation on the subgrid, shock-driven instabilities, such as Richtmyer–Meshkov, are not captured on the subgrid itself. This is currently an area of active research in the framework of one-dimensional turbulence, an alternative grid-within-a-grid approach for LES (Jozefik, Kerstein & Schmidt Reference Jozefik, Kerstein and Schmidt2016). For the high-aspect-ratio flows considered here, the large-scale 2D flow instabilities are sufficient to generate the bulk of the subgrid kinetic energy, which influences stirring events on the subgrid scales accordingly. The second caveat is that the LES scale is assumed to be sufficiently resolved to the inertial range of the Kolmogorov cascade (Frisch Reference Frisch2000). If this were the case, one might expect isotropic shear-driven mixing to dominate on the subgrid scales. However, it is noted that, while the integral scales of turbulence have been resolved here, it is not clear to what extent the turbulence characteristics of the shear layers have been captured, with respect to the Kolmogorov cascade. Furthermore, vortex breakdown, according to the Kolmogorov cascade, depends on the ability of vortices to stretch in all three dimensions. Flows that are predominantly 2D lack this ability and tend to experience significant backscatter as a result (Kraichnan Reference Kraichnan1967; Leith Reference Leith1968; Batchelor Reference Batchelor1969). It is also noted that Kolmogorov’s theory of turbulence was developed for incompressible flow. It is not yet understood how these assumptions, regarding isotropic shear-driven mixing, apply to highly compressible flows.
$\dot{F_{Y}}$
, in (3.10) and (3.11) (Kerstein Reference Kerstein1991a
). To this effect, the LEM subgrid simulates 3D isotropic turbulent mixing according to the large-scale flow conditions. The principal caveat here is that, owing to the low-Mach-number approximation on the subgrid, shock-driven instabilities, such as Richtmyer–Meshkov, are not captured on the subgrid itself. This is currently an area of active research in the framework of one-dimensional turbulence, an alternative grid-within-a-grid approach for LES (Jozefik, Kerstein & Schmidt Reference Jozefik, Kerstein and Schmidt2016). For the high-aspect-ratio flows considered here, the large-scale 2D flow instabilities are sufficient to generate the bulk of the subgrid kinetic energy, which influences stirring events on the subgrid scales accordingly. The second caveat is that the LES scale is assumed to be sufficiently resolved to the inertial range of the Kolmogorov cascade (Frisch Reference Frisch2000). If this were the case, one might expect isotropic shear-driven mixing to dominate on the subgrid scales. However, it is noted that, while the integral scales of turbulence have been resolved here, it is not clear to what extent the turbulence characteristics of the shear layers have been captured, with respect to the Kolmogorov cascade. Furthermore, vortex breakdown, according to the Kolmogorov cascade, depends on the ability of vortices to stretch in all three dimensions. Flows that are predominantly 2D lack this ability and tend to experience significant backscatter as a result (Kraichnan Reference Kraichnan1967; Leith Reference Leith1968; Batchelor Reference Batchelor1969). It is also noted that Kolmogorov’s theory of turbulence was developed for incompressible flow. It is not yet understood how these assumptions, regarding isotropic shear-driven mixing, apply to highly compressible flows.

Figure 35. The p.d.f.s of a detonation wave having a certain velocity (
![]() $D/D_{avg}$
) at any given moment and location. These p.d.f.s have been compiled from both 2D and 3D simulations where
$D/D_{avg}$
) at any given moment and location. These p.d.f.s have been compiled from both 2D and 3D simulations where
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
and
$C_{\unicode[STIX]{x1D705}}=6.7$
and
![]() $H=10$
. Also shown is a p.d.f. compiled from Kiyanda & Higgins (Reference Kiyanda and Higgins2013). Note that
$H=10$
. Also shown is a p.d.f. compiled from Kiyanda & Higgins (Reference Kiyanda and Higgins2013). Note that
![]() $D_{avg}=5.53$
(
$D_{avg}=5.53$
(
![]() $1969.1~\text{m}~\text{s}^{-1}$
) for the experiment and
$1969.1~\text{m}~\text{s}^{-1}$
) for the experiment and
![]() $D_{avg}=6.30\pm 0.05$
(
$D_{avg}=6.30\pm 0.05$
(
![]() $2243.3\pm 17.8~\text{m}~\text{s}^{-1}$
) for the simulations.
$2243.3\pm 17.8~\text{m}~\text{s}^{-1}$
) for the simulations.

Figure 36. ZND temperature profiles computed for
![]() $\text{CH}_{4}+2\text{O}_{2}$
using the one-step reaction mechanism (3.13) compared to the SD Toolbox ZND solver (Kao & Shepherd Reference Kao and Shepherd2008) using the GRI-3.0 mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016).
$\text{CH}_{4}+2\text{O}_{2}$
using the one-step reaction mechanism (3.13) compared to the SD Toolbox ZND solver (Kao & Shepherd Reference Kao and Shepherd2008) using the GRI-3.0 mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016).
5.7 Validity and limitations of the global one-step reaction mechanism
In the current study, the global one-step ignition reaction mechanism, given by (3.13), although simplistic, was calibrated to reproduce the correct ZND half reaction length for a detonation travelling at the CJ velocity. Figure 36 shows the theoretical ZND temperature profile, computed using both the one-step model and the GRI-3.0 reaction mechanism (Smith et al.
Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016), for a detonation travelling at the CJ velocity of
![]() $D_{CJ}=6.30$
(
$D_{CJ}=6.30$
(
![]() $2240~\text{m}~\text{s}^{-1}$
). Clearly, the correct reaction length is recovered by the one-step model, where the chemical reactions terminate around
$2240~\text{m}~\text{s}^{-1}$
). Clearly, the correct reaction length is recovered by the one-step model, where the chemical reactions terminate around
![]() $1\unicode[STIX]{x1D6E5}_{1/2}$
(10 mm) downstream from the shock location, shown at
$1\unicode[STIX]{x1D6E5}_{1/2}$
(10 mm) downstream from the shock location, shown at
![]() $x=0$
. However, notable differences in temperature are observed, between the two reaction mechanisms, in the post-shock and fully burned states. Differences in the state variables of these two locations arise from the perfect-gas assumptions adopted in the governing equations, where
$x=0$
. However, notable differences in temperature are observed, between the two reaction mechanisms, in the post-shock and fully burned states. Differences in the state variables of these two locations arise from the perfect-gas assumptions adopted in the governing equations, where
![]() $\unicode[STIX]{x1D6FE}$
was assumed constant. In reality, however,
$\unicode[STIX]{x1D6FE}$
was assumed constant. In reality, however,
![]() $\unicode[STIX]{x1D6FE}$
varies across the shock and reaction zone. Despite this, the amount of heat release,
$\unicode[STIX]{x1D6FE}$
varies across the shock and reaction zone. Despite this, the amount of heat release,
![]() $Q$
, is consistent between the two models, yielding the correct propagation velocity. Another notable difference between the two reaction mechanisms is the temperature profile within the reaction zone itself. While the GRI-3.0 mechanism has a very distinct induction zone, with very little heat release until
$Q$
, is consistent between the two models, yielding the correct propagation velocity. Another notable difference between the two reaction mechanisms is the temperature profile within the reaction zone itself. While the GRI-3.0 mechanism has a very distinct induction zone, with very little heat release until
![]() $x<-0.5$
(
$x<-0.5$
(
![]() $-$
5 mm), the one-step model begins releasing heat as soon as the gas is shocked. This is observed by a gradual increase in temperature from
$-$
5 mm), the one-step model begins releasing heat as soon as the gas is shocked. This is observed by a gradual increase in temperature from
![]() $x<0$
onwards. As a result, the exothermicity of the GRI-3.0 model is confined to a much smaller layer towards the end of the reaction phase compared to the one-step model. Thus, there may be implications on the turbulence–chemistry interactions, and therefore the required value of
$x<0$
onwards. As a result, the exothermicity of the GRI-3.0 model is confined to a much smaller layer towards the end of the reaction phase compared to the one-step model. Thus, there may be implications on the turbulence–chemistry interactions, and therefore the required value of
![]() $C_{\unicode[STIX]{x1D705}}$
, since the one-step model does not accurately capture the very short-duration energy release of methane combustion. Furthermore, this may explain the lack of substructure observed in the numerical soot foil records shown in § 5.4. Despite this deficiency, the correct post-shock ignition delay is captured by the one-step model for the range of shock velocities expected during detonation propagation. Figure 37 shows how the constant-volume ignition delays, computed from the one-step and GRI-3.0 reaction mechanisms, compare for shock speeds in the range
$C_{\unicode[STIX]{x1D705}}$
, since the one-step model does not accurately capture the very short-duration energy release of methane combustion. Furthermore, this may explain the lack of substructure observed in the numerical soot foil records shown in § 5.4. Despite this deficiency, the correct post-shock ignition delay is captured by the one-step model for the range of shock velocities expected during detonation propagation. Figure 37 shows how the constant-volume ignition delays, computed from the one-step and GRI-3.0 reaction mechanisms, compare for shock speeds in the range
![]() $D=4{-}9$
(1400–
$D=4{-}9$
(1400–
![]() $3200~\text{m}~\text{s}^{-1}$
). Although there exists a slight underprediction of ignition times at low shock speeds, and overprediction at high speeds, the one-step model performs well at capturing the correct order of magnitude for the ignition delay times across the range of values. In fact, the one-step model works well for predicting ignition delays of methane chemistry, since there are no chain-branching cross-over effects (Browne, Liang & Shepherd Reference Browne, Liang and Shepherd2005). The sensitivity of the mixture to changes in temperature and pressure remain relatively unchanged, for the range of post-shock conditions expected.
$3200~\text{m}~\text{s}^{-1}$
). Although there exists a slight underprediction of ignition times at low shock speeds, and overprediction at high speeds, the one-step model performs well at capturing the correct order of magnitude for the ignition delay times across the range of values. In fact, the one-step model works well for predicting ignition delays of methane chemistry, since there are no chain-branching cross-over effects (Browne, Liang & Shepherd Reference Browne, Liang and Shepherd2005). The sensitivity of the mixture to changes in temperature and pressure remain relatively unchanged, for the range of post-shock conditions expected.

Figure 37. Ignition delay times for various shock speeds, computed using the one-step reaction mechanism (3.13) compared to the GRI-3.0 mechanism (Smith et al. Reference Smith, Golden, Frenklach, Moriarty, Eiteneer, Goldenberg, Bowman, Hanson, Song and Gardiner2016).
5.8 Kolmogorov constant
 $C_{\unicode[STIX]{x1D705}}$
as a tuning parameter
$C_{\unicode[STIX]{x1D705}}$
as a tuning parameter
From the numerical soot foils presented figure 15, it is clear that the
![]() $C_{\unicode[STIX]{x1D705}}$
parameter requires tuning in order to match the desired cell size and behaviour observed in the experiments of this study and Kiyanda & Higgins (Reference Kiyanda and Higgins2013). From a quantitative perspective, figures 30 and 31 have shown that numerically obtained p.d.f.s of detonation velocity distributions matched well the trends obtained through experiments when
$C_{\unicode[STIX]{x1D705}}$
parameter requires tuning in order to match the desired cell size and behaviour observed in the experiments of this study and Kiyanda & Higgins (Reference Kiyanda and Higgins2013). From a quantitative perspective, figures 30 and 31 have shown that numerically obtained p.d.f.s of detonation velocity distributions matched well the trends obtained through experiments when
![]() $C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
. In general, higher values of
$C_{\unicode[STIX]{x1D705}}\geqslant 6.7$
. In general, higher values of
![]() $C_{\unicode[STIX]{x1D705}}$
allowed below-average velocities to be favoured along the wave front, as was the case experimentally. As a result, it is clear that
$C_{\unicode[STIX]{x1D705}}$
allowed below-average velocities to be favoured along the wave front, as was the case experimentally. As a result, it is clear that
![]() $C_{\unicode[STIX]{x1D705}}$
requires tuning in order to ensure the correct velocity distribution, and consequently the correct expected reaction zone thickness. Furthermore, as observed in figures 17–28, a value of
$C_{\unicode[STIX]{x1D705}}$
requires tuning in order to ensure the correct velocity distribution, and consequently the correct expected reaction zone thickness. Furthermore, as observed in figures 17–28, a value of
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
was found to be adequate to form qualitative cells and burning patterns comparable to experiments. For smaller values of
$C_{\unicode[STIX]{x1D705}}=6.7$
was found to be adequate to form qualitative cells and burning patterns comparable to experiments. For smaller values of
![]() $C_{\unicode[STIX]{x1D705}}$
, only much smaller cells appear. For larger values of
$C_{\unicode[STIX]{x1D705}}$
, only much smaller cells appear. For larger values of
![]() $C_{\unicode[STIX]{x1D705}}$
, the cells increase in size until they are mode-locked by the channel height. It should be noted, however, that specific ‘matching’ of
$C_{\unicode[STIX]{x1D705}}$
, the cells increase in size until they are mode-locked by the channel height. It should be noted, however, that specific ‘matching’ of
![]() $C_{\unicode[STIX]{x1D705}}$
values can prove difficult due to the stochastic nature of both the experiments and the numerical simulations. For this, better-converged statistics would be required. It should be further noted that, even though the value of
$C_{\unicode[STIX]{x1D705}}$
values can prove difficult due to the stochastic nature of both the experiments and the numerical simulations. For this, better-converged statistics would be required. It should be further noted that, even though the value of
![]() $C_{\unicode[STIX]{x1D705}}=6.7$
was found to give good agreement with experimental observation,
$C_{\unicode[STIX]{x1D705}}=6.7$
was found to give good agreement with experimental observation,
![]() $C_{\unicode[STIX]{x1D705}}=1.4{-}2.0$
is a more universally accepted value (Chasnov Reference Chasnov1991; Bradley Reference Bradley1992). This difference may be due to several reasons.
$C_{\unicode[STIX]{x1D705}}=1.4{-}2.0$
is a more universally accepted value (Chasnov Reference Chasnov1991; Bradley Reference Bradley1992). This difference may be due to several reasons.
First of all, low values of
![]() $C_{\unicode[STIX]{x1D705}}$
correspond to Kolmogorov’s theory of the turbulence cascade in the incompressible limit (Frisch Reference Frisch2000). The detonation phenomenon under investigation here, on the other hand, is highly compressible. It is possible that highly compressible regimes generate much more turbulent fluctuations than incompressible theory predicts. This is especially true for Richtmyer–Meshkov instability, where turbulent motion is generated from shock waves interacting with material interfaces. Secondly, the large-scale motions of the experimental flow fields are essentially 2D due to the thin channel cross-section widths. In fact, the aspect ratios of the channel heights to widths (
$C_{\unicode[STIX]{x1D705}}$
correspond to Kolmogorov’s theory of the turbulence cascade in the incompressible limit (Frisch Reference Frisch2000). The detonation phenomenon under investigation here, on the other hand, is highly compressible. It is possible that highly compressible regimes generate much more turbulent fluctuations than incompressible theory predicts. This is especially true for Richtmyer–Meshkov instability, where turbulent motion is generated from shock waves interacting with material interfaces. Secondly, the large-scale motions of the experimental flow fields are essentially 2D due to the thin channel cross-section widths. In fact, the aspect ratios of the channel heights to widths (
![]() $H/W$
) in the experiments are
$H/W$
) in the experiments are
![]() ${\sim}10$
(this study) and
${\sim}10$
(this study) and
![]() ${\sim}4$
(Kiyanda & Higgins Reference Kiyanda and Higgins2013). In both cases, the channel widths are much smaller than the observed cell sizes. Thus, straining and decay of turbulent motions along the cross-sectional width may not be as prominent as would be expected in a full-scale 3D experiment. Furthermore, turbulence in two dimensions has been shown, theoretically, to exhibit backscatter (Kraichnan Reference Kraichnan1967; Leith Reference Leith1968; Batchelor Reference Batchelor1969), and hence generate more turbulent motions. This has also been assumed to be the case for atmospheric flows, which are also considered essentially 2D at planetary scales (Lilly Reference Lilly1966). In this sense, small-scale turbulence is able to feed into, and amplify, larger-scale turbulent motions. Although 3D burning does occur in the wake of the detonation wave at smaller scales, a 3D simulation conducted in the previous section suggested that the rate of fuel burn-up is largely governed by the large-scale fluid motions along the channel length and height. Since the experiments of this study and Kiyanda & Higgins (Reference Kiyanda and Higgins2013) are quasi-2D, it is possible that there are more turbulent motions behind the detonation front than would be expected in a naturally occurring 3D detonation wave propagation. In this sense, it is possible that the corresponding 2D simulation would also require a higher
${\sim}4$
(Kiyanda & Higgins Reference Kiyanda and Higgins2013). In both cases, the channel widths are much smaller than the observed cell sizes. Thus, straining and decay of turbulent motions along the cross-sectional width may not be as prominent as would be expected in a full-scale 3D experiment. Furthermore, turbulence in two dimensions has been shown, theoretically, to exhibit backscatter (Kraichnan Reference Kraichnan1967; Leith Reference Leith1968; Batchelor Reference Batchelor1969), and hence generate more turbulent motions. This has also been assumed to be the case for atmospheric flows, which are also considered essentially 2D at planetary scales (Lilly Reference Lilly1966). In this sense, small-scale turbulence is able to feed into, and amplify, larger-scale turbulent motions. Although 3D burning does occur in the wake of the detonation wave at smaller scales, a 3D simulation conducted in the previous section suggested that the rate of fuel burn-up is largely governed by the large-scale fluid motions along the channel length and height. Since the experiments of this study and Kiyanda & Higgins (Reference Kiyanda and Higgins2013) are quasi-2D, it is possible that there are more turbulent motions behind the detonation front than would be expected in a naturally occurring 3D detonation wave propagation. In this sense, it is possible that the corresponding 2D simulation would also require a higher
![]() $C_{\unicode[STIX]{x1D705}}$
value to artificially generate more turbulence. Furthermore, Kraichnan (Reference Kraichnan1971) predicts a theoretical value of
$C_{\unicode[STIX]{x1D705}}$
value to artificially generate more turbulence. Furthermore, Kraichnan (Reference Kraichnan1971) predicts a theoretical value of
![]() $C_{\unicode[STIX]{x1D705}}=6.69$
for 2D turbulence, compared to 1.4 for 3D turbulence. Another review of 2D turbulence (Danilov & Gurarie Reference Danilov and Gurarie2000) indicates that a
$C_{\unicode[STIX]{x1D705}}=6.69$
for 2D turbulence, compared to 1.4 for 3D turbulence. Another review of 2D turbulence (Danilov & Gurarie Reference Danilov and Gurarie2000) indicates that a
![]() $C_{\unicode[STIX]{x1D705}}$
value of 5.8–7 should be adopted due to the increased turbulence associated with backscatter. It should be noted, however, that in the current work this agreement is simply treated as a coincidence and has not been investigated further.
$C_{\unicode[STIX]{x1D705}}$
value of 5.8–7 should be adopted due to the increased turbulence associated with backscatter. It should be noted, however, that in the current work this agreement is simply treated as a coincidence and has not been investigated further.
Other sources of discrepancy may arise from discrepancies associated with experimental losses, and errors associated with limitations of the chemical model used. Turbulence–flame interactions of the artificially stretched reaction zone structure, obtained from the one-step model chemistry, may have an effect on the distribution of hotspots during subgrid stirring. This should be investigated further in future work. Despite this potential deficiency, the one-step model was found to produce the correct post-shock ignition delays for the range of shock speeds expected on the wave front. Therefore, while the exact value of
![]() $C_{\unicode[STIX]{x1D705}}$
may not be captured correctly by the one-step model, the methodology is able to capture the underlying physics of how turbulence–reaction layer interactions affect changes in the detonation structure for the unsteady wave front, with varying shock speeds.
$C_{\unicode[STIX]{x1D705}}$
may not be captured correctly by the one-step model, the methodology is able to capture the underlying physics of how turbulence–reaction layer interactions affect changes in the detonation structure for the unsteady wave front, with varying shock speeds.
Finally, in terms of calibration, it should be noted that it is possible to implement a dynamic procedure to obtain the
![]() $C_{\unicode[STIX]{x1D705}}$
value, i.e. the localized dynamic kinetic energy model (LDKM) method (Schumann Reference Schumann1975; Menon & Calhoon Reference Menon and Calhoon1996; Menon & Kerstein Reference Menon and Kerstein2011). Although this is possible, validation and verification would still be required. Furthermore, the method may be more appropriate for 3D simulations and would therefore increase computational expense significantly. Also, the dynamic procedure may not adequately account for increased turbulent fluctuations due to compressibility effects. For now, the static method of prescribing
$C_{\unicode[STIX]{x1D705}}$
value, i.e. the localized dynamic kinetic energy model (LDKM) method (Schumann Reference Schumann1975; Menon & Calhoon Reference Menon and Calhoon1996; Menon & Kerstein Reference Menon and Kerstein2011). Although this is possible, validation and verification would still be required. Furthermore, the method may be more appropriate for 3D simulations and would therefore increase computational expense significantly. Also, the dynamic procedure may not adequately account for increased turbulent fluctuations due to compressibility effects. For now, the static method of prescribing
![]() $C_{\unicode[STIX]{x1D705}}$
proves advantageous in two dimensions for examining the effect of turbulence intensity on detonation propagation patterns and behaviours.
$C_{\unicode[STIX]{x1D705}}$
proves advantageous in two dimensions for examining the effect of turbulence intensity on detonation propagation patterns and behaviours.
6 Conclusions
In this work, experiments and numerical simulations involving methane–oxygen have been conducted to identify the mechanisms that contribute to irregular detonation propagation. Of particular interest was to determine the mechanisms leading to the formation of unburned pockets of reactive fuel in the wake of an irregular detonation, and how the burning of these pockets influence the overall cell pattern, size and structure during propagation. Furthermore, the burning rate on the surface of such pockets was determined through both experiment and simulation to be of the order of
![]() ${\sim}60{-}120~\text{m}~\text{s}^{-1}$
(
${\sim}60{-}120~\text{m}~\text{s}^{-1}$
(
![]() $S_{t}/S_{L}\approx 3.7{-}7.3$
), and was found to vary proportionally to the local turbulence intensity. To this effect, experiments provided a general qualitative insight into the role of turbulent mixing on the propagation characteristics, as well as the necessary data, qualitatively and quantitatively, to validate the numerical strategy, from which a detailed investigation was carried out.
$S_{t}/S_{L}\approx 3.7{-}7.3$
), and was found to vary proportionally to the local turbulence intensity. To this effect, experiments provided a general qualitative insight into the role of turbulent mixing on the propagation characteristics, as well as the necessary data, qualitatively and quantitatively, to validate the numerical strategy, from which a detailed investigation was carried out.
From experiments, the Richtmyer–Meshkov flow instability, behind triple-point paths, plays a major role in the burning of such pockets. On the other hand, KH instability is believed to contribute only a minor role in such burning. In fact, KH instability growth rates, in the presence of burned and unburned fuel interfaces along slip lines behind triple points, can actually be damped by the decoupling of velocity and thermal gradients in high-activation-energy mixtures (Massa et al.
Reference Massa, Austin and Jackson2007). In general, flow instabilities were found to generate turbulent mixing behind the front of the wave, thus influencing the overall burning rate of the pockets. Furthermore, turbulent motions were found to entrain burned products into regions of shocked and unburned gas, also contributing to the overall burning rate of unburned fuel in the wake. In order to investigate, in detail, how the turbulent mixing rates of these pockets affect the overall propagation characteristics of the wave, in terms of cell pattern and size, irregularity and reaction zone thickness, numerical simulations have been carried out. In order to resolve the small-scale mixing and chemical reactions, which are often very challenging to resolve for flows that are highly compressible, reactive and contain rapid transients in pressure and energy, the compressible linear eddy model for large-eddy simulation (CLEM-LES) is applied. The strategy itself serves as extended work to a previously developed linear eddy model formulation for large-eddy simulation (Menon & Calhoon Reference Menon and Calhoon1996; Chakravarthy & Menon Reference Chakravarthy and Menon2000; Sankaran & Menon Reference Sankaran and Menon2005; Menon & Kerstein Reference Menon and Kerstein2011) whose capabilities were limited to modelling only weakly compressible flows in multiple dimensions. To this effect, the CLEM-LES strategy was validated against experiments accordingly. The major contribution of the current work, in terms of advancing numerical strategies, was to provide adequate closure of the reaction rate term,
![]() $\overline{\dot{\unicode[STIX]{x1D714}}}$
, in (3.3) for modelling and understanding detonation behaviour. In fact, the CLEM-LES was found to qualitatively and quantitatively capture experimental observations conducted in this study, and also Kiyanda & Higgins (Reference Kiyanda and Higgins2013), in terms of detonation cell structure and irregularity.
$\overline{\dot{\unicode[STIX]{x1D714}}}$
, in (3.3) for modelling and understanding detonation behaviour. In fact, the CLEM-LES was found to qualitatively and quantitatively capture experimental observations conducted in this study, and also Kiyanda & Higgins (Reference Kiyanda and Higgins2013), in terms of detonation cell structure and irregularity.
Given the success of CLEM-LES for capturing experimental observations of multi-dimensional detonation propagation, the strategy is promising for gaining insight into the physical influence of turbulent mixing rates on other compressible and reactive problems. For planar detonation propagation in a thin channel, numerical simulations have shown that turbulent mixing rates have significantly influenced the observed cell patterns and detonation structure. Furthermore, for increased levels of turbulence intensity, such turbulent wave fronts were found to favour local velocities below the CJ value. This led to a favouring of much longer ignition delays, compared to ZND theory, for the unburned gas that passed through the front. This, in turn, contributed to the formation of unburned pockets in the wake, thus lengthening the overall hydrodynamic structure. Furthermore, the presence of such unburned pockets was found to give rise to larger and more irregular cell patterns. These findings thus support previous postulates that turbulence gives rise to a large variation of shock-induced ignition delays, and thus the formation of unburned pockets. In the current work, however, the role of turbulence intensity on the resulting cellular flow patterns, structure thickness and irregularity were clarified. All of these qualitative features were found to be significantly altered by the degree of turbulence intensity present.
Finally, in terms of investigation of the role of turbulent mixing itself on highly compressible combustion, it remains an open question why the optimum
![]() $C_{\unicode[STIX]{x1D705}}$
value to match experiments is higher than theory predicts for incompressible three-dimensional Kolmogorov turbulence. It is possible that the predominant two-dimensional nature of the simulated flow field generates more backscatter, resulting in less subgrid kinetic energy generated at smaller scales. Furthermore, the compressible nature of the phenomena investigated probably generates backscatter through amplification of pressure waves that originate from reactive events, which thus feed into larger low-frequency fluid motions (Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). Thus, compressible problems may inherently require a higher
$C_{\unicode[STIX]{x1D705}}$
value to match experiments is higher than theory predicts for incompressible three-dimensional Kolmogorov turbulence. It is possible that the predominant two-dimensional nature of the simulated flow field generates more backscatter, resulting in less subgrid kinetic energy generated at smaller scales. Furthermore, the compressible nature of the phenomena investigated probably generates backscatter through amplification of pressure waves that originate from reactive events, which thus feed into larger low-frequency fluid motions (Radulescu et al.
Reference Radulescu, Sharpe, Lee, Kiyanda, Higgins and Hanson2005). Thus, compressible problems may inherently require a higher
![]() $C_{\unicode[STIX]{x1D705}}$
value. This should be investigated in future work.
$C_{\unicode[STIX]{x1D705}}$
value. This should be investigated in future work.
Acknowledgements
Funding for the work presented in this paper has been provided by the Ontario Ministry of Training, Colleges and Universities via an Ontario Graduate Scholarship, a CFD Society of Canada Graduate Scholarship, and NSERC through an Alexander Graham Bell Scholarship, the Discovery Grant, and the H2Can strategic network. Further acknowledgement is given to A. Pekalski from Shell for financial support in the later stages of the project. Finally, two academic visits to the University of Leeds, UK, were made possible through additional funding from the University of Ottawa Mobility Scholarship, NSERC Michael Smith Foreign Study Supplement, and also the H2Can strategic network.