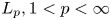1. Introduction
We consider the following eigenvalue problem
where ![]() $\lambda \in \mathbb {C}\,$ is a spectral parameter,
$\lambda \in \mathbb {C}\,$ is a spectral parameter, ![]() $Ty \equiv y''' - qy'$,
$Ty \equiv y''' - qy'$, ![]() $q(x)$ is a positive absolutely continuous function on
$q(x)$ is a positive absolutely continuous function on ![]() $[0,1]$,
$[0,1]$, ![]() $a, c$ and
$a, c$ and ![]() $\gamma$ are real constants such that
$\gamma$ are real constants such that ![]() $a < 0$,
$a < 0$, ![]() $c < 0$ and
$c < 0$ and ![]() $\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$.
$\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$.
The study of spectral problems for ordinary differential equations with boundary conditions depending on the spectral parameter has a long history which is well reflected in [Reference Aliyev and Namazov10, Reference Courant and Hilbert21]. Problems of this type arise when solving various specific problems of mechanics, physics and mathematical physics. The eigenvalue problem (1.1)–(1.5) describes the bending vibrations of a homogeneous rod, in cross-sections of which the longitudinal force acts, on the left end of which a mass is concentrated. Moreover, the right end of the rod is fixed elastically by a spring that prevents it from turning (the case of ![]() $\gamma \in ( {0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}} ))$, and on this end a tracking force acts (see [Reference Binding, Browne and Watson19, pp. 152–154]).
$\gamma \in ( {0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}} ))$, and on this end a tracking force acts (see [Reference Binding, Browne and Watson19, pp. 152–154]).
The general theory of spectral problems for ordinary differential equations with polynomial occurrence of the spectral parameter in the equations and boundary conditions was constructed in [Reference Schneider38] and [Reference Shkalikov39]. In these papers, various classes of boundary value problems (normal, regular and strongly regular) were distinguished, and spaces ![]() $W_{2,U}^{r} \oplus \mathbb {C}^{N_r}$ were constructed in which these problems admit natural linearization. For strongly regular problems, in [Reference Schneider38] the Riesz basis property (after normalization) of the system of eigenvectors and associated vectors of linearizing operators in the space
$W_{2,U}^{r} \oplus \mathbb {C}^{N_r}$ were constructed in which these problems admit natural linearization. For strongly regular problems, in [Reference Schneider38] the Riesz basis property (after normalization) of the system of eigenvectors and associated vectors of linearizing operators in the space ![]() $W_{2,U}^{r} \oplus \mathbb {C}^{N_r}$ was established, and in [Reference Shkalikov39] a condition was found under which the system of eigen- and associated functions of the original problem form a defective Riesz basis (with a finite number of defects) in space
$W_{2,U}^{r} \oplus \mathbb {C}^{N_r}$ was established, and in [Reference Shkalikov39] a condition was found under which the system of eigen- and associated functions of the original problem form a defective Riesz basis (with a finite number of defects) in space ![]() $W_2^{r}$.
$W_2^{r}$.
Oscillatory properties of eigenfunctions and basis properties in various functional spaces of root functions of Sturm-Liouville problems with a spectral parameter in the boundary conditions were investigated in [Reference Aliyev1, Reference Aliev3, Reference Aliev4, Reference Aliyev and Namazov11, Reference Banks and Kurowski15–Reference Binding, Browne and Watson18, Reference Courant and Hilbert21, Reference Gao and Ran24, Reference Ilin26–Reference Kapustin28, Reference Kerimov and Aliev31, Reference Möller and Zinsou34, Reference Naimark36–Reference Schneider38, Reference Tretter40]. These properties of the root functions of eigenvalue problems for ordinary differential equations of the fourth order, one of the boundary conditions of which depends on the spectral parameter, were studied in detail in [Reference Aliyev2, Reference Altinisik, Kadakal and Mukhtarov12, Reference Ben Amara and Vladimirov13, Reference Fulton22, Reference Gao, Li and Ma23, Reference Kapustin and Moiseev29, Reference Kerimov and Aliev30, Reference Kerimov and Poladov32, Reference Mekhrabov33, Reference Shkalikov39]. In the case when two of the boundary conditions contain a spectral parameter, these problems were studied in [Reference Aliev and Dunyamalieva5, Reference Aliyev and Guliyeva6, Reference Aliyev and Mamedova9, Reference Aliyev and Namazov10, Reference Kerimov and Poladov32], and when three of the boundary conditions contain a spectral parameter, they were studied in [Reference Aliyev, Kerimov and Mekhrabov8]. The problems studied in these works describe bending vibrations of a rod, the left end of which is either fixed or at this end a load is concentrated or a tracking force acts, and at the right end an inertial load is concentrated (the tracking force can also act at this end) (see. [Reference Binding, Browne and Watson19, Ch. 8, § 5]). In [Reference Aliyev, Kerimov and Mekhrabov7], the authors establish conditions under which the Fourier series expansions of continuous functions in the system of eigenfunctions of the problem converge uniformly.
The aim of this work is to study the position of the eigenvalues on the real axis, the structure of root subspaces, and the oscillatory properties of the eigenfunctions, and also to obtain asymptotic formulas for the eigenvalues and eigenfunctions of problem (1.1)–(1.5). Moreover, using these properties and the operator interpretation of this problem, we establish sufficient conditions for the subsystems of root functions to form a basis in the space ![]() $L_p, \, 1 < p < \infty$. It should be noted that the results of this paper will allow us in the future to investigate the eigenvalue problem for the equation (1.1) with boundary conditions, three of which depend on the spectral parameter.
$L_p, \, 1 < p < \infty$. It should be noted that the results of this paper will allow us in the future to investigate the eigenvalue problem for the equation (1.1) with boundary conditions, three of which depend on the spectral parameter.
The structure of this paper is as follows. In § 2, we consider the initial-boundary value problem (1.1), (1.2), (1.4), (1.5), in contrast to [Reference Ben Amara and Vladimirov14] where initial-boundary value problem (1.1)–(1.4) is considered for ![]() $\gamma = {{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}}$. This is due to the fact that great difficulties arise in the study of the oscillatory properties of the solution to the problem (1.1)–(1.4) for
$\gamma = {{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}}$. This is due to the fact that great difficulties arise in the study of the oscillatory properties of the solution to the problem (1.1)–(1.4) for ![]() $\lambda < 0$. Here we show the existence and uniqueness of a solution of problem (1.1), (1.2), (1.4), (1.5) for each
$\lambda < 0$. Here we show the existence and uniqueness of a solution of problem (1.1), (1.2), (1.4), (1.5) for each ![]() $\lambda \in \mathbb {C}$, and investigate some properties of this solution, including its oscillatory properties depending on the parameter
$\lambda \in \mathbb {C}$, and investigate some properties of this solution, including its oscillatory properties depending on the parameter ![]() $\lambda \in \mathbb {R}$. In § 3, we study the location of the eigenvalues on the real axis, the structure of root subspaces and the oscillation properties of the eigenfunctions corresponding to both positive and negative eigenvalues of problem (1.1)–(1.5). In § 4, using the oscillatory properties of the eigenfunctions, we find asymptotic formulas for the eigenvalues and eigenfunctions of the considered problem. In § 5, problem (1.1)–(1.5) is reduced to the eigenvalue problem for a some nonself-adjoint operator in a Hilbert space
$\lambda \in \mathbb {R}$. In § 3, we study the location of the eigenvalues on the real axis, the structure of root subspaces and the oscillation properties of the eigenfunctions corresponding to both positive and negative eigenvalues of problem (1.1)–(1.5). In § 4, using the oscillatory properties of the eigenfunctions, we find asymptotic formulas for the eigenvalues and eigenfunctions of the considered problem. In § 5, problem (1.1)–(1.5) is reduced to the eigenvalue problem for a some nonself-adjoint operator in a Hilbert space ![]() $H = L_2 (0, 1) \oplus {\mathbb {C}}^{2}$ with corresponding scalar product. This operator is
$H = L_2 (0, 1) \oplus {\mathbb {C}}^{2}$ with corresponding scalar product. This operator is ![]() $J$ -self-adjoint in the Pontryagin space
$J$ -self-adjoint in the Pontryagin space ![]() $\Pi _1 = L_2 (0, 1) \,\oplus \,{\mathbb {C}}^{2}$ with the corresponding inner product, and the system of its root vectors forms an unconditional basis in
$\Pi _1 = L_2 (0, 1) \,\oplus \,{\mathbb {C}}^{2}$ with the corresponding inner product, and the system of its root vectors forms an unconditional basis in ![]() $H$. We also find the system adjoint to the system of root vectors of this operator. Next, with the use of these results and oscillatory properties of eigenfunctions we establish sufficient conditions for the system of root functions of problem (1.1)–(1.5) to form a basis in the space
$H$. We also find the system adjoint to the system of root vectors of this operator. Next, with the use of these results and oscillatory properties of eigenfunctions we establish sufficient conditions for the system of root functions of problem (1.1)–(1.5) to form a basis in the space ![]() $L_p(0, 1), 1 < p < \infty$ after removing two functions.
$L_p(0, 1), 1 < p < \infty$ after removing two functions.
2. The existence and main properties of the solution of problem (1.1), (1.2), (1.4), (1.5)
We consider the boundary condition
Alongside the problem (1.1)–(1.5) we also consider the eigenvalue problem (1.1), (1.2), (2.1), (1.4), (1.5). The spectral properties of this problem in a more general form of boundary conditions were investigated in [Reference Kapustin and Moiseev29, Reference Kerimov and Aliev30].
It follows from [Reference Kerimov and Aliev30, lemma 2.2 and theorem 2.2] that the following result holds for this problem.
Theorem 2.1 For each ![]() $\beta$ and each
$\beta$ and each ![]() $\gamma$ the eigenvalues of the boundary value problem (1.1), (1.2), (2.1), (1.4), (1.5) are real and simple, and form an unbounded increasing sequence
$\gamma$ the eigenvalues of the boundary value problem (1.1), (1.2), (2.1), (1.4), (1.5) are real and simple, and form an unbounded increasing sequence ![]() $\{\lambda _{k} (\beta ,\gamma )\}_{k=1}^{\infty }$ such that
$\{\lambda _{k} (\beta ,\gamma )\}_{k=1}^{\infty }$ such that
and
Moreover, the eigenfunction ![]() $y_{k,\beta , \,\gamma } (x)$,
$y_{k,\beta , \,\gamma } (x)$, ![]() $k \in \mathbb {N}$, corresponding to the eigenvalue
$k \in \mathbb {N}$, corresponding to the eigenvalue ![]() $\lambda _k (\beta , \gamma )$ has
$\lambda _k (\beta , \gamma )$ has ![]() $k - 1$ simple zeros in the interval
$k - 1$ simple zeros in the interval ![]() $(0, 1)$.
$(0, 1)$.
Let ![]() $\tilde H = L_2 (0,1) \oplus \mathbb {C}$ be the Hilbert space with the scalar product
$\tilde H = L_2 (0,1) \oplus \mathbb {C}$ be the Hilbert space with the scalar product
As is known [Reference Aliyev2] that problem (1.1), (1.2), (2.1), (1.4), (1.5) is equivalent the following eigenvalue problem
where ![]() $L$ is a self-adjoint bounded below operator in
$L$ is a self-adjoint bounded below operator in ![]() $\tilde H$ defined by
$\tilde H$ defined by
with the domain
 \begin{align*} &D (\tilde L ) = \left\{ {\tilde y = \{y,n\} \in \tilde H : y \in W_2^{4} (0,1),\ell y \in L_2 (0,1), y''(0) = 0,}\right.\\ &\left.{y (0) \cos \beta + T y(0) \sin \beta = y (1) \cos \gamma + y''(1) \sin \gamma = 0,n = c y (1)}\right \}. \end{align*}
\begin{align*} &D (\tilde L ) = \left\{ {\tilde y = \{y,n\} \in \tilde H : y \in W_2^{4} (0,1),\ell y \in L_2 (0,1), y''(0) = 0,}\right.\\ &\left.{y (0) \cos \beta + T y(0) \sin \beta = y (1) \cos \gamma + y''(1) \sin \gamma = 0,n = c y (1)}\right \}. \end{align*}It is known that the eigenvalues of problem (2.2) are given by the max-min principle [Reference Bolotin20]
where ![]() $R\,[\tilde y]$ is the Rayleigh quotient
$R\,[\tilde y]$ is the Rayleigh quotient
 \begin{align*} R\,[\tilde y] &= \frac{(\tilde L \tilde y, \tilde y)}{(\tilde y, \tilde y)} = \frac {\int_0^{1} {\left( {y''^{2} (x) + q(x)y'^{2} (x)} \right)}\,\textrm{d}x + N[y] }{\int_0^{1} {y^{2} (x)\,\textrm{d}x - cy^{2} (1)}}, \\
N [y] &= y^{2} (0) \cot \beta + y'^{2} (1) \cot \gamma, \end{align*}
\begin{align*} R\,[\tilde y] &= \frac{(\tilde L \tilde y, \tilde y)}{(\tilde y, \tilde y)} = \frac {\int_0^{1} {\left( {y''^{2} (x) + q(x)y'^{2} (x)} \right)}\,\textrm{d}x + N[y] }{\int_0^{1} {y^{2} (x)\,\textrm{d}x - cy^{2} (1)}}, \\
N [y] &= y^{2} (0) \cot \beta + y'^{2} (1) \cot \gamma, \end{align*}
(we use the convention that if any of the parameters ![]() $\beta$ or
$\beta$ or ![]() $\gamma$ is zero, then the boundary value of
$\gamma$ is zero, then the boundary value of ![]() $y$ at
$y$ at ![]() $0$ or
$0$ or ![]() $y'$ at
$y'$ at ![]() $1$ is taken to be zero and the corresponding term in
$1$ is taken to be zero and the corresponding term in ![]() $N [y]$ does not appear),
$N [y]$ does not appear), ![]() $\mathfrak {L}$ is the set of vectors
$\mathfrak {L}$ is the set of vectors ![]() $\tilde y = \{y,n\} \in \tilde H$ such that the function
$\tilde y = \{y,n\} \in \tilde H$ such that the function ![]() $y$ satisfies the boundary conditions (1.2), (2.1), (1.4),
$y$ satisfies the boundary conditions (1.2), (2.1), (1.4), ![]() $\tilde V^{(k-1)}$ is an arbitrary set of linearly independent vectors
$\tilde V^{(k-1)}$ is an arbitrary set of linearly independent vectors ![]() $\tilde v_j = \{v_j,t_j\}$,
$\tilde v_j = \{v_j,t_j\}$, ![]() $1 \le j \le k-1$, such that the functions
$1 \le j \le k-1$, such that the functions ![]() $v_j$,
$v_j$, ![]() $1 \le j \le k-1$, satisfy the boundary conditions (1.2), (2.1), (1.4).
$1 \le j \le k-1$, satisfy the boundary conditions (1.2), (2.1), (1.4).
Using this max-min characterization, by following the argument in theorem 9 of [Reference Bolotin20, p. 419] for eigenvalues of (1.1), (1.2), (2.1), (1.4), (1.5) we have the following property.
Lemma 2.2 The eigenvalues of problem (1.1), (1.2), (2.1), (1.4), (1.5) are continuous, strictly decreasing functions of ![]() $\beta$ and
$\beta$ and ![]() $\gamma$ for
$\gamma$ for ![]() $\beta ,\gamma \in [0, {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$.
$\beta ,\gamma \in [0, {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$.
By virtue of theorem 2.1 and lemma 2.2 for each ![]() $\gamma \in [0, {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ we have
$\gamma \in [0, {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ we have
Theorem 2.3 For each fixed ![]() $\lambda \in \mathbb {C}$ there exists a nontrivial solution
$\lambda \in \mathbb {C}$ there exists a nontrivial solution ![]() $y(x, \lambda )$ of (1.1), (1.2), (1.4), (1.5) which is unique up to a constant coefficient.
$y(x, \lambda )$ of (1.1), (1.2), (1.4), (1.5) which is unique up to a constant coefficient.
Proof. Let ![]() $\psi _{k} (x, \lambda ), k = 1,2,3,4$, denote the solutions of equation (1.1) normalized for
$\psi _{k} (x, \lambda ), k = 1,2,3,4$, denote the solutions of equation (1.1) normalized for ![]() $x = 1$ by the Cauchy conditions
$x = 1$ by the Cauchy conditions
where ![]() $\delta _{ks}$ is the Kronecker delta.
$\delta _{ks}$ is the Kronecker delta.
As in [Reference Aliyev, Kerimov and Mekhrabov8, Reference Mekhrabov33], we will seek the solution ![]() $y (x, \lambda )$ of (1.1), (1.2), (1.4), (1.5) in the form
$y (x, \lambda )$ of (1.1), (1.2), (1.4), (1.5) in the form
 \begin{equation} y (x,\lambda ) = \sum \limits_{k = 1}^{4} {A_k } \psi _k (x,\lambda), \end{equation}
\begin{equation} y (x,\lambda ) = \sum \limits_{k = 1}^{4} {A_k } \psi _k (x,\lambda), \end{equation}
where ![]() $A_{k}, \,k = 1, \,2,3,4$, are some constants.
$A_{k}, \,k = 1, \,2,3,4$, are some constants.
By (1.4), (1.5) and (2.4) it follows from (2.5) that ![]() $A_2 \cos \gamma + A_3 \sin \gamma = 0$,
$A_2 \cos \gamma + A_3 \sin \gamma = 0$, ![]() $A_4 - c \lambda A_1 = 0$. Consequently, for the function
$A_4 - c \lambda A_1 = 0$. Consequently, for the function ![]() $y (x, \lambda )$ we have
$y (x, \lambda )$ we have
 \begin{equation}
y(x,\lambda ) = \begin{cases}
A_1 \left\{{\psi_1
(x,\lambda) + c \lambda \psi_4 (x,\lambda)}\right\} + A_3
\,\psi_3 (x,\lambda) \quad \textrm{if}\ \gamma = 0, \\
A_1
\left\{{\psi_1 (x,\lambda) + c \lambda \psi_4
(x,\lambda)}\right\}\\
\quad + A_2 \{\psi_2
(x,\lambda) - \psi_3 (x,\lambda)\,\cot \gamma\}
\quad \textrm{if}\, \gamma \in (0,{\pi /2}].
\end{cases}
\end{equation}
\begin{equation}
y(x,\lambda ) = \begin{cases}
A_1 \left\{{\psi_1
(x,\lambda) + c \lambda \psi_4 (x,\lambda)}\right\} + A_3
\,\psi_3 (x,\lambda) \quad \textrm{if}\ \gamma = 0, \\
A_1
\left\{{\psi_1 (x,\lambda) + c \lambda \psi_4
(x,\lambda)}\right\}\\
\quad + A_2 \{\psi_2
(x,\lambda) - \psi_3 (x,\lambda)\,\cot \gamma\}
\quad \textrm{if}\, \gamma \in (0,{\pi /2}].
\end{cases}
\end{equation}For brevity, we use the following notations:
 \begin{align} C_1 (\lambda) &= \psi''_1 (0,\lambda ) + c \lambda \psi''_4 (0,\lambda ),\notag\\ C_2 (\lambda ) &= \begin{cases}\psi''_3 (0,\lambda ) & \textrm{if}\ \gamma = 0, \\ \psi ''_2 (0,\lambda ) - \psi ''_3 \,(0,\lambda )\cot \gamma & \textrm{if} \ \gamma \in (0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}]. \end{cases} \end{align}
\begin{align} C_1 (\lambda) &= \psi''_1 (0,\lambda ) + c \lambda \psi''_4 (0,\lambda ),\notag\\ C_2 (\lambda ) &= \begin{cases}\psi''_3 (0,\lambda ) & \textrm{if}\ \gamma = 0, \\ \psi ''_2 (0,\lambda ) - \psi ''_3 \,(0,\lambda )\cot \gamma & \textrm{if} \ \gamma \in (0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}]. \end{cases} \end{align} It can be seen from (2.7) that to complete the proof of theorem it suffices to show that for each ![]() $\lambda \in \mathbb {C}$ the relation
$\lambda \in \mathbb {C}$ the relation
holds.
If ![]() $\lambda > 0$, then by the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we get
$\lambda > 0$, then by the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we get
 \begin{equation}
\begin{aligned}\psi_1 (0,\lambda) > 0, \,\psi'_1
(0,\lambda) < 0, \,\psi''_1 (0,\lambda ) > 0, \,T \psi_1
(0,\lambda) < 0,\\ \psi_2 (0,\lambda) < 0, \,\psi'_2
(0,\lambda) > 0, \,\psi''_2 (0,\lambda ) < 0, \,T \psi_2
(0,\lambda) > 0,\\ \psi_3 (0,\lambda) > 0, \,\psi'_3
(0,\lambda) < 0, \,\psi''_3 (0,\lambda ) > 0, \,T \psi_3
(0,\lambda) < 0,\\ \psi_4 (0,\lambda) < 0, \,\psi'_4
(0,\lambda) > 0, \,\psi''_4 (0,\lambda ) < 0, \,T \psi_4
(0,\lambda) > 0.\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}\psi_1 (0,\lambda) > 0, \,\psi'_1
(0,\lambda) < 0, \,\psi''_1 (0,\lambda ) > 0, \,T \psi_1
(0,\lambda) < 0,\\ \psi_2 (0,\lambda) < 0, \,\psi'_2
(0,\lambda) > 0, \,\psi''_2 (0,\lambda ) < 0, \,T \psi_2
(0,\lambda) > 0,\\ \psi_3 (0,\lambda) > 0, \,\psi'_3
(0,\lambda) < 0, \,\psi''_3 (0,\lambda ) > 0, \,T \psi_3
(0,\lambda) < 0,\\ \psi_4 (0,\lambda) < 0, \,\psi'_4
(0,\lambda) > 0, \,\psi''_4 (0,\lambda ) < 0, \,T \psi_4
(0,\lambda) > 0.\end{aligned}
\end{equation}
Indeed, by (1.1) and (2.4) for the function ![]() $\psi _1 (x,\lambda )$ we have
$\psi _1 (x,\lambda )$ we have
which implies that there exists ![]() $(T \psi _1)' (1,\lambda ) = \lambda > 0$. Consequently, there exists
$(T \psi _1)' (1,\lambda ) = \lambda > 0$. Consequently, there exists ![]() $\psi _1^{(4)} (1,\lambda ) = (T \psi _1)' (1,\lambda ) + q(1) \psi ''_1 (1,\lambda ) + q'(1) \psi '_1 (1,\lambda ) = (T \psi _1)' (1,\lambda ) > 0$. Hence
$\psi _1^{(4)} (1,\lambda ) = (T \psi _1)' (1,\lambda ) + q(1) \psi ''_1 (1,\lambda ) + q'(1) \psi '_1 (1,\lambda ) = (T \psi _1)' (1,\lambda ) > 0$. Hence ![]() $T \psi _1 (x,\lambda ) < 0$ and
$T \psi _1 (x,\lambda ) < 0$ and ![]() $\psi '''_1 (x,\lambda ) < 0$ in a sufficiently small left punctured neighbourhood
$\psi '''_1 (x,\lambda ) < 0$ in a sufficiently small left punctured neighbourhood ![]() $V_1^{-}$ of the point
$V_1^{-}$ of the point ![]() $x = 1$. Since
$x = 1$. Since ![]() $x = 1$ is a triple zero of the function
$x = 1$ is a triple zero of the function ![]() $\psi _1' (x,\lambda )$ it follows that
$\psi _1' (x,\lambda )$ it follows that ![]() $\psi _1'' (x,\lambda ) > 0$,
$\psi _1'' (x,\lambda ) > 0$, ![]() $\psi _1' (x,\lambda ) < 0$ for
$\psi _1' (x,\lambda ) < 0$ for ![]() $x \in V_1^{-}$. Moreover,
$x \in V_1^{-}$. Moreover, ![]() $\psi _1 (x,\lambda ) > 0$ for
$\psi _1 (x,\lambda ) > 0$ for ![]() $x \in V_1^{-}$. Then it follows from the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] that
$x \in V_1^{-}$. Then it follows from the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] that ![]() $\psi _1 (0,\lambda ) > 0$,
$\psi _1 (0,\lambda ) > 0$, ![]() $\psi '_1 (0,\lambda ) < 0$,
$\psi '_1 (0,\lambda ) < 0$, ![]() $\psi ''_1 (0,\lambda ) > 0$,
$\psi ''_1 (0,\lambda ) > 0$, ![]() $T \psi _1 (0,\lambda ) < 0$. The remaining relations in (2.10) for the functions
$T \psi _1 (0,\lambda ) < 0$. The remaining relations in (2.10) for the functions ![]() $\psi _2 (x,\lambda )$,
$\psi _2 (x,\lambda )$, ![]() $\psi _3 (x,\lambda )$ and
$\psi _3 (x,\lambda )$ and ![]() $\psi _4 (x,\lambda )$ are proved similarly.
$\psi _4 (x,\lambda )$ are proved similarly.
Let ![]() $\lambda > 0$. Then, in view of
$\lambda > 0$. Then, in view of ![]() $c < 0$, by (2.8) we have
$c < 0$, by (2.8) we have ![]() $C_1 (\lambda ) = \psi ''_1 (0,\lambda ) + c \lambda \psi ''_4 (0,\lambda ) > 0$, and consequently, (2.9) holds.
$C_1 (\lambda ) = \psi ''_1 (0,\lambda ) + c \lambda \psi ''_4 (0,\lambda ) > 0$, and consequently, (2.9) holds.
Now let ![]() $\lambda \in \mathbb {C} \,\backslash ({\,0, + \infty })$. If (2.8) fails for some such
$\lambda \in \mathbb {C} \,\backslash ({\,0, + \infty })$. If (2.8) fails for some such ![]() $\lambda$, then
$\lambda$, then ![]() $C_1 (\lambda ) = C_2 (\lambda ) = 0$. Hence the functions
$C_1 (\lambda ) = C_2 (\lambda ) = 0$. Hence the functions ![]() $\psi _1 (x,\lambda ) + c \lambda \psi _4 (x,\lambda )$ and
$\psi _1 (x,\lambda ) + c \lambda \psi _4 (x,\lambda )$ and ![]() $\psi _3 (x,\lambda )$ for
$\psi _3 (x,\lambda )$ for ![]() $\gamma = 0$,
$\gamma = 0$, ![]() $\psi _2 (x,\lambda ) - \psi _3 (x,\lambda ) \cot \gamma$ for
$\psi _2 (x,\lambda ) - \psi _3 (x,\lambda ) \cot \gamma$ for ![]() $\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ are solutions of problem (1.1), (1.2), (1.4), (1.5) for such
$\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ are solutions of problem (1.1), (1.2), (1.4), (1.5) for such ![]() $\lambda$. We consider the function
$\lambda$. We consider the function ![]() $u (x,\lambda )$ which is defined as follows:
$u (x,\lambda )$ which is defined as follows:
 \[ u\,(x,\lambda ) =
\begin{cases}
\psi_3 (0,\lambda) \left(
{\psi_1 (x,\lambda) + c \lambda \psi_4 (x,\lambda)} \right)
- \left( {\psi_1 (0,\lambda) + c \lambda \psi_4
(0,\lambda)} \right)\\
\psi_3 (x,\lambda)
\ \textrm{for}\ \gamma = 0,\\
\left({\psi_2
\,(0,\lambda ) - \psi_3 \,(0,\lambda ) \cot \gamma}\right)
\left( {\psi_1 (x,\lambda) + c \lambda \psi_4 (x,\lambda)}
\right)\\
\quad - \left( {\psi_1 (0,\lambda) + c \lambda \psi_4
(0,\lambda)} \right) \\ \left({\psi_2 \,(x,\lambda )
- \psi_3 \,(x,\lambda ) \cot \gamma}\right)
\ \textrm{for}\ \gamma \in (0,{\pi \mathord{\left/
{\vphantom {\pi 2}} \right. } 2}].
\end{cases}\]
\[ u\,(x,\lambda ) =
\begin{cases}
\psi_3 (0,\lambda) \left(
{\psi_1 (x,\lambda) + c \lambda \psi_4 (x,\lambda)} \right)
- \left( {\psi_1 (0,\lambda) + c \lambda \psi_4
(0,\lambda)} \right)\\
\psi_3 (x,\lambda)
\ \textrm{for}\ \gamma = 0,\\
\left({\psi_2
\,(0,\lambda ) - \psi_3 \,(0,\lambda ) \cot \gamma}\right)
\left( {\psi_1 (x,\lambda) + c \lambda \psi_4 (x,\lambda)}
\right)\\
\quad - \left( {\psi_1 (0,\lambda) + c \lambda \psi_4
(0,\lambda)} \right) \\ \left({\psi_2 \,(x,\lambda )
- \psi_3 \,(x,\lambda ) \cot \gamma}\right)
\ \textrm{for}\ \gamma \in (0,{\pi \mathord{\left/
{\vphantom {\pi 2}} \right. } 2}].
\end{cases}\]
Note that ![]() $u (0, \lambda ) = 0$. Hence the function
$u (0, \lambda ) = 0$. Hence the function ![]() $u (x, \lambda )$ is an eigenfunction of the eigenvalue problem (1.1), (1.2), (2.1), (1.4), (1.5) for
$u (x, \lambda )$ is an eigenfunction of the eigenvalue problem (1.1), (1.2), (2.1), (1.4), (1.5) for ![]() $\beta = 0$ and
$\beta = 0$ and ![]() $\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$. Then by theorem 2.1 we have
$\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$. Then by theorem 2.1 we have ![]() $\lambda > 0$ which contradicts the condition
$\lambda > 0$ which contradicts the condition ![]() $\lambda \in \mathbb {C} \, \backslash ({\,0, + \infty })$. The proof of this theorem is complete.
$\lambda \in \mathbb {C} \, \backslash ({\,0, + \infty })$. The proof of this theorem is complete.
Remark 2.4 By (2.6)–(2.8), for each ![]() $\lambda \in \mathbb {C}$ the nontrivial solutions
$\lambda \in \mathbb {C}$ the nontrivial solutions ![]() $y (x,\lambda )$ of problem (1.1), (1.2), (1.4), (1.5) are nonzero multiples of
$y (x,\lambda )$ of problem (1.1), (1.2), (1.4), (1.5) are nonzero multiples of
 \begin{align} v (x,\lambda) &= C_2 (\lambda) \left\{{\psi_1 (x,\lambda) + c \lambda \psi_4 (x,\lambda)}\right\}\notag\\ &\quad - C_1 (\lambda) \left\{{ \textrm{sgn} \gamma \, \psi_2 (x,\lambda) - ({-}1)^{1- \textrm{sgn} \gamma} \left({1 + \textrm{sgn} \gamma \, (\cot \gamma - 1) }\right) \,\psi_3 (x,\lambda) }\right\}. \end{align}
\begin{align} v (x,\lambda) &= C_2 (\lambda) \left\{{\psi_1 (x,\lambda) + c \lambda \psi_4 (x,\lambda)}\right\}\notag\\ &\quad - C_1 (\lambda) \left\{{ \textrm{sgn} \gamma \, \psi_2 (x,\lambda) - ({-}1)^{1- \textrm{sgn} \gamma} \left({1 + \textrm{sgn} \gamma \, (\cot \gamma - 1) }\right) \,\psi_3 (x,\lambda) }\right\}. \end{align} As is known (see [Reference Naimark35, Ch. 1, § 2.1]) that for each fixed ![]() $x \in [0,1]$ the functions
$x \in [0,1]$ the functions ![]() $\psi _{k} (x, \lambda )$,
$\psi _{k} (x, \lambda )$, ![]() $k = 1,2,3,4$, and their derivatives are entire functions of
$k = 1,2,3,4$, and their derivatives are entire functions of ![]() $\lambda$, and consequently,
$\lambda$, and consequently, ![]() $v (x,\lambda )$ is also an entire function of
$v (x,\lambda )$ is also an entire function of ![]() $\lambda$ for each fixed
$\lambda$ for each fixed ![]() $x \in [0,1]$.
$x \in [0,1]$.
Lemma 2.5 Let ![]() $y(x, \lambda )$,
$y(x, \lambda )$, ![]() $\lambda \in \mathbb {C}$, be nontrivial solutions of problem (1.1), (1.2), (1.4), (1.5). Then
$\lambda \in \mathbb {C}$, be nontrivial solutions of problem (1.1), (1.2), (1.4), (1.5). Then ![]() $y(1, \lambda ) \ne 0$ for
$y(1, \lambda ) \ne 0$ for ![]() $\lambda > 0$ and
$\lambda > 0$ and ![]() $y(0, \lambda ) \ne 0$ for
$y(0, \lambda ) \ne 0$ for ![]() $\lambda \le 0$.
$\lambda \le 0$.
Proof. If ![]() $y (1,\lambda ) = 0$ for some
$y (1,\lambda ) = 0$ for some ![]() $\lambda > 0$, then from (1.5) we get
$\lambda > 0$, then from (1.5) we get ![]() $T y (1,\lambda ) = 0$. Since
$T y (1,\lambda ) = 0$. Since ![]() $\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ it follows from (1.4) that
$\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ it follows from (1.4) that ![]() $y'(1,\lambda ) y''(1,\lambda ) \le 0$. Then by the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we have
$y'(1,\lambda ) y''(1,\lambda ) \le 0$. Then by the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we have ![]() $y' (0,\lambda ) \, y'' (0,\lambda ) < 0$ which contradicts the condition (1.2).
$y' (0,\lambda ) \, y'' (0,\lambda ) < 0$ which contradicts the condition (1.2).
If ![]() $y (0,\lambda ) = 0$ for some
$y (0,\lambda ) = 0$ for some ![]() $\lambda \le 0$, then
$\lambda \le 0$, then ![]() $y (x,\lambda )$ is an eigenfunction of problem (1.1), (1.2), (2.1), (1.4), (1.5) for
$y (x,\lambda )$ is an eigenfunction of problem (1.1), (1.2), (2.1), (1.4), (1.5) for ![]() $\beta = 0$ and
$\beta = 0$ and ![]() $\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$. Then by theorem 2.1 we have
$\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$. Then by theorem 2.1 we have ![]() $\lambda > 0$ which contradicts the condition
$\lambda > 0$ which contradicts the condition ![]() $\lambda \le 0$. The proof of this lemma is complete.
$\lambda \le 0$. The proof of this lemma is complete.
Now, using lemma 2.5, we can normalize the function ![]() $y(x,\lambda ),x \in [0,1],\lambda \in \mathbb {R}$, as follows:
$y(x,\lambda ),x \in [0,1],\lambda \in \mathbb {R}$, as follows:
if ![]() $\lambda > 0$, and
$\lambda > 0$, and
if ![]() $\lambda \le 0$.
$\lambda \le 0$.
For ![]() $\lambda \in \mathbb {R}$ we consider the following equation
$\lambda \in \mathbb {R}$ we consider the following equation
It is obvious that the zeros of this equation are functions of the parameter ![]() $\lambda$.
$\lambda$.
Lemma 2.6 The zeros of function ![]() $y (x, \lambda )$ contained in the half-open interval
$y (x, \lambda )$ contained in the half-open interval ![]() $[0,1)$ are simple and continuously differentiable functions of
$[0,1)$ are simple and continuously differentiable functions of ![]() $\lambda$,
$\lambda$, ![]() $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.
Proof. Let ![]() $\lambda _0$ be an arbitrary fixed positive number. If
$\lambda _0$ be an arbitrary fixed positive number. If ![]() $y (x_0,\lambda _0) = 0$ for
$y (x_0,\lambda _0) = 0$ for ![]() $x_0 \in (0,1)$, then it follows from [Reference Ben Amara and Vladimirov14, lemma 2.2] that
$x_0 \in (0,1)$, then it follows from [Reference Ben Amara and Vladimirov14, lemma 2.2] that ![]() $y' (x_0,\lambda _0) \ne 0$. If
$y' (x_0,\lambda _0) \ne 0$. If ![]() $y (0,\lambda _0) = y' (0,\lambda _0) = 0$, then in view of (1.2), by the first part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we have
$y (0,\lambda _0) = y' (0,\lambda _0) = 0$, then in view of (1.2), by the first part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we have ![]() $y ' (1,\lambda _0) y '' (1,\lambda _0) > 0$ in contradiction with the boundary condition (1.4).
$y ' (1,\lambda _0) y '' (1,\lambda _0) > 0$ in contradiction with the boundary condition (1.4).
Let ![]() $\lambda _0 \le 0$ and
$\lambda _0 \le 0$ and ![]() $x_0 \in [0, 1)$ such that
$x_0 \in [0, 1)$ such that ![]() $y (x_0,\lambda _0) = y' (x_0,\lambda _0) = 0$. Then
$y (x_0,\lambda _0) = y' (x_0,\lambda _0) = 0$. Then ![]() $y (x,\lambda _0)$ solves the eigenvalue problem defined on
$y (x,\lambda _0)$ solves the eigenvalue problem defined on ![]() $[x_0, 1]$ and determined by equation (1.1) with the boundary conditions
$[x_0, 1]$ and determined by equation (1.1) with the boundary conditions ![]() $y (x_0) = y' (x_0) = 0$ and (1.4), (1.5). By theorem 2.1 the eigenvalues of this problem are simple and positive which contradicts the condition
$y (x_0) = y' (x_0) = 0$ and (1.4), (1.5). By theorem 2.1 the eigenvalues of this problem are simple and positive which contradicts the condition ![]() $\lambda _0 \le 0$.
$\lambda _0 \le 0$.
The continuous differentiability of the zeros contained in ![]() $[0,1)$ of the function
$[0,1)$ of the function ![]() $y (x, \lambda )$ follows from the well-known implicit function theorem, and the proof of this lemma is complete.
$y (x, \lambda )$ follows from the well-known implicit function theorem, and the proof of this lemma is complete.
By lemma 2.5, lemma 2.6 implies the following statement.
Corollary 2.7 As ![]() $\lambda > 0$
$\lambda > 0$ ![]() $(\lambda \le 0)$ varies the function
$(\lambda \le 0)$ varies the function ![]() $y (x,\lambda )$ can lose or gain zeros only by these zeros leaving or entering the interval
$y (x,\lambda )$ can lose or gain zeros only by these zeros leaving or entering the interval ![]() $[0, 1]$ through its endpoint
$[0, 1]$ through its endpoint ![]() $x = 0$
$x = 0$ ![]() $(x = 1)$.
$(x = 1)$.
We consider the function
By theorem 2.3, remark 2.4 and lemma 2.6 the function ![]() $H (x,\lambda )$ is a finite order meromorphic function of
$H (x,\lambda )$ is a finite order meromorphic function of ![]() $\lambda$ for each fixed
$\lambda$ for each fixed ![]() $x \in [\,0,1]$.
$x \in [\,0,1]$.
Let ![]() $\mathcal {D}_k = ( {\lambda _{k - 1} (0,\gamma ),\lambda _k (0,\gamma )} )$,
$\mathcal {D}_k = ( {\lambda _{k - 1} (0,\gamma ),\lambda _k (0,\gamma )} )$, ![]() $k \in \mathbb {N}$, where
$k \in \mathbb {N}$, where ![]() $\lambda _{0} (0,\gamma ) = -\, \infty$.
$\lambda _{0} (0,\gamma ) = -\, \infty$.
Obviously, the function
which is well defined for
 \[ \lambda \in \mathcal{D} \equiv \left( {\mathbb{C}\backslash \mathbb{R}} \right) \cup \left( {\bigcup\limits_{k = 1}^{\infty} {\mathcal{D}_k} } \right) \]
\[ \lambda \in \mathcal{D} \equiv \left( {\mathbb{C}\backslash \mathbb{R}} \right) \cup \left( {\bigcup\limits_{k = 1}^{\infty} {\mathcal{D}_k} } \right) \]
and is a meromorphic function of finite order. The eigenvalues ![]() $\lambda _k (0,\gamma )$ and
$\lambda _k (0,\gamma )$ and ![]() $\lambda _k ( {{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}, \gamma }),k = 1,2,.\,.\,.\,,$ of problem (1.1), (1.2), (2.1), (1.4), (1.5) for
$\lambda _k ( {{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}, \gamma }),k = 1,2,.\,.\,.\,,$ of problem (1.1), (1.2), (2.1), (1.4), (1.5) for ![]() $\beta = 0$ and
$\beta = 0$ and ![]() $\beta = {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}$ are poles and zeros of function
$\beta = {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}$ are poles and zeros of function ![]() $F (\lambda )$, respectively.
$F (\lambda )$, respectively.
Lemma 2.8 For each ![]() $\lambda \in \mathcal {D}$ the relation
$\lambda \in \mathcal {D}$ the relation
holds.
Proof. By virtue of equation (1.1) we have
Integrating equality (2.15) from ![]() $0$ to
$0$ to ![]() $1$, using the formula for the integration by parts and taking boundary conditions (1.2), (1.4) and (1.5) into account we obtain
$1$, using the formula for the integration by parts and taking boundary conditions (1.2), (1.4) and (1.5) into account we obtain
 \begin{align} &-Ty (0, \mu )\,y (0,\lambda ) + T y (0,\lambda )\,y (0,\mu )\notag\\ &\quad =(\mu - \lambda ) \left\{ {\int_0^{1} y(x,\mu )\,y(x,\lambda )\textrm{d}x - c y(1,\mu)\,y(1,\lambda )} \right\}. \end{align}
\begin{align} &-Ty (0, \mu )\,y (0,\lambda ) + T y (0,\lambda )\,y (0,\mu )\notag\\ &\quad =(\mu - \lambda ) \left\{ {\int_0^{1} y(x,\mu )\,y(x,\lambda )\textrm{d}x - c y(1,\mu)\,y(1,\lambda )} \right\}. \end{align}
By (2.16) for ![]() $\mu ,\lambda \in \mathcal {D},\mu \ne \lambda$, we have
$\mu ,\lambda \in \mathcal {D},\mu \ne \lambda$, we have
 \begin{align} &\frac{Ty(0,\mu )}{y(0,\mu)} - \frac{Ty(0,\lambda)}{y(0,\lambda )}\notag\\ &\quad = - (\mu - \lambda) \frac{1} {y(0,\mu)\,y(0,\lambda)} \left\{ {\int_0^{1} {y(x,\mu )y(x,\lambda )\textrm{d}x} - cy(1,\mu )y(1,\lambda )} \right\}. \end{align}
\begin{align} &\frac{Ty(0,\mu )}{y(0,\mu)} - \frac{Ty(0,\lambda)}{y(0,\lambda )}\notag\\ &\quad = - (\mu - \lambda) \frac{1} {y(0,\mu)\,y(0,\lambda)} \left\{ {\int_0^{1} {y(x,\mu )y(x,\lambda )\textrm{d}x} - cy(1,\mu )y(1,\lambda )} \right\}. \end{align}
Dividing both sides of relation (2.17) by ![]() $\mu - \lambda$ (
$\mu - \lambda$ (![]() $\mu \ne \lambda$) and by passing to the limit as
$\mu \ne \lambda$) and by passing to the limit as ![]() $\mu \to \lambda$ we get (2.14). The proof of this lemma is complete.
$\mu \to \lambda$ we get (2.14). The proof of this lemma is complete.
Corollary 2.9 The function ![]() $F (\lambda )$ strictly decreases on each of intervals
$F (\lambda )$ strictly decreases on each of intervals ![]() $\mathcal {D}_k,\ k = 1,2,\ldots\ .$
$\mathcal {D}_k,\ k = 1,2,\ldots\ .$
Lemma 2.10 The following relation holds:
Proof. In equation (1.1) we set ![]() $\lambda = \rho ^{4}$. By theorem 1 of [Reference Mukhtarov and Aydemir35, Ch. II, § 4.5] in each subdomain
$\lambda = \rho ^{4}$. By theorem 1 of [Reference Mukhtarov and Aydemir35, Ch. II, § 4.5] in each subdomain ![]() $\mathcal {T}$ of the complex
$\mathcal {T}$ of the complex ![]() $\rho$-plane this equation has four linearly independent solutions
$\rho$-plane this equation has four linearly independent solutions ![]() $\varphi _{k}(x, \rho ), k = 1,2,3,4$, which are regular with respect to
$\varphi _{k}(x, \rho ), k = 1,2,3,4$, which are regular with respect to ![]() $\rho$ (for sufficiently large
$\rho$ (for sufficiently large ![]() $|\,\rho |$) and satisfying the following relations
$|\,\rho |$) and satisfying the following relations
where ![]() $\omega _{k},k = 1,2,3,4$, are distinct fourth roots of unity.
$\omega _{k},k = 1,2,3,4$, are distinct fourth roots of unity.
Let ![]() $\lambda < 0$. Then, without loss of generality, we can assume that
$\lambda < 0$. Then, without loss of generality, we can assume that ![]() $\rho$ lies on the bisector of the first quadrant, and the numbers
$\rho$ lies on the bisector of the first quadrant, and the numbers ![]() $\omega _{k},k = 1,2,3,4$, are numbered in the following order:
$\omega _{k},k = 1,2,3,4$, are numbered in the following order: ![]() $\omega _1 = - 1$,
$\omega _1 = - 1$, ![]() $\omega _2 = i$,
$\omega _2 = i$, ![]() $\omega _3 = - i$ and
$\omega _3 = - i$ and ![]() $\omega _4 = 1$.
$\omega _4 = 1$.
For brevity, we introduce the notation
Assuming that the initial condition ![]() $y(0, \lambda ) = 1$ is imposed, the unique solution of (1.1), (1.2), (1.4), (1.5) together with the initial condition
$y(0, \lambda ) = 1$ is imposed, the unique solution of (1.1), (1.2), (1.4), (1.5) together with the initial condition ![]() $y(0, \lambda ) = 1$ can be written in the form
$y(0, \lambda ) = 1$ can be written in the form
 \[ y(x, \lambda) = \sum\limits_{k = 1}^{4} {B_k } (\rho )\,\varphi _k (x,\rho ). \]
\[ y(x, \lambda) = \sum\limits_{k = 1}^{4} {B_k } (\rho )\,\varphi _k (x,\rho ). \]
Writing ![]() $B = (B_1,B_2,B_3,B_4)^{T}$, the coefficients
$B = (B_1,B_2,B_3,B_4)^{T}$, the coefficients ![]() $C_k(\rho )$ are solution of the linear algebraic system
$C_k(\rho )$ are solution of the linear algebraic system
where the matrix ![]() $M (\rho )$ is given by
$M (\rho )$ is given by
 \[ M (\rho) = \left( \begin{array}{rrrr}
{[}1] & -[1] & -[1] & [1]\\
-e^{-\rho}[1] & ie^{ i\rho }[1] & -ie^{-i\rho }[1] & e^{\rho}[1] \\
e^{-\rho}[1] & e^{i\rho} [1] & e^{- i\rho} [1] & e^{\rho}[1] \\
{[}1] & [1] & [1] & [1]
\end{array} \right) \]
\[ M (\rho) = \left( \begin{array}{rrrr}
{[}1] & -[1] & -[1] & [1]\\
-e^{-\rho}[1] & ie^{ i\rho }[1] & -ie^{-i\rho }[1] & e^{\rho}[1] \\
e^{-\rho}[1] & e^{i\rho} [1] & e^{- i\rho} [1] & e^{\rho}[1] \\
{[}1] & [1] & [1] & [1]
\end{array} \right) \]
for ![]() $\gamma = 0$, and
$\gamma = 0$, and
 \[
M (\rho) = \left( \begin{array}{rrrr}
{[}1] & -[1] & -[1] & [1]\\
e^{-\rho}[1] & -e^{ i\rho }[1] & -e^{-i\rho}[1] & e^{\rho}[1]\\
e^{-\rho}[1] & e^{i\rho} [1] & e^{- i\rho} [1] & e^{\rho}[1]\\
{[}1] & [1] & [1] & [1]
\end{array} \right) \]
\[
M (\rho) = \left( \begin{array}{rrrr}
{[}1] & -[1] & -[1] & [1]\\
e^{-\rho}[1] & -e^{ i\rho }[1] & -e^{-i\rho}[1] & e^{\rho}[1]\\
e^{-\rho}[1] & e^{i\rho} [1] & e^{- i\rho} [1] & e^{\rho}[1]\\
{[}1] & [1] & [1] & [1]
\end{array} \right) \]
for ![]() $\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2].}}} \right .} {2]}}$.
$\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2].}}} \right .} {2]}}$.
The solution of the system ![]() $M (\rho ) \,B (\rho ) = (0,0,0,1)^{T}$ is
$M (\rho ) \,B (\rho ) = (0,0,0,1)^{T}$ is
 \begin{align*} B_1 (\rho) &=
\frac{1}{2} [1],\quad B_2 (\rho)
={-}\frac{{\,(1+i)\,e^{-\,i\rho}}}{{2 ((1-i) e^{i\rho} -
(1+i)e^{{-}i\rho})}}[1],\\
B_3 (\rho) &= \frac{{(1-i)\,e^{ i\rho}}}{{2 ((1-i) e^{i\rho} - (1+i)e^{{-}i\rho})}}[1],\quad B_4 (\rho) ={-}\frac{2ie^{-\,\rho}}{2 ((1-i) e^{i\rho} - (1+i)e^{{-}i\rho})}[1],
\end{align*}
\begin{align*} B_1 (\rho) &=
\frac{1}{2} [1],\quad B_2 (\rho)
={-}\frac{{\,(1+i)\,e^{-\,i\rho}}}{{2 ((1-i) e^{i\rho} -
(1+i)e^{{-}i\rho})}}[1],\\
B_3 (\rho) &= \frac{{(1-i)\,e^{ i\rho}}}{{2 ((1-i) e^{i\rho} - (1+i)e^{{-}i\rho})}}[1],\quad B_4 (\rho) ={-}\frac{2ie^{-\,\rho}}{2 ((1-i) e^{i\rho} - (1+i)e^{{-}i\rho})}[1],
\end{align*}
if ![]() $\gamma = 0$, and
$\gamma = 0$, and
 \begin{align*} B_1 (\rho) &=
\frac{1}{2} [1],\quad B_2 (\rho) = \frac{{-\,e^{-\,i\rho}}}{{2
(e^{i\rho} - e^{-\,i\rho})}}[1],\\
B_3 (\rho) &= \frac{{\,e^{
i\rho}}}{{2 (e^{i\rho} - e^{-\,i\rho})}}[1],B_4 (\rho) =
\frac{1}{2}\,e^{{-}2\,\rho}[1]. \end{align*}
\begin{align*} B_1 (\rho) &=
\frac{1}{2} [1],\quad B_2 (\rho) = \frac{{-\,e^{-\,i\rho}}}{{2
(e^{i\rho} - e^{-\,i\rho})}}[1],\\
B_3 (\rho) &= \frac{{\,e^{
i\rho}}}{{2 (e^{i\rho} - e^{-\,i\rho})}}[1],B_4 (\rho) =
\frac{1}{2}\,e^{{-}2\,\rho}[1]. \end{align*}
if ![]() $\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2].}}} \right .} {2]}}$. Then for
$\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2].}}} \right .} {2]}}$. Then for ![]() $F (\lambda ) = {{Ty(0,\lambda )} \mathord {\left / {\vphantom {{Ty(0,\lambda )} {y(0,\lambda )}}} \right .} {y(0,\lambda )}}$ we get the following representation
$F (\lambda ) = {{Ty(0,\lambda )} \mathord {\left / {\vphantom {{Ty(0,\lambda )} {y(0,\lambda )}}} \right .} {y(0,\lambda )}}$ we get the following representation
 \begin{equation} \begin{array}{l} F(\lambda) = \{((1\,{-}\,i) e^{i\rho} - (1\,{+}\,i)e^{{-}i\rho}) [1] - (1\,{+}\,i) \, e^{- i\rho } [1] + (1-i) \,e^{i \rho} [1] + 2i e^{- \rho}[1]\}^{{-}1} \\ \\\,\, \rho^{3} \{-((1-i) e^{i\rho} - (1+i)e^{{-}i\rho}) [1] - (1-i) \, e^{- i\rho } [1] + (1+i) \,e^{i \rho} [1] + 2ie^{-\rho} [1]\} \\ \end{array} \end{equation}
\begin{equation} \begin{array}{l} F(\lambda) = \{((1\,{-}\,i) e^{i\rho} - (1\,{+}\,i)e^{{-}i\rho}) [1] - (1\,{+}\,i) \, e^{- i\rho } [1] + (1-i) \,e^{i \rho} [1] + 2i e^{- \rho}[1]\}^{{-}1} \\ \\\,\, \rho^{3} \{-((1-i) e^{i\rho} - (1+i)e^{{-}i\rho}) [1] - (1-i) \, e^{- i\rho } [1] + (1+i) \,e^{i \rho} [1] + 2ie^{-\rho} [1]\} \\ \end{array} \end{equation}
if ![]() $\gamma = 0$, and
$\gamma = 0$, and
 \begin{equation} \begin{array}{l} F (\lambda) = \rho^{3} \{(e^{i\rho} - e^{{-}i\rho}) [1] - \, e^{- i\rho } [1] + \,e^{i \rho} [1] - e^{{-}2\rho}(e^{i\rho} - e^{{-}i\rho}) [1]\}^{{-}1} \\ \\ \,\,\, \{-( e^{i\rho} - e^{{-}i\rho}) [1] + i \, e^{- i\rho } [1] + i \,e^{i \rho} [1] - e^{{-}2\rho}(e^{i\rho} - e^{{-}i\rho}) [1] \} \\ \end{array} \end{equation}
\begin{equation} \begin{array}{l} F (\lambda) = \rho^{3} \{(e^{i\rho} - e^{{-}i\rho}) [1] - \, e^{- i\rho } [1] + \,e^{i \rho} [1] - e^{{-}2\rho}(e^{i\rho} - e^{{-}i\rho}) [1]\}^{{-}1} \\ \\ \,\,\, \{-( e^{i\rho} - e^{{-}i\rho}) [1] + i \, e^{- i\rho } [1] + i \,e^{i \rho} [1] - e^{{-}2\rho}(e^{i\rho} - e^{{-}i\rho}) [1] \} \\ \end{array} \end{equation}
if ![]() $\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2].}}} \right .} {2]}}$.
$\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2].}}} \right .} {2]}}$.
Since ![]() $\rho$ lies on the bisector of the first quadrant it follows that
$\rho$ lies on the bisector of the first quadrant it follows that ![]() $\rho = (1 + i) u$, where
$\rho = (1 + i) u$, where ![]() $u > 0$, and consequently,
$u > 0$, and consequently, ![]() $|\rho | = \sqrt 2\,u$. Then, from (2.20) and (2.21) by a straightforward computation, we obtain
$|\rho | = \sqrt 2\,u$. Then, from (2.20) and (2.21) by a straightforward computation, we obtain
 \begin{align}
F(\lambda ) &={-} (1-i)^{{-}1}\rho^{3} [1]
={-} (1-i)^{{-}1}(1+i)^{3} u^{3} [1] = (\sqrt
2)^{{-}1}|\rho|^{3} (1 + O(|\rho|^{{-}1})\notag\\
& = (\sqrt{2})^{{-}1}\,\sqrt[4]{{\,|\lambda |^{3} }}
\left({ 1 + O \left(
{\left({\sqrt[4]{|\lambda|}\,}\right)^{{-}1} } \right)
}\right)\, \textrm{as} \,\lambda \to - \infty.
\end{align}
\begin{align}
F(\lambda ) &={-} (1-i)^{{-}1}\rho^{3} [1]
={-} (1-i)^{{-}1}(1+i)^{3} u^{3} [1] = (\sqrt
2)^{{-}1}|\rho|^{3} (1 + O(|\rho|^{{-}1})\notag\\
& = (\sqrt{2})^{{-}1}\,\sqrt[4]{{\,|\lambda |^{3} }}
\left({ 1 + O \left(
{\left({\sqrt[4]{|\lambda|}\,}\right)^{{-}1} } \right)
}\right)\, \textrm{as} \,\lambda \to - \infty.
\end{align}The proof of this lemma is complete.
Lemma 2.11 Let ![]() $x \in [0,1)$ and
$x \in [0,1)$ and ![]() $\lambda > 0$ such that
$\lambda > 0$ such that ![]() $y (x,\lambda ) = 0$. Then
$y (x,\lambda ) = 0$. Then
Proof. Let ![]() $y (x,\lambda ) = 0$ for some
$y (x,\lambda ) = 0$ for some ![]() $x \in [0,1)$ and
$x \in [0,1)$ and ![]() $\lambda > 0$. If
$\lambda > 0$. If ![]() $x \in (0,1)$, then it follows from [Reference Ben Amara and Vladimirov14, lemma 2.2] that
$x \in (0,1)$, then it follows from [Reference Ben Amara and Vladimirov14, lemma 2.2] that ![]() $y' (x,\lambda ) \,Ty (x,\lambda ) < 0$. If
$y' (x,\lambda ) \,Ty (x,\lambda ) < 0$. If ![]() $y (0,\lambda ) = 0$, then in view of (1.2), by the first part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we have
$y (0,\lambda ) = 0$, then in view of (1.2), by the first part of [Reference Ben Amara and Vladimirov14, lemma 2.1] we have ![]() $y' (0,\lambda ) Ty (0,\lambda ) < 0$. Therefore, by virtue of (1.1), we get
$y' (0,\lambda ) Ty (0,\lambda ) < 0$. Therefore, by virtue of (1.1), we get
The proof of lemma 2.11 is complete.
By ![]() $\tau (\lambda )$ we denote the number of zeros of the function
$\tau (\lambda )$ we denote the number of zeros of the function ![]() $y (x, \lambda )$ contained in
$y (x, \lambda )$ contained in ![]() $(0, 1)$.
$(0, 1)$.
Lemma 2.12 Let ![]() $0 < \mu < \nu$. Then
$0 < \mu < \nu$. Then ![]() $\tau (\mu ) \le \tau (\nu )$.
$\tau (\mu ) \le \tau (\nu )$.
Proof. By corollary 2.7 as ![]() $\lambda > 0$ varies the zeros of the function
$\lambda > 0$ varies the zeros of the function ![]() $y(x,\lambda )$ can enter or leave the interval
$y(x,\lambda )$ can enter or leave the interval ![]() $(0, 1)$ only through the endpoint
$(0, 1)$ only through the endpoint ![]() $x = 0$. Moreover, by lemma 2.6 and the implicit function theorem for every zero
$x = 0$. Moreover, by lemma 2.6 and the implicit function theorem for every zero ![]() $x (\lambda )$ of the function
$x (\lambda )$ of the function ![]() $y (x,\lambda )$ the following relation holds:
$y (x,\lambda )$ the following relation holds:
If ![]() $x (\lambda ) = 0$, then it follows from this and relations (2.14), (2.23) that
$x (\lambda ) = 0$, then it follows from this and relations (2.14), (2.23) that
Therefore, as ![]() $\lambda > 0$ increases the zeros of the function
$\lambda > 0$ increases the zeros of the function ![]() $y (x, \lambda )$ cannot leave the interval
$y (x, \lambda )$ cannot leave the interval ![]() $(0, 1)$ through the point
$(0, 1)$ through the point ![]() $x = 0$. Hence, as
$x = 0$. Hence, as ![]() $\lambda$,
$\lambda$, ![]() $\mu < \lambda < \nu$, increases the number of zeros of the function
$\mu < \lambda < \nu$, increases the number of zeros of the function ![]() $y (x, \lambda )$ cannot decrease, i.e.
$y (x, \lambda )$ cannot decrease, i.e. ![]() $\tau (\mu ) \le \tau (\nu )$. The proof of this lemma is complete.
$\tau (\mu ) \le \tau (\nu )$. The proof of this lemma is complete.
Theorem 2.13 If ![]() $\lambda \in [0, + \infty ) \cap (\lambda _{k-1} (0, \gamma ),\lambda _{k-1} (0, \gamma )$, then
$\lambda \in [0, + \infty ) \cap (\lambda _{k-1} (0, \gamma ),\lambda _{k-1} (0, \gamma )$, then ![]() $\tau (\lambda ) = k - 1$.
$\tau (\lambda ) = k - 1$.
Proof. It is obvious that ![]() $\psi _1 (x,0) \equiv 1$. Then by (2.8), (2.13) it follows from (2.11) that
$\psi _1 (x,0) \equiv 1$. Then by (2.8), (2.13) it follows from (2.11) that ![]() $y (x,0) \equiv 1$. Hence, for all
$y (x,0) \equiv 1$. Hence, for all ![]() $\lambda \in \mathbb {R}$ sufficiently close to zero, the function
$\lambda \in \mathbb {R}$ sufficiently close to zero, the function ![]() $y (x,\lambda )$ has no zeros in
$y (x,\lambda )$ has no zeros in ![]() $(0,1)$. Moreover, by theorem 2.1 we have
$(0,1)$. Moreover, by theorem 2.1 we have ![]() $\tau (\lambda _k (0,\gamma ) = k - 1$,
$\tau (\lambda _k (0,\gamma ) = k - 1$, ![]() $k = 1,2,.\,.\,.\,$. Therefore, by lemma 2.12 it follows that if
$k = 1,2,.\,.\,.\,$. Therefore, by lemma 2.12 it follows that if ![]() $\lambda > 0$ and
$\lambda > 0$ and ![]() $\lambda \in (\lambda _{k-1} (\gamma ,0),\lambda _{k-1} (\gamma ,0)$, then
$\lambda \in (\lambda _{k-1} (\gamma ,0),\lambda _{k-1} (\gamma ,0)$, then ![]() $\tau (\lambda ) = k - 1$. The proof of theorem 2.13 is complete.
$\tau (\lambda ) = k - 1$. The proof of theorem 2.13 is complete.
It follows from lemma 2.6 that as ![]() $\lambda < 0$ varies then the zeros of the function
$\lambda < 0$ varies then the zeros of the function ![]() $y(x,\lambda )$ can enter or leave the interval
$y(x,\lambda )$ can enter or leave the interval ![]() $(0, 1)$ only through the endpoint
$(0, 1)$ only through the endpoint ![]() $x = 1$. To find the number of zeros contained in the interval
$x = 1$. To find the number of zeros contained in the interval ![]() $(0, 1)$ of the function
$(0, 1)$ of the function ![]() $y (x,\lambda )$ for
$y (x,\lambda )$ for ![]() $\lambda < 0$ consider the following spectral problem
$\lambda < 0$ consider the following spectral problem
It follows from the second part of [Reference Ben Amara and Vladimirov14, lemma 2.1] that the eigenvalues of problem (2.24) cannot be positive. Let ![]() $\eta$ be a real eigenvalue of this problem and
$\eta$ be a real eigenvalue of this problem and ![]() $\epsilon > 0$ be the fixed sufficiently small number. The oscillation index of the eigenvalue
$\epsilon > 0$ be the fixed sufficiently small number. The oscillation index of the eigenvalue ![]() $\eta$ which denotes by
$\eta$ which denotes by ![]() $i (\eta )$ is the difference between the number of zeros of the function
$i (\eta )$ is the difference between the number of zeros of the function ![]() $y (x,\lambda )$ for
$y (x,\lambda )$ for ![]() $\lambda \in (\eta - \epsilon ,\eta )$ contained in the interval
$\lambda \in (\eta - \epsilon ,\eta )$ contained in the interval ![]() $(0, 1)$ and the number of the same zeros for
$(0, 1)$ and the number of the same zeros for ![]() $\lambda \in (\eta , \eta + \epsilon )$. This definition directly implies that the number of zeros of the function
$\lambda \in (\eta , \eta + \epsilon )$. This definition directly implies that the number of zeros of the function ![]() $y (x,\lambda )$ for
$y (x,\lambda )$ for ![]() $\lambda < 0$ contained in the interval
$\lambda < 0$ contained in the interval ![]() $(0, 1)$ is equal to the sum of the oscillation indices of all eigenvalues of problem (2.24) contained in the interval
$(0, 1)$ is equal to the sum of the oscillation indices of all eigenvalues of problem (2.24) contained in the interval ![]() $(\lambda , 0)$ (see [Reference Ben Amara and Vladimirov13, § 4]).
$(\lambda , 0)$ (see [Reference Ben Amara and Vladimirov13, § 4]).
By following the arguments in theorem 4.1 of [Reference Ben Amara and Vladimirov13] one can justify the following statement.
Theorem 2.14 There exists ![]() $\xi < 0$ such that the eigenvalues
$\xi < 0$ such that the eigenvalues ![]() $\eta _k$,
$\eta _k$, ![]() $k =1,2,.\,.\,.\,$, of problem (2.24) are simple, lying on the interval
$k =1,2,.\,.\,.\,$, of problem (2.24) are simple, lying on the interval ![]() $(-\,\infty , \xi )$, form an unbounded decreasing sequence
$(-\,\infty , \xi )$, form an unbounded decreasing sequence ![]() $\{\eta _k\}_{k=1}^{\infty }$ such that
$\{\eta _k\}_{k=1}^{\infty }$ such that ![]() $i (\eta _k) = 1$,
$i (\eta _k) = 1$, ![]() $k \in \mathbb {N}$, and
$k \in \mathbb {N}$, and
Now, based on the above reasoning, we obtain the following formula for the number of zeros contained in ![]() $(0, 1)$ of the function
$(0, 1)$ of the function ![]() $y (x,\lambda )$ for
$y (x,\lambda )$ for ![]() $\lambda < 0$:
$\lambda < 0$:
3. The location of eigenvalues and the oscillatory properties of eigenfunctions of problem (1.1)–(1.5)
Lemma 3.1 The eigenvalues of the boundary value problem (1.1)–(1.5) are real and form an at most countable set without finite limit point.
Proof. Note that the eigenvalues of problem (1.1)–(1.5) are the roots of the equation
Let ![]() $\lambda$ be the nonreal eigenvalue of this problem. Then
$\lambda$ be the nonreal eigenvalue of this problem. Then ![]() $\bar \lambda$ is also eigenvalue of (1.1)–(1.5) because the coefficients
$\bar \lambda$ is also eigenvalue of (1.1)–(1.5) because the coefficients ![]() $q(x)$,
$q(x)$, ![]() $a$,
$a$, ![]() $c$ and
$c$ and ![]() $\gamma$ are real. Moreover, in this case
$\gamma$ are real. Moreover, in this case ![]() $y(x, \bar \lambda ) = \overline {y(x,\lambda )}$, and consequently, equality (3.1) holds for
$y(x, \bar \lambda ) = \overline {y(x,\lambda )}$, and consequently, equality (3.1) holds for ![]() $\bar \lambda \,$.
$\bar \lambda \,$.
Setting ![]() $\mu = \bar \lambda$ in relation (2.16) and taking (1.4) into account we get
$\mu = \bar \lambda$ in relation (2.16) and taking (1.4) into account we get
whence, by ![]() ${\overline \lambda } \ne \lambda$, implies that
${\overline \lambda } \ne \lambda$, implies that
Putting ![]() $y (x,\lambda )$ in (1.1)–(1.5), then multiplying both sides of (1.1) by
$y (x,\lambda )$ in (1.1)–(1.5), then multiplying both sides of (1.1) by ![]() $\overline {y (x,\lambda )}$, integrating this relation from
$\overline {y (x,\lambda )}$, integrating this relation from ![]() $0$ to
$0$ to ![]() $1$, using the formula for the integration by parts, and taking into account conditions (1.2)–(1.5), we obtain
$1$, using the formula for the integration by parts, and taking into account conditions (1.2)–(1.5), we obtain
 \begin{align}
&\int_0^{1} {\,|y'' (x,\lambda)|^{2}
\textrm{d}x + \int_0^{1} {q(x)\,|y' (x,\lambda )|^{2}}}
\textrm{d}x + \mathcal{N} [y (x, \lambda)]\notag\\
&\quad = \lambda
\left\{ { \int_0^{1} |y(x,\lambda)|^{2} \textrm{d}x + a
\,|y (0,\lambda)|^{2}- c |y(1,\lambda)|^{2} } \right\},
\end{align}
\begin{align}
&\int_0^{1} {\,|y'' (x,\lambda)|^{2}
\textrm{d}x + \int_0^{1} {q(x)\,|y' (x,\lambda )|^{2}}}
\textrm{d}x + \mathcal{N} [y (x, \lambda)]\notag\\
&\quad = \lambda
\left\{ { \int_0^{1} |y(x,\lambda)|^{2} \textrm{d}x + a
\,|y (0,\lambda)|^{2}- c |y(1,\lambda)|^{2} } \right\},
\end{align}
where ![]() $\mathcal {N} [y (x,\lambda )] = 0$ for
$\mathcal {N} [y (x,\lambda )] = 0$ for ![]() $\gamma = 0$,
$\gamma = 0$, ![]() $\mathcal {N} [y (x,\lambda )] = |y' (1,\lambda )|^{2} \cot \gamma$ for
$\mathcal {N} [y (x,\lambda )] = |y' (1,\lambda )|^{2} \cot \gamma$ for ![]() $\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2]}}} \right .} {2]}}$. Hence it follows from (3.3) and (3.4) that
$\gamma \in (0,{\pi \mathord {\left / {\vphantom {\pi {2]}}} \right .} {2]}}$. Hence it follows from (3.3) and (3.4) that
By the boundary condition (1.3), relation (3.5) implies that ![]() $y (x,\lambda ) \equiv 0$, a contradiction.
$y (x,\lambda ) \equiv 0$, a contradiction.
By the above arguments the entire function on the left-hand side of (3.1) does not vanish for non-real ![]() $\lambda$. Consequently, it does not vanish identically. Therefore, its zeros form an at most countable set without finite limit point. The proof of this lemma is complete.
$\lambda$. Consequently, it does not vanish identically. Therefore, its zeros form an at most countable set without finite limit point. The proof of this lemma is complete.
Remark 3.2 If ![]() $\lambda$ is an eigenvalue of (1.1)–(1.5), then
$\lambda$ is an eigenvalue of (1.1)–(1.5), then ![]() $y (0,\lambda ) \ne 0$. Indeed, if
$y (0,\lambda ) \ne 0$. Indeed, if ![]() $y (0,\lambda ) = 0$, then it follows from (1.2) that
$y (0,\lambda ) = 0$, then it follows from (1.2) that ![]() $T y (0,\lambda ) = 0$. Consequently,
$T y (0,\lambda ) = 0$. Consequently, ![]() $\lambda$ is an eigenvalue of problem (1.1), (1.2), (2.1), (1.4), (1.5) for
$\lambda$ is an eigenvalue of problem (1.1), (1.2), (2.1), (1.4), (1.5) for ![]() $\beta = 0$ and
$\beta = 0$ and ![]() $\beta = {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}$ in contradiction with relation (2.3).
$\beta = {\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}$ in contradiction with relation (2.3).
Proof. Let ![]() $\lambda$ be an eigenvalue of (1.1)–(1.5). Then by remark 3.2 we have
$\lambda$ be an eigenvalue of (1.1)–(1.5). Then by remark 3.2 we have ![]() $y (0,\lambda ) \ne 0$. Therefore each root (with regard of multiplicities) of equation (3.1) is a root of the equation
$y (0,\lambda ) \ne 0$. Therefore each root (with regard of multiplicities) of equation (3.1) is a root of the equation
Let ![]() $\lambda = \lambda ^{*}$ be a multiple root of (3.6). Then the following relations hold:
$\lambda = \lambda ^{*}$ be a multiple root of (3.6). Then the following relations hold:
By remark 3.2 and formula (2.14), the second relation of (3.7) implies that
Since ![]() $\lambda ^{*} \in \mathbb {R}$ it follows from (3.4) that
$\lambda ^{*} \in \mathbb {R}$ it follows from (3.4) that
 \begin{align}
&\int_0^{1} {\,y''^{2} (x,\lambda^{*})
\textrm{d}x + \int_0^{1} {q(x)\,y'^{2} (x,\lambda^{*})}}
\textrm{d}x + \mathcal{N} [y (x,\lambda^{*})]\notag\\
&\quad =\lambda \left\{ { \int_0^{1} y^{2} (x,\lambda^{*})
\textrm{d}x + a \,y^{2} (0,\lambda^{*})- c \,y^{2}
(1,\lambda^{*}) } \right\},
\end{align}
\begin{align}
&\int_0^{1} {\,y''^{2} (x,\lambda^{*})
\textrm{d}x + \int_0^{1} {q(x)\,y'^{2} (x,\lambda^{*})}}
\textrm{d}x + \mathcal{N} [y (x,\lambda^{*})]\notag\\
&\quad =\lambda \left\{ { \int_0^{1} y^{2} (x,\lambda^{*})
\textrm{d}x + a \,y^{2} (0,\lambda^{*})- c \,y^{2}
(1,\lambda^{*}) } \right\},
\end{align}whence, by virtue of (3.8), we get
Consequently, by condition (1.3), from (3.10) we obtain ![]() $y (x,\lambda ^{*}) \equiv 0$ which contradicts the condition
$y (x,\lambda ^{*}) \equiv 0$ which contradicts the condition ![]() $y (x,\lambda ^{*}) \not \equiv 0$. The proof of this lemma is complete.
$y (x,\lambda ^{*}) \not \equiv 0$. The proof of this lemma is complete.
Following the reasoning in [Reference Aliyev and Guliyeva6, lemma 3.3], we can justify the following result.
Lemma 3.4 One has the following representation:
 \begin{equation} F(\lambda ) = \sum\limits_{k = 1}^{\infty} {\frac{{\lambda c_k }}{{\lambda _k (0,\gamma )\left( {\lambda - \lambda _k (0,\gamma )} \right)}}}\,, \end{equation}
\begin{equation} F(\lambda ) = \sum\limits_{k = 1}^{\infty} {\frac{{\lambda c_k }}{{\lambda _k (0,\gamma )\left( {\lambda - \lambda _k (0,\gamma )} \right)}}}\,, \end{equation}
where ![]() $c_k = \mathop {\textrm {res}}\limits _{\lambda = \lambda _k (0,\gamma )} F(\lambda )$ and
$c_k = \mathop {\textrm {res}}\limits _{\lambda = \lambda _k (0,\gamma )} F(\lambda )$ and ![]() $c_k > 0$,
$c_k > 0$, ![]() $k =1, \,2,.\,.\,.\,$.
$k =1, \,2,.\,.\,.\,$.
We have the following oscillation theorem for problem (1.1)–(1.5).
Theorem 3.5 For each ![]() $\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ the eigenvalues of problem (1.1)–(1.5) form an unbounded nondecreasing sequence
$\gamma \in [0,{\pi \mathord {\left / {\vphantom {\pi 2}} \right .} 2}]$ the eigenvalues of problem (1.1)–(1.5) form an unbounded nondecreasing sequence ![]() $\{\lambda _{k} (\gamma )\}_{k = 1}^{\infty }$ such that
$\{\lambda _{k} (\gamma )\}_{k = 1}^{\infty }$ such that
 \begin{align*} &\lambda_1 (\gamma) < 0 = \lambda_2 (\gamma) < \lambda_3 (\gamma) < \ldots < \lambda_k (\gamma)< \ldots\ {if}\ a > c - 1,\\
&\lambda_1 (\gamma) = \lambda_2 (\gamma) = 0 < \lambda_3 (\gamma) < \ldots < \lambda_k (\gamma)< \ldots\ {if}\ a = c - 1,\\
&\lambda_1 (\gamma) = 0 < \lambda_2 (\gamma) < \lambda_3 (\gamma) < \ldots < \lambda_k (\gamma)< \ldots\ {if}\ a < c - 1, \end{align*}
\begin{align*} &\lambda_1 (\gamma) < 0 = \lambda_2 (\gamma) < \lambda_3 (\gamma) < \ldots < \lambda_k (\gamma)< \ldots\ {if}\ a > c - 1,\\
&\lambda_1 (\gamma) = \lambda_2 (\gamma) = 0 < \lambda_3 (\gamma) < \ldots < \lambda_k (\gamma)< \ldots\ {if}\ a = c - 1,\\
&\lambda_1 (\gamma) = 0 < \lambda_2 (\gamma) < \lambda_3 (\gamma) < \ldots < \lambda_k (\gamma)< \ldots\ {if}\ a < c - 1, \end{align*}
![]() $($in the case
$($in the case ![]() $c = a + 1$ the eigenvalue
$c = a + 1$ the eigenvalue ![]() $\lambda _1 (\gamma ) = 0$ is double, and it corresponds to the chain consisting of the eigenfunction
$\lambda _1 (\gamma ) = 0$ is double, and it corresponds to the chain consisting of the eigenfunction ![]() $y_{1,\gamma } (x)$ and the associated function
$y_{1,\gamma } (x)$ and the associated function ![]() $y_{2,\gamma } (x))$. The eigenfunction
$y_{2,\gamma } (x))$. The eigenfunction ![]() $y_k (x)$, corresponding to the eigenvalue
$y_k (x)$, corresponding to the eigenvalue ![]() $\lambda _k$, for
$\lambda _k$, for ![]() $k \ge 3$ has exactly
$k \ge 3$ has exactly ![]() $k - 2$ simple zeros in
$k - 2$ simple zeros in ![]() $(0,1)$; moreover, if
$(0,1)$; moreover, if ![]() $a < c - 1$, then the eigenfunctions
$a < c - 1$, then the eigenfunctions ![]() $y_{1,\gamma } (x)$ and
$y_{1,\gamma } (x)$ and ![]() $y_{2,\gamma } (x)$ have no zeros in
$y_{2,\gamma } (x)$ have no zeros in ![]() $(0,1)$, if
$(0,1)$, if ![]() $a = c - 1$, then the eigenfunction
$a = c - 1$, then the eigenfunction ![]() $y_{1,\gamma } (x)$ has no zeros in
$y_{1,\gamma } (x)$ has no zeros in ![]() $(0,1)$, if
$(0,1)$, if ![]() $a > c - 1$, then
$a > c - 1$, then ![]() $y_{2,\gamma } (x)$ has no zeros in
$y_{2,\gamma } (x)$ has no zeros in ![]() $(0,1)$ and the number of zeros of the eigenfunction
$(0,1)$ and the number of zeros of the eigenfunction ![]() $y_{1,\gamma } (x)$ in
$y_{1,\gamma } (x)$ in ![]() $(0,1)$ is equal
$(0,1)$ is equal ![]() $\sum \limits _{\eta _k \in (\lambda _1 (\gamma ),0)} {i(\eta _k )}$.
$\sum \limits _{\eta _k \in (\lambda _1 (\gamma ),0)} {i(\eta _k )}$.
Proof. Recall that the eigenvalues of problem (1.1)–(1.5), taking into account their multiplicities, are the roots of equation (3.6). It follows from (3.11) that
 \[ F''(\lambda) = 2 \sum\limits_{k = 1}^{\infty} {\frac{{ c_k }}{{\left( {\lambda - \lambda _k (0,\gamma )} \right)^{3}}}},\lambda \in \mathcal{D}. \]
\[ F''(\lambda) = 2 \sum\limits_{k = 1}^{\infty} {\frac{{ c_k }}{{\left( {\lambda - \lambda _k (0,\gamma )} \right)^{3}}}},\lambda \in \mathcal{D}. \]From this we obtain the relation
i.e. the function ![]() $F(\lambda )$ is concave in
$F(\lambda )$ is concave in ![]() $\mathcal {D}_1$. Moreover, by (2.14), (2.18) and (3.11) we have
$\mathcal {D}_1$. Moreover, by (2.14), (2.18) and (3.11) we have
Let ![]() $f(\lambda ) = F (\lambda ) - a \lambda$. Then it follows from relations (3.12)–(3.14) that
$f(\lambda ) = F (\lambda ) - a \lambda$. Then it follows from relations (3.12)–(3.14) that
Moreover, by (2.22) and (3.14) we have
If ![]() $a > c- 1$, then
$a > c- 1$, then ![]() $f' (0) < 0$. Since
$f' (0) < 0$. Since ![]() $f'' (\lambda ) < 0$ in
$f'' (\lambda ) < 0$ in ![]() $\mathcal {D}_1$ it follows that
$\mathcal {D}_1$ it follows that ![]() $f' (\lambda ) < f' (0) < 0$ for
$f' (\lambda ) < f' (0) < 0$ for ![]() $\lambda \in (0,\lambda _1 (0,\gamma ))$. Then
$\lambda \in (0,\lambda _1 (0,\gamma ))$. Then ![]() $f (\lambda ) < 0$ for
$f (\lambda ) < 0$ for ![]() $\lambda \in (0,\lambda _1 (0,\gamma ))$. By the relations
$\lambda \in (0,\lambda _1 (0,\gamma ))$. By the relations ![]() $f(0) = 0$ and
$f(0) = 0$ and ![]() $f' (0) < 0$ we have
$f' (0) < 0$ we have ![]() $f (\lambda ) > 0$ for all
$f (\lambda ) > 0$ for all ![]() $0 > \lambda$ small. Then it follows from the first relation of (3.15) that there exists
$0 > \lambda$ small. Then it follows from the first relation of (3.15) that there exists ![]() $\lambda _{*} (\gamma ) \in (-\,\infty ,0)$ such that
$\lambda _{*} (\gamma ) \in (-\,\infty ,0)$ such that ![]() $f (\lambda _{*} (\gamma )) = 0$. Hence there exists
$f (\lambda _{*} (\gamma )) = 0$. Hence there exists ![]() $\lambda _{**} (\gamma ) \in (\lambda _{*} (\gamma ),0)$ such that
$\lambda _{**} (\gamma ) \in (\lambda _{*} (\gamma ),0)$ such that ![]() $f' (\lambda _{**} (\gamma )) = 0$. Consequently,
$f' (\lambda _{**} (\gamma )) = 0$. Consequently, ![]() $f' (\lambda ) > 0$ for
$f' (\lambda ) > 0$ for ![]() $\lambda \in (-\infty ,\lambda _{**} (\gamma ))$ and
$\lambda \in (-\infty ,\lambda _{**} (\gamma ))$ and ![]() $f' (\lambda ) < 0$ for
$f' (\lambda ) < 0$ for ![]() $\lambda \in (\lambda _{**} (\gamma ), \lambda _1 (0,\gamma ))$. Therefore, in this case equation (3.6) in the interval
$\lambda \in (\lambda _{**} (\gamma ), \lambda _1 (0,\gamma ))$. Therefore, in this case equation (3.6) in the interval ![]() $\mathcal {D}_1$ has two simple roots
$\mathcal {D}_1$ has two simple roots ![]() $\lambda _1 (\gamma ) < \lambda _2 (\gamma )$, where
$\lambda _1 (\gamma ) < \lambda _2 (\gamma )$, where ![]() $\lambda _1 (\gamma ) = \lambda _{*} (\gamma ) < 0$ and
$\lambda _1 (\gamma ) = \lambda _{*} (\gamma ) < 0$ and ![]() $\lambda _2 (\gamma ) = 0$.
$\lambda _2 (\gamma ) = 0$.
Let ![]() $a = c- 1$. Then we have
$a = c- 1$. Then we have ![]() $f' (0) = 0$. Since
$f' (0) = 0$. Since ![]() $f'' (\lambda ) < 0$ in
$f'' (\lambda ) < 0$ in ![]() $\mathcal {D}_1$ it follows that
$\mathcal {D}_1$ it follows that ![]() $f' (\lambda ) > 0$ for
$f' (\lambda ) > 0$ for ![]() $\lambda \in (-\infty ,0)$ and
$\lambda \in (-\infty ,0)$ and ![]() $f' (\lambda ) < 0$ for
$f' (\lambda ) < 0$ for ![]() $\lambda \in (0, \lambda _1 (0,\gamma ))$. Hence by relations (3.15)
$\lambda \in (0, \lambda _1 (0,\gamma ))$. Hence by relations (3.15) ![]() $f (\lambda ) < 0$ for
$f (\lambda ) < 0$ for ![]() $\lambda \in (-\infty ,0) \cup (0, \lambda _1 (0,\gamma ))$. Therefore, in this case
$\lambda \in (-\infty ,0) \cup (0, \lambda _1 (0,\gamma ))$. Therefore, in this case ![]() $f (0) = f'(0) = 0$,
$f (0) = f'(0) = 0$, ![]() $f'' (0) < 0$ and
$f'' (0) < 0$ and ![]() $f (\lambda ) \ne 0$ for
$f (\lambda ) \ne 0$ for ![]() $\lambda \in D_1 \backslash \{0\}$, i.e. equation (3.6) has one double root
$\lambda \in D_1 \backslash \{0\}$, i.e. equation (3.6) has one double root ![]() $\lambda _1 (\gamma ) = \lambda _2 (\gamma ) = 0$ for
$\lambda _1 (\gamma ) = \lambda _2 (\gamma ) = 0$ for ![]() $a = c - 1$.
$a = c - 1$.
If ![]() $a < c- 1$, then
$a < c- 1$, then ![]() $f' (0) > 0$. Hence
$f' (0) > 0$. Hence ![]() $f' (\lambda ) > f' (0) > 0$ for
$f' (\lambda ) > f' (0) > 0$ for ![]() $\lambda \in (-\,\infty , 0)$. Then
$\lambda \in (-\,\infty , 0)$. Then ![]() $f (\lambda ) < 0$ for
$f (\lambda ) < 0$ for ![]() $\lambda < 0$. Since
$\lambda < 0$. Since ![]() $f(0) = 0$ and
$f(0) = 0$ and ![]() $f' (0) > 0$ it follows that
$f' (0) > 0$ it follows that ![]() $f (\lambda ) > 0$ for all
$f (\lambda ) > 0$ for all ![]() $0 < \lambda$ small. Then by virtue of second relation of (3.15) there exists
$0 < \lambda$ small. Then by virtue of second relation of (3.15) there exists ![]() $\lambda ^{*} (\gamma ) \in (0,\lambda _1 (0,\gamma )$ such that
$\lambda ^{*} (\gamma ) \in (0,\lambda _1 (0,\gamma )$ such that ![]() $f (\lambda ^{*} (\gamma )) = 0$. Hence there exists
$f (\lambda ^{*} (\gamma )) = 0$. Hence there exists ![]() $\lambda ^{**} (\gamma ) \in (0,\lambda ^{*} (\gamma ))$ such that
$\lambda ^{**} (\gamma ) \in (0,\lambda ^{*} (\gamma ))$ such that ![]() $f' (\lambda ^{**} (\gamma )) = 0$. Then
$f' (\lambda ^{**} (\gamma )) = 0$. Then ![]() $f' (\lambda ) > 0$ for
$f' (\lambda ) > 0$ for ![]() $\lambda \in (-\infty ,\lambda ^{**} (\gamma ))$ and
$\lambda \in (-\infty ,\lambda ^{**} (\gamma ))$ and ![]() $f' (\lambda ) < 0$ for
$f' (\lambda ) < 0$ for ![]() $\lambda \in (\lambda ^{**} (\gamma ), \lambda _1 (0,\gamma ))$. Thus, in this case equation (3.6) in the interval
$\lambda \in (\lambda ^{**} (\gamma ), \lambda _1 (0,\gamma ))$. Thus, in this case equation (3.6) in the interval ![]() $\mathcal {D}_1$ has two simple root
$\mathcal {D}_1$ has two simple root ![]() $\lambda _1 (\gamma ) < \lambda _2 (\gamma )$, where
$\lambda _1 (\gamma ) < \lambda _2 (\gamma )$, where ![]() $\lambda _1 (\gamma ) = 0$ and
$\lambda _1 (\gamma ) = 0$ and ![]() $\lambda _2 (\gamma ) = \lambda ^{*} (\gamma ) > 0$.
$\lambda _2 (\gamma ) = \lambda ^{*} (\gamma ) > 0$.
By theorem 2.13 and formula (2.25) it follows from the above reasoning that ![]() $\tau (\lambda _1 (\gamma )) = \sum _{\eta _k \in \,(\lambda _1 (\gamma ), 0)} {i (\eta _k )}$ and
$\tau (\lambda _1 (\gamma )) = \sum _{\eta _k \in \,(\lambda _1 (\gamma ), 0)} {i (\eta _k )}$ and ![]() $\tau (\lambda _2 (\gamma )) = 0$ for
$\tau (\lambda _2 (\gamma )) = 0$ for ![]() $a > c - 1$,
$a > c - 1$, ![]() $\tau (\lambda _1 (\gamma )) = 0$ for
$\tau (\lambda _1 (\gamma )) = 0$ for ![]() $a = c - 1$, and
$a = c - 1$, and ![]() $\tau (\lambda _1 (\gamma )) = \tau (\lambda _2 (\gamma )) = 0$ for
$\tau (\lambda _1 (\gamma )) = \tau (\lambda _2 (\gamma )) = 0$ for ![]() $a < c - 1$.
$a < c - 1$.
From representation (3.11) we obtain the following relations
If equation (3.6) has a root in the interval ![]() $\mathcal {D}_k$ for
$\mathcal {D}_k$ for ![]() $k \ge 2$, then by lemma 3.3 this root must be simple. Since
$k \ge 2$, then by lemma 3.3 this root must be simple. Since ![]() $F (\lambda )$ is continuous in each of intervals
$F (\lambda )$ is continuous in each of intervals ![]() $\mathcal {D}_k$,
$\mathcal {D}_k$, ![]() $k \in \mathbb {N}$, by (3.16) it follows that equation (3.6) has at least one root in each of intervals
$k \in \mathbb {N}$, by (3.16) it follows that equation (3.6) has at least one root in each of intervals ![]() $\mathcal {D}_k$,
$\mathcal {D}_k$, ![]() $k \ge 2$. Let us show that this equation has only one simple root in
$k \ge 2$. Let us show that this equation has only one simple root in ![]() $\mathcal {D}_k$ for
$\mathcal {D}_k$ for ![]() $k \ge 2$. Indeed, if (3.6) has more than one root, then the two smallest roots
$k \ge 2$. Indeed, if (3.6) has more than one root, then the two smallest roots ![]() $\lambda _{k1}^{*} < \lambda _{k2}^{*}$ satisfy
$\lambda _{k1}^{*} < \lambda _{k2}^{*}$ satisfy
On the other hand it follows from (3.4) that
 \begin{align*} &\int_0^{1} {\,y''^{2} (x,\lambda_{k2}^{*}) \textrm{d}x + \int_0^{1} {q(x)\,y'^{2} (x,\lambda_{k2}^{*})}} \textrm{d}x + \mathcal{N} [y(x,\lambda_{k2}^{*})]\\ &\quad = \lambda_{k2}^{*} \left\{ { \int_0^{1} y^{2}(x,\lambda_{k2}^{*}) \textrm{d}x + a \,y^{2} (0,\lambda_{k2}^{*})- c \,y^{2}(1,\lambda_{k2}^{*}) } \right\}, \end{align*}
\begin{align*} &\int_0^{1} {\,y''^{2} (x,\lambda_{k2}^{*}) \textrm{d}x + \int_0^{1} {q(x)\,y'^{2} (x,\lambda_{k2}^{*})}} \textrm{d}x + \mathcal{N} [y(x,\lambda_{k2}^{*})]\\ &\quad = \lambda_{k2}^{*} \left\{ { \int_0^{1} y^{2}(x,\lambda_{k2}^{*}) \textrm{d}x + a \,y^{2} (0,\lambda_{k2}^{*})- c \,y^{2}(1,\lambda_{k2}^{*}) } \right\}, \end{align*}
whence, by ![]() $\lambda _{k2}^{*} > 0$, we get
$\lambda _{k2}^{*} > 0$, we get
By (2.14) we obtain from the last relation
which contradicts the second relation of (3.17). Therefore, problem (1.1)–(1.5) in each interval ![]() $\mathcal {D}_k$,
$\mathcal {D}_k$, ![]() $k \ge 2$, has a unique simple eigenvalue
$k \ge 2$, has a unique simple eigenvalue ![]() $\lambda _{k + 1} (\gamma )$. Then it follows from theorem 2.13 that
$\lambda _{k + 1} (\gamma )$. Then it follows from theorem 2.13 that ![]() $\tau (\lambda _{k + 1} (\gamma )) = k - 1$. The proof of theorem 3.5 is complete.
$\tau (\lambda _{k + 1} (\gamma )) = k - 1$. The proof of theorem 3.5 is complete.
4. Asymptotic behaviour of eigenvalues and eigenfunctions of problem (1.1)–(1.5)
Let
By [Reference Kerimov and Aliev30, theorem 3.1] we have the following asymptotic formulas
where relation ( 4.2) holds uniformly for ![]() $x \in [\,0,1]$.
$x \in [\,0,1]$.
Theorem 4.1 The following asymptotic formulas hold:
where relation (4.4) holds uniformly for ![]() $x \in [\,0,1]$.
$x \in [\,0,1]$.
Proof. Taking (2.19) into account in the boundary conditions (1.2)–(1.4) we get
where ![]() $i$ is some fixed integer. Then using (2.19) and (4.5), and following the arguments in pp. 84–87 of [Reference Mukhtarov and Aydemir35] we obtain the following asymptotic formula
$i$ is some fixed integer. Then using (2.19) and (4.5), and following the arguments in pp. 84–87 of [Reference Mukhtarov and Aydemir35] we obtain the following asymptotic formula
 \begin{align} y_{k
+ i,\gamma} (x) &= \sin \left({k - \nu_{\gamma} + 1}\right)
\pi x + (1 - \textrm{sgn} \gamma) ({-}1)^{k} \left( {\sqrt
2\,} \right)^{ - 1} e^{\left({k - \nu_{\gamma} + 1
}\right)\pi (x-1)}\notag\\ &\quad + O \left( { k^{{-}1} } \right),
\end{align}
\begin{align} y_{k
+ i,\gamma} (x) &= \sin \left({k - \nu_{\gamma} + 1}\right)
\pi x + (1 - \textrm{sgn} \gamma) ({-}1)^{k} \left( {\sqrt
2\,} \right)^{ - 1} e^{\left({k - \nu_{\gamma} + 1
}\right)\pi (x-1)}\notag\\ &\quad + O \left( { k^{{-}1} } \right),
\end{align}
which holds uniformly for ![]() $x \in [\,0,1]$. Next, using the oscillation properties of the eigenfunctions of problem (1.1)–(1.5) and following the proof of [Reference Kerimov and Aliev30, theorem 3.1] we get
$x \in [\,0,1]$. Next, using the oscillation properties of the eigenfunctions of problem (1.1)–(1.5) and following the proof of [Reference Kerimov and Aliev30, theorem 3.1] we get ![]() $i = 2$. Hence by setting
$i = 2$. Hence by setting ![]() $i = 2$ in (4.5) and (4.6) we obtain (4.3) and (4.4) respectively. The proof of this theorem is complete.
$i = 2$ in (4.5) and (4.6) we obtain (4.3) and (4.4) respectively. The proof of this theorem is complete.
5. Operator interpretation and basis properties of the root functions of problem (1.1)–(1.5)
Let ![]() $H = L_{2} (0, 1) \oplus \,\mathbb {C}^{2}$ be the Hilbert space with the scalar product
$H = L_{2} (0, 1) \oplus \,\mathbb {C}^{2}$ be the Hilbert space with the scalar product
In ![]() $H$ we define the operator
$H$ we define the operator
with the domain
 \begin{align*} &D(L) = \left\{ {\{ y} \right.(x),m,n\} \in H \,: \,y \in W_2^{4} (0,1),\ell (y) \in L_2 (0,1),y'' (0) = 0,\\ &y'(1) \cos \gamma + y''(1) \sin \gamma = 0,m = a y(0),n = c y(1)\}, \end{align*}
\begin{align*} &D(L) = \left\{ {\{ y} \right.(x),m,n\} \in H \,: \,y \in W_2^{4} (0,1),\ell (y) \in L_2 (0,1),y'' (0) = 0,\\ &y'(1) \cos \gamma + y''(1) \sin \gamma = 0,m = a y(0),n = c y(1)\}, \end{align*}
which dense everywhere in ![]() $H$. Then problem (1.1)–(1.5) is equivalent to the eigenvalue problem
$H$. Then problem (1.1)–(1.5) is equivalent to the eigenvalue problem
In this the eigenvalues ![]() $\lambda _{k,\gamma },k \in \mathbb {N}$, of problems (1.1)–(1.5) and (5.2) coincide considering their multiplicity, and between the root functions, there is a one-to-one correspondence
$\lambda _{k,\gamma },k \in \mathbb {N}$, of problems (1.1)–(1.5) and (5.2) coincide considering their multiplicity, and between the root functions, there is a one-to-one correspondence
We define the operator ![]() $J:H \to H$ by
$J:H \to H$ by
Note that operator ![]() $J$ generates the Pontryagin space
$J$ generates the Pontryagin space ![]() $\Pi _1 = L_2 (0, 1) \oplus \mathbb {C}^{2}$ equipped with an inner product
$\Pi _1 = L_2 (0, 1) \oplus \mathbb {C}^{2}$ equipped with an inner product
where ![]() $\hat y = \{ y, m, n\}$,
$\hat y = \{ y, m, n\}$, ![]() $\hat v = \{ v, s, t\}$.
$\hat v = \{ v, s, t\}$.
Theorem 5.1 (see [9, lemma 4.1, theorem 4.2]) ![]() $L$ is a
$L$ is a ![]() $J$-self-adjoint operator in
$J$-self-adjoint operator in ![]() $\Pi _1$;
$\Pi _1$; ![]() $L^{*} = JLJ$, where
$L^{*} = JLJ$, where ![]() $L^{*}$ is an adjoint operator of
$L^{*}$ is an adjoint operator of ![]() $L$ in
$L$ in ![]() $H$; the system of root vectors
$H$; the system of root vectors ![]() $\{\hat y_{k,\gamma }\}_{k=1}^{\infty }$,
$\{\hat y_{k,\gamma }\}_{k=1}^{\infty }$, ![]() $\hat y_{k,\gamma } = \{ y_{k,\gamma } (x),m_{k,\gamma } ,n_{k,\gamma }\}$,
$\hat y_{k,\gamma } = \{ y_{k,\gamma } (x),m_{k,\gamma } ,n_{k,\gamma }\}$, ![]() $m_{k,\gamma } = a y_{k,\gamma }(0)$,
$m_{k,\gamma } = a y_{k,\gamma }(0)$, ![]() $n_{k,\gamma } = c y_{k,\gamma } (1)$, of problem ( 5.2) forms an unconditional basis in
$n_{k,\gamma } = c y_{k,\gamma } (1)$, of problem ( 5.2) forms an unconditional basis in ![]() $H$.
$H$.
Theorem 4.1 implies that
 \begin{align} y_{k,\gamma} (x) &= y(x, \lambda_k
(\gamma))\,\textrm{if}\, a \ne c - 1, \,k \in \mathbb{N},
\,\textrm{and}\, a = c - 1, \,k \ge 3;\notag\\
y_{1,\gamma}
(x) &= y(x, \lambda_1 (\gamma)),y_{2,\gamma} (x) =
y_{2,\gamma}^{*} (x) + b \,y_{1,\gamma} (x) \ \textrm{if}\
a = c - 1, \end{align}
\begin{align} y_{k,\gamma} (x) &= y(x, \lambda_k
(\gamma))\,\textrm{if}\, a \ne c - 1, \,k \in \mathbb{N},
\,\textrm{and}\, a = c - 1, \,k \ge 3;\notag\\
y_{1,\gamma}
(x) &= y(x, \lambda_1 (\gamma)),y_{2,\gamma} (x) =
y_{2,\gamma}^{*} (x) + b \,y_{1,\gamma} (x) \ \textrm{if}\
a = c - 1, \end{align}
where ![]() $y_{2,\gamma }^{*} (x) = y'_{\lambda } (x, \lambda _1 (\gamma ))$ and
$y_{2,\gamma }^{*} (x) = y'_{\lambda } (x, \lambda _1 (\gamma ))$ and ![]() $b$ is an arbitrary constant
$b$ is an arbitrary constant
Let ![]() $\{ \hat v^{*}_{k,\gamma } \} _{k = 1}^{\infty }$,
$\{ \hat v^{*}_{k,\gamma } \} _{k = 1}^{\infty }$, ![]() $\hat v^{*}_{k,\gamma } = \{ v^{*}_{k,\gamma } ,s^{*}_{k,\gamma } ,t^{*}_{k,\gamma } \}$, is the system of root vectors of the operator
$\hat v^{*}_{k,\gamma } = \{ v^{*}_{k,\gamma } ,s^{*}_{k,\gamma } ,t^{*}_{k,\gamma } \}$, is the system of root vectors of the operator ![]() $L^{*}$. Then by [Reference Hinton25, formula (7)] we have
$L^{*}$. Then by [Reference Hinton25, formula (7)] we have
 \begin{align}
L \hat y_{k,\gamma} &= \lambda_{k} (\gamma)
\,\hat y_{k,\gamma}, \,L^{*} \hat v^{*}_{k,\gamma} =
\lambda_k (\gamma) \,\hat v^{*}_{k,\gamma},\textrm{if}\, a
\ne c - 1, \,k \in \mathbb{N}, \,\textrm{and}\, a = c - 1,
\,k \ge 3; \notag\\
L \hat y_{1,\gamma} &=
\lambda_{1} (\gamma) \,\hat y_{1,\gamma},L \hat
y_{2,\gamma} = \lambda_{1} (\gamma) \,\hat y_{2,\gamma} +
\hat y_{1,\gamma}, L^{*} \hat v^{*}_{1,\gamma} =
\lambda_{1} (\gamma) \,\hat v^{*}_{1,\gamma} + \hat
v^{*}_{2,\gamma},\notag\\
L^{*} \hat v^{*}_{1,\gamma} &= \lambda_{1}
(\gamma)\, \hat v^{*}_{1,\gamma}. \end{align}
\begin{align}
L \hat y_{k,\gamma} &= \lambda_{k} (\gamma)
\,\hat y_{k,\gamma}, \,L^{*} \hat v^{*}_{k,\gamma} =
\lambda_k (\gamma) \,\hat v^{*}_{k,\gamma},\textrm{if}\, a
\ne c - 1, \,k \in \mathbb{N}, \,\textrm{and}\, a = c - 1,
\,k \ge 3; \notag\\
L \hat y_{1,\gamma} &=
\lambda_{1} (\gamma) \,\hat y_{1,\gamma},L \hat
y_{2,\gamma} = \lambda_{1} (\gamma) \,\hat y_{2,\gamma} +
\hat y_{1,\gamma}, L^{*} \hat v^{*}_{1,\gamma} =
\lambda_{1} (\gamma) \,\hat v^{*}_{1,\gamma} + \hat
v^{*}_{2,\gamma},\notag\\
L^{*} \hat v^{*}_{1,\gamma} &= \lambda_{1}
(\gamma)\, \hat v^{*}_{1,\gamma}. \end{align}
In view of (5.2), by (5.3) we obtain
 \begin{align}
\hat v^{*}_{k,\gamma} &= J \hat
y_{k,\gamma} \,\textrm{if}\,a \ne c - 1, k \in \mathbb{N},
\,\textrm{and}\, a = c - 1, k \ge 3;\notag\\
\hat
v^{*}_{1,\gamma} &= J \hat y^{*}_{2,\gamma} + \tilde b J
\hat y_{1,\gamma}, \hat v^{*}_{2,\gamma} = J \hat
y_{1,\gamma}, \,\textrm{if}\,c = a + 1,
\end{align}
\begin{align}
\hat v^{*}_{k,\gamma} &= J \hat
y_{k,\gamma} \,\textrm{if}\,a \ne c - 1, k \in \mathbb{N},
\,\textrm{and}\, a = c - 1, k \ge 3;\notag\\
\hat
v^{*}_{1,\gamma} &= J \hat y^{*}_{2,\gamma} + \tilde b J
\hat y_{1,\gamma}, \hat v^{*}_{2,\gamma} = J \hat
y_{1,\gamma}, \,\textrm{if}\,c = a + 1,
\end{align}
where ![]() $\tilde b$ is an arbitrary constant.
$\tilde b$ is an arbitrary constant.
By following the arguments in lemma 4.1 of [Reference Aliyev and Mamedova9, pp. 15–16] we can show that the following assertion holds.
Lemma 5.2 Let ![]() $\{ \hat v_{k,\gamma } \} _{k = 1}^{\infty }$,
$\{ \hat v_{k,\gamma } \} _{k = 1}^{\infty }$, ![]() $\hat v_{k,\gamma } = \{ v_{k,\gamma }, s_{k,\gamma }, t_{k,\gamma } \}$, be the system that is adjoint to the system
$\hat v_{k,\gamma } = \{ v_{k,\gamma }, s_{k,\gamma }, t_{k,\gamma } \}$, be the system that is adjoint to the system ![]() $\{ \hat y_{k,\gamma } \} _{k = 1}^{\infty }$. Then
$\{ \hat y_{k,\gamma } \} _{k = 1}^{\infty }$. Then
where ![]() $\delta _{k,\gamma } = (y_{k,\gamma }, y_{k,\gamma })_{\Pi _1}$, if
$\delta _{k,\gamma } = (y_{k,\gamma }, y_{k,\gamma })_{\Pi _1}$, if ![]() $a \ne c -1, k \in \mathbb {N}$, and
$a \ne c -1, k \in \mathbb {N}$, and ![]() $a = c - 1, k \ge 3$;
$a = c - 1, k \ge 3$; ![]() $\delta _{1,\gamma } = \delta _{2,\gamma } = (\hat y_{1,\gamma }, \hat y^{*}_{2,\gamma })_{\Pi _1}$ if
$\delta _{1,\gamma } = \delta _{2,\gamma } = (\hat y_{1,\gamma }, \hat y^{*}_{2,\gamma })_{\Pi _1}$ if ![]() $a = c - 1$, and
$a = c - 1$, and ![]() $\delta _{k,\gamma } \ne 0$ for
$\delta _{k,\gamma } \ne 0$ for ![]() $k \in \mathbb {N}$, and
$k \in \mathbb {N}$, and ![]() $\tilde b = - ( {b + \delta _{1,\gamma }^{-1} \,(\hat y^{*}_{2,\gamma }, \hat y^{*}_{2,\gamma })_{\Pi _1}} )$.
$\tilde b = - ( {b + \delta _{1,\gamma }^{-1} \,(\hat y^{*}_{2,\gamma }, \hat y^{*}_{2,\gamma })_{\Pi _1}} )$.
Let
where ![]() $r$ and
$r$ and ![]() $l$ (
$l$ (![]() $r \ne l$) are arbitrary fixed positive integers.
$r \ne l$) are arbitrary fixed positive integers.
Theorem 5.3 If ![]() $\Delta _{r,l,\gamma } \ne 0$, then the system of root functions
$\Delta _{r,l,\gamma } \ne 0$, then the system of root functions ![]() $\{ y_{k,\gamma } (x) \} _{k = 1, k \ne r,l}^{\infty }$ of problem (1.1)–(1.5) forms a basis in
$\{ y_{k,\gamma } (x) \} _{k = 1, k \ne r,l}^{\infty }$ of problem (1.1)–(1.5) forms a basis in ![]() $L_{p} (0,1),1 < p < \infty$, which is an unconditional basis for
$L_{p} (0,1),1 < p < \infty$, which is an unconditional basis for ![]() $p = 2$; if
$p = 2$; if ![]() $\Delta _{r,l,\gamma } = 0$ then this system is incomplete and nonminimal in
$\Delta _{r,l,\gamma } = 0$ then this system is incomplete and nonminimal in ![]() $L_{p} (0,1),1 < p < \infty$.
$L_{p} (0,1),1 < p < \infty$.
Proof. The assertions of this theorem for ![]() $p = 2$ follow from [Reference Aliyev1, theorems 3.1, 3.2 and corollary 3.1]. The proof of theorem 5.3 for
$p = 2$ follow from [Reference Aliyev1, theorems 3.1, 3.2 and corollary 3.1]. The proof of theorem 5.3 for ![]() $p \in (1, + \infty ), p \ne 2$, is similar to that of [Reference Kerimov and Aliev30, theorem 5.1] by using asymptotic formulas (4.1)–(4.4). The proof of this theorem is complete.
$p \in (1, + \infty ), p \ne 2$, is similar to that of [Reference Kerimov and Aliev30, theorem 5.1] by using asymptotic formulas (4.1)–(4.4). The proof of this theorem is complete.
Using the oscillatory properties of the eigenfunctions of problem (1.1)–(1.5), by theorem 5.3 we can establish sufficient conditions for the system ![]() $\{ y_{k,\gamma } (x) \} _{k = 1, k \ne r,l}^{\infty }$ of root functions of this problem to form a basis in
$\{ y_{k,\gamma } (x) \} _{k = 1, k \ne r,l}^{\infty }$ of root functions of this problem to form a basis in ![]() $L_{p} (0, 1), \, 1 < p < \infty$.
$L_{p} (0, 1), \, 1 < p < \infty$.
Theorem 5.4 Let ![]() $r$ and
$r$ and ![]() $l$
$l$ ![]() $(r < l)$ be arbitrary fixed natural numbers. Then in the cases (i)
$(r < l)$ be arbitrary fixed natural numbers. Then in the cases (i) ![]() $r,l \ge 3$ and have different parities; (ii)
$r,l \ge 3$ and have different parities; (ii) ![]() $a < c - 1$,
$a < c - 1$, ![]() $r = 1$ or
$r = 1$ or ![]() $r = 2$, and
$r = 2$, and ![]() $l$ is odd; (iii)
$l$ is odd; (iii) ![]() $a > c - 1$,
$a > c - 1$, ![]() $r = 2$ and
$r = 2$ and ![]() $l$ is odd; (iv)
$l$ is odd; (iv) ![]() $a > c - 1$,
$a > c - 1$, ![]() $r = 1$,
$r = 1$, ![]() $\tau (\lambda _1 (\gamma ))$ and
$\tau (\lambda _1 (\gamma ))$ and ![]() $l$ have different parities; (v)
$l$ have different parities; (v) ![]() $a = c - 1$,
$a = c - 1$, ![]() $r = 2$ and
$r = 2$ and ![]() $l$ is odd; (vi)
$l$ is odd; (vi) ![]() $a = c - 1$,
$a = c - 1$, ![]() $r = 1$ and
$r = 1$ and ![]() $y_{2,\gamma }^{*} (0) - y_{2,\gamma }^{*} (1)\, y_{\,l,\gamma } (0) \ne 0$, the system
$y_{2,\gamma }^{*} (0) - y_{2,\gamma }^{*} (1)\, y_{\,l,\gamma } (0) \ne 0$, the system ![]() $\{ y_{k,\gamma } (x) \} _{k = 1, k \ne r,l}^{\infty }$ is a basis in
$\{ y_{k,\gamma } (x) \} _{k = 1, k \ne r,l}^{\infty }$ is a basis in ![]() $L_{p} (0,1),1 < p < \infty$, which is an unconditional basis in
$L_{p} (0,1),1 < p < \infty$, which is an unconditional basis in ![]() $L_{2} (0,1)$.
$L_{2} (0,1)$.
Proof. By relations (5.4) and (5.5), it follows from (5.6) that
 \begin{align} \Delta _{r,l,\gamma} &= \left| \begin{array}{l} - \delta _{r,\gamma}^{{-}1}\,m_{r,\gamma} \, - \,\delta_{l,\gamma}^{{-}1}\,m_{l,\gamma} \\ \delta _{r,\gamma}^{{-}1}\,n_{r,\gamma} \delta _{l,\gamma}^{{-}1}\,n_{l,\gamma}\end{array} \right| ={-} \,\delta _{r,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} m_{r,\gamma} \,m_{l,\gamma} \\ \,n_{r,\gamma} \,\,n_{l,\gamma} \end{array} \right|\notag\\ & = - \,\delta _{r,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} a \,y_{r,\gamma} (0) \,a \,y_{l,\gamma} (0) \\ c \,y_{r,\gamma} (1)\,\,c\,y_{l,\gamma} (1) \end{array} \right| ={-} a\,c\,\delta _{r,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} \,y_{r,\gamma} (0) \, \,y_{\,l,\gamma} (0) \\ \,y_{r,\gamma} (1)\,\,y_{\,l,\gamma} (1) \end{array} \right| \end{align}
\begin{align} \Delta _{r,l,\gamma} &= \left| \begin{array}{l} - \delta _{r,\gamma}^{{-}1}\,m_{r,\gamma} \, - \,\delta_{l,\gamma}^{{-}1}\,m_{l,\gamma} \\ \delta _{r,\gamma}^{{-}1}\,n_{r,\gamma} \delta _{l,\gamma}^{{-}1}\,n_{l,\gamma}\end{array} \right| ={-} \,\delta _{r,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} m_{r,\gamma} \,m_{l,\gamma} \\ \,n_{r,\gamma} \,\,n_{l,\gamma} \end{array} \right|\notag\\ & = - \,\delta _{r,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} a \,y_{r,\gamma} (0) \,a \,y_{l,\gamma} (0) \\ c \,y_{r,\gamma} (1)\,\,c\,y_{l,\gamma} (1) \end{array} \right| ={-} a\,c\,\delta _{r,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} \,y_{r,\gamma} (0) \, \,y_{\,l,\gamma} (0) \\ \,y_{r,\gamma} (1)\,\,y_{\,l,\gamma} (1) \end{array} \right| \end{align}
for ![]() $\,r, l \in \mathbb {N}$ in the case
$\,r, l \in \mathbb {N}$ in the case ![]() $a \ne c - 1$, and for
$a \ne c - 1$, and for ![]() $\,r, l \ge 3$ in the case
$\,r, l \ge 3$ in the case ![]() $a = c - 1$.
$a = c - 1$.
By (2.12) and (2.13), relation (5.7) implies that
for ![]() $\,r, l \in \mathbb {N}$ in the case
$\,r, l \in \mathbb {N}$ in the case ![]() $a < c - 1$, for
$a < c - 1$, for ![]() $r,l \ge 2$ in the case
$r,l \ge 2$ in the case ![]() $a > c - 1$, and for
$a > c - 1$, and for ![]() $r,l \ge 3$ in the case
$r,l \ge 3$ in the case ![]() $a = c - 1$, and
$a = c - 1$, and
for ![]() $l \ge 2$ in the case
$l \ge 2$ in the case ![]() $a > c - 1$.
$a > c - 1$.
Moreover, in the case ![]() $a = c - 1$ for
$a = c - 1$ for ![]() $r = 2$,
$r = 2$, ![]() $l \ge 3$, and for
$l \ge 3$, and for ![]() $r = 1$ and
$r = 1$ and ![]() $l \ge 2$ we have
$l \ge 2$ we have
 \begin{align} \Delta _{2,l,\gamma} &={-} \,\delta_{2,\gamma}^{{-}1} \delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} m_{1,\gamma} \,m_{\,l,\gamma} \\ \,n_{1,\gamma} \,\,n_{\,l,\gamma} \end{array} \right| ={-} \,\delta_{2,\gamma}^{{-}1} \delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} a\,y_{1,\gamma} (0) \,a \,y_{\,l,\gamma} (0) \\ c\,y_{1,\gamma} (1) \,\,c\,y_{\,l,\gamma} (1) \\ \end{array} \right|\notag\\ & = - a\,c\,\delta_{2,\gamma}^{{-}1} \delta_{l,\gamma}^{{-}1} \left| \begin{array}{cc} y_{1,\gamma} (0) & y_{\,l,\gamma} (0) \\ 1 & 1 \\ \end{array} \right| = \, - a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left({y_{\,1,\gamma} (0) - y_{\,l,\gamma} (0)}\right), \end{align}
\begin{align} \Delta _{2,l,\gamma} &={-} \,\delta_{2,\gamma}^{{-}1} \delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} m_{1,\gamma} \,m_{\,l,\gamma} \\ \,n_{1,\gamma} \,\,n_{\,l,\gamma} \end{array} \right| ={-} \,\delta_{2,\gamma}^{{-}1} \delta_{l,\gamma}^{{-}1} \left| \begin{array}{l} a\,y_{1,\gamma} (0) \,a \,y_{\,l,\gamma} (0) \\ c\,y_{1,\gamma} (1) \,\,c\,y_{\,l,\gamma} (1) \\ \end{array} \right|\notag\\ & = - a\,c\,\delta_{2,\gamma}^{{-}1} \delta_{l,\gamma}^{{-}1} \left| \begin{array}{cc} y_{1,\gamma} (0) & y_{\,l,\gamma} (0) \\ 1 & 1 \\ \end{array} \right| = \, - a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left({y_{\,1,\gamma} (0) - y_{\,l,\gamma} (0)}\right), \end{align}and
 \begin{align} \Delta _{1,l,\gamma} &={-}\left| \begin{array}{l} \delta_{1,\gamma}^{{-}1}\,\{m_{2,\gamma}^{*} + \tilde b\, m_{1,\gamma}\} \, \,\delta_{l,\gamma}^{{-}1}\,m_{l,\gamma} \\ \delta _{1,\gamma}^{{-}1}\,\{\,n_{2,\gamma}^{*} + \,\tilde b \,n_{1,\gamma}\} \,\delta _{l,\gamma}^{{-}1}\,n_{l,\gamma} \\ \end{array} \right| ={-}\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left| \begin{array}{l} m_{2,\gamma}^{*} + \tilde b\, m_{1,\gamma} \,m_{l,\gamma} \\n_{2,\gamma}^{*} + \,\tilde b \,n_{1,\gamma}\,n_{l,\gamma} \\ \end{array} \right|\notag\\ &= - a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left| \begin{array}{l} y_{2,\gamma}^{*} (0) + \tilde b\, y_{1,\gamma} (0) \,y_{l,\gamma} (0) \\y_{2,\gamma}^{*} (1) + \tilde b \,y_{1,\gamma} (1)\,y_{\,l,\gamma} (1) \\ \end{array} \right| ={-}\,a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left| \begin{array}{l} y_{2,\gamma}^{*} (0) \,y_{\,l,\gamma} (0) \\ y_{2,\gamma}^{*} (1) \,\,\,1 \\ \end{array} \right|\notag\\ & = - a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\{\,y_{2,\gamma}^{*} (0) - y_{2,\gamma}^{*} (1)\, y_{\,l,\gamma} (0) \}. \end{align}
\begin{align} \Delta _{1,l,\gamma} &={-}\left| \begin{array}{l} \delta_{1,\gamma}^{{-}1}\,\{m_{2,\gamma}^{*} + \tilde b\, m_{1,\gamma}\} \, \,\delta_{l,\gamma}^{{-}1}\,m_{l,\gamma} \\ \delta _{1,\gamma}^{{-}1}\,\{\,n_{2,\gamma}^{*} + \,\tilde b \,n_{1,\gamma}\} \,\delta _{l,\gamma}^{{-}1}\,n_{l,\gamma} \\ \end{array} \right| ={-}\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left| \begin{array}{l} m_{2,\gamma}^{*} + \tilde b\, m_{1,\gamma} \,m_{l,\gamma} \\n_{2,\gamma}^{*} + \,\tilde b \,n_{1,\gamma}\,n_{l,\gamma} \\ \end{array} \right|\notag\\ &= - a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left| \begin{array}{l} y_{2,\gamma}^{*} (0) + \tilde b\, y_{1,\gamma} (0) \,y_{l,\gamma} (0) \\y_{2,\gamma}^{*} (1) + \tilde b \,y_{1,\gamma} (1)\,y_{\,l,\gamma} (1) \\ \end{array} \right| ={-}\,a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\left| \begin{array}{l} y_{2,\gamma}^{*} (0) \,y_{\,l,\gamma} (0) \\ y_{2,\gamma}^{*} (1) \,\,\,1 \\ \end{array} \right|\notag\\ & = - a\,c\,\delta _{1,\gamma}^{{-}1} \,\delta_{l,\gamma}^{{-}1} \,\{\,y_{2,\gamma}^{*} (0) - y_{2,\gamma}^{*} (1)\, y_{\,l,\gamma} (0) \}. \end{align}respectively.
Next, by (2.12) and (2.25), theorem 3.5 implies that
 \begin{align} &y_{1,\gamma} (0) = 1\ \textrm{for}\ a \le c - 1,y_{2,\gamma} (0) > 0 \ \textrm{for}\ a < c - 1,\notag\\ &\textrm{sgn}\,y_{1,\gamma} (1) = ({-}1)^{\tau \,(\lambda_1 (\gamma))}, y_{2,\gamma} (0) = 1\ \textrm{for}\ a > c - 1, \end{align}
\begin{align} &y_{1,\gamma} (0) = 1\ \textrm{for}\ a \le c - 1,y_{2,\gamma} (0) > 0 \ \textrm{for}\ a < c - 1,\notag\\ &\textrm{sgn}\,y_{1,\gamma} (1) = ({-}1)^{\tau \,(\lambda_1 (\gamma))}, y_{2,\gamma} (0) = 1\ \textrm{for}\ a > c - 1, \end{align}
where ![]() $\tau \,(\lambda _1 (\gamma )) = \sum \limits _{\xi _k \in (\lambda _1 (\gamma ),0)} {i(\xi _k)}$.
$\tau \,(\lambda _1 (\gamma )) = \sum \limits _{\xi _k \in (\lambda _1 (\gamma ),0)} {i(\xi _k)}$.
Now the statements (i)–(vi) of this theorem follow from (5.8)–(5.13) in view of theorem 5.3. The proof of this theorem is complete.
Acknowledgments
The authors express their deep gratitude to the referee, whose comments and suggestions contributed to a significant improvement in the presentation of the text of the article and the obtained results.